一种混合负二进制编码的光学矩阵乘法系统
矩阵乘法快速幂 样例

矩阵乘法快速幂样例矩阵乘法快速幂是一种用于高效计算矩阵幂次的算法,它在一些数学问题和计算机科学领域中具有重要的应用。
本文将介绍矩阵乘法快速幂的原理和算法,并通过实例来说明其在解决实际问题中的作用。
我们来了解一下矩阵乘法快速幂的基本原理。
在数学中,矩阵乘法是指将两个矩阵相乘得到一个新的矩阵的操作。
而矩阵幂是指将一个矩阵连乘多次得到的结果。
传统的方法是通过多次循环来实现矩阵的连乘,但这种方法的时间复杂度较高。
而矩阵乘法快速幂则通过将矩阵幂转化为二进制形式来降低计算量,从而提高计算效率。
具体来说,矩阵乘法快速幂的算法如下:首先,将矩阵幂的指数转化为二进制形式。
例如,将指数3转化为二进制形式为11。
然后,通过不断将矩阵的平方乘到结果中,最终得到最终的结果。
以计算矩阵A的幂次为例,假设其幂次为3,那么根据二进制形式,我们可以将矩阵A表示为A^3 = A^(2^0) * A^(2^1)。
在计算过程中,我们可以通过不断将A的平方乘到结果中来得到最终的结果。
通过这种方法,我们可以将时间复杂度从O(n)降低到O(log n),大大提高计算效率。
矩阵乘法快速幂在实际问题中有着广泛的应用。
例如,在图论中,我们经常需要计算图的幂次。
通过将图的邻接矩阵表示为一个矩阵,我们可以使用矩阵乘法快速幂来计算图的幂次,从而解决一些与图相关的问题。
此外,在密码学中,矩阵乘法快速幂也被用于计算一些加密算法中的幂次操作,保护数据的安全性。
为了更好地理解矩阵乘法快速幂的应用,我们来看一个具体的例子。
假设我们需要计算一个矩阵A的幂次,其中A的大小为2x2,幂次为100。
如果使用传统的方法,需要进行99次矩阵乘法运算,计算量较大。
而如果使用矩阵乘法快速幂的方法,只需要进行7次矩阵乘法运算,大大降低了计算量。
通过这个例子,我们可以看到矩阵乘法快速幂在解决实际问题中的优势。
矩阵乘法快速幂是一种用于高效计算矩阵幂次的算法。
通过将矩阵幂转化为二进制形式,并通过不断将矩阵的平方乘到结果中,我们可以大大降低计算量,提高计算效率。
数学与通信技术编码与加密

数学与通信技术编码与加密在当今数字化时代,信息的传输与保密问题备受关注。
数学与通信技术的结合使得编码与加密成为信息安全的关键技术。
本文将重点讨论数学与通信技术在编码与加密领域的应用。
一、编码技术1. 线性编码线性编码是基于矩阵运算的一种编码方式。
在通信领域中,二进制数据通常通过编码方式转换为模拟信号进行传输。
线性编码通过将数据表示为向量,并通过矩阵乘法实现编码过程。
这种编码方式简单高效,被广泛应用于数字通信系统中。
2. 奇偶校验码奇偶校验码是一种简单的错误检测编码方式。
在数据传输过程中,可能会发生传输错误。
奇偶校验码通过在数据中添加一个校验位,使得数据的位数为奇数或偶数。
接收端根据校验位的奇偶性判断传输是否正确。
虽然奇偶校验码无法纠正错误,但是它可以有效地检测传输错误,提高数据传输的可靠性。
3. 哈夫曼编码哈夫曼编码是一种变长编码方式,常用于数据压缩。
在哈夫曼编码中,出现频率较高的字符使用较短的编码,而出现频率较低的字符使用较长的编码。
这种编码方式可以有效地减少数据的存储和传输空间,提高数据传输的效率。
二、加密技术1. 对称加密对称加密是一种加密方式,使用同一个密钥进行加密和解密操作。
在对称加密中,发送方和接收方使用相同的密钥对数据进行加密和解密。
优点是加密解密速度快,但是密钥的传输需要安全通道,且密钥的管理较为复杂。
2. 公钥加密公钥加密是一种使用两个密钥进行加密和解密的方式。
发送方使用接收方的公钥进行加密,而接收方使用自己的私钥进行解密。
公钥加密方式安全性较高,但是加密解密速度较慢。
3. 数字签名数字签名是一种用于验证信息完整性和真实性的技术。
发送方使用自己的私钥对信息进行加密,接收方可以使用发送方的公钥对信息进行解密和验证。
数字签名可以保证信息在传输过程中不被篡改,确保信息的可靠性。
三、数学与通信技术的应用案例1. 移动通信中的编码与加密在移动通信中,编码与加密技术被广泛应用于数据传输过程中。
二进制矩阵乘法 matlab

二进制矩阵乘法 matlab英文回答:Binary matrix multiplication is a mathematical operation that involves multiplying two matrices where the elements can only be either 0 or 1. It is commonly used in various fields such as computer science, cryptography, and image processing.In MATLAB, we can perform binary matrix multiplication using the "bitand" and "bitor" functions. The "bitand" function performs a bitwise AND operation on corresponding elements of two matrices, while the "bitor" function performs a bitwise OR operation. By combining these two operations, we can achieve binary matrix multiplication.Here is an example to illustrate the process:Matrix A:1 0 1。
0 1 0。
1 1 0。
Matrix B:1 1 0。
0 1 1。
1 0 1。
To perform binary matrix multiplication, we can use the following MATLAB code:C = bitand(A, B);D = bitor(A, B);E = bitand(C, D);The resulting matrix E will be the binary matrix product of A and B.中文回答:二进制矩阵乘法是一种数学运算,涉及将元素只能是0或1的两个矩阵相乘。
计算机导论-5-二进制-进制计算-编码

【计导非课系列】第五节二进制进制计算编码对于计算机来说,数字只有两个——0和1。
数据对于计算机来说是相当重要的,而电路的通断两种状态决定了计算机只能通过1和0来进行一切事情的处理。
所以,我们见到的计算机的一切都是通过二进制才能呈现出来的。
这次就会着重介绍一下进制的计算和编码。
博文目录•什么是数据•数的进制•二进制•进制的转换•逻辑运算•计算机对数据的处理•常用编码•数的表示•符号数的机器码表示before we start…计算机为什么采用二进制?计算机中,数是用物理器件的状态表示的,二进制只有两种状态,0和1,容易用电路表示。
二进制规则简单,容易用数字逻辑电路实现。
二进制还可以表示逻辑值,进行逻辑计算。
To say it simply, 这本来就是电路决定的。
而这样一决定之后,正好带来了许多好处:比如0代表假的,没发生过的;比如所有数字只有两种状态,便于管理,写起来程序还方便……总之,二进制就是强!自动计算要解决的问题数据的存储、表示、运算,以及自动执行的计算模型计算机主要技术指标•字长:计算机一次存取传递或加工的数据长度。
也就是系统是多少位的。
•主存容量:内存(主存储器)所能存储的二进制容量,主存越大,交换越少,处理速度越快。
•计算机指令执行速度:(MIPS),每秒钟执行加减法有几百万次,可以通过时钟频率间接估计。
•时钟周期(频率、主频)CPU主频速度:CPU在单位时间内发出的脉冲数。
•数据输入/输出最高速率:计算机的数据吞吐量。
例题:下面的特点分别对应哪些技术指标?数据什么是数据数据:反应客观世界事物属性的原始记录。
需要对数据做什么•存储数据:数据怎样做才能被记到计算机上?用0和1。
•组织数据:怎样存储这些0和1对我最有用?数据结构。
存储容量单位换算在计算机里面,“千”不是所谓的103,而是210!也就是1024。
存储容量指的是存储器有多少个存储单元。
最基本的存储单元是位,bit,可以存放1个0或者1。
光电信息处理论文

题目:光子信息处理技专业:电子信息科学与技术学生姓名:贾玉新学号:20121601010212光子信息处理技术(一)光子信息处理技术的定义:光子学信息处理是一门研究以光子为载体对信息进行处理的科学分支,是光子学的一个主要研究领域。
60年代初,由于发射相干光的激光器的问世以及记录和再现三维波面的全息技术的发明,使得光子不仅作为零维信息的载体而且作为多维信息的相干载体变为现实,同时也为信息的光子直接处理开辟了实质意义上的新途径,并显示出光子比电子处理的无以比拟的优点,从而开拓和迅速地发展了以图像处理为主要内容的光信息处理学科。
近十年来,由于通信和计算的需要,信息的处理从模拟量向数字量转化,信息的传递从空不变到空变交换转化;由于大批生产的微电子工艺的渗人,光学元件的制作从单个冷加工工艺向大批量复制工艺转化;由于半导体光子学器件的发展,光学分立式块结构器件向集成化微结构器件转化。
这些变化促使子信息处理技术成为研究内容广泛、目标明确并涉及光学、通信学、计算机学、微电子学、材料学、生物学等的一门交叉性高科技学科。
充分利用光子作为信息载体所具有的高速、高效率、高并行能力等,以完成信息处理的诸多功能,这是光子信息处理的主要研究内容,而数字化和微结构化是当代光子信息处理的主要技术特征。
1, 光子信息处理的发展光子信息处理技术的主要研究内容及其发展情况可概括为以下四个领域:光信息处理,光互连技术,空间光调制器,光子系统的微型化和集成化.(1) 光信息处理:以光子为载体对信息进行加工处理,目前大体上有三种方式,即模拟光学方式、数字光学方式和光电子学处理。
模拟光学和数字光学处理都可分为对数值进行计算和对图像进行处理的两大应用领域。
光电子处理可分为光电混合处理和光互连的电子处理两大类。
A 模拟光学处理模拟光学信息处理由于具有大信息容量,并行高速等特点已在光信息处理领域获得广泛应用。
具有代表性的系统有:a, 特征识别的光学相关器原理基于光学傅里叶变换,基本结构有两种,在频谱面上直接综合的全息匹配滤波和用特征图像变换综合的光学联合变换。
信息论与编码第三版答案

信息论与编码第三版答案《信息论与编码》是一本非常经典的书籍,已经成为了信息科学领域中的经典教材。
本书的第三版已经出版,相比于前两版,第三版的变化不小,主要是增加了一些新内容,同时也对一些旧内容做了修改和完善。
作为一本教材,上面的题目和习题都是非常重要的,它们可以帮助读者更好地理解书中的相关概念和知识点,同时也可以帮助读者更好地掌握理论和技术。
因此,本文将介绍《信息论与编码》第三版中部分习题的答案,方便读者快速查阅和学习。
第一章:信息量和熵1.1 习题1.1Q:两个随机变量的独立性和无关性有什么区别?A:独立性和无关性是两个不同的概念。
两个随机变量是独立的,当且仅当它们的联合概率分布等于乘积形式的边缘概率分布。
两个随机变量是无关的,当且仅当它们的协方差等于0。
1.2 习题1.7Q:什么样的随机变量的熵等于0?A:当随机变量的概率分布是确定的(即只有一个概率为1,其余全为0),其熵等于0。
第二章:数据压缩2.5 习题2.9Q:为什么霍夫曼编码比熵编码更加高效?A:霍夫曼编码能够更好地利用信源的统计特征,将出现频率高的符号用较短的二进制编码表示,出现频率低的符号用较长的二进制编码表示。
这样一来,在编码过程中出现频率高的符号会占用较少的比特数,从而能够更加高效地表示信息。
而熵编码则是针对每个符号分别进行编码,没有考虑符号之间的相关性,因此相比于霍夫曼编码更加低效。
第四章:信道编码4.2 习题4.5Q:在线性块码中,什么是生成矩阵?A:在线性块码中,生成矩阵是一个包含所有二元线性组合系数的矩阵。
它可以用来生成码字,即任意输入信息序列可以通过生成矩阵与编码器进行矩阵乘法得到相应的编码输出序列。
4.3 习题4.12Q:简述CRC校验的原理。
A:CRC校验是一种基于循环冗余校验的方法,用于检测在数字通信中的数据传输错误。
其基本思想是将发送数据看作多项式系数,通过对这个多项式进行除法运算,得到余数,将余数添加到数据尾部,发送给接收方。
一种混合负二进制编码的光学矩阵乘法系统

第5卷 第3期 2007年6月光学与光电技术OPTICS &OP TO EL ECTRON IC TECHNOLO GYVol.5,No.3 J une ,2007 收稿日期 2006207226; 收到修改稿日期 2006210213作者简介 张锐(1981-),男,硕士,助理工程师,主要研究方向是信息光学、光计算。
E 2mail :zr5337@文章编号:167223392(2007)0320066203一种混合负二进制编码的光学矩阵乘法系统张 锐1,2 李修建1 杨建坤1 胡文华1(1国防科学技术大学技术物理研究所,长沙410073;2北京军区66222部队,北京102202)摘要 将数学中的编码方法与光学原理相结合,利用光折变晶体的四波混频效应,提出了一种可实现矩阵2矩阵的混合负二进制编码的光学系统。
介绍了该系统的工作原理,分析了其工作性能。
研究表明,此系统的矩阵面编码信息简单,便于扩展,可实现大规模矩阵乘法运算,对光计算的研究有一定的指导作用。
关键词 光计算;光学矩阵乘法;混合负二进制;光折变晶体中图分类号 O438 文献标识码 A1 引 言在电子计算机中许多复杂的运算都可以分解为乘法和卷积运算,用光学的方法来高效地实现。
光学矩阵乘法一直是光计算领域中的一个很重要的部分。
早期的一些研究主要都是进行光学模拟式的矩阵乘法系统,这类系统大都精度低。
例如,Heinz 最早提出用相干空间滤波技术实现矩阵乘法[1],由于光输出时损失太大,它的技术很难实现大规模的矩阵乘法。
后来由Schneider 提出一种由球面柱面透镜组与光孔阵列组合成的非相干系统,当矩阵维数增加时,衍射现象限制了系统的精度[2]。
为了提高其精度,引入了许多的编码方法,实现了数字式的矩阵乘法系统。
例如,由D.saltis 提出的二进制乘法转化技术[3],周常河教授提出二进制补码编码技术[4],刘立人教授提出运用混合负二进制编码实现向量矩阵乘法[5]等。
马赫_曾德尔干涉仪的应用研究_陈勇

[7] FENG S,XU O,LU S,et al. Switchable multi-wavelength erbiumdoped fiber lasers based on a Mach-Zehnder interferometer using a twin-core fiber[J]. Chin Phys Lett, 2009,26( 6) : 064-208.
法分析可得输出端的光强为
I1
=
I0 2
(
1
+ αcosφ( t) )
( 1)
收稿日期: 2012-11-01
I2
=
I0 2
(
1
-
αcosφ(
t)
)
( 2)
图 1 M-Z 干涉仪的结构
2 M-Z 应用于传感解调
解调系统是整个传感系统的核心,解调是指通
过检测信号波长的偏移量来检测被测参数的变化,
图 2 为 M-Z 干涉仪用于传感解调的系统图。
后,在输出 的 探 测 器 上 可 观 察 到 干 涉 条 纹 的 移 动,
从这个移动中就能获得待测环境中物理量的变化。
图 3 为全光纤马赫-曾德尔干涉仪的温度传感图。
恒温箱作用于传感臂 L1,改变干涉仪中干涉光
的相位,引 起 输 出 光 强 的 变 化,反 映 到 干 涉 谱 上 就
是波长的漂移,通过测量波长的漂移进而得到温度
[2] JIA Zhenan,LI Li,QIAO Xueguang,et al. Study on ASE gain flattening filter based on all-fiber M-Z interferometer[J]. Journal of Optoelectro-nics·Laser,2010,21 ( 1) : 1-4.
onehot矩阵运算

onehot矩阵运算一、引言在机器学习和自然语言处理等领域中,经常需要将离散特征转化为数字特征,以便进行进一步的分析和处理。
而onehot矩阵就是一种常用的编码方式,它能够将离散特征转化为稀疏向量表示,方便后续的计算和使用。
本文将介绍onehot矩阵的定义、生成方法以及常见的运算操作。
二、onehot矩阵的定义onehot矩阵是一种特殊的二进制矩阵,它的每一行表示一个离散特征的取值情况,每一列表示一个离散特征的一个取值。
矩阵中的元素只能取0或1,其中1表示该样本具有该离散特征的该取值,0表示不具有。
例如,假设有一个特征表示颜色,可能的取值有红、黄、蓝三种,那么onehot矩阵的形式为:红黄蓝1 0 00 1 00 0 1三、onehot矩阵的生成方法生成onehot矩阵的方法有多种,下面介绍两种常见的方法。
1. 使用sklearn库的OneHotEncoder类sklearn库是Python中常用的机器学习库,其中的OneHotEncoder 类可以方便地生成onehot矩阵。
首先,需要对离散特征进行编码,将其转化为数值形式。
然后,使用OneHotEncoder类对编码后的特征进行onehot编码,即可得到对应的onehot矩阵。
2. 使用numpy库的eye函数numpy库是Python中常用的科学计算库,其中的eye函数可以生成对角线上为1的矩阵。
利用该函数,可以先生成一个全0矩阵,然后根据离散特征的取值个数,在对应位置上将元素置为1,即可得到onehot矩阵。
四、onehot矩阵的运算操作onehot矩阵可以进行多种运算操作,下面介绍其中的三种常见操作。
1. onehot矩阵的加法onehot矩阵的加法是指将两个onehot矩阵对应位置的元素相加。
由于onehot矩阵中的元素只能取0或1,因此加法运算实际上就是逻辑或运算。
例如,对于两个onehot矩阵:矩阵A:红黄蓝1 0 00 0 1矩阵B:红黄蓝0 1 00 0 1它们的加法运算结果为:矩阵A + 矩阵B:红黄蓝1 1 00 0 22. onehot矩阵的乘法onehot矩阵的乘法是指将两个onehot矩阵对应位置的元素相乘。
矩阵快速幂与同余定理

矩阵快速幂与同余定理矩阵快速幂和同余定理是计算机科学和数学领域的重要概念,在算法设计和数论问题中有广泛的应用。
本文将分别介绍矩阵快速幂和同余定理,并说明它们的相关性。
一、矩阵快速幂矩阵快速幂是一种高效计算矩阵乘法的方法,它通过将指数转化为二进制形式,从而降低了计算复杂性。
具体来说,对于一个矩阵A和非负整数n,矩阵快速幂算法能够在O(log(n))的时间内计算出A的n次幂,而传统的幂运算需要O(n)的时间。
矩阵快速幂的基本思想是通过不断地平方和相乘来快速计算幂次。
首先将指数n用二进制表示,然后按照二进制形式的每一位进行计算。
具体步骤如下:1. 初始化结果矩阵res为单位矩阵,即矩阵对角线上的元素全为1,其余元素全为0;2. 将矩阵A赋值给临时矩阵tmp;3. 从二进制的最低位开始,如果该位为1,则将res与tmp相乘并将结果赋值给res;4. 不断地将tmp自乘,即将tmp与自身相乘,并将结果赋值给tmp;5. 将指数n右移一位,即将二进制表示的n向右移动一位;6. 重复步骤3-5,直到n变为0。
矩阵快速幂的时间复杂度为O(log(n)),其中n为指数的位数。
这种算法在求解庞大的矩阵乘法和幂运算问题时非常高效。
二、同余定理同余定理是数论中的重要定理,它描述了两个整数在除以一个正整数的情况下的余数之间的关系。
具体来说,对于给定的整数a、b和正整数m,如果a与b对m取余得到的余数相等,即a ≡ b (mod m),则称a和b同余于模m。
同余关系具有如下性质:1. 若a ≡ b (mod m),则对于任意的整数k,有a+km ≡ b (mod m),即同余关系在加法运算下封闭;2. 若a ≡ b (mod m),则对于任意的正整数n,有a^n ≡ b^n (mod m),即同余关系在乘法运算下封闭。
同余定理在数论中有广泛的应用,如计算组合数、求解线性同余方程、判定素数等。
通过同余定理,我们可以将原问题转化为与余数相关的问题,从而简化计算过程。
矩阵乘法运算效率

矩阵乘法运算效率摘要近年来,处理器运行速度的增长和存储器访问速度的增长之间存在着巨大的差距,这使得两者之间的速度差距越来越大,现代计算机体系结构中广泛采用高速缓冲存储器(Cache)来缓解这两者之间的速度差距。
本文根据矩阵乘法运算的六种不同程序代码,构建了矩阵乘法运算时间的测试程序,得到矩阵乘法运算六种不同版本的运行时间;并通过分析六种不同矩阵乘法运算程序代码中的空间局部性与时间局部性,得出由于高速缓冲存储器和程序访问的局部性差异,同一算法的不同程序代码运行时间相差很大。
为了充分利用高速缓冲存储器,提高程序运行效率,在编写程序时需要考虑程序和数据的空间局部性和时间局部性。
为了充分利用高速缓冲存储器,论文又给出了分块矩阵乘法运算程序,它可以进一步提高矩阵乘法运算效率。
关键字:高速缓冲存储器;矩阵乘法;分块矩阵;局部性原理;时间局部性;空间局部性AbstractRecent years, there has been a big gap between the growth of processor and memory runs access speed, which makes the speed difference between them is more and more big . In modern computer system structure, Cache is widely used to alleviate the speed gap.Based on the six different program code of matrix multiplication, constructs the matrix multiplication time test procedures, obtaining the running time of matrix multiplication six different versions; And through the analysis of space localized and time localized in six different program code of matrix multiplication, it is concluded that due to the cache memory and the local differences of programs access, there is a huge difference in the running time of the same algorithm of different program code. In order to make full use of cache memory and improve program efficiency, it is needed to consider the space and time localized when programming.In order to make full use of cache memory, paper gives the program of partitioned matrix multiplication, which could further improve the matrix multiplication efficiency.Key words: Cache; matrix multiplication; block matrix; principle of locality; temporal locality; spatial locality目录摘要 0Abstract 0第一章概述 (3)1.1 研究背景及意义 (3)1.2 研究内容 (4)第二章基础知识 (5)2.1 矩阵乘法运算 (5)2.2 高速缓冲存储器 (6)2.2.1 设置Cache的理论依据 (6)2.2.2 Cache的体系结构 (8)2.2.3 Cache的相关知识 (8)2.3 开发平台 (9)第三章测试程序 (10)3.1.数据区的设定 (10)3.2.程序执行时间的计算方法 (10)3.3.测试程序的运行结果保存方式 (11)3.4.测试程序代码 (12)第四章结果和分析 (16)4.1实验结果图 (16)4.2实验结果分析 (17)第五章改进的矩阵乘法运算 (18)5.1分块的矩阵乘法运算 (18)5.2分块的矩阵乘法运算实验结果和分析 (19)第六章总结 (21)参考文献 (23)致谢 (25)第一章概述1.1 研究背景及意义在应用程序中,如何提高程序的效率?这是很现实的问题。
矩阵 按位乘法

矩阵按位乘法
(最新版)
目录
1.矩阵的定义与基本概念
2.矩阵的按位乘法
3.按位乘法在矩阵运算中的应用
正文
矩阵是数学中的一个重要概念,广泛应用于物理、计算机科学、信号处理等领域。
矩阵可以看作是一个由数值排列成的矩形阵列,通常用方括号表示。
矩阵的每一个元素都是一个实数或复数,它们按照横行和纵列的方式排列,这些横行和纵列被称为矩阵的行和列。
矩阵的行数和列数决定了矩阵的大小,通常用“m×n 矩阵”表示一个具有 m 行 n 列的矩阵。
在矩阵运算中,有一种特殊的乘法运算叫做按位乘法。
按位乘法是一种基于二进制的计算方法,它将两个二进制数每一位相乘,然后将结果相加得到最终的乘积。
矩阵的按位乘法是将矩阵中的每一个元素看作一个二进制数,然后将对应的行和列的二进制数相乘,最后将结果相加得到新的矩阵。
按位乘法在矩阵运算中有广泛的应用,其中最常见的是用于矩阵的缩放。
矩阵的缩放是指将矩阵中的所有元素按照一定的比例进行缩放,这是矩阵处理中常见的操作之一。
通过按位乘法,我们可以快速地将一个矩阵按照一定的比例进行缩放,从而得到一个新的矩阵。
矩阵的按位乘法还可以用于矩阵的加密和解密。
在计算机科学中,加密和解密是常见的安全措施,矩阵的按位乘法可以用于实现矩阵的加密和解密,从而提高数据的安全性。
第1页共1页。
01编码 矩阵乘法

01编码矩阵乘法01编码矩阵乘法是一种基于二进制编码的矩阵乘法算法。
在普通矩阵乘法的基础上,将矩阵中的元素用二进制表示,并按照二进制位进行相乘和相加的操作。
具体来说,对于两个大小为n×m和m×p的矩阵A和B,它们的01编码矩阵乘法可以按照以下步骤进行:1. 初始化一个n×p的零矩阵ans,用于存储结果。
2. 对于A矩阵中的每个元素a(i,j),将其转换为二进制编码,并存储为一个长度为m的二进制串a_str。
3. 对于B矩阵中的每个元素b(i,j),将其转换为二进制编码,并存储为一个长度为n的二进制串b_str。
4. 对于ans矩阵中的每个位置(i,j),计算a_str和b_str的按位与运算,并将结果转换为十进制数,然后加到ans(i,j)中。
5. 重复步骤2-4,直到遍历完所有元素。
下面是一个示例代码,演示如何使用01编码矩阵乘法计算两个矩阵的乘积:```pythonimport numpy as npdef matrix_multiplication(A, B):n = len(A)m = len(A[0])p = len(B[0])ans = np.zeros((n, p))for i in range(n):for j in range(p):a_str = ''.join(str(int(x)) for x in A[i]) b_str = ''.join(str(int(x)) for x in B[j]) ans[i][j] += int(a_str & b_str)return ans```需要注意的是,01编码矩阵乘法的计算复杂度较高,因此在处理大规模矩阵时可能会比较耗时。
此外,由于采用了二进制编码,需要使用按位与运算符(&)来进行相乘操作,这可能会增加代码的复杂性。
8种乘法计算方法

8种乘法计算方法乘法是数学中的一个基本运算。
它用于计算两个数的乘积,表示为a×b=c,其中a和b是被乘数,c是积。
乘法可以用多种方式进行计算,下面将介绍8种常用的乘法计算方法。
方法一:竖式乘法竖式乘法是最常见的乘法计算方法,适用于任意大小的数字乘法运算。
它的基本原理是从右到左分别将每个位上的数相乘,并将结果按位相加得到最终的乘积。
具体步骤如下:1.将两个数写在竖式中,被乘数在上面,乘数在下面,对齐各位。
2.从被乘数的个位开始,依次将每一位与乘数相乘。
3.将每一位乘积按照对应的位数写在下面。
4.对所有位数的乘积进行相加,得到最终的乘积。
方法二:横式乘法横式乘法也称为“十字相乘法”,它适用于两位数或以上的数字乘法。
这种方法可以有效地减少计算过程中的错误。
具体步骤如下:1.将两个数分别写在乘法式的左侧和上方,对齐各位。
2.从乘法式的右下角开始,将每一位上的数两两相乘,然后将结果按位写在对应的位置上。
3.将每一列的结果相加,并按位排列,得到最终的乘积。
方法三:折线乘法折线乘法是一种可以简化计算的乘法方法,适用于多位数的乘法运算。
它的基本原理是将被乘数和乘数分别分解成整数和分数部分,并通过计算整数和分数的乘积得到最终结果。
具体步骤如下:1.将被乘数和乘数分别拆分成整数和分数部分。
2.计算整数部分的乘积。
3.计算分数部分的乘积。
4.将整数部分的乘积和分数部分的乘积相加,得到最终的乘积。
方法四:长方体法长方体法是一种用物理模型来解释乘法的方法。
它适用于多位数的乘法计算。
这种方法通过将被乘数和乘数表示为长方体的长度和宽度,并通过计算长方体的体积得到最终的乘积。
具体步骤如下:1.将被乘数和乘数分别表示为长方体的长度和宽度。
2.计算长方体的体积,即被乘数乘以乘数。
3.得到长方体的体积即为最终的乘积。
方法五:分配律法则分配律法则是一种利用代数运算的法则来计算乘法的方法。
它适用于涉及到多个因数的乘法运算。
具体步骤如下:1.将乘数分解成两个或多个分量。
矩阵乘法是一种高效的算法可以把一些一维递推优化到log
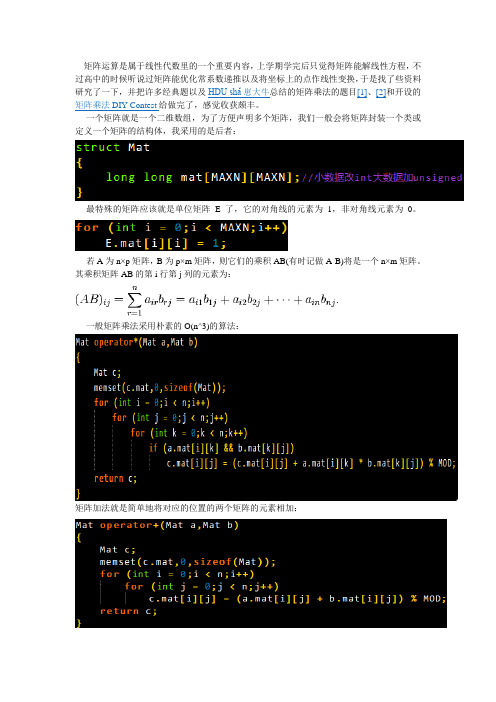
矩阵运算是属于线性代数里的一个重要内容,上学期学完后只觉得矩阵能解线性方程,不过高中的时候听说过矩阵能优化常系数递推以及将坐标上的点作线性变换,于是找了些资料研究了一下,并把许多经典题以及HDU shǎ崽大牛总结的矩阵乘法的题目[1]、[2]和开设的矩阵乘法DIY Contest给做完了,感觉收获颇丰。
一个矩阵就是一个二维数组,为了方便声明多个矩阵,我们一般会将矩阵封装一个类或定义一个矩阵的结构体,我采用的是后者:最特殊的矩阵应该就是单位矩阵E了,它的对角线的元素为1,非对角线元素为0。
若A为n×p矩阵,B为p×m矩阵,则它们的乘积AB(有时记做A·B)将是一个n×m矩阵。
其乘积矩阵AB的第i行第j列的元素为:一般矩阵乘法采用朴素的O(n^3)的算法:矩阵加法就是简单地将对应的位置的两个矩阵的元素相加:在ACM的题目中,我们一般考虑的是n阶方阵之间的乘法以及n阶方阵与n维向量(把向量看成n×1的矩阵)的乘法。
矩阵乘法最重要的性质就是满足结合律,同时它另一个很重要的性质就是不满足交换率,这保证了矩阵的幂运算满足快速幂取模(A^k % MOD)算法:假设k = 27,则k的二进制表示为11011,所以按二进制展开,乘以相应的权值,可以看出:k的二进制的每一位矩阵A都要平方,在k二进制为1的位:末矩阵×平方后的A,在k二进制为0的位则末矩阵×E(单位矩阵),即不变。
代码如下:重载按位与(乘方)和加法时注意,加法的优先级高于按位与*->+->^许多题目还要求S = A + A2 + A3+ … + A k.。
其实再作一次二分即可:只需计算log(n)个A 的幂即可。
()()343251A6231=+++++将二分+⨯+AAAeA+AAAAA若A中=m表示从i到j有m条有向边,则kA中=n表示从i经过k条有向边到达j,这样的走法有n种矩阵在ACM 里用处最大的就是加速常系数递推方程的计算,最经典的例子就是Fibonacci 数列,如果普通的递推,计算第n 项复杂度为o(n),显然对于10^9左右的数据就力不从心了。
LDPC码全面介绍

LDPC码全面介绍LDPC(Low-Density Parity-Check)码是一种稀疏图码,是一种在通信和存储系统中广泛使用的前向纠错码。
它的特点是可以实现接近香农极限的通信性能,且译码算法相对简单。
一、LDPC码的原理LDPC码又可分为二进制LDPC码和非二进制LDPC码。
其中,二进制LDPC码是最常用的类型,其每个码字由0和1组成。
以二进制LDPC码为例,其编码过程可以被表示为矩阵乘法,公式为:c=mG,其中c是码字,m是原始信息向量,G是生成矩阵。
译码算法是LDPC码的关键。
现代LDPC码的主要译码算法是迭代译码算法,其中最常用的是和位翻转(Bit-Flip)算法和置信传播(Belief Propagation)算法。
这些算法通过迭代反复修正和更新变量节点和校验节点上的概率信息来进行译码,最终得到最有可能的原始信息。
二、LDPC码的特点1.接近香农极限:LDPC码是一种接近香农极限的前向纠错码,能够提供接近于理论信道容量的通信性能,有效地减小了误码率。
2.译码算法简单:通过迭代的译码算法,LDPC码的译码过程相对简单、低延迟。
3.结构可调:通过调整生成矩阵的结构和参数,可以生成不同结构、不同长度的LDPC码,以适应不同应用场景的需求。
4.物理层实现方便:LDPC码可以通过布尔电路实现,也可以通过矩阵运算进行计算,便于硬件实现。
5.适应多种信道:LDPC码适用于多种信道环境,如高斯信道、AWGN信道、混合信道等。
三、应用领域1.无线通信系统:LDPC码被广泛应用于无线通信系统中,如Wi-Fi系统、蜂窝网络(LTE、5G)等。
它们通过在无线传输中引入LDPC码,提高了系统的传输容量和抗干扰能力,从而提供更高的传输速率和更好的通信质量。
2.光通信系统:LDPC码也被应用于光通信系统中,如光纤通信和光存储系统。
在高速光纤通信中,由于信道噪声和光纤非线性等因素的影响,译码算法的复杂度较低的LDPC码成为了较为理想的纠错码选项。
光学向量矩阵乘法实验研究

0 引 言
向量矩阵乘 法 ( MM) V 在傅 立 叶变 换 、 解线 性 求 方程组 、 图像处理 、 知识 推理 、 字 信号处 理等许 多 领 数 域 里发挥着重要作用 , 期受 到计算 机科 学工作 者 的 长
能够实 现的向量矩 阵乘法 的规模很有 限。作者受三值 光计算机研究成果 的启示 , 出了一 种新方法 , 提
第2 2卷
第 3期
计 算 机 技 术 与 发 展
COMPU r ER ECHN0LOGY T AND DEVEL OPMEN T
21 0 2年 3月
V0 . 2 No 3 】2 . Ma . 2 2 r 0l
光 学 向量 矩 阵乘 法 实验 研 究
李 梅
( 西安工业大学 计算机学院, 陕西 西安 7 02 ) 10 1
c sigt ec ret e sn O b o r c .
Ke r s v c 0 — arx mu tp i ai n; p i a e t 卜 m x mu t l a o l u d c t ra y wo d : e t r m ti l l t i c o o t l V co c l p i t n;i i  ̄s a ar y i ci q l
A src : t a vco- txmut lr( VMM )cnb p l di a e f ed. h r c l o oma ’ VMM t — bta tOp cl et mar lp e O i r i ii a eap e avr t o lsT ep ni e f i n i y f i i p God n SO ii r sn o
该方法 理论上 能有 效解 决 现行 系统 中普遍 存 在 的问
二进制编码计算矩阵

二进制编码计算矩阵可以使用二进制运算来代替常规的乘法运算,从而提高计算速度。
具体方法如下:1. 将矩阵中的每个数字表示为一个二进制数,例如,数字3 可以表示为二进制数11(即2^2 + 2^1 = 4 + 2 = 6),数字1 可以表示为二进制数01(即2^0 + 2^0 = 1 + 1 = 2)。
2. 对于矩阵中的每个元素,将左侧的数字与上方的数字进行乘法运算,并将结果存入目标矩阵中对应的单元格。
需要注意的是,二进制数的乘法运算可以使用异或(XOR)运算来实现,因为异或运算可以满足乘法运算的交换律和结合律。
3. 如果计算过程中出现进位的情况,将进位保存下来,并加到下一个单元格中。
具体来说,如果当前单元格的值为c,下一个单元格的值为n,那么将c 与n 进行异或运算得到结果后,再将进位与结果进行异或运算。
4. 重复上述步骤,直到计算完矩阵中的所有元素。
例如,对于一个3x3 的矩阵,其元素分别为3、1、2 和1、0、1,那么可以按照以下步骤进行计算:1. 将3 表示为二进制数11,将1 表示为二进制数01,将2 表示为二进制数10。
2. 将第一行中的三个数字分别与左上角的数字进行乘法运算,并将结果存入目标矩阵中对应的单元格:* 第一行中的第一个数字3 与左上角的数字3 进行乘法运算,得到6,即11 * 11 = 100(二进制),将进位0 保存下来。
* 第一行中的第二个数字1 与左上角的数字3 进行乘法运算,得到3,即01 * 11 = 011(二进制),将进位0 保存下来。
* 第一行中的第三个数字2 与左上角的数字3 进行乘法运算,得到6,即10 * 11 = 101(二进制),将进位0 保存下来。
3. 将第二行中的三个数字分别与左上角的数字进行乘法运算,并将结果存入目标矩阵中对应的单元格:* 第二行中的第一个数字1 与左上角的数字6 进行乘法运算,得到6,即01 * 100(二进制)= 0100(二进制)= 4(十进制),将进位0 保存下来。
一套二进制向量-矩阵乘法运算的光计算系统

中图分类 号 : 4 9 0 3 文献标 识码 : A 文章 编号 :6 3 2 X(0 7 1 —0 4 —0 1 7 —6 9 2 0 ) 0 1 1 3
An Op ia mp t g S se wih P r o m i g Bi a y tc lCo u i y tm t e f r n n r n
0 引 言
随着计算机性 能需 求的提 高 , 以及微 电子技术 和
采用光作为传输信息媒 质的新 型计算 技术 , 与 电子 光
相 比, 具有与电子几 乎完全不 同的特性 , 如具有更快 的
集成 电路制备工艺 的发展 , 了提高计 算机 的计算能 为 力和计算速度 , 因此 , 提高单片处理器 的集成度在过 去
Ve t r ‘M a rx M u tplc to co t i li ia in
Z HANG i-, Ru -GUO e , io , W i LIM a 3 YANG in k n Ja — u 4
( .62 r f eigMit yB in 0 2 2 C ia2 64 9A myo e i layB i g12 0 , hn ; 16 2 2A myo i la , ei 1 20 , h ; .6 6 r f in Mi r , ei 0 30 C ia Bj n ir jg n B jg i t j n
zemax binary phase 相位

zemax binary phase 相位摘要:1.Zemax 二进制相位简介2.Zemax 二进制相位的应用3.Zemax 二进制相位的优势与特点4.如何使用Zemax 二进制相位5.实践案例分享6.总结与展望正文:【1.Zemax 二进制相位简介】Zemax 二进制相位是一种在光学设计领域广泛应用的数值计算方法。
它通过将相位信息编码为二进制格式,实现了对光学系统的高效建模、分析和优化。
这种方法在Zemax 光学设计软件中得到了很好的支持,为光学工程师提供了一个强大的工具。
【2.Zemax 二进制相位的应用】Zemax 二进制相位广泛应用于以下领域:1.光学系统设计与优化:通过高效地处理光学元件的相位信息,实现对光学系统的快速建模、分析和优化。
2.光学元件制造:指导光学元件的制造过程,如薄膜制备、光刻等。
3.光学检测与测量:通过分析二进制相位数据,实现对光学系统的性能检测与评价。
4.光学信号处理:在光纤通信、光信号处理等领域,利用二进制相位实现对光信号的调制、解调等操作。
【3.Zemax 二进制相位的优势与特点】1.高效性:相较于传统方法,Zemax 二进制相位能够显著提高光学系统分析和优化的速度。
2.准确性:二进制相位能够精确地反映光学元件的相位信息,有利于获得更准确的分析结果。
3.通用性:Zemax 二进制相位适用于多种光学系统和应用场景。
4.易于操作:在Zemax 软件中,用户可以方便地实现二进制相位的加载、处理和分析。
【4.如何使用Zemax 二进制相位】1.准备数据:获取光学元件的相位数据,将其转换为二进制格式。
2.加载数据:在Zemax 软件中,选择“相位”菜单,导入二进制相位数据。
3.应用二进制相位:在光学系统建模、分析和优化过程中,启用二进制相位功能。
4.分析与优化:利用Zemax 软件的强大功能,对光学系统进行性能分析与优化。
【5.实践案例分享】以下是一个使用Zemax 二进制相位的实践案例:案例:设计一款用于光纤通信的光学系统,要求高分辨率、低损耗。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5卷 第3期 2007年6月光学与光电技术OPTICS &OP TO EL ECTRON IC TECHNOLO GYVol.5,No.3 J une ,2007 收稿日期 2006207226; 收到修改稿日期 2006210213作者简介 张锐(1981-),男,硕士,助理工程师,主要研究方向是信息光学、光计算。
E 2mail :zr5337@文章编号:167223392(2007)0320066203一种混合负二进制编码的光学矩阵乘法系统张 锐1,2 李修建1 杨建坤1 胡文华1(1国防科学技术大学技术物理研究所,长沙410073;2北京军区66222部队,北京102202)摘要 将数学中的编码方法与光学原理相结合,利用光折变晶体的四波混频效应,提出了一种可实现矩阵2矩阵的混合负二进制编码的光学系统。
介绍了该系统的工作原理,分析了其工作性能。
研究表明,此系统的矩阵面编码信息简单,便于扩展,可实现大规模矩阵乘法运算,对光计算的研究有一定的指导作用。
关键词 光计算;光学矩阵乘法;混合负二进制;光折变晶体中图分类号 O438 文献标识码 A1 引 言在电子计算机中许多复杂的运算都可以分解为乘法和卷积运算,用光学的方法来高效地实现。
光学矩阵乘法一直是光计算领域中的一个很重要的部分。
早期的一些研究主要都是进行光学模拟式的矩阵乘法系统,这类系统大都精度低。
例如,Heinz 最早提出用相干空间滤波技术实现矩阵乘法[1],由于光输出时损失太大,它的技术很难实现大规模的矩阵乘法。
后来由Schneider 提出一种由球面柱面透镜组与光孔阵列组合成的非相干系统,当矩阵维数增加时,衍射现象限制了系统的精度[2]。
为了提高其精度,引入了许多的编码方法,实现了数字式的矩阵乘法系统。
例如,由D.saltis 提出的二进制乘法转化技术[3],周常河教授提出二进制补码编码技术[4],刘立人教授提出运用混合负二进制编码实现向量矩阵乘法[5]等。
本文跟踪目前国际上的研究热点———光折变晶体的研究[6],利用其光学性质,提出了一种运用数学编码技术实现混合负二进制可编码的矩阵乘法的光学系统。
2 混合负二进制编码光学矩阵乘法系统2.1 编码技术在光学矩阵乘法研究领域中,编码问题一直是人们研究的热点。
光强编码采用数字编码数制有:二进制、二进制补码、混合负二进制等。
二进制编码是利用计算机算法的思路衍变过来的一种编码方法,利用这种方法来实现光学矩阵乘法运算,必须考虑进位和反馈回路等问题,不但结构复杂而且误码率高。
在此基础上提出的用二进制补码编码技术实现矩阵乘法运算,无需进位。
但是由于此类系统对透镜的尺寸要求很高,因此很难实现大规模的矩阵乘法。
结合以上两种编码方法的优缺点,人们又提出了混合负二进制编码。
任何一个十进制的数a 都可以表示为a =∑Mn =-N a n (-2)n (a n 是混合负二进制中的第n 位数,N 和M 都是整数)。
这种编码算法无需进位,无需正负号,既能表示实数,也能表示复数。
更重要的是,它便于光路的实现,是矩阵乘法系统编码的最佳选择。
2.2 光折变晶体的光学特性光折变晶体在光辐射下由光强的空间分布会引起材料折射率的相关变化,典型的应用就是相位共轭装置[7]。
当三束相干的入射光同时照射在光折变晶体中某点时,会产生第四束相干光波,这也就是四波混频效应,其原理如图1如所示。
其中k 1和k 2是同频率、同强度、方向相反的写入光,k 3是与之同频但强度略小的读出光。
当k 3以特定的角度入射时,就会同时出现反射光k 4和共轭光k 5,最后经半透半反镜得到输出光k 6。
只要当k 1、k 2、k 3其中一个不存在时,就不会有输出光产生。
第3期张锐等:一种混合负二进制编码的光学矩阵乘法系统图1 相位共轭器原理图Fig.1 Schematic diagram of phase conjugate system2.3 光学矩阵乘法系统在矩阵2矩阵乘法系统中实现两个矩阵A 和B 的相乘。
首先把矩阵表示在两个大小相等的平面上,并在其上面完成编码,然后通过光路使它们完成相乘,最后由输出装置得到探测结果。
若A =a 11a 12…a 1q a 21a 22…a 2q………am 1a m 2…a mqm ×qB =b 11b 12…b 1q b 21b 22…b 2q………b n 1b n 2…b nqq ×n则C =AB =c 11c 12…c 1n c 21c 22…c 2n………c m 1c m 2…c mnm ×n其中,矩阵C 中每个元素c ik =a i 1b 1k +a i 2b 2k +…+a ikb ik (i =1,2,3,…,p ;k =1,2,3,…,n )。
当A和B 中的元素都用混合负二进制表示时,所得到的结果也必定是混合二进制的。
现以A =521-8,B =-10-74-2为例,为了实现两个矩阵的乘法,首先将矩阵的信息分别加载到两个大小相等的矩阵平面上,如图2所示。
再对矩阵A 和B 中元素进行混合负二进制编码。
同时将编码后的信息按图3、4的形式重复排列,其中1代表发光,0和空格代表不发光。
利用这样的编排方法,只要将两个矩阵面中的矩阵元素对应相乘即可,无需考虑进位问题。
将光折变晶体相对平行地置于两个矩阵面正中间,且其中元素与矩阵面的元素一一对应,最后经透镜组传输到接收平面。
系统原理如图5所示。
a 11a 11a 12a 12a 21a 21a 22a 22b 11b 11b 21b22b 11b 12b21b 22图2 矩阵A 和矩阵B 中元素分布Fig.2 Arrangement of element ofmatrix A and B图3 矩阵A 混合负二进制编码图Fig.3 Negative binary of matrix A图4 矩阵B 混合负二进制编码图Fig.4 Negative binary of matrix B图5 混合负二进制编码矩阵乘法系统原理图Fig.5 Schematic diagram of optical matrix multiplicationscheme with negative binary encoding若在晶体某个位置同时有方向相反频率相同的写入光时,则当读出光以合适角度照射时,会出现共轭光。
以a 11b 11+a 12b 21=c 11为例,若两个矩阵面的相互对应的点同时为1时,则在这两点中间的光折变晶体面的对应位置上会有读出光的共轭光束产生。
例如第2行第4、6列,第4行第2、4列,76光学与光电技术第5卷第7行第3、4列位置。
同一列的8束共轭光经过柱面镜后会聚为一点,在光折变晶体C 11位置的7列就会在接收面C 11位置处得到7个点的光强分布信息,如图6所示。
第2、3、6个点的光强基本相同,而第4个点的光强是它们的3倍,因此光强信息代表混合负二进制0113010,转化为十进制为-42,且符合乘法规则。
同理,可以得到接收面其他各点的光强信息。
所以此光学系统验证式(1)成立,实现了矩阵2矩阵乘法。
C =A ×B =521-8×-10-74-2混合负二进制0101011000011001×1010100101000001混合负二进制0113010010121101010100002001十进制-42-39-428(1)图6 C 11处的光强分布Fig.6 Arrangement of optical intensity on C 113 结 论利用了光折变晶体的特性与混合负二进制编码的方法,提出了一种矩阵乘法系统。
不但可以实现实数的编码而且可以实现复数的编码,无需光电转换即可实现高度并行的矩阵2矩阵乘法运算,是一种全光学光计算系统。
由于矩阵面编码信息简单,便于扩展,可用于实现大规模矩阵乘法运算。
但是仍有许多待解决的问题,最重要的就是工艺实现。
要产生共轭光,读出光必须在合适的角度入射,入射角度和位置需做精确调整。
另外,两矩阵面上发光位置的一一对应点方向是否完全反向和激光光束之间的相干性都会影响共轭光的产生。
在此基础上,可以研发“与”、“或”、“非”等逻辑运算,为研制高速并行的光计算机做铺垫。
参考文献[1] R A Heinz ,J O Artman ,S H Lee.Matrix multipli 2cation by optical methods[J ].Appl.Opt.,1970(9):216122164.[2] W Schneider ,W Fink.Incoherent optical matrixmultiplication[J ].Opt.Acta.,1975(22):8792883.[3] D Psaltis ,D Casasent.Accurate numerical omputa 2tion by optical convolution photo 2opt [J ].Instrum.Eng.,1980,(232):1512153.[4] Changhe Zhou ,Liren Liu ,Zhijiang Wang.Binary 2enco 2ded vector 2matrix multiplica 2tion architecture [J ].Opt.Let.,1992,(17):180021802.[5] Liren Liu ,Guoqiang Li ,Yaozu Y in.Optical complexmatrix 2vector mult 2iplication [J ].Opt.Let.,1994,(19):175921761.[6] A K Das ,S Mukhopaadhyay.All 2optical time 2domainmultiplexing de 2multiplexing scheme with nonlinear ma 2terial[J ].Opt .Eng.,2005,(44):2012203[7] Archan Kumar Das ,Sourangshu Mukhopadhyay.Anall 2optical matrix multiplication scheme with non 2line 2ar material based swithching system [J ].Chinese Opt.Let.,2005,(30):1722175.Optical Matrix Multiplication System With N egative Binary E ncodingZHAN G Rui 1,2 L I Xiu 2jian 1 YAN G Jian 2kun 1 HU Wen 2hua 1(1Tech 2Physical Research Center ,National University of Defence Technology ,Changsha 410073,China ;266222Army of Beijing Military Command ,Beijing 102202,China )Abstract In this paper we apply the encoding in mathematics to the optical principle and propose a new optical matrix multi 2plication system with negative binary encoding by using four 2wave mixing of photoref ractive crystal.Its principle is intro 2duced and its operating performance is analyzed.The research shows that the matrix encoding of the system is easy and it can realize the matrix multiplication cosmically.And it is useful for the research on optical calculation.K ey w ords optical calculation ;optical matrix multiplication ;negative binary ;photoref ractive crystal86。
