冲刺训练一(答案)

合集下载

2023届重庆高考冲刺训练数学试题及参考答案

2023年重庆高考冲刺训练数学试题及参考答案一、选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．设集合A ＝{y |y ＝x }，B ＝{x |y ＝x }，全集为R ，则A ∩(∁R B )等于()A ．[0，＋∞)B ．(－∞，0)C ．{0,1}D ．{(0,0)，(1,1)}2．已知复数z 的共轭复数为z ，若z ＋z ＝4，(z －z )i ＝2(i 为虚数单位)，则z 等于()A ．2＋iB ．2－iC ．－2＋iD ．－2－i3．已知|a |＝5，b ＝(1,2)，且a ∥b ，a ·b <0，则a 的坐标为()A ．(1,2)B ．(－1,2)C ．(1，－2)D ．(－1，－2)4．甲、乙、丙三人参加社区义工活动，每人从编号为1到6的社区中任选一个，所选社区编号数各不相同且不相邻，则不同的选择方案的种数为()A ．12B ．24C ．36D ．485．已知数列{a n }满足a 1＝2，S n ＋1＝2(1＋S n )，若a 6是a m ，a 2n 的等比中项，m ，n ∈N *，则m ＋2n 等于()A ．12B ．123C ．22D ．46．如图所示，F 1，F 2是双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的左、右焦点，过F 1的直线与C 的左、右两支分别交于A ，B 两点．若|AB |∶|BF 2|∶|AF 2|＝3∶4∶5，则双曲线的离心率为()A ．2B .15 C.13 D.37．如图，已知三棱锥P －ABC 的四个顶点都在球O 的表面上，PA ⊥平面ABC ，AC ＝BC ＝2，AB ＝2，球心O 到平面ABC 的距离为3，则球O 的体积为()A.32π3B.16π3C ．16πD ．32π8．已知f(x)＝x(l n x－a)，不等式f(x)≥x2－e x－1恒成立，则实数a的取值范围是() A．(－∞，－1]B．(－∞，0]C．(－∞，1]D．(－∞，e]二、选择题(本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求的．全部选对得5分，部分选对得2分，有选错的得0分)9．已知函数f(x)＝sin2x＋3cos2x，则下列四个命题正确的是()A．f(x)的最小值为－2B．f(x)向右平移π3个单位长度后得到的函数是奇函数C．f(x)在0，π12上单调递增D．f(x)关于直线x＝7π12对称10．已知x>0，y>0，且x＋y＋xy－3＝0，则()A．x y的取值范围是[1,9]B．x＋y的取值范围是[2，＋∞)C．x＋4y的最小值是3D．x＋2y的最小值是42－311．有两个箱子，第1个箱子有3个白球，2个红球，第2个箱子有4个白球，4个红球，现从第1个箱子中随机地取1个球放到第2个箱子里，再从第2个箱子中随机取1个球放到第1个箱子里，则下列判断正确的是()A．从第2个箱子里取出的球是白球的概率为2345B．从第2个箱子里取出的球是红球的概率为2245C．若从第2个箱子里取出的球是白球，则从第1个箱子里取出的是白球的概率为1523D．两次取出的球颜色不同的概率为5912．如图，正方体ABCD－A1B1C1D1的棱长为a，线段B1D1上有两个动点E，F，且EF＝2a2.则下列结论正确的是()A．当E与D1重合时，异面直线AE与BF所成的角为π3B．三棱锥B－AEF的体积为定值C．EF在平面ABB1A1内的射影长为a2D．当E向D1运动时，二面角A－EF－B的平面角保持不变三、填空题(本大题共4小题，每小题5分，共20分)13．在的二项展开式中，所有项的系数之和为81，则常数项为________．14．设曲线y＝12x2在点A1，12y＝x l n x在点P处的切线互相平行，则点P的坐标为________．15．以模型y＝c e k x(c>0)去拟合一组数据时，设z＝l n y，将其变换后得到经验回归方程z ＝2x－1，则c＝________.16．在△ABC中，AB＝2，AC＝23，BC＝4，点O为△ABC的外心，则AO→·BC→＝________，P是△ABC外接圆圆O上一动点，则PA→·(PB→＋PC→)的最小值为________．四、解答题(本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(10分)在①a3＋a11＝20，②a3S10＝310这两个条件中任选一个，补充到下面问题中，若1a n a n＋1n∈N*)的前2023项和；若问题中的数列不存在，说明理由．问题：是否存在正项等差数列{a n}(n∈N*)，其前n项和为S n，且a1＝1，________？18．(12分)在△ABC中，内角A，B，C所对的边分别为a，b，c，△ABC的面积为S，已知a c o s C＋c c o s A＝3，a＝2b.(1)求a；(2)若S＝312(a2＋c2－b2)，求A.19．(12分)如图，在四棱锥P－ABCD中，底面ABCD是边长为2的正方形，△PAB为正三角形，且侧面PAB⊥底面ABCD，M为PD的中点．(1)求证：PB∥平面ACM；(2)求直线BM与平面PAD所成角的正弦值．20．(12分)某新华书店将在六一儿童节进行有奖促销活动，凡在该书店购书达到规定金额的小朋友可参加双人PK赢取“购书券”的游戏．游戏规则为：游戏共三局，每局游戏开始前，在不透明的箱中装有5个号码分别为1,2,3,4,5的小球(小球除号码不同之外，其余完全相同)．每局由甲、乙两人先后从箱中不放回地各摸出一个小球(摸球者无法摸出小球号码)．若双方摸出的两球号码之差为奇数，则甲被扣除2个积分，乙增加2个积分；若号码之差为偶数，则甲增加n(n∈N*)个积分，乙被扣除n个积分．PK游戏开始时，甲、乙的初始积分均为零，PK游戏结束后，若双方的积分不等，则积分较大的一方视为获胜方，将获得“购书券”奖励；若双方的积分相等，则均不能获得奖励．(1)设PK游戏结束后，甲的积分为随机变量ξ，求ξ的分布列；(2)以(1)中的随机变量ξ的均值为决策依据，当游戏规则对甲获得“购书券”奖励更为有利时，记正整数n的最小值为n0.①求n0的值，并说明理由；②当n＝n0时，求在甲至少有一局被扣除积分的情况下，甲仍获得“购书券”奖励的概率．21．(12分)在平面直角坐标系中，已知F为抛物线C：y2＝2px(p>0)的焦点，点P(t，s)(s>0)为抛物线C上一点，P关于x轴对称的点为Q，且△OPQ和△OPF的面积分别为16和2.(1)求C的方程；(2)设点D(a,2)，A，B为抛物线C上不同的三点，直线DA，DB的倾斜角分别为α，β，且满足tanα＋tanβ＝1，证明：直线AB经过定点．22．(12分)已知函数f(x)＝ln x＋ax－b(其中a，b为参数)．(1)求函数f(x)的单调区间；(2)若a＝1，函数g(x)＝f(x e x)有且仅有2个零点，求b的取值范围．参考答案1．B 2.B 3.D4.B5.A6.C7．A[如图，因为AC ＝BC ＝2，AB ＝2，所以AC 2＋BC 2＝AB 2，所以AC ⊥BC .因为PA ⊥平面ABC ，AB ，BC ⊂平面ABC ，所以PA ⊥AB ，PA ⊥BC .又AC ∩PA ＝A ，PA ，AC ⊂平面PAC ，所以BC ⊥平面PAC ，所以BC ⊥PC ，所以球心O 是PB 的中点．取AB 的中点D ，连接OD ，则OD ∥PA ，所以OD ⊥平面ABC ，所以OD ＝ 3.设球O 的半径为R ，在Rt △ODB 中，R ＝OB ＝OD 2＋DB 2＝(3)2＋12＝2，所以球O 的体积为43πR 3＝43×π×23＝32π3.]8．B[由题意可知x >0，由f (x )≥x 2－e x －1，可得a ≤e x －1x＋l n x －x .∵e x －1x ＋l n x －x ＝1e ·e x x ＋l n x e x ，令t ＝e xx ，则t ′＝e x x －e x x 2＝e x (x －1)x 2，∴t ＝e xx在(0,1)上单调递减，在(1，＋∞)上单调递增，∴t ≥t (1)＝e ，因此令φ(t )＝1e t ＋ln 1t ＝1e t －ln t (t ≥e)，φ′(t )＝t －e t e ≥0，∴φ(t )在[e ，＋∞)上单调递增，故φ(t )≥φ(e)＝0，∴a ≤0.]9．ACD 10．BD[因为x >0，y >0，所以x ＋y ≥2xy ，所以3－xy ≥2xy ，解得0<xy ≤1，即0<xy ≤1，故A 错误；因为x >0，y >0，所以x y ，所以3－(x ＋y )，即(x ＋y )2＋4(x ＋y )－12≥0，解得x ＋y ≥2，故B 正确；因为x ＋y ＋x y －3＝0，所以x ＝－y ＋3y ＋1＝－1＋4y ＋1，则x ＋4y ＝－1＋4y ＋1＋4y ＝4y ＋1＋4(y ＋1)－5≥2×4－5＝3，当且仅当4y ＋1＝4(y ＋1)，即y ＝0时等号成立．因为y >0，所以x ＋4y >3，故C 错误；x ＋2y ＝－1＋4y ＋1＋2y ＝4y ＋1＋2(y ＋1)－3≥42－3，当且仅当4y ＋1＝2(y ＋1)，即y ＝2－1时等号成立，故D 正确．]11．ABC[从第2个箱子里取出的球是白球的概率为35×59＋25×49＝2345，故A 正确；从第2个箱子里取出的球是红球的概率为35×49＋25×59＝2245，故B 正确；设从第2个箱子取出的球是白球为事件A ，从第1个箱子取出的球是白球为事件B ，则P (B |A )＝P (AB )P (A )＝35×592345＝1523，故C 正确；两次取出的球颜色不同的概率为35×49＋25×49＝49，故D 错误．]12．BCD[当E 与D 1重合时，因为EF ＝22a ，此时F 为B 1D 1的中点，记BD中点为O ，连接D 1O ，如图，由正方体性质可知，BO ∥D 1F ，BO ＝D 1F ，所以四边形BOD 1F 为平行四边形，所以D 1O ∥BF ，所以AE 与BF 所成的角为∠AD 1O .又D 1O＝6a 2，AD 1＝2a ，AO ＝2a 2，所以cos ∠AD 1O ＝3a 22＋2a 2－a 222×6a2×2a＝32，故A 错误；V B －AEF ＝V A －BEF ，易知点A 到平面BB 1D 1D 的距离和点B 到直线B 1D 1的距离为定值，且EF ＝2a2为定值，所以三棱锥A －BEF 的体积为定值，故B 正确；易知∠A 1B 1D 1＝π4，EF 在平面ABB 1A 1内的射影在A 1B 1上，所以射影长为2a 2×cos π4＝a2，故C 正确；二面角A －EF －B 即为二面角A －B 1D 1－B ，显然其平面角不变，故D 正确．]13．8；14.(1,0)；15.1e 解析由z ＝l n y ，得l n y ＝2x －1，y ＝e 2x －1＝e －1·e 2x ，所以c ＝e －1＝1e.16．40解析因为AB 2＋AC 2＝BC 2，所以AB ⊥AC ，所以O 是BC 的中点．以A 为原点，AB ，AC 所在直线分别为x 轴、y 轴建立平面直角坐标系，如图所示，则A (0,0)，B (2,0)，C (0,23)，O (1，3)，AO →＝(1，3)，BC →＝(－2,23)，所以AO →·BC →＝4.圆O 的方程为(x －1)2＋(y －3)2＝4.设P (x ，y )，则PA →＝(－x ，－y )，PB →＝(2－x ，－y )，PC →＝(－x ,23－y )，所以圆上点P d min ＝r －1＝2－1＝1，所以PA →·(PB →＋PC →)的最小值为2×12－2＝0.17．解若选择①1＝1，3＋a 11＝a 1＋2d ＋a 1＋10d ＝20，所以d ＝32，所以a n ＝1＋(n －1)×32＝32n －12.由a 3S 10＝(1＋2d＋10×92d 310，得d ＝32(舍负)，因此a n ＝1＋(n －1)×32＝32n －12.因为1a n a n ＋1＝所以1a 1a 2＋1a 2a 3＋1a 3a 4＋…＋1a 2023a 2024＝－1a 2＋1a 2－1a 3＋…＋1a 2023＝23×＝40466071.18．解(1)在△ABC 中，由a cos C ＋c cos A ＝3及余弦定理，可得a ·a 2＋b 2－c 22ab ＋c ·b 2＋c 2－a 22bc ＝3，即2b 2＝23b ，则b ＝3，而a ＝2b ，所以a ＝ 6.(2)由S ＝312(a 2＋c 2－b 2)，得S ＝312×2ac ×cos B ＝36ac cos B ，又S ＝12ac sin B ，所以12ac sin B ＝36ac cos B ，则tan B ＝33，因为B ∈(0，π)，故B ＝π6，根据a ＝2b ，得sin A ＝2sin B ＝22，又A >B ，A ∈(0，π)，所以A ＝π4或3π4.19．(1)证明连接BD 交AC 于点N ，连接MN ，如图，在正方形ABCD 中，N 为BD 的中点，而M 为PD 的中点，则PB ∥MN ，而MN ⊂平面ACM ，PB ⊄平面ACM ，所以PB ∥平面ACM .(2)解取AB 的中点O ，连接PO ，如图，在正△PAB 中，PO ⊥AB ，因为侧面PAB ⊥底面ABCD ，侧面PAB ∩底面ABCD ＝AB ，PO ⊂侧面PAB ，则PO ⊥平面在平面ABCD 内，过点O 作OE ⊥AB 交CD 于点E ，则射线OB ，OE ，OP 两两垂直，以O 为原点，射线OB ，OE ，OP 分别为x ，y ，z 轴的非负半轴建立空间直角坐标系，则B (1,0,0)，A (－1,0,0)，D (－1,2,0)，P (0,0，3)，－12，1AD →＝(0,2,0)，AP →＝(1,0，3)，BM →－32，1设平面PAD 的法向量为m ＝(x 1，y 1，z 1)·AD →＝2y 1＝0，·AP →＝x 1＋3z 1＝0，令z 1＝1，得m ＝(－3，0,1)，设直线BM 与平面PAD 所成的角为θ，则sin θ＝|cos 〈m ，BM →〉|＝|m ·BM →||m ||BM →|＝232×2＝32，所以直线BM 与平面PAD 所成角的正弦值为32.20．解(1)记“一局游戏后甲被扣除2个积分”为事件A ，“一局游戏后乙被扣除n 个积分”为事件B ，由题意可知P (A )＝C 12C 13A 22A 25＝35，则P (B )＝1－P (A )＝25，当三局均为甲被扣除2个积分时，ξ＝－6，当两局为甲被扣除2个积分，一局为乙被扣除n 个积分时，ξ＝n －4，当一局为甲被扣除2个积分，两局为乙被扣除n 个积分时，ξ＝2n －2，当三局均为乙被扣除n 个积分时，ξ＝3n ，所以P (ξ＝－6)＝27125，P (ξ＝n －4)＝C 23×25＝54125，P (ξ＝2n －2)＝C 13×35×＝36125，P (ξ＝3n )＝8125，所以随机变量ξ的分布列为ξ－6n －42n －23n P2712554125361258125(2)①由(1)易得E (ξ)＝(－6)×27125＋(n －4)×54125＋(2n －2)×36125＋3n ×8125＝6n －185，显然甲、乙双方的积分之和恒为零，当游戏规则对甲获得“购书券”奖励更为有利时，则需E (ξ)＝6n －185>0，所以n >3，即正整数n 的最小值n 0＝4.②当n ＝4时，记“甲至少有一局被扣除积分”为事件C ，则P (C )＝1＝117125，由题设可知若甲获得“购书券”奖励，则甲被扣除积分的局数至多为1，记“甲获得‘购书券’奖励”为事件D ，易知事件CD 为“甲恰好有一局被扣除积分”，则P (CD )＝C 13×35×＝36125，所以P (D |C )＝P (CD )P (C )＝36125×125117＝413，即在甲至少有一局被扣除积分的情况下，甲仍获得“购书券”奖励的概率为413.21．(1)解由题意知|PQ |＝2s ，所以△OPQ 的面积为12×t ×2s ＝ts ，则ts ＝16.①又因为焦点|OF |＝p 2，则△OPF 的面积为12×p 2×s ＝ps 4，则ps4＝2.②由①②联立解得t ＝2p ，s ＝8p，则p将P 点坐标代入抛物线方程得＝2p ·2p ，解得p ＝2，故C 的方程为y 2＝4x .(2)证明将D (a ,2)代入抛物线C 的方程得22＝4a ，解得a ＝1，所以D (1,2)．设A (x 1，y 1)，B (x 2，y 2)，直线AB 的方程为x ＝my ＋n ，＝my ＋n ，2＝4x ，消去x 得y 2－4my －4n ＝0，所以y 1＋y 2＝4m ，y 1y 2＝－4n .因为tan α＋tan β＝1，即k DA ＋k DB ＝1，所以y 1－2x 1－1＋y 2－2x 2－1＝1，所以y 1－2y 214－1＋y 2－2y 224－1＝4y 1＋2＋4y 2＋2＝1，整理得y 1y 2－2(y 1＋y 2)－12＝0，所以－4n －2×4m －12＝0，则n ＝－2m －3，所以直线AB 的方程为x ＝my －2m －3，即x ＋3＝m (y －2)，所以直线AB 经过定点(－3,2)．22．解(1)函数f (x )的定义域为(0，＋∞)，f ′(x )＝x －ax2.当a ≤0时，f ′(x )>0，所以f (x )的单调递增区间为(0，＋∞)，无单调递减区间；当a >0时，令f ′(x )>0，解得x >a ，令f ′(x )<0，解得0<x <a ，11所以f (x )的单调递减区间为(0，a )，单调递增区间为(a ，＋∞)．(2)当a ＝1时，g (x )＝f (x e x )＝ln x e x ＋1x e x －b ＝ln x ＋x ＋1x ex －b ，g ′(x )＝1x ＋1－x ＋1x 2e x ＝(x ＋1)(x e x －1)x 2ex .令g ′(x )＝0，则x e x ＝1(x ＝－1舍去)，令h (x )＝x e x －1(x >0)，则h ′(x )＝(x ＋1)e x >0，所以h (x )在(0，＋∞)上单调递增．又＝12e －1<0，h (1)＝e －1>0，且函数h (x )在(0，＋∞)上的图象是连续不断的曲线，所以根据零点存在定理，存在唯一的x 0h (x 0)＝x 00e x －1＝0，并且当x ∈(0，x 0)时，h (x )<0，当x ∈(x 0，＋∞)时，h (x )>0，所以当x ∈(0，x 0)时，g ′(x )<0，函数g (x )单调递减；当x ∈(x 0，＋∞)时，g ′(x )>0，函数g (x )单调递增，所以g (x )min ＝g (x 0)＝ln x 0＋x 0＋1e x x 00－b ＝1－b .因为函数g (x )有且仅有2个零点，所以必须有g (x )min <0，即b >1.下面证明当b >1时，函数g (x )有且仅有2个零点．因为g (x 0)＝1－b <0，g (b )＝ln b ＋1b eb >0，且g (x )在(x 0，＋∞)上单调递增且连续，所以g (x )在(x 0，＋∞)上有且仅有1个零点，因为g (x )＝f (x e x )＝ln x e x ＋1x e x －b ，令x e x ＝t (0<t <x 0)，则F (t )＝ln t ＋1t－b .因为b >1，所以0<e －b <1e <12，F (e －b )＝ln e －b ＋e b －b ＝e b －2b ，令φ(b )＝e b －2b ，b >1，显然φ(b )＝e b －2b 在(1，＋∞)上单调递增，所以φ(b )＝e b －2b >e －2>0，又g (x 0)＝1－b <0，所以g (x )在(0，x 0)上有且仅有1个零点．综上，b >1.。

2022一建《建筑》巅峰模拟题1参考答案

2022年一级建造师巅峰冲刺训练(一)参考答案《建筑工程管理与实务》一、单项选择题(共20题，每题1分。

每题的备选项中，只有一个最正确或最符合题意；选对每题得1分；没选或错选均不得分)。

1.【参考答案】D【解析】如下图所示，民用建筑单层即低层。

除单层以外，住宅按27m划分，公共按24m划分。

本题为住宅建筑(按27m划分)，且为非单层(八层)，且＞27m，所以为高层建筑。

(1)建筑高度不大于27m的住宅建筑、建筑高度不大于24m的公共建筑及建筑高度大于24m的单层公共建筑为低层或多层民用建筑。

(2)建筑高度大于27m的住宅建筑和建筑高度大于24m的非单层公共建筑，且高度不大于100m，为高层民用建筑。

(3)建筑高度大于100m的民用建筑为超高层建筑。

2.【参考答案】C【解析】防水混凝土的水泥品种宜采用硅酸盐水泥、普通硅酸盐水泥，采用其他品种水泥时应经试验确定。

宜选用坚固耐久、粒形良好的洁净石子，其最大粒径不宜大于40mm。

砂宜选用坚硬、抗风化性强、洁净的中粗砂，含泥量不应大于3%，泥块含量不宜大于1%。

不宜使用海砂。

用于拌制混凝土的水，应符合相关标准规定。

相似考点：水泥砂浆防水层施工，水泥砂浆应使用硅酸盐水泥、普通硅酸盐水泥或特种水泥。

砂宜采用中砂，含泥量不应大于1%。

3.【参考答案】B【解析】和易性是指混凝土拌合物易于施工操作(搅拌、运输、浇筑、捣实)并能获得质量均匀、成型密实的性能，又称工作性。

和易性是一项综合的技术性质，包括流动性、黏聚性和保水性三方面的含义。

4.【参考答案】D【解析】国家标准规定，六大常用水泥的初凝时间均不得短于45min，硅酸盐水泥的终凝时间不得长于6.5h，其他五类常用水泥的终凝时间不得长于10h。

5.【参考答案】A【解析】箍筋下料长度=箍筋周长+箍筋调整值=1.3+0.25=1.55m。

可以加工的箍筋套数：1000÷1.55=645.16，即最多可以加工645套，只取整数，不遵循四舍五入原则。

初中语文中考基础知识冲刺训练(一)(含答案)

2021年中考基础知识冲刺训练（一）语文姓名：__________班级：__________考号：__________一、选择题（本大题共30小题，共计80分。

在每小题给出的四个选项中，只有一个选项是符合题目要求的）1.下列句中标点符号使用有误的一项是（2分）( )A.多么美丽呀，这满地的野花！B.是他说得对呢，还是我说得对？C.明天还去北京吗？如果下雨的话。

D.这究竟是怎么回事？1.下列句中标点符号使用有误的一项是（3分）( )A.鲁迅先生团起浸湿的纸，揉烂了，把它放进炉子里。

B.万人大礼堂，里面宽76米，深60米，中部高33米。

C.他穿上那套漂亮的礼服，原来是为了纪念这最后一课！D.“一年之计在于春，”刚起头儿，有的是工夫，有的是希望。

1.下列句中标点符号使用恰当的一项是（3分） ( )A.每天，我望着掩盖着我的种子的那片土地，想象着它将发芽生长开花结果。

B.人们无聊的时候，不妨读来解闷；怀恨我的人，也可以幸灾乐祸地骂声“活该！”C.我怀着希望播种：——那希望绝不比任何一个智者的希望更为谦卑。

D.古语云：“舟必漏而后入水，土必湿而后生苔。

”几处渗漏，可使巨轮倾覆；一处管涌，能让长堤崩溃。

1.下列句中标点符号使用正确的一项是（3分）( )A.哪一架班机几点起飞？它停在哪条跑道上？他都记得一清二楚。

B.我哪儿都不去，你能把我怎么样？C.我不知道他今天为什么不去图书馆？D.我不管你们是怎么想的？我的态度是不会改变了。

1.下列句中标点符号使用不正确的一项是（2分）( )A.我问那个卖牡蛎的人：“应该付您多少钱，先生？”B.生活教我认识了桥——与水形影不离的过河的建筑。

C.无名战士小心翼翼地一根根拨弄着火柴，口里小声数着：“一，二，三，四……”D.诸葛亮在“诫子书”中说：“静以修身，俭以养德。

”1.下列句子中标点符号的使用，正确的一句是（3分）( )A.教授激动极了，说，“你是我见到的最优秀的中国男孩，我相信今后会存中国驻丹麦大使馆里见到你”。

牛津译林版七年级上册英语期末冲刺训练(1)(含答案)

期末冲刺训练（1）一、单词辩音( ) 1. A. sugar B. sure C. usually D. shoe( ) 2.A.with B.brother C.those D.three( ) 3.A.building B.cute C.student ually( ) 4.A.design B.centre C.wallet D.pretty( ) 5.A.boot B.pool C.wool D.cool( ) 6. A. sport B. comfortable C. morning D. more( ) 7.A.always B.chalk C.salt D.also( ) 8.A.orange B.uncle C.bank D.drink二、单项选择( )1.Do you know __________a child?A.how do you look afterB.how are you look afterC.how to look afterD.how to look carefully ( )2.Excuse me. Could you please tell me how to _______fish_______ Japanese?A.speak, inB.speak, withC.say, inD.say, with ( )3.Yes, I make sure that I will go to visit her _________.A.sometimesB.some timeC.some timesD.sometime( )4.Which kind of music would you like _________?A.listen toB.listening toC.to listen toD.listening ( )5.---Could I borrow your new bike?---I’m sorry ________it’s not here at present.A.orB.andC.butD.because ( )6.You will _________tired after _________ walk.A.feel also, two hoursB.also feel, two hour’sC.also feel, two hours ofD.feel also, two hours’( )7. It’s easy for us _________ him because we know __________.A.finding, where’s heB.to find, where does he liveC.to find, where he livesD.finding, where he is( )8.How _________ do you go to the fitness centre(健身中心)__________?A.much time, a monthB.many times, in every monthC.many times, each timeD.much times, a month( )9.For breakfast , the dancer usually has _________ and two pieces of bread.A.half a glass of milkB.a half milk glassC.a glass of milk halfD.half a milk glass( )10.Jason, there won’t _____________________, so just cook a bit more.A.have enough soup for everyoneB.be soup enough for everyoneC.be enough soup for anyoneD.have soup enough for anyone ( )11._________ wonderful news report he writes! All of us are proud of (以…为荣) him.A.What aB.WhatC.HowD.How a ( )12.---____________ is the school?--- Only a few minutes by bike.A.How oldB.How muchC.How longD.How far ( )13.---___________?---Because it is very cute.A.What is the panda look likeB.What’s the panda likeC.Why do you like the pandaD.What do you think of the panda ( )14.________is your new e-friend called in _______?A.How, EnglishB.What, EnglishC.Who, ChineseD.What, China( )15.I am _________holiday in New York now. I often go to large cities _______a holiday.A.on, onB.in, forC.in, onD.on, for ( )16.---Do you think the Rocket will beat the Bulls?---Yes. They have better players, so I _________them to win.A.hopeB.wishC.likeD.need( )17.Daniel goes to the Reading Club ________every Wednesday afternoon and goes to the Computer Club _________Fridays.A.on, /B.in, onC./, onD.at, in( )18.You can see lots of buildings on _________ sides of the road.A.bothB.eachC.allD.every ( )19.I want to ________ after class to have a rest. I can’t always do maths ________.A.take exercises, exerciseB.take exercises, exercisesC.exercise, exerciseD.exercise, exercises ( )20.---I will go to the USA for a holiday after last exam.---______________.A.It’s nice of youB.Enjoy yourselfC.Thank youD.That’s right三、词汇运用1.Our school has three ________(年级) and all get good ________(分数)at every subject.2.How __________(happy) the girls are dancing at the party!3.---Can I help you?---No , thanks. I __________(只是)need some time.4.The book ________(call) “Fan Xin Chun Shui” is my favourite.5.There are a lot of people in the classroom, ___________(包括)my parents.6. There is a wallet _____________ (躺) on the ground. Is it yours, Sandy?7.How much did you ___________(花钱) on this beautiful cup?8.Which of the ___________(大门) should we meet at?9.The ___________(价格) of houses in different areas change a lot these years.10.Can you help me work out the ___________(总的) cost of the trip.四、用所给词的适当形式填空1.My mother often tell us __________(not speak) to strangers on your way to school.2.My dream is ___________(help) poor children go back to school.3.Would the boy with a pair of glasses like __________(look) after our books?4.I will spend as much time as I can ___________(do) my homework.5.Everyone gets __________(excite) when they see so many animals in the zoo.6.A lot of people lose their __________(life) in the earthquake.7.---Whose are these hats? ---Maybe the ____________(lady) over there.8.Each of us always ___________(dress) up as a ghost on Halloween.五、翻译句子1.读完这本书后，我确信你会学到很多关于中国的历史。

上海华育中学初三英语一模冲刺复习试卷附答案

华育中学一模考冲刺训练(一)（满分150分，考试时间100分钟）Part2Phonetics,VocabularyandGrammar（第二部分语音、词汇和语法）Ⅱ.Choosethebestanswer(选择最恰当的答案)(共20分)()26.TuYouyouwasawarded2015NobelPrizeforhercontributiontohealthofmankind.Whichofthefoll owingiscorrectfortheunderlinedword?A)/priz/B)/praiz/C)/pris/D)/prais/()27.Thefisherman’swifesaidthatshewantedtobe_________mayorofthecity?A)aB)anC)/D)the()28.“DoyouwanttoseemyIDcardormydriver’slicense?”“_____willdo.”A)Every B)EachC)EitherD)Neither()29.Youwillfind_______importanttolearnasecondforeignlanguage.A)thoseB)thatC)itD)this()30.Ahealthydietisessential_______everybody.Youshouldcaremoreaboutwhatyoudailyeat.A)forB)on C)inD)over()31.Areportsaysthatabout________oftheEnglishteachersinShanghaiareundertheageof35.A)three-fifthB)third-fifthsC)thirds-fifthD)three-fifths()32.Theoldwomancan’tseethemessageonthemobilephone_________.A)clearenough B)enoughclearC)clearlyenough D)enoughclearly()33.Wethoughttheideasounded__________,yetcommonsensetoldusitwouldn’twork.A)wellB)badC)goodD)badly()34.I t’srainingsohardthatthewaterintherivercanbeseen________A)riseB)raiseC)raisingD)rising()35.Johnnyadmitted__________thewindow,soMr.KarldecidedtolethimgobecausehethoughtJohnn ywasanhonestboy.A)tobreakB)breakingC)brokeD)broken()36.UnlessI________itwithmyowneyes,I__________it.A)see…won’tbelieveB)willsee…believeC)see…willbelieveD)see….don’tbelieve()37.ThefilmWaroftheWordshas__________foraweek.A)beenoverB)finishedC)endedD)beenoff()38.“__________frighteningexperience!”thewomanwhosurvivedtheearthquakesaidwit hafrighten edlookonherface.A)WhataB)WhatC)HowD)Howa()39.-Idon’tthinkIrunanyfarther.-___________,Let’shavearest.A)SodoI.B)SocanI.C)NeitherdoID)NeithercanI()40.Iwasreadinganewspaper________hecameinA)assoonasB)sinceC)whileD)when()41.It’ssocoldhere.Pleasegoandfindsomewood_________.A)tobemadeafireB）tomakeafireC)tobemadeafirewithD)tomakeafirewith()42.Youshouldbecareful,themedicine__________inwetplaces.A)needn’tkeptB)mustbekeptC)can’tbekeptD)can’tbekeeping()43.Shewondered_________.A)whatwasthematterwithJohn.B)whatthematterwaswithJohnC)whatwrongwaswithJohnD)whatwasthewrongwithJohn()44.---DoyoumindtakingmetoFifthAvenue.---____________.Whenshallweleave?A)NevermindB)Itdoesn’tmatterC)Yes,Ido.D)Notatall()45—Jim,canyouworkthisSunday?—________?I’vebeenworkingtwoweeksonend.A)Whyme B)Whynot C)Whatif D)Sowhat.Ⅲ.Completethefollowingpassagewiththewordsorphrasesinthebox.Eachcanonlybeusedonce (将下列单词或词组填入空格。

2023年新高考数学大一轮复习专题七考前冲刺一 12类二级结论高效解题(含答案)

新高考数学大一轮复习专题：考前冲刺一 12类二级结论高效解题高中数学二级结论在解题中有其高明之处，不仅简化思维过程，而且可以提高解题速度和准确度，记住这些常用二级结论，可以帮你理清数学套路，节约做题时间，从而轻松拿高分.结论1 奇函数的最值性质已知函数f (x )是定义在区间D 上的奇函数，则对任意的x ∈D ，都有f (x )＋f (－x )＝0.特别地，若奇函数f (x )在D 上有最值，则f (x )max ＋f (x )min ＝0，且若0∈D ，则f (0)＝0. 【例1】设函数f (x )＝（x ＋1）2＋sin xx 2＋1的最大值为M ，最小值为m ，则M ＋m ＝________.解析显然函数f (x )的定义域为R ， f (x )＝（x ＋1）2＋sin x x 2＋1＝1＋2x ＋sin x x 2＋1，设g (x )＝2x ＋sin xx 2＋1，则g (－x )＝－g (x )，∴g (x )为奇函数，由奇函数图象的对称性知g (x )max ＋g (x )min ＝0， ∴M ＋m ＝[g (x )＋1]max ＋[g (x )＋1]min ＝2＋g (x )max ＋g (x )min ＝2. 答案 2【训练1】已知函数f (x )＝ln(1＋9x 2－3x )＋1，则f (lg 2)＋f ⎝ ⎛⎭⎪⎫lg 12＝( )A.－1B.0C.1D.2解析令g (x )＝ln(1＋9x 2－3x )，x ∈R ，则g (－x )＝ln(1＋9x 2＋3x )，因为g (x )＋g (－x )＝ln(1＋9x 2－3x )＋ln(1＋9x 2＋3x )＝ln(1＋9x 2－9x 2)＝ln 1＝0，所以g (x )是定义在R 上的奇函数.又lg 12＝－lg 2，所以g (lg 2)＋g ⎝ ⎛⎭⎪⎫lg 12＝0，所以f (lg 2)＋f ⎝ ⎛⎭⎪⎫lg 12＝g (lg 2)＋1＋g ⎝ ⎛⎭⎪⎫lg 12＋1＝2.答案 D结论2 函数周期性问题已知定义在R 上的函数f (x )，若对任意的x ∈R ，总存在非零常数T ，使得f (x ＋T )＝f (x )，则称f (x )是周期函数，T 为其一个周期. 常见的与周期函数有关的结论如下：(1)如果f (x ＋a )＝－f (x )(a ≠0)，那么f (x )是周期函数，其中的一个周期T ＝2a . (2)如果f (x ＋a )＝1f （x ）(a ≠0)，那么f (x )是周期函数，其中的一个周期T ＝2a . (3)如果f (x ＋a )＋f (x )＝c (a ≠0)，那么f (x )是周期函数，其中的一个周期T ＝2a .【例2】 (1)已知定义在R 上的函数f (x )满足f ⎝ ⎛⎭⎪⎫x ＋32＝－f (x )，且f (－2)＝f (－1)＝－1，f (0)＝2，则f (1)＋f (2)＋f (3)＋…＋f (2 019)＋f (2 020)＝( )A.－2B.－1C.0D.1(2)(多选题)(2020·济南模拟)函数f (x )的定义域为R ，且f (x ＋1)与f (x ＋2)都为奇函数，则( ) A.f (x )为奇函数B.f (x )为周期函数C.f (x ＋3)为奇函数D.f (x ＋4)为偶函数解析 (1)因为f ⎝ ⎛⎭⎪⎫x ＋32＝－f (x )，所以f (x ＋3)＝－f ⎝ ⎛⎭⎪⎫x ＋32＝f (x )，则f (x )的周期T ＝3. 则有f (1)＝f (－2)＝－1，f (2)＝f (－1)＝－1，f (3)＝f (0)＝2，所以f (1)＋f (2)＋f (3)＝0，所以f (1)＋f (2)＋f (3)＋…＋f (2 019)＋f (2 020)＝f (1)＋f (2)＋f (3)＋…＋f (2 017)＋f (2 018)＋f (2 019)＋f (2 020) ＝673×[f (1)＋f (2)＋f (3)]＋f (2 020)＝0＋f (1)＝－1.(2)法一由f (x ＋1)与f (x ＋2)都为奇函数知，函数f (x )的图象关于点(1，0)，(2，0)对称，所以f (－x )＋f (2＋x )＝0，f (－x )＋f (4＋x )＝0，所以f (2＋x )＝f (4＋x )，即f (x )＝f (2＋x )，所以f (x )是以2为周期的周期函数.又f (x ＋1)与f (x ＋2)都为奇函数，所以f (x )，f (x＋3)，f (x ＋4)均为奇函数.故选ABC.法二由f (x ＋1)与f (x ＋2)都为奇函数知，函数f (x )的图象关于点(1，0)，(2，0)对称，所以f (x )的周期为2|2－1|＝2，所以f (x )与f (x ＋2)，f (x ＋4)的奇偶性相同，f (x ＋1)与f (x ＋3)的奇偶性相同，所以f (x )，f (x ＋3)，f (x ＋4)均为奇函数.故选ABC.答案 (1)B (2)ABC【训练2】奇函数f (x )的定义域为R .若f (x ＋2)为偶函数，且f (1)＝1，则f (8)＋f (9)＝( ) A.－2B.－1C.0D.1解析由f (x ＋2)是偶函数可得f (－x ＋2)＝f (x ＋2)，又由f (x )是奇函数得f (－x ＋2)＝－f (x －2)，所以f (x ＋2)＝－f (x －2)，f (x ＋4)＝－f (x )，f (x ＋8)＝f (x ). 故f (x )是以8为周期的周期函数，所以f (9)＝f (8＋1)＝f (1)＝1.又f (x )是定义在R 上的奇函数，所以f (0)＝0，所以f (8)＝f (0)＝0，故f (8)＋f (9)＝1. 答案 D结论3 函数的对称性已知函数f (x )是定义在R 上的函数.(1)若f (a ＋x )＝f (b －x )恒成立，则y ＝f (x )的图象关于直线x ＝a ＋b2对称，特别地，若f (a＋x )＝f (a －x )恒成立，则y ＝f (x )的图象关于直线x ＝a 对称.(2)若函数y ＝f (x )满足f (a ＋x )＋f (a －x )＝0，即f (x )＝－f (2a －x )，则f (x )的图象关于点(a ，0)对称.(3)若f (a ＋x )＋f (a －x )＝2b 恒成立，则y ＝f (x )的图象关于点(a ，b )对称.【例3】 (1)函数y ＝f (x )对任意x ∈R 都有f (x ＋2)＝f (－x )成立，且函数y ＝f (x －1)的图象关于点(1，0)对称，f (1)＝4，则f (2 016)＋f (2 017)＋f (2 018)的值为________. (2)(多选题)已知定义在R 上的函数f (x )满足f (x )＝2－f (2－x )，且f (x )是偶函数，下列说法正确的是( )A.f (x )的图象关于点(1，1)对称B.f (x )是周期为4的函数C.若f (x )满足对任意的x ∈[0，1]，都有f （x 2）－f （x 1）x 1－x 2<0，则f (x )在[－3，－2]上单调递增D.若f (x )在[1，2]上的解析式为f (x )＝ln x ＋1，则f (x )在[2，3]上的解析式为f (x )＝1－ln(x －2)解析 (1)因为函数y ＝f (x －1)的图象关于点(1，0)对称，所以f (x )是R 上的奇函数，又f (x ＋2)＝－f (x )，所以f (x ＋4)＝－f (x ＋2)＝f (x )，故f (x )的周期为4.所以f (2 017)＝f (504×4＋1)＝f (1)＝4，所以f (2 016)＋f (2 018)＝－f (2 014)＋f (2 014＋4) ＝－f (2 014)＋f (2 014)＝0，所以f (2 016)＋f (2 017)＋f (2 018)＝4.(2)根据题意，f (x )的图象关于点(1，1)对称，A 正确；又f (x )的图象关于y 轴对称，所以f (x )＝f (－x )，则2－f (2－x )＝f (－x )，f (x )＝2－f (x ＋2)，从而f (x ＋2)＝2－f (x ＋4)，所以f (x )＝f (x ＋4)，B 正确；由f （x 2）－f （x 1）x 1－x 2<0可知f (x )在[0，1]上单调递增，又f (x )的图象关于点(1，1)对称，所以f (x )在[1，2]上单调递增，因为f (x )的周期为4，所以f (x )在[－3，－2]上单调递增，C 正确；因为f (x )＝f (－x )，x ∈[－2，－1]时，－x ∈[1，2]，所以f (x )＝f (－x )＝ln(－x )＋1，x ∈[－2，－1]，因为f (x )的周期为4，f (x )＝f (x －4)，x ∈[2，3]时，x －4∈[－2，－1]，所以f (x )＝f (x －4)＝ln(4－x )＋1，x ∈[2，3]，D 错误.综上，正确的是ABC. 答案 (1)4 (2)ABC【训练3】 (1)若函数y ＝f (x )的图象如图所示，则函数y ＝f (1－x )的图象大致为( )(2)若偶函数y ＝f (x )的图象关于直线x ＝2对称，且f (3)＝3，则f (－1)＝________. 解析 (1)作出y ＝f (x )的图象关于y 轴对称的图象，得到y ＝f (－x )的图象，将y ＝f (－x )的图象向右平移1个单位，得y ＝f [－(x －1)]＝f (1－x )的图象.因此图象A 满足.(2)因为f (x )的图象关于直线x ＝2对称，所以f (x )＝f (4－x )，f (－x )＝f (4＋x )，又f (－x )＝f (x )，所以f (x )＝f (x ＋4)，则f (－1)＝f (3)＝3. 答案 (1)A (2)3 结论4 两个经典不等式(1)对数形式：x ≥1＋ln x (x >0)，当且仅当x ＝1时，等号成立. (2)指数形式：e x≥x ＋1(x ∈R )，当且仅当x ＝0时，等号成立. 进一步可得到一组不等式链：e x>x ＋1>x >1＋ln x (x >0，且x ≠1). 【例4】已知函数f (x )＝x －1－a ln x . (1)若f (x )≥0，求a 的值；(2)证明：对于任意正整数n ，⎝ ⎛⎭⎪⎫1＋12⎝ ⎛⎭⎪⎫1＋122…⎝ ⎛⎭⎪⎫1＋12n <e. (1)解 f (x )的定义域为(0，＋∞)，①若a ≤0，因为f ⎝ ⎛⎭⎪⎫12＝－12＋a ln 2<0，所以不满足题意. ②若a >0，由f ′(x )＝1－a x ＝x －ax知，当x ∈(0，a )时，f ′(x )<0；当x ∈(a ，＋∞)时，f ′(x )>0；所以f (x )在(0，a )上单调递减，在(a ，＋∞)上单调递增，故x ＝a 是f (x )在(0，＋∞)的唯一最小值点.因为f (1)＝0，所以当且仅当a ＝1时，f (x )≥0，故a ＝1. (2)证明由(1)知当x ∈(1，＋∞)时，x －1－ln x >0. 令x ＝1＋12n ，得ln ⎝ ⎛⎭⎪⎫1＋12n <12n .从而ln ⎝ ⎛⎭⎪⎫1＋12＋ln ⎝ ⎛⎭⎪⎫1＋122＋…＋ln ⎝ ⎛⎭⎪⎫1＋12n <12＋122＋…＋12n ＝1－12n <1.故⎝ ⎛⎭⎪⎫1＋12⎝ ⎛⎭⎪⎫1＋122…⎝ ⎛⎭⎪⎫1＋12n <e.【训练4】 (1)已知函数f (x )＝1ln （x ＋1）－x，则y ＝f (x )的图象大致为( )解析由⎩⎪⎨⎪⎧x ＋1>0，ln （x ＋1）－x ≠0，得{x |x >－1，且x ≠0}，所以排除选项D. 当x >0时，由经典不等式x >1＋ln x (x >0)，以x ＋1代替x ，得x >ln(x ＋1)(x >－1，且x ≠0)，所以ln(x ＋1)－x <0(x >－1，且x ≠0)，排除A ，C ，易知B 正确. 答案 B(2)已知函数f (x )＝e x，x ∈R .证明：曲线y ＝f (x )与曲线y ＝12x 2＋x ＋1有唯一公共点.证明令g (x )＝f (x )－⎝ ⎛⎭⎪⎫12x 2＋x ＋1＝e x －12x 2－x －1，x ∈R ，则g ′(x )＝e x－x －1，由经典不等式e x≥x ＋1恒成立可知，g ′(x )≥0恒成立，所以g (x )在R 上为增函数，且g (0)＝0.所以函数g (x )有唯一零点，即两曲线有唯一公共点. 结论5 三点共线的充要条件设平面上三点O ，A ，B 不共线，则平面上任意一点P 与A ，B 共线的充要条件是存在实数λ与μ，使得OP →＝λOA →＋μOB →，且λ＋μ＝1.特别地，当P 为线段AB 的中点时，OP →＝12OA →＋12OB →.【例5】在△ABC 中，AE →＝2EB →，AF →＝3FC →，连接BF ，CE ，且BF 与CE 交于点M ，AM →＝xAE →＋yAF →，则x －y 等于( ) A.－112B.112C.－16D.16解析因为AE →＝2EB →，所以AE →＝23AB →，所以AM →＝xAE →＋yAF →＝23xAB →＋yAF →.由B ，M ，F 三点共线得23x ＋y ＝1.①因为AF →＝3FC →，所以AF →＝34AC →，所以AM →＝xAE →＋yAF →＝xAE →＋34yAC →.由C ，M ，E 三点共线得x ＋34y ＝1.②联立①②解得⎩⎪⎨⎪⎧x ＝12，y ＝23，所以x －y ＝12－23＝－16.答案 C【训练5】在梯形ABCD 中，已知AB ∥CD ，AB ＝2CD ，M ，N 分别为CD ，BC 的中点.若AB →＝λAM →＋μAN →，则λ＋μ＝________.解析如图，连接MN 并延长交AB 的延长线于T .由已知易得AB ＝45AT ，∴45AT →＝AB →＝λAM →＋μAN →， ∴AT →＝54λAM →＋54μAN →，∵T ，M ，N 三点共线，∴54λ＋54μ＝1，∴λ＋μ＝45.答案 45结论6 三角形“四心”向量形式的充要条件设O 为△ABC 所在平面上一点，内角A ，B ，C 所对的边分别为a ，b ，c ，则 (1)O 为△ABC 的外心⇔|OA →|＝|OB →|＝|OC →|＝a2sin A. (2)O 为△ABC 的重心⇔OA →＋OB →＋OC →＝0.(3)O 为△ABC 的垂心⇔OA →·OB →＝OB →·OC →＝OC →·OA →.(4)O 为△ABC 的内心⇔aOA →＋bOB →＋cOC →＝0.【例6】 P 是△ABC 所在平面内一点，若PA →·PB →＝PB →·PC →＝PC →·PA →，则P 是△ABC 的( ) A.外心B.内心C.重心D.垂心解析由PA →·PB →＝PB →·PC →，可得PB →·(PA →－PC →)＝0，即PB →·CA →＝0，∴PB →⊥CA →，同理可证PC →⊥AB →，PA →⊥BC →.∴P 是△ABC 的垂心. 答案 D【训练6】 O 是平面上一定点，A ，B ，C 是平面上不共线的三个点，动点P 满足OP →＝OB →＋OC→2＋λAP →，λ∈R ，则P 点的轨迹一定经过△ABC 的( )A.外心B.内心C.重心D.垂心解析设BC 的中点为M ，则OB →＋OC →2＝OM →，则有OP →＝OM →＋λAP →，即MP →＝λAP →. ∴P 的轨迹一定通过△ABC 的重心. 答案 C结论7 与等差数列相关的结论已知等差数列{a n }，公差为d ，前n 项和为S n .(1)若S m ，S 2m ，S 3m 分别为等差数列{a n }的前m 项、前2m 项、前3m 项的和，则S m ，S 2m －S m ，S 3m －S 2m 成等差数列.(2)若等差数列{a n }的项数为偶数2m ，公差为d ，所有奇数项之和为S 奇，所有偶数项之和为S 偶，则所有项之和S 2m ＝m (a m ＋a m ＋1)，S 偶－S 奇＝md ，S 偶S 奇＝a m ＋1a m.(3)若等差数列{a n }的项数为奇数2m －1，所有奇数项之和为S 奇，所有偶数项之和为S 偶，则所有项之和S 2m －1＝(2m －1)a m ，S 奇－S 偶＝a m ，S 奇S 偶＝m m －1. 【例7】 (1)设等差数列{a n }的前n 项和为S n ，若S m －1＝－2，S m ＝0，S m ＋1＝3，则m ＝( ) A.3B.4C.5D.6(2)等差数列{a n }的前n 项和为S n ，已知a m －1＋a m ＋1－a 2m ＝0，S 2m －1＝38，则m ＝________. 解析 (1)∵数列{a n }为等差数列，且前n 项和为S n ，∴数列⎩⎨⎧⎭⎬⎫S n n 也为等差数列.∴S m －1m －1＋S m ＋1m ＋1＝2S m m ，即－2m －1＋3m ＋1＝0，解得m ＝5. 经检验，m ＝5符合题意.(2)由a m －1＋a m ＋1－a 2m ＝0得2a m －a 2m ＝0，解得a m ＝0或2. 又S 2m －1＝（2m －1）（a 1＋a 2m －1）2＝(2m －1)a m ＝38，显然可得a m ≠0，所以a m ＝2.代入上式可得2m －1＝19，解得m ＝10. 答案 (1)C (2)10【训练7】 (1)等差数列{a n }的前n 项和为S n ，若S 10＝20，S 20＝50，则S 30＝________. (2)一个等差数列的前12项和为354，前12项中偶数项的和与奇数项的和的比为32∶27，则数列的公差d ＝________.解析 (1)(S 20－S 10)－S 10＝(S 30－S 20)－(S 20－S 10)，S 30＝3S 20－3S 10＝3×50－3×20＝90. (2)设等差数列的前12项中奇数项和为S 奇，偶数项的和为S 偶，等差数列的公差为d .由已知条件，得⎩⎪⎨⎪⎧S 奇＋S 偶＝354，S 偶∶S 奇＝32∶27，解得⎩⎪⎨⎪⎧S 偶＝192，S 奇＝162. 又S 偶－S 奇＝6d ，所以d ＝192－1626＝5.答案 (1)90 (2)5结论8 与等比数列相关的结论已知等比数列{a n }，公比为q ，前n 项和为S n .(1)数列⎩⎨⎧⎭⎬⎫1a n 也为等比数列，其公比为1q.(2)公比q ≠－1或q ＝－1且n 为奇数时，S n ，S 2n －S n ，S 3n －S 2n ，…成等比数列(n ∈N *). (3)若等比数列的项数为2n (n ∈N *)，公比为q ，奇数项之和为S 奇，偶数项之和为S 偶，则S 偶＝qS 奇.(4)已知等比数列{a n }，公比为q ，前n 项和为S n .则S m ＋n ＝S m ＋q mS n (m ，n ∈N *). 【例8】 (1)设等比数列{a n }的前n 项和为S n ，若S 6S 3＝3，则S 9S 6＝( ) A.2 B.73 C.83D.3解析由已知S 6S 3＝3，得S 6＝3S 3且q ≠－1，因为S 3，S 6－S 3，S 9－S 6也为等比数列，所以(S 6－S 3)2＝S 3(S 9－S 6)，则(2S 3)2＝S 3(S 9－3S 3).化简得S 9＝7S 3，从而S 9S 6＝7S 33S 3＝73.答案 B(2)已知等比数列{a n }的前n 项和为S n ，且满足S 3＝72，S 6＝632.①求数列{a n }的通项公式；②求log 2a 1＋log 2a 2＋log 2a 3＋…＋log 2a 25的值.解 ①由S 3＝72，S 6＝632，得S 6＝S 3＋q 3S 3＝(1＋q 3)S 3，∴q ＝2.又S 3＝a 1(1＋q ＋q 2)，得a 1＝12.故通项公式a n ＝12×2n －1＝2n －2.②由①及题意可得log 2a n ＝n －2，所以log 2a 1＋log 2a 2＋log 2a 3＋…＋log 2a 25＝－1＋0＋1＋2＋…＋23＝25×（－1＋23）2＝275.【训练8】已知{a n }是首项为1的等比数列，S n 是{a n }的前n 项和，且9S 3＝S 6，则数列⎩⎨⎧⎭⎬⎫1a n 的前5项和为( ) A.158或5 B.3116或5 C.3116D.158解析设等比数列{a n }的公比为q ，易知S 3≠0. 则S 6＝S 3＋S 3q 3＝9S 3，所以q 3＝8，q ＝2.所以数列⎩⎨⎧⎭⎬⎫1a n 是首项为1，公比为12的等比数列，其前5项和为1－⎝ ⎛⎭⎪⎫1251－12＝3116. 答案 C结论9 多面体的外接球和内切球(1)长方体的体对角线长d 与共点的三条棱长a ，b ，c 之间的关系为d 2＝a 2＋b 2＋c 2；若长方体外接球的半径为R ，则有(2R )2＝a 2＋b 2＋c 2. (2)棱长为a 的正四面体内切球半径r ＝612a ，外接球半径R ＝64a . 【例9】已知一个平放的各棱长为4的三棱锥内有一个小球O (重量忽略不计)，现从该三棱锥顶端向内注水，小球慢慢上浮，若注入的水的体积是该三棱锥体积的78时，小球与该三棱锥的各侧面均相切(与水面也相切)，则小球的表面积等于( ) A.7π6B.4π3C.2π3D.π2解析当注入水的体积是该三棱锥体积的78时，设水面上方的小三棱锥的棱长为x (各棱长都相等).依题意，⎝ ⎛⎭⎪⎫x 43＝18，得x ＝2，易得小三棱锥的高为263.设小球半径为r ，则13S 底面·263＝4×13S 底面·r (S 底面为小三棱锥的底面积)，得r ＝66.故小球的表面积S ＝4πr 2＝2π3. 答案 C【训练9】 (1)已知直三棱柱的底面是等腰直角三角形，直角边长是1，且其外接球的表面积是16π，则该三棱柱的侧棱长为( ) A.14B.2 3C.4 6D.3(2)已知球O 的直径PA ＝2r ，B ，C 是该球面上的两点，且BC ＝PB ＝PC ＝r ，三棱锥P －ABC 的体积为3223，则球O 的表面积为( )A.64πB.32πC.16πD.8π解析 (1)由于直三棱柱ABC －A 1B 1C 1的底面ABC 为等腰直角三角形.把直三棱柱ABC －A 1B 1C 1补成正四棱柱，则正四棱柱的体对角线是其外接球的直径，因为外接球的表面积是16π，所以外接球半径为2，因为直三棱柱的底面是等腰直角三角形，斜边长2，所以该三棱柱的侧棱长为16－2＝14.(2)如图，取PA 的中点O ，则O 为球心，连接OB ，OC ，则几何体O －BCP 是棱长为r 的正四面体，所以V O －BCP ＝212r 3，于是V P －ABC ＝2V O －BCP ＝26r 3，令26r 3＝3223，得r ＝4.从而S 球＝4π×42＝64π.答案 (1)A (2)A结论10 焦点三角形的面积公式(1)在椭圆x 2a 2＋y 2b2＝1(a >b >0)中，F 1，F 2分别为左、右焦点，P 为椭圆上一点，则△PF 1F 2的面积S △PF 1F 2＝b 2·tan θ2，其中θ＝∠F 1PF 2.(2)在双曲线x 2a 2－y 2b2＝1(a >0，b >0)中，F 1，F 2分别为左、右焦点，P 为双曲线上一点，则△PF 1F 2的面积S △PF 1F 2＝b 2tanθ2，其中θ＝∠F 1PF 2.【例10】如图，F 1，F 2是椭圆C 1：x 24＋y 2＝1与双曲线C 2的公共焦点，A ，B 分别是C 1，C 2在第二、四象限的公共点.若四边形AF 1BF 2为矩形，则C 2的离心率是( )A. 2B. 3C.32D.62解析设双曲线C 2的方程为x 2a 22－y 2b 22＝1，则有a 22＋b 22＝c 22＝c 21＝4－1＝3.又四边形AF 1BF 2为矩形，所以△AF 1F 2的面积为b 21tan 45°＝b 22tan 45°，即b 22＝b 21＝1.所以a 22＝c 22－b 22＝3－1＝2. 故双曲线的离心率e ＝c 2a 2＝32＝62. 答案 D【训练10】已知F 1，F 2是椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的两个焦点，P 为椭圆C 上一点，且PF 1→⊥PF 2→.若△PF 1F 2的面积为9，则b ＝________. 解析在焦点三角形PF 1F 2中，PF 1→⊥PF 2→，所以∠F 1PF 2＝90°，故S △PF 1F 2＝b 2tan ∠F 1PF 22＝b 2tan 45°＝9，则b ＝3.答案 3结论11 圆锥曲线的切线问题(1)过圆C ：(x －a )2＋(y －b )2＝R 2上一点P (x 0，y 0)的切线方程为(x 0－a )(x －a )＋(y 0－b )(y －b )＝R 2.(2)过椭圆x 2a 2＋y 2b 2＝1上一点P (x 0，y 0)的切线方程为x 0x a 2＋y 0yb2＝1.(3)已知点M (x 0，y 0)，抛物线C ：y 2＝2px (p ≠0)和直线l ：y 0y ＝p (x ＋x 0). ①当点M 在抛物线C 上时，直线l 与抛物线C 相切，其中M 为切点，l 为切线.②当点M 在抛物线C 外时，直线l 与抛物线C 相交，其中两交点与点M 的连线分别是抛物线的切线，即直线l 为切点弦所在的直线.【例11】已知抛物线C ：x 2＝4y ，直线l ：x －y －2＝0，设P 为直线l 上的点，过点P 作抛物线C 的两条切线PA ，PB ，其中A ，B 为切点，当点P (x 0，y 0)为直线l 上的定点时，求直线AB 的方程.解联立方程得⎩⎪⎨⎪⎧x 2＝4y ，x －y －2＝0，消去y ，整理得x 2－4x ＋8＝0，Δ＝(－4)2－4×8＝－16<0，故直线l 与抛物线C 相离.由结论知，P 在抛物线外，故切点弦AB 所在的直线方程为x 0x ＝2(y ＋y 0)，即y ＝12x 0x －y 0.【训练11】 (1)过点(3，1)作圆(x －1)2＋y 2＝1的两条切线，切点分别为A ，B ，则直线AB 的方程为( ) A.2x ＋y －3＝0 B.2x －y －3＝0 C.4x －y －3＝0D.4x ＋y －3＝0(2)设椭圆C ：x 24＋y 23＝1，点P ⎝ ⎛⎭⎪⎫1，32，则椭圆C 在点P 处的切线方程为________________.解析 (1)如图，圆心坐标为C (1，0)，易知A (1，1).又k AB ·k PC ＝－1，且k PC ＝1－03－1＝12，∴k AB ＝－2.故直线AB 的方程为y －1＝－2(x －1)，即2x ＋y －3＝0.(2)由于点P ⎝ ⎛⎭⎪⎫1，32在椭圆x 24＋y 23＝1上，故切线方程为x 4＋32y 3＝1，即x ＋2y －4＝0.答案 (1)A (2)x ＋2y －4＝0结论12 过抛物线y 2＝2px (p >0)焦点的弦设AB 是过抛物线y 2＝2px (p >0)焦点F 的弦，若A (x A ，y A )，B (x B ，y B )，则 (1)x A ·x B ＝p 24.(2)y A ·y B ＝－p 2.(3)|AB |＝x A ＋x B ＋p ＝2psin 2α(α是直线AB 的倾斜角).【例12】过抛物线y 2＝4x 的焦点F 的直线l 与抛物线交于A ，B 两点，若|AF |＝2|BF |，则|AB |等于( ) A.4B.92C.5D.6解析由对称性不妨设点A 在x 轴的上方，如图设A ，B 在准线上的射影分别为D ，C ，作BE ⊥AD 于E ，设|BF |＝m ，直线l 的倾斜角为θ，则|AB |＝3m ，由抛物线的定义知|AD |＝|AF |＝2m ，|BC |＝|BF |＝m ，所以cos θ＝|AE ||AB |＝13，∴sin 2θ＝89.又y 2＝4x ，知2p ＝4，故利用弦长公式|AB |＝2p sin 2θ＝92.答案 B【训练12】设F 为抛物线C ：y 2＝3x 的焦点，过F 且倾斜角为30°的直线交C 于A ，B 两点，O 为坐标原点，则△OAB 的面积为( )A.334B.938C.6332D.94解析法一由已知得焦点坐标为F ⎝ ⎛⎭⎪⎫34，0，因此直线AB 的方程为y ＝33⎝ ⎛⎭⎪⎫x －34，即4x －43y －3＝0.与抛物线方程联立，化简得4y 2－123y －9＝0，故|y A －y B |＝（y A ＋y B ）2－4y A y B ＝6. 因此S △OAB ＝12|OF ||y A －y B |＝12×34×6＝94.法二由2p ＝3，及|AB |＝2psin 2α得|AB |＝2p sin 2α＝3sin 230°＝12. 原点到直线AB 的距离d ＝|OF |·sin 30°＝38，故S △AOB ＝12|AB |·d ＝12×12×38＝94.答案 D。

2024年广州市普通高中毕业班冲刺训练题(一)含答案

★启用前注意保密试卷类型：B 2024年广州市普通高中毕业班冲刺训练题（一）历史本试卷共6页，20小题，满分100分。

考试用时75分钟。

注意事项：1. 答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号、考场号和座位号填写在答题卡上，并用2B铅笔在答题卡上的相应位置填涂考生号。

2. 作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3. 非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4. 考生必须保证答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题：本题共16小题，每小题3分，共48分。

在每小题给出的四个选项中，只有一项符合题目要求。

1．商王朝在与方国交战时要祭祀先王，如武丁伐土方时祭祀先王汤，伐虎方时祭祀先王大甲、祖乙等。

这说明商朝A. 统治范围在不断扩大B．注重维护封建等级秩序C．对方国实行直接统治D．利用神权巩固强化王权2．敦煌悬泉汉简记载：甘露二年七月，敦煌九个驿站的马匹累死368匹，超过西汉政府为驿站配置的定额8匹；汉元帝时将敦煌郡九个厩置马匹定额从360匹提高到480匹，还为驿站配置马医。

这A. 促进了区域间商业贸易发展B. 提高了边疆地区的农业技术C. 确保了军令和政令畅通无阻D. 加速了西南地区的民族交融3．西晋鼓吹曲辞仿造汉短箫铙歌有所新变。

西晋官方制作的鼓吹曲辞按照宣、景、文、武的顺序梳理帝王功绩，与晋宣帝司马懿相关的五首曲辞分别描述其剿灭孟达、抵御诸葛亮、剿灭辽东公孙渊之战，赞其击退吴军对魏的攻伐后，又征吴之事，肇创帝基。

西晋官方制作鼓吹曲辞反映了A. 统治者重构权力的更替过程B. 儒学成为了官方正统C. 艺术审美与史料价值的统一D. 宫廷文化传播到民间4．下表是宋代江南西路改乡名表（部分）原名改名时间原因永昌文昌庆历中(1041—1048) 以其乡多文士康乐欧桂宋代欧阳修伯祖欧阳仪进士及第，里间荣之文霸儒林南宋周必大中进士太平孝感淳祐十二年(1252) 朝廷因杨懋卿纯孝，“诏旌表其门闾”材料反映了宋朝A.科举制度的完善B. 对文教事业推崇C. 重文轻武的政策D. 乡里制度的变化5．明万历三十六年大水，大量农田被毁，河北柏乡县引种籼谷（水稻），并从福建引种甘薯；清代江汉平原民众在灾年时，种植茭米、荞麦等生长期较短的植物代替水稻，洞庭湖区的民众大量采集水蒿、菱角等水生植物。

2020浙教版科学七年级上册“期中冲刺”专题训练(一)：实验探究(1)【含答案】

1、细菌的生长繁殖是否受酸碱性影响呢？科学兴趣小组找来面包，探究细菌的生长繁殖与酸碱性的关系。

在A 、B 、C 三个培养皿中分别加入适量的酸液、蒸馏水、碱液，分别放入一块等大的面包。

A B C（1）实验中需要控制相同的量有（写出一个即可）。

（2）下表是兴趣小组观察后记录的细菌数，“+”的多少表示细菌数量的多少。

培养皿A （酸液）B （蒸馏水）C （碱液）细菌数目 ++ +++++ +实验可得到的结论是：该细菌的生长繁殖。

（3）小组成员中有人提出，是不是所有的细菌都适合在中性环境中生长呢？他们通过查资料获得甲、乙、丙三种细菌与酸碱性的关系图。

下列分析正确的是（答案不止一个）。

（备注：PH 的大小代表液体不同的酸碱性。

PH=7中性，PH>7碱性，PH<7酸性；）A 、甲细菌对酸碱性的适应范围最广B 、乙、丙两种细菌在中性环境中不能生长C 、乙细菌适合在酸性环境中生活D 、不同细菌生活环境对酸碱性的要求是不同的2020浙教版科学七年级上册“期中复习”过关（一）：实验探究（1）细菌数目甲乙丙2、蝙蝠是一种分布很广的哺乳动物，几乎所有蝙蝠均于白犬憩息，夜出觅食。

蝙蝠通常喜欢栖息于孤立的地方，如山洞、缝隙、地洞或建筑物内。

为了研究“蝙蝠主要是通过眼、耳、皮肤中的什么来发现障碍物的，”科学家在一个大房间内竖起金属丝制成的障碍物，然后记录撞击或避开障碍物的蝙蝠数量，实验方法和结果见下表。

实验处理方法被观察的蝙蝠数量避开障碍物蝙蝠的百分比(％)A 不做任何处理1000 71B 蒙住蝙蝠的双眼1000 70C 蒙住蝙蝠的双耳1000 35(1)设计实验A的目的是__________________。

(2)从实验A和B中，你能得出的结论是___________________________________________。

(3)分析表中的数据，蝙蝠是通过__________来发现障碍物的。

(4)是什么生活环境促使蝙蝠在长期的进化过程中形成了这样的功能，答：_________ 3、某同学将甲、乙两种植物种植在成份相同的土壤中，分成A、B、C、D四组（如下图所示），其中B与C组遮光，降低光照30%。

人教版七年级数学上册期末冲刺训练(一)(含答案)

人教版七年级数学上册期末冲刺训练（一）一．选择题1．在下列分数中，不能化成有限小数的是（）A．B．C．D．2．2020年新冠肺炎席卷全球．据经济日报3月8日报道，为支持发展中国家应对新冠肺炎疫情，中国向世卫组织捐款2000万美元．其中的2000万用科学记数法表示为（）A．20×106B．2×107C．2×108D．0.2×1083．下列说法正确的是（）A．绝对值等于它本身的数是零B．零的相反数没有意义C．互为相反数的两数，绝对值一定相等D．互为相反数的两数，它们的符号一定是异号4．在﹣（﹣8），（﹣1）2019，﹣32，0，﹣|﹣1|，﹣中，负数的个数有（）A．2个B．3个C．4个D．5个5．一个长方形的长是2a，宽是a+1，则这个长方形的周长等于（）A．6a+1 B．2a2+2a C．6a D．6a+26．下列结论正确的是（）A．abc的系数是0B．1﹣3x2﹣x中二次项系数是1C．﹣ab3c的次数是5D．的次数是57．下列各组单项式中，不是同类项的是（）A．32与23B．﹣5m4与0.36m4C．与﹣23a3bc D．与﹣0.19x3m8．在下列说法中，正确的是（）A．不是整式B．﹣系数是﹣3，次数是3C．3是单项式D．多项式2x2y﹣xy是五次二项式9．解方程1﹣＝，去分母，去括号得（）A．1﹣2x+2＝x B．1﹣2x﹣2＝x C．4﹣2x+2＝x D．4﹣2x﹣2＝x 10．若关于y的一元一次方程的解是y＝﹣2，则a的值是（）A．﹣50 B．﹣40 C．40 D．5011．中国古代人民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有个问题，原文：今有三人共车，二车空；二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，求共有多少人？设有x人，根据题意可列方程为（）A．﹣2＝B．+2＝C．+2＝D．﹣2＝12．一列火车正在匀速行驶，它先用20秒的时间通过了一条长为160米的隧道（即从车头进入入口到车尾离开出口），又用15秒的时间通过了一条长为80米的隧道，求这列火车的长度．设这列火车的长度为x米，根据题意可列方程为（）A．＝B．＝C．＝D．＝二．填空题13．单项式的系数是．14．某产品原价为n元，涨价30%之后，销量下降，于是又降价20%销售，则该产品现价为元．15．代数式3x+2比4﹣x大4，则x＝．16．一艘轮船从甲码头到乙码头顺流行驶用3小时，从乙码头到甲码头逆流行驶用4小时，已知轮船在静水中的速度为30千米/时，求水流的速度，若设水流的速度为x千米/时，则可列一元一次方程为．17．铁路旁的一条平行小路上有一行人与一骑车人同时向东行驶，行人速度为3.6千米/时，骑车人速度为10.8千米/时，如果有一列火车从他们背后开过来，他通过行人用了22秒，通过骑车人用了26秒，则这列火车长度为米．三．解答题18．（1）（﹣2）+（﹣3）﹣（+1）﹣（﹣6）（2）（3）﹣14﹣32÷[（﹣2）3+4]（4）﹣9÷3+（﹣）×12+（﹣3）219．先化简，再求值．（1）﹣（4x2+2x﹣1）+3x2﹣3x．其中x＝﹣；（2）（3a2﹣ab+5）﹣2（5ab﹣4a2+2），其中a2﹣ab＝2．20．解方程：（1）5x﹣4＝2（2x﹣3）（2）﹣＝121．某水果批发市场苹果的价格如表：购买苹果（千克）不超过20千克20千克以上但不超40千克以上过40千克每千克的价格6元5元4元表格说明：苹果价格分段计算，如：某人购买苹果25千克，则总费用＝20×6+（25﹣20）×5＝145元．（1）小明购买苹果45千克，需付费元；（2）若小明两次共购买100千克苹果，设小明第一次购买苹果x千克，且x≤50，求小明两次共需付费多少元（用含x的式子表示）．22．2020年“新冠肺炎”疫情的蔓延，使得医用口罩销量大幅增加．某口罩加工厂为满足市场需求，计划在本周每日生产5000个医用口罩，但是由于各种原因，实际每日生产量与计划生产量相比情况如表（增加的口罩数为正数，减少的口罩数为负数）：星期一二三四五六日增减（单位：个）+100 ﹣200 +300 ﹣150 ﹣100 +350 +150（1）该口罩加工厂本周产量最多的一日比产量最少的一日多生产多少个口罩？（2）请你根据记录求出该口罩加工厂本周前三日共生产多少个口罩；（3）该加工厂实行计件工资，每生产一个医用口罩，工资为0.2元，则该口罩加工厂本周应支付的工资总额是多少元？23．列方程解应用题：如图，现有两条乡村公路AB、BC，AB长为1200米，BC长为1600米，一个人骑摩托车从A处以20m/s的速度匀速沿公路AB、BC向C处行驶；另一人骑自行车从B处以5m/s的速度从B向C行驶，并且两人同时出发．（1）求经过多少秒摩托车追上自行车？（2）求两人均在行驶途中时，经过多少秒两人在行进路线上相距150米？参考答案一．选择题1．解：A、的分母中只含有质因数2，所以能化成有限小数，故本选项不合题意；B、＝，分母中只含有质因数2，所以能化成有限小数，故本选项不合题意；C、的分母中含有质因数3和2，所以不能化成有限小数，故本选项符合题意；D、的分母中只含有质因数5，所以能化成有限小数，故本选项不合题意．故选：C．2．解：2000万＝20000000＝2×107．故选：B．3．解：A、绝对值等于它本身的数是所有非负数，故此选项错误；B、根据零的相反数是0，零的相反数有意义，故此选项错误；C、互为相反数的绝对值一定相等，故此选项正确；D、互为相反数的两数，有可能是0，故此选项错误．故选：C．4．解：﹣（﹣8）＝8，是正数；（﹣1）2019＝﹣1，是负数；﹣32＝﹣9，是负数；0既不是正数也不是负数；﹣|﹣1|＝﹣1，是负数；﹣是负数；故选：C．5．解：根据题意得：2（2a+a+1）＝2（3a+1）＝6a+2，故选：D．6．解：A、abc的系数是1，选项错误；B、1﹣3x2﹣x中二次项系数是﹣3，选项错误；C、﹣ab3c的次数是5，选项正确；D、的次数是6，选项错误．故选：C．7．解：A、常数项也是同类项，故A不符合题意；B、所含字母相同且相同字母的指数也相同的项是同类项，故B不符合题意；C、所含字母相同且相同字母的指数也相同的项是同类项，故C不符合题意；D、字母不同不是同类项，故D符合题意；故选：D．8．解：A、是整式；B、﹣系数是﹣，次数是3；C、3是单项式，正确；D、多项式2x2y﹣xy是三次二项式；故选：C．9．解：解方程1﹣＝，去分母，去括号得4﹣2（x+1）＝x，即4﹣2x﹣2＝x．故选：D．10．解：把y＝﹣2代入方程，得：﹣1＝，解得：a＝﹣50．则a的值为﹣50．故选：A．11．解：设有x人，依题意，得：+2＝．故选：C．12．解：设这列火车的长度为x米，依题意，得：＝．故选：B．二．填空题（共5小题）13．解：单项式﹣的系数是：﹣．故答案为：﹣．14．解：涨价30%之后的价格：（1+30%）n＝1.3n，降价20%后的价格：1.3n×（1﹣20%）＝1.04n，故答案为1.04n．15．解：根据题意得：（3x+2）﹣（4﹣x）＝4，去括号得：3x+2﹣4+x＝4，移项得：3x+x＝4﹣2+4，合并得：4x＝6，解得：x＝1.5．故答案为：1.5．16．解：设水流的速度为x千米/时，则顺流行驶的速度为（x+30）千米/时，逆流行驶的速度为（30﹣x）千米/时，依题意，得：3（x+30）＝4（30﹣x）．故答案为：3（x+30）＝4（30﹣x）．17．解：设这列火车长度为x米，3.6千米/小时＝1米/秒，10.8千米/小时＝3米/秒，＝，解得x＝286，即这列火车长度为286米，故答案为：286．三．解答题（共6小题）18．解：（1）原式＝﹣2﹣3﹣1+6＝0（2）原式＝（﹣+﹣）×（﹣24）＝2﹣8+12＝6（3）原式＝﹣1﹣32÷（﹣8+4）＝﹣1+8＝7（4）原式＝﹣3+（﹣）×12+9＝﹣3﹣2+9＝419．解：（1）原式＝﹣6x2﹣3x++3x2﹣3x＝﹣3x2﹣6x+，∴当x＝﹣时，原式＝﹣3×（﹣）2﹣6×（﹣）+＝﹣+4+＝4；（2）原式＝3a2﹣ab+5﹣10ab+8a2﹣4＝11a2﹣11ab+1＝11（a2﹣ab）+1，∴当a2﹣ab＝2时，原式＝22+1＝23．20．解：（1）去括号得：5x﹣4＝4x﹣6，移项合并得：x＝﹣2；（2）去分母得：5x﹣15﹣8x﹣2＝10，移项合并得：﹣3x＝27，解得：x＝﹣9．21．解：（1）由题意可得，小明购买苹果45千克，需付费：20×6+（40﹣20）×5+（45﹣40）×4＝240（元），故答案为：240元；（2）当0＜x≤20时，小明两次共需付费：6x+20×6+20×5+（100﹣x﹣40）×4＝（460+2x）（元），当20＜x≤40时，小明两次共需付费：20×6+（x﹣20）×5+20×6+20×5+4（100﹣x﹣40）＝（480+x）（元），当40＜x≤50时，小明两次共需付费：20×6+20×5+（x﹣40）×4+20×6+20×5+4（100﹣x﹣40）＝520（元）．22．解：（1）根据题意知，星期六产量最多，星期二产量最低，（+350）﹣（﹣200）＝550（个），答：产量最多的一天比产量最少的一天多生产550个口罩；（2）（+100）+（﹣200）+（300）＝200，5000×3＝15000，200+15000＝15200（个），答：前三天共生产15200个口罩；（3）（+100）+（﹣200）+（+300）+（﹣150）+（﹣100）+（+350）+（+150）＝450，5000×7＝35000，450+35000＝35450，35450×0.2＝7090（元），答：口罩加工厂本周应支付工人的工资总额是7090元．23．解：（1）设经过x秒摩托车追上自行车，20x＝5x+1200，解得x＝80．答：经过80秒摩托车追上自行车．（2）设经过y秒两人相距150米，第一种情况：摩托车还差150米追上自行车时，20y﹣1200＝5y﹣150解得y＝70．第二种情况：摩托车超过自行车150米时，20y＝150+5y+1200解得y＝90．答：经过70秒或90秒两人在行进路线上相距150米．。

九年级数学中考提升冲刺训练(一)(含答案)

九年级数学中考提升冲刺训练（一）姓名：___________班级：___________考号：___________注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第Ⅰ卷（选择题）一．选择题1．|﹣|的值是（）A．2020 B．﹣2020 C．﹣D．2．2019年末到2020年3月16日截止，世界各国感染新冠状肺炎病毒患者达到15万人，将数据15万用科学记数表示为（）A．1.5×104B．1.5×103C．1.5×105D．1.5×1023．如图，这是一个机械模具，则它的左视图是（）A．B．C．D．4．下列运算中，错误的是（）A．x2•x3＝x6B．x2+x2＝2x2C．（x2）3＝x6D．（﹣3x）2＝9x2 5．下列图形中，是轴对称图形，也是中心对称图形的是（）A．B．C．D．6．一组数据：3、6、7、5、4，则这组数据的中位数是（）A．4 B．4.5 C．5 D．67．实数a，b，c在数轴上的对应点的位置如图所示，则下列结论正确的是（）A．|c|＞|a| B．ac＞0 C．c﹣b＞0 D．b+c＜08．已知3+m＝n，则m可能是（）A．3B．C．D．9．若α，β是关于x的一元二次方程x2﹣2x+m＝0的两实根，且+＝﹣，则m等于（）A．﹣2 B．﹣3 C．2 D．310．如图，E、F分别是正方形ABCD的边BC、CD的中点，连接AF、DE交于点P，过B作BG ∥DE交AD于G，BG与AF交于点M．对于下列结论：①AF⊥DE；②G是AD的中点；③∠GBP＝∠BPE；④S△AGM ：S△DEC＝1：4．正确的个数是（）A．1个B．2个C．3个D．4个第Ⅱ卷（非选择题）二．填空题11．计算：（﹣3）﹣1+（﹣4）0＝．12．如图，△ABC的两条中线AD，BE交于点G，EF∥BC交AD于点F．若FG＝1，则AD＝．13．一个n边形的内角和等于720°，则n＝．14．若a＝2019，b＝2020，则[a2（a﹣2b）﹣a（a﹣b）2]÷b2的值为．15．某数学兴趣小组为测量河对岸树AB的高，在河岸边选择一点C．从C处测得树梢A的仰角为45°，沿BC方向后退10米到点D，再次测得树梢A的仰角为30°，则树高为米．（结果精确到0.1米，参考数据：≈1.414，≈1.732）16．如图1所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按图2所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用9个这样的图形（图1）拼出来的图形的总长度是（结果用含a，b代数式表示）．三．解答题17．解不等式组：18．先化简，再求值：（+）÷，其中x＝6．19．如图，在△ABC中，（1）求作：∠BAD＝∠C，AD交BC于D．（用尺规作图法，保留作图痕迹，不要求写作法）．（2）在（1）条件下，求证：AB2＝BD•BC．20．今年3月，某集团随机抽取所属的m家商业连锁店进行评估，将各连锁店按照评估成绩分成了A、B、C、D四个等级，绘制了如图尚不完整的统计图表．评估成绩n（分）评定等级频数90≤n≤100 A 280≤n＜90 B b70≤n＜80 C15n＜70 D 6根据以上信息解答下列问题：（1）求m，b的值；（2）在扇形统计图中，求B等级所在扇形的圆心角的大小；（3）从评估成绩不少于80分的连锁店中，任选2家介绍营销经验，用树状图或列表法求其中至少有一家是A等级的概率．21．某商场购进一批LED灯泡与普通白炽灯泡，其进价与标价如下表．该商场购进LED灯泡与普通白炽灯泡共300个，LED灯泡按标价进行销售，而普通白炽灯泡按标价打九折销售，销售完这批灯泡后可以获利3200元．（1）求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个？（2）由于春节期间热销，很快将两种灯泡销售完，若该商场计划再次购进两种灯泡120个，并在不打折的情况下销售完．若销售完这两批灯泡的获利不超过总进货价的28%，则最多再次购进LED灯泡多少个？LED灯泡普通白炽灯泡进价（元）45 25标价（元）60 3022．在如图所示的网格中，每个小正方形的边长为1，每个小正方形的顶点叫格点，△ABC 的三个顶点均在格点上，以点A为圆心的与BC相切于点D，分别交AB、AC于点E、F．（1）求△ABC三边的长；（2）求图中由线段EB、BC、CF及所围成的阴影部分的面积．23．在平面直角坐标系xOy中，直线y＝kx+b（k≠0）与双曲线y＝（m≠0）相交于A，B 两点，点A坐标为（﹣3，2），点B坐标为（n，﹣3）．（1）求一次函数和反比例函数的表达式；（2）如果点P是x轴上一点，且△ABP的面积是5，求点P的坐标．（3）利用函数图象直接写出关于x的不等式kx+b＜的解集．24．定义：如果三角形的两个内角α与β满足α+2β＝90°，那么称这样的三角形为“类直角三角形”．尝试运用（1）如图1，在Rt△ABC中，∠C＝90°，BC＝3，AB＝5，BD是∠ABC的平分线．①证明△ABD是“类直角三角形”；②试问在边AC上是否存在点E（异于点D），使得△ABE也是“类直角三角形”？若存在，请求出CE的长；若不存在，请说明理由．类比拓展（2）如图2，△ABD内接于⊙O，直径AB＝13，弦AD＝5，点E是弧AD上一动点（包括端点A，D），延长BE至点C，连结AC，且∠CAD＝∠AOD，当△ABC是“类直角三角形”时，求AC的长．25．如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+c的图象与x轴交于A（﹣3，0）、B（2，0）两点，与y轴交于点C（0，3）．（1）求抛物线的解析式；（2）点E（m，2）是直线AC上方的抛物线上一点，连接EA、EB、EC，EB与y轴交于D．①点F是x轴上一动点，连接EF，当以A、E、F为顶点的三角形与△BOD相似时，求出线段EF的长；②点G为y轴左侧抛物线上一点，过点G作直线CE的垂线，垂足为H，若∠GCH＝∠EBA，请直接写出点H的坐标．参考答案一．选择题1．解：，故选：D．2．解：15万＝15×104＝1.5×105．故选：C．3．解：从左边看，得到的图形只有一列两层，第一层是正方形，第二层的正方形里面有实心的圆圈，故选：B．4．解：A．x2•x3＝x5，故本选项符合题意；B．x2+x2＝2x2，故本选项不合题意；C．（x2）3＝x6，故本选项不合题意；D．（﹣3x）2＝9x2，故本选项不合题意．故选：A．5．解：A、不是中心对称图形，是轴对称图形，故本选项不合题意；B、是中心对称图形，也是轴对称图形，故本选项符合题意；C、是中心对称图形，不是轴对称图形，故本选项不合题意；D、不是中心对称图形，是轴对称图形，故本选项不合题意．故选：B．6．解：把数据按从小到大的顺序排列为：3，4，5，6，7，则中位数是5．故选：C．7．解：由数轴可知，﹣4＜a＜﹣3，﹣1＜b＜0，2＜c＜3，∴|c|＜|a|，A错误；ac＜0，B错误；c﹣b＞0，C正确；b+c＞0，D错误；故选：C．8．解：根据3+m＝n，得到3与m为同类二次根式，则m可能是3，故选：A．9．解：α，β是关于x的一元二次方程x2﹣2x+m＝0的两实根，∴α+β＝2，αβ＝m，∵+＝＝＝﹣，∴m＝﹣3；故选：B．10．解：∵正方形ABCD，E，F均为中点∴AD＝BC＝DC，EC＝DF＝BC，∵在△ADF和△DCE中，，∴△ADF≌△DCE（SAS），∴∠AFD＝∠DEC，∵∠DEC+∠CDE＝90°，∴∠AFD+∠CDE＝90°＝∠DGF，∴AF⊥DE，故①正确，∵BG∥DE，GD∥BE，∴四边形GBED为平行四边形，∴GD＝BE，∵BE＝BC，∴GD＝AD，即G是AD的中点，故②正确，∵BG∥DE，∴∠GBP＝∠BPE，故③正确．∵BG∥DG，AF⊥DE，∴AF⊥BG，∴∠ANG＝∠ADF＝90°，∵∠GAM＝∠FAD，∴△AGM∽△AFD，设AG＝a，则AD＝2a，AF＝a，∴＝．∵△ADF≌△DCE，∴S△AGM ：S△DEC＝1：5．故④错误．故选：C．二．填空题11．解：原式＝+1＝，故答案为：12．解：∵△ABC的两条中线AD，BE交于点G，∴BD＝CD，AE＝CE，∵EF∥CD，∴＝＝1，即AF＝FD，∴EF为△ADC的中位线，∴EF＝CD，∴EF＝BD，∵EF∥BD，∴＝＝，∴DG＝2FG＝2，∴FD＝2+1＝3，∴AD＝2FG＝6．故答案为6．13．解：依题意有：（n﹣2）•180°＝720°，解得n＝6．故答案为：6．14．解：原式＝（a3﹣2a2b﹣a3+2a2b﹣ab2）]÷b2＝﹣a，当a＝2019时，原式＝﹣2019．故答案为：﹣201915．解：根据题意可知：∠ABC＝90°，CD＝10，在Rt△ABC中，∠ACB＝45°，∴AB＝CB，在Rt△ABD中，∠ADB＝30°，BD＝CD+BC＝10+AB，∴tan30°＝，即＝，解得AB≈13.7（米）．答：树高约为13.7米．故答案为：13.716．解：方法1、如图，由图可得，拼出来的图形的总长度＝5a+4[a﹣2（a﹣b）]＝a+8b 故答案为：a+8b．方法2、∵小明用9个这样的图形（图1）拼出来的图形∴口朝上的有5个，口朝下的有四个，而口朝上的有5个，长度之和是5a，口朝下的有四个，长度为4[b﹣（a﹣b）]＝8b﹣4a，即：总长度为5a+8b﹣4a＝a+8b，故答案为a+8b．三．解答题17．解：解不等式①，得x＜2，解不等式②，得x≥﹣，∴原不等式组的解集为﹣5≤x＜2．18．解：（+）÷＝＝﹣＝，当x＝6时，原式＝＝＝．19．（1）解：如图，∠BAD为所作；（2）证明：∵∠BAD＝∠C，∠B＝∠B∴△ABD∽△CBA，∴AB：BC＝BD：AB，∴AB2＝BD•BC．20．解：（1）∵C等级频数为15，占60%，∴m＝15÷60%＝25；∴b＝25﹣15﹣2﹣6＝2；（2）∵B等级频数为2，∴B等级所在扇形的圆心角的大小为：×360°＝28.8°；（3）评估成绩不少于80分的连锁店中，有两家等级为A，有两家等级为B，画树状图得：∵由图可知，共有12种等可能的结果，其中至少有一家是A等级的有10种情况，∴P（至少有一家是A等级）＝＝．21．解：（1）设该商场购进LED灯泡x个，普通白炽灯泡y个．根据题意，得：，解得，答：该商场购进LED灯泡200个，普通白炽灯泡100个．（2）设再次购进LED灯泡m个．（60﹣45）m+（30﹣25）（120﹣m）+3200≤28%[45×200+25×100+45m+25（120﹣m）] 解得：m≤59，∵m取正整数，∴m的最大值为59则最多再次购进LED灯泡59个．22．解：（1）AB＝＝2，AC＝＝2，BC＝＝4；（2）由（1）得，AB2+AC2＝BC2，∴∠BAC＝90°，连接AD，AD＝＝2，∴S阴＝S△ABC﹣S扇形AEF＝AB•AC﹣π•AD2＝20﹣5π．23．解：（1）∵双曲线y＝（m≠0）过点A（﹣3，2），∴m＝﹣3×2＝﹣6，∴反比例函数表达式为y＝﹣，∵点B（n，﹣3）在反比例函数y＝﹣的图象上，∴n＝2，∴B（2，﹣3）．∵点A（﹣3，2）与点B（2，﹣3）在直线y＝kx+b上，∴解得∴一次函数表达式为y＝﹣x﹣1；（2）如图，在x轴上任取一点P，连接AP，BP，由（1）知点B的坐标是（2，﹣3）．在y＝﹣x﹣1中令y＝0，解得x＝﹣1，则直线与x轴的交点是（﹣1，0）．设点P的坐标是（a，0）．∵△ABP的面积是5，∴•|a+1|•（2+3）＝5，则|a+1|＝2，解得a＝﹣3或1．则点P的坐标是（﹣3，0）或（1，0）；（3）关于x的不等式kx+b＜的解集是﹣3＜x＜0或x＞2．24．（1）①证明：如图1中，∵BD是∠ABC的角平分线，∴∠ABC＝2∠ABD，∵∠C＝90°，∴∠A+∠ABC＝90°，∴∠A+2∠ABD＝90°，∴△ABD为“类直角三角形”．②如图1中，假设在AC边设上存在点E（异于点D），使得△ABE是“类直角三角形”．在Rt△ABC中，∵AB＝5，BC＝3，∴AC＝＝＝4，∵∠AEB＝∠C+∠EBC＞90°，∴∠ABE+2∠A＝90°，∵∠ABE+∠A+∠CBE＝90°∴∠A＝∠CBE，∴△ABC∽△BEC，∴＝，∴CE＝＝，（2）∵AB是直径，∴∠ADB＝90°，∵AD＝5，AB＝13，∴BD＝＝＝12，①如图2中，当∠ABC+2∠C＝90°时，作点D关于直线AB的对称点F，连接FA，FB．则点F在⊙O上，且∠DBF＝∠DOA，∵∠DBF+∠DAF＝180°，且∠CAD＝∠AOD，∴∠CAD+∠DAF＝180°，∴C，A，F共线，∵∠C+∠ABC+∠ABF＝90°∴∠C＝∠ABF，∴△FAB∽△FBC，∴＝，即＝，∴AC＝．②如图3中，由①可知，点C，A，F共线，当点E与D共线时，由对称性可知，BA平分∠FBC，∴∠C+2∠ABC＝90°，∵∠CAD＝∠CBF，∠C＝∠C，∴△DAC∽△FBC，∴＝，即＝，∴CD＝（AC+5），在Rt△ADC中，CD2+AD2＝AC2，∴AC＝（舍去负值），综上所述，当△ABC是“类直角三角形”时，AC的长为或．25．解：（1）将A（﹣3，0）、B（2，0）、C（0，3）代入y＝ax2+bx+c得，，解得：，∴抛物线的解析式为：y＝﹣x+3；（2）①将E（m，2）代入y＝﹣x+3中，得﹣m+3＝0，解得m＝﹣2或1（舍去），∴E（﹣2，2），∵A（﹣3，0）、B（2，0），∴AB＝5，AE＝，BE＝2，∴AB2＝AE2+BE2，∴∠AEB＝∠DOB＝90°，∴∠EAB+∠EBA＝∠ODB+∠EBA＝90°，∴∠EAB＝∠ODB，（Ⅰ）当△FEA∽△BOD时，∴∠AEF＝∠DOB＝90°，∴F与B点重合，∴EF＝BE＝2，（Ⅱ）当△EFA∽△BOD时，∴∠AFE＝∠DOB＝90°，∵E（﹣2，2），∴EF＝2，故：EF的长为2或2；②点H的坐标为（﹣，）或（﹣，），（Ⅰ）过点H作HN⊥CO于点N，过点G作GM⊥HN于点M，∴∠GMN＝∠CNH＝90°，又∠GHC＝90°，∴∠CHN+∠GHM＝∠MGH+∠GHM＝90°，∴∠CHN＝∠MGH，∵HN⊥CO，∠COP＝90°，∴HN∥AB，∴∠CHN＝∠APE＝∠MGH，∵E（﹣2，2），C（0，3），∴直线CE的解析式为y＝x+3，∴P（﹣6，0），∴EP＝EB＝2，∴∠APE＝∠EBA，∵∠GCH＝∠EBA，∴∠GCH＝∠APE＝∠EBA＝∠CHN＝∠MGH，∴GC∥PB，又C（0，3），∴G点的纵坐标为3，代入y＝﹣x+3中，得：x＝﹣1或0（舍去），∴MN＝1，∵∠AEB＝90°，AE＝，BE＝2，∴tan∠EBA＝tan∠CHN＝tan∠MGH＝，设CN＝MG＝m，则HN＝2m，MH＝m，∴MH+HN＝2m+m＝1，解得，m＝，∴H点的橫坐标为﹣，代入y＝x+3，得：y＝，∴点H的坐标为（﹣，）．（Ⅱ）过点H作MN⊥PB，过点C作CN⊥MH于点N，过点G作GM⊥HM于点M，∴CN∥PB，∴∠NCH＝∠APE，由（Ⅰ）知：∠APE＝∠EBA，则∠NCH＝∠EBA，∵∠GMN＝∠CNH＝90°，又∠GHC＝90°，∴∠HCN+∠NHC＝∠MHG+∠NHC＝90°，∴∠HCN＝∠MHG，∵∠GCH＝∠EBA，∴∠GCH＝∠EBA＝∠HCN＝∠MHG，由（Ⅰ）知：tan∠EBA＝，则tan∠MHG＝＝tan∠GCH＝，设MG＝a，则MH＝2a，∵∠NCH＝∠MHG，∠N＝∠M，∴△HMG∽△CNH，∴，∴NH＝2a，CN＝4a，又C（0，3），∴G（﹣3a，3﹣4a），代入y＝﹣x+3中，得，a＝或0（舍去），∴CN＝，∴H点的橫坐标为﹣，代入y＝x+3，得，y＝．∴点H的坐标为（﹣）．综合以上可得点H的坐标为（﹣，）或（﹣）．。

湖北省2023届高三地理考前冲刺训练含答案

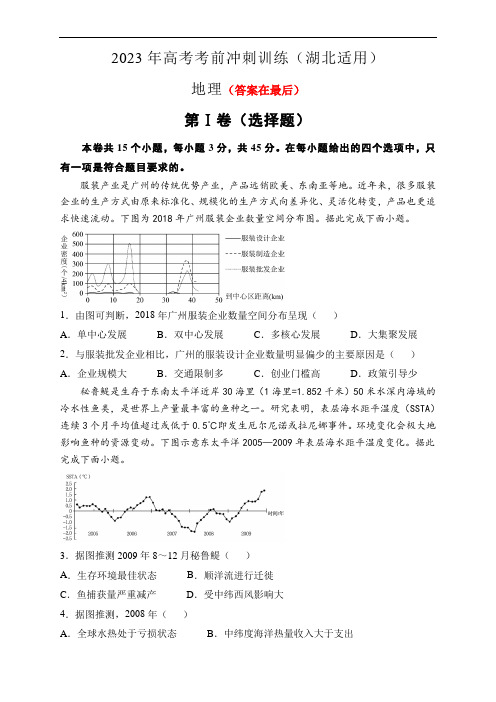
2023年高考考前冲刺训练（湖北适用）地理（答案在最后）第Ⅰ卷（选择题）本卷共15个小题，每小题3分，共45分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

服装产业是广州的传统优势产业，产品远销欧美、东南亚等地。

近年来，很多服装企业的生产方式由原来标准化、规模化的生产方式向差异化、灵活化转变，产品也更追求快速流动。

下图为2018年广州服装企业数量空间分布图。

据此完成下面小题。

1．由图可判断，2018年广州服装企业数量空间分布呈现（）A．单中心发展B．双中心发展C．多核心发展D．大集聚发展2．与服装批发企业相比，广州的服装设计企业数量明显偏少的主要原因是（）A．企业规模大B．交通限制多C．创业门槛高D．政策引导少秘鲁鳀是生存于东南太平洋近岸30海里（1海里=1.852千米）50米水深内海域的冷水性鱼类，是世界上产量最丰富的鱼种之一。

研究表明，表层海水距平温度（SSTA）连续3个月平均值超过或低于0.5℃即发生厄尔尼诺或拉尼娜事件。

环境变化会极大地影响鱼种的资源变动。

下图示意东太平洋2005—2009年表层海水距平温度变化。

据此完成下面小题。

3．据图推测2009年8～12月秘鲁鳀（）A．生存环境最佳状态B．顺洋流进行迁徙C．鱼捕获量严重减产D．受中纬西风影响大4．据图推测，2008年（）A．全球水热处于亏损状态B．中纬度海洋热量收入大于支出C．我国冬季气温相对偏低D．在一定程度上延缓了全球变暖随着时间的推移，城市中的住区逐渐出现建筑设施老化、环境风貌杂乱、治理水平低下等问题，成为居住品质低下的老旧住区。

城市老旧住区的空间分布与建设时序、功能区划、土地价格等因素息息相关。

且老旧住区具有“传染”性，呈集聚分布态势。

下图示意哈尔滨市区街道层面的老旧住区空间分布。

读图完成下面小题。

5．哈尔滨老旧住区多呈现集聚分布态势，结合材料，其原因表述正确的有（）①同一片住区开发时间接近，老化程度相当②生态脆弱，影响周边地区③住区老化，导致人口外迁，加速周边住区老化④住区老化传染，导致周边住区地价低迷，维护动力不足A．①②④B．②③④C．①③④D．①②③6．甲地附近主要的城市功能区类型与该地住区老化严重的原因，匹配正确的是（）A．住宅区——城市发展早，配套设施老化B．商业区——随着城市规模的扩大，原有商业区活力不足，逐渐老化C．工业区——早期工业发展，配套住宅随工业衰败而老化D．交通与仓储区——位于郊区，土地面积较大且地租较低廉，仓储区因时间推移缺乏维护而老八字门滑坡（下图）是三峡库区重点监测滑坡之一，由于每年受强降雨或持续性降雨影响，目前该滑坡仍处于位移变形状态。

《运动生理学》人体版冲刺卷(一)- 答案

2019年《运动生理学》人体版冲刺卷（一）（150分）注意：考生须将试题答案写在答题纸上，写在试卷上无效！一、名词解释（共5题，每题4分，共20分)1.反应时【参考答案】从感受器接受刺激产生兴奋并沿反射弧传递开始，到引起效应器发生反应所需要的时间称为反应时。

2.最大摄氧量（最大吸氧量）【参考答案】最大摄氧量是指人体在进行有大量肌肉群参加的长时间剧烈运动中，当心肺功能和肌肉利用氧的能力达到人体极限水平时，单位时间内（通常以每分钟为计算单位）所能摄取的氧量，也称最大耗氧量。

3.极点【参考答案】在进行持续时间较长的剧烈运动中，由于运动开始阶段内脏器官的功能不能满足运器官的需要，运动者常常产生一些非常难受的生理反应，如呼吸困难、胸闷、头晕肌肉酸软无力、动作迟缓不协调、精神低落，甚至产生停止运动的念头等，这种现象称为“极点”。

4.运动单位【参考答案】一个a一运动神经元和受其支配的肌纤维所组成的最基本的肌肉收缩单位。

5.突触【参考答案】神经元之间在结构上并没有原生质相通，前一个神经元的轴突末梢分枝与后一个神经元的胞体或突起相互接触的部位，称为突触。

二、简答题（共3题，每题10分，共30分）1.简述力量素质的生理学基础？【参考答案】影响肌肉力量的生物学因素很多，除年龄和性别外，主要受“肌源性”因素和“神经源性”因素的影响。

“肌源性”因素包括肌肉的生理横断面积、肌纤维类型、肌肉收缩时的初长度等，“神经源性”因素包括中枢激活水平、中枢神经对肌肉的协调和控制能力、神经系统的兴奋状态等方面。

（1）肌肉生理横断面积（2）肌纤维类型（3）肌肉收缩时的初长度（4）中枢激活（5）中枢神经系统的兴奋状态（6）中枢神经对肌肉活动的协调和控制能力（7）年龄与性别（8）体重（9）其他2.试述神经——肌肉接点处兴奋的传递过程？【参考答案】当动作电位沿神经纤维传到轴突末梢时，引起轴突末梢处的接头前膜上的Ca2（钙离子）通道开放，Ca2从细胞外液进入轴突末梢，促使轴浆中含有乙酰胆碱的突触小泡向接头前膜移动。

中考数学冲刺专题训练(附答案)：应用题

精品基础教育教学资料，仅供参考，需要可下载使用！中考数学冲刺专题训练（附答案）：应用题一、选择题（本大题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．某种衬衫因换季打折出售，如果按原价的六折出售，那么每件赔本40元；按原价的九折出售，那么每件盈利20元，则这种衬衫的原价是( ) A ．160元 B ．180元 C ．200元 D ．220元【答案】C 【解析】设这种衬衫的原价是x 元，依题意，得：0.6x+40=0.9x-20，解得：x=200．故选：C ．2．某校“研学”活动小组在一次野外实践时，发现一种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是43，则这种植物每个支干长出的小分支个数是（） A ．4 B ．5 C ．6 D ．7【答案】C 【解析】设这种植物每个支干长出x 个小分支，依题意，得：2143x x ++=，解得： 17x =-（舍去），26x =．故选：C ．3．学校计划购买A 和B 两种品牌的足球，已知一个A 品牌足球60元，一个B 品牌足球75元．学校准备将1500元钱全部用于购买这两种足球（两种足球都买），该学校的购买方案共有（）A ．3种B ．4种C ．5种D ．6种【答案】B 【解析】设购买A 品牌足球x 个，购买B 品牌足球y 个，依题意，得：60751500x y +=，∴4205y x =-．x ，y 均为正整数，∴11516x y =⎧⎨=⎩，221012x y =⎧⎨=⎩，33158x y =⎧⎨=⎩，44204x y =⎧⎨=⎩，∴该学校共有4种购买方案．故选：B ．4．为提高市民的环保意识，某市发出“节能减排，绿色出行”的倡导，某企业抓住机遇投资20万元购买并投放一批A 型“共享单车”，因为单车需求量增加，计划继续投放B 型单车，B 型单车的投放数量与A 型单车的投放数量相同，投资总费用减少20%，购买B 型单车的单价比购买A 型单车的单价少50元，则A 型单车每辆车的价格是多少元？设A 型单车每辆车的价格为x 元，根据题意，列方程正确的是（）A ．200000200000(120%)50x x -=- B ．200000200000(120)50x x x +=- C ．200000200000(120%)50x x -=+ D ．200000200000(120)50x x x +=+ 【答案】A 【解析】设A 型单车每辆车的价格为x 元，则B 型单车每辆车的价格为(50)x -元，根据题意，得200000200000(120)50x x x -=- 故选A ．5．《九章算术》中有这样一个题：今有甲乙二人持钱不知其数．甲得乙半而钱五十，乙得甲太半而钱亦五十．问甲、乙持钱各几何？其意思为：今有甲乙二人，不如其钱包里有多少钱，若乙把其一半的钱给甲，则甲的数为50；而甲把其23的钱给乙．则乙的钱数也为50，问甲、乙各有多少钱？设甲的钱数为x ，乙的钱数为y ，则可建立方程组为（）A ．15022503x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩B ．15022503x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩C ．15022503x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩D ．15022503x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩【答案】A【解析】设甲的钱数为x ，乙的钱数为y ；由甲得乙半而钱五十，可得：1x y 502+= 由甲把其23的钱给乙，则乙的钱数也为50；可得：2503x y += 故答案为:A6．红星商店计划用不超过4200元的资金，购进甲、乙两种单价分别为60元、100元的商品共50件，据市场行情，销售甲、乙商品各一件分别可获利10元、20元，两种商品均售完．若所获利润大于750元，则该店进货方案有( ) A ．3种 B ．4种C ．5种D ．6种【答案】C 【解析】设该店购进甲种商品x 件，则购进乙种商品()50x -件，根据题意，得：()()60100504200102050750x x x x ⎧+-≤⎪⎨+->⎪⎩，解得：2025x ≤<， ∵x 为整数，∴20x、21、22、23、24，∴该店进货方案有5种，故选：C ．7．甲、乙二人做某种机械零件，已知每小时甲比乙少做8个，甲做120个所用的时间与乙做150个所用的时间相等，设甲每小时做x 个零件，下列方程正确的是（） A ．1201508x x =- B ．1201508x x=+ C ．1201508x x=- D ．1201508x x =+ 【答案】D 【解析】∵甲每小时做x 个零件，∴乙每小时做（x+8）个零件， ∵甲做120个所用的时间与乙做150个所用的时间相等，∴1201508x x =+，故选D.8．为了落实精准扶贫政策，某单位针对某山区贫困村的实际情况，特向该村提供优质种羊若干只．在准备配发的过程中发现：公羊刚好每户1只；若每户发放母羊5只，则多出17只母羊，若每户发放母羊7只，则有一户可分得母羊但不足3只．这批种羊共（）只． A ．55 B ．72C ．83D ．89【答案】C 【解析】设该村共有x 户，则母羊共有()517x +只，由题意知，()()517710517713x x x x ⎧+-->⎪⎨+--<⎪⎩解得：21122x <<， ∵x 为整数， ∴11x =，则这批种羊共有115111783+⨯+=（只），故选C ．二、填空题（本大题共4个小题，每小题6分，共24分）9．《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”译文大致是：“用一根绳子去量一根木条，绳子剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺？”如果设木条长x 尺，绳子长y 尺，可列方程组为_____．【答案】 4.5112x yx y +=⎧⎪⎨-=⎪⎩【解析】设木条长x 尺，绳子长y 尺，依题意，得： 4.5112x yx y +=⎧⎪⎨-=⎪⎩10．某市为了扎实落实脱贫攻坚中“两不愁、三保障”的住房保障工作，去年已投入5亿元资金，并计划投入资金逐年增长，明年将投入7.2亿元资金用于保障性住房建设，则这两年投入资金的年平均增长率为________. 【答案】20%.【解析】设这两年中投入资金的平均年增长率是x ，由题意得： 5(1+x )2＝7.2，解得：x 1＝0.2＝20%，x 2＝﹣2.2(不合题意舍去). 答：这两年中投入资金的平均年增长率约是20%. 故答案是：20%.11．一艘轮船在静水中的最大航速为30/km h ，它以最大航速沿江顺流航行120km 所用时间，与以最大航速逆流航行60km 所用时间相同，则江水的流速为______/km h ．【答案】10 【解析】设江水的流速为/x km h ，根据题意可得：120603030x x=+-，解得：10x =，经检验：10x =是原方程的根，答：江水的流速为10/km h ．故答案为：10．12．有一种落地晾衣架如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度. 图2是支撑杆的平面示意图，AB 和CD 分别是两根不同长度的支撑杆，夹角∠BOD=α. 若AO=85cm ，BO=DO=65cm. 问: 当74α=︒，较长支撑杆的端点A 离地面的高度h 约为_____cm .(参考数据:sin 370.6,≈cos30.8≈，sin530.8,cos530.6≈≈.)【答案】120. 【解析】过O 作OE ⊥BD ，过A 作AF ⊥BD ，可得OE ∥AF ，∵BO=DO ， ∴OE 平分∠BOD ， ∴∠BOE=12∠BOD=12×74°=37°，∴∠FAB=∠BOE=37°，在Rt △ABF 中，AB=85+65=150cm ， ∴h=AF=AB•cos ∠FAB=150×0.8=120cm ，故答案为：120三、解答题（本大题共3个小题，每小题12分，共36分. 解答应写出文字说明、证明过程或演算步骤）13．小明同学在综合实践活动中对本地的一座古塔进行了测量．如图，他在山坡坡脚P 处测得古塔顶端M 的仰角为60︒，沿山坡向上走25m 到达D 处，测得古塔顶端M 的仰角为30︒．已知山坡坡度3:4i =，即3tan 4θ=，请你帮助小明计算古塔的高度ME ．（结果精确到0.1m ，参考数据：3 1.732≈）【答案】古塔的高度ME 约为39.8m ．【解析】解：作DC EP ⊥交EP 的延长线于点C ，作DF ME ⊥于点F ，作PH DF ⊥于点H ，则DC PH FE ==，DH CP =，HF PE =，设3DC x =，∵3tan 4θ=，∴4CP x =，由勾股定理得，222PD DC CP =+，即22225(3)(4)x x =+，解得，5x =，则315DC x ==，420CP x ==， ∴20DH CP ==，15FE DC ==，设MF y =，则15ME y =+，在Rt MDF 中，tan MF MDF DF∠=，则3tan 30MFDF y ==，在Rt MPE 中，tan ME MPE PE ∠=，则3(15)tan 603ME PE y ==+， ∵DH DF HF =-， ∴33(15)203y y -+=，解得，7.5103y =+， ∴7.51031539.8ME MF FE =+=++≈. 答：古塔的高度ME 约为39.8m ．14．某蔬菜种植基地为提高蔬菜产量，计划对甲、乙两种型号蔬菜大棚进行改造，根据预算，改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元，改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元．（1）改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元？（2）已知改造1个甲种型号大棚的时间是5天，改造1个乙种型号大概的时间是3天，该基地计划改造甲、乙两种蔬菜大棚共8个，改造资金最多能投入128万元，要求改造时间不超过35天，请问有几种改造方案？哪种方案基地投入资金最少，最少是多少？【答案】（1）改造1个甲种型号大棚需要12万元，改造1个乙种型号大棚需要18万元；（2）共有3种改造方案，方案1：改造3个甲种型号大棚，5个乙种型号大棚；方案2：改造4个甲种型号大棚，4个乙种型号大棚；方案3：改造5个甲种型号大棚，3个乙种型号大棚；方案3投入资金最少，最少资金是114万元．【解析】（1）设改造1个甲种型号大棚需要x万元，改造1个乙种型号大棚需要y万元，依题意，得：26248 x yx y-=⎧⎨+=⎩，解得：1218 xy=⎧⎨=⎩．答：改造1个甲种型号大棚需要12万元，改造1个乙种型号大棚需要18万元．（2）设改造m个甲种型号大棚，则改造（8﹣m）个乙种型号大棚，依题意，得：53(8)35 1218(8)128 m mm m+-⎧⎨+-⎩，解得：83≤m≤112．∵m为整数，∴m＝3，4，5，∴共有3种改造方案，方案1：改造3个甲种型号大棚，5个乙种型号大棚；方案2：改造4个甲种型号大棚，4个乙种型号大棚；方案3：改造5个甲种型号大棚，3个乙种型号大棚．方案1所需费用12×3+18×5＝126（万元）；方案2所需费用12×4+18×4＝120（万元）；方案3所需费用12×5+18×3＝114（万元）．∵114＜120＜126，∴方案3改造5个甲种型号大棚，3个乙种型号大棚基地投入资金最少，最少资金是114万元．15．超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件．根据市场调查发现，销售单价每增加2元，每天销售量会减少1件．设销售单价增加x元，每天售出y件．（1）请写出y与x之间的函数表达式；（2）当x为多少时，超市每天销售这种玩具可获利润2250元？（3）设超市每天销售这种玩具可获利w元，当x为多少时w最大，最大值是多少？【答案】（1）1502y x=-+（2）当x为10时，超市每天销售这种玩具可获利润2250元（3）当x为20时w 最大，最大值是2400元【解析】（1）根据题意得，1502y x =-+；（2）根据题意得，()1405022502x x ⎛⎫+-+= ⎪⎝⎭，解得：150x =，210x =， ∵每件利润不能超过60元， ∴10x =，答：当x 为10时，超市每天销售这种玩具可获利润2250元；（3）根据题意得，()211405030200022w x x x x ⎛⎫=+-+=-++ ⎪⎝⎭()213024502x =--+，∵102a =-<， ∴当30x <时，w 随x 的增大而增大，∴当20x时，2400w =增大，答：当x 为20时w 最大，最大值是2400元．。

2021届高考语文正确使用成语冲刺训练卷(1)

2021届高考语文正确使用成语冲刺训练卷（1）一、选择题1.下列各句中，加点粗成语使用恰当的一项是( )A.这位姑娘天生就眼睛深凹，鼻梁挺直，头发卷曲，身材苗条，好似芝兰玉树，在黄皮肤黑眼睛的国度里，很容易被人认出。

B.为化解部分旅客的不满情绪，他们设立了"旅客投诉中心"，此举说明他们不光有良好的服务意识，还有闻过则喜的雅量。

C.一名惯偷在车站行窃后正要逃跑，两位守候多时的反扒队员突然拦住他的去路，二人上下其手地将他摁倒，结果人赃俱获。

D.旧的梦想总是被新的梦想代替，很少有人能从一而终地记住自己做过的华丽缥缈的梦，因为现实需要人们不断调整梦想。

2.下列语句中加粗的成语，使用不正确的一项是( )A.沈从文有着丰富的“乡下”经验，这就使边地生活和民间文化成了他创作的最重要的源泉，尤其是沅水，在沈从文创作生涯中扮演了举足轻重的角色。

B.小说精心设计了主要情节发生的时节——端午和中秋，充分营造了具有地域色彩的民俗环境和背景，这一切生成了一个美轮美奂的湘西世界。

C.小说结尾写到作为小城标志的白塔在渡船老人死去的那个夜晚轰然坍塌，预示了一个田园牧歌神话的必然终结。

D.沈从文笔下的边城是湘西乡土地域文化的一个缩影，它虽然具体而微，但能帮助我们懂得地域特征是中国历史中的一股社会力量。

3.下列各句中加粗成语的使用，全都不正确的一项是( )①生活在这个快节奏时代的我们，已经很少能静下心来好好读书了，即便读也是东鳞西爪、浮光掠影的文字信息的汇集，难得有对着美食大快朵颐式的阅读快感。

②临到要离开伦敦的前夕，在一个美丽的黄昏，徐志摩漫步于康桥，举步维艰，几个月后，在归国途中写下了《再别康桥》。

③夕阳下流淌的康河，波光潋滟，栩栩如生；河畔的金柳姿态婀娜，如妩媚的新娘，让人心生向往④艾青写了《大堰河——我的保姆》成名作以后，便一发不可收拾，连续写下了《向太阳》《火把》等名篇。

⑤修复长城是一份既危险又辛苦的工作，工人们却甘之如饴，因为他们觉得这是一种荣誉，他们在用汗水和勇气，维护着长城的荣光。

广东英语中考笔试部分冲刺训练1(含答案)

2020年广东英语中考笔试部分满分冲刺（一）二、语法选择(本大题有10小题，每小题1分，共10分)The first time I saw Kai, she was sitting in my front yard, hugging my dog Harley. She and her husband Sean moved ____31____ a small house next to us a few days ago. From the moment I talked to her, I knew Kai would be a wonderful friend. Her smile made ____32____ feel comfortable. Her voice was always full of happiness.It didn't take long before Kai ____33____ by everyone in our neighborhood. Children and adults visited her home often. ____34____ we visited her, she listened to all of our troubles ___35____ and then said something so wise that we would leave her home with our hearts ___36____. Sometimes I read her my stories, and she always encouraged me to keep writing.All of this time, though, Kai was slowly ___37____ from cancer (癌症). She told me the first time we talked ___38____ she was terminal (晚期). But she lived each day with such cheer that I often forgot just how ill she was. Still, she died on 39 cold winter day with heavy snow falling down. During the short time we had together, I learned ____40____ from Kai about how to truly live. She taught us so many lessons about kindness, happiness, hope and cheer.()31. A. into B. on C. for D. at()32. A. I B. we C. me D. us()33. A. loved B. is loved C. was loved D. is loving()34. A. When B. If C. Since D. As()35. A. kind B. kindness C. kindly D. kinds()36. A. sing B. sang C. sings D. singing()37. A. die B. died C. dying D. dead()38. A. that B. when C. how D. why()39. A. a B. an C. the D. /()40. A. so many B. so much C. so little D. so few三、完形填空(本大题有10小题，每小题1分，共10分)(2019深圳）Nowadays, lots of foreigners are learning Chinese. Like many of them, I 41 knew two words of Chinese (“Ni Hao” and “Xie Xie”) when I first came to Beijing, China in 2009. As you can guess, my life was 42 for a while after I arrived. Simple tasks like ordering food or taking ataxi were quite stressful.I knew I had to learn more Chinese, so I 43 a Chinese class. My teacher was 44 , although I didn’t learn enough to have a real conversation. Later I studied on my own as well, but my progress was still slow. And I decided to 45 .Around this time, I started playing in a band with a Chinese man who became one of my best friends in Beijing. He taught me a lot of 46 about music, such as “melody”. He learned a lot of English from me in return, so it was a good way to 47 language and culture.I have learned enough Chinese to 48 many problems like booking train tickets. These days. there are more foreigners who are studying Chinese. I can49 why it’s an amazing language. Finally, I found that the best way to learn a 50 is to make friends with native speakers and spend time with them.( ) 41. A. usually B. only C. hardly( ) 42. A. easy B. interesting C. difficult( ) 43. A. missed B. attended C. taught( ) 44. A. helpful B. cheerful C. thankful( )45. A. make up B. put up C. give up( ) 46. A. words B. names C. jokes( ) 47. A. change B. imagine C. exchange( ) 48. A. deal with B. look for C. think of( ) 49. A. hope B. realize C. doubt( ) 50. A. language B. subjectC. task四、阅读理解(本大题有15小题，每小题2分，共30分)AWould you like to live in a city where buildings turn the lights off for you, and self-driving cars will find the nearest parking space themselves? Although it might sound a little far from you, living in a “smart” city like this could happen sooner than you think.Great changes have taken place in towns that we have lived in for centuries, while completely new cities are being built. One such place is the city of Songdo. Every home there will have a “telepresence” system (远程遥控系统)—allowing users to control the heating and looks, take part in video meetings, and receive education, health care and government services. Around the city, escalators (自动扶梯) will onlymove when someone is on them, and offices and schools will all be connected to the system.The great mind behind Songdo is from the company Cisco. In fact, technology companies around the world such as IBM, Siemens and Microsoft are already in the business.About 75% of the world's population will live in cities by 2050, so cities will need to be more modern to deal with the coming problems. “Making cities smarter is one way out, and I think this will in turn make cities greener,” said Dan Hill, head of a research company.()51. According to the text, living in a “smart” city ____.A. is not a green wayB. will be far from youC. will soon become trueD. is completely impossible()52. Paragraph 2 is mainly about ____.A. a city of the futureB. a meeting in SongdoC. a plan to build a houseD. a report on public health()53. Which company offers the great mind to build Songdo?A. Cisco.B. IBM.C. Siemens.D. Microsoft.()54. Dan Hill thinks that making cities smarter is one way to ____.A. drive people out of citiesB. control the world's populationC. develop his own companyD. solve the cities' coming problems()55. Which of the following might be the best title for the passage?A. Future EducationB. Smart CitiesC. Government ServicesD. Famous CompaniesBHow quickly can you count from one to ten? Do you use ten different words to do it? Can you do it in English or do you have to use your first language? Do you count on your fingers? Many people think that numbers and math are the same all over the world. But scientists have discovered that it is not true.People in different parts of the world use different ways to count on their fingers. In the United States,people begin counting with their first finger which they extend or stick out. They then extend the rest of their fingers and finally the thumb to count to five. Then they repeat this with the other hand to get to ten. In China, people count by using different finger positions. In this way, a Chinese person can easily count to ten on only one hand.Besides ways of finger counting, scientists have found that cultures and languages are also different when it comes to numbers. Some languages have only a few words for numbers and others have no words for numbers. A group of scientists studied aboriginal（土著的）people in Australia. These people don't have hand movements to stand for numbers. They don't even have words for numbers. However, they are still able to understand different ideas about numbers.In a similar study, researchers from the Massachusetts Institute of Technology discovered that people of the Piraha tribe（部落）in northwestern Brazil don't have words for numbe rs, such as “one” or “three”. They are not able to say “five trees” or “ten trees”, but can say “some trees”, “more trees” or “many trees”. Professor Edward Gibson said that most people believe that everyone knows how to count, “But here is a group that does not count. They could learn, but it's not useful in their culture, so they've never picked it up. ”Although all humans are able to understand quantities（数量）, not all languages have numbers and not all people use counting. Number words in a certain language are a result of people needing numbers in their daily lives. Now we know that people have different ideas about numbers and math, too.()56. The writer begins with the four questions in order to ________.A. make a surveyB. interest readersC. tell a storyD. solve math problems()57. What do we learn from the difference in finger counting between the U. S. and China?A. People from China count much faster than people from the U. S.B. People from China need two hands to count from one to ten.C. People from the U. S. count to ten with two hands.D. People of different cultures use the same way of finger counting.()58. Which of the following is TRUE about aboriginal Australians?A. They have only a few words for numbers.B. They have hand movements to stand for numbers.C. They can only count to five on their fingers.D. They can understand different ideas about numbers.()59. What is the meaning of underlined (划线) phrases “picked up”?A. 捡起来B. 使用C. 学习D. 交流()60. What's the main idea of the passage?A. People from different cultures have different ideas about numbers and math.B. Chinese people can count more easily on their fingers than Americans.C. In some aboriginal cultures, people don't even know how to count.D. Some languages don't have number words because people don't need numbers.C配对阅读。

九年级数学中考基础冲刺训练(一)(含答案) (2)

2020年数学中考基础冲刺训练（一）一．选择题1．下列计算或运算中，正确的是（）A．a6÷a2＝a3B．（﹣2a2）3＝﹣8a3C．（a﹣b）2＝a2﹣b2D．（a﹣3）（3+a）＝a2﹣92．已知实数a，b满足a+1＞b+1，则下列选项错误的是（）A．a＞b B．﹣a＞﹣b C．a+2＞b+2 D．2a＞2b3．下列函数中，y总随x的增大而减小的是（）A．y＝﹣4x B．y＝x﹣4 C．y＝D．y＝x24．小明家1至6月份的用水量统计如下表：月份 1 2 3 4 5 6 用水量（吨） 4 6 3 5 6 6 关于这组数据，下列说法中错误的（）A．众数是6 B．平均数是5 C．中位数是5 D．方差是5．下列命题中，真命题是（）A．两对角线相等的四边形是矩形B．两对角线互相垂直的四边形是菱形C．两对角线互相垂直平分且相等的四边形是正方形D．一组对边相等另一组对边平行的四边形是平行四边形6．在△ABC中，AB＝9，BC＝2AC＝12，点D、E分别在边AB、AC上，且DE∥BC，AD ＝2BD，以AD为半径的⊙D和以CE为半径的⊙E的位置关系是（）A．外离B．外切C．相交D．内含二．填空题7．计算：（）3＝．8．已知函数y＝，当x＝2时，函数值y为．9．已知≈1.766，≈5.586，则≈．10．已知关于x方程3x2+2（1﹣a）x﹣a（a+2）＝0至少有一实根大于1，则a的取值范围是．11．书架上有3本小说、2本散文，从中随机抽取2本都是小说的概率是．12．在幻方拓展课程探中，小明在如图的3×3方格内填入了一些表示数的代数式，若圈中各行、各列及对角线上的三个数之和都相等，则x﹣2y＝．x2y﹣2 y 613．已知某地的地面气温是20℃，如果每升高1000m气温下降6℃，则气温t（℃）与高度h（m）的函数关系式为．14．“成都马拉松”活动组委会计划制作运动衫分发给参与者，为此，调查了部分参与者，以决定制作橙色、黄色、白色、红色四种颜色运动衫的数量．根据得到的调查数据，绘制成如图所示的扇形统计图．若本次活动共有50000名参与者，则估计其中选择红色运动衫的约有名．15．如图，△ABC中，AB＝AC，BC＝8，AD平分∠BAC交BC于点D，过D作DE∥AB 交AC于E，当△CDE的周长为14时，则AB长为．16．如图，已知D是△ABC的边AC上一点，且AD＝2DC，如果＝，＝，那么向量关于、的分解式是．17．如图，正方形ABCD的边长为6，点E，F分别为AB、BC的中点，点H是AD边上一点，将△DCF沿DF折叠得△DC′F，将△AEH沿EH折叠后点A的对应点A′刚好落在DC′上，则cos∠DA′H＝．18．在△ABC和△A1B1C1中，已知∠C＝∠C1＝90°，AC＝A1C1＝3，BC＝4，B1C1＝2，点D、D1分别在边AB、A1B1上，且△ACD≌△C1A1D1，那么AD的长是______三．解答题19．计算：4﹣+（﹣1）2++|1﹣|．20．解方程：+＝121．在平面直角坐标系中，直线l1：y＝kx+b（k、b为常数，且k≠0）经过A、B两点，点A 在y轴上．（1）若B点坐标为（﹣1，2）．①b＝（用含有字母k的代数式表示）②当△OAB的面积为2时，求直线l1的表达式；（2）若B点坐标为（k﹣2b，b﹣b2），点C（﹣1，s）也在直线l1上，①求s的值；②如果直线l1：y＝kx+b（k≠0）与直线l2：y＝x交于点（x1，y1），且0＜x1＜2，求k的取值范围．22．小明准备用一块矩形材料剪出如图所示的四边形ABCD（阴影部分），作为要制作的风筝的一个翅膀，请你根据图中的数据帮小明计算出CD的长度．（结果精确到0.1cm）（参考数据：sin60°＝0.87，cos60°＝0.50，tan60°＝1.73）23．如图，AB是⊙O的直径，弦CD⊥AB于点H，点F是上一点，连接AF交CD的延长线于点E．（1）求证：△AFC∽△ACE；（2）若AC＝5，DC＝6，当点F为的中点时，求AF的值．24．如图，直线y＝﹣x+5与x轴交于点B，与y轴交于点C，抛物线y＝﹣x2+bx+c与直线y＝﹣x+5交于B，C两点，已知点D的坐标为（0，3）（1）求抛物线的解析式；（2）点M，N分别是直线BC和x轴上的动点，则当△DMN的周长最小时，求点M，N 的坐标，并写出△DMN周长的最小值；（3）点P是抛物线上一动点，在（2）的条件下，是否存在这样的点P，使∠PBA＝∠ODN？若存在，请直接写出点P的坐标；若不存在，请说明理由．25．在矩形ABCD中，AB＝a，AD＝b，点E为对角线AC上一点，连接DE，以DE为边，作矩形DEFG，点F在边BC上；（1）观察猜想：如图1，当a＝b时，＝，∠ACG＝；（2）类比探究：如图2，当a≠b时，求的值（用含a、b的式子表示）及∠ACG的度数；（3）拓展应用：如图3，当a＝6，b＝8，且DF⊥AC，垂足为H，求CG的长．参考答案一．选择题1．解：A、原式＝a4，不符合题意；B、原式＝﹣8a6，不符合题意；C、原式＝a2﹣2ab+b2，不符合题意；D、原式＝a2﹣9，符合题意，故选：D．2．解：由不等式的性质得a＞b，a+2＞b+2，﹣a＜﹣b，2a＞2b．故选：B．3．解：A、k＝﹣4＜0，y随x的增大而减小，故A符合题意；B、k＝1＞0，y随x的增大而增大，故B不符合题意；C、k＝4＞0，在每一象限，y随x的增大而减小，故C不符合题意；D、a＝1，当x＜0时，y随x增大而减小，当x＞0时，y随x增大而增大，故D不符合题意；故选：A．4．解：A、众数是6是正确的，不符合题意；B、平均数＝（4+6+3+5+6+6）÷6＝5是正确的，不符合题意；C、这组数据按照从小到大排列是：3，4，5，6，6，6，则这组数据的中位数是（5+6）÷2＝5.5，原来的说法错误，符合题意；D、方差是：＝是正确的，不符合题意．故选：C．5．解：A、两对角线相等的平行四边形是矩形，所以A选项为假命题；B、两对角线互相垂直平分的四边形是菱形，所以B选项为假命题；C、两对角线互相垂直平分且相等的四边形是正方形，所以C选项为真命题；D、一组对边相等另一组对边也相等的四边形是平行四边形，所以D选项为假命题；故选：C．6．解：如图，∵DE∥BC，∴，∵BC＝12，AD＝2BD，∴，DE＝8，∵⊙D的半径为AD＝6，⊙E的半径CE＝2，∴AD+CE＝6+2＝8＝DE，∴以AD为半径的⊙D和以CE为半径的⊙E的位置关系是外切，故选：B．二．填空题7．解：（）3＝﹣a6b3，故答案为：﹣a6b3．8．解：当x＝2时，y＝2×2﹣3＝4﹣3＝1．故答案为：1．9．解：∵≈5.586，∴≈55.86，故答案为：55.8610．解：将方程左边因式分解得：（x﹣a）（3x+a+2）＝0，∴方程的解为：x1＝a，x2＝﹣，∵方程3x2+2（1﹣a）x﹣a（a+2）＝0至少有一实根大于1，∴a＞1或﹣＞1，解得：a＞1或a＜﹣5，故答案为：a＞1或a＜﹣5．11．解：画树状图为：（用A、B、C表示三本小说，a、b表示两本散文）共有20种等可能的结果数，其中从中随机抽取2本都是小说的结果数为6，所以从中随机抽取2本都是小说的概率＝＝．故答案为．12．解：由题意可得：，解得：，则x﹣2y＝8﹣4＝4．故答案为：4．13．解：∵每升高1000m气温下降6℃，∴每升高1m气温下降0.006℃，∴气温t（℃）与高度h（m）的函数关系式为t＝﹣0.006h+20，故答案为：t＝﹣0.006h+20．14．解：若本次活动共有12000名参与者，则估计其中选择红色运动衫的约有50000×20%＝10000（名），故答案为：10000．15．解：∵AB＝AC，AD平分∠BAC，∴AD⊥BC，CD＝BC＝4，∵DE∥AB，BD＝CD，∴AE＝EC，在Rt△ADC中，∠ADC＝90°，AE＝EC，∴DE＝AE，∵△CDE的周长＝14，即DE+EC+CD＝14，∴AE+EC+CD＝AC+CD＝14，∴AC＝10，∴AB＝10，故答案为：10．16．解：∵AD＝2CD，∴＝＝，∵＝+，＝﹣，∴＝﹣，故答案为﹣．17．解：如图，延长DC'交AB于K，连接FK，分别过H，E作DK的垂线，垂足分别为M，N，∵四边形ABCD为正方形，∴∠A＝∠B＝∠C＝90°，AB＝BC＝6，∵E，F分别为AB，BC的中点，∴AE＝BE＝BF＝FC＝×6＝3，由翻折知，△DCF≌△DC'F，△AEH≌△A'EH，∴∠FC'D＝∠C＝90°，∠A＝∠HA'E＝90°，AE＝A'E＝3，C'F＝CF＝BF＝3，DC'＝DC ＝6，∴∠B＝∠FC'K＝90°，又∵KF＝KF，∴Rt△FBK≌Rt△FC'K（HL），∴KB＝KC'，设KB＝KC'＝x，在Rt△ADK中，AD＝6，AK＝6﹣x，DK＝6+x，∵DK2＝AD2+AK2，∴（6+x）2＝62+（6﹣x）2，解得，x＝，∴BK＝C'K＝，∴DK＝DC'+KC'＝6+＝，EK＝BE﹣BK＝，在Rt△KNE与Rt△KAD中，sin∠EKN＝，即，解得，EN＝，∵∠DA'H+∠EA'N＝90°，∠EA'N+∠NEA'＝90°，∴∠HA'D＝∠NEA'，在Rt△EA'N中，cos∠A'EN＝＝＝，即cos∠DA'H＝，故答案为：．18．解：如图，∵在△ABC和△A1B1C1中，∠C＝∠C1＝90°，AC＝A1C1＝3，BC＝4，B1C1＝2，∴AB＝＝5，设AD＝x，则BD＝5﹣x，∵△ACD≌△C1A1D1，∴C1D1＝AD＝x，∠A1C1D1＝∠A，∠A1D1C1＝∠CDA，∴∠C1D1B1＝∠BDC，∵∠B＝90°﹣∠A，∠B1C1D1＝90°﹣∠A1C1D1，∴∠B1C1D1＝∠B，∴△C1B1D1∽△BCD，∴＝，即＝2，解得x＝，∴AD的长为，故答案为．三．解答题19．解：原式＝+（2+1﹣2）+（﹣）+﹣1 ＝+3﹣2+﹣+﹣1＝+﹣2．20．解：方程两边乘（x﹣3）（x+3），得x（x+3）+6 （x﹣3）＝x2﹣9，解得：x＝1，检验：当x＝1 时，（x﹣3）（x+3）≠0，所以，原分式方程的解为x＝1．21．解：（1）①把B（﹣1，2）代入y＝kx+b，得b＝2+k．故答案为2+k；②∵点A在y轴上，∴A（0，b），当b＞0时，S＝×b×1＝2△OAB解得b＝4，∵b＝2+k，∴k＝2∴直线l1的表达式为：y＝2x+4，当b＜0时，S＝×（﹣b）×1＝2△OAB解得b＝﹣4，∵b＝2+k，∴k＝﹣6∴直线l1的表达式为：y＝﹣6x﹣4，综上，直线l1的表达式为：y＝2x+4或y＝﹣6x﹣4；（2）①∵直线l1：y＝kx+b经过点B（k﹣2b，b﹣b2）和点C（﹣1，s）．∴k（k﹣2b）+b＝b﹣b2，﹣k+b＝s整理得，（b﹣k）2＝0，所以s＝b﹣k＝0．②∵直线l1：y＝kx+b（k≠0）与直线l2：y＝x交于点（x1，y1），∴kx1+b＝x1（1﹣k）x1＝b，∵b﹣k＝0∴b＝k∴x1＝∵0＜x1＜2，∴＞0或＜2解得0＜k＜．答：k的取值范围是0＜k＜．22．解：由题意，在Rt△BEC中，∠E＝90°，∠EBC＝60°，∴∠BCE＝30°，tan30°＝，∴BE＝EC tan30°＝51×＝17（cm）；∴CF＝AE＝34+BE＝（34+17）cm，在Rt△AFD中，∠FAD＝45°，∴∠FDA＝45°，∴DF＝AF＝EC＝51cm，则CD＝FC﹣FD＝34+17﹣51＝17﹣17≈12.5（cm），答：CD的长度为12.5cm．23．解：（1）∵CD⊥AB，AB是⊙O的直径∴∴∠AFC＝∠ACD．∵在△ACF和△AEC中，∠AFC＝∠ACD，∠CAF＝∠EAC∴△AFC∽△ACE．（2）∵四边形ACDF内接于⊙O∴∠AFD+∠ACD＝180°∵∠AFD+∠DFE＝180°∴∠DFE＝∠ACD∵∠AFC＝∠ACD∴∠AFC＝∠DFE．∵△AFC∽△ACE∴∠ACF＝∠DEF．∵F为的中点∴AF＝DF．∵在△ACF和△DEF中，∠ACF＝∠DEF，∠AFC＝∠DFE，AF＝DF ∴△ACF≌△DEF（AAS）∴AC＝DE＝5∵CD⊥AB，AB是⊙O的直径∴CH＝DH＝3．∴EH＝8在Rt△AHC中，AH2＝AC2﹣CH2＝16，在Rt△AHE中，AE2＝AH2+EH2＝80，∴．∵△AFC∽△ACE∴，即，∴．24．解：（1）y＝﹣x+5，令x＝0，则y＝5，令y＝0，则x＝5，故点B、C的坐标分别为（5，0）、（0，5），则二次函数表达式为：y＝﹣x2+bx+5，将点B坐标代入上式并解得：b＝4，故抛物线的表达式为：y＝﹣x2+4x+5…①，令y＝0，则x＝﹣1或5，故点A（﹣1，0），而OB＝OC＝2，故∠OCB＝45°；（2）过点D分别作x轴和直线BC的对称点D′（0，﹣3）、D″，∵∠OCB＝45°，则CD″∥x轴，则点D″（2，5），连接D′D″交x轴、直线BC于点N、M，此时△DMN的周长最小，将点D′、D″的坐标代入一次函数表达式：y＝mx+n并解得：m＝4，n＝﹣3，故：直线D′D″的坐标代入一次函数表达式为：y＝4x﹣3，则点M、N的坐标分别为（，）、（，0），△DMN周长的最小值＝DM+DN+MN＝D′D″＝＝2；（3）①当点P在x轴上方时，如图2，tan∠ODN＝＝＝tan∠PBA，则直线BP的表达式为：y＝﹣x+s，将点B的坐标代入上式并解得：直线BP的表达式为：y＝﹣x+…②，联立①②并解得：x＝5或﹣（舍去5）故：点P（﹣，）；②当点P在x轴下方时，同理可得点P（﹣，﹣）；综上，点P（﹣，）或（﹣，﹣）．25．解：（1）如图1，作EM⊥BC于M，EN⊥CD于N，∴∠MEN＝90°，∵a＝b，∴AB＝AD，∴矩形ABCD是正方形，∴∠ACD＝∠DAE＝45°，∵点E是正方形ABCD对角线上的点，∴EM＝EN，∵∠DEF＝90°，∴∠DEN＝∠MEF，在△DEN和△FEM中，，∴△DEN≌△FEM（ASA），∴EF＝DE．∵四边形DEFG是矩形，∴矩形DEFG是正方形；∵四边形ABCD是正方形，∴DE＝DG，AD＝DC，∵∠CDG+∠CDE＝∠ADE+∠CDE＝90°，∴∠CDG＝∠ADE，在△ADE和△CDG中，，∴△ADE≌△CDG（SAS），∴AE＝CG．∠DAE＝∠DCG＝45°，∴＝1，∠ACG＝∠ACD+∠DCG＝90°，故答案为：1；90°；（2）如图2，作EM⊥BC于M，EN⊥CD于N，则EM∥AB，EN∥AD，四边形EMCN是矩形，∴EM：AB＝CE：AC，EN：AD＝CE：AC，∠MEN＝90°，∴EM：AB＝EN：AD，∴＝＝，∵四边形ABCD、四边形DEFG是矩形，∴∠ADC＝∠DEF＝∠EDG＝90°，∴∠DEN＝∠FEM，∠ADE＝∠CDG，∵∠END＝∠EMF＝90°，∴△DEN∽△FEM，∴＝＝＝，∴△ADE∽△CDG，∴＝＝，∠DAE＝∠DCG，∵AB∥CD，∴∠BAC＝∠ACD，∵∠BAC+∠DAE＝90°，∴∠ACD+∠DCG＝90°，即∠ACG＝90°；（3）∵a＝6，b＝8，∴CD＝AB＝6，BC＝AD＝8，∴AC＝＝10，∵DF⊥AC，∴DH＝＝＝，∴CH＝＝＝，∵∠FHC＝∠B＝90°，∠FCH＝∠ACB，∴△CFH∽△CAB，∴＝，即＝，解得：FH＝，∴DF＝DH+FH＝，由（2）得：＝＝＝，设DE＝4x，则EF＝3x，∵∠DEF＝90°，∴DF＝＝5x＝，∴x＝，∴DE＝4x＝6＝DC，∴EH＝CH，∴CE＝2CH＝，∴AE＝AC﹣CE＝10﹣＝，由（2）得：＝＝＝＝，∴CG＝AE＝．。

青于蓝高考英语核按钮·综合冲刺训练(一)答案及详解

青于蓝高考英语核按钮·综合冲刺训练(一)答案及详解.txt第一次笑是因为遇见你，第一次哭是因为你不在，第一次笑着流泪是因为不能拥有你。

青于蓝高考英语核按钮·综合冲刺训练（一）答案及详解第一部分英语知识运用1-5 DAABC 6-10 BDCAA 11-15 CBDDD 16-20 CABBB21-25 CADBA 26-30 CDDAA 31-35 BCBDC 36-40 ABCDB第二部分阅读理解41-45 ACBAA 46-50 CDCAD 51-55 CBABD 56-60 BCBAC第一部分英语知识运用第二节语法和词汇知识6. B。

考查冠词。

抽象名词前一般不加任何冠词，如果不定冠词与抽象名词结合，则表示“一种”，“一类”，“一下子”等意义。

句意：他在听我说话时，脸上显出惊讶的神色。

7. D。

考查副词。

entirely 完全地，accurately精确地，previously 以前地，positively 积极地。

句意：他一生耽于玩乐，结果毁了他的事业。

8. C。

考查代词。

在本句中theirs相当于their pictures。

句意：他们看了我们的照片，但没有把他们的照片给我们看。

9. A。

考查句型。

There is+ no +抽象名词+ that从句。

句意：人类被“机器控制”的可能性并不存在。

10. A。

考查情景对话。

A 第一个人要对方猜(Guess what?)，对方猜不出，原来是她得了奖，奖励是到一家餐馆免费吃一餐。

Mmm, really？表示惊异；How awful! 表示赞赏；Then what? 后来怎么样了?11. C。

考查虚拟语气。

与requirement关联的同位语从句用should型虚拟语气，并且should 可以省略。

句意：他不得不满足先买房，后结婚的要求。

12. B。

考查动词。

根据主句, 不可能有消防队员来救圣诞老人，可知他被“卡住(got stuck)了”。

九年级数学中考基础冲刺训练(一)(含答案)

2020年数学中考基础冲刺训练（一）一．选择题（每题4分，满分48分）1．下列四个数中，最小的是（）A．﹣|﹣3| B．|﹣32| C．﹣（﹣3 ）D．﹣322．如图，该立体图形的主视图为（）A．B．C．D．3．如图，Rt△AOB∽Rt△DOC，∠ABO＝30°，∠AOB＝∠COD＝90°，M为OA的中点，OA＝6，将△COD绕点O旋转一周，直线AD，CB交于点P，连接MP，则MP的最小值是（）A．6﹣3B．6﹣6 C．3 D．4．如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于D，且∠D＝40°，则∠PCA 等于（）A．50°B．60°C．65°D．75°5．下面命题正确的是（）A．矩形对角线互相垂直B．方程x2＝14x的解为x＝14C．六边形内角和为540°D．一条斜边和一条直角边分别相等的两个直角三角形全等6．估计（）×（）A．3和4之间B．4和5之间C．5和6之间D．6和7之间7．用一块A型钢板可制成2块C型钢板、3块D型钢板；用一块B型钢板可制成1块C 型钢板、4块D型钢板．某工厂现需14块C型钢板、36块D型钢板，设恰好用A型钢板x块，B型钢板y块，根据题意，则下列方程组正确的是（）A．B．C．D．8．按下面的程序计算，若开始输入的值x为正整数，输出结果86，那么满足条件的x的值有（）A．2个B．3个C．4个D．5个9．如图，在平面直角坐标系中，矩形ABCD四个顶点的坐标分别为A（﹣1，2），B（﹣1，﹣1，），C（3，﹣1），D（3，2），当双曲线y＝（k＞0）与矩形有四个交点时，k 的取值范围是（）A．0＜k＜2 B．1＜k＜4 C．k＞1 D．0＜k＜110．如图，某建筑物CE上挂着“巴山渝水，魅力重庆”的宣传条幅CD，王同学利用测倾器在斜坡的底部A处测得条幅底部D的仰角为60°，沿斜坡AB走到B处测得条幅顶部C 的仰角为50°，已知斜坡AB的坡度i＝1：2.4，AB＝13米，AE＝12米（点A、B、C、D、E在同一平面内，CD⊥AE，测倾器的高度忽略不计），则条幅CD的长度约为（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19，≈1.73）（）A．12.5米B．12.8米C．13.1米D．13.4米11．若数a既使关于x的不等式组无解，又使关于x的分式方程＝1的解小于4，则满足条件的所有整数a的个数为（）A．2 B．3 C．4 D．512．如图，将矩形OABC置于平面直角坐标系中，点A的坐标为（8，0），点D在BC上，且CD＝2，将矩形OABC沿AD折叠，使点B落在点E处，DE与y轴交于M点，点M 恰好为DE中点，连接OE，则OE的长度（）A．2B．2C．2D．2二．填空题（每题4分，满分24分）13．（π﹣1）0＝，（）﹣2＝．14．2019年12月27日20点45分，长征五号遥三运载火箭﹣﹣“胖五”复飞，把实践二十号卫星准确送入近地点192千米、远地点68000千米的预定轨道，发射飞行试验圆满成功，举国欢腾．其中68000千米用科学记数法表示是千米．15．一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1、2、3、4．随机摸取一个小球然后放回，再随机摸出一个小球，两次取出的小球标号的和等于5的概率是．16．如图，菱形ACBD中，AB与CD相交于点O，∠ACB＝120°，以C为圆心，CA为半径作弧AB，再以C为圆心，CO为半径作弧EF，分别交CA、CB于点F、E，若CB＝2，则图中阴影部分的面积是．17．已知A、B两地之间的路程为3000米，甲、乙两人分别从A、B两地同时出发，相向而行，甲到B地停止，乙到A地停止，出发10分钟后，甲原路原速返回A地取重要物品，取到该物品后立即原路原速前往B地（取物品的时间忽略不计），结果到达B地的时间比乙到达A地的时间晚，在整个行走过程中，甲、乙两人均保持各自的速度匀速行走，甲、乙两人相距的路程y（m）与甲运动的时间x（min）之间的关系如图所示，则乙到达A地时，甲与B地相距的路程是米．18．某中学去年举办竞赛，颁发一二三等奖各若干名，获奖人数依次增加，各获奖学生获得的奖品价值依次减少（奖品单价都是整数元），其中有3人获得一等奖，每人获得的奖品价值34元，二等奖的奖品单价是5的倍数，获得三等奖的人数不超过10人，并且获得二三等奖的人数之和与二等奖奖品的单价相同．今年又举办了竞赛，获得一二三等奖的人数比去年分别增加了1人、2人、3人，购买对应奖品时发现单价分别上涨了6元、3元、2元．这样，今年购买奖品的总费用比去年增加了159元．那么去年购买奖品一共花了元．三．解答题19．（10分）化简：（1）（﹣a﹣2b）2﹣a（a+4b）（2）÷（﹣）20．（10分）已知：如图，在等腰三角形ADC中，AD＝CD，且AB∥DC，CB⊥AB于B，CE⊥AD交AD的延长线于E．（1）求证：CE＝CB；（2）如果连结BE，请写出BE与AC的关系并证明．21．（10分）在新的教学改革的推动下，某中学初三年级积极推进走班制教学．为了了解一段时间以来“至善班”的学习效果，年级组织了多次定时测试，现随机选取甲、乙两个“至善班”，从中各抽取20名同学在某一次定时测试中的数学成绩，其结果记录如下：收集数据至善班”甲班的20名同学的数学成绩统计（满分为100分）（单位：分）86 90 60 76 92 83 56 76 85 7096 96 90 68 78 80 68 96 85 81“至善班”乙班的20名同学的数学成绩统计（满分为100分）（单位：分）78 96 75 76 82 87 60 54 87 72100 82 78 86 70 92 76 80 98 78整理数据：（成绩得分用x表示）0≤x＜60 60≤x＜70 70≤x＜80 80≤x＜90 90≤x＜100 分数数量班级甲班（人数） 1 3 4 6 6乙班（人数） 1 1 8 6 4 分析数据，并回答下列问题：（1）完成下表：平均数中位数众数甲班80.6 83 a＝乙班80.35 b＝78 （2）在“至善班”甲班的扇形图中，成绩在70≤x＜80的扇形中，所对的圆心角α的度数为，估计全部“至善班”的1600人中优秀人数为人．（成绩大于等于80分为优秀）（3）根据以上数据，你认为“至善班”班（填“甲”或“乙”）所选取做样本的同学的学习效果更好一些，你所做判断的理由是：①．②．22．（10分）仔细观察，找出规律，并计算：2＝1×2；（1）2+4+6+ (18)2+4＝6＝2×3；（2）2+4+6+…+2n＝2+4+6＝12＝3×4；（3）2+4+6+ (198)2+4+6+8＝20＝4×5；（4）200+202+204+ (1998)2+4+6+8+10＝30＝5×6．23．（10分）某工厂有两批数量相同的产品生产任务，分别交给甲、乙两个小组同时进行生产．如图是反映生产数量y（件）与生产时间x（h）之间关系的部分图象．请解答下列问题：（1）乙小组生产到30 件时，用了h．生产6h时，甲小组比乙小组多生产了件；（2）请你求出：①甲小组在0≤x≤6的时段内，y与x之间的函数关系式；（直接写出结论）②乙小组在2≤x≤6的时段内，y与x之间的函数关系式；（直接写出结论）③生产几小时后，甲小组所生产的数量开始超过乙小组？（要求写出过程）（3）如果甲小组生产速度不变，乙小组在生产6h后，生产速度增加到12 件/h，结果两小组同时完成了任务．问甲小组从开始生产到完工所生产的数量为多少件？（要求写出过程）24．（10分）（1）解方程：4x（2x+1）＝3（2x+1）（2）某快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同，求该快递公司投递总件数的月平均增长率．25．（10分）在▱ABCD中，BE平分∠ABC交AD于点E．（1）如图1，若∠D＝30°，AB＝，求△ABE的面积；（2）如图2，过点A作AF⊥DC，交DC的延长线于点F，分别交BE，BC于点G，H，且AB＝AF．求证：ED﹣AG＝FC．四．解答题26．（8分）如图，已知抛物线y＝﹣x2+bx+c经过点A（3，0），点B（0，3）．点M（m，0）在线段OA上（与点A，O不重合），过点M作x轴的垂线与线段AB交于点P，与抛物线交于点Q，联结BQ．（1）求抛物线表达式；（2）联结OP，当∠BOP＝∠PBQ时，求PQ的长度；（3）当△PBQ为等腰三角形时，求m的值．参考答案一．选择题1．解：∵﹣|﹣3|＝﹣3，|﹣32|＝9，﹣（﹣3）＝3，﹣32＝﹣9，∴|﹣32|＞﹣（﹣3）＞﹣|﹣3|＞﹣32．故选：D．2．解：从正面看可得到左边第一竖列为2个正方形，第二竖列为2个正方形，第三竖列为1个正方形．故选：B．3．解：取AB的中点S，连接MS、PS，则PS﹣MS≤PM≤MS+PS，∵∠AOB＝90°，OA＝6，∠ABO＝30°，∴AB＝2OA＝12，OB＝6∵∠AOB＝∠COD＝90°，∴∠COB＝∠DOA，∵△AOB∽△DOC，∴＝，∴△COB∽△DOA，∴∠OBC＝∠OAD，∵∠OBC+∠PBO＝180°，∴∠OAD+∠PBO＝180°，∠AOB+∠APB＝180°，∴∠APB＝∠AOB＝90°，又S是AB的中点，∴PS＝AB＝6，∵M为OA的中点，S是AB的中点，∴MS＝OB＝3，∴MP的最小值为6﹣3，故选：A．4．解：∵PD切⊙O于点C，∴OC⊥CD，∴∠OCD＝90°，∵∠D＝40°，∴∠DOC＝90°﹣40°＝50°，∵OA＝OC，∴∠A＝∠ACO，∵∠COD＝∠A+∠ACO，∴∠A＝∠COD＝25°，∴∠PCA＝∠A+∠D＝25°+40°＝65°．故选：C．5．解：A．矩形对角线互相垂直，不正确；B．方程x2＝14x的解为x＝14，不正确；C．六边形内角和为540°，不正确；D．一条斜边和一条直角边分别相等的两个直角三角形全等，正确；故选：D．6．解：（）×＝1+，∵3＜＜4，∴4＜+1＜5，．故选：B．7．解：设恰好用A型钢板x块，B型钢板y块，根据题意，得：，故选：A．8．解：设输入x，则直接输出4x﹣2，且4x﹣2＞0，那么就有（1）4x﹣2＝86，解得：x＝22．若不是直接输出4x﹣2＞0，那么就有：①4x﹣2＝22，解得：x＝6；（2）4x﹣2＝6，解得：x＝2；（3）4x﹣2＝2，解得：x＝1．（4）4x﹣2＝1，解得：（舍去）∵x为正整数，因此符合条件的一共有4个数，分别是22，6，2，1故选：C．9．解：根据反比例函数的对称性，双曲线y＝（k＞0）与矩形有四个交点，只要反比例函数在第四象限的图象与矩形有2个交点即可，当反比例函数过点B（﹣1，﹣1）时，此时k＝1，反比例函数图象与矩形有三个交点，当反比例函数图象与AB有交点时，则当x＝﹣1时，y＝﹣k＞﹣1，即k＜1；当反比例函数图象与BC有交点时，则当y＝﹣1时，x＝﹣k＞﹣1，即k＜1；又∵k＞0，∴0＜k＜1，故选：D．10．解：过B作BF⊥AE，交EA的延长线于F，作BG⊥DE于G．Rt△ABF中，i＝tan∠BAF＝＝，AB＝13米，∴BF＝5（米），AF＝12（米），∴BG＝AF+AE＝24（米），Rt△BGC中，∠CBG＝50°，∴CG＝BG•tan50°≈24×1.19＝28.56（米），Rt△ADE中，∠DAE＝60°，AE＝12米，∴DE＝AE＝12m，∴CD＝CG+GE﹣DE＝28.56+5﹣12≈12.8（米）故选：B．11．解：解不等式+1≤，得：x≤5a﹣6，解不等式x﹣2a＞6，得：x＞2a+6，∵不等式组无解，∴2a+6≥5a﹣6，解得：a≤4，解方程＝1，得：x＝2﹣2a，∵方程的解小于4，∴2﹣2a＜4且2﹣2a≠±2，解得：a＞﹣1且a≠0、a≠2，则﹣1＜a≤4且a≠0、a≠2，所以满足条件的所有整数a有1、3、4这3个，故选：B．12．解：如图，作EH⊥AB于H，交OC于F．∵四边形OABC是矩形，∴AB∥OC，AB＝OC，OA＝BC，∠BCO＝90°，∵CD＝2，A（8，0），∴OA＝BC＝8，BD＝6，由翻折的性质可知：BD＝DE＝6，∵EM＝DM，∴EM＝DM＝3，CM＝＝＝，∵EH⊥AB，AB∥OC，∴EH⊥OC，∴∠EFM＝∠DCM＝90°，∵∠EMF＝∠CMD，ME＝MD，∴△MEF≌△MDC（AAS），∴EF＝CD＝2，MF＝CM＝，∵∠B＝∠BHF＝∠BCF＝90°，∴四边形BCFH是矩形，∴BH＝CF＝2，设AB＝AE＝x，在Rt△EHA中，则有x2＝102+（x﹣2）2，∴x＝6，∴OF＝AH＝4，∴OE＝＝＝2，故选：D．二．填空题13．解：（π﹣1）0＝1、（）﹣2＝＝＝9，故答案为：1、9．14．解：68000千米用科学记数法表示是6.8×104千米．故答案为：6.8×104．15．解：画树状图如下：随机地摸出一个小球，然后放回，再随机地摸出一个小球，共有16种等可能的结果数，其中两次摸出的小球标号的和等于5的占4种，所有两次摸出的小球标号的和等于5的概率为＝，故答案为：．16．解：∵四边形ACBD是菱形，∠ACB＝120°，∴DB＝DA，∠BCO＝60°，∴OC＝BC×cos60°＝1，OB＝BC×sin60°＝，∴图中阴影部分的面积＝﹣×1×＝﹣，故答案为：﹣．17．解：设甲的速度为am/min，乙的速度为bm/min，，解得，，则乙到达A地时用的时间为：3000÷40＝75min，∴乙到达A地时，甲与B地相距的路程是：3000﹣50×（75﹣20）＝250m，故答案为：250．18．解：设二等奖人数为m，三等奖人数为n，二等奖单价为a，三等奖单价为b，根据题意列表分析如下：∵今年购买奖品的总费用比去年增加了159元∴4×40+（m+2）（a+3）+（n+3）（b+2）﹣34×3﹣ma﹣nb＝159整理得：3m+2a+2n+3b＝89∵3＜m＜n≤10，m+n＝a，a为5的倍数∴a的值为10或15当a＝10时，m＝4，n＝6代入3m+2a+2n+3b＝89得3×4+2×10+2×6+3b＝89解得b＝15＞a不符合题意，舍去；当a＝15时，有3种情况：①m＝5，n＝10，代入3m+2a+2n+3b＝89得3×5+2×15+2×10+3b＝89解得b＝8＜a，符合题意此时去年购买奖品一共花费3×34+5×15+10×8＝257（元）；②m＝6，n＝9，代入3m+2a+2n+3b＝89得3×6+2×15+2×10+2×9+3b＝89解得b＝，不符合题意，舍去；③m＝7，n＝8，代入3m+2a+2n+3b＝89得3×7+2×15+2×8+3b＝89，解得b＝，不符合题意，舍去；综上可得，去年购买奖品一共花费257元．故答案为：257．三．解答题19．解：（1）原式＝a2+4ab+4b2﹣a2﹣4ab＝4b2．（2）原式＝÷[﹣]＝÷＝•＝．20．（1）证明：∵AD＝CD，∴∠DAC＝∠DCA，∵AB∥CD，∴∠DCA＝∠CAB，∴∠DAC＝∠CAB，∴AC是∠EAB的角平分线，∵CE⊥AE，CB⊥AB，∴CE＝CB；（2）AC垂直平分BE，证明：由（1）知，CE＝CB，∵CE⊥AE，CB⊥AB，∴∠CEA＝∠CBA＝90°，在Rt△CEA和Rt△CBA中，，∴Rt△CEA≌Rt△CBA（HL），∴AE＝AB，CE＝CB，∴点A、点C在线段BE的垂直平分线上，∴AC垂直平分BE．21．解：（1）将甲班成绩重新整理如下：56 60 68 68 70 76 76 78 80 81 83 85 85 86 90 90 92 96 96 96，其中96出现次数做多，∴众数a＝96（分），将乙班成绩重新整理如下：54 60 70 72 75 76 76 78 78 78 80 82 82 86 87 87 92 96 98 100，其中中位数b＝＝79（分），故答案为：96，79；（2）成绩在70≤x＜80的扇形中，所对的圆心角α的度数为360°×＝72°，估计全部“至善班”的1600人中优秀人数为1600×＝880（人）．（3）甲所选取做样本的同学的学习效果更好一些，你所做判断的理由是：甲的优秀率高，甲的中位数比乙的中位数大，故答案为：甲，甲的优秀率高，甲的中位数比乙的中位数大．22．解：由题意可得，（1）2+4+6+…+18＝（18÷2）（18÷2+1）＝9×10，故答案为：9×10；（2）2+4+6+…+2n＝n（n+1），故答案为：n（n+1）；（3）2+4+6+…+198＝（198÷2）（198÷2+1）＝99×100，故答案为：99×100；（4）200+202+204+…+1998＝（1998÷2）（1998÷2+1）﹣99×100＝999×1000﹣99×100，故答案为：999×1000﹣99×100．23．解：（1）利用图象点的坐标得出：乙小组生产到30 件时，用了2h．生产6h时，甲小组比乙小组多生产了10件；故答案为：2，10；（2）①甲队在0≤x≤6的时段内y＝10x，②乙队在2≤x≤6的时段内y＝5x+20．③设x小时时，甲乙所生产的数量相等，则30+5×（x﹣2）＝10x，解得x＝4．答：生产4小时后，甲小组所生产的数量开始超过乙小组．（3）设生产x′小时后，两小组同时完成了任务，则10x′＝50+12×（x′﹣6），解得x′＝11．∴甲小组从开始生产到完工所生产的数量为110件．24．解：（1）∵4x（2x+1）﹣3（2x+1）＝0，∴（4x﹣3）（2x+1）＝0，则4x﹣3＝0或2x+1＝0，解得；（2）设该快递公司投递总件数的月平均增长率为x，根据题意得10（1+x）2＝12.1，解得x1＝0.1，x2＝﹣2.1（不合题意舍去），答：该快递公司投递总件数的月平均增长率为10%．25．（1）解：作BO⊥AD于O，如图1所示：∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AB＝CD，∠ABC＝∠D＝30°，∴∠AEB＝∠CBE，∠BAO＝∠D＝30°，∴BO＝AB＝，∵BE平分∠ABC，∴∠ABE＝∠CBE，∴∠ABE＝∠AEB，∴AE＝AB＝，∴△ABE的面积＝AE×BO＝××＝；（2）证明：作AQ⊥BE交DF的延长线于P，垂足为Q，连接PB、PE，如图2所示：∵AB＝AE，AQ⊥BE，∴∠ABE＝∠AEB，BQ＝EQ，∴PB＝PE，∴∠PBE＝∠PEB，∴∠ABP＝∠AEP，∵AB∥CD，AF⊥CD，∴AF⊥AB，∴∠BAF＝90°，∵AQ⊥BE，∴∠ABG＝∠FAP，在△ABG和△FAP中，，∴△ABG≌△AFP（ASA），∴AG＝FP，∵AB∥CD，AD∥BC，∴∠ABP+∠BPC＝180°，∠BCP＝∠D，∵∠AEP+∠PED＝180°，∴∠BPC＝∠PED，在△BPC和△PED中，，∴△BPC≌△PED（AAS），∴PC＝ED，∴ED﹣AG＝PC﹣AG＝PC﹣FP＝FC．四．解答题26．解：（1）将A（3，0），B（0，3）分别代入抛物线解析式，得．解得．故该抛物线解析式是：y＝﹣x2+2x+3；（2）设直线AB的解析式是：y＝kx+t（k≠0），把A（3，0），B（0，3）分别代入，得．解得k＝﹣1，t＝3．则该直线方程为：y＝﹣x+3．故设P（m，﹣m+3），Q（m，﹣m2+2m+3）．则BP＝m，PQ＝﹣m2+3m．∵OB＝OA＝3，∴∠BAO＝45°．∵QM⊥OA，∴∠PMA＝90°．∴∠AMP＝45°．∴∠BPQ＝∠AMP＝∠BAO＝45°．又∵∠BOP＝∠QBP，∴△POB∽△QBP．于是＝，即＝．解得m1＝，m2＝0（舍去）．∴PQ＝﹣m2+3m＝；（3）由两点间的距离公式知，BP2＝2m2，PQ2＝（﹣m2+3m）2，BQ2＝m2+（﹣m2+2m）2．①若BP＝BQ，2m2＝m2+（﹣m2+2m）2，解得m1＝1，m2＝3（舍去）．即m＝1符合题意．②若BP＝PQ，2m2＝（﹣m2+3m）2，解得m1＝3﹣，m2＝3+（舍去）．即m＝3﹣符合题意．③若PQ＝BQ，（﹣m2+3m）2＝m2+（﹣m2+2m）2，解得m＝2．综上所述，m的值为1或3﹣或2．。

天学网高考英语听力冲刺训练一答案

天学网高考英语听力冲刺训练一答案(Text 1)W: What’s new with you,Jack?M:Well,I met a really nice woman.We’ve been going out for three months and things look good now.(Text 2)M: When did you first find the door broken and things missing?W:After I got up,around 5:20.Then I called the police station.(Text 3)W: Pass me the flour,please.M:Which tin is it in?W:The one at the end of the shelf.It’s slightly smaller than the others.M:Oh,right.(Text 4)W:Do you know why George hasn’t come ye t?M:Yes.He was planning to come,but his wife’s father fell down some stairs and they had to take him to a hospital.W:I’m sorry to hear that.(Text 5)W:Hi,Tony.How did your experiment go yesterday?M: Well,it wasn’t as easy as I had thought.I have to con tinue doing it tonight.(Text 6)M:Is that Ann?W:Yes.M:This is Mike.How are things with you?W:Oh,very well,but I’m very busy.M:Busy? But you’ve finished all your exams?W:Yes,but I have to help my little sister with her foreign language.M:How about coming out with me this evening?There’s a new film on.W:I’m afraid I can’t.A friend of mine is coming from the south and I have to go to the station to meet him.M:What a pity!How about the weekend then?W:No,I’ve arranged to go to an art exhi bition with my parents.M:What about next week sometime?W:Maybe.(Text 7)W:I hear there will be a football competition between all senior schools next month.Is that so?M:That’s true.W:Would you please go into some more details?M:Well,the competition will be held in our school and it will begin on August 11.The competition will last a whole week.W:Anything else?M:Yes,both the girls and boys competition will be held at the same time.The girls competition will be held in the morning and the boys competition will be held in the afternoon.W:Yes? Sounds exciting.M:We are both members of our school football team.We should be ready for it.W:Of course.It’s a long time since we had the last football competition last time.I’m really looking forward to another competition.M:Me,too.(Text 8)W: Excuse me.I am from STM.We are carrying out a survey on the traffic in our city.Do you mind if I ask you some questions?M:No,not at all.Go ahead.W:Good,thanks.What do you do,sir?M:I am a teacher.I teach children French.W:Great.Do you live far from the school? I mean,how do you usually go to work?M:Well,mostly by car.But once in a while,I prefer to ride my bike.You know,I live quite far from the school,about 20 miles.And I have to spend about an hour riding to school.But it only takes me less than a quarter of an hour to drive my car,unless the traffic is very bad.W:I see.Does this happen often? I mean the bad traffic.M:Yes,sure! I often get stuck on the way,and the problem’s getting worse and worse.W:That’s all of my questions.Thank you very much.M:You are welcome.M: Customer service.Andney Grant speaking.How may I help you?W:I can’t believe this is happening.I called and ordered a 32?inch bag last Friday.But today I found that you sent me a 24?inch one.I was planning to use that bag during our vacation in Mexico,but it doesn’t seem possible any more because we will take off on Saturday.It’s only two days away.What am I supposed to do?M:I’m really sorry,madam. I’ll check right away.Would you please tell me your order number?W:It’s CE2938.M:Just a minute.I do apologize,madam.There did seem to be a mistake.I’ll have the corre ct size bag sent to you by overnight mail right away.It will arrive in time for your Saturday trip.Again I apologize for any inconvenience caused by our mistake.I promise it won’t happen again.W:OK.Well,thank you.M:Thank you,madam,for choosing Linch mail.I hope you will have a wonderful vacation.I wasn’t too fond of the lecture classes of 400 students in my general course.Halfway through my second term when I was considering whether or not to come back in the fall,I went on the Internet and came across Americorp.Then I joined in an organization,and that’s what I did last school year.I worked on making roads,building a house,serving as a teacher’s assistant and working as a camp officer in several projects in South Carolina and Florida.It’s been a great experience,and I’ve almost learned more than what I could have in college since I didn’t really want to be at that school and wasn’t interested in my major anyway,I thought this was better for me.After 1,700 hours of service I received 4,750 dollars.I can use that to pay off the money I borrowed from the bank or for what is needed when I go back to school this fall at Columbus State in Ohio.Classes are smaller there and I’ll be majoring in German education.After working with the kids,now I know,I want to be a teacher.一、听力第一节(共5小题，每小题1分)听下面5段对话。