PB5-8
牛津译林8年级上册 期末复习Unit5-8易错题集合 (含解析)

牛津译林8上期末复习U5-8易错题集合1.Lucy, if you want to join the Painting Society, you should fill in the form.-Thanks for your advice!A.applicationB.instructionpetitionD.action2. -Mum, what's wrong with Dad?serious. He has just got a cold.A. SomethingB. EverythingC.AnythingD. Nothing3. My father is busy. Every year, he only has 10 days off while we have 30.A. at firstB.at mostC.at leastD.at last4.-Look! The girl long hair is building a snow house. Is she Sandy?-It be her. I'm not sure.A. has; mustB. has; can'tC. with; mayD. with; mustn't5. The bus is coming. Oh, my God! It's full. I'm afraid we can't it.A. get upB. get onC.get offD. get out6. You should study hard. No one can a good future you. It's you who shape your life and your future.A. provide; withB. provide; forC. offer; forD. offer; with7.The sentence structure of "Simon watched Tom eating some ice cream."is “A.S+V+PB.S+V+OC.S+V+DO+OCD.S+V+IO+DO8. -Jim spends the most time on English,but he always gets the marks.-It's a great pity. Maybe he needs to find a way.A. lowest; goodB.fewest; bestC.lowest; betterD. fewest; good9.Amy met Peter, she with her mum for the bus at the bus station.A. When; were waitingB. When; was waitingC.While; were waitingD. While; was waiting10.-Did you get WeChat Red Packets the Spring Festival?-Yes. It's usually the most popular way of sending holiday presents now.A.withB. forC.duringD.after11.There are sharing bikes in many cities. So there will be pollution.A. less and less; more and moreB. less and less; fewer and fewerC. fewer and fewer; less and lessD. more and more; less and less12,-When will Mr Green Beijing?-In a week.A. GeteC.arriveD.reach13.Lucy the fire in the kitchen with a blanket.A. put outB. put inC.put onD. put up14. Our teacher often tells us time because it never goes back.A.not wasteB.not to wasteC.not useD.not to use15. -Who do you think l can talk with a final decision?-No one.You'd better it yoursell.A. to makes not makeB. makingi makeC. to make: makeD. makingi not make16. They were talking in the classroom Mr Wu walked in.A. noise: asB. Noisily; whileC. Noisy; whenD.noisily; when17. Children get presents from Santa Claus the evening of December 25th.A.onB. atC.inD.by18. Tom has more free time because he is in clubs than Daniel.A.fewB. lessC. moreD.fewer19. Bring your geography book here tomorrow. Don't it at home again.A.forgetB. rememberC.leaveD. bring20. 一is it since you left your primary school?-Two years.A. How oldB.How farC.How longD.How soon21. He tried to a poster on the wall by himself, but he failed.A. put outB. put offC.put upD. put in22. -Can she be a good nurse?-I don't think so. Because she is not enough to take care of the sick.A. PatientB.impatientC.activeD.inactive23.You had better talk with each other loudly while watching a film.A.notB. don'tC.noD.doesn't24.-Are you still reading the book Gulliver's Travels?-Yes,it is long. I still need time to finish it.A. a bit; a bit ofB. a bit of; a bit ofC.a bit; a bitD. a bit of; a bit25.-Could you tell me what he meant just now?-Sorry,I what was happening outside.A. had thoughtB. was thinkingC.thoughtD.think26.-is the Golden Gate Bridge?-About 90 feet. And it is very long, about 1.7 miles.A.How farB.How muchC.How wideD.How long27. He isn't good at English. ,he tries to read stories in English in his free time.A.YetB. OtherwiseC.ButD.However28. Which sentence has the same structure as “The wise man gives us some useful advice."?A. Eddie is watching Hobo work.B. Hobo brought Eddie his clothes.C. They are quite different.D. We have four seasons in a year.29.Wow! You've got so many boots.-But of them are in fashion now.A.allB.bothC.neitherD. none30. The bushes make good for animals to hide in.A.coverB.homeC.gardensD. parks31.“I found him a clever student.” The sentence structure isA.S+V+OB. S+V+DO+OCC.S+V+IO+DOD.S+V+P32. The deadline is coming! I finísh the report in two days!A. CanB. mayC.mustD.should33. This famous company a well-paid job to him.A. OfferedB. providedC.showedD.had34. great fun Simon has a snowman in the yard!A. What; makingB. What: madeC.How; makingD.How: made35.-What your English teacher ?-He is friendly and patient.A. does: likeB.is: likeC.does: lookD.are, like36. The weather report says it is going to rain. your raincoat here.A. Forget to bringB.Forget bringingC.Remember to bringD.Remember bringing37. he's too tired, he doesn't want to go with us.A. Because, soB. Because;/C.Because of; soD.Because of; /38.Shanghai is larger than in China.A. any cityB. any other cityC.any other citiesD. another city39. -Which of the three dresses will you take?-I'll take . Let's go to another shop.A. BothB. neitherC.noneD.all40.-How is the in your city?-Awful. There are always long lines of cars on roads.A.cultureB.foodC.weatherD. traffic41.I feel hungry. Can you give me something to eat?A. a littleB.a bitC.a bit ofD.both A &B42. I have so few friends that I have to live at this school,so I sometimes feel and helpless.A. lonely; aloneB. lonely; lonelyC. alone; aloneD. alone; lonely43.-What do you think of the model plane?-Oh,it's I have ever seen.A. the better oneB.a better oneC. the best oneD.a best one44. When Xi Wang was , she started to go outside for the first time.A. four months oldB. four month oldC.four-month-oldD.four-months-old45. -Is the film interesting?-I thought it would be. But ,it's very boring.A. in allB.at firstC. in factD. in the future46. His grandfather had to stay at home because ofA.sickB.illC.sicknessD.sicking47. Zhalong Nature Reserve provides a lot of wildlife food and cover.A.onB. withC.toD.for48. May is patient her classmates and never says a bad word anyone.A. to; ofB. with; ofC.with; aboutD.about; to49.-What the number of the students in your school?-About two thousand. A number of them from the countryside.A.is; areB.is; isC.are; isD. are; are50. The birds don't have to eat because people keep fishing in rivers.A. enough spaceB. space enoughC. enough foodD.food enough【参考答案】1.A 句意:-Lucy,如果你想加人画社,你应该填写申请表。
《国家标准》铸造锡青铜的化学成分(GBT1176-1987)

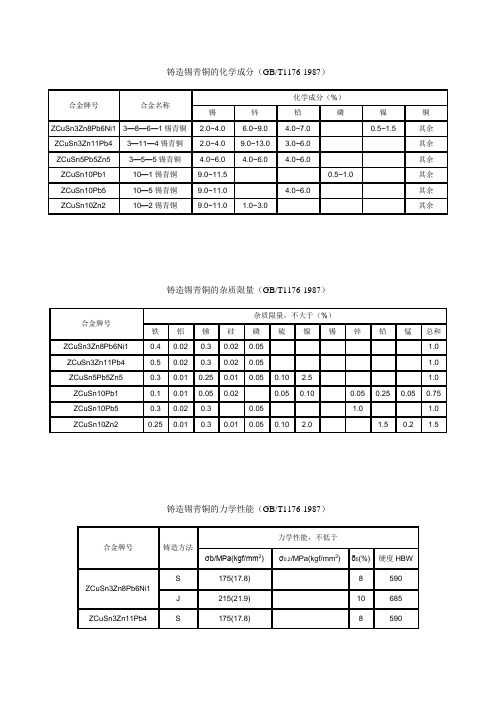
铸造锡青铜的化学成分(GB/T1176-1987)
铸造锡青铜的杂质限量(GB/T1176-1987)
铸造锡青铜的力学性能(GB/T1176-1987)
铸造锡青铜的主要特性和应用举例(GB/T1176-1987)
铸造铝青铜的化学成分(GB/T1176-1987)
铸造铝青铜的杂质限量(GB/T1176-1987)
铸造铝青铜的力学性能(GB/T1176-1987)
铸造铝青铜的主要特性和应用举例(GB/T1176-1987)
铅青铜的化学成分(GB/T1176-1987)
铸造铅青铜的力学性能(GB/T1176-1987)
铸造铅青铜的主要特性和应用举例(GB/T1176-1987)
铸造黄铜的化学成分(GB/T1176-1987)
铸造黄铜的杂质限量(GB/T1176-1987)
铸造黄铜的力学性能(GB/T1176-1987)
铸造黄铜的主要特性和应用举例(GB/T1176-1987)
资讯来源:国家标准化管理委员会。
计算理论-5-8章定义定理

第五章可归约性定理5.1:HALT TM是不可判定的。
证明:为得到矛盾,假设TM R判定HALT TM,由之可以构造TM S来判定A TM, 其构造如下:S=“在输入<M,w >上,此处<M,w >是TM M和串w的编码:1) 在输入<M,w >上运行TM R。
2)如果R拒绝,则拒绝。
3)如果R接受,则在w上模拟M,直到它停机。
4)如果M已经接受,则接受;如果M已经拒绝,则拒绝。
显然,如果R判定HALT TM,则S判定A TM。
因为A TM是不可判定的,故HALT TM也必定是不可判定的。
定理5.2:E TM是不可判定的。
构造TM M1:M1=“在输入x上:1)如果x≠w,则拒绝。
2)如果x=w,则在x上运行M,当M接受时,就接受。
”假设TM R判定E TM。
如下构造判定A TM的TM S:S=“在输入<M,w >上,此处<M,w >是TM M和串w的编码:1) 用M和w的描述来构造上述TM M1。
2)在输入< M1 >上运行R。
3)如果R接受,则拒绝;如果R拒绝,则接受。
”定理5.3:REGULARTM是不可判定的。
设R是判定REGULAR TM的一个TM,下面构造判定A TM的TM S。
S的运行方式如下:S=“对于输入<M,w>,其中M是TM,w是串:1)构造下述TM M2:M2=“在输入x上:a) 如果x具有形式0n1n,则接受。
b)如果x不具有此形式,则在输入w上运行M。
如果M接受w,则接受。
”2)在输入<M2>上运行R。
3) 如果R接受,则接受;如果R拒绝,则拒绝。
”定理5.4:EQ TM是不可判定的。
设TM R判定EQ TM。
如下构造判定E TM的TM S:S=“对于输入<M>,其中M是TM:1)在输入<M,M1>上运行R,其中M1是拒绝所有输入的图灵机。
2)如果R接受,则接受;如果R拒绝,则拒绝。
铸铜材料(GB-T-1176)
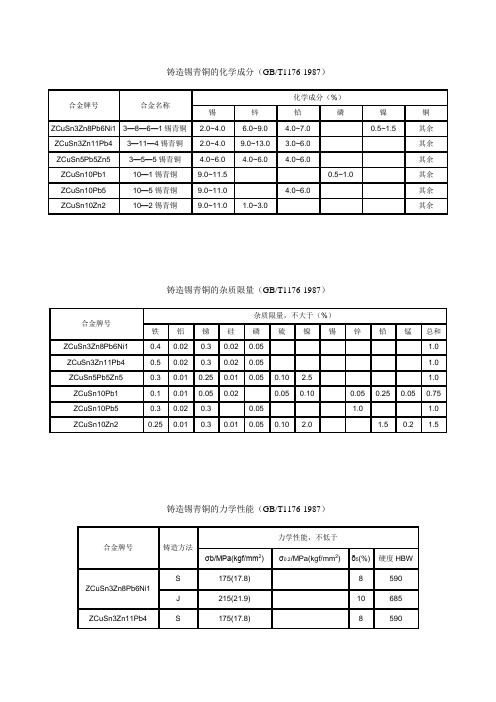
铸造锡青铜的化学成分(GB/T1176-1987)
铸造锡青铜的杂质限量(GB/T1176-1987)
铸造锡青铜的力学性能(GB/T1176-1987)
铸造锡青铜的主要特性和应用举例(GB/T1176-1987)
铸造铝青铜的化学成分(GB/T1176-1987)
铸造铝青铜的杂质限量(GB/T1176-1987)
铸造铝青铜的力学性能(GB/T1176-1987)
铸造铝青铜的主要特性和应用举例(GB/T1176-1987)
铅青铜的化学成分(GB/T1176-1987)
铸造铅青铜的力学性能(GB/T1176-1987)
铸造铅青铜的主要特性和应用举例(GB/T1176-1987)
铸造黄铜的化学成分(GB/T1176-1987)
铸造黄铜的杂质限量(GB/T1176-1987)
铸造黄铜的力学性能(GB/T1176-1987)
铸造黄铜的主要特性和应用举例(GB/T1176-1987)
资讯来源:国家标准化管理委员会。
贵州省黔东南苗族侗族自治州2023-2024学年八年级下学期期末数学试题(含答案)

黔东南州2023—2024学年度第二学期期末文化水平测试八年级数学试卷同学你好!答题前请认真阅读以下内容:1.本卷为数学试题卷,全卷共6页,三大题25小题,满分150分,考试时间为120分钟.2.一律在《答题卡》相应位置作答,在试题卷上答题视为无效.3.不能使用计算器.一、选择题:以下每小题均有A、B、C、D、四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每题3分,共36分.1)A.4B.-4C.8D.2.下列计算中,正确的是A.B.CD3.某学校在6月6日全国爱眼日当天,组织学生进行了视力测试.小红所在的学习小组每人视力测试的结果分别为:5.0,4.8,4.5,4.8,4.6,这组数据的众数和中位数分别为()A.4.8,4.74B.4.8,4.5C.5.0,4.5D.4.8,4.84.下列函数中,是正比例函数的是()A.B.C.D.5.如图,平地上、两点被池塘隔开,测量员在岸边选一点,并分别找到和的中点、,测量得米,则、两点间的距离为()A.30米B.32米C.36米D.48米6.下列曲线中,不能表示是的函数的是()A.B.C.D.7.若,且,则函数的图象可能是()4±2-=3==5= 23y x=5y x=6yx=1y x=-A B C AC BC D E16DE=A By xkb<k b<y kx b=+A .B .C .D .8.如图,在平面直角坐标系中,已知点,,以点为圆心,长为半径画弧,交轴的正半轴于点,则点的坐标是()A .B .C .D .9.下列命题中:①对角线垂直且相等的四边形是正方形;②对角线互相垂直平分的四边形为菱形;③一组对边平行,另一组对边相等的四边形是平行四边形;④若顺次连接四边形各边中点得到的是矩形,则该四边形的对角线相等.是真命题的有( )A .1个B .2个C .3个D .4个10.如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形、、、的面积分别为2、5、1、2.则最大的正方形的面积是()A .5B .10C .15D .2011.如图,在中,对角线,相交于点,若,,,则的长为()A .8B .9C .10D .1212.如图1,将正方形置于平面直角坐标系中,其中边在轴上,其余各边均与坐标轴平行,直线沿轴的负方向以每秒1个单位长度的速度平移,在平移的过程中,该直线被正方形的边所截得的线段长为,平移的时间为(秒),与的函数图象如图2所示,则图2中的值为()(0,0)O (1,3)A O OA x BB(3,0)A B C D E ABCD AC BD O 90ADB ∠=︒6BD =4AD =ACABCD AD x :3l y x =-x ABCD m t m t bA .B .C .D .二、填空题:每小题4分,共16分.13的取值范围是______.14.某校学生期末美术成绩满分为100分,其中课堂表现占,平时绘画作业占,期末手工作品占,小花的三项成绩依次为90,85,95,则小花的期末美术成绩为______分.15.已知甲、乙两地相距,,两人沿同一公路从甲地出发到乙地,骑摩托车,骑电动车,图中,分别表示,两人离开甲地的路程与时间的关系图象.则两人相遇时,是在出发后______小时.16.在矩形中,点,分别是,上的动点,连接,将沿折叠,使点落在点处,连接,若,,则的最小值为______.三、解答题:本大题9小题,共98分.17.(8分)计算:(1)(2)18.(10分)如图,每个格子都是边长为1的小正方形,,四边形的四个顶点都在格点上.(1)求四边形的周长;(2)连接,试判断的形状,并求四边形的面积.x 30%50%20%90km A B A B DE OC A B (km)S (h)t B ABCD E F AB AD EF AEF △EF A P BP 2AB =3BC =BP 90ABC ∠=︒ABCD ABCD AC ACD △ABCD19.(10分)如图,在平行四边形中,点是边的中点,的延长线与的延长线相交于点.(1)求证:;(2)连接、,试判断四边形的形状,并证明你的结论.20.(12分)2024年4月30日,“神舟十七号”载人飞船成功着陆,激发了同学们的爱国热情.某校为了解七、八年级学生对“航空航天”知识的掌握情况,对七、八年级学生进行了测试,此次“航空航天”知识测试采用百分制,并规定90分及以上为优秀;80~89分为良好;60~79分为及格;59分及以下为不及格.现从七、八年级各随机抽取20名学生的测试成绩,并将数据进行以下整理与分析.①抽取的七年级20名学生的成绩如下:57 58 65 67 69 69 77 78 79 81838788898994969797100②抽取的七年级20名学生的成绩的频数分布直方图如图1所示,数据分成5组:,,,,)③抽取的八年级20名学生的成绩的扇形统计图如图2所示.④七、八年级各抽取的20名学生成绩的平均数、中位数、方差如下表所示.年级平均数中位数方差七年级81167.9八年级8281106.3请根据以上信息,解答下列问题.(1)______,______.并补全抽取的七年级20名学生的成绩的频数分布直方图.(2)目前该校七年级学生有300人,八年级学生有200人,估计两个年级此次测试成绩达到优秀的学生总人数.(3)从平均数和方差的角度分析,你认为哪个年级的学生成绩较好?请说明理由.21.(10分)如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°为30°.已知原传送带长为.(1)求新传送带的长度;(2)若需要在货物着地点的左侧留出2m 的通道,试判断和点相距5m (即)的货物是否需要挪走,并说明理由.)ABCD E AD BE CD F ABE DFE △≌△BD AF ABDF 5060x ≤<6070x ≤<7080x ≤<8090x ≤<90100x ≤≤aa =m =AB AC C B 5PB =MNQP 1.4≈ 1.7≈22.(12分)某小型企业获得授权生产甲、乙两种奥运吉祥物,生产每种吉祥物所需材料及所获利润如下表:种材料种材料所获利润(元)每个甲种吉祥物0.30.510每个乙种吉祥物0.60.220该企业现有种材料,种材料,用这两种材料生产甲、乙两种吉祥物共2000个.设生产甲种吉祥物个,生产这两种吉祥物所获总利润为元.(1)求出(元)与(个)之间的函数关系式,并求出自变量的取值范围;(2)该企业如何安排甲、乙两种吉祥物的生产数量,才能获得最大利润?最大利润是多少?23.(12分)如图,在矩形中,延长到,使,延长到,使,连接.(1)求证:四边形是菱形;(2)连接,若,,求的长.24.(12分)如图,在平面直角坐标系中,一次函数的图象与轴交于点,与轴交于点,且与正比例函数的图象的交点为.(1)求一次函数的解析式;(2)根据图像直接写出:当时,的取值范围.(3)一次函数的图象上有一动点,连接,当的面积为5时,求点的坐标.25.(12分)在正方形中,点是线段上的动点,连接,过点作(点在直线的下方),且,连接.A ()2m B ()2m A 2900m B 2850m x y y x x ABCO AO D DO AO =CO E EO CO =AE ED DC CA 、、、AEDC EB 4AE =60AED ∠=︒EB xOy 1y kx b =+x (3,0)A -y B 243y x =(,4)C m 1y kx b =+12y y >x 1y kx b =+P OP OPC △P ABCD E AB DE D DF DE ⊥F DE DF DE =EF(1)【动手操作】在图①中画出线段,;与的数量关系是:______;(2)【问题解决】利用(1)题画出的图形,在图②中试说明,,三点在一条直线上;(3)【问题探究】取的中点,连接,利用图③试求的值.黔东南州2023-2024学年度第二学期期末考试八年级数学参考答案一、选择题123456789101112ACDBBADAABCA二、填空题13、14、88.515、1.816、三、解答题17.(8分)(1)解:原式(2)解:原式18.(10分)解:(1),,,,(2),,,,,∴,∴△ACD 是直角三角形,19.(10分)(1)四边形ABCD 是平行四边形,AB //CDAB //CF ,ABE =∠DFE ,E 是边AD 的中点,AE =DEDF EF ADE ∠CDF ∠B C F EF P CP CPBE2≥x 313-4=-+432+===4=AB 3=BC 54322=+=CD 257122=+=AD 251225534+=+++=ABCD C 四边形5=AC 5=CD 25=AD 5022=+CD AC 502=AD 222AD CD AC =+2136225=-=-=ABC ACD ABCD S S S △△四边形 ∴∴∴∠ ∴在△ABE 与△DFE 中,△ABE ≌△DFE (AAS )(2)四边形ABDF 是平行四边形,如图:由(1)得:△ABE ≌△DFE ,则BE =EFBE = EF ,AE =ED ,四边形ABDF 是平行四边形20.(12分)(1)82;30(2)七年级优秀人数人,八年级优秀人数人75+60=135人,答:两个年级此次测试成绩达到优秀的学生总人数为135人.(3)八年级学生的成绩较好.理由:八年级学生成绩的平均数较大,而且方差较小,说明平均成绩较高,并且波动较小,所以八年级学生的成绩较好.21.(10分)(1),∴AD =BD ,∴解得:AD =4,在Rt △ACD 中∵∠ACD =30°,∴AC =2AD =8(2)货物MNQP 不需要挪走.理由:在Rt △ABD 中,BD =AD =4(米).在Rt△ACD 中,2.2>2∴货物MNQP 不需要挪走.22.(12分)AE DE ABE FAEB DEF =∠=∠∠=∠⎧⎪⎨⎪⎩∴ ∴75205300=⨯6030200=⨯%︒=∠45ABD ABD Rt 中,△在()222242==AB AD 2.28.258.24343422≈-≈-=∴≈-=-=∴=-=CB PB PC BD CD CB AD AC CD(1)解:根据题意得,,由题意,解得:,自变量的取值范围是,且是整数;(2)由(1),,随的增大而减小,又且是整数,当时,有最大值,最大值是(元),生产甲种吉祥物个,乙种吉祥物个,所获利润最大,最大为元.23.(12分)(1)证明:∵四边形是矩形,∴,∴,即,∵,,∴四边形是菱形.(2)解:连接,如图:∵四边形是菱形,,∴,∵,∴,∴,∴,∵四边形是矩形,∴,,∴.24.(12分)解(1)把,,∴C (3,4)把A (-3,0),C (3,4)代入得,解得∴解析式是()10202000y x x =+-1040000y x ∴=-+()()0.30.620009000.50.22000850x x x x +-≤⎧⎪⎨+-≤⎪⎩10001500x ≤≤∴x 10001500x ≤≤x 1040000y x =-+100k =-< y ∴x 10001500x ≤≤x ∴1000x =y 1010004000030000-⨯+=∴1000100030000ABCO =90AOC ∠︒AO OC ⊥AD EC ⊥DO AO =EO CO =AEDC EB AEDC 60AED ∠=︒30AEO ∠=︒904AOE AE ∠=︒=,122OA AE ==EO ===2CE EO ==ABCO 2BC OA ==90BCE ∠=︒EB ===()x y m C 3442=代入,443m =3m =b kx y +=13034k b k b -+=⎧⎨+=⎩232k b ⎧=⎪⎨⎪=⎩2321+=x y(2)<3(3)设点P ,∵B (0,2),C (3,4),所以或25.(12分)(1)如图,∠ADE =∠CDF(2)证明:如图②,连接CF .∵四边形ABCD 是正方形,∴AD =CD ,∠ADC =,即∠ADE+∠EDC=,∵∠EDF =,即∠EDC+∠CDF=,∴∠ADE=∠CDF ∵DE =DF ,∴△ADE ≌△CDF ,∠DAE=∠DCF=∴∠BCD+∠DCF=,即B ,C ,F 三点在一条直线上(3)连接PB ,PD .在Rt △EDF 和Rt △EBF 中∵P 是斜边EF 的中点,∴x ⎪⎭⎫ ⎝⎛+232,m m 232-⋅=∴m S OPC △2,821-==m m ⎪⎭⎫ ⎝⎛-32,21P ⎪⎭⎫⎝⎛322,82P 90 90 90 90 90 180EF PB PD 21==又∵BC =DC ,PC =PC ,∴△BCP ≌△DCP ∴∠BCP=∠DCP=取BF 的中点P ,连接PG ,则PG ∥EB .∴∠PGF=∠EBF=,∴△PGC 是等腰直角三角形.设PG =x ,则CP =,BE =2x ,∴4521=∠BCD 90x 22222==x x BE CP。
物理化学核心教程第二版(沈文霞)课后习题答案5-8

第五章 化学平衡一.基本要求1.掌握化学反应等温式的各种形式,并会用来判断反应的方向和限度。
2.了解标准平衡常数的定义,掌握标准平衡常数的各种表示形式和计算方法。
3.掌握标准平衡常数K 与r m G ∆ 在数值上的联系,熟练用热力学方法计算r m G ∆,从而获得标准平衡常数的数值。
4.了解标准摩尔生成Gibbs 自由能f m G ∆ 的定义和它的应用。
5.掌握温度对化学平衡的影响,记住van ’t Hoff 公式及其应用。
6.了解压力和惰性气体对化学平衡的影响。
二.把握学习要点的建议把本章放在多组分系统之后的目的,就是要利用多组分系统中介绍的化学势的概念和各种表示方式,来导出化学反应等温式,从而用来判断化学反应的方向与限度。
本章又用到了反应进度的概念,不过其值处在0 1 m ol -的区间之内。
因为在利用化学势的表示式来计算反应的Gibbs 自由能的变化值时,是将化学势看作为一个定值,也就是在有限的反应系统中,化学进度为d ξ,如果在一个很大的系统中, 1 mol ξ=。
严格讲,标准平衡常数应该用绝对活度来定义,由于本教材没有介绍绝对活度的概念,所以利用标准态化学势来对标准平衡常数下定义,其含义是一样的。
从标准平衡常数的定义式可知,标准平衡常数与标准化学势一样,都仅是温度的函数,因为压力已指定为标准压力。
对于液相反应系统,标准平衡常数有其相应的形式。
对于复相化学反应,因为纯的凝聚态物质本身就作为标准态,它的化学势就是标准态化学势,已经归入r m G ∆中,所以在计算标准平衡常数时,只与气体物质的压力有关。
学习化学平衡的主要目的是如何判断反应的方向和限度,知道如何计算平衡常数,了解温度、压力和惰性气体对平衡的影响,能找到一个经济合理的反应条件,为科研和工业生产服务。
而不要过多地去考虑各种浓度表示式和各种平衡常数表示式之间的换算,否则会把自己搞糊涂了,反而没抓住主要内容。
由于标准平衡常数与r m G ∆ 在数值上有联系,r m ln p G RT K ∆=-,所以有了r m G ∆的值,就可以计算p K 的值。
2023-2024学年北京市海淀区中国人民大学附属中学本部中考模拟数学试题+答案解析

2023-2024学年北京市海淀区中国人民大学附属中学本部中考模拟数学试题一、选择题:本题共8小题,每小题3分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.2022年5月18日是第46个国际博物馆日,今年国际博物馆日的宣传主题是“博物馆的力量”,在以下几幅古代纹样图案中,利用中心对称进行整体构图的是()A. B.C. D.2.在第46个国际博物馆日来临之际.中国国家博物馆推出了丰富多彩的“云上观展”活动.观众有机会在屏幕上欣赏国博140万余件藏品的真容,将140万用科学记数法表示为()A. B. C. D.3.下列各组角中,互为余角的是()A.与B.与C.与D.与4.下列说法中错误的是()A.成轴对称的两个图形的对应点连线的垂直平分线是它们的对称轴B.关于某条直线对称的两个图形全等C.两个全等三角形的对应高相等D.两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧5.有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的点数记为x,则的概率是()A. B. C. D.6.实数a、b在数轴上的对应点的位置如图所示,下列式子成立的是()A. B. C. D.7.李老师是一位运动达人,他通过佩戴智能手环来记录自己一个月天每天所走的步数,并绘制成如右统计表:在每天所走的步数这组数据中,众数和中位数分别是()A.,B.,C.,D.,8.某学校对教室采用药薰消毒法进行消毒.现测得不同时刻的y与x的数据如表:时间分钟0246810121620含药量毫克03643则下列图象中,能表示y与x的函数关系的图象可能是()A. B.C. D.二、填空题:本题共8小题,每小题3分,共24分。
9.若有意义,则x的取值范围是__________.10.把多项式分解因式的结果是__________.11.若n为整数,且,则n的值为__________.12.分式方程的解__________.13.如图,点A,B,C,D在上,,,则__________.14.如图,在中,按以下步骤作图:①以点A为圆心,适当长为半径作弧,分别交于点M,N;②分别以点M,N为圆心,大于的长为半径作弧,两弧交于点P;③作射线AP交BC于点若,的面积为4,则的面积为__________.15.如图,已知等腰三角形ABC,,,若以点B为圆心,BC长为半径画弧,则__________16.以下是小亮的妈妈做晚饭的食材准备及加工时间列表,有一个炒菜锅,一个电饭煲,一个煲汤锅,两个燃气灶可用,做好这顿晚餐一般情况下至少需要__________分钟.用时种类准备时间分钟加工时间分钟米饭330炒菜156炒菜258汤56三、计算题:本大题共1小题,共6分。
八年级数学第一次月考卷01(解析:八年级上册第十一章~第十二章】人教版-25年初中上学期第一次月考

2024-2025学年八年级数学上学期第一次月考卷01(考试时间:120分钟试卷满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:人教版八年级上册第十一章~第十二章。
5.难度系数:0.85。
一、选择题(本题共12小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.下列长度的三条线段能组成三角形的是()A.6,2,3B.3,3,3C.4,3,8D.4,3,72.如图,生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的()A.全等形B.稳定性C.灵活性D.对称性【详解】解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性,故选:B.3.如图,CM是△ABC的中线,AB=10cm,则BM的长为()A.7cm B.6cm C.5cm D.4cm4.画△ABC的BC边上的高AD,下列画法中正确的是()A.B.C.D.【答案】D【详解】解∶A、选项A不是△ABC的高,故不符合题意;B、选项B不是△ABC的高,故不符合题意;C、选项C不是△ABC的高,故不符合题意;D、选项D为△ABC中BC边上的高,故符合题意.故选:D.5.一个多边形的内角和等于540°,则它的边数为()A.4B.5C.6D.8【答案】B【详解】解:设这个多边形的边数为n,∴(n―2)·180°=540°,故选:B .6.请仔细观察用直尺和圆规作一个角∠A ′O ′B ′等于已知角∠AOB 的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A ′O ′B ′=∠AOB 的依据是( )A .SASB .ASAC .AASD .SSS【答案】D【详解】解:由作法易得OD =O ′D ′,OC =O ′C ′,CD =C ′D ′,在△ODC 和△O ′D ′C ′中,∵ OC =O ′C′OD =O ′D ′CD =C ′D ′ ,∴△COD≌△C ′O ′D ′(SSS ),∴∠D ′O ′C ′=∠DOC .故选:D7.如图,△ABE ≌△ACF ,若AB=5,AE=2,则EC 的长度是( )A .2B .3C .4D .5【答案】B【详解】解:∵△ABE ≌△ACF ,AB =5,AE =2,∴AB =AC =5,∴EC=AC-AE=5-2=3,故选:B .8.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件()A.∠BAC=∠BAD B.∠C=∠D C.AC=AD D.BC=AD【答案】C【详解】解:∵∠C=∠D=90°,在Rt△ABC和Rt△ABD中,AB=ABAC=AD∴Rt△ABC≌Rt△ABD(HL).故选:C.9.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,CD=3,则点D到AB的距离是()A.6B.2C.3D.4【答案】C【详解】解:如图,过D作DE⊥AB于E,∵∠C=90°,∠BAC的平分线AD交BC于点D,CD=3,∴DE=CD=3,∴点D到AB的距离是3.故选C.10.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2的度数为()A.210°B.250°C.270°D.300°11.某同学把一块三角形的玻璃打碎了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是()A.带①去B.带②去C.带③去D.带①②③去【答案】C【详解】解:A. 第①块只保留了原三角形的一个角和部分边,不符合任何判定方法,不合题意;B. 第②块仅保留了原三角形的一部分边,不符合任何判断方法,不合题意;C. 第③块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃,符合题意;D. 带①②③去,可以得到一块一样的玻璃,但不如直接带③省事,不合题意.故选:C12.如图1,∠DEF=20°,将长方形纸片ABCD沿直线EF折叠成图2,再沿折痕为BF折叠成图3,则∠CFE 的度数为()A.100°B.120°C.140°D.160°二、填空题(本题共6小题,每小题2分,共12分.)13.在Rt△ABC中,∠C=90°,∠A=40°,则∠B= .【答案】50°/50度【详解】解:因为在Rt△ABC中,∠C=90°,∠A=40°,所以∠B=90°-40°=50°,故答案为:50°.14.如图,CD是△ABC的高,∠ACB=90°.若∠A=35°,则∠BCD的度数是.【答案】35°/35度【详解】∵CD是△ABC的高,∴CD⊥AB,∴∠ADC=90°,∵在△ACD中,∠A+∠ADC+∠ACD=180°,∠A=35°,∠ACB=90°,∴∠ACD=55°∵∠ACB=∠ACD+∠BCD=90°∴∠BCD=35°.故答案为:35°.15.如图所示的两个三角形全等,则∠1的度数是.16.如果一个正多边形的一个外角是60°,那么这个正多边形的边数是.【答案】6【详解】解:根据多边形的外角和等于360°和正多边形的每一个外角都相等,得多边形的边数为360°÷60°=6.故答案为:6.17.如图,BP 是△ABC 中∠ABC 的平分线,CP 是∠ACB 的外角的平分线,如果∠ABP=15°,∠ACP=50°,则∠P=°.【答案】35【详解】解:∵BP 是△ABC 中∠ABC 的平分线,CP 是∠ACB 的外角的平分线,∴∠CBP=∠ABP=15°,∠MCP=∠ACP=50°,∵∠CBP+∠P=∠MCP,∴∠P=∠MCP-∠CBP=50°-15°=35°,故答案为:35.18.如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1、B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=α,则∠A2023B2023O=.三、解答题(本题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)19.(6分)计算:|―2|―6×―+(―4)2+8.2021.(8分)如图,AC 和BD 相交于点0,OA =OC , OB=OD ,求证:DC //AB .【详解】解:∵⎪⎩⎪⎨⎧=∠=∠=OD OB COD AOB OC OA ,∴△AOB ≌△COD (SAS ).(6分)∴∠A =∠C .∴AB ∥CD .(8分)22.(8分)如图△ABC 中,∠A =40° , ∠ABC =∠C .(1)作∠ABC的平分线,交AC于点D(用直尺和圆规按照要求作图,不写作法,保留作图痕迹);(2)在(1)的条件下,求∠BDC的大小.23.(10分)某校学生处为了了解全校1200名学生每天在上学路上所用的时间,随机调查了30名学生,下面是某一天这30名学生上学所用时间(单位:分钟):20,20,30,15,20,25,5,15,20,10,15,35,45,10,20,25,30,20,15,20,20,10,20,5,15,20,20,20,5,15.通过整理和分析数据,得到如下不完全的统计图.根据所给信息,解答下列问题:(1)补全条形统计图;(2)这30名学生上学所用时间的中位数为______ 分钟,众数为______ 分钟;(3)若随机问这30名同学中其中一名学生的时间,最有可能得到的回答是______ 分钟;(4)估计全校学生上学所用时间在20分钟及以下的人数.名学生用时数据从小到大排列,处在中间位置的两个数都是20分钟,,即m=20,名学生用时数据出现次数最多的是20分钟,n=20,;(6分))解:由于众数是20分钟,分钟的学生最多,所以最有可能得到的回答是20分钟;24.(10分)中央大街工艺品店销售冰墩墩徽章和冰墩墩摆件,若购买4个冰墩墩徽章和2个冰墩墩摆件需要130元,购买3个冰墩墩徽章和5个冰墩墩摆件需要220元.(1)求每个冰墩墩徽章和每个冰墩墩摆件各需要多少钱?(2)若某旅游团计划买冰墩墩徽章和冰墩墩摆件共50个,所用钱数不超过1150元,则该旅游团至少买多少个冰墩墩徽章?25.(12分)如图,已知△ABC中,AC=CB=20cm,AB=16cm,点D为AC的中点.(1)如果点P在线段AB上以6cm/s的速度由A点向B点运动,同时,点Q在线段BC上由点B向C点运动.①若点Q的运动速度与点P的运动速度相等,经过1s后,△APD与△BQP是否全等?说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△APD与△BQP全等?(2)若点Q以②中的运动速度从点B出发,点P以原来的运动速度从点A同时出发,都逆时针沿△ABC 三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?26.(12分)如图,在△ABC中,∠BAC=90°,AB=AC,点D为BC的中点.点E是直线AB上的一动点,连接DE,作DF⊥DE交直线AC于点F.(1)如图1,若点E与点A重合时,请你直接写出线段DE与DF的数量关系;(2)如图2,若点E在线段AB上(不与A、B重合)时,请判断线段DE与DF的数量关系并说明理由;(3)若点E在AB的延长线上时,线段DE与DF的数量关系是否仍然满足上面(2)中的结论?请利用图3画图并说明理由.由(1)可知,△ABD≌△∴∠ADB=∠ADC=90°,∵DF ⊥DE ,∴∠EDF =90°,∵∠BDE +∠ADE =90°,∠ADE +∠ADF =90°,∴∠BDE =∠ADF ,(4分)在△BDE 和△ADF 中,∠B =∠DAF BD =AD ∠BDE =∠ADF,∴△BDE≌△ADF (ASA ),(6分)∴DE =DF ;(7分)(3)解:DE =DF ,(8分)如图2,理由如下;由(1)(2)可知∠DBE =∠DAF =135°,∵DF ⊥DE ,∴∠EDF =90°,∵∠BDE +∠BDF =90°,∠BDF +∠ADF =90°,∴∠BDE =∠ADF ,在△BDE 和△ADF 中,∠DBE =∠DAF BD =DA ∠BDE =∠ADF,∴△BDE≌△ADF (ASA ),∴DE =DF .(12分)。
上教版八年级数学(上)暑假讲义 第12讲--勾股定理及两点间的距离公式
!"#$%&'()*+,-.内容分析!"#$%&'()*+,-./0121342567849:;<=> @A-BC>?@A4DEF GHIJ@A4DEKGH(LMN O/(P8 4QRSTU VP/>?@A4DEIGH-W/'X012132678;< 4YHLZ-/.[\]ST-^_`4abcdHeYfgUh知识结构!"#$%&'()*+,-./知识精讲1、勾股定理:(1)直角三角形中,两条直角边的平方和,等于斜边的平方.利用勾股定理往往构造方程,已达到解决问题的目的;(2)应用勾股定理解决实际问题,要注意分析题目的条件,关注其中是否存在直角三角形,如果存在直角三角形,根据所给的三边条件,建立方程,从而解决问题;如果问题中没有直角三角形,可以通过添加辅助线构造出直角三角形,寻求等量关系,再根据勾股定理建立相应的方程,因此,在解决直角三角形中有关边长的问题时,要灵活的运用方程的思想.【例1】 (1)在直角△ABC 中,∠C =90°,∠A =30°,BC =1,则AB =_________;(2)在直角△ABC 中,∠C =90°,∠A =45°,AB =3,则AC =_________.【例2】 (1)等边三角形的边长是3,则此三角形的面积是___________;(2)等腰三角形底边上的长为2,腰长为4,则它底边上的高为__________.【例3】 (1)直角三角形两边长为3和4,则此三角形第三边长为_________;(2)直角三角形两直角边长为3和4,则此三角形斜边上的高为_________; (3)等腰三角形两边长是2、4,则它腰上的高是____________.【例4】 (1)若直角三角形的三边长分别为N +1,N +2,N +3则N 的值是____________;(2)如果直角三角形的三边长为连续偶数,则此三角形的周长为______________.【例5】 如图,在直角△ABC 中,∠ACB =90°,∠B=60°,D 是斜边AB 的中点,BC =2,求△ADC 的周长.【例6】 如图,已知:R △ABC 中,∠ACB 是直角,BC =15,AB 比AC 大9,CD ⊥AB 于点D ,求CD 的长.【例7】 已知已直角三角形的周长为斜边上的中线为2,求这个直角三角形的面积.t例题解析ABC DCD【例8】 如图,直线MN 是沿南北方向的一条公路,某施工队在公路的点A 测得北偏西30°的方向上有一栋别墅C ,朝正北方向走了400米到达点B 后,测得别墅C 在北偏西75°的方向上,如果要从别墅C 修一条通向MN 的最短小路,请你求出这条小路的长(结果保留根号).【例9】 如图,公路MN 和公里PQ 在点P 处交汇,且∠QPN =30°,点A 处有一所中学,AP =160米,假设拖拉机行驶时,周围100米以内会受到噪音的影响,那么拖拉机在MN 上沿PN 方向行驶时,学校是否会受到噪音的影响?请说明理由;如果受影响,已知拖拉机的速度是18千米/时,那么学校受影响的时间是多少秒?【例10】 如图,矩形ABCD 中,AB =8,BC =4,将矩形沿AC 进行翻折,点D 落在E 处,求出重叠部分△AFC 的面积.ABMMNAPF【例11】 如图,AB 两个村子在河边CD 的同侧,A 、B 两村到河边的距离分别为AC =1千米,BD =3千米,CD =3千米.现在河边CD 建一座水厂,建成后的水厂,可以直接向A 、B 两村送水,也可以将水送一村再转送另一村.铺设水管费用为每千米2万元,试在河边CD 选择水厂位置P 确定方案,使铺设水管费用最低,并求出铺设水管的总费用(精确到0.01万元).【例12】 如图,在直角△ABC 中,∠BAC =90°,AB =AC ,E 、F 是BC 上的两点,且∠EAF =45°,求证:.222+=BE CFEFA BCDA B C DP2、 逆定理:(1) 如果三角形一条边的平方等于其他两边的平方和,那么这个三角形是直角三角形;利用逆定理来判断三角形是否为直角三角形.(2) 在直角三角形的三边中,首先弄清楚哪条边是斜边,另外应用逆定理时,最大边的平方和等于较小两边的平方和.【例13】 下列命题中是假命题的是( )A . 在△ABC 中,若∠B =∠C -∠A ,则△ABC 是直角三角形 B . 在△ABC 中,若,则△ABC 是直角三角形 C . 在△ABC 中,若∠B :∠C :∠A =3:4:5,则△ABC 是直角三角形D . △ABC 中,若,则△ABC 是直角三角形【例14】 (1)将直角三角形的三边都扩大相同的倍数后,得到的三角形是______三角形;(2)若△ABC 的三边A 、B 、C 满足则△ABC 是________三角形. 【例15】 (1)一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,则旗杆折断之前有多少米?(2)如果梯子的底端离建筑物8米,那么17米长的梯子可以到达建筑物的高度是__________米.【例16】 的三边分别为A 、B 、C ,且满足,判断△ABC的形状.2()()a b c b c =+-::5:4:3a b c =222()()0a b a b c -+-=ABC D 222506810a b c a b c +++=++!"0$%&'()1'()*+,-./例题解析知识精讲【例17】 如图,公路上A 、B 两点相距25千米,C 、D 为两村庄,DA ⊥AB 于点A ,CB ⊥AB 于点B ,已知DA =15千米,CB =10千米,现要在公路AB 上建一车站E . (1) 若使得C 、D 两村到E 站的距离相等,E 站建在离A 站多少千米处? (2) 若使得C 、D 两村到E 站的距离和最小,E 站建在离A 站多少千米处?【例18】 如图,在四边形ABCD 中,AB =BC =2,CD =3,DA =1,且∠B =90°,求∠DAB的度数.【例19】 如图,已知在△ABC 中,∠B =90°,AB =BC ,AD 是BC 边上的中线,EF 是AD的垂直平分线,交AB 于点E ,交AC 于点F ,求AE :BE 的值.【例20】 如图,ABC 是等边三角形,P 是三角形内一点,P A =3,PB =4,PC =5,求∠APB 的度数.D ABCD ABCDE FBPA BCDE【例21】 如图,P 是凸四边形内一点,过点P 作AB 、BC 、CD 、DA 的垂线,垂足分别为E 、F 、G 、H ,已知AH =3,DH =4,DG =1,GC =5,CF =6,BF =4,且BE -AE =1,求四边形ABCD 的周长.【例22】 已知,如图,在△ABC 中,∠ACB =90°,CD ⊥AB 于点D ,设AC =,BC =,AB =,CD = . 求证:(1);(2)以、、为三边可构成一个直角三角形.b ac h c h a b +>+a b +c h +h ABCDEFGHPAB CD3、 距离公式:如果平面内有两点、,则A 、B 两点间的距离为:(1) 当、两点同在轴上或平行于轴的直线上,则有,AB =;(2) 当、两点同在轴上或平行于轴的直线上,则有,AB =.【例23】 已知点A (2,2)、B (5,1).(1) 求A 、B 两点间的距离; (2) 在轴上找一点C ,使AC =BC .【例24】 (1)已知A (,3)、B (3,+1)之间的距离为5,则的值是_________;(2)已知点P 在第二、四象限的平分线上,且到Q (2,-3)的距离为5,则点P 的坐标为_________.【例25】 (1)以点A (1,2)、B (-2,-1),C (4,-1)为顶点的三角形是________;(2)已知点A (0,3)、B (0,-1),△ABC 是等边三角形,则点C 的坐标是_______.【例26】 已知直角坐标平面内的点A (4,1)、B (6,3),在坐标轴上求点P ,使P A =PB .11()A x y ,22()B x y ,11()A x y ,22()B x y ,x x 12y y =12||x x -11()A x y ,22()B x y ,y y 12x x =12||y y -x x x x 例题解析!"2$345)6789/知识精讲【例27】 已知直角坐标平面内的点P (4,),且点P 到点A (-2,3)、B (-1,-2)的距离相等,求点P 的坐标.【例28】 已知点A (2,3)B (4,5),在轴上是否存在点P ,使得的值最小?若存在,求出这个最小值;若不存在,说明理由.【例29】 已知直角坐标平面内的点A (4,)、B (6,3),在轴上求一点C ,使得 △ABC 是等腰三角形.【例30】已知点A (4,0)、B (2,-1),点C 的坐标是(,2-),若△ABC 是等腰三角形,求C 的坐标.m x PA PB +32x x x【习题1】 六根细木棒,她们的长度分别是2、4、6、8、10、12(单位:)从中取出三根,首尾顺次连接搭成一个直角三角形,则这些木棒的长度分别为().A . 2、4、8B .4、8、10C .6、8、10D .8、10、12【习题2】 已知点A (2,4)B (-1,-3)C (-3,-2),那么△ABC 的形状是()A .等腰三角形B .直角三角形C .等腰直角三角形D .以上都不是【习题3】 (1)如果等腰直角三角形一边长为2,另外两边长为_________;(2)如果直角三角形两边长为5和12,第三边长度为_______________.【习题4】 如图,将长方形ABCD 沿AE 折叠,使得点D 落在BC 上的点F 处,AB =8,AD =10.求EC 的长.【习题5】 如图,在四边形ABCD 中,AB ⊥BC ,AB =9,BC =12,CD =15,DA =四边形ABCD 的面积.【习题6】 如图,在△ABC 中,AD 为BC 边上的中线,AB =5,AC =3,AD =2.求:△ABC的面积.cm 随堂检测ABCDAB D CABC DEF【习题7】 若A 、B 、C 是三角形的边长且关于的方程有两个相等的实数根,试判断这个三角形的形状.【习题8】 如图,在一条公路上有P 、Q 两个车站,相距27,A 、B 是两个村庄,AP ⊥PQ ,BQ ⊥PQ ,且AP =15,BQ =24,现在要在公路上建立一个商场M 使得A 、B 两个村庄到商场M 的距离相等,求PM 的长 .【习题9】 已知点,点C 在轴上,使为直角直角三角形,求满足条件的点C 的坐标.【习题10】 如图,在中,是内一点,且 ,求的度数.x 222()20x a b x c ab -+++=km km km ()()2814A B -,,y ABC D ABC D 90ACB AC BC M Ð==!,,ABC D 312AM BM CM ===,,BMC Ð ABCMABQP M【习题11】 若在△ABC 中,AB =c ,AC =b ,BC =a ,∠ACB =90°,则试用两种方法证明.【作业1】 下列命题中,正确的有()个(1) 腰长及底边上的高对应相等的两个等腰三角形全等 (2) 有一直角边和斜边上对应相等的两个直角三角形全等 (3) 有两边和其中一边上的高对应相等的两个三角形全等 A .0 B .1 C .2 D .3【作业2】 如图,图中的字母、数代表正方形的面积,则A =______.【作业3】 如图,中,斜边,则的值是iiiiiiiii . 【作业4】 已知点,点B 的横坐标为-3,且A 、B 两点之间的距离为10,那么点B的坐标是iiiiiiiiiiii .【作业5】 现将直角三角形ABC 的直角边AC 沿直线AD 折叠,使它落在斜边AB 上,C 与E 重合,且AC =3,BC =4,则CD 等于_____________.【作业6】 如果的周长为12,而那么的形状是____________.【作业7】 已知等腰直角三角形斜边BC 的长为2,为等边三角形,那么A 、D两点的距离为______ij222a b c +=Rt ABC D 1AB =222AB BC AC ++()35A -,ABC D 22AB BC AC AB BC +=-=,,ABC D ABC DBC D 课后作业5072A【作业8】 已知:如图,已知在中,,将绕点逆时针旋转后得到,若,则两个三角形重叠部分的面积为_________.【作业9】 已知:如图,四边形ABCD 的三边(、、)和都为5厘米,动点P 从A 出发(),速度为2厘米/秒,动点Q 从点D 出发()到A ,速度为2.8厘米/秒,5秒后P 、Q 相距3厘米,试确定5秒时的形状.【作业10】 阅读下列题目的解题过程: 已知、、为的三边,且满足,试判断的形状. 解:(A ),(B )(C ),是直角三角形.问:(1)上述解题过程中,从哪一步开始出错? 请写出该步的代号:____________; (2)错误的原因:_______________;(3)本题正确的结论为:iiiiiiiiiiiijhh h h h hRt ABC D 9030B C Ð=Ð=!!,ABC D A 30!APQ D 1AB =AB BC CD BD A B D ®®D C B A ®®®APQ D a b c ABC D 222244a c b c a b -=-ABC D !222244a c b c a b -=-()()()2222222c a b a b a b \-=+-222c a b \=+\ABC D ABCDQPABQP【作业11】 如图,一根长度为50CM 的木棒的两端系着一根长度为70CM 的绳子,现准备在绳子上找一点,然后将绳子拉直,使拉直后的绳子与木棒构成一个直角三角形,求满足条件的点有几个,并且这个点将绳子分成的两段各有多长?【作业12】 在直角坐标平面内,已知,在坐标轴上求一点P ,使得为直角三角形,求点P 的坐标.()()1054A B -,,,PAB D。
苏科版八年级上册数学期中考试试题含答案

苏科版八年级上册数学期中考试试卷一、单选题1.在以下回收、绿色食品、节能、节水四个标志中,是轴对称图形的是()A.B.C.D.2.下列长度的三条线段能组成直角三角形的是()A.4,6,8B.6,8,10C.6,9,10D.5,11,133.已知:△ABC≌△DEF,AB=DE,∠A=70°,∠E=30°,则∠F的度数为()A.80°B.70°C.30°D.100°4.若等腰三角形中有两边的长分别为5和8,则这个三角形的周长为()A.18B.21C.18或21D.21或165.在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在ABC()A.三边中线的交点B.三边垂直平分线的交点C.三条角平分线的交点D.三边上高的交点6.如图,在△ABC和△DEF中,AC=DF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是()A.∠A=∠D B.BE=CF C.∠ACB=∠DFE=90°D.∠B=∠DEF 7.如图,矩形ABCD边AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积为24,则EC等于()A.2B.103C.4D.838.下列说法:①等腰三角形的两底角相等;②角的对称轴是它的角平分线;③成轴对称的两个图形中,对应点的连线被对称轴垂直平分;④全等三角形的对应边上的高相等;⑤在直角三角形中,如果有一条直角边长等于斜边长的一半.那么这条直角边所对的角等于30°.以上结论正确的个数()A.1个B.2个C.3个D.4个9.如图,在△ABC中,AB=13,BC=14,S△ABC=84,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为()A.15B.12C.10D.910.如图,如果把△ABC沿AD折叠,使点C落在边AB上的点E处,那么折痕(线段AD)是△ABC的()A.中线B.角平分线C.高D.既是中线,又是角平分线二、填空题11.如图,∠1=∠2,要使△ABE≌△ACE,需添加一个条件是__________.(填上一个条件即可)12.若一个直角三角形的两直角边长分别为6和8,则其斜边上的高为________.13.如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长为___________.14.如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=6,AD=4,则DE的长为________________.15.如图,∠ABC=∠ACD=90°,BC=2,AC=CD,则△BCD的面积为_________.16.已知长方形ABCD中,∠A=∠ABC=∠C=∠D=90°,AB=8,BC=5,点E为射.线.CD上一点,将△BCE沿BE翻折得到△BC′E,当点C′落在边AB的垂直平分线上时,点C/到边CD的距离为_____.17.爱动脑筋的小明某天在家玩遥控游戏时遇到下面的问题:已知,如图一个棱长为8cm 无盖的正方体铁盒,小明通过遥控器操控一只带有磁性的甲虫玩具,他先把甲虫放在正方体盒子外壁A处,然后遥控甲虫从A处出发沿外壁面正方形ABCD爬行,爬到边CD上后再在边CD上爬行3cm,最后在沿内壁面正方形ABCD上爬行,最终到达内壁BC的中点M,甲虫所走的最短路程是______cm三、解答题18.如图,阴影部分是由5个小正方形组成的一个直角图形,请用3种方法分别在下图方格内涂黑2个小正方形,使它们成为轴对称图形.19.已知:如图,AC∥DF,AC=DF,AB=DE.求证:(1)△ABC≌△DEF;(2)BC∥EF.20.已知:如图,△ABC中,∠A=90°,现要在AC边上确定一点D,使点D到BA、BC 的距离相等.(1)请你按照要求,在图上确定出点D的位置(尺规作图,不写作法,保留作图痕迹);(2)若BC =5,AB =4,则AC =,AD =(直接写出结果).21.如图,在△ABC 中,AB =AC ,D 为BC 边上一点,∠B =30°,∠DAB =45°.(1)求∠DAC 的度数;(2)求证:DC =AB .22.如图,小明爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算这块土地的面积,以便估算产量.小明测得AB 8m =,AD 6m =,CD 24m =,BC 26m =,又已知A 90∠=︒,求这块土地的面积.23.已知,如图,AC =BD ,∠1=∠2.(1)求证:△ABC ≌△BAD ;(2)若∠2=∠3=25°,求∠D 的度数.24.如图是一个零件的示意图,测量AB =4cm ,BC =3cm ,CD =12cm ,AD =13cm ,∠ABC =90°,根据这些条件,你能求出∠ACD 的度数吗?试说明理由.25.如图,△ABC 中,∠C =90°,AC =8cm ,BC =6cm ,若动点P 从点C 开始,按C→A→B→C 的路径运动,且速度为每秒1cm ,设运动的时间为t 秒.(1)当t=秒时,CP把△ABC的面积分成相等的两部分,此时CP=cm;(2)当t为何值时,△ABP为等腰三角形.(3)若点P在线段AC上运动,点Q是线段AB上的动点,求PB+PQ的最小值.26.在四边形ABCD中,∠A=∠B=∠C=∠D=90°,AB=CD=10,BC=AD=6,P为BC上一点,将△ABP沿直线AP翻折至△AEP的位置,使点B落在点E处.射线..(1)若P为BC上一点.①如图1,当点E落在边CD上时,利用尺规作图,在图1中作出满足条件的点E(不写作法,保留作图痕迹),并直接写出此时CE=;②如图2,连接CE,若CE∥AP,则BP与BC有何数量关系?请说明理由;(2)如果点P在BC的延长线上,当△PEC为直角三角形时,求PB的长.参考答案1.B【解析】【分析】根据轴对称图形的概念对各选项分析判断,利用排除法求解.【详解】解:A 、不是轴对称图形,故本选项错误;B 、是轴对称图形,故本选项正确;C 、不是轴对称图形,故本选项错误;D 、不是轴对称图形,故本选项错误.故选:B .【点睛】本题主要考查轴对称图形,掌握轴对称图形的概念是解题的关键.2.B【解析】【分析】根据勾股定理的逆定理:两边的平方和等于第三边的平方,即可完成解答.【详解】A 、22246528+=≠,故不能组成直角三角形;B 、2226810010+==,故能组成直角三角形;C 、2226911710+=≠,故不能组成直角三角形;D 、22251114613+=≠,故不能组成直角三角形;故选:B【点睛】本题考查了勾股定理的逆定理,熟练掌握此定理是关键.3.A【解析】【分析】根据全等三角形对应角相等求出∠D=∠A ,再利用三角形的内角和等于180°列式进行计算即可得解.【详解】∵△ABC≌△DEF,AB=DE,∠A=70°,∴∠D=∠A=70°,在△DEF中,∠F=180°-∠D-∠E=180°-70°-30°=80°,故选A.【点睛】本题考查了全等三角形对应角相等的性质,三角形的内角和定理,根据全等三角形对应顶点的字母写在对应位置上准确找出对应角是解题的关键.4.C【解析】【分析】分5是腰长和底边长两种情况讨论求解.【详解】解:5是腰长时,三角形的三边分别为5、5、8,能组成三角形,周长=5+5+8=18,5是底边长时,三角形的三边分别为5、8、8,能组成三角形,周长=5+8+8=21,综上所述,这个等腰三角形的周长是18或21.故选:C.【点睛】本题考查了等腰三角形的性质,三角形的三边关系,难点在于要分情况讨论.5.B【解析】【分析】为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.【详解】解:∵三角形的三条边的垂直平分线的交点到中间的凳子的距离相等,∴凳子应放在△ABC的三边中垂线的交点最适当.故选:B.【点睛】本题主要考查了游戏的公平性与线段垂直平分线的性质的应用;利用所学的数学知识解决实际问题是一种能力,要注意培养.想到要使凳子到三个人的距离相等是正确解答本题的关键.6.D【解析】【分析】根据全等三角形的判定,利用ASA、SAS、AAS即可得答案.【详解】解:∵AC=DF,AB=DE,∴添加∠A=∠D,可利用SAS证明△ABC≌△DEF,故A不符合题意;∴添加BE=CF,得出BC=EF,利用SSS证明△ABC≌△DEF,故B不符合题意;∴添加∠ACB=∠DFE=90°,利用HL证明Rt△ABC≌Rt△DEF,故C不符合题意;添加∠B=∠DEF,不能证明△ABC≌△DEF,故D符合题意;故选:D.【点睛】本题考查了全等三角形的判定,掌握全等三角形的判定方法:SSS、ASA、SAS、AAS和HL是解题的关键.7.D【解析】【分析】先根据三角形的面积公式求得BF的长,然后根据勾股定理可求得AF=10,由翻折的性质和矩形的性质可知BC=10,故此FC=2,最后在△EFC中,由勾股定理列方程求解即可.【详解】∵S△ABF=24,∴12AB•BF=24,即12×6•BF=24.解得:BF=8,在Rt△ABF中由勾股定理得:AF10.由翻折的性质可知:BC=AD=AF=10,ED=FE.∴FC =10﹣8=2.设DE =x ,则EC =6﹣x .在Rt △EFC 中,由勾股定理得:EF 2=FC 2+EC 2,x 2=4+(6﹣x )2.解得:x =103,∴CE =83.故选D .【点睛】本题主要考查了翻折问题,矩形的性质,勾股定理,熟练运用勾股定理是解题的关键.8.D【解析】【分析】根据直角三角形性质,等边对等角,全等三角形的性质定理,轴对称图形的概念判断即可.【详解】解:等腰三角形的两底角相等,①正确;角的对称轴是它的角平分线所在的直线,②错误;成轴对称的两个图形中,对应点的连线被对称轴垂直平分,③正确;全等三角形的对应边上的高相等④正确;在直角三角形中,如果有一条直角边长等于斜边长的一半.那么这条直角边所对的角等于30°,⑤正确;故选D .【点睛】本题考查的是直角三角形性质,全等三角形的性质,轴对称图形,掌握全等三角形的性质定理,轴对称图形的概念是解题的关键.9.A【解析】【分析】如图,连接AD ,作AM BC ⊥,CN l ⊥垂足分别为M N ,,可证()BDF CDN AAS ≌,BF CN =;由1842ABC S BC AM =⨯⨯= ,求得AM 的值,在Rt ABM 中,由勾股定理得22BM AB AM =-,求得BM 的值,CM BC BM =-,求得CM 的值,在Rt ACM △中,由勾股定理得22AC AM CM =+,求得AC 的值;12CDH ADH ABC S S S += ,可得12ABC S ()12DH CN AE =⨯⨯+,可知当l AC ⊥时,DH 最小,CN AE +最大,此时有111222ABC S DH CN DH AE =⨯⨯+⨯ ,解得DH 的值,进而求解CN AE +的值,故可知BF AE +的最大值.【详解】解:如图,连接AD ,作AM BC ⊥,CN l ⊥垂足分别为M N,由题意知BD CD=在BDF 和CDN △中∵90BFD CND BDF CDN BD CD ∠=∠=︒⎧⎪∠=⎨⎪=⎩∴()BDF CDN AAS ≌∴BF CN=∵1842ABC S BC AM =⨯⨯= ∴12AM =在Rt ABM 中,由勾股定理得225BM AB AM =-=∴9CM BC BM =-=在Rt ACM △中,由勾股定理得15AC ==∵12CDH ADH ABC S S S += ∴111222ABC S DH CN DH AE =⨯⨯+⨯ ()12DH CN AE =⨯⨯+∴当l AC ⊥时,DH 最小,CN AE +最大∴此时1122ADCS CD AM AC DH =⨯⨯=⨯⨯ 解得285DH =∴5841528CN AE +=⨯=∴BF AE +的最大值为15故选A .【点睛】本题考查了全等三角形的判定与性质,勾股定理等知识.解题的关键在于将线段和与面积联系求解.10.B【解析】【分析】根据折叠的性质即可得到结论.【详解】解:∵把△ABC 沿AD 折叠得到△ADE ,∴△ACD ≌△AED ,∴∠CAD=∠EAD ,∴AD 是△ABC 的角平分线.故选择:B .【点睛】本题考查折叠图形的性质,掌握折叠图形的性质是解题关键.11.∠B=∠C(或BE=CE或∠BAE=∠CAE)【解析】【分析】根据题意,易得∠AEB=∠AEC,又AE公共,所以根据全等三角形的判定方法容易寻找添加条件.【详解】解:∵∠1=∠2,∴∠AEB=∠AEC,又AE是公共边,∴当∠B=∠C时,△ABE≌△ACE(AAS);当BE=CE时,△ABE≌△ACE(SAS);当∠BAE=∠CAE时,△ABE≌△ACE(ASA).故答案为:∠B=∠C(或BE=CE或∠BAE=∠CAE).【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.12.24 5【解析】【分析】10=,根据面积不变,得斜边上的高为16821102⨯⨯⨯,计算求解即可.【详解】10=,根据面积不变,得斜边上的高为16824 215102⨯⨯=⨯,故答案为:24 5.【点睛】本题考查了勾股定理,等面积法求三角形的高,解题的关键在于正确的计算.13.10【解析】【分析】根据线段垂直平分线的性质得到EA=EB,根据三角形的周长公式计算,得到答案.【详解】解:∵DE是AB的垂直平分线,∴EA=EB,∵△BCE的周长为18,∴BC+CE+BE=BC+CE+AE=BC+AC=18,∵BC=8,∴AC=10,故答案为:10.【点睛】本题考查的是线段的垂直平分线的性质、三角形的周长计算,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.14.5 2【解析】【分析】利用勾股定理求出AB,再利用直角三角形斜边中线的性质求解即可.【详解】解:∵AB=AC,AD平分∠BAC,∴AD⊥BC,BD=CD=3,∴∠ADB=90°,∴AB5,∵AE=EB,∴1522DE AB ==,故答案为52.15.2【解析】如图,作DE 垂直于BC 的延长线,垂足为E ,可知BAC DCE ∠=∠,可证()ABC CED AAS ≌,有2BC DE ==,进而可知122BCDS BC DE =⨯⨯= .【详解】解:如图,作DE 垂直于BC 的延长线,垂足为E ∵90ACB BAC ∠+∠=︒,90ACB DCE ∠+∠=︒∴BAC DCE∠=∠在ABC 和CED 中∵90BAC DCE ABC CED AC CD ∠=∠⎧⎪∠==︒⎨⎪=⎩∴()ABC CED AAS ≌∴2BC DE ==∴122BCD S BC DE =⨯⨯= 故答案为:2.16.2或8【解析】根据题意分类讨论:当E 点在线段AB 垂直平分线左侧时和当E 点在线段AB 垂直平分线右侧时,根据翻折的性质得出5BC BC '==.根据垂直平分线得出90BFC '∠=︒,142BF AB ==,5FG BC ==.再在Rt BFC ' 中,利用勾股定理可求出FC '的长,从而求出'C G 的长,即点C '到边CD 的距离.【详解】分类讨论:①当E 点在线段AB 垂直平分线左侧时,如图,由翻折可知,5BC BC '==,∵FG 为线段AB 的垂直平分线,∴90BFC '∠=︒,142BF AB ==,5FG BC ==,∴在Rt BFC ' 中,3FC '===,∴532C G FG FC ''=-=-=.②当E 点在线段AB 垂直平分线右侧时,如图,同理可知5BC BC '==,90BFC '∠=︒,5FG BC ==,142BF AB ==∴在Rt BFC ' 中,3FC '===,∴538C G FG FC ''=+=+=.综上可知,点C '到边CD 的距离为2或8.故答案为:2或8.【点睛】本题考查翻折的性质,垂直平分线的性质,勾股定理.利用分类讨论的思想是解答本题的关键.17.16【解析】【分析】将正方形ABCD 沿着CD 翻折得到正方形''A B CD ,过点M 在正方形ABCD 内部作'MM BC ⊥,使'3cm MM =,连接QM ,过'M 作'''M N A B ⊥于点N ,此时''''AP PQ QM A P PQ PM A M PQ ++=++=+最小,运用勾股定理求解即可.【详解】如图,将正方形ABCD 沿着CD 翻折得到正方形''A B CD ,过点M 在正方形ABCD 内部作'MM BC ⊥,使'3cm MM =,连接QM ,过'M 作'''M N A B ⊥于点N ,则四边形''MM NB 是矩形,四边形'PQMM 是平行四边形,∴'''M N MB =,'PM QM =,''B N MM =,''90A NM ∠=︒,此时''''AP PQ QM A P PQ PM A M PQ ++=++=+最小,∵点M 是BC 中点,∴142CM BC ==cm ,∴''12M N MB ==cm ,''''5A N A B B N =-=cm ,在''Rt A M N △中,''13A M =cm ,∴''16A M PQ +=cm ,故答案为:16.【点睛】本题考查最短路径问题,考查了正方形的性质,矩形的性质,平行四边形的性质和判定,勾股定理,轴对称性质等,解题的关键是将立体图形中的最短距离转换为平面图形的两点之间线段长度进行计算.18.见解析【解析】【分析】如果一个图形沿着某条直线对折后,直线两旁的部分能够重合,则这个图形是轴对称图形,这条直线是对称轴,根据轴对称图形的含义,按照要求完成即可.【详解】【点睛】本题考查了轴对称图形,掌握轴对称图形的含义是本题的关键.19.(1)见解析;(2)见解析【解析】【分析】(1)由平行线的性质可得∠A=∠FDE ,再由已知即可证得结论;(2)由全等三角形的性质可得∠ABC=∠E ,由平行线的判定定理即可得到结论.(1)∵AC ∥DF∴∠A=∠FDE在△ABC 和△DEF 中AC DF A FDE AB DE =⎧⎪∠=∠⎨⎪=⎩∴△ABC≌△DEF(SAS)(2)∵△ABC≌△DEF∴∠ABC=∠E∴BC∥EF【点睛】本题考查了全等三角形的判定与性质、平行线的判定与性质,掌握这两个判定与性质是关键.20.(1)见解析;(2)AC=3,AD=4 3【解析】【分析】(1)由题意可知以点B为圆心,适当长为半径画弧,交AB、BC于两点,然后再以这两个点为圆心,大于这两个点距离的一半为半径画弧,交于一点,连接点B与这个点,交AC 于点D,进而问题可求解;(2)过点D作DH⊥BC于点H,由勾股定理可得AC,然后根据角平分线的性质定理可得AD=DH,进而根据面积法可求解.(1)解:由题意可得如图所示:(2)解:过点D作DH⊥BC于点H,如(1)图:∵∠A=90°,BC=5,AB=4,∴由勾股定理得:3AC=,∵BD平分∠ABC,∴AD=DH,∴162ABCS AB AC=⋅=△,∵11622ABCADB BCD S S S AB AD BC DH =+=⋅+⋅= ,∴()162AB BC AD +⋅=,解得:43AD =;故答案为3,43.【点睛】本题主要考查勾股定理及角平分线的性质定理,熟练掌握勾股定理及角平分线的性质定理是解题的关键.21.(1)75°(2)证明见解析【解析】【分析】(1)由AB=AC 可得∠C=∠B=30°,可求得∠BAC ,再利用角的和差可求得∠DAC ;(2)由外角的性质得到∠ADC=75°,即可得到∠ADC=∠DAC ,从而有AC=DC ,即可得到结论.【详解】(1)∵AB=AC ,∠B=30°,∴∠C=30°,∴∠BAC=180°﹣30°﹣30°=120°,∵∠DAB=45°,∴∠DAC=∠BAC ﹣∠DAB=120°﹣45°=75°;(2)∵∠ADC=∠B+∠DAB=30°+45°=75°,∴∠ADC=∠DAC ,∴AC=DC ,∵AB=AC ,∴AB=CD .【点睛】考点:1.等腰三角形的性质;2.三角形的外角性质.22.2144m 【解析】【分析】本题要先把解四边形的问题转化成解三角形的问题,再用勾股定理解答.【详解】解:连接BD,A 90∠=︒ ,222BD AD AB 100∴=+=则2222BD CD 10057667626BC +=+===,因此CDB 90∠=︒,ADB CBD ABCD 1111S S S AD AB BD CD 682410144(2222=+=⋅+⋅=⨯⨯+⨯⨯= 四边形平方米).【点睛】此题考查勾股定理,解答此题的关键是解四边形的问题转化成运用勾股定理解直角三角形的问题再解答.23.(1)见解析(2)∠D =105°【解析】【分析】(1)直接根据SAS 证明三角形全等即可;(2)由△ABC ≌△BAD 可得,∠DAB=∠CBA=2∠2=50°,通过三角形内角和可得.(1)解:在△ABC 和△BAD 中=1=2=AC BD AB BA ⎧⎪∠∠⎨⎪⎩∴△ABC ≌△BAD (SAS )(2)解:由(1)△ABC ≌△BAD 得,∠DAB=∠CBA∵∠2=∠3=25°∴∠DAB=∠CBA=2∠2=50°∴∠D=180°-∠DAB-∠2=105°【点睛】本题考查了三角形全等判定的证明,及性质的运用,解题的关键是熟练掌握三角形全等的判定方法.24.∠ACD=90°,理由:见解析【解析】【分析】在Rt△ABC中,由勾股定理求出AC的长,然后在△ACD中,根据勾股定理的逆定理即可判断△ACD的形状,进而求出∠ACD的度数.【详解】∠ACD=90°,理由:∵∠ABC=90°,AB=4厘米,BC=3厘米,∴在Rt△ABC中,由勾股定理得:,在△ACD中,∵AC2+CD2=52+122=169=132=AD2,∴△ACD是直角三角形,且∠ACD=90°.【点睛】此题考查了勾股定理和勾股定理的逆定理,勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.25.(1)t=13,CP=5(2)t=7 4(3)48 5【解析】【分析】(1)先根据勾股定理得出AB的长,再根据CP把△ABC的面积分成相等的两部分,得出P为AB的中点,从而求出x的值和CP的长;(2)△ABP为等腰三角形,点P只能在AC上且PA=PB,在RtΔPBC中运用勾股定理列出方程即可.(3)作点B关于AC的对称点B′,过点B′作AB的垂线段,交AC于点P,交AB于点Q,连接AB′,则垂线段B′Q即为所求的PB+PQ的最小值.(1)解:在直角三角形ACB中,由勾股定理得AB10=,∵CP把△ABC的面积分成相等的两部分,∴P为AB的中点,CP=15 2AB=.∴运动的路径长为AC+AP=8+5=13.运动的时间为13÷1=13(秒)所以t=13;CP=5.(2)解:△ABP为等腰三角形,点P只能在AC上且PA=PB,设CP=t,则AP=BP=8﹣t,在Rt△BCP中,BC2+CP2=BP2,即62+t2=(8﹣t)2,解得,t=7 4,∴当t=74时,△ABP为等腰三角形;(3)作点B关于AC的对称点B′,过点B′作AB的垂线段,交AC于点P,交AB于点Q,连接AB′,则垂线段B′Q即为所求的PB+PQ的最小值,∵S△ABB′=12×BB′×AC=12×12×8=48,S△ABB′=12×AB×B′Q,∴B′Q=485,即PB+PQ最小值为485.【点睛】本题考查三角形综合题、勾股定理、等腰三角形的判定和性质、直角三角形的性质等知识,解题的关键是学会构建方程,把问题转化为方程解决.26.(1)见解析,①2CE =,②2B C B P =,见解析;(2)10BP =或30【解析】【分析】(1)①以点A 为圆心,AB 为半径交CD 于点E ,利用勾股定理求出DE 的长即可;②根据平行线的性质和翻折的性质可证EP=CP ,BP=PE ,从而BP=PC ;(2)由△PEC 是直角三角形,当∠EPC=90°时,则四边形ABPE 是正方形,得PB=AB=10;当∠ECP=90°时,设BP=x ,则PC=x-6,在Rt △ECP 中,利用勾股定理列方程即可求解,当∠PEC=90°时,点P 在线段BC 上,不符合题意,舍去.(1)解:(1)①如图:以点A 为圆心,AB 为半径交CD 于点E ,∵AE=AB=10,AD=6,∠D=90°,∴22AE AD -22106-,∴CE=DC-DE=10-8=2;故答案为:2;②BC =2BP ,理由如下:∵将△ABP 沿直线AP 翻折至△AEP 的位置,∴∠APB =∠APE ,PE =BP ,∵CE ∥AP ,∴∠CEP =∠APE ,∠ECP =∠APB ,∴∠PEC =∠ECP ,∴EP=CP,∴BP=BC,∴BC=2BP;(2)(2)∵△PEC是直角三角形,当∠EPC=90°时,∵∠EPC=∠AEP=∠B=90°,且EP=BP,∴四边形ABPE是正方形,∴PB=AB=10;当∠ECP=90°时,由翻折知AE=AB =10,根据勾股定理得DE=8,∴EC=18,设BP=x,则PC=x﹣6,在Rt△ECP中,由勾股定理得:182+(x﹣6)2=x2,解得x=30,∴PB=30;当∠PEC=90°时,点P在线段BC上,不符合题意,舍去,综上:BP=10或30.。
物理化学答案——第五章-相平衡[1]
![物理化学答案——第五章-相平衡[1]](https://img.taocdn.com/s3/m/0243f86d58fafab069dc0265.png)
第五章 相平衡一、基本公式和内容提要基本公式1. 克劳修斯—克拉贝龙方程m mH dp dT T V ∆=∆相相(克拉贝龙方程,适用于任何纯物质的两相平衡) 2ln m H d p dT RT∆=相(克劳修斯—克拉贝龙方程,适用与其中一相为气相,且服从理想气体状态方程的两相间平衡)2.特鲁顿(Trouton)规则1188vap mvap m bH S J mol k T --∆=∆≈⋅⋅(T b 为该液体的正常沸点)3.相律 f+Φ=C+n C=S-R-R ′f+Φ=C+2 (最普遍形式)f* +Φ=C+1 (若温度和压力有一个固定,f * 称为“条件自由度”)*4. Ehrenfest 方程2112()p p C C dp dT TV αα-=-(C p ,α为各相的恒压热容,膨胀系数) 基本概念1. 相:体系中物理性质和化学性质完全均匀的部分,用Φ表示。
相的数目叫相数。
2. 独立组分数C =S -R -R ′,S 为物种数,R 为独立化学反应计量式数目,R ′ 为同一相中独立的浓度限制条件数。
3. 自由度:指相平衡体系中相数保持不变时,所具有独立可变的强度变量数,用字母 f 表示。
单组分体系相图相图是用几何图形来描述多相平衡系统宏观状态与 T 、p 、X B (组成)的关系。
单组分体系,因 C =1 ,故相律表达式为 f =3-Φ。
显然 f 最小为零,Φ 最多应为 3 ,因相数最少为 1 ,故自由度数最多为 2 。
在单组分相图中,(如图5-1,水的相图)有单相的面、两相平衡线和三相平衡的点,自由度分别为 f =2、f =1、f =0。
两相平衡线的斜率可由克拉贝龙方程求得。
图5-1二组分体系相图根据相律表达式f=C-Φ+2=4-Φ,可知f最小为零,则Φ最多为 4 ,而相数最少为 1 ,故自由度最多为 3 。
为能在平面上显示二组分系统的状态,往往固定温度或压力,绘制压力-组成(p-x、y)图或温度-组成(T-x、y)图,故此时相律表达式为f*=3-Φ,自然f*最小为 0 ,Φ最多为 3,所以在二组分平面图上最多出现三相共存。
锡青铜化学成分
8
590
ZCuSn5Pb5Zn5 ZCuSn10Pb1 ZCuSn10Pb5 ZCuSn10Zn2
J S、J Li、La
S J Li La S J S J Li、La
215(21.9) 200(20.4) 250(25.5) 220(22.4) 310(31.6) 330(33.6) 360(36.7) 195(19.9) 245(25.0) 240(24.5) 245(25.0) 270(27.5)
S
630(64.3)
250(25.5)
16
1570
S
490(50.0)
180(18.4)
13
980
ZCuAl10Fe3
J Li、La
540(55.1) 540(55.1)
200(20.4) 200(20.4)
15
1080
15
1080
S ZCuAl10Fe3Mn2
J
490(50.0) 540(55.1)
有较好的铸造性能和切削加工性能,在大气 (8m/s)下工作的耐磨零件,如连杆、衬套、
和淡水中有良好的耐蚀性
轴瓦、齿轮、蜗轮等
ZCuSn10Pb5
结构材料,耐蚀、耐酸的配件以及破碎机衬套、 耐腐蚀,特别对稀硫酸、盐酸和脂肪酸
轴瓦
ZCuSn10Zn2
在中等及较高负荷和小滑动速度下工作的重要 耐蚀性、耐磨性和切削加工性能好,铸造性
0.05 0.10 0.01 0.01
0.1 0.5 0.3
0.75
铸造铝青铜的力学性能(GB/T1176-1987)
合金牌号
铸造方法 σb/MPa(kgf/mm2)
力学性能,不低于 σ0.2/MPa(kgf/mm2) δ5(%) 硬度 HBW
2022-2023学年八年级数学上学期期中考前必刷卷含答案解析(人教版)(一)
第Ⅰ卷
一、选择题:本大题共 14 个小题,每题 2 分,共 28 分,在每个小题的四个选项中只有一项是符合题目要求 的.
1.(2021·重庆市璧山中学校八年级期中)在一些美术字中,有的汉字是轴对称图形.下列 4 个汉字中,可以 看作“沿某一条直线折叠后,直线两旁的部分能够互相重合”的是( )
A.①②
B.①②③
C.①②④
第Ⅱ卷
D.①②③④
二、填空题:本题共 4 个小题;每个小题 3 分,共 12 分,把正确答案填在横线上.
15.(2020·福建省福州延安中学八年级期中)已知点 Р(a,3)和点 Q(4,b)关于 x 轴对称,则 a b 2021 ________.
A. 35
B. 40
高,则 CD 的长( )
A.只有①②③ B.只有①②④ C.只有①③④ D.①②③④ 13.(2021·重庆市璧山中学校八年级期中)如图,过边长为1的等边三角形 ABC 的边 AB 上一点 P ,作
PE AC 于点 E , Q 为 BC 延长线上一点,当 AP CQ 时, PQ 交 AC 于点 D ,则 DE 的长为( )
D.不能确定
14.(2022·陕西·西安爱知初级中学七年级期末)如图,在 VABC 中, BAC 90, AB 2AC ,点 D 是线段
AB 的中点,将一块锐角为 45 的直角三角板按如图 VADE 放置,使直角三角板斜边的两个端点分别与 A 、
D 重合,连接 BE 、 CE , CE 与 AB 交于点 F. 下列判断正确的有( )
△A1B1C1 ,第二次将等边 △A1B1C1 的三边向外延长一倍,得到第二个新的 △A2B2C2 ,依此规律继续延长下去, 若△ABC 的面积 S0 1,则第 2022 个新的三角形的面积 S2022 为________
jpma色卡对照表

2
FN-55
N5.5
30
F25—50B
5Y5/1
58
F69-40D
10B4/2
2
FN—50
N5
30
F25-30B
5Y3/1
58删
F69—20D
10B2/2
3
FN-45
N4。5
31
F25—92B
5Y9。2/1
59删
F69-80B
10B8/1
3
FN-40
N4
31
F25-90B
5Y9/1
59
F69—80H
2。5BG6/10
新色
25—90H
5Y9/4
新色
69—60T
10B6/10
新色
69—60T
10B6/10
新色
27-85V
7。5Y8.5/12
新色
69-70P
10B7/8
新色
69—70P
10B7/8
新色
27—90P
7。5Y9/8
新色
82—70H
2.5P7/4
新色
82—70H
2.5P7/4
新色
42-50T
60
F75—20B
5PB2/1
5
F05-90A
5R9/0。5
33
F25-90D
5Y9/2
61
F75-90A
5PB9/0。5
5
F05—85A
5R8.5/0。5
33
F25—85F
5Y8.5/3
61
F75-85A
5PB8。5/0.5
5
F05—80A
2022-2023学年四川省成都市武侯区西川中学八年级(上)期末数学试卷

2022-2023学年四川省成都市武侯区西川中学八年级(上)期末数学试卷一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项1.(4分)下列各数中是无理数的是()A.3.5B.C.D.2.(4分)下列计算正确的是()A.B.C.D.3.(4分)下列句子是命题的是()A.作线段AB=aB.a与b谁大C.你喜欢数学吗D.任何一个三角形一定有直角4.(4分)点P(﹣3,5)关于y轴的对称点的坐标是()A.(﹣3,﹣5)B.(3,﹣5)C.(5,﹣3)D.(3,5)5.(4分)已知A(﹣2,a),B(1,b)是一次函数y=﹣2x+3的图象上的两个点,则a与b的大小关系是()A.a>b B.a<b C.a=b D.不能确定6.(4分)对于一次函数y=3x+2,①图象必经过点(﹣1,﹣1);②图象经过第一、二、四象限;③当x >1时,y<0;④y的值随着x值的增大而增大,以上结论正确的个数是()A.0个B.1个C.2个D.3个7.(4分)如果方程组的解是方程2x﹣3y+a=5的解,那么a的值是()A.20B.﹣15C.﹣10D.58.(4分)我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是()A.B.C.D.二、填空题(本大题共4个小题,每小题4分:共16分,答案写在答题卡上)9.(4分)函数y=的自变量x的取值范围是.10.(4分)如图,将长方形ABCD沿对角线AC折叠,得到如图所示的图形,点B的对应点是点B′,B′C与AD交于点E.若AB=2,BC=4,则AE的长是.11.(4分)如图,长方形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是﹣1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则这个点E表示的实数是.12.(4分)如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解是.三、解答题(本大题共6个小题,共52分,解答过程写在答题卡上)13.(12分)计算:(1);(2).14.(6分)解方程组:.15.(8分)如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).(1)把△ABC向上平移3个单位后得到△A1B1C1,请画出△A1B1C1,并写出点B1的坐标;(2)若△ABC与△A2B2C2关于直线成轴对称,且点A的对称点为A2(2,1),请画出直线l及△A2B2C2,并求出线段AA2的长度.16.(8分)我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示:(1)根据图示填写下表:平均数(分)中位数(分)众数(分)初中部85高中部85(2)结合两队成绩的平均数中中位数,分析哪个队的决赛成绩较好;(3)计算两队决赛成绩的方差,并判断哪一个代表队选手的成绩较为稳定.17.(8分)已知:如图所示,AB∥CD,∠A=∠F,∠D=∠E.求证:AF⊥DE.18.(10分)如图,在长方形ABCD中,AB=6,BC=8,点O在对角线AC上,且OA=OC,点P是边CD上的一个动点,连接OP,过点O作OQ⊥OP,交BC于点Q.(1)求OB的长度;(2)设DP=y,CQ=x,4求y与x的函数表达式(不要求写自变量的取值范围);(3)当△OCQ是等腰三角形时,求CP的长度.一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)19.(4分)已知方程组和的解相同,则2m﹣n=.20.(4分)定义一种新的运算“※”,规定:x※y=mx+ny2,其中m、n为常数,已知2※3=﹣1,3※2=8,则m※n=.21.(4分)已知,则值为.22.(4分)在直角坐标系中,如图所示,把∠BAO放在直角坐标系中,使射线AO与x轴重合,已知∠BAO =30°,OA=OB=1,过点B作BA1⊥OB交x轴于A1,过A1作B1A1⊥BA1交直线AB于点B1,过点B1作B1A2⊥B1A1交x轴于点A2,再过A2依次作垂线…,则△A1B1A2的面积为,△A n B n A n+1的面积为.23.(4分)如图,∠MON=90°,已知△ABC中,AC=BC=25,AB=14,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为.二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)24.(8分)甜蜜公司要把240吨白砂糖运往江浙的A,B两地,先用大小两种货车共20辆,恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨每辆和10吨每辆,运往A地的费用为:大车630元每辆,小车420元每辆,运往B地的费用为:大车750元每辆,小车550元每辆.(1)求这两种货车各多少辆?(2)如果安排10辆货车前往A地,其余货车前往B地,且运往A地的白砂糖不少于115吨.请你设计出使总运费最少的方案并求出最少的总运费?25.(10分)已知∠ACB=90°,AC=2,CB=4.点P为线段CB上一动点,连接AP,△APC与△APC′关于直线AP对称,其中点C的对称点为点C′.直线m过点A且平行于CB(1)如图①:连接AB,当点C落在线段AB上时,求BC′的长;(2)如图②:当PC=BC时,延长PC′交直线m于点D,求△ADC′面积;(3)在(2)的条件下,连接BC′,直接写出线段BC′的长.26.(12分)如图,已知直线l1:y=﹣x+8与直线l2:y=x交于点M,直线l1与坐标轴分别交于A,C两点.(1)分别求点A和点M的坐标;(2)在直线y=x上找一点D,使△ADM的面积等于△AOM的面积的2倍,求出点D的坐标;(3)若点P是线段OM上的一动点(不与端点重合),过点P作PB∥x轴交CM于点B.①在x轴上是否存在一点H,使得△PBH为等腰直角三角形,若存在,求出点P的坐标;若不存在,请说明理由;②设点P的纵坐标为n,以点P为直角顶点作等腰直角△PBF(点F在直线PB下方),设△PBF与△MOC 重叠部分的面积为S,求S与n之间的函数关系式,并写出相应n的取值范围.。
Pb同位素

一、铅稳定同位素组成
• 铅有4种稳定同位素: • 204Pb、206Pb、207Pb、208Pb 204Pb尚未被发现有放射性母体,普遍被认为代 表原始铅。 • 206Pb、207Pb、208Pb都是由放射性母体产生的: • 238U206Pb+84He+6-+Q 235U207Pb+74He+4-+Q 232Th208Pb+64He+4-+Q
•
(4) 在增长曲线图中,异常铅的数据点 或是沿某一原始等时线分布,但落在不 同μ值的演化线上;或是落在不同的原始 等时线上,但μ值差别不大,数据点都位 于增长曲线的弦上,不超出增长曲线;或 落在具有不同μ值的增长曲线和不同年龄 的原始等时线上。
•
(5) 在异常铅的源区中,通过计算所获 得的U/Pb或Th/Pb变化明显。 • (6) 在很多具有异常铅的矿床中,铅同 位素组成的变化具有一定的规律性。如 在横山岭铅锌矿床中,206Pb/204Pb或 208Pb/204Pb随矿体埋藏深度增加而有升高 的趋势 (据陈好寿,1979)
• m是等时线的斜率。当t=0时,称为地球 年龄线,等时线通过地球原始铅同位素组 成点。
5T
5t
• 前述方程式是一个超越方程,不能用代 数方法来求解,可用作图或制表的办法 来求解,同样可以得到很好的精度。 • 求解模式年龄的步骤: • 用斜率公式,按一定的时间间隔代入到 斜率公式中的t,计算出相应的斜率值, 制成表格。 • 用样品的比值求出等时线的斜率,在用 插值法求出年龄值——模式年龄
下表是单阶段铅等时线斜率与 模式年龄对照表:
计算出模式年龄后,将他代入下式,计算、W和k值:
Pb a0 204 8Pb 8t t0 e e
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Cambridge Young Learners English Test
Pre-starters B Unit 5-8
Class:___________Name:____________ Score: ____________ Listening Part
一.Listen and match. (2’*5=10’)
Bobby Kim Lucy Tim Bill
二.Listen and order. (2’*5=10’)
( ) ( ) ( )
( ) ( )
三.Listen and write the letters.(2’*6=12’)
1 _________________
2 _________________
3 _________________
4 _________________
5 _________________
6 _________________
Writing Part
一.Look, read and put ‘√’or ‘×’. (2’*5=10’)
1. You can brush teeth here. ( )
2. This is a lemon. ( )
3. It’s a pet. ( )
4. They are sausages. ( )
5. I like to eat a pizza with some carrots. ( )
二.Look and match.(2’*6=12’)
mango carrot peach sheep tomato mouse ( s ) ( es ) (特殊)
三. Fill in the blanks. ( (1’*21=21’)
1. p___ ___ ___
2. b ___ ___ n
3. o ___ i ___ ___
4. s l ___ ___ p
5. l ___ m ___ ___
6. p ___ ___ c h
7. p ___ t ___ t ___
8. t ___ ___ t l ___
四Look, read and find the different one: (2’*5=10’)
( ) 1 A cat B snake C mouse D pea
( ) 2 A kitchen B zoo C bedroom D bathroom
( ) 3 A pineapple B orange C carrot D banana
( ) 4 A ball B ice cream C pizza D sausage
( ) 5 A eat B brush C big D watch
五Choose the correct answer: (3’*5=15’)
( )1 What animal do you like?
A I like apples.
B I like parrots
C I like peas. ( )2 What fruit do you like?
A I like grapes.
B I like orange.
C I like tomatoes. ( )3 Do you like mice?
A Yes, I don’t.
B Yes, I do.
C No, I do. ( )4 What’s in the pizza?
A Some tomatos.
B Some sausages.
C Some bean. ( )5 What’s Bobby doing?
A He is watch TV.
B He is sleeping.
C He sleeping.
听力材料:
一Listen and match
1 Hello, Bobby! What are you doing? I’m taking a bath.
2 Kim, do you like potatoes? No, I like tomatoes.
3 Lucy, what’s that? That’s an animal, a spider.
4 What’s in the pizza, Tim? Some beans.
5 Is that a peach, Bill? Yes, it is.
二Listen and order:
Today is a sunny day. It’s seven o’clock. Bobby is cooking meals. It’s eight o’clock, and he is having breakfast. It’s four o’clock in the afternoon, he is watching TV. It’s eight o’clock in the evening, and he is taking a bath. It’s ten o’clock, and he’s going to sleep.
三Listen and write the letters:
1 UXYV
2 BDGH
3 QSRJ
4 EATW
5 IKMO
6 NPCF。
