2011年高考数学天津卷(理科)

合集下载

2011年天津高考数学试题及答案(理科)

2011年高考理科数学试题及答案（天津卷）本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

答卷前，考生务必将自己的姓名、准考号填写在答题卡上，并在规定位置粘贴考试用条形码答卷时，考生务必将答案涂写在答题卡上，答在试卷上的无效.考试结束后，将本试卷和答题卡一并交回.第Ⅰ卷注意事项：1．每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.2．本卷共8小题，每小题5分，共40分.参考公式：如果事件A ，B 互斥，那么如果事件A ，B 相互独立，那么()()()P A B P A P B =+U ()()().P AB P A P B =棱柱的体积公式.V Sh = 圆锥的体积公式1.3V Sh =其中S 表示棱柱的底面面积其中S 表示圆锥的底面面积h 表示棱柱的高 h 表示圆锥的高一、选择题：在每小题给出的四个选项中只有一项是符合题目要求的．1．i 是虚数单位，复数131ii --=A ．2i +B ．2i -C ．12i -+D ．12i --2．设,,x y R ∈则“2x ≥且2y ≥”是“224x y +≥”的 A ．充分而不必要条件 B ．必要而不充分条件C ．充分必要条件D ．即不充分也不必要条件3．阅读右边的程序框图，运行相应的程序，则输出i 的值为A ．3B ．4C ．5D ．64．已知{}n a 为等差数列，其公差为-2，且7a 是3a 与9a 的等比中项，n S 为 {}n a 的前n 项和，*n N ∈，则10S 的值为A ．-110B ．-90C ．90D ．1105．在6x x ⎛⎫- ⎪ ⎪⎝⎭的二项展开式中，2x 的系数为 A ．154- B ．154 C ．38- D ．386．如图，在△ABC 中，D 是边AC 上的点，且,23,2AB CD AB BD BC BD ===，则sin C 的值为A ．33B ．36C ．6D ．67．已知324log 0.3log 3.4log 3.615,5,,5a b c ⎛⎫=== ⎪⎝⎭则A ．a b c >>B ．b a c >>C ．a c b >>D ．c a b >>8．对实数a 和b ，定义运算“⊗”：,1,, 1.a a b a b b a b -≤⎧⊗=⎨->⎩ 设函数()()22()2,.f x x x x x R =-⊗-∈若函数()y f x c =-的图像与x 轴恰有两个公共点，则实数c 的取值范围是A ．(]3,21,2⎛⎫-∞-⋃- ⎪⎝⎭ B ．(]3,21,4⎛⎫-∞-⋃-- ⎪⎝⎭C ．111,,44⎛⎫⎛⎫-⋃+∞ ⎪ ⎪⎝⎭⎝⎭D ．311,,44⎛⎫⎡⎫--⋃+∞ ⎪⎪⎢⎝⎭⎣⎭。

2011年普通高等学校招生全国统一考试高考数学教师精校版含详解天津理

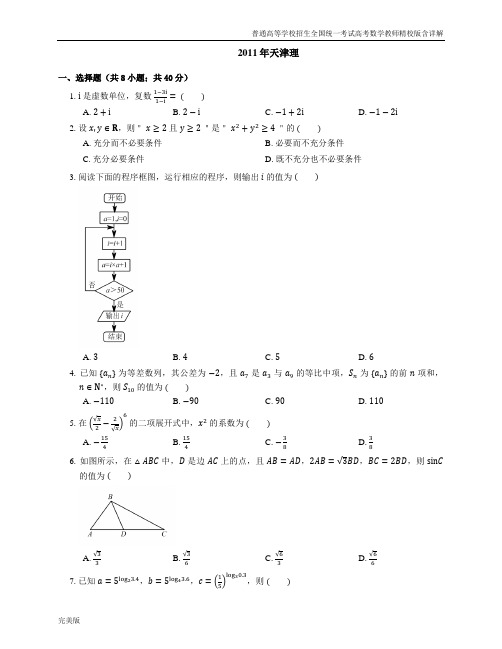
2011年天津理一、选择题（共8小题；共40分）1. i是虚数单位，复数1−3i1−i= A. 2+iB. 2−iC. −1+2iD. −1−2i2. 设x,y∈R，则＂x≥2且y≥2＂是＂x2+y2≥4＂的 A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件3. 阅读下面的程序框图，运行相应的程序，则输出i的值为 A. 3B. 4C. 5D. 64. 已知a n为等差数列，其公差为−2，且a7是a3与a9的等比中项，S n为a n的前n项和，n∈N∗，则S10的值为 A. −110B. −90C. 90D. 1105. 在x2x 6的二项展开式中，x2的系数为 A. −154B. 154C. −38D. 386. 如图所示，在△ABC中，D是边AC上的点，且AB=AD，2AB=3BD，BC=2BD，则sin C的值为 A. 33B. 36C. 63D. 667. 已知a=5log23.4，b=5log43.6，c=15log30.3，则 A. a>b>cB. b>a>cC. a>c>bD. c>a>b8. 对实数a与b，定义运算“ ⊗”：a⊗b=a,a−b≤1,b,a−b>1.设函数f x=x2−2⊗x−x2,x∈R．若函数y=f x−c的图象与x轴恰有两个公共点，则实数c的取值范围是 A. −∞,−2∪ −1,32B. −∞,−2∪ −1,−34C. −∞,14∪14,+∞ D. −1,−34∪14,+∞二、填空题（共6小题；共30分）9. 一支田径队有男运动员48人，女运动员36人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，则抽取男运动员的人数为．10. 一个几何体的三视图如图所示（单位：m），则这个几何体的体积为m3．11. 已知抛物线C的参数方程为x=8t2y=8t（t为参数），若斜率为1的直线经过抛物线C的焦点，且与圆x−42+y2=r2r>0相切，则r=．12. 如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=2，AF:FB:BE=4:2:1．若CE与圆相切，则CE的长为．13. 已知集合A=x∈R x+3+x−4≤9，B= x∈R x=4t+1t−6,t∈0,+∞，则集合A∩B=．14. 已知直角梯形ABCD中，AD∥BC，∠ADC=90∘，AD=2，BC=1，P是腰DC上的动点，则PA+3PB的最小值为．三、解答题（共6小题；共78分）15. 已知函数f x=tan2x+π4．（1）求f x的定义域与最小正周期；（2）设α∈0,π4，若fα2=2cos2α，求α的大小．16. 学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）（1）求在一次游戏中，①摸出3个白球的概率；②获奖的概率；（2）求在两次中获奖次数X的分布列及数学期望E X．17. 如图，在三棱柱ABC−A1B1C1中，H是正方形AA1B1B的中心，AA1=22，C1H⊥平面AA1B1B，且C1H=5．（1）求异面直线AC与A1B1所成角的余弦值；（2）求二面角A−A1C1−B1的正弦值；（3）设N为棱B1C1的中点，点M在平面AA1B1B内，且MN⊥平面A1B1C1，求线段BM的长．18. 在平面直角坐标系xOy中，点P a,b a>b>0为动点，F1，F2分别为椭圆x2a +y2b=1的左右焦点．已知△F1PF2为等腰三角形．（1）求椭圆的离心率e；（2）设直线PF2与椭圆相交于A，B两点，M是直线PF2上的点，满足AM⋅BM=−2，求点M的轨迹方程．19. 已知a>0，函数f x=ln x−ax2，x>0．（f x的图象连续不断）（1）求f x的单调区间；（2）当a=18时，证明：存在x0∈2,+∞，使f x0=f32；（3）若存在均属于区间1,3的α，β，且β−α≥1，使fα=fβ，证明：ln3−ln25≤a≤ln23．20. 已知数列a n与b n满足：b n a n+a n+1+b n+1a n+2=0，b n=3+−1n2，n∈N∗，且a1=2，a2=4．（1）求a3，a4，a5的值；（2）设c n=a2n−1+a2n+1，n∈N∗，证明：c n是等比数列；（3）设S k=a2+a4+⋯+a2k，k∈N∗，证明：S ka k <76n∈N∗4nk=1．答案第一部分1. B2. A 【解析】当x≥2且y≥2时，一定有x2+y2≥4；反过来，当x2+y2≥4时，不一定有x≥2且y≥2，例如x=−4，y=0也可以．3. B 【解析】i=1时，a=1×1+1=2；i=2时，a=2×2+1=5；i=3时，a=3×5+1=16；i=4时，a=4×16+1=65>50．所以输出i=4．4. D 【解析】由a72=a3⋅a9，d=−2，得a1−122=a1−4a1−16,解得a1=20，从而S10=10×20+10×92−2=110.5. C【解析】由二项式展开式得：T k+1=C6k x26−kxk=−1k22k−6C6k x3−k，令k=1，则x2的系数为−1⋅22−6C61=−38．6. D 【解析】设AB=a，所以AD=a，BD=3，BC=2BD=3，故cos A=AB2+AD2−BD22AB⋅AD=2a2−43a22a =13，所以sin A=1−cos2A=223．由正弦定理知sin C=ABBC ⋅sin A=34×223=66．7. C 【解析】因为a=5log23.4，b=5log43.6，c=5log310，所以只需要比较它们的指数即可．由对数函数的性质知log43.6=log2 3.6<1<log3103<log33.4<log23.4，从而有a>c>b．8. B 【解析】f x=x2−2,x2−2−x−x2≤1 x−x2,x2−2−x−x2>1=x2−2,−1≤x≤3x−x2,x<−1,或x>3则f x的图象如图：∵y=f x−c的图象与x轴恰有两个公共点，∴y=f x与y=c的图象恰有两个公共点，由图象知c≤−2，或−1<c<−34．第二部分9. 12【解析】设抽取男运动员人数为n，则n48=2148+36，解之得n=12．10. 6+π【解析】如图：该几何体为一个棱柱与一个圆锥的组合体．所以V=3×2×1+1π×12×3=6+π.11. 212. 72【解析】设AF=4k，BF=2k，BE=k，由DF⋅FC=AF⋅BF，得2=8k2，即k=12，从而AF=2，BF=1，BE=12，AE=72，由切割线定理得CE2=BE⋅EA=12×72=74，故CE=72．13. x∈R−2≤x≤5【解析】因为A=x∈R−4≤x≤5，B= x∈R x≥24t×1t−6,t∈0,+∞=x∈R x≥−2，所以A∩B=x∈R−4≤x≤5∩x∈R x≥−2=x∈R−2≤x≤5．14. 5【解析】建立如图所示的坐标系，设DC= ，则A2,0，B1, ．设P0,y0≤y≤ ，则PA=2,−y，PB=1, −y，所以PA+3PB=25+3 −4y2≥第三部分15. （1）由2x +π4≠π2+kπ，k ∈Z ，得x ≠π8+kπ2,k ∈Z ,所以f x 的定义域为 x ∈R x ≠π8+kπ2,k ∈Z ，f x 的最小正周期为π2．（2）由f α2 =2cos2α，得tan α+π4=2cos2α，sin α+π4cos α+4=2 cos 2α−sin 2α ,整理得sin α+cos αcos α−sin α=2 cos α+sin α cos α−sin α . 因为α∈ 0,π4 ，所以sin α+cos α≠0.因此 cos α−sin α 2=12.即sin2α=12.由α∈ 0,π4 ，得2α∈ 0,π2 ，所以2α=π6，即α=π12.16. （1）①设“在1次游戏中摸出i 个白球”为事件A i i =0,1,2,3 ，则P A 3 =C 3252⋅C 2132=1.②设“在1次游戏中获奖”为事件B ，则B =A 2∪A 3，又P A 2 =C 32C 52⋅C 22C 32+C 31C 21C 52⋅C 21C 32=12,且A 2，A 3互斥，所以P B =P A 2 +P A 3 =1+1=7.（2）由题意可知X 的所有可能取值为0，1，2．P X =0 = 1−7 2=9,P X =1 =C 21⋅7⋅ 1−7 =21,P X =2 = 7 2=49.所以X 的分布列是X 012P92149E X =0×9+1×21+2×49=7.17. （1）方法一：由于AC ∥A 1C 1，故∠C 1A 1B 1是异面直线AC 与A 1B 1所成的角．因为C 1H ⊥平面AA 1B 1B ，又H 为正方形AA 1B 1B 的中心，AA 1=2 2，C 1H = 5．可得A 1C 1=B 1C 1=3.因此cos ∠C 1A 1B 1=A 1C 12+A 1B 12−B 1C 122A 1C 1⋅A 1B 1= 23.所以异面直线AC 与A 1B 1所成角的余弦值为 23．方法二：如图所示，建立空间直角坐标系，点B 为坐标原点．依题意得A 2 2,0,0 ,B 0,0,0 ，C 2,− 2, 5 ，A 1 2 2,2 2,0 ，B 1 0,2 2,0 ，C 1 2, 2, 5 ．易得AC= − 2,− 2, 5 ,A 1B 1= −2 2,0,0 ,于是cos AC ,A 1B 1 =AC ⋅A 1B 1AC ⋅ A 1B 1 =3×2 2= 2, 所以异面直线AC 与A 1B 1所成角的余弦值为 23．（2）方法一：连接AC 1，易知AC1=B1C1，又由于AA1=B1A1，A1C1=A1C1，所以△AC1A1≌△B1C1A1，过点A作AR⊥A1C1于点R，连接B1R，于是B1R⊥A1C1，故∠ARB1为二面角A—A1C1—B1的平面角．在Rt△A1RB1中，B1R=A1B1⋅sin∠RA1B1=22⋅1−22=214.连接AB1，在△ARB1中，AB1=4，AR=B1R，cos∠ARB1=AR2+B1R2−AB12 2AR⋅B1R=−2 ,从而sin∠ARB1=35.所以二面角A—A1C1—B1的正弦值为357．方法二：易知AA1=0,22,0,A1C1= − 2,− 2,5.设平面AA1C1的法向量m=x1,y1,z1，则m⋅A1C1=0,m⋅AA1=0,即− 2x1−2y1+5z1=0,22y1=0.不妨令x1=5，可得m=5,0,2,n⋅A1C1=0,n⋅A1B1=0.即− 2x2−2y2+5z2=0,−22x2=0.不妨令y2=5，可得n=0,5,2.于是cos m,n=m⋅nm⋅n=27⋅7=27,从而sin m,n=35.所以二面角A—A1C1—B的正弦值为357．（3）方法一：因为MN⊥平面A1B1C1，所以MN⊥A1B1．取HB1中点D，连接ND，由于N是棱B1C1中点，所以ND∥C1H且ND=12C1H=52.又C1H⊥平面AA1B1B，所以ND⊥平面AA1B1B，故ND⊥A1B1．又MN∩ND=N，所以A1B1⊥平面MND，连接MD并延长交A1B1于点E，则由DE AA1=B1EB1A1=B1DB1A=14,得DE=B1E=2 ,延长EM交AB于点F，可得BF=B1E=2 .连接NE，在Rt△ENM中，所以DM=ND2=52.可得FM=2 4 .连接BM，在Rt△BFM中，BM= FM2+BF2=104.方法二：由N为棱B1C1的中点，得N22,322,52．设M a,b,0，则MN=22−a,322−b,52.由MN⊥平面A1B1C1，得MN⋅A1B1=0,MN⋅A1C1=0.即22−a ⋅ −22=0,2 2−a ⋅ − 2+322−b ⋅ − 2+52⋅5=0.解得a=2 ,b=2 4 .故M22,24,0，因此BM=22,24,0,所以线段BM的长为BM=10 4 .18. （1）设F1−c,0，F2c,0c>0，由题意，可得PF2=F1F2,即a−c2+b2=2c.整理得2c2+c−1=0,即c a =−1舍,或 ca=12.所以e=1 2 .（2）由（1）知a=2c,b=3c,可得椭圆方程为3x2+4y2=12c2,直线PF2方程为y=3x−c. A,B两点的坐标满足方程组3x2+4y2=12c2,y=3x−c.消去y并整理，得5x2−8cx=0.解得x1=0,x2=8 5 c.得方程组的解x1=0,y1=− 3c, x2=8c,y2=335c.不妨设A85c,335c ，B 0,−3c ，设点M的坐标为x,y，AM= x−85c,y−335c ,BM= x,y+3c ,由y=3x−c，得c=x−3 y.于是AM=83y−3x,8y−33x ,BM= x,3x .由AM⋅BM=−2，即83y−3x ⋅x+8y−33x ⋅3x=−2,化简得18x2−163xy−15=0.将y=2163xc=x−33y，得c=10x2+5>0.所以x>0．因此，点M的轨迹方程是18x2−163xy−15=0x>0.19. （1）fʹx=1x−2ax=1−2ax2x,x∈0,+∞,令fʹx=0，解得x=2a 2a.当x变化时，fʹx,f x的变化情况如下表：x0,2a2a2a2a2a2a,+∞fʹx+0−f x↗极大值↘所以，f x的单调递增区间是0,2a2a ，f x的单调递减区间是2a2a,+∞ ．（2）当a=18时，f x=ln x−18x2.由（1）知f x在0,2内单调递增，在2,+∞内单调递减．令g x=f x−f32．由于f x在0,2内单调递增，故f2>f 3 2 ,即g2>0.取xʹ=32e>2，则g xʹ=41−9e232<0.所以存在x0∈2,xʹ，使g x0=0，即存在x0∈2,+∞，使f x0=f32．（3）由fα=fβ及（1）的结论知α<2a2a<β,从而f x在α,β上的最小值为fα．又由β−α≥1，α,β∈1,3，知1≤α≤2≤β≤3.故f2≥fα≥f1,f2≥fβ≥f3.即ln2−4a≥−a,ln2−4a≥ln3−9a.从而ln3−ln2≤a≤ln2.20. （1）由b n=3+−1n2,n∈N∗，可得b n=1, n为奇数, 2, n为偶数.又b n a n+a n+1+b n+1a n+2=0，当n=1时，a1+a2+2a3=0,由a1=2，a2=4，可得a3=−3;当n=2时，2a2+a3+a4=0,可得a4=−5;当n=3时，a3+a4+2a5=0,可得a5=4.（2）对任意n∈N∗，a2n−1+a2n+2a2n+1=0, ⋯⋯①2a2n+a2n+1+a2n+2=0, ⋯⋯②a2n+1+a2n+2+2a2n+3=0, ⋯⋯③②−③，得a2n=a2n+3. ⋯⋯④将④代入①，可得a2n+1+a2n+3=−a2n−1+a2n+1,即c n+1=−c n n∈N∗.又c1=a1+a3=−1，故c n≠0，因此c n+1c n=−1,所以c n是等比数列．（3）由（2）可得a 2k−1+a 2k +1= −1 k ,于是，对任意k ∈N ∗且k ≥2，有a 1+a 3=−1,− a 3+a 5 =−1,a 5+a 7=−1,⋮ −1 k a 2k−3+a 2k−1 =−1.将以上各式相加，得a 1+ −1 k a 2k−1=− k −1 ,即a 2k−1= −1 k +1 k +1 ,此式当k =1时也成立．由④式得a 2k = −1 k +1 k +3 .从而S 2k= a 2+a 4 + a 6+a 8 +⋯+ a 4k−2+a 4k =−k ,S 2k−1=S 2k −a 4k =k +3.所以，对任意n ∈N ∗，n ≥2，S ka k4nk =1= S 4m−3a 4m−3+S 4m−2a 4m−2+S 4m−1a 4m−1+S 4ma 4mnm =1= 2m +2−2m −1−2m +3+2mnm =1= 22m 2m +1 +32m +2 2m +3n m =1=22×3+ 52m 2m +1 +3 2n +2 2n +3 nm =2<1+ 5 +3 nm =2=1+5⋅ 1−1 + 1−1 +⋯+ 1−1 +3 =13+56−52⋅12n +1+3 2n +2 2n +3 <7.对于n =1，不等式显然成立．。

2011年普通高等学校招生全国统一考试(天津卷)数学试题 (理科)(解析版)

【答案】B
【解析】
f
(x)
x 2 2, x x 2 ,
x2 x2
2 2
x x2 x x2
1 1
x
2
2,1
x
3 2
x
x2, x
1, 或x
3 2
则 f x 的图象如图
y
o x
-1
-2
∵ y f (x) c 的图象与 x 轴恰有两个公共点，
第 3页（共 13页）
∴ y f (x) 与 y c 的图象恰有两个公共点，由图象知 c 2 ，或 1 c 3 . 4
【答案】A.
1 3i
【解析】
1i
(1 3i)(1 i) (1 i)(1 i)
4 2i 2
2
i
.
2．设 x, y R, 则“ x 2 且 y 2 ”是“ x2 y2 4 ”的( )
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件
D．即不充分也不必要条件
【答案】A
【解析】当 x 2且y 2 时，一定有 x 2 y 2 4 ；反过来当
【答案】C
10
【解析】令 m
log
3.4 2
，
n
log
3.6 4
，l
log
3 3
，在同一坐标系下作出三个函数的图象，
由图象可得 m l n ，
第 2页（共 13页）
=log3x
y
y=log2x
o
x
y=log4x
又∵ y 5x 为单调递增函数， ∴a c b.
8．对实数
a
和
b
，定义运算“
【答案】 6
【解析】该几何体为一个棱柱与一个圆锥的组合体，

2011年天津高考数学试题及答案(理科)

野草中的梦与幻我有幸拜读了鲁迅先生所写的散文诗《野草》，诗中有的词藻华丽，有的依旧言辞犀利，在作者的梦幻中依旧有残酷现实的倩影，美丽的景物却要用血腥的言语来抨击现实依旧是个可怕的世界，他在虚幻中道出了真实，而这真是就反映在他的梦里面。

他在预计未来的死亡中，把握现在的生命，领悟着生之要义，有死亡感知生命。

在绝望与希望中挣扎，在作者的眼中一切的矛盾，一方的尽头即是另一方的开端，希望的尽头便是绝望，绝望到了极点便又有了希望：死亡的尽头才又有了重生；“沉舟侧畔千帆过，病树前头万木春”斗转星移的变迁中，都为另一个新的开始而始终前进着。

在《野草》中，多篇都以“我梦见”为开头，如《死火》，《狗的驳洁》，《失掉的好地狱》，《墓碣文》，《颓败线的颤动》，《立论》，《死后》。

在《好的故事》中虽未以“我梦见”为开头，但也在“我在蒙胧中，看见一个好的故事”中知道这是作者的想象了。

现实若用虚幻的梦境来显现，更是清晰得可怕。

然而作者的这些梦境如此奇丽，如此狂乱的恐怖，使得它们简直成了梦魇。

虽然这些写梦境的篇章，皆以梦境开头，让人明白这并非现实，可他所诉说的内容，又无不让人联想到现实。

将我们从现实中推开，自己置身在奇异的想象中。

这些梦不来自光明，不来自天上，却来自黑暗，来自地狱与深渊。

因为鲁迅认为不能“光梦‘大同世界’之类的光明，不要只做将来的梦，还要梦到目前的‘阶级斗争，白色恐怖，轰炸，虐杀，鼻子里灌辣椒水，电刑……’。

于是《野草》没有叫人完全轻松的好梦。

死亡，地狱，黑暗，挣扎，斗争……无不是极让人感觉很冷得意象。

在《好的故事》中，作者闭上眼睛感知到一片朦胧的世界，各种美丽的景色跃然于眼前，俨然是一片乡村祥和图，但“骤然一惊，睁开眼”，瞬间化为几点虹霓色的碎影，似乎说明这融汇着一切美丽事物的完满世界只是幻想，在现实世界中是不可能存在的。

一旦醒来，一切便难追回。

《墓碣文》中的梦境，给人一种恐怖的感觉，也只能疾走，不要回顾，仿佛生活中的一些令人畏惧的的事情，让人敬而远之。

2011天津数学高考试题及答案

2011年普通高等学校夏季招生全国统一考试数学(天津卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试用时120分钟．第Ⅰ卷本卷共8小题，每小题5分，共40分．参考公式：·如果事件A 、B 互斥，那么P (A ∪B )＝P (A )＋P (B )．·如果事件A ，B 相互独立，那么P (AB )＝P (A )P (B )．·棱柱的体积公式V ＝Sh .其中S 表示棱柱的底面面积，h 表示棱柱的高．·圆锥的体积公式1.3V Sh =.其中S 表示棱锥的底面面积，h 表示圆锥的高．一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．i 是虚数单位，复数1-3i 1-i ＝( ) A ．2＋i B ．2－i C ．－1＋2iD ．－1－2i 2．设,,x y R ∈则“2x ≥且2y ≥”是“224x y +≥”的…( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件3．阅读如图的程序框图，运行相应的程序，则输出i 的值为( )A ．3B ．4C ．5D ．64．已知{a n }为等差数列，其公差为－2，且a 7是a 3与a 9的等比中项，S n 为{a n }的前n 项和，n ∈N *，则S 10的值为 …( )A ．－110B ．－90C ．90D ．110 5．在622x x ⎛⎫- ⎪ ⎪⎝⎭的二项展开式中，x 2的系数为( ) A ．154- B ． 154 C ．38- D ． 38 6．如图，在△ABC 中，D 是边AC 上的点，且,23,2AB CD AB BD BC BD ===则sin C 的值为( )A ．33 B ．36C ．63D ．667．已知324log0.3log 3.4log 3.615,5,,5a b c⎛⎫=== ⎪⎝⎭则()A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞a＞b8．对实数a和b，定义运算“⊗”：,1,, 1.a a ba bb a b-≤⎧⊗=⎨->⎩设函数()()22()2,.f x x x x x R=-⊗-∈，x∈R.若函数()y f x c=-的图象与x轴恰有两个公共点，则实数c的取值范围是()A．(－∞，－2]∪(－1，3 2 )B．(－∞，－2]∪(－1，3 4 -)C．(－1，14)∪(14，＋∞)D．(－1，34-)∪[14，＋∞)第Ⅱ卷本卷共12小题，共110分．二、填空题：本大题共6小题，每小题5分，共30分．9．一支田径队有男运动员48人，女运动员36人．若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，则抽取男运动员的人数为________．10．一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________ m3.11．已知抛物线C的参数方程为28,8.x ty t⎧=⎨=⎩(t为参数)．若斜率为1的直线经过抛物线C的焦点，且与圆(x－4)2＋y2＝r2(r＞0)相切，则r＝________.12．如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且2,::4:2:1DF CF AF FB BE===，若CE与圆相切，则线段CE的长为________．13．已知集合{}|349, A x R x x=∈++-≤1|46,(0,)B x R x t tt⎧⎫=∈=+-∈+∞⎨⎬⎩⎭，则集合A∩B＝________.。

2011年高考天津市数学试卷-理科(含详细答案)

2011年高考天津市数学试卷-理科(含详细答案)2011年普通高等学校招生全国统一考试天津卷（理科）第Ⅰ卷本卷共8小题，每小题5分，共40分一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．i 是虚数单位,复数13i 1i-=-( )． A ．2i+ B ．2i- C ．12i-+D ．12i --【解】()()()()13i 1i 13i 42i2i 1i 1i 1i 2-+--===---+．故选Ｂ． 2．设,x y ∈R ，则“2x ≥且2y ≥”是“224x y +≥”的( )．A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【解】因为2x ≥且2y ≥，则24x≥且24y≥，因而224x y +≥，所以“2x ≥且2y ≥”是“224xy +≥”的充分条件，取3x y ==，则满足224xy +≥，但不满足2x ≥且2y ≥，所以“2x ≥且2y ≥”不是“224xy +≥”的必要条件．因此“2x ≥且2y ≥”是“224xy +≥”的充分而于是()1011091010204521102Sa d ⨯=+=⨯+⨯-=．故选Ｄ．5．在6x x ⎫⎝的二项展开式中，2x 的系数为( )．A ．154-B ．154C ．38-D ．38【解】()6326166C 1C 2rrr r r r r r x T x x ---+⎛==- ⎝⎝⎭，令32r -=，则1r =．()112262226631C 2168Tx x x -=-=-=-．所以，2x 的系数38-，故选Ｃ．6．如图，在ABC ∆中，D 是边AC 上的点，且AB AD =，23AB BD=，2BC BD=，则sin C 的值为( )．A 3B 3C．6D 6【解】解法１．取BD 的中点E ，因为AB AD =，所以AE BD ⊥，因为23AB BD=，3AB BE=．所以3cos cos BE ABE ADB AB=∠==∠，CBDAECBDA于是6sin sin 3ADB CDB ∠=∠=．在BDC ∆中，由正弦定理得sin sin BC BDCDB C=∠， sin 6BDC=，所以6sin C =．故选Ｄ．解法2．设1BD =，由题设32AB AD ==，2BC =．在ABD∆中，由余弦定理得222331144cos 32324AB AD BD BAD AB AD +-+-∠===⋅⨯，所以22sin BAD ∠=在ABC ∆中，由正弦定理得sin sin BC ABBAD C=∠，即32sin 22C =，所以6sin 6C =．故选Ｄ．7．2log 3.45a =，4log 3.65b =，3log 0.315c ⎛⎫= ⎪⎝⎭，则( )．A ．a b c >>B ．b a c >>C ．a c b >>D ．c a b >> 【解】解法1．33310log 0.3log log 0.331555c -⎛⎫=== ⎪⎝⎭，下面比较2log 3.4a '=，4log 3.6b '=和310log 3c '=的大小．因为1a '>，1c '>，1b '<，则b '最小．2310lg10lg 3.43log 3.4log 3lg 2lg 3a c ''-=-=-，因为10lg 3.4lg 03>>，0lg 2lg3<<，所以11lg 2lg 3>，因此10lglg 3.430lg 2lg 3a c ''-=->．所以a c ''>，因而a cb '''>>．由于函数5x y =是R 上的增函数，所以a c b >>．故选Ｃ．解法2．33310log 0.3log log 0.331555c -⎛⎫=== ⎪⎝⎭，下面比较2log 3.4a '=，4log 3.6b '=和310log 3c '=的大小．因为1a '>，1c '>，1b '<，则b '最小．因为3310log log 3.43c '=<，所以233lg3.4lg3.410log 3.4log 3.4log lg 2lg33a c ''==>>>=，因而a cb '''>>．由于函数5x y =是R 上的增函数，所以a c b >>．故选Ｃ．解法3．由解法2，3310log log 3.43c '=<,画出函数2log y x =和3log y x =的图象,比较 3.4x =的纵坐标，可得23log 3.4log 3.4>，于是23310log 3.4log 3.4log 3a c ''=>>=．因而a cb '''>>．由于函数5x y =是R 上的增函数，所以ac b >>．故选Ｃ．8．对实数a 和b ，定义运算“⊗”：,1,,1.a ab a b b a b -≤⎧⊗=⎨->⎩设函数()()()222f x x x x =-⊗-，x ∈R ．若函数()y f x c =-的图象与x 轴恰有两个公共点，则实数c 的取值范围是( )． A ．()3,21,2⎛⎫-∞-- ⎪⎝⎭ B ．(]3,21,4⎛⎫-∞--- ⎪⎝⎭ C ．111,,44⎛⎫⎛⎫-+∞ ⎪⎪⎝⎭⎝⎭ D ．311,,44⎛⎫⎡⎫--+∞ ⎪⎪⎢⎝⎭⎣⎭【解】由题设()2232,1,23,12x x f x x x x x ⎧--≤≤⎪⎪=⎨⎪-<->⎪⎩或画出函数的图象，函数图象的四个端点（如图）为()1,1A --，31,24D ⎛⎫⎪⎝⎭，()1,2B --，33,24C ⎛⎫- ⎪⎝⎭，从图象中可以看出，直线y c =穿过点C ，点A 之间时，直线y c =与图象有且只有两个公共点，同时，直线y c =穿过点B 及其下方时，直线y c =与图象有且只有两个公共点，所以实数c 的取值范围是(]3,21,4⎛⎫-∞--- ⎪⎝⎭．故选Ｂ．第Ⅱ卷二、填空题：本答题共6小题，每小题5分,共30分．9．一支田径队有男运动员48人，女运动员36人．若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，则抽取男运动员的人数为．【解】12．抽取男运动员的人数为2121484812483684⨯=⨯=+（人）．10．一个几何体的三视图如右图所示（单位：m），则该几何体的体积为3m ．【解】6π+．几何体是由一个长方体与一个圆锥组合的．体积为213211363V ππ=⨯⨯+⨯⨯⨯=+．俯视图侧视图正视图12233311．已知抛物线C 的参数方程为28,8x t y t ⎧=⎨=⎩(t 为参数）．若斜率为1的直线经过抛物线C 的焦点，且与圆()()22240x y r r -+=>相切，则r = ．2抛物线C 的普通方程为28y x=，其焦点为()2,0F ．直线方程为2y x =-．因为直线与圆()()22240x y r r -+=>相切，则圆心到直线的距离等于半径，即40222r --==12．如图，已知圆中两条弦AB 与CD 相交于点F ，E 是AB 延长线上一点，且2DF CF ==::4:2:1AF FB BE =，若CE 与圆相切，则线段CE 的长为．【解】72．因为::4:2:1AF FB BE =，所以设BE a =，2FB a =，4AF a =．由相交弦定理，242DF CF AF FB a a ⋅=⋅==⋅，所以12a =，12BE =，772AE a ==．因为CE与圆相切，由切割线定理，2177224CE AE BE =⋅=⋅=．所以72CE =．FDCB A13．已知集合{}349A x x x =∈++-≤R ，()146,0,B x x t t t ⎧⎫=∈=+-∈+∞⎨⎬⎩⎭R ，则集合A B =．【解】{}25x x -≤≤．解集合A ．当3x <-时，不等式化为349x x --+-≤，解得4x ≥-．所以解为43x -≤<-；当34x -≤≤时，不等式化为349x x ++-≤，即79≤．所以解为34x -≤≤；当4x >时，不等式化为349x x ++-≤，解得5x ≤，所以解为45x <≤．综合以上，{}45A x x =-≤≤．解集合B ．因为0t >，所以1146246462x t t t t=+-≥⋅=-=-，所以{}2B x x =≥-，因而{}25AB x x =-≤≤．14．已知直角梯形ABCD 中，//AD BC ，90ADC ∠=︒，2AD =，1BC =，P 是腰DC 上的动点，则3PA PB +的最小值为．【解】5．解法1 ．以D 为坐标原点，DA 所在直线为x 轴，DC 所在直线为y 轴，y xPD C BA建立如图的直角坐标系．由题设，()2,0A ，设()0,C c ，()0,P y ，则()1,B c ．()2,PA y =-，()1,PB c y =-．()35,34PA PB c y +=-．()2235345PA PB c y +=+-，当且仅当34c y =时，等号成立，于是，当34c y =时，3PA PB+有最小值5．解法2 ．以相互垂直的向量DP ，DA 为基底表示PB PA 3+，得()533332PA PB DA DP PC CB DA PC DP +=-++=+-．又P 是腰DC 上的动点，即PC 与DP 共线，于是可设DP PC λ=，有DP DA PB PA )13(253-+=+λ．所以2222553(31)(31)42PA PB DA DP DA DP λλ⎡⎤+=+-+⨯-⋅⎣⎦即[]2)13(25)13(4253DP DPDA PB PA -+=-+=+λλ．由于P 是腰DC 上的动点，显然当31=λ，即DP PC 31=时，所以3PA PB +有最小值5．解法3 ．如图，3PB PF =，设E 为AF1a FB的中点，Q 为AB 的中点，则12QE BF PB ==， 32PA PB PA PF PE+=+=， ①因为PB PQ PE +=，PB PQ QB -=．则22222222PB PQ PB PQ PB PQ PE QB++-=+=+． ②（实际上，就是定理：“平行四边形的对角线的平方和等于各边的平方和”）设T 为DC 的中点，则TQ 为梯形的中位线，()1322TQ AD BC =+=．设P 为CT 的中点，且设,CP a PT b ==，则221PBa =+，2294PQ b =+，()2214QB a b =++，代入式②得()()222222912221244PB PQ a b PE a b ⎛⎫+=+++=+++⎪⎝⎭，于是()22252544PEa b =+-≥，于是25PE ≥，当且仅当a b=时，等号成立．由式①，325PA PB PE +=≥，所以3PA PB +有最小值5．三、解答题：本大题共6小题，共80分。

2011年天津市高考数学试卷(理科)答案与解析

2011年天津市高考数学试卷（理科）参考答案与试题解析一、选择题（共8小题，每小题5分，满分40分）1 一1. --------------------------------------------------------------------- （5分）（2011?天津）i是虚数单位，复数-------------------------------------------------- =（）1_1A . 2+i B. 2 - i C.- 1+2i D . - 1 - 2i【考点】复数代数形式的乘除运算.【专题】数系的扩充和复数.【分析】要求两个复数的除法运算，分子和分母同乘以分母的共轭复数，分子和分母上进行复数的乘法运算，最后结果要化简成最简形式.【解答】解：复数= -：：'=2 - i1-i （1-i）（1+i） 2故选B .【点评】本题考查复数的代数形式的乘除运算，是一个基础题，这种题目运算量不大，解题应用的原理也比较简单，是一个送分题目.2 22. （5分）（2011?天津）设x, y€R，贝U X丝且y多堤x +y台”的（）A •充分而不必要条件B •必要而不充分条件C.充分必要条件D •既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【专题】简易逻辑.2 2 2 2【分析】由X支且y多”推出X +y台”可证明充分性；由满足X +y台”可举出反例推翻X多且y 支”，则证明不必要性，综合可得答案.【解答】解：若X》且y呈，则x2台,y2呂，所以x2+y2%，即x2+y2呂；2 2 右x +y台，则如（-2,- 2）满足条件，但不满足x支且y支.2 2 所以X呈且y支”是X +y绍”的充分而不必要条件.故选A .【点评】本题主要考查充分条件与必要条件的含义.3. （5分）（2011?天津）阅读程序框图，运行相应的程序，则输出i的值为（）£7 = J X CT*1/输出］L/A . 3B . 4C . 5D . 6【考点】程序框图. 【专题】算法和程序框图.【分析】通过程序框图的要求，写出前四次循环的结果得到输出的值. 【解答】解：该程序框图是循环结构经第一次循环得到 i=1 , a=2; 经第二次循环得到 i=2, a=5;经第三次循环得到 i=3, a=16;经第四次循环得到 i=4, a=65满足判断框的条件，执行是，输出4故选B【点评】本题考查解决程序框图中的循环结构时，常采用写出前几次循环结果，找规律.4. （ 5分）（2011?天津）已知｛a n ｝为等差数列，其公差为- 2,且a 是a s 与a 9的等比中项, S n 为｛an ｝的前n 项和，n€N ，则S io 的值为（）A . - 110B . - 90C . 90D . 110【考点】等差数列的前n 项和；等比数列的性质. 【专题】等差数列与等比数列.【分析】通过a 7是a 3与a 9的等比中项，公差为-2，求出【解答】解：a 7是a 3与a 9的等比中项，公差为-2，所以a 72=a 3?a 9,T ｛a n ｝公差为-2,二 a 3=a 7- 4d=a 7+8, a 9=a 7+2d=a 7 - 4,所以 a 7 = （a 7+8）（a 7 - 4）,所以 a 7=8，所以 a 1 =20, 所以 S 10=「「二亠八 ' 「-=110故选D【点评】本题是基础题，考查等差数列的前 n 项和，等比数列的应用，考查计算能力，常考题型.故选C【点评】本题考查利用二项展开式的通项公式解决二项展开式的特定项问题.【考点】二项式定理. 【专题】二项式定理.【分析】利用二项展开式的通项公式求出展开式的通项，令 x 2的系数，即得答案.【解答】解：展开式的通项为 T r+1= （- 1） r 22r -6C 6r x 3-rx 的指数为2，求出展开式中,令 3 - r=2 得 r=1所以项展开式中,x 2的系数为-..\ '-° O5. （ 5分）（2011?天津）在x 2的系数为（2V5 r V6BD _ BC * c _ 3V6sinC sin-ZBDC 4逅兀 3故选：D .【点评】本题主要考查了在三角形中，综合运用正弦定理、余弦定理、识解三角形的问题，反复运用正弦定理、余弦定理，要求考生熟练掌握基本知识, 选择基本工具解决问题.7. （ 5 分）（2011?天津）已知二:r 丄. 八］则（）5A . a > b > cB . b > a > cC . a > c >bD . c > a > b 【考点】指数函数的单调性与特殊点.【专题】函数的性质及应用.6. （5分）（2011?天津）如图，在 △ ABC 中，D 是边AC 上的点，且 AB=AD , 2AB= ■:BD ,BC=2BD ，则sinC 的值为（ A .匚3【考点】【专题】【分析】B .亘C .丄D .6 3三角形中的几何计算.解三角形.根据题中条件，在 △ ABD 中先由余弦定理求出 cosA ，利用同角关系可求 sinA ,利用正弦定理可求 sin /BDC ，然后在△ BDC 中利用正弦定理求解 sinC 即可【解答】解：设AB=x ，由题意可得 AD=x , BD=—■，.-V3 <3△ ABD 中，由余弦定理可得cosA=2 _ 4 X 2AB 2 + AD 2- BD 2 2x ~~_1••• sinA = _△ ABD 中，由正弦定理可得AB1? sin / ADB=sin^ADB sinA霁in 么孟X 竽暮V3BC △ BDC 中，由正弦定理可得同角基本关系式等知并能灵活【分析】比较大小的方法：找1或者0做中介判断大小,指数幕的运算法则和对数的运算法则对 c 进行化简，得到b ,再借助于中间值log 2丄进行比较大小，从而得到结果.，3【解答】解:••Tog 23.4 > 1, Iog 43.6v 1, 又y=5x 是增函数，••• a > b ,沁)W5103T Y二5影>5】呃昇二51=5"隔4〉5"阴"归b而 ge |og J >IogJ'，• a > c故 a >c >b . 故选C .【点评】此题是个中档题.本题考查对数函数单调性、指数函数的单调性及比较大小，以及中介值法，考查学生灵活应用知识分析解决问题的能力.自，a - b^l.设函数fb, a - bJ>l2 2(x ) = (x - 2) ? (X - x ), x €R .若函数y=f (x )- c 的图象与x 轴恰有两个公共点，则实数c 的取值范围是()A .| 一 •； 1. " 1 B. ' 一. . 二2 4C .-二「「D.'-卩：■-4444【考点】函数与方程的综合运用. 【专题】函数的性质及应用.【分析】根据定义的运算法则化简函数f (x ) = (x 2- 2) ? (x - x 2)的解析式，并求出 f(x )的取值范围，函数 y=f (x ) - c 的图象与x 轴恰有两个公共点转化为 y=f (x ), y=c 图象的交点问题，结合图象求得实数c 的取值范围.£ a - b<l【解答】解：•••已毗二J|、■.，b, a ~ b^>l.X.由图可知，当函数f (x )与y=c 的图象有两个公共点, ••• c 的取值范围是 -,｛•函数 f ( x ) = (x 2- 2)(x - x 2)Iog 43.6v 1, Iog 23.4> 1，利用分数- K £4【点评】本题考查二次函数的图象特征、函数与方程的综合运用，及数形结合的思想.属于基础题.二、填空题（共6小题，每小题5分，满分30分）9. （5分）（2011?天津）一支田径队有男运动员48人，女运动员36人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，则抽取男运动员的人数为12 . 【考点】分层抽样方法.【专题】概率与统计.【分析】根据田径队的男女运动员数目和用分层抽样要抽取的数目，得到每个个体被抽到的概率，利用每个个体被抽到的概率乘以男运动员的数目，得到结果.【解答】解：：•田径队有男运动员48人，女运动员36人，•••这支田径队共有48+36=84人，用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，•每个个体被抽到的概率是——84 4•••田径队有男运动员48人，•••男运动员要抽取48X =12人，4故答案为：12.【点评】本题考查分层抽样，在抽样过程中每个个体被抽到的概率相等，这是解决这种问题的依据，本题是一个基础题.10. （5分）（2011?天津）一个几何体的三视图如图所示（单位：m）,则这个几何体的体积为6+ n m3.正视圏犒视圏【考点】由三视图求面积、体积.【专题】立体几何.【分析】由已知中的三视图，我们易判断已知中几何体的形状，然后根据已知的三视图分析出几何体的相关几何量，代入体积公式，即可求出该几何体的体积.【解答】解：由已知可得已知的几何体是一个圆锥和长方体的组合体其中上部的圆锥的底面直径为2,高为3，下部的长方体长、宽高分别为：2，3, 1贝U V圆锥=* ? n?= nV长方体=1 >2X3=6则V=6+ n故答案为：6+ n【点评】本题考查的知识是由三视图求体积，其中根据已知中的三视图分析几何体的形状是解答本题的关键.11. （5分）（2011?天津）已知抛物线C的参数方程为X=St（t为参数），若斜率为1的直线经过抛物线C的焦点，且与圆（x-4）2+y2=r2（r> 0）相切，则r=_ . ：_ .【考点】直线与圆的位置关系；抛物线的简单性质；直线的参数方程.【专题】圆锥曲线的定义、性质与方程；坐标系和参数方程.f 2【分析】由抛物线C的参数方程为X"St我们易求出抛物线的标准方程，进而根据斜率L y=8t为1的直线经过抛物线C的焦点，且与圆（x- 4）2+y2=r2（r>0）相切，我们根据直线与圆相切，贝U 圆心到直线的距离等于半径，求出直线方程后，代入点到直线距离公式，构造关于r的方程，解方程即可得到答案.【解答】解：•••抛物线C的参数方程为，x=St则抛物线的标准方程为：y2=8x则抛物线C的焦点的坐标为（2, 0）又•••斜率为1的直线经过抛物线C的焦点则直线的方程为 y=x - 2,即经x - y - 2=0 由直线与圆（x - 4） 2+y 2=r 2，则故答案为：-其中根据直线与圆相切，则圆心到直线的距离等于半径，求出直线方程后，代入点到直线距离公式，构造关于r 的方程，是解答本题的关键.12. （ 5分）（2011?天津）如图，已知圆中两条弦 AB 与CD 相交于点F , E 是AB 延长线上一点，且 DF=CF= 二 AF : FB : BE=4 : 2: 1.若CE 与圆相切，则 CE 的长为.【考点】圆的切线方程. 【专题】直线与圆.【分析】设出AF=4k , BF=2k , BE=k ，由DF?FC=AF?BF 求出k 的值，禾U 用切割定理求出 CE .2 1【解答】解：设 AF=4k , BF=2k , BE=k ，由 DF?FC=AF ?BF ，得 2=8k ，即 k=,2••• AF=2 , BF=1 , BE= , AE=,2 22 17 7由切割定理得CE =BE?EA= =—，2 2 4• CE ==.2【点评】本题是基础题，考查直线与圆的位置关系，考查计算能力，基本知识掌握的情况，常考题型.13. （ 5 分）（2011?天津）已知集合 A={x €R||x+3|+|x - 4|电}, B= . T _ I ： — - |I ' ，则集合 A QB= _【考点】交集及其运算. 【专题】集合.【分析】求出集合A ，求出集合B ,然后利用集合的运算法则求出 A AB .【解答】解：集合A={x €R||x+3|+|x - 40}，所以A={x| - 4纟老}; 集合-.■' -'. ■ . ； .•-，--_ -■■■■. '| _ _ - - - ■-- ,当且仅当t=〔时取等号，所以 B={x|x A 2},2所以 A AB={x| - 4$W5} A{x|x A 2}={x| - 2$老}, 故答案为：{x| - 2<x<5}.r=4-2【点评】本题考查的知识点是直线与的圆位置关系,抛物线的简单性质及抛物线的参数方程,【点评】本题是基础题，考查集合的基本运算，注意求出绝对值不等式的解集，基本不等式求出函数的值域，是本题解题是关键，考查计算能力.14. (5 分)(2011?天津)已知直角梯形ABCD 中，AD // BC,/ ADC=90 ° AD=2 , BC=1 ,P是腰DC上的动点，则|的最小值为 5 .【考点】向量的模.【专题】平面向量及应用.【分析】根据题意，利用解析法求解，以直线DA , DC分别为x, y轴建立平面直角坐标系，则A (2, 0), B (1 , a) , C (0 , a) , D (0 , 0),设P (0 , b) (0电弟)，求出包+3瓦,根据向量模的计算公式，即可求得_ J : ：■.<■' | ,利用完全平方式非负，即可求得其最小值.【解答】解：如图，以直线DA, DC分别为x , y轴建立平面直角坐标系，则A (2 , 0), B (1 , a) , C ( 0 , a) , D (0 , 0)设P ( 0 , b) ( 04)毛)则」■■= (2 , - b), -1= (1, a- b),•••「'd「用=(5 , 3a- 4b)••• C「二* 「一二；l.. .「为.故答案为5.【点评】此题是个基础题•考查向量在几何中的应用，以及向量模的求法，同时考查学生灵活应用知识分析解决问题的能力.三、解答题(共6小题，满分80分)15. (13 分)(2011?天津)已知函数f (x) =tan (2x+——),(1 )求f (x)的定义域与最小正周期；(2)设a€ ( 0,——)，若f (二)=2cos2 a ,求a 的大小.4 2【考点】正切函数的周期性；同角三角函数基本关系的运用；二倍角的余弦；正切函数的定义域.【专题】解三角形.【分析】(I)利用正切函数的定义域求出函数的定义域，利用周期公式求出最小正周期；(n)通过f (2) -2cos2Cl ，化简表达式，结合 a€ ( 0,丄L ),求出a 的大小.241解答,解：⑴由吩即n 迪.所以x 专呼，k 厘.所以f (x )的定义域/. f (x )的最小正周期为:sin ( a +令)---------- 二2 (co s 2a - si cos ( □ +—)4整理得—L' ] 1 J _ 二 i -二二: cos a 一 sin Cl(cos a+sind )因为 a€ (0,匹)，所 4以 sin a +cos a 0 因此(COS a — sin a) 即 sin2 a —因为 a€ (0,二_),2 4所以a_—12【点评】本题考查两角和的正弦函数、余弦函数、式，二倍角公式等基本知识，考查基本运算能力.16. (13分)(2011?天津)学校游园活动有这样一个游戏项目：甲箱子里装有 3个白球、2 个黑球，乙箱子里装有 1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出 2个球，若摸出的白球不少于 2个，则获奖.(每次游戏结束后将球放回原箱)(I)求在1次游戏中，(i) 摸出3个白球的概率； (ii) 获奖的概率；(n)求在2次游戏中获奖次数 X 的分布列及数学期望 E (X ).【考点】离散型随机变量的期望与方差；互斥事件与对立事件；古典概型及其概率计算公式；离散型随机变量及其分布列. 【专题】概率与统计.【分析】(1)( i )甲箱子里装有3个白球、2个黑球，乙箱子里装有 1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出 2个球，事件数是 C 52C 32,摸出3个白球事件数为C 32C 21C 21；由古典概型公式，代入数据得到结果，(ii )获奖包含摸出2个白球和摸出3个白球，且它们互斥，根据(i )求出摸出2个白球的概率，再相加即可求得结果，注意运算为:2_丄=:正切函数公式，同角三角函数的基本关系 - ■-.-：=：'得 tan (=2cos2 a,要正确，因为第二问要用本问的结果.(II )连在2次游戏中获奖次数 X 的取值是0、1、2,根据上面的结果，代入公式得到结果，写出分布列，求出数学期望.【点评】此题是个中档题. 本题考查古典概型及共概率计算公式，离散型随机变量的分布列数学期望、互斥事件和相互独立事件等基础知识，考查运用概率知识解决实际问题的能力.17. (13分)(2011?天津)如图所示，在三棱柱 ABC - A 1B 1C 1中，H 是正方形AA 伯伯的中心，AA 仁2*：「，C 1H 丄平面 AA 1B 1B ，且 C 1H=".(1) 求异面直线 AC 与A 1B 1所成角的余弦值； (2) 求二面角 A - A 1C 1 - B 1的正弦值；(3) 设N 为棱B 1C 1的中点，点 M 在平面AA 1B 1B 内，且MN 丄平面A 1B 1C 1,求线段BM【考点】二面角的平面角及求法；异面直线及其所成的角；直线与平面垂直的性质. 【专题】空间位置关系与距离；空间角；空间向量及应用；立体几何.【解答】解：(I) (i )设在一次游戏中摸出i 个白球”为事件A i (i= , 0, 1, 2, 3),则2 1 C3 c 21P (A 3).(ii )设在一次游戏中获奖2 2 11 C 电 C 9C C nP (A 2)=厂丁- - - ■ c 5 c 3 c 5”为事件B , 1.一-3则 B=A 2U A 3,又且 A 2、A 3 互斥，所以 P ( B ) =P (A 2)(H)由题意可知 X 的所有可能取值为+P ( A 3)=:」］ 0, 1, 2.P (X=0 )==(1 - \ 2=,10 100P (X=2 )==(')「，10 10012.p910021 50 49 100X 的数学期望E (X ) =0X " . ■ 一100 50100^5P (X =1)"吒(1 甘疇，所以X 的分布列是【分析】方法一：如图所示，建立空间直角坐标系，点B 为坐标原点.(I)求出心中的有关向量，然后求出异面直线 AC 与A 1B 1所成角的余弦值；□二0T(H)利用,「: 求出平面AA i C i 的法向量IT ,通过*AA ［二 0 的法向量」然后利用MN-AiBi=O(川)设N 为棱B i C i 的中点，设M ( a, b, 0),利用MN 丄平面A i B i C i,结合［一 fHN-A^^O求出a , b ,然后求线段BM 的长.方法二：(I )说明/ C i A i B i 是异面直线AC 与A i B i 所成的角，通过解三角形 C i A i B i ,利用余弦定理， cosZC l A l B l- 2A 1C 1-A 1B 1-3求出异面直线 AC 与A i B i 所成角的余弦值为士I3(II )连接AC i ,过点A 作AR 丄A i C i 于点R ，连接B i R ，说明/ ARB i 为二面角A - A i C iA "+E E - AB !-B i 的平面角.连接 AB i ,在厶ARB i 中，通过「 • •,1ZAK* D j K求出二面角A -A i C i - B i 的正弦值为 -7(III )首先说明MN 丄A i B i .取HB i 中点D ,连接ND ，由于N 是棱B i C i 中点，推出ND 丄A i B i .证明A i B i 丄平面MND ,连接MD 并延长交A i B i 于点E ,延长EM 交AB 于点F,_连接NE .连接BM ，在Rt △ BFM 中，求出【解答】方法一：如图所示，建立空间直角坐标系，点 B 为坐标原点. 依题意得A (2^2. 0, 0) ,B (0, 0, 0),C (近，-伍，真)A t (2A /2 * 2^2* 0)，B ］ (CL 2品 0) , Cj (V2 * V2 * Vs )cos 疋，盘磴［B ；〉二,一.’, ----- .,1 1|人1匚1二Q求出平面 A I B I C I i 二0［一求二面角A - A i C i - B i 的正弦值；(I )解：易得-- 冷「 —.:—► -------►AC p A 1B 14 V?是，所以异面直线AC 与A 1B1所成角的余弦值为匚.(H )解：易知.I .... ■--: =匸设平面AA 1C 1的法向量 =(x , y , z ),不妨令」二，可得.. - ■ 同样地，设平面 A i B i C i 的法向量-i=(x , y , z ),n p A t C t =0( -^/2x - V23^V5Z ~0、厂则* f ______ * 即《不妨令尸，n-A^^O l - 2V2K =0.可得-厂•「 ■■: 1所以二面角A - A 1C 1 - B 的正弦值为in* Ai Ci=O则-丄即(■后-品*12727=0.从而:j(III )解：由N 为棱B i C i 的中点,方法二：(I )解：由于AC // A 1C 1，故/ C i A i B i 是异面直线AC 与A I B I 所成的角. 因为CiH 丄平面AAlBlB ,又H 为正方形AAlBlB 的中心，「.二-C . H--可得 A i C 仁B i C i =3 .因此-M--G 曲厶n 1 2打所以异面直线AC 与A i B i 所成角的余弦值为 1.3(II )解：连接 AC i ，易知 AC I =B I C I , 又由于 AA I =B I A I , A i C i =A i C i ,所以△ AC i A i ^A B i C i A i ,过点A 作AR 丄A i C i 于点R ,连接B i R ，于是B i R 丄A i C i ，故/ ARB i 为二面角A - A i C i - B i 的平面角.由MN 丄平面A I B I C I ，得、MN-B!=0连接 AB I ，在△ ARB I 中，上「门-一 A7.:.-AR 2+B 1R 2 - ABj 2祁•石百=°c在Rt △ A IRBI中，•-…..-(I)求椭圆的离心率 e ;【考点】直线与圆锥曲线的综合问题；轨迹方程；椭圆的简单性质. 【专题】圆锥曲线的定义、性质与方程.所以二面角A - A i C i - B i 的正弦值为-7(III )解：因为 MN 丄平面A i B i C l ，所以MN 丄A i B i . 取HB i 中点D ,连接ND ，由于N 是棱B i C i 中点，所以 ND // C i H 且、一-厂--.2 2又C i H 丄平面AA i B i B , 所以ND 丄平面AA i B i B ，故ND 丄A i B i . 又 MN AND=N ,所以A i B i 丄平面MND ，连接MD 并延长交A i B i 于点E , 则 ME 丄A iB i ，故 ME // AA i .得---：--，延长EM 交AB 于点F ,2可得-_ ：)2在 Rt △ ENM 中，ND 丄 ME ，故 ND 2=DE?DMD 厝晋 F 闻所以可得BM ，在 Rt △ BFM 中，：丫_ y 二］；一 . 【点评】本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识，考查用空间向量解决立体几何问题的方法，考查空间想象能力、运算能力和推理论证能力.连接 i8. (i3分)(20ii?天津)在平面直角坐标系2 2F2分别为椭圆1的左、右焦点.已知a 2b 2xOy 中，点 P (a , b ) (a > b > 0)为动点,△ F i PF 2为等腰三角形.F i ,(H)设直线PF 2与椭圆相交于 A , B 两点,M 是直线PF 2上的点，满足f ；：,.连接NE .点M 的轨迹方程.【分析】(I)直接利用△ F 1PF 2为等腰三角形得离心率e ;将① 代入化简得18x 2- 16 7y - 15=0, ? y='代入① 化简得c=丄」>0.所1&V3X16x以 x >0 , 因此点M 的轨迹方程为18x 2- 16 ■:xy - 15=0 (x >0). 【点评】本题主要考查椭圆的方程和几何性质，直线的方程，平面向量等基础知识，考查用代数方法研究圆锥曲线的性质和数形结合的数学思想，考查解决问题的能力和运算能力.219. (14分)(2011?天津)已知a >0，函数f (x ) =lnx - ax , x >0. (f (x )的图象连续不断)(I)求f (x )的单调区间；(n)当手g 时，证明：存在Xo € (2, + 8),使f (耳)=f (冷);(川)若存在均属于区间［1,3］的a 且B- a 丰,使(a)=f( B),证明 — ■ ■-：一匚一5 3|PF 2|=|F 1F 2|,解其对应的方程即可求椭圆的 (n)先把直线方程与椭圆方程联立，求得A ,B 两点的坐标，代入二,即可求点M 的轨迹方程.【解答】解：(I)设 F i (- c , 0) , F 2 (c , 0)(C >0).由题得 |PF 2|=|F i F 2|，即:'=2c ，整理得 2a2+ :-仁0,得：=-1 (舍),或=,a 2所以e=.2(n)由(I)知a=2c , b= 7c ,可得椭圆方程为y 2=12c 2 Cx-d '消y 并整理得5x 2- 8xc=0 ,3x 2+4y 2=12c 2，直线方程为 y= '； (x - c ).解得x =0, x鲁得方程组的解为x=08c5v=—■—c不妨设 A ( c 二一c ), B (0, - 7 c )5 5*p设点M 的坐标为(x , y ),则AH = (x - — c , 5y -— c ) , M= (x , y+■:c )5由.「，丫 * f'= - 2 即(x -x+ (y --C) 5(y+* ?c ) =- 2.A ,B 的坐标满足方程组①，由 Y =W (x - c ) 得 c=x -【考点】利用导数研究函数的单调性；函数的零点；不等式的证明.【专题】导数的综合应用.【分析】(I)求导数f/(x)；在函数的定义域内解不等式f/(x)> 0和f/(x)v 0确定函数的单调区间，若在函数式中含字母系数，往往要分类讨论.(II )由(I)知f (x)在(0, 2)内单调递增，在(2, +8)内单调递减•令-二.■' I I .利用函数f (x)在(0, 2)内单调递增，得到2.■- ■ .- 「•最后取I:「「一「从而得到结论;(III )先由f (a) =f (份及( :1)的结论知P，从而f (x )在［a, 3上的最小值为f (a).再依1Wa2<B3建立关于a的不等关系即可证得结论.2【解答】解: (I) : :. - ・■X X令-:< ■.-11^ /'.za当x变化时，f (x), f (X)的变化情况如下表：x(0, ^^)2a 7 2刁2a(V^, + 8)2af' (x) +0—f ( x) 增极大值减所以，f( x)的单调递增区间是I I, --1 . ，:的单调递减区间是2a(II )证明：当-厂"「一丄' :, •s y由(I)知f (x)在(0, 2)内单调递增，在(2, + 8)内单调递减.令H ；■一•'':.由于f (x)在(0, 2)内单调递增，故..取:,'■■■■ ■' : - -J- -'r- 1.1所以存在x°€ (2, x'),使g (xo) =0,即存在- . . ' : 1■, -1 ,.(说明：x'的取法不唯一，只要满足x'> 2，且g (x')v 0即可)(Ill )证明：由f (a) =f (B)及(I )的结论知,, 2a 从而f (x )在［a B 上的最小值为f (a ). 又由 a 1 a, ^€［1 , 3］，知 1 Wa 2^B 3.,,ff (2) Af ( Ct ) >f (1) An fln2 -- af (2) CP) C3) . ^In2 - 4a^ln3 - 9a.【点评】本小题主要考查导数的运算、禾U 用导数研究函数的单调性、解不等式、函数的零点等基础知识，考查运算能力和运用函数思想分析解决问题的能力及分类讨论的思想方法.20. (14分)(2011?天津)已知数列｛a n ｝与｛b n ｝满足:(I)求 a 3, a 4, a 5 的值；(n)设 C n =a 2n -1+a 2n+1, n €N ，证明：｛c n ｝是等比数列;(川)设 S k =a 2+a 4+ --+a 2k , k€N ，证明:【考点】数列与不等式的综合；等比关系的确定. 【专题】等差数列与等比数列.【分析】(I)要求a 3, a 4, a 5的值；通过赋值方法，利用已知条件化简求解即可.(n)化简出a 2n - 1+a 2n+1, a 2n+1+a 2n+3的关系，即：C n+1与C n 的关系，从而证明｛C n ｝是等比数列；就是利用(I)的 b 二'1" 吟覚豎，用2n — 1, 2n , 2n+1 ,替换n匕且为偶数1,.r -———中的n ,化简出只含a n'的关系式，就是a 2n-1+a 2n +2a 2n+1=0,① 2a 2n +a 2n+1+a 2n+2=0,② a 2n+1+a 2n+2+2a 2n+3=0,③ 然后推出 a 2n+1+a 2n+3= —(a 2n - 1+a 2n+1),得到5+1= — C n ( n €N ),从而证明｛C n ｝是等比数列； (川)先研究通项公式a 2k ,推出S k 的表达式，然后计算 '，结合证明的表达式，利用表达式的特征，通过裂项法以及放缩法证明即可；就是：根据a 2k -1+a 2k+1= (— 1) k ,对任意k+1k€N 且k 多，列出n 个表达式，利用累加法求出 a 2k = (— 1) (k+3).化简S 2k = ( a 2+a 4)、 / x . . <KI * 3 兀 JJ r 场m-3 ^4jn-2 1 】皿计+ (a 6+a 8)+ ••+ ( a 4k -2+a 4k ) = — k , k €N ，二k=l a k m=l两皿-？屯1 対皿加 S T , 7通过裂项法以及放缩法证明：::\'k=i a k 6【解答】20、满分14 分.b n a n +an+l + b n +l a n+2=°7''■'，n €N *，且 a 1=2,a 2=4.% Si, 7可得b =(lf n?Sn u，ii为偶数又b n a n+a n+1+b n+1a n+2=0,当n=l时，a1-l-a2+2a3=：0i由31~2, a2=4s可得a3= - 3；当口二£时，2a2 + a3+a4=0* 可得a4= - 5i当HF3时,&3+a4+2a5=0* 可得屯=4.(II)证明：对任意n€N , a2n-i+a2n+2a2n+仁0,①2a2n+a2n+1+a2n+2=0, ②a2n+l+a2n+2+2a2n+3=0,③②-③，得a2n=a2n+3-④将④ 代入①，可得a2n+1+a2n+3=-( a2n- 1+a2n+1)即C n+1= - c n ( n€N )又c1 =a1+a3= - 1,故C n M D,因此:. ■ ■I是等比数列.c n n（III ）证明：由（II）可得a2k- 1+a2k+1= （- 1）, 于是，对任意k €N*且k逖有aj + a^ - l t-（巧+叫）二巧+ a亍~1，(-1 ) k ( a2t-3+ a2k - 1^ = _ 1-将以上各式相加，得a1+ (- 1) k a2k-1= -( k - 1),即a2k-1= (- 1) k+1(k+1),k+1此式当k=1时也成立.由④ 式得a2k= (- 1) ( k+3).从而S2k= (a2+a4) + (a6+a8) + ••+ ( a4k-2+a4k) = - k, S2k-仁S2k- a4k=k+3.所以，对任意n €N*, n老芒( 3如「3 | S如_2 ] $仏「打5-机)(2nH~2 _ 加- 1 _ 2nrh3 十2m)k=l a k Jii=l 为m-3 ^-2 1 m=l 加2时2 2^1 2nr+3「： =... . =—(——+____________________ 3 _______ )2*3 ±2 加(2nri-l) (2时2) (2时3). =3急(2m-l) (2^1) (2^2) (2时3)孚订(1-1) + (1-1) +…+] ——-2 ------------- —3 2 3 5 5 7 2n- 1 2n+l (2n+2) (2n+3)^5.5 ] 3 _______飞陀2*2n+l (2n+2) (2n+3)对于n=1，不等式显然成立.【点评】本小题主要考查等比数列的定义、数列求和等基础知识，考查运算能力、推理论证能力、综合分析和解决问题的能力及分类讨论的思想方法. 赋值法是求数列前几项的常用方法，注意n=1的验证，裂项法和放缩法的应用.。

2011年天津理解析

2011年普通高等学校招生全国统一考试（天津卷）数学（理工类）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的。

1、(2011·天津·理,1)i 是虚数单位，复数131i i-=- ( )(A)2i + ( B)2i - (C)12i -- (D)12i - 2、(2011·天津·理,2)设,x y R ∈，则“2x ≥且2y ≥”时“224x y +≥”的 ( ) (A)充分而不必要条件（B ）必要而不充分条件 (C)充分必要条件（D ）既不充分而也不必要条件3、(2011·天津·理,3)阅读右边的程序框图，运行相应的程序，则输出i 的值为 ( ) （A ）3 （B ）4 （C ）5 （D ）64、(2011·天津·理,4)已知{}n a 为等差数列，其公差为-2，且7a 是3a 与9a 的等比中项，n S 为{}n a 的前n 项和，n N *∈,则10S 的值为 ( ) （A ）-110 （B ）-90 （C ）90 （D ）1105、(2011·天津·理,5)在62⎛⎫- ⎝的二项展开式中，2x 的系数为 ( ) （A ）154-（B ）154（C ）38-（D ）386、(2011·天津·理,6)如图，在ABC ∆中，D 是边AC 上的点，且AB=AD ，2AB=，BC=2BD ，则sinC 的值为（）（A ）3（B 6（C 3（D67、(2011·天津·理,7)已知2log3.45a =，4log3.65b =，3log0.31()5c =，则( )（A ）a b c >> （B ）b a c >> （C ）a c b >> （D ）c a b >> 8、(2011·天津·理,8)对实数a 和b ，定义运算“⊗”：,1,,1.a a b a b b a b -≤⎧⊗=⎨->⎩设函数22()(2)()f x x x x =-⊗-，x R ∈。

2011年天津高考数学试题及答案(理科)

BABDCDCB二、填空题：本题考查基本知识和基本运算，每小题5分，满分30分.9．12 10．6π+ 11．213．{|25}x x-≤≤ 14．5三、解答题15．本小题主要考查两角和的正弦、余弦、正切公式，同角三角函数的基本关系，二倍角的正弦、余弦公式，正切函数的性质等基础知识，考查基本运算能力.满分13分.（I）解：由2,42x k k Zπππ+≠+∈，得,82kx k Zππ≠+∈.所以()f x的定义域为{|,}82kx R x k Zππ∈≠+∈()f x的最小正周期为.2π（II）解：由()2cos2,2af a=得tan()2cos2,4a aπ+=22sin()42(cos sin),cos()4aa aaππ+=-+整理得sin cos2(cos sin)(cos sin).cos sina aa a a aa a+=+--因为(0,)4aπ∈，所以sin cos0.a a+≠因此211(cos sin),sin2.22a a a-==即由(0,)4aπ∈，得2(0,)2aπ∈.所以2,.612a aππ==即16．本小题主要考查古典概型及其概率计算公式、离散型随机变量的分布列、互斥事件和相互独立事件等基础知识，考查运用概率知识解决简单的实际问题的能力.满分13分.（I）（i）解：设“在1次游戏中摸出i个白球”为事件(0,1,2,3),iA i==则2132322531().5C CP AC C=⋅=（ii）解：设“在1次游戏中获奖”为事件B，则23B A A= ，又22111322222222253531(),2C C C C CP AC C C C=⋅+⋅=且A2，A3互斥，所以23117()()().2510P B P A P A=+=+=（II）解：由题意可知X的所有可能取值为0，1，2.2122(0)(1),101007721(1)(1),101050749(2)().10100P X P X C P X ==-===-==== 所以X 的分布列是X0 1 2 P 9100 215049100X 的数学期望921497()012.100501005E X =⨯+⨯+⨯=17．本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识，考查用空间向量解决立体几何问题的方法，考查空间想象能力、运算能力和推理论证能力.满分13分.方法一：如图所示，建立空间直角坐标系，点B 为坐标原点.依题意得(0,0,0),AB C111A B C （I ）解：易得11((AC AB==- ，于是111111cos ,3||||AC A B AC A B AC A B ⋅===⋅所以异面直线AC 与A 1B 1（II ）解：易知111(AA AC ==设平面AA 1C 1的法向量(,,)m x y z =，则11100m AC mAA ⎧⋅=⎪⎨⋅=⎪⎩ 即0,0.⎧+=⎪⎨=⎪⎩不妨令x =可得m =，同样地，设平面A 1B 1C 1的法向量(,,)n x y z =，则11110,0.n AC n A B⎧⋅=⎪⎨⋅=⎪⎩即0,0.⎧+=⎪⎨-=⎪⎩不妨令y =可得n = 于是2cos ,,||||7m n m n m n ⋅===⋅从而sin ,7m n = 所以二面角A —A 1C 1—B的正弦值为7（III ）解：由N 为棱B 1C 1的中点，得(22N 设M （a ，b ，0），则(,22MN a b =--中学教育大家谈h t t p://b1327668.x i c i.n e t由MN⊥平面A1B1C1，得11110, 0.MN A BMN A C⎧⋅=⎪⎨⋅=⎪⎩即()(0,2()(()(0.22aa b⎧-⋅-=⎪⎪⎨⎪-⋅+-⋅+⎪⎩解得24ab⎧=⎪⎪⎨⎪=⎪⎩故M因此(,,0)24BM=，所以线段BM的长为||4BM=方法二：（I）解：由于AC//A1C1，故111C A B∠是异面直线AC与A1B1所成的角.因为1C H⊥平面AA1B1B，又H为正方形AA1B1B的中心，11AA C H==可得11113.AC B C==因此2221111111111111cos2AC A BB CC A BAC A B+-∠==⋅所以异面直线AC与A1B1（II）解：连接AC1，易知AC1=B1C1，又由于AA1=B1A1，A1C1=A1=C1，所以11AC A∆≌11BC A∆，过点A作11AR AC⊥于点R，连接B1R，于是111B R AC⊥，故1ARB∠为二面角A—A1C1—B1的平面角.在11Rt A RB∆中，11111sin3B R A B RA B=⋅∠=连接AB1，在1ARB∆中，2221111114,,cos2AR B RABAB AR B R ARBAR B R+-==∠=⋅27=-，从而1sin7ARB∠=所以二面角A—A1C1—B1的正弦值为7（III）解：因为MN⊥平面A1B1C1，所以11.MN A B⊥取HB1中点D，连接ND，由于N是棱B1C1中点，所以ND//C1H且112ND C H==.又1C H⊥平面AA1B1B，所以ND⊥平面AA1B1B，故11.ND A B⊥又,MN ND N=所以11平面MND ，连接MD 并延长交A 1B 1于点E ，则111,//.ME A B ME AA ⊥故由1111111,4B E B D DE AA B A B A ===得12DE B E ==EM 交AB 于点F ，可得1BF B E ==连接NE. 在Rt ENM ∆中，2,.ND ME ND DE DM⊥=⋅故所以2ND DMDE ==可得4FM = 连接BM ，在Rt BFM ∆中，BM == 18．本小题主要考查椭圆的标准方程和几何性质、直线的方程、平面向量等基础知识，考查用代数方法研究圆锥曲线的性质及数形结合的数学思想，考查解决问题能力与运算能力.满分13分.（I ）解：设12(,0),(,0)(0)F c F c c ->由题意，可得212||||,PF F F =2.c =整理得22()10,1c c c aa a+-==-得（舍），或1.2c a =所以1.2e = （II ）解：由（I ）知2,,a cb == 可得椭圆方程为2223412,x yc +=直线PF 2方程为).y x c =-A ，B 两点的坐标满足方程组2223412,).x y c y x c ⎧+=⎪⎨=-⎪⎩消去y 并整理，得2580.x cx-=解得1280,.5x x c == 得方程组的解21128,0,5,.5x cx y y c ⎧=⎪=⎧⎪⎪⎨⎨=⎪⎪⎩=⎪⎩不妨设8(,),(0,)55A cB 设点M 的坐标为8(,),(,),(,)55x y AM x c y BM x y =--=+ 则，于是38(,),555AMy x y x =--().BM x = 由2,AM BM ⋅=-即38)()255y xx y x -⋅+=-，化简得218150.x --= 将22105,0.316x y c x y c x +==-=>得所以0.x >因此，点M 的轨迹方程是218150(0).x x --=>19．本小题主要考查导数的运算、利用导数研究函数的单调性、解不等式、函数的零点等基础知识，考查运算能力和运用函数思想分析解决问题的能力及分类讨论的思想方法.满分14分.（I ）解：2112'()2,(0,)2ax f x ax x x -=-=∈+∞，令'()0,fx =解得当x 变化时，'(),()f x f x 的变化情况如下表：x(0,)2a 2a()2a+∞ '()f x+ 0 - ()f x 极大值所以，()f x 的单调递增区间是(0,()2f x a 的单调递减区间是().2a+∞ （II ）证明：当211,()ln .88a f x x x ==-时由（I ）知()f x 在（0，2）内单调递增，在(2,)+∞内单调递减. 令3()()().2g x f x f =- 由于()f x 在（0，2）内单调递增，故3(2)(),2f f >即g(2)>0. 取23419'2,(')0.232e x e g x -=>=<则所以存在00(2,'),()0,x x g x ∈=使即存在003(2,),()().2x f x f ∈+∞=使（说明：的取法不唯一，只要满足即可）（III ）证明：由()()f f αβ=及（I ）的结论知αβ<<，从而()[,]f x αβ在上的最小值为().f a又由1βα-≥，,[1,3],αβ∈知12 3.αβ≤≤≤≤ 故(2)()(1),ln 24,(2)()(3).ln 24ln39.f f f a a f f f a a αβ≥≥-≥-⎧⎧⎨⎨≥≥-≥-⎩⎩即从而ln 3ln 2ln 2.53a -≤≤20．本小题主要考查等比数列的定义、数列求和等基础知识，考查运算能力、推理论证能力、综合分析和解决问题的能力及分类讨论的思想方法.满分14分.（I ）解：由*3(1),,2nn b n N +-=∈ 可得1,n n b ⎧=⎨⎩为奇数2,n 为偶数又1120,n n n n n b a a b a +++++=123123234434543;5;4.=-=-=当n=1时,a +a +2a =0,由a =2,a =4,可得a 当n=2时,2a +a +a =0,可得a 当n=3时,a +a +2a =0,可得a （II ）证明：对任意*,n N ∈2122120,n n n a a a -+++=① 2212220,n n n a a a ++++=② 21222320,n n n a a a +++++=③ ②—③，得 223.n n a a +=④ 将④代入①，可得21232121()n n n n a a a a ++-++=-+即*1()n n c c n N +=-∈又1131,0,n c a a =+=-≠故c因此11,{}n n nc c c +=-所以是等比数列. （III ）证明：由（II ）可得2121(1)k k k a a -++=-，于是，对任意*2k N k ∈≥且，有133********,()1,1,(1)() 1.k k k a a a a a a a a --+=--+=-+=--+=-将以上各式相加，得121(1)(1),k k a a k -+-=--即121(1)(1)k k a k +-=-+，此式当k=1时也成立.由④式得12(1)(3).k k a k +=-+从而22468424()()(),k k k S a a a a a a k -=++++++=-2124k k k -所以，对任意*,2n N n ∈≥，44342414114342414()n nk m m m m k m k m m m m S S S S S a a a a a ---==---=+++∑∑12221232()2222123nm m m m mm m m m =+-+=--++++∑123()2(21)(22)(22)nm m m m m ==++++∑ 2253232(21)(22)(23)nm m m n n ==++⨯+++∑ 21533(21)(21)(22)(23)n m m m n n =<++-+++∑151111113[()()()]3235572121(22)(23)n n n n =+⋅-+-++-+-+++1551336221(22)(23)7.6n n n =+-⋅++++<对于n=1，不等式显然成立.所以，对任意*,n N ∈2121212212n nn nS S S S a a a a --++++32121241234212()()()n n n n S S S S S S a a a a a a --=++++++22211121(1)(1)(1)41244(41)4(41)n n n=--+--++-----22211121()()()41244(41)44(41)n n n nn =-+-+--+--111().4123n n ≤-+=-。

2011年高考数学天津理(word版含答案)

【选择题】【1】．i 是虚数单位，复数i1i31--=（）. (A)2+i(B)2i -(C)12i -+ (D)12i --【2】．设R ∈y x ,，则“x ≥2且y ≥2”是“22y x +≥4”的（）.（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件【3】．阅读下面的程序框图，运行相应的程序，则输出i 的值为（）. （A ）3 （B ）4 （C ）5 （D ）6【4】．已知{}n a 为等差数列，其公差为-2，且937a a a 与是的等比中项，{}n n a S 为的前n 项和，*n ∈N ，则10S 的值为（）.（A ）—110（B ）—90 （C ）90（D ）110【5】．在622⎪⎪⎭⎫⎝⎛-x x 的二项展开式中，2x 的系数为（）. （A ）415- （B ）415 （C ）83- （D ）83 【6】．如下图，在△ABC 中，D 是边AC 上的点，且AB AD =，2,2AB BC BD ==，则C sin 的值为（）. （A ）33 (B) 63 (C) 36 (D) 66【7】．已知4.3log 25=a ，6.3log 45=b ，3.0log 351⎪⎭⎫ ⎝⎛=c ，则（）.（A ）c b a >>（B ）c a b >>（C ）b c a >> （D ）b a c >>【8】．对实数a 与b ，定义新运算“⊗”：,1,,1.aab a b b a b -≤⎧⊗=⎨->⎩ 设函数)()2()(22x x x x f -⊗-=R ∈x ,，若函数()y f x c =-的图像与x 轴恰有两个公共点，则实数c 的取值范围是（）.（A ）(]3,21,2⎛⎫-∞-⋃- ⎪⎝⎭ （B ）(]3,21,4⎛⎫-∞-⋃-- ⎪⎝⎭（C ）111,,44⎛⎫⎛⎫-⋃+∞ ⎪ ⎪⎝⎭⎝⎭ （D ）311,,44⎛⎫⎡⎫--⋃+∞ ⎪⎪⎢⎝⎭⎣⎭【填空题】【9】．一支田径队有男运动员48人，女运动员36人.若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，则抽取男运动员的人数为___________.【10】．一个几何体的三视图如下图所示（单位：m ），则该几何体的体积为__________3m .【11】．已知抛物线C 的参数方程为28,8x t y t ⎧=⎨=⎩，（t 为参数）．若斜率为1的直线经过抛物线C 的焦点，且与圆()2224(0)x y r r -+=>相切，则r =________.【12】．如下图，已知圆中两条弦AB 与CD 相交于点F ，E 是AB 延长线上一点，且::4:2:1.DF CF AF FB BE ===若CE 与圆相切，则线段CE 的长为__________.【13】．已知集合|4||3| |{-++∈=x x x A R ≤19},|46,(0,)B x x t t t ⎧⎫=∈=+-∈+∞⎨⎬⎩⎭R ，则集合A B ⋂=________.【14】．已知直角梯形ABCD 中，P BC AD ADC BC AD ,1,2,90,//==︒=∠是腰DC 上的动点，则|3|PB PA +的最小值为______. 【解答题】【15】．已知函数π()tan(2).4f x x =+（Ⅰ）求()f x 的定义域与最小正周期；（Ⅱ）设π0,4α⎛⎫∈ ⎪⎝⎭，若()2cos 2,2f αα=求α的大小. 【16】．学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖.（每次游戏结束后将球放回原箱）（Ⅰ）求在一次游戏中，（i ）摸出3个白球的概率；（ii ）获奖的概率；（Ⅱ）求在两次游戏中获奖次数X 的分布列及数学期望()E X .【17】．如下图，在三棱柱111ABC A B C -中，H 是正方形11AA B B 的中心，1AA =1C H ⊥平面11AA B B ，且1C H=（Ⅰ）求异面直线AC 与11A B 所成角的余弦值；（Ⅱ）求二面角111B C A A --的正弦值；（Ⅲ）设N 为棱11B C 的中点，点M 在平面11AA B B 内，且MN ⊥平面111A B C ，求线段BM 的长.【18】．在平面直角坐标系xOy 中，点(,)P a b (0)a b >>为动点，12,F F 分别为椭圆22221x y a b +=的左、右焦点．已知△12F PF 为等腰三角形．（Ⅰ）求椭圆的离心率e ；（Ⅱ）设直线2PF 与椭圆相交于,A B 两点，M 是直线2PF 上的点，满足2AM BM ⋅=-，求点M 的轨迹方程. 【19】．已知0a >，函数2()ln ,0.f x x ax x =->（()f x 的图像连续不断）（Ⅰ）求()f x 的单调区间；（Ⅱ）当18a =时，证明：存在0(2,)x ∈+∞，使03()()2f x f =；（Ⅲ）若存在均属于区间[]1,3的,αβ，且βα-≥1，使()()f f αβ=，证明ln 3ln 25-≤a ≤ln 23. 【20】．已知数列{}n a 与{}n b 满足1123(1)0,2nn n n n n n b a a b a b ++++-++==，*n ∈N ，且122,4a a ==.（Ⅰ）求345,,a a a 的值；（Ⅱ）设121-2++=n n n a a c ，n ∈*N ，证明{}n c 是等比数列；（Ⅲ）设242,,kk S a a a k =++⋅⋅⋅+∈*N 证明：417()6nk k kS n a =<∈∑*N .【参考答案】【1】．B 提示：i 22i24)i 1)(i 1()i 1)(i 31(i 1i 31-=-=+-+-=--.故选（B ）. 【2】．A提示：充分性显然成立，而存在反例43122≥+，可知必要性不成立.故选（A ）. 【3】．B提示：根据条件执行4次，过程如下：当1=i 时，2a =，不合题意；当2=i 时，5=a ，不合题意；当3=i 时，16=a ，不合题意；当4=i 时，65=a ，适合题意. 故应选（B ）. 【4】．D提示：⎩⎨⎧-=⋅=，，29327d a a a 解得201=a ，则110291010110=⨯⨯+=d a S . 【5】．C提示：6326166C ((1)C 2rr r r r r r r T x ---+==-，令23=-r ，则,1=r 故2x 的系数为1463C (1)28--⨯=-. 【6】．D提示：设x AB =，则,332,x BD x AD ==可求31co s =A ,那么322s i n =A ,又A C BC AB sin sin 43==,求得66sin =C .【7】．C提示：首先确定16.3log 04<<，则5<b ，而310log 3.0log 33551=⎪⎭⎫⎝⎛=c ，又1310log 4.3log 4.3log 332>>>，从而5>>c a ，故选（C ）. 【8】．B提示：解1)()2(22≤---x x x ，得1-≤x ≤32，则⎪⎪⎩⎪⎪⎨⎧>-<-≤≤--=.231,,231,2)(22x x x x x x x f 或如下图,由图像可看出函数c y =与函数有两个交点时，c 的取值范围为(]3,21,4⎛⎫-∞-⋃-- ⎪⎝⎭.故应选（B ）.【9】．12提示：男女比例为：4:3，则样本中抽取男运动员的人数为127421=⨯. 【10】．π6+提示：根据所给的几何体的三视图，可以想到这个几何体是一个复合体.底座是一个长、宽、高分别为3,2,1的长方体，上面是一个半径为1的圆锥，且底面是长方体的上地面的内切圆,可得π63π31123+=⨯⨯+⨯⨯=V .【11】．2提示：抛物线方程为x y 82=，那么直线方程为2-=x y ，由相切可得：22|24|==-r .【12】．27提示：设,x BE =则,2,4x FB x AF ==圆的相交弦定理得FC DF FB AF ⋅=⋅,解得.21=x 由切割线定理知，2,CE EB EA =⋅解得27=CE . 【13】．2|{-x ≤x ≤5} 提示：|)4()3(|-++x x ≤|3||4|x x ++-≤9，即|12|-x ≤9，可得4|{-∈=R x A ≤x ≤5}，而x x B |{=≥2}-,所以A B ⋂=2|{-x ≤x ≤5}.【14】．5提示：建立直角坐标系如下图所示，则),0,2(A 设),0(),,0(a C y P ，),1(a B ，那么),1(),,2(y a PB y PA -=-=，)43,5(3y a -=+，从而22)43(25|3|y a PB PA -+=+≥25，当且仅当a y 43=时，取等号.【15】．解（Ⅰ）因为由ππ2π,42x k k +≠+∈Z, 得ππ,82k x k ≠+∈Z . 所以()f x 的定义域为ππ{|,}82k x x k ∈≠+∈R Z . ()f x 的最小正周期为π.2（Ⅱ）由()2cos 2,2f αα=得πtan()2cos 2,4αα+= 即22πsin()42(cos sin ),πcos()4αααα+=-+ 整理得sin cos 2(cos sin )(cos sin ).cos sin αααααααα+=+--因为π(0,)4α∈，所以sin cos 0.αα+≠因此21(cos sin ),2αα-=即1sin 2.2α= 由π(0,)4α∈，得π2(0,)2α∈.所以π2,6α=即π.12α=【16】．解：（Ⅰ）（i ）设“在1次游戏中摸出i 个白球”为事件(0,1,2,3),i A i =则213232253C C 1().C C 5P A =⋅= （ii ）设“在1次游戏中获奖”为事件B ，则23B A A =，又2112133222222225353C C C C C 1(),C C C C 2P A =⋅+⋅= 且23A A ，互斥，所以23117()()().2510P B P A P A =+=+= （Ⅱ）由题意可知X 的所有可能取值为0，1，2.212279(0)(1),101007721(1)C (1),101050749(2)().10100P X P X P X ==-===⨯-====XX的数学期望()012.100501005E X =⨯+⨯+⨯=【17】．解：如下图所示，建立空间直角坐标系，点B为坐标原点.依题意得111A B C ,(0,0,0),A B C ,（Ⅰ）易得11(2,2,5),(22,0,0)AC AB =--=-，于是111111cos,3||||3AC A B AC A B AC A B ⋅===⋅⨯所以异面直线AC 与11A B （Ⅱ）易知111(0,22,0),(2,AA AC ==-设平面11AAC 的法向量(,,)x y z=m ，则11100.AC AA ⎧⋅=⎪⎨⋅=⎪⎩，m m即0,0.⎧+=⎪⎨=⎪⎩不妨令x =可得=m ，同样地，设平面111A B C 的法向量(,,)x y z =n ，则11110,0.AC A B ⎧⋅=⎪⎨⋅=⎪⎩n n即0,0.⎧+=⎪⎨-=⎪⎩不妨令y =可得=n于是2cos,,||||7⋅===⋅m n m n mn从而sin ,=m n 所以二面角111A AC B --（Ⅲ）由N 为棱11B C 的中点，得N 设(,,0)M a b ，则2(,,222MNa b =--. 由MN ⊥平面111A B C ，得11110,0.MN A BMN AC ⋅=⎧⎨⋅=⎩即)(0,()(()(0.222a ab ⎧-⨯-=⎪⎪⎨⎪-⨯+-⨯+=⎪⎩解得4a b ⎧=⎪⎪⎨⎪=⎪⎩故M因此2(24BM=，所以线段BM 的长为10||BM = 【18】．解：（Ⅰ）设12(,0),(,0)(0)F c F c c ->.由题意，可得212||||,PF F F =即2.c = 整理得22()10,1cc c aa a +-==-得（舍），或1.2c a =所以1.2e = （Ⅱ）由（Ⅰ）知2,,a c b ==可得椭圆方程为2223412,x y c +=直线2PF方程为).y x c =-,A B 两点的坐标满足方程组2223412,).x y c y x c ⎧+=⎪⎨=-⎪⎩消去y 并整理，得2580.x cx -=解得1280,.5x x c ==所以方程组的解21128,0,5,.x c x y y ⎧=⎪=⎧⎪⎪⎨⎨=⎪⎪⎩=⎪⎩不妨设8(),(0,)5A c B 设点M的坐标为833(,),(,),(,)55xy AMx c y c BM x y =--=则，由),.3y x c c x y =-=-得于是838(,),55AM y x y x =--().BM x=由2,AM BM ⋅=- 即38)()255y x x y x -⋅+=-，化简得218150.x --=将22105,0.16x y c x y c x +===>得所以0.x >因此，点M 的轨迹方程是218150(0).xx --=>【19】．（Ⅰ）解：2112()2,(0,)ax f x ax x x x-'=-=∈+∞. 令()0,f x '=解得2x a=当x 变化时，(),()f x f x '的变化情况如下表：所以，()f x 的单调递增区间是()f x 的单调递减区间是).+∞ （Ⅱ）证明：当211,()ln .88a f x x x ==-时由（Ⅰ）知()f x 在（0，2）内单调递增，在(2,)+∞内单调递减. 令3()()().2g x f x f =-由于()f x 在（0，2）内单调递增，故3(2)(),2f fg >即(2)>0.取23419e e 2,()0232x g x -''=>=<则，所以存在00(2,),()0,x x g x '∈=使即存在003(2,),()().2x f x f ∈+∞=使（说明：x '的取法不唯一，只要满足2,()0x g x ''><且即可）.（Ⅲ）证明：由()()f f αβ=及（I ）的结论知αβ<<，从而()[,]f x αβ在上的最小值为().f α又由βα-≥1，,[1,3],αβ∈知1≤α≤2≤β≤3.故(2)()(1),ln 24,(2)()(3).ln 24ln39.f f f a a f f f a a αβ≥≥-≥-⎧⎧⎨⎨≥≥-≥-⎩⎩即从而ln 3ln 25-≤a ≤ln 2.3【20】．（Ⅰ）解：由*3(1),,2nn b n +-=∈N 可得1,n n b n ⎧=⎨⎩为奇数，2,为偶数.又1120,n n n n n b a a b a +++++=123123234434553;5;4.n a a a a a a n a a a a n a a a a =-=-=当=1时,++2=0,由=2,=4,可得当=2时,2++=0,可得当=3时,++2=0,可得（Ⅱ）证明：对任意*,n ∈N2122120,n n n a a a -+++= ① 2212220,n n n a a a ++++= ② 21222320.n n n a a a +++++= ③②-③，得223.nn a a += ④将④代入①，可得21232121()n n n n a a a a ++-++=-+，即*1()n n c c n +=-∈N ,又1131,0,n c a a c =+=-≠故因此11,n nc c +=-所以{}n c 是等比数列. （Ⅲ）证明：由（Ⅱ）可得2121(1)k k k a a -++=-，于是，对任意*k k ∈N 且≥2，有133********,()1,1,(1)() 1.k k k a a a a a a a a --+=--+=-+=--+=-将以上各式相加，得121(1)(1),kk a a k -+-=--即121(1)(1)k k a k +-=-+，此式当k =1时也成立. 由④式得12(1)(3).k k a k +=-+从而22468424()()(),kk k S a a a a a a k -=++++++=-2124 3.k k k S S a k -=-=+所以，对任意*,n n ∈N≥2，44342414114342414()nnk m m m mk m k m m m mS S S S S a a a a a ---==---=+++∑∑ 12221232()2222123nm m m m mm m m m =+-+=--++++∑ 123()2(21)(22)(22)nm m m m m ==++++∑2253232(21)(22)(23)nm m m n n ==++⨯+++∑21533(21)(21)(22)(23)n m m m n n =<++-+++∑ (151111113()())]3235572121(22)(23)n n n n =+⨯-+-++-+-+++ 155137.36221(22)(23)6n n n =+-⨯+<+++ 对于n =1，不等式显然成立. 【End 】。

2011年高考数学(理)真题(Word版)——天津卷(试题+答案解析)

2011年普通高等学校招生全国统一考试（天津卷）数学（理）试题本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

第Ⅰ卷参考公式：如果事件A ，B 互斥，那么如果事件A ，B 相互独立，那么()()()P A B P A P B =+()()().P AB P A P B =棱柱的体积公式.V Sh =圆锥的体积公式1.3V Sh =其中S 表示棱柱的底面面积其中S 表示圆锥的底面面积 h 表示棱柱的高 h 表示圆锥的高一、选择题：在每小题给出的四个选项中只有一项是符合题目要求的． 1．i 是虚数单位，复数131ii--= A ．2i + B ．2i -C ．12i -+D ．12i --2．设,,x y R ∈则“2x ≥且2y ≥”是“224x y +≥”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．即不充分也不必要条件 3．阅读右边的程序框图，运行相应的程序，则输出i 的值为 A ．3 B ．4 C ．5 D ．6 4．已知{}n a 为等差数列，其公差为-2，且7a 是3a 与9a 的等比中项，n S 为{}n a 的前n 项和，*n N ∈，则10S 的值为A ．-110B ．-90C ．90D ．1105．在622x x ⎛⎫- ⎪ ⎪⎝⎭的二项展开式中，2x 的系数为 A ．154- B ．154 C ．38- D ．386．如图，在△ABC 中，D 是边AC 上的点，且AB=AD ，2AB=BD ，BC=2BD ，则sin C的值为A ．33B ．36 C ．63D ．667．已知324log 0.3log 3.4log 3.615,5,,5a b c ⎛⎫=== ⎪⎝⎭则A ．a b c >>B ．b a c >>C ．a c b >>D ．c a b >>8．对实数a 和b ，定义运算“⊗”：,1,, 1.a a b a b b a b -≤⎧⊗=⎨->⎩设函数()()22()2,.f x x x x x R =-⊗-∈若函数()y f x c =-的图像与x 轴恰有两个公共点，则实数c 的取值范围是A ．(]3,21,2⎛⎫-∞-⋃- ⎪⎝⎭B ．(]3,21,4⎛⎫-∞-⋃--⎪⎝⎭ C ．111,,44⎛⎫⎛⎫-⋃+∞ ⎪ ⎪⎝⎭⎝⎭D ．311,,44⎛⎫⎡⎫--⋃+∞ ⎪⎪⎢⎝⎭⎣⎭第II 卷二、填空题：本大题共6小题，每小题5分，共30分．9．一支田径队有男运动员48人，女运动员36人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，则抽取男运动员的人数为___________ 10．一个几何体的三视图如右图所示（单位：m ），则该几何体的体积为__________3m11．已知抛物线C 的参数方程为28,8.x t y t ⎧=⎨=⎩（t 为参数）若斜率为1的直线经过抛物线C 的焦点，且与圆()2224(0)x y r r -+=>相切，则r =________.12．如图，已知圆中两条弦AB 与CD 相交于点F ，E 是AB 延长线上一点，且2,::4:2:1.DF CF AF FB BE ===若CE 与圆相切，则线段CE 的长为__________.13．已知集合{}1|349,|46,(0,)A x R x x B x R x t t t⎧⎫=∈++-≤=∈=+-∈+∞⎨⎬⎩⎭，则集合A B ⋂=________.14．已知直角梯形ABCD 中，AD //BC ,090ADC ∠=,2,1AD BC ==,P 是腰DC 上的动点，则3PA PB +的最小值为____________.三、解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤． 15．（本小题满分13分）已知函数()tan(2),4f x x π=+（Ⅰ）求()f x 的定义域与最小正周期；（II ）设0,4πα⎛⎫∈ ⎪⎝⎭，若()2cos 2,2f αα=求α的大小．16．（本小题满分13分）学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）（Ⅰ）求在1次游戏中，（i ）摸出3个白球的概率；（ii ）获奖的概率；（Ⅱ）求在2次游戏中获奖次数X 的分布列及数学期望()E X . 17．（本小题满分13分）如图，在三棱柱111ABC A B C -中，H 是正方形11AA B B 的中心，122AA =，1C H ⊥平面11AAB B ，且1 5.C H =（Ⅰ）求异面直线AC 与A 1B 1所成角的余弦值；（Ⅱ）求二面角111A AC B --的正弦值；（Ⅲ）设N 为棱11B C 的中点，点M 在平面11AA B B 内，且MN ⊥平面11A B C ，求线段BM 的长．18．（本小题满分13分）在平面直角坐标系xOy 中，点(,)P a b (0)a b >>为动点，12,F F 分别为椭圆22221x y a b+=的左右焦点．已知△12F PF 为等腰三角形．（Ⅰ）求椭圆的离心率e ；（Ⅱ）设直线2PF 与椭圆相交于,A B 两点，M 是直线2PF 上的点，满足2AM BM ⋅=-，求点M 的轨迹方程．19．（本小题满分14分）已知0a >，函数2()ln ,0.f x x ax x =->（()f x 的图像连续不断）（Ⅰ）求()f x 的单调区间；（Ⅱ）当18a =时，证明：存在0(2,)x ∈+∞，使03()()2f x f =；（Ⅲ）若存在均属于区间[]1,3的,αβ，且1βα-≥，使()()f f αβ=，证明ln 3ln 2ln 253a -≤≤．20．（本小题满分14分）已知数列{}n a 与{}n b 满足：1123(1)0,2n n n n n n n b a a b a b ++++-++==， *n ∈N ，且122,4a a ==．（Ⅰ）求345,,a a a 的值；（Ⅱ）设*2121,n n n c a a n N -+=+∈，证明：{}n c 是等比数列；（III ）设*242,,k k S a a a k N =++⋅⋅⋅+∈证明：4*17()6nk k kS n N a =<∈∑．答案解析一、选择题( 本大题共8 题, 共计40 分)1、(5分) B.2、(5分) A∵x≥2，∴x2≥4.∵y≥2，∴y2≥4.∴x2＋y2≥8≥4.∴x≥2且y≥2?x2＋y2≥4，反之令x2＋y2＝5≥4，可取x＝2，y＝1，无法推出y≥2.故选A项．3、(5分) B第一次运算：i＝1，a＝2，a＜50；第二次运算：i＝2，a＝5，a＜50；第三次运算：i＝3，a ＝16，a＜50；第四次运算：i＝4，a＝65，a＞50.所以输出i＝4.4、(5分) D设等差数列{a n}的首项为a，公差d＝－2.则a7＝a1＋6d＝a1－12；a3＝a1＋2d＝a1－4；a9＝a1＋8d＝a1－16.∵a7是a3与a9的等比中项，∴＝a3·a9，∴(a1－12)2＝(a1－4)(a1－16)，∴a1＝20.∴S10＝10a1＋d＝110.5、(5分) C设含x2的项是二项展开式中第r＋1项，则.令3－r＝2，得r＝1.∴x2的系数为.6、(5分) D设BD＝a，则BC＝2a，AB＝AD＝A．在△ABD中，由余弦定理，得cos A＝＝＝.又∵A为△ABC的内角，∴sin A＝.在△ABC中，由正弦定理得，.∴sin C＝·sin A＝·＝.7、(5分) C，log23.4＞log22＝1，log43.6＜log44＝1，＞log3 3＝1，又log23.4＞＞，∴log23.4＞＞log43.6.又∵y＝5x是增函数，∴a＞c＞b．8、(5分) B由题意得，即在同一坐标系内画出函数y＝f(x)与y＝c的图象如图所示，结合图象可知，当c∈(－∞，－2]∪(－1，)时两个函数的图象有两个公共点，从而方程f(x)－c＝0有两个不同的根，即y＝f(x)－c与x轴有两个不同交点．二、填空题( 本大题共6 题, 共计30 分)9、(5分) 12解析：设抽取男运动员人数为n，则女运动员人数21－n.由分层抽样知：，∴n＝12.10、(5分) 6＋π解析：由几何体的三视图可知，原几何体是一个长方体和一个圆锥的组合体．下面的长方体的长、宽、高分别是3 m，2 m，1 m，∴体积为3×2×1＝6(m3)．上面的圆锥底面圆半径为1 m，高为3 m，∴圆锥的体积为π×12×3＝π(m3)．∴该几何体的体积为(6＋π) m3.11、(5分)解析：消去参数t，得抛物线标准方程y2＝8x，其焦点F(2，0)，∴过抛物线焦点斜率为1的直线方程：x－y－2＝0，∵直线与圆(x－4)2＋y2＝r2相切，∴r＝d＝.12、(5分)解析：设BE＝m，则BF＝2m，AF＝4m.∵AB与CD是圆的两条相交弦，交点为F，∴由相交弦定理，得AF·FB＝CF·FD＝＝2，∴4m·2m＝2，∴m2＝.又∵CE是圆的切线，根据切割弦定理，得CE2＝EB·EA＝m(m＋2m＋4m)＝7m2＝，∴CE＝.13、(5分) {x|－2≤x≤5}解析：解不等式|x＋3|＋|x－4|≤9.(1)当x＜－3时，|x＋3|＋|x－4|＝－x－3＋4－x≤9，∴x≥－4，即－4≤x＜－3；(2)当－3≤x≤4时，|x＋3|＋|x－4|＝x＋3＋4－x≤9恒成立，∴－3≤x≤4；(3)当x＞4时，|x＋3|＋|x－4|＝x＋3＋x－4≤9，∴x≤5，即4＜x≤5.综上所述，A＝{x∈R|－4≤x≤5}．∵t∈(0，＋∞)，∴x＝4t＋－6≥2－6＝－2，当且仅当t＝时等号成立．∴B＝{x∈R|x≥－2}．∴A∩B＝{x∈R|－4≤x≤5}∩{x∈R|x≥－2}＝{x∈R|－2≤x≤5}．14、(5分) 5解析：根据题意，以AD为x轴，DC为y轴，建立平面直角坐标系，如图所示．∵AD＝2，∴A(－2，0)．∵BC＝1，∴可设B(－1，n)．∴点P在DC上运动，∴可设P(0，y)(0≤y≤n)．∴＝(－2，－y)，＝(－1，n－y)，∴＝(－5，3n－4y)．∴.∴当3n＝4y，即y＝n时，取得最小值5.三、解答题( 本大题共6 题, 共计80 分)15..解：（1）由，得，所以f(x)的定义域为．f(x)的最小正周期为（2）由得，，整理得．因为，所以.因此由，得．所以16.解：（1）①设“在1次游戏中摸出i个白球”为事件A i(i＝0，1，2，3)，则②设“在1次游戏中获奖”为事件B，则B＝A2∪A3.又且A2，A3互斥，所以.（2）由题意可知X的所有可能取值为0，1，2.所以X的分布列是X0 1 2PX的数学期望17. 解：(方法1)如图所示，建立空间直角坐标系，点B为坐标原点.依题意得（1）解：易得，于是所以异面直线AC与A1B1所成角的余弦值为（2）解：易知设平面AA1C1的法向量，则即不妨令可得，同样地，设平面A1B1C1的法向量，则即不妨令，可得于是从而所以二面角A—A1C1—B的正弦值为（3）解：由N为棱B1C1的中点，得设M（a，b，0），则由平面A1B1C1，得即解得故因此，所以线段BM的长为(方法2)（1）解：由于AC//A1C1，故是异面直线AC与A1B1所成的角. 因为平面AA1B1B，又H为正方形AA1B1B的中心，可得因此所以异面直线AC与A1B1所成角的余弦值为（2）解：连接AC1，易知AC1=B1C1，又由于AA1=B1A1，A1C1=A1=C1，所以≌，过点A作于点R，连接B1R，于是，故为二面角A—A1C1—B1的平面角. 在中，连接AB1，在中，，从而所以二面角A—A1C1—B1的正弦值为（3）解：因为平面A1B1C1，所以取HB1中点D，连接ND，由于N是棱B1C1中点，所以ND//C1H且.又平面AA1B1B，所以平面AA1B1B，故又所以平面MND，连接MD并延长交A1B1于点E，则由得，延长EM交AB于点F，可得连接NE.在中，所以可得连接BM，在中，18. 解：（1）设F1(－c，0)，F2(c，0)(c＞0)．由题意，可得|PF2|＝|F1F2|，即整理得(舍)，或，所以.（2）由(1)知，可得椭圆方程为3x2＋4y2＝12c2，直线PF2方程为．A，B两点的坐标满足方程组，消去y并整理，得5x2－8cx＝0.解得得方程组的解.不妨设．设点M的坐标为．由于是由，即，化简得将，所以x＞0.因此，点M的轨迹方程是18x2－16xy－15＝0(x＞0)．19. 解：（1）．令.当x变化时，f′(x)，f(x)的变化情况如下表：xf′(x) ＋0 －f(x) ↗极大值↘所以，f(x)的单调递增区间是的单调递减区间是．（2）证明：当由(1)知f(x)在(0，2)内单调递增，在(2，＋∞)内单调递减．令由于f(x)在(0，2)内单调递增，故.取所以存在x0∈(2，x′)，使g(x0)＝0，即存在(说明：x′的取法不唯一，只要满足x′＞2，且g(x′)＜0即可．)（3）证明：由f(α)＝f(β)及(1)的结论知，从而f(x)在[α，β]上的最小值为f(α)．又由β－α≥1，α，β∈[1，3]，知1≤α≤2≤β≤3.故从而20. 解：（1）由可得又b n a n＋a n＋1＋b n＋1a n＋2＝0，当n＝1时，a1＋a2＋2a3＝0，由a1＝2，a2＝4，可得a3＝－3；当n＝2时，2a2＋a3＋a4＝0，可得a4＝－5；当n＝3时，a3＋a4＋2a5＝0，可得a5＝4.（2）证明：对任意n∈N*，a2n－1＋a2n＋2a2n＋1＝0，①2a2n＋a2n＋1＋a2n＋2＝0，②a2n＋1＋a2n＋2＋2a2n＋3＝0.③②－③，得a2n＝a2n＋3.④将④代入①，可得a2n＋1＋a2n＋3＝－(a2n－1＋a2n＋1)．即c n＋1＝－c n(n∈N*)．又c1＝a1＋a3＝－1，故c n≠0，因此是等比数列．（3）证明：由(2)可得a2k－1＋a2k＋1＝(－1)k，于是，对任意k∈N*且k≥2，有a1＋a3＝－1，－(a3＋a5)＝－1，a5＋a7＝－1，(－1)k(a2k－3＋a2k－1)＝－1.将以上各式相加，得a1＋(－1)k a2k－1＝－(k－1)，即a2k－1＝(－1)k＋1(k＋1)，此式当k＝1时也成立．由④式得a2k＝(－1)k＋1·(k＋3)．从而S2k＝(a2＋a4)＋(a6＋a8)＋…＋(a4k－2＋a4k)＝－k，S2k－1＝S2k－a4k＝k＋3所以，对任意n∈N*，n≥2，对于n＝1，不等式显然成立．。

2011年天津市高考数学试卷(理科)及答案

2011年天津市高考数学试卷（理科）一、选择题（共8小题，每小题5分，满分40分）1．（5分）i是虚数单位，复数=（）A．2+i B．2﹣i C．﹣1+2i D．﹣1﹣2i2．（5分）设x，y∈R，则“x≥2且y≥2”是“x2+y2≥4”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件3．（5分）阅读程序框图，运行相应的程序，则输出i的值为（）A．3 B．4 C．5 D．64．（5分）已知{a n}为等差数列，其公差为﹣2，且a7是a3与a9的等比中项，S n 为{a n}的前n项和，n∈N*，则S10的值为（）A．﹣110 B．﹣90 C．90 D．1105．（5分）在的二项展开式中，x2的系数为（）A．B．C．D．6．（5分）如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=BD，BC=2BD，则sinC的值为（）A．B．C．D．7．（5分）已知，则（）A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞a＞b8．（5分）对实数a与b，定义新运算“⊗”：．设函数f（x）=（x2﹣2）⊗（x﹣x2），x∈R．若函数y=f（x）﹣c的图象与x轴恰有两个公共点，则实数c的取值范围是（）A．B．C． D．二、填空题（共6小题，每小题5分，满分30分）9．（5分）一支田径队有男运动员48人，女运动员36人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，则抽取男运动员的人数为．10．（5分）一个几何体的三视图如图所示（单位：m），则这个几何体的体积为m3．11．（5分）已知抛物线C的参数方程为（t为参数），若斜率为1的直线经过抛物线C的焦点，且与圆（x﹣4）2+y2=r2（r＞0）相切，则r=．12．（5分）如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=，AF：FB：BE=4：2：1．若CE与圆相切，则CE的长为．13．（5分）已知集合A={x∈R||x+3|+|x﹣4|≤9}，B=，则集合A∩B=．14．（5分）已知直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=1，P是腰DC上的动点，则|+3|的最小值为．三、解答题（共6小题，满分80分）15．（13分）已知函数f（x）=tan（2x+），（1）求f（x）的定义域与最小正周期；（2）设α∈（0，），若f（）=2cos2α，求α的大小．16．（13分）学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）（Ⅰ）求在1次游戏中，（i）摸出3个白球的概率；（ii）获奖的概率；（Ⅱ）求在2次游戏中获奖次数X的分布列及数学期望E（X）．17．（13分）如图所示，在三棱柱ABC﹣A1B1C1中，H是正方形AA1B1B的中心，AA1=2，C1H⊥平面AA1B1B，且C1H=．（1）求异面直线AC与A1B1所成角的余弦值；（2）求二面角A﹣A1C1﹣B1的正弦值；（3）设N为棱B1C1的中点，点M在平面AA1B1B内，且MN⊥平面A1B1C1，求线段BM的长．18．（13分）在平面直角坐标系xOy中，点P（a，b）（a＞b＞0）为动点，F1，F2分别为椭圆的左、右焦点．已知△F1PF2为等腰三角形．（Ⅰ）求椭圆的离心率e；（Ⅱ）设直线PF2与椭圆相交于A，B两点，M是直线PF2上的点，满足，求点M的轨迹方程．19．（14分）已知a＞0，函数f（x）=lnx﹣ax2，x＞0．（f（x）的图象连续不断）（Ⅰ）当a=时①求f（x）的单调区间；②证明：存在x0∈（2，+∞），使f（x0）=f（）；（Ⅱ）若存在均属于区间[1，3]的α，β，且β﹣α≥1，使f（α）=f（β），证明．20．（14分）已知数列{a n}与{b n}满足：，n∈N*，且a1=2，a2=4．（Ⅰ）求a3，a4，a5的值；（Ⅱ）设c n=a2n﹣1+a2n+1，n∈N*，证明：{c n}是等比数列；（Ⅲ）设S k=a2+a4+…+a2k，k∈N*，证明：．2011年天津市高考数学试卷（理科）参考答案与试题解析一、选择题（共8小题，每小题5分，满分40分）1．（5分）（2011•天津）i是虚数单位，复数=（）A．2+i B．2﹣i C．﹣1+2i D．﹣1﹣2i【分析】要求两个复数的除法运算，分子和分母同乘以分母的共轭复数，分子和分母上进行复数的乘法运算，最后结果要化简成最简形式．【解答】解：复数===2﹣i故选B．2．（5分）（2011•天津）设x，y∈R，则“x≥2且y≥2”是“x2+y2≥4”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【分析】由“x≥2且y≥2”推出“x2+y2≥4”可证明充分性；由满足“x2+y2≥4”可举出反例推翻“x≥2且y≥2”，则证明不必要性，综合可得答案．【解答】解：若x≥2且y≥2，则x2≥4，y2≥4，所以x2+y2≥8，即x2+y2≥4；若x2+y2≥4，则如（﹣2，﹣2）满足条件，但不满足x≥2且y≥2．所以“x≥2且y≥2”是“x2+y2≥4”的充分而不必要条件．故选A．3．（5分）（2011•天津）阅读程序框图，运行相应的程序，则输出i的值为（）A．3 B．4 C．5 D．6【分析】通过程序框图的要求，写出前四次循环的结果得到输出的值．【解答】解：该程序框图是循环结构经第一次循环得到i=1，a=2；经第二次循环得到i=2，a=5；经第三次循环得到i=3，a=16；经第四次循环得到i=4，a=65满足判断框的条件，执行是，输出4故选B4．（5分）（2011•天津）已知{a n}为等差数列，其公差为﹣2，且a7是a3与a9的等比中项，S n为{a n}的前n项和，n∈N*，则S10的值为（）A．﹣110 B．﹣90 C．90 D．110【分析】通过a7是a3与a9的等比中项，公差为﹣2，求出【解答】解：a7是a3与a9的等比中项，公差为﹣2，所以a72=a3•a9，∵{a n}公差为﹣2，∴a3=a7﹣4d=a7+8，a9=a7+2d=a7﹣4，所以a72=（a7+8）（a7﹣4），所以a7=8，所以a1=20，所以S10==110故选D5．（5分）（2011•天津）在的二项展开式中，x2的系数为（）A．B．C．D．【分析】利用二项展开式的通项公式求出展开式的通项，令x的指数为2，求出展开式中，x2的系数，即得答案．=（﹣1）r22r﹣6C6r x3﹣r【解答】解：展开式的通项为T r+1令3﹣r=2得r=1所以项展开式中，x2的系数为﹣故选C6．（5分）（2011•天津）如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=BD，BC=2BD，则sinC的值为（）A．B．C．D．【分析】根据题中条件，在△ABD中先由余弦定理求出cosA，利用同角关系可求sinA，利用正弦定理可求sin∠BDC，然后在△BDC中利用正弦定理求解sinC 即可【解答】解：设AB=x，由题意可得AD=x，BD=△ABD中，由余弦定理可得∴sinA=△ABD中，由正弦定理可得⇒sin∠ADB=∴△BDC中，由正弦定理可得故选：D．7．（5分）（2011•天津）已知，则（）A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞a＞b【分析】比较大小的方法：找1或者0做中介判断大小，log43.6＜1，log23.4＞1，利用分数指数幂的运算法则和对数的运算法则对c进行化简，得到＞1＞b，再借助于中间值log2进行比较大小，从而得到结果．，【解答】解：∵log23.4＞1，log43.6＜1，又y=5x是增函数，∴a＞b，＞==b而log23.4＞log2＞log3，∴a＞c故a＞c＞b．故选C．8．（5分）（2011•天津）对实数a与b，定义新运算“⊗”：．设函数f（x）=（x2﹣2）⊗（x﹣x2），x∈R．若函数y=f（x）﹣c的图象与x轴恰有两个公共点，则实数c的取值范围是（）A．B．C． D．【分析】根据定义的运算法则化简函数f（x）=（x2﹣2）⊗（x﹣x2）的解析式，并求出f（x）的取值范围，函数y=f（x）﹣c的图象与x轴恰有两个公共点转化为y=f（x），y=c图象的交点问题，结合图象求得实数c的取值范围．【解答】解：∵，∴函数f（x）=（x2﹣2）⊗（x﹣x2）=，由图可知，当c∈函数f（x）与y=c的图象有两个公共点，∴c的取值范围是，故选B．二、填空题（共6小题，每小题5分，满分30分）9．（5分）（2011•天津）一支田径队有男运动员48人，女运动员36人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，则抽取男运动员的人数为12．【分析】根据田径队的男女运动员数目和用分层抽样要抽取的数目，得到每个个体被抽到的概率，利用每个个体被抽到的概率乘以男运动员的数目，得到结果．【解答】解：∵田径队有男运动员48人，女运动员36人，∴这支田径队共有48+36=84人，用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，∴每个个体被抽到的概率是，∵田径队有男运动员48人，∴男运动员要抽取48×=12人，故答案为：12．10．（5分）（2011•天津）一个几何体的三视图如图所示（单位：m），则这个几何体的体积为6+πm3．【分析】由已知中的三视图，我们易判断已知中几何体的形状，然后根据已知的三视图分析出几何体的相关几何量，代入体积公式，即可求出该几何体的体积．【解答】解：由已知可得已知的几何体是一个圆锥和长方体的组合体其中上部的圆锥的底面直径为2，高为3，下部的长方体长、宽高分别为：2，3，1=•π•3=π则V圆锥V长方体=1×2×3=6则V=6+π故答案为：6+π11．（5分）（2011•天津）已知抛物线C的参数方程为（t为参数），若斜率为1的直线经过抛物线C的焦点，且与圆（x﹣4）2+y2=r2（r＞0）相切，则r=．【分析】由抛物线C的参数方程为我们易求出抛物线的标准方程，进而根据斜率为1的直线经过抛物线C的焦点，且与圆（x﹣4）2+y2=r2（r＞0）相切，我们根据直线与圆相切，则圆心到直线的距离等于半径，求出直线方程后，代入点到直线距离公式，构造关于r的方程，解方程即可得到答案．【解答】解：∵抛物线C的参数方程为则抛物线的标准方程为：y2=8x则抛物线C的焦点的坐标为（2，0）又∵斜率为1的直线经过抛物线C的焦点则直线的方程为y=x﹣2，即经x﹣y﹣2=0由直线与圆（x﹣4）2+y2=r2，则r==故答案为：12．（5分）（2011•天津）如图，已知圆中两条弦AB与CD相交于点F，E是AB 延长线上一点，且DF=CF=，AF：FB：BE=4：2：1．若CE与圆相切，则CE的长为．【分析】设出AF=4k，BF=2k，BE=k，由DF•FC=AF•BF求出k的值，利用切割定理求出CE．【解答】解：设AF=4k，BF=2k，BE=k，由DF•FC=AF•BF，得2=8k2，即k=，∴AF=2，BF=1，BE=，AE=，由切割定理得CE2=BE•EA==，∴CE=．13．（5分）（2011•天津）已知集合A={x∈R||x+3|+|x﹣4|≤9}，B=，则集合A∩B={x|﹣2≤x≤5} ．【分析】求出集合A，求出集合B，然后利用集合的运算法则求出A∩B．【解答】解：集合A={x∈R||x+3|+|x﹣4|≤9}，所以A={x|﹣4≤x≤5}；集合，，当且仅当t=时取等号，所以B={x|x≥﹣2}，所以A∩B={x|﹣4≤x≤5}∩{x|x≥﹣2}={x|﹣2≤x≤5}，故答案为：{x|﹣2≤x≤5}．14．（5分）（2011•天津）已知直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=1，P是腰DC上的动点，则|+3|的最小值为5．【分析】根据题意，利用解析法求解，以直线DA，DC分别为x，y轴建立平面直角坐标系，则A（2，0），B（1，a），C（0，a），D（0，0），设P（0，b）（0≤b≤a），求出，根据向量模的计算公式，即可求得，利用完全平方式非负，即可求得其最小值．【解答】解：如图，以直线DA，DC分别为x，y轴建立平面直角坐标系，则A（2，0），B（1，a），C（0，a），D（0，0）设P（0，b）（0≤b≤a）则=（2，﹣b），=（1，a﹣b），∴=（5，3a﹣4b）∴=≥5．故答案为5．三、解答题（共6小题，满分80分）15．（13分）（2011•天津）已知函数f（x）=tan（2x+），（1）求f（x）的定义域与最小正周期；（2）设α∈（0，），若f（）=2cos2α，求α的大小．【分析】（Ⅰ）利用正切函数的定义域求出函数的定义域，利用周期公式求出最小正周期；（Ⅱ）通过，化简表达式，结合α∈（0，），求出α的大小．【解答】解：（Ⅰ）由2x+≠+kπ，k∈Z．所以x≠，k∈Z．所以f （x）的定义域为：f（x）的最小正周期为：．（Ⅱ）由得tan（）=2cos2α，整理得因为α∈（0，），所以sinα+c osα≠0 因此（cosα﹣sinα）2=即sin2α=因为α∈（0，），所以α=16．（13分）（2011•天津）学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）（Ⅰ）求在1次游戏中，（i）摸出3个白球的概率；（ii）获奖的概率；（Ⅱ）求在2次游戏中获奖次数X的分布列及数学期望E（X）．【分析】（I）（i）甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，事件数是C52C32，摸出3个白球事件数为C32C21C21；由古典概型公式，代入数据得到结果，（ii）获奖包含摸出2个白球和摸出3个白球，且它们互斥，根据（i）求出摸出2个白球的概率，再相加即可求得结果，注意运算要正确，因为第二问要用本问的结果．（II）连在2次游戏中获奖次数X的取值是0、1、2，根据上面的结果，代入公式得到结果，写出分布列，求出数学期望．【解答】解：（Ⅰ）（i）设“在一次游戏中摸出i个白球”为事件A i（i=，0，1，2，3），则P（A3）=，（ii）设“在一次游戏中获奖”为事件B，则B=A2∪A3，又P（A2）=，且A2、A3互斥，所以P（B）=P（A2）+P（A3）=；（Ⅱ）由题意可知X的所有可能取值为0，1，2．P（X=0）=（1﹣）2=，P（X=1）=C21（1﹣）=，P（X=2）=（）2=，所以X的分布列是X012pX的数学期望E（X）=0×．17．（13分）（2011•天津）如图所示，在三棱柱ABC﹣A1B1C1中，H是正方形AA1B1B 的中心，AA1=2，C1H⊥平面AA1B1B，且C1H=．（1）求异面直线AC与A1B1所成角的余弦值；（2）求二面角A﹣A1C1﹣B1的正弦值；（3）设N为棱B1C1的中点，点M在平面AA1B1B内，且MN⊥平面A1B1C1，求线段BM的长．【分析】方法一：如图所示，建立空间直角坐标系，点B为坐标原点．（Ⅰ）求出中的有关向量，然后求出异面直线AC与A1B1所成角的余弦值；（Ⅱ）利用求出平面AA1C1的法向量，通过求出平面A1B1C1的法向量，然后利用求二面角A﹣A1C1﹣B1的正弦值；（Ⅲ）设N为棱B1C1的中点，设M（a，b，0），利用MN⊥平面A1B1C1，结合求出a，b，然后求线段BM的长．方法二：（I）说明∠C1A1B1是异面直线AC与A1B1所成的角，通过解三角形C1A1B1，利用余弦定理，．求出异面直线AC与A1B1所成角的余弦值为．（II）连接AC1，过点A作AR⊥A1C1于点R，连接B1R，说明∠ARB1为二面角A ﹣A1C1﹣B1的平面角．连接AB1，在△ARB1中，通过，求出二面角A﹣A1C1﹣B1的正弦值为．（III）首先说明MN⊥A1B1．取HB1中点D，连接ND，由于N是棱B1C1中点，推出ND⊥A1B1．证明A1B1⊥平面MND，连接MD并延长交A1B1于点E，延长EM 交AB于点F，连接NE．连接BM，在Rt△BFM中，求出．【解答】方法一：如图所示，建立空间直角坐标系，点B为坐标原点．依题意得（I）解：易得，于是，所以异面直线AC与A1B1所成角的余弦值为．（II）解：易知．设平面AA1C1的法向量=（x，y，z），则即不妨令，可得，同样地，设平面A1B1C1的法向量=（x，y，z），则即不妨令，可得．于是，从而．所以二面角A﹣A1C1﹣B的正弦值为．（III）解：由N为棱B1C1的中点，得．设M（a，b，0），则由MN⊥平面A1B1C1，得即解得故．因此，所以线段BM的长为．方法二：（I）解：由于AC∥A1C1，故∠C1A1B1是异面直线AC与A1B1所成的角．因为C 1H⊥平面AA1B1B，又H为正方形AA1B1B的中心，，可得A1C1=B1C1=3．因此．所以异面直线AC与A1B1所成角的余弦值为．（II）解：连接AC1，易知AC1=B1C1，又由于AA1=B1A1，A1C1=A1C1，所以△AC1A1≌△B1C1A1，过点A作AR⊥A1C1于点R，连接B1R，于是B1R⊥A1C1，故∠ARB1为二面角A﹣A1C1﹣B1的平面角．在Rt△A1RB1中，．连接AB1，在△ARB1中，=，从而．所以二面角A﹣A1C1﹣B1的正弦值为．（III）解：因为MN⊥平面A1B1C1，所以MN⊥A1B1．取HB1中点D，连接ND，由于N是棱B1C1中点，所以ND∥C1H且．又C1H⊥平面AA1B1B，所以ND⊥平面AA1B1B，故ND⊥A1B1．又MN∩ND=N，所以A1B1⊥平面MND，连接MD并延长交A1B1于点E，则ME⊥A1B1，故ME∥AA1．由，得，延长EM交AB于点F，可得．连接NE．在Rt△ENM中，ND⊥ME，故ND2=DE•DM．所以．可得．连接BM，在Rt△BFM中，．18．（13分）（2011•天津）在平面直角坐标系xOy中，点P（a，b）（a＞b＞0）为动点，F1，F2分别为椭圆的左、右焦点．已知△F1PF2为等腰三角形．（Ⅰ）求椭圆的离心率e；（Ⅱ）设直线PF2与椭圆相交于A，B两点，M是直线PF2上的点，满足，求点M的轨迹方程．【分析】（Ⅰ）直接利用△F1PF2为等腰三角形得|PF2|=|F1F2|，解其对应的方程即可求椭圆的离心率e；（Ⅱ）先把直线方程与椭圆方程联立，求得A，B两点的坐标，代入，即可求点M的轨迹方程．【解答】解：（Ⅰ）设F1（﹣c，0），F2（c，0）（c＞0）．由题得|PF2|=|F1F2|，即=2c，整理得2+﹣1=0，得=﹣1（舍），或=，所以e=．（Ⅱ）由（Ⅰ）知a=2c，b=c，可得椭圆方程为3x2+4y2=12c2，直线方程为y=（x﹣c）．A，B的坐标满足方程组，消y并整理得5x2﹣8xc=0，解得x=0，x=，得方程组的解为，，不妨设A（c，c），B（0，﹣c）．设点M的坐标为（x，y），则=（x﹣c，y﹣c），=（x，y+c）由y=（x﹣c）得c=x﹣y ①，由=﹣2即（x﹣c）x+（y﹣c）（y+c）=﹣2．将①代入化简得18x2﹣16xy﹣15=0，⇒y=代入①化简得c=＞0．所以x＞0，因此点M的轨迹方程为18x2﹣16xy﹣15=0 （x＞0）．19．（14分）（2011•天津）已知a＞0，函数f（x）=lnx﹣ax2，x＞0．（f（x）的图象连续不断）（Ⅰ）当a=时①求f（x）的单调区间；②证明：存在x0∈（2，+∞），使f（x0）=f（）；（Ⅱ）若存在均属于区间[1，3]的α，β，且β﹣α≥1，使f（α）=f（β），证明．【分析】（I）将a=代入可得函数的解析式，①求导数fˊ（x）；在函数的定义域内解不等式fˊ（x）＞0和fˊ（x）＜0确定的单调区间②由（I）知f（x）在（0，2）内单调递增，在（2，+∞）内单调递减．令g（x）=f（x）﹣f（）．利用函数f（x）在（0，2）内单调递增，得到f（2）＞f（），即g（2）＞0．最后取x′=e＞2，则g（x′）=＜0．从而得到结论；（II）先由f（α）=f（β）及（I）的结论知α＜＜β，从而f（x）在[α，β]上的最小值为f（a）．再依1≤α≤2≤β≤3建立关于a的不等关系即可证得结论．【解答】解：（I）①当a=时，f（x）=lnx﹣x2．∴f′（x）=﹣x=，x∈（0，+∞），令f′（x）=0，解得x=2．当x变化时，f'（x），f（x）的变化情况如下表：所以，f（x）的单调递增区间是（0，2），f（x）的单调递减区间是（2，+∞）．证明：②由（I）知f（x）在（0，2）内单调递增，在（2，+∞）内单调递减．令g（x）=f（x）﹣f（）．由于f（x）在（0，2）内单调递增，故f（2）＞f（），即g（2）＞0．取x′=e＞2，则g（x′）=＜0．所以存在x0∈（2，x'），使g（x0）=0，即存在x0∈（2，+∞），使f（x0）=f（）．（II）证明：由f（α）=f（β）及（I）的结论知α＜＜β，从而f（x）在[α，β]上的最小值为f（a）．又由β﹣α≥1，α，β∈[1，3]，知1≤α≤2≤β≤3．故即从而≤a≤．20．（14分）（2011•天津）已知数列{a n}与{b n}满足：，n∈N*，且a1=2，a2=4．（Ⅰ）求a3，a4，a5的值；（Ⅱ）设c n=a2n﹣1+a2n+1，n∈N*，证明：{c n}是等比数列；（Ⅲ）设S k=a2+a4+…+a2k，k∈N*，证明：．【分析】（Ⅰ）要求a3，a4，a5的值；通过赋值方法，利用已知条件化简求解即可．（Ⅱ）化简出a2n+a2n+1，a2n+1+a2n+3的关系，即：c n+1与c n的关系，从而证明{c n}﹣1是等比数列；就是利用（Ⅰ）的，用2n﹣1，2n，2n+1，替换中的n，化简出只含“a n”的关系式，就+a2n+2a2n+1=0，①2a2n+a2n+1+a2n+2=0，②a2n+1+a2n+2+2a2n+3=0，③然后推出是a2n﹣1a2n+1+a2n+3=﹣（a2n﹣1+a2n+1），得到c n+1=﹣c n（n∈N*），从而证明{c n}是等比数列；（Ⅲ）先研究通项公式a2k，推出S k的表达式，然后计算，结合证明的表达式，+a2k+1=利用表达式的特征，通过裂项法以及放缩法证明即可；就是：根据a2k﹣1（﹣1）k，对任意k∈N*且k≥2，列出n个表达式，利用累加法求出a2k=（﹣1）k+1（k+3）．化简S2k=（a2+a4）+（a6+a8）+…+（a4k+a4k）=﹣k，k∈N*，﹣2，通过裂项法以及放缩法证明：．【解答】20、满分14分．（I）解：由，可得又b n a n+a n+1+b n+1a n+2=0，（II）证明：对任意n∈N*，a2n+a2n+2a2n+1=0，①﹣12a2n+a2n+1+a2n+2=0，②a2n+1+a2n+2+2a2n+3=0，③②﹣③，得a2n=a2n+3．④+a2n+3=﹣（a2n﹣1+a2n+1）将④代入①，可得a2n+1=﹣c n（n∈N*）即c n+1又c1=a1+a3=﹣1，故c n≠0，因此是等比数列．+a2k+1=（﹣1）k，（III）证明：由（II）可得a2k﹣1于是，对任意k∈N*且k≥2，有将以上各式相加，得a1+（﹣1）k a2k﹣1=﹣（k﹣1），=（﹣1）k+1（k+1），即a2k﹣1此式当k=1时也成立．由④式得a2k=（﹣1）k+1（k+3）．从而S2k=（a2+a4）+（a6+a8）+…+（a4k﹣2+a4k）=﹣k，S2k﹣1=S2k﹣a4k=k+3．所以，对任意n∈N*，n≥2，====对于n=1，不等式显然成立．。

(完整版)2011年高考数学天津卷(理科)

2011年天津市高考数学（理科）试题一、选择题：在每小题给出的四个选项中只有一项是符合题目要求的． 1．i 是虚数单位，复数131i i --= A ．2i + B ．2i - C ．12i -+ D ．12i --2．设,,x y R ∈则“2x ≥且2y ≥”是“224x y +≥”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．即不充分也不必要条件3．阅读右边的程序框图，运行相应的程序，则输出i 的值为A ．3B ．4C ．5D ．64．已知{}n a 为等差数列，其公差为-2，且7a 是3a 与9a 的等比中项，n S 为{}n a 前n 项和，*n N ∈，则10S 的值为A ．-110B ．-90C ．90D ．1105．在62x x ⎛⎫- ⎪ ⎪⎝⎭的二项展开式中，2x 的系数为 A ．154- B ．154C ．38-D ．38 6．如图，在△ABC 中，D 是边AC 上的点，且,23,2AB CD AB BD BC BD ===，则sin C 的值为A ．3B ．3C ．6D ．6 7．已知324log 0.3log 3.4log 3.615,5,,5a b c ⎛⎫=== ⎪⎝⎭则 A ．a b c >> B ．b a c >> C ．a c b >> D ．c a b >>8．对实数a 与b ，定义新运算“⊗”：,1,, 1.a ab a b b a b -≤⎧⊗=⎨->⎩ 设函数()()22()2,.f x x x x x R =--∈若函数()y f xc =-的图像与x 轴恰有两个公共点，则实数c 的取值范围是A ．(]3,21,2⎛⎫-∞-⋃- ⎪⎝⎭B ．(]3,21,4⎛⎫-∞-⋃-- ⎪⎝⎭C ．11,,44⎛⎫⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎭⎝⎭D ．311,,44⎛⎫⎡⎫--⋃+∞ ⎪⎪⎢⎝⎭⎣⎭二、填空题：本大题共6小题，每小题5分，共30分．9．一支田径队有男运动员48人，女运动员36人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，则抽取男运动员的人数为___________10．一个几何体的三视图如图所示（单位：m ），则这个几何体的体积为__________3m 11．已知抛物线C 的参数方程为28,8.x t y t ⎧=⎨=⎩（t 为参数），若斜率为1的直线经过抛物线C 的的焦点，且与圆()2224(0)x y r r -+=>相切，则r =________12．如图已知圆中两条弦AB 与CD 相交于点F ，E 是AB 延长线上一点，且 2,::4:2:1.DF CF AF FB BE ===若CE 与圆相切，则CE 的长为__________13．已知集合{}1|349,|4,(0,)A x R x x B x R x t t t ⎧⎫=∈++-≤=∈=+∈+∞⎨⎬⎩⎭，则集合A B ⋂=________14．已知直角梯形ABCD 中，AD //BC ,090ADC ∠=,2,1AD BC ==,P 是腰DC 上的动点，则3PA PB +u u u r u u u r 的最小值为____________三、解答题：本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．15．（本小题满分13分）已知函数()tan(2),4f x x π=+，（Ⅰ）求()f x 的定义域与最小正周期；（Ⅱ）设0,4πα⎛⎫∈ ⎪⎝⎭，若()2cos 2,2f αα=求α的大小．16．（本小题满分13分）学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖.（每次游戏结束后将球放回原箱）（Ⅰ）求在一次游戏中，（i ）摸出3个白球的概率；（ii ）获奖的概率；（Ⅱ）求在两次游戏中获奖次数X 的分布列及数学期望()E X17．（本小题满分13分）如图，在三棱柱111ABC A B C -中，H 是正方形11AA B B 的中心，122AA =，1C H ⊥平面11AA B B ，且1 5.C H =（Ⅰ）求异面直线与所成角的余弦值；（Ⅱ）求二面角111A AC B --的正弦值；（Ⅲ）设N 为棱11B C 的中点，点M 在平面11AA B B 内，且MN ⊥平面11A B C ，求线段BM 的长．18．（本小题满分13分）在平面直角坐标系xOy 中，点(,)P a b (0)a b >>为动点，12,F F 分别为椭圆22221x y a b+=的左右焦点．已知△12F PF 为等腰三角形．（Ⅰ）求椭圆的离心率e ；（Ⅱ）设直线2PF 与椭圆相交于,A B 两点，M 是直线2PF 上的点，满足2AM BM ⋅=-u u u u r u u u u r ，求点M 的轨迹方程．19．（本小题满分14分）已知0a >，函数2()ln ,0.f x x ax x =->（()f x 的图像连续不断）（Ⅰ）求()f x 的单调区间；（Ⅱ）当18a =时，证明：存在0(2,)x ∈+∞，使03()()2f x f =；（Ⅲ）若存在均属于区间[]1,3的,αβ，且1βα-≥，使()()f f αβ=，证明ln 3ln 2ln 253a -≤≤．20．（本小题满分14分）已知数列{}n a 与{}n b 满足： 1123(1)0,2n n n n n n n b a a b a b ++++-++==， *n ∈N ，且122,4a a ==．（Ⅰ）求345,,a a a 的值；（Ⅱ）设*2121,n n n c a a n N -+=+∈，证明：{}n c 是等比数列；（Ⅲ）设*242,,k k S a a a k N =++⋅⋅⋅+∈证明：4*17()6n k k k S n N a =<∈∑．。

2011年天津高考数学试题及答案(理科)

数学教研组：阿布都西库尔.吐逊9.1．2不等式的性质（第1课时）说课稿1、教育教学目标：根据上述教材分析，考虑到学生已有的认知结构心理特征，制定如下教学目标：2、重点，难点以及确定依据：重点：理解不等式的三个性质。

通过探究规律，交流讨论突出重点。

难点：对不等式的性质3的认识。

通过探索、交流、总结，练习突破难点关键：经历探究不等式性质的过程，用类比的方法使学生体会不等式与等式的异同，掌握不等式的性质。

一、教法分析（说教法）1、教学手段及方法：本课采用多媒体辅助教学。

如何突出重点，突破难点，从而实现教学目标。

在教学过程中拟计划进行如下操作：基于本节课的特点应着重采用类比-实验-交流的教学方法。

2、教学方法及其理论依据：坚持“以学生为主体，以教师为主导”的原则，根据学生的心理发展规律，采用教类比-实验-交流的教学方法。

在学生探究，讨论的基础上，在老师启发引导下，激发学生学习热情。

有效的开发各层次学生的潜在智能，力求使学生能在原有的基础上得到发展。

在教学中积极培养学生学习兴趣和动机，明确的学习目的，激发来自学生主体的最有力的动力。

二、说教学过程（一）、回顾交流，指导观察教师提问：同学们还记得等式的性质吗？学生举手回答，交流联想。

投影显示：等式的性质设计意图：通过回顾等式的性质，类比等式的性质，为探索不等式的性质做好铺垫，并且从学生已有的数学经验出发，建立新旧知识之间的联系，培养学生梳理知识体系的习惯。

交流在探索不等式性质的过程中的心得和体会，不断积累数学活动经验。

通过课后作业，教师及时了解学生对本节知识的掌握情况，对教学进度和方法进行适当调整。

三、说教学后记：本节课主要采用了类比-实验-交流的教学方法，采用多媒体教学手段，学生参与课堂的积极性很高，课堂气氛非常活跃，大多数学生掌握了不等式的三条基本性质并能简单运用。

但这节课，在探索新知上花的时间较多，以至于学生的练习时间太短了，以后我在安排教学内容时应注意教学时间的把握，充分利用好课堂时间。