考点16...
广东省中考高分突破鉴赏比较、开放题型

语文
外面真冷啊!一出门,一股凛冽的寒意扑面而来,院子里是一 片白茫茫的寒霜,我忍不住打了个寒战,我看到哥哥的身子也抖动了 一下,我知道,这样的寒夜,刚刚从温暖的被窝里出来,置身在这寒意 袭人的院子里,无论是谁都会感到寒冷。
我漫不经心地抬头朝夜空望去,只见一轮朦胧的月亮挂在天 上,照得到处都在亮晶晶地闪烁着光芒。
返回
语文
“总有几百只大雁呢!”父亲提高了声音对我和哥哥说。 我入迷地看着美丽的雁阵,竟然忘记了寒冷。 雁阵很快就飞过去了。 我依然怔怔地站在那里,沉浸在一份难以言说的美妙情境里, 直到哥哥喊了我一声,我才回过神来。 父亲带着我和哥哥回屋。上床,继续睡觉。
返回
语文
父亲躺在了床上,对我和哥哥又说了一句:“我想,能够看到这 夜晚月下的雁阵,咱们受一点寒冷也是值得的。”
2021广东中考高分突破 语文
文学作品阅读考点突破
考点突破六:鉴赏比较、开放题型
语文
一、解题技巧 考点16:鉴赏比较 考点溯源 (教材母题)
统编教材七上第9课《从百草园到三味书屋》 课文原题: 有人认为美女蛇的故事是赘笔,没必要写。你是否同意?简要 说明理由。
返回
语文
参考答案: 美女蛇的故事虽然与百草园中的赤练蛇没有关系,作者却由 此开始生发出联想。先由百草园的草联想到草中的赤练蛇, 再由赤练蛇联想到长妈妈讲述的美女蛇的故事。很明显,美 女蛇的故事深深地吸引着“我”,而这故事让“我”产生了“做人 之险”的感受,同时也给百草园增添了更多的神秘色彩,所以多 年以后“我”还清楚地记得。这一段看似闲笔,却写出了儿童 的心理,写出了童年的“我”的心目中世界奇特的色彩,是全文 不可或缺的组成部分。
返回
语文
没想到,今天又是同样的情形。下午出门时,他就曾叮嘱过 儿子,晚上在家吃哦。他分明看到儿子瞥了他一眼,轻轻地嗯 了一声的。眼下,儿子却又撒腿走了,他站在窗前,看着窗外雨 雾迷蒙,天色渐渐昏暗,竟无语凝噎。
中考物理高频考点精练16 机械效率

精品基础教育教学资料,仅供参考,需要可下载使用!中考物理高频考点精练专题16 机械效率★考点一:机械效率的概念及大小比较1.下列各选项是小明整理的物理笔记,错误的是()A.做功快的机械,效率不一定高B.动滑轮既能省力又能改变力的方向C.不透明物体的颜色由它反射的色光决定D.沙漠地区昼夜温差大与砂石的比热容小有关【解析】A、做功快的机械,表示其功率大;但机械效率是指有用功与总功的比值,做功快的机械,机械效率不一定高,二者没有直接关系。
故A正确;B、使用动滑轮可以省力,但不能改变力的方向。
故B错误;C、不透明的物体可以反射与它相同的色光,而吸收其它色光,所以物体颜色是由反射的色光决定的。
故C正确;D、沙漠地区的昼夜温差大,主要是因为砂石的比热容小,在同样吸放热的情况下,其温度变化大。
故D正确。
故选:B。
2.如图所示的吊车有大小两个吊钩,在确保安全的前提下,下列关于吊车机械效率说法正确的是()A.吊起相同货物,使用小吊钩机械效率高B.吊起相同货物,上升速度快机械效率高C.每次吊起的货物越少,机械效率越高D.货物升高的高度越高,机械效率越高【解析】(1)使用小吊钩吊起相同货物时,小吊钩(小动滑轮)的重力小,做的额外功少,在有用功一定的情况下,总功小,其机械效率高,故A正确;(2)由机械效率公式η===可知,机械效率的高低与上升速度、货物升高的高度无关,故BD错误;(3)每次吊起的货物越少,有用功越少,有用功在总功中所占比例越小,所以机械效率越低,故C错误。
故选:A。
3.人类从刀耕火种,经过几次工业革命,走向了科技大发展的今天。
简单机械和内燃机的使用,为我们的生活带来了极大便利。
下列几种简单机械和内燃机,其机械效率大于百分之七十的是()A.用滑轮匀速拉一个重为5N的物体到高处(不计绳重,摩擦)B.利用斜面,用平行于斜面的大小为2N拉力,将一个重为5N的物体匀速拉到高处,斜面高1.2m,斜面长5mC.用滑轮组拉一个重为5N的物体到高处,重物在拉力F作用下匀速上升,动滑轮质量100g(不计绳重,摩擦)D.四冲程四缸内燃机,气缸内汽油燃烧产生高温高压燃气推动活塞向下运动,若燃气对活塞平均推力为400N,活塞向下运动距离为30cm,内燃机转速为600r/min ,内燃机每一个循环完成四个冲程,每分钟需要消耗热值为4.6×107J/kg 的汽油5.2g【解析】A 、由于不计绳重和摩擦,用定滑轮提升物体过程不做额外功,总功等于有用功,机械效率为100%,故A 符合题意; B 、有用功:W 有=Gh =5N×1.2m =6J , 总功:W 总=Fs =2N×5m =10J , 则斜面的机械效率:η=×100%=×100%=60%,故B 不符合题意;C 、动滑轮的质量m =100g =0.1kg ,其重力:G 动=mg =0.1kg×10N/kg =1N , 不计绳重和摩擦,则动滑轮的机械效率:η====×100%≈83.3%,故C 符合题意; D 、一个做功冲程燃气对活塞做的功: W 1=Fs =400N×0.3m =120J ,因为飞轮转2r ,对外做功1次,内燃机转速为600r/min , 所以,1min 飞轮转600r ,对外做功300次,1min 做的机械功:W =300W 1=300×120J =3.6×104J , 5.2g 汽油完全燃烧放出的热量:Q =mq =5.2×10﹣3kg×4.6×107J/kg =2.392×105J , 则汽油机的效率:η=×100%=×100%≈15%,故D 不符合题意。
人教高中历史高考复习考点规范练16改革开放与社会主义现代化建设的新时期(含答案)

考点规范练16改革开放与社会主义现代化建设的新时期一、选择题1.1979年3月15日,《人民日报》在头版头条位置发表了题为《“三级所有、队为基础”应该稳定》的文章,明确指出不能从“队为基础”退回去,搞“分田到组”“包产到组”。
已经发现“分田到组”“包产到组”的地方,应坚决纠正。
这说明了()A.家庭联产承包责任制得到推广B.围绕农村体制改革出现分歧C.国家改革开放战略遭到了质疑D.农村经济体制改革初见成效答案:B解析:根据题干材料“已经发现‘分田到组’‘包产到组’的地方,应坚决纠正”,可知当时部分领导人对农村包产到组还是持抵制态度,说明围绕农村体制改革出现分歧,故选B项;题干材料说明包产到组遭到了部分人的抵制,而非得到推广,排除A项;不认同包产到组并不等同于质疑改革开放的战略,C项属于过度推断,排除;题干材料说明包产到组遭到部分人的抵制陷于停滞,而非农村的经济体制改革初见成效,排除D项。
2.到1982年底,河北省某县在全县社队企业中实行了责任制,形式有“定额承包,超包全留,自主分配”“定额承包,超额分成,计件工资”“定额承包,超额提奖,固定工资”“定额生产,超额奖励,利润分成”等等。
这些举措()A.奠定了家庭联产承包责任制的基础B.促进了农村经济结构的重大调整C.丰富了农村经济体制改革的经验D.适应了社会主义市场经济的要求答案:C解析:根据题干材料,可知河北省某县在全县社队企业中实行了责任制。
自主承包经营的做法有利于提高生产积极性,同时丰富了农村经济体制改革关于发展乡镇企业的内容,故C项正确;1978年,安徽、四川一些农村,开始实行包产到组、包干到户的农业生产责任制,与题干时间不符,故A项错误;题干材料不能反映农村经济结构的重大调整,故B项错误;1993年,中共十四届三中全会审议通过了《中共中央关于建立社会主义市场经济体制若干问题的决定》,确立了我国社会主义市场经济体制的基本框架,故D项错误。
3.中华人民共和国出现千万人以上规模的人口迁徙,主要有“大跃进”运动、1959—1961年经济困难时期的精简下放和20世纪80年代中期以来的农民工流动。
生物中考考点专题训练及答案解析16:植物的光合作用

考点16 植物的光合作用中考频度:★★★★★难易程度:★★★★☆一、探究绿叶在光下制造有机物1.过程及图示(1)主要过程步骤操作目的结论暗处理将天竺葵放到黑暗处一昼夜将叶片内原有的淀粉运走或耗尽见光部分产生了淀粉,光是合成淀粉不可缺少的条件遮光将部分叶片上下两面用黑纸板遮盖并照光设置有光和无关的对照实验脱色酒精水浴加热,脱色成黄白色完全溶解叶绿素染色清水漂洗后用碘液染色遇碘变蓝的部分证明有淀粉冲洗清水冲掉碘液后观察去掉碘液便于观察(2)图示2.实验原理淀粉具有遇碘变蓝色的特性。
归纳总结用数字记忆法巧记“绿叶在光下制造有机物”实验的方法步骤实验步骤可概括为“一昼夜,两面遮,三步走”。
具体地说,“一昼夜”就是把天竺葵放在黑暗处一昼夜;“两面遮”强调用黑纸板遮盖叶片的一部分,要把上下两面都遮盖住;“三步走”是“隔水加热→清水漂洗→碘液检验”三个连续的操作步骤。
二、光合作用1.概念:绿色植物通过叶绿体,利用光能,把二氧化碳和水转化成储存能量的有机物,并且释放出氧气的过程。
学科-网2.场所:叶绿体3.实质(1)物质转化:将二氧化碳和水转化成有机物,并释放氧气。
(2)能量转化:将太阳能转化为储存在有机物中的化学能。
4.影响因素(1)光照强度:在一定范围内,光合作用随着光照的增强而增强,当增强到一定程度后,光合作用不再增强,因此中午光照最强的时候并不一定是光合作用最强的时候。
(2)二氧化碳浓度:在一定范围内,光合作用随着二氧化碳浓度的增强而增强。
温室大棚通常采用增加大棚内二氧化碳浓度的方法以提高产量。
(3)温度:在一定范围内,光合作用随着温度的增强而增强。
植物在10~35℃正常进行光合作用,其中,25~35℃最适宜。
5.应用:合理密植、间作套种等。
6.意义:(1)为动物和人提供有机物。
(2)是动植物和人类生活所必需的能量来源。
(3)维持大气中氧气和二氧化碳含量的相对稳定。
考向一绿叶在光下制造有机物1.在“绿叶在光下制造淀粉”的实验中,下列叙述中不正确的是A.图二的作用是褪去叶片中的绿色B.图一中遮光部分滴加碘酒后变蓝色C.图一中遮光部分和未遮光部分形成对照D.此实验的结论是光合作用需要光,光合作用能产生淀粉【答案】B【解析】酒精的作用是溶解叶绿素,A正确;遮光部分不能进行光合作用,没有制造有机物,滴加碘酒后不变蓝,B错误;图一中遮光部分和未遮光部分形成对照,C正确;此实验的结论是光合作用需要光,光合作用能产生淀粉,D正确。
19年秋人教部编版九年级语文上册考点手册:16 孤独之旅

16* 孤独之旅1.重点字嬉.闹(xī) 掺.杂(chān) 胆怯.(qiè) 给予..(jǐ yǔ) 空旷.(kuàng) 驱.除(qū) 觅.食(mì) 撩.逗(liáo) 镰.刀(lián) 歇.斯底里(xiē) 2.多音字撩⎩⎨⎧(liāo )撩起(liáo )撩逗 嚼⎩⎪⎨⎪⎧(jiáo )嚼东西(jué)咀嚼(jiào )倒嚼 扎⎩⎪⎨⎪⎧(zhā)扎针(zhá)挣扎(zā)扎辫子“扎”为“捆,缠束”“把儿,捆儿”义时,一般读zā;为“勉强支持”义时,一般读zhá;为其他义时,一般读zhā。
3.形近字⎩⎪⎨⎪⎧掺(chān)掺杂渗(shèn)渗透碜(chěn)牙碜⎩⎪⎨⎪⎧怯(qiè)胆怯却(què)退却祛(qū)祛病4.重点词语眺望:从高处往远处看。
嬉闹:嬉笑打闹。
撩逗:挑逗;招惹。
茫然:完全不知道的样子。
乖巧:(言行等)合人心意;讨人喜欢。
驱除:赶走;除掉。
一落千丈:形容地位、景况、声誉等下降得很快。
置之不理:放在一边儿不理不睬。
歇斯底里:形容情绪异常激动,举止失常。
文中指暴风雨来势猛烈,超乎寻常。
1.黄昏,船舱里的小泥炉飘起第一缕炊烟,它是这里的唯一的炊烟。
(“第一”“唯一”这两个词表现出芦苇丛中的寂寞,再次点出了人物所处环境的荒凉,烘托了杜小康凄苦、孤独的心情,交代了杜小康的成长环境)2.芦荡如万重大山围住了小船。
杜小康有一种永远逃不走了的感觉。
(用“万重大山”形容芦荡,生动地表现出陌生的环境带给杜小康压抑、沉重、无处逃遁的感觉。
芦荡越幽深繁茂,越反衬出小船的孤小,杜小康那种“永远逃不走了的感觉”才越真切) 3.除了必要的对话,他们几乎不知道再说些其他什么话,而且,原先看来是必要的对话,现在也可以通过眼神或者干脆连眼神都不必给予,双方就能明白一切。
高考生物一轮复习考点练16生物的进化(含解析)

生物的进化考试要求1.现代生物进化理论的主要内容2.用数学方法讨论基因频率的变化3.生物进化与生物多样性的形成[题组冲关]题组一现代生物进化理论的主要内容1.(2021·1月广东学业水平合格考)下列关于现代生物进化理论的叙述,错误..的是( ) A.个体是生物进化的基本单位B.自然选择导致种群基因频率的定向改变C.突变与基因重组为进化提供原材料D.生物多样性是共同进化的结果[答案] A2.(2021·6月广东学业水平合格考)下列关于达尔文自然选择学说的叙述,错误..的是( ) A.生物都有过度繁殖的倾向B.生物个体间普遍存在差异C.自然选择是通过生存斗争来实现的D.自然选择学说能解释遗传和变异的本质[答案] D3.(2021·7月广东学业水平合格考)达尔文发现兰花(虫媒传粉)都具有唇瓣结构,但不同种的兰花其唇瓣形态差异极大。
如图是3种兰花的唇瓣。
下列叙述正确的是( )A.唇瓣形态的差异是定向变异的结果B.唇瓣形态的演化与其它物种无关C.具有不同唇瓣的兰花可能有共同祖先D.兰花唇瓣的形态在未来不会继续变化C 变异是不定向的,A错误;生物之间存在协同进化,B错误;兰花唇瓣的形态可能会继续随环境变化而变化,D错误。
4.下列关于生物进化和生物多样性的叙述,错误的是( )A.化石为研究生物进化提供了直接证据B.自然选择导致种群基因频率的定向改变C.生物的多样性就是指生物的种类多种多样D.生物多样性是协同进化的结果[答案] C5.下列关于生物进化的叙述,错误的是( )A.环境改变使生物产生了定向变异B.突变和基因重组为生物进化提供原材料C.自然选择使种群基因频率发生定向改变D.隔离是新物种形成的必要条件[答案] A题组二种群基因频率的计算1.某昆虫种群有100个个体,其中基因型为AA的个体有50只,aa的个体有40只,则该种群中A 的基因频率为( )A.40% B.45%C.50% D.55%D 由题意知,AA=50%,Aa=10%,aa=40%,因此该种群的基因频率为A=50%+1/2×10%=55%,故选D。
中考政治红色主观题知识考点

中考政治红色主观题知识考点考点1建党100周年
考点2反食品浪费法
考点3乡村振兴促进法
考点4三牛精神
考点5三星堆
考点6祝融号火星车
考点7致敬戍边英雄
考点8新疆棉花
考点9第七次全国人口普查
考点10袁隆平
考点11伟大抗疫精神
考点12伟大抗美援朝精神
考点13修改《中华人民共和国教育法》
考点14刑法修正案(十一)草案
考点15新修订的未成年人保护法
考点16《网络直播营销行为规范》
考点17加强中小学生睡眠管理工作
考点18首届中国国际消费品博览会
考点19博鳌亚洲论坛2021年年会
考点20领导人气候峰会。
中考物理知识点总结(按考试大纲整理16个大考点)

中考物理考点总结■考点一质量和密度1·质量♥质量是物体的属性。
物体的质量不随形状,状态,位置和温度而改变。
质量(m):物体中含有物质的多少叫质量。
♥质量国际单位是:千克。
其他有:吨,克,毫克,1吨=103千克=106克=109毫克♥质量测量工具:实验室常用天平测质量.常用的天平有托盘天平和物理天平.♥估测常见物体的质量:大象2___,中学生60____,一只苹果100____,一个一元硬币5____2·密度♥密度:某种物质单位体积的质量叫做这种物质的密度。
用ρ表示密度,m表示质量,V 表示体积,密度单位是千克/米3,(还有:克/厘米3),1克/厘米3=1000千克/米3;质量m的单位是:千克;体积V的单位是米3.♥密度是物质的一种特性,不同种类的物质密度一般不同。
♥水的密度ρ=1.0×103千克/米3♥密度知识的应用: (1)鉴别物质:用天平测出质量m和用量筒测出体积V就可据公式:ρ= m/V求出物质密度。
再查密度表。
(2)求质量:m=ρV.(3)求体积:V=m/ρ♥物质的物理属性包括:密度、比热容、状态、透光性、导热性、导电性、磁性、弹性等。
■考点二力1·力的概念♥什么是力:力是一个物体对另一个物体的作用.♥物体间力的作用是相互的。
(一个物体对别的物体施力时,也同时受到后者对它的力). ♥力的作用效果:①改变物体的运动状态,②使物体发生形变。
(物体形状或体积的改变,叫做形变。
)♥力的单位是:牛顿(简称:牛),符合是N。
1牛顿大约是你拿起两个鸡蛋所用的力.♥实验室测力的工具是:弹簧测力计。
♥弹簧测力计的原理:在弹性限度内,弹簧的伸长与受到的拉力成正比。
♥弹簧测力计的用法:(1)要检查指针是否指在零刻度,如果不是,则要调零;(2)认清最小刻度和测量范围;(3)轻拉秤钩几次,看每次松手后,指针是否回到零刻度,(4)一般要求竖直使用,非竖直使用时应使弹簧测力计内弹簧的轴线与所测力的方向一致;⑸观察读数时,视线必须与刻度盘垂直。
【精品】备战2020年高考理科数学之高频考点专题专题16 空间向量与立体几何(学生版)

专题16 空间向量与立体几何考点1 利用空间向量证明平行与垂直调研1 如图,在正方体1111ABCD A B C D-中,O是AC的中点,E是线段1D O上一点,且1D E EOλ=⋅u u u u r u u u r.(1)求证:11DB CD O⊥平面;(2)若平面CDE ⊥平面1CD O ,求λ的值. 【答案】(1)证明见解析;(2)2λ=.【解析】(1)不妨设正方体的棱长为1,如图建立空间直角坐标系,则1111(0,0,0),(1,1,1),(,,0),(0,1,0),(0,0,1)22D B O C D ,于是1111(1,1,1),(,,0),(0,1,1)22DB OC CD ==-=-u u u u r u u u u r u u u r ,因为1110,0DB CD DB OC ⋅=⋅=u u u r u u u r u u u u u u ru r ,所以111,DB CD DB OC ⊥⊥, 故11DB CD O ⊥平面.(2)由(1)可知1CD O 平面的一个法向量为1(1,1,1)DB ==u u u u rm , 由1D E EO λ=⋅u u u u r u u u r,则1(,,)2(1)2(1)(1)E λλλλλ+++,设平面CDE 的法向量为(,,)x y z =n ,由·0,0CD DE =⋅=u u u r u u u r n n ,得0,02(1)2(1)(1)y x y zλλλλλ=⎧⎪⎨++=⎪+++⎩∴可取(2,0,)λ=-n ,因为1CD O CED ⊥平面平面,所以·0,2λ=∴=m n .☆技巧点拨☆直线与平面、平面与平面的平行与垂直的向量判定方法设直线l 的方向向量为a =(a 1,b 1,c 1),平面α,β的法向量分别为μ=(a 2,b 2,c 2),v =(a 3,b 3,c 3),则 (1)线面平行:l ∥α⇔a ⊥μ⇔a·μ=0⇔a 1a 2+b 1b 2+c 1c 2=0; (2)线面垂直:l ⊥α⇔a ∥μ⇔a =k μ⇔a 1=ka 2,b 1=kb 2,c 1=kc 2; (3)面面平行:α∥β⇔μ∥v ⇔μ=λv ⇔a 2=λa 3,b 2=λb 3,c 2=λc 3; (4)面面垂直:α⊥β⇔μ⊥v ⇔μ·v =0⇔a 2a 3+b 2b 3+c 2c 3=0.注意:用向量知识证明立体几何问题,仍然离不开立体几何中的定理.如要证明线面平行,只需要证明平面外的一条直线和平面内的一条直线平行,即化归为证明线线平行,用向量方法证明直线a ∥b ,只需证明向量a =λb (λ∈R )即可.若用直线的方向向量与平面的法向量垂直来证明线面平行,仍需强调直线在平面外.考点2 求空间角题组一 求异面直线所成的角调研1 如图所示,在三棱锥P –ABC 中,P A ⊥平面ABC ,D 是棱PB 的中点,已知P A =BC =2,AB =4,CB ⊥AB ,则异面直线PC ,AD 所成角的余弦值为A .−3010 B .−305 C .305D .3010【答案】D【解析】因为P A ⊥平面ABC ,所以P A ⊥AB ,P A ⊥BC .过点A 作AE ∥CB ,又CB ⊥AB ,则AP ,AB ,AE 两两垂直.如图,以A 为坐标原点,分别以AB ,AE ,AP 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系,则A (0,0,0),P (0,0,2),B (4,0,0),C (4,−2,0).因为D 为PB 的中点,所以D (2,0,1).故CP uu r =(−4,2,2),AD uuu r =(2,0,1).所以cos 〈AD uuu r ,CP uu r 〉=||||AD CPAD CP ⋅⋅uuu r uu ruuur uu r =-65×26=−3010. 设异面直线PC ,AD 所成的角为θ,则cos θ=|cos 〈AD uuu r ,CP uu r〉|=3010.调研 2 在正方体1111ABCD A B C D -中,点P 在1A C 上运动(包括端点),则BP 与1AD 所成角的取值范围是ABCD 【答案】D【解析】以点D 为原点,DA 、DC 、1DD 所在直线分别为x y z 、、轴建立空间直角坐标系,设正方体棱长为1,点P 坐标为(),1,x x x -,则()()11,,,1,0,1BP x x x BC =--=-u u u r u u u u r ,设1BP BC u u u ru u u u r、的夹角为α,则所以当13x =时,cos α取最大值当1x =时,cos α因为11BC AD ∥,所以BP 与1AD 所成角的取值范围是故选D. 【名师点睛】空间向量的引入为求空间角带来了方便,解题时只需通过代数运算便可达到解题的目的,由于两向量夹角的范围为[0,π],因此向量的夹角不一定等于所求的空间角,因此在解题时求得两向量的夹角(或其余弦值)后还要分析向量的夹角和空间角大小间的关系.解题时要根据所求的角的类型得到空间角的范围,并在此范围下确定出所求角(或其三角函数值).☆技巧点拨☆利用向量求异面直线所成的角一是几何法:作—证—算;二是向量法:把角的求解转化为向量运算,应注意体会两种方法的特点,“转化”是求异面直线所成角的关键,一般地,异面直线AC ,BD 的夹角β的余弦值为cos β=||||AC BD AC BD ⋅⋅uuu r uu u ruuur uu u r . 注意:两条异面直线所成的角α不一定是两直线的方向向量的夹角β,即cos α=|cos β|.题组二 求线面角调研3 如图,四棱锥P –ABCD 中,底面ABCD 是直角梯形,∠DAB =90°,AD ∥BC ,AD ⊥侧面P AB ,△P AB 是等边三角形,DA =AB =2,BC =12AD ,E 是线段AB 的中点.(1)求证:PE ⊥CD ;(2)求PC 与平面PDE 所成角的正弦值. 【答案】(1)见解析;(2) 35.【解析】(1)因为AD ⊥侧面P AB ,PE ⊂平面P AB ,所以AD ⊥PE . 又△P AB 是等边三角形,E 是线段AB 的中点,所以PE ⊥AB . 因为AD ∩AB =A ,所以PE ⊥平面ABCD , 而CD ⊂平面ABCD ,所以PE ⊥CD .(2)以E 为坐标原点,建立如图所示的空间直角坐标系E −xyz . 则E (0,0,0),C (1,−1,0),D (2,1,0),P (0,0,3). 所以ED →=(2,1,0),EP →=(0,0,3),PC →=(1,−1,−3). 设n =(x ,y ,z )为平面PDE 的法向量.由,得⎩⎨⎧2x +y =0,3z =0.令x =1,可得n =(1,−2,0).设PC 与平面PDE 所成的角为θ,则sin θ=|cos 〈PC →,n 〉|=|||||PC PC ⋅⋅uu u ruu ur n n |=35. 所以PC 与平面PDE 所成角的正弦值为35.调研4 如图,四棱锥P ABCD -中,PD ABCD ⊥平面,底面ABCD 是梯形,AB ∥CD ,BC CD ⊥,AB=PD=4,CD=2,AD =M 为CD 的中点,N 为PB 上一点,且(01)PN PB λλ=<<u u u r u u u r.(1)若14λ=时,求证:MN ∥平面P AD ; (2)若直线AN 与平面PBCAD 与直线CN 所成角的余弦值. 【答案】(1)见解析;(2. 【解析】(114PN PB =u u u r u u u r .在P A 上取点EEN ,DE ,Q 1444PN PB PE PA AB ===u u u r u u u r u u r ,,,∴EN ∥AB ,且14EN AB ==,Q M 为CD 的中点,CD=2,∴112DM CD ==,又AB ∥CD ,∴EN ∥DM ,EN =DM ,∴四边形DMNE 是平行四边形,∴MN ∥DE ,又DE ⊂平面P AD ,MN ⊄平面P AD ,∴MN ∥平面P AD .(2)如图所示,过点D 作DH ⊥AB 于H ,则DH ⊥CD .以D 为坐标原点建立空间直角坐标系D −xyz . 则D (0,0,0),M (0,1,0),C (0,2,0),B (2,2,0),A (2,−2,0),P (0,0,4),∴()()2,0,0,0,2,4CB CP ==-u u u r u u u r ,()()2,2,42,2,4AN AP PN AP PB λλ=+=+=-+-u u u r u u u r u u u r u u u r u u u r()22,22,44λλλ=-+-.该平面PBC 的法向量为(),,x y z =n ,则由20240CB x CP y z ⎧⋅==⎪⎨⋅=-+=⎪⎩u u u r u u u r n n ,得02x y z =⎧⎨=⎩,令z =1,得()0,2,1=n .该直线AN 与平面PBC 所成的角为θ,则 ,解得1,3λ=∴()228248,,,,2,2,0333333N CN AD ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭u u ur u u u r ,,, 设直线AD 与直线CN 所成的角为α所以直线AD 与直线CN.☆技巧点拨☆利用向量求直线与平面所成的角①分别求出斜线和它所在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角); ②通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角.注意:直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值,即注意函数名称的变化.直线与平面的夹角计算设直线l 的方向向量为a =(a 1,b 1,c 1),平面α的法向量为μ=(a 3,b 3,c 3),直线l 与平面α的夹角为θ⎝⎛⎭⎫0≤θ≤π2,则sin θ=|a·μ||a ||μ|=|cos 〈a ,μ〉|.题组三 求二面角调研5 二面角的棱上有A ,B 两点,直线AC ,BD 分别在这个二面角的两个半平面内,且都垂直于AB ,已知2AB =,3AC =,4BD =,CD = A .45︒ B .60︒ C .120︒D .150︒【答案】B【解析】由已知可得:0,0AB AC AB BD ⋅=⋅=u u u r u u u r u u u r u u u r ,CD CA AB BD =++u u u r u u u u r u u r u u u r,,∴cos CA 12,即CA ,∴二面角的大小为60°,故选B.【名师点睛】这个题目考查的是立体几何中空间角的求法;解决立体几何的小题,通常有以下几种方法:一是建系法,二是用传统的方法,利用定义直接在图中找到要求的角;还有就是利用空间向量法来解决问题.注意向量夹角必须是共起点的,还有就是异面直线夹角必须是锐角或直角.调研6 如图,在四棱锥P ABCD -中,AP ,AB ,AD 两两垂直,BC AD ∥,且4AP AB AD ===,2BC =.(1)求二面角P CD A --的余弦值;(2)已知点H 为线段PC 上异于C 的点,且DC DH =,求PHPC的值. 【答案】(1)23;(2【思路分析】(1)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解得各平面法向量,利用向量数量积求向量夹角,最后根据二面角与向量夹角关系求结果;(2)设PH PC λ=u u u v u u u v,根据向量坐标表示距离,再根据距离相等解得λ,即为PHPC的值. 【解析】以{},,A AB AP D u u u r u u u r u u u r为正交基底,建立如图所示的空间直角坐标系A xyz -.则()0,0,0A ,()4,0,0B ,()4,2,0C ,()0,4,0D ,()0,0,4P .(1)易知()0,4,4DP =-u u u r ,()4,2,0DC =-u u u r.设平面PCD 的法向量为()1,,x y z =n ,则1100DP DC ⎧⋅=⎪⎨⋅=⎪⎩u u u v u u u v n n ,即440420y z x y -+=⎧⎨-=⎩,令1x =,则2y =,2z =.所以()11,2,2=n .易知平面ACD 的法向量为()20,0,1=n ,P CD A --的余弦值为23. (2)由题意可知,()4,2,4PC =-u u u r ,()4,2,0DC =-u u u r ,设()4,2,4PH PC λλλλ==-u u u r u u u r,则DH DP PH =+=u u u u r u u u r u u u r()4,24,44λλλ--, 因为DC DH ==,化简得23410λλ-+=,所以1λ=或13λ=.点H 异于点C ,所以13λ=调研7 如图,在三棱柱111ABC A B C -中,侧棱1CC ⊥底面ABC ,且122,CC AC BC AC BC ==⊥,D 是棱AB 的中点,点M 在侧棱1CC 上运动.(1)当M 是棱1CC 的中点时,求证:CD ∥平面1MAB ; (2)当直线AM 与平面ABC 所成的角的正切值为32时,求二面角11A MB C --的余弦值.【答案】(1)见解析;(2)14-. 【思路分析】(1)取线段1AB 的中点E ,连接,DE EM ,可得四边形CDEM 是平行四边形,CD EM ∥,即可证明CD ∥平面1MAB ;(2)以C 为原点,CA ,CB ,1CC 所在直线分别为x ,y ,z 轴建立空间直角坐标系,利用向量法求二面角11A MB C --的余弦值. 【解析】(1)取线段1AB 的中点E ,连接,DE EM . ∵1,AD DB AE EB ==,∴1DE BB ∥,且112DE BB =. 又M 为1CC 的中点,∴1CM BB ∥,且112CM BB =, ∴CM DE ∥,且CM DE =,∴四边形CDEM 是平行四边形,∴CD EM ∥. 又EM ⊂平面1,AB M CD ⊄平面1AB M ,∴CD ∥平面1MAB .(2)∵1,,CA CB CC 两两垂直,∴以C 为原点,1,,CA CB CC 所在直线分别为x ,y ,z 轴,建立空间直角坐标系C xyz -,如图,∵三棱柱111ABC A B C -中,1CC ⊥平面ABC ,∴MAC ∠即为直线AM 与平面ABC 所成的角. 设1AC =,则由3tanMAC ∠=,得3CM =.设平面1AMB 的一个法向量为(),,x y z =n ,2z =,得3,1x y ==-,即()3,1,2=-n .又平面11BCC B 的一个法向量为()1,0,0CA =u u ur,∴,又二面角11A MB C --的平面角为钝角,∴二面角11A MB C --的余弦值为14-.☆技巧点拨☆利用向量求二面角求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐角还是钝角.注意:两平面的法向量的夹角不一定是所求的二面角,有可能为两法向量夹角的补角.运用空间向量坐标运算求空间角的一般步骤(1)建立恰当的空间直角坐标系; (2)求出相关点的坐标; (3)写出向量坐标;(4)结合公式进行论证、计算;(5)转化为几何结论.平面与平面的夹角计算公式设平面α,β的法向量分别为μ=(a 3,b 3,c 3),v =(a 4,b 4,c 4),平面α,β的夹角为θ(0≤θ≤π),则|cos θ|=|μ·v ||μ||v |=|cos 〈μ,v 〉|.题组四 解决探索性问题调研8 如图,在五面体ABCDPE 中,PD ⊥平面ABCD ,∠ADC =∠BAD =90°,F 为棱P A 的中点,PD =BC =2,AB =AD =1,且四边形CDPE 为平行四边形.(1)判断AC 与平面DEF 的位置关系,并给予证明;(2)在线段EF 上是否存在一点Q ,使得BQ 与平面PBC 所成角的正弦值为36?若存在,请求出QE 的长;若不存在,请说明理由.【答案】(1) AC ∥平面DEF ,证明见解析;(2) 在线段EF 上存在一点Q ⎝⎛⎭⎫14,1,324,使得BQ 与平面PBC 所成角的正弦值为36,此时QE =194. 【解析】(1)AC ∥平面DEF .理由如下: 设线段PC 交DE 于点N ,连接FN ,如图所示,因为四边形PDCE 为平行四边形,所以点N 为PC 的中点, 又点F 为P A 的中点,所以FN ∥AC , 因为FN ⊂平面DEF ,AC ⊄平面DEF , 所以AC ∥平面DEF .(2)假设在线段EF 上存在一点Q ,使得BQ 与平面PBC 所成角的正弦值为36,设FQ →=λFE →(0≤λ≤1),如图,以D 为坐标原点,分别以DA ,DC ,DP 所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系. 因为PD =BC =2,AB =AD =1,所以CD =2,所以P (0,0,2),B (1,1,0),C (0,2,0),A (1,0,0),所以PB →=(1,1,−2),BC →=(−1,1,0). 设平面PBC 的法向量为m =(x ,y ,z ),则,即⎩⎨⎧ x +y -2z =0,-x +y =0,解得⎩⎨⎧x =y ,z =2x ,令x =1,得平面PBC 的一个法向量为m =(1,1,2). 假设存在点Q 满足条件.由F ⎝⎛⎭⎫12,0,22,E (0,2,2),可得FE →=⎝⎛⎭⎫-12,2,22.由FQ→=λFE →(0≤λ≤1),整理得1)(,2,)22Q λλλ-+,则BQ →=1)(,21,)22λλλ-+--, 因为直线BQ 与平面PBC 所成角的正弦值为36,所以|cos 〈BQ →,m 〉|=|||||BQ BQ ⋅⋅uu u ruu ur m m |=|5λ-1|219λ2-10λ+7=36, 化简可得14λ2-5λ-1=0, 又0≤λ≤1,所以λ=12,故在线段EF 上存在一点Q ⎝⎛⎭⎫14,1,324,使得BQ 与平面PBC 所成角的正弦值为36, 且QE=194.调研9 棱台1111ABCD A B C D -的三视图与直观图如图所示. (1)求证:平面11ACC A ⊥平面11BDD B ;(2)在线段1DD 上是否存在一点Q ,使CQ 与平面11BDDB ?若存在,指出点Q 的位置;若不存在,说明理由.【答案】(1)见解析;(2)存在,点Q 在1DD 的中点位置,理由见解析.【思路分析】(1)首先根据三视图特征可得1AA ⊥平面ABCD ,四边形ABCD 为正方形,所以AC BD ⊥.再由1AA BD ⊥即可得线面垂直,从而得出面面垂直;(2)直接建立空间直角坐标系写出各点坐标求出法向量,再根据向量的夹角公式列等式求出12λ=. 【解析】(1)根据三视图可知1AA ⊥平面ABCD ,四边形ABCD 为正方形,所以AC BD ⊥. 因为BD ⊂平面ABCD ,所以1AA BD ⊥, 又1AA AC A =I ,所以BD ⊥平面11ACC A .因为BD ⊂平面11BDD B ,所以平面11ACC A ⊥平面11BDD B .(2)以A 为坐标原点,1,,AB AD AA 所在直线分别为,,x y z 轴建立空间直角坐标系,如图所示,根据三视图可知四边形ABCD 为边长为2的正方形,四边形1111A B C D 为边长为1的正方形,1AA ⊥平面ABCD ,且11AA =.所以()11,0,1B ,()10,1,1D ,()2,0,0B ,()0,2,0D ,()2,2,0C . 因为Q 在1DD 上,所以可设()101DQ DD λλ=≤≤u u u r u u u u r.因为()10,1,1DD =-u u u u r ,所以1AQ AD DQ AD DD λ=+=+u u u r u u u u u r u u r u u u r u u u r()()()0,2,00,1,10,2,λλλ=+-=-. 所以()0,2,Q λλ-,()2,,CQ λλ=--u u u r.设平面11BDD B 的法向量为(),,x y z =n ,根据()()()()1,,2,2,00,0,,0,1,10,0x y z BD x y z DD ⎧⎧⋅-=⋅=⎪⎪⇒⎨⎨⋅-=⋅=⎪⎪⎩⎩u u u r u u u ur n n令1x =,可得1y z ==,所以()1,1,1=n .设CQ 与平面11BDD B 所成的角为θ,9==. 所以12λ=,即点Q 在1DD 的中点位置. 调研10 如图(1),在边长为4的菱形ABCD 中,∠BAD =60°,DE ⊥AB 于点E ,将△ADE 沿DE 折起到△A 1DE 的位置,使A 1D ⊥DC ,如图(2).(1)求证:A 1E ⊥平面BCDE . (2)求二面角E −A 1B −C 的余弦值.(3)判断在线段EB 上是否存在一点P ,使平面A 1DP ⊥平面A 1BC ?若存在,求出EPPB 的值;若不存在,说明理由.【答案】(1)见解析;(2) −77;(3)在线段EB 上不存在点P ,使得平面A 1DP ⊥平面A 1BC . 【解析】(1)∵DE ⊥BE ,BE ∥DC ,∴DE ⊥DC .又∵A 1D ⊥DC ,A 1D ∩DE =D ,∴DC ⊥平面A 1DE ,∴DC ⊥A 1E . 又∵A 1E ⊥DE ,DC ∩DE =D ,∴A 1E ⊥平面BCDE . (2)∵A 1E ⊥平面BCDE ,DE ⊥BE ,∴以EB ,ED ,EA 1所在直线分别为x 轴,y 轴和z 轴,建立空间直角坐标系(如图).易知DE =23,则A 1(0,0,2),B (2,0,0),C (4,23,0),D (0,23,0),∴1BA uuu r =(−2,0,2),BC uu u r=(2,23,0),易知平面A 1BE 的一个法向量为n =(0,1,0).设平面A1BC的法向量为m =(x ,y ,z ),由1BA uuu r ·m =0,BC uu u r·m =0,得⎩⎨⎧-2x +2z =0,2x +23y =0.令y =1,得m =(−3,1,−3),∴cos 〈m ,n 〉=m·n|m |·|n |=17×1=77.由图得二面角E −A 1B −C 为钝二面角, ∴二面角E −A 1B −C 的余弦值为−77.(3)假设在线段EB 上存在一点P ,使得平面A 1DP ⊥平面A 1BC .设P (t ,0,0)(0≤t ≤2),则1A P uuu r =(t ,0,−2),1A D uuu r=(0,23,−2),设平面A 1DP 的法向量为p =(x 1,y 1,z 1),由得⎩⎨⎧23y 1-2z 1=0,tx 1-2z 1=0.令x 1=2,得p =⎝⎛⎭⎫2,t 3,t .∵平面A 1DP ⊥平面A 1BC ,∴m·p =0,即23−t3+3t =0,解得t =−3. ∵0≤t ≤2,∴在线段EB 上不存在点P ,使得平面A 1DP ⊥平面A 1BC .☆技巧点拨☆用向量解决探索性问题的方法1.确定点在线段上的位置时,通常利用向量共线来求.2.确定点在平面内的位置时,充分利用平面向量基本定理表示出有关向量的坐标而不是直接设出点的坐标. 3.解题时,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等,所以为使问题的解决更简单、有效,应善于运用这一方法解题.1.(山东省泰安第二中学2019-2020学年高三上学期9月月考数学试题)已知(2,1,3)=-a ,(1,4,2)=--b ,(7,5,)x =c ,若a ,b ,c 三向量共面,则实数x =A .627 B .637C .607D .6572.(四川省成都市树德中学2019-2020学年高三11月阶段性检测数学试题)如图三棱锥S ABC -中,SA ⊥底面ABC ,AB BC ⊥,2AB BC ==,SA =SC 与AB 所成角的大小为A .90︒B .60︒C .45︒D .30°3.(甘肃省天水市第一中学2020年高三上学期12月月考数学试题)如图1四边形ABCD 与四边形ADEF分别为正方形和等腰梯形,,AD EF AF =∥4,2AD EF ==,沿AD 边将四边形ADEF 折起,使得平面ADEF ⊥平面ABCD ,如图2,动点M 在线段EF 上,,N G 分别是,AB BC 的中点,设异面直线MN 与AG 所成的角为α,则cos α的最大值为A BC D 4.(山东省泰安第二中学2019-2020学年高三上学期9月月考数学试题)在正方体1111ABCD A B C D -中,点M 是1AA 的中点,已知AB =u u u r a ,AD =u u u rb ,1AA =u u u r c ,用a ,b ,c 表示CM u u u u r ,则CM =u u u u r ______. 5.(河南省天一大联考2019-2020学年高三阶段性测试(三)数学试题)在直四棱柱1111ABCD A B C D -中,底面ABCD 是菱形,60BAD ∠=o ,1122AB AA ==,E 、F 分别是线段1AA 、11C D 的中点.(1)求证:BD CE ⊥;(2)求平面ABCD 与平面CEF 所成锐二面角的余弦值.6.(四川省南充市高中2019-2020学年高三第一次高考适应性考试数学试题)如图,在四棱锥P ABCD -中,底面ABCD 是矩形,2AB =,BC a =,PA ABCD 底面⊥.(1)当a 为何值时,BD PAC ⊥平面?证明你的结论; (2)当122PA a ==时,求面PDC 与面PAB 所成二面角的正弦值.7.(河北省承德市第一中学2019-2020学年高三上学期12月月考数学试题)如图,已知点H 在正方体1111ABCD A B C D -的对角线11B D 上,∠HDA =60︒.(1)求DH 与1CC 所成角的大小;(2)求DH 与平面1A BD 所成角的正弦值.8.(湖北省“荆、荆、襄、宜四地七校考试联盟2019-2020学年高三上学期10月联考数学试题)已知在多面体ABCDE 中,DE AB ∥,AC BC ⊥,24BC AC ==,2AB DE =,DA DC =且平面DAC ⊥平面ABC .(1)设点F 为线段BC 的中点,试证明EF ⊥平面ABC ;(2)若直线BE 与平面ABC 所成的角为60o ,求二面角B AD C --的余弦值.9.(广东省广州市番禺区广东仲元中学2019-2020年高三上学期11月月考数学试题)如图1,PAD △是以AD 为斜边的直角三角形,1PA =,BC AD ∥,CD AD ⊥,22AD DC ==,12BC =,将PAD △沿着AD 折起,如图2,使得2PC =.(1)证明:平面PAD ⊥平面ABCD ; (2)求二面角A PB C --大小的余弦值.10.(天津市部分区2019-2020学年高三上学期期末数学试题)如图,在三棱柱111ABC A B C -中,P 、O 分别为AC 、11A C 的中点,11PA PC ==1111A B B C =1PB ==114A C =.(1)求证:PO ⊥平面111A B C ; (2)求二面角111B PA C --的正弦值;(3)已知H 为棱11B C 上的点,若11113B H BC =u u u u r u u u u r,求线段PH 的长度.1.(2018新课标全国Ⅱ理科)在长方体1111ABCD A B C D -中,1AB BC ==,1AA =则异面直线1AD 与1DB 所成角的余弦值为A .15 BC .5D .22.(2017新课标全国Ⅲ理科)a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论: ①当直线AB 与a 成60°角时,AB 与b 成30°角; ②当直线AB 与a 成60°角时,AB 与b 成60°角; ③直线AB 与a 所成角的最小值为45°; ④直线AB 与a 所成角的最大值为60°.其中正确的是________________.(填写所有正确结论的编号)3.(2018新课标全国Ⅰ理科)如图,四边形ABCD 为正方形,,E F 分别为,AD BC 的中点,以DF 为折痕把DFC △折起,使点C 到达点P 的位置,且PF BF ⊥. (1)证明:平面PEF ⊥平面ABFD ; (2)求DP 与平面ABFD 所成角的正弦值.4.(2018新课标全国Ⅱ理科)如图,在三棱锥P ABC -中,AB BC ==4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且二面角M PA C --为30︒,求PC 与平面PAM 所成角的正弦值.5.(2018新课标全国Ⅲ理科)如图,边长为2的正方形ABCD 所在的平面与半圆弧»CD 所在平面垂直,M 是»CD上异于C ,D 的点. (1)证明:平面AMD ⊥平面BMC ;(2)当三棱锥M ABC -体积最大时,求面MAB 与面MCD 所成二面角的正弦值.6.(2017新课标全国Ⅰ理科)如图,在四棱锥P−ABCD 中,AB//CD ,且90BAP CDP ∠=∠=o . (1)证明:平面P AB ⊥平面P AD ;C(2)若P A =PD =AB =DC ,90APD ∠=o ,求二面角A −PB −C 的余弦值.7.(2017新课标全国Ⅱ理科)如图,四棱锥P −ABCD 中,侧面P AD 为等边三角形且垂直于底面ABCD ,o 1,90,2AB BC AD BAD ABC ==∠=∠= E 是PD 的中点. (1)证明:直线CE ∥平面P AB ;(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成角为o 45,求二面角M AB D --的余弦值.8.(2017新课标全国Ⅲ理科)如图,四面体ABCD 中,△ABC 是正三角形,△ACD 是直角三角形,∠ABD =∠CBD ,AB =BD .(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.9.(2019年高考全国Ⅰ卷理数)如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求二面角A−MA1−N的正弦值.10.(2019年高考全国Ⅱ卷理数)如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B–EC–C1的正弦值.11.(2019年高考全国Ⅲ卷理数)图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的二面角B−CG−A的大小.。
三角函数的图象与性质-备战高考数学(理)一轮复习考点

(1)形如y=asinx+bcosx+k的三角函数化为y=Asin(ωx+φ)+k的形式,再求最值(值域);
(2)形如y=asin2x+bsinx+k的三角函数,可先设sinx=t,化为关于t的二次函数求值域(最值);
(3)形如y=asinxcosx+b(sinx±cosx)+c的三角函数,可先设t=sinx±cosx,化为关于t的二次函数求值域(最值).
D.函数 的一个单调递减区间为
7.已知函数 (其中 , , )的部分图象如图所示,则下列结论正确的是()
A.函数 的最小正周期为 B.函数 的图象关于点 对称C.函数 在区间 上单调递减D.若 ,则 的值为
8.已知函数 的部分图象如图所示,下列结论正确的有()
A.函数 的最小正周期为
B.直线 为函数 的一条对称轴
【解析】由题图可知A=2,T=4π,故 =4π,解得ω= .所以f(x)=2sin .
把点 代入可得2sin =2,即sin =1,所以φ- =2kπ+ (k∈Z),
解得φ=2kπ+ (k∈Z).又0<φ<π,所以φ= .所以f(x)=2sin .
5.已知函数 ( )的部分图象如图所示,若 ,则 的最小值为。
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2
解得 .
8.函数 的最小正周期为。
【答案】
【解析】因为 ,所以最小正周期为 .
2023年中考语文一轮复习考点突破 要点16 文言文阅读之句子翻译(答案带解析)

要点16 文言文阅读之句子翻译例1:【2022·陕西·中考真题】阅读下面的文言文,完成下面小题。
【甲】嗟夫!予尝求古仁人之心,或异二者之为,何哉?不以物喜,不以已悲,居庙堂之高则忧其民,处江湖之远则忧其君。
是.进亦忧,退亦忧。
然则何时而乐耶?其必曰“先.天下之忧而忧,后天下之乐而乐”乎!噫!微斯人,吾谁与归?时六年九月十五日。
(节选自范仲淹《岳阳楼记》)【乙】亭以雨名,志喜也。
……予至扶风之明年,始治.官舍。
为亭于堂之北,而凿池其南。
引流.种树,以为休息之所。
是岁之春,雨麦①于岐山之阳,其占为有年②。
既而弥月不雨,民方以为忧。
越三月,乙卯乃雨,甲子又雨,民以为未足。
丁卯大雨,三日乃止。
官吏相与庆于庭,商贾相与歌于市,农夫相与忭③于野。
忧者以喜,病者以愈,而吾亭适成。
(节选自苏轼《喜雨亭记》)【注释】①雨麦:下麦雨。
②有年:丰年。
③忭(biàn):喜乐,欢欣。
1.解释下列句子中加点的词语。
(1)是.进亦忧,退亦忧( )(2)先.天下之忧而忧( )(3)始治.官舍( )(4)引流.种树( )2.下列句子中加点的“之”,与“予尝求古仁人之心”中“之”的意义和用法不同的一项是()A.或异二者之.为B.处江湖之.远则忧其君C.予至扶风之.明年D.以为休息之.所★3.请将文中画横线的句子翻译成现代汉语。
(1)微斯人,吾谁与归?(2)亭以雨名,志喜也。
4.两位作者在文中表现出的“忧乐观”,有何不同?【答案】1.这在……之前修建水,水流2.B3.(1)如果没有这种人,我同谁一道呢?(2)亭子用雨来命名,是为了记载这件喜事。
4.范仲淹:“先天下之忧而忧,后天下之乐而乐”;苏轼:“与民同乐”。
【解析】1.本题考查文言实词理解。
(1)句意为:这(他)进入朝廷做官也忧虑,退处江湖也忧虑。
是,这。
(2)句意为:在天下人忧愁之前先忧愁。
先,在……之前。
(3)句意为:开始修建官邸。
治,修建。
(4)句意为:引来流水,种上树木。
高考数学总复习考点知识专题讲解16 圆锥曲线光学性质

高考数学总复习考点知识专题讲解专题16 圆锥曲线光学性质知识点一:光学性质概念椭圆的光学性质:从一个焦点发出的照射到椭圆上其反射光线会经过另一个焦点。
双曲线有一个光学性质:从一个焦点发出的照射到双曲线上其反射光线的反向延长线会经过另一个焦点。
抛物线有一个光学性质:从焦点发出的照射到抛物线上其反射光线平行于抛物线开口方向。
知识点二:光学性质定理定理1点P 为椭圆上任一点,1F 、2F 为椭圆的两焦点,则椭圆在P 点处的切线与12F PF ∠的平分线垂直.由于本题证明方法很多,如果是解决小题,我们按照小题小作来解读,根据物理学的反射原理,反射光线等于入射光线,即把椭圆上的点P 处切线看成镜面,那么法线就是12F PF ∠的平分线,所以它们垂直就自然而然了,同理也能推导双曲线.推论1:设椭圆22221x y a b+=(0a >,0b >)的两焦点为1F ,2F ,00(,)P x y (0x ,00y ≠)为椭圆上一点,则12F PF ∠的角平分线所在直线l 的方程为22220000(0)a y x b x y a b x y ---=.根据光学性质可知00(,)P x y 处切线方程为12020=+b yy a xx ,由于P 点处的切线与12F PF ∠的平分线垂直,故12F PF ∠的角平分线所在直线l 的方程为000022()a y b x y y x x =--,即22220000(0)a y x b x ya b x y ---=.【例1】已知点P 为椭圆上任一点,1F 、2F 为椭圆的两焦点,求证椭圆在P 点处的切线与12F PF ∠的平分线垂直.定理2点P 为双曲线上任一点.1F 、2F 为双曲线的两焦点,则双曲线在P 点处的切线与12F PF ∠的平分线重合.推论2 设双曲线22221x y a b-=±(0a >,0b >)的两焦点为1F ,2F ,00(,)P x y (0x ,00y ≠)为双曲线上一点,则12F PF ∠的角平分线所在直线l 的方程.为222200b x x a y y a b -=±. 【例2】已知点P 为双曲线上任一点,1F 、2F 为椭圆的两焦点,求证双曲线在P 点处的切线与12F PF ∠的平分线重合.定理3点P 为抛物线上任一点,F 为拋物线的焦点,过P 作拋物线的准线的垂线,垂足为P ',则拋物线在点P 处的切线与FPP ∠'的平分线重合.证明:设拋物线的方程为22y px =,200(,)2y P y p.利用导数知识易得抛物线在P 点处的切线斜率存在时为0PQ P k y =.又(,0)2pF ,则02202PP py k y p'=-,0PP k '=.由夹角公式可得:0tan ||||1PP PQ PP PQk k PQPP k k y ∠''-=+'=,0220002202tan ||||121PP PQ PP PQ py pk k y y p FPQ py p k k y y p ''---∠==++⋅-2222232000022222220000021||||()2py p py y p p py y y y p y p p y p -----=⋅=⋅--++22022000()1||||p p y p y y y p -+=⋅=+. 即有tan tan QPP FPQ ∠∠'=,所以PQ 为FPP ∠'的平分线.【例3】(2011年高考全国卷II 理15)已知1F 、2F 分别为双曲线C :221927x y -=的左、右焦点,点A C ∈,点M 的坐标为(2,0),AM 为12F AF ∠的平分线.则2||AF =________.【例4】(2023•东莞市期末)如图,从椭圆的一个焦点1F 发出的光线射到椭圆上的点P ,反射后光线经过椭圆的另一个焦点2F ,事实上,点0(P x ,0)y 处的切线00221xx yy a b+=垂直于12F PF ∠的角平分线.已知椭圆22:143x y C +=的两个焦点是1F ,2F ,点P 是椭圆上除长轴端点外的任意一点,12F PF ∠的角平分线PT 交椭圆C 的长轴于点(,0)T t ,则t 的取值范围是.【例5】(2023•老唐说题教师群探讨)如图,椭圆焦点三角形的1290F AF ∠=︒,AB 为12F AF ∠的角平分线且2AB BD =,则椭圆离心率为.【例6】(2023•广东期末)我国首先研制成功的“双曲线新闻灯”,如图,利用了双曲线的光学性质:1F 、2F 是双曲线的左、右焦点,从2F 发出的光线m 射在双曲线右支上一点P ,经点P 反射后,反射光线的反向延长线过1F ;当P 异于双曲线顶点时,双曲线在点P 处的切线平分12F PF ∠.若双曲线C 的方程为221916x y -=,则下列结论不正确的是()A .射线n 所在直线的斜率为k ,则44(,)33k ∈-B .当m n ⊥时,12||||32PF PF ⋅= C .当n 过点(7,5)Q 时,光线由2F 到P 再到Q 所经过的路程为13 D .若点T 坐标为(1,0),直线PT 与C 相切,则2||12PF =【例7】(2023•阳信期末)已知椭圆22143x y +=上一点P 位于第一象限,左、右焦点分别为1F ,2F ,左、右顶点分别为1A ,2A ,12F PF ∠的角平分线与x 轴交于点G ,与y 轴交于点1(0,)2H -,则()A .四边形12HF PF 的周长为4+.直线1A P ,2A P 的斜率之积为34- C .12||:||3:2FG F G =D .四边形12HF PF 的面积为2【例8】(2023•天河区期末)抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.反之,平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.已知抛物线2:C y x =,O 为坐标原点.一束平行于x 轴的光线1l 从点(P m ,1)(1)m >射入,经过C 上的点1(A x ,1)y 反射后,再经C 上另一点2(B x ,2)y 反射后,沿直线2l 射出,经过点Q ,则()A .121y y =-B .延长AO 交直线14x =-于点D ,则D ,B ,Q 三点共线 C .25||16AB =D .若PB 平分ABQ ∠,则4116m =知识点三:光学定理与内心旁心 定理一:椭圆焦点三角形内心如图,I 为12PF F △内切圆的圆心,PI 和12F F 相交于点N (区分切点M ),则①INe IP=.②121212IF F PF F IF F S e S S =-△△△证明:法一(利用角平分线定理+等比定理):1212121222F N F N F N F N IN c e IP F P F P F P F P a+=====+. 法二:(光学定理+中垂线)PI 是)(00y x P ,处切线(切点弦)的中垂线(考虑极限情况,切点看为两个交点的中点),根据中垂线截距定理202ax c x N =,再根据角平分线定理可知e ex a c a x c P F N F IP IN =++==020211,根据等面积法,121212IF F N N P NP NPF F IF F S y c y IN IPy y c y y S S ===---△△△.中垂线截距定理:若B A 、关于直线PQ 对称,可以知道线段AB 被直线PQ 垂直平分,其中(0)P n ,,(0)Q m ,则能得出以下定理(不妨设焦点在x 轴上): 202y c m b =-(椭圆),202y c m b =(双曲线);202x c n a =(椭圆),202x c n a=(双曲线).因为22AB OM b k ak =-⋅(点差法),1AB PQ k k =-⋅,所以22OMPQb a k k =,故220000b a y x y m x =-,即202y c m b =-;同理220000b a y x y x n=-,即202x c n a =.定理二:双曲线焦点三角形旁心旁心定理:I 是12PF F △的旁心,1F I 、2F I 分别是1PF D ∠、2PF D ∠的角平分线.如图,则:ID e IP =,11IF D PF IS e S =△△.证明:法一:(利用外角平分线定理+等比定理):111212121222DIF PIF S ID DF F D DF F D ce S PIPF PF PF PF a -======-△△,法二:(光学定理+中垂线)PD 是)(00y x P ,处切线(切点弦)的中垂线,根据中垂线截距定理202ax c x D =,再根据角平分线定理可知,e a ex c a x c PF DF IP ID =--==020222 【例9】(2023•思明区期末)已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1(,0)F c -和2(,0)F c,1(M x 为C 上一点,且△12MF F 的内心为2(I x ,1),则椭圆C 的离心率为()A .35B .25C .13D .12【例10】(2023哈三中高三一模16题)如图,椭圆)0(12222>>=+b a by a x与双曲线)00(12222>>=-n m ny m x ,有公共焦点)0(1,c F -,)0(2,c F ,椭圆的离心率为1e ,双曲线的离心率为2e ,点P 为两曲线的一个公共点,︒=∠6021PF F ,则=+222131e e ;I 为21F PF ∆的内心,G I F 、、1三点共线,且0=⋅IP GP ,x 轴上点A 、B 满足IP AI λ=,GP BG μ=,则22μλ+的最小值为.知识点四:光学定理与大圆小圆问题1. 椭圆的大圆焦点作椭圆切线的垂线,垂足轨迹是以长轴为直径的圆.这个圆我们称之为大圆.如图,已知椭圆()222210x y a b a b+=>>上点P 处的切线为l ,则过焦点12F F 、作直线l 的垂线,垂足H 的轨迹是以长轴为直径的圆,即为222x y a +=.证明: 如图,作2F H l ⊥,1F H l '⊥.当点P 不在长轴的两个端点时,延长1F P 交2F H 于点Q ,根据椭圆的光学性质可知:切线l 平分2F PQ ∠,故2PQF △是等腰三角形,点H是线段2F Q 的中点.因此,在12F F Q 中,1112222FQ F P PQF P PF OH a ++====,故点H 的轨迹是222()x y a x a +=≠±,同理,H`的轨迹也符合此轨迹方程,当点P 在长轴的两个端点时,此时的射影点(,0)a ±亦满足上述方程.【例11】(2023•连城县月考)如图所示,已知1F ,2F 是椭圆2222:1(0)x y a b a bΓ+=>>的左,右焦点,P 是椭圆Γ上任意一点,过2F 作12F PF ∠的外角的角平分线的垂线,垂足为Q ,则点Q 的轨迹为()A .直线B .圆C .椭圆D .双曲线2.大圆性质拓展如图,已知椭圆()222210x y C a b a b+=>>:上点P 处的切线为l ,且焦点12F F 、在直线l 上的垂足分别为G 、H ,设12F PF θ∠=,椭圆的上顶点为B ,左右顶点分别为1A 、2A ,则:(1) 212FG F H b =; (2)直角梯形12F F GH 的面积的为2sin S a θ=,又12F BF θ≤∠,故212max12,22,02a F BF S bc F BF ⎧π⎛⎫∠≥ ⎪⎪⎪⎝⎭=⎨π⎛⎫⎪<∠< ⎪⎪⎝⎭⎩;证明(1) 法一:设1F P m =,2F P n =,则2cos 11θPF G F =,2cos 22θPF H F =222222212411cos ()42cos 2224m n c m n c mn FG F H mn mn mn b θθ+-+++-=====.法二延长1MF 交大圆222x y a +=于点I ,根据对称性,有21F H F I =,再利用相交弦定理,则212111112()()FG F H FG F I A F F A a c a c b ===-+=.(2) 利用椭圆的光学性质,如图所示,延长1F P 交2F H 于点N ,过点N 作//GH MN 交G F 1延长线于点M,因此,2121111111()()sin cos 222222S FG F H MN FG MG MN F M MN F N θθ=+=+==,又1122F N F P PF a =+=,则2214sin cos sin 222S a a θθθ==. 注意:大题在证明光学性质时比较麻烦,建议参考例题方式书写大题,那样其实也不难.【例12】已知椭圆22143x y +=,圆224x y +=,直线2y x =与椭圆交于点A ,过A 作椭圆的切线交圆于M 、N 两点(M 在N 的左侧),则12MF NF =.【例13】(2023•南充模拟)设点1(,0)F c -,2(,0)F c 分别是椭圆222:1(1)x C y a a+=>的左、右焦点,P 为椭圆C 上任意一点,且12PF PF ⋅的最小值为0. (1)求椭圆C 的方程;(2)如图,动直线:l y kx m =+与椭圆C 有且仅有一个公共点,点M ,N 是直线l 上的两点,且1F M l ⊥,2F N l ⊥,求四边形12F MNF 面积S 的最大值.3.双曲线的小圆焦点在双曲线切线上的垂足轨迹是以实轴为直径的圆,我们称之为小圆.如图,已知双曲线()222210,0x y a b a b-=>>上点P 处的切线为l ,则焦点12F F 、在直线l上的射影点H 的轨迹是以实轴为直径的圆,即为222x y a +=.【例14】已知双曲线221916x y -=的两焦点分别为12F F 、,P 为双曲线上一动点,过点1F 作12F PF ∠平分线所在直线的垂线,则垂足M 的轨迹方程为( ).A .229x y +=B .2216x y +=C .229x y -=D .2216x y -=【例15】(多选)设双曲线22:14x C y -=左右焦点分别为1F ,2F ,设右支上一点P 与2F 所连接的线段为直径的圆为圆1O ,以实轴为直径的圆为圆2O ,则下列结论正确的有() A .圆1O 与圆2O 始终外切B .若2F P 与渐近线垂直,则2F P 与圆2O 相切 C .12F PF ∠的角平分线与圆1O 相切D .三角形12F PF 的内心和外心最短距离为2【例16】(2023•江苏模拟)已知椭圆22:143y x C +=,点0(P x ,0)y 为椭圆C 在第一象限的点,12F F 为椭圆的左、右焦点,点P 关于原点的对称点为Q . (1)设点Q 到直线1PF ,2PF 的距离分别为1d ,2d ,求12d d 取值范围; (2)已知椭圆在0(P x ,0)y 处的切线l 的方程为:00143x x y y+=,射线1QF 交l 于点R .求证:11F RP RPF ∠=∠.【例17】(2022•湖北21校)平面直角坐标系xOy 中,已知点(2,0)M -,(2,0)N 点A 满足||||AM AN -=A 的轨迹C . (1)求C 的方程;(2)设点T 与点A 关于原点O 对称,MTN ∠的角平分线为直线l ,过点A 作l 的垂线,垂足为H ,交C 于另一点B ,求:||||AH BH 的最大值.【例18】(2023•闵行区期中)如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC 是椭圆的一部分,灯丝位于椭圆的一个焦点1F 上,片门位于该椭圆的另一个焦点2F 上.椭圆有光学性质:从一个焦点出发的光线,经过椭圆面反射后经过另一个焦点,即椭圆上任意一点P 处的切线与直线1PF 、2PF 的夹角相等.已知12BC F F ⊥,垂足为1F ,1||3F B m =,12||4F F cm =,以12F F 所在直线为x 轴,线段12F F 的垂直平分线为y 轴,建立如图的平面直角坐标系. (1)求截口BAC 所在椭圆C 的方程;(2)点P 为椭圆C 上除长轴端点和短轴端点外的任意一点.①是否存在m ,使得P 到2F 和P 到直线x m =的距离之比为定值,如果存在,求出的m 值,如果不存在,请说明理由;②若12F PF ∠的角平分线PQ 交y 轴于点Q ,设直线PQ 的斜率为k ,直线1PF 、2PF 的斜率分别为1k ,2k ,请问21k kk k +是否为定值,若是,求出这个定值,若不是,请说明理由.【例19】(2023•上海模拟)椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别是点1F ,2F ,过点1F 且垂直于x 轴的直线被椭圆C 截得的线段长为1,点2F 与短轴两个顶点构成等边三角形.(1)求椭圆C 的方程;(2)已知过椭圆上点0(M x ,0)y 的椭圆的切线方程为00221xx yy a b+=.求证:过椭圆C 上任一点0(M x ,0)y 的切线与直线1MF 和2MF 所成角都相等;(3)点P 是椭圆C 上除长轴端点外的任一点连接1PF ,2PF ,设12F PF ∠的角平分线PQ 交C 的长轴于点(,0)Q q ,求q 的取值范围.同步训练1.(2022•怀化二模)若点P 是椭圆22221(0)4x y b b b+=>上的点,且点I 是焦点三角形△12PF F 的内心,12F PF ∠的角平分线交线段12F F 于点M ,则||PIIM等于()A C .122.(2023•贵州模拟)根据圆锥曲线的光学性质:从双曲线的一个焦点发出的光线,经双曲线反射后,反射光线的反向延长线过双曲线的另一个焦点.由此可得,过双曲线上任意一点的切线,平分该点与两焦点连线的夹角.请解决下面问题:已知1F ,2F 分别是双曲线22:12y C x -=的左、右焦点,若从点2F 发出的光线经双曲线右支上的点0(A x ,2)反射后,反射光线为射线AM ,则2F AM ∠的角平分线所在的直线的斜率为() A..CD3.(2022•南昌三模)已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别是1F ,2F ,P 是椭圆上的动点,I 和G 分别是△12PF F 的内心和重心,若IG 与x 轴平行,则椭圆的离心率为() A .12B3.(2022•焦作一模)已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1F ,2F ,M 为C 上一点,且△12MF F 的内心为0(I x ,2),若△12MF F 的面积为4b ,则1212||||(||MF MF F F +=) A .32B .53C.434.(2023•建邺区期中)已知抛物线24y x =的焦点为F ,直线l 过点F 且与抛物线交于A ,B 两点,过点A 作抛物线准线的垂线,垂足为M ,MAF ∠的角平分线与抛物线的准线交于点P ,线段AB 的中点为Q .若||16AB =,则||(PQ =) A .2B .4C .6D .85.(2022•衡阳二模)圆锥曲线的光学性质:从双曲线的一个焦点发出的光线,经双曲线反射后,反射光线的反向延长线过双曲线的另一个焦点、由此可得,过双曲线上任意一点的切线,平分该点与两焦点连线的夹角、请解决下面问题:已知1F ,2F 分别是双曲线22:12y C x -=的左、右焦点,点P 为C 在第一象限上的点,点M 在1F P 延长线上,点Q的坐标为,且PQ 为12F PF ∠的平分线,则下列正确的是() A .12||2||PF PF =B .12||23PF PF +=C .点P到x .2F PM ∠的角平分线所在直线的倾斜角为150︒6.(2023•阳信县期末)已知椭圆22143x y +=上一点P 位于第一象限,左、右焦点分别为1F ,2F ,左、右顶点分别为1A ,2A ,12F PF ∠的角平分线与x 轴交于点G ,与y 轴交于点1(0,)2H -,则()A .四边形12HFPF 的周长为4+.直线1A P ,2A P 的斜率之积为34- C .12||:||3:2FG F G =D .四边形12HF PF 的面积为2 7.(2023•佛山期末)圆锥曲线具有丰富的光学性质,从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线过椭圆的另一个焦点.如图,胶片电影放映机的聚光灯有一个反射镜.它的形状是旋转椭圆.为了使影片门(电影胶片通过的地方)处获得最强的光线,灯丝2F ,与影片门1F 应位于椭圆的两个焦点处.已知椭圆22:143x y C +=,椭圆的左右焦点分别为1F ,2F ,一束光线从2F 发出,射向椭圆位于第一象限上的P 点后反射光线经过点1F ,且124tan 3F PF ∠=,则12F PF ∠的角平分线所在直线方程为.8.(2023•诸暨市期末)圆锥曲线有着令人惊奇的光学性质,这些性质均与它们的焦点有关.如:从椭圆的一个焦点处出发的光线照射到椭圆上,经过反射后通过椭圆的另一个焦点;从抛物线的焦点处出发的光线照射到抛物线上,经反射后的光线平行于抛物线的轴.某次科技展览中某展品的一个截面由抛物线的一部分1C 和一个“双孔”的椭圆2C 构成(小孔在椭圆的右上方).如图,椭圆22212:1,,43x y C F F +=为2C 的焦点,B 为下顶点,2F 也为1C 的焦点,若由1F 发出一条光线经过点B 反射后穿过一个小孔再经抛物线上的点D 反射后平行于x 轴射出,由1F 发出的另一条光线经由椭圆2C 上的点P 反射后穿过另一个小孔再经抛物线上的点E 反射后平行于x轴射出,若两条平行光线间隔,则1cos BF P ∠=.11.已知P是双曲线221168x y -=右支上一点,12F F 、分别是双曲线的左、右焦点,O 为坐标原点,1(0)F P PM λλ=>,22PF PM PN PM PF μ⎛⎫⎪=+⎪⎝⎭,20PN F N =.若22PF =,则ON =.12.已知双曲线22221x y a b-=的左右焦点分别为12F F 、,O 为双曲线的中心,P 是双曲线右支上的点,12PF F △的内切圆的圆心为I ,且圆I 与x 轴相切于点A ,过2F 作直线PI 的垂线,垂足为B ,若e 为双曲线的离心率,则( ).A .OB e OA =B .OA e OB=C .OA OB =D .OA 与OB 关系不确定。
高考化学一轮复习:考点剖析专题卷:专题六 非金属及其化合物

考点剖析专题卷专题六非金属及其化合物考点16 碳、硅及其化合物(2、3、5、6、9、12、20、21题)考点17 富集在海水中的元素——氯(1、4、13、16、18题)考点18 硫及其化合物(8、10、15~17、19、22题)考点19 氮及其化合物(7、10、11、14、16、23题)考试时间:90分钟满分:100分一、选择题(本题共15小题,每小题2分,共30分。
在每小题给出的四个选项中,只有一项是最符合题目要求的。
)1.化学与生产、生活密切相关,下列说法正确的是( )A.溴化银是一种重要的感光材料,常用于人工降雨B.水玻璃是建筑行业常用的一种黏合剂C.工业上可采用向澄清石灰水中通入氯气的方法来生产漂白粉D.氯化钙、生石灰、硫酸亚铁等都是食品包装袋中常用的干燥剂2.下列关于硅的说法不正确的是( )A.高纯度的单质硅被广泛用于制作计算机芯片B.自然界中硅元素的贮量丰富,是地壳中含量最高的元素C.常温时硅与水、空气和绝大多数酸不反应,但能与氢氟酸反应D.硅可由二氧化硅还原制得3.科学家将含有石墨烯和碳纳米管两种纳米材料的水溶液在低温环境下冻干得到“全碳气凝胶”,该固态材料的密度仅为3⋅,是迄今为止世界上最轻的材料。
下列有关说0.18mg cm-法正确的是( )A. “全碳气凝胶”可用作处理海上原油泄漏的吸油材料B. “全碳气凝胶”与石墨互为同位素C. “全碳气凝胶”中含有碳碳双键,属于烯烃D. “全碳气凝胶”的性质稳定,能在热的浓硫酸中稳定存在4.在2020年初抗击新型冠状病毒肺炎(COVID-19)疫情中,化学品发挥了重要的作用,如75%酒精、“84”消毒液等。
“84”消毒液是主要用于环境和物体表面消毒的含氯消毒剂。
下列判断不正确的是( )A.制备“84”消毒液的离子方程式为22Cl 2OH Cl ClO H O ---+++B.“84”消毒液的有效成分是NaClOC.“84”消毒液是利用NaClO 的还原性进行杀菌消毒D.将氯气通入石灰乳中可制得漂白粉,漂白粉的有效成分是2Ca(ClO),可作纸张的漂白剂5.据报道,科学家已经研制出世界上最薄的材料——碳膜片,其厚度只有一根头发的二十万分之一。
细胞16.细胞的社会联系知识考点

细胞16.细胞的社会联系知识考点●细胞连接多细胞生物体内,细胞间通过细胞通信、细胞黏着、细胞连接以及细胞与胞外基质的相互作用构成复杂的细胞社会●cell junction 细胞连接●定义:在细胞质膜的特化区域,通过膜蛋白、细胞骨架蛋白、胞外基质形成的细胞与细胞之间、细胞与胞外基质之间的连接结构●功能:细胞社会性的结构基础,是多细胞有机体中相邻细胞之间协同作用的重要组织方式,主要存在于上皮细胞间●occluding junction 封闭连接(tight junction 紧密连接)●定义:相邻上皮细胞的质膜紧密地连接在一起,阻止溶液中的小分子沿细胞间隙从细胞一侧渗透到另一侧的连接方式,典型代表:紧密连接●结构特点●一般存在与上皮细胞之间,紧密连接处的相邻细胞质膜紧紧地靠在一起,没有间隙●成串排列的特殊跨膜蛋白在相邻细胞间形成嵴线,嵴线相互交联封闭了细胞之间的间隙●有关蛋白质:occludin 闭合蛋白、claudin 密封蛋白●功能●形成渗透屏障,阻止可溶性物质从上皮细胞层一侧通过细胞间隙扩散到另一侧,起封闭作用●小肠上皮细胞的阻碍●血脑屏障大脑毛细血管内皮细胞形成血脑屏障,阻止离子或水分子等通过血管内皮进入大脑,保证大脑内环境的稳定性但免疫细胞通过分泌信号分子可以打开紧密连接●形成上皮细胞膜蛋白与膜脂分子侧向扩散的屏障,从而维持上皮细胞的极性小肠上皮细胞游离面与基底面的膜蛋白以及膜脂分子只能够在各自的膜区域流动●anchoring junction 锚定连接●定义:通过细胞膜蛋白及细胞骨架系统将相邻细胞,或细胞与胞外基质间黏着起来的连接方式,分为与中间丝相关的锚定连接(桥粒、半桥粒)和与肌动蛋白纤维相关的锚定连接(黏着带、黏着斑)●功能:细胞间或细胞与胞外基质间通过锚定连接分散作用力,从而增强细胞承受机械力的能力●蛋白质构成●anchor protein 细胞内锚蛋白●形成盘状致密斑(胞质斑)●一侧与胞内骨架纤维(中间丝、微丝)相连,另一侧与跨膜黏附性蛋白相连●adhesion protein 跨膜黏附性蛋白质●细胞膜蛋白●一端与胞内膜蛋白相连,另一端与胞外基质蛋白或与相邻细胞特异的跨膜黏附性蛋白质相连●与中间丝相连的锚定连接●desmosome 桥粒连接相邻细胞间的锚定连接方式●最明显的形态特征:细胞内锚蛋白形成独特的盘状致密斑,一侧与细胞内的中间丝相连,另一侧与跨膜黏着蛋白质相连,在两个细胞之间形成纽扣样结构,将相邻细胞铆接在一起●功能:一个细胞内的中间丝与相邻细胞内的中间丝通过桥粒相互作用,从而将相邻细胞连成一体,增强了细胞抵抗外界压力与张力的机械强度●hemidesmosome 半桥粒胞内到胞外:中间丝-盘状致密斑-整联蛋白-层粘连蛋白-胶原●细胞骨架是中间丝●跨膜黏附性蛋白质是integrin 整联蛋白,与其相连的胞外基质是laminin,LN 层粘连蛋白●功能:通过半桥粒,上皮细胞可以黏着在基膜上●与肌动蛋白纤维相连的锚定连接●adhesion belt 黏着带●位于上皮细胞紧密连接的下方,相邻细胞间形成一个连续的带状结构,由cadhesin 钙黏蛋白形成胞间横桥而相连●结构组分●细胞内锚蛋白包括联蛋白、黏着斑蛋白及α-辅肌动蛋白等●与黏着带相连的骨架纤维是肌动蛋白纤维●功能:在动物胚胎发育形态建成过程中,黏着带能促使上皮细胞层弯曲形成神经管等结构●focal adhesion 黏着斑●结构组分●胞内锚蛋白包括踝蛋白、α-辅肌动蛋白、细丝蛋白和纽蛋白等●跨膜黏附性蛋白质是integrin 整联蛋白,与其相连的胞外基质主要是胶原和纤连蛋白●细胞骨架组分是微丝●功能:有助于维持细胞在运动过程中的张力以及影响细胞生长的信号传递●communicating junction 通信连接●定义:介导相邻细胞间的物质转运、化学或电信号的传递的连接方式,主要包括间隙连接、化学突触和胞间连丝●gap junction 间隙连接●结构连接子蛋白→ 连接子→ 间隙连接●基本结构单位是连接子,每个连接子由6个连接子蛋白呈环状排列而成●相邻细胞质膜上的两个连接子对接便形成完整的间隙连接结构●功能●代谢偶联间隙连接允许通过小分子代谢物和信号分子,以实现细胞间代谢偶联或细胞通信●神经冲动信息传递神经元之间或神经元与效应细胞之间通过突触完成神经冲动的传导,间隙连接在电突触中形成,使电冲动可直接通过间隙连接从突触前向突触后传导●胚胎早期发育间隙连接出现在动物胚胎发育的早期,其建立的电偶联为影响细胞分化的信号物质的传递提供了重要的通路●通透性的调节●间隙连接对小分子物质的通透能力具有底物选择性●间隙连接通透性受细胞质Ca^{2+}浓度、pH调节Ca^{2+}浓度升高、pH降低可以使间隙连接通透性降低●两侧电压梯度的调控、细胞外化学信号的调控●plasmodesma 胞间连丝●定义:高等植物细胞间的通信连接方式,胞间连丝形成了物质从一个细胞进入另一个细胞的通路,在植物细胞的物质运输和信号传递中起作用●结构特点●胞间连丝穿越细胞壁,由相邻细胞的细胞质膜共同组成直径为20~40nm的管状结构,中央是由光面内质网延伸形成的链样管(desmotubule)●链样管与管状质膜之间是由细胞液构成的环孔,两端狭窄用以调节细胞间的物质交换●物质运输有选择性,并且可以调节●功能●在植物细胞的物质运输和信号传递中起着非常重要的作用●在协调其基因表达与生理功能中起重要的作用●细胞黏着及其分子基础●cell adhesion 细胞黏着●定义:通过细胞表面的细胞黏着分子(CAM),介导细胞与细胞间的黏着或细胞与细胞外基质间的黏着,细胞黏着有助于胚胎发育和形态建成●细胞识别与黏着的分子基础是细胞表面的cell adhesion molecule, CAM 细胞黏着分子●黏着分子作用的方式●同亲型结合——同种黏着分子间的相互识别与黏着●异亲型结合——不同黏着分子间的相互识别与黏着●衔接分子依赖性结合——同种黏着分子借助其他衔接分子的相互识别与黏着●cell adhesion molecule, CAM 细胞黏着分子整合膜蛋白,介导细胞与细胞间的黏着或细胞与细胞外基质间的黏着●cadhesin 钙黏蛋白●定义:一种同亲型结合、Ca^{2+}依赖的细胞黏着糖蛋白,对胚胎发育中的细胞识别、迁移和组织分化以及成体组织器官构成具有重要作用●分类●典型钙黏蛋白具有细胞黏着和信号转导功能,其胞内或胞外结构域在序列组成上高度相似 E-、N-、P-钙黏蛋白●非典型钙黏蛋白序列上组成差异较大,主要功能是介导细胞黏着原钙黏蛋白、桥粒芯蛋白、桥粒芯胶黏蛋白●功能●介导高度选择性的细胞识别与黏着,通过调控钙黏蛋白的种类与数量能影响细胞间的黏着与迁移,从而影响组织分化●epothelial-mesenchymal transition, EMT 上皮-间质转型定义:上皮细胞与间质细胞间相互转化的受控的可逆的过程,其分子机制涉及E-钙黏蛋白的表达在表达E-钙黏蛋白后,分散的间质细胞会聚集在一起形成上皮组织,不表达E-钙黏蛋白的上皮细胞则转化为游离的间质细胞●selectin 选凝素●定义:一类异亲型结合,Ca^{2+}依赖性的细胞黏着分子,能与特异糖基识别并结合,其胞外部分具有高度保守并能识别其他细胞表面特异性寡糖链的凝集素(lectin)结构域●功能:主要参与白细胞与血管内皮细胞之间的识别与黏着,帮助白细胞经血流进入炎症部位由于选凝素与白细胞表面特异亲和力较小,加上血流速度的影响,白细胞在血管中不断黏着-分离,呈现滚动式运动,直到活化自身整联蛋白后,最终于血管内皮细胞较强地结合●immunoglobulin superfamily, IgSF 免疫球蛋白超家族●定义:分子结构中具有与免疫球蛋白类似结构域的细胞黏着分子超家族,介导不依赖于Ca^{2+}的同亲型细胞黏着或者异亲型细胞黏着●功能●大多数IgSF细胞黏着分子介导淋巴细胞和免疫应答所需要的细胞之间的黏着●一些IgSF成员介导非免疫细胞的黏着,在神经系统发育中有重要作用●integrin 整联蛋白●定义:普遍存在于脊椎动物细胞表面,属于异亲型结合、Ca^{2+}或Mg^{2+}依赖性的细胞黏着分子,主要介导细胞与胞外基质间的黏着●相连的结构●胞内:肌动蛋白纤维●胞外:含有RGD三肽序列的胞外基质成分●介导黏着的结构:focal adhesion 黏着斑、hemidesmosome 半桥粒●信号传递方向●“由内向外”信号传递细胞内信号传递启动后,PIP_2激活踝蛋白,引起踝蛋白与整联蛋白β链结合能力增强,整联蛋白胞外构象的改变而增强与其他胞外配体的结合能力,最后介导细胞黏着●“由外向内”信号传递一旦与配体结合,整联蛋白快速与肌动蛋白骨架产生联系,聚集在一起形成黏着斑,FAK被募集到黏着斑部位,为胞内酪氨酸激酶家族提供位点。
高考化学复习考点知识专项突破讲解16 弱电解质的电离平衡

高考化学复习考点知识专项突破讲解专题16 弱电解质的电离平衡考向分析:以图像分析的形式综合考查外界因素对电离平衡的影响,根据信息计算弱电解质的平衡常数,强调用动态平衡的观点看待和分析微粒变化的过程。
(一)必备知识和方法1.影响弱电解质电离平衡的因素:内因:弱电解质本身的性质,是决定因素。
外因:①温度:升高温度,电离程度增大。
②浓度:越稀越电离,加水稀释,电离平衡向电离方向移动。
③同离子效应:在弱电解质溶液中加入与弱电解质电离出相同离子的强电解质,电离平衡向生成弱电解质分子的方向移动。
④化学反应:若外加物质能与弱电解质电离出的离子发生反应,电离平衡向电离方向移动。
COOH⇌CH3COO-+H+ΔH>0以醋酸电离为例:CH31 / 292.电离平衡常数K a(或K b)及其应用:(1)影响因素:与溶液的浓度、酸碱性无关。
决定因素:①弱电解质本身的性质。
②温度:升高温度电离平衡常数增大。
(2)意义:相同条件下,K值越大,表示该弱电解质越容易电离,所对应的酸性或碱性相对越强。
例如,相同条件下常见弱酸的酸性强弱:H2SO3>H3PO4>HF>CH3COOH>H2CO3 >H2S>HClO。
(3)应用:①判断弱酸酸性(或弱碱碱性)的相对强弱:电离常数越大,酸性(或碱性)越强。
②判断盐溶液的酸性(或碱性)强弱:电离常数越小,对应的盐水解程度越大,碱性(或酸性)越强。
3 / 29③判断复分解反应能否发生:一般符合“强酸制弱酸”规律。
④判断微粒浓度比值的变化:弱电解质加水稀释时,能促进弱电解质的电离,溶液中离子和分子的浓度会发生相应的变化,但电离常数不变,可利用电离常数来判断溶液中微粒浓度比值的变化情况。
3.判断HA 是弱酸的依据:(1)测钠盐NaA 溶液的pH ,若常温下pH>7,则说明HA 为弱酸。
(2)测一定物质的量浓度的HA 溶液,常温下若0.01 mol·L-1 HA 溶液的pH>2,则说明HA 为弱酸。
2020高考历史核心考点专题16 西方人文主义的起源与发展(解析版)

专题16 西方人文主义的起源与发展(解析版)考点一:西方人文主义思想的起源母题1.(2017年新课标全国卷Ⅰ)在公元前9至前8世纪广为流传的希腊神话中,诸神的形象和性情与人相似,不仅具有人的七情六欲,而且还争权夺利,没有一个是全知全能和完美无缺的。
这反映了在古代雅典A.宗教信仰意识淡薄B.人文思想根植于传统文化C.理性占据主导地位D.神话的影响随民主进程而削弱【答案】B【解析】结合题干与所学知识,显然这不是反映宗教信仰意识淡薄,排除A;材料突出的是诸神的人性而非理性,排除C;题干涉及的是经济体制的问题,没有反映阐明融入经济全球化的必要,排除;公元前9至前8世纪,雅典民主还没有确立,排除D;根据“诸神的形象和性情与人相似,不仅具有人的七情六欲,而且还争权夺利,没有一个是全知全能和完美无缺的”,可见神话文化中凸显的是诸神的人性而非神性,具有早期的人文思想,故B项正确。
本题命题意图是考查考生阅读和获取信息、调动和运用知识的能力。
本题以希腊神话为切入点,深入考查了考生对古希腊人文思想的认识和理解。
前几年全国卷Ⅰ的32小题基本上是考查古代雅典民主或罗马法,2017年的32小题却是考查古希腊人文思想,这似乎也说明命题者在命题方向上力图有所创新突破。
本题难度不大,事实上类似的架构在2016年全国卷Ⅰ中也出现过,如2016年全国卷Ⅰ的24小题就考查了儒学思想植根于久远的历史传统,显然与本题都是考查思想文化对传统文化的传承这一角度。
这就要求学生不仅要分析和理解如人文主义等概念的内涵,也要注意对近几年高考题的回顾或训练。
【智者学派——普罗塔戈拉】:“人是万物的尺度” 西方第一次思想解放运动的先驱。
主张把人置于世界和社会的中心,是西方历史上第一次思想解放运动;是在原始宗教和自然统治下人类自我意识的第一次觉醒;是西方人文精神的滥觞。
【苏格拉底】:“认识你自己”;哲学的创造者;智慧的化身;启蒙思想家的先驱和战友。
①、反对智者忽视道德、追求功利,提出“美德即知识” ;②、强调人类的理性、否认绝对权威(这点与智者一致);③、“认识你自己”,第一次在哲学意义上发现了“自我”;④、对理性的尊崇和对思想自由的追求,并为此付出了生命(与18世纪启蒙思想的特点极为相似)。
中考物理精选考点专项突破专题16画力的示意图 (原卷版)
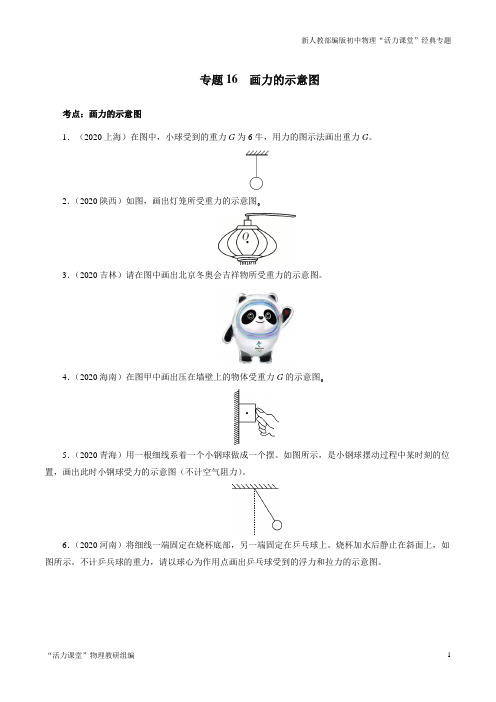
专题16 画力的示意图考点:画力的示意图1.(2020上海)在图中,小球受到的重力G为6牛,用力的图示法画出重力G。
2.(2020陕西)如图,画出灯笼所受重力的示意图。3.(2020吉林)请在图中画出北京冬奥会吉祥物所受重力的示意图。
4.(2020海南)在图甲中画出压在墙壁上的物体受重力G的示意图。____5.(2020青海)用一根细线系着一个小钢球做成一个摆。
如图所示,是小钢球摆动过程中某时刻的位置,画出此时小钢球受力的示意图(不计空气阻力)。
6.(2020河南)将细线一端固定在烧杯底部,另一端固定在乒乓球上。
烧杯加水后静止在斜面上,如图所示。
不计乒兵球的重力,请以球心为作用点画出乒乓球受到的浮力和拉力的示意图。
7.(2020云南)如图丙所示,画出物体静止在斜面上时对斜面压力F的示意图。
______8.(2020孝感)如图所示,放在水平地面上的小车B与弹簧相连,弹簧处于伸长状态,物体A与小车B均静止。
请画出:①物体A的重力示意图(O为物体A的重心);②弹簧对小车B的弹力示意图。
9.(2020咸宁)(1)如图甲所示,木棒在手指上平衡,画出它所受重力的示意图(力的作用点画在木棒的重心上)10.(2020襄阳)请画出木块所受重力的示意图。
11.(2020随州)如图所示,在体育课上小明从被竖直的绳子吊着的爬杆上匀速下滑,请画出此时爬杆在竖直方向的受力示意图。
12.(2020黄石)一个质量分布均匀的小球放在光滑的水平地面上,左边与竖直光滑墙壁接触,小球处于静止状态,如图,在图中画出小球受力示意图。
13.(2020三市一企)如图所示,穿着早冰鞋的小梅同学用手推墙,手离开墙后,小梅开始减速后退。请画出小梅后退过程中受力的示意图。(力的作用点在O点)14.(2020内江)如图所示,小明同学用一水平推力推静止在水平地面上的木箱,木箱没有动,请你在O点画出木箱所受力的示意图。
15.(2020广安)如图所示,一物体在水平地面上处于静止状态,请画出它的受力示意图。16.(2020遂宁)一木箱静止于斜面,请作出木箱对斜面的压力示意图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一编考点161.[2015·天津高考]低温诱导可使二倍体草鱼卵原细胞在减数第一次分裂时不形成纺锤体,从而产生染色体数目加倍的卵细胞,此卵细胞与精子结合发育成三倍体草鱼胚胎。
上述过程中产生下列四种细胞,下图所示四种细胞的染色体行为(以二倍体草鱼体细胞含两对同源染色体为例)可出现的是()答案 B解析A项,根据题干信息可知,卵原细胞在减数第一次分裂时不形成纺锤体,因此同源染色体不能移向两极;B项,由于减数第一次分裂时不形成纺锤体,所以形成的次级卵母细胞中的染色体数目与体细胞相同,即次级卵母细胞在减数第二次分裂后期时含有8条染色体;C项,减数第二次分裂形成的卵细胞中染色体数目为4条;D项,染色体数目加倍的卵细胞与精子结合发育成三倍体草鱼胚胎,因此胚胎细胞有丝分裂中期应含有6条染色体,三个染色体组。
2.[2015·浙江高考]下列有关细胞周期和细胞分裂的叙述,正确的是()A.不同生物的细胞大小和数目不同,但细胞周期长短相同B.同一生物各种组织的细胞周期长短相同,但G1、S、G2和M期长短不同C.若在G2期加入DNA合成抑制剂,则有丝分裂前期每条染色体仍含有2条染色单体,子细胞染色体数目与母细胞的相同D.减数分裂前期Ⅰ同源染色体配对,每条染色体含有4条染色单体,子细胞染色体数目为母细胞的一半答案 C解析不同生物和同一生物不同组织的细胞周期长短都不相同,G1、S、G2和M期长短也不相同,故A、B错误;DNA复制发生在分裂间期中的S期,在G2期加入DNA合成抑制剂不会影响DNA的复制,染色体的行为和数目不受影响,C正确;减数第一次分裂前期同源染色体配对形成一个四分体,每个四分体含有4条染色单体,每条染色体含有两条染色单体,故D错误。
3.[2014·上海高考]正常情况下,在人的初级卵母细胞经减数分裂形成卵细胞的过程中,一个细胞中含有的X染色体条数最多为()A.1 B.2C.3 D.4答案 B解析正常情况下,人的卵原细胞有X染色体两条,初级卵母细胞进行减数第一次分裂过程中由于着丝点不分裂,染色体数目不加倍,所以一个初级卵母细胞中含有的X染色体条数仍为2条,产生的次级卵母细胞或第一极体在减数第二次分裂过程中含有X染色体1条或2条(后期着丝点分裂,染色体数目加倍),卵细胞或第二极体中X染色体只有1条。
B 正确。
4.[2014·安徽高考]某种植物细胞减数分裂过程中几个特定时期的显微照片如下。
下列叙述正确的是()A.图甲中,细胞的同源染色体之间发生了基因重组B.图乙中,移向细胞两极的染色体组成相同C.图丙中,染色体的复制正在进行,着丝点尚未分裂D.图丁中,细胞的同源染色体分离,染色体数目减半答案 A解析图示为植物细胞减数分裂过程,根据图甲的联会现象,可知该图处于减数第一次分裂的前期,细胞的同源染色体之间可因交叉互换而发生基因重组,A项正确;图乙同源染色体分离,为减数第一次分裂的后期,移向细胞两极的染色体为同源染色体,B项错误;丙为减数第一次分裂末期后进入减数第二次分裂的间期,而减数第二次分裂的间期短暂,并无染色体的复制,C项错误;丁图为减数第二次分裂的后期,此时着丝点分裂,姐妹染色单体分离,导致细胞中染色体数目暂时加倍,而此时细胞中已没有同源染色体,D项错误。
5.[2013·课标全国卷Ⅰ]关于同一个体中细胞有丝分裂和减数第一次分裂的叙述,正确的是()A.两者前期染色体数目相同,染色体行为和DNA分子数目不同B.两者中期染色体数目不同,染色体行为和DNA分子数目相同C.两者后期染色体数目和染色体行为不同,DNA分子数目相同D.两者末期染色体数目和染色体行为相同,DNA分子数目不同答案 C解析本题主要考查有丝分裂和减数第一次分裂过程中染色体行为、染色体数目以及核DNA分子数目的相关知识。
两者的前期,染色体数目均与体细胞相同,核DNA分子数目均为体细胞的两倍,但减数第一次分裂前期发生了同源染色体的联会,而有丝分裂前期没有此行为;两者的中期,染色体数目均与体细胞相同,核DNA分子数目均为体细胞的两倍,有丝分裂中期,每条染色体的着丝点排列在赤道板上,减数第一次分裂中期,每对同源染色体排列在赤道板上;有丝分裂后期染色体数目、核DNA分子数目均为体细胞的两倍,姐妹染色单体分开,减数第一次分裂后期染色体数目与体细胞相同,核DNA分子数目为体细胞的两倍,同源染色体分开;两者的末期,核DNA分子的数目均与体细胞相同,有丝分裂末期,染色体数目与体细胞相同,减数第一次分裂末期,染色体数目为体细胞的一半。
6.[2015·海南高考]回答下列关于遗传和变异的问题:(1)高等动物在产生精子或卵细胞的过程中,位于非同源染色体上的基因会发生________,同源染色体的非姐妹染色单体之间可能会发生________,这两种情况都可能导致基因重组,从而产生基因组成不同的配子。
(2)假设物种的染色体数目为2n,在其减数分裂过程中,会出现不同的细胞,甲、乙2个模式图仅表示出了Aa、Bb基因所在的常染色体,那么,图甲表示的是________(填“初级精母细胞”“次级精母细胞”或“精细胞”),图乙表示的是________(填“初级精母细胞”“次级精母细胞”或“精细胞”)。
(3)某植物的染色体数目为2n,其产生的花粉经培养可得到单倍体植株。
单倍体是指________________________________________________________________________。
答案(1)自由组合交叉互换(2)初级精母细胞精细胞(3)体细胞内含有本物种配子染色体数目的个体解析 (1)高等动物在产生精子或卵细胞的过程中,减数第一次分裂后期,位于非同源染色体上的基因会发生自由组合;减数第一次分裂前期,同源染色体的非姐妹染色单体之间可能会发生交叉互换,这两种情况都可能导致基因重组,从而产生基因组成不同的配子。
(2)根据题意,二倍体生物精子形成过程中,减数第一次分裂的前期同源染色体联会形成四分体,根据图甲中基因的数量和位置可知,图甲表示初级精母细胞;图乙中没有同源染色体,也无染色单体,表示精细胞。
(3)单倍体是指体细胞内含有本物种配子染色体数目的个体。
7.[2014·江苏高考]某研究者用非洲爪蟾性腺为材料进行了下列实验。
请回答下列问题:(1)对非洲爪蟾的精巢切片进行显微观察,绘制了以下示意图。
上图中甲、乙、丙、丁细胞含有同源染色体的有________;称为初级精母细胞的有________。
丁细胞中染色体的互换区段内同一位点上的基因__________________(填“相同”、“不相同”或“不一定相同”)。
(2)如对卵巢切片进行显微观察,无法看到和乙细胞同时期的细胞,其原因是________________________________________________________________________。
(3)该研究者进行了一系列“诱导早期卵母细胞成熟的物质”实验,结果如下:实验一⎩⎪⎨⎪⎧ 早期卵母细胞――→注射早期卵母细胞少量细胞质早期卵母细胞早期卵母细胞――→注射成熟卵细胞少量细胞质成熟卵细胞实验二⎩⎨⎧ 早期卵母细胞――→孕酮成熟卵细胞早期卵母细胞――→孕酮+蛋白质合成抑制剂早期卵母细胞由实验一可得出推论:_____________________含有可以诱导卵母细胞成熟的物质。
由实验二可得出推论:这种诱导早期卵母细胞成熟的“促成熟因子”的化学成分是________;孕酮在实验二中的作用是___________________________________________。
答案 (1)甲、丙、丁 甲、丁 不一定相同(2)卵母细胞在卵巢中不能分裂到该时期(3)成熟卵细胞的细胞质蛋白质诱导早期卵母细胞合成“促成熟因子”解析(1)根据有丝分裂和减数分裂的特征可以判断:甲为减数第一次分裂的中期、乙为减数第二次分裂的后期、丙为有丝分裂的后期、丁为减数第一次分裂的后期。
二倍体生物有丝分裂(图丙)和减数第一次分裂(图甲、图丁)有同源染色体,减数第二次分裂(图乙)无同源染色体;雄性生物减数第一次分裂的前期、中期(图甲)、后期(图丁)的细胞均称为初级精母细胞。
丁中同源染色体的姐妹染色单体之间交叉互换,互换区段内同一位点上的基因是否相同与同源染色体相同位置含的基因有关,如果同源染色体上含相同基因,则互换区段内同一位点仍是相同基因,如果同源染色体上含等位基因,则互换区段内同一位点是不同基因。
(2)排卵排出的卵子先是在输卵管中发育到减数第二次分裂的中期,只有在受精的过程中才能继续进行减数第二次分裂,发生图乙的减数第二次分裂后期。
因此在输卵管中发生减数第二次分裂的后期,卵巢中观察不到。
(3)由实验一的相互对照可知,当含有成熟卵细胞的细胞质才能使早期卵母细胞发育成成熟卵细胞,说明成熟卵细胞的细胞质中含有可以诱导卵母细胞成熟的物质。
由实验二孕酮处理组,可以得出孕酮有诱导早期卵母细胞成熟的功能;当蛋白质合成抑制剂与孕酮同时处理时,蛋白质合成抑制剂抑制蛋白质的合成,早期卵母细胞就不能发育成熟,说明蛋白质的合成与促进早期卵母细胞成熟有关。
由此可以做出推测:诱导早期卵母细胞成熟的“促成熟因子”的化学成分是一种蛋白质;孕酮可是诱导早期卵母细胞合成“促成熟因子”从而促进其发育成熟的。
1.[2016·四川成都模拟]下列对四分体的描述,不正确的是()A.一个四分体有两个着丝点B.四分体中的非姐妹染色单体之间可能发生染色体交叉互换C.一个四分体有4条脱氧核苷酸长链D人体细胞进行减数分裂可形成23个四分体答案 C解析减数第一次分裂过程中联会后的同源染色体含有四条染色单体,称为四分体,因此一个四分体含有两个着丝点,四分体时期同源染色体的非姐妹染色单体之间可以发生交叉互换;一个四分体含有4个DNA分子,8条脱氧核苷酸长链;人体细胞含有23对同源染色体,因此联会时可以形成23个四分体。
2.[2016·黄山质检]C1、C2、C3、C4是某动物(2N)的4个细胞,其染色体数分别是N、2N、2N、4N,下列相关叙述错误的是()A.C1、C2可能是C4的子细胞B.C1、C3不一定是C4的子细胞C.C1、C2、C3、C4可能存在于一个器官中D.C1、C3、C4的核DNA分子比例可以是1∶2∶2答案 A解析由C1、C2、C3、C4是某动物的4个细胞,其染色体数分别是N、2N、2N、4N 可知,C1可能为减数第二次分裂前期、中期的细胞或减数分裂结束后形成的细胞,C2、C3的染色体数相同,但DNA数可能不同,C4为有丝分裂后期的细胞,故C1不可能是C4的子细胞。
