土壤地面不平度及接触分形模型
分形几何在工程地质中的应用

分形几何在工程地质中的应用分形几何是一种数学理论,它可以描述自然界中的复杂形态和非线性因素。
随着工程技术的发展,分形几何在地质领域中的应用越来越广泛。
本文将探讨分形几何在工程地质中的应用。
1. 地质形态分析地质形态是指地面或地下土地的形态。
通过对地质形态的分析,可以了解地下地形和地质构造,从而为地质灾害预防和工程设计提供有效的参考。
分形几何可以用于分析地质形态。
通过计算地质构造的分形维度,可以确定地质形态的复杂程度。
分形维度越高,表明地质构造越复杂,反之亦然。
因此,分形几何可以为地震风险评价、山体滑坡预警、土壤侵蚀评估等提供重要的参考。
工程地质中最常见的问题之一是地层的变形问题。
分形几何可以应用于变形分析中。
工程师可以通过计算地层的分形维度,来确定地层是否发生变形。
如果地层的分形维度发生了变化,则说明地层发生了变形。
这种方法可以用于诊断地层的变形类型,以及确定变形的程度和范围。
3. 地下水运动模拟水文地质与地下水文学是工程地质的一个重要领域。
分形几何可以用于模拟地下水运动。
在地下水运动模拟中,分形几何可以用于计算水流路径和地下水位线的分形维度。
这种方法可以诊断水文地质问题,并提供有效的预测和管理方法。
4. 土壤侵蚀预测土壤侵蚀是一种普遍存在的自然现象。
它对生态环境和农业生产都有极大的影响。
分形几何可以用于预测和评估土壤侵蚀的危害程度。
通过计算土壤质地和斜坡的分形维度,可以确定土壤侵蚀的发生和程度。
这种方法可以为土地使用和管理提供重要的参考。
5. 岩土工程设计岩土工程是工程地质的重要分支。
分形几何可以用于岩土工程的设计和评估。
例如,分形几何可以用于考虑地面沉降的影响,以及土壤的渗透性和压缩性。
这种方法可以为岩土工程设计提供更准确的数据,从而提高工程质量和安全性。
6. 地震监测与预测地震是一种普遍存在的自然灾害。
地震发生的时间、强度和范围都是难以确定的。
分形几何可以用于地震监测和预测。
通过计算地震波和岩土体的分形维度,可以预测地震的频率和强度,从而提供有效的预防和应对措施。
两种土壤粒径分形模型的对比研究

s mp e,b c u et e dfe e tg a u a iy g o p a e t e smi rpe c n fmie a o o iin,t ea r g e a l e s h i r n r n lrt r u sh v h i l r e to n r lc mp sto a f a h vea ed n— st fg an i i lra d t e fe i i t fa s mp i n i o d i o r i ssmi n h lx bl y o s u to sg o . y a i Ke r s:s l sz i t i to fa t lm o e ; r c a i nso l n ld o1 y wo d oi; ie d srbu i n;r c a d 1 f a t ld me i n;a dsi e s i
分形理论数学模型在土壤学中的应用研究

与传导 , 包括人渗与通气 , 还影响土壤的机械性质 , 这 对于种子萌发 , 根系生长 , 土壤耕作 , 陆上交通和土壤 侵蚀以及其他一些问题 的研究也不可缺少。
土 壤 水 分 运 动 参 数 主要 包 括 水 分 特 征 曲线 , 饱 和、 非饱 和 导水 率 及 土 壤水 分 扩 散 率 , 关 这 些 参 数 有
的生命力和广阔的发展前景。
1 分形 理论 的提 出
对于 自然界常见的 、 变幻莫测的, 不稳定的、 非常 不规则的现象 , 欧氏几何学将其贬为“ 病态结构 ” 。但 是, 这些“ 病态结构” 似乎 比经典 的 、 光滑的几何 图形 能更 好 的反 映 自然现 象 的本 质规 律 。在 研究 这 些 “ 病
S HAN AT XIW ER RES J ES OIRC
分 形理 论数 学模 型在 土壤 学 中的应 用研 究
梁青 丽
( 城 市 盐 湖 区水 利局 , 运 山西 运城 000 ) 4 0 1
[ 要] 摘 分形理论作为非线性科 学中的普适性理论之 一, 研究工作 十分活跃 , 该理论 为研 究土壤 结构的复杂性
基本框架 , 开辟了这一数学研究的新领域。 分形理论一经提出, 便受到 自然科学诸多领域的 广泛关注。现在 , 对分形的研究 已远远超 出了几何学 的范 围 。分 形 理论 已被 应用 到 物理 学 , 学 , 物学 , 化 生
地 质学 以及 诸 多动 力学 系统 , 甚至 社 会经 济 的理 论 和
自然 现 象 多样 性 和复 杂 性 的 根 源 在 于 世 界 本 质 上是 非线 性 的 。 线性科 学 ( ol er cec ) 非 N ni a ine已成 为 n S 蓬勃 发 展 的前 沿科 学 。其 中以研 究非线 性 图形 自相 似
【浙江省自然科学基金】_分形模型_期刊发文热词逐年推荐_20140812
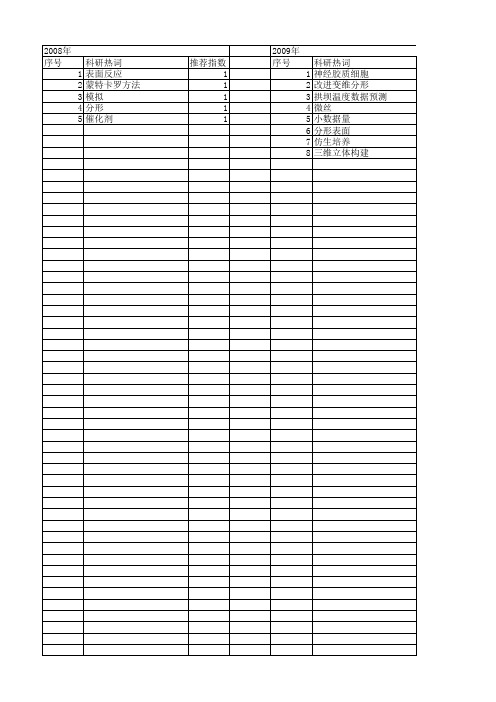
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5
2014年 科研热词 高速列车 降噪 多尺度表面织构 复合表面织构 koch雪花表面织构 推荐指数 1 1 1 1 1
科研热词 遥操作机器人 轴向间隙 趋化因子 表面肌电信号 肌电信号 经验模态分解 神经网络 港口物流 涡旋压缩机 泄漏量 模式识别 机械手 最大分形长度 最佳分形参数 支持向量机 多重分形分析 呼吸道合胞病毒 分维数 分形预测 pparγ 激动剂 lempel-ziv复杂度 k最近邻模型法 5 6 7 8 9
科研热词 静电纺丝法 花式纱线 纳米纤维 纳米压痕 真实感模拟 分形理论 分形 光照模型 dla模型
推荐指数 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10
2011年 科研热词 分形维数 自然保护区 肤色建模 纹理粗糙度 空间变异 皮肤纹理 皮肤检测 常绿阔叶林 土壤学 土壤养分 推荐指数 2 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8
科研热词 迭代函数系统 裂缝型多孔介质 渗流 树木模拟 径向 分形维数 分形模型 ifs
推荐指数 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
2008年 序号 1 2 3 4 5
科研热词 表面反应 蒙特卡罗方法 模拟 分形 催化剂
推荐指数 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8
科研热词 神经胶质细胞 改进变维分形 拱坝温度数据预测 微丝 小数据量 分形表面 仿生培养 三维立体构建
土壤颗粒结构的分形模型及其渗透性

d .Bae n p r—oi a tlmo e fs i srcu ,amo ie to f e eaigt esmpeo rn a ol t cuewi y a s d o oe sl f ca d lo ol tu tr dr e df dmeh do n rt a l f a u rsi sr tr t i g n h g l u h crua an,whc a e u e ie t o i lt n o c a ia h vo fg a ua olb srt lme tmeh d,i i lr g i c r ihc n b s d drcl frsmuai fme h nc lb a iro r n r si y d c eee n to y o e l i e s s g e td h r .T ec aa tr fp r n nefc ewe n p r n oi ftega ua ol l n y e n dt efr uafr u g se e e h h rceso o ea ditr eb t e o a ds l o h rn r si ae a a zd,a m l a e d l l h o o p r a it sgv n b s d o zn - r e n Koe y Ca n fm l i m o
Ke wo d :g a u a ol olsr cu e;fa tlm o l ic ee p r il o e ;p r a i t y r s r n lr s i;s i tu t r r ca de;ds r t a t e m d l e me bl y c i
1 简
介
本文 基于 PF模型 , 虑到土壤 结构 的实 际生 成过程是 S 考 由有 限次复制完成 , 析 了最后 一次 复制完 成后 , 分 叠代 子域 分别指配 为固体颗粒或孔 隙时所形成 的颗 粒数量 、 隙数量 孔 及孔 隙度 的差异 , 进一 步完 善 了 P F模型 。考虑到现有 离散 S
常用土体本构模型及其特点小结

常用土体本构模型及其特点小结山中一草线弹性模型线弹性模型遵从虎克定律,只有2个参数,即弹性模量E和泊松比V,它是最简单的应力-应变关系,但无法描述土的很多特征,主要应用于早期的有限元分析及解析方法中,可用来近似模拟较硬的材料如岩土。
Duncan-Chang( DC 模型DC模型是一种非线性弹性模型,它用双曲线来模拟土的三轴排水试验的应力-应变关系(图1)。
它侧重于刻画土体应力-应变曲线非线性的简单特征,通过弹性参数的调整来近似地考虑土体的塑性变形。
但所用的理论仍然是弹性理论而没有涉及到任何塑性理论,故仍不能反映如应力路径对变形的影响、土体的剪胀特性和球应力对剪应变的影响等土体的很多重要性质。
由于DC模型是在二为常数的常规三轴试验基础上提出的,比较适用于围压不变或变化不大、轴压增大的情况,如模拟土石坝和路堤的填筑。
图】IK模型关于三轴试验的应力-应变关系Fig.l Duncan-Chang approxiniathm of the siress-strainrd nt kinship Ln ft standard drained triAxt*! te&lMohr-Coulomb (MC)模型MC模型是一种弹-理想塑性模型,它综合了胡克定律和Coulomb破坏准则。
有5个参数,即控制弹性行为的2个参数:弹性模量E和泊松比v及控制塑性行为的3个参数:有效黏聚力c、有效内摩擦角和剪胀角。
MC模型采用了弹塑性理论,能较好地描述土体的破坏行为但却认为土体在达到抗剪强度之前的应力-应变关系符合胡克定律,因而并不能较好地描述土体在破坏之前的变形行为,且不能考虑应力历史的影响及区分加荷和卸荷。
故MC模型能较好地模拟土体的强度问题,MC模型的六凌锥形屈服面(图2)与土样真三轴试验的应力组合形成的屈服面吻合得较好,因此MC模型适合于低坝、边坡等稳定性问题的分析。
Drucker -Prager( DP)模型DP模型对MC模型的屈服面函数作了适当的修改,采用圆锥形屈服面(图3)来代替MC模型的六凌锥屈服面,易于程序的编制和进行数值计算。
农田地面不平度测量与分析_徐竹凤

路面不平度能量的 分 布 ,以 及 路 面 波 的 结 构 与 路 面 的 总体特征[10]。因 此,研 究 者 一 般 通 过 研 究 路 面 谱 来
研究路面不平度 。 同 样 地 ,可 以 通 过 研 究 农 田 地 面 功
率谱密 度 来 研 究 农 田 地 面 不 平 度。 根 据 标 准 ISO / TC108[11]和标准《车辆振动输入—路面平度的表示方 法 》[12]两 个 文 件 ,拟 定 路 面 不 平 度 的 路 面 位 移 功 率 谱
2. 2 数据预处理 数据预处理是在 数 据 准 备 完 成 之 后 进 行 ,以 测 得
的 3 种地面的试验数据为分析对象,对数据进行预处 理分 析,即 提 取 路 面 不 平 度 曲 线 的 趋 势 项 、去 除 所 有 数据中的 毛 刺、进 行 分 段 路 面 数 据 间 的 平 滑 过 渡 连 接、将 等 时 间 间 隔 采 样 数 据 转 换 为 等 距 离 间 隔 数 据 , 得到有效的地面不平度曲线,如图 6 所示。
师,( E-mail) 735178312@ qq. com。
实土路及石子路进行了测量,以验证系统量原理[9] 图 1 中,包括质量 M,弹簧刚度 K,阻尼 C,测量轮
·171·
2017 年 1 月
农机化研究
w。测量仪安装在农机上( 农机后车桥位置为宜) ,随 着农 机 行 驶,测 量 轮 跟 随 地 面 的 起 伏 而 升 降 ,测 量 过 程中,为确保测 量 轮 始 终 保 持 与 地 面 接 触 ,要 求 测 量 轮组件的质量小,以提高其自振频率; 控制测量行驶 的速度 ,使所测量的 地 面 谐 量 的 激 励 频 率 低 于 测 量 轮 的自振频率 。 测量时 ,由 于 测 量 轮 跟 随 地 面 不 平 而 运 动,所以测量轮产生的垂直位移 W 就是被测地面的不 平度。图 2 为自行设计研制的测量仪三维图。
土壤表面不平度分形特性的图像分析方法

土壤表面不平度分形特性的图像分析方法侯占峰,韩进玉,韩宝生(内蒙古农业大学机电工程学院,呼和浩特010018)摘要:研究了分形几何理论和图像处理技术在土壤表面不平度分形维数计算方法中的应用。
利用分形几何的相关理论针对图像预处理后的表面形貌的图像数据建立数学模型,得到可以表征土壤表面不平度的分形参数。
为此,共选择了3种不同耕作方式的土壤表面作为研究对象,运用自行设计的程序进行了表面分形维数的计算。
结果表明:不同类型表面的分形维数相差较大,利用分形维数能够进行土壤表面不平度的有效表征,同时能对不同类型的土壤表面进行准确分类。
关键词:土壤;图像;分形维数中图分类号:T P391.41文献标识码:A 0引言土壤表面不平度对土壤颗粒的形成以及土壤表面磨蚀、风蚀等起着重要作用…。
由于土壤空间变异性的存在,使得土壤的表面结构具有随机性和空间相关的特征,因此通过土壤表面不平度分析可进行土壤风蚀预测及对土壤中溶质的时空分布和变化进行预测预报口J。
另外,根据地面不平度还可模拟研究土壤与轮胎之间的相互作用规律及土壤的变形量∞J。
所以,土壤不平度是农业工程人员与汽车工程人员长期以来研究的对象。
这些都表明研究土壤表面不平度的特性具有重大意义。
近20年来,分形的应用渗透到了各个领域,并不断得到发展,这主要是分形可以将以前不能定量描述或难以定量描述的复杂对象用一种较为便捷的定量方法表述出来。
传统的分析方法是对利用专门的测量仪器测到的表面轮廓高度进行分形分析¨J,这种方法费时费工。
随着计算机技术的发展,数字图像技术已经越来越广泛地应用到各个生产和科技领域。
如果将表面不平度的信息通过图像的形式获取,然后进行分形分析,则不仅可以节省时间与资金,还可以为人们提供形象化的信息。
本文作为图像技术在农业工程中应用的尝试,利用分形理论,计算了不同耕作方式土壤表面图像的分形维数。
结果表明:土壤表面不平度与分维值之间具收稿日期:2011—03—11基金项目:内蒙古自然科学基金项目(2010K S0718)作者简介:侯占峰(1980一),男,呼和浩特人,讲师,硕士,(E—m ai l) nj au-haf@163.c or n。
耙地土壤表面分形特征及不同测量精度下形貌恢复研究

m aue et cuay ae ni te r t nl rw ’ i e oao er a pl d te e t aa e e otepyigo y esrm n acr .B sdo ,h a i a Bo n Sn r ltnt o w s pi ,h i t sr s fh hs nm c t fco tp i h y a e h g d i h o
摘
Hale Waihona Puke 要: 分析 了经耙地后 的土壤表 面的分形特征 , 结果表明 : 在不同测量精度下 , 分形维数 与无标度 区间 2项分形数值特
征都具有高度的一致性 ; 拟合线性后 直线截距具有显著阶梯 分布的特点 , 表明截距能够反映测量精度信息 , 于该特 点, 基 应用 分数布朗插值原理 , 对比插值前后地貌高度数据列, 统计特征 中的均值 、 标差、 偏度 系数、 峰度 系数 , 拟合 线性后 的直线截 距和
Ab t a t h rc a c a a tr t s o u a e s i at rh ro i g wee a ay e .T e r s h n iae h t n e i ee t sr c :T e fa t h r ce i i fs r c ol fe ar w n r l z d l sc f n h e u s id c t d t a :u d rd f rn me s r me ta c r ce .t e dme so a n c e—f e r go a a t u rc h rc e siswee h g l o sse t ie ri — a u e n c u a is h i n in a d s a l l r e i n l r ca n meia c a a tr t r ihy c n i n .L n a n e f l l i c t tr e th d t e sg i c t u e o tp d s i u in atr l e r s lt n h w n h t te itr e tc u d r f c h n o main o ec p a h in f a l fs it b t f i a i ai ,s o i g t a h n e c p o l e e tte if r t f in r e r o e n mu o l o
土壤模型

无定形的土壤有机质(软碳)
凝聚态的土壤有机质(硬碳)
土壤固相——吸附
随后,Weber和Huang将土壤(沉积物)中吸附有机污染物的组份分 成无机矿物表面、无定形的土壤有机质(软碳)和凝聚态的土壤有机质 (硬碳)3个部分。这样多端元反应模型就变成了三端元反应模型,有机 污染物通过不同的吸附方式进入到土壤的上述3个部分。 无定形——其内部原子或分子的排列无周期性,如同液体那样杂乱无章 地分布,可看作过冷液体,如玻璃、松香、明胶等。 凝聚态——由大量粒子组成,并且粒子间有很强相互作用。
土壤孔隙
土粒或者团聚体之间以及团聚体内部的孔隙,称为土壤孔隙。 土壤中孔隙的容积占整个土体容积的百分数,称为土壤孔隙度:
土壤孔隙度=[孔隙容积/土壤容积]×100% =[(土壤容积-土粒容积)/土壤容积]×100% =[1-(土粒容积/土壤容积)]×100%
=[1-(土粒重量/比重)/(土壤重量/容重)]×100%
土壤固相——吸附
吸附是化合物从气相或液相向固体表面凝集的一种物理化学过程,可分为 物理吸附、静电吸附和离子交换吸附。 土壤吸附有机污染物机理的主要研究是从土壤中有机质的角度进行的,目 前为止的模型有: 1.线性分配模型 2.非线性分配模型 3.双模式吸附模型
4.多端元反应模型
5.三端元反应模型 ……
土壤固相——土壤胶体
2.带电性 一般来讲,土壤胶体带负电荷,某些情况下也会带正电荷。土壤中许多重要 的理化性质和其有关,其所带的表面电荷是土壤具有一系列化学、物理化学性质 的根本原因。土壤中的化学反应主要为界面反应,这是由于表面结构不同的胶体 所产生的电荷,能与溶液中的离子、质子、电子发生相互作用。
详述土壤颗粒体积单重分形理论模型计算过程

科技与创新┃Science and Technology &Innovation·64·2021年第02期文章编号:2095-6835(2021)02-0064-02详述土壤颗粒体积单重分形理论模型计算过程*孟婷婷(1.陕西省土地工程建设集团有限责任公司,陕西西安710075;2.陕西地建土地工程技术研究院有限责任公司,陕西西安710075;3.国土资源部退化及未利用土地整治工程重点实验室,陕西西安710075;4.陕西省土地整治工程技术研究中心,陕西西安710075)摘要:土壤颗粒分形理论被广泛用来描述土壤的自相似特征,目前很多文献中常用王国梁推导的土壤颗粒体积单重分形理论模型来计算土壤分形维数D 。
但是,很大一部分人对模型参数的理解有误。
因此,选用笔者已发表的论文数据,对模型各参数意义和计算过程进行了详细概述,可为后面的研究者提供直观便捷的参考资料。
关键词:土壤;土壤粒径;分形模型;参数计算中图分类号:S152文献标志码:A DOI :10.15913/ki.kjycx.2021.02.0211引言土壤作为一种由水分、空气和不同颗粒等各类物质所组成的多孔介质,其本身是具有不规则的形状和自相似性特征的复杂几何体[1]。
基于土壤颗粒的自相似特征,分形理论被引入到土壤学中来,更好地反映土壤性质及结构的变化。
自杨培岭等[2]和王国梁等[3]学者提出并不断优化土壤颗粒分形维数计算模型以来,土壤颗粒分形维数被广泛应用。
虽然关于土壤颗粒体积单重分形理论模型的文献很多,但缺乏对模型计算过程的详细概述。
2土壤分形模型本文根据王国梁等[3]推导的土壤颗粒体积单重分形理论模型计算出土壤分形维数D ,公式为:D3V T -⎪⎪⎭⎫⎝⎛=λR V R r V )<((1)式(1)中:V (r <R )为所有小于R 的土粒的粒径体积之和;V T 为土壤颗粒的总体积;R 为某一粒径特征尺度,计算时用该区间上下限算数平均值表示;λV 为土壤粒径分级中最大的粒级值;D 为土壤颗粒的体积分形维数。
土壤结构的分形特征及土壤水分运动模型研究

土壤结构的分形特征及土壤水分运动模型研究下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!土壤结构的分形特征及土壤水分运动模型研究引言在农业生产和环境保护中,土壤是一个至关重要的因素。
土壤水分特性曲线的研究与理论模型的构建

土壤水分特性曲线的研究与理论模型的构建土壤是农业生产中不可或缺的资源之一。
为了优化土地利用效益,掌握土壤的水分特性曲线是必不可少的。
这不仅有助于农民掌握土壤水分情况,提高农作物产量,也有助于生态环境的保护和土地资源的可持续利用。
本文将围绕土壤水分特性曲线的研究与理论模型的构建展开论述。
一、土壤水分特性曲线的概念与意义土壤水分特性曲线是描述土壤保水能力的一种重要指标。
它是指土壤水分含量与土壤水势之间的关系,通俗地说就是描述土壤在不同水分状况下蓄水和利用水的能力。
土壤水分特性曲线可以反映土壤的蓄水能力、渗透能力、干旱抗性及土壤孔隙结构等特点,是科学测定土壤水分与理解生态环境关系的核心内容。
土壤水分特性曲线所反映出的水分状态,对于人们对土壤肥力进行评估和土地利用的选择具有重要的意义。
同时,也可以指导农民科学地排灌水,化肥,农药,以达到节约用水,防止污染和减轻土地环境压力等多方面的作用。
二、土壤水分特性曲线的影响因素土壤水分特性曲线的形态与土壤固体颗粒及孔隙形状、分布有关,是土壤研究中的重要内容之一。
影响土壤水分特性曲线的要素主要有以下几点:1. 土壤颗粒的多寡,大小及分布情况;2. 土壤孔隙的分布、尺度和连通性;3. 土壤类型及其化学成分;4. 环境因素(如空气温度、相对湿度、降雨量与土壤表面温度)等。
以上要素可以单独或联合作用,从而影响土壤水分特性曲线的形态和特征。
三、土壤水分特性曲线的实验研究土壤水分特性曲线的实验研究是农学、水文学等多个学科领域的重要内容之一,其研究主要围绕土壤蓄水性能和滞集能力开展。
实验方法通常采用高精密的水分计设备,通过多组水分势数据和对应的土壤含水量数据,确定土壤水分特性曲线。
在实验方法上,根据在土壤中施加的负水势的可控程度,以及反映土壤物理力学特性的方法和数据的可测定性和可靠性等方面的要求,目前土壤水分特性曲线的实验方法主要有压滤法、压缩法和张力悬浮法三种方法。
四、土壤水分特性曲线的理论模型土壤水分特性曲线的理论模型构建是研究土壤物理力学特性的重要方法之一。
土坡动力稳定的空间模型分析

土坡动力稳定的空间模型分析土壤坡度是坡面稳定性关键因素之一,对于中小型滑坡或山体滑坡研究,土壤坡度的影响是必不可少的。
几十年来,土壤动力稳定性在空间上的分析方法一直是为地质和工程领域提供了最重要的研究和设计能力。
本文将介绍一种土坡动力稳定性空间模型分析方法,旨在提供一种新的理解土壤坡度对坡面稳定性和滑坡危险性的重要性。
在空间上分析土壤动力稳定性的基本思想是,测量一定的土壤坡度后,计算可能的滑坡杆长范围。
以滑坡杆长范围为空间坐标,确定土壤坡度下的稳定性,用来反映土壤坡度的空间分布的稳定性特征。
该模型分析方法可将空间上的滑坡意义联系起来,可以对某一地质,气象,地貌等条件下的滑坡进行分析,从而了解土壤坡度在滑坡过程中所发挥的重要作用。
在《土坡动力稳定的空间模型分析》中,土壤坡度是指其坡度的垂直度,是土壤坡面的空间特征。
土壤坡度的高度可以从野外实测、工程仿真或模型计算中测量得到,并以平面度为指标,计算滑坡杆长范围。
给定土壤坡度,可以确定土壤动力稳定性的滑坡杆长。
空间模型分析方法能够有效探知土壤坡度对坡面稳定性的影响。
空间模型分析可以提供详细的滑坡杆长范围,从而使地质工程师和规划师更加清楚地了解水文地质条件下坡面的稳定性状态,从而有效地控制坡面的安全性。
此外,空间模型分析还可以提供滑坡预测模型,可以在一定范围内预测滑坡大小,从而有效控制其发展。
坡面稳定性的安全性取决于土壤坡度的测量和空间模型分析的准确性。
因此,对于坡面稳定性研究来说,土壤坡度的测量不仅要准确而便捷,还要有足够的空间来识别土壤坡度的空间分布特征。
合理的土壤坡度测量应考虑在不同地貌条件下,土壤坡度可能变化的一般性及特殊性,如挡土墙,剖面等。
此外,测量时应当考虑自然界的动态变化因素,如时间和季节因素。
在空间模型分析中,考虑土壤动力稳定性的参数可以提供更精确的滑坡杆长空间分布。
该参数包括推力系数、荷载系数、荷载均匀度系数、抗剪系数等。
这些参数可以更具体地反映出土壤坡度对滑坡意义的重要性。
土壤表层模型的构建及其在气候变化中的应用

土壤表层模型的构建及其在气候变化中的应用一、概述土壤表层(topsoil)是土壤的上部层,通常为土壤厚度的前0-30厘米之间。
土壤表层是植物根系生长和养分吸收的重要区域,同时也是土壤中有机质和养分富集的地方。
因此,建立土壤表层模型有助于研究和分析土壤生态系统的功能,对区域气候变化的响应也有所帮助。
二、土壤表层模型构建1. 数据采集土壤表层模型最基础的需要是土壤数据的采集。
一般需要采集土壤的化学和物理性质数据,如有机质含量、氮、磷、钾等元素含量、土壤温度、含水量和pH值等。
还需要考虑到土地利用方式和植被类型,以及人类活动对土地的影响(如施肥、排水等)。
2. 样品分析土壤数据的样品分析包括土壤干重、水分含量、样品制备、土壤有机质含量、卡方检验等。
这些数据需要经过准确检测和统计分析,作为构建模型的基础数据。
3. 模型建立建立一个高效准确的土壤表层模型需要考虑多种因素,如随机森林法、支持向量机法(SVM)、人工神经网络法(ANN)和多元回归分析法等。
主要考虑因素包括预测模型的准确性、鲁棒性等。
三、土壤表层模型在气候变化中的应用1. 模型在气候变化预测中的应用建立的土壤表层模型可以用于对大气和降水中的碳、氮、磷等有机和无机元素的变化进行预测,从而可以为气候变化研究提供公开的参考数据。
2. 模型在土地管理中的应用由于土壤表层中的有机质非常重要,可以作为衡量土地健康程度的指标。
如果我们建立了一个良好的土壤表层模型,就可以帮助我们识别哪些土壤需要改进,提高生产力和营养水平。
3. 模型在生态系统管理中的应用合理管理生态系统可以帮助提高土壤质量、丰富生物多样性。
通过利用先前建立的模型来辅助学习土地和生态系统结构和功能之间的关系,我们就可以建立模型,来预测不同的生态系统管理方法和外部陆地利用变化对生态系统的影响。
结语综上所述,本文讨论了如何建立土壤表层模型,以及该模型在气候变化中的应用。
建立土壤表层模型可以帮助我们更好地了解土地和生态系统的结构和功能之间的关系,同时也为能做出更好的决策和政策提供了帮助。
土壤地面不平度的三维分形模型

( c )驱 动 耙 耙 地
图 1 不 同耕 作 方 式 的地 表 不 平 度 图
Fi g. 1 Pr of i l e s o f di f f e r e n t t i l l ag e s o i l s u r f a c e
收稿 日期 : 2 0 1 4年 2月 2 4日
的凸峰 与 凹谷 组 成 的粗 糙 表 面 , 它 的结 构 从 微 观 尺 度
到 宏观 尺度都 具 有 自组 织 分 层 性 质 ] , 它 具 有 自形 似
结 构 。耕 作地 表 的不 平度 、 孔 隙表 面 、 团聚体 、 变性、 水 分 运移等 土壤 特性 , 都属 于此类 不规 则 、 不稳 定及 具 有 高度 复杂结 构 的现象 _ 5 ] 。作 为探 索不 规则 结构 和 形 态
论 和方法之 一 l 6 J 。
形相关理论与布朗模 型建立土壤地面 的三维模型 , 旨在为 适用于评定农用车辆振动激励的输入模型提供理论基础。
本文利 用 自制 的激光非 接触 式不 平度 测试 仪 测取
农 田耕作 后 的 地 表 不 平 度 。测 试 仪 有 效 测 试 长 度 为
1 0 2 4 mm, 测试 精 度 为 l mm ・次- 。 , 每次测定 l m 长
! 璺 奎 兰 塑
分形 参 数 D 可 以控 制 地 面 的 不平 度 。该 模 型 具 有 一
定的灵 活 性 , 可 以 作 为 车 辆 仿 真 测 试 的 激 励 输 入 模 型。
修 回 日期 : 2 0 1 4年 4月 4日
*基 金 项 目 : 内蒙 古 自治 区 高 等 学校 科 学 研 究 项 目( N J Z Y1 3 0 6 8 ) 第一作者 : 侯 占峰 , 男, 1 9 8 0年 生 , 内蒙 古 呼 和 浩 特 人 , 硕士 , 副教 授 ; 研 究 方 向 为 汽 车地 面力 学 。E — ma i l
采用土壤孔隙表面分形维数预测土壤水分特征曲线

采用土壤孔隙表面分形维数预测土壤水分特征曲线刘亚磊;梁杏;朱常坤;李静【摘要】采用土壤颗粒体积累积曲线按照不同的粒径分级方法计算表面分形维数,避免了原始计算过程中颗粒密度不变的假设,改进了计算中的缺陷.结合土壤水分特征曲线分形模型—de Gennes模型,预测试样的SWRC.结果发现:不同颗粒分级只会影响表面分形维数的大小;相同颗粒分级情况下,计算得出的分形维数随着土壤粘粒含量降低而减小;采用D2(最大半径为lmm)的分级情况计算出的表面分形维数,预测得出的结果与实测值相差偏大,RMSE≥2.11E-02cm3/cm3只适合粗略估计田间土壤的水分特征曲线;通过D1(最大半径为0.1mm)计算出的表面分形维数,结合deGennes模型预测水分特征曲线结果与实测值非常接近,RMSE≤0.0l05cm3/cm3.研究表明采用土壤颗粒体积累积曲线计算表面分形维数,并预测土壤水分特征曲线是合理的,具有较高的预测精度.【期刊名称】《水文地质工程地质》【年(卷),期】2014(041)003【总页数】6页(P125-130)【关键词】颗粒体积累积曲线;表面分形维数;土壤水分特征曲线(SWRC)【作者】刘亚磊;梁杏;朱常坤;李静【作者单位】中国地质大学(武汉)环境学院,湖北武汉430074;中国地质大学(武汉)环境学院,湖北武汉430074;中国地质大学(武汉)生物地质与环境地质国家重点实验室,湖北武汉430074;中国地质大学(武汉)环境学院,湖北武汉430074;中国地质大学(武汉)环境学院,湖北武汉430074【正文语种】中文【中图分类】P642.68分形理论是由 Mandelbrot[1]提出,用来研究无规则图形以及复杂结构特征的方法。
分形是度量上述土壤物理因素的一种手段,分形维数则是其具体的表现形式[2]。
Bartoli[3]和 Tyler等人[4]发现:反映土壤质地和结构的物理因素,如容重、粒径分布、孔隙度及孔隙的连通状况等,都表现出分形特征,这些物理因素对土壤的水力参数存在直接或者间接的影响。
仿生挖掘斗_土壤接触二维有限元分析_郭志军

仿生挖掘斗O土壤接触二维有限元分析郭志军,邓志强,陈海燕(河南科技大学!车辆与动力工程学院,河南!洛阳!,#’""%)!摘要"研究切削性能更为优良的挖掘斗对减小挖掘机工作阻力意义重大#运用二维有限元方法$对比分析了普通挖掘斗和仿生挖掘斗的土壤接触模型使土壤产生位移的差异#对比结果表明$本文所分析的仿生挖掘斗的切削性能理论上优于某公司生产的(H液压挖掘机铲斗的切削性能#!关键词"挖掘斗%有限元%仿生!中图分类号").’##)O’’%$!!!!文献标识码".!!!文章编号"’""’/&&,0$!""#%"%/""#,/",!2*C’5#+4’*+$&F B<*,D’*+’(#P($6$)*0D-(3#)4*’&*+)"#’+)#0$()’+1%0*D;-PS54/U6E$@T;9S54/b4B E R$N O T;O B4/c B E在对各种材料实施切削作业时$优化作业工具的几何形状$减少被切削材料对切削工具的粘附$降低工作阻力&提高工作效率$是人们一直关注的问题’’$!(#现代仿生学研究表明$许多生物经过长期的进化$造就了适应生态环境的优良系统#其中的某些动物在长期的土壤环境生活过程中$其爪趾经过亿万年的进化$逐步形成了优化的几何形状和优良的生物力学功能$使其在挖掘过程中能够获得最低的切削阻力$这为切削工具几何形状及力学性能的优化提供了仿生研究的基础#挖掘斗曲面形式对切削阻力具有重要影响$设计良好的铲斗曲面是减小切削阻力的主要途径#空间曲面可以看作是由一条曲线!母线"沿着另一条曲线!导线"按一定规律运动而成的$挖掘斗和深松部件&松土铲等切削工具的触土面也不例外#本文研究的仿生挖掘斗应用动物爪的轮廓曲线作为触土面导线$与普通挖掘机铲斗进行比较$分析其切削性能的差异$以期为切削工具的仿生设计提供可靠的依据#7!分析方法电子计算机的发展$各种非线性计算模型的改进以及对土壤本构关系的深入认识$使有限元法成为最近’"多年切削工具)土壤接触系统研究中应用最多的分析方法’%$,$&(#由于它们普遍考虑了切削工具)土壤接触系统的几何&物理及边界非线性问题$使得这些有限元分析的结果比以往的模型预测值更接近于实测值#将有限元法正确用于切削过程的动态模拟需要考虑以下!个问题*一是选择合适的土壤应力)应变关系$即土壤的本构关系%二是采用合理的切削工具)土壤相互作用计算模型#在对空间力学问题进行有限元分析时$根据研究对象的特殊情况$常对其作适当的简化和力学模型的抽象处理#由于考虑到挖掘机铲斗实际工作过程的复杂性和随机性$本文将挖掘机铲斗的工作过程分解为水平和旋转两个过程$分别考虑这两种不同状态下的挖掘斗的切削性能#9!仿生曲线本文引用文献’!(中研究的田鼠右前爪中趾内轮廓线作为挖掘机铲斗的触土面导线$图’为田鼠右前爪中趾经扫描电镜放大("倍的照片#田鼠爪趾内轮廓线的,次多项式拟合方程为* $F"$"""""&6,7"$"""&6%+"$"!!6!7"$(=’%67’($=,$拟合度0!F"$???’$据此绘制如图!所示的田鼠爪趾内轮廓曲线#!收稿日期"!""#$"*$!!!基金项目""’!’!!"&+!!通讯地址"郭志军,河南科技大学车辆与动力工程学院图7!田鼠右前爪中趾图9!田鼠爪趾内轮廓曲线:!挖掘斗O 土壤接触系统的二维有限元模型对于挖掘斗#土壤接触系统而言$其有限元模型主要包括土壤模型%挖掘斗模型以及挖掘斗#土壤接触模型&:87!土壤模型土壤计算模型的核心是土壤的本构关系以及具体参数&土壤的本构关系一般呈非线性性质$它不仅取决于土壤的类别$而且与应力历程%加载路线以及应力水平等有关$正是由于这种复杂性$对土壤的研究需根据其实际工作状况采用与之相适应的本构关系或模型&迄今已提出许多种土的本构模型$目前应用最多的两种土壤本构关系为@6E G B E 7N 5B E R 的双曲线应力#应变本构关系和@\6G L Z \7*\B R Z \非线性弹塑性本构关系$研究结果说明它们大多能够给出满足适当精度要求的结果&实践证明$根据所研究的具体问题$为了简化计算$采用理想弹塑性材料本构关系来模拟切削工具#土壤接触问题是可行的&本文采用如图%所示的理想弹塑性本构关系和2W E A 4X Z X 屈服准则$且不考虑切削速度对切削阻力的影响&土壤弹性模量为’!&"L *B $剪切模量为&,%$,#=L *B ’!($泊松比为"$’&$切削工具#土壤摩擦角为&"d ’&(&图:!土壤的应力O 应变关系示意图:89!挖掘斗模型采用的挖掘斗为某公司生产的(H 液压挖掘机铲斗$挖掘斗触土面导线形式为复合型$中部为圆弧$上下各有一段与之相切的线段&圆弧半径为!#’C C $弧形角为?"d $上部相切的线段长!?C C $在上切线端画长%,,C C 与下切线夹角为,"d 的线$下部相切的线段!连同铲刃部分"长,%"C C &铲壁材料为’(A E $其弹性模量为!$’"‘’"=L *B $剪切模量为=$"’(‘’"#L *B $泊松比为"$!?&:8:!挖掘斗O 土壤接触模型土壤模型的网格划分采用四边形等参单元$采用自动划分方式&为了在保证计算精度的前提下降低计算量$在靠近接触区域部分的有限元网格划分得比较密集$而远离接触区域的网格分布比较稀疏&整个土壤模型单元数为?"!个$节点数’"’’个&挖掘斗模型网格也采用自动划分的四边形等参单元$单元数=!个$节点数’!=个$如图,所示&图;!挖掘斗O 土壤接触二维有限元模型模拟挖掘斗与土壤在接触界面的接触状态可用杆单元%间隙单元%弹性单元等几种形式$本文采用间隙为"$’C C 的二维间隙单元来模拟挖掘斗与土壤的接触状态&在间隙单元的物理属性中将挖掘斗与土壤间的摩擦系数设为"$,,&#为了便于分析$规定挖掘斗水平向前的移动方向为J轴正向$垂直向上方向为K轴正向$依右手螺旋定则确定.轴正向#为了模拟挖掘机铲斗与土壤的接触过程$将挖掘机铲斗的工作过程分解为水平和旋转两个过程$分别对铲斗施加水平方向!;的力和绕.轴的!;C转矩#;!仿生挖掘斗O土壤接触系统的二维有限元模型仿生挖掘斗%土壤接触二维有限元模型如图&所示$仿生挖掘斗触土面导线形式为复合型$中部为圆弧$上方有一段与之相切的线段#圆弧半径为!#’C C$弧形角为,&d$上部相切的线段长!?C C$在上切线端画长%,,C C与下切线夹角为,"d的线$下部相切曲线为仿生曲线!田鼠爪趾内轮廓线"$弦长,%"C C#铲壁材料为’(A E#图>!仿生挖掘斗O土壤接触二维有限元模型>!有限元分析结果比较与讨论为了便于比较$两接触模型取相同的&"d切削角$土壤切削深度&&"C C#将水平面内土壤单元的右向位移定为正值$垂直向上的位移为正值#>87!挖掘斗!土壤接触系统分析结果当挖掘斗%土壤接触系统采用平板型壳单元分析方法$对切削工具施加!;的水平力时$土壤单元位移场的水平分量和垂直分量如图(和图#所示#图中箭头的长度和方向分别表示相应位置土壤单元位移的大小和方向$土壤的最大水平位移为’$=(C C$发生在与切削工具相接触的土壤单元部分&土壤的最大垂直位移为"$%%#C C$发生在切削刃尖后下方的土壤单元处#图?!施加9Q的水平力时土壤位移场水平分量图@!施加9Q的水平力时土壤位移场垂直分量挖掘斗%土壤接触系统采用平板型壳单元分析方法$对切削工具施加!;C的绕S轴的转矩时$土壤单元位移场的水平分量和垂直分量如图=和图?所示#图中箭头的长度和方向分别表示相应位置土壤单元位移的大小和方向$土壤的最大水平位移为($,’C C$发生在与切削工具相接触的土壤单元部分&土壤的最大垂直位移为($,,C C$发生在切削刃尖正前方的土壤单元处#图A!施加9Q5的转矩时土壤位移场水平分量图H !施加9Q 5的转矩时土壤位移场垂直分量>89!仿生挖掘斗O 土壤接触系统分析结果采用平板型壳单元的分析方法#对切削工具施加!;的水平力时#土壤的最大水平位移为!$%?C C #发生在与切削工具相接触的土壤单元部分$土壤的最大垂直位移"$,##C C #发生在切削刃尖后下方的土壤单元处%对切削工具施加!;C 的绕.轴的转矩时#土壤的最大水平位移为&$%%CC #发生在与切削工具相接触的土壤单元部分$土壤的最大垂直位移?$(&CC #发生在切削刃尖正前方的土壤单元处%>8:!两个接触系统分析结果的对比由表’和表!可以看出#当给切削工具加载!;水平力时#仿生挖掘斗最大水平位移比(H 挖掘斗大!=$(M #最大垂直位移大,’$&M #合成位移大!=$&M %而当给切削工具加载!;C 的转矩时#仿生挖掘斗最大水平位移小’($=M #但最大垂直位移大,?$=M #合成位移大#$,M %表’和表!的对比结果表明#本文所采用的田鼠爪趾内轮廓作为触土面导线的挖掘机铲斗#其切削性能优于(H 液压挖掘机铲斗%表7!加载9Q 水平力时两模型分析结果土壤位移(H 挖掘斗仿生挖掘斗相对差值J 正向最大位移&C C’$=&!$%=!=$(MK 正向最大位移&C C "$%%#"$,##,’$&M合成位移&C C’$=(!$%?!=$&M表9!加载9Q 5转矩时两模型分析结果土壤位移(H 挖掘斗仿生挖掘斗相对差值J 正向最大位移&C C($,’&$%%7’($=MK 正向最大位移&C C ($,,?$(&,?$=M合成位移&C C?$"??$#(#$,M!参考文献"’’(郭志军#周志立#佟金等$抛物线型切削面刀具切削性能二维有限元分析’Y ($洛阳工学院学报#!""!#!%!,")’7,$’!(V 6X 5_B 5B>1#K 5Z E Y $<4E 4H Z Z I Z C Z E H B E B I cX 4X W e H 5Z 4E /H Z \B G H 4W E J Z H _Z Z EX W 4IB E DH 4I I B R ZH W W I $)\B E X $W eH 5Z 8K 8T #’??&#%#!,")’%’&7’%’?$’%(郭志军#佟金#周志立#任露泉$耕作部件*土壤接触问题研究方法分析’Y ($农业机械报#!""’#%!!,")’"!7’",$’,(94I I]>#2B E D Z E.Z \R 9T $K W 4I @c E B C 4G X 4E)4I I B RZ B E D )\B G H 4W E $8R \4G 6I H 6\ZO B E D J W W L #-E 4H Z DK H B H Z X@Z Q B \H /C Z E H W e8R\4G 6I H 6\Z #’?(#$’&(K 5Z E Y #V 6X 5_B 5B>1$K W 4I 7C B G 54E Z 4E H Z \B G H 4W E )B<4/E 4H ZT I Z C Z E H*Z \X Q Z G H 4f Z $;Z _g W \L )A B \G Z I@Z L L Z \#’??=$!责任编辑#贺彩宏"。
数学建模 土地平整问题

土地平整问题摘要随着社会的快速发展,对于山区的土地整理显得格外重要。
为了更好地合理利用土地,选择合适的土地整理地点,达到节约成本的目的。
我们会建立模型,根据几个重要的制约因素,使得土石方量最小,而且成本最低,在实际的操作过程中更接近于科学实施。
针对问题一:利用软件MATLAB中的绘图功能,对数据进行处理,得到这片土地的三维图形与等高线图。
针对问题二:采用二重积分的意义,即曲顶柱体的体积。
利用分割、取值、求和、取极限的思想,将山地分割成无数个小曲顶柱体,然后对这些小曲顶柱体进行求和,并结合土石方量最小,挖填土时费用使用的最少限制条件,从而求得在什么海拔高度进行平整。
对于平面位置的确定,利用枚举法,总费用最少,求得在什么位置,什么海拔高度平整,已达到最优的标准。
针对问题三:类比于问题二,采用相同的方法,在不同的海拔高度上平整,已满足二层的台阶状地块的要求,达到挖填土石方量最小的目标。
最后,对所建立的模型和求解方法的优缺点给出了客观的评价,并指出了改进的方法。
关键词:土石方量最小;二重积分;枚举法;一、问题重述与分析1.1问题的重述十堰市是一个山区城市,向山要地是十堰市发展的一个必然的选择,但是如何在一片山地之中选择合适的方位与开挖深度,从而使总的土石方量最小,就是一个有意义的命题了!某工厂为了在一片长度为1500米,宽度为1000米的山地之中,开挖出一个800米×600米平坦连续的长方形地块作为工厂的厂房地基,前期已经在本块土地上测量出长、宽每隔30米的网格的对应网格点的海拔高度。
问题:①用附件(1)中的数据画出工厂的这片土地的三维图形与等高线图;②从什么地方,什么海拔高度平整一块800米×600米的连片土地能使总的土石方量最小?③如果允许平整出来的土地为二层的台阶状地块,要求各地块的长、宽不少于60米,又将从什么地方、什么海拔高度分别开挖,能使总的土石方量最小?1.2问题的分析1.2.1问题一我们可以利用MATLAB软件直接调用surf函数和contour函数分别画出这片土地的三维图形和等高线图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行 驶时 的 主要激 励 , 它对 车辆 的附着 性 能 、 制 动 距 离 以
及悬 架 系统 的力 学 性能 都有 影 响 。地 面 不平 度 对 车辆 产 生 的振 动 冲击 也 通 过 轮胎 、 悬 架 等元 件 传 递 给 车辆
和乘 客 , 从 而影 响乘 客 乘 坐 车 辆 的舒 适性 与 行 驶 平顺
对 独立 的参 数来 表 征土壤 表 面不 平度 。对 于研 究 非线 性 方法 的分 形几 何 理论 对描 述具 有标 度 律 特征 的 自然 现 象具 有很 好 的适 用性 。本 文对 采集 的土 壤地 面 不 平 度 数据 进行 分 形 特 性 分 析 , 以期 望 获得 全 面 的 对 地 面
性, 同时 对汽 车 的使用 质量 、 疲 劳寿 命 和安 全性 能 等 也
有 重要 影 响 。理 论 与 实践 研 究 均 表 明 , 对 土 壤 地 面 不
平 度进 行 研究 , 对 于改 进 车辆 的性 能 , 提高 其零 件 的使 用寿命 和汽 车行 驶安 全性 能等 都有 重 要 的意 义 。在 对
第 3 6 卷
第 4 期
中 国 农 机 化 学 报
J o u r n a l o f Ch i n e s e Ag r i c u l t u r a l Me c h a n i z a t i o n
Vo 1 . 3 6 No . 4
2 0 1 5年 7月
J u 1 . 2 0 1 5
土壤 地 面不平 度 的研 究 中发 现 , 土 壤 表 面 高 程 是 一 种
图 1 实 测 地 面 不 平 度 的 数 据 信 息
Fi g .1 Me a s u r e d s u r { a c e r o u g h n e s s d a t a i n f o r ma t i o n
摘要 : 采 用 均方 根 法计 算 对 实 测 土壤 地 面不 平 度 数 据 进 行 分 形 维 数 值 的计 算 。结 果 显 示 , 土壤表面不平度具有典型的分形特征 , 可 以利 用 w — M 分 形 函数 进 行 土 壤 表 面 的 模 拟 。根 据 分 形 接 触 模 型 理 论 , 建立车轮与土壤表面接触发生弹 、 塑性 变 形 时 的 分形 模 型 。
采 集 的一组 典 型 耕 作 土 壤 地 面 不 平 度 数 据 如 图 1所 示 。土壤 表面不平 度测试 仪 有效测 试 长 度为 1 0 2 4 mm,
测 试精 度 为 l mm/ 次, 文 中测 定 2 O 0 0 mm 长 的 地 表 不
平度。
车辆 进 行舒 适性 、 平 顺性 研究 时 , 地 面不 平度 成 为 车辆
Ag r i c u l t u r a l Me c ha n i z a t i o n,2 0 1 5,36 ( 4):2 7 9 ~2 8 1
O 引 言
土壤 表 面不 平 度 Ⅲ 1 是对 地面的微小峰谷、 微 小 间 距 以及 微观 几何 尺 寸特性 进 行评 价 的主 要 指标 。在对
特 征进 行 描述 的方 法 。
令 人满 意 的结果方法 进行 了对 比研 究 , 对 比结 果 显示 ,
在 计算 土壤 地 面 不平 度 的分 维 值 时 , 均 方 根 法 具 有 较
高 的计算 精度 , 而且 其 时物理 意 义 明确 [ 4 ] 。因此 , 本 文
为 了全 面表 征分 形 , 人们 引 入 了许 多 不 同 的分 维
随机 非平 稳 的过 程 ] , 利 用 传 统 的几 何 评 定 参 数 和 形
状评 定 参数 进行 表 征 时 , 会 出现 参 数 随着 测 量 仪 器 及
定 义 。截止 现在 , 对 复 杂 轮 廓 进 行 分 形 维数 计 算 的 方
土壤 地 面 不 平 度 及 接 触 分 形 模 型 *
侯 占峰 ,薛晶 ,闰建 国 ,朱利 忠 ,陈 智
( 1 .内蒙 古 农 业 大 学 机 电工 程 学 院 , 呼和浩特市 , 0 1 0 0 1 8 ; 2 .呼 和 浩 特 市 交 通 科 研 所 , 呼和浩特市 , 0 1 0 0 5 1 )
法 有很 多 , 每种计 算 方法 都有 其特 点 和适 用 的范 围 , 对 于不 同 的复杂 轮廓需 要采 用合 适 的计算 方 法 才能 得 到
采样 长 度 等 的 变 化 而 表 现 出参 数 的不 稳 定 性 ] 。 因 此, 对表 面 不平 度进 行表 征 时 , 有 必要 找 到一 种 尺 度相
关键词 : 分形维数 ; w —M 函数 ; 弹、 塑 性 变 形
中图分类号 : S 1 5 2 . 9 文献标识码 : A 文章编号 : 2 0 9 5 - 5 5 5 3 ( 2 0 1 5 )0 4 - 0 2 7 9 — 0 3
侯 占 峰 ,薛 晶 ,闰 建 国 ,朱利 忠 ,陈 智 .土 壤 地 面 不 平 度 及 接 触分 形模 型 J - j ] .中 国农 机 化 学 报 ,2 o 1 5 ,3 6 ( 4 ) :2 7 9  ̄2 8 1 Ho u Z h a n f e n g ,X u e J i n g , Ya h J i a n g u o , Z h u L i z h o n g ,C h e n Z h i .S o i l s u r f a c e r o u g h n e s s a n d f r a c t a l c o n t a c t mo d e l I - J 3 .J o u r n a l o f C h i n e s e
