湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考 数学理-含答案
湖北省重点中学2014届高三10月统一阶段性考试 数学试题(理) 含解析

第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U R =,设集合(){}ln 31A x y x ==-,集合(){}sin 2B y y x ==+,则()UA B为( )A.1,3⎛⎫+∞ ⎪⎝⎭B 。
10,3⎛⎤ ⎥⎝⎦C 。
11,3⎡⎤--⎢⎥⎣⎦D 。
∅2。
.已知函数()()()()cos 0260x x f x f x x ππ⎧⎛⎫+≥⎪ ⎪=⎝⎭⎨⎪-<⎩,则()2013f -等于( )A 。
12B 。
12- C.32D 。
3考点:1。
分段函数;2.诱导公式3.若函数()tan y x N ωω*=∈的一个对称中心是,06π⎛⎫⎪⎝⎭,则ω的最小值为 ( )A 。
2 B.3 C.6 D 。
9考点:三角函数的对称性4.已知命题:p x R∃∈,2lg x x->,命题:q x R∀∈,sin x x<,则 ( ) A。
命题p q∨是假命题B 。
命题p q ∧是真命题C.命题()p q ⌝∧是真命题D 。
命题()p q ⌝∨是假命题 【答案】C5。
若()tan lg 10a α=,1tan lgaβ=,且4παβ+=,则实数a的值为( )A.1 B 。
110C 。
1或110D.1或10【答案】C6。
,42ππα⎛⎫∀∈ ⎪⎝⎭,()log cos sin x παα=,()log sin cos y παα=,则x 与y 的大小关系为( )A 。
x y >B 。
x y <C 。
x y = D.不确定7。
在ABC ∆中,“()()sin cos cos sin 1A B B A B B -+-≥”是 “ABC ∆是直角三角形”的( ) A 。
充分不必要条件 B 。
必要不充分条件C。
充分必要条件D.既不充分也不必要条件 【答案】A件,故选A.考点:1。
两角和的正弦公式;2。
湖北省襄阳市第四中学2014届高三收心考试数学(理)试题及答案

一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合}|,1||{},1,0,1{A a a x x B A ∈-==-=,则B A 中的元素的个数为( ▲ ) A.2 B.4 C.6 D.8 2.设a 是实数,若复数112a ii -+-(i 为虚数单位)在复平面内对应的点在直线0x y +=上,则a 的值为( ▲ )A .1-B .0C .1D .23.将4名同学录取到3所大学,每所大学至少要录取一名,则不同的录取方法共有( ▲ ) A. 12B. 24C. 36D. 724.已知命题:(,0),34x x p x ∃∈-∞<;命题:(0,),tan 2q x x xπ∀∈>则下列命题中真命题是( ▲ )A .p q ∧ B.()p q ∨⌝ C.()p q ∧⌝ D.()p q ⌝∧5.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M 的值是( ▲ )A .5B .6C .7D .8 6. 等差数列{}n a 中564a a +=,则310122log (2222)a a aa ⋅⋅⋅⋅=…( ▲ )A. 10B. 20C. 40D. 22log 5+7.若在直线l 上存在不同的三点A 、B 、C ,使得关于实数x 的方程20x OA xOB BC ++=有解(点O 不在直线l 上),则此方程的解集为( ▲ )A .φB .{一1,0}C .{-1}D . ⎪⎪⎩⎭8.已知双曲线2222100(,)x y a b a b-=>>,12A A 、是实轴顶点, F 是右焦点,0(,)B b 是虚轴端点,若在线段BF 上(不含端点)存在不同的两点12(,)i P i =,使得1212(,)i P A A i ∆=构成以12A A 为斜边的直角三角形,则双曲线离心率e 的取值范围是( ▲ )A .)+∞ B. 12(,)+∞ C. 112(,) D. 12)9.在区间[0,2]上随机取两个数x 、y ,则[0,2]xy ∈的概率是( ▲ )CA.1ln 22- B. 32ln 24- C. 1ln 22+ D. 12ln 22+ 10.一只小球放入一长方体容器内,且与共点的三个面相接触.若小球上一点到这三个面的距离分别为4、5、5,则这只小球的半径是 ( ▲ ) A .3或8B .8或11C .5或8D .3或11二.填空题:本大题共6小题,考生共需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分. (一)必做题(11~14题) 11.已知611e n dx x =⎰,那么3()n x x-展开式中含2x 项的系数为__▲__. 12.已知实数x ,y 满足⎪⎩⎪⎨⎧-≥≤+≤11y y x xy ,则函数y x z 24=的最大值为 ▲ .13.若一个棱锥的三视图如右图所示,则它的体积为 ▲ . 14.将含有3n 个正整数的集合M 分成元素个数相等且两两没有公共元素的三个集合A 、B 、C ,其中12{,,,}n A a a a =,12{,,,}n B b b b =,12{,,,}n C c c c =,若A 、B 、C 中的元素满足条件:12n c c c <<<,k k k a b c +=,k =1,2,…,n ,则称M 为“完并集合”.(1)若{1,,3,4,5,6}M x =为“完并集合”,则x 的一个可能值为__▲__.(写出一个即可) (2)对于“完并集合”{1,2,3,4,5,6,7,8,9,10,11,12}M =,在所有符合条件的集合C 中, 其元素乘积最小的集合是__▲__.(二)选考题(请考生在第15、16两题中任选一题作答,请先在答题卡指定位置将你所选的题目序号后的方框用2B 铅笔涂黑.如果全选,则按第15题作答结果计分.) 15.(《几何证明选讲》选做题)如图:直角三角形ABC 中,∠B =90 o ,AB =4,以BC为直径的圆交边AC 于点D ,AD =2,则∠C 的大小为.16. (《坐标系与参数方程选讲》选做题)已知直线的极坐标方程为sin()4πρθ+则点7(2,)4A π到这条直线的距离为 . 三.解答题:(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)17(本小题满分12分)在如图所示的平面直角坐标系中,已知点(1,0)A 和点(1,0)B -,||1OC =,且AOC x ∠=,其中O 为坐标原点. (1)若34x π=,设点D 为线段OA 上的动点,求||OC OD +的最小值; (2)若[0,]2x π∈,向量m BC =,(1cos ,sin 2cos )n x x x =--,求m n ⋅的最小值及对应的x 值. 18(本小题满分12分)O车速70 75 80 85 90 95 1000.01 0.02 0.040.06 0.05 频率 组距 我市某中学一研究性学习小组,在某一高速公路服务区,从小型汽车中按进服务区的先后,每间隔5辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h )分成六段: [70,75),[75,80),[80,85),[85,90),[90,95),[95,100],统计后得到如图的频率分布直方图. (1)此研究性学习小组在采样中,用到的是什么抽样方法?并求这40辆小型汽车车速的众数和中位数的估计值.(2)从车速在[80,90)的车辆中任意抽取3辆车,求车速在[80,85),[85,90)内都有车辆的概率.(3)若从车速在[70,80)的车辆中任意抽取3辆,求车速在[75,80)的车辆数的数学期望.19(本小題满分12分)如图,直角梯形ABCD 中,090=∠=∠B A ,A D = A B = 2, B C = 3,E ,F 分别是AD,BC 上的两点,且AE =BF =1,G 为AB 中点,将四边形ABCD 沿EF 折起到(如图2)所示的位置,使得EG 丄GC ,连接 A D 、B C 、AC 得(图2)所示六面体.(1)求证:EG 丄平面CFG; (2)求二面角A —CD-E 的余弦值. 20(本小題满分12分)已知数列{},()n a n N ∈满足11a =,且对任意非负整数,()m n m n ≥均有:2211()2m n m n mn a a m n a a +-++--=+. (1)求02,a a ;(2)求证:数列*1{}()m m a a m N +-∈是等差数列,并求*()n a n N ∈的通项; (3)令*31()n n c a n n N =+-∈,求证:1134nk kc =<∑ 21(本小題满分13分)已知椭圆C :22221(0)x y a b a b +=>>的焦距为,离心率为2,其右焦点为F ,过点(0,)B b 作直线交椭圆于另一点A .(1)若6AB BF ⋅=-,求ABF ∆外接圆的方程;(2)若过点(2,0)M 的直线与椭圆:N 222213x y a b +=相交于两点G 、H ,设P 为N 上一点,且满足OG OH tOP +=(O 为坐标原点),当253PG PH -<时,求实数t 的取值范围. 22(本小题满分14分)已知函数f (x )=x ln x (x ∈(0,+∞)). (1)求(+1)()+1f xg x x x =-(x ∈(-1,+∞))的单调区间与极大值; (2)任取两个不等的正数x 1、x 2,且x 1<x 2,若存在x 0>0使21021()()()f x f x f x x x -'=-成立,求证:x 1<x 0<x 2;(3)已知数列{a n }满足a 1=1,1211(1)2n n n a a n+=++(n ∈N +),求证:114n a e <(e 为自然对数的底数).三.解答题17解:(Ⅰ) 设(,0)D t (01t ≤≤),又(C所以(OC OD t +=-+所以 22211||122OC OD t t +=-++=-+21((01)22t t =-+≤≤所以当t =||OC OD +………………6分 (Ⅱ)由题意得(cos ,sin )C x x ,(cos 1,sin )m BC x x ==+ 则221cos sin 2sin cos 1cos2sin 2m n x x x x x x ⋅=-+-=--1)4x π=+ ……………9分因为[0,]2x π∈,所以52444x πππ≤+≤所以当242x ππ+=,即8x π=时,sin(2)4x π+取得最大值1所以8x π=时,1)4m n x π⋅=-+取得最小值1所以m n ⋅的最小值为18x π=…………………………12分18. 解:(Ⅰ)此研究性学习小组在采样中,用到的抽样方法是系统抽样.………2分∴这40辆小型汽车车速众数的计值为87.5,中位数的估计值为87.5.………4分 (Ⅱ)车速在[80,90)的车辆共有(0.2+0.3)⨯40=20辆.速在[80,85),[85,90)内的车辆分别有8辆和12辆.记从车速在[80,90)的车辆中任意抽取3辆车,车速在[80,85)内的有2辆,在[85,90)内的有1辆为事件A ,车速在[80,85)内的有1辆,在[85,90)内的有2辆为事件B ,则211281281233202086472()()114095C C C C P A P B C C 鬃+=+==.………………………8分 (Ⅲ)车速在[70,80)的车辆共有6辆,车速在[70,75)和[75,80)的车辆分别有2辆和4辆,设若从车速在[70,80)的车辆中任意抽取3辆,车速在[75,80)的车辆数为x ,则x 的可能取值为1,2,3.21243641(1)205C C P C x ×====,…………………………………………………9分 122436123(2)205C C P C x ×====,…………………………………………………10分 03243641(3)205C C P C x ×====,…………………………………………………11分 故分布列为∴车速在[75,80)的车辆数的数学期望为1311232555E x =???.………12分19.证明:(Ⅰ)F 、E 分别是BC AD ,上的两点,1==BF AE∴四边形ABFE 为矩形∴折叠后BF EF FC EF ⊥⊥,,即⊥EF 平面BFC连接GF ︒=∠∴===902,1,1EGF AB BF AE 由已知得GC EG ⊥⊥∴EG 平面CFG …………………………6分(Ⅱ)由(Ⅰ)知EG FC ⊥EF FC ⊥⊥∴FC 平面ABFEBF FC ⊥∴ ………………………………………7分方法一:如图建系xyz F -则A (1,0,2)C (0,2,0)D (0,1,2)设1=()z y x ,,为平面ACD 的法向量,)2,1,0(),0,1,1(-=-=⎩⎨⎧=+-=+-∴020z y y x 得⎩⎨⎧==zy xy 2.则令1=z 得)1,2,2(1=n …………………9分 又)0,0,1(2=n 为平面CDEF 的法向量,设二面角E CD A --为θ,则321442=++=,即32cos =θ …12分方法二:延长CD 与FE 的延长线交于P 点,过E 作DP EH ⊥垂足为H 点,连结EH 、AH ,则EHA ∠为二面角E CD A --的平面角, 设二面角E CD A --为θ,由DE =1,得EP =2,则EH =52,53,1=∴=AH AE =∠∴AHE cos 32即32cos =θ……………12分 20解:(1)令m n =得01a =,…………………………1分 令0n =,得2423m m a a m =+-,∴23a =……………………2分(2)令1n =,得:112212()22m m m m a a m a a a m +-++-=+=+∴112m m m m a a a a +--=-+,又212a a -=,∴数列1{}m m a a +-是以2为首项,2为公差的等差数列.∴*12()m m a a m m N +-=∈∴1*111()(1)1()m m k k k a a aa m m m N -+==+-=-+∈∑∴*(1)1()n a n n n N =-+∈………………………………8分 (3)2*312()n n c a n n n n N =+-=+∈∴11(2)n c n n =+ ∴111111113113(1)232424212(2)4nk kcn n n n ==-+-++-=--<+++∑()…………12分 21解:(Ⅰ)由题意知:c =2c e a ==,又222a b c -=,解得:a b 椭圆C 的方程为:22163x y += …………………………2分 可得:B,F ,设00(,)A x y ,则00()AB x y=-,(3,BF =,6AB BF ⋅=-,00)6y =-,即00y x =由220000163x yy x ⎧+=⎪⎨⎪=⎩000x y =⎧⎪⇒⎨=⎪⎩0x y ⎧=⎪⎪⎨⎪=⎪⎩即(0,A,或A …………………………………………………………4分 ①当A 的坐标为(0,时,OA OB OF ==∴ABF ∆外接圆是以O 为圆心,223x y +=……………………………………………………………5分②当A 的坐标为(33时,1AF k =,1BF k =-,所以ABF ∆为直角三角形,其外接圆是以线段AB 为直径的圆,圆心坐标为,半径为12AB =,ABF ∴∆外接圆的方程为225((3x y -+=综上可知:ABF ∆外接圆方程是223x y +=,或225((3x y += ……7分22121222882,1212k k x x x x k k -+==++253PG PH -<,253HG ∴<12x -<214k ∴>,结合(*)得: ………………………………………………11分 OG OH tOP +=,1212(,)(,)x x y y t x y ∴++=从而21228(12)x x k x t t k +==+,1212214[()4](12)y y ky k x x k t t t k +-==+-=+ 点P 在椭圆上,2222284[]2[]2(12)(12)k k t k t k -∴+=++,整理得:22216(12)k t k =+即228812t k =-+,2t ∴-<<2t <<………………………………13分22.解:(Ⅰ)由已知有(+1)()+1f xg x x x =-=ln(+1)x x -, 于是1()1=+11xg x x x '=--+. 故当x ∈(-1,0)时,()g x '>0;当x ∈(0,+∞)时,()g x '<0.所以g (x )的单调递增区间是(-1,0),单调递减区间是(0,+∞),g (x )的极大值是g (0)=0. ……………………………………………………………………4分(Ⅱ)因为()ln +1f x x '=,所以0ln +1x =2121()()f x f x x x --,于是02ln ln x x -=21221()()ln 1f x f x x x x ----=2211221ln ln ln 1x x x x x x x ----=121121ln ln 1x x x x x x ---=2121ln11x x x x --,令21x x =t (t >1),ln ln 1()111t t t h t t t -+-=--=, 因为10t ->,只需证明ln +10t t -<.令ln +1t t t ϕ=-(),则110t tϕ'=-<(),∴ t ϕ()在(1+)t ∈∞,递减,所以10t ϕϕ<()()=, 于是h (t )<0,即02ln ln x x <,故02x x <.仿此可证10x x <,故102x x x <<.……………………………………………10分 (Ⅲ)因为11a =,1211(1)2n n n n a a a n +=++>,所以{}n a 单调递增,n a ≥1. 于是1222111111(1)(1)=(1)222n n n n n n n n a a a a a n n n+=++≤++++, 所以1211ln ln ln(1)2n n n a a n +≤+++. (*) 由(Ⅰ)知当x >0时,ln 1+x ()<x . 所以(*)式变为1211ln ln 2n n n a a n +<++. 即11211ln ln 2(1)k k k a a k ---<+-(k ∈N ,k ≥2), 令k =2,3,…,n ,这n -1个式子相加得1121222111111ln ln +++)[]22212(1)n n a a n --<++++-(1221111111)[]2122334(2)(1)n n n -<++++++⨯⨯--(-=1111111111)[1()()()]24233421n n n -+++-+-++---(- =111111)1)2421n n -+++--(-(1111111=4214n n --<--, 即11111ln ln 44n a a <+=,所以114n a e <.……………………………………14分。
湖北省襄阳四中、龙泉中学、荆州中学高三物理10月联考

2013~2014学年度襄阳四中、荆州中学、龙泉中学高三10月联考物理试题本试卷共四大题18小题。
总分110分,考试用时90分钟一.单项选择题(本题共8小题,每小题4分。
以下各题中仅有一项符合要求)1.在物理学建立、发展的过程中,许多物理学家的科学发现推动了人类历史的进步.关于科学家和他们的贡献,下列说法中错误..的是( )A.古希腊学者亚里士多德认为物体下落的快慢由它们的重量决定,伽利略在他的《两种新科学的对话》中利用逻辑推断,使亚里士多德的理论陷入了困境B.德国天文学家幵普勒对他的导师——第谷观测的行星数据进行了多年研究,得出了开普勒三大行星运动定律C.英国物理学家卡文迪许利用“卡文迪许扭秤”首先较准确的测定了万有引力常量D.伽利略猜想自由落体的运动速度与下落时间成正比,并直接用实验进行了验证【答案】 D【解析】 D选项中,伽利略并没有用试验得到验证【考点】物理学史2.物体以40m/s的初速度竖直上抛,不计空气阻力,g取10m/s2。
5秒内,关于物体的运动,下列说法中正确的是( )A.路程为90m B.位移大小为75m,方向向上C.速度改变量为30m/s,方向向下 D.平均速度为25m/s,方向向上【答案】 B【解析】路程为85m,速度改变量为向下50m/s,平均速度为向上15m/s【考点】匀变速直线运动3.如图所示,a、b、c三物体在力F的作用下一起向右匀速运动,所受的摩擦力分别为f a、f b、f c,ab间绳子的拉力为T,下列正确的是()A.F= f a+f b+f c+TB.F= f a+f b+f c—TC.f c不等于0D.F= f a+ T【答案】 D【解析】 AB选项用整体法得F= f a+f b; C选项用隔离法单独分析c物体,可知f c=0;D选项单独分析a物体,由平衡条件可得出答案。
【考点】物体的平衡4.质量为m 的物体以v 0的速度水平抛出,经过一段时间速度大小变为2v 0,不计空气阻力,重力加速度为g ,以下说法正确的是( ) A .该过程平均速度大小为221+ v 0 B .运动位移的大小为gv 2520C .物体机械能的变化量为2021mv D .速度大小变为2v 0时,重力的瞬时功率为2mgv 0 【答案】 B 【解析】只适用在匀变速直线运动中,故A 错;竖直方向:gt v =得gv t 0=,g v h 220=,水平方向g v x 20=,所以合位移为22h x S +=,故B 对;机械能守恒,所以C 错;速度大小变为2v 0时,由瞬时功率θcos Fv P =得出重力的瞬时功率为2mgv 0cos45°,故D 错。
湖北省襄阳市襄州一中等四校2014届高三数学上学期期中联考试题 理(含解析)新人教A版

湖北省襄阳市襄州一中等四校2014届高三数学上学期期中联考试题理(含解析)新人教A 版第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{(,)|2},{(,)|4}M x y x y N x y x y =+==-=,那么集合MN 为( )A 、3,1x y ==-B 、{(3,1)}-C 、{3,1}-D 、(3,1)-2.已知命题:,23x x p x R ∀∈<;命题32:,1q x R x x ∃∈=-,则下列命题中为真命题的是( )A 、p q ∧B 、p q ∧⌝C 、p q ⌝∧D 、p q ⌝∧⌝3.在同一坐标系中画出函数x y a log =,xa y =,a x y +=的图象,可能正确的是( ).【答案】D【解析】试题分析:分10<<a 和1>a 两种情形,易知ABC 均错,选D. 考点:基本初等函数的图像4.函数()x e x f x cos =的图像在点()()0,0f 处的切线的倾斜角为( ) A 、4π B 、0 C 、43π D 、15.若42ππθ⎡⎤∈⎢⎥⎣⎦,,37sin 2=θ,则sin θ=( )A 、35 B 、45 C 、74 D 、346.对于函数()c bx x a x f ++=sin (其中Z c R b a ∈∈,,),选取c b a ,,的一组值计算()1f 和()1-f ,所得出的正确结果一定不可能是( ) A 、4和6 B 、2和1 C 、2和4D 、1和3【答案】B7.奇函数()x f 在()+∞,0上为单调递减函数,且()02=f ,则不等式()()0523≤--xx f x f 的解集为( ) A 、(](]2,02,⋃-∞- B 、[][)+∞⋃-,20,2 C 、(][)+∞⋃-∞-,22,D 、[)(]2,00,2⋃-8.已知函数()x f 是定义在实数集R 上的不恒为零的偶函数,且对任意实数x 都有())()1(1x f x x xf +=+,则⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛25f f 的值是( )A 、0B 、12C 、1D 、529.已知函数()()()cos 0,2f x x x π=∈有两个不同的零点12,x x ,方程()f x m =有两个不同的实根34,x x .若这四个数按从小到大排列构成等差数列,则实数m 的值为( ) A 、23-B 、23C 、21- D 、2110.设函数()f x 满足2()2()x e x f x xf x x '+=,2(2)8e f =,则当0x >时,()f x ( )A 、有极大值,无极小值B 、有极小值,无极大值C 、既无极大值,也无极小值D 、既有极大值,又有极小值第Ⅱ卷(共100分)二、填空题(本大题共5个小题,每小题5分,共25分,将答案填在答题纸上)11.已知函数()()⎩⎨⎧<>=)0(,20,log 2x x x x f x ,则()241-+⎪⎭⎫⎝⎛f f 的值等于_______.12.由曲线y x =,直线2y x =-及y 轴所围成的图形的面积为_______.【答案】316【解析】 试题分析:曲线y=,直线y=x-2及y 轴所围成的图形如图所示,故:=.考点:定积分的计算13.在ABC ∆中,三内角C B A ,,满足C B C B A sin sin sin sin sin 222-+<,则角A 的取值范围为 .14.如果对于函数()x f 的定义域内任意两个自变量的值21,x x ,当21x x <时,都有()()21x f x f ≤且存在两个不相等的自变量21,m m ,使得()()21m f m f =,则称()x f 为定义域上的不严格的增函数.已知函数()x g 的定义域、值域分别为A ,B ,{}3,2,1=A ,A B ⊆且()x g 为定义域A 上的不严格的增函数,那么这样的函数()x g 共有________个. 【答案】9 【解析】试题分析:由题意,若函数g (x )是三对一的对应,则有{1,2,3}对应1;{1,2,3}对应2;{1,2,3}对应3三种方式,故此类函数有三种,若函数是二对一的对应,则有{1,2}对1,3对2;;{1,2}对1,3对3,有两种;1对1,{2,3}对2;1对1,{2, 3}对3,有两种;1对2,{2,3}对3,有一种;若函数是一对一的对应,则1对1,2对2, 3对3,共一种;综上,这样的g (x )共有3+2+2+1+1=9种.考点:1.函数单调性的性质;2.分类讨论的思想方法15.下列五个命题中,正确的命题的序号是_____________. ①函数2tanxy =的图象的对称中心是Z k k ∈),0,(π; ②)(x f 在()b a ,上连续,()()0)()(0,,00<=∈b f a f x f b a x 则且; ③函数)32sin(3π+=x y 的图象可由函数x y 2sin 3=的图象向右平移3π个单位得到; ④)(x f 在R 上的导数)1(2)2(,0)()(),(f f x f x f x x f <<-''则且; ⑤函数)2cos 21ln(x y +=的递减区间是⎪⎭⎫⎢⎣⎡+4,πππk k ()Z k ∈.三、解答题 (本大题共6小题,满分75分.解答须写出文字说明证明过程或演算步骤.)16.(本小题满分12分) 设函数2()lg(2)f x x x =--的定义域为集合A ,函数()3g x x =-的定义域为集合B .(1)求A B ;(2)若{}R m m x m x C ∈+<<-=,121,B C ⊆,求实数m 的取值范围.17.(本小题满分12分)已知函数()23sin()2cos()cos 22f x x x x x ππ=⋅--+⋅+.(1)求)(x f 的最小正周期;(2)在ABC ∆中,c b a ,,分别是∠A 、∠B 、∠C 的对边,若4)(=A f ,1=b ,ABC ∆的面积为23,求a 的值. 【答案】(1)π; (2)3 【解析】试题分析:(1)由已知条件由三角恒等变换化简得3)62sin(2)(++=πx x f ,可得最小正18.(本小题满分12分) 已知函数()2()1x x af x a a a -=--,其中0,1a a >≠ (1)写出()x f 的奇偶性与单调性(不要求证明);(2)若函数()x f y =的定义域为()1,1-,求满足不等式()()0112<-+-m f m f 的实数m 的取值集合;(3)当(),2x ∈-∞时,()4f x -的值恒为负,求a 的取值范围.【答案】(1))(x f 是在R 上的奇函数,且在R 上单调递增.(2))2,1(.(3)]32,1()1,32[+-【解析】试题分析:(1)先由解析式分析定义域为R ,再根据奇偶函数的定义由)()(x f x f -=-可知是奇函数;(2)函数()x f y =的定义域为()1,1-,结合(1)的奇偶性和单调性,可得关19.(本小题满分12分)设函数()()8613223+++-=ax x a x x f ,其中a R ∈.(1)若()f x 在3=x 处取得极值,求常数a 的值; (2)设集合(){}0<'=x f x A ,⎭⎬⎫⎩⎨⎧>--=034x x x B ,若B A ⋂元素中有唯一的整数,求a 的取值范围.20.(本小题满分13分)如图,某市准备在一个湖泊的一侧修建一条直路OC ,另一侧修建一条观光大道,它的前一段OD 是以O 为顶点,x 轴为对称轴,开口向右的抛物线的一部分,后一段DBC 是函数)2,0,0)(sin(πφωφω<>>+=A x A y ,[]8,4∈x 时的图象,图象的最高点为⎪⎪⎭⎫ ⎝⎛338,5B ,OC DF ⊥,垂足为F .(1)求函数)sin(φω+=x A y 的解析式;(2)若在湖泊内修建如图所示的矩形水上乐园PMFE ,问:点P 落在曲线OD 上何处时,水上乐园的面积最大?21.(本小题满分14分)设函数21()ln .2f x x ax bx =-- (1)当12a b ==时,求函数)(x f 的最大值; (2)令21()()2a F x f x ax bx x=+++(03x <≤)其图象上任意一点00(,)P x y 处切线的斜率k ≤21 恒成立,求实数a 的取值范围; (3)当0a =,1b =-,方程22()mf x x =有唯一实数解,求正数m 的值.【答案】(1)43-;(2)),21[+∞∈; (3)21=m(3)因为方程有唯一实数解,所以有唯一实数解,设,则,令,因为,当上单调递减;当上单调递增;当,。
湖北省教学合作高三数学10月联考试题 理(含解析)

湖北省教学合作2014届高三数学10月联考试题 理(含解析)第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合={x||x|2,x Z}A ≤∈,1={x|>0,x R}1B x ∈+,则A B 是( ) A .(1,2]- B .[0,2]C .{1,0,1,2}-D .{0,1,2}2. 已知3sin()35x π-=,则cos()6x π+=( ) A .35 B .45 C .35- D .45-3. 下列给出的四个命题中,说法正确的是( )A .命题“若21x =,则1x =”的否命题是“若21x =,则1x ≠”; B .“1x =-”是“2560x x --=”的必要不充分条件;C .命题“存在x R ∈,使得210x x ++<”的否定是“对任意x R ∈,均有210x x ++<”; D .命题“若x y =,则sin sin x y =”的逆否命题为真. 【答案】D 【解析】试题分析:本题考查命题的相关概念. 选项A ,“若21x =,则1x =”的否命题为:“若21x ≠,则1x ≠”; 1x =-可以推出2560x x --=,反之不成立,故“1x =-”是“2560x x --=”的充分不必要条件,故选项B 错;命题“存在x R ∈,使得210x x ++<”的否定应为:“对任意x R ∈,均有210x x ++≥”,故选项C 错,正确答案为D . 考点:1.四种命题及其关系;2.充分与必要条件;3.全程量词与存在量词.4. 把函数sin ()y x x R =∈的图像上所有的点向左平移6π个单位长度,再把图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)得到的图像所表示的函数为( )A .sin(2),3y x x R π=-∈ B .1sin(),26y x x R π=+∈ C .sin(2),3y x x R π=+∈ D .1sin(),26y x x R π=-∈5. 已知()()()()f x x a x b a b =-->的图像如图所示,则函数()xg x a b =+的图像是( )6. 已知1(,1)x e -∈,ln a x =,ln 1()2xb =,ln xc e=,则,,a b c 的大小关系为( )A .c b a >>B .b c a >>C .a b c >>D .b a c >>7. 某出租车公司计划用450万元购买A 型和B 型两款汽车投入营运,购买总量不超过50辆,其中购买A 型汽车需要13万元/辆,购买B 型汽车需要8万元/辆,假设公司第一年A 型汽车的纯利润为5万元/辆,B 型汽车的纯利润为1.5万元/辆,为使该公司第一年纯利润最大,则需安排购买( )A .8辆A 型汽车,42辆B 型汽车 B .9辆A 型汽车,41辆B 型汽车C .11辆A 型汽车,39辆B 型汽车D .10辆A 型汽车,40辆B 型汽车 【答案】D 【解析】试题分析:解法一:A 时,成本为813428440⨯+⨯=万元,利润为8242 1.579⨯+⨯=万元;B 时,成本为913418445⨯+⨯=万元,利润为9241 1.579.5⨯+⨯=万元;C 时,成本为1113398455⨯+⨯=万元,利润为11239 1.580.5⨯+⨯=万元;而1113398455450⨯+⨯=>,选D .解法二:设购买A 型出租车x 辆,购买B 型出租车y 辆,第一年纯利润为z ,则50138450x y x y x N y N +++≤⎧⎪+≤⎪⎨∈⎪⎪∈⎩2 1.5z x y =+,作出可行域,由50138450x y x y +=⎧⎨+=⎩解得1040x y =⎧⎨=⎩,此时z 取得最大值,选D .考点:线性规划问题.8. 已知二次函数2()1f x ax bx =++的导数为'()f x ,'(0)0f >,()f x 与x 轴恰有一个交点,则'(1)(0)f f 的最小值为( ) A .3 B .52 C .2 D .329. 设,,1,1x y R a b ∈>>,若2,28xya b a b ==+=,则11x y+的最大值为( ) A .2 B .3 C .4 D .2log 3 【答案】B 【解析】试题分析:由2xya b ==得log 2a x =,log 2b y =,∴2221111log log log ()log 2log 2a b a b ab x y +=+=+=,又1,1a b >>,∴2s a b =+≥8ab ≤,当且仅当2a b =,即2,4a b ==时取等号, 所以2211log ()log 83ab x y +=≤=. 故max 11()3x y+=. 考点:基本不等式.10. 在直角坐标系中,定义两点1122(,),(,)P x y Q x y 之间的“直角距离”为1212(,)||||d P Q x x y y =-+-,现给出四个命题:①已知22(1,3),(sin ,cos ),()P Q x x x R ∈,则(,)d P Q 为定值;②用||PQ 表示,P Q 两点间的“直线距离”,那么||(,)2PQ d P Q ≥;③已知P 为直线2y x =+上任一点,O 为坐标原点,则(,)d P Q ④已知,,P Q R 三点不共线,则必有(,)(,)(,)d P Q d Q R d P Q +>. A .②③ B .①④ C .①② D .①②④第Ⅱ卷(共100分)二、填空题(每题5分,满分25分,将答案填在答题纸上)11.=⎰.【答案】π【解析】试题分析:根据积分的几何意义,由图可得⎰=-224πdx x ,故填π.考点:1.积分的几何意义;2.积分的计算.12. 不等式组|21|32113x x x-<⎧⎪+⎨≤⎪-⎩的解集为 .【答案】]32,1(-14. 若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法计算,其参考数据如下:那么方程32220x x x +--=的一个近似根(精确到0.1)为15. 定义在N +上的函数()f x ,满足1(),(1)22(),nf n f n f n n ⎧⎪+=⎨⎪⎩为偶数为奇数, (1)若1(11)4f =,则(1)f = . (2)若(1)1f =,则(2)n f = (用含n 的式子表示).三、解答题 (本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.) 16. (本小题满分12分) 函数()sin()(,0)22f x x ππωϕϕω=+-<<>的最小正周期为π,其图像经过点(,1)12π(1)求()f x 的解析式;(2)若24()()325f a f a π+-=且a 为锐角,求sin cos αα+的值.【答案】(1)()sin(2)3f x x π=+;(2)7sin cos 5αα+=.【解析】试题分析:本题考查三角函数的性质,主要考查三角函数的周期、两角和与差的三角函数、倍角公式等基础知识,考查运算能力,考查数型结合思想.第一问,先利用周期求出ω,再利用点的坐标求出ϕ,注意已知条件中ϕ的取值范围;第二问,先利用两角和与差的三角函数公式展开化简表达式,得到24sin 225α=,然后求sin cos αα+,但是注意sin cos αα+的正负符号.试题解析: (1)∵()f x 的最小正周期为π,0ω>,∴2ππω=,2ω=,又()y f x =的图象经过点(,1)12π∴22122k ππϕπ⨯+=+,即2,3k k Z πϕπ=+∈,又||2πϕ<∴3πϕ=∴()sin(2)3f x x π=+(2)24()()325f f παα+-=,∴24sin(2)sin(2)3325ππαα++-=整理得24sin 225α=即249sin cos 25αα+=(),又α为锐角,sin cos 0αα+>∴7sin cos 5αα+=.考点:1.三角函数的周期;2.三角函数的对称轴;3.三角函数值.17.(本小题满分12分)已知函数()f x =(1)计算53115(),(),(),()4242f f f f 的值,据此提出一个猜想,并予以证明;(2)证明:除点(2,2)外,函数()f x 2y =的下方.试题解析: (1)∵()f x =∴5111()()442f f ==;35()()222f f == 猜想:()f x 的图象关于2x =对称,下面证明猜想的正确性;∵(4)()f x f x -= ∴()f x 的图象关于2x =对称 (2)∵()f x =[1,3],由(1)知()f x 的图象关于2x =对称设1212x x ≤<≤∴12()()f x f x -==12(x x =-∵12x x < ∴120x x ->0+>∴12()()f x f x <∴()f x 为[1,2]上的增函数,由对称性知()f x 在[2,3]上为减函数, ∴()(2)2f x f ≤=∴()y f x =的图象除点(2,2)外均在直线2y =的下方. 考点:1.证明函数的对称性;2.函数单调性的定义.18. (本小题满分12分)已知角A B C 、、是ABC ∆的内角,,,a b c 分别是其对边长,且3A π=.(1)若2,cos a B ==b 的长; (2)设A ∠的对边1a =,求ABC ∆面积的最大值. 【答案】(1)3;(2)4.19. (本小题满分12分)已知二次函数2()f x ax bx k =++满足,()(0)x R f x f ∀∈≥且()y f x =的图像在(1,(1))f 处的切线垂直于直线210x y ++=. (1)求,a b 的值;(2)若方程()2|()(1)|f x x f x f =--有实数解,求k 的取值范围.考点:1.用导数求切线方程;2.求分段函数值域.20. (本小题满分13分)某校内有一块以O 为圆心,R (R 为常数,单位为米)为半径的半圆形(如图)荒地,该校总务处计划对其开发利用,其中弓形BCDB 区域(阴影部分)用于种植学校观赏植物,OBD ∆区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.(1)设BOD θ∠=(单位:弧度),用θ表示弓形BCDB 的面积()S f θ=弓;(2)如果该校总务处邀请你规划这块土地,如何设计BOD ∠的大小才能使总利润最大?并求出该最大值. (参考公式:扇形面积公式21122S R Rl θ==,l 表示扇形的弧长)【答案】(1)21(sin )2S R θθ=-弓;(2)当园林公司把扇形的圆心角设计成3π时,总利润取最大值245(3R π-.(2)设总利润为y 元,种植草皮利润为1y 元,种植花卉利润为2y ,种植学校观赏植物成本为3y2211130()22y R R πθ=-,221sin 802y R θ=⋅,231(sin )202y R θθ=-⋅, 2222123111130()sin 80(sin )202222y y y y R R R R πθθθθ∴=+-=-+⋅--⋅ . 25[3(510sin )]R πθθ=--设()510sin g θθθ=- (0,)θπ∈. '()510cos g θθ=-'1()0,cos ,()2g g πθθθθ<>∈在(0, )3上为减函数; '1()0,cos ,()2g g πθθθθπ><∈在(,)3上为增函数. 当3πθ=时,()g θ取到最小值,此时总利润最大:225[3(510sin )]=5-y R R ππθθ=--4(3.答:所以当园林公司把扇形的圆心角设计成3π时,总利润取最大值25-R π4(3。
湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考 数学文试题 word版含答案(修改,图片无他网标志)-推
A.3
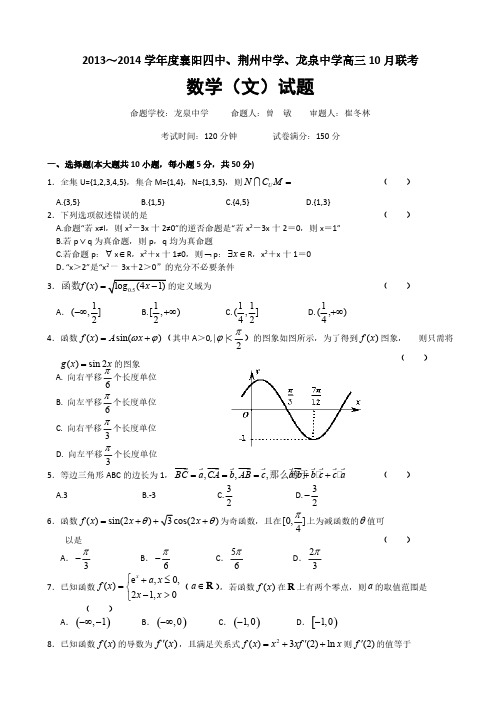
6.函数 f (x) sin(2x )
以是
A. 3
7.已知函数
()
A. , 1
f
(x)B.-33 NhomakorabeaC.
2
试卷满分:150 分
3 cos(2x ) 为奇函数,且在[0, ]上为减函数的 值可 4
B. 6
ex a, x
2
x
1,
G 型装置和 3 个 H 型装置配套组成,每个工人每小时能加工 6 个 G 型装置或 3 个 H 型装置。现将工人分成 两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组)。设加工 G 型装置的工 人有 x 人,他们加工完 G 型装置所需时间为 g(x),其余工人加工完 H 型装置所需时间为 h(x)(单位: 小时,可不为整数)
2013~2014 学年度襄阳四中、荆州中学、龙泉中学高三 10 月联考
数学(文)试题
命题学校:龙泉中学 命题人:曾 敏 审题人:崔冬林
考试时间:120 分钟
一、选择题(本大题共 10 小题,每小题 5 分,共 50 分)
1.全集 U={1,2,3,4,5},集合 M={1,4},N={1,3,5},则 N CU M
f
(x)
在R
D.{1,3}
D. 3
2
D.
3
D. (1 ,) 4
2
上有两个零点,则 a
D.1, 0
()
()
()
() ()
()
的取值范围是
则只需将
A. 2
9.已知函数
A.
C.
f
f
(
()
5
3
湖北省襄阳四中、龙泉中学、宜昌一中、荆州中学高三数学下学期期中四校联考试题 理

2014~2015学年度下学期期中联考高 二 数 学(理)本试题卷共4页,三大题22小题。
全卷满分150分。
考试用时120分钟。
★ 祝考试顺利 ★ 注意事项:1.答卷前,考生务必将自己的姓名、班级、准考证号填写在答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3.非选择题的作答:用黑色墨水签字笔直接答在答题卡上对应的答题区域内。
答在试题卷、草稿纸上无效。
4.考生必须保持答题卡的整洁。
考试结束后,请将答题卡上交。
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是满足题目要求的.1.命题“0200(0,),2x x x ∃∈+∞<”的否定为 A .2(0,),2x x x ∀∈+∞< B .2(0,),2x x x ∀∈+∞> C .2(0,),2x x x ∀∈+∞≥D .2(0,),2x x x ∃∈+∞≥2.已知随机变量ξ服从正态分布2(0,)N σ,若(2)0.023P ξ>=,则(22)P ξ-<≤= A .0.477 B .0.628 C .0.954 D .0.9773.已知平面α的法向量为(2,2,4),(3,1,2)n AB =-=-,点A 不在α内,则直线AB 与平面的位置关系为 A .AB α⊥B . AB α⊂C .AB 与α相交不垂直D .//AB α4.为防止某种疾病,今研制一种新的预防药.任选取100只小白鼠作试验,得到如下的列联表:经计算得2 3.2079K 的观测值为,则在犯错误的概率不超过( )的前提下认为“药物对防止某种疾病有效”。
A .0.025 B .0.10C . 0.01D . 0.05参考数据:5.某咖啡厂为了了解热饮的销售量y (个)与气温x (℃)之间的关系,随机统计了某4天的销售量与气温,并制作了对照表:由表中数据,得线性回归方程为y ^=2-x a +,,当气温为-4℃时,预测销售量约为 A .68 B .66 C .72 D .706.抛掷两枚骰子,当至少有一枚5点或6点出现时,就说试验成功,则在30次独立重复试验中成功的次数X 的数学期望是A .403B .503C .10D .207.下列选项中,说法正确的是 A .若命题“p q ∨”为真命题,则命题p 和命题q 均为真命题B .22am bm <是a b <的必要不充分条件C .2()4x k k Z ππ=+∈是(sin )(cos )x x ''-=的充要条件D .命题“若{,,}a b b c c a +++构成空间的一个基底,则{,,}a b c 构成空间的一个基底”的否命题为真命题8.已知中心在原点,焦点在坐标轴上的双曲线与圆2217x y +=有公共点(1,4)A -,且圆在A 点的切线与双曲线的渐近线平行,则双曲线的离心率为A .4BC.4D .以上都不对9.某校在高二年级开设选修课,选课结束后,有四名同学要求改选物理,现物理选修课开有三个班,若每个班至多可再接收2名同学,那么不同的接收方案共有 A .72种B .54种C .36种D .18种10.已知函数3axy e x =+有平行于x 轴的切线且切点在y 轴右侧,则a 的范围为 A .(),3-∞-B .(),3-∞C .()3,+∞D .()3,-+∞11.抛物线22(0)y px p =>的焦点为F ,准线为l ,,A B 是抛物线上的两个动点,且满足32π=∠AFB .设线段AB 的中点M 在l 上的投影为N ,则||||MN AB 的最大值是A .3B .23C .33D .4312.在棱长为1的正方体1111CD C D AB -A B 中,M 是11D A 的中点,点P 在侧面11CC B B 上运动.现有下列命题:①若点P 总保持1D PA ⊥B ,则动点P 的轨迹所在的曲线是直线;②若点P 到点A的距离为3,则动点P 的轨迹所在的曲线是圆; ③若P 满足1C ∠MAP =∠MA ,则动点P 的轨迹所在的曲线是椭圆;④若P 到直线C B 与直线11C D 的距离比为2:1,则动点P 的轨迹所在的曲线是双曲线; ⑤若P 到直线D A 与直线1CC 的距离相等,则动点P 的轨迹所在的曲线是抛物线.其中真命题的个数为( )A .4B .3C .2D .1二、填空题:本大题共4小题,每小题5分,共20分。
【解析】湖北版01期2014届高三名校数学理试题分省分项汇编专题05平面向量Word版含解析

一.基础题组1.【2013年湖北七市(州)高三年级联合考试理科数学】已知向量(2,1)a =,(,2)b x =-,若a ∥b ,则a +b =( )A .(-2,-1)B .(2,1)C .(3,-1)D .(-3,1)2.【湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考理科数学】已知点()1,3A ,()4,1B -则与AB 同方向的单位向量是( ) A.34,55⎛⎫- ⎪⎝⎭ B.43,55⎛⎫- ⎪⎝⎭ C.34,55⎛⎫- ⎪⎝⎭D.43,55⎛⎫- ⎪⎝⎭3.【湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考理科数学】已知向量()2,8a b +=-,()8,16a b -=-,则a 与b 夹角的余弦值为( ) A.6365 B.6365- C.6365±D.5134.【湖北省黄冈市黄冈中学2013届高三下学期6月适应性考试数学理试题(B 卷)】已知向量(2,3)=a ,(2,1)=-b ,则a 在b 方向上的投影等于 .二.能力题组1.【湖北省黄冈市黄冈中学2013届高三下学期6月适应性考试数学理试题(B 卷)】如图,在扇形O A B 中,︒=∠60AOB ,C 为弧.AB 上且与B A ,不重合...的一个动点,且y x +=,若(0)u x y λλ=+>存在最大值,则λ的取值范围为( )A .)3,1(B .)3,31( C .)1,21( D .)2,21(三.拔高题组1.【2013届高中毕业生四月调研理科数学测试题】在Rt ABC ∆中,90C ∠=,若ABC ∆所在平面内一点P 满0PA PB PC λ++=(第10题图)(1)当1λ=时,222||||||PA PB PC += (2)222||||||PA PB PC +的最小值为2.【湖北稳派教育2014届高三10月联合调研考试数学理科试题】已知O 为坐标原点,向量)1,(sin α=,)0,(cos α=,)2,sin (α-=,点P 满足BP AB =. (Ⅰ)记函数CA PB f ∙=)(α,)2,8(ππα-∈,讨论函数)(αf 的单调性,并求其值域; (Ⅱ)若C P O ,,三点共线,求||OB OA +的值.(Ⅱ)由C P O ,,三点共线可得)sin cos 2(2)sin ()1(ααα-⨯=-⨯-得34tan =α,(9分) ∴2524tan 1tan 2cos sin cos sin 22sin 222=+=+=ααααααα, ∴5742sin 21)cos (sin ||2=+=++=+αααOB OA . (12分) 考点:三角函数的性质,两角和的正、余弦公式和向量基本定理,三角恒等变换.。
湖北省部分重点中学2014届高三10月联考数学理试题 Word版含答案

秘密★启用前2013~2014年度湖北省部分重点中学高三十月联考数学(理科)试题★祝考试顺利★注意事项:1. 答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用统一提供的2B 铅笔将答题卡上的方框涂黑。
2. 选择题的作答:每小题选出答案后,用统一提供的2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3.用统一提供的签字笔直接答在答题卡上对应的答题区域内。
答在试题卷、草稿纸上无效。
4. 考生必须保持答题卡的整洁。
考试结束后,请将本试题卷和答题卡一并上交。
一、(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知全集=N ,集合P ={},6,4,3,2,1Q={}1,2,3,5,9则()P C Q =( )A .{}3,2,1B .{}6,4C .{}9,5D {}6,4,3,2,12.已知集合A ={}5,4,3,2,1,(){},/,,B x y x A y A x y A =∈∈-∈,则B 中所含元素的个数为 A .6 B .12C .16D .203.下列命题中错误的是A .命题“若2560x x -+=,则3x =”的逆否命题是“若3x ≠,则2560x x -+≠” B .若x 、y ∈R ,则“x y =”是2()2x y xy +≥成立的充要条件 C .已知命题p 和q ,若p ∨q 为假命题,则命题p 与q 中必一真一假D .对命题p :x R ∃∈,使220x x ++<,则:p x R ⌝∀∈,则220x x ++≥4.将函数()sin()f x x ωϕ=+的图象向左平移2π个单位,若所得图象与原图象重合,则ω的值不可能等于( ) A.4 B.6C.8D.125.已知函数()f x 的图象向右平移()0a a >个单位后关于1x a =+对称,当211x x >>时,[]2121()()()f x f x x x --<0恒成立,设1()2a f =-,(2)b f =,()c f e =,则,,a b c 的大小关系为 A .c >a >bB .c >b >aC .a >c >bD .b >a >c6.已知函数32()f x ax bx cx d =+++的图象如图所示,k R ∈,则()()f k f k +-的值一定A .等于0B .不小于0C .小于0D .不大于07.若),0(π∈α,且)4sin(2cos 3α-π=α,则α2sinA .1或1817-B .1C .1817 D .1817-8.已经函数21()()sin ,23x f x x a R a a =-∈++,则()f x 在[0,2π]上的零点个数为 A .1B .2C .3D .49.已知()||x f x x e =⋅,方程()2()()10f x tf x t R ++=∈有四个实数根,则t 的取值范围为A .21(,)e e++∞B .21,e e ⎛⎫+-∞- ⎪⎝⎭C .21,2e e ⎛⎫+-- ⎪⎝⎭D .212,e e ⎛⎫+ ⎪⎝⎭10.定义在R 上的奇函数()f x 满足(2)()f x f x -=,当[]0,1x ∈时,()f x =又()cos2xg x π=,则集合{}|()()x f x g x =等于A .1|4,2x x k k z ⎧⎫=+∈⎨⎬⎩⎭B .1|2,2x x k k z ⎧⎫=+∈⎨⎬⎩⎭C .1|4,2x x k k z ⎧⎫=±∈⎨⎬⎩⎭D .{}|21,x x k k z =+∈二、填空题:本大题共5小题,每小题5分,共25分.11.设有两个命题:p :不等式1()42x +>m >22x x -对一切实数x 恒成立;q :()(92)x f x m =--是R 上的减函数,如果p 且q 为假命题,则实数m 的取值范围是;12. 在△ABC 中,060,C AB AB ∠==边上的高为83,则AC BC += ; 13. 已知函数()()()222,log ,log 2x f x x g x x x h x x =+=+=-的零点依次为a , b , c ,则a ,b ,c 的大小关系是 。
2014年湖北省高三数学十月联考试卷(理科含答案)

2014年湖北省高三数学十月联考试卷(理科含答案)2014年湖北省高三数学十月联考试卷(理科含答案) 考生注意: 1、本试卷分第Ⅰ卷(选择题)和第Ⅱ(非选择题)两部分,共150分,考试时间120分钟 2、请将各题答案填在卷后面的答案卡上. 3、本试卷主要考试内容:集合与常用逻辑用语、函数与导数(60%);三角函数与平面向量(40%)第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1、已知集合,则等于 A. B. C. D. 2、的值为 A. B. C. D. 3、已知为常数,则使得成立的一个充分而不必要条件是() A. B. C. D. 4、已知为第三象限角,且,则的值为 A. B. C. D. 5、在中,角角的对边分别为,若且,则等于 A. B. C. D. 6、已知定义在R上的奇函数满足,且当时,,则等于 A. B. C.1 D.2 7、给出下列命题,其中错误的是 A.在中,若,则 B.在锐角中, C.把函数的图象沿x 轴向左平移个单位,可以得到函数的图象 D.函数最小正周期为的充要条件是 8、已知幂函数的图象如图所示,则在的切线与两坐标轴围成的面积为 A. B. C. D.4 9、已知,函数在处于直线相切,设,若在区间上,不等式恒成立,则实数 A.有最小值B.有最小值 C.有最大值 D.有最大值 10、对于函数,若,为某一三角形的三边长,则称为“可构造三角形函数”,已知函数是“可构造三角形函数”,则实数的取值范围是 A. B. C. D.第Ⅱ卷二、填空题:本大题共7小题,每小题5分,共35分,把答案填在答案卡中的横线上 11、已知,则 12、化简的结果为 13、已知关于的方程有两个不等的负实数根;关于的方程的两个实数根,分别在区间与内(1)若是真命题,则实数的取值范围为(2)若是真命题,则实数的取值范围为 14、在中,角的对边分别为,且,若的面积为,则的最小值为 15、已知函数,,给出下列结论:①函数的值域为;②函数在上是增函数;③对任意,方程在内恒有解;④若存在,使得,则实数的取值范围是.其中所有正确的结论的序号是三、解答题:本大题共5小题,满分65分,解答应写出文字说明、证明过程或演算步骤 16、(本小题满分11分)已知函数的部分图象如图所示.(1)试确定函数的解析式;(2)若,求的值.17、(本小题满分12分) 2014世界园艺博览会在青岛举行,某展销商在此期间销售一种商品,根据市场调查,当每套商品售价为x元时,销售量可达到万套,供货商把该产品的供货价格分为来那个部分,其中固定价格为每套30元,浮动价格与销量(单位:万套)成反比,比例系数为,假设不计其它成本,即每套产品销售利润=售价-供货价格(1)若售价为50元时,展销商的总利润为180元,求售价100元时的销售总利润;(2)若,求销售这套商品总利润的函数,并求的最大值. 18、(本小题满分12分)如图,在直角坐标系中,角的顶点是原点,始边与轴正半轴重合,终边交单位圆于点A,且,将角的终边按逆时针方向旋转,交单位圆于点B,记.(1)若,求;(2)分别过作x轴的垂线,垂足一次为C、D,记的面积为,的面积为,若,求角的值.19、(本小题满分12分)已知函数是定义在R上的奇函数.(1)若,求在上递增的充要条件;(2)若对任意的实数和正实数恒成立,求实数的取值范围.20、(本小题满分14分)已知(1)求的单调区间与极值;(2)若,试分析方程在上是否有实根,若有实数根,求出的取值范围;否则,请说明理由.21、(本小题满分14分)已知为常数,在处的切线方程为.(1)求的单调区间;(2)若任意实数,使得对任意的上恒有成立,求实数的取值范围;(3)求证:对任意正整数,有.。
襄阳四中、荆门龙泉中学、宜昌一中、荆州中学四校2014年10月联考理数试卷PDF版

1 ,2) 2
x
B. ( −1,− ]
x 3
1 2
D. (2, e)
B. 极大值点为 e D. 既有极大值点,又有极小值点
4.已知命题 p : ∀x ∈ R , 2 < 3 ;命题 q : ∃x ∈ R , x = 1 − x ,则下列命题中为真命题的是(
2
A. p ∧ q
B. p ∧ q
¬
C. p ∧ q
2015 届
襄阳四中 荆州中学
龙泉中学 高三年级十月联考 宜昌一中
审题人:襄阳四中 谢明铎 陈辉
A. f (sin1) < f (cos1) C. f (sin ) < f (cos ) 8.关于函数 f ( x) = sin(2 x −
B. f (sin
数学试题(理工类)
命题人:襄阳四中 陈辉 谢明铎 本试卷共 4 页, 共 22 题(2 个选做题只做 1 个) ,满分 150 分, 考试用时 120 分钟.
x k
5. 以下四图,都是同一坐标系中三次函数及其导函数的图象,其中一定不 正 确 的序号是( . . .
f ( x) = e 的一个承托函数,记实数 a 的取值范围为集合 M,则有( ) −1 −1 −1 A. e ∉ M , e ∉ M B. e ∉ M , e ∈ M C. e ∈ M , e ∉ M
x2 . 2
∑ (e k
k =1
n
1
+ ln 2
1 − 2 g ( )) > 2n + 2 ln(n + 1) (n ∈ N + ) . k
2
g ( x)
π
4
个单位得到;
B.2-i
湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考 生物试题 word版含答案(修改,图片无他网标志)-推荐

2013~2014学年度襄阳四中、荆州中学、龙泉中学高三10月联考生物试题命题学校:荆州中学命题人:董中辉审题人:李淑方本试卷共两大题33小题。
总分90分,考试用时90分钟一、单选题(共28小题,共42分,其中第1~14题每题1分,15~28题每题2分)1.下列各组物质可能在人体同一个细胞中产生的是()A.血红蛋白和淋巴因子B.抗体和ATP水解酶C.抗利尿激素和促性腺激素D.胰岛素和胰高血糖素2.阿胶被称为“中药三宝”之一,是利用驴皮为主要原材料熬制而成,因含有大量的胶原蛋白呈暗红的凝胶状,对于贫血、营养不良等有明显的疗效,下列有关分析正确的是()A.驴胶能用于治疗贫血、营养不良等症状是因为驴胶中含有Fe、Zn、Ca等微量元素,并能为人体提供多种必需氨基酸B.驴皮熬制出来的驴胶呈凝胶状,说明驴皮细胞内含量最多的化合物是蛋白质C.驴的遗传物质是DNA,而无细胞结构的生物遗传物质是RNAD.驴皮细胞内的某种蛋白质含有n条肽链,由m个氨基酸参与合成,则该蛋白质至少含有m+n个氧原子3.葡萄糖穿越细胞膜进入红细胞的运输速度存在一个饱和值,该值的大小取决于()A.细胞内的氧浓度B.细胞膜外的糖蛋白数量C.细胞膜上相应载体的数量D.细胞内外葡萄糖浓度差值4.下列实验中,细胞始终处于生活状态的是()①观察根尖分生组织细胞的有丝分裂②观察洋葱表皮细胞的质壁分离和复原现象③探究酵母菌细胞呼吸的方式④恩格尔曼用水绵观察光合作用的场所⑤观察口腔上皮细胞中线粒体的形态和分布⑥观察DNA和RNA在细胞中的分布A.②③⑤B.②④⑤C.②③④⑤D.①②④⑥5.下列有关酶的叙述,正确的是()A.酶具有高效性,酶比无机催化剂提高活化能的作用更显著B.酶和激素的作用原理相同,且起作用后均会被灭活C.酶的作用条件较温和,酶催化的反应只能在细胞内进行D.酶是所有活细胞都含有的有机物,其合成包括转录过程6.下列对应关系错误的是()A.纸层析法——提取菠菜叶片叶绿体中的四种色素B.对比实验法——探究酵母菌的呼吸方式C.差速离心法——分离细胞中各种细胞器D.假说-演绎法——孟德尔的豌豆杂交实验7.关于细胞的衰老、凋亡、坏死与癌变,下面选项中表述正确的是()A.衰老细胞内的各种酶的活性降低,故代谢变慢B.原癌基因或抑癌基因发生多次变异累积可导致癌症,因此癌症都可以遗传C.机体效应T细胞攻击被结核杆菌侵染的肺组织细胞,使之裂解死亡,属于细胞坏死D.良好心态有利于神经、内分泌系统发挥正常的调节功能,从而延缓衰老8.下列与绿色植物新陈代谢有关的叙述中,正确的是()A.绿色植物的光反应可以在暗处进行,暗反应也可以在光下进行B.大豆根吸收矿质元素所需的ATP可以直接来源于光合作用C.水果贮存时充入N2和C02的目的主要是抑制无氧呼吸,延长水果的贮存时间D.即使给予叶绿素提取液适宜的温度、光照和C02,也无法检测到有氧气生成9.下列关于细胞的结构和生理描述正确的是()A.拍摄洋葱鳞叶表皮细胞显微照片就是构建了细胞的物理模型B.生物膜是对生物体内所有膜结构的统称C.运用台盼蓝染液能将死细胞染成蓝色,是因为死细胞的细胞膜选择透过性丧失,染液分子进入细胞内而着色D.新宰的畜、禽类的肉放置一段时间后口味变好,是因为细胞中的核糖体合成了新的蛋白质而引起的10.下列为减少实验误差而采取的措施,不合理的是()选项实验内容减少实验误差采取的措施A探索影响淀粉酶的最适温度设置多组梯度较小的温度条件B性状分离比模拟实验重复多次抓取小球后再统计结果C调查人群中红绿色盲发病率在足够多的患病家族中调查并统计D比较有丝分裂细胞周期不同时期的时间长短观察多个视野的细胞并统计11.某些植物在早春开花时,花序细胞的耗氧速率高出其它细胞100倍以上,但单位质量葡萄糖生成ATP 的量却只有其它细胞的40%,此时的花序细胞()A.主要通过无氧呼吸生成ATP B.产生的热量远多于其它细胞C.线粒体基质不参与有氧呼吸D.没有进行有氧呼吸第三阶段12.下图表示某生物膜结构,图中A、B、C、D、E、F表示某些物质,a、b、c、d表示物质跨膜的运输方式。
湖北省教学合作2014届高三10月月联考数学(理)试题

高三年级十月联考理科数学试题参考答案1~10 DADBA BDCBC11.π 12.]32,1(- 13.12- 14.1.415.(1)f(1)=1;(2)f(2n )=121-n1.D[解析] A ={x||x|≤2,x ∈Z}={-2,-1,0,1,2},B ={x|x>-1},所以A∩B ={0,1,2},答案选D. 2. A [解析])6cos(π+x 3cos()sin()2335x x πππ=--=-=(),选A 。
3. D[解析]本题考查命题的相关概念. 选项A ,“若x2=1,则x=1”的否命题为:“若x2≠1,则x≠1”;x=-1可以推出x2―5x―6=0,反之不成立,故“x=-1”是“x2―5x―6=0”的充分不必要条件,故选项B 错;命题“存在x ∈R ,使得x2+x+1<0”的否定应为:“对任意x ∈R ,均有x2+x+1≥0”,故选项C 错,正确答案为D.4. B[解析]把函数y=sinx(x ∈R)的图象上所有的点向左平移6π个单位长度,得到y=sin(x+6π),再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y=sin(x 21+6π),x ∈R ,选择B. 5. A[解析]f(x)的零点为a,b ,由图可知0<a<1,b<-1,则g(x)是一个减函数,可排除C ,D ,再根据g(0)=1+b<0,可排除B ,故正确选项为A.6. B[解析] ∵x ∈(e -1,1),∴lnx ∈(-1,0) ∴a ∈(-1,0),b ∈(1,2),c ∈(e -1,1) ∴b>c>a. 选B. 7. D[解析]解法一:A 时,成本为8×13+42×8=440万元,利润为8×2+42×1.5=79万元; B 时,成本为9×13+41×8=445万元,利润为9×2+41×1.5=79.5万元;C 时,成本为11×13+39×8=455万元,利润为11×2+39×1.5=80.5万元; 而11×13+39×8=455>450,选D. 解法二:设购买A 型出租车x 辆,购买B 型出租车y 辆,第一年纯利润为z ,则⎪⎪⎩⎪⎪⎨⎧∈∈≤+≤+++,,,450813,50N y N x y x y x z=2x+1.5y ,作出可行域,由⎩⎨⎧==⎩⎨⎧=+=+,40,10,450813,50y x ,y x y x 解得此时z 取得最大值,选D.8. A[解析]本题考查二次函数与导数的内容,0)0(,2)(>='∴+='b f b ax x f ,因为f(x)与x 轴恰有一个交点,所以b 2-4a=0,bb b b b b b b a f f 1421141141)0()1(2⋅≥++=++=++='+1=2,故选A. 9. B[解析]由a x =b y =2得x=log a 2,y=log b 2,∴2log 12log 111b a y x +=+=log 2a+log 2b=lob 2(ab),又a>1,b>1,∴8=2a+b≥2ab 2,即ab≤8,当且仅当2a=b ,即a=2,b=4时取等号,所以yx 11+=log 2(ab)≤log 28=3. 故(yx 11+)max=3.10. C[解析] ①d(p,q)=|1-sin 2x |+|3-cos 2x |=(1-sin 2x )+(3-cos 2x )=4-1=3;②∵|PQ|2=|x 1-x 2|2+|y 1-y 2|2≧12(|x 1-x 2|+|y 1-y 2|)=d(P,Q)11.π[解析]根据积分的几何意义,由图可得⎰=-224πdx x ,故填π.12.]32,1(- [解析]解分式不等式和绝对值不等式。
湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考 数学理试题 Word版含答案

2013~2014学年度襄阳四中、荆州中学、龙泉中学高三10月联考数学(理)试题命题学校:龙泉中学 命题人:陈信金 审题人:陆晓峰总分150分,考试用时120分钟。
一、选择题: 本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题意要求的. 1.已知全集{}1,2,3,4,5,6,7,8,9U = 集合{}1,2,3,4,5,6A = 集合{}3,4,5,6,7,8B =,则集合U UAB 痧为( )A . {}3,4,5,6B . {}1,2,7,8,9C . {}1,2,3,4,5,6,7,8D . {}9 2.已知点()1,3A ,()4,1B -则与AB 同方向的单位向量是( ) A . 34,55⎛⎫-⎪⎝⎭ B . 43,55⎛⎫- ⎪⎝⎭C . 34,55⎛⎫- ⎪⎝⎭ D . 43,55⎛⎫- ⎪⎝⎭3.命题“对任意x R ∈都有21x ≥”的否定是( ) A .对任意x R ∈,都有21x <B .不存在x R ∈,使得21x <C .存在0x R ∈,使得201x ≥D .存在0x R ∈,使得201x <4.已知函数()21f x +的定义域为12,2⎛⎫- ⎪⎝⎭,则()f x 的定义域为( ) A . 31,24⎛⎫-⎪⎝⎭ B . 31,2⎛⎫- ⎪⎝⎭ C . ()3,2- D . ()3,3-5.已知角x 的终边上一点坐标为55sin ,cos 66ππ⎛⎫⎪⎝⎭,则角x 的最小正值为( ) A .56π B . 53π C . 116π D . 23π 6.已知函数()f x 的导函数为()f x ',且满足关系式()()2=32ln f x x xf x '++,则()2f '的值等于( )A .2B . 2-C .94 D . 94- 7.已知向量()2,8a b +=-,()8,16a b -=-,则a 与b 夹角的余弦值为( )A .6365 B . 6365- C . 6365± D . 5138.已知点(),a b 在圆221x y +=上,则函数()2cos sin cos 12af x a x b x x =+--的最小正周期和最小值分别为( ) A . 32,2π-B . 3,2π-C . 5,2π- D . 52,2π-9.函数()f x m =-有零点,则实数m 的取值范围是( )A . ⎛ ⎝⎭B .⎡⎢⎣⎦C .⎡⎢⎣⎦D .⎛ ⎝⎭10.设分程220xx ++=和方程2log 20x x ++=的根分别为p 和q ,函数()()()2f x x p x q =+++,则( )A . ()()()203f f f =<B . ()()()023f f f <<C . ()()()302f f f <=D . ()()()032f f f <<二、填空题:本大题共5小题,每小题5分,共25分.请把答案填在答题卡上. 11.已知()tan 2θπ-=,则22sin sin cos 2cos 3θθθθ+-+的值为13.ABC 中,60A =︒,1b =,三角形ABC 面积S =sin sin sin a b cA B C++=++14.已知函数()322f x x ax bx a =+++在1x =处取得极值10,则a b +取值的集合为 15.若关于x 的方程43210x ax ax ax ++++=有实根,则实数a 的取值范围是三、解答题:本大题共6小题,共75分.请在答题卡指定区域内作答,解答应写出必要的文字说明.证明过程或演算步骤. 16.(本小题满分12分)17.(本小题满分12分)已知函数()2cos cos f x x x x ωωω=-,其中ω为使()f x 能在23x π=时取得最大值的最小正整数. (1)求ω的值;(2)设ABC 的三边长a 、b 、c 满足2b ac =,且边b 所对的角θ的取值集合为A ,当x A∈时,求()f x 的值域.18.(本小题满分12分)ABC 中,设a 、b 、c 分别为角A 、B 、C 的对边,角A 的平分线AD 交BC 边于D ,60A =︒. (1)求证:AD =; (2)若2BD DC =,AD =a 、b 、c 的值. 19.(本小题满分12分)工厂生产某种产品,次品率P 与日产量x (万件)间的关系()()10623x c xP x c ⎧<≤⎪⎪-=⎨⎪>⎪⎩(c 为常数,且06c <<),已知每生产一件合格产品盈利3元,每出现一件次品亏损1.5元(1)将日盈利额y (万元)表示为日产量x (万件)的函数; (2)为使日盈利额最大,日产量应为多少万件?(注: 100⨯次品数次品率=%产品总数)20.(本小题满分13分)已知()()20f x ax bx c a =++>,当1x ≤时,()1f x ≤. (1)证明1c ≤;(2)若224442a b a b ab ++=+-成立,请先求出c 的值,并利用c 值的特点求出函数()f x 的表达式. 21.(本小题满分14分)已知函数()()()()()1212ln ,x f x a x x g x xe -=---=(a 为常数,e 为自然对数的底)(1)当1a =时,求()f x 的单调区间;(2)若函数()f x 在10,2⎛⎫⎪⎝⎭上无零点,求a 的最小值;(3)若对任意的(]00,x e ∈,在(]0,e 上存在两个不同的()1,2i x i =使得()()0i f x g x =成立,求a 的取值范围.2013~2014学年度襄阳四中、荆州中学、龙泉中学高三10月联考数学(理)参考答案11.19512.3,32⎡⎤⎢⎥⎣⎦13.314.{}7-15.[)2,2,3⎛⎤-∞-+∞ ⎥⎝⎦16.若命题p 为真 ()()210a x a x +-= 显然0a ≠ 2x a ∴=-或1x a= []1,1x ∈- 故有21a -≤或11a≤ 1a ∴≥ (5)分若命题q 为真,就有()22420a x a -=0a ∴=或2a =∴命题“p 或q ”为假命题时,()()1,00,1a ∈- (12)分17.(1)()1sin 262f x x πω⎛⎫=-- ⎪⎝⎭,依题意有()42362k k Z πωπππ-=+∈ 即()312k k Z ω+=∈ ω的最小正整数值为22ω∴= (5)分(2)2b ac = 又 2222c o s b a c a B =+-222cos a c ac B ac ∴+-= 即22212cos 2a c acB ac ac++=≥= 12cos 2B ∴+≥ 1c o s 2B ∴≥ 03B π∴<≤即0,3A π⎛⎤= ⎥⎝⎦……………………………………8分()1sin 462f x x π⎛⎫=-- ⎪⎝⎭ 03x π<≤74666x πππ∴-<-≤1sin 4,162x π⎛⎫⎡⎤∴-∈- ⎪⎢⎥⎝⎭⎣⎦ (10)分()11,2f x ⎡⎤∴∈-⎢⎥⎣⎦故函数()f x 的值域是11,2⎡⎤-⎢⎥⎣⎦…………………………12分18.(1)S ABC S ABD S ACD =+ 即111sin 60sin 30sin 30222b c cADbAD ︒=︒+︒AD b c∴=+………………………………5分 (2)2BD DC = 2c B D b D C∴== 2cb ∴= ①……………………7分又()4bc b c =∴=+ ②…………………………9分 由①②解得6,12b c == …………………………………………10分又在ABC 中 2222212c o s 61226122a b c b B =+-=+-⨯⨯⨯ a ∴= ……………………………………………………12分 19.(1)当x c >时,23p =,222130333y x x ⎛⎫=--= ⎪⎝⎭…………2分 当0x c <≤时,16p x=-()()23921131366226x x y x xx x x -⎛⎫⎛⎫∴=--= ⎪ ⎪---⎝⎭⎝⎭……………4分∴日盈利额y (万元)与日产量x (万件)的函数关系式为()()()()23920260x x x c y x x c ⎧-⎪<≤=-⎨⎪>⎩……………………………………5分(2)当x c >时,日盈利额为0当0x c <≤时,()()239226x x y x -=-()()()2239326x x y x --'∴=- 令0y '=得3x =或9x =(舍去)∴当03c <<时,0y '> ∴y 在(]0,c 上单增 ∴y 最大值()()()239226c c f c c -==- ………………………………9分当36c ≤<时,y 在()0,3上单增,在()3,c 上单减∴y 最大值()932f ==……………………………………10分综上:当03c <<时,日产量为c 万件y 日盈利额最大当36c ≤<时,日产量为3万件时日盈利额最大20.(1)1x ≤时 ()()101f x f ≤∴≤0c ∴≤ ……………………………………………………4分(2)由224442a b a b ab ++=+-得到()220a b +-=2a b ∴+= ……………………………………………………5分 又1x ≤时 ()11f ∴≤ 即11a b c -≤++≤将2a b +=代入上式得31c -≤≤- 又 11c -≤≤1c ∴=- ……………………………………………………8分又()01f c ==- 1x ≤时()1f x ≥()()0f x f ∴≥对1x ≤均成立0x ∴=为函数()f x 为对称轴 ………………………………10分002bb a∴-=∴= 又22a b a +=∴= 201a b c ∴===- ………………………………………………12分 ()221f x x ∴=- ………………………………………………13分21.(1)1a =时,()()22ln 11f x x x f x x'=--=- 由()0f x '>得2x > ()0f x '<得02x <<故()f x 的减区间为()0,2 增区间为()2,+∞ …………………………3分 (2)因为()0f x <在10,2⎛⎫ ⎪⎝⎭上恒成立不可能故要使()f x 在10,2⎛⎫ ⎪⎝⎭上无零点,只要对任意的10,2x ⎛⎫∈ ⎪⎝⎭,()0f x >恒成立 即10,2x ⎛⎫∈ ⎪⎝⎭时,2ln 21xa x >-- …………………………………5分 令()2ln 120,12x l x x x ⎛⎫=-∈ ⎪-⎝⎭则()()222ln 21x x l x x +-'=- 再令()212ln 20,2m x x x x⎛⎫=+-∈ ⎪⎝⎭()()2210x m x x --'=< 于是在10,2⎛⎫⎪⎝⎭上()m x 为减函数故()122ln 202m x m ⎛⎫>=-> ⎪⎝⎭ ()0l x '∴>在10,2⎛⎫⎪⎝⎭上恒成立()l x ∴在10,2⎛⎫⎪⎝⎭上为增函数()12l x l ⎛⎫∴< ⎪⎝⎭ 在10,2⎛⎫⎪⎝⎭上恒成立又124ln 22l ⎛⎫=- ⎪⎝⎭故要使ln 21xa x >--恒成立,只要[)24ln 2,a ∈-+∞若函数()f x 在10,2⎛⎫⎪⎝⎭上无零点,a 的最小值为24ln 2-………………8分(3)()()11xf x x e -'=-当()0,1x ∈时,()0g x '>,()g x ∴为增函数 当()1,x e ∈时,()0g x '<,()g x ∴为减函数()()()100,110e g g g e e e -===>∴函数()g x 在(]0,e 上的值域为(]0,1 …………………………………9分 当2a =时,不合题意当2a ≠时,()()()2220,a x a f x x e x⎛⎫-- ⎪-⎝⎭'=∈ 故202e a <<- 22a e∴<-① (10)分此时,当x 变化时,()f x ',()f x 的变化情况如下0x →时,()f x →+∞,2ln 22f a a a ⎛⎫⎛⎫=- ⎪ ⎪--⎝⎭⎝⎭()()()212f e a e =---∴任意定的(]00,x e ∈,在区间(]0,e 上存在两个不同的()1,2i x i =使得()()0i f x g x =成立, 当且仅当a 满足下列条件202f a ⎛⎫< ⎪-⎝⎭即22ln 02a a ⎛⎫-< ⎪-⎝⎭②()1f e >即()()2121a e ---≥ ③……………………11分令()222ln ,22h a a a a e ⎛⎫⎛⎫=-∈-∞-⎪ ⎪-⎝⎭⎝⎭()2ah a a '=- 令()0h a '=得0a = 当(),0a ∈-∞时,()0h a '> 函数()h a 为增函数 当20,2a e ⎛⎫∈-⎪⎝⎭时,()0h a '< 函数()h a 为减函数 所以在任取2,2a e ⎛⎫∈-∞- ⎪⎝⎭时有()()00h a h ≤=即②式对2,2a e ⎛⎫∈-∞- ⎪⎝⎭恒成立 ……………………………………13分由③解得3,21a e ⎛⎫∈-∞- ⎪-⎝⎭ ④由①④ 当3,21a e ⎛⎫∈-∞- ⎪-⎝⎭时对任意(]00,x e ∈,在(]0,e 上存在两个不同的()1,2i x i =使()()0i f x g x =成立。
湖北省襄阳四中、龙泉中学、荆州中学2014届高三10月联考 化学试题 word版含答案(修改,图片无他网标志)

2013~2014学年度襄阳四中、荆州中学、龙泉中学高三10月联考化学试题命题学校:龙泉中学命题人:刘正雄审题人:李旭考试时间:90分钟试卷满分:100分注意事项:1.本次考试使用条形码粘贴,学生需认真核对条形码上的信息,确定无误后粘到答题卡上指定位置;2.客观题填涂必须使用2B铅笔,且按要求填满填涂点;3.答题内容必须全部书写在答题卡题目规定的答题区域内(每题的答题区域以方框为界);4.必须保持卷面整洁、平整,不得揉、搓或折叠试卷。
可能用到的相对原子质量:H—1 C—12 N—14 O—16 Na—23 Mg—24 Al—27 Si—28 S—32 Cl—35.5 Ca—40 Mn —55 Fe—56 Cu—64 Ba—137第Ⅰ卷选择题(共45分)一、选择题(在每题给出的四个选项中,只有一项符合题目要求,每题3分,共45分)1.化学与科学、技术、社会、环境密切相关。
下列有关说法中错误..的是()A.国庆节期间燃放的焰火是某些金属元素焰色反应所呈现出来的色彩B.小苏打是制作馒头和面包等糕点的膨松剂,还是治疗胃酸过多的一种药剂C.为防止中秋月饼等富脂食品因被氧化而变质,常在包装袋中放入生石灰或硅胶D.青铜是我国使用最早的合金材料,目前世界上使用量最大的合金材料是钢铁2.室温时,两个容积相同的烧瓶中分别盛有M和N两种气体(同温同压),取下弹簧夹A,使两烧瓶内的气体接触(如图),容器内的压强由大到小的顺序是()A.③①④②B.①②③④C.④①②③D.①④③②3.下列各组物质相互混合反应后,最终有白色沉淀生成的是()①金属钠投入到FeCl2溶液中②过量NaOH溶液和明矾溶液混合③少量Ca(OH)2投入过量NaHCO3溶液中④向NaAlO2溶液中通入过量CO2⑤向饱和Na2CO3溶液中通入过量CO2A.①③④⑤B.只有①④C.只有②③D.只有③④⑤4.下列说法正确..的是()①标准状况下,6.02×1023个分子所占的体积约是22.4 L ②0.5 mol N 2所占体积为11.2 L③标准状况下,1 mol H 2O 的体积为22.4 L④常温常压下,28 g CO 与N 2的混合气体的所含的原子数为2N A ⑤各种气体的气体摩尔体积都约为22.4 L/mol ⑥标准状况下,体积相同的两种气体的分子数一定相同 A .①③⑤B .④⑥ C.③④⑥ D .①④⑥5.硅被誉为无机非金属材料的主角。
2014-2015学年湖北省襄阳四中、龙泉中学、宜昌一中、荆州中学高三(下)期中数学试卷(理科)

2014-2015学年湖北省襄阳四中、龙泉中学、宜昌一中、荆州中学高三(下)期中数学试卷(理科)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 设集合,,若,则集合等于( ) A. B. C. D.2. 下列说法正确的是( )A.命题“若,则”的否命题为“若,则”B.命题“,”的否定是“,”C.命题“若,则 ”的逆否命题为假命题D.若“”为真命题,则,中至少有一个为真命题3. 设等差数列的前项和为,若,则的值等于( ) A. B. C. D.4. 某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是( )A.B.C.D.5. 曲线与曲线的( ) A.长轴长与实轴长相等 B.短轴长与虚轴长相等 C.焦距相等 D.离心率相等6. 在矩形中,,,如果向该矩形内随机投一点,那么使得与的面积都不小于的概率为( ) A. B. C. D.7. 运行如图的程序框图,则输出的结果是( )A. B. C. D.8. 如图,偶函数的图象形如字母(图),奇函数的图象形如字母(图),若方程().()的实根个数分别为,,则A. B. C. D.9. 中,,,,是边上的一点(包括端点),则的取值范围是( ) A. B. C. D.10. 下面四个图象中,有一个是函数的导函数的图象,则等于( )A. B. C. D.或11. 函数在的图象大致为( ) A.B.C.D.12. 已知由不等式组,确定的平面区域的面积为,定点的坐标为,若,为坐标原点,则的最小值是()A. B. C. D.二、填空题(本大题共4个小题,每小题4分,共16分,把正确答案填在题中横线上.)1. 若为锐角,且,则的值为________.2. 设等差数列前项和为,若,,,则________.3. 点是不等式组表示的平面区域内的一动点,使的值取得最小的点为,则(为坐标原点)的取值范围是________.4. 给出下列命题(1)对于命题,使得,则¬,均有;(2)是直线与直线互相垂直的充要条件;(3)已知回归直线的斜率的估计值为,样本点的中心为,则回归直线方程为;(4)若函数是定义在上的奇函数,且,则.其中真命题的序号是________.(把所有真命题的序号都填上)三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证明过程或演算步骤.)1. 已知平面向量,,,其中,且函数的图象过点.(1)求的值;(2)将函数图象上各点的横坐标变为原来的倍,纵坐标不变,得到函数的图象,求函数在上的最大值和最小值.2. 设数列的前项和为,且,.(1)求数列的通项公式;(2)若数列的各项均为正数,且是与的等比中项,求的前项和.3. 已知几何体的三视图如图所示,其中俯视图和侧视图都是腰长为的等腰直角三角形,正视图为直角梯形,已知几何体的体积为.(1)求实数的值;(2)将直角三角形绕斜边旋转一周,求该旋转体的表面积.4. 甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满局时停止.设在每局中参赛者胜负的概率均为,且各局胜负相互独立.求:(1)打满局比赛还未停止的概率;(2)比赛停止时已打局数的分布列与期望.5. 设函数定义在上,,导函数,.(1)求的单调区间和最小值;(2)讨论与的大小关系;(3)是否存在,使得对任意成立?若存在,求出的取值范围;若不存在请说明理由.6. 已知椭圆的焦距为,离心率为.(1)求椭圆方程;(2)设过椭圆顶点,斜率为的直线交椭圆于另一点,交轴于点,且,,成等比数列,求的值.参考答案与试题解析2014-2015学年四川省达州市大竹县文星中学高三(下)期中数学试卷(理科)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.【答案】D【考点】集合的包含关系判断及应用【解析】根据子集的定义,得出,利用排除法即可得出答案.【解答】解:∵集合,,且,∴;∴选项满足条件.故选:.2.【答案】D【考点】复合命题的真假四种命题间的逆否关系命题的否定【解析】通过复合命题的定义,四种命题的关系,命题的否定,逐项进行判断.【解答】解:对于:否命题为“若,则”,故错误;对于:否定是“,”,故错误;对于:逆否命题为:若“,则”,是真命题,故错误;,,,都错误,故正确,故选:.3.【答案】A【考点】等差数列的前n项和【解析】由已知,结合等差数列的性质可得,从而可得,,代入等差数列的前项和,然后利用利用等差数列的性质及所求的的值代入可求得答案.【解答】解:∵由等差数列的性质可得,从而可得,由等差数列的前项和可得,故选:4.【答案】D【考点】简单空间图形的三视图【解析】由图可知,此几何体为组合体,对照选项分别判断组合体的结构,能吻合的排除,不吻合的为正确选项【解答】解:依题意,此几何体为组合体,若上下两个几何体均为圆柱,则俯视图为若上边的几何体为正四棱柱,下边几何体为圆柱,则俯视图为;若上边的几何体为底面为等腰直角三角形的直三棱柱,下面的几何体为正四棱柱时,俯视图为;若俯视图为,则正视图中上图中间还有一条虚线,故该几何体的俯视图不可能是故选5.【答案】C【考点】椭圆的性质双曲线的标准方程【解析】由曲线的标准方程分别计算其焦距即可判断出.【解答】解:曲线是焦点在轴上的椭圆,半焦距.曲线表示焦点在轴上的双曲线,半焦距.∴两曲线的截距相等.故选:.6.【答案】A【考点】几何概型【解析】本题是一个几何概型的概率,以为底边,要使面积不小于,则三角形的高要,高即为点到和的距离要不小于和,得到结果.【解答】解:由题意知本题是一个几何概型的概率,以为底边,要使面积不小于,由于,则三角形的高要,高即为点到的距离要不小于,同样,点到的距离要不小于,其表示的区域为图中阴影部分,它的面积是,∴概率为.故选.7.【答案】B【考点】程序框图【解析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【解答】解:当时,满足进入循环的条件,执行循环体后,,;当时,满足进入循环的条件,执行循环体后,,;当时,满足进入循环的条件,执行循环体后,,;当时,满足进入循环的条件,执行循环体后,,;当时,不满足进入循环的条件,故输出的值为,故选:8.【答案】A【考点】函数奇偶性的性质【解析】结合函数图象把方程根的个数转化为函数图象的交点个数,可分别求得,进而可得答案.【解答】解:由图象知,有个根,,,有个根,,(假设与轴交点横坐标为),由(),得或,由图象可知所对每一个值都能有个根,因而;由(),知或,由图象可可以看出时对应有个根,而时有个,而时只有个,加在一起也是个,即,∴,故选:.9.【答案】D【考点】平面向量数量积的运算【解析】由于是边上的一点(包括端点),利用向量共线定理:可设.由,,,可得.代入利用数量积运算性质即可得出.再利用一次函数的单调性即可得出.【解答】解:∵是边上的一点(包括端点),∴可设.∵,,,∴.∴ •.∵,∴.∴的取值范围是.故选:.10.【答案】D【考点】导数的运算法则【解析】先求出,根据开口方向,对称轴,判断哪一个图象是导函数的图象,再根据图象求出的值,最后求出.【解答】解:函数的的导数,则的图象开口向上,排除,若是则,对称轴关于轴对称,则,即,,∴,若对应的图象应为,则函数过原点,,解得,或且对称轴,即,∴∴,∴,故选:.11.【答案】C【考点】函数的图象与图象变化【解析】由函数的奇偶性可排除,再由时,,可排除,求导数可得,可排除,进而可得答案.【解答】由题意可知:,故函数为奇函数,故可排除,又因为当时,,,故,可排除,又,故可得,可排除,12.【答案】B【考点】简单线性规划【解析】首先作出不等式组所表示的平面区域,然后根据直线恒过点,且原点的坐标恒满足,当时,,此时平面区域的面积为,由于,由此可得.联立方程组求出的坐标,根据三角形的面积公式求得的值,最后把转化为线性目标函数解决.【解答】解:依题意画出不等式组所表示的平面区域(如右图所示)可知其围成的区域是等腰直角三角形面积为,由直线恒过点,且原点的坐标恒满足,当时,,此时平面区域的面积为,由于,由此可得.由可得,依题意应有,因此(,舍去).故有,设,由,可化为,∵,∴当直线过点时,截距最大,即取得最小值.故选:.二、填空题(本大题共4个小题,每小题4分,共16分,把正确答案填在题中横线上.)1.【答案】【考点】两角和与差的正弦公式【解析】由同角三角函数的基本关系可求,而,代入化简即可.【解答】解:∵为锐角,∴,又∵,∴,∴故答案为:.2.【答案】【考点】等差数列的前n项和【解析】利用等差数列的前项和公式即可得出;【解答】解:解法一:∵等差数列前项和为,满足,,,∴,解得.解法二:由等差数列的性质可得:为等差数列,∴,解得.解法三:,,所以公差,所以,解得,故答案为.3.【答案】【考点】简单线性规划平面向量数量积的运算【解析】画出满足约束条件的平面区域,然后利用角点法求出满足条件使的值取得最小的点的坐标,结合平面向量的数量积运算公式,即可得到结论.【解答】解:满足约束条件的平面区域如下图所示:由图可知,当,时,取得最小值故设则,则当与重合时,取最小值;当点坐标为时,取最大值故则(为坐标原点)的取值范围是故答案为:4.【答案】(3)(4).【考点】命题的真假判断与应用【解析】直接写出特称命题的否定判断(1);由两直线垂直与斜率的关系判断(2);由回归直线方程恒过样本中心点求得判断(3);利用函数的周期性求得判断(4).【解答】解:(1)对于命题,使得,则¬,均有,故(1)错误;(2)由,得两直线分别为和,两直线斜率互为负倒数,两直线垂直,由直线与直线互相垂直,也可能,∴是直线与直线互相垂直的充分不必要条件,故(2)错误;(3)已知回归直线的斜率的估计值为,则回归直线方程为,代入样本点的中心,得,则回归直线方程为,故(3)正确;(4)若函数是定义在上的奇函数,且,则,故(4)正确.三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证明过程或演算步骤.)1.【答案】解:(1)∵ ……∴,…即∴,而,∴.…(2)由(1)得,,于是,即.…当时,,所以,…即当时,取得最小值,当时,取得最大值.…【考点】函数y=Asin(ωx+φ)的图象变换数量积的坐标表达式两角和与差的余弦公式余弦函数的定义域和值域【解析】(1)先根据两个向量数量积的坐标公式求出以及,再代入求出的表达式;根据图象过点即可求出的值;(2)根据函数图象的变换规律求出函数的表达式,再根据变量的范围结合函数的单调性即可求出函数在上的最大值和最小值.【解答】解:(1)∵ ……∴,…即∴,而,∴.…(2)由(1)得,,于是,即.…当时,,所以,…即当时,取得最小值,当时,取得最大值.…2.【答案】解:(1)由,得,两式作差得:,即.又,∴.∴数列是以为首项,以为公比的等比数列.则;(2)∵数列的各项均为正数,且是与的等比中项,∴,.∴..作差得:.∴.【考点】数列的求和【解析】(1)由数列递推式得到另一递推式,作差后得到,再求出后由综合得到数列是等比数列,由此得到等比数列的通项公式;(2)由是与的等比中项求得的通项公式,然后利用错位相减法求得的前项和.【解答】解:(1)由,得,两式作差得:,即.又,∴.∴数列是以为首项,以为公比的等比数列.则;(2)∵数列的各项均为正数,且是与的等比中项,∴,.∴..作差得:.∴.3.【答案】解:(1)由该几何体的三视图知面,且,,体积,解得;(2)在中,,,,过作的垂线,垂足为,得,该旋转体由两个同底的圆锥构成,圆锥底面半径为,所以圆锥底面周长为,两个圆锥的母线长分别为和,故该旋转体的表面积为.【考点】由三视图求面积、体积旋转体(圆柱、圆锥、圆台)【解析】(1)由该几何体的三视图知面,且,,利用几何体的体积为,求实数的值;(2)过作的垂线,垂足为,得,求出圆锥底面周长为,两个圆锥的母线长分别为和,即可求该旋转体的表面积.【解答】解:(1)由该几何体的三视图知面,且,,体积,解得;(2)在中,,,,过作的垂线,垂足为,得,该旋转体由两个同底的圆锥构成,圆锥底面半径为,所以圆锥底面周长为,两个圆锥的母线长分别为和,故该旋转体的表面积为.4.【答案】解:令,,分别表示甲、乙、丙在第局中获胜.(1)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满局比赛还未停止的概率为:.…(各分)(2)由题设知的所有可能值为,,,,,且,,,,,…故的布列为【考点】离散型随机变量的期望与方差相互独立事件的概率乘法公式【解析】(1)令,,分别表示甲、乙、丙在第局中获胜,由独立事件同时发生与互斥事件至少有一个发生的概率公式,能求出打满局比赛还未停止的概率.(2)由题设知的所有可能值为,,,,,利用独立事件同时发生与互斥事件至少有一个发生的概率公式分别求出,,,,,由此能求出比赛停止时已打局数的分布列与期望.【解答】解:令,,分别表示甲、乙、丙在第局中获胜.(1)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满局比赛还未停止的概率为:.…(各分)(2)由题设知的所有可能值为,,,,,且,,,,,…故的布列为.5.【答案】解:(1)由题设易知,,∴,令,得,当时,,故的单调递减区间是,当时,,故的单调递增区间是,因此是的唯一极值点,且为极小值点,从而是最小值点,∴最小值为;(2),设,则,当时,,即,当时,,,因此,在内单调递减,当,时,,即,当,时,,即,(3)满足条件的不存在.证明如下:证法一假设存在,使成立,即对任意,有,但对上述,取时,有,这与左边不等式矛盾,因此,不存在,使成立.证法二假设存在,使成立.由(1)知,的最小值为.又,而时,的值域为,∴时,的值域为,从而可取一个,使,即,故,与假设矛盾.∴不存在,使成立.【考点】利用导数研究函数的单调性指、对数不等式的解法【解析】(1)根据题意求出的解析式,代入.求出,求导,令导数等于零,解方程,跟据,随的变化情况即可求出函数的单调区间和最小值;(2)构造函数,利用导数求该函数的最小值,从而求得与的大小关系;(3)证法一:假设存在,使成立,即对任意,解此绝对值不等式,取时,得出矛盾;证法二假设存在,使成立,转化为求函数的值域,得出矛盾.【解答】解:(1)由题设易知,,∴,令,得,当时,,故的单调递减区间是,当时,,故的单调递增区间是,因此是的唯一极值点,且为极小值点,从而是最小值点,∴最小值为;(2),设,则,当时,,即,当时,,,因此,在内单调递减,当,时,,即,当,时,,即,(3)满足条件的不存在.证明如下:证法一假设存在,使成立,即对任意,有,但对上述,取时,有,这与左边不等式矛盾,因此,不存在,使成立.证法二假设存在,使成立.由(1)知,的最小值为.又,而时,的值域为,∴时,的值域为,从而可取一个,使,即,故,与假设矛盾.∴不存在,使成立.6.【答案】解:(1)由已知,.…解得,…所以,椭圆的方程为.…(2)由(1)得过点的直线为,由得,…所以,所以,…依题意,.因为,,成等比数列,所以,…所以,即,…当时,,无解,…当时,,解得,…所以,解得,所以,当,,成等比数列时,.…【考点】直线与圆锥曲线的综合问题椭圆的标准方程【解析】(1)由已知,可求,结合即可求,进而可求椭圆方程(2)由(1)得过点的直线为,联立直线与椭圆方程可求的坐标,及的取值范围,由,,成等比,可得,即,解方程可求【解答】解:(1)由已知,.…解得,…所以,椭圆的方程为.…(2)由(1)得过点的直线为,由得,…所以,所以,…依题意,.因为,,成等比数列,所以,…所以,即,…当时,,无解,…当时,,解得,…所以,解得,所以,当,,成等比数列时,.…。
襄阳四中、龙泉中学、荆州中学高三数学10月联考试题 文 新人教A版
2013~2014学年度襄阳四中、荆州中学、龙泉中学高三10月联考数学(文)试题考试时间:120分钟 试卷满分:150分一、选择题(本大题共10小题,每小题5分,共50分) 1.全集U={1,2,3,4,5},集合M={1,4},N={1,3,5},则U N C M =( )A.{3,5}B.{1,5}C.{4,5}D.{1,3} 2.下列选项叙述错误的是( )A.命题“若x≠l,则x 2-3x 十2≠0”的逆否命题是“若x 2-3x 十2=0,则x =1” B.若p ∨q 为真命题,则p ,q 均为真命题C.若命题p :∀x ∈R ,x 2+x 十1≠0,则⌝p :x ∃∈R ,x 2+x 十1=0D .“x>2”是“x 2一3x +2>0”的充分不必要条件3.()f x =函数的定义域为( )A .]21,(-∞ B.1[,)2+∞ C.]21,41( D.),41(+∞ 4.函数()sin()f x A x ωϕ=+(其中A >0,2||πϕ<)的图象如图所示,为了得到()f x 图象,则只需将()sin 2g x x =的图象 ( ) A. 向右平移6π个长度单位B. 向左平移6π个长度单位 C. 向右平移3π个长度单位 D. 向左平移3π个长度单位5.等边三角形ABC 的边长为1,,,,BC a CA b AB c a b b c c a ===++那么等于( )A.3B.-3C.32 D.32-6.函数()sin(2))f x x x θθ=+++为奇函数,且在[0,]4π上为减函数的θ值可以是( )A .3π-B .6π-C .56π D .23π 7.已知函数e ,0,()21,0x a x f x x x ⎧+≤=⎨->⎩(a ∈R ),若函数()f x 在R 上有两个零点,则a 的取值范围是 ( )A .(),1-∞-B .(),0-∞C .()1,0-D .[)1,0-8.已知函数()f x 的导数为()f x ',且满足关系式2()3(2)ln f x x xf x '=++则(2)f '的值等于( ) A.2- B.2 C.94-D. 949.已知函数()sin f x x x =,∈x R ,则)5(πf ,)1(f ,)(3π-f 的大小关系为( ) A .)5()1()3(ππf f f >>-B .)5()3()1(ππf f f >->C .)3()1()5(ππ->>f f f D .)1()5()3(f f f >>-ππ10.函数2()2||2f x x x =-+的定义域是[a ,b ] (a<b),值域是[2a,2b ],则符合条件的数组(a ,b )的组数为 ( )A . 0B .1C . 2D . 3二、填空题:(本大题共7小题,每小题5分,共35分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013~2014学年度襄阳四中、荆州中学、龙泉中学高三10月联考数学(理)试题命题学校:龙泉中学 命题人:陈信金 审题人:陆晓峰总分150分,考试用时120分钟。
一、选择题: 本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题意要求的. 1.已知全集{}1,2,3,4,5,6,7,8,9U = 集合{}1,2,3,4,5,6A = 集合{}3,4,5,6,7,8B =,则集合U UAB 痧为( )A . {}3,4,5,6B . {}1,2,7,8,9C . {}1,2,3,4,5,6,7,8D . {}9 2.已知点()1,3A ,()4,1B -则与AB 同方向的单位向量是( ) A . 34,55⎛⎫-⎪⎝⎭ B . 43,55⎛⎫- ⎪⎝⎭C . 34,55⎛⎫- ⎪⎝⎭ D . 43,55⎛⎫- ⎪⎝⎭3.命题“对任意x R ∈都有21x ≥”的否定是( ) A .对任意x R ∈,都有21x <B .不存在x R ∈,使得21x <C .存在0x R ∈,使得201x ≥D .存在0x R ∈,使得201x <4.已知函数()21f x +的定义域为12,2⎛⎫- ⎪⎝⎭,则()f x 的定义域为( ) A . 31,24⎛⎫-⎪⎝⎭ B . 31,2⎛⎫- ⎪⎝⎭ C . ()3,2- D . ()3,3-5.已知角x 的终边上一点坐标为55sin ,cos 66ππ⎛⎫ ⎪⎝⎭,则角x 的最小正值为( ) A .56π B . 53π C . 116π D . 23π6.已知函数()f x 的导函数为()f x ',且满足关系式()()2=32ln f x x xf x '++,则()2f '的值等于( )A .2B . 2-C .94 D . 94-7.已知向量()2,8a b +=-,()8,16a b -=-,则a 与b 夹角的余弦值为( ) A .6365 B . 6365- C . 6365± D . 5138.已知点(),a b 在圆221x y +=上,则函数()2cos sin cos 12af x a x b x x =+--的最小正周期和最小值分别为( ) A . 32,2π-B . 3,2π-C . 5,2π- D . 52,2π-9.函数()3f x m x =-+有零点,则实数m 的取值范围是( )A . 0,2⎛⎫⎪ ⎪⎝⎭ B . 0,2⎡⎢⎣⎦ C . 0,4⎡⎢⎣⎦ D . 0,4⎛ ⎝⎭10.设分程220xx ++=和方程2log 20x x ++=的根分别为p 和q ,函数()()()2f x x p x q =+++,则( )A . ()()()203f f f =<B . ()()()023f f f <<C . ()()()302f f f <=D . ()()()032f f f <<二、填空题:本大题共5小题,每小题5分,共25分.请把答案填在答题卡上. 11.已知()tan 2θπ-=,则22sin sin cos 2cos 3θθθθ+-+的值为13.ABC 中,60A =︒,1b =,三角形ABC 面积S =sin sin sin a b cA B C++=++14.已知函数()322f x x ax bx a =+++在1x =处取得极值10,则a b +取值的集合为 15.若关于x 的方程43210x ax ax ax ++++=有实根,则实数a 的取值范围是三、解答题:本大题共6小题,共75分.请在答题卡指定区域内作答,解答应写出必要的文字说明.证明过程或演算步骤. 16.(本小题满分12分)17.(本小题满分12分)已知函数()2cos cos f x x x x ωωω=-,其中ω为使()f x 能在23x π=时取得最大值的最小正整数. (1)求ω的值;(2)设ABC 的三边长a 、b 、c 满足2b ac =,且边b 所对的角θ的取值集合为A ,当x A ∈时,求()f x 的值域.18.(本小题满分12分)ABC 中,设a 、b 、c 分别为角A 、B 、C 的对边,角A 的平分线AD 交BC 边于D ,60A =︒.(1)求证:AD =;(2)若2BD DC =,AD =a 、b 、c 的值. 19.(本小题满分12分)工厂生产某种产品,次品率P 与日产量x (万件)间的关系()()10623x c xP x c ⎧<≤⎪⎪-=⎨⎪>⎪⎩(c 为常数,且06c <<),已知每生产一件合格产品盈利3元,每出现一件次品亏损1.5元(1)将日盈利额y (万元)表示为日产量x (万件)的函数; (2)为使日盈利额最大,日产量应为多少万件?(注: 100⨯次品数次品率=%产品总数)20.(本小题满分13分)已知()()20f x ax bx c a =++>,当1x ≤时,()1f x ≤.(1)证明1c ≤;(2)若224442a b a b ab ++=+-成立,请先求出c 的值,并利用c 值的特点求出函数()f x 的表达式. 21.(本小题满分14分)已知函数()()()()()1212ln ,x f x a x x g x xe -=---=(a 为常数,e 为自然对数的底)(1)当1a =时,求()f x 的单调区间;(2)若函数()f x 在10,2⎛⎫⎪⎝⎭上无零点,求a 的最小值;(3)若对任意的(]00,x e ∈,在(]0,e 上存在两个不同的()1,2i x i =使得()()0i f x g x =成立,求a的取值范围.2013~2014学年度襄阳四中、荆州中学、龙泉中学高三10月联考数学(理)参考答案11.19512.3,32⎡⎤⎢⎥⎣⎦13 14.{}7-15.[)2,2,3⎛⎤-∞-+∞ ⎥⎝⎦16.若命题p 为真 ()()210a x a x +-= 显然0a ≠2x a ∴=-或1x a=[]1,1x ∈- 故有21a -≤或11a≤ 1a ∴≥………………………5分若命题q 为真,就有()22420a x a -=0a ∴=或2a =∴命题“p 或q ”为假命题时,()()1,00,1a ∈-………………………12分17.(1)()1sin 262f x x πω⎛⎫=-- ⎪⎝⎭,依题意有()42362k k Z πωπππ-=+∈ 即()312k k Z ω+=∈ ω的最小正整数值为22ω∴=………………………5分 (2)2b ac = 又 2222c o s b a c a B =+-222cos a c ac B ac ∴+-= 即22212cos 2a c ac B ac ac++=≥= 12cos 2B ∴+≥ 1c o s2B ∴≥ 03B π∴<≤ 即0,3A π⎛⎤= ⎥⎝⎦……………………………………8分()1sin 462f x x π⎛⎫=-- ⎪⎝⎭ 03x π<≤74666x πππ∴-<-≤1sin 4,162x π⎛⎫⎡⎤∴-∈- ⎪⎢⎥⎝⎭⎣⎦ …………………………10分()11,2f x ⎡⎤∴∈-⎢⎥⎣⎦故函数()f x 的值域是11,2⎡⎤-⎢⎥⎣⎦…………………………12分18.(1)S ABC S ABD S ACD =+ 即111sin 60sin 30sin 30222b c cAD bAD ︒=︒+︒AD ∴=………………………………5分 (2)2BD DC = 2c B D b D C∴== 2cb ∴= ①……………………7分又()4bc b c b c=∴=++ ② …………………………9分由①②解得6,12b c == …………………………………………10分又在ABC 中 2222212c o s 61226122a b c b B =+-=+-⨯⨯⨯a ∴= ……………………………………………………12分19.(1)当x c >时,23p =,222130333y x x ⎛⎫=--= ⎪⎝⎭…………2分当0x c <≤时,16p x=-()()23921131366226x x y x xx x x -⎛⎫⎛⎫∴=--= ⎪ ⎪---⎝⎭⎝⎭……………4分 ∴日盈利额y (万元)与日产量x (万件)的函数关系式为()()()()23920260x x x c y x x c ⎧-⎪<≤=-⎨⎪>⎩……………………………………5分(2)当x c >时,日盈利额为0当0x c <≤时,()()239226x x y x -=-()()()2239326x x y x --'∴=- 令0y '=得3x =或9x =(舍去)∴当03c <<时,0y '> ∴y 在(]0,c 上单增 ∴y 最大值()()()239226c c f c c -==- ………………………………9分当36c ≤<时,y 在()0,3上单增,在()3,c 上单减 ∴y 最大值()932f ==……………………………………10分综上:当03c <<时,日产量为c 万件y 日盈利额最大当36c ≤<时,日产量为3万件时日盈利额最大20.(1)1x ≤时 ()()101f x f ≤∴≤0c ∴≤ ……………………………………………………4分(2)由224442a b a b ab ++=+-得到()220a b +-=2a b ∴+= ……………………………………………………5分 又1x ≤时 ()11f ∴≤ 即11a b c -≤++≤将2a b +=代入上式得31c -≤≤- 又 11c -≤≤1c ∴=- ……………………………………………………8分又()01f c ==- 1x ≤时()1f x ≥()()0f x f ∴≥对1x ≤均成立0x ∴=为函数()f x 为对称轴 ………………………………10分002bb a∴-=∴= 又22a b a +=∴= 201a b c ∴===- ………………………………………………12分 ()221f x x ∴=- ………………………………………………13分21.(1)1a =时,()()22ln 11f x x x f x x'=--=-由()0f x '>得2x > ()0f x '<得02x <<故()f x 的减区间为()0,2 增区间为()2,+∞ …………………………3分 (2)因为()0f x <在10,2⎛⎫ ⎪⎝⎭上恒成立不可能故要使()f x 在10,2⎛⎫ ⎪⎝⎭上无零点,只要对任意的10,2x ⎛⎫∈ ⎪⎝⎭,()0f x >恒成立 即10,2x ⎛⎫∈ ⎪⎝⎭时,2ln 21xa x >-- …………………………………5分 令()2ln 120,12x l x x x ⎛⎫=-∈ ⎪-⎝⎭则()()222ln 21x x l x x +-'=-再令()212ln 20,2m x x x x⎛⎫=+-∈ ⎪⎝⎭()()2210x m x x --'=< 于是在10,2⎛⎫ ⎪⎝⎭上()m x 为减函数故()122ln 202m x m ⎛⎫>=-> ⎪⎝⎭()0l x '∴>在10,2⎛⎫⎪⎝⎭上恒成立()l x ∴在10,2⎛⎫⎪⎝⎭上为增函数()12l x l ⎛⎫∴< ⎪⎝⎭ 在10,2⎛⎫⎪⎝⎭上恒成立又124ln 22l ⎛⎫=- ⎪⎝⎭故要使ln 21xa x >--恒成立,只要[)24ln 2,a ∈-+∞若函数()f x 在10,2⎛⎫⎪⎝⎭上无零点,a 的最小值为24ln 2-………………8分(3)()()11xf x x e -'=-当()0,1x ∈时,()0g x '>,()g x ∴为增函数 当()1,x e ∈时,()0g x '<,()g x ∴为减函数()()()100,110e g g g e e e -===>∴函数()g x 在(]0,e 上的值域为(]0,1 …………………………………9分当2a =时,不合题意 当2a ≠时,()()()2220,a x a f x x e x⎛⎫--⎪-⎝⎭'=∈故202e a <<- 22a e∴<-① ……………………………………………………10分此时,当x 变化时,()f x ',()f x 的变化情况如下0x →时,()f x →+∞,222ln 22f a a a ⎛⎫⎛⎫=- ⎪ ⎪--⎝⎭⎝⎭()()()212f e a e =---∴任意定的(]00,x e ∈,在区间(]0,e 上存在两个不同的()1,2i x i =使得()()0i f x g x =成立, 当且仅当a 满足下列条件202f a ⎛⎫< ⎪-⎝⎭即22ln 02a a ⎛⎫-< ⎪-⎝⎭② ()1f e >即()()2121a e ---≥ ③……………………11分令()222ln ,22h a a a a e ⎛⎫⎛⎫=-∈-∞-⎪ ⎪-⎝⎭⎝⎭()2ah a a '=- 令()0h a '=得0a = 当(),0a ∈-∞时,()0h a '> 函数()h a 为增函数 当20,2a e ⎛⎫∈-⎪⎝⎭时,()0h a '< 函数()h a 为减函数 所以在任取2,2a e ⎛⎫∈-∞- ⎪⎝⎭时有()()00h a h ≤=即②式对2,2a e ⎛⎫∈-∞- ⎪⎝⎭恒成立 ……………………………………13分由③解得3,21a e ⎛⎫∈-∞- ⎪-⎝⎭ ④由①④ 当3,21a e ⎛⎫∈-∞- ⎪-⎝⎭时对任意(]00,x e ∈,在(]0,e 上存在两个不同的()1,2i x i =使()()0i f x g x =成立。
