专题八__几何图形的类比探究

2020中考数学专题《几何变式探究和类比变换综合类问题》

2020中考数学专题《几何变式探究和类比变换综合类问题》【方法指导】图形的类比变换是近年来中考的常考点，常以三角形、四边形为背景，与翻折、旋转相结合，考查三角形全等或相似的性质与判定，难度较大．此类题目第一问相对简单，后面的问题需要结合第一问的方法进行类比解答．根据其特征大致可分为：几何变换类比探究问题、旋转综合问题、翻折类问题等．解决此类问题要善于将复杂图象分解为几个基本图形，通过添加副主席补全或构造基本图形，借助转化、方程、数形结合、分类讨论等数学思想解决几何证明问题，计算则把几何与代数知识综合起来，渗透数形结合思想，考查学生分析问题的能力、逻辑思维和推理能力. 【题型剖析】【类型1】几何类比变换综合题【例1】（2018秋•盐都区期中）【阅读理解】截长补短法，是初中数学几何题中一种辅助线的添加方法．截长就是在长边上截取一条线段与某一短边相等，补短是通过在一条短边上延长一条线段与另一短边相等，从而解决问题．（1）如图1，ABC∆是等边三角形，点D是边BC下方一点，120∠=︒，探索线段DA、BDCDB、DC之间的数量关系．解题思路：延长DC到点E，使CE BD∠+∠=︒，可证=，连接AE，根据180BAC BDC ∠=∠易证得ABD ACEABD ACE∆≅∆，得出ADE=，从而∆是等边三角形，所以AD DE 探寻线段DA、DB、DC之间的数量关系．根据上述解题思路，请直接写出DA、DB、DC之间的数量关系是____；【拓展延伸】（2）如图2，在Rt ABC∆中，90∠=︒，=．若点D是边BC下方一点，90BDCBAC∠=︒，AB AC探索线段DA、DB、DC之间的数量关系，并说明理由；【知识应用】（3）如图3，两块斜边长都为14cm的三角板，把斜边重叠摆放在一起，则两块三角板的直角顶点之间的距离PQ的长分别为____cm．【变式1-1】（2019•亭湖区二模）【阅读材料】小明遇到这样一个问题：如图1，点P 在等边三角形ABC 内，且150APC ∠=︒，3PA =，4PC =，求PB 的长．小明发现，以AP 为边作等边三角形APD ，连接BD ，得到ABD ∆；由等边三角形的性质，可证ACP ABD ∆≅∆，得PC BD =；由已知150APC ∠=︒，可知PDB ∠的大小，进而可求得PB 的长．（1）请回答：在图1中，PDB ∠=________︒，PB =____．【问题解决】（2）参考小明思考问题的方法，解决下面问题：如图2，ABC ∆中，90ACB ∠=︒，AC BC =，点P 在ABC ∆内，且1PA =，17PB =，22PC =，求AB 的长．【灵活运用】（3）如图3，在Rt ABC ∆中，90ACB ∠=︒，BAC α∠=，且4tan 3α=，点P 在ABC ∆外，且3PB =，1PC =，直接写出PA 长的最大值．【变式1-2】（2018•亭湖区二模）如图，在等腰Rt ABC ∆与等腰Rt ADE ∆中，90BAC DAE ∠=∠=︒．（1）连接BD ，CE （如图①)，请直接写出线段BD ，CE 的数量关系____；（2）在（1）的基础上，延长BD 交CE 于点F ，连接AF （如图②)，试探究线段AF ，BF ，CF 的数量关系，并证明你的结论；（3）连接BE ，取BE 的中点O ，连接AO （如图③)，若5AD =，2AO =，3tan 4DAO ∠=，求AB 的长．【类型2】几何旋转变换综合题【例2】（2019•海州区一模）如图1，将两个完全相同的三角形纸片ABC 和DEC 重合放置，其中90C ∠=︒，30B E ∠=∠=︒．（1）操作发现：如图2，固定ABC ∆，使DEC ∆绕点C 旋转，当点D 恰好落在AB 边上时，填空： ①线段DE 与AC 的位置关系是____；②设BDC ∆的面积为1S ，AEC ∆的面积为2S ，则1S 与2S 的数量关系是____．（2）猜想论证：当DEC ∆绕点C 旋转到如图3所示的位置时，小明猜想（1）中1S 与2S 的数量关系仍然成立，并尝试分别作出了BDC ∆和AEC ∆中BC 、CE 边上的高，请你证明小明的猜想．（3）拓展探究已知60ABC ∠=︒，点D 是角平分线上一点，6BD CD ==，//DE AB 交BC 于点E （如图4)，若在射线BA 上存在点F ，使DCF BDE S S ∆∆=，请求出相应的BF 的长．【变式2-1】（2019•辽阳模拟）旋转变换是解决数学问题中一种重要的思想方法，通过旋转变换可以将分散的条件集中到一起，从而方便解决问题．已知，ABC ∆中，AB AC =，BAC α∠=，点D 、E 在边BC 上，且12DAE α∠=．（1）如图1，当60α=︒时，将AEC ∆绕点A 顺时针旋转60︒到AFB ∆的位置，连接DF ， ①求DAF ∠的度数；②求证：ADE ADF ∆≅∆；（2）如图2，当90α=︒时，猜想BD 、DE 、CE 的数量关系，并说明理由；（3）如图3，当120α=︒，4BD =，5CE =时，请直接写出DE 的长为____．【变式2-2】（2019•宜兴市二模）【问题提出】如图1，四边形ABCD 中，AD CD =，120ABC ∠=︒，60ADC ∠=︒，2AB =，1BC =，求四边形ABCD 的面积．【尝试解决】旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．（1）如图2，连接BD ，由于AD CD =，所以可将DCB ∆绕点D 顺时针方向旋转60︒，得到DAB ∆'，则BDB ∆'的形状是____________．（2）在（1）的基础上，求四边形ABCD 的面积．[类比应用]如图3，四边形ABCD 中，AD CD =，75ABC ∠=︒，60ADC ∠=︒，2AB =，2BC =，求四边形ABCD 的面积．【类型3】几何翻折变换综合题【例3】（2019•江都区三模）如图1，有一张矩形纸片ABCD ，已知5AB =，6AD =，现将纸片进行如下操作：首先将纸片沿折痕BF 进行折叠，使点A 落在BC 边上的点E 处，点F 在AD 上（如图2)；然后将纸片沿折痕DH 进行第二次折叠，使点C 落在第一次的折痕BF 上的点G 处，点H 在BC 上（如图3)．（1）如图2，判断四边形ABEF 的形状，并说明理由；（2）如图3，求BG 的长．【变式3-1】（2019•广陵区校级二模）如图，将矩形ABCD 先过点A 的直线1L 翻折，点DA 的对应点D '刚好落在边BC 上，直线1L 交DC 于点F ；再将矩形ABCD 沿过点A 的直线2L 翻折，使点B 的对应点G 落在AD '上，EG 的延长线交AD 于点H ．（1）当四边形AED H '是平行四边形时，求AD H ∠'的度数．（2）当点H 与点D 刚好重合时，试判断AEF ∆的形状，并说明理由．【变式3-2】（2018•深圳模拟）已知矩形纸片ABCD 中，2AB =，3BC =．操作：将矩形纸片沿EF 折叠，使点B 落在边CD 上．探究：（1）如图1，若点B 与点D 重合，你认为1EDA ∆和FDC ∆全等吗？如果全等，请给出证明，如果不全等，请说明理由；（2）如图2，若点B 与CD 的中点重合，请你判断1FCB ∆、△1B DG 和△1EAG 之间的关系，如果全等，只需写出结果，如果相似，请写出结果和相应的相似比；（3）如图2，请你探索，当点B 落在CD 边上何处，即1B C 的长度为多少时，1FCB ∆与△1B DG 全等．【达标检测】1．如图1，在Rt △ABC 中，AB ＝AC ，D 、E 是斜边BC 上两动点，且∠DAE ＝45°，将△ABE 绕点A 逆时针旋转90后，得到△AFC ，连接DF ．（1）试说明：△AED ≌△AFD ；（2）当BE ＝3，CE ＝9时，求∠BCF 的度数和DE 的长；（3）如图2，△ABC 和△ADE 都是等腰直角三角形，∠BAC ＝∠DAE ＝90°，D 是斜边BC 所在直线上一点，BD ＝3，BC ＝8，求DE 2的长．2．如图①，在等腰△ABC和△ADE中，AB＝AC，AD＝AE，且∠BAC＝∠DAE＝120°．（1）求证：△ABD≌△ACE；（2）把△ADE绕点A逆时针方向旋转到图②的位置，连接CD，点M、P、N分别为DE、DC、BC的中点，连接MN、PN、PM，判断△PMN的形状，并说明理由；（3）在（2）中，把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝6，请分别求出△PMN周长的最小值与最大值．3．如图，在平面直角坐标系xOy中，点A（0，4），B（﹣4，0），C（4，0），D（0，﹣4），连接AB，AC，BD，点P是线段AB上的一个动点，连接PD，过点P作PE⊥PD，交线段AC于点E，将线段EP绕点E逆时针旋转90°至EF．（1）过点P的横坐标为，则AE＝__________；（2）当点P在线段AB上运动到何处时，线段AE最长？求出此时点P的坐标；（3）连接OF．当点P在线段AB上运动时，线段OF的长度随之变化，求线段OF长度的最小值．4．如图1，Rt△ABC中，∠C＝90°，AB＝15，BC＝9，点D，E分别在AC，BC上，CD ＝4x，CE＝3x，其中0＜x＜3．（1）求证：DE∥AB；（2）当x＝1时，求点E到AB的距离；（3）将△DCE绕点E逆时针方向旋转，使得点D落在AB边上的D′处．在旋转的过程中，若点D′的位置有且只有一个，求x的取值范围．5．在△ABC中，∠B＝45°，∠C＝30°，作AP⊥AB，交BC于P点．（1）如图1，若AB＝3，求BC的长；（2）点D是BC边上一点，连接AD，将线段AD绕点A逆时针旋转90°，得到线段AE．①如图2，当点E落在AC边上时，求证：CE＝2BD；②如图3，当AD⊥BC时，直接写出的值．6．【操作发现】如图1，△ABC为等边三角形，点D为AB边上的一点，∠DCE＝30°，将线段CD绕点C顺时针旋转60°得到线段CF，连接AF、EF，请直接写出下列结果：①∠EAF的度数为________；②DE与EF之间的数量关系为__________；【类比探究】如图2，△ABC为等腰直角三角形，∠ACB＝90°，点D为AB边上的一点，∠DCE＝45°，将线段CD绕点C顺时针旋转90°得到线段CF，连接AF、EF．①则∠EAF的度数为__________；②线段AE，ED，DB之间有什么数量关系？请说明理由；【实际应用】如图3，△ABC是一个三角形的余料，小张同学量得∠ACB＝120°，AC＝BC，他在边BC上取了D、E两点，并量得∠BCD＝15°、∠DCE＝60°，这样CD、CE 将△ABC分成三个小三角形，请求△BCD、△DCE、△ACE这三个三角形的面积之比．7．综合与实践：如图1，已知△ABC为等边三角形，点D，E分别在边AB、AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点．（1）观察猜想在图1中，线段PM与PN的数量关系是______________，∠MPN的度数是____________；（2）探究证明把△ADE绕点A逆时针方向旋转到图2的位置，①判断△PMN的形状，并说明理由；②求∠MPN的度数；（3）拓展延伸若△ABC为直角三角形，∠BAC＝90°，AB＝AC＝10，点DE分别在边AB，AC上，AD ＝AE＝4，连接DC，点M，P，N分别为DE，DC，BC的中点．把△ADE绕点A在平面内自由旋转，如图3，请直接写出△PMN面积的最大值．8．【问题提出】在△ABC中，AB＝AC≠BC，点D和点A在直线BC的同侧，BD＝BC，∠BAC＝α，∠DBC＝β，且α+β＝120°，连接AD，求∠ADB的度数．（不必解答）【特例探究】小聪先从特殊问题开始研究，当α＝90°，β＝30°时，利用轴对称知识，以AB为对称轴构造△ABD的轴对称图形△ABD′，连接CD′（如图2），然后利用α＝90°，β＝30°以及等边三角形等相关知识便可解决这个问题．请结合小聪研究问题的过程和思路，在这种特殊情况下填空：△D′BC的形状是________三角形；∠ADB的度数为________．【问题解决】在原问题中，当∠DBC＜∠ABC（如图1）时，请计算∠ADB的度数；【拓展应用】在原问题中，过点A作直线AE⊥BD，交直线BD于E，其他条件不变若BC＝7，AD＝2．请直接写出线段BE的长为________________．9．点D为△ABC外一点，∠ACB＝90°，AC＝BC．（1）如图1，∠DCE＝90°，CD＝CE，求证：∠ADC＝∠BEC；（2）如图2，若∠CDB＝45°，AE∥BD，CE⊥CD，求证：AE＝BD；（3）如图3，若∠ADC＝15°，CD，BD＝n，请直接用含n的式子表示AD的长．10．如图，△ABC是等边三角形，D是BC边的中点，以D为顶点作一个120°的角，角的两边分别交直线AB、直线AC于M、N两点．以点D为中心旋转∠MDN（∠MDN的度数不变），当DM与AB垂直时（如图①所示），易证BM+CN＝BD．（1）如图②，当DM与AB不垂直，点M在边AB上，点N在边AC上时，BM+CN＝BD是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（2）如图③，当DM与AB不垂直，点M在边AB上，点N在边AC的延长线上时，BM+CN＝BD是否仍然成立？若不成立，请写出BM，CN，BD之间的数量关系，不用证明．11．在△ABC中，∠ACB＝90°，AC＝BC，点P在边AB上，点D、Q分别为边BC上的点，线段AD的延长线与线段PQ的延长线交于点F，连接CP交AF于点E，若∠BPF ＝∠APC，FD＝FQ．（1）如图1，求证：AF⊥CP；（2）如图2，作∠AFP的平分线FM交AB于点M，交BC于点N，若FN＝MN，求证：DQ BC；（3）在（2）的条件下，连接DM、MQ，分别交PC于点G、H，求的值．12．已知△ABC和△ADE都是等腰直角三角形，∠ACB＝∠ADE＝90°，点F为BE中点，连结DF，CF．（1）如图1，点D在AC上，请你判断此时线段DF，CF的关系，并证明你的判断；（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45时，若AD＝DE＝2，AB ＝6，求此时线段CF的长．13．如图①，将一个矩形纸片OABC放置在平面直角坐标系中，点A坐标是（3，0），点C 坐标是（0，2），点O的坐标是（0，0），点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．（1）求点E、F的坐标；（2）如图2，若点P是线段DA上的一个动点（点P不与点D，A重合），过P作PH⊥DB于H，设OP的长为x，△DPH的面积为S，试用关于x的代数式表示S．14．如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A，点D重合）将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC 于H，折痕为EF，连接BP，BH．（1）求证：BP平分∠APH；（2）当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论．15．已知：矩形ABCD中，AB＝4，BC＝3，点M、N分别在边AB、CD上，直线MN交矩形对角线AC于点E，将△AME沿直线MN翻折，点A落在点P处，且点P在射线CB 上（Ⅰ）如图①，当EP⊥BC时，①求证CE＝CN；②求CN的长；（Ⅱ）请写出线段CP的长的取值范围，及当CP的长最大时MN的长．【题型剖析】【类型1】几何类比变换综合题【例1】（2018秋•盐都区期中）【阅读理解】截长补短法，是初中数学几何题中一种辅助线的添加方法．截长就是在长边上截取一条线段与某一短边相等，补短是通过在一条短边上延长一条线段与另一短边相等，从而解决问题．（1）如图1，ABC∆是等边三角形，点D是边BC下方一点，120BDC∠=︒，探索线段DA、DB、DC之间的数量关系．解题思路：延长DC到点E，使CE BD∠+∠=︒，可证BAC BDC=，连接AE，根据180∠=∠易证得ABD ACEABD ACE∆≅∆，得出ADE=，从而∆是等边三角形，所以AD DE 探寻线段DA、DB、DC之间的数量关系．根据上述解题思路，请直接写出DA、DB、DC之间的数量关系是；【拓展延伸】（2）如图2，在Rt ABC ∆中，90BAC ∠=︒，AB AC =．若点D 是边BC 下方一点，90BDC ∠=︒，探索线段DA 、DB 、DC 之间的数量关系，并说明理由；【知识应用】（3）如图3，两块斜边长都为14cm 的三角板，把斜边重叠摆放在一起，则两块三角板的直角顶点之间的距离PQ 的长分别为 cm ．【分析】（1）由等边三角形知AB AC =，60BAC ∠=︒，结合120BDC ∠=︒知180ABD ACD ∠+∠=︒，由180ACE ACD ∠+∠=︒知ABD ACE ∠=∠，证ABD ACE ∆≅∆得AD AE =，BAD CAE ∠=∠，再证ADE ∆是等边三角形得DA DE DC CE DC DB ==+=+．（2）延长DC 到点E ，使CE BD =，连接AE ，先证ABD ACE ∆≅∆得AD AE =，BAD CAE ∠=∠，据此可得90DAE BAC ∠=∠=︒，由勾股定理知222DA AE DE +=，继而可得222()DA DB DC =+；（3）由直角三角形的性质知172QN MN ==，2273MQ MN QN -，利用（2）中的273PQ QN QM =+=+ 【解析】（1）如图1，延长DC 到点E ，使CE BD =，连接AE ，ABC ∆Q 是等边三角形， AB AC ∴=，60BAC ∠=︒， 120BDC ∠=︒Q ，180ABD ACD ∴∠+∠=︒，又180ACE ACD ∠+∠=︒Q ，ABD ACE ∴∠=∠，()ABD ACE SAS ∴∆≅∆，AD AE ∴=，BAD CAE ∠=∠，60ABC ∠=︒Q ，即60BAD DAC ∠+∠=︒，60DAC CAE ∴∠+∠==︒，即60DAE ∠=︒，ADE ∴∆是等边三角形，DA DE DC CE DC DB ∴==+=+，即DA DC DB =+，故答案为：DA DC DB =+；（2）2DA DB DC =+，如图2，延长DC 到点E ，使CE BD =，连接AE ，90BAC ∠=︒Q ，90BDC ∠=︒， 180ABD ACD ∴∠+∠=︒， 180ACE ACD ∠+∠=︒Q ， ABD ACE ∴∠=∠， AB AC =Q ，CE BD =， ABD ACE ∴∆≅∆，AD AE ∴=，BAD CAE ∠=∠， 90DAE BAC ∴∠=∠=︒， 222DA AE DE ∴+=，222()DA DB DC ∴=+， ∴2DA DB DC =+；（3）如图3，连接PQ ，14MN =Q ，30QMN ∠=︒，172QN MN ∴==，MQ ∴由（27QN QM =+=+，PQ ∴==【点评】此题是三角形的综合题，主要考查了考查的是全等三角形的判定和性质、直角三角形的性质、等边三角形的性质，掌握全等三角形的判定定理和性质定理是解题的关键．【变式1-1】（2019•亭湖区二模）【阅读材料】小明遇到这样一个问题：如图1，点P 在等边三角形ABC 内，且150APC ∠=︒，3PA =，4PC =，求PB 的长．小明发现，以AP 为边作等边三角形APD ，连接BD ，得到ABD ∆；由等边三角形的性质，可证ACP ABD ∆≅∆，得PC BD =；由已知150APC ∠=︒，可知PDB ∠的大小，进而可求得PB 的长．（1）请回答：在图1中，PDB ∠= ︒，PB = ．【问题解决】（2）参考小明思考问题的方法，解决下面问题：如图2，ABC ∆中，90ACB ∠=︒，AC BC =，点P 在ABC ∆内，且1PA =，PB =PC =AB 的长．【灵活运用】（3）如图3，在Rt ABC ∆中，90ACB ∠=︒，BAC α∠=，且4tan 3α=，点P 在ABC ∆外，且3PB =，1PC =，直接写出PA 长的最大值．【分析】（1）由ACP ABD ∆≅∆，得150ADB APC ∠=∠=︒，4PC BD ==，3AD AP ==，因为ADP ∆为等边三角形，所以60ADP ∠=︒，3DP AD ==，可得90BDP ∠=︒，在Rt BDP ∆中，用勾股定理可求得PB 的长；（2）如图2中，把ACP ∆绕点C 逆时针旋转90︒得到BCD ∆．首先证明90PDB ∠=︒，再证明A ，P ，D 共线，利用勾股定理即可解决问题．（3）如图3中，作CD CP ⊥，使得3344CD PC ==，则2254PD PC CD =+=，利用相似三角形的性质求出AD ，即可解决问题．【解析】（1）如图1中，ACP ABD ∆≅∆Q ，150PDB APC ∴∠=∠=︒，4PC BD ==，3AD AP ==，ADP ∆Q 为等边三角形， 60ADP ∴∠=︒，3DP AD ==， 1506090BDP ∴∠=︒-︒=︒，22345PB ∴=+=．故答案为：90︒，5；（2）如图2中，把ACP ∆绕点C 逆时针旋转90︒得到BCD ∆．由旋转性质可知；1BD PA ==，22CD CP ==，90PCD ∠=︒，PCD ∴∆是等腰直角三角形，22224PD PC ∴==⨯=，45CDP ∠=︒，22224117PD BD +=+=Q ，22(17)17PB ==，222PD BD PB ∴+=，90PDB ∴∠=︒， 135BDC ∴∠=︒，135APC CDB ∴∠=∠=︒，45CPD ∠=︒Q ， 180APC CPD ∴∠+∠=︒，A ∴，P ，D 共线， 5AD AP PD ∴=+=，在RtADB 中，22225126AB AD BD =+=+=．（3）如图3中，作CD CP ⊥，使得3344CD PC ==，则2254PD PC CD =+=，4tan 3BC BAC AC ∠==Q ， ∴BC PCAC CD=， 90ACB PCD ∠=∠=︒Q ， ACD BCP ∴∠=∠， ACD BCP ∴∆∆∽，∴34AD CD PB PC ==， 94AD ∴=， Q93954444PA -+剟，∴3722PA 剟， PA ∴的最大值为72．【变式1-2】（2018•亭湖区二模）如图，在等腰Rt ABC ∆与等腰Rt ADE ∆中，90BAC DAE ∠=∠=︒．（1）连接BD ，CE （如图①)，请直接写出线段BD ，CE 的数量关系；（2）在（1）的基础上，延长BD 交CE 于点F ，连接AF （如图②)，试探究线段AF ，BF ，CF 的数量关系，并证明你的结论；（3）连接BE ，取BE 的中点O ，连接AO （如图③)，若5AD =，2AO =，3tan 4DAO ∠=，求AB 的长．【分析】（1）结论：BD EC =．只要证明BAD CAE ∆≅∆即可解决问题；（2）结论：2BF FA FC =．如图②中，作AM AF ⊥交BF 于M ．想办法证明BM FC =，MAF ∆是等腰直角三角形即可解决问题；（3）如图③中，作DM AO ⊥交AO 的延长线于M ，作EN OA ⊥交OA 的延长线于N ，作AH EO ⊥于H ．想办法求出AH ，BH 即可解决问题；【解析】（1）结论：BD CE =．理由：如图①中，AB AC =Q ，AD AE =，90BAC DAE ∠=∠=︒， BAD CAE ∴∆≅∆， BD EC ∴=．故答案为BD EC =．（2）结论：2BF FA FC =．理由：如图②中，作AM AF ⊥交BF 于M ．BAD CAE∆≅∆Q，ABM ACF∴∠=∠，90BAC MAF∠=∠=︒Q，BAM CAF∴∠=∠，AB AC=Q，BAM CAF∴∆≅∆，BM CF∴=，AM AF=，AMF∴∆是等腰直角三角形，2FM FA∴=，2FB FM BM CF AF∴=+=+，2BF AF FC∴-=．（3）如图③中，作DM AO⊥交AO的延长线于M，作EN OA⊥交OA的延长线于N，作AH EO⊥于H．在Rt ADM∆中，3tan4DMDAMAM∠==，设3DM k=，4AM k=，则有222(3)(4)5k k+=，解得1k=±，k>Q，1k∴=，3DM∴=，4AM=，2OA =Q ， 2OM ∴=，由ADM EAN ∆≅∆，可得4NE AM ==，3AN DM ==，在Rt ENO ∆中，EO =OH x =， 22222AH OA OH AE EH =-=-Q ，222225)x x ∴-=-，解得x =，OH ∴AH ，在Rt ABH ∆中，AB ==【类型2】几何旋转变换综合题【例2】（2019•海州区一模）如图1，将两个完全相同的三角形纸片ABC 和DEC 重合放置，其中90C ∠=︒，30B E ∠=∠=︒．（1）操作发现：如图2，固定ABC ∆，使DEC ∆绕点C 旋转，当点D 恰好落在AB 边上时，填空： ①线段DE 与AC 的位置关系是；②设BDC ∆的面积为1S ，AEC ∆的面积为2S ，则1S 与2S 的数量关系是．（2）猜想论证：当DEC ∆绕点C 旋转到如图3所示的位置时，小明猜想（1）中1S 与2S 的数量关系仍然成立，并尝试分别作出了BDC ∆和AEC ∆中BC 、CE 边上的高，请你证明小明的猜想．（3）拓展探究已知60ABC ∠=︒，点D 是角平分线上一点，6BD CD ==，//DE AB 交BC 于点E （如图4)，若在射线BA 上存在点F ，使DCF BDE S S ∆∆=，请求出相应的BF 的长．【分析】（1）①证明60EDC DCA ∠=∠=︒即可判断．②首先证明AD BD =，推出ADC ∆与BDC ∆的面积相等，再证明ADC ∆与ACE ∆的面积相等即可．（2）作AN EC ⊥交EC 的延长线于N ，DM BC ⊥于M ，证明()ACN DCM AAS ∆≅∆即可解决问题．（3）分两种情形分别求解即可解决问题．【解析】（1）①如图1中，由旋转可知：CA CD =，90ACB ∠=︒Q ，30B ∠=︒， 60CAD ∴∠=︒， ADC ∴∆是等边三角形， 60DCA ∴∠=︒，90ECD ∠=︒Q ，30DEC ∠=︒， 60CDE ∴∠=︒， EDC DCA ∴∠=∠，//DE AC ∴，②2AB AC =Q ，AD AC =，AD BD ∴=，BDC ADC S S ∆∆∴=，//DE AC Q ，ADC ACE S S ∆∆∴=， 12S S ∴=．故答案为：//DE AC ，12S S =．（2）如图3中，DEC ∆Q 是由ABC ∆绕点C 旋转得到， BC CE ∴=，AC CD =，90ACN BCN ∠+∠=︒Q ，1809090DCM BCN ∠+∠=︒-︒=︒， ACN DCM ∴∠=∠，在ACN ∆和DCM ∆中， 90ACN DCM ANC DMC AC CD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ()ACN DCM AAS ∴∆≅∆，AN DM ∴=，BDC AEC S S ∆∆∴=．（3）如图4中，作//DF BC 交AB 于F ．延长CD 交AB 于H ．//DF BE Q ，//DE BF ，∴四边形DEBF 是平行四边形，BDF BDE S S ∆∆∴=，BDF DFC S S ∆∆=， DFC BDE S S ∆∆∴=，60ABC ∠=︒Q ，BD 平分ABC ∠， 30ABD DBE ∴∠=∠=︒， //DF BE Q ， 30FDB ∴∠=︒， 30FBD FDB ∴∠=∠=︒，FB FD ∴=，∴四边形DEBF 是菱形，6BD CD ==Q ， 30DBC DCB ∴∠=∠=︒， 60DEC ABC ∠=∠=︒Q ， 90CDE ∴∠=︒，3tan30623DE CD ∴=︒==g 23BF DE ∴==//DE AB Q ，90BHC EDC ∴∠=∠=︒，CH AB ∴⊥，作点F 关于CH 的对称点F '，连接DF '，易知DFC DF C S S ∆'=V ，在Rt DFH ∆中，sin303FH HF DF ='=︒=g ， 43BF ∴'=综上所述，满足条件的BF 的值为23或43．【点评】本题属于几何变换综合题，考查了旋转变换，全等三角形的判定和性质，菱形的判定和性质，等边三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造特殊四边形解决问题，属于中考压轴．【变式2-1】（2019•辽阳模拟）旋转变换是解决数学问题中一种重要的思想方法，通过旋转变换可以将分散的条件集中到一起，从而方便解决问题．已知，ABC ∆中，AB AC =，BAC α∠=，点D 、E 在边BC 上，且12DAE α∠=．（1）如图1，当60α=︒时，将AEC ∆绕点A 顺时针旋转60︒到AFB ∆的位置，连接DF ， ①求DAF ∠的度数； ②求证：ADE ADF ∆≅∆；（2）如图2，当90α=︒时，猜想BD 、DE 、CE 的数量关系，并说明理由；（3）如图3，当120α=︒，4BD =，5CE =时，请直接写出DE 的长为．【分析】（1）①利用旋转的性质得出FAB CAE ∠=∠，再用角的和即可得出结论； ②利用SAS 判断出ADE ADF ∆≅∆，即可得出结论；（2）先判断出BF CE =，ABF ACB ∠=∠，再判断出90DBF ∠=︒，即可得出结论；（3）同（2）的方法判断出60DBF ∠=︒，再用含30度角的直角三角形求出BM ，FM ，最后用勾股定理即可得出结论．【解析】（1）①由旋转得，FAB CAE ∠=∠，603030BAD CAE BAC DAE ∠+∠=∠-∠=︒-︒=︒Q ， 30DAF BAD BAF BAD CAE ∴∠=∠+∠=∠+∠=︒；②由旋转知，AF AE =，BAF CAE ∠=∠，BAF BAD CAE BAD BAC DAE DAE ∴∠+∠=∠+∠=∠-∠=∠，在ADE ∆和ADF ∆中，AF AEDAF DAE AD AD =⎧⎪∠=∠⎨⎪=⎩，()ADE ADF SAS ∴∆≅∆；（2）222BD CE DE +=，理由：如图2，将AEC ∆绕点A 顺时针旋转90︒到AFB ∆的位置，连接DF ，BF CE ∴=，ABF ACB ∠=∠，由（1）知，ADE ADF ∆≅∆，DE DF ∴=，AB AC =Q ，90BAC ∠=︒， 45ABC ACB ∴∠=∠=︒，90DBF ABC ABF ABC ACB ∴∠=∠+∠=∠+∠=︒，根据勾股定理得，222BD BF DF +=，即：222BD CE DE +=；（3）如图3，将AEC ∆绕点A 顺时针旋转120︒到AFB ∆的位置，连接DF ，BF CE ∴=，ABF ACB ∠=∠，由（1）知，ADE ADF ∆≅∆，DE DF ∴=，5BF CE ==， AB AC =Q ，120BAC ∠=︒， 30ABC ACB ∴∠=∠=︒，60DBF ABC ABF ABC ACB ∴∠=∠+∠=∠+∠=︒，过点F 作FM BC ⊥于M ，在Rt BMF ∆中，9030BFM DBF ∠=︒-∠=︒，5BF =，52BM ∴=，FM = 4BD =Q ，32DM BD BM ∴=-=，根据勾股定理得，DF ==DE DF ∴==【变式2-2】（2019•宜兴市二模）【问题提出】如图1，四边形ABCD 中，AD CD =，120ABC ∠=︒，60ADC ∠=︒，2AB =，1BC =，求四边形ABCD 的面积．【尝试解决】旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．（1）如图2，连接BD ，由于AD CD =，所以可将DCB ∆绕点D 顺时针方向旋转60︒，得到DAB ∆'，则BDB ∆'的形状是．（2）在（1）的基础上，求四边形ABCD 的面积．[类比应用]如图3，四边形ABCD 中，AD CD =，75ABC ∠=︒，60ADC ∠=︒，2AB =，2BC =，求四边形ABCD 的面积．【分析】（1）易证DEB DAB ∆≅∆'，则BD DB ='，60BDB ∠'=︒，所以BDB ∆'是等边三角形；（2）知等边三角形的边长为3，求出S BDB ∆'即可；【类比应用】类比（1），连接BD ，由于AD CD =，所以可将BCD ∆绕点D 逆时针方向旋转60︒，得到DAB ∆'，连接BB '，延长BA ，作B E BE '⊥；易证AFB ∆'是等腰直角三角形，AEB ∆是等腰直角三角形，利用勾股定理计算1AE B E ='=，10BB '=ABB ∆'和BDB ∆'的面积和即可．【解析】（1）如图2，连接BD ，由于AD CD =，所以可将DCB ∆绕点D 顺时针方向旋转60︒，得到DAB ∆'，BD B D ='Q ，60BDB ∠'=︒BDB ∴∆'是等边三角形；（2）由（1）知，BCD ∆≅△B AD '，∴四边形ABCD 的面积=等边三角形BDB '的面积，1BC AB ='=Q213BB AB AB ∴'=+'=+=，132BDB ABCD S S ∆'∴==⨯=四边形；【类比应用】如图3，连接BD ，由于AD CD =，所以可将BCD ∆绕点D 逆时针方向旋转60︒，得到DAB ∆'，连接BB '，延长BA ，作B E BE '⊥； Q AD CDCDB ADB BD B D =⎧⎪∠=∠'⎨⎪='⎩， BCD ∴∆≅△B AD 'ABCD BDB A S S '∴=四边形四边形，75ABC ∠=︒Q ，60ADC ∠=︒， 135BAB ∴∠'=︒45B AE ∴∠'=︒，B A BC '=Q1B E AE ∴'==，213BE AB AE ∴=+=+=，BB ∴'，1121122ABB S AB B E ∆'∴='=⨯⨯=g g ，12S BDB ∆'==，1ABB ABCD BDB A S S S BDB S ∆''∴==∆'-=四边形四边形．【类型3】几何翻折变换综合题【例3】（2019•江都区三模）如图1，有一张矩形纸片ABCD ，已知5AB =，6AD =，现将纸片进行如下操作：首先将纸片沿折痕BF 进行折叠，使点A 落在BC 边上的点E 处，点F 在AD 上（如图2)；然后将纸片沿折痕DH 进行第二次折叠，使点C 落在第一次的折痕BF 上的点G 处，点H 在BC 上（如图3)．（1）如图2，判断四边形ABEF 的形状，并说明理由；（2）如图3，求BG 的长．【分析】（1）由折叠可得：AB BE =，且90A ABE BEF ∠=∠=∠=︒，即可得出结论；’ （2）过G 点作//MN AB ，交AD 、BC 于点M 、N ，由四边形ABEF 为正方形，可求得AF 的长，得出BNG ∆和FMG ∆为等腰直角三角形，设BN x =，则可表示出GN 、MG 、MD ，利用折叠的性质可得到CD DG =，在Rt MDG ∆中，利用勾股定理可求得x ，即可得出结果．【解析】（1）四边形ABEF 是正方形，理由如下： Q 四边形ABCD 为矩形，5AB CD ∴==，6BC AD ==，由折叠可得：AB BE =，且90A ABE BEF ∠=∠=∠=︒， ∴四边形ABEF 为正方形；（2）过点G 作//MN AB ，分别交AD 、BC 于点M 、N ，如图3所示：Q 四边形ABEF 是正方形，5AF AB ∴==， //MN AB Q ，BNG ∴∆和FMG ∆为等腰直角三角形，且5MN AB ==，设BN x =，则GN AM x ==，5MG MN GN x =-=-，6MD AD AM x =-=-，又由折叠的性质可知：5DG DC ==，在Rt MDG ∆中，由勾股定理可得222MD MG GD +=，即222(6)(5)5x x -+-=，解得：2x =，2GN BN ∴==，222BG BN ∴==．【点评】本题考查了翻折变换的性质、矩形的性质、正方形的判定和性质、等腰直角三角形的性质、勾股定理等知识；熟练掌握正方形的判定与性质，由勾股定理得出方程是解题的关键．【变式3-1】（2019•广陵区校级二模）如图，将矩形ABCD 先过点A 的直线1L 翻折，点DA 的对应点D '刚好落在边BC 上，直线1L 交DC 于点F ；再将矩形ABCD 沿过点A 的直线2L 翻折，使点B 的对应点G 落在AD '上，EG 的延长线交AD 于点H ．（1）当四边形AED H '是平行四边形时，求AD H ∠'的度数．（2）当点H 与点D 刚好重合时，试判断AEF ∆的形状，并说明理由．【分析】（1）如图1中，在RT ABC ∆中，由2AD AB '=推出30AD B ∠'=︒，再证明四边形AED H '是菱形即可解决问题．（2）如图2中，先证明△DD G '≅△DD C '得出DG DC AB AG ===，发现AGD ∆、GED ∆'、DEC ∆都是等腰直角三角形，再证明ABE ECF ∆≅∆即可解决问题．【解析】（1）如图1中，Q 四边形AED H '是平行四边形，AG GD ∴=，EH AD ⊥Q ，∴四边形AED H '是菱形，AD H AD B ∴∠'=∠'，AEG ∆Q 是由AEB ∆翻折得到， AB AG D G ∴=='，Q 四边形ABCD 是矩形，90B ∴∠=︒， 30AD B ∴∠'=︒， 30AD H ∴∠'=︒．（2）结论：AEF ∆是等腰直角三角形．理由：如图2中，连接DD '． Q 四边形ABCD 是矩形，//AD BC ∴，ADD DD C ∠'=∠'，AB DC =，90B C ∠=∠=︒，AD AD ='Q ， ADD AD D ∴∠'=∠'， DD A DD C ∴∠'=∠'，在△DD G ' 和△DD C '中，DGD DCD DD G DD C DD DD ∠'=∠'⎧⎪∠'=∠'⎨⎪'='⎩， ∴△DD G '≅△DD C '，DG DC AB AG ∴===，90AGD ∠=︒Q ，45GAD GDA AD E DED ∴∠=∠=∠'=∠'=︒， EG GD BE CD ∴='=='， 90AD B FD C ∠'+∠'=︒Q ， 45FD C D FC ∴∠'=''=︒， CD CF BE ∴'==，45CED CDE ∠=∠=︒Q ， EC CD AB ∴==，在ABE ∆和ECF ∆中， 90AB EC B C BE CF =⎧⎪∠=∠=︒⎨⎪=⎩， ABE ECF ∴∆≅∆，AE EF ∴=，BAE CEF ∠=∠， 90BAE AEB ∠+∠=︒Q ， 90AEB CEF ∴∠+∠=︒， 90AEF ∴∠=︒，AEF ∴∆是等腰直角三角形．【点评】本题考查翻折变换、矩形的性质、菱形的判定和性质、全等三角形的判定和性质、等腰直角三角形的判定等知识，第一问的关键是菱形性质的应用，第二个问题的关键是正确寻找全等三角形，利用特殊三角形解决问题，属于中考常考题型．【变式3-2】（2018•深圳模拟）已知矩形纸片ABCD 中，2AB =，3BC =．操作：将矩形纸片沿EF 折叠，使点B 落在边CD 上．探究：（1）如图1，若点B 与点D 重合，你认为1EDA ∆和FDC ∆全等吗？如果全等，请给出证明，如果不全等，请说明理由；（2）如图2，若点B 与CD 的中点重合，请你判断1FCB ∆、△1B DG 和△1EAG 之间的关系，如果全等，只需写出结果，如果相似，请写出结果和相应的相似比；（3）如图2，请你探索，当点B 落在CD 边上何处，即1B C 的长度为多少时，1FCB ∆与△1B DG 全等．【分析】（1）由四边形ABCD 是矩形，可得90A B C ADC ∠=∠=∠=∠=︒，AB CD =，由折叠的性质可得：1A A ∠=∠，190B A DF ∠=∠=︒，1CD A D =，然后利用同角的余角相等，可证得1A DE CDF ∠=∠，则可利用ASA 证得1EDA ∆和FDC ∆全等；（2）易得△1B DG 和△1EAG 全等，1FCB ∆与△1B DG 相似，然后设FC x =，由勾股定理可得方程2221(3)x x +=-，解此方程即可求得答案；（3）设1B C a =，则有12FC B D a ==-，11B F BF a ==+，在直角1FCB ∆中，可得222(1)(2)a a a +=-+，解此方程即可求得答案．【解析】（1）全等．证明：Q 四边形ABCD 是矩形，90A B C ADC ∴∠=∠=∠=∠=︒，AB CD =，由题意知：1A A ∠=∠，190B A DF ∠=∠=︒，1CD A D =， 190A C ∴∠=∠=︒，90CDF EDF ∠+∠=︒， 1A DE CDF ∴∠=∠，在1EDA ∆和FDC ∆中， 111A C A D CDA DE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩，1()EDA FDC ASA ∴∆≅∆；（2）△1B DG 和△1EAG 全等，1FCB ∆与△1B DG 相似，设FC x =，则13B F BF x ==-，1112B C DC ==， 2221(3)x x ∴+=-，43x ∴=， 1FCB ∴∆与△1B DG 相似，相似比为4:3．（3）1FCB ∆与△1B DG 全等．设1B C a =，则有12FC B D a ==-，11B F BF a ==+，在直角1FCB ∆中，可得222(1)(2)a a a +=-+，整理得2630a a -+=，解得：36a =-（另一解舍去），∴当136B C =-时，1FCB ∆与△1B DG 全等．【达标检测】1．如图1，在Rt △ABC 中，AB ＝AC ，D 、E 是斜边BC 上两动点，且∠DAE ＝45°，将△ABE 绕点A 逆时针旋转90后，得到△AFC ，连接DF ．（1）试说明：△AED ≌△AFD ；（2）当BE ＝3，CE ＝9时，求∠BCF 的度数和DE 的长；（3）如图2，△ABC 和△ADE 都是等腰直角三角形，∠BAC ＝∠DAE ＝90°，D 是斜边BC 所在直线上一点，BD ＝3，BC ＝8，求DE 2的长．【分析】（1）想办法证明∠DAE ＝∠DAF ，由DA ＝DA ，AE ＝AF ，即可证明；（2）如图1中，设DE＝x，则CD＝9﹣x．在Rt△DCF中，由DF2＝CD2+CF2，CF＝BE＝3，推出x2＝（9﹣x）2+32，解方程即可；（3）分两种情形①当点E在线段BC上时，如图2中，连接BE．由△EAD≌△ADC，推出∠ABE＝∠C＝∠ABC＝45°，EB＝CD＝5，推出∠EBD＝90°，推出DE2＝BE2+BD2＝52+32＝34；②当点D在CB的延长线上时，如图3中，同法可得DE2＝130；【解析】（1）如图1中，∵△BAE≌△CAF，∴AE＝AF，∠BAE＝∠CAF，∵∠BAC＝90°，∠EAD＝45°，∴∠CAD+∠BAE＝∠CAD+∠CAF＝45°，∴∠DAE＝∠DAF，∵DA＝DA，AE＝AF，∴△AED≌△AFD；（2）如图1中，设DE＝x，则CD＝9﹣x．∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝45°，∵∠ABE＝∠ACF＝45°，∴∠DCF＝90°，∵△AED≌△AFD，∴DE＝DF＝x，在Rt△DCF中，∵DF2＝CD2+CF2，CF＝BE＝3，∴x2＝（9﹣x）2+32，∴x＝5，∴DE＝5．（3）①当点E在线段BC上时，如图2中，连接BE．∵∠BAC＝∠EAD＝90°，∴∠EAB＝∠DAC，∵AE＝AD，AB＝AC，∴△EAD≌△ADC，∴∠ABE＝∠C＝∠ABC＝45°，EB＝CD＝5，∴∠EBD＝90°，∴DE2＝BE2+BD2＝52+32＝34，②当点D在CB的延长线上时，如图3中，连接BE．同法可证△DBE是直角三角形，EB＝CD＝11，DB＝3，∴DE2＝EB2+BD2＝121+9＝130，综上所述，DE2的值为34或130．2．如图①，在等腰△ABC和△ADE中，AB＝AC，AD＝AE，且∠BAC＝∠DAE＝120°．（1）求证：△ABD≌△ACE；（2）把△ADE绕点A逆时针方向旋转到图②的位置，连接CD，点M、P、N分别为DE、DC、BC的中点，连接MN、PN、PM，判断△PMN的形状，并说明理由；（3）在（2）中，把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝6，请分别求出△PMN周长的最小值与最大值．【分析】（1）根据全等三角形的判定证明即可；（2）根据平行线的性质和等边三角形的判定解答即可；（3）根据点D在AB上时，BD最小和点D在BA延长线上时，BD最大矩形分析解答即可．【解答】证明：（1）∵∠BAC＝∠DAE＝120°，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ABD≌△ADE；（2）△PMN是等边三角形．理由：∵点P，M分别是CD，DE的中点，∴PM CE，PM∥CE，∵点N，M分别是BC，DE的中点，∴PN BD，PN∥BD，同理可得BD＝CE，∴PM＝PN，∴△PMN是等腰三角形，∵PM∥CE，∴∠DPM＝∠DCE，∵PN∥BD，∴∠PNC＝∠DBC，∵∠DPN＝∠DCB+∠PNC＝∠DCB+∠DBC，。

八数类比探究专题

八数类比探究专题(人教）知识点睛1. 类比探究是一类共性条件与特殊条件相结合，由特殊情形到一般情形（或由简单到复杂）逐步深入，解决思想方法一脉相承的综合性题目，常以几何综合题为主——“条件类似、图形结构类似、问法类似”．2. 类比探究的处理思路：（1）类比是解决类比探究的第一原则，即类比上一问思路，迁移解决下一问；（2）对比前后条件变化，寻找并利用不变特征，考虑相关几何结构解决问题．①若属于类比探究常见结构，调用结构类比解决；②若不属于常见结构，依据不变特征大胆猜测、尝试、验证、构造． 3. 类比探究常见结构举例（1）中点结构直角+中点平行夹中点见中点，要倍长多个中点，斜边中线延长证全等倍长之后证全等考虑中位线（2）旋转结构常见模型1如图，△ABC ，△ADE 均为等边三角形，则出现了AB =AC ，AD =AE 等线段共端点的结构，所以连接BD ，CE ，可以证明△ABD ≌△ACE ，即把 △ABD 绕点A 逆时针旋转60°得到△ACE ．常见模型2CEDC B AEDC B A如图，正方形ABCD 中，点E ，F 分别在边BC ，CD 上，且∠EAF =45°，则EF =BE +DF ．思路提示：正方形四条边都相等，提供了等线段共端点，所以考虑构造旋转解决问题，即找到等线段AD =AB ，把线段AD 绕点A 顺时针旋转90°，与线段AB 重合，则AD 所在△ADF 绕着点A 顺时针旋转90°得到△ABG ．（3）直角结构直角结构——斜直角放正FEFG E B C ABCD E DECBA精讲精练【中点结构】1. 已知P 是Rt △ABC 的斜边AB 上一动点（不与点A ，B 重合），分别过点A ，B 向直线CP 作垂线，垂足分别为点E ，F ，Q 为斜边AB 的中点．（1）如图1，当点P 与点Q 重合时，AE 与BF 的位置关系是___________，QE 与QF 的数量关系是______________．（2）如图2，当点P 不与点Q 重合时，试判断QE 与QF 的数量关系，并给予证明．（3）如图3，当点P 在线段BA （或AB ）的延长线上时，（2）中的结论是否仍然成立？请画出图形并给予证明．2. 如图，四边形ABCD 和四边形CGEF 均为正方形，M 是线段AE 的中点．图1BCQ (P )EF A AFE PQCB 图2（1）如图1所示，点B ，C ，G 在同一条直线上，DM 的延长线交EF 于点N ，连接FM ，则DM 与FM 的数量关系为____________，位置关系为___________（直接写出答案，无需写证明过程）．（2）如图2，当点B ，C ，F 在同一条直线上，DM 的延长线交EG 于点N ，其余条件不变，试探究线段DM 与FM 有怎样的关系？请写出猜想，并给予证明．（3）如图3，当点E ，B ，C 在同一条直线上，DM 的延长线交CE 的延长线于点N ，若此时点A 恰好为CG 的中点，AB =1，其余条件不变，请直接写出FM 的长度．3. 已知等腰三角形ABC 中，∠ACB =90°，点E 在AC 的延长线上，且∠DEC =45°，M ，N 分别是DE ，AE 的中点，连接MN ，交直线BE 于点F ．当点D 在CB图1NMG FED CBA 图2N MG FEDCB A图3NMGFEDCBA的延长线上时，如图1所示，易证．（1）如图2，当点D 在CB 边上时，上述结论是否成立？若成立，请给出证明；若不成立，请写出你的猜想，并说明理由．（2）当点D 在BC 的延长线上时，如图3所示，请直接写出线段MF ，FN ，BE 之间的数量关系（不需要证明）．12MF FN BE +=图1ADBCNMEF 图2A DBCN M EF图3ADBC NMEF4. 已知点O 是△ABC 内任意一点，连接OA 并延长到点E ，使得AE =OA ，以OB ，OC 为邻边作□OBFC ，连接OF ，与BC 交于点H ，连接EF ．（1）问题发现如图1，若△ABC 为等边三角形，线段EF 与BC 的位置关系是________，数量关系为__________．（2）拓展探究如图2，若△ABC 为等腰直角三角形（BC 为斜边），（1）中的两个结论是否成立？若成立，请给予证明；若不成立，请写出正确结论再给予证明．（3）解决问题如图3，若△ABC 是等腰三角形，AB =AC =2，BC =3，请你直接写出线段EF 的长．ABCEF HO图1图2F BAOHCE图3F BHOCAE5. 操作与证明：如图1，把一个含45°角的直角三角板ECF 和一个正方形ABCD 摆放在一起，使三角形的直角顶点和正方形的顶点C 重合，点E ，F 分别在正方形的边CB ，CD 上，连接AF ，取AF 中点M ，EF 的中点N ，连接MD ，MN ．（1）连接AE ，求证：△AEF 是等腰三角形．猜想与发现：（2）在（1）的条件下，请判断MD ，MN 的数量关系和位置关系．（不需要证明）结论1：MD ，MN 的数量关系是____________________；结论2：MD ，MN 的位置关系是____________________．拓展与探究：（3）如图2，将图1中的直角三角板ECF 绕点C 顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．图1AB CD EFM N 图2N M F EDCBA6.已知，在四边形ABCD中，点E，点F分别为AD，BC的中点，链接EF．（1）如图1，AB∥CD，连接AF并延长交DC的延长线于点G，则AB，CD，EF之间的数量关系为________________；（2）如图2，∠B=90°，∠C=150°，求AB，CD，EF之间的数量关系？AB C DEFG 图1AB CDEF图2图1ABDEFG图2ABCDEFG图3AB CD EFG 【旋转结构】7. 以四边形ABCD 的边AB ，AD 为边分别向外侧作等边△ABF 和等边△ADE ，连接EB ，FD ，交点为G ．（1）问题发现：当四边形ABCD 为正方形时（如图1），EB 和FD 的数量关系是___________．（2）拓展探究：当四边形ABCD 为矩形时（如图2），EB 和FD 具有怎样的数量关系？请加以证明．（3）问题解决：四边形ABCD 由正方形到矩形到一般平行四边形的变化过程中，∠EGD 是否发生变化？如果改变，请说明理由；如果不变，请在图3中求出∠EGD 的度数．图1A BCDE F图2AB EC FD图3B A DCEF8. 已知四边形ABCD 是菱形，AB =4，∠ABC =60°，∠EAF 的两边分别与射线CB ，DC 相交于点E ，F ，且∠EAF =60°．（1）如图1，当点E 是线段CB 的中点时，直接写出．．．．线段AE ，EF ，AF 之间的数量关系；（2）如图2，当点E 是线段CB 上任意一点时（点E 不与B ，C 重合），求证：BE =CF ；（3）如图3，当点E 在线段CB 的延长线上，且∠EAB =15°时，求点F 到BC 的距离．图1GF ED CBA 图2ED CB A图3GFED CBA9. 如图1，在正方形ABCD 中，点E ，F 分别为DC ，BC 边上的点，且满足∠EAF =45°，连接EF ，求证：DE +BF =EF ．小明是这样解决的：延长CB 到点G ，使BG =DE ，连接AG ，再证明△GAF ≌△EAF ，可证得结论．感悟小明的解题方法，运用你所积累的经验和知识，完成下题：（1）如图2，在四边形ABCD 中，AD ∥BC （AD ＞BC ），∠D =90°，AD =CD =10，E 是CD 上一点，且∠BAE =45°，DE =4，求BE 的长．（2）类比（1）证明思想完成下列问题：在同一平面内，将两个全等的等腰直角三角形ABC 和AFG 摆放在一起，A 为公共顶点，∠BAC =∠AGF =90°，若△ABC 固定不动，△AFG 绕点A 旋转，AF ，AG 与边BC 的交点分别为D ，E （点D 不与点B 重合，点E 不与点C 重合），在旋转过程中，等式 BD 2+CE 2=DE 2始终成立，请说明理由．G FEDCBA图1FED CBA图210. 问题背景如图1，在四边形ABCD 中，AB =AD ，∠BAD =120°，∠B =∠ADC =90°，EF 分别是BC ，CD 上的点，且∠EAF =60°，探究图中线段BE ，EF ，FD 之间的数量关系．小王同学探究此问题的方法是延长FD 到点G ，使DG =BE ，连接AG ，先证明△ABE ≌△ADG ，再证明△AEF ≌△AGF ，可得出结论，他的结论应是_______．（2）探索延伸如图2，在四边形ABCD 中，AB =AD ，∠B +∠D =180°，E ，F 分别是BC ，CD 上的点，且∠EAF =12∠BAD ，上述结论是否仍然成立，并说明理由．（3）结论应用如图3，在某次军事演习中，舰艇甲在指挥中心（O 处）北偏西30°的A 处，舰艇乙在指挥中心南偏东70°的B 处，并且两舰艇到指挥中心的距离相等．接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E ，F 处，且两舰艇与指挥中心O 之间夹角∠EOF =70°，试求此时两舰艇之间的距离.【直角结构】11. （1）观察猜想如图1，点B ，A ，C 在同一条直线上，DB ⊥BC ，EC ⊥BC 且∠DAE =90°，AD =AE ，则BC ，BD ，CE 之间的数量关系为_______________；（2）问题解决如图2，在Rt △ABC 中，∠ABC =90°，CB =4，AB =2，以AC 为直角边向外作等腰Rt △DAC ，连接BD ，求BD 的长；图1 图2（3）拓展延伸如图3，在四边形ABCD 中，∠ABC =∠ADC =90°，CB =4，AB =2，DC =DA ，请直接写出BD 的长．EDCBADCB ADCBA12. 情境创设：如图1，两块全等的直角三角板，△ABC ≌△DEF ，且∠C =∠F =90°，现如图放置，则∠ABE =___________．问题探究：如图2，△ABC 中，AH ⊥BC 于点H ，以A 为直角顶点，分别以AB ，AC 为直角边，向△ABC 外作等腰直角△ABE 和等腰直角△ACF ，过点E ，F 作射线HA 的垂线，垂足分别为M ，N ，试探究线段EM 和FN 之间的数量关系，并说明理由．拓展延伸：如图，△ABC 中，AH ⊥BC 于点H ，以A 为直角顶点，分别以AB ，AC 为一边，向△ABC 外作正方形ABME 和正方形ACNF ，连接EF 交射线HA 于点G ，试探究线段EG 和FG 之间的数量关系，并说明理由．图1AB (D )CEF图2AB CEFHN M 图3M13.的正方形ABCD中，P是对角线AC上的一个动点（与点A，C不重合），过点P作PE⊥PB，PE交射线DC于点E，过点E作EF⊥AC，垂足为点F．（1）求证：PB=PE．（2）在点P的运动过程中，PF的长度是否发生变化？若不变，试求出这个不变的值，写出解答过程；若变化，试说明理由．（3）在点P的运动过程中，△PEC能否为等腰三角形？如果能，直接写出此时AP的长；如果不能，试说明理由．AB CDPEF备用图FEPDCBA【其他类型】14.如图1，点A(a，b)在平面直角坐标系xOy中，点A到坐标轴的垂线段AB，AC与坐标轴围成矩形OBAC，当这个矩形的一组邻边长的和与积相等时，点A称作“垂点”，矩形称作“垂点矩形”．（1）在点P(1，2)，Q(2，-2)，N(12，-1)中，是“垂点”的点为______；（2）点M(-4，m)是第三象限的“垂点”，直接写出m的值______；（3）如果“垂点矩形”的面积是163，且“垂点”位于第二象限，写出满足条件的“垂点”的坐标______；（4）如图2，平面直角坐标系的原点O是正方形DEFG的对角线的交点，当正方形DEFG的边上存在“垂点”时，GE的最小值为______．图1图215. 如图1，在正方形ABCD 中，P 是对角线BD 上的一点，点E 在AD 的延长线上，且PA =PE ，PE 交CD 于F ．（1）证明：PC =PE ；（2）求∠CPE 的度数；（3）如图2，把正方形ABCD 改为菱形ABCD ，其他条件不变，当∠ABC =120°时，连接CE ，试探究线段AP 与线段CE 的数量关系，并说明理由．图1ABC PD EF图2APDEFBC16. 如图，在等边三角形ABC 中，点D 在直线BC 上，连接AD ，作∠ADN =60°，直线DN 交射线AB 于点E ，过点C 作CF ∥AB ，交直线DN 于点F ．（1）当点D 在线段BC 上，∠NDB 为锐角时，如图1，求证：CF +BE =CD ．（提示：过点F 作FM ∥BC ，交射线AB 于点M ）（2）当点D 在线段BC 的延长线上，∠NDB 为锐角时，如图2；当点D 在线段CB 的延长线上，∠NDB 为钝角时，如图3．请分别写出线段CF ，BE ，CD 之间的数量关系，不需要证明．（3）在（2）的条件下，若∠ADC =30°，ABC S △，则BE =_________，CD =________．图1N MFEDC B ADCABFEN图2D CABFEN图3。

几何类比探究题型-2024年中考数学答题技巧与模板构建(解析版)

几何类比探究题型题型解读|模型构建|通关试练几何的类比探究题型是近年中招解答题的必考题型，该题型往往以压轴题的形式出现，有一定的难度。

探究型问题是指命题中缺少一定的条件或无明确的结论，需要经过推断，补充并加以证明的一类问题．根据其特征大致可分为：条件探究型、结论探究型、规律探究型和存在性探究型等四类。

由于探究型试题的知识覆盖面较大，综合性较强，灵活选择方法的要求较高，再加上题意新颖，构思精巧，具有相当的深度和难度，所以要求同学们在复习时，首先对于基础知识一定要复习全面，并力求扎实牢靠；其次是要加强对解答这类试题的练习，注意各知识点之间的因果联系，选择合适的解题途径完成最后的解答．模型01图形旋转模型模型一、A字形(手拉手)及其旋转模型二、K字型及其旋转手拉手模型是有两个等腰的三角形或者两个等边的三角形，他们有一个共同的顶点，且两个等腰三角形的顶角是相等的，那么就可以用角的和差求得共顶点的另外两个角相等等，然后利用等腰的边对应相等，可证明两个三角形全等(边角边)组成这样的图形模样的我们就说他是手拉手模型。

在类比探究题型中，往往会对等腰三角形或者等边三角形进行演变，变成一般三角形进行旋转，通常全等三角形变为相似三角形。

模型特征：双等腰；共顶点；顶点相等；绕着顶点作旋转解题依据：等腰共顶手拉手，旋转全等马上有；左手拉左手，右手拉右手，两根拉线抖一抖，它们相等不用愁；拉线夹角与顶角，相等互补答案有。

模型02图形平移模型探究1.四边形平移变换四边形的平移变换题型中主要考查了全等三角形的判定和性质，相似三角形的判定和性质，平移几何性质、三角形内角和定理的应用，勾股定理，解题的关键是熟练掌握三角形全等或相似的判定方法，画出相应的图形，注意分类讨论．2.三角形平移变换三角形平移变换主要利用三角形全等和三角形相似的判定和性质，勾股定理，矩形的判定和性质，平移性质、平行线的判定和性质，解题的关键是作出辅助线，熟练掌握三角形相似的判定方法.3.其它图形平移类比探究问题综合考查了全等三角形的判定和性质，相似三角形的判定和性质，三角形内角和定理的应用，勾股定理，解题的关键是熟练掌握三角形相似的判定方法，画出相应的图形，注意分类讨论.模型03动点引起的题型探究动点型问题是指题设中的图形中存在一个或多个动点，它们在线段、射线、直线、抛物线、双曲线、弧线等上运动的一类非常具有开放性的题目。

四川省中考数学复习难题突破专题八：类比、拓展探究题

难题突破专题八类比、拓展探究题类比、拓展探究题是近两年中考热门考题，题型的模式基本分为三步：初步尝试、类比发现、深入探究，考查的知识点有：三角形旋转、平行四边形性质、相似、全等、矩形折叠、勾股定理等．此类问题解答往往是层层深入，从特殊到一般，然后是拓展运用．在解题时需要牢牢把握特殊情况、特殊位置下的结论，然后探寻一般情况下是否也成立，最后是类比应用．类比模仿是解决此类问题的重要手段．1 [2019·湖州] 数学活动课上，某学习小组对有一内角为120°的平行四边形ABCD(∠BAD＝120°)进行探究：将一块含60°的直角三角板如图Z8－1放置在平行四边形ABCD 所在平面内旋转，且60°角的顶点始终与点C 重合，较短的直角边和斜边所在的两直线分别交线段AB ，AD 于点E ，F(不包括线段的端点)．(1)初步尝试如图①，若AD ＝AB ，求证：①△BCE≌△ACF，②AE ＋AF ＝AC ； (2)类比发现如图②，若AD ＝2AB ，过点C 作CH⊥AD 于点H ，求证：AE ＝2FH ； (3)深入探究如图③，若AD ＝3AB ，探究得AE ＋3AFAC的值为常数t ，则t ＝________．图Z8－1例题分层分析(1)①先证明△ABC，△ACD 都是________三角形，再证明∠BCE＝________，即可解决问题． ②根据①的结论得到________，由此可证明．(2)设DH ＝x ，由题意，可得CD ＝________，CH ＝________(用含x 的代数式表示)，由△ACE∽△HCF，得AE FH ＝ACCH，由此即可证明． (3)如图③，过点C 作CN⊥AD 于N ，CM ⊥BA ，交BA 的延长线于点M ，CM 与AD 交于点H.先证明△CFN∽△CEM，得CN CM ＝FN EM ，由AB·CM＝AD·CN，AD ＝3AB ，推出CM ＝3CN ，所以CN CM ＝FN EM ＝13，设CN ＝a ，FN＝b ，则CM ＝3a ，EM ＝3b ，想办法求出AC ，AE ＋3AF 即可解决问题．2 [2019·舟山] 我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”．(1)概念理解请你根据上述定义举一个等邻角四边形的例子；(2)问题探究如图Z8－2①，在等邻角四边形ABCD中，∠DAB＝∠ABC，AD，BC的中垂线恰好交于AB边上一点P，连结AC，BD，试探究AC与BD的数量关系，并说明理由；(3)应用拓展如图②，在Rt△ABC与Rt△ABD中，∠C＝∠D＝90°，BC＝BD＝3，AB＝5，将Rt△ABD绕着点A顺时针旋转角α(0°＜∠α＜∠BAC)得到Rt△AB′D′(如图③)，当凸四边形AD′BC为等邻角四边形时，求出它的面积．图Z8－2例题分层分析(1)矩形或正方形邻角相等，满足“等邻角四边形”的条件；(2)连结PD，PC，根据PE，PF分别为AD，BC的垂直平分线，可得到PA＝________，PB＝________，∠DAP＝________＝∠ABC＝________，从而可得∠APC＝∠DPB，利用SAS可证得△APC≌△DPB，即可得到AC＝BD.(3)分两种情况考虑：(i)当∠AD′B＝∠D′BC时，延长AD′，CB交于点E，由S四边形ACBD′＝S△ACE－S△BED′，求出四边形ACBD′的面积；(ii)当∠D′BC＝∠ACB＝90°时，过点D′作D′E⊥AC于点E，由S四边形ACBD′＝S△AED′＋S矩形ECBD′，求出四边形ACBD′的面积即可．专题训练1．[2019·淮安] 【操作发现】如图Z8－3，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．图Z8－3(1)请按要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连结BB′；(2)在(1)所画图形中，∠AB′B＝________．【问题解决】如图Z8－4，在等边三角形ABC中，AC＝7，点P在△ABC内，且∠APC＝90°，∠BPC＝120°，求△APC 的面积．图Z8－4小明同学通过观察、分析、思考，对上述问题形成了如下想法：想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连结PP′，寻找PA，PB，PC三条线段之间的数量关系；想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，连结PP′，寻找PA，PB，PC三条线段之间的数量关系．……请参考小明同学的想法，完成该问题的解答过程．(―种方法即可)【灵活运用】如图Z8－5，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD＝5，AD＝kAB(k 为常数)，求BD的长(用含k的式子表示)．图Z8－52．[2019·连云港] 问题呈现：如图Z8－6①，点E，F，G，H分别在矩形ABCD的边AB，BC，CD，DA上，AE＝DG.求证：2S四边形EFGH＝S矩形ABCD.(S表示面积)图Z8－6实验探究：某数学实验小组发现：若图①中AH≠BF，点G在CD上移动时，上述结论会发生变化．分别过点E，G 作BC边的平行线，再分别过点F，H作AB边的平行线，四条平行线分别相交于点A1，B1，C1，D1，得到矩形A1B1C1D1.如图②，当AH＞BF时，若将点G向点C靠近(DG>AE)，经过探索，发现：2S四边形EFGH＝S矩形ABCD＋S矩形A1B1C1D1.如图③，当AH＞BF时，若将点G向点D靠近(DG<AE)，请探索S四边形EFGH、S矩形ABCD与S矩形A1B1C1D1之间的数量关系，并说明理由．迁移应用：请直接应用“实验探究”中发现的结论解答下列问题．(1)如图Z8－7，点E，F，G，H分别是面积为25的正方形ABCD各边上的点，已知AH>BF，AE>DG，S 四边形EFGH＝11，HF＝29，求EG的长．图Z8－7(2)如图Z8－8，在矩形ABCD中，AB＝3，AD＝5，点E，H分别在边AB，AD上，BE＝1，DH＝2，点F，G分别是边BC，CD上的动点，且FG＝10，连结EF，HG，请直接写出四边形EFGH面积的最大值．图Z8－83.[2019·盐城]【探索发现】如图Z8－9①是一张直角三角形纸片，∠B＝90°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE，EF剪下时，所得的矩形的面积最大．随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为________．图Z8－9【拓展应用】如图②，在△ABC中，BC＝a，BC边上的高AD＝h，矩形PQMN的顶点P，N分别在边AB，AC上，顶点Q，M在边BC上，则矩形PQMN面积的最大值为________．(用含a，h的代数式表示) 【灵活应用】如图③，有一块“缺角矩形”ABCDE，AB＝32，BC＝40，AE＝20，CD＝16，小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角)，求该矩形的面积．【实际应用】如图Z8－10，现有一块四边形的木板余料ABCD，经测量AB＝50 cm，BC＝108 cm，CD＝60 cm，且tanB＝tanC＝43，木匠徐师傅从这块余料中裁出了顶点M，N在边BC上且面积最大的矩形PQMN，求该矩形的面积．图Z8－10参考答案例1 【例题分层分析】(1)①等边∠ACF②BE＝AF (2)2x 3x解：(1)证明：①∵四边形ABCD是平行四边形，∠BAD＝120°，∴∠D＝∠B＝60°.∵AD＝AB，∴▱ABCD是菱形，∴△ABC，△ACD都是等边三角形，∴∠B＝∠CAD＝60°，∠ACB＝60°，BC＝AC.∵∠ECF ＝60°，∴∠BCE ＋∠ACE＝∠ACF＋∠ACE＝60°， ∴∠BCE ＝∠ACF. 在△BCE 和△ACF 中， ⎩⎪⎨⎪⎧∠B＝∠CAF，BC ＝AC ，∠BCE ＝∠ACF， ∴△BCE ≌△ACF.②∵△BCE ≌△ACF ，∴BE ＝AF ， ∴AE ＋AF ＝AE ＋BE ＝AB ＝AC.(2)证明：设DH ＝x ，由题意，CD ＝2x ，CH ＝3x ， ∴AD ＝2AB ＝4x ，∴AH ＝AD －DH ＝3x. ∵CH ⊥AD ，∴AC ＝AH 2＋CH 2＝2 3x ， ∴AC 2＋CD 2＝AD 2，∴∠ACD ＝90°， ∴∠BAC ＝∠ACD＝90°，∴∠CAD ＝30°， ∴∠ACH ＝60°，∵∠ECF ＝60°，∴∠HCF ＝∠ACE，∴△ACE ∽△HCF ，∴AE FH ＝ACCH＝2，∴AE ＝2FH. (3)如图，过点C 作CN⊥AD 于N ，CM ⊥BA ，交BA 的延长线于M ，CM 与AD 交于点H.∵∠ECF ＋∠EAF＝180°， ∴∠AEC ＋∠AFC＝180°. ∵∠AFC ＋∠CFN＝180°， ∴∠CFN ＝∠AEC.∵∠M ＝∠CNF＝90°，∴△CFN ∽△CEM ， ∴CN CM ＝FN EM. ∵AB ·CM ＝AD·CN，AD ＝3AB ， ∴CM ＝3CN ，∴CN CM ＝FN EM ＝13. 设CN ＝a ，FN ＝b ，则CM ＝3a ，EM ＝3b ， ∵∠MAH ＝60°，∠M ＝90°，∴∠AHM ＝∠CHN＝30°， ∴HC ＝2a ，HM ＝a ，HN ＝3a ， ∴AM ＝33a ，AH ＝2 33a ， ∴AC ＝AM 2＋CM 2＝2 213a ， AE ＋3AF ＝(EM －AM)＋3(AH ＋HN －FN)＝EM －AM ＋3AH ＋3HN －3FN ＝3AH ＋3HN －AM ＝14 33a ，∴AE ＋3AFAC ＝14 33a 2 213a ＝7.故答案为7.例2 【例题分层分析】(2)PD PC ∠ADP ∠BCP 解：(1)矩形或正方形． (2)AC ＝BD ，理由如下：连结PD ，PC ，如图①所示：∵PE 是AD 的垂直平分线，PF 是BC 的垂直平分线，∴PA ＝PD ，PC ＝PB ， ∴∠PAD ＝∠PDA，∠PBC ＝∠PCB， ∴∠DPB ＝2∠PAD，∠APC ＝2∠PBC，又∠PAD＝∠PBC， ∴∠APC ＝∠DPB， ∴△APC ≌△DPB(SAS)， ∴AC ＝BD.(3)分两种情况考虑：(i)当∠AD′B＝∠D′BC 时，延长AD′，CB 交于点E ，如图②所示，∴∠ED ′B ＝∠EBD′， ∴EB ＝ED′.∵BC ＝B ′D′＝3，AB ＝AB′＝5， ∴AC ＝AD′＝4. 设EB ＝ED′＝x ，由勾股定理得42＋(3＋x)2＝(4＋x)2，解得x ＝4.5.过点D′作D′F⊥CE 于F ， ∴D ′F ∥AC ，∴△ED ′F ∽△EAC ， ∴D′F AC ＝ED′AE ，即D′F 4＝ 4.54＋4.5，解得D′F＝3617，∴S △ACE ＝12AC×EC＝12×4×(3＋4.5)＝15，S △BED ′＝12BE×D′F＝12×4.5×3617＝8117，∴S 四边形ACBD′＝S △ACE －S △BED ′＝15－8117＝10417. (ii)当∠D′BC＝∠ACB＝90°时，过点D′作D′E⊥AC 于点E ，如图③所示，∴四边形ECBD′是矩形， ∴ED ′＝BC ＝3.在Rt △AED ′中，根据勾股定理得 AE ＝42－32＝7，∴S △AED ′＝12AE×ED′＝12×7×3＝3 72，S 矩形ECBD′＝CE×CB＝(4－7)×3＝12－3 7，则S 四边形ACBD′＝S △AED ′＋S 矩形ECBD′＝3 72＋12－3 7＝12－3 72. 专题训练1．解：【操作发现】 (1)如图①所示．(2)45°. 【问题解决】如图②，将△APC 绕点A 按顺时针方向旋转60°，得到△AP′B，连结PP′，则AP′＝AP ，∠PAP ′＝60°，∠AP ′B ＝∠APC.∴△APP′是等边三角形．∴∠APP′＝∠AP′P＝60°.∵AP⊥PC，∴∠APC＝90°.又∵∠BPC＝120°，∴∠APB＝360°－∠APC－∠BPC＝360°－90°－120°＝150°. ∴∠BPP′＝∠APB－∠APP′＝150°－60°＝90°.∴∠BP′P＝∠AP′B－∠AP′P＝∠APC－∠AP′P＝90°－60°＝30°.设BP＝a.在Rt△BPP′中，∵∠BP′P＝30°，∴P′B＝2a，P′P＝3a，∴AP＝3a，PC＝2a.在Rt△APC中，由勾股定理得AP2＋PC2＝AC2，∴(3a)2＋(2a)2＝72.解得a＝7.∴AP＝21，PC＝2 7.∴S△APC＝12AP·PC＝12×21×2 7＝7 3.【灵活运用】连结AC.∵AE⊥BC，BE＝CE，∴AB＝AC.又∵AE⊥BC，∴∠BAE＝∠CAE.设∠BAE＝α，则∠CAE＝α，∠ABE＝90°－α，∠ADC＝α.如图③，将△ACD绕点A顺时针旋转2α，得到△ABD′，则BD′＝CD＝5，AD＝AD′，∠DAD′＝2α，∠BD′A＝α.过点A作AF⊥DD′，垂足为点F，则∠D′AF＝α，∠AD′F＝90°－α，DD′＝2D′F，∴∠BD ′D ＝∠BD′A＋∠AD′F＝α＋90°－α＝90°.在Rt △AD ′F 中，D ′F ＝AD′·cos ∠AD ′F ＝AD·cos(90°－α)＝kAB·cos(90°－α)＝k·BE＝2k.∴DD ′＝4k.在Rt △BDD ′中，由勾股定理得BD ＝BD′2＋D′D 2＝52＋（4k ）2＝25＋16k 2. 2．解：问题呈现：证明：因为四边形ABCD 是矩形，所以AB∥CD，∠A ＝90°，又因为AE ＝DG ，所以四边形AEGD 是矩形，所以S △HEG ＝12EG·AE＝12S 矩形AEGD ，同理可得S △FEG ＝12S 矩形BCGE .因为S 四边形EFGH ＝S △HEG ＋S △FEG ，所以2S 四边形EFGH ＝S 矩形ABCD .实验探究：由题意得，当点G 向点D 靠近(DG<AE)时，如图所示，S △HEC 1＝12S 矩形HAEC 1，S △EFB 1＝12S 矩形EBFB 1，S △FGA 1＝12S 矩形FCGA 1，S △GHD 1＝12S 矩形GDHD 1，所以S 四边形EFGH ＝S △HEC 1＋S △EFB 1＋S △FGA 1＋S △GHD 1－S 矩形A 1B 1C 1D 1，所以2S 四边形EFGH ＝S 矩形HAEC 1＋S 矩形EBFB 1＋S 矩形FCGA 1＋S 矩形GDHD 1－2S 矩形A 1B 1C 1D 1，即2S 四边形EFGH ＝S 矩形ABCD －S 矩形A 1B 1C 1D 1. 迁移应用：(1)如图所示，由“实验探究”的结论可知2S 四边形EFGH ＝S 矩形ABCD －S 矩形A 1B 1C 1D 1，所以S 矩形A 1B 1C 1D 1＝S 矩形ABCD －2S 四边形EFGH ＝25－2×11＝3＝A 1B 1·A 1D 1. 因为正方形面积是25，所以边长为5，又A 1D 12＝HF 2－52＝29－25＝4，所以A 1D 1＝2，A 1B 1＝32，所以EG 2＝A 1B 12＋52＝94＋25＝1094，所以EG ＝1092.(2)四边形EFGH 面积的最大值为172. 3．解：【探索发现】12.【拓展应用】14ah.【灵活应用】如图①，设四边形BFGK 是从“缺角矩形”中剪出的一个矩形，显然，当顶点G 在线段DE 上时，矩形的面积才可取最大值．作直线DE ，分别交线段BA ，BC 的延长线于点P ，Q ，过点E 作EH⊥BC 于点H. ∵四边形ABCM 是矩形，∴AM ∥BC ， ∴△DEM ∽△DQC ，∴EM CQ ＝MDCD.∵CD ＝16，CM ＝AB ＝32，∴MD ＝CD ＝16， ∴EMCQ＝1，即CQ ＝EM. ∵AE ＝20，AM ＝BC ＝40， ∴EM ＝AE ＝20.∴AE＝CQ. 同理PA ＝MD ＝CD ＝16.∴当BK ＝12PB ＝24，即当顶点G 在DE 中点处时，矩形的面积最大，最大面积为14×60×48＝720.【实际应用】分三种情形：(Ⅰ)如图②，当矩形的另两个顶点P ，Q 分别在边AB ，CD 上时，延长BA ，CD 相交于点E. ∵∠EBC ＝∠DCG，∴EB ＝EC. 过点E 作EH⊥BC 于点H ， ∴BH ＝12BC ＝12×108＝54(cm)．在Rt △EBH 中，EH ＝BH·tanB ＝54×43＝72(cm)，∴EB ＝90 cm.由结论知，当PB ＝12EB ＝45 cm ＜AB 时，矩形面积有最大值为14×108×72＝1944(cm 2)．(Ⅱ)如图③，当矩形的另两个顶点P，Q分别在边AD，CD上时，延长BA，CD相交于点E，延长QP交AE于点F，过点F作FG⊥BC于点G，则矩形PQMN的面积小于矩形FQMG的面积．由(Ⅰ)知，矩形FQMG的面积＜1944 cm2.(Ⅲ)当矩形另两个顶点P，Q分别在边AB，AD上时，此时不能裁出矩形．综上所述，矩形面积的最大值为1944 cm2.2019-2020学年数学中考模拟试卷一、选择题1．关于x 的方程2(5)410a x x ---=有实数根，则a 满足（）A ．1a ≥B ．1a >且5a ≠C ．1a ≥且5a ≠D ．5a ≠2．如图，在平面直角坐标系中，点A （0，6），点B 在x 轴的负半轴上，将线段AB 绕点A 逆时针旋转90°至AB'，点M 是线段AB'的中点，若反比例函数ky x=(k≠0)的图象恰好经过点B'，M ，则k ＝（）A.4B.6C.9D.123．某市连续10天的最低气温统计如下（单位：℃）：4，5，4，7，7，8，7，6，5，7，该市这10天的最低气温的中位数是（） A ．6℃B ．6.5℃C ．7℃D ．7.5℃4．一般地，当α、β为任意角时，sin （α+β）与sin （α﹣β）的值可以用下面的公式求得：sin （α+β）＝sin α•cos β+cos α•sin β；sin （α﹣β）＝sin α•co s β﹣cos α•sin β．例如sin90°＝sin （60°+30°）1122+⨯＝1．类似地，可以求得sin15°的值是（）A B C D 5．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图：根据该折线图，下列结论错误的是（） A ．月接待游客量逐月增加 B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7，8月份D ．各年1月至6月的月接待游客量相对7月至12月，波动性更小，变化比较平稳6．电影《流浪地球》从2月5日上映以来，凭借其气势磅礴的特效场面与动人的父子情获得大众的喜爱与支持，截止3月底，中国电影票房高达4559000000元．数据4559000000用科学记数法表示为（） A ．845.5910⨯；B ．945.5910⨯；C ．94.55910⨯；D ．104.55910⨯．7．在同一平面内，⊙O 的半径为5cm ，点A 到圆心O 的距离OA ＝3cm ，则点A 与圆O 的位置关系为（） A ．点A 在圆内B ．点A 在圆上C ．点A 在圆外D ．无法确定8．如图，二次函数y ＝ax 2+bx+c 的图象与x 轴的一个交点坐标是（3，0），对称轴为直线x ＝1，下列结论：①abc ＞0；②2a+b ＝0；③4a ﹣2b+c ＞0；④当y ＞0时，﹣1＜x ＜3；⑤b ＜c ．其中正确的个数是（）A ．2B ．3C ．4D ．59．如图，□ABCD 中，对角线AC 和BD 相交于点O ，如果AC=26,BD=18,AB=x,那么x 的取值范围是（）A ．4< m <13B ．4< m <22C ．9< m <13D ．4< m <910．用计算器求35值时，需相继按“133”，“y x ”，“5”，“＝”键，若小颖相继按“””4”，“y x ”，“（﹣）”，“3”，“＝”键，则输出结果是（） A ．8B ．4C ．﹣6D ．0.12511．如图，在△ABC 中，AB ＝AC ＝5，BC ＝6，将△ABC 绕点B 逆时针旋转60°得到△A'BC’，连接A'C ，则A'C 的长为（）A ．6B ．C ．D ．12．某校对部分参加研学旅行社会实践活动的中学生的年龄（单位：岁）进行统计，结果如表：则这些学生年龄的众数和中位数分别是（） A ．15，14 B ．15，13C ．14，14D ．13，14二、填空题13．把多项式a 3b-ab 分解因式的结果为______．14．如图，a//b，点B在直线b上，且AB⊥BC，∠1=35°，那么∠2=______．15．某公司向银行申请了甲、乙两种贷款，共计68万元，每年需付出8.42万元利息。

几何类比专题

中考几何类比探究专题24．已知四边形ABCD 和四边形CEFG 都是正方形，且AB>CE ．（1）如图1，连接BG 、DE ．求证：BG =DE ；（2）如图2，如果正方形ABCD 的边长为2，将正方形CEFG 绕着点C 旋转到某一位置时恰好使得CG //BD ，BG=BD . ①求BDE ∠的度数；②请直接写出正方形CEFG 的边长的值.24. （本小题满分7分）解：（1）证明：∵四边形ABCD 和CEFG 为正方形，∴BC DC =，CG CE =，90BCD GCE ∠=∠=︒. ∴BCD DCG GCE DCG ∠+∠=∠+∠.BCG DCE ∠=∠即：. ……………………1分 ∴△BCG ≌△DCE .∴BG DE =.………………………………2分（2）①连接BE .由（1）可知：BG=DE . ∵//CG BD ，∴=45DCG BDC ∠∠=︒.∴9045135BCG BCD GCD ∠=∠+∠=︒+︒=︒. ∵90GCE ∠=︒,GFEDCBA图2ABCDEFG图1 ABCDEFG∴36036013590135BCE BCG GCE∠=︒-∠-∠=︒-︒-︒=︒.∴=BCG BCE∠∠.…………………………3分∵BC BC CG CE==，,∴△BCG≌△BCE.∴BG BE=.………………………………4分∵BG BD DE==,∴BD BE DE==.∴△BDE为等边三角形.∴60.BDE∠=︒…………………………5分②正方形CEFG的边长为31-. ……………………………………………7分22．阅读理解：如图1，若在四边形ABCD的边AB上任取一点E（点E与点A，B不重合），分别连结ED，EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的相似点；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的强相似点．解决问题：（1）如图1，若∠A=∠B=∠DEC=55°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；（2）如图2，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD的边AB上的一个强相似点E；拓展探究：（3）如图3，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处．若点E恰好是四边形ABCM的边AB上的一个强相似点，请直接写出BCAB的值．GFEDCB A图1 图2 图3 24．如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中90,C∠=︒B E∠=∠=︒.30（1）操作发现如图2，固定△ABC，使△DEC绕点C顺时针旋转．当点D恰好落在AB边上时，填空：图1 图2①线段DE与AC的位置关系是；② 设△BDC 的面积为1S ，△AEC 的面积为2S ，则1S 与2S 的数量关系是，证明你的结论；（2）猜想论证当△DEC 绕点C 旋转到图3所示的位置时，小明猜想（1）中1S 与2S 的数量关系仍然成立，并尝试分别作出了△BDC 和△AEC 中BC ，CE 边上的高，请你证明小明的猜想．图322．解：（1）点E 是四边形ABCD 的边AB 上的相似点．理由：∵∠A = 55°， ∴∠ADE +∠DEA = 125°． ∵∠DEC = 55°，∴∠BEC +∠DEA =125°． ∴∠ADE =∠BEC ． ∵∠A =∠B ，∴△ADE ∽△BEC ．∴点E 是四边形ABCD 的AB 边上的相似点． ………………..2分（2）作图如下：图1 图2 ………………..4分（3）32BC AB=． ………….. 5分24．解：（1）①线段DE 与AC 的位置关系是平行． …………………..1分②S 1与S 2的数量关系是相等．证明：如图2，过D 作DN ⊥AC 交AC 于点N ，过E 作EM ⊥AC 交AC 延长线于M ，过C 作CF ⊥AB 交AB 于点F ．由①可知 △ADC 是等边三角形，DE ∥AC ， ∴DN =CF , DN =EM ． ∴CF =EM ．∵90,30ACB B ∠=︒∠=︒，∴2AB AC =．又∵AD AC =,∴BD AC =．图2∵112S CF BD =，212S AC EM =，∴1S =2S ． …………………..3分（2）证明：如图3，作DG ⊥BC 于点G ，AH ⊥CE 交EC 延长线于点H .∵90,180DCE ACB DCG ACE ∠=∠=︒∴∠+∠=︒．又∵180,ACH ACE ACH DCG ∠+∠=︒∴∠=∠．又∵90,CHA CGD AC CD ∠=∠=︒=,∴△AHC ≌△DGC ．∴AH =DG ．又∵CE =CB ,图3∴12S S =． ……………………..7分20．如图，在矩形ABCD 中，E 是CD 边上任意一点（不与点C ，D 重合），作AF ⊥AE 交CB 的延长线于点F ．（1）求证：△ADE ∽△ABF ；（2）连接EF ，M 为EF 的中点，AB ＝4，AD ＝2，设DE ＝x ， ①求点M 到FC 的距离（用含x 的代数式表示）； ②连接BM ，设2BM y =，求y 与x 之间的函数关系式，并直接写出BM 的长度的最小值．24．已知：△ABC，△DEF都是等边三角形，M是BC与EF的中点，连接AD，BE.（1）如图1，当EF与BC在同一条直线上时，直接写出AD与BE的数量关系和位置关系；（2）△ABC固定不动，将图1中的△DEF绕点M顺时针旋转α（o0≤α≤o90）角，如图2所示，判断（1）中的结论是否仍然成立，若成立，请加以证明；若不成立，说明理由；（3）△ABC固定不动，将图1中的△DEF绕点M旋转α（o0≤α≤o90）角，作DH⊥BC于点H．设BH＝x，线段AB，BE，ED，DA所围成的图形面积为S．当AB＝6，DE＝2时，求S关于x的函数关系式，并写出相应的x的取值范围．图1图2备用图25．将ABC △绕点A 按逆时针方向旋转,旋转角为）（︒<α<︒α900，旋转后使各边长变为原来的n 倍，得到C B A ''△,我们将这种变换记为[n ,α]．（1）如图①,对ABC △作变换[3,60 ]得C B A ''△，则C B A S ''△：ABC S △= ___；直线BC 与直线C B ''所夹的锐角为 __ °；（2）如图②，ABC △中，330,90==∠=∠AC BAC ACB ，，对A B C △作变换[n ,α]得C B A ''△，使得四边形C B AB ''为梯形，其中AB ∥C B '',且梯形C B AB ''的面积为312，求α和n 的值．25. 已知ABD ∆和CBD ∆关于直线BD 对称(点A 的对称点是点C )，点E 、F 分别是线段BC 和线段BD 上的点，且点F 在线段EC 的垂直平分线上，联结AF 、AE ，AE 交BD 于点G ．（1）如图（1），求证：ABD EAF ∠=∠；（2）如图（2），当AD AB =时，M 是线段AG 上一点，联结BM 、图①图②654321G FCBDA EED 、MF ，MF 的延长线交ED 于点N ，BAF MBF ∠=∠21，AD AF 32=，试探究线段FM 和FN 之间的数量关系，并证明你的结论．图（1）图（2）25.(1)证明：如图1 连接FE 、FC∵点F 在线段EC 的垂直平分线上,∴ FE=FC ∴∠l=∠2 ………………………1分∵△ABD 和△CBD 关于直线BD 对称． ∴AB =CB ,∠4=∠3，又BF =BF∴△ABF ≌△CBF ， ∴∠BAF =∠2，F A =FC∴FE =F A ，∠1=∠BAF ． …………………………2分G FEDCBA NMGF EDCBAQ NMG F CBDA E∴∠5=∠6，∵ ∠l+∠BEF =1800，∴∠BAF +∠BEF =1800∵∠BAF +∠BEF +∠AFE +∠ABE =3600∴∠AFE +∠ABE =1800………………………………3分图1又∵∠AFE +∠5+∠6=1800， ∴∠5+∠6=∠3+∠4∴∠5=∠4，即∠EAF =∠ABD ………………………4分(2)解：FM =72FN ……………………………………………5分证明：如图2，由(1)可知∠EAF =∠ABD ，又∵∠AFB =∠GF A ∴△AFG ∽△BF A ∴∠AGF =∠BAF又∵∠MBF =12∠BAF ，∴∠MBF =12∠AGF 又∵∠AGF =∠MBG +∠BMG ∴∠MBG =∠BMG∴BG =MG …………………………6分 ∵AB =AD ∴∠ADB =∠ABD =∠EAF又∵∠FGA =∠AGD ．∴△AGF ∽△DGA ．GF AG AFGA DG DA∴==∵AF =23AD23GF AG GA DG ∴== 图2设GF =2a ，则AG =3a ，∴GD =92a ，∴FD =DG -GF =922a a -=52a ∵∠CBD =∠ABD ，∠ABD =∠ADB ，∴∠CBD =∠ADB .∴//BE AD ．∴BG EG GD AG =23EG AG BG GD ∴==，设EG =2k ，则MG =BG =3k 过点F 作FQ ∥ED 交AE 于Q ，24552GQ GF a a QE FD ∴=== 45GQ QE ∴=……………………7分∴GQ =49EG =89k ．∴QE =109k ， MQ =MG +GQ =3k +89k =359k∵FQ ∥ED ，35791029kMF MQ FN QE k ∴===.∴FM =72FN ……………8分22. 阅读下面的材料：小明遇到一个问题：如图（1），在□ABCD 中，点E 是边BC 的中点，点F 是线段AE 上一点，BF 的延长线交射线CD 于点G . 如果3AF EF =，求CDCG的值.他的做法是：过点E 作EH ∥AB 交BG 于点H ，则可以得到△BAF ∽△HEF .请你回答：（1）AB 和EH 的数量关系为，CG 和EH 的数量关系为，CDCG的值为 .（2）如图（2），在原题的其他条件不变的情况下，如果(0)AFa a EF=>，那么CDCG的值为（用含a 的代数式表示）. （3）请你参考小明的方法继续探究：如图（3），在四边形ABCD 中，DC ∥AB ，点E 是BC 延长线上一点，AE 和BD 相交于点F . 如果(00)AB BC m n m n CD BE ==>>，，，那么AFEF的值为（用含m ，n 的代数式表示）.H (1)ABCD E FGG F E D CBA(2)(3)ABCDEF25.已知：四边形ABCD 中，AD ∥BC ，AD =AB =CD ，∠BAD =120°，点E 是射线CD上的一个动点（与C、D不重合），将△ADE绕点A顺时针旋转120°后，得到△ABE'，连接EE'.（1）如图1，∠AEE'= °；（2）如图2，如果将直线AE绕点A顺时针旋转30°后交直线BC于点F，过点E作EM∥AD交直线AF于点M，写出线段DE、BF、ME之间的数量关系；（3）如图3，在（2）的条件下，如果CE=2，AE =27，求ME的长.E'MFEDC BAE'EDCBA图1图2E'MFEDC BA图322. 已知：△ABC 中，ACB ABC ∠=∠，以AB 为直径的⊙O 交BC 于点D. （1）如图1，当∠A 为锐角时，AC 与⊙O 交于点E ，联结BE ，则∠∠BAC CBE 与的数量关系是∠BAC = ∠CBE ；图1 （2）如图2，若AB 不动，AC 绕点A 逆时针旋转，当∠BAC 为钝角时，CA 的延长线与⊙O 交于点E ，联结BE ，（1）中∠∠BAC CBE 与的数量关系是否依然成立？若成立，请加以证明；若不成立，请说明理由.图224．已知：如图，Rt MPN ∆的顶点P 在正方形ABCD 的边AB 上，∠MPN=90°，PN 经过点C ，PM 与AD 交于点Q ．（1）在不添加字母和辅助线的情况下，图中△APQ ∽△ ；（2）若P 为AB 的中点，联结CQ ，求证：AQ +BC =CQ ；（3）若14=AQ AD 时，试探究线段PC 与线段PQ 的数量关系，并加以证明.22．已知：如图，在⊙O 中，直径AB ⊥CD 于点E ，连接BC ．（1）线段BC 、BE 、AB 应满足的数量关系是；（2）若点P 是优弧CAD 上一点（不与点C 、A 、D 重合），连接BP 与CD交于点G .请完成下面四个任务：①根据已知画出完整图形，并标出相应字母；②在正确完成①的基础上，猜想线段BC 、BG 、BP 应满足的数量关系是；③证明你在②中的猜想是正确的；④点P ′恰恰是你选择的点P 关于直径AB 的对称点，那么按照要求画出图形后在②中的猜想仍然正确吗？；（填正确或者不正确，不需证明）D ACB OE。

中考几何中的类比探究解题方法分析

（1）作 EH⊥CD，EQ⊥AB，利用 AAS 先证△AEQ≌△ECH，易得 EQ=EH，把 EQ=EH 作为一个条件，再利用 ASA 易证 Rt△EFQ≌Rt△EGH，从而有 EF=EG；
（2）作 EH⊥CD，EQ⊥AB，先证△EFQ∽△EGH，易得 EF EQ ， EG EH
再证△AQE∽△EHC，那么 EA EQ 2 ， EC EH 1
CD m
∴=
CG 2
（3）拓展迁移
第 2页，共 7页
如图 3，梯形 ABCD 中，DC//AB，点 E 是 BC 的延长线上一点，AE 和 BD 相交于点 F。
若
AB
a
BC
，
b(a
0,b 0) ，则
AF
的值是
AF
ab（用含 a，b
的代数式表示）。
CD
BE
EF
EF
E
【解析】过 E 作 EH∥AB，交 BD 延长线于点 H
∴ EA EQ 2 EG EH 1
∴ EF 2 EG
∴EF=2EG；
（3）EF=kEG．
第 6页，共 7页
【上题基本思路：过直角顶点，作横平竖直的线，找全等或相似。】
中考数学类比探题思维误区：第一问通常是特殊的图形，题中的条件比较充分，而且一般有提示，所以学生做的时，
基本上能得心应手，但做第二、三问时，往往有部分学生，没有按照第一问的思路去思考，而且是对着题干思考第二、三问，这样就陷入了“自己布置的陷阱”结果做不出来，把一道题当成三道题来做了。
H
由题意可知:EH∥DC∥AB
∴ BC CD BE EH
∴CD = b EH
D
C
F
又∵ AB a CD
∴AB=a CD

几何难点突破之类比探究讲义及答案

几何难点突破之类比探究（讲义）一、知识点睛识别类比探究题型特征：1.题目中一般有三问或者更多，每小问的条件和图形相似度很高，因此可以“照搬”第一问的方法；2.每一问的图形或点的位置会有所变化（通常条件从特殊走向一般），但可以在这些变化过程中按照第一问的思路和对应关系找角、找边、找全等．二、精讲精练1. 如图1所示，在△ABC 和△ADE 中，AB =AC ，AD =AE ，∠BAC =∠DAE ，且点B 、A 、D 在一条直线上，连接BE 、CD ，M 、N 分别为BE 、CD 的中点．（1）求证：①BE =CD ；②△AMN 是等腰三角形．（2）在图1的基础上，将△ADE 绕点A 按顺时针方向旋转180°，其他条件不变，得到图2所示的图形．（1）中的两个结论是否仍然成立，若成立，请给予证明；若不成立，请说明理由．图2ME CBNDA图1CBMN ED A2. 已知△ABC 为等边三角形，点D 为直线BC 上一动点（点D 不与B ，C 重合），以AD 为边作菱形ADEF （A 、D 、E 、F 按逆时针排列），使∠DAF ＝60°，连接CF ．（1）如图1，当点D 在边BC 上时，求证：①BD ＝CF ；②AC ＝CF ＋CD ；（2）如图2，当点D 在边BC 的延长线上且其他条件不变时，结论AC ＝CF ＋CD 是否成立？若不成立，请写出AC 、CF 、CD 之间存在的数量关系，并说明理由；（3）如图3，当点D 在边CB 的延长线上且其他条件不变时，探究AC 、CF 、CD 之间存在的数量关系．图1AFECDB图2ABC DFEABCD F3. 如图1，四边形ABCD 是正方形，点E 是边BC 的中点．且90AEF ∠=，且EF 交正方形外角DCG ∠的平分线CF 于点F ．（1）求证：AE =EF ；（2）如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立吗？如果成立，写出证明过程；如果不成立，请说明理由；（3）如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”是否成立？如果成立，写出证明过程；如果不成立，请说明理由．图1GFE DC B A图2A B CDE FG图3GFE DCBA4.如图1，在△ABC 中，点P 为BC 边的中点，直线a 绕顶点A 旋转，若B 、P 在直线a 的异侧，BM ⊥直线a 于点M ，CN ⊥直线a 于点N ，连接PM 、PN ；（1）求证：PM =PN ；（2）若直线a 绕点A 旋转到图2的位置时，点B 、P 在直线a 的同侧，其它条件不变．此时PM =PN 还成立吗？若成立，请给予证明；若不成立，请说明理由；（3）如图3，若直线a 绕点A 旋转到与BC 边平行的位置时，其它条件不变．请判断四边形MBCN 的形状及此时PM =PN 还成立吗？图1ABCP aMN图2ABCP aM N图3NMaP CBA5.如图1所示,已知A、B为直线l上两点，点C为直线l上方一动点，连接AC、BC，分别以AC 、BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作DD1⊥l于点D1，过点E作EE1⊥l于点E1.(1)如图2，当点E恰好在直线l上时(此时E1与E重合)，试说明DD1=AB；(2)在图1中，当D、E两点都在直线l的上方时，试探求三条线段DD1、EE1、AB之间的数量关系，并说明理由；(3)如图3，当点E在直线l的下方时，请探究三条线段DD1、EE1、AB之间的数量关系.DA BGEFCl D1E1图1GEBACFD1DE1()l图2图3lFGEBACD1DE16. 如图，点P 是正方形ABCD 对角线AC 上一动点，点E 在射线BC 上，且PE ＝PB ，连接PD ，O 为AC 中点．（1）如图1，当点P 在线段AO 上时，试猜想PE 与PD 的数量关系和位置关系，不用说明理由；（2）如图2，当点P 在线段OC 上时，（1）中的猜想还成立吗？请说明理由；（3）如图3，当点P 在AC 的延长线上时，判断（1）中的猜想是否成立？若成立，请直接写出结论；若不成立，请说明理由．图1BB图2三、课后作业1．已知：如图所示，直线MA∥NB，∠MAB与∠NBA的平分线交于点C，过点C作一条直线l与两条直线MA、NB分别相交于点D、E．（1）如图1所示，当直线l与直线MA垂直时，猜想线段AD、BE、AB之间的数量关系，请直接写出结论，不用证明；（2）如图2所示，当直线l与直线MA不垂直且交点D、E都在AB的同侧时，（1）中的结论是否成立？如果成立，请证明：如果不成立，请说明理由；（3）如图3所示，当直线l与直线MA不垂直且交点D、E在AB的异侧时，（1）中的结论是否仍然成立？如果成立，请说明理由；如果不成立，那么线段AD、BE、AB之间还存在某种数量关系吗？如果存在，请写出它们之间的数量关系．【几何难点突破之类比探究参考答案】二、精讲精练图1A lCEBDNM图2M NDBElACMNDBEClA图3(1)lCENM1.提示：（1）①证△CAD≌△BAE（SAS）；②证△ACN≌△ABM（SAS）；或证△MEA≌△NDA（SAS）；（2）成立，同（1）可证．2.证明：（1）如图1，在等边△ABC中，AB=AC=BC，∠BAC=60°∴ ∠BAD+∠DAC=60°∵ 在菱形ADEF中，∠DAF=60°∴ AD=AF，∠DAC+∠CAF=60°∴ ∠BAD=∠CAF∴ △ABD≌△ACF（SAS）∴ BD=CF∵ BC=BD+DC∴ BC=CF+CD即AC= CF+CD（2）此时AC=CF+CD不成立，CF = AC +CD.理由如下：如图2，在等边△ABC中，AB=AC=BC，∠BAC=60°∵ 在菱形ADEF中，∠DAF=60°∴ AD=AF∴ ∠BAC+∠CAD=∠DAF+∠CAD∴ ∠BAD=∠CAF∴ △ABD≌△ACF（SAS）∴ BD=CF∵ BD=BC+CD∴ CF= BC+CD即CF = AC +CD（3）CF = CD-AC.理由如下：如图3，在等边△ABC中，AB=AC=BC，∠BAC=60°∴ ∠CAF+∠BAF=60°∵ 在菱形ADEF中，∠DAF=60°∴ AD=AF，∠DAB+∠BAF=60°∴ ∠DAB+∠BAF =∠CAF+∠BAF∴ ∠DAB=∠F AC∴△ABD≌△ACF（SAS）∴ BD=CF图1AFECDB图2AB C DFE图3AB CDEF∵ BD=CD-CB∴ CF= CD-CB即CF = CD-AC3.提示：（1）在AB上取点M，使得AM=CE，证△AME≌△ECF（ASA）；（2）成立，同（1）可证；（3）成立，在BA的延长线上取点M，使得AM=CE，证△AME≌△ECF（ASA）．4.提示：（1）延长MP交CN于点E，证△BPM≌△CPE（ASA），直角三角形斜边中线等于斜边一半；（2）延长MP交NC的延长线于点E，同（1）可证；（3）四边形MBCN为矩形；成立，同（1）可证．5.提示：（1）△ADD1≌△CAB；（2）AB＝DD1＋EE1，过点C作CM⊥AB于点M，证△ADD1≌△CAM，△EBE1≌△BCM；（3）DD1=AB＋EE1，同（2）可证．6.提示：（1）过P作PM⊥BC于点M，PN⊥DC于点N．证△APB≌△APD（SAS），△PME≌△PND（HL）即可；（2）成立，同（1）可证；（3）作图略；成立，过P分别作BC，DC的垂线，交BE于点M，DC的延长线于点N，同（1）可证．四、课后作业1．解：（1）AD+BE＝AB（2）成立．证明：（方法一）：在AB上截取AG=AD，连接CG．∵ ∠1＝∠2，AC＝AC∴△ADC≌△AGC（SAS）∴∠5＝∠6∵ AM∥BN∴ ∠1+∠2+∠3+∠4=180°图1A lCEBDNM876541C lEDNM∵∠1＝∠2，∠3＝∠4∴ ∠2+∠3=90°∴ ∠ACB＝90°即∠6＋∠7＝90°∵ ∠5+∠6+∠7+∠8=180°∴ ∠5＋∠8＝90°∴∠7＝∠8∵∠3＝∠4，BC＝BC∴△BGC≌△BEC（ASA）∴BG＝BE∴AG+BG＝AD+BE∴AD+BE＝AB（方法二）：过点C作直线FG⊥AM，垂足为点F，交BN于点G．作CH⊥AB，垂足为点H．由（1）得AF+BG=AB∵AM∥BN，∠AFG＝90°∴ ∠BGF＝∠FGE＝90°∵∠1＝∠2，∠3＝∠4∴ CF＝CH，CH＝CG∴ CF＝CG∵ ∠FCD＝∠GCE∴△CFD≌△CGE（ASA）∴DF＝EG∴ AD+BE=AF-DF+GE+BG=AF+BG=AH+BH=AB （方法三）：延长BC，交AM于点F．∵AM∥BN∴∠5＝∠4∵ ∠3＝∠4∴∠5＝∠3HFG1234CAlEBDNM图2方法二51234FCAlEBDNM∴ AF =AB∵ ∠1＝∠2，∴ CF ＝CB∵∠FCD ＝∠BCE∴ △FCD ≌△BCE （ASA ）∴ DF ＝BE∴ AD +BE =AD +DF =AF =AB（3）不成立．存在．当点D 在射线AM 上，点E 在射线BN 的反向延长线上时（如图3（1）），AD -BE =AB当点D 在射线AM 的反向延长线上，点E 在射线BN 上时（如图3（2）），BE -AD =AB图3(2)图3(1)A l C E B D N M MN DBEClA。

平面几何命题与立体几何命题的类比

平面几何命题与立体几何命题的类比著名的哲学家康德曾经讲过：“每当理智缺乏可靠论证思路的时候，类比就像一位大师指引我们前进。

”这段话深刻地说明了类比推理的重要性。

现在新课程标准已经把类比推理当作合情推理的一种重要形式，要求学生掌握，高考也已经把类比推理作为一个重要的内容来考察。

立体几何与平面几何的教学应统一起来，不仅仅是因为立体几何中的许多问题需要转化成平面几何中的问题来完成，更重要的立体几何与平面几何研究问题的思路与方法是相似的，而且许多定理在平面中成立，在空间中也成立。

但是，有些命题在平面中成立，在空间中不成立。

应注意区别。

如果在教学过程中注意类比，那么不但有助于理解定理的适用范围，梳理和理解对于几何命题的认识，有助于大学学习射影几何——笛沙革原理。

教师在教学过程中应注意研究整理，研究它的思维过程体现了逻辑思维中的类比思维，类比是进行合情推理的一种重要方法。

在数学中，类比是发现概念﹑方法﹑定理和公式的重要手段，也是开拓新领域和创造数学新分支的重要途径。

学生在数学的学习中应该学会运用这种独特的思维方法，教师在教学过程中应努力培养学生运用类比方法进行合情推理的能力。

并将此意识渗透给学生，培养学生用联系的观点，对立统一的观点认识事物，这也从一个侧面，体现了数学的结构美﹑对称美﹑和谐美。

如果学生能体会到数学的美感，那么他学习数学的兴趣就会越来越浓，热情会越来越高。

正如罗素所说：“数学，如果正确地看它，不但拥有真理，而且拥有至高的美。

”为了便于学生在学习过程中进行对比，培养学生类比推理的能力，在教学过程中我尝试设立了平面几何与立体几何命题的专题课，师生共同探讨，下面把学生归纳的部分命题列举如下：一、平面几何与立体几何都成立的命题1、两点之间线段最短，两点确定一条直线；2、平行于同一条直线的两条直线平行；3、如果一个角的两边分别平行于另一个角的两边，并且方向相同，那么这两个角相等；4、如果一条直线垂直于两条平行线中的一条，那么它也垂直于另一条直线；5、过直线外一点有且只有一条直线与已知直线平行；6、垂线段最短；7、顺次连接四边形各边中点得到的四边形为平行四边形；8、三角形的全等、相似的公理和定理。

人教版数学八下压轴题研究之四边形之类比探究

四边形之类比探究（一）➢ 知识点睛1. 类比探究问题的处理思路：①根据题干条件，结合____________先解决第一问．②用解决__________的方法类比解决下一问．类比的关键是把握住变化过程中的__________． 2. 类比探究问题中常见不变特征举例ABCE MDA BMCNM C BA（类）倍长中线平行夹中点中位线➢ 精讲精练1. 已知，在△ABC 中，∠BAC =90°，∠ABC =45°，D 为直线BC 上一动点（不与点B ，C 重合），以AD 为边作正方形ADEF ，连接CF ．（1）如图1，当点D 在线段BC 上时，求证：BC=CF+CD ．（2）如图2，当点D 在线段BC 的延长线上时，其他条件不变，请直接写出BC ，CD ，CF 三条线段之间的数量关系．（3）如图3，当点D 在线段BC 的反向延长线上时，点A ，F 分别在直线BC 的两侧，其他条件不变．①请直接写出BC ，CD ，CF 三条线段之间的数量关系；②若正方形ADEF的边长为AE ，DF 相交于点O ，求OC 的长．图1D F EC B A B E C FD A 图2图3DF E C BA 2. 如图1，在正方形ABCD 中，E ，F 分别是BC ，CD 上的点，且∠EAF =45°，则有结论EF =BE +DF成立．（1）如图2，在四边形ABCD 中，AB =AD ，∠B =∠D =90°，E ，F 分别是BC ，CD 上的点，12EAF BAD ∠=∠，那么结论EF =BE +DF 是否仍然成立？若成立，请证明；若不成立，请说明理由．（2）如图3，若将（1）中的条件改为：在四边形ABCD 中，AB =AD ，∠B +∠ADC =180°，延长BC 到点E ，延长CD 到点F ，使得12EAF BAD ∠=∠，则结论EF =BE +DF 是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．3. 在菱形ABCD 和正三角形BEF 中，∠ABC =60°，P 是DF 的中点，连接PE ，PC ．（1）如图1，当点E 在BC边上时，求证：PE =．（2）如图2，当点F 在AB 的延长线上时，线段PC ，PE 有怎样的数量关系？写出你的猜想，并给予证明．图1EPDCBAABCDP E F图24. 如图1，在四边形ABCD 中，AB =CD ，E ，F 分别为BC ，AD 的中点，连接EF 并延长，与BA ，CD 的延长线分别交于点M ，N ，则∠BME =∠CNE ．（1）如图2，在四边形ADBC 中，AB 与CD 相交于点O ，AB =CD ，E ，F 分别为BC ，AD 的中点，连接EF ，与CD ，AB 分别交于点M ，N ，判断OM ，ON 之间的数量关系，并证明你的结论．（2）如图3，在△ABC 中，AC AB ，点D 在AC 边上，且AB =CD ．E ，F 分别为BC ，AD 的中点，连接EF 并延长，与BA 的延长线交于点G ，连接DG ，若∠EFC =60°，判断△ADG 的形状，并证明你的结论．GE F DCBA 图1图2图3E FNMOCBDANM FE DBA【参考答案】➢ 知识点睛 1．①分支条件②第一问，不变特征 ➢ 精讲精练 1．（1）证明略．提示：题目中有旋转结构，证明△ABD ≌△ACF （SAS ），得到BD =CF ，进而得证．（2）BC CF CD =-．（3）①BC CD CF =-；②2OC =． 2．（1）成立，证明略．提示：题目中有旋转结构，证明△ADF ≌△ABH （SAS ），得到DF =BH ，进而得证．（2）不成立，BE EF DF =+.提示：题目中有旋转结构，证明△ABH ≌△ADF （SAS ），得到AH =AF ，∠BAH=∠DAF ，可证△AHE ≌△AFE （SAS ）, EF =EH ，得到BE EF DF =+.3．（1）PE =，证明略．提示：延长EP ，交CD 于点H ．证明△EFP ≌△HDP （ASA ），得到FE DH =，EP HP =，可得CE CH =，由三线合一得，CP ⊥EH ，进而可得PE =．（2）PE =．4．（1）OM ON =，证明略．提示：取BD 的中点G'，连接EG'，FG'．则FG'∥AB ，12FG AB '=，EG'∥CD ，12EG CD '=，由AB CD =得EG FG ''=，进而可得OM ON =．（2）△ADG 是含30°角的直角三角形，证明略．提示：连接BD ，取BD 的中点G'，连接EG'，FG'．四边形之类比探究（二）（讲义）➢ 知识点睛类比探究问题的处理思路：①根据题干条件，结合__________先解决第一问．②用解决第一问的方法类比解决下一问．如果不能，分析条件变化，寻找__________． ③结合所求目标，依据__________，大胆猜测、尝试、验证．➢ 精讲精练1. （1）问题探究如图1，分别以△ABC 的边AC 与边BC 为边，向△ABC 外作正方形ACD 1E 1和正方形BCD 2E 2，过点C 作直线K H 交直线A B 于点H ，使∠A H K =∠A C D 1．作D1M ⊥K H ，D 2N ⊥KH ，垂足分别为点M ，N ．试探究线段D 1M 与线段D 2N 的数量关系，并加以证明．（2）拓展延伸①如图2，若将“问题探究”中的“正方形”改为“正三角形”，过点C 作直线K 1H 1，K 2H 2，分别交直线AB 于点H 1，H 2，使∠AH 1K 1=∠BH 2K 2=∠ACD 1．作D 1M ⊥K 1H 1，D 2N ⊥K 2H 2，垂足分别为点M ，N ．D 1M =D 2N 是否仍成立？若成立，给出证明；若不成立，说明理由．②如图3，若将①中的“正三角形”改为“正五边形”，其他条件不变，D 1M =D 2N 是否仍成立？（要求：在图3中补全图形，注明字母，直接写出结论，不需证明）BCD 1E 1E 2D 2F 2F 1图2图1ABCD 1K 1K 2D 2MNH 2H 1NM KHD 2E 2E 1D 1CB A2. （1）问题背景如图1，Rt △ABC 中，∠BAC =90°，AB =AC ，∠ABC 的平分线交直线AC 于点D ，过点C 作CE ⊥BD ，交直线BD 于点E ．请探究线段BD 与CE 之间的数量关系．结论：线段BD 与CE 之间的数量关系为_______________（请直接写出结论）．（2）类比探索在（1）中，如果把BD 改为△ABC 的外角∠ABF 的平分线，其他条件均不变（如图2），（1）中的结论还成立吗？若成立，请写出证明过程；若不成立，请说明理由．DE AFAB CD图1 图23. 如图1，将两个完全相同的三角形纸片ABC 和DEC 重合放置，其中∠C =90°，∠B =∠E =30°．（1）操作发现如图2，固定△ABC ，使△DEC 绕点C 旋转，当点D 恰好落在AB 边上时，填空： ①线段DE 与AC 的位置关系是_______________；②设△BDC 的面积为S 1，△AEC 的面积为S 2，则S 1与S 2的数量关系是_______________．（2）猜想论证当△DEC 绕点C 旋转到图3所示的位置时，小明猜想（1）中S 1与S 2的数量关系仍然成立，并尝试分别作出了△BDC 和△AEC 中BC ，CE 边上的高，请你证明小明的猜想．图2图1C B (E )A (D )（3）拓展探究已知∠ABC =60°，点D 是其角平分线上一点，BD =CD =4， DE ∥AB 交BC 于点E （如图4）．若在射线BA 上存在点F ，使S △DCF =S △BDE ，请直接写出．．．．相应的BF 的长．4. 在□ABCD 中，∠BAD 的平分线交直线BC 于点E ，交直线DC 于点F ．（1）在图1中证明CE =CF ；（2）如图2，若∠ABC =90°，G 是EF 的中点，求∠BDG 的度数；（3）如图3，若∠ABC =120°，FG ∥CE ，且FG =CE ，求∠BDG 的度数．DFEC BA图1GDFEC BA图2G DFE C BA图3【参考答案】➢知识点睛①分支条件；②不变特征；③不变特征．➢精讲精练1．（1）D1M=D2N，证明略．提示：证明△CMD1≌△AHC，△CND2≌△BHC．（2）D1M=D2N仍成立，证明略．（3）D1M=D2N仍成立，图形略．2．（1）BD=2CE．提示：延长CE，交BA的延长线于点M，由角平分线+垂直可以得到BM=BC，之后证明△ABD ≌△ACM即可．（2）（1）中的结论仍成立，证明略．提示：延长CE，交AB的延长线于点M，由角平分线+垂直可以得到BM=BC，之后证明△ABD ≌△ACM即可．3．（1）①AC∥DE；②S1=S2．（2）证明略．提示：证明△ANC≌△DMC，可得AN=DM，根据等底等高即可得证．．（3）BF的长为334．（1）证明略．（2）∠BDG=45°．（3）∠BDG=60°．。

河南数学热点专题突破专题八：几何图形的类比探究

末页
3.（2015德州）（1）问题
如图①，在四边形ABCD 中，点P 为AB 上一点，
∠DPC = ∠A = ∠B = 90°，求证：AD·BC = AP·BP.
（2）探究
如图②，在四边形ABCD 中，点P 为AB 上一点，
当∠DPC = ∠A = ∠B = θ 时，上述结论是否依然成立？
并说明理由.
2013 22
图形的旋转；全等三角形的
10
解答题
几何图形的类比探究
判定和性质；三角形的面积；等边三角形及菱形的判定和
性质
目录
上一页
下一页
末页
续表
年份题号分值题型
考点
2012 22
10
解答题
几何图形的类比探究
2011 —— —— ——
——
考查内容
平行四边形的性质；相似三角形的判定和性质
上一页
下一页
末页
解：
目录
上一页
下一页
末页
目录
上一页
下一页
末页
目录
上一页
下一页
末页

解：
目录
上一页
下一页
末页
目录
上一页
下一页
末页
目录
上一页
下一页
末页
目录
上一页
下一页
末页
解：（1）同意
目录
上一页
下一页
末页
目录
上一页
下一页
末页
目录
上一页
下一页
末页
目录
上一页
下一页
末页
目录
上一页
下一页
末页

2020中考数学专题《几何变式探究和类比变换综合类问题》

2020中考数学专题《几何变式探究和类比变换综合类问题》【方法指导】图形的类比变换是近年来中考的常考点，常以三角形、四边形为背景，与翻折、旋转相结合，考查三角形全等或相似的性质与判定，难度较大．此类题目第一问相对简单，后面的问题需要结合第一问的方法进行类比解答．根据其特征大致可分为：几何变换类比探究问题、旋转综合问题、翻折类问题等．解决此类问题要善于将复杂图象分解为几个基本图形，通过添加副主席补全或构造基本图形，借助转化、方程、数形结合、分类讨论等数学思想解决几何证明问题，计算则把几何与代数知识综合起来，渗透数形结合思想，考查学生分析问题的能力、逻辑思维和推理能力. 【题型剖析】【类型1】几何类比变换综合题【例1】（2018秋•盐都区期中）【阅读理解】截长补短法，是初中数学几何题中一种辅助线的添加方法．截长就是在长边上截取一条线段与某一短边相等，补短是通过在一条短边上延长一条线段与另一短边相等，从而解决问题．（1）如图1，ABC∆是等边三角形，点D是边BC下方一点，120∠=︒，探索线段DA、BDCDB、DC之间的数量关系．解题思路：延长DC到点E，使CE BD∠+∠=︒，可证=，连接AE，根据180BAC BDC ∠=∠易证得ABD ACEABD ACE∆≅∆，得出ADE=，从而∆是等边三角形，所以AD DE 探寻线段DA、DB、DC之间的数量关系．根据上述解题思路，请直接写出DA、DB、DC之间的数量关系是____；【拓展延伸】（2）如图2，在Rt ABC∆中，90∠=︒，=．若点D是边BC下方一点，90BDCBAC∠=︒，AB AC探索线段DA、DB、DC之间的数量关系，并说明理由；【知识应用】（3）如图3，两块斜边长都为14cm的三角板，把斜边重叠摆放在一起，则两块三角板的直角顶点之间的距离PQ的长分别为____cm．【变式1-1】（2019•亭湖区二模）【阅读材料】小明遇到这样一个问题：如图1，点P 在等边三角形ABC 内，且150APC ∠=︒，3PA =，4PC =，求PB 的长．小明发现，以AP 为边作等边三角形APD ，连接BD ，得到ABD ∆；由等边三角形的性质，可证ACP ABD ∆≅∆，得PC BD =；由已知150APC ∠=︒，可知PDB ∠的大小，进而可求得PB 的长．（1）请回答：在图1中，PDB ∠=________︒，PB =____．【问题解决】（2）参考小明思考问题的方法，解决下面问题：如图2，ABC ∆中，90ACB ∠=︒，AC BC =，点P 在ABC ∆内，且1PA =，17PB =，22PC =，求AB 的长．【灵活运用】（3）如图3，在Rt ABC ∆中，90ACB ∠=︒，BAC α∠=，且4tan 3α=，点P 在ABC ∆外，且3PB =，1PC =，直接写出PA 长的最大值．【变式1-2】（2018•亭湖区二模）如图，在等腰Rt ABC ∆与等腰Rt ADE ∆中，90BAC DAE ∠=∠=︒．（1）连接BD ，CE （如图①)，请直接写出线段BD ，CE 的数量关系____；（2）在（1）的基础上，延长BD 交CE 于点F ，连接AF （如图②)，试探究线段AF ，BF ，CF 的数量关系，并证明你的结论；（3）连接BE ，取BE 的中点O ，连接AO （如图③)，若5AD =，2AO =，3tan 4DAO ∠=，求AB 的长．【类型2】几何旋转变换综合题【例2】（2019•海州区一模）如图1，将两个完全相同的三角形纸片ABC 和DEC 重合放置，其中90C ∠=︒，30B E ∠=∠=︒．（1）操作发现：如图2，固定ABC ∆，使DEC ∆绕点C 旋转，当点D 恰好落在AB 边上时，填空： ①线段DE 与AC 的位置关系是____；②设BDC ∆的面积为1S ，AEC ∆的面积为2S ，则1S 与2S 的数量关系是____．（2）猜想论证：当DEC ∆绕点C 旋转到如图3所示的位置时，小明猜想（1）中1S 与2S 的数量关系仍然成立，并尝试分别作出了BDC ∆和AEC ∆中BC 、CE 边上的高，请你证明小明的猜想．（3）拓展探究已知60ABC ∠=︒，点D 是角平分线上一点，6BD CD ==，//DE AB 交BC 于点E （如图4)，若在射线BA 上存在点F ，使DCF BDE S S ∆∆=，请求出相应的BF 的长．【变式2-1】（2019•辽阳模拟）旋转变换是解决数学问题中一种重要的思想方法，通过旋转变换可以将分散的条件集中到一起，从而方便解决问题．已知，ABC ∆中，AB AC =，BAC α∠=，点D 、E 在边BC 上，且12DAE α∠=．（1）如图1，当60α=︒时，将AEC ∆绕点A 顺时针旋转60︒到AFB ∆的位置，连接DF ， ①求DAF ∠的度数；②求证：ADE ADF ∆≅∆；（2）如图2，当90α=︒时，猜想BD 、DE 、CE 的数量关系，并说明理由；（3）如图3，当120α=︒，4BD =，5CE =时，请直接写出DE 的长为____．【变式2-2】（2019•宜兴市二模）【问题提出】如图1，四边形ABCD 中，AD CD =，120ABC ∠=︒，60ADC ∠=︒，2AB =，1BC =，求四边形ABCD 的面积．【尝试解决】旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．（1）如图2，连接BD ，由于AD CD =，所以可将DCB ∆绕点D 顺时针方向旋转60︒，得到DAB ∆'，则BDB ∆'的形状是____________．（2）在（1）的基础上，求四边形ABCD 的面积．[类比应用]如图3，四边形ABCD 中，AD CD =，75ABC ∠=︒，60ADC ∠=︒，2AB =，2BC =，求四边形ABCD 的面积．【类型3】几何翻折变换综合题【例3】（2019•江都区三模）如图1，有一张矩形纸片ABCD ，已知5AB =，6AD =，现将纸片进行如下操作：首先将纸片沿折痕BF 进行折叠，使点A 落在BC 边上的点E 处，点F 在AD 上（如图2)；然后将纸片沿折痕DH 进行第二次折叠，使点C 落在第一次的折痕BF 上的点G 处，点H 在BC 上（如图3)．（1）如图2，判断四边形ABEF 的形状，并说明理由；（2）如图3，求BG 的长．【变式3-1】（2019•广陵区校级二模）如图，将矩形ABCD 先过点A 的直线1L 翻折，点DA 的对应点D '刚好落在边BC 上，直线1L 交DC 于点F ；再将矩形ABCD 沿过点A 的直线2L 翻折，使点B 的对应点G 落在AD '上，EG 的延长线交AD 于点H ．（1）当四边形AED H '是平行四边形时，求AD H ∠'的度数．（2）当点H 与点D 刚好重合时，试判断AEF ∆的形状，并说明理由．【变式3-2】（2018•深圳模拟）已知矩形纸片ABCD 中，2AB =，3BC =．操作：将矩形纸片沿EF 折叠，使点B 落在边CD 上．探究：（1）如图1，若点B 与点D 重合，你认为1EDA ∆和FDC ∆全等吗？如果全等，请给出证明，如果不全等，请说明理由；（2）如图2，若点B 与CD 的中点重合，请你判断1FCB ∆、△1B DG 和△1EAG 之间的关系，如果全等，只需写出结果，如果相似，请写出结果和相应的相似比；（3）如图2，请你探索，当点B 落在CD 边上何处，即1B C 的长度为多少时，1FCB ∆与△1B DG 全等．【达标检测】1．如图1，在Rt △ABC 中，AB ＝AC ，D 、E 是斜边BC 上两动点，且∠DAE ＝45°，将△ABE 绕点A 逆时针旋转90后，得到△AFC ，连接DF ．（1）试说明：△AED ≌△AFD ；（2）当BE ＝3，CE ＝9时，求∠BCF 的度数和DE 的长；（3）如图2，△ABC 和△ADE 都是等腰直角三角形，∠BAC ＝∠DAE ＝90°，D 是斜边BC 所在直线上一点，BD ＝3，BC ＝8，求DE 2的长．2．如图①，在等腰△ABC和△ADE中，AB＝AC，AD＝AE，且∠BAC＝∠DAE＝120°．（1）求证：△ABD≌△ACE；（2）把△ADE绕点A逆时针方向旋转到图②的位置，连接CD，点M、P、N分别为DE、DC、BC的中点，连接MN、PN、PM，判断△PMN的形状，并说明理由；（3）在（2）中，把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝6，请分别求出△PMN周长的最小值与最大值．3．如图，在平面直角坐标系xOy中，点A（0，4），B（﹣4，0），C（4，0），D（0，﹣4），连接AB，AC，BD，点P是线段AB上的一个动点，连接PD，过点P作PE⊥PD，交线段AC于点E，将线段EP绕点E逆时针旋转90°至EF．（1）过点P的横坐标为，则AE＝__________；（2）当点P在线段AB上运动到何处时，线段AE最长？求出此时点P的坐标；（3）连接OF．当点P在线段AB上运动时，线段OF的长度随之变化，求线段OF长度的最小值．4．如图1，Rt△ABC中，∠C＝90°，AB＝15，BC＝9，点D，E分别在AC，BC上，CD ＝4x，CE＝3x，其中0＜x＜3．（1）求证：DE∥AB；（2）当x＝1时，求点E到AB的距离；（3）将△DCE绕点E逆时针方向旋转，使得点D落在AB边上的D′处．在旋转的过程中，若点D′的位置有且只有一个，求x的取值范围．5．在△ABC中，∠B＝45°，∠C＝30°，作AP⊥AB，交BC于P点．（1）如图1，若AB＝3，求BC的长；（2）点D是BC边上一点，连接AD，将线段AD绕点A逆时针旋转90°，得到线段AE．①如图2，当点E落在AC边上时，求证：CE＝2BD；②如图3，当AD⊥BC时，直接写出的值．6．【操作发现】如图1，△ABC为等边三角形，点D为AB边上的一点，∠DCE＝30°，将线段CD绕点C顺时针旋转60°得到线段CF，连接AF、EF，请直接写出下列结果：①∠EAF的度数为________；②DE与EF之间的数量关系为__________；【类比探究】如图2，△ABC为等腰直角三角形，∠ACB＝90°，点D为AB边上的一点，∠DCE＝45°，将线段CD绕点C顺时针旋转90°得到线段CF，连接AF、EF．①则∠EAF的度数为__________；②线段AE，ED，DB之间有什么数量关系？请说明理由；【实际应用】如图3，△ABC是一个三角形的余料，小张同学量得∠ACB＝120°，AC＝BC，他在边BC上取了D、E两点，并量得∠BCD＝15°、∠DCE＝60°，这样CD、CE 将△ABC分成三个小三角形，请求△BCD、△DCE、△ACE这三个三角形的面积之比．7．综合与实践：如图1，已知△ABC为等边三角形，点D，E分别在边AB、AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点．（1）观察猜想在图1中，线段PM与PN的数量关系是______________，∠MPN的度数是____________；（2）探究证明把△ADE绕点A逆时针方向旋转到图2的位置，①判断△PMN的形状，并说明理由；②求∠MPN的度数；（3）拓展延伸若△ABC为直角三角形，∠BAC＝90°，AB＝AC＝10，点DE分别在边AB，AC上，AD ＝AE＝4，连接DC，点M，P，N分别为DE，DC，BC的中点．把△ADE绕点A在平面内自由旋转，如图3，请直接写出△PMN面积的最大值．8．【问题提出】在△ABC中，AB＝AC≠BC，点D和点A在直线BC的同侧，BD＝BC，∠BAC＝α，∠DBC＝β，且α+β＝120°，连接AD，求∠ADB的度数．（不必解答）【特例探究】小聪先从特殊问题开始研究，当α＝90°，β＝30°时，利用轴对称知识，以AB为对称轴构造△ABD的轴对称图形△ABD′，连接CD′（如图2），然后利用α＝90°，β＝30°以及等边三角形等相关知识便可解决这个问题．请结合小聪研究问题的过程和思路，在这种特殊情况下填空：△D′BC的形状是________三角形；∠ADB的度数为________．【问题解决】在原问题中，当∠DBC＜∠ABC（如图1）时，请计算∠ADB的度数；【拓展应用】在原问题中，过点A作直线AE⊥BD，交直线BD于E，其他条件不变若BC＝7，AD＝2．请直接写出线段BE的长为________________．9．点D为△ABC外一点，∠ACB＝90°，AC＝BC．（1）如图1，∠DCE＝90°，CD＝CE，求证：∠ADC＝∠BEC；（2）如图2，若∠CDB＝45°，AE∥BD，CE⊥CD，求证：AE＝BD；（3）如图3，若∠ADC＝15°，CD，BD＝n，请直接用含n的式子表示AD的长．10．如图，△ABC是等边三角形，D是BC边的中点，以D为顶点作一个120°的角，角的两边分别交直线AB、直线AC于M、N两点．以点D为中心旋转∠MDN（∠MDN的度数不变），当DM与AB垂直时（如图①所示），易证BM+CN＝BD．（1）如图②，当DM与AB不垂直，点M在边AB上，点N在边AC上时，BM+CN＝BD是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（2）如图③，当DM与AB不垂直，点M在边AB上，点N在边AC的延长线上时，BM+CN＝BD是否仍然成立？若不成立，请写出BM，CN，BD之间的数量关系，不用证明．11．在△ABC中，∠ACB＝90°，AC＝BC，点P在边AB上，点D、Q分别为边BC上的点，线段AD的延长线与线段PQ的延长线交于点F，连接CP交AF于点E，若∠BPF ＝∠APC，FD＝FQ．（1）如图1，求证：AF⊥CP；（2）如图2，作∠AFP的平分线FM交AB于点M，交BC于点N，若FN＝MN，求证：DQ BC；（3）在（2）的条件下，连接DM、MQ，分别交PC于点G、H，求的值．12．已知△ABC和△ADE都是等腰直角三角形，∠ACB＝∠ADE＝90°，点F为BE中点，连结DF，CF．（1）如图1，点D在AC上，请你判断此时线段DF，CF的关系，并证明你的判断；（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45时，若AD＝DE＝2，AB ＝6，求此时线段CF的长．13．如图①，将一个矩形纸片OABC放置在平面直角坐标系中，点A坐标是（3，0），点C 坐标是（0，2），点O的坐标是（0，0），点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．（1）求点E、F的坐标；（2）如图2，若点P是线段DA上的一个动点（点P不与点D，A重合），过P作PH⊥DB于H，设OP的长为x，△DPH的面积为S，试用关于x的代数式表示S．14．如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A，点D重合）将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC 于H，折痕为EF，连接BP，BH．（1）求证：BP平分∠APH；（2）当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论．15．已知：矩形ABCD中，AB＝4，BC＝3，点M、N分别在边AB、CD上，直线MN交矩形对角线AC于点E，将△AME沿直线MN翻折，点A落在点P处，且点P在射线CB 上（Ⅰ）如图①，当EP⊥BC时，①求证CE＝CN；②求CN的长；（Ⅱ）请写出线段CP的长的取值范围，及当CP的长最大时MN的长．【题型剖析】【类型1】几何类比变换综合题【例1】（2018秋•盐都区期中）【阅读理解】截长补短法，是初中数学几何题中一种辅助线的添加方法．截长就是在长边上截取一条线段与某一短边相等，补短是通过在一条短边上延长一条线段与另一短边相等，从而解决问题．（1）如图1，ABC∆是等边三角形，点D是边BC下方一点，120BDC∠=︒，探索线段DA、DB、DC之间的数量关系．解题思路：延长DC到点E，使CE BD∠+∠=︒，可证BAC BDC=，连接AE，根据180∠=∠易证得ABD ACEABD ACE∆≅∆，得出ADE=，从而∆是等边三角形，所以AD DE 探寻线段DA、DB、DC之间的数量关系．根据上述解题思路，请直接写出DA、DB、DC之间的数量关系是；【拓展延伸】（2）如图2，在Rt ABC ∆中，90BAC ∠=︒，AB AC =．若点D 是边BC 下方一点，90BDC ∠=︒，探索线段DA 、DB 、DC 之间的数量关系，并说明理由；【知识应用】（3）如图3，两块斜边长都为14cm 的三角板，把斜边重叠摆放在一起，则两块三角板的直角顶点之间的距离PQ 的长分别为 cm ．【分析】（1）由等边三角形知AB AC =，60BAC ∠=︒，结合120BDC ∠=︒知180ABD ACD ∠+∠=︒，由180ACE ACD ∠+∠=︒知ABD ACE ∠=∠，证ABD ACE ∆≅∆得AD AE =，BAD CAE ∠=∠，再证ADE ∆是等边三角形得DA DE DC CE DC DB ==+=+．（2）延长DC 到点E ，使CE BD =，连接AE ，先证ABD ACE ∆≅∆得AD AE =，BAD CAE ∠=∠，据此可得90DAE BAC ∠=∠=︒，由勾股定理知222DA AE DE +=，继而可得222()DA DB DC =+；（3）由直角三角形的性质知172QN MN ==，2273MQ MN QN -，利用（2）中的273PQ QN QM =+=+ 【解析】（1）如图1，延长DC 到点E ，使CE BD =，连接AE ，ABC ∆Q 是等边三角形， AB AC ∴=，60BAC ∠=︒， 120BDC ∠=︒Q ，180ABD ACD ∴∠+∠=︒，又180ACE ACD ∠+∠=︒Q ，ABD ACE ∴∠=∠，()ABD ACE SAS ∴∆≅∆，AD AE ∴=，BAD CAE ∠=∠，60ABC ∠=︒Q ，即60BAD DAC ∠+∠=︒，60DAC CAE ∴∠+∠==︒，即60DAE ∠=︒，ADE ∴∆是等边三角形，DA DE DC CE DC DB ∴==+=+，即DA DC DB =+，故答案为：DA DC DB =+；（2）2DA DB DC =+，如图2，延长DC 到点E ，使CE BD =，连接AE ，90BAC ∠=︒Q ，90BDC ∠=︒， 180ABD ACD ∴∠+∠=︒， 180ACE ACD ∠+∠=︒Q ， ABD ACE ∴∠=∠， AB AC =Q ，CE BD =， ABD ACE ∴∆≅∆，AD AE ∴=，BAD CAE ∠=∠， 90DAE BAC ∴∠=∠=︒， 222DA AE DE ∴+=，222()DA DB DC ∴=+， ∴2DA DB DC =+；（3）如图3，连接PQ ，14MN =Q ，30QMN ∠=︒，172QN MN ∴==，MQ ∴由（27QN QM =+=+，PQ ∴==【点评】此题是三角形的综合题，主要考查了考查的是全等三角形的判定和性质、直角三角形的性质、等边三角形的性质，掌握全等三角形的判定定理和性质定理是解题的关键．【变式1-1】（2019•亭湖区二模）【阅读材料】小明遇到这样一个问题：如图1，点P 在等边三角形ABC 内，且150APC ∠=︒，3PA =，4PC =，求PB 的长．小明发现，以AP 为边作等边三角形APD ，连接BD ，得到ABD ∆；由等边三角形的性质，可证ACP ABD ∆≅∆，得PC BD =；由已知150APC ∠=︒，可知PDB ∠的大小，进而可求得PB 的长．（1）请回答：在图1中，PDB ∠= ︒，PB = ．【问题解决】（2）参考小明思考问题的方法，解决下面问题：如图2，ABC ∆中，90ACB ∠=︒，AC BC =，点P 在ABC ∆内，且1PA =，PB =PC =AB 的长．【灵活运用】（3）如图3，在Rt ABC ∆中，90ACB ∠=︒，BAC α∠=，且4tan 3α=，点P 在ABC ∆外，且3PB =，1PC =，直接写出PA 长的最大值．【分析】（1）由ACP ABD ∆≅∆，得150ADB APC ∠=∠=︒，4PC BD ==，3AD AP ==，因为ADP ∆为等边三角形，所以60ADP ∠=︒，3DP AD ==，可得90BDP ∠=︒，在Rt BDP ∆中，用勾股定理可求得PB 的长；（2）如图2中，把ACP ∆绕点C 逆时针旋转90︒得到BCD ∆．首先证明90PDB ∠=︒，再证明A ，P ，D 共线，利用勾股定理即可解决问题．（3）如图3中，作CD CP ⊥，使得3344CD PC ==，则2254PD PC CD =+=，利用相似三角形的性质求出AD ，即可解决问题．【解析】（1）如图1中，ACP ABD ∆≅∆Q ，150PDB APC ∴∠=∠=︒，4PC BD ==，3AD AP ==，ADP ∆Q 为等边三角形， 60ADP ∴∠=︒，3DP AD ==， 1506090BDP ∴∠=︒-︒=︒，22345PB ∴=+=．故答案为：90︒，5；（2）如图2中，把ACP ∆绕点C 逆时针旋转90︒得到BCD ∆．由旋转性质可知；1BD PA ==，22CD CP ==，90PCD ∠=︒，PCD ∴∆是等腰直角三角形，22224PD PC ∴==⨯=，45CDP ∠=︒，22224117PD BD +=+=Q ，22(17)17PB ==，222PD BD PB ∴+=，90PDB ∴∠=︒， 135BDC ∴∠=︒，135APC CDB ∴∠=∠=︒，45CPD ∠=︒Q ， 180APC CPD ∴∠+∠=︒，A ∴，P ，D 共线， 5AD AP PD ∴=+=，在RtADB 中，22225126AB AD BD =+=+=．（3）如图3中，作CD CP ⊥，使得3344CD PC ==，则2254PD PC CD =+=，4tan 3BC BAC AC ∠==Q ， ∴BC PCAC CD=， 90ACB PCD ∠=∠=︒Q ， ACD BCP ∴∠=∠， ACD BCP ∴∆∆∽，∴34AD CD PB PC ==， 94AD ∴=， Q93954444PA -+剟，∴3722PA 剟， PA ∴的最大值为72．【变式1-2】（2018•亭湖区二模）如图，在等腰Rt ABC ∆与等腰Rt ADE ∆中，90BAC DAE ∠=∠=︒．（1）连接BD ，CE （如图①)，请直接写出线段BD ，CE 的数量关系；（2）在（1）的基础上，延长BD 交CE 于点F ，连接AF （如图②)，试探究线段AF ，BF ，CF 的数量关系，并证明你的结论；（3）连接BE ，取BE 的中点O ，连接AO （如图③)，若5AD =，2AO =，3tan 4DAO ∠=，求AB 的长．【分析】（1）结论：BD EC =．只要证明BAD CAE ∆≅∆即可解决问题；（2）结论：2BF FA FC =．如图②中，作AM AF ⊥交BF 于M ．想办法证明BM FC =，MAF ∆是等腰直角三角形即可解决问题；（3）如图③中，作DM AO ⊥交AO 的延长线于M ，作EN OA ⊥交OA 的延长线于N ，作AH EO ⊥于H ．想办法求出AH ，BH 即可解决问题；【解析】（1）结论：BD CE =．理由：如图①中，AB AC =Q ，AD AE =，90BAC DAE ∠=∠=︒， BAD CAE ∴∆≅∆， BD EC ∴=．故答案为BD EC =．（2）结论：2BF FA FC =．理由：如图②中，作AM AF ⊥交BF 于M ．BAD CAE∆≅∆Q，ABM ACF∴∠=∠，90BAC MAF∠=∠=︒Q，BAM CAF∴∠=∠，AB AC=Q，BAM CAF∴∆≅∆，BM CF∴=，AM AF=，AMF∴∆是等腰直角三角形，2FM FA∴=，2FB FM BM CF AF∴=+=+，2BF AF FC∴-=．（3）如图③中，作DM AO⊥交AO的延长线于M，作EN OA⊥交OA的延长线于N，作AH EO⊥于H．在Rt ADM∆中，3tan4DMDAMAM∠==，设3DM k=，4AM k=，则有222(3)(4)5k k+=，解得1k=±，k>Q，1k∴=，3DM∴=，4AM=，2OA =Q ， 2OM ∴=，由ADM EAN ∆≅∆，可得4NE AM ==，3AN DM ==，在Rt ENO ∆中，EO =OH x =， 22222AH OA OH AE EH =-=-Q ，222225)x x ∴-=-，解得x =，OH ∴AH ，在Rt ABH ∆中，AB ==【类型2】几何旋转变换综合题【例2】（2019•海州区一模）如图1，将两个完全相同的三角形纸片ABC 和DEC 重合放置，其中90C ∠=︒，30B E ∠=∠=︒．（1）操作发现：如图2，固定ABC ∆，使DEC ∆绕点C 旋转，当点D 恰好落在AB 边上时，填空： ①线段DE 与AC 的位置关系是；②设BDC ∆的面积为1S ，AEC ∆的面积为2S ，则1S 与2S 的数量关系是．（2）猜想论证：当DEC ∆绕点C 旋转到如图3所示的位置时，小明猜想（1）中1S 与2S 的数量关系仍然成立，并尝试分别作出了BDC ∆和AEC ∆中BC 、CE 边上的高，请你证明小明的猜想．（3）拓展探究已知60ABC ∠=︒，点D 是角平分线上一点，6BD CD ==，//DE AB 交BC 于点E （如图4)，若在射线BA 上存在点F ，使DCF BDE S S ∆∆=，请求出相应的BF 的长．【分析】（1）①证明60EDC DCA ∠=∠=︒即可判断．②首先证明AD BD =，推出ADC ∆与BDC ∆的面积相等，再证明ADC ∆与ACE ∆的面积相等即可．（2）作AN EC ⊥交EC 的延长线于N ，DM BC ⊥于M ，证明()ACN DCM AAS ∆≅∆即可解决问题．（3）分两种情形分别求解即可解决问题．【解析】（1）①如图1中，由旋转可知：CA CD =，90ACB ∠=︒Q ，30B ∠=︒， 60CAD ∴∠=︒， ADC ∴∆是等边三角形， 60DCA ∴∠=︒，90ECD ∠=︒Q ，30DEC ∠=︒， 60CDE ∴∠=︒， EDC DCA ∴∠=∠，//DE AC ∴，②2AB AC =Q ，AD AC =，AD BD ∴=，BDC ADC S S ∆∆∴=，//DE AC Q ，ADC ACE S S ∆∆∴=， 12S S ∴=．故答案为：//DE AC ，12S S =．（2）如图3中，DEC ∆Q 是由ABC ∆绕点C 旋转得到， BC CE ∴=，AC CD =，90ACN BCN ∠+∠=︒Q ，1809090DCM BCN ∠+∠=︒-︒=︒， ACN DCM ∴∠=∠，在ACN ∆和DCM ∆中， 90ACN DCM ANC DMC AC CD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ()ACN DCM AAS ∴∆≅∆，AN DM ∴=，BDC AEC S S ∆∆∴=．（3）如图4中，作//DF BC 交AB 于F ．延长CD 交AB 于H ．//DF BE Q ，//DE BF ，∴四边形DEBF 是平行四边形，BDF BDE S S ∆∆∴=，BDF DFC S S ∆∆=， DFC BDE S S ∆∆∴=，60ABC ∠=︒Q ，BD 平分ABC ∠， 30ABD DBE ∴∠=∠=︒， //DF BE Q ， 30FDB ∴∠=︒， 30FBD FDB ∴∠=∠=︒，FB FD ∴=，∴四边形DEBF 是菱形，6BD CD ==Q ， 30DBC DCB ∴∠=∠=︒， 60DEC ABC ∠=∠=︒Q ， 90CDE ∴∠=︒，3tan30623DE CD ∴=︒==g 23BF DE ∴==//DE AB Q ，90BHC EDC ∴∠=∠=︒，CH AB ∴⊥，作点F 关于CH 的对称点F '，连接DF '，易知DFC DF C S S ∆'=V ，在Rt DFH ∆中，sin303FH HF DF ='=︒=g ， 43BF ∴'=综上所述，满足条件的BF 的值为23或43．【点评】本题属于几何变换综合题，考查了旋转变换，全等三角形的判定和性质，菱形的判定和性质，等边三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造特殊四边形解决问题，属于中考压轴．【变式2-1】（2019•辽阳模拟）旋转变换是解决数学问题中一种重要的思想方法，通过旋转变换可以将分散的条件集中到一起，从而方便解决问题．已知，ABC ∆中，AB AC =，BAC α∠=，点D 、E 在边BC 上，且12DAE α∠=．（1）如图1，当60α=︒时，将AEC ∆绕点A 顺时针旋转60︒到AFB ∆的位置，连接DF ， ①求DAF ∠的度数； ②求证：ADE ADF ∆≅∆；（2）如图2，当90α=︒时，猜想BD 、DE 、CE 的数量关系，并说明理由；（3）如图3，当120α=︒，4BD =，5CE =时，请直接写出DE 的长为．【分析】（1）①利用旋转的性质得出FAB CAE ∠=∠，再用角的和即可得出结论； ②利用SAS 判断出ADE ADF ∆≅∆，即可得出结论；（2）先判断出BF CE =，ABF ACB ∠=∠，再判断出90DBF ∠=︒，即可得出结论；（3）同（2）的方法判断出60DBF ∠=︒，再用含30度角的直角三角形求出BM ，FM ，最后用勾股定理即可得出结论．【解析】（1）①由旋转得，FAB CAE ∠=∠，603030BAD CAE BAC DAE ∠+∠=∠-∠=︒-︒=︒Q ， 30DAF BAD BAF BAD CAE ∴∠=∠+∠=∠+∠=︒；②由旋转知，AF AE =，BAF CAE ∠=∠，BAF BAD CAE BAD BAC DAE DAE ∴∠+∠=∠+∠=∠-∠=∠，在ADE ∆和ADF ∆中，AF AEDAF DAE AD AD =⎧⎪∠=∠⎨⎪=⎩，()ADE ADF SAS ∴∆≅∆；（2）222BD CE DE +=，理由：如图2，将AEC ∆绕点A 顺时针旋转90︒到AFB ∆的位置，连接DF ，BF CE ∴=，ABF ACB ∠=∠，由（1）知，ADE ADF ∆≅∆，DE DF ∴=，AB AC =Q ，90BAC ∠=︒， 45ABC ACB ∴∠=∠=︒，90DBF ABC ABF ABC ACB ∴∠=∠+∠=∠+∠=︒，根据勾股定理得，222BD BF DF +=，即：222BD CE DE +=；（3）如图3，将AEC ∆绕点A 顺时针旋转120︒到AFB ∆的位置，连接DF ，BF CE ∴=，ABF ACB ∠=∠，由（1）知，ADE ADF ∆≅∆，DE DF ∴=，5BF CE ==， AB AC =Q ，120BAC ∠=︒， 30ABC ACB ∴∠=∠=︒，60DBF ABC ABF ABC ACB ∴∠=∠+∠=∠+∠=︒，过点F 作FM BC ⊥于M ，在Rt BMF ∆中，9030BFM DBF ∠=︒-∠=︒，5BF =，52BM ∴=，FM = 4BD =Q ，32DM BD BM ∴=-=，根据勾股定理得，DF ==DE DF ∴==【变式2-2】（2019•宜兴市二模）【问题提出】如图1，四边形ABCD 中，AD CD =，120ABC ∠=︒，60ADC ∠=︒，2AB =，1BC =，求四边形ABCD 的面积．【尝试解决】旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．（1）如图2，连接BD ，由于AD CD =，所以可将DCB ∆绕点D 顺时针方向旋转60︒，得到DAB ∆'，则BDB ∆'的形状是．（2）在（1）的基础上，求四边形ABCD 的面积．[类比应用]如图3，四边形ABCD 中，AD CD =，75ABC ∠=︒，60ADC ∠=︒，2AB =，2BC =，求四边形ABCD 的面积．【分析】（1）易证DEB DAB ∆≅∆'，则BD DB ='，60BDB ∠'=︒，所以BDB ∆'是等边三角形；（2）知等边三角形的边长为3，求出S BDB ∆'即可；【类比应用】类比（1），连接BD ，由于AD CD =，所以可将BCD ∆绕点D 逆时针方向旋转60︒，得到DAB ∆'，连接BB '，延长BA ，作B E BE '⊥；易证AFB ∆'是等腰直角三角形，AEB ∆是等腰直角三角形，利用勾股定理计算1AE B E ='=，10BB '=ABB ∆'和BDB ∆'的面积和即可．【解析】（1）如图2，连接BD ，由于AD CD =，所以可将DCB ∆绕点D 顺时针方向旋转60︒，得到DAB ∆'，BD B D ='Q ，60BDB ∠'=︒BDB ∴∆'是等边三角形；（2）由（1）知，BCD ∆≅△B AD '，∴四边形ABCD 的面积=等边三角形BDB '的面积，1BC AB ='=Q213BB AB AB ∴'=+'=+=，132BDB ABCD S S ∆'∴==⨯=四边形；【类比应用】如图3，连接BD ，由于AD CD =，所以可将BCD ∆绕点D 逆时针方向旋转60︒，得到DAB ∆'，连接BB '，延长BA ，作B E BE '⊥； Q AD CDCDB ADB BD B D =⎧⎪∠=∠'⎨⎪='⎩， BCD ∴∆≅△B AD 'ABCD BDB A S S '∴=四边形四边形，75ABC ∠=︒Q ，60ADC ∠=︒， 135BAB ∴∠'=︒45B AE ∴∠'=︒，B A BC '=Q1B E AE ∴'==，213BE AB AE ∴=+=+=，BB ∴'，1121122ABB S AB B E ∆'∴='=⨯⨯=g g ，12S BDB ∆'==，1ABB ABCD BDB A S S S BDB S ∆''∴==∆'-=四边形四边形．【类型3】几何翻折变换综合题【例3】（2019•江都区三模）如图1，有一张矩形纸片ABCD ，已知5AB =，6AD =，现将纸片进行如下操作：首先将纸片沿折痕BF 进行折叠，使点A 落在BC 边上的点E 处，点F 在AD 上（如图2)；然后将纸片沿折痕DH 进行第二次折叠，使点C 落在第一次的折痕BF 上的点G 处，点H 在BC 上（如图3)．（1）如图2，判断四边形ABEF 的形状，并说明理由；（2）如图3，求BG 的长．【分析】（1）由折叠可得：AB BE =，且90A ABE BEF ∠=∠=∠=︒，即可得出结论；’ （2）过G 点作//MN AB ，交AD 、BC 于点M 、N ，由四边形ABEF 为正方形，可求得AF 的长，得出BNG ∆和FMG ∆为等腰直角三角形，设BN x =，则可表示出GN 、MG 、MD ，利用折叠的性质可得到CD DG =，在Rt MDG ∆中，利用勾股定理可求得x ，即可得出结果．【解析】（1）四边形ABEF 是正方形，理由如下： Q 四边形ABCD 为矩形，5AB CD ∴==，6BC AD ==，由折叠可得：AB BE =，且90A ABE BEF ∠=∠=∠=︒， ∴四边形ABEF 为正方形；（2）过点G 作//MN AB ，分别交AD 、BC 于点M 、N ，如图3所示：Q 四边形ABEF 是正方形，5AF AB ∴==， //MN AB Q ，BNG ∴∆和FMG ∆为等腰直角三角形，且5MN AB ==，设BN x =，则GN AM x ==，5MG MN GN x =-=-，6MD AD AM x =-=-，又由折叠的性质可知：5DG DC ==，在Rt MDG ∆中，由勾股定理可得222MD MG GD +=，即222(6)(5)5x x -+-=，解得：2x =，2GN BN ∴==，222BG BN ∴==．【点评】本题考查了翻折变换的性质、矩形的性质、正方形的判定和性质、等腰直角三角形的性质、勾股定理等知识；熟练掌握正方形的判定与性质，由勾股定理得出方程是解题的关键．【变式3-1】（2019•广陵区校级二模）如图，将矩形ABCD 先过点A 的直线1L 翻折，点DA 的对应点D '刚好落在边BC 上，直线1L 交DC 于点F ；再将矩形ABCD 沿过点A 的直线2L 翻折，使点B 的对应点G 落在AD '上，EG 的延长线交AD 于点H ．（1）当四边形AED H '是平行四边形时，求AD H ∠'的度数．（2）当点H 与点D 刚好重合时，试判断AEF ∆的形状，并说明理由．【分析】（1）如图1中，在RT ABC ∆中，由2AD AB '=推出30AD B ∠'=︒，再证明四边形AED H '是菱形即可解决问题．（2）如图2中，先证明△DD G '≅△DD C '得出DG DC AB AG ===，发现AGD ∆、GED ∆'、DEC ∆都是等腰直角三角形，再证明ABE ECF ∆≅∆即可解决问题．【解析】（1）如图1中，Q 四边形AED H '是平行四边形，AG GD ∴=，EH AD ⊥Q ，∴四边形AED H '是菱形，AD H AD B ∴∠'=∠'，AEG ∆Q 是由AEB ∆翻折得到， AB AG D G ∴=='，Q 四边形ABCD 是矩形，90B ∴∠=︒， 30AD B ∴∠'=︒， 30AD H ∴∠'=︒．（2）结论：AEF ∆是等腰直角三角形．理由：如图2中，连接DD '． Q 四边形ABCD 是矩形，//AD BC ∴，ADD DD C ∠'=∠'，AB DC =，90B C ∠=∠=︒，AD AD ='Q ， ADD AD D ∴∠'=∠'， DD A DD C ∴∠'=∠'，在△DD G ' 和△DD C '中，DGD DCD DD G DD C DD DD ∠'=∠'⎧⎪∠'=∠'⎨⎪'='⎩， ∴△DD G '≅△DD C '，DG DC AB AG ∴===，90AGD ∠=︒Q ，45GAD GDA AD E DED ∴∠=∠=∠'=∠'=︒， EG GD BE CD ∴='=='， 90AD B FD C ∠'+∠'=︒Q ， 45FD C D FC ∴∠'=''=︒， CD CF BE ∴'==，45CED CDE ∠=∠=︒Q ， EC CD AB ∴==，在ABE ∆和ECF ∆中， 90AB EC B C BE CF =⎧⎪∠=∠=︒⎨⎪=⎩， ABE ECF ∴∆≅∆，AE EF ∴=，BAE CEF ∠=∠， 90BAE AEB ∠+∠=︒Q ， 90AEB CEF ∴∠+∠=︒， 90AEF ∴∠=︒，AEF ∴∆是等腰直角三角形．【点评】本题考查翻折变换、矩形的性质、菱形的判定和性质、全等三角形的判定和性质、等腰直角三角形的判定等知识，第一问的关键是菱形性质的应用，第二个问题的关键是正确寻找全等三角形，利用特殊三角形解决问题，属于中考常考题型．【变式3-2】（2018•深圳模拟）已知矩形纸片ABCD 中，2AB =，3BC =．操作：将矩形纸片沿EF 折叠，使点B 落在边CD 上．探究：（1）如图1，若点B 与点D 重合，你认为1EDA ∆和FDC ∆全等吗？如果全等，请给出证明，如果不全等，请说明理由；（2）如图2，若点B 与CD 的中点重合，请你判断1FCB ∆、△1B DG 和△1EAG 之间的关系，如果全等，只需写出结果，如果相似，请写出结果和相应的相似比；（3）如图2，请你探索，当点B 落在CD 边上何处，即1B C 的长度为多少时，1FCB ∆与△1B DG 全等．【分析】（1）由四边形ABCD 是矩形，可得90A B C ADC ∠=∠=∠=∠=︒，AB CD =，由折叠的性质可得：1A A ∠=∠，190B A DF ∠=∠=︒，1CD A D =，然后利用同角的余角相等，可证得1A DE CDF ∠=∠，则可利用ASA 证得1EDA ∆和FDC ∆全等；（2）易得△1B DG 和△1EAG 全等，1FCB ∆与△1B DG 相似，然后设FC x =，由勾股定理可得方程2221(3)x x +=-，解此方程即可求得答案；（3）设1B C a =，则有12FC B D a ==-，11B F BF a ==+，在直角1FCB ∆中，可得222(1)(2)a a a +=-+，解此方程即可求得答案．【解析】（1）全等．证明：Q 四边形ABCD 是矩形，90A B C ADC ∴∠=∠=∠=∠=︒，AB CD =，由题意知：1A A ∠=∠，190B A DF ∠=∠=︒，1CD A D =， 190A C ∴∠=∠=︒，90CDF EDF ∠+∠=︒， 1A DE CDF ∴∠=∠，在1EDA ∆和FDC ∆中， 111A C A D CDA DE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩，1()EDA FDC ASA ∴∆≅∆；（2）△1B DG 和△1EAG 全等，1FCB ∆与△1B DG 相似，设FC x =，则13B F BF x ==-，1112B C DC ==， 2221(3)x x ∴+=-，43x ∴=， 1FCB ∴∆与△1B DG 相似，相似比为4:3．（3）1FCB ∆与△1B DG 全等．设1B C a =，则有12FC B D a ==-，11B F BF a ==+，在直角1FCB ∆中，可得222(1)(2)a a a +=-+，整理得2630a a -+=，解得：36a =-（另一解舍去），∴当136B C =-时，1FCB ∆与△1B DG 全等．【达标检测】1．如图1，在Rt △ABC 中，AB ＝AC ，D 、E 是斜边BC 上两动点，且∠DAE ＝45°，将△ABE 绕点A 逆时针旋转90后，得到△AFC ，连接DF ．（1）试说明：△AED ≌△AFD ；（2）当BE ＝3，CE ＝9时，求∠BCF 的度数和DE 的长；（3）如图2，△ABC 和△ADE 都是等腰直角三角形，∠BAC ＝∠DAE ＝90°，D 是斜边BC 所在直线上一点，BD ＝3，BC ＝8，求DE 2的长．【分析】（1）想办法证明∠DAE ＝∠DAF ，由DA ＝DA ，AE ＝AF ，即可证明；（2）如图1中，设DE＝x，则CD＝9﹣x．在Rt△DCF中，由DF2＝CD2+CF2，CF＝BE＝3，推出x2＝（9﹣x）2+32，解方程即可；（3）分两种情形①当点E在线段BC上时，如图2中，连接BE．由△EAD≌△ADC，推出∠ABE＝∠C＝∠ABC＝45°，EB＝CD＝5，推出∠EBD＝90°，推出DE2＝BE2+BD2＝52+32＝34；②当点D在CB的延长线上时，如图3中，同法可得DE2＝130；【解析】（1）如图1中，∵△BAE≌△CAF，∴AE＝AF，∠BAE＝∠CAF，∵∠BAC＝90°，∠EAD＝45°，∴∠CAD+∠BAE＝∠CAD+∠CAF＝45°，∴∠DAE＝∠DAF，∵DA＝DA，AE＝AF，∴△AED≌△AFD；（2）如图1中，设DE＝x，则CD＝9﹣x．∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝45°，∵∠ABE＝∠ACF＝45°，∴∠DCF＝90°，∵△AED≌△AFD，∴DE＝DF＝x，在Rt△DCF中，∵DF2＝CD2+CF2，CF＝BE＝3，∴x2＝（9﹣x）2+32，∴x＝5，∴DE＝5．（3）①当点E在线段BC上时，如图2中，连接BE．∵∠BAC＝∠EAD＝90°，∴∠EAB＝∠DAC，∵AE＝AD，AB＝AC，∴△EAD≌△ADC，∴∠ABE＝∠C＝∠ABC＝45°，EB＝CD＝5，∴∠EBD＝90°，∴DE2＝BE2+BD2＝52+32＝34，②当点D在CB的延长线上时，如图3中，连接BE．同法可证△DBE是直角三角形，EB＝CD＝11，DB＝3，∴DE2＝EB2+BD2＝121+9＝130，综上所述，DE2的值为34或130．2．如图①，在等腰△ABC和△ADE中，AB＝AC，AD＝AE，且∠BAC＝∠DAE＝120°．（1）求证：△ABD≌△ACE；（2）把△ADE绕点A逆时针方向旋转到图②的位置，连接CD，点M、P、N分别为DE、DC、BC的中点，连接MN、PN、PM，判断△PMN的形状，并说明理由；（3）在（2）中，把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝6，请分别求出△PMN周长的最小值与最大值．【分析】（1）根据全等三角形的判定证明即可；（2）根据平行线的性质和等边三角形的判定解答即可；（3）根据点D在AB上时，BD最小和点D在BA延长线上时，BD最大矩形分析解答即可．【解答】证明：（1）∵∠BAC＝∠DAE＝120°，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ABD≌△ADE；（2）△PMN是等边三角形．理由：∵点P，M分别是CD，DE的中点，∴PM CE，PM∥CE，∵点N，M分别是BC，DE的中点，∴PN BD，PN∥BD，同理可得BD＝CE，∴PM＝PN，∴△PMN是等腰三角形，∵PM∥CE，∴∠DPM＝∠DCE，∵PN∥BD，∴∠PNC＝∠DBC，∵∠DPN＝∠DCB+∠PNC＝∠DCB+∠DBC，。

平面几何与立体几何的类比

平面几何与立体几何的类比一．目标定位“强调本质，注意适度形式化”是高中数学课程改革的一个基本理念 .虽然形式化是数学的基本特征之一，学会形式化表达是数学教学的一项基本要求，但更重要的是对数学本质的认识，是生动活泼的数学思维活动 .高中数学课程应该返璞归真，努力揭示数学概念、法则、结论的发展过程的本质，除了要讲逻辑推理，更要讲道理（合情推理） .为此，高中数学课程中的立体几何初步，其内容设计将合情推理与演绎推理有机地结合在一起，体现了直观几何与论证几何的结合，避免了以往课程中以论证几何为主线展开几何内容的形式化的问题，让学生在自主探索的过程中，理解有关数学概念、结论，体会数学思想方法 .根据《数学课程标准》的要求，本节课的目标要求定位如下：1、通过比较、分析平面几何与立体几何的相似性，进行类比推理，构造新的概念、创建新命题、拓展新结论和寻找解题途径 .2、了解类比在科学上的运用 .通过研究过程，培养学生“主动探索、敢于实践、勇于发现、合作交流”的能力，发展学生的合情推理能力 .3、通过创设和谐、协作的教学氛围，让学生体验成功，增强自信，增强运用类比推理的自觉性，并在探究与体验活动中感受几何学中的结构美和对称美 .二．多向对比（无）三．案例聚焦本节内容为教材（立体几何初步）中的一个阅读材料，编排这个阅读材料是为了扩展学生的知识，提高学生的兴趣 .通过该阅读材料，可使学生体会类比这种合情推理在猜测和发现结论、探索和提供思路方面的作用 .在本专题的教学中，教师还可以根据实际情况对一部分有兴趣的同学作进一步的指导和要求，让这部分同学查找、阅读有关资料，了解类比在科学研究中的作用、意义和重要性 .由于本专题蕴涵着丰富的数学思想方法，故本专题内容除了是知识上的拓展，更应看成是方法上的拓展 .类比思想应受到足够的重视，因为它能激发学生的兴趣，培养学生进行探索、发现的意识和能力 .因此，要充分利用和挖掘教材中的有关内容，创造机会学习和运用类比的方法 .但也要让学生思考类比方法在拓展和推广方面的可靠性和正确性，辨证地理解创新和严谨的关系 .事实上，合情推理与演绎推理的有机结合，有助于学生对数学基本知识的理解，有助于学生对数学思想方法的认识，只有这样，才能真正提高学生的数学思维能力 .本节课的教学重点是类比的对象间的结构特征（类的界定、比的内容）、规则和方式以及运用类比推理思想解决有关问题，而教学难点则是类比中命题变化的内容、规则、特点及命题不变的结构、关系、属性，另外，类比中的新元素、新关系、新图形的构建、定义和约定也是难点所在 .在教学的过程中，应使学生逐步学会观察分析数学对象、数学问题间的联系和区别，寻找数学结构中的“改变”与“不变”、“个性”与“共性” .加强学生对数学内容框架的宏观认识 .四．教学示例（苏教版）（一）提出问题，引导思考：平面几何与立体几何的关系？1、由平面几何与立体几何的相似性引发的思考，是否可以类比 .平面几何和立体几何在研究对象和方法、构成图形的基本元素等方面是相同或相似的，因此，在两者之间进行类比是研究他们性质的一种非常有效的方法 .2、什么是类比？类比是根据两个对象在某些方面的相同或相似，推出它们在其他方面的相同或相似点的一种推理方法 .波利亚指出：类比就是一种相似 .类比思维的认识依据是客观事物或对象之间存在的普遍联系------相似形 .举例：为什么人的老年称为生命的黄昏？3、类比在科学研究中的作用、意义和重要性 .由于类比推理所得结论的真实性并不可靠，因此它不能作为严格的数学推理方法 .尽管如此，我们丝毫不能由此忽视类比法 .为什么呢？因为它是提出新问题和获得新发现取之不竭的源泉 .还是波利亚说的好：如果把类比猜想的结论的似真性当作肯定性，那将是愚蠢的 .但是，忽视这种似真的猜想更为愚蠢 .让我们欣赏一段名人名言（Kepler ）：“我珍惜类比胜于任何别的东西，它是我最信赖的老师，它能揭示自然界的秘密，在几何中它应该是最不容忽视的 .”（二）研究课题：立体几何与平面几何的类比1、如何进行类比为了对二者进行类比，可以在它们的基本元素之间建立如下的类比关系：平面空间点点或直线直线直线或平面平面图形平面图形或立体图形例如：线段长面积面积体积平面角二面角三角形四面体（三棱锥）多边形多面体2、类比构造命题例1、（1）在平面几何中，若两个角的边对应平行或垂直，则这两个角相等或互补 .那么推广到空间，又有怎么样的一个命题，并判断该命题是否成立 .（2）在平面几何中，三角形具有性质：三角形的中线平分三角形的面积 .试将该性质推广到空间，写出相应的一个真命题，并加以证明 .点评：在进行类比时要了解一些平面几何研究对象与立体几何研究对象常用的类比关系，如直线类比平面，三角形类比四面体，长度类比面积，面积类比体积等等 .但要注意的是这些类比关系又不是唯一的 .例2、（2004年高考广东卷）在图1所示的三角形PAB 中，有面积关系：，则推广到空间，在图2所示的三棱锥P-ABC 中，有体积关系：.从元素的度量关系入手从元素的结构特征入手从元素的相对关系入手3、类比拓展结论例3、对勾股定理的拓展引申 .勾股定理：在直角边长为a,b，斜边长为c的直角三角形中，有 .类比Ⅰ：长、宽、高分别为a、b、c，对角线长为l的长方体中，有.类比Ⅱ：设三棱锥的三个侧面ABC、ACD、ADB两两互相垂直，则4、类比推理论证由立体几何问题，用类比的方法构造辅助的平面几何问题，通过这个问题的解决，类比猜想立体几何问题的解决方法 .例4、求证：正四面体内任一点到四个面的距离之和为定值 .第一步类比构造一个辅助平面几何问题“求证:正三角形内任意一点到三边的距离之和为定值”.第二步通过分割的方法,利用面积的关系解决平面几何问题(图3).图3 图4第三步类比猜想,所给立体几何问题是否也可以通过分割的方法,利用体积的关系来证明(图4)?这个猜想是正确的(证明留给学生课外完成).（三）学生自主探索，尝试体验类比平面几何与立体几何的许多概念、性质是相似的，如：“长方形的每一边恰好与另一边平行，而与其余的边垂直”；“长方体的每一面恰好与另一面平行，而与其余的面垂直”.问题1：请你用类比法写出更多相似的命题 .问题2：请你先写出平面几何中的一个结论，然后用类比法拓展推广到空间的情形，并加以证明 .问题3：你会运用类比推理论证来解题吗？不妨举例一试！学生分组研究，由各小组推选学生展示有关研究成果 .（四）归纳总结有关内容1、类比的方式：类比构造命题；类比拓展结论；类比推理论证 .2、类比方法的简单阐述：类比的存在性、可行性（合情推理）；类比的必然性、偶然性（演绎推理）；类比的探索性、创造性（创新思维）；类比方法的联想意识和运用意识 .3、类比是一个伟大的引路人，求解立体几何问题往往有赖于平面几何中的类比问题，正如波利亚所说：“对平面几何和立体几何作类比，是提出新问题和获得新发现取之不竭的源泉” .五、资源点击课后作业建议1、请你用类比法写出一组平面几何与立体几何相似的命题 .2、请你用类比法将平面几何的有关结论拓展推广到空间的情形，并加以证明 .3、请你举一例运用类比推理论证来解决的立体几何问题 .4、在平面几何中，存在性质：三角形的三条中线交于一点，这点倒顶点的距离与它到对边中点的距离之比为；在立体几何中，如果定义：四面体的顶点与其相对底面的重心连线也叫四面体的中线 .请你判断，四面体的四条中线是否也存在着类似的性质 .若存在，请用简练语言叙述，并给予证明；若不存在，请说明理由 .5、空间有n个平面，每三个平面交于一点，但无四面共点，试问：这些平面将空间分成几部分？（以上5题任选2题即可）拓展资源1、借助类比推理，可望形成有关问题答案的猜想，从而找到有用的探索方向 .例如：已知，求证：（提示：先与“若则”这个结论作类比，然后用三角代换的方法证明）2、类比是富于创造性的方法之一拉普拉斯说：“甚至在数学里，发现真理的主要工具也是归纳和类比 .”徐利治教授对归纳与类比在从事数学创造性科学研究活动过程中的作用作了充分肯定，画了如下的图：在数学史上，类比推理给人的启示是巨大的 .数学发展史上充满了类比，我们随时可以找到许多例证 .我们想用一个不太初等的例子来说明这点，但是这是一个比我所能想出的任何太初等的例子更能使人难忘和具有历史意义的有趣的例子（波利亚语），瑞士数学家伯努利，他发现过几个无穷级数的和，但是他未能求出所有的正整数平方的倒数之和，即未能找出：的和，这个问题引起了另一个瑞士数学家欧拉的注意，他发现了这个和的各式各样表达式（定积分、级数），但没有一个能使他满意，他用了这些表达式之一，算出了有七位有效数字的和（1.644934），然而这仅仅是一个近似值，而他的目的是要求出准确值，最后他发现了它，类比推理引导他作出了一个非常大胆的猜想 .数学家欧拉用类比法猜想的过程给人们以启发，他的基本思想是拿三角方程与代数方程类比，从而大胆地回答了当时无人回答的难题 .他的“思路”是：（1）设代数方程：有2n个不同的根则 .比较两边的的系数，得： .（2）三角方程sinx=0，有无穷多个根：0，①欧拉抛去0这个根，用x除这个方程两边，。

平面几何的立体几何类比讲解

从三角形到三棱锥性质1:在平面上到△ ABC三个顶点距离相等的点是三角形三边的垂直平分线的交点，这个点也称为三角形的外心（外接圆圆心）•如果把“在平面上”几个字去掉，再来研究到三角形三个顶点距离相等的点会是一种什么情形呢？首先这样的点肯定存在（三角形外心就是一例），在平面ABC外是否还有这样的点呢？我们先把研究的问题具体化•ABC所在平面外满足PA=PB=PC的点P是否存在？先考虑到A、B距离相等的点.在平面中这样的点的轨迹为线段AB的垂直平分线，不难证明在空间满足此条件的点的轨迹为线段AB的垂直平分面（即过AB中点且与AB垂直的平面.记为:-）.同理，到A、C两点距离相等的点的轨迹为线段AC的垂直平分面（记为0 .显然这两个平面不平行，记交线为m,因为直线m上的任意一点P都满足PA=PB，PA=PC，所以有PB=PC，可知点P也应在线段BC的垂直平分面上，即直线m是AB、AC、BC三条线段的垂直平分面的交线.由此可得：在空间到三角形三个顶点距离相等的点在其三边的垂直平分面的交线上，易证，这条直线垂直于三角形所在平面且通过三角形的外心，这条直线我们不妨称之为三角形的外心线•这个结论还可以如下的角度来表述: 如图1,如果平面ABC外有一点P且PA=PB=PC,那么点P在过△ ABC外心且与平面ABC垂直的直线上.也可以说，到△ ABC三个顶点距离相等的点在平面ABC内的射影是△ABC的外心.思考：三角形还有哪些类似的性质可以推广到空间去?不难想到三角形的内心（三条角平分线的交点）、垂心（三条高线的交点）都可以在空间找到对应的图形.对这些性质我们不妨先大胆写出结论，再进行严格证明.在类比中，我们看到，平面中的点常对应空间中的线，平面中的线则常对应空间中的面.在平面几何中有这样一个性质:如图2,8BC中，B '和C 分别在边AB、AC上，则有S AB C ■ AB -ACS ABC AB AC1（用公式S4ABc = ?bcsin A易证）将这一性质类比到空间得到相应结论:图2 性质2:如图3,已知四面体A —BCD中，棱AB、AD上各有一点B '、C'、D '，则有V A_BC L _ AB AC ADS A _BCD AB AC AD证明：作DP丄平面ABC于P,连结A、P并延长AP交BC于E.则平面APD丄平面ABC.过D '作D Q 1AP于Q，贝U D Q丄平面ABC，于是有V A _B C DS.AB C ，DQ,3 1V ^CD =3S ABC DP.所以 V A _BCD AB A C AD练习：下面这些平面中的性质类比到空间应怎样叙述？它是正确的吗? 如果正确，你能证明它吗？性质3：如图4,正△ABC ，过其内任一点P 作三边垂线，垂足分别为D 、E 、F ,贝U PE+PF+PD 为定值.性质4:如图5,点0是△ABC 内任意一点，连结 AO 、BO 、CO 并延性质3、4向空间类比所得命题都是正确的，它们分别可表述为性质3':如图6,过正四面体内一点P 向四个面作垂线，垂足分别为M i 、M 2、M 3、M 4,贝U PM 1+PM 2+PM 3+PM 4 为定值.性质4'如图7, P 为四面体A — BCD 内任意一点，连结AP 、BP 、CP 、DP 并延长分别交A 、B 、C 、D 所对的平面于A 1、B 1、C 1、D 1,则又因为 S曲BL _ AB" AC ，D'QAD' AB AC DPADV A _BCDAB AC ADc c图6 图7竺+豎+ZC1 +竺=「A、A B! B CQ DQ这些性质的证明方法与性质本身的证明类似可以从相应平面性质的证明中类比得到.如性质3、4的证明用到了面积割补思想，类比到空间就是体积割补思想，性质3'、4'的证明问题就迎刃而解了.一、转化的思想方法研究问题时，将研究对象在一定条件下转化为熟悉的、简单的、基本的研究对象的思维方法称为转化的思想方法。

几何类比探究问题

几何类比探究问题几何探究问题是中考必考题型,考查知识全面,综合性强,它把几何知识与代数知识有机结合起来,渗透数形结合思想,重在考查分析问题的能力、逻辑思维推理能力.如折叠类型、探究型、开放型、运动型、情境型等,背景鲜活,具有实用性和创造性,在考查考生计算能力的同时,考查考生的阅读理解能力、动手操作能力、抽象思维能力、建模能力,力求引导考生将数学知识运用到实际生活中去.需要通过观察、分析、比较、概括、推理、判断等来确定所需求的结论、条件或方法,因而解题的策略是将其转化为封闭性问题.常常符合“瓜豆原理”,常用的解题策略:1.找特征或模型:如中点、特殊角、折叠、相似结构、三线合一、三角形面积等;2.找思路:借助问与问之间的联系,寻找条件和思路;3.照搬:照搬前一问的方法和思路解决问题,如照搬字母、照搬辅助线、照搬全等、照搬相似等;4.找结构:寻找不变的结构,利用不变结构的特征解决问题.常见的不变结构及方法:有直角,作垂线,找全等或相似;有中点,作倍长,通过全等转移边和角;有平行,找相似,转比例.1.(1)问题发现如图1,△ABC和△ADE均为等边三角形,点D在BC的延长线上,连接CE,请填空:①∠ACE的度数为________; ②线段AC,CD,CE之间的数量关系为_________.(2)拓展探究如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在边BC的延长线上,连接CE,请判断∠ACE的度数及线段AC,CD,CE之间的数量关系,并说明理由.(3)问题解决如图3,在Rt△ABC中,AC=3,BC=5,∠ACB=90°,若点P满足PA=PB,∠APB=90°,请直接写出线段PC的长度.2.(1)阅读理解:如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD 绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断中线AD的取值范围是____;(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF 交AC于点F,连接EF,求证:BE+CF>EF;(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF 之间的数量关系,并加以证明.3．已知△ABC是等腰三角形，AB=AC．（1）特殊情形：如图1，当DE∥BC时，有DB EC．（填“＞”，“＜”或“=”）（2）发现探究：若将图1中的△ADE绕点A顺时针旋转α（0°＜α＜180°）到图2位置，则（1）中的结论还成立吗？若成立，请给予证明；若不成立，请说明理由．（3）拓展运用：如图3，P是等腰直角三角形ABC内一点，∠ACB=90°，且PB=1，PC=2，PA=3，求∠BPC的度数．4．我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”（1）概念理解：请你根据上述定义举一个等邻角四边形的例子；（2）问题探究；如图1，在等邻角四边形ABCD中，∠DAB=∠ABC，AD，BC的中垂线恰好交于AB边上一点P，连结AC，BD，试探究AC与BD的数量关系，并说明理由；（3）应用拓展；如图2，在Rt△ABC与Rt△ABD中，∠C=∠D=90°，BC=BD=3，AB=5，将Rt△ABD绕着点A 顺时针旋转角α（0°＜∠α＜∠BAC）得到Rt△AB′D′（如图3），当凸四边形AD′BC为等邻角四边形时，求出它的面积．5．△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．（1）观察猜想如图1，当点D在线段BC上时，①BC与CF的位置关系为：．②BC，CD，CF之间的数量关系为：；（将结论直接写在横线上）（2）数学思考如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．（3）拓展延伸如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=22,CD=1BC，请求出GE的长．4。

中考数学复习几何图形旋转中的类比探究解析版

例6．（2019•自贡）（1）如图1，E 是正方形ABCD 边AB 上的一点，连接BD 、DE ，将∠BDE 绕点D 逆时针旋转90°，旋转后角的两边分别与射线BC 交于点F 和点G .∠线段DB 和DG 之间的数量关系是；∠写出线段BE ，BF 和DB 之间的数量关系.（2）当四边形ABCD 为菱形，∠ADC =60°，点E 是菱形ABCD 边AB 所在直线上的一点，连接BD 、DE ，将∠BDE 绕点D 逆时针旋转120°，旋转后角的两边分别与射线BC 交于点F 和点G .∠如图2，点E 在线段AB 上时，请探究线段BE 、BF 和BD 之间的数量关系，写出结论并给出证明；∠如图3，点E 在线段AB 的延长线上时，DE 交射线BC 于点M ，若BE =1，AB =2，直接写出线段GM 的长度.图1 图2 图3【答案】（1）①DB =DG②BE BF +=（2）见解析.【解析】解：（1）由旋转知：∠GDB =90°，∵四边形ABCD 是正方形，BD 为对角线，∴∠DBG =45°，∴∠DGB =45°，∴DG =DB ，②在△DBE 和△DGF 中，BDE FDG BD DG DBE G =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△DBE ≌△DGF ，∴BE =GF ，由①知，BD =DG ，∠BDG =90°，即△BDG 是等腰直角三角形，∴BG，即BE BF +=.（2）∠BD BF BE 3=+理由如下：在菱形ABCD 中，∠ABD =∠CBD =21∠ABC =30°，由旋转可得，∠EDF =∠BDG =120°，∴∠EDF -∠BDF =∠BDG -∠BDF ，即∠FDG =∠BDE . 在△DBG 中，∠G =180°-∠BDG -∠DBG =30°， ∴∠DBG =∠G =30°，∴BD =DG .在△BDE 和△GDF 中，⎪⎩⎪⎨⎧∠=∠=∠=∠DGF DBE DGBD BDE GDF∴△BDE ≌△△GDF （ASA ），∴BE =GF ，∴BE +BF =BF +GF =BG .过点D 作DM ⊥BG 于点M ，如下图所示，∵BD =DG ，∴BG =2BM .在Rt △BMD 中，∠DBM =30°，∴BD =2DM ，设DM =a ，则BD =2a ，BM =a 3. ∴BG =a 32， ∴3232==aa BD BG ∴BF +BE =3BD .∠GM 的长度为319. 理由：∵GF =BE =1，FC =2CD =4，CM =23BC =43, ∴GM =GF +FC +CM =1+4+43=193.。

类比思想在几何中的应用

结合期末试卷中的综合题，设计了本节课。通过本节课的学习，希望学生能用类比的思想方法解几何综合题。
教学目标
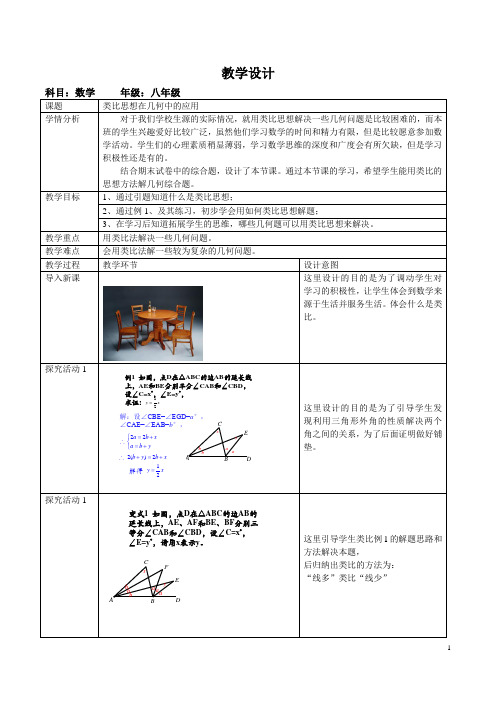
1、通过引题知道什么是类比思想；
2、通过例1、及其练习，初步学会用如何类比思想解题；
3、在学习后知道拓展学生的思维，哪些几何题可以用类比思想来解决。
教学重点
用类比法解决一些几何问题。
教学难点
会用类比法解一些较为复杂的几何问题。
教学过程
教学环节
设计意图
导入新课
这里设计的目的是为了调动学生对学习的积极性，让学生体会到数学来源于生活并服务生活。体会什么是类比。
探究活动1
这里设计的目的是为了引导学生发现利用三角形外角的性质解决两个角之间的关系，为了后面证明做好铺垫。
探究活动1
这里引导学生类比例1的解题思路和方法解决本题，
后归纳出类比的方法为：
这里设计的目的是为了让学生了解点在x轴同侧时，可类比点在x轴异侧时的解题思路方法及书写格式。
后归纳出类比的方法为：
“同侧”类比“异侧”
。
探究活动4
这里学生基本已有解题思路，让学生自己解决，为了后面证明做好铺垫。
这里设计的目的是为了让学生类比前一题的解题思路方法及解题格式解决此题。
后归纳出类比的方法为：
教学设计
科目：数学年级：八年级
课题
类比思想在几何中的应用
学情分析
对于我们学校生源的实际情况，就用类比思想解决一些几何问题是比较困难的，而本班的学生兴趣爱好比较广泛，虽然他们学习数学的时间和精力有限，但是比较愿意参加数学活动。学生们的心理素质稍显薄弱，学习数学思维的深度和广度会有所欠缺，但是学习积极性还是有的。
“线多”类比“线少”
探究活动2
这里设计的目的是为对应点在三角形内时求三个角的关系，可以类比例1的解题思路：三角形外角的性质。