人教版八年级上学期第一次大联考数学试题
八年级上第一次大联考数学试卷
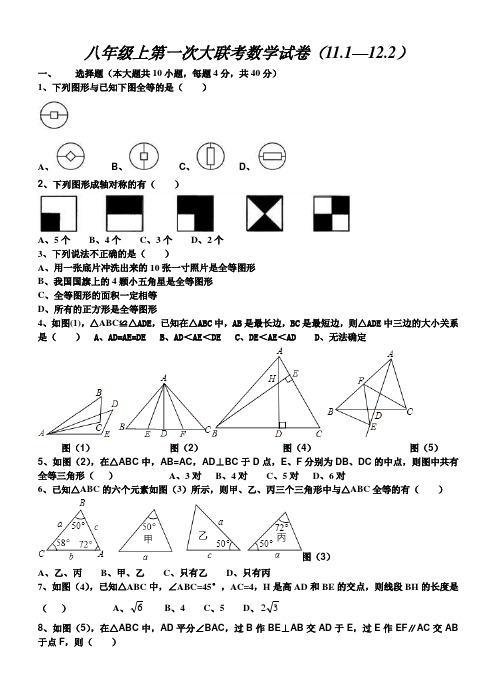
八年级上第一次大联考数学试卷(11.1—12.2)一、选择题(本大题共10小题,每题4分,共40分)1、下列图形与已知下图全等的是()A、B、C、D、2、下列图形成轴对称的有()A、5个B、4个C、3个D、2个3、下列说法不正确的是()A、用一张底片冲洗出来的10张一寸照片是全等图形B、我国国旗上的4颗小五角星是全等图形C、全等图形的面积一定相等D、所有的正方形是全等图形4、如图(1),△ABC≌△ADE,已知在△ABC中,AB是最长边,BC是最短边,则△ADE中三边的大小关系是() A、AD=AE=DE B、AD<AE<DE C、DE<AE<AD D、无法确定图(1)图(2)图(4)图(5)5、如图(2),在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形()A、3对B、4对C、5对D、6对6、已知△ABC的六个元素如图(3)所示,则甲、乙、丙三个三角形中与△ABC全等的有()图(3)A、乙、丙B、甲、乙C、只有乙D、只有丙7、如图(4),已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度是2()A、6B、4 C、5 D、3A 、AF=2BFB 、AF=BFC 、AF >BFD 、AF <BF9、如图(6)所示为跳棋盘,其中格点上的黑点为棋子,剩余没有.我们约定游戏规则是:把在棋内,沿着对称跳行,跳行一次称一步.己知A 己方一枚,欲将A 跳进对方区域(阴影部分),则跳行最少步数为( )A 、5步B 、4步C 、3步D 、2步图(6) 图(7)10、全等三角形又叫合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC 和△A 1B 1C 1是全等(合同)三角形,点A 与点A 1对应,点B 与点B 1对应,点C 与点C 1对应,当沿周界A→B→C→A ,及A 1→B 1→A 1环绕时,若运动方向相同,则称它们是真正合同三角形 如图,若运动方向相反,则称它们是镜面合同三角形 如图,两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180° 如图,下列各组合同三角形中,是镜面合同三角形的是( )A 、B 、C 、D 、二、填空题(本大题共6小题,每题4分,计24分)11、26个英文字母中,有很多都具有轴对称结构,请你写出具有轴对称结构的字母 。
人教版2019-2020学年八年级上学期第一次大联考数学试题(I)卷

人教版2019-2020学年八年级上学期第一次大联考数学试题(I)卷姓名:________ 班级:________ 成绩:________一、单选题1 . 如图1,园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是()A.24米2B.36米2C.48米2D.72米22 . 给出下列命题:①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;②三角形的三边a、b、c 满足a2+c2=b2,则∠C=90°;③命题“菱形的四条边都相等”的逆命题是四条边相等的四边形是菱形.④△ABC中,若 a:b:c=1:2:,则这个三角形是直角三角形.其中,正确命题的个数为()A.1个B.2个C.3个D.4个3 . 实数,在数轴上的位置如图所示,以下说法正确的是()A.B.C.D.4 . 如图所示的是小杰使用微信告诉小宇从小宇家到小杰家的方式.根据小杰所说的,最后应向东走()A.5千米B.6千米C.7千米D.8千米5 . 已知m=,则以下对m的估算正确的是()A.3<m<4B.4<m<5C.5<m<6D.6<m<76 . 下列各数中不是无理数的是()A.B.πC.D.7 . 如下图,在长方形ABCD中,放入六个形状相同的长方形,所标尺寸如图,图中阴影部分面积()A.36cm2B.96cm2C.44cm2D.84cm28 . 用字母a表示任意一个有理数,下列四个代数式中,值不可能为0的是()A.1+|a|B.|a+1|C.a2D.a3+19 . 如图,在中,,以AB,AC,BC为边作等边,等边.等边.设的面积为,的面积为,的面积为,四边形DHCG的面积为,则下列结论正确的是()A.B.C.D.10 . 如果a与3互为相反数,则是()A.3B.﹣3C.D.二、填空题11 . 观察等式:①0×2+1=1,(2)1×3+1=4,③2×4+1=9,④3×5+1=16,…,则第n个式子为_______.12 . 如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为_______cm.13 . 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.(1)计算AB 的长等于__,(2)请在如图所示的网格中,用无刻度的直尺,画出一个△ADE,使△ADE~△ABC,且满足点D在AC边上,点E在AB边上,AE=2.简要说明画图方法(不要求证明)__.14 . 平方等于本身的数是__________,立方等于本身的数是__________.15 . (-2)2的算术平方根是________.三、解答题16 . 如图,一学校(点M)距公路(直线l)的距离(MA)为1km,在公路上距该校2km处有一车站(点N),该校拟在公路上建一个公交车停靠点(点p),以便于本校职工乘车上下班,要求停靠站建在AN之间且到此校与车站的距离相等,请你计算停靠站到车站的距离.17 . 如图,Rt△ABC中,∠B=90°,点D在边AC上,且DE⊥AC交BC于点A.(1)求证:△CDE∽△CBA;(2)若AB=3,AC=5,E是BC中点,求DE的长.18 . 先观察下列等式,然后用你发现的规律(n≥1且n为整数)解答下列问题:,,,……(1)计算:= ;(2)若的值为,求n的值.19 . (1)计算:;(2)一次函数的图像与平行且与x轴交于点(-2,0)求解析式20 . 如图,在中,,是边上的高,,,.求(1)的面积.(2)的长.21 . 已知5a﹣1的算术平方根是3,3a+b﹣1的立方根为2.(1)求a与b的值;(2)求2a+4b的平方根.22 . 阅读材料:我们知道:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.所以式子|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离;同理式子|x+2|的几何意义是数轴上表示有理数x的点与表示有理数-2的点之间的距离.试探索:(1)|x﹣5|的几何意义是.(2)若|x﹣2|=5,则x的值是.(3)同理|x﹣5|+|x+3|=8表示数轴上有理数x所对应的点到5和﹣3所对应的两点距离之和为8,则所有符合条件的整数x是.(4)由以上探索猜想,若点P表示的数为x,|x﹣3|+|x﹣6|最小值是.23 . 如图所示,在Rt△ABC中,∠C=90°,AM是中线,MN⊥AB,垂足为N,试说明.AN2-BN2=AC2参考答案一、单选题1、2、3、4、5、6、7、8、9、10、二、填空题1、2、3、4、5、三、解答题1、2、3、4、5、6、7、8、。
八年级数学上学期第一次联考试卷(含解析) 新人教版

2016-2017学年吉林省长春市五校八年级(上)第一次联考数学试卷一.选择题(每小题3分,共30分)1.8的平方根和立方根分别是()A.8和4 B.±4和2 C.和8 D.±和22.下列各数是无理数的是()A.B.C.πD.﹣13.化简(a2b m)n,结果正确的是()A.a2n b mn B.a b C.a b mn D.a2n b4.(﹣5ab)2的化简结果是()A.﹣25ab2B.25a2b2C.﹣25a2b2D.25a2b5.下列计算正确的是()A.2a2•4ab2=6a3b2B.3a3•4a4=7a12C.3x2•2x5=6a10D.0.1x•10x2=x36.y3n+1可写成()A.(y3)n+1B.(y n)3+1C.y•y3n D.(y n)n+17.计算(2a2)3•a正确的结果是()A.3a7B.4a7C.a7D.4a68.计算(6×103)•(8×105)的结果是()A.48×109B.4.8×109C.4.8×108D.48×10159.计算(x2+2)2的结果正确的是()A.x4+2x2+4 B.x4+4x2+4 C.x2+4x+4 D.x2+2x+410.已知9a n﹣3b2n与﹣2a3m b5﹣n的积和5a4b9是同类项,则m+n的值是()A.7 B.6 C.5 D.4二、填空题(每小题3分,共30分)11.请将下列各数:,0,﹣1.5,﹣,2按从小到大排列为:.12.若a、b互为相反数,c、d互为倒数,则= .13.计算(3+2a)(3﹣2a)= .14.已知3x=4,则3x+2= .15.计算:﹣3x•(2x2﹣x+4)= .16.如果(3x m y m﹣n)3=27x12y9成立,那么整数m= ,n= .17.已知以a m=2,a n=4,a k=32.则a3m+2n﹣k的值为.18.设M=(x﹣2)(x﹣3),N=(x+3)(x﹣8),则M与N的关系为.19.如果关于x的多项式x+2与x2+mx+1的乘积中不含一次项,则m= .20.若a2+a﹣1=5,则(5﹣a)(6+a)= .三、解答题(21题每小题20分;22-25每小题20分;26-27题每小题20分,共60分)21.计算(1)|﹣2|+﹣(﹣6)×(﹣)(2)(m2n)4•(﹣m2n)3÷(m2n)5(3)(﹣2x2)•(3xy2﹣5xy3)(4)(a+2)(a﹣3)﹣a(a﹣2)﹣9.22.化简求值:2(2x﹣1)(2x+1)﹣5x(﹣x+3y)+4x(﹣4x+y),其中x=﹣1,y=2.23.已知3×9m×27m=321,求(﹣m2)3÷(m3•m2)的值.24.数学课堂上,王老师给同学们出了道题:若(x2﹣px+3)(x﹣q)中不含x2项,请同学们探究一下p与q的关系.请你根据所学知识帮助同学们解决一下.25.将4个数a、b、c、d排成2行2列,两边各加一条竖直线记成,定义=ad﹣bc,上述记号就叫做2阶行列式.若=﹣20,求x的值.26.已知有理数a,b,c满足|a﹣b﹣3|+(b+1)2+=0,求a+2b﹣c的值.27.先阅读,再填空解题:(x+5)(x+6)=x2+11x+30;(x﹣5)(x﹣6)=x2﹣11x+30;(x﹣5)(x+6)=x2+x﹣30;(x+5)(x﹣6)=x2﹣x﹣30.(1)观察积中的一次项系数、常数项与两因式中的常数项有何关系?答:.(2)根据以上的规律,用公式表示出来:.(3)根据规律,直接写出下列各式的结果:(a+99)(a﹣100)= ;(y﹣80)(y﹣81)= .2016-2017学年吉林省长春市五校八年级(上)第一次联考数学试卷参考答案与试题解析一.选择题(每小题3分,共30分)1.8的平方根和立方根分别是()A.8和4 B.±4和2 C.和8 D.±和2【考点】立方根;平方根.【分析】根据平方根和立方根定义求出即可.【解答】解:8的平方根和立方根分别是±和2.故选:D.2.下列各数是无理数的是()A.B.C.πD.﹣1【考点】无理数.【分析】根据无理数的三种形式求解.【解答】解: =2,则无理数为π.故选C.3.化简(a2b m)n,结果正确的是()A.a2n b mn B.a b C.a b mn D.a2n b【考点】幂的乘方与积的乘方.【分析】结合幂的乘方与积的乘方的概念和运算法则进行求解即可.【解答】解:(a2b m)n=a2n b mn.故选A.4.(﹣5ab)2的化简结果是()A.﹣25ab2B.25a2b2C.﹣25a2b2D.25a2b【考点】幂的乘方与积的乘方.【分析】结合幂的乘方与积的乘方的概念和运算法则进行求解即可.【解答】解:(﹣5ab)2=(﹣5)2×a2b2=25a2b2.故选B.5.下列计算正确的是()A.2a2•4ab2=6a3b2B.3a3•4a4=7a12C.3x2•2x5=6a10D.0.1x•10x2=x3【考点】单项式乘单项式.【分析】根据同底数幂的乘法底数不变指数相加,可得答案.【解答】解:A、2a2•4ab2=8a3b2,故错误;B、3a3•4a4=12a7,故错误;C、3x2•2x5=6a7,故错误;D、0.1x•10x2=x3,故正确.6.y3n+1可写成()A.(y3)n+1B.(y n)3+1C.y•y3n D.(y n)n+1【考点】幂的乘方与积的乘方.【分析】直接利用幂的乘方与同底数幂的乘法的性质求解即可求得答案;注意掌握排除法在选择题中的应用.【解答】解:A、(y3)n+1=y3n+3,故本选项错误;B、(y n)3+1=y4n,故本选项错误;C、y•y3n=y3n+1,故本选项正确;D、(y n)n+1=y n(n+1),故本选项错误.故选C.7.计算(2a2)3•a正确的结果是()A.3a7B.4a7C.a7D.4a6【考点】单项式乘单项式;幂的乘方与积的乘方.【分析】根据幂的乘方与积的乘方、单项式与单项式相乘及同底数幂的乘法法则进行计算即可.【解答】解:原式==4a7,故选:B.8.计算(6×103)•(8×105)的结果是()A.48×109B.4.8×109C.4.8×108D.48×1015【考点】整式的混合运算.【分析】本题需先根据同底数幂的乘法法则进行计算,即可求出答案.【解答】解:(6×103)•(8×105),=48×108,=4.8×109;故选B9.计算(x2+2)2的结果正确的是()A.x4+2x2+4 B.x4+4x2+4 C.x2+4x+4 D.x2+2x+4【考点】完全平方公式.【分析】根据完全平方公式即可求出答案.【解答】解:原式=x4+4x2+4,故选(B)10.已知9a n﹣3b2n与﹣2a3m b5﹣n的积和5a4b9是同类项,则m+n的值是()A.7 B.6 C.5 D.4【考点】单项式乘单项式;同类项.【分析】先根据单项式乘以单项式的法则计算9a n﹣3b2n与﹣2a3m b5﹣n的积,再根据同类项的概念,可得,解关于m、n的方程组,进而可求m+n.【解答】解:9a n﹣3b2n×(﹣2a3m b5﹣n)=﹣18a3m+n﹣3b n+5,∵﹣18a3m+n﹣3b n﹣5与5a4b9是同类项,∴,解得,∴m+n=5.故选C.二、填空题(每小题3分,共30分)11.请将下列各数:,0,﹣1.5,﹣,2按从小到大排列为:﹣<﹣1.5<0<<2.【考点】实数大小比较.【分析】根据实数大小比较的方法进行比较即可求解.【解答】解:,0,﹣1.5,﹣,2按从小到大排列为:﹣<﹣1.5<0<<2.故答案为:﹣<﹣1.5<0<<2.12.若a、b互为相反数,c、d互为倒数,则= 1 .【考点】实数的运算.【分析】由互为相反数的两数之和为0得到a+b=0,由互为倒数两数之积为1得到cd=1,代入所求式子中计算即可得到结果.【解答】解:由题意得:a+b=0,cd=1,则+=0+1=1.故答案为:1.13.计算(3+2a)(3﹣2a)= 9﹣4a2.【考点】平方差公式.【分析】原式利用平方差公式计算即可得到结果.【解答】解:原式=9﹣4a2,故答案为:9﹣4a214.已知3x=4,则3x+2= 36 .【考点】同底数幂的乘法.【分析】根据同底数幂的运算公式即可求出答案,.【解答】解:由题意可知:3x+2=3x×32=4×9=36,故答案为:3615.计算:﹣3x•(2x2﹣x+4)= ﹣6x3+3x2﹣12x .【考点】单项式乘多项式.【分析】根据单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加,计算即可.【解答】解:﹣3x•(2x2﹣x+4)=﹣6x3+3x2﹣12x.故答案为:﹣6x3+3x2﹣12x.16.如果(3x m y m﹣n)3=27x12y9成立,那么整数m= 4 ,n= 1 .【考点】幂的乘方与积的乘方.【分析】由(3x m y m﹣n)3=27x3m y3(m﹣n)=27x12y9,可得,继而求得答案.【解答】解:∵(3x m y m﹣n)3=27x3m y3(m﹣n)=27x12y9,∴,解得:.故答案为:4,1.17.已知以a m=2,a n=4,a k=32.则a3m+2n﹣k的值为 4 .【考点】同底数幂的除法;同底数幂的乘法;幂的乘方与积的乘方.【分析】根据幂的乘方,可得同底数幂的乘除法,根据同底数幂的乘除法,可得答案.【解答】解:a3m=23=8,a2n=42=16,a3m+2n﹣k=a3m•a2n÷a k=8×16÷32=4,故答案为:4.18.设M=(x﹣2)(x﹣3),N=(x+3)(x﹣8),则M与N的关系为M>N .【考点】多项式乘多项式.【分析】根据多项式乘多项式的运算法则进行计算,比较即可得到答案.【解答】解:M=(x﹣2)(x﹣3)=x2﹣5x+6,N=(x+3)(x﹣8)=x2﹣5x﹣24,M﹣N=(x2﹣5x+6)﹣(x2﹣5x﹣24)=30,则M>N.故答案为:M>N.19.如果关于x的多项式x+2与x2+mx+1的乘积中不含一次项,则m= ﹣.【考点】多项式乘多项式.【分析】原式利用多项式乘多项式法则计算,根据乘积中不含x的一次项,则一次项系数为0,求出m的值即可.【解答】解:(x+2)(x2+mx+1)=x3+(m+2)x2+(1+2m)x+2∵乘积中不含一次项,∴1+2m=0,∴m=,故答案为:﹣.20.若a2+a﹣1=5,则(5﹣a)(6+a)= 24 .【考点】多项式乘多项式.【分析】原式利用多项式乘以多项式法则计算,整理后将已知等式变形后代入计算即可求出值.【解答】解:原式=30+5a﹣6a﹣a2=﹣(a2+a)+30,由a2+a﹣1=5,得到a2+a=6,则原式=﹣6+30=24.故答案为:24.三、解答题(21题每小题20分;22-25每小题20分;26-27题每小题20分,共60分)21.计算(1)|﹣2|+﹣(﹣6)×(﹣)(2)(m2n)4•(﹣m2n)3÷(m2n)5(3)(﹣2x2)•(3xy2﹣5xy3)(4)(a+2)(a﹣3)﹣a(a﹣2)﹣9.【考点】整式的混合运算;实数的运算.【分析】(1)分别根据绝对值的性质、数的开方法则计算出各数,再根据实数混合运算的法则进行计算即可;(2)根据单项式的乘法与除法法则进行计算即可;(3)根据单项式乘以多项式的法则进行计算即可;(4)先根据多项式乘以多项式,单项式乘以多项式的法则分别计算出各数,再合并同类项即可.【解答】解:(1)原式=2﹣3﹣(﹣6)×(﹣)=2﹣3﹣3=﹣4;(2)原式=m8n4•(﹣m6n3)÷(m10n5)=﹣m8+6﹣10 n 4+3﹣5=﹣m4n2;(3)原式=﹣6x3y2+10x3y3;(4)原式=a2﹣3a+2a﹣6﹣a2+2a﹣9=a2+a﹣15.22.化简求值:2(2x﹣1)(2x+1)﹣5x(﹣x+3y)+4x(﹣4x+y),其中x=﹣1,y=2.【考点】整式的混合运算—化简求值.【分析】先算乘法,再合并同类项,最后代入求出即可.【解答】解:2(2x﹣1)(2x+1)﹣5x(﹣x+3y)+4x(﹣4x+y)=8x2﹣2+5x2﹣15xy﹣16x2+10xy=﹣3x2﹣5xy﹣2,当x=﹣1,y=2时,原式=5.23.已知3×9m×27m=321,求(﹣m2)3÷(m3•m2)的值.【考点】同底数幂的除法;同底数幂的乘法;幂的乘方与积的乘方.【分析】转化为同底数幂的乘法,求出m的值,即可解答.【解答】解:3×9m×27m=3×32m×33m=31+5m=321,∴1+5m=21,∴m=4,∴(﹣m2)3÷(m3•m2)=﹣m6÷m5=﹣m=﹣4.24.数学课堂上,王老师给同学们出了道题:若(x2﹣px+3)(x﹣q)中不含x2项,请同学们探究一下p与q的关系.请你根据所学知识帮助同学们解决一下.【考点】多项式乘多项式.【分析】原式利用多项式乘以多项式法则计算,根据结果不含x2项,求出p与q的关系即可.【解答】解:原式=x3﹣(p+q)x2+(pq+3)x﹣3q,由结果不含x2项,得到p+q=0,则p与q的关系为p=﹣q.25.将4个数a、b、c、d排成2行2列,两边各加一条竖直线记成,定义=ad﹣bc,上述记号就叫做2阶行列式.若=﹣20,求x的值.【考点】多项式乘多项式;解一元一次方程.【分析】根据所给的例子,按照多项式乘以多项式,进行解答即可.【解答】解: =﹣20,(6x﹣5)2﹣(6x﹣1)2=﹣20(6x﹣5+6x﹣1)(6x﹣5﹣6x+1)=﹣20(12x﹣6)×(﹣4)=﹣20﹣48x+24=﹣20﹣48x=﹣44x=26.已知有理数a,b,c满足|a﹣b﹣3|+(b+1)2+=0,求a+2b﹣c的值.【考点】非负数的性质:算术平方根;非负数的性质:绝对值;非负数的性质:偶次方.【分析】首先依据非负数的性质得到c﹣1=0,b+1=0,a﹣b﹣3=0,然后可求得c=1,b=﹣1,a=2,最后代入所求代数式进行计算即可.【解答】解:由非负数的性质可知:c﹣1=0,b+1=0,a﹣b﹣3=0.解得:c=1,b=﹣1,a=2.所以a+2b﹣c=2+2×(﹣1)﹣1=﹣1.27.先阅读,再填空解题:(x+5)(x+6)=x2+11x+30;(x﹣5)(x﹣6)=x2﹣11x+30;(x﹣5)(x+6)=x2+x﹣30;(x+5)(x﹣6)=x2﹣x﹣30.(1)观察积中的一次项系数、常数项与两因式中的常数项有何关系?答:一次项系数是两因式中的常数项的和,常数项是两因式中的常数项的积..(2)根据以上的规律,用公式表示出来:(a+b)(a+c)=a2+(b+c)a+bc .(3)根据规律,直接写出下列各式的结果:(a+99)(a﹣100)= a2﹣a﹣9900 ;(y﹣80)(y﹣81)= y2﹣161y+6480 .【考点】多项式乘多项式.【分析】(1)根据所给的式子,找出积中的一次项系数、常数项是两因式中的常数项的和与积,即可求出答案.(2)根据(1)中所得的结论,即可找出规律,得出公式;(3)根据(2)中的公式即可求出(a+99)(a﹣100)与(y﹣80)(y﹣81)的值.【解答】解:(1)观察积中的一次项系数、常数项与两因式中的常数项有何关系是:一次项系数是两因式中的常数项的和,常数项是两因式中的常数项的积;(2)根据以上的规律,用公式表示出来:(a+b)(a+c)=a2+(b+c)a+bc;(3)根据(2)中得出的公式得:(a+99)(a﹣100)=a2﹣a﹣9900;(y﹣80)(y﹣81)=y2﹣161y+6480.故填:一次项系数是两因式中的常数项的和,常数项是两因式中的常数项的积;(a+b)(a+c)=a2+(b+c)a+bc; a2﹣a﹣9900,y2﹣161y+6480.。
精选八年级数学上学期第一次联考试题新人教版

山东省德州市六校2017-2018学年八年级数学上学期第一次联考试题本试卷考试时间120分钟分值150分一、 选择题(每题4分,共48分)1、下列多项式中,可以提取公因式的是( )A. 22y x -B. x x +2C. y x -2D. 222y xy x ++2、化简33)(x x -⋅的结果是( )A. 6x -B.C.D. 5x -3、下列计算中正确的是().A .a 2+b 3=2a 5B .a 4÷a =a 4C .a 2·a 4=a 8D .(-a 2)3=-a 64、下列两个多项式相乘,不能用平方差公式的是()A. )32)(32(b a b a --+-B. )32)(32(b a b a ++-C. )32)(32(b a b a --+D. )32)(32(b a b a ---5、若2249x mxy y ++是完全平方式,则=()A. 26B. ±26C. ±12D. ±66、若3x =15,3y =5,则3x -y 等于().A .5B .3C .15D .107、已知实数,x y 满足30x -=,则代数式()2017x y -的值为()A.1B.-1C.2017D.-20178、如(x +m )与(x +3)的乘积中不含x 的一次项,则m 的值为().A .0B .3C .-3D .19、若代数式2a 2+3a+1的值是6,则代数式6a 2+9a+5的值为(). A .17 B .11 C .20 D .1510、下列各式中,相等关系一定成立的是( )A.(x -y)2 =(y -x)2B.(x+6)(x -6)=x 2-6C.(x+y)2 =x 2 +y 2D.x 2 +2xy 2 -y 2 =(x+y) 2 11、下列因式分解中,正确的是()A.()()2222x y z x y z y z -=+- B.()224545x y xy y y x x -+-=-++ C.()()()2951x y x x +-=+- D.()22912432a a a -+=-- 12、在边长为的正方形中挖去一个边长为的小正方形(如图①),把余下的部分拼成一个矩形(如图②),根据两个图形中阴影部分的面积相等,可以验证( )A .()2222a b a ab b -=-+ B.()2222a b a ab b +=++ C.()()22a b a b a b -=+- D.()()222a b a b a ab b +-=+-二、填空题(每小题4分,共24分)13、计算:2007200831()(1)43⨯-=. 14、计算:()(()023220172-+--=______. 15、若523m x y +与7n x y 的和是单项式,则=_________.16、若多项式x 2+ax +b 分解因式的结果为(x +1)(x -2),则a +b 的值为__________.17、已知a +1a =3,则a 2+21a的值是__________. 18、定义运算ab =a (1-b ),下面给出了关于这种运算的四个结论:①2(-2)=6 ②ab =ba ③若a +b =0,则(aa )+(bb )=22a b --④若ab =0,则a =0.其中正确结论的序号是(填上你认为正确的所有结论的序号).三、解答题:(共78分)19.计算:(每小题5分,共20分)第12题。
人教版八年级上册第一次联考试题含答案

初中数学试题2ABCDE第4题图安徽省淮南市潘集区2017-2018学年八年级数学上学期第一次联考试题(满分:100分 时间:100分钟)题号 选择题 填空题 17 18 19 20 21 22 23 总分 得分一、选择题:(每小题3分,共30分)每小题只有一个选符合题目的要求,请你把你认为正确的选项的代号填入题后所给的括号内。
1. 下列长度的三条线段能组成三角形的是 ( ) A .1cm , 2cm , 3cm B .4cm 11cm 6cm C .5cm 5cm 10cm D .6cm 7cm 8cm2.如图,小亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是 ( ) A . SSS B .SAS C .AAS D .ASA3.如图所示,已知AB ∥CD ,∠A=55°,∠C=20°,则∠P 的度数是( )A .55°B .75°C .35°D .125° 第2题4.如图,AD,CE 是△ABC 的两条高,已知AD=10,CE=9,AB=12,则BC 的长是( ) A .10 B .10.8 C .12 D .155.两个三角形只有以下元素对应相等,不能判定两个三角形全等的( ) A .两角和一边 B .两边及夹角 C .三个角 D .三条边6.下列条件能判定△ABC ≌△DEF 的是 ( )A .∠A=∠D ∠B=∠E ∠C=∠FB .AB=BC DE=EF AC=DF第3题图3C . AB=DE AC=DF ∠C=∠FD .∠B=∠E ∠C=∠F BC=EF 7.已知一个多边形内角和为720°,则该多边形的对角线条数为( )A .9B .12C .15D .188. 如图所示,E 、B 、F 、C 四点在一条直线上,EB=CF ,∠A=∠D ,再添一个条件仍不能证明△ABC ≌△DEF 的是 ( )A .AB=DEB . DF ∥AC C . ∠E=∠ABCD . AB ∥DE 9. 一个正多边形的一个内角等于144°,则该多边形的边数为( ) A .8 B .9 C .10 D .1110. 如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址总共有几处 ( )A .1处B .2处C .3处D .4处 二、填空题:(每小题3分,共18分)11. 等腰三角形两边长分别为3,7,则它的周长为 。
人教版八年级数学上册第一次联考试卷

HE DC B AC D AE B θ第17题图 第18题图 ED F C B A选择第4题图 P D C B A初中数学试卷2010年大冶市西畈中学八年级第一次联考数学试卷一、选择题(每小题3分,共30分)1、用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A ′O ′B ′=∠AOB 的依据是( ) A 、(S .S .S .) B 、(S .A .S .) C 、(A .S .A .) D 、(A .A .S .)2、如图, ∠C=90°,AD 平分∠BAC 交BC 于D,若BC=5cm,BD=3cm,则点D 到AB 的距离为( ) A 、5cm B 、3cm C 、2cm D 、不能确定3、下列条件能判定△ABC ≌△DEF 的一组是( )A 、∠A=∠D , ∠C=∠F , AC=DF B.AB=DE , BC=EF , ∠A=∠DC 、∠A=∠D , ∠B=∠E , ∠C=∠F D.AB=DE ,△ABC 的周长等于△DEF 的周长4、如图, AD 是△ABC 的中线, E 、F 分别是AD 和AD 延长线上的点,且DE =DF ,连结BF 、CE.下列说法:① CE =BF ;② △ABD 和△ACD 面积相等;③BF ∥CE ;④△BDF ≌△CDE .其中正确的有( ).A 、1个B 、2个C 、3个D 、4个5、如图,在△ABC 中,AD 是∠A 的外角平分线,P 是AD 上异于A 的任意一点,设PB =m ,PC =n ,AB =c ,AC =b ,则)(n m +与)(c b +的大小关系是( )A 、n m +>c b +B 、n m +<c b +C 、n m +=c b +D 、无法确定 6、如图,△ABC 中AB=AC ,AD 是角平分线,BE=CF ,则下列说法正确的有( )个 (1)AD 平分∠EDF ;(2)△EBD ≌△FCD ; (3)BD=CD ;(4)AD ⊥BC .A 、1个B 、2个C 、3个D 、4个 7、以下说法:①有两个角和其中一个角的对边对应相等的两个三角形全等;②有一边和一个角对应相等的两个三角形全等;③有一边相等的两个等边三角形全等; ④一个锐角和一条对应边相等的两个直角三角形全等。
八年级数学上学期第一次联考试题(含解析) 新人教版-新人教版初中八年级全册数学试题

某某市铁厂中学2015-2016学年八年级数学上学期第一次联考试题一、选择题:(共10小题,每小题3分,本题满分30分)1.以下列长度的三条线段为边,能组成三角形的是()A.3,3,3 B.3,3,6 C.3,2,5 D.3,2,62.方程2x﹣1=5的解是()A.x=3 B.x=2 C.x=﹣3 D.x=﹣23.2008年5月12日,某某汶川发生8.3级大地震,据统计这次地震直接经济损失大约600 000 000 000元,这个数据用科学记数法表示为()A.0.6×1012元B.6×1012元C.6×1011元D.60×1010元4.下列图形中有稳定性的是()A.正方形B.直角三角形C.长方形D.平行四边形5.如图已知:△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数为()A.80° B.70° C.60° D.50°6.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是()A.带①去B.带②去C.带③去D.①②③都带去7.如图所示,AB=CD,AD=BC,则图中的全等三角形共有()A.4对B.3对C.2对D.1对8.在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D,CD=2,则点D到AB的距离是()A.1 B.2 C.3 D.49.如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=()A.90° B.120°C.160°D.180°10.如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是()A.35° B.70° C.110°D.130°二、填空题(共8小题,每小题3分,本题满分24分)11.已知方程(a﹣2)x|a|﹣1+4=0是关于x的一元一次方程.则a的值为.12.等腰三角形的两边长分别为4和9,则第三边长为.13.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是.14.一个多边形的每个外角都是60°,则这个多边形边数为.15.如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=度.16.如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是(填上你认为适当的一个条件即可).17.已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为.18.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是.三、解答题(共9小题,本大题满分66分)19.(1)计算:3×(﹣)×﹣|﹣2|(2)解方程组:.20.按要求画图,并描述所作线段.(1)过点A画三角形的高线AD;(2)过点B画三角形的中线BE;(3)过点C画三角形的角平分线CF.21.如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.∵AD平分∠BAC∴∠=∠(角平分线的定义)在△ABD和△ACD中∴△ABD≌△ACD.22.已知:如图,AD=BC,BD=AC.求证:∠D=∠C.23.如图,点F是△ABC的边BC延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF的度数.24.如图,在平面直角坐标系中,O为坐标原点,△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(1,1),C(﹣3,1),△A1B1C1是△ABC向下平移2个单位,向右平移3个单位得到的.(1)写出点A1、B1、C1的坐标,并在图中画出△A1B1C1;(2)求△A1B1C1的面积.25.如图,AB∥CD,∠A=45°,∠C=∠E,求∠C.26.雅西高速公路于2012年4月29日正式通车,某某到某某全长420千米,一辆小汽车和一辆客车同时从某某、某某两地相向开出,经过2.5小时相遇,相遇时,小汽车每小时比客车每小时多行驶28千米,求出小汽车和客车的平均速度.27.如图:AB∥CD,∠ABD,∠BDC的平分线交于E,试猜想△BED的形状并说明理由.2015-2016学年某某市铁厂中学八年级(上)第一次联考数学试卷参考答案与试题解析一、选择题:(共10小题,每小题3分,本题满分30分)1.以下列长度的三条线段为边,能组成三角形的是()A.3,3,3 B.3,3,6 C.3,2,5 D.3,2,6【考点】三角形三边关系.【分析】三角形的三条边必须满足:任意两边之和>第三边,任意两边之差<第三边.【解答】解:A中,3+3>3,能构成三角形;B中,3+3=6,不能构成三角形;C中,3+2=5,不能构成三角形;D中,3+2<6,不能构成三角形.故选A.【点评】本题主要考查对三角形三边关系的理解应用.判断是否可以构成三角形,只要判断两个较小的数的和<最大的数就可以.2.方程2x﹣1=5的解是()A.x=3 B.x=2 C.x=﹣3 D.x=﹣2【考点】解一元一次方程.【专题】计算题.【分析】方程移项合并,把x系数化为1,即可求出解.【解答】解:方程2x﹣1=5,移项合并得:2x=6,解得:x=3,故选A【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.3.2008年5月12日,某某汶川发生8.3级大地震,据统计这次地震直接经济损失大约600 000 000 000元,这个数据用科学记数法表示为()A.0.6×1012元B.6×1012元C.6×1011元D.60×1010元【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将600 000 000 000用科学记数法表示为:6×1011.故选:C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a的值以及n的值.4.下列图形中有稳定性的是()A.正方形B.直角三角形C.长方形D.平行四边形【考点】三角形的稳定性.【分析】根据三角形具有稳定性可得答案.【解答】解:直角三角形有稳定性,故选:B.【点评】此题主要考查了三角形的稳定性,是需要识记的内容.5.如图已知:△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数为()A.80° B.70° C.60° D.50°【考点】全等三角形的性质.【专题】数形结合.【分析】在△ABE中,利用外角的知识求出∠BAE的度数,再根据△ABC≌△ACD,得出∠BAE=∠DAC,这样即可得出答案.【解答】解:由题意得:∠B=50°,∠AEC=120°,又∵∠AEC=∠B+∠BAE(三角形外角的性质),∴∠BAE=120°﹣50°=70°,又∵△ABE≌△ACD,∴∠BAE=∠DAC=70°.故选B.【点评】本题考查全等三角形的性质,属于基础题,比较简单,解答本题用到的三角形的外角的性质及全等三角形的对应边、对应角分别相等的性质.6.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是()A.带①去B.带②去C.带③去D.①②③都带去【考点】全等三角形的应用.【分析】本题就是已知三角形破损部分的边角,得到原来三角形的边角,根据三角形全等的判定方法,即可求解.【解答】解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.故选:C.【点评】此题主要考查了全等三角形的判定方法的开放性的题,要求学生将所学的知识运用于实际生活中,要认真观察图形,根据已知选择方法.7.如图所示,AB=CD,AD=BC,则图中的全等三角形共有()A.4对B.3对C.2对D.1对【考点】全等三角形的判定.【分析】两组对边分别对应相等的四边形是平行四边形,平行四边形的两条对角线和它的四条边共构成4对全等的三角形.【解答】解:∵AB=CD,AD=BC∴四边形ABCD是平行四边形,∴OC=OA,OB=OD;∵OD=OB,OB=OD,∠AOD=∠BOC;∴△AOD≌△COB(SAS);①同理可得出△AOB≌△COD(SAS);②∵AD=BC,CD=AB,BD=BD;∴△ABD≌△CDB(SSS);③同理可得:△ABC≌△CDA(SSS).④因此本题共有4对全等三角形.故选择A.【点评】本题考查了对全等三角形的性质和判定,平行四边形的性质和判定等知识点的理解和运用,关键是根据平行四边形的性质得出边相等,再根据全等三角形的判定定理进行证明.全等三角形的判定方法有SSS,SAS,ASA,AAS.8.在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D,CD=2,则点D到AB的距离是()A.1 B.2 C.3 D.4【考点】角平分线的性质.【分析】根据角平分线的性质“角的平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D 到AC的距离=CD=2.【解答】解:由角平分线的性质,得点D到AB的距离=CD=2.故选B.【点评】本题主要考查平分线的性质,由已知能够注意到D到AB的距离即为CD长是解决的关键.9.如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=()A.90° B.120°C.160°D.180°【考点】角的计算.【分析】因为本题中∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.【解答】解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,所以∠AOC+∠BOD=90°+a+90°﹣a=180°.故选D.【点评】本题考查了角度的计算问题,在本题中要注意∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.10.如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是()A.35° B.70° C.110°D.130°【考点】平行线的性质.【分析】由三角形的外角性质得出∠ABD=35°,由角平分线的定义求出∠ABC=2∠ABD=70°,再由平行线的性质得出同旁内角互补∠BED+∠ABC=180°,即可得出结果.【解答】解:∵∠BDC=∠A+∠ABD,∴∠ABD=95°﹣60°=35°,∵BD是∠ABC的角平分线,∴∠ABC=2∠ABD=70°,∵DE∥BC,∴∠BED+∠ABC=180°,∴∠BED=180°﹣70°=110°.故选C.【点评】本题考查了平行线的性质、三角形的外角性质;熟练掌握平行线的性质,运用三角形的外角性质求出∠ABD的度数是解决问题的关键.二、填空题(共8小题,每小题3分,本题满分24分)11.已知方程(a﹣2)x|a|﹣1+4=0是关于x的一元一次方程.则a的值为﹣2 .【考点】一元一次方程的定义.【专题】计算题.【分析】只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程,它的一般形式是ax+b=0(a,b是常数且a≠0),高于一次的项系数是0.据此可得出关于a的方程,继而可求出a 的值.【解答】解:由一元一次方程的特点得,解得:a=﹣2.故答案是:﹣2.【点评】本题主要考查了一元一次方程的一般形式,只含有一个未知数,未知数的指数是1,一次项系数不是0,这是这类题目考查的重点.12.等腰三角形的两边长分别为4和9,则第三边长为9 .【考点】等腰三角形的性质;三角形三边关系.【分析】题目给出等腰三角形有两条边长为4和9,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【解答】解:当4是腰时,因4+4<9,不能组成三角形,应舍去;当9是腰时,4、9、9能够组成三角形.则第三边应是9.故答案为:9.【点评】本题考查等腰三角形的性质及三角形三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形,这点非常重要,也是解题的关键.13.如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是利用三角形的稳定性.【考点】三角形的稳定性.【分析】三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变.【解答】解:这样做的道理是利用三角形的稳定性.【点评】本题考查三角形稳定性的实际应用,三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.14.一个多边形的每个外角都是60°,则这个多边形边数为 6 .【考点】多边形内角与外角.【分析】利用外角和除以外角的度数即可得到边数.【解答】解:360÷60=6.故这个多边形边数为6.故答案为:6.【点评】此题主要考查了多边形的外角和,关键是掌握任何多边形的外角和都360°.15.如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=270 度.【考点】三角形内角和定理;多边形内角与外角.【专题】应用题.【分析】根据三角形的内角和与平角定义可求解.【解答】解:如图,根据题意可知∠5=90°,∴∠3+∠4=90°,∴∠1+∠2=180°+180°﹣(∠3+∠4)=360°﹣90°=270°.【点评】本题主要考查了三角形的内角和定理和内角与外角之间的关系.要会熟练运用内角和定理求角的度数.16.如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是∠B=∠C(填上你认为适当的一个条件即可).【考点】全等三角形的判定.【专题】开放型.【分析】根据题意,易得∠AEB=∠AEC,又AE公共,所以根据全等三角形的判定方法容易寻找添加条件.【解答】解:∵∠1=∠2,∴∠AEB=∠AEC,又 AE公共,∴当∠B=∠C时,△ABE≌△ACE(AAS);或BE=CE时,△ABE≌△ACE(SAS);或∠BAE=∠CAE时,△ABE≌△ACE(ASA).【点评】此题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.17.已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为3:2 .【考点】角平分线的性质.【专题】压轴题.【分析】本题需先利用角平分线的性质可知点D到AB、AC的距离相等,即两三角形的高相等,观察△ABD 与△ACD,面积比即为已知AB、AC的比,答案可得.【解答】解:∵AD是△ABC的角平分线,∴点D到AB的距离等于点D到AC的距离,又∵AB:AC=3:2,则△ABD与△ACD的面积之比为 3:2.故答案为:3:2.【点评】本题考查了角平分线的性质;此题的关键是根据角平分线的性质,求得点D到AB的距离等于点D 到AC的距离,即△ABD边AB上的高与△ACD边AC上的高相等.18.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是 5 .【考点】角平分线的性质.【分析】要求△ABD的面积,有AB=5,可为三角形的底,只求出底边上的高即可,利用角的平分线上的点到角的两边的距离相等可知△ABD的高就是CD的长度,所以高是2,则可求得面积.【解答】解:∵∠C=90°,AD平分∠BAC,∴点D到AB的距离=CD=2,∴△ABD的面积是5×2÷2=5.故答案为:5.【点评】本题主要考查了角平分线上的一点到两边的距离相等的性质.注意分析思路,培养自己的分析能力.三、解答题(共9小题,本大题满分66分)19.(1)计算:3×(﹣)×﹣|﹣2|(2)解方程组:.【考点】实数的运算;解二元一次方程组.【专题】计算题.【分析】(1)原式利用立方根及绝对值的代数意义化简,计算即可得到结果;(2)方程组利用加减消元法求出解即可.【解答】解:(1)原式=3×(2﹣)×﹣2+=4﹣2﹣2+=2﹣;(2),①+②得:3x=6,即x=2,把x=2代入①得:y=2,则方程组的解为.【点评】此题考查了实数的运算,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.20.按要求画图,并描述所作线段.(1)过点A画三角形的高线AD;(2)过点B画三角形的中线BE;(3)过点C画三角形的角平分线CF.【考点】作图—复杂作图;三角形的角平分线、中线和高.【分析】(1)延长CB,过点A作AD⊥BC即可;(2)找到AC中点E,连接BE,即为所求;(3)作出∠BCA的角平分线,进而得出答案.【解答】解:(1)如图所示:AD即为所求;(2)如图所示:BE即为所求;(3)如图所示:CF即为所求.【点评】此题主要考查了复杂作图,正确掌握钝角三角形高线作法是解题关键.21.如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.∵AD平分∠BAC∴∠BAD =∠CAD (角平分线的定义)在△ABD和△ACD中∴△ABD≌△ACD SAS .【考点】全等三角形的判定;等腰三角形的性质.【专题】推理填空题.【分析】根据角平分线的定义及全等三角形的判定定理,填空即可.【解答】解:∵AD平分∠BAC∴∠BAD=∠CAD(角平分线的定义),在△ABD和△ACD中,,∴△ABD≌△ACD(SAS).【点评】本题考查了全等三角形的判定,解答本题的关键是掌握全等三角形的判定定理及角平分线的定义.22.已知:如图,AD=BC,BD=AC.求证:∠D=∠C.【考点】全等三角形的判定与性质.【专题】证明题.【分析】连接AB,根据SSS推出△ADB和△BCA全等,再根据全等三角形的性质得出即可.【解答】证明:连接AB,在△ADB和△BCA中,,∴△ADB≌△BCA(SSS),∴∠D=∠C.【点评】本题考查了全等三角形的性质和判定的应用,能正确作出辅助线是解此题的关键,注意:全等三角形的对应边相等,对应角相等.23.如图,点F是△ABC的边BC延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF的度数.【考点】三角形内角和定理;三角形的外角性质.【分析】在直角三角形DFB中,根据三角形内角和定理,求得∠B的度数;再在△ABC中,根据内角与外角的性质求∠ACF的度数即可.【解答】解:在△DFB中,∵DF⊥AB,∴∠FDB=90°,∵∠F=40°,∠FDB+∠F+∠B=180°,∴∠B=50°.在△ABC中,∵∠A=30°,∠B=50°,∴∠ACF=30°+50°=80°.【点评】本题主要考查了三角形的内角和定理,以及三角形的外角等于不相邻的两个内角的和,此题基础题,比较简单.24.如图,在平面直角坐标系中,O为坐标原点,△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(1,1),C(﹣3,1),△A1B1C1是△ABC向下平移2个单位,向右平移3个单位得到的.(1)写出点A1、B1、C1的坐标,并在图中画出△A1B1C1;(2)求△A1B1C1的面积.【考点】作图-平移变换.【专题】作图题.【分析】(1)在平面直角坐标系中描出A,B,C三点,连接得到△ABC,根据平移法则画出△A1B1C1,并求出点A1、B1、C1的坐标即可;(2)结合网格求出△A1B1C1的面积即可.【解答】解:(1)画出△A1B1C1,如图所示,点A1、B1、C1的坐标分别为(2,﹣4);(4,﹣1);(0,﹣1)’(2)根据网格得:B1C1=4,边B1C1上的高为3,则△A1B1C1的面积S=×4×3=6.【点评】此题考查了作图﹣平移变换,作平移图形时,找关键点的对应点也是关键的一步.平移作图的一般步骤为:①确定平移的方向和距离,先确定一组对应点;②确定图形中的关键点;③利用第一组对应点和平移的性质确定图中所有关键点的对应点;④按原图形顺序依次连接对应点,所得到的图形即为平移后的图形.25.如图,AB∥CD,∠A=45°,∠C=∠E,求∠C.【考点】平行线的性质;三角形的外角性质.【分析】根据平行线的性质求出关于∠1,然后根据外角的性质求解.【解答】解:∵AB∥CD,∠A=45°,∴∠A=∠1=45°,∵∠1=∠C+∠E,即∠C=∠1﹣∠E,又∵∠E=∠C,∴∠C==22.5°.【点评】本题比较简单,考查的是平行线的性质及三角形内角与外角的关系.两直线平行,内错角相等;三角形的一个外角等于和它不相邻的两个内角的和.26.雅西高速公路于2012年4月29日正式通车,某某到某某全长420千米,一辆小汽车和一辆客车同时从某某、某某两地相向开出,经过2.5小时相遇,相遇时,小汽车每小时比客车每小时多行驶28千米,求出小汽车和客车的平均速度.【考点】分式方程的应用;一元一次方程的应用.【分析】设客车的平均速度为x千米/小时,小汽车的速度为(x+28)千米/小时,根据两车相向而行,2.5小时走了420千米,列方程求解.【解答】解:设客车的平均速度为x千米/小时,小汽车的速度为(x+28)千米/小时,由题意得,2.5(x+x+28)=420,解得:x=70,则x+28=70+28=98.答:客车的平均速度为70千米/小时,小汽车的速度为98千米/小时.【点评】本题考查了一元一次方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解.27.如图:AB∥CD,∠ABD,∠BDC的平分线交于E,试猜想△BED的形状并说明理由.【考点】平行线的性质;角平分线的定义;三角形内角和定理.【专题】探究型.【分析】根据平行线的性质,求出∠ABD+∠CDB=180°,然后根据角平分线的性质,求∠EBD+∠EDB的度数,然后根据三角形内角和定理解答.【解答】解:△BED为直角三角形.理由如下:∵AB∥CD∴∠ABD+∠CDB=180°(两直线平行,同旁内角互补)又∵∠ABD,∠BDC的平分线交于E,∴∠EBD=∠ABD,∠EDB=∠BDC,∴∠EBD+∠EDB=(∠ABD+∠BDC)=×180°=90°,∴△BED为直角三角形.【点评】两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.。
人教版2019-2020年度八年级上学期第一次大联考数学试题A卷

人教版2019-2020年度八年级上学期第一次大联考数学试题A卷姓名:________ 班级:________ 成绩:________一、单选题1 . 将点向右平移2个单位长度,再向上平移3个单位长度得点,则点的坐标是()A.B.C.D.2 . 从车站向东走400 m,再向北走500 m到小红家;从车站向北走500 m,再向西走200 m到小强家,若以车站为原点,以正东、正北方向为正方向建立平面直角坐标系,则小红家、小强家的坐标分别为()A.(400,500),(500,200)B.(400,500),(200,500)C.(400,500),(-200,500)D.(500,400),(500,-200)3 . 星期6,小亮从家里骑自行车到同学家去玩,然后返回,图是他离家的路程y(千米)与时间x(分钟)的函数图象。
下列说法不一定正确的是()A.小亮家到同学家的路程是3千米B.小亮在同学家返回的时间是1小时C.小亮去时走上坡路,回家时走下坡路D.小亮回家时用的时间比去时用的时间少4 . 若点A(2,4)在函数y=kx的图象上,则下列各点在此函数图象上的是()A.(1,2)B.(-2,-1)C.(-1,2)D.(2,-4)5 . 在平面直角坐标系中,点P(-3,1)在()A.第一象限B.第二象限C.第三象限D.第四象限6 . 若是关于的一次函数,则的值为()A.B.C.D.7 . 一台机器原价万元,如果每年的折旧率为,两年后这台机器的价位为万元,则关于的函数关系式为()A.B.C.D.8 . 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2;④当x>3时,y1≥y2中正确的个数是()A.0B.1C.2D.39 . 不等式组的解集在数轴上表示正确的是A.B.C.D.10 . 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是()A.B.C.D.二、填空题11 . 已知点m(3a-9,1-a),将m点向左平移3个单位长度后落在y轴上,则a= __________ .12 . .如图,在反比例函数上有两点A(3,2),B(6,1),在直线上有一动点P,当P点的坐标为时,PA+PB有最小值.13 . 在平面直角坐标系中,若点 M(﹣1,4)与点 N(x,4)之间的距离是 5,则x的值是________.14 . 当______时,在实数范围内有意义三、解答题15 . 如图,已知一条直线经过点A(0,2),点B(1,0),将这条直线向左平移与x轴y轴分别交于点C、点A.若DB=DC,求直线CD对应的函数解析式.16 . 有一条直线y=kx+b,它与直线y=x+3交点的纵坐标为5,而与直线y=3x-9的交点的横坐标也是5.求该直线与两坐标轴围成的三角形面积.17 . △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.(1)将△ABC向右平移2个单位长度,作出平移后的△A1B1C1,并写出△A1B1C1各顶点的坐标.(2)若将△ABC绕点(-1,0)顺时针旋转180°后得到△A2B2C2,并写出△A2B2C2各顶点的坐标.(3)观察△A1B1C1和△A2B2C2,它们是否关于某点成中心对称?若是,请写出对称中心的坐标;若不是,说明理由.18 . 已知正比例函数的图像经过第二、四象限,求这个正比例函数的解析式.19 . 仙游度尾文旦柚,是莆田四大名果之一,获得“国家地理标志保护产品”。
等四校八年级数学上学期第一次联考试题-人教版初中八年级全册数学试题

某某省南安市九都中学等四校2015-2016学年八年级数学上学期第一次联考试题(考试X 围:第11、12章;考试时间:120分钟;满分:150分)一、选择题(每小题3分,共21分)1.把64开平方得( )A 8B –8C ±8D 322.下列各式正确的是()A 、981±=B 、14.314.3-=-ππC 、3927-=-D 、235=- ……,π,4,32其中无理数有 ( )个A 2B 3C 4D 54.有理数中,算术平方根最小的是( )A 、1B 、0C 、0.1D 、不存在5.下列各式计算正确的是( )A.3)3)(3(2-=-+x x xB.92)32)(32(2-=-+x x xC.92)3)(32(2-=-+x x xD.125)15)(15(22-=-+b a ab ab6.如果x 2+kxy+4y 2是关于x 、y 的完全平方式,那么k 的值是( ).(A)2 (B)4 (C) -4 (D)4或-47.如果()()b x a x ++中不含有x 的一次项,则b a ,一定满足( )A. 互为相反数B. 互为倒数C.0==b aD.0=ab二、填空题(每小题4分,共40分)8.-27的立方根是9.比较大小:8310.若42-x 有意义,则x11.(a+8)2+|b -5|+c -3=0,则a +b +c =12. 若最简根式x +1和y 3是同类根式,则 x +y =__________。
13.计算:(m+4) (m -4)=_______.14.利用因式分解简便计算:。
-=2271.229.7. 15..3)3(a -=16. 已知x +y =6,xy =4,则x 2y +xy 2的值为。
17.请你观察、思考下列计算过程:因为121112=,所以11121=,同样,因为123211112=,所以11112321=…由此猜想(1)(2)76543211234567898=_________________.三、解答题(共89分)18.(9分)计算:(32-23)219.(9分)计算:(x+3)(x-1)-x(x-1)20.(9分)先化简,再求值:(x -2y )(x +2y )-(x +2y )2,其中x=0.5,y=-221.(9分)因式分解(第(1)题4分,第(2)题5分).(1)224y x - (2)22242b ab a ++22.(9分)23. (9分)若x -y =3,xy =1.(1) 求(x+y )2的值;(2)求x 2+y 2的值 ;24.(9分)如图,是X 老师买的经济适用房平面结构示意图,图中标明了有关尺寸(墙体厚度忽略不计,单位:m ),房主计划把卧室以外的地面都铺上地砖,(1)求出该经济适用房的面积。
2020-2021学年八年级上学期第一次大联考数学试卷(含解析)

2020-2021学年八年级上学期第一次大联考数学试卷一、选择题(本大题共10小题,共40.0分)1.在平面直角坐标系中,若点A(a,−b)在第一象限内,则点B(−a,b)所在的象限是()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.第四象限中的点P(a,b)到x轴的距离是()A. aB. −aC. −bD. b3.不等式组{x<1x≤4的解集在数轴上表示正确的是()A. B.C. D.4.下列各图象中,表示y是x的函数的是()A. B.C. D.5.△ABC三个顶点的坐标分别为A(−6,1),B(−3,1),C(−3,3),将△ABC先向左平移1个单位,再向上平移3个单位得到△A′B′C′,则点B的对应点B′的坐标为()A. (−4,4)B. (−3,3)C. (−2,4)D. (−3,5)6.已知一次函数y=ax+b的图象过第一、二、四象限,且与x轴交于点(2,0),则关于x的不等式a(x−1)−b>0的解集为()A. x<−1B. x>−1C. x>1D. x<17.如图所示是温度计的示意图,左边的刻度表示摄氏温度,右边的刻度表示华氏湿度,华氏温度y(∘F)与摄氏温度x(∘C)之间的一次函数表达式为()x+32A. y=95B. y=x+40x+32C. y=59x+31D. y=598.当kb<0时,一次函数y=kx+b的图像一定经过()A. 第一、四象限B. 第二、四象限C. 第二、三象限D. 第三、四象限9.函数y=x+3的图象不经过()A. 第四象限B. 第三象限C. 第二象限D. 第一象限10.教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:①当放水时间10分钟时饮水机的存水量9.8升;②饮水机里的水全部放完,需要20分钟;③如果打开第一个水管后,2分钟时恰好有4个同学接水结束,则前22个同学接水结束共需要7分钟;④如果打开第一个水管后,2分钟时恰好有4个同学接水结束,在课间10分钟内班级中最多有32个同学能及时接完水;以上结论正确的有()个.A. 1B. 2C. 3D. 4二、填空题(本大题共4小题,共20.0分)11.函数y=√x−1中,自变量x的取值范围是______ .x−212.已知点M在y轴上,点P(3,−2),若线段MP的长为5,则点M的坐标为____________.13.如图:在由边长为1个单位的小正方形组成的方格纸中,△A1B1C1是由△ABC平移______ 个单位得.14.已知二次函数y=−x2−2x+3图象如图,与x轴交于A,B两点(A在B的左侧),与y轴交于C,图象顶点为D,则直线CD的解析式为______.三、解答题(本大题共9小题,共90.0分)15.21、如图,一次函数y=k1x+3与x轴、y轴分别交于点A和点B,与一次函数y=k2x−1交于点M。
人教版八年级(上)第一次联考数学试卷

初中数学试卷八年级(上)第一次联考数学试卷(满分100分,考试时间120分钟)一、选择题(每小题3分,共30分)1.下列图形具有稳定性的是( ) A.正方形B.三角形C.长方形D.平行四边形2.下面四个图形中,线段BE是△ABC的高的图是()A B C D3.已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是()A.13cm B.6cm C.5cm D.4cm4.等腰三角形中,一个角为50°,则这个等腰三角形的顶角的度数为()A.150°B.80°C.50°或80°D.70°第5题第7题140801ABCDE5.如图,将一副三角板叠放在一起,使直角的顶点重合于O ,则∠AOC+∠DOB=( ) A 、900B 、1200C 、1600D 、1806.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 ( )A 、4B 、5C 、6D 、77.用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A'O'B'=∠AOB 的依据是 A .SSS B.SAS C.ASA D.AAS ( )8. 已知△ABC 中,∠ABC 和∠ACB 的平分线交于点O ,则∠BOC 一定( ) A.小于直角 B .等于直角 C .大于直角 D.不能确定9.如图,在△ABC 中,若AD ⊥BC ,点E 是BC 边上一点,且不与点B 、C 、D 重合,则AD 是几个三角形的高线( )A .4个B .5个C .6个D .8个10. 如图,将含30°角的三角板的直角顶点放在直尺的一边上,若∠1=40°,则∠2的度数为( ) A .90° B .80° C .75° D .70° 题 号 1 2 3 4 5 6 7 8 910 答 案二、填空题(每题3分,共21分) 11.如图,∠1=_____。
人教版八年级数学上册第一次联考试卷

H E DC B A CD AE B θ 第17题图 第18题图 ED F C B A 选择第4题图 P DC B A初中数学试卷2010年大冶市西畈中学八年级第一次联考数学试卷一、选择题(每小题3分,共30分)1、用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A ′O ′B ′=∠AOB 的依据是( ) A 、(S .S .S .) B 、(S .A .S .) C 、(A .S .A .) D 、(A .A .S .)2、如图, ∠C=90°,AD 平分∠BAC 交BC 于D,若BC=5cm,BD=3cm,则点D 到AB 的距离为( ) A 、5cm B 、3cm C 、2cm D 、不能确定3、下列条件能判定△ABC ≌△DEF 的一组是( )A 、∠A=∠D , ∠C=∠F , AC=DF B.AB=DE , BC=EF , ∠A=∠DC 、∠A=∠D , ∠B=∠E , ∠C=∠F D.AB=DE ,△ABC 的周长等于△DEF 的周长4、如图, AD 是△ABC 的中线, E 、F 分别是AD 和AD 延长线上的点,且DE =DF ,连结BF 、CE.下列说法:① CE =BF ;② △ABD 和△ACD 面积相等;③BF ∥CE ;④△BDF ≌△CDE .其中正确的有( ).A 、1个B 、2个C 、3个D 、4个5、如图,在△ABC 中,AD 是∠A 的外角平分线,P 是AD 上异于A 的任意一点,设PB =m ,PC =n ,AB =c ,AC =b ,则)(n m +与)(c b +的大小关系是( ) A 、n m +>c b + B 、n m +<c b + C 、n m +=c b + D 、无法确定 6、如图,△ABC 中AB=AC ,AD 是角平分线,BE=CF ,则下列说法正确的有( )个(1)AD 平分∠EDF ;(2)△EBD ≌△FCD ; (3)BD=CD ;(4)AD ⊥BC .A 、1个B 、2个C 、3个D 、4个 7、以下说法:①有两个角和其中一个角的对边对应相等的两个三角形全等;②有一边和一个角对应相等的两个三角形全等;③有一边相等的两个等边三角形全等; ④一个锐角和一条对应边相等的两个直角三角形全等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版八年级上学期第一次大联考数学试题
姓名:________ 班级:________ 成绩:________
一、单选题
1 . 如图,若象棋盘上建立直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点()
A.(1,-1)B.(-1,1)C.(-1,2)D.(1,-2)
2 . 下列不等式组中,解集在数轴上表示出来如图所示的不等式组为()
A.B.C.D.
3 . 某超市将进货单价为l8元的商品按每件20元销售时,每日可销售100件,如果每件提价1元,日销售就要减少10件,那么把商品的售出价定为多少元时,才能使每天获得的利润最大?()
A.22元B.24元C.26元D.28元
4 . 在函数y=kx(k>0)的图象上有三点A1(x1,y1),A2(x2,y2),A3(x3,y3),已知x1<x2<0<x3,则下列各式中正确的是()
A.y1<y2<0<y3B.y3<0<y1<y2
C.y2<y1<y3<0D.y3<y1<0<y2
5 . 若把点A(-5m,2m-1)向上平移3个单位后得到的点在x轴上,则点A在()
A.x轴上B.第三象限C.y轴上D.第四象限
6 . 甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,乙从B地到A地需要()分钟
A.12B.14C.18D.20
7 . 若一次函数y=kx+b的图象与y轴的负半轴相交,且函数值y随自变量x的增大而增大,则函数y=bx﹣k 的图象只能是图中的()
A.B.
C.D.
8 . 点P(-1,3)在
A.第一象限.B.第二象限.C.第三象限.D.第四象限
9 . 若点在函数的图象上,则的值是()
A.B.
C.D.
10 . 梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含l0千克)的种子,超过l0千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示.下列四种说法:
①一次购买种子数量不超过l0千克时,销售价格为5元/千克;
②一次购买30千克种子时,付款金额为100元;
③一次购买10千克以上种子时,超过l0千克的那部分种子的价格打五折:
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱.
其中正确的个数是
A.1个B.2个C.3个D.4个
二、填空题
11 . 要使二次根式有意义,则x的取值范围为____________.
12 . 在圆O中,弦AB∥弦CD,AB=24,CD=10,弦AB的弦心距为5,则AB和CD之间的距离是_____ .
13 . 在平面直角坐标系中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标(1,0),顶点A 的坐标为(0, 2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该
双曲线上时停止运动,则此时点C的对应点的坐标为__________
14 . 已知长方形ABCD在平面直角坐标系中的位置如图所示,将长方形ABCD沿x轴向左平移到使点C与坐标原点重合后,再沿y轴向下平移到使点D与坐标原点重合,此时点A的坐标是______,点B的坐标是______,点C
的坐标是______.
三、解答题
15 . 为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段以达到节约用水的目的. 该市规定了如下的用水标准:每户每月的用水不超过6m3时,水费按每立方米a元收费;超过6m3时,不超过部分每立方米仍按a元收费,超过部分每立方米按b元收费. 该市居民张大爷一家今年3、4月份的用水量和水费如下表:
月份用水量/m3水费/元
357.5
4915
设该户每月用水量为x(m3),应缴水费y(元).
(1)求a、b的值,写出用水不超过6m3和超过6m3时,y与x之间的代数表达式;
(2)若张大爷一家今年5月份的用水量为8m3,该户5月份应缴的水费是多少?
16 . 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲、y乙与x之间的函数图象如图所示.
(1)甲的速度是_____km/h;
(2)当1≤x≤5时,求y乙关于x的函数解析式;
(3)当乙与A地相距240km时,甲与A地相距_____km.
17 . 如图,直线AB的函数解析式为y=-2x+8,与x轴交于点A,与y轴交于点B。
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接E,若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围。
18 . 已知y=y1+y2,其中y1与x成正比例,y2与(x﹣2)成反比例.当x=1时,y=2;x=3时,y=10.求:
(1)y与x的函数关系式;
(2)当x=﹣1时,y的值.
19 . 如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,﹣1).
(1)作出△ABC关于原点对称的△A1B1C1,并写出点A1的坐标;
(2)把△ABC绕点C逆时针旋转90°,得△A2B2C,画出△A2B2C,并写出点A2的坐标;
(3)直接写出△A2B2C的面积.
20 . 在同一直角坐标系中画出下列函数的图象:y=2x,y=-2x.
21 . 如图,在△ABC中,∠C=90°,AB=10,AC=8,将线段AB绕点A按逆时针方向旋转90°到线段AD.△EFG 由△ABC沿CB方向平移得到,且直线EF过点D.
(I)求∠1的大小.
(Ⅱ)求AE的长.
22 . 如图,矩形OABC中, A(0,5),C(4,0),正比例函数的图象经过点B.
(1)求正比例函数的表达式;
(2)反比例函数的图象与正比例函数的图象和边BC围成的阴影区域BNM如图所示,请直接写出阴影区域中横纵坐标都是整数的点的坐标(不包括边界).
23 . 某经销商从市场得知如下信息:
A品牌手表B品牌手表
进价(元/块)700100
售价(元/块)900160
他计划用4万元资金一次性购进这两种品牌手表共100块,设该经销商购进A品牌手表x块,这两种品牌手表全部销售完后获得利润为y元.
(1)试写出y与x之间的函数关系式;
(2)若要求全部销售完后获得的利润不少于1.26万元,该经销商有哪几种进货方案;
(3)选择哪种进货方案,该经销商可获利最大;最大利润是多少元.
参考答案一、单选题
1、
2、
3、
4、
5、
6、
7、
8、
9、
10、
二、填空题
1、
2、
3、
4、
三、解答题
1、2、3、4、5、6、7、8、9、。
