切线练习题
切线长定理练习题

切线长定理练习题一、选择题1.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( ) A.21 B.20 C.19 D.182. 如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角(不包括∠PAB本身)有( )A.1个B.2个C.3个D.4个2题图3题图4题图3.如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的( ) A.三条中线的交点B.三条高的交点C.三条角平分线的交点D.三条边的垂直平分线的交点4.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( )A.21 B.20 C.19 D.18二、填空题5.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________.5题图6题图7题图6.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.7.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.三、解答题9. 如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.P BAO10. 如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC= 12,∠P=60o,求弦AB的长.11.如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.(1)求∠APB的度数;(2)当OA=3时,求AP的长.12.已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长.13.已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.14.如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2 cm,AD=4 cm.(1)求⊙O的直径BE的长;(2)计算△ABC的面积.正多边形和圆习题一、填空题判断:①正多边形的中心角等于它的每一个外角.( )②若一个正多边形的每一个内角是150°,则这个正多边形是正十二边形.( )⑤各角相等的圆外切多边形是正多边形.( )4.判断下列各种图形是否一定是正多边形(是打“√”,不是打“×”)。
切线长定理练习题

A切线长定理练习题一、选择题1. 一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( ) A .21 B .20 C .19 D .182. 如图,PA 、PB 分别切⊙O 于点A 、B ,AC 是⊙O 的直径,连结AB 、BC 、OP ,则与∠PAB 相等的角(不包括∠PAB 本身)有 ( ) A .1个 B .2个 C .3个 D .4个3.如图,已知△ABC 的内切圆⊙O 与各边相切于点D 、E 、F ,则点O 是△DEF 的( ) 交点 A .三条中线B .三条高C .三条角平分线D .三条边的垂直平分线4. 一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( ) A .21 B .20 C .19 D .185.△ABC 中,AB =AC ,∠A 为锐角,CD 为AB 边上的高,I 为△ACD 的内切圆圆心,则∠AIB 的度数是( )A .120° B .125°C .135°D .150°6.一个钢管放在V 形架内,右图是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN = 60︒,则OP =( )A .50 cm B .253cm C .3350cm D .503cm7.如图,在△ABC 中,5cm AB AC ==,cos B 35=.如果⊙O ,且经过点B 、C ,那么线段AO = cm .二、填空题1.如图,⊙I 是△ABC 的内切圆,切点分别为点D 、E 、F ,若∠DEF=52o,则∠A 的度为________. 2.如图,一圆内切于四边形ABCD ,且AB=16,CD=10,则四边形ABCD 的周长为________. 3.如图,已知⊙O 是△ABC 的内切圆,∠BAC=50o,则∠BOC 为____________度.4.如图,⊙O 内切于△ABC ,∠BOC =105°,∠ACB =90°,AB =20cm .则BC=___________5.如图,PA 、PB 是⊙O 的两条切线,切点分别为点A 、B ,若直径AC= 12,∠P=60o ,.则AB 的长=___________.6.如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,则△ABC 的周长=___________. 三、解答题1. 如图,在△ABC 中,已知∠ABC=90o ,在AB 上取一点E ,以BE 为直径的⊙O 恰与AC 相切于点D ,若AE=2 cm ,AD=4 cm . (1)求⊙O 的直径BE 的长; (2)计算△ABC 的面积.2、如图,AB 、CD 分别与半圆O 切于点A 、D ,BC 切⊙O 于点E ,若AB =4,CD =9,求⊙O 的半径。
圆的切线综合练习题与答案完整版

圆的切线综合练习题与答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】切线的判定与性质练习题一、选择题(答案唯一,每小题3分)1.下列说法中,正确的是( )A.与圆有公共点的直线是圆的切线 B.经过半径外端的直线是圆的切线C.经过切点的直线是圆的切线 D.圆心到直线的距离等于半径的直线是圆的切线2. 如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )A.70° B.35° C.20° D.40°第2题第3题第4题第5题3. 如图,线段AB是⊙O的直径,点C,D为⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠CDB等于( )A.20° B.25° C.30° D.40°4.如图,等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为( )A.8 B.6 C.5 D.45.如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )A.AG=BG B.AB∥EF C.AD∥BC D.∠ABC=∠ADC二.填空题(每小题3分)6.如图,在⊙O中,弦AB=OA,P是半径OB的延长线上一点,且PB=OB,则PA与⊙O的位置关系是_________.第6题第7题第8题7.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为________________.8.如图,AB是⊙O的直径,O是圆心,BC与⊙O切于点B,CO交⊙O于点D,且BC=8,CD=4,那么⊙O的半径是______.9. 如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=_______度.第9题第10题第11题10. 如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC,BE.若AE=6,OA=5,则线段DC的长为______.11.如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=________度.三、解答题(写出详细解答或论证过程)12.(7分)如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.求证:AC是⊙O的切线.第12题第13题第14题13.(7分)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.求证:∠BDC=∠A.14.(7分)如图,在Rt△ABC中,∠ABC=90°,∠BAC的平分线交BC于D,以D为圆心,DB长为半径作⊙D,求证:AC与⊙D相切.15.(10分)如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.(1)求∠D的度数;(2)若CD=2,求BD的长.第15题第16题16.(12分)已知△ABC内接于⊙O,过点A作直线EF.(1)如图①,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种):__________________________或者_______________________;(2)如图②,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.17.(12分)如图,已知直线PA交⊙O于A,B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.(1)求证:CD为⊙O的切线;(2)若DC+DA=6,⊙O的直径为10,求AB的长.答案:DDADC 6. 相切 7. ∠ABC=90°不排除等效答案 8. 6 9. 45 10. 4 11. 6012. 解:连接OD,∵BD为∠ABC平分线,∴∠OBD=∠CBD,∵OB=OD,∴∠OBD=∠ODB,∴∠CBD=∠ODB,∴OD∥BC,∵∠C=90°,∴∠ODA=90°,则AC为⊙O的切线13. 解:连接OD,∵CD是⊙O的切线,∴∠ODC=90°,∴∠ODB+∠BDC=90°,∵AB是⊙O的直径,∴∠ADB=90°,即∠ODB+∠ADO=90°,∴∠BDC=∠ADO,∵OA=OD,∴∠ADO=∠A,∴∠BDC=∠A14. 解:过D作DH⊥AC于H,由角平分线的性质可证DB=DH,∴AC与⊙D相切15. 解:(1)∵∠COD=2∠CAD,∠D=2∠CAD,∴∠D=∠COD.∵PD与⊙O相切于点C,∴OC⊥PD,即∠OCD=90°,∴∠D=45°(2)由(1)可知△OCD是等腰直角三角形,∴OC=CD=2,由勾股定理,得OD=22+22=22,∴BD=OD-OB=22-216. (1) ∠BAE=90°∠EAC=∠ABC(2) (2)EF是⊙O的切线.证明:作直径AM,连接CM,则∠ACM=90°,∠M=∠B,∴∠M+∠CAM=∠B+∠CAM=90°,∵∠CAE=∠B,∴∠CAM+∠CAE=90°,∴AE⊥AM,∵AM为直径,∴EF是⊙O的切线17. 解:(1)连接OC,证∠DAC=∠CAO=∠ACO,∴PA∥CO,又∵CD⊥PA,∴CO⊥CD,∴CD为⊙O 的切线(2)过O作OF⊥AB,垂足为F,∴四边形OCDF为矩形.∵DC+DA=6,设AD=x,则OF=CD=6-x,AF=5-x,在Rt△AOF中,有AF2+OF2=OA2,即(5-x)2+(6-x)2=25,解得x1=2,x2=9,由AD<DF知0<x<5,故x=2,从而AD=2,AF=5-2=3,由垂径定理得AB=2AF=6。
切线的判定及性质练习题

切线的判定及性质练习题1、⊙O 的半径为2cm,直线MN 上有一点P,且PO=2cm,则⊙O 与直线MN 的位置关系是_______。
2、Rt △ABC, ∠C=90°,AC=6cm,BC=8cm,以点C 为圆心的⊙C 与AB 所在的直线相切,则⊙C 的半径为_______。
3、设⊙O 的半径为3,点O 到直线AB 的距离为d,若直线AB 与⊙O 至少有一个公共点,则d 应满足的条件是_______。
4、如图1,已知AB 是⊙O 的直径,PB 是⊙O 的切线,PA 交⊙O 于点C,AB=3cm,PB=4cm,则BC 的长是﹍﹍。
5、如图2,AB 是⊙O 的直径,CD 切⊙O 于C,若∠BCD=25°,则∠B= ﹍﹍。
6、如图1、⊙O 的直径AB 与弦AC 的夹角为25°,切线CD 与AB 的延长线交与点D ,则∠ADC=﹍﹍。
7.如图2、点P 为⊙O 外一点,PA 且⊙O 与点A,OP 交⊙O 于点B,PA=6,BP=4,则⊙O 的半径为﹍﹍。
8、如图3、知⊙O 半径为6cm,AB 是⊙O 的直径,D 为AB 延长线上的一点,DC 切⊙O 于点C ,连接AC ,若∠CAB=30 °,则 ∠ADC=﹍﹍,BD=﹍﹍。
1、以等腰△ABC 的腰AB 为直径作⊙O 交底边BC 与点D ,DE ⊥ AC 于E , 求证:DE 为⊙O 的切线AODCB ●●O PAB(2)●C DOAB(3)B DCA●OE●AOCBP(1)●ACB OD (2)2、如图⊙O 是Rt △ABC 外接圆,点O 在AB 上,BD ⊥AB,点B 是垂足,OD ∥AC ,连接CD 。
求证:CD 是⊙O 的切线。
3、如图1,MP 切⊙O 于点M ,直线PO 交⊙O 于A 、B ,弦AC ∥MP , 求证: MO ∥BC3、如图:AB 是⊙O 的直径,C 为⊙O 上一点,AD 和过点C 的切线互相垂直,垂足为点D,求证:AC 平分∠DAB .OACB DOABDC●CBOAP M(1)●4、如图2,CD 是△ABC 的边AB 上的高,以CD,为直径的⊙O 分别交CA 、CB 于点E 、F ,点G 是AD 的中点。
新教材切线长定理练习题

3切线长定理习题1、如图,PA,PB,分别切⊙O于点A,B,∠P=70°,∠C等于。
1.在△ABC中,AB=5cm BC=7cm AC=8cm,⊙O与BC、AC、 AB分别相切于 D、 E 、F,那么 AF=_____, BD=_______ 、CF=________2.PA、PB切⊙O于A、B,∠APB=60º,PA=4,那么⊙O的半径为。
4.如图1,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,那么∠ACB=〔〕.A.60°B.75°C.105°D.120°(1) (2)5.圆外一点P,PA、PB分别切⊙O于A、B,C为优弧AB上一点,假设∠ACB=a,那么∠APB=〔〕A.180°-a B.90°-a C.90°+a D.180°-2a6.如图2,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,•PA=7cm,那么△PCD的周长等于_________.7.:如图,从两个同心圆O的大圆上一点A,作大圆的弦AB切小圆于C点,大圆的弦AD切小圆于E点.求证:(1)AB=AD; (2)DE=BC.8.如图,PA,PB为⊙O的切线,A、B是切点,OP与⊙O交于C,∠APB=60°,求证:OC=PC9、如图在△ABC中,圆I与边BC、CA、AB分别相切于点D、E、F,∠B=60°,∠C=70°,求∠EDF的度数。
FEIBACPBCAOBCDP OBACPOABCD E O123BA C DPO 10.如下图,EB 、EC 是⊙O 的两条切线,B 、C 是切点,A 、D 是⊙O 上两点,如果∠E=46°,∠DCF=32°,求∠A 的度数.BA ED O11.:Rt △ABC 中,∠ABC=90°,以AB 为直径的⊙O 交AC 于D ,过D 作⊙O 的切线DE ,交BC于E ,求证:BE=CE .12.如图,PA 、PB 分别切圆O 于A 、B ,并与圆O 的切线,分别相交于C 、D ,•PA=7cm ,求△PCD 的周长.13.:如图,在三角形ABC 中,内切圆O 与△ABC 的三边分别切于D ,E ,F 三点,∠DFE=56°,求∠A 得度数。
(完整版)切线长定理练习题

切线长定理练习题一、选择题1.下列说法中,不正确的是( ) A.三角形的内心是三角形三条内角平分线的交点B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部C.垂直于半径的直线是圆的切线D.三角形的内心到三角形的三边的距离相等2.给出下列说法:①任意一个三角形一定有一个外接圆,并且只有一个外接圆;②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③任意一个三角形一定有一个内切圆,并且只有一个内切圆;④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.其中正确的有( ) A.1个B.2个C.3个D.4个3.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( ) A.21 B.20 C.19 D.184. 如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角(不包括∠PAB本身)有( ) A.1个B.2个C.3个D.4个4题图5题图6题图5.如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的( )C.三条角平分线的交点D.三条边的垂直平分线的交点6.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( )A.21 B.20 C.19 D.18二、填空题6.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________.6题图7题图8题图7.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.8.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.三、解答题9. 如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.10. 如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC= 12,∠P=60o,求弦AB的长.PBAO11. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°.(1)求∠APB 的度数;(2)当OA =3时,求AP 的长.12.已知:如图,⊙O 内切于△ABC ,∠BOC =105°,∠ACB =90°,AB =20cm .求BC 、AC 的长.13.已知:如图,△ABC 三边BC =a ,CA =b ,AB =c ,它的内切圆O 的半径长为r .求△ABC 的面积S .14. 如图,在△ABC 中,已知∠ABC=90o ,在AB 上取一点E ,以BE 为直径的⊙O 恰与AC 相切于点D ,若AE=2 cm ,AD=4 cm . (1)求⊙O 的直径BE 的长; (2)计算△ABC 的面积.15.已知:如图,⊙O 是Rt △ABC 的内切圆,∠C =90°.(1)若AC =12cm ,BC =9cm ,求⊙O 的半径r ; (2)若AC =b ,BC =a ,AB =c ,求⊙O 的半径r .四、体验中考16.(2011年安徽)△ABC 中,AB =AC ,∠A 为锐角,CD 为AB 边上的高,I 为△ACD 的内切圆圆心,则∠AIB 的度数是( )A .120°B .125°C .135°D .150°17.(2011年绵阳)一个钢管放在V 形架内,右图是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN = 60︒,则OP =( ) A .50 cm B .253cm C .3350cm D .503cm 18. (2011年甘肃定西)如图,在△ABC 中,5cm AB AC ==,cos B 35=.如果⊙O 的半径为10cm ,且经过点B 、C ,那么线段AO = cm .17题图 18题图 19题图19. (2011年湖南怀化)如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,参考答案◆随堂检测1. C2. B (提示:②④错误)3. 760(提示:连接ID,IF ∵∠DEF=520∴∠DIF=1040∵D、F是切点∴DI ⊥AB,IF⊥AC∴∠ADI=∠AFI=900∴∠A=1800-1040=760)4. 52 (提示:AB+CD=AD+BC)5. 1150(提示:∵∠A=500∴∠ABC+∠ACB=1300∵OB,OC分别平分∠ABC,∠ACB ∴∠OBC+∠OCB=650∴∠BOC=1800-650=1150)◆课下作业1. D (提示:AD=AF,BD=BE,CE=CF ∴周长=821218⨯+⨯=)2. C3. D4. 解:∵AD,AE 切于⊙O 于D,E ∴AD=AE=20 ∵AD,BF 切于⊙O 于D,F ∴BD=BF 同理:CF=CE∴C △ABC =AB+BC+AC=AB+BF+FC+AC=AB+BD+EC+AC=AD+AE=405. 解:连接BC ∵PA,PB 切⊙O 于A,B ∴PA=PB ∵∠P=600 ∴△ABC 是正三角形 ∵∠PAB=600∵PA 是⊙O 切线 ∴CA ⊥AP ∴∠CAP=900 ∴∠CAB=300 ∵直径AC ∴∠ABC=900∴cos300=ABAC∴AB=6. 解:(1)∵在△ABO 中,OA =OB ,∠OAB =30°∴∠AOB =180°-2×30°=120°∵PA 、PB 是⊙O 的切线∴OA ⊥PA ,OB ⊥PB .即∠OAP =∠OBP =90° ∴在四边形OAPB 中,∠APB =360°-120°-90°-90°=60°.(2)如图①,连结OP∵PA 、PB 是⊙O 的切线∴PO 平分∠APB ,即∠APO =12∠APB =30°又∵在Rt △OAP 中,OA =3, ∠APO =30°∴AP =tan 30OA°=7. 解:(1)连接OD ∴OD ⊥AC ∴△ODA 是Rt △解之得:r=3 ∴BE=6(2) ∵∠ABC=900 ∴OB ⊥BC ∴BC 是⊙O 的切线 ∵CD 切⊙O 于D ∴CB=CD 令CB=x∴AC=x+4,BC=4,AB=x ,AB=8 ∵2228(4)x x +=+ ∴6x = ∴S △ABC =186242⨯⨯= ●体验中考 1. C2. A (提示:∠MPN=600可得∠OPM=300 可得OP=2OM=50)3.3(提示:连接OB ,易得:∠ABC=∠AOB ∴cos ∠AOB=cos ∠35=OBOA AO=)4. ∠P=600。
切线长定理练习题

切线长定理—巩固练习(基础)一、选择题1. 下列说法中,不正确的是 ( )A .三角形的内心是三角形三条内角平分线的交点B .锐角三角形、直角三角形、钝角三角形的内心都在三角形内部C .垂直于半径的直线是圆的切线D .三角形的内心到三角形的三边的距离相等2.△ABC 的三边长分别为a 、b 、c ,它的内切圆的半径为r ,则△ABC 的面积为( )A.(a +b +c )rB.2(a +b +c )C.(a +b +c )rD.(a +b +c )r 3.(2016•西城区)如图,PA 、PB 分别切⊙O 于A 、B 两点,如果∠P=60°,PA=2,那么AB 的长为( )A .1B .2C .3D .44. 如图所示,⊙O 的外切梯形ABCD 中,如果AD ∥BC ,那么∠DOC 的度数为( )A.70°B.90°C.60°D.45°第4题图 第5题图21315.如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为()A.35°B.45°C.65°D.70°6.已知如图所示,等边△ABC的边长为2cm,下列以A为圆心的各圆中,半径是3cm 的圆是( )二、填空题7.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________.第7题图第8题图第9题图8.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.9.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.10.如图,、分别切⊙于点、,点是⊙上一点,且,则____度.PA PB O A B E O60=∠AEB=∠P第10题图第11题图11.如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为 .12.(2016秋•淮安校级期中)如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径为6cm,OP的长为10cm,则△PDE的周长是.三、解答题13.已知,如图,A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,P是BC上任意一点,过点P作⊙O的切线,交AB于点M,交AC于点N,设AO=d,BO=r.求证:△AMN 的周长是一个定值,并求出这个定值.14. 已知:如图,PA,PB,DC分别切⊙O于A,B,E点.(1)若∠P=40°,求∠COD;(2)若PA=10cm,求△PCD的周长.15.(2015•南丹县一模)如图,∠C=90°,⊙O是Rt△ABC的内切圆,分别切BC,AC,AB于点E,F,G,连接OE,OF.AO的延长线交BC于点D,AC=6,CD=2.(1)求证:四边形OECF为正方形;(2)求⊙O的半径;(3)求AB的长.【答案与解析】一、选择题1.【答案】C.【解析】经过半径的外端,并且垂直于这条半径的直线是圆的切线.2.【答案】A.【解析】连结内心与三个顶点,则△ABC 的面积等于三个三角形的面积之和,所以△ABC的面积为a ·r +b ·r +c ·r =(a +b +c )r . 3.【答案】B【解析】∵PA 、PB 分别切⊙O 于A 、B ,∴PA=PB ;∵∠P=60°,∴△PAB 是等边三角形;∴AB=PA=2,故选B .4.【答案】B ;【解析】由AD ∥BC ,得∠ADC+∠BCD=180°,又AD 、DC 、BC 与⊙O 相切,所以∠ODC=∠ADC ,∠OCD=∠BCD ,所以∠ODC+∠OCD=×180°=90°,所以∠DOC=90°.故选B.5.【答案】D ; 21212121212121【解析】根据切线的性质定理得∠PAC=90°,∴∠PAB=90°﹣∠BAC=90°﹣35°=55°.根据切线长定理得PA=PB,所以∠PBA=∠PAB=55°,所以∠P=70°.6.【答案】C;【解析】易求等边△ABC的高为3cm等于圆的半径,所以圆A与BC相切,故选C. 二、填空题7.【答案】76°;【解析】连接ID,IF ∵∠DEF=52°,∴∠DIF=104°,∵D、F是切点,∴DI⊥AB,IF⊥AC ,∴∠ADI=∠AFI=90°,∴∠A=1800-1040=76°.8.【答案】52;【解析】提示:AB+CD=AD+BC.9.【答案】115°;【解析】∵∠A=500∴∠ABC+∠ACB=130°,∵OB,OC分别平分∠ABC,∠ACB,∴∠OBC+∠OCB=65°,∴∠BOC=1800-650=115°.10.【答案】60°;【解析】连结OA、OB,则∠AOB=120°,在四边形OAPB中,∠P=360°-90°-90°-120°=60°.11.【答案】26°;【解析】连结OA,则∠AOC=64°,∠P=90°-64°=26°.12.【答案】16cm【解析】连接OA.∵PA、PB、DE分别切⊙O于A、B、C点,∴BD=CD,CE=AE,PA=PB,OA⊥AP.在直角三角形OAP中,根据勾股定理,得AP=8,∴△PDE的周长为2AP=16.故选答案为16cm.三、解答题13.【答案与解析】解:∵AB,AC分别与⊙O相切,∴OB⊥AB,∵AO=d,BO=r,∴AB==,∵MN切圆O于点P,∴MP=MB,NP=NC,∴△AMN的周长=AM+AN+MN=AM+PM+PN+AN=AM+BM+AN+PN=AB+AC=2AB=2,∴△AMN的周长是一个定值,这个定值为2.14. 【答案与解析】(1)∵PA,PB,DC 分别切圆O 于A,B,E 点∴OC 与OD 就是△PCD 的两个外角的平分线∴∠COD=90°- ∠P=90°-20°=70° (2)∵PA 与PB 分别切⊙O 于A 、B 两点,CD 切⊙O 于E ,∴PA=PA=10cm ,CA=CE ,DE=DB ,∴△PCD 的周长=PD+DE+EC+PC=PD+DB+CA+PC=PA+PB=20cm .故答案为20 cm .15. 【答案与解析】(1)证明:∵⊙O 是Rt△ABC 的内切圆,分别切BC ,AC ,AB 于点E ,F ,G , ∴∠C=∠CFO=∠CEO=90°,∴四边形CFOE 是矩形,∵OF=OE,∴四边形OECF 为正方形;(2)解:由题意可得:EO∥AC,∴△DEO∽△DCA,∴=,设⊙O 的半径为x ,则=,解得:x=1.5,12故⊙O的半径为1.5;(3)解:∵⊙O的半径为1.5,AC=6,∴CF=1.5,AF=4.5∴AG=4.5,设BG=BE=y,∴在Rt△ACB中AC2+BC2=AB2,∴62+(y+1.5)2=(4.5+y)2,解得:y=3,∴AB=AG+BG=4.5+3=7.5.。
高考数学切线经典练习题

高考数学切线经典练习题例题1、设曲线C 的方程为321()1,3f x x x =-+求曲线C 上在点(3,1)的切线。
变式1、设曲线C 的方程为321()1,3f x x x =-+求曲线C 上经过点(3,1)的切线。
变式2、若过点(3,1)的直线与曲线32113y x x =-+和21(0)y ax x a =++≠ 都相切,求a 的值。
练习、已知有且仅有一条直线与抛物线C 1:y=x 2+2x 和C :y=-x 2+a都相切,求a 的值。
变式3、已知曲线C 的方程为3211,32a y x x =-+若过点(0,2)曲线C 有三条不同的切线,求a 的范围。
练习、若过点(1,)P m -可作曲线32()x 69f x x x =-+-的三条切线,求实数m 的取值范围.变式4、已知函数3()f x x x =-.设0a >,若过点()a b ,可作曲线....()y f x =的三条切线.....,证明:()a b f a -<<变式6、已知定义在正实数集上的函数,ex x x f 221)(2+=b x e x g +=ln 3)(2(其中为常数,),若这两个函数的图象有公共点,且在该点处的切线相同. 求实数b 的值;抛物线()y g x =经过点(0,0)O 、(,0)A m 与点(1,1)P m m ++,其中0>>n m ,a b <,设函数)()()(x g n x x f -=在a x =和b x =处取到极值。
(1)用,m x 表示()y g x =;(2) 比较n m b a ,,,的大小(要求按从小到大排列);(3)若22≤+n m ,且过原点存在两条互相垂直的直线与曲线)(x f y =均相切,求)(x f y =。
e 2.71828e =⋅⋅⋅。
切线长定理练习题

一.选择题(1)若⊙O的切线长和半径相等,则两条切线所夹角的度数为()A.30°B.45°C.60° D.90°(2)若AB、AC分别切⊙O于B、C,延长OB到D使BD=OB,连AD,∠DAC =78°,则∠ADO=()A.56°B.39°C.64°D.78°(3)如图7—153,AB、AC切⊙O于B、C,AO交⊙O于D,过D作⊙O切线分别交AB、AC于E、F,若OB=6,AO=10,则△AEF的周长是()A.10B.12C.14D.16(4). 如图:△ABC与⊙O分别切于D、E、F,DE∥BC,AB=8,AD=5,则BC的长为()A.3B.6C.3D.无法求出(5)⊙O的半径为2,弦AB=23,过A、B两点的⊙O的切线相交于点P,PO与圆相交于C,则C到PA的距离是_______;(5)PA、PC分别切⊙O于A、C两点,B为⊙O上与A、C不重合的点,若∠P =50°,则∠AB C=_______.(6)已知:PA、PB分别切⊙O于点A和B,C为弧AB上一点,过C与⊙O 相切的直线分别交PA、PB于点D和E,若PA=2cm,∠APB=60°则(1)△PDE的周长= (2)∠DOE= .二、填空题:1.已知两圆半径分别为8、6,若两圆内切,则圆心距为______;若两圆外切,则圆心距为___.2.已知两圆的圆心距d=8,两圆的半径长是方程x2-8x+1=0的两根,则这两圆的位置关系是______.3.圆心都在y轴上的两圆⊙O1、⊙O2,⊙O1的半径为5,⊙O2的半径为1,O1 的坐标为(0,-1),O2的坐标为(0,3),则两圆⊙O1与⊙O2的位置关系是________.4.⊙O1和⊙O2交于A、B两点,且⊙O1经过点O,若∠AO1B=90°,那么∠AO2B 的度数是__.5.矩形ABCD中,AB=5,BC=12,如果分别以A、C为圆心的两圆相切,点D 在⊙C内, 点B在⊙C外,那么圆A的半径r的取值范围是__________.6.两圆半径长分别是R和r(R>r),圆心距为d,若关于x的方程x2-2rx+(R-d)2=0 有相等的两实数根,则两圆的位置关系是_________.二、选择题7.⊙O的半径为2,点P是⊙O外一点,OP的长为3,那么以P为圆心,且与⊙O 相切的圆的半径一定是( )A.1或5B.1C.5D.1或48.直径为6和10的两上圆相外切,则其圆心距为( )A.16B.8C.4D.29.如图1,在以O为圆心的两个圆中,大圆的半径为5,小圆的半径为3, 则与小圆相切的大圆的弦长为( )A.4B.6C.8D.1010.⊙O1、⊙O2、⊙O3两两外切,且半径分别为2cm,3cm,10cm,则△O1O2O3 的形状是( )A.锐角三角形B.等腰直角三角形;C.钝角三角形D.直角三角形11.如图2,⊙O1和⊙O2内切,它们的半径分别为3和1,过O1作⊙O2的切线, 切点为A,则O1A的长为( )A.2B.4C.D.12.半径为1cm和2cm的两个圆外切,那么与这两个圆都相切且半径为3cm 的圆的个数是( ) A.5个 B.4个 C.3个 D.2个13.如图3,⊙O的半径为r,⊙O1、⊙O2的半径均为r1,⊙O1与⊙O内切,沿⊙O 内侧滚动m圈后回到原来的位置,⊙O2与⊙O外切并沿⊙O外侧滚动n圈后回到原来的位置,则m、n的大小关系是( )A.m>nB.m=nC.m<nD.与r,r1的值有关三、解答题14.若两圆的圆心距d满足等式│d-4│=3,且两圆的半径是方程x2-7x+12=0 的两个根,试判断这两圆的位置关系.15.某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上, 向内放入两个半径为5cm的钢球,测得上面一个钢球顶部高DC=16cm(钢管的轴截面如图所示), 求钢管的内直径AD的长.三,解答题1. 已知如图:在△ABC中,∠ACB=Rt∠,⊙O的O点在BC上,且AB切⊙O于D,若OC∶OB=1∶3,AD=2.求BE的长.2.如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,再过A点作半圆的切线,与半圆相切于F点,与DC相交于E点.求:△ADE的面积.四.思考题在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8厘米,AD=24厘米,BC=26厘米,AB是⊙O的直径,动点P从点A开始沿AD边向点D以1厘米/秒的速度运动.动点Q从点C开始沿CB边向点B以3厘米/秒的速度运动,P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒,求:(1)t分别为何值时,四边形PQCD为平行四边形、等腰梯形?(2)t分别为何值时,直线PQ与⊙O相切、相交、相离?。
切线练习题

切线练习1、以△ABC 的边AB 为直径作⊙O ,如果⊙O 经过AC 的中点D,然后过D 作DE ⊥BC ,垂足为点E ,DE 是⊙O 的切线吗?2、在Rt △ABC,∠B=90°,∠A 的平分线交BC 于D,以D 为圆心,DB 长为半径作⊙D.试说明:AC 是⊙D 的切线.3、已知:如图,AB 是⊙O 的直径,P 是⊙O 外一点,PA ⊥AB ,弦BC ∥OP ,求证:PC 为⊙O 的切线4、已知:如图,在Rt △ABC 中,∠ABC=900,以AB 为直径的⊙O 交AC 于E 点,D 为BC 的中点。
求证:DE 与⊙O 相切。
5、已知:以等腰△ABC 的一腰AB 为直径的⊙O 交BC 于D ,,过D 作DE ⊥AC 于E , 求证:DE 是⊙O 的切线。
CD6、直线l上的一点到圆心O的距离等于⊙O的半径,则直线l与⊙O的位置关系是()(A)相切(B)相交(C)相离(D)相切或相交7、圆O的直径4,圆心O到直线L的距离为3,则直线L与圆O的位置关系是()(A)相离(B)相切(C)相交(D)相切或相交8、RtABC中,∠C=90°,AB=10,AC=6,以C为圆心作圆C与AB相切,则圆C的半径为()(A)8 (B)4 (C)9.6 (D)4.89、⊙O的半径为6,⊙O的一条弦AB为63,以3为半径的同心圆与直线AB的位置关系是10.Rt△ABC中,∠C=90°,AB=10,AC=6,以C为圆心作⊙C和AB相切,则⊙C的半径长为()A.8 B.4 C.9.6 D.4.811、.如图直线AB与半径为2的⊙O的相切于点C,D是⊙O上一点且∠EDC=30°,弦EF∥AB,则EF长为()A. 2 B 2 C. D. 2√212、.如图,PA切⊙O于A,PB切⊙O于B,∠APB=90°,OP=4,则⊙O的半径=_________.。
大学切线方程练习题

大学切线方程练习题大学切线方程练习题在大学数学课程中,切线方程是一个重要的概念。
它是用来描述曲线上某一点处的切线的方程。
切线方程的求解需要运用导数的知识,因此对于学习者来说,掌握切线方程的求解方法是非常重要的。
下面我们来看一些关于大学切线方程的练习题。
练习题一:求曲线的切线方程已知曲线C的方程为y = x^3 + 2x + 1,求曲线C在点(1, 4)处的切线方程。
解析:要求曲线C在点(1, 4)处的切线方程,首先需要求出曲线C在该点的斜率。
曲线C的斜率可以通过求导来得到。
对曲线C的方程y = x^3 + 2x + 1求导,得到y' = 3x^2 + 2。
将x = 1代入y' = 3x^2 + 2,得到y' = 3(1)^2 + 2 = 5。
因此,曲线C在点(1, 4)处的切线的斜率为5。
接下来,我们可以利用切线的斜率和已知点(1, 4)来求出切线方程。
切线方程的一般形式为y - y1 = m(x - x1),其中m为切线的斜率,(x1, y1)为切线上的一点。
代入已知点(1, 4)和切线的斜率5,得到切线方程为y - 4 = 5(x - 1)。
练习题二:求曲线的切线方程与法线方程已知曲线C的方程为y = 2x^2 + 3x - 1,求曲线C在点(-1, -2)处的切线方程和法线方程。
解析:与练习题一类似,首先需要求出曲线C在点(-1, -2)处的斜率。
对曲线C的方程y = 2x^2 + 3x - 1求导,得到y' = 4x + 3。
将x = -1代入y' = 4x + 3,得到y' = 4(-1) + 3 = -1。
因此,曲线C在点(-1, -2)处的切线的斜率为-1。
利用切线的斜率和已知点(-1, -2),可以求出切线方程。
代入已知点(-1, -2)和切线的斜率-1,得到切线方程为y + 2 = -1(x + 1),即y + 2 = -x - 1。
圆的切线综合练习题与答案

切线的判定与性质练习题一、选择题(答案唯一,每小题3分)1.下列说法中,正确的是( )A.与圆有公共点的直线是圆的切线 B.经过半径外端的直线是圆的切线C.经过切点的直线是圆的切线 D.圆心到直线的距离等于半径的直线是圆的切线2. 如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )A.70° B.35° C.20° D.40°第2题第3题第4题第5题3. 如图,线段AB是⊙O的直径,点C,D为⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠CDB等于( )A.20° B.25° C.30° D.40°4.如图,等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为( )A.8 B.6 C.5 D.45.如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )A.AG=BG B.AB∥EF C.AD∥BC D.∠ABC=∠ADC二.填空题(每小题3分)6.如图,在⊙O中,弦AB=OA,P是半径OB的延长线上一点,且PB=OB,则PA与⊙O的位置关系是_________.第6题第7题第8题7.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为________________.8.如图,AB是⊙O的直径,O是圆心,BC与⊙O切于点B,CO交⊙O于点D,且BC=8,CD=4,那么⊙O的半径是______.9. 如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=_______度.第9题第10题第11题10. 如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC,BE.若AE=6,OA=5,则线段DC的长为______.11.如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=________度.三、解答题(写出详细解答或论证过程)12.(7分)如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.求证:AC是⊙O的切线.第12题第13题第14题13.(7分)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.求证:∠BDC=∠A.14.(7分)如图,在Rt△ABC中,∠ABC=90°,∠BAC的平分线交BC于D,以D为圆心,DB长为半径作⊙D,求证:AC与⊙D相切.15.(10分)如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.(1)求∠D的度数;(2)若CD=2,求BD的长.第15题第16题16.(12分)已知△ABC内接于⊙O,过点A作直线EF.(1)如图①,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种):__________________________或者_______________________;(2)如图②,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.17.(12分)如图,已知直线PA交⊙O于A,B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.(1)求证:CD为⊙O的切线;(2)若DC+DA=6,⊙O的直径为10,求AB的长.答案:DDADC 6. 相切 7. ∠ABC=90°不排除等效答案 8. 6 9. 45 10. 4 11. 60 12. 解:连接OD,∵BD为∠ABC平分线,∴∠OBD=∠CBD,∵OB=OD,∴∠OBD=∠ODB,∴∠CBD=∠ODB,∴OD∥BC,∵∠C=90°,∴∠ODA=90°,则AC为⊙O的切线13. 解:连接OD,∵CD是⊙O的切线,∴∠ODC=90°,∴∠ODB+∠BDC=90°,∵AB是⊙O的直径,∴∠ADB=90°,即∠ODB+∠ADO=90°,∴∠BDC=∠ADO,∵OA=OD,∴∠ADO=∠A,∴∠BDC=∠A14. 解:过D作DH⊥AC于H,由角平分线的性质可证DB=DH,∴AC与⊙D相切15. 解:(1)∵∠COD=2∠CAD,∠D=2∠CAD,∴∠D=∠COD.∵PD与⊙O相切于点C,∴OC⊥PD,即∠OCD=90°,∴∠D=45°(2)由(1)可知△OCD是等腰直角三角形,∴OC=CD=2,由勾股定理,得OD=22+22=22,∴BD =OD-OB=22-216. (1) ∠BAE=90°∠EAC=∠ABC(2) (2)EF是⊙O的切线.证明:作直径AM,连接CM,则∠ACM=90°,∠M=∠B,∴∠M+∠CAM =∠B+∠CAM=90°,∵∠CAE=∠B,∴∠CAM+∠CAE=90°,∴AE⊥AM,∵AM为直径,∴EF是⊙O 的切线17. 解:(1)连接OC,证∠DAC=∠CAO=∠ACO,∴PA∥CO,又∵CD⊥PA,∴CO⊥CD,∴CD为⊙O的切线(2)过O作OF⊥AB,垂足为F,∴四边形OCDF为矩形.∵DC+DA=6,设AD=x,则OF=CD=6-x,AF =5-x,在Rt△AOF中,有AF2+OF2=OA2,即(5-x)2+(6-x)2=25,解得x1=2,x2=9,由AD<DF知0<x<5,故x=2,从而AD=2,AF=5-2=3,由垂径定理得AB=2AF=6。
关于切线的习题
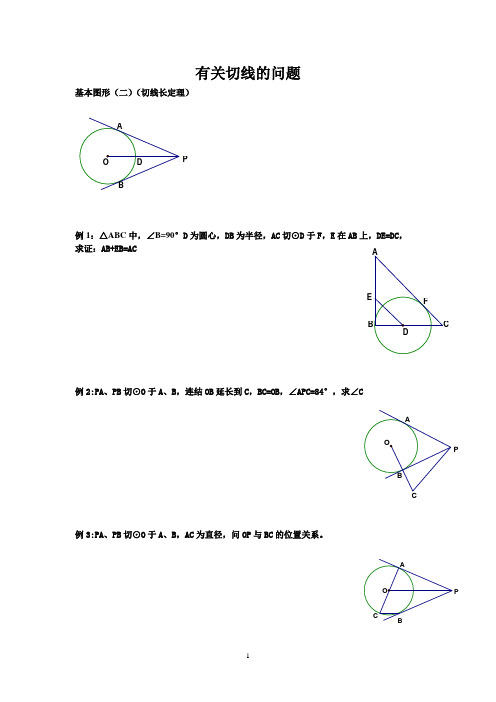
有关切线的问题基本图形(二)(切线长定理)例1:△ABC 中,∠B=90°D 为圆心,DB 为半径,AC 切⊙D 于F ,E 在AB 上,DE=DC , 求证:AB+EB=AC例2:PA 、PB 切⊙O 于A 、B ,连结OB 延长到C ,BC=OB ,∠APC=84°,求∠C例3:PA 、PB 切⊙O 于A 、B ,AC 为直径,问OP 与BC 的位置关系。
EPPP例4: PA、PB切⊙O于A、B,∠P=40°,E在⊙O上,求∠AEB的度数。
例5: PA、PB切⊙O于A、B,求证:∠1=∠2基本图形(三)⑴例1:已知AC、BD、CD切⊙于A、B、E三点,AC=a,BD=9,求半径PPDDC例2:已知AC 、BD 、CD 切⊙于A 、B 、E 三点,求证:OC ⊥OD.例3:正方形ABCD ,以AB 为直径,CF 切⊙O 于E ,求DF ∶DC ∶CF例4: 正方形ABCD ,以AD 为直径,E 在AB 上,为:E 在AB 上什么位置时,直线CE 与⊙O 相离、相切、相交.注意:此题与基本图形(三)⑵的区别.................已知:CD 切⊙O 于E ,AC ⊥CD ,BD ⊥CD ,AB 为直径,AC=4,BD=9,求半径.DCF COC B⑶三角形的内切圆例1:已知△ABC的内心为I,∠A=α,求∠BIC的度数。
例2:⊙O为△ACF的内切圆,B、D、E为切点,PE过圆心,∠A+∠C=100°,求∠BPE的度数CIAB C例3:△ABC 的内切圆与BC 、CA 、AB 相切于点D 、E 、F ,AB=9,BC=14,CA=13,求AF 、BD 、CE 的长例4:△ABC 中,AB=AC=13,60=∆ABC S ,求△ABC 内切圆的半径.例5:∠A=50°,I 为内心,O 为外心,求∠BIC 和∠BOC 的度数例6:△ABC 中, I 为内心,AI 的延长线交△ABC 的外接圆于E ,求证IE=EC.C例7: ⊙O 为△ABC 的内切圆,D 、E 、F 为切点,∠A ∶∠B ∶∠C=2∶3∶4,求∠1∶∠2∶∠3的度数.例8:直角三角形两直角边长为3和4,求①内切圆的半径;②外接圆的半径;③内外心之间的距离.例9: 等边△ABC ,边长为a ,求①内切圆的半径;②外接圆的半径;③高;④?=∆ABC SBAB CC基本图形(四)例10:已知⊙O 外切等腰梯形ABCD ,AD ∥BC ,AB=CD ,中位线EF 。
曲线切线练习题

曲线切线练习题曲线切线是微积分中的重要概念,它在解决实际问题和数学推导中都具有广泛的应用。
本文将介绍一些曲线切线的练习题,帮助读者更好地理解与掌握这一概念。
练习题1:已知曲线方程为 y = x^2 + 2x + 1,求该曲线在点 x = 2 处的切线方程。
解答:首先,我们需要求出曲线在点 x = 2 处的斜率,即切线的斜率。
切线的斜率可以通过求曲线的导数得到。
对 y = x^2 + 2x + 1 进行求导,得到 y' = 2x + 2。
然后将 x = 2 代入导数表达式求得切线的斜率:y' = 2(2) + 2 = 6所以,曲线在点 x = 2 处的切线斜率为 6。
接下来,我们需要求取点(2, y)。
将 x = 2 代入曲线方程,可以求得 y = 9。
现在我们有了切线的斜率和一点坐标,可以使用点斜式来写出切线方程。
切线方程的点斜式为 y - y1 = m(x - x1),其中 (x1, y1) 是切线上的一点。
代入已知条件,得到:y - 9 = 6(x - 2)将等式进行变形,得到切线方程的一般式:y = 6x - 3练习题2:已知曲线方程为 y = 2x^3 + 3x^2 - 4x,求该曲线在点 x = -1 处的切线方程。
解答:与练习题1类似,我们需要先求出曲线在点 x = -1 处的斜率,即切线的斜率。
对 y = 2x^3 + 3x^2 - 4x 进行求导,得到 y' = 6x^2 + 6x - 4。
将 x = -1 代入导数表达式求得切线的斜率:y' = 6(-1)^2 + 6(-1) - 4 = -2所以,曲线在点 x = -1 处的切线斜率为 -2。
接下来,我们需要求取点 (-1, y)。
将 x = -1 代入曲线方程,可以求得 y = -1。
现在我们有了切线的斜率和一点坐标,可以使用点斜式来写出切线方程。
代入已知条件,得到:y - (-1) = -2(x - (-1))将等式进行变形,得到切线方程的一般式:y = -2x通过以上两个练习题的解答,我们可以看出,对于已知曲线方程,求解切线方程的关键是求取切线的斜率和一个切线上的点,而切线的斜率可以通过求导得到。
完整版切线长定理练习试题

切线长定理练习题一、选择题1.以下说法中,不正确的选项是 ( )A .三角形的心里是三角形三条内角均分线的交点B.锐角三角形、直角三角形、钝角三角形的心里都在三角形内部C.垂直于半径的直线是圆的切线D.三角形的心里到三角形的三边的距离相等2.给出以下说法:①随意一个三角形必定有一个外接圆,而且只有一个外接圆;②随意一个圆必定有一个内接三角形,而且只有一个内接三角形;③随意一个三角形必定有一个内切圆,而且只有一个内切圆;④随意一个圆必定有一个外切三角形,而且只有一个外切三角形.此中正确的有 ( )A .1 个 B.2 个 C.3 个 D.4 个3. 一个直角三角形的斜边长为 8,内切圆半径为 1,那么这个三角形的周长等于 ( )A .21 B.20 C.19 D.184. 如图, PA、PB 分别切⊙ O 于点 A、B,AC 是⊙O 的直径,连结 AB 、BC、OP,那么与∠ PAB 相等的角 (不包含∠ PAB 自己)有 ( )A .1 个 B.2 个 C.3 个 D.4 个4 题图5 题图6 题图5.如图,△ ABC 的内切圆⊙ O 与各边相切于点 D、E、F,那么点 O 是△DEF 的 ( )A .三条中线的交点 B.三条高的交点C.三条角均分线的交点 D.三条边的垂直均分线的交点6. 一个直角三角形的斜边长为 8,内切圆半径为 1,那么这个三角形的周长等于 ( )A .21 B.20 C.19 D.18二、填空题6.如图,⊙ I 是△ABC 的内切圆,切点分别为点 D、E、F,假定∠ DEF=52 o,那么∠A 的度为________.6 题图7 题图8 题图7.如图,一圆内切于四边形 ABCD ,且 AB=16 ,CD=10 ,那么四边形 ABCD 的周长为________.o,那么∠ BOC 为____________度. 8.如图,⊙ O 是△ ABC 的内切圆,∠ BAC=50三、解答题9. 如图, AE 、AD 、BC 分别切⊙ O 于点 E、D、F,假定 AD=20 ,求△ ABC 的周长.o,10. 如图, PA、PB 是⊙O 的两条切线,切点分别为点 A、B,假定直径 AC= 12 ,∠P=60求弦 AB 的长.11. 如图, PA、PB是⊙O的切线, A、B 为切点,∠ OAB=30°.A〔1〕求∠ APB的度数;PO〔2〕当 OA=3 时,求 AP的长.B12.:如图,⊙ O 内切于△ ABC,∠BOC =105°,∠ ACB =90°,AB =20cm.求 BC、AC 的长.13.:如图,△ ABC 三边 BC=a,CA= b,AB =c,它的内切圆 O 的半径长为 r.求△ABC 的面积 S.14. 如图,在△ ABC 中,∠ ABC=90 o,在 AB 上取一点 E,以 BE 为直径的⊙ O 恰与AC 相切于点 D,假定 AE=2 cm ,AD=4 cm .(1) 求⊙O 的直径 BE 的长;(2) 计算△ ABC 的面积.15.:如图,⊙ O 是 Rt△ABC 的内切圆,∠ C=90°.(1)假定 AC=12cm ,BC=9cm ,求⊙ O 的半径 r;(2)假定 AC= b,BC= a,AB =c,求⊙ O 的半径 r.四、体验中考16.〔2021 年安徽〕△ ABC 中,AB=AC,∠ A 为锐角, CD 为 AB 边上的高, I 为△ACD的内切圆圆心,那么∠ AIB 的度数是〔〕A .120° B.125° C.135° D.150°17.〔2021 年绵阳〕一个钢管放在 V 形架内,右图是其截面图, O 为钢管的圆心.假如钢管的半径为 25 cm,∠MPN = 60 ,那么 OP =( )A .50 cm B.25 3 cm C.5033cm D.50 3 cm18. (2021 年甘肃定西 )如图,在△ ABC 中,AB AC 5cm,cosB 35.假如⊙ O 的半径为10 cm,且经过点 B、C,那么线段 AO= cm.17 题图 18 题图 19 题图19. 〔2021 年湖南怀化〕如图,PA、PB分别切⊙O于点A、B ,点E 是⊙O 上一点,且AEB 60 ,那么P __ ___度.参照答案◆随堂检测1. C2. B (提示:②④错误 )3. 760 〔提示:连结 ID,IF ∵∠DEF=52 0 ∴∠DIF=104 0 ∵D、F 是切点∴DI ⊥AB,IF ⊥AC∴∠ADI= ∠AFI=90 0 ∴∠ A=180 0-1040=760〕4. 52 (提示: AB+CD=AD+BC)5. 1150 (提示:∵∠ A=50 0 ∴∠ ABC+ ∠ACB=130 0 ∵OB,OC 分别均分∠ ABC, ∠ACB ∴∠OBC+ ∠OCB=65∴∠BOC=180 0-650=1150)◆课下作业●拓展提升1. D 〔提示: AD=AF,BD=BE,CE=CF ∴周长 =8 2 1 2 18〕2. C3. D4. 解:∵ AD,AE 切于⊙ O 于 D,E ∴AD=AE=20 ∵AD,BF 切于⊙ O 于 D,F ∴ BD=BF 同理: CF=CE∴C △ABC =AB+BC+AC=AB+BF+FC+AC=AB+BD+EC+AC=AD+AE=400 ∴△ABC 是正 5.解:连结 BC ∵PA,PB 切⊙O 于 A,B ∴PA=PB ∵∠P=60 三角形 ∵∠PAB=60 0∵PA 是⊙O 切线 ∴CA ⊥AP ∴∠CAP=90 0∴∠CAB=30 0∵直径AC ∴∠ABC=90∴cos300=A B AC∴AB= 6 36. 解:〔1〕∵在△ ABO 中,O A =O B ,∠OAB =30°∴∠AOB =180° -2× 30° =120° ∵PA 、PB 是⊙O 的切线A∴O A ⊥PA ,OB ⊥PB .即∠ OAP =∠OBP =90°PO∴在四边形 OAPB 中,∠APB =360° -120° -90° -90° = 60° .B〔2〕如图①,连结 OP ∵PA 、PB 是⊙O 的切线∴P O 均分∠ APB ,即∠ APO = 1 2∠APB =30°A PO又∵在 Rt △OAP 中, O A =3, ∠APO =30°∴AP =OAtan30°=3 3 .B7. 解:〔1〕连结 OD ∴OD⊥AC∴△ ODA 是 Rt△设半径为 r ∴AO=r+2 ∴〔 r+2〕2—r2=16解之得: r=3 ∴BE=6(2) ∵∠ ABC=90 0 ∴OB⊥BC ∴BC 是⊙ O 的切线∵CD 切⊙O 于 D ∴CB=CD 令 CB=x∴AC=x+4 ,BC=4 ,AB=x ,AB=8 ∵ 2 82 ( 4)2x x ∴x 6 ∴S△ABC =128 6 24●体验中考1. C2. A 〔提示:∠ MPN=60 0 可得∠ OPM=30 0 可得 OP=2OM=50 〕3. 5 103〔提示:连结 OB,易得:∠ABC= ∠AOB ∴cos∠AOB=cos ∠35=O B10OA AO〕04. ∠P=60。
高二求切线方程练习题

高二求切线方程练习题1. 给定函数y = 3x^2 + 2x - 1,求过点P(1, 4)的切线方程。
解析:首先,我们需要求出函数在点P(1, 4)处的切线斜率。
切线的斜率等于函数在该点的导数值。
所以,我们先计算函数的导数。
y = 3x^2 + 2x - 1y' = 6x + 2将x = 1代入导数公式中,我们可以得到在点P(1, 4)处的斜率。
y'(1) = 6(1) + 2 = 8接下来,我们可以根据点斜式来写出切线方程。
点斜式的一般形式为:y - y1 = m(x - x1)将已知的点P(1, 4)和切线斜率8代入方程中,得到切线方程的具体表达式。
y - 4 = 8(x - 1)对该方程进行化简,我们可以得到切线方程的最简形式:y = 8x - 4因此,过点P(1, 4)的切线方程为y = 8x - 4。
2. 设函数f(x) = x^3 - 5x + 3,求函数f(x)的所有切线方程。
解析:为了求函数f(x)的所有切线方程,我们需要求出函数的导数,并找到导数的零点,然后使用这些零点来确定切线的斜率和切线方程。
首先,我们计算函数f(x)的导数。
f'(x) = 3x^2 - 5接下来,我们找到导数的零点。
导数的零点即为函数f(x)的驻点或拐点。
我们需要解方程f'(x) = 0。
3x^2 - 5 = 03x^2 = 5x^2 = 5/3x = ±√(5/3)得到导数的零点为x = ±√(5/3)。
然后,我们根据导数的零点来确定切线的斜率。
切线的斜率等于函数的导数在零点处的值。
斜率1:x = √(5/3)f' (√(5/3)) = 3(√(5/3))^2 - 5 = 3(5/3) - 5 = 0斜率2:x = -√(5/3)f' (-√(5/3)) = 3(-√(5/3))^2 - 5 = 3(5/3) - 5 = 0我们可以看到,函数f(x)在x = √(5/3)和x = -√(5/3)处的导数为0,因此在这两个点处存在切线。
