【计算机应用】_拓扑排序_期刊发文热词逐年推荐_20140726
【计算机应用】_tc_期刊发文热词逐年推荐_20140726
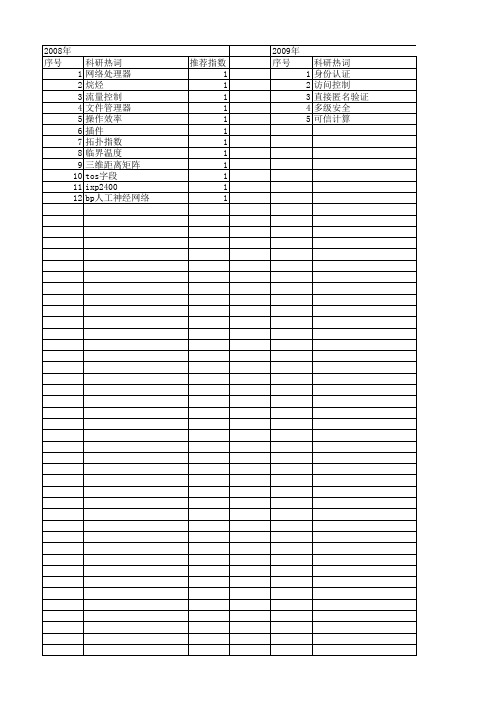
科研热词 自相关 移动 核属性 无模糊 支付平台 捕获 手机支付 容差关系 多普勒补偿 冲突域 不完备决策表 n) boc(n app
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5 6 7 8
2014年 科研热词 语法特征 话题句 编辑距离 粗糙集 属性约简 可邻接性 冲突域 不完备决策表 推荐指数 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
2011年 科研热词 距离像 自组织网络 模糊c-均值 模块化 数据传输 拒绝服务攻击 嵌入式 密钥协商 字典攻击 地址自动配置 可信计算 口令 双向匿名性 原型法 分类水平 关键线 关键点 传递闭包 二阶模糊聚类 个性化 tc/ip s3c2440 olsr路由协议 linux操作系统 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 网络处理器 烷烃 流量控制 文件管理器 操作效率 插件 拓扑指数 临界温度 三维距离矩阵 tos字段 ixp2400 bp人工神经网络
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5
2012年 序号 1 2 3 4 5 6 7 8 9
科研热词 推荐指数 轨道交通 1 自动售检票系统 1 自动售检票清算管理中心 1 线路票务中心 1 管理 1 手机平台 1 多线共用线路中心 1 totalcommander 1 tc 1
拓扑排序了解拓扑排序的概念和实现方式

拓扑排序了解拓扑排序的概念和实现方式拓扑排序:了解拓扑排序的概念和实现方式拓扑排序是一种用于有向无环图(DAG)中对节点进行排序的算法,它将图中所有节点按照一种线性排序的方式排列,使得任意一条有向边从排在前面的节点指向排在后面的节点。
本文将介绍拓扑排序的概念和实现方式。
一、拓扑排序的概念拓扑排序的概念是基于拓扑排序图的。
拓扑排序图是一个有向图,其中每个节点表示一个任务,有向边表示任务之间的依赖关系。
如果任务A依赖于任务B完成,那么在拓扑排序图中就有一条从B指向A的有向边。
拓扑排序的目标是找到一种任务排序的方式,使得排在前面的任务不依赖于排在后面的任务。
这样,我们可以按照拓扑排序中节点的顺序依次执行任务,确保任务的依赖关系得以满足。
二、拓扑排序的实现方式拓扑排序有两种主要的实现方式:Kahn算法和深度优先搜索(DFS)算法。
1. Kahn算法Kahn算法是一种基于贪心策略的拓扑排序算法,它通过不断删除没有入度的节点来构建拓扑排序。
Kahn算法的实现步骤如下:步骤1:初始化一个队列Q,并将所有入度为0的节点加入队列Q。
步骤2:当队列Q非空时,执行以下操作:1)从队列Q中取出一个节点u;2)将节点u添加到排序结果中;3)遍历u的所有邻接节点v,将v的入度减1;4)若节点v的入度减为0,则将节点v加入队列Q。
步骤3:返回排序结果。
2. 深度优先搜索算法深度优先搜索(DFS)是另一种常用的拓扑排序算法。
它通过递归地访问节点和其邻接节点来构造拓扑排序。
DFS算法的实现步骤如下:步骤1:初始化一个空的结果列表res和一个记录节点状态的字典visited。
步骤2:对于图中的每个节点v,执行DFS(v):1)若节点v未被访问,则执行步骤3。
2)将节点v标记为已访问。
3)递归地访问v的所有未被访问的邻接节点,并将它们加入结果列表res。
4)将节点v添加到结果列表res的最前面。
步骤3:返回结果列表res的逆序。
三、总结拓扑排序是一种对有向无环图中节点进行排序的算法。
【计算机工程与设计】_多样性_期刊发文热词逐年推荐_20140726
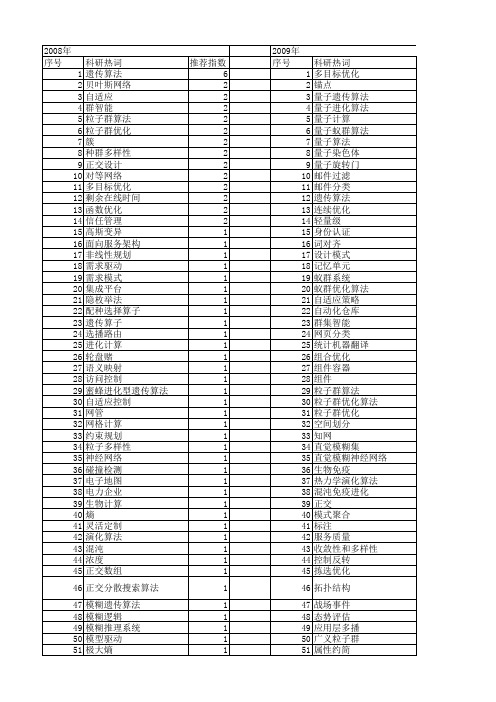
推荐指数 6 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89
机械仿真 最短路径 时延约束 改进遗传算法 收敛性 授权 指导变异 异构 建模 工作流引擎 局部搜索 对象建模 多样性 基因重组 基于角色的访问控制 变异 参数选择 参数调整 动画 动态规划法 动态惩罚 办制模型 体系结构 优化选址 优化算法 亲和力 交互协同 web服务 web services技术 pareto解 mof bp算法
安全性 多策略 多播路由 多处理机系统 垃圾邮件 图形化 同构环境 可疑行为 可定制 变异 反编译 双语词典 双层过滤 分裂算子 六峰值驼背函数优化问题 全局最优 免疫 克隆进化选择 元数据 信息集成 任务调度 人工免疫 亲和度 交叉 事件检测 xml wrapper web services tsp svg jdom
【计算机应用研究】_网格研究_期刊发文热词逐年推荐_20140726
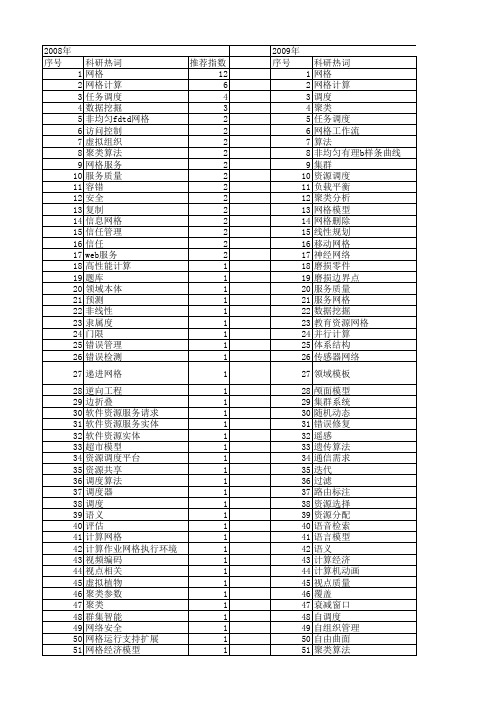
107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
科研热词 网格 网格计算 调度 聚类 任务调度 网格工作流 算法 非均匀有理b样条曲线 集群 资源调度 负载平衡 聚类分析 网格模型 网格删除 线性规划 移动网格 神经网络 磨损零件 磨损边界点 服务质量 服务网格 数据挖掘 教育资源网格 并行计算 体系结构 传感器网络 领域模板 颅面模型 集群系统 随机动态 错误修复 遥感 遗传算法 通信需求 迭代 过滤 路由标注 资源选择 资源分配 语音检索 语言模型 语义 计算经济 计算机动画 视点质量 覆盖 衰减窗口 自调度 自组织管理 自由曲面 聚类算法 置信度
推荐指数 12 6 4 3 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
拓扑算法应用

拓扑算法应用
拓扑排序是对一个有向无环图(DAG)的所有顶点进行线性排序,它必须满足两个条件:每个顶点出现且只出现一次,若存在一条从顶点A到顶点B的路径,那么在序列中顶点A出现在顶点B的前面。
拓扑排序常常用于确定事物发生的顺序。
这种算法在多个领域有实际应用:
1.项目管理:在工程项目或系统过程中,可以将每个子工程视为
一个顶点,如果一个子工程的开始必须在另一个子工程完成之
后,那么就在这两个子工程之间画一条有向边。
通过拓扑排序,可以确定所有子工程的执行顺序,从而确保工程能顺利进行,
并计算出整个工程完成所需的最短时间。
2.编译器优化:在编译器设计中,拓扑排序也被广泛应用。
例如,
在VS中创建一个MVC的解决方案XMedia,如果项目A引用项
目B,则表示A依赖B,所以必须先编译项目B,再编译项目A。
通过拓扑排序,可以确定项目的编译顺序,从而优化编译过程,提高编译效率。
3.表达式优化:在描述含公共子式的表达式的工具中,拓扑排序
也可以用于实现对相同子式的共享,从而节省存储空间。
总的来说,拓扑排序算法在项目管理、编译器优化、表达式优化等多个领域都有重要的应用。
拓扑排序算法的应用解决任务调度和依赖关系问题

拓扑排序算法的应用解决任务调度和依赖关系问题拓扑排序是一种常用的算法,用于解决与有向无环图(Directed Acyclic Graph,简称DAG)相关的任务调度和依赖关系问题。
该算法通过对图中的节点进行排序,使得所有有向边从排在前面的节点指向排在后面的节点。
这种排序方法在实际应用中具有广泛的用途,本文将详细介绍拓扑排序算法的原理和应用。
一、拓扑排序算法原理拓扑排序算法的原理基于有向无环图的性质。
在一个有向无环图中,节点表示任务或事件,有向边表示任务间的依赖关系。
拓扑排序的目标是找到一种排序方式,使得所有有向边的起始节点都排在终止节点之前。
为了实现这个目标,拓扑排序算法采用了以下步骤:1. 初始化:首先,需要对图中的每个节点进行初始化,将所有节点的入度(即指向该节点的有向边的数量)统计出来。
同时,创建一个队列或栈,用于保存入度为0的节点。
2. 循环处理:从队列或栈中取出一个入度为0的节点,并将其加入结果中。
然后,将该节点的所有邻接节点的入度减1。
如果邻接节点的入度变为0,将其加入队列或栈中。
3. 重复上述步骤:重复以上步骤,直到队列或栈为空。
如果此时仍有节点的入度不为0,则证明图中存在环路,无法进行拓扑排序。
二、任务调度问题的应用拓扑排序算法可以应用于任务调度问题,其中任务表示为图中的节点,依赖关系表示为有向边。
通过进行拓扑排序,可以确定任务的执行顺序,保证所有的前置任务都已完成。
例如,假设有5个任务需要执行,它们之间的依赖关系如下图所示:```A ---> B| ^| |v |C ----||vD|vE```通过拓扑排序算法,可以得到一个可行的任务执行顺序,即 A -> C -> B -> D -> E。
这个顺序保证了所有前置任务都已完成,可以顺利执行。
三、依赖关系问题的应用除了任务调度问题,拓扑排序算法还可以应用于解决依赖关系问题。
在软件开发中,经常会存在不同模块之间的依赖关系,需要按照一定顺序进行编译或加载。
【计算机系统应用】_开源_期刊发文热词逐年推荐_20140726

推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
53 54 55 56 57
dicom dcmtk dbscan bootloader dm320 linux内核 arm
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44
科研热词 工作流 面向服务计算 近似度 身份认证 虚拟局域网技术 聚类分析 网络模拟测试 网络模拟 网构软件 组装 物流生产 混合系统 流媒体文件 松耦合 权限控制 时间控制 底层设备驱动 应用程序接口 嵌入式linux 嵌入式internet 嵌入式 句群相似度 单点登录 功能仿真 任务分配 互连度 主程序 三维仿真 weka uip协议栈 osg opnet ns2 map/reduce hadoop gnu gnash flv ffmpeg flash chameleon ces c序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
拓扑排序应用场景

拓扑排序应用场景拓扑排序是一种常用的图算法,用于解决一些特定的应用场景。
它的主要作用是对有向无环图(DAG)中的节点进行排序,使得所有的边从前向后指向排列的顺序。
在实际应用中,拓扑排序被广泛应用于任务调度、依赖关系分析、编译优化等领域。
在任务调度中,拓扑排序可以用来确定任务的执行顺序。
假设有一组任务,每个任务都有一些依赖关系,即某些任务必须在其他任务执行之后才能开始。
这时候,我们可以将任务看作图中的节点,依赖关系看作图中的边,利用拓扑排序算法确定任务的执行顺序。
通过拓扑排序,我们可以确保没有任务在其依赖任务执行之前开始,从而保证任务的正确执行。
拓扑排序也可以应用于依赖关系分析。
在软件开发中,各个模块之间可能存在依赖关系,即某些模块需要依赖其他模块的输出结果才能正常工作。
通过使用拓扑排序,可以分析模块之间的依赖关系,找出模块之间的依赖顺序,从而保证软件的正确运行。
另一个应用场景是编译优化。
在编译过程中,源代码会经过多个阶段的处理,例如词法分析、语法分析、语义分析等。
这些处理过程之间也存在依赖关系,必须按照一定的顺序进行。
通过拓扑排序,可以确定编译过程中各个阶段的执行顺序,从而提高编译的效率和准确性。
除了上述应用场景,拓扑排序还可以用于解决其他问题。
例如,可以用拓扑排序来判断一个有向图是否存在环路,如果拓扑排序中存在环路,则图中存在环路;反之,如果拓扑排序中不存在环路,则图中不存在环路。
此外,拓扑排序还可以用于确定关键路径,即在一组任务中找出耗时最长的路径,从而可以优化任务的执行时间。
拓扑排序是一种非常实用的图算法,广泛应用于任务调度、依赖关系分析、编译优化等领域。
通过拓扑排序,可以确定任务的执行顺序,分析模块之间的依赖关系,优化编译过程,判断图中是否存在环路,确定关键路径等。
这些应用场景都可以通过拓扑排序来解决,从而提高工作效率和准确性。
拓扑排序——精选推荐

拓扑排序在百度百科中的解释是:对⼀个有向⽆环图(Directed Acyclic Graph简称DAG)G进⾏拓扑排序,是将G中所有顶点排成⼀个线性序列,使得图中任意⼀对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。
转换为显⽰中⽐较容易理解的例⼦就是,在⼤学有学过课程需要学习,例如要想学习数据结构,⾸先就需要学习完C语⾔才可以,那么我们就可以将课程看成图中的点,将先学习c语⾔再学习数据结构看成是⼀条C语⾔指向数据结构的有向边。
那么我们只需要找到⼀个线性的排列顺序,使得这个顺序满⾜所有的课程的前置要求(就是要想学习这门课程,需要将该课程的所有前置课程学完)。
那么我们也⽐较容易的知道,拓扑排序并不⼀定是⼀个唯⼀的线性顺序。
在学习拓扑排序的算法之前,我们需要先了解⼏个基本概念出度:以点u为起点的边的数量是u的出度⼊度:以点u为终点的边的数量是u的⼊度对于拓扑排序⽽⾔有BFS和DFS两种算法BFS基于BFS的拓扑排序也可以分为两类:⽆前驱的顶点优先、⽆后继的顶点优先⽆前驱的顶点优先拓扑排序:1:预处理,遍历每个边,计算出所有顶点的出度和⼊度。
复杂度O(V+E),其中包含每个顶点的初始化2:找到所有⼊度为0的顶点,放进队列,作为起点(这些点的先后顺序⽆所谓)。
如果找不到⼊度为0的点,那么这个图不是DAG,不存在拓扑排序3:弹出队⾸元素,将队⾸的所有直接邻居点(队⾸元素指向的邻居节点)的⼊度减⼀,把⼊度变为0的结点放⼊队列。
4:重复操作3,直到队列为空。
这个时候队列的所有弹出顺序就是⼀个拓扑排序。
拓扑排序⽆解的判定条件:如果队列为空时,仍旧有点没有进⼊过队列,那么这些点的⼊度都不可能为0,⼀定存在⼀个有向环⽆后继的顶点优先拓扑排序:相当于是⽆前驱的反向执⾏1:预处理,计算出所有顶点的出度和⼊度2:找到所有出度为0的顶点,放⼊队列。
如果找不到,则不存在拓扑排序3:弹出队⾸元素,将队⾸的所有直接邻居结点(指向对⼿的邻居节点)的出度减⼀,把出度为0的结点放⼊队列4:重复操作3,直到队列为空。
【计算机工程与设计】_免疫算法_期刊发文热词逐年推荐_20140726

2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
科研热词 遗传算法 自适应 免疫遗传算法 免疫算法 人工免疫 高频变异 路由搜索与优化 资源平衡 航班延误 网络计划图 组合预测 粒子群算法 疫苗 状态感知 活跃度 波长选取 木马 智能化 智能优化 智能manet 整数规划模型 排课问题 拓扑排序 抗体 应急通信 并行计算 多项目选择计划 多样性 多抗体集 原子化 动态指数平滑法 动态克隆选择算法 制造元设计 全局收敛 入侵检测 免疫微粒群算法 免疫 克隆选择 光谱分析 个性化
53 54 55 56 57 58 59 60 61 62 63 64 65
Байду номын сангаас
伪并行 优化搜索 人工免疫聚类 人工免疫网络 人工免疫分类器 人工免疫 亲和力 交通流 事件检测 中医诊断 不确定理论 prüfer数 k.均值
1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70
推荐指数 6 3 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
【计算机系统应用】_代码_期刊发文热词逐年推荐_20140726

2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 线程同步 特定领域建模 元模型 代码生成 代码模板 面向方面编程 链路结构 重叠i/o模型 逻辑判别 连接方面 连接件 远程控制实验室 调试 语义模板 规则引擎 草图 芯片驱动 自定义未处理异常过滤器 脚本 网络驱动程序 缓冲区溢出 维度表 维度类型 维度值 维度 经验库 组合解决方案 线程池 系统框架 程序流程图 监控系统 皮尔逊卡方检验 特征因子 深度遍历 模糊物元 核心业务逻辑 样例代码 栈 构件组装 构件 机器学习 服务器端应用程序 服务器 有序解集 无线mesh网络 数据结构 数据挖掘 攻击代码检测 搜索引擎 拓扑排序 恶意代码 性能优化
科研热词 状态转换 状态机 售货机控制 领域工程 重构代码 通用性 软件体系结构 身份认证 跨站脚本攻击 语义概念 角色 行为规范 自动挖掘 网络安全 编辑器 编译 缓冲区溢出 结构化数据 管理信息系统 知识诠释 知识挖掘 监测终端 界面开发 独立线程分配模型 源代码自动生成 渲染引擎 流程图 正则表达式 模式学习 框架 校园网 权限控制 本体 智能问答 数据读取 数字证书 攻击 指令集扩展 指令选择 报表模型 报表 循环匹配 底层设备驱动 应用程序接口 嵌入式internet 封装技术 封装 客户端 安全 多执行路径 复合文本 图形算法控件
科研热词 推荐指数 页间传递 1 集群 1 过程模型 1 软件设计 1 组件 1 糖尿病信息管理系统 1 混合模式 1 测试用例自动生成 1 模块性 1 柜面交易系统 1 柔性业务管理系统管理逻辑通用业务管理 1 服务器控件值 1 方面 1 数据预处理 1 数据传递 1 操作系统 1 控件 1 持久层 1 引擎 1 开源 1 工作流管理 1 对象嵌入 1 实时操作系统 1 双向过程切片 1 单点登录 1 协议栈 1 动态数据表 1 动态数据库 1 关注点分离 1 健身计划 1 代码生成 1 从节点 1 交易界面 1 业务流程管理 1 xml 1 word对象模型 1 web服务 1 txul 1 soa设计 1 saml 1 ole技术 1 mda行为建模扩展活动图 1 jndi 1 j2ee 1 data 1 canopen 1 canfestival 1 aspectc 1 apache 1 ajax 1 .net 1
拓扑排序在代码中的应用

拓扑排序在代码中的应用拓扑排序是一种常用的算法,用来对有向图进行排序。
在实际代码中,拓扑排序经常被用来解决诸如工程规划、任务调度等问题。
在本文中,我们将详细介绍拓扑排序在代码中的应用。
一、什么是拓扑排序拓扑排序是一种对有向无环图(DAG)进行排序的算法,其实现原理是通过不断“剥离”入度为0的节点,并更新其余节点的入度,直到所有节点都被“剥离”完毕,从而得到一个有序序列。
在实际应用中,拓扑排序常常被用来解决任务调度、工程规划等问题。
例如,我们可以将工程中的任务抽象为DAG中的节点,而任务间的依赖关系则以边的方式表示。
二、拓扑排序的实现实际上,实现拓扑排序并不复杂。
我们可以通过维护一个队列来实现,具体步骤如下:1. 将所有入度为0的节点加入队列。
2. 对于队列中每一个节点,将其从图中删除,并将其所有相邻节点的入度减1。
3. 如果某个节点的入度变为0,将其加入队列中。
4. 重复步骤2和步骤3,直到队列为空为止。
最终,我们可以得到一个有序的节点序列,这就是拓扑排序的结果。
三、代码实现示例以下是一段用Java实现的拓扑排序代码示例:```javaimport java.util.*;public class TopologicalSort {public List<Integer> sort(int numCourses, int[][] prerequisites) {List<Integer> result = new ArrayList<>();int[] inDegree = new int[numCourses];Map<Integer, List<Integer>> map = new HashMap<>();for (int[] p : prerequisites) {int prerequisite = p[1];int course = p[0];inDegree[course]++;if (map.containsKey(prerequisite)) {map.get(prerequisite).add(course);} else {List<Integer> list = new ArrayList<>();list.add(course);map.put(prerequisite, list);}}Queue<Integer> q = new LinkedList<>();for (int i = 0; i < numCourses; i++) {if (inDegree[i] == 0) {q.offer(i);}}while (!q.isEmpty()) {int prerequisite = q.poll();result.add(prerequisite);if (map.containsKey(prerequisite)) {for (int course : map.get(prerequisite)) {inDegree[course]--;if (inDegree[course] == 0) {q.offer(course);}}}}return result.size() == numCourses ? result : new ArrayList<>();}public static void main(String[] args) {int[][] prerequisites = {{1,0},{2,0},{3,1},{3,2}};TopologicalSort ts = new TopologicalSort();System.out.println(ts.sort(4, prerequisites));}}```此代码实现就是一种最常见的实现方式,其核心思路与上述算法流程一致。
计算机应用的计算机网络拓扑

计算机应用的计算机网络拓扑计算机网络拓扑是计算机网络的基础架构,是网络的物理形式。
拓扑的设计直接影响着网络的性能和可靠性。
在计算机网络中,拓扑提供了一个抽象概括,用于描述网络节点之间的连接关系。
在计算机网络拓扑设计中,有一些经典的拓扑结构,包括总线、星型、环形、树型和网状。
总线型拓扑是最简单的拓扑结构之一。
它由一组计算机与一条主要的、中央的通信线路组成。
每台计算机都连接到主线上,多个计算机共享同一个通信通道。
总线型拓扑的优点在于简单、易于安装和扩展。
然而,缺点也显而易见,当线路中出现故障,整个网络将无法正常工作。
因此,总线型拓扑不太适用于大型企业网络,而更适用于小型网络或家庭网络。
星型拓扑是一种常见的拓扑结构,也是企业网络中使用最广泛的拓扑结构之一。
它是由一组计算机与一个中心节点组成。
每台计算机都与中心节点相连,而中心节点则负责转发数据包和控制网络流量。
星型拓扑的优点在于易于管理和扩展,其中出现故障也不会对整个网络造成影响。
然而,它也存在一些缺点,单点故障可能会导致整个网络瘫痪。
环形拓扑是由一组计算机按照环形连接方式互相连接而成。
每台计算机都连接到相邻的两台计算机上。
因此,环形拓扑的数据传输效率比较高,但同时也有同样的单点故障问题。
除非拓扑设计体现了高度的重叠部分,否则如果发生了任何一个节点故障,整个系统都会陷入瘫痪。
树型拓扑是由多个星型拓扑结构组成的。
每个星型拓扑都有自己的中心节点,而这些中心节点又组成提供更大、更分散、更完整网络结构的中心节点。
树形拓扑由于分层结构的原因,因此可以在分开的网段块中有效地控制因公开性问题而产生的访问限制,它的优点是可靠性高和能够快速分配全局带宽,非常适合在高度分散的网络环境中进行。
网状拓扑是一种分布式拓扑结构,由分散节点的所有计算机组成,并采用多个连接节点的方式相互链接。
正如网络的名称所示,这种拓扑结构由许多相互关联的节点组成,每个节点同时也充当中继器的角色,意味着在某种程度上具有自我纠错能力。
拓扑排序定义

拓扑排序定义嘿,朋友们!今天咱来唠唠拓扑排序这个有意思的玩意儿。
你说拓扑排序像不像给一堆事情排排队呀!咱生活中不也经常要给各种事儿安排个先后顺序嘛。
比如说,早上起来,你得先穿衣服吧,总不能先穿鞋再穿裤子呀,这就乱套啦!拓扑排序就是这么个理儿。
想象一下,有好多任务,它们之间有着各种关系,有的任务得等其他任务完成了才能开始。
这就好像是搭积木,下面的积木不搭好,上面的可就没法放稳喽。
拓扑排序就是要找到一个合理的顺序,让这些任务一个接一个地顺利进行下去。
咱举个例子哈,比如盖房子。
你得先打地基吧,然后才能砌墙,墙砌好了才能装窗户啥的。
要是顺序搞错了,那房子不就盖得歪七扭八啦?拓扑排序就是要保证这种事情不会发生。
它可不是随随便便就能搞定的哦!得仔细研究那些任务之间的关系,找出那个正确的顺序。
就像解一道复杂的谜题一样,得动脑子呢!要是没整好,那可就麻烦大啦。
你想想,如果一个系统里的任务都乱了套,那还不得乱成一锅粥呀!比如说,电脑程序里的任务要是没按拓扑排序来,那程序可能就运行不起来,或者运行出一堆莫名其妙的结果。
这多让人头疼啊!再比如说,在一个项目里,各种工作环节都有先后顺序。
要是不按拓扑排序来安排,那不就可能导致有的工作没法开展,或者前面的工作白做了,这得浪费多少时间和精力呀!拓扑排序虽然听起来有点高大上,但其实和咱的生活息息相关呢。
它能让事情变得有条理,让一切都按部就班地进行。
所以说呀,拓扑排序可真是个好东西呢!它能让复杂的事情变得简单,让混乱的关系变得清晰。
咱可得好好琢磨琢磨它,让它为我们的生活和工作服务呀!这就是我对拓扑排序的理解,你们觉得呢?。
拓扑排序在代码中的应用

拓扑排序在代码中的应用拓扑排序是一种在有向图中解决任务排序问题的算法。
它可以找到一个节点的线性顺序,使得图中所有的有向边都按照它们的方向指向的顺序排列。
拓扑排序在很多领域都有广泛的应用,特别是在软件工程和任务调度中。
下面是一些拓扑排序在代码中的应用:1. 任务调度:拓扑排序可以用来解决任务调度问题。
例如,在一个多线程的程序中,不同的任务可能有依赖关系,一个任务必须在另一个任务之前执行。
通过对任务之间的依赖关系进行拓扑排序,可以确定执行任务的顺序,以确保每个任务在执行之前满足其依赖的条件。
2. 编译器优化:在编译器中,源代码会被转换成中间代码,然后再生成目标代码。
中间代码中的指令也可能存在依赖关系,需要按照拓扑排序的顺序进行执行,以确保指令的执行顺序正确。
3. 依赖管理:在软件开发中,代码库通常会有很多模块和依赖关系。
通过分析这些依赖关系,可以使用拓扑排序来确定模块之间的构建顺序或加载顺序。
4. 数据流分析:在编程语言的静态分析中,可以使用数据流分析技术来找出代码中的数据依赖关系。
通过对数据依赖图进行拓扑排序,可以获得数据的传递路径,从而进行更深入的代码优化。
5. 继承关系分析:在面向对象的编程语言中,类之间可能存在继承关系。
通过对类之间的继承关系进行拓扑排序,可以确定类的实例化顺序或类的加载顺序。
6. 数据库查询优化:在数据库中,查询语句之间可能有依赖关系。
通过对查询语句的依赖关系进行拓扑排序,可以确定查询语句的执行顺序,从而优化查询的性能。
拓扑排序的代码实现通常使用深度优先搜索(DFS)或广度优先搜索(BFS)算法。
在DFS算法中,通过递归地访问节点的后继节点,并在递归返回时将节点存入一个栈中,最后通过出栈的顺序得到拓扑排序的结果。
在BFS算法中,通过将节点的后继节点入队,然后依次出队并访问这些节点,直到队列为空为止,最后得到的节点顺序即为拓扑排序的结果。
以下是一段示例代码,演示了如何使用DFS算法实现拓扑排序:```pythondef topo_sort(graph):visited = set()stack = []def dfs(node):visited.add(node)for neighbor in graph[node]:if neighbor not in visited:dfs(neighbor)stack.append(node)for node in graph:if node not in visited:dfs(node)return stack[::-1]```在这段代码中,`graph`表示有向图的邻接表表示,函数`dfs`实现了DFS算法,将已访问的节点存入`visited`集合中,并递归地访问后继节点。
拓扑排序方法

拓扑排序方法嘿,朋友们!今天咱们来聊聊拓扑排序这个超有趣的东西,就像是在一个神秘的迷宫里给小怪兽们排队一样。
拓扑排序啊,就像是给一群性格各异的超级英雄排座次。
每个超级英雄都有自己的专长和依赖关系呢。
比如说,钢铁侠得先造好他的战甲才能去和灭霸干架,这战甲制造的步骤就像是拓扑排序里的前置任务。
你不能让他穿着个半成品就冲上去,那就像让厨师拿着生食材直接上菜一样滑稽。
想象一下,拓扑排序是一场盛大的音乐会安排。
各种乐器演奏者就像是一个个节点。
鼓手不能先敲起来,要是他一上来就“咚咚咚”,而其他乐手还没准备好,那整个音乐会就乱套了,就如同一场群魔乱舞的闹剧。
必须得先让弦乐组调好音,就像在拓扑排序里先处理那些没有前置依赖的任务。
再把拓扑排序比作一场魔法学校的课程安排。
魔法防御术得在学会一些基础魔法之后才能学吧。
要是一年级的小巫师一上来就学习高级的防御魔法,那估计他们的魔杖都会抗议,就像一个还不会走路的小娃娃就想参加马拉松一样荒谬。
在这个拓扑排序的世界里,每个元素都像是一个调皮的小精灵。
有些小精灵很独立,自己就能先行动起来,就像那些独自闯荡江湖的大侠。
而有些小精灵则要等其他小精灵做完事情才能开始,就像那些需要长辈带着才能出门的小孩子。
这拓扑排序还像是搭建乐高城堡。
你得先把地基打好,那些大块的、作为基础的乐高积木得先放好位置,这就好比拓扑排序里的初始任务。
要是你先把城堡的尖顶放上去,那整个城堡就会摇摇欲坠,就像一个头重脚轻的大怪物,随时都会倒下,那场面简直比小丑的滑稽表演还搞笑。
它也像一场复杂的美食制作过程。
你得先把食材准备好,比如先洗菜切菜,才能下锅烹饪。
要是你把顺序弄反了,就像把还没洗的泥巴萝卜直接扔进锅里煮,那煮出来的东西估计连最贪吃的小猪都不会看一眼。
而且拓扑排序就像是一场接力赛跑。
每个选手都得等前一个选手把接力棒交到手里才能跑。
要是有个心急的选手提前跑了,那整个比赛就全乱套了,就像一群没头的苍蝇到处乱飞。
拓扑排序——精选推荐

拓扑排序基本概念拓扑序:如果图中从V到W有⼀条有向路径,则V⼀定排在W之前。
满⾜此条件的顶点序列称为⼀个拓扑序,那么拓扑排序就是获得⼀个拓扑序的过程。
另外,如果有合理的拓扑序,则必定是有向⽆环图。
拓扑排序算法下⾯介绍⼀个⽐较好的拓扑排序算法伪代码如下:void TopSort(){for(图中每个顶点V)if(Indegree[V]==0)Enqueue(Q,V);while(!IsEmpty(Q)){V=Dequeue(Q);输出V,或者记录V的输出序号;cnt++;for(V的每个邻接点W)if(--Indegree[W]==0)Enqueue(Q,W);}if(cnt!=|V|)ERROR("图中有回路");}C语⾔实现如下:bool TopSort(LGraph Graph, Vertex TopOrder[]){ //对Graph进⾏拓扑排序,TopOrder[]顺序存储排序后的顶点下标int Indegree[MaxVertexNum],cnt;Vertex V;PtrToAdjVNode W;Queue Q=CreateQueue(Graph->Nv);for(V=0;V<Graph->Nv;V++) //初始化Indegree[]Indegree[V]=0;for(V=0;V<Graph->Nv;V++) //遍历图,得到Indegree[]for(W=Graph->G[V].FirstEdge;W;W=W->Next)Indegree[W->AdjV]++; //对有向边<V,W->AdjV>累计终点的⼊度for(V=0;V<Graph->Nv;V++)if(Indegree[V]==0) //将所有⼊度为0的顶点⼊队AddQ(Q,V);cnt=0;while(!IsEmpty(Q)){V=DeleteQ(Q); //弹出⼀个⼊度为0的顶点TopOrder[cnt++]=V; //将V存为结果序列的下⼀个元素for(W=Graph->G[V].FirstEdge;W;W=W->Next) //对于V的每⼀个邻接点W->AdjVif(--Indegree[W->AdjV]==0) //若删除V使得W->AdjV的⼊度为0AddQ(Q,W->AdjV); //则将W->AdjV⼊队}if(cnt!=Graph->Nv) //图中有回路return fasle;elsereturn true;}时间复杂度T=O(|V|+|E|),此算法也可以⽤来检测有向图是否是⽆环图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年 科研热词 重叠 资源均衡 自适应分层算法 算法 梯形图 无向环搜索 搜索 接触 指令表 拓扑排序 承继约束 快速成形 影响域 多项目多任务选择计划 可编程控制器 区域增长 免疫遗传算法 二叉排序树 三角面片 三角网格化 三角形网格 一致性 stl模型 k近邻 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4
科研热词 边界排序 夹角判断 多边形 vct
推荐指数 1 1 1 1
2013年 序号 1 2 3 4 5
科研热词 骨架 骨切点 部分遮挡 路径轮廓 三维物体
推荐指数 2 2 2 2 2
Hale Waihona Puke 2014年 序号 1 2 3 4 5 6 7 8 9
2014年 科研热词 隐朴素贝叶斯 链接预测 社会网络 排序 形式化验证 同步数据流 关系预测 关系推荐 coq 推荐指数 1 1 1 1 1 1 1 1 1
2008年 序号 1 2 3 4 5 6 7 8 9
科研热词 推荐指数 调度 1 线性时间复杂度 1 拓扑关系 1 扩展拓扑排序 1 工作流 1 多边形 1 单调多边形 1 三角化 1 extended qd-sufferage算法 1
2009年 序号 1 2 3 4 5 6
科研热词 拟合 拓扑空间 彩色结构光 实时三维重建 优先排序神经网络 三维
推荐指数 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8
科研热词 递归调用 测试用例生成 有向无圈图 文本分类 拓扑排序 嵌入式c编译器 层次分类 多标记分类
推荐指数 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
