2.3 三角函数的蛋白质
人教版高中数学目录(文科)

人教 A 版高中数学(文)目录表必修 1 第一章会合与函数观点1.1 会合1.2 函数及其表示1.3 函数的基天性质阅读与思虑广告中数据的靠谱性阅读与思虑怎样获得敏感性问题的诚实反响2.2 用样本预计整体阅读与思虑生产过程中的质量控制图2.3 变量间的有关关系阅读与思虑有关关系的强与弱第二章基本初等函数(Ⅰ)2.1 指数函数2.2 对数函数2.3 幂函数第三章概率3.1 随机事件的概率阅读与思虑天气变化的认识过程3.2 古典概型3.3 几何概型第三章函数的应用3.1 函数与方程3.2 函数模型及其应用必修 4 第一章三角函数1.1 随意角和弧度制1.2 随意角的三角函数必修21.3 三角函数的引诱公式第一章空间几何体1.4 三角函数的图象与性质1.1 空间几何体的构造1.2 空间几何体的三视图和直观图1.5 函数 y=Asin(ωx+ψ)1.3 空间几何体的表面积与体积1.6 三角函数模型的简单应用第二章平面向量第二章点、直线、平面之间的地点关2.1 平面向量的实质背景及基本概牵挂2.1 空间点、直线、平面之间的位2.2 平面向量的线性运算置关系2.3 平面向量的基本定理及坐标表2.2 直线、平面平行的判断及其性示质2.4 平面向量的数目积2.3 直线、平面垂直的判断及其性2.5 平面向量应用举例质第三章直线与方程第三章三角恒等变换3.1 直线的倾斜角与斜率3.1 两角和与差的正弦、余弦和正3.2 直线的方程切公式3.3 直线的交点坐标与距离公式3.2 简单的三角恒等变换必修 3 第一章算法初步1.1 算法与程序框图1.2 基本算法语句1.3 算法事例阅读与思虑割圆术必修 5 第一章解三角形1.1 正弦定理和余弦定理1.2 应用举例1.3 实习作业第二章数列第二章统计2.1 随机抽样阅读与思虑一个有名的事例 1 人教 A 版高中数学(文)目录表2.1 数列的观点与简单表示法2.2 等差数列2.3 等差数列的前 n 项和2.4 等比数列2.5 等比数列的前 n 项和第三章不等式3.1 不等关系与不等式3.2 一元二次不等式及其解法3.3 二元一次不等式(组)与简单的线性规划问题3.3.1 二元一次不等式(组)与平面地区3.3.2 简单的线性规划问题3.4 基本不等式第一章统计事例1.1 回归剖析的基本思想及其初步应用1.2 独立性查验的基本思想及其初步应用第二章推理与证明2.1 合情推理与演绎证明2.2 直接证明与间接证明第三章数系的扩大与复数的引入3.1 数系的扩大和复数的观点3.2 复数代数形式的四则运算第四章框图4.1 流程图4.2 构造图选修 1-1 第一章常用逻辑用语1.1 命题及其关系1.2 充足条件与必需条件1.3 简单的逻辑联络词1.4 全称量词与存在量词第二章圆锥曲线与方程2.1 椭圆2.2 双曲线2.3 抛物线第三章导数及其应用3.1 变化率与导数3.2 导数的计算3.3 导数在研究函数中的应用3.4 生活中的优化问题举例选修4-1 第一讲相像三角形的判断及有关性质第二讲直线与圆的地点关系第三讲圆锥曲线性质的商讨选修 4-4 第一讲坐标系第二讲参数方程选修 1-22。
北师大版(2019)高中数学必修第二册课程目录与教学计划表

北师大版(2019)高中数学必修第二册课程目录与教学计划表教材课本目录是一本书的纲领,是教与学的路线图。
不管是做教学计划、实施教学活动,还是做学习计划、复习安排、工作总结,都离不开目录。
目录是一本书的知识框架,要做到心中有书、胸有成竹,就从目录开始吧!课程目录教学计划、进度、课时安排必修第二册第一章三角函数1 周期变化2 任意角2.1 角的概念推广2.2 象限角及其表示本节综合与测试3 弧度制3.1 弧度概念3.2 弧度与角度的换算本节综合与测试4 正弦函数和余弦函数的概念及其性质4.1 单位圆与任意角的正弦函数、余弦函数定义4.2 单位圆与正弦函数、余弦函数的基本性质4.3 诱导公式与对称4.4 诱导公式与旋转本节综合与测试5 正弦函数、余弦函数的图象与性质再认识5.1 正弦函数的图象与性质再认识5.2 余弦函数的图象与性质再认识本节综合与测试6 函数y=Asin(wx+φ)性质与图象6.1 探究w对y=sinwx的图象的影响6.2 探究φ对y=sin(x+φ)的图象的影响第六章立体几何初步1 基本立体图形1.1 构成空间几何体的基本元素1.2 简单多面体——棱柱、棱锥和棱台1.3 简单旋转体——球、圆柱、圆锥和圆台本节综合与测试2 直观图3 空间点、直线、平面之间的位置关系3.1 空间图形基本位置关系的认识3.2 刻画空间点、线、面位置关系的公理本节综合与测试4 平行关系4.1 直线与平面平行4.2 平面与平面平行本节综合与测试5 垂直关系5.1 直线与平面垂直5.2 平面与平面垂直本节综合与测试6 简单几何体的再认识6.1 柱、锥、台的侧面展开与面积6.2 柱、锥、台的体积6.3 球的表面积和体积本节综合与测试本章综合与测试本册综合。
蛋白质的化学—蛋白质的理化性质(生物化学课件)

蛋白质的化学
1
蛋白质的分子组成
2
蛋白质的分子结构
3
蛋白质的理化性质
血糖
**
蛋白质的化学
3.蛋白质的理化性质
3.1
等电点
目录 3.2
沉淀
CONTENTS
3.3
变性
三级结构和四级结构
**
3.1
等电点
一、蛋白质的两性电离及等电点
蛋白质分子中具有可解离基团,分别可以使其带上 正、负电荷,因此蛋白质也具有两性,在电场中也可以 电泳。
条件 pH = pI pH = pI pH > pI pH < pI
能沉淀各类生物碱的化学试剂叫做生物碱试剂。 如:单宁酸、苦味酸、钼酸、钨酸、三氯乙酸能沉 淀各类生物碱
湖北职业技术学院 医学院《人体机能学》教学课件
人体机能学
• 蛋白质沉淀的实践应用 1.分离制备有活性的天然蛋白制品 2.从制品中除去杂蛋白,或者制备失去活性的蛋白质 制品
湖北职业技术学院 医学院《人体机能学》教学课件
+++
酸
+
+碱
++
带正电荷的蛋白质 在等电点的蛋白质
碱
--
-
-
酸
- --
-
带负电荷的蛋白质
脱水作用
++ +
+
+
+ ++
带正电荷的蛋白质
脱水作用
脱水作用
--
碱
酸-
-
-
-- -
不稳定的蛋白质颗粒
带负电荷的蛋白质
食品生物化学-2.3蛋白质化学ppt课件

2.3.2氨基酸
蛋白质的相对分子量非常大,但是用酸水解后, 蛋白质分子产生一系列相对分子质量低的简单有 机化合物——α-氨基酸,构成蛋白质的α-氨基 酸共有20种,称为天然氨基酸或基本氨基酸。
不参与蛋白质组成的氨基酸称为非蛋白氨基酸 (稀有氨基酸)。
(1)蛋白质氨基酸的结构特点即表示方法
2.3.4.3蛋白质的变性
大多数蛋白质分子只有在一定的温度和pH范围内 才能保持其生物学活性。将蛋白质分子暴露在极 端的温度或pH中就会使它们发生变化,称为变性。
球蛋白变性最显著的效应就是溶解度下降。大多 数蛋白质加热到50~60℃以上即发生变性,有些 蛋白质冷却到10~15℃以下也会发生变性。
超滤是利用压力或离心力使小分子溶质通过半透 膜而蛋白质被截留在膜上而分离。
图 超滤装置
离心沉降法
原理:不同蛋白质颗粒在质量、密度和 性状上存在差异,在一定的强离心力场 中表现出不同的下沉速度-沉降速度。
许多蛋白质的变性之所以表现为不可逆,是由于 重新折叠成天然状态往往是极慢的过程。
细胞或组织蛋白质变性后不能复性。
核糖核酸酶变性与复性作用
Native ribonuclease
8 M urea and -mercapotoethanol
变性
Denative reduced ribonuclease
丝氨酸-缬氨酸-酪氨酸-谷氨酰胺
2.3.3.2蛋白质分子的二级结构
概念:蛋白质的二级结构,是指多肽链中 彼此靠近的氨基酸残基之间由于氢键相互 作用而形成的空间关系;是指蛋白质分子 中多肽链本身的折叠方式。
主要是α-螺旋结构,其次是β-折叠结构和β转角。
(1)α-螺旋
蛋白质的理化性质ppt课件

蛋白质的热变性与凝固作用
2、蛋白质的凝固作用
天然蛋白质变性后,变性蛋 白质分子互相凝集或相互穿插 缠绕在一起的现象成为蛋白质 的凝固(coagulation) 。
凝固作用分两个阶段: 首先是变性; 其次失去规律性的肽链聚集缠绕在一起而凝固或结絮;
45
淀,加热后变成红色 31
六、蛋白质的颜色反应
7. 乙醛酸反应—色氨酸的特有反应
在蛋白质溶液中加入HCOCOOH,将 浓硫酸沿管壁缓慢加入,不使相混, 在液面交界处,即有紫色环形成
色氨酸的反应(吲哚环的反应) 鉴定蛋白质中是否含有色氨酸 明胶中不含色氨酸
32
六、蛋白质的颜色反应
8. 坂口反应—精氨酸特有的反应
19
蛋白质仍能保持生物活性的沉淀方法
(1)盐析—中性盐沉淀 What’s salt precipitation of protein? 盐溶作用 盐析作用
20
蛋白质仍能保持生物活性的沉淀方法
(1)盐析—中性盐沉淀
What’s salt precipitation of protein? 定义:在蛋白质溶液中加入大量中性盐,以
沉淀原理:
① 脱水作用——破坏水化膜; ② 使水的介电常数降低,蛋白质溶解度降低。
24
蛋白质仍能保持生物活性的沉淀方法
(2)有机溶剂沉淀法 处理条件: ① 低温操作;
② 沉淀完全后尽快分离;
(3)酸沉淀法 机制:破坏电荷,等电点沉淀。
25
四、蛋白质的沉淀作用
3.沉淀方法:
沉淀后蛋白质仍能保持生物活性的沉淀方法 沉淀后蛋白质失去生物活性的沉淀方法
同性电荷蛋白质分子互相排斥。
7
蛋白质颗粒的表面电荷和水化膜
蛋白质理化性质

原体的吞噬作用、补体系统的激活等免疫效应,从而清除病原体并促进
受损细胞的修复。
05 蛋白质的分离纯化
沉淀法
盐析法
在蛋白质溶液中加入高浓度的盐溶液, 使蛋白质发生沉淀,常用的盐有硫酸 铵、硫酸钠和氯化钠等。
有机溶剂沉淀法
加入有机溶剂降低水的介电常数,使 蛋白质发生沉淀,常用的有机溶剂有 乙醇、丙酮和丁醇等。
ห้องสมุดไป่ตู้解性
蛋白质的溶解性主要取决于其氨基酸组成和分子结构。一般来说,蛋白质在极性溶剂如水中的溶解度 较高,而在非极性溶剂如有机溶剂中的溶解度较低。
蛋白质的溶解度还受到温度、pH值和离子强度的影响。在适宜的pH值和离子强度下,加热可以提高蛋 白质的溶解度。
不同蛋白质具有不同的溶解度,这与其功能和用途密切相关。例如,酶的活性与其在水中的溶解度密切 相关,因此需要选择适当的条件以保持酶的活性。
萃取法
要点一
液-液萃取
利用两种不混溶的溶剂,将蛋白质从一种溶剂转移到另一 种溶剂中。
要点二
液-固萃取
利用固体吸附剂将蛋白质吸附,然后用适当的溶剂将蛋白 质洗脱下来。
感谢您的观看
THANKS
抗体活性
01
抗体定义
抗体是免疫系统中的一种蛋白质,能够与抗原特异性结合,发挥免疫防
御和清除作用。
02
抗体活性调节
抗体的活性受到多种因素的影响,如抗原的种类和浓度、抗体与抗原的
亲和力等。通过调节这些因素,可以影响抗体的免疫应答效果。
03
抗体活性与免疫反应
抗体在免疫反应中发挥重要作用,通过与抗原结合,触发吞噬细胞对病
三级结构决定蛋白质的生物学活性和功能。
四级结构
四级结构是指蛋白质复合物中 各亚基的空间排布及亚基之间 的相互关系。
蛋白质的理化性质课件参考.ppt

精选课件
4
练习
• 下列哪种蛋白质在pH5.0的溶液 中带负电荷?
• A.pI为5.5的蛋白质 B.pI为4.0的蛋白质 C.pI为7.0的蛋白质 D.pI为5.0的蛋白质
精选课件
5
体内大多数蛋白质的等电点在pH5.0 左右,
因而在生理条件下以阴离子形式存在 。
精选课件
6
3.电泳
定义: 带电粒子在电场中向电性相反的电极移动的现象。
若蛋白质变性程度较轻,去除变性因素,有些
可恢复其天然构象和生物活性,称为蛋白质的复性。
精选课件
25
核糖核酸酶的变性与复性示意图
8M尿素或 β-巯基乙醇
透析
精选课件
26
(五)、变性与复性
过核 程糖
核 酸 酶 的 变 性
精选课件
27
蛋白质沉淀
概念 蛋白质从溶液中析出的现象称为沉淀。
方法 盐析法、有机溶剂的沉淀、重金属盐沉淀、
蛋白质在带电场中泳动的速度和方向与其所 带电荷的性质、数量及分子的大小、形状有关。
带电荷多,分子小的泳动速度较快;反之则泳动 较慢,从而达到分离蛋白质的目的。
血清蛋白醋酸纤维素薄膜电泳可将血清蛋白
分为清蛋白、α1球蛋白、α2球蛋白、β球蛋白
、γ球蛋白。
精选课件
7
精选课件
8
A:染色后显示的蛋白质区带 B:光密度扫描定量分析
精选课件
9
精选课件
10
精选课件
11
正常
肝硬化
精选课件
12
精选课件
13
二、蛋白质的胶体性 质
1.蛋白质有胶体性质
蛋白质是生物大分子,分子量在1万~10万 kD(千道尔顿)之间,分子直径在胶体颗粒 的范围(1—100nm)
5蛋白质2
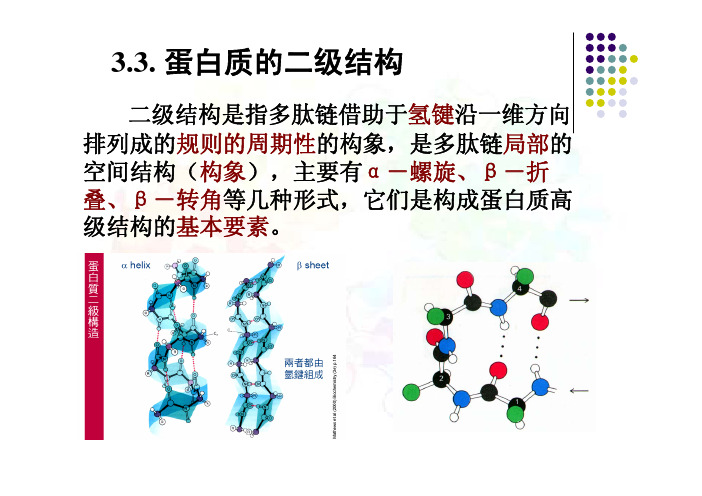
3.3. 蛋白质的二级结构二级结构是指多肽链借助于氢键沿一维方向排列成的规则的周期性的构象,是多肽链局部的空间结构(构象),主要有α-螺旋、β-折叠、β-转角等几种形式,它们是构成蛋白质高级结构的基本要素。
3.3.1 酰胺平面与Cα的二面角(φ和ψ)Cα的二面角两相邻酰胺平面之间,能以共同的Cα为定点而旋转,绕Cα-N键旋转的角度称φ角,绕C-Cα键旋转的角度称ψ角。
φ和ψ称作二面角,亦称构象角。
二面角的定义二面角的一般定义在A-B-C-D四个原子依次相连的系统中,含A、B、C的平面和含B、C、D的平面之间的夹角。
Φ=0°Ψ=0°Φ=180°Ψ=180°完全重叠完全伸展完全伸展的多肽主链构象α-碳原子肽平面Φ=1800,ψ=1800Φ=00,ψ=00的多肽主链构象酰胺平面Φ=00,ψ=00侧链非键合原子接触半径二面角(Φ,ψ)所决定的构象能否存在,主要取决于相邻两肽单位中非共价原子间有无位阻。
Ramachandran Plot 拉氏图允许区:7.7%最大允许区:20.3%αβl拉氏图是判断蛋白质模型正误的重要参考。
R 基团的电荷、大小限制使肽平面不能任意转动,二面角只能限制在一定范围内1950年,Pauling等人根据晶体衍射的数据、肽键数据,考虑到氢键的重要性,预测出了α螺旋结构,1951年又提出了β折叠结构。
1954Chemistry1962 PeaceBooks by Pauling:The Nature of the Chemical Bond, and the Structure of Molecules and Crystals (1939);General Chemistry(1947, 1953);No More War!(1958, 1959,1962); Vitamin C, the Common cold and the Flu; How to Live Longer and Feel Better The ability to imagine a different answer, one that nobody else has though of, is critical to scientific advancement.First, have a lot of ideas. Then,throw away the bad onesthe Nuclear TestBan TreatyPauling became anobject of suspicion forhis opposition to theUnited States'involvement in thearms race."orthomolecular"/.../pauling.html稳定二级结构的最主要作用力是氢键3.3.2 α-螺旋(α-helix)特征:1.右手螺旋,一圈3.6个AA;螺距0.54nm;2.>C=0 和>N-H近乎平行于螺旋轴;3.R基在外侧;4.第n个aa的>C=O基与第n+4个aa的>N-H形成氢键。
第一节三角函数基因指导蛋白落叶质的合成教学设计

第一节 基因指导蛋白质的合成 教学设计ȠȠȠȠȠȠȱȮ教学重点ȠȠ站立松岗桥头,仰视二碉,一雄踞村北山脊上,一耸峙村中,相距50米。
碉为石木结构,八角整体由下向上中国版的“比萨斜塔ʔ[1]渐内收尾台锥形,其中一座高31米,如直刺蓝天的无尘墨剑,另一座高28米,如从空而落,玉笋刺空,各有一势。
另两碉已残败不堪了。
两碉对峙,可敌万军,有一夫当关,万夫莫开之势。
据传双碉内有暗道相通,碉底有井可储粮食数月不腐。
对面上坡上的官寨遗址是显赫一时的松岗土司官寨遗址。
当时修建的富丽堂皇,所耗人力和才力在当时四土地区来说是“四土之最”,有“布达拉宫第二”之称。
可惜,如此美丽、宏伟的建筑其命运同阿房宫一般毁于一场无情的大火。
如今所见残缺不全双碉和遗址也算后人来凭吊夕日的一种见证。
编辑本段旅游信息松岗直波古碉群ȠȠ位于距县城17公里的松岗镇,始建于清朝初年,共由四个风格各异,沿河两岸对峙的古碉组成,是第五批全国重点文物保护单位。
在距离马尔康县城15公里的松岗镇,有个松岗碉群,共有4座碉楼,分别位于梭磨河两岸。
其中,两个碉楼位于直波村,被称为直波碉楼。
[1] ȠȠ碉为石木结构,八角碉整体由下向上渐内收尾呈锥形。
其中一座高31米,如直刺蓝天的无尘墨剑;另一座高28米,如从空而落、玉笋刺空,各有一势。
两碉对峙,可敌万军,有一夫当关万夫莫开之势。
双碉内有暗道相通,碉底有井且储存粮食可保数月不腐。
官寨遗址ȠȠȠȠȠ(1)了解基因控制蛋白质合成的中间物质──ɒɎɁ的基本单位、化学组成和种类,以及它与ɄɎɁ在组成、结构、功能和分布等方面的异同;ȠȠȠȠȠ(2)理解基因表达的转录和翻译的概念和过程;ȠȠȠȠȠ(3)比较转录和翻译的异同;ȠȠȠȠȠ(4)认知和区分相关概念:遗传信息、遗传密码、反密码子;ȠȠȠȠȠ(5)计算问题:基因ȨɄɎɁȩ碱基、ɒɎɁ碱基和氨基酸的对应关系。
ȠȠȠȠȠȲȮ教学重难点ȠȠȠȠȠ(1)理解基因表达的转录和翻译的概念和过程ȠȠȠȠȠ(2)认知和区分相关概念:遗传信息、遗传密码、反密码子;ȠȠȠȠȠ(3)计算问题:基因ȨɄɎɁȩ碱基、ɒɎɁ碱基和氨基酸的对应关系,以图解方法解决。
2-3蛋白质的理化性质

2-3蛋白质的理化性质蛋白质是由氨基酸组成的大分子化合物,其理化性质一部分与氨基酸相似,如两性电离、等电点、呈色反应等,也有一部分又不同于氨基酸,如高分子量、胶体性质、变性等。
一、蛋白质的两性电离蛋白质是由氨基酸组成的,其分子中除两端的游离氨基和羧基外,侧链中尚有一些解离基,如谷氨酸、天门冬氨酸残基中的γ和β-羧基,赖氨酸残基中的ε-氨基,精氨酸残基的胍基和组氨酸的咪唑基。
作为带电颗粒它可以在电场中移动,移动方向取决于蛋白质分子所带的电荷。
蛋白质颗粒在溶液中所带的电荷,既取决于其分子组成中碱性和酸性氨基酸的含量,又受所处溶液的pH影响。
当蛋白质溶液处于某一pH时,蛋白质游离成正、负离子的趋势相等,即成为兼性离子(净电荷为O),此时溶液的pH值称为蛋白质的等电点(简写pI,)。
处于等电点的蛋白质颗粒,在电场中并不移动。
蛋白质溶液的pH大于等电点,该蛋白质颗粒带负电荷,反之则带正电荷。
各种蛋白质分子由于所含的碱性氨基酸和酸性氨基酸的数目不同,因而有各自的等电点。
凡碱性氨基酸含量较多的蛋白质,等电点就偏碱性,如组蛋白、精蛋白等。
反之,凡酸性氨基酸含量较多的蛋白质,等电点就偏酸性,人体体液中许多蛋白质的等电点在pH5.0左右,所以在体液中以负离子形式存在。
二、蛋白质的胶体性质蛋白质分子量颇大,介于一万到百万之间,故其分子的大小已达到胶粒1~100nm范围之内。
球状蛋白质的表面多亲水基团,具有强烈地吸引水分子作用,使蛋白质分子表面常为多层水分子所包围,称水化膜,从而阻止蛋白质颗粒的相互聚集。
与低分子物质比较,蛋白质分子扩散速度慢,不易透过半透膜,粘度大,在分离提纯蛋白质过程中,我们可利用蛋白质的这一性质,将混有小分子杂质的蛋白质溶液放于半透膜制成的囊内,置于流动水或适宜的缓冲液中,小分子杂质皆易从囊中透出,保留了比较纯化的囊内蛋白质,这种方法称为透析。
三、蛋白质的沉淀蛋白质凝聚从溶液中析出的现象称为蛋白质沉淀,变性蛋白质一般易于沉淀,但也可不变性而使蛋白质沉淀,在一定条件下,变性的蛋白质也可不发生沉淀。
《蛋白质》人教版高中化学实用课件3

《蛋白质》人教版高中化学实用课件3
《蛋白质》人教版高中化学实用课件3
2、胰岛素是一种蛋白质分子,结构如下:
-S-SA链
S
S A链有21个氨基酸
B链 S
S
B链有30个氨基酸
①该胰岛素分子含有肽键 49 个;
②理论上分析,胰岛素分子至少含有 2 个
氨基, 2 个羧基;
③51个氨基酸形成胰岛素后,分子量比原来 减少了 888 。
物水解时最多消耗多少个水分子?
13(链)
14(环)
《蛋白质》人教版高中化学实用课件3
《蛋白质》人教版高中化学实用课件3
蛋白质知识体系
占细胞鲜重7%-10% 占细胞干重50%以上
与双缩脲试剂显紫色反应
DN
含量
鉴定
A
mRNA 控制合成 蛋白质 结构
化学元素 氨基酸 肽链
蛋白质
《蛋白质》人教版高中化学实用课件3
思考:下列哪个分子不是组成蛋白质的氨基酸?
CH3 CH CH COOH
OH NH2 A
CH2 CH
COOH
NH2 B
CH3 CH3 CH O
H2N C C OH
H C
CH2—CH2—CH2—COOH
NH2
XD
NH2— CH—(CH2)2—COOH
COOH E
思考: 氨基酸是如何构成蛋白质的呢?
四、脱水缩合
总结
失去的水分子数=肽键数=氨基酸数-肽链数、 至少含有的氨基数=羧基数=肽链数、 至少含有的氮原子数=氨基酸数、 至少含有的氧原子数=氨基酸数+肽链数
变式: 由n个氨基酸脱水缩合形成1个环状肽中或m个环状肽中:
形成的肽键数是 n ,失去的水分子数是 n ,至少含有 的氨基数是 0 、羧基数是 0 、氧原子数是 n 、 氮原子数是 n 。
三角函数的积化和

三角函数的积化和三角函数是数学中的重要概念,它在解决各种实际问题和求解各种数学方程中扮演着关键的角色。
三角函数的积化和是一种常见的技巧和方法,用于将一个三角函数的乘积转化为和式或积分形式。
在本文中,我们将探讨三角函数的积化和方法及其应用。
一、三角函数的积化和方法1.1 正弦函数的积化和我们首先来研究正弦函数的积化和。
假设我们有一个正弦函数的乘积sin(x)sin(y),我们可以通过以下公式将其转化为和式的形式:sin(x)sin(y) = (1/2)[cos(x-y)-cos(x+y)]这个公式可以通过使用三角函数的和差化积公式来推导。
通过这个公式,我们可以将一个正弦函数的乘积转化为两个余弦函数的差的形式。
这样的转化在一些数学计算和问题求解中非常有用。
1.2 余弦函数的积化和接下来我们来研究余弦函数的积化和。
假设我们有一个余弦函数的乘积cos(x)cos(y),我们可以通过以下公式将其转化为和式的形式:cos(x)cos(y) = (1/2)[cos(x-y)+cos(x+y)]这个公式同样可以使用三角函数的和差化积公式来推导得出。
通过这个公式,我们可以将一个余弦函数的乘积转化为两个余弦函数的和的形式。
同样地,这样的转化在数学计算和问题求解中非常有用。
1.3 正切函数的积化和最后我们来研究正切函数的积化和。
假设我们有一个正切函数的乘积tan(x)tan(y),我们可以通过以下公式将其转化为和式的形式:tan(x)tan(y) = (1/2)[tan(x+y)-tan(x-y)]这个公式同样可以通过使用三角函数的和差化积公式来推导得出。
通过这个公式,我们可以将一个正切函数的乘积转化为两个正切函数的和的形式。
这个转化在某些数学计算和问题求解中也是非常有用的。
二、三角函数的积化和的应用三角函数的积化和方法在数学和物理学中有着广泛的应用。
以下是一些常见的应用领域:2.1 解方程通过将一个三角函数的乘积转化为和式的形式,我们可以简化一些复杂的三角方程的求解过程。
