届全国各省市高三上期数学联考试题重组专题题型三立体几何(学生版)

合集下载

全国名校大联考2022-2023学年高三上学期第三次联考数学试卷

一、单选题二、多选题1. 已知数列为递减数列，其前n 项和，则实数m 的取值范围是（）．A．B．C．D．2. 已知点，，在半径为5的球面上，且，，为球面上的动点，则三棱锥体积的最大值为（）A．B．C．D．3.已知等差数列的前项和为，，则（）A．B ．13C ．-13D ．-184. 已知函数的图像向左平移个单位后，得到函数的图像，则函数的单调递增区间为（）A．，B ．，C．，D ．，5.在的展开式中，除常数项外，其余各项系数的和为（）A ．63B ．-517C ．-217D ．-1776. 对于定义域为的函数，若同时满足下列三个条件：①；②当，且时，都有；③当，且时，都有，则称为“偏对称函数”．现给出下列三个函数：；；，则其中是“偏对称函数”的函数个数为（）A．B．C．D．7.已知圆锥的表面积为，母线与底面所成角为，若，则圆锥的体积为（）．A．B．C．D．8. 若直线是曲线与曲线的公切线，则（）A ．11B ．12C．D．9. 已知的展开式中的所有项的二项式系数之和为64，记展开式中的第项的系数为，二项式系数为，，则下列结论正确的是（）A ．数列是等比数列B ．数列的所有项之和为729C ．数列是等差数列D ．数列的最大项为2010. 已知函数，则以下结论正确的是（）A．的零点个数的可能取值为0，2，3，4B ．当时，恒成立C．的极大值点为D ．的值域为11. 如图，长方体中，底面是边长为的正方形，，动点在线段上运动，则下列判断正确的是（）全国名校大联考2022-2023学年高三上学期第三次联考数学试卷三、填空题四、解答题A．三棱锥的体积为定值B ．当为中点时，最短C．三棱锥外接球表面积的最小值为D ．与所成角的范围是12. 已知直线l：与圆C：相交于A ，B 两点，则（）A ．直线l恒过点B ．当时，圆C 关于直线l 对称C．的取值范围为D ．若，则13. 已知，且，则向量与的夹角___14. 已知a ，b 为实数，若对任意，都有恒成立，则的最小值为__________．15.已知向量满足，且向量在向量上的投影向量为，则__________.16. 新一代新冠病毒奥密克戎致病性与原始毒株相比显著降低，但传染力显著增强.已知我国沿海某特区人口约为800万，其中感染过新冠的人口占比.(1)以频率估计概率，从该地区所有人口中随机抽出60人，则这60个人中感染过新冠的人数最有可能是多少？(2)从该地区所有新冠患者中随机抽出1000人，统计得到轻症患者有960人，重症患者有40人，其中轻症患者有600人接种过新冠疫苗，重症患者有12人接种过新冠疫苗，是否有99.5%的把握认为接种新冠疫苗可以减少新冠重症率？(3)若该地区人口失业率与感染过新冠人员的重症率均为4%（失业率指失业人口占总人口比例），失业与是否感染过新冠独立，该地区政府出台政策，对所有感染过新冠且轻症的失业人员每人发放400元补助，对所有感染过新冠且重症的人员无论是否失业每人发放1000元补助，预计总的资金投入是多少？参考公式：，.0.100.050.010.0052.7063.8416.6357.87917. 2022年6月5日是世界环境日，十三届全国人大常委会第三十二次会议表决通过的《中华人民共和国噪声污染防治法》今起施行.噪声污染已经成为影响人们身体健康和生活质量的严重问题，为了解声音强度（单位：）与声音能量（单位：）之间的关系，将测量得到的声音强度和声音能量的数据作了初步处理，得到如图所示的散点图：(1)根据散点图判断，与哪一个适宜作为声音强度关于声音能量的回归模型？（能给出判断即可，不必说明理由）(2)求声音强度关于声音能量的非线性经验回归方程（请使用题后参考数据作答）；(3)假定当声音强度大于45dB时，会产生噪声污染，城市中某点处共受到两个声源的影响，这两个声源的声音能量分别是和，且.已知点处的声音能量等于与之和，请根据（2）中的非线性经验回归方程，判断点处是否受到噪声污染，并说明理由.参考数据：，，令，有，，，，，，，，.18. 设函数，其中；（1）若的最小正周期为，求的单调增区间；（2）若函数的图象的一条对称轴为，求的值．19. 已知动点到定直线的距离比到定点的距离大.(1)求动点的轨迹的方程；(2)过点的直线交轨迹于，两点，直线，分别交直线于点，，证明：以为直径的圆被轴截得的弦长为定值，并求出此定值.20. 年月日，国家统计局公布全国规模以上工业企业月累计营业收入利润率数据如表：月份累计月月月月月月月月月月月份累计代码营业收入利润率（1）根据表中有关数据请在下图中补充完整与的折线图，判断与哪一个更适宜作为关于的回归方程类型，并说明理由；（2）根据（1）的判断结果及表中数据，建立关于的回归方程（系数精确到）；（3）根据（2）得出的回归方程，预测月月累计营业收入利润率的值为多少？参考公式：对于一组数据、、、，其回归直线的斜率和截距的最小二乘估计分别为，.参考数据：表中，，．21. 已知数列满足且．(1)求的通项公式；(2)设，求数列的前项和．。

2022学年高三上(编号1-25)立体几何大题汇编(学生版)

AEB图2图1NCDCB BDF2022学年高三上（编号1-25）立体几何大题汇编（学生版）1：（2023届广东省高三上学期开学联考解析第19题）1：（本小题满分12分）如图所示，在直三棱柱111ABC A B C -中，底面ABC ∆ 是边长为2的等边三角形，14AA =，D 是AB 的中点，E 是1CC 上一点．（1）求证：平面CDE ⊥平面11AA B B ；（2）若//CD 平面1A BE ，求平面1A BE 与平面ABC 所成的锐二面角的余弦值．．2：（2023届湖北圆创第一次联合测试解析第20题）2：如图，四棱锥F ABCD -的底面ABCD 是菱形，其对角线2AC =，2BD =AE ，CF 都与平面ABCD 垂直，1AE =，2CF =（1）求二面角角B AF D --的大小；（2）求三棱锥E ABD -与四棱锥F ABCD -公共部分的体积3：（2023届湖北九师联盟高三开学考解析第20题） 3：如图，四边形ABCD 是梯形，//AB CD ，142AD DC CB AB ====，M 是AB 的中点，将ADM △沿DM 折起至'A DM △，如图2，点N 在线段'A C 上．（1）若N 是'A C 的中点，求证：平面DNM ⊥平面'A BC ；（2）若'26A C =DNM 与平面CDM 25，求'A N NC ．4：（20234：如图，在四棱锥B ACFM -中，四边形ACFM 为直角梯形，//FM AC ，90ACF ∠=︒，平面ACFM ⊥E平面ABC ，1BC CF ==，3AC =，60ABC ∠=︒．（1）证明：BC AM ⊥；（2）若四棱锥B ACFM -3，求平面MAB 与平面FCB 所成的锐二面角的余弦值．5：（2023届湖北省九校教研协作体高三起点考试解析第19题）5：查找并阅读关于蜂房结构的资料，建立数学模型说明蜂房正面采用正六边形面，底端是封闭的六角棱锥体的底，由三个相同的菱形组成（菱形的锐角为'7032，钝角为'10928）的原因6：（2023届南京市一中高三上学期数学模拟卷1解析第20题）6：在三棱锥ABCD 中，已知平面ABD ⊥平面BCD ，且6BD =2AD ，22AB =，BC AC ⊥．（1）求证：BC ⊥平面ACD ；（2）若E 为ABC △的重心，3CD =，求平面CDE 与平面ABD 所成锐二面角的正弦值．7：（2023届南京市高三年级学情调研1解析第21题）B 17：(本小题满分12分)如图，四棱锥P -ABCD 的体积为34，平面P AD ⟘平面ABCD ，△P AD 是面积为3ABCD 是等腰梯形，1BC =，E 为棱P A 上一动点． (1)若直线EC 与平面ABCD 的夹角为60°，求二面角B -CE -D 的正弦值； (2)求EDEC的取值范围．8：（2023届湖北省二十一所重点中学高三上第二次联考解析第19题）8：已知四棱锥P ABCD -的底面为直角梯形，//AB DC ，90DAB ∠=，PA ⊥平面ABCD ，112PA AD DC AB ====；（1）若点M 是棱PB 上的动点请判断下列条件：①直线AM 与平面ABCD 所成角的正切值为12； ②12PM MB =中哪一个条件可以推断出//PD 平面ACM (无需说明理由)，并用你的选择证明该结论；（2）若点N 为棱PC 上的一点(不含端点)，试探究PC 上是否存在一点N ，使得平面ADN ⊥平面BDN ?若存在，请求出PNNC的值，若不存在，请说明理由．9：（2023届武汉市高三上7月新起点考试解析第19题）9：在直三棱柱111ABC A B C -中，已知侧面11ABB A 为正方形，2BA BC ==，D ，E ，F 分别为AC ，BC ，1CC 的中点，1BF B D ⊥．（1）证明：平面1B DE ⊥平面11BCC B ；（2）求平面1BC D 与平面1B DE 夹角的余弦值．10：（2023届重庆市巴蜀中学月考卷（一）解析第19题）10：如图4，在多面体ABCDEF 中，四边形ABCD 是一个矩形，//EF AC ，2AC EF =，2AB AE ==，4AD =，120BAE ∠=︒．（1）求证：//AE 平面BFD ；（2）若平面EAB ⊥平面ABCD ，求平面EAB 与平面FCD 的夹角的余弦值．11：（2023届广东惠州高三第一次调研考解析第20题）11:（本小题满分12分）如图，在四棱锥P ABCD -中，已知//AB CD ，AD CD ⊥，BC BP =，24CD AB ==，ADP ∆是等边三角形，E 为DP 的中点．（1）证明：AE ⊥平面PCD ；（2）若42PA =PBC 与平面PAD 夹角的余弦值．12：（2023届江苏省盐城中学8月高三上开学考解析第19题）12：如图，四棱锥P ABCD -的底面是等腰梯形，//AD BC ，2BC AD =，60ABC ∠=︒，E 是棱PBA 1ABB 11P的中点，F 是棱PC 上的点，且A 、D 、E 、F 四点共面．（1）求证：F 为PC 的中点；（2）若PAD △为等边三角形，二面角P AD B --的大小为120︒，求直线BD 与平面ADFE 所成角的正弦值．13：（2022年8月福建福安一中高三上第一次检测解析第20题）13:（本小题满分12分）如图，C 是以AB 为直径的圆O 上异于,A B 的点，平面PAC ⊥平面ABC ，PAC ∆为正三角形，,E F 分别是,PC PB 上的动点．（1）求证：BC AE ⊥；（2）若,E F 分别是,PC PB 的中点且异面直线AF 与BC 所成角 3，记平面AEF 与平面ABC 的交线为直线l ，点Q 为直线l 上动点，求直线PQ 与平面AEF 所成角的取值范围．14：（2023届广州市真光中学高三上8月开学考解析第19题）14：如图，在直三棱柱111ABC A B C -中，90ACB ∠=︒，且12AC BC CC ===，点P 为线段1B C 上的动点．（1）当P 为线段1B C 中点时，求点1B 到平面ABP 的距离；（2）当直线AP 与平面11BCC B 32求二面角P AB C --的余弦值．15：（2023届浙江省新高考研究高三上8月测试解析第20题）15：如图，在四棱锥P ABCD -中，底面ABCD 是等腰梯形，2224CD AB BC AD ====，平面ADP ⊥平面ABCD ，E 是PC 的中点，且ADP ∆为等边三角形，平面ADP ⋂平面PBC m =．（1）设m ⋂直线BC M =，求点M 到平面PDC 的距离；（2）求二面角P BE D --的正弦值．16：（2023届浙江省A9协作体高三暑假返校考解析第20题）16：（本题满分12分）如图, 在平面四边形ABCD 中，AD AB =，CD CB =．现将ABD ∆沿BD 翻折到A BD '∆的位置, 且二面角A BD C '--的平面角大小为120．（I ）求证:A C BD '⊥；（II ）若2BD =, 且BC 与平面A BD '所成角的大小为45, 求BC 的长．17：（2023届长沙市一中入学摸底考解析第19题）17：如图，在直三棱柱111ABC A B C -中，O ，M ，N 分别为线段BC ，1AA ，1BB 的中点，P 为线段FCDABE1AC 上的动点，12AO BC =，3AB =，4AC =，18AA = （1）求点C 到平面1C MN 的距离；（2）试确定动点P 的位置，使线段MP 与平面11BB C C 所成角的正弦值最大．18：（2023届金太阳联考数学试题解析第19题）18：在多面体EF ABCD -中，平面EDCF ⊥平面ABCD ，EDCF 3//CD AB ，1AD DC CB ===，2AB =．（1）证明：BD EA ⊥；（2）求平面EDCF 与平面EAB 夹角的余弦值．19：（2022年8月Z20联盟数学解析第19题）19:（本题满分12分）如图, 在四棱锥P ABCD -中, 平面PAD ⊥平面ABCD ，2PA AD ==，4BD =，23AB =BD 是ADC ∠的平分线，且BD BC ⊥．（I ）若点E 为棱PC 的中点, 证明：//BE 平面PAD ；（II ）已知二面角P AB D --的大小为60，求平面PBD 和平面PCD 的夹角的余弦值．20：（2022年8月南京市六校联合体高三联合调研解析第20题）20：如图，在四棱锥S ABCD -中，四边形ABCD 是矩形，SAD ∆是正三角形，且平面SAD ⊥平面ABCD ，AE1AB =，P 为棱AB 的中点，四棱锥S ABCD - （1）若E 为棱SA 的中点，求证：//PE 平面SCD ；（2）在棱SA 上是否存在点M ，使得平面PMB 与平面SAD 所成？若存在，指出点M 的位置并给以证明；若不存在，请说明理由．21：（2023届南海区摸底考试解析第19题）21：在如图所示的圆柱MN 中，AB 为圆M 的直径，C ，D 是AB 上的两个三等分点，EA ，FC ，GB 都是圆柱MN 的母线．（1）求证：//FM 平面ADE ；（2）若1BC =，已知直线AF 与平面ABCD 所成的角为30︒，求二面角A FB C --的余弦值．。

各省份历年高考立体几何3及答案

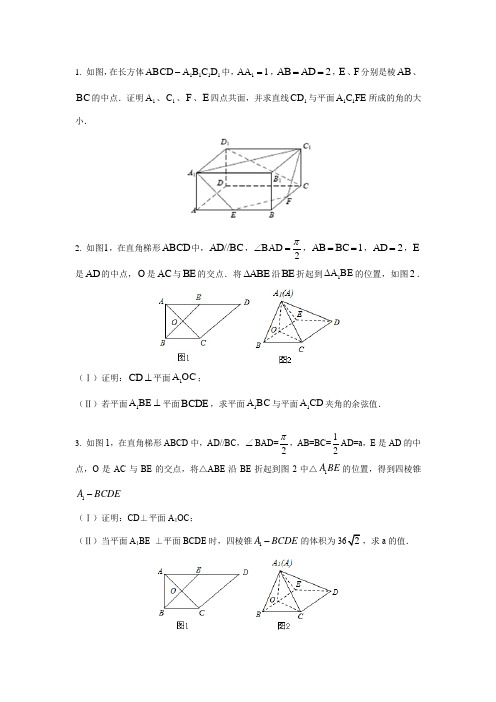
1. 如图，在长方体1111CD C D AB -A B 中，11AA =，D 2AB =A =，E 、F 分别是棱AB 、C B 的中点．证明1A 、1C 、F 、E 四点共面，并求直线1CD 与平面11C F AE 所成的角的大小．2. 如图1，在直角梯形CD AB 中，D//C A B ，D 2π∠BA =，C 1AB =B =，D 2A =，E是D A 的中点，O 是C A 与BE 的交点．将∆ABE 沿BE 折起到1∆A BE 的位置，如图2．（Ⅰ）证明：CD ⊥平面1C A O ；（Ⅱ）若平面1A BE ⊥平面CD B E ，求平面1C A B 与平面1CD A 夹角的余弦值．3. 如图1，在直角梯形ABCD 中，AD//BC ，∠BAD=2π，AB=BC=12AD=a ，E 是AD 的中点，O 是AC 与BE 的交点，将△ABE 沿BE 折起到图2中△1A BE 的位置，得到四棱锥1A BCDE -（Ⅰ）证明：CD ⊥平面A 1OC ；（Ⅱ）当平面A 1BE ⊥平面BCDE 时，四棱锥1A BCDE -的体积为a 的值．4. 如图，三棱台ABC -DEF 中，2,,AB DE G H =分别为BC AC ,的中点，（Ⅰ）求证：//BD 平面FGH ；（Ⅱ）若BC AB BC CF ⊥⊥,，求证：平面⊥BCD 平面FGH .5. 如图，在三棱台DEF-ABC 中，AB=2DE,G,H 分别为AC,BC 的中点。

（Ⅰ）求证：BC//平面FGH ；（Ⅱ）若CF ⊥平面ABC ，AB ⊥BC ，CF=DE, ∠BAC=045 ,求平面FGH 与平面ACFD 所成的角（锐角）的大小．6. 如图，在四棱锥P ABCD -中，已知PA ⊥平面ABCD ，且四边形ABCD 为直角梯形，2ABC BAD π∠=∠=,2,1PA AD AB BC ====（1）求平面PAB 与平面PCD 所成二面角的余弦值；（2）点Q 是线段BP 上的动点，当直线CQ 与DP 所成角最小时，求线段BQ 的长7. 如图，在直三棱柱111ABC A B C -中，已知1,AC BC BC CC ⊥=．设1AB 的中点为D ，11.B C BC E ⋂=求证：（1）DE//平面C C AA 11；（2）11BC AB ⊥8. 如图，已知四棱台1111ABCD A BC D -上、下底面分别是边长为3和6的正方形，16AA =，且1AA ⊥底面ABCD ，点P 、Q 分别在棱1DD 、BC 上．（1）若P 是1DD 的中点，证明：1AB PQ ⊥；（2）若PQ//平面11ABB A ，二面角P-QD-A 的余弦值为37，求四面体ADPQ 的体积．参考答案：9. 解：如图，以D 为原点建立空间直角坐标系，可得有关点的坐标为A 1(2，0，1)、C 1(0，2，1)、E(2，1，0)、F （1，2,0）、C （0、2、0）、D （0,0,1）．因为()0,2,211-=C A ,()0,1,1-=EF ，所以11//EF AC，因此直线11C A 与EF 共面，即，、、、四点共面．设平面EF C A 11的法向量为(,,)n u v w =，则n ⊥EF ，n ⊥1FC ，又(1,1,0)EF =-，1FC =(1,0,1)-, 故0,u .0,u v v w u w -+=⎧==⎨-+=⎩解得取u=1，则平面EF C A 11的一个法向量n =(1,1,1)．又1(0,2,1)CD =-,故11||CD n CD n ⋅=⋅因此直线与平面所成的角的大小1515arcsin ．10. （I ）在图1中，因为AB=BC=1,AD=2,E 是AD 的中点，∠BAD=2π，所以BE ⊥AC 即在图2中，BE ⊥1OA ，BE ⊥OC 从而BE ⊥平面1AOC1A 1C F E 1CD FE C A 11又CD//BE ，所以CD ⊥平面1AOC ．（II ）由已知，平面1A BE ⊥平面BCDE ，又由（1）知，BE⊥1OA ，BE ⊥OC 所以1AOC ∠为二面角1--C A BE 的平面角，所以1OC 2A π∠=．如图，以O 为原点，建立空间直角坐标系，因为11B=E=BC=ED=1A A ,BC//ED所以1((0,0,2222B -得BC(-1A -，CD BE (== ．设平面1BC A 的法向量1111(,,)n x y z = ，平面1CD A 的法向量2222(,,)n x y z =，平面1BC A 与平面1CD A 夹角为θ，则1110n BC n A C ⎧⋅=⎪⎨⋅=⎪⎩，得111100x y y z -+=⎧⎨-=⎩，取1(1,1,1)n = ，2210n CD n A C ⎧⋅=⎪⎨⋅=⎪⎩，得22200x y z =⎧⎨-=⎩，取2(0,1,1)n = ，从而12cos |cos ,|n n θ=〈〉==即平面1BC A 与平面1CD A夹角的余弦值为311. 解（Ⅰ）在图1中，因为 AB=BC=12AD=a,E 是AD 的中点∠BAD=2π,所以BE ⊥AC, 即在图2中，BE ⊥A 1O, BE ⊥OC,从而BE ⊥平面A 1OC又CD//BE,所以 CD ⊥平面A 1OC ．（Ⅱ）由已知，平面A 1BE ⊥平面BCDE=BE且平面A 1BE ∩平面BCDE=BE, 又由（I ），A 1O ⊥BE, 所以 A 1O ⊥平面BCDE, 即 A 1O 是四棱锥A 1-BCE 的高。

立体几何初步空间几何与点线面章节综合检测提升试卷(三)含答案人教版高中数学高考真题汇编

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃，匠心巨制！独家原创，欢迎下载！注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）请点击修改第I 卷的文字说明评卷人得分一、选择题1．已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（） A ．1 B ．2C ．3D ．2(2020全国2理)2．四面体ABCD 四个面的重心分别为E 、F 、G 、H ，则四面体EFGH 的表面积与四面体ABCD 的表面积的比值是（） A ．271B ．161 C ．91 D ．81(2020湖北文)3．直三棱柱111ABC A B C -中，若90BAC ∠=︒，1AB AC AA ==，则异面直线1BA 与1AC 所成的角等于A ．30°B ．45°C ．60°D ．90°(2020全国1文) 4．已知空间三条直线.l m n 、、若l 与m 异面,且l 与n 异面,则（） A ．m 与n 异面. B ．m 与n 相交.C ．m 与n 平行.D ．m 与n 异面、相交、平行均有可能.（2020上海春）5．1l ，2l ，3l 是空间三条不同的直线，则下列命题正确的是( ) (A)12l l ⊥，23l l ⊥13l l ⇒ （B ）12l l ⊥，23l l ⇒13l l ⊥ (C)233l l l ⇒ 1l ，2l ，3l 共面（D ）1l ，2l ，3l 共点⇒1l ，2l ，3l 共面(2020年高考四川卷理科3)6．1．下面给出四个命题中正确命题的个数是----------------------------------------------------------（）①若a b ∥，b c ∥，则a c ∥；②若a b ⊥，b c ⊥，则a c ⊥；③若a b 、相交，b c 、相交，则a c 、也相交；④若a b 、是异面直线，b c 、是异面直线，则a c 、也是异面直线(A) 1 (B) 2 (C) 3 (D)7．已知平面αβαβα∈=⊥P m 点平面,, 直线n 过点P ，则β⊥⊥n m n 是的（）A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．非充分非必要条件 8．2．用一个平面去截正方体，所得截面一定不是---------------------------------------------------（）(A)正三角形 (B)正方形 (C)正五边形 (D)正六边 9．3．下列说法中正确的是----------------------------------------------------------------------------------（）(A)互相垂直的两条直线的直观图仍然是互相垂直的两条直线 (B)梯形的直观图可能是平行四边形 (C)矩形的直观图可能是梯形(D)正方形的直观图可能是平行四边10．过正方体1111ABCD A B C D -的对角线1BD 的截面面积为S ，max S 和min S 分别为S 的最大值和最小值，则maxminS S 的值为（） A ．32B ．62 C ．233D ．263第II 卷（非选择题）请点击修改第II 卷的文字说明评卷人得分二、填空题11．已知,,αβγ是三个互不重合的平面， l 是一条直线，给出下列四个命题： ①若,l αββ⊥⊥，则//l α ②若,//l l αβ⊥，则αβ⊥③若l 上有两个点到α的距离相等，则//l α； ④若,//,αβαγ⊥则γβ⊥ 其中正确命题的序号是12．设,m n 为空间的两条直线，,αβ为空间的两个平面，给出下列命题： ①若m ∥α,m ∥β , 则α∥β； ②若m ⊥α，m ⊥β，则α∥β; ③若m ∥α，n ∥α，则m ∥n ； ④若m ⊥α，n ⊥α，则m ∥n ; 上述命题中，其中假命题．．．的序号是 ▲ ．13．在正方体1111ABCD A B C D -中，M 为1BB 的中点，AC 、B D 交于点O ，则1D O 与平面AMC 成的角为度．14．已知二面角AB αβ--的平面角是锐角θ，α内一点C 到β的距离为3，点C 到棱AB 的距离为4，那么tan θ的值等于15．正四面体ABCD 的体积为1，O 为其中心。

立体几何(学生版)--2025新高考数学新题型

立体几何题型01 空间几何体的有关计算题型02 点线面位置关系、空间角及距离题型03 内切球、外接球问题题型04 空间向量题型01 空间几何体的有关计算1(2024·山西晋城·统考一模)若一个正n棱台的棱数大于15，且各棱的长度构成的集合为{2,3}，则n 的最小值为，该棱台各棱的长度之和的最小值为．2(2024·浙江·校联考一模)已知圆台的上下底面半径分别是1，4，且侧面积为10π，则该圆台的母线长为．3(2024·安徽合肥·合肥一六八中学校考一模)球O的半径与圆锥M的底面半径相等，且它们的表面积也相等，则圆锥M的侧面展开图的圆心角大小为，球O的体积与圆锥M的体积的比值为．4(2024·湖南长沙·雅礼中学校考一模)已知圆锥的母线长为2，则当圆锥的母线与底面所成的角的余弦值为时，圆锥的体积最大，最大值为．5(2024·广东深圳·校考一模)已知圆锥的侧面展开图是一个半径为4的半圆.若用平行于圆锥的底面，且与底面的距离为3的平面截圆锥，将此圆锥截成一个小圆锥和一个圆台，则小圆锥和圆台的体积之比为.6(2024·辽宁沈阳·统考一模)正方体的8个顶点分别在4个互相平行的平面内，每个平面内至少有一个顶点，且相邻两个平面间的距离为1，则该正方体的棱长为()A.2B.3C.2D.57(2024·云南曲靖·统考一模)为努力推进“绿美校园”建设，营造更加优美的校园环境，某校准备开展校园绿化活动．已知栽种某绿色植物的花盆可近似看成圆台，圆台两底面直径分别为18厘米，9厘米，母线长约为7.5厘米．现有2000个该种花盆，假定每一个花盆装满营养土，请问共需要营养土约为( )(参考数据：π≈3.14)A.1.702立方米B.1.780立方米C.1.730立方米D.1.822立方米8(2024·新疆乌鲁木齐·统考一模)某广场设置了一些石凳供大家休息，这些石凳是由棱长为40cm的正方体截去八个一样的四面体得到的，则()A.该几何体的顶点数为12B.该几何体的棱数为24C.该几何体的表面积为(4800+8003)cm 2D.该几何体外接球的表面积是原正方体内切球、外接球表面积的等差中项9(2024·山西晋城·统考一模)如图，在正四棱柱ABCD -A 1B 1C 1D 1中，AB =2，AA 1=4，C 1 E =3EC，平面ABE 将该正四棱柱分为上、下两部分，记上部分对应的几何体为Ω上，下部分对应的几何体为Ω下，则()A.Ω下的体积为2B.Ω上的体积为12C.Ω下的外接球的表面积为9πD.平面ABE 截该正四棱柱所得截面的面积为25题型02 点线面位置关系、空间角及距离10(2024·河北·校联考一模)已知直线l 、m 、n 与平面α、β，下列命题正确的是()A.若α⎳β，l ⊂α，n ⊂β，则l ⎳nB.若α⊥β，l ⊂α，则l ⊥βC.若l ⊥n ，m ⊥n ，则l ⎳mD.若l ⊥α，l ⎳β，则α⊥β11(2024·浙江·校联考一模)已知直线a ,b 和平面α,a ⊄α,b ∥α，则“a ∥b ”是“a ∥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件12(2024·广东深圳·校考一模)已知α，β是两个不同的平面，m ，n 是两条不同的直线，则下列说法正确的是()A.若m ⊥n ，m ⊥α，n ⊥β，则α⊥βB.若m ⎳n ，m ⎳α，n ⎳β，则α⎳βC.若m ⊥n ，m ⎳α，α⊥β，则n ⊥βD.若m ⎳n ，m ⊥α，α⊥β，则n ⎳β13(2024·吉林白山·统考一模)正八面体可由连接正方体每个面的中心构成，如图所示，在棱长为2的正八面体中，则有()A.直线AE与CF是异面直线B.平面ABF⊥平面ABEC.该几何体的体积为432 D.平面ABE与平面DCF间的距离为26314(2024·河南郑州·郑州市宇华实验学校校考一模)如图，在四棱锥P-ABCD中，PA⊥平面ABCD,PA=AB=2,∠BAD=120°,AC⊥BD，△BCD是等边三角形.(1)证明：平面PAD⊥平面PCD.(2)求二面角B-PC-D的正弦值.15(2024·辽宁沈阳·统考一模)如图，在三棱锥A-BCD中，平面ABC⊥平面BCD，且BC=BD= BA，∠CBA=∠CBD=120°，点P在线段AC上，点Q在线段CD上.(1)求证：AD⊥BC；(2)若AC⊥平面BPQ，求BPBQ的值；(3)在(2)的条件下，求平面ABD与平面PBQ所成角的余弦值.16(2024·重庆·统考一模)如图，四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD中，AB= AP，AB⊥AD,AB+AD=6,CD=2,∠CDA=45°．(1)若E为PB的中点，求证：平面PBC⊥平面ADE；(2)若平面PAB与平面PCD所成的角的余弦值为66．(ⅰ)求线段AB的长；(ⅱ)设G为△PAD内(含边界)的一点，且GB=2GA，求满足条件的所有点G组成的轨迹的长度．17(2024·云南曲靖·统考一模)在图1的直角梯形ABCD中，∠A=∠D=90°,AB=BC=2,DC=3，点E是DC边上靠近于点D的三等分点，以BE为折痕将△BCE折起，使点C到达C1的位置，且AC1= 6，如图2．(1)求证：平面BC1E⊥平面ABED；(2)在棱DC1上是否存在点P，使得二面角P-EB-C1的大小为45°？若存在，求出线段DP的长度，若不存在说明理由．18(2024·云南曲靖·统考一模)如图所示，正方体ABCD -A B C D 的棱长为1，E ,F 分别是棱AA ,CC 的中点，过直线EF 的平面分别与棱BB ,DD 交于点M ,N ，以下四个命题中正确的是()A.四边形EMFN 一定为菱形B.四棱锥A -MENF 体积为13C.平面EMFN ⊥平面DBB DD.四边形EMFN 的周长最小值为419(2024·山东济南·山东省实验中学校考一模)如图，在四棱锥P -ABCD 中，PA ⊥平面ABCD ，PB 与底面ABCD 所成的角为π4，底面ABCD 为直角梯形，∠ABC =∠BAD =π2,AD =2,PA =BC =1，点E 为棱PD 上一点，满足PE =λPD0≤λ≤1 ，下列结论正确的是()A.平面PAC ⊥平面PCD ；B.在棱PD 上不存在点E ，使得CE ⎳平面PABC.当λ=12时，异面直线CE 与AB 所成角的余弦值为255；D.点P 到直线CD 的距离3；20(2024·新疆乌鲁木齐·统考一模)如图，在四棱锥P -ABCD 中，底面ABCD 为正方形，PA ⊥平面ABCD ，PA =AB ，点E ，F 分别是棱PB ，BC 的中点．(1)求直线AF 与平面PBC 所成角的正弦值；(2)在截面AEF 内是否存在点G ，使DG ⊥平面AEF ，并说明理由．21(2024·山西晋城·统考一模)如图，P 是边长为2的正六边形ABCDEF 所在平面外一点，BF 的中点O 为P 在平面ABCDEF 内的射影，PM =2MF．(1)证明：ME ⎳平面PBD ．(2)若PA =2，二面角A -PB -D 的大小为θ，求cos2θ．22(2024·河南郑州·郑州市宇华实验学校校考一模)如图，在正方体ABCD -A 1B 1C 1D 1中，点P 是AD 1的中点，点Q 是直线CD 1上的动点，则下列说法正确的是()A.△PBD 是直角三角形B.异面直线PD 与CD 1所成的角为π3C.当AB 的长度为定值时，三棱锥D -PBQ 的体积为定值D.平面PBD ⊥平面ACD123(2024·浙江·校联考一模)在三棱柱ABC-A1B1C1中，四边形BCC1B1是菱形，△ABC是等边三角形，点M是线段AB的中点，∠ABB1=60°．(1)证明：B1C⊥平面ABC1；(2)若平面ABB1A1⊥平面ABC，求直线B1C与平面A1MC1所成角的正弦值．24(2024·广东深圳·校考一模)如图，在圆锥SO中，AB是圆O的直径，且△SAB是边长为4的等边三角形，C,D为圆弧AB的两个三等分点，E是SB的中点.(1)证明：DE⎳平面SAC；(2)求平面SAC与平面SBD所成锐二面角的余弦值.25(2024·广西南宁·南宁三中校联考一模)在如图所示的五面体ABCDEF中，ABEF共面，△ADF是正三角形，四边形ABCD为菱形，∠ABC=2π3,EF⎳平面ABCD,AB=2EF=2，点M为BC中点．(1)证明：EM∥平面BDF；(2)已知EM=2，求平面BDF与平面BEC所成二面角的正弦值．26(2024·安徽合肥·合肥一六八中学校考一模)如图，菱形ABCD的对角线AC与BD交于点O，AB =5，AC=6，点E，F分别在AD，CD上，AE=CF=54，EF交BD于点H，将△DEF沿EF折到△DEF 位置，OD =10．(1)证明：D H⊥平面ABCD；(2)求平面BAD 与平面ACD 的夹角的余弦值．27(2024·安徽合肥·合肥一六八中学校考一模)设b、c表示两条直线，α、β表示两个平面，则下列命题正确的是()A.若b⎳α，c⊂α，则b⎳cB.若b⊂α，b⎳c，则c⊂αC.若c⎳α，α⊥β，则c⊥βD.若c⎳α，c⊥β，则α⊥β28(2024·吉林延边·统考一模)已知三棱柱ABC-A1B1C1，侧面AA1C1C是边长为2的菱形，∠CAA1 =πA1是矩形，且平面AA1C1C⊥平面ABB1A1，点D是棱A1B1的中点．3，侧面四边形ABB1(1)在棱AC上是否存在一点E，使得AD∥平面B1C1E，并说明理由；(2)当三棱锥B-A1DC1的体积为3时，求平面A1C1D与平面CC1D夹角的余弦值．29(2024·黑龙江齐齐哈尔·统考一模)如图1，在平面四边形PABC中，PA⊥AB,CD⎳AB，CD=2AB=2PD=2AD=4.点E是线段PC上靠近P端的三等分点，将△PDC沿CD折成四棱锥P-ABCD，且AP=22，连接PA,PB,BD，如图2.(1)在图2中，证明：PA⎳平面BDE；(2)求图2中，直线AP与平面PBC所成角的正弦值.30(2024·重庆·统考一模)如图，在边长为1的正方体ABCD-A1B1C1D1中，E是C1D1的中点，M是线段A1E上的一点，则下列说法正确的是()A.当M点与A1点重合时，直线AC1⊂平面ACMB.当点M移动时，点D到平面ACM的距离为定值C.当M点与E点重合时，平面ACM与平面CC1D1D夹角的正弦值为53D.当M点为线段A1E中点时，平面ACM截正方体ABCD-A1B1C1D1所得截面面积为73332 31(2024·福建厦门·统考一模)如图，在四棱锥E-ABCD中，AD⎳BC，2AD=BC=2，AB=2，AB⊥AD，EA⊥平面ABCD，过点B作平面α⊥BD．(1)证明：平面α⎳平面EAC；(2)已知点F为棱EC的中点，若EA=2，求直线AD与平面FBD所成角的正弦值．32(2024·吉林延边·统考一模)如图，在多面体ABCDEF 中，底面ABCD 是边长为2的正方形，DE =BF =1,DE ∥BF ,DE ⊥平面ABCD ，动点P 在线段EF 上，则下列说法正确的是()A.AC ⊥DPB.存在点P ，使得DP ∥平面ACFC.三棱锥A -CDE 的外接球被平面ACF 所截取的截面面积是9π2D.当动点P 与点F 重合时，直线DP 与平面ACF 所成角的余弦值为3101033(2024·福建厦门·统考一模)如图所示，在五面体ABCDEF 中，四边形ABCD 是矩形，△ABF 和△DCE 均是等边三角形，且AB =23，EF =x (x >0)，则()A.EF ⎳平面ABCDB.二面角A -EF -B 随着x 的减小而减小C.当BC =2时，五面体ABCDEF 的体积V (x )最大值为272D.当BC =32时，存在x 使得半径为32的球能内含于五面体ABCDEF 题型03 内切球、外接球问题34(2024·黑龙江齐齐哈尔·统考一模)已知四面体ABCD 的各个面均为全等的等腰三角形，且CA =CB =2AB =4.设E 为空间内任一点，且A ,B ,C ,D ,E 五点在同一个球面上，则()A.AB ⊥CDB.四面体ABCD 的体积为214C.当AE =23时，点E 的轨迹长度为4πD.当三棱锥E -ABC 的体积为146时，点E 的轨迹长度为32π35(2024·吉林白山·统考一模)在四面体A -BCD 中，BC =22，BD =23，且满足BC ⊥BD ，AC ⊥BC ，AD ⊥BD ．若该三棱锥的体积为863，则该锥体的外接球的体积为．36(2024·吉林延边·统考一模)已知一个圆锥的侧面展开图是一个圆心角为25π5，半径为5的扇形.若该圆锥的顶点及底面圆周都在球O 的表面上，则球O 的体积为.37(2024·河南郑州·郑州市宇华实验学校校考一模)已知正三棱柱ABC-A1B1C1的底面边长为2，以A1为球心、3为半径的球面与底面ABC的交线长为3π6，则三棱柱ABC-A1B1C1的表面在球内部分的总面积为．38(2024·江西吉安·吉安一中校考一模)已知球O的直径PQ=4，A，B，C是球O球面上的三点，△ABC是等边三角形，且∠APQ=∠BPQ=∠CPQ=30°，则三棱锥P-ABC的体积为( ).A.334B.934C.332D.273439(2024·湖南长沙·雅礼中学校考一模)如图所示，有一个棱长为4的正四面体P-ABC容器，D是PB的中点，E是CD上的动点，则下列说法正确的是()A.直线AE与PB所成的角为π2B.△ABE的周长最小值为4+34C.如果在这个容器中放入1个小球(全部进入)，则小球半径的最大值为63D.如果在这个容器中放入4个完全相同的小球(全部进入)，则小球半径的最大值为26-25 40(2024·江西吉安·吉安一中校考一模)如图，在正三棱锥P-ABC中，有一半径为1的半球，其底面圆O与正三棱锥的底面贴合，正三棱锥的三个侧面都和半球相切．设点D为BC的中点，∠ADP=α．(1)用α分别表示线段BC和PD长度；(2)当α∈0,π2时，求三棱锥的侧面积S的最小值．41(2024·江西吉安·吉安一中校考一模)地球仪是地理教学中的常用教具.如图1所示，地球仪的赤道面(与转轴垂直)与黄道面(与水平面平行)存在一个夹角，即黄赤交角，大小约为23.5°.为锻炼动手能力，某同学制作了一个半径为4cm 的地球仪(不含支架)，并将其放入竖直放置的正三棱柱ABC -A 1B 1C 1中(姿态保持不变)，使地球仪与该三棱柱的三个侧面相切，如图2所示.此时平面AB 1C 恰与地球仪的赤道面平行，则三棱柱ABC -A 1B 1C 1的外接球体积为.(参考数据：tan23.5°≈0.43)题型04 空间向量42(2024·福建厦门·统考一模)已知平面α的一个法向量为n=(1,0,1)，且点A (1,2,3)在α内，则点B (1,1,1)到α的距离为．43(2024·广西南宁·南宁三中校联考一模)在边长为2的正方体ABCD -A 1B 1C 1D 1中，动点M 满足AM =xAB +yAD +zAA 1 ，(x ,y ,z ∈R 且x ≥0,y ≥0,z ≥0)，下列说法正确的是()A.当x =14,z =0,y ∈0,1 时，B 1M +MD 的最小值为13B.当x =y =1,z =12时，异面直线BM 与CD 1所成角的余弦值为105C.当x +y +z =1，且AM =253时，则M 的轨迹长度为42π3D.当x +y =1,z =0时，AM 与平面AB 1D 1所成角的正弦值的最大值为6344(2024·湖南长沙·雅礼中学校考一模)如图，在平行六面体ABCD -A 1B 1C 1D 1中，AB =AD =AA 1=1，∠DAB =90°，cos <AA 1 ，AB >=22，cos <AA 1 ，AD >=12，点M 为BD 中点.(1)证明：B 1M ⎳平面A 1C 1D ；(2)求二面角B -AA 1-D 的正弦值.。

历年(2019-2023)全国高考数学真题分项(立体几何)汇编(附答案)

历年（2019-2023）全国高考数学真题分项（立体几何）汇编考点一空间几何体的侧面积和表面积1．（2021( )A ．2B ．C ．4D ．2．（2022•上海）已知圆柱的高为4，底面积为9π，则圆柱的侧面积为．3．（2021•上海）已知圆柱的底面圆半径为1，高为2，AB 为上底面圆的一条直径，C 是下底面圆周上的一个动点，则ABC ∆的面积的取值范围为．4．（2021•上海）已知圆柱的底面半径为1，高为2，则圆柱的侧面积为．5．（2019•上海）一个直角三角形的两条直角边长分别为1和2，将该三角形分别绕其两个直角边旋转得到的两个圆锥的体积之比为( ) A ．1B ．2C ．4D ．86．（2020•浙江）已知圆锥的侧面积（单位：2)cm 为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：)cm 是．7．（2022•新高考Ⅱ）已知正三棱台的高为1，上、下底面边长分别为，其顶点都在同一球面上，则该球的表面积为( ) A ．100πB ．128πC ．144πD ．192π8．（2021•新高考Ⅱ）北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步轨道卫星的轨道位于地球赤道所在平面，轨道高度为36000km （轨道高度是指卫星到地球表面的距离）．将地球看作是一个球心为O ，半径r 为6400km 的球，其上点A 的纬度是指OA 与赤道平面所成角的度数．地球表面上能直接观测到的一颗地球静止同步轨道卫星点的纬度最大值为α，该卫星信号覆盖地球表面的表面积22(1cos )S r πα=-（单位：2)km ，则S 占地球表面积的百分比约为( ) A ．26%B ．34%C ．42%D ．50%考点二空间几何体的体积9．（2022•新高考Ⅰ）已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上．若该球的体积为36π，且3l 剟，则该正四棱锥体积的取值范围是( )A ．[18，81]4B ．27[4，814C ．27[4，643D ．[18，27]10．（2022•新高考Ⅰ）南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库．已知该水库水位为海拔148.5m 时，相应水面的面积为2140.0km ；水位为海拔157.5m 时，相应水面的面积为2180.0km ．将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5m 上升到157.5m 时，增加的水量约为 2.65)(≈ ) A ．931.010m ⨯B ．931.210m ⨯C ．931.410m ⨯D ．931.610m ⨯11．（2021•新高考Ⅱ）正四棱台的上、下底面的边长分别为2，4，侧棱长为2，则其体积为( )A ．20+B ．C ．563D ．312．【多选】（2023•新高考Ⅰ）下列物体中，能够被整体放入棱长为1（单位：)m 的正方体容器（容器壁厚度忽略不计）内的有( ) A ．直径为0.99m 的球体 B ．所有棱长均为1.4m 的四面体C ．底面直径为0.01m ，高为1.8m 的圆柱体D ．底面直径为1.2m ，高为0.01m 的圆柱体13．【多选】（2022•新高考Ⅱ）如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，//FB ED ，2AB ED FB ==．记三棱锥E ACD -，F ABC -，F ACE -的体积分别为1V ，2V ，3V ，则( )A ．322V V =B ．31V V =C ．312V V V =+D ．3123V V =14．【多选】（2021•新高考Ⅰ）在正三棱柱111ABC A B C -中，11AB AA ==，点P 满足1BP BC BB λμ=+ ，其中[0λ∈，1]，[0μ∈，1]，则( ) A ．当1λ=时，△1AB P 的周长为定值 B ．当1μ=时，三棱锥1P A BC -的体积为定值C ．当12λ=时，有且仅有一个点P ，使得1A P BP ⊥D ．当12μ=时，有且仅有一个点P ，使得1A B ⊥平面1AB P 15．（2023•新高考Ⅱ）底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为．16．（2023•新高考Ⅰ）在正四棱台1111ABCD A B C D -中，2AB =，111A B =，1AA =，则该棱台的体积为． 17．（2020•海南）已知正方体1111ABCD A B C D -的棱长为2，M 、N 分别为1BB 、AB 的中点，则三棱锥1A NMD -的体积为．18．（2022•上海）如图所示三棱锥，底面为等边ABC ∆，O 为AC 边中点，且PO ⊥底面ABC ，2AP AC ==．（1）求三棱锥体积P ABC V -；（2）若M 为BC 中点，求PM 与面PAC 所成角大小．19．（2020•上海）已知四棱锥P ABCD -，底面ABCD 为正方形，边长为3，PD ⊥平面ABCD ．（1）若5PC =，求四棱锥P ABCD -的体积；（2）若直线AD 与BP 的夹角为60︒，求PD 的长．考点三空间中直线与直线之间的位置关系20．（2022•上海）如图正方体1111ABCD A B C D -中，P 、Q 、R 、S 分别为棱AB 、BC 、1BB 、CD 的中点，联结1A S ，1B D ．空间任意两点M 、N ，若线段MN 上不存在点在线段1A S 、1B D 上，则称MN 两点可视，则下列选项中与点1D 可视的为( )A ．点PB ．点BC ．点RD ．点Q21．（2021•浙江）如图，已知正方体1111ABCD A B C D -，M ，N 分别是1A D ，1D B 的中点，则( )A ．直线1A D 与直线1DB 垂直，直线//MN 平面ABCD B ．直线1A D 与直线1D B 平行，直线MN ⊥平面11BDD BC ．直线1AD 与直线1D B 相交，直线//MN 平面ABCDD ．直线1A D 与直线1D B 异面，直线MN ⊥平面11BDD B22．（2020•上海）在棱长为10的正方体1111ABCD A B C D -中，P 为左侧面11ADD A 上一点，已知点P 到11A D 的距离为3，P 到1AA 的距离为2，则过点P 且与1A C 平行的直线交正方体于P 、Q 两点，则Q 点所在的平面是( )A ．11AAB BB ．11BBC CC ．11CCD DD ．ABCD23．（2023•上海）如图所示，在正方体1111ABCD A B C D -中，点P 为边11A C 上的动点，则下列直线中，始终与直线BP 异面的是( )A ．1DDB ．ACC ．1ADD ．1B C考点四异面直线及其所成的角24．【多选】（2022•新高考Ⅰ）已知正方体1111ABCD A B C D -，则( ) A ．直线1BC 与1DA 所成的角为90︒ B ．直线1BC 与1CA 所成的角为90︒ C ．直线1BC 与平面11BB D D 所成的角为45︒D ．直线1BC 与平面ABCD 所成的角为45︒考点五空间中直线与平面之间的位置关系25．（2019•上海）已知平面α、β、γ两两垂直，直线a 、b 、c 满足：a α⊆，b β⊆，c γ⊆，则直线a 、b 、c 不可能满足以下哪种关系( )A ．两两垂直B ．两两平行C ．两两相交D ．两两异面26．【多选】（2021•新高考Ⅱ）如图，下列正方体中，O 为底面的中心，P 为所在棱的中点，M ，N 为正方体的顶点，则满足MN OP ⊥的是( )A ．B ．C ．D ．考点六直线与平面所成的角27．（2020•山东）日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球（球心记为)O ，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面．在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40︒，则晷针与点A 处的水平面所成角为( )A ．20︒B ．40︒C ．50︒D ．90︒28．（2021•上海）如图，在长方体1111ABCD A B C D -中，已知2AB BC ==，13AA =．（1）若P 是棱11A D 上的动点，求三棱锥C PAD -的体积；（2）求直线1AB 与平面11ACC A 的夹角大小．29．（2021•浙江）如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，120ABC ∠=︒，1AB =，4BC =，PA =M ，N 分别为BC ，PC 的中点，PD DC ⊥，PM MD ⊥．（Ⅰ）证明：AB PM ⊥；（Ⅱ）求直线AN 与平面PDM 所成角的正弦值．30．（2020•海南）如图，四棱锥P ABCD -的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知1PD AD ==，Q 为l 上的点，QB =，求PB 与平面QCD 所成角的正弦值．31．（2020•上海）已知ABCD 是边长为1的正方形，正方形ABCD 绕AB 旋转形成一个圆柱．（1）求该圆柱的表面积；（2）正方形ABCD 绕AB 逆时针旋转2π至11ABC D ，求线段1CD 与平面ABCD 所成的角．32．（2020•山东）如图，四棱锥P ABCD -的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知1PD AD ==，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值．33．（2020•浙江）如图，在三棱台ABC DEF -中，平面ACFD ⊥平面ABC ，45ACB ACD ∠=∠=︒，2DC BC =．（Ⅰ）证明：EF DB ⊥；（Ⅱ）求直线DF 与平面DBC 所成角的正弦值．34．（2019•上海）如图，在长方体1111ABCD A B C D -中，M 为1BB 上一点，已知2BM =，3CD =，4AD =，15AA =．（1）求直线1A C 和平面ABCD 的夹角；（2）求点A 到平面1A MC 的距离．35．（2019•浙江）如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ，90ABC ∠=︒，30BAC ∠=︒，11A A A C AC ==，E ，F 分别是AC ，11A B 的中点．（Ⅰ）证明：EF BC ⊥；（Ⅱ）求直线EF 与平面1A BC 所成角的余弦值．考点七二面角的平面角及求法36．（2022•浙江）如图，已知正三棱柱111ABC A B C -，1AC AA =，E ，F 分别是棱BC ，11A C 上的点．记EF 与1AA 所成的角为α，EF 与平面ABC 所成的角为β，二面角F BC A --的平面角为γ，则( )A ．αβγ剟B ．βαγ剟C ．βγα剟D ．αγβ剟37．（2019•浙江）设三棱锥V ABC -的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点）．记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P AC B --的平面角为γ，则( )A ．βγ<，αγ<B ．βα<，βγ<C ．βα<，γα<D ．αβ<，γβ<38．【多选】（2023•新高考Ⅱ）已知圆锥的顶点为P ，底面圆心为O ，AB 为底面直径，120APB ∠=︒，2PA =，点C 在底面圆周上，且二面角P AC O --为45︒，则( )A ．该圆锥的体积为πB ．该圆锥的侧面积为C ．AC =D ．PAC ∆39．（2023•上海）已知直四棱柱1111ABCD A B C D -，AB AD ⊥，//AB CD ，2AB =，3AD =，4CD =．（1）证明：直线1//A B 平面11DCC D ；（2）若该四棱柱的体积为36，求二面角1A BD A --的大小．40．（2023•新高考Ⅱ）如图，三棱锥A BCD -中，DA DB DC ==，BD CD ⊥，60ADB ADC ∠=∠=︒，E 为BC 中点．（1）证明BC DA ⊥；（2）点F 满足EF DA =，求二面角D AB F --的正弦值．41．（2023•新高考Ⅰ）如图，在正四棱柱111ABCD A B C D -中，2AB =，14AA =．点2A ，2B ，2C ，2D 分别在棱1AA ，1BB ，1CC ，1DD 上，21AA =，222BB DD ==，23CC =．（1）证明：2222//B C A D ；（2）点P 在棱1BB 上，当二面角222P A C D --为150︒时，求2B P ．42．（2022•浙江）如图，已知ABCD 和CDEF 都是直角梯形，//AB DC ，//DC EF ，5AB =，3DC =，1EF =，60BAD CDE ∠=∠=︒，二面角F DC B --的平面角为60︒．设M ，N 分别为AE ，BC 的中点．（Ⅰ）证明：FN AD ⊥；（Ⅱ）求直线BM 与平面ADE 所成角的正弦值．43．（2022•新高考Ⅱ）如图，PO 是三棱锥P ABC -的高，PA PB =，AB AC ⊥，E 为PB 的中点．（1）证明：//OE 平面PAC ；（2）若30ABO CBO ∠=∠=︒，3PO =，5PA =，求二面角C AE B --的正弦值．44．（2022•新高考Ⅰ）如图，直三棱柱111ABC A B C -的体积为4，△1A BC 的面积为（1）求A 到平面1A BC 的距离；（2）设D 为1A C 的中点，1AA AB =，平面1A BC ⊥平面11ABB A ，求二面角A BD C --的正弦值．45．（2021•新高考Ⅱ）在四棱锥Q ABCD -中，底面ABCD 是正方形，若2AD =，QD QA ==3QC =．（Ⅰ）求证：平面QAD ⊥平面ABCD ；（Ⅱ）求二面角B QD A --的平面角的余弦值．46．（2021•新高考Ⅰ）如图，在三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点．（1）证明：OA CD ⊥；（2）若OCD ∆是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D --的大小为45︒，求三棱锥A BCD -的体积．考点八立体几何的交线问题47．（2020•山东）已知直四棱柱1111ABCD A B C D -的棱长均为2，60BAD ∠=︒．以1D 为半径的球面与侧面11BCC B 的交线长为．参考答案考点一空间几何体的侧面积和表面积1．（2021，其侧面展开图为一个半圆，则该圆锥的母线长为( )A ．2B ．C ．4D ．【详细解析】由题意，设母线长为l ，因为圆锥底面周长即为侧面展开图半圆的弧长，圆锥的母线长即为侧面展开图半圆的半径，则有2l ππ=⋅，解得l =所以该圆锥的母线长为故选：B ．2．（2022•上海）已知圆柱的高为4，底面积为9π，则圆柱的侧面积为．【详细解析】因为圆柱的底面积为9π，即29R ππ=，所以3R =，所以224S Rh ππ==侧．故答案为：24π．3．（2021•上海）已知圆柱的底面圆半径为1，高为2，AB 为上底面圆的一条直径，C 是下底面圆周上的一个动点，则ABC ∆的面积的取值范围为．【详细解析】如图1，上底面圆心记为O ，下底面圆心记为O '，连接OC ，过点C 作CM AB ⊥，垂足为点M ，则12ABC S AB CM ∆=⨯⨯，根据题意，AB 为定值2，所以ABC S ∆的大小随着CM 的长短变化而变化，如图2所示，当点M 与点O 重合时，CM OC ==，此时ABC S ∆取得最大值为122⨯=；如图3所示，当点M 与点B 重合，CM 取最小值2，此时ABC S ∆取得最小值为12222⨯⨯=．综上所述，ABC S ∆的取值范围为．故答案为：．4．（2021•上海）已知圆柱的底面半径为1，高为2，则圆柱的侧面积为．【详细解析】圆柱的底面半径为1r =，高为2h =，所以圆柱的侧面积为22124S rh πππ==⨯⨯=侧．故答案为：4π．5．（2019•上海）一个直角三角形的两条直角边长分别为1和2，将该三角形分别绕其两个直角边旋转得到的两个圆锥的体积之比为( ) A ．1B ．2C ．4D ．8【详细解析】如图，则21142133V ππ=⨯⨯=，22121233V ππ=⨯⨯=，∴两个圆锥的体积之比为43223ππ=．故选：B ．6．（2020•浙江）已知圆锥的侧面积（单位：2)cm 为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：)cm 是．【详细解析】圆锥侧面展开图是半圆，面积为22cm π，设圆锥的母线长为acm ，则2122a ππ⨯=，2a cm ∴=，∴侧面展开扇形的弧长为2cm π，设圆锥的底面半径OC rcm =，则22r ππ=，解得1r cm =．故答案为：1cm ．7．（2022•新高考Ⅱ）已知正三棱台的高为1，上、下底面边长分别为，其顶点都在同一球面上，则该球的表面积为( ) A ．100πB ．128πC ．144πD ．192π3=4=，如图，设球的半径为R 1=，解得5R =， ∴该球的表面积为24425100R πππ=⨯=．当球心在台体内时，如图，1=，无解．综上，该球的表面积为100π．故选：A ．8．（2021•新高考Ⅱ）北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步轨道卫星的轨道位于地球赤道所在平面，轨道高度为36000km （轨道高度是指卫星到地球表面的距离）．将地球看作是一个球心为O ，半径r 为6400km 的球，其上点A 的纬度是指OA 与赤道平面所成角的度数．地球表面上能直接观测到的一颗地球静止同步轨道卫星点的纬度最大值为α，该卫星信号覆盖地球表面的表面积22(1cos )S r πα=-（单位：2)km ，则S 占地球表面积的百分比约为( ) A ．26%B ．34%C ．42%D ．50%【详细解析】由题意，作出地球静止同步卫星轨道的左右两端的竖直截面图，则36000640042400OP =+=，那么64008cos 4240053α==；卫星信号覆盖的地球表面面积22(1cos )S r πα=-，那么，S 占地球表面积的百分比为222(1cos )4542%4106r r παπ-=≈．故选：C ．考点二空间几何体的体积9．（2022•新高考Ⅰ）已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上．若该球的体积为36π，且3l 剟，则该正四棱锥体积的取值范围是( )A ．[18，814B ．27[4，814C ．27[4，643D ．[18，27]【详细解析】如图所示，正四棱锥P ABCD -各顶点都在同一球面上，连接AC 与BD 交于点E ，连接PE ，则球心O 在直线PE 上，连接OA ，设正四棱锥的底面边长为a ，高为h ，在Rt PAE ∆中，222PA AE PE =+，即222221(22l h a h =+=+，球O 的体积为36π，∴球O 的半径3R =，在Rt OAE ∆中，222OA OE AE =+，即222(3)(2R h =-+， ∴221602a h h +-=，∴22162a h h +=，26l h ∴=，又3l 剟∴3922h剟， ∴该正四棱锥体积2232112()(122)4333V h a h h h h h h ==-=-+，2()282(4)V h h h h h '=-+=- ，∴当342h <…时，()0V h '>，()V h 单调递增；当942h <…时，()0V h '<，()V h 单调递减，()max V h V ∴=（4）643=，又327(24V = ，981()24V =，且278144<，∴2764()43V h 剟，即该正四棱锥体积的取值范围是27[4，643，故选：C ．10．（2022•新高考Ⅰ）南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库．已知该水库水位为海拔148.5m 时，相应水面的面积为2140.0km ；水位为海拔157.5m 时，相应水面的面积为2180.0km ．将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5m 上升到157.5m 时，增加的水量约为 2.65)(≈ )A ．931.010m ⨯B ．931.210m ⨯C ．931.410m ⨯D ．931.610m ⨯【详细解析】26214014010km m =⨯，26218018010km m =⨯，根据题意，增加的水量约为661401018010(157.5148.5)3⨯+⨯⨯-9=6693(32060 2.65)103143710 1.410m ≈+⨯⨯⨯=⨯≈⨯．故选：C ．11．（2021•新高考Ⅱ）正四棱台的上、下底面的边长分别为2，4，侧棱长为2，则其体积为( )A ．20+B ．C ．563D 【详细解析】解法一：如图1111ABCD A B C D -为正四棱台，2AB =，114A B =，12AA =．在等腰梯形11A B BA 中，过A 作11AE A B ⊥，可得14212A E -==，AE ==．连接AC ，11A C ，AC ==，11A C ==，过A 作11AG A C ⊥，12A G -==AG ==， ∴正四棱台的体积为：V h =22243+== 解法二：作出图形，连接该正四棱台上下底面的中心，如图，该四棱台上下底面边长分别为2，4，侧棱长为2，∴该棱台的记h ==下底面面积116S =，上底面面积24S =，则该棱台的体积为：1211((16433V h S S =++=+=故选：D ．12．【多选】（2023•新高考Ⅰ）下列物体中，能够被整体放入棱长为1（单位：)m 的正方体容器（容器壁厚度忽略不计）内的有( )A ．直径为0.99m 的球体B ．所有棱长均为1.4m 的四面体C ．底面直径为0.01m ，高为1.8m 的圆柱体D ．底面直径为1.2m ，高为0.01m 的圆柱体【详细解析】对于A ，棱长为1的正方体内切球的直径为10.99>，选项A 正确；对于B ，如图，正方体内部最大的正四面体11D A BC - 1.4=>，选项B 正确；对于C ，棱长为1 1.8<，选项C 错误；对于D ，如图，六边形EFGHIJ 为正六边形，E ，F ，G ，H ，I ，J 为棱的中点，高为0.01米可忽略不计，看作直径为1.2米的平面圆，六边形EFGHIJ 棱长为2米，30GFH GHF ∠=∠=︒，所以FH ===米，故六边形EFGHIJ而223()(1.2) 1.4422=>=，选项D 正确．故选：ABD ．13．【多选】（2022•新高考Ⅱ）如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，//FB ED ，2AB ED FB ==．记三棱锥E ACD -，F ABC -，F ACE -的体积分别为1V ，2V ，3V ，则( )A ．322V V =B ．31V V =C ．312V V V =+D ．3123V V =【详细解析】设22AB ED FB ===， 114||33ACD V S ED ∆=⨯⨯=，212||33ABC V S FB ∆=⨯⨯=，如图所示，连接BD 交AC 于点M ，连接EM 、FM ，则FM =EM =，3EF =，故12EMF S ∆==，3112332EMF V S AC ∆=⨯=⨯⨯=，故C 、D 正确，A 、B 错误．故选：CD ．14．【多选】（2021•新高考Ⅰ）在正三棱柱111ABC A B C -中，11AB AA ==，点P 满足1BP BC BB λμ=+ ，其中[0λ∈，1]，[0μ∈，1]，则( )A ．当1λ=时，△1AB P 的周长为定值 B ．当1μ=时，三棱锥1P A BC -的体积为定值C ．当12λ=时，有且仅有一个点P ，使得1A P BP ⊥D ．当12μ=时，有且仅有一个点P ，使得1A B ⊥平面1AB P 【详细解析】对于A ，当1λ=时，1BP BC BB μ=+ ，即1CP BB μ= ，所以1//CP BB，故点P 在线段1CC 上，此时△1AB P 的周长为11AB B P AP ++，当点P 为1CC 的中点时，△1AB P ，当点P 在点1C 处时，△1AB P 的周长为1，故周长不为定值，故选项A 错误；对于B ，当1μ=时，1BP BC BB λ=+ ，即1B P BC λ= ，所以1//B P BC，故点P 在线段11B C 上，因为11//B C 平面1A BC ，所以直线11B C 上的点到平面1A BC 的距离相等，又△1A BC 的面积为定值，所以三棱锥1P A BC -的体积为定值，故选项B 正确；对于C ，当12λ=时，取线段BC ，11B C 的中点分别为M ，1M ，连结1M M ，因为112BP BC BB μ=+，即1MP BB μ= ，所以1//MP BB ，则点P 在线段1M M 上，当点P 在1M 处时，1111A M B C ⊥，111A M B B ⊥，又1111B C B B B = ，所以11A M ⊥平面11BB C C ，又1BM ⊂平面11BB C C ，所以111A M BM ⊥，即1A P BP ⊥，同理，当点P 在M 处，1A P BP ⊥，故选项C 错误；对于D ，当12μ=时，取1CC 的中点1D ，1BB 的中点D ，因为112BP BC BB λ=+ ，即DP BC λ= ，所以//DP BC ，则点P 在线的1DD 上，当点P 在点1D 处时，取AC 的中点E ，连结1A E ，BE ，因为BE ⊥平面11ACC A ，又1AD ⊂平面11ACC A ，所以1AD BE ⊥，在正方形11ACC A 中，11AD A E ⊥，又1BE A E E = ，BE ，1A E ⊂平面1A BE ，故1AD ⊥平面1A BE ，又1A B ⊂平面1A BE ，所以11A B AD ⊥，在正方体形11ABB A 中，11A B AB ⊥，又11AD AB A = ，1AD ，1AB ⊂平面11AB D ，所以1A B ⊥平面11AB D ，因为过定点A 与定直线1A B 垂直的平面有且只有一个，故有且仅有一个点P ，使得1A B ⊥平面1AB P ，故选项D 正确．故选：BD ．15．（2023•新高考Ⅱ）底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为．【详细解析】如图所示，根据题意易知△11SO A SOA ∆∽，∴11112SO O A SO OA ===，又13SO =， 6SO ∴=，13OO ∴=，又上下底面正方形边长分别为2，4，∴所得棱台的体积为1(4163283⨯++⨯=．故答案为：28．16．（2023•新高考Ⅰ）在正四棱台1111ABCD A B C D -中，2AB =，111A B =，1AA =，则该棱台的体积为．【详细解析】如图，设正四棱台1111ABCD A B C D -的上下底面中心分别为M ，N ，过1A 作1A H AC ⊥，垂足点为H ，由题意易知12A M HN ==，又AN =，2AH AN HN ∴=-=，又1AA =，1A H MN ∴==∴该四棱台的体积为1(143⨯++故答案为：6．17．（2020•海南）已知正方体1111ABCD A B C D -的棱长为2，M 、N 分别为1BB 、AB 的中点，则三棱锥1A NMD -的体积为．【详细解析】如图，正方体1111ABCD A B C D -的棱长为2，M 、N 分别为1BB 、AB 的中点， ∴111122ANM S ∆=⨯⨯=， ∴111112323A NMD D AMN V V --==⨯⨯=．故答案为：13．18．（2022•上海）如图所示三棱锥，底面为等边ABC ∆，O 为AC 边中点，且PO ⊥底面ABC ，2AP AC ==．（1）求三棱锥体积P ABC V -；（2）若M 为BC 中点，求PM 与面PAC 所成角大小．【详细解析】（1）在三棱锥P ABC -中，因为PO ⊥底面ABC ，所以PO AC ⊥，又O 为AC 边中点，所以PAC ∆为等腰三角形，又2AP AC ==．所以PAC ∆是边长为2的为等边三角形，PO ∴=，三棱锥体积2112133P ABC ABC V S PO -∆=⋅==，（2）以O 为坐标原点，OB 为x 轴，OC 为y 轴，OP 为z 轴，建立空间直角坐标系，则(0P ，0，B 0，0)，(0C ，1，0)，M 12，0)，(2PM = ，12，，平面PAC的法向量OB =0，0)，设直线PM 与平面PAC 所成角为θ，则直线PM 与平面PAC所成角的正弦值为3sin ||||||PM OB PM OB θ⋅===⋅所以PM 与面PAC所成角大小为arcsin4． 19．（2020•上海）已知四棱锥P ABCD -，底面ABCD 为正方形，边长为3，PD ⊥平面ABCD ．（1）若5PC =，求四棱锥P ABCD -的体积；（2）若直线AD 与BP 的夹角为60︒，求PD 的长．【详细解析】（1）PD ⊥ 平面ABCD ，PD DC ∴⊥． 3CD = ，5PC ∴=，4PD ∴=，2134123P ABCD V -∴=⨯⨯=，所以四棱锥P ABCD -的体积为12．（2）ABCD 是正方形，PD ⊥平面ABCD ， BC PD ∴⊥，BC CD ⊥又PD CD D = BC ∴⊥平面PCDBC PC ∴⊥异面直线AD 与PB 所成角为60︒，//BC AD ∴在Rt PBC ∆中，60PBC ∠=︒，3BC =故PC =在Rt PDC ∆中，3CD =PD ∴=考点三空间中直线与直线之间的位置关系20．（2022•上海）如图正方体1111ABCD A B C D -中，P 、Q 、R 、S 分别为棱AB 、BC 、1BB 、CD 的中点，联结1A S ，1B D ．空间任意两点M 、N ，若线段MN 上不存在点在线段1A S 、1B D 上，则称MN 两点可视，则下列选项中与点1D 可视的为( )A ．点PB ．点BC ．点RD ．点Q【详细解析】线段MN 上不存在点在线段1A S 、1B D 上，即直线MN 与线段1A S 、1B D 不相交，因此所求与1D 可视的点，即求哪条线段不与线段1A S 、1B D 相交，对A 选项，如图，连接1A P 、PS 、1D S ，因为P 、S 分别为AB 、CD 的中点， ∴易证11//A D PS ，故1A 、1D 、P 、S 四点共面，1D P ∴与1A S 相交，A ∴错误；对B 、C 选项，如图，连接1D B 、DB ，易证1D 、1B 、B 、D 四点共面，故1D B 、1D R 都与1B D 相交，B ∴、C 错误；对D 选项，连接1D Q ，由A 选项分析知1A 、1D 、P 、S 四点共面记为平面11A D PS ， 1D ∈ 平面11A D PS ，Q ∉平面11A D PS ，且1A S ⊂平面11A D PS ，点11D A S ∉， 1D Q ∴与1A S 为异面直线，同理由B ，C 选项的分析知1D 、1B 、B 、D 四点共面记为平面11D B BD ， 1D ∈ 平面11D B BD ，Q ∉平面11D B BD ，且1B D ⊂平面11D B BD ，点11D B D ∉，1D Q ∴与1B D 为异面直线，故1D Q 与1A S ，1B D 都没有公共点，D ∴选项正确．故选：D ．21．（2021•浙江）如图，已知正方体1111ABCD A B C D -，M ，N 分别是1A D ，1D B 的中点，则( )A ．直线1A D 与直线1DB 垂直，直线//MN 平面ABCD B ．直线1A D 与直线1D B 平行，直线MN ⊥平面11BDD BC ．直线1AD 与直线1D B 相交，直线//MN 平面ABCDD ．直线1A D 与直线1D B 异面，直线MN ⊥平面11BDD B【详细解析】连接1AD ，如图：由正方体可知11A D AD ⊥，1A D AB ⊥，1A D ∴⊥平面1ABD ， 11A D D B ∴⊥，由题意知MN 为△1D AB 的中位线，//MN AB ∴，又AB ⊂ 平面ABCD ，MN ⊂/平面ABCD ，//MN ∴平面ABCD ．A ∴对；由正方体可知1A D 与平面1BDD 相交于点D ，1D B ⊂平面1BDD ，1D D B ∉， ∴直线1A D 与直线1D B 是异面直线，B ∴、C 错；//MN AB ，AB 不与平面11BDD B 垂直，MN ∴不与平面11BDD B 垂直，D ∴错．故选：A ．22．（2020•上海）在棱长为10的正方体1111ABCD A B C D -中，P 为左侧面11ADD A 上一点，已知点P 到11A D 的距离为3，P 到1AA 的距离为2，则过点P 且与1A C 平行的直线交正方体于P 、Q 两点，则Q 点所在的平面是( )A ．11AAB B B ．11BBC C C ．11CCD DD ．ABCD【详细解析】如图，由点P 到11A D 的距离为3，P 到1AA 的距离为2，可得P 在△1AA D 内，过P 作1//EF A D ，且1EF AA 于E ，EF AD 于F ，在平面ABCD 中，过F 作//FG CD ，交BC 于G ，则平面//EFG 平面1A DC ．连接AC ，交FG 于M ，连接EM ，平面//EFG 平面1A DC ，平面1A AC ⋂平面11A DC A C =，平面1A AC ⋂平面EFM EM =， 1//EM A C ∴．在EFM ∆中，过P 作//PQ EM ，且PQ FM 于Q ，则1//PQ A C ．线段FM 在四边形ABCD 内，Q 在线段FM 上，Q ∴在四边形ABCD 内． ∴则Q 点所在的平面是平面ABCD ．故选：D ．23．（2023•上海）如图所示，在正方体1111ABCD A B C D -中，点P 为边11A C 上的动点，则下列直线中，始终与直线BP 异面的是( )A ．1DDB ．ACC ．1ADD ．1B C【详细解析】对于A ，当P 是11A C 的中点时，BP 与1DD 是相交直线；对于B ，根据异面直线的定义知，BP 与AC 是异面直线；对于C ，当点P 与1C 重合时，BP 与1AD 是平行直线；对于D ，当点P 与1C 重合时，BP 与1B C 是相交直线．故选：B ．考点四异面直线及其所成的角24．【多选】（2022•新高考Ⅰ）已知正方体1111ABCD A B C D -，则( ) A ．直线1BC 与1DA 所成的角为90︒ B ．直线1BC 与1CA 所成的角为90︒ C ．直线1BC 与平面11BB D D 所成的角为45︒D ．直线1BC 与平面ABCD 所成的角为45︒ 【详细解析】如图，连接1B C ，由11//A B DC ，11A B DC =，得四边形11DA B C 为平行四边形，可得11//DA B C ，11BC B C ⊥ ，∴直线1BC 与1DA 所成的角为90︒，故A 正确；111A B BC ⊥ ，11BC B C ⊥，1111A B B C B = ，1BC ∴⊥平面11DA B C ，而1CA ⊂平面11DA B C ，11BC CA ∴⊥，即直线1BC 与1CA 所成的角为90︒，故B 正确；设1111A C B D O = ，连接BO ，可得1C O ⊥平面11BB D D ，即1C BO ∠为直线1BC 与平面11BB D D 所成的角，1111sin 2OC C BO BC ∠== ，∴直线1BC 与平面11BB D D 所成的角为30︒，故C 错误； 1CC ⊥ 底面ABCD ，1C BC ∴∠为直线1BC 与平面ABCD 所成的角为45︒，故D 正确．故选：ABD ．考点五空间中直线与平面之间的位置关系25．（2019•上海）已知平面α、β、γ两两垂直，直线a 、b 、c 满足：a α⊆，b β⊆，c γ⊆，则直线a 、b 、c 不可能满足以下哪种关系( )A ．两两垂直B ．两两平行C ．两两相交D ．两两异面【详细解析】如图1，可得a 、b 、c 可能两两垂直；如图2，可得a 、b 、c 可能两两相交；如图3，可得a 、b 、c 可能两两异面；故选：B ．26．【多选】（2021•新高考Ⅱ）如图，下列正方体中，O 为底面的中心，P 为所在棱的中点，M ，N 为正方体的顶点，则满足MN OP ⊥的是( )A ．B ．C ．D ．【详细解析】对于A ，设正方体棱长为2，设MN 与OP 所成角为θ，则1tan 12θ==，∴不满足MN OP ⊥，故A 错误；对于B ，如图，作出平面直角坐标系，设正方体棱长为2，则(2N ，0，0)，(0M ，0，2)，(2P ，0，1)，(1O ，1，0)，(2MN = ，0，2)-，(1OP = ，1-，1)，0MN OP ⋅= ，∴满足MN OP ⊥，故B 正确；对于C ，如图，作出平面直角坐标系，设正方体棱长为2，则(2M ，2，2)，(0N ，2，0)，(1O ，1，0)，(0P ，0，1)，(2MN =- ，0，2)-，(1OP =- ，1-，1)，0MN OP ⋅= ，∴满足MN OP ⊥，故C 正确；对于D ，如图，作出平面直角坐标系，设正方体棱长为2，则(0M ，2，0)，(0N ，0，2)，(2P ，1，2)，(1O ，1，0)，(0MN = ，2-，2)，(1OP = ，0，2)，4MN OP ⋅= ，∴不满足MN OP ⊥，故D 错误．故选：BC ．考点六直线与平面所成的角27．（2020•山东）日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球（球心记为)O ，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面．在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40︒，则晷针与点A 处的水平面所成角为( )A ．20︒B ．40︒C ．50︒D ．90︒【详细解析】可设A 所在的纬线圈的圆心为O '，OO '垂直于纬线所在的圆面，由图可得OHA ∠为晷针与点A 处的水平面所成角，又OAO '∠为40︒且OA AH ⊥，在Rt OHA ∆中，O A OH '⊥，40OHA OAO '∴∠=∠=︒，另解：画出截面图，如下图所示，其中CD 是赤道所在平面的截线．l 是点A 处的水平面的截线，由题意可得OA l ⊥，AB 是晷针所在直线．m 是晷面的截线，由题意晷面和赤道面平行，晷针与晷面垂直，根据平面平行的性质定理可得//m CD ，根据线面垂直的定义可得AB m ⊥，由于40AOC ∠=︒，//m CD ，所以40OAG AOC ∠=∠=︒，由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒，所以40BAE OAG ∠=∠=︒，也即晷针与A 处的水平面所成角为40BAE ∠=︒，故选：B ．28．（2021•上海）如图，在长方体1111ABCD A B C D -中，已知2AB BC ==，13AA =．（1）若P 是棱11A D 上的动点，求三棱锥C PAD -的体积；（2）求直线1AB 与平面11ACC A 的夹角大小．【详细解析】（1）如图，在长方体1111ABCD A B C D -中，1112322332C PAD PAD C PAD V S h -∆-⎛⎫=⋅=⨯⨯⨯⨯= ⎪⎝⎭平面；（2）连接1111A C B D O = ，AB BC = ，∴四边形1111A B C D 为正方形，则11OB OA ⊥，又11AA OB ⊥，111OA AA A = ，1OB ∴⊥平面11ACC A ，∴直线1AB 与平面11ACC A 所成的角为1OAB ∠，∴111sin OB OAB AB ∠=== ∴直线1AB 与平面11ACC A所成的角为29．（2021•浙江）如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，120ABC ∠=︒，1AB =，4BC =，PA =M ，N 分别为BC ，PC 的中点，PD DC ⊥，PM MD ⊥．（Ⅰ）证明：AB PM ⊥；（Ⅱ）求直线AN 与平面PDM 所成角的正弦值．【详细解析】（Ⅰ）证明：在平行四边形ABCD 中，由已知可得，1CD AB ==，122CM BC ==，60DCM ∠=︒， ∴由余弦定理可得，2222cos60DM CD CM CD CM =+-⨯⨯︒11421232=+-⨯⨯⨯=，则222134CD DM CM +=+==，即CD DM ⊥，又PD DC ⊥，PD DM D = ，CD ∴⊥平面PDM ，而PM ⊂平面PDM ，CD PM ∴⊥，//CD AB ，AB PM ∴⊥；（Ⅱ）解：由（Ⅰ）知，CD ⊥平面PDM ，又CD ⊂平面ABCD ，∴平面ABCD ⊥平面PDM ，且平面ABCD ⋂平面PDM DM =，PM MD ⊥ ，且PM ⊂平面PDM ，PM ∴⊥平面ABCD ，连接AM ，则PM MA ⊥，在ABM ∆中，1AB =，2BM =，120ABM ∠=︒，可得2114212(72AM =+-⨯⨯⨯-=，又PA =Rt PMA ∆中，求得PM ==，取AD 中点E ，连接ME ，则//ME CD ，可得ME 、MD 、MP 两两互相垂直，以M 为坐标原点，分别以MD 、ME 、MP 为x 、y 、z 轴建立空间直角坐标系，则(A ，2，0)，(0P ，0，，1,0)C -，又N 为PC的中点，1(22N ∴-，5(,22AN =- ，平面PDM 的一个法向量为(0,1,0)n = ，设直线AN 与平面PDM 所成角为θ，则5||sin |cos ,|6||||AN n AN n AN n θ⋅=<>===⋅ ．故直线AN 与平面PDM所成角的正弦值为6．30．（2020•海南）如图，四棱锥P ABCD -的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知1PD AD ==，Q 为l上的点，QB =，求PB 与平面QCD 所成角的正弦值．【详细解析】（1）证明：过P 在平面PAD 内作直线//l AD ，由//AD BC ，可得//l BC ，即l 为平面PAD 和平面PBC 的交线，PD ⊥ 平面ABCD ，BC ⊂平面ABCD ，PD BC ∴⊥，又BC CD ⊥，CD PD D = ，BC ∴⊥平面PCD ，设m 为平面PCD 中任意一条直线，则BC m ⊥，//l BC ，l m ∴⊥，由线面垂直的定义是l ⊥平面PCD ；（2）解：如图，以D 为坐标原点，直线DA ，DC ，DP 所在的直线为x ，y ，z 轴，建立空间直角坐标系D xyz -，1PD AD == ，Q 为l上的点，QB =，PB ∴=，1QP =，则(0D ，0，0)，(1A ，0，0)，(0C ，1，0)，(0P ，0，1)，(1B ，1，0)，作//PQ AD ，则PQ 为平面PAD 与平面PBC 的交线为l，因为QB =，QAB ∆是等腰直角三角形，所以(1Q ，0，1)，则(1DQ = ，0，1)，(1PB = ，1，1)-，(0DC = ，1，0)，设平面QCD 的法向量为(n a = ，b ，)c ，则00n DC n DQ ⎧⋅=⎪⎨⋅=⎪⎩ ，∴00b a c =⎧⎨+=⎩，取1c =，可得(1n =- ，0，1)，|cos n ∴<，||||||||n PB PB n PB ⋅>=== ， PB ∴与平面QCD所成角的正弦值为3． 31．（2020•上海）已知ABCD 是边长为1的正方形，正方形ABCD 绕AB 旋转形成一个圆柱．（1）求该圆柱的表面积；（2）正方形ABCD 绕AB 逆时针旋转2π至11ABC D ，求线段1CD 与平面ABCD 所成的角．【详细解析】（1）该圆柱的表面由上下两个半径为1的圆面和一个长为2π、宽为1的矩形组成， 221214S πππ∴=⨯⨯+⨯=．故该圆柱的表面积为4π．（2）正方形11ABC D ，1AD AB ∴⊥，又12DAD π∠=，1AD AD ∴⊥，AD AB A = ，且AD 、AB ⊂平面ADB ，1AD ∴⊥平面ADB ，即1D 在面ADB 上的投影为A ，连接1CD ，则1D CA ∠即为线段1CD 与平面ABCD 所成的角，而11cos 3AC D CA CD ∠==， ∴线段1CD 与平面ABCD所成的角为3． 32．（2020•山东）如图，四棱锥P ABCD -的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知1PD AD ==，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值．【详细解析】（1）证明：过P 在平面PAD 内作直线//l AD ，由//AD BC ，可得//l BC ，即l 为平面PAD 和平面PBC 的交线， PD ⊥ 平面ABCD ，BC ⊂平面ABCD ，PD BC ∴⊥，又BC CD ⊥，CD PD D = ，BC ∴⊥平面PCD ，设平面PCD 中有任一直线l '，则BC ⊥直线l '，//l BC ，l ∴⊥直线l '，∴由线面垂直的定义得l ⊥平面PCD ；（2）如图，以D 为坐标原点，直线DA ，DC ，DP 所在的直线为x ，y ，z 轴，建立空间直角坐标系D xyz-则(0D ，0，0)，(1A ，0，0)，(0C ，1，0)，(0P ，0，1)，(1B ，1，0)，设(Q m ，0，1)，(DQ m = ，0，1)，(1PB = ，1，1)-，(0DC = ，1，0)，设平面QCD 的法向量为(n a = ，b ，)c ，则00n DC n DQ ⎧⋅=⎪⎨⋅=⎪⎩ ，∴00b am c =⎧⎨+=⎩，取1a =-，可得(1n =- ，0，)m ， cos n ∴<，||||n PB PB n PB ⋅>==⋅ ， PB ∴与平面QCD。

高中数学复习提升-高中数学专题——立体几何专题(学生版)

立体几何专题【命题趋向】高考对空间想象能力的考查集中体现在立体几何试题上，着重考查空间点、线、面的位置关系的判断及空间角等几何量的计算．既有以选择题、填空题形式出现的试题，也有以解答题形式出现的试题．选择题、填空题大多考查概念辨析、位置关系探究、空间几何量的简单计算求解，考查画图、识图、用图的能力；解答题一般以简单几何体为载体，考查直线与直线、直线与平面、平面与平面的位置关系，以及空间几何量的求解问题，综合考查空间想象能力、推理论证能力和运算求解能力．试题在突出对空间想象能力考查的同时，关注对平行、垂直关系的探究，关注对条件或结论不完备情形下的开放性问题的探究．【考点透析】立体几何主要考点是柱、锥、台、球及其简单组合体的结构特征、三视图、直观图，表面积体积的计算，空间点、直线、平面的位置关系判断与证明，（理科）空间向量在平行、垂直关系证明中的应用，空间向量在计算空间角中的应用等．【例题解析】题型1 空间几何体的三视图以及面积和体积计算一、看图选择正确的三视图1、（2010广东理数）6.如图1，△ABC为三角形，AA'//BB'//CC' ,CC'⊥平面ABC且3AA'=32BB'=CC'=AB,则多面体△ABC -A B C'''的正视图（也称主视图）是2、（2010北京理数）一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为二、根据三视图求几何体的面积、体积1、（2010安徽理数）8、一个几何体的三视图如图，该几何体的表面积为A、280B、292C、360D、372A B C D2、（江苏省苏州市2009届高三教学调研测试第12题）已知一个正三棱锥P ABC -的主视图如图所示，若32AC BC ==， 6PC =_________．3、（2010全国卷1文数）已知在半径为2的球面上有A 、B 、C 、D 四点，若AB=CD=2,则四面体ABCD 的体积的最大值为 2343 (C) 2383题型2 空间点、线、面位置关系的判断例1 （江苏苏州市2009届高三教学调研测试7）已知n m ,是两条不同的直线，βα,为两个不同的平面，有下列四个命题：①若βα⊥⊥n m ,，m n ⊥，则βα⊥；②若n m n m ⊥,//,//βα，则βα//； ③若n m n m ⊥⊥,//,βα，则βα//；④若βαβα//,//,n m ⊥，则n m ⊥．其中正确的命题是（填上所有正确命题的序号）_______________．分析：根据空间线面位置关系的判定定理和性质定理逐个作出判断．例2 （浙江省2009年高考省教研室第一次抽样测试理科第5题）设,m n 是两条不同的直线，,αβ是两个不同的平面，下列命题正确的是A ．若,,//m n m n αβ⊥⊥，则//αβB ．若//,//,//,m n αβαβ则//m nC ．若,//,//m n αβαβ⊥，则m n ⊥D ．若//,//,//,m n m n αβ则//αβ题型3 空间平行与垂直关系的证明、空间几何体的有关计算例1．(2009江苏泰州期末16)如图所示，在棱长为2的正方体 1111ABCD A B C D -中，E 、F 分别为1DD 、DB 的中点．（1）求证：EF //平面11ABC D ；（2）求证：1EF B C ⊥；（3）求三棱锥EFC B V -1的体积．例2．（江苏省苏州市2009届高三教学调研测试第17题）在四棱锥P ABCD -中，90ABC ACD ∠=∠=，60BAC CAD ∠=∠=，PA ⊥平面ABCD ，E 为PD 的中点，22PA AB ==．（1）求四棱锥P ABCD -的体积V ；（2）若F 为PC 的中点，求证PC ⊥平面AEF ；（3）求证CE ∥平面PAB ．题型4 求空间的角的大小一、异面直线所成的角例1（2007年广东理数）如图6所示，等腰三角形△ABC 的底边AB=66CD=3，点E 是线段BD 上异于B 、D 的动点，点F 在BC 边上，且E F ⊥AB ，现沿EF 将△BEF 折起到△PEF 的位置，使P E ⊥AE ，记BE=x ，V （x ）表示四棱锥P-ACEF 的体积。

全国各省市高三数学上学期联考试题重组专题题型五解析几何(学生版)

2012届全国各省市高三上学期数学联考试题重组专题题型五解析几何（学生版）【备考要点】考情分析从近几年高考来看，本讲高考命题具有以下特点：1．圆锥曲线是高考中每年必考内容，是高考的重点和热点，选择题、填空题和解答题均有涉及，所占分数在12～18分．主要考查圆锥曲线的标准方程、几何性质等．2．由于新课标对此部分的考查增加了“理解数形结合思想”的要求，所以考查数形结合、等价转化、分类讨论等数学思想方法的问题有所加强．3．以向量为载体的解析几何问题已成为高考的重中之重，联系方程、不等式以及圆锥曲线的转化，题型灵活多样．解答题的题型设计主要有三类：圆锥曲线的有关元素计算．关系证明或范围的确定；涉及与圆锥曲线平移与对称变换、最值或位置关系的问题；求平面曲线（整体或部分）的方程或轨迹．近年来，高考中解析几何综合题的难度有所下降．随着高考的逐步完善，结合上述考题特点分析，预测今后高考的命题趋势是：将加强对于圆锥曲线的基本概念和性质的考查，加强对于分析和解决问题能力的考查．因此，教学中要注重对圆锥曲线定义、性质、以及圆锥曲线基本量之间关系的掌握和灵活应用．高考第二阶段的复习，应在继续作好知识结构调整的同时，抓好数学基本思想、数学基本方法的提炼，进行专题复习；做好“五个转化”，即从单一到综合、从分割到整体、从记忆到应用、从慢速摸仿到快速灵活、从纵向知识到横向方法.这一复习过程，要充分体现分类指导、分类要求的原则，内容的选取一定要有明确的目的性和针对性，要充分发挥教师的创造性，更要充分考虑学生的实际，要密切注意学生的信息反馈，防止过分拔高，加重负担. 要点知识整合【2011高考题型】根据近年来各地高考的情况，解析几何高考考查特点(1)题型稳定:近几年来高考解析几何试题一直稳定在三(或二)个选择题,一个填空题,一个解答题上,分值约为30分左右, 占总分值的20%左右。

(2)整体平衡,重点突出:对直线、圆、圆锥曲线知识的考查几乎没有遗漏,通过对知识的重新组合,考查时既注意全面,更注意突出重点, 对支撑数学科知识体系的主干知识, 考查时保证较高的比例并保持必要深度。

高三数学全国各地模拟试题专题汇编立体几何解答题(一)

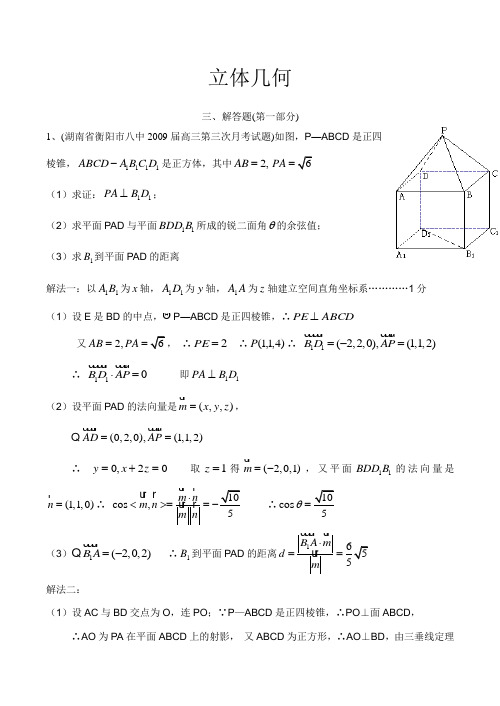
立体几何三、解答题(第一部分)1、(湖南省衡阳市八中2009届高三第三次月考试题)如图，P —ABCD 是正四棱锥，1111ABCD A B C D -是正方体，其中2,AB=PA =（1）求证：11PA B D ⊥；（2）求平面PAD 与平面11BDD B 所成的锐二面角θ的余弦值；（3）求1B 到平面PAD 的距离解法一：以11B A 为x 轴，11D A 为y 轴，A A 1为z 轴建立空间直角坐标系…………1分（1）设E 是BD 的中点， P —ABCD 是正四棱锥，∴ABCD PE ⊥又2,AB PA ==， ∴2=PE ∴)4,1,1(P ∴ 11(2,2,0),(1,1,2)B D AP =-=∴ 110B D AP ⋅= 即11PA B D ⊥ （2）设平面PAD 的法向量是(,,)m x y z =，(0,2,0),(1,1,2)AD AP ==∴ 02,0=+=z x y 取1=z 得(2,0,1)m =-，又平面11BDD B 的法向量是(1,1,0)n =∴10cos ,5m n m n m n⋅<>==-∴cos 5θ=（3）1(2,0,2)B A =- ∴1B 到平面PAD 的距离15B A m d m⋅==解法二：（1）设AC 与BD 交点为O ，连PO ；∵P —ABCD 是正四棱锥，∴PO ⊥面ABCD ，∴AO 为PA 在平面ABCD 上的射影，又ABCD 为正方形，∴AO ⊥BD ，由三垂线定理知PA ⊥BD ，而BD ∥B 1D 1；∴11PA B D ⊥（2）由题意知平面PAD 与平面11BDD B 所成的锐二面角为二面角A-PD-B ；∵AO ⊥面PBD ，过O 作OE 垂直PD 于E ，连AE ，则由三垂线定理知∠AEO 为二面角A-PD-B 的平面角；可以计算得，cos θ= （3）设B 1C 1与BC 的中点分别为M 、N ；则1B 到平面PAD 的距离为M 到平面PAD 的距离；由V M-PAD =V P-ADM 求得556=d 。

高三数学上学期考试试题分类汇编立体几何

学习资料汇编江苏省13市2017高三上学期考试数学试题分类汇编立体几何一、填空题 1、（南京市、盐城市2017届高三第一次模拟）将矩形ABCD 绕边AB 旋转一周得到一个圆柱，3AB =，2BC =，圆柱上底面圆心为O ，EFG ∆为下底面圆的一个内接直角三角形，则三棱锥O EFG -体积的最大值是 ▲ . 2、（南通、泰州市2017届高三第一次调研测）如图，在正四棱柱ABCD –A 1B 1C 1D 1中，3cm AB =，11cm AA =，则三棱锥D 1–A 1BD 的体积为 ▲ 3cm ．3、（苏北四市（淮安、宿迁、连云港、徐州）2017届高三上学期期中）将斜边长为4的等腰直角三角形绕其斜边所在直线旋转一周，则所形成的几何体体积是 ▲ ．4、（苏北四市（徐州、淮安、连云港、宿迁）2017届高三上学期期末）已知圆锥的底面直径与高都是2，则该圆锥的侧面积为5、（苏州市2017届高三上学期期末调研）一个长方体的三条棱长分别为983,,，若在该长方体上面钻一个圆柱形的孔后其表面积没有变化，则圆孔的半径为．6、（无锡市2017届高三上学期期末）已知圆锥的侧面展开图为一个圆心角为120，且面积为3π的扇形，则该圆锥的体积等于 .7、（扬州市2017届高三上学期期末）若正四棱锥的底面边长为2（单位：cm ），侧面积为8（单位：2cm ），则它的体积为 ▲ （单位：3cm ）. 8、（扬州市2017届高三上学期期末）已知一个长方体的表面积为48（单位：2cm ），12条棱长度之和为36（单位：cm ），则这个长方体的体积的取值范围是 ▲ （单位：3cm ）．9、（镇江市2017届高三上学期期末）若圆锥底面半径为2，高为5，则其侧面积为二、解答题1、（南京市、盐城市2017届高三第一次模拟）如图，在直三棱柱111ABC A B C -中，BC AC ⊥，D ,E 分别是AB ,AC 的中点．（1）求证：11B C ∥平面1A DE ；（2）求证：平面1A DE ⊥平面11ACC A ．2、（南通、泰州市2017届高三第一次调研测）如图，在四棱锥P -ABCD 中，四边形ABCD 为平行四边形，AC ，BD 相交于点O ，点E 为PC 的中点，OP =OC ，PA ⊥PD ．求证：（1）直线PA ∥平面BDE ；（2）平面BDE ⊥平面PCD ．3、（苏北四市（淮安、宿迁、连云港、徐州）2017届高三上学期期中）如图，在正三棱柱111ABC A B C -中，已知D ，E 分别为BC ，11B C 的中点，点F 在棱1CC 上，且1EF C D ⊥．求证：（1）直线1A E ∥平面1ADC ；（2）直线EF ⊥平面1ADC ．4、（苏北四市（淮安、宿迁、连云港、徐州）2017届高三上学期期中）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，90ABC BAD ∠=∠=︒， 4AD AP ==，2AB BC ==，M 为PC 的中点．（1）求异面直线AP ，BM 所成角的余弦值；（2）点N 在线段AD 上，且AN λ=，若直线MN 与平面PBC 所成角的正弦值为45，求λ的值．5、（苏北四市（徐州、淮安、连云港、宿迁）2017届高三上学期期末）如图，在四棱锥E ABCD -中，平面EAB ⊥平面ABCD ，四边形ABCD 为矩形，EA EB ⊥，点,M N 分别是,AE CD 的中点．求证：（1）直线MN ∥平面EBC ；（2）直线EA ⊥平面EBC ．6、（苏州市2017届高三上学期期中调研）在如图所示的四棱锥S ABCD -中，SA ⊥底面ABCD ，90DAB ABC ︒∠=∠=，SA AB BC a ===，3AD a =(0)a >，E 为线段BS 上的一个动点．（1）证明：DE 和SC 不可能垂直；（2）当点E 为线段BS 的三等分点（靠近B ）时，求二面角S CD E --的余弦值．DBC7、（无锡市2017届高三上学期期末）在四棱锥P ABCD -中，底面ABCD 为矩形，AP ⊥平面PCD ，E,F 分别为PC,AB 的中点.求证：（1）平面PAD ⊥平面ABCD ；（2）//EF 平面PAD .8、（无锡市2017届高三上学期期末）如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 为直角梯形，//,90,1,2,,,AD BC BAD CBA PA AB BC AD E F G∠=∠=====分别为,,BC PD PC的中点.（1）求EF与DG所成角的余弦值；（2）若M为EF上一点，N为DG上一点，是否存在MN,使得MN⊥平面PBC?若存在，求出点M,N的坐标；若不存在，请说明理由.9、（扬州市2017届高三上学期期中）如图，在四棱锥P – ABCD中，底面ABCD为正方形，侧棱PA⊥底面ABCD，AB=1，PA=2，E为PB的中点，点F在棱PC上，且PF=λPC。

高三数学上学期第三次联考试题理含解析试题

二中2021届高三数学上学期第三次联考试题理〔含解析〕制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日第一卷一、选择题：此题一共12小题，每一小题5分，一共60分.在每一小题给出的四个选项里面，只有一项是哪一项符合题目要求的1.设{}11A x x =-<<，{}0B x x a =->，假设A B ⊆，那么a 的取值范围是〔〕 A. (,1]-∞-B. (,1)-∞-C. [1,)+∞D.(1,)+∞【答案】A 【解析】【分析】根据A B ⊆，得到1a ≤-，即可求解实数a 的取值范围，得到答案。

【详解】由题意，集合{}11A x x =-<<，{}{}0B x x a x x a =->=，因为A B ⊆，那么1a ≤-，即实数a 的取值范围是(,1]-∞-。

应选：A 。

【点睛】此题主要考察了利用集合的包含关系求解参数问题，其中解答中纯熟集合的包含关系，列出相应的不等式是解答的关键，着重考察了推理与运算才能，属于根底题。

2.己知命题p ：,21000nn N ∃∈>，那么p ⌝为〔〕A. ,21000nn N ∀∈< B. ,21000nn N ∀∉< C. ,21000nn N ∀∈≤ D. ,21000nn N ∀∉≤【答案】C【解析】【分析】先改存在量词为全称量词,再否认结论. 【详解】p ⌝:,21000nn N ∀∈≤.应选C.【点睛】此题考察了含有一个量词的命题的否认,属于根底题. 解题方法:先改量词,再否认结论. 3.己知复数z 满足2019(1)i z i-=-〔其中i 为虚数单位〕，那么||z =〔〕A.12B.2C. 1【答案】B 【解析】【分析】根据i 的幂运算性质可得2019i i =-，再由复数的除法运算可求得z ，从而求出||z . 【详解】2019(1)i i z i-=-=，那么(1)1111(1)(1)222i i i i z i i i i +-+====-+--+，所以，||z ==所以此题答案为B.【点睛】此题考察复数的乘除法和复数的模，解决复数问题，要通过复数的四那么运算将复数表示为一般形式，结合复数相关知识求解，考察计算才能，属于根底题.4.中国当代数学著作?算法统宗?中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还．〞其意思为；“有一个人走378里路，第一天健步行走，从第二天起脚痛每天走的路程为前一天的一半，走了6天后到达目的地，请问第一天走了〔〕 A. 24里 B. 48里C. 96里D. 192里【答案】D 【解析】【分析】每天行走的步数组成公比为12的等比数列,根据前6项和为378列式可解得. 【详解】设第n 天行走了n a 步,那么数列{}n a 是等比数列,且公比12q =,因为123456378a a a a a a +++++=,所以23451(1)378a q q q q q +++++=,所以12345378111111()()()()22222a =+++++ 6378378192111()2(1)264112===--- , 所以第一天走了192里. 应选D【点睛】此题考察了等比数列的前n 项和公式中的根本量的计算,属于根底题. 5.函数()f x 为偶函数，且对于任意的()12,0,x x ∈+∞，都有1212()()f x f x x x --()120x x >≠,设(2)a f =，3(log 7)b f =，0.1(2)c f -=-那么〔〕A. b a c <<B. c a b <<C. c b a <<D.a cb <<【答案】C 【解析】【分析】首先判断函数在()0,∞+的单调性，然后根据偶函数化简()()0.10.122f f ---=，然后比拟2，3log 7，0.12-的大小，比拟,,a b c 的大小关系.【详解】假设()()()1212120f x f x x x x x ->≠-，那么函数在()0,∞+是单调递增函数，并且函数是偶函数满足()()f x f x -=，即()()0.10.122f f ---=，0.1021-<<，31log 72<<()f x 在()0,∞+单调递增，()()()0.132log 72f f f -∴<<，即c b a <<. 应选C.【点睛】此题考察利用函数的奇偶性和函数的单调性比拟函数值的大小，意在考察函数性质的应用，意在考察转化和变形才能，属于根底题型.6.假设函数()sin(2)6f x x π=-的图像向左平移ϕ〔0ϕ>〕个单位，所得的图像关于y 轴对称，那么当ϕ最小时，tan ϕ=〔〕C. D.【答案】B 【解析】【分析】根据平移变换得到解析式后,利用所得的图像关于y 轴对称列式,再求最小值.【详解】将函数()sin(2)6f x x π=-的图像向左平移ϕ〔0ϕ>〕个单位后,得到函数sin[2()]sin(22)66y x x ππϕϕ=+-=+-,因为其图像关于y 轴对称,所以262k ππϕπ-=+,k Z ∈,即23k ππϕ=+,k Z ∈, 因为0ϕ>,所以0k =时,ϕ获得最小值3π,此时tan tan 33πϕ==. 应选B .【点睛】此题考察了三角函数图像的平移变换,以及对称轴,属于中档题. 7.函数21()cos 4f x x x =+的图象在点()t f t （，）处的切线的斜率为k ，那么函数()k g t =的大致图象是〔〕A. B.C. D.【答案】A 【解析】【分析】求得1()sin 2f x x x '=-，得到函数在点()t f t （，）处的切线的斜率为1()sin 2k f t t t ='=-，得出函数()1sin 2t g t t -=，利用函数的奇偶性和特殊的函数的值，即可求解。

全国各省市高三上期数学联考试题重组专题题型三立体几何(教师版)

2012届全国各省市高三上学期数学联考试题重组专题题型三立体几何（教师版）【备考要点】立体几何在数学高考中占有重要的地位，近几年高考对立体几何考察的重点与难点稳定（也是考生的基本得分点）：高考始终把直线与直线、直线与平面、平面与平面的平行的判断与性质、垂直的判断与性质作为考察的重点。

新课标教材对立体几何要求虽有所降低，但考察的重点一直没有变，常常考察线线、线面、面面的平行与垂直的位置关系和空间角与距离的计算。

（1）从考题的数量看，一般为2-3题，其中一大一小的设置更符合课时比例；从所占分值来看，同一省份不同年份差异不大，不同省份略有差异。

（2）文理科差异较大，文科以三视图、面积与体积、平行与垂直关系的判断与证明为主要的考查对象，三视图几乎每年必考（其实，三视图是考察学生空间想象能力的良好素材，大部分省份的情况是文、理同题，位置调整难度）。

（3）理科在文科的基础上重点考查空间角的计算，由此可见“空间角的计算”受到的关注程度最高，与考纲要求吻合。

解答题的命制特点是“一题两法”，各地标准答案都给出了向量解法。

（4）在“空间角”的考查中，主要考查的是“二面角”，高于教材要求，但对线面角的考查也有加大的趋势。

预测2012年高考的可能情况是：(1)以选择题或者填空题的形式考查空间几何体的三视图以及表面积和体积的计算．对空间几何体的三视图的考查有难度加大的趋势，通过这个试题考查考生的空间想象能力；空间几何体的表面积和体积计算以三视图为基本载体，交汇考查三视图的知识和面积、体积计算，试题难度中等．(2)以解答题的方式考查空间线面位置关系的证明，在解答题中的一部分考查使用空间向量方法求解空间的角和距离，以求解空间角为主，特别是二面角．【2011高考题型】立体几何大题一般出现在试卷中第18、19题，难度中等，少数省份出现在20、21或17题位置，难度中等偏上或偏下。

小题通常为容易题、中等题，中上难度的题也时有出现。

2021年高三(上)第三次联考数学试卷 Word版含解析

2021年高三（上）第三次联考数学试卷 Word版含解析一、填空题：本大题共14小题，每小题5分，共70分．不需要写出解答过程，请把答案直接填在答题卡相应位置上．1．（5分）集合{0，1，2}的所有子集个数为8 ．考点：子集与真子集．专题：计算题．分析：根据题意，易得集合M中有3个元素，由集合的元素数目与其子集数目的关系，可得答案．解答：解：集合{0，1，2}中有3个元素，则其子集有23=8个，故答案为8．点评：本题考查集合的元素数目与其子集数目的关系，牢记若一个集合有n个元素，则其有2n个子集．2．（5分）设（2+i）z=5i（i为虚数单位），则|z|=．考点：复数求模．专题：计算题．分析：把给出的等式两边同时乘以，然后运用复数的除法运算化简，最后利用求复数模的公式求模．解解：∵复数z满足（2+i）z=5i （i为虚数单位），答：∴z====1+2i．则|z|==．故答案为．点评：本题考查复数的模的定义，考查了复数的乘除法运算，复数的除法，采用分子分母同时乘以分母的共轭复数，此题是基础题．3．（5分）（2011•徐州模拟）在某个容量为300的样本的频率分布直方图中，共有9个小长方形，若中间一个小长方形的面积等于其他8个小长方形面积和的，则中间一组的频数为50．考点：频率分布直方图．专题：计算题．分析：由已知中频率分布直方图中，共有9个小长方形，若中间一个小长方形的面积等于其他8个小长方形面积和的，根据这9个小正方形的面积（频率）和为1，进而求出该组的频率，进而根据频数=频率×样本容量，即可得到中间一组的频数．解答：解：由于中间一个小长方形的面积等于其他8个小长方形面积和的，这9个长方形的面积和为1故中间一个小长方形的面积等于即中间一组的频率为双有样本容量为300故中间一组的频数为300×=50故答案为：50点评：本题考查的知识点是频率分布直方图，其中根据已知条件结合频率分布直方图中各矩形面积的和为1，求出中间一组的频率，是解答本题的关键．4．（5分）（2011•南通一模）根据如图的算法，输出的结果是55．考点：伪代码．专题：阅读型．分析：先读懂程序的算法，再据算法规则依次算出结果．可以看出这是一个for循环结构，循环执行10此，依其特点求解即可．解答：解：程序是一个循环结构，步长是1，每循环一次就加进i，初始i=1，可循环十次，故S=0+1+2+3+…+10=55故答案为：55．点评：本题主要考查算法语言的结构，此类题的做法通常是把值代入，根据其运算过程求出值，属于基础题．5．（5分）（2011•西安模拟）设变量x，y满足约束条件，则z=x﹣3y的最小值﹣8．考点：简单线性规划．专题：计算题．分析：作出变量x，y满足约束条件所对应的平面区域，采用直线平移的方法，将直线l：平移使它经过区域上顶点A（﹣2，2）时，目标函数达到最小值﹣8解答：解：变量x，y满足约束条件所对应的平面区域为△ABC如图，化目标函数z=x﹣3y 为将直线l：平移，因为直线l在y轴上的截距为﹣，所以直线l越向上移，直线l在y轴上的截距越大，目标函数z的值就越小，故当直线经过区域上顶点A时，将x=﹣2代入，直线x+2y=2，得y=2，得A（﹣2，2）将A（﹣2，2）代入目标函数，得达到最小值z min=﹣2﹣3×2=﹣8故答案为：﹣8点评：本题考查了用直线平移法解决简单的线性规划问题，看准直线在y轴上的截距的与目标函数z符号的异同是解决问题的关键．6．（5分）（2011•江苏模拟）已知α、β表示两个不同的平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的必要不充分条件．考点：必要条件、充分条件与充要条件的判断；空间中直线与平面之间的位置关系；平面与平面之间的位置关系．分直线和平面垂直，平面和平面垂直的判定，二者的关系搞清楚，析：解答：解：由平面与平面垂直的判定定理知，m为平面α内的一条直线，如果m⊥β，则α⊥β；反过来m为平面α内的一条直线，则“α⊥β”可能有m∥β，m∩β=p，可能有m⊥β三种情况．所以“α⊥β”是“m⊥β”的必要不充分条件．故答案为：必要不充分点评：考查定理的理解，分析问题时：考虑要全面，有时可以借助实物，动手动脑，简化问题．7．（5分）（2011•江苏二模）若以连续掷两次骰子分别得到的点数m、n作为点P的坐标，则点P落在圆x2+y2=16内的概率是．考点：古典概型及其概率计算公式．专题：计算题．分析：本题是一个古典概型，试验发生包含的事件是连续掷两次骰子分别得到的点数m、n 作为点P的坐标，共有6×6种结果，而满足条件的事件是点P落在圆x2+y2=16内，列举出落在圆内的情况共有8种结果，求比值得到结果．解答：解：由题意知，本题是一个古典概型，试验发生包含的事件是连续掷两次骰子分别得到的点数m、n作为点P的坐标，共有6×6=36种结果，而满足条件的事件是点P落在圆x2+y2=16内，列举出落在圆内的情况：（1，1）（1，2）（1，3）（2，1）（2，2）（2，3）（3，1）（3，2），共有8种结果，根据古典概型概率公式得到P==，故答案为：点评：本题是一个古典概型问题，这种问题在高考时可以一道解答题，古典概型要求能够列举出所有事件和发生事件的个数，本题可以列举出所有事件．8．（5分）已知，则tanα=．考点：两角和与差的正切函数．专题：计算题．分析：把已知，直接代入tanα=tan[（α+β）﹣β]，利用两角差的正切公式运算求得结果．解答：解：已知，则tanα=tan[（α+β）﹣β]===．故答案为：．点评：本题主要考查两角差的正切公式的应用以及角的变换，属于基础题．9．（5分）（2011•扬州模拟）在平面直角坐标系xOy中，已知A、B分别是双曲线的左、右焦点，△ABC的顶点C在双曲线的右支上，则的值是．考点：双曲线的简单性质．专题：计算题．分析：首先由正弦定理，可得=，进而根据双曲线的几何性质，可得|AB|=2c=4，|CB|﹣|CA|=﹣2a=﹣2；代入中，可得答案．解答：解：根据正弦定理：在△ABC中，有=；又由题意A、B分别是双曲线的左、右焦点，则|AB|=2c=4，且△ABC的顶点C在双曲线的右支上，又可得|CB|﹣|CA|=﹣2a=﹣2；故则===﹣；故答案为：﹣．点评：本题考查双曲线的几何性质，注意点C在双曲线的右支上，则有|CA|＞|CB|，即|CB|﹣|CA|=﹣2a，这是一个易错点．10．（5分）如图，在△ABC中，∠BAC=120°，AB=AC=2，D为BC边上的点，且•=0，=2，则=1．考点：向量加减混合运算及其几何意义．专题：平面向量及应用．分析：由题意可知：⊥，且D为BC中点，∠B=∠C=30°，且易求得AD=1，，而==代入可得结果．解答：解：由题意可知：⊥，且D为BC中点，∠B=∠C=30°故在直角三角形ABD中可求得AD=1，，∴====1．故答案为：1点评：本题为向量的数量积的运算，把向量适当转化时解决问题的关键，属基础题．11．（5分）已知，若对任意两个不等的正实数m，n都有＞3恒成立，则实数a的取值范围是a≥．考函数的单调性与导数的关系．点：专题：导数的概念及应用．分析：由题意易得f′（x）＞3恒成立，求导数，分离a，只需求x（3﹣x）的最小值即可．解答：解：因为对任意两个不等的正实数m，n都有＞3恒成立，所以函数f（x）图象上每点切线的斜率＞3恒成立，故f′（x）＞3恒成立，又已知，定义域为（0，+∞）求导数可得，故＞3恒成立，所以a＞x（3﹣x）恒成立，只需求x（3﹣x）的最小值，而当x=时，[x（3﹣x）]min=，故答案为：a≥点评：本题考查函数的单调性和导数的关系，涉及恒成立问题，属中档题．12．（5分）设，a＞0，函数f（θ）=的最小值为25，则实数a=16．考点：三角函数的最值．专题：三角函数的求值．分析：由题意可得cosθ＞0，＞0，函数f（θ）=[]•[cosθ+（1﹣cosθ）]=1+a++，利用基本不等式求得最小值为1+a+2=25，由此求得实数a 的值．解答：解：∵，a＞0，∴cosθ＞0，＞0，∴函数f（θ）==[]•[cosθ+（1﹣cosθ）]=1+a++≥1+a+2，当且仅当=时，取等号，故函数的最小值为1+a+2=25，解得a=16，故答案为16．点评：本题主要考查基本不等式的应用，求函数的最值，属于中档题．13．（5分）已知数列{a n}，{b n}满足a1=1，a2=2，b1=2，且对任意的正整数i，j，k，l，当i+j=k+l时，都有a i+b j=a k+b l，则的值是xx．考点：数列的求和．专题：计算题；点列、递归数列与数学归纳法．分析：先求出b2的值，然后分别判定数列{a n}，{b n}的特征，然后利用求和公式分别求出两数列的和，将xx代入求出所求即可．解答：解：∵对任意的正整数m，n，p，q，当m+n=p+q时，都有a m+b n=a p+b q，∴a2+b1=a1+b2，将a1=1，a2=2，b1=2，代入可得b2=3∵1+（n+1）=2+n∴a1+b n+1=a2+b n，即b n+1﹣b n=1∴数列{b n}是等差数列首项为1，公差为1，则T n=∵（n+1）+1=n+2∴a n+1+b1=a n+b2则a n+1﹣a n=1∴数列{a n}是等差数列首项为2，公差为1，则S n=∴=Sxx+Txx=（1006×xx+1006+xx）=xx故答案为：xx点评：本题主要考查了数列的求和，以及数列的判定，同时考查了计算能力，属于中档题14．（5分）（2011•延安模拟）我们把形如的函数因其图象类似于汉字“囧”字，故生动地称为“囧函数”，并把其与y轴的交点关于原点的对称点称为“囧点”，以“囧点”为圆心凡是与“囧函数”有公共点的圆，皆称之为“囧圆”，则当a=1，b=1时，所有的“囧圆”中，面积的最小值为3π．考点：直线和圆的方程的应用．专题：计算题；新定义．分析：根据已知中关于“囧函数”、“囧点”、“囧圆”的定义，根据a=1，b=1我们易求出“囧点”坐标，并设出“囧圆”的方程，根据求出圆心到“囧函数”图象上的最小距离后，即可得到结论．解答：解：当a=1，b=1时，则函数与Y轴交于（0，﹣1）点则“囧点”坐标为（0，1）令“囧圆”的标准方程为x2+（y﹣1）2=r2，令“囧圆”与函数图象的左右两支相切则切点坐标为（±，±）此时r=；令“囧圆”与函数图象的下支相切则切点坐标为（0，﹣1）此时r=2；故所有的“囧圆”中，面积的最小值为3π故答案为：3π点评：本题考查的知识点是抽象函数及其应用，其中根据“囧圆”的圆心坐标及“囧函数”的解析式，求出“囧圆”的圆心到函数图象距离的最小值是解答本题的关键，属中档题．二、解答题：本大题共6小题，共90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（14分）（xx•台州二模）已知函数．（1）求函数f（x）的单调增区间；（2）已知f（α）=3，且α∈（0，π），求α的值．考点：正弦函数的单调性；三角函数的化简求值．专题：计算题．分析：先把函数进行化简，f（x）=2sin（）+2（1），解不等式可求（2）把已知代入可得，求解即可．解答：解：（1）=．由；得；．∴函数f（x）的单调增区间为．（2）由f（α）=3，得．∴．∴，或（k1，k2∈Z），即α=k1π或（k1，k2∈Z）．∵α∈（0，π），∴．点评：本题考查了三角函数的性质：单调性，还考查了三角公式中的二倍角及和差角公式的综合运用，在处理三角函数的单调区间的问题时，常用整体思想，类比正（余）弦函数的性质．16．（14分）（xx•南京二模）如图，四边形ABCD是矩形，平面ABCD⊥平面BCE，BE⊥EC．（1）求证：平面AEC⊥平面ABE；（2）点F在BE上．若DE∥平面ACF，求的值．考点：平面与平面垂直的判定；直线与平面平行的性质．专题：综合题；空间位置关系与距离．分析：（1）根据平面ABCD⊥平面BCE，利用面面垂直的性质可得AB⊥平面BCE，从而可得CE⊥AB，由CE⊥BE，根据线面垂直的判定可得CE⊥平面ABE，从而可得平面AEC⊥平面ABE；（2）连接BD交AC于点O，连接OF．根据DE∥平面ACF，可得DE∥OF，根据O为BD中点，可得F为BE中点，从而可得结论．解答：（1）证明：因为ABCD为矩形，所以AB⊥BC．因为平面ABCD⊥平面BCE，平面ABCD∩平面BCE=BC，AB⊂平面ABCD，所以AB⊥平面BCE．…（3分）因为CE⊂平面BCE，所以CE⊥AB．因为CE⊥BE，AB⊂平面ABE，BE⊂平面ABE，AB∩BE=B，所以CE⊥平面ABE．…（6分）因为CE⊂平面AEC，所以平面AEC⊥平面ABE．…（8分）（2）解：连接BD交AC于点O，连接OF．因为DE∥平面ACF，DE⊂平面BDE，平面ACF∩平面BDE=OF，所以DE∥OF．…（12分）又因为矩形ABCD中，O为BD中点，所以F为BE中点，即=．…（14分）点评：本题考查线面、面面垂直的判定与性质，考查线面平行，掌握线面、面面垂直的判定与性质是关键．17．（14分）如图，某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”，其中AB长为定值a，BD长可根据需要进行调节（BC足够长）．现规划在△ABD的内接正方形BEFG内种花，其余地方种草，且把种草的面积S1与种花的面积S2的比值称为“草花比y”．（Ⅰ）设∠DAB=θ，将y表示成θ的函数关系式；（Ⅱ）当BE为多长时，y有最小值，最小值是多少．考点：函数模型的选择与应用；函数的最值及其几何意义．专题：综合题；函数思想．分析：（1）由于题目中“设∠DAB=θ，”，故可利用解三角形的知识解决“草花比y”；（2）由于式子“”括号中两式的积是定值，故利用二元不等式求其最小值．解答：解：（Ⅰ）因为BD=atanθ，所△ABD的面积为a2tanθ（）（2分）设正方形BEFG的边长为t，则由，得，（4分）解得，则（5分）所以a2tanθ﹣S2，则（8分）（Ⅱ）因为tanθ∈（0，+∞），所以（10分）当且仅当tanθ=1，时取等号，此时BE=．所以当BE长为时，y有最小值1．（12分）点评：本题主要考查函数在实际生活中的应用、解三角形以及利用二元不等式求函数最值的方法，解决实际问题通常有几个步骤：（1）阅读理解，认真审题；（2）引进数学符号，建立数学模型；（3）利用数学的方法，得到数学结果，其中关键是建立数学模型．18．（16分）（2011•重庆模拟）已知椭圆E：+=1的左焦点为F，左准线l与x轴的交点是圆C的圆心，圆C恰好经过坐标原点O，设G是圆C上任意一点．（Ⅰ）求圆C的方程；（Ⅱ）若直线FG与直线l交于点T，且G为线段FT的中点，求直线FG被圆C所截得的弦长；（Ⅲ）在平面上是否存在一点P，使得=？若存在，求出点P坐标；若不存在，请说明理由．考点：圆与圆锥曲线的综合；椭圆的简单性质．专题：计算题．分析：（1）由题易知圆C的圆心为（）而a=，b=2可求出圆心为（﹣4，0）又圆C恰好经过坐标原点O故半径为4所以圆C的方程为（x+4）2+y2=16（2）可利用直线FG与直线l联立求出t点坐标再利用中点坐标公式求出G（﹣3，y G）再代入圆C的方程求出y G进而求出FG的方程为y=（x+2），然后利用圆心到直线的距离公式求出C（﹣4，0）到FG的距离d=再利用勾股定理即可求出弦长的一半进而求解．（3）假设存在P（s，t），G（x0，y0）使得=成立利用两点间的距离公式化简可得方程3（x02+y02）+（16+2s）x0+2ty0+16﹣s2﹣t2=0再结G（x0，y0）在圆C即x02+y02+8x0=o可得（2s﹣8）x0+2ty0+16﹣s2﹣t2=0对所有的x0，y0．成立故2s﹣8=0，2t=0，16﹣s2﹣t2=0所以s=4，t=0即存在p（4，0）满足题意．解答：解：（1）∵a=，b=2∴c=2∴左准线方程为x==﹣4∴圆心为（﹣4，0）∵圆C恰好经过坐标原点O故半径为4∴圆C的方程为（x+4）2+y2=16（2）由题意知，得G（﹣3，y G），代入（x+4）2+y2=16，得y= 所以FG的斜率为K=y=，FG的方程为y=（x+2）所以C（﹣4，0）到FG的距离d=，直线FG被圆C截得弦长为2=7故直线FG被圆C截得弦长为7．（3）设P（s，t），G（x0，y0），则由，得，整理得3（x02+y02）+（16+2s）x0+2ty0+16﹣s2﹣t2=0①又G（x0，y0）在圆C：（x+4）2+y2=16上，所以x02+y02+8x0=o②②代入①得（2s ﹣8）x0+2ty0+16﹣s2﹣t2=0又G（x0，y0）为圆C上任意一点可知，2s﹣8=0，2t=0，16﹣s2﹣t2=0解得s=4，t=0．所以在平面上存在一点p，其坐标为（4，0）．点评：此题第一问主要考查了利用椭圆的有关知识求圆的方程关键是要知道椭圆的左准线方程是x=．第二问考查了利用圆心到直线的距离公式求出d再利用半径，d，弦长的一半构成直角三角形再采用勾股定理即可求解．对于第三问较难但思路较简单即假设存在P（s，t），G（x0，y0）使得=成立，关键是得出（2s﹣8）x0+2ty0+16﹣s2﹣t2=0后怎么办是难点！实质上这是恒成立的问题只需系数和常数项为0即可求出s，t．19．（16分）（xx•江苏模拟）已知函数f（x）=alnx﹣bx2图象上一点P（2，f（2））处的切线方程为y=﹣3x+2ln2+2（1）求a，b的值；（2）若方程f（x）+m=0在内有两个不等实根，求实数m的取值范围（其中e为自然对数的底，e≈2.7）；（3）令g（x）=f（x）﹣nx，如果g（x）图象与x轴交于A（x1，0），B（x2，0），x1＜x2，AB中点为C（x0，0），求证：g′（x0）≠0．考点：函数与方程的综合运用；利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．专题：计算题；证明题；压轴题．分析：（1）由切线方程得函数在x=2处的切线斜率为﹣3，即f′（2）=﹣3，由函数f（x）=alnx﹣bx2得其导函数，进而得f′（2），由f′（2）=﹣3得关于a、b的方程，又切点在函数图象上，也在切线上，当x=2时分别代入两个函数方程，函数值相等，得第二个关于a、b的方程，求解方程组，得a，b的值；（2）设h（x）=f（x）+m=2lnx﹣x2+m，求h′（x），令h′（x）＞0，h′（x）＜0，得函数h（x）的单调区间，得出h（x）的图象的大致走向，得出满足题意的不等式组，解得实数m的取值范围；（3）由点A（x1，0），B（x2，0）在g（x）图象上，把点的坐标代入g（x）的解析式得方程组，两式相减得关于x1、x2、n的方程，假设g′（x）=0成立，求导，得关于x0、n的方程，由中点坐标公式转化关于x1、x2、n的方程，两方程消去n，得关于x1、x2的方程，整理此方程，分子分母同除以x2，整理方程，右边为0，设t=，左边得关于t的函数，求此函数的导数，得函数的单调性，得函数值恒小于0，所以方程不成立，所以假设不成立，所以g′（x0）≠0．解答：解：（1），所以，且aln2﹣4b=﹣6+2ln2+2，解得a=2，b=1．（2）f（x）=2lnx﹣x2，令h（x）=f（x）+m=2lnx﹣x2+m，则=，令h'（x）=0，得x=1（x=﹣1舍去）．在内，当时，h'（x）＞0，所以h（x）是增函数；当x∈（1，e]时，h'（x）＜0，所以h（x）是减函数则方程h（x）=0在内有两个不等实根的充要条件是即1＜m≤e2﹣2．（3）．假设结论成立，则有，（1）﹣（2），得．所以．由（4）得，所以，即，即=，令．则，所以u（t）在0＜t＜1上是增函数，u（t）＜u（1）=0，所以（5）式不成立，与假设矛盾，所以g'（x0）≠0．点评：此题考查函数与方程的综合运用，求未知数的值，几个未知数需几个方程构成方程组求解；注意把方程解的个数问题转化为对应函数图象的交点个数问题，可使问题直观易懂；也可把函数图象的交点个数问题转化为方程组得各量之间的关系，把未知量转化为一种形式，令一边为0，另一边再转化为函数，利用函数单调性解题；用反证法证明问题时，先假设结论不正确，得出与假设相反的结论，从而结论是正确的．20．（16分）已知数列．（I）试证数列是等比数列，并求数列{b n}的通项公式；（II）在数列{b n}是，是否存在连续三项成等差数列？若存在，求出所有符合条件的项；若不存在，说明理由．（III）试证在数列{b n}中，一定存在满足条件1＜r＜s的正整数r，s，使得b1，b r，b s成等差数列；并求出正整数r，s之间的关系．考点：函数与方程的综合运用；数列的应用；等比关系的确定．专题：综合题；等差数列与等比数列．分析：（I）由a n+a n+1=2n，得a n+1=2n﹣a n，从而可证=﹣1，即可证得数列是等比数列，并可求数列{b n}的通项公式；（II）解：假设在数列{b n}中，存在连续三项b k﹣1，b k，b k+1（k∈N*，k≥2）成等差数列，则b k﹣1+b k+1=2b k，即2k﹣1=4（﹣1）k﹣1．分类讨论，可得在数列{b n}中，有且仅有连续三项b2，b3，b4成等差数列；（III）证明：要使b1，b r，b s成等差数列，只需b1+b s=2b r，即2s﹣2r+1=（﹣1）s ﹣2（﹣1）r﹣3，（﹡），分类讨论，可知存在不小于4的正偶数s，且s=r+1，使得b1，b r，b s成等差数列．解答：（I）证明：由a n+a n+1=2n，得a n+1=2n﹣a n，所以==﹣1又因为a1﹣=，所以数列{a n﹣×2n}是首项为，公比为﹣1的等比数列．所以a n﹣×2n=×（﹣1）n﹣1，即a n=[2n﹣（﹣1）n]，所以b n=2n﹣（﹣1）n．（5分）（II）解：假设在数列{b n}中，存在连续三项b k﹣1，b k，b k+1（k∈N*，k≥2）成等差数列，则b k﹣1+b k+1=2b k，即[2k﹣1﹣（﹣1）k﹣1]+[2k+1﹣（﹣1）k+1]=2[2k﹣（﹣1）k]，即2k﹣1=4（﹣1）k﹣1．①若k为偶数，则2k﹣1＞0，4（﹣1）k﹣1=﹣4＜0，所以，不存在偶数k，使得b k﹣1，b k，b k+1成等差数列．（7分）②若k为奇数，则当k≥3时，2k﹣1≥4，而4（﹣1）k﹣1=4，所以，当且仅当k=3时，b k﹣1，b k，b k+1成等差数列．综上所述，在数列{b n}中，有且仅有连续三项b2，b3，b4成等差数列．（9分）（III）证明：要使b1，b r，b s成等差数列，只需b1+b s=2b r，即3+2s﹣（﹣1）s=2[2r﹣（﹣1）r]，即2s﹣2r+1=（﹣1）s﹣2（﹣1）r﹣3，（﹡）（10分）①若s=r+1，在（﹡）式中，左端2s﹣2r+1=0，右端（﹣1）s﹣2（﹣1）r﹣3=（﹣1）s+2（﹣1）s﹣3=3（﹣1）s﹣3，要使（﹡）式成立，当且仅当s为偶数时．又s＞r＞1，且s，r为正整数，所以当s为不小于4的正偶数，且s=r+1时，b1，b r，b s成等差数列．（12分）②若s≥r+2时，在（﹡）式中，左端2s﹣2r+1≥2r+2﹣2r+1=2r+1，由（II）可知，r≥3，所以r+1≥4，所以左端2s﹣2r+1≥16（当且仅当s为偶数、r为奇数时取“=”）；右端（﹣1）s﹣2（﹣1）s﹣3≤0．所以当s≥r+2时，b1，b r，b s不成等差数列．综上所述，存在不小于4的正偶数s，且s=r+1，使得b1，b r，b s成等差数列．（14分）点评：本题主要考查等比数列的判定和等差数列的应用，考查函数与方程，分类讨论思想，考查推理论证能力．24795 60DB 惛25072 61F0 懰!38998 9856 顖21947 55BB 喻,35342 8A0E 討3O21500 53FC 叼40169 9CE9 鳩35426 8A62 詢26050 65C2 旂S39445 9A15 騕。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2012届全国各省市高三上学期数学联考试卷重组专题题型三立体几何（学生版）【备考要点】立体几何在数学高考中占有重要的地位，近几年高考对立体几何考察的重点与难点稳定（也是考生的基本得分点）：高考始终把直线与直线、直线与平面、平面与平面的平行的判断与性质、垂直的判断与性质作为考察的重点。

新课标教材对立体几何要求虽有所降低，但考察的重点一直没有变，常常考察线线、线面、面面的平行与垂直的位置关系和空间角与距离的计算。

（1）从考题的数量看，一般为2-3题，其中一大一小的设置更符合课时比例；从所占分值来看，同一省份不同年份差异不大，不同省份略有差异。

（3）理科在文科的基础上重点考查空间角的计算，由此可见“空间角的计算”受到的关注程度最高，与考纲要求吻合。

解答题的命制特点是“一题两法”，各地规范答案都给出了向量解法。

（4）在“空间角”的考查中，主要考查的是“二面角”，高于教材要求，但对线面角的考查也有加大的趋势。

预测2012年高考的可能情况是：(1)以选择题或者填空题的形式考查空间几何体的三视图以及表面积和体积的计算．对空间几何体的三视图的考查有难度加大的趋势，通过这个试卷考查考生的空间想象能力；空间几何体的表面积和体积计算以三视图为基本载体，交汇考查三视图的知识和面积、体积计算，试卷难度中等．(2)以解答题的方式考查空间线面位置关系的证明，在解答题中的一部分考查使用空间向量方法求解空间的角和距离，以求解空间角为主，特别是二面角．【2011高考题型】立体几何大题一般出现在试卷中第18、19题，难度中等，少数省份出现在20、21或17题位置，难度中等偏上或偏下。

小题通常为容易题、中等题，中上难度的题也时有出现。

占分比重全国绝大多数省份是两小题一大题21-22分，占全卷的14%左右。

考查重点直线与平面的位置关系判定、证明及角度与距离的计算。

直线平面的平行、垂直作为知识体系的轴心，在考查中地位突出，贯穿整个大题。

角度的计算：线线角、线面角、二面角是必考内容，线面角、二面角的出现频率更高些。

距离以点面距、异面直线的距离为主，前者的出现频率更高。

另外还应注意非规范图形的识别、三视图的运用、图形的翻折、求体积时的割补思想等，以及把运动的思想引进立体几何。

最近几年综合分析全国及各省高考真题，立体几何开放题是高考命题的一个重要方向，开放题更能全面的考查学生综合分析问题的能力。

考查内容一般有以下几块内容：1、平行：包括线线平行，线面平行，面面平行；2、垂直：包括线线垂直，线面垂直，面面垂直；3、角度：包括线线（主要是异面直线）所成的角，线面所成的角，面面所成的角；4、求距离或体积；高考中的立体几何题的解法通常一题多解，同一试卷的解题途径和方法中常常潜藏着极其巧妙的解法，尤其是空间向量这一工具性的作用体现的更为明显。

因此，这就要求考生通过“周密分析、明细推理、准确计算、猜测探求”等具有创造性思维活动来选择其最佳解法以节约做题时间，从而适应最新高考要求。

立体几何解答题的设计，注意了求解方法既可用向量方法处理，又可用传统的几何方法解决，并且向量方法比用传统方法解决较为简单，对中学数学教案有良好的导向作用，符合数学教材改革的要求，有力地支持了新课程的改革..【2012 命题方向】【原题】（本题满分13分）如图，在四棱锥S ABCD -中，平面SAD ⊥平面ABCD ．底面ABCD 为矩形，,AD AB ，SA SD a ==．（Ⅰ）求证：CD SA ⊥；（Ⅱ）求二面角C SA D --的大小.【试卷出处】北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷【原题】(本小题满分12分) 如图，在三棱柱ABC —A 1B 1C 1中，AA 1⊥平面A 1B 1C 1，∠B 1A 1C 1=90°，D 、E 分别为CC 1和A 1B 1的中点，且A 1A=AC=2AB=2． (I)求证：C 1E∥平面A 1BD ； (Ⅱ)求点C 1到平面A 1BD 的距离．【试卷出处】河北省石家庄市2012届高三上学期教案质量检测(一)数学（文）试卷【原题】(本小题满分12分) 如图，在四棱锥P —ABCD 中，底面ABCD是正方形，PA ⊥底面ABCD ，且PA=AB ，M 、N 分别是PA 、BC 的中点．(I)求证：MN∥平面PCD ；(II)在棱PC 上是否存在点E ，使得AE 上平面PBD?若存在，求出AE 与平面PBC 所成角的正弦值，若不存在，请说明理由．【试卷出处】河北省石家庄市2012届高三上学期教案质量检测(一)数学（理）试卷【原题】（本小题满分13分）如图，在四棱锥ABCD P －中，底面ABCD 是菱形，060BAD ＝∠，2AB ＝，1PA ＝,⊥PA 平面ABCD ，E 是PC 的中点，F 是AB 的中点.(Ⅰ) 求证：B E ∥平面PDF ；（Ⅱ）求证：平面PDF ⊥平面PA B ；（Ⅲ）求平面PA B 与平面PCD 所成的锐二面角的大小.说明：（Ⅲ）小题用几何法，解答只要言之有理均应按步给分.【试卷出处】福建省三明市普通高中2011-2012学年第一学期联合命题考试高三数学（理科）试卷【原题】（本题满分12分）如图1，平面四边形ABCD 关于直线AC 对称，2,90,60==∠=∠CD C A ，把△ABD 沿BD 折起（如图2），使二面角A ―BD ―C 2，完成以下各小题：（1）求A ，C 两点间的距离；（2）证明：AC ⊥平面BCD ；（3）求直线AC 与平面ABD 所成角的正弦值。

【试卷出处】山东省烟台市2012届高三上学期期末检测数学（理）试卷【原题】（本题满分12分）本题共有2个小题，第1小题满分5分，第2小题满分7分．如图，在直三棱柱111C B A ABC -中，2=AB ，41==AA AC ，︒=∠90ABC ．（1）求三棱柱111C B A ABC -的表面积S ；（2）求异面直线B A 1与AC 所成角的大小（结果用反三角函数表示）．【试卷出处】2011学年嘉定区高三年级第一次质量调研数学试卷（理）【原题】（本小题满分12分）如图，四边形ABCD 为矩形，DA ⊥平面ABE ,2AE EB BC ===，BF ⊥平面ACE 于点F ，且点F 在CE 上.（Ⅰ）求证：DE BE ⊥；（Ⅱ）求四棱锥E ABCD -的体积；（Ⅲ）设点M 在线段AB 上，且AM MB =，试在线段CE 上确定一点N ，使得//MN 平面DAE .【试卷出处】山东省青岛市2012届高三期末检测数学 (文科)【原题】（本小题满分12分）已知四边形ABCD 满足AD ∥BC ，12BA AD DC BC a ====，E 是BC 的中点，将BAE ∆沿着AE 翻折成1B AE ∆，使面1B AE ⊥面AECD ，F 为1B D 的中点.（Ⅰ）求四棱1B AECD -的体积；（Ⅱ）证明：1B E ∥面ACF ；（Ⅲ）求面1ADB 与面1ECB 所成二面角的余弦值.【试卷出处】山东省青岛市2012届高三期末检测数学 (理科)【原题】（本小题满分12分）如图，在四棱锥S —ABCD 中，SD ⊥底面ABCD ，底面ABCD是矩形，且SD AD ==，E 是SA 的中点。

（1）求证：平面BED ⊥平面SAB ；（2）求平面BED 与平面SBC 所成二面角（锐角）的大小。

【试卷出处】唐山市2012届高三上学期期末考试数学试卷（理）【原题】（本小题满分14分）如图，在直三棱柱111ABC A B C -中，AB=AC=5,BB 1=BC=6,D,E 分别是AA 1和B 1C 的中点（Ⅰ）求证：D E ∥平面ABC ；（Ⅱ）求三棱锥E-BCD 的体积。

【试卷出处】江苏省苏北四市（徐、连、宿、淮）2012届高三元月调研测试（数学）【原题】（本题满分14分）如图，在梯形ABCD 中，//AB CD ， 2===CB DC AD ， 30=∠CAB ，四边形ACFE 为矩形，平面ACFE ⊥平面ABCD ，3=CF ．（Ⅰ）求证：BC ⊥平面ACFE ；（Ⅱ）设点M 为EF 中点，求二面角C AM B --的余弦值．【试卷出处】浙江省宁波市2012届高三第一学期期末考试数学（文）试卷【原题】（本题满分14分）已知四棱锥P ABCD -中，PA ABCD ⊥平面，底面ABCD 是边长为a 的菱形，120BAD ∠=︒，PA b =．（I ）求证：PBD PAC ⊥平面平面；（II ）设AC 与BD 交于点O ，M 为OC 中点，若二面角O PM D --的正切值为，求:a b 的值．【试卷出处】浙江省宁波市2012届高三第一学期期末考试数学（理）试卷（第20题）A B C D E M F E D B 1C 1A 1CB AF ED P 【原题】（本小题满分14分）如图①边长为1的正方形ABCD 中，点E 、F 分别为AB 、BC 的中点，将△BEF 剪去，将△AED 、△DCF 分别沿DE 、DF 折起，使A 、C 两点重合于点P 得一三棱锥如图②示.（1）求证：PD EF ⊥；（2）求三棱锥P DEF -的体积；（3）求点E 到平面PDF 的距离．【试卷出处】广东省揭阳市2011—2012学年度高三学业水平考试数学文试卷【原题】（本小题满分14分）如图，一简单组合体的底面ABCD 为正方形，PD ⊥平面ABCD ，EC //PD ，PD =2EC(1)PDA BE 平面求证：//(2)若2=ADPD ，求DE 与平面PDB 所成角的正弦值。

【试卷出处】温州市十校联合体2011学年第一学期高三期末联考数学试卷【原题】（本小题满分12分）如图，已知四棱台ABCD –A 1B 1C 1D 1的侧棱AA 1垂直于底面ABCD ，底面ABCD 是边长为2的正方形，四边形A 1B 1C 1D 1是边长为1的正方形，DD 1=2。

（ I ）求证：平面A 1ACC 1⊥平面B 1BDD 1；（Ⅱ）求四棱台ABCD -A 1B 1C 1D 1的体积；（Ⅲ）求二面角B —C 1C —D 的余弦值．【试卷出处】湖北省武昌区2012届高三年级元月调研测试数学（理）试卷【原题】(本小题满分13分)在三棱柱ABC —A 1B 1C 1中，底面是边长为32的正三角形，点A 1在底面ABC 上的射影O恰是BC 的中点．（Ⅰ）求证：A 1A ⊥BC ；（Ⅱ）当侧棱AA 1和底面成45°角时，求二面角A 1—A C —B 的大小余弦值；D P A B C E（Ⅲ）若D 为侧棱A 1A 上一点，当DAD A 1为何值时，BD ⊥A 1C 1．【试卷出处】2012届厦门市高三上期末质量检查数学模拟试卷（理）【原题】（本小题满分12分）如图，在四棱锥S-ABCD 中，底面ABCD 是正方形，四个侧面都是等边三角形，AC 与BD的交点为O ，E 为侧棱SC 上一点。