数学建模 戒烟问题
影响戒烟成功因素的分析--数学建模

影响戒烟成功因素的分析高利(理学院11信科1班)摘要:为了分析影响戒烟成功的主要因素,原题提供了包括234人的调查数据。
涉及的影响因素包括年龄、性别、每日抽烟只数、CO浓度和调整的CO浓度。
本文就是以234人的调查数据为基础,对数据进行处理和分析,利用计算机编程和数学模型的方法,探寻影响戒烟成功的主要因素,并在最后根据文本的相关研究结果对广大烟民提出建议。
问题一主要分析了不同年龄和不同性别的累加发病率分布情况,主要利用计算机编程,对原始数据进行分组、筛选和统计,并作出分布直方图。
经过分析得知男性的累加发病率为84.55%,女性的累加发病率为87.10%,略高于男性,青年人(18---40岁)累加发病率最高,为87.72%,中年人(41---65岁)次之,为84.68%,老年人(66岁)以后很少,为77.78%。
问题二是判断年龄、性别、每日抽烟支数、调整的CO浓度等因素哪些对戒烟时间有影响,并要求给出定量的分析。
针对此问题,本文只取戒烟天数小于365天的被调查者为研究对象,并把原始数据中空缺的数据行排除,首先画出个因素与戒烟天数的散点图,直接观察数据间的关系,再通过计算两组数据的相关,比较其绝对值的大小,定量的给个影响因素对戒烟天数的影响程度初系数ρxy步排序,处理结果为影响程度有大到小排序:CO浓度,每日抽烟支数,调整CO 浓度,年龄。
问题三利用建立适当的数学模型,讨论影响戒烟成功的主要因数,并对模型进行可靠性分析。
在这里主要建立了统计回归模型。
由于原始数据散点图比较散乱,不容易直接看出两组数据间的关系,也不方便直接处理,所以首先对原始数据做了预处理,等距分组,并求出每组戒烟天数的均值,以减小数据的波动,方便观察数据之间的宏观关系,再利用处理后的数据建模分析,通过建立统计回归模型对处理后的数据做了二次函数拟合,再进行回归分析,比较回归方程的决定系数R2等,进一步量化和判断不同因素对戒烟成功影响程度的大小,得到的结论是每天抽烟支数和CO浓度是影响戒烟成功的最主要因素。
一类具有阶段结构的戒烟模型的全局渐近稳定性

世 所共 知 , 吸烟 对公 共 卫 生 健康 有 严 重 的潜 在
在 吸烟者 与吸烟 者 的传 染 接触 率 系 数 , K 为 吸 烟者
危害. 虽然如此 , 仍然有很大 比例的成年公民和青少 年对此熟视无睹, 继续保持着铤而走险的抽烟习惯. G u l Z a ma n [ 1 ] 根据 吸烟数 量 的多 少把 研究 的人 群 分
在传染病动力 学 的研究 中, 基本 再生数 R 。 是
O O O O , 个非常重要的概念 , 它表示在发病初期 当所有人 均为易感者时, 一个病人在其平均患病期 内所传染 的人数 , 通常 R 。 一1 可作为决定疾病是否消亡的一 个 阈值. R。 < 1时 , 疾 病 逐步 消 亡 , 而 当 R。 > 1时 , 疾
S 1 S 2
‘ — —1 2 1
一
口2
系统( 1 ) 的各 个 方 程 相 加得 d N —o 因此 , 总人数 N
.
为常数 , 为方便起见 , 设 N_ -1 . 模型 中的 5 个方程都 是对 人 口的描述 ,因此 当 £ 一0时 , 所有 的变 量 和参
数都是正数 , 更进一步可 以得到系统( 1 ) 的解都在可 行域 : D={ ( S 1 , S 2 , I , T, 尺)∈ 群 : 0<
f o u n d t h a t i f R0 >1 ,t h e r e wi l l e x i s t a u n i q u e s mo k i n g - p r e s e n t e q u i l i b r i u m.C o r r e s p o n d i n g n u me r i c a l s i mu —
关键词 :无烟平衡 点;吸烟平衡点;基本再生数 ; 稳定 性 中图分类号 : 01 7 5 文献标识码 : A
2014年学校数学建模模拟赛(戒烟)

分析:由图表分析可得,距离抽最后一支烟的分钟数为 100-150 之间时累计发病率最高, 在 100-150 分钟段之前累积发病率逐渐升高,在其之后,累积发病率显著降低。
5.1.2 各因素交互作用影响下的累加发病率分布情况
对于之前的模型分析,我们只是考虑到单个因素对累加发病率的影响,并没有考虑到各 个因素之间可能会有交互作用,为此,我们利用 spss 的双因素相关性分析来分析每个因素 之间的相关性,并在此分析各因素之间的交互作用对累加发病率的影响,从而作出相关分 布图。 spss 的双因素相关性分析结果如下表 7 所示: 表7 x1 Pearson 相关 性 显著性 (双侧) N 1 双因素相关性分析表 相关性 x2 x4 x3 -.052 .476 193 .115 .111 193
我们参赛选择的题号是(从 A/B/C/D 中选择一项填写) : 我们的参赛报名号为(如果赛区设置报名号的话) : 所属学校(请填写完整的全名) : 参赛队员 (打印并签名) :1. 2. 3. 指导教师或指导教师组负责人 (打印并签名): 日期: 2014 年
B
8 月
27 日
赛区评阅编号(由赛区组委会评阅前进行编号):
6
分析:通过图表可得,20-30 岁抽烟支数在 10-20 支之间累积发病率最高,30-70 岁抽 烟支数在 20-30 支之间累计发病率最高, 70-80 岁抽烟支数在 10-20 支之间累计发病率最高, 综合观察可知 30-40 岁抽烟支数在 20-30 支之间累计发病率最高。 b. 不同性别下每日抽烟支数对累加发病率的影响
分析:有图表可以看出,累加发病率在 CO 浓度为 150-300 段达到最高,并在此之后, 随着 CO 浓度段的增加,累加发病率反而逐渐降低,累加发病率在 CO 浓度超过 750 之后累 加发病率极低, 这可能是因为 CO 浓度大于 300 的人数逐渐减少, 超过 750 的人数极少导致。
【原创】R语言广义回归模型戒烟对体重案例附代码数据

R语言广义回归模型戒烟对体重案例随机的实验不会有这种误差。
随机实验可以设计成,随机从一个总体中抽出一定数量的样本点,观测他们的各种变量如年龄,性别,名族,体重与是否戒烟等的关系。
随机戒烟实验和这个实验的主要差别在于,这个实验主要观测是否戒烟对体重的变化,而其他的变量会相互作用从而对是否戒烟这个变量产生干扰,从而产生潜在误差。
比较是有偏差的。
因为戒烟的样本和没有戒烟的样本除了是否戒烟这个变量的区别,还有其他的变量如性别,教育程度,第一次调查时的初始的体重,民族等都会影响样本的体重变化,因此如果直接以是否戒烟为自变量来分析体重的变化会导致结果不准确。
(c)prop.model<-glm(qsmk~sex+race+age+education.code+smokeintensity+smokeyrs+exercise+activ e+wt71, family = binomial(), data = nhefshwdat)#对我们要对总体样本执行广义回归模型(logit 回归),以是否戒烟为因变量,性别种族年龄教育程度等8个变量作为协变量,然后估计出每一个观测对象戒烟的概率是多少。
可以得到是否戒烟这个二元逻辑变量与其他协变量的线性回归关系。
nhefshwdat$p.qsmk.obs <- ifelse(qsmk == 0, 1 - predict(prop.model, type = "response"),+ predict(prop.model, type = "response"))#用上一步得到的模型预测每一个观测对象的戒烟概率为多少,并赋值给p.qsmk.obs这个变量。
X <- prop.model$fitted#对nhefshwdat数据集中原始数据进行拟合Y <- nhefshwdat$wt82_71#Y为观测对象从71年到82年的体重变化Tr <-nhefshwdat$qsmk#Tr为观测对象是否戒烟library(Matching)#读取Matching包rr <-Match(Y=Y,Tr=Tr,X=X,M=1)#使用Match命令,对于每个戒烟的观测对象,找出一个与之具有最接近的概率值的,可是抽烟的观测对象,使得任何戒烟的观察对象的对照对象都具有唯一性,换言之,只能1对1匹配。
2012-2013上学期:数学建模期末测试问题
请用数学建模的方法解决下列问题(选做一题)
1.(盐水混合问题)一个圆柱形的容器,内装350L的均匀混合的盐水溶液,如果纯水以每秒14L的速度从容器顶部流入,同时,容器内的混合的盐水以每秒10.5L的速度从容器底部流出.开始时,容器内盐的含量为7kg.求经过时间t后容器内盐的含量.
2.(吸烟与健康问题)调查了339名50岁以上人群中吸烟习惯与患慢性气管炎的关系后,结果如表1所示.
试问吸烟习惯与慢性气管炎是否有关?
3.某饮料厂生产甲、乙两种产品,一件甲用A原料1kg,B原料5kg;一件乙用A原料2kg,B原料4kg.现有A原料20kg,B原料70kg.甲、乙产品每件售价分别为20元和30元.试问如何安排生产使收入最大?
(注)数学建模方法应包括以下步骤:“问题分析——模型假设——模型建立——模型检验与求解——结论及应用”.(不少于1500字,要求交电子版和纸质版.)。
戒烟影响因素分析模型与实证研究

戒烟影响因素分析模型与实证研究戒烟影响因素分析模型与实证研究【摘要】目的:探讨影响戒烟成功的主要因素,以此引起烟民对戒烟的重视,从而成功从根本上进行戒烟。
方法:使用偏相关分析、多元线性回归、t检验、因子分析等方法,分别构建了多元线性回归、因子分析等模型,使用EXCEL、MATLAB、SPSS 等软件处理数据和编程,在此根底上建立多元回归模型而后进行评价。
结果:多元线性回归模型说明了各个影响因素与戒烟成功之间的定量的关系,因子分析模型阐述了影响戒烟成功的主要因素。
结论:通过建立的多元回归模型,找出了各个影响因素对戒烟的定量影响关系,同时因子分析得出了每日抽烟支数、CO浓度和调整的CO浓度就是影响戒烟成功的主要因素,故而降低抽烟数量可以有效地进行戒烟。
【关键词】戒烟影响因素评价因子分析吸烟有害健康,不仅仅危害自身健康,尤其是周围被迫吸收二手烟的人群,他们的身心都会被受到伤害。
目前全世界约有11亿吸烟者,其中70%以上的烟民分布在开展中国家。
而作为最大的开展中国家,中国是全球最大的卷烟生产国和消费国,中国吸烟人数占世界吸烟者总数的近30%,居首位,我国每年吸烟导致的死亡人数超过100万,如此现状不加改变,到2021年,我国归因于吸烟的死亡人数将上升至200万,占总死亡的比重将上升33%。
同时,我国每年还有10万人死于二手烟。
近年来我国虽然先后在154个地区颁发了禁止吸烟的规定,但是效果甚微。
为此,如何帮助相关人士摆脱烟瘾的困扰也就成为一个重要的研究课题。
从现有的研究结果看,国外研究显示,吸烟者戒烟与吸烟者的人口学特征、戒烟的决心、尼古丁依赖程度和既往的戒烟经历有关。
国内的研究相对较少,李恂【8】研究的吸烟者自身意愿因素,文其岭的研究中说明戒烟受人们所处的社会环境的因素的影响,导致戒烟成功率较低,有调查显示认为吸烟者的知识水平与每日抽烟支数有关。
前人的研究成果给予了研究重要的参考,但是本文运用了同前人不同的定量分析方法,并运用因子分析法使结果更加准确科学。
九年级数学上册23.3方差戒烟素材冀教版(new)

戒烟10个人在戒烟前和戒烟五星期后的体重记录如下(单位:kg)人员: .戒烟前:67,80,69,52,52,60,55,54,64,60。
戒烟后:70,81,68,55,57,62,54,52,67,58。
(1)求这10人在戒烟前和戒烟后的体重的平均数和中位数;(2)求这10人在戒烟前和戒烟后的体重的方差.解:因涉及中位数,故需要将数据按从小到大的顺序重排:戒烟前:52,52,55,55,60,60,64,67,69,80。
戒烟后:52,54,55,57,58,62,67,68,70,81.戒烟前: (kg)。
戒烟后: (kg)。
中位数分别为:戒烟前中位数。
戒烟后中位数。
方差分别为:戒烟前。
戒烟后。
说明:从戒烟前后两组数据的统计量进行对比可知,戒烟后,这10人的平均体重增加了1kg,中位数没有变化,说明这两组数据集中趋势变化不大.从方差可知,戒烟后数据的波动比戒烟前数据的波动大,说明戒烟对不同的人所发生的变化程度不同。
通过对这两组数据的统计分析,可以得出戒烟对身体健康有益的结论,从而为实现方便决策服务。
尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
戒烟干预模型
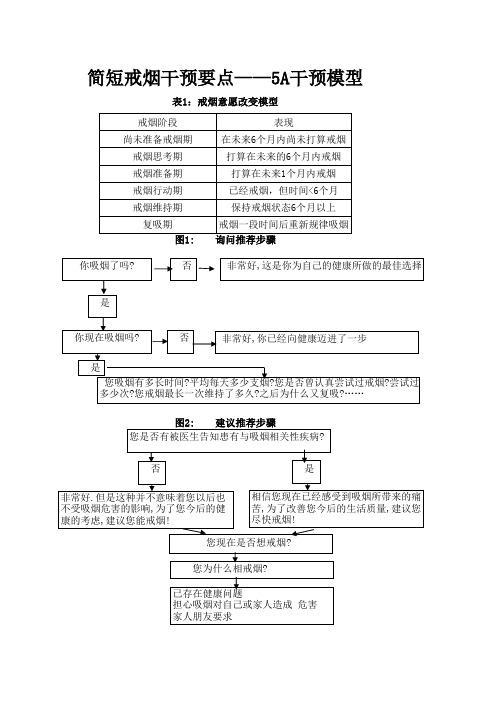
表2:尼古丁依赖检验量表(FTND)
问题 你早晨醒来后多长时间吸第一支 烟? 您是否在许多禁烟场所很难控制吸 烟的需求? 您认为哪一支烟您最不愿意放弃?
您每天抽多少支烟?
您卧病在床时仍旧吸烟吗? 您早晨醒来后第1个小时是否比 其他时间吸烟多?
答案 5分钟内 5—30分钟 31—60分钟 60分钟
是 否 早晨第一支 其他 ≤10支 10—20支 21—30支 ≥31支 是 否 是 否
相信您现在已经感受到吸烟所带来的痛 苦,为了改善您今后的生活质量,建议您 尽快戒烟!
您现在是否想戒烟?
您为什么相戒烟?
已存在健康问题 担心吸烟对自己或家人造成 危害 家人朋友要求
图3:评估推荐步骤 您是否打算在未来1个月内开始戒烟?
是
否
准备戒烟者
尚未准备戒烟者
您早晨起床之后是否马上就想吸烟? 在禁止吸烟的场所,您能否控制烟瘾?
分值 3 2 1 0 1 0 1 0 0 1 2 3 1 0 1 0
图4:帮助推荐步骤
图5:随访推荐步骤
准备戒烟
尚未准备戒烟者 过去1周(1个月,3个月)内,您是否还在戒烟?
我们是否可以讨论 我们是否可以讨
一下制定一份戒烟 论一下您对吸烟
计划?
危害的认
提供戒烟材料 转诊到戒烟门
提供戒烟材料 简短的动机干
简短戒烟干预要点——5A干预模型
表1:戒烟意愿改变模型
戒烟阶段 尚未准备戒烟期
戒烟思考期 戒烟准备期 戒烟行动期 戒烟维持期
复吸期 图1:
表现 在未来6个月内尚未打算戒烟 打算在未来的6个月内戒烟
打算在未来1个月内戒烟 已经戒烟,但时间<6个月 保持戒烟状态6个月以上 戒烟一段时间后重新规律吸烟 询问推荐步骤
数学建模 戒烟问题

2014高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料我赛):2014高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):摘要本文针对戒烟和各种相关因素关系,解决影响戒烟成功的因素有哪些的问题,我们利用Excel,spss,Matlab软件对相关数据进行分析,利用主成分分析法、层次分析法建立模型,并进行可靠性检验,得到影响戒烟成功的重要因素,对有志于戒烟的人士提供戒烟对策和建议。
针对问题一,首先观察数据发现数据残缺,运用spss中缺失值替换的线性插值法将缺失数据补充完整。
然后求出在不同年龄段、不同性别、不同调整CO浓度下、不同每日抽烟数的条件下的发病累加率,并运用Excel,Matlab,Spss的等软件做出图像,结合图像对发病累加率的分布进行分析,得到累加发病率的基本趋势为随着每日抽烟数和调整CO浓度的增加而提高,男性比女性的累加发病率略低。
浓yy一、问题的重述众所周知,吸烟不仅危害自身健康,而且由此引起的被动吸烟更是危害公众身心健康的主要原因。
为此,如何帮助相关人士摆脱烟瘾的困扰也就成为一个重要的研究课题。
本文研究数据涉及234人,他们都自愿表示戒烟但还未戒烟。
在他们戒烟的这一天,测量了每个人的CO(一氧化碳)水平并记下他们抽最后一支烟到CO测定时间.。
CO的水平提供了一个他们先前抽烟数量的客观指标,但其值也受到抽最后一支烟的时间的影响,因此抽最后一支烟的时间可以用来调整CO的水平。
记录下研究对象的性别、年龄及自述每日抽烟支数。
最新影响戒烟成功的因素分析数模26545507

影响戒烟成功的因素分析数模26545507影响戒烟成功的因素分析数学建模论文摘要本论文通过对戒烟者的年龄、性别、每日抽烟支数及调整的CO 浓度等因素的数量变化分析说明影响戒烟成功的因素,分段讨论不同因素下的累加发病率分布情况,用相关系数讨论影响戒烟时间的因素,用多元线性回归讨论影响戒烟成功的主要因素有哪些,建立出三个相应的模型。
针对问题一,利用数理统计与概率的知识分别在不同年龄段、不同性别等因素下对234名烟民进行分段,设再次吸烟的人数为p ,总人数为p 总,统计累加发病率∑P ,建立一个较为简单的模型。
∑=P 总p p针对问题二,利用相关系数和平均数的方法分两步来讨论分析影响戒烟时间的因素:(1)对于戒烟时间受年龄、每日抽烟支数及调整的CO 浓度等因素的影响的差异,首先分别求戒烟时间y 与年龄、每日抽烟支数及调整的CO 浓度等因素即x n 的相关系数。
以戒烟时间与不同因素分别对应的相关系数r 为基础,建立相应的模型.∑∑∑----=22)()())((y y x x y y x x r然后根据不同的r 讨论影响戒烟时间的因素。
(2)对于性别对戒烟天数的影响,我们分别求出不同性别对应的戒烟天数t 的平均值,再进行比较,由此得出性别对戒烟天数的影响。
x =nt(n 为不同性别对应的人数) (3)另外,我们分别绘制出戒烟时间与年龄、每日抽烟支数及调整的CO 浓度等因素的散点图,由点的分布更直观地体现不同因素对戒烟时间的影响程度。
针对问题三,把戒烟天数作为戒烟成功的标准,运用多元线性回归的知识,由于在问题一和二的解答中,我们得知性别对戒烟情况影响不大,所以只把年龄,每日抽烟支数,CO 浓度,调整的CO 浓度四个因素作为自变量X ,戒烟天数作为Y ,建立新的模型:Y=εβββββ+++++LogCoadj co Day Cig Age X X X X 43_210通过本模型分析各种因素与成功戒烟之间的关系,确定了影响戒烟成功的因素。
数学建模影响戒烟成功因素的分析

题目:影响戒烟成功的因素分析姓名1:许沛韩姓名2:马雪瑜姓名3:秦栋2012年8月20日星期一目录摘要 (3)关键词 (3)问题重述 (4)问题分析 (5)建模过程 (5)问题一 (5)模型假设与约定 (5)符号说明及名词定义 (6)模型建立与求解 (6)问题二 (9)模型假设与约定 (9)符号说明及名词定义 (9)建立模型进行求解 (9)问题三 (15)模型假设与约定 (15)符号说明及名词定义 (15)建立模型进行求解 (16)问题四 (18)模型优缺点 (19)参考文献及参考书籍和网站 (19)附录 (20)摘要据调查,中国是烟草生产和消费大国,生产和消费均占全球三分之一以上。
目前,中国约有3.5亿吸烟者,尽管与之前相比吸烟率略有下降,但是随着中国总人口的增加,吸烟人数仍然在增加。
为了帮助相关人士摆脱烟瘾的困扰,研究小组对234个自愿表示戒烟但还未戒烟的人进行调查,并记录下了调查的数据。
根据数据,我们对戒烟成功的因素、再次吸烟的累加发病率和影响戒烟时间长短的因素进行分析。
在分析过程中,我们利用MATLAB和SAS统计工具对数据进行拟合并进行逐步多元回归分析和方差分析,其次在建立模型时我们还利用了残差分析法发现了模型的缺陷,并及时引入交互作用项来对模型进行修改。
而在分析再次吸烟的累加发病率时,我们用控制变量法对各个影响因素的数据进行控制并在Excel中用直方图表现出来,使其看起来直观易懂。
最后,通过了对其建立起模型分析,得出了影响戒烟成功的因素有每天抽烟的支数、CO的浓度和调整的CO 浓度等三个因素,而影响戒烟时间长短除了上述三个因素外则还有性别的因素在影响。
关键词累加发病率、CO的浓度、调整的CO浓度为了帮助相关人士摆脱烟瘾的困扰,研究小组展开了调查,对234个自愿表示戒烟但还未戒烟的人进行调查. 在他们戒烟的这一天, 测量了每个人的CO(一氧化碳)水平并记下他们抽最后一支烟到CO 测定的时间. CO的水平提供了一个他们先前抽烟数量的客观指标,但其值也受到抽最后一支烟的时间的影响, 因此抽最后一支烟的时间可以用来调整CO 的水平. 记录下研究对象的性别、年龄及自述每日抽烟支数.这个调查跟踪1年, 考察他们一直保持戒烟的天数, 由此估计这些人中再次吸烟的累加发病率, 也就是原吸烟者戒烟一段时间后又再吸烟的比例. 戒烟天数是从0到他(她)退出戒烟或研究截止时间(1 年)的天数.假定他们全部没有人中途退出研究.1)试分析上述234人中再次吸烟的累加发病率在不同因素下的分布情况。
利用模型进行_拒绝吸烟_一节概念教学_洪剑

因,理解长期吸烟对人体呼吸道和肺部刺激,可能 诱发慢性支气管炎和肺癌。
前概念 2:吸烟只是个人行为,不会伤害到别 人。学生往往将吸烟看成是个人行为,其实吸烟已 经危害到公共卫生。 吸烟不仅仅是个人生活方式 的选择,还可能对别人造成危害。吸烟时直接呼出 或香烟燃烧产生的烟雾中含有一氧化碳、尼古丁、 刺激性物质、致癌物质等,可导致周围人群被动吸 二手烟,危害其身体健康;吸烟者“吞云吐雾”后 会在衣服、墙壁、地毯、家具甚至头发和皮肤等表 面残留致癌物质。此外,吸烟还会对下一代产生影 响。 孕妇吸烟将会使胎儿患先天严重畸形的风险 增 加 50%。 大 量 研 究 显 示 , 与 父 母 不 吸 烟 的 儿 童 相比,父母吸烟的儿童成年后更容易成为吸烟者。 因此,教学时,教师可通过提问:为什么我国通过 《公共场所控制吸烟条例》, 以法令的形式禁止在 室内和公共场所吸烟?引导学生思考探索,从而转 变学生错误的前概念,构建“二手烟会污染环境, 危害周围人健康”的科学概念。
“拒绝‘朋友’的第 1 支烟”,形成“珍爱生命,远离 6 教学过程
香烟,选择健康”的生活方式的情感态度。
6.1 创设情境,导入新课 首先,学生通过观看
本节课的概念构建设计如图 1 所示。
《禁烟》宣传片,初步了解吸烟有害身体健康。 教
重要概念 选择健康的生活方式 (个人的生活习惯与行为 选择能对一生的健康产生
对自身的身体健康会造成极大危害。
丰富内涵
转化
转化
转化
前概念 1 吸烟有害健康
前概念 2 吸烟只是自己的事,
不会伤害到别人
前概念 3 吸烟能增加 自身的吸引力
对吸烟的危害数学建模

对吸烟的危害数学建模摘要众所周知,吸烟不仅危害自身健康,而且由此引起的被动吸烟更是危害公众身心健康的主要原因。
为此,如何帮助相关人士摆脱烟瘾的困扰也就成为一个重要的研究课题。
本文对题中所给数据进行深入细致的处理和分析,利用EXCEL 作图,MATLAB 拟合和SPSS 相关性检验建立数学模型,探寻影响戒烟成功的主要因素,并在最后根据本文的相关研究结果对广大有志于戒烟的烟民提出了几条科学合理的建议。
针对问题一,为了能够直观的看出再次吸烟者的累加发病率的分布情况,利用数理统计分析知识和EXCEL 知识对各影响因素的调查数据进行的筛选、分组和数值统计,采用控制变量法分别对性别,年龄,每日抽烟支数,CO 浓度和调整CO 浓度分别进行分析,用数理统计知识进行分组、统计,整理出再次吸烟者累加发病率条形分布图,即得到再次吸烟者的累加发病率分布情况。
针对问题二,考虑到要定量分析年龄、性别、每日抽烟支数及调整的CO 浓度等因素会影响戒烟时间即天数的长短。
首先用EXCEL 进行数据筛选,删掉缺失的数据,其次,对224名戒烟时间一样的研究对象的不同影响因素的数据求均值,建立统计回归模型,并结合MATLAB 统计工具进行多次去点拟合,得到回归系数,用多重判断系数2R 评价模型拟合的优度,用检验统计量F 、p 等判断自变量对因变量的影响是否显著,最后,用SPSS 的Pearson 相关性检验,找出可靠性较高的模型,用控制变量法对线性回归模型进行定量分析,得出关系式为:2354313402.00842.01984.03477.166518.13730.207x x x x x d ++---=针对问题三,在问题二分析的基础上可知戒烟是否成功可用戒烟时间的长短来刻画,则戒烟成功的因素有研究对象的每日抽烟支数、CO 浓度及调整的CO 浓度,建立多元线性统计回归模型,并结合MATLAB 统计工具进行统计回归分析,经过多次去点拟合, 得到回归系数,进一步写成回归方程,经过可靠性分析,即可得出影响戒烟成功的主要因素为每日抽烟支数。
基于“5R、5A”模型的综合戒烟软件框架设计

交互 、渠道推送 、群体干预等功能的干预服务 。结论 :综合戒烟软件设计遵循最新 临床戒烟指南, 以科学的理论 为依据 ,采
取科学 的实践方法 ,综合运用健康管理 的各种手段方法 ,提升健康干 预的互动性 ,为有效控烟开辟新路径 。
关键词 干预 模型 戒烟 软件 框架设计
Doi:10.3969/j.issn.1673 号 】R319;TP391
【文献 标识码】A
Design of the Comprehensive Smoking Cessation Software Framework Based on”5R and 5A”Model/CHEN Li—chao.SUN Jin— hai,CHEN Li—fu//China Digital M edicine.一2018 13(8):73 tO 75 Abstract Objective:Design a comprehensive anti——smoking software based on the clinical guidelines for smoking cessation tO guide
指 导,综 合运用心理 、行为 、社会支持和 临床等干预手段 ,为戒烟者提供教育、咨询 、心理疏导 、随访和线上线下结合 的戒
烟服 务。结果:综合戒烟软件包括数据采集评估 、戒烟认知干预 、制定 戒烟 方案 、戒烟过 程干 预、戒烟复吸干预5项基本流
程 ,根据戒烟者 的具体情况提供立即戒断法 、逐 日减量法 、逐 日推迟法三种戒烟方法 ,并提供集数据分析、反馈激励 、社群
基于 ‘5G 模型的综合戎烟袄件框架设计
陈礼 潮 ①② 孙金 海 陈立 富①
摘 要 目的:设计一款基于 临床戒烟指南的综合 戒烟软件 ,指 导吸烟者科学戒烟。方法 :该戒烟软件设计 以 《中国临床 戒
基于IMB模型的江苏省青少年吸烟预防行为影响因素结构方程模型分析

目前 ,烟草 危 害 已成 为 我 国重要 的公 共卫 生 问题 。 预 防控 制 中心根 据 我 国 国情 增加 了部 分 问题 形成 最终
调 查显 示 ,我 国每年 有 近 136.6万人 死 于 吸 烟 相 关疾 问卷 ,最终 问卷 通 过 了 GYTS调 查 问卷 审 查 委 员会 的
病 ,其 中超 过 10万 人 死 于 二手 烟暴 露 ¨ ,给 家 庭 和 社 批 准 。
会带来沉重的疾病和经济负担 。青少年好 奇心强 ,从
3.调查 内容 问卷 内容 包 括 :(1)性 别 、年 龄 、年
众心理 明显 ,缺乏对长期吸烟导致慢性健康危 害的认 级等 一 般人 口学 特 征 ;(2)青 少 年 的 吸 烟 及 二 手 烟 暴 知 ,并 且 由于尼古 丁 的致 瘾 性 ,一 旦 开 始 吸 烟 ,大 部 分 露情 况 ;(3)青少 年控 烟 的知识 、态 度情 况 等 。
查 ,首次 建立 青 少年 吸烟 预 防行 为结 构方 程模 型 ,阐明 信息 、动 机 以及行 为 技 巧 各 个 变 量 间 的关 系并 探 讨 青
结 果
少 年吸 烟 预防行 为 的 影 响 因 素 ,为 制 定 青 少 年 控 烟 策
1.基 本 情 况 共 发放 5702份调 查 问 卷 ,回 卷 5697份 ,有 效 回收 率 99.9l%。其 中,男 生
资料 与方 法
3083人 (54.1% ),女 生 2614人 (45.9% );城 市 学 生 2289人 (40.2% ),农 村学 生 3408人 (59.8% );初 一 学
1.资料来 源 选 取 2013年 9月 一11月 在江 苏 省 生 1896人 (33.3% ),初 二 学 生 1949人 (34.2% ),初
影响戒烟成功的因素分析数模论文

影响戒烟成功的因素分析数学建模论文摘要本论文通过对戒烟者的年龄、性别、每日抽烟支数及调整的CO 浓度等因素的数量变化分析说明影响戒烟成功的因素,分段讨论不同因素下的累加发病率分布情况,用相关系数讨论影响戒烟时间的因素,用多元线性回归讨论影响戒烟成功的主要因素有哪些,建立出三个相应的模型。
针对问题一,利用数理统计与概率的知识分别在不同年龄段、不同性别等因素下对234名烟民进行分段,设再次吸烟的人数为p ,总人数为p 总,统计累加发病率∑P ,建立一个较为简单的模型。
∑=P 总p p针对问题二,利用相关系数和平均数的方法分两步来讨论分析影响戒烟时间的因素:(1)对于戒烟时间受年龄、每日抽烟支数及调整的CO 浓度等因素的影响的差异,首先分别求戒烟时间y 与年龄、每日抽烟支数及调整的CO 浓度等因素即x n 的相关系数。
以戒烟时间与不同因素分别对应的相关系数r 为基础,建立相应的模型.∑∑∑----=22)()())((y y x x y y x x r然后根据不同的r 讨论影响戒烟时间的因素。
(2)对于性别对戒烟天数的影响,我们分别求出不同性别对应的戒烟天数t 的平均值,再进行比较,由此得出性别对戒烟天数的影响。
x =nt(n 为不同性别对应的人数) (3)另外,我们分别绘制出戒烟时间与年龄、每日抽烟支数及调整的CO 浓度等因素的散点图,由点的分布更直观地体现不同因素对戒烟时间的影响程度。
针对问题三,把戒烟天数作为戒烟成功的标准,运用多元线性回归的知识,由于在问题一和二的解答中,我们得知性别对戒烟情况影响不大,所以只把年龄,每日抽烟支数,CO 浓度,调整的CO 浓度四个因素作为自变量X ,戒烟天数作为Y ,建立新的模型:Y=εβββββ+++++LogCoadj co D ay Cig Age X X X X 43_210通过本模型分析各种因素与成功戒烟之间的关系,确定了影响戒烟成功的因素。
最后,我们对模型的科学性和现实性进行了阐述,并得到了对模型的整体评价,及急需改进之处。
数学建模-吸烟

问题 • 过滤嘴的作用与它的材料和长度有什么关系
• 人体吸入的毒物量与哪些因素有关,其中哪 些因素影响大,哪些因素影响小。
模型 • 分析吸烟时毒物进入人体的过程,建立吸 分析 烟过程的数学模型。
• 设想一个“机器人”在典型环境下吸烟, 吸烟方式和外部环境认为是不变的。
模型 假设
1)l1~烟草长, l2~过滤嘴长, l = l1+ l2, 毒物量M均匀分布,密度v q(x), 0 x l1
q(x), l x l
v
1
q(0) aH 0 H 0 uw0
1) 求q(x,0)=q(x)
q(x) a aH H 0 0e e b bvv1lx,e(xvl1),
2) 求q(l,t)
0xl1 l1 xl
t时刻,香烟燃至 x=ut H (t)u(w u,tt)
模 t=0, x=0,点燃香烟
q( x) q(xx)
型 q(x,t) ~ 毒物流量
v
建 w(x,t) ~ 毒物密度
立 w(x,0)w 0
0
x xx l 1
lx
1) 求q(x,0)=q(x) Q 0 Tq (l,t)d,tT l1/u
q ( x ) q ( x x ) b q ( ( x x ) q ) , ,0 l 1 x x l l 1 , , v x
aw v l2
Q
e 0
v
1 ab
1ea'v b1l
不带过滤嘴
Q2 aa'w b 0vebv2l 1ea'v b1l
Q
( b )l2
1 e v
Q2
b Q 1Q 2
提高 -b 与加长l2,效果相同
2023深圳杯数学建模赛题

2023深圳杯数学建模赛题摘要:1.2023年深圳杯数学建模赛题概述2.问题1:分析居民饮食习惯的合理性3.问题2:分析生活习惯与年龄、性别、婚姻状况、文化程度、职业等因素的关系4.问题3:分析慢性病与吸烟、饮酒、饮食习惯、生活习惯、工作性质、运动等因素的关系及程度5.问题4:对居民进行合理分类并提出有利于身体健康的膳食、运动等方面的建议正文:2023年深圳杯数学建模赛题主要关注慢性非传染性疾病对我国居民身体健康的影响。
慢性非传染性疾病,如心脑血管疾病、糖尿病、恶性肿瘤以及慢性阻塞性肺病等,已经成为影响我国居民身体健康的重要问题。
随着人们生活方式的改变,慢性病的患病率持续攀升。
本题要求分析居民的饮食习惯、生活习惯与各种因素的相关性,以及慢性病与吸烟、饮酒、饮食习惯、生活习惯、工作性质、运动等因素的关系。
问题1要求参考附件A3,分析附件A2中居民的饮食习惯的合理性,并说明存在的主要问题。
通过分析,我们可以发现居民在饮食方面存在的一些不合理之处,如摄入盐分过多、油脂摄入不当等。
这些问题需要引起广泛关注,以促进居民饮食习惯的改善。
问题2要求分析居民的生活习惯和饮食习惯是否与年龄、性别、婚姻状况、文化程度、职业等因素相关。
通过统计分析,我们可以得出这些因素与居民的生活习惯和饮食习惯确实存在一定的相关性。
例如,年龄较大的居民更可能存在慢性病,而文化程度较高的居民往往更加注重健康饮食。
问题3要求深入分析常见慢性病(如高血压、糖尿病等)与吸烟、饮酒、饮食习惯、生活习惯、工作性质、运动等因素的关系以及相关程度。
通过多元线性回归等方法,我们可以得出这些因素与慢性病的发生存在不同程度的关联。
例如,吸烟与高血压的关系最为密切,饮酒与糖尿病的关系也相当显著。
问题4要求根据附件A2中居民的具体情况,对居民进行合理分类,并针对各类人群提出有利于身体健康的膳食、运动等方面的合理建议。
我们可以根据居民的年龄、性别、生活习惯等因素将其分类,然后针对不同类别的人群给出相应的膳食和运动建议,以帮助他们改善生活习惯,预防慢性病的发生。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B题我们的参赛报名号为(如果赛区设置报名号的话): 79 所属学校(请填写完整的全名):河南理工大学参赛队员 (打印并签名) :1.2.3.指导教师或指导教师组负责人 (打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期: 2014 年 9 月 3 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):摘要本文针对戒烟和各种相关因素关系,解决影响戒烟成功的因素有哪些的问题,我们利用Excel ,spss ,Matlab 软件对相关数据进行分析,利用主成分分析法、层次分析法建立模型,并进行可靠性检验,得到影响戒烟成功的重要因素,对有志于戒烟的人士提供戒烟对策和建议。
针对问题一,首先观察数据发现数据残缺,运用spss 中缺失值替换的线性插值法将缺失数据补充完整。
然后求出在不同年龄段、不同性别、不同调整CO 浓度下、不同每日抽烟数的条件下的发病累加率,并运用Excel ,Matlab ,Spss 的等软件做出图像,结合图像对发病累加率的分布进行分析,得到累加发病率的基本趋势为随着每日抽烟数和调整CO 浓度的增加而提高,男性比女性的累加发病率略低。
针对问题二,首先用spss 做其它各变量与戒烟天数的相关性分析,得到显著性(双侧)值,CO 浓度和戒烟天数0.01水平显著相关,距离最后一支烟的分钟数和调整的CO 浓度与戒烟天数0.05水平显著相关;然后,根据题意,CO 浓度和距离最后一支烟的分钟数共同影响调整的CO 浓度;可以得到每日抽烟数和调整的CO 浓度会影响戒烟时间(天数)长短。
最后,对相关变量的数据进行分组,在不同区间对戒烟天数求平均值,然后用spss 回归分析中曲线估计对数据进行拟合,再用MATLAB 拟合求回归方程中系数的置信区间来分析拟合效果。
得到每日抽烟和戒烟天数的回归方程为33323008.0760.0711.22633.278x x x y -+-=,2R =0.948,F=12.038,Sig=0.078,可得拟合效果较好;调整的CO 浓度和戒烟天数的回归方程为34824610784.110436.6306.117x x y --⨯-⨯+=,2R =0.785,F=12.799,Sig=0.005,拟合的较好。
针对问题三,我们认为CO 浓度和距抽最后一支烟的分钟数是来控制调整CO 浓度的,这两个因素可以用调整CO 浓度说明,因此在考虑戒烟成功主要因素时没有针对这两个因素讨论,那么可以假定戒烟成功受年龄,性别,每日抽烟数以及调整CO 浓度影响。
就这四个因素建立层次分析,探究每个因素对戒烟成功的影响。
先用主成分分析法对影响因素探究,再运用层次分析法,根据主成分分析得到的累计贡献率来建立判断矩阵,并算出各成分的权向量。
结果显示影响戒烟成功的因素主要为每天抽烟数,调整CO 浓度和年龄。
其比重分别为37.15%,25.00%,23.22%。
通过一致性检验,判断矩阵具有满意一致性,可以为模型提供可靠分析。
针对问题四,我们根据前三问所得结果向有志于戒烟的人士提供相应的戒烟对策及建议,撰写的报告具体见5.4问题四的求解。
关键字:线性插值法 相关性分析 回归分析 主成分分析 层次分析法一、问题的重述众所周知,吸烟不仅危害自身健康,而且由此引起的被动吸烟更是危害公众身心健康的主要原因。
为此,如何帮助相关人士摆脱烟瘾的困扰也就成为一个重要的研究课题。
本文研究数据涉及 234人,他们都自愿表示戒烟但还未戒烟。
在他们戒烟的这一天,测量了每个人的CO(一氧化碳)水平并记下他们抽最后一支烟到CO测定时间.。
CO的水平提供了一个他们先前抽烟数量的客观指标,但其值也受到抽最后一支烟的时间的影响, 因此抽最后一支烟的时间可以用来调整CO的水平。
记录下研究对象的性别、年龄及自述每日抽烟支数。
这个调查跟踪1年, 考察他们一直保持戒烟的天数, 由此估计这些人中再次吸烟的累加发病率, 也就是原吸烟者戒烟一段时间后又再吸烟的比例. 其中假设原烟民戒烟的可信度是很低的(更恰当地说多数是再犯者)戒烟天数是从0到他(她)退出戒烟或研究截止时间(1年)的天数。
假定他们全部没有人中途退出研究。
请回答下列问题:1)试分析上述234人中再次吸烟的累加发病率分布情况(如不同年龄段、不同性别等因素下的累加发病率分布情况)。
2)你认为年龄、性别、每日抽烟支数及调整的CO浓度等因素会影响戒烟时间(天数)长短吗?如果影响请利用附录中的数据,分别给出戒烟时间与上述你认为有影响的因素之间的定量分析结果。
3)请利用附录中的数据建立适当的数学模型,讨论影响戒烟成功的主要因素有哪些,并对你的模型进行可靠性分析。
4)请根据你的模型,撰写一篇500字左右的短文,向有志于戒烟的人士提供戒烟对策和建议。
二、模型的假设1、原烟民戒烟天数不足365天的数据都是可靠的;2、原烟民戒烟的可信度很低,可以说他们多数是再犯者;3、自愿者中全部没有人中途退出研究。
四、问题的分析4.1问题一的分析针对问题一,首先对缺失数据进行补充,然后求出在不同因素下,不同年龄段、不同性别、不同每日抽烟数、不同调整CO浓度条件下的累加发病率的分布情况,并作出图表,进行分析。
4.2问题二的分析针对问题二,首先对其它各变量与戒烟天数的相关性分析,得到和戒烟天数相关的变量,然后根据题意,得到会对戒烟天数长短的变量。
对相关变量的数据进行分组处理,求不同区间内戒烟天数的平均值,把组距中间值作为那一组的数值,用spss和MATLAB 对数据进行处理得到相关变量和戒烟天数的定量分析结果。
4.3问题三的分析我们认为CO浓度和距抽最后一支烟的分钟数是来控制调整CO浓度的,这两个因素可以用调整CO浓度说明,因此在考虑戒烟成功主要因素时没有针对这两个因素讨论,那么可以假定戒烟成功受年龄,性别,每日抽烟数以及调整CO浓度影响。
就这四个因素建立层次分析,探究每个因素对戒烟成功的影响。
五、模型的建立与求解5.1问题一的求解5.1.1问题一模型的建立观察附录可以发现,附录中所给数据缺失,为了更加全面的进行分析,首先我们使用spss中缺失值分析命令对于数据进行分析,结果如下。
所给数据缺失率为0.0446,缺失率较小,可以利用spss 进行补充,然后使用缺失值替换命令进行数据的补充,经过对已有数据的分析,决定使用线性差值法进行补充,补充后数据见附表。
为了直观得了解所有234人的总体戒烟情况,作出如下散点图:图5.1.1由图5.1.1看出,被调查的234人中大多数经过很短时间后又再次抽烟,只有少数人戒烟天数达到365天,只占总人数的14.10%,本文假设在研究截止时间内没有再抽烟的烟民戒烟成功,所以累加发病率的具体定义为戒烟天数小于365的烟民数量占研究样本总人数的比例,本文据此对在不同性别、年龄、每日抽烟数、调整后CO 浓度的情况下对累加发病率进行比较和分析。
首先运用spss 做出男性与女性吸烟者的戒烟天数频率分布图,并求出男性与女性的累加发病率,做出图像,图表如下。
图5.1.2表5.1.2由图5.1.2看出男性与女性再次吸烟的累加发病率分布情况相差不大,而由表5.1.1可以发现男性累加发病率为0.845,略低于女性的0.871。
年龄:通过对所给数据进行分析可以得到参与研究人员的年龄跨度为22—72,所以本文将所有参与研究人员的年龄分为6段,分别为20—29、30—39、40—49、50—59、60—69、70—79,经过统计可以得到不同年龄段的累加发病率的分布,如图所示。
通过表5.1.3和图5.1.1可以看出30-59年龄段的累加发病率较低,70岁以上的被研究者累加发病率最低,60-69年龄段的被研究者的累加发病率最高。
每日抽烟数:首先用Matlab 做出每日抽烟数跟戒烟天数的散点图图5.1.5通过对数据的分析可发现每日抽烟数的跨度为2—90,所以将每日抽烟数分为7个档次,分别为1—10、11—20、31—40、41—50、51—60、60以上,求出其累加发病率,并做成图表,如下。
通过观察图表可得,每日抽烟数60以上的样本数过少具有偶然性,所以在分析时,可适当忽略,由图表可以看出,基本趋势为每日抽烟数越多则累加发病率越高。
调整CO浓度:首先用Excel做出调整CO浓度跟戒烟天数的散点图,如下图。
图5.1.7通过对数据的分析可以得到调整CO浓度的跨度为682—1951,所以将调整CO浓度分为7个区段,分别为600-799、800-999、1000-1199、1200-1399、1400-1599、1600-1799、1800-2000,求出其累加发病率,并做成统计图,图表如下。
通过图表可以发现累加发病率的趋势是随着调整后CO浓度的增加而提高。
5.2问题二模型的建立与求解5.2.1问题二模型的建立由图5.1.2可以看出戒烟天数的长短与性别的关系不明显,由spss软件得到它们的相关系数为0.006,所以可以认为戒烟天数和性别无关。
由spss中双变量相关系分析得到的每个变量之间的相关性数据(见附表),得到变量Age、Gender、Cig_Day、CO 、Min_last、 LogCOadj和戒烟天数的显著性(双侧)值分别为0.458、0.925、0.686、0.002、0.019、0.037。
根据题意变量CO和Min_last可得到LogCOadj。
LogCOadj水平提供了一个自愿者们先前抽烟数量的客观标准,在一定程度上,LogCOadj和Cig_Day有一定的关系。
