2019全国各地中考数学考试真题及答案

合集下载

2019年数学中考试卷(含答案)

（2）如图 2，当 6<t<10 时，DE 是否存在最小值？若存在，求出 DE 的最小值；若不存在，请说明理由. （3）当点 D 在射线 OM 上运动时，是否存在以 D，E，B 为顶点的三角形是直角三角形？若存在，求出此时 t 的值；若不存在，请说明理由.
【参考答案】***试卷处理标记，请不要删除
24．某公司销售两种椅子，普通椅子价格是每把 180 元，实木椅子的价格是每把 400 元． (1)该公司在 2019 年第一月销售了两种椅子共 900 把，销售总金额达到了 272000 元，求两种椅了各销售了多少把？ (2)第二月正好赶上市里开展家俱展销活动，公司决定将普通椅子每把降 30 元后销售，实木椅子每把降价 2a%(a＞0)后销售，在展销活动的第一周，该公司的普通椅子销售量比上
22．4 月 18 日，一年一度的“风筝节”活动在市政广场举行，如图，广场上有一风筝 A，小江抓着风筝线的一端站在 D 处，他从牵引端 E 测得风筝 A 的仰角为 67°，同一时刻小芸在附近一座距地面 30 米高(BC＝30 米)的居民楼顶 B 处测得风筝 A 的仰角是 45°，已知小江与居民楼的距离 CD＝40 米，牵引端距地面高度 DE＝1.5 米，根据以上条件计算风筝距地
7．D
解析：D 【解析】【分析】【详解】
解：A 选项中，根据对顶角相等，得 1与 2 一定相等； B、C 项中无法确定 1与 2 是否相等；
D 选项中因为∠1=∠ACD，∠2＞∠ACD，所以∠2＞∠1．故选：D
8．A
解析：A 【解析】
【分析】
【详解】
该班男生有
x
人，女生有
y
人．根据题意得：
x y 30 3x 2y 78

2019年全国中考数学真题分类汇编：正多边形、弧长与扇形面积(含答案)

2019年全国中考数学真题分类汇编：正多边形、弧长与扇形面积一、选择题1.（2019年山东省青岛市）如图，线段AB经过⊙O的圆心，AC，BD分别与⊙O相切于点C，D．若AC＝BD＝4，∠A＝45°，则的长度为（）A．πB．2πC．2πD．4π【考点】切线的性质、等腰直角三角形的判定和性质、弧长的计算【解答】解：连接OC、OD，∵AC，BD分别与⊙O相切于点C，D．∴OC⊥AC，OD⊥BD，∵∠A＝45°，∴∠AOC＝45°，∴AC＝OC＝4，∵AC＝BD＝4，OC＝OD＝4，∴OD＝BD，∴∠BOD＝45°，∴∠COD＝180°﹣45°﹣45°＝90°，∴的长度为：＝2π，故选：B．2.（2019年山东省枣庄市）如图，在边长为4的正方形ABCD中，以点B为圆心，AB为半径画弧，交对角线BD于点E，则图中阴影部分的面积是（结果保留π）（）A ．8﹣πB ．16﹣2πC ．8﹣2πD ．8﹣π【考点】正方形的性质、扇形的面积【解答】解：S 阴＝S △ABD ﹣S 扇形BAE ＝×4×4﹣＝8﹣2π，故选：C ．3. （2019年云南省）一个圆锥的侧面展开图是半径为8的半圆，则该圆锥的全面积是（）A.48πB.45πC.36πD.32π【考点】圆锥的全面积【解答】设圆锥底面圆的半径为r ，母线长为l ，则底面圆的周长等于半圆的弧长8π，∴ ππ82=r ，∴4=r ，圆锥的全面积等于πππππ4832162=+=+=+r rl S S 底侧，故选A4. (2019年浙江省温州市)若扇形的圆心角为90°，半径为6，则该扇形的弧长为（）A ．πB ．2πC ．3πD ．6π【考点】弧长公式计算．【解答】解：该扇形的弧长＝＝3π．故选：C ．5. （2019年湖北省荆州市）如图，点C 为扇形OAB 的半径OB 上一点，将△OAC 沿AC 折叠，点O 恰好落在上的点D 处，且l ：l ＝1：3（l 表示的长），若将此扇形OAB 围成一个圆锥，则圆锥的底面半径与母线长的比为（）A ．1：3B ．1：πC ．1：4D ．2：9【考点】圆锥的侧面积【解答】解：连接OD 交OC 于M ．由折叠的知识可得：OM＝OA，∠OMA＝90°，∴∠OAM＝30°，∴∠AOM＝60°，∵且：＝1：3，∴∠AOB＝80°设圆锥的底面半径为r，母线长为l，＝2πr，∴r：i＝2：9．故选：D．6. （2019年西藏）如图，从一张腰长为90cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的底面半径为（）A．15cm B．12cm C．10cm D．20cm【考点】圆锥的侧面积【解答】解：过O作OE⊥AB于E，∵OA＝OB＝90cm，∠AOB＝120°，∴∠A＝∠B＝30°，∴OE＝OA＝45cm，∴弧CD的长＝＝30π，设圆锥的底面圆的半径为r，则2πr＝30π，解得r＝15．故选：A．二、填空题1.（2019年重庆市）如图，在菱形ABCD中，对角线AC，BD交于点O，∠ABC＝60°，AB＝2，分别以点A、点C为圆心，以AO的长为半径画弧分别与菱形的边相交，则图中阴影部分的面积为．（结果保留π）【考点】扇形面积公式、菱形的性质【解答】解：∵四边形ABCD是菱形，∴AC⊥BD，∠ABO＝∠ABC＝30°，∠BAD＝∠BCD＝120°，∴AO＝AB＝1，由勾股定理得，OB＝＝，∴AC＝2，BD＝2，∴阴影部分的面积＝×2×2﹣×2＝2﹣π，故答案为：2﹣π．2. （2019年山东省滨州市）若正六边形的内切圆半径为2，则其外接圆半径为．【考点】正多边形和圆、等边三角形的判定与性质、三角函数【解答】解：如图，连接OA、OB，作OG⊥AB于G；则OG＝2，∵六边形ABCDEF正六边形，∴△OAB是等边三角形，∴∠OAB＝60°，∴OA＝＝＝，∴正六边形的内切圆半径为2，则其外接圆半径为．故答案为：．3. （2019年山东省青岛市）如图，五边形ABCDE是⊙O的内接正五边形，AF是⊙O的直径，则∠BDF的度数是°．【考点】正多边形和圆、圆周角定理【解答】解：连接AD，∵AF是⊙O的直径，∴∠ADF＝90°，∵五边形ABCDE是⊙O的内接正五边形，∴∠ABC＝∠C＝108°，∴∠ABD＝72°，∴∠F＝∠ABD＝72°，∴∠FAD＝18°，∴∠CDF＝∠DAF＝18°，∴∠BDF＝36°+18°＝54°，故答案为：54．4. （2019年广西贵港市）如图，在扇形OAB中，半径OA与OB的夹角为120°，点A与点B的距离为2，若扇形OAB恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为______．【考点】圆锥面积公式【解答】解：连接AB ，过O 作OM ⊥AB 于M ，∵∠AOB=120°，OA=OB ，∴∠BAO=30°，AM=， ∴OA=2，∵=2πr ， ∴r=故答案是：5. （2019年广西贺州市）已知圆锥的底面半径是1，高是，则该圆锥的侧面展开图的圆心角是度．【考点】圆锥面积公式【解答】解：设圆锥的母线为a ，根据勾股定理得，a ＝4，设圆锥的侧面展开图的圆心角度数为n °，根据题意得2π•1＝，解得n ＝90，即圆锥的侧面展开图的圆心角度数为90°．故答案为：90．6. （2019年江苏省泰州市）如图，分别以正三角形的3个顶点为圆心，边长为半径画弧，三段弧围成的图形称为莱洛三角形.若正三角形边长为6cm ，则该莱洛三角形的周长为 cm ．【考点】扇形弧长公式【解答】∵l=180R n π=1806120⨯π=4π, ∴4π×3=12π. 故答案为：12π.7.（2019年江苏省无锡市）已知圆锥的母线成为5cm ，侧面积为15πcm 2，则这个圆锥的底面圆半径为 cm ．【考点】圆锥侧面积【解答】圆锥底面圆的半径r=15π÷5π=3.8. （2019年江苏省扬州市）如图，AC 是⊙O 的内接正六边形的一边，点B 在弧AC 上，且BC 是⊙O 的内接正十边形的一边，若AB 是⊙O 的内接正n 边形的一边，则n=__15_。

2019年中考数学真题试题(含答案)

A CC2019年中考数学真题试题（总分120分考试时间120分钟）注意事项：1．本试题分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷为选择题，30分；第Ⅱ卷为非选择题，90分；本试题共6页．2．数学试题答题卡共8页．答题前，考生务必将自己的姓名、准考证号、座号等填写在试题和答题卡上，考试结束，试题和答题卡一并收回．3．第Ⅰ卷每题选出答案后，都必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑．如需改动，先用橡皮擦干净，再改涂其它答案．第Ⅱ卷按要求用0.5mm碳素笔答在答题卡的相应位置上.第Ⅰ卷（选择题共30分）一、选择题：本大题共10小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均记零分．1．51-的倒数是（）A．5- B．5 C．51- D．512．下列运算正确的是（）A.()2222yxyxyx---=-- B.422aaa=+C.632aaa=⋅ D.4222yxxy=）（3．下列图形中，根据AB∥CD，能得到∠1=∠2的是（）A B C D4．在平面直角坐标系中，若点P（2-m，1+m）在第二象限，则m的取值范围是（）A．1-＜m B．2＞m C．21＜＜m- D．1-＞m5．为了帮助市内一名患“白血病”的中学生，东营市某学校数学社团15名同学积极捐款，捐款情况如下表所示，下列说法正确的是（）A．众数是100 B．中位数是30 C．极差是20 D．平均数是306．小岩打算购买气球装扮学校“毕业典礼”活动会场，气球的种类有笑脸和爱心两种，两种气球的价格不同，但同一种气球的价格相同．由于会场布置需要，购买时以一束（4个气球）为单位，已知第一、二束气球的价格如图所示，则第三束气球的价格为（）A．19 B．18 C．16 D．15B7．如图，在四边形ABCD 中，E 是BC 边的中点，连接DE 并延长，交AB 的延长线于点F ，AB =BF ．添加一个条件使四边形ABCD 是平行四边形，你认为下面四个条件中可选择的是（） A. AD =BC B. CD =BF C. ∠A =∠C D. ∠F =∠CDF8．如图所示，圆柱的高AB =3，底面直径BC =3，现在有一只蚂蚁想要从A 处沿圆柱表面爬到对角C 处捕食，则它爬行的最短距离是（）A ．π+13B ．23C ．2432π+ D ．213π+9．如图所示，已知△ABC 中，BC =12，BC 边上的高h =6，D 为BC 上一点，EF ∥BC ，交AB 于点E ，交AC 于点F ，设点E 到边BC 的距离为x ．则△DEF 的面积y 关于x 的函数图象大致为 ( )10．如图，点E 在△DBC 的边DB 上，点A 在△DBC 内部，∠DAE =∠BAC =90°，AD =AE ，AB =AC ．给出下列结论：①CE BD =；②∠ABD +∠ECB =45°；③BD ⊥CE ；④2222)(2CD AB AD BE -+=.其中正确的是（） A. ①②③④ B. ②④ C. ①②③第Ⅱ卷（非选择题共90分）二、填空题：本大题共8小题，其中11-14题每小题3分，15-18题每小题4分，共28分．只要求填写最后结果．11．东营市大力推动新旧动能转换，产业转型升级迈出新步伐．建立了新旧动能转换项目库，筛选论证项目377（第6题图）（第7题图）（第9题图）（第10题图）（第8题图）个，计划总投资4147亿元．4147亿元用科学记数法表示为元．12. 分解因式：234xyx-= ．13. 有五张背面完全相同的卡片，其正面分别画有等腰三角形、平行四边形、矩形、正方形、菱形，将这五张卡片背面朝上洗匀，从中随机抽取一张，卡片上的图形是中心对称图形的概率是 .14．如图，B（3，-3），C（5，0），以OC，CB为边作平行四边形OABC，则经过点A的反比例函数的解析式为 .15．如图，在Rt△ABC中，∠B＝90°，以顶点C为圆心，适当长为半径画弧，分别交AC，BC于点E，F，再分别以点E，F为圆心，大于21EF的长为半径画弧，两弧交于点P，作射线CP交AB于点D，若BD＝3，AC＝16．已知一个圆锥体的三视图如图所示，则这个圆锥体的侧面积为．17．在平面直角坐标系内有两点A、B，其坐标为A），（11--，B（2，7），点M为x轴上的一个动点，若要使MAMB-的值最大，则点M的坐标为．18．如图，在平面直角坐标系中，点1A，2A，3A，…和1B，2B，3B，…分别在直线bxy+=51和x轴上．△OA1B1，△B1A2B2，△B2A3B3，…都是等腰直角三角形，如果点1A（1，1），那么点2018A的纵坐标是．19． (本题满分7分，第⑴题4分，第⑵题3分)(第15题图)(第14题图) (第16题图)（1）计算：12018o 0)21()1(3tan30)12(32---+-++-；（2）解不等式组：⎩⎨⎧≥+-+.331203x x x ）（，＞并判断-1，2这两个数是否为该不等式组的解.20.（本题满分8分）2018年东营市教育局在全市中小学开展了“情系疏勒书香援疆”捐书活动，200多所学校的师生踊跃参与，向新疆疏勒县中小学共捐赠爱心图书28.5万余本．某学校学生社团对本校九年级学生所捐图书进行统计，根据收集的数据绘制了下面不完整的统计图表．请你根据统计图表中所提供的信息解答下列问题：（1）求该校九年级共捐书多少本；（2）统计表中的a = ，b = ，c = ，d = ；（3）若该校共捐书1500本，请估计“科普图书”和“小说”一共多少本；（4）该社团3名成员各捐书1本，分别是1本“名人传记”，1本“科普图书”，1本“小说”，要从这3人中任选2人为受赠者写一份自己所捐图书的简介，请用列表法或树状图求选出的2人恰好1人捐“名人传记”，1人捐“科普图书”的概率.21．(本题满分8分)小明和小刚相约周末到雪莲大剧院看演出，他们的家分别距离剧院1200m 和2000m ，两人分别从家中同时出发，已知小明和小刚的速度比是3:4，结果小明比小刚提前4min 到达剧院．求两人的速度．22．(本题满分8分)如图，CD 是⊙O 的切线，点C 在直径AB 的延长线上．(第20题图)（1）求证：∠CAD=∠BDC；（2）若BD=32AD，AC=3，求CD的长．23．(本题满分9分)关于的方程有两个相等的实数根，其中∠A是锐角三角形ABC的一个内角．（1）求sin A 的值；（2）若关于y的方程的两个根恰好是△ABC的两边长，求△ABC的周长．24．(本题满分10分)（1）某学校“智慧方园”数学社团遇到这样一个题目：如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=33，BO：CO=1:3，求AB的长．经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．请回答：∠ADB= °，AB= ．（2）请参考以上解决思路，解决问题：如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO=33，∠ABC=∠ACB=75°， BO：OD=1:3，求DC的长．25．(本题满分12分)如图，抛物线y=a（a0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC．（1）求线段OC的长度；（2）设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；(第24题图1) (第24题图2) (第24题图3)数学试题参考答案及评分标准评卷说明：1. 选择题和填空题中的每小题，只有满分和零分两个评分档，不给中间分．2. 解答题中的每小题的解答中所对应的分数，是指考生正确解答到该步骤所应得的累计分数．本答案对每小题只给出一种解法，对考生的其他解法，请参照评分标准相应评分．3. 如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部分酌情给分，但最多不超过正确解答分数的一半；若出现严重的逻辑错误，后续部分就不再给分．一．选择题：本大题共10小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，共30分．选错、不选或选出的答案超过一个均记零分．二、填空题：本大题共8小题，其中11-14题每小题3分，15-18题每小题4分，共28分．只要求填写最后结果．11.1110147.4⨯； 12. )2)(2(y x y x x -+ ； 13.54； 14. xy 6=； 15. 15； 16. π20； 17. ），（023-； 18. 201723）（．三、解答题：本大题共7小题，共62分．解答要写出必要的文字说明、证明过程或演算步骤．19．(本题满分7分，第（1）题4分，第（2）题3分) 解：（1）原式=2-1333-13-2+⨯+ …………………3分 =32-2 ……………………………………………4分....（2） 302133x x x +⎧⎨-+≥⎩＞①（）②解不等式①得：x>-3，解不等式②得：x ≤1………………………………………1分所以不等式组的解集为： -3<x ≤1. …………………………………………………2分则-1是不等式组的解，2不是不等式组的解.…………………………………………3分 20．（本题满分8分）解：（1）该校九年级共捐书：（本）500360126175=÷……………………………………1分（2）a =0.35………………………………………………………………………………1.5分b =150…………………………………………………………………………………2分c =0.22………………………………………………………………………………2.5分d =0.13…………………………………………………………………………………3分（3）78022.03.01500=+⨯）（（本）…………………………………………………5分（4）分别用“1、2、3”代表“名人传记”、“科普图书”、“小说”三本书，可用列表法表示如下：则所有等可能的情况有6种，其中2人恰好1人捐“名人传记”，1人捐“科普图书”的情况有2种．…………………………………………………………………… …………7分所以所求的概率：3162==P ………………………………………………………8分 21．(本题满分8分)解：设小明和小刚的速度分别是3x 米/分和4 x 米/分…………………………………1分则44200031200-=xx …………………………………………………………………3分解得 x =25………………………………………………………………………………5分检验：当x =25时，3x ≠0，4 x ≠0所以分式方程的解为x =25……………………………………………………………6分则3x =75 4x =100………………………………………………………………………7分答：小明的速度是75米/分，小刚的速度是100米/分.………………………………8分 22．(本题满分8分) （1）证明：连接OD ∵OB =OD....∴∠OBD=∠ODB …………………………1分 ∵CD 是⊙O 的切线，OD 是⊙O 的半径∴∠ODB +∠BDC =90°……………………2分 ∵AB 是⊙O 的直径∴∠ADB =90°∴∠OBD +∠CAD = 90°………………………………………3分 ∴∠CAD=∠BDC ………………………………………………4分（2）解:∵∠C =∠C ，∠CAD=∠BDC∴△CDB ∽ △CAD ………………………………………………5分∴ACCD ADBD =…………………………………………………6分∵32=AD BD ∴32=ACCD …………………………………………………7分 ∵ AC =3∴ CD =2…………………………………………………8分 23. (本题满分9分) 解：（1）因为关于x 的方程有两个相等的实数根，则△=25sin 2A -16=0………………………………………1分∴sin 2A =2516， ∴sin A =54±，……………………………………………2分∵∠A 为锐角， ∴sin A =54；………………………………………………3分（2）由题意知，方程y 2﹣10y +k 2-4k +29=0有两个实数根，则△≥0，………………………………………………4分 ∴100﹣4（k 2-4k +29）≥0， ∴﹣（k -2）2≥0， ∴（k -2）2≤0，又∵（k -2）2≥0，∴k =2．…………………………………………………5分把k =2代入方程，得y 2﹣10y +25=0，解得y 1=y 2=5，∴△ABC 是等腰三角形,且腰长为5. …………6分(第22题答案图)....分两种情况：① ∠A 是顶角时:如图，过点B 作BD ⊥AC 于点D , 在Rt △ABD 中，AB =AC =5 ∵sin A =54, ∴AD =3 ，BD =4∴DC =2, ∴BC =52. ∴△ABC 的周长为5210+. ……………………………7分 AB =5 ∵sin A =54, ② ∠A 是底角时：如图，过点B 作BD ⊥AC 于点D , 在Rt △ABD 中，∴A D =DC =3, ∴AC =6.∴△ABC 的周长为16. …………………………8分综合以上讨论可知：△ABC 的周长为或16……………9分24．(本题满分10分)(1)75，……………………………………………1分2分(2)解：过点B 作BE ∥AD 交AC 于点E ∵AC ⊥AD∴∠DAC =∠BEA =90° ∵∠AOD =∠EOB∴△AOD ∽△EOB ……………………………………………3分 ∴=BO EO BE DO AO DA = ∵BO:OD =1:3∴1=3EO BE AO DA = (4)分 ∵AO=∴∴AE =……………………………………………5分 ∵∠ABC =∠ACB =75°∴∠BAC =30°,AB=AC ……………………………………………6分 ∴AB =2BE在Rt △AEB 中，222BE AE AB +=即222)2(34BE BE =+）（,得BE =4……………………………………………7分 ∴AB =AC =8,AD =12……………………………………………8分在Rt △CAD 中，222AC AD CD +=即2228+12CD=,得CD =10分 25．(本题满分12分)(第23题答案图1)(第23题答案图2)(第24题答案图)....解：（1）由题可知当y =0时，a =0解得：x 1=1，x 2=3则A （1,0），B （3,0）于是OA =1，OB =3∵△OCA ∽△OBC ∴OC ∶OB =OA ∶OC ∴OC 2=OA •OB =3即OC =（2）因为C 是BM 的中点 ∴OC =BC 从而点C 的横坐标为23又OC =，点C 在x 轴下方∴C），（2323-设直线BM 的解析式为y =kx +b ，因其过点B （3，0），C），（2323-，则有⎪⎩⎪⎨⎧-=+=+.232303b k b k ，∴，33=k ∴333-=x y ……………………5分又点C），（2323-在抛物线上,代入抛物线解析式，解得a =332……………………6分 ∴抛物线解析式为：323383322+-=x x y ……………………7分（3）点P 存在.……………………8分设点P 坐标为（x ，323383322+-x x ），过点P 作PQ x 轴交直线BM 于点Q ，则Q （x ,333-x ）,....11PQ =33333322-+-x x ……………………9分当△BCP 面积最大时，四边形ABPC ）（）（△2321321-+-=x PQ x PQ S BCP ）（23321-+-=x x PQ PQ 43= 43943923 2-+-=x x 当492=-=a b x 时，BCP S △此时点P 的坐标为）385-，49（。

2019年全国各地中考数学试题分类汇编专题5 二元一次方程(组)及其应用(含解析)

二元一次方程(组)及其应用一.选择题1. （2019•天津•3分）方程组⎩⎨⎧=-=+1126723y x y x ，的解是A.⎩⎨⎧=-=51y xB.⎩⎨⎧==21y xC.⎩⎨⎧==1-3y xD.⎪⎩⎪⎨⎧==212y x【答案】D【解析】用加减消元法，⎩⎨⎧=-=+②①1126723y x y x①+②=1172623+=-++y x y x189=x 2=x 代入2=x 到①中，726=+y 则21=y ，故选D.2. （2019•广西贺州•3分）已知方程组，则2x +6y 的值是（） A ．﹣2B ．2C ．﹣4D ．4【分析】两式相减，得x +3y ＝﹣2，所以2（x +3y ）＝﹣4，即2x +6y ＝﹣4．【解答】解：两式相减，得x +3y ＝﹣2， ∴2（x +3y ）＝﹣4，即2x +6y ＝﹣4，故选：C ．【点评】本题考查了二元一次方程组，对原方程组进行变形是解题的关键．二.填空题1. （2019•河北•4分）勘测队按实际需要构建了平面直角坐标系，并标示了A ，B ，C 三地的坐标，数据如图（单位：km ）．笔直铁路经过A ，B 两地．（1）A ，B 间的距离为 km ；（2）计划修一条从C 到铁路AB 的最短公路l ，并在l 上建一个维修站D ，使D 到A ，C 的距离相等，则C ，D 间的距离为 km ．【解答】解：（1）由A、B两点的纵坐标相同可知：AB∥x轴，∴AB＝12﹣（﹣8）20；（2）过点C作l⊥AB于点E，连接AC，作AC的垂直平分线交直线l于点D，由（1）可知：CE＝1﹣（﹣17）＝18，AE＝12，设CD＝x，∴AD＝CD＝x，由勾股定理可知：x2＝（18﹣x）2+122，∴解得：x＝13，∴CD＝13，故答案为：（1）20；（2）13；2. （2019•江苏宿迁•3分）下面3个天平左盘中“△”“□”分别表示两种质量不同的物体，则第三个天平右盘中砝码的质量为10．【分析】设“△”的质量为x，“□”的质量为y，由题意列出方程：，解得：，得出第三个天平右盘中砝码的质量＝2x+y＝10．【解答】解：设“△”的质量为x，“□”的质量为y，由题意得：，解得：，∴第三个天平右盘中砝码的质量＝2x+y＝2×4+2＝10；故答案为：10．【点评】本题考查了二元一次方程组的应用以及二元一次方程组的解法；设出未知数，根据题意列出方程组是解题的关键．3. （2019•四川自贡•4分）某活动小组购买了4个篮球和5个足球，一共花费了466元，其中篮球的单价比足球的单价多4元，求篮球的单价和足球的单价．设篮球的单价为x元，足球的单价为y元，依题意，可列方程组为．【分析】根据题意可得等量关系：①4个篮球的花费+5个足球的花费＝466元，②篮球的单价﹣足球的单价＝4元，根据等量关系列出方程组即可．【解答】解：设篮球的单价为x元，足球的单价为y元，由题意得：，故答案为：，【点评】此题主要考查了由实际问题抽象出二元一次方程组，关键是正确理解题意，找出题目中的等量关系．三.解答题1. （2019•贵阳•10分）某文具店最近有A，B两款毕业纪念册比较畅销，近两周的销售情况是：第一周A款销售数量是15本，B款销售数量是10本，销售总价是230元；第二周A 款销售数量是20本，B款销售数量是10本，销售总价是280元．（1）求A，B两款毕业纪念册的销售单价；（2）若某班准备用不超过529元购买这两种款式的毕业纪念册共60本，求最多能够买多少本A款毕业纪念册．【分析】（1）直接利用第一周A款销售数量是15本，B款销售数量是10本，销售总价是230元；第二周A款销售数量是20本，B款销售数量是10本，销售总价是280元，分别得出方程求出答案；（2）利用不超过529元购买这两种款式的毕业纪念册共60本，得出不等式求出答案．【解答】解：（1）设A款毕业纪念册的销售为x元，B款毕业纪念册的销售为y元，根据题意可得：，解得：，答：A款毕业纪念册的销售为10元，B款毕业纪念册的销售为8元；（2）设能够买a本A款毕业纪念册，则购买B款毕业纪念册（60﹣a）本，根据题意可得：10a+8（60﹣a）≤529，解得：a≤24.5，则最多能够买24本A款毕业纪念册．【点评】此题主要考查了一元一次不等式的应用以及二元一次方程组的应用，正确得出等量关系是解题关键．2. （2019•海南•10分）时下正是海南百香果丰收的季节，张阿姨到“海南爱心扶贫网”上选购百香果，若购买2千克“红土”百香果和1千克“黄金”百香果需付80元，若购买1千克“红土”百香果和3千克“黄金”百香果需付115元．请问这两种百香果每千克各是多少元？【分析】设“红土”百香果每千克x元，“黄金”百香果每千克y元，由题意列出方程组，解方程组即可．【解答】解：设“红土”百香果每千克x元，“黄金”百香果每千克y元，由题意得：，解得：；答：“红土”百香果每千克25元，“黄金”百香果每千克30元．【点评】本题考查了二元一次方程组的应用以及二元一次方程组的解法；根据题意列出方程组是解题的关键．3. （2019•河南•9分）学校计划为“我和我的祖国”演讲比赛购买奖品．已知购买3个A奖品和2个B奖品共需120元；购买5个A奖品和4个B奖品共需210元．（1）求A，B两种奖品的单价；（2）学校准备购买A，B两种奖品共30个，且A奖品的数量不少于B奖品数量的．请设计出最省钱的购买方案，并说明理由．【分析】（1）设A的单价为x元，B的单价为y元，根据题意列出方程组，即可求解；（2）设购买A奖品z个，则购买B奖品为（30﹣z）个，购买奖品的花费为W元，根据题意得到由题意可知，z≥（30﹣z），W＝30z+15（30﹣z）＝450+15z，根据一次函数的性质，即可求解；【解答】解：（1）设A的单价为x元，B的单价为y元，根据题意，得，∴，∴A的单价30元，B的单价15元；（2）设购买A奖品z个，则购买B奖品为（30﹣z）个，购买奖品的花费为W元，由题意可知，z≥（30﹣z），∴z≥，W＝30z+15（30﹣z）＝450+15z，当z＝8时，W有最小值为570元，即购买A奖品8个，购买B奖品22个，花费最少；【点评】本题考查二元一次方程组的应用，一次函数的应用；能够根据条件列出方程组，将最优方案转化为一次函数性质解题是关键．4. （2 019·江苏盐城·10分）体育器材室有A、B两种型号的实心球，1只A型球与1只B 型球的质量共7千克，3只A型球与1只B型球的质量共13千克.(1)每只A型球、B型球的质量分别是多少千克?(2)现有A型球、B型球的质量共17千克，则A型球、B型球各有多少只?5. （2019•广东省广州市•9分）解方程组：．【分析】运用加减消元解答即可．【解答】解：，②﹣①得，4y＝2，解得y＝2，把y＝2代入①得，x﹣2＝1，解得x＝3，故原方程组的解为．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．6. （2019•甘肃省庆阳市•6分）小甘到文具超市去买文具．请你根据如图中的对话信息，求中性笔和笔记本的单价分别是多少元？【分析】根据对话分别利用总钱数得出等式求出答案．【解答】解：设中性笔和笔记本的单价分别是x 元、y 元，根据题意可得：，解得：，答：中性笔和笔记本的单价分别是2元、6元．【点评】此题主要考查了二元一次方程组的应用，正确得出等量关系是解题关键．7.（2019•天津•10分）甲、乙两个批发店销售同一种苹果，在甲批发店，不论一次购买数量是多少，价格均为6元/kg 。

2019全国各市中考真题(含解析)—福建省中考数学试卷

2019年全国各省市中考数学真题（函解析）2019年福建省中考数学试卷4A . 72 X 10 5B . 7.2X 10 - c -6C. 7.2X10 6D. 0.72X 10（4分）下列图形中，一定既是轴对称图形又是中心对称图形的是（C. 8（4分）如图是某班甲、乙、丙三位同学最近 5次数学成绩及其所在班级相应平均分的折线统方t 图，则下列判断错误的是（」丁宇成般分104-A .甲的数学成绩高于班级平均分，且成绩比较稳定 B.乙的数学成绩在班级平均分附近波动，且比丙好C.丙的数学成绩低于班级平均分，但成绩逐次提高、选择题（每小题4分共40分）（4分）计算22+ （-1）0的结果是（A. 5C. 3D. 22. （4分）北京故宫的占地面积约为720000m 2将720000用科学记数法表示为（ 3. A.等边三角形B.直角三角形C.平行四边形D.正方形4. （4分）如图是由一个长方体和一个球组成的几何体，它的主视图是5. （4分）已知正多边形的一个外角为D.36。

，则该正多边形的边数为（D.6. A .C.70审丙■班氢用均D.就甲、乙、丙三个人而言，乙的数学成绩最不稳10. （4 分）若二次函数 y= |a|x 2+bx+c 的图象经过 A （m,n ）、B （0,y 1）、C （3-m,n ）、D（N''2,y 2）、E （2,y 3）,则y 1、y 2、y 3的大小关系是（）A . y 1V y 2〈y 3B . y 1V y 3〈y 2C. y 3V y 2〈y 1D. y 2V y 3〈y 1二、填空题（每小题 4分共24分）2 -11. （4分）因式分解：x -9 =.12.（4分）如图，数轴上A 、B 两点所表示的数分别是- 4和2,点C 是线段AB 的中点，则点C 所表示的数是.AC Bt I n副〉-4213. （4分）某校征集校运会会徽，遴选出甲、乙、丙三种图案.为了解何种图案更受欢迎，随机调查了该校100名学生，其中60名同学喜欢甲图案，若该校共有2000人,根据所学的统7. （4分）下列运算正确的是（ A. a?a 3=a 3 B.(2a) 3= 6a 3 8. C. a 6+a 3=a 2D.（4分）《增删算法统宗》记载：“有个学生资性好 (a 2) 3- (- a3) 2=0，一部孟子三日了，每日增添一倍多，问若每日读多少？”其大意是：有个学生天资聪慧前一天的两倍，问他每天各读多少个字？已知，三天读完一部《孟子》，每天阅读的字数是《孟子》一书共有34685个字,设他第一天读x 个字，则下面所列方程正确的是（A . x+2x+4x= 34685C. x+2x+2x= 34685B. x+2x+3x= 346859.4分）如图，PA 、PB 是。

2019年中考数学试题含答案

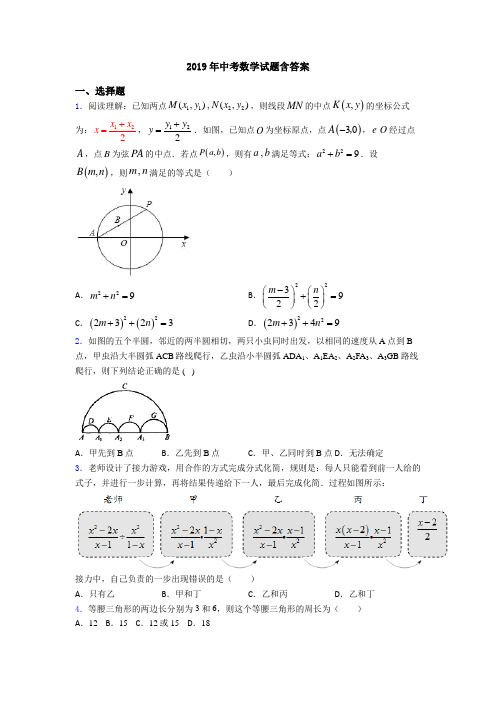
2019年中考数学试题含答案一、选择题1．阅读理解：已知两点1122,,()(),M x y N x y ，则线段MN 的中点(),K x y 的坐标公式为：122x x x +=，122y y y +=．如图，已知点O 为坐标原点，点()30A -,，O e 经过点A ，点B 为弦PA 的中点．若点(),P a b ，则有,a b 满足等式：229a b +=．设(),B m n ，则,m n 满足的等式是（）A ．229m n +=B ．223922m n -⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭ C ．()()222323m n ++= D ．()222349m n ++= 2．如图的五个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度从A 点到B 点，甲虫沿大半圆弧ACB 路线爬行，乙虫沿小半圆弧ADA 1、A 1EA 2、A 2FA 3、A 3GB 路线爬行，则下列结论正确的是 ( )A ．甲先到B 点 B ．乙先到B 点C ．甲、乙同时到B 点D ．无法确定3．老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：接力中，自己负责的一步出现错误的是（）A ．只有乙B ．甲和丁C ．乙和丙D ．乙和丁4．等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为（）A ．12B ．15C ．12或15D ．185．如图，长宽高分别为2，1，1的长方体木块上有一只小虫从顶点A出发沿着长方体的外表面爬到顶点B，则它爬行的最短路程是（）A．10B ．5C ．22D．36．我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+43与x轴、y轴分别交于A 、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P 在线段OA上运动时，使得⊙P成为整圆的点P个数是（）A．6B．8C．10D．127．如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．若AC=5，BC=2，则sin∠ACD的值为（）A．5B．25C．5D．238．不等式组213312xx+⎧⎨+≥-⎩＜的解集在数轴上表示正确的是（）A．B．C．D．9．下列各曲线中表示y是x的函数的是（）A．B．C．D．10．如图，两根竹竿AB和AD斜靠在墙CE上，量得∠ABC=α，∠ADC=β，则竹竿AB与AD的长度之比为()A．tan tanαβB．sinsinβαC．sinsinαβD．coscosβα11．如图，正比例函数1y=k x与反比例函数2ky=x的图象相交于点A、B两点，若点A的坐标为（2，1），则点B的坐标是（）A．（1，2）B．（－2，1）C．（－1，－2）D．（－2，－1）12．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中正确结论的个数是（）A．4个B．3个C．2个D．1个二、填空题13．一列数123,,,a a a……na，其中1231211111,,,,111nna a a aa a a-=-===---L L，则1232014a a a a++++=L L__________.14．如图，矩形ABCD中，AB=3，对角线AC，BD相交于点O，AE垂直平分OB于点E，则AD的长为____________．15．如图，在平面直角坐标系中，菱形OABC 的面积为12，点B 在y 轴上，点C 在反比例函数y =k x 的图象上，则k 的值为________.16．半径为2的圆中，60°的圆心角所对的弧的弧长为_____.17．如图，在Rt △AOB 中，OA=OB=32，⊙O 的半径为1，点P 是AB 边上的动点，过点P 作⊙O 的一条切线PQ （点Q 为切点），则切线PQ 的最小值为．18．若一个数的平方等于5，则这个数等于_____．19．已知圆锥的底面圆半径为3cm ，高为4cm ，则圆锥的侧面积是________cm 2.20．对于有理数a 、b ，定义一种新运算，规定a ☆b ＝a 2﹣|b|，则2☆（﹣3）＝_____．三、解答题21．如图，AD 是ABC ∆的中线，AE BC ∥，BE 交AD 于点F ，F 是AD 的中点，连接EC .（1）求证：四边形ADCE 是平行四边形；（2）若四边形ABCE 的面积为S ，请直接写出图中所有面积是13S 的三角形.22．先化简，再求值： 233212-),322x x x x x x （其中+-+÷=++ 23．直线AB 交⊙O 于C 、D 两点，CE 是⊙O 的直径，CF 平分∠ACE 交⊙O 于点F ，连接EF ，过点F 作FG∥ED 交AB 于点G ．（1）求证：直线FG 是⊙O 的切线；（2）若FG ＝4，⊙O 的半径为5，求四边形FGDE 的面积．24．解方程：3x x +﹣1x =1． 25．计算：（1）2（m ﹣1）2﹣（2m+1）（m ﹣1）（2）（1﹣）【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【解析】【分析】根据中点坐标公式求得点B 的坐标，然后代入,a b 满足的等式进行求解即可.【详解】∵点()30A -,，点(),P a b ，点(),B m n 为弦PA 的中点， ∴32a m -+=，02b n +=， ∴23,2a m b n =+=，又,a b 满足等式：229a b +=，∴()222349m n ++=，故选D ．【点睛】本题考查了坐标与图形性质，解题的关键是理解中点坐标公式． 2．C解析：C【解析】1 2π(AA1+A1A2+A2A3+A3B)=12π×AB，因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等，因此两个同时到B点。

2019年中考数学试题(及答案)

2019年中考数学试题(及答案)一、选择题1．“厉行勤俭节约，反对铺张浪费”势在必行,最新统计数据显示,中国每年浪费食物总量折合粮食大约是230000000人一年的口粮,将230000000用科学记数法表示为( ) A．2.3×109 B．0.23×109 C．2.3×108 D．23×1072．预计到2025年，中国5G用户将超过460 000 000，将460 000 000用科学计数法表示为（）A．94.610⨯D．94.610⨯C．84610⨯B．7⨯0.46103．下列命题正确的是（）A．有一个角是直角的平行四边形是矩形B．四条边相等的四边形是矩形C．有一组邻边相等的平行四边形是矩形D．对角线相等的四边形是矩形4．如图，将▱ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B为（）A．66°B．104°C．114°D．124°5．如图，在△ABC中，AC＝BC，有一动点P从点A出发，沿A→C→B→A匀速运动．则CP的长度s与时间t之间的函数关系用图象描述大致是（）A．B．C．D．6．如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．若AC5BC=2，则sin∠ACD的值为（）A ．5B ．25C ．5D ．237．在某篮球邀请赛中，参赛的每两个队之间都要比赛一场，共比赛36场，设有x 个队参赛，根据题意，可列方程为（）A ．()11362x x -=B ．()11362x x +=C ．()136x x -=D ．()136x x += 8．不等式组213312x x +⎧⎨+≥-⎩＜的解集在数轴上表示正确的是（） A ．B ．C ．D ．9．一副直角三角板如图放置，点C 在FD 的延长线上，AB//CF ，∠F=∠ACB=90°，则∠DBC 的度数为( )A ．10°B ．15°C ．18°D ．30°10．下面的几何体中，主视图为圆的是（）A ．B ．C ．D ．11．把一副三角板如图（1）放置，其中∠ACB ＝∠DEC ＝90°，∠A ＝45°，∠D ＝30°，斜边AB ＝4，CD ＝5．把三角板DCE 绕着点C 顺时针旋转15°得到△D 1CE 1（如图2），此时AB 与CD 1交于点O ，则线段AD 1的长度为（）A ．13B ．5C ．22D ．412．下列由阴影构成的图形既是轴对称图形，又是中心对称图形的是（） A ． B ．C ．D ．二、填空题13．已知62x =+，那么222x x -的值是_____．14．当直线()223y k x k =-+-经过第二、三、四象限时，则k 的取值范围是_____．15．某品牌旗舰店平日将某商品按进价提高40%后标价，在某次电商购物节中，为促销该商品，按标价8折销售，售价为2240元，则这种商品的进价是______元.16．关于x 的一元二次方程(a ＋1)x 2－2x ＋3＝0有实数根，则整数a 的最大值是_____.17．如图，把三角形纸片折叠，使点B ，点C 都与点A 重合，折痕分别为,DE FG ，若15,2C AE EG ︒∠===厘米，ABC △则的边BC 的长为__________厘米。

2019年数学中考试卷(附答案)

2019年数学中考试卷(附答案)一、选择题1．地球与月球的平均距离为384 000km ，将384 000这个数用科学记数法表示为（） A ．3.84×103 B ．3.84×104 C ．3.84×105 D ．3.84×1062．在同一坐标系内，一次函数y ax b =+与二次函数2y ax 8x b =++的图象可能是A ．B ．C ．D ．3．一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（） A ．108°B ．90°C ．72°D ．60°4．下表是某学习小组一次数学测验的成绩统计表：分数/分 70 80 90100 人数/人13x1已知该小组本次数学测验的平均分是85分，则测验成绩的众数是（） A ．80分B ．85分C ．90分D ．80分和90分5．老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：接力中，自己负责的一步出现错误的是（） A ．只有乙B ．甲和丁C ．乙和丙D ．乙和丁6．如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图是( )A ．B ．C ．D ．7．如图，矩形纸片ABCD 中，4AB =，6BC =，将ABC V 沿AC 折叠，使点B 落在点E 处，CE 交AD 于点F ，则DF 的长等于（）A ．35B ．53C ．73D ．548．方程21(2)304m x mx ---+=有两个实数根，则m 的取值范围（） A ．52m >B ．52m ≤且2m ≠ C ．3m ≥ D ．3m ≤且2m ≠9．如图中的几何体是由一个圆柱和个长方体组成的，该几何体的俯视图是( )A ．B ．C ．D ．10．如图，已知⊙O 的半径是2，点A 、B 、C 在⊙O 上，若四边形OABC 为菱形，则图中阴影部分面积为（）A ．23π﹣3B ．13π3 C ．43π﹣3 D ．43π3 11．51-是一个很奇妙的数，大量应用于艺术、建筑和统计决策等方面，请51的值（） A ．在1.1和1.2之间B ．在1.2和1.3之间C．在1.3和1.4之间D．在1.4和1.5之间12．为了帮助市内一名患“白血病”的中学生，东营市某学校数学社团15名同学积极捐款，捐款情况如下表所示，下列说法正确的是（）捐款数额10203050100人数24531A．众数是100B．中位数是30C．极差是20D．平均数是30二、填空题13．已知a，b，c是△ABC的三边长，a，b满足|a﹣7|+（b﹣1）2=0，c为奇数，则c=_____．14．如图，△ABC的三个顶点均在正方形网格格点上，则tan∠BAC=_____________．15．如图，小明的父亲在相距2米的两棵树间拴了一根绳子，给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为米.16．如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝3， BC＝2，tanA＝43，则CD＝_____．17．如图，在平面直角坐标系中，菱形OABC的面积为12，点B在y轴上，点C在反比例函数y=kx的图象上，则k的值为________.18．计算：2cos45°﹣（π+1）0+111()42-+=______． 19．如图，将矩形ABCD 沿CE 折叠，点B 恰好落在边AD 的F 处，如果AB 2BC 3=，那么tan ∠DCF 的值是____．20．如图是两块完全一样的含30°角的直角三角尺，分别记做△ABC 与△A′B′C′，现将两块三角尺重叠在一起，设较长直角边的中点为M ，绕中点M 转动上面的三角尺ABC ，使其直角顶点C 恰好落在三角尺A′B′C′的斜边A′B′上．当∠A ＝30°，AC ＝10时，两直角顶点C ，C′间的距离是_____．三、解答题21．两个全等的直角三角形 ABC 和 DEF 重叠在一起，其中∠A=60°，AC=1．固定△ABC 不动，将△DEF 进行如下操作：（1）如图，△DEF 沿线段 AB 向右平移（即 D 点在线段 AB 内移动），连接 DC 、CF 、FB ，四边形 CDBF 的形状在不断的变化，但它的面积不变化，请求出其面积．（2）如图，当 D 点移到 AB 的中点时，请你猜想四边形CDBF 的形状，并说明理由．（3）如图，△DEF 的 D 点固定在 AB 的中点，然后绕 D 点按顺时针方向旋转△DEF，使DF 落在 AB 边上，此时 F 点恰好与 B 点重合，连接 AE，请你求出sinα的值．22．“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况，在本校学生中随机抽取部分学生作调查，把收集的数据分为以下4类情形：A．仅学生自己参与；B．家长和学生一起参与；C．仅家长自己参与； D．家长和学生都未参与.请根据图中提供的信息，解答下列问题：（1）在这次抽样调查中，共调查了________名学生；（2）补全条形统计图，并在扇形统计图中计算C类所对应扇形的圆心角的度数；（3）根据抽样调查结果，估计该校2000名学生中“家长和学生都未参与”的人数.23．某公司推出一款产品，经市场调查发现，该产品的日销售量y（个）与销售单价x （元）之间满足一次函数关系．关于销售单价，日销售量，日销售利润的几组对应值如下表：销售单价x（元）8595105115日销售量y（个）17512575m日销售利润w87518751875875（元）（注：日销售利润=日销售量×（销售单价﹣成本单价））（1）求y关于x的函数解析式（不要求写出x的取值范围）及m的值；（2）根据以上信息，填空：该产品的成本单价是元，当销售单价x=元时，日销售利润w最大，最大值是元；（3）公司计划开展科技创新，以降低该产品的成本，预计在今后的销售中，日销售量与销售单价仍存在（1）中的关系．若想实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？24．对垃圾进行分类投放，能提高垃圾处理和再利用的效率，减少污染，保护环境．为了检查垃圾分类的落实情况，某居委会成立了甲、乙两个检查组，采取随机抽查的方式分别对辖区内的A，B，C，D四个小区进行检查，并且每个小区不重复检查．（1）甲组抽到A小区的概率是多少；（2）请用列表或画树状图的方法求甲组抽到A小区，同时乙组抽到C小区的概率．25．如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A，D的⊙O分别交AB，AC于点E，F，连接OF交AD于点G．(1)求证：BC是⊙O的切线；(2)设AB＝x，AF＝y，试用含x，y的代数式表示线段AD的长；(3)若BE＝8，sinB＝513，求DG的长，【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【解析】试题分析：384 000=3.84×105．故选C．考点：科学记数法—表示较大的数．2．C解析：C【解析】【分析】x=0，求出两个函数图象在y轴上相交于同一点，再根据抛物线开口方向向上确定出a＞0，然后确定出一次函数图象经过第一三象限，从而得解．【详解】x=0时，两个函数的函数值y=b，所以，两个函数图象与y轴相交于同一点，故B、D选项错误；由A、C选项可知，抛物线开口方向向上，所以，a＞0，所以，一次函数y=ax+b经过第一三象限，所以，A选项错误，C选项正确．故选C．3．C解析：C【解析】【分析】首先设此多边形为n边形，根据题意得：180（n-2）=540，即可求得n=5，再由多边形的外角和等于360°，即可求得答案．【详解】解：设此多边形为n边形，根据题意得：180（n-2）=540，解得：n=5，∴这个正多边形的每一个外角等于：3605=72°．故选C．【点睛】此题考查了多边形的内角和与外角和的知识．注意掌握多边形内角和定理：（n-2）•180°，外角和等于360°．4．D解析：D【解析】【分析】先通过加权平均数求出x的值，再根据众数的定义就可以求解．【详解】解：根据题意得：70+80×3+90x+100=85（1+3+x+1），x=3∴该组数据的众数是80分或90分．故选D．【点睛】本题考查了加权平均数的计算和列方程解决问题的能力，解题的关键是利用加权平均数列出方程．通过列方程求出x是解答问题的关键．5．D解析：D【解析】【分析】根据分式的乘除运算步骤和运算法则逐一计算即可判断．【详解】∵22211x x x x x -÷--=2221·1x x x x x ---=() 2212·1xx xx x----=()()221·1x x xx x----=()2xx --=2xx-，∴出现错误是在乙和丁，故选D．【点睛】本题考查了分式的乘除法，熟练掌握分式乘除法的运算法则是解题的关键.6．B解析：B【解析】试题分析：从左面看易得第一层有2个正方形，第二层最左边有一个正方形．故选B．考点：简单组合体的三视图．7．B解析：B【解析】【分析】由折叠的性质得到AE=AB，∠E=∠B=90°，易证Rt△AEF≌Rt△CDF，即可得到结论EF=DF；易得FC=FA，设FA=x，则FC=x，FD=6-x，在Rt△CDF中利用勾股定理得到关于x的方程x2=42+（6-x）2，解方程求出x即可．【详解】∵矩形ABCD沿对角线AC对折，使△ABC落在△ACE的位置，∴AE=AB，∠E=∠B=90°，又∵四边形ABCD为矩形，∴AB=CD，∴AE=DC，而∠AFE=∠DFC，∵在△AEF与△CDF中，AFE CFD E DAE CD ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△AEF ≌△CDF （AAS ）， ∴EF=DF ；∵四边形ABCD 为矩形， ∴AD=BC=6，CD=AB=4， ∵Rt △AEF ≌Rt △CDF ， ∴FC=FA ，设FA=x ，则FC=x ，FD=6-x ，在Rt △CDF 中，CF 2=CD 2+DF 2，即x 2=42+（6-x ）2，解得x ＝133，则FD ＝6-x=53. 故选B ．【点睛】考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应边相等．也考查了矩形的性质和三角形全等的判定与性质以及勾股定理．8．B解析：B 【解析】【分析】根据一元二次方程的定义、二次根式有意义的条件和判别式的意义得到20m -≠，30m -≥，(()214204m ∆=--⨯≥，然后解不等式组即可．【详解】解：根据题意得20m -≠， 30m -≥，(()214204m ∆=--⨯≥，解得m ≤52且m ≠2．故选B ． 9．D解析：D 【解析】【分析】根据从上边看得到的图形是俯视图，可得答案．【详解】解：从上边看是一个圆形，圆形内部是一个虚线的正方形.故选：D．【点睛】本题考查了简单组合体的三视图，从上边看得到的图形是俯视图．10．C解析：C【解析】分析：连接OB和AC交于点D，根据菱形及直角三角形的性质先求出AC的长及∠AOC 的度数，然后求出菱形ABCO及扇形AOC的面积，则由S菱形ABCO﹣S扇形AOC可得答案．详解：连接OB和AC交于点D，如图所示：∵圆的半径为2，∴OB=OA=OC=2，又四边形OABC是菱形，∴OB⊥AC，OD=12OB=1，在Rt△COD中利用勾股定理可知：22213-=，3∵sin∠COD=3 CDOC=∴∠COD=60°，∠AOC=2∠COD=120°，∴S菱形ABCO=12B×AC=12×2×33S扇形AOC=2120243603ππ⨯⨯=，则图中阴影部分面积为S菱形ABCO﹣S扇形AOC=423 3π-故选C．点睛：本题考查扇形面积的计算及菱形的性质，解题关键是熟练掌握菱形的面积=12 a•b（a、b是两条对角线的长度）；扇形的面积=2360n rπ，有一定的难度．11．B 解析：B【解析】【分析】根据4.84<5<5.29，可得答案．【详解】∵4.84<5<5.29，∴，∴，故选B．【点睛】是解题关键．12．B解析：B【解析】分析：根据中位数、众数和极差的概念及平均数的计算公式，分别求出这组数据的中位数、平均数、众数和极差，得到正确结论．详解：该组数据中出现次数最多的数是30，故众数是30不是100，所以选项A不正确；该组共有15个数据，其中第8个数据是30，故中位数是30，所以选项B正确；该组数据的极差是100-10=90，故极差是90不是20，所以选项C不正确；该组数据的平均数是102204305503100100245313⨯+⨯+⨯+⨯+=++++不是30，所以选项D不正确．故选B．点睛：本题考查了中位数、平均数、众数和极差的概念．题目难度不大，注意勿混淆概念．二、填空题13．7【解析】【分析】根据非负数的性质列式求出ab的值再根据三角形的任意两边之和大于第三边两边之差小于第三边求出c的取值范围再根据c是奇数求出c的值【详解】∵ab满足|a﹣7|+（b﹣1）2=0∴a﹣7解析：7【解析】【分析】根据非负数的性质列式求出a、b的值，再根据三角形的任意两边之和大于第三边，两边之差小于第三边求出c的取值范围，再根据c是奇数求出c的值．【详解】∵a，b满足|a﹣7|+（b﹣1）2=0，∴a﹣7=0，b﹣1=0，解得a=7，b=1，∵7﹣1=6，7+1=8，∴68c <<，又∵c 为奇数，∴c=7，故答案为7．【点睛】本题考查非负数的性质：偶次方，解题的关键是明确题意，明确三角形三边的关系．14．【解析】分析：在图形左侧添加正方形网格分别延长ABAC 连接它们延长线所经过的格点可构成直角三角形利用正切的定义即可得出答案详解：如图所示由图形可知∴tan∠BAC=故答案为点睛：本题考查了锐角三角函解析：13【解析】分析：在图形左侧添加正方形网格，分别延长AB 、AC ，连接它们延长线所经过的格点，可构成直角三角形，利用正切的定义即可得出答案.详解：如图所示，由图形可知，90AFE ∠=︒，3AF AC =，EF AC =，∴tan ∠BAC =133EF AC AF AC ==. 故答案为13. 点睛：本题考查了锐角三角函数的定义. 利用网格构建直角三角形进而利用正切的定义进行求解是解题的关键.15．5【解析】【分析】根据题意运用待定系数法建立适当的函数解析式代入求值即可解答【详解】以左边树与地面交点为原点地面水平线为x 轴左边树为y 轴建立平面直角坐标系由题意可得A(025)B(225)C(051解析：5【解析】【分析】根据题意，运用待定系数法，建立适当的函数解析式，代入求值即可解答．【详解】以左边树与地面交点为原点，地面水平线为x 轴，左边树为y 轴建立平面直角坐标系，由题意可得A(0,2.5),B(2,2.5),C(0.5,1)设函数解析式为y=ax2+bx+c把A. B. C三点分别代入得出c=2.5同时可得4a+2b+c=2.5，0.25a+0.5b+c=1解得a=2，b=−4，c=2.5.∴y=2x2−4x+2.5=2(x−1)2+0.5.∵2>0∴当x=1时,y min=0.5米.16．【解析】【分析】延长AD和BC交于点E在直角△ABE中利用三角函数求得BE 的长则EC的长即可求得然后在直角△CDE中利用三角函数的定义求解【详解】如图延长ADBC相交于点E∵∠B=90°∴∴BE=∴解析：6 5【解析】【分析】延长AD和BC交于点E，在直角△ABE中利用三角函数求得BE的长，则EC的长即可求得，然后在直角△CDE中利用三角函数的定义求解．【详解】如图，延长AD、BC相交于点E，∵∠B=90°，∴4 tan3BEAAB==，∴BE=44 3AB⋅=，∴CE=BE-BC=2，225AB BE+=，∴3 sin5ABEAE==，又∵∠CDE=∠CDA=90°，∴在Rt △CDE 中，sin CD E CE =， ∴CD=36sin 255CE E ⋅=⨯=. 17．-6【解析】因为四边形OABC 是菱形所以对角线互相垂直平分则点A 和点C 关于y 轴对称点C 在反比例函数上设点C 的坐标为(x)则点A 的坐标为(－x)点B 的坐标为(0)因此AC=－2xOB=根据菱形的面积等解析：-6【解析】因为四边形OABC 是菱形,所以对角线互相垂直平分,则点A 和点C 关于y 轴对称,点C 在反比例函数上,设点C 的坐标为(x ,k x ),则点A 的坐标为(－x ,k x ),点B 的坐标为(0,2k x ),因此AC=－2x,OB=2K X,根据菱形的面积等于对角线乘积的一半得: ()OABC 122122k S x x=⨯-⨯=菱形,解得 6.k =- 18．【解析】解：原式==故答案为：32．【解析】解：原式=121222⨯-++3232． 19．【解析】【分析】【详解】解：∵四边形ABCD 是矩形∴AB ＝CD ∠D ＝90°∵将矩形ABCD 沿CE 折叠点B 恰好落在边AD 的F 处∴CF ＝BC ∵∴∴设CD ＝2xCF ＝3x ∴∴tan ∠DCF ＝故答案为：【点【解析】【分析】【详解】解：∵四边形ABCD 是矩形，∴AB ＝CD ，∠D ＝90°，∵将矩形ABCD 沿CE 折叠，点B 恰好落在边AD 的F 处，∴CF ＝BC ， ∵AB 2BC 3=，∴CD 2CF 3=．∴设CD ＝2x ，CF ＝3x ，∴．∴tan ∠DCF ＝DF =CD 2x 2=．故答案为：5．【点睛】本题考查翻折变换(折叠问题)，翻折对称的性质，矩形的性质，勾股定理，锐角三角函数定义．20．5【解析】【分析】连接CC1根据M是ACA1C1的中点AC=A1C1得出CM=A1M=C1M=AC=5再根据∠A1=∠A1CM=30°得出∠CMC1=60°△MCC1为等边三角形从而证出CC1=CM解析：5【解析】【分析】连接CC1，根据M是AC、A1C1的中点，AC=A1C1，得出CM=A1M=C1M=12AC=5，再根据∠A1=∠A1CM=30°，得出∠CMC1=60°，△MCC1为等边三角形，从而证出CC1=CM，即可得出答案．【详解】解：如图，连接CC1，∵两块三角板重叠在一起，较长直角边的中点为M，∴M是AC、A1C1的中点，AC=A1C1，∴CM=A1M=C1M=12AC=5，∴∠A1=∠A1CM=30°，∴∠CMC1=60°，∴△CMC1为等边三角形，∴CC1=CM=5，∴CC1长为5．故答案为5．考点：等边三角形的判定与性质．三、解答题21．（1）过点C作CG⊥AB于G 在Rt△ACG中∵∠A＝60°∴sin60°＝∴……………1分在Rt△ABC中∠ACB＝90°∠ABC＝30°∴AB=2 …………………………………………2分∴………3分（2）菱形………………………………………4分∵D是AB的中点∴AD=DB=CF=1在Rt△ABC中，CD是斜边中线∴CD=1……5分同理 BF=1 ∴CD=DB=BF=CF∴四边形CDBF是菱形…………………………6分（3）在Rt△ABE中∴……………………………7分过点D作DH⊥AE 垂足为H则△ADH∽△AEB ∴即∴ DH=……8分在Rt△DHE中sinα==…=…………………9分【解析】（1）根据平移的性质得到AD=BE，再结合两条平行线间的距离相等，则三角形ACD的面积等于三角形BEF的面积，所以要求的梯形的面积等于三角形ABC的面积．根据60度的直角三角形ABC中AC=1，即可求得BC的长，从而求得其面积；（2）根据直角三角形斜边上的中线等于斜边的一半和平移的性质，即可得到该四边形的四条边都相等，则它是一个菱形；（3）过D点作DH⊥AE于H，可以把要求的角构造到直角三角形中，根据三角形ADE的面积的不同计算方法，可以求得DH的长，进而求解．22．（1）400；（2）补全条形图见解析；C类所对应扇形的圆心角的度数为54°；（3）该校2000名学生中“家长和学生都未参与”有100人.【解析】分析：（1）根据A 类别人数及其所占百分比可得总人数；（2）总人数减去A 、C 、D 三个类别人数求得B 的人数即可补全条形图，再用360°乘以C 类别人数占被调查人数的比例可得；（3）用总人数乘以样本中D 类别人数所占比例可得．详解：（1）本次调查的总人数为80÷20%=400人；（2）B 类别人数为400-（80+60+20）=240，补全条形图如下：C 类所对应扇形的圆心角的度数为360°×60400=54°；（3）估计该校2000名学生中“家长和学生都未参与”的人数为2000×0N F N ==100人．点睛：本题考查了条形统计图、扇形统计图及用样本估计总体的知识，解题的关键是从统计图中整理出进一步解题的信息．23．（1）25；（2）80，100，2000；（3）该产品的成本单价应不超过65元．【解析】分析：（1）根据题意和表格中的数据可以求得y 关于x 的函数解析式；（2）根据题意可以列出相应的方程，从而可以求得生产成本和w 的最大值；（3）根据题意可以列出相应的不等式，从而可以取得科技创新后的成本．详解；（1）设y 关于x 的函数解析式为y=kx+b ，8517595125k b k b +⎧⎨+⎩＝＝，得5600k b ＝＝-⎧⎨⎩，即y 关于x 的函数解析式是y=-5x+600，当x=115时，y=-5×115+600=25，即m 的值是25；（2）设成本为a 元/个，当x=85时，875=175×（85-a ），得a=80，w=（-5x+600）（x-80）=-5x 2+1000x-48000=-5（x-100）2+2000，∴当x=100时，w 取得最大值，此时w=2000，（3）设科技创新后成本为b 元，当x=90时，（-5×90+600）（90-b ）≥3750，解得，b≤65，答：该产品的成本单价应不超过65元．点睛：本题考查二次函数的应用、一元二次方程的应用、不等式的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用函数和数形结合的思想解答．24．（1）甲组抽到A小区的概率是14；（2）甲组抽到A小区，同时乙组抽到C小区的概率为1 12．【解析】【分析】（1）直接利用概率公式求解可得；（2）画树状图列出所有等可能结果，根据概率公式求解可得．【详解】（1）甲组抽到A小区的概率是14，故答案为：14．（2）画树状图为：共有12种等可能的结果数，其中甲组抽到A小区，同时乙组抽到C小区的结果数为1，∴甲组抽到A小区，同时乙组抽到C小区的概率为1 12．【点睛】此题考查列表法与树状图法，解题关键在于根据题意画出树状图.25．(1)证明见解析；xy(3)DG=3013 23．【解析】【分析】（1）连接OD，由AD为角平分线得到一对角相等，再由等边对等角得到一对角相等，等量代换得到内错角相等，进而得到OD与AC平行，得到OD与BC垂直，即可得证；（2）连接DF，由（1）得到BC为圆O的切线，由弦切角等于夹弧所对的圆周角，进而得到三角形ABD与三角形ADF相似，由相似得比例，即可表示出AD；（3）连接EF，设圆的半径为r，由sinB的值，利用锐角三角函数定义求出r的值，由直径所对的圆周角为直角，得到EF与BC平行，得到sin∠AEF=sinB，进而求出DG的长即可．【详解】(1)如图，连接OD，∵AD为∠BAC的角平分线，∴∠BAD=∠CAD，∵OA=OD ，∴∠ODA=∠OAD ，∴∠ODA=∠CAD ，∴OD ∥AC ，∵∠C=90°，∴∠ODC=90°，∴OD ⊥BC ，∴BC 为圆O 的切线；(2)连接DF ，由(1)知BC 为圆O 的切线，∴∠FDC=∠DAF ，∴∠CDA=∠CFD ，∴∠AFD=∠ADB ，∵∠BAD=∠DAF ，∴△ABD ∽△ADF ， ∴AB AD AD AF=，即AD 2=AB•AF=xy ，则；(3)连接EF ，在Rt △BOD 中，sinB=513OD OB =，设圆的半径为r ，可得5813r r =+，解得：r=5，∴AE=10，AB=18，∵AE 是直径，∴∠AFE=∠C=90°，∴EF ∥BC ，∴∠AEF=∠B ，∴sin ∠AEF=513AF AE =， ∴AF=AE•sin ∠AEF=10×513=5013， ∵AF ∥OD ， ∴501013513AG AF DG OD ===，即DG=1323AD ，∴13==，则DG=133033013 231323⨯=．【点睛】圆的综合题，涉及的知识有：切线的判定与性质，相似三角形的判定与性质，锐角三角函数定义，勾股定理，以及平行线的判定与性质，熟练掌握各自的性质是解本题的关键．。

2019年中考数学试题含答案 (12)

2019年中考数学试卷一、选择题（本大题共10小题，共30分）1.比1小2的数是()A. −1B. −2C. −3D. 1【答案】A【解析】解：1−2=−1．故选：A．求比1小2的数就是求1与2的差．本题主要考查有理数的减法法则：减去一个数等于加上这个数的相反数.这是需要熟记的内容．2.下列运算正确的是()A. a3⋅a4=a12B. a6÷a3=a2C. 2a−3a=−aD. (a−2)2=a2−4【答案】C【解析】解：A、应为a3⋅a4=a7，故本选项错误；B、应为a6÷a3=a3，故本选项错误；C、2a−3a=−a，正确；D、应为(a−2)2=a2−4a+4，故本选项错误．故选：C．根据同底数的幂的运算法则、合并同类项法则及完全平方公式计算．本题考查同底数幂的乘法，同底数幂的除法，合并同类项法则，完全平方公式，计算时要认真．3.长度单位1纳米=10−9米，目前发现一种新型病毒直径为25 100纳米，用科学记数法表示该病毒直径是()A. 25.1×10−6米B. 0.251×10−4米C. 2.51×105米D. 2.51×10−5米【答案】D【解析】解：2.51×104×10−9=2.51×10−5米.故选D．先将25100用科学记数法表示为2.51×104，再和10−9相乘．a×10n中，a的整数部分只能取一位整数，1≤|a|<10.此题中的n应为负数．4.小红上学要经过三个十字路口，每个路口遇到红、绿灯的机会都相同，小红希望上学时经过每个路囗都是绿灯，但实际这样的机会是()A. 12B. 18C. 38D. 12+12+12【答案】B【解析】解：画树状图，得∴共有8种情况，经过每个路口都是绿灯的有一种，∴实际这样的机会是1，8故选：B．列举出所有情况，看个路口都是绿灯的情况占总情况的多少即可．此题考查了树状图法求概率，树状图法适用于三步或三步以上完成的事件，解题时要注意列出所有的情形.用到的知识点为：概率=所求情况数与总情况数之比．5.一个正方体的平面展开图如图所示，将它折成正方体后“建”字对面是()A. 和B. 谐C. 凉D. 山【答案】D【解析】解：对于正方体的平面展开图中相对的面一定相隔一个小正方形，由图形可知，与“建”字相对的字是“山”．故选：D．本题考查了正方体的平面展开图，对于正方体的平面展开图中相对的面一定相隔一个小正方形，据此作答．注意正方体的空间图形，从相对面入手，分析及解答问题．6.一组数据：3，2，1，2，2的众数，中位数，方差分别是()A. 2，1，0.4B. 2，2，0.4C. 3，1，2D. 2，1，0.2【答案】B【解析】解：从小到大排列此数据为：1，2，2，2，3；数据2出现了三次最多为众数，[(3−2)2+2处在第3位为中位数.平均数为(3+2+1+2+2)÷5=2，方差为153×(2−2)2+(1−2)2]=0.4，即中位数是2，众数是2，方差为0.4．故选：B．找中位数要把数据按从小到大的顺序排列，位于最中间的一个数(或两个数的平均)数为中位数；众数是一组数据中出现次数最多的数据，注意众数可以不只一个.利用方差公式计算方差．本题属于基础题，考查了确定一组数据的中位数、方差和众数的能力.注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数．7.若ab<0，则正比例函数y=ax与反比例函数y=b在同一坐标系中的大致图象可x能是()A. B. C. D.【答案】B【解析】解：∵ab<0，∴分两种情况：(1)当a>0，b<0时，正比例函数y=ax数的图象过原点、第一、三象限，反比例函数图象在第二、四象限，无此选项；(2)当a<0，b>0时，正比例函数的图象过原点、第二、四象限，反比例函数图象在第一、三象限，选项B符合．故选：B．根据ab<0及正比例函数与反比例函数图象的特点，可以从a>0，b<0和a<0，b>0两方面分类讨论得出答案．本题主要考查了反比例函数的图象性质和正比例函数的图象性质，要掌握它们的性质才能灵活解题．8.下列图形中既是轴对称图形，又是中心对称图形的是()A. B. C. D.【答案】D【解析】解：A、不是轴对称图形，是中心对称图形，故本选项错误；B、既不是轴对称图形，也不是中心对称图形，故本选项错误；C、既不是轴对称图形，也不是中心对称图形，故本选项错误；D、既是轴对称图形，又是中心对称图形．故选：D．根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．9.如图将矩形ABCD沿对角线BD折叠，使C落在C′处，BC′交AD于点E，则下到结论不一定成立的是()A. AD=BC′B. ∠EBD=∠EDBC. △ABE∽△CBDD. sin∠ABE=AEED【答案】C【解析】解：A、BC=BC′，AD=BC，∴AD=BC′，所以正确．B、∠CBD=∠EDB，∠CBD=∠EBD，∴∠EBD=∠EDB正确．D、∵sin∠ABE=AE，BE∴∠EBD=∠EDB∴BE=DE∴sin∠ABE=AE．ED故选：C．主要根据折叠前后角和边相等找到相等的边之间的关系，即可选出正确答案．本题主要用排除法，证明A，B，D都正确，所以不正确的就是C，排除法也是数学中一种常用的解题方法．10.如图，⊙O是△ABC的外接圆，已知∠ABO=50∘，则∠ACB的大小为()A. 40∘B. 30∘C. 45∘D. 50∘【答案】A【解析】解：△AOB中，OA=OB，∠ABO=50∘，∴∠AOB=180∘−2∠ABO=80∘，∠AOB=40∘，∴∠ACB=12故选：A．首先根据等腰三角形的性质及三角形内角和定理求出∠AOB的度数，再利用圆周角与圆心角的关系求出∠ACB的度数．本题主要考查了圆周角定理的应用，涉及到的知识点还有：等腰三角形的性质以及三角形内角和定理．二、填空题（本大题共6小题，共24分）11.分解因式：9a−a3=______，2x2−12x+18=______．【答案】a(3+a)(3−a)；2(x−3)2【解析】解：9a−a3=a(9−a2)=a(3+a)(3−a)；2x2−12x+18=2(x2−6x+9)=2(x−3)2．观察原式9a−a3，找到公因式a后，发现9−a2符合平方差公式的形式，直接运用公式可得；观察原式2x2−12x+18，找到公因式2后，发现x2−6x+9符合完全平方差公式的形式，直接运用公式可得．本题考查整式的因式分解.一般地，因式分解有两种方法，提公因式法，公式法，能提公因式先提公因式，然后再考虑公式法．12.已知△ABC∽△A′B′C′且S△ABC：S△A′B′C′=1：2，则AB：A′B′=______．【答案】1：√2【解析】解：∵△ABC∽△A′B′C′，∴S△ABC：S△A′B′C′=AB2：A′B′2=1：2，∴AB：A′B′=1：√2．根据相似三角形的面积比等于相似比的平方求解即可．本题的关键是理解相似三角形的面积比等于相似比的平方．13.有两名学员小林和小明练习射击，第一轮10枪打完后两人打靶的环数如图所示，通常新手的成绩不太稳定，那么根据图中的信息，估计小林和小明两人中新手是______．【答案】小林【解析】解：由于小林的成绩波动较大，根据方差的意义知，波动越大，成绩越不稳定，故新手是小林．故填小林．观察图象可得：小明的成绩较集中，波动较小，即方差较小；故小明的成绩较为稳定；根据题意，一般新手的成绩不太稳定，故新手是小林．本题考查方差的意义.方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．14. 已知一个正数的平方根是3x −2和5x +6，则这个数是______．【答案】494【解析】解：根据题意可知：3x −2+5x +6=0，解得x =−12，所以3x −2=−72，5x +6=72，∴(±72)2=494故答案为：494．由于一个非负数的平方根有2个，它们互为相反数.依此列出方程求解即可．本题主要考查了平方根的逆运算，平时注意训练逆向思维．15. 若不等式组{b −2x >0x−a>2的解集是−1<x <1，则(a +b)2009=______．【答案】−1【解析】解：由不等式得x >a +2，x <12b ， ∵−1<x <1， ∴a +2=−1，12b =1∴a =−3，b =2，∴(a +b)2009=(−1)2009=−1．故答案为−1．解出不等式组的解集，与已知解集−1<x <1比较，可以求出a 、b 的值，然后相加求出2009次方，可得最终答案．本题是已知不等式组的解集，求不等式中另一未知数的问题.可以先将另一未知数当作已知处理，求出解集与已知解集比较，进而求得零一个未知数．16. 将△ABC 绕点B 逆时针旋转到△A′BC′，使A 、B 、C′在同一直线上，若∠BCA =90∘，∠BAC =30∘，AB =4cm ，则图中阴影部分面积为______cm 2．【答案】4π【解析】解：∵∠BCA =90∘，∠BAC =30∘，AB =4cm ， ∴BC =2，AC =2√3，∠A′BA =120∘，∠CBC′=120∘， ∴阴影部分面积=(S △A′BC′+S 扇形BAA ′)−S 扇形BCC′−S △ABC =120π360×(42−22)=4πcm 2．故答案为：4π．易得整理后阴影部分面积为圆心角为120∘，两个半径分别为4和2的圆环的面积．本题利用了直角三角形的性质，扇形的面积公式求解．三、计算题（本大题共3小题，共24分）17.先化简，再选择一个你喜欢的数(要合适哦!)代入求值：(1+1x )÷x2−1x．【答案】解：(1+1x )÷x2−1x=x+1x⋅x(x+1)(x−1)=1x−1，当x=2时，原式=12−1=1．【解析】根据分式的加法和除法可以化简题目中的式子，再选取一个使得原分式有意义的值代入即可解答本题．本题考查分式的化简求值，解答本题的关键是明确分式的化简求值的计算方法．18.如图，要在木里县某林场东西方向的两地之间修一条公路MN，已知C点周围200米范围内为原始森林保护区，在MN上的点A处测得C在A的北偏东45∘方向上，从A向东走600米到达B处，测得C在点B的北偏西60∘方向上．(1)MN是否穿过原始森林保护区，为什么？(参考数据：√3≈1.732)(2)若修路工程顺利进行，要使修路工程比原计划提前5天完成，需将原定的工作效率提高25%，则原计划完成这项工程需要多少天？【答案】解：(1)理由如下：如图，过C作CH⊥AB于H．设CH=x，由已知有∠EAC=45∘，∠FBC=60∘，则∠CAH=45∘，∠CBA=30∘．在Rt△ACH中，AH=CH=x，在Rt△HBC中，tan∠HBC=CHHB∴HB=CHtan30∘=x√33=√3x，∵AH+HB=AB，∴x+√3x=600，解得x=6001+√3≈220(米)>200(米)．∴MN不会穿过森林保护区．(2)设原计划完成这项工程需要y天，则实际完成工程需要(y−5)天．根据题意得：1y−5=(1+25%)×1y解得：y=25．经检验知：y=25是原方程的根．答：原计划完成这项工程需要25天．【解析】(1)要求MN是否穿过原始森林保护区，也就是求C到MN的距离.要构造直角三角形，再解直角三角形；(2)根据题意列方程求解．考查了构造直角三角形解斜三角形的方法和分式方程的应用．19.我们常用的数是十进制数，如4657=4×103+6×102+5×101+7×100，数要用10个数码(又叫数字)：0、1、2、3、4、5、6、7、8、9，在电子计算机中用的二进制，只要两个数码：0和1，如二进制中110=1×22+1×21+0×20等于十进制的数6，110101=1×25+1×24+0×23+1×22+0×21+1×20等于十进制的数53.那么二进制中的数101011等于十进制中的哪个数？【答案】解：101011=1×25+0×24+1×23+0×22+1×21+1×20=43，所以二进制中的数101011等于十进制中的43．【解析】利用新定义得到101011=1×25+0×24+1×23+0×22+1×21+1×20，然后根据乘方的定义进行计算．本题考查了有理数的乘方：有理数乘方的定义：求n个相同因数积的运算，叫做乘方．四、解答题（本大题共7小题，共72分）20.计算：|3.14−π|+3.14÷(√32+1)0−2cos45∘+(√2−1)−1+(−1)2009．【答案】解：原式=π−3.14+3.14−2×√22+1√2−1−1=π−√2+√2+1−1=π．【解析】直接利用二次根式的性质以及特殊角的三角函数值、绝对值的性质、负指数幂的性质进而化简得出答案．此题主要考查了实数运算，正确化简各数是解题关键．21.观察下列多面体，并把如表补充完整．名称三棱柱四棱柱五棱柱六棱柱图形顶点数a61012棱数b912面数c58观察表中的结果，你能发现、、之间有什么关系吗？请写出关系式．【答案】解：填表如下：名称三棱柱四棱柱五棱柱六棱柱图形顶点数a681012棱数b9121518面数c5678根据上表中的规律判断，若一个棱柱的底面多边形的边数为n，则它有n个侧面，共有n+2个面，共有2n个顶点，共有3n条棱；故a，b，c之间的关系：a+c−b=2．【解析】结合三棱柱、四棱柱和五棱柱的特点，即可填表，根据已知的面、顶点和棱与几棱柱的关系，可知n棱柱一定有(n+2)个面，2n个顶点和3n条棱，进而得出答案，利用前面的规律得出a，b，c之间的关系．此题主要考查了欧拉公式，熟记常见棱柱的特征，可以总结一般规律：n棱柱有(n+2)个面，2n个顶点和3n条棱是解题关键．22.如图，△ABC在方格纸中(1)请在方格纸上建立平面直角坐标系，使A(2,3)，C(6,2)，并求出B点坐标；(2)以原点O为位似中心，相似比为2，在第一象限内将△ABC放大，画出放大后的图形△A′B′C′；(3)计算的面积S．【答案】解：(1)如图所示，即为所求的直角坐标系；B(2,1)；(2)如图：即为所求；．【解析】(1)直接利用A，C点坐标得出原点位置进而得出答案；(2)利用位似图形的性质即可得出；(3)直接利用(2)中图形求出三角形面积即可．此题主要考查了位似变换以及三角形面积求法，正确得出对应点位置是解题的关键.画位似图形的一般步骤为：①确定位似中心；②分别连接并延长位似中心和关键点；③根据位似比，确定位似图形的关键点；④顺次连接上述各点，得到放大或缩小的图形．23.我国沪深股市交易中，如果买、卖一次股票均需付交易金额的0.5%作费用.张先生以每股5元的价格买入“西昌电力”股票1000股，若他期望获利不低于1000元，问他至少要等到该股票涨到每股多少元时才能卖出？(精确到0.01元)【答案】解：设涨到每股x元时卖出，根据题意得1000x−(5000+1000x)×0.5%≥5000+1000，(4分)解这个不等式得x≥1205199，即x≥6.06.(6分)答：至少涨到每股6.06元时才能卖出.(7分)【解析】根据关系式：总售价−两次交易费≥总成本+1000列出不等式求解即可．本题考查的是一元一次不等式在生活中的实际运用，解决本题的关键是读懂题意根据“总售价−两次交易费≥总成本+1000”列出不等关系式．24.已知一个口袋中装有7个只有颜色不同的球，其中3个白球，4个黑球．(1)求从中随机抽取出一个黑球的概率是多少？(2)若往口袋中再放入x个白球和y个黑球，从口袋中随机取出一个白球的概率是14，求y与x之间的函数关系式．【答案】解：(1)∵一个口袋中装有7个只有颜色不同的球，其中3个白球，4个黑球，∴从中随机抽取出一个黑球的概率是：47；(2)∵往口袋中再放入x个白球和y个黑球，从口袋中随机取出一个白球的概率是14，∴x+37+x+y =14，则y=3x+5．【解析】(1)直接利用概率公式直接得出取出一个黑球的概率；(2)直接利用从口袋中随机取出一个白球的概率是14，进而得出答案函数关系式．此题主要考查了概率公式，正确掌握概率求法是解题关键．25.如图，在平面直角坐标系中，点O1的坐标为(−4,0)，以点O1为圆心，8为半径的圆与x轴交于A，B两点，过A作直线l与x轴负方向相交成60∘的角，且交y轴于C 点，以点O2(13,5)为圆心的圆与x轴相切于点D．(1)求直线l的解析式；(2)将⊙O2以每秒1个单位的速度沿x轴向左平移，当⊙O2第一次与⊙O1外切时，求⊙O2平移的时间．【答案】解：(1)由题意得OA =|−4|+|8|=12， ∴A 点坐标为(−12,0)．∵在Rt △AOC 中，∠OAC =60∘，OC =OAtan∠OAC =12×tan60∘=12√3． ∴C 点的坐标为(0,−12√3).设直线l 的解析式为y =kx +b ，由l 过A 、C 两点，得{−12√3=b 0=−12k +b ，解得{b =−12√3k =−√3∴直线l 的解析式为：y =−√3x −12√3．(2)如图，设⊙O 2平移t 秒后到⊙O 3处与⊙O 1第一次外切于点P ，⊙O 3与x 轴相切于D 1点，连接O 1O 3，O 3D 1．则O 1O 3=O 1P +PO 3=8+5=13． ∵O 3D 1⊥x 轴，∴O 3D 1=5，在Rt △O 1O 3D 1中，O 1D 1=√O 1O 32−O 3D 12=√132−52=12．∵O 1D =O 1O +OD =4+13=17，∴D 1D =O 1D −O 1D 1=17−12=5， ∴t =51=5(秒)．∴⊙O 2平移的时间为5秒．【解析】(1)求直线的解析式，可以先求出A 、C 两点的坐标，就可以根据待定系数法求出函数的解析式．(2)设⊙O 2平移t 秒后到⊙O 3处与⊙O 1第一次外切于点P ，⊙O 3与x 轴相切于D 1点，连接O 1O 3，O 3D 1．在直角△O 1O 3D 1中，根据勾股定理，就可以求出O 1D 1，进而求出D 1D 的长，得到平移的时间．本题综合了待定系数法求函数解析式，以及圆的位置关系，其中两圆相切时的辅助线的作法是经常用到的．26. 如图，已知抛物线y =x 2+bx +c 经过A(1,0)，B(0,2)两点，顶点为D ．(1)求抛物线的解析式；(2)将△OAB 绕点A 顺时针旋转90∘后，点B 落到点C 的位置，将抛物线沿y 轴平移后经过点C ，求平移后所得图象的函数关系式；(3)设(2)中平移后，所得抛物线与y 轴的交点为B 1，顶点为D 1，若点N 在平移后的抛物线上，且满足△NBB1的面积是△NDD1面积的2倍，求点N的坐标．【答案】解：(1)已知抛物线y=x2+bx+c经过A(1,0)，B(0,2)，∴{2=0+0+c0=1+b+c，解得{c=2b=−3，∴所求抛物线的解析式为y=x2−3x+2；(2)∵A(1,0)，B(0,2)，∴OA=1，OB=2，可得旋转后C点的坐标为(3,1)，当x=3时，由y=x2−3x+2得y=2，可知抛物线y=x2−3x+2过点(3,2)，∴将原抛物线沿y轴向下平移1个单位后过点C．∴平移后的抛物线解析式为：y=x2−3x+1；(3)∵点N在y=x2−3x+1上，可设N点坐标为(x0,x02−3x0+1)，将y=x2−3x+1配方得y=(x−32)2−54，∴其对称轴为直线x=32．①0≤x0≤32时，如图①，∵S△NBB1=2S△NDD1，∴12×1×x0=2×12×1×(32−x0)∵x0=1，此时x02−3x0+1=−1，∴N点的坐标为(1,−1)．②当x0>32时，如图②，同理可得12×1×x0=2×12×(x0−32)，∴x0=3，此时x02−3x0+1=1，∴点N的坐标为(3,1)．③当x<0时，由图可知，N点不存在，∴舍去．综上，点N的坐标为(1,−1)或(3,1)．【解析】(1)利用待定系数法，将点A，B的坐标代入解析式即可求得；(2)根据旋转的知识可得：A(1,0)，B(0,2)，∴OA=1，OB=2，可得旋转后C点的坐标为(3,1)，当x=3时，由y=x2−3x+2得y=2，可知抛物线y= x2−3x+2过点(3,2)∴将原抛物线沿y轴向下平移1个单位后过点C.∴平移后的抛物线解析式为：y=x2−3x+1；(3)首先求得B1，D1的坐标，根据图形分别求得即可，要注意利用方程思想．此题属于中考中的压轴题，难度较大，知识点考查的较多而且联系密切，需要学生认真审题．此题考查了二次函数与一次函数的综合知识，解题的关键是要注意数形结合思想的应用．。

2019年中考数学试卷及答案

2019年中考数学试卷及答案一、选择题1．下列计算正确的是（） A ．2a ＋3b ＝5abB ．( a －b )2＝a 2－b 2C ．( 2x 2 )3＝6x 6D ．x 8÷x 3＝x 5 2．在数轴上，与表示6的点距离最近的整数点所表示的数是( ) A ．1B ．2C ．3D ．43．如图，若一次函数y ＝﹣2x +b 的图象与两坐标轴分别交于A ，B 两点，点A 的坐标为（0，3），则不等式﹣2x +b ＞0的解集为（）A ．x ＞32B ．x ＜32C ．x ＞3D ．x ＜34．小军旅行箱的密码是一个六位数，由于他忘记了密码的末位数字，则小军能一次打开该旅行箱的概率是（） A ．110B ．19C ．16D ．155．如图，将△ABC 绕点C （0，1）旋转180°得到△A'B'C ，设点A 的坐标为(,)a b ，则点的坐标为（）A ．(,)a b --B ．(,1)a b ---C ．(,1)a b --+D ．(,2)a b --+6．下列命题中，其中正确命题的个数为（）个．①方差是衡量一组数据波动大小的统计量；②影响超市进货决策的主要统计量是众数；③折线统计图反映一组数据的变化趋势；④水中捞月是必然事件． A ．1B ．2C ．3D ．47．老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：接力中，自己负责的一步出现错误的是（）A．只有乙B．甲和丁C．乙和丙D．乙和丁8．如图，AB是一垂直于水平面的建筑物，某同学从建筑物底端B出发，先沿水平方向向右行走20米到达点C，再经过一段坡度（或坡比）为i=1：0.75、坡长为10米的斜坡CD 到达点D，然后再沿水平方向向右行走40米到达点E（A，B，C，D，E均在同一平面内）．在E处测得建筑物顶端A的仰角为24°，则建筑物AB的高度约为（参考数据：sin24°≈0.41，cos24°≈0.91，tan24°=0.45）（）A．21.7米B．22.4米C．27.4米D．28.8米9．如图，是一个几何体的表面展开图，则该几何体是（）A．三棱柱B．四棱锥C．长方体D．正方体10．如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．若AC=5，BC=2，则sin ∠ACD的值为（）A．53B．255C．52D．2311．如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是()A ．24B ．16C ．413D ．2312．如图，O 为坐标原点，菱形OABC 的顶点A 的坐标为(34)-，，顶点C 在x 轴的负半轴上，函数(0)ky x x=<的图象经过顶点B ，则k 的值为（）A ．12-B ．27-C ．32-D ．36-二、填空题13．如图，△ABC 的三个顶点均在正方形网格格点上，则tan ∠BAC =_____________．14．如图，小明的父亲在相距2米的两棵树间拴了一根绳子，给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为米.15．如图，在平面直角坐标系中，菱形OABC 的边OA 在x 轴上，AC 与OB 交于点D （8，4），反比例函数y=的图象经过点D ．若将菱形OABC 向左平移n 个单位，使点C落在该反比例函数图象上，则n 的值为___．16．如图，⊙O的半径为6cm，直线AB是⊙O的切线，切点为点B，弦BC∥AO，若∠A=30°，则劣弧BC的长为 cm．17．用一个圆心角为180°，半径为4的扇形围成一个圆锥的侧面，则这个圆锥的底面圆的半径为_______．18．如图，正方形ABCD的边长为2，点E为边BC的中点，点P在对角线BD上移动，则PE+PC的最小值是．19．等腰三角形一腰上的高与另一腰的夹角的度数为20°，则顶角的度数是．20．从﹣2，﹣1，1，2四个数中，随机抽取两个数相乘，积为大于﹣4小于2的概率是_____．三、解答题21．电器专营店的经营利润受地理位置、顾客消费能力等因素的影响，某品牌电脑专营店设有甲、乙两家分店，均销售A、B、C、D四种款式的电脑，每种款式电脑的利润如表1所示．现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式，统计各种款式电脑的销售数量，如表2所示．表1：四种款式电脑的利润电脑款式A B C D利润（元/台）160200240320表2：甲、乙两店电脑销售情况电脑款式A B C D甲店销售数量（台）2015105乙店销售数量（台）88101418试运用统计与概率知识，解决下列问题：（1）从甲店每月售出的电脑中随机抽取一台，其利润不少于240元的概率为；（2）经市场调查发现，甲、乙两店每月电脑的总销量相当．现由于资金限制，需对其中一家分店作出暂停营业的决定，若从每台电脑的平均利润的角度考虑，你认为应对哪家分店作出暂停营业的决定？并说明理由．22．如图，在Rt△ACB中，∠C=90°，AC=3cm，BC=4cm，以BC为直径作⊙O交AB于点D．（1）求线段AD的长度；（2）点E是线段AC上的一点，试问：当点E在什么位置时，直线ED与⊙O相切？请说明理由．23．某数学小组到人民英雄纪念碑站岗执勤，并在活动后实地测量了纪念碑的高度，方法如下：如图，首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN项部M的仰角为37°，然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M 的仰角为45°，最后测量出A，B两点间的距离为15m，并且N，B，A三点在一条直线上，连接CD并延长交MN于点E．请你利用他们的测量结果，计算人民英雄纪念碑MN 的高度．（参考数据：sin37°≈0.60，cos37°≈0.80，tan35°≈0.75）24．今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图：等级成绩（s）频数（人数）A90＜s≤1004B80＜s≤90xC70＜s≤8016D s≤706根据以上信息，解答以下问题：（1）表中的x= ；（2）扇形统计图中m= ，n=，C等级对应的扇形的圆心角为度；（3）该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用a1，a2表示）和两名女生（用b1，b2表示），请用列表或画树状图的方法求恰好选取的是a1和b1的概率．25．某烘焙店生产的蛋糕礼盒分为六个档次，第一档次(即最低档次)的产品每天生产76件，每件利润10元，调查表明：生产提高一个档次的蛋糕产品，该产品每件利润增加2元(1)若生产第五档次的蛋糕，该档次蛋糕每件利润为多少元？(2)由于生产工序不同，蛋糕产品每提高一个档次，一天产量会减少4件．若生产的某档次产品一天的总利润为1024元，该烘焙店生产的是第几档次的产品？【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【解析】分析：A．原式不能合并，错误；B．原式利用完全平方公式展开得到结果，即可做出判断；C．原式利用积的乘方运算法则计算得到结果，即可做出判断；D．原式利用同底数幂的除法法则计算得到结果，即可做出判断．详解：A．不是同类项，不能合并，故A错误；B．（a﹣b）2=a2﹣2ab+b2，故B错误；C．（2x2）3＝8x6，故C错误；D．x8÷x3＝x5，故D正确．故选D．点睛：本题考查了完全平方公式，合并同类项，幂的乘方及积的乘方，以及同底数幂的除法，熟练掌握公式及法则是解答本题的关键．2．B解析：B【解析】【分析】6的大小，即可得到结果．【详解】<<，46 6.2526 2.5∴<<，则在数轴上，与表示6的点距离最近的整数点所表示的数是2，故选：B．【点睛】此题考查了实数与数轴，以及算术平方根，熟练掌握各自的性质是解本题的关键．3．B解析：B【解析】【分析】根据点A的坐标找出b值，令一次函数解析式中y=0求出x值，从而找出点B的坐标，观察函数图象，找出在x轴上方的函数图象，由此即可得出结论．【详解】解：∵一次函数y＝﹣2x+b的图象交y轴于点A（0，3），∴b＝3，令y＝﹣2x+3中y＝0，则﹣2x+3＝0，解得：x＝32，∴点B（32，0）．观察函数图象，发现：当x＜32时，一次函数图象在x轴上方，∴不等式﹣2x+b＞0的解集为x＜32．故选：B．【点睛】本题考查了一次函数与一元一次不等式，解题的关键是找出交点B的坐标．本题属于基础题，难度不大，解决该题型题目时，根据函数图象的上下位置关系解不等式是关键．4．A解析：A【解析】∵密码的末位数字共有10种可能（0、1、 2、 3、4、 5、 6、 7、 8、 9、 0都有可能），∴当他忘记了末位数字时，要一次能打开的概率是1 10.故选A.5．D解析：D 【解析】试题分析：根据题意，点A 、A′关于点C 对称，设点A 的坐标是（x ，y ），则0122a xb y++==，，解得2x a y b =-=-+，，∴点A 的坐标是(2)a b --+，．故选D ．考点：坐标与图形变化-旋转．6．C解析：C 【解析】【分析】利用方差的意义，众数的定义、折线图及随机事件分别判断后即可确定正确的选项．【详解】①方差是衡量一组数据波动大小的统计量，正确，是真命题； ②影响超市进货决策的主要统计量是众数，正确，是真命题； ③折线统计图反映一组数据的变化趋势，正确，是真命题； ④水中捞月是随机事件，故错误，是假命题，真命题有3个，故选C ．【点睛】本题考查了命题与定理的知识，解题的关键是了解方差的意义，众数的定义、折线图及随机事件等知识，难度不大．7．D解析：D 【解析】【分析】根据分式的乘除运算步骤和运算法则逐一计算即可判断．【详解】∵22211x x x x x-÷--=2221·1x x x x x --- =()2212·1x x x x x---- =()()221·1x x x x x ---- =()2x x--=2xx-，∴出现错误是在乙和丁，故选D．【点睛】本题考查了分式的乘除法，熟练掌握分式乘除法的运算法则是解题的关键. 8．A解析：A【解析】【分析】作BM⊥ED交ED的延长线于M，CN⊥DM于N．首先解直角三角形Rt△CDN，求出CN，DN，再根据tan24°=AMEM，构建方程即可解决问题.【详解】作BM⊥ED交ED的延长线于M，CN⊥DM于N．在Rt△CDN中，∵140.753CNDN==，设CN=4k，DN=3k，∴CD=10，∴（3k）2+（4k）2=100，∴k=2，∴CN=8，DN=6，∵四边形BMNC是矩形，∴BM=CN=8，BC=MN=20，EM=MN+DN+DE=66，在Rt△AEM中，tan24°=AM EM，∴0.45=866AB +，∴AB=21.7（米），故选A．【点睛】本题考查的是解直角三角形的应用-仰角俯角问题，根据题意作出辅助线，构造出直角三角形是解答此题的关键．9．A解析：A【解析】【分析】本题可以根据三棱柱展开图的三类情况分析解答【详解】三棱柱的展开图大致可分为三类：1.一个三角在中间,每边上一个长方体,另一个在某长方形另一端.2.三个长方形并排,上下各一个三角形.3.中间一个三角形,其中两条边上有长方形,这两个长方形某一个的另一端有三角形,在这三角形的一条(只有一条,否则拼不上)边有剩下的那个长方形.此题目中图形符合第2种情况故本题答案应为：A 【点睛】熟练掌握几何体的展开图是解决本题的关键，有时也可以采用排除法．10．A解析：A 【解析】【分析】在直角△ABC 中，根据勾股定理即可求得AB ，而∠B ＝∠ACD ，即可把求sin ∠ACD 转化为求sin B ．【详解】在直角△ABC 中，根据勾股定理可得：AB ===3．∵∠B +∠BCD ＝90°，∠ACD +∠BCD ＝90°，∴∠B ＝∠ACD ，∴sin ∠ACD ＝sin ∠B AC AB ==．故选A ．【点睛】本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系，难度适中．11．C解析：C 【解析】【分析】由菱形ABCD 的两条对角线相交于O ，AC=6，BD=4，即可得AC ⊥BD ，求得OA 与OB 的长，然后利用勾股定理，求得AB 的长，继而求得答案．【详解】∵四边形ABCD 是菱形，AC=6，BD=4， ∴AC ⊥BD ，OA=12AC=3， OB=12BD=2，AB=BC=CD=AD ，∴在Rt △AOB 中，AB=222+3=13，∴菱形的周长为413．故选C ．12．C 解析：C【解析】【分析】【详解】∵A （﹣3，4），∴OA=2234+=5，∵四边形OABC 是菱形，∴AO=CB=OC=AB=5，则点B 的横坐标为﹣3﹣5=﹣8，故B 的坐标为：（﹣8，4），将点B 的坐标代入k y x=得，4=8k -，解得：k=﹣32．故选C ．考点：菱形的性质；反比例函数图象上点的坐标特征．二、填空题13．【解析】分析：在图形左侧添加正方形网格分别延长ABAC 连接它们延长线所经过的格点可构成直角三角形利用正切的定义即可得出答案详解：如图所示由图形可知∴tan∠BAC=故答案为点睛：本题考查了锐角三角函解析：13【解析】分析：在图形左侧添加正方形网格，分别延长AB 、AC ，连接它们延长线所经过的格点，可构成直角三角形，利用正切的定义即可得出答案.详解：如图所示，由图形可知，90AFE ∠=︒，3AF AC =，EF AC =，∴tan ∠BAC =133EF AC AF AC ==.故答案为1 3 .点睛：本题考查了锐角三角函数的定义. 利用网格构建直角三角形进而利用正切的定义进行求解是解题的关键.14．5【解析】【分析】根据题意运用待定系数法建立适当的函数解析式代入求值即可解答【详解】以左边树与地面交点为原点地面水平线为x轴左边树为y轴建立平面直角坐标系由题意可得A(025)B(225)C(051解析：5【解析】【分析】根据题意，运用待定系数法，建立适当的函数解析式，代入求值即可解答．【详解】以左边树与地面交点为原点，地面水平线为x轴，左边树为y轴建立平面直角坐标系，由题意可得A(0,2.5),B(2,2.5),C(0.5,1)设函数解析式为y=ax2+bx+c把A. B. C三点分别代入得出c=2.5同时可得4a+2b+c=2.5，0.25a+0.5b+c=1解得a=2，b=−4，c=2.5.∴y=2x2−4x+2.5=2(x−1)2+0.5.∵2>0∴当x=1时,y min=0.5米.15．【解析】试题分析根据菱形的性质得出CD=ADBC∥OA根据D（84）和反比例函数的图象经过点D求出k=32C点的纵坐标是2×4=8求出C的坐标即可得出答案∵四边形ABCO是菱形∴CD=ADBC∥OA解析：【解析】试题分析根据菱形的性质得出CD=AD，BC∥OA，根据D （8，4）和反比例函数的图象经过点D求出k=32，C点的纵坐标是2×4=8，求出C的坐标，即可得出答案．∵四边形ABCO是菱形，∴CD=AD，BC∥OA，∵D （8，4），反比例函数的图象经过点D，∴k=32，C点的纵坐标是2×4=8，∴，把y=8代入得：x=4，∴n=4﹣2=2，∴向左平移2个单位长度，反比例函数能过C点，故答案为2．16．【解析】根据切线的性质可得出OB⊥AB从而求出∠BOA的度数利用弦BC∥AO及OB=OC可得出∠BOC的度数代入弧长公式即可得出∵直线AB是⊙O 的切线∴OB⊥AB（切线的性质）又∵∠A=30°∴∠B解析：2π．【解析】根据切线的性质可得出OB⊥AB，从而求出∠BOA的度数，利用弦BC∥AO，及OB=OC可得出∠BOC的度数，代入弧长公式即可得出∵直线AB是⊙O的切线，∴OB⊥AB（切线的性质）．又∵∠A=30°，∴∠BOA=60°（直角三角形两锐角互余）．∵弦BC∥AO，∴∠CBO=∠BOA=60°（两直线平行，内错角相等）．又∵OB=OC，∴△OBC是等边三角形（等边三角形的判定）．∴∠BOC=60°（等边三角形的每个内角等于60°）．又∵⊙O的半径为6cm，∴劣弧BC的长=606=2180ππ⋅⋅（cm）．17．2【解析】【分析】设这个圆锥的底面圆的半径为R根据扇形的弧长等于这个圆锥的底面圆的周长列出方程即可解决问题【详解】设这个圆锥的底面圆的半径为R由题意：2πR=解得R=2故答案为2解析：2【解析】【分析】设这个圆锥的底面圆的半径为R，根据扇形的弧长等于这个圆锥的底面圆的周长，列出方程即可解决问题.【详解】设这个圆锥的底面圆的半径为R，由题意：2πR=1804 180π⨯，解得R=2．故答案为2.18．【解析】试题分析：要求PE+PC的最小值PEPC不能直接求可考虑通过作辅助线转化PEPC的值从而找出其最小值求解试题解析：如图连接AE∵点C关于BD 的对称点为点A∴PE+PC=PE+AP根据两点之间【解析】试题分析：要求PE+PC的最小值，PE，PC不能直接求，可考虑通过作辅助线转化PE，PC的值，从而找出其最小值求解．试题解析：如图，连接AE，∵点C关于BD的对称点为点A，∴PE+PC=PE+AP，根据两点之间线段最短可得AE就是AP+PE的最小值，∵正方形ABCD的边长为2，E是BC边的中点，∴BE=1，∴AE=22125+=．考点：1．轴对称-最短路线问题；2．正方形的性质．19．110°或70°【解析】试题分析：此题要分情况讨论：当等腰三角形的顶角是钝角时腰上的高在外部根据三角形的一个外角等于与它不相邻的两个内角的和即可求得顶角是90°+20°=110°；当等腰三角形的顶角解析：110°或70°．【解析】试题分析：此题要分情况讨论：当等腰三角形的顶角是钝角时，腰上的高在外部．根据三角形的一个外角等于与它不相邻的两个内角的和，即可求得顶角是90°+20°=110°；当等腰三角形的顶角是锐角时，腰上的高在其内部，故顶角是90°﹣20°=70°．故答案为110°或70°．考点：1．等腰三角形的性质；2．分类讨论．20．【解析】【分析】列表得出所有等可能结果从中找到积为大于-4小于2的结果数根据概率公式计算可得【详解】列表如下：-2 -1 1 2 -2 2 -2 -4 -1 2 -1 -2 1 -2 -解析：1 2【解析】【分析】列表得出所有等可能结果，从中找到积为大于-4小于2的结果数，根据概率公式计算可得．【详解】列表如下：∴积为大于-4小于2的概率为612=12，故答案为12．【点睛】此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；用到的知识点为：概率=所求情况数与总情况数之比．三、解答题21．（1）310（2）应对甲店作出暂停营业的决定【解析】【分析】（1）用利润不少于240元的数量除以总数量即可得；（2）先计算出每售出一台电脑的平均利润值，比较大小即可得．【详解】解：（1）从甲店每月售出的电脑中随机抽取一台，其利润不少于240元的概率为1053201510510+=+++，故答案为310；（2）甲店每售出一台电脑的平均利润值为160202001524010320550⨯+⨯+⨯+⨯＝204（元），乙店每售出一台电脑的平均利润值为160820010240143201850⨯+⨯+⨯+⨯＝248（元），∵248＞204，∴乙店每售出一台电脑的平均利润值大于甲店；又两店每月的总销量相当，∴应对甲店作出暂停营业的决定．【点睛】本题主要考查概率公式的应用，解题的关键是熟练掌握概率＝所求情况数与总情况数之比及加权平均数的定义．22．（1）AD=95；（2）当点E是AC的中点时，ED与⊙O相切；理由见解析.【解析】【分析】（1）由勾股定理易求得AB的长；可连接CD，由圆周角定理知CD⊥AB，易知△ACD∽△ABC，可得关于AC、AD、AB的比例关系式，即可求出AD的长．（2）当ED与 O相切时，由切线长定理知EC=ED，则∠ECD=∠EDC，那么∠A和∠DEC就是等角的余角，由此可证得AE=DE，即E是AC的中点．在证明时，可连接OD，证OD⊥DE 即可．【详解】（1）在Rt△ACB中，∵AC=3cm，BC=4cm，∠ACB=90°，∴AB=5cm；连接CD，∵BC为直径，∴∠ADC=∠BDC=90°；∵∠A=∠A，∠ADC=∠ACB，∴Rt△ADC∽Rt△ACB；∴，∴；（2）当点E是AC的中点时，ED与⊙O相切；证明：连接OD，∵DE是Rt△ADC的中线；∴ED=EC，∴∠EDC=∠ECD；∵OC=OD，∴∠ODC=∠OCD；∴∠EDO=∠EDC+∠ODC=∠ECD+∠OCD=∠ACB=90°；∴ED⊥OD，∴ED与⊙O相切．【点睛】本题考查了圆周角定理、切线的判定、相似三角形的判定与性质，熟练掌握该知识点是本题解题的关键.23．人民英雄纪念碑MN的高度约为36.5米．【解析】【分析】在Rt△MED中，由∠MDE＝45°知ME＝DE，据此设ME＝DE＝x，则EC＝x+15，在Rt△MEC 中，由ME＝EC•tan∠MCE知x≈0.7（x+15），解之求得x的值，根据MN＝ME+EN可得答案．【详解】由题意得四边形ABDC、ACEN是矩形，∴EN＝AC＝1.5，AB＝CD＝15，在Rt△MED中，∠MED＝90°，∠MDE＝45°，∴ME＝DE，设ME＝DE＝x，则EC＝x+15，在Rt△MEC中，∠MEC＝90°，∠MCE＝35°，∵ME＝EC•tan∠MCE，∴x≈0.7（x+15），解得：x≈35，∴ME≈35，∴MN＝ME+EN≈36.5，答：人民英雄纪念碑MN的高度约为36.5米．【点睛】本题考查了解直角三角形中的仰俯角问题，解题的关键是从实际问题中整理出直角三角形并利用解直角三角形的知识解题．24．（1）14；（2）10、40、144；（3）恰好选取的是a1和b1的概率为16．【解析】【分析】（1）根据D组人数及其所占百分比可得总人数，用总人数减去其他三组人数即可得出x的值；（2）用A、C人数分别除以总人数求得A、C的百分比即可得m、n的值，再用360°乘以C等级百分比可得其度数；（3）首先根据题意列出表格，然后由表格求得所有等可能的结果与恰好选取的是a1和b1的情况，再利用概率公式即可求得答案．【详解】（1）∵被调查的学生总人数为6÷15%=40人，∴x=40﹣（4+16+6）=14，故答案为14；（2）∵m%=440×100%=10%，n%=1640×10%=40%，∴m=10、n=40，C等级对应的扇形的圆心角为360°×40%=144°，故答案为10、40、144；（3）列表如下：a1和b1的有2种结果，∴恰好选取的是a1和b1的概率为21 126．【点睛】本题考查的是条形统计图和扇形统计图的综合运用，列表法或树状图法求概率，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小；概率=所求情况数与总情况数之比．25．（1该档次蛋糕每件利润为18元;（2）该烘焙店生产的是四档次的产品．【解析】【分析】（1）依题意可求出产品质量在第五档次的每件的利润．（2）设烘焙店生产的是第x档次的产品，根据单件利润×销售数量=总利润，即可得出关于x的一元二次方程，解之即可得出结论．【详解】（1）10＋2×（5－1）＝18（元）．答：该档次蛋糕每件利润为18元．（2）设烘焙店生产的是第x档次的产品，根据题意得：[10＋2（x－1）]×[76－4(x－1）]＝1024，整理得：x2﹣16x＋48＝0，解得：x1＝4，x2＝12（不合题意，舍去）．答：该烘焙店生产的是四档次的产品．【点睛】本题考查了一元二次方程的应用，解题的关键是：（1）根据数量关系，列式计算；（2）根据单件利润×销售数量=总利润，列出关于x的一元二次方程．。

2019年数学中考试卷及答案

2019年数学中考试卷及答案一、选择题1．通过如下尺规作图，能确定点D是BC边中点的是（）A．B．C．D．2．下列几何体中，其侧面展开图为扇形的是( )A．B．C．D．3．有31位学生参加学校举行的“最强大脑”智力游戏比赛，比赛结束后根据每个学生的最后得分计算出中位数、平均数、众数和方差，如果去掉一个最高分和一个最低分，则一定不发生变化的是（）A．中位数B．平均数C．众数D．方差4．如图，在矩形ABCD中，AD=2AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①∠AED=∠CED；②OE=OD；③BH=HF；④BC﹣CF=2HE；⑤AB=HF，其中正确的有（）A．2个B．3个C．4个D．5个5．如图，⊙O的半径为5，AB为弦，点C为AB的中点，若∠ABC=30°，则弦AB的长为（）A．12B．5C53D．36．在某篮球邀请赛中，参赛的每两个队之间都要比赛一场，共比赛36场，设有x 个队参赛，根据题意，可列方程为（）A ．()11362x x -=B ．()11362x x += C ．()136x x -= D ．()136x x +=7．如图，是由四个相同的小正方体组成的立体图形，它的左视图是（）A ．B ．C ．D ．8．估6的值应在（） A ．3和4之间 B ．4和5之间 C ．5和6之间 D ．6和7之间9．如图，将▱ABCD 沿对角线BD 折叠，使点A 落在点E 处，交BC 于点F ，若ABD 48∠=，CFD 40∠=，则E ∠为( )A ．102B ．112C ．122D ．9210．“绿水青山就是金山银山”．某工程队承接了60万平方米的荒山绿化任务，为了迎接雨季的到来，实际工作时每天的工作效率比原计划提高了25%，结果提前30天完成了这一任务．设实际工作时每天绿化的面积为x 万平方米，则下面所列方程中正确的是（） A ．606030(125%)x x -=+ B ．606030(125%)x x -=+ C ．60(125%)6030x x ⨯+-= D ．6060(125%)30x x⨯+-= 11．如图中的几何体是由一个圆柱和个长方体组成的，该几何体的俯视图是( )A ．B ．C ．D ．12．如图，在平行四边形ABCD 中，M 、N 是BD 上两点，BM DN =，连接AM 、MC 、CN 、NA ，添加一个条件，使四边形AMCN 是矩形，这个条件是( )A ．12OM AC =B ．MB MO =C ．BD AC ⊥ D ．AMB CND ∠=∠二、填空题13．如图，直线l x ⊥轴于点P ，且与反比例函数11k y x=（0x >）及22k y x =（0x >）的图象分别交于A 、B 两点，连接OA 、OB ，已知OAB ∆的面积为4，则12k k =﹣________．14．如图：已知AB=10，点C 、D 在线段AB 上且AC=DB=2； P 是线段CD 上的动点，分别以AP 、PB 为边在线段AB 的同侧作等边△AEP 和等边△PFB ，连结EF ，设EF 的中点为G ；当点P 从点C 运动到点D 时，则点G 移动路径的长是________．15．如图，在平面直角坐标系中，点O 为原点，菱形OABC 的对角线OB 在x 轴上，顶点A 在反比例函数y=2x的图像上，则菱形的面积为_______．16．如图所示，过正五边形ABCDE 的顶点B 作一条射线与其内角EAB ∠的角平分线相交于点P ，且60ABP ∠=︒，则APB ∠=_____度．17．不等式组3241112x x x x ≤-⎧⎪⎨--<+⎪⎩的整数解是x= ． 18．如图，在平行四边形ABCD 中，连接BD ，且BD ＝CD ，过点A 作AM ⊥BD 于点M ，过点D 作DN ⊥AB 于点N ，且DN ＝32，在DB 的延长线上取一点P ，满足∠ABD ＝∠MAP ＋∠PAB ，则AP ＝_____.19．正六边形的边长为8cm ，则它的面积为____cm 2．20．对于有理数a 、b ，定义一种新运算，规定a ☆b ＝a 2﹣|b|，则2☆（﹣3）＝_____．三、解答题21．解方程：x 21x 1x-=-. 22．某种蔬菜的销售单价y 1与销售月份x 之间的关系如图1所示，成本y 2与销售月份x 之间的关系如图2所示（图1的图象是线段，图2的图象是抛物线）（1）已知6月份这种蔬菜的成本最低，此时出售每千克的收益是多少元？（收益=售价﹣成本）（2）哪个月出售这种蔬菜，每千克的收益最大？简单说明理由．（3）已知市场部销售该种蔬菜4、5两个月的总收益为22万元，且5月份的销售量比4月份的销售量多2万千克，求4、5两个月的销售量分别是多少万千克？23．“端午节”是我国的传统佳节，民间历来有吃“粽子”的习俗．我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽（以下分别用A 、B 、C 、D 表示）这四种不同口味粽子的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）．请根据以上信息回答：（1）本次参加抽样调查的居民有多少人？（2）将两幅不完整的图补充完整；（3）若居民区有8000人，请估计爱吃D 粽的人数；（4）若有外型完全相同的A 、B 、C 、D 粽各一个，煮熟后，小王吃了两个．用列表或画树状图的方法，求他第二个吃到的恰好是C 粽的概率．24．解方程组：226,320.x y x xy y +=⎧⎨-+=⎩25．将平行四边形纸片ABCD 按如图方式折叠，使点C 与A 重合，点D 落到D '处，折痕为EF ．（1）求证：ABE AD F '≌；（2）连结CF ，判断四边形AECF 是什么特殊四边形？证明你的结论．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【解析】【分析】作线段BC的垂直平分线可得线段BC的中点．【详解】作线段BC的垂直平分线可得线段BC的中点．由此可知：选项A符合条件，故选A．【点睛】本题考查作图﹣复杂作图，解题的关键是熟练掌握五种基本作图．2．C解析：C【解析】【分析】根据特殊几何体的展开图逐一进行分析判断即可得答案．【详解】A、圆柱的侧面展开图是矩形，故A错误；B、三棱柱的侧面展开图是矩形，故B错误；C、圆锥的侧面展开图是扇形，故C正确；D、三棱锥的侧面展开图是三个三角形拼成的图形，故D错误，故选C．【点睛】本题考查了几何体的展开图，熟记特殊几何体的侧面展开图是解题关键．3．A解析：A【解析】【分析】根据中位数的定义：位于中间位置或中间两数的平均数可以得到去掉一个最高分和一个最低分不影响中位数．【详解】去掉一个最高分和一个最低分对中位数没有影响，故选A．【点睛】考查了统计量的选择，解题的关键是了解中位数的定义.4．C解析：C【解析】【分析】【详解】试题分析：∵在矩形ABCD中，AE平分∠BAD，∴∠BAE=∠DAE=45°，∴△ABE是等腰直角三角形，∴AB，∵AB，∴AE=AD，又∠ABE=∠AHD=90°∴△ABE≌△AHD（AAS），∴BE=DH，∴AB=BE=AH=HD，∴∠ADE=∠AED=12（180°﹣45°）=67.5°，∴∠CED=180°﹣45°﹣67.5°=67.5°，∴∠AED=∠CED，故①正确；∵∠AHB=12（180°﹣45°）=67.5°，∠OHE=∠AHB（对顶角相等），∴∠OHE=∠AED，∴OE=OH，∵∠OHD=90°﹣67.5°=22.5°，∠ODH=67.5°﹣45°=22.5°，∴∠OHD=∠ODH，∴OH=OD，∴OE=OD=OH，故②正确；∵∠EBH=90°﹣67.5°=22.5°，∴∠EBH=∠OHD，又BE=DH，∠AEB=∠HDF=45°∴△BEH≌△HDF（ASA），∴BH=HF，HE=DF，故③正确；由上述①、②、③可得CD=BE、DF=EH=CE，CF=CD-DF，∴BC-CF=（CD+HE）-（CD-HE）=2HE，所以④正确；∵AB=AH，∠BAE=45°，∴△ABH不是等边三角形，∴AB≠BH，∴即AB≠HF，故⑤错误；综上所述，结论正确的是①②③④共4个．故选C．【点睛】考点：1、矩形的性质；2、全等三角形的判定与性质；3、角平分线的性质；4、等腰三角形的判定与性质5．D解析：D【解析】【分析】连接OC、OA，利用圆周角定理得出∠AOC=60°，再利用垂径定理得出AB即可．【详解】连接OC、OA，∵∠ABC=30°，∴∠AOC=60°，∵AB为弦，点C为AB的中点，∴OC⊥AB，53在Rt△OAE中，∴AB=53，故选D．【点睛】此题考查圆周角定理，关键是利用圆周角定理得出∠AOC=60°．6．A解析：A【解析】【分析】共有x个队参加比赛，则每队参加（x-1）场比赛，但2队之间只有1场比赛，根据共安排36场比赛，列方程即可．【详解】解：设有x个队参赛，根据题意，可列方程为：1x（x﹣1）＝36，2故选：A．【点睛】此题考查由实际问题抽象出一元二次方程，解题关键在于得到比赛总场数的等量关系. 7．A【解析】【分析】【详解】从左面看，这个立体图形有两层，且底层有两个小正方形，第二层的左边有一个小正方形．故选A ．8．C解析：C【解析】【分析】先化简后利用的范围进行估计解答即可．【详解】 =6-3=3， ∵1.7<<2， ∴5<3<6，即5<<6，故选C ．【点睛】此题主要考查了无理数的估算能力，现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．9．B解析：B【解析】【分析】由平行四边形的性质和折叠的性质，得出ADB BDF DBC ∠∠∠==，由三角形的外角性质求出1BDF DBC DFC 202∠∠∠===，再由三角形内角和定理求出A ∠，即可得到结果．【详解】 AD //BC ，ADB DBC ∠∠∴=，由折叠可得ADB BDF ∠∠=，DBC BDF ∠∠∴=，又DFC 40∠=，DBC BDF ADB 20∠∠∠∴===，又ABD 48∠=，ABD ∴中，A 1802048112∠=--=，E A 112∠∠∴==，【点睛】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理的综合应用，熟练掌握平行四边形的性质，求出ADB ∠的度数是解决问题的关键．10．C解析：C【解析】分析：设实际工作时每天绿化的面积为x 万平方米，根据工作时间=工作总量÷工作效率结合提前 30 天完成任务，即可得出关于x 的分式方程．详解：设实际工作时每天绿化的面积为x 万平方米，则原来每天绿化的面积为125%x +万平方米，依题意得：606030125%x x -=+，即()60125%6030x x ⨯+-=．故选C ．点睛：考查了由实际问题抽象出分式方程．找到关键描述语，找到合适的等量关系是解决问题的关键．11．D解析：D【解析】【分析】根据从上边看得到的图形是俯视图，可得答案．【详解】解：从上边看是一个圆形，圆形内部是一个虚线的正方形.故选：D ．【点睛】本题考查了简单组合体的三视图，从上边看得到的图形是俯视图．12．A解析：A【解析】【分析】由平行四边形的性质可知：OA OC =，OB OD =，再证明OM ON =即可证明四边形AMCN 是平行四边形．【详解】∵四边形ABCD 是平行四边形，∴OA OC =，OB OD =，∵对角线BD 上的两点M 、N 满足BM DN =，∴OB BM OD DN -=-，即OM ON =，∴四边形AMCN 是平行四边形， ∵12OM AC =， ∴MN AC =，∴四边形AMCN 是矩形．故选：A ．【点睛】本题考查了矩形的判定，平行四边形的判定与性质，解题的关键是灵活运用所学知识解决问题．二、填空题13．【解析】【分析】根据反比例函数的几何意义可知：的面积为的面积为然后两个三角形面积作差即可求出结果【详解】解：根据反比例函数的几何意义可知：的面积为的面积为∴的面积为∴∴故答案为8【点睛】本题考查反比解析：【解析】【分析】根据反比例函数k 的几何意义可知：AOP ∆的面积为112k ，BOP ∆的面积为212k ，然后两个三角形面积作差即可求出结果．【详解】解：根据反比例函数k 的几何意义可知：AOP ∆的面积为112k ，BOP ∆的面积为212k ， ∴AOB ∆的面积为121122k k -，∴1211422k k -=，∴128k k -=. 故答案为8．【点睛】本题考查反比例函数k 的几何意义，解题的关键是正确理解k 的几何意义，本题属于基础题型． 14．3【解析】【分析】分别延长AEBF 交于点H 易证四边形EPFH 为平行四边形得出G 为PH 中点则G 的运行轨迹为三角形HCD 的中位线MN 再求出CD 的长运用中位线的性质求出MN 的长度即可【详解】如图分别延长A解析：3【解析】【分析】分别延长AE 、BF 交于点H ，易证四边形EPFH 为平行四边形，得出G 为PH 中点，则G 的运行轨迹为三角形HCD 的中位线MN ．再求出CD 的长，运用中位线的性质求出MN 的长度即可．【详解】如图，分别延长AE、BF交于点H．∵∠A=∠FPB=60°，∴AH∥PF，∵∠B=∠EPA=60°，∴BH∥PE，∴四边形EPFH为平行四边形，∴EF与HP互相平分．∵G为EF的中点，∴G也正好为PH中点，即在P的运动过程中，G始终为PH的中点，所以G的运行轨迹为三角形HCD的中位线MN．∵CD=10-2-2=6，∴MN=3，即G的移动路径长为3．故答案为：3.【点睛】本题考查了等腰三角形及中位线的性质，以及动点问题，是中考的热点．15．4【解析】【分析】【详解】解：连接AC交OB于D∵四边形OABC是菱形∴AC⊥OB∵点A在反比例函数y=的图象上∴△AOD的面积=×2=1∴菱形OABC的面积=4×△AOD的面积=4故答案为：4解析：4【解析】【分析】【详解】解：连接AC交OB于D．∵四边形OABC是菱形，∴AC⊥OB．∵点A 在反比例函数y=2x 的图象上， ∴△AOD 的面积=12×2=1， ∴菱形OABC 的面积=4×△AOD 的面积=4故答案为：416．66【解析】【分析】首先根据正五边形的性质得到度然后根据角平分线的定义得到度再利用三角形内角和定理得到的度数【详解】解：∵五边形为正五边形∴度∵是的角平分线∴度∵∴故答案为：66【点睛】本题考查了多解析：66【解析】【分析】首先根据正五边形的性质得到108EAB ∠=度，然后根据角平分线的定义得到54PAB ∠=度，再利用三角形内角和定理得到APB ∠的度数．【详解】解：∵五边形ABCDE 为正五边形，∴108EAB ∠=度，∵AP 是EAB ∠的角平分线，∴54PAB ∠=度，∵60ABP ∠=︒，∴180605466APB ∠=︒-︒-︒=︒．故答案为：66．【点睛】本题考查了多边形内角与外角，题目中还用到了角平分线的定义及三角形内角和定理．17．﹣4【解析】【分析】先求出不等式组的解集再得出不等式组的整数解即可【详解】解：∵解不等式①得：x≤﹣4解不等式②得：x ＞﹣5∴不等式组的解集为﹣5＜x≤﹣4∴不等式组的整数解为x=﹣4故答案为﹣4【解析：﹣4．【解析】【分析】先求出不等式组的解集，再得出不等式组的整数解即可．【详解】解：3241112x x x x ≤-⎧⎪⎨--<+⎪⎩①②, ∵解不等式①得：x≤﹣4，解不等式②得：x ＞﹣5，∴不等式组的解集为﹣5＜x≤﹣4，∴不等式组的整数解为x=﹣4，故答案为﹣4．【点睛】本题考查了解一元一次不等式组和不等式组的整数解，能根据不等式的性质求出不等式组的解集是解此题的关键．18．6【解析】分析：根据BD=CDAB=CD可得BD=BA再根据AM⊥BDDN⊥AB即可得到DN=AM=3依据∠ABD=∠MAP+∠PAB∠ABD=∠P+∠BAP即可得到△APM是等腰直角三角形进而得到解析：6【解析】分析：根据BD=CD，AB=CD，可得BD=BA，再根据AM⊥BD，DN⊥AB，即可得到，依据∠ABD=∠MAP+∠PAB，∠ABD=∠P+∠BAP，即可得到△APM是等腰直角三角形，进而得到AM=6．详解：∵BD=CD，AB=CD，∴BD=BA，又∵AM⊥BD，DN⊥AB，∴，又∵∠ABD=∠MAP+∠PAB，∠ABD=∠P+∠BAP，∴∠P=∠PAM，∴△APM是等腰直角三角形，∴AM=6，故答案为6．点睛：本题主要考查了平行四边形的性质以及等腰直角三角形的性质的运用，解决问题给的关键是判定△APM是等腰直角三角形．19．【解析】【分析】【详解】如图所示正六边形ABCD中连接OCOD过O作OE⊥CD；∵此多边形是正六边形∴∠COD=60°；∵OC=OD∴△COD是等边三角形∴OE=CE•tan60°=cm∴S△OCD【解析】【分析】【详解】如图所示，正六边形ABCD中，连接OC、OD，过O作OE⊥CD；∵此多边形是正六边形，∴∠COD=60°；∵OC=OD，∴△COD是等边三角形，∴OE=CE•tan60°=83432⨯=cm，∴S△OCD=12CD•OE=12×8×43=163cm2．∴S正六边形=6S△OCD=6×163=963cm2．考点：正多边形和圆20．1【解析】解：2☆（﹣3）=22﹣|﹣3|=4﹣3=1故答案为1点睛：此题考查有理数的混合运算掌握规定的运算方法是解决问题的关键解析：1【解析】解：2☆（﹣3）=22﹣|﹣3|=4﹣3=1．故答案为1．点睛：此题考查有理数的混合运算，掌握规定的运算方法是解决问题的关键．三、解答题21．2x=.【解析】【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【详解】去分母得：x2-2x+2=x2-x，解得：x=2，检验：当x=2时，方程左右两边相等，所以x=2是原方程的解．【点睛】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．22．（1）6月份出售这种蔬菜每千克的收益是2元．（2）5月份出售这种蔬菜，每千克的收益最大．（3）4月份的销售量为4万千克，5月份的销售量为6万千克．【解析】分析：（1）找出当x=6时，y1、y2的值，二者作差即可得出结论；（2）观察图象找出点的坐标，利用待定系数法即可求出y1、y2关于x的函数关系式，二者作差后利用二次函数的性质即可解决最值问题；（3）求出当x=4时，y1﹣y2的值，设4月份的销售量为t万千克，则5月份的销售量为（t+2）万千克，根据总利润=每千克利润×销售数量，即可得出关于t 的一元一次方程，解之即可得出结论．详解：（1）当x=6时，y 1=3，y 2=1，∵y 1﹣y 2=3﹣1=2，∴6月份出售这种蔬菜每千克的收益是2元．（2）设y 1=mx+n ，y 2=a （x ﹣6）2+1．将（3，5）、（6，3）代入y 1=mx+n ，3563m n m n +=⎧⎨+=⎩，解得：237m n ⎧=-⎪⎨⎪=⎩， ∴y 1=﹣23x+7；将（3，4）代入y 2=a （x ﹣6）2+1，4=a （3﹣6）2+1，解得：a=13， ∴y 2=13（x ﹣6）2+1=13x 2﹣4x+13． ∴y 1﹣y 2=﹣23x+7﹣（13x 2﹣4x+13）=﹣13x 2+103x ﹣6=﹣13（x ﹣5）2+73． ∵﹣13＜0， ∴当x=5时，y 1﹣y 2取最大值，最大值为73，即5月份出售这种蔬菜，每千克的收益最大．（3）当t=4时，y 1﹣y 2=﹣13x 2+103x ﹣6=2．设4月份的销售量为t 万千克，则5月份的销售量为（t+2）万千克，根据题意得：2t+73（t+2）=22，解得：t=4，∴t+2=6．答：4月份的销售量为4万千克，5月份的销售量为6万千克．点睛：本题考查了待定系数法求一次（二次）函数解析式、二次函数的性质以及一元一次方程的应用，解题的关键是：（1）观察函数图象，找出当x=6时y 1﹣y 2的值；（2）根据点的坐标，利用待定系数法求出y 1、y 2关于x 的函数关系式；（3）找准等量关系，正确列出一元一次方程．23．（1）600（2）见解析（3）3200（4）【解析】（1）60÷10%=600（人）．答：本次参加抽样调查的居民有600人．（2分）（2）如图；…（5分）（3）8000×40%=3200（人）．答：该居民区有8000人，估计爱吃D 粽的人有3200人．…（7分）（4）如图；（列表方法略，参照给分）．…（8分）P （C 粽）==．答：他第二个吃到的恰好是C 粽的概率是．…（10分）24．114,2;x y =⎧⎨=⎩223,3.x y =⎧⎨=⎩ 【解析】【分析】先对x 2-3xy+2y 2=0分解因式转化为两个一元一次方程，然后联立①，组成两个二元一次方程组，解之即可．【详解】将方程22320x xy y -+= 的左边因式分解，得20x y -=或0x y -=．原方程组可以化为6,20x y x y +=⎧⎨-=⎩或6,0.x y x y +=⎧⎨-=⎩解这两个方程组得114,2;x y =⎧⎨=⎩ 223,3.x y =⎧⎨=⎩ 所以原方程组的解是114,2;x y =⎧⎨=⎩ 223,3.x y =⎧⎨=⎩ 【点睛】本题考查了高次方程组，将高次方程化为一次方程是解题的关键．25．（1）证明见解析；（2）四边形AECF 是菱形．证明见解析.【解析】【分析】（1）根据平行四边形的性质及折叠的性质我们可以得到∠B=∠D′，AB=AD′，∠1=∠3，从而利用ASA 判定△ABE ≌△AD′F ；（2）四边形AECF 是菱形，我们可以运用菱形的判定，有一组邻边相等的平行四边形是菱形来进行验证．【详解】解:（1）由折叠可知：∠D=∠D′，C D=AD′，∠C=∠D′AE ．∵四边形ABCD 是平行四边形，∴∠B=∠D ，AB=CD ，∠C=∠BAD ．∴∠B=∠D′，AB=AD′，∠D′AE=∠BAD ，即∠1+∠2=∠2+∠3．∴∠1=∠3．在△ABE 和△AD′F 中∵{13D BAB AD ∠'=∠='∠=∠∴△ABE ≌△AD′F （ASA ）．（2）四边形AECF 是菱形．证明：由折叠可知：AE=EC ，∠4=∠5．∵四边形ABCD 是平行四边形，∴AD ∥BC ．∴∠5=∠6．∴∠4=∠6．∴AF=AE ．∵AE=EC ，∴AF=EC ．又∵AF ∥EC ，∴四边形AECF 是平行四边形．又∵AF=AE ，∴平行四边形AECF是菱形．考点：1.全等三角形的判定；2.菱形的判定．。

(3套)2019年中考数学试题(解析版)

2019年河南省中考数学试卷一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的。

1．（3分）﹣的绝对值是（）A．﹣B．C．2 D．﹣22．（3分）成人每天维生素D的摄入量约为0.0000046克．数据“0.0000046”用科学记数法表示为（）A．46×10﹣7B．4.6×10﹣7C．4.6×10﹣6D．0.46×10﹣53．（3分）如图，AB∥CD，∠B＝75°，∠E＝27°，则∠D的度数为（）A．45°B．48°C．50°D．58°4．（3分）下列计算正确的是（）A．2a+3a＝6a B．（﹣3a）2＝6a2C．（x﹣y）2＝x2﹣y2D．3﹣＝25．（3分）如图①是由大小相同的小正方体搭成的几何体，将上层的小正方体平移后得到图②．关于平移前后几何体的三视图，下列说法正确的是（）A．主视图相同B．左视图相同C．俯视图相同D．三种视图都不相同6．（3分）一元二次方程（x+1）（x﹣1）＝2x+3的根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．只有一个实数根D．没有实数根7．（3分）某超市销售A，B，C，D四种矿泉水，它们的单价依次是5元、3元、2元、1元．某天的销售情况如图所示，则这天销售的矿泉水的平均单价是（）A．1.95元B．2.15元C．2.25元D．2.75元8．（3分）已知抛物线y＝﹣x2+bx+4经过（﹣2，n）和（4，n）两点，则n的值为（）A．﹣2 B．﹣4 C．2 D．49．（3分）如图，在四边形ABCD中，AD∥BC，∠D＝90°，AD＝4，BC＝3．分别以点A，C为圆心，大于AC长为半径作弧，两弧交于点E，作射线BE交AD于点F，交AC于点O．若点O是AC的中点，则CD的长为（）A．2B．4 C．3 D．10．（3分）如图，在△OAB中，顶点O（0，0），A（﹣3，4），B（3，4），将△OAB与正方形ABCD组成的图形绕点O顺时针旋转，每次旋转90°，则第70次旋转结束时，点D的坐标为（）A．（10，3）B．（﹣3，10）C．（10，﹣3）D．（3，﹣10）二、填空题（每小题3分，共15分。

2019年中考数学试卷带答案

∴该组数据的众数是80分或90分．
故选D．
【点睛】
本题考查了加权平均数的计算和列方程解决问题的能力，解题的关键是利用加权平均数列出方程．通过列方程求出x是解答问题的关键．
7．C
解析：C
【解析】
试题分析：根据轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．据此对图中的图形进行判断．
故轴对称图形有4个．
故选C．
考点：轴对称图形．
8．A
解析：A
【解析】
【分析】
作BM⊥ED交ED的延长线于M，CN⊥DM于N．首先解直角三角形Rt△CDN，求出CN，DN，再根据tan24°= ，构建方程即可解决问题.
【详解】
作BM⊥ED交ED的延长线于M，CN⊥DM于N．
在Rt△CDN中，∵ ，设CN=4k，DN=3k，
A．21.7米B．22.4米C．27.4米D．28.8米
9．已知为矩形的对角线，则图中与一定不相等的是（）
A． B． C． D．
10．若关于x的一元二次方程有两个实数根，则k的取值范围是（）
A． B． C． D．
11．如图，是由四个相同的小正方体组成的立体图形，它的左视图是（）
A． B． C． D．
9．D
解析：D
【解析】
【分析】
【详解】
解：A选项中，根据对顶角相等，得与一定相等；
B、C项中无法确定与是否相等；
D选项中因为∠1=∠ACD，∠2＞∠ACD，所以∠2＞∠1．
故选：D
10．D
解析：D
【解析】
【分析】
运用根的判别式和一元二次方程的定义，组成不等式组即可解答
【详解】

2019年数学中考试题(附答案)

C．（﹣1.5）8÷（﹣1.5）7=﹣1.5D．﹣1.58÷（﹣1.5）7=﹣1.5
9．如图，已知，那么下列结论正确的是（）
A． B． C． D．
10．若关于x的一元二次方程kx2﹣4x+3=0有实数根，则k的非负整数值是（）
A．1B．0，1C．1，2D．1，2，3
11．二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为( )
2019年数学中考试题(附答案)
一、选择题
1．下列命题中，其中正确命题的个数为（）个．
①方差是衡量一组数据波动大小的统计量；②影响超市进货决策的主要统计量是众数；③折线统计图反映一组数据的变化趋势；④水中捞月是必然事件．
A．1B．2C．3D．4
2．不等式组的解集在数轴上表示正确的是（）
A． B． C． D．
∴∠DAB=90°，
∴∠DAM=30°，
∴AM= ，
故选：B．
【点睛】
本题考查了矩形的性质及折叠的性质，解题的关键是利用折叠的性质求得∠MAN=∠DAM,
4．A
解析：A
【解析】
试题分析：∵今后项目的数量﹣今年的数量=20，∴ ．故选A．
考点：由实际问题抽象出分式方程．
5．C
解析：C
【解析】
试题解析：A、的主视图是矩形，故A不符合题意；
（收集数据）
甲班15名学生测试成绩统计如下：（满分100分）
68，72，89，85，82，85，74，92，80，85，78，85，69，76，80
乙班15名学生测试成绩统计如下：（满分100分）
86，89，83，76，73，78，67，80，80，79，80，84，82，80，83
（整理数据）

【中考真题】2019年全国中考数学试卷(含答案及解析)

【中考真题】2019年全国中考数学试卷(含答案及解析)2019年全国中考数学试卷(含答案及解析)。

一、选择题。

1.已知函数y=2x+3，那么当x=5时，y的值是多少？A. 8B. 10C. 13D. 15。

解析，将x=5代入y=2x+3中，得到y=25+3=13，因此答案为C。

2.下列各数中，最小的是（）。

A. -5B. -3C. 1D. 2。

解析，-5是负数中最小的，因此答案为A。

3.已知集合A={x|x是2的倍数}，集合B={x|x是3的倍数}，则A∪B是（）。

A. {x|x是2和3的公倍数}B. {x|x是2或3的倍数} 。

C. {x|x是2和3的公因数}D. {x|x是2和3的倍数}。

解析，A∪B表示A和B的并集，即A和B中所有的元素的集合。

A={...,-4,-2,0,2,4,...}，B={...,-6,-3,0,3,6,...}，A∪B={...,-6,-4,-3,-2,0,2,3,4,6,...}，即A∪B是2和3的倍数的集合，因此答案为D。

4.已知△ABC中，AB=BC=6cm，AC=8cm，则△ABC的周长是（）。

A. 12cmB. 20cmC. 24cmD. 30cm。

解析，△ABC的周长为AB+BC+AC=6+6+8=20cm，因此答案为B。

5.已知直角三角形的两条直角边分别为3cm和4cm，则斜边长为（）。

A. 5cmB. 7cmC. 9cmD. 12cm。

解析，根据勾股定理，斜边长为√(3^2+4^2)=√(9+16)=√25=5cm，因此答案为A。

6.已知a:b=3:4，b:c=2:5，则a:b:c=（）。

A. 3:4:5B. 6:8:10C. 12:16:20D. 15:20:25。

解析，根据比例的性质，a:b=3:4，b:c=2:5，将两个比例相连结，得到a:b:c=32:42:45=6:8:20，因此答案为B。

7.已知(-2)×(-3)×(-4)×(-5)的结果是（）。

2019年中考数学试题含答案

2019年中考数学试题含答案一、选择题1．如图A ，B ，C 是上的三个点，若，则等于（）A ．50°B ．80°C ．100°D ．130° 2．下列四个实数中，比1-小的数是（）A ．2-B ．0C ．1D ．23．二次函数y ＝x 2﹣6x +m 满足以下条件：当﹣2＜x ＜﹣1时，它的图象位于x 轴的下方；当8＜x ＜9时，它的图象位于x 轴的上方，则m 的值为（） A ．27B ．9C ．﹣7D ．﹣164．小军旅行箱的密码是一个六位数，由于他忘记了密码的末位数字，则小军能一次打开该旅行箱的概率是（） A ．110B ．19C ．16D ．155．定义一种新运算：1an n n bn xdx a b -⋅=-⎰，例如：222khxdx k h ⋅=-⎰，若m252mx dx --=-⎰，则m =（）A ．-2B ．25-C ．2D ．256．肥皂泡的泡壁厚度大约是0.0007mm ，0.0007用科学记数法表示为（） A ．0.7×10﹣3 B ．7×10﹣3 C ．7×10﹣4 D ．7×10﹣5 7．下列命题中，真命题的是（） A ．对角线互相垂直的四边形是菱形 B ．对角线互相垂直平分的四边形是正方形 C ．对角线相等的四边形是矩形D ．对角线互相平分的四边形是平行四边形8．如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB ，垂足为D ．若AC 5BC =2，则sin ∠ACD 的值为（）A ．5 B ．25C ．5 D ．239．若关于x 的一元二次方程()2110k x x -++=有两个实数根，则k 的取值范围是（）A ．54k ≤B ．54k ＞C ．514k k ≠＜且D ．514k k ≤≠且 10．如图，在直角坐标系中，矩形OABC 的顶点O 在坐标原点，边OA 在x 轴上，OC 在y 轴上，如果矩形OA′B′C′与矩形OABC 关于点O 位似，且矩形OA′B′C′的面积等于矩形OABC 面积的14，那么点B′的坐标是（）A ．（－2，3）B ．（2，－3）C ．（3，－2）或（－2，3）D ．（－2，3）或（2，－3）11．根据以下程序，当输入x ＝2时，输出结果为（）A ．﹣1B ．﹣4C ．1D ．11 12．已知关于x 的方程2x+a-9=0的解是x=2，则a 的值为A ．2B ．3C ．4D ．5二、填空题13．色盲是伴X 染色体隐性先天遗传病，患者中男性远多于女性，从男性体检信息库中随机抽取体检表，统计结果如表：抽取的体检表数n 501002004005008001000120015002000色盲患者的频数m3 7 13 29 37 55 69 85 105 138色盲患者的频率m/n0.0600.0700.0650.0730.0740.0690.0690.0710.0700.069根据表中数据，估计在男性中，男性患色盲的概率为______（结果精确到0.01）．14．如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝3， BC＝2，tanA＝43，则CD＝_____．15．已知关于x的方程3x n22x1+=+的解是负数，则n的取值范围为．16．如图：已知AB=10，点C、D在线段AB上且AC=DB=2； P是线段CD上的动点，分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB，连结EF，设EF的中点为G；当点P从点C运动到点D时，则点G移动路径的长是________．17．如图，在△ABC中E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC、△ADF、△BEF的面积分别为S△ABC，S△ADF，S△BEF，且S△ABC=12，则S△ADF－S△BEF=_________．18．如图，在△ABC中，BC边上的垂直平分线DE交边BC于点D，交边AB于点E．若△EDC的周长为24，△ABC与四边形AEDC的周长之差为12，则线段DE的长为_____．19．一批货物准备运往某地，有甲、乙、丙三辆卡车可雇用.已知甲、乙、丙三辆车每次运货量不变，且甲、乙两车单独运完这批货物分别用2, a a 次；甲、丙两车合运相同次数，运完这批货物，甲车共运180吨；乙、丙两车合运相同次数，运完这批货物乙车共运270吨，现甲、乙、丙合运相同次数把这批货物运完，货主应付甲车主的运费为___________ 元.(按每吨运费20元计算)20．在一个不透明的口袋中，装有A ，B ，C ，D4个完全相同的小球，随机摸取一个小球然后放回，再随机摸取一个小球，两次摸到同一个小球的概率是___．三、解答题21．如图，AB 是⊙O 的直径，点C 是的中点，连接AC 并延长至点D ，使CD ＝AC ，点E 是OB 上一点，且，CE 的延长线交DB 的延长线于点F ，AF 交⊙O 于点H ，连接BH ．（1）求证：BD 是⊙O 的切线；（2）当OB ＝2时，求BH 的长．22．如图是某市一座人行天桥的示意图，天桥离地面的高BC 是10米，坡面AC 的倾斜角45CAB ∠=︒，在距A 点10米处有一建筑物HQ .为了方便行人推车过天桥，市政府部门决定降低坡度，使新坡面DC 的倾斜角30BDC ∠=︒，若新坡面下D 处与建筑物之间需留下至少3米宽的人行道，问该建筑物是否需要拆除（计算最后结果保留一位小数）.（参考数据：2 1.414≈，3 1.732≈）23．某市某中学积极响应创建全国文明城市活动，举办了以“校园文明”为主题的手抄报比赛.所有参赛作品均获奖，奖项分为一等奖、二等奖、三等奖和优秀奖，将获奖结果绘制成如右两幅统计图.请你根据图中所给信息解答意）（1）等奖所占的百分比是________；三等奖的人数是________人；（2）据统计，在获得一等奖的学生中，男生与女生的人数比为11:，学校计划选派1名男生和1名女生参加市手抄报比赛，请求出所选2位同学恰是1名男生和1名女生的概率；（3）学校计划从获得二等奖的同学中选取一部分人进行集训使其提升为一等奖，要使获得一等奖的人数不少于二等奖人数的2倍，那么至少选取多少人进行集训？24．材料：解形如（x+a）4+（x+b）4＝c的一元四次方程时，可以先求常数a和b的均值，然后设y＝x+．再把原方程换元求解，用种方法可以成功地消去含未知数的奇次项，使方程转化成易于求解的双二次方程，这种方法叫做“均值换元法．例：解方程：（x﹣2）4+（x﹣3）4＝1解：因为﹣2和﹣3的均值为，所以，设y＝x﹣，原方程可化为（y+）4+（y﹣）4＝1，去括号，得：（y2+y+）2+（y2﹣y+）2＝1y4+y2++2y3+y2+y+y4+y2+﹣2y3+y2﹣y＝1整理，得：2y4+3y2﹣＝0（成功地消去了未知数的奇次项）解得：y2＝或y2＝（舍去）所以y＝±，即x﹣＝±．所以x＝3或x＝2．（1）用阅读材料中这种方法解关于x的方程（x+3）4+（x+5）4＝1130时，先求两个常数的均值为______．设y＝x+____．原方程转化为：（y﹣_____）4+（y+_____）4＝1130．（2）用这种方法解方程（x+1）4+（x+3）4＝70625．计算：（1）2（m﹣1）2﹣（2m+1）（m﹣1）（2）（1﹣）【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【解析】试题分析：根据圆周的度数为360°，可知优弧AC的度数为360°-100°=260°，然后根据同弧所对的圆周角等于它所对的圆心角的一半，可求得∠B=130°．故选D考点：圆周角定理2．A解析：A【解析】试题分析：A．﹣2＜﹣1，故正确；B．0＞﹣1，故本选项错误；C．1＞﹣1，故本选项错误；D．2＞﹣1，故本选项错误；故选A．考点：有理数大小比较．3．D解析：D【解析】【分析】先确定抛物线的对称轴为直线x＝3，根据抛物线的对称性得到x＝−2和x＝8时，函数值相等，然后根据题意判断抛物线与x轴的交点坐标为（−2，0），（8，0），最后把（−2，0）代入y＝x2−6x＋m可求得m的值．【详解】解：∵抛物线的对称轴为直线x＝，∴x＝−2和x＝8时，函数值相等，∵当−2＜x＜−1时，它的图象位于x轴的下方；当8＜x＜9时，它的图象位于x轴的上方，∴抛物线与x轴的交点坐标为（−2，0），（8，0），把（−2，0）代入y＝x2−6x＋m得4＋12＋m＝0，解得m＝−16．故选：D．【点睛】本题考查了抛物线与x 轴的交点：把求二次函数y ＝ax 2＋bx ＋c （a ，b ，c 是常数，a≠0）与x 轴的交点坐标问题转化为解关于x 的一元二次方程．也考查了二次函数的性质．4．A解析：A 【解析】∵密码的末位数字共有10种可能（0、1、 2、 3、4、 5、 6、 7、 8、 9、 0都有可能）， ∴当他忘记了末位数字时，要一次能打开的概率是110. 故选A.5．B解析：B 【解析】【分析】根据新定义运算得到一个分式方程，求解即可. 【详解】根据题意得，5211m11(5)25m x dx m m m m---⎰-=-=-=-，则25m =-，经检验，25m =-是方程的解，故选B. 【点睛】此题考查了解分式方程，弄清题中的新定义是解本题的关键．6．C解析：C 【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n ，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【详解】解：0.0007=7×10﹣4 故选C ．【点睛】本题考查科学计数法，难度不大．7．D解析：D【分析】根据平行四边形、矩形、菱形、正方形的判定定理进行判断即可．【详解】对角线互相垂直且平分的四边形是菱形，故A 是假命题；对角线互相垂直平分且相等的四边形是正方形，故B 是假命题；对角线相等且平分的四边形是矩形，故C 是假命题；对角线互相平分的四边形是平行四边形，故D 是真命题．故选D ．【点睛】本题考查了命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．8．A解析：A 【解析】【分析】在直角△ABC 中，根据勾股定理即可求得AB ，而∠B ＝∠ACD ，即可把求sin ∠ACD 转化为求sin B ．【详解】在直角△ABC 中，根据勾股定理可得：AB ===3．∵∠B +∠BCD ＝90°，∠ACD +∠BCD ＝90°，∴∠B ＝∠ACD ，∴sin ∠ACD ＝sin ∠B AC AB ==．故选A ．【点睛】本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系，难度适中．9．D解析：D 【解析】【分析】运用根的判别式和一元二次方程的定义，组成不等式组即可解答【详解】解：∵关于x 的一元二次方程（k ﹣1）x 2+x +1＝0有两个实数根，∴210=1-41)10k k -⎧⎨∆⨯-⨯≥⎩≠（，解得：k ≤54且k ≠1．故选：D ．此题考查根的判别式和一元二次方程的定义，掌握根的情况与判别式的关系是解题关键10．D解析：D【解析】如果两个图形不仅是相似图形，而且每组对应点的连线交于一点，对应边互相平行或在一条直线上，那么这两个图形叫做位似图形。

2019年中考数学试题及答案

10．B
解析：B 【解析】【分析】根据 4.84<5<5.29，可得答案．【详解】 ∵4.84<5<5.29，
∴2.2< 5 <2.3，
∴1.2< 5 -1<1.3，
故选 B．【点睛】
本题考查了估算无理数的大小，利用 5 ≈2.236 是解题关键． 11．D
解析：D 【解析】【分析】将特殊角的三角函数值代入求解．【详解】
5．B
解析：B 【解析】试题分析：根据题意，要分情况讨论：①、3 是腰；②、3 是底．必须符合三角形三边的关系，任意两边之和大于第三边．解：①若 3 是腰，则另一腰也是 3，底是 6，但是 3+3=6，∴不构成三角形，舍去． ②若 3 是底，则腰是 6，6． 3+6＞6，符合条件．成立． ∴C=3+6+6=15．故选 B．考点：等腰三角形的性质．
（2）如图 2，当 6<t<10 时，DE 是否存在最小值？若存在，求出 DE 的最小值；若不存在，请说明理由. （3）当点 D 在射线 OM 上运动时，是否存在以 D，E，B 为顶点的三角形是直角三角形？若存在，求出此时 t 的值；若不存在，请说明理由.
【参考答案】***试卷处理标记，请不要删除
A．12cm2
B． 12 πcm2
C． 6π cm2
D． 8π cm2
9．均匀的向一个容器内注水，在注水过程中，水面高度 h 与时间 t 的函数关系如图所示，
则该容器是下列中的（）
A．
B．
C．
D．
10．黄金分割数 5 1 是一个很奇妙的数，大量应用于艺术、建筑和统计决策等方面，请 2
你估算 5 ﹣1 的值（）

2019全国中考数学真题分类汇编：与圆的有关计算及参考答案

一、选择题1．（2019·德州）如图，点O为线段BC的中点，点A，C，D到点O的距离相等，若∠ABC＝40°，则∠ADC的度数是（）A．130°B．140°C．150°D．160°【答案】B．【解析】由题意得到OA＝OB＝OC＝OD，作出圆O，如图所示，∴四边形ABCD为圆O的内接四边形，∴∠ABC+∠ADC＝180°，∵∠ABC＝40°，∴∠ADC＝140°，故选B．2．（2019·滨州）如图，AB为⊙O的直径，C，D为⊙O上两点，若∠BCD＝40°，则∠ABD的大小为（）A．60°B．50°C．40°D．20°【答案】B【解析】如图，连接AD，∵AB为⊙O的直径，∴∠ADB=90°．∵∠A和∠BCD都是弧BD所对的圆周角，∴∠A=∠BCD=40°，∴∠ABD=90°－40°=50°．故选B．3、（2019·遂宁）如图，△ABC 内接于⊙O ，若∠A=45°，⊙O 的半径r=4，则阴影部分的面积为 ( )A.4π-8B. 2πC.4πD. 8π-8 【答案】A【解析】由题意可知∠BOC=2∠A=45°2⨯=90°，S 阴=S 扇-S △OBC ，S 扇=14S 圆=14π42=4π， S △OBC =2142⨯=8，所以阴影部分的面积为4π-8，故选A. 4．(2019·广元)如图,AB,AC 分别是 O 的直径和弦,OD ⊥AC 于点D,连接BD,BC,且AB ＝10,AC ＝8,则BD 的长为( )A.B.4C.D.4.8第6题图【答案】C【解析】∵AB 是直径,∴∠C ＝90°,∴BC ＝6,又∵OD ⊥AC,∴OD ∥BC,∴△OAD ∽△BAC,∴CD ＝AD＝12AC ＝4,∴BD =故选C.5．（2019·温州）若扇形的圆心角为90°，半径为6，则该扇形的弧长为（） A ．32π B ．2π C ．3π D ．6π 【答案】D【解析】扇形的圆心角为90°，它的半径为6，即n=90°，r=6，根据弧长公式l=180n rπ，得6π．故选D. 6．（2019·绍兴）如图，△ABC 内接于圆O ，∠B=65°，∠C=70°，若BC=22，则弧BC 的长为 ( )A.πB.π2C.π2D.π22【答案】A【解析】在△ABC 中，得∠A＝180°-∠B -∠C＝45°，连接OB ，OC ，则∠BOC＝2∠A＝90°，设圆的半径为r ，由勾股定理，得22r r +＝（22）2，解得r=2，所以弧BC 的长为902180π⨯=π．7．（2019·山西）如图,在Rt △ABC 中,∠ABC ＝90°,AB ＝＝2,以AB 的中点O 为圆心,OA 的长为半径作半圆交AC 于点D,则图中阴影部分的面积为( )2π- 2πC.πD.2π第10题图【答案】A【解题过程】在Rt △ABC 中,连接OD,∠ABC ＝90°,AB ＝＝2,∴∠A ＝30°,∠DOB ＝60°,过点D 作DE ⊥AB 于点E,∵AB ＝∴AO ＝OD＝∴DE ＝32,∴S 阴影＝S △ABC －S △AOD －S扇形BOD＝－2π2π-,故选A.8．（2019·长沙）一个扇形的半径为6，圆心角为120°，则该扇形的面积是【】A ．2π B．4π C．12π D．24π 【答案】C【解析】根据扇形的面积公式，S=120×π×62360=12π，故本题选：C ．9．（2019·武汉）如图，AB 是⊙O 的直径，M 、N 是弧AB （异于A 、B ）上两点，C 是弧MN 上动点，∠ACB 的角平分线交⊙O 于点D ，∠BAC 的平分线交CD 于点E ．当点C 从点M 运动到点N 时，则C 、E 两点的运动路径长的比是（）A ．2B ．2πC ．23 D ．25【答案】A【解题过程】由题得∠1＝∠2＝12∠C ＝45°，∠3＝∠4，∠5＝∠6 设∠3＝∠4＝m ，∠5＝∠6＝n ，得m ＋n ＝45°，∴∠AEB ＝∠C ＋m ＋n90°＋45°＝135°∴E 在以AD 为半径的⊙D 上（定角定圆）4t 2t t165432QP EDAOBC MN如图，C的路径为MN,E的路径为PQ设⊙O的半径为1，则⊙D，∴MNPQ＝42136022360ttππ⨯⨯⨯10. (2019·泰安)如图,将O沿弦AB折叠,AB恰好经过圆心O,若O的半径为3,则AB的长为A.12π B.π C.2π D.3π【答案】C【解析】连接OA,OB,过点O作OD⊥AB交AB于点E,由题可知OD＝DE＝12OE＝12OA,在Rt△AOD中,sinA＝ODOA＝1 2,∴∠A＝30°,∴∠AOD＝60°,∠AOB＝120°,AB＝180n rπ＝2π,故选C.11. (2019·枣庄)如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,交对角线BD与点E,则图中阴影部分的面积是(结果保留π)A.8－πB.16－2πC.8－2πD.8－1 2π【答案】C【解析】在边长为4的正方形ABCD 中,BD 是对角线,∴AD ＝AB ＝4,∠BAD ＝90°,∠ABE ＝45°,∴S △ABD ＝12AD AB⋅⋅＝8,S 扇形ABE ＝2454360π⋅⋅＝8－2π,故选C.12. (2019·巴中)如图,圆锥的底面半径r ＝6,高h ＝8,则圆锥的侧面积是( )A.15πB.30πC.45πD.60π【答案】D【解析】圆锥的高,母线和底面半径构成直角三角形,其中r ＝6,h ＝8,所以母线为10,即为侧面扇形的半径,底面周长为12π,即为侧面扇形的弧长,所以圆锥的侧面积＝12×10×12π＝60π,故选D.13. （2019·凉山）如图，在△AOC 中，OA =3cm ，OC =lcm ，将△AOC 绕点D 顺时针旋转90 °后得到△BOD ，则AC 边在旋转过程中所扫过的图形的面积为( ▲ )cm 2 A ．2πB ．2πC ．178πD ．198π【答案】B【解析】AC 边在旋转过程中所扫过的图形的面积=S △OCA +S 扇形OAB - S 扇形OCD - S △ODB ①,由旋转知：△OCA ≌△ODB ，∴S △OCA =S△ODB ,∴①式=S 扇形OAB - S 扇形OCD =3603902⨯π-3601902⨯π=2π，故选B .14.（2019·自贡）图中有两张型号完全一样的折叠式饭桌，将正方形桌面边上的四个弓形面板翻折起来后，就能形成一个圆形桌面（可近似看作正方形的外接圆），正方形桌面与翻折成的圆形桌面的面积之比最接近（）A. B. C. D.【答案】C.【解析】由题意可知，⊙O是正方形ABCD的外接圆，过圆心O点作OE⊥BC于E，在Rt△OEC中，∠COE=45°，∴sin∠COE=,设CE=k，则OC=CE=k，∵OE⊥BC，∴CE=BE=k，即BC=2k.∴S正方形ABCD=BC2=4k2，⊙O的面积为πr2=π×(k)2=2πk2.∴正方形==≈.15.（2019·湖州）已知圆锥的底面半径为5cm，母线长为13cm，则这个圆锥的侧面积是（）A．60πcm2 B．65πcm2 C．120πcm2 D．130πcm2【答案】B．【解析】∵r＝5，l＝13，∴S锥侧＝πrl＝π×5×13＝65π（cm2）．故选B．16. （2019·金华）如图，物体由两个圆锥组成，其主视图中，∠A=90°，∠ABC=105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（）32【答案】D．【解析】∵∠A=90°，∠ABC=105°，∴∠ABD=45°，∠CBD =60°，∴△ABD是等腰直角三角形，△CBD是等边三角形．设AB长为R，则BDR．∵上面圆锥的侧面积为1，即1＝12lR，∴l＝2R·∴下面圆锥的侧面积为12lR＝12·2R．故选D．17.(2019·宁波)如图所示,矩形纸片ABCD中,AD＝6cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的底面和侧面,则AB的长为A.3.5cmB.4cmC.4.5cmD.5cm【答案】BDCBA【解析】AE＝124ABπ⋅⋅,右侧圆的周长为DEπ⋅,∵恰好能作为一个圆锥的底面和侧面,∴,124ABπ⋅⋅＝DEπ⋅,AB＝2DE,即AE＝2ED,∵AE+ED＝AD＝6,∴AB＝4,故选B.18. （2019·衢州）如图，取两根等宽的纸条折叠穿插，拉紧，可得边长为2的正六边形。

2019年数学中考试题及答案

2019年数学中考试题及答案一、选择题1．如图，下列四种标志中，既是轴对称图形又是中心对称图形的为（）A ．B ．C ．D ．2．在数轴上，与表示6的点距离最近的整数点所表示的数是()A．1B．2C．3D．43．如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm，则菱形ABCD的周长为（）A．5cm B．10cm C．20cm D．40cm4．有31位学生参加学校举行的“最强大脑”智力游戏比赛，比赛结束后根据每个学生的最后得分计算出中位数、平均数、众数和方差，如果去掉一个最高分和一个最低分，则一定不发生变化的是（）A．中位数B．平均数C．众数D．方差5．我国古代数学著作《增删算法统宗》记载”绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托“其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x 尺，竿长y尺，则符合题意的方程组是（）A．5{152x yx y=+=-B．5{1+52x yx y=+=C．5{2-5x yx y=+=D．-5{2+5x yx y==6．已知二次函数y＝ax2+bx+c(a≠0)的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是( )A．③④B．②③C．①④D．①②③7．如图，在矩形ABCD中，2AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①∠AED=∠CED；②OE=OD；③BH=HF；④BC﹣CF=2HE；⑤AB=HF，其中正确的有（）A．2个B．3个C．4个D．5个8．下表是某学习小组一次数学测验的成绩统计表：分数/分708090100人数/人13x1已知该小组本次数学测验的平均分是85分，则测验成绩的众数是（）A．80分B．85分C．90分D．80分和90分9．下列命题中，真命题的是（）A．对角线互相垂直的四边形是菱形B．对角线互相垂直平分的四边形是正方形C．对角线相等的四边形是矩形D．对角线互相平分的四边形是平行四边形10．将两个大小完全相同的杯子（如图甲）叠放在一起（如图乙），则图乙中实物的俯视图是（）.A．B．C．D．11．不等式组213312xx+⎧⎨+≥-⎩＜的解集在数轴上表示正确的是（）A．B．C．D．12．如图，直线//AB CD ，AG 平分BAE ∠，40EFC ∠=，则GAF ∠的度数为( )A ．110 B ．115 C ．125 D ．130二、填空题13．已知扇形的圆心角为120°，半径等于6，则用该扇形围成的圆锥的底面半径为_________．14．如图，添加一个条件：，使△ADE ∽△ACB ，（写出一个即可）15．不等式组0125x a x x ->⎧⎨->-⎩有3个整数解，则a 的取值范围是_____．16．如图所示，图①是一个三角形，分别连接三边中点得图②，再分别连接图②中的小三角形三边中点，得图③……按此方法继续下去．在第n 个图形中有______个三角形（用含n 的式子表示）17．不等式组3241112x x x x ≤-⎧⎪⎨--<+⎪⎩的整数解是x= ．18．在Rt△ABC 中，∠C=90°，AC=6，BC=8，点E 是BC 边上的动点，连接AE ，过点E 作AE 的垂线交AB 边于点F ，则AF 的最小值为_______19．如图，把三角形纸片折叠，使点B ，点C 都与点A 重合，折痕分别为,DE FG ，若15,2C AE EG ︒∠===厘米，ABC △则的边BC 的长为__________厘米。