梁的许用挠度
材料力学作业题集(学院)

一、求图示图形形心的位置。
二、计算半圆形对形心轴 的惯性矩。
三、试确定图示平面图形的形心主惯性轴的位置,并求形心主惯性矩。
一、试求图示各梁中截面1-1、2-2、3-3上的剪力和弯矩,这些截面无限接近于截面 或截面 。设 、 、 均为已知。
五、平面直角折杆在C端受到铅直力P作用,如图所示。材料的[σ]=160MPa。若P=10kN,l=2m,a=1.2m。试根据第四强度理论设计轴AB的直径d。
六、下图示圆轴直径d=15mm,受弯矩My与扭矩Mx共同作用。测得轴表面上点A沿轴线方向的线应变 ,点B沿与轴线成45o方向的线应变 ,E=210GPa, , MPa。试求My与Mx,并用第四强度理论校核轴的强度。
五、已知受力构件表面某点处沿三个方向的线应变为: , , 。材料的弹性模量 ,泊松比 ,试求该点的主应力。
一、从低碳钢零件中某点取出一单元体,其应力状态如图所示,试按第三和第四强度理论计算单元体的相当应力。图中应力单位是 。
(1)、 , ,
(2)、 , ,
二、上题中若材料为铸铁,试按第一和第二强度理论计算单元体的相当应力。图中应力单位是 ,泊松比 。
一、作图示杆的扭矩图
二、已知传动轴为钢制实心轴,最大扭矩MT=7kN•m,材料的许可切应力[]=30MPa,切变模量G=80GPa,许可扭角[]=0.2/m,试按强度条件和刚度条件设计轴径d。
四、已知圆轴受外力偶矩m=5kN·m,材料的许可切应力[]=80MPa。
(1)试设计实心圆轴的直径D1;
(2)若该轴改为=d/D=0.9的空心圆轴,试设计空心圆轴的内、外径d2、D2。
梁的强度校核

σ max
(
)
超过许用弯曲正应力的百分数为(175-170)/170≈3%,未超过 5%,故允许。事实上即使把梁的自重 (2×22.63 kg/m=0.4435 kg/m)考虑进去,超过许用弯曲正应力的百分数仍不到5%。
2011-11-7
6
2. 按切应力强度条件校核 最大剪力FS,max=138 kN,在左支座以右0.4 m范围内各 横截面上。每根槽钢承受的最大剪力为
[σ ]
2011-11-7
5
而每根槽钢所需的弯曲截面系数Wz≥367×10-6 m3/2=183.5× 10-6m3。由型钢表查得20a号槽钢其Wz=178 cm3,虽略小于所需 的Wz=183.5×10-6 m3而最大弯曲正应力将略高于许用弯曲正应 力[σ],但如超过不到5%,则工程上还是允许的。 现加以检验: 62.4 × 103 N ⋅ m = = 175 ×106 Pa = 175 MPa 2 × 178 × 10 −6 m 3
其值小于许用切应力[τ]=100 MPa,故选用20a号槽钢满足切
2011-11-7
应力强度条件。
8
3. 按刚度条件校核 此简支梁上各集中荷载的指向相同,故可将跨中截 面C的挠度wC作为梁的最大挠度wmax。本教材附录Ⅳ序号 11中给出了简支梁受单个集中荷载F 时,若荷载离左支座 的距离a大于或等于离右支座的距离b,跨中挠度wC的计 算公式为 Fb 3l 2 − 4b 2 wC = 48EI
§5-5梁的刚度校核 .提高弯曲刚度的措施
Ⅰ. 梁的刚度校核 对于产生弯曲变形的杆件,在满足强度条件的同时, 为保证其正常工作还需对弯曲位移加以限制,即还应该满 足刚度条件(stiffness condition):
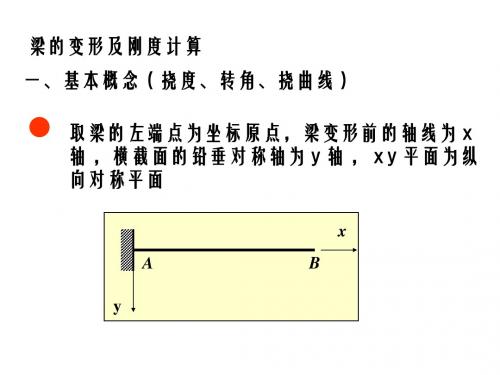
梁的变形与刚度计算
f2B qa 4 qa3 ( L a) 8EI z 6 EI z
c L (1) L a
f2c
B
B
2c
B B
A
q
c
(2)
由叠加原理
f B f1B f 2 B
qL4 qa 4 qa3 ( L a) 8EI z 8EI z 6EI z
材料——梁的位移与材料的弹性模量 E 成反比; 截面——梁的位移与截面的惯性矩 I 成反比; 跨长——梁的位移与跨长 L 的 n 次幂成正比。 (转角为 L 的 2 次幂,挠度为 L的 3 次幂) 1、增大梁的抗弯刚度(EI) 2、调整跨长和改变结构 方法——同提高梁的强度的措施相同
3、预加反弯度(预变形与受力时梁的变形方向相反,目的起到 一定的抵消作用)
w max L w L
max
、设计截面尺寸: (对于土建工程,强度常处于主要地位,刚度
、设计载荷:
常处于从属地位。特殊构件例外)
三、提高梁的刚度的措施 由梁在简单荷载作用下的变形表和前面的变形计算可看:
梁的挠度和转角除了与梁的支座和荷载有关外还取决于
下面三个因素:
式中 ,x 为梁变形前轴线上任一点的横坐标 ,y为该点的挠度。
B
A
C
x
挠曲线
C'
B
转角
y挠度
y
4、挠度和转角的符号约定
挠度:向下为正,向上为负。
转角:自x 转至切线方向,顺时针转为正,逆时针转为负。
A
C
B
x
挠曲线
C'
工程力学(材料力学)8 弯曲变形与静不定梁

B
ql4 RBl3 0
8EI 3EI
q 约束反力为
B
RB
3 8
ql
RB
用变形比较法求解静不定梁的一般步骤:
(1)选择基本静定系,确定多余约束及反力。 (2)比较基本静定系与静不定梁在多余处的变形、确定 变形协调条件。 (3)计算各自的变形,利用叠加法列出补充方程。 (4)由平衡方程和补充方程求出多余反力,其后内力、 强度、刚度的计算与静定梁完全相同。
教学重点
• 梁弯曲变形的基本概念; • 挠曲线的近似微分方程; • 积分法和叠加法计算梁的变形; • 梁的刚度条件。
教学难点
• 挠曲线近似微分方程的推导过程; • 积分法和叠加法计算梁的变形; • 变形比较法求解静不定梁。
第一节 弯曲变形的基本概念
齿轮传动轴的弯曲变形
轧钢机(或压延机)的弯曲变形
例13-4 用叠加法求图示梁的 yC、A、B ,EI=常量。
M
P
解 运用叠加法
A
C
l/2
l/2
A
=
q
5ql4 Pl3 ml2
B
yC
384EI
48EI
16EI
A
ql3 24EI
Pl 2
16EI
ml 3EI
B
B
ql3 24EI
Pl2 16EI
ml 3EI
M
+
q
A
+
BA
B
二、梁的刚度条件
y max y,
A
max
A ql3
B
24EI
RA
q
A
θB
l
B θB RB
在梁跨中点 l /2 处有 最大挠度值
工程力学c材料力学部分第六章 弯曲变形

A l/2
C l
B
解:此梁上的荷载可视为 正对称和反对称荷载的叠加, 正对称和反对称荷载的叠加, 如图所示。 如图所示。 正对称荷载作用下:
q/2
5(q / 2)l 4 5ql 4 wC1 = − =− 384 EI 768 EI
B
(q / 2)l 3 ql 3 θ A1 = −θ B1 = =− 24 EI 48EI
w P A a D
a
A C a H a B
EI
Pl 3 wB = − 3 EI
P
B
l
Pl 2 θB = − 2 EI
P A a 2a 2a C B
P/2
P/2 B
P/2
=
A
+
P/2
力分解为关于中截面的对称和反对称力( )之和的形式。 解:将P力分解为关于中截面的对称和反对称力(P/2)之和的形式。 力分解为关于中截面的对称和反对称力 显然,在反对称力( / )作用下, 显然,在反对称力(P/2)作用下,wc=0 对称力作用的简支梁, 对称力作用的简支梁,可以等效为悬臂梁受到两个力的作用 的问题。 的问题。
wA=0 θA=0
B
②、变形连续条件 变形连续条件: 连续条件
P A C θC左 wC左= wC右, =θ C右 B
的悬臂梁, 例1:图示一弯曲刚度为 的悬臂梁,在自由端受一集中力 作 :图示一弯曲刚度为EI的悬臂梁 在自由端受一集中力F 试求梁的挠曲线方程,并求最大挠度及最大转角。 用,试求梁的挠曲线方程,并求最大挠度及最大转角。 解:① 建立坐标系并写出弯矩方程 ①
在小变形情况下, 曲线弯曲平缓, 在小变形情况下,挠曲线弯曲平缓,
∴ w′ ≪ 1
2
理论力学11梁的位移计算

dvM dxEI ( z x)
θ ( x) = = ∫
⎛ M ( x) ⎞ v( x) = ∫ dxEI ⎜∫ z
dx + C
dx ⎟dx + Cx + D C,D 为积分常数,由梁的位移约束条件确定。 ⎝ EI z⎠ 挠曲线近似微分方程通解的积分常数确定以后,就得 到了挠曲线方程和转角方程,这种求梁变形的方法称为积 分法。
本章小结
挠曲线、挠度、转角、挠曲线方程、转角方程
v = f ( x)
θ = θ ( x)
挠曲线微分方程
dv θ ≈ tgθ = dx
dv ±
2
2
dx dv 2 ⎤⎡ 1+ ( ) ⎥⎢ dx ⎦⎣
将b处约束去掉基本静定系静定基相当系统加上q及约束力变形协调条件marblqlvbeirb39梁的位移计算本章小结挠曲线挠度转角挠曲线方程转角方程dx挠曲线微分方程dxdv40梁的位移计算积分法求梁的位移边界条件和连续条件dvmdxdx叠加法求梁的位移梁的刚度条件4041梁的位移计算提高梁的刚度的主要措施增大截面惯性矩
23
梁的位移计算
24
梁的位移计算
25
梁的位移计算
思考:
应用叠加法求梁的位移,必须满足的条件是什么? 答:小变形,材料符合胡克定律。
26
梁的位移计算
4 3
已知图1B点的挠度和转角分别为 ql / 8 EI , ql / 6 EI , 图2C截面的转角为多少?
q
A
l
B
ql / 8 EI
3
q
A B
3
16
例
3
求简支梁最大挠度,F已知,EI为常数。
解
1、建立挠曲线微分方程
第五章 弯曲位移

材料的弹性模量
E 200GPa 20 106 N/cm2
因P和q而引起的最大挠度均 位于梁的中点C,由表6-1查得:
Pl 3 55 1000 9203 yCP 1.38cm 6 48EI 48 20 10 32240 5ql 4 5 8.04 9204 yCq 0.116cm 6 384EI 384 20 10 32240
由表 查得,因P2在C处引起的挠度 和在B处引起的转角(d)为:
BP
P2 l 2 1000 402 2.53 105 rad 6 16EI 16 21 10 188 BP2 a 2.53 105 20 5.06 104 cm
2
Me
Me
Me
Me
A
l 2
B
l 2
C
l 2
D
A
l 2
B
l 2
C
l 2
D
(a)
Me Me Me Me
A
l 2
B
l 2
C
l 2
D
A
l 2
B
l 2
C
l 2
D
(b)
(C)
Me
Me
A
l 2
B
l 2
C
l 2
D
AB,CD段弯矩为零,所以这两段保持直 线不发生弯曲变形。AB,BC,CD三段变 形曲线在交界处应有共切线。
查表:选16号工字钢
I z 1130cm4 , Wz 141cm3
41qa 4 24 EI Z
2.按刚度选择 q
q
B
max B1 B 2 B3
A
L 2a
梁的刚度计算

l=400mm,a=100mm,E=210GPa,
l/2 l/2 a
F1=2kN,F2=1kN, [yC]=0.0002l,
[B]=0.001rad。 试校核主轴的刚度。
解 Iz=1.88106mm4
A
应用叠加法计算C截面的挠度和
B截面的转角为 。yC=5.9110-3mm
F2 BF1
D
B
BF2
F1 yCF1
Fl 2 16 EI z
ql3 24 EI z
B=BF+Bq=
Fl2 16 EI z
ql 3 24 EI z
q
机械工业出版社
A
C
B
Aq
yCq Bq
AF yCF
BF
A
C
B
F
Bq
ql 3 24 EI z
上一页 返回首页 下一页
在一经简化处理的机床空心主轴 A
上一页 返回目录 下一页
1.挠度和转角
y
度量梁的变形的两个基
本物理量是挠度和转角。它 A 们主要因弯矩而产生, 剪
力的影响可以忽略不计。
机械工业出版社
m Fm1 C BF x
挠曲线 n1
C1 B1 n
以悬臂梁为例,变形前梁的轴线为直线AB,mn 是梁的某一横截面,变形后AB变为光滑的连续曲线 AB1。mn转到了m1n1的位置。
退出
上一页 返回首页 下一页
设全轴(包括外伸端)可近似视为等
机械工业出版社
DB
C
例7-17 截面梁,且刀具与齿轮受力恰在同一
平面内。已知轴的外径D=80mm,内 径d=40mm,AB跨长l=400mm ,外伸 A 长a=100mm,材料的弹性模量
(修订)第9章 弯曲应力与弯曲变形-习题解答

第9章 弯曲应力与弯曲变形 习题解答题9 – 1 试计算下列各截面图形对z 轴的惯性矩I z (单位为mm )。
解:(a )mm 317400250500350200400250250500350≈⨯-⨯⨯⨯-⨯⨯=c y()()49323mm 107314002502003171240025050035025031712500350⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z (b )mm 431550400800500375550400400800500≈⨯-⨯⨯⨯-⨯⨯=c y()()410323mm 1054615504003754311255040080050040043112800500⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z (c )()mm 3060202060506020102060=⨯+⨯⨯⨯+⨯⨯=c y()()46323mm103616020503012602020601030122060⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯+⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.Z I(a)(b) (c)题9-1图题9–2 悬臂梁受力及截面尺寸如图所示。
设q = 60kN/m ,F = 100kN 。
试求(1)梁1– 1截面上A 、B 两点的正应力。
(2)整个梁横截面上的最大正应力和最大切应力。
解:(1)求支反力kN 220100260=+⨯=A F (↑)m kN 32021001260⋅=⨯+⨯⨯=A M ( ) (2)画F S 、M 图(3)求1-1截面上A 、B 两点的正应力 m kN 1305016011001⋅=⨯⨯+⨯=.MF MA 点:MPa 254Pa 1025412150100550101306331=⨯≈⨯⨯⨯==...I y M zA t σB 点:MPa 162Pa 107816112150100*********331=⨯≈⨯⨯⨯==....I y M σzB c (4)求最大正应力和最大切应力M P a 853Pa 10385361501010320623max max =⨯≈⨯⨯==...W M σzM P a 22Pa 10221501010220232363max =⨯≈⨯⨯⋅=⋅=..A F τS 题9 - 3 简支梁受力如图所示。
工程力学(第二版)章图文 (6)

(1) 一体重为700 N (2) 要求两名体重均为700 N的工人抬着1500 N的货物安全 走过,木板的宽度不变,重新设计木板厚度h。
第6章 弯 曲
解 (1) 计算弯矩的最大值Mmax。当工人行走到跳板中央
(2) 横截面上的弯矩在数值上等于该截面左侧(或右侧)所 有外力对该截面形心的力矩的代数和。
第6章 弯 曲
为了使所求得的剪力与弯矩符合前面的符号规定,按此 规律计算剪力时,截面左侧梁上外力向上取正值,向下取负 值,截面右侧梁上外力向下取正值,向上取负值;计算弯矩 时,截面左侧梁上外力对该截面形心的力矩顺时针转向取正 值,逆时针转向取负值,截面右侧外力对该截面形心的力矩 逆时针转向取正值,顺时针转向取负值。可以将这个规则归 纳为一个简单的口诀:左上右下,剪力为正;左顺右逆,弯 矩为正。
第6章 弯 曲 图 6.10
第6章 弯 曲 解 设截面m-m与B端之间的距离为x,取m-m截面的右段
为研究对象,画出受力图,如图6.10(b)所示。 根据平衡条件:
由Fs=qx可绘出剪力图,如图6.10(c)所示;由 描点可绘出弯矩图,如图6.10(d)
第6章 弯 曲
6.3 弯曲时的正应力与强度计算
m,材料的许用应力[σ]=150 MPa, 求此悬臂梁的许可载荷。
图 6.15
第6章 弯 曲 解 绘出悬臂梁的弯矩图,如图6.15(b)所示。 图中,Mmax=Fl=4000F 梁的横截面抗弯截面系数为
由梁的弯曲正应力强度条件得
因此, 悬臂梁的许可载荷为F=25 000 N。
第6章 弯 曲 【例6.5】 某建筑工地上, 用长l=3 m的矩形截面木板做
梁弯曲变形的计算

第7章 梁弯曲变形的计算§7-1 挠度与转角及梁的刚度条件梁变形前后形状的变化称为变形,一般用各段梁曲率的变化表示。
梁变形前后位置的变化称为位移,位移包括线位移和角位移,如图7-1所示。
在小变形和忽略剪力影响的条件下,线位移是截面形心沿垂直于梁轴线方向的位移,称为挠度,用v 表示;角位移是横截面变形前后的夹角,称为转角,用θ表示。
而dxx dv x )()(=θ,可见确定梁的位移,关键是确定挠曲线方程Y=f(x)。
梁的设计中,除了需要满足强度条件外,在很多情况下,还要将其弹性变形限制在一定范围内,即满足刚度条件][][max max θθ≤≤v v式中的和][v ][θ分别为梁的许用挠度和许用转角,可从有关设计手册中查得。
§7-2 挠度曲线的近似微分方程忽略剪力对变形的影响,梁平面弯曲的曲率公式为: 式(a)表明梁轴线上任一点的曲率)(1x ρ与该点处横截面上的弯矩成正比,而与该截面的抗弯刚度)(x M EI 成反比。
如图7-2所示。
而梁轴线上任一点的曲率与挠曲线方程v 之间存在下列关系:)(xEIx M x )()(1=ρ (a) 232221)(1⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛+±dx dv dx vd x ρ (b)将上式代入式(a),得到EIx M dx dv dx v d )(12322=⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛+±(c) 小挠度条件下,1<<=θdxdv,式(c)可简化为: EI x M dxv d )(22=±(d)在图7-3所示的坐标系中,正弯矩对应着22dx vd 的正值(图7-3a),负弯矩对应着22dxvd 的负值(图7-3b),故式(d)左边的符号取正值EI x M dx v d )(22= (8-1)式(7-1)称为小挠度曲线微分方程,简称小挠度微分方程。
显然,小挠度微分方程仅适用于线弹性范围内的平面弯曲问题。
架桥机计算书

40米160吨架桥机计算书一、主梁过孔时强度计算:1、自重荷载:(1)单桁架主梁自重q主=5.76KN/m(2) 前支承自重q前=20.5KN(3) 前支自重q前支=70KN(4)天车横移、纵移q横纵=100KN过孔时梁中的最大弯矩:Mmax=q前/2×41×104+41×0.49×41/2×104=2.05/2×41×104+41×0.575×41/2×104+23×7×104=(42.025+483+161) ×104=686×104N.m上下弦所承受的最大轴力:Nmax=Mmax/h=686×104N·m/2.415m=284×104N上弦杆(上弦杆32b槽钢对扣,上贴12*240钢板,侧贴12*300钢板)的面积为: A=(12*300*10-6+12*240*10-6+55.1*10-4)*2=239.8*10-4上弦杆的工作应力σmax= Nmax/A=284×104N/(239.8×10-4)m=118 MPa考虑组合因素安全系数n=1.33,上下弦材料采用:Q235-B σS=210 MPa许用应力[σ]= σS/1.3=161Mpa工作应力: σmax=118 Mpa<161Mpa, 过孔时上弦满足强度条件下弦杆(下弦杆22b槽钢对扣,上贴10*230钢板,侧贴10*220钢板)的面积为: A=(10*230*10-6+10*220*10-6+2*39.91*10-4)*2=124.82*2*10-4=249.64*10-4上弦杆的工作应力σmax= Nmax/A=284×104N/(249.64×10-4)m=113.8 Mpa考虑组合因素安全系数n=1.33,上下弦材料采用:Q235-B σS=210 MPa许用应力[σ]= σS/1.3=161Mpa工作应力: σmax=113.8Mpa<161Mpa, 过孔时上弦满足强度条件2、过孔时悬臂达到最长时,悬臂端处的挠度:主梁截面对中性轴的惯性矩:上弦截面积为A!=239.8, 下弦截面积为A2=249.6,主梁上下截面合计为:A=489.4×10-4Iy=489.4×(2.415/2)2×10-4=713.6×10-4m4E=210*109 Mpa考虑简单计算:桥机过孔时为悬臂的外伸梁,图中为过孔时为保证不倾覆所加的配重,利用叠加原理计算悬臂端的挠度。
弯曲刚度问题

第9章弯曲刚度问题9.1 基本概念9.1.1 梁弯曲后的挠曲线吊车梁若变形过大,将使小车行走困难,还会引起梁的严重振动。
因此,必须对梁的变形加以限制若梁的变形在弹性范围内,梁的轴线在梁弯曲后变为一条连续光滑曲线,该曲线称为弹性曲线或挠度曲线,简称弹性线或挠曲线。
挠曲线:梁变形后的轴线。
性质:连续、光滑、弹性、极其平坦的平面曲线。
9.1.2梁的挠度与转角设有一具有纵向对称面的悬臂梁,在自由端处作用一集中力F p。
F p力作用在梁的纵向对称面内,使梁发生平面弯曲。
一、挠度与转角梁的变形可用以下两个基本量来度量。
tan"二dw ,、w(x)二 w ‘ dxtan0-W⑴挠度挠度:横截面形心沿垂直于轴线方向的位移梁轴线上各点(各截面)的挠度w 随着点(截面)的位置 x 的不同而改变,即各截面的挠度是截面位置坐标x 的函数。
因小变形时,u 与w 相比为高阶无穷小,故忽略不计。
、挠度w 于转角二间的关系w = w(x)d挠曲线方程 单位:mm挠度 w 符号规定:向下为正⑵转角,向上为负。
转角:横截面绕中性轴转过的角度。
用“,”表示。
梁不同横截面其转角是不相同的,二是横截面位置坐标x 的函数 6 = &(兀)转角方程 单位:rad71的符号规定:由变形前的横截面转到变形后,顺时针为正;逆时针为负。
⑶ 水平位移:横截面形心沿水平方向的位移,用 u 表示。
9.2 小挠度微分方程及其积分9.2.1 小挠度微分方程1梁发生平面弯曲时,其轴线由直线变成一条曲率为7的平面曲线1 M 1 M (x)纯弯曲EI细长梁横力弯曲(x) El12d w d2w M(x)2dx2El 由高数知(x)dxM (x)与W的符号总是相反的JElM (x)dx C _______ 转角方程dw w解上二阶微分方程可求得挠度 w ,再根据dx,可求得截面转角71。
等截面梁:EI =常数。
Elw …M (x) Elw dx …M (x)dxElw = El — - 严(x)dx C Elw dx 二[j M (x)dx]dx Cdx Elw 二 」| M (x)dx]dx Cx Dd 2w M (x) dx 2 El尸EIw” = -M (工)求梁的变形:d 2w Eldx 2-M (x)挠曲线近似微分方程1 5 / 28w[ M (x)dx]dx Cx DE| i i ''____ 挠度方程其中C 、D 为积分常数。
第9章_直梁

max
IZ 1.067106 ymax
M max 141 MN/m2 150MN/m2 WZ
故压板的强度足够
第九章 直梁弯曲
例9-8 一起重量原为 50kN 的吊车,其跨度l = 10.5m (如图),由 45a号工字钢制成。为发挥其潜力,现欲将 起重量提高到Q =70kN,试校核梁的强度;若强度不足, 再计算其可能承载的起重量。设梁的材料为 Q235钢, 许用应力[σ]=140MN/m2,电葫芦自重G = 15kN,梁
第九章 直梁弯曲
推断和假设
假设:(1) 梁在纯弯曲时,各横截 面始终保持为平面,并垂直于梁轴。
此即弯曲变形的平面假设。
(2) 纵向纤维之间没有相互挤压,每 根纵向纤维只受到简单拉伸或压缩。 中性层:从伸长到缩短区,中间必有一层纤维既不伸长也不缩短。这 一长度不变的过渡层称为中性层。 中性轴:中性层与横截面的交线 在纯弯曲的条件下,所有横截面仍保持平面,只是绕中性轴作 相对转动,横截面之间并无互相错动的变形,而每根纵向纤维 则处于简单的拉伸或压缩的受力状态。
Q max P M max Pl
Q O
x P
第九章 直梁弯曲
例9-3
一简支梁 AB ,受均布载荷 q 的作用,试作此梁的弯矩图。
解: 1、求支反力
由对称性知: ql FA FB 2
2、建立剪力方程和弯矩方程
ql Q = FA qx = qx (0 < x < 1) 2 qx2 qlx qx2 M = FA x = (0 ≤x < 1) 2 2 2
非对称弯曲:若梁不具有纵向对称面,或梁有纵向对称面上但 外力并不作用在纵向对称面内的弯曲。
第九章 直梁弯曲
第七章梁的位移转角、挠度

第七章 梁的弯曲变形
§7-2 挠曲线的近似微分方程
2.挠曲线的近似微分方程
推导弯曲正应力时,得到:
1M
ρ EIz
忽略剪力对变形的影响
1 M(x)
( x) EIz
5
第七章 梁的弯曲变形
§7-2 挠曲线的近似微分方程
1 M (x)
EI Z
1
d2 y dx2
1
(
dy dx
边界条件
x0 0
x0 y 0
xL
B
qL3 6EI z
C1
qL3 6EI z
C2
qL3 24 EI z
yB
qL4 8 EI z
EIz
y
1 24
qL
x4
C1x
C2
q L x3 L3 6EI z
y q L x4 4L3x L4 24 EIz 12
C
1 5q0L4 2 384EIZ
5q0 L4 768EI Z
21
第七章 梁的弯曲变形
§7-4 用叠加法求梁的变形
A
B
L 2a
q
L 2a
例7-6 已知:悬臂梁受力如图
示,q、l、EI均为已知。求C 截面的挠度yC和转角C
C 解 1)首先,将梁上的载荷
变成有表可查的情形
为了利用梁全长承受均
Fb L
x
F b
C
l
y
x
最大转角 y'' 0 M x 0
A
材料力学-梁的挠度

F 3 Fl 2 x1 x1 12EI 12EI y 2 3 F 3 1 5 Fl Fl 2 3 ( lx2 x2 ) x2 6 6 EI 4 EI EI 4
F 2 Fl 2 (x ) x1 1 1 4 EI 12EI 2 F 3 1 Fl 2 2 ( x2 ) ( lx2 x2 ) EI 2 2 3EI Fl 2 由此可知: A 1 ( x1 0) (逆时针方向 ); 12 EI 3 Fl 3 yC y2 ( x2 l ) (向下) 2 8 EI
二、挠曲线:变形后,轴线变为光滑曲线,该曲线称为挠曲线。
其方程为:v =f (x)
小变形
三、转角与挠曲线的关系:
df tg dx
f
(1)
§7-2
梁的挠曲线近似微分方程
M z ( x) EI z 1
(1)
小变形
3
一、挠曲线 0
f
1
梁的刚度校核
max
1 1 f (对土建工程 : ( ~ )) 250 1000 L
其中[]称为许用转角;[f/L]称为许用挠跨比。通常依此条 件进行如下三种刚度计算: 、校核刚度:
f
max
L
f L
max
、设计截面尺寸: (对于土建工程,强度常处于主要地位,刚度
二、结构形式叠加(逐段刚化法)
P
A C
q B
[例4] 按叠加原理求A点转角 和C点挠度。 解、① 载荷分解如图
a
P A
a
②
由梁的简单载荷变形表, 查简单载荷引起的变形。
=
B
