Matlab二维数组及其应用
matlab 数组积分

matlab 数组积分摘要:一、引言1.1 MATLAB简介1.2 数组在MATLAB中的重要性1.3 积分运算在数学和工程领域的应用二、MATLAB数组积分概念2.1 数组积分定义2.2 数组积分的性质2.3 数组积分与传统积分的关系三、MATLAB数组积分操作3.1 数组积分的创建3.2 数组积分元素的访问与修改3.3 数组积分运算符3.4 数组积分函数四、MATLAB数组积分应用实例4.1 二维数组积分示例4.2 三维数组积分示例4.3 数组积分在实际问题中的应用五、MATLAB数组积分与其他数学工具的联系5.1 MATLAB与数学软件包的集成5.2 数组积分与其他数学概念的关联六、总结6.1 数组积分在MATLAB中的重要性6.2 数组积分的优缺点6.3 对未来MATLAB数组积分的展望正文:一、引言MATLAB是一种广泛应用于科学计算和工程设计的数学软件,其强大的矩阵运算功能使得用户可以轻松地处理复杂数学问题。
在MATLAB中,数组是矩阵的一种扩展,可以存储和管理大量数据。
积分运算在数学和工程领域具有广泛的应用,如求解定积分、计算面积和体积等。
因此,了解MATLAB数组积分对于更好地应用该软件具有重要意义。
二、MATLAB数组积分概念数组积分是MATLAB中一种特殊的积分运算,它可以对数组中的每个元素进行积分。
数组积分具有以下性质:1.数组积分是逐个元素进行的,即对数组中的每个元素求积分。
2.数组积分的结果是一个新的数组,其元素是原数组中对应元素的积分结果。
数组积分与传统积分之间的关系可以通过以下例子说明:假设有一个二维数组A,对其进行数组积分得到结果B。
则B的元素b_ij 表示A中元素a_ij的积分结果。
若A是一个n×m的矩阵,则传统积分的结果为一个标量值,而数组积分的结果是一个n×m的矩阵。
三、MATLAB数组积分操作在MATLAB中,数组积分的创建、访问、修改和运算等操作均非常简便。
MATLAB实验二《一维二维数组的创建和寻访》

实验二一维二维数组的创建和寻访一、实验目的1、掌握一维数组、二维数组创建和寻访的几种方法。
2、区别数组运算和矩阵运算的差别。
3、熟悉执行数组运算的常用数组操作函数。
4、掌握数组运算中的关系和逻辑操作及常用的关系、逻辑函数。
5、掌握“非数”、“空”数组在MA TLAB中的应用。
二、实验主要仪器与设备装配有MA TLAB7.6软件的计算机三、预习要求做实验前必须认真复习第三章MATLAB的数值数组及向量化运算功能。
四、实验内容及实验步骤1、一维数组的创建方法有哪几种?举例说明。
答:(1)“冒号”生成法;(2)线性(或对数)定点法;(3)逐个元素输入法;(4)运用MA TLAB 函数生成法。
例子:b1=linspace(0,pi,4)b2=logspace(0,3,4)运行结果:b1 =0 1.0472 2.0944 3.1416b2 =1 10 100 10002、根据要求补充输入指令,并写出运行结果。
本例演示:数组元素及子数组的各种标识和寻访格式;冒号的使用;end的作用。
A= zeros(2,6)%创建(2×6)的全零数组A(:)=1:12 %赋值号左边:单下标寻访(2×6) 数组A的全部12个元素%赋值号右边:拥有12个元素的一维数组A( 2,4 ) %双下标:A数组的第2行第4列元素A(8) %单下标:数组A的第8个元素A(: , [1,3]) %双下标:显示A的“第1列和第3列上全部行的元素”A([1, 2, 5, 6]') %单下标:把A数组第1,2,5,6个元素排成列向量A(: , 4:end) %双下标:显示A的“从第4起到最后一列上全部行的元素”%在此end用于“列标识”,它表示“最后一列”A(2,1:2:5)=[-1, -3, -5] %把右边的3个数分别赋向A数组第2行的第1,3,5个元素位置B=A([1, 2, 2, 2], [1, 3, 5]) %取A数组的1,3,5列的第1行元素作为B的第1行%取A数组的1,3,5列的第2行分别作为B的第2,3,4行L=A<3 %产生与A维数相同的“0,1”逻辑数组A(L)=NaN %把逻辑1标识的位置上的元素赋为“非数”运行结果:A =0 0 0 0 0 00 0 0 0 0 0A =1 3 5 7 9 112 4 6 8 10 12ans =8ans =8ans =1 52 6ans =1256ans=7 9 118 10 12A =1 3 5 7 9 11-1 4 -3 8 -5 12B =1 5 9-1 -3 -5-1 -3 -5-1 -3 -5L =1 0 0 0 0 01 0 1 0 1 0A =NaN 3 5 7 9 11NaN 4 NaN 8 NaN 123、补充输入以下指令,写出运行结果并说明reshape,diag,repmat,flipud,fliplr,rot90的作用。
matlab2011教程之二数值数组及向量化运算

第 2 章 数值数组及向量化运算本章集中讲述两个数据类型(数值数组和逻辑数组)、两个特有概念变量(非数和空)、以及MATLAB的数组运算和向量化编程。
值得指出:本章内容是读者今后编写各种科学计算M码的基本构件。
数值数组(Numeric Array)是MATLAB最重要的数据类型数组。
在各种维度的数值数组中,二维数组为最基本、最常用。
本章对二维数组创建、标识、寻访、扩充、收缩等方法进行了详尽细腻的描述,并进而将这些方法推广到高维数组。
本章讲述的逻辑数组主要产生于逻辑运算和关系运算。
它是MATLAB 援引寻访数据、构成数据流控制条件、、编写复杂程序所不可或缺的重要构件。
数组运算是MATLAB区别于其它程序语言的重要特征,是MATLAB绝大多数函数指令、Simulink许多库模块的本性,是向量化编程的基础。
为此,本章专辟第2.2节用于阐述MATLAB的这一重要特征。
在此提醒读者注意:随书光盘mbook目录上保存着本章相应的电子文档“ch02_数值数组及向量化运算.doc”。
该文档中有本章全部算例的可执行指令,以及相应的运算结果。
2.1数值数组的创建和寻访2.1.1一维数组的创建1递增/减型一维数组的创建(1)“冒号”生成法(2)线性(或对数)定点法2其他类型一维数组的创建(1)逐个元素输入法(2)运用MATLAB函数生成法【例2.1-1】一维数组的常用创建方法举例。
a1=1:6a2=0:pi/4:pia3=1:-0.1:0a1 =1 2 3 4 5 6a2 =0 0.7854 1.5708 2.3562 3.1416a3 =Columns 1 through 81.0000 0.9000 0.8000 0.7000 0.6000 0.5000 0.4000 0.3000Columns 9 through 110.2000 0.1000 0b1=linspace(0,pi,4)b2=logspace(0,3,4)b1 =0 1.0472 2.0944 3.1416b2 =1 10 100 1000c1=[2 pi/2 sqrt(3) 3+5i]c1 =2.0000 1.5708 1.73213.0000 + 5.0000i rng defaultc2=rand(1,5)c2 =0.8147 0.9058 0.1270 0.9134 0.6324〖说明〗x1=(1:6)' , x2=linspace(0,pi,4)'y1=rand(5,1)z1=[2; pi/2; sqrt(3); 3+5i]2.1.2二维数组的创建1小规模数组的直接输入法【例2.1-2】在MATLAB环境下,用下面三条指令创建二维数组C。
matlab多维数组形状

matlab多维数组形状MATLAB多维数组的形状MATLAB是一种功能强大的数值计算和科学数据可视化工具,它以其多维数组操作而闻名。
在MATLAB中,多维数组是其中最重要的数据结构之一。
它们允许我们以一种清晰而简洁的方式处理和分析具有多个维度的数据。
一维数组是最简单的数组形状。
它由一系列按顺序排列的元素组成。
我们可以使用一对方括号和逗号分隔的元素列表表示一维数组。
例如,以下是一个包含5个元素的一维数组的定义:arr = [1, 2, 3, 4, 5]二维数组则是由多行和多列组成的矩阵。
我们也可以使用一对方括号表示,每行的元素由逗号分隔,每行之间用分号分隔。
以下是一个包含3行2列的二维数组的定义:matrix = [1, 2;3, 4;5, 6]三维数组是由多个二维数组组成的集合。
我们可以将三维数组看作是一个立方体,其中每个面都是一个二维数组。
在MATLAB中,我们可以使用一对方括号和分号分隔的二维数组定义每个面。
以下是一个包含2个2行3列的二维数组的三维数组的定义:cube = [1, 2, 3;4, 5, 6],[7, 8, 9;10, 11, 12]对于更高维度的数组,我们可以将其看作是一个更大的数据容器,其中嵌套了更小的维度。
同样,我们可以使用一对方括号和分号分隔的多维数组定义每个较低维度的数组。
下面是一个包含2个2行3列的二维数组的两个三维数组的定义:array = [1, 2, 3;4, 5, 6],[7, 8, 9;10, 11, 12];[13, 14, 15;16, 17, 18],[19, 20, 21;22, 23, 24]除了上述示例中使用的方括号表示数组外,我们还可以使用函数来创建不同形状的多维数组。
例如,我们可以使用zeros函数创建一个全为零的数组,使用ones函数创建一个全为一的数组,或使用rand函数创建一个随机数数组。
创建一个具有特定形状的多维数组后,我们可以对其进行各种操作,如元素索引、切片和重塑等。
matlab中array的用法

matlab中array的用法Matlab中的array(数组)是一种重要的数据结构,它可以存储和处理一组数据。
一、创建数组在Matlab中可以通过以下方式创建数组:1.使用[]来创建数组如:A = [1,2,3,4,5],表示创建了一个包含5个元素的数组,分别是1,2,3,4,5。
2.使用linspace函数创建等差数列如:A = linspace(1,10,10),表示创建了一个长度为10的等差数列,从1到10。
3.使用logspace函数创建等比数列如:A = logspace(1,3,3),表示创建了一个长度为3的等比数列,从10到1000。
二、访问和操作数组1.通过索引访问数组元素如:A(2)表示对数组A中第二个元素进行访问、修改或运算。
2.在数组中添加、移除元素可以使用 append 函数在数组末尾添加元素;可以使用 remove 函数删除数组中的指定元素。
3.数组运算Matlab中的数组支持很多数学运算,例如:加、减、乘、除、矩阵乘积等,可以使用加减乘除符号或者对应的函数进行运算。
如:C = A + B;D = A * B。
三、应用实例以下以一个简单的数组排序为例,来介绍数组的应用。
我们要将一个包含5个随机数的数组从小到大排序。
使用sort函数可以对数组进行排序,如:A = [5,4,3,1,2],B =sort(A);则B的值为[1,2,3,4,5]。
如果我们要实现一个基于插入排序的程序,来达到同样的效果,可以按照以下步骤操作:1.设定一个数组A;2.循环从第二个元素开始到最后一个元素,每次取出一个元素;3.将待排序元素插入有序数组中,得到新的有序数组。
四、总结数组是Matlab中一个重要的数据结构,我们可以使用数组来存储和处理一组数据。
通过索引访问数组元素、数组运算、添加、移除元素,我们可以完成对数组的操作。
在本文的实例中,我们通过Matlab中的sort函数和自己实现的算法两种方式,对一个数组进行了排序,体现了数组的应用的实际意义。
Matlab二维数组及其应用

Matlab:二维数组及其应用二维数组实际上也是一个矩阵。
应此直接创建一个矩阵就行。
创建的方法你应该会吧,就是直接按行方式输入每个元素:同一行中的元素用逗号(,)或者用空格符来分隔,且空格个数不限;不同的行用分号(;)分隔。
所有元素处于一方括号([ ])内。
比如,创建一个3×5的矩阵(对应3×5的二维数组)A = [12 62 93 -8 22; 16 2 87 43 91; -4 17 -72 95 6]A =12 62 93 -8 2216 2 87 43 91-4 17 -72 95 6当然也可以用专门用来创建多维数组的cat函数来创建。
具体如下:函数cat格式A=cat(n,A1,A2,…,Am)说明n=1和n=2时分别构造[A1;A2]和[A1,A2],都是二维数组,而n=3时可以构造出三维数组。
例如:>> A1=[1,2,3;4,5,6;7,8,9];A2=A1';>> A3=cat(2,A1,A2)A3 =1 2 3 1 4 74 5 6 2 5 87 8 9 3 6 9这样A3就是一个二维数组此外还有诸如特殊矩阵的创建方法等这里就不列举了你可以百度或者Google一下二维数组的变换我还不太确定你的意思:这里就提供几个矩阵的操作:1.矩阵的变维矩阵的变维有两种方法,即用“:”和函数“reshape”,前者主要针对2个已知维数矩阵之间的变维操作;而后者是对于一个矩阵的操作。
(1)“:”变维例1-48> A=[1 2 3 4 5 6;6 7 8 9 0 1]A =1 2 3 4 5 66 7 8 9 0 1>> B=ones(3,4)B =1 1 1 11 1 1 11 1 1 1>> B(:)=A(:)B =1 7 4 06 3 9 62 8 5 1(2)Reshape函数变维格式 B = reshape(A,m,n) %返回以矩阵A的元素构成的m×n矩阵BB = reshape(A,m,n,p,…) %将矩阵A变维为m×n×p×…B = reshape(A,[m n p…]) %同上B = reshape(A,siz) %由siz决定变维的大小,元素个数与A中元素个数相同。
matlab中二维插值函数用法

matlab中二维插值函数用法Matlab是一种强大的数学软件,可以对数据进行各种操作和分析。
在Matlab 中,二维插值函数是一种非常常用的工具,它可以帮助我们在已知数据点的基础上,估计其它位置的数值。
在本文中,我们将一步一步介绍二维插值函数的用法,希望对你有所帮助。
首先,我们需要明确一点,二维插值是用于处理二维平面上的数据,即x和y坐标都是变化的。
插值的目的是在这样的二维数据上,估计其它位置的数值,使得整个平面上的数值分布更加密集。
在Matlab中,二维插值函数主要是interp2函数。
该函数的基本语法如下:Vq = interp2(X, Y, V, Xq, Yq, method)其中,X和Y是已知数据点的x和y坐标,V是对应的数值;Xq和Yq是我们要估计数值的位置,Vq是估计得到的数值;method是插值方法,可以是‘linear’、‘nearest’、‘spline’等。
接下来,我们来演示一个具体的例子,以说明interp2函数的用法。
假设我们有一组二维数据如下:X = [1, 2, 3; 1, 2, 3; 1, 2, 3]Y = [1, 1, 1; 2, 2, 2; 3, 3, 3]V = [0, 1, 0; 1, 4, 1; 0, 1, 0]这里,X和Y分别是数据点的x和y坐标,V是对应的数值。
现在我们想要在位置(1.5, 1.5)处进行插值,估计其数值。
我们可以使用interp2函数来完成这个任务:Vq = interp2(X, Y, V, 1.5, 1.5, 'linear')这里,我们使用了‘linear’插值方法,得到的估计值Vq为2。
这就是在位置(1.5, 1.5)处的估计数值。
除了‘linear’插值方法,我们还可以尝试其它方法,比如‘nearest’和‘spline’。
这些方法在实际应用中有着不同的特点,需要根据具体情况选择合适的方法。
例如,‘nearest’方法会选择最近的数据点的数值作为估计值,‘spline’方法则会使用样条插值进行估计。
MATLAB基础教程 第2章 数组、矩阵及其运算

写出MATLAB表达式。 解:根据MATLAB的书写规则,以上MATLAB表达式为: (1)y=1/(a*log(1-x-1)+C1) (2)f=2*log(t)*exp(t)*sqrt(pi) (3)z=sin(abs(x)+abs(y))/sqrt(cos(abs(x+y))) (4)F=z/(z-exp(T*log(8)))
命令:X(3:-1:1)
命令:X(find(X>0.5)) 命令:X([1 2 3 4 4 3 2 1])
第二章 数组、矩阵及其运算
2.1 数组(矩阵)的创建和寻访
2. 二维数组的创建和寻访
例2-3 综合练习。将教材P.31~P.44的实例按顺序在MATLAB的 command窗口中练习一遍,观察并体会其输出结果。 (注意变量的大小写要和教材上的严格一致。)
A./B
B.\A
A的元素被B的对应元素相除
(与上相同)
第二章 数组、矩阵及其运算
2.3 数组、矩阵的其他运算
1. 乘方开方运算
数组的乘方运算与power函数 格式:c=a.^k或c=power(a,k) 例如: >> g=[1 2 3;4 5 6] >>g.^2 矩阵的乘方运算与mpower函数 格式:C=A^P或C=mpower(A,P) 注意:A必须为方阵
第二章 数组、矩阵及其运算
2.2 数组、矩阵的运算
3. 矩阵的加法、减法
运算规则是:若A和B矩阵的维数相同,则可以执行矩阵的加减运算, A和B矩阵的相应元素相加减。如果维数不相同,则MATLAB将给出
出错信息。
第二章 数组、矩阵及其运算
2.2 数组、矩阵的运算
3. 矩阵的乘法
matlab 二维坐标数组求解连通区域-概述说明以及解释

matlab 二维坐标数组求解连通区域-概述说明以及解释1.引言概述部分的内容可以如下编写:1.1 概述在数字图像处理和计算机视觉领域中,连通区域是常见的概念,它代表了具有相同像素值或特定属性的像素的集合。
本文将主要介绍使用MATLAB对二维坐标数组进行连通区域的求解方法。
二维坐标数组是一种常见的数据结构,用于存储和表示二维平面上的图像、地理信息等。
连通区域的求解在许多应用中都具有重要意义。
例如,在图像处理中,我们经常需要对目标进行分割和提取,而连通区域的求解可以帮助我们实现这一目标。
此外,在计算机视觉领域,连通区域的应用也非常广泛,如对象识别、目标跟踪等。
在正文部分,我们将首先介绍二维坐标数组的定义和特点,包括如何表示和访问数组中的元素。
然后,我们将详细解释连通区域的概念和应用,以及常见的连通区域求解算法和技术。
最后,在结论部分,我们将总结本文所介绍的二维坐标数组求解连通区域的方法,并给出相关实验结果和分析。
通过本文的阅读,读者将能够了解和掌握使用MATLAB对二维坐标数组进行连通区域求解的方法和技巧,从而在实际应用中能够灵活运用和扩展相关算法。
希望本文能够对读者在数字图像处理和计算机视觉领域的学习和研究工作有所帮助。
文章结构部分可以根据文章的主要内容和逻辑,介绍文章的主要章节和各个章节的内容概要。
下面是1.2 文章结构部分的内容示例:1.2 文章结构本文将按照以下结构进行叙述:第二部分:正文本部分主要介绍了二维坐标数组的定义和特点,并深入探讨了连通区域的概念和应用。
首先,我们将对二维坐标数组进行详细的定义,并解释其在实际问题中的应用。
其次,我们将介绍连通区域的概念和特点,并展示其在图像处理、地理信息系统等领域的广泛应用。
第三部分:结论本部分将重点讨论二维坐标数组求解连通区域的方法,并对实验结果进行分析。
我们将介绍一种有效的算法,基于二维坐标数组的特点,实现连通区域的快速求解。
同时,我们将通过实验结果验证该算法的准确性和效率,并分析不同参数对算法性能的影响。
matlab 数组或运算

matlab 数组或运算
在Matlab中,数组和运算是非常常见的操作。
以下是一些常见的数组操作和运算:
1. 创建数组:可以使用“[]”或“zeros”、“ones”函数创建数组。
例如,a = [1 2 3],b = zeros(2,3)。
2. 访问数组元素:可以使用索引或切片来访问数组元素。
例如,a(1)表示访问数组a的第1个元素,b(1:2,1:3)表示访问数组b中第1-2行、1-3列的元素。
3. 运算:可以对数组进行加、减、乘、除等运算,例如a + b、
a - b、a .* b、a ./ b。
4. 矩阵运算:可以对矩阵进行转置、求逆、特征值等运算,例如a'表示对矩阵a进行转置,det(a)表示求矩阵a的行列式,eig(a)表示求矩阵a的特征值。
5. 数组函数:Matlab中提供了许多有用的数组函数,例如sum、mean、max、min等函数,可以对数组进行求和、平均值、最大值、最小值等操作。
6. 条件选择:可以使用条件语句(如if、else)和逻辑运算符(如&&、||)对数组进行条件选择。
7. 循环:可以使用for和while循环对数组进行遍历和操作。
循环中可以使用break和continue关键字进行控制。
8. 数据类型转换:可以使用类型转换函数(如int8、double、char等)将数组转换为不同的数据类型。
MATLAB应用 MATLAB数据及运算
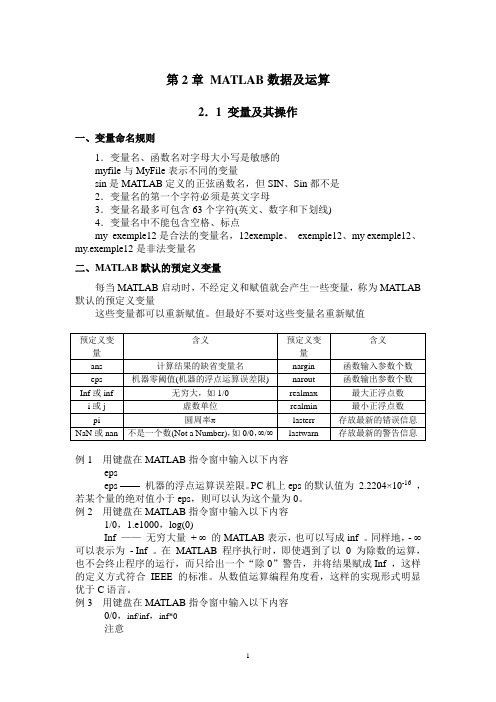
第2章MATLAB数据及运算2.1 变量及其操作一、变量命名规则1.变量名、函数名对字母大小写是敏感的myfile与MyFile表示不同的变量sin是MATLAB定义的正弦函数名,但SIN、Sin都不是2.变量名的第一个字符必须是英文字母3.变量名最多可包含63个字符(英文、数字和下划线)4.变量名中不能包含空格、标点my_exemple12是合法的变量名,12exemple、_exemple12、my exemple12、my.exemple12是非法变量名二、MATLAB默认的预定义变量每当MATLAB启动时,不经定义和赋值就会产生一些变量,称为MATLAB 默认的预定义变量这些变量都可以重新赋值。
但最好不要对这些变量名重新赋值例1 用键盘在MATLAB指令窗中输入以下内容epseps ——机器的浮点运算误差限。
PC机上eps的默认值为2.2204×10-16,若某个量的绝对值小于eps,则可以认为这个量为0。
例2 用键盘在MATLAB指令窗中输入以下内容1/0,1.e1000,log(0)Inf ——无穷大量+ ∞的MATLAB表示,也可以写成inf 。
同样地,- ∞可以表示为- Inf 。
在MATLAB 程序执行时,即使遇到了以0 为除数的运算,也不会终止程序的运行,而只给出一个“除0”警告,并将结果赋成Inf ,这样的定义方式符合IEEE 的标准。
从数值运算编程角度看,这样的实现形式明显优于C语言。
例3 用键盘在MATLAB指令窗中输入以下内容0/0,inf/inf,inf*0注意在MATLAB 中,即使遇到以0为除数的运算,程序也不会终止运行。
这时只给出一个警告,并将结果赋给inf 或NaNNaN —— 不定式( not a number ) ,通常由 0 / 0 运算、Inf / Inf 及其他可能的运算得出。
NaN 是一个很奇特的量,如 NaN 与Inf 的乘积仍为 NaN 。
《MATLAB程序设计》第4章数组及应用

0x0012FF68 a[0] 0x0012FF6C a[1] 0x0012FF70 a[2] 0x0012FF74 a[3]
数组元素
0x0012FF78 a[4]
0x0012FF7C a[5]
8
一维数组在内存中的存储形式
说明:
(1)数组名a表示内存首地址,是地址常量。
(2)数组a中每个数组元素占的内存空间根据 数组类型确定,整个数组占的内存为:数组元 素个数乘以每个元素所占内存空间如: int a[10]; 4×10=40 float b[20]; 4×20=80 double c[5]; 8×5=40 char d[8]; 1×8=8
第4章 数组
教学内容
数组的定义及应用
字符串处理函数
几个常用算法:排序算法(选择排序、
冒泡排序)
1
第4章 数组
重点、难点
数组的定义及应用
常用算法的设计(选择排序、
冒泡排序)
2
第4章 数组
教学目标
熟练掌握数组的定义及应用
掌握字符数组的定义及应用
掌握常用的字符串处理函数
熟练掌握几个常用算法:排序
算法(选择排序、冒泡排序)
分析:所谓转置就是将矩阵的行列互换,即将 a矩阵 的a[i][j]元素变成b矩阵的b[j][i]。
24
#include <iostream> using namespace std; int main() { int a[3][4] ={{1,2,3,4},{3,4,5,6},{5,6,7,8}}; int b[4][3],i,j; for(i=0;i<3;i++) //输出二维数组a[3][4] { for(j=0;j<4;j++) cout<<a[i][j]<<" "; cout<<endl; } for(i=0;i<4;i++) //将矩阵a转置给矩阵b for(j=0;j<3;j++) b[i][j]=a[j][i]; for(i=0;i<4;i++) //输出二维数组b[4][3] { for(j=0;j<3;j++) cout<<b[i][j]<<" "; cout<<endl; } return 0;}
matlab cell2struct用法

Matlab是一种强大的技术计算软件,广泛应用于工程、科学和数学等领域。
在Matlab中,有许多有用的函数和工具,其中cell2struct就是其中之一。
本文将重点介绍cell2struct的用法和功能,帮助读者更好地理解和应用这一功能。
1. cell2struct的概念在Matlab中,cell2struct是一个非常实用的函数,用于将cell数组转换为结构体数组。
结构体数组是Matlab中一种非常方便的数据类型,它可以存储不同类型的数据,并且可以根据字段名进行访问和操作。
而cell数组是一种特殊的数据类型,可以存储不同类型的数据,类似于一个二维数组。
通过cell2struct函数,我们可以方便地将cell 数组转换为结构体数组,从而更方便地对数据进行管理和操作。
2. cell2struct的基本用法使用cell2struct函数非常简单,基本语法如下:```matlabS = cell2struct(C, fields, dim)```其中,C是待转换的cell数组,fields是字段名的数组,dim是指定的维度。
通过这个基本的语法,我们可以将一个cell数组转换为一个结构体数组,并且可以指定字段名和维度,非常灵活和方便。
3. cell2struct的高级用法除了基本用法之外,cell2struct还有一些高级的用法,可以更灵活地对数据进行转换和处理。
我们可以通过指定字段名的方式,将cell数组中的数据转换为一个结构体数组,方便进行后续的操作和分析。
另外,我们还可以通过指定维度的方式,实现多维数据的转换,适应不同类型的数据存储和处理需求。
这些高级用法可以帮助我们更好地利用cell2struct函数,实现更灵活和高效的数据处理和管理。
4. 个人观点与总结cell2struct是Matlab中一个非常有用的函数,可以帮助我们更好地管理和处理数据。
通过本文的介绍,相信读者对cell2struct的用法和功能有了更深入的了解。
matlab二维插值

matlab二维插值--interp2与griddatafrom:matlab功能强大,以至于不知道他不能做什么,只是怨自己没有找到相应的函数。
二者均是常用的二维差值方法,两者的区别是,interp2的插值数据必须是矩形域,即已知数据点(x,y)组成规则的矩阵,或称之为栅格,可使用meshgid生成。
而griddata函数的已知数据点(X,Y)不要求规则排列,特别是对试验中随机没有规律采取的数据进行插值具有很好的效果。
griddata(X,Y,XI,YI,'v4') v4是一种插值算法,没有具体的名字,原文称为“MATLAB 4 griddata method”,是一种很圆滑的差值算法,效果很好。
X和Y提供的已知数据点,XI和YI是需要插值的数据点,一般使用meshgrid生成,当然也可以其他数据,但是那样绘图的时候就比较麻烦,不能使用mesh等,只能使用trimesh。
示例如下:a=[3 3 1.53003 27 0.42105 17 0.59809 9 0.590013 25 0.447015 15 117 5 0.383021 21 0.310025 13 0.283027 3 0.282027 27 0.1200];x=a(:,1);y=a(:,2);z=a(:,3);xtemp=linspace(min(x),max(x),100);ytemp=linspace(min(y),max(y),100);[X,Y]=meshgrid(xtemp,ytemp);Z=griddata(x,y,z,X,Y,'v4');surf(X,Y,Z)shading interp为了方便理解,先考虑一维情况下的线性插值对于一个数列c,我们假设c[a]到c[a+1]之间是线性变化的那么对于浮点数x(a<=x<a+1),c(x)=c[a+1]*(x-a)+c[a]*(1+a-x);这个好理解吧?把这种插值方式扩展到二维情况对于一个二维数组c,我们假设对于任意一个浮点数i,c(a,i)到c(a+1,i)之间是线性变化的,c(i,b)到c(i,b+1)之间也是线性变化的(a,b都是整数)那么对于浮点数的坐标(x,y)满足(a<=x<a+1,b<=y<b+1),我们可以先分别求出c(x,b)和c(x,b+1):c(x,b) = c[a+1][b]*(x-a)+c[a][b]*(1+a-x);c(x,b+1) = c[a+1][b+1]*(x-a)+c[a][b+1]*(1+a-x);好,现在已经知道c(x,b)和c(x,b+1)了,而根据假设c(x,b)到c(x,b+1)也是线性变化的,所以:c(x,y) = c(x,b+1)*(y-b)+c(x,b)*(1+b-y)这就是双线性插值,不知道我这么讲是否将明白了我不太明白画板取值是什么意思如果直接理解成亮度值的话就这么写://返回x,y的像素值,c[a][b]表示(a,b)的像素值int getColor(double x,double y,int[][] c){int a = (int)x;int b = (int)y;double dx = x-a;double dy = y-b;return(int)((c[a][b]*(1-dx)+c[a+1][b]*dx)*(1-dy)+(c[a][b+1]*(1-dx)+c[a+1][b +1]*dx)*dy);}我觉得这样的代码好像写不了注释Matlab 一维,二维及多维插值插值就是已知一组离散的数据点集,在集合内部某两个点之间预测函数值的方法。
Matlab基本使用方法详解

Matlab基本使用方法详解Matlab(Matrix Laboratory)是一种面向数值计算和编程的高级语言和环境,由MathWorks公司开发。
它在科学、工程以及其他领域广泛应用,可以进行各种数值计算、数据分析、绘图以及编写复杂的算法等。
本文将详细介绍Matlab的基本使用方法,帮助初学者快速上手。
一、Matlab基础知识在开始之前,我们先了解一些Matlab的基础知识。
Matlab的代码文件以.m为后缀名,并通过Matlab编译器执行。
它是一种解释性的语言,每一行代码都可以立即执行。
Matlab提供了丰富的数学函数和工具箱,可以简化复杂的数值计算。
同时,Matlab还具备强大的矩阵运算能力,使得处理矩阵和向量的运算更加高效。
二、Matlab环境和命令行窗口当我们打开Matlab时,会出现一个包含命令行窗口的集成开发环境界面。
命令行窗口是一个交互式的界面,可以直接输入和执行Matlab命令。
我们可以在命令行窗口中进行简单的计算,例如输入"2+2"并按回车键执行,Matlab将返回计算结果"4"。
此外,通过命令行窗口,我们还可以执行脚本文件、调试代码、查看变量等。
三、基本操作和数据类型1. 变量的定义和赋值在Matlab中,使用等号(=)将数值或表达式赋值给一个变量。
例如,"x = 5"将5赋值给变量x。
同时,Matlab还支持复数、字符串、矩阵等多种数据类型。
2. 数组和矩阵Matlab中的数组和矩阵是最基本的数据结构。
数组中的元素可以是数值、字符串、逻辑值等。
矩阵是一个二维数组,可以进行各种线性代数运算。
创建矩阵可以使用方括号([])和分号(;)对元素进行分隔。
例如,"A = [1,2,3;4,5,6;7,8,9]"创建了一个3x3的矩阵A。
3. 访问矩阵元素可以使用下标访问矩阵中的元素。
在Matlab中,下标从1开始。
matlab基础及其应用

matlab基础及其应用MATLAB基础及其应用摘要:MATLAB是一种强大的计算机程序设计语言,可以使用它来进行简单的程序编写,绘图,数学建模,数据分析,科学计算等,广泛应用于工程,科研,教育等领域。
本文讲述了MATLAB的基础知识,并以实际的例子说明了MATLAB的应用领域,如:信号处理、电子信号仿真、计算物理、人工智能等。
关键词:MATLAB;计算机程序;信号处理;仿真MATLAB基础及其应用一、MATLAB简介MATLAB(Matrix Laboratory)是由美国MathWorks公司出版的商业数值计算软件,是一个用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,它拥有完善的算法库和强大的图形绘制工具,主要被用于科学计算。
MATLAB提供了一个强大的编程接口,可以用于代码编写,程序测试、程序调试,解决大量的复杂科学计算问题。
二、MATLAB方面1、变量MATLAB提供了丰富的变量,包括标量(单个数值)、矢量(一维数组)、矩阵(二维数组)、多维数组(三维及以上数组)。
MATLAB的变量不需要预定义,该变量在程序中第一次使用时就被自动创建。
2、输入输出MATLAB有丰富的输入输出指令,可以使用输入指令(input)输入数据,使用输出指令(disp)输出结果,也可以使用文件输入输出指令(load,save)进行文件的读写操作。
3、语法MATLAB的语法与传统的程序设计语言大致相同,它也是一种基于程序流程控制的程序设计语言。
MATLAB的语法也有一些特殊之处,如:数组元素的下标从1开始,加号(+)表示数学上的加法,减号(-)表示数学上的减法,乘号(*)表示数学上的乘法,除号(/)表示数学上的除法。
三、MATLAB的应用1、信号处理MATLAB作为一种多功能的计算机语言,常常用于信号处理,如:正弦波分析,信号采集,声音处理,图像处理等。
2、电子信号仿真MATLAB也常用于电子信号仿真,电路模拟,信号发生器模拟等,可以使用MATLAB来设计复杂的电子电路,例如:数字逻辑电路、滤波器、时钟电路等,并进行仿真。
matlab 二维数组 定义

matlab 二维数组定义二维数组是一种常见的数据结构,它由多行多列的元素组成。
在Matlab中,我们可以使用矩阵来表示二维数组。
本文将从定义、特性、操作等方面介绍二维数组在Matlab中的应用。
一、定义二维数组是由相同类型的元素按照行和列排列形成的矩形表格。
在Matlab中,我们可以使用方括号和分号来定义二维数组。
例如,下面的代码定义了一个3行4列的二维数组A:A = [1, 2, 3, 4; 5, 6, 7, 8; 9, 10, 11, 12];二、特性1. 二维数组的元素可以是任意类型,包括数字、字符、字符串等。
2. 二维数组的行和列的数目可以不相等,但同一行或同一列的元素个数必须相等。
3. 二维数组的行和列的索引从1开始,行在前,列在后。
4. 二维数组可以通过行和列的索引来访问和修改元素。
三、操作1. 访问元素我们可以使用行和列的索引来访问二维数组中的元素。
例如,要访问二维数组A中的第2行第3列的元素,可以使用下面的代码:A(2, 3)2. 修改元素我们可以通过赋值的方式来修改二维数组中的元素。
例如,要将二维数组A中的第1行第2列的元素修改为10,可以使用下面的代码:A(1, 2) = 103. 求和我们可以使用sum函数来对二维数组的元素进行求和。
例如,要求二维数组A中每一列的和,可以使用下面的代码:sum(A)4. 求最大值和最小值我们可以使用max函数和min函数来求二维数组的最大值和最小值。
例如,要求二维数组A中的最大值和最小值,可以使用下面的代码:max(A)min(A)5. 求平均值我们可以使用mean函数来求二维数组的平均值。
例如,要求二维数组A中每一行的平均值,可以使用下面的代码:mean(A, 2)6. 转置我们可以使用'运算符来对二维数组进行转置操作。
例如,要将二维数组A进行转置,可以使用下面的代码:A'四、应用举例下面通过一个简单的例子来展示二维数组在Matlab中的应用。
Matlab实验报告13

301,302,303,304,305,306,307,308,309];
(3)
仿照问题
1
中方法找出数组
A
4 3
2 1
0 1
2 3
4
5
中所有绝对值大于
3
的元素。
(4)在命令窗口执行下面指令,体味二维数组的子数组寻访和赋值
A=zeros(2,4)
% 创建(2*4)的全零数组
二行是“ has multiple rows. ”。
6 .利用串操作函数 char、str2mat、strvcat 分别写出使以下这段文字成为字符串的程序,
注意保持这段文字的格式。
在英式用法中,引号通常是单引号,如‘Fire!’。
In GB usage quotation marks are usually single: ’Fire!’ .
whos
% 观察变量 a,b 在内存中所占字节
2 .已知串数组 a=”This is an example.”, 试将其到序输出。
3 .接上题,试执行 ascii_a=double(a),观察其 ASCII 码,并将 ASCII 码变回字符串。
4 .设 A=”这是一个算例”,重复上面的 2-3。
5 .尝试用直接输入法在命令窗口创建字符串 s ,第一行时“ This string array ” , 第
全赋为 1
(5) 运行指令
rand(‘state ’,11),A=rand(3,10000);B=(A>0.5);C=2*B-1;
首先预测( C*C’)/100 的运行结果,然后再在机器上验证。(本方法提供了产
生通信等仿真中常需若干独立的双随机码的方法原型。)
二维数组元素的存储顺序matlab

一、介绍二维数组二维数组是一种常见的数据结构,它由多行和多列的元素组成。
在Matlab中,二维数组也称为矩阵,它是一个重要的数据类型,常用于存储和处理二维数据。
二、二维数组的存储顺序在Matlab中,二维数组的存储是按列优先的方式进行的。
这意味着数组的元素是按照列的顺序依次存储的,而不是按照行的顺序。
这一点与其他编程语言中的存储方式可能有所不同,需要注意。
三、优点和缺点1. 优点按列优先的存储方式有利于Matlab进行矩阵运算和向量化操作。
由于在实际应用中,矩阵运算和向量化操作是Matlab经常需要进行的操作,这种存储方式可以提高运算效率和性能。
2. 缺点但是,按列优先的存储方式在访问数组元素时可能会导致不连续访问内存,从而降低缓存命中率,影响性能。
另外,在某些特定场景下,按行优先的存储方式可能更加高效。
四、存储顺序的影响存储顺序的不同可能会对代码性能产生影响。
在Matlab中,如果对一个二维数组进行迭代操作,尤其是较大规模的数组,需要注意存储顺序对性能的影响。
1. 一般性建议通常情况下,Matlab中的许多函数和操作都是针对按列优先的存储方式进行优化的,因此在大多数情况下,存储顺序的影响并不明显。
但在性能要求较高的场景下,还是需要仔细评估存储顺序的影响。
2. 特殊场景注意如果在Matlab中遇到需要自己手动对二维数组进行迭代的情况,例如使用循环逐个处理数组元素,需要考虑存储顺序对性能的影响。
在这种情况下,可以对数组进行转置,以适应按行优先的存储方式。
五、如何确定存储顺序在Matlab中,可以使用函数`isrowmajor`来确定存储顺序。
这个函数会返回一个逻辑值,表示数组的存储方式是按行优先还是按列优先。
通过这个函数,可以帮助我们更好地理解数组的存储方式,并在需要时进行适当的调整。
六、总结在Matlab中,二维数组的存储顺序是按列优先的。
这种存储方式对于矩阵运算和向量化操作有利,但在某些特定场景下可能会对性能产生影响。
matlabfor数组

matlabfor数组
Matlab的数组是一组具有相同数据类型的元素。
可以使用不同的方法来创建数组。
例如,可以使用一系列数字创建数组,也可以使用Matlab提供的函数。
创建数组后,可以使用许多操作来处理它们,例如索引、切片、排序等。
Matlab中的数组可以是一维数组、二维数组、多维数组等。
一维数组是最简单的数组类型,类似于Python中的列表或NumPy中的一维数组。
二维数组是最常见的数组类型,类似于Excel中的表格或Python中的二维数组。
多维数组可以包含任意数量的维度。
在操作数组时,可以使用许多有用的函数来处理它们。
例如,可以使用sum函数计算数组的总和,使用max函数找到数组中的最大值,使用sort函数对数组进行排序等。
在使用Matlab时,了解如何创建和操作数组是非常重要的。
掌握这些基本技能可以帮助您更有效地编写代码和解决问题。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab:二维数组及其应用
二维数组实际上也是一个矩阵。
应此直接创建一个矩阵就行。
创建的方法你应该会吧,就是直接按行方式输入每个元素:同一行中的元素用逗号(,)或者用空格符来分隔,且空格个数不限;不同的行用分号(;)分隔。
所有元素处于一方括号([ ])内。
比如,创建一个3×5的矩阵(对应3×5的二维数组)
A = [12 62 93 -8 22; 16 2 87 43 91; -4 17 -72 95 6]
A =
12 62 93 -8 22
16 2 87 43 91
-4 17 -72 95 6
当然也可以用专门用来创建多维数组的cat函数来创建。
具体如下:
函数cat
格式A=cat(n,A1,A2,…,Am)
说明n=1和n=2时分别构造[A1;A2]和[A1,A2],都是二维数组,而n=3时可以构造出三维数组。
例如:
>> A1=[1,2,3;4,5,6;7,8,9];A2=A1';
>> A3=cat(2,A1,A2)
A3 =
1 2 3 1 4 7
4 5 6 2 5 8
7 8 9 3 6 9
这样A3就是一个二维数组
此外还有诸如特殊矩阵的创建方法等这里就不列举了你可以百度或者Google一下
二维数组的变换我还不太确定你的意思:
这里就提供几个矩阵的操作:
1.矩阵的变维
矩阵的变维有两种方法,即用“:”和函数“reshape”,前者主要针对2个已知维数矩阵之间的变维操作;而后者是对于一个矩阵的操作。
(1)“:”变维
例1-48
> A=[1 2 3 4 5 6;6 7 8 9 0 1]
A =
1 2 3 4 5 6
6 7 8 9 0 1
>> B=ones(3,4)
B =
1 1 1 1
1 1 1 1
1 1 1 1
>> B(:)=A(:)
B =
1 7 4 0
6 3 9 6
2 8 5 1
(2)Reshape函数变维
格式 B = reshape(A,m,n) %返回以矩阵A的元素构成的m×n矩阵B
B = reshape(A,m,n,p,…) %将矩阵A变维为m×n×p×…
B = reshape(A,[m n p…]) %同上
B = reshape(A,siz) %由siz决定变维的大小,元素个数与A中元素个数相同。
矩阵变维例子:
>> a=[1:12];
>> b=reshape(a,2,6)
b =
1 3 5 7 9 11
2 4 6 8 10 12
2.矩阵的变向
(1)矩阵旋转
函数
格式 B = rot90 (A) %将矩阵A逆时针方向旋转90°
B = rot90 (A,k) %将矩阵A逆时针方向旋转(k×90°),k可取正负整数。
例如:
>> A=[1 2 3;4 5 6;7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> Y1=rot90(A),Y2=rot90(A,-1)
Y1 = %逆时针方向旋转
3 6 9
2 5 8
1 4 7
Y2 = %顺时针方向旋转
7 4 1
8 5 2
9 6 3
(2)矩阵的左右翻转
函数fliplr
格式 B = fliplr(A) %将矩阵A左右翻转
(3)矩阵的上下翻转
函数flipud
格式 B = flipud(A) %将矩阵A上下翻转
例如:
>> A=[1 2 3;4 5 6]
A =
1 2 3
4 5 6
>> B1=fliplr(A),B2=flipud(A)
B1 =
3 2 1
6 5 4
B2 =
4 5 6
1 2 3
(4)按指定维数翻转矩阵
函数flipdim
格式 B = flipdim(A,dim) % flipdim(A,1) = flipud(A),并且flipdim(A,2)=fliplr(A)。
例如
>> A=[1 2 3;4 5 6]
A =
1 2 3
4 5 6
>> B1=flipdim(A,1),B2=flipdim(A,2)
B1 =
4 5 6
1 2 3
B2 =
3 2 1
6 5 4
(5)复制和平铺矩阵
函数repmat
格式 B = repmat(A,m,n) %将矩阵A复制m×n块,即B由m×n块A平铺而成。
B = repmat(A,[m n]) %与上面一致
B = repmat(A,[m n p…]) %B由m×n×p×…个A块平铺而成
repmat(A,m,n) %当A是一个数a时,该命令产生一个全由a组成的m×n矩阵。
例如
>> A=[1 2;5 6]
A =
1 2
5 6
>> B=repmat(A,3,4)
B =
1 2 1 2 1 2 1 2
5 6 5 6 5 6 5 6
1 2 1 2 1 2 1 2
5 6 5 6 5 6 5 6
1 2 1 2 1 2 1 2
5 6 5 6 5 6 5 6
3.矩阵元素的数据变换
对于小数构成的矩阵A来说,如果我们想对它取整数,有以下几种方法:(1)按-∞方向取整
函数floor
格式floor(A) %将A中元素按-∞方向取整,即取不足整数。
(2)按+∞方向取整
函数ceil
格式ceil(A) %将A中元素按+∞方向取整,即取过剩整数。
(3)四舍五入取整
函数round
格式round (A) %将A中元素按最近的整数取整,即四舍五入取整。
(4)按离0近的方向取整
函数fix
格式fix (A) %将A中元素按离0近的方向取整
例如:
>> A=-1.5+4*rand(3)
A =
2.3005 0.4439 0.3259
-0.5754 2.0652 -1.4260
0.9274 1.5484 1.7856
>> B1=floor(A),B2=ceil(A),B3=round(A),B4=fix(A)
B1 =
2 0 0
-1 2 -2
0 1 1
B2 =
3 1 1
0 3 -1
1 2 2
B3 =
2 0 0
-1 2 -1
1 2 2
B4 =
2 0 0
0 2 -1
0 1 1
(5)矩阵的有理数形式
函数rat
格式[n,d]=rat (A) %将A表示为两个整数矩阵相除,即A=n./d。
例如:对于上例中的A
>> [n,d]=rat(A)
n =
444 95 131
-225 2059 -472
166 48 1491
d =
193 214 402
391 997 331
179 31 835
(6)矩阵元素的余数
函数rem
格式 C = rem (A, x) %表示A矩阵除以模数x后的余数。
若x=0,则定义rem(A, 0)=NaN,若x≠0,则整数部分由fix(A./x)表示,余数C=A-x.*fix (A./x)。
允许模x为小数。
