考研数学历年真题(2008-2017)年数学二

合集下载

2017年考研(数学二)真题试卷(题后含答案及解析)

2017年考研（数学二）真题试卷(题后含答案及解析)题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．若函数f(x)=在x=0处连续，则( )A．ab=1／2B．ab=-C．ab=0D．ab=2正确答案：A解析：=1／2a，∵f(x)在x=0处连续，1／2a=bab=1／2，选A．2．设二阶可导函数f(x)满足f(1)=f(-1)=1，f(0)=-1且f”(x)＞0，则( ) A．∫-11f(x)dx＞0B．∫-11f(x)dx＜0C．∫-10f(x)dx＞∫01f(x)dxD．∫-10f(x)dx＜∫01f(x)dx正确答案：B解析：f(x)为偶函数时满足题设条件，此时∫-10f(x)dx=∫01f(x)dx，排除C，D．取f(x)=2x2-1满足条件，则∫-11f(x)dx=∫-11(2x2-1)dx=-＜0，选B．3．设数列{xn}收敛，则( )A．B．C．D．正确答案：D解析：特值法：A取xn=π，有xn=π，A错；取xn=-1，排除B，C．所以选D．4．微分方程y”-4y’+8y=e2x(1+cos2x)的特解可设为yk=( )A．Ae2x+e2x(Bcos2x+Csin2x)B．Axe2x+e2x(Bcos2x+Csin2x)C．Ae2x+xe2x(Bcos2x+Csin2x)D．Axe2x+xe2x(Bcos2x+Csin2x)正确答案：C解析：特征方程为：λ2-4λ+8=0λ1．2=2±2i∵f(x)=e2x(1+cos2x)=e2x+e2xcos2x，∴y1*=Ae2x，y2*=xe2x(Bcos2x+Csin2x)，故特解为：y*=y1*+y2*=Ae2x+xe2x(Bcos2x+Csin2x)，选C．5．设f(x，y)具有一阶偏导数，且对任意的(x，y)，都有＞0，则( )A．f(0，0)＞f(1，1)B．f(0，0)＜f(1，1)C．f(0，1)＞f(1，0)D．f(0，1)＜f(1，0)正确答案：D解析：f(x，y)是关于y的单调递减函数，所以有f(0，1)＜f(1，1)＜f(1，0)，故答案选D．6．甲、乙两人赛跑，计时开始时，甲在乙前方10(单位：m)处，图中实线表示甲的速度曲线v=v1(t)(单位：m／s)，虚线表示乙的速度曲线v=v2(t)，三块阴影部分面积的数值依次为10，20，3计时开始后乙追上甲的时刻记为t0(单位：s)，则( )A．t0=10B．15＜t0＜20C．t0=25D．t0＞25正确答案：C解析：从0到t0这段时间内甲乙的位移分别为∫0t0v1(t)dt，∫0t0v2(t)dt，则乙要追上甲，则∫0t0v2(t)dt-v1(t)dt=10，当t0=25时满足，故选C．7．设A为三阶矩阵，P=(α1，α2，α3)为可逆矩阵，使得P-1AP=，则A(α1，α2，α3)=( )A．α1+α2B．α2+2α3C．α2+α3D．α1+2α2正确答案：B解析：P-1AP=A(α1，α2，α3)=(α1，α2，α3)=α2+2α3，因此B正确．8．已知矩阵A=，则( )A．A与C相似，B与C相似B．A与C相似，B与C不相似C．A与C不相似，B与C相似D．A与C不相似，B与C不相似正确答案：B解析：由|λE-A|=0可知A的特征值为2，2，1，因为3-r(2E-A)=1，∴A可相似对角化，即A～由|λE-B|=0可知B特征值为2，2，1．因为3-r(2E-B})=2，∴B不可相似对角化，显然C可相似对角化，∴A～C，但B不相似于C．填空题9．曲线y=x(1+arcsin)的斜渐近线方程为_______．正确答案：y=x+2解析：∵=2，∴y=x+2．10．设函数y=y(x)由参数方程确定，则d2y／dx2=|t=0_______．正确答案：解析：11．∫0+∞dx=_______．正确答案：1解析：12．设函数f(x，y)具有一阶连续偏导数，且af(x，y)=yeydx+x(1+y)eydy，f(0，0)=0，则f(x，y)=_______．正确答案：xyey解析：f’x=yey，f’y1=x(1+y)ey，f(x，y)=∫yeydx=xyey+c(y)，故f’y=xey+xyey+c’(y)=xey+xyey，故c’(y)=0，即c(y)=c，由f(0，0)=0，即f(x，y)=xyey．13．∫01dy∫y1dx=_______．正确答案：lncos1解析：∫01dy∫y1dx=∫01dx∫0xdy=∫01tanxdx=lncos1．14．设矩阵A=的一个特征向量为，则a=_______．正确答案：-1解析：设α=，由题设知Aα=λα，故(1 1 2)T=λ(1 1 2)T故a=1．解答题解答应写出文字说明、证明过程或演算步骤。

考研数学二真题(2008年)

2008年全国硕士研究生入学统一考试
数学二试题
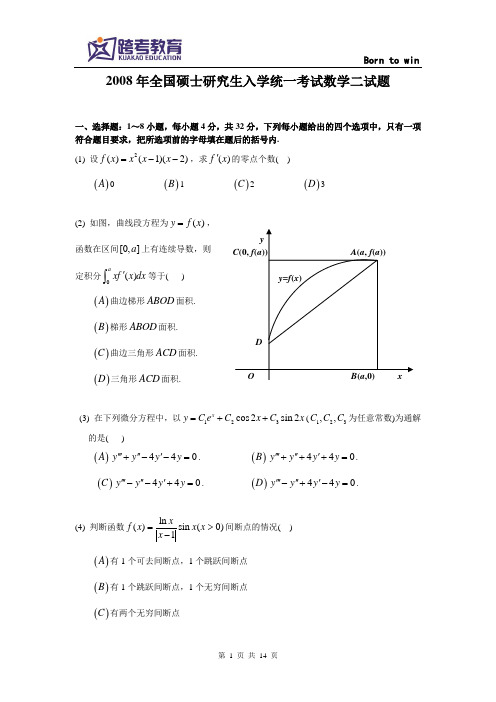
一、选择题：1～10小题，每小题4分，共40分. 在每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.
1.
2.
3.
4.
6.
7.
8.
二、填空题：9～14小题，每小题4分，共24分. 把答案填在题中横线上.
9.
11.
12.
13.
14.
三、解答题：15～22小题，共86分. 解答应写出文字说明、证明过程或演算步骤.
15.
17.
19.
21.
2008年全国硕士研究生入学统一考试
数学二试题答案
一、选择题：1～10小题，每小题4分，共40分. 在每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.
1. D
2. C
3. D
4. A
5. B
6. A
7. C
8. D
二、填空题：9～14小题，每小题4分，共24分. 把答案填在题中横线上.
9. 2
10. y=-xe-x+Cx
11. y=x+1
12. (-1，-6)
14. λ=-1
三、解答题：15～22小题，共86分. 解答应写出文字说明、证明过程或演算步骤.
16.
17.
18.
19.
20.
21.
22.
23.。

2008年全国硕士研究生入学统一考试数学二真题及答案

故线性无关．
（Ⅱ）记则可逆，
即 .
【难易度】★★
【详解】
解析：
则。记，则
则，正、负惯性指数相同，故选
二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.
（9）已知函数连续，且，则
【答案】2
【考点】等价无穷小
【难易度】★★
【详解】
解析：利用等价无穷小因子替换有
.
（10）微分方程的通解是 .
【答案】y＝Cx－xe－x，其中C为任意常数
2个无穷间断点
2个跳跃间断点
【答案】
【考点】函数间断点的类型
【难易度】★★
Hale Waihona Puke 【详解】解析：的间断点为，而，故是可去间断点；
，，故是跳跃间断点
故选 .
（5）设函数在内单调有界，为数列，下列命题正确的是（）
若收敛，则收敛. 若单调，则收敛.
若收敛，则收敛. 若单调，则收敛.
【详解】
解析：令
得方程组即，解得或
得 .
.
（22）（本题满分11分）
设元线性方程组，其中，， .
（Ⅰ）证明行列式；
（Ⅱ）当为何值时，该方程组有唯一解，求；
（Ⅲ）当为何值时，该方程组有无穷多解，求通解.
【考点】行列式的基本性质，非齐次线性方程组解的判定
【难易度】★★★
【详解】
解析：（Ⅰ）证明：消元法．记
．
（Ⅱ）由克莱姆法则，时方程组有唯一解，故时方程组有唯一解.
由克莱姆法则，将得第一列换成，得行列式为
所以，．
（Ⅲ）当时，方程组为
此时方程组系数矩阵的秩和增广矩阵的秩均为，所以方程组有无穷多组解，其通解为，其中为任意常数．

考研数二历年真题答案

考研数二历年真题答案为了帮助考研数学二科目的学生更好地备考，以下整理了近几年的考研数学二历年真题及其详细答案。

通过仔细研究和解析这些真题，考生们可以更好地了解考试内容和出题思路，从而更有针对性地复习和备考。

一、2000年考研数学二真题及答案（下面是2000年考研数学二的真题及其答案，请考生查看。

）二、2001年考研数学二真题及答案（下面是2001年考研数学二的真题及其答案，请考生查看。

）三、2002年考研数学二真题及答案（下面是2002年考研数学二的真题及其答案，请考生查看。

）四、2003年考研数学二真题及答案（下面是2003年考研数学二的真题及其答案，请考生查看。

）五、2004年考研数学二真题及答案（下面是2004年考研数学二的真题及其答案，请考生查看。

）六、2005年考研数学二真题及答案（下面是2005年考研数学二的真题及其答案，请考生查看。

）七、2006年考研数学二真题及答案（下面是2006年考研数学二的真题及其答案，请考生查看。

）八、2007年考研数学二真题及答案（下面是2007年考研数学二的真题及其答案，请考生查看。

）九、2008年考研数学二真题及答案（下面是2008年考研数学二的真题及其答案，请考生查看。

）十、2009年考研数学二真题及答案（下面是2009年考研数学二的真题及其答案，请考生查看。

）十一、2010年考研数学二真题及答案（下面是2010年考研数学二的真题及其答案，请考生查看。

）十二、2011年考研数学二真题及答案（下面是2011年考研数学二的真题及其答案，请考生查看。

）十三、2012年考研数学二真题及答案（下面是2012年考研数学二的真题及其答案，请考生查看。

）十四、2013年考研数学二真题及答案（下面是2013年考研数学二的真题及其答案，请考生查看。

）十五、2014年考研数学二真题及答案（下面是2014年考研数学二的真题及其答案，请考生查看。

）十六、2015年考研数学二真题及答案（下面是2015年考研数学二的真题及其答案，请考生查看。

2008年数学二考研数学真题及解析

2008年全国硕士研究生入学统一考试数学二试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内. (1)设2()(1)(2)f x x x x =--，求()f x '的零点个数（）()A 0()B 1 ()C 2()D 3（2）曲线方程为()y f x =函数在区间[0,]a 上有连续导数，则定积分'()axf x dx ⎰（）()A 曲边梯形ABCD 面积. ()B 梯形ABCD 面积.()C 曲边三角形ACD 面积.()D 三角形ACD 面积.（3）在下列微分方程中，以123cos2sin 2x y C e C x C x =++（123,,C C C 为任意常数）为通解的是（）()A 440y y y y ''''''+--=.()B 440y y y y ''''''+++=.()C 440y y y y ''''''--+=.()D 440y y y y ''''''-+-=.（4）判断函数ln ()sin (0)1xf x x x x =>-间断点的情况( ) ()A 有1个可去间断点，1个跳跃间断点 ()B 有1个跳跃间断点，1个无穷间断点 ()C 有两个无穷间断点 ()D 有两个跳跃间断点（5）设函数()f x 在(,)-∞+∞内单调有界，{}n x 为数列，下列命题正确的是（）()A 若{}n x 收敛，则{}()n f x 收敛. ()B 若{}n x 单调，则{}()n f x 收敛.()C 若{}()n f x 收敛，则{}n x 收敛.()D 若{}()n f x 单调，则{}n x 收敛.（6）设f 连续，221x y +=，222x y u +=，1u >，则()22,Df u v F u v +=，则Fu∂=∂（） ()A ()2vf u()B ()vf u()C ()2vf u u()D ()vf u u（7）设A 为n 阶非零矩阵，E 为n 阶单位矩阵. 若30A =，则（）()A E A -不可逆，E A +不可逆.()B E A -不可逆，E A +可逆.()C E A -可逆，E A +可逆.()D E A -可逆，E A +不可逆.（8）设1221A ⎛⎫=⎪⎝⎭，则在实数域上与A 合同的矩阵为（） ()A 2112-⎛⎫⎪-⎝⎭.()B 2112-⎛⎫⎪-⎝⎭.()C 2112⎛⎫⎪⎝⎭.()D 1221-⎛⎫⎪-⎝⎭.二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）()f x 连续，21cos(sin )lim1(1)()x x x e f x →-=-，则(0)f =（10）曲线()()sin ln xy y x x +-=在点()0,1处的切线方程为 . （11）求函数23()(5)f x x x =-的拐点______________. （12）已知xyy z x ⎛⎫=⎪⎝⎭，则(1,2)_______z x ∂=∂. （13）矩阵A 的特征值是,2,3λ，其中λ未知，且2A =-48，则λ=_______.（14）设A 为2阶矩阵，12,a a 为线性无关的2维列向量，12120,2Aa Aa a a ==+，则A 的非零特征值为 .三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)（本题满分10分）求极限()40sin sin sin sin lim x x x x x →-⎡⎤⎣⎦. (17)（本题满分10分）求积分21⎰(18)（本题满分10分）求函数222u x y z =++在在约束条件22z x y =+和4x y z ++=下的最大和最小值. (19)（本题满分10分）曲线()y f x =满足(0)1f =对于任意的t 曲线是严格递增，在x 轴上0t >，该曲线与直线0,(0)x x t t ==>及0y =围成一曲边梯形.该曲边梯形绕x 轴旋转一周得一旋转体，其体积为()V t ,侧面积为()S t .如果()f x 二阶可导,且()2()S t V t =，求曲线()y f x =. (20)（本题满分11分）求二重积分max(,1),Dxy dxdy ⎰⎰其中{(,)02,02}D x y x y =≤≤≤≤（21）（本题满分11分）证明(1)积分中值定理；(2)已知()x ϕ在[1,3]上连续且可导，32(2)(1),(2)()x dx ϕϕϕϕ>>⎰证明至少存在一点(1,3)ξ∈，()0ϕξ'=使得. （22）（本题满分11分）设矩阵2221212n n a a a A a a ⨯⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭ ，现矩阵A 满足方程AX B =，其中()1,,T n X x x = ，()1,0,,0TB = ，（1）求证()1nA n a =+（2）a 为何值，方程组有唯一解，求1x （3）a 为何值，方程组有无穷多解，求通解（23）（本题满分11分）设A 为3阶矩阵，12,a a 为A 的分别属于特征值1,1-特征向量，向量3a 满足323Aa a a =+，证明（1）123,,a a a 线性无关；（2）令()123,,P a a a =，求1P AP -。

2008年考研数学二试题答案与解析

(B) E − A 不可逆, E + A可逆. (D) E − A 可逆, E + A不可逆.
[C]
(8)
设
A
=
⎛ ⎜ ⎝
1 2
2 1
⎞ ⎟ ⎠
,则在实数域上与
A
合同的矩阵为
(A)
⎛ −2
⎜ ⎝
1
1 −2
⎞ ⎟ ⎠
.
(B)
⎛2
⎜ ⎝
−1
−1⎞
2
⎟ ⎠
.
(C)
⎛2
⎜ ⎝
1
1⎞
2
⎟ ⎠
.
(D)
⎛1
⎜ ⎝
NBF 辅导，真正为考研人着想的辅导!
由定积分性质,有
m(b
−
a)
≤
b
∫a
f
(
x )dx
≤
M
(b
−
a)
即
m
≤
b
1 −
a
b
∫a
f
(
x)dx
≤
M
由连续函数介值定理可知,至少存在一点η ∈[a,b] ,使得
f
(η
)
=
b
1 −
a
b
∫a
f
( x)dx
即
b
∫a
f
( x)dx
=
f
(η )(b − a)
x = ln (1+ t2 )
dy dx
=
dy
dt dx
=
ln (1+ t2 ) ⋅ 2t
2t
=
(1+ t2 ) ln (1+ t2 )
dt

2017年考研数学二真题与解析

x lim
1x 2
1
， lim
f (x) b
f (0) ，要使函数在 x 0 处连续，
x0
x0
ax
x0 ax 2a x0
必须满足 1 b ab 1 ．所以应该选（A）
2a
2
2．设二阶可导函数 f (x) 满足 f (1) f (1) 1 ， f (0) 1 ，且 f (x) 0 ，则（）
2 1
a
1
1 2
1
2
3
2a
2
，解得 a
1 ．
三、解答题
15．（本题满分 10 分）
x
求极限 lim 0 x0
x tetdt x3
【详解】令 x t u ，则 t x u , dt du ， x x tetdt x uexudu
0
0
x
lim 0
x0
x tetdt
A(1 , 2 , 3 )
AP
P
0
1
0
1,
2
,3
0
1
0
0,2, 23
0 0 2
0 0 2
所以 A(1 2 3) A1 A2 A3 2 23 ，所以可知选择（B）．
2 0 0
2 1 0
1 0 0
8．已知矩阵
A
0
2
1
，
B
0
2
0
，C
0
2
0
，则
0 0 1
0 0 1
19．（本题满分 10 分）
设函数 f (x) 在区间 0,1上具有二阶导数，且 f (1) 0 ， lim f (x) 0 ，证明：
x x0

2008考研数学二真题及答案

2008考研数学二真题及答案一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）设2()(1)(2)f x x x x =--，则'()f x 的零点个数为（）()A 0 ()B 1. ()C 2 ()D 3（2）曲线方程为()y f x =函数在区间[0,]a 上有连续导数，则定积分0()at af x dx ⎰（）()A 曲边梯形ABCD 面积.()B 梯形ABCD 面积. ()C 曲边三角形ACD 面积.()D 三角形ACD 面积.（3）在下列微分方程中，以123cos 2sin 2xy C e C x C x =++（123,,C C C 为任意常数）为通解的是（）()A ''''''440y y y y +--= ()B ''''''440y y y y +++=()C ''''''440y y y y --+=()D ''''''440y y y y -+-=（5）设函数()f x 在(,)-∞+∞内单调有界，{}n x 为数列，下列命题正确的是（）()A 若{}n x 收敛，则{}()n f x 收敛. ()B 若{}n x 单调，则{}()n f x 收敛. ()C 若{}()n f x 收敛，则{}n x 收敛.()D 若{}()n f x 单调，则{}n x 收敛.（6）设函数f 连续，若2222()(,)uvD f x y F u v dxdy x y+=+⎰⎰，其中区域uv D 为图中阴影部分，则Fu∂=∂ ()A 2()vf u ()B 2()vf u u ()C ()vf u ()D ()vf u u（7）设A 为n 阶非零矩阵，E 为n 阶单位矩阵. 若30A =，则（）()A E A -不可逆，E A +不可逆.()B E A -不可逆，E A +可逆. ()C E A -可逆，E A +可逆.()D E A -可逆，E A +不可逆.（8）设1221A ⎛⎫=⎪⎝⎭，则在实数域上与A 合同的矩阵为（） ()A 2112-⎛⎫⎪-⎝⎭.()B 2112-⎛⎫ ⎪-⎝⎭. ()C 2112⎛⎫⎪⎝⎭.()D 1221-⎛⎫⎪-⎝⎭.二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9）已知函数()f x 连续，且21cos[()]lim1(1)()x x xf x e f x →-=-，则(0)____f =.（10）微分方程2()0xy x e dx xdy -+-=的通解是____y =.（11）曲线()()sin ln xy y x x +-=在点()0,1处的切线方程为 . （12）曲线23(5)y x x =-的拐点坐标为______. （13）设xyy z x ⎛⎫=⎪⎝⎭，则(1,2)____z x ∂=∂.（14）设3阶矩阵A 的特征值为2,3,λ.若行列式248A =-，则___λ=.三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)（本题满分9分）求极限()4sin sin sin sin limx x x x x →-⎡⎤⎣⎦.(16)（本题满分10分）设函数()y y x =由参数方程20()ln(1)t x x t y u du =⎧⎪⎨=+⎪⎩⎰确定，其中()x t 是初值问题020xt dx te dtx --⎧-=⎪⎨⎪=⎩的解.求22y x ∂∂.(17)（本题满分9分）求积分1⎰.(18)（本题满分11分）求二重积分max(,1),Dxy dxdy ⎰⎰其中{(,)02,02}D x y x y =≤≤≤≤(19)（本题满分11分）设()f x 是区间[)0,+∞上具有连续导数的单调增加函数，且(0)1f =.对任意的[)0,t ∈+∞，直线0,x x t ==，曲线()y f x =以及x 轴所围成的曲边梯形绕x 轴旋转一周生成一旋转体.若该旋转体的侧面积在数值上等于其体积的2倍，求函数()f x 的表达式. (20)（本题满分11分）(1) 证明积分中值定理：若函数()f x 在闭区间[,]a b 上连续，则至少存在一点[,]a b η∈，使得()()()baf x dx f b a η=-⎰(2)若函数()x ϕ具有二阶导数，且满足32(2)(1),(2)()x dx ϕϕϕϕ>>⎰，证明至少存在一点(1,3),()0ξϕξ''∈<使得（21）（本题满分11分）求函数222u x y z =++在约束条件22z x y =+和4x y z ++=下的最大值与最小值. （22）（本题满分12分）设矩阵2221212n na a a A a a ⨯⎛⎫⎪⎪= ⎪⎪⎝⎭OO O ，现矩阵A 满足方程AX B =，其中()1,,Tn X x x =L ，()1,0,,0B =L ，（1）求证()1nA n a =+；（2）a 为何值，方程组有唯一解，并求1x ；（3）a 为何值，方程组有无穷多解，并求通解. （23）（本题满分10分）设A 为3阶矩阵，12,αα为A 的分别属于特征值1,1-特征向量，向量3α满足323A ααα=+，（1）证明123,,ααα线性无关；（2）令()123,,P ααα=，求1P AP -. 参考答案一、选择题 (1)【答案】D【详解】因为(0)(1)(2)0f f f ===，由罗尔定理知至少有1(0,1)ξ∈，2(1,2)ξ∈使12()()0f f ξξ''==，所以()f x '至少有两个零点. 又()f x '中含有因子x ，故0x =也是()f x '的零点， D 正确.本题的难度值为0.719. (2)【答案】C 【详解】00()()()()()()aa a aaxf x dx xdf x xf x f x dx af a f x dx '==-=-⎰⎰⎰⎰其中()af a 是矩形ABOC 面积，0()af x dx ⎰为曲边梯形ABOD 的面积，所以0()axf x dx '⎰为曲边三角形的面积．本题的难度值为0.829.(3)【答案】D【详解】由微分方程的通解中含有xe 、cos2x 、sin 2x 知齐次线性方程所对应的特征方程有根1,2r r i ==±，所以特征方程为(1)(2)(2)0r r i r i --+=，即32440r r r -+-=. 故以已知函数为通解的微分方程是40y y y ''''''-+-= 本题的难度值为0.832. (4) 【答案】A【详解】0,1x x ==时()f x 无定义，故0,1x x ==是函数的间断点因为 000ln 11lim ()lim lim lim csc |1|csc cot x x x x x xf x x x x x++++→→→→=⋅=-- 200sin lim lim 0cos cos x x x xx x x++→→=-=-=同理 0lim ()0x f x -→= 又 1111ln 1lim ()lim lim sin lim sin1sin11x x x x x f x x x x ++++→→→→⎛⎫=⋅== ⎪-⎝⎭所以 0x =是可去间断点，1x =是跳跃间断点. 本题的难度值为0.486.(5)【答案】B【详解】因为()f x 在(,)-∞+∞内单调有界，且{}n x 单调. 所以{()}n f x 单调且有界. 故{()}n f x 一定存在极限.本题的难度值为0.537. (6)【答案】A【详解】用极坐标得 ()222()2011,()vu uf r r Df u v F u v dv rdr v f r dr +===⎰⎰⎰所以()2Fvf u u∂=∂ 本题的难度值为0.638. (7) 【答案】C【详解】23()()E A E A A E A E -++=-=，23()()E A E A A E A E +-+=+= 故,E A E A -+均可逆．本题的难度值为0.663. (8) 【答案】D【详解】记1221D -⎛⎫=⎪-⎝⎭，则()2121421E D λλλλ--==---，又()2121421E A λλλλ---==----所以A 和D 有相同的特征多项式，所以A 和D 有相同的特征值.又A 和D 为同阶实对称矩阵，所以A 和D 相似．由于实对称矩阵相似必合同，故D 正确. 本题的难度值为0.759. 二、填空题 (9)【答案】2【详解】222220001cos[()]2sin [()2]2sin [()2]()lim lim lim ()[()2]4(1)()x x x x xf x xf x xf x f x x f x xf x e f x →→→-⋅==⋅- 011lim ()(0)122x f x f →=== 所以 (0)2f = 本题的难度值为0.828. (10)【答案】()xx eC --+【详解】微分方程()20x y x e dx xdy -+-=可变形为x dy yxe dx x--= 所以 111()dx dx x x xx x y e xe e dx C x xe dx C x e C x ----⎡⎤⎛⎫⎰⎰=+=⋅+=-+⎢⎥ ⎪⎝⎭⎣⎦⎰⎰本题的难度值为0.617. (11)【答案】1y x =+【详解】设(,)sin()ln()F x y xy y x x =+--，则1cos()11cos()x yy xy F dy y xdx F x xy y x--'-=-=-'+-，将(0)1y =代入得1x dy dx==，所以切线方程为10y x -=-，即1y x =+本题的难度值为0.759. (12)【答案】(1,6)-- 【详解】53235y xx =-⇒23131351010(2)333x y x x x -+'=-=⇒134343101010(1)999x y x x x --+''=+=1x =-时，0y ''=；0x =时，y ''不存在在1x =-左右近旁y ''异号，在0x =左右近旁0y ''>，且(1)6y -=- 故曲线的拐点为(1,6)-- 本题的难度值为0.501. (13)【答案】21)2- 【详解】设,y xu v x y==，则v z u = 所以121()ln v v z z u z v y vu u u x u x v x x y-∂∂∂∂∂=⋅+⋅=-+⋅∂∂∂∂∂ 2ln 11ln x yv vy u y y u uxy x y x ⎛⎫⎛⎫⎛⎫=-+=⋅-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭ 所以(1,2)21)z x ∂=-∂本题的难度值为0.575. (14)【答案】-1【详解】||236A λλ =⨯⨯=Q 3|2|2||A A = 32648λ∴ ⨯=- 1λ⇒=- 本题的难度值为0.839.三、解答题 (15)【详解】方法一：4300[sin sin(sin )]sin sin sin(sin )limlim x x x x x x x x x→→--= 22220001sin cos cos(sin )cos 1cos(sin )12lim lim lim 3336x x x xx x x x x x x →→→--==== 方法二：331sin ()6x x x o x =-+Q 331sin(sin )sin sin (sin )6x x x o x =-+4444400[sin sin(sin )]sin sin (sin )1lim lim 66x x x x xx o x x x x →→⎡⎤-∴ =+=⎢⎥⎣⎦本题的难度值为0.823. (16)【详解】方法一：由20x dx te dt--=得2x e dx tdt =，积分并由条件0t x =得21x e t =+，即2ln(1)x t =+ 所以 2222ln(1)2(1)ln(1)21dydy t tdt t t dxt dx dt t +⋅===+++222222[(1)ln(1)]2ln(1)221dt t d y d dy t t tdt dx t dx dx dx dt t ++++⎛⎫=== ⎪⎝⎭+ 22(1)[ln(1)1]t t =+++方法二：由20x dx te dt--=得2x e dx tdt =，积分并由条件0t x =得21x e t =+，即2ln(1)x t =+ 所以 2222ln(1)2(1)ln(1)21x dydy t tdt t t e x dxt dx dt t +⋅===++=+所以 22(1)xd ye x dx=+本题的难度值为0.742.(17)【详解】方法一：由于21x -→=+∞，故21⎰是反常积分.令arcsin x t =，有sin x t =，[0,2)t π∈22122220000sin cos 2cos sin ()cos 22t t t t t tdt t tdt dt t πππ===-⎰⎰⎰⎰2222220001sin 21sin 2sin 2441644tt t td t tdt πππππ=-=-+⎰⎰ 222011cos 2168164t πππ=-=+方法二：21⎰12201(arcsin )2x d x =⎰ 121122220001(arcsin )(arcsin )(arcsin )28x x x x dx x x dx π=-=-⎰⎰令arcsin x t =，有sin x t =，[0,2)t π∈1222200011(arcsin )sin 2cos 224x x dx tdt t d t ππ==-⎰⎰⎰ 222200111(cos 2)cos 242164t t t tdt πππ=-+=-⎰故，原式21164π=+ 本题的难度值为0.631.(18)【详解】曲线1xy =将区域分成两个区域1D 和23D D +，为了便于计算继续对区域分割，最后为()max ,1Dxy dxdy ⎰⎰123D D D xydxdy dxdy dxdy =++⎰⎰⎰⎰⎰⎰112222211102211x xdx dy dx dy dx xydy =++⎰⎰⎰⎰⎰⎰1512ln 2ln 24=++-19ln 24=+ 本题的难度值为0.524. (19)【详解】旋转体的体积20()tV f x dx π=⎰，侧面积02(tS f x π=⎰，由题设条件知20()(ttf x dx f x =⎰⎰上式两端对t 求导得2()(f t f t = 即y '=由分离变量法解得1ln(y t C =+，即t y Ce =将(0)1y =代入知1C =，故t y e =，1()2t t y e e -=+于是所求函数为 1()()2x xy f x e e -==+本题的难度值为0.497.(20)【详解】(I) 设M 与m 是连续函数()f x 在[,]a b 上的最大值与最小值，即()m f x M ≤≤ [,]x a b ∈由定积分性质，有 ()()()bam b a f x dx M b a -≤≤-⎰，即 ()baf x dx m M b a≤≤-⎰由连续函数介值定理，至少存在一点[,]a b η∈，使得 ()()b af x dx f b aη=-⎰即()()()baf x dx f b a η=-⎰(II) 由(I)的结论可知至少存在一点[2,3]η∈，使 32()()(32)()x dx ϕϕηϕη=-=⎰又由 32(2)()()x dx ϕϕϕη>=⎰，知 23η<≤对()x ϕ在[1,2][2,]η上分别应用拉格朗日中值定理，并注意到(1)(2)ϕϕ<，()(2)ϕηϕ<得1(2)(1)()021ϕϕϕξ-'=>- 112ξ<<2()(2)()02ϕηϕϕξη-'=<- 123ξη<<≤在12[,]ξξ上对导函数()x ϕ'应用拉格朗日中值定理，有2121()()()0ϕξϕξϕξξξ''-''=<- 12(,)(1,3)ξξξ∈⊂本题的难度值为0.719. (21)【详解】方法一：作拉格朗日函数22222(,,,,)()(4)F x y z x y z x y z x y z λμλμ=++++-+++-令 2222022020040x y z F x x F y y F z F x y z F x y z λμλμλμλμ'=++=⎧⎪'=++=⎪⎪'=-+=⎨⎪'=+-=⎪'=++-=⎪⎩解方程组得111222(,,)(1,1,2),(,,)(2,2,8)x y z x y z ==-- 故所求的最大值为72，最小值为6.方法二：问题可转化为求2242242u x y x x y y =++++在224x y x y +++=条件下的最值设44222222(,,)2(4)F x y u x y x y x y x y x y λλ==++++++++-令 323222442(12)0442(12)040x y F x xy x x F y x y y y F x y x y λλλ'⎧=++++=⎪'=++++=⎨⎪'=+++-=⎩解得1122(,)(1,1),(,)(2,2)x y x y ==--，代入22z x y =+，得122,8z z == 故所求的最大值为72，最小值为6. 本题的难度值为0.486. (22)【详解】(I)证法一：2222122212132101221221122a a a a a a a a a A r ar aaa a =-=O O L OO O OO O OO OO121301240134(1)2(1)3231(1)0n n n a a an a a n a r ar a n a nnn a n--+-=⋅⋅⋅=++O K O OO OO证法二：记||n D A =，下面用数学归纳法证明(1)nn D n a =+．当1n =时，12D a =，结论成立．当2n =时，2222132a D a a a==，结论成立．假设结论对小于n 的情况成立．将n D 按第1行展开得2212102121212n n a a a a D aD a a-=-OO O OO21221222(1)(1)n n n n n aD a D ana a n a n a ---- =-=--=+故 ||(1)nA n a =+证法三：记||n D A =，将其按第一列展开得 2122n n n D aD a D --=-，所以 211212()n n n n n n D aD aD a D a D aD ------=-=-222321()()n n n n a D aD a D aD a ---=-==-=L即 12122()2n n n n n n n n D a aD a a a aD a a D ----=+=++=++2121(2)(1)n n n n n a a D n a a D --==-+=-+L1(1)2(1)n n n n a a a n a -=-+⋅=+(II)因为方程组有唯一解，所以由Ax B =知0A ≠，又(1)nA n a =+，故0a ≠．由克莱姆法则，将n D 的第1列换成b ，得行列式为2221122(1)(1)112102*********n n n nn n a a a aa a a a D na a a a a --⨯-⨯-===O O OO O OO O OO OO所以 11(1)n n D nx D n a-==+ (III)方程组有无穷多解，由0A =，有0a =，则方程组为12101101001000n n x x x x -⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭M O O M此时方程组系数矩阵的秩和增广矩阵的秩均为1n -，所以方程组有无穷多解，其通解为()()10000100,TTk k +L L为任意常数．本题的难度值为0.270.(23)【详解】(I)证法一：假设123,,ααα线性相关．因为12,αα分别属于不同特征值的特征向量，故12,αα线性无关，则3α可由12,αα线性表出，不妨设31122l l ααα=+，其中12,l l 不全为零(若12,l l 同时为0，则3α为0，由323A ααα=+可知20α=，而特征向量都是非0向量，矛盾)Q 11,A αα=-22A αα=∴32321122A l l αααααα=+=++，又311221122()A A l l l l ααααα=+=-+ ∴112221122l l l l ααααα-+=++，整理得：11220l αα+=则12,αα线性相关，矛盾. 所以，123,,ααα线性无关.证法二：设存在数123,,k k k ，使得1122330k k k ααα++= (1)用A 左乘(1)的两边并由11,A αα=-22A αα=得1123233()0k k k k ααα-+++= (2)(1)—(2)得 113220k k αα-= (3) 因为12,αα是A 的属于不同特征值的特征向量，所以12,αα线性无关，从而130k k ==，代入(1)得220k α=，又由于20α≠，所以20k =，故123,,ααα线性无关.(II) 记123(,,)P ααα=，则P 可逆，123123(,,)(,,)AP A A A A αααααα==1223(,,)αααα=-+123100(,,)011001ααα-⎛⎫ ⎪= ⎪ ⎪⎝⎭100011001P -⎛⎫ ⎪= ⎪ ⎪⎝⎭所以 1100011001P AP --⎛⎫ ⎪= ⎪ ⎪⎝⎭.本题的难度值为0.272.。

2017考研数学二真题及答案

2017考研数学二真题及答案一、选择题（本题共8小题，每小题4分，满分32分）（1）若函数⎪⎩⎪⎨⎧≤>-=0,,0,cos 1)(x b x axxx f 在0=x 处连续，则（） )(A 21=ab 。

)(B 21-=ab 。

)(C 0=ab 。

D (2=ab 。

【答案】)(A【解】aax x f x 21cos 1lim)00(0=-=++→，b f f =-=)00()0(，因为)(x f 在0=x 处连续，所以)00()0()00(-==+f f f ，从而21=ab ，应选)(A 。

（2）设二阶可导函数)(x f 满足1)1()1(=-=f f ，1)0(-=f ，且0)(>''x f ，则（）)(A ⎰->110)(x f 。

)(B ⎰-<110)(x f 。

)(C ⎰⎰->101)()(dx x f x f 。

)(D ⎰⎰-<11)()(dx x f x f 。

【答案】)(B【解】取12)(2-=x x f ，显然⎰-<110)(x f ，应选)(B 。

（3）设数列}{n x 收敛，则（）)(A 当0sin lim =∞→n n x 时，0lim =∞→n n x 。

)(B 当0)||(lim =+∞→n n n x x 时，0lim =∞→n n x 。

)(C 当0)(lim 2=+∞→nn n x x 时，0lim =∞→n n x 。

)(D 当0)sin (lim =+∞→n n n x x 时，0lim =∞→n n x 。

【答案】)(D【解】令A x n n =∞→lim ，由0sin )sin (lim =+=+∞→A A x x n n n 得0=A 。

（4）微分方程)2cos 1(842x e y y y x+=+'-''的特解可设为=*y （）)(A )2sin 2cos (22x C x B e Ae x x ++。

历年数学2考研试题及答案

历年数学2考研试题及答案试题：一、选择题（每题3分，共30分）1. 下列哪个选项是最小的正整数？A. -2B. 0C. 1D. 22. 如果函数 \( f(x) = ax^2 + bx + c \) 在 \( x = 1 \) 处取得极值，那么 \( b \) 的值应该是：A. \( a + c \)B. \( -a + c \)C. \( -2a \)D. \( 0 \)3. 已知 \( \sin(\alpha + \beta) = \frac{3}{5} \)，\( \cos(\alpha + \beta) = -\frac{4}{5} \)，且 \( \alpha < \alpha + \beta < \pi \)，那么 \( \sin\alpha \) 的值是：A. \( \frac{4}{5} \)B. \( -\frac{3}{5} \)C. \( \frac{3}{5} \)D. \( -\frac{4}{5} \)4. 极限 \( \lim_{x \to 0} \frac{\sin x}{x} \) 的值是：A. 0B. 1C. \( \frac{\pi}{2} \)D. \( \infty \)5. 以下哪个序列是发散的？A. \( \{ \frac{1}{n} \} \)B. \( \{ (-1)^n \} \)C. \( \{ \frac{1}{1+n^2} \} \)D. \( \{ \sqrt{n} \} \)6. 设 \( A \) 是 \( m \) 行 \( n \) 列的矩阵，\( B \) 是 \( n \) 行 \( p \) 列的矩阵，那么 \( AB \) 的维度是：A. \( m \times n \)B. \( m \times p \)C. \( n \times p \)D. \( p \times n \)7. 以下哪个选项不是有理数？A. \( \sqrt{2} \)B. \( \frac{3}{4} \)C. \( \pi \)D. \( -\frac{2}{3} \)8. 已知 \( e^x = 1 \)，则 \( x \) 的值是：A. 0B. 1C. -1D. \( \ln 1 \)9. 以下哪个函数在区间 \( (0, +\infty) \) 上是增函数？A. \( f(x) = \frac{1}{x} \)B. \( f(x) = x^2 \)C. \( f(x) = \ln x \)D. \( f(x) = \cos x \)10. 以下哪个级数是收敛的？A. \( \sum_{n=1}^{\infty} \frac{1}{n^2} \)B. \( \sum_{n=1}^{\infty} \frac{1}{n} \)C. \( \sum_{n=1}^{\infty} (-1)^n \frac{1}{n} \)D. \( \sum_{n=1}^{\infty} n \)答案：一、选择题1. C2. D3. A4. B5. B6. B7. A8. C9. C10. A。

2017考研数学二真题及答案

一、选择题（每小题4分，共32分）（1）若函数21cos ,0(),0xx f x axb x ⎧->⎪=⎨⎪≤⎩在0x =处连续，则（）。

A. 12ab = B. 12ab =-C. 0ab =D. 2ab = 【答案】A【解析】由连续的定义可知：-0lim ()lim ()(0),x x f x f x f +→→==其中-0(0)lim ()x f f x b →==，2000112lim ()lim lim 2x x x f x ax a+++→→→===，从而12b a =，也即12ab =，故选A. 【试题点评】本题考查函数的连续性。

此知识点在冲刺阶段的数学冲刺串讲班中第一部分高等数学有重点讲解，在强化阶段数学强化班高等数学第一章函数、极限、连续和强化阶段数学重点题型精讲班也均有涉及。

（2）设二阶可导函数()f x 满足(1)(1)1,(0)1f f f =-==-，且''()0f x >，则（）。

A. 11()0f x dx ->⎰ B. 12()0f x dx -<⎰ C. 0110()()f x dx f x dx ->⎰⎰D.11()()f x dx f x dx -<⎰⎰【答案】B【解析】由于'()0f x ＜，可知其中()f x 的图像在其任意两点连线的曲线下方，也即()(0)[(1)(0)]21f x f f f x x ≤+-=-，(0,1)x ∈，因此11()(21)=0f x dx f x dx -⎰⎰＜，同理()(0)[(0)(1)]21(1,0)f x f f f x x x ≤+--=--∈-，，因此 0111()(21)=0f x dx f x dx ----⎰⎰＜，从而11()0f x dx -⎰＜，故选B.【试题点评】本题考查二阶导数与拐点的关系。

此知识点在冲刺阶段的数学冲刺串讲班中第一部分高等数学有重点讲解，在强化阶段数学强化班高等数学第二章导数与微分和强化阶段数学重点题型精讲班也均有涉及。

考研数学(二)历年真题详解【圣才出品】

2．如图 1 所示，曲线方程为 y＝f（x），函数在区间[0，a]上有连续导数，则定积分
a xf ( x)dx 在几何上表示（）。 0
1 / 287
圣才电子书十万种考研考证电子书、题库视频学习平台

图1
A．曲边梯形 ABOD 面积
B．梯形 ABOD 的面积
C．曲边三角形 ACD 面积
9．已知函数 f（x）连续，且
lim
x0
1 cos[xf (ex 1) f
4 / 287
圣才电子书十万种考研考证电子书、题库视频学习平台

6．设函数 f（x）连续，
F (u, v) f (x2 y2 )dxdy
Duv x2 y 2
其中区域 Duv 如图 2 阴影部分所示，则∂F/∂u＝（）。 A．vf（u2） B．vf（u） C．vf（u2）/u D．vf（u）/u
1
所以∂F/∂u＝vf（u2）。
7．设 A 为 n 阶非零矩阵，E 为 n 阶单位矩阵。若 A3＝O，则下列结论正确的是（）。 A．E－A 不可逆，则 E＋A 不可逆 B．E－A 不可逆，则 E＋A 可逆 C．E－A 可逆，则 E＋A 可逆 D．E－A 可逆，则 E＋A 不可逆【答案】C 【考点】可逆的定义【解析】（E－A）（E＋A＋A2）＝E－A3＝E，（E＋A）（E－A＋A2）＝E＋A3＝E。故 E －A，E＋A 均可逆。
8．设
A
1 2
2
1
则在实数域上，与 A 合同的矩阵为（）。
2 1
A．
1
2
2 1
B．
1
2
6 / 287
圣才电子书

2 1
C．
1

2008考研数二真题及解析

2008年全国硕士研究生入学统一考试数学二试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.(1) 设2()(1)(2)f x x x x =--，求()f x '的零点个数( )()A 0()B 1 ()C 2()D 3(2) 如图，曲线段方程为()y f x =，函数在区间[0,]a 上有连续导数，则定积分()axf x dx '⎰等于( )()A 曲边梯形ABOD 面积.()B 梯形ABOD 面积. ()C 曲边三角形ACD 面积.()D 三角形ACD 面积.(3) 在下列微分方程中，以123cos 2sin 2xy C e C x C x =++(123,,C C C 为任意常数)为通解的是( )()A 440y y y y ''''''+--=. ()B 440y y y y ''''''+++=. ()C 440y y y y ''''''--+=.()D 440y y y y ''''''-+-=.(4) 判断函数ln ()sin (0)1xf x x x x =>-间断点的情况( ) ()A 有1个可去间断点，1个跳跃间断点 ()B 有1个跳跃间断点，1个无穷间断点 ()C 有两个无穷间断点yC (0, f (a )) A (a , f (a ))y =f (x )O B (a ,0) xD()D 有两个跳跃间断点(5) 设函数()f x 在(,)-∞+∞内单调有界，{}n x 为数列，下列命题正确的是( )()A 若{}n x 收敛，则{}()n f x 收敛. ()B 若{}n x 单调，则{}()n f x 收敛. ()C 若{}()n f x 收敛，则{}n x 收敛.()D 若{}()n f x 单调，则{}n x 收敛.(6) 设函数f 连续. 若()2222,uvD f x y F u v dxdy x y+=+⎰⎰，其中区域uv D 为图中阴影部分，则Fu∂=∂( ) ()A ()2vf u()B ()2vf u u()C ()vf u()D ()vf u u(7) 设A 为n 阶非零矩阵，E 为n 阶单位矩阵. 若3A O =，则( )()A E A -不可逆，E A +不可逆.()B E A -不可逆，E A +可逆. ()C E A -可逆，E A +可逆.()D E A -可逆，E A +不可逆.(8) 设1221A ⎛⎫= ⎪⎝⎭，则在实数域上与A 合同的矩阵为( )()A 2112-⎛⎫⎪-⎝⎭.()B 2112-⎛⎫⎪-⎝⎭.()C 2112⎛⎫ ⎪⎝⎭.()D 1221-⎛⎫⎪-⎝⎭.二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. (9) ()f x 连续，21cos(sin )lim1(1)()x x x e f x →-=-，则(0)f =O xvx 2+y 2=u 2 x 2+y 2=1 D uvy(10) 微分方程2()0xy x e dx xdy -+-=的通解是y = (11) 曲线()()sin ln xy y x x +-=在点()0,1处的切线方程为 . (12) 求函数23()(5)f x x x =-的拐点______________. (13) 已知xyy z x ⎛⎫=⎪⎝⎭，则(1,2)_______z x ∂=∂. (14) 矩阵A 的特征值是,2,3λ，其中λ未知，且248A =-，则λ=_______.三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求极限()40sin sin sin sin lim x x x x x →-⎡⎤⎣⎦.(16) (本题满分10分)设函数()y y x =由参数方程20()ln(1)t x x t y u du =⎧⎪⎨=+⎪⎩⎰确定，其中()x t 是初值问题 020|0xt dx te dtx -=⎧-=⎪⎨⎪=⎩的解. 求22d y dx .(17)(本题满分9分)计算2121dx x-⎰(18)(本题满分11分)计算{}max ,1,Dxy dxdy ⎰⎰其中{(,)02,02}D x y x y =≤≤≤≤(19)(本题满分11分)设()f x 是区间[0,)+∞上具有连续导数的单调增加函数，且(0)1f =. 对于任意的[0,)t ∈+∞，直线0,x x t ==，曲线()y f x =以及x 轴所围成曲边梯形绕x 轴旋转一周生成一旋转体. 若该旋转体的侧面面积在数值上等于其体积的2倍，求函数()f x 的表达式.(20)(本题满分11分)(I) 证明积分中值定理：若函数()f x 在闭区间[,]a b 上连续，则至少存在一点[,]a b η∈，使得()()()baf x dx f b a η=-⎰；(II) 若函数()x ϕ具有二阶导数，且满足，32(2)(1),(2)()x dx ϕϕϕϕ>>⎰，则至少存在一点(1,3)ξ∈，()0ϕξ''<使得.(21)(本题满分11分)求函数222u x y z =++在约束条件22z x y =+和4x y z ++=下的最大和最小值.(22)(本题满分12分)设n 元线性方程组Ax b =，其中2221212n n a a a A a a ⨯⎛⎫ ⎪⎪= ⎪⎪⎝⎭，12n x x x x ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭，100b ⎛⎫⎪⎪= ⎪ ⎪⎝⎭(I) 证明行列式()1nA n a =+(II) 当a 为何值时，该方程组有唯一解，并求1x (III) 当a 为何值时，该方程组有无穷多解，并求通解(23)(本题满分10分)设A 为3阶矩阵，12,αα为A 的分别属于特征值1,1-的特征向量，向量3α满足323A ααα=+，(I) 证明123,,ααα线性无关； (II) 令()123,,P ααα=，求1P AP -2008年全国硕士研究生入学统一考试数学二试题解析一、选择题 (1)【答案】D【详解】因为(0)(1)(2)0f f f ===，由罗尔定理知至少有1(0,1)ξ∈，2(1,2)ξ∈使12()()0f f ξξ''==，所以()f x '至少有两个零点. 由于()f x '是三次多项式，三次方程()0f x '=的实根不是三个就是一个，故D 正确.(2)【答案】C 【详解】00()()()()()()aa a aaxf x dx xdf x xf x f x dx af a f x dx '==-=-⎰⎰⎰⎰其中()af a 是矩形ABOC 面积，0()af x dx ⎰为曲边梯形ABOD 的面积，所以0()axf x dx '⎰为曲边三角形的面积．(3)【答案】D【详解】由微分方程的通解中含有xe 、cos2x 、sin 2x 知齐次线性方程所对应的特征方程有根1,2r r i ==±，所以特征方程为(1)(2)(2)0r r i r i --+=，即32440r r r -+-=. 故以已知函数为通解的微分方程是440y y y ''''''-+-=(4) 【答案】A【详解】0,1x x ==时()f x 无定义，故0,1x x ==是函数的间断点因为 000ln 11lim ()lim lim lim csc |1|csc cot x x x x x xf x x x x x++++→→→→=⋅=-- 200sin lim lim 0cos cos x x x xx x x++→→=-=-=同理 0lim ()0x f x -→= 又 1111ln 1lim ()lim lim sin lim sin1sin11x x x x x f x x x x ++++→→→→⎛⎫=⋅== ⎪-⎝⎭ 111ln lim ()lim lim sin sin11x x x xf x x x--+→→→=⋅=--所以 0x =是可去间断点，1x =是跳跃间断点.(5)【答案】B【详解】因为()f x 在(,)-∞+∞内单调有界，且{}n x 单调. 所以{()}n f x 单调且有界. 故{()}n f x 一定存在极限.(6)【答案】A【详解】用极坐标得 ()222()22211,()vu uf r r Df u v F u v dudv dv rdr v f r dr u v +===+⎰⎰⎰所以()2Fvf u u∂=∂(7) 【答案】C【详解】23()()E A E A A E A E -++=-=，23()()E A E A A E A E +-+=+= 故,E A E A -+均可逆．(8) 【答案】D【详解】记1221D -⎛⎫= ⎪-⎝⎭，则()2121421E D λλλλ--==---，又()2121421E A λλλλ---==----所以A 和D 有相同的特征多项式，所以A 和D 有相同的特征值.又A 和D 为同阶实对称矩阵，所以A 和D 相似．由于实对称矩阵相似必合同，故D 正确.二、填空题 (9)【答案】2【详解】222220001cos[()]2sin [()2]2sin [()2]()lim lim lim ()[()2]4(1)()x x x x xf x xf x xf x f x x f x xf x e f x →→→-⋅==⋅- 011lim ()(0)122x f x f →=== 所以 (0)2f =(10)【答案】()xx eC --+【详解】微分方程()20x y x e dx xdy -+-=可变形为x dy yxe dx x--= 所以 111()dx dx x x x x xy e xe e dx C x xe dx C x e C x ----⎡⎤⎛⎫⎰⎰=+=⋅+=-+⎢⎥ ⎪⎝⎭⎣⎦⎰⎰(11)【答案】1y x =+【详解】设(,)sin()ln()F x y xy y x x =+--，则1cos()11cos()x y y xy F dy y xdx F x xy y x--'-=-=-'+-，将(0)1y =代入得01x dy dx==，所以切线方程为10y x -=-，即1y x =+(12)【答案】(1,6)-- 【详解】53235y xx =-⇒2311351010(2)333x y x x x -+'=-= ⇒134343101010(1)999x y x x x--+''=+= 1x =-时，0y ''=；0x =时，y ''不存在在1x =-左右近旁y ''异号，在0x =左右近旁0y ''>，且(1)6y -=- 故曲线的拐点为(1,6)--(13)【答案】2(ln 21)2- 【详解】设,y xu v x y==，则v z u = 所以121()ln v v z z u z v y vu u u x u x v x x y-∂∂∂∂∂=⋅+⋅=-+⋅∂∂∂∂∂ 2ln 11ln x yv vy u y y u ux y x y x ⎛⎫⎛⎫⎛⎫=-+=⋅-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭所以(1,2)2(ln 21)2z x ∂=-∂(14)【答案】-1【详解】||236A λλ =⨯⨯= 3|2|2||A A =32648λ∴⨯=- 1λ⇒=-三、解答题 (15)【详解】方法一：4300[sin sin(sin )]sin sin sin(sin )limlim x x x x x x x x x→→--= 22220001sin cos cos(sin )cos 1cos(sin )12lim lim lim 3336x x x xx x x x x x x →→→--==== 方法二：331sin ()6x x x o x =-+ 331sin(sin )sin sin (sin )6x x x o x =-+4444400[sin sin(sin )]sin sin (sin )1lim lim 66x x x x xx o x x x x →→⎡⎤-∴ =+=⎢⎥⎣⎦(16)【详解】方法一：由20x dx te dt--=得2x e dx tdt =，积分并由条件0t x =得21x e t =+，即2ln(1)x t =+ 所以 2222ln(1)2(1)ln(1)21dydy t tdt t t dxt dx dt t +⋅===+++222222[(1)ln(1)]2ln(1)221dt t d y d dy t t tdt dx t dx dx dx dt t ++++⎛⎫=== ⎪⎝⎭+ 22(1)[ln(1)1]t t =+++方法二：由20x dx te dt--=得2x e dx tdt =，积分并由条件0t x =得21x e t =+，即2ln(1)x t =+ 所以 2222ln(1)2(1)ln(1)21x dydy t tdt t t e x dxt dx dt t +⋅===++=+所以 22(1)x d ye x dx=+(17)【详解】方法一：由于2211x x-→=+∞-，故2121dx x-⎰是反常积分.令arcsin x t =，有sin x t =，[0,2)t π∈221222220000sin cos 2cos sin ()cos 221t t t t t dx tdt t tdt dt t xπππ===--⎰⎰⎰⎰2222220001sin 21sin 2sin 2441644tt t td t tdt πππππ=-=-+⎰⎰ 222011cos 2168164t πππ=-=+ 方法二：2121dx x -⎰12201(arcsin )2x d x =⎰ 121122220001(arcsin )(arcsin )(arcsin )28x x x x dx x x dx π=-=-⎰⎰令arcsin x t =，有sin x t =，[0,2)t π∈12222200011(arcsin )sin 2cos 224x x dx t tdt t d t ππ==-⎰⎰⎰ 222200111(cos 2)cos 242164t t t tdt πππ=-+=-⎰故，原式21164π=+(18)【详解】曲线1xy =将区域分成两个区域1D 和23D D +，为了便于计算继续对区域分割，最后为()max ,1Dxy dxdy ⎰⎰D 1123D D D xydxdy dxdy dxdy =++⎰⎰⎰⎰⎰⎰112222211102211x xdx dy dx dy dx xydy =++⎰⎰⎰⎰⎰⎰1512ln 2ln 24=++-19ln 24=+(19)【详解】旋转体的体积20()tV f x dx π=⎰，侧面积202()1()tS f x f x dx π'=+⎰，由题设条件知220()()1()ttf x dx f x f x dx '=+⎰⎰上式两端对t 求导得 22()()1()f t f t f t '=+ 即 21y y '=-由分离变量法解得 21ln(1)y y t C -=+，即 21t y y Ce -=将(0)1y =代入知1C =，故21t y y e -=，1()2t t y e e -=+于是所求函数为 1()()2t t y f x e e -==+(20)【详解】(I) 设M 与m 是连续函数()f x 在[,]a b 上的最大值与最小值，即()m f x M ≤≤ [,]x a b ∈由定积分性质，有 ()()()bam b a f x dx M b a -≤≤-⎰，即 ()baf x dx m M b a≤≤-⎰由连续函数介值定理，至少存在一点[,]a b η∈，使得 ()()b af x dx f b aη=-⎰即()()()baf x dx f b a η=-⎰(II) 由(I)的结论可知至少存在一点[2,3]η∈，使 32()()(32)()x dx ϕϕηϕη=-=⎰又由 32(2)()()x dx ϕϕϕη>=⎰，知 23η<≤对()x ϕ在[1,2][2,]η上分别应用拉格朗日中值定理，并注意到(1)(2)ϕϕ<，()(2)ϕηϕ<得 1(2)(1)()021ϕϕϕξ-'=>- 112ξ<<2()(2)()02ϕηϕϕξη-'=<- 123ξη<<≤在12[,]ξξ上对导函数()x ϕ'应用拉格朗日中值定理，有2121()()()0ϕξϕξϕξξξ''-''=<- 12(,)(1,3)ξξξ∈⊂(21)【详解】方法一：作拉格朗日函数22222(,,,,)()(4)F x y z x y z x y z x y z λμλμ=++++-+++-令 2222022020040x y z F x x F y y F z F x y z F x y z λμλμλμλμ'=++=⎧⎪'=++=⎪⎪'=-+=⎨⎪'=+-=⎪'=++-=⎪⎩解方程组得111222(,,)(1,1,2),(,,)(2,2,8)x y z x y z ==-- 故所求的最大值为72，最小值为6.方法二：问题可转化为求2242242u x y x x y y =++++在224x y x y +++=条件下的最值设44222222(,,)2(4)F x y u x y x y x y x y x y λλ==++++++++-令 323222442(12)0442(12)040x y F x xy x x F y x y y y F x y x y λλλ'⎧=++++=⎪'=++++=⎨⎪'=+++-=⎩解得1122(,)(1,1),(,)(2,2)x y x y ==--，代入22z x y =+，得122,8z z == 故所求的最大值为72，最小值为6.(22)【详解】(I)证法一：2222122212132101221221122a a a a a a aa aA r ar aaa a =-=121301240134(1)2(1)3231(1)0n n n a a a n a a n ar ar a n a nnn a n--+-=⋅⋅⋅=++ 证法二：记||n D A =，下面用数学归纳法证明(1)nn D n a =+．当1n =时，12D a =，结论成立．当2n =时，2222132a D a aa==，结论成立．假设结论对小于n 的情况成立．将n D 按第1行展开得2212102121212n n a a a aD aD a a-=-21221222(1)(1)n n n n n aD a D ana a n a n a ---- =-=--=+故 ||(1)nA n a =+证法三：记||n D A =，将其按第一列展开得 2122n n n D aD a D --=-，所以 211212()n n n n n n D aD aD a D a D aD ------=-=-222321()()n n n n a D aD a D aD a ---=-==-=即 12122()2n n n n n n n n D a aD a a a aD a a D ----=+=++=++2121(2)(1)n n n n n a a D n a a D --==-+=-+1(1)2(1)n n n n a a a n a -=-+⋅=+(II)因为方程组有唯一解，所以由Ax B =知0A ≠，又(1)n A n a =+，故0a ≠．由克莱姆法则，将n D 的第1列换成b ，得行列式为2221122(1)(1)112102*********n n n nn n a a a aa aa aD na a a a a --⨯-⨯-===所以 11(1)n n D nx D n a-==+ (III)方程组有无穷多解，由0A =，有0a =，则方程组为12101101001000n n x x x x -⎛⎫⎛⎫⎛⎫⎪⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 此时方程组系数矩阵的秩和增广矩阵的秩均为1n -，所以方程组有无穷多解，其通解为()()10000100,TTk k +为任意常数．(23)【详解】(I)证法一：假设123,,ααα线性相关．因为12,αα分别属于不同特征值的特征向量，故12,αα线性无关，则3α可由12,αα线性表出，不妨设31122l l ααα=+，其中12,l l 不全为零(若12,l l 同时为0，则3α为0，由323A ααα=+可知20α=，而特征向量都是非0向量，矛盾)11,A αα=-22A αα=∴32321122A l l αααααα=+=++，又311221122()A A l l l l ααααα=+=-+ ∴112221122l l l l ααααα-+=++，整理得：11220l αα+=则12,αα线性相关，矛盾. 所以，123,,ααα线性无关.证法二：设存在数123,,k k k ，使得1122330k k k ααα++= (1)用A 左乘(1)的两边并由11,A αα=-22A αα=得1123233()0k k k k ααα-+++= (2)(1)—(2)得 113220k k αα-= (3) 因为12,αα是A 的属于不同特征值的特征向量，所以12,αα线性无关，从而130k k ==，代入(1)得220k α=，又由于20α≠，所以20k =，故123,,ααα线性无关.(II) 记123(,,)P ααα=，则P 可逆，123123(,,)(,,)AP A A A A αααααα==1223(,,)αααα=-+123100(,,)011001ααα-⎛⎫ ⎪= ⎪ ⎪⎝⎭100011001P -⎛⎫ ⎪= ⎪ ⎪⎝⎭所以 1100011001P AP --⎛⎫ ⎪= ⎪ ⎪⎝⎭.。

考研数学二真题及解析

2017年全国硕士研究生入学统一考试数学二试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸．．．指定位置上. （1））若函数1,0(),0x f x axb x ⎧->⎪=⎨⎪≤⎩在0x =处连续，则（） (A)12ab =(B)12ab =-(C)0ab = (D)2ab =【答案】A【解析】001112lim lim ,()2x x xf x ax ax a++→→-==在0x =处连续11.22b ab a ∴=⇒=选A. （2）设二阶可导函数()f x 满足(1)(1)1,(0)1f f f =-==-且''()0f x >，则（）【答案】B【解析】()f x 为偶函数时满足题设条件，此时011()()f x dx f x dx -=⎰⎰，排除C,D.取2()21f x x =-满足条件，则()112112()2103f x dx x dx --=-=-<⎰⎰，选B. （3）设数列{}n x 收敛，则（）()A 当limsin 0n n x →∞=时，lim 0n n x →∞=()B当lim(0n n x →∞=时，lim 0n n x →∞=()C 当2lim()0n n n x x →∞+=时，lim 0n n x →∞=()D 当lim(sin )0n n n x x →∞+=时，lim 0n n x →∞=【答案】D【解析】特值法：（A ）取n x π=，有limsin 0,lim n n n n x x π→∞→∞==，A 错；取1n x =-，排除B,C.所以选D. （4）微分方程的特解可设为（A ）22(cos 2sin 2)x x Ae e B x C x ++（B ）22(cos 2sin 2)x x Axe e B x C x ++ （C ）22(cos 2sin 2)x x Ae xe B x C x ++（D ）22(cos 2sin 2)x x Axe e B x C x ++ 【答案】A【解析】特征方程为：21,248022i λλλ-+=⇒=± 故特解为：***2212(cos 2sin 2),x x y y y Ae xe B x C x =+=++选C.（5）设(,)f x y 具有一阶偏导数，且对任意的(,)x y ，都有(,)(,)0,0f x y f x y x y∂∂>>∂∂，则（A ）(0,0)(1,1)f f >（B ）(0,0)(1,1)f f <（C ）(0,1)(1,0)f f >（D ）(0,1)(1,0)f f < 【答案】C 【解析】(,)(,)0,0,(,)f x y f x y f x y x y∂∂><⇒∂∂是关于x 的单调递增函数，是关于y 的单调递减函数，所以有(0,1)(1,1)(1,0)f f f <<，故答案选D.（6）甲乙两人赛跑，计时开始时，甲在乙前方10（单位：m ）处，图中实线表示甲的速度曲线1()v v t =（单位：/m s ），虚线表示乙的速度曲线2()v v t =，三块阴影部分面积的数值依次为10,20,3，计时开始后乙追上甲的时刻记为0t （单位：s ），则（）（A ）010t =（B ）01520t <<（C ）025t =（D ）025t >【答案】B【解析】从0到0t 这段时间内甲乙的位移分别为0120(t),(t),t t v dt v dt ⎰⎰则乙要追上甲，则210(t)v (t)10t v dt -=⎰，当025t =时满足，故选C.（7）设A 为三阶矩阵，123(,,)P ααα=为可逆矩阵，使得1012P AP -⎛⎫⎪= ⎪ ⎪⎝⎭，则123(,,)A ααα=（）（A ）12αα+（B ）232αα+（C ）23αα+（D ）122αα+ 【答案】B【解析】11231232300011(,,)(,,)12222P AP AP P A αααααααα-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=⇒=⇒==+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,因此B 正确。

2008考研数二真题

2008考研数二真题2008年的考研数学二真题是考研数学考试中的一道经典题目。

这道题目涉及到概率论和统计学的知识，考察了考生对于概率分布、随机变量和样本调查等方面的理解和应用能力。

本文将对这道题目进行分析和解答，并探讨其中涉及的一些数学概念和方法。

首先，让我们来看一下这道题目的具体内容。

题目要求我们考虑一个随机变量X，它的概率密度函数为f(x) = 2x (0<x<1)，否则为0。

同时，给出了一个样本调查的结果，样本量为n，其中有k个样本的取值大于0.5。

我们需要根据这些信息回答几个问题。

首先，我们来计算X的分布函数F(x)。

根据概率密度函数的定义，我们可以得到F(x) = ∫[0,x] 2t dt = x^2 (0<x<1)，否则为0。

这里，我们利用了定积分的性质，将概率密度函数积分得到分布函数。

接下来，我们需要计算P(X>0.5)。

根据分布函数的定义，我们可以得到P(X>0.5) = 1 - P(X≤0.5) = 1 - F(0.5) = 1 - (0.5)^2 = 0.75。

这里，我们利用了分布函数的性质，将概率转化为1减去另一个概率的形式。

然后，我们需要计算样本调查中k个样本的取值大于0.5的概率。

根据题目给出的信息，我们可以知道每个样本的取值大于0.5的概率为P(X>0.5) = 0.75。

由于样本之间是独立同分布的，所以k个样本的取值大于0.5的概率可以表示为P(X>0.5)^k = 0.75^k。

接下来，我们需要计算样本调查中至少有一个样本的取值大于0.5的概率。

根据概率的加法法则，我们可以得到至少有一个样本的取值大于0.5的概率为1减去所有样本的取值都小于等于0.5的概率。

根据样本的独立性，我们可以得到所有样本的取值都小于等于0.5的概率为P(X≤0.5)^n = (1 - P(X>0.5))^n = (1 - 0.75)^n = 0.25^n。

2008年全国硕士研究生入学统一考试数学二试题及答案详解

2008年全国硕士研究生入学统一考试数学二试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内. (1)设2()(1)(2)f x x x x =--，求()f x '的零点个数（）()A 0()B 1 ()C 2()D 3解：()D分析：()()()()()()22221212494f x x x x x x x x x x x '=--+-+-=-+令()0f x '=，则可得()f x '零点的个数为3.（2）曲线方程为()y f x =函数在区间[0,]a 上有连续导数，则定积分'()axf x dx ⎰（）()A 曲边梯形ABCD 面积.()B 梯形ABCD 面积.()C 曲边三角形ACD 面积.()D 三角形ACD 面积.解：()C分析：0()()()()aaaxf x dx xdf x af a f x dx '==-⎰⎰⎰，其中()af a 是矩形面积，0()af x dx⎰为曲边梯形的面积，所以()axf x dx '⎰为曲边三角形的面积。

（3）在下列微分方程中，以123cos2sin 2x y C e C x C x =++（123,,C C C 为任意常数）为通解的是（）()A 440y y y y ''''''+--=.()B 440y y y y ''''''+++=. ()C 440y y y y ''''''--+=.()D 440y y y y ''''''-+-=.解：()D .分析；由123cos2sin 2x y C e C x C x =++可知其特征根为12,31,2i λλ==±.故对应的特征方程为 2(1)(2)(2)(1)(4)i i λλλλλ-+-=-+，即32440λλλ-+-=所以所求微分方程为440y y y y ''''''-+-=, 选()D . （4）判断函数ln ()sin (0)1xf x x x x =>-间断点的情况( )()A 有1个可去间断点，1个跳跃间断点 ()B 有1个跳跃间断点，1个无穷间断点 ()C 有两个无穷间断点 ()D 有两个跳跃间断点解：()A分析：()f x 的间断点为1,0x =，而0lim ()0x f x →+=，故0x =是可去间断点；1lim ()sin1x f x →+=，1lim ()sin1x f x →+=-，故1x =是跳跃间断点故选()A 。

2017考研数学二真题及答案

一、选择题（每小题4分，共32分）（1）若函数21cos ,0(),0xx f x axb x ⎧->⎪=⎨⎪≤⎩在0x =处连续，则（）。

（2）设二阶可导函数()f x 满足(1)(1)1,(0)1f f f =-==-，且''()0f x >，则（）。

2017数学二考研真题

2017数学二考研真题2017年数学二考研真题是考研数学二科目中的一道经典题目，涉及到概率与统计、线性代数、高等数学等多个数学领域的知识点。

本文将从不同角度对该题进行解析和讨论。

首先，我们来看一下这道题的具体内容：已知某公司员工的薪资服从正态分布，平均薪资为5000元，标准差为1000元。

现从该公司随机抽取10名员工，求这10名员工的平均薪资不超过5500元的概率。

从概率与统计的角度来看，我们可以利用正态分布的性质来解答这道题。

根据中心极限定理，当样本量足够大时，样本均值的分布将近似服从正态分布。

而题目中已知员工薪资服从正态分布，因此我们可以利用正态分布的性质来求解。

根据题目中给出的信息，我们可以计算出每个员工的平均薪资的标准差为1000/√10≈316.23元。

接下来，我们需要计算出标准正态分布中平均薪资不超过5500元的概率。

我们可以通过查表或使用计算机软件来得到这个概率值，假设为P(Z≤(5500-5000)/316.23)。

接下来，我们需要计算出10名员工的平均薪资不超过5500元的概率。

根据中心极限定理的推论，样本均值的标准差等于总体标准差除以样本量的平方根。

因此，我们可以计算出10名员工的平均薪资的标准差为316.23/√10≈99.79元。

然后，我们可以计算出10名员工的平均薪资不超过5500元的概率，假设为P(Z≤(5500-5000)/99.79)。

通过计算，我们可以得到10名员工的平均薪资不超过5500元的概率为P(Z≤0.501)≈0.6915。

这意味着从该公司随机抽取10名员工，其平均薪资不超过5500元的概率约为69.15%。

从线性代数的角度来看，我们可以将这道题转化为矩阵运算的问题。

假设该公司的员工薪资向量为X=[X1, X2, ..., Xn]，其中Xi表示第i名员工的薪资。

根据题目中给出的信息，我们可以知道X服从均值为μ=5000，协方差矩阵为Σ=1000^2的多元正态分布。

考研数学历年真题(2008-2017)年数学二

2017年考研(数学二)真题试卷(题后含答案及解析)

考研数学二真题(2008年)

2008年全国硕士研究生入学统一考试数学二真题及答案

考研数二历年真题答案

2008年数学二 考研数学真题及解析

2008年考研数学二试题答案与解析

2017年考研数学二真题与解析

2008考研数学二真题及答案

2017考研数学二真题及答案

历年数学2考研试题及答案

2017考研数学二真题及答案

考研数学(二)历年真题详解【圣才出品】

2008考研数二真题及解析

考研数学二真题及解析

2008考研数二真题

2008年全国硕士研究生入学统一考试数学二试题及答案详解

2017考研数学二真题及答案

2017数学二考研真题

2008年数学二考研数学真题及解析