组合图形的面积(含练习题) PPT
《组合图形的面积》练习题(含答案)

助学堂组合图形的面积测试题1、下面的图形是由两个三角形组成的,请画出这两个三角形。
AB DC2、已知平行四边形的面积是48平方分米,求阴影部分的面积。
3dm8dm3、求下面个图形的面积、(单位:分米)(1)(2)1486 6123 612(3)(4)82.55.4 4 1.54.2 634、如图所示,梯形的周长是52厘米,求阴影部分的面积。
1014165、校园里有一块花圃,(如图所示),算出它的面积。
(单位:米)6 2256、大小正方形如图放置,阴影部分为重叠部分,求空白部分面积。
(单位:厘米)1577助学堂227、有一块土地如图所示,你能用几种方法求出它的面积?(单位:米)12158227、如图所示,一个平行四边形背分成A、B两被封,A的面积比B的面积打40平方米,A的上底是多少?BA8米【参考答案】1 解:AB DC2 解:48÷8×3÷2=9(平方分米)3(1)解:8×6+(8+12)×3÷2=78(平方分米)3(2)解:(14+12)×6÷2+12×6÷2=114(平方分米)3(3)解:5.4×4.2+5.4×6÷2=38.88(平方分米)3(4)解:2.5×1.5+(2.5+4)×(8-3-1.5)÷2+4×3=27.125(平方分米)4 解:10×(52-10-14-16)÷2=60(平方厘米)5 解:2×2+(5-2)×6=22(平方米)6 解:大正方形面积为:22×22=484(平方厘米)小正方形面积为:15×15=225(平方厘米)阴影部分面积为:7×7=49(平方厘米)空白部分的面积为:484+225-2×49=611(平方厘米)7 解:方法一:12 15助学堂82212×8+(15+8)×(22-12)÷2=211(平方米)方法二:1215822(15-8)×(22-2)÷2+22×8=211(平方米)8 解:40÷8=5(平方米)。
《组合图形的面积》练习题(含答案)
组合图形的面积
测试题
1、下面的图形是由两个三角形组成的,请画出这两个三角形。
A
B D
C
2、已知平行四边形的面积是48平方分米,求阴影部分的面积。
3dm
8dm
3、求下面个图形的面积、(单位:分米)
(1)(2)14 8
6 6
12
3 6
12
(3)(4)8
2.5
5.4 4 1.5
4.2 6
3
4、如图所示,梯形的周长是52厘米,求阴影部分的面积。
16
5、校园里有一块花圃,(如图所示),算出它的面积。
(单位:米)
6 2
2
5
6、大小正方形如图放置,阴影部分为重叠部分,求空白部分面积。
(单位:厘米)
15
7、有一块土地如图所示,你能用几种方法求出它的面积?(单位:米)
12
15
8
22
7、如图所示,一个平行四边形背分成A、B两被封,A的面积比B的面积打40平方米,A的上底是多少?
B
A
8米
【参考答案】。
《组合图形的面积》 优秀课件 (共31张PPT)

思考题:计算下面图形的面 积,你能想出不同的解法吗?
单位:米
6 10
5
12 S = S梯形 + S长方形
=(10+5)×6÷2+6×5
思考题:计算下面图形的面 积,你能想出不同的解法吗?
单位:米
6 10
5
12 S = S三角形 + S长方形
=5×6÷2+12×5
思考题:计算下面图形的面 积,你能想出不同的解法吗?
要计算下图的面积,你认为哪种方法是对 的?为什么?(单位:厘米)
8
5
向下
10 ①10×8-5×4
②8×5+5×4
4
③(8+4)×5÷2+(10+5)×4÷2
8
10 ①10×8-5×4
5 4
8
5
10 5
4
②8×5+5×4
③(8+4)×5÷2+(10+5)×4÷2
8
5
45
10
4
这是我们少先队的中队旗,怎样算 出它的面积。(你能想出不同的方法 吗?)
15、最终你相信什么就能成为什么。因为世界上最可怕的二个词,一个叫执着,一个叫认真,认真的人改变自己,执着的人改变命运。只要在路上,就没有到不了的地方。 16、你若坚持,定会发光,时间是所向披靡的武器,它能集腋成裘,也能聚沙成塔,将人生的不可能都变成可能。 17、人生,就要活得漂亮,走得铿锵。自己不奋斗,终归是摆设。无论你是谁,宁可做拼搏的失败者
答:它的面积是30平方米。
例4 右图表示的是一间房子
侧面墙的形状。它的面积是 多少平方米?
2米
5 米
5×2÷2+5×5÷2×2 =5+25 =30(平方米)5米Biblioteka 答:它的面积是30平方米。
组合图形的面积及练习题

方法二:
梯形×2
上底: 5m
2m
下底: 5+2=7m 5m 高: 5÷2=2.5m
5m
(5+5+2)×(5÷2)÷2×2 =12×2.5÷2×2 =30(平方米) 答:它的面积是30平方米。
方法三:
2m
5m
5m
长方形 - 两个三角形
(5+2)×5 -(5÷ 2)×2÷2×2 =35-5 =30(平方米)
虚线把组合图形分割或填补成我们知道的 简单的图形,从而方便我们的计算。在数 学中这些虚线叫做辅助线。
求组合图形面积的一般方法: ⑴分割法:可以把一个组合图形分成几个简 单的图形,分别求出这几个简单图形的面 积,再求和。 ⑵添补法:可以把一个组合图形看作是从一 个简单图形中减去几个简单的图形,求出 它们的面积差。
4m
3m 3m
(2) (7-4+7)×3÷2=15 ( m2 ) (3)18+15=33( m2 ) 答:这个图形的面积是33平方米。
6m
3m 7m
(6-3+6)×4÷2+(7-4+7)×3÷2 =9×4÷2+10×3÷2 =18+15 =33(m2)
方法4:
补上一个小的正方形,使 它成了一个大的长方形
已经学过的几种平面图形的面积计算公式
b a
S=ab
a
a
S=a2
h a
平行四边形的面积=底×高 长方形的面积=长×宽 正方形的面积=边长×边长
S=ah
a h a
三角形的面积=底×高 ÷2
b
h b a
梯形的面积=﹙上底+下底﹚×高÷2
S=ah÷2
S=(a+b)h÷2
这些都是简单的、基本的图形。
《组合图形的面积》练习题(含答案)

3(4)
解:2.5×1.5+(2.5+4)×(8-3-1.5)÷2+4×3=27.125(平方分米)
4
解:10×(52-10-14-16)÷2=60(平方厘米)
5
解:2×2+(5-2)×6=22(平方米)
6பைடு நூலகம்
解:大正方形面积为:22×22=484(平方厘米)
7.如图所示,一个平行四边形背分成A.B两被封,A的面积比B的面积打40平方米,A的上底是若干?
B
A
8米
【参考答案】
1
解:
A
B D
C
2
解:48÷8×3÷2=9(平方分米)
3(1)
解:8×6+(8+12)×3÷2=78(平方分米)
3(2)
解:(14+12)×6÷2+12×6÷2=114(平方分米)
3(3)
4.如图所示,梯形的周长是52厘米,求暗影部分的面积.
10
14
16
5.校园里有一块花园,(如图所示),算出它的面积.(单位:米)
6 2
2
5
6.大小正方形如图放置,暗影部分为重叠部分,求空白部分面积.(单位:厘米)
15
7
7
22
7.有一块地盘如图所示,你能用几种办法求出它的面积?(单位:米)
12
15
8
22
小正方形面积为:15×15=225(平方厘米)
暗影部分面积为:7×7=49(平方厘米)
空白部分的面积为:484+225-2×49=611(平方厘米)
7
解:办法一:
组合图形的面积——小学奥数专题

组合图形的面积(一)例1一个等腰直角三角形,最长的边是12厘米,这个三角形的面积是多少平方厘米?练习一1、求四边形ABCD的面积。
(单位:厘米)2、已知正方形ABCD的边长是7厘米,求正方形EFGH的面积。
3、有一个梯形,它的上底是5厘米,下底7厘米。
如果只把上底增加3厘米,那么面积就增加4.5平方厘米。
求原来梯形的面积。
例2正图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的2倍。
求中间长方形的面积。
练习二1、已知大正方形的边长是12厘米,求中间最小正方形的面积。
2、如下图长方形ABCD的面积是16平方厘米,E、F都是所在边的中点,求三角形AEF的面积。
3、求下图长方形ABCD的面积(单位:厘米)。
例3四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积是7平方厘米。
三角形CDH的面积是多少平方厘米?练习三1、图中两个正方形的边长分别是6厘米和4厘米,求阴影部分面积。
2、下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。
3、下图中,甲三角形的面积比乙三角形的面积大多少平方厘米?例4下图中正方形的边长为8厘米,CE为20厘米,梯形BCDF的面积是多少平方厘米?练习四1、如下图,正方形ABCD中,AB=4厘米,EC=10厘米,求阴影部分的面积。
2、在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(单位:厘米)3、图中BC=10厘米,EC=8厘米,且阴影部分面积比三角形EFG的面积大10平方厘米。
求平行四边形的面积。
例5图中ABCD是长方形,三角形EFD的面积比三角形ABF的面积大6平方厘米,求ED的长。
练习五1、如图,平行四边形BCEF中,BC=8厘米,直角三角形中,AC=10厘米,阴影部分面积比三角形ADH的面积大8平方厘米。
求AH长多少厘米?2,图中三个正方形的边长分别是1厘米、2厘米和3厘米,求图中阴影部分的面积。
《组合图形的面积》练习题(含答案)

组合图形的面积测试题1、下面的图形是由两个三角形组成的,请画出这两个三角形。
AB DC2、已知平行四边形的面积是48平方分米,求阴影部分的面积。
3dm8dm3、求下面个图形的面积、(单位:分米)(1)(2)14 86 6123 612(3)(4)82.55.4 4 1.54.2 634、如图所示,梯形的周长是52厘米,求阴影部分的面积。
1014165、校园里有一块花圃,(如图所示),算出它的面积。
(单位:米)6 2256、大小正方形如图放置,阴影部分为重叠部分,求空白部分面积。
(单位:厘米)1577227、有一块土地如图所示,你能用几种方法求出它的面积?(单位:米)12158227、如图所示,一个平行四边形背分成A、B两被封,A的面积比B的面积打40平方米,A的上底是多少?BA8米【参考答案】1 解:AB DC2 解:48÷8×3÷2=9(平方分米)3(1)解:8×6+(8+12)×3÷2=78(平方分米)3(2)解:(14+12)×6÷2+12×6÷2=114(平方分米)3(3)解:5.4×4.2+5.4×6÷2=38.88(平方分米)3(4)解:2.5×1.5+(2.5+4)×(8-3-1.5)÷2+4×3=27.125(平方分米)4 解:10×(52-10-14-16)÷2=60(平方厘米)5 解:2×2+(5-2)×6=22(平方米)6 解:大正方形面积为:22×22=484(平方厘米)小正方形面积为:15×15=225(平方厘米)阴影部分面积为:7×7=49(平方厘米)空白部分的面积为:484+225-2×49=611(平方厘米)7 解:方法一:121582212×8+(15+8)×(22-12)÷2=211(平方米)方法二:1215822(15-8)×(22-2)÷2+22×8=211(平方米)8 解:40÷8=5(平方米)。
求与圆有关的组合图形的面积ppt课件

说说你知道了哪些数学信 息?要解决的问题是什么 ?
03
任务一
学校阅览室的窗户上面是半圆,下面是正方形(如下图)。窗
户的面积约是多少平方米?(得数保留整数。)
怎样算出这个图形的面积
?小 提 示 先分解,把它变成我们学过
的简单图形,然后再算这些简单
图形的面积的和。
03
任务一
学校阅览室的窗户上面是半圆,下面是正方形(如下图)。窗
板书设计
求与圆有关的组合图形的面积(1)
半圆的面积+正方形的面积=窗户的面积 圆环的面积=大圆的面积-小圆的面积 S环=π(R2-r2)
S=ah÷2
S=(a+b)h÷2
S=πr2
02
新知导入
根据这些平面图形,我们能够拼出很多不同形状的图形。
三角形+长方形
三角形+长方形+正方形+圆
02
新知导入
小提示
像这些由几个简单的平 面图形组合而成的图形,叫 做组合图形。
学习任务一
求与圆有关的组合图形的面积
03
任务一
学校阅览室的窗户上面是半圆,下面是正方形(如下图)。窗 户的面积约是多少平方米?(得数保留整数。)
户的面积约是多少平方米?(得数保留整数。)
思考: 这个图形可以分解成什么图形
?窗户的面积怎么计算?
03
任务一
学校阅览室的窗户上面是半圆,下面是正方形(如下图)。窗
户的面积约是多少平方米?(得数保留整数。)
半圆
1.2m
正方形
窗户的面积是1个半圆 与1个正方形面积的和。
上半部分半圆的直径与正 方形的边长有什么关系?
2米 8米
3.14×(102-82) =3.14×36 =113.04(m2)
第二讲组合图形的面积

二、多边形的面积例1 求下列组合图形的面积。
(单位:厘米)例一题图例二图例5题图例2下面是一个长方形的草坪,中间有两个人行道。
求草坪面积。
(单位:米)例3一个长方形若长增加2厘米,面积就增加10平方厘米;若宽减少2厘米,则面积就减少18平方厘米,求原来长方形的面积。
例4有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米,两个正方形的面积各是多少?例5如图,长方形ABCD的长是9,宽是6。
三角形ABE、三角形AFD和四边形AECF的面积相等。
求三角形AEF的面积。
例6已知正方形对角线长10厘米,它的面积是多少平方厘米?第七题图第八题图第九题图例7 如图,三个正方形的边长分别是5cm,7cm,10cm,求四边形ABCD的面积。
例8 如图,已知大正方形ABCD的边长是9厘米,小正方形CEFG的边长是6厘米。
求三角形BDF 的面积。
例9如图,三角形ABC和三角形ABD都是直角三角形。
AD=4cm,AB=8cm,BC=6cm。
三角形AOD 的面积比三角形BOC的面积少多少平方厘米?例10如图,四边形ABCD为正方形,边长为8厘米,已知三角形ADF比三角形CEF的面积大10平方厘米,求阴影部分面积。
例11 如下图,三角形ABE的面积比梯形BCDE的面积小180平方米,BC=30米,CD=20米。
请问三角形ABE的面积是多少平方米?第十题图第十一图第十二题图例12三角形ABC和三角形DEF的面积相等,BC=DE=30cm,BG=10cm,DG=5cm。
梯形ABGF的面积是多少平方厘米?例13如图,四边形ABCD是长方形,长(AD)为8.4cm,宽(AB)为5cm,四边形ABEF是平行四边形。
如果DH长4cm,那么图中阴影部分的面积是多少平方厘米?第十三题图第十四图第十五题图例14如图,一个直角三角形ABC中有一个长方形CDEF,其中AD=4,BF=6。
求长方形CDEF的面积。
例15 如图,把三角形ABC的各边延长至原来的2倍,得到一个大三角形DEF。
组合图形面积(课件)-2021-2022学年数学五年级上册
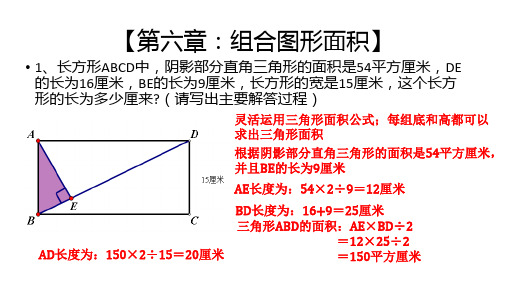
以AD为底,FB为高,同样可以求出平行四边形ABCD的面积 AD=平行四边形ABCD的面积÷FB
=24÷4.8 =5厘米
• 4、如图,BE=EF=FD,GF=CF,甲乙两个三角形的面积之和为12.9 平方分米,那么四边形ABCD的面积是( 38.7 )平方分米。
• 5、一个直角梯形,它的下底是5.6米,如果上底增加3米,它就变 成了正方形,求这个直角梯形的面积?
下底是5.6米,如果上底增加3米,它就变成了正方形 这个直角梯形的高是:5.6米 这个直角梯形的上底:5.6-3=2.6米 梯形的面积公式:(上底+下底)×高÷2 这个直角梯形的面积:(2.6+5.6)×5.6÷2=22.96m²
AE长度为:54×2÷9=12厘米
BD长度为:16+9=25厘米
三角形ABD的面积:AE×BD÷2
=12×25÷2
AD长度为:150×2÷15=20厘米
=150平方厘米
• 2、在下图,三个边长分别为10、12、8的正方形并放在一起,已 知直线BC将整个图形分为面积相等的两部分,求AB的长。
D
AB=DB-DA =29-10 =19
5、单位换算
• 23公顷=( 230000 )平方米 60078平方米=(0.060078 )平方千米 • 1.87平方分米=( 187 )平方厘米 350000平方米=( 35 )公顷 • 42.56平方米=( 4256 )平方分米=( 425600 )平方厘米
• 1、(如图)边长为3厘米的正方形的每条边都被平均分成3份。 以这8个点中的4个为顶点的可以连出很多四边形,请连出一个面
苏教版五年级下册数学圆的面积组合图形的面积计算课件ppt

正方形的面积:
1.8×1.8=3.24(m2) 半圆形的面积:
0.9×0.9×3.14÷2=1.2717(m2)
这扇窗户的面积:
3.24+1.2717=4.5117(m2) 答:
经 营者提 供商品 或者服 务有欺 诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经 营者提 供商品 或者服 务有欺 诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
复习
圆的面积的计算公式:
s = r²
背诵(13道) 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
求图形中涂色部分的面积。 (单位:cm)
经 营者提 供商品 或者服 务有欺 诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
涂色部分的面积=长方 形的面积-半圆的面积
经 营者提 供商品 或者服 务有欺 诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经 营者提 供商品 或者服 务有欺 诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
下面两个图形,你见过吗?
经 营者提 供商品 或者服 务有欺 诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
《组合图形的面积》练习题(含答案)

组合图形的面积之吉白夕凡创作
测试题
1、下面的图形是由两个三角形组成的,请画出这两个三角形。
A
B D
C
2、已知平行四边形的面积是48平方分米,求阴影部分的面积。
3dm
8dm
3、求下面个图形的面积、(单位:分米)
(1)(2) 14
8
6 6
12
3 6
12
(3)(4) 8
5.4 4 1.5
4.2 6
3
4、如图所示,梯形的周长是52厘米,求阴影部分的面积。
10
14
16
5、校园里有一块花圃,(如图所示),算出它的面积。
(单位:米)
6 2
2
5
6、大小正方形如图放置,阴影部分为重叠部分,求空白部分面积。
(单位:厘米)
7
7、如图所示,一个平行四边形背分成A 、B 两被封,A 的面积比B 的面积打40平方米,A 的上底是多少?
B
A
8米
【参考答案】。
《组合图形面积》优秀课件(共20张PPT)

3、等底等高的两个三角形的面积一定相等. ( ∨ )
4,、周长相等的长方形和平行四边形,他们的面积一定
相等.
(× )
5、底和高都是0.2厘米的三角形的面积是0.2平方厘米.
( ×)
6、下图中,两个完全一样的长方形中有 ① 、 ②两个
三角形,比较①和②的面积是 ①>②. ( ×)
①
②
练一练
求下列图形的面积。 (单位:cm)
27
10
下图是一个机器零件横截面图,
求黑色部分的面积。
20毫米
54×27—(20+30)×10÷2 =1458—50×10÷2 =1458—250
毫
米
30毫米
毫
米
=1208(平方毫米)
54毫米
答:黑色部分的面积是1208平方毫米。
判断
1、面积相等的两个梯形一定可以拼成一个平行四边形.
( ×) 2、面积相等的两个三角形形状也相同. (× )
15、最终你相信什么就能成为什么。因为世界上最可怕的二个词,一个叫执着,一个叫认真,认真的人改变自己,执着的人改变命运。只要在路上,就没有到不了的地方。 16、你若坚持,定会发光,时间是所向披靡的武器,它能集腋成裘,也能聚沙成塔,将人生的不可能都变成可能。 17、人生,就要活得漂亮,走得铿锵。自己不奋斗,终归是摆设。无论你是谁,宁可做拼搏的失败者
2、人生就有许多这样的奇迹,看似比登天还难的事,有时轻而易举就可以做到,其中的差别就在于非凡的信念。 3、影响我们人生的绝不仅仅是环境,其实是心态在控制个人的行动和思想。同时,心态也决定了一个人的视野和成就,甚至一生。
4、无论你觉得自己多么了不起,也永远有人比更强;无论你觉得自己多么不幸,永远有人比你更不幸。 5、也许有些路好走是条捷径,也许有些路可以让你风光无限,也许有些路安稳又有后路,可是那些路的主角,都不是我。至少我会觉得,那些路不是自己想要的。 6、在别人肆意说你的时候,问问自己,到底怕不怕,输不输的起。不必害怕,不要后退,不须犹豫,难过的时候就一个人去看看这世界。多问问自己,你是不是已经为了梦想而竭尽全力了?
组合图形的面积及练习题

80cm
20cm
30cm (80+80-200(平方厘米)
中队旗面积 = 梯形面积 ×2
(80-20)×(30+30)+30×20÷2×2 =3600+600 =4200(平方厘米)
中队旗面积 = 长方形面积 + 三角形面积 × 2
(12+20) ×(16-10)÷2 12×10
=96+120 =216(cm2)
人教课标版五年级数学上册
练习课
复习导入
1、上节课我们学习了什么?谁能说说求组合 图形面积的一般方法?
求组合图形面积的一般方法: ⑴分割法:可以把一个组合图形分成几个简
单的图形,分别求出这几个简单图形的面 积,再求和。 ⑵添补法:可以把一个组合图形看作是从一 个简单图形中减去几个简单的图形,求出 它们的面积差。
练一练1. 下面图形可以分成哪些已学过的图形?
长方形+三角形
梯形+三角形
长方形+梯形 正方形-梯形
练一练2. 下面图形可以分成哪些已学过的图形?
大长方形-小长方形
长方形×2+正方形
大长方形+小长方形×2
45cm 60cm
学校开运动会要制作一些锦旗,式样如图所示。 一面锦旗需要多少平方厘米的布料?
已经学过的几种平面图形的面积计算公式
a
h
b
a
a
a
长方形的面积=长×宽 正方形的面积=边长×边长平行四边形的面积=底×高
S=ab
S=a2
S=ah
a
b
h
h
a
三角形的面积=底×高 ÷2
S=ah÷2
ba
梯形的面积=﹙上底+下底﹚×高÷2
五年级奥数-组合图形的面积(二)PPT课件

3,图中三角形ABC的面积是36平方厘米, AC长8厘米,DE长3厘米,求阴影部分 的面积(ADFC不是正方形)。
8
CHENLI
例3、两条对角线把梯形ABCD分割
成四个三角形。已知两个三角形的 面积(如图所示),求另两个三角 形的面积各是多少?(单位:平方 厘米)
三角形ADC的面积是:10×15÷2=75, 而三角形ABC的高是三角形BCD高的 15÷10=1.5倍, 它们都以BC为边为底,所以,三角形 ABC的面积是三角形BCD的1.5倍。 阴影部分的面积是:
7.5÷(1+1.5)×1.5=45。
7
CHENLI
练习二
1,下图中,三角形ABC的面积是36平方厘米,三角形ABE 与三角形AEC的面积相等,如果AB=9厘米, FB=FE,求三角形AFE的面积。
16
CHENLI
练习五
1,边长是8厘米的正三角形的面积是边长为2厘米的 正三角形面积的多少倍? 2,一个梯形与一个三角形等高,梯形下底的长是上 底的2倍,梯形上底的长又是三角形底长的2倍。这 个梯形的面积是三角形面积的多少倍? 3,有两种自然的放法将正方形内接于等腰直角三角 形。已知等腰直角三角形的面积是36平方厘米,两 个正方形的面积分别是多少?
14
CHENLI
例5 、边长是9厘米的正 三角形的面积是边长为3 厘米的正三角形面积的 多少倍?
15
CHENLI
分析:
题中的已知条件不能计算出两种三 角形的面积,我们可以用边长是3厘 米的正三角形拼一个边长是9厘米的 正三角形,从而看出它们之间的倍 数关系。从下图中可以看出:边长9 厘米的正三角形是边长3厘米的正三 角形面积的9倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绿色圃中小学教育网 绿色圃中小学教育网 绿色圃中小学教育网 绿色圃中小学教育网
6m 3m
4m
7m
1
2
3
4
?
绿色圃中小学教育网 绿色圃中小学教育网 绿色圃中小学教育网
? ?
?
? ?
1.中国少年先锋队的中队旗 是五角星加火炬的红旗, 如右图。(单位:cm)
⑴估一估,这面中队旗的面 积大约有多大?与同伴交 流你的想法。
⑵如果刷漆每平方米需要花 费5元,那么刷漆共要花费 多少元?
大家应该也有点累了,稍作休息
大家有疑问的,可以询问和交流
求组合图形面积的一般方法: ⑴分割法:
可以把一个组合图形分成几个简单 的图形,分别求出这几个简单图形 的面积,再求和。 ⑵添补法:
可以把一个组合图形看作是从一个 简单图形中减去几个简单的图形, 求出它们的面积差。
1、求组合图形面积的方法有: 分割法和添补法
2、求组合图形面积的步骤:
(1)分解图形
(2)寻找条件 (3)计算面积
图形的特点
长方形、平行四边形:对边相等 正方形、等边三角形:
所有边都相等 等腰梯形、等腰三角形:
两条腰相等
1、求下列图形中的面积(单位:cm)
20
16-10
10 12 16
12
1、求下列图形中的面积(单位:cm)
70m
15 m
5、下图是一个 零件的横截面, 计算它的面积。
27mm
20mm 10mm 30mm
54mm
6、求下列图形中阴影部分的面积。
20
10
16
12
1、求下列图形中的面积(单位:cm)Biblioteka 122016-10
10
16
12
2、求下列图形中的面积(单位:cm)
8
12
14
25
3、求下列图形中阴影部分的面积 (单位:cm)。
4、在一块梯形的地中间有一个长方 形的游泳池,其余的地方是草地。 草地的面积是多少平方米?
40m
30m 30m
⑵计算中队旗的面积,说一 说你是怎么想的。
2.把下面各个图形分成已学过的图形,并与同伴 交流你的想法。
3.如图一张硬纸板剪下4个边长是4cm的小正方形 后,可以做成一个没有盖子的盒子。你知道剪 后的硬纸板面积是多少吗?
4.学校要给30扇教室门的正面刷漆。(单位:m)
⑴需要刷漆的面积一共是多 少?
