有理数课前小测
有理数的测试题

小卷(一)1、下列说法正确的是( )A 、零是正数不是负数B 、零既不是正数也不是负数C 、零既是正数也是负数D 、不是正数的数一定是负数,不是负数的数一定是正数2、下列说法正确的是( )A 、整数就是正整数和负整数B 、分数包括正分数、负分数C 、正有理数和负有理数组成全体有理数D 、一个数不是正数就是负数。
3、把下列各数分别填入相应的大括号内:24,32.0,10,213,03.0,1713,0,,1415.3,5.3,7----- π 自然数集合{ …};整数集合{ …};正分数集合{ …};非正数集合{ …};有理数集合{ …};4.____、_____和____统称为整数;____和____统称为分数; _______和_______统称为有理数;____和____统称为非负数;_____和_____统称为非正数; ____和____统称为非正整数;_____和_____统称为非负整数;5.下列说法中正确的是 ……………………………………………………………〖 〗A .有最小的负整数,有最大的正整数B .有最小的负数,没有最大的正数C .有最大的负数,没有最小的正数D .没有最大的有理数和最小的有理数6.大于-3.5小于4.7的整数有_______个.7.在数轴上到表示-2的点相距8个单位长度的点表示的数为_________.8.______的相反数是它本身,_____的绝对值是它本身,_______的绝对值是它的相反数.9.一个数的绝对值是32,那么这个数为______. 10.当a a -=时,0______a ;当0>a 时,______=a . 11.绝对值等于4的数是______.12.绝对值等于其相反数的数一定是 ( )A .负数B .正数C .负数或零D .正数或零13.如果3-=a ,则______=-a ,______=a .14. 最大的负整数是___________;小于3的非负整数有______________________。
第一章《有理数》测试卷(含答案)-

a 10第一章《有理数》测试卷(时间:90分钟 总分:120分)一、选择题:(每题2分,共30分)1.下列说法正确的是( ) A.所有的整数都是正数 B.不是正数的数一定是负数C.0不是最小的有理数D.正有理数包括整数和分数2.12的相反数的绝对值是( ) A.-12 B.2 C.-2 D.12 3.有理数a 、b 在数轴上的位置如图所示,那么下列式子中成立的是( )A.a>bB.a<bC.ab>0D.0a b> 4.在数轴上,原点及原点右边的点表示的数是( ) A.正数 B.负数 C.非正数 D.非负数5.如果一个有理数的绝对值是正数,那么这个数必定是( )A.是正数B.不是0C.是负数D.以上都不对6.下列各组数中,不是互为相反意义的量的是( )A.收入200元与支出20元B.上升10米和下降7米C.超过0.05mm 与不足0.03mD.增大2岁与减少2升7.下列说法正确的是( )A.-a 一定是负数;B.│a │一定是正数;C.│a │一定不是负数;D.-│a │一定是负数8.如果一个数的平方等于它的倒数,那么这个数一定是( )A.0B.1C.-1D.±19.如果两个有理数的和除以它们的积,所得的商为零,那么,这两个有理数( )A.互为相反数但不等于零;B.互为倒数;C.有一个等于零;D.都等于零10.若0<m<1,m 、m 2、1m 的大小关系是( ) A.m<m 2<1m ; B.m 2<m<1m ; C.1m <m<m 2; D.1m<m 2<m 11.4604608取近似值,保留三个有效数字,结果是( )A.4.60×106B.4600000;C.4.61×106D.4.605×10612.下列各项判断正确的是( )A.a+b 一定大于a-b;B.若-ab<0,则a 、b 异号;C.若a 3=b 3,则a=b;D.若a 2=b 2,则a=b 13.下列运算正确的是( ) A.-22÷(-2)2=1; B. 31128327⎛⎫-=- ⎪⎝⎭ C.1352535-÷⨯=- D. 133( 3.25)6 3.2532.544⨯--⨯=- 14.若a=-2×32,b=(-2×3)2,c=-(2×)2,则下列大小关系中正确的是( )A.a>b>0B.b>c>a;C.b>a>cD.c>a>b15.若│x │=2,│y │=3,则│x+y │的值为( )A.5B.-5C.5或1D.以上都不对二、填空题:(每空2分,共30分)16.某地气温不稳定,开始是6℃,一会儿升高4℃,再过一会儿又下降11℃, 这时气温是__.17.一个数的相反数的倒数是113-,这个数是________.18.数轴上到原点的距离是3个单位长度的点表示的数是______.19.-2的4次幂是______,144是____________的平方数.20.若│-a │=5,则a=________. 21.若ab>0,bc<0,则ac________0.22.绝对值小于5的所有的整数的和_______.23.用科学记数法表示13040000应记作_______________________,若保留3个有效数字, 则近似值为__________. 24.若│x-1│+(y+2)2=0,则x-y=___________; 25.(-5)×145⎛⎫- ⎪⎝⎭=_________. 26. 31277⎛⎫÷- ⎪⎝⎭=___________; 27. 1564358-÷⨯=___________. 28. 22128(2)2⎛⎫-⨯-+÷- ⎪⎝⎭=_______. 三、解答题:(共60分)29.列式计算(每题5分,共10分)(1)-4、-5、+7三个数的和比这三个数绝对值的和小多少?(2)从-1中减去573,,1284---的和,所得的差是多少?30.计算题(每题5分,共30分)(1)(-12)÷4×(-6)÷2; (2) 235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭;(3) 111311123124244⎛⎫⎛⎫⎛⎫⎛⎫--+----- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭; (4) 222121(3)242433⎛⎫⎛⎫-÷⨯-+-⨯- ⎪ ⎪⎝⎭⎝⎭;(5) 2242(12)6(3)24(3)(5)53+⨯-÷--++-⨯-; (6)1+3+5+…+99-(2+4+6+…+98).31.若│a │=2,b=-3,c 是最大的负整数,求a+b-c 的值.(10分)32.检修组乘汽车,沿公路检修线路,约定向东为正,向西为负,某天自A 地出发, 到收工时,行走记录为(单位:千米):+8、-9、+4、+7、-2、-10、+18、-3、+7、+5回答下列问题:(每题5分,共10分)(1)收工时在A 地的哪边?距A 地多少千米?(2)若每千米耗油0.3升,问从A 地出发到收工时,共耗油多少升?答案:一、1.C 2.D 3.A 4.D 5.B 6.D 7.C 8.B 9.A 10.B 11.A 12. C 13.D 14.C15.C二、16.评析:负数的意义,升高和降低是一对意义相反的量,借助数轴可以准确无误地得出正确结果-1℃,数无数不形象,形无数难入微, 数形结合是数学的基本思想,在新课标中有重要体现,是中考命题的重要指导思想,多以综合高档题出现,占分比例较大.17.评析:利用逆向思维可知本题应填34. 18.评析:绝对值的几何意义.在数轴上绝对值的代名词就是距离,绝对值是一个“一学就会一做就错”的难点概念,其原因是没有把握好绝对值的几何意义.19.1620.评析:可以设计两个问题理解本题.①什么数的绝对值等于5, 学生可顺利得出正确结论±5.②什么数的相反数等于±5,学生也可顺利得出正确结论-5和5,在解题的过程中学生自然会概括出│-a │=│a │,把一个问题转化成两个简单的问题,这种方法和思想是数学学习的核心思想,这一思想在历届中考中都有体现.21.<22.023.用科学记数法表示一个数,要把它写成科学记数的标准形式a ×10n , 这里的a 必须满足1≤a<10条件,n 是整数,n 的确定是正确解决问题的关键,在这里n 是一个比位数小1的数,因为原数是一个8位数,所以可以确定n=7,所以13040000=1.304×107,对这个数按要求取近似值,显然不能改变其位数,只能对其中的a 取近似值,保留3个有效数字为1.30×107,而不能误认为 1.30,通过这类问题,学生可概括出较大的数取近似值的基本模式应是:先用科学记数法将其表示为a ×10n (1≤a<10,n 是整数), 然后按要求对a 取近似值,而n 的值不变. 24.3 25.21 26.15- 27.252- 28.4 三、29.本题根据题意可列式子:(1)(│-4│+│-5│+│7│)-(-4-5+7)=18. (2) 573251128424⎛⎫-----= ⎪⎝⎭. 30.(1)属同一级运算,计算这个题按题的自然顺序进行(-12)÷4×(-6)÷2=(-12)×14×(-6)×12=9. (2)是一个含有乘方的混合运算 235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭=25160.25(4)(5)(4)1080908-⨯-⨯-⨯-⨯-=--=-.这里把-4同0.25结合在一起,利用了凑整法可以简化计算.(3)这一题只含同一级运算,计算中要统一成加法的计算, 然后把可以凑整的结合在一起进行简便计算,具体做法是: 111311123124244⎛⎫⎛⎫⎛⎫⎛⎫--+----- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭=111311123124244---++ =1111331111230434422444⎛⎫⎛⎫-++--+=-+=- ⎪ ⎪⎝⎭⎝⎭ (4)本题是一个混合运算题,具体解法如下: 232121(3)242433⎛⎫⎛⎫-÷⨯-+-⨯- ⎪ ⎪⎝⎭⎝⎭ =4412744993⎛⎫-⨯⨯+-⨯- ⎪⎝⎭=1644033-++= (5) 2242(12)6(3)24(3)(5)53+⨯-÷--++-⨯- =421(12)9249(5)536+⨯-⨯-++⨯- =4487933(5)9165155531515--+⨯-=--=- (6)1+3+5+...99-(2+4+6+ (98)=1+(3-2)+(5-4)+…(99-98)=1+1+1+…1=50.此题有多种简便方法,请你探索.31.∵│a │=2,∴a=±2,c 是最大的负整数,∴c=-1,当a=2时,a+b-c=2-3-(-1)= 0;当a=-2时a+b-c=-2-3-(-1)=-4.32.(1)∵8-9+4+7-2+10+18-3+7+5=8+4+7+18+7+5-9-10-2-3=25,∴在A 处的东边25米处.(2)∵│8│+│-9│+│4│+│7│+│-2│+│-10│+│18│+│-3│+│7│+│5│=73千米,73×0.3=21.9升,∴从出发到收工共耗油21.9升.。
1.第一章有理数当堂检测

1第一章 有理数1.1 正数和负数1. 下列说法:(1)正数前加上负号就是负数,(2)不是正数的数就是负数,(3)只有带“+”的数才是正数,(4)0既不是正数也不是负数,其中正确的有( )A.一个B.二个C.三个D.四个2. 【2012•河北】下列各数中,为负数的是( )A .0B .-2C .1D .21 3. 【2012•陕西】如果零上5 ℃记作+5 ℃,那么零下7 ℃可记作( )A .-7 ℃B .+7 ℃C .+12 ℃D .-12 ℃4. 2012年6月24日,我国自行研制的“蛟龙”号载人潜水器在马里亚纳海域成功突破7000米深度,再创中国载人深潜新纪录.如果把“蛟龙”号下潜350米记为-350米,那么正数:{ …};负数:{ …}.2参考答案:1. B2. B3. A4. 1005. 解:正数:{3.14,+72,227, …}; 负数:{-2.5,-2,-0.6, …}.31.2 有理数1.2.1 有理数1. 下列关于“0”的说法中不正确的是( )A .0不只是表示没有B .0是正数也是有理数C .0是非负数D .0既不是正数,也不是负数2. 有公共部分的两个数集是( )A .正数集和负数集B .正数集和整数集C .整数集和分数集D .正整数集和负数集3. 下列说法:(1)正数和负数统称有理数,(2)整数和分数统称有理数,(3)有理数包括:正有理数、负有理数和0,(4)有理数可以有不同的分类方法.其中正确的有( )A. 1个B. 2个C.3个D. 4个4 在 -2013,227,0,π,3.14,0.33,0.020020002…中,有理数有( ) A. 2个 B. 3个 C. 4个 D. 5个45. 写出3个负有理数与3个整数,分别填入下面的集合中,且使两集合重叠部分中的数有两个.5 参考答案:1. B2. B3. C6 1.2.2 数轴1.下列说法:(1)数轴是一条直线,(2)数轴是一条射线,(3)数轴是一条有正方向的直线,(4)规定了原点,单位长度和正方向的直线叫数轴.其中正确的有( )A .一个, B. 二个, C. 三个, D.四个。
有理数的运算经典测试题附解析

有理数的运算经典测试题附解析一、选择题1.设n 是自然数,则n n 1(1)(1)2+-+-的值为( ) A .0B .1C .﹣1D .1或﹣1 【答案】A【解析】试题分析:当n 为奇数时,(n +1)为偶数, n n 1(1)(1)2+-+-=(1)12-+=0; 当n 为偶数时,(n +1)为奇数,n n 1(1)(1)2+-+-=1(1)2+-=0. 故选A .点睛:本题考查有理数乘方,解答本题的关键是明确有理数乘方的计算方法,利用分类讨论的数学思想解答.2.已知一天有86400秒,一年按365天计算共有31536000秒,用科学记数法表示31536000正确的是( )A .63.153610⨯B .73.153610⨯C .631.53610⨯D .80.3153610⨯ 【答案】B【解析】【分析】科学记数法的表示形式为10n a ⨯的形式,其中1||10a ≤<,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值1<时,n 是负数.【详解】将31536000用科学记数法表示为73.153610⨯.故选B .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为10n a ⨯的形式,其中1<10a ≤,n 为整数,表示时关键要正确确定a 的值以及n 的值.3.据央视网报道,2019年1~4月份我国社会物流总额为88.9万亿元人民币,“88.9万亿”用科学记数法表示为( )A .138.8910⨯B .128.8910⨯C .1288.910⨯D .118.8910⨯【解析】【分析】利用科学记数法的表示形式进行解答即可【详解】4.广西北部湾经济区包括南宁、北海、钦州、防城港、玉林、崇左六个市,户籍人口约2400万,该经济区户籍人口用科学记数法可表示为( )A .2.4×103B .2.4×105C .2.4×107D .2.4×109【答案】C【解析】【分析】科学记数法的表示形式为a ×10n 的形式,其中1≤|a |<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>10时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】将2400万用科学记数法表示为:2.4×107.故选C .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a ×10n 的形式,其中1≤|a |<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.5.在数轴上,实数a ,b 对应的点的位置如图所示,且这两个点到原点的距离相等,下列结论中,正确的是( )A .0a b +=B .0a b -=C .a b <D .0ab >【答案】A【解析】由题意可知a<0<1<b ,a=-b ,∴a+b=0,a-b=2a<0,|a|=|b|,ab<0,∴选项A 正确,选项B 、C 、D 错误,故选A.6.现在网购是人们喜爱的一种消费方式,2018年天猫“双11”全球狂欢节某网店的总交易额超过1207000元,1207000用科学记数法表示为( )A .61.20710⨯B .70.120710⨯C .512.0710⨯D .51.20710⨯【答案】A【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】1207000=1.207×106,故选A .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.7.如图是张小亮的答卷,他的得分应是( )A .40分B .60分C .80分D .100分【答案】A【解析】【分析】 根据绝对值、倒数、相反数、立方以及平均数进行计算即可.【详解】解:①若ab=1,则a 与b 互为倒数,②(-1)3=-1,③-12=-1,④|-1|=-1,⑤若a+b=0,则a 与b 互为相反数,故选A .【点睛】本题考查了实数,掌握绝对值、倒数、相反数、立方根以及平均数的定义是解题的关键.8.为应对疫情,许多企业跨界抗疫,生产口罩.截至2月29日,全国口罩日产量达到116000000只.将116000000用科学记数法表示应为( )A .611610⨯B .711.610⨯C .71.1610⨯D .81.1610⨯【解析】【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】将116000000用科学记数法表示应为1.16×108.故选:D .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.9.若2(1)210x y -++=,则x +y 的值为( ).A .12B .12-C .32D .32- 【答案】A【解析】解:由题意得:x -1=0,2y +1=0,解得:x =1,y =12-,∴x +y =11122-=.故选A . 点睛:本题考查了非负数的性质.几个非负数的和为0,则每个非负数都为0.10.地球上海洋面积约为361000000平方公里,361000000用科学记数法可表示为( ) A .90.36110⨯B .73.6110⨯C .83.6110⨯D .736110⨯【答案】C【解析】【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】 361000000=83.6110⨯,故选:C .【点睛】本题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.11.-2的倒数是( )A.-2 B.12-C.12D.2【答案】B【解析】【分析】根据倒数的定义求解.【详解】-2的倒数是-1 2故选B【点睛】本题难度较低,主要考查学生对倒数相反数等知识点的掌握12.大量事实证明,治理垃圾污染刻不容缓.据统计,全球每分钟约有8500000吨污水排入江河湖海,这个排污量用科学记数法表示为()A.8.5×105 B.8.5×106C.85×105 D.85×106【答案】B【解析】【分析】根据科学记数法的表示形式:a×10n,其中1≤|a|<10,n为整数.解答即可.【详解】8500000=8.5×106,故选B.【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.13.去年端午节假期第一天,国内游客人数达3050万人次,将数据“3050万”用科学记数法表示为()A.63.0510⨯B.630.510⨯C.73.0510⨯D.83.0510⨯【答案】C【解析】【分析】根据科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.【详解】3050万=30500000=73.0510⨯,故选:C .【点睛】此题考查科学记数法的表示方法.解题关键在于掌握科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.14.根据制定中的通州区总体规划,将通过控制人口总量上限的方式,努力让副中心远离“城市病”.预计到2035年,副中心的常住人口规模将控制在130万人以内,初步建成国际一流的和谐宜居现代化城区.130万用科学记数法表示为( )A .61.310⨯B .413010⨯C .51310⨯D .51.310⨯【答案】A【解析】【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值是易错点,由于130万有7位,所以可以确定n=7-1=6.【详解】130万=1 300 000=1.3×106.故选A .【点睛】此题考查科学记数法表示较大的数的方法,准确确定a 与n 值是关键.15.将数47300000用科学记数法表示为( )A .547310⨯B .647.310⨯C .74.7310⨯D .54.7310⨯【答案】C【解析】【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】解:将47300000用科学记数法表示为74.7310⨯,故选:C .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.16.2019年3月3日至3月15日,中国进入“两会时间”,根据数据统计显示,2019年全国两会热点传播总量达829.8万条,其中数据“829.8万”用科学记数法表示为( ) A .8.298×107 B .82.98×105 C .8.298×106 D .0.8298×107【答案】C【解析】【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】数据“829.8万”用科学记数法表示为8.298×106.故选C .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.17.如果a+b >0,ab >0,那么( )A .a >0,b >0B .a <0,b <0C .a >0,b <0D .a <0,b >0【答案】A【解析】解:因为ab >0,可知ab 同号,又因为a +b >0,可知a >0,b >0.故选A .18.2018年4月8日11-日,博鳌亚洲论坛2018年年会在海南博鳌句型,本次年会的主题为“开放创新的亚洲,繁荣发展的世界”.开幕式上,博鳌亚洲论坛副理事长周小川致辞中提到:“一带一路”区域基础设施投资缺口每年超过6000亿美元.6000亿用科学计数法可以表示为( )A .3610⨯亿B .4610⨯亿C .30.610⨯亿D .40.610⨯亿 【答案】A【解析】【分析】科学计数法的表示形式为n a 10⨯的形式,其中1a 10≤<,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值1>时,n 是正数;当原数的绝对值1<时,n 是负数.【详解】解:6000亿3610=⨯⨯亿,故选A .【点睛】此题考查科学计数法的表示方法.科学计数法的表示形式为n a 10⨯的形式,其中1a 10≤<,n 为整数,表示时关键要正确确定a 的值以及n 的值.19.如图,是一个计算流程图.当16x =时,y 的值是( )A2B.2C.2±D.2±【答案】A【解析】【分析】观察流程图的箭头指向,根据判断语句,当结果是无理数时输出,当结果是有理数时重复上述步骤,即可得到答案.【详解】x=后,取算术平方根的结果为2,判断2不是无理数,再取2的算术平方根解:输入1622是无理数,数出结果.故A为答案.【点睛】本题主要考查流程图的知识点、无理数的基本概念(无限不循环小数)、算术平方根的基本概念,看懂流程图是做题的关键,注意算术平方根只有正数.20.x是最大的负整数,y是最小的正整数,则x-y的值为( )A.0 B.2 C.-2 D.±2【答案】C【解析】【分析】根据有理数的概念求出x、y,再根据减去一个数等于加上这个数的相反数进行计算即可得解.【详解】∵x是最大的负整数,y是最小的正整数,∴x=-1,y=1,∴x-y=-1-1=-2.故选C.【点睛】本题考查了有理数的减法,熟记有理数的概念求出a、b的值是解题的关键.。
新人教版七年级数学试题第一章《有理数》全章检测120分钟150分

第一章《有理数》全章检测测试题(时间120分钟 满分150分)一、选择题(每题3分,共45分)1、大于–3.5,小于2.5的整数共有( )个。
A.6B.5C.4D.32、如果一个数的相反数比它本身大,那么这个数为 ( )A 、正数B 、负数C 、整数D 、不等于零的有理数3、在有理数中,绝对值等于它本身的数有 ( )A. 1个B. 2个C. 3个D. 无穷多个4. 若ab≠0,则a/b 的取值不可能是 ( )A 0B 1C 2D -25. 在-2,0,1,3这四个数中,比0小的数是( )A 、-2B 、0C 、1D 、36、已知点A 和点B 在同一数轴上, 点A 表示数2-, 又已知点B 和点A 相距5个单位长度, 则点B 表示的数是 ( )A.3B.-7C.3或-7D.3或77、 若两个有理数的和是正数,那么一定有结论( )A . 两个加数都是正数;B .两个加数有一个是正数;C . 一个加数正数,另一个为零D .两个加数不能同为负数8. 下列说法正确的个数是 ( ) ①一个有理数不是整数就是分数 ②一个有理数不是正数就是负数 ③一个整数不是正的,就是负的 ④一个分数不是正的,就是负的。
A 1B 2C 3D 4 2.9、甲、乙、丙三地的海拔高度分别为20米,-15米和-10米,那么最高的地方比最低的地方高( )A.10米B.15米C.35米D.5米10、下列说法中正确的是 ( )A.a -一定是负数B.a 一定是负数C.a -一定不是负数D.2a -一定是负数11、每天供给地球光和热的太阳与我们的距离非常遥远,它距地球的距离约为15000000千米,将150000000千米用科学记数法表示为( )A .0.15×910千米B .1.5×810千米C .15×710千米D .1.5×710千米12. 下列说法正确的是 ( )。
①0是绝对值最小的有理数 ②相反数大于本身的数是负数③数轴上原点两侧的数互为相反数 ④两个数比较,绝对值大的反而小 。
有理数测试题及答案

有理数测试题及答案一、选择题1. 下列哪个数是有理数?A. √2B. πC. 1/3D. 0.8080080008…(每两个8之间依次增加一个0)答案:C2. 有理数的英文是什么?A. Rational numberB. Irrational numberC. Real numberD. Complex number答案:A3. 若a和b是有理数,且a/b ≠ 0,那么a和b至少有一个数是?A. 正数B. 负数C. 零D. 整数答案:D4. 两个有理数相加,结果必然是?A. 有理数B. 无理数C. 整数D. 零答案:A5. 以下哪个操作不会改变一个有理数的值?A. 乘以一个非零有理数B. 加上一个无理数C. 除以一个非零有理数D. 减去一个相同的有理数答案:D二、填空题1. 请写出一个有理数的例子:__________。
答案:2/32. 有理数可以表示为两个整数的比,即 a/b,其中a和b都是__________。
答案:整数3. 若一个有理数的分母为零,则该有理数是__________。
答案:未定义4. 一个有理数可以是__________或__________。
答案:正数负数5. 请写出一个无限循环小数的有理数例子:__________。
答案:1/3 = 0.33333…三、简答题1. 请简述什么是有理数。
答案:有理数是可以表示为两个整数的比的数,其中分母不为零。
这包括有限小数、无限循环小数以及整数。
2. 有理数和无理数有什么区别?答案:有理数可以表示为两个整数的比,而无理数则不能。
有理数可以是有限小数或无限循环小数,而无理数则是无限不循环小数。
3. 如何判断一个数是否是有理数?答案:如果一个数可以表示为两个整数的比,并且分母不为零,那么这个数就是有理数。
例如,所有整数、分数和无限循环小数都是有理数。
4. 请举例说明有理数的加法和减法。
答案:例如,1/2 + 1/3 = 5/6,这是一个有理数的加法例子。
第二章 有理数 检测试卷(二)及答案

第二章 有理数 检测试卷(二)一、用你的慧眼选一选(每小题3分,共30分)1.下列各数中,是负数的是( )A.)51(--B.|41|-- C. 2)31(- D.|61|- 2.下列结论正确的是( )A.有理数包括正数和负数B.有理数包括整数和分数C.0是最小的整数D.两个有理数的绝对值相同,则这两个有理数也相等 3.如果0)1(|2|2=-++b a ,那么2011)(b a +的值是( ) A. -2011 B. 2011 C. -1 D.1 4.如果一个数的平方等于它的倒数,那么这个数一定是( )A.0B.1 C .-1 D.1或-1 5.下列说法正确的是( )A.一个数的相反数一定是负数B.若| a |= b ,则a = bC.若-|m |=-2,则m =±2 D .-a 一定是负数 6.已知|x |=3,|y |=2,x y <0,则y x +的值等于( )A.5或-5B.1或-1C.5或1 D .-5或-17.有理数a 、b 、c 在数轴上对应点位置如下图所示,则下列关系式成立的是( )A. a +b +c <0B. a +b +c >0C. a b <a cD. a c >a b8.某种品牌的彩电降价30%以后,每台售价为a 元,则该品牌彩电每台原价应为( )A.0.7a 元B.0.3a 元C.3.0a 元 D.7.0a 元 9.用代数式表示“比m 的平方的3倍大1的数”是( )A.1)3(2+mB.132+m C.2)1(3+m D.2)13(+m10.当代数式532++x x 的值为7时,代数式2932-+x x 的值是( )A.4B.0 C .-2 D. -4二、用你敏锐的思维填一填(每小题3分,共30分)11.用科学记数法表示-526000= . 12.大于311-且小于2的所有整数是 . 13.)23(-的倒数是 ,)3(-n 得相反数是 ,|32|-的相反数的倒数是 . 14.有理数1,321,2.1,73,0,31,5.0+----按从小到大的顺序排列是 . 15.若数轴上的点A 所对应的有理数是322-,那么与A 点相距5个单位长度的点所对应的有理数是 .· · · · a b 0 c16.在32,1,45,4,0|,5.3|,4---π中,负数有 ,分数有 . 17.在有理数中,最大的负整数是 ,最小的正整数是 ,绝对值最小的数是 . 18.如果212=-y x ,那么|2|y x +-= . 19.计算:20062007)5()51(-⨯-= .20.若x 、y 互为相反数,则3-2006x -2006y = ;若a 、b 互为倒数,则ab2007-= ;若,0)4(|2|4=-+-b a 那么ab 2= .三、开动你的脑筋圆满解答(本大题共40分)21.计算题(每题4分,共12分)4.654.18)4.6()54.26).(1(+--+- )2(541)3()211()2.(324÷-+-⨯-|4|)313133.0(121).3(-÷+⨯+-22(本题5分).已知a 、b 互为相反数,c 、d 互为倒数,x 的绝对值为5. 试求:200320022)()()(cd b a x cd b a x -+++++-的值.23.(本题5分)球的体积公式是:球体体积=.343r π请用公式计算直径为2.45米的球的体积(用计算器计算,保留两个有效数字,π取3.14.)24.(本题8分)计算下列各式(可以使用计算器) 6×7= ,66×67= ,666×667= ,6666×6667= ,66666×66667= . 观察上述结果,你发现了什么规律?25.(本题10分)一辆汽车沿着一条南北向的公路来回行驶,某一天早晨从A 地出发,晚上最后到达B 地.约定向北为正方向(如:+7.4表示汽车向北行驶7.4千米,-6则表示汽车向南行驶6千米),当天的行驶记录如下(单位:千米):+18.3,-9.5,+7.1,-14,-6.2,+13,-6.8,-8.5.请你根据计算回答以下问题: (1)B 地在A 地何方,相距多少千米?(2)若汽车行驶每千米耗油0.0642升,那么这一天共耗油多少升?(结果保留两位有效数字)四、拓广探索,更上一层楼(每题10分,共20分)26.十边形有多少条对角线?若将十边形的对角线全部画出比较麻烦,我们可以通过边数较你发现规律了吗?请总结你发现的规律,并写出十边形对角线的条数.27.在计算10023331++++ 的值时,可设S =10023331++++ ,①则3S=101323333++++ ②,②-①得 2S=13101-,∴S=213101- .试利用上述方法求200428881++++ 的值,并求一般地)1(12≠++++x x x x n的值.第二章 有理数 检测试卷(二)参考答案1.B2.B3.C4.B5.C6.B7.A8.D9.B 10.A11.51026.5⨯- 12.-1,0,1 13.23,3,32---n 14.73,5.0,321---2.1,1,0,31+- 15.327-或312 16.32,45|,5.3|;32,4---- 17.-1,1,0 18.21 19.51- 20.3,-2007,1621.(1)-45.08 (2)21 (3)4122. 19或29 23. 7.7 24.42,4422,444222,44442222,4444422222;最后的乘积由4和2组成,4和2的位数分别与因数的位数相同 25.(1)B 地在A 地正南方,与A 地相距6.6千米.(2)这一天共耗油约为5.4升.26.充分观察表,从表中可以看出对角线随多边形边数增加的规律:四边形的对角线2条;五边形的对角线5条,即5=2+3;六边形的对角线9条,即9=2+3+4;七边形的对角线14条,即14=2+3+4+5;八边形的对角线20条,即20=2+3+4+5+6;n 边形的对角线条数: 2+3+4+5+…+(n -2)=2)3(-n n 条(n ≥3).所以十边形有352)310(10=-(条). 27. 设S=200428881++++ ① 则8S=2005328888++++ ②②-①得 7S=182005-,所以S=7182005-一般地)1(11112≠--=+++++x x x x x x n n。
人教七年级数学上课堂(课前)五分钟练习资料

第一章 有理数1.1 正数和负数(第一课时)(基础训练)1.任意写出5个正数:________________;任意写出5个负数:_______________. 2.在银行存入款存入3万元记作+3万元,那么支取2万元应记作_______,-4万元表示________________. 3.已知下列各数:51-,432-,3.14,+305,0,-23. 则正数有___________ _;负数有______ ______.4.向东行进-50m 表示的意义是( )A .向东行进50m C .向北行进50mB .向南行进50m D .向西行进50m 5.下列结论中正确的是( )A .0既是正数,又是负数B .O 是最小的正数C .0是最大的负数D .0既不是正数,也不是负数6.给出下列各数:-3,0,+5,213-,+3.1,21-,2004,+2008.其中是负数的有 ( ) A .2个 B .3个 C .4个 D .5个7.下列各数中,哪些是正数?哪些是负数?+8,-25,68,O ,722,-3.14,0.001,-889. (综合训练)1.写出比O 小4的数,比4小2的数,比-4小2的数.2.如果海平面的高度为0米,一潜水艇在海水下40米处航行,一条鲨鱼在潜水艇上方10米处游动,试用正负数分别表示潜水艇和鲨鱼的高度.1.1 正数和负数(第二课时)(课前小测)1.如果向南走5米,记作+5米,那么向北走8米应记作___________. 2.零下15℃,表示为_____,比O℃低4℃的温度是_____.3.地图上标有甲地海拔高度30米,乙地海拔高度为20米,丙地海拔高度为-5米,其中最高处为_______地,最低处为_______地. 4.“甲比乙大-3岁”表示的意义是________________. 5.在-7,0,-3,34,+9100,-0.27中,负数有( )A .0个B .1个C .2个D .3个(基础训练)1.如果全班某次数学测试的平均成绩为83分,某同学考了85分,记作+2分,得分90分和80分应分别记作__________.2.如果把+210元表示收入210元,那么-60元表示______________.3.粮食产量增产11%,记作+11%,则减产6%应记作______________.4.如果把公元2008年记作+2008年,那么-205年表示______________.5.如果向西走12米记作+12米,则向东走-120米表示的意义是__________________.6.甲、乙两人同时从A地出发,如果甲向南走50m记为+50m,则乙向北走30m记为;这时甲、乙两人相距米。
有理数测试题及答案

有理数测试题及答案一、选择题(每题2分,共10分)1. 下列数中,属于有理数的是()。
A. πB. √2C. 0.33333...D. 0.12. 有理数的乘法法则是()。
A. 同号得正,异号得负B. 同号得正,异号得负,绝对值相乘C. 同号得负,异号得正D. 绝对值相乘,符号相加3. 两个有理数相除,其结果为()。
A. 正数B. 负数C. 非负数D. 非正数4. 绝对值的定义是()。
A. 一个数的相反数B. 一个数到原点的距离C. 一个数的平方D. 一个数的立方5. 有理数的加法法则是()。
A. 同号相加,取相同的符号,并把绝对值相加B. 同号相加,取相反的符号,并把绝对值相加C. 异号相加,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值D. 异号相加,取绝对值较小的数的符号,并用较大的绝对值减去较小的绝对值二、填空题(每题2分,共10分)1. 一个有理数的绝对值是它到原点的距离,即 |-3| = ____。
2. 有理数的乘法法则是同号得____,异号得____,绝对值相乘。
3. 有理数的除法法则是同号得____,异号得____,绝对值相除。
4. 有理数的加法法则是同号相加,取相同的符号,并把绝对值____。
5. 有理数的减法法则是减去一个数等于加上这个数的____。
三、解答题(每题10分,共20分)1. 计算下列有理数的和:-3 + 4 + (-5) + 6。
2. 计算下列有理数的积:(-2) × 3 × 4 × (-1)。
四、判断题(每题1分,共10分)1. 有理数包括正整数、负整数、正分数、负分数和零。
()2. 0是正数。
()3. 有理数的绝对值一定是正数。
()4. 有理数的乘法法则是同号得正,异号得负,绝对值相乘。
()5. 有理数的除法法则是同号得正,异号得负,绝对值相除。
()答案:一、选择题1. C2. B3. C4. B5. A二、填空题1. 32. 正,负3. 正,负4. 相加5. 相反数三、解答题1. -3 + 4 + (-5) + 6 = 22. (-2) × 3 × 4 × (-1) = 24四、判断题1. 正确2. 错误3. 错误4. 正确5. 正确。
有理数及代数式小测试A

有理数及代数式小测试A 班级姓名学号一、填空题(25分)1.商店运来一批梨,共9箱,每箱n个,则共有_______个梨.2.一辆客车行驶在长240千米的公路,设它行驶完共用a个小时,则它的速度是每小时_______千米.3.“龟兔赛跑”,龟兔每小时的行程分别为a千米,b千米,经过t小时后,龟兔相距_____千米.4.全班总人数为y,其中男生占56%,那么女生人数是_____.5.若|a-2|+|b+3|=0,则3a+2b= .二、选择题(25分)1.原产量n千克增产20%之后的产量应为()A.(1-20%)n千克B.(1+20%)n千克C.n+20%千克D.n×20%千克2.代数式a2+b2的意义是()A.a与b的和的平方B.a+b的平方C.a与b的平方和D.以上都不对3.一个两位数,个位是a,十位比个位大1,这个两位数是()A.a(a+1)B.(a+1)aC.10(a+1)aD.10(a+1)+a4.一个数的平方是81,这个数是()A、9B、-9C、+9D、815.在-(-5),-(-5)2,-|-5|,(-5)3中负数有()A、0个B、1个C、2个D、3个三、计算题(30分)(2)(15)(9)(12)---+--+ 10+(-2)×(-5)21-2+3-4+5-6+----+2007-2008四、解答题(20分)1.小明今年x岁,爸爸y岁,3年后小明和爸爸的年龄之和是多少?2.某一出租车一天下午以鼓楼为出发地在东西方向运营,向东走为正,向西走为负,行车里程(单位:㎞)依先后次序记录如下:+9,-3,-5,+4,-8,+6,-3,-6,-4,+10.⑴将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?⑵若每千米的价格为2.4元,司机一个下午的营业额是多少?。
人教版数学七年级上册第一章《有理数》检测试试题(含答案)

人教版数学七年级上册第一章《有理数》检测试题一、选择题1.-1的相反数是( )A.-1B.0C.1D.-1或12.计算(-1)2020的结果是( )A.-1B.1C.-2020D.20203.若x =-(-2)×3,则x 的倒数是( )A.-16B.16C.-6D.64.已知有理数a 、b 在数轴上对应点如图所示,则下列式子正确的是( )A .ab >0B .︱a ︱>︱b ︱C .a -b >0D .a +b >05.比较-12,-13,14的大小,下列选项中正确的结果是( ) A.-12<-13<14 B.-12<14<-13C.14<-13<-12D.-13<-12<14 6.有以下两个结论:①任何一个有理数和它的相反数之间至少有一个有理数;②如果一个有理数有倒数,则这个有理数与它的倒数之间至少有一个有理数.则( )A.①,②都不对B.①对,②不对C.①,②都对D.①不对,②对7.若a +b <0,ab <0,则( )A.a >0,b >0B.a <0,b <0C.a ,b 两数一正一负,且正数的绝对值大于负数的绝对值D.a ,b 两数一正一负,且负数的绝对值大于正数的绝对值8.某粮店出售的三种品牌的面粉袋上分别标有质量为(25±0.1)kg ,(25±0.2)kg ,(25±0.3)kg 的字样,从中任意拿出两袋,它们的质量最多相差( )BA.0.8kgB.0.6kgC.0.5kgD.0.4kg9.一根1m 长的小棒,第一次截去它的13,第二次截去剩下的13,如此截下去,第五次后剩下的小棒的长度是( )C A.513⎛⎫ ⎪⎝⎭m B.[1-513⎛⎫ ⎪⎝⎭]m C.523⎛⎫ ⎪⎝⎭m D.[1-523⎛⎫ ⎪⎝⎭]m 10.若ab ≠0,则a a +b b的取值不可能是( ) A.0 B.1C.2D.-2 二、填空题11.-15的绝对值是_______;立方等于-8的数是_______. 12.一种商品原价120元,按八折(即原价的80%)出售,则现售价应为_______元. 0 1 -1 b a13.对于式子-(-4),下列理解:①可表示-4的相反数;②可表示-1与-4的乘积;③可表示-4的绝对值;④运算结果等于4.其中理解错误的有_______个.14.数轴距离原点3个单位的点有_______个,他们分别表示数是_______.15.比-312大而比213小的所有整数的和为_______.16.多伦多与北京的时间差为-12小时(正数表示同一时刻比北京时间早的时数),如果北京时间是10月1日14:00,那么多伦多时间是_______.17.某校师生在为某地地震灾区举行的爱心捐款活动中总计捐款18.49 万元.把18.49 万用科学记数法表示并保留两个有效数字为_______.18.规定a※b=5a2+2b-1,则(-4)※6的值为_______.19.大家知道5=50-,它在数轴上的意义是表示5的点与原点(即表示0的点)之间的距离.又如式子63-,它在数轴上的意义是表示6的点与表示3的点之间的距离.类似地,式子5a+在数轴上的意义是_______.20.为了求1+2+22+23+…+22020的值,可令S=1+2+22+23+…+22020,则2S=2+22+23+24+…+22021,因此2S-S=22021-1,所以1+2+22+23+24+…+22020=22021-1,仿照以上推理计算出1+5+52+53+…+52020的值是_______.三、解答题21.计算:(1)-9÷3+(12-23)×12+32;(2)713×(-9)+713×(-18)+713;(3)-691516×8.22.一条小虫沿一根东西方向放着的长杆向东以2.5米/分的速度爬行4分钟后,又向西爬行6分钟.问此时它距出发点的距离是多少?23.马虎同学在做题时画一条数轴,数轴上原有一点A,其表示的数是-2,由于一时粗心把数轴上的原点标错了位置,使A点正好落在-2的相反数的位置,请你帮帮马虎同学,借助于这个数轴要把这个数轴画正确,原点应向哪个方向移动几个单位长度.24.我们常用的数是十进制数,如4657=4×103+6×102+5×101+7×100,数要用10个数码(又叫数字):0、1、2、3、4、5、6、7、8、9,在电子计算机中用的二进制,只要两个数码:0和1,如二进制中110=1×22+1×21+0×20等于十进制的数6,110101=1×25+1×24+0×23+1×22+0×21+1×20等于十进制的数53.那么二进制中的数101011等于十进制中的哪个数?25.若1+2+3+…+31+32+33=17×33,试求1-3+2-6+3-9+4-12+…+31-93+32-96+33-99的值.26.我国古代有一道有趣的数学题,“井深10米,一只蜗牛从井底向上爬,白天向上爬2米,夜间又滑下1米,问小蜗牛几天可以爬出深井?”27.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向(1)求收工时距A地多远?(2)在第几次纪录时距A地最远?(3若每km耗油0.3升,问共耗油多少升?参考答案:一、1.C;2.B;3.A;4.C.点拨:由数轴上a、b对应点的位置可知0<a<1,b<-1,故a、b异号,即ab<0,否定A选项;又︱a︱<1,︱b︱>1,即︱a︱<︱b︱,选项B 错误;因为a>0>b,所以a-b>0,选项C正确;由︱a︱<︱b︱且a>0,b<0,得a+b<0,选项D错误;5.A.点拨:因为正数大于一切负数,所以三个数中14最大.又因为︱-1 2︱=12=36,︱-13︱=13=26,︱-12︱>︱-13︱,所以-12<-13,即-12<-13<14;6.A.点拨:①中的说法我们可以想象在一条数轴上原点的两边如±1,±2,…这样的两个非零有理数之间存在“间隙”,也就是说它们之间一定有另外的有理数.但是0的相反数是0,0和它的相反数0之间就没有“间隙”了,所以①错;②中按照①的分析方法,如果一个数的倒数等于它本身,那么说法②就是错的,我们知道1的倒数是1,-1的倒数是-1,显然②这种说法也不对;7.D;8.B;9.C;10.B.点拨:本题可利用分析的方法考虑.因为ab≠0,所以ab>0或ab<0.若ab>0,则可能有两种情况:a>0,b>0或a<0,b<0.当a>0,b>0时,aa+bb=1+1=2;当a<0,b<0时,aa+bb=-1-1=-2;若ab<0,则可能有两种情况:a>0,b<0或a<0,b>0;当a>0,b<0时,aa+bb=1-1=0;当a<0,b>0时,aa+bb=-1+1=0.可能出现的结果有0,2,-2,所以应选B.二、11.15、-2;12.96;13.2.点拨:②和③理解错误;14.2个、+3和-3;15.-3;16.2:00;17.1.8×105.点拨:因为18.49万=184900,所以用科学记数可表示为1.849×105,保留两个有效数字在8后的数要舍去为1.8×105;18.61.点拨:因为a※b=2a2+5b-1,所以(-4)※6=2×(-4)2+5×6-1=61;19.表示a的点与表示-5的点之间的距离;20.4152021-.点拨:不妨模仿条件中的求解方法,设S=1+5+52+53+…+52020,再在两边同乘以5,得5S=5+52+53+…+52021,两式相减,得5S-S=52021-1,即S=4152021-.三、21.(1)-9÷3+(12-23)×12+32=-3+12×12-23×12+9=-3+6-8+9=4.(2)7 13×(-9)+713×(-18)+713=713×(-9-18+1)=713×(-26)=-14.(3)-691516×8=-(70-116)×8=-(70×8-116×8)=-55912.点拨:(1)中涉及有理数的加、减、乘、除与乘方,用运算法则进行运算,其中可以运用分配律简化运算,(12-23)×12=12×12-23×12=6-8=-2;(2)中各部分含有相同因数713,所以可想到逆用分配律计算;(3)题先确定符号,然后把绝对值691516化成(70-116)再与8相乘比较简便.解:评析:在进行有理数的计算时,切记要灵活.在拿到题目之前先要看看题目的特点,选择恰当的运算性质,尤其是分配律的正向和反向应用,正确应用运算律会起到事半功倍的效果.22.设向东速度为2.5米/分,向西为-2.5米/分.2.5×4+(-2.5)×6=10-15=-5(米).答:它在距出发点西边5米的地方.点拨:我们一般规定向东为正,即向东速度为2.5米/分;向西为负,即向西速度为-2.5米/分.评析:本题是一道有理数乘法与数轴知识综合运用的应用题,可以利用数轴的直观性使问题变得简单.23.向左移动4个单位长度.24.101011=1×25+0×24+1×23+0×22+1×21+1×20=32+0+8+0+2+1=43.25.1-3+2-6+3-9+4-12+…+31-93+32-96+33-99=(1+2+3+…+31+32+33)+(-3-6-9-…-99)=17×33-3(1+2+3+…+31+32+33)=17×33-3×17×33=-2×17×33.26.把向上爬记为正数,向下滑记为负数,由蜗牛一天爬1米;蜗牛最后一天可以爬出井,在此之前它要爬10-2=8(米);所以蜗牛要先爬8天,加上最后一天,总共是9天.答:蜗牛要9天可以爬出深井.点拨:如果把向上爬记为正数,向下滑记为负数,则蜗牛一天爬(2+(-1)=1)米,那么蜗牛爬了8天,就爬8米,剩下2米,第9天就可以爬出来了.27.(1)因为(-4)+(+7)+(-9)+(+8)+(+6)+(-5)+(-2)=+1,所以收工时距A 地1 km.(2)五.(3)因为一天中共行驶的路程=4-+7++9-+8++6++5-+2-发=41(km ),而41×0.3=12.3(升),所以共耗油12.3升.。
有理数基础知识识记与小测
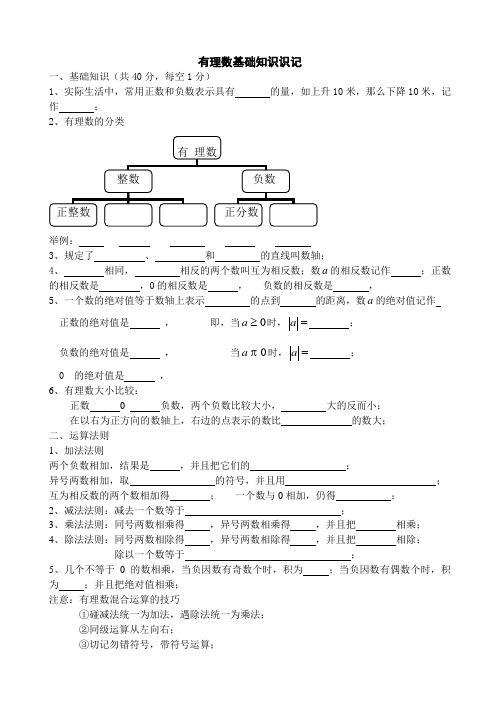
有理数基础知识识记一、基础知识(共40分,每空1分)1、实际生活中,常用正数和负数表示具有的量,如上升10米,那么下降10米,记作;2、有理数的分类{ SHAPE \* MERGEFORMAT |举例:3、规定了、和的直线叫数轴;4、相同,相反的两个数叫互为相反数;数的相反数记作;正数的相反数是,0的相反数是,负数的相反数是,5、一个数的绝对值等于数轴上表示的点到的距离,数的绝对值记作正数的绝对值是,即,当时,;负数的绝对值是,当时,;0 的绝对值是,6、有理数大小比较:正数0 负数,两个负数比较大小,大的反而小;在以右为正方向的数轴上,右边的点表示的数比的数大;二、运算法则1、加法法则两个负数相加,结果是,并且把它们的;异号两数相加,取的符号,并且用;互为相反数的两个数相加得;一个数与0相加,仍得;2、减法法则:减去一个数等于;3、乘法法则:同号两数相乘得,异号两数相乘得,并且把相乘;4、除法法则:同号两数相除得,异号两数相除得,并且把相除;除以一个数等于;5、几个不等于0的数相乘,当负因数有奇数个时,积为;当负因数有偶数个时,积为;并且把绝对值相乘;注意:有理数混合运算的技巧①碰减法统一为加法,遇除法统一为乘法;②同级运算从左向右;③切记勿错符号,带符号运算;班级:姓名:得分:1、3的绝对值是,相反数是,倒数是,(3分)的绝对值是 ,相反数是 ,倒数是 ,2、比较大小(4分):3、有理数加减法(12分)-3+(-8)= , -2.6+(+3.6)= , 0+(-12.564)= ,, =⎪⎭⎫⎝⎛-+-43)21( , ,, , ,, , ,4、有理数乘除法(12分)-6×7= , -25×(-6)= , 0×(-3.5)= , , =⨯-58415, ,, , ,, , ,5、乘方运算(8分), , , ,, , , ,6、用科学记数法表示下列各数(3分)1280000= , -21600= ,-315000= , 7、混合运算(12分)⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-⨯-⨯-23232328、(6分)已知:与互为相反数,求的值。
第1章 有理数测试题 (含答案)

七年级上册第1章有理数测试题一.选择题1.下列四个选项,其中的数不是分数的选项是()A.﹣4B.C.D.50%2.在数轴上,点A,B分别表示数a,3,点A关于原点O的对称点为点C.如果C为AB 的中点,那么a的值为()A.﹣3B.﹣1C.1D.33.在数轴上,点A表示数a,将点A向右平移4个单位长度得到点B,点B表示数b.若|a|=|b|,则a的值为()A.﹣3B.﹣2C.﹣1D.14.5G是第五代移动通信技术,5G网络下载速度可以达到每秒1300000KB以上,这意味着下载一部高清电影只需1秒.将1300000用科学记数法表示应为()A.13×105B.1.3×105C.1.3×106D.1.3×1075.四个有理数﹣2,3,0,﹣,其中最小的是()A.﹣2B.3C.0D.﹣6.下列各数中,不能和2,3,4组成比例的是()A.1B.C.2D.67.如图,点A、B、C、O在数轴上表示的数分别为a、b、c、0,且OA+OB=OC,则下列结论中:其中正确的有()①abc>0.第1页(共13页)②a(b+c)=0③a﹣c=b.④++=﹣1,A.①③④B.①②④C.②③④D.①②③④8.定义运算a⨂b=,则(﹣2)⨂4=()A.﹣1B.﹣3C.5D.39.已知实数a、b、c满足a+b+c=0,abc<0,x=++,则x2019的值为()A.1B.﹣1C.32019D.﹣3201910.如果一个正整数可以表示为两个连续奇数的立方差,则称这个正整数为“和谐数”.如:2=13﹣(﹣1)3,26=33﹣13,2和26均为和谐数.那么,不超过2019的正整数中,所有的“和谐数”之和为()A.6858B.6860C.9260D.9262二.填空题11.计算:20﹣(﹣7)+|﹣2|=.12.点A在数轴上表示的数是﹣2,AB=3,则点B表示的数为.13.港珠澳大桥是中国境内一座连接着香港、珠海和澳门的桥隧工程,工程投资总额126900000000元,126900000000用科学记数法表示为.14.用四舍五入法得到的近似数14.0精确到位,它表示原数大于或等于,而小于.第2页(共13页)15.定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为(其中k是使为奇数的正整数)并且运算重复进行,例如,n=66时,其“C运算”如下:若n=26,则第2019次“C运算”的结果是.三.解答题16.用简便方法计算:(1)23.23×47+46.46×30﹣7×23.23;(2).17.已知ab2>0,a+b=0,且|a|=2,求|a﹣|+(b﹣1)2的值.第3页(共13页)18.已知a,b,c在数轴上的位置如图所示,所对应的点分别为A、B、C.(1)在数轴上表示﹣1的点与表示3的点之间的距离为;由此可得点A、B之间的距离为;(2)化简:﹣|a+b|+2|c﹣b|﹣|b﹣a|;(3)若c2=4,﹣b的倒数是它本身,a的绝对值的相反数是﹣2,M是数轴上表示x的一点,且|x﹣a|+|x﹣b|+|x﹣c|=20,求x所表示的数.19.出租车司机小王国庆节当天上午看阅兵式,下午的营运全是在东西走向的公路上进行的.如果向东记作“+”,向西记作“﹣”.他这天下午行车情况如下:(单位:千米:每次行车都有乘客)+8,+4,﹣10,﹣3,+6,﹣5,﹣3,+6,﹣5,+10.请回答:(1)将第几名乘客送到目的地时,小王刚好回到下午出发点?(2)小王将最后一名乘客送到目的地时,小王在下午出车的出发地的什么方向?距下午出车的出发地多远?(3)若小王的出租车每千米耗油0.3升,每升汽油6元,不计汽车的损耗,那么小王这天下午共需要多少油费?第4页(共13页)20.在学习完《有理数》后,小奇对运算产生了浓厚的兴趣,借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.(1)求2⊕(﹣1)的值;(2)求﹣3⊕(﹣4⊕)的值.第5页(共13页)参考答案一.选择题1.解:A、﹣4是分数,与要求不符;B、是分数,与要求不符;C、是无理数,不是分数,与要求相符;D、50%=是分数,与要求不符.故选:C.2.解:∵点A,B分别表示数a,3,点A关于原点O的对称点为点C.∴点C表示的数为﹣a,∵C为AB的中点,∴|a﹣(﹣a)|=|3+a|,∴2a=3+a,或﹣2a=3+a,∴a=3(舍去,因为此时点A与点B重合,则点C为AB中点,但又要与点A关于原点对称,矛盾),或a=﹣1.故选:B.3.解:∵点A表示数a,将点A向右平移4个单位长度得到点B,∴b=a+4,∵|a|=|b|,∴|a|=|a+4|,第6页(共13页)∴a=a+4或a=﹣a﹣4,当a=a+4时,无解,当a=﹣a﹣4时,a=﹣2,故选:B.4.解:将数据1300000用科学记数法可表示为:1.3×106.故选:C.5.解:四个数大小关系为﹣2<﹣<0<3,则最小的数为﹣2,故选:A.6.解:根据比例的基本性质,两内项之积等于两外项之积,A选项:1×4≠2×3,不可以组成比例;B选项:2×3=×4,两个数的积等于另外两个数的积,所以能组成比例;C选项:2×4=3×2,可以组成比例.D选项:2×6=3×4,可以组成比例.故选:A.7.解:∵c<a<0,b>0,∴abc>0,∴选项①符合题意.∵c<a<0,b>0,|a|+|b|=|c|,第7页(共13页)∴b+c<0,∴a(b+c)>0,∴选项②不符合题意.∵c<a<0,b>0,|a|+|b|=|c|,∴﹣a+b=﹣c,∴a﹣c=b,∴选项③符合题意.∵++=﹣1+1﹣1=﹣1,∴选项④符合题意.∴正确的有①③④.故选:A.8.解:根据题中的新定义得:﹣2﹣4=﹣6<1,则有(﹣2)⨂4=4﹣1=3,故选:D.9.解:已知a,b,c是有理数,a+b+c=0,abc<0,则b+c=﹣a,a+c=﹣b,a+b=﹣c,a、b、c两正一负,则++==1﹣1﹣1=﹣1.x2019=(﹣1)2019=﹣1.故选:B.第8页(共13页)10.解:由(2n+1)3﹣(2n﹣1)3=24n2+2≤2019,可得n2≤,∵和谐数为正整数,∴0≤n≤9,则在不超过2019的正整数中,所有的“和谐数”之和为13﹣(﹣1)3+33﹣13+53﹣33+…+193﹣173=193﹣(﹣1)3=6860.故选:B.二.填空题11.解:20﹣(﹣7)+|﹣2|=27+2=29故答案为:29.12.解:由题意得,AB=3,即A,B之间的距离是3个单位长度,在数轴上到A的距离是3个单位长度的点有两个,分别表示的数是﹣5或1.故答案为:﹣5或1.13.解:126900000000=1.269×1011,故答案为:1.269×1011.14.解:用四舍五入法得到的近似数14.0精确到十分位,它表示原数大于或等于13.95,而小于14.05.故答案为:十分,13.95,14.05.第9页(共13页)15.解:由题意可得,当n=26时,第一次输出的结果为:13,第二次输出的结果为:40,第三次输出的结果为:5,第四次输出的结果为:16,第五次输出的结果为:1,第六次输出的结果为:4,第七次输出的结果为:1第八次输出的结果为:4…,∵(2019﹣4)÷2=2015÷2=1007…1,∴第2019次“C运算”的结果是1,故答案为:1.三.解答题16.解:(1)23.23×47+46.46×30﹣7×23.23=23.23×47+23.23×60﹣7×23.23=23.23×(47+60﹣7)=23.23×100=2323;第10页(共13页)(2)==﹣48+18+15﹣14=﹣29.17.解:∵ab2>0,∴a>0,∵|a|=2,∴a=2,又∵a+b=0,∴b=﹣2,∴|a﹣|+(b﹣1)2=|2﹣|+(﹣2﹣1)2=1+9=10.18.解:(1)由数轴的定义得:在数轴上表示﹣1的点与表示3的点之间的距离为3﹣(﹣1)=4;点A,B之间的距离为a﹣b;故答案为:4;a﹣b;(2)由a,b,c在数轴上的位置可知:c<b<0<a,|a|>|b|,则﹣|a+b|+2|c﹣b|﹣|b﹣a|=﹣(a+b)+2(b﹣c)﹣(a﹣b)=﹣a﹣b+2b﹣2c﹣a+b =﹣第11页(共13页)2a+2b﹣2c;(3)由a,b,c在数轴上的位置可知:c<b<0<a,由c2=4得,c=﹣2或c=2(舍去),由﹣b的倒数是它本身得,﹣b•(﹣b)=1,解得b=﹣1或b=1(舍去),由a的绝对值的相反数是﹣2得,﹣|a|=﹣2,解得a=2或a=﹣2(舍去),将a=2,b=﹣1,c=﹣2代入得|x﹣2|+|x+1|+|x+2|=20,根据数轴的定义、绝对值运算分以下四部分讨论:①当x≤﹣2时,2﹣x﹣x﹣1﹣x﹣2=20,解得x=﹣7,符合题设,②当﹣2<x≤﹣1时,2﹣x﹣x﹣1+x+2=20,解得x=﹣17,不符题设,舍去,③当﹣1<x≤2时,2﹣x+x+1+x+2=20,解得x=15,不符题设,舍去,④当x>2时,x﹣2+x+1+x+2=20,解得,符合题设,综上,x所表示的数为﹣3或.19.解:(1)8+4=12,12﹣10=2,2﹣3=﹣1,﹣1+6=5,第12页(共13页)5﹣5=0,∴将第6名乘客送到目的地时,小王刚好回到下午出发点;(2)+8+4﹣10﹣3+6﹣5﹣3+6﹣5+10=8.∴小王在下午出车的出发地的东边,距下午出车的出发地8km.(3)|+8|+|+4|+|﹣10|+|﹣3|+|+6|+|﹣5|+|﹣3|+|+6|+|﹣5|+|+10|=60.60×0.3×6=108元.∴小王这天下午共需要108元油费.20.解:(1)根据题中的新定义得:原式=2×(﹣1)+2×2=﹣2+4=2;(2)根据题中的新定义得:原式=﹣3⊕[﹣4×+2×(﹣4)]=﹣3⊕(﹣10)=30﹣6=24.第13页(共13页)。
有理数测试题

有理数测试题一、选择题1、下列说法正确的是( )A 整数就是正整数和负整数B 负整数的相反数就是非负整数C 有理数中不是负数就是正数D 零是自然数,但不是正整数2.下列各图中,是数轴的是( ) A.-1 0 1 -1 0 1 3.下列个组数中,数值相等的是( )A 32和23 ;B -23和(-2)3C -32和(-3)2 ;D —(3×2)2和-3×224.下列四组有理数的大小比较正确的是( )A. —32 =(—3)2B. -->-+||||11C. —(—2)= —2-D. 43->54- 5、下列各对数中,数值相等的是( )A -27与(-2)7B -32与(-3)2C -3×23与-32×2 D ―(―3)2与―(―2)36.a,b,c 三个数在数轴上的位置如图所示,则下列结论中错误的是 ( ) (A)a+b<0 (B)a+c<0(C)a -b>0 (D)b -7.下列算式正确的是( );A 、—32=9 ;B 、1441=-÷-)()( ; C 、1682-=-)(;D 、325-=---)( 8.下列计算正确的是( )(A )1313÷= (B )-2-2=0 (C )10111-=-() (D ) (5)(3)15-⨯-=- 9.下列各对数中,不是相反数的是( )A +(-3)与 –[-(-3)]B 41-与4(1)-C -(-8)与 -|-8 |D -5.2与-[+(-5.2)]1.在下列各数 :()2+-,23-,315231200124------,)(,,)(中,负数有( )个。
2、在-5,-9,-3.5,-0.01,-2,-212各数中,最大的数是( ) 3. 平方等于16的数是 ( )4、若其中至少有一个正数的5个有理数的积是负数,这五个因数中有( )个正数。
5、绝对值大于或等于1,而小于4的所有的正整数的和是( )6、比-7.1大,而比1小的整数的个数是( )7、在数轴上,a 表示的点在b 表示的点的右边,且6,3a b ==,则a b -的值为( ) 8、2003年5月19日,国家邮政局特别发行万众一心,抗击“非典”邮票,收入全部捐赠给卫生部门用以支持抗击“非典”斗争,其邮票发行为12050000枚,用科学记数法表示正确的是( ) 9、有这样5个数:-3,-5 , 0 , 3 ,41从中取出2个数,这2个数的乘积最小值是( ) 10、如果数轴上的点A 对应有理数为-2,那么与A 点相距3个单位长度的点所对应的有理数为___________。
有理数1-3节10分钟小测

比0小的数测试班级姓名1.如果收入100元记作+100元,那么支出180元记作___________;如果电梯上升了两层记作+2,那么-3表示电梯__________________。
2.某校初一年级举行乒乓球比赛,一班获胜2局记作+2,二班失败3局记作_________,三班不胜不败记作_______.3.下列各数中既不是正数又不是负数的是()A.-1 B. -3 C.-0.13 D.04. -206不是()A.有理数 B.负数 C.整数 D.自然数5.既是分数,又是正数的是()A.+5 B.-514C.0 D.83106.下列说法正确的是()A.有理数是指整数、分数、正有理数、零、负有理数这五类数B.有理数不是正数就是负数C.有理数不是整数就是分数; D.以上说法都正确7.一潜水艇所在的高度为-100米,如果它再下潜20米,则高度是_______,如果在原来的位置上再上升20米,则高度是________.8.判断:①所有整数都是正数;()②所有正数都是整数:()③奇数都是正数;()④分数是有理数:()9.把下列各数填入相应的大括号内:-13,2,0, 3.14,+27,,-15%,-112,227.正数集合{ …},负数集合{ …},整数集合{ …},分数集合{ …},非负整数集合{ …}.10.如果用m表示一个有理数,那么-m是()A.负数 B.正数 C.零 D.以上答案都有可能对班级 姓名1. 如图所示的图形为四位同学画的数轴,其中正确的是( )2. 如图所示,点M 表示的数是( )A. 2.5B. -15.C. -25.D. 1.53. 下列说法正确的是( )A. 有原点、正方向的直线是数轴B. 数轴上两个不同的点可以表示同一个有理数C. 有些有理数不能在数轴上表示出来D. 任何一个有理数都可以用数轴上的点表示4. 下列各组数中,大小关系正确的是( )A. -<-<-752B. ->->752C. -<-<-725D. ->->-2755. 数轴上点M 到原点的距离是5,则点M 表示的数是( )A. 5B. -5C. 5或-5D. 不能确定6. 在数轴上表示-206315,,,.的点中,在原点右边的点有( )A. 0个B. 1个C. 2个D. 3个7.在数轴上表示下列各数,并用“<”连接起来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学
6.在数43,-1,0,3.14,-412,-0.02中, (1)正数:__43_,_3_.1_4___; (2)负数:_-_1_,_-_4_12_,-_0_._0_2__;
(3)整数:__-_1_,0___; (4)分数:__43_,_3_.1_4_,_-_4_12_,-_0_._0_2___.
2020七年级上册(BS) 数学
数学
第二章 有理数及其运算
第1课时 有理数
返回
数学
1.下列各数中,为负数的是( B )
A.14
B.-14
C.4ห้องสมุดไป่ตู้
D.0
返回
数学
2.若火箭发射前15 s记为-15 s,那么发射后10 s应记为( D ) A.-5 s B.+5 s C.-10 s D.+10 s
返回
返回
谢谢观看
数学
3.如果+20%表示增加20%,那么-8%表示( A ) A.减少8% B.减少20% C.增加20% D.增加8%
返回
数学
4.水库的水位高于标准水位时用正数表示,低于标准水位时用 负数表示,则0 m表示水库的水位__等__于____标准水位.(填“高 于”“等于”或“低于”)
返回
数学
5.某药品说明书上标明药品保存的温度是(20±2)℃,该药品 在__1_8_℃__~_2_2__℃___ (填温度范围)保存才合适.
