3.2020年中考模拟卷(三)(含答案)
北京市2020年中考数学模拟试卷三含答案

北京市2020年中考数学模拟试卷三一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有..一个. 1.“蛟龙号”是一艘由中国自行设计、自主集成研制的载人潜水器,也是“863”计划中的一个重大研究专项.2010年5月至7月,“蛟龙号”在中国南海中进行了多次下潜任务,其中最大下潜深度超过了7 000米.将7 000用科学记数法表示为 A .7 × 104B .7 × 103C .0.7 × 105D .70×1022.如果2350m m --=,那么代数式29().3m m m m -+的值是A .﹣5B .﹣1C .1D .53.实数a ,b ,c 在数轴上的对应点的位置如图所示,则正确的结论是A .a+c >0B . |a|<|b|C .bc>1 D. ac >0 4.如图,正五边形ABCDE ,点F 是AB 延长线上的一点,则∠CBF 的度数是A . 60°B . 72°C . 108°D . 120°5.京剧是我国的国粹,是介绍、传播中国传统艺术文化的重要媒介.在下面的四个京剧脸谱中,不是轴对称图形的是A B C D6.如图是北京地铁部分线路图.若车公庄坐标为(-3,3),崇文门站坐标为(8,-2),则雍和宫站的坐标为A.(8,6)B.(6,8)C.(-6,-8)D.(-8,-6)7.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图:根据该折线图,下列结论错误的是 A .月接待游客量逐月增加B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 8.如图,二次函数y =ax 2+bx +c (a ≠0)的图象经过点A ,B ,C .现有下面四个推断: ①抛物线开口向下; ②当x =-2时,y 取最大值;③当m <4时,关于x 的一元二次方程ax 2+bx +c =m 必有两 个不相等的实数根;④直线y=kx+c (k ≠0)经过点A ,C ,当kx+c> ax 2+bx +c 时, x 的取值范围是-4<x <0; 其中推断正确的是 (A) ①② (B) ①③ (C) ①③④ (D) ②③④二、填空题(本题共16分,每小题2分)9.如图所示的网格是正方形网格,则线段AB 和CD 的长度关系为:AB___ CD (填“>”,“<”或“=”)10.分式2xx - 有意义,则x 的取值范围是____________. 11.如图,在△ABC 中,射线AD 交BC 于点D ,BE ⊥AD 于E ,CF ⊥AD 于F ,请补充一个条件,使△BED ≌△CFD ,你补充的条件是 (填出一个即可).12.如果在多项式241a +中添加一个单项式,可使其成为一个完全平方式,那么添加的单13.如图,点A ,B ,C ,D 在⊙O 上,AC 是⊙O 的直径,∠BAC =40°,则∠D 的度数是 .(第13题图) (第14题图)14.如图,从一个边长为a 的正方形的一角上剪去一个边长为b (a>b )的正方形,则剩余(阴影)部分正好能够表示一个乘法公式,则这个乘法公式是 (用含a ,b 的等式表示).15..新能源汽车环保节能,越来越受到消费者的喜爱.某品牌新能源汽车2017年销售总额为500万元,2018年销售总额为960万元,2018年每辆车的销售价格比2017年降低1万元,2018年销售量是2017年销售量的2倍.求2018年每辆车的销售价格是多少万元?若设2018年每辆车的销售价格x 万元,则可列出方为 . 16.顾客请一位工艺师把A 、B 两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这ABCD项任务.每件原料先由徒弟完成粗加工,再由工艺师进行精加工完成制作,两件工艺品都完成后交付顾客,两件原料每道工序所需时间(单位:工作日)如下:粗加工 精加工 原料A 9 15 原料B621那么最短交货期为 工作日.三、解答题(本题共68分,第17-22题,每小题5分;第23-26题,每小题6分;第27-28题,每小题7分)解答应写出文字说明、演算步骤或证明过程. 17.下面是小元设计的“作已知角的角平分线”的尺规作图过程.已知:如图,∠AOB . 求作:∠AOB 的角平分线OP . 作法:如图,①在射线OA 上任取点C ; ②作∠ACD =∠AOB ;③以点C 为圆心CO 长为半径画圆,交射线CD 于点P ; ④作射线OP ;所以射线OP 即为所求.根据小元设计的尺规作图过程,完成以下任务. (1)补全图形; (2)完成下面的证明:证明:∵ ∠ACD =∠AOB ,∴ CD ∥OB (____________)(填推理的依据). ∴∠BOP =∠CPO . 又∵ OC=CP ,∴∠COP =∠CPO (____________)(填推理的依据). ∴∠COP =∠BOP . ∴ OP 平分∠AOB .OBA CD工 序时间原料18.计算:116cos30()|2|2-︒+ .19.解不等式组 {4(x +1)≤7x +10x −5≤x−83 ,并求该不等式组的所有非负整数解.20.已知关于x 的一元二次方程2(1)20x k x k +-+-=(1)求证:方程总有两个实数根;(2)若方程有一根为正数,求实数k 的取值范围.21.如图,在△ABD 中,∠ABD = ∠ADB ,分别以点B ,D 为圆心,AB 长为半径在BD 的右侧作弧,两弧交于点C ,连接BC ,D C 和AC ,AC 与BD 交于点O . (1)用尺规补全图形,并证明四边形ABCD 为菱形; (2)如果AB = 5,3cos 5ABD ∠=,求B D 的长.22.如图,AB 为⊙O 的直径,E 为OB 中点,过E 作AB 垂线与⊙O 交于C 、D 两点.过点C 作⊙O 的切线CF 与DB 延长线交于点F. (1)求证:CF ⊥DF (2)若OF 长.DBA23.如图,在平面直角坐标系xOy 中,一次函数y kx b =+的图象与反比例函数6y x=的图象交于点A (m ,3)和B (6-,n ),与x 轴交于点C . (1)求直线y kx b =+的表达式; (2)如果点P 在x 轴上,且S △ACP =32S △BOC ,直接写出点P 的坐标.24.费尔兹奖是国际上享有崇高荣誉的一个数学奖项,每4年评选一次,在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家,美籍华人丘成桐1982年获得费尔兹奖.为了让学生了解费尔兹奖得主的年龄情况,我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据,并对数据进行整理、描述和分析.下面给出了部分信息. a .截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如下 (数据分成5组,各组是28≤x <31,31≤x <34,34≤x <37,37≤x <40,x ≥40):Fb.如图,在a的基础上,画出扇形统计图;c.截止到2018年费尔兹奖得主获奖时的年龄在34≤x<37这一组的数据是:3635343535343435363636363435d.截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下:根据以上信息,回答下列问题:(1)依据题意,补全频数直方图;(2)31≤x<34这组的圆心角度数是度,并补全扇形统计图;(3)统计表中中位数m的值是;(4)根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征.25. 如图,点P是⌒AB所对弦AB上一动点,点Q是⌒AB与弦AB所围成的图形的内部的一定点,作射线PQ交⌒AB于点C,连接BC.已知AB=6cm,设A,P两点间的距离为x cm,P,C两点间的距离为y1cm,B,C两点间的距离为y2cm.(当点P与点A重合时,x 的值为0).小平根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小平的探究过程,请补充完整:(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y与x的几组对应值;的值是 (保留一位小数)(2)在同一平面直角坐标系xOy 中,描出补全后的表中各组数值所对应的点(x ,y 1),(x ,y 2),并画出函数y 1,y 2的图象;(3)结合函数图象,解决问题:当△BCP 为等腰三角形时,AP 的长度约为 cm .26.已知抛物线2224y x mx m =-+-,抛物线的顶点为P.(1)求点P 的纵坐标.(2)设抛物线x 轴交于A 、B 两点,1122(,),(,)A x y B x y ,21x x >.①判断AB 长是否为定值,并证明.②已知点M (0,-4),且MA≥5,求21-x x m +的取值范围.27.在△ABC 中,∠ABC =120°,线段AC 绕点A 逆时针旋转60°得到线段AD ,连接CD ,BD 交AC 于P .(1)若∠BAC =α,直接写出∠BCD 的度数 (用含α的代数式表示); (2)求AB ,BC ,BD 之间的数量关系; (3)当α=30°时,直接写出AC ,BD 的关系.28.对于平面直角坐标系xOy 中的线段MN 和点P ,给出如下定义:点A 是线段MN 上一个动点,过点A 作线段MN 的垂线l ,点P 是垂线l 上的另外一个动点.如果以点P 为旋转中心,将垂线l 沿逆时针方向旋转60°后与线段MN 有公共点,我们就称点P 是线段MN 的“关联点”.如图,M (1,2),N (4,2).(1) 在点P 1(1,3),P 2(4,0),P 3(3,2)中,线段MN 的“关联点”有 ; (2) 如果点P 在直线1y x =+上,且点P 是线段MN 的“关联点”,求点P 的横坐标x的取值范围;(3) 如果点P 在以O (1,1-)为圆心,r 为半径的⊙O 上,且点P 是线段MN 的“关联点”,直接写出⊙O半径r的取值范围.备用图答案一、选择题(本题共16分,每小题2分)二、填空题(本题共16分,每小题2分)9. < 10.2x ≠11.答案不唯一,如BD=DC ;12.答案不唯一,如4x . 13.60°14.()()22a b a b a b -=+-15.96010001x x =+ 16.42; 三、解答题(本题共68分,第17-22题,每小题5分;第23-26题,每小题6分;第27-2817.(1 (1)(2)同位角相等,两直线平行; ································································ 3 等边对等角. ·················································································· 5 18.(本小题满分5分)原式=116cos30()|2|2-︒+=622+ ..................................4分=0 ..................................5分19.(本小题满分5分)解:原不等式组为()41710,853x xxx⎧++⎪⎨--⎪⎩≤<解不等式①,得x≥2-.……………………………………1分解不等式②,得72x<.……………………………………2分∴该不等式组的解集为2-≤x<72.……………………………………3分∴该不等式组的非负整数解为0,1,2,3.……………………5分20.(本小题满分5分)解:(1)22148k k k∆=-+-+ (1)()23k=- (2)()230k-≥Q,∴方程总有两个实数根. (3)(2) ∵x=,∴11x=-,22x k=-. (4)∵方程有一个根为正数,∴20k->2k<. (5)21.(本小题满分5分)(1)补全的图形如图所示.…………1分证明:由题意可知BC = DC = AB.∵在△ABD中,=ABD ADB∠∠,∴AB = AD.∴BC = DC = AD = AB.①②∴ 四边形ABC D 为菱形. …………… 3分 (2)解:∵ 四边形ABC D 为菱形,∴ BD ⊥AC ,O B=OD . …………… 4分 在Rt △ABO 中,90AOB ∠=︒,AB =5,3cos 5ABD ∠=,∴ cos 3OB AB ABD =⋅∠=.∴ 2=6BD OB =. ………………… 5分22.(本小题满分5分) 证明:连结OC.∵AB 为⊙O 直径,CD 为弦,AB⊥CD 于E ∴CE=ED又∵OE=EB ,∠CEO=∠BED ∴△OCE ≌△BDE ∴∠OCE=∠CDB ∵CF 切⊙O 于点C ∴∠OCF=90° ∴∠ODB+∠OCF =90° ∴∠CFD=90° 即CF⊥FD.................................3分(2) ∵1,2OE OB OB OC == ∴12OE OC =∵在Rt △OEC 中,1sin 2OCE ∠= ∴∠OCE=30° ∴∠CDF=30° ∴12FC CD =.................................6分即. 在Rt △OEC中,2cos CEOC OCE===∠ 在Rt △OCF中,OF =23.(本小题满分6分)解:(1)由题意可求:m = 2,n = -1. ……………………… 2分将(2,3),B (-6,-1)带入y kx b =+,得 32,16.k b k b =+⎧⎨-=-+⎩ 解得 1,22.k b ⎧=⎪⎨⎪=⎩ ∴ 直线的解析式为122y x =+. …………………… 3分 (2)(-2,0)或(-6,0). …………………… 5分24.(本小题满分6分)(1)如图; …………………… 1分(2)31≤x <34这组的圆心角度数是 78 度, ……………………… 2分如图(画图1分,数据1分); …………………… 4分 (3)统计表中中位数m 的值是 36 ; …………………… 5分 (4)答案不唯一,如:费尔兹奖得主获奖时年龄集中在37岁至40岁.…………6分25.(本小题满分6分)(1)3.0;…………………… 1分 (2)如图;…………………… 3分(3)1.2或1.6或3.0.…………………… 6分26.(本小题满分6分) (1)2()4(,4)y x m P m =--∴-Q 即顶点P 的纵坐标为-4…………………… 2分(2)①AB 长为定值.令y=0,则22240x mx m -+-= 则2()4x m -=解得22x m x m =+=-或 AB 长为:2(2)4m m +--=…………………… 4分②当MA=5时,可求A 点坐标为(-3,0)或(3,0) ∵AB=4,∴MA=5时,m=-1或m=1 ∵214x x m m -+=+结合图象可知,21x x m -+的取值范围为…………………… 6分212115x x m x x m -+≤--+≥或27.(本小题满分7分)(1)∠BCD =120°-α.…………………… 2分 (2)解:方法一:延长BA 使AE=BC ,连接DE . ······ 3分 由(1)知△ADC 是等边三角形,∴AD=CD .∵∠DAB +∠DCB =∠DAB +∠DAE =180°, ∴∠DAB =∠DAE .∴△ADE ≌△CDB . ···················· 5分 ∴BD=BE .∴BD=AB+BC . ·························· 5分方法二:延长AB 使AF=BC ,连接CF . ······ 3分∠BDC =∠ADE . ∵∠ABC =120°, ∴∠CBF =60°.∴△BCF 是等边三角形. ∴BC=CF .∵∠DCA =∠BCF =60°,∴∠DCA +∠ACB =∠BCF +∠ACB . 即∠DCB =∠ACF . ∵CA=CD ,∴△ACF ≌△DCB .····················· 4分 ∴BD=AF .∴BD=AB+BC . ·························· 5分(3)AC ,BD的数量关系是:AC =;……………………6分 位置关系是:AC ⊥BD 于点P .……………………7分28.(本小题满分7分)(1)P 1和P 3; ………………………… 2分 (2)线段MN 的“关联点”P 的位置如图所示,∵ 直线1y x =+经过点M (1,2),∴ x ≥1. ……………………… 3分 设直线1y x =+与P 4N 交于点A .过点A 作AB ⊥MN 于B ,延长AB 交x 轴于C .由题意易知,在△AMN 中,MN = 3,∠AMN = 45°,∠ANM = 30°. 设AB = MB = a ,∴ tanAB ANM BN ∠=,即tan303a a︒=-,解得a =………………………4分 ∴ 点A 的横坐标为11x a =++=∴x …………………………5分 综上1x ≤ …………………… 6分 (33r ≤ ……………………… 7分说明:若考生的解法与给出的解法不同,正确者可参照评分参考相应给分。
2020年初三中考物理三模试卷(有答案)

中考物理模拟试题(含答案)一、选择题:(每题2分,共24分)1.(2分)如图是科学家最新研制的薄片扬声器,外形像一张金属片,但在音色上却可以媲美专业的发声设备,目前已经应用在手机、家庭影院等方面。
关于薄片扬声器说法错误的是()A.薄片扬声器体积可以做的很小,所以应用前景很广泛B.正常情况下我们听到薄片扬声器发出的声音,是通过空气传声的C.薄片扬声器的声音是由电流发出的,不是振动产生的D.薄片扬声器发声时,消耗的电能有一部分转化为声能2.(2分)百年老字号“绿杨春茶”是扬州市的特色农业品牌。
下列对于沏茶和品茶过程中情境的解释,正确的是()A.沏茶时,杯内水面上方出现白雾,这是汽化现象B.沏茶时,透过玻璃杯的外壁会看见茶叶好像放大了,这是光的反射现象C.品茶时茶香四溢,这是一种升华现象D.品茶时茶香四溢,这说明了分子在不停地做无规则运动3.(2分)下列作图,错误的是()A.平面镜成像B.凸透镜对光线的作用C.静止在水面上的物体的受力D.磁体的磁场4.(2分)下列数据最接近实际的是()A.一枚1元硬币的直径大约2cmB.通常情况下,健康人的心率约为每分钟1次C.通常情况下酒精的凝固点大约是0℃D.家用电冰箱的正常工作电流约为5A5.(2分)为了揭示大自然的奥秘,无数科学家进行了不懈的探索。
下列说法正确的是()A.谱线红移现象说明我们观察到的天体在远离我们而去B.宇宙是一个有层次的天体结构,光年是天文学中的常用时间单位C.中子的发现,让人们认识到原子还可以再分D.大自然中无论是宏观的天体还是微观的粒子都在不停地运动,其中太阳是宇宙的中心6.(2分)关于光现象与形成原因的对应关系,下列说法正确的是()A.手影游戏﹣﹣光的折射B.镜花水月﹣﹣光的漫反射C.海市蜃楼﹣﹣光的反射D.小孔成像﹣﹣光沿直线传播7.(2分)关于温度、热量和内能,下列说法正确的是()A.早晨去富春茶社吃早茶,我们不敢大口咬热气腾腾的汤包,是因为汤包含有的热量多B.生活中有时内能小的物体也可以将热量传递给内能大的物体C.从冰箱中取出的正在熔化的冰块,内能不断增大,温度也不断升高D.五一假期,小明一家驱车到京华城时,汽油机做功冲程中,燃气的内能不断增大8.(2分)如图,重为500N的小科沿着竖直的直杆匀速上爬,此阶段他受到的摩擦力为f1;小科停在A处稍作休息,此阶段他受到的摩擦力为f2;之后沿杆匀速下滑,此阶段他受到的摩擦力为f3.下列说法正确的是()A.f1>500N,方向竖直向下B.f2=500N,方向竖直向下C.f3<500N,方向竖直向上D.f1=f2=f3,方向都竖直向上9.(2分)“跨越时空,漫游地球”离不开电磁波和能源,下列相关认识,正确的是()A.“嫦娥四号”探测器能从月球上发回月背的影像图;说明电磁波能在真空中传播B.我国5G技术世界领先,该技术采用无线电波传输信息,但无线电波不是电磁波C.太阳是人类的“能源之母”,煤、石油、风能、核能等能源都是间接来自太阳能D.能量在转化或转移过程中总量保持不变,所以不必担心能源危机10.(2分)地磅工作时,重物越重,电表的示数就越大。
2020年初三中考物理三模试卷(含解析)

中考物理一模试卷及解析一、选择题(每小题3分,共60分,每小题只有一个选项符合题意)1.(3分)下列关于正常成年人的估测,最接近实际的是()A.体积约为0.5立方米B.双脚站立时对地面的压强约为500帕C.正常的步行速度约为1.3千米/小时D.平静时心脏每分钟跳动约75次2.(3分)以下事例在改变物体内能的方式上与其他三项不同的是()A.冬天,通过搓手来取暖B.划火柴时,火柴燃烧C.把袋装牛奶放在热水中加热D.铁丝反复弯折,弯折处变热3.(3分)甲、乙、丙三辆车一起以各自的速度向东匀速直线行驶,t1时刻甲乙丙的位置如图所示,甲乙、乙丙之间的距离均为1千米。
行驶一段时间后,t2时刻乙在甲后方800米的位置,丙在乙后方1200米的位置,则在t1和t2这段时间内()A.以甲车为参照物,丙车向西运动B.以甲车为参照物,丙车向东运动C.以乙车为参照物,甲车向东运动D.以乙车为参照物,甲车向西运动4.(3分)小金用水平拉力F将一物体在草地上匀速移动了一段距离,所做的功为W1,后用同样大小的水平拉力F将该物体在水泥地上加速移动了同样的距离,所做的功为W2,则()A.W1=W2B.W1<W2C.W1>W2D.无法比较5.(3分)甲、乙两个相同规格的烧杯,分别装有等质量的食盐水和清水,将两个体积相同的实心铅块用细线拴住浸没在液体中(不接触烧杯底部),甲、乙两个烧杯对桌面的压力大小关系为()A.F甲大于F乙B.F甲小于F乙C.F甲等于F乙D.无法确定6.(3分)将一个木块从粗糙的斜面A点静止释放,下滑到B点时的速度为v,则从A点到B点的下滑过程中()A.木块的机械能守恒B.木块动能不变,重力势能减少C.木块动能的增加量等于重力势能的减少量D.木块动能的增加量小于重力势能的减少量7.(3分)水是生命之源,自然界中有许多科学现象与水相关,下列描述正确的是()A.甲图:桥在平静的水面成像,是由于光的折射形成的B.乙图:水电解产生氢气和氧气,因此水是由氢气和氧气组成的C.丙图:利用该实验能测量出土壤中水的体积分数D.丁图:比较A种子和B种子可以探究水分对种子萌发的影响二、填空题(本大题共26分)8.(4分)如图是小金设计的甲醛污染的检测电路,当甲醛浓度高于0.1毫克/立方米时,电铃发声报警,图中气敏电阻R1的阻值随甲醛浓度的增大而减小。
2020年中考英语模拟考试试卷(三模有答案)

2020年初中学业水平模拟考试(三模)英语(试题卷)温馨提示:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4. 试题卷由听力技能、阅读技能、知识运用和写作技能四个部分组成,共75个小题,其中听力材料读两遍。
第一部分听力技能(共两节,满分20分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上,并在答题卡上将该编号字母涂黑。
第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
1. What is the woman?A B C2. What animal does the boy want to see first?A B C3. How will Paul go to Hong Kong?A B C4. What was the boy doing when Linda called him?A B C5. How was the weather yesterday?A B C第二节(共15小题;每小题1分,满分15分)听下面6段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
听第6段材料,回答第6、7题。
6. Where does the man like to go?A. To the farm.B. To a beach.C. To his parents’ home.7. What does the woman prefer to do?A. Feed the animals.B. Pick fresh fruit.C. Go swimming.听第7段材料,回答第8、9题。
2020年中考数学模拟试卷(三)(含解析)
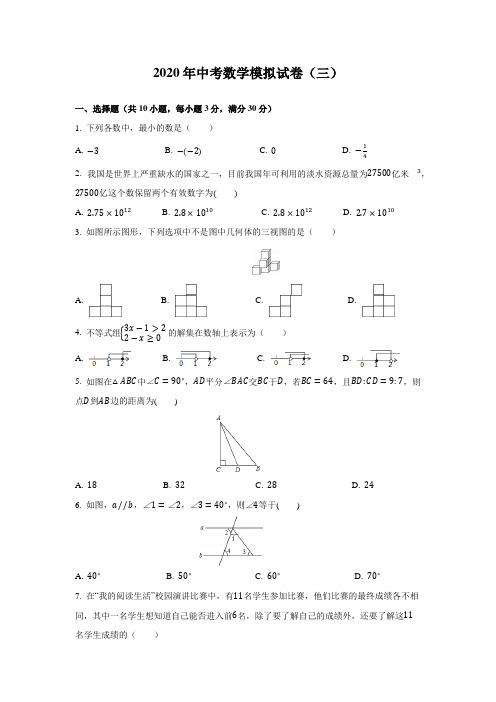
2020年中考数学模拟试卷(三)一、选择题(共10小题,每小题3分,满分30分)1. 下列各数中,最小的数是( )A. −3B. −(−2)C. 0D. −14 2. 我国是世界上严重缺水的国家之一,目前我国年可利用的淡水资源总量为27500亿米3,27500亿这个数保留两个有效数字为( )A. 2.75×1012B. 2.8×1010C. 2.8×1012D. 2.7×1010 3. 如图所示图形,下列选项中不是图中几何体的三视图的是( )A. B. C. D.4. 不等式组{3x −1>22−x ≥0的解集在数轴上表示为( ) A. B. C. D. 5. 如图在△ABC 中∠C =90∘,AD 平分∠BAC 交BC 于D ,若BC =64,且BD:CD =9:7,则点D 到AB 边的距离为( )A. 18B. 32C. 28D. 24 6. 如图,a // b ,∠1=∠2,∠3=40∘,则∠4等于( )A. 40∘B. 50∘C. 60∘D. 70∘ 7. 在“我的阅读生活”校园演讲比赛中,有11名学生参加比赛,他们比赛的最终成绩各不相同,其中一名学生想知道自己能否进入前6名,除了要了解自己的成绩外,还要了解这11名学生成绩的( )A. 众数B. 方差C. 平均数D. 中位数8. 如图,在ABCD中,用直尺和圆规作∠BAD的平分线AC交BC于点E.若∠BCD=80∘,则∠AEC的度数为()A. 80∘B. 100∘C. 120∘D. 140∘9. 现有三张质地大小完全相同的卡片,上面分别标有数字−2,−1,1,把卡片背面朝上洗匀,从中任意抽取一张卡片,记下数字后放回,洗匀,再任意抽取一张卡片,则第一次抽取的卡片上的数字大于第二次抽取的卡片上的数字的概率是()A. 13B. 12C. 23D. 4910. 如图,将边长为2cm的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为()A. (√3,−1)B. (2, −1)C. (1, −√3)D. (−1, √3)二、填空题(共5小题,每小题3分,满分15分)11. √273−|−1|=________.12. 关于x的一元二次方程x2−6x+b=0有两个不相等的实数根,则实数b的取值范围是________.13. 若关于x的方程x2−2ax+a−2=0的一个实数根为x1≥1,另一个实数根x2≤−1,则抛物线y=−x2+2ax+2−a的顶点到x轴距离的最小值是________169.14. 如图,在Rt△AOB中,∠AOB=90∘,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90∘后得到Rt△FOE,将线段EF绕点E逆时针旋转90∘后得到线段ED,分別以O、E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分的面积是________.15. 如图,在菱形ABCD中,AB=√3,∠B=120∘,点E是AD边上的一个动点(不与A,D重合),EF // AB交BC于点F,点G在CD上,DG=DE.若△EFG是等腰三角形,则DE的长为________.三、解答题(共8小题,满分0分)16. 先化简,再求值:(2a+1−1a)÷2a2b−2ba2+2a+1,其中a=√3+1,b=√3−1.17. 某小学开展寒假争星活动,学生可以从“自理星”、“读书星”、“健康星”、“孝敬星”等中选一个项目参加争星竞选,根据该校一年级某班学生的“争星”报名情况,绘制成了如下两幅不完整的统计图,请根据图中信息回答下列问题:(1)参加调查的学生共有________人.(2)将条形统计图补充完整;(3)请计算扇形统计图中“读书星”对应的扇形圆心角度数;(4)根据调查结果,试估计该小学全校3600名学生中争当“健康星”的学生人数.18. 如图,在Rt△ABC中,∠ACB=90∘,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.(1)求证:BE=EC(2)填空:①若∠B=30∘,AC=2√3,则DB=________;②当∠B =________度时,以O ,D ,E ,C 为顶点的四边形是正方形.19. 4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A ,小江抓着风筝线的一端站在D 处,他从牵引端E 测得风筝A 的仰角为67∘,同一时刻小芸在附近一座距地面30米高(BC =30米)的居民楼顶B 处测得风筝A 的仰角是45∘,已知小江与居民楼的距离CD =40米,牵引端距地面高度DE =1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67∘≈1213,cos67∘≈513,tan67∘≈125,√2≈1.414).20. 如图,一次函数y =−12x +52的图象与反比例函数y =kx(k >0)的图象交于A ,B 两点,过A 点作x 轴的垂线,垂足为M ,△AOM 面积为1.(1)求反比例函数的解析式;(2)在y 轴上求一点P ,使PA +PB 的值最小,并求出其最小值和P 点坐标.21. 一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:(1)甲、乙两组工作一天,商店各应付多少钱?(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?(3)装修完毕第二天即可正常营业,且每天仍可盈利200元(即装修前后每天盈利不变),你认为商店应如何安排施工更有利?说说你的理由.(可用(1)(2)问的条件及结论) 22. (1)观察猜想如图①,点B 、A 、C 在同一条直线上,DB ⊥BC ,EC ⊥BC 且∠DAE =90∘,AD =AE ,则BC 、BD 、CE 之间的数量关系为________;(2)问题解决如图②,在Rt△ABC中,∠ABC=90∘,CB=4,AB=2,以AC为直角边向外作等腰Rt△DAC,连结BD,求BD的长;(3)拓展延伸如图③,在四边形ABCD中,∠ABC=∠ADC=90∘,CB=4,AB=2,DC=DA,请直接写出BD的长.23. 已知:直线y=12x−3与x轴、y轴分别交于点A、B,抛物线y=13x2+bx+c经过点A、B,且交x轴于点C.(1)求抛物线的解析式;(2)点P为抛物线上一点,且点P在AB的下方,设点P的横坐标为m.①试求当m为何值时,△PAB的面积最大;②当△PAB的面积最大时,过点P作x轴的垂线PD,垂足为点D,问在直线PD上是否存在点Q,使△QBC为直角三角形?若存在,直接写出符合条件的Q的坐标,若不存在,请说明理由.参考答案1. A2. C3. B4.5. C6. D7. D8. D9. A10.11. 212. b<913. 169.14. 10−π415. 1或√3316. 解:原式=2a−(a+1)a(a+1)⋅(a+1)22b(a2+1)=a−1a(a+1)⋅(a+1)22b(a+1)(a−1)=12ab,当a=√3+1,b=√3−1时,原式=2×(√3+1)(√3−1)=14.17. 50“自理星”的人数为50×30%=15人,补全图形如下:=72∘;扇形统计图中“读书星”对应的扇形圆心角度数为360∘×10503600×12=864,50答:该小学全校3600名学生中争当“健康星”的学生人数为864人.18. ②当∠B=45∘时,四边形ODEC是正方形,理由如下:∵∠ACB=90∘,∴∠A=45∘,∵OA=OD,∴∠ADO=45∘,∴∠AOD=90∘,∴∠DOC=90∘,∵∠ODE=90∘,∴四边形DECO是矩形,∵OD=OC,∴矩形DECO是正方形.故答案为:45.3√3,4519. 如图,作AM⊥CD于M,作BF⊥AM于F,EH⊥AM于H.∵∠ABF=45∘,∠AFB=90∘,∴AF=BF,设AF=BF=x,则CM=BF=x,DM=HE=40−x,AH=x+30−1.5=x+28.5,在Rt△AHE中,tan67∘=AHHE,∴125=x+28.540−x,解得x=19.9m.∴AM=19.9+30=49.9m.∴风筝距地面的高度49.9m.20. 解:(1)设A点坐标为A(a,ka ),则AM=ka,OM=a,∵ △AOM的面积为1,∴12OM⋅AM=1,即12a⋅ka=1,∴ k=2,∴反比例函数的解析式为y=2x;(2)如图,取B点关于y轴的对称点C,连接AC,与y轴交于点P,此时PA+PB的值最小= PA+PC=AC.联立方程组{y =2x y =−12x +52, 解得{x 1=1y 1=2,{x 2=4y 2=12, ∴ A (1,2),B (4,12) ∴ B 点关于y 轴的对称点C 的坐标为C (−4,12), 设直线AC 的解析式为 y =mx +n ,将A (1,2),C (−4,12) 代入得:{m +n =2−4m +n =12 ,解得{m =310n =1710. ∴ 直线AC 的解析式为 y =310x +1710, 当 x =0时, y =1710,∴ P 点的坐标为 P (0,1710), ∴ PA +PB 的最小值为 AC = √(1+4)2+(2−12)2=√1092. 21. 设甲组工作一天商店应付x 元,乙组工作一天商店应付y 元,根据题意得:{8x +8y =35206x +12y =3480, 解得:{x =300y =140. 答:甲组工作一天商店应付300元,乙组工作一天商店应付140元. 单独请甲组所需费用为:300×12=3600(元),单独请乙组所需费用为:140×24=3360(元),∵ 3600>3360,∴ 单独请乙组所需费用最少.商店请甲乙两组同时装修,才更有利,理由如下:单独请甲组完成,损失钱数为:200×12+3600=6000(元), 单独请乙组完成,损失钱数为:200×24+3360=8160(元), 请甲乙两组同时完成,损失钱数为:200×8+3520=5120(元).∵ 8160>6000>5120,∴ 商店请甲乙两组同时装修,才更有利.22. (1)BC =BD +CE(2)如图②,过点D 作DE ⊥AB 交BA 的延长线于点E ,易证△ABC ≅△DEA ,∴ DE =AB =2,AE =BC =4,∴ BE =AB +AE =6,在Rt △BDE 中,由勾股定理得BD =√62+22=2√10;(3)如图③,过D 作DE ⊥BC 于E ,作DF ⊥AB 于F , 同理得:△CED ≅△AFD ,∴ CE =AF ,ED =DF ,设AF =x ,DF =y ,则{x +y =42+x =y ,解得:{x =1y =3, ∴ BF =2+1=3,DF =3,由勾股定理得:BD =√32+32=3√2.23. ∵ 直线y =12x −3与x 轴、y 轴分别交于点A 、B , ∴ 点A 的坐标为(6, 0),点B 的坐标为(0, −3). 将A(6, 0)、B(0, −3)代入y =13x 2+bx +c ,得:{c =−312+6b +c =0 ,解得:{b =−32c =−3, ∴ 抛物线的解析式为y =13x 2−32x −3.①过点P 作PD ⊥x 轴于D ,交AB 于点E ,如图1所示. 设点P 的横坐标为m ,则点P 的坐标为(m, 13m 2−32m −3),点E 的坐标为(m, 12m −3), ∴ PE =12m −3−(13m 2−32m −3)=−13m 2+2m , ∴ S △PAB =12×PE ×(AD +DO)=12×(−13m 2+2m)×6=−m 2+6m =−(m −3)2+9, ∴ 当m =3时,△PAB 的面积最大,最大值是9. ②当y =0时,有13x 2−32x −3=0, 解得:x 1=−32,x 2=6,∴ 点C 的坐标为(−32, 0). 设点Q 的坐标为(3, y),则CQ 2=(92)2+y 2,BC 2=9+94,BQ 2=9+(y +3)2. 当∠QCB =90∘时,有CQ 2+BC 2=BQ 2, 即(92)2+y 2+9+94=9+(y +3)2,解得:y =94;当∠CBQ =90∘时,有BC 2+BQ 2=CQ 2, 即9+94+9+(y +3)2=(92)2+y 2,解得:y =−32;当∠CQB =90∘时,有BQ 2+CQ 2=BC 2, 即(92)2+y 2+9+(y +3)2=9+94,方程无解.综上所示:在直线PD 上存在点Q(3, 94)或(3, −32),使△QBC 为直角三角形.。
安徽省2020年九年级中考语文模拟卷三附答案解析

安徽省2020年九年级中考语文模拟卷三时间:150分钟满分:150(含卷面书写5分)一、语文积累与综合运用(35分)1.默写。
(10分)(1)了却君王天下事,。
(辛弃疾《破阵子》)(2),长河落日圆。
(王维《使至塞上》)(3)东风不与周郎便,。
(杜牧《赤壁》)(4),星河欲转千帆舞。
(李清照《渔家傲》)(5)《次北固山下》描写江水浩渺、视野开阔的景色的诗句是“,。
”(6)第五次反围剿失败后,毛泽东在遵义会议上临危受命,接管中央军事工作,这和《出师表》中诸葛亮“,”的境况何其相似。
(7)郦道元在《三峡》中,用江船的日行千里侧面衬托江流之急的句子是“,。
”2.请运用所积累的知识,完成(1)—(4)题。
(12分)但是逮捕总司令却流了血。
蒋介石下榻在十英里外著名温泉胜地临潼,把所有其他客人都驱赶一空。
张少帅的卫队长、26岁的孙铭九上尉午夜前往临潼,他在半路上带了200名东北军,清晨3点钟开车到临潼郊外。
他们在那里等到5点钟,第一辆卡车载着15个人开到宾馆门口,被岗哨喝止,就开起火来。
东北军这批先遣人员的增援部队马上开到,孙上尉率部进攻总司令住处。
警卫人员猝不及防,没有久战,不过有足够时间让吃惊的总司令逃跑。
孙上尉到蒋介石的寝室时,他已经逃跑了。
孙率部搜索,爬上了宾馆后面的白雪掩盖、岩石嶙峋的小山。
他们马上就发现了总司令的贴身仆人,接着不久就找到了总司令本人。
他只穿着睡衣睡裤,外面披着一件长袍,赤裸的手脚在急急忙忙爬上山时给划破了,嘴里也没有假牙,身子索索地在寒冷中哆嗦着,躲在一块大岩石旁的小洞里——这块大岩石是长城建筑者秦始皇陵寝所在的标志。
(1)以上文段选自《》,作者是。
(2分)(2)“嶙峋”在句子中的意思是:。
(2分)(3)画线句子运用了描写,生动形象地表现了蒋介石此时的状态。
(2分)(4)请结合原著回答:①文段中描写的是哪一历史事件?②这一事件的领导者是谁?③说说这一事件结果的历史意义。
(6分)3.九(1)班开展以“发展地方戏曲,弘扬传统文化”为主题的综合实践活动,下面是活动中的一些问题,请你参与解决。
2020年初三中考物理三模试卷及答案

初三中考物理一模试卷(有答案)一、选择题(本题共14小题,每小题2分,共28分)意:第1~11小题中,每题只有一个选项正确1.(2分)我们很容易分辨出熟人的声音,主要根据声音的()A.响度B.音色C.音调D.传播速度2.(2分)下列实例中,属于通过热传递改变物体内能的是()A.搓手会发热B.铁锤敲打铁钉,铁钉变热C.钻木取火D.勺子放热汤里,勺子变热3.(2分)小明同在探究凸透镜成像规律的实验中,光屏上得到发光体清晰的像,但他不小心用手指指尖触摸到了凸透镜,则光屏上会出现的情形中正确的是()A.光屏上有指尖的像B.光屏上有指尖的影子C.光屏上不会出现指尖的像D.以上都有可能出现4.(2分)下列工具中主要不是利用大气压工作的是()A.活塞式抽水机B.卫生间里的塑料吸盘C.医生用针筒把药水推入病人肌肉中D.饮料吸管5.(2分)下列四幅图中能说明电动机工作原理的是()A.B.C.D.6.(2分)小明在湖边树荫下乘凉,想到了所学的物理知识。
其中合理的是()A.看到池水“变”浅,是光的反射引起的B.水中出现树的倒影,水中的“树”比岸上的树小C.阳光中的紫外线可以灭菌,也可以用来遥控D.树下的圆形光斑,是光沿直线传播形成的7.(2分)关于物体的内能,下列说法中正确的是()A.物体的内能增加,一定是从外界吸收了热量B.0℃的冰熔化成0℃的水内能变大C.物体吸收热量,它的温度一定会升高D.热量总是从内能大的物体向内能小的物体转移8.(2分)如图所示,在光滑的水平台面上,一轻弹簧左端固定,右端连接一金属小球,O 点是弹簧保持原长时小球的位置。
压缩弹簧使小球至A位置,然后释放小球,小球就在AB间做往复运动(已知AO=OB)。
小球从A位置运动到B位置的过程中,下列判断正确的是()A.小球的动能不断增加B.弹簧的弹性势先变小后变大C.小球运动到O点时的动能与此时弹簧的弹性势能相等D.小球的动能先变小后变大9.(2分)如图所示做法中符合安全用电原则的是()A.导线绝缘层破损继续使用B.湿衣服晾晒在电线上C.电动机的金属外壳不接地线D.触电后立即切断电源10.(2分)如图所示,A、B两物块叠放在水平桌面上保持静止。
2020年中考物理三模试卷(有答案)

初三中考物理一模试卷(含解析)一、选择题:本题共16小题,每小题2分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2分)在科学探索的道路上,有众多的科学巨人披荆斩棘,铺路架桥,为后人留下了丰硕的知识园地、科学的探究方法及不朽的科学精神。
下列关于物理学家的说法正确的是()A.亚里士多德提出力不是维持物体运动的原因B.牛顿提出了相对论学说C.马德堡最先测出了大气压强值D.欧姆揭示电流与电压和电阻之间的关系2.(2分)厦门是全国文明城市,公共场所不要大声喧哗。
这里的“大声”是指声音的()A.频率B.响度C.音调D.音色3.(2分)用3D打印技术可以打印钛合金眼镜架。
在高能激光的作用下,钛合金粉末吸收热量变成液态,再定型成为镜架。
在此过程中发生的物态变化是()A.熔化和凝固B.升华和凝华C.汽化和液化D.液化和凝固4.(2分)对于密度公式ρ=的正确理解为()A.某种物质的密度ρ跟其质量m成正比B.某种物质的质量m跟其体积V成反比C.某种物质的密度ρ跟其体积V成反比D.密度是物质的一种特性,与其质量、体积无关5.(2分)如图所示的四种光现象中,属于光的反射现象的是()A.透镜下的花B.水中倒影C.笔“折断”了D.海市蜃楼6.(2分)如图所示的机械中,同属于一类杠杆的是()A.①④B.②③C.①③D.②④7.(2分)如图所示的简单机械,忽略杠杆和滑轮的自重及它们与轴之间的摩擦,当提起相同重物时,最省力的是()A.B.C.D.8.(2分)超市里,小明用水平方向的力,推着购物车在水平地面上做匀速直线运动,下列说法正确的是()A.购物车对地面的压力与地面对购物车的支持力是一对平衡力B.购物车所受的推力与地面对购物车的摩擦力是一对平衡力C.购物车所受的重力与购物车对地面的压力是一对相互作用力D.购物车对小明的力与地面对小明的摩擦力是一对相互作用力9.(2分)“歼﹣20”作为我国新一代隐形战机,改进了形状与材料方面的技术,能有效避开雷达的探测,如图所示为其在珠海航展上的首次公开亮相。
2020年中考第三次模拟考试语文试卷(word版,含答案)

2020年中考第三次模拟考试语文试卷(时间:150分钟满分:150分,其中卷面分5分)一、语文积累与运用(35分)1.默写。
(10分)(1)城阙辅三秦,____________。
(王勃《送杜少府之任蜀州》)(2)____________,归雁入胡天。
(王维《使至塞上》)(3)角声满天秋色里,____________。
(李贺《雁门太守行》)(4)____________,天与云与山与水,上下一白。
(张岱《湖心亭看雪》)(5)崔颍在《黄鹤楼》中运用对偶的修辞手法,描绘出登楼所见的明丽之景的句子是“_______________,______________”。
(6)勇扛“文以明道”大旗的“唐宋八大家”在诗词创作方面也独具一格。
登高望远,“_______________,______________”尽显一展抱负的雄心壮志;怀乡忆亲,“____________,______________”抒发对亲人的美好祝愿。
(请结合题干,从《登飞来峰》《望岳》《江城子·密州出猎》《水调歌头》四首诗词中选择符合要求的句子作答)2.请运用所积累的知识,完成(1)~(4)题。
(12分)“胡扯!为了薪金,大多数自由人对什么都会屈服。
因此,只说你自己吧,不要妄谈普遍现象,你对此一无所知。
尽管你的回答并不确切,但因为你回答了我,我在心里同你握手言好,同样还因为你回答的内容和回答的态度。
这种态度担率诚恳,并不常见。
不,恰恰相反,矫揉造作或者冷漠无情,或者对你的意思愚蠢而粗俗地加以误解,常常是坦率正直所得到的报答。
三千个初出校门的女学生式家庭教师中,像你刚才那么回答我的不到三个。
不过我无意恭wéi你,要说你是从跟大多数人不同的模子里浇制出来的,这不是你的功劳,而是造化的圣绩。
再说我的结论毕竟下得过于匆忙。
就我所知,你也未必胜过其他人。
也许有难以容忍的缺点,抵消你不多的长处。
”(1)以上文段的作者是来自___________(国名)的__________________(人名)。
陕西省2020年中考数学模拟试卷(三)及解析

2020年陕西省中考数学模拟试卷(三)一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.(3分)9的倒数是()A.9B.C.﹣9D.2.(3分)如图所示,该几何体的俯视图是()A.B.C.D.3.(3分)下列计算正确的是()A.2x+3y=5xy B.(﹣2x2)3=﹣6x6C.3y2•(﹣y)=﹣3y2D.6y2÷2y=3y4.(3分)将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为()A.75°B.65°C.45°D.30°5.(3分)已知:点A(a,b),B(a+1,b﹣2)均在正比例函数y=kx(k≠0)的图象上,则k值为()A.﹣1B.﹣2C.﹣3D.﹣46.(3分)如图,在Rt△ABC中,∠C=30°,AB=4,D,F分别是AC,BC的中点,等腰直角三角形DEH的边DE经过点F,EH交BC于点G,且DF=2EF,则CG的长为()A.2B.2﹣1C.D.+17.(3分)直线y=﹣x+1与y=2x+a的交点在第一象限,则a的取值不可能是()A.B.﹣C.﹣D.﹣8.(3分)如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为()A.3B.C.D.49.(3分)如图,在半径为6的⊙O内有两条互相垂直的弦AB和CD,AB=8,CD=6,垂足为E,则tan∠OEA的值是()A.B.C.D.10.(3分)在平面直角坐标系中,有两条抛物线关于x轴对称,且它们的顶点相距6个单位长度,若其中一条抛物线的函数表达式为y=﹣x2+4x+m,则m的值是()A.1或7B.﹣1或7C.1或﹣7D.﹣1或﹣7二、填空题(共4小题,每小题3分,计12分)11.(3分)在﹣2,,,,这5个数中,无理数有个.12.(3分)在正六边形中,其较短对角线与较长对角线的比值为.13.(3分)如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(8,4),反比例函数y=(k >0)的图象分别交边BC、AB于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是.14.(3分)如图,在正方形ABCD中,AB=4,E,F分别为BC,AD上的点,过点E,F的直线将正方形ABCD 的面积分为相等的两部分,过点A作AG⊥EF于点G,连接DG,则线段DG的最小值为.三、解答题(共11小题,计78分.解答应写出过程)15.(5分)计算:(π﹣2020)0+|1﹣|+2﹣1﹣2sin60°.16.(5分)化简:(x)17.(5分)赵凯想利用一块三角形纸片ABC裁剪一个菱形ADEF,要求一个顶点为A,顶点D在三角形的AC边上,点E在三角形的BC边上,点F在三角形的AB边上,请你利用尺规作图把这个菱形作出来.(不写作法,保留作图痕迹)18.(5分)如图,点A、E、F、C在一直线上,DE∥BF,DE=BF,AE=CF.求证:AB∥CD.19.(7分)为了给顾客提供更好的服务,某商场随机对部分顾客进行了关于“商场服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.满意度人数所占百分比非常满意1210%满意54m比较满意n40%不满意65%根据图表信息,解答下列问题:(1)本次调查的总人数为,表中m的值为;(2)请补全条形统计图;(3)根据统计,该商场平均每天接待顾客约3600名,若将“非常满意”和“满意”作为顾客对商场服务工作的肯定,请你估计该商场服务工作平均每天得到多少名顾客的肯定.20.(7分)为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度约为多少米(精确到0.1米).21.(7分)春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.(1)求甲、乙两种商品每件的进价分别是多少元?(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.22.(7分)小明最喜欢吃芝麻馅的汤圆了,一天早晨小明妈妈给小明下了四个大汤圆,一个花生馅,一个水果馅,两个芝麻馅,四个汤圆除内部馅料不同外,其他一切均相同.(1)求小明吃第一个汤圆恰好是芝麻馅的概率;(2)请利用树状图或列表法,求小明吃前两个汤圆恰好是芝麻馅的概率.23.(8分)如图,已知⊙O经过平行四边形ABCD的顶点A,B及对角线的交点M,交AD于点E且圆心〇在AD 边上,∠BCD=45°.(1)求证:BC为⊙O的切线;(2)连接ME,若ME=﹣1,求⊙O的半径.24.(10分)综合与探究:如图,抛物线y=ax2+bx﹣4与x轴交于A(﹣3,0)、B(4,0)两点,与y轴交于点C.(1)求抛物线解析式;(2)抛物线对称轴上存在一点H,连接AH、CH,当|AH﹣CH|值最大时,求点H坐标;(3)若抛物线上存在一点P(m,n),mn>0,当S△ABC=S△ABp时,求点P坐标;(4)若点M是∠BAC平分线上的一点,点N是平面内一点,若以A、B、M、N为顶点的四边形是矩形,请直接写出点N坐标.25.(12分)问题提出(1)如图1,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有处.问题探究(2)如图2,在△ABC中,内角∠ABC的平分线BE和外角∠ACF的平分线CE,相交于点E,连接AE,若∠BEC=40°,请求出∠EAC的度数.问题解决(3)如图3,某地在市政工程施工中需要对一直角区域(∠AOB=90°)内部进行围挡,直角区域∠AOB内部有一棵大树(点P),工作人员经过测量得到点P到OA的距离PC为10米,点P到OB的距离PD为20米,为了保护大树及节约材料,设计要求围挡牌要经过大树位置(点P)并且所用材料最少,即围挡区域△EOF周长最小,请你根据以上信息求出符合设计的△EOF周长的最小值,并说明理由.参考答案与试题解析1.B.2.C.3.D.4.A.5.B.6.B.7.D.8.C.9.D.10.D.11.3.12.:2.13.12.14.2﹣2.15.解:原式=1+﹣1+﹣2×=.16.解:原式=•=•=x(x﹣1)=x2﹣x.17.解:如图所示:先作∠BAC的平分线交BC边于点E,再作线段AE的垂直平分线交AC于点D,交AB于点F 连接DE、EF,易证△EAD≌△EAF(SAS),则F A=DA而由线段的垂直平分线的性质可得DA=DE、F A=FE∴F A=DA=DE=FE∴四边形ADEF为菱形则菱形ADEF即为所求作的菱形.18.证明:∵DE∥BF∴∠DEF=∠BFE∵AE=CF∴AF=CE,且DE=BF,∠DEF=∠BFE∴△AFB≌△CED(SAS)∴∠A=∠C∴AB∥CD19.解:(1)本次调查的总人数为:12÷10%=120,m=54÷120×100%=45%,故答案为:120,45%;(2)比较满意的人数为:120×40%=48,补全的条形统计图如右图所示;(3)3600×(10%+45%)=3600×55%=1980(名),答:该商场服务工作平均每天得到1980名顾客的肯定.20.解:∵∠CED=∠AEB,CD⊥DB,AB⊥BD,∴△CED∽△AEB,∴=,∵CD=1.6米,DE=2.4米,BE=8.4米,∴=,∴AB==5.6米.故答案为:5.6米.21.解:(1)设甲、乙两种商品每件的进价分别是x元、y元,,解得,,即甲、乙两种商品每件的进价分别是30元、70元;(2)设购买甲种商品a件,获利为w元,w=(40﹣30)a+(90﹣70)(100﹣a)=﹣10a+2000,∵a≥4(100﹣a),解得,a≥80,∴当a=80时,w取得最大值,此时w=1200,即获利最大的进货方案是购买甲种商品80件,乙种商品20件,最大利润是1200元.22.解:(1)小明吃第一个汤圆,可能的结果有4种,其中是芝麻馅的结果有2种,∴小明吃第一个汤圆恰好是芝麻馅的概率==;(2)分别用A,B,C表示花生馅,水果馅,芝麻馅的大汤圆,画树状图得:∵共有12种等可能的结果,小明吃前两个汤圆恰好是芝麻馅的有2种情况,∴小明吃前两个汤圆恰好是芝麻馅的概率为=.23.(1)证明:连接OB,∵四边形ABCD是平行四边形,∴∠BAD=∠BCD=45°,∴∠BOD=2∠BAD=90°,∵AD∥BC,∴∠DOB+∠OBC=180°,∴∠OBC=90°,∴OB⊥BC,∴BC为⊙O切线;(2)解:连接OM,∵四边形ABCD是平行四边形,∴BM=DM,∵∠BOD=90°,∴OM=BM,∵OB=OM,∴OB=OM=BM,∴∠OBM=60°,∴∠ADB=30°,连接EM,过M作MF⊥AE于F,∵OM=DM,∴∠MOF=∠MDF=30°,设OM=OE=r,∴FM=r,OF=r,∴EF=r﹣r,∵EF2+FM2=EM2,∴(r﹣r)2+(r)2=(﹣1)2,解得:r=(负值舍去),∴⊙O的半径为.24.解:(1)∵抛物线与y轴交于点C,∴点C坐标为(0,﹣4),把A(﹣3,0)、B(4,0)坐标代入y=ax2+bx﹣4得解得∴抛物线解析式为:.(2)抛物线的对称轴为:x=,由三角形任意两边之差小于第三边,可知抛物线对称轴上存在一点H,连接AH、CH,当|AH﹣CH|值最大时,点H为AC直线与对称轴的交点,由A(﹣3,0)、C(0,﹣4)易得直线AC解析式为:,当x=时,y=,故点H的坐标为:(,﹣).(3)∵抛物线上存在一点P(m,n),mn>0,当S△ABC=S△ABp时,∴点P(m,n)只能位于第一象限,C(0,﹣4)∴n=4∴由4=﹣4解得x=或x=(舍)故点P坐标为(,4).(4)若以A、B、M、N为顶点的四边形是矩形,则点M和点N的位置有两种如图所示点M和点M’点N和点N’易得OA=3,OC=4,AC=5,点M是∠BAC平分线上的一点,作QF⊥AC,则OQ=QF,∴OQ=QF=1.5,∴在直角三角形AOQ和直角三角形ABM中,,∴,∴BM=3.5,∴点N(﹣3,﹣3.5)同理在直角三角形AEN’和直角三角形ABN’中,可解得点N’(﹣,).故点N的坐标为(﹣3,﹣3.5)或(﹣,).25.解:作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.故答案为:4;(2)解:∵∠ABC与∠ACD的角平分线相交于点E,∴∠CBE=∠ABC,∠ECD=∠ACD,由三角形的外角性质得,∠ACD=∠ABC+∠BAC,∠ECD=∠BEC+∠CBE,∴∠ACD=∠BEC+∠ABC,∴(∠ABC+∠BAC)=∠BEC+∠ABC,整理得,∠BAC=2∠BEC,∵∠BEC=40°,∴∠BAC=2×40°=80°,过点E作EH⊥BA交延长线于H,作EG⊥AC于G,作EF⊥BC于F,∵BE平分∠ABC,∴EF=EH,∵CE平分∠ACD,∴EG=EF,∴EH=EG,∴AE是∠CAF的平分线,∴∠CAE=(180°﹣∠BAC)=(180°﹣80°)=50°;(3)如图,设∠AOB、∠AEF、∠BFE的角平分线交于点Q,作QN⊥OB于N,QM⊥OA于M,QH⊥EF于H.连接QP.则QN=QH=QM=y,FH=FN,EH=EM,∴△OEF的周长:OE+OF+EF=OF+FN+OE+EM=ON+OM=QN+QM=2QN=2y,∵PDOC是矩形,且PD=20,PC=10,∴ND=y﹣10,CM=y﹣20,∴QP2=(y﹣10)2+(y﹣20)2∵PQ≥QH,∴(y﹣10)2+(y﹣20)2≥y2∴y2﹣60y+500≥0,∴(y﹣30)2≥400,∴y≥50或y≤10(舍),∴2y≥100,当且仅当P、H重合时取等号.即△OEF的周长的最小值为100.。
2020年中考物理模拟试题(三)含答案解析

秘密★启用前人教版2020年中考模拟测试卷(三)九年级物理考生注意:1.一律用黑色笔或2B铅笔将答案填写或填涂在答题卷指定位置内。
2.本试卷共4页,满分90分,答题时间75分钟。
一、选择题(共6小题,每小题3分,共18分。
每小题的4个选项中只有一个选项符合题意,多选、不选、错选均不得分)1.下列物理量中,以科学家的名字“焦耳”作为单位的物理量是A.电压B.电阻C.电流D.电功2.下列关于声现象说法中正确的是A.随着科技进步,物体不振动也能发声B.医生用“B超”给病人做检查,说明声音可以传递信息C.熟悉的人,听声音我们就知道他是谁,是根据不同人的音调来判断的D.学校路段“禁鸣喇叭”,是在传播过程中阻断噪声3.图甲测凸透镜的焦距,图乙“探究凸透镜成像的规律”,在图乙所示的位置光屏上成清晰的像,下列说法正确的是A.图乙中若用遮光板挡住凸透镜的上半部分,光屏上只出现像的下半部分B.图乙中若在凸透镜左侧“戴”上近视眼镜,光屏向右移动才能找到清晰的像C.由图甲可知凸透镜的焦距是40cmD.图乙的成像特点与照相机的成像特点相同4.下列有关热和能的说法中,正确的是A.发生热传递时,温度总是从内能大的物体传递给内能小物体B.一块0℃的冰熔化成0℃的水后,温度不变,内能变大C.内燃机的压缩冲程,主要通过热传递增加了气缸内物质的内能D.夏天在室内洒水降温,利用了水的比热容较大的性质5.图甲所示,放水地面上体,受到方向不变的水平拉F的作用F的大小与时间关如图乙示;物体运动的速度v与时间的如图丙示.则下列说法中正确的()A.0)2s内物体受摩擦力的作用B.2)4s内物体受到的摩擦力与拉力是一对平衡力C.2)4s内物体做匀速直线运动D.4)6s内拉力做功16J6.如图所示,电源电压为4.5V且保持不变,电压表量程为0)3V,电流表量程为0)0.6A,滑动变阻器R 的规格为“20Ω 1A”,灯泡L标有“2.5V 1.25W”的字样,忽略灯丝电阻的变化,闭合开关S,为了保证各元件都安全,则下列说法中正确的是()A.向左移动滑片,两表示数都变大B.电流表示数的变化范围是0.3A)0.5AC.滑动变阻器的阻值变化范围是4Ω)20ΩD.整个电路消耗的总功率变化范围是1W)2.25W二、填空题(共7小题,每空1分,共18分。
2020年中考语文模拟试题三(pdf,含解析)

精品文档!精品文档!初三语文全国中考真题汇编(三)积累与运用第I卷一、基础知识(8分,每题2分)1.加点字的注音不正确的是()A.咨诹.(zōu)攘.除(rǍng)倾颓.(tuí)崩殂.(cú)B.聘.请(pìn)书斋.(zhāi)眺.望(ti o)矜.持(jīn)C.阴鸷.(zhì)祸殃.(yāng)狡黠.(xi)挑衅.(xìn)D.鼎.沸(dǐng)缄.默(xi n)孱.弱(ch n)坍.塌(dān)2.作家、作品搭配不正确的是()A.鲁迅——《藤野先生》——《朝花夕拾》B.马克•吐温——《奥伊达的理想》——《马克•吐温中短篇小说选》C.契诃夫——《变色龙》——《契诃夫小说选》D.韩愈——《师说》——《昌黎先生集》3.加点词语解释不正确的是()A.①实在标.致.极了。
(漂亮.这里是反语,丑陋的意思)②我亲眼看到渔民们安.之.若.素.,举止泰然。
(安然相处,和往常一样,不觉得有什么不合适。
)B.①它让人讨厌,复又令人哑.然.失.笑.。
(禁不住笑出声来,有轻视的意思。
)②而民主党的权威报纸则将一桩大.事.渲.染.的讹诈案硬栽到我头上。
(大力夸张形容。
)C.①请看这位声.名.狼.藉.的伪证犯。
(声音和名誉乱七八糟。
)②我偃.旗.息.鼓.,甘拜下风。
(这里指停止竞选。
)D.①而卒赖其力以脱于虎.豹.之.秦.。
(像老虎和豹子一样凶残的秦国。
)②唐、虞尚仁,天下之民从.而.帝.之.。
(顺从他们并拥护他们做皇帝。
)4.与原文不一致的是()A.江山如此多娇,引无数英雄竞折腰B.有的人活着,他已经死了;有的人死了,他还活着C.然侍卫之臣不懈于外,忠志之士忘身于内者,盖追先帝之殊遇,欲报之于陛下也D.孔乙己是站着喝酒而穿长衫的唯一的人二、填空简答题(16分,每题4分)5.在下列词语中的错别字下画线,并按顺序工整地改正在横线上。
①炊烟袅袅②咸言碎语③暗然失色④自惭形秽⑤鸠占雀巢⑥潸然泪下⑦盘根错节⑧无精打彩答:、、、。
2020年初三中考物理三模试卷(含解析)

初三中考物理一模试卷一.选择题(本大题共16小题,每小题1.5分,共24分.每小题只有一个选项符合题意)1.(1.5分)以下四幅图都跟声音的知识有关,其中你认为解释正确的是()A.图甲:吹奏笛子时,演奏者用手指按住不同气孔,是为了改变声音的音调B.图乙:使用麦克风时,声信号转换成电信号,这说明电流可以产生磁场C.图丙:鼓面上泡沫小球弹起的高度形象地反映了鼓面振动的频率,这里用了放大法D.图丁:由表格的数据知:高音C比中央C的音调要高,所以高音C是噪音2.(1.5分)以下时光现象解释正确的是()A.图甲:阳光照在海面上。
海水是蓝的,说明海水吸收蓝光反射其他颜色的光B.图乙:用“太阳观察镜“看日偏食,利用了深色玻璃对光的反射和光的直线传播原理C.图丙:战士通过潜望镜可以看到墙外的景象,这是平面镜成像,看到的是正立等大的虚像D.图丁:图中的水晶球是一个凸透镜,此时成倒立缩小的像,球离眼睛越近,像越大3.(1.5分)轿车的设计和使用包含许多物理原理,其中解释不正确的是()A.图甲:乘车时系安全带﹣可以防止急刹车时由于惯性人飞出窗外B.图乙:汽车的方向盘﹣一种省力的简单机械,与门把手的使用原理相同C.图丙:轮胎上的花纹﹣可以增大与地面之间的摩擦D.图丁:挡风玻璃外面起雾﹣车内温度高于室外,使水蒸气液化而成的4.(1.5分)如图是一辆电动车行驶过程中的v﹣t图象。
根据图象得出的信息如下:①在0﹣5s,电动车做加速运动②在5﹣10s时,电动车的动能最大③在5﹣10s,电动车行驶了150m④若已知10﹣15s,电动车行驶了125m,则电动车在5﹣20s之间的平均速度约为18.3m/s则以上分析正确的是()A.①和②B.②和③C.①②③D.①②③④5.(1.5分)体温计(如图甲)中封闭着一定量的水银,其横截面(如图乙)是椭圆形的,通过水银热胀冷缩的多少,可以反映体温的高低。
在体温计的使用过程中,下列说法不正确的是()A.体温计中水银的密度不变B.体温计的玻璃外壳可以起到放大镜的作用C.甲图中体温计的示数是39.8℃D.体温计玻璃泡做得比较大可以提高精确度6.(1.5分)在一个长3米的跷跷板(支点在木板中点)的两瑞分别放置两个木箱,它们的质量分别为m1=30kg,m2=20kg,为了使跷跷板在水平位置平衡,以下做法可行的是()A.把m1向右移动0.5米B.把m2向左移动0.5米C.把m1向右移动0.2米D.把m2向左移动0.3米7.(1.5分)小球向左运动与左端固定在墙上的弹簧接触后,经历了如图甲、乙所示过程,下列说法正确的是()①压缩过程中,小球的形状和运动状态都发生了改变②压缩过程中,弹簧对小球做了功,小球的动能在增大③弹开过程中,弹簧的弹性势能减小,小球的动能增加④弹开过程中,小球受向右的推力,推力的大小逐渐增大A.只有②③④B.只有①③C.只有①②③D.只有①②④8.(1.5分)在生活中水有多种用途,这些用途的背后也包含着许多物理原理,以下水的作用与运用原理都正确的是()A.气温骤降时,果农给没有成熟的橘子喷水﹣水的凝固吸热,防止橘子冻伤B.汽车装有水箱作为散热器帮助气缸降温﹣水的比热容比较大,可以吸收较多的热量C.炎热的夏天,在地上洒水可以降低室内气温﹣水的液化吸热,带走空气的热量D.寒冷地区,岩石裂隙中的水结冰后会使岩石崩裂﹣水结冰密度变大,体积膨胀9.(1.5分)如图所示,底面积不同的圆性形容器分别盛有质量相等的甲、乙两种液体,则甲,乙容器底部受到的压力和压强的大小关系为()A.F甲>F乙;p甲=p乙B.F甲<F乙;p甲=p乙C.F甲>F乙;p甲>p乙D.F甲=F乙;p甲<p乙10.(1.5分)A、B是两个质量完全相同的长方体铝块,轻轻放入水中后,静止时如图所示,则下列说法正确的是()A.两物体排开水的体积大小关系是:V球A=V球BB.两物体受到水的浮力大小关系是:F球A>F球BC.两物体的体积不等,V A<V BD.A一定是空心的,B一定是实心的11.(1.5分)如图是手电筒工作的实物图(电池是新的)。
2020年中考数学三模试卷(含答案)

2020年中考数学三模试卷一、选择题:本大题有10个小题,每小题3分,共30分。
1.-23等于( )A. -6B. 6C. -8D. 82.在平面直角坐标系中,点关于原点对称的点的坐标是A. B. C. D.3.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形的上底AD、下底BC以及腰AB均相切,切点分别是D、C、E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是().A. 9B. 10C. 12D. 144.A种饮料比B种饮料单价少1元,小峰买了2瓶A种饮料和3瓶B种饮料,一共花了13元,如果设B 种饮料单价为x元/瓶,那么下面所列方程正确的是( )A. 2(x-1)+3x=13B. 2(x+1)+3x=13C. 2x+3(x+1)=13D. 2x+3(x-1)=135.如图,这是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,根据统计图提供的信息,可得到该班40名同学一周参加体育锻炼时间的众数、中位数分别是()A. 8,9B. 8,8.5C. 16,8.5D. 16,10.56.如图,AB和CD表示两根直立于地面的柱子,AC和BD表示起固定作用的两根钢筋,AC与BD相交于点M,已知AB=8m,CD=12m,则点M离地面的高度MH为( )A. 4 mB. mC. 5mD. m7.若等腰三角形中有一个角等于110°,则其它两个角的度数为().A. 70°B. 110°和70°C. 35°和35°D. 30°和70°8.已知点A,点B在一次函数y=kx+b(k,b为常数,且k≠0)的图象上,点A在第三象限,点B在第四象限,则下列判断一定正确的是()A. b<0B. b>0C. k<0D. k>09.身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是()同学甲乙丙丁放出风筝线长140m 100m 95m 90m线与地面夹角30°45°45°60°A. 甲B. 乙C. 丙D. 丁10.已知抛物线与轴交于点A、B,与轴交于点C,则能使△ABC为等腰三角形抛物线的条数是()A. 5B. 4C. 3D. 2二、填空题:本大题有6个小题,每小题4分,共24分11.把多项式2x2y﹣4xy2+2y3分解因式的结果是________12.一组数据7,x,8,y,10,z,6的平均数为4,则x,y,z的平均数是________.13.若圆锥的地面半径为,侧面积为,则圆锥的母线是________ .14.如图,和分别是的直径和弦,且,,交于点,若,则的长是________.15.一次函数y = kx + b ,当- 3 £x £ 1时,对应的y 值为1 £y £ 9 ,则k + b =________;16.已知等腰中,,,,在线段上,是线段上的动点,的最小值是________.三、解答题:本大题有7个小题,共66分17.化简:18.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表:(1)把表中所空各项数据填写完整;选手选拔成绩/环中位数平均数甲 10 9 8 8 10 9 ________ ________乙 10 10 8 10 7 ________ ________ 9(2)分别计算甲、乙六次测试成绩的方差;(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.19.如图,已知:,,,点,分别在,上,连接,且,是上一点,的延长线交的延长线于点.(1)求证:;(2)求证:.20.大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:x(天) 1 2 3 (50)p(件)118 116 114 (20)销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+ .(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.(3)这50天中,该超市第几天获得利润最大?最大利润为多少?21.某校数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=4,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.(1)求证:AP=CQ;(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;(3)在(2)的条件下,若AP=1,求PE的长.22.已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A (10,0),B(8,2 ),C(0,2 ),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S.(1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式;(2)当纸片重叠部分的图形是四边形时,求t的取值范围;(3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由.23.如图,在⊙中,弦,相交于点,且.(1)求证:;(2)若,,当时,求:①图中阴影部分面积.②弧的长.答案解析部分一、选择题1.C2.C3.D4.A5.A6.B7.C8.A9.D10.B二、填空题11.2y(x﹣y)2【解答】解:原式=2y(x2﹣2xy+y2)=2y(x﹣y)2.故答案为:2y(x﹣y)2.12.-1【解答】解:∵一组数据7,x,8,y,10,z,6的平均数为4,∴=4,解得,x+y+z=﹣3,∴=﹣1,故答案为:﹣1.13.13【解答】设母线长为R,则:解得:故答案为13.14.5【解答】连接CD;Rt△AOB中,∠A=30°,OB=5,则AB=10,OA=5 ;在Rt△ACD中,∠A=30°,AD=2OA=10 ,∴AC=cos30°×10 =15,∴BC=AC-AB=15-10=5.故答案为515.9或1【解答】解:①当x=-3时,y=1;当x=1时,y=9,则解得:所以k + b =2+7=9;②当x=-3时,y=9;当x=1时,y=1,则解得:,所以k + b=-2+3=1.故答案为9或1.16.【解答】解:∵AC=BC,OC⊥AB,∴AB=2OB=6,∵OC=4,∴BC=5,∴A,B关于y轴对称,过A作AM⊥BC于M,交y轴于P,则此时,PM+PB的值最小且PM+PB的最小值=AM,∵∠AMB=∠COB=90°,∠ABM=∠CBO,∴△ABM∽△CBO,∴,即,∴AM=,∴PM+PB的最小值是,故答案为:.三、解答题:本大题有7个小题,共66分.17. 解:===1【分析】根据同分母分式的减法法则计算,再根据完全平方公式展开,合并同类项后约分计算即可求解.18. (1)9,9,9,9.5(2)解:s2甲= [2×(8﹣9)2+2×(9﹣9)2+2×(10﹣9)2]=;s2乙= [(7﹣9)2+(8﹣9)2+(9﹣9)2+3×(10﹣9)2]=(3)解:我认为推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适【解答】解:(1)甲:将六次测试成绩按从小到大的顺序排列为:8,8,9,9,10,10,中位数为(9+9)÷2=9,平均数为(10+9+8+8+10+9)÷6=9;乙:第6次成绩为9×6﹣(10+10+8+10+7)=9,将六次测试成绩按从小到大的顺序排列为:7,8,9,10,10,10,中位数为(9+10)÷2=9.5;填表如下:选手选拔成绩/环中位数平均数甲10 9 8 8 10 9 9 9乙10 10 8 10 7 9 9.5 919. (1)证明:∵,,∴,,又∵,∴(2)证明:∵在△BGF中,∴∠HGF>∠GBF,∵,∴∠ADE=∠GBF,∴20. (1)解:设销售量p件与销售的天数x的函数解析式为p=kx+b,代入(1,118),(2,116)得解得因此销售量p件与销售的天数x的函数解析式为p=﹣2x+120(2)解:当1≤x<25时,y=(60+x﹣40)(﹣2x+120)=﹣2x2+80x+2400,当25≤x≤50时,y=(40+ ﹣40)(﹣2x+120)= ﹣2250(3)解:当1≤x<25时,y=﹣2x2+80x+2400,=﹣2(x﹣20)2+3200,∵﹣2<0,∴当x=20时,y有最大值y1,且y1=3200;当25≤x≤50时,y= ﹣2250;∵135000>0,∴随x的增大而减小,当x=25时,最大,于是,x=25时,y= ﹣2250有最大值y2,且y2=5400﹣2250=3150.∵y1>y2∴这50天中第20天时该超市获得利润最大,最大利润为3200元21. (1)证明:∵四边形ABCD是正方形,∴∠ADC=∠A=∠B=∠BCD=∠DCQ=90°,AD=BC=CD=AB=4,∵∠PDQ=90°,∴∠ADP=∠CDQ,在△APD和△CQD中,,∴△APD≌△CQD(ASA),∴AP=CQ(2)解;PE=QE,理由如下:由(1)得:△APD≌△CQD,∴PD=QD,∵DE平分∠PDQ,∴∠PDE=∠QDE,在△PDE和△QDE中,,∴△PDE≌△QDE(SAS),∴PE=QE(3)解:由(2)得:PE=QE,由(1)得:CQ=AP=1,∴BQ=BC+CQ=5,BP=AB﹣AP=3,设PE=QE=x,则BE=5﹣x,在Rt△BPE中,由勾股定理得:32+(5﹣x)2=x2,解得:x=3.4,即PE的长为3.422. (1)解:∵A,B两点的坐标分别是A(10,0)和B(8,2 ),∴tan∠OAB= = ,∴∠OAB=60°,当点A′在线段AB上时,∵∠OAB=60°,TA=TA′,∴△A′TA是等边三角形,且TP⊥AA′,∴TP=(10﹣t)sin60°= (10﹣t),A′P=AP= AT= (10﹣t),∴S=S△ATP= A′P•TP= (10﹣t)2,当A´与B重合时,AT=AB==4,所以此时6≤t<10(2)解:当点A′在线段AB的延长线上,且点P在线段AB(不与B重合)上时,纸片重叠部分的图形是四边形(如图①,其中E是TA′与CB的交点),假设点P与B重合时,AT=2AB=8,点T的坐标是(2,0),由(1)中求得当A´与B重合时,T的坐标是(6,0),则当纸片重叠部分的图形是四边形时,2<t<6(3)解:S存在最大值.①当6≤t<10时,S= (10﹣t)2,在对称轴t=10的左边,S的值随着t的增大而减小,∴当t=6时,S的值最大是2 ;②当2≤t<6时,由图①,重叠部分的面积S=S△A′TP﹣S△A′EB,∵△A′EB的高是A′B•sin60°,∴S= (10﹣t)2﹣(10﹣t﹣4)2×+ (﹣4)2×= (﹣t2+2t+30)=﹣(t﹣2)2+4 ,当t=2时,S的值最大是4 ;③当0<t≤2,即当点A′和点P都在线段AB的延长线上是(如图②,其中E是TA´与CB的交点,F是TP 与CB的交点),∵∠EFT=∠ETF,四边形ETAB是等腰梯形,∴EF=ET=AB=4,∴S= EF•OC= ×4×2 =4 .综上所述,S的最大值是4 ,此时t的值是t=2.23. (1)证明:连接,,∵,∴,∵,∴,∵,∴,∵,∴≌,∴.(2)解:作于,于,由()可知,∴,∵,,,,∴四边形是正方形,∴,∵,∴≌,∴,∵,,∴,,,∵,∴.①.②,∴,∴.。
2020年中考数学模拟试卷03含解析

2020年中考数学模拟试卷03一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知点M(1﹣m,2﹣m)在第三象限,则m的取值范围是()A.m>3 B.2<m<3 C.m<2 D.m>22.已知x=2是方程2x﹣3a+2=0的根,那么a的值是()A.﹣2 B.C.2 D.3.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC相似的是()A.B.C.D.4.2020年5月5日18时整,海南文昌发射中心成功发射一枚长征五号B运载火箭,运载火箭起飞质量约849000kg,请将849000kg用科学记数法表示为()A.8.49×104kg B.8.49×105kg C.0.849×106kg D.84.9×104kg5.已知圆锥的底面半径为6cm,高为8cm,则圆锥的侧面积为()A.36πcm2B.48πcm2C.60πcm2D.80πcm26.已知,且﹣1<x﹣y<0,则k的取值范围为()A.﹣1<k<﹣B.0<k<C.0<k<1 D.<k<17.如图所示实数a,b在数轴上的位置,以下四个命题中是假命题的是()A.a3﹣ab2<0 B.C.D.a2<b28.如图,⊙P内含于⊙O,⊙O的弦AB切⊙P于点C,且AB∥OP,若阴影部分的面积为9π,则弦AB的长为()A.3 B.4 C.6 D.99.因为sin30°=,sin210°=,所以sin210°=sin(180°+30°)=﹣sin30°;因为sin45°=,sin225°=,所以sin225°=sin(180°+45°)=﹣sin45°,由此猜想,推理知:一般地当α为锐角时有sin(180°+α)=﹣sinα,由此可知:sin240°=()A.B.C.D.10.如图,两个反比例函数和(其中k1>k2>0)在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是()①△ODB与△OCA的面积相等;②四边形P AOB的面积等于k2﹣k1;③P A与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.A.①②B.①②④C.①④D.①③④第二部分非选择题(共110分)二.填空题(本大题共6小题,每小题4分,共24分.)11.当x时,|3﹣x|=x﹣3.12.在中,有理数的个数是个.13.一组数据3,1,2,1,3的平均数是,方差是.14.抛物线开口向下,则a=.15.如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为.16.如图,直线l:y=,经过点M(0,),一组抛物线的顶B1(1,y1),B2(2,y2),B3(3,y3)…B n(n,y n)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0).,A n+1(x n+1,0)(n为正整数),设x1=d(0<d<1)若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则我们把这种抛物线就称为:“美丽抛物线”.则当d(0<d<1)的大小变化时美丽抛物线相应的d的值是.三、解答题(本大题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分8分)计算:()-1﹣(π﹣2012)0+2sin45°﹣.18.(本小题满分8分)解分式方程:.19.(本小题满分8分)联合国规定每年的6月5日是“世界环境日”,为配合今年的“世界环境日”宣传活动,某校课外活动小组对全校师生开展了以“爱护环境,从我做起”为主题的问卷调查活动,将调查结果分析整理后,制成了上面的两个统计图.其中:A:能将垃圾放到规定的地方,而且还会考虑垃圾的分类;B:能将垃圾放到规定的地方,但不会考虑垃圾的分类;C:偶尔会将垃圾放到规定的地方;D:随手乱扔垃圾.根据以上信息回答下列问题:(1)该校课外活动小组共调查了多少人?并补全上面的条形统计图;(2)如果该校共有师生2400人,那么随手乱扔垃圾的约有多少人?20.(本小题满分8分)如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD 为45°.(1)求两建筑物底部之间水平距离BD的长度;(2)求建筑物CD的高度(结果保留根号).21.(本小题满分8分)如图,四边形ABCD是正方形,E是BC延长线上的一点,且AC=EC.(1)求证:AE平分∠CAD;(2)设AE交CD于点F,正方形ABCD的边长为1,求DF的长.(结果保留根号)22.(本小题满分10分)已知:反比例函数和一次函数y=2x﹣1,其中一次函数的图象经过点(k,5).(1)试求反比例函数的解析式;(2)若点A在第一象限,且同时在上述两函数的图象上,求A点的坐标.23.(本小题满分10分)绿谷商场“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示:类别冰箱彩电进价(元/台)2320 1900售价(元/台)2420 1980(1)按国家政策,农民购买“家电下乡”产品可享受售价13%的政府补贴.农民田大伯到该商场购买了冰箱、彩电各一台,可以享受多少元的政府补贴?(2)为满足农民需求,商场决定用不超过85000元采购冰箱、彩电共40台,且冰箱的数量不少于彩电数量的.①请你帮助该商场设计相应的进货方案;②哪种进货方案商场获得利润最大(利润=售价﹣进价),最大利润是多少?24.(本小题满分12分)如图,已知AB是⊙O的切线,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F(1)求证:ED是⊙O的切线;(2)求证:△CFP∽△CPD;(3)如果CF=1,CP=2,sin A=,求O到DC的距离.25.(本小题满分14分)如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C(0,3),点P是OA边上的动点(与点O、A不重合).现将△P AB沿PB翻折,得到△PDB;再在OC边上选取适当的点E,将△POE沿PE翻折,得到△PFE,并使直线PD、PF重合.(1)设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值;(2)如图2,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式;(3)在(2)的情况下,在该抛物线上是否存在点Q,使△PEQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.2020年中考数学模拟试卷03答案一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.D 2.C 3.B 4.B 5.C 6.D7.B【解析】由数轴可知a>0,b<0,且|a|<|b|,由此可判断a+b<0,a﹣b>0,再逐一检验.依题意,得a>0,b<0,且|a|<|b|,∴a+b<0,a﹣b>0,A、a3﹣ab2=a(a+b)(a﹣b)<0,正确;B、∵a+b<0,∴=﹣(a+b),错误;C、∵0<a<a﹣b,∴<,正确;D、∵(a+b)(a﹣b)<0,∴a2﹣b2<0,即a2<b2,正确.故选:B.8.C【解析】本题可先由题意OD=PC=r,再根据阴影部分的面积为9π,得出R2﹣r2=9,即AD==3,进而可知AB=2×3=6.设PC=r,AO=R,连接PC,⊙O的弦AB切⊙P于点C,故AB⊥PC,作OD⊥AB,则OD∥PC.又∵AB∥OP,∴OD=PC=r,∵阴影部分的面积为9π,∴πR2﹣πr2=9π,即R2﹣r2=9,于是AD==3.∵OD⊥AB,∴AB=3×2=6.故选:C.9.C【解析】阅读理解:240°=180°+60°,因而sin240°就可以转化为60°的角的三角函数值.根据特殊角的三角函数值,就可以求解.∵当α为锐角时有sin(180°+α)=﹣sinα,∴sin240°=sin(180°+60°)=﹣sin60°=﹣.故选:C.10.C【解析】根据反比例函数系数k所表示的意义,对①②③④分别进行判断.①A、B为上的两点,则S△ODB=S△OCA=k2,正确;②由于k1>k2>0,则四边形P AOB的面积应等于k1﹣k2,错误;③只有当P的横纵坐标相等时,P A=PB,错误;④当点A是PC的中点时,点B一定是PD的中点,正确.故选:C.第二部分非选择题(共110分)二.填空题(本大题共6小题,每小题4分,共24分.)11.≥312.313.2,14.﹣115.4﹣π【解析】根据题意得点M到正方形各顶点的距离都为1,点M所走的运动轨迹为以正方形各顶点为圆心,以1为半径的四个扇形,∴点M所经过的路线围成的图形的面积为正方形ABCD的面积减去4个扇形的面积.而正方形ABCD的面积为2×2=4,4个扇形的面积为4×=π,∴点M所经过的路线围成的图形的面积为4﹣π.故答案为4﹣π.16.【答案】或【解析】将(0,)代入直线l:y=得:b=∴y=∵当x=1时,y=<1 ∴B1(1,)∵当x=2时,y=<1 ∴B2(2,)∵当x=3时,y=>1 ∴美丽抛物线的顶点只有B1,B2若B1为顶点,则d=1﹣=;若B2为顶点,则d=1﹣[(2﹣)﹣1]=;故答案为:或.三、解答题(本大题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤)17.解:原式=3﹣1+2•﹣(﹣1)=3﹣1+﹣+1=3.18.【解析】解:去分母,得x(x+2)+6(x﹣2)=(x﹣2)(x+2).化简得:8x=8,解得x=1.经检验,x=1是原方程的解.∴原方程的解是x=1.考查分式方程的解法,先去分母化成整式方程,再解这个整式方程,注意验根.19.【解析】解:(1)由统计图可知B种情况的有150人,占总人数的50%,所以调查的总人数为150÷50%=300(人),D种情况的人数为300﹣(150+30+90)=30(人),补全图形如图所示(2)因为该校共有师生2400人,所以随手乱扔垃圾的人约为2400×=240(人)答:随手乱扔垃圾的约有240人20.解:(1)根据题意得:BD∥AE,∴∠ADB=∠EAD=45°,∵∠ABD=90°,∴∠BAD=∠ADB=45°,∴BD=AB=60,∴两建筑物底部之间水平距离BD的长度为60米;(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,∴AF=BD=DF=60,在Rt△AFC中,∠F AC=30°,∴CF=AF•tan∠F AC=60×=20,又∵FD=60,∴CD=60﹣20,∴建筑物CD的高度为(60﹣20)米.21.(1)证明:∵四边形ABCD是正方形,AC是对角线,∴∠BCA=∠DAC=45°,又∵AC=EC,∴∠CAE=∠E,∵四边形ABCD是正方形,∴AD∥BC,∴∠E=∠DAF,∴∠DAF=∠CAF,∴AE平分∠CAD;(2)解:∵四边形ABCD是正方形,∴∠B=90°,∠D=∠DCE=90°,∴AC==,∴CE=AC=,又∵∠AFD=∠EFC,∴△AFD∽△EFC,∴=,∴=,解得:DF=﹣1.22.【解析】解:(1)因为一次函数y=2x﹣1的图象经过点(k,5)所以有5=2k﹣1解得k=3所以反比例函数的解析式为y=;(2)由题意得:,解这个方程组得:,因为点A在第一象限,则x>0,y>0所以点A的坐标为(,2).23.【解析】解:(1)(2420+1980)×13%=572,答:可以享受政府572元的补贴;(2)①设冰箱采购x台,则彩电采购(40﹣x)台,根据题意得2320x+1900(40﹣x)≤85000 ①,x≥(40﹣x)②,解不等式组得≤x≤,∵x为正整数.∴x=19,20,21.∴该商场共有3种进货方案,方案一:冰箱购买19台,彩电购买21台.方案二:冰箱购买20台,彩电购买20台,方案三:冰箱购买21台,彩电购买19台;②设商场获得总利润y元,根据题意得y=(2420﹣2320)x+(1980﹣1900)(40﹣x)=20x+3200,∵20>0,∴y随x的增大而增大,=20×21+3200=3620元,∴当x=21时,y最大答:方案三商场获得利润最大,最大利润是3620元.24.(1)证明:连接OD.∵BC为直径,∴△BDC为直角三角形.在Rt△ADB中,E为AB中点,∴BE=DE,∴∠EBD=∠EDB.又∵OB=OD,∴∠OBD=∠ODB,∵∠OBD+∠ABD=90°,∴∠ODB+∠EDB=90°.∴ED是⊙O的切线.(2)证明:∵PF⊥BC,∴∠FPC=90°﹣∠BCP(直角三角形的两个锐角互余).∵∠PDC=90°﹣∠PDB(直径所对的圆周角是直角),∠PDB=∠BCP(同弧所对的圆周角相等),∴∠FPC=∠PDC(等量代换).又∵∠PCF是公共角,∴△PCF∽△DCP.(3)解:过点O作OM⊥CD于点M,∵△PCF∽△DCP,∴PC2=CF•CD(相似三角形的对应边成比例).∵CF=1,CP=2,∴CD=4.可知sin∠DBC=sin A=sin∠MOC=,∴=,即=,∴直径BC=5,∴=,∴MC=2,∴MO=,∴O到DC的距离为.25.解:(1)由已知PB平分∠APD,PE平分∠OPF,且PD、PF重合,则∠BPE=90度.∴∠OPE+∠APB=90°.又∵∠APB+∠ABP=90°,∴∠OPE=∠PBA,∴Rt△POE∽Rt△BP A.∴,即.∴y=x(4﹣x)=﹣x2+x(0<x<4).且当x=2时,y有最大值.(2)由已知,△P AB、△POE均为等腰直角三角形,可得P(1,0),E(0,1),B(4,3).设过此三点的抛物线为y=ax2+bx+c,则∴y=x2﹣x+1.(3)由(2)知∠EPB=90°,即点Q与点B重合时满足条件.直线PB为y=x﹣1,与y轴交于点(0,﹣1).将PB向上平移2个单位则过点E(0,1),∴该直线为y=x+1.由得,∴Q(5,6).故该抛物线上存在两点Q(4,3)、(5,6)满足条件.。
2020年中考模拟试题(3)及参考答案

2020年中考模拟试题(3)及参考答案听力测试(20%)一、听对话,回答问题(每题1分)1. A Size 24 B Size 25 C Neither size D Both sizes2. A In 1985 B In 1983 C In 1987 D In 19863. A It was sunny B It was fine C It was cloudy D It was hot4. A She’s mending her bike. B She’s driving a car.C She’s helping Mr.Black mend a car.D She’s mending her car.5. A Thirty-nine BThirty-seven C Two D None二、听选同义句(每题1分)6. A The heavy rain stopped us from goingout.B We were staying at home when it began to rain.C It rained hard, so we had to leave home.D When we arrived home, it was raining hard.7. A Maths is the easiest subject. B Maths is the most difficult subject of all.C Maths isn’t as hard as any other subject. DMaths is as easy as any other subject.8. A It takes me fifteen minutes to walkhome.B I go home b y bike because my h ouse is about fifteen kilometres away.C It takes me about a quarter to go home by bike.D It takes me a bout fifty minutes to go home by bike.9. A Tom is too old to dress himself. B Tom is so old that he can’t dress himself.C Tom is old, but he can’t dress himself.D Tom is too young to dress himself.10. A The baby began to cry when the mothercame in.B The baby didn’t cry any more when the m other came in.C The baby cried harder when the mother came in.D The mother saw the baby crying when she came in三、短文理解(每题1分)根据所听到的短文内容选择正确答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年中考模拟卷(三) 【河北卷】考生注意:1.本试卷共四个大题,满分60分,考试时间45分钟。
2.-35.5Zn-65题号一二三四总分得分一、选择题(本大题共14个小题,共28分。
每小题的四个选项中,只有一个选项符合题意,每小题2分)1.空气中含量最多的是()A.O2B.N2C.He D.CO22.下列食物中富含糖类的是()A.白菜B.鸡蛋C.牛肉D.米饭3.下列实验基本操作正确的是()4.下列对化肥的认识正确的是()A.NH4HCO3是一种复合肥B.磷肥可以从外观上与其他化肥相区别C.铵态氮肥能与碱性肥料混合施用D.施用钾肥可增强作物抗寒、抗旱能力5.硒元素具有抗衰老、抑制癌细胞生长的功能。
其原子结构示意图及在元素周期表的信息如图,下列说法错误的是()A.硒属于非金属元素B.硒原子核内有34个质子C.硒原子核外有4个电子层D.硒的相对原子质量是78.96g6.某同学根据铜绿的成分Cu(OH)2CO3做出猜想:金属铜锈蚀的条件除有氧气和水外,还必须有二氧化碳。
为证明“必须有二氧化碳”,需要进行如图所示实验中的()A.甲和乙B.甲和丁C.乙和丁D.丙和丁7.在一密闭容器中,有X、O2、CO2、H2O四种物质,在一定条件下发生某种反应,反应一段时间后,测得反应前后各物质的质量如表。
下列说法正确的是()物质X O2CO2H2O反应前的质量/g 19 34 6 2反应后的质量/g 11 待测28 20A.B.X中一定含有C、H、O元素C.该反应是置换反应D.反应中CO2和H2O的质量比为11∶98.下列做法不符合低碳行为的是()A.购物时自带包装袋,减少塑料袋的使用B.骑“共享单车”出行C.就地焚烧垃圾D.纸张双面打印9.下列物质的用途,利用了物理性质的是()A.O2供给呼吸B.盐酸用于除锈C.用钢材制作高压锅D.氢气用作燃料10.下列科学家与他的贡献对应不正确的是()A.安培——安培定则B.沈括——磁偏角C.拉瓦锡——元素周期表D.侯德榜——联合制碱法11.下列关于分子、原子和离子的说法不正确的是()A.“花香四溢”说明分子在不断运动B.化学变化前后原子的种类和数目都不变C.原子核不都是由质子和中子构成D.带电的微粒都是离子12.下列物质归类不正确的是()A.纯碱——碱B.玻璃——晶体C.石墨——导体D.空气——混合物选项实验操作实验目的A 高温煅烧除去碳酸钙中混有的氧化钙B 滴加石蕊溶液鉴别稀盐酸和稀硫酸C 向平行且自由下垂的两张纸中间吹气探究气体流速与压强的关系D 将两根用毛皮摩擦过的橡胶棒相互靠近探究两种电荷间的相互作用14.如图所示实验中得出的结果正确的是()A.甲:水不能从杯中溢出,说明水和纸的分子之间存在引力B.乙:铜片上白磷燃烧,红磷不燃烧,说明燃烧需要达到着火点C.丙:温度计示数减小,说明NH4NO3固体溶于水时放出热量D.丁:敲击音叉乒乓球被弹起,说明振幅越大音调越高二、填空及简答题(本大题共5个小题,共20分,每空1分)15.请用下列物质的序号填空:a.生石灰b.熟石灰c.氢氧化钠d.金刚石e.石墨f.活性炭g.钨h.氢气(1)________可用作电极材料。
(2)________常用来制作灯丝。
(3)________是常见的建筑材料,也常用于改良酸性土壤。
16.利用如图装置我们认识了水的组成:(1)在实验室中用自来水制取净化程度较高的水的方法是____________。
(2)试管“2”中的气体是________。
(3)水是生命之源,我国水资源总量虽位居世界第六位,但人均占水量很少。
请你写出一条节约用水的方法:______________________________________________。
17.利用所学的知识填空:(1)硬水和软水常用______________来区分。
(2)自来水厂用______________吸附水中的色素和异味。
(3)用来制作保鲜膜的聚乙烯具有______________(选填“热塑性”或“热固性”)。
(4)钢比生铁的含碳量________(选填“高”或“低”)。
(5)洗涤剂能除去油污利用的是其____________作用。
18.根据如图所示的实验回答问题。
(1)甲图实验验证了二氧化碳的物理性质:____________________________;化学性质____________________________。
(2)通过乙图实验得出铁锈蚀的条件是________________________________________,请你写出防止家中菜刀生锈的方法:________________________________________。
(3)小海同学用丙图进行实验,当观察到________________________________________时,证明酸碱恰好完全反应。
19.A~F均为初中化学常见的物质,他们之间的关系如图所示(“→”表示转化关系,所涉及反应均为初中常见的化学反应),其中A俗称生石灰,C是最常用的溶剂,C与F元素组成相同。
(1)C的化学式是__________。
(2)D的一种用途是______________________________。
(3)A→B反应的基本类型是__________________。
(4)F→E反应的化学方程式为____________________________________。
三、实验探究题(本大题共1个小题,共7分)20.小维与家人聚餐时,对火锅燃料“固体酒精”产生了好奇,于是他与同学对其成分进行如下探究。
【查阅资料】(1)该固体酒精是用酒精、氯化钙和氢氧化钠按一定的质量比混合制成的。
(2)氯化钙、氯化钡溶液均呈中性。
【提出问题】(1)酒精中是否含有碳元素?(2)固体酒精中氢氧化钠是否变质?【做出猜想】猜想一:酒精中含有碳元素。
猜想二:固体酒精中氢氧化钠已变质。
【实验探究】(1)如图所示进行实验,发现澄清石灰水________________,可得出酒精中含有碳元素的结论。
(2)取少量固体酒精于烧杯中,加足量的水充分溶解后静置,发现杯底有白色沉淀。
取沉淀于试管中加入稀盐酸,固体溶解并有气泡产生,则生成气体的化学方程式为________________________________________________。
【实验结论】(1)酒精中含有碳元素。
(2)固体酒精中氢氧化钠已经变质。
【拓展延伸】为进一步确定固体酒精中是否还含有氢氧化钠,小维与同学继续探究。
(1)他另取少量固体酒精,加水溶解后,取上层清液,滴加酚酞溶液,酚酞溶液________,于是得出固体酒精中还含有氢氧化钠。
(2)小维的同学认为他的实验不能证明固体酒精中一定有氢氧化钠剩余,理由是________________________________________。
(3)他们另取上层清液,加入足量的氯化钡溶液,充分反应后滴加氯化铁溶液,生成红褐色沉淀,他们一致认为固体酒精中氢氧化钠有剩余。
【反思交流】(1)实验中,加入足量氯化钡溶液的目的是____________________________ _________________________________________________。
(2)实验室中氢氧化钠应______________保存。
四、计算应用题(本大题共1个小题,共5分。
解答时,要求有必要的文字说明、公式和计算步骤等,只写最后结果不得分)21.向133.4g稀盐酸中加入锌粉(仅含不溶于酸的杂质),所加锌粉的质量与产生气体的质量的关系如图所示。
求:(1)此过程产生气体的最大质量是________。
(2)原稀盐酸中溶质的质量分数为多少?参考答案与点拨1.B 2.D 3.C 4.B 5.D6.B 点拨:甲中的铜片与氧气、水和二氧化碳同时接触发生了锈蚀;乙中的铜片与二氧化碳和水接触,没有锈蚀,说明铜的锈蚀与氧气有关;丙中的铜片与二氧化碳和氧气接触,没有锈蚀,说明铜的锈蚀与水有关;丁中的铜片与氧气和水接触没有锈蚀,说明了铜的锈蚀与二氧化碳有关。
由以上分析可知,通过实验甲与丁的对比得出:铜的锈蚀必须有二氧化碳参与。
故选B 。
7.D 点拨:根据质量守恒定律可知,待测值=19+34+6+2-11-28-20=2,故A 错误;22g 二氧化碳中含有氧元素的质量为22g ×3244=16g ,18g 水中含氧元素的质量为18g ×1618=16g ;生成物中氧元素的质量为16g +16g =32g ,与参加反应的氧气的质量正好相等,说明X 中一定只含有碳、氢两种元素,故B 错误;根据反应前后质量的变化可以判断二氧化碳和水为生成物,而X 和氧气为反应物,一定不是置换反应,故C 错误;反应中生成二氧化碳的质量为28g -6g =22g ,生成水的质量为20g -2g =18g ,其质量比为11∶9,故D 正确。
答案选D 。
8.C 9.C 10.C 11.D 12.A13.C 点拨:高温条件下,碳酸钙分解生成氧化钙和二氧化碳,不能除去碳酸钙中混有的氧化钙,A 不正确;滴加石蕊溶液时,两种溶液都变红色,不能鉴别稀盐酸和稀硫酸,B 不正确;向平行且自由下垂的两张纸中间吹气时,两张纸向中间靠拢,说明气体流速越大,压强越小,可以探究气体流速与压强的关系,C 正确;两根用毛皮摩擦过的橡胶棒带相同性质的电荷,不能探究两种电荷间的相互作用,D 不正确。
正确答案选C 。
14.B 点拨:水不能流出,是因为大气压强对水向上的压力和水的重力相等,A 不正确;铜片上白磷燃烧,红磷不燃烧,说明白磷的着火点比红磷低,即燃烧需要达到可燃物的着火点,B 正确;温度计示数减小,说明NH 4NO 3固体溶于水时吸收热量,C 不正确;音调取决于振动的频率,因此敲击音叉乒乓球被弹起,不能说明振幅越大音调越高,D 不正确。
答案选B 。
15.(1)e (2)g (3)b16.(1)蒸馏 (2)氧气(或O 2)(3)洗菜水浇花(其他答案合理均可)17.(1)肥皂水 (2)活性炭 (3)热塑性 (4)低 (5)乳化 18.(1)密度比空气大 不可燃,也不支持燃烧(2)铁与水、氧气(或空气)同时接触 洗净擦干(其他答案合理均可) (3)溶液刚好由红色变为无色19.(1)H 2O (2)用作建筑材料等 (3)化合反应(4)2H 2O 2=====MnO 22H 2O +O 2↑20.【实验探究】(1)变浑浊(2)CaCO 3+2HCl===CaCl 2+H 2O +CO 2↑ 【拓展延伸】(1)变红(2)碳酸钠溶液也能使酚酞溶液变红【反思交流】(1)除去碳酸钠(或CO 2-3)(合理即可) (2)密封21.(1)0.4g(2)解:设HCl的质量为x。
