五年级奥数——第六讲长度与角度.ppt

(完整版)五年级奥数平面图形面积计算

1 / 4五年级奥数第六讲———平面图形面积的计算一、知识重点1. 基本平面图形特点及面积公式特点面积公式① 四条边都相等。

正方形② 四个角都是直角。

S=aa③ 有四条对称轴。

①对边相等。

长方形②四个角都是直角。

S=ab③有二条对称轴。

平行四边形三角形梯形① 两组对边平行且相等。

② 对角相等，相邻的两个角之和为180°③ 平行四边形简单变形。

①两边之和大于第三条边。

②两边之差小于第三条边。

③三个角的内角和是④有三条边和三个角，拥有稳固性。

① 只有一组对边平行。

② 中位线等于上下底和的一半。

S=ahS=ah ÷ 2S=(a+b)h ÷22. 基本解题方法：由两个或多个简单的基本几何图形组合成的组合图形，要计算这样的组合图形面积，先依据图形的基本关系，再运用分解、组合、平移、割补、添协助线等几种方法将图形变为基本图形分别计算。

【典型例题】【例 1】已知平行四边表的面积是28 平方厘米，【练一练】假如用铁丝围成以下列图同样的求暗影部分的面积。

平行四边形，需要用多少厘米铁丝？（单位：厘米）1 / 4180°。

【例 2】求图中暗影部分的面积。

【练一练】下列图中甲和乙都是正方形，求暗影部分（单位：厘米）的面积。

（单位：厘米）【例 3】以下图，甲三角形的面积比【练一练】平行四边形ABCD 的边长乙三角形的面积大 6 平方厘米，求CE 的长度。

BC=10 厘米，直角三角形 BCE 的直角边 EC 长 8 厘米，已知暗影部分的面积比三角形 EFG 的面积大10 平方厘米。

求 CF 的长。

【例 4】两条对角线把梯形 ABCD 切割成四个三角形。

【练一练】下边的梯形 ABCD 中，下底是已知两个三角形的面积（以下图），求另两个三角形上底的 2 倍， E 是 AB 的中点，求梯形 ABCD 的面积各是多少？（单位：厘米）的面积是三角形EDB 面积的多少倍？B【练一练】【练一练】计算下边图形的面积。

高斯小学奥数五年级下册含答案第06讲_钟表问题

第六讲钟表问题常见的钟表问题主要是讨论钟表上的时针、分针和秒针之间的位置关系，这和我们前面学习过的环形路线问题是很像的．就像前面漫画中画的一样，可以将三种针想象成绕着钟表不断奔跑的三个人，时针是一位老人，他慢悠悠的，12个小时才能在钟表上散步一圈；分针是一位中年人，他有条不紊的，一个小时走过钟表上的一圈；而秒针就像少年们，活力无限，每分钟都绕着钟表欢快的跑过．但同学们会发现，这样的速度表示法并没有明确的说明三种针的速度，所以我们考虑能不能将各个针的速度统一来表示？以前计算一个人或一个物体的速度，所用的单位总是/米秒或/千米时，很明显，在钟表问题中这样的表示法是不适用的，那我们用什么来表示时针、分针和秒针的速度呢？我们仔细观察钟表，会发现除了表示小时的12个大格，在每个大格中还有一些小格，数一数，每个大格都包含了5个小格，那整个钟面上就包含了60个小格，于是，利用这个“格”来表示分针、时针和秒针的速度．经过计算，我们容易得出：时针的速度：5格/时=格/分；分针的速度：60格/时=1格/分；秒针的速度：3600格/时=60格/分=1格/秒．知道了速度，就可以根据以前学过的环形路线问题来分析时针和分针的运动过程，从而解决问题．练一练在下图的钟面上标出时间，并写出分针与时针相差的格数．9:00 10:00分针在时针后_____格分针在时针后_____格1124:30 12:24分针在时针后_____格分针在时针后_____格例题1．一个时钟现在显示的时间是3点整，请问：（1）多少分钟后，时针与分针第一次重合？（2）多少分钟后，时针与分针第一次张开成一条直线？（3）多少分钟后，时针与分针第一次垂直？第二次垂直呢？分析：3点整时，分针落后时针多少格？到了重合、张成直线或者垂直的时候，又分别落后多少格？在这个过程中，分针比时针多走了多少格？练习1．2点到3点之间，什么时候时针和分针重合？什么时候时针与分针张开成一条直线？什么时候时针与分针垂直？通过前面的例题，同学们应该已经学会了最基本的钟表问题解题方法．简单钟表问题求解的关键在于计算分针和时针的路程差，要算清这一点，一定要把出发点两针之间的距离和结束点两针之间的距离算清楚．这个问题中的出发点和结束点都很清楚，因此过程比较简单，但也有很多问题出发点和结束点没有直接给出，这就需要我们自己会合理地选择．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题2．现在是10点23分，多少分钟后，时针与分针第一次垂直？分析：10点23分分针与时针相差的格数很难计算，那我们可以换一个起始时刻．练习2．现在是11点5分，多少分钟后，时针与分针第一次垂直？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -只要是涉及到钟面上分针与时针之间相差多少格的题目，都可以转化成追及问题来处理．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3．小高晚上去超市买东西，到的时候是7点24分，买完出来的时候仍然是7点多，且分针和时针所夹的角度与到超市时相同．请问：小高出来的时候是7点几分？买东西一共花了多少分钟？分析：7点24分时，分针落后时针多少格？练习3．小高晚上去超市买东西，到的时候是7点30分，买完出来的时候仍然是7点多，且分针和时针所夹的角度与到超市时相同．请问：小高出来的时候是7点几分？买东西一共花了多少分钟？钟表用上一段时间之后，有可能会变慢或变快．碰到这种类型的题目应该怎么处理呢？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题4．（1）墨莫的闹钟比标准时间每小时快3分钟．一天晚上11点，墨莫把钟校准，并把闹铃定在第二天早上6点．试问：当闹铃响起时，标准时间是几点几分？（2）萱萱的手表比标准时间每小时慢4分钟．一天早上8点，萱萱将表校准．试问：当这只表指向下午3点的时候，标准时间是几点几分？分析：比标准时间每小时快3分钟，是指标准钟的分针走了60格的同时，快钟的分针走了63格，两针的速度比时20:21．那么“比标准时间每小时慢4分钟”，说明两针的速度比是多少呢？练习4．某手表每小时比标准时间慢3分钟，若在早上4点30分校准，则手表指示为上午10点50分时，标准时间是几点几分？在一些钟表问题中，路程差的想法并不能帮助我们解决问题．这时需要我们发挥想象力，找出分针与时针的路程和．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题5．小明上了一节课，时间不到1小时，他发现下课时与上课时手表上时针与分针的位置刚好对调．请问：这一堂课上了多少分钟？分析：不妨假设上课时是三点多，下课时是四点多．我们可以在钟面上画出上课与下课时分针与时针大概的位置，然后观察在这段时间内它们分别走过的路程．例题6．在早晨6点到7点之间有一个时刻，钟面上的数字“6”恰好在时针与分针的正中央．请问：这时是6点几分？分析：同样的，画图吧，但是题目中给的信息只能知道时针和分针最后的结果，这对我们解决问题是不利的，所以考虑找到一个时针和分针开始运动的时刻，那么，你能想到找哪个时间对我们解题比较有利吗？古代的计时工具日晷是最早报“标准时”的仪器，它由晷盘和晷针组成．晷盘是一个有刻度的盘，其中央装有一根与盘面垂直的晷针，针影随太阳运转而移动在盘上的位置．那时，有钱人家里自己也装有这种钟表．埃及是第一个漏壶钟出口国．它由两个互相叠置的圆筒组成．水从上面的圆筒穿过一个小孔滴入下面的圆筒．水滴完了，就是某个时辰过去了．大一点儿的漏壶灌一次水可报六个小时，然后再重新装满水．古埃及法老王朝的钟表巧匠甚至制做了装有指针和鸣击装置的钟表，每隔一小时，一定数量的圆球便滚落到金属盖上，发出大声的鸣响．罗马人是埃及漏壶钟的主要买主．清晨，报时人大声地报出钟点，然后，每家每户便往漏壶钟里装满水．罗马诗人普拉图斯对这样的计时方法很不满意．他写道：“但愿上帝杀死发明钟点的人，……因为钟点把我的整天撕成了碎块．以前，我的肚子便是我的报时钟，在所有的钟表中它是最好和最准确的．”据说君士坦丁大帝曾经有一只奇妙的钟，即使在今天看来它也是一只极不寻常的、复杂的计时器．它有一棵树木的形状，在枝桠上坐满所有可能的动物，下面蹲着许多的狮子，时钟一敲，狮子便张开大口，发出吼声．柏拉图是第一个借助埃及的漏壶制成闹钟的人．他把下面的圆筒挂起来，使它可以旋转，过一定的时间，圆筒便翻倒，把水倒出，水又流往一个哨管，水流的冲击造成的气流使哨管吱吱作响．每隔同样的时间，柏拉图的闹钟便准时地“吹响”，催促着这位伟大哲学家的学生去上课．漏壶计时的方法持续了几千年．查理大帝在位时还从诃伦哈里发那里得到过一只装有时针和鸣击器的漏壶钟，它用纯金制成，做工精巧，富有艺术性．直到十二世纪，一名僧侣发明了沙时钟，漏壶才逐渐被沙时钟取代．最后，彼得·亨兰发明了平衡轮，克里斯蒂安·海根斯发明了摆锤，在此基础上，才制成了类似于今天的钟表．值得一提的是，沙时钟原先只用于给说教台上的神父掌握说教时间的．据考证，早在公元前2000年，中国就有了漏壶．一张公元前2679年的图样证明中国早有了类似于印度人和阿兹台克人所拥有的日晷．除此之外，中国人还用另外的方法制做了他们的计时器，例如，他们通过燃烧刻有时间标记的薰烛计算时间．另外，据说中国的一位制做钟表的能工巧匠，用各种各样的薰料制成了一种香味钟，它每小时散发出一种不同的味道．作业1.现在时刻为1:24，钟面上，时针与分针所成的角度是多少度？作业2.现在是九点整，那么多少分钟之后时针和分针第一次重合？多少分钟之后时针和分针第一次张开成一条直线？作业3.10点12分，时针和分针的夹角是多少度？之后，时针和分针第一次垂直在什么时刻？作业4.在10点至11点之间，钟面上的时针和分针可能在什么时刻相互垂直？作业5.一个快钟每小时比标准时间快4分钟．小高在标准时间晚上10:00把这个钟调到标准时间．第二天早上小高醒来时，钟面显示的时间是6:00．那么小高醒来时实际是几点几分？第六讲钟表问题例题1. 答案：（1）41611；（2）14911；（3）83211，56511详解：3点整时，分针在时针后面15格．（1）从3点整到重合，分针比时针多走了15格，用了14151161211⎛⎫÷-= ⎪⎝⎭分．（2）第一次张开成直线时，分针在时针前面30格．从3点整算起，分针比时针多走了45格，用了11451491211⎛⎫÷-= ⎪⎝⎭分．（3）第一次垂直时，分针在时针前面15格．从3点整算起，分针比时针多走了30格，用了183********⎛⎫÷-= ⎪⎝⎭分．第二次垂直时，分针在时针前面45格．用了156********⎛⎫÷-= ⎪⎝⎭分．（3点整时针与分针垂直，这不算第一次）例题2. 答案：21511详解：以10点整为起始点，这时分针在时针后面50格．分针与时针第一次垂直时，分针在时针后面45格，用了155151211⎛⎫÷-= ⎪⎝⎭分．但是这时还没有到10点23分，也就是说我们要求的是10整之后时针与分针第二次垂直的时刻．第二次垂直时，分针在时针后面15格，用了12351381211⎛⎫÷-= ⎪⎝⎭分．223823151111-=分．例题3. 答案：7点45211分，42811分详解：7点24分时分针在时针后面13格．小高出来时夹角与到超市时相同，说明出来时分针在时针前面13格，逛超市用了14261281211⎛⎫÷-= ⎪⎝⎭分，出来的时候是7点45211分．例题4. 答案：（1）5时40分；（2）15时30分详解：（1）标准钟分针走60格，闹钟分针可走63格，速度比为20:21．闹钟响起时，闹钟的分针走了760420⨯=格，标准钟的分针可走400格，用时6时40分，标准时间是5点40分．（2）标准钟分针走60格，手表分针可走56格，速度比是15:14．手表下午3点时，手表的分针走了760420⨯=格，标准钟的分针可走450格，用时7个半小时，标准时间是下午3点半．例题5. 答案：55513详解：分针与时针刚好对调，那么分针与时针的路程和刚好是1圈，即60格，这一堂课上了156********⎛⎫÷+= ⎪⎝⎭分．例题6. 答案：92713详解：如图所示，从6点整到这个时刻，时针与分针共走了30格，用了19301271213⎛⎫÷+= ⎪⎝⎭分．练习1. 答案：2点101011分；2点74311分；2点32711分简答：（1）110101101211⎛⎫÷-= ⎪⎝⎭；（2）17401431211⎛⎫÷-= ⎪⎝⎭；（3）132********⎛⎫÷-= ⎪⎝⎭．练习2. 答案：10511简答：从11点开始算起，需要过110101101211⎛⎫÷-= ⎪⎝⎭分时针与分针第一次垂直，101010551111-=．练习3. 答案：44611；41611简答：7点30分时，分针在时针后面7.5格，那么出来时分针在时针前面7.5格．14151161211⎛⎫÷-= ⎪⎝⎭，说明用了41611分，出来时是7点44611分．练习4. 答案：11点10分简答：标准钟分针走60格，手表分针走57格，速度比是20:19．从早上4点30到手表显示的10点50分，手表的分针一共走了380格．3801920400÷⨯=，说明这段时间实际是400分钟，实际时间是11点10分．作业1. 答案：102简答：1:24时，时针与分针相差17格，176102⨯=．作业2. 答案：14911，简答：11451491211⎛⎫÷-= ⎪⎝⎭，14151161211⎛⎫÷-= ⎪⎝⎭．作业3. 答案：126；10点分简答：10点12分时时针与分针相差21格，216126⨯=．12241261211⎛⎫÷-= ⎪⎝⎭． 22611 41611分针路程时针路程作业4.答案：10时5511分；10时23811分简答：155151211⎛⎫÷-=⎪⎝⎭，12351381211⎛⎫÷-=⎪⎝⎭．作业5.答案：5点30分简答：快钟与标准钟的速度比是16:15．到小高醒来时，快钟的分针走了480格，那么标准钟的分针走了450格，需要7.5个小时．所以小高醒来的标准时间是5点30分．。

五年级上册奥数第六讲能被30以下质数整除的数的特征 _通用版(例题含答案)

第六讲能被30以下质数整除的数的特征课本、报刊杂志中的成语、名言警句等俯首皆是，但学生写作文运用到文章中的甚少，即使运用也很难做到恰如其分。

为什么?还是没有彻底“记死”的缘故。

要解决这个问题，方法很简单，每天花3-5分钟左右的时间记一条成语、一则名言警句即可。

可以写在后黑板的“积累专栏”上每日一换，可以在每天课前的3分钟让学生轮流讲解，也可让学生个人搜集，每天往笔记本上抄写，教师定期检查等等。

这样，一年就可记300多条成语、300多则名言警句，日积月累，终究会成为一笔不小的财富。

这些成语典故“贮藏”在学生脑中，自然会出口成章，写作时便会随心所欲地“提取”出来，使文章增色添辉。

大家知道，一个整数能被2整除，那么它的个位数能被2整除；反过来也对，也就是一个数的个位数能被2整除，那么这个数本身能被2整除.因此，我们说“一个数的个位数能被2整除”是“这个数能被2整除”的特征.在这一讲中，我们通过寻求对于某些质数成立的等式来导出能被这些质数整除的数的特征。

课本、报刊杂志中的成语、名言警句等俯首皆是，但学生写作文运用到文章中的甚少，即使运用也很难做到恰如其分。

为什么?还是没有彻底“记死”的缘故。

要解决这个问题，方法很简单，每天花3-5分钟左右的时间记一条成语、一则名言警句即可。

可以写在后黑板的“积累专栏”上每日一换，可以在每天课前的3分钟让学生轮流讲解，也可让学生个人搜集，每天往笔记本上抄写，教师定期检查等等。

这样，一年就可记300多条成语、300多则名言警句，日积月累，终究会成为一笔不小的财富。

这些成语典故“贮藏”在学生脑中，自然会出口成章，写作时便会随心所欲地“提取”出来，使文章增色添辉。

为了叙述方便起见，我们把所讨论的数N记为：观察内容的选择，我本着先静后动，由近及远的原则，有目的、有计划的先安排与幼儿生活接近的，能理解的观察内容。

随机观察也是不可少的，是相当有趣的，如蜻蜓、蚯蚓、毛毛虫等，孩子一边观察，一边提问，兴趣很浓。

《角的度量》PPT课件

注意环境因素对测量的影响，如温度、湿度等，尽量在稳定的环境条件下进行测量。
04
CHAPTER
角的计算与应用
角的和差公式及其应用
角的和差公式
介绍了角的和差公式，即两个角的和或差的正弦、余弦、正切等三角函数值可以通过这两个角的三角函数值计算得出。
应用举例
通过具体实例，展示了如何利用角的和差公式解决与角度计算相关的问题，如测量角度、计算角度等。
02这个Βιβλιοθήκη 享的端点被称为角的顶点，而两条射线被称为角的边。
角的分类
01
锐角
角度小于90度的角。
02
03
04
直角
角度等于90度的角。
钝角
角度大于90度但小于180度的角。
平角
角度等于180度的角。
角的基本性质
角的大小是由其度数来衡量的，度数越大，角越大。
在同一平面内，如果两个角的和等于180 度，则这两个角互为补角。
钝角和直角三角函数
钝角和直角三角函数是高中数学的延伸内容，同样需要借助角的度量进行计算和应用。
三角函数的图像和性质
通过角的度量和三角函数的计算，可以绘制三角函数的图像，并研究其性质和应用。
角在物理问题中的应用
1 2 3
角度与力的关系
在物理学中，角度常常与力的大小和方向有关。通过角的度量，可以计算力之间的夹角，进而解决与力学相关的问题。
角度与速度的关系
在运动学中，角度可以表示速度的方向。通过角的度量，可以计算速度的方向角，进而解决与运动学相关的问题。
角度与光学的关系
在光学中，角度与光的反射、折射等现象密切相关。通过角的度量，可以研究光的传播路径和光学器件的性能。

五年级奥数——第六讲长度与角度

• 例6：图6-14①是两个紧贴的转动较轮的开始位置（大胶轮上画出的一条直径为竖直线，小胶轮上画出的一条直径为水平线）。胶轮周长是小胶轮的3倍，问大胶轮转过多少度后，两轮的这两条直径第一次平行？两轮的这两条直• 例5：纸板上已经画出了一个60 °的角，请你用一个正方形的模板作工具，在纸板上画出一个75 °的角？
•例6：图6-14①是两个紧贴的转动较轮的开始位置（大胶轮上画出的 ①是两个紧贴的转动较轮的开始位置（
一条直径为竖直线，小胶轮上画出的一条直径为水平线）一条直径为竖直线，小胶轮上画出的一条直径为水平线） •胶轮周长是小胶轮的倍，问大胶轮转过多少度后，两轮的这两条直胶轮周长是小胶轮的3倍问大胶轮转过多少度后，胶轮周长是小胶轮的径第一次平行？两轮的这两条直径从平行位置转到再次平行，大胶径第一次平行？两轮的这两条直径从平行位置转到再次平行，轮要转多少度？轮要转多少度？
• 例1：1条1米长的纸条，在距离一端0.618 米的地方有一个红点，把纸条对折起来，在对准红点的地方涂一个黄点，然后打开纸条从红点的地方剪断，再把有黄点的一段对折起来，再对准黄点的地方剪一刀，使纸条断成三段，问四段纸条中最短的一段长度是多少米？
• 例2：一把长为9厘米的直尺，你能不能在上面只刻上三条刻度线，使得这把直尺可以量出1至9厘米的所有整厘米的长度？
• 例3：图6-3是由风筝形和镖形两种不同的砖铺设而成，请仔细观察这个美丽的图案，并且回答风筝形砖的四个内角各是多少度？
• 例4：两条直线相交，四个交角中的一个锐角或一个直角称为这条直线的“夹角” （见图6-8），现平面上有若干条直线，它们两两相交，并且“夹角”只能是30°， 60 °或90 ° ，问：至多有多少条直线？

《角的度量》课件

《角的度量》
如何度量三个角的大小呢？
1厘米
1厘米
1厘米
1厘米
我用尺子试一试。
有专门量角的工具吗？
如何度量三个角的大小呢？
淘气是这么量∠2的，你也试一试。
如果折的角再小一点，会更准确。
如何度量三个角的大小呢？
人们将圆平均分成360份，将其中的1份所对的角作为度量角的单位，它的大小就是1度，记作1°。
每一份所对的角的大小是1°。
人们将圆平均分成360份，将其中的1份所对的角作为度量角的单位，它的大小就是1度，记作1°。1周角=360°，1平角=180°，1直角=90°。
想一想，认一认。
123ຫໍສະໝຸດ ∠1＜∠2＜∠3比较三个角的大小
1
已知∠1=70度，
那么∠2=（）度。
因为∠1和∠2组成了一个平角，是180度，其中∠1是70度，因此∠2是180度减70度。
110
2
算一算
数一数，说一说，比较下面∠1，∠2，∠3的大小。
∠1<∠2<∠3
3
估一估，下面的角有多少度？
30°
80°
4
30°
60°
90°
120°
180°
270°
50°
（1）你能在图上分别标出30°，60°，90°，120°，180°，270°的角吗？
（2）你能在图上标出两个50°的角吗？标一标。
50°
5
（）（）（）（）（）（）（）（）
把一张圆形的纸对折三次。想一想，填一填。
180°
平角
90°
直角
45°
锐角
360°
周角
6
人们将圆平均分成360份，将其中的1份所对的角作为度量角的单位，它的大小就是1度，记作1°。1周角=360°，1平角=180°，1直角=90°。

06五年级奥数第六讲-长度与角度

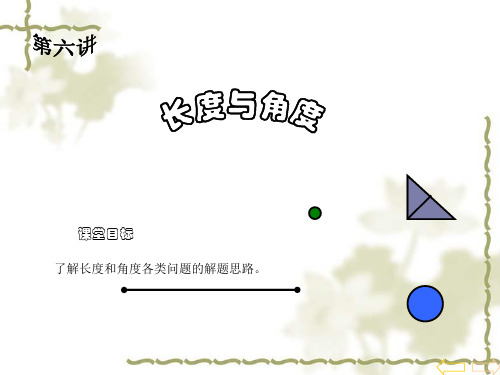
综上所述，我们可以有4种刻法：
0
1
2
3ห้องสมุดไป่ตู้
4
5
6
7
8
9

例3：下图是由风筝形和镖形两种不同的砖铺设而成，请仔细观察这个美丽的图案，并且回答风筝形砖的四个内角各是多少度？
根据多边形内角和公式：n边形内角和=180×（n-2）我们可以看到图中5个风筝形组成一个正10边形，则每个风筝形的钝角 =180×（10-2）÷10=144度，而5个风筝形顶角组成360度，则每个顶角为360÷5=72度，风筝形剩余两个角相等，且内角和一共为360度，所以剩余的角为（360-144-72）÷2=72度。所以，风筝形砖中，有一个钝角144度，其余都是72度。

例4：两条直线相交，四个交角中的一个锐角或一个直角称为这条直线的“夹角”，现平面上有若干条直线，它们两两相交，并且“夹角”只能是30°，60°或者 90°，问：至多有多少条直线？夹角
1
2 3
4 5 6

例5：纸板上已经画出了一个60 °的角，请你用一个正方形的模板作工具，在纸板上画出一个75 °的角？
课堂目标
了解长度和角度各类问题的解题思路。

例1：1条1米长的纸条，在距离一端0.618米的地方有一个红点，把纸条对折起来，在对准红点的地方涂一个黄点，然后打开纸条从红点的地方剪断，再把有黄点的一段对折起来，再对准黄点的地方剪一刀，使纸条断成三段，问四段纸条中最短的一段长度是多少米？
0.382 0.146

1 2
同样道理，当第二次重合时（绿线处），1线右转到绿线+2线左转道到绿线处刚好是180°，则可以求出n+3n=180,n=45° 所以第一次平行大胶轮转了22.5°，第二次平行大胶轮转过45°。

角的大小课件

一个角是另一个角的倍数，其度数等于一个角的度数乘以倍数的值。例如，如果一个角是30度，3倍的角是90度。
角的半数
一个角是另一个角的半数，其度数等于一个角的度数除以2。例如，如果一个角是60度，半的角是30 度。
角的补角和余角
补角
两个角的和为90度，这两个角互为补角。例如，如果一个角是30度，另一个角是60度，它们互为补角。
在日常生活中，角度的应用还涉及到安全问题，如车辆的转向角度、电梯的倾斜角度等，都需要控制在安全范围内，以保障人们的生命安全。
角度在科学中的应用
角度在科学中有着广泛的应用，如物理学中的力矩、化学中的键角、生物学中的关节角度等。这些角度的大小和方向对科学现象的解释和预测具有重要意义。
在科学实验中，角度的测量和控制也是非常重要的，如光谱分析中的入射角和折射角、望远镜的指向角等，都需要精确测量和控制，以保证实验结果的准确性和可靠性。
角度在机械设计中的应用
01
02பைடு நூலகம்
03
机械零件的配合
在机械设计中，许多零件需要精确的角度配合，如齿轮、轴承等，以确保机器的正常运转。
机械运动的控制
通过调整机械运动中的角度，可以精确控制机器的运动轨迹和方向。
机械强度与刚度
合理的角度设计可以提高机械零件的强度和刚度，从而提高机器的整体性能和使用寿命。
角度在运动学中的应用
运动轨迹的控制
在运动学中，角度是一个重要的参数，通过调整角度可以精确控
制物体的运动轨迹和方向。
运动员技术的提高
在体育比赛中，许多技术动作需要精确的角度控制，如投掷、跳高等，通过训练可以提高运动员
的角度控制能力。
运动伤害的预防

角的度量课件

角的度量课件
• 角的基本概念与类型 • 角度的度量方法 • 角的应用 • 角的变换与计算 • 角的研究与探索 • 角的度量练习与思考
目录
01
角的基本概念与类型
角的基本概念
角是由两条射线或线段在一个端点相交而构成的图形。
角的大小是指从一条射线或线段到另一条射线或线段的距离。
角通常用三个大写英文字母或一个希腊字母表示。
角的类型与定义
直角
等于90°的角。
平角
等于180°的角。
锐角
小于90°的角。
钝角
大于90°但小于180° 的角。
周角
等于360°的角。
角的度量单位
度
最基本的单位，通常用“°”表示。
分
1度的十分之一，通常用“′”表示。
秒
1分的十分之一，通常用“″”表示。
02
角度的度量方法
量角器的使用方法
角在日常生活中的应用
角度测量
如何使用量角器等工具进行角度测量，如测量角度大小、角度之间的数量关系等。
角度与生活的关系
角在生活中无处不在，如房屋结构、家具设计、车辆行驶等，这些都需要考虑角度问题。
角度与运动的关系
角在运动学中的应用，如速度、加速度等，这些都需要考虑角度问题。
角在科学领域中的应用
现代角的度量技术
随着科技的发展，现代的测量仪器越来越精密和准确，如电子测角仪、全站仪等，这些仪器可以提供高精度的角度测量数据。
角度测量在科技中的应用
角度测量在科技中有着广泛的应用，如地理测量、航空测量、工程测量等，这些领域都需要高精度的角度数据来支持。
角的应用的未来展望
角在数学中的进一步应用

高斯小学奥数五年级下册含答案第06讲_钟表问题

第六讲钟表问题常见的钟表问题主要是讨论钟表上的时针、分针和秒针之间的位置关系，这和我们前面学习过的环形路线问题是很像的．就像前面漫画中画的一样，可以将三种针想象成绕着钟表不断奔跑的三个人，时针是一位老人，他慢悠悠的，12个小时才能在钟表上散步一圈；分针是一位中年人，他有条不紊的，一个小时走过钟表上的一圈；而秒针就像少年们，活力无限，每分钟都绕着钟表欢快的跑过．但同学们会发现，这样的速度表示法并没有明确的说明三种针的速度，所以我们考虑能不能将各个针的速度统一来表示？以前计算一个人或一个物体的速度，所用的单位总是/米秒或/千米时，很明显，在钟表问题中这样的表示法是不适用的，那我们用什么来表示时针、分针和秒针的速度呢？我们仔细观察钟表，会发现除了表示小时的12个大格，在每个大格中还有一些小格，数一数，每个大格都包含了5个小格，那整个钟面上就包含了60个小格，于是，利用这个“格”来表示分针、时针和秒针的速度．经过计算，我们容易得出：时针的速度：5格/时=格/分；分针的速度：60格/时=1格/分；秒针的速度：3600格/时=60格/分=1格/秒．知道了速度，就可以根据以前学过的环形路线问题来分析时针和分针的运动过程，从而解决问题．练一练在下图的钟面上标出时间，并写出分针与时针相差的格数．9:00 10:00分针在时针后_____格分针在时针后_____格1124:30 12:24分针在时针后_____格分针在时针后_____格例题1．一个时钟现在显示的时间是3点整，请问：（1）多少分钟后，时针与分针第一次重合？（2）多少分钟后，时针与分针第一次张开成一条直线？（3）多少分钟后，时针与分针第一次垂直？第二次垂直呢？分析：3点整时，分针落后时针多少格？到了重合、张成直线或者垂直的时候，又分别落后多少格？在这个过程中，分针比时针多走了多少格？练习1．2点到3点之间，什么时候时针和分针重合？什么时候时针与分针张开成一条直线？什么时候时针与分针垂直？通过前面的例题，同学们应该已经学会了最基本的钟表问题解题方法．简单钟表问题求解的关键在于计算分针和时针的路程差，要算清这一点，一定要把出发点两针之间的距离和结束点两针之间的距离算清楚．这个问题中的出发点和结束点都很清楚，因此过程比较简单，但也有很多问题出发点和结束点没有直接给出，这就需要我们自己会合理地选择．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题2．现在是10点23分，多少分钟后，时针与分针第一次垂直？分析：10点23分分针与时针相差的格数很难计算，那我们可以换一个起始时刻．练习2．现在是11点5分，多少分钟后，时针与分针第一次垂直？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -只要是涉及到钟面上分针与时针之间相差多少格的题目，都可以转化成追及问题来处理．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3．小高晚上去超市买东西，到的时候是7点24分，买完出来的时候仍然是7点多，且分针和时针所夹的角度与到超市时相同．请问：小高出来的时候是7点几分？买东西一共花了多少分钟？分析：7点24分时，分针落后时针多少格？练习3．小高晚上去超市买东西，到的时候是7点30分，买完出来的时候仍然是7点多，且分针和时针所夹的角度与到超市时相同．请问：小高出来的时候是7点几分？买东西一共花了多少分钟？钟表用上一段时间之后，有可能会变慢或变快．碰到这种类型的题目应该怎么处理呢？- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题4．（1）墨莫的闹钟比标准时间每小时快3分钟．一天晚上11点，墨莫把钟校准，并把闹铃定在第二天早上6点．试问：当闹铃响起时，标准时间是几点几分？（2）萱萱的手表比标准时间每小时慢4分钟．一天早上8点，萱萱将表校准．试问：当这只表指向下午3点的时候，标准时间是几点几分？分析：比标准时间每小时快3分钟，是指标准钟的分针走了60格的同时，快钟的分针走了63格，两针的速度比时20:21．那么“比标准时间每小时慢4分钟”，说明两针的速度比是多少呢？练习4．某手表每小时比标准时间慢3分钟，若在早上4点30分校准，则手表指示为上午10点50分时，标准时间是几点几分？在一些钟表问题中，路程差的想法并不能帮助我们解决问题．这时需要我们发挥想象力，找出分针与时针的路程和．- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题5．小明上了一节课，时间不到1小时，他发现下课时与上课时手表上时针与分针的位置刚好对调．请问：这一堂课上了多少分钟？分析：不妨假设上课时是三点多，下课时是四点多．我们可以在钟面上画出上课与下课时分针与时针大概的位置，然后观察在这段时间内它们分别走过的路程．例题6．在早晨6点到7点之间有一个时刻，钟面上的数字“6”恰好在时针与分针的正中央．请问：这时是6点几分？分析：同样的，画图吧，但是题目中给的信息只能知道时针和分针最后的结果，这对我们解决问题是不利的，所以考虑找到一个时针和分针开始运动的时刻，那么，你能想到找哪个时间对我们解题比较有利吗？古代的计时工具日晷是最早报“标准时”的仪器，它由晷盘和晷针组成．晷盘是一个有刻度的盘，其中央装有一根与盘面垂直的晷针，针影随太阳运转而移动在盘上的位置．那时，有钱人家里自己也装有这种钟表．埃及是第一个漏壶钟出口国．它由两个互相叠置的圆筒组成．水从上面的圆筒穿过一个小孔滴入下面的圆筒．水滴完了，就是某个时辰过去了．大一点儿的漏壶灌一次水可报六个小时，然后再重新装满水．古埃及法老王朝的钟表巧匠甚至制做了装有指针和鸣击装置的钟表，每隔一小时，一定数量的圆球便滚落到金属盖上，发出大声的鸣响．罗马人是埃及漏壶钟的主要买主．清晨，报时人大声地报出钟点，然后，每家每户便往漏壶钟里装满水．罗马诗人普拉图斯对这样的计时方法很不满意．他写道：“但愿上帝杀死发明钟点的人，……因为钟点把我的整天撕成了碎块．以前，我的肚子便是我的报时钟，在所有的钟表中它是最好和最准确的．”据说君士坦丁大帝曾经有一只奇妙的钟，即使在今天看来它也是一只极不寻常的、复杂的计时器．它有一棵树木的形状，在枝桠上坐满所有可能的动物，下面蹲着许多的狮子，时钟一敲，狮子便张开大口，发出吼声．柏拉图是第一个借助埃及的漏壶制成闹钟的人．他把下面的圆筒挂起来，使它可以旋转，过一定的时间，圆筒便翻倒，把水倒出，水又流往一个哨管，水流的冲击造成的气流使哨管吱吱作响．每隔同样的时间，柏拉图的闹钟便准时地“吹响”，催促着这位伟大哲学家的学生去上课．漏壶计时的方法持续了几千年．查理大帝在位时还从诃伦哈里发那里得到过一只装有时针和鸣击器的漏壶钟，它用纯金制成，做工精巧，富有艺术性．直到十二世纪，一名僧侣发明了沙时钟，漏壶才逐渐被沙时钟取代．最后，彼得·亨兰发明了平衡轮，克里斯蒂安·海根斯发明了摆锤，在此基础上，才制成了类似于今天的钟表．值得一提的是，沙时钟原先只用于给说教台上的神父掌握说教时间的．据考证，早在公元前2000年，中国就有了漏壶．一张公元前2679年的图样证明中国早有了类似于印度人和阿兹台克人所拥有的日晷．除此之外，中国人还用另外的方法制做了他们的计时器，例如，他们通过燃烧刻有时间标记的薰烛计算时间．另外，据说中国的一位制做钟表的能工巧匠，用各种各样的薰料制成了一种香味钟，它每小时散发出一种不同的味道．作业1.现在时刻为1:24，钟面上，时针与分针所成的角度是多少度？作业2.现在是九点整，那么多少分钟之后时针和分针第一次重合？多少分钟之后时针和分针第一次张开成一条直线？作业3.10点12分，时针和分针的夹角是多少度？之后，时针和分针第一次垂直在什么时刻？作业4.在10点至11点之间，钟面上的时针和分针可能在什么时刻相互垂直？作业5.一个快钟每小时比标准时间快4分钟．小高在标准时间晚上10:00把这个钟调到标准时间．第二天早上小高醒来时，钟面显示的时间是6:00．那么小高醒来时实际是几点几分？第六讲钟表问题例题1. 答案：（1）41611；（2）14911；（3）83211，56511详解：3点整时，分针在时针后面15格．（1）从3点整到重合，分针比时针多走了15格，用了14151161211⎛⎫÷-= ⎪⎝⎭分．（2）第一次张开成直线时，分针在时针前面30格．从3点整算起，分针比时针多走了45格，用了11451491211⎛⎫÷-= ⎪⎝⎭分．（3）第一次垂直时，分针在时针前面15格．从3点整算起，分针比时针多走了30格，用了183********⎛⎫÷-= ⎪⎝⎭分．第二次垂直时，分针在时针前面45格．用了156********⎛⎫÷-= ⎪⎝⎭分．（3点整时针与分针垂直，这不算第一次）例题2. 答案：21511详解：以10点整为起始点，这时分针在时针后面50格．分针与时针第一次垂直时，分针在时针后面45格，用了155151211⎛⎫÷-= ⎪⎝⎭分．但是这时还没有到10点23分，也就是说我们要求的是10整之后时针与分针第二次垂直的时刻．第二次垂直时，分针在时针后面15格，用了12351381211⎛⎫÷-= ⎪⎝⎭分．223823151111-=分．例题3. 答案：7点45211分，42811分详解：7点24分时分针在时针后面13格．小高出来时夹角与到超市时相同，说明出来时分针在时针前面13格，逛超市用了14261281211⎛⎫÷-= ⎪⎝⎭分，出来的时候是7点45211分．例题4. 答案：（1）5时40分；（2）15时30分详解：（1）标准钟分针走60格，闹钟分针可走63格，速度比为20:21．闹钟响起时，闹钟的分针走了760420⨯=格，标准钟的分针可走400格，用时6时40分，标准时间是5点40分．（2）标准钟分针走60格，手表分针可走56格，速度比是15:14．手表下午3点时，手表的分针走了760420⨯=格，标准钟的分针可走450格，用时7个半小时，标准时间是下午3点半．例题5. 答案：55513详解：分针与时针刚好对调，那么分针与时针的路程和刚好是1圈，即60格，这一堂课上了156********⎛⎫÷+= ⎪⎝⎭分．例题6. 答案：92713详解：如图所示，从6点整到这个时刻，时针与分针共走了30格，用了19301271213⎛⎫÷+= ⎪⎝⎭分．练习1. 答案：2点101011分；2点74311分；2点32711分简答：（1）110101101211⎛⎫÷-= ⎪⎝⎭；（2）17401431211⎛⎫÷-= ⎪⎝⎭；（3）132********⎛⎫÷-= ⎪⎝⎭．练习2. 答案：10511简答：从11点开始算起，需要过110101101211⎛⎫÷-= ⎪⎝⎭分时针与分针第一次垂直，101010551111-=．练习3. 答案：44611；41611简答：7点30分时，分针在时针后面7.5格，那么出来时分针在时针前面7.5格．14151161211⎛⎫÷-= ⎪⎝⎭，说明用了41611分，出来时是7点44611分．练习4. 答案：11点10分简答：标准钟分针走60格，手表分针走57格，速度比是20:19．从早上4点30到手表显示的10点50分，手表的分针一共走了380格．3801920400÷⨯=，说明这段时间实际是400分钟，实际时间是11点10分．作业1. 答案：102简答：1:24时，时针与分针相差17格，176102⨯=．作业2. 答案：14911，简答：11451491211⎛⎫÷-= ⎪⎝⎭，14151161211⎛⎫÷-= ⎪⎝⎭．作业3. 答案：126；10点分简答：10点12分时时针与分针相差21格，216126⨯=．12241261211⎛⎫÷-= ⎪⎝⎭． 22611 41611分针路程时针路程作业4.答案：10时5511分；10时23811分简答：155151211⎛⎫÷-=⎪⎝⎭，12351381211⎛⎫÷-=⎪⎝⎭．作业5.答案：5点30分简答：快钟与标准钟的速度比是16:15．到小高醒来时，快钟的分针走了480格，那么标准钟的分针走了450格，需要7.5个小时．所以小高醒来的标准时间是5点30分．。

五年级第六讲火车行程问题省公开课获奖课件说课比赛一等奖课件

两列火车错车用旳时间是：
(A旳车身长+B旳车身长)÷(A车旳速度+B车旳速度)
练习：
在有上、下行旳轨道上，两列火车相对开来，甲列车旳车身长235米，每秒行驶25米，乙列车旳车身长 215米，每秒行驶20米。求这两列火车从车头相遇到车尾离开需要多少秒钟。
例4、一列客车经过250米长旳隧道用25秒，经过210米长旳隧道用23秒.已知在客车旳前方有一列行驶方向与它相同旳货车，车身长为320米，速度每秒17米.求列车与客车从相遇到离开所用旳时间.
客车速度是每秒
（250－210）÷（25－23）＝20(米)，车身长＝20×23－210＝250(米) 客车与火车从相遇到离开旳时间是
（250＋320）÷（20－17）＝190（秒）答:客车与火车从相遇到离开旳时间是190秒.
两列火车超车用旳时间是：
(A旳车身长+B旳车身长)÷(A车旳速度-B车旳速度) (注：A车追B车)
解：队伍长：1×(528÷4-1)=131(米) 队伍行进旳旅程： 25×16=400(米) 桥长：400-131=269(米)
答：这座桥长269米。
练习：
少先队员346人排成两路纵队去参观科技成果展览，队伍行进旳速度是每分23米，前后两人都相距1米，目前经过一座长 702米旳大桥，整个队伍从上桥到离开桥用多长时间？
火车行程问题涉及火车过桥（或隧道），火车错车问题及火车超车问题。
例1.一列火车长180米，每秒钟行25米. 全车经过一条120米旳山洞，需要多少时间?
（180＋120）÷25＝12（秒）答：需要12秒钟.
火车过桥（或隧道）问题，可用下面旳关系式求火车经过旳时间：
[列车长度+桥（或隧道）旳长度]÷列车速度

奥数第六讲行程问题

奥数第六讲行程问题行程问题是小学奥数中变化最多的一个专题，不论在奥数竞赛中还是在“小升初”的升学考试中，都拥有非常重要的地位。

行程问题中包括：火车过桥、流水行船、沿途数车、猎狗追兔、环形行程、多人行程，等等。

每一类问题都有自己的特点，解决方法也有所不同，但是，行程问题无论怎么变化，都离不开“三个量，三个关系”：这三个量是：路程(s)、速度(v)、时间(t)三个关系：1. 简单行程：路程 = 速度× 时间2. 相遇问题：路程和 = 速度和× 时间3. 追击问题：路程差 = 速度差× 时间牢牢把握住这三个量以及它们之间的三种关系，就会发现解决行程问题还是有很多方法可循的。

①追击及相遇问题一、例题与方法指导例1. 有甲、乙、丙三人同时同地出发，绕一个花圃行走，乙、丙二人同方向行走，甲与乙、丙相背而行。

甲每分钟走40米，乙每分钟走38米，丙每分钟走36米。

在途中，甲和乙相遇后3分钟和丙相遇。

问：这个花圃的周长是多少米？思路导航：这个三人行程的问题由两个相遇、一个追击组成，题目中所给的条件只有三个人的速度，以及一个“3分钟”的时间。

第一个相遇：在3分钟的时间里，甲、丙的路程和为（40+36）×3=228（米）第一个追击：这228米是由于在开始到甲、乙相遇的时间里，乙、丙两人的速度差造成的，是逆向的追击过程，可求出甲、乙相遇的时间为228÷ （38-36）=114（分钟）第二个相遇：在114分钟里，甲、乙二人一起走完了全程所以花圃周长为（40+38）×114=8892（米）我们把这样一个抽象的三人行程问题分解为三个简单的问题，使解题思路更加清晰。

例2. 东西两地间有一条公路长217.5千米，甲车以每小时25千米的速度从东到西地，1.5小时后，乙车从西地出发，再经过3小时两车还相距15千米。

乙车每小时行多少千米？思路导航：从图中可以看出，要求乙车每小时行多少千米，关键要知道乙车已经行了多少路程和行这段路程所用的时间。

五年级奥数第六、七讲--行程问题

第六讲行程问题（二）知识要点：相遇问题两个物体由于相向运动而相遇。

解答此类问题的关键是求出两个运动物体的速度和。

基本关系式有:速度和×相遇时间＝相遇路程相遇路程÷速度和＝相遇时间相遇路程÷相遇时间＝速度和相遇路程：两个运动物体从两地同时相向运动所行的路程.例题精讲：【例1】一辆客车和一辆货车同时从A、B两城相对开出.客车的速度是62每小时千米,货车的速度是50千米每小时，经过4小时相遇，A、B两城相距多远？每小时62千米每小时50千米客车货车？千米小结：这是一道典型的相遇问题，还可以尝试直接套用相遇问题的公式：速度和×相遇时间=相遇路程进行解答。

【例2】解放军某部通讯兵在一次演习中，摩托车每小时行60千米，汽车每小时行40千米，汽车出发1.5小时后，摩托车沿同路去追赶汽车，需要几小时追上？小结：这是典型的求追及时间的问题：可根据公式速度差×追及时间=追及距离进行求解。

【例2】运动场的跑道400米，王芳和陈月两名运动员从起跑线同时出发,王芳每分钟跑390米,陈月每分钟跑310米,求多少分钟后王芳超过陈月一周？小结：本题是典型的环形跑道问题追及问题的综合。

基础巩固：1、小亚和小巧同时从自己家里走向学校。

小亚每分钟走65米,小巧每分钟走70米,经过4分钟两人在校门相遇,他们两家相距多少米？2、客车和货车同时从甲、乙两地相向开出，客车每小时行40千米，货车每小时行32千米，4小时后两车相遇，甲、乙两地相距多少千米?3、甲、乙两地相距288千米，客车和货车同时从甲、乙两地相向开出,客车每小时行40千米，货车每小时行32千米，几小时后两车相遇？4、一辆拖拉机要去拉货，每小时走30千米，出发30分钟后,家中有事派一辆小轿车50千米/小时的速度去追拖拉机，问小轿车用多少时间可以追上拖拉机？5、一条环形跑道长400米,甲骑自行车平均每分钟骑300米,乙跑步,平均每分钟跑250米，两人同时同地同向出发,经过多少分钟两人相遇？6、客车和货车同时从丙地开出,向相反方向开出，客车每小时行40千米，货车每小时行32千米，开出4小时后,两车相距多少千米？7、甲、乙二人骑自行车从环形公路上同一地点同时出发，背向而行,环形公路的一周是360米。

《角以及角的度量》PPT优秀课件

(2) 16°59′15″.
解：(1)75°24′36″＝75.41°
(2)16°59′15″＝16.987 5°
2. 计算：(1) 70°56′－26°31′
(2) 90°－32°51′18″.
解：(1)70°56′－26°31′＝44°25′ (2)90°－32°51′18″＝57°8′42″
3 1°等于（ C ）
1. 如图所示． (1)写出能用一个字母表示的角； (2)写出以B为顶点的角； (3)图中共有几个角？(不包括平角和周角)
解：(1)∠A，∠C. (2)∠ABC，∠ABD，∠CBD. (3)共有9个角．
2. 如图，下列说法中错误的是（ B ） A.∠1与∠AOB表示同一个角 B.∠AOC也可用∠O来表示 C.图中共有三个角：∠AOB、∠AOC、∠BOC D.∠β表示的是∠BOC
0.2′ = 60"×0.2 = 12". 所以57. 32°=57°19′12".
总结
注意度、分、秒是六十进制.
例4 将 10°6′36" 用度表示.
解：先把36" 化为分，
36″=
1 60
×36=0.6′
，6′
+0.6′
=
6.6′.
再把6.6' 化为度，
3.6′=
1 60
×6.6=0.11°，
问题（二）
你能举出几个在现实生活中反映角是由一条射线绕其端点旋转而成的例子吗?
定义有公共端点的两条射线所组成的图形叫做角，这个公共端点叫做角的顶点，这两条射线叫做角的边. 如图，点O是角的顶点，射线OA和OB是角的边. 角可以看做一条射线绕着端点旋转到另一个位置所形成的图形.

人教五年级数学上册《角的度量》课件PPT(最新)

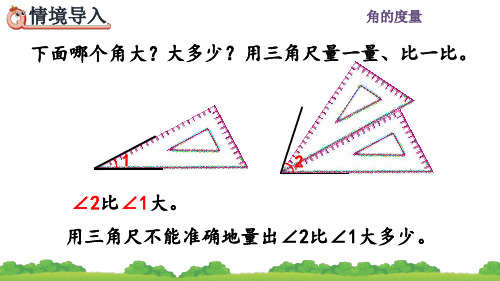
1时＝6分 1分＝60秒
课堂小结这节课你们都学会了哪些知识？
角的度量
如何计算经过时间？ 1、数格后，用格数乘5来计算； 2、经过时间＝结束时刻－开始时刻。
课堂练习
角的度量
如图，学校操场的跑道由正方形的两条对边和两个半圆组
成。小晨在操场上跑了5圈，一共是多少米？
操场跑道的长度等于一个整圆的周长与两条直的跑道的长度之和。
50 m
（3.14×50＋50×2）×5＝1285（m）答：一共是1285米。

课堂练习
角的度量
如图所示，一块边长为8m的正方形草地，在图中相对的顶点处各拴有一只羊，拴羊的绳长都是8m．两只羊都能吃到草的草地面积（阴影部分）是多少平方米？
举例
比较大小。 9分＝540秒 9分○> 90秒 60＋15＝75秒 1分15秒 ○> 65秒
探究新知
比大小。
○ 30分 < 3时 ○ 40秒 < 1分 ○ 60分 = 1时
练习
角的度量
○ 80分 > 1时 ○ 120分 = 2时 ○ 90分 < 3时
探究新知
角的度量
结束时刻－开始时刻＝经过时间
练习
开始时刻＝结束时刻－经过时间 7时50分－16分=7时34分答：他最晚7时34分出发。
课堂练习
填一填。
先统一单位，再填写。
角的度量
2时＝( 120 )分 2时15分＝( 135 )分 5分＝( 300 )秒 130秒－10秒＝( 2 )分
课堂练习
角的度量
在（）里填上“＞”“＜”或“＝”。
○ 30分 < 3时 ○ 40秒 < 1分 ○ 60分 = 1时

长度和角度计量演示文稿

L4
L1
L
L2 L3
量块平晶
图3-4量块
量块的用途：量块在机械制造厂和各级计量部门中应
用较广，常作为尺寸传递的长度标准和计量仪器示值误差的检定标准，也可作为精密机械零件测量、精密机床和夹具调整时的尺寸基准。
量块的精度（级）：GB/T6093－2001按制造精度将量块分为00，0，1，2，3和K级共6级，其中00级精度最高，3级精度最低，K级为校准级。主要根据量块长度极限偏差、测量面的平面度、粗糙度及量块的研合性等指标来划分的。量块按“级”使用时，以量块的标称长度为工作尺寸，该尺寸包含了量块的制造误差，并将被引入到测量结果中。由于不需要加修正值，故使用较方便。
度与环境温度相同后方可使用。 5. 轻拿、轻放量块，杜绝磕碰、跌落等情况的发生。 6. 不得用手直接接触量块，以免造成汗液对量块的腐蚀及
手温对测量精确度的影响。 7. 使用完毕，应用航空汽油清洗所用量块，并擦干后涂上
防锈脂存于干燥处。
第五节测量误差与数据处理
• 一、测量误差的概述（自学）
二、随机误差 1. 随机误差的分布规律及其特性
x=xi±δlim = xi±3σ
式中 xi
某次测得值。
（3-14）
4. 测量列中随机误差的处理
（1）测量列的算术平均值 x
在评定有限测量次数测量列的随机误差时，必须获
得真值，但真值是不知道的，因此只能从测量列中找到一个接近真值的数值加以代替，这就是测量列的算术平均值。
随机误差可用试验方法来确定。实践表明，大多数情况下，随机误差符合正态分布。为便于理解，现举例说明。
表3-2 测量数据统计表
尺寸分组区间 / mm
19.990～19.992 19.992～19.994 19.994～19.996 19.996～19.998 19.998～20.000 20.000～20.002 20.002～20.004 20.004～20.006 20.006～20.008 20.008～20.010 20.010～20.012

五年级奥数——第六讲长度与角度.ppt

(完整版)五年级奥数平面图形面积计算

高斯小学奥数五年级下册含答案第06讲_钟表问题

五年级上册奥数第六讲 能被30以下质数整除的数的特征 _通用版(例题含答案)

《角的度量》PPT课件

五年级奥数——第六讲长度与角度

《角的度量》课件

06五年级奥数第六讲-长度与角度

角的大小课件

角的度量课件

高斯小学奥数五年级下册含答案第06讲_钟表问题

五年级第六讲火车行程问题省公开课获奖课件说课比赛一等奖课件

奥数第六讲 行程问题

五年级奥数第六、七讲--行程问题

《角以及角的度量》PPT优秀课件

人教五年级数学上册《角的度量》课件PPT(最新)

长度和角度计量演示文稿

五年级上册奥数第六讲能被30以下质数整除的数的特征 _通用版(例题含答案)

奥数第六讲行程问题