最新平行线与三角形内角和(计算(人教版含答案
2022年中考数学真题-专题11 平行线与三角形(1)(全国通用解析版)

专题11 平行线与三角形一.选择题(2022·湖北宜昌·中考真题)1. 如图,在ABC 中,分别以点B 和点C 为圆心,大于12BC 长为半径画弧,两弧相交于点M ,N .作直线MN ,交AC 于点D ,交BC 于点E ,连接BD .若7AB =,12AC =,6BC =,则ABD △的周长为( )A. 25B. 22C. 19D. 18【答案】C【解析】 【分析】由垂直平分线的性质可得BD =CD ,由△ABD 的周长=AB +AD +BD =AB +AD +CD =AB +AC 得到答案.【详解】解:由作图的过程可知,DE 是BC 的垂直平分线,∴BD =CD ,∵7AB =,12AC =,∴ △ABD 的周长=AB +AD +BD=AB +AD +CD=AB +AC=19.故选:C【点睛】此题考查了线段垂直平分线的作图、线段垂直平分线的性质、三角形的周长等知识,熟练掌握线段垂直平分线的性质是解题的关键.(2022·浙江台州·中考真题)2. 如图,点D 在ABC 的边BC 上,点P 在射线AD 上(不与点A ,D 重合),连接PB ,PC .下列命题中,假命题是( )A. 若AB AC =,AD BC ⊥,则PB PC =B. 若PB PC =,AD BC ⊥,则AB AC =C. 若AB AC =,12∠=∠,则PB PC =D. 若PB PC =,12∠=∠,则AB AC =【答案】D【解析】【分析】根据等腰三角形三线合一的性质证明PD 是否是BC 的垂直平分线,判断即可.【详解】因为AB=AC ,且AD ⊥BC ,得AP 是BC 的垂直平分线,所以PB=PC ,则A 是真命题;因为PB=PC ,且AD ⊥BC ,得AP 是BC 的垂直平分线,所以AB=AC ,则B 是真命题;因为AB=AC ,且∠1=∠2,得AP 是BC 的垂直平分线,所以PB=PC ,则C 是真命题;因为PB=PC ,△BCP 是等腰三角形,∠1=∠2,不能判断AP 是BC 的垂直平分线,所以AB 和AC 不一定相等,则D 是假命题.故选:D .【点睛】本题主要考查了等腰三角形的性质和判定,掌握性质定理是解题的关键. (2022·江苏宿迁·中考真题)3. 若等腰三角形的两边长分别是3cm 和5cm ,则这个等腰三角形的周长是( )A. 8cmB. 13cmC. 8cm 或13cmD. 11cm 或13cm 【答案】D【解析】【分析】题目给出等腰三角形有两条边长为3和5,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【详解】解:当3是腰时,∵3+3>5,∴3,3,5能组成三角形,此时等腰三角形的周长为3+3+5=11(cm),当5是腰时,∵3+5>5,5,5,3能够组成三角形,此时等腰三角形的周长为5+5+3=13(cm),则三角形的周长为11cm或13cm.故选:D【点睛】本题考查等腰三角形的性质及三角形三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.(2022·浙江杭州·中考真题)4. 如图,CD⊥AB于点D,已知∠ABC是钝角,则()A. 线段CD是ABC的AC边上的高线B. 线段CD是ABC的AB边上的高线C. 线段AD是ABC的BC边上的高线D. 线段AD是ABC的AC边上的高线【答案】B【解析】【分析】根据高线的定义注意判断即可.【详解】∵线段CD是ABC的AB边上的高线,∴A错误,不符合题意;∵线段CD是ABC的AB边上的高线,∴B正确,符合题意;∵线段AD是ACD的CD边上的高线,∴C错误,不符合题意;∵线段AD是ACD的CD边上的高线,∴D错误,不符合题意;故选B.【点睛】本题考查了三角形高线的理解,熟练掌握三角形高线的相关知识是解题的关键.(2022·湖南邵阳·中考真题)5. 下列长度的三条线段能首尾相接构成三角形的是()A. 1cm,2cm,3cmB. 3cm,4cm,5cmC. 4cm,5cm,10cmD. 6cm,9cm,2cm【答案】B【解析】【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.【详解】解:根据三角形的三边关系,知A、1+2=3,不能组成三角形,故选项错误,不符合题意;B、3+4>5,能够组成三角形,故选项正确,符合题意;C、5+4<10,不能组成三角形,故选项错误,不符合题意;D、2+6<9,不能组成三角形,故选项错误,不符合题意;故选:B.【点睛】此题考查了三角形的三边关系.解题的关键是看较小的两个数的和是否大于第三个数.(2022·云南·中考真题)6. 如图,OB平分∠AOC,D、E、F分别是射线OA、射线OB、射线OC上的点,D、E、F与O点都不重合,连接ED、EF若添加下列条件中的某一个.就能使DOE FOE,你认为要添加的那个条件是()A. OD =OEB. OE =OFC. ∠ODE =∠OEDD. ∠ODE =∠OFE【答案】D【解析】【分析】根据OB 平分∠AOC 得∠AOB =∠BOC ,又因为OE 是公共边,根据全等三角形的判断即可得出结果.【详解】解:∵OB 平分∠AOC∴∠AOB =∠BOC当△DOE ≌△FOE 时,可得以下结论:OD =OF ,DE =EF ,∠ODE =∠OFE ,∠OED =∠OEF .A 答案中OD 与OE 不是△DOE ≌△FOE 的对应边,A 不正确;B 答案中OE 与OF 不是△DOE ≌△FOE 的对应边,B 不正确;C 答案中,∠ODE 与∠OED 不是△DOE ≌△FOE 的对应角,C 不正确; D 答案中,若∠ODE =∠OFE ,在△DOE 和△FOE 中, DOE FOE OE OEODE OFE =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△DOE ≌△FOE (AAS )∴D 答案正确.故选:D .【点睛】本题考查三角形全等的判断,理解全等图形中边和角的对应关系是解题的关键.(2022·浙江湖州·中考真题)7. 如图,已知在锐角△ABC 中,AB =AC ,AD 是△ABC 的角平分线,E 是AD 上一点,连结EB ,E C .若∠EBC =45°,BC =6,则△EBC 的面积是( )A. 12B. 9C. 6D. 【答案】B【解析】【分析】根据三线合一可得ED BC ⊥,根据垂直平分线的性质可得EB EC =,进而根据∠EBC =45°,可得BEC △为等腰直角三角形,根据斜边上的中线等于斜边的一半可得132DE BC ==,然后根据三角形面积公式即可求解. 【详解】解: AB =AC ,AD 是△ABC 的角平分线,,AD BD BD DC ∴⊥=,EB EC ∴=,∠EBC =45°,45ECB EBC ∠=∠=︒,∴BEC △为等腰直角三角形,6BC =, ∴132DE BC ==, 则△EBC 的面积是13692⨯⨯=.故选B .【点睛】本题考查了等腰三角形的性质与判定,垂直平分线的性质,直角三角形中斜边上的中线等于斜边的一半,掌握等腰三角形的性质与判定是解题的关键. (2022·江苏扬州·中考真题)8. 如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为ABC ∆,提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )A. ,,AB BC CAB. ,,AB BC B ∠C. ,,AB AC B ∠D. ,,∠∠A B BC【答案】C【解析】 【分析】根据SSS ,SAS ,ASA 逐一判定,其中SSA 不一定符合要求.【详解】A. ,,AB BC CA .根据SSS 一定符合要求;B. ,,AB BC B ∠.根据SAS 一定符合要求;C. ,,AB AC B ∠.不一定符合要求;D. ,,∠∠A B BC .根据ASA 一定符合要求.故选:C .【点睛】本题考查了三角形全等的判定,解决问题的关键是熟练掌握判定三角形全等的SSS ,SAS ,ASA 三个判定定理.(2022·山东泰安·中考真题)9. 如图,30AOB ∠=︒,点M 、N 分别在边OA OB 、上,且3,5OM ON ==,点P 、Q 分别在边OB OA 、上,则MP PQ QN ++的最小值是( )A. 2- 2-【答案】A【解析】 【分析】作M 关于OB 的对称点M ′,作N 关于OA 的对称点N ′,连接M ′N ′,即为MP +PQ +QN 的最小值;证出△ONN ′为等边三角形,△OMM ′为等边三角形,得出∠N ′OM ′=90°,由勾股定理求出M ′N ′即可.【详解】解:作M 关于OB 的对称点M ′,作N 关于OA 的对称点N ′,如图所示:连接M ′N ′,即为MP +PQ +QN 的最小值.根据轴对称的定义可知:5ON ON '==,3OM OM '==,∠N ′OQ =∠M ′OB =30°, ∴∠NON ′=60°,'60MOM ∠=︒,∴△ONN ′为等边三角形,△OMM ′为等边三角形,∴∠N ′OM ′=90°,∴在Rt △M ′ON ′中,M ′N=故选:A .【点睛】本题考查了轴对称--最短路径问题,根据轴对称的定义,找到相等的线段,得到等边三角形是解题的关键.(2022·浙江金华·中考真题)10. 如图,AC 与BD 相交于点O ,,OA OD OB OC ==,不添加辅助线,判定ABO DCO △≌△的依据是( )A. SSSB. SASC. AASD. HL【答案】B【解析】 【分析】根据OA OD =,OB OC =,AOB COD ∠=∠正好是两边一夹角,即可得出答案.【详解】解:∵在△ABO 和△DCO 中,OA OD AOB COD OB OC =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABO DCO ≌△△,故B 正确. 故选:B .【点睛】本题主要考查了全等三角形的判定,熟练掌握两边对应相等,且其夹角也对应相等的两个三角形全等,是解题的关键.(2022·浙江金华·中考真题)11. 已知三角形的两边长分别为5cm 和8cm ,则第三边的长可以是( )A. 2cmB. 3cmC. 6cmD. 13cm【答案】C【解析】【分析】先确定第三边的取值范围,后根据选项计算选择.【详解】设第三边的长为x ,∵ 角形的两边长分别为5cm 和8cm ,∴3cm <x <13cm ,故选C .【点睛】本题考查了三角形三边关系定理,熟练确定第三边的范围是解题的关键. (2022·安徽·中考真题) 12. 已知点O 是边长为6的等边△ABC 的中心,点P 在△ABC 外,△ABC ,△P AB ,△PBC ,△PCA 的面积分别记为0S ,1S ,2S ,3S .若12302S S S S ++=,则线段OP 长的最小值是( )A. 2C.【答案】B【解析】【分析】根据12302S S S S ++=,可得1012S S =,根据等边三角形的性质可求得△ABC 中AB 边上的高1h 和△P AB 中AB 边上的高2h 的值,当P 在CO 的延长线时,OP 取得最小值,OP =CP -OC ,过O 作OE ⊥BC ,求得OC =【详解】解:如图,2PDB BDC S S S ,3PDA ADC S S S , ∴1231()()PDB BDC PDA ADC S S S S SS S S ++=++++ =1()()PDB PDA BDC ADC S SS S S ++++ =1PAB ABC S S S ++=110S S S ++=102S S +=02S , ∴1012S S =, 设△ABC 中AB 边上的高为1h ,△P AB 中AB 边上的高为2h , 则0111116322S AB h h h ,1222116322S AB h h h , ∴211332h h ,∴122h h =,∵△ABC 是等边三角形, ∴22166()332h , 2113322h h ,∴点P 在平行于AB ,且到AB ∴当点P 在CO 的延长线上时,OP 取得最小值,过O 作OE ⊥BC 于E , ∴12932CP h h , ∵O 是等边△ABC 的中心,OE ⊥BC ∴∠OCE =30°,CE =132BC = ∴OC =2OE∵222OE CE OC +=,∴2223(2)OE OE ,解得OE∴OC =∴OP =CP -OC 52332. 故选B .【点睛】本题考查了等边三角形的性质,勾股定理,三角形的面积等知识,弄清题意,找到P 点的位置是解题的关键.(2022·四川南充·中考真题) 13. 如图,在Rt ABC 中,90,C BAC ∠=︒∠的平分线交BC 于点D ,DE //AB ,交AC 于点E ,DF AB ⊥于点F ,5,3DE DF ==,则下列结论错误的是( )A. 1BF =B. 3DC =C. 5AE =D. 9AC =【答案】A【解析】 【分析】根据角平分线的性质得到CD =DF =3,故B 正确;根据平行线的性质及角平分线得到AE =DE =5,故C 正确;由此判断D 正确;再证明△BDF ≌△DEC ,求出BF =CD =3,故A 错误.【详解】解:在Rt ABC 中,90,C BAC ∠=︒∠的平分线交BC 于点D ,DF AB ⊥,∴CD =DF =3,故B 正确;∵DE =5,△CE =4,∵DE //AB ,∴∠ADE =∠DAF ,∵∠CAD =∠BAD ,∴∠CAD =∠ADE ,∴AE =DE =5,故C 正确;∴AC =AE +CE =9,故D 正确;∵∠B =∠CDE ,∠BFD =∠C =90°,CD =DF ,∴△BDF ≌△DEC ,∴BF =CD =3,故A 错误;故选:A .【点睛】此题考查了角平分线的性质定理,平行线的性质,等边对等角证明角相等,全等三角形的判定及性质,熟记各知识点并综合应用是解题的关键. (2022·四川德阳·中考真题)14. 八一中学校九年级2班学生杨冲家和李锐家到学校的直线距离分别是5km 和3km .那么杨冲,李锐两家的直线距离不可能...是( ) A. 1kmB. 2kmC. 3kmD. 8km【答案】A【解析】【分析】利用构成三角形的条件即可进行解答.【详解】以杨冲家、李锐家以及学校这三点来构造三角形,设杨冲家与李锐家的直线距离为a ,则根据题意有:5-353a +<<,即28a <<,当杨冲家、李锐家以及学校这三点共线时,538a =+=或者532a =-=, 综上a 的取值范围为:28a ≤≤,据此可知杨冲家、李锐家的距离不可能是1km ,故选:A .【点睛】本题考查了构成三角形的条件的知识,构成三角的条件:三角形中任意的两边之和大于第三边,任意的两边之差小于第三边.(2022·山东泰安·中考真题) 15. 如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ,若∠BPC =40°,则∠CAP =( )A. 40°B. 45°C. 50°D. 60°【答案】C【解析】 【分析】根据外角与内角性质得出∠BAC 的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP =∠F AP ,即可得出答案.【详解】解:延长BA ,作PN ⊥BD ,PF ⊥BA ,PM ⊥AC ,设∠PCD =x °,∵CP 平分∠ACD ,∴∠ACP =∠PCD =x °,PM =PN ,∵BP 平分∠ABC ,∴∠ABP =∠PBC ,PF =PN ,∴PF =PM ,∵∠BPC =40°,∴∠ABP =∠PBC =∠PCD ﹣∠BPC =(x ﹣40)°,∴∠BAC =∠ACD ﹣∠ABC =2x °﹣(x °﹣40°)﹣(x °﹣40°)=80°,∴∠CAF =100°,在Rt △PF A 和Rt △PMA 中,{PA PAPM PF ==,∴Rt △PF A ≌Rt △PMA (HL ),∴∠F AP =∠P AC =50°.故选C .【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM =PN =PF 是解题的关键.(2022·浙江绍兴·中考真题)16. 如图,把一块三角板ABC 的直角顶点B 放在直线EF 上,30C ∠=︒,AC ∥EF ,则1∠=( )A. 30°B. 45°C. 60°D. 75°【答案】C【解析】【分析】根据三角板的角度,可得60A ∠=︒,根据平行线的性质即可求解. 【详解】解:30C ∠=︒,9060A C ∴∠=︒-∠=︒AC ∥EF ,160A ∴∠=∠=︒故选C【点睛】本题考查了平行线的性质,掌握平行线的性质是解题的关键. (2022·安徽·中考真题)17. 两个矩形的位置如图所示,若1∠=α,则2∠=( )A. 90α-︒B. 45α-︒C. 180α︒-D. 270α︒-【答案】C【解析】 【分析】用三角形外角性质得到∠3=∠1-90°=α-90°,用余角的定义得到∠2=90°-∠3=180°-α.【详解】解:如图,∠3=∠1-90°=α-90°,∠2=90°-∠3=180°-α.故选:C .【点睛】 本题主要考查了矩形,三角形外角,余角,解决问题的关键是熟练掌握矩形的角的性质,三角形的外角性质,互为余角的定义.(2022·浙江杭州·中考真题)18. 如图,已知AB CD ∥,点E 在线段AD 上(不与点A ,点D 重合),连接CE .若∠C =20°,∠AEC =50°,则∠A =( )A. 10°B. 20°C. 30°D. 40°【答案】C【解析】 【分析】根据三角形外角的性质、平行线的性质进行求解即可;【详解】解:∵∠C +∠D =∠AEC ,∴∠D =∠AEC -∠C =50°-20°=30°,∵AB CD ∥,∴∠A =∠D=30°,故选:C .【点睛】本题主要考查三角形外角的性质、平行线的性质,掌握相关性质并灵活应用是解题的关键.(2022·湖南娄底·中考真题)19. 一条古称在称物时的状态如图所示,已知180∠=︒,则2∠=( )A. 20︒B. 80︒C. 100︒D. 120︒【答案】C【解析】【分析】如图,由平行线的性质可得80,BCD ∠=︒ 从而可得答案.【详解】解:如图,由题意可得:,AB CD ∥ 180∠=︒,180,BCD218080100,故选C 【点睛】本题考查的是平行线的性质,邻补角的含义,掌握“两直线平行,内错角相等”是解本题的关键.(2022·江苏苏州·中考真题)20. 如图,直线AB 与CD 相交于点O ,75AOC ∠=︒,125∠=︒,则2∠的度数是( )A. 25°B. 30°C. 40°D. 50°【答案】D【解析】【分析】根据对顶角相等可得75BOD ∠=︒,之后根据125∠=︒,即可求出2∠.【详解】解:由题可知75BOD AOC ∠=∠=︒,125∠=︒∵,217525BOD ∴∠=∠-∠=︒-︒=50︒.故选:D .【点睛】本题主要考查对顶角和角的和与差,掌握对顶角相等是解决问题的关键.二.填空题(2022·湖南株洲·中考真题)21. 如图所示,点O 在一块直角三角板ABC 上(其中30ABC ∠=︒),OM AB ⊥于点M ,ON BC ⊥于点N ,若OM ON =,则ABO ∠=_________度.【答案】15【解析】【分析】根据ON BC ⊥,OM AB ⊥,OM ON =判断OB 是ABC ∠的角平分线,即可求解.【详解】解:由题意,ON BC ⊥,OM AB ⊥,OM ON =,即点O 到BC 、AB 的距离相等,△ OB 是ABC ∠的角平分线,△ 30ABC ∠=︒, △1152ABO ABC ∠=∠=︒. 故答案为:15.【点睛】本题考查角平分线的定义及判定,熟练掌握“到一个角的两边距离相等的点在这个角的平分线上”是解题的关键.(2022·浙江嘉兴·中考真题)22. 小曹同学复习时将几种三角形的关系整理如图,请帮他在横线上____填上一个适当的条件.【答案】60A ∠=︒(答案不唯一)【解析】【分析】利用等边三角形的判定定理即可求解.【详解】解:添加60A ∠=︒,理由如下: ABC 为等腰三角形,180602A B C ︒-∠∴∠=∠==︒, ABC ∴为等边三角形,故答案为:60A ∠=︒(答案不唯一).【点睛】本题考查了等边三角形的判断,解题的关键是掌握三角形的判断定理. (2022·浙江绍兴·中考真题)23. 如图,在ABC 中,40ABC ∠=︒,80BAC ∠=︒,以点A 为圆心,AC 长为半径作弧,交射线BA 于点D ,连接CD ,则BCD ∠的度数是______.【答案】10°或100°【解析】【分析】分两种情况画图,由作图可知得AC AD =,根据等腰三角形的性质和三角形内角和定理解答即可.【详解】解:如图,点D 即为所求;在ABC ∆中,40ABC ∠=︒,80BAC ∠=︒,180408060ACB ∴∠=︒-︒-︒=︒,由作图可知:AC AD =,1(18080)502ACD ADC ∴∠=∠=︒-︒=︒, 605010BCD ACB ACD ∴∠=∠-∠=︒-︒=︒;由作图可知:AC AD =',ACD AD C ∴∠'=∠',80ACD AD C BAC ∠'+∠'=∠=︒,40AD C ∴∠'=︒,1801804040100BCD ABC AD C ∴∠'=︒-∠-∠'=︒-︒-︒=︒.综上所述:BCD ∠的度数是10︒或100︒.故答案为:10︒或100︒.【点睛】本题考查了作图-复杂作图,三角形内角和定理,等腰三角形的判定与性质,解题的关键是掌握基本作图方法.(2022·云南·中考真题)24. 已知△ABC 是等腰三角形.若∠A =40°,则△ABC 的顶角度数是____.【答案】40°或100°【解析】【分析】分∠A 为三角形顶角或底角两种情况讨论,即可求解.【详解】解:当∠A 为三角形顶角时,则△ABC 的顶角度数是40°;当∠A 为三角形底角时,则△ABC 的顶角度数是180°-40°-40°=100°;故答案为:40°或100°.【点睛】本题考查了等腰三角形的性质,此类题目,难点在于要分情况讨论. (2022·山东滨州·中考真题)25. 如图,屋顶钢架外框是等腰三角形,其中AB AC =,立柱AD BC ⊥,且顶角120BAC ∠=︒,则C ∠的大小为_______.【答案】30°##30度【解析】【分析】先由等边对等角得到B C ∠=∠,再根据三角形的内角和进行求解即可.【详解】AB AC =,B C ∴∠=∠,120BAC ∠=︒,180BAC B C ∠+∠+∠=︒,180120302C ︒-︒∴∠==︒, 故答案为:30°.【点睛】本题考查了等腰三角形的性质及三角形的内角和定理,熟练掌握知识点是解题的关键.(2022·山东泰安·中考真题)26. 如图,△ ABC 中,∠BAC =90°,AB =3,AC =4,点 D 是 BC 的中点,将△ ABD 沿 AD 翻折得到△ AED ,连 CE ,则线段 CE 的长等于_____【答案】75【解析】【详解】如图,过点A 作AH △BC 于点H ,连接BE 交AD 于点O △△△ABC 中,△BAC =90°△AB =3△AC =4,点D 是BC 的中点,△BC 5=△AD =BD =2.5△ △12BC ·AH =12AC ·AB △即2.5AH =6△△AH =2.4△由折叠的性质可知,AE =AB △DE =DB =DC △△AD 是BE 的垂直平分线,△BCE 是直角三角形,△S △ADB =12AD ·OB =12BD ·AH △△OB =AH =2.4△△BE =4.8△△CE 75=. 故答案为△75. 【点睛】本题的解题要点有△△1△读懂题意,画出符合要求的图形;(2)作AH △BC 于点H ,连接BE 交AD 于点O ,利用面积法求出AH 和OB 的长;(3)一个三角形中,若一边上的中线等于这边的一半,则这边所对的角是直角. (2022·湖北武汉·中考真题)27. 如图,沿AB 方向架桥修路,为加快施工进度,在直线AB 上湖的另一边的D 处同时施工.取150ABC ∠=︒,1600m BC =,105BCD ∠=︒,则C ,D 两点的距离是_________m .【答案】【解析】【分析】如图所示:过点C 作CE BD ⊥于点E ,先求出800m CE =,再根据勾股定理即可求出CD 的长.【详解】如图所示:过点C 作CE BD ⊥于点E ,则∠BEC =∠DEC =90°, 150ABC ∠=︒,30CBD ∴∠=︒,∴∠BCE =90°-30°=60°,又105BCD ∠=︒,45CDB ∴∠=︒,∴∠ECD =45°=∠D ,∴CE DE =,1600m BC =,111600800m 22CE BC ∴==⨯=,22222CD CE DE CE ∴=+=,即CD ==.故答案为:【点睛】本题考查三角形内角和定理、等腰三角形的判定与性质、直角三角形的性质及勾股定理,解题的关键是熟练掌握相关内容并能灵活运用.(2022·湖北黄冈·中考真题)28. 勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1,柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m (m ≥3,m 为正整数),则其弦是________(结果用含m 的式子表示).【答案】m 2+1【解析】【分析】2m 为偶数,设其股是a ,则弦为a +2,根据勾股定理列方程即可得到结论.【详解】∵2m 为偶数,∴设其股是a ,则弦为a +2,根据勾股定理得,(2m )2+a 2=(a +2)2,解得a =m 2-1,∴弦长为m 2+1,故答案为:m 2+1.【点睛】本题考查了勾股数,勾股定理,熟练掌握勾股定理是解题的关键. (2022·江苏苏州·中考真题)29. 定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰△ABC 是“倍长三角形”,底边BC 的长为3,则腰AB 的长为______.【答案】6【解析】【分析】分类讨论:AB =AC =2BC 或BC =2AB =2AC ,然后根据三角形三边关系即可得出结果.【详解】解:∵△ABC 是等腰三角形,底边BC =3∴AB =AC当AB =AC =2BC 时,△ABC 是“倍长三角形”;当BC =2AB =2AC 时,AB +AC =BC ,根据三角形三边关系,此时A 、B 、C 不构成三角形,不符合题意;所以当等腰△ABC 是“倍长三角形”,底边BC 的长为3,则腰AB 的长为6. 故答案为6.【点睛】本题考查等腰三角形,三角形的三边关系,涉及分类讨论思想,结合三角形三边关系,灵活运用分类讨论思想是解题的关键.(2022·江苏扬州·中考真题)30. 将一副直角三角板如图放置,已知60E ∠=︒,45C ∠=︒,EF BC ∥,则BND ∠=________°.【答案】105【解析】【分析】根据平行线的性质可得45FAN B ∠=∠=︒,根据三角形内角和定理以及对顶角相等即可求解.【详解】45B C ∠︒∠==,EF BC ∥,∴45FAN B ∠=∠=︒,△△E =60°△△△F =30°△180105BND ANF F BAF ∴∠=∠=︒-∠-∠=︒故答案为:105【点睛】本题考查了平行线的性质,三角形内角和定理,掌握平行线的性质是解题的关键.(2022·湖北黄冈·中考真题)31. 如图,直线a ∥b ,直线c 与直线a ,b 相交,若∠1=54°,则∠3=________度.【答案】54【解析】【分析】根据对顶角相等和平行线的性质“两直线平行同位角相等”,通过等量代换求解.【详解】因为a△b ,所以23∠=∠,因为12∠∠,是对顶角,所以12∠=∠,所以31∠=∠,因为154∠=︒,所以354∠=︒,故答案为:54.【点睛】本题考查了平行线的性质和对顶角的性质,熟练掌握对顶角相等,两直线平行同位角相等、内错角相等,加以灵活运用求解相关角的度数是解题关键. (2022·四川达州·中考真题)32. 如图,在Rt ABC 中,90C ∠=︒,20B ∠=︒,分别以点A ,B 为圆心,大于12AB 的长为半径作弧,两弧分别相交于点M ,N ,作直线MN ,交BC 于点D ,连接AD ,则CAD ∠的度数为_____.【答案】50︒##50度【解析】【分析】根据作图可知DA DB =,20DAB B ∠=∠=︒,根据直角三角形两个锐角互余,可得70CAB ∠=︒,根据CAD CAB DAB ∠=∠-∠即可求解.【详解】解:∵在Rt ABC 中,90C ∠=︒,20B ∠=︒,∴70CAB ∠=︒,由作图可知MN 是AB 的垂直平分线,DA DB ∴=,∴20DAB B ∠=∠=︒,∴CAD CAB DAB∠=∠-∠702050︒-︒=︒,故答案为:50︒.【点睛】本题考查了基本作图,垂直平分线的性质,等边对等角,直角三角形的两锐角互余,根据题意分析得出MN是AB的垂直平分线,是解题的关键.(2022·湖北黄冈·中考真题)33. 如图,点B、E、C、F在一条直线上,AB∥DE,且AB=DE,请添加一个条件_____,使△ABC≌△DEF.【答案】∠A=∠D或BC=EF或BE=CF或∠ACB=∠F【解析】【分析】判定一般三角形全等一共有四种方法,根据这四种方法一一选择即可.【详解】解:添加BE=CF∵BE=CF,∴BC=EF,∵AB∥DE,∴∠B=∠DEF,∵AB=DE,∴△ABC≌△DEF(SAS).故答案为:AB=DE(答案不唯一).视频【点睛】本题考查的是三角形全等的判定,根据判定的方法选择合适的方法,关键是要能熟练运用三角形的判定方法.三.解答题(2022·浙江温州·中考真题)∥,交AB于点E.34. 如图,BD是ABC的角平分线,DE BC(1)求证:EBD EDB ∠=∠.(2)当AB AC =时,请判断CD 与ED 的大小关系,并说明理由.【答案】(1)见解析 (2)相等,见解析【解析】【分析】(1)利用角平分线的定义和平行线的性质可得结论;(2)利用平行线的性质可得ADE AED ∠=∠, 则AD= AE ,从而有CD = BE ,由(1) 得,EBD EDB ∠=∠,可知BE = DE ,等量代换即可.【小问1详解】证明:△BD 是ABC 的角平分线,△CBD EBD ∠=∠.△DE BC ∥,△CBD EDB ∠=∠,△EBD EDB ∠=∠.【小问2详解】CD ED =.理由如下:△AB AC =,△C ABC ∠=∠.△DE BC ∥,△,ADE C AED ABC ∠=∠∠=∠,△ADE AED ∠=∠,△AD AE =,△AC AD AB AE -=-,即CD BE =.由(1)得EBD EDB ∠=∠,△BE ED =,△CD ED =.【点睛】本题主要考查了平行线的性质,等腰三角形的判定与性质,角平分线的定义等知识,熟练掌握平行与角平分线可推出等腰三角形是解题的关键. (2022·四川乐山·中考真题)35. 如图,B 是线段AC 的中点,,AD BE BD CE ∥∥,求证:ABD BCE △≌△.【答案】证明过程见详解【解析】【分析】运行平行线的性质可证△A =△EBC ,△DBA =△C ,结论即可得证.【详解】证明△B 是AC 中点,△AB =BC ,△AD BE ∥,△△A =△EBC ,△BD EC ∥,△△DBA =△C ,在△ABD 和△BCE 中,A EBC AB BC DBA C ∠=∠⎧⎪=⎨⎪∠=∠⎩,△△ABD ≌△BCE (ASA).【点睛】本题考查了全等三角形的判定、平行线的性质,掌握两直线平行同位角相等的知识是解答本题的关键.(2022·浙江杭州·中考真题)36. 如图,在Rt △ACB 中,∠ACB =90°,点M 为边AB 的中点,点E 在线段AM上,EF⊥AC于点F,连接CM,CE.已知∠A=50°,∠ACE=30°.(1)求证:CE=CM.(2)若AB=4,求线段FC的长.【答案】(1)见解析(2【解析】【分析】(1)根据直角三角形的性质可得MC=MA=MB,根据外角的性质可得∠MEC=∠A+∠ACE,∠EMC=∠B+∠MCB,根据等角对等边即可得证;(2)根据CE=CM先求出CE的长,再解直角三角形即可求出FC的长.【小问1详解】证明:∵∠ACB=90°,点M为边AB的中点,∴MC=MA=MB,∴∠MCA=∠A,∠MCB=∠B,∵∠A=50°,∴∠MCA=50°,∠MCB=∠B=40°,∴∠EMC=∠MCB+∠B=80°,∵∠ACE=30°,∴∠MEC=∠A+∠ACE=50°,∴∠MEC=∠EMC,∴CE=CM;【小问2详解】解:∵AB=4,∴CE=CM=12AB=2,∵EF⊥AC,∠ACE=30°,∴FC=CE•cos30°=【点睛】本题考查了直角三角形的性质,涉及三角形外角的性质,解直角三角形等,熟练掌握并灵活运用直角三角形的性质是解题的关键.(2022·陕西·中考真题)37. 如图,在△ABC 中,点D 在边BC 上,CD =AB ,DE ∥AB ,∠DCE =∠A .求证:DE =BC .【答案】证明见解析【解析】【分析】利用角边角证明△CDE ≌△ABC ,即可证明DE =BC .【详解】证明:∵DE ∥AB ,∴∠EDC =∠B .又∵CD =AB ,∠DCE =∠A ,∴△CDE ≌△ABC (ASA).∴DE =BC .【点睛】本题考查了全等三角形的判定和性质,掌握全等三角形的判定是本题的关键.(2022·湖南衡阳·中考真题)38. 如图,在ABC 中,AB AC =,D 、E 是BC 边上的点,且BD CE =,求证:AD AE =.【答案】见解析【解析】【分析】利用等腰三角形的性质可得B C ∠=∠,再由SAS 证明ABD ACE △≌△,从而得AD AE =.【详解】证明:∵AB AC =,∴B C ∠=∠,在ABD △和ACE 中,AB AC B C BD CE =⎧⎪∠=∠⎨⎪=⎩,∴()ABD ACE SAS △≌△,∴AD AE =.【点睛】本题考查等腰三角形的性质,全等三角形的性质与判定,熟练掌握相关性质定理是解题的关键.(2022·湖南怀化·中考真题)39. 如图,在等边三角形ABC 中,点M 为AB 边上任意一点,延长BC 至点N ,使CN =AM ,连接MN 交AC 于点P ,MH ⊥AC 于点H .(1)求证:MP =NP ;(2)若AB =a ,求线段PH 的长(结果用含a 的代数式表示).【答案】(1)见详解;(2)0.5a .【解析】【分析】(1)过点M 作MQ ∥CN ,证明MQP NCP ≅△△即可;(2)利用等边三角形的性质推出AH =HQ ,则PH =HQ +PQ =0.5(AQ +CQ ).【小问1详解】如下图所示,过点M 作MQ ∥CN ,△ABC 为等边三角形,MQ ∥CN , △1AM AB AQ AC==, 则AM =AQ ,且△A =60°,△AMQ △为等边三角形,则MQ =AM =CN ,又△MQ ∥CN ,△△QMP =△CNP ,在MQP NCP △与△中,MPQ NPC QMP CNP QM CN ∠=∠⎧⎪∠=∠⎨⎪=⎩△MQP NCP ≅△△,则MP =NP ;【小问2详解】△AMQ △为等边三角形,且MH △AC ,△AH =HQ ,又由(1)得,MQP NCP ≅△△,则PQ =PC ,△PH =HQ +PQ =0.5(AQ +CQ )=0.5AC =0.5a .【点睛】本题考查了等边三角形的性质与判定、三角形全等的判定,正确作出辅助线是解题的关键.(2022·浙江丽水·中考真题)40. 如图,将矩形纸片ABCD 折叠,使点B 与点D 重合,点A 落在点P 处,折痕为EF .(1)求证:PDE CDF △≌△;(2)若4cm,5cm CD EF ==,求BC 的长.【答案】(1)证明见解析(2)163cm 【解析】【分析】(1)利用ASA 证明即可;(2)过点E 作EG ⊥BC 交于点G ,求出FG 的长,设AE =x ,用x 表示出DE 的长,在Rt △PED 中,由勾股定理求得答案.【小问1详解】∵四边形ABCD 是矩形,∴AB =CD ,∠A =∠B =∠ADC =∠C =90°,由折叠知,AB =PD ,∠A =∠P ,∠B =∠PDF =90°,∴PD =CD ,∠P =∠C ,∠PDF =∠ADC ,∴∠PDF -∠EDF =∠ADC -∠EDF ,∴∠PDE =∠CDF ,在△PDE 和△CDF 中,P C PD CDPDE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴PDE CDF △≌△(ASA );【小问2详解】如图,过点E 作EG ⊥BC 交于点G ,∵四边形ABCD 是矩形,∴AB =CD =EG =4cm ,又∵EF =5cm ,∴3GF ==,设AE =x ,∴EP =x ,由PDE CDF △≌△知,EP =CF =x ,∴DE =GC =GF +FC =3+x ,在Rt △PED 中,222PE PD DE +=,即()22243x x +=+, 解得,76x =, ∴BC =BG +GC =77163663++=cm . 【点睛】本题考查了翻折变换,矩形的性质,勾股定理,全等三角形的判定和性质,根据翻折变换的性质将问题转化到直角三角形中利用勾股定理是解题的关键. (2022·四川自贡·中考真题)41. 如图,△ABC 是等边三角形,,D E 在直线BC 上,DB EC =.求证:D E ∠=∠ .【答案】详见解析【解析】【分析】由等边三角形的性质以及题设条件,可证△ADB ≌△AEC ,由全等三角形的性质可得D E ∠=∠.【详解】证明:△△ABC 是等边三角形,∴AB=AC ,∠ABC =∠ACB ,∴∠ABD =∠ACE ,在△ADB 和△AEC 中,AB AC ABD ACE DB EC =⎧⎪=⎨⎪=⎩∠∠∴△ADB ≌△AEC (SAS ),∴D E ∠=∠.【点睛】本题考查等边三角形的性质、补角的性质、全等三角形的判定和性质,综合性强,但是整体难度不大.(2022·重庆·中考真题)42. 我们知道,矩形的面积等于这个矩形的长乘宽,小明想用其验证一个底为a ,高为h 的三角形的面积公式为12S ah =.想法是:以BC 为边作矩形BCFE ,点A 在边FE 上,再过点A 作BC 的垂线,将其转化为证三角形全等,由全等图形面积相等来得到验证.按以上思路完成下面的作图与填空:证明:用直尺和圆规过点A 作BC 的垂线AD 交BC 于点D .(只保留作图痕迹)在ADC 和CFA △中,∵AD BC ⊥,∴90ADC ∠=︒.∵90F ∠=︒,。
中考数学最新真题专项汇总—平行线与三角形(含解析)

中考数学最新真题专项汇总—平行线与三角形(含解析)一.选择题1.(2022·内蒙古通辽)如图,一束光线AB 先后经平面镜OM ,ON 反射后,反射光线CD 与AB 平行,当35ABM ∠=︒时,DCN ∠的度数为( )A .55︒B .70︒C .60︒D .35︒【答案】A 【分析】根据题意得:∠ABM =∠OBC , ∠BCO =∠DCN ,然后平行线的性质可得∠BCD =70°,即可求解.【详解】解:根据题意得:∠ABM =∠OBC , ∠BCO =∠DCN ,∠∠ABM =35°,∠∠OBC =35°,∠∠ABC =180°-∠ABM -∠OBC =180°-35°-35°=110°, ∠CD ∠AB ,∠∠ABC +∠BCD =180°,∠∠BCD =180°-∠ABC =70°,∠∠BCO +∠BCD +∠DCN =180°, ∠BCO =∠DCN , ∠1(180)552DCN BCD ︒︒-∠=∠=.故选:A【点睛】本题主要考查了平行线的性质,熟练掌握两直线平行,同旁内角互补是解题的关键.2.(2022·河北)要得知作业纸上两相交直线AB ,CD 所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图1和图2):对于方案∠、∠,说法正确的是()A.∠可行、∠不可行B.∠不可行、∠可行C.∠、∠都可行D.∠、∠都不可行【答案】C【分析】用夹角可以划出来的两条线,证明方案∠和∠的结果是否等于夹角,即可判断正误【详解】方案∠:如下图,BPD∠即为所要测量的角∠HEN CFG∥∠AEM BPD∠=∠∠MN PD∠=∠故方案∠可行方案∠:如下图,BPD∠即为所要测量的角在EPF中:180∠+∠+∠=︒BPD PEF PFE则:180∠=︒-∠-∠故方案∠可行故选:CBPD AEH CFG【点睛】本题考查平行线的性质和判定,三角形的内角和;本题的突破点是用可画出夹角的情况进行证明3.(2022·河南)如图,直线AB,CD相交于点O,EO∠CD,垂足为O.若∠1=54°,则∠2的度数为()A.26°B.36°C.44°D.54°【答案】B【分析】根据垂直的定义可得90∠=︒,根据平角的定义即可求解.COE【详解】解:EO∠CD,90∴∠=︒,COE12180∠+∠+∠=︒,2180905436∴∠=︒-︒-︒=︒.故选:B .COE【点睛】本题考查了垂线的定义,平角的定义,数形结合是解题的关键.4.(2022·湖北鄂州)如图,直线l1∥l2,点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )A .10°B .15°C .20°D .30°【答案】B 【分析】由作图得ABC ∆为等腰三角形,可求出15ABC ∠=︒,由l 1∥l 2得1ABC ∠=∠,从而可得结论.【详解】解:由作图得,CA CB =,∠ABC ∆为等腰三角形,∠ABC CAB ∠=∠ ∠∠BCA =150°,∠11(180)(180150)1522ABC ACB ∠=︒-∠=︒-︒=︒∠l 1∥l 2∠115ABC ∠=∠=︒故选B【点睛】本题主要考查了等腰三角形的判定与性质,平行线的性质等知识,求出15ABC ∠=︒是解答本题的关键. 5.(2022·湖南郴州)如图,直线a b ∥,且直线a ,b 被直线c ,d 所截,则下列条件不能..判定直线c d ∥的是( )A .34∠=∠B .15180∠+∠=︒C .12∠=∠D .14∠=∠【答案】C 【分析】利用平行线的判定条件进行分析即可得出结果.【详解】解:A 、当34∠=∠时,c d ∥;故A 不符合题意;B 、当15180∠+∠=︒时,c d ∥;故B 不符合题意;C 、当12∠=∠时,a b ∥;故C 符合题意;D 、∠a b ∥,则12∠=∠,∠14∠=∠,则24∠∠=,∠c d ∥;故D 不符合题意;故选:C【点睛】本题主要考查平行线的判定,解答的关键是熟记平行线的判定条件并灵活运用.6.(2022·山东潍坊)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面AB 与CD 平行,入射光线l 与出射光线m 平行.若入射光线l 与镜面AB 的夹角14010'∠=︒,则6∠的度数为( )A .10040'︒B .9980'︒C .9940'︒D .9920'︒【答案】C 【分析】由入射光线与镜面的夹角等于反射光线与镜面的夹角,可得∠1=∠2,可求出∠5,由l //m 可得∠6=∠5【详解】解:由入射光线与镜面的夹角等于反射光线与镜面的夹角,可得∠1=∠2,∠14010'∠=︒∠24010'∠=︒∠518012180401040109940'''∠=︒-∠-∠=︒-︒-︒=︒ ∠l //m ∠659940'∠=∠=︒ 故选:C【点睛】本题主要考查了平行线的性质,熟记两直线平行,内错角相等是解答本题的关键.7.(2022·北京)如图,利用工具测量角,则1∠的大小为( )A .30°B .60°C .120°D .150°【答案】A 【分析】利用对顶角相等求解.【详解】解:量角器测量的度数为30°,由对顶角相等可得,130∠=︒.故选A .【点睛】本题考查量角器的使用和对顶角的性质,掌握对顶角相等是解题的关键.8.(2022·黑龙江)如图,ABC 中,AB AC =,AD 平分BAC ∠与BC 相交于点D ,点E 是AB 的中点,点F 是DC 的中点,连接EF 交AD 于点P .若ABC 的面积是24, 1.5PD =,则PE 的长是( )A.2.5B.2C.3.5D.3【答案】A【分析】连接DE,取AD的中点G,连接EG,先由等腰三角形“三线合一“性质,证得AD∠BC,BD=CD,再由E是AB的中点,G是AD的中点,求出S∠EGD=3,然后证∠EGP∠∠FDP(AAS),得GP=CP=1.5,从而得DG=3,即可由三角形面积公式求出EG长,由勾股定理即可求出PE长.【详解】解:如图,连接DE,取AD的中点G,连接EG,∠AB=AC,AD平分BAC∠与BC相交于点D,∠AD∠BC,BD=CD,∠S∠ABD=112422ABCS=⨯=12,∠E是AB的中点,∠S∠AED=111222ABDS=⨯=6,∠G是AD的中点,∠S△EGD=11622AEDS=⨯=3,∠E是AB的中点,G是AD的中点,∠EG∥BC,EG=12BD=12CD,∠∠EGP=∠FDP=90°,∠F是CD的中点,∠DF=12CD,∠EG=DF,∠∠EPG=∠FPD,∠∠EGP∠∠FDP(AAS),∠GP=PD=1.5,∠GD=3,∠S△EGD=12GD EG⋅=3,即1332EG⨯=,∠EG=2,在Rt∠EGP中,由勾股定理,得PE=,故选:A.【点睛】本题考查等腰三角形的性质,三角形面积,全等三角形判定与性质,勾股定理,熟练掌握三角形中线分三角形两部分的面积相等是解题的关键.9.(2022·贵州遵义)如图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若1AB BC==,30AOB∠=︒,则点B到OC的距离为()A B C .1 D .2【答案】B【分析】根据题意求得2OB =,进而求得OC【详解】解:在Rt ,Rt ABO BOC 中,30AOB ∠=︒,1AB BC ==,2OB ∴=,OC ∴设B 到OC 的距离为h ,1122OC h BC BO ∴⋅=⋅,h ∴==, 故选B .【点睛】本题考查了勾股定理,含30度角的直角三角形的性质,掌握以上知识是解题的关键.10.(2022·广西)活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等,如己知∠ABC 中,∠A =30°, AC =3,∠A 所对的边为满足已知条件的三角形有两个(我们发现其中如图的∠ABC 是一个直角三角形),则满足已知条件的三角形的第三边长为( )A.B .3C .D .3【答案】C 【分析】分情况讨论,当∠ABC 是一个直角三角形时,当∠AB 1C 是一个钝角三角形时,根据含30°的直角三角形的性质及勾股定理求解即可.【详解】如图,当∠ABC 是一个直角三角形时,即90C ∠=︒,30,A BC ∠=︒=2∴==AB BC如图,当∠AB 1C 是一个钝角三角形时,过点C 作CD ∠AB 1,90CDA CDB ∴∠=︒=∠,1CB CB =,1BD B D ∴=,30,3A AC ∠=︒=,1322CD AC ∴==, 3BC =1B D BD ∴===,1BB ∴11AB AB BB ∴=-综上,满足已知条件的三角形的第三边长为故选:C . 【点睛】本题考查了根据已知条件作三角形,涉及含30°的直角三角形的性质及勾股定理,熟练掌握知识点是解题的关键.11.(2022·山东烟台)如图,某海域中有A ,B ,C 三个小岛,其中A 在B 的南偏西40°方向,C 在B 的南偏东35°方向,且B ,C 到A 的距离相等,则小岛C 相对于小岛A 的方向是( )A .北偏东70°B .北偏东75°C .南偏西70°D .南偏西20°【答案】A 【分析】根据题意可得∠ABC =75°,AD ∠BE ,AB =AC ,再根据等腰三角形的性质可得∠ABC =∠C =75°,从而求出∠BAC 的度数,然后利用平行线的性质可得∠DAB =∠ABE =40°,从而求出∠DAC 的度数,即可解答.【详解】解:如图:由题意得:∠ABC=∠ABE+∠CBE=40°+35°=75°,AD∠BE,AB=AC,∠∠ABC=∠C=75°,∠∠BAC=180°﹣∠ABC﹣∠C=30°,∠AD∠BE,∠∠DAB=∠ABE=40°,∠∠DAC=∠DAB+∠BAC=40°+30°=70°,∠小岛C相对于小岛A的方向是北偏东70°,故选:A..【点睛】本题考查了方向角,等腰三角形的性质,熟练掌握等腰三角形的性质是解题的关键.12.(2022·河北)如图,将∠ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是∠ABC的()A.中线B.中位线C.高线D.角平分线【答案】D【分析】根据折叠的性质可得CAD BAD∠=∠,作出选择即可.【详解】解:如图,∠由折叠的性质可知CAD BAD∠=∠,∠AD是BAC∠的角平分线,故选:D.【点睛】本题考查折叠的性质和角平分线的定义,理解角平分线的定义是解答本题的关键.13.(2022·广西贺州)如图,在Rt∠ABC中,∠C=90°,∠B=56°,则∠A的度数为()A.34︒B.44︒C.124︒D.134︒【答案】A【分析】根据直角三角形的两个锐角互余,即可得出∠A的度数.【详解】解:∠Rt∠ABC中,∠C=90°,∠B=56°,∠∠A=90°-∠B=90°-56°=34°;故选:A.【点睛】本题考查了直角三角形的性质:直角三角形的两个锐角互余;熟练掌握直角三角形的性质,并能进行推理计算是解决问题的关键.14.(2022·湖南永州)如图,在Rt ABC∠=°,点D为边AC∠=︒,60C△中,90ABC的中点,2BD=,则BC的长为()B.C.2D.4A【答案】C【分析】根据三角形内角和定理可得∠A=30°,由直角三角形斜边上的中线的性质得出AC=2BD=4,再利用含30度角的直角三角形的性质求解即可.【详解】解:∠∠ABC=90°,∠C=60°,∠∠A=30°,∠点D为边AC的中点,BD=2∠AC=2BD=4,∠BC=12AC=,2故选:C.【点睛】题目主要考查三角形内角和定理及直角三角形斜边上中线的性质,含30度角的直角三角形的性质等,理解题意,综合运用这些知识点是解题关键.15.(2022·湖南永州)下列多边形具有稳定性的是()A.B.C.D.【答案】D【分析】利用三角形具有稳定性直接得出答案.【详解】解:三角形具有稳定性,四边形、五边形、六边形都具有不稳定性,故选D.【点睛】本题考查三角形的特性,牢记三角形具有稳定性是解题的关键.16.(2022·广西玉林)请你量一量如图ABC中BC边上的高的长度,下列最接近的是()A.0.5cm B.0.7cm C.1.5cm D.2cm【答案】D【分析】作出三角形的高,然后利用刻度尺量取即可.【详解】解:如图所示,过点A作AO∠BC,用刻度尺直接量得AO更接近2cm,故选:D.【点睛】题目主要考查利用刻度尺量取三角形高的长度,作出三角形的高是解题关键.17.(2022·黑龙江大庆)下列说法不正确...的是()A.有两个角是锐角的三角形是直角或钝角三角形B.有两条边上的高相等的三角形是等腰三角形C.有两个角互余的三角形是直角三角形D.底和腰相等的等腰三角形是等边三角形【答案】A【分析】利用等腰三角形的性质与判定、等边三角形的性质与判定、直角三角形的判定,对各选项逐项分析可得出正确答案.【详解】解:A、设∠1、∠2为锐角,因为:∠1+∠2+∠3=180°,所以:∠3可以为锐角、直角、钝角,所以该三角形可以是锐角三角形,也可以是直角或钝角三角形,故A选项不正确,符合题意;B、如图,在∠ABC中,BE∠AC,CD∠AB,且BE=CD.∠BE ∠AC ,CD ∠AB ,∠∠CDB =∠BEC =90°,在Rt ∠BCD 与Rt ∠CBE 中,CD BE BC CB=⎧⎨=⎩, ∠Rt ∠BCD ∠Rt ∠CBE (HL ),∠∠ABC =∠ACB ,∠AB =AC ,即∠ABC 是等腰三角形.,故B 选项正确,不符合题意;C 、根据直角三角形的判定:有两个角互余的三角形是直角三角形,, 故C 选项正确,不符合题意;D 、底和腰相等的等腰三角形是等边三角形,故D 选项正确,不符合题意;故选:A .【点睛】本题综合考查了等腰三角形的性质与判定、等边三角形的性质与判定、直角三角形的判定,要求学生在学习过程中掌握三角形的各种性质及推论,不断提升数学学习的能力.18.(2022·广西梧州)如图,在ABC 中,,AB AC AD =是ABC 的角平分线,过点D 分别作,DE AB DF AC ,垂足分别是点E ,F ,则下列结论错误..的是( )A .90ADC ∠=B .DE DF =C .AD BC = D .BD CD =【答案】C【分析】根据等腰三角形底边上的高线、顶角的角平分线、底边上的中线这三线合一及角平分线的性质即可判断求解.【详解】解:∠,AB AC AD =是ABC 的角平分线,∠,AD BC BD CD , ∠90ADC ∠=,故选项A 、D 结论正确,不符合题意;又AD 是BAC ∠的角平分线,,DE AB DF AC ,∠DE DF =,故选项B 结论正确,不符合题意;由已知条件推不出AD BC =,故选项C 结论错误,符合题意;故选:C .【点睛】本题考察了等腰三角形的性质及角平分线的性质,属于基础题,熟练掌握其性质即可.19.(2022·四川乐山)如图,等腰∠ABC 的面积为AB =AC ,BC =2.作AE ∠BC 且AE =12BC .点P 是线段AB 上一动点,连接PE ,过点E 作PE 的垂线交BC 的延长线于点F ,M 是线段EF 的中点.那么,当点P 从A 点运动到B 点时,点M 的运动路径长为( )AB .3C .D .4【答案】D【分析】当P 与A 重合时,点F 与C 重合,此时点M 在N 处,当点P 与B 重合时,如图,点M 的运动轨迹是线段MN .求出CF 的长即可解决问题.【详解】解:过点A 作AD ∠BC 于点D ,连接CE ,∠AB =AC ,∠BD =DC =12BC =1,∠AE =12BC ,∠AE =DC =1,∠AE ∠BC ,∠四边形AECD 是矩形,∠S ∠ABC =12BC ×AD =12×2×AD∠ADCE =AD当P 与A 重合时,点F 与C 重合,此时点M 在CE 的中点N 处,当点P 与B 重合时,如图,点M 的运动轨迹是线段MN .∠BC =2,CE由勾股定理得BE =4,cos∠EBC =BC BE BE BF =,即244BF =, ∠BF =8,∠点N 是CE 的中点,点M 是EF 的中点,∠MN =12BF =4,∠点M 的运动路径长为4,故选:D .【点睛】本题考查点的轨迹、矩形的判定和性质、解直角三角形、勾股定理等知识,解题的关键是正确寻找点M 的运动轨迹,学会利用起始位置和终止位置寻找轨迹,属于中考填空题中的压轴题.20.(2022·四川凉山)下列长度的三条线段能组成三角形的是( ) A .3,4,8B .5,6,11C .5,6,10D .5,5,10 【答案】C【分析】根据三角形的三边关系定理(任意两边之和大于第三边)逐项判断即可得.【详解】解:A 、3478+=<,不能组成三角形,此项不符题意;B 、5611+=,不能组成三角形,此项不符题意;C 、561110+=>,能组成三角形,此项符合题意;D 、5510+=,不能组成三角形,此项不符题意;故选:C .【点睛】本题考查了三角形的三边关系定理,熟练掌握三角形的三边关系定理是解题关键.21.(2022·四川成都)如图,在ABC 和DEF 中,点A ,E ,B ,D 在同一直线上,AC DF ∥,AC DF =,只添加一个条件,能判定ABC DEF △≌△的是( )A .BC DE =B .AE DB =C .A DEF ∠=∠D .ABC D ∠=∠【答案】B 【分析】根据三角形全等的判定做出选择即可.【详解】A 、BC DE =,不能判断ABC DEF △≌△,选项不符合题意;B 、AE DB =,利用SAS 定理可以判断ABC DEF △≌△,选项符合题意; C 、A DEF ∠=∠,不能判断ABC DEF △≌△,选项不符合题意;D 、ABC D ∠=∠,不能判断ABC DEF △≌△,选项不符合题意;故选:B .【点睛】本题考查三角形全等的判定,根据SSS 、SAS 、ASA 、AAS 判断三角形全等,找出三角形全等的条件是解答本题的关键.22.(2022·山东聊城)如图,ABC 中,若80BAC ∠=︒,70ACB ∠=︒,根据图中尺规作图的痕迹推断,以下结论错误的是( )A .40BAQ ∠=︒B .12DE BD = C .AF AC = D .25EQF ∠=︒【答案】D【分析】根据线段的垂直平分线的性质,角平分线的定义,三角形外角的性质,直角三角形的性质判断即可.【详解】∠80BAC ∠=︒,70ACB ∠=︒,∠∠B =180°-∠BAC -∠ACB =30°,A .由作图可知,AQ 平分BAC ∠,∠1402BAP CAP BAC ∠=∠=∠=︒,故选项A 正确,不符合题意;B .由作图可知,MQ 是BC 的垂直平分线,∠90DEB ∠=︒,∠30B ∠=︒,∠12DE BD =,故选项B 正确,不符合题意;C .∠30B ∠=︒,40BAP ∠=︒,∠70AFC ∠=︒,∠70C ∠=︒,∠AF AC =,故选项C 正确,不符合题意;D .∠70EFQ AFC ∠=∠=︒,90QEF ∠=︒,∠20EQF ∠=︒;故选项D 错误,符合题意.故选:D .【点睛】本题考查了线段的垂直平分线的性质,角平分线的定义,三角形外角的性质,直角三角形的性质等知识,解题的关键是读懂图象信息.23.(2022·海南)如图,直线m n∥,ABC是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F,若1140∠=︒,则2∠的度数是()A.80︒B.100︒C.120︒D.140︒【答案】B【分析】根据等边三角形的性质可得∠A=60°,再由三角形外角的性质可得∠AEF=∠1-∠A=80°,从而得到∠BEF=100°,然后根据平行线的性质,即可求解.【详解】解:∠ABC是等边三角形,∠∠A=60°,∠∠1=140°,∠∠AEF=∠1-∠A=80°,∠∠BEF=180°-∠AEF=100°,∠m n∥,∠∠2=∠BEF=100°.故选:B【点睛】本题主要考查了等边三角形的性质,三角形外角的性质,平行线的性质,熟练掌握等边三角形的性质,三角形外角的性质,平行线的性质是解题的关键.24.(2022·黑龙江齐齐哈尔)如图所示,直线a∠b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为()A .57°B .63°C .67°D .73°【答案】D【分析】根据等腰三角形的性质可求出30ABC ∠=︒,可得出+173ABC ∠∠=︒,再根据平行线的性质可得结论.【详解】解:∠AC =BC ,∠ABC ∆是等腰三角形,∠=120C ∠︒ ∠11(180)(180120)3022ABC C ∠=︒-∠=︒-︒=︒∠1304373ABC ∠+∠=︒+︒=︒∠a ∠b ,∠2173ABC ∠=∠+∠=︒ 故选:D【点睛】本题主要考查了等腰三角形的判定与性质,以及平行线的性质,求出173ABC ∠+∠=︒是解答本题的关键. 25.(2022·湖北恩施)已知直线12l l ∥,将含30°角的直角三角板按图所示摆放.若1120∠=︒,则2∠=( )A.120°B.130°C.140°D.150°【答案】D【分析】根据平行线的性质可得∠3=∠1=120°,再由对顶角相等可得∠4=∠3=120°,然后根据三角形外角的性质,即可求解.【详解】解:如图,根据题意得:∠5=30°,∥,∠∠3=∠1=120°,∠∠4=∠3=120°,∠12l l∠∠2=∠4+∠5,∠∠2=120°+30°=150°.故选:D【点睛】本题主要考查了平行线的性质,对顶角相等,三角形外角的性质,熟练掌握平行线的性质,对顶角相等,三角形外角的性质是解题的关键.二.填空题26.(2022·辽宁锦州)如图,在ABC中,,30=∠=︒,点D为BC的中AB AC ABC点,将ABC绕点D逆时针旋转得到A B C''',当点A的对应点A'落在边AB上时,点C'在BA的延长线上,连接BB',若1AA'=,则BB D'△的面积是____________.【分析】先证明A AD ' 是等边三角形,再证明AO BC '⊥,再利用直角三角形30角对应的边是斜边的一般分别求出A B ''和A O ',再利用勾股定理求出OD ,从而求得BB D '△的面积.【详解】解:如下图所示,设A B ''与BD 交于点O ,连接A D '和AD ,∠点D 为BC 的中点,,30AB AC ABC =∠=︒,∠AD BC ⊥,A D B C '''⊥,A D '是B A C '''∠的角平分线,AD 是BAC ∠,∠120B A C ︒'''∠=,120BAC ︒∠=∠60BAD B A D ︒'∠'=∠=∠A D AD '=,∠A AD ' 是等边三角形,∠1A A AD A D ''===,∠18060BA B B A C ︒︒'''''∠=-∠=,∠BA B A AD '''∠=∠,∠//A B AD '',∠AO BC '⊥, ∠1122A O A D ''==,∠OD ==∠22A B A D '''==∠30A BD A DO ︒''∠=∠=,∠BO OD = ∠13222OB '=-=,2BD OD ==∠113222BB D S BD B O ''=⨯⨯==. 【点睛】本题考查等腰三角形、等边三角形和直角三角形的性质,证明A AD ' 是等边三角形是解本题的关键.27.(2022·湖南郴州)如图.在ABC 中,90C ∠=︒,AC BC =.以点A 为圆心,以任意长为半径作弧交AB ,AC 于D ,E 两点;分别以点D ,E 为圆心,以大于12DE 长为半径作弧,在BAC ∠内两弧相交于点P ;作射线AP 交BC 于点F ,过点F 作FG AB ⊥,垂足用G .若8cm AB =,则BFG 的周长等于________cm .【答案】8【分析】由角平分线的性质,得到CF GF=,然后求出BFG的周长即可.【详解】解:根据题意,在ABC中,90=,C∠=︒,AC BC由角平分线的性质,得CF GF=,∠BFG的周长为:()8++=-+=-+==;BG BF FG AB AG BC AB AC BC AB故答案为:8【点睛】本题考查了角平分线的性质,解题的关键是掌握角平分线的性质.28.(2022·江苏常州)如图,在ABC中,E是中线AD的中点.若AEC△的面积是1,则ABD△的面积是______.【答案】2【分析】根据ACE∆的面积DCE=∆的面积计算出各部=∆的面积,ABD∆的面积ACD分三角形的面积.【详解】解:AD是BC边上的中线,E为AD的中点,根据等底同高可知,ACE ∆的面积DCE =∆的面积1=,ABD ∆的面积ACD =∆的面积2AEC =∆的面积2=,故答案为:2.【点睛】本题考查了三角形的面积,解题的关键是利用三角形的中线平分三角形面积进行计算.29.(2022·黑龙江哈尔滨)在ABC 中,AD 为边BC 上的高,30ABC ∠=︒,20CAD ∠=︒,则BAC ∠是___________度.【答案】40或80##80或40【分析】根据题意,由于ABC 类型不确定,需分三种情况:高在三角形内部、高在三角形边上和高在三角形外部讨论求解.【详解】解:根据题意,分三种情况讨论:∠高在三角形内部,如图所示:在ABD ∆中,AD 为边BC 上的高,30ABC ∠=︒,90903060BAD ABC ∴∠=︒-∠=︒-︒=︒,20CAD ∠=︒,602080BAC BAD CAD ∴∠=∠+∠=︒+︒=︒;∠高在三角形边上,如图所示:可知0CAD ∠=︒,20CAD ∠=︒,故此种情况不存在,舍弃;∠高在三角形外部,如图所示:在ABD ∆中,AD 为边BC 上的高,30ABC ∠=︒,90903060BAD ABC ∴∠=︒-∠=︒-︒=︒,20CAD ∠=︒,602040BAC BAD CAD ∴∠=∠-∠=︒-︒=︒;综上所述:80BAC ∠=︒或40︒,故答案为:40或80.【点睛】本题考查求角度问题,在没有图形的情况下,必须考虑清楚各种不同的情况,根据题意分情况讨论是解决问题的关键.30.(2022·四川成都)如图,在ABC 中,按以下步骤作图:∠分别以点B 和C 为圆心,以大于12BC 的长为半径作弧,两弧相交于点M 和N ;∠作直线MN 交边AB 于点E .若5AC =,4BE =,45B ∠=︒,则AB 的长为_________.【答案】7【分析】连接EC,依据垂直平分线的性质得EB EC=.由已知易得∠∠=︒=,在Rt∠AEC中运用勾股定理求得AE,即可求得答案.BEC CEA90【详解】解:由已知作图方法可得,MN是线段BC的垂直平分线,连接EC,如图,所以BE CE=,所以45∠=∠=︒,ECB B所以∠BEC=∠CEA=90°,因为5AC=,4BE=,所以4CE=,在AEC△中,2222AE AC EC,543所以347AB AE BE=+=+=,因此AB的长为7.故答案为:7.【点睛】本题主要考查中垂线性质,等腰三角形的性质,勾股定理等知识,解题的关键是掌握中垂线上一点到线段两端点距离相等,由勾股定理求得AE 即可. 31.(2022·内蒙古通辽)在Rt ABC 中,90C ∠=︒,有一个锐角为60︒,6AB =,若点P 在直线..AB 上(不与点A ,B 重合),且30PCB ∠=︒,则AP 的长为_______. 【答案】92或9或3【分析】分∠ABC =60、∠ABC =30°两种情况,利用数形结合的方法,分别求解即可.【详解】解:当∠ABC =60°时,则∠BAC =30°, ∠132BC AB ==,∠AC =,当点P 在线段AB 上时,如图,∠30PCB ∠=︒,∠∠BPC =90°,即PC ∠AB ,∠9cos 2AP AC BAC =⋅∠==; 当点P 在AB 的延长线上时,∠30PCB ∠=︒,∠PBC =∠PCB +∠CPB ,∠∠CPB =30°,∠∠CPB =∠PCB ,∠PB =BC =3,∠AP =AB +PB =9;当∠ABC =30°时,则∠BAC =60°,如图,∠132AC AB ==,∠30PCB ∠=︒,∠∠APC =60°,∠∠ACP =60°,∠∠APC =∠P AC =∠ACP ,∠∠APC 为等边三角形,∠P A =AC =3.综上所述,AP 的长为92或9或3. 故答案为:92或9或3【点睛】本题是解直角三角形综合题,主要考查了含30度角的直角三角形、解直角三角形,等边三角形的判定和性质等,分类求解是本题解题的关键.32.(2022·湖南岳阳)如图,在ABC中,AB AC=,AD BCBC=,⊥于点D,若6则CD=______.【答案】3【分析】根据等腰三角形的性质可知D是BC的中点,即可求出CD的长.【详解】解:∠AB AC=,AD BC⊥,∠CD BD=,∠6BC=,∠3CD=,故答案为:3.【点睛】本题考查了等腰三角形的性质,熟练掌握等腰三角形三线合一是解题的关键.33.(2022·江苏无锡)∠ABC是边长为5的等边三角形,∠DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在∠ABC内,∠DBC=20°,则∠BAF=________°;现将∠DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是________.【答案】804##4【分析】利用SAS证明∠BDC∠∠AEC,得到∠DBC=∠EAC=20°,据此可求得∠BAF 的度数;利用全等三角形的性质可求得∠AFB=60°,推出A、B、C、F四个点在同一个圆上,当BF是圆C的切线时,即当CD∠BF时,∠FBC最大,则∠FBA 最小,此时线段AF长度有最小值,据此求解即可.【详解】解:∠∠ABC和∠DCE都是等边三角形,∠AC=BC,DC=EC,∠BAC=∠ACB=∠DCE=60°,∠∠DCB+∠ACD=∠ECA+∠ACD=60°,即∠DCB =∠ECA,在∠BCD和∠ACE中,CD CEBCD ACEBC AC=⎧⎪∠=∠⎨⎪=⎩,∠∠ACE∠∠BCD(SAS),∠∠EAC=∠DBC,∠∠DBC=20°,∠∠EAC=20°,∠∠BAF=∠BAC+∠EAC=80°;设BF与AC相交于点H,如图:∠∠ACE ∠∠BCD∠AE =BD ,∠EAC =∠DBC ,且∠AHF =∠BHC ,∠∠AFB =∠ACB =60°,∠A 、B 、C 、F 四个点在同一个圆上,∠点D 在以C 为圆心,3为半径的圆上,当BF 是圆C 的切线时,即当CD ∠BF 时,∠FBC 最大,则∠FBA 最小,∠此时线段AF 长度有最小值,在Rt ∠BCD 中,BC =5,CD =3,∠BD=4,即AE =4,∠∠FDE =180°-90°-60°=30°,∠∠AFB =60°,∠∠FDE =∠FED =30°,∠FD =FE ,过点F 作FG ∠DE 于点G ,∠DG =GE =32,∠FE =DF =cos30DG ︒∠AF=AE-FE=4故答案为:80;4【点睛】本题考查了旋转的性质,等边三角形的性质,圆周角定理,切线的性质,解直角三角形,解答本题的关键是明确题意,找出所求问题需要的条件.34.(2022·湖南永州)我国古代数学家赵爽创制了一幅“赵爽弦图”,极富创新意识地给出了勾股定理的证明.如图所示,“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是25,小正方形的面积是1,则AE=______.【答案】3【分析】根据题意得出AB=BC=CD=DA=5,EF=FG=GH=HE=1,设AF=DE=CH=BG=x,结合图形得出AE=x-1,利用勾股定理求解即可得出结果.【详解】解:∠大正方形的面积是25,小正方形的面积是1,∠AB=BC=CD=DA=5,EF=FG=GH=HE=1,根据题意,设AF=DE=CH=BG=x,则AE=x-1,在Rt∆AED中,222+=,AE ED AD即()222-+=,x x15解得:x =4(负值已经舍去),∠x -1=3,故答案为:3.【点睛】题目主要考查正方形的性质,勾股定理解三角形,一元二次方程的应用等,理解题意,综合运用这些知识点是解题关键.35.(2022·黑龙江齐齐哈尔)在∠ABC 中,AB =6AC =,45B ∠=,则BC =______________.【答案】3或3【分析】画出图形,分∠ABC 为锐角三角形和钝角三角形两种情况讨论即可.【详解】解:情况一:当∠ABC 为锐角三角形时,如图1所示:过A 点作AH ∠BC 于H ,∠∠B =45°,∠∠ABH 为等腰直角三角形, ∠363322ABAH BH ,在Rt∠ACH 中,由勾股定理可知:2236273CHAC AH , ∠333BC BH CH . 情况二:当∠ABC 为钝角三角形时,如图2所示:由情况一知:363322ABAH BH ,2236273CH AC AH , ∠333BC BH CH .故答案为:3或3.【点睛】本题考察了等腰直角三角形的性质及勾股定理的应用,本题的关键是能将∠ABC 分成锐角三角形或钝角三角形分类讨论.36.(2022·贵州遵义)如图,在等腰直角三角形ABC 中,90BAC ∠=︒,点M ,N分别为BC ,AC 上的动点,且AN CM =,AB 当AM BN +的值最小时,CM 的长为__________.【答案】2【分析】过点A 作AD BC ∥,且AD AC =,证明AND CMA ≌△△,可得AM DN =,当,,B N D 三点共线时,BN AM +取得最小值,证明AB BM =,即可求解.【详解】如图,过点A 作AD BC ∥,且AD AC =,连接DN ,如图1所示, DAN ACM ∴∠=∠,又AN CM =,AND CMA ∴≌,AM DN ∴=,BN AM BN DN BD ∴+=+≥,当,,B N D 三点共线时,BN AM +取得最小值,此时如图2所示,在等腰直角三角形ABC 中,90BAC ∠=︒,AB =2BC ∴==,AND CMA ≌△△,ADN CAM ∴∠=∠,AD AC AB ==,ADN ABN ∴∠=∠,AD BC ∥,ADN MBN ∴∠=∠,ABN MBN ∴∠=∠,设MAC α∠=,90BAM BAC αα∴∠=∠-=︒-,245ABM ABN NBM α∴∠=∠+∠==︒,22.5α∴=︒,180180904567.5AMB BAM ABM α∴∠=︒-∠-∠=︒-︒+-︒=︒,9022.567.5BAM ∠=︒-︒=︒,AB BM ∴==2CM BC BM ∴=-=即BN AM +取得最小值为2 故答案为:2图1 图2【点睛】本题考查了等腰直角三角的性质,勾股定理,两点之间线段最短,转化线段是解题的关键.37.(2022·广西)如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC 的大小为______【答案】135°##135度【分析】根据三角板及其摆放位置可得180,45BAO BAC OAC OAC ∠=︒=∠+∠∠=︒,求解即可.【详解】180,45BAO BAC OAC OAC ∠=︒=∠+∠∠=︒,18045135BAC ∴∠=︒-︒=︒,故答案为:135°.【点睛】本题考查了求一个角的补角,即两个角的和为180度时,这两个角互为补角,熟练掌握知识点是解题的关键.38.(2022·广西桂林)如图,点C是线段AB的中点,若AC=2cm,则AB=_____cm.【答案】4【分析】根据中点的定义可得AB=2AC=4cm.【详解】解:根据中点的定义可得:AB=2AC=2×2=4cm,故答案为:4.【点睛】本题主要考查中点的定义,熟知中点的定义是解题关键.39.(2022·贵州遵义)数学小组研究如下问题:遵义市某地的纬度约为北纬28°,求北纬28纬线的长度.小组成员查阅相关资料,得到如下信息:信息一:如图1,在地球仪上,与赤道平行的圆圈叫做纬线;信息二:如图2,赤道半径OA约为6400千米,弦BC OA∥,以BC为直径的圆的周长就是北纬28°纬线的长度;(参考数据:π3≈,sin280.47︒≈,︒≈,cos280.88︒≈)tan280.53根据以上信息,北纬28°纬线的长度约为__________千米.【答案】33792【分析】根据平行线的性质可知28∠=∠=︒,在Rt BOD中,利用锐角三角B BOA函数求出BD ,即为以BC 为直径的圆的半径,求出周长即可.【详解】解:如图,过点O 作OD BC ,垂足为D ,根据题意6400OB OA ==,∠BC OA ∥,∠28B BOA ∠=∠=︒,∠在Rt BOD 中, 28B ∠=︒,∠cos28BD OB =︒,∠OD BC ,∠由垂径定理可知:12BD DC BC ==,∠以BC 为直径的圆的周长为22364000.8833792BD π⨯≈⨯⨯⨯=,故答案为:33792.【点睛】本题考查解直角三角形,平行线的性质,解题的关键是熟练三角函数的含义与解直角三角形的方法.三.解答题40.(2022·广东)如图,已知AOC BOC ∠=∠,点P 在OC 上,PD OA ⊥,PE OB ⊥,垂足分别为D ,E .求证:OPD OPE ≌.【答案】见解析【分析】根据角平分线的性质得PD PE =,再用HL 证明OPD OPE ≌.【详解】证明:∠AOC BOC ∠=∠,∠OC 为AOB ∠的角平分线,又∠点P 在OC 上,PD OA ⊥,PE OB ⊥,∠PD PE =,90PDO PEO ∠=∠=︒,又∠PO PO =(公共边),∠()HL OPD OPE ≌.【点睛】本题考查角平分线的性质,全等三角形的判定,利用合适的条件证明三角形全等是本题的关键.41.(2022·广西)校园内有一块四边形的草坪造型,课外活动小组实地测量,并记录数据,根据造型画如图的四边形ABCD ,其中 AB =CD =2米,AD =BC =3米,∠B =30(1)求证:∠ABC ∠∠CDA ;(2)求草坪造型的面积.【答案】(1)见解析(2)草坪造型的面积为23m【分析】(1)根据“SSS ”直接证明三角形全等即可;(2)过点A 作AE ∠BC 于点E ,利用含30°的直角三角形的性质求出AE 的长度,继而求出ABC 的面积,再由全等三角形面积相等得出32ABC CDASS ==,即可求出草坪造型的面积.(1)在ABC 和CDA 中,AB CD AC CA BC AD =⎧⎪=⎨⎪=⎩, ()ABC CDA SSS ∴≅;(2)过点A 作AE ∠BC 于点E ,90AEB ∴∠=︒,30,2m B AB ∠=︒=,11m 2AE AB ∴==, 3m BC =,211331m 222ABCS BC AE ∴=⋅=⨯⨯=, ABC CDA ≅,23m 2ABC CDA S S ∴==, ∴草坪造型的面积23m ABC CDA S S =+=,所以,草坪造型的面积为23m .【点睛】本题考查了全等三角形的判定和性质,含30°的直角三角形的性质,熟。
平行线与三角形内角

平行线与三角形内角平行线与三角形内角的关系是几何学中的基本概念之一。
在解决与三角形相关问题时,研究平行线与三角形内角的相互作用,可以帮助我们更好地理解与计算三角形的属性和关系。
1. 平行线与三角形内角的基本概念在平面几何中,如果两条直线在同一个平面上,且不相交,我们就称这两条直线为平行线。
平行线之间的距离保持不变,它们永远不会相交。
当平行线与三角形的两边相交时,根据平行线切割定理,我们可以得到如下结论:- 两条平行线与三角形两边形成的内角相等。
- 平行线切割三角形两边所得的线段成比例。
2. 平行线与三角形内角的应用平行线与三角形内角的关系在解决几何问题中经常被应用。
以下是几个常见的应用场景:2.1 平行线的判定使用平行线与三角形内角的关系,我们可以通过内角相等的性质来判定直线是否平行。
若两条直线切割三角形的两边所得的内角相等,则这两条直线为平行线。
2.2 确定线段的长度比例平行线切割三角形的两边,使得线段成比例。
利用这一性质,我们可以通过已知比例来计算其他线段的长度,或者通过已知线段的长度来推算其他线段的长度。
2.3 解决面积相关问题平行线切割三角形后,将三角形分割成多个简单的几何形状,如梯形、平行四边形等。
通过计算这些形状的面积,可以进一步求解原三角形面积的问题。
3. 实例分析为了更好地理解平行线与三角形内角的关系,下面通过一个实例进行分析。
假设有一个三角形ABC,其中AD与平行线EF相交(D为BC上的点)。
已知∠ABE = 70°,∠BED = 35°,以及AB:BC = 3:4。
我们可以利用平行线与三角形内角的关系来计算其他角度的度数。
首先,根据平行线切割定理,我们知道∠DAE = ∠ABE = 70°,∠BED与∠DEC也是由平行线切割所得,因此∠BED = ∠DEC = 35°。
接下来,我们以∠BAD为例进行计算。
由三角形内角和定理可知,∠BAD + ∠ABD + ∠ADB = 180°。
平行线与三角形内角和的综合应用(讲义及答案)
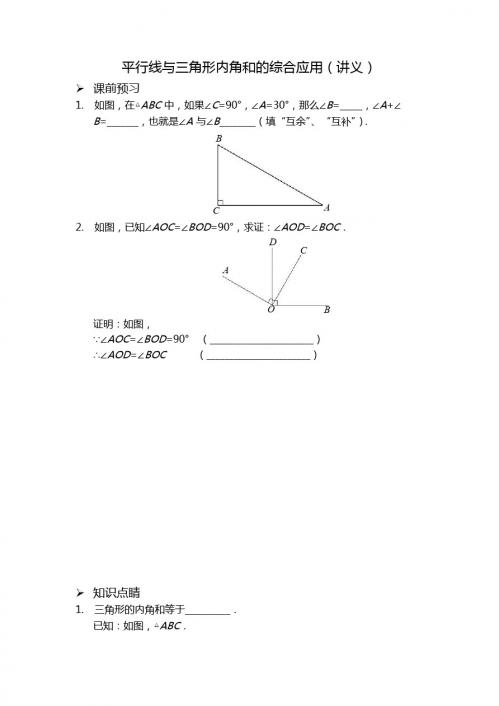
2. 直角三角形两锐角___________.
精讲精练
1. 如图,在△ABC 中,∠A=50°,∠C=72°,BD 是△ABC 的一条角平分线,则∠ ABD=__________.
C D
A
F E
A
B
B
DC
第 1 题图
第 2 题图
2. 如图,在△ABC 中,∠B=∠C,E 是 AC 上一点,ED⊥BC,DF⊥AB,垂足分
解:如图,
在△ABC 中,∠B=40°,∠BAC=68°(已知)
∴∠C=180°-______-______
=180°-_____-_____
=______(_______________________)
∵AD⊥BC(已知) ∴∠ADC=90°(垂直的定义)
B
∴∠C+_____=90°(直角三角形两锐角互余)
FAD=60°,则∠EAB=_______.
5. 如图,在△ABC 中,CD 平分∠ACB 交 AB 于点 D,过点 D 作 DE∥BC 交 AC
于点 E.若∠A=75°,∠ADE=35°,则
∠EDC=_________.
A
D
E
B
C
6. 如图,在△ABC 中,∠B=40°,∠BAC=68°,AD⊥BC 于点 D,求∠DAC 的度 数.
别为 D,F.若∠AED=140°,则∠C=_____,∠BDF=______,∠A=______.
3. 如图,AE∥BD,∠1=110°,∠2=30°,则∠C=______.
F
A
E
1
2
B
D
A
D
C
E
B
C
第 3 题图
2021全国各地中考数学真题专项汇编: 平行线与三角形 (含答案解析)

专题11.平行线与三角形一、单选题1.(2021·山东临沂市)如图,在//AB CD 中,40AEC ∠=︒,CB 平分DCE ∠,则ABC ∠的度数为( )A .10︒B .20︒C .30D .40︒【答案】B 【分析】根据平行线的性质得到∠ABC =∠BCD ,再根据角平分线的定义得到∠ABC =∠BCD ,再利用三角形外角的性质计算即可.【详解】解:∵AB ∥CD ,∴∠ABC =∠BCD ,∵CB 平分∠DCE ,∴∠BCE =∠BCD ,∴∠BCE =∠ABC , ∵∠AEC =∠BCE +∠ABC =40°,∴∠ABC =20°,故选B .【点睛】本题考查了平行线的性质,角平分线的定义和外角的性质,掌握平行线的性质:两直线平行,内错角相等是解题的关键.2.(2021·四川眉山市)如图,将直角三角板放置在矩形纸片上,若148∠=︒,则2∠的度数为( )A .42°B .48°C .52°D .60°【答案】A 【分析】先通过作辅助线,将∠1转化到∠BAC ,再利用直角三角形两锐角互余即可求出∠2.【详解】解:如图,延长该直角三角形一边,与该矩形纸片一边的交点记为点A ,由矩形对边平行,可得∠1=∠BAC ,因为BC ⊥AB ,∴∠BAC +∠2=90°,∴∠1+∠2=90°,因为∠1=48°,∴∠2=42°;故选:A .【点睛】本题考查了矩形的性质、平行线的性质、直角三角形的性质等内容,要求学生能根据题意理解其中的隐含关系,解决本题的关键是对角进行的转化,因此需要牢记并能灵活应用相关性质等.3.(2021·四川乐山市)七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为4的正方形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”(即阴影部分)的面积为()A.3 B.72C.2 D.52【答案】A【分析】根据由边长为4的正方形分割制作的七巧板,可得共5种图形,然后根据阴影部分的构成图形,计算阴影部分面积即可.【详解】解:如下图所示,由边长为4的正方形分割制作的七巧板,共有以下几种图形:○1腰长是2的等腰直角三角形,2,顶角分别是45和135的平行四边形,根据图2可知,图中抬起的“腿”的等腰直角三角形,和一个边长分别是2,顶角分别是45和135的平行四边形组成,如下图示,根据平行四边形的性质可知,顶角分别是45和135的平行四边形的高是DB,且DB=的等腰直角三角形的面积是:112=,顶角分别是45和1352=,∴阴影部分的面积为:123+=,故选:A.【点睛】本题考查了七巧板中的图形的构成和面积计算,熟悉七巧板中图形的分类是解题的关键.4.(2021·湖南岳阳市)下列命题是真命题的是()A.五边形的内角和是720︒B.三角形的任意两边之和大于第三边C.内错角相等D.三角形的重心是这个三角形的三条角平分线的交点【答案】B【分析】根据相关概念逐项分析即可.【详解】A、五边形的内角和是540︒,故原命题为假命题,不符合题意;B、三角形的任意两边之和大于第三边,原命题是真命题,符合题意;C、两直线平行,内错角相等,故原命题为假命题,不符合题意;D、三角形的重心是这个三角形的三条中线的交点,故原命题为假命题,不符合题意;故选:B.【点睛】本题考查命题判断,涉及多边形的内角和,三角形的三边关系,平行线的性质,以及三角形的重心等,熟记基本性质和定理是解题关键.5.(2021·安徽)两个直角三角板如图摆放,其中90BAC EDF ∠=∠=︒,45E ∠=︒,30C ∠=︒,AB 与DF 交于点M .若//BC EF ,则BMD ∠的大小为( )A .60︒B .67.5︒C .75︒D .82.5︒【答案】C 【分析】根据//BC EF ,可得45FDB F ∠=∠=︒,再根据三角形内角和即可得出答案.【详解】由图可得6045B F ∠=︒∠=︒,,∵//BC EF ,∴45FDB F ∠=∠=︒, ∴180180456075BMD FDB B ∠=︒-∠-∠=︒-︒-︒=︒,故选:C .【点睛】本题考查了平行线的性质和三角形的内角和,掌握平行线的性质和三角形的内角和是解题的关键. 6.(2021·浙江金华市)某同学的作业如下框,其中※处填的依据是( )A .两直线平行,内错角相等B .内错角相等,两直线平行C .两直线平行,同位角相等D .两直线平行,同旁内角互补 【答案】C【分析】首先准确分析题目,已知12//l l ,结论是34∠=∠,所以应用的是平行线的性质定理,从图中得知∠3和∠4是同位角关系,即可选出答案.【详解】解:∵12//l l ,∴34∠=∠(两直线平行,同位角相等).故选C .【点睛】本题主要考查了平行线的性质的应用,解题的关键是理解平行线之间内错角的位置,从而准确地选择出平行线的性质定理.7.(2021·云南)如图,直线c 与直线a 、b 都相交.若//a b ,155∠=︒,则2∠=( )A .60︒B .55︒C .50︒D .45︒【答案】B 【分析】直接利用平行线的性质:两直线平行,同位角相等,即可得出答案.【详解】解:如图,1=55∠︒,3=55,∴∠︒ ∵a ∥b ,∠3=55°,∴∠2=∠3=55°.故选B .【点睛】此题主要考查了平行线的性质,正确掌握平行线的基本性质是解题关键.8.(2021·山东)如图,AB ∥CD ∥EF ,若∠ABC =130°,∠BCE =55°,则∠CEF 的度数为( )A .95°B .105°C .110°D .115°【答案】B 【分析】由//AB CD 平行的性质可知ABC DCB ∠=∠,再结合//EF CD 即可求解.【详解】解://AB CD 130ABC DCB ∴∠=∠=︒1305575ECD DCB BCE ∴∠=∠-∠=︒-︒=︒//EF CD 180ECD CEF ∴∠+∠=︒18075105CEF ∴∠=︒-︒=︒故答案是:B .【点睛】本题考查平行线的性质和角度求解,难度不大,属于基础题.解题的关键是掌握平行线的性质.9.(2021·山东泰安市)如图,直线//m n ,三角尺的直角顶点在直线m 上,且三角尺的直角被直线m 平分,若160∠=︒,则下列结论错误的是( )A .275∠=︒B .345∠=︒C .4105∠=︒D .5130∠=︒【答案】D 【分析】根据角平分线的定义求出∠6和∠7的度数,再利用平行线的性质以及三角形内角和求出∠3,∠8,∠2的度数,最后利用邻补角互补求出∠4和∠5的度数.【详解】首先根据三角尺的直角被直线m 平分,∴∠6=∠7=45°;A 、∵∠1=60°,∠6=45°,∴∠8=180°-∠1-∠6=180-60°-45°=75°,m ∥n ,∴∠2=∠8=75°结论正确,选项不合题意;B 、∵∠7=45°,m ∥n ,∴∠3=∠7=45°,结论正确,选项不合题意;C 、∵∠8=75°,∴∠4=180-∠8=180-75°=105°,结论正确,选项不合题意;D 、∵∠7=45°,∴∠5=180-∠7=180-45°=135°,结论错误,选项符合题意.故选:D .【点睛】本题考查了角平分线的定义,平行线的性质,三角形内角和,邻补角互补,解答本题的关键是掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.10.(2021·四川资阳市)如图,已知直线//,140,230m n ∠=︒∠=︒,则3∠的度数为( )A .80︒B .70︒C .60︒D .50︒【答案】B 【分析】如图,由题意易得∠4=∠1=40°,然后根据三角形外角的性质可进行求解.【详解】解:如图,∵//,140m n ∠=︒,∴∠4=∠1=40°,∵230∠=︒,∴34270∠=∠+∠=︒;故选B .【点睛】本题主要考查平行线的性质及三角形外角的性质,熟练掌握平行线的性质及三角形外角的性质是解题的关键.11.(2021·四川广元市)如图,在ABC 中,90ACB ∠=︒,4AC BC ==,点D 是BC 边的中点,点P 是AC 边上一个动点,连接PD ,以PD 为边在PD 的下方作等边三角形PDQ ,连接CQ .则CQ 的最小值是( )A B .1 C D .32【答案】B【分析】以CD 为边作等边三角形CDE ,连接EQ ,由题意易得∠PDC =∠QDE ,PD =QD ,进而可得△PCD ≌△QED ,则有∠PCD =∠QED =90°,然后可得点Q 是在QE 所在直线上运动,所以CQ 的最小值为CQ ⊥QE 时,最后问题可求解.【详解】解:以CD 为边作等边三角形CDE ,连接EQ ,如图所示:∵PDQ 是等边三角形,∴60,,CED PDQ CDE PD QD CD ED ∠=∠=∠=︒==,∵∠CDQ 是公共角,∴∠PDC =∠QDE ,∴△PCD ≌△QED (SAS ),∵90ACB ∠=︒,4AC BC ==,点D 是BC 边的中点,∴∠PCD =∠QED =90°,122CD DE CE BC ====,∴点Q 是在QE 所在直线上运动, ∴当CQ ⊥QE 时,CQ 取的最小值,∴9030QEC CED ∠=︒-∠=︒,∴112CQ CE ==;故选B . 【点睛】本题主要考查等边三角形的性质、含30°直角三角形的性质及最短路径问题,熟练掌握等边三角形的性质、含30°直角三角形的性质及最短路径问题是解题的关键.12.(2021·河北)定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,ACD ∠是ABC 的外角.求证:ACD A B ∠=∠+∠.下列说法正确的是( )A .证法1还需证明其他形状的三角形,该定理的证明才完整B .证法1用严谨的推理证明了该定理C .证法2用特殊到一般法证明了该定理D .证法2只要测量够一百个三角形进行验证,就能证明该定理【答案】B【分析】根据三角形的内角和定理与平角的定义可判断A 与B ,利用理论与实践相结合可判断C 与D .【详解】解:A . 证法1给出的证明过程是完整正确的,不需要分情况讨论,故A 不符合题意;B . 证法1给出的证明过程是完整正确的,不需要分情况讨论,故选项B 符合题意;C . 证法2用量角器度量两个内角和外角,只能验证该定理的正确性,用特殊到一般法证明了该定理缺少理论证明过程,故选项C 不符合题意;D . 证法2只要测量够一百个三角形进行验证,验证的正确性更高,就能证明该定理还需用理论证明,故选项D 不符合题意.故选择:.B【点睛】本题考查三角形外角的证明问题,命题的正确性需要严密推理证明,三角形外角分三种情形,锐角、直角、和钝角,证明中应分类才严谨.13.(2021·四川凉山州)如图,ABC 中,90,8,6ACB AC BC ∠=︒==,将ADE 沿DE 翻折,使点A 与点B 重合,则CE 的长为( )A .198B .2C .254D .74【答案】D【分析】先在RtABC 中利用勾股定理计算出AB =10,再利用折叠的性质得到AE =BE ,AD =BD =5,设AE =x ,则CE =AC -AE =8-x ,BE =x ,在Rt △BCE 中根据勾股定理可得到x 2=62+(8-x )2,解得x ,可得CE .【详解】解:∵∠ACB =90°,AC =8,BC =6,∴AB ,∵△ADE 沿DE 翻折,使点A 与点B 重合,∴AE =BE ,AD =BD =12AB =5, 设AE =x ,则CE =AC -AE =8-x ,BE =x ,在Rt △BCE 中∵BE 2=BC 2+CE 2,∴x 2=62+(8-x )2,解得x =254,∴CE =2584-=74,故选:D . 【点睛】本题考查了折叠的性质:折叠前后两图象全等,即对应角相等,对应边相等.也考查了勾股定理. 14.(2021·陕西)如图,点D 、E 分别在线段BC 、AC 上,连接AD 、BE .若35A ∠=︒,25B ∠=︒,50C ∠=︒,则1∠的大小为( )A .60°B .70°C .75°D .85°【答案】B 【分析】由题意易得105BEC ∠=︒,然后根据三角形外角的性质可进行求解.【详解】解:∵25B ∠=︒,50C ∠=︒,∴在Rt △BEC 中,由三角形内角和可得105BEC ∠=︒,∵35A ∠=︒,∴170BEC A ∠=∠-∠=︒;故选B .【点睛】本题主要考查三角形内角和及外角的性质,熟练掌握三角形内角和及外角的性质是解题的关键. 15.(2021·安徽)在△ABC 中,90ACB ∠=︒,分别过点B ,C 作BAC ∠平分线的垂线,垂足分别为点D ,E ,BC 的中点是M ,连接CD ,MD ,ME .则下列结论错误的是( )A .2CD ME =B .//ME ABC .BD CD = D .ME MD = 【答案】A【分析】设AD 、BC 交于点H ,作HF AB ⊥于点F ,连接EF .延长AC 与BD 并交于点G .由题意易证△CAE ≌△FAE ,从而证明ME 为△CBF 中位线,即//ME AB ,故判断B 正确;又易证△AGD ≌△ABD ,从而证明D 为BG 中点.即利用直角三角形斜边中线等于斜边一半即可求出CD BD =,故判断C 正确;由90HDM DHM ∠+∠=︒、90HCE CHE ∠+∠=︒和DHM CHE ∠=∠可证明HDM HCE ∠=∠.再由90HEM EHF ∠+∠=︒、EHC EHF ∠=∠和90EHC HCE ∠+∠=︒可推出 HCE HEM ∠=∠,即推出HDM HEM ∠=∠,即MD ME =,故判断D 正确;假设2CD ME =,可推出2CD MD =,即可推出30DCM ∠=︒.由于无法确定DCM ∠的大小,故2CD ME =不一定成立,故可判断A 错误.【详解】如图,设AD 、BC 交于点H ,作HF AB ⊥于点F ,连接EF .延长AC 与BD 并交于点G .∵AD 是BAC ∠的平分线,HF AB ⊥,HC AC ⊥,∴HC =HF ,∴AF =AC .∴在△CAE 和△FAE 中,AF AC CAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△CAE ≌△FAE ,∴CE FE =,∠AEC =∠AEF =90°,∴C 、E 、F 三点共线,∴点E 为CF 中点.∵M 为BC 中点,∴ME 为△CBF 中位线,∴//ME AB ,故B 正确,不符合题意;∵在AGD △和ABD △中,90GAD BAD AD AD ADG ADB ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩,∴△AGD ≌△ABD , ∴12GD BD BG ==,即D 为BG 中点.∵在BCG 中,90BCG ∠=︒,∴12CD BG =, ∴CD BD =,故C 正确,不符合题意;∵90HDM DHM ∠+∠=︒,90HCE CHE ∠+∠=︒,DHM CHE ∠=∠,∴HDM HCE ∠=∠. ∵HF AB ⊥,//ME AB ,∴HF ME ⊥,∴90HEM EHF ∠+∠=︒.∵AD 是BAC ∠的平分线,∴EHC EHF ∠=∠.∵90EHC HCE ∠+∠=︒, ∴HCE HEM ∠=∠, ∴HDM HEM ∠=∠,∴MD ME =,故D 正确,不符合题意;∵假设2CD ME =,∴2CD MD =,∴在Rt △CDM 中,30DCM ∠=︒.∵无法确定DCM ∠的大小,故原假设不一定成立,故A 错误,符合题意.故选A .【点睛】本题考查角平分线的性质,三角形全等的判定和性质,直角三角形的性质,三角形中位线的判定和性质以及含30角的直角三角形的性质等知识,较难.正确的作出辅助线是解答本题的关键. 16.(2021·重庆)如图,在△ABC 和△DCB 中,ACB DBC ∠=∠ ,添加一个条件,不能..证明和△ABC 和△DCB 全等的是( )A .ABC DCB ∠=∠ B .AB DC = C .AC DB =D .A D ∠=∠【答案】B【分析】根据已知条件和添加条件,结合全等三角形的判断方法即可解答.【详解】选项A ,添加ABC DCB ∠=∠,在△ABC 和△DCB 中,ABC DCB BC CB ACB DBC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC ≌△DCB (ASA ),选项B ,添加 AB DC =,在△ABC 和△DCB 中, AB DC =,BC CB =,ACB DBC ∠=∠,无法证明△ABC ≌△DCB ;选项C ,添加AC DB =,在ABC 和DCB 中,BC CB ACB DBC AC DB =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DCB (SAS );选项D ,添加A D ∠=∠,在ABC 和DCB 中,A D ACB DBC BC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DCB (AAS );综上,只有选项B 符合题意.故选B .【点睛】本题考查了全等三角形的判定方法,熟知全等三角形的判定方法是解决问题的关键. 17.(2021·浙江丽水市)如图,在Rt ABC △纸片中,90,4,3ACB AC BC ∠=︒==,点,D E 分别在,AB AC 上,连结DE ,将△ADE 沿DE 翻折,使点A 的对应点F 落在BC 的延长线上,若FD 平分EFB ∠,则AD 的长为( )A .259B .258C .157D .207【答案】D【分析】先根据勾股定理求出AB ,再根据折叠性质得出∠DAE=∠DFE ,AD=DF ,然后根据角平分线的定义证得∠BFD=∠DFE =∠DAE ,进而证得∠BDF=90°,证明Rt △ABC ∽Rt △FBD ,可求得AD 的长.【详解】解:∵90,4,3ACB AC BC ∠=︒==,∴AB ==,由折叠性质得:∠DAE=∠DFE ,AD=DF ,则BD =5﹣AD ,∵FD 平分EFB ∠,∴∠BFD =∠DFE=∠DAE ,∵∠DAE +∠B =90°,∴∠BDF +∠B =90°,即∠BDF =90°,∴Rt △ABC ∽Rt △FBD ,∴BD BC DF AC =即534AD AD -=,解得:AD =205,故选:D . 【点睛】本题考查折叠性质、角平分线的定义、勾股定理、相似三角形的判定与性质、三角形的内角和定理,熟练掌握折叠性质和相似三角形的判定与性质是解答的关键.18.(2021·四川自贡市)如图,()8,0A,()2,0C -,以点A 为圆心,AC 长为半径画弧,交y 轴正半轴于点B ,则点B 的坐标为( )A .()0,5B .()5,0C .()6,0D .()0,6【答案】D 【分析】先根据题意得出OA =8,OC =2,再根据勾股定理计算即可【详解】解:由题意可知:AC =AB ∵()8,0A,()2,0C -∴OA =8,OC =2∴AC =AB =10在Rt △OAB 中,6OB ==∴B (0,6)故选:D【点睛】本题考查勾股定理、正确写出点的坐标,圆的半径相等、熟练进行勾股定理的计算是关键 19.(2021·重庆)如图,点B ,F ,C ,E 共线,∠B =∠E ,BF =EC ,添加一个条件,不等判断△ABC ≌△DEF 的是( )A .AB =DEB .∠A =∠DC .AC =DFD .AC ∥FD【答案】C 【分析】根据全等三角形的判定与性质逐一分析即可解题. 【详解】解:BF =EC ,BC EF ∴=A. 添加一个条件AB =DE ,又,BC EF B E =∠=∠()ABC DEF SAS ∴△≌△ 故A 不符合题意;B. 添加一个条件∠A =∠D ,又,BC EF B E =∠=∠,∴△ABC ≌△DEF (AAS ),故B 不符合题意;C. 添加一个条件AC =DF ,不能判断△ABC ≌△DEF ,故C 符合题意;D. 添加一个条件AC ∥FD , ACB EFD ∴∠=∠,又,BC EF B E =∠=∠,△ABC ≌△DEF (ASA ),故D 不符合题意,故选:C .【点睛】本题考查添加条件使得三角形全等即全等三角形的判定,是重要考点,难度较易,掌握相关知识是解题关键.20.(2021·江苏扬州市)如图,在44⨯的正方形网格中有两个格点A 、B ,连接AB ,在网格中再找一个格点C ,使得ABC 是等腰直角....三角形,满足条件的格点C 的个数是( )A .2B .3C .4D .5【答案】B 【分析】根据题意,结合图形,分两种情况讨论:①AB 为等腰直角△ABC 底边;②AB 为等腰直角△ABC 其中的一条腰.【详解】解:如图:分情况讨论:①AB 为等腰直角△ABC 底边时,符合条件的C 点有0个;②AB 为等腰直角△ABC 其中的一条腰时,符合条件的C 点有3个.故共有3个点,故选:B .【点睛】本题考查了等腰三角形的判定;解答本题关键是根据题意,画出符合实际条件的图形,数形结合的思想是数学解题中很重要的解题思想.21.(2021·浙江宁波市)如图,在△ABC 中,45,60,B C AD BC ∠=︒∠=︒⊥于点D ,BD =.若E ,F 分别为AB ,BC 的中点,则EF 的长为( )A B C .1 D 【答案】C【分析】根据条件可知△ABD 为等腰直角三角形,则BD =AD ,△ADC 是30°、60°的直角三角形,可求出AC 长,再根据中位线定理可知EF =2AC . 【详解】解:因为AD 垂直BC ,则△ABD 和△ACD 都是直角三角形,又因为45,60,B C ∠=︒∠=︒所以AD =BD =,因为sin ∠C =2AD AC =,所以AC =2, 因为EF 为△ABC 的中位线,所以EF =2AC =1,故选:C . 【点睛】本题主要考查了等腰直角三角形、锐角三角形函数值、中位线相关知识,根据条件分析利用定理推导,是解决问题的关键.22.(2021·青海)如图,在四边形ABCD 中,∠A=90°,AD=3,BC=5,对角线BD 平分∠ABC ,则△BCD 的面积为( )A .7.5B .8C .15D .无法确定【答案】A 【详解】如图,过点D 作DE ⊥BC 于点E .∵∠A=90°,∴AD ⊥AB .∴AD=DE=3.又∵BC=5,∴S △BCD =12BC•DE=12×5×3=7.5.故选A . 考点:角平分线的性质;全等三角形的判定与性质.二、填空题 1.(2021·浙江)由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分).则图中AB 的长应是______.1【分析】据裁剪和拼接的线段关系可知CD =,1BD CE ==,在Rt ACD △中应用勾股定理即可求解.【详解】解:∵地毯平均分成了3=CD =在Rt ACD △中,根据勾股定理可得AD =,根据裁剪可知1BD CE ==,∴1AB AD BD =-=1.【点睛】本题考查勾股定理,根据裁剪找出对应面积和线段的关系是解题的关键.2.(2021·河北)下图是可调躺椅示意图(数据如图),AE 与BD 的交点为C ,且A ∠,B ,E ∠保持不变.为了舒适,需调整D ∠的大小,使110EFD ∠=︒,则图中D ∠应___________(填“增加”或“减少”)___________度.【答案】减少 10【分析】先通过作辅助线利用三角形外角的性质得到∠EDF 与∠D 、∠E 、∠DCE 之间的关系,进行计算即可判断.【详解】解:∵∠A +∠B =50°+60°=110°,∴∠ACB =180°-110°=70°,∴∠DCE =70°,如图,连接CF 并延长,∴∠DFM =∠D +∠DCF =20°+∠DCF ,∠EFM =∠E +∠ECF =30°+∠ECF , ∴∠EFD =∠DFM +∠EFM =20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°,要使∠EFD =110°,则∠EFD 减少了10°,若只调整∠D 的大小,由∠EFD =∠DFM +∠EFM =∠D +∠DCF +∠E +∠ECF =∠D +∠E +∠ECD =∠D +30°+70°=∠ D +100°,因此应将∠D 减少10度;故答案为:①减少;②10.【点睛】本题考查了三角形外角的性质,同时涉及到了三角形的内角和与对顶角相等的知识;解决本题的关键是理解题意,读懂图形,找出图形中各角之间的关系以及牢记公式建立等式求出所需的角,本题蕴含了数形结合的思想方法.3.(2021·青海)如图,AB ∥CD ,FE ⊥DB ,垂足为E ,∠1=50°,则∠2的度数是_____.【答案】40°【分析】由EF ⊥BD ,∠1=50°,结合三角形内角和为180°,即可求出∠D 的度数,再由“两直线平行,同位角相等”即可得出结论.【详解】解:在△DEF 中,∠1=50°,∠DEF=90°,∴∠D=180°-∠DEF-∠1=40°.∵AB ∥CD ,∴∠2=∠D=40°.故答案为40°.【点睛】本题考查平行线的性质以及三角形内角和为180°,解题关键是求出∠D=40°.解决该题型题目时,根据平行线的性质,找出相等或互补的角是解题技巧.4.(2021·山东聊城市)如图,在△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为点D 和点E ,AD 与CE 交于点O ,连接BO 并延长交AC 于点F ,若AB =5,BC =4,AC =6,则CE :AD :BF 值为____________.【答案】12:15:10【分析】由题意得:BF ⊥AC ,再根据三角形的面积公式,可得5432ABC SAD CE BF ===,进而即可得到答案.【详解】解:∵在△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为点D 和点E ,AD 与CE 交于点O ,∴BF ⊥AC ,∵AB =5,BC =4,AC =6,∴111222ABC SBC AD AB CE AC BF =⋅=⋅=⋅, ∴5432ABC S AD CE BF ===,∴CE :AD :BF =12:15:10,故答案是:12:15:10. 【点睛】本题主要考查三角形的高,掌握“三角形的三条高交于一点”是解题的关键.5.(2021·江苏南京市)如图,在四边形ABCD 中,AB BC BD ==.设ABC α∠=,则ADC ∠=______(用含α的代数式表示).【答案】11802α︒- 【分析】由等腰的性质可得:∠ADB =1902ABD ︒-∠,∠BDC =1902CBD ︒-∠,两角相加即可得到结论. 【详解】解:在△ABD 中,AB =BD ∴∠A =∠ADB =11(180)9022ABD ABD ︒-∠=︒-∠ 在△BCD 中,BC =BD ∴∠C =∠BDC =11(180)9022CBD CBD ︒-∠=︒-∠ ∵ABC ABD CBD α∠=∠+∠= ∴ADC ADB CBD ∠=∠+∠ =11909022ABD CBD ︒-∠+︒-∠ =1180()2ABD CBD ︒-∠+∠=11802ABC ︒-∠=11802α︒-故答案为:11802α︒-. 【点睛】此题主要考查了等腰三角形的性质和三角形内角和定理,分别求出∠ADB=1902ABD ︒-∠,∠BDC=1902CBD ︒-∠是解答本题的关键. 6.(2021·江苏连云港市)如图,BE 是ABC 的中线,点F 在BE 上,延长AF 交BC 于点D .若3BF FE =,则BD DC=______.【答案】32【分析】连接ED ,由BE 是ABC 的中线,得到BE BCE S S =△A △,AED EDC S S =,由3BF FE =,得到3,3ABF BFD AFEFEDS S SS ==,设=,AEF EFDSx Sy =,由面积的等量关系解得53x y =,最后根据等高三角形的性质解得ABD ADCS BDSDC=,据此解题即可. 【详解】解:连接EDBE 是ABC 的中线,ABEBCESS∴=,AEDEDCSS=3BF FE =3,3ABF BFD AFEFEDS S SS∴==设=,AEFEFDSx Sy =,33ABFBFDSx Sy ∴==,4,4,4ABE BECBEDSx Sx Sy ∴===44EDCBECBEDSSSx y ∴=-=-ADEEDCSS=44x y x y ∴+=-53x y∴=ABD 与ADC 是等高三角形,53+33333833=516445325333ABD ADCy yS BD x y x y y SDC x y x y x y y y y ⨯++∴=====++--⨯-,故答案为:32. 【点睛】本题考查三角形的中线、三角形面积等知识,是重要考点,难度一般,掌握相关知识是解题关键.7.(2021·浙江绍兴市)如图,在ABC 中,AB AC =,70B ∠=︒,以点C 为圆心,CA 长为半径作弧,交直线BC 于点P ,连结AP ,则BAP ∠的度数是_______.【答案】15︒或75︒【分析】分①点P 在BC 的延长线上,②点P 在CB 的延长线上两种情况,再利用等腰三角形的性质即可得出答案.【详解】解:①当点P 在BC 的延长线上时,如图∵AB AC =,70B ∠=︒,∴70B ACB ∠=∠=︒∴40CAB ∠=︒∵以点C 为圆心,CA 长为半径作弧,交直线BC 于点P ,∴AC =PC ∴∠=∠P CAP∵70∠=∠+∠=︒ACB B CAP ∴35∠=∠=P CAP ∴403575∠=∠+∠=+=BAP BAC CAP②当点P 在CB 的延长线上时,如图由①得70C ∠=︒,40CAB ∠=︒∵AC =PC ∴=55∠=∠P CAP ∴-55-4015∠=∠∠==BAP CAP BAC 故答案为:15︒或75︒【点睛】本题主要考查了等腰三角形的性质,分类讨论不重不漏是解题的关键.8.(2021·四川广安市)如图,将三角形纸片ABC 折叠,使点B 、C 都与点A 重合,折痕分别为DE 、FG .已知15ACB ∠=︒,AE EF =,DE =BC 的长为_______.【答案】4+【分析】由折叠的性质得出BE =AE ,AF =FC ,∠F AC =∠C =15°,得出∠AFE =30°,由等腰三角形的性质得出∠EAF =∠AFE =30°,证出△ABE 是等边三角形,得出∠BAE =60°,求出AE =BE =2,证出∠BAF =90°,利用勾股定理求出AF ,即CF ,可得BC .【详解】解:∵把三角形纸片折叠,使点B 、点C 都与点A 重合,折痕分别为DE ,FG , ∴BE =AE ,AF =FC ,∠F AC =∠C =15°,∴∠AFE =30°,又AE =EF ,∴∠EAF =∠AFE =30°,∴∠AEB =60°,∴△ABE 是等边三角形,∠AED =∠BED =30°,∴∠BAE =60°,∵DE AE =BE =AB =cos30DE︒=2,∴BF =BE +EF =4,∠BAF =60°+30°=90°,∴FC =AF =BC =BF +FC =4+,故答案为:4+.【点睛】此题考查了翻折变换的性质、等腰三角形的性质、等边三角形的判定与性质、直角三角形的性质;根据折叠的性质得出相等的边和角是解题关键.9.(2021·四川遂宁市)如图,在△ABC 中,AB =5,AC =7,直线DE 垂直平分BC ,垂足为E ,交AC 于点D ,则△ABD 的周长是 _____ .【答案】12.【分析】根据线段的垂直平分线的性质得到DB DC =,根据三角形的周长公式计算即可. 【详解】解:∵直线DE 垂直平分BC ,∴DB DC =,∴△ABD 的周长5712AB AD BD AB AD DC AB AC =++=++=+=+=,故答案为:12.【点睛】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.10.(2021·江苏宿迁市)《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AB 生长在它的中央,高出水面部分BC 为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B 恰好碰到岸边的B '(示意图如图,则水深为__尺.【答案】12【分析】依题意画出图形,设芦苇长AB =AB '=x 尺,则水深AC =(x ﹣1)尺,因为B 'E =10尺,所以B 'C =5尺,利用勾股定理求出x 的值即可得到答案..【详解】解:依题意画出图形,设芦苇长AB =AB '=x 尺,则水深AC =(x ﹣1)尺, 因为B 'E =10尺,所以B 'C =5尺,在Rt △AB 'C 中,52+(x ﹣1)2=x 2,解之得x =13,即水深12尺,芦苇长13尺.故答案为:12.【点睛】此题考查勾股定理的实际应用,正确理解题意,构建直角三角形利用勾股定理解决问题是解题的关键. 三、解答题1.(2021·湖北武汉市)如图,//AB CD ,B D ∠=∠,直线EF 与AD ,BC 的延长线分别交于点E ,F .求证:DEF F ∠=∠.【答案】见解析【分析】根据已知条件//AB CD ,B D ∠=∠,得到DCF D ∠=∠,从而得到//AD BC ,即可证明DEF F ∠=∠.【详解】证明:∵//AB CD ,∴DCF B ∠=∠.∵B D ∠=∠,∴DCF D ∠=∠.∴//AD BC .∴DEF F ∠=∠.【点睛】本题考查平行线的性质和判定.平行线的性质:两直线平行,内错角相等.平行线的判定:同位角相等,两直线平行.2.(2021·浙江温州市)如图,BE 是ABC 的角平分线,在AB 上取点D ,使DB DE =. (1)求证://DE BC .(2)若65A ∠=︒,45AED ∠=︒,求EBC ∠的度数.【答案】(1)见解析;(2)35°【分析】(1)直接利用角平分线的定义和等边对等角求出BED EBC ∠=∠,即可完成求证; (2)先求出∠ADE ,再利用平行线的性质求出∠ ABC ,最后利用角平分线的定义即可完成求解. 【详解】解:(1)BE 平分ABC ∠,∴ABE EBC ∠=∠.DB DE =,∴ABE BED ∠=∠,∴BED EBC ∠=∠,∴//DE BC .(2)65A ∠=︒,45AED ∠=︒,∴18070ADE A AED ∠=︒-∠-∠=︒.//DE BC .∴70ABC ADE ∠=∠=︒.BE 平分ABC ∠,∴1352EBC ABC ∠=∠=︒,即35EBC ∠=︒. 【点睛】本题综合考查了角平分线的定义、等腰三角形的性质、平行线的判定与性质等内容,解决本题的关键是牢记概念与性质,本题的解题思路较明显,属于几何中的基础题型,着重考查了学生对基本概念的理解与掌握.3.(2021·四川南充市)如图,90BAC ∠=︒,AD 是BAC ∠内部一条射线,若AB AC =,BE AD ⊥于点E ,CF AD ⊥于点F .求证:AF BE =.【答案】见详解【分析】根据AAS 证明△BAE ≌△ACF ,即可得AF BE =. 【详解】证明:∵90BAC ∠=︒,∴∠BAE +∠CAF =90°, ∵BE ⊥AD ,CF ⊥AD ,∴∠BEA =∠AFC =90°, ∴∠BAE +∠EBA =90°,∴∠CAF =∠EBA , ∵AB =AC ,∴△BAE ≌△ACF ,∴AF BE =.【点睛】本题主要考查全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键. 4.(2021·浙江绍兴市)如图,在ABC 中,40A ∠=︒,点D ,E 分別在边AB ,AC 上,BD BC CE ==,连结CD ,BE .(1)若80ABC ∠=︒,求BDC ∠,ABE ∠的度数.(2)写出BEC ∠与BDC ∠之间的关系,并说明理由.【答案】(1)50BDC ∠=︒;20ABE ∠=︒;(2)110BEC BDC ∠+∠=︒,见解析【分析】(1)利用三角形的内角和定理求出ACB ∠的大小,再利用等腰三角形的性质分别求出BDC ∠,ABE ∠.(2)利用三角形的内角和定理、三角形外角的性质和等腰三角形的性质,求出用含ABE ∠分别表示BEC ∠,BDC ∠,即可得到两角的关系.【详解】(1)80ABC ∠=︒,BD BC =,50BDC BCD ∴∠=∠=︒. 在ABC 中,180A ABC ACB ∠+∠+∠=︒,40A ∠=︒,60ACB ∠=︒∴,CE BC =,60EBC ∴∠=︒.20ABE ABC EBC ∴∠=∠-∠=︒.(2)BEC ∠,BDC ∠的关系:110BEC BDC ∠+∠=︒.理由如下:设BEC α∠=,BDC β∠=.在ABE △中,40A ABE ABE α=∠+∠=︒+∠,CE BC =,CBE BEC α∴∠=∠=.2402ABC ABE CBE A ABE ABE ∴∠=∠+∠=∠+∠=︒+∠,在BDC 中,BD BC =,2402180BDC BCD DBC ABE β∴∠+∠+∠=+︒+∠=︒.70ABE β︒∴=-∠.4070110ABE ABE αβ∴+=︒+∠+︒-∠=︒.110BEC BDC ∴∠+∠=︒.【点睛】本题主要通过求解角和两角之间的关系,考查三角形的内角和定理、三角形外角的性质和等腰三角形的性质.三角形的内角和等于180︒ .三角形的外角等于与其不相邻的两个内角之和.等腰三角形等边对等角.5.(2021·陕西中考真题)如图,//BD AC ,BD BC =,点E 在BC 上,且BE AC =.求证:D ABC ∠=∠.【答案】见解析【分析】由题意易得EBD C ∠=∠,进而可证EDB ABC ≌△△,然后问题可求证. 【详解】证明:∵//BD AC ,∴EBD C ∠=∠.∵BD BC =,BE AC =,∴()EDB ABC SAS ≌.∴D ABC ∠=∠.【点睛】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键. 6.(2021·湖南衡阳市)如图,点A 、B 、D 、E 在同一条直线上,,//,//AB DE AC DF BC EF =.求证:ABC DEF △≌△.【答案】见解析【分析】根据//,//AC DF BC EF ,可以得到,A FDE ABC DEF ∠=∠∠=∠,然后根据题目中的条件,利用ASA 证明△ABC ≌△DEF 即可.【详解】证明:点A ,B ,C ,D ,E 在一条直线上 ∵//,//AC DF BC EF ∴,A FDE ABC DEF ∠=∠∠=∠在△ABC 与△DEF 中CAB FDEAB DE ABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ABC DEF ASA △≌△【点睛】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS 、ASA 、SAS、SSS ,直角三角形可用HL 定理,但AAA 、SSA ,无法证明三角形全等,本题是一道较为简单的题目. 7.(2021·浙江)已知在ACD △中,Р是CD 的中点,B 是AD 延长线上的一点,连结,BC AP .(1)如图1,若90,60,,ACB CAD BD AC AP ︒∠=︒∠===,求BC 的长.(2)过点D 作//DE AC ,交AP 延长线于点E ,如图2所示.若60,CAD BD AC ∠︒==,求证:2BC AP =. (3)如图3,若45CAD ∠=︒,是否存在实数m ,当BD mAC =时,2BC AP =?若存在,请直接写出m 的值;若不存在,请说明理由.【答案】(1)(2)见解析;(3)存在,m =【分析】(1)先解直角三角形ABC 得出2AB AC =,从而得出△ADC 是等边三角形,再解直角三角形ACP 即可求出AC 的长,进而得出BC 的长;(2)连结BE ,先利用AAS 证出△CPA ≌△DPE ,得出AE =2PE ,AC =DE ,再得出△ADC 是等边三角形,然后由SAS 得出△CAB ≌△EBA ,得出AE =BC 即可得出结论; (3)过点D 作//DE AC ,交AP 延长线于点E ,连接BE ,过C 作CG ⊥AB 于G ,过E 作EN ⊥AB 于N ,由(2)得AE =2AP ,DE =AC ,再证明△AEN ≌△BCG ,从而得出△CAB ≌△EBA 得出DE =BE ,然后利用勾股定理即可得出m 的值. 【详解】(1)解90,60ACB CAD ∠=∠=︒︒,2cos60ACAB AC ︒==,BD AC =,AD AC =∴,∴△ADC 是等边三角形,60ACD ∴∠=︒Р是CD 的中点,AP CD ∴⊥,在Rt APC 中,AP =2sin 60APAC ∴==︒,tan 60BC AC =︒=∴(2)证明:连结BE ,//DE AC ,CAP DEP ∴∠=∠,,CP DP CPA DPE =∠=∠,∴△CPA ≌△DPE , 1,2AP EP AE DE AC ∴===, BD AC =,BD DE ∴=,又//DE AC ,60BDE CAD ∴∠=∠=︒,∴△BDE 是等边三角形,,60BD BE EBD ∴=∠=︒BD AC =,AC BE ∴=,又60,CAB EBA AB BA ∠=∠=︒=,∴△CAB ≌△EBA , AE BC ∴=,2BC AP ∴=.。
人教版八年级数学上册第一单元《三角形的内角和》同步练习2(含参考答案)

人教版八年级数学上册第一单元《三角形的内角和》同步练习2(含参考答案)一.选择题1.已知在Rt△ABC中,∠B=90°,∠C=35°,则∠A等于()A.35°B.45°C.55°D.65°2.如右图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为()A.40°B.50°C.60°D.70°3.如右图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是()A.∠1+∠2=90°B.∠2=∠3 C.∠1=∠4 D.∠1=30°4.直角三角形两个锐角平分线相交所成的钝角的度数为()A.90°B.135°C.120°D.45°或135°5.如右图△ABC中,∠BAC=90°,AD⊥BC,AE平分∠BAC,∠B=2∠C,∠DAE的度数是()A.45°B.20°C.30°D.15°二.填空题6.若直角三角形的一个锐角为15°,则另一个锐角等于.7.如右图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=54°,∠2=24°,则∠B的度数为.8.在直角三角形中,两个锐角的度数比为2:3,那么较小锐角的度数是.9.如右图,在△ABC中,∠ACB=90°,AD平分∠CAB,交边BC于点D,过点D作DE⊥AB,垂足为E.若∠CAD=20°,则∠EDB的度数是.10.将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,则∠1+∠2=.三.解答题11.AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.12.解方程组:.参考答案一.选择题1.已知在Rt△ABC中,∠B=90°,∠C=35°,则∠A等于()A.35°B.45°C.55°D.65°【分析】根据直角三角形的两锐角互余计算即可.【解答】解:在Rt△ABC中,∠B=90°,∠C=35°,则∠A=90°﹣35°=55°,故选:C.【点评】本题考查的是直角三角形的性质,掌握直角三角形的两锐角互余是解题的关键.2.如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为()A.40°B.50°C.60°D.70°【分析】根据直角三角形的性质求出∠AEB的度数,根据对顶角相等求出∠DEC,根据直角三角形的两个锐角互余计算即可.【解答】解:∵AB⊥BD,∠A=40°,∴∠AEB=50°,∴∠DEC=50°,又AC⊥CD,∴∠D=40°,故选:A.【点评】本题考查的是直角三角形的性质,掌握直角三角形的两个锐角互余是解题的关键.3.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是()A.∠1+∠2=90°B.∠2=∠3C.∠1=∠4D.∠1=30°【分析】根据垂直得出∠ADC=∠BDC=90°,再根据直角三角形的性质逐个判断即可.【解答】解:A.∵∠ACB=90°,∴∠1+∠2=90°,故本选项不符合题意;B.∵CD⊥AB,∴∠ADC=90°,∴∠1+∠3=90°,∵∠1+∠2=90°,∴∠2=∠3,故本选项不符合题意;C.∵CD⊥AB,∴∠BDC=90°,∴∠2+∠4=90°,∵∠1+∠2=90°,∴∠1=∠4,故本选项不符合题意;D.根据已知条件不能推出∠1=30°,故本选项符合题意;故选:D.【点评】本题考查了垂直定义和直角三角形的性质,注意:直角三角形的两锐角互余.4.直角三角形两个锐角平分线相交所成的钝角的度数为()A.90°B.135°C.120°D.45°或135°【分析】本题可根据直角三角形内角的性质和三角形内角和为180°进行求解.【解答】解:如图:∵AE、BD是直角三角形中两锐角平分线,∴∠OAB+∠OBA=90°÷2=45°,两角平分线组成的角有两个:∠BOE与∠EOD这两个角互补,根据三角形外角和定理,∠BOE=∠OAB+∠OBA=45°,∴∠EOD=180°﹣45°=135°,故选:B.【点评】本题考查的是直角三角形的性质,熟知直角三角形的性质是解答此题的关键.5.△ABC中,∠BAC=90°,AD⊥BC,AE平分∠BAC,∠B=2∠C,∠DAE的度数是()A.45°B.20°C.30°D.15°【分析】根据三角形的内角和∠B=60°,根据角平分线的定义得出∠BAE=45°,根据直角三角形的两锐角互余得出∠BAD=30°,即可根据角的和差得解.【解答】解:∵∠BAC=90°,∠B=2∠C,∴∠B=60°,∵AD⊥BC,AE平分∠BAC,∴∠ADB=90°,∠BAE=∠BAC=45°,∴∠BAD=90°﹣60°=30°,∴∠DAE=45°﹣30°=15°.故选:D.【点评】此题考查了直角三角形的性质,熟记直角三角形的两锐角互余是解题的关键.二.填空题6.若直角三角形的一个锐角为15°,则另一个锐角等于75°.【分析】根据直角三角形的两锐角互余列式计算即可.【解答】解:∵直角三角形的一个锐角为15°,∴另一个锐角=90°﹣15°=75°,故答案为:75°.【点评】本题考查的是直角三角形的性质,掌握直角三角形的两锐角互余是解题的关键.7.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=54°,∠2=24°,则∠B的度数为60°.【分析】利用平行线的性质,三角形的外角的性质求出∠A即可解决问题.【解答】解:如图,∵a∥b,∴∠1=∠3=54°,∵∠3=∠2+∠A,∴∠A=54°﹣24°=30°,∵∠ACB=90°,∴∠B=90°﹣30°=60°,故答案为60°.【点评】本题考查平行线的性质,三角形的外角的性质,三角形的内角和定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.8.在直角三角形中,两个锐角的度数比为2:3,那么较小锐角的度数是36°.【分析】根据比例设两锐角分别为2k、3k,然后利用直角三角形两锐角互余列方程求解即可.【解答】解:设两锐角分别为2k、3k,由题意得2k+3k=90°,解得k=18°,所以较小锐角的度数为18×2=36°.故答案为:36°.【点评】本题考查了直角三角形的性质,解题时注意:在直角三角形中,两个锐角互余.9.如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交边BC于点D,过点D作DE⊥AB,垂足为E.若∠CAD=20°,则∠EDB的度数是40°.【分析】根据角平分线的定义得∠CAB=40°,由直角三角形的性质计算即可得解.【解答】解:∵AD平分∠CAB,∠CAD=20°,∴∠CAB=2∠CAD=40°,∵∠ACB=90°,∴∠B=90°﹣40°=50°,∵DE⊥AB,∴∠DEB=90°,∴∠EDB=90°﹣50°=40°,故答案为:40°.【点评】本题考查了角平分线的定义和直角三角形的性质,熟记性质是解题的关键.10.将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,则∠1+∠2=90°.【分析】如图,连接两交点,根据两直线平行,同旁内角互补和直角三角形两锐角互余的性质解答.【解答】解:如图,连接两交点,根据矩形两边平行,得∠1+∠2+∠3+∠4=180°,又矩形的角等于90°,∴∠3+∠4=90°,∴∠1+∠2=180°﹣90°=90°.故答案为:90.【点评】本题主要考查平行线的性质和直角三角形两锐角互余的性质.三.解答题11.AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.【分析】根据同角的余角相等求出∠BHD=∠C,从而得解.【解答】解:∵AD是△ABC的高,∴∠BHD+∠HBD=90°,∵BE是△ABC的高,∴∠HBD+∠C=90°,∴∠BHD=∠C,∵∠C=50°,∴∠BHD=50°.【点评】本题考查了直角三角形两锐角互余的性质,同角的余角相等的性质,熟记性质并准确识图是解题的关键.12.解方程组:.【分析】运用加减消元解答即可.【解答】解:,②﹣①得,4y=8,解得y=2,把y=2代入①得,x﹣2=1,解得x=3,故原方程组的解为.【点评】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.。
三角形内角和、外角定理(含详细解答)

三角形内角和、外角定理(含详细解答)-CAL-FENGHAI.-(YICAI)-Company One1三角形内角和、外角和定理一.选择题(共10小题)1.(2013?泉州)在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是()A .等边三角形B.锐角三角形C.直角三角形D.钝角三角形2.(2012?滨州)一个三角形三个内角的度数之比为2:3:7,这个三角形一定是()A .等腰三角形B.直角三角形C.锐角三角形D.钝角三角形3.(2012?河源)如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=()A .150°B.210°C.105°D.75°4.(2012?云南)如图,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为()A .40°B.45°C.50°D.55°5.(2012?南通)如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=()A .360°B.250°C.180°D.140°6.(2012?梧州)如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是()A .10°B.12°C.15°D.18°7.(2011?日照)如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为()A .70°B.80°C.90°D.100°8.(2011?台湾)如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下列何者正确()A .∠2=∠4+∠7B.∠3=∠1+∠6C.∠1+∠4+∠6=180°D.∠2+∠3+∠5=360°9.(2011?台湾)若△ABC中,2(∠A+∠C)=3∠B,则∠B的外角度数为何()A .36B.72C.108D.14410.(2011?台湾)若钝角三角形ABC中,∠A=27°,则下列何者不可能是∠B的度数()A .37B.57C.77D.97二.填空题(共4小题)11.(2014?抚顺)将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2= _________度.12.(2013?河池)如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是_________.13.(2008?安徽)如图,已知a∥b,∠1=70°,∠2=40°,则∠3=_________度.14.(2003?金华)如图,平面镜A与B之间夹角为120°,光线经过平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1=_________度.三.解答题(共16小题)15.(2014?六盘水)(1)三角形内角和等于_________.(2)请证明以上命题.16.(2001?海南)如图,在△ABC中,已知∠ABC=46°,∠ACB=80°,延长BC至D,使CD=CA,连接AD,求∠BAD的度数.17.(2000?内蒙古)如图,已知在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.18.(2011?青海)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线∴∴又∵∠ABC+∠ACB=180°﹣∠A∴∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系请说明理由.探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系(只写结论,不需证明)结论:_________.19.(2010?玉溪)平面内的两条直线有相交和平行两种位置关系(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图b,以上结论是否成立若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.20.(2013?响水县一模)探究与发现:探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.探究三:若将△ADC改为任意四边形ABCD呢已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:_________.21.已知:如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.22.如图,求∠A+∠B+∠C+∠D+∠E的度数和.23.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=63°,试求∠DAC,∠ADC的度数.24.已知:如图所示,∠ABC=66°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,求:∠ABE,∠ACF和∠BHC的度数.25.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠A=50°,∠C=60°,求∠DAC及∠BOA.26.如图,AF是△ABC的高,AD是△ABC的角平分线,∠B=36°,∠C=76°,求∠DAF的度数.27.一个零件的形状如图,按规定∠A=90°,∠C=25°,∠B=25°,检验已量得∠BDC=150°,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由.28.一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠C应分别是30°和20°,李叔叔量得∠BDC=142°,就判定这个零件不合格,你能说出其中的道理吗29.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.30.如图,在三角形ABC中,∠A=35°,求∠1+∠2+∠3+∠4的度数和.三角形内角和、外角和定理参考答案与试题解析一.选择题(共10小题)1.(2013?泉州)在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是()A .等边三角形B.锐角三角形C.直角三角形D.钝角三角形考点:三角形内角和定理.分析:根据三角形的内角和定理求出∠C,即可判定△ABC的形状.解答:解:∵∠A=20°,∠B=60°,∴∠C=180°﹣∠A﹣∠B=180°﹣20°﹣60°=100°,∴△ABC是钝角三角形.故选D.点评:本题考查了三角形的内角和定理,比较简单,求出∠C的度数是解题的关键.2.(2012?滨州)一个三角形三个内角的度数之比为2:3:7,这个三角形一定是()A .等腰三角形B.直角三角形C.锐角三角形D.钝角三角形考点:三角形内角和定理.专题:方程思想.分析:已知三角形三个内角的度数之比,根据三角形内角和定理,可求得三角的度数,由此判断三角形的类型.解答:解:三角形的三个角依次为180°×=30°,180°×=45°,180°×=105°,所以这个三角形是钝角三角形.故选:D.点评:本题考查三角形的分类,这个三角形最大角为180°×>90°.本题也可以利用方程思想来解答,即2x+3x+7x=180,解得x=15,所以最大角为7×15°=105°.3.(2012?河源)如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=()A .150°B.210°C.105°D.75°考点:三角形内角和定理;翻折变换(折叠问题).专题:压轴题.分析:先根据图形翻折变化的性质得出△ADE≌△A′DE,∠AED=∠A′ED,∠ADE=∠A′DE,再根据三角形内角和定理求出∠AED+∠ADE及∠A′ED+∠A′DE的度数,然后根据平角的性质即可求出答案.解答:解:∵△A′DE是△ABC翻折变换而成,∴∠AED=∠A′ED,∠ADE=∠A′DE,∠A=∠A′=75°,∴∠AED+∠ADE=∠A′ED+∠A′DE=180°﹣75°=105°,∴∠1+∠2=360°﹣2×105°=150°.故选A.点评:本题考查的是图形翻折变换的性质,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.4.(2012?云南)如图,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为()A .40°B.45°C.50°D.55°考点:三角形内角和定理.分析:首先利用三角形内角和定理求得∠BAC的度数,然后利用角平分线的性质求得∠CAD的度数即可.解答:解:∵∠B=67°,∠C=33°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣67°﹣33°=80°∵AD是△ABC的角平分线,∴∠CAD=∠BAC=×80°=40°故选A.点评:本题考查了三角形的内角和定理,属于基础题,比较简单.三角形内角和定理在小学已经接触过.5.(2012?南通)如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=()A .360°B.250°C.180°D.140°考点:三角形内角和定理;多边形内角与外角.分析:先利用三角形内角与外角的关系,得出∠1+∠2=∠C+(∠C+∠3+∠4),再根据三角形内角和定理即可得出结果.解答:解:∵∠1、∠2是△CDE的外角,∴∠1=∠4+∠C,∠2=∠3+∠C,即∠1+∠2=∠C+(∠C+∠3+∠4)=70°+180°=250°.故选B.点评:此题主要考查了三角形内角和定理及外角的性质,三角形内角和是180°;三角形的任一外角等于和它不相邻的两个内角之和.6.(2012?梧州)如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是()A .10°B.12°C.15°D.18°考点:三角形内角和定理;三角形的角平分线、中线和高.分析:根据直角三角形两锐角互余求出∠CAD,再根据角平分线定义求出∠CAE,然后根据∠DAE=∠CAE ﹣∠CAD,代入数据进行计算即可得解.解答:解:∵AD⊥BC,∠C=36°,∴∠CAD=90°﹣36°=54°,∵AE是△ABC的角平分线,∠BAC=128°,∴∠CAE=∠BAC=×128°=64°,∴∠DAE=∠CAE﹣∠CAD=64°﹣54°=10°.故选A.点评:本题考查了三角形的内角和定理,三角形的角平分线,高线的定义,准确识图,找出各角度之间的关系并求出度数是解题的关键.7.(2011?日照)如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为()A .70°B.80°C.90°D.100°考点:三角形内角和定理;平行线的性质.专题:计算题.分析:根据两直线平行,同旁内角互补,求得∠EFA=55°,再利用三角形内角和定理即可求得∠E的度数.解答:解:∵AB∥CD,∠C=125°,∴∠EFB=125°,∴∠EFA=180﹣125=55°,∵∠A=45°,∴∠E=180°﹣∠A﹣∠EFA=180°﹣45°﹣55°=80°.故选B.点评:本题应用的知识点为:两直线平行,同旁内角互补;三角形内角和定理.8.(2011?台湾)如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下列何者正确()A .∠2=∠4+∠7B.∠3=∠1+∠6C.∠1+∠4+∠6=180°D.∠2+∠3+∠5=360°考点:三角形内角和定理;对顶角、邻补角;三角形的外角性质.分析:根据对顶角的性质得出∠1=∠AOB,再用三角形内角和定理得出∠AOB+∠4+∠6=180°,即可得出答案.解答:解:∵四条互相不平行的直线L1、L2、L3、L4所截出的七个角,∵∠1=∠AOB,∵∠AOB+∠4+∠6=180°,∴∠1+∠4+∠6=180°.故选C.点评:此题主要考查了对顶角的性质以及三角形的内角和定理,正确的应用三角形内角和定理是解决问题的关键.9.(2011?台湾)若△ABC中,2(∠A+∠C)=3∠B,则∠B的外角度数为何()A .36B.72C.108D.144考点:三角形内角和定理;解二元一次方程组;对顶角、邻补角.专题:计算题.分析:由∠A+∠B+∠C=180°,得到2(∠A+∠C)+2∠B=360°,求出∠B=72°,根据∠B的外角度数=180°﹣∠B即可求出答案.解答:解:∵∠A+∠B+∠C=180°,∴2(∠A+∠B+∠C)=360°,∵2(∠A+∠C)=3∠B,∴∠B=72°,∴∠B的外角度数是180°﹣∠B=108°,故选C.点评:本题主要考查对二元一次方程组,三角形的内角和定理,邻补角等知识点的理解和掌握,能根据三角形的内角和定理求出∠B的度数是解此题的关键.10.(2011?台湾)若钝角三角形ABC中,∠A=27°,则下列何者不可能是∠B的度数()A .37B.57C.77D.97考点:三角形内角和定理.专题:推理填空题.分析:根据钝角三角形有一内角大于90°且三角形内角和为180°,①∠C>90°,②∠B>90°,分类讨论解答.解答:解:∵钝角三角形△ABC中,∠A=27°,∴∠B+∠C=180°﹣27°=153°,又∵△ABC为钝角三角形,有两种可能情形如下:①∠C>90°,∴∠B<153°﹣90°=63°,∴选项A、B合理;②∠B>90°,∴选项D合理,∴∠B不可能为77°.故选C.点评:本题考查了钝角三角形的定义及三角形的内角和定理,体现了分类讨论思想.二.填空题(共4小题)11.(2014?抚顺)将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2=70度.考点:三角形内角和定理;多边形内角与外角.专题:几何图形问题.分析:分别根据正三角形、正四边形、正五边形各内角的度数及平角的定义进行解答即可.解答:解:∵∠3=32°,正三角形的内角是60°,正四边形的内角是90°,正五边形的内角是108°,∴∠4=180°﹣60°﹣32°=88°,∴∠5+∠6=180°﹣88°=92°,∴∠5=180°﹣∠2﹣108° ①,∠6=180°﹣90°﹣∠1=90°﹣∠1 ②,∴①+②得,180°﹣∠2﹣108°+90°﹣∠1=92°,即∠1+∠2=70°.故答案为:70°.点评:本题考查的是三角形内角和定理,熟知正三角形、正四边形、正五边形各内角的度数是解答此题的关键.12.(2013?河池)如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是56°.考点:三角形内角和定理.分析:先根据三角形内角和定理求出∠1+∠2的度数,再根据角平分线的定义求出∠ABC+∠ACB的度数,由三角形内角和定理即可得出结论.解答:解:∵△BOC中,∠BOC=118°,∴∠1+∠2=180°﹣118°=62°.∵BO和CO是△ABC的角平分线,∴∠ABC+∠ACB=2(∠1+∠2)=2×62°=124°,在△ABC中,∵∠ABC+∠ACB=124°,∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣124°=56°.故答案为:56°.点评:本题考查的是角平分线的定义,三角形内角和定理,即三角形的内角和是180°.13.(2008?安徽)如图,已知a∥b,∠1=70°,∠2=40°,则∠3=70度.考点:三角形内角和定理;平行线的性质.专题:计算题.分析:把∠2,∠3转化为△ABC中的角后,利用三角形内角和定理求解.解答:解:由对顶角相等可得∠ACB=∠2=40°,在△ABC中,由三角形内角和知∠ABC=180°﹣∠1﹣∠ACB=70°.又a∥b,∴∠3=∠ABC=70°.点评:本题考查了平行线与三角形的相关知识.14.(2003?金华)如图,平面镜A与B之间夹角为120°,光线经过平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1=30度.考点:三角形内角和定理;角平分线的定义.专题:压轴题.分析:因为入射角等于反射角,所以∠1=∠2=(180°﹣120°)÷2.解答:解:如图所示,作出入射光线的法线,根据“入射角等于反射角”可知∠1=∠3,∠2=∠4,∵∠1=∠2,∠AOB=120°,∴1=∠2=(180°﹣120°)÷2=30°.故答案为:30°.点评:此题由题意得出“入射角等于反射角”是关键.三.解答题(共16小题)15.(2014?六盘水)(1)三角形内角和等于180°.(2)请证明以上命题.考点:三角形内角和定理;平行线的性质.专题:证明题.分析:(1)直接根据三角形内角和定理得出结论即可;(2)画出△ABC,过点C作CF∥AB,再根据平行线的性质得出∠2=∠A,∠B+∠BCF=180°,再通过等量代换即可得出结论.解答:解:(1)三角形内角和等于180°.故答案为:180°;(2)已知:如图所示的△ABC,求证:∠A+∠B+∠C=180°.证明:过点C作CF∥AB,∵CF∥AB,∴∠2=∠A,∠B+∠BCF=180°,∵∠1+∠2=∠BCF,∴∠B+∠1+∠2=180°,∴∠B+∠1+∠A=180°,即三角形内角和等于180°.点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.16.(2001?海南)如图,在△ABC中,已知∠ABC=46°,∠ACB=80°,延长BC至D,使CD=CA,连接AD,求∠BAD的度数.考点:三角形内角和定理;三角形的外角性质;等腰三角形的性质.分析:要求∠BAD的度数,只要求出∠C的度数就行了,根据三角形内角和为180°,求出∠BAD的度数,根据三角形内角和外角关系及等腰三角形性质,易求∠C的度数.解答:解:∵∠ACB=80°∴∠ACD=180°﹣∠ACB=180°﹣80°=100°又∵CD=CA∴∠CAD=∠D∵∠ACD+∠CAD+∠D=180°∴∠CAD=∠D=40°在△ABC内∴∠BAD=180°﹣∠ABC﹣∠D=180°﹣46°﹣40°=94°.点评:此题主要考三角形内角与外角的关系及等腰三角形的性质;找出角之间的关系利用内角和求解是正确解答本题的关键.17.(2000?内蒙古)如图,已知在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.考点:三角形内角和定理.专题:数形结合.分析:根据三角形的内角和定理与∠C=∠ABC=2∠A,即可求得△ABC三个内角的度数,再根据直角三角形的两个锐角互余求得∠DBC的度数.解答:解:∵∠C=∠ABC=2∠A,∴∠C+∠ABC+∠A=5∠A=180°,∴∠A=36°.则∠C=∠ABC=2∠A=72°.又BD是AC边上的高,则∠DBC=90°﹣∠C=18°.点评:此题主要是三角形内角和定理的运用.三角形的内角和是180°.18.(2011?青海)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线∴∴又∵∠ABC+∠ACB=180°﹣∠A∴∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系请说明理由.探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系(只写结论,不需证明)结论:∠BOC=90°﹣∠A.考点:三角形的外角性质;三角形内角和定理.专题:压轴题.分析:(1)根据提供的信息,根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠O与∠1表示出∠2,然后整理即可得到∠BOC与∠A的关系;(2)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB,然后再根据三角形的内角和定理列式整理即可得解.解答:解:(1)探究2结论:∠BOC=∠A,理由如下:∵BO和CO分别是∠ABC和∠ACD的角平分线,∴∠1=∠ABC,∠2=∠ACD,又∵∠ACD是△ABC的一外角,∴∠ACD=∠A+∠ABC,∴∠2=(∠A+∠ABC)=∠A+∠1,∵∠2是△BOC的一外角,∴∠BOC=∠2﹣∠1=∠A+∠1﹣∠1=∠A;(2)探究3:∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),∠BOC=180°﹣∠0BC﹣∠OCB,=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),=180°﹣∠A﹣(∠A+∠ABC+∠ACB),结论∠BOC=90°﹣∠A.点评:本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键,读懂题目提供的信息,然后利用提供信息的思路也很重要.19.(2010?玉溪)平面内的两条直线有相交和平行两种位置关系(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图b,以上结论是否成立若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.考点:三角形的外角性质;平行线的性质;三角形内角和定理.专题:综合题;压轴题.分析:(1)延长BP交CD于E,根据两直线平行,内错角相等,求出∠PED=∠B,再利用三角形的一个外角等于和它不相邻的两个内角的和即可说明不成立,应为∠BPD=∠B+∠D;(2)作射线QP,根据三角形的外角性质可得;(3)根据三角形的外角性质,把角转化到四边形中再求解.解答:解:(1)不成立.结论是∠BPD=∠B+∠D延长BP交CD于点E,∵AB∥CD∴∠B=∠BED又∵∠BPD=∠BED+∠D,∴∠BPD=∠B+∠D.(2)结论:∠BPD=∠BQD+∠B+∠D.(3)连接EG并延长,根据三角形的外角性质,∠AGB=∠A+∠B+∠E,又∵∠AGB=∠CGF,在四边形CDFG中,∠CGF+∠C+∠D+∠F=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.点评:本题是信息给予题,利用平行线的性质和三角形的一个外角等于和它不相邻的两个内角的和解答.20.(2013?响水县一模)探究与发现:探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.探究三:若将△ADC改为任意四边形ABCD呢已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:∠P=(∠A+∠B+∠E+∠F)﹣180°.考点:三角形的外角性质;三角形内角和定理.专题:探究型.分析:探究一:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和定理整理即可得解;探究二:根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据三角形内角和定理列式整理即可得解;探究三:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;探究四:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.解答:解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;探究二:∵DP、CP分别平分∠ADC和∠ACD,∴∠PDC=∠ADC,∠PCD=∠ACD,∴∠DPC=180°﹣∠PDC﹣∠PCD,=180°﹣∠ADC﹣∠ACD,=180°﹣(∠ADC+∠ACD),=180°﹣(180°﹣∠A),=90°+∠A;探究三:∵DP、CP分别平分∠ADC和∠BCD,∴∠PDC=∠ADC,∠PCD=∠BCD,∴∠DPC=180°﹣∠PDC﹣∠PCD,=180°﹣∠ADC﹣∠BCD,=180°﹣(∠ADC+∠BCD),=180°﹣(360°﹣∠A﹣∠B),=(∠A+∠B);探究四:六边形ABCDEF的内角和为:(6﹣2)180°=720°,∵DP、CP分别平分∠ADC和∠ACD,∴∠P=∠ADC,∠PCD=∠ACD,∴∠P=180°﹣∠PDC﹣∠PCD,=180°﹣∠ADC﹣∠ACD,=180°﹣(∠ADC+∠ACD),=180°﹣(720°﹣∠A﹣∠B﹣∠E﹣∠F),=(∠A+∠B+∠E+∠F)﹣180°,即∠P=(∠A+∠B+∠E+∠F)﹣180°.点评:本题考查了三角形的外角性质,三角形的内角和定理,多边形的内角和公式,此类题目根据同一个解答思路求解是解题的关键.21.已知:如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.考点:三角形的外角性质;三角形内角和定理.分析:根据三角形的内角和定理和三角形的外角性质即可解决.解答:解:∵∠BAC=120°,∴∠2+∠3=60°①∵∠1=∠2,∴∠4=∠3=∠1+∠2=2∠2②把②代入①得:3∠2=60°,∠2=20°.∴∠DAC=120°﹣20°=100°.点评:注意三角形的内角和定理以及推论的运用,还要注意角之间的等量代换.22.如图,求∠A+∠B+∠C+∠D+∠E的度数和.考点:三角形的外角性质;三角形内角和定理.分析:由三角形的一个外角等于与它不相邻的两个内角的和,得∠4=∠A+∠2,∠2=∠D+∠C,进而利用三角形的内角和定理求解.解答:解:如图可知:∵∠4是三角形的外角,∴∠4=∠A+∠2,同理∠2也是三角形的外角,∴∠2=∠D+∠C,在△BEG中,∠B+∠E+∠4=180°,即∠B+∠E+∠A+∠D+∠C=180°.点评:本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.23.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=63°,试求∠DAC,∠ADC的度数.考点:三角形的外角性质;三角形内角和定理.分析:由三角形的内角和是180°,和三角形的一个外角等于与它不相邻的两个内角的和,可求∠1=39°,∠3=78°,所以∠DAC=24°,∠ADC=∠3=78°.解答:解:∵∠1=∠2,∴∠3=∠1+∠2=2∠1=∠4,∴2∠3+∠CAD=2∠1+2∠2+∠BAC﹣∠1=4∠1+63°﹣∠1=3∠1+63°=180°,∴∠1=39°=∠2,∠3=∠4=78°,∴∠DAC=63°﹣∠1=63°﹣39°=24°,∠ADC=∠3=78°.点评:本题考查三角形外角的性质及三角形的内角和定理.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;以及三角形的一个外角等于与它不相邻的两个内角的和.24.已知:如图所示,∠ABC=66°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,求:∠ABE,∠ACF和∠BHC的度数.考点:三角形的外角性质;三角形内角和定理.分析:由三角形的内角和是180°,可求∠A=60°.又因为BE是AC边上的高,所以∠AEB=90°,所以∠ABE=30°.同理,∠ACF=30度,又因为∠BHC是△CEH的一个外角,所以∠BHC=120°.解答:解:∵∠ABC=66°,∠ACB=54°,∴∠A=180°﹣∠ABC﹣∠ACB=180°﹣66°﹣54°=60°.又∵BE是AC边上的高,所以∠AEB=90°,∴∠ABE=180°﹣∠BAC﹣∠AEB=180°﹣90°﹣60°=30°.同理,∠ACF=30°,∴∠BHC=∠BEC+∠ACF=90°+30°=120°.点评:本题考查三角形外角的性质及三角形的内角和定理,求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;三角形的外角通常情况下是转化为内角来解决.25.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠A=50°,∠C=60°,求∠DAC及∠BOA.考点:三角形的外角性质;三角形内角和定理.专题:计算题.分析:先利用三角形内角和定理可求∠ABC,在直角三角形ACD中,易求∠DAC;再根据角平分线定义可求∠CBF、∠EAF,然后利用三角形外角性质,可先求∠AFB,再次利用三角形外角性质,容易求出∠BOA.解答:解:∵∠A=50°,∠C=60°∴∠ABC=180°﹣50°﹣60°=70°,又∵AD是高,∴∠ADC=90°,∴∠DAC=180°﹣90°﹣∠C=30°,∵AE、BF是角平分线,∴∠CBF=∠ABF=35°,∠EAF=25°∴∠AFB=∠C+∠CBF=60°+35°=95°,∴∠BOA=∠EAF+∠AFB=25°+95°=120°,∴∠DAC=30°,∠BOA=120°.点评:本题考查了三角形内角和定理、角平分线定义、三角形外角性质.关键是利用角平分线的性质解出∠EAF、∠CBF,再运用三角形外角性质求出∠AFB.26.如图,AF是△ABC的高,AD是△ABC的角平分线,∠B=36°,∠C=76°,求∠DAF的度数.考点:三角形的外角性质;角平分线的定义;三角形内角和定理.分析:在△ADF中,由三角形的外角性质知:∠ADF=∠B+∠BAC,所以∠B+∠BAC+∠FAD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠DAF,∠B,∠C的关系,再代值求解即可.解答:解:由三角形的外角性质知:∠ADF=∠B+∠BAC,故∠B+∠BAC+∠DAF=90°;①△ABC中,由三角形内角和定理得:∠C+∠B+∠BAC=180°,即:∠C+∠B+∠BAC=90°,②②﹣①,得:∠DAF=(∠C﹣∠B)=20°.点评:此题主要考查了三角形的外角性质、角平分线的性质以及三角形内角和定理等知识,熟记此题的结论在解选择和填空题时会加快解题效率.27.一个零件的形状如图,按规定∠A=90°,∠C=25°,∠B=25°,检验已量得∠BDC=150°,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由.考点:三角形的外角性质.分析:根据三角形外角的性质求出∠BDC的度数,与测量所得的度数对比即可得出结论.解答:解:如图,∠CDE是△ADC的外角,∠BDE是△ABD的外角,∵∠CDE=∠C+∠CAD,∠BDE=∠B+∠DAB,∴∠BDC=∠CDE+∠BDE=∠C+∠CAD+∠B+∠DAB,即∠BDC=∠B+∠C+∠A=25°+25°+90°=140°.检验已量得∠BDC=150°,就判断这个零件不合格.点评:考查了三角形的外角性质,三角形的外角等于和它不相邻的两个内角的和.28.一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠C应分别是30°和20°,李叔叔量得∠BDC=142°,就判定这个零件不合格,你能说出其中的道理吗考点:三角形的外角性质.分析:连接AD并延长,根据三角形的一个外角等于和它不相邻的两个内角的和求出∠1=∠B+∠BAD,∠2=∠C+∠CAD,然后求出∠1+∠2的度数,根据零件规定数据,只有140°才是合格产品.解答:解:如图,连接AD并延长,∴∠1=∠B+∠BAD,∠2=∠C+∠CAD,∵∠A=90°,∠B=30°,∠C=20°,∴∠BDC=∠1+∠2,=∠B+∠BAD+∠DAC+∠C,=∠B+∠BAC+∠C,=30°+90°+20°,=140°,∵140°≠142°,∴这个零件不合格.点评:本题主要利用三角形的一个外角等于和它不相邻的两个内角的和的性质,熟练掌握性质是解题的关键.29.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.考点:三角形的外角性质;三角形内角和定理.分析:连接BE,由三角形内角和外角的关系可知∠C+∠D=∠CBE+∠DEB,由四边形内角和是360°,即可求∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.解答:解:如图连接BE.∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,∴∠C+∠D=∠CBE+∠DEB,∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F=∠A+∠ABE+∠BEF+∠F.又∵∠A+∠ABE+∠BEF+∠F=360°,∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.点评:本题考查的是三角形内角与外角的关系,涉及到四边形及三角形内角和定理,比较简单.30.如图,在三角形ABC中,∠A=35°,求∠1+∠2+∠3+∠4的度数和.考点:三角形的外角性质;三角形内角和定理.分析:根据三角形的内角和是180°,可分别求出∠1+∠2=∠3+∠4=145°,即可求出∠1+∠2+∠3+∠4的度数和.解答:解:∵∠A=35°,在△ABC中,∠A+∠1+∠2=180°,∴∠1+∠2=180°﹣∠A=145°,同理可证∠3+∠4=145°,∴∠1+∠2+∠3+∠4=290°.点评:本题考查了三角形的内角和定理,求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.。
平行线与三角形 试题及答案

平行线与三角形一、单选题1.如图(1),在//AB CD 中,40AEC ∠=︒,CB 平分DCE ∠,则ABC ∠的度数为()A .10︒B .20︒C .30°D .40︒2.如图(2),将直角三角板放置在矩形纸片上,若148∠=︒,则2∠的度数为()A .42°B .48°C .52°D .60°3.七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为4的正方形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”(即阴影部分)的面积为()A .3B .72C .2D .524.下列命题是真命题的是()A .五边形的内角和是720︒B .三角形的任意两边之和大于第三边C .内错角相等D .三角形的重心是这个三角形的三条角平分线的交点5.两个直角三角板如图(5)摆放,其中90BAC EDF ∠=∠=︒,45E ∠=︒,30C ∠=︒,AB 与DF 交于点M .若//BC EF ,则BMD ∠的大小为()(1)A .60︒B .67.5︒C .75︒D .82.5︒6.某同学的作业如下框,其中※处填的依据是()如图,已知直线1234,,,l l l l .若12∠=∠,则34∠=∠.请完成下面的说理过程.解:已知12∠=∠,根据(内错角相等,两直线平行),得12//l l .再根据(※),得34∠=∠.A .两直线平行,内错角相等B .内错角相等,两直线平行C .两直线平行,同位角相等D .两直线平行,同旁内角互补7.如图(7),直线c 与直线a 、b 都相交.若//a b ,155∠=︒,则2∠=()A .60︒B .55︒C .50︒D .45︒8.如图(8),AB ∥CD ∥EF ,若∠ABC =130°,∠BCE =55°,则∠CEF 的度数为()A .95°B .105°C .110°D .115°9.如图(9),直线//m n ,三角尺的直角顶点在直线m 上,且三角尺的直角被直线m 平分,若160∠=︒,则下列结论错误的是()A .275∠=︒B .345∠=︒C .4105∠=︒D .5130∠=︒10.如图(10),已知直线//,140,230m n ∠=︒∠=︒,则3∠的度数为()A .80︒B .70︒C .60︒D .50︒11.如图(11),在ABC 中,90ACB ∠=︒,4AC BC ==,点D 是BC 边的中点,点P 是AC 边上一个动点,连接PD ,以PD 为边在PD 的下方作等边三角形PDQ ,连接CQ .则CQ 的最小值是()A .2B .1C D .3212.定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图(12),ACD ∠是ABC 的外角.求证:ACD A B ∠=∠+∠.下列说法正确的是()A .证法1还需证明其他形状的三角形,该定理的证明才完整B .证法1用严谨的推理证明了该定理C .证法2用特殊到一般法证明了该定理D .证法2只要测量够一百个三角形进行验证,就能证明该定理13.如图(13),ABC 中,90,8,6ACB AC BC ∠=︒==,将ADE 沿DE 翻折,使点A 与点B 重合,则CE 的长为()A .198B .2C .254D .7414.如图(14),点D 、E 分别在线段BC 、AC 上,连接AD 、BE .若35A ∠=︒,25B ∠=︒,50C ∠=︒,则1∠的大小为()A .60°B .70°C .75°D .85°15.在ABC 中,90ACB ∠=︒,分别过点B ,C 作BAC ∠平分线的垂线,垂足分别为点D ,E ,BC 的中点是M ,连接CD ,MD ,ME .则下列结论错误的是()A .2CD ME=B .//ME ABC .BD CD=D .ME MD=16.如图(16),在ABC 和DCB 中,ACB DBC ∠=∠,添加一个条件,不能..证明ABC 和DCB 全等的是()A .ABC DCB∠=∠B .AB DC=C .AC DB=D .A D∠=∠17.如图(17),在Rt ABC △纸片中,90,4,3ACB AC BC ∠=︒==,点,D E 分别在,AB AC 上,连结DE ,将ADE 沿DE 翻折,使点A 的对应点F 落在BC 的延长线上,若FD 平分EFB ∠,则AD 的长为()A .259B .258C .157D .20718.如图(18),()8,0A ,()2,0C -,以点A 为圆心,AC 长为半径画弧,交y 轴正半轴于点B ,则点B 的坐标为()A .()0,5B .()5,0C .()6,0D .()0,6(16)(17)19.如图(19),点B ,F ,C ,E 共线,∠B =∠E ,BF =EC,添加一个条件,不等判断△ABC ≌△DEF 的是()A .AB =DEB .∠A =∠DC .AC =DFD .AC ∥FD20.如图(20),在44⨯的正方形网格中有两个格点A 、B ,连接AB ,在网格中再找一个格点C ,使得ABC 是等腰直角....三角形,满足条件的格点C 的个数是()A .2B .3C .4D .521.如图(21),在ABC 中,45,60,B C AD BC ∠=︒∠=︒⊥于点D ,3BD =.若E ,F 分别为AB ,BC 的中点,则EF 的长为()A .33B .32C .1D .6222.如图(22),在四边形ABCD 中,∠A=90°,AD=3,BC=5,对角线BD 平分∠ABC ,则△BCD 的面积为()A .7.5B .8C .15D .无法确定23.如图(23)所示,直线EF //GH ,射线AC 分别交直线EF 、GH 于点B 和点C ,AD ⊥EF 于点D ,如果∠A =20°,则∠ACG =()A .160°B .110°C .100°D .70°(18)(19)(20)(21)(22)24.如图(24),直线a ,b 被直线c 所截,则∠1与∠2的位置关系是()A .同位角B .内错角C .同旁内角D .邻补角25.将一副三角尺如图(25)摆放,点E 在AC 上,点D 在BC 的延长线上,//,90,45,60EF BC B EDF A F ∠=∠=︒∠=︒∠=︒,则CED ∠的度数是()A .15°B .20°C .25°D .30°26.有两个直角三角形纸板,一个含45°角,另一个含30°角,如图①所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A 顺时针旋转,使BC ∥DE ,如图②所示,则旋转角∠BAD 的度数为()A .15°B .30°C .45°D .60°27.如图(27),在ABC 中,AB =AC ,分别以点A 、B 为圆心,以适当的长为半径作弧,两弧分别交于E ,F ,作直线EF ,D 为BC 的中点,M 为直线EF 上任意一点.若BC =4,ABC 面积为10,则BM +MD 长度的最小值为()A .52B .3C .4D .5(23)(24)(25)(27)28.如图(28),ABC 中,90,40ACB ABC ︒︒∠=∠=.将ABC 绕点B 逆时针旋转得到A BC ''△,使点C 的对应点C '恰好落在边AB 上,则CAA '∠的度数是()A .50︒B .70︒C .110︒D .120︒29.如图(29),在△ABC 中,AB =2,∠ABC =60°,∠ACB =45°,D 是BC 的中点,直线l 经过点D ,AE ⊥l ,BF ⊥l ,垂足分别为E ,F ,则AE +BF 的最大值为()A 6B .2C .3D .230.如图(30),在四边形ABCD 中,//AD BC ,90D ∠= ,8AD =,6BC =,分别以点A ,C 为圆心,大于12AC 长为半径作弧,两弧交于点E ,作射线BE 交AD 于点F ,交AC 于点O .若点O 是AC 的中点,则CD 的长为()A .42B .6C .210D .831.如图(31),在一个宽度为AB 长的小巷内,一个梯子的长为a ,梯子的底端位于AB 上的点P ,将该梯子的顶端放于巷子一侧墙上的点C 处,点C 到AB 的距离BC 为b ,梯子的倾斜角BPC ∠为45︒;将该梯子的顶端放于另一侧墙上的点D 处,点D 到AB 的距离AD 为c ,且此时梯子的倾斜角APD ∠为75︒,则AB 的长等于()(28)(29)(30)(31)(33)A .aB .bC .2bc +D .c32.等腰三角形的一个内角为70°,则另外两个内角的度数分别是()A .55°,55°B .70°,40°或70°,55°C .70°,40°D .55°,55°或70°,40°33.如图(33),已知ABC 和ADE 都是等腰三角形,90BAC DAE ∠=∠=︒,,BD CE 交于点F ,连接AF ,下列结论:①BD CE =;②BF CF ⊥;③AF 平分CAD ∠;④45AFE ∠=︒.其中正确结论的个数有()A .1个B .2个C .3个D .4个34.如图(34),,ABC ECD ∆∆都是等边三角形,且B ,C ,D 在一条直线上,连结,BE AD ,点M ,N 分别是线段BE ,AD 上的两点,且11,33BM BE AN AD ==,则CMN ∆的形状是()A .等腰三角形B .直角三角形C .等边三角形D .不等边三角形35.如图(35)所示的网格由边长相同的小正方形组成,点A 、B 、C 、D 、E 、F 、G 在小正方形的顶点上,则ABC ∆的重心是()A .点DB .点EC .点FD .点G36.如图(36),在CEF △中,80E ∠=︒,50F ∠=︒,AB CF ,AD CE ,连接BC ,CD ,则A ∠的度数是()A .45°B .50°C .55°D .80°二、填空题(34)(35)(36)37.由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图(37),三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分).则图中AB的长应是______.38.下图(38)是可调躺椅示意图(数据如图),AE与BD的交点为C,且A∠,BÐ,E∠保持不变.为了舒适,需调整D∠的大小,使110EFD∠=︒,则图中D∠应___________(填“增加”或“减少”)___________度.39.如图(39),AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是_____.40.如图(40),在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D和点E,AD与CE交于点O,连接BO 并延长交AC于点F,若AB=5,BC=4,AC=6,则CE:AD:BF值为____________.41.如图(41),在四边形ABCD中,AB BC BD==.设ABCα∠=,则ADC∠=______(用含α的代数式表示).42.如图(42),BE是ABC的中线,点F在BE上,延长AF交BC于点D.若3BF FE=,则BDDC=______.(37)(38)(39)(40)(41)43.如图(43),在ABC 中,AB AC =,70B ∠=︒,以点C 为圆心,CA 长为半径作弧,交直线BC 于点P ,连结AP ,则BAP ∠的度数是_______.44.如图(44),将三角形纸片ABC 折叠,使点B 、C 都与点A 重合,折痕分别为DE 、FG .已知15ACB ∠=︒,AE EF =,DE =,则BC 的长为_______.45.如图(45),在△ABC 中,AB =5,AC =7,直线DE 垂直平分BC ,垂足为E ,交AC 于点D ,则△ABD 的周长是_____.46.《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AB 生长在它的中央,高出水面部分BC 为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B 恰好碰到岸边的B '(示意图如图(46),则水深为__尺.47.如图(47),四边形ABCD 中,AB ∥CD ,∠ABC =60°,AD =BC =CD =4,点M 是四边形ABCD 内的一个动点,满足∠AMD =90°,则点M 到直线BC 的距离的最小值为_____.48.如图(48),在ABC 中,5,8,9===AB AC BC ,以A 为圆心,以适当的长为半径作弧,交AB(42)(44)(45)(46)(47)(48)(43)于点M ,交AC 于点N ,分别以,M N 为圆心,以大于12MN 的长为半径作弧,两弧在BAC ∠的内部相交于点G ,作射线AG ,交BC 于点D ,点F 在AC 边上,AFAB =,连接DF ,则CDF 的周长为___________.49.如图(49),在ABC 中,9,4BC AC ==,分别以点A B 、为圆心,大于12AB 的长为半径画弧,两弧相交于点,M N 、作直线MN ,交BC 边于点D ,连接AD ,则ACD △的周长为________.50.如图(50),△ABC 为等边三角形,边长为6,AD ⊥BC ,垂足为点D ,点E 和点F 分别是线段AD 和AB 上的两个动点,连接CE ,EF ,则CE +EF 的最小值为_____.51.如图(51),在ABC 中,84C ∠=︒,分别以点A 、B 为圆心,以大于12AB 的长为半径画弧,两弧分别交于点M 、N ,作直线MN 交AC 点D ;以点B 为圆心,适当长为半径画弧,分别交BA 、BC 于点E 、F ,再分别以点E 、F 为圆心,大于12EF 的长为半径画弧,两弧交于点P ,作射线BP ,此时射线BP 恰好经过点D ,则A ∠=_____度.52.由4个直角边长分别为a ,b 的直角三角形围成的“赵爽弦图”如图(52)所示,根据大正方形的面积2c 等于小正方形的面积2()a b -与4个直角三角形的面积2ab 的和证明了勾股定理222+=a b c ,还可以用来证明结论:若0a >、0b >且22a b +为定值,则当a _______b 时,ab 取得最大值.53.如图(53),在ABC 中,90,ACB AC BC ∠=︒=,点P 在斜边AB 上,以PC 为直角边作等腰直角三角形PCQ ,90PCQ ∠=︒,则222,,PA PB PC 三者之间的数量关系是_____.54.如图(54),D 是等边三角形ABC 外一点.若8,6BD CD ==,连接AD ,则AD 的最大值与最小值(49)(50)(51)(53)的差为_____.55.勘测队按实际需要构建了平面直角坐标系,并标示了A ,B ,C 三地的坐标,数据如图(55)(单位:km ).笔直铁路经过A ,B 两地.(1)A ,B 间的距离为______km ;(2)计划修一条从C 到铁路AB 的最短公路l ,并在l 上建一个维修站D ,使D 到A ,C 的距离相等,则C ,D 间的距离为______km .三、解答题56.如图(56),//AB CD ,B D ∠=∠,直线EF 与AD ,BC 的延长线分别交于点E ,F .求证:DEF F ∠=∠.57.如图(57),BE 是ABC 的角平分线,在AB 上取点D ,使DB DE =.(1)求证://DE BC .(2)若65A ∠=︒,45AED ∠=︒,求EBC ∠的度数.58.如图(58),90BAC ∠=︒,AD 是BAC ∠内部一条射线,若AB AC =,BE AD ⊥于点E ,CF AD ⊥于点F .求证:AF BE =.(54)(55)(56)(57)59.如图(59),在ABC 中,40A ∠=︒,点D ,E 分別在边AB ,AC 上,BD BC CE ==,连结CD ,BE .(1)若80ABC ∠=︒,求BDC ∠,ABE ∠的度数.(2)写出BEC ∠与BDC ∠之间的关系,并说明理由.60.如图(60),//BD AC ,BD BC =,点E 在BC 上,且BE AC =.求证:D ABC ∠=∠.61.如图(61),点A 、B 、D 、E 在同一条直线上,,//,//AB DE AC DF BC EF =.求证:ABC DEF △≌△.(58)(59)(60)62.已知在ACD △中,Р是CD 的中点,B 是AD 延长线上的一点,连结,BC AP .(1)如图1,若90,60,,ACB CAD BD AC AP ︒∠=︒∠===BC 的长.(2)过点D 作//DE AC ,交AP 延长线于点E ,如图2所示.若60,CAD BD AC ∠︒==,求证:2BC AP =.(3)如图3,若45CAD ∠=︒,是否存在实数m ,当BD mAC =时,2BC AP =?若存在,请直接写出m的值;若不存在,请说明理由.63.如图(63),AC 是四边形ABCD 的对角线,∠1=∠B ,点E 、F 分别在AB 、BC 上,BE =CD ,BF =CA ,连接EF .(1)求证:∠D =∠2;(2)若EF ∥AC ,∠D =78°,求∠BAC的度数.64.阅读与思考(61)(63)下面是小宇同学的数学日记,请仔细阅读并完成相应的任务.×年×月×日星期日没有直角尺也能作出直角今天,我在书店一本书上看到下面材料:木工师傅有一块如图①所示的四边形木板,他已经在木板上画出一条裁割线AB ,现根据木板的情况,要过AB 上的一点C ,作出AB 的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢?办法一:如图①,可利用一把有刻度的直尺在AB 上量出30CD cm =,然后分别以D ,C 为圆心,以50cm 与40cm 为半径画圆弧,两弧相交于点E ,作直线CE ,则DCE ∠必为90︒.办法二:如图②,可以取一根笔直的木棒,用铅笔在木棒上点出M ,N 两点,然后把木棒斜放在木板上,使点M 与点C 重合,用铅笔在木板上将点N 对应的位置标记为点Q ,保持点N 不动,将木棒绕点N 旋转,使点M 落在AB 上,在木板上将点M 对应的位置标记为点R .然后将RQ 延长,在延长线上截取线段QS MN =,得到点S ,作直线SC ,则90RCS ∠=︒.我有如下思考:以上两种办法依据的是什么数学原理呢?我还有什么办法不用直角尺也能作出垂线呢?……任务:(1)填空;“办法一”依据的一个数学定理是_____________________________________;(2)根据“办法二”的操作过程,证明90RCS ∠=︒;(3)①尺规作图:请在图③的木板上,过点C 作出AB 的垂线(在木板上保留作图痕迹,不写作法);②说明你的作法依据的数学定理或基本事实(写出一个即可)65.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射,如图(65),水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知20,45HFB FED∠=︒∠=︒,求GFH∠的度数.66.已知D是Rt△ABC斜边AB的中点,∠ACB=90°,∠ABC=30°,过点D作Rt△DEF使∠DEF=90°,∠DFE=30°,连接CE并延长CE到P,使EP=CE,连接BE,FP,BP,设BC与DE交于M,PB与EF 交于N.(1)如图1,当D,B,F共线时,求证:①EB=EP;②∠EFP=30°;(2)如图2,当D,B,F不共线时,连接BF,求证:∠BFD+∠EFP=30°.(65)67.已知AOB 和MON △都是等腰直角三角形22OM ON ⎛⎫<< ⎪⎝⎭,90AOB MON ︒∠=∠=.(1)如图1:连,AM BN ,求证:AOM BON ≌;(2)若将MON △绕点O 顺时针旋转,①如图2,当点N 恰好在AB 边上时,求证:2222BN AN ON =+;②当点,,A M N 在同一条直线上时,若4,3OB ON ==,请直接写出线段BN 的长.68.如图1,在等边三角形ABC 中,点E 是边AC 上一定点,点D 是直线BC 上一动点,以DE 为一边作等边三角形DEF ,连接CF .(问题解决)(1)如图1,若点D 在边BC 上,求证:CE+CF =CD ;(类比探究)(2)如图2,若点D 在边BC 的延长线上,请探究线段CE ,CF 与CD 之间存在怎样的数量关系?并说明理由.69.(1)如图①,在四边形ABCD 中,AB CD ∥,点E 是BC 的中点,若AE 是BAD ∠的平分线,试判断AB ,AD ,DC 之间的等量关系.解决此问题可以用如下方法:延长AE 交DC 的延长线于点F ,易证AEB FEC ∆∆≌得到AB FC =,从而把AB ,AD ,DC 转化在一个三角形中即可判断.AB ,AD ,DC 之间的等量关系________;(2)问题探究:如图②,在四边形ABCD 中,AB CD ∥,AF 与DC 的延长线交于点F ,点E 是BC 的中点,若AE 是BAF ∠的平分线,试探究AB ,AF ,CF 之间的等量关系,并证明你的结论.70.小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.(一)猜测探究:在ABC ∆中,AB AC =,M 是平面内任意一点,将线段AM 绕点A 按顺时针方向旋转与BAC ∠相等的角度,得到线段AN ,连接NB .(1)如图1,若M 是线段BC 上的任意一点,请直接写出NAB ∠与MAC ∠的数量关系是,NB 与MC 的数量关系是;(2)如图2,点E 是AB 延长线上点,若M 是CBE ∠内部射线BD 上任意一点,连接MC ,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.(二)拓展应用:如图3,在111A B C ∆中,118A B =,11160A B C ∠= ,11175B A C ∠= ,P 是11B C 上的任意点,连接1A P ,将1A P 绕点1A按顺时针方向旋转75 ,得到线段1AQ ,连接1B Q .求线段1B Q 长度的最小值.答案1、【答案】B解:∵AB∥CD,∴∠ABC=∠BCD,∵CB平分∠DCE,∴∠BCE=∠BCD,∴∠BCE=∠ABC,∵∠AEC=∠BCE+∠ABC=40°,∴∠ABC=20°,故选B.2、【答案】A解:如图,延长该直角三角形一边,与该矩形纸片一边的交点记为点A,由矩形对边平行,可得∠1=∠BAC,因为BC⊥AB,∴∠BAC+∠2=90°,∴∠1+∠2=90°,因为∠1=48°,∴∠2=42°;故选:A.3、【答案】A解:如下图所示,由边长为4的正方形分割制作的七巧板,共有以下几种图形:○1腰长是的等腰直角三角形,②腰长是2的等腰直角三角形,的正方形,⑤边长分别是2,顶角分别是45 和135 的平行四边形,根据图2可知,图中抬起的“腿”的等腰直角三角形,和一个边长分别是2,顶角分别是45 和135 的平行四边形组成,如下图示,根据平行四边形的性质可知,顶角分别是45 和135 的平行四边形的高是DB ,且DB =,的等腰直角三角形的面积是:112=,顶角分别是45 和135 2=,∴阴影部分的面积为:123+=,故选:A.4、【答案】BA、五边形的内角和是540︒,故原命题为假命题,不符合题意;B、三角形的任意两边之和大于第三边,原命题是真命题,符合题意;C、两直线平行,内错角相等,故原命题为假命题,不符合题意;D、三角形的重心是这个三角形的三条中线的交点,故原命题为假命题,不符合题意;故选:B.5、【答案】C由图可得6045B F ∠=︒∠=︒,,∵//BC EF ,∴45FDB F ∠=∠=︒,∴180180456075BMD FDB B ∠=︒-∠-∠=︒-︒-︒=︒,故选:C.6、【答案】C解:∵12//l l ,∴34∠=∠(两直线平行,同位角相等).故选C .7、【答案】B解:如图,1=55∠︒ ,3=55,∴∠︒∵a ∥b ,∠3=55°,∴∠2=∠3=55°.故选B.8、【答案】B解://AB CD 130ABC DCB ∴∠=∠=︒1305575ECD DCB BCE ∴∠=∠-∠=︒-︒=︒//EF CD 180ECD CEF ∴∠+∠=︒18075105CEF ∴∠=︒-︒=︒故答案是:B.9、【答案】D首先根据三角尺的直角被直线m 平分,∴∠6=∠7=45°;A 、∵∠1=60°,∠6=45°,∴∠8=180°-∠1-∠6=180-60°-45°=75°,m∥n ,∴∠2=∠8=75°结论正确,选项不合题意;B 、∵∠7=45°,m ∥n ,∴∠3=∠7=45°,结论正确,选项不合题意;C 、∵∠8=75°,∴∠4=180-∠8=180-75°=105°,结论正确,选项不合题意;D 、∵∠7=45°,∴∠5=180-∠7=180-45°=135°,结论错误,选项符合题意.故选:D.10、【答案】B 解:如图,∵//,140m n ∠=︒,∴∠4=∠1=40°,∵230∠=︒,∴34270∠=∠+∠=︒;故选B.11.(2021·四川广元市·中考真题)如图,在ABC 中,90ACB ∠=︒,4AC BC ==,点D 是BC 边的中点,点P 是AC 边上一个动点,连接PD ,以PD 为边在PD 的下方作等边三角形PDQ ,连接CQ .则CQ 的最小值是()A.2B.1D.3211、【答案】B解:以CD 为边作等边三角形CDE ,连接EQ ,如图所示:∵PDQ 是等边三角形,∴60,,CED PDQ CDE PD QD CD ED ∠=∠=∠=︒==,∵∠CDQ 是公共角,∴∠PDC =∠QDE ,∴△PCD ≌△QED (SAS ),∵90ACB ∠=︒,4AC BC ==,点D 是BC 边的中点,∴∠PCD =∠QED =90°,122CD DE CE BC ====,∴点Q 是在QE 所在直线上运动,∴当CQ ⊥QE 时,CQ 取的最小值,∴9030QEC CED ∠=︒-∠=︒,∴112CQ CE ==;故选B.12、【答案】BA .证法1给出的证明过程是完整正确的,不需要分情况讨论,故A 不符合题意;B .证法1给出的证明过程是完整正确的,不需要分情况讨论,故选项B 符合题意;C .证法2用量角器度量两个内角和外角,只能验证该定理的正确性,用特殊到一般法证明了该定理缺少理论证明过程,故选项C 不符合题意;D .证法2只要测量够一百个三角形进行验证,验证的正确性更高,就能证明该定理还需用理论证明,故选项D 不符合题意.故选择:.B 13、【答案】D解:∵∠ACB =90°,AC =8,BC =6,∴AB∵△ADE 沿DE 翻折,使点A 与点B 重合,∴AE =BE ,AD =BD =12AB =5,设AE =x ,则CE =AC -AE =8-x ,BE =x ,在Rt △BCE 中∵BE 2=BC 2+CE 2,∴x 2=62+(8-x )2,解得x =254,∴CE =2584-=74,故选:D.14、【答案】B解:∵25B ∠=︒,50C ∠=︒,∴在Rt △BEC 中,由三角形内角和可得105BEC ∠=︒,∵35A ∠=︒,∴170BEC A ∠=∠-∠=︒;故选B.15、【答案】A如图,设AD 、BC 交于点H ,作HF AB ⊥于点F ,连接EF .延长AC 与BD 并交于点G.∵AD 是BAC ∠的平分线,HF AB ⊥,HC AC ⊥,∴HC =HF ,∴AF =AC .∴在CAE V 和FAE 中,AF AC CAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩,∴()CAE FAE SAS ≅ ,∴CE FE =,∠AEC =∠AEF =90°,∴C、E、F 三点共线,∴点E 为CF 中点.∵M 为BC 中点,∴ME 为CBF V 中位线,∴//ME AB ,故B 正确,不符合题意;∵在AGD △和ABD △中,90GAD BAD AD AD ADG ADB ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩,∴()AGD ABD ASA ≅ ,∴12GD BD BG ==,即D 为BG 中点.∵在BCG 中,90BCG ∠=︒,∴12CD BG =,∴CD BD =,故C 正确,不符合题意;∵90HDM DHM ∠+∠=︒,90HCE CHE ∠+∠=︒,DHM CHE ∠=∠,∴HDM HCE ∠=∠.∵HF AB ⊥,//ME AB ,∴HF ME ⊥,∴90HEM EHF ∠+∠=︒.∵AD 是BAC ∠的平分线,∴EHC EHF ∠=∠.∵90EHC HCE ∠+∠=︒,∴HCE HEM ∠=∠,∴HDM HEM ∠=∠,∴MD ME =,故D 正确,不符合题意;∵假设2CD ME =,∴2CD MD =,∴在Rt CDM 中,30DCM ∠=︒.∵无法确定DCM ∠的大小,故原假设不一定成立,故A 错误,符合题意.故选A.16、【答案】B选项A,添加ABC DCB ∠=∠,在ABC 和DCB 中,ABC DCB BC CB ACB DBC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴ABC ≌DCB (ASA),选项B,添加 AB DC =,在ABC 和DCB 中, AB DC =,BC CB =,ACB DBC ∠=∠,无法证明ABC ≌DCB ;选项C,添加AC DB =,在ABC 和DCB 中,BC CB ACB DBC AC DB =⎧⎪∠=∠⎨⎪=⎩,∴ABC ≌DCB (SAS);选项D,添加A D ∠=∠,在ABC 和DCB 中,A D ACB DBC BC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴ABC ≌DCB (AAS);综上,只有选项B 符合题意.故选B.17、【答案】D解:∵90,4,3ACB AC BC ∠=︒==,∴AB ==由折叠性质得:∠DAE=∠DFE ,AD=DF ,则BD =5﹣AD ,∵FD 平分EFB ∠,∴∠BFD =∠DFE=∠DAE ,∵∠DAE +∠B =90°,∴∠BDF +∠B =90°,即∠BDF =90°,∴Rt△ABC ∽Rt△FBD ,∴BD BC DF AC =即534AD AD -=,解得:AD =205,故选:D.18、【答案】D解:由题意可知:AC =AB ∵()8,0A,()2,0C -∴OA =8,OC =2∴AC =AB =10在Rt △OAB 中,6OB ===∴B (0,6)故选:D19、【答案】C解: BF =EC ,BC EF∴=A.添加一个条件AB =DE ,又,BC EF B E =∠=∠ ()ABC DEF SAS ∴△≌△故A 不符合题意;B.添加一个条件∠A =∠D 又,BC EF B E =∠=∠ ()ABC DEF AAS ∴≌故B 不符合题意;C.添加一个条件AC =DF ,不能判断△ABC ≌△DEF ,故C 符合题意;D.添加一个条件AC ∥FD ACB EFD ∴∠=∠又,BC EF B E =∠=∠ ()ABC DEF ASA ∴≌故D 不符合题意,故选:C.20、【答案】B解:如图:分情况讨论:①AB 为等腰直角△ABC 底边时,符合条件的C 点有0个;②AB 为等腰直角△ABC 其中的一条腰时,符合条件的C 点有3个.故共有3个点,故选:B.21、【答案】C解:因为AD 垂直BC ,则△ABD 和△ACD 都是直角三角形,又因为45,60,B C ∠=︒∠=︒所以AD =BD =,因为sin∠C =32AD AC =,所以AC =2,因为EF 为△ABC 的中位线,所以EF =2AC =1,故选:C.22、【答案】A如图,过点D 作DE⊥BC 于点E.∵∠A=90°,∴AD⊥AB.∴AD=DE=3.又∵BC=5,∴S △BCD =12BC•DE=12×5×3=7.5.故选A.23、【答案】B 解:∵AD ⊥EF ,∠A =20°,∴∠ABD =180°﹣∠A ﹣∠ABD =180°﹣20°﹣90°=70°,∵EF ∥GH ,∴∠ACH =∠ABD =70°,∴∠ACG =180°﹣∠ACH =180°﹣70°=110°,故选:B .24、【答案】A解:如图所示,∠1和∠2两个角都在两被截直线直线b 和a 同侧,并且在第三条直线c(截线)的同旁,故∠1和∠2是直线b、a 被c 所截而成的同位角.故选:A.25、【答案】A解:由三角板的特点可知∠ACB=45°、∠DEF=30°∵//EF BC ∴∠CEF=∠ACB=45°,∴∠CED=∠CEF-∠DEF=45°-30°=15°.故答案为A.26、【答案】B解:如图,设AD 与BC 交于点F ,∵BC ∥DE ,∴∠CFA =∠D =90°,∵∠CFA =∠B +∠BAD =60°+∠BAD ,∴∠BAD =30°故选:B .27、【答案】D解:由作法得EF 垂直平分AB ,∴MB =MA ,∴BM +MD =MA +MD ,连接MA 、DA ,如图,∵MA +MD ≥AD (当且仅当M 点在AD 上时取等号),∴MA +MD 的最小值为AD ,∵AB =AC ,D 点为BC 的中点,∴AD ⊥BC ,∵110,2ABC S BC AD == ∴1025,4AD ⨯==∴BM +MD 长度的最小值为5.故选:D .28、【答案】D解:在ABC 中,90,40ACB ABC ︒︒∠=∠=,∴∠CAB=50°,由旋转的性质,则40ABA '∠=︒,AB A B '=,∴1(18040)702BAA '∠=⨯︒-︒=︒,∴''50+70=120CAA CAB BAA ∠=∠+∠=︒︒︒;故选:D.29、【答案】A解:如图,过点C 作CK⊥l 于点K,过点A 作AH⊥BC 于点H,在Rt△AHB在Rt△AHC==,∵点D 为BC 中点,∴BD=CD,在△BFD 与△CKD 中,90BFD CKD BDF CDK BD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△BFD≌△CKD(AAS),∴BF=CK,延长AE,过点C 作CN⊥AE 于点N,可得AE+BF=AE+CK=AE+EN=AN,在Rt△ACN 中,AN<AC,当直线l⊥AC,综上所述,AE+BF.故选:A.30、【答案】A解:如图,连接FC ,∵点O 是AC 的中点,由作法可知,OE 垂直平分AC ,∴AF =FC.∵AD ∥BC ,∴∠FAO =∠BCO .在△FOA 与△BOC 中,FAO BCO OA OC AOF COB ∠∠⎧⎪⎨⎪∠∠⎩===,∴△FOA ≌△BOC (ASA ),∴AF =BC =6,∴FC =AF =6,FD =AD -AF =8-6=2.在△FDC 中,∵∠D =90°,∴CD 2+DF 2=FC 2,∴CD 2+22=62,∴CD =42.故选:A .31、【答案】D过点C 作CE⊥AD 于点E,则CE//AB,45PCE BPC ∴∠=∠=︒180754560DPC ∠=︒-︒-︒=︒ ,且PD=PC,PCD ∴ 为等边三角形,CD PD a ∴==,60PCD CDP ∠=∠=︒,45PCE ∠=︒ ,604515DCE DCP PCE ∴∠=∠-∠=︒-︒=︒,75APD =︒∠ ,90DAP ∠=︒,∴907515PDA ∠=︒-︒=︒,∴15DCE PDA ∠=∠=︒,∴601575CDE PDC PDA ∠=∠+∠=︒+︒=︒,APD CDE ∴∠=∠,在Rt APD 和Rt CDE △中,DCE PDA CD PD CDE DPA ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴Rt APD ≌Rt CDE △,CE DA c ==,故选:D.32、【答案】D(1)当70︒的内角为这个等腰三角形的顶角则另外两个内角均为底角,它们的度数为18070552︒-︒=︒(2)当70︒的内角为这个等腰三角形的底角,则另两个内角一个为底角,一个为顶角底角为70︒,顶角为180707040︒-︒-︒=︒综上,另外两个内角的度数分别是55,55︒︒或70,40︒︒故选:D.33、【答案】C解:∵∠BAC=∠EAD∴∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE在△BAD 和△CAE 中AB=AC,∠BAD=∠CAE,AD=AE∴△BAD≌△CAE∴BD=CE 故①正确;∵△BAD≌△CAE∴∠ABF=∠ACF∵∠ABF+∠BGA=90°、∠BGA=∠CGF∴∠ACF+∠BGA=90°,∴∠BFC=90°故②正确;分别过A 作AM⊥BD、AN⊥CE 垂足分别为M、N∵△BAD≌△CAE∴S △BAD =S △CAE ,∴1122BD AM CE AN ⋅=⋅∵BD=CE∴AM=AN∴AF 平分∠BFE,无法证明AF平分∠CAD.故③错误;∵AF 平分∠BFE,BF CF ⊥∴45AFE ∠=︒故④正确.故答案为C.34、【答案】C∵,ABC ECD ∆∆都是等边三角形,∴BC AC =,CE CD =,60BCA DCE ∠=∠=︒,∴+BCA ACE DCE ACE ∠∠=∠+∠,∴BCE ACD ∠=∠,在BCE 和ACD △中,BC AC BCE ACD CE CD ⎧=⎪∠=∠⎨⎪=⎩,∴()△△BCE ACD SAS ≅,∴BE AD =,CBM ACN ∠=∠,又∵11,33BM BE AN AD ==,∴BM AN =,在BCM 和ACN △中,BM AN CBM ACN BC AC ⎧=⎪∠=∠⎨⎪=⎩,∴()△△BCM ACN SAS ≅,∴BCM ACN ∠=∠,MC NC =,∴+60BCM ACM ACN ACM ∠∠=∠+∠=︒,∴CMN ∆是等边三角形.故答案选C.35、【答案】A根据题意可知,直线CD 经过ABC ∆的AB 边上的中点,直线AD 经过ABC ∆的BC 边上的中点,∴点D 是ABC ∆重心.故选A.36、【答案】B解:连接AC 并延长交EF 于点M.AB CF ,31∴∠=∠,AD CE ,24∴∠=∠,3412BAD FCE ∴∠=∠+∠=∠+∠=∠,180180805050FCE E F ∠=︒-∠-∠=︒-︒-︒=︒ ,50BAD FCE ∴∠=∠=︒,故选B.37、1解:∵地毯平均分成了33=,∴CD =在Rt ACD △中,根据勾股定理可得AD ==,根据裁剪可知1BD CE ==,∴1AB AD BD =-=-1-.38、【答案】减少10解:∵∠A +∠B =50°+60°=110°,∴∠ACB =180°-110°=70°,∴∠DCE =70°,如图,连接CF 并延长,∴∠DFM =∠D +∠DCF =20°+∠DCF ,∠EFM =∠E +∠ECF =30°+∠ECF ,∴∠EFD =∠DFM +∠EFM =20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°,要使∠EFD =110°,则∠EFD 减少了10°,若只调整∠D 的大小,由∠EFD =∠DFM +∠EFM =∠D +∠DCF +∠E +∠ECF =∠D +∠E +∠ECD =∠D +30°+70°=∠D +100°,因此应将∠D 减少10度;故答案为:①减少;②10.39、【答案】40°解:在△DEF 中,∠1=50°,∠DEF=90°,∴∠D=180°-∠DEF-∠1=40°.∵AB∥CD,∴∠2=∠D=40°.故答案为40°.40、【答案】12:15:10解:∵在△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为点D 和点E ,AD 与CE 交于点O ,∴BF ⊥AC ,∵AB =5,BC =4,AC =6,∴111222ABC S BC AD AB CE AC BF =⋅=⋅=⋅ ,∴5432ABC S AD CE BF === ,∴CE :AD :BF =12:15:10,故答案是:12:15:10.41、【答案】11802α︒-解:在△ABD 中,AB =BD ∴∠A =∠ADB =11(180)9022ABD ABD ︒-∠=︒-∠在△BCD 中,BC =BD ∴∠C =∠BDC =11(180)9022CBD CBD ︒-∠=︒-∠∵ABC ABD CBD α∠=∠+∠=∴ADC ADB CBD ∠=∠+∠=11909022ABD CBD ︒-∠+︒-∠=1180()2ABD CBD ︒-∠+∠=11802ABC ︒-∠=11802α︒-故答案为:11802α︒-.42、【答案】32解:连接ED BE 是ABC 的中线,ABE BCE S S ∴= ,AED EDCS S = 3BF FE = 3,3ABF BFD AFE FEDS S S S ∴== 设=,AEF EFD S x S y = ,33ABF BFD S x S y ∴== ,4,4,4ABE BEC BED S x S x S y ∴=== 44EDC BEC BED S S S x y∴=-=- ADE EDC S S = 44x y x y ∴+=-53x y ∴= ABD 与ADC 是等高三角形,53+33333833=516445325333ABD ADC y y S BD x y x y y S DC x y x y x y y y y ⨯++∴=====++--⨯- ,故答案为:32.43、【答案】15︒或75︒解:①当点P 在BC 的延长线上时,如图∵AB AC =,70B ∠=︒,∴70B ACB ∠=∠=︒∴40CAB ∠=︒∵以点C 为圆心,CA 长为半径作弧,交直线BC 于点P ,∴AC =PC ∴∠=∠P CAP∵70∠=∠+∠=︒ACB B CAP ∴35∠=∠= P CAP ∴403575∠=∠+∠=+= BAP BAC CAP ②当点P 在CB 的延长线上时,如图由①得70C ∠=︒,40CAB ∠=︒∵AC =PC ∴=55∠=∠P CAP ∴-55-4015∠=∠∠== BAP CAP BAC 故答案为:15︒或75︒44、【答案】4+解:∵把三角形纸片折叠,使点B 、点C 都与点A 重合,折痕分别为DE ,FG ,∴BE =AE ,AF =FC ,∠FAC =∠C =15°,∴∠AFE =30°,又AE =EF ,∴∠EAF =∠AFE =30°,∴∠AEB =60°,∴△ABE 是等边三角形,∠AED =∠BED =30°,∴∠BAE =60°,∵DE ,∴AE =BE =AB =cos30DE ︒=2,∴BF =BE +EF =4,∠BAF =60°+30°=90°,∴FC =AF =BC =BF +FC =4+4+.45、【答案】12.解:∵直线DE 垂直平分BC ,∴DB DC =,∴△ABD 的周长5712AB AD BD AB AD DC AB AC =++=++=+=+=,故答案为:12.46、【答案】12解:依题意画出图形,设芦苇长AB =AB '=x 尺,则水深AC =(x ﹣1)尺,因为B 'E =10尺,所以B 'C =5尺,在Rt△AB 'C 中,52+(x ﹣1)2=x 2,解之得x =13,即水深12尺,芦苇长13尺.故答案为:12.47、【答案】2解:取AD 的中点O,连接OM,过点M 作ME⊥BC 交BC 的延长线于E,点点O 作OF⊥BC 于F,交CD 于G,则OM+ME≥OF.∵∠AMD=90°,AD=4,OA=OD,∴OM=12AD=2,∵AB∥CD,∴∠GCF=∠B=60°,∴∠DGO=∠CGE=30°,∵AD=BC,∴∠DAB=∠B=60°,∴∠ADC=∠BCD=120°,∴∠DOG=30°=∠DGO,∴DG=DO=2,∵CD=4,∴CG=2,﹣2,∴当O,M,E 共线时,ME 的值最小,最小值为﹣2.48、【答案】12解:根据题意可知,AD 是∠BAC 的角平分线,∴∠BAD=∠FAD,∵AB=AF=5,AD=AD,∴△ABD≌△AFD,∴BD=FD,∴FD+DC=BD+DC=BC=9,∵FC=AC -AF=8-5=3,∴CDF ∆的周长为:FD+DC+FC=9+3=12;故答案为:12.49、【答案】13∵在ABC 中,分别以A、B 为圆心,大于1AB 2的长为半径画弧,两弧交于M,N,作直线MN,交BC 边于D,连接AD;∴MN 为AB 的垂直平分线,∴AD=BD,∴ACD 的周长为:AD+DC+AC=BC+AC=13;故答案为13.50、【答案】解:过C 作CF ⊥AB 交AD 于E ,则此时,CE +EF 的值最小,且CE +EF 的最小值为CF ,∵△ABC 为等边三角形,边长为6,∴BF =12AB =12⨯6=3,∴CF ,∴CE +EF 的最小值为.51、【答案】32由作图可得,MN 是线段AB 的垂直平分线,BD 是∠ABC 的平分线,∴AD=BD,1=2ABD CBD ABC ∠=∠∠∴A ABD ∠=∠∴A ABD CBD ∠=∠=∠∵+180A ABC C ∠∠+∠=︒,且84C ∠=︒,∴+2180A ABD C ∠∠=︒-∠,即318084A ∠=︒-︒,∴32A ∠=︒.故答案为:32.52、【答案】=设22a b +为定值k ,则222kc a b +==由“张爽弦图”可知,2222()()ab c a b k a b =--=--即2()2k a b ab --=要使ab 的值最大,则2()a b -需最小又2()0a b -≥ ∴当a b =时,2()a b -取得最小值,最小值为0则当a b =时,ab 取得最大值,最大值为2k 故答案为:=.53、【答案】PA 2+PB 2=2PC 2解:过点C 作CD⊥AB,交AB 于点D ∵△ACB 为等腰直角三角形,CD⊥AB,∴CD=AD=DB,∵PA 2=(AD-PD)2=(CD-PD)2=CD 2-2CD•PD+PD 2,PB 2=(BD+PD)2=(CD+PD)2=CD 2-2CD•PD+PD 2,∴PA 2+PB 2=2CD 2+2PD 2=2(CD 2+PD 2),在Rt△PCD 中,由勾股定理可得PC 2=CD 2+PD 2,∴PA 2+PB 2=2PC 2,故答案为PA 2+PB 2=2PC 2.54、【答案】12解:如图1,以CD 为边向外作等边三角形CDE,连接BE,∵CE=CD,CB=CA,∠ECD=∠BCA=60°,∴∠ECB=∠DCA,∴△ECB≌△DCA(SAS),∴BE=AD,∵DE=CD=6,BD=8,∴8-6<BE<8+6,∴2<BE<14,∴2<AD<14.∴则AD 的最大值与最小值的差为12.故答案为:1255、【答案】2013(1)由A 、B 两点的纵坐标相同可知:AB ∥x 轴,∴AB =12﹣(﹣8)=20;(2)过点C 作l ⊥AB 于点E ,连接AC ,作AC 的垂直平分线交直线l 于点D ,由(1)可知:CE =1﹣(﹣17)=18,AE =12,设CD =x ,∴AD =CD =x ,由勾股定理可知:x 2=(18﹣x )2+122,∴解得:x =13,∴CD =13.故答案为(1)20;(2)13.56、【答案】见解析证明:∵//AB CD ,∴DCF B ∠=∠.∵B D ∠=∠,∴DCF D ∠=∠.∴//AD BC .∴DEF F ∠=∠.57、【答案】(1)见解析;(2)35°解:(1) BE 平分ABC ∠,∴ABE EBC ∠=∠.DB DE =,∴ABE BED ∠=∠,∴BED EBC ∠=∠,∴//DE BC .(2) 65A ∠=︒,45AED ∠=︒,∴18070ADE A AED ∠=︒-∠-∠=︒.//DE BC .∴70ABC ADE ∠=∠=︒.BE 平分ABC ∠,∴1352EBC ABC ∠=∠=︒,即35EBC ∠=︒.58、【答案】见详解证明:∵90BAC ∠=︒,∴∠BAE +∠CAF =90°,∵BE ⊥AD ,CF ⊥AD ,∴∠BEA =∠AFC =90°,∴∠BAE +∠EBA =90°,∴∠CAF =∠EBA ,∵AB =AC ,∴△BAE ≌△ACF ,∴AF BE =.59、【答案】(1)50BDC ∠=︒;20ABE ∠=︒;(2)110BEC BDC ∠+∠=︒,见解析(1)80ABC ∠=︒ ,BD BC =,50BDC BCD ∴∠=∠=︒.在ABC 中,180A ABC ACB ∠+∠+∠=︒,40A ∠=︒ ,60ACB ∠=︒∴,CE BC = ,60EBC ∴∠=︒.20ABE ABC EBC ∴∠=∠-∠=︒.(2)BEC ∠,BDC ∠的关系:110BEC BDC ∠+∠=︒.理由如下:设BEC α∠=,BDC β∠=.在ABE △中,40A ABE ABE α=∠+∠=︒+∠,CE BC = ,CBE BEC α∴∠=∠=.2402ABC ABE CBE A ABE ABE ∴∠=∠+∠=∠+∠=︒+∠, 在BDC 中,BD BC =,2402180BDC BCD DBC ABE β∴∠+∠+∠=+︒+∠=︒.70ABE β︒∴=-∠.4070110ABE ABE αβ∴+=︒+∠+︒-∠=︒.110BEC BDC ∴∠+∠=︒.60、【答案】见解析证明:∵//BD AC ,∴EBD C ∠=∠.∵BD BC =,BE AC =,∴()EDB ABC SAS ≌.∴D ABC ∠=∠.61、【答案】见解析证明:点A ,B ,C ,D ,E 在一条直线上∵//,//AC DF BC EF ∴,A FDE ABC DEF∠=∠∠=∠在ABC 与DEF 中CAB FDE AB DE ABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ABC DEF ASA △≌△62、【答案】(1);(2)见解析;(3)存在,m =(1)解90,60ACB CAD ∠=∠=︒︒ ,2cos60AC AB AC ︒==,BD AC = ,AD AC =∴,ADC ∴ 是等边三角形,60ACD ∴∠=︒Р 是CD 的中点,AP CD ∴⊥,在Rt APC 中,3AP =,2sin 60AP AC ∴==︒,tan 6023BC AC =︒=∴.(2)证明:连结BE ,//DE AC ,CAP DEP ∴∠=∠,,CP DP CPA DPE =∠=∠ ,()CPA DPE AAS ∴ ≌,1,2AP EP AE DE AC ∴===,BD AC = ,BD DE ∴=,又//DE AC ,60BDE CAD ∴∠=∠=︒,BDE ∴ 是等边三角形,,60BD BE EBD ∴=∠=︒BD AC = ,AC BE ∴=,又60,CAB EBA AB BA ∠=∠=︒= ,()CAB EBA SAS ∴≌,AE BC ∴=,2BC AP ∴=.(3)存在这样的,2m m =.过点D 作//DE AC ,交AP 延长线于点E ,连接BE ,过C 作CG ⊥AB 于G ,过E 作EN ⊥AB 于N ,则45∠=∠=︒BDE CAD ,sin 45∴=⨯ CG AC ,sin 45=⨯ EN DE 由(2)得AE =2AP ,DE =AC ,∴CG =EN ,∵2BC AP =,∴AE =BC ,∵∠ANE =∠BGC =90°,≌∴ AEN BCG ,∴∠EAN =∠CBG∵AE =BC ,AB =BA ,∴≌ CAB EBA ∴AC =BE ,∴DE =BE ,∴∠EDB =∠EBD =45°,∴∠DEB =90°,∴2=BD AC ,∵BD mAC =∴2m =63、【答案】(1)证明见解析;(2)78°.证明:(1)在△BEF 和△CDA 中,1BE CD B BF CA =⎧⎪∠=∠⎨⎪=⎩,∴△BEF ≌△CDA (SAS ),∴∠D =∠2;(2)∵∠D =∠2,∠D =78°,∴∠D =∠2=78°,。
专题 与平行线有关的角度计算(四大题型)(解析版 )

(人教版)七年级下册数学《第五章相交线与平行线》专题与平行线有关的角度计算1.(2023秋•惠安县期末)如图,直线l1和l2被l3所截,若l1∥l2,∠1+∠2=232°,则∠3的度数为()A.64°B.66°C.84°D.86°【分析】根据对顶角相等结合已知可求出∠1的度数,再根据两直线平行,同旁内角互补即可求出∠4的度数,再根据对顶角相等即可得出∠3的度数.【解答】解:如图,∵∠1+∠2=232°,又∵∠1=∠2,∴∠1=116°,∵l1∥l2,∴∠1+∠4=180°,∴∠4=64°,∵∠3=∠4,∴∠3=64°,故选:A.【点评】本题考查了平行线的性质,对顶角的性质,熟练掌握平行线的性质及对顶角的性质是解题的关键.2.如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数是()A.154°B.144°C.134°D.124°【分析】根据平行线的判定和性质定理即可得到结论.【解答】解:∵DA⊥AB,CD⊥DA,∴∠A=∠D=90°,∴∠A+∠D=180°,∴AB∥CD,∴∠B+∠C=180°,∵∠B=56°,∴∠C=180°﹣∠B=124°,故选:D.【点评】本题考查了平行线的判定和性质,熟练掌握平行线的判定和性质定理是解题的关键.3.(2023秋•遂平县期末)如图.直线a∥b,直线L与a、b分别交于点A、B,过点A作AC⊥b于点C.若∠1=50°,则∠2的度数为()A.130°B.50°C.40°D.25°【分析】直接利用垂直的定义得出∠ACB=90°,再利用平行线的性质得出答案.【解答】解:∵AC⊥b,∴∠ACB=90°,∵∠1=50°,∴∠ABC=40°,∵a∥b,∴∠ABC=∠2=40°.故选:C.【点评】此题主要考查了垂线以及平行线的性质,正确得出∠ABC的度数是解题关键.4.如图,直线l1∥l2,CD⊥AB于点D,∠1=44°,则∠2的度数为()A.30°B.44°C.46°D.56°【分析】根据直角三角形的两个锐角互余,可以得到∠CBD的度数,再根据直线l1∥l2,可以得到∠CBD =∠2,从而可以得到∠2的度数,本题得以解决.【解答】解:∵CD⊥AB于点D,∠1=44°,∴∠CBD=46°,∵直线l1∥l2,∴∠CBD=∠2,∴∠2=46°,故选:C.【点评】本题考查平行线的性质、垂线,解答本题的关键是明确题意,利用数形结合的思想解答.5.如图,一个由4条线段a,b,c,d组成的“鱼”形图案,若∠1=45°,∠2=45°,∠3=140°,则∠4的度数为()A.35°B.40°C.45°D.50°【分析】先由∠1、∠2的关系得到b与c的关系,再利用平行线的性质求出∠4.【解答】解:∵∠1=45°,∠2=45°,∴∠1=∠2.∴b∥c.∴∠3+∠4=180°.∵∠3=140°,∴∠4=180°﹣140°=40°.故选:B.【点评】本题考查了平行线的判定与性质,解决本题的关键是注意平行线的性质和判定定理的综合运用.6.(2023秋•泰兴市期末)如图,AB∥CD,直线EF和AB、CD分别交于点G、H,若∠EGB=(2x+30)°,∠CHF=(80﹣3x)°,则x的值为()A.10B.20C.100D.110【分析】根据平行线的性质和对顶角的性质,可以得到∠EGB和∠CHF的关系,然后即可求得x的值.【解答】解:∵AB∥CD,∴∠EGB=∠EHD,∵∠EHD=∠CHF,∴∠EGB=∠CHF,∵∠EGB=(2x+30)°,∠CHF=(80﹣3x)°,∴2x+30=80﹣3x,解得x=10,故选:A.【点评】本题考查平行线的性质、对顶角的性质,解答本题的关键是明确题意,利用数形结合的思想解答.7.如图,DE∥BC,点A在直线DE上,∠DAB=78°,∠ACF=135°,∠BAC=度.【分析】由DE∥BC可知∠DAC=∠ACF=135°,再利用角的差求∠BAC即可.【解答】解:∵DE∥BC,∴∠DAC=∠ACF=135°,∵∠DAB=78°,∴∠BAC=∠DAC﹣∠DAB=57°.故答案为:57.【点评】本题考查平行线的性质,解题关键是结合图形利用平行线的性质进行角的转化和计算.8.(2023秋•东坡区期末)如图,AB∥CD,∠ACD=155°,∠AFE=26°,则∠CEF的度数为.【分析】先利用平行线的性质可得∠A=25°,然后利用三角形的外角性质进行计算,即可解答.【解答】解:∵AB∥CD,∠ACD=155°,∴∠A=180°﹣∠ACD=25°,∵∠CEF是△AEF的一个外角,∠AFE=26°,∴∠CEF=∠A+∠AFE=51°,故答案为:51°.【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.9.如图,直线AB∥EF,直线AG,BD分别交直线EF于点C,D.若∠A=2∠B,∠ECG=108°,则∠BDF的度数为°.【分析】由∠ECG=108°,AB∥EF,可得∠A=72°,而∠A=2∠B,知∠B=12∠A=36°;故∠BDF=∠B=36°.【解答】解:∵∠ECG=108°,∴∠ACD=108°,∵AB∥EF,∴∠A=180°﹣∠ACD=72°,∵∠A=2∠B,∴∠B=12∠A=36°;∵AB∥EF,∴∠BDF=∠B=36°;故答案为:36.【点评】本题考查平行线的性质,掌握两直线平行,内错角相等,同旁内角互补是解题的关键.10.(2022春•五莲县期末)如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,则∠BCD的度数为.【分析】由AB∥CF,∠ABC=70°,易求∠BCF,又DE∥CF,∠CDE=130°,那么易求∠DCF,于是∠BCD=∠BCF﹣∠DCF可求.【解答】解:∵AB∥CF,∠ABC=70°,∴∠BCF=∠ABC=70°,又∵DE∥CF,∴∠DCF+∠CDE=180°,∴∠DCF=50°,∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.故答案为:20°.【点评】本题主要考查了平行线的性质,两直线平行,内错角相等;两直线平行,同旁内角互补.11.(2023秋•商水县期末)如图,已知DE∥CB,∠B=∠D.(1)判断AB、CD是否平行,并说明理由.(2)若∠B+∠F=102°,求∠DEF的度数.【分析】(1)由平行线的性质可得∠D=∠BCF,从而可求得∠BCF=∠B,即可判定AB∥CD;(2)由平行线的性质可得∠B+∠BED=180°,∠F=∠BEF,结合条件即可求解.【解答】解:(1)AB∥CD,理由如下:∵DE∥CB,∴∠D=∠BCF,∵∠B=∠D,∴∠BCF=∠B,∴AB∥CD;(2)∵DE∥CB,∴∠B+∠BED=180°,∴∠B+∠BEF+∠DEF=180°,∵AB∥CD,∴∠F=∠BEF,∴∠B+∠F+∠DEF=180°,∵∠B+∠F=102°,∴∠DEF=78°.【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的判定定理与性质并灵活运用.12.(2023秋•长沙期末)如图,直线EF与CD交于点O,OA平分∠COE交直线l于点A,OB平分∠DOE交直线l于点B,且∠1+∠2=90°.(1)求∠AOB的度数;(2)求证:AB∥CD;(3)若∠2:∠3=2:5,求∠AOF的度数.【分析】(1)利用角平分线的定义可得∠A=12∠A,∠A=12∠A,然后利用平角定义,以及角的和差关系进行计算,即可解答;(2)利用(1)的结论可得:∠AOB=90°,从而利用平角定义可得:∠AOC+∠2=90°,然后利用同角的余角相等可得∠AOC=∠1,从而利用内错角相等,两直线平行可得AB∥CD,即可解答;(3)利用角平分线的定义可得∠2=12∠DOE,从而可得∠DOE:∠3=4:5,然后利用平角定义可得∠DOE+∠3=180°,从而可得∠3=100°,进而可得∠COE=∠3=100°,最后利用角平分线的定义可得∠AOE =50°,从而利用平角定义进行计算,即可解答.【解答】(1)解:∵OA,OB分别平分∠COE和∠DOE,∴∠A=12∠A,∠A=12∠A,∴∠AOE+∠BOE=12∠COE+12∠DOE=12(∠COE+∠DOE)=12×180°=90°,∴∠AOB=90°,∴∠AOB的度数为90°;(2)证明:由(1)得:∠AOB=90°,∴∠AOC+∠2=180°﹣∠AOB=180°﹣90°=90°,∵∠1+∠2=90°,∴∠AOC=∠1,∴AB∥CD;(3)解:∵OB平分∠DOE,∴∠2=12∠DOE,∵∠2:∠3=2:5,∴∠DOE:∠3=4:5,∵∠DOE+∠3=180°,∴∠3=180°×59=100°,∴∠COE=∠3=100°,∵OA平分∠COE,∠A=12∠A=50°,∴∠AOF=180°﹣∠AOE=130°,∴∠AOF的度数为130°.【点评】本题考查了平行线的性质,三角形的外角性质,根据题目的已知条件并结合图形进行分析是解题的关键.1.(2023秋•南关区校级期末)如图,一把长方形直尺沿直线断开并错位摆放,点E、D、B、F在同一条直线上,若∠ADE=131°,则∠DBC的度数为.【分析】由平行线是的性质推出∠GED=∠ADE=131°,∠DBC+∠GED=180°,即可求出∠DBC的度数.【解答】解:∵AD∥EG,∴∠GED=∠ADE=131°,∵EG∥BC,∴∠DBC+∠GED=180°,∴∠DBC=49°.故答案为:49°.【点评】本题考查平行线的性质,关键是由平行线的性质得到∠GED=∠ADE,∠DBC+∠GED=180°.2.(2023秋•威宁县期末)一把直尺按如图所示摆放,AB∥CD,且∠1=70°,则∠2的度数是()A.70°B.60°C.30°D.80°【分析】根据题意可得:EF∥HG,从而利用平行线的性质可得∠1=∠3=70°,然后再利用平行线的性质可得∠3=∠2=70°,即可解答.【解答】解:如图:由题意得:EF∥HG,∴∠1=∠3=70°,∵AB∥CD,∴∠3=∠2=70°,故选:A.【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.3.(2023秋•海安市期末)将一直尺和一块含30°角的三角尺按如图放置,若∠CDE=40°,则∠BF A 的度数为()A.40°B.50°C.130°D.140°【分析】先求∠CFA的度数,再求∠BFA的度数.【解答】解:∵DE∥AF,∴∠CDE=∠CFA,∵∠CDE=40°,∴∠CFA=40°,∴∠BFA=180°﹣∠CFA=140°.故选:D.【点评】本题主要考查平行线的性质,解决本题的关键是熟练运用平行线的性质.4.(2023秋•铜官区期末)如图,将一块含有45°角的三角板的两个顶点放在直尺的一组对边上.如果∠2=65°,那么∠1的度数为()A.15°B.20°C.25°D.30°【分析】根据题意∠2=65°即可算出∠3度数,再利用平行性质即可算出本题答案.【解答】解:如下图所示:∵∠2=65°,一块含有45°角的三角板,∴∠3=90°﹣65°=25°,∵两个顶点放在直尺的一组对边上,∴∠3=∠4=25°,∴∠1=45°﹣25°=20°,故选:B.【点评】本题考查平行线性质,关键是余角定义,角度计算.5.(2023秋•锦江区校级期末)一块含30°角的直角三角板,按如图所示方式放置,顶点A,C分别落在直线a,b上,若直线a∥b,∠1=35°,则∠2的度数是()A.45°B.35°C.30°D.25°【分析】先根据题意得出∠1+∠BAC的度数,再由平行线的性质即可得出结论.【解答】解:∵∠1=35°,∴∠1+∠BAC=35°+30°=65°,∵a∥b,∴∠2+∠ACB+∠1+∠BAC=180°,即∠2+90°+35°+30°=180°,∴∠2=25°.故选:D.【点评】本题考查的是平行线的性质,熟知两直线平行,同旁内角互补是解题的关键.6.如图,将一副三角尺按如图所示的位置在同一平面内摆放,其中∠ACB=∠CED=90°,∠B=30°,∠ECD=45°.若AB∥CE,CB与DE相交于点F,则∠BCD的度数为()A.15°B.20°C.25°D.30°【分析】根据平行线的性质得出∠ECA=120°,进而利用角的关系解答即可.【解答】解:∵AB∥CE,∴∠ECA=180°﹣∠A=180°﹣60°=120°,∵∠ECD=45°,∴∠DCA=120°﹣45°=75°,∵∠BCA=90°,∴∠BCD=90°﹣75°=15°,故选:A.【点评】此题考查平行线的性质,关键是根据两直线平行,同旁内角互补解答.7.(2023秋•新都区期末)如图,将含有30°的直角三角尺CAB(∠C=60°)直角顶点A放到矩形DEFH 的边DE上,若∠EAB=15°,则∠FQG的度数是()A.25°B.30°C.35°D.45°【分析】先根据∠EAB=15°,∠CAB=90°得出∠CAE的度数,再由HF∥DE得出∠CMF的度数,由三角形内角和定理得出∠CQM的度数,进而可得出结论.【解答】解:∵∠EAB=15°,∠CAB=90°,∴∠CAE=90°﹣15°=75°,∵HF∥DE,∴∠CMF=∠CAE=75°,∵∠C=60°,∴∠CQM=180°﹣60°﹣75°=45°,∴∠FQG=∠CQM=45°.故选:D.【点评】本题考查的是平行线的性质,熟知两直线平行,同位角相等是解题的关键.8.将一副三角尺如图放置,其中∠D=∠BAC=90°,∠F=30°,∠B=45°,则∠BCF的度数为()A.105°B.120°C.150°D.165°【分析】由∠D=∠BAC,利用“同位角相等,两直线平行”,可得出AC∥DF,利用“两直线平行,同位角相等”,可求出∠ACE的度数,结合∠BCE=∠ACB﹣∠ACE,可求出∠BCE的度数,再利用邻补角互补,即可求出∠BCF的度数.【解答】解:∵∠D=∠BAC=90°,∴AC∥DF,∴∠ACE=∠F=30°,∴∠BCE=∠ACB﹣∠ACE=45°﹣30°=15°.又∵∠BCE+∠BCF=180°,∴∠BCF﹣180°﹣∠BCE=180°﹣15°=165°.故选:D.【点评】本题考查了平行线的判定与性质以及邻补角,根据各角之间的关系,求出∠BCE的度数是解题的关键.9.一副三角形板如图放置,DE∥BC,∠C=∠DBE=90°,∠E=45°,∠A=30°,则∠ABD的度数为()A.5°B.15°C.20°D.25°【分析】根据三角形内角和定理以及平行线的性质,即可得到∠DC=45°,∠AB=60据此可得∠ABD的度数.【解答】解:Rt△ABC中,∠A=30°,∴∠ABC=60,∵BC∥DE,∠EDB=∠E=45°,∴∠DBC=45°,∴∠ABD=60°﹣45°=15°,故选:B.【点评】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,内错角相等.10.如图,将一副三角尺按图中所示位置摆放,点F在AC上,∠ACB=90°,∠ABC=60°,∠EFD=90°,∠DEF=45°,AB∥DE.则∠AFD的度数是()A.25°B.20°C.15°D.10°【分析】利用三角板的度数可得∠A=30°,∠D=45°,由平行线的性质定理可得∠1=∠D=45°,利用三角形外角的性质可得结果.【解答】解:如图,∵∠ACB=90°,∠ABC=60°,∴∠A=180°﹣∠ACB﹣∠ABC=180°﹣90°﹣60°=30°,∵∠EFD=90°,∠DEF=45°,∴∠D=180°﹣∠EFD﹣∠DEF=180°﹣90°﹣45°=45°,∵AB∥DE,∴∠1=∠D=45°,∴∠AFD=∠1﹣∠A=45°﹣30°=15°,故选:C.【点评】本题主要考查了平行线的性质定理和外角的性质,求出∠A,∠D的度数是解本题的关键.11.(2023秋•莲湖区期末)如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠2=55°,求∠1的度数.【分析】先根据两直线平行的性质,得到∠3=∠2,再根据平角的定义,即可得出∠1的度数.【解答】解:∵AB∥CD,∴∠2=∠3.∵∠2=55°,∴∠3=55°.∵∠1+60°+∠3=180°,∴∠1=65°.【点评】本题主要考查了平行的性质,解题的关键是掌握:两直线平行,同位角相等.12.将一副直角三角板如图1摆放在直线MN上(直角三角板ABC和直角三角板EDC,∠EDC=90°,∠DEC=60°,∠ABC=90°,∠BAC=45°),保持三角板EDC不动,将三角板ABC绕点C以每秒5°的速度顺时针旋转,旋转时间为t秒,当AC与射线CN重合时停止旋转.(1)如图2,当AC为∠DCE的角平分线时,t=.(2)当t=18时,求∠BCD的度数?(3)在旋转过程中,当三角板ABC的AB边平行于三角板EDC的某一边时(不包含重合的情形),求此时t的值为.(直接写出答案即可)【分析】(1)当AC为∠DCE的角平分线时,可以求出旋转角,再根据旋转的速度即可求解.(2)当t=18时,旋转角为90°,可求出∠ACD,即可求出∠BCD.(3)数形结合,分情况进行讨论即可.【解答】解:(1)当AC为∠DCE的角平分线时,旋转角为15°,∴t=155=3,故答案为3.(2)当t=18时,旋转角为90°,如图:∵∠DCE=30°,∠ACB=45°,∴∠ACD=60°,∠BCD=60°﹣45°=15°.(3)当三角板ABC的AB边平行于三角板EDC的某一边时,有3种情况:①当AB∥DE时,如图:此时,BC与CD重合,t=(30+40)÷5=15,②当AB∥CE时,如图:∵AB∥CE,∴∠BCE=∠B=90°,∴∠ACE=90°+45°=135°,∴t=135÷5=27,③当AB∥CD时,如图:∵AB∥CD,∴∠BCD=∠D=90°,∴∠ACE=30°+90°+45°=165°,∴t=165÷3=33.综上所述,t=15或27或33.【点评】本题考查旋转的性质,角平分线的性质,平行线的性质,关键在于数形结合,分类讨论.1.如图,在弯形管道ABCD中,若AB∥CD,拐角∠ABC=122°,则∠BCD的大小为()A.58°B.68°C.78°D.122°【分析】根据平行线的性质得出∠ABC+∠BCD=180°,代入求出即可.【解答】解:∵AB∥CD,∴∠ABC+∠BCD=180°,∵∠ABC=122°,∴∠BCD=180°﹣122°=58°,故选:A.【点评】本题考查了平行线的性质,能熟练地运用平行线的性质定理进行推理是解此题的关键,注意:两直线平行,同旁内角互补.2.如图,万岁山大宋武侠城的两条小路AB∥CD,则∠BAE+∠AEC+∠ECD=()A.180°B.270°C.360°D.540°【分析】作辅助线EF∥AB,然后根据平行线的性质,可以得到∠BAE+∠AEC+∠ECD的度数.【解答】解:过点E作EF∥AB,如图:∵AB∥CD,∴AB∥CD∥EF,∴∠BAE+∠AEF=180°,∠FEC+∠ECD=180°,∵∠AEF+∠FEC=∠AEC,∴∠BAE+∠AEC+∠ECD=360°,故选:C.【点评】本题考查平行线的性质,解答本题的关键是熟练掌握平行线的性质,明确题意,利用数形结合的思想解答.3.(2023秋•海门区期末)如图,两面镜子AB,BC的夹角为∠α,入射光线OM经过镜子两次反射后的出射光线NO平行于AB,图中∠1=∠2,∠3=∠4.当OM∥BC时,∠α的度数是()A.30°B.45°C.60°D.75°【分析】由平行线的性质推出∠4=∠α,∠1=∠α,又∠3=∠4,∠2=∠1,得到∠1=∠2=∠α,判定△MNB是等边三角形,得到∠α=60°.【解答】解:∵ON∥AB,∴∠4=∠α,∵∠3=∠4,∴∠3=∠α,∵OM∥BN,∴∠1=∠α,∵∠2=∠1,∴∠2=∠α,∴∠3=∠2=∠α,∴△MNB是等边三角形,∴∠α=60°.故选:C.【点评】本题考查平行线的性质,关键是由平行线的性质推出∠3=∠2=∠α.4.(2023秋•即墨区期末)生活中的椅子一般依据人体工学原理设计,如图为生活中一把椅子的侧面图,从人体脊柱的形势而言,当靠背角度∠DEF=115°时,能产生较为接近自然腰部的形状,此时最舒适.已知DE与地面平行,支撑杆BD与地面夹角∠ABD=50°,则制作时用螺丝固定时支撑杆BD和AF需构成夹角∠ACB为()A.70°B.65°C.60°D.50°【分析】先求出∠DEC的度数,再求出∠CAB的度数,最后求出∠ACB的度数.【解答】解:∵∠DEF=115°,∴∠DEC=180°﹣∠DEF=65°,∵DE∥AB,∴∠CAB=∠DEC=65°,∵∠ABD=50°,∴∠ACB=180°﹣∠ABD﹣∠CAB=65°.故选:B.【点评】本题主要考查了平行线的性质,解题的关键是熟练运用平行线的性质.5.当光从一种介质射向另一种介质时,光线会发生折射,不同介质的折射率不同.如图,水平放置的水槽中装有适量水,空气中两条平行光线射入水中,两条折射光线也互相平行.若∠1=110°,则∠2的度数为()A.70°B.60°C.50°D.40°【分析】根据题意可得:AB∥CE,然后利用平行线的性质可得∠ACE=70°,再利用两直线平行,内错角相等可得∠2=∠ACE=70°,即可解答.【解答】解:如图:由题意得:AB∥CE,∴∠1+∠ACE=180°,∴∠ACE=180°﹣∠1=70°,∵AC∥BE,∴∠2=∠ACE=70°,故选:A.【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.6.(2023秋•鹿寨县期末)如图1是某景区电动升降门,将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,当CD平行于地面AE时,则∠ABC+∠BCD=.【分析】过点B作BF∥AE,如图,由于CD∥AE,则BF∥CD,根据两直线平行,同旁内角互补得∠BCD+∠CBF=180°,由AB⊥AE得AB⊥BF,所以∠ABF=90°,于是有∠ABC+∠BCD=∠ABF+∠CBF+∠BCD =270°.【解答】解:过点B作BF∥AE,如图:∵CD∥AE,∴BF∥CD,∴∠BCD+∠CBF=180°,∵AB⊥AE,∴AB⊥BF,∴∠ABF=90°,∴∠ABC+∠BCD=∠ABF+∠CBF+∠BCD=90°+180°=270°.故答案为:270°.【点评】本题主要考查了平行线的性质,正确作出辅助线,并熟记两直线平行,同旁内角互补是解决问题的关键.7.(2023秋•鼓楼区校级期末)如图是路灯维护工程车的工作示意图,工作篮底部与支撑平台平行.若∠1=30°,则∠2+∠3的度数为.【分析】过∠2顶点做直线l∥支撑平台,直线l将∠2分成两个角,根据平行的性质即可求解.【解答】解:过∠2顶点做直线l∥支撑平台,∴l∥支撑平台∥工作篮底部,∴∠1=∠4=30°、∠5+∠3=180°,∴∠4+∠5+∠3=30°+180°=210°,∵∠4+∠5=∠2,∴∠2+∠3=210°.故答案为:210°.【点评】本题考查平行线的性质,熟练掌握平行线的性质是解题的关键.8.某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知∠BAC=130°,AB∥DE,∠D=70°,则∠ACD=.【分析】过点C作CF∥AB,先证明CF∥DE,然后根据平行线的性质求出∠ACF=130°,∠DCF=110°,最后利用角的和差关系求解即可.【解答】解:过点C作CF∥AB,∵AB∥DE,∴CF∥DE,∴∠ACF=∠BAC,∠D+∠DCF=180°,又∠BAC=130°,∠D=70°,∴∠ACF=130°,∠DCF=110°,∴∠ACD=∠ACF﹣∠DCF=20°.故答案为:20°.【点评】本题考查了平行线的判定与性质,添加合适的辅助线是解题的关键.9.乐乐观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=121°,则∠AEC的度数是()A.30°B.29°C.28°D.27°【分析】延长DC交AE于F,依据AB∥CD,∠BAE=92°,可得∠CFE=92°,再根据三角形外角性质,即可得到∠AEC=∠DCE﹣∠CFE.【解答】解:如图,延长DC交AE于F,∵AB∥CD,∠BAE=92°,∴∠CFE=92°,又∵∠DCE=121°,∴∠AEC=∠DCE﹣∠CFE=121°﹣92°=29°.故选:B.【点评】本题主要考查了平行线的性质,解决问题的关键是掌握:两直线平行,同位角相等.10.(2023秋•鹰潭期末)生活现象如图1,杆秤是中国最古老也是现今人们仍然在使用的衡量工具,是利用杠杆原理来称质量的简易衡器,由木制的带有秤星的秤杆、金属秤砣、提绳等组成.数学模型如图2,是杆秤的示意图,AC∥BD,经测量发现∠A=104°,∠BOE=76°,请判断OE与BD的位置关系,并说明理由.【分析】由AC∥BD可得∠A+∠ABD=180°,进而得出∠ABD=76°,再根据内错角相等,两直线平行可得答案.【解答】解:OE∥BD,理由如下:∵AC∥BD,∴∠A+∠ABD=180°,∴∠ABD=180°﹣104°=76°,∴∠ABD=∠BOE,∴OE∥BD.【点评】本题考查了平行线的判定和性质,熟练掌握这些判定和性质解题的关键.11.如图所示①是一种网红弹弓的示意图,在两头系上皮筋,拉动皮筋可形成如图②所示的平面示意图,弹弓的两边可看成平行的,即AB∥CD.活动小组在探索∠APD与∠A,∠D的数量关系时,有如下发现:当拉起皮筋使∠A=∠D时,瞄准最准确.现测得∠A=160°,∠APD=40°,判断此时瞄准是否最准确,请说明理由.【分析】如图所示,过点P作PQ∥AB,利用平行线的性质得到∠APQ=180°﹣∠A=20°,∠D=180°﹣∠DPQ,在求出∠DPQ的度数即可得到答案.【解答】解:此时瞄准最准确.如图所示,过点P作PQ∥AB,∵AB∥CD,∴AB∥PQ∥CD,∴∠APQ=180°﹣∠A=20°,∠D=180°﹣∠DPQ,∵∠APD=40°,∴∠DPQ=∠APD﹣∠APQ=20°∴∠D=160°,此时瞄准最准确.【点评】本题主要考查了平行线的性质,正确作出辅助线是解题的关键.1.(2023秋•天元区期末)如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFC=125°,则∠1=()A.35°B.55°C.70°D.65°【分析】根据两直线平行,同旁内角互补可得∠DEF+∠EFC=180°,再根据翻折的性质和平角的定义列式计算,即可求出∠1.【解答】解:∵长方形对边AD∥BC,∴∠DEF+∠EFC=180°,∴∠DEF=180°﹣∠EFC=180°﹣125°=55°,由翻折的性质得:∠DEF=∠MEF=55°,∴∠1=180°﹣55°×2=70°,故选:C.【点评】本题主要考查平行线的性质,折叠的性质,熟练掌握平行线的性质和折叠的性质是解题的关键.2.如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=30°,则∠EFC′的度数为()A.120°B.100°C.150°D.90°【分析】根据折叠的性质知∠BEF=∠DEF,而∠AEB的度数可在Rt△ABE中求得,根据平角定义可求出∠BED的度数,即得∠BEF的度数,再根据平行线的性质即可得解.【解答】解:Rt△ABE中,∠ABE=30°,∴∠AEB=60°,由折叠的性质知:∠BEF=∠DEF=12∠BED,∵∠BED=180°﹣∠AEB=120°,∴∠BEF=60°,∵BE∥C′F,∴∠BEF+∠EFC′=180°,∴∠EFC′=180°﹣∠BEF=120°.故选:A.【点评】本题考查平行线的性质,熟记折叠的性质及“两直线平行,同旁内角互补”是解题的关键.2.如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A'处,点B落在点B'处,若∠1=115°,则图中∠2的度数为()A.40°B.45°C.50°D.60°【分析】由邻补角概念和翻折变换性质得出∠EFB′=∠1=115°,∠EFC=65°,据此知∠CFB′=50°,结合∠B=∠B′=90°知∠2=90°﹣∠CFB′,从而得出答案.【解答】解:∵∠1=115°,∴∠EFB′=∠1=115°,∠EFC=65°,∴∠CFB′=50°,又∵∠B=∠B′=90°,∴∠2=90°﹣∠CFB′=40°,故选:A.【点评】本题主要考查翻折变换的性质,解题的关键是掌握翻折变换的对应边、对应角相等的性质及直角三角形两锐角互余、对顶角相等的性质.3.(2022•南京模拟)如图,将一块长方形纸条折成如图的形状,若已知∠1=α,则∠2的度数为()A.90°﹣αB.45°+αC.45°+2D.90°−2【分析】根据平行线的性质即可求解.【解答】解:如图,作过点B的射线AF',∵AB∥CD,∴∠1+∠FBC+∠2=180°,∠F'BC=∠2∵纸条是对折,∴∠FBC=∠F'BC=∠2,∴2∠2+∠1=180°,∵∠1=α,∴∠2=12×(180°﹣α),∴∠2=90°−12α,故选:D.【点评】本题考查了平行线的性质,本题的解题关键找出是纸条对折后的角度关系.4.(2022秋•宛城区校级期末)如图,把一个长方形纸片沿OG折叠后,C,D两点分别落在C',D'两点处,若∠AOD':∠D'OG=4:3,则∠BGO=度.【分析】设∠AOD'=4x,则∠D'OG=3x,由翻折可知∠DOG=∠D'OG=3x,根据平角的定义解出x,由矩形的性质进而可以得出∠BGO的度数.【解答】解:∵∠AOD':∠D'OG=4:3,设∠AOD'=4x,则∠D'OG=3x,由翻折可知∠DOG=∠D'OG=3x∵∠AOD'+∠D'OG+∠DOG=180°,即10x=180°,解得x=18°,∵AD∥BC,∴∠BGO=∠DOG=3x=54°,故答案为:54.【点评】本题考查了折叠的性质和平角的等于180°,解题关键是发现图中折叠前后重合的角相等.5.(2023秋•北林区校级期末)将长方形ABCD纸片沿AE折叠得到如图所示的图形,已知∠CED′=68°,则∠EAB的度数是.【分析】由折叠可得∠DEA=∠D'EA,再由已知的条件可求得∠DEA的度数,从长方形可得AB∥CD,从而可求∠EAB的度数.【解答】解:由折叠得:∠DEA=∠D'EA,∵∠CED′=68°,∴∠DED'=180°﹣∠CED'=112°,∴∠DEA=12∠DED'=56°,∵四边形ABCD是长方形,∴AB∥CD,∴∠EAB=∠DEA=56°.故答案为:56°.【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的性质:两直线平行,内错角相等.6.(2023秋•萍乡期末)如图,△ABC中,∠B=40°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠ADE的度数为°.【分析】根据平行线的性质得到∠BDE=∠B=40°,根据折叠的性质得到∠ADE=∠ADC,根据平角的定义可得∠ADB+∠ADC=180°,由此可以求出∠ADC的度数即可得到答案.【解答】解:∵DE∥AB,∠B=40°,∴∠BDE=40°,由折叠的性质得∠ADE=∠ADC,∵∠ADB+∠ADC=180°,∠ADB=∠ADE﹣∠BDE=∠ADC﹣40°,∴∠ADC﹣40°+∠ADC=180°,∴∠ADC=110°,∴∠ADE=∠ADC=110°.故答案为:110.【点评】本题考查了折叠的性质,平行线的性质,熟练掌握平行线的性质、折叠的性质是解题的关键.7.(2023秋•淮南期末)如图,在Rt△ABC中,∠C=90°,∠1=76°,D、E分别在AB、AC上,将△ADE沿DE折叠得△FDE,且满足EF∥AB,则∠B的度数为.【分析】由折叠的性质得∠FED=∠1,∠A=∠F,根据平角的定义求出∠FEC的度数,再根据平行线的性质求出∠F的度数,即可得出∠A的度数,从而求出∠B的度数.【解答】解:由折叠的性质得∠FED=∠1,∠A=∠F,∵∠1=76°,∴∠FED=76°,∴∠FEC=180°﹣∠FED﹣∠1=180°﹣76°﹣76°=28°,∵EF∥AB,∴∠F=∠FEC=28°,∴∠A=28°,∵∠C=90°,∴∠B=90°﹣∠A=90°﹣28°=62°,故答案为:62°.【点评】本题考查了平行线的性质,折叠的性质,平角的定义,三角形内角和定理,熟练掌握这些知识点是解题的关键.8.(2023秋•丹徒区期末)如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠EFC =30°,则∠DAE等于.【分析】由长方形的性质得出∠D=90°,AD∥BC,再由折叠的性质得出∠DAE=∠FAE,∠AFE=∠D =90°,结合已知∠EFC=30°即可求出∠AFB的度数,从而求出∠DAE的度数.【解答】解:∵四边形ABCD为长方形,∴∠D=90°,AD∥BC,由折叠得,∠DAE=∠FAE,∠AFE=∠D=90°,∵∠EFC=30°,∴∠AFB=180°﹣∠AFE﹣∠EFC=180°﹣90°﹣30°=60°,∵AD∥BC,∴∠AFB=∠DAF,即60°=2∠DAE,∴∠DAE=30°,故答案为:30°.【点评】本题考查了平行线的性质,长方形的性质,折叠的性质,熟练掌握这些图形的性质是解题的关键.9.(2022•郑州模拟)如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为C'、D'.若∠DEF =α,用含α的式子可以将∠C'FG表示为()A.2αB.90°+αC.180°﹣αD.180°﹣2α【分析】由折叠的性质可得:∠DEG=2α,C'F∥D'E,由AD∥BC可得∠D'GF=∠DEG=2α,从而有∠C'FG=180°﹣∠D'GF,即可得出结果.【解答】解:由长方形纸带ABCD及折叠性质可得:∠D'EF=∠DEF=α,C'F∥D'E,∴∠DEG=2∠DEF=2α,∠C'FG=180°﹣∠D'GF,∵AD∥BC,∴∠D'GF=∠DEG=2α,∴∠C'FG=180°﹣2α.故选:D.【点评】本题主要考查平行线的性质,折叠的性质,解答的关键是熟记折叠的性质.10.(2023秋•泉州期末)如图,四边形ABCD是一条两边互相平行的纸带,将其沿着EG折叠,使得点B,C分别落在点H,I处,EH与DG相交于点F,若∠EGF=56°,求∠EFD的度数.【分析】利用平行线的性质可得∠BEG=∠EGD=56°,再利用折叠的性质可得:∠BEF=2∠BEG=112°,然后利用平行线的性质可得∠BEF=∠EFD=112°,即可解答.【解答】解:∵AB∥CD,∴∠BEG=∠EGD=56°,由折叠得:∠BEF=2∠BEG=112°,∵AB∥CD,∴∠BEF=∠EFD=112°,∴∠EFD的度数为112°.【点评】本题考查了平行线的性质,根据题目的已知条件并结合图形进行分析是解题的关键.11.在图中,图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3.(1)若在图1中,∠DEF=20°,则图3中∠C2FE的度数是多少?(2)若∠DEF=α,请用α表示图3中的∠C2FE的度数.【分析】(1)根据两直线平行,同旁内角互补可得∠CFE=160°,根据两直线平行,内错角相等可得∠BFE=∠DEF,然后求出∠BFC1,再根据翻折的性质可得∠CFE=∠EFC1,∠C2FB+∠BFC1,即可得解;(2)同(1)的方法求解即可.【解答】解:(1)∵矩形对边AD∥BC,∴CF∥DE,∴∠CFE=180°﹣∠DEF=180°﹣20°=160°,∵AD∥BC,∴∠BFE=∠DEF=20°,由翻折的性质得,∠CFE=∠EFC1,∴∠BFC1=160°﹣20°=140°,由翻折的性质得,∠C2FB+∠BFC1,所以,∠C2FE=140°﹣20°=120°;(2)∵矩形对边AD∥BC,∴CF∥DE,∴∠CFE=180°﹣∠DEF=180°﹣α,∵AD∥BC,∴∠BFE=∠DEF=α,由翻折的性质得,∠CFE=∠EFC1,∴∠BFC1=180°﹣α﹣α=180°﹣2α,由翻折的性质得,∠C2FB+∠BFC1,所以,∠C2FE=180°﹣2α﹣α=180°﹣3α.【点评】本题考查了平行线的性质,翻折变换的性质,熟记各性质并准确识图,理清翻折前后重叠的角是解题的关键.12.(2022秋•东阳市期末)如图,长方形纸片ABCD中,G、H分别是AB、CD边上的动点,连GH,将长方形纸片ABCD沿着GH翻折,使得点B,C分别落在点E,F位置.(1)若∠BGH=110°,求∠AGE的度数.(2)若∠FHD=20°,求∠CHG的度数.(3)已知∠BGH和∠CHG始终互补,若∠BGH=α,请直接写出∠FHC的度数(含α的代数式).【分析】(1)根据折叠得到∠BGH=∠EGH=110°,再根据平角的定义,利用∠AGE=∠BGH+∠EGH ﹣180°计算可得;(2)根据折叠得到∠CHG=∠FHG,再根据平角的定义计算即可;(3)根据互补得到∠BGH+∠CHG=180°,从而求出∠CHG=∠FHG=180°﹣α,分情况继而可得结果.【解答】解:(1)由折叠可得:∠BGH=∠EGH=110°,∵∠BGH+∠AGH=180°,∴∠AGE=∠BGH+∠EGH﹣180°=40°;(2)由折叠可得:∠CHG=∠FHG,∴∠C=12(180°−∠Cp=80°;(3)情况一:∵∠BGH和∠CHG始终互补,∴∠BGH+∠CHG=180°,∵∠BGH=α,∴∠CHG=180°﹣α,∴∠FHG=180°﹣α,∴∠FHC=∠FHG+∠CHG=360°﹣2α.情况二:由第一种情况可知:∠1=360°﹣2α,∴∠FHC=360°﹣(360°﹣2α)=2α.【点评】本题考查了折叠的性质,平角的定义,解题的关键是掌握折叠前后对应角相等.。
三角形内角和

三角形内角和三角形是几何学中最基本的图形之一,它由三条线段组成,每个线段都与其他两条线段相连接形成三个内角。
本文将讨论三角形的内角和,并对其性质进行探究。
一、三角形的内角和性质设三角形的三个内角分别为A、B、C,其内角和为180度。
也就是说,A + B + C = 180度。
这个性质被称为三角形内角和定理,是几何学中最基本的性质之一。
二、证明三角形内角和性质要证明三角形内角和为180度,可以通过多种方法进行证明。
本文将介绍两种常用的证明方法。
方法一:三角形内角和与直线平行性质结合在三角形ABC中,延长边AC,分别延长到点D和E上,使得AD和BE与BC平行。
根据平行线性质,∠BED与∠EBC为内错角、∠CAD与∠ACB为内错角。
考虑△ADC,对内角A进行角度求和,则∠CAD + ∠ADC = 180度。
考虑△BEC,对内角B进行角度求和,则∠BED + ∠BEC = 180度。
观察△ADC和△BEC的内角和,有∠CAD + ∠ADC + ∠BED +∠BEC = 360度。
将上述两个等式相减,得到∠CAD + ∠ADC - (∠CAD + ∠ACB) +∠BED + ∠BEC - (∠BEC + ∠ACB) = 360度 - 180度。
化简可得∠ADC - ∠ACB + ∠BED - ∠ACB = 180度。
即有∠ADC + ∠BED = 2∠ACB。
继续化简,得到2∠ACB = 180度,即∠ACB = 90度。
由此可得,三角形ABC中的一个内角为90度。
结合前面提到的三角形内角和定理,可推知三角形的另外两个内角之和也为90度。
所以,三角形的内角和为180度。
方法二:三角形内角和与直线平行性质相结合在三角形ABC中,延长边AC,接下来在边BC的延长线上取一点D,使得AD与AC重合。
根据三角形内角和定理,∠ABC + ∠BAC + ∠BCA = 180度。
在三角形ABC中,AD || BC,根据平行线性质,可知∠ABC +∠ACD = 180度。
人教版_部编版八年级数学上册第十一章第二节三角形的内角复习试题(含答案) (76)

人教版_部编版八年级数学上册第十一章第二节三角形的内角试题(含答案)如图,AD 是∆ABC 的高,BE 平分∠ABC 交AD 于点E .若∠C = 76︒,∠BED = 64︒.求∠BAC 的度数.【答案】58°【解析】【分析】由已知条件,首先得出∠DAC=20°,再利用∠ABE=∠EBD,进而得出∠ABE+∠BAE=64°,求出∠EBD=26°,进而得出答案.【详解】∵AD是△ABC的高,∠C=70°,∴∠DAC=20°,∵BE平分∠ABC交AD于E,∴∠ABE=∠EBD,∵∠BED=64°,∴∠ABE+∠BAE=64°,∴∠EBD+64°=90°,∴∠EBD=26°,∴∠BAE=38°,∴∠BAC=∠BAE+∠CAD=38°+20°=58°. 【点睛】此题主要考查了三角形的外角与三角形内角和定理等知识,题目综合性较强,注意从已知条件得出所有结论是解决问题的关键.52.(1)在锐角ABC ∆中,AC 边上的高所在直线和AB 边上的高所在直线的交点为P ,110BPC ∠=︒,求A ∠的度数.(2)如图,AF 和CE 分别平分BAD ∠和BCD ∠,当点D 在直线AC 上时,100APC ∠=︒,则B ∠=_________.(3)在(2)的基础上,当点D 在直线AC 外时,如下图:130ADC ∠=︒,100APC ∠=︒,求B 的度数.【答案】(1)70︒;(2)20︒;(3)70︒.【解析】 【分析】(1)根据对顶角相等以及四边形的内角和进行判断即可;(2)根据100APC ∠=︒以及AF 和CE 分别平分BAD ∠和BCD ∠,算出BAD ∠和BCD ∠,从而算出B【详解】如图AC 边上的高所在直线和AB 边上的高所在直线的交点为P ∴90BDA CEA ∠=∠=︒ 又∴110BPC ∠=︒ ∴110EPD BPC ∠=∠=︒∴在四边形AEPD 中,内角和为360︒ ∴=360-110-90-90=70A ∠︒︒︒︒︒(2)∵AF 和CE 分别平分BAD ∠和BCD ∠ ∴,BAP FAC BCE ACE ∠=∠∠=∠又∵100APC ∠=︒∴+18010080FAC ACE ∠∠=︒-︒=︒ ∴160BAC BCA ∠+∠=︒ ∴=180-160=20B (3)如图:连接AC∵130ADC ∠=︒,100APC ∠=︒∴18013050,18010080DAC DCA PAC PCA ∠+∠=︒-︒=︒∠+∠=︒-︒=︒ ∴2+3=30∠∠︒又∵AF 和CE 分别平分BAD ∠和BCD ∠ ∴1+4=2+3=30∠∠∠∠︒ ∴110BAC BCA ∠+∠=︒ ∴=180-110=70B 【点睛】三角形的内角和定理以及角平分线的定义是解决本题的关键.53.小学我们已经知道三角形三个内角和是180°,对于如图1中,AC ,BD 交于O 点,形成的两个三角形中的角存在以下关系:①DOC AOB ∠=∠;②D C A B ∠+∠=∠+∠.试探究下面问题:已知BAD ∠的平分线AE 与BCD ∠的平分线CE 交于点E ,(1)如图2,若AB CD ∥,30D ∠=︒,40B ∠=︒,则E ∠=_________; (2)如图3,若AB 不平行CD ,30D ∠=︒,50B ∠=︒,则E ∠=_______. (3)在总结前两问的基础上,借助图3,探究E ∠与D ∠、B 之间是否存在某种等量关系?若存在,请说明理由;若不存在,请举例说明.【答案】(1)35°;(2)40°;(3)∠D+∠B=2∠E ,理由见解析 【解析】 【分析】(1)(2)在∴CDF 和△AEF 中,有:∴D+∠DCF= ∴E+∠DAE ∴;在∴ABG 和△CEG 中, ∴B+∠EAB= ∴E+∠BCE ∴;∴+∴再结合BAD ∠的平分线AE 与BCD ∠的平分线CE 交于点E ,进行化简得到∴E=12(∠B+∠D ),然后将∴B 和∴D 代入即可解答;(3)根据(1)(2)的推导即可得到∴D+∴B=2∴E . 【详解】解:(1)如图2在∴CDF 和△AEF 中,有∴D+∠DCF= ∴E+∠DAE ① ∴ABG 和△CEG 中, 有∴B+∠EAB= ∴E+∠BCE ∴∴+∴得:∴D+∠DCF +∴B+∠EAB =∴E+∠DAE +∴E+∠BCE 又∵BAD ∠的平分线AE 与BCD ∠的平分线CE 交于点E ∴∠DCF =∠BCE ,∠EAB =∠DAE∴∴E=12(∠B+∠D )∵30D ∠=︒,40B ∠=︒ ∴∴E =35°(2)如图3:同(1)可得∴E=12(∠B+∠D )∵30D ∠=︒,50B ∠=︒ ∴∴E =40°(3)解:∴D+∴B=2∴E . 理由如下:在∴CDF 和△AEF 中,有∠D+∠DCF= ∠E+∠DAE ① ∴ABG 和△CEG 中, 有∠B+∠EAB= ∠E+∠BCE ∴∴+∴得:∠D+∠DCF +∠B+∠EAB =∠E+∠DAE +∠E+∠BCE 又∵BAD ∠的平分线AE 与BCD ∠的平分线CE 交于点E ∴∠DCF =∠BCE ,∠EAB =∠DAE∴∴E=12(∠B+∠D )∴∴D+∴B=2∴E 【点睛】考查了平行线的性质、三角形内角和定理、对顶角相等的性质,解题方法较多,关键在于选择合适的解题方法.54.如图,平面直角坐标系中, 4,2, 6()(4),,B C --//BE x 轴,点A 从原点O 出发在x 轴上以1单位/秒的速度向x 轴的正方向运动,运动的时间为t秒.,OAB m BD ∠=︒平分ABC ∠. (提示:ABC ∆中,90︒∠=C ,若,AC BC =则45A B ︒∠=∠=,反之亦然)(1)当4t =时,m = ;(2)当ABC ∆的面积为3时,求A 点运动的时间t ;(3)当0t >时,求DBE ∠的度数(用含m 的式子表示,且不含绝对值).【答案】(1)90m ︒=;(2)()5t s =;(3)当02t <<时,4052m DBE ︒︒-∠=;当2t =时,45DBE ︒∠=或135︒;当26t ≤≤时,452m DBE ︒︒-∠=;当6t >时,452m DBE ︒︒-∠=.【解析】 【分析】(1)求出点A 的坐标即可判断.(2)如图2中,延长CB 交x 轴于K ,则看(2,0).设A (n ,0).根据S △ABC =S △AKC −S △AKB =3,解方程求出n 即可解决问题.(3)分四种情形:如图3−1中,当0<t <2时,∠DBE =∠CBD +∠CBE .如图3−2中,当t =2时,∠DBE =45°或135°.如图3−3中,当2<t ≤6时,∠DBE =∠ABE =∠ABD .如图3−4中,当t >6时,∠DBE =∠CBE −∠CBD ,分别求解即可解决问题.【详解】(1)如图1中,当t =4时,OA =4, ∴A (4,0), ∵B (4,−2), ∴AB ⊥OA ,∴∠OAB =90°,即m =90. 故答案为90.()2延长CB 交x 轴于点K ,过C 作CT BE ⊥于点T 连接KTLTC LBT BTC S S S ∆∆∆=+()2,0K ∴ 设A (n ,0).又S △ABC =S △AKC −S △AKB =3112422322n n ∴⨯-⨯=⨯-⨯+ 解得n=5或n=-1(舍去)()551t s ∴==时,ABC ∆的面积为3; (3)如图3−1中,当0<t <2时,∵∠ABC =(180°−m °)+(180°−45°)=315−m °,BD 平分∠ABC ,∴∠CBD =12∠ABC =3152m ︒-︒ ∴∠DBE =∠CBD +∠CBE =2180135m ︒-︒+︒+45°=4052m ︒-︒如图3−2中,当t =2时,∠DBE =45°或135°如图3−3中,当2<t ≤6时, ∵OA ∥BE ,∴∠ABE =∠OAB =m °, ∴∠ABC =45°+m °,∵BD 平分∠ABC , ∴∠ABD =452m ︒+︒, ∴∠DBE =∠ABE −∠ABD =m °−452m ︒+︒=452m ︒-︒如图3−4中,当t >6时,同法可得:∠DBE =∠CBE −∠CBD =45°−452m ︒+︒=452m ︒-︒;综上,当02t <<时,4052D E m B ︒-∠︒=;当2t =时,45DBE ∠=︒或135︒;当26t ≤≤时,452DBE m ︒-∠︒=;当6t >时,452DBE m ︒-∠︒=.【点睛】本题属于三角形综合题,考查了坐标图图形的性质,三角形的面积,角平分线,平行线的性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.55.如图,//,84AB CD ABE ︒∠=.(1)求:EFC ∠的大小;(2)若3ABE DCE =∠∠,求:E ∠的大小.【答案】(1)96EFC ︒∠=;(2)56BEC ∠=︒.【解析】【分析】(1)根据两直线平行,同位角相等,即可求得∠DFE 的度数,又由邻补角的定义,即可求得∠EFC 的大小.(2)由∠ABE =3∠DCE ,可得∠DCE =28°,又由三角形内角和为180°,即可求得∠E 的度数.【详解】(1)∵AB ∥CD ,∴∠DFE =∠ABE =84°,∴∠EFC =180°−∠DFE =96°;(2)∵∠ABE =3∠DCE ,∴∠DCE =28°,∴∠E =180°−∠EFC −∠DCE =56°.【点睛】 此题考查了平行线的性质.此题比较简单,解题的关键是熟悉两直线平行,同位角相等,注意数形结合思想的应用.56.如图1,已知ABC ∆.(1)求证:180A B C ∠+∠+∠=︒;(2)如图2,ABC ∆中,CD AB ⊥,点,,E F G 分别在BC ,AB ,AC 上,且EF AB ⊥,DG BC .若35B ∠=︒,求1∠、2∠的度数.【答案】(1)证明见解析;(2)2155∠=∠=︒【解析】【分析】(1)要证明180A B C ∠+∠+∠=︒,即证明三角形的内角形是180°,可以通过做BC 的平行线,根据直线平行的性质,得到答案.(2)根据三角形内角和等于180°,35B ∠=︒,EF AB ⊥,可以计算出1∠的度数,根据DG BC ,和等量替换原则可以得到2∠的度数.【详解】解:(1)证明:如图,过A 作BC 的平行线EF,∴EF ∴BC ,∴BAE B ∠=∠,FAC C ∠=∠(两直线平行,内错角相等),∴180BAE FAC BAC ∠+∠+∠=︒,∴180A B C ∠+∠+∠=︒(等量替换).(2)∴EF AB ⊥,∴90BFE ∠=︒.又35B ∠=︒,∴1903555∠=︒-︒=︒∴EF AB ⊥,CD AB ⊥,∴EF CD ∥,∴1BCD ∠=∠,∴DG BC ,∴2BCD ∠=∠,∴2155∠=∠=︒.【点睛】本题反复运用了平行线的性质(两直线平行,内错角相等,同位角相等,同旁内角互补)、等量替换原则,灵活运用所学知识是解题的关键.57.在ABC 中,90,C D ∠=为直线AC 上一点,E 为直线AB 上一点,ADE B ∠=∠(1)如图1,当D 在AC 上,E 在AB 上时,求证DE AB ⊥;(2)如图2,当D 在CA 的延长线上,E 在BA 的延长线上时,点G 在EF 上,连接AG ,且1452EAG D ∠-∠=,求证:2F DGA ∠=∠(3)如图3,在(2)的条件下,连接,BG 当BG 平分ABC ∠时,将AGB 沿着AG 折至,AGH 探究HGD ∠与F ∠的数量关系.【答案】(1)见解析(2)见解析(3)∠F +2∠HGD =90°,理由见解析【解析】【分析】(1)通过三角形内角和定理,可得∠AED =∠ACB =90°,可得结论;(2)由直角三角形的性质和三角形内角和定理可得∠EAG +∠AGE =90°①,∠D+∠F=90°③,且2∠EAG−∠D=90°②,可以组成方程组,可得结论;(3)由角平分线的性质和折叠的性质可得∠ADE=2∠H,由外角性质可得∠ADE=2∠DGH,由直角三角形的性质可得∠F+2∠HGD=90°.【详解】(1)∵∠ADE=∠B,∠A=∠A,且∠ADE+∠A+∠AED=180°,∠B+∠A+∠ACB=180°,∴∠AED=∠ACB=90°,∴DE⊥AB(2)∵∠ADE=∠B,∠DAE=∠BAC,∴∠AED=∠ACB=90°,∴∠EAG+∠AGE=90°①,∵∠EAG−12∠D=45°,∴2∠EAG−∠D=90°②,∵∠D+∠F=90°③,∴②+③得:2∠EAG+∠F=180°④,④−①×2得:∠F−2∠AGE=0°,∴∠F=2∠AGE,(3)如图3,∵BG平分∠ABC,∴∠ABG=12∠ABC,∵将△AGB沿着AG折至△AGH,∴∠H=∠ABG=12∠ABC,∵∠ADE=∠B,∴∠ADE=2∠H,且∠ADE=∠H+∠DGH,∴∠H=∠DGH,∴∠ADE=2∠DGH,∵∠F+∠CDF=90°,∴∠F+2∠HGD=90°.【点睛】本题是三角形综合题,考查了三角形内角和定理,折叠的性质,利用方程的思想解决问题是本题的关键.58.已知:如图,//,,AD BC B D∠=∠求证:E F∠=∠.【答案】见解析【解析】【分析】根据平行线的性质得到∠DAB+∠B=∠BCD+∠D=180°,∠2=∠3,等量代换得到∠DAB=∠BCD,根据对顶角的性质得到∠1=∠2,∠3=∠4,等量代换得到∠1=∠4,根据三角形的外角的性质得到∠E=∠DAB-∠1,∠F=∠BCD-∠4,于是得到结论.【详解】如下图:∵AD∥BC,∴∠DAB+∠B=∠BCD+∠D=180°,∠2=∠3,∵∠B=∠D,∴∠DAB=∠BCD,∵∠1=∠2,∠3=∠4,∴∠1=∠4,∴∠E=∠DAB-∠1,∠F=∠BCD-∠4,∴∠E=∠F.【点睛】此题主要查了平行线的性质与判定以及三角形内角和定理等知识,熟练正确平行线的性质是解决问题的关键.59.如图①,点D E 、是ABC 的边AB AC 、上一点,连结,DE 把ABC 沿DE 折叠,使点A 落在'A 处,令'1'2AD B A EC ∠=∠∠=∠,.(1)如图②,当点A 落在四边形BCED 内部时,若'30DA E ∠=︒,则12∠+∠的度数为 ;(2)事实上,当点A 落在四边形BCED 内部时,DA E '∠与12∠∠、之间的数量关系始终保持不变,请写出DA E '∠与1 2∠∠、之间的数量关系,并利用图②进行证明;(3)如图③,当点A 落在四边形BCED 外部时,直接写出DA E '∠与1 2∠∠、之间的数量关系为 .【答案】(1)60;(2)212DA E '∠=∠+∠,证明见解析;(3)212DA E '∠=∠-∠. 【解析】【分析】(1)根据翻折变换的性质用∠1、∠2表示出∠ADE 和∠AED ,再根据三角形的内角和定理列式整理即可得解;(2)设','A DE A ED αβ∠=∠=,分别用含α和β的式子表示出'A ∠、1∠和2∠,求出12∠+∠即可得解;(3)设','A DE DEA αβ∠=∠=,分别用含α和β的式子表示出'A ∠、1∠和2∠,分别对式子变形整理可得答案.【详解】解:(1)由折叠的性质得:∠ADE =∠A ′DE ,∠AED =∠A ′ED ,'30DA E A ∠=∠=︒,∴∠ADE =12(180°−∠1),∠AED =12(180°−∠2), 在△ADE 中,∠A +∠ADE +∠AED =180°,∴30°+12(180°−∠1)+12(180°−∠2)=180°, 整理得:∠1+∠2=60°;(2)设','A DE A ED αβ∠=∠=,则()'180A αβ∠=-+①,11802,28021αβ∠=-∠=︒-,∴1236)0(2αβ∠+∠=︒-+②,由①和②得:122A '∠+∠=∠,即212DA E '∠=∠+∠;(3)设','A DE DEA αβ∠=∠=,则11802,22180αβ∠=︒-∠=-,()'180A αβ∠=︒-+,∴()212360αβ∠-∠=+-,()2'3602A αβ∠=︒-+∵2'12A ∠=∠-∠,即212DA E '∠=∠-∠.【点睛】本题考查了翻折变换的性质,三角形内角和定理,难度不大,熟记性质并准确识图是解题的关键.60.如图,在ABC 中,4460CAB CBA CD ∠=︒∠=︒,,平分ACB ∠交AB 于点D DE AC ⊥,交AC 于点,E 求CDE ∠的度数.【答案】52CDE ∠=【解析】【分析】根据三角形内角和定理求出ACB ∠的度数,然后利用角平分线的定义得到DCE ∠的度数,再在CED 中利用三角形内角和定理即可求出CDE ∠.【详解】解:在ABC 中,80176ACB A B ∠=︒-∠-∠=︒, CD 平分ACB ∠,1382DCE ACB ∴∠=∠=︒, DE AC ⊥,90CED ∴∠=︒,在CED 中,18052CDE CED DCE ∠=-∠-∠=︒.【点睛】本题考查了角平分线的定义以及三角形内角和定理的应用,熟练掌握三角形内角和定理是解题的关键.。
平行线与三角形内外角

平行线与三角形内外角在初中数学学习中,平行线与三角形内外角是一个重要的知识点。
理解和掌握这些概念对于解题和推理都有着重要的作用。
本文将以指导性和鼓励性的语气,通过举例、分析和说明的方式,帮助中学生和他们的父母更好地理解和应用平行线与三角形内外角的知识。
一、平行线的定义和性质平行线是指在同一个平面中,永不相交的两条直线。
在数学中,我们用符号“||”来表示两条平行线。
平行线具有以下性质:1. 平行线的任意两条直线除了平行于它们自身外,不可能同时与同一条直线相交。
2. 平行线之间的距离是始终相等的,即平行线上的任意两点之间的距离相等。
3. 平行线与一条横截线所夹的内角和外角相等。
举例来说,假设有两条平行线AB和CD,以及一条横截线EF。
如果我们分别连接AE和CF,那么∠EAF和∠FCB是内角,∠EAB和∠FCD是外角。
根据平行线的性质,我们可以得出结论:∠EAF = ∠FCB,∠EAB = ∠FCD。
二、三角形内外角的关系在三角形中,内角和外角是密切相关的。
下面我们来详细讨论一下它们之间的关系:1. 三角形内角和为180度对于任意一个三角形ABC,它的三个内角∠A、∠B和∠C的和始终等于180度。
这是因为三角形的内角是平面内两条直线的夹角,而平面内两条直线的夹角和为180度。
举例来说,如果一个三角形的∠A = 60度,∠B = 80度,那么∠C = 180度 - 60度 - 80度 = 40度。
2. 三角形外角等于其对应内角的补角三角形的外角是指在三角形的一条边上,与另外两条边的延长线所夹的角。
根据这一性质,我们可以得出结论:三角形的外角等于其对应内角的补角。
举例来说,如果一个三角形的∠A = 60度,那么∠D = 180度- 60度 = 120度。
3. 三角形内角与外角的关系三角形的内角和外角之间存在着一定的关系。
具体来说,一个三角形的一个内角与其对应的外角之和始终等于180度。
举例来说,如果一个三角形的∠A = 60度,那么∠A + ∠D = 60度 + 120度 = 180度。
《三角形的内角和》2024新版

多边形内角和的计算方法可以用于解决与多边形相关的各种问题,如多边形划分、多边形 面积计算等。同时,多边形内角和的计算方法也是学习更高级数学知识的基础。
THANKS
感谢观看
按边可分为不等边三角形、等腰 三角形;按角可分为锐角三角形 、直角三角形、钝角三角形。
三角形边与角关系
三角形边的关系
任意两边之和大于第三边,任意两边 之差小于第三边。
三角形角的关系
三个内角之和等于180度,外角等于 与它不相邻的两个内角之和。
特殊三角形性质
等腰三角形性质
两腰相等,两底角相等;三线合 一(即顶角的平分线、底边上的
构造辅助线简化问题
作高线
通过作三角形的高线,将 复杂问题转化为简单的直 角三角形问题,便于求解 。
作中线
利用中线的性质(中线平 分对边),将原三角形划 分为两个面积相等的小三 角形,从而简化问题。
作角平分线
通过作角的平分线,将问 题转化为与角平分线相关 的简单问题,便于求解。
典型例题解析
例题1
解析
三角形内角和定理的推论
直角三角形的两个锐角互余。
证明方法及思路
01
02
03
拼图法
将三角形的三个内角剪下 拼在一起,组成一个平角 来加以证明。
平行线法
过三角形的一个顶点做对 边的平行线,利用平行线 的性质进行证明。
折叠法
将三角形纸片的三个角折 向同一点,利用折叠后形 成的平角进行证明。
应用举例
计算三角形中未知角 的度数。
中线、底边上的高重合)。
等边三角形性质
三边相等,三个内角均为60度;三 线合一(即任意一边上的中线、高 和这边所对的角的平分线重合)。
《三角形的内角和》

研究三角形内角和的意义
数学理论的发展
研究三角形的内角和是数 学几何学发展的基础,有 助于推动数学理论和几何 学理论的深入和完善。
实际应用
在实际生活中,研究三角 形的内角和有着广泛的应 用,如建筑设计、航空航 天、交通运输等。
数学思维培养
通过研究三角形的内角和 ,有助于培养学生的数学 思维和逻辑推理能力。
04
三角形内角和的应用
在几何学中的应用
定理证明
三角形内角和定理是几何学中 的重要定理之一,它可以用于 证明其他几何定理,如平行线
定理、三角形相似定理等。
多边形分解
三角形内角和定理可以用于将多边 形分解成三角形,从而简化多边形 的角度计算和面积计算。
图形拼接
三角形内角和定理可以用于判断两 个三角形是否可以拼接成一个完整 的三角形。
《三角形的内角和》
汇报人: 日期:
• 引言 • 三角形内角和的几何证明方法 • 三角形内角和的代数证明方法 • 三角形内角和的应用 • 结论
01
引言
什么是三角形的内角和
三角形的内角和是指三角形内部三个角的度数之和。 三角形的内角和等于180度。
为什么研究三角形的内角和
了解三角形的内角和是几何学的基础知识。
在物理学中的应用
01
02
03
光学研究
三角形内角和定理可以用 于研究光的反射、折射和 散射等现象,帮助我们更 好地理解光学原理。
力学研究
三角形内角和定理可以用 于研究物体的稳定性和平 衡性,如三角形的稳定性 。
电学研究
三角形内角和定理可以用 于研究电磁波的传播和散 射等现象,帮助我们更好 地理解电学原理。
研究三角形内角和的应用前景
人教版八年级上册数学第11章 三角形 三角形的内角——三角形内角和

知2-练
2 (中考·邵阳)如图,在△ABC中,∠B=46°,∠C= 54°,AD平分∠BAC,交BC于点D,DE∥AB,交 AC于点E,则∠ADE的大小是( C ) A.45°B.54°C.40°D.50°
知2-练
3 (中考·威海)直线l1∥l2,一块含45°角的直角三角 尺如图放置,∠1=85°,则∠2=__4_0_°____.
辅助线 通过本课时的学习,需要我们掌握:
三角形的 内角和等 于180°
证法 应用
转化为一个平角 或同旁内角互补
求角度
完成教材P16T1、T3P17T7、T9
第十一章三角形
11.2与三角形有关的角
第1课时三角形的内角——三 角形的内角和
1 课堂讲解 2 课时流程
三角形内角和定理 三角形内角和的应用
逐点 导讲练
课堂 小结
作业 提升
知识点 1 三角形内角和定理
知1-导
问题1 在小学我们已经知道任意一个三角形三个内 角的和等于180°,你还记得是怎么发现这个结论的 吗?请大家利用手中的三角形纸片进行探究.
数.
解:由∠BAC=40°,AD是
C
△ABC的角平分线,
得∠BAD=∠12 BAC=20°.
在△ABD中,
A
D B
∠ADB=180°-∠B-∠BAD
=180°-75°-20°=85°.
知2-讲
三角形的三内角和是180º,所以三内角可能出现的情况:
一个钝角两个锐角 一个直角两个锐角
三个都为锐角
钝角三角形 直角三角形 锐角三角形
线l,直线l与边BC有什么位置关系?
直线l与边BC平行.
部编数学八年级上册专题02三角形内角外角问题(解析版)含答案

2023--2024学年度人教版数学八年级上册期末复习核心考点三种题型精炼专题02 三角形内角外角问题一、选择题1. (2023湖北宜昌)如图,小颖按如下方式操作直尺和含30°角的三角尺,依次画出了直线a ,b ,c .如果170=°∠,则2Ð的度数为( )A. 110°B. 70°C. 40°D. 30°【答案】C 【解析】可求34570Ð=Ð+Ð=°,由25Ð=Ð,即可求解.如图,由题意得:430Ð=°,a b ∥,3170\Ð=Ð=°,34570Ð=Ð+Ð=°Q ,540\Ð=°,2540\Ð=Ð=°,故选:C .【点睛】本题考查了平行线的性质,对顶角的性质,三角形外角定理,掌握平行线的性质是解题的关键.2. (2023大连)如图,直线,45,20AB CD ABE D Ð=Ð=°°∥,则E Ð的度数为( )A. 20°B. 25°C. 30°D. 35°【答案】B 【解析】先根据平行线的性质可得45ABE BCD ÐÐ==°,再根据三角形的外角性质即可得.,45AB CD ABE Ð=°Q ∥,45ABE BCD \=Ð=а,20D Ð=°Q ,25BCD D E Ð-Ð==\а,故选:B .【点睛】本题考查了平行线的性质、三角形的外角性质,熟练掌握平行线的性质是解题关键.3. (2023内蒙古包头)如图,直线a b P ,直线l 与直线,a b 分别相交于点,A B ,点C 在直线b 上,且CA CB =.若132Ð=°,则2Ð的度数为( )A. 32°B. 58°C. 74°D. 75°【答案】C 【解析】由CA CB =,132Ð=°,可得1801742CBA CAB °-ÐÐ=Ð==°,由a b P ,可得2CBA Ð=Ð,进而可得2Ð的度数.∵CA CB =,132Ð=°,∴1801742CBA CAB °-ÐÐ=Ð==°,∵a b P ,∴274CBA Ð=Ð=°,故选:C .【点睛】本题考查了等边对等角,三角形的内角和定理,平行线的性质.解题的关键在于明确角度之间的数量关系.4. (2023山东东营)如图,AB CD ∥,点E 在线段BC 上(不与点B ,C 重合),连接DE ,若40D Ð=°,60BED Ð=°,则B Ð=( )A. 10°B. 20°C. 40°D. 60°【答案】B 【解析】根据三角形的外角的性质求得20C Ð=°,根据平行线的性质即可求解.∵40D Ð=°,60BED Ð=°,∴20C BED D Ð=Ð-Ð=°,∵AB CD ∥,∴B Ð=20C Ð=°,故选:B .【点睛】本题考查了三角形的外角的性质,平行线的性质,熟练掌握以上知识是解题的关键.5. (2023山东聊城)如图,分别过ABC V 的顶点A ,B 作AD BE P .若25CAD Ð=°,80EBC Ð=°,则ACB Ð的度数为( )A. 65°B. 75°C. 85°D. 95°【答案】B 【解析】根据两直线平行,同位角相等,得到80E ADC BC =°Ð=Ð,利用三角形内角和定理计算即可.∵AD BE P ,80EBC Ð=°,∴80E ADC BC =°Ð=Ð,∵25CAD Ð=°,∴71805ACB ADC CAD =°Ð=°-Ð-Ð,故选B .【点睛】本题考查了平行线的性质,三角形内角和定理,熟练掌握平行线性质是解题的关键.6. (2023深圳)如图为商场某品牌椅子侧面图,120DEF Ð=°,DE 与地面平行,50ABD Ð=°,则ACB =∠( )A. 70°B. 65°C. 60°D. 50°【答案】A 【解析】根据平行得到50ABD EDC Ð=Ð=°,再利用外角的性质和对顶角相等,进行求解即可.由题意,得:DE AB ∥,∴50ABD EDC Ð=Ð=°,∵120DEF EDC DCE Ð=Ð+Ð=°,∴70DCE Ð=°,∴70ACB DCE Ðа==;故选A .【点睛】本题考查平行线的性质,三角形外角的性质,对顶角.熟练掌握相关性质,是解题的关键.7. (2023湖北荆州)如图所示的“箭头”图形中,AB CD ∥,80B D Ð=Ð=o ,47E F Ð=Ð=o ,则图中G Ð的度数是( )的A. 80oB. 76oC. 66oD. 56o【答案】C 【解析】延长AB 交EG 于点M ,延长CD 交GF 于点N ,过点G 作AB 的平行线GH ,根据平行线的性质即可解答.如图,延长AB 交EG 于点M ,延长CD 交GF 于点N ,过点G 作AB 的平行线GH ,4780,E F EBA FDC Ð=Ð=Ð=Ð=o o Q ,33EMA EBA E \Ð=Ð-Ð=°,33FNC FDC F Ð=Ð-Ð=°,,AB CD AB HG ∥∥Q ,HG CD \∥,33MGH EMA \Ð=Ð=°,33NGH FND Ð=Ð=°,333366EGF \Ð=°+°=°,故选:C .【点睛】本题考查了平行线的判定及性质,三角形外角的定义和性质,作出正确的辅助线是解题的关键.8. 如图,已知AB CD ∥,点E 在线段AD 上(不与点A ,点D 重合),连接CE .若∠C =20°,∠AEC =50°,则∠A =( )A. 10°B. 20°C. 30°D. 40°【答案】C 【解析】根据三角形外角的性质、平行线的性质进行求解即可;∵∠C +∠D =∠AEC ,∴∠D =∠AEC -∠C =50°-20°=30°,∥,∵AB CD∴∠A=∠D=30°,故选:C.【点睛】本题主要考查三角形外角的性质、平行线的性质,掌握相关性质并灵活应用是解题的关键.9.将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )A.70°B.75°C.80°D.85°【答案】B【解析】利用三角形内角和定理和平行线的性质解题即可.如图,∵∠2=90°﹣30°=60°,∴∠3=180°﹣45°﹣60°=75°,∵a∥b,∴∠1=∠3=75°.10.如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )A.15°B.25°C.30°D.10°【答案】A.【解析】本题考查的是三角形外角的性质,熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键。
人教版_部编版八年级数学上册第十一章第二节三角形的内角试题(含答案) (48)

人教版_部编版八年级数学上册第十一章第二节三角形的内角试题(含答案)如图①,BE 、DF 分别平分四边形ABCD 的外角MBC ∠和NDC ∠,设BAD ∠=α,BCD β∠=.(1)若110αβ+=︒,则MBC NDC ∠+∠= ︒;(2)若BE 与DF 相交于点G ,且25BGD ∠=︒,求α、β所满足的等量关系式,并说明理由;(3)如图②,若αβ=,试判断BE 、DF 的位置关系,并说明理由.【答案】(1)110;(2)50βα-=︒,理由见解析;(3)BE DF ∥,理由见解析【解析】【分析】(1)根据四边形的内角和与邻补角的性质即可求解;(2)连接BD ,先得到1()2CBG CDG αβ∠+∠=+,再根据三角形的内角和得到角度的关系即可求解;(3)由(1)有,∠MBC +∠NDC =αβ+,BE 、DF 分别平分四边形的外角∠MBC 和∠NDC ,则∠CBE +∠CDH =12(αβ+),∠CBE +β−∠DHB =12(αβ+),根据α=β,则有∠CBE +β−∠DHB =12(β+β)=β,得到∠CBE =∠DHB ,故可得到BE ∥DF .【详解】解:(1)∵∠ABC +∠ADC =360°−(αβ+)=250°,∴∠MBC +∠NDC =180°−∠ABC +180°−∠ADC =360°-(∠ABC +∠ADC )=αβ+=110°.故答案为:110;(2)50βα-=︒.理由如下:如解图①,连接BD ,由(1)知,MBC NDC αβ∠+∠=+, BE 、DF 分别平分四边形ABCD 的外角MBC ∠和NDC ∠, ∴12CBG MBC ∠=∠,12CDG NDC ∠= ()1111()2222CBG CDG MBC NDC MBC NDC αβ∴∠+∠=∠+=∠+=+. 在△BCD 中,∠BDC +∠CBD =180°−∠BCD =180°−β,在△BDG 中,∠GBD +∠GDB +∠BGD =180°,∴∠CBG +∠CBD +∠CDG +∠BDC +∠BGD =180°,∴(∠CBG +∠CDG )+(∠BDC +∠CBD )+∠BGD =180°, ∴12(αβ+)+180°−β+25°=180°, 整理得50βα-=︒;(3)BE DF ∥.理由如下,如解图①所示,延长BC 交DF 于点H ,由(1)、(2)可知,MBC NDC αβ∠+∠=+,1()2CBE CDH αβ∠+∠=+. BCD CDH DHC ∠=∠+∠,CDH BCD DHC DHC β∴∠=∠-∠=-∠,1()2CBE DHC βαβ∴∠+-∠=+. αβ=,1()2CBE DHB ββββ∴∠+-∠=+=, CBE DHB ∴∠=∠,BE DF ∴∥.【点睛】此题考查了平行线的性质及其判定,多边形的内角和公式,利用多边形的内角和公式倒角为解题关键.72.如图,在ABC ,AD BC ⊥于点D ,AE 平分BAC ∠.(1)若70C ∠=︒,40B ∠=︒,求DAE ∠的度数;(2)若20C B ∠-∠=︒,求DAE ∠的度数.【答案】(1)15︒;(2)10︒【解析】【分析】(1)根据角平分线的定义和互余进行计算;(2)根据三角形内角和定理和角平分线定义得出∠DAE 的度数等于∠B 与∠C 差的一半解答即可.【详解】解:(1)70C ∠=︒,40B ∠=︒,180407070BAC ∴∠=︒-︒-︒=︒,AE ∵平分BAC ∠,35EAC ∴∠=︒.AD BC ⊥,90ADC ∴∠=︒,907020CAD ∴∠=︒-︒=︒,352015DAE EAC CAD ∴∠=∠-∠=︒-︒=︒;(2)∵∠B +∠C +∠BAC =180°,∴∠BAC =180°−∠B −∠C ,∵AE 平分∠BAC ,∴∠BAE =12∠BAC =12(180°−∠B −∠C )=90°−12(∠B +∠C ), ∵AD ⊥BC ,∴∠ADE =90°,而∠ADE =∠B +∠BAD ,∴∠BAD =90°−∠B ,∴∠DAE =∠BAD −∠BAE =90°−∠B )−[90°−12(∠B +∠C )]=12(∠C −∠B ),∵∠C −∠B =20°,∴∠DAE =12×20°=10°. 【点睛】本题考查了三角形内角和定理,关键是根据三角形内角和是180°和三角形外角性质解答.73.如图,AB BD ⊥于点B ,点C 在BD 上,且BAC DCE ∠=∠,ACE △是直角三角形吗?为什么?【答案】是直角三角形,理由见解析【解析】【分析】根据已知得到90ACB DCE ∠+∠=︒,即可求出90ACE ∠=︒,故可求解.【详解】解:ACE △是直角三角形,理由如下:AB BD ⊥,90ABC ∴∠=︒,90ACB BAC ∴∠+∠=︒.BAC DCE ∠=∠,90ACB DCE ∴∠+∠=︒.180()90ACE ACB DCE ∴∠=︒-∠+∠=︒,ACE ∴是直角三角形.【点睛】此题主要考查直角三角形的判定,解题的关键是熟知三角形的内角和及平角的性质.74.已知ABC ∆中,B C ∠=∠,D 为边BC 上一点(不与,B C 重合),点E 为边AC 上一点,ADE AED ∠=∠,44BAC ∠=︒.(1)求C ∠的度数;(2)若75ADE ∠=︒,求CDE ∠的度数.【答案】(1)68C ∠=︒;(2)7CDE ∠=︒.【解析】【分析】(1)根据已知及三角形的内角和定理进行计算即可得解;(2)根据三角形的内角和定理进行角度的计算即可得解.【详解】(1)∵44BAC ∠=︒,180BAC B C ∠+∠+∠=︒,∴18044136B C ∠+∠=︒-︒=︒,∵B C ∠=∠,∴2136C ∠=︒,∴68C ∠=︒;(2)∵ADE AED ∠=∠,75ADE ∠=︒,∴75AED ∠=︒,∵180AED CED ∠+∠=︒,∴18075105CED ∠=︒-︒=︒,∵180CDE CED C ∠+∠+∠=︒,∴180105687CDE ∠=︒-︒-︒=︒.【点睛】本题主要考查了三角形的内角和定理,熟练掌握角度的和差计算是解决本题的关键.75.已知:在ABC 中,AD ,AE 分别是ABC 的高和角平分线,若3050B C ∠=︒∠=︒,.你能帮助工人师傅解决下面的问题吗.(1)求DAE ∠的度数;(2)试写出DAE ∠与C B ∠-∠有何关系.(不必证明)【答案】(1)10°;(2)1DAE (C B)2∠=∠-∠ 【解析】【分析】(1)先根据三角形内角和定理求出BAC ∠的度数,再利用角平分线的定义求得CAE ∠的度数,然后由直角三角形两锐角互余求出CAD ∠的度数,两角相减即可得解;(2)先根据三角形内角和定理用含B 、C ∠的式子表示出BAC ∠的度数,再利用角平分线的定义求得CAE ∠的度数,然后由直角三角形两锐角互余求出CAD ∠的度数,两角相减即可得解.【详解】解:(1)∵3050B C ∠=︒∠=︒,∴1803050100BAC ∠=︒-︒-︒=︒∵AE 是ABC 的角平分线 ∴110050212CAE BAC ∠=∠=⨯︒=︒ ∵AD 是ABC 的高,50C ∠=︒∴905040CAD ∠=︒-︒=︒∴504010DAE CAE CAD ∠=∠-∠=︒-︒=︒.(2)同(1)的思路, ∵()1111CAE BAC 180B C 90B C 2222︒︒∠=∠=-∠-∠=-∠-,CAD 90C ︒∠=-∠ ∴()111DAE CAE CAD 90B C 90C (C B)222︒︒∠=∠-∠=-∠---∠=∠-∠. 故答案是:(1)10︒;(2)1()2DAE C B ∠=∠-∠ 【点睛】本题考查了三角形内角和定理、角平分线定义以及直角三角形两锐角互余等知识点,属基础题目,两问解题思路是一样的,体现了从特殊到一般的思想方法.76.如图,ABC 中,90ACB ∠=︒,点F 在AC 上,点D 在AB 上,FE AB ⊥于点,E DG BC ⊥于点G ,且12∠=∠.求证:90ADC ∠=︒.【答案】见解析【解析】【分析】根据三角形内角和相等得到∠1=∠B ,再由∠1=∠2得出∠2=∠B ,推出∠2+∠BDG=90°,即∠CDB=90°,从而得出∠ADC=90°.【详解】解:如图,∵EF ⊥AB ,DG ⊥BC ,∴∠AEF=∠DGB=90°,∵∠ACB=90°,∠A=∠A,∴∠1=∠B ,又∵∠1=∠2,∴∠B=∠2,∵∠B+∠BDG=90°,∴∠2+∠BDG=90°,∴∠CDB=90°,∴∠ADC=90°.【点睛】本题考查了三角形内角和定理,余角的性质,解题的关键是找到∠B ,通过∠1、∠2与∠B 的关系推出结论.77.如图,点A 在MN 上,点B 在PQ 上,连接AB ,过点A 作AC AB ⊥交PQ 于点C ,过点B 作BD 平分ABC ∠交AC 于点D ,且NAC ABC ∠+∠90=︒.(1)求证://MN PQ ;(2)若10ABC NAC ∠=∠+︒,求ADB ∠的度数.【答案】(1)见解析;(2)65°【解析】【分析】(1)根据垂直的定义得到∠BAC=90°,推出∠NAC=∠ACB ,根据平行线的判定定理即可得到结论;(2)根据三角形的内角和列方程得到∠ABC=50°,根据角平分线的定义得到∠ABD=12∠ABC=25°,于是得到结论. 【详解】解:(1)证明:∵AC ⊥AB ,∴∠BAC=90°,∴∠ABC+∠ACB=90°,∵∠NAC+∠ABC=90°,∴∠NAC=∠ACB,∴MN∥PQ;(2)解:∵∠ABC=∠NAC+10°=∠ACB+10°,∵∠ACB+∠ABC=90°,∴∠ACB+∠ACB+10°=90°,∴∠ACB=40°,∴∠ABC=50°,∵BD平分∠ABC,∴∠ABD=12∠ABC=25°,∵∠BAC=90°,∴∠ADB=90°-25°=65°.【点睛】本题考查了三角形的内角和,垂直的定义,平行线的判定和性质,正确的识别图形是解题的关键.78.阅读下面的材料图1,在△ABC中,试说明∠A+∠B+∠C=180°分析:通过画平行线,将∠A、∠B、∠C作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法:解:如图2,延长BC到点D,过点C作CE∥BA因为BA∥CE(作图所知)所以∠B=∠2,∠A=∠1(两直线平行,同位角、内错角相等)又因为∠BCD=∠BCA+∠2+∠1=180°(平角的定义)所以∠A+∠B+∠ACB=180°(等量代换)(1)如图3,过BC上任一点F,作FH∥AC,FG∥AB,这种添加辅助线的方法能说∠A+∠B+∠C=180°吗?并说明理由.(2)还可以过点A作直线MN∥BC,或在三角形内取点P过P作三边的平行线,请选择一种方法,画出相应图形,并说明∠A+∠B+∠C=180°.【答案】(1)可以,理由详见解析;(2)详见解析【解析】【分析】(1)利用平角的定义以及平行线的性质即可解决问题.(2)过点A作直线MN∥BC,利用平角的定义以及平行线的性质即可解决问题.【详解】解:(1)可以,因为FH∥AC所以∠1=∠C,∠2=∠FGC,因为FG∥AB所以∠3=∠B,∠FGC=∠A所以∠2=∠A因为∠1+∠2+∠3=180°所以∠A+∠B+∠C=180°.(2)过点A作直线MN∥BC.则∠MAB=∠B,∠NAC=∠C,因为∠MAB+∠BAC+∠NAC=180°,所以∠BAC+∠B+∠C=180°.【点睛】本题考查三角形内角和定理、平行线的性质和平角的定义等知识,解题的关键是熟练掌握平行线的性质和平角的定义.79.如图,在△ABC中,CD△AB,垂足为D,点E在BC上,EF△AB,垂足为F.(1)CD与EF平行吗?为什么?(2)如果△1=△2,CD平分△ACB,且△3=120°,求△ACB与△1的度数.【答案】(1)详见解析;(2)①ACB=120°,①1=60°【解析】【分析】(1)根据垂直于同一直线的两直线平行判定;(2)根据平行线的性质和已知求出∠1=∠2=∠DCB,推出DG∥BC,根据平行线的性质得出∠ACB的度数即可;再由∠ACB的度数和已知得∠DCG的度数,利用三角形的外角的性质即可求出∠1的度数.【详解】解:(1)CD∥EF,理由是:∵CD⊥AB,EF⊥AB,∴CD∥EF;(2)∵CD∥EF,∴①2=①DCB,∵①1=①2,∴①1=①DCB,∴DG∥BC,∴①ACB=①3,∵①3=120°,∴①ACB=120°.∵CD平分①ACB,∴①DCG=12①ACB=60°,∵①3=①1+①DCG,∴①1=120°-60°=60°.∴①ACB=120°,①1=60°. 【点睛】本题考查了对平行线的性质和判定的应用,三角形的内角和定理以及三角形外角的性质,角平分线的定义.熟练掌握平行线的判定与性质是解决本题的关键.80.(1)如图,在ABC 中,AD 是高,,AE BF 是角平分线,它们相交于点O ,4060ABC C ∠=︒∠=︒,.求AOB ∠和DAE ∠的度数.(2)一个多边形的内角和是外角和的3倍,它是几边形?若这个多边形的各个内角都相等,求这个多边形的每个内角的度数.【答案】(1)AOB ∠=120°,DAE ∠=10°;(2)多边形为8边形;每个内角的度数为135°.【解析】【分析】(1)根据三角形的内角和定理,可求出∠BAC 的度数,结合AE 是角平分线,求出∠EAC 的度数,由AD 是高,可以依据直角三角形两锐角互余,可求出∠DAC 的度数,代入=EAC DA D C AE ∠-∠∠中求解;运用角平分线的定义及三角形内角和定理即可求出AOB ∠;(2)依据多边形内角和公式和外角和为360°,结合已知条件,列出关于边数的方程,解出即可;多边形内角和÷边数即得每个内角的度数.【详解】解:(1)AD 是ABC ∆的高,∴90ADC ∠=︒,∴在ADC ∆中,90906030DAC C ∠=︒-∠=︒-︒=︒,在ABC ∆中,180180406080BAC ABC C ∠=︒-∠-∠=︒-︒-︒=︒, ∵AE 、BF 是角平分线,11402022ABO ABC ∴∠=∠=⨯︒=︒, 11=804022BAO EAC BAC ∠=∠∠=⨯︒=︒, ∴=EAC DA D C AE ∠-∠∠=40°-30°=10°,在ABC ∆中,1801802040120BOA ABO BAO ∠=︒-∠-∠=︒-︒-︒=︒. 答:AOB ∠=120°,DAE ∠=10°.(2)设多边形为n 边形.依题意得:(n -2)×180°=3×360°,解之得:n =8,∴多边形为8边形,若这个多边形的各个内角都相等,则每个内角的度数=3×360°÷8=135°.答:多边形为8边形;每个内角的度数为135°.【点睛】(1)本题考查了三角形中的角度计算,熟练掌握高和角平分线的定义、三角形内角和定理以及直角三角形两锐角互余是解答本题的关键.(2)本题考查了多边形的内角和与外角和,熟练掌握多边形的内角和公式、外角和为360度是解题的基础,列出关于边数的方程是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线与三角形内角和(计算)(人教
版)含答案
平行线与三角形内角和(计算)(人教版)
一、单选题(共10道,每道10分)
1.如图,在△ABC中,AD平分∠BAC,且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C的度数为( )
A.80°
B.90°
C.100°
D.110°
答案:A
解题思路:
试题难度:三颗星知识点:三角形内角和定理
2.已知在△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A的度数为( )
A.30°
B.40°
C.60°
D.80°
答案:B
解题思路:
试题难度:三颗星知识点:三角形内角和定理
3.如图,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E.若
∠AFD=158°,则∠EDF=( )
A.42°
B.44°
C.68°
D.79°
答案:C
解题思路:
试题难度:三颗星知识点:互余
4.如图,在△ABC中,AE平分∠BAC,AD⊥BC,垂足为D,若∠BAC=128°,∠C=36°,则∠DAE的度数为( )
A.10°
B.12°
C.15°
D.18°
答案:A
解题思路:
试题难度:三颗星知识点:三角形内角和定理
5.如图,在△ABC中,∠BAC=4∠1=4∠C,BD⊥CA于点D,则∠DBA=( )
A.20°
B.60°
C.45°
D.30°
答案:D
解题思路:
试题难度:三颗星知识点:三角形内角和定理
6.如图,直线BD∥EF,AE与BD交于点C,若∠B=30°,∠A=75°,则∠CEF 的度数为( )
A.60°
B.75°
C.90°
D.105°
答案:D
解题思路:
试题难度:三颗星知识点:三角形内角和定理
7.如图,在四边形ABCD中,点E在BC上,AB∥DE,∠B=78°,∠C=60°,则∠EDC的度数为( )
A.42°
B.60°
C.78°
D.80°
答案:A
解题思路:
试题难度:三颗星知识点:三角形内角和定理
8.如图,直线AB∥CD,∠EFA=28°,∠EHC=50°,则∠E=( )
A.28°
B.22°
C.32°
D.38°
答案:B
解题思路:
试题难度:三颗星知识点:三角形内角和定理
9.如图,AB∥CD,AE平分∠CAB,CE平分∠ACD,则∠E=( )
A.60°
B.75°
C.90°
D.105°
答案:C
解题思路:
试题难度:三颗星知识点:三角形内角和定理
10.将一副直角三角板如图放置,已知AE∥BC,则∠AFE的度数为( )
A.95°
B.100°
C.110°
D.105°
答案:D
解题思路:
精品好文档,推荐学习交流
试题难度:三颗星知识点:三角形内角和定理仅供学习与交流,如有侵权请联系网站删除谢谢9。
