第五章 化学平衡
第五章 化学平衡

第五章化学平衡授课时数:8学时主要内容:1. 化学反应的等温方程式和化学反应的亲的势2. 理想气体化学反应的标准平衡常数3. 温度对标准平衡常数的影响4. 其它因素对理想气体化学平衡的影响5. 同时反应平衡6. 真实气体反应及混合物和溶液中反应的化学平衡重点:1. 化学反应标准平衡常数的定义;2. 平衡常数和平衡组成的计算;3. 化学反应的等温方程式和等压方程式及其应用;4. 温度、压力及惰性气体等因素对化学平衡的影响。
难点:1. 利用等温方程式判断一定条件下化学反应可能进行的方向;2. 范特霍夫方程式的推导及其应用。
教学方式:1. 采用CAI 课件与黑板讲授相结合的教学方式;2. 合理运用问题教学或项目教学的教学方法;3. 作业:1,3,4,5,8,10,11,14,15,18,20,21,22,24,26,27,28;4. 答疑:(a) 课后答疑;(b) 通过网络答疑。
5.1化学反应的等温方程1.摩尔反应吉布斯函数和化学反应亲和势在一定的温度、压力和非体积功为零的条件下,化学反应B0BB ∑=ν的摩尔反应吉布斯函数为⎪⎭⎫ ⎝⎛=∆<=自发平衡0m r G定义化学反应的亲和势A 为m r G A ∆-=A 代表在恒温、恒压和'0W =的条件下反应的推动力。
A >0反应能自动进行;A =0反应处于平衡态;A < 0反应不能自动进行。
2.摩尔反应吉布斯函数与反应进度的关系,平衡条件对于化学反应B0BB ∑=ν,随着反应的进行,各物质的量均发生变化,对多组分系统BBB d d d d n p V T S G ∑++-=μ如果在恒温恒压下BBB d d n G ∑=μ根据反应进度的定义 BBd d νξn =,得ξνd n B B d =,代入上式,则ξμνd d BB B ∑=Gmr BB B ,)/(G G P T ∆=∑=∂∂μνξ式中的()pξ∂∂T,G 表示在T ,p 及组成一定的条件下,反应系统的吉布斯函数随反应进度的变化率, 恒温恒压下均相反应的G -ξ曲线示意图称为摩尔反应吉布斯函数变。
化学平衡

p
B
B
neq
B' B'
p
B
B
Kn
neq
B' B'
例1 已知反应
1 2
N
2
3 2
H
2
NH
3
在400℃、
30.4MPa时Kp=18.1×10-5kPa-1,原料气中N2
与H2的物质的量之比为1:3,试求N2的理论
转化率与平衡时NH3的摩尔分数。
解:
初始 1mol
3mol
0
平衡 (1-α)mol 3(1-α)mol
d
B
B
def
Kf
B
(
f
eq B
) B
( fGeq )g ( fReq )r L
(
f
eq D
)d
(
fEeq
)e
L
量纲为: p
B
B
以逸度表示 的平衡常数
K f =K d
pd
B
B
exp
ΔrGmd RT
pd
B
B
K f 只决定于反应本性和温度,与总压以及各物
质的平衡组成无关,也不受 pd 选取的影响
0
B
BB
DDEE
GG RR
B
B
B
DD
EE
GG
RR
< 0;未达到平衡 = 0;达到平衡 > 0;未达到平衡
1.标准平衡常数
K d def exp
B
B
Bd
RT
d B
BB
量纲为一
Bd
exp Bd
RT
K d 仅决定于反应本性和温度 p d 的不同取法也会影响 K d 的数值
物理化学 第五章 化学平衡

压力商Jp: 前式中的后一项的加和Σ υ BRTln(pB/pθ )可以用 乘积的形式表示: Σ υ BRTln(pB/pθ )=RTΣ υ Bln(pB/pθ ) B B =RTlnП (pB/pθ )υ B B 式中,П (pB/pθ )υ B为各反应物及反应产物的 B (pB/pθ )υ B的连乘积,称为压力商,用Jp表示。
←Δ rGm=(əG/əξ )T,p
0
1
图5.1.1 恒温、恒压下G随ξ 的变化
由图中曲线可以看出,在反应开始即ξ =0时,G 值最大;随着反应的进行,反应系统的G值逐渐 降低。曲线上任一点处的斜率(əG/əξ )T,p代表 在 T、p一定且反应进度为ξ 处的反应Δ rGm: Δ rGm=(əG/əξ )T,p 随着反应的进行,ξ 渐渐增大,曲线斜率的绝对 值渐渐变小。反应达平衡时,Δ rGm=0,即反应系 统的G达到极小。所以,恒温恒压不作非体积功 条件下,化学反应的平衡条件为: Δ rGm=(əG/əξ )T,p=0
代入摩尔反应吉布斯函数的关系式中,可得: Δ rGm=(əG/əξ )T,p=Σ υ Bμ θ B+Σ υ BRTln(pB/pθ ) B B 标准摩尔反应吉布斯函数Δ rGθ m: 上式中Σ υ Bμ θ B为各反应组分均处于标准态 B (pθ =100kPa的纯理想气体)时每摩尔反应进度吉 布斯函数变,以Δ rGθ m表示,称为标准摩尔反应 吉布斯函数,即: Δ rGθ m=Σ υ Bμ θ B
调节Jp改变反应方向和反应产率的局限性: Jp的可调性提供了控制、甚至改变反应方向的可 能性。但是对于Δ rGθ m«0的反应,Kθ »1,反应达 到平衡时反应物的分压几乎为0,因此可以认为 反应能进行到底;而Δ rGθ m»0的反应,Kθ «1,反 应达到平衡时反应产物的分压几乎为0,可以认 为反应不能发生;只有Δ rGθ m接近于0的反应, Kθ 与1相差不太大时,才有可能通过调节Jp来改 变化学反应的方向和影响反应的产率。
物理化学:05 化学平衡

B(T )
RT
ln
fB P
K
f
fG P
fD P
g
d
fH P
fE P
h
e
(2)液相反应
a) aA(l) bB(l) gG(l) hH(l)
如果参加反应的物质是构成理想溶液,物质的化学势
表示式:
B
B
RT
ln
B
代入
K
G g H h A a B b
如果参加反应的物质均溶于一溶剂中,而溶液为稀
2、用作判据
化学反应等温式主要用作判据。等温方程式可以判断
一个化学反应是否能自发进行。因为用 rGm 作判据,
在等温、等压、只作膨胀功(体积功)不作其它功的情况
下,如果一热力学过程的:
G 0 G 0 G 0
能自发进行 达平衡 反应不能自发进行
将此结论推广应用于任意一气相反应,则从 等温方程式可以看出:
平衡时:CaO(s) CO2 ( g ) CaCO3 (s) 0
对于凝聚相(液体或固体),其化学势随压力变化不
大,并且凝聚相均处于纯态不形成固溶体或溶液。则
CaO(s)
CaO( s )
CaCO3 (s)
CaCO3 (s)
CO2 ( g )
CO2 (T )
RT
ln
PCO2 P
P )
P2 SO3
P P 2
SO2
O2
(1/
(1/ P )2 P )2 (1/ P )
KP
1 P
2 ( 2 1)
KP
(P
B )B
B
PB P
B
B=产物的系数和-反应物的系数和 B
K
05章 化学平衡

.a
h H
a
a A
.a
b B
exp[rGm ]常数
RT
令:
aGg
.a
h H
a
a A
.a
b B
B aBB K
得:K a a G g A a..a a H h B b eex prG (m/R)T*
上式即为标准平衡常数K 定义式。
上一内容 下一内容 回主目录
返回
5.1.4 化学反应等温方程式
2、这说明 rGm>0的反应能通过调节Qa的大小而使 其向正向进行。因此,rGm 的大小并不能用来判断化
学反应的方向。
上一内容 下一内容 回主目录
返回
化学反应等温方程式
例题
理想气体反应 2 H 2 O ( g ) =6.45×10-8,试求:
2 H 2 ( g ) O 2 ( g ) ,在2000K时K
Kx的大小不仅与温度有关,而且与系统的压力也 有关。严格地讲,Kx不是平衡常数。
上一内容 下一内容 回主目录
返回
5.2.2 实际气体反应
aB=fB/p
K ( fB B )p () B B K f(p) B B K f
B
因 fB = γB.pB, Kf=ПpBνB.ПγBνB = KP.Kγ
KP= Kf/ Kγ
g(GRlT n aG )h(HRlT n aH )
a(ARlT n aA )b(BRlT n aB)
整理得:
lnaaG gA aaaH hB b R 1T[(gGhH)(aAbB)]
R 1TrGm
上一内容 下一内容 回主目录
返回
化学反应的平衡常数:
式中 rG m(T)BB (意义?)
第5章 化学平衡原理要点

上一内容 下一内容 回主目录
rGmΘ
r
H
Θ m
Tr SmΘ
41.16 673 (0.042 )
12.89kJ mol 1
②求Kθ
lnK(T) ΔrGm T
RT
12.89 103 2.304 8.314 673
=-41.16kJ·mol-1 △Sθ(298.15K)={Sθ(CO2, g, 298.15K) + Sθ(H2, g, 298.15K)}
-{Sθ(CO, g, 298.15K) + Sθ(H2O, g, 298.15K)} ={213.64+130.574-197.56-188.72)}J·mol-1·K-1
用符号KΘ表示。
上一内容 下一内容 回主目录
标准平衡常数
K
pEeq pAeq
p e pFeq p a pDeq
p p
f d
B
pBeq p vB
0 rGm (T ) RT ln K
rGm (T ) RT ln K 或 ln K rGm (T ) RT
上一内容 下一内容 回主目录
上一内容 下一内容 回主目录
如合成氨的反应:
N2(g) + 3H2(g)
2NH3(g)
K1
p p eq
2
NH3
peq N2
p
peq H2
p 3
1/2N2(g) + 3/2H2(g)
NH3(g)
K
2
peq N2
p p eq
NH3
1
p p 2 eq H2
05章 化学平衡

例:N2O4(g) ⇌ 2 NO2(g) 无色 红棕色 在 373K 恒温槽中反应一段时间后,反应 混合物颜色不再变化,显示已达平衡,测 得平衡时N2O4、NO2浓度
N2O4(g) ⇌ 2 NO2(g)
N2O4-NO2体系的平衡浓度(373K) 0.100 0 0 0.100 0.100 0.100 -0.060 +0.120 +0.014 -0.028 -0.030 +0.060 0.040 0.120 0.014 0.072 0.072 0.160
三、与“平衡常数”有关的计算
例:C2H5OH + CH3COOH ⇌ CH3COOC2H5 + H2O 若起始浓度c (C2H5OH) = 2.0 mol.dm-3 , c (CH3COOH ) = 1.0 mol.dm-3 , 室温测得经验平衡常数Kc =4.0 , 求平衡时C2H5OH的转化率α。 解:反应物的平衡转化率 α% = (反应物起始浓度 - 反应物平衡浓度) / (反应物起始浓度) × 100
C2H5OH + CH3COOH ⇌ CH3COOC2H5 + H2O 起始浓度/ 2.0 1.0 0 0 平衡浓度/ 2.0- 1.0- Kc = 2 / [(2.0- ) (1,得 = 0.845 mol.dm-3 C2H5OH平衡转化率
pi = ciRT , 代入KP表达式 KP = ( pDd pEe) / ( pAa pB b)
经验平衡常数存在两大问题 : ①多值性; ②△n≠0时,量纲≠1. (2)相对平衡常数:Kr (或标准平衡常数Kø )
定义:“标准压力”为p ø
“标准(物质的量)浓度”为c ø SI制规定:p ø= 1 ×105 Pa(旧:101325 Pa) c ø = 1 mol· dm-3
第五章化学平衡常数

Kc r 、Kpr 、K杂r 统一为 K r(或 K ø):
优点:①量纲为1; ②在SI制中单值。
反应的自由能变化与平衡常数的关系
由范特霍夫等温方程:
rG m (T ) r G (T) RTlnJ m
平衡状态: △G = 0, Jp r = K r △G ø = - RT ln K r (△G ø K r) 而 △G ø = ∑i △fG iø (二)Van’t Hoff等温式的应用 把△G ø = - RT ln K r 代入 △G = △G ø + RT lnJp r 得:△G = - RT ln K r + RT lnJp r △G = RT ln(Jp r /K r )
(3) 计算平衡时各物种的组成
实验平衡常数
平衡常数的获得除了由热力学计算外,还可以通过实验测定。 实验平衡常数(经验平衡常数) —— 由实验得到的平衡常数。
表6-1 500oC下的合成氨实验测定的平衡浓度与实验平衡常数(Kc)
[ H 2 ] / mol.dm
3
[ N 2 ] / mol.dm
3
第5章 化学平衡
Chapter 5 Equilibrium
本章要求
1、建立化学平衡常数的概念。 2、掌握反应产率或反应物转化为产物的转化率的计算。 3、学会讨论浓度、分压、总压和温度对化学平衡的影响。
内容提要
● 化学平衡状态
● 平衡常数
● 浓度对化学平衡的影响 ● 压力对化学平衡的影响 ● 温度对化学平衡的影响
H2(g) + I2(g) = 2 HI (g) K = 50.3 (713 K)
第五章 化学平衡

• 反应: SO2(g)+0.5O2(g) SO3(g) SO2分子与O2分子会化合生成 SO3分子;但同 时, SO3分子也会分解为SO2和O2分子.
• 若体系的初始组成是原料SO2和O2, 那么在反应初期, 体系中主要 为SO2和O2分子, 它们之间的碰撞频率较高, 而SO3的分子数很少, 其分解的速率自然较低, 故在宏观上,反应向正方进行. • 随着反应进行, SO3分子的浓度逐步提高, 其分解速率也随之提高; SO2和O2的浓度逐步降低, 故合成SO3的速率也随之降低, 当达到 一定程度时, 两者的速率相等。此时,从宏观上看,体系的组成 不再变化,化学反应达到了平衡。
• rGm的单位是: J.mol-1.
• 化学反应通常在恒温、恒压下进行, rGm 可作为反应 过程进行方向的判据 。 1、若 rGm < 0 ,即∑B B < 0
反应物的化学势大于产物的化学势,反应自发正向进行; 2、若 rGm > 0 ,即∑B B > 0
反应物的化学势小于产物的化学势,反应自发逆向进行; 3、若 rGm = 0 ,即∑B B = 0
• 产物与反应物的标准态化学势之差决定了反应在给定条件下的反
应限度,即 eq的大小。
当反应进度 大于 0而小于 1时,由于反应物及产物以混合的方 式存在,产生了负值的混合吉布斯自由能改变量,使G总对的曲 线表现为有最低点的曲线而不是一条直线。 • 若反应物与产物并不相混合,则反应是有可能进行到底的,如一 定条件下碳酸钙的热分解反应或爆炸性反应。
底的=1处,而是在其左侧= eq<1的某处。
• 当反应进行到总自由能达到最低值,就达到了化学平衡而不能使 再加大了. 因为假若反应继续进行,就形成了自发地进行一个dG>
物理化学第五章化学平衡

G ξ = ∑ν B B = r Gm B T ,P
B
化学反应的亲和势,用A来表示,A只取决于系统的始、终态,是系统的强 度性质 二、化学平衡的热力学原因 在一定的条件下,自发的化学反应总是向着一定的方向进行,并进行到一 定的限度即达到平衡为止
r m p
J p (气) 只包括气体组分的分压商 平衡时
r Gm = 0
§5-2 等温方程及标准平衡常数
0 r Gm = RTLnJ p (平衡,g )
定义:
0 r Gm K ≡ exp RT 0
PB (g , 平衡) γ B ) 0 P PL 0 P = a PA 0 P
( ξ 增大),则系统的Gibbs函数降低,这就是说,此时反应的倾向是自左 而右进行,即向生成产物的方向进行。 G G 若 > ,表明反应在反应进度 ξ 时,若反应继续正向进行,( ξ 增 0
ξ T , P
大),则系统的Gibbs函数增大,此时反应不能向右进行,只能向左进行, 即向生成反应物的方向进行。 G 若 ξ = 0时,表明反应向右进行和向左进行的趋势相等,此时反应将达
§5-2 等温方程及标准平衡常数
0 Ky
0
PB = P y B
P K = ∏ B 0 BP
γB
K y = ∏ yB
B
P yB = ∏ P0 B
γB
γB
∑B ∑ P P γB = 0 ∏ yB = 0 P P B
γ
γB
Ky
Kn
PB = P
nB ∑ nB
P K = ∏ B 0 B P
§5-1 化学反应的方向和限度 一、化学反应的摩尔Gibbs函变 多组分封闭系统发生微小变化 ,系统的Gibbs函变表示为:
第五章化学平衡要点

K = B(pB /p )B K c = B(cB /c )B K y = B yB B Kn = B nB B
(c = 1moldm-3)
K K c : K = B(pB /p ) B
K = B ((cB /c) c RT/p )B = K c (c RT / p ) B
2. 摩尔反应Gibbs函数与化学反应进度的 关系,平衡条件
对任一反应 0 BB
B
设恒T、p且W’ = 0,有 dG μBdnB
B
因为:dnBBdξ
所以: d G T,p = (BB B ) d
( G / ) T,p = BB B
= rG m
对如下反应: N2 (g) + H2 (g) = NH3(g)
式中第二项 BB RT ln (pB/p )
= RT BB ln (pB/p )
= RT lnB (pB /p )B
令
压力商Jp = B (pB /p )B
rG m = BB B + BB RT ln (pB/p ) = rG m + RT ln Jp
此即理想气体反应的等温方程。
2.标准平衡常数
K Ky: K = B(pB /p ) B = B(ptotal yB /p ) B = B yB B (ptotal /p ) B = K y (ptotal /p ) B (ptotal为总压)
K Kn: K = B(pB /p ) B = B(ptotal yB /p ) B
Jp = K 处于平衡;
Jp > K 反应逆向进行。
K 与化学计量式的写法有关。例如合成氨:
1. N2(g)+3H2(g) = 2NH3(g);
第五章吉布斯自由能和化学平衡

ΔG判据:
ΔG < 0, 能自发进行
ΔG > 0 不自发进行,要进行需外力推动,
但反向是自发的。
ΔG = 0 处于平衡状态。
2、化学反应的标准摩尔吉布斯自由能变
a) 物质的标准生成吉布斯自由能ΔfGm
与焓一样,在特定状态下物质(所含)的吉布斯自由能的绝对值 是无法求得的。人们采取的办法是求取其相对值。规定:
只是说需要外力的推动。
b)自发的过程进行有一定的限度,即最终达到平衡。
c)自发的过程的内在推动力是什么?
A、能量倾向于较低,例如放热反应 B、混乱度倾向于增加
历史上曾有人,用焓变作为化学反应的方向 性的判据。 但对有些情况,遭到了失败。例如:
水的蒸发(吸热)
NH4Cl的溶解
N2O5 = 2 NO2 + 1/2 O2 这种失败,其原因是,只考虑了化学反应能量这一个方 面的因素。但决定整个化学反应方向的还有另外一个重要因 素,即:“混乱度”的因素。因此,要全面考察化学反应的 方向,还必须引入一个新的热力学状态函数——熵。
# 冰的融化,水的气化 # 锌粒在酸溶液中反应溶解
2、热力学第三定律与物质的标准摩尔规定熵
既然熵指的是体系的混乱度,那么,对于一个特定的物质体 系,什么时候物质的微粒排列最整齐,物质的熵值为零?热力学 第三定律就给我们指出了物质熵的零点:
热力学第三定律:任何物质的完美晶体,在绝对0 K时的熵值为零。
ΔS体系 + ΔS环境 > 0
三、吉布斯自由能
?吉布斯自由能变与自发反应的方向
? 化学反应的标准摩尔吉布斯自由能变 ? 温度对化学反应的吉布斯自由能变 及
化学反应方向的影响
无机化学教学5章化学平衡PPT课件

05
沉淀溶解平衡
沉淀溶解平衡常数
沉淀溶解平衡常数(Ksp)
表示在一定温度下,难溶电解质在水中的溶解度。
Ksp的表达式
Ksp = [Ca2+][CO32-] / [CaCO3],其中 [Ca2+][CO32-]和[CaCO3]分别代表溶液中钙离子、 碳酸根离子和碳酸钙的浓度。
Ksp的意义
用于判断沉淀的生成和溶解,以及计算溶液中离子 的浓度。
影响沉淀溶解平衡的因素
温度
温度升高,沉淀溶解平衡常数增大,沉淀溶解度 增大。
同离子效应
当溶液中存在与沉淀溶解平衡相同的离子时,会 降低沉淀的溶解度。
浓度
溶液中离子浓度的改变会影响沉淀溶解平衡常数 ,进而影响沉淀的生成和溶解。
盐效应
当溶液中加入强电解质时,会增大沉淀的溶解度 。
沉淀溶解平衡的应用
80%
影响因素
总结词
化学平衡常数受温度、压力、反应物浓度等因素的影响。
详细描述
温度对化学平衡常数的影响较大,温度升高,平衡常数一般会增大;压力对平衡常数的影响较小,但在高压条件 下,平衡常数可能会有所增大;反应物浓度对平衡常数的影响取决于反应的特性,对于可逆反应,反应物浓度的 变化会影响平衡常数的数值。
详细描述
酸碱平衡常数(通常用K表示)是温度的函数,反映了在一定温度下,酸和碱达 到平衡时各自的浓度。这个常数对于理解酸碱反应的本质和预测反应结果至关重 要。
酸碱平衡的移动
总结词
酸碱平衡的移动是化学反应动态平衡的表现,受到温度、压 力、物质的性质和浓度等多种因素的影响。
详细描述
当一个酸碱反应达到平衡状态时,平衡可能会因为温度、压 力、物质的性质或浓度的变化而发生移动。了解平衡移动的 规律对于预测和控制化学反应结果具有重要意义。
物理化学-第五章化学平衡

ΔG1=0
ΔG2=RTln(bθ/b)
C4H6O4(饱和溶液, b=0.715 mol/kg)
G
f
G
θ m
(aq)
f
G
θ m
(s)
G1
G2
ΔfG
θ m
(aq)
Δf
G
θ m
(s)
RTln(bθ /b)
5.4 各种因素对化学平衡的影响 问题:
1. 对于已经达到平衡的反应,可否改变其平衡位置?
2. 如何选择最适宜的反应条件? 工业合成氨 3H2(g) + N2(g) = 2NH3(g) 工业生产中的工艺条件一般是在520ºC, 30MPa,
B
pBeq
vB
pθ
平衡分压积
标准平衡常数, 简称平衡常数
rGmθ RT ln K θ 标准平衡常数Kθ热
力学定义式
K θ exp( rGmθ )
适用于任何类型的 化学反应
RT
任意化学反应
0 B BB
当化学反应处于平衡时:rGmeq
v
B
eq
B
0
B
化学势通式:
μB μBθ RTlnaB FB
(1) 根据反应的ΔrHmθ 和ΔrSmθ 计算
rGmθ
r
H
θ m
Tr Smθ
其中:
r
H
θ m
vB
f
H
θ m,
B
标准摩尔生成焓
B
Δr Smθ
vB Smθ , B
B
标准摩尔规定熵
由表中298.15K数据如何求T 下的ΔrGmθ?
T
r
H
θ m
第5章化学平衡
1
第五章 化学平衡(Chemical Equilibrium)
热力学在物理化学中两个重要的应用:相平衡、 化学平衡。
所有的化学反应可同时向正反两个方向进行。在 一定条件下,当正反两个方向的反应速率相等时, 就达到了平衡状态(有些反应逆向程度很小,可忽 略,称为单向反应) 。
• ΔrGm0 f (T ) • ΔrG与m Δ均rG与m0 化学反应写法有关
②等温方程应用于平衡态: ΔrGm 0
③等温方程应用于标准态:ΔrG=m ΔrGm0
15
2.理气反应的标准平衡常数(Standard Equilibrium Constant)
恒温恒压理想气体反应的等温方程:
ΔrGm ΔrGm0 RT ln J P
9
2.化学反应的方向与平衡条件
1)判据
r Gm
用(
G
)
T
判断:相当于
,p
A
G
T
,P
G ~ 图 上曲线的斜率。
G
(
)T , p
0
反应自发向右进 行,趋向平衡;
(
G
)T
,
p
0
反应自发向左进 行,趋向平衡。
G
( )T , p
0
反应达到平衡;
10
2.化学反应的方向与平衡条件
2)化学反应的限度(平衡条件) 化学反应的平衡条件是?
解决方法:将上式转变为用T , p等, y宏观
可测量表示的公式,达到便于使用的目的。
12
1.理想气体反应的等温方程(Isothermal Equation)
•对于理想气体反应 0 B B( g)
物理化学 第5章 化学平衡-讲稿
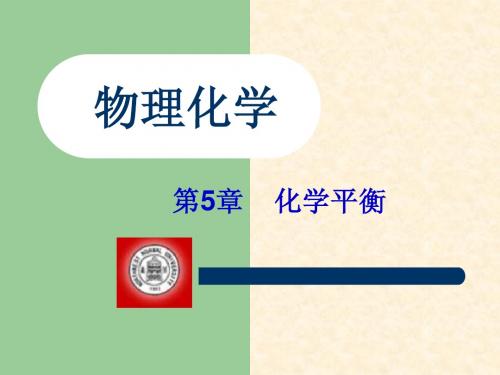
∆rG (T) 反应的标准摩尔Gibbs函数变化值,与标准化学势 反应的标准摩尔Gibbs函数变化值 标准摩尔Gibbs函数变化值, m
一样, 一样,仅是温度函数
Qp
称为压力商, 称为压力商,由参与反应的气体的压力决定
§5.2 化学反应等温方程式
(∆ r Gm), p = ∆ r Gm (T ) + RT ln Qp T
∑ν
B
B
∑ν
B
B
µB > 0
§5.2 化学反应等温方程式
1、理想气体反应系统: 理想气体反应系统:
dD ( p D ) + eE ( p E ) = fF ( p F ) + gG ( p G )
等温等压下, 等温等压下,
∆ rG m =
∅ B
∑ν
B
B
µB
组分B在反应条件的化学势为: 组分B在反应条件的化学势为:
aB = γ B xB = xB
∅ K x = ∏ ( xB )ν B = K x e B
即以液相物质的量分数代替活度 代入标准平衡常数定义式: 代入标准平衡常数定义式: ▲
该式为理想液态混合物反应的标准平衡常数 该式为理想液态混合物反应的标准平衡常数
化学反应等温式的用途: 化学反应等温式的用途:若已知 ∆ r Gm (T ) 和 Q p ,就可以 来判断反应的方向和限度。 计算 (∆ r Gm), p,来判断反应的方向和限度。 T
( 只能用 ∆ r G m) , p 来判断反应的方向和限度,不能用 来判断反应的方向和限度, T ∆r Gm (T ) 来判断反应的方向和限度,除非系统都处于标准 来判断反应的方向和限度, 态。 是一个绝对值较大的负数时, 当 ∆ r Gm (T ) 是一个绝对值较大的负数时,基本上决定 的正、负号, 了 ∆ r Gm), p 的正、负号,可近似用来判断反应的方向和 ( T 限度。 限度。
物理化学-第五章-化学平衡
( g )
3. 增加反应物的量对平衡移动的影响
aA bB yY zZ 恒温恒容条件下增加反应物量对反应平衡的影响:
在已达到平衡的系统中,加入反应物A,瞬间A的分压增加,其他组分分压不变,结果Jp减小, 温度一定,Kϴ不变,反应右移。 恒温恒压条件下增加反应物量并不总是使平衡右移: 当起始反应物配比1:1时,平衡后加入反应物,会使平衡左移。
Kθ的实验测定和平衡组成的计算
Kθ的计算 1. Kθ可由热力学计算得到,由△rGθm=-RTlnKθ计算 2. Kθ 可由实验测定得到,由平衡时Kθ= ∏(PB/Pθ)vB( 理想气 体)可得
平衡组成的特点
1. 反应条件不变,平衡组成不变 2. 一定温度下,正向与逆向反应平衡组成算出的Kθ应一致 3. 温度不变,改变原料配比所得的Kθ应相同
注意:溶剂A和溶质B的标准态不同。
A
B
B
(r b
B
B B
/ b )B
习题
五氯化磷分解反应 在200℃时的Kθ =0.312,计算: (1)200℃、200kPa下PCl5的离解度; ( 2 )组成 1 ∶ 5 的 PCl5 与 Cl2 的混合物,在 200 ℃ 、 101.325kPa下PCl5的离解度。
上式中△rHθ m=∑vB△fHθ m,B=-∑vB△cHθ m,B,△rSθ m=∑vBSθ m,B (2)通过△fGθ m来计算△rGθ m
△rGθ m=∑vB△fGθ m
(3)由相关线性反应计算,如果一个反应可由其他反应线 性组合得到,那么该反应的△rGm也可由相应反应的△rGm线
性组合得到
如 (3)=(1)+ 2*(2),那么 △rGθ m,3=△rGθ m,1+2△rGθ m,2
化学平衡(全)

0
e
0
1
系统的Gibbs自由能和ξ的关系
为什么化学反应通常不能进行到底?
严格讲,反应物与产物处于同一系统的反应都 是可逆的,不能进行到底。
只有逆反应与正反应相比小到可以忽略不计的 反应,可以粗略地认为可以进行到底。这主要是由 于存在混合Gibbs自由能的缘故。
为什么化学反应通常不能进行到底?
以反应 D E 2F 为例,在反应过程中Gibbs自 由能随反应过程的变化如图所示。
判断化学反应的方向与限度
用
(
G
)T
,
p
,
BB
B
或
(rGm )T , p
作判据都是等效的
(rGm )T, p 0
BB 0
B
(rGm)T,p 0
BB > 0
B
反应自发地向右进行 反应自发地向左进行
(rGm )T , p 0
BB = 0
B
反应达到平衡
判断化学反应的方向与限度
用
G
T , p
Gg
h H
Dd
e E
Kp
Kf B
K ( p ) B
气体反应的经验平衡常数的表示法有:
1. 用压力表示的经验平衡常数 K p
Kp
Kf B
K ( p ) B
Kp
B
p B B
K
B
B B
因为 所以
BB (T ) rGm (T ) RT ln K f
B
K f 仅是温度的函数
K 与温度和压力有关
混合理想气体中B的化学势表达式为:
B (T ,
p)
B
(T )
RT
ln
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 化学平衡 考研辅导题答案说明:如果答案有问题,请及时联系1、化学反应体系的ΔrGmθ是指( B )。
天津工业2006A 、 反应体系处于平衡状态下,体系G 的改变量;B 、由标准状态下各自独立的反应物变为标准状态下各自独立的产物,Δξ=1mol 假想变化中体系G 的改变量;C 、与ΔrGm 有相同的物理含义及数值;D 、总压力为101.325kPa 下,Δξ=1mol 的化学反应体系G 的改变量。
2、根据某一反应的ΔrGmθ,下列( D )不能确定。
浙江工业2005A 、 标准状态下,反应自发变化的方向;B 、在ΔrGmθ下所对应的平衡位置;C 、在标准状态下,系统所能做的最大非膨胀功;D 、提高温度反应速率的变化趋势。
3、摩尔反应吉布斯函数变∆rGm 不仅是___T__ 的函数,而且还是__P__ 的函数。
在G-ξ曲线上的最低点处∆rGm__=0_,此点即为系统的平衡点。
在平衡点的左边∆rGm<0_;在平衡点的右边∆rGm_>0__。
4、在恒T 、恒P 、非体积功为零的条件下,某反应的△G 负值很大,表明该反应进行的程度大,反应速度也快 ( 错 )5、在 中, 是化学反应达到平衡时的摩尔吉布斯函数的变化值。
( 错 )6、在T 、P 条件下化学反应2A(g)+B(g)Û3C(g)自发地由反应物变为产物,则反应体系中化学势之间应满足( A )A 、 2mA+mB>3mCB 、2mA+mB<3mC C 、2mA+mB=3mCD 、 mA+mB>mC 7、在恒T ,恒P ,非体积功为零的条件下,反应2O3 =3O2在任何温度下都能自发进行,这说明该反应的( C )A 、 △H>0△S>0B 、△H>0 △S<0 C、△H<0 △S>0 D、△H<0 △S<0θθK RT G m r ln -=∆θmr G ∆8. 若某一化学反应的ΣνBμB <0,那该反应能自发向正反应方向进行,此叙述能成立的条件是体系处于( C )A 、等温B 、等压.等温C 、等温等压,除膨胀功外无其它功D 、等温无非膨胀功9、化学反应CaCO3=CaO+CO2,在某温度下若将CO2的压力保持在这样一个值,使得µ(CaCO3 )> µ(CaO) + µ(CO2),则CaCO3将_分解_.10、恒温恒压下,某反应的 =5kJ/mol ,无法判断该反应是否自发。
( 对 )11、反应器中盛有液态Sn 和SnCl 2,相互溶解度可以忽略,在900 K 通入总压为101.325 kPa的H 2—Ar 混合气体。
H 2与SnCl 2起反应,实验测出逸出反应器的气体组成是:50% H 2,7% HCl ,43% Ar(均为体积分数),试问在反应器中气相与液相达到平衡没有?已知: H 2+Cl 2==== 2HCl(g) Θ∆m r G =(-188289-13.134T)J·mol -1Sn (l)+Cl 2==== SnCl 2 (l) Θ∆m r G =(-333062+118.4T)J·mol -1解:反应:H 2+Cl 2==== 2HCl(g) (1)Θ∆m1r G = -188289-13.134×900= -200109.6 J=-200110JSn (l)+Cl 2==== SnCl 2 (l) (2)Θ∆m2r G = -333062+118.4×900= -226502 JSnCl 2(l) +H 2(g)= Sn (l)+2HCl(g) (3)Θ∆m3r G =?由(1)-(2)得(3):∴Θ∆m3r G = -200110-(-226502)= 26392 J lnK 3Θ=-26392/(8.314×900)=-3.5271 K 3Θ=2.94×10-2J P =(P HCl /P Θ)2/(P H2/P Θ)=0.072/(0.5)= 9.8×10-5∵ K Θ与 J P 相差很远θmr G ∆∴ 未达平衡。
12、反应CO(g)+H2O(g)=CO2(g)+H2(g)在973K 时压力平衡常数Kp=0.71,若各物质分压为CO 100kPaH2O 50kPa,CO2和H2各10kPa ,则反应( A )浙江工业2003 A 、向右进行 B 、向左进行 C 、处于平衡 D 、反应方向难确定13、某反应A(s) == Y(g) + Z(g)的ΔrGm 与温度的关系为ΔrGm = (-45000+110 T/K)J ·mol -1,在标准压力下,要防止该反应发生,温度必须 ( A )A 、高于136 ℃ B、低于184 ℃ C、高于184 ℃ D、低于136 ℃14、在T = 600K ,总压p = 3×105Pa,反应A(g) + B(g)= 2D(g),达平衡时,各气体物质的量之比为n A/n B = n B/n D =1,则此反应的 ( 0 ); ( 0 ) ( 1 ) 15、16、Ag 可能受到H2S(g)的腐蚀,发生下列反应H2S(g)+2Ag(s)=Ag2S(s)+H2(g)25℃,将Ag(s)放到总压为p θ的H2与H2S 混合气体中,求在什么浓度下H2S 不使Ag 腐蚀。
已知此温度下 分别为Ag2S(s)=-40.25kJ/mol ,H2S=-32.93kJ/mol解:得p(H2S)≤4.96kPa所以混合气体中H2S 的摩尔分数应低于x(H2S) ≤0.049617、反应 MgO(s)+H 2O(g)=== Mg(OH)2(s), Θ∆m r G =(-46024+100.42T) J·mol -1,试问:(1)在298 K 、相对湿度64%的空气中MgO(s)是否会水解成Mg(OH)2(s)?r mG ∆=r m G θ∆=K θ=θmf G ∆)2()2(100ln 1015.298314.893.3225.40)()(ln)()(/)(/)(ln)()(0ln 322222222S H p S H p S H p H p RT S H G S Ag G p S H p p H p RT S H G S Ag G J RT G G m f m f m f m f p m r m r -⨯⨯⨯++-=+∆-∆=+∆-∆=≥+∆=∆-θθθθθθθ(2)在298 K ,为避免MgO 的水解,允许的最大相对湿度为多少? 已知298 K 时水的饱和蒸气压为2338 Pa 。
解: (1) MgO(s)+H 2O(g)=== Mg(OH)2(s)rGm ∆=-46024+100.42T=-46024+100.42×298=-16098.8 J·mol -1相对湿度 RH=P H2O /P’H2O =0.64 P H2O =0.64 P’H2O =0.64×2338=1496.3 ParGm ∆= rGm ∆+RTln(P o /P H2O )=-16098.8+8.314×298ln(100000/1496.3) =-5687.6 J·mol -1 rGm ∆<0 故 MgO(s)会水解(2) rGm ∆=rGm ∆+RTln (P o /P H2O )≥0-16098.8+8.314×298ln(100000/ P H2O ) ≥0 ln P H2O ≤5.015, P H2O ≤150.66即相对湿度 RH= P H2O /P’H2O =150.66/2338=0.0644=6.44%18、潮湿的Ag 2CO 3在383 K 时于空气流中干燥,为防止分解,空气中CO 2的分压应为多少?已查得有关热力学数据如下:解:232Θ∆mr H (298)=-393510-30543+501660=77607 J Θ∆mr S (298)=213.68+121.75-167.4=168.03 J/KCp ∆=37.6+65.7-109.6=-6.3 J/K∴ Θ∆m r G (298)=77607-168.03×298=27534 J因为:Θ∆mr H (T)= 77607+⎰-TdT298)3.6(= 79484-6.3TΘ∆mr G /T=27534/298+⎰--TdTT T 2982/)3.679484(=79484/T+6.3lnT-210.22T∴ Θ∆m r G (T)=79484+6.3TlnT-25.48RT则:Θ∆m r G (383)= 13322 J, Kp o (383)=0.01524=P(CO 2)/P o所以Ag 2CO 3(s)的分解压为:P(CO 2)=1545Pa ,故CO 2的压力应大于1545 Pa 。
求Θ∆m r G 还有另外一种方法,想想?19、固体化合物A 放入抽空的容器中,发生分解反应:A(s)=B(g)+C(g).298K 测得系统总压(分解压)为90kPa,假设B 、C 为理想气体,则该条件下反应的标准平衡常数为(0.2025 )20、某反应的 =0,则该反应的标准平衡常数 =( 1 )21、已知反应:FeO(s)+H 2(g)=== Fe(s)+ H 2O(g) 的 Θ∆m r G =(13180-7.74T)J·mol -1;CO 2(g)+H 2(g)=== CO(g)+ H 2O(g) 的Θ∆m r G =(35982-32.63T)J·mol -1(1)试计算1000 K 时下列反应的平衡常数:FeO(s)+CO(g)==== Fe(s)+CO 2(g)(2) 如果薄钢板在1000 K 下于含有10% CO 、2% CO 2和88% N 2(均为体积分数)的气氛中退火,会不会生成FeO? 解:(1) 已知 1000K 时:FeO(s)+H 2(g)==== Fe(s)+ H 2O(g) (1)1rGm ∆=13180-7.74×1000=5440 JCO 2(g)+H 2(g)==== CO(g)+ H 2O(g) (2)2rGm ∆=35 982-32.63×1000=3350 J由(1)-(2) 得 (3):FeO(s)+CO 2(g) ==== Fe(s)+CO(g) (3)∴ 3rGm ∆= 1rGm ∆-2rGm ∆=5440-3352=2088 JlnK 3o = -3rGm ∆/(RT)= -2088/(8.314×1000)= -0.2511K 3o =0.778θm r G ∆θK(2) rGm ∆=rGm ∆+RTln[(P CO /P o )/(P CO2/P o )]=rGm ∆+ RTln (P CO / P CO2)=2088+8.314×1000ln(0.1/0.02)= 15.469k J·mol -1rGm ∆>0∴ 钢板在所给气氛下退火会生成FeO 。
