线性规划对偶问题__运筹学__胡运权__清华大学出版社
《运筹学》胡运权清华版-2-01对偶问题

一、对偶问题的提出
二、原问题与对偶问题的数学模型
继续
三、原问题与对偶问题的对应关系
返回
一、对偶问题的提出
题对
偶 问
实例:某家电厂家利用现有资源生产两种
产品, 有关数据如下表:
上页 下页 返回
设备A 设备B 调试工序
产品Ⅰ 产品Ⅱ
0
5
6
2
1
1
利润(元) 2
1
D
15时 24时 5时
a11x1 a12x2 ... a1n xn b1 .a..21x1 a22x2 ... a2n xn b2 am1x1 am2 x2 ... amn xn bm xi 0,i 1,2,..., n
题对 偶 问
上页 下页 返回
对偶问题
min w b1 y1 b2 y2 ... bm ym
y 调试工序 –––– 元/3时
付出的代价最小, 且对方能接受。
厂家觉得比
收
自己生产有利。
购
题对 偶 问
上页 下页 返回
厂家能接受的条件:
出 用同让等代6 y数价2量应的不y资低3 源于 2 5 y自1己生2产y的2 利润y3。 1
收购方的意愿:
单位产品Ⅰ出租 收入不低于2元
单位产品Ⅱ出租 收入不低于1元
y1 a11
a12...
a1n ≤ b1
偶 问
y2 a21 ... ...
a22... ...
a2n
≤
... b2
... ...
题
ym am1 am2 ... amn ≤ bm
≥ ≥ ≥
max c1 c2 ... cn
题对 偶 问
运筹学课程03-线性规划对偶理论及其应用(胡运权 清华大学)

15
二、线性规划的对偶模型
2、非对称型对偶问题
NEUQ
矩阵形式:P max Z CX AX b X 0
D min W Y b AY C Y 无符号限制(无约束)
16
NEUQ 例二、原问题 max Z 2 x1 3 x 2 4 x 3
2 x1 3 x 2 5 x 3 2 3 x1 x 2 7 x 3 3 x1 4 x 2 6 x 3 5 x1 , x 2 , x 3 0
解:对偶问题为 minW 2 y1 3 y 2 5 y 3 2 y1 3 y 2 y 3 2 3 y1 y 2 4 y 3 3 5 y1 7 y 2 6 y 3 4 y , y , y 无约束 2 3 1
NEUQ
minW 4 y1 2 y 2 y1 y 2 2 y1 y 2 1 (对) y1 0, y 2 0
无界
无可 行解
28
例:已知
NEUQ
D : minW 2 y1 y2 y1 2 y2 1 y1 y2 2 y1 y2 0 y1 , y2 0
对偶问题: max W 5 y1 4 y 2 6 y 3 y1 2 y 2 2 y1 y3 3 3 y1 2 y 2 y 3 5 y1 4 y 2 y 3 1 y1 0, y 2 0, y 3无 约 束
__
__
NEUQ
推论1 原问题的任何可行解目标函数值是其对偶问题目 标函数值的下限 对偶问题的任何可行解目标函数值是其原问题目
运筹学教程(第二版)(胡运权)课后答案(清华大学出版社)

运筹学教程(第⼆版)(胡运权)课后答案(清华⼤学出版社)运筹学教程(第⼆版)习题解答第⼀章习题解答运筹学教程1.1 ⽤图解法求解下列线性规划问题。
并指出问题具有惟⼀最优解、⽆穷多最优解、⽆界解还是⽆可⾏解。
1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5 x 1 + 6 x 2≤ 82 5 ≤ x ? 1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3) 1 2 x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 21 2 ? ≥ 12 2 1 ? x , x ≥ 0 .? ?2 x 1 + x 2 ≤ 2st ?3x + 4 x (2) max Z = 3x 1 + 2 x 2x , x ≥ 0 1 2该问题⽆解≥ 12 2 1 ? ? 2 x 1 + x 2 ≤ 2st .?3 x +4 x ( 2 ) max Z = 3 x 1 + 2 x 2第⼀章习题解答3 2 1x = 1, x = 1, Z = 3是⼀个最优解⽆穷多最优解,1 2x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 2该问题有⽆界解1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5x 1 + 6 x 2第⼀章习题解答唯⼀最优解, x 1 = 10, x 2 = 6, Z = 16 ≤ 82 5 ≤ x ?1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3)第⼀章习题解答运筹学教程1.2 将下述线性规划问题化成标准形式。
运筹学(一)

第三节
单纯形法原理
一、线性规划问题的解
可行解:满足约束条件的解称为可行解,可行解的集合称
a m 1 x1
a
m
2
x2
amnxn (,)bm
x1, x2 , , xn 0
n : 变 量 个 数 ; m:约 束 行 数 ;
n:变量个数 m:约束个数 cj:价值系数 bi:资源拥有量 aij :工艺系数
n m :线性规划问题的规模
c j : 价 值 系 数 ; b j : 右 端 项 ; aij : 技 术 系 数
2x1 x2 x3 x3 x4 9
st.34xx11
x2 2x3 2x3 x5 2x2 3x3 3x3 6
4
x1, x2, x3, x3, x4, x5 0
第二节
图解法
一、图解法的步骤
1.画出直角平面坐标系; 2.图示约束条件,找出可行域; 3.图示目标函数; 4.最优解的确定。
x2 2x2
2x3 3x3
4 6
x1 0, x2 0, x3取值无约束
解: z令 z,x1x1,x3x3 x3 ,其x中 3 , x3 0, 同时引入x4松 和弛 剩变 余 x5,标 量 变准 量形式
m z x a 1 2 x 2 x 3 x 3 3 x 3 0 x 4 0 x 5
1940年,英国军事部门成立了第一个由一些数学家、物理学家 和工程专家等组成的OR小组,负责研究一些武器有效使用的问题。
1942年,美国也成立了由17人组成的OR小组,研究反潜艇策 略等问题。
(3)二战后:推广与发展
战时从事运筹学研究的许多专家转到了经济部门、民用企业、大 学或研究所,继续从事决策的数量方法的研究,运筹学作为一门学 科逐步形成并得以迅速发展。运筹学发展到今天,已成为分支学科 众多的一个繁荣昌盛的大家族。随着电子计算机的发展和使用,运 筹学处理复杂性问题的能力大大加强,成为解决实际问题的有力工 具,广泛地应用于企业管理、交通运输、公共服务等领域。
运筹学清华大学出版社胡运权着课后答案

�12 x1 � 3 x2 � 6 x3 � 3 x4 � 9
(1)
st
��8 ��3
x1 x1
� �
x2 x6
� 4 x3 �0
�
2 x5
� 10
�� x j � 0�, j � 1,� ,6�
min Z � 5 x1 � 2 x2 � 3 x3 � 2 x4
� x1 � 2 x2 � 3 x3 � 4 x4 � 7
运筹学教程�第二版� 习题解答
运筹学教程
1.1 用图解法求解下列线性规划问题。并指出问 题具有惟一最优解、无穷多最优解、无界解还是无可 行解。
min Z � 2 x1 � 3 x2 � 4 x1 � 6 x2 � 6
(1) st .�� 2 x1 � 2 x2 � 4 �� x1 , x2 � 0
Z
0
0.5
2
0
5
0
0
1
1
5
2/5
0
11/5
0
43/5
page 10 6 January 2011
School of Management
运筹学教程
1.4 分别用图解法和单纯形法求解下述线性规划 问题�并对照指出单纯形表中的各基可行解对应图解 法中可行域的哪一顶点。
max Z � 10 x1 � 5 x2 �3 x1 � 4 x2 � 9
max Z � x1 � x2 �6 x1 � 10 x2 � 120 (3) st.�� 5 � x1 � 10 �� 5 � x2 � 8
max Z � 3x1 � 2 x2 �2 x1 � x2 � 2
(2) st.��3x1 � 4 x2 � 12 �� x1, x2 � 0
运筹学胡运权第五版课件-第二章

min Z 3 x1 2 x2 3 x3 4 x4 x1 2 x2 3 x3 4 x4 3 x2 3x3 4 x4 5 s.t. 2 x1 3 x2 7 x3 4 x4 2 x1 0,x2 0, x3、x4无约束 解:对偶问题为: max W 3 y1 5 y2 2 y3
3、矩阵形式: P max z CX AX b s.t. X 0
其中
D min w bT Y AT Y C T s.t. Y 0
a1n a2 n amn
C (c1 , c2 , , cn )
b1 b2 b bm
T T
A Y C C Y A
T T T
CX Y AX Y b b Y
T T T
2、最优性: 若 X* 和 Y* 分别是 P 和 D 的可行解且 CX* = bT Y* , 则X*,Y*分别是问题 P和D 的最优解。
对偶问题(D):
max z 2 x1 3 x2 2 x1 2 x2 12 4 x 16 1 s.t. 5 x2 15 x1 , x2 0
min w 12 y1 16 y2 15 y3 2 2 y1 4 y2 s.t. 2 y1 5 y3 3 y , y , y 0 1 2 3
解:第一步 改写为 min 的基本形式
令x1 x1,x2 x2 x2 min z 7 x1 ( 4 x2 x2) 3x3 4 x ( 2 x2 x2) 6 x3 24 1 3x1 ( 6 x2 x2) 4 x3 15 s.t. ( 5 x2 x2) 3x3 30 ( 5 x2 x2) 3x3 30 x1 ,x2,x2,x3 0
《运筹学》胡运权 第版 第二章 线性规划的对偶理论及灵敏度分析

maZxCX 对
对
AX b
称
偶
s.t.
X
0
形
问 题
式
mW inbTYT
的
对
的 定
s.t.YATT
YT 0
CT
偶 问
题
义
对偶问题的特点
对 •若原问题目标是求极大化,则对偶问题的 偶 目标是极小化,反之亦然
问
•原问题的约束系数矩阵与对偶问题的约束 系数矩阵互为转置矩阵
题 •极大化问题的每个约束对应于极小化问题
出让自己的资源?
问 题 的 导 出
例2-1
条件:出让代价应不低于用同等数量资源由自己组织生 产活动时获取的赢利。
y1,y2,y3分别代表单位时间(h)设备A、设备B和调试工 序的出让代价。 y1,y2,y3的取值应满足:
5y 1
6y 2
2y 2
y 3
y 3
2
1
美佳公司用6h设备B和1h调试可 生产一件家电I,赢利2元
项目
Ⅰ
Ⅱ
每天可用能力
设备A(h)
0
5
15
设备B(h)
6
2
24
调试工序(h)
1
1
5
利润(元)
2
1
其线性规划问题为:
m ax z 2x x
1
2
5 x215
s
.t
.
6
x 2 1 x
x 2
x
24 5
1
2
x1,x2 0
(LP1)
假定有某个公司想把美佳公 司的资源收买过来,它至少 应付出多大代价,才能使美 佳公司愿意放弃生产活动,
对
《运筹学》胡运权第4版线性规划的对偶理论及灵敏度分析省名师优质课赛课获奖课件市赛课一等奖课件

13
2
y3
2 3
题
y1符号不限, y 2 0, y3 0
非 对 偶 形 式 旳 原对 偶 问 题
例2-4 写出下列问题旳对偶问题
max z c1x1 c2 x2 c3x3
a11x a12 x a13x3 b1
s.t.
a21x1 a31x1
a22 x2 a32 x2
a23 x3 a33 x3
出让自己旳资源?
问 题 旳 导 出
例2-1
条件:出让代价应不低于用同等数量资源由自己组织生 产活动时获取旳获利。
y1,y2,y3分别代表单位时间(h)设备A、设备B和调试工 序旳出让代价。 y1,y2,y3旳取值应满足:
6y 2
y 3
2
5y 1
2y 2
y 3
1
美佳企业用6h设备B和1h调试可 生产一件家电I,获利2元
y1, y2 , y3 0
LP1和LP2两个线性规划问题,一般称LP1为原问题, LP2为前者旳对偶问题。
max Z c1x1 c2 x2 cn xn
对 偶 问 题
s.t.
a11 a21
am1
a12 a22
am2
a1n x1 b1
a2n
x2
b2
amn xn bm
规 划 问
minW b1 y1 b2 y2 bm ym
a11 y1 a21 y2 am1 ym (, )c1
a12y1
a22 y2
am2
ym
(,
)c2
题 旳 对 偶 问
a1n y1 a2n y2 amn ym (, )cn
题
y j 0(符号不限,或 0)i 1 ~ m
运筹学(胡运权第二版)习题答案(第二章)

对偶问题: st34yy11
y2 4y3 2 3y2 3y3 4
y1 0, y2 0, y3无限制
School of Management
运筹学教程
page 3 5/17/2021
第二章习题解答
maxZ 5x1 6x2 3x3
x1 2x2 2x3 5
(2)
st
4xx1175xx22
3x3 3x3
运筹学教程
第二章习题解答
page 2 5/17/2021
2.1 写出下列线性规划问题的对偶问题。
min Z 2x1 2x2 4x3
x1 3x2 4x3 2
(1)
st
2x1x3
3 5
x1, x2 , 0, x3无约束
maxW 2y1 3y2 5y3
y1 2y2 y3 2
page 4 5/17/2021
School of Management
运筹学教程
第二章习题解答
m
maxZ cjxj
j1
n
aijxj
bi
(i 1,,m1 m)
(4)
j1 st n aijxj bi
(i m1 1,m1 2,,m)
j1
xj 0 (j 1,,n1,n),xj无约束j( n1 1,,n)
(4)
由于(1)和(4)是矛盾约束,故对偶问题无可行解。 所以原问题目标函数值无界。
page 16 5/17/2021
School of Management
运筹学教程
第二章习题解答
2.7 给出线性规划问题
min Z 2 x1 4 x 2 x3 x 4
x1 3 x2 x4 8
st .
《运筹学》胡运权清华版-2-01对偶问题

对应关系进行求解。
3
对偶定理
运用对偶定理将原问题转化为对偶问题, 从而获得解的有效信息。
优化算法
利用优化算法对对偶问题进行求解,如 单纯运输网络、供应链管理等领域有着广泛的应用。它提供了一种分析和解决实际问题的思 路和方法。
对偶问题在线性规划中的应用
在线性规划中,对偶问题可以通过对偶定理求解,从而获得原问题的最优解。 对偶问题的解释和分析在实际问题中具有重要的意义。
总结
对偶问题是运筹学中一个重要的概念和研究方向。掌握对偶问题的特征、性质、求解方法和应用,将有助于我 们在实际问题中更好地进行分析、建模和决策。
对偶问题的特征
对偶性质
对偶问题与原问题具有相关性,其解与原问题 的解有一定的对应关系。
约束条件
对偶问题的约束条件通常是原问题的目标函数 的系数的线性组合。
目标函数
对偶问题的目标函数通常是原问题的约束条件 的线性组合。
解的含义
对偶问题的解可以提供有关原问题的附加信息, 如原问题的可行域范围。
对偶问题的性质
数学抽象
对偶问题的性质通过数学模型进 行抽象表示,便于分析和求解。
问题解决
对偶问题的性质可以帮助我们从 不同的角度思考和解决现实生活 中的复杂问题。
方程系统
对偶问题的性质可以转化为一组 等式和不等式的方程系统,使得 问题的求解更加简化。
求解对偶问题的方法
1
线性规划方法
2
运用线性规划的方法,通过对偶问题的
《运筹学》胡运权清华版 -2-01对偶问题
在运筹学中,对偶问题是一个重要的概念。它具有独特的特征和性质,可以 通过特定的方法求解。本讲座将介绍对偶问题的定义、特征、求解方法以及 在线性规划中的应用。
《运筹学》胡运权清华版-2-01对偶问题

应用场景限制
对偶问题在某些应用场景中可能存在限制, 需要探索更广泛的应用领域和场景。
对偶问题的未来发展方向
交叉学科融合
对偶问题将与数学、物理、工程等多个学科交叉融合,形成新的 研究领域和方向。
算法优化与并行计算
针对大规模对偶问题的求解,将发展更高效的算法和并行计算技 术,提高求解效率。
应用领域拓展
02
对偶问题在优化、机器学习、大数据等领域的应用将进一步深
化,推动相关领域的发展。
算法创新
03
针对对偶问题的求解算法将不断创新,提高求解效率,满足大
规模复杂问题的求解需求。
对偶问题的研究难点与挑战
理论证明
对偶理论中的一些基本定理和性质仍需进一 步证明和完善,以增强其数学严谨性。
求解难度
求解动态规划对偶问题的方法包括状态转移方程、最优子结构、备忘录法等。这些方法可以帮助我们找 到最优解,并避免重复计算。
在求解动态规划对偶问题时,需要注意对偶问题的最优解并不一定对应原问题的最优解,因此需要对解 进行验证和调整。
博弈论对偶问题的求解方法
01
博弈论是研究多个决策者之间 决策问题的学科,而博弈论对 偶问题则是将原问题转化为求 最大值的问题。
题
非线性规划对偶问题是将原非线 性规划问题的目标函数和约束条 件转换为对偶形式后得到的新问 题。
对偶问题的重要性
理论意义
对偶问题在运筹学理论中具有重要的 地位,它揭示了原问题与对偶问题之 间的内在联系,有助于深入理解运筹 学的基本原理。
应用价值
在实际应用中,对偶问题可以用于求 解原问题的近似解或启发式解,提高 求解效率,尤其在处理大规模优化问 题时具有显著的优势。
线性规划对偶问题__运筹学__胡运权__清华大学出版社

6 互补松弛性
20
1 单纯形法的矩阵描述
max z CX AX b
A, I B, N
C CB,CN
X
XB XN
X 0
max z CX 0X s AX IX s b X 0, X s 0
max z CB X B CN X N BX B NX N b X B 0, X N 0
4
2、 换个角度审视生产计划问题
例 要求制定一个生产计划方案,在劳动力和原材料可能供应的
范围内,使得产品的总利润最大 。
MaxZ 2x1 3x2 3x3
s.t.xx11
x2 x3 3 4x2 7x3
9
x1, x2 , x3 0
它的对偶问题就是一个价格系统,使在平衡了劳动力和原材料 的直接成本后,所确定的价格系统最具有竞争力:
设 y1, y2, y3 分别为设备A、B、C的每台时的租金。为了叙述方便,这里把租金定义为扣 除 原成 利本润后50的元利,润即。y1作 2为y出2 租50者,来否说则,就把不生出产租单还位是用产于品生所产需各产设品备以的获台利时5各0元总;租同金样不把应低于
生产一单位产品所需各设备的台时的总租金也不应当低于原利润100元, 即 y1 y2 y3 100 ,否则这些设备台时就不出租,还是用于生产 产品以获利100元。但对于租用者来说,他要 求在满足上述要求的前提下,也就是在出租者愿意出租的前提下尽量要求全部设备台时的总 租金越低越好,即min 300 y1 400 y2 250 y3 ,这样我们得到了该问题的数学模型:
y1, y2 , , ym 0
这两个式子之间的变换关系称为“对称
形式的对偶关系”。
8
(2)对称形式的对偶关系的矩阵描述
运筹学 第三版 (胡运权版) 黄皮版 清华大学出版社

五、学科体系
2. 学科内容
模型类型 线性规划 整数规划 目标规划 动态规划 网络分析 网络计划 管理决策 方案排序 库存模型 统计方法 排队理论 仿真模拟
21
解决的典型办法 在线性目标和约束条件间取得最优化结果 在线性目标和约束条件间寻求整数决策最优 在相对立的目标间寻得多目标妥协的满意解 寻求多阶段动态系统的整体决策优化问题 寻求网络路径、流量分布、网络瓶颈及其改进 用各种作业和结点的网络排列来说明项目实施计划 依据决策准则权衡比较备选方案的决策结果 综合各方案的优势与不足寻求多指标排名次序 寻求订货、存储和缺货等库存成本降至最低的经济批量 从一个抽样得到普遍结果的推论和曲线拟合 分析正在等待的队列特点及其运行指标 动态观察复杂的管理问题的行为,模拟管理系统的结构关系
MC: 定量解决方法
应用统计 线性规划 整数规划 目标规划 网络计划 网络分析 决策分析 动态规划 ……
教材与参考书籍
• 教材:
谢家平编著.管理运筹学:管理科学方法, 中国人民大学出版社,2010
• 参考书:
David et al. 数据、模型与决策,机械工业出版社,2004 费雷德里克. 数据、模型与决策,中国财政经济出版社,2004 James et al. 数据、模型与决策,中国人民大学出版社,2006
9 OR:SM
决策
二、学科作用
2. 量化思考使人理性
• 冰淇淋实验: 一杯A有70克,装在50克的杯子里,看上去要溢出了 一杯B是80克,装在100克的杯子里,看上去还没装满
单独凭经验判断时,在相同的价格上,人们普遍选择A
• 听一场音乐会:网络订票的票价500元,不去可退票 情况1:在你马上要出发的时候,发现你把最近的价值 500元的电话卡弄丢了。你是否还会去听这场音乐会?
运筹学基础及应用第四版胡运权主编课后练习答案
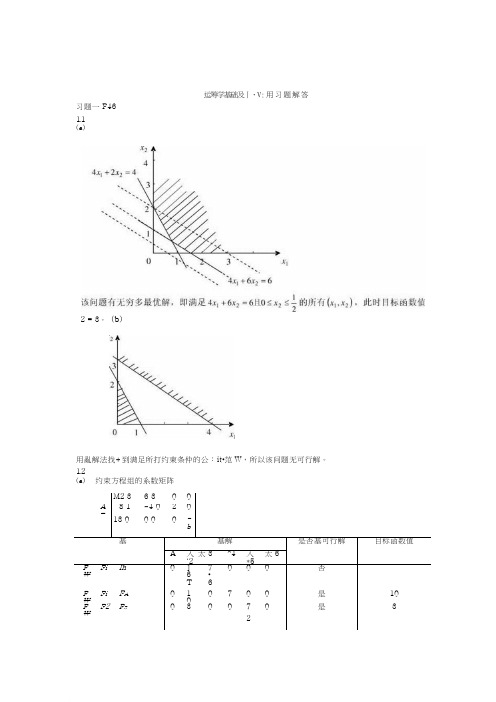
运筹学基础及丨、V:用习题解答习题一 P461.1(a)2 = 3。
(b)用亂解法找+到满足所打约柬条仲的公:it•范W,所以该问题无可行解。
1.2(a)约束方程组的系数矩阵最优解A.=(o,i a o,7,o,o)r(b)约束方程组的系数矩阵 f I 2 3 4、4 = l2 2 I 2,最优解1 = (^,0,11,0^ V55 )"1.3(a)(1)图解法⑵单纯形法首先在各约朿条件上添加松弛变铽,将问题转化为标准形式max z = 10a-, +5a'2 +0x3 +0a4[3a-. +4 义2 + A3 = 9 si.<[5a-j + 2X2 + a'4 = 8则A,P4组成个猫《=令 A = ;c2 = 0得-站可行解a_ = (0.0.9,8),山此列出初始单纯形表cr 2 >0, 0 - minj 2Ax2xi =~,a-3 =0, a 4最优解即为严+2X2=24的解x =卩,2V 最大值z : IA"i + X y =5I 2 2 /新的单纯形农为A', Xo X A14 14_5_ _25M ~T?q.qcO ,表明已找到问题垴优解.(b)(1)图解法17(2)单纯形法苘先在外约朿条件.h 添加松弛变M ,将问题转化为标准形式 max z = 2.v, + x 2 + Ox 3 + 0.v 4 + Oa 5 5a'2 + = 15 6.y, + 2x 2 + .v 4 = 240 00 --2 *^4o A :5、Q 0 一4(7,^2 <0,表明已找到问题最优解^ =1,X 2=- , A-32L估• 17Hi Z =——21.6(a)在约朿条件中添加松弛变量或剩余变量,且令k = jc 2 -a :; (a*2 > 0,.v ; > o)Xx = ~X->该问题转化为max z' = -3a, - x 2 + .v 2 - 2a 3 + 0.v 4 + (Xv 5 2x | + 3a -2 - 3a 2+ 4a 3 +a 4 =12攀 M I4a'| +x 2 -A*2 -2a*3 —^5 =8 3a*, -X 2 +X 2 — 3a*3 = 6A*,, A '2,X 2, x 3,A-4 , A 3 ^ 0-K 约朿系数矩陴为23 -34 I 0 4 丨-1-20-13 -丨丨一3 0 0在A 屮人为地添加两列单位向虽/>7,2 3 -3 4 1 0 0 0 4 丨-1 -2 t) -1 丨 0 3-1 I -3 0 0 0 1令 max z'= -3a -i - x 2 +x 2- 2.v 3 + Oa:., + 0.v 5 - Mx 6 - Mx 7 得初始单纯形表15最大a 4 = 0,x 5SS ^ Xi x 2x 4 x 5 x 6-2 0 0M -M4 10 -I 0 00 0 0-3 + 7M -J 1 -2-5M 0 -M 0 0-I-5(b)在约朿条件中添加松弛变M 或剩余变M ,.R 令a:3 (jc 3>0,.x ;>0)该问题转化为max z • = 一3^ - 5.v 2 + x ?- x ? + 0,v 4 + Ox 5 x, + 2X 2 + x^- x^-x 4 =6 2.v, + x 2- 3jc 3 - 3^:3 + a*5 = 16 x 2+ 5 a*3 一 5a*3= 10 •v p A :2,“x 4,A 5^0艽约柬系数矩阵为213-30-1 115-50 0v/ft A 屮人为地添加两列单位向觉p 7, 121-1-1010、2 13-30 100 115 -5 0 0 01、 /令 max z , = -3a*, 一 5,v 2 + .v 3 一 x 3 + 0x 4 + 0x s 一 Mx b - Mx 1衍初始单纯形表0 0 -M - M X. X, X,X, X, X, X, x n-A/ x 616-M x 7 10-3 + 2A/ 5 + 3M 1+6M -1-6M -M 0 0 0(a)解1:大\1法在上述线性规划问题中分别减去剩余变萤x 4,x 6,〜再加上人工变蛩15,17,',得max z = 2x t - x2 + 2x3 + 0,v4 - Mx s + 0,v6 - Mx7 + 0a8- Mx^-3 + 7M -J 1 -2-5M 0 -M 0 0A', + X 2 + A :3 - + JC 5 = 6 -2x l + jc 3 — a*6 + x 1 —2 2x z — j c 3 - a *8+ j c 9 =0a-,,.v 2,a*3,j:4,a:5,^6,x 7,x 8,a-9 >0,r,其中MS 个任意人的正数-据此可列出单纯形表22MMMjc, x 2x 4X5 X6 A-M x s 6 -M x 7一2 —Ma 、00 0 0[2]0 M 02-M 3A/-1 2 + A/ -M 1/2 -1/2 0 0-1/2 -1/2x s-M x,—Ix\ [1]1/2^ 5M 3 … ^… A/ I 1 3A/ 2-M0 ----- + — - M0 -M 0 ------------------ 一十 ---2 2 2 2 2 2-M jr 5 3 2 .v 3 2 -I x 2 I 3/2 -3/2 1/2 -1/2 -11-1/2 1/2 -1/2 1/20 0 0 1 1 03/40 0?>M +3 -5M -3 M-3M4Af+5 0 ■M22 2x, 3/4 A 3 7/2 7/40 00 1 0| 43/8 - 8 8-5/4 -M8山单纯形表计算结果可以ft 出,ct 4 >0且%<0(/ =丨,2,3),所以该线性规划问题有无界解 解2:两阶段法。
运筹学(胡运权第二版)习题答案(第二章)

2.9 用对偶单纯形法求解下列线性规划问题。
minZ 4x1 12x2 18x3
(1)
st.
x1 3x3 3 2x2 2x3 5
xj 0,( j 1,,3)
minZ 5x1 2x2 4x3
3x1 x2 2x3 4
(2) st.6x1 3x2 5x3 10
xj
0, (
j
1,,3)
School of Management
page 11 5/17/2021
School of Management
运筹学教程
第二章习题解答
min W 2 y1 3 y2
y1 2 y2 2
(1)
对偶问题:
st
.
2 3
y1 y1
y2 y2
3 5
y1
3y2
6
y1 0, y2 0
(2) 最优解是:y1=-8/5,y2=1/5,目标函数值-19/5。 (3)由于 y1=-8/5,y2=1/5都不等于零,原问题中的约 束取等号。又上面第4个约束不等号成立,故x4=0,令 x3=0就可以得到最优解: x1=8/5,x2=1/5。
page 5 5/17/2021
School of Management
运筹学教程
第二章习题解答
minWb1y1b2y2 bmym
m
aijyi
cj
(j 1,2,,n1)
对偶问题s: tim 1 aijyi cj
(j n11,n12,,n)
i1 yi 0
(i 1,,m1)
yi无约束j( m1 1,,m)
2x3 5x3
4 10
xj
0, (
j
1,,3)
运筹学线性规划与对偶问题PPT.

2021/12/24
8
运筹学与管理科学的关系
从管理的角度看,可以说运筹学是用定量方法为管 理决策提供依据的一门学科。以便实现有效管理、 正确决策和现代化管理可简单地归结为一句话: “依照给定条件和目标,从众多方案中选择最佳方 案”。
解 释 实施方案
运筹学解决问题的关键—建立模型
10
按照模型特征的分类:
线性规划 整数规划 网络规划 动态规划 非线性规划 多目标规划 存贮论 决策论 排队论 博弈论 搜索论, 等等
2021/12/24
11
第四个等级就是,客户想买车,但是不知道买什么样的车。他拿不定主意是买十万块钱左右的,还是买十万块钱以下的,或是十万块 钱以上的,他自己的购车目的还不明确。除了价钱没确定,品牌也没确定,他未确定的因素还有很多,但是他想买车,有买车的需求
运筹学模型求解的软件介绍 ,至于买什么样的车自己还没定位,究竟哪一款车适合自己他不知道,他现在正处于调研阶段,这种客户属于第四个等级,他可能需
要一个月以上的时间才能决定购买。
EXCEL (2)跳远时,必须严格按老师的指导助跑、起跳。起跳前前脚要踏中木制的起跳板,起跳后要落入沙坑之中。这不仅是跳远训练的技
现在普遍认为,运筹学是近代应用数学的一个分支, 主要是将生产、管理等事件中出现的一些带有普遍 性的运筹问题加以提炼,然后利用数学方法进行解 决。
运筹学已成为管理科学中最重要的组成部分之一。
2021/12/24
9
0.2 运筹学的模型化方法论
2021/12/24
确定现实问题
建 摸 模型
分 析 求 解 模型解
《运筹学》胡运权清华版-2-02单纯形算法的矩阵表示

?
-1 -2 1/2 1/2
-1/2 1/2
解:
cj CB 0 0 0 XB x4 x5 b 60 10 2 x1 3 1 1 2 -1 x2 1 -1 1 -1 1 x3 1 2 -1 1 0 x4 1 0 0 0 0 x5 0 1 0 0 0 x6 0 0 1 0
.............................................................
1. 两者的最优值相同 z w 17 / 2 2. 从任一个问题的最优表,可以直接 找到另一个问题的最优解,对应关系 原问题决策变量 原问题松弛变量
对偶问题剩余变量 对偶问题决策变量
例2、用单纯形表求解 x1 LP问题所得最优表如下, 4 x1 试直接写出对偶问题最 优解。 x1 , x2
单纯形法的矩阵描述
一、初始单纯形表 线性规划问题:
标准型:
max
z CX
max
z CX 0 X S
AX b s.t. X 0
初始单纯形表
AX I X S b s.t. X , XS 0
C 0
基系数
0
基列
XS
常数列
b
X
A
XS
I
cj- zj
C
0
二、迭代后的单纯形表(当前可行基——B)
结论:当采用单纯形法求得原问题的一个 最优解的时候,检验行上同时得到对偶问 题的一个可行解,且两者具有相同的目标 值。利用对偶性质,可以证明这个对偶问 题的解也为最优解。
例、以求解下面LP问题以及它的对偶问题过程为 例,验证前述结论
原 问 题
max z 2 x1 x 2 s.t. 5 x 2 15 6 x1 2 x 2 24 x1 x 2 5 x1, x 2 0 min w 15 y 24 y 5 y s.t 6y y 2 5y 2y y 1 y ,y ,y 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
约束条件数:m个
对偶变量数:m个
第 i 个 约 束 条 件 类 型 为 “ ≤ ”第i个变量≥0
不等式变号,“极大”变“极小”
(4) 对称性: 对偶问题的对偶是原问题. 9
例:写出下面线性规划的对偶规划模型:
max z c1x1 c2 x2 c3x3
a11x1 a12 x2 a13x3 b1
s.t.aa3211xx11
a22 x2 a32 x2
a23 x3 a33 x3
b2 b3
2
每一个线性规划问题,都存在每一个与它密切相关的线性规划的问题,我们称其为原问题, 另一个为对偶问题。
例题1 某工厂在计划期内安排Ⅰ、Ⅱ两种产品,生产单位产品所需设备A、B、C台时如表所示
设备 A
1
设备 B
2
设备 C
0
资源限量
1
300 台时
1
400 台时
1
250 台时
该工厂每生产一单位产品 可获利50元,每生产一单位产品Ⅱ可获利100元,问工厂应分别 生产多少 产品和Ⅱ产品,才能使工厂获利最多?
5
MinW 3y1 9 y2
y1 y2 2
s.t.
y1 y1
4y2 7 y2
3 3
y1, y2 0
(用于生产第i种产品的资源转让收益不 小于生产该种产品时获得的利润)
对偶变量的经济意义可以解释为对工时及原材料的单位定价 ;
若工厂自己不生产产品A、B和C,将现有的工时及原材料转 而接受外来加工时,那么上述的价格系统能保证不亏本又最富 有竞争力(包工及原材料的总价格最低)
am1x1 am2 x2 amn xn bm
x1, x2 , , xn 0
7
则定义其对偶问题为
min W b1 y1 b2 y2 bm ym
a11 y1 a21 y2
s.t.
a12
y1
a22
y2
am1 ym c1 am2 yn c2
a1n y1 a2n y2
amn yn cn
y1 0, y2无约束, y3 0
11
2、非对称形式的对偶关系:
(1) 原问题
对偶问题
n
max Z cj xj j 1
s.t.
n j 1
aij x j
bi
i 1, 2, , m
x
j
0
j 1, 2, , n
m
minW bixi i1
s.t.Βιβλιοθήκη m i1aijyi
cj
j 1,2, ,n
yi符号不限, i 1,2, , m
目标函数:min f 300 y1 400 y2 250 y3
约束条件: y1 2 y2 50 y1 y2 y3 100 y1, y2 , y3 0
这样从两个不同的角度来考虑同一个工厂的最大利润(最小租金)的问题,所建立起来 的两个线性模型就是一对对偶问题,其中一个叫做原问题,而另外一个叫对偶问题。
当原问题和对偶问题都取得最优解时,这一对线性规划对应的 目标函数值是相等的:
Zmax Wmin 8
6
二、原问题和对偶问题的关系
1、对称形式的对偶关系 (1)定义:若原问题是
max Z c1x1 c2 x2 cn xn
a11x1 a12 x2
s.t.
a21
x1
a22
x2
a1n xn b1 a2n xn b2
设 y1, y2, y3 分别为设备A、B、C的每台时的租金。为了叙述方便,这里把租金定义为扣 除 原成 利本润后50的元利,润即。y1作 2为y出2 租50者,来否说则,就把不生出产租单还位是用产于品生所产需各产设品备以的获台利时5各0元总;租同金样不把应低于
生产一单位产品所需各设备的台时的总租金也不应当低于原利润100元, 即 y1 y2 y3 100 ,否则这些设备台时就不出租,还是用于生产 产品以获利100元。但对于租用者来说,他要 求在满足上述要求的前提下,也就是在出租者愿意出租的前提下尽量要求全部设备台时的总 租金越低越好,即min 300 y1 400 y2 250 y3 ,这样我们得到了该问题的数学模型:
y1, y2 , , ym 0
这两个式子之间的变换关系称为“对称
形式的对偶关系”。
8
(2)对称形式的对偶关系的矩阵描述
max Z CX
minW Yb
(LP)s.t.
AX b X 0
YA C (DP) s.t. Y 0
(3)怎样从原始问题写出其对偶问题?
按照定义; 记忆法则:
“上、下”交换,“左、右”换位,
(特点:等式约束)
(特点:对偶变量符号 不限,系数阵转置)
12
(2)怎样写出非对称形式的对偶问题? 把一个等式约束写成两个不等式约束,再 根据对称形式的对偶关系定义写出; 按照原始-对偶表直接写出 ; (3)原始-对偶表
13
原问题(或对偶问题) 对偶问题(或原问题)
目标函数 MaxZ
目标函数 MinW
解:设x1为产品 的计划产量,x2为产品Ⅱ的计划产量,则有
目标函数:
Max z=50x1 +100x2
约束条件:
x1 x2 300 2x1 x2 400
x2 250
x1 ,x2 0
3
现在我们从另一个角度来考虑这个问题。假如有另外一个工厂要求租用该厂的设备A、B、 C,那么该厂的厂长应该如何来确定合理的租金呢?
4
2、 换个角度审视生产计划问题
例 要求制定一个生产计划方案,在劳动力和原材料可能供应的
范围内,使得产品的总利润最大 。
MaxZ 2x1 3x2 3x3
s.t.xx11
x2 x3 3 4x2 7x3
9
x1, x2 , x3 0
它的对偶问题就是一个价格系统,使在平衡了劳动力和原材料 的直接成本后,所确定的价格系统最具有竞争力:
第二章 线性规划的对偶理论与灵敏度 分析
• §1 线性规划的对偶问题 • §2 对偶规划的基本性质 • §3 影子价格 • §4 对偶单纯形法 • §5 线性规划的灵敏度分析
1
§1 线性规划的对偶问题
一、对偶问题的提出 1、 对偶思想举例 周长一定的矩形中,以正方形面积最大;面积一定的矩
形中,以正方形周长最小;
x1 0, x2 0, x3无约束
10
解:设对偶变量为 y , y , y ,对偶目标为w ,则
min w b1 y1 b2 y2 b3 y3
a11 y1 a21 y2 a31 y3 c1
s.t.aa1132
y1 y1
a22 a23
y2 y2
a32 y3 a33 y3
c2 c3
