(完整版)实数应用题
实数运算100道题

实数运算100道题1. 计算:(-3) + 5 = ?2. 计算:2.5 - 1.3 = ?3. 计算:4 × 3.2 = ?4. 计算:7 ÷ 2 = ?5. 计算:(-2) × (-4) = ?6. 计算:(-5) ÷ 2 = ?7. 计算:3.5 + 2.7 = ?8. 计算:(-6) - (-3) = ?9. 计算:1.2 × 0.5 = ?10. 计算:(-8) ÷ (-2) = ?11. 计算:(-4) + 6 = ?12. 计算:3.8 - 2.1 = ?13. 计算:5 × (-2) = ?14. 计算:(-9) ÷ 3 = ?15. 计算:2.5 + (-1.7) = ?16. 计算:(-5) - 3 = ?18. 计算:(-7) ÷ (-1) = ?19. 计算:(-2) + (-3) = ?20. 计算:4.9 - 1.2 = ?21. 计算:(-6) × 2 = ?22. 计算:7 ÷ (-2) = ?23. 计算:1.5 + 2.3 = ?24. 计算:(-4) - (-7) = ?25. 计算:0.8 × (-0.5) = ?26. 计算:(-9) ÷ (-3) = ?27. 计算:(-3) + (-4) = ?28. 计算:2.7 - 1.4 = ?29. 计算:6 × (-2) = ?30. 计算:(-8) ÷ 4 = ?31. 计算:(-5) + 7 = ?32. 计算:3.9 - 2.6 = ?33. 计算:4 × (-3) = ?35. 计算:1.7 + (-2.5) = ?36. 计算:(-4) - 2 = ?37. 计算:0.5 × 0.3 = ?38. 计算:(-7) ÷ 1 = ?39. 计算:(-2) + 3 = ?40. 计算:4.2 - 1.9 = ?41. 计算:(-6) × (-3) = ?42. 计算:7 ÷ (-3) = ?43. 计算:1.8 + 2.6 = ?44. 计算:(-4) - (-6) = ?45. 计算:0.9 × (-0.4) = ?46. 计算:(-9) ÷ (-1) = ?47. 计算:(-3) + (-5) = ?48. 计算:2.9 - 1.7 = ?49. 计算:5 × (-3) = ?50. 计算:(-8) ÷ (-4) = ?52. 计算:3.5 - 2.2 = ?53. 计算:4 × (-4) = ?54. 计算:(-6) ÷ (-3) = ?55. 计算:1.9 + (-2.3) = ?56. 计算:(-5) - 4 = ?57. 计算:0.4 × 0.2 = ?58. 计算:(-7) ÷ (-1) = ?59. 计算:(-2) + (-4) = ?60. 计算:4.5 - 1.8 = ?61. 计算:(-6) × 3 = ?62. 计算:7 ÷ (-4) = ?63. 计算:1.2 + 2.8 = ?64. 计算:(-4) - (-8) = ?65. 计算:0.7 × (-0.3) = ?66. 计算:(-9) ÷ (-3) = ?67. 计算:(-3) + (-6) = ?69. 计算:6 × (-3) = ?70. 计算:(-8) ÷ 2 = ?71. 计算:(-5) + 9 = ?72. 计算:3.2 - 2.1 = ?73. 计算:4 × (-2) = ?74. 计算:(-6) ÷ (-2) = ?75. 计算:1.5 + (-2.7) = ?76. 计算:(-4) - 1 = ?77. 计算:0.6 × 0.5 = ?78. 计算:(-7) ÷ 2 = ?79. 计算:(-2) + 4 = ?80. 计算:4.8 - 1.3 = ?81. 计算:(-6) × (-2) = ?82. 计算:7 ÷ (-2) = ?83. 计算:1.3 + 2.7 = ?84. 计算:(-4) - (-5) = ?85. 计算:0.8 × (-0.6) = ?86. 计算:(-9) ÷ (-3) = ?87. 计算:(-3) + (-7) = ?88. 计算:2.7 - 1.3 = ?89. 计算:5 × (-2) = ?90. 计算:(-8) ÷ 4 = ?91. 计算:(-5) + 6 = ?92. 计算:3.8 - 2.5 = ?93. 计算:4 × (-3) = ?94. 计算:(-6) ÷ (-3) = ?95. 计算:1.7 + (-2.3) = ?96. 计算:(-4) - 3 = ?97. 计算:0.5 × 0.4 = ?98. 计算:(-7) ÷ 1 = ?99. 计算:(-2) + 3 = ?100. 计算:4.2 - 1.5 = ?这是一百道实数运算题,涵盖了加法、减法、乘法和除法。
实数和有理数应用题

实数和有理数应用题
实数和有理数在数学中扮演着重要的角色,广泛应用于各种实际问题的解决中。
本文将通过一些应用题目,来展示实数和有理数在现实生活中的实际应用。
1. 购物问题
小明去商场购买了一双球鞋,原价400元,现正值打折活动,打八折。
请问小明购买该球鞋后需要支付多少钱?
解:打八折即为原价的80%,因此小明购买该球鞋需要支付的金额为400元 x 80% = 320元。
所以小明购买该球鞋后需支付320元。
2. 温度计问题
某地的气温为摄氏20度,请问这个温度转换为华氏度是多少?
解:华氏度与摄氏度的转换公式为F = C x 9/5 + 32,代入C = 20,得到F = 20 x 9/5 + 32 = 68度。
所以摄氏20度对应的华氏度为68度。
3. 基础运算问题
已知有理数a = -5,b = 3,c = 4,请计算表达式a + b - c的值。
解:将a, b, c代入表达式得到-5 + 3 - 4 = -6。
因此表达式a + b - c的值为-6。
通过以上几个应用题目,我们可以看到实数和有理数在日常生活中的广泛运用,不仅能够帮助我们解决实际问题,还能够锻炼我们的逻
辑思维能力。
希望读者在平时的学习和生活中多多应用数学知识,提升自己的解决问题的能力。
专题02 实数的运算(三大题型,50题)(解析版)

专题02实数的运算(三大题型,50题)(解析版)学校:___________姓名:___________班级:___________考号:___________一、用数轴上的点表示实数,中档题20题,难度三星1.如图,若5x =,则表示2211(1)x x x x -+÷-的值的点落在()A .段①B .段②C .段③D .段④【答案】C 【分析】首先对原式进行化简,然后代入x 的值,最后根据5 2.236≈即可判断.【详解】原式=2211()x x x x x-+-÷=()211x xx x -- =1x -当5x =时,原式=51-∵5 2.236≈∴51 1.236-≈故选C .【点睛】本题考查了分式的乘除法化简,无理数的估算,无理数的估算是难点,关键是要熟记一些常用的完全平方数,和一些常用无理数的近似值.2.若实数p ,q ,m ,n 在数轴上的对应点的位置如图所示,且满足0p q m n +++=,则绝对值最小的数是()A .pB .qC .mD .n【答案】C 【分析】根据0p q m n +++=,并结合数轴可知原点在q 和m 之间,且离m 点最近,即可求解.A.a b>B.π+A.πB.1【答案】B【分析】根据数轴与实数的一一对应关系解答即可.A .a b-+B .a b +C .a 【答案】21π--【分析】求出圆的周长,再根据实数与数轴上的点的对应关系解答即可.【答案】﹣2a﹣b【分析】直接利用数轴结合绝对值以及平方根的性质化简得出答案.【答案】32-或32+【分析】分顺时针旋转和逆时针旋转,两种情况讨论求解即可.【详解】解:∵点A 表示的数为3,点B 表示的数为4,∴1AB =,此时C '表示的数为:32-;当正方形ABCD 绕点A 逆时针旋转,使得点C 落在数轴上的点C '处时,如图:此时C '表示的数为:32+;【答案】2π2+【分析】先求出圆的周长为2π,再利用数轴的性质求解即可得.【详解】解:由题意可知,将圆沿数轴向右转动一周,转动的距离为∴点A 向右移动了2π个单位长度,【答案】280905--+/809052【分析】本题考查的是数轴的一个知识,解题的关键是找到规律:第移动25个单位,从第2次落在数轴上开始,比上一次又向右多移动了(1)图1中的阴影部分为正方形,它的面积是_________;(2)请利用(1)的解答,在图1的数轴上画出表示10的点;并简洁地说明理由.(3)如图2,请你利用正方形网格,设计一个面积方案,在数轴上画出表示理由.【答案】(1)10(3)解:如图,阴影部分为正方形,面积为所以,其边长为5,在数轴上截取5==,CDOC OK则点K表示的数为5,点D表示的数【点睛】本题主要考查正方形的性质以及网格,熟练掌握正方形的性质是解题的关键.20.阅读下面的文字,解答问题.大家知道,2是无理数,而无理数是无限不循环小数,因此【点睛】此题考查的是估算无理数及求代数式的值,能够得到一个无理数的整数部分与小数部分是解决此题的关键.二、实数的大小比较,中档题15题,难度三星π-<-<根据数轴上点的特点可得: 1.5333.在数轴上表示数0,π-303π-<-<<.2【点睛】本题考查了实数与数轴,实数的大小比较,能利用数轴比较实数的大小是解此题的关键,注意:。
实数经典例题+习题(最全)

经典例题类型一.有关概念的识别1.下面几个数:0.23,1.010010001…,,3π,,,其中,无理数的个数有()A、1B、2C、3D、4解析:本题主要考察对无理数概念的理解和应用,其中,1。
010010001…,3π,是无理数故选C举一反三:【变式1】下列说法中正确的是()A、的平方根是±3B、1的立方根是±1C、=±1D、是5的平方根的相反数【答案】本题主要考察平方根、算术平方根、立方根的概念,∵=9,9的平方根是±3,∴A正确.∵1的立方根是1,=1,是5的平方根,∴B、C、D都不正确.【变式2】如图,以数轴的单位长线段为边做一个正方形,以数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是()A、1B、1。
4C、D、【答案】本题考察了数轴上的点与全体实数的一一对应的关系.∵正方形的边长为1,对角线为,由圆的定义知|AO|=,∴A表示数为,故选C.【变式3】【答案】∵π= 3。
1415…,∴9<3π<10因此3π—9>0,3π-10<0∴类型二.计算类型题2.设,则下列结论正确的是()A. B。
C. D。
解析:(估算)因为,所以选B举一反三:【变式1】1)1.25的算术平方根是__________;平方根是__________.2)—27立方根是__________。
3)___________,___________,___________.【答案】1);。
2)—3。
3),,【变式2】求下列各式中的(1)(2)(3)【答案】(1)(2)x=4或x=—2(3)x=-4类型三.数形结合3. 点A在数轴上表示的数为,点B在数轴上表示的数为,则A,B两点的距离为______解析:在数轴上找到A、B两点,举一反三:【变式1】如图,数轴上表示1,的对应点分别为A,B,点B关于点A的对称点为C,则点C表示的数是( ).A.-1 B.1-C.2-D.-2【答案】选C[变式2]已知实数、、在数轴上的位置如图所示:化简【答案】:类型四.实数绝对值的应用4.化简下列各式:(1) |—1。
[数学]-专题 实数的运算计算题(共45小题)(原版)
![[数学]-专题 实数的运算计算题(共45小题)(原版)](https://img.taocdn.com/s3/m/7fc1e82e793e0912a21614791711cc7930b77863.png)
七年级下册数学《第六章 实 数》 专题 实数的运算计算题(共45小题)1.(2022秋•招远市期末)计算:(1)(√5)2+√(−3)2+√−83; (2)(﹣2)3×18−√273×(−√19).2.(2022•庐江县二模)计算:√0.04+√−83−√1−925.3.(2022春•上思县校级月考)计算:(1)−12+√16+|√2−1|+√−83;(2)2√3+|√3−2|−√643+√9.4.(2022春•渝中区校级月考)实数的计算:(1)√16+√(−3)2+√273;(2)√−33+|1−√33|﹣(−√3)2.5.(2022秋•原阳县月考)计算:(1)√−83+√4−(−1)2023;(2)(−√9)2−√643+|−5|−(−2)2.6.(2022春•牡丹江期中)计算:(1)−12−√0.64+√−273−√125; (2)√3+√(−5)2−√−643−|√3−5|.7.(2022秋•南关区校级期末)计算:√16−(−1)2022−√273+|1−√2|.8.(2022秋•成武县校级期末)计算:﹣12022−√643+|√3−2|.9.(2022春•昌平区校级月考)√1253+√(−3)2−√1−35273.10.(2022春•舒城县校级月考)计算:√−273+12√16+|−√2|+1.11.(2022春•舒城县校级月考)计算:﹣12+|﹣2|+√−83+√(−3)2.12.(2021秋•镇巴县期末)计算:(−1)10+|√2−2|+√49+√(−3)33.13.(2022春•阳新县期末)计算:|√3−2|+√−83×12+(−√3)2.14.(2022春•十堰期中)计算:﹣12022+√(−4)2+√83+10√925.15.(2021秋•峨边县期末)计算:|√5−3|+√(−2)2−√−83+√5.16.(2021秋•乳山市期末)计算:√(−3)2−2×√94+52×√−0.0273.17.(2022秋•横县期中)计算:(﹣1)2022+√9−(2﹣3)÷12.18.(2022秋•儋州校级月考)计算:(1)√643−√81+√1253+3;(2)|−3|−√16+√83+(−2)2.19.(2022秋•海曙区校级期中)计算:(1)﹣23+√−273−(﹣2)2+√1681; (2)(﹣3)2×(﹣2)+√643+√9.20.(2022秋•安岳县校级月考)计算:(1)(√3)2−√16+√−83; (2)(﹣2)3×√1214+(﹣1)2013−√273; (3)√(−4)2+√214+√3383−√32+42.21.(2022秋•隆昌市校级月考)计算:(1)|−3|−√16+√−83+(−2)2;(2)√−273+|2−√3|−(−√16)+2√3.22.(2021秋•泉州期末)计算:√(−3)2×√−183−(12)2+(−1)2022.23.(2022秋•新野县期中)计算:√−83+√9−√1916+(−1)2022+|1−√2|.24.(2021秋•新兴区校级期末)计算下列各题:(1)√1−19273+√(14−1)2; (2)√53−|−√53|+2√3+3√3.25.(2022秋•绥德县期中)计算:2(√3−1)−|√3−2|−√643.26.(2022秋•义乌市校级期中)计算:﹣22×(﹣112)2−√−643−√169×|﹣3|.27.(2022秋•西湖区校级期中)计算:(1)|7−√2|﹣|√2−π|−√(−7)2;(2)﹣22×√(−4)2+√(−8)33×(−12)−√273.28.(2022秋•沈丘县校级月考)计算:√0.01×√121+√−11253−√0.81.29.(2022春•西山区校级期中)计算:5−2×(√7−2)+√−83+|√3−2|.30.(2022春•东莞市期中)计算:√(−3)2+(﹣1)2020+√−83+|1−√2|31.(2022秋•安溪县月考)计算:√16+√−273−√3−|√3−2|+√(−5)2.32.(2022秋•仁寿县校级月考)计算:√−8273+√(−4)2×(−12)3−|1−√3|.33.(2022春•海淀区校级期中)计算:√81+√−273−2(√3−3)−|√3−2|.34.(2022春•梁平区期中)计算:√(−1)33+√−273+√(−2)2−|1−√3|.35.(2022春•东莞市校级期中)计算:﹣12020+√(−2)2−√643+|√3−2|.36.计算下列各题:(1)√1+√−273−√14+√0.1253+√1−6364(2)|7−√2|﹣|√2−π|−√(−7)237.计算:√0.0083×√1916−√172−82÷√−11253.38.计算:3√3−2(1+√3)+√(−2)2+|√3−2|39.计算:(1)√(−2)2×√214−23×√(−18)23(2)√9+|1−√2|−√125273×√(−3)2+|4√0.25−√2|40.计算:(﹣2)2×√14+|√−83|+√2×(﹣1)202241.计算:﹣22+√16+√83+1014×934.42.计算:|﹣5|−√273+(﹣2)2+4÷(−23).43.(2022秋•城关区校级期中)计算:(1)√12+(√3)2+14√48−9√13; (2)√(−3)2+(−1)2022+√83+|1−√2|.44.(2021春•濉溪县期末)计算:√49−√273+|1−√2|+√(1−43)2.45.(2022秋•岳麓区校级月考)计算−12022+(12)2+|√2−3|−√(−3)2.。
实数应用题35道及答案

1、已知一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子多288元,一张桌子和一把椅子各多少元?2、3箱苹果重45千克。
一箱梨比一箱苹果多5千克,3箱梨重多少千克?3、甲乙二人从两地同时相对而行,经过4小时,在距离中点4千米处相遇。
甲比乙速度快,甲每小时比乙快多少千米?4、刘军和张强付同样多的钱买了同一种铅笔,刘军要了13支,张强要了7支,刘军又给张强0.6元钱。
每支铅笔多少钱?5、甲乙两辆客车上午8时同时从两个车站出发,相向而行,经过一段时间,两车同时到达一条河的两岸。
由于河上的桥正在维修,车辆禁止通行,两车需交换乘客,然后按原路返回各自出发的车站,到站时已是下午2点。
甲车每小时行40千米,乙车每小时行45千米,两地相距多少千米?(交换乘客的时间略去不计)6、学校组织两个课外兴趣小组去郊外活动。
第一小组每小时走4.5千米,第二小组每小时行3.5千米。
两组同时出发1小时后,第一小组停下来参观一个果园,用了1小时,再去追第二小组。
多长时间能追上第二小组?7、有甲乙两个仓库,每个仓库平均储存粮食32.5吨。
甲仓的存粮吨数比乙仓的4倍少5吨,甲、乙两仓各储存粮食多少吨?8、甲、乙两队共同修一条长400米的公路,甲队从东往西修4天,乙队从西往东修5天,正好修完,甲队比乙队每天多修10米。
甲、乙两队每天共修多少米?9、学校买来6张桌子和5把椅子共付455元,已知每张桌子比每把椅子贵30元,桌子和椅子的单价各是多少元?10.一列火车和一列慢车,同时分别从甲乙两地相对开出。
快车每小时行75千米,慢车每小时行65千米,相遇时快车比慢车多行了40千米,甲乙两地相距多少千米?11、某玻璃厂托运玻璃250箱,合同规定每箱运费20元,如果损坏一箱,不但不付运费还要赔偿100元。
运后结算时,共付运费4400元。
托运中损坏了多少箱玻璃?12、五年级一中队和二中队要到距学校20千米的地方去春游。
第一中队步行每小时行4千米,第二中队骑自行车,每小时行12千米。
初中数学:专题1 实数的运算专项训练50道(举一反三)(解析版)

专题6.5 实数的运算专项训练(50道)参考答案与试题解析3+(﹣1)2021.1.(1分)(2021春•陆河县校级期末)计算:√9+|√5−3|+√−64【分析】先求算术平方根、绝对值、立方根运算,再进行计算即可.3+(﹣1)2021【解答】解:√9+|√5−3|+√−64=3+3−√5−4﹣1=1−√5.3+|√3−2|.2.(1分)(2021春•珠海期中)计算:(﹣2)2+√(−3)2−√27【分析】运用负数的平方、二次根式、三次根式,绝对值的定义及性质进行计算.3+2−√3【解答】解:原式=4+√32−√33=4+3﹣3+2−√3=6−√3.3.(1分)(2021•天心区开学)计算:|7−√2|−|√2−π|−√(−7)2.【分析】由去绝对值及算术平方根运算法则计算即可.【解答】解:原式=7−√2−(π−√2)﹣7=7−√2−π+√2−7=﹣π.3+|2−√5|+|3−√5|.4.(1分)(2021春•浏阳市期末)计算:√81+√−27【分析】本题涉及绝对值、二次根式化简、三次根式化简3个知识点.在计算时,需要针对每个知识点分别进行计算,然后根据实数的运算法则求得计算结果.3+|2−√5|+|3−√5|【解答】解:√81+√−27=9﹣3+√5−2+3−√5=7.3+(﹣3)2−√25+|√3−2|+(√3)2.5.(1分)(2021春•淮北期末)√(−5)3【分析】先计算开方、乘方、绝对值的运算,再合并即可得到答案.【解答】解:原式=−5+9−5+2−√3+3=4−√3.3−√4.6.(1分)(2021春•昆明期末)计算:(﹣1)3+|−√2|+√27【分析】直接利用立方根的性质以及绝对值的性质、有理数的乘方运算法则分别化简得出答案.【解答】解:原式=﹣1+√2+3﹣2=√2. 7.(1分)(2021春•宁乡市期末)计算:√−13+√49+|3−π|−(−√3)2.【分析】直接利用立方根的性质以及绝对值的性质和二次根式的性质分别化简,再利用实数加减运算法则计算得出答案.【解答】解:原式=﹣1+7+π﹣3﹣3=π. 8.(1分)(2021春•临沧期末)计算:√83−(−1)2021+√(−3)2−|1−√3|.【分析】首先计算乘方、开方、开立方和绝对值,然后从左向右依次计算,求出算式的值是多少即可.【解答】解:√83−(−1)2021+√(−3)2−|1−√3|=2﹣(﹣1)+3﹣(√3−1)=6−√3+1=7−√3.9.(1分)(2021春•曲靖期末)计算:﹣22×√14−√83+√9×(﹣1)2021. 【分析】先化简有理数的乘方,算术平方根,立方根,然后先算乘法,再算加减.【解答】解:原式=﹣4×12−2+3×(﹣1)=﹣2﹣2﹣3=﹣7. 10.(1分)(2021春•海拉尔区期末)计算:√−83÷√0.04+√14×(−2)2−(−1)2020.【分析】先化简立方根,算术平方根,有理数的乘方,然后先算乘除,再算加减.【解答】解:原式=﹣2÷0.2+12×4﹣1=﹣10+2﹣1=﹣9.11.(1分)(2021春•红塔区期末)计算:(﹣1)2020﹣(﹣2)2+√4+√−273. 【分析】直接利用有理数的乘方运算法则以及立方根的性质、算术平方根分解化简得出答案.【解答】解:原式=1﹣4+2﹣3=﹣4.12.(1分)(2021春•盘龙区期末)计算:(﹣1)2021+|3﹣π|+√16+√−83−π.【分析】根据﹣1的奇、偶次方,绝对值、算术平方根、立方根的运算法则进行计算即可得出答案.【解答】解:原式=﹣1﹣(3﹣π)+4﹣2﹣π=﹣1﹣3+π+2﹣π=﹣2. 13.(1分)(2021春•开福区校级期末)√(−1)2+√273+(−1)2021+|√3−3|.【分析】先计算平方根、乘方和绝对值运算,再合并同类项即可.【解答】解:原式=|﹣1|+3+(﹣1)+3−√3=1+3﹣1+3−√3=6−√3.14.(1分)(2021春•利川市期末)计算|√2−√3|﹣2(14+√22)−√−183. 【分析】根据绝对值的性质、立方根的定义以及实数的加减运算以及乘除运算法则即可求出答案. 【解答】解:原式=√3−√2−12−√2+12 =√3−2√2. 15.(1分)(2021春•永城市期末)计算:√16+√−643−√1−(35)2−|π﹣3.2|. 【分析】直接利用立方根的性质以及二次根式的性质、绝对值的性质分别化简得出答案.【解答】解:原式=4﹣4−45−(3.2﹣π)=4﹣4−45−3.2+π=﹣4+π. 16.(1分)(2021春•鹿邑县期末)计算:√(−1)33−√3116+√(1−78)23. 【分析】首先计算开方,然后从左向右依次计算,求出算式的值是多少即可.【解答】解:√(−1)33−√3116+√(1−78)23=﹣1−74+14=−52. 17.(1分)(2021春•恩平市期末)计算:√25+√−83−√49+√8273+(−1)2021. 【分析】利用实数的运算法则对所求式子进行求解即可.【解答】解:√25+√−83−√49+√8273+(−1)2021 =5﹣2−23+23−1=2.18.(1分)(2021春•潮阳区期末)计算:−12021+√(−2)2−√−1253+|√2−3|.【分析】直接利用绝对值的性质和立方根的性质和二次根式的性质分别化简得出答案.【解答】解:原式=﹣1+2+5+3−√2=9−√2. 19.(1分)(2021春•白云区期末)计算:√−273−√256−√116+√1−63643. 【分析】实数的混合运算,先分别化简立方根,算术平方根,然后再计算.【解答】解:原式=﹣3﹣16−14+√1643 =﹣3﹣16−14+14=﹣19. 20.(1分)(2021春•杨浦区期中)计算:√−0.0013−(√23−√10003)−√162.【分析】直接利用立方根以及二次根式的性质分别化简得出答案.【解答】解:原式=﹣0.1−√23+10−42 =﹣0.1−√23+10﹣2 =7.9−√23.21.(2分)(2021春•青川县期末)计算:(1)(﹣3)2+2×(√2−1)﹣|﹣2√2|;(2)√−83−√1−1625+|2−√5|+√(−4)2.【分析】(1)先算乘方,化简绝对值,去括号,然后再算加减;(2)先化简立方根,算术平方根,绝对值,然后再计算.【解答】解:(1)原式=9+2√2−2﹣2√2=7; (2)原式=﹣2−√925+√5−2+4=﹣2−35+√5−2+4=√5−35.22.(2分)(2021春•西城区校级期中)计算:(1)(−√7)2−√62+√−83;(2)√49−√273+|1−√2|+√(1−54)2.【分析】(1)先化简,再计算加减法;(2)先算二次根式、三次根式,再计算加减法.【解答】解:(1)原式=7﹣6+(﹣2)=7﹣6﹣2=﹣1;(2)原式=7﹣3+√2−1+54−1=2+54+√2=134+√2. 23.(2分)(2021春•抚顺期末)计算:(1)√−83+√36−√49;(2)√254+√−273−|2−√3|+√(−2)2. 【分析】(1)根据立方根,算术平方根的运算法则进行运算,即可得出答案;(2)根据算术平方根,立方根,绝对值的法则进行运算,即可得出答案.【解答】解:(1)解:原式=﹣2+6﹣7=﹣3;(2)原式=52−3﹣2+√3+2 =−12+√3. 24.(2分)(2021春•乾安县期末)计算:(1)|√3−2|−(√3−1)+√−643;(2)√9+|﹣2|+√273+(﹣1)2021. 【分析】(1)直接利用绝对值的性质以及立方根的性质分别化简得出答案;(2)直接利用绝对值的性质以及立方根的性质、有理数的乘方运算法则分别化简得出答案.【解答】解:(1)原式=2−√3−√3+1﹣4=﹣2√3−1;(2)原式=3+2+3﹣1=7.25.(2分)(2021春•曾都区期末)计算下列各式:(1)√(−1)2+√14×(﹣2)2−√−643;(2)|√3−√2|+|√3−2|﹣|√2−1|.【分析】(1)直接利用二次根式的性质以及立方根的性质分别化简得出答案;(2)直接利用绝对值的性质化简,再合并二次根式得出答案.【解答】解:(1)原式=1+12×4+4=1+2+4=7;(2)原式=√3−√2+2−√3−(√2−1)=√3−√2+2−√3−√2+1=3﹣2√2.26.(2分)(2021春•林州市期末)计算:(1)|3−√13|+√−273−√13+√25;(2)−12−(−2)3×18+√−273×|−13|+|1−√3|.【分析】(1)直接利用绝对值的性质、立方根的性质、二次根式的性质分别化简得出答案;(2)直接利用绝对值的性质、立方根的性质、二次根式的性质分别化简得出答案.【解答】解:(1)原式=√13−3﹣3−√13+5=﹣1;(2)原式=﹣1+8×18−3×13+√3−1=﹣1+1﹣1+√3−1=√3−2.27.(2分)(2021春•黄冈期末)计算:(1)(−√2)2+|1−√2|+√−83; (2)﹣22+√(−4)2+√32+42−(﹣1)2021.【分析】(1)首先计算乘方、开立方和绝对值,然后从左向右依次计算,求出算式的值是多少即可.(2)首先计算乘方和开方,然后从左向右依次计算,求出算式的值是多少即可.【解答】解:(1)(−√2)2+|1−√2|+√−83=2+√2−1+(﹣2)=√2−1.(2)﹣22+√(−4)2+√32+42−(﹣1)2021=﹣4+4+5﹣(﹣1)=6.28.(2分)(2021春•越秀区期末)(1)计算:√183+√(−2)2+√14;(2)计算:2(√3−1)﹣|√3−2|−√−643.【分析】(1)根据立方根以及算术平方根的定义解决此题.(2)由|√3−2|=2−√3,√−643=−4,得2(√3−1)−|√3−2|−√−643=3√3.【解答】解:(1)√183+√(−2)2+√14=12+2+12=3.(2)2(√3−1)−|√3−2|−√−643=2√3−2−(2−√3)−(−4)=2√3−2−2+√3+4=3√3.29.(2分)(2021春•西城区校级期末)计算题(1)√83+√0−√14+√−183+|3−√2|; (2)√−273−√0−√14+√0.1253+√1−63643.【分析】(1)根据立方根,算术平方根,绝对值的性质计算即可;(2)先化简,再求这个数的立方根,化简即可.【解答】解:(1)原式=2+0−12−12+3−√2=4−√2;(2)原式=﹣3﹣0−12+√183+√1643 =﹣3−12+12+14=−114.30.(2分)(2020春•合川区期末)计算:(1)|﹣2|+(﹣1)2020+√214−√−183; (2)(﹣24)﹣(12−23)÷(−16)×[﹣2−√(−3)2]﹣|14−0.52|. 【分析】(1)直接利用有理数的乘方运算法则以及立方根的性质、算术平方根、绝对值的性质分别化简得出答案;(2)直接利用有理数的混合运算以及二次根式的性质、绝对值的性质分别化简得出答案. 【解答】解:(1)原式=2+1+√94+12=2+1+32+12=5;(2)原式=﹣16﹣(36−46)×(﹣6)×(﹣2﹣3)﹣|14−(12)2| =﹣16+16×(﹣6)×(﹣5)﹣0=﹣16+5﹣0=﹣11.31.(2分)(2020春•甘南县期中)计算下列各式:(1)√16−√273+√−183+√94 (2)|1−√2|+√−8273×√14−√2【分析】(1)原式利用平方根、立方根定义计算即可求出值;(2)原式利用绝对值的代数意义,平方根、立方根定义计算即可求出值.【解答】解:(1)原式=4﹣3−12+32=2;(2)原式=√2−1−23×12−√2=−43.32.(2分)(2020春•岳麓区校级月考)计算:(1)√83−√4−√(−3)2+|1−√2|(2)√6×(√6−√6)−√214−|2﹣π| 【分析】(1)首先计算立方根,化简二次根式,计算绝对值,然后再计算加减即可;(2)首先计算乘法、化简二次根式,计算绝对值,然后再计算加减即可.【解答】解:(1)原式=2﹣2﹣3+√2−1=√2−4;(2)原式=1﹣6−32−(π﹣2),=1﹣6−32−π+2,=﹣412−π. 33.(2分)(2020春•蕲春县期中)计算:(1)√−273+√(−3)2+√−13;(2)√16+√−27643×√(−43)2−|2−√5|. 【分析】(1)首先根据二次根式和立方根的性质进行化简,再计算加减即可;(2)首先根据二次根式和立方根和绝对值的性质进行化简,再计算乘法,后算加减即可.【解答】解:(1)原式=﹣3+3﹣1=﹣1;(2)原式=4−34×43−(√5−2)=4﹣1−√5+2=5−√5.34.(2分)(2020春•西市区期末)计算:(1)√−13−√83÷√(−6)2;(2)(2−√3)2020×(2+√3)2021﹣2√34.【分析】(1)首先计算乘方、开方,然后计算除法,最后计算减法,求出算式的值是多少即可.(2)首先根据积的乘方计算,然后计算乘法、减法,求出算式的值是多少即可.【解答】解:(1)√−13−√83÷√(−6)2=﹣1﹣2÷6=﹣1−13=−43.(2)(2−√3)2020×(2+√3)2021﹣2√34 =[(2−√3)×(2+√3)]2020×(2+√3)﹣2×√32=2+√3−√3=2.35.(2分)(2020春•渝北区校级月考)计算下列各题. (1)|3−2√3|−√643+(√6)2;(2)√1.44+√1033−√0.04−√83−√−13.【分析】(1)直接利用立方根的性质以及二次根式的性质、绝对值的性质等知识分别化简得出答案;(2)直接利用立方根的性质以及二次根式的性质等知识分别化简得出答案.【解答】解:(1)原式=2√3−3﹣4+6=2√3−1;(2)原式=1.2+10﹣0.2﹣2+1=10.36.(2分)(2020春•牡丹江期中)计算题:(1)√81+√−273+√(−2)2+|√3−2|;(2)√22−√214+√78−13−√−13. 【分析】各式利用算术平方根、立方根性质计算即可求出值.【解答】解:(1)原式=9﹣3+2+2−√3=10−√3;(2)原式=2−32−12−(﹣1)=2﹣2+1=1.37.(2分)(2020春•凉州区校级期中)计算:(1)√2549+|﹣5|+√−643−(﹣1)2020; (2)√16+√−273−√3−|√3−2|+√(−5)2.【分析】利用二次根式的性质、绝对值得先年改制、立方根的性质、乘方的意义进行计算,再算加减即可.【解答】解:(1)原式=57+5﹣4﹣1=57;(2)原式=4﹣3−√3−2+√3+5=4.38.(2分)(2020秋•东港市期中)(1)(√6−√7)2019×(√6+√7)2020.(2)√32−√−273−√(−23)2+|1−√2|.【分析】(1)直接利用积的乘方运算法则,将原式变形得出答案;(2)直接利用立方根以及算术平方根的性质、绝对值的性质分别化简得出答案.【解答】解:(1)原式=[(√6−√7)(√6+√7)]2019×(√6+√7)=﹣1×(√6+√7) =−√6−√7;(2)原式=4√2+3−23+√2−1 =5√2+43.39.(2分)(2020春•越秀区校级月考)计算:(1)√36−√273+√(−2)2−√214;(2)|√3−2|−√4−(3−√3).【分析】(1)直接利用立方根的定义和算术平方根的定义分别化简得出答案;(2)直接利用绝对值的性质以及算术平方根的定义分别化简得出答案.【解答】解:(1)原式=6﹣3+2−32=3.5;(2)原式=2−√3−2﹣3+√3=﹣3.40.(2分)(2020春•和平区校级月考)计算(1)√273+|3−√5|﹣(√9−√83)2+√5; (2)√16−√83−√13+√1+916+|1−√2|﹣|√3−√2|.【分析】(1)直接利用立方根的性质以及绝对值的性质分别化简得出答案;(2)直接利用立方根的性质以及绝对值的性质分别化简得出答案.【解答】解:(1)原式=3+3−√5−(3﹣2)2+√5=3+3−√5−1+√5=5;(2)原式=4﹣2﹣1+54+√2−1﹣(√3−√2)=4﹣2﹣1+54+√2−1−√3+√2 =2√2−√3+54.41.(4分)(2020春•硚口区期中)(1)计算:①√−8273×√14−√(−2)2;②√3−√25+|√3−3|+√1−63643.(2)求下列式子中的x 的值:①4(x ﹣2)2=49;②(x ﹣1)3=64.【分析】(1)①直接利用立方根以及二次根式的性质分别化简得出答案;②直接利用立方根以及二次根式的性质分别化简得出答案;(2)①直接利用平方根的定义化简得出答案;②直接利用立方根的定义化简得出答案.【解答】解:(1)①原式=−23×12−2=﹣213;②原式=√3−5+3−√3+14=−74;(2)①∵4(x ﹣2)2=49, ∴(x −2)2=494, ∴x −2=±72,∴x =2±72,∴x =112或x =−32.②∵(x ﹣1)3=64,∴x ﹣1=4,∴x =5.42.(4分)(2020秋•射洪市月考)(1)计算:√16+√−643−√(−3)2+|√3−1|;(2)解方程:18﹣2x 2=0;(3)解方程:(x +1)3+27=0;(4)(2−√3)2020×(2+√3)2021﹣2√1−(35)2.【分析】(1)利用平方根与立方根的定义及绝对值的意义,先化简,再利用实数混合运算进行运算即可;(2)对方程进行转化,利用平方根的定义即可解答;(3)对方程进行转化,利用立方根的定义即可解答;(4)先利用幂运算法则和平方差公式进行简便运算,利用算术平方根的定义进行化简,再利用实数混合运算进行运算即可;【解答】解:(1)原式=4﹣4﹣3+√3−1=﹣4+√3;(2)∵18﹣2x 2=0,∴2x 2=18,即x 2=9,∴x =±3;(3)∵(x +1)3+27=0,∴(x +1)3=﹣27,∴x +1=﹣3,∴x =﹣4;(4)(2−√3)2020×(2+√3)2021﹣2√1−(35)2 =[(2−√3)×(2+√3)]2020×(2+√3)﹣2×45=2+√3−85=25+√3.43.(4分)(2021春•南开区期中)(1)化简|1−√2|+|√2−√3|+|√3−2|.(2)计算:√−643+√16×√94÷(−√2)2.(3)解方程(x ﹣1)3=27.(4)解方程2x 2﹣50=0.【分析】(1)去掉绝对值符号,合并同类二次根式即可;(2)利用实数的混合运算法则进行运算即可;(3)利用立方根的意义解答;(4)利用平方根的意义解答.【解答】解:(1)原式=√2−1+√3−√2+2−√3=1;(2)原式=﹣4+4×32÷2=﹣4+3=﹣1;(3)两边开立方得:x ﹣1=3.∴x =4.∴原方程的解为:x =4.(4)原方程变为:2x 2=50.∴x 2=25.两边开平方得:x =±5.∴原方程的解为:x 1=5,x 2=﹣5.44.(4分)(2021春•红桥区期中)计算:(1)3√2+√2−6√2;(2)√5(√5+1√5); (3)√−273+√(−2)2−|1−√3|;(4)√9−√−83+√(−3)2−(√2)2. 【分析】(1)直接利用二次根式的加减运算法则计算得出答案;(2)直接利用二次根式的混合运算法则计算得出答案;(3)直接利用立方根以及二次根式、绝对值的性质分别化简得出答案;(4)直接利用立方根以及二次根式、绝对值的性质分别化简得出答案.【解答】解:(1)原式=﹣2√2;(2)原式=5+1=6;(3)原式=﹣3+2﹣(√3−1)=﹣3+2−√3+1=−√3;(4)原式=3+2+3﹣2=6.45.(4分)(2021春•硚口区期中)(1)计算:①√16−√273+√214;②√3(√3√3)+|2−√5|. (2)求下列式子中的x 的值:①(x ﹣2)2=9;②3(x +1)3+81=0.【分析】(1)①首先计算开方,然后从左向右依次计算即可.②首先计算绝对值和乘法,然后从左向右依次计算即可.(2)①根据平方根的含义和求法,求出x 的值是多少即可.②根据立方根的含义和求法,求出x 的值是多少即可.【解答】解(1)①√16−√273+√214=4﹣3+32=52.②√3(√31√3)+|2−√5| =3﹣1+√5−2=√5.(2)①∵(x ﹣2)2=9,∴x ﹣2=±3,解得:x =5或﹣1.②∵3(x +1)3+81=0,∴3(x +1)3=﹣81,∴(x +1)3=﹣27,∴x +1=﹣3,解得:x =﹣4.46.(4分)(2021春•岷县月考)计算:(1)√−8×(−0.5).(2)√4+√225−√400.(3)√−13+√(−1)33+√(−1)23.(4)√183−52×√−11253+√−3433−√−273. 【分析】根据算术平方根和立方根的定义,分别计算即可.【解答】解:(1)原式=√4=2;(2)原式=2+15﹣20=﹣3;(3)原式=﹣1+√−13+√13=﹣1+(﹣1)+1=﹣1;(4)原式=12−52×(−15)+(﹣7)﹣(﹣3)=12−(−12)+(﹣7)+3=12+12+(﹣7)+3 =1﹣7+3=﹣3.47.(4分)(2020秋•海曙区期中)计算.(1)−34×(−8+23−13).(2)17﹣8÷(﹣4)+4×(﹣5).(3)√25+(√−1273+13)−6. (4)−32×[−32×(−23)2−2].【分析】(1)利用乘法分配律使得计算简便;(2)先算乘除,然后再算加减;(3)先化简算术平方根,立方根,然后算小括号里面的,再算括号外面的;(4)先算乘方,然后算乘除,最后算加减,有小括号先算小括号里面的.【解答】解:(1)原式=34×8−34×23+34×13=6−12+14 =512+14=524+14 =534;(2)原式=17+2﹣20=19﹣20=﹣1; (3)原式=5+(−13+13)﹣6=5+0﹣6=5﹣6=﹣1;(4)原式=−32×(﹣9×49−2)=−32×(﹣4﹣2)=−32×(﹣6)=9.48.(4分)(2020秋•嵊州市期中)计算:(1)(+1013)+(﹣11.5)+(﹣1013)﹣4.5; (2)(﹣6)2×(13−12)﹣23; (3)(﹣270)×14+0.25×21.5+(﹣812)×(﹣0.25); (4)−√36+6÷(−23)×√−83.【分析】(1)直接利用有理数的加减运算法则计算得出答案;(2)直接利用乘法分配律以及有理数的混合运算法则计算得出答案;(3)直接提取公因式14,进而计算得出答案; (4)直接利用算术平方根的性质以及立方根的性质分别化简得出答案.【解答】解:(1)原式=﹣11.5﹣4.5+(1013−1013) =﹣16+0=﹣16;(2)(﹣6)2×(13−12)﹣23 =36×13−36×12−8=12﹣18﹣8=﹣14;(3)(﹣270)×14+0.25×21.5+(﹣812)×(﹣0.25) =14×(﹣270+21.5+812) =14×(﹣240)=﹣60;(4)−√36+6÷(−23)×√−83=﹣6﹣9×(﹣2)=﹣6+18=12.49.(4分)(2020秋•北仑区期中)计算:(1)(﹣3)2﹣(112)3×29−6÷|−23|; (2)﹣12020+|﹣3|+√−1273−√(−4)2; (3)3×(√3−√5)+2×(−32×√3+32);(4)|√6−√2|+|√2−1|﹣|3−√6|.【分析】(1)直接利用有理数的混合运算法则计算得出答案;(2)直接利用立方根以及绝对值的性质、算术平方根的性质分别化简得出答案;(3)直接利用二次根式的混合运算法则计算得出答案;(4)直接利用绝对值的性质化简,进而得出答案.【解答】解:(1)(﹣3)2﹣(112)3×29−6÷|−23|=9−278×29−6×32=9−34−9=−34;(2)﹣12020+|﹣3|+√−1273−√(−4)2=﹣1+3−13−4=﹣213; (3)3×(√3−√5)+2×(−32×√3+32)=3√3−3√5−3√3+3=﹣3√5+3;(4)|√6−√2|+|√2−1|﹣|3−√6|=√6−√2+√2−1﹣(3−√6)=√6−√2+√2−1﹣3+√6=2√6−4.50.(4分)(2020秋•下城区校级期中)计算.(1)(+15)﹣(+11)﹣(﹣18)+(﹣15);(2)(﹣72)×(49−38+512−13); (3)﹣12﹣(1﹣0.5)÷15×[2﹣(﹣2)2];(4)|1−√2|+|√2−√3|+|√3−√4|+……+|√2019−√2020|.(结果保留根号形式)【分析】(1)直接利用有理数的加减运算法则计算得出答案;(2)直接利用乘法分配律进而计算得出答案;(3)直接利用有理数的混合运算法则计算得出答案;(4)直接去绝对值进而计算得出答案.【解答】解:(1)(+15)﹣(+11)﹣(﹣18)+(﹣15)=15﹣11+18﹣15=7;(2)(﹣72)×(49−38+512−13) =(﹣72)×49+(﹣72)×(−38)+(﹣72)×512+(﹣72)×(−13)=﹣32+27﹣30+24=﹣11;(3)﹣12﹣(1﹣0.5)÷15×[2﹣(﹣2)2]=﹣1−12×5×(2﹣4)=﹣1−52×(﹣2)=﹣1+5=4;(4)|1−√2|+|√2−√3|+|√3−√4|+……+|√2019−√2020| =√2−1+√3−√2+√4−√3+⋯+√2020−√2019 =√2020−1.。
七年级数学实数测试题及答案

七年级数学实数测试题及答案一、选择题(每题2分,共10分)1. 下列哪个数不是实数?A. -3B. √2C. πD. i(虚数单位)2. 实数a和b满足a < b,那么a + 1与b + 1的大小关系是:A. a + 1 < b + 1B. a + 1 > b + 1C. a + 1 = b + 1D. 不能确定3. 以下哪个表达式表示的是实数的乘方?A. √9B. 3^2C. 1/2^3D. -2^34. 实数x满足|x| < 1,那么x的取值范围是:A. x > 1B. x < -1C. -1 < x < 1D. x ≥ 1 或x ≤ -15. 两个实数相除,如果除数为负数,商的符号与:A. 被除数相同B. 被除数相反C. 除数相同D. 除数相反二、填空题(每题2分,共10分)6. 若a = -2,则a的相反数是______。
7. 一个数的绝对值是5,这个数可以是______。
8. 一个数的平方根是3,那么这个数的立方根是______。
9. 一个数的立方是-8,这个数是______。
10. 若√x = 3,则x = ______。
三、解答题(每题10分,共40分)11. 计算下列各题,并简化结果:(1) √25(2) (-3)^2(3) √(-4)^212. 已知a = -1,b = 3,求下列表达式的值:(1) a + b(2) a - b(3) a * b13. 根据题目条件,求解以下不等式:(1) |x - 2| < 3(2) |x + 1| ≥ 414. 证明:如果a > 0,b < 0,且|a| > |b|,则a + b > 0。
四、应用题(每题15分,共30分)15. 一个数的平方根是4,求这个数,并计算它的立方根。
16. 某工厂在生产过程中,发现一个零件的长度在-2到2厘米之间波动。
如果这个零件的长度超过1.5厘米,就会影响机器的正常运转。
实数练习题及答案

实数练习题及答案一、选择题1. 下列各数中,不是实数的是()。
A. πB. -3C. iD. √2答案:C2. 若a > 0,b < 0,且|a| < |b|,则a + b()。
A. 一定大于0B. 一定小于0C. 等于0D. 大小不确定答案:B3. 实数x满足|x-1| + |x-2| = 1,x的取值范围是()。
A. x = 1B. 0 ≤ x ≤ 2C. x = 2D. x ≥ 1答案:B二、填空题4. 若a是实数,且a^2 = 4,则a的值是()。
答案:±25. 若x是实数,且x^2 - 4x + 4 = 0,求x的值。
答案:x = 2三、解答题6. 已知实数a和b,a + b = 5,a - b = 3,求a和b的值。
解:由题意得,将两个方程相加,得到2a = 8,所以a = 4。
将a的值代入第一个方程,得到4 + b = 5,所以b = 1。
7. 已知实数x满足方程x^2 - 5x + 6 = 0,求x的值。
解:首先将方程因式分解,得到(x - 2)(x - 3) = 0。
所以x的值为2或3。
四、应用题8. 某工厂生产一批零件,已知零件的合格率为90%,不合格率为10%。
若工厂生产了1000个零件,求不合格的零件数量。
解:不合格的零件数量为1000 × 10% = 100个。
9. 若一个数的平方根等于这个数本身,求这个数。
解:设这个数为x,则有√x = x。
解这个方程,我们得到x = 0或 x = 1。
五、综合题10. 某公司计划在两个不同的地点设立仓库,仓库A和仓库B。
已知仓库A的租金为每年10万元,仓库B的租金为每年15万元。
公司计划在两个仓库中存放的货物总价值为1000万元。
如果仓库A的货物价值是仓库B的两倍,求仓库A和仓库B各自存放的货物价值。
解:设仓库B存放的货物价值为x万元,则仓库A存放的货物价值为2x万元。
根据题意,我们有x + 2x = 1000,解得x = 333.33(万元)。
实数理论应用题

实数理论应用题在数学领域中,实数理论是一个非常重要的分支,它涉及到了实数的性质、运算规则等方面。
实数理论的应用非常广泛,可以用于解决各种实际问题。
本文将通过几个实数理论应用题的例子,来探讨实数理论在解决实际问题中的重要性。
例题一:某人从A地出发,以每小时60公里的速度向B地行进,另一人从B地以每小时40公里的速度向A地行进。
两人同时出发,问他们相遇的时间是多久?解析:假设两人相遇的时间为t小时,则根据题意可知,第一个人行驶的距离为60t公里,第二个人行驶的距离为40t公里。
由于两人相遇时行驶距离之和等于A地到B地的距离,因此可以得到以下方程:60t + 40t = AB100t = ABt = AB / 100因此,他们相遇的时间为AB / 100小时。
例题二:若一根绳子被均分为5段,第一段长度为1/6米,第二段长度为1/5米,第三段长度为1/4米,依此类推,问这根绳子总长是多少?解析:根据题意可知,将绳子分成5段后,每段的长度依次为1/6米、1/5米、1/4米、1/3米、1/2米。
因此,总长为1/6 + 1/5 + 1/4 + 1/3 + 1/2 = 127/60米。
例题三:现有一组数列{an},其中第一个数a1 = 3,公比为2,求该数列的第n项an的表达式。
解析:根据数列的定义,可知an = a1 * q^(n-1),其中a1为首项,q 为公比。
代入题目中给出的数据,可得到an的表达式为an = 3 * 2^(n-1)。
通过以上例题的解答,我们可以看到实数理论在解决实际问题中的应用。
实数理论不仅仅是一种抽象的概念,更是一种解决实际问题的重要工具。
只有深入理解实数理论的性质和规律,才能更好地应用于实际问题的解决中。
希望通过本文的介绍,读者们对实数理论的应用有了更深入的了解。
(完整版)实数应用题
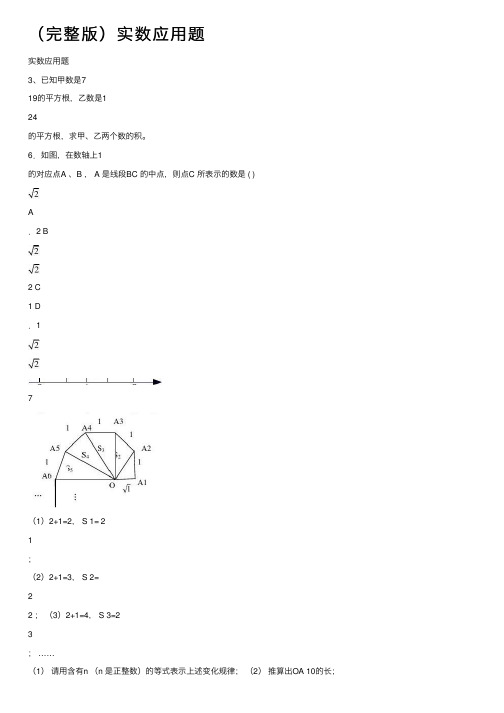
(完整版)实数应⽤题实数应⽤题3、已知甲数是719的平⽅根,⼄数是124的平⽅根,求甲、⼄两个数的积。
6.如图,在数轴上1的对应点A 、B , A 是线段BC 的中点,则点C 所表⽰的数是 ( )A.2 B2 C1 D.17(1)2+1=2, S 1= 21;(2)2+1=3, S 2=22 ;(3)2+1=4, S 3=23; ……(1)请⽤含有n (n 是正整数)的等式表⽰上述变化规律;(2)推算出OA 10的长;(3)推算出S 12+ S 2 2+ S 32+…+S 102 的值。
8.已知21a -的平⽅根是3±,4是31a b +-的算术平⽅根,求2a b +的值. 9.已知322+-+-=x x y ,求x y 的平⽅根.10.已知a , b , 求2(a b 的值.11、已知实数 a 、b 试化简:(a -b)2-|a +b |x12、若(2x +3)2和y +2互为相反数,求 x -y 的值。
13、如果A 的平⽅根是2x -1与3x -4,求A 的值?14、已知321x -与323-y 互为相反数,求yx21+的值。
15、已知28-++=b a a M 是()8+a 的算术平⽅根,423+--=b a b N 是()3-b 的⽴⽅根N M +的平⽅根。
16、已知x 、y 都是实数,且422+-+-=x x y ,求x y 的平⽅根17、如果⼀个数的平⽅根是3+a 和152-a ,求这个数。
18、已知a 、b 满⾜0382=-++b a ,解关于x 的⽅程()122-=++a b x a 。
19、⼀个正⽅形的表⾯积为24002cm ,求这个正⽅形的体积。
22、已知a 、b 满⾜0382=-++b a ,解关于x 的⽅程()122-=++a b x a 。
关于初中实数试题及答案

关于初中实数试题及答案一、选择题1. 下列哪个数是实数?A. √2B. -3.14C. 3iD. 1/0答案:A2. 计算下列哪个表达式的结果不是实数?A. (-3)^2B. √(-4)C. 2/3D. √9答案:B3. 以下哪个选项是正确的?A. √16 = 4B. √16 = ±4C. √16 = -4D. √16 = 2答案:B二、填空题4. 计算√25的值是______。
答案:55. 计算(-5)^2的值是______。
答案:256. 计算√(-1)^2的值是______。
答案:1三、解答题7. 已知a是实数,且a^2 = 9,求a的值。
答案:a = ±38. 计算√(2^2 * 3^2)的值。
答案:√(4 * 9) = √36 = 69. 已知x是实数,且x^2 - 4x + 4 = 0,求x的值。
答案:x = 2四、应用题10. 一个物体从高度为h的建筑物上自由下落,其下落时间t(秒)与高度h(米)之间的关系为h = 1/2 * g * t^2,其中g是重力加速度,取g = 9.8 m/s^2。
如果一个物体从20米高的建筑物上自由下落,求它下落的时间。
答案:t = √(2 * h / g) = √(2 * 20 / 9.8) ≈ 2.02秒11. 一个数的平方是25,求这个数。
答案:这个数是±512. 一个数的立方是-27,求这个数。
答案:这个数是-3五、证明题13. 证明:对于任意实数a和b,(a + b)^2 = a^2 + 2ab + b^2。
答案:证明如下:(a + b)^2 = (a + b)(a + b) = a^2 + ab + ba + b^2由于ab = ba,所以上式可以简化为:a^2 + 2ab + b^214. 证明:√a * √b = √(ab),其中a和b都是非负实数。
答案:证明如下:√a * √b = √(a * b),因为√(a * b)的定义就是a和b 的乘积的平方根。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实数应用题
3、已知甲数是7
19的平方根,乙数是1
24
的平方根,求甲、乙两个数的积。
6.如图,在数轴上1
的对应点A 、B , A 是线段BC 的中点,则点C 所表示的数是 ( )
A
.2 B
2 C
1 D
.1
7
(1)2+1=2, S 1= 2
1
;
(2)2+1=3, S 2=
2
2 ; (3)2+1=4, S 3=2
3
; ……
(1) 请用含有n (n 是正整数)的等式表示上述变化规律; (2) 推算出OA 10的长;
(3) 推算出S 12+ S 2 2+ S 32+…+S 102 的值。
8.已知21a -的平方根是3±,4是31a b +-的算术平方根,求2a b +的值. 9.已知322+-+-=x x y ,求x y 的平方根.
10.已知a , b , 求2(a b 的值.
11、已知实数 a 、b 试化简:(a -b)2-|a +b |
x
12、若(2x +3)2和y +2互为相反数,求 x -y 的值。
13、如果A 的平方根是2x -1与3x -4,求A 的值?
14、已知321x -与323-y 互为相反数,求y
x
21+的值。
15、已知2
8-++=
b a a M 是()8+a 的算术平方根,423+--=b a b N 是()3-b 的立方根
N M +的平方根。
16、已知x 、y 都是实数,且422+-+-=
x x y ,求x y 的平方根
17、如果一个数的平方根是3+a 和152-a ,求这个数。
18、已知a 、b 满足0382=-++b a ,解关于x 的方程()122
-=++a b x a 。
19、一个正方形的表面积为24002
cm ,求这个正方形的体积。
22、已知a 、b 满足0382=-++b a ,解关于x 的方程()122
-=++a b x a 。
