八年级上册期末统考试卷
八年级上册语文期末考试试卷(含答案)

八年级上册语文期末考试试卷(满分150分,时间150分钟)一、语文积累与综合运用(40分)1. 下列加点字的注音全部正确的一项是( )(3分)A. 翘.首(qi áo) 粗糙.(z ào) 锐不可当.(d āng) 络绎.不绝(y ì) B. 锃.亮(z èng) 禁锢.(g ù) 深恶.痛疾(è) 杳.无消息(y ǎo) C. 恹.恹(y àn) 滞.留(zh ì) 潜.滋暗长(qi ǎn) 鸢飞戾.天(l ì) D. 炽.热(ch ì) 缥.碧(pi ǎo) 殚.精竭虑(d ān) 纵横.决荡(h éng) 2.下列词语中没有错别字的一项是( )(3分) A .琐屑 泄气 长途跋涉 诚惶诚恐 B .俯瞰 颁发 春寒料峭 自出新裁 C .序幕 落第 重峦叠障 妙手偶得 D .妨御 斟酌 摧枯拉朽 一丝不苟 3. 下列各句中,加点词语使用不正确的一项是( )(3分) A .八路军出其不意的反击,使敌人有些张皇失措....。
B .看着家中日渐衰败的景象,我不禁触目伤怀....。
C .小明为人诚实,待人接物坦荡如砥....,深得同学好评。
D .他生性刚直,一身傲骨,从不对权贵唯命是从....。
4. 下列句子没有语病的一项是( )(3分) A .屠呦呦全身心投入世界性流行疾病——疟疾的防治研究。
B. 只有对老师所提的问题理解到位,就能回答得清楚明了。
C. 新时代教育应培养学生善于观察、善于思考、善于创造的水平。
D. 经过三年的努力学习,他对自己能否考上理想的高中充满信心。
5. 将下列句子组成语段,顺序排列正确的一项是( )(3分) ①寻根求源,乃是一种不愿与流俗同流合污的理想。
②耐寒草木,说到底,没有超过松柏的。
③自孔老夫子以缓舒纡徐的口吻道出:“岁寒,然后知松柏之后凋”之后。
人教版八年级上册数学期末考试试卷带答案

人教版八年级上册数学期末考试试题一、单选题1.下列所述图形中,不是轴对称图形的是()A .矩形B .平行四边形C .正五边形D .正三角形2.在平面直角坐标系中,点(3,2)关于x 轴对称的点的坐标为()A .(3,2)-B .(2,3)-C .(2,3)-D .(3,2)-3.若一个多边形的内角和是540°,则该多边形的边数为 ()A .4B .5C .6D .74.下面因式分解错误的是()A .22()()x y x y x y -=+-B .22816(4)x x x -+=-C .2222()x xy x x y -=-D .222()x y x y +=+5.以下列各组线段为边,能组成三角形的是()A .1cm ,2cm ,4cmB .4cm ,6cm ,8cmC .5cm ,6cm ,12cmD .2cm ,3cm ,5cm6.解分式方程22311x x x++=--时,去分母后变形为A .()()2231x x ++=-B .()2231x x -+=-C .()()2231x x -+=-D .()()2231x x -+=-7.下列计算正确的是()A .2a +3b =5abB .x 8÷x 2=x 6C .(ab 3)2=ab 6D .(x +2)2=x 2+48.将0.0000025用科学记数法表示为()A .2.5×10﹣5B .2.5×10﹣6C .25×10﹣7D .1.2×10﹣89.若分式242x x -+的值为0,则x 的值为()A .-2B .0C .2D .±210.如图,△ABC 中,AB=5,AC=8,BD 、CD 分别平分∠ABC ,∠ACB ,过点D 作直线平行于BC ,分别交AB 、AC 于E 、F ,则△AEF 的周长为()A.12B.13C.14D.18二、填空题11.计算:|﹣2|﹣20210+(12)﹣1=______________.12.分解因式:xy―x=_____________.13.如图,AC与BD相交于点O,且AB=CD,请添加一个条件_____________,使得△ABO≌△CDO.14.等腰三角形有两条边长为4cm和9cm,则该三角形的周长是__________.15.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=2,BC =7,则△BDC的面积是________.16.如图,在△ABC中,AB=AC.在AB、AC上分别截取AP,AQ,使AP=AQ.再分别以点P,Q为圆心,以大于12PQ的长为半径作弧,两弧在∠BAC内交于点R,作射线AR,交BC于点D.若BC=6,则BD的长为______________.17.如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB 边于E ,F 点.若点D 为BC 边的中点,点M 为线段EF 上动点,则CMD △周长的最小值为______.18.如图,将一个边长为3的正方形纸片进行分割,部分①的面积是边长为3的正方形纸片的一半,部分②的面积是部分①的一半,部分③的面积是部分②的一半,以此类推,n 部分的面积是______.(用含n 的式子表示)三、解答题19.计算:()()()222x y x y x y x +++--20.先化简,再求值:221224xx x x x x -⎛⎫-÷ ⎪---⎝⎭,其中x =.21.解方程:28124x x x -=--.22.如图,AB AD =,25BAC DAC ∠=∠=︒,80D ∠=︒.求BCA ∠的度数.23.某公司购买了一批A 、B 型芯片,其中A 型芯片的单价比B 型芯片的单价少9元,已知该公司用3120元购买A 型芯片的条数与用4200元购买B 型芯片的条数相等.(1)求该公司购买的A 、B 型芯片的单价各是多少元?(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条A 型芯片?24.如图,已知ABC 中,10cm AB AC ==,8cm BC =,点D 为AB 的中点.(1)如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1s 后,BPD △与CQP V 是否全等,请说明理由.②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP V 全等.(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC 三边运动,求经过多长时间点P 与点Q 第一次在ABC 的哪条边上相遇.25.已知:22214816x x x A x x x +-=÷--+,221x m B x -=-(1)化简分式A ;(2)若关于x 的分式方程:1A B +=的解是非负数,求m 的取值范围;(3)当x 取什么整数时,分式A 的值为整数.26.如图,90ACB ∠=︒,AC BC =,AD CE ⊥,BE CE ⊥,垂足分别为D ,E .(1)求证:ACD CBE △△≌;(2)试探究线段AD ,DE ,BE 之间有什么样的数量关系,请说明理由.27.如图,AB BC CD DA ===,60A ∠=︒,点E ,F 分别为线段AD ,CD 上的动点,且60EBF ∠=︒.(1)当BE AD ⊥时,求证:12AE AD =;(2)连接EF ,判断BEF 的形状,并作证明;(3)当AB 的长度为定值时,四边形BEDF 的面积是否为定值?请说明理由.参考答案1.B【分析】由轴对称图形的定义对选项判断即可.【详解】矩形为轴对称图形,不符合题意,故错误;平行四边形不是轴对称图形,符合题意,故正确;正五边形为轴对称图形,不符合题意,故错误;正三角形为轴对称图形,不符合题意,故错误;故选:B .【点睛】本题考查了轴对称图形的概念,如果一个平面图形沿着一条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.识别轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.2.D【分析】利用关于x 轴对称的点坐标特征:横坐标不变,纵坐标互为相反数解答即可.【详解】点(3,2)关于x 轴对称的点的坐标为(3,-2),故选:D.【点睛】本题主要考查了关于坐标轴对称的点的坐标特征,熟练掌握关于坐标轴对称的点的坐标特征是解答的关键.3.B【分析】根据多边形的内角和公式可直接求出多边形的边数.【详解】设这个多边形的边数为n,根据多边形内角和定理得(n-2)×180°=540°,解得n=5;故选:B.【点睛】本题考查了多边形的内角和定理,熟记多边形的内角和为(n-2)×180°是解题的关键.4.D【分析】分别利用完全平方公式、平方差公式以及提公因式法分解因式,进而判断得出答案.【详解】解:A、x2﹣y2=(x+y)(x﹣y),正确,不合题意;B、x2﹣8x+16=(x﹣4)2,正确,不合题意;C、2x2﹣2xy=2x(x﹣y),正确,不合题意;D、无法进行因式分解,此选项错误,符合题意.故选:D.【点睛】此题主要考查了公式法以及提取公因式法分解因式,熟练应用乘法公式是解题关键.5.B【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.【详解】解:根据三角形的三边关系,知A、1+2<4,不能组成三角形;B、4+6>8,能组成三角形;C、5+6<12,不能够组成三角形;D、2+3=5,不能组成三角形.故选:B.【点睛】此题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.6.D【详解】解:方程223 11xx x++=--,两边都乘以x-1去分母后得:2-(x+2)=3(x-1),故选D.7.B【分析】由相关运算法则计算判断即可.【详解】2a和3b不是同类项,无法计算,与题意不符,故错误;x8÷x2=x6,与题意相符,故正确;(ab3)2=a2b6,与题意不符,故错误;(x+2)2=x2+2x+4,与题意不符,故错误.故选:B.【点睛】本题考查了合并同类项、同底数幂的除法、幂的乘方运算、完全平方公式,熟练掌握运算法则是解题的关键.8.B【分析】由题意依据绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定进行分析即可.【详解】解:0.0000025=2.5×10-6.故选:B.【点睛】本题考查用科学记数法表示较小的数,注意掌握其一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.9.C【详解】由题意可知:24020 xx=⎧-⎨+≠⎩,解得:x=2,故选C.10.B【分析】根据平行线的性质得到∠EDB=∠DBC,∠FDC=∠DCB,根据角平分线的性质得到∠EBD=∠DBC,∠FCD=∠DCB,等量代换得到∠EDB=∠EBD,∠FDC=∠FCD,于是得到ED=EB,FD=FC,即可得到结果.【详解】解:∵EF BC,∴∠EDB=∠DBC,∠FDC=∠DCB,∵△ABC中,∠ABC和∠ACB的平分线相交于点D,∴∠EBD=∠DBC,∠FCD=∠DCB,∴∠EDB=∠EBD,∠FDC=∠FCD,∴ED=EB,FD=FC,∵AB=5,AC=8,∴△AEF的周长为:AE+EF+AF=AE+ED+FD+AF=AE+EB+FC+AF=AB+AC=5+8=13.故选B.【点睛】此题考查了等腰三角形的判定与性质.此题难度适中,注意证得△BDE与△CDF 是等腰三角形是解此题的关键.11.3【分析】先化简绝对值、零指数幂和负整数指数幂,再算加减即可【详解】解:|﹣2|﹣20210+(12)﹣1=2-1+2=3.故答案为:3.【点睛】本题考查了有理数的意义,熟练掌握绝对值、零指数幂和负整数指数幂的意义是解答本题的关键,非零数的负整数指数幂等于这个数的正整数次幂的倒数;非零数的零次幂等于1.12.x(y-1)【详解】试题解析:xy―x=x(y-1)13.∠A=∠C(答案不唯一)【分析】根据全等三角形的判定定理得出即可.【详解】∵∠AOB、∠COD是对顶角,∴∠AOB=∠COD,又∵AB=CD,∴要使得△ABO≌△CDO,则只需添加条件:∠A=∠C.故答案为:∠A=∠C(答案不唯一)考点:1.全等三角形的判定;2.开放型.【点睛】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL.14.22cm【分析】分两种情况讨论:当4cm为腰时,而449,+<不合题意,舍去,当9cm为腰时,而4+99,>符合题意,从而可得答案.【详解】解:等腰三角形有两条边长为4cm和9cm,当4cm为腰时,而449,+<不合题意,舍去,当9cm为腰时,而4+99,>符合题意,所以三角形的周长为:49922++=(cm),故答案为:22cm【点睛】本题考查的是三角形三边关系的应用,等腰三角形的定义,掌握“等腰三角形的定义及清晰的分类讨论”是解本题的关键.15.7【分析】过点D作DE⊥BC于E,根据角平分线上的点到角的两边距离相等可得DE=AD,然后利用三角形的面积公式列式计算即可得解.【详解】如图,过点D作DE⊥BC于E,∵∠A=90°,BD是∠ABC的平分线,∴DE=AD=2,∴△BDC的面积=12BC•DE=12×7×2=7.故答案为:7【点睛】本题考查角平分线的性质,熟练掌握角平分线上的点到角的两边距离相等的性质是解题关键.16.3【分析】根据题意依据等腰三角形的性质,即可得到BD=12BC,进而分析计算即可得出结论.【详解】解:由题可得,AR平分∠BAC,又∵AB=AC,∴AD是三角形ABC的中线,∴BD=12BC=12×6=3.故答案为:3.【点睛】本题主要考查基本作图以及等腰三角形的性质,注意掌握等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.17.10【分析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AC的垂直平分线可知,点C关于直线EF的对称点为点A,故AD的长为CM+MD的最小值,由此即可得出结论.【详解】连接AD,∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S△ABC=12BC•AD=12×4×AD=16,解得AD=8,∵EF是线段AC的垂直平分线,∴点C关于直线EF的对称点为点A,∴CM=AM,∴CD+CM+DM=CD+AM+DM,∵AM+DM≥AD,∴AD的长为CM+MD的最小值,∴△CDM的周长最短=(CM+MD)+CD=AD+12BC=8+12×4=8+2=10.故答案为10.【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.18.92n【分析】根据图形和题意,求出①、②、③、④的面积从而可以推出n 部分的面积;【详解】解:19922=⨯=①面积21199222=⨯⨯=②面积3111992222=⨯⨯⨯=③面积411119922222=⨯⨯⨯⨯=④面积以此类推可知n 部分的面积为92n 故答案为:92n【点睛】本题考查图形的变化规律、有理数的混合运算、列代数式,解答本题的关键是明确题意,求出所求式子的值.19.2xy【分析】先根据完全平方公式计算,再合并同类项即可【详解】解:()()()222x y x y x y x +++--=2222222x xy y x y x +++--=2xy .【点睛】本题考查了整式的混合运算,熟练掌握运算顺序及乘法公式是解答本题的关键.完全平方公式是(a±b)2=a 2±2ab+b 2;平方差公式是(a+b)(a-b)=a 2-b 2.20.22x +1+.【分析】括号内先进行分式的加减运算,然后再进行分式的乘除法运算,最后把数值代入化简后的结果进行计算即可.【详解】原式()()()22121x x x x x x +--=⋅--=2x x+,当x =时,原式1=.【点睛】本题考查了分式的化简求值,熟练掌握分式混合运算的运算顺序以及运算法则是解题的关键.21.无解【分析】根据解分式方程的步骤去解答:去分母将分式方程化为整式方程、解整式方程、检验、回答.【详解】解:原方程可化为:812(2)(2)x x x x -=-+-.方程两边同时乘以(2)(2)x x +-,得(2)(2)(2)8x x x x +-+-=.化简,得248x +=.解得2x =.检验:2x=时(2)(2)0x x +-=,所以2x =不是原分式方程的解,所以原分式方程无解.【点睛】本题考查解分式方程,熟练掌握解分式方程的步骤,尤其是检验是解分式方程的重要步骤.22.75°.【分析】由三角形的内角和定理求出∠DCA=75°,再证明△ABC ≌△ADC ,即可得到答案.【详解】∵25DAC ∠=︒,80D ∠=︒,∴∠DCA=75°,∵AB AD =,25BAC DAC ∠=∠=︒,AC=AC ,∴△ABC ≌△ADC ,∴∠BCA=∠DCA=75°.【点睛】此题考查三角形的内角和定理,全等三角形的判定及性质,这是一道比较基础的三角形题.23.(1)A 型芯片的单价为26元/条,B 型芯片的单价为35元/条;(2)80.【分析】(1)设B 型芯片的单价为x 元/条,则A 型芯片的单价为(x ﹣9)元/条,根据数量=总价÷单价结合用3120元购买A 型芯片的条数与用4200元购买B 型芯片的条数相等,即可得出关于x 的分式方程,解之经检验后即可得出结论;(2)设购买a 条A 型芯片,则购买(200﹣a )条B 型芯片,根据总价=单价×数量,即可得出关于a 的一元一次方程,解之即可得出结论.【详解】(1)设B 型芯片的单价为x 元/条,则A 型芯片的单价为(x ﹣9)元/条,根据题意得:312042009x x=-,解得:x =35,经检验,x =35是原方程的解,∴x ﹣9=26.答:A 型芯片的单价为26元/条,B 型芯片的单价为35元/条.(2)设购买a 条A 型芯片,则购买(200﹣a )条B 型芯片,根据题意得:26a+35(200﹣a )=6280,解得:a =80.答:购买了80条A 型芯片.【点睛】本题考查了分式方程的应用以及一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)找准等量关系,正确列出一元一次方程.24.(1)①BPD CQP V V ≌,理由见解析;②15cm /s 4Q v =;(2)经过80s 3点P 与点Q 第一次在边AB 上相遇【分析】(1)①根据时间和速度分别求得两个三角形中的边的长,根据SAS 判定两个三角形全等.②根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P 运动的时间,再求得点Q 的运动速度;(2)根据题意结合图形分析发现:由于点Q 的速度快,且在点P 的前边,所以要想第一次相遇,则应该比点P 多走等腰三角形的两个腰长.【详解】解:(1)①∵1s t =,∴313cm BP CQ ==⨯=,∵10cm AB =,点D 为AB 的中点,∴5cm BD =.又∵PC BC BP =-,8cm BC =,∴835cm PC =-=,∴PC BD =.又∵AB AC =,∴B C ∠=∠,在BPD △和CQP V 中,PC BD B C BP CQ =⎧⎪∠=∠⎨⎪=⎩,∴()SAS BPD CQP ≌△△.②∵P Q v v ≠,∴BP CQ≠若BPD CPQ △≌△,B C ∠=∠,则4cm BP PC ==,5cm CQ BD ==,∴点P ,点Q 运动的时间4s 33BP t ==,∴515cm /s 443Q CQ v t ===.(2)设经过x 秒后点P 与点Q 第一次相遇,由题意,得1532104x x =+⨯,解得803x =.∴点P 共运动了80380cm 3⨯=.ABC 周长为:1010828cm ++=,若是运动了三圈即为:28384cm ⨯=,∵84804cm AB -=<的长度,∵点P 、点Q 在AB 边上相遇,∴经过80s 3点P 与点Q 第一次在边AB 上相遇.【点睛】此题主要是运用了路程=速度×时间的公式,解题的关即使熟练运用全等三角形的判定和性质,能够分析出追及相遇的问题中的路程关系.25.(1)241x x x --(2)12m ≥-且2m ≠(3)当2x =-时,分式的值为4-;当0x =时,分式的值为0;当2x =时,分式的值为4-;当4x =时,分式的值为0【分析】(1)将分式的分子、分母分解因式,将除法化为乘法,约分计算即可;(2)将A 、B 的值代入解方程,根据解是非负数,得到21055m +≥,计算即可;(3)将A 利用完全平方公式及整式加减法添括号法则变形为331x x ---,由值为整数得到x 的值,代入计算.(1)解:()()()21114(4)x x x x A x x ++-=÷--()()()()214411x x x x x x +-=⋅-+-241x x x -=-;(2)解:由题意:2242111x x x m A B x x--+=+=--2242111x x x m x x ---=--,22421x x x m x --+=-,2155x m =+.∵解是非负数,∴21055m +≥∴12m ≥-.∵10x -≠即1x ≠,∴25511m +≠,解得2m ≠,∴12m ≥-且2m ≠;(3)解:241x x A x -=-()21211x x x ---=-2111x x x +=---()21311x x x -+=---331x x =---.当2x =-时,分式的值为4-;当0x =时,分式的值为0;当2x =时,分式的值为4-;当4x =时,分式的值为0.【点睛】此题考查了分式的除法运算法则,解分式方程,正确掌握分式的分解,运算法则,完全平方公式是解题的关键.26.(1)见解析(2)BE DE AD +=,见解析【分析】(1)由“AAS”可证ACD CBE △△≌;(2)由全等三角形的性质可得CD BE =,AD CE =,即可求解.(1)证明:∵AD CE ⊥,BE CE ⊥,∴90E ADC ∠=∠=︒,∴1290∠+∠=︒,∵90ACB ∠=︒,∴3290∠+∠=︒,∴13∠=∠,在ACD △和CBE △中,13ADC E AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ACD CBE △△≌(AAS ).(2)解:BE DE AD +=,理由如下:∵ACD CBE △△≌,∴CD BE =,AD CE =.∵CD DE CE +=,∴BE DE AD +=.【点睛】本题考查了全等三角形的判定和性质,直角三角形两锐角互余,掌握全等三角形的判定是本题的关键.27.(1)见解析(2)等边三角形,见解析(3)是定值,见解析【分析】(1)连接BD ,可证ABD △是等边三角形,再由等边三角形的三线合一即可得证;(2)由ABD △是等边三角形,可得FBD ABE ∠=∠,由BCD △是等边三角形,可得60BDC ∠=︒.由ASA 可证得ABE △和DBF 全等,从而BE BF =,即可证明BEF 是等边三角形;(3)由ABE DBF △△≌,可得面积相等,故ABD BEDF S S = 四边形,当AB 的长度为定值时,ABD △的面积为定值,四边形BEDF 的面积也为定值.(1)证明:连接BD .∵AB AD =,60A ∠=︒,∴ABD △是等边三角形.∵BE AD ⊥,∴12AE AD =.(2)解:BEF是等边三角形,理由如下:∵ABD △是等边三角形,∴AB BD =,60ABD ∠=︒,∴60ABE EBD ∠+∠=︒.∵60EBF ∠=︒,∴60FBD EBD ∠+∠=︒,∴FBD ABE ∠=∠,∵AB BC CD ==,∴BD BC CD ==,∴BCD △是等边三角形,∴60BDC ∠=︒.在ABE △和DBF 中,60ABE DBFAB DB A BDF ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴ABE DBF △△≌(ASA ).∴BE BF =,∴BEF 是等边三角形.(3)解:四边形BEDF 的面积是定值,理由如下:∵ABE DBF △△≌,∵DBF BED ABE BED ABD BEDF S S S S S S =+=+= 四边形∴当AB 的长度为定值时,ABD △的面积为定值,四边形BEDF 的面积也为定值.。
【3套】八年级上册数学期末考试试题(答案)

八年级上册数学期末考试试题(答案)一、填空题:(每小题3分,共30分)1.科学家发现一种病毒的直径为0.000104米,用科学记数法表示为米.2.当x时,分式有意义.3.分解因式:4m2﹣16n2=.4.计算:﹣=.5.如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上,已知BD=2,AB=4,则DE =.6.x+=3,则x2+=.7.当x时,分式的值为正.8.已知:如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC的中点,AE=BF.若BC =8,则四边形AFDE的面积是.9.等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角为.10.如图,第1个图形有1个三角形,第2个图形中有5个三角形,第3个图形中有9个三角形,……,则第2019个图形中有个三角形.二、选择题:(每小题3分,共30分)11.下列运算正确的是()A.a2•a3=a6B.(2a)2=2a2C.(a2)3=a6D.(a+1)2=a2+112.下列图形中,是轴对称图形的是()A.B.C.D.13.若关于x的方程无解,则m的值是()A.3 B.2 C.1 D.﹣114.在,,﹣3xy+y2,,,分式的个数为()A.2 B.3 C.4 D.515.若把分式中的x和y都扩大2倍,则分式的值()A.扩大2倍B.缩小4倍C.缩小2倍D.不变16.下列二次根式中最简二次根式是()A.B.C.D.17.若x2+kx+9是完全平方式,则k的值是()A.6 B.﹣6 C.9 D.6或﹣618.八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是()A.﹣=20 B.﹣=20C.﹣=D.﹣=19.如图,等边三角形ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则=()A.B.2 C.D.20.如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有()A.2个B.3个C.4个D.无数个三、简答题:(共60分21.(8分)计算(1)4(x+y)(x﹣y)﹣(2x﹣y)2(2)(+)﹣(﹣)22.(5分)解方程:=+23.(5分)先化简,再求值:,其中x=.24.(7分)△ABC在平面直角坐标系中的位置如图.A、B、C三点在格点上.(1)作出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;(2)在y轴上找点D,使得AD+BD最小,作出点D并写出点D的坐标.25.(7分)已知=3,求的值.26.(8分)已知a,b,c都是实数,且满足(2﹣a)2+=0,且ax2+bx+c =0,求代数式3x2+6x+1的值.27.(10分)欧城物业为美化小区,要对面积为9600平方米的区域进行绿化,计划安排甲、乙两个园林队完成,已知甲园林队每天绿化面积是乙园林队每天绿化面积的2倍,并且甲、乙两园林队独立完成面积为800平方米区域的绿化时,甲园林队比乙园林队少用2天.(1)求甲、乙两园林队每天能完成绿化的面积分别是多少平方米.(2)物业每天需付给甲园林队的绿化费用为0.4万元,乙园林队的绿化费用为0.25万元,如果这次绿化总费用不超过10万元,那么欧城物业至少应安排甲园林队工作多少天?28.(10分)已知△ABC为等边三角形,E为射线BA上一点,D为直线BC上一点,ED=EC.(1)当点E在AB的上,点D在CB的延长线上时(如图1),求证:AE+AC=CD;(2)当点E在BA的延长线上,点D在BC上时(如图2),猜想AE、AC和CD的数量关系,并证明你的猜想;(3)当点E在BA的延长线上,点D在BC的延长线上时(如图3),请直接写出AE、AC 和CD的数量关系.参考答案一、填空题1.科学家发现一种病毒的直径为0.000104米,用科学记数法表示为 1.04×10﹣4米.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.解:0.000104=1.04×10﹣4,故答案为:1.04×10﹣4.【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.2.当x≠﹣时,分式有意义.【分析】根据,分式有意义,可得答案.解:由题意,得3x+5≠0,解得x≠﹣,故答案为:≠﹣.【点评】本题考查了分式有意义的条件,利用分母不能为零得出不等式是解题关键.3.分解因式:4m2﹣16n2=4(m+2n)(m﹣2n).【分析】原式提取4后,利用平方差公式分解即可.解:原式=4(m+2n)(m﹣2n).故答案为:4(m+2n)(m﹣2n)【点评】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.4.计算:﹣=﹣.【分析】先化简,再进一步合并同类二次根式即可.解:原式=﹣=﹣【点评】此题考查二次根式的加减,注意先化简再合并.5.如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上,已知BD=2,AB=4,则DE = 6 .【分析】因为AD⊥BC,BD=DC,点C在AE的垂直平分线上,由垂直平分线的性质得AB=AC=CE,即可得到结论.解:∵AD⊥BC,BD=DC,∴AB=AC;又∵点C在AE的垂直平分线上,∴AC=EC,∴AB=AC=CE=5;∵BD=CD=3,∴DE=CD+CE=2+4=6,故答案为6.【点评】本题主要考查线段的垂直平分线的性质等几何知识,利用线段的垂直平分线上的点到线段的两个端点的距离相等是解答此题的关键.6.x+=3,则x2+=7 .【分析】直接利用完全平方公式将已知变形,进而求出答案.解:∵x+=3,∴(x+)2=9,∴x2++2=9,∴x2+=7.故答案为:7.【点评】此题主要考查了分式的混合运算,正确应用完全平方公式是解题关键.7.当x>且x≠0 时,分式的值为正.【分析】同号为正,异号为负.分母≠0.解:分式的值为正,即>0,解得x>,因为分母不为0,所以x≠0.故当x>且x≠0时,分式的值为正.【点评】由于该类型的题易忽略分母不为0这个条件,所以常以这个知识点来命题.8.已知:如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC的中点,AE=BF.若BC =8,则四边形AFDE的面积是8 .【分析】连接AD,求出△DAE≌△DBF,得到四边形AFDE的面积=S△ABD=S△ABC,于是得到结论解:连接AD,∵Rt△ABC中,∠BAC=90°,AB=AC,∴∠B=∠C=45°,∵AB=AC,DB=CD,∴∠DAE=∠BAD=45°,∴∠BAD=∠B=45°,∴AD=BD,∠ADB=90°,在△DAE和△DBF中,,∴△DAE≌△DBF(SAS),∴四边形AFDE的面积=S△ABD=S△ABC,∵BC=8,∴AD=BC=4,∴四边形AFDE的面积=S△ABD=S△ABC=××8×4=8,故答案为:8.【点评】本题主要考查了全等三角形的判定和等腰三角形的判定.考查了学生综合运用数学知识的能力,连接AD,构造全等三角形是解决问题的关键.9.等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角为60°或120°.【分析】等腰三角形的高相对于三角形有三种位置关系,三角形内部,三角形的外部,三角形的边上.根据条件可知第三种高在三角形的边上这种情况不成了,因而应分两种情况进行讨论.解:当高在三角形内部时,顶角是120°;当高在三角形外部时,顶角是60°.故答案为:60°或120°.【点评】此题主要考查等腰三角形的性质,熟记三角形的高相对于三角形的三种位置关系是解题的关键,本题易出现的错误是只是求出120°一种情况,把三角形简单的认为是锐角三角形.因此此题属于易错题.10.如图,第1个图形有1个三角形,第2个图形中有5个三角形,第3个图形中有9个三角形,……,则第2019个图形中有8073 个三角形.【分析】根据题目中的图形,可以发现三角形个数的变化规律,从而可以解答本题.解:由图可得,第1个图形有1个三角形,第2个图形中有1+4=5个三角形,第3个图形中有1+4+4=1+4×2=9个三角形,……,则第2019个图形中有:1+4×(2019﹣1)=8073个三角形,故答案为:8073.【点评】本题考查图形的变化类,解答本题的关键是明确题意,发现题目中的三角形个数的变化规律,利用数形结合的思想解答.二、选择题:(每小题3分,共30分)11.下列运算正确的是()A.a2•a3=a6B.(2a)2=2a2C.(a2)3=a6D.(a+1)2=a2+1【分析】直接利用同底数幂的乘法运算法则以及积的乘方运算法则、幂的乘方运算法则、完全平方公式分别计算得出答案.解:A、a2•a3=a5,故此选项错误;B、(2a)2=4a2,故此选项错误;C、(a2)3=a6,正确;D、(a+1)2=a2+2a+1,故此选项错误;故选:C.【点评】此题主要考查了同底数幂的乘法运算以及积的乘方运算、幂的乘方运算、完全平方公式等知识,正确掌握运算法则是解题关键.12.下列图形中,是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称,进而得出答案.解:A、不是轴对称图形,故A错误;B、是轴对称图形,故B正确;C、不是轴对称图形,故C错误;D、不是轴对称图形,故D错误.故选:B.【点评】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.13.若关于x的方程无解,则m的值是()A.3 B.2 C.1 D.﹣1【分析】方程两边都乘以最简公分母(x﹣1)把分式方程化为整式方程,再根据方程无解,最简公分母等于0求出x的值吗,然后代入整式方程进行计算即可得解.解:方程两边都乘以(x﹣1)得,m﹣1﹣x=0,∵分式方程无解,∴x﹣1=0,解得x=1,∴m﹣1﹣1=0,解得m=2.故选:B.【点评】本题考查了分式方程的解,通常方法是:(1)把分式方程化为整式方程,(2)根据分式方程无解,最简公分母等于0求出x的值,(3)把求出的x的值代入整式方程求解得到所求字母的值.14.在,,﹣3xy+y2,,,分式的个数为()A.2 B.3 C.4 D.5【分析】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.解:分式有:,,共2个.故选:A.【点评】本题主要考查分式的定义,注意判断分式的条件是:含有分母,且分母中含有未知数.15.若把分式中的x和y都扩大2倍,则分式的值()A.扩大2倍B.缩小4倍C.缩小2倍D.不变【分析】利用分式的基本性质求解即可判定.解:分式中的x和y都扩大2倍,得.故选:D.【点评】本题主要考查了分式的基本性质,解题的关键是熟记分式的基本性质.16.下列二次根式中最简二次根式是()A.B.C.D.【分析】直接利用最简二次根式的定义分析得出答案.解:A、=2,故此选项错误;B、==,故此选项错误;C、,是最简二次根式,故此选项正确;D、=|mn|,故此选项错误;故选:C.【点评】此题主要考查了最简二次根式,正确把握定义是解题关键.17.若x2+kx+9是完全平方式,则k的值是()A.6 B.﹣6 C.9 D.6或﹣6【分析】本题是完全平方公式的应用,这里首末两项是x和9这两个数的平方,那么中间一项为加上或减去x和9乘积的2倍.解:∵x2+kx+9是一个完全平方式,∴这两个数是x和3,∴kx=±2×3x=±6x,解得k=±6.故选:D.【点评】本题考查的是完全平方公式,两数平方和再加上或减去它们乘积的2倍,是完全平方式的主要结构特征,本题要熟记完全平方公式,注意积的2倍的符号,有正负两种情况,避免漏解.18.八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是()A.﹣=20 B.﹣=20C.﹣=D.﹣=【分析】根据八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,可以列出相应的方程,从而可以得到哪个选项是正确的.解:由题意可得,﹣=,故选:C.【点评】本题考查由实际问题抽象出分式方程,解题的关键是明确题意,找出题目中的等量关系,列出相应的方程.19.如图,等边三角形ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则=()A.B.2 C.D.【分析】根据等边三角形性质得出AC=AB,∠BAC=∠B=60°,证△ABE≌△CAD,推出∠BAE=∠ACD求出∠AFD=∠BAC=60°求出∠FAG=30°,即可求出答案.证明:∵△ABC 是等边三角形, ∴AC =AB ,∠BAC =∠B =60°, 在△ABE 和△CAD 中∴△ABE ≌△CAD (SAS ), ∴∠BAE =∠ACD ,∴∠AFD =∠CAE +∠ACD =∠CAE +∠BAE =∠BAC =60°, ∵AG ⊥CD , ∴∠AGF =90°, ∴∠FAG =30°,∴sin30°==,即=.【点评】本题考查了全等三角形的性质和判定等边三角形性质,特殊角的三角函数值,含30度角的直角三角形性质的应用,主要考查学生的推理能力.20.如图,∠AOB =120°,OP 平分∠AOB ,且OP =2.若点M ,N 分别在OA ,OB 上,且△PMN 为等边三角形,则满足上述条件的△PMN 有( )A .2个B .3个C .4个D .无数个【分析】如图在OA 、OB 上截取OE =OF =OP ,作∠MPN =60°,只要证明△PEM ≌△PON 即可推出△PMN 是等边三角形,由此即可得结论解:如图在OA 、OB 上截取OE =OF =OP ,作∠MPN =60°.∵OP 平分∠AOB ,∴∠EOP=∠POF=60°,∵OP=OE=OF,∴△OPE,△OPF是等边三角形,∴EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,∴∠EPM=∠OPN,在△PEM和△PON中,,∴△PEM≌△PON(ASA).∴PM=PN,∵∠MPN=60°,∴△PNM是等边三角形,∴只要∠MPN=60°,△PMN就是等边三角形,故这样的三角形有无数个.故选:D.【点评】本题考查等边三角形的判定和性质、全等三角形的判定和性质、角平分线的定义等知识,解题的关键是正确添加辅助线,构造全等三角形,属于中考常考题型.三、简答题:(共60分21.(8分)计算(1)4(x+y)(x﹣y)﹣(2x﹣y)2(2)(+)﹣(﹣)【分析】(1)根据平方差和完全平方公式计算即可;(2)根据二次根式的加减法的法则计算即可.解:(1)4(x+y)(x﹣y)﹣(2x﹣y)2=4(x2﹣y2)﹣(4x2﹣4xy+y2)=4x2﹣4y2﹣4x2+4xy ﹣y2=4xy﹣5y2;(2)(+)﹣(﹣)=2+﹣+=3+.【点评】本题考查了二次根式的加减法,完全平方公式,平方差公式,熟记法则和乘法公式是解题的关键,22.(5分)解方程: =+【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.解:去分母得:3x =2x ﹣4+6, 解得:x =2,经检验x =2是增根,分式方程无解.【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.23.(5分)先化简,再求值:,其中x =.【分析】根据分式的运算法则即可求出答案.解:由于x ==﹣2原式=×﹣=﹣== =【点评】本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型. 24.(7分)△ABC 在平面直角坐标系中的位置如图.A 、B 、C 三点在格点上. (1)作出△AB C 关于x 轴对称的△A 1B 1C 1,并写出点C 1的坐标 (3,﹣2) ; (2)在y 轴上找点D ,使得AD +BD 最小,作出点D 并写出点D 的坐标 (0,2) .【分析】(1)根据网格结构找出点A 、B 、C 关于x 轴的对称的A 1、B 1、C 1的位置,然后顺次连接即可,再根据平面直角坐标系写出点C1的坐标;(2)确定出点B关于y轴的对称点B′,根据轴对称确定最短路线问题连接AB′,与y轴的交点即为所求的点D,然后求出OD的长度,再写出坐标即可.解:(1)△A1B1C1如图所示,C1(3,﹣2);(2)点D如图所示,OD=2,所以,点D的坐标为(0,2).故答案为:(3,﹣2);(0,2).【点评】本题考查了利用轴对称变换作图,利用轴对称确定最短路线问题,熟练掌握网格结构准确找出对应点的位置是解题的关键.25.(7分)已知=3,求的值.【分析】由题意可知:b﹣a=3ab,然后整体代入原式即可求出答案.解:由题意可知:b﹣a=3ab,∴a﹣b=﹣3ab∴原式===【点评】本题考查分式的值,解题的关键是由题意得出a﹣b=﹣3ab,本题属于基础题型.26.(8分)已知a,b,c都是实数,且满足(2﹣a)2+=0,且ax2+bx+c =0,求代数式3x2+6x+1的值.【分析】利用非负数的性质求出a,b,c的值,代入已知等式求出x2+2x的值,原式变形后代入计算即可求出值.解:∵(2﹣a)2++|c+8|=0,∴a=2,b=4,c=﹣8,代入ax2+bx+c=0得:2x2+4x﹣8=0,即x2+2x﹣4=0,∴x2+2x=4,则3x2+6x+1=3(x2+2x)+1=12+1=13.【点评】此题考查了代数式求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.27.(10分)欧城物业为美化小区,要对面积为9600平方米的区域进行绿化,计划安排甲、乙两个园林队完成,已知甲园林队每天绿化面积是乙园林队每天绿化面积的2倍,并且甲、乙两园林队独立完成面积为800平方米区域的绿化时,甲园林队比乙园林队少用2天.(1)求甲、乙两园林队每天能完成绿化的面积分别是多少平方米.(2)物业每天需付给甲园林队的绿化费用为0.4万元,乙园林队的绿化费用为0.25万元,如果这次绿化总费用不超过10万元,那么欧城物业至少应安排甲园林队工作多少天?【分析】(1)设乙工程队每天能完成的绿化面积为x平方米,则甲工程队每天能完成的绿化面积为2x平方米,根据工作时间=工作总量÷工作效率结合甲队比乙队少用2天,即可得出关于x的分式方程,解之并检验后即可得出结论;(2)设应安排甲工程队工作y天,则乙工程队工作(48﹣2y)天,根据总费用=0.4×甲工程队工作天数+0.25×乙工程队工作天数结合总费用不超过10万元,即可得出关于y 的一元一次不等式,解之即可得出y的取值范围,取其内的最小值即可.解:(1)设乙园林队每天能完成绿化的面积为x平方米,则甲园林队每天能完成绿化的面积为2x平方米,根据题意得:﹣=2,解得:x=200,经检验,x=200是原分式方程的解,∴当x=200时,2x=400;答:甲、乙两园林队每天能完成绿化的面积分别是400平方米和200平方米;(2)设欧城物业应安排甲园林队工作y天,则乙园林队工作=(48﹣2y)天,根据题意得:0.4y+0.25(48﹣2y)≤10,解得:y≥20,∴y的最小值为20.答:甲工程队至少应工作20天.【点评】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据数量关系,列出一元一次不等式.28.(10分)已知△ABC为等边三角形,E为射线BA上一点,D为直线BC上一点,ED=EC.(1)当点E在AB的上,点D在CB的延长线上时(如图1),求证:AE+AC=CD;(2)当点E在BA的延长线上,点D在BC上时(如图2),猜想AE、AC和CD的数量关系,并证明你的猜想;(3)当点E在BA的延长线上,点D在BC的延长线上时(如图3),请直接写出AE、AC 和CD的数量关系.【分析】(1)在CD上截取CF=AE,连接EF.运用“AAS”证明△ECF≌△EDB得AE=BD,从而得证;(2)在BC的延长线上截取CF=AE,连接EF.同理可得AE、AC和CD的数量关系;(3)同(2)的探究过程可得AE、AC和CD的数量关系.(1)证明:在CD上截取CF=AE,连接EF.∵△ABC是等边三角形,∴∠ABC=60°,AB=BC.∴BF=BE,△BEF为等边三角形.∴∠EBD=∠EFC=120°.又∵ED=EC,∴∠D=∠ECF.∴△EDB≌△ECF(AAS)∴CF=BD.∴AE=BD.∵CD=BC+BD,BC=AC,∴AE+AC=C D;(2)解:在BC的延长线上截取CF=AE,连接EF.同(1)的证明过程可得AE=BD.∵CD=BC﹣BD,BC=AC,∴AC﹣AE=CD;(3)解:AE﹣AC=CD.(在BC的延长线上截取CF=AE,连接EF.证明过程类似(2)).【点评】此题考查全等三角形的判定与性质及等边三角形的性质,运用了类比的数学思想进行探究,有利于培养分散思维习惯和举一反三的能力.八年级上册数学期末考试试题及答案一、单选题(本题共12小题,每题只有一个正确选项,每小题3分,共36分)1.下面4个图案,其中不是轴对称图形的是()A. B. C. D.2.计算232a b -()的结果是( ) A . 636a b - B . 638a b - C . 638a b D .53 8a b - 3.在平面直角坐标系中,点P (3,﹣2)关于y 轴的对称点在( ) A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限 4.一个三角形的两边长为3和7,第三边长为偶数,则第三边为( ) A . 6 B . 6或8 C . 4 D . 4或6 5.下列从左到右的变形,属于分解因式的是( )A . 2(3)(3)9a a a +--=B . 25(1)5x x x x +-=--C . 2 (1)a a a a =++D . 32x y x x y =⋅⋅ 6.如图,点A 在DE 上,AC =CE ,∠1=∠2=∠3,则DE 的长等于( ) A . DC B . BC C . AB D . AE +AC7.若分式2424x x --的值为零,则x 等于( )A. 0B. 2C. 2或-2D. -28.如图(1)是一个长为2a ,宽为2b (a >b )的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )A . 2abB . 2()a b +C . 2()a b -D . 22 a b - 9.如图,AB =AC =AD ,若∠BAD =80°,则∠BCD =( )A . 80°B . 100°C . 140°D . 160°10.如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 的外部时,则∠A 与∠1 和∠2之间有一种数量关系始终保持不变,请试着找一找这个结论,你发现的结论是( ) A . 2∠A =∠1-∠2 B . 3∠A =2(∠1-∠2) C . 3∠A =2∠1-∠2 D . ∠A =∠1-∠2第8题图第9题图第10题图第6题图11.如图,在△ABC 中,∠A =20°,∠ABC 与∠ACB 的角平分线交于D 1, ∠ABD 1与∠ACD 1的角平分线交于点D 2,依此类推,∠ABD 4与∠ACD 4的角平分线交于点D 5,则∠BD 5C 的度数是( )A . 24°B . 25°C . 30°D . 36° 12.如图,点E 是BC 的中点,AB ⊥BC ,DC ⊥BC ,AE 平分∠BAD ,下列结论:①∠AED =90°②∠ADE =∠CDE ③DE =BE ④AD =AB +CD ,四个结论中成立的是( ) A . ①②④ B . ①②③ C . ②④ D . ①②③④二、填空题(本题共8小题,每小题3分,共24分) 13.(1)若要使分式34x+有意义,则x 的取值范围是________ (2)数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1=______(3)如图,在△ABC 中,D 是BC 边上的中点,∠BDE =∠CDF ,请你添加一个条件,使DE=DF 成立.你添加的条件是________.(不再添加辅助线和字母)(4)化简22244x xx x --+的结果是________(5)已知关于x 的分式方程112a x -=+无实数解,则a =________ (6)如图,AB=AC ,DB=DC ,若∠ABC 为60°,BE =3cm ,则AB =________cm .(7)如图,∠AOE =∠BOE =15°,EF ∥OB ,EC ⊥OB ,若EC =2,则S △OFE =________ (8)如图,已知点P 是射线ON 上一动点(即P 可在射线ON 上运动),∠AON =45°, 当∠A =________时,△AOP 为等腰三角形.第12题图第11题图第13(7)题图 第13(6)题图 第13(3)题图第13(2)题图第13(8)题图三、解答题(共60分)14.(本题共3小题,每小题4分,共12分)(1)因式分解:244xyz xyz xy -+- (2)因式分解:229()()m n m n +--(3)解方程:2133x x x x-+=--15.(本小题6分)化简求值 已知113x y +=,求222x xy y x xy y-+-+的值16.(本小题9分)如图,(1)在网格中画出△ABC 关于y 轴对称的△A 1B 1C 1; (2)写出△ABC 关于x 轴对称的△A 2B 2C 2的各顶点坐标;(3)在y 轴上确定一点P ,使△PAB 周长最短.(只需作图,保留作图痕迹)第16题图17.(本小题9分)已知等边三角形ABC ,延长BA 至E ,延长BC 至D ,使得AE =BD ,求证:EC =ED18.(本小题12分)某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.(1)求第一批购进书包的单价是多少元?(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?B第17题图19.(本小题12分)在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP 于点D,交直线BC于点Q.第19题图(1)如图1,当P在线段AC上时,求证:BP=AQ;(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?________(填“成立”或“不成立”)(3)在(2)的条件下,当∠DBA=________时,存在AQ=2BD,说明理由.2017—2018学年度上学期期末学业水平质量调研试题八年级数学参考答案2018.01说明:本答案仅供参考,阅卷时以小组统一答案为准13(1)x ≠﹣4 (2)60° (3)答案不唯一,如AB=AC 或∠B =∠C 或∠BED =∠CFD 或∠AED =∠AFD (4)2xx - (5) 1 (6) 6 (7) 4 (8) 45°或67.5°或90° 三、解答题14.(1)因式分解244xyz xyz xy -+-22(44)(2)xy z z xy z =--+=--……………4分(2)22()9m n m n +--() =223()m n m n +--⎡⎤⎣⎦() =33()()m n m n m n m n ⎡⎤⎡⎤⎣⎦+⎦+---⎣+()()=()422m n m n ++()……………4分(3)解:两边乘(3)x -得到(2)3x x x --=-, 23x x x -+=-,1x =-, 检验:当1x =-时,(3)0x -≠,故1x =-是分式方程的根……………4分 15.解:11222()653,3,3,52()232x y x xy y x y xy xy xy xy x y xy x y xy x xy y x y xy xy xy xy+-++--+==+=====-++-- ……………6分16.(1)解:如图所示:……………3分(2)解:A 2(﹣3,﹣2),B 2(﹣4,3),C 2(﹣1,1)……………6分(3)解:连结AB 1或BA 1交y 轴于点P ,则点P 即为所求……………9分17.证明:延长BD 到F ,使BF=BE ,连接EF .则BF-BC =BE-BA . 即CF=AE ;又AE=BD . 故CF=BD , DF=BC . ∵∠B =60°.∴△BEF 为等边三角形,BE=EF ;∠B =∠F =60°.∴△EBC ≌△EFD (SAS),EC=ED .……………9分 18.(1)解:设第一批购进书包的单价是x 元.则:2000630034x x ⨯=+ 解得:x =80.经检验:x =80是原方程的根.答:第一批购进书包的单价是80元 ……………7分 (2)解:20006300120801208437008084⨯+⨯=(﹣)(﹣)(元).答:商店共盈利3700元……………12分19.(1)证明:∵∠ACB=∠ADB=90°,∠APD=∠BPC,∴∠DAP=∠CBP,在△ACQ和△BCP中∴△ACQ≌△BCP(ASA),∴BP=AQ ……………5分(2)成立……………7分(3)22.5°……………9分当∠DBA=22.5°时,存在AQ=2BD,理由:∵∠BAC=∠DBA+∠APB=45°,∴∠PBA=∠APB=22.5°,∴AP=AB,∵AD⊥BP,∴BP=2BD,在△PBC与△QAC中,,∴△PBC≌△ACQ,∴AQ=PB,∴AQ=2BD.故答案为:22.5°……………12分人教版八年级(上)期末模拟数学试卷【答案】一、选择题(本大题共16个小题,每小题3分,共48分)1.下列图形中,不是轴对称图形的是()2.下列根式中是最简二次根式的是()A. B. C. D.3.下列各数中,没有平方根的是()A. B. C. D.4.下列运算结果正确的是()A. B. C. D.5.若代数式在实数范围内有意义,则x的取值范围是()A. B. C. D.6.解分式方程,去分母得()A.B.C.D.7.已知等腰三角形的两边x,y满足,则等腰三角形的周长为()A.16 B.12 C.20 D.20或168.下列二次根式中,与可以合并的根式是()A. B. C. D.9.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是()A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°10.如图是一个以O为对称中心的中心对称图形,若∠A=30°,∠C=90°,OC=1,则AB的长为()A.2 B.4 C. D.11.如图,AB∥FC,E是DF的中点,若AB=20,CF=12,则BD等于()A.12 B.8 C.6 D.1012.已知,,则的值为()A.10 B.8 C.6 D.413.如图,在△ABC中,AB=AC,∠A=20°,以B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则∠ADB=()A.100° B.160° C.80° D.20°14.如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C’处,P为直线AD上的一点,则线段BP的长不可能是()A.3 B.4 C.5.5 D.1015.如图,△ABC的顶点A,B,C在连长为1的正方形网格的格点上,BD⊥AC 于点D,则BD的长为()A. B. C. D.16.如图,△ABC的面积为10,BP是∠ABC的平分线,AP⊥BP于P,则△PBC 的面积为()A.4 B.5 C.6 D.7二、填空(每小题3分,共12分)17.化简:的结果为 .18.已知的平方根是,则m= .19.若,则代数式的值是 .20.如图,Rt△ABC中,∠B=90°,AB=8cm,BC=6cm,D点从A出发以每秒1cm 的速度向B点运动,当D点运动到AC的中垂线上时,运动时间为秒.三、(共12分)21.(1)化简,再求值:,其中.(2)计算:.四、(本题8分)22.如图,在△ABC中,AB=AC=8cm.(1)作AB的垂直平分线,交AC于点M,交AB于点N;(尺规作图,保留作图痕迹)(2)在(1)的条件下,连接MB,若△MBC的周长是14cm,求BC的长.五、(本题8分)23.某八年级计划用360元购买笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,结果买的笔记本比打折前多10本.(1)请利用分工方程求出每本笔记本原来的标价;(2)恰逢文具店周年庆典,每本笔记本可以按原价打8折,这样该校最多可购入多少笔记本?六、(8分)24.如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.(1)求证:△ABC≌△DCB;(2)△OBC是何种三角形?证明你的结论.七、(12分)25.先阅读,再解答由可以看出,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式,在进行二次根式计算时,利用有理化因式,有时可以化去分母中的根号,例如:,请完成下列问题:(1)的有理化因式是;(2)化去式子分母中的根号:, .(3)(填或)(4)利用你发现的规律计算下列式子的值:八、(12分)26.已知:如图,Rt△ABC中,∠C=90°,AC=6,AB=10.(1)求BC的长;(2)有一动点P从点C开始沿C→B→A方向以1cm/s的速度运动到点A后停止运动,设运动时间为t秒;求:①当t为几秒时,AP平分∠CAB;②当t为几秒时,△ACP是等腰三角形(直接写答案).。
江苏省宝应县2024届八上数学期末统考试题含解析

江苏省宝应县2024届八上数学期末统考试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每题4分,共48分)1.如图,若在象棋盘上建立直角坐标系,使“帅”位于点.“馬”位于点,则“兵”位于点( )A .(1?1)-, B .(2?1)--, C .(3?1)-, D .(1?2)-, 2.某种细菌的半径是0.00000618米,用科学记数法把半径表示为( )A .618×10﹣6B .6.18×10﹣7C .6.18×106D .6.18×10﹣63.下面计算正确的是( )A .33645x x x +=B .236a a a ⋅=C .()4312216x x -=D .()()22222x y x y x y +-=- 4.如图点,,A B C 在同一条直线上,,CBE ADC ∆∆都是等边三角形,,AE BD 相交于点O ,且分别与,CD CE 交于点,M N ,连接,M N ,有如下结论:①DCB ACE ∆≅∆;②AM DN =;③CMN ∆为等边三角形;④60︒∠=EOB .其中正确的结论个数是( )A .1个B .2个C .3个D .4个5.长度为下列三个数据的三条线段,能组成直角三角形的是( )A .1,2,3B .3,5,7C .12 3D .1,53,436.某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x 件,则x 应满足的方程为( )A .72072054848x -=+B .72072054848x +=+C .720720548x -=D .72072054848x -=+ 7.下列命题属于真命题的是( )A .同旁内角相等,两直线平行B .相等的角是对顶角C .平行于同一条直线的两条直线平行D .同位角相等8.以下列各组线段为边,能组成三角形的是().A .2cm ,3cm ,5cmB .5cm ,6cm ,10cmC .1cm ,1cm ,3cmD .3cm ,4cm ,9cm9.下列各数是无理数的是( )A .B .C .D . 10.如图①,把4个长为a ,宽为b 的长方形拼成如图②所示的图形,且a=3b ,则根据这个图形不能得到的等式是( )A .(a+b)2=4ab+(a-b)2B .4b 2+4ab=(a+b)2C .(a-b)2=16b 2-4abD .(a-b)2+12a 2=(a+b)211.如图,将一张含有30︒角的三角形纸片的两个顶点放在直尺的两条对边上,若120∠=︒,则2∠的度数是( )A .30︒B .40︒C .50︒D .60︒12.如图所示,AO CO 分别平分BAC ∠和,100ACB B ∠∠=︒,则AOC ∠的度数为( )A .120︒B .90︒C .140︒D .135︒二、填空题(每题4分,共24分)13.如图,,3,5ABC EBD AB cm BD cm ==≌,则CE 的长度为__________.14.计算:169=_____. 15.如图,在ABC 中,AB AC =,30A ∠=︒,AB 的垂直平分线交AC 于点E ,垂足是D ,连接BE ,则EBC ∠的度数为______.16.如图,已知△ABC 的周长是22,OB 、OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,且OD =3,△ABC 的面积是_____.17.如图,在△ABC 中,AB=3,AC=4,则BC 边上的中线AD 的长x 取值范围是___;18.将点M (﹣5,m )向上平移6个单位得到的点与点M 关于x 轴对称,则m 的值为_____.三、解答题(共78分)19.(8分)计算:-1432-(π-3.14) 06÷220.(8分)两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,其中AB AC =,AE AD =,90BAC EAD ∠=∠=︒,45ABC ACB AED ADE ∠=∠=∠=∠=︒,B 、C 、E 在同一条直线上,连结DC .(1)请在图2中找出与ABE ∆全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)证明:DC BE ⊥.21.(8分)先化简(22444a a a -+-﹣2a a +)÷12a a -+,再从a ≤2的非负整数解中选一个适合的整数代入求值. 22.(10分)如图,直线27y x =-+与x 轴、y 轴分别相交于点C 、B ,与直线32y x =相交于点A . (1)求A 点坐标;(2)如果在y 轴上存在一点P ,使OAP ∆是以OA 为底边的等腰三角形,求P 点坐标;(3)在直线27y x =-+上是否存在点Q ,使OAQ ∆的面积等于6?若存在,请求出Q 点的坐标,若不存在,请说明理由.23.(10分)如图,Rt △ABC 中,∠ACB =90°.(1)作∠BAC 的平分线,交BC 于点D ;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的条件下,若BD =5,CD =3,求AC 的长.24.(10分)如图,已知△ABC 的顶点分别为A (-2,2)、B (-4,5)、C (-5,1)和直线m (直线m 上各点的横坐标都为1).(1)作出△ABC 关于x 轴对称的图形111A B C ∆,并写出点1A 的坐标;(2)作出点C 关于直线m 对称的点2C ,并写出点2C 的坐标;(3)在x 轴上画出点P ,使PA +PC 最小.25.(12分)先化简再求值:(a +2﹣52a -)•243a a --,其中a =12-. 26.如图,已知A (-1,2),B (-3,1),C (-4,3).(1)作△ABC 关于x 轴的对称图形△A 1B 1C 1,写出点C 关于x 轴的对称点C 1的坐标;(2)作△ABC 关于直线l 1:y=-2(直线l 1上各点的纵坐标都为-2)的对称图形△A 2B 2C 2,写出点C 关于直线l 1的对称点C 2的坐标.(3)作△ABC 关于直线l 2:x=1(直线l 2上各点的横坐标都为1)的对称图形△A 3B 3C 3,写出点C 关于直线l 2的对称点C 3的坐标.(4)点P (m ,n )为坐标平面内任意一点,直接写出:点P 关于直线x=a (直线上各点的横坐标都为a )的对称点P 1的坐标;点P 关于直线y=b (直线上各点的纵坐标都为b )的对称点P 2的坐标.参考答案一、选择题(每题4分,共48分)1、C【解题分析】试题解析:如图,“兵”位于点(−3,1).故选C.2、D【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,n的值由原数左边起第一个不为零的数字前面的0的个数所决定.【题目详解】0.00000118=1.18×10﹣1.故选D.【题目点拨】本题考查了用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.3、C【解题分析】A.合并同类项得到结果;B.利用同底数幂的乘法法则计算得到结果;C.利用幂的乘方与积的乘方运算法则计算得到结果;D.利用平方差公式计算得到结果,即可作出判断.5x,错误;【题目详解】A.原式=3B.原式=5a,错误;C.原式=1216x ,正确;D.原式=224x y -,错误.故选C.【题目点拨】本题主要考查同底数幂的乘法,合并同类项,幂的乘方与积的乘方,平方差公式运算,熟知其运算法则是解题的关键. 4、D【分析】由SAS 即可证明DCB ACE ∆≅∆,则①正确;有∠CAE=∠CDB ,然后证明△ACM ≌△DCN ,则②正确;由CM=CN ,∠MCN=60°,即可得到CMN ∆为等边三角形,则③正确;由AD ∥CE ,则∠DAO=∠NEO=∠CBN ,由外角的性质60EOB OAC CBN ∠=∠+∠=︒,即可得到答案.【题目详解】解:∵△DAC 和△EBC 均是等边三角形,∴AC=CD ,BC=CE ,∠ACD=∠BCE=60°,∴∠ACD+∠DCE=∠BCE+∠DCE ,即∠ACE=∠BCD ,在△ACE 和△DCB 中,AC CD ACE BCD BC CE =⎧⎪∠=∠⎨⎪=⎩∴△ACE ≌△DCB (SAS ),则①正确;∴AE=BD ,∠CAE=∠CDB ,在ACM 和△DCN 中,ACD DCE AC CDCAE CDB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ACM ≌△DCN (ASA ),∴CM=CN ,AM DN =;则②正确;∵∠MCN=60°,∴CMN ∆为等边三角形;则③正确;∵∠DAC=∠ECB=60°,∴AD ∥CE ,∴∠DAO=∠NEO=∠CBN ,∴60EOB OAC CBN OAC DAO ∠=∠+∠=∠+∠=︒;则④正确;∴正确的结论由4个;故选:D .【题目点拨】本题考查了等边三角形的性质,全等三角形的判定与性质,平行线的判定,综合性较强,但难度不是很大,准确识图找出全等三角形是解题的关键.5、D【分析】根据勾股定理的逆定理逐项判断即可.【题目详解】由直角三角形的性质知,三边中的最长边为斜边A 、2221253+=≠,不满足勾股定理的逆定理,此项不符题意B 、22235347+=≠,不满足勾股定理的逆定理,此项不符题意C 、222133+=≠,不满足勾股定理的逆定理,此项不符题意D 、22242551()()393+==,满足勾股定理的逆定理,此项符合题意 故选:D .【题目点拨】本题考查了勾股定理的逆定理的应用,熟记勾股定理的逆定理是解题关键.6、D【分析】本题的关键是要弄清因客户要求工作量提速后的工作效率和工作时间,然后根据题目给出的关键语“提前5天”找到等量关系,然后列出方程. 【题目详解】因客户的要求每天的工作效率应该为:(48+x )件,所用的时间为:72048x+,根据“因客户要求提前5天交货”,用原有完成时间72048,减去提前完成时间72048x +,可以列出方程:72072054848x -=+ 故选:D .【题目点拨】这道题的等量关系比较明确,直接分析题目中的重点语句即可得知,再利用等量关系列出方程.7、C【解题分析】要找出正确命题,可运用相关基础知识分析找出正确选项,也可以通过举反例排除不正确选项,从而得出正确选项.【题目详解】A 、同旁内角互补,两直线平行,是假命题;B 、相等的角不一定是对顶角,是假命题;C 、平行于同一条直线的两条直线平行,是真命题;D、两直线平行,同位角相等,是假命题;故选C.【题目点拨】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.2、有些命题的正确性是用推理证实的,这样的真命题叫做定理.8、B【分析】根据三角形的三边关系对各选项进行逐一分析即可.【题目详解】A.∵2+3=5,∴不能组成三角形,故本选项错误;B.∵5+6=11>10,∴能组成三角形,故本选项正确;C.∵1+1=2<3,∴不能组成三角形,故本选项错误;D.∵3+4=7<9,∴不能组成三角形,故本选项错误.故选B.【题目点拨】本题考查了三角形的三边关系,熟知三角形任意两边之和大于第三边,任意两边之差小于第三边是解答此题的关键.9、D【解题分析】由于无理数就是无限不循环小数.初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及0.1010010001…,等有这样规律的数.由此即可判定选择项.【题目详解】解:A、是有理数,故选项错误;B、是有理数,故选项错误;C、C. 是有理数,故选项错误;D、是无理数,故选项正确.故选:D.【题目点拨】此题主要考查了无理数的定义.注意带根号的数与无理数的区别:带根号的数不一定是无理数,带根号且开方开不尽的数一定是无理数.10、D【分析】根据题意得出大正方形边长为(a+b),面积为(a+b)2,中间小正方形的边长为(a-b),面积为(a-b)2,然后根据图形得出不同的等式,对各选项进行验证即可.【题目详解】图②中的大正方形边长为(a+b),面积为(a+b)2,中间小正方形的边长为(a-b),面积为(a-b)2,由题意可知,大正方形的面积=四个小长方形的面积+小正方形的面积,即=(a+b)2=4ab+(a-b)2,故A项正确;∵a=3b,∴小正方形的面积可表示为4b2,即四个小长方形的面积+小正方形的面积=大正方形的面积,可表示为4b2+4ab=(a+b)2,故B项正确;大正方形的面积可表示为16b2,即大正方形的面积-四个小长方形的面积=小正方形的面积,可表示为(a-b)2=16b2-4ab,故C项正确;只有D选项无法验证,故选:D.【题目点拨】本题考查了等式的性质及应用,正方形的性质及应用,根据图形得出代数式是解题关键.11、C【分析】利用平行线的性质,三角形的外角的性质解决问题即可;【题目详解】解:如图,∵AB∥CD,∴∠3=∠2,∴∠3=∠1+30°,∵∠1=20°,∴∠3=∠2=50°;故选:C.【题目点拨】本题主要考查平行线的性质,三角形的外角等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.12、C【分析】首先根据三角形的内角和求出∠BAC、∠BCA的度数和,然后根据三角形的角平分线的定义,用∠BAC、∠BCA 的度数和除以2,求出∠OAC,∠OCA的度数和,最后根据三角形的内角和可求出∠AOC的度数.【题目详解】解:∵∠B=100°,∴∠BAC+∠BCA =180°-∠B=180°-100°=80°,又∵AO平分∠BAC,CO平分∠BCA,∴∠OAC+∠OCA =12(∠BAC+∠BCA)=40°,∴∠AOC=180°-(∠OAC+∠OCA )=180°-40°=140°.故答案为:C .【题目点拨】此题主要考查了三角形内角和定理,以及三角形角平分线的定义,解答此题的关键是求出∠OAC ,∠OCA 的度数和.二、填空题(每题4分,共24分)13、2cm【分析】根据全等三角形的对应边都相等,得到BC 、BE 的长,即可求出CE 的长.【题目详解】解:,3,5ABC EBD AB cm BD cm ∆∆==≌5,3BC BD cm EB AB cm ∴====532CE BC EB cm ∴=-=-=故答案为:2cm .【题目点拨】本题考查的主要是全等三角形的性质,对应的边都相等,注意到全等三角形的对应顶点写在对应的位置,正确判断对应边即可.14、43【解题分析】根据算术平方根的定义求解可得.【题目详解】解:=43故答案为:43【题目点拨】本题考查算术平方根,解题关键是熟练掌握算术平方根的定义.15、45【分析】先利用线段垂直平分线的性质得到EA=EB ,则根据等腰三角形的性质得∠ABE=∠A=30°,再利用三角形内角和计算出∠ABC 的度数,然后计算∠ABC-∠ABE 即可.【题目详解】解:∵DE 垂直平分AB ,∴EA=EB ,∴∠ABE=∠A=30°,∵AB=AC ,∴∠ABC=∠C ,∴∠ABC=12(180°-30°)=75°, ∴∠EBC=∠ABC-∠ABE=75°-30°=45°.故答案为:45°.【题目点拨】本题考查了等腰三角形的性质:等腰三角形的两腰相等;等腰三角形的两个底角相等;等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.也考查了线段垂直平分线的性质.16、1【分析】根据角平分线上的点到角的两边的距离相等可得点O 到AB 、AC 、BC 的距离都相等,从而可得到△ABC 的面积等于周长的一半乘以OD ,然后列式进行计算即可求解.【题目详解】解:如图,连接OA ,作OE ⊥AB 于E ,OF ⊥AC 于F .∵OB 、OC 分别平分∠ABC 和∠ACB ,∴OD=OE=OF ,∴S △ABC =S △BOC +S △AOB +S △AOC=111222BC OD AC OF AB OE ⋅+⋅+⋅ =()12BC AC AB OD ++⋅ =12×22×3=1. 故答案为:1.【题目点拨】本题考查了角平分线上的点到角的两边的距离相等的性质,判断出三角形的面积与周长的关系是解题的关键. 17、0.1<x<3.1【解题分析】延长AD 到E ,使AD=DE ,连接BE ,∵AD 是△ABC 的中线,∴BD=CD,在△ADC 和△EDB 中,BD CD ADC BDE AD DE =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△EDB (SAS ),∴EB=AC=4,∵AB=3,∴1<AE <7,∴0.1<AD <3.1.故答案为0.1<AD <3.1.18、-1.【分析】直接利用平移的性质得出平移后点的坐标,再利用关于x 轴对称点的性质得出答案.【题目详解】解:∵点M (﹣5,m )向上平移6个单位长度,∴平移后的点的坐标为:(﹣5,m +6),∵点M (﹣5,m )向上平移6个单位长度后所得到的点与点M 关于x 轴对称,∴m +m +6=0,解得:m =﹣1.故答案为:﹣1.【题目点拨】本题考查了平移的问题,掌握平移的性质以及关于x 轴对称点的性质是解题的关键.三、解答题(共78分)19、0【分析】首先计算乘方,然后计算除法,最后从左向右依次计算,求出算式的值是多少即可.【题目详解】原式 =-1+2--= 0【题目点拨】 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.20、(1)与ABE ∆全等的三角形为△ACD ,理由见解析;(2)见解析【分析】(1)根据等式的基本性质可得∠BAE=∠CAD ,然后利用SAS 即可证出ABE ∆≌△ACD ;(2)根据全等三角形的性质和已知条件可得∠ABE=∠ACD=45°,从而求出∠DCB=90°,然后根据垂直的定义即可证出结论.【题目详解】解:(1)与ABE ∆全等的三角形为△ACD ,理由如下∵90BAC EAD ∠=∠=︒∴∠BAC +∠CAE=∠EAD +∠CAE∴∠BAE=∠CAD在ABE ∆和△ACD 中AB AC BAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩∴ABE ∆≌△ACD(2)∵ABE ∆≌△ACD ,45ABC ACB AED ADE ∠=∠=∠=∠=︒∴∠ABE=∠ACD=45°∴∠DCB=∠ACD +∠ACB=90°∴DC BE ⊥【题目点拨】此题考查的是全等三角形的判定及性质和垂直的判定,掌握利用SAS 判定两个三角形全等、全等三角形的对应角相等和垂直的定义是解决此题的关键.21、21a --,1 【分析】先将分式的分子和分母分解因式,再根据分式的化简求值的过程计算即可求解. 【题目详解】解:原式=2(2)2(2)(2)21a a a a a a a ⎡⎤-+-⋅⎢⎥-++-⎣⎦, 22()221a a a a a a -+=-⋅++-,2221a a a +=-⋅+-, 21a =--. ∵a ≤1的非负整数解有0,1,1,又∵a ≠1,1,∴当a =0时,原式=1.【题目点拨】此题考察分式的化简求值,化简时需先分解因式约去公因式得到最简分式,求值时选的数需满足分母不为0的数才可代入求值.22、(1)(23)A ,;(2)P 点坐标是13(0,)6;(3)存在;点Q 的坐标是245(,)77或263(,)77- 【分析】(1)联立方程组即可解答; (2)设P 点坐标是0y (,),表达出OP=PA 在解方程即可;(3)对Q 点分类讨论,①当点Q 在线段AB 上;②当点Q 在AC 的延长线上,表达出OAQ ∆的面积即可求解.【题目详解】解:(1)解方程组:2732y x y x =-+⎧⎪⎨=⎪⎩,得23x y =⎧⎨=⎩ ∴23A (,); (2)设P 点坐标是0y (,),∵OAP ∆是以OA 为底边的等腰三角形,∴OP PA =,∴22223y y +-=() 解得136y = ∴P 点坐标是13(0,)6(3)存在; 由直线27y x =-+可知07B (,),702C (,), ∵172136224AOC S ∆=⨯⨯=<,172762AOB S ∆=⨯⨯=< ∴Q 点有两个位置:Q 在线段AB 上和AC 的延长线上设点Q 的坐标是x y (,),①当点Q 在线段AB 上:作QD y ⊥轴于点D ,如图①,则QD x =,∴761OBQ OAB OAQ S S S ∆∆∆=-=-= ∴112OB QD •=,即1271x ⨯= ∴27x = 把27x =代人了27y x =-+,得7457y =, ∵Q 的坐标是245(,)77 ②当点Q 在AC 的延长线上:作QD x ⊥轴于点D ,如图②,则QD y =-,∴213644OCQ OAQ OAC S S S ∆∆∆=-=-= ∴1324OC QD •=,即173()224y ⨯⨯-= ∴37y =- 把37y =-代入27y x =-+,得267x =, ∴Q 的坐标是263(,)77- 综上所述:点Q 的坐标是245(,)77或263(,)77-【题目点拨】本题考查了一次函数与几何综合问题,解题的关键是灵活运用函数的图象与性质,熟知直角坐标系中不规则三角形面积的求法.23、 (1)见解析;(2)6.【分析】(1)先以A 为圆心,小于AC 长为半径画弧,交AC ,AB 运用H 、F ;再分别以H 、F 为圆心,大于12HF 长为半径画弧,两弧交于点M ,最后画射线AM 交CB 于D ;(2)过点D 作DE ⊥AB ,垂足为E ,先证明△ACD ≌△AED 得到AC=AE ,CD=DE=3,再由勾股定理得求的BE 长,然后在Rt △ABC 中,设AC=x ,则AB=AE+BE=x+4,最后再次运用勾股定理求解即可.【题目详解】解:(1)如图:(2)过点D作DE⊥AB,垂足为E.则∠AED=∠BED=90°∵AD平分∠BAC∴CD=DE在RtACD和RtAED中CD=DE,AD=AD∴△CDE≌△AED(HL)∴AC=AE,CD=DE=3在Rt△BDE中,由勾股定理得:DE2+BE2=BD2∴BE2=BD2-DE2=52-32=16.∴BE=4在Rt△ABC中,设AC=x,则AB=AE+BE=x+4.由勾股定理得:AC2+BC2=AB2,即x2+82=(x+4)2解得:x=6,即AC=6.【题目点拨】本题主要考查了作角平分线、以及角平分线的性质、勾股定理的应用、全等三角形的判定和性质.解题的关键在于作出角平分线并利用其性质证明三角形全等.24、(1)图见解析,A(-2,-2);(2)图见解析,C2(7,1);(3)图见解析【分析】(1)根据轴对称关系确定点A1、B1、C1的坐标,顺次连线即可;(2)根据轴对称的性质解答即可;(3)连接AC1,与x轴交点即为点P.【题目详解】(1)如图,A1(-2,-2);(2)如图,C2的坐标为(7,1);(3)连接AC1,与x轴交点即为所求点P.【题目点拨】此题考查轴对称的性质,利用轴对称关系作图,确定直角坐标系中点的坐标,最短路径问题作图,正确理解轴对称的性质是解题的关键.25、﹣2a﹣6,-1【分析】原式括号中两项通分并利用同分母分式的减法法则计算,然后约分得到最简结果,再把a的值代入计算即可.【题目详解】解:(a+2﹣52a-)•243aa--=(2)(2)52(2)×223-a a aa a a+--⎡⎤-⎢⎥--⎣⎦=(3)(3)2(2)×23-a a aa a+--⎡⎤⎢⎥-⎣⎦=﹣2a﹣6,当a=12-时,原式=﹣2a﹣6=﹣1.【题目点拨】本题考查了分式的化简求值,熟练掌握分式的运算法则是解本题的关键.26、(1)图见解析;C1的坐标为(-4,-3);(2)图见解析;C2的坐标为(-4,-7);(3)图见解析;C3的坐标为(6,3);(4)点P1的坐标为(2a-m,n);P2的坐标为(m,2b-n)【分析】(1)根据x轴为对称轴,利用轴对称的性质,即可得到△ABC关于x轴的对称图形△A1B1C1,进而得到点C 关于x轴的对称点C1的坐标;(2)根据直线l1:y=-2为对称轴,利用轴对称的性质,即可得到△ABC关于直线l1:y=-2的对称图形△A2B2C2,进而得到点C关于直线l1的对称点C2的坐标.(3)根据直线l2:x=1为对称轴,利用轴对称的性质,即可得到△ABC关于直线l2:x=1的对称图形△A3B3C3,进而得到点C关于直线l2的对称点C3的坐标.(4)根据对称点到对称轴的距离相等,即可得到点P关于直线x=a的对称点P1的坐标;以及点P关于直线y=b的对称点P2的坐标.【题目详解】(1)如图所示,△A1B1C1即为所求,C1的坐标为(-4,-3);(2)如图所示,△A2B2C2即为所求,C2的坐标为(-4,-7);(3)如图所示,△A3B3C3即为所求,C3的坐标为(6,3);(4)点P(m,n)关于直线x=a的对称点P1的坐标为(2a-m,n);点P(m,n)关于直线y=b的对称点P2的坐标为(m,2b-n).【题目点拨】本题主要考查了利用轴对称变换进行作图以及轴对称性质的运用,几何图形都可看做是由点组成,画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的,连接这些对称点,就得到原图形的轴对称图形.。
八年级上册数学期末考试卷附答案

八年级上册数学期末考试卷附答案一、选择题1. 下列哪个数是素数?A. 11B. 15C. 18D. 20答案:A2. 下列哪个数是合数?A. 7B. 13C. 17D. 21答案:D3. 下列哪个数是偶数?A. 5B. 9C. 12D. 15答案:C4. 下列哪个数是奇数?A. 8B. 10C. 14D. 16答案:A5. 下列哪个数是整数?A. 3.5B. 4.8C. 5.6D. 6.7答案:D二、填空题6. 3的平方是_________。
答案:97. 4的立方是_________。
答案:648. 5的平方根是_________。
答案:±√59. 6的立方根是_________。
答案:∛610. 7的平方根是_________。
答案:±√7三、解答题11. 解方程:2x + 3 = 9。
答案:x = 312. 解方程:3x 2 = 8。
答案:x = 313. 解方程:4x + 5 = 17。
答案:x = 314. 解方程:5x 6 = 19。
答案:x = 515. 解方程:6x + 7 = 23。
答案:x = 216. 解方程:7x 8 = 21。
答案:x = 517. 解方程:8x + 9 = 35。
答案:x = 418. 解方程:9x 10 = 29。
答案:x = 519. 解方程:10x + 11 = 41。
答案:x = 320. 解方程:11x 12 = 39。
答案:x = 5八年级上册数学期末考试卷附答案四、应用题21. 小华买了5个苹果,每个苹果重200克,请问小华买的苹果总重量是多少克?答案:1000克22. 小红家有一个长方形花园,长为10米,宽为5米,请问花园的面积是多少平方米?答案:50平方米23. 小刚骑自行车去学校,速度为每小时15公里,请问他从家到学校需要多长时间?答案:30分钟24. 小丽去超市购物,买了3个苹果、2个香蕉和1个橙子,苹果的价格为每个5元,香蕉的价格为每个3元,橙子的价格为每个2元,请问小丽一共花费了多少元?答案:24元五、简答题25. 请简述勾股定理的内容。
八年级上册期末试卷(实用11篇)

八年级上册期末试卷(实用11篇)八年级上册期末试卷(1)1、选择题(下列各题的四个选项中,只有一项是最符合题意的。
每小题1分,共20分)与水生环境相比,陆地环境要复杂得多,一般来讲,陆生动物适应陆地生活的结构特点有①体表具有防止水分散失的结构②有辅助呼吸的气囊③有能在空气中呼吸的器官④有发达的感觉器官和神经系统⑤有支持躯体和运动的器官⑥有防寒皮毛②③④⑥ B①③④⑤ C①③④⑥①②①⑤下列对动物特征的叙述,准确的是水螅、涡虫和蝈虫都有口无肛门,属于低等动物B河蚌、蜗牛和乌贼身体柔软,都有大的贝壳保护蝗虫、蜘蛛和蜈蚣的足和触角均分节,且体表都有外骨骼,适应环境的能力较强就鱼、章鱼、鲨鱼、娃娃鱼、鯨鱼和美人鱼都不属于鱼类乳酸菌在自然界广泛分布,与人类关系密切,有关乳酸菌的叙述正确的是A单细胞个体,有细胞核,是真核生物B乳酸菌能利用二氧化碳和水制造乳酸乳酸菌主要通过产生芽孢来繁殖后代D用其制作泡菜时,要使泡菜坛内缺氧下列诗句中的各种动物,不具备“体表都有外骨骼,足和触角均分节”特征的是正是河豚欲上时儿童急走追黄蝶C蝉噪林逾静 D早有蜻蜓立上头下列关于人体运动的说法,错误的是运动系统主要是由骨、关节和肌肉组成的B运动是骨骼肌受到神经传来的刺激收缩,牵动骨绕关节活动而产生的C运动的完成不仅依靠运动系统,还需要其他系统的协调配合屈肘时,肱三头肌收缩为运动提供动力关于社会行为的叙述,哪一项是错误的A社会行为有利于动物的生存和繁衍社会行为是群体内形成了一定的组织,成员间有明确分工的动物集群行为所有高等动物都有社会行为具有社会行为的群体,组织内一定有传递信息的“语言”当蚂蚁发现新食物源或要迁移到新的巢址时,都要通知同伴。
下列关于这种行为的说法错误的是A这种行为与小鼠走迷宫获取食物的行为均属于学习行为这种行为直接反映了蚂蚁个体之间能够进行信息交流C蚂蚁的这种行为叫通讯,靠嗅觉和触觉实现D蚂蚁的这种行为是由体内的遗传物质决定的吃剩的饭菜放在冰箱内不易腐败变质且能保存较长时间,其主要原因是低温把微生物冻死了B低温抑制了微生物的生长、繁殖冰箱内含杀死微生物的物质D冰箱内无空气,微生物无法生存如图①~⑤表示五种不同的生物,有关叙述错误的是①是酵母菌,②是细菌,③是病毒,④是草履虫,⑤是衣藻有细胞壁的是①②⑤,有成形细胞核的是①②④⑤,无细胞膜的是③有蛋白质外壳的是③,有叶绿体的是⑤,有伸缩泡的是④,有纤毛的是④⑤进行自养生活,①②③④进行异养生活,③营寄生生活,①营腐生活如图是部分蝶形花科植物分类图解,据此分析正确的是蝶形花科所包含的植物种类比紫檀属少紫檀、绿豆和菜豆属于同一个分类等级绿豆和菜豆的亲缘关系比绿豆和紫檀更远紫檀、绿豆和菜豆三种植物中,前两者形态结构更相似下列对于生物分类单位的叙述,正确的是分类单位越小,生物间的亲缘关系越近分类单位越大,所包含的生物种类越少“科”是生物分类中最小的单位同一分类单位中,生物的特征完全相同下列有关生物多样性的说法,正确的是生物多样性是指生物种类的多样性B科研人员将油桃和蟠桃进行杂交,培育出油蟠桃,利用的是遗传的多样性保护生物的多样性可大量引进外来物种要保护生物多样性,必须禁止对生物资源的开发和利用下列现象与活动,与真菌无关的是制作腐乳发面蒸馒头脏衣服受潮发霉幼儿患手足口病完成屈肘动作的正确顺序是①骨骼肌收缩②骨受到肌肉牵拉绕着关节产生动作③骨骼肌接受神经传来的兴奋③①② B②③①①③②②①③下列关于动物在生物圈中的作用的叙述,错误的是维持生态平衡 B促进物质循环帮助植物传粉、传播种子 D动物能产生二氧化碳下列表示骨,关节和肌肉关系的模式图中,正确的是下列关于病毒的说法,错误的是A由蛋白质外壳和内部的遗传物质构成B十分微小,没有细胞结构可以在人体细胞内繁殖可以在空气中独立生活酸奶的制作过程需要加入乳酸菌、嗜热杆菌等益生菌,因此需要专门进行菌种培养。
八年级上册期末考试试卷含详细答案
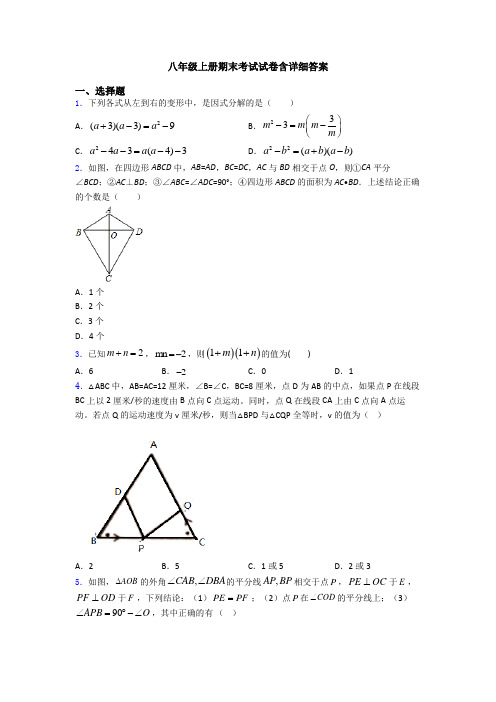
八年级上册期末考试试卷含详细答案一、选择题1.下列各式从左到右的变形中,是因式分解的是( )A .2(3)(3)9a a a +-=-B .233m m m m ⎛⎫-=- ⎪⎝⎭C .243(4)3a a a a --=--D .22()()a b a b a b -=+-2.如图,在四边形ABCD 中,AB =AD ,BC =DC ,AC 与BD 相交于点O ,则①CA 平分∠BCD ;②AC ⊥BD ;③∠ABC =∠ADC =90°;④四边形ABCD 的面积为AC •BD .上述结论正确的个数是( )A .1个B .2个C .3个D .4个3.已知2m n +=,m n 2=-,则()()11m n ++的值为( )A .6B .2-C .0D .14.△ABC 中,AB=AC=12厘米,∠B=∠C ,BC=8厘米,点D 为AB 的中点,如果点P 在线段BC 上以2厘米/秒的速度由B 点向C 点运动。
同时,点Q 在线段CA 上由C 点向A 点运动。
若点Q 的运动速度为v 厘米/秒,则当△BPD 与△CQP 全等时,v 的值为( )A .2B .5C .1或5D .2或35.如图,AOB ∆的外角,CAB DBA ∠∠的平分线,AP BP 相交于点P ,PE OC ⊥于E ,PF OD ⊥于F ,下列结论:(1)PE PF =;(2)点P 在COD ∠的平分线上;(3)90APB O ∠=︒-∠,其中正确的有 ( )A .0个B .1个C .2个D .3个6.如图,△ABC 中,AB =AC ,AD ⊥BC 于点D ,点E 是AB 的中点,点F 在AD 上,当△BEF 周长最小时,点F 的位置在( )A .AD 的中点B .△ABC 的重心 C .△ABC 三条高线的交点D .△ABC 三边中垂线的交点 7.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是3:1,这个多边形的边数是( )A .8B .9C .10D .12 8.有下列说法:①轴对称的两个三角形形状相同;②面积相等的两个三角形是轴对称图形;③轴对称的两个三角形的周长相等;④经过平移、翻折或旋转得到的三角形与原三角形是形状相同的.其中正确的有( )A .4个B .3个C .2个D .1个 9.如图,在ABC ∆中,AD 平分BAC ∠,2B ADB ∠=∠,4,7AB CD ==,则AC 的长为( )A .3B .11C .15D .910.设,,a b c 是三角形的三边长,且满足222a b c ab bc ca ++=++,关于此三角形的形状有以下判断:①是直角三角形; ②是等边三角形; ③是锐角三角形;④是钝角三角形,其中正确的说法的个数有( )A .1个B .2个C .3个D .4个二、填空题11.如图,在△ABC 中,AB =10,AC =8,∠ABC 、∠ACB 的平分线相交于点O ,MN 过点O ,且MN ∥BC ,分别交AB 、AC 于点M 、N .则△AMN 的周长为_______.12.如图,已知:AB ∥CD ,DB ⊥BC ,∠1=40°,求∠2的度数.完成下面的证明过程: 证明:∵AB ∥CD ( ), ∴∠1=∠BCD =40°( ).∵BD ⊥BC ,∴∠CBD = .∵∠2+∠CBD+∠BCD = ( ),∴∠2= .13.化简分式22214ac a bc- 的结果为_____. 14.如图,直线a 平移后得到直线b ,若170∠=,则23∠-∠=______.15.()()()243232121211++⋯++计算结果的个位数字是______________. 16.已知直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为___________.17.求220191222++++的值,可令22019S 1222=++++,则23202022222S =++++,因此2020221S S -=-.仿照以上推理,计算出23201911112222++++的值为______. 18.从A 沿北偏东60︒的方向行驶到B ,再从B 沿南偏西20︒方向行驶到C ,则ABC ∠=______.19.在多项式241x +中添加一个单项式,使其成为一个完全平方式,则添加的单项式是______(只写出一个即可).20.当 x_____ 时,分2x x+式有意义. 三、解答题21.如图,等边ABC 中,D 为BC 边中点,CP 是BC 的延长线.按下列要求作图并回答问题:(要求:尺规作图,不写作法,保留作图痕迹)(1)作ACP ∠的平分线CF ;(2)作60ADE ∠=︒,且DE 交CF 于点E ;(3)在(1),(2)的条件下,可判断AD 与DE 的数量关系是__________;请说明理由.22.已知:如图,AD 垂直平分BC ,D 为垂足,DM ⊥AB ,DN ⊥AC ,M 、N 分别为垂足.求证:DM=DN .23.先化简,再求值:2()()(2)()x y x y y x y x y +-++--,其中3x =,13y =-.24.如图,点B ,E ,C ,F 在一条直线上,AB=DE ,AC=DF ,BE=CF .试说明:(1)ABC DEF ≅;(2)A EGC ∠=∠.25.先化简,再求值:(a +2)2-(a +1)(a -1),其中a =32-. 26.如图,四边形ABCD 是长方形,E 是边CD 的中点,连接AE 并延长交边BC 的延长线于F ,过点E 作AF 的垂线交边BC 于M ,连接AM .(1)请说明 ΔADE ≌ ΔFCE ;(2)试说明AM = BC + MC ;(3)设S △AEM = S 1,S △ECM = S 2,S △ABM = S 3,试探究S 1,S 2,S 3三者之间的等量关系,并说明理由.27.已知,//AB CD ,点M 在AB 上,点N 在CD 上.(1)如图1中,BME E END ∠∠∠、、的数量关系为:________;(不需要证明) 如图2中,BMF F FND ∠∠∠、、的数量关系为:__________;(不需要证明)(2)如图3中,NE 平分FND ∠,MB 平分FME ∠,且2180E F ∠+∠=︒,求FME ∠的度数;(3)如图4中,60BME ∠=︒,EF 平分MEN ∠,NP 平分END ∠,且//EQ NP ,则FEQ ∠的大小是否发生变化,若变化,请说明理由,若不变化,求出FEQ ∠的度数.28.如图①所示是一个长为2m ,宽为2n(m n)>的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的方式拼成一个正方形()1如图②中的阴影部分的正方形的边长等于______(用含m 、n 的代数式表示); ()2请用两种不同的方法列代数式表示图②中阴影部分的面积:方法①:______;方法②:______;()3观察图②,试写出2(m n)+、2(m n)-、mn 这三个代数式之间的等量关系:______;()4根据()3题中的等量关系,若m n 12+=,mn 25=,求图②中阴影部分的面积.29.在学习分式计算时有这样一道题:先化简1(1+)2x -÷22214x x x -+-,再选取一个你喜欢且合适的数代入求值.张明同学化简过程如下:解:1(1+)2x -÷22214x x x -+- =212x x -+-÷2(1)(2)(2)x x x -+-( ) =21(2)(2)2(1)x x x x x -+-⋅-- ( ) =21x x +- ( ) (1)在括号中直接填入每一步的主要依据或知识点;(2)如果你是张明同学,那么在选取你喜欢且合适的数进行求值时,你不能选取的数有__________.30.如图,△ACF ≌△DBE ,其中点A 、B 、C 、D 在一条直线上.(1)若BE ⊥AD ,∠F=62°,求∠A 的大小.(2)若AD=9cm ,BC=5cm ,求AB 的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】【分析】直接利用因式分解的定义得出答案.【详解】A 、2(3)(3)9a a a +-=-,是整式乘法,故此选项不合题意;B 、233m m m m ⎛⎫-=- ⎪⎝⎭,不符合因式分解的定义,故此选项不合题意; C 、243(4)3a a a a --=--,不符合因式分解的定义,故此选项不合题意;D 、22()()a b a b a b -=+-是分解因式,符合题意;故选:D .【点睛】此题主要考查了因式分解的意义,正确分解因式是解题关键.2.B解析:B【解析】【分析】证明△ABC 与△ADC 全等,即可解决问题.【详解】解:在△ABC 与△ADC 中,AB AD BC DC AC AC =⎧⎪=⎨⎪=⎩, ∴△ABC ≌△ADC (SSS ),∴∠ACB =∠ACD ,故①正确,∵AB =AD ,BC =DC∴AC 是BD 的垂直平分线,即AC ⊥DB ,故②正确;无法判断∠ABC =∠ADC =90°,故③错误,四边形ABCD 的面积=S △ADB +S △BCD =12DB ×OA +12DB ×OC =12AC •BD , 故④错误;故选B .【点睛】此题考查全等三角形的判定和性质,关键是根据SSS 证明△ABC 与△ADC 全等. 3.D解析:D【解析】【分析】根据整式乘法法则去括号,再把已知式子的值代入即可.【详解】∵2m n +=,m n 2=-,∴原式()11221m n mn =+++=+-=.故选:D .解析:D【解析】【分析】此题要分两种情况:①当BD=PC时,△BPD与△CQP全等,计算出BP的长,进而可得运动时间,然后再求v;②当BD=CQ时,△BDP≌△QCP,计算出BP的长,进而可得运动时间,然后再求v.【详解】解:当BD=PC时,△BPD与△CQP全等,∵点D为AB的中点,∴BD=12AB=6cm,∵BD=PC,∴BP=8-6=2(cm),∵点P在线段BC上以2厘米/秒的速度由B点向C点运动,∴运动时间时1s,∵△DBP≌△PCQ,∴BP=CQ=2cm,∴v=2÷1=2;当BD=CQ时,△BDP≌△QCP,∵BD=6cm,PB=PC,∴QC=6cm,∵BC=8cm,∴BP=4cm,∴运动时间为4÷2=2(s),∴v=6÷2=3(m/s).故v的值为2或3.故选择:D.【点睛】此题主要考查了全等三角形的判定,关键是要分情况讨论,不要漏解,掌握全等三角形的判定方法:SSS、SAS、ASA、AAS、HL.5.C解析:C【解析】【分析】过点P作PG⊥AB,由角平分线的性质定理,得到PE PG PF==,可判断(1)(2)正确;由12APB EPF∠=∠,180EPF O∠+∠=︒,得到1902APB O∠=︒-∠,可判断(3)错误;即可得到答案.解:过点P 作PG ⊥AB ,如图:∵AP 平分∠CAB ,BP 平分∠DBA ,PE OC ⊥,PF OD ⊥,PG ⊥AB ,∴PE PG PF ==;故(1)正确;∴点P 在COD ∠的平分线上;故(2)正确; ∵12APB APG BPG EPF ∠=∠+∠=∠, 又180EPF O ∠+∠=︒,∴11(180)9022APB O O ∠=⨯︒-∠=︒-∠;故(3)错误; ∴正确的选项有2个;故选:C .【点睛】本题考查了角平分线的判定定理和性质定理,解题的关键是熟练掌握角平分线的判定和性质进行解题.6.B解析:B【解析】【分析】连接EC ,与AD 交于点P ,由题意易得BD=DC ,根据等腰三角形的“三线合一”可得当△BEF 周长最小时,即为BE+CE 的长,最后根据中线的交点可求解.【详解】解:连接EC ,与AD 交于点P ,如图所示:△ABC 中,AB =AC ,AD ⊥BC 于点D ,∴BD=DC ,点F 在AD 上,当△BEF 周长最小时,即BE+BF+EF 为最小,由轴对称的性质及两点之间线段最短可得:BE+BF+EF 为最小时即为BE+CE 的长;点F的位置即为点P的位置,根据三角形的重心是三角形三条中线的交点;故选B.【点睛】本题主要考查等腰三角形及轴对称的性质和三角形的重心,熟练掌握等腰三角形及轴对称的性质和三角形的重心是解题的关键.7.A解析:A【解析】试题分析:设这个多边形的外角为x°,则内角为3x°,根据多边形的相邻的内角与外角互补可的方程x+3x=180,解可得外角的度数,再用外角和除以外角度数即可得到边数.解:设这个多边形的外角为x°,则内角为3x°,由题意得:x+3x=180,解得x=45,这个多边形的边数:360°÷45°=8,故选A.考点:多边形内角与外角.8.B解析:B【解析】【分析】根据平移、翻折或旋转的性质逐项判断可求解.【详解】解:①轴对称的两个三角形形状相同,故正确;②面积相等的两个三角形形状不一定相同,故不是轴对称图形,故错误;③轴对称的两个三角形的周长相等,故正确;④经过平移、翻折或旋转得到的三角形与原三角形是形状相同的,故正确.故选:B.【点睛】本题考查了图形的变换,掌握平移、翻折或旋转的性质是解题的关键.9.B解析:B【解析】【分析】在AC上截取AE=AB,连接DE,如图,先根据SAS证明△ABD≌△AED,然后根据全等三角形的性质和已知条件可得∠BDE=∠AED,进而可得CD=EC,再代入数值计算即可.【详解】解:在AC上截取AE=AB,连接DE,如图,∵AD平分∠BAC,∴∠BAD=∠DAC,又∵AD=AD,∴△ABD ≌△AED (SAS ),∴∠B =∠AED ,∠ADB =∠ADE ,∵∠B =2∠ADB ,∴∠AED =2∠ADB ,而∠BDE =∠ADB +∠ADE =2∠ADB ,∴∠BDE =∠AED ,∴∠CED =∠EDC ,∴CD =CE ,∴AC =AE +CE =AB +CD =4+7=11.故选:B .【点睛】本题考查了全等三角形的判定和性质、等腰三角形的判定、角平分线的性质,正确作出辅助线、构造全等三角形是解题的关键.10.B解析:B【解析】【分析】先将原式转化为完全平方公式,再根据非负数的性质得出a b c ==.进而判断即可.【详解】∵222a b c ab bc ca ++=++,∴222222222a b c ab bc ca ++=++,即()()()2220a b b c a c -+-+-=,∴a b c ==,∴此三角形为等边三角形,同时也是锐角三角形.故选:B .【点睛】本题考查了因式分解的应用,根据式子特点,将原式转化为完全平方公式是解题的关键. 二、填空题11.18【解析】【分析】由在△ABC 中,∠ABC 与∠ACB 的平分线相交于点O ,过点O 作MN∥BC,易证得△BOM 与△CON 是等腰三角形,继而可得△AMN 的周长等于AB+AC .【详解】解析:18【解析】【分析】由在△ABC中,∠ABC与∠ACB的平分线相交于点O,过点O作MN∥BC,易证得△BOM 与△CON是等腰三角形,继而可得△AMN的周长等于AB+AC.【详解】∵在△ABC中,∠ABC、∠ACB的平分线相交于点O,∴∠ABO=∠OBC,∵MN∥BC,∴∠MOB=∠OBC,∴∠ABO=∠MOB,∴BM=OM,同理CN=ON,∴△AMN的周长是:AM+NM+AN=AM+OM+ON+AN=AM+BM+CN+AN=AB+AC=10+8=18.故答案为:18.【点睛】本题考查等腰三角形的判定与性质,角平分线的性质,平行线的判定,三角形周长的求法,等量代换等知识点.12.已知;两直线平行,同位角相等;90°;180°;三角形内角和定理;50°【解析】【分析】由平行线的性质和垂线的定义可得∠1=∠BCD=40°,∠CBD=90°,由三角形内角和定理可求∠2的度数解析:已知;两直线平行,同位角相等;90°;180°;三角形内角和定理;50°【解析】【分析】由平行线的性质和垂线的定义可得∠1=∠BCD=40°,∠CBD=90°,由三角形内角和定理可求∠2的度数.【详解】∵AB∥CD(已知),∴∠1=∠BCD=40°(两直线平行,同位角相等).∵BD⊥BC,∴∠CBD=90°.∵∠2+∠CBD+∠BCD=180°(三角形内角和定理),∴∠2=50°.故答案为:已知,两直线平行,同位角相等,90°,180°,三角形内角和定理,50°.本题考查了平行线的性质,垂线的定义,三角形内角和定理,熟练运用三角形内角和定理是本题的关键.13.【解析】【分析】把分子分母中的公因式2ac约去即可.【详解】解:原式==.故答案为:.【点睛】本题考查约分:约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约解析:7c ab-【解析】【分析】把分子分母中的公因式2ac约去即可.【详解】解:原式=227ac c ac ab -=7c ab-.故答案为:7c ab-.【点睛】本题考查约分:约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.14.110°.【解析】【分析】延长直线后根据平行线的性质和三角形的外角性质解答即可.【详解】延长直线,如图:∵直线a平移后得到直线b,∴a∥b,∴∠5=180°−∠1=180°−70°解析:110°.【解析】【分析】延长直线后根据平行线的性质和三角形的外角性质解答即可.【详解】延长直线,如图:∵直线a平移后得到直线b,∴a∥b,∴∠5=180°−∠1=180°−70°=110°,∵∠2=∠4+∠5,∠3=∠4,∴∠2−∠3=∠5=110°,故答案为110°.【点睛】此题考查平移的性质,解题关键在于作辅助线.15.6【解析】【分析】根据平方差公式化简所求,再根据2的n次幂的变化规律即可求解.【详解】=====∵21=2,22=4,23=8,24=16,25=32,26=64,27=128解析:6【解析】【分析】根据平方差公式化简所求,再根据2的n 次幂的变化规律即可求解.【详解】()()24323212121(1++⋯++)=()()()()22432212121211-++⋯++ =()()()44322121211-+⋯++=323221)2((1)1-++=64211-+=642∵21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…∴64÷4=16∴个位数为6故答案为:6.【点睛】本题考查了平方差公式的应用,解此题的关键是熟知平方差公式的特点,题型较好,难度适中,是一道不错的题目,通过此题能培养学生的观察能力.16.40°【解析】【分析】如图,过E 作EF∥AB,则AB∥EF∥CD,根据平行线的性质和三角形的内角和定理即可求得答案.【详解】解:如图,过E 作EF∥AB,则AB∥EF∥CD,∴∠1=∠3,解析:40°【解析】【分析】如图,过E 作EF ∥AB ,则AB ∥EF ∥CD ,根据平行线的性质和三角形的内角和定理即可求得答案.【详解】解:如图,过E 作EF ∥AB ,则AB ∥EF ∥CD ,∴∠1=∠3,∠2=∠4,∵∠3+∠4=180°-90°-30°=60°,∴∠1+∠2=60°,∵∠1=20°,∴∠2=40°.故答案为:40°.【点睛】本题以三角板为载体,主要考查了平行线的性质和三角形的内角和定理,正确添加辅助线、熟练掌握平行线的性质是解题的关键.17.【解析】【分析】根据题目所给计算方法,令,再两边同时乘以,求出,用,求出的值,进而求出的值.【详解】解:令,则,∴,∴,则.故答案为:【点睛】本题考查了同底数幂的乘法,利用错 解析:2019112【解析】【分析】 根据题目所给计算方法,令23201911112222S,再两边同时乘以12,求出12S ,用12S S ,求出12S 的值,进而求出S 的值. 【详解】 解:令23201911112222S , 则22023401111122222S , ∴2020111222S S , ∴2020111222S , 则2019112S .故答案为:2019112【点睛】 本题考查了同底数幂的乘法,利用错位相减法,消掉相关值,是解题的关键.18.40【解析】【分析】根据方位角的概念,画图正确表示出行驶的过程,再根据已知转向的角度结合三角形的内角和与外角的关系求解.【详解】如图,A 沿北偏东60°的方向行驶到B ,则∠BAC=90°-解析:40【解析】【分析】根据方位角的概念,画图正确表示出行驶的过程,再根据已知转向的角度结合三角形的内角和与外角的关系求解.【详解】如图,A 沿北偏东60°的方向行驶到B ,则∠BAC=90°-60°=30°,B 沿南偏西20°的方向行驶到C ,则∠BCO=90°-20°=70°,又∵∠ABC=∠BCO-∠BAC ,∴∠ABC=70°-30°=40°.故答案为40°【点睛】解答此类题需要从运动的角度,正确画出方位角,再结合三角形的内角和与外角的关系求解.19.或【解析】【分析】【详解】设这个单项式为Q ,如果这里首末两项是2x 和1这两个数的平方,那么中间一项为加上或减去2x 和1积的2倍,故Q=±4x;如果这里首末两项是Q 和1,则乘积项是4x2=2解析:4x ±或416x【解析】【分析】【详解】设这个单项式为Q ,如果这里首末两项是2x 和1这两个数的平方,那么中间一项为加上或减去2x 和1积的2倍,故Q=±4x ;如果这里首末两项是Q 和1,则乘积项是4x 2=2⋅2x 2,所以Q=4x 4;如果该式只有4x 2项或1,它也是完全平方式,所以Q=-1或-4x 2.解:∵4x 2+1±4x=(2x±1)2;4x 2+1+4x 4=(2x 2+1)2;4x 2+1-1=(±2x )2;4x 2+1-4x 2=(±1)2.∴加上的单项式可以是±4x 、4x 4、-4x 2、-1中任意一个.20.【解析】【分析】直接利用分式有意义的条件分析得出即可.【详解】解:根据分式有意义得:2+x≠0,解得:x≠-2.故答案为:≠-2.【点睛】本题考查了分式有意义的条件,关键是熟练掌握解析:2≠-【解析】【分析】直接利用分式有意义的条件分析得出即可.【详解】解:根据分式有意义得:2+x≠0,解得:x≠-2.故答案为:≠-2.【点睛】本题考查了分式有意义的条件,关键是熟练掌握知识点:分式有意义,分母不为0.三、解答题21.(1)见解析;(2)见解析;(3)AD DE =,见解析【解析】【分析】(1)根据角平分线的作法作图即可;(2)根据作一个角等于已知角的方法作图即可;(3)连接AE ,首先根据等边三角形的性质计算出30BAD EDC ∠=∠=︒,30DEC EDC ∠=∠=︒,进而得到CE CD BD ==,然后证明ABD ACE ∆≅∆可得AD AE =,再由60ADE ∠=︒,可得ADE ∆是等边三角形,进而得到AD DE =.【详解】(1)尺规作图,如下图;(2)尺规作图,如下图;(3)AD DE =理由如下:如图,连接AE∵等边ABC 中,D 为BC 边中点,∴BD DC =,90ADB ADC ∠=∠=︒,∵60B ADE ∠=∠=︒,∴30BAD EDC ∠=∠=︒,∵120ACP ∠=︒,CE 为ACP ∠的平分线,∴60ACE ECP ∠=∠=︒,∴30DEC ECP EDC ∠=∠-∠=︒,∴30DEC EDC ∠=∠=︒,∴CE CD BD ==,在ABD △和ACE △中,∵AB AC =,60B ACE ∠=∠=︒,BD CE =,∴ABD ACE SAS △≌△(),∴AD AE =,又∵60ADE ∠=︒,∴ADE 是等边三角形,∴AD DE =.【点睛】此题主要考查了基本作图,以及全等三角形的判定与性质,解题的关键是正确掌握全等三角形的判定方法.22.见解析.【解析】【分析】根据垂直平分线的性质得到AC=AB ,再利用等腰三角形的性质得到AD 是角平分线,最后利用角平分线的性质即可得到结论.【详解】证明:∵AD 垂直平分BC ,∴AC=AB ,即ABC 是等腰三角形,∴AD 平分∠BAC ,∵DM ⊥AB ,DN ⊥AC ,∴DM=DN .【点睛】本题考查了垂直平分线的性质,等腰三角形的判定与性质,角平分线的性质,熟练掌握各性质判定定理是解题的关键.23.3xy ,3-.【解析】【分析】先计算平方差公式、完全平方公式、整式的乘法,再计算整式的加减法,然后将x 、y 的值代入即可得.【详解】原式222222(2)x y xy y x xy y =-++--+,2222222x y xy y x xy y =-++-+-,3xy =,将3x =,13y =-代入得:原式133333xy ⎛⎫==⨯⨯-=- ⎪⎝⎭.【点睛】本题考查了平方差公式、完全平方公式、整式的加减法与乘法,熟记公式和整式的运算法则是解题关键.24.(1)见解析;(2)见解析【解析】【分析】(1)根据等式性质,由BE=CF 得BC=EF ,再根据SSS 定理得△ABC ≌△DEF 即可;(2)由全等三角形得∠B=∠DEF ,由平行线的判定定理得AB ∥DE ,再根据平行线的性质得∠A=∠EGC .【详解】(1)∵BE CF =,∴BE EC CF EC +=+,即BC EF =,在△ABC 与△DEF 中,AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩, ∴(SSS)ABC DEF ≅△△;(2)∵△ABC ≌△DEF ,∴∠B=∠DEF ,∴AB ∥DE ,∴∠A=∠EGC .【点睛】本题考查了全等三角形的判定和性质,平行线的性质与判定,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.25.-1.【解析】分析:原式利用完全平方公式,以及平方差公式化简,去括号合并得到最简结果,把a 的值代入计算即可求出值.详解:原式=a 2+4a +4﹣a 2+1=4a +5当a =32-时,原式=﹣6+5=﹣1. 点睛:本题考查了整式的混合运算﹣化简求值,熟练掌握运算法则是解答本题的关键.26.(1)见解析;(2)见解析;(3)S 3=2S 1-4S 2,理由见解析.【解析】【分析】(1)根据ASA 可证得 ΔADE ≌ ΔFCE ;(2)由(1)可得AE=EF ,AD=CF ,根据垂直平分线的性质可得再由线段等量关系即可说明AM = BC + MC ;(3)由AE=EF 得出S △ECF =S 1-S 2,再由底和高的倍数关系得到S △ABF =4S △ECF =4S 1-4S 2,从而根据S 3=S △ABF -S △MAF 得到结果.【详解】解:(1)∵E 是边CD 的中点,∴DE=CE ,∵∠D=∠DCF=90°,∠DEA=∠ECF ,∴△ADE ≌△FCE (ASA );(2)由(1)得AE=EF ,AD=CF ,∴点E 为AF 中点,∵ME ⊥AF ,∴AM=MF ,∵MF=CF+MC ,∵AD=BC=CF ,∴MF=BC+MC ,即AM=BC+MC ;(3)S 3=2S 1-4S 2,理由是:由(2)可知:AE=EF ,AD=BC=CF ,∴S 1=S △MEF =S 2+S △ECF ,∴S △ECF =S 1-S 2,∵AB=2EC ,BF=2CF ,∠B=∠ECF=90°,∴S △ABF =4S △ECF =4S 1-4S 2,∴S 3=S △ABF -S △MAF =S △ABF -2S 1=2S 1-4S 2.【点睛】本题考查了长方形的性质,全等三角形的判定与性质,线段垂直平分线的性质,勾股定理。
八年级上册语文期末考试试卷及答案

八年级上册语文期末考试试卷及答案一、选择题(本题共 20 分)1. 下列成语中,不属于“形容坚定不移”的是:A. 坚如磐石B. 坚不可摧C. 坚贞不屈D. 坚定不移2. 下列哪个不是《道德经》的思想?A. 大道废,有仁义B. 论语说得好,不如实践好C. 天行健,君子以自强不息D. 为道日损,为物日益3. “彼”指代的是什么?A. 武松B. 花和尚C. 杨志D. 小宝4. “半江瑟瑟半江红”的上半句是?A. 半江瑟瑟B. 半江红C. 半江瑟瑟半江雨D. 半江瑟瑟半江月5. “俯仰之间,已发千言”一句的俯仰是指什么?A. 低头B. 抬头C. 转头D. 点头6. “床前明月光”下一句是?A. 疑是地上霜B. 疑是天上花C. 问君能有几多愁D. 举头望明月7. “稻花香里说丰年”的下一句是?A. 庄稼满仓禾稻香B. 梧桐更兼细雨C. 今年无恙,明年更难D. 看取眼底无人心8. “破釜沉舟”出自哪个故事?A. 《神雕侠侣》B.《红楼梦》C. 《三国演义》D. 《吕洞宾》9. 下列哪项不是状元及第的标志?A. 宴请文人墨客B. 分发赏赐C. 庆祝酒宴D. 论及元戎无不齐10. 下列哪一个不是《孙子兵法》所注重的原则?A. 内外勾结B. 知己知彼C. 以战止战D. 远交近攻二、问答题(本题共 30 分)1. 著名的《阿Q正传》是由谁所写?2. “生的伟大,死的光荣”这句话是什么意思?3. 写一篇关于如何保护野生动物的短文(不少于 100 字)。
三、阅读理解题(本题共 25 分)请阅读下面这篇文章,并回答问题:北京西城区新街口北邻近的“兰馨苑”,是年代比较久远的一处老小区,虽然是政府保障房,小区环境及设施却一直没有得到改善,走进来让人很失望。
居住在这里老年人们一直很渴望小区的环境能够变得更优美。
“环境太差了,改改肯定好。
”一位六十多岁的老人说,“我们一年四季都是绿泥巴,月台上还常年停着死车,连车都不让我们停。
”据悉,这栋楼的厕所一直使用灶油炉取暖,对于安全隐患,老人们深感担忧。
人教版数学八年级上册期末考试试卷附答案

人教版数学八年级上册期末考试试题一、选择题(每小题只有一个正确答案。
每小题2分,共12分)1.(2分)下列平面图形中,不是轴对称图形的是()A.B.C.D.2.(2分)计算(﹣2x2y)3的结果是()A.﹣2x5y3B.﹣8x6y3C.﹣2x6y3D.﹣8x5y33.(2分)如果代数式有意义,那么x的取值范围是()A.x≥0B.x≠1C.x>0D.x≥0且x≠1 4.(2分)一个三角形的三条边长分别为1、2、x,则x的取值范围是()A.1≤x≤3B.1<x≤3C.1≤x<3D.1<x<3 5.(2分)如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是()A.180°B.220°C.240°D.300°6.(2分)如图,已知∠1=∠2,∠B=∠C,下列结论:(1)AB=AC;(2)∠BAE=∠CAD;(3)BE=DC;(4)AD=DE.中正确的个数是()A.1B.2C.3D.4二、填空题(每小题3分,共24分)7.(3分)芝麻作为食品和药物,均广泛使用.经测算,一粒芝麻约有0.00000201千克,用科学记数法表示为.8.(3分)因式分解:ax2﹣ay2=.9.(3分)已知等腰三角形两边的长分别是9和4,则它的周长为.10.(3分)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,需添加一个条件是.(只需添加一个条件即可)11.(3分)如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为米.12.(3分)将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF =90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=.13.(3分)计算+的结果是.14.(3分)如图,在△ABC中,CD是它的角平分线,DE⊥AC于点E.若BC=6cm,DE =2cm,则△BCD的面积为cm2.三、解答题(每题5分,共20分)15.(5分)计算:(π﹣3.14)0+()﹣1﹣|﹣2|﹣(﹣1)2020.16.(5分)计算:(a+3)(a﹣1)+a(a﹣2)17.(5分)已知一个多边形的内角和与外角和之比为9:2,求它的边数.18.(5分)解分式方程:﹣=1.四、解答题(每小题7分,共28分)19.(7分)如图,在平面直角坐标系中.(1)请画出△ABC关于y轴对称的△AB1C1,并写出B1、C1的坐标;=;(2)直接写出△ABC的面积:S△ABC(3)在x轴上找到一点P,使PA+PC的值最小,请标出点P在坐标轴上的位置.20.(7分)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.(1)从图中任找两组全等三角形;(2)从(1)中任选一组进行证明.21.(7分)已知:a+b=4,ab=2,求下列式子的值:①a2+b2②(a﹣b)222.(7分)如图所示,在△ABC中,BO,CO分别平分∠ABC和∠ACB;BD、CD分别平分∠ABC和∠ACB的外角.(1)若∠BAC=70°,求:∠BOC的度数;(2)探究∠BDC与∠A的数量关系.(直接写出结论,无需说明理由)五、解答题(每小题8分,共16分)23.(8分)学校在假期内对教室内的黑板进行整修,需在规定日期内完成.如果由甲工程小组做,恰好按期完成;如果由乙工程小组做,则要超过规定日期3天.结果两队合作了2天,余下部分由乙组独做,正好在规定日期内完成,问规定日期是几天?24.(8分)如图1,等边△ABC中,AD是BC边上的中线,E为AD上一点(点E与点A 不重合),以CE为一边且在CE下方作等边△CEF,连接BF.(1)猜想线段AE,BF的数量关系:(不必证明);(2)当点E为AD延长线上一点时,其它条件不变.①请你在图2中补全图形;②(1)中结论成立吗?若成立,请证明;若不成立请说明理由.六、解答题(每小题10分,共20分)25.(10分)如图①所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿虚线AB剪开,把剪成的两张纸片拼成如图②所示的等腰梯形.(1)设图①中阴影部分的面积为S1,图②中阴影部分面积为S2,请直接用含a,b的式子表示S1和S2.(2)请写出上述过程中所揭示的乘法公式;(3)用这个乘法公式计算:①(x﹣)(x+)(x2+);②107×93.26.(10分)在△ABC中,AB=AC=2,∠B=40°,D是线段BC上一动点(不与B、C 两点重合),且∠ADE=40°.(1)若∠BDA=115°,则∠CDE=,∠AED=;(2)当DC等于多少时,△ABD≌△DCE?试说明理由;(3)在D点运动过程中,能使△ADE是等腰三角形吗?若能,请求出使△ADE是等腰三角形时的∠ADB的度数;若不能,请说明理由.答案与解析一、单项选择题1.(2分)下列平面图形中,不是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析.【解答】解:A、是轴对称图形,故此选项不合题意;B、是轴对称图形,故此选项不合题意;C、不是轴对称图形,故此选项符合题意;D、是轴对称图形,故此选项不合题意;故选:C.【点评】此题主要考查了轴对称图形,判断轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.2.(2分)计算(﹣2x2y)3的结果是()A.﹣2x5y3B.﹣8x6y3C.﹣2x6y3D.﹣8x5y3【分析】积的乘方法则,把每一个因式分别乘方,再把所得的幂相乘,据此求解即可.【解答】解:(﹣2x2y)3=(﹣2)3(x2)3y3=﹣8x6y3.故选:B.【点评】本题主要考查了幂的乘方与积的乘方,熟记幂的运算法则是解答本题的关键.3.(2分)如果代数式有意义,那么x的取值范围是()A.x≥0B.x≠1C.x>0D.x≥0且x≠1【分析】代数式有意义的条件为:x﹣1≠0,x≥0.即可求得x的范围.【解答】解:根据题意得:x≥0且x﹣1≠0.解得:x≥0且x≠1.故选:D.【点评】式子必须同时满足分式有意义和二次根式有意义两个条件.分式有意义的条件为:分母≠0;二次根式有意义的条件为:被开方数≥0.此类题的易错点是忽视了二次根式有意义的条件,导致漏解情况.4.(2分)一个三角形的三条边长分别为1、2、x,则x的取值范围是()A.1≤x≤3B.1<x≤3C.1≤x<3D.1<x<3【分析】已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围.【解答】解:根据题意得:2﹣1<x<2+1,即1<x<3.故选:D.【点评】考查了三角形三边关系,本题需要理解的是如何根据已知的两条边求第三边的范围.5.(2分)如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是()A.180°B.220°C.240°D.300°【分析】本题可先根据等边三角形顶角的度数求出两底角的度数和,然后在四边形中根据四边形的内角和为360°,求出∠α+∠β的度数.【解答】解:∵等边三角形的顶角为60°,∴两底角和=180°﹣60°=120°;∴∠α+∠β=360°﹣120°=240°;故选:C.【点评】本题综合考查等边三角形的性质及三角形内角和为180°,四边形的内角和是360°等知识,难度不大,属于基础题6.(2分)如图,已知∠1=∠2,∠B=∠C,下列结论:(1)AB=AC;(2)∠BAE=∠CAD;(3)BE=DC;(4)AD=DE.中正确的个数是()A.1B.2C.3D.4【分析】先证AB=AC,再证△ABE≌△ACD(AAS)得AD=AE,BE=CD,∠BAE =∠CAD,即可得出结论.【解答】解:∵∠B=∠C,∴AB=AC,故(1)正确;在△ABE和△ACD中,,∴△ABE≌△ACD(AAS),∴AD=AE,BE=CD,∠BAE=∠CAD,故(2)(3)正确,(4)错误,正确的个数有3个,故选:C.【点评】本题考查了全等三角形的判定与性质、等腰三角形的判定等知识,熟练掌握全等三角形的判定与性质是本题的关键.二、填空题(每小题3分,共24分)7.(3分)芝麻作为食品和药物,均广泛使用.经测算,一粒芝麻约有0.00000201千克,用科学记数法表示为 2.01×10﹣6.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.00000201=2.01×10﹣6.故答案为:2.01×10﹣6.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.8.(3分)因式分解:ax2﹣ay2=a(x+y)(x﹣y).【分析】首先提取公因式a,再利用平方差公式分解因式得出答案.【解答】解:ax2﹣ay2=a(x2﹣y2)=a(x+y)(x﹣y).故答案为:a(x+y)(x﹣y).【点评】此题主要考查了提取公因式法以及公式法分解因式,正确应用平方差公式是解题关键.9.(3分)已知等腰三角形两边的长分别是9和4,则它的周长为22.【分析】因为等腰三角形的两边分别为4和9,但没有明确哪是底边,哪是腰,所以有两种情况,需要分类讨论.【解答】解:当4为底时,其它两边都为9,即:9、9、4可以构成三角形,周长为22;当4为腰时,其它两边为9和4,因为4+4=8<9,所以不能构成三角形,故舍去.所以答案只有22.故答案为:22.【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.10.(3分)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,需添加一个条件是∠D=∠B.(只需添加一个条件即可)【分析】利用全等三角形的判定与性质进而得出当∠D=∠B时,△ADF≌△CBE.【解答】解:当∠D=∠B时,在△ADF和△CBE中∵,∴△ADF≌△CBE(SAS),故答案为:∠D=∠B.(答案不唯一)11.(3分)如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为6米.【分析】先过点C作CE⊥AB,交AB的延长线于E,易求∠CBE=30°,在Rt△BCE中可知CE=BC,进而可求CE.【解答】解:过点C作CE⊥AB,交AB的延长线于E,如右图,∵∠ABC=150°,∴∠CBE=30°,在Rt△BCE中,∵BC=12,∠CBE=30°,∴CE=BC=6.故答案是6.【点评】本题考查了含30°角的直角三角形的性质,解题的关键是作辅助线构造直角三角形.12.(3分)将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF =90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=25°.【分析】由∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,可求得∠ACE的度数,又由三角形外角的性质,可得∠CDF=∠ACE﹣∠F=∠BCE+∠ACB﹣∠F,继而求得答案.【解答】解:∵AB=AC,∠A=90°,∴∠ACB=∠B=45°,∵∠EDF=90°,∠E=30°,∴∠F=90°﹣∠E=60°,∵∠ACE=∠CDF+∠F,∠BCE=40°,∴∠CDF=∠ACE﹣∠F=∠BCE+∠ACB﹣∠F=45°+40°﹣60°=25°.故答案为:25°.13.(3分)计算+的结果是.【分析】利用分式加减法的计算方法进行计算即可.【解答】解:原式=﹣===,故答案为:.14.(3分)如图,在△ABC中,CD是它的角平分线,DE⊥AC于点E.若BC=6cm,DE =2cm,则△BCD的面积为6cm2.【分析】作DF⊥BC于F,根据角平分线的性质求出DF,根据三角形的面积公式计算即可.【解答】解:作DF⊥BC于F,∵CD是它的角平分线,DE⊥AC,DF⊥BC,∴DF=DE=2,∴△BCD的面积=×BC×DF=6(cm2),故答案为:6.【点评】本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.三、解答题(每题5分,共20分)15.(5分)计算:(π﹣3.14)0+()﹣1﹣|﹣2|﹣(﹣1)2020.【分析】先算零指数幂、负整数指数幂、绝对值、乘方,再算加减法即可求解.【解答】解:(π﹣3.14)0+()﹣1﹣|﹣2|﹣(﹣1)2020=1+2﹣2﹣1=0.【点评】考查了实数的运算,解决此类题目的关键是熟练掌握零指数幂、负整数指数幂、绝对值、乘方等知识点的运算.16.(5分)计算:(a+3)(a﹣1)+a(a﹣2)【分析】根据整式混合运算的顺序和法则分别进行计算,再把所得结果合并即可.【解答】解:(a+3)(a﹣1)+a(a﹣2)=a2+2a﹣3+a2﹣2a=2a2﹣3;【点评】此题考查了整式的混合运算,在计算时要注意混合运算的顺序和法则以及运算结果的符号,是一道基础题.17.(5分)已知一个多边形的内角和与外角和之比为9:2,求它的边数.【分析】根据多边形的内角和与外角和之间的关系列出有关边数n的方程求解即可.【解答】解:设该多边形的边数为n则(n﹣2)×180°:360=9:2,解得:n=11.故它的边数为11.【点评】本题考查了多边形的内角与外角,解题的关键是牢记多边形的内角和公式与外角和定理.18.(5分)解分式方程:﹣=1.【分析】先去分母,再解整式方程,一定要验根.【解答】解:﹣=1(x+1)2﹣4=x2﹣1x2+2x+1﹣4=x2﹣1x=1,检验:把x=1代入x2﹣1=1﹣1=0,∴x=1不是原方程的根,原方程无解.【点评】本题考查了解分式方程,掌握分式方程一定要验根是解题的关键.四、解答题(每小题7分,共28分)19.(7分)如图,在平面直角坐标系中.(1)请画出△ABC关于y轴对称的△AB1C1,并写出B1、C1的坐标;=5;(2)直接写出△ABC的面积:S△ABC(3)在x轴上找到一点P,使PA+PC的值最小,请标出点P在坐标轴上的位置.【分析】(1)利用关于y轴对称的点的坐标特征写出B1、C1的坐标,然后描点即可;(2)用一个矩形的面积分别减去三个直角三角形的面积去计算△ABC的面积;(3)作A点关于x轴的对称点A′,然后连接A′C交x轴于P点.【解答】解:(1)如图,△AB1C1为所作,B1(﹣2,﹣4),C1(﹣4,﹣1);=3×4﹣×2×2﹣×2×3﹣×4×1=5;(2)S△ABC故答案为5;(3)如图,点P为所作.【点评】本题考查了作图﹣轴对称变换:几何图形都可看做是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的.也考查了最短路径问题.20.(7分)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.(1)从图中任找两组全等三角形;(2)从(1)中任选一组进行证明.【分析】(1)根据题目所给条件可分析出△ABE≌△CDF,△AFD≌△CEB;(2)根据AB∥CD可得∠1=∠2,根据AF=CE可得AE=FC,然后再证明△ABE≌△CDF即可.【解答】解:(1)△ABE≌△CDF,△AFD≌△CEB;(2)∵AB∥CD,∴∠1=∠2,∵AF=CE,∴AF+EF=CE+EF,即AE=FC,在△ABE和△CDF中,,∴△ABE≌△CDF(AAS).【点评】此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.21.(7分)已知:a+b=4,ab=2,求下列式子的值:①a2+b2;②(a﹣b)2.【分析】①根据(a+b)2=a2+2ab+b2,可得a2+b2=(a+b)2﹣2ab,再把a+b=4,ab=2代入计算即可;②根据(a﹣b)2=a2﹣2ab+b2=(a+b)2﹣4ab,再把a+b=4,ab=2代入计算即可.【解答】解:∵a+b=4,ab=2,∴①a2+b2=(a+b)2﹣2ab=42﹣2×2=16﹣4=12;②(a﹣b)2=a2﹣2ab+b2=(a+b)2﹣4ab=42﹣4×2=16﹣8=8.【点评】本题考查完全平方公式的应用,根据题中条件,变换形式即可.22.(7分)如图所示,在△ABC中,BO,CO分别平分∠ABC和∠ACB;BD、CD分别平分∠ABC和∠ACB的外角.(1)若∠BAC=70°,求:∠BOC的度数;(2)探究∠BDC与∠A的数量关系.(直接写出结论,无需说明理由)【分析】(1)根据三角形的角平分线定义和三角形的内角和定理求出∠OBC+∠OCB的度数,再根据三角形的内角和定理即可求出∠BOC的度数;(2)根据三角形外角平分线的性质可得∠BCD=(∠A+∠ABC)、∠DBC=(∠A+∠ACB);根据三角形内角和定理可得∠BDC=90°﹣∠A.【解答】解:(1)∵OB、OC分别是∠ABC和∠ACB的角平分线,∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB),∵∠A=70°,∴∠OBC+∠OCB=(180°﹣70°)=55°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°;(2)∠BDC=90°﹣∠A.理由如下:∵BD、CD为△ABC两外角∠ABC、∠ACB的平分线,∴∠BCD=(∠A+∠ABC)、∠DBC=(∠A+∠ACB),由三角形内角和定理得,∠BDC=180°﹣∠BCD﹣∠DBC,=180°﹣[∠A+(∠A+∠ABC+∠ACB)],=180°﹣(∠A+180°),=90°﹣∠A;【点评】本题考查的是三角形内角和定理,涉及到三角形内角与外角的关系,角平分线的性质,三角形内角和定理,结合图形,灵活运用基本知识解决问题.五、解答题(每小题8分,共16分)23.(8分)学校在假期内对教室内的黑板进行整修,需在规定日期内完成.如果由甲工程小组做,恰好按期完成;如果由乙工程小组做,则要超过规定日期3天.结果两队合作了2天,余下部分由乙组独做,正好在规定日期内完成,问规定日期是几天?【分析】由题意可知甲的工作效率=1÷规定日期,乙的工作效率=1÷(规定日期+3);根据“结果两队合作了2天,余下部分由乙组独做,正好在规定日期内完成”可知甲做两天的工作量+乙做规定日期的工作量=1,由此可列出方程.【解答】解:设规定日期为x天,根据题意,得2(+)+×(x﹣2)=1解这个方程,得x=6经检验,x=6是原方程的解.∴原方程的解是x=6.答:规定日期是6天.【点评】找到关键描述语,找到等量关系是解决问题的关键.本题主要考查的等量关系为:工作时间=工作总量÷工作效率,当题中没有一些必须的量时,为了简便,应设其为1.24.(8分)如图1,等边△ABC中,AD是BC边上的中线,E为AD上一点(点E与点A 不重合),以CE为一边且在CE下方作等边△CEF,连接BF.(1)猜想线段AE,BF的数量关系:AE=BF(不必证明);(2)当点E为AD延长线上一点时,其它条件不变.①请你在图2中补全图形;②(1)中结论成立吗?若成立,请证明;若不成立请说明理由.【分析】(1)利用等边三角形的性质得出AC=BC,CE=CF,∠ACB=∠ECF=60°,进而得出∠ACE=∠BCF,进而判断出△ACE≌△BCF,即可得出结论;(2)①由题意补全图形,即可得出结论;②同(1)的方法,即可得出结论.【解答】解:(1)AE=BF,理由:∵△ABC和△CEF是等边三角形,∴AC=BC,CE=CF,∠ACB=∠ECF=60°,∴∠ACB﹣∠BCE=∠ECF﹣∠BCE,∴∠ACE=∠BCF,在△ACE和△BCF中,,∴△ACE≌△BCF(SAS),∴AE=BF,故答案为:AE=BF;(2)①补全图形如图2所示;②AE=BF仍然成立,理由:∵△ABC和△CEF是等边三角形,∴AC=BC,CE=CF,∠ACB=∠ECF=60°,∴∠ACB+∠BCE=∠ECF+∠BCE,∴∠ACE=∠BCF,在△ACE和△BCF中,,∴△ACE≌△BCF(SAS),∴AE=BF.【点评】此题是三角形综合题,主要考查了等边三角形的性质,全等三角形的判定和性质,判断出△ACE≌△BCF是解本题的关键.六、解答题(每小题10分,共20分)25.(10分)如图①所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿虚线AB剪开,把剪成的两张纸片拼成如图②所示的等腰梯形.(1)设图①中阴影部分的面积为S1,图②中阴影部分面积为S2,请直接用含a,b的式子表示S1和S2.(2)请写出上述过程中所揭示的乘法公式;(3)用这个乘法公式计算:①(x﹣)(x+)(x2+);②107×93.【分析】(1)图①中的阴影部分的面积为两个正方形的面积差,图②中的阴影部分是上底为2b,下底为2a,高为a﹣b的梯形,利用梯形面积公式可得答案;(2)图①、图②面积相等可得等式;(3)①连续两次利用平方差公式可求结果;②将107×93转化为(100+7)(100﹣7),即可利用平方差公式求出结果.【解答】解:(1)S1=a2﹣b2,S2=(2a+2b)(a﹣b)=(a+b)(a﹣b);(2)a2﹣b2=(a+b)(a﹣b);(3)①原式=(x2﹣)(x2+)=x4﹣;②107×93=(100+7)(100﹣7)=1002﹣72=10000﹣49=9951.【点评】本题考查平方差公式的几何背景,掌握平方差公式的结构特征是解决问题的关键.26.(10分)在△ABC中,AB=AC=2,∠B=40°,D是线段BC上一动点(不与B、C 两点重合),且∠ADE=40°.(1)若∠BDA=115°,则∠CDE=25°,∠AED=65°;(2)当DC等于多少时,△ABD≌△DCE?试说明理由;(3)在D点运动过程中,能使△ADE是等腰三角形吗?若能,请求出使△ADE是等腰三角形时的∠ADB的度数;若不能,请说明理由.【分析】(1)利用等腰三角形的性质和三角形的外角性质解答即可;(2)先求出∠ADB=∠DEC,再由∠B=∠C,AB=DC=2,即可得出△ABD≌△DCE (AAS);(3)分两种情况讨论即可.【解答】解:(1)∵AB=AC,∴∠B=∠C=∠40°,∵∠BDA=115°,∴∠ADC=180°﹣115°=65°,∴∠CDE=∠ADC﹣∠ADE=65°﹣40°=25°,∴∠AED=∠CDE+∠C=25°+40°=65°,故答案为:25°,65°;(2)当DC=2时,△ABD≌△DCE,理由如下:∵∠C=40°,∴∠DEC+∠EDC=140°,∵∠ADE=40°,∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC,在△ABD和△DCE中,,∴△ABD≌△DCE(AAS);(3)△ADE能成为等腰三角形,理由如下:∵∠ADE=∠C=40°,∠AED>∠C,∴△ADE为等腰三角形时,只能是AD=DE或AE=DE,当AD=DE时,∠DAE=∠DEA=(180°﹣40°)=70°,∴∠EDC=∠AED﹣∠C=70°﹣40°=30°,∴∠ADB=180°﹣40°﹣30°=110°;当EA=ED时,∠ADE=∠DAE=40°,∴∠AED=180°﹣40°﹣40°=100°,∴∠EDC=∠AED﹣∠C=100°﹣40°=60°,∴∠ADB=180°﹣40°﹣60°=80°;综上所述,当∠ADB的度数为110°或80°时,△ADE是等腰三角形.【点评】此题考查了等腰三角形的判定与性质,全等三角形的判定与性质,三角形外角的性质等知识点,此题涉及到的知识点较多,综合性较强.21。
初中八年级数学上册期末考试卷及答案【完美版】

初中八年级数学上册期末考试卷及答案【完美版】班级: 姓名:一、选择题(本大题共10小题, 每题3分, 共30分)1. -5的相反数是()A. B. C. 5 D. -52. 计算: (a-b)(a+b)(a2+b2)(a4-b4)的结果是( )A. a8+2a4b4+b8B. a8-2a4b4+b8C. a8+b8D. a8-b83.解分式方程时, 去分母变形正确的是()A. B.C. D.4.《孙子算经》中有一道题, 原文是: “今有木, 不知长短.引绳度之, 余绳四足五寸;屈绳量之, 不足一尺.木长几何?”意思是: 用一根绳子去量一根长木, 绳子还剩余尺.将绳子对折再量长木, 长木还剩余尺, 问木长多少尺, 现设绳长尺, 木长尺, 则可列二元一次方程组为()A. B. C. D.5.“绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务, 为了迎接雨季的到来, 实际工作时每天的工作效率比原计划提高了25%, 结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x万平方米, 则下面所列方程中正确的是()A. B.C. D.6.欧几里得的《原本》记载, 形如的方程的图解法是: 画, 使, , , 再在斜边上截取.则该方程的一个正根是()A. 的长B. 的长C. 的长D. 的长7.如图, 某小区计划在一块长为32m, 宽为20m的矩形空地上修建三条同样宽的道路, 剩余的空地上种植草坪, 使草坪的面积为570m2.若设道路的宽为xm, 则下面所列方程正确的是()A. (32﹣2x)(20﹣x)=570B. 32x+2×20x=32×20﹣570C. (32﹣x)(20﹣x)=32×20﹣570D. 32x+2×20x﹣2x2=5708.如图, △ABC中, AB⊥BC, BE⊥AC, ∠1=∠2, AD=AB, 则下列结论不正确的是()A. BF=DFB. ∠1=∠EFDC. BF>EFD. FD∥BC9.如图, 在△ABC和△DEF中, ∠B=∠DEF, AB=DE, 若添加下列一个条件后, 仍然不能证明△ABC≌△DEF, 则这个条件是()A. ∠A=∠DB. BC=EFC. ∠ACB=∠FD. AC=DF10.如图, 点P是边长为1的菱形ABCD对角线AC上的一个动点, 点M, N分别是AB, BC边上的中点, 则MP+PN的最小值是()A. B. 1 C. D. 2二、填空题(本大题共6小题, 每小题3分, 共18分)1. 若, 则二次根式化简的结果为________.2. 将命题“同角的余角相等”, 改写成“如果…, 那么…”的形式_____.3. 若一个正数的两个平方根分别是a+3和2﹣2a, 则这个正数的立方根是________.4. 如图, 在△ABC中, AD⊥BC于D, BE⊥AC于E, AD与BE相交于点F, 若BF =AC, 则∠ABC=________度.5. 如图, 菱形ABCD中, ∠B=60°, AB=3, 四边形ACEF是正方形, 则EF的长为__________.6.如图, 已知正方形ABCD的边长为5, 点E、F分别在AD、DC上, AE=DF=2, BE与AF相交于点G, 点H为BF的中点, 连接GH, 则GH的长为_______.三、解答题(本大题共6小题, 共72分)1. 解不等式(1)7252x x-+≥(2)111 32x x-+-<2. (1)已知x=, y=, 试求代数式2x2-5xy+2y2的值.(2)先化简, 再求值:, 其中x=, y=.3. 已知关于x的方程x2 -(m+1)x+2(m-1)=0,(1)求证: 无论m取何值时, 方程总有实数根;(2)若等腰三角形腰长为4, 另两边恰好是此方程的根, 求此三角形的另外两条边长.4. 如图, 在四边形中, , , 对角线, 交于点, 平分, 过点作交的延长线于点, 连接.(1)求证: 四边形是菱形;(2)若, , 求的长.5. 已知和位置如图所示, , , .(1)试说明: ;(2)试说明:.6. 某学校为改善办学条件, 计划采购A.B两种型号的空调, 已知采购3台A型空调和2台B型空调, 需费用39000元;4台A型空调比5台B型空调的费用多6000元.(1)求A型空调和B型空调每台各需多少元;(2)若学校计划采购A.B两种型号空调共30台, 且A型空调的台数不少于B 型空调的一半, 两种型号空调的采购总费用不超过217000元, 该校共有哪几种采购方案?(3)在(2)的条件下, 采用哪一种采购方案可使总费用最低, 最低费用是多少元?参考答案一、选择题(本大题共10小题, 每题3分, 共30分)1.C2.B3.D4.B5.C6.B7、A8、B9、D10、B二、填空题(本大题共6小题, 每小题3分, 共18分)1.-2、如果两个角是同一个角的余角, 那么这两个角相等3.44.455.36.三、解答题(本大题共6小题, 共72分)1.(1);(2)2、(1)42, (2)3. 略 4和24.(1)略;(2)2.5、(1)略;(2)略.6、(1)A型空调和B型空调每台各需9000元、6000元;(2)共有三种采购方案, 方案一:采购A型空调10台, B型空调20台, 方案二:采购A型空调11台, B型空调19台, 案三:采购A型空调12台, B型空调18台;(3)采购A型空调10台, B型空调20台可使总费用最低, 最低费用是210000元.。
2024年最新人教版八年级数学(上册)期末试卷及答案(各版本)

2024年最新人教版八年级数学(上册)期末试卷及答案(各版本)一、选择题(每题5分,共20分)1. 若x是实数,下列不等式恒成立的是()A. x² > 0B. x² ≥ 0C. x² < 0D. x² ≤ 02. 下列函数中,其图像是直线的是()A. y = x²B. y = xC. y = 1/xD. y = x³3. 下列图形中,属于轴对称图形的是()A. 正方形B. 圆C. 等腰三角形D. 正六边形4. 下列关于圆的命题中,正确的是()A. 圆的直径等于半径的两倍B. 圆的周长等于直径的四倍C. 圆的面积等于半径的平方D. 圆的周长等于半径的四倍5. 下列关于角的命题中,正确的是()A. 直角是90度B. 钝角是大于90度小于180度的角C. 锐角是小于90度的角D. 平角是180度的角二、填空题(每题5分,共20分)6. 若a² = b²,则a和b的关系是__________。
7. 下列函数中,其图像是抛物线的是__________。
8. 下列图形中,属于中心对称图形的是__________。
9. 下列关于圆的命题中,错误的是__________。
10. 下列关于角的命题中,错误的是__________。
三、解答题(每题10分,共40分)11. 解方程:2x 5 = 3x + 4。
12. 解不等式:3x 2 < 2x + 5。
13. 解三角形:已知三角形的两边长分别为5cm和8cm,夹角为60度,求第三边的长度。
14. 解圆的方程:x² + y² 6x 8y + 9 = 0。
四、证明题(每题10分,共20分)15. 证明:若a² = b²,则a = b或a = b。
16. 证明:若x² + y² = r²,则x和y是半径为r的圆上的点。
八年级上册期末考试卷及答案【含答案】

八年级上册期末考试卷及答案【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪种物质在空气中不支持燃烧?A. 氧气B. 二氧化碳C. 氮气D. 氢气2. 八进制数110转换为十进制数是?A. 72B. 74C. 76D. 783. 在光合作用中,植物释放出的气体是?A. 二氧化碳B. 氧气C. 氮气D. 氢气4. 下列哪个不是我国的四大发明?A. 指南针B. 火药C. 印刷术D. 电视5. 地球公转的方向是?A. 自西向东B. 自东向西C. 自南向北D. 自北向南二、判断题(每题1分,共5分)1. 鸟类是哺乳动物。
()2. 长江是我国最长的河流。
()3. 光的传播速度在真空中是最慢的。
()4. 地球是太阳系中唯一有生命存在的星球。
()5. 人类最早使用的金属是铜。
()三、填空题(每题1分,共5分)1. 地球上的淡水主要分布在______、______和______。
2. 人体最大的消化腺是______。
3. 我国的国旗是______。
4. 八进制数111转换为十进制数是______。
5. 氢气和氧气在点燃的条件下______。
四、简答题(每题2分,共10分)1. 请简述光合作用的过程。
2. 请简述血液循环的过程。
3. 请简述牛顿三大定律。
4. 请简述我国的历史朝代顺序。
5. 请简述欧姆定律。
五、应用题(每题2分,共10分)1. 小明有10个苹果,他吃掉了3个,还剩下多少个?2. 一个长方形的长是8厘米,宽是4厘米,求这个长方形的面积。
3. 一个数加上5等于10,求这个数。
4. 一辆汽车以60公里/小时的速度行驶,行驶了2小时,求这辆汽车行驶的路程。
5. 一个正方形的边长是6厘米,求这个正方形的周长。
六、分析题(每题5分,共10分)1. 请分析影响植物生长的因素。
2. 请分析影响化学反应速率的因素。
七、实践操作题(每题5分,共10分)1. 请设计一个实验,验证植物的光合作用。
2. 请设计一个实验,验证影响化学反应速率的因素。
初二上册期末考试试卷及答案

初二上册期末考试试卷及答案一、选择题(共20分)1、下列不属于中国的四大发明之一的是()。
A、造纸术B、印刷术C、指南针D、火药2、阅读下面的诗句,找出其中的典故()。
微山湖畔菊花开,天A、缺兵少将的故事B、屈原放逐的故事C、梁祝的故事D、白蛇传的故事3、黄河流域是我国的()文明发祥地之一。
A、华夏B、中华C、少数民族D、西域4、下列可代表北京传统文化的是()。
A、元宵节B、清明节C、端午节D、中秋节5、《论语》是()的书。
A、老子B、孔子C、墨子D、庄子二、填空题(共30分)1、我国的国旗是红色旗帜,旗面上绣着()黄色的大星星。
2、人们能够看到的最深的星座是()座。
3、黄河的源头位于()。
4、玄奘法师是唐朝时期的()。
5、《聊斋志异》是我国()小说的代表作。
三、解答题(共50分)1、简述唐三彩的特点和用途。
(10分)唐三彩是唐代的一种陶器,最初仅用于皇室的仪式和礼仪用品,后来在民间普及。
其特点是色彩斑斓、形态生动、线条优美,主要用于盛装食物、饮料等日常生活器皿,也可以用于装饰和供奉。
2、阐述改革开放政策对中国经济的影响。
(15分)改革开放政策的实施,使中国经济迎来了高速发展的新时期。
在政策的推动下,国内外资本大量进入,国有企业逐步转制、股份制改革,私营企业的兴起,都极大地推动了中国经济的发展。
同时,国家也鼓励和支持科技创新和高技术产业的发展,加速了技术升级和工业化进程。
今天,中国已经成为全球第二大经济体,对世界经济的稳定和发展有着重要的贡献。
3、回答“绿水青山就是金山银山”这一名言的含义。
(25分)该名言的含义是,保护生态环境和自然资源就是最大的财富。
在环保节能逐渐成为全球主流趋势的今天,绿色发展已经成为各国发展的必经之路。
过度开采和污染环境不仅会危害人们的健康,也会带来沉重的经济损失。
相反,注重生态环保和资源可持续利用,可以让人们享有更美好的生活,也可以为全球的可持续发展创造更加广阔的前景。
人教版数学八年级上册期末考试试卷带答案

人教版数学八年级上册期末考试试题一、选择题(30分)1.下列图形中,不是轴对称图形的是()A.B.C.D.2.某病毒直径约为0.00012毫米,则这个数字用科学记数法表示正确的是()A.1.2×104B.1.2×10﹣4C.0.12×105D.0.12×10﹣5 3.分式有意义的条件是()A.x=0B.x≠0C.x=﹣1D.x≠﹣14.点P(﹣1,2)关于y轴对称点的坐标是()A.(1,2)B.(﹣1,﹣2)C.(1,﹣2)D.(2,﹣1)5.下列计算正确的是()A.a2•a3=a6B.(2a)3=6a3C.(a+b)2=a2+b2D.(﹣a2)3=﹣a66.如图,四边形ABCD中,∠A=80°,BC、CD的垂直平分线交于A点,则∠BCD的度数为()A.150°B.140°C.130°D.120°7.已知a+b=2,则a2﹣b2+4b的值是()A.2B.3C.4D.68.小明上月在某文具店正好用20元钱买了几本笔记本,本月再去买时,恰遇此文具店搞优惠酬宾活动,同样的笔记本,每本比上月便宜1元,结果小明只比上次多用了4元钱,却比上次多买了2本.若设他上月买了x本笔记本,则根据题意可列方程()A.=1B.=1C.=1D.=19.当x分别取2020、2018、2016、…、2、0、、、…、、、时,计算分式的值,再将所得结果相加,其和等于()A.﹣1B.1C.0D.202010.如图,四边形ABCD中,∠DAB+∠ABC=90°,对角线AC、BD相交于O点,且分别平分∠DAB和∠ABC,若BO=4OD,则的值为()A.B.C.D.二、填空题(18分)11.计算:x2y÷xy2=.12.若x2+6x+m是完全平方式,则m=.13.已知x﹣=3,则x2+=.14.若某三角形两边长为2,4,第三边上的中线为x,则x的取值范围为.15.若关于x的方程=+1无解,则a的值是.16.如图,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,D为BC上一动点,EF垂直平分AD分别交AC于E、交AB于F,则BF的最大值为.三、解答题(72分)17.(8分)计算:(1)(2x+y)(2xy);(2)(4x6y﹣6x3)÷2x3.18.(8分)因式分解:(1)2x2﹣2;(2)x3﹣4x2y+4xy2.19.(8分)解方程:﹣1=.20.(8分)先化简,再求值:(1﹣)÷,其中a=﹣1.21.(8分)如图,是由边长为1的小正方形组成的网格,网格线的交点称为格点,△AOB 的顶点在格点上,以O为原点建立平面直角坐标系.(1)∠OAB=;O点关于直线AB的对称点的坐标为;(2)作A点关于OB的对称点F可按下列操作,要求:仅用无刻度直尺作图(保留作图过程与痕迹);①在网格中取格点C,连接AC,使AC⊥OB,则C的坐标为;②延长AO使OD=OA,则D的坐标为;③在网格中取格点E,连接DE,使DE⊥AC,则E的坐标为,AC与DE的交点F即为A点关于OB的对称点.22.(10分)某道路工程项目,若由甲、乙两工程队合作20天可完工;若甲工程队先单独施工40天,再由乙工程队单独施工10天也可完工.(1)求甲、乙两工程队单独完成此项工程各需要多少天?(2)如果甲、乙工程队合作施工时对道路交通有影响,独施工时对交通无影响,且要求整个工期不能超过24天,问如何安排两队施工,对道路交通的影响会最小?23.(10分)已知△ABC中,∠BAC=60°,以AB和BC为边向外作等边△ABD和等边△BCE.(1)连接AE、CD,如图1,求证:AE=CD;(2)若N为CD中点,连接AN,如图2,求证:CE=2AN;(3)若AB⊥BC,延长AB交DE于M,DB=,如图3,则BM =.(直接写出结果)24.(12分)已知点A(0,4)、B(﹣4,0)分别为面直角坐标中y、x轴上一点,将线段OA绕O点顺时针旋转至OC,连接AC、BC.(1)如图1,求∠ACB的度数;(2)若∠AOC=60°,∠AOB的平分线OD交BC于D,如图2,求证:OD+BD=CD;(3)若∠AOC=30°,过A作AE⊥AC交BC于E,如图3,求BE的长.参考答案与试题解析一、选择题(30分)1.下列图形中,不是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形进行分析即可.【解答】解:A、不是轴对称图形,符合题意;B、是轴对称图形,不合题意;C、是轴对称图形,不合题意;D、是轴对称图形,不合题意.故选:A.【点评】此题主要考查了轴对称图形,正确掌握轴对称图形的性质是解题关键.2.目前发现的新冠病毒其直径约为0.00012毫米,则这个数字用科学记数法表示正确的是()A.1.2×104B.1.2×10﹣4C.0.12×105D.0.12×10﹣5【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.00012=1.2×10﹣4.故选:B.【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.3.分式有意义的条件是()A.x=0B.x≠0C.x=﹣1D.x≠﹣1【分析】根据分式的分母不为0列出不等式,解不等式得到答案.【解答】解:分式有意义的条件是x+1≠0,解得x≠﹣1,故选:D.【点评】本题考查的是分式有意义的条件,掌握分式的分母不为0是解题的关键.4.点P(﹣1,2)关于y轴对称点的坐标是()A.(1,2)B.(﹣1,﹣2)C.(1,﹣2)D.(2,﹣1)【分析】根据关于y轴对称,横坐标互为相反数,纵坐标不变.【解答】解:点P(﹣1,2)关于y轴对称点的坐标为(1,2).故选:A.【点评】本题考查了关于x轴、y轴对称点的坐标,注:关于y轴对称,横坐标互为相反数,纵坐标不变;关于x轴对称,纵坐标互为相反数,横坐标不变;关于原点对称,横纵坐标都互为相反数.5.下列计算正确的是()A.a2•a3=a6B.(2a)3=6a3C.(a+b)2=a2+b2D.(﹣a2)3=﹣a6【分析】分别根据同底数幂的乘法法则,幂的乘方与积的乘方运算法则,完全平方公式逐一判断即可.【解答】解:A、a2•a3=a5,故本选项不合题意;B、(2a)3=8a3,故本选项不合题意;C、(a+b)2=a2+2ab+b2,故本选项不合题意;D、(﹣a2)3=﹣a6,故本选项符合题意.故选:D.【点评】本题主要考查了同底数幂的乘法,完全平方公式以及幂的乘方与积的乘方,熟记相关公式与运算法则是解答本题的关键.6.如图,四边形ABCD中,∠A=80°,BC、CD的垂直平分线交于A点,则∠BCD的度数为()A.150°B.140°C.130°D.120°【分析】根据垂直平分线的性质及等腰三角形的性质求解即可.【解答】解:连接AC,∵BC、CD的垂直平分线交于A点,∴AB=AC,AC=AD,∴∠B=∠ACB,∠D=∠ACD,在△ABC中,∠ACB=(180°﹣∠BAC)=90°﹣∠BAC,同理,∠ACD=90°﹣∠CAD,∴∠BCD=∠ACB+∠ACD=180°﹣(∠BAC+CAD)=180°﹣∠BAD,∵∠BAD=80°,∴∠BCD=140°.故选:B.【点评】此题考查了多边形的内角与外角,熟练掌握多边形内角和公式及等腰三角形的性质是解题的关键.7.已知a+b=2,则a2﹣b2+4b的值是()A.2B.3C.4D.6【分析】把a2﹣b2+4b变形为(a﹣b)(a+b)+4b,代入a+b=2后,再变形为2(a+b)即可求得最后结果.【解答】解:∵a+b=2,∴a2﹣b2+4b=(a﹣b)(a+b)+4b,=2(a﹣b)+4b,=2a﹣2b+4b,=2(a+b),=2×2,=4.故选:C.【点评】本题考查了代数式求值的方法,同时还利用了整体思想.8.小明上月在某文具店正好用20元钱买了几本笔记本,本月再去买时,恰遇此文具店搞优惠酬宾活动,同样的笔记本,每本比上月便宜1元,结果小明只比上次多用了4元钱,却比上次多买了2本.若设他上月买了x本笔记本,则根据题意可列方程()A.=1B.=1C.=1D.=1【分析】由设他上月买了x本笔记本,则这次买了(x+2)本,然后可求得两次每本笔记本的价格,由等量关系:每本比上月便宜1元,即可得到方程.【解答】解:设他上月买了x本笔记本,则这次买了(x+2)本,根据题意得:﹣=1,即:﹣=1.故选:B.【点评】此题考查了分式方程的应用.注意准确找到等量关系是关键.9.当x分别取2020、2018、2016、…、2、0、、、…、、、时,计算分式的值,再将所得结果相加,其和等于()A.﹣1B.1C.0D.2020【分析】把互为倒数的两个数代入分式可得它们的和是0,把0代入分式得﹣1,故得出结果为﹣1.【解答】解:当x=a(a≠0)时,=,当x=时,==﹣,即互为倒数的两个数代入分式的和为0,当x=0时,=﹣1,故选:A.【点评】本题考查数字的变化规律,总结出数字的变化规律是解题的关键.10.如图,四边形ABCD中,∠DAB+∠ABC=90°,对角线AC、BD相交于O点,且分别平分∠DAB和∠ABC,若BO=4OD,则的值为()A.B.C.D.【分析】在AB上截取AE=AD,BF=BC,连接OE、OF,根据题意易证△AOD≌△AOE (SAS),△BOC=△BOF(SAS),即得出结论∠AOD=∠AOE,∠BOC=∠BOF,OD =OE,OC=OF.继而求出∠AOD=∠BOC=∠AOE=∠BOF=∠EOF=45°,再由题意可知,==4,即又可推出,AE=AB,BE=AB,由OF平分∠BOE,得===4,可推出BF=×AB=AB,最后由BO平分∠ABC,可得==,即可求出的值.【解答】解:如图,在AB上截取AE=AD,BF=BC,连接OE,OF,∵AC、BD相交于O点,且分别平分∠DAB和∠ABC,∴∠OAB=∠OAD=∠DAB,∠OBC=∠OBA=∠ABC,在△AOD和△AOE中,,∵AD=AE,BC=BF,∴△AOD≌△AOE(SAS),同理,△BOC≌△BOF,∴∠AOD=∠AOE,OD=OE,∠BOC=∠BOF,OC=OF,∵∠DAB+∠ABC=90°,∴∠OAB+∠OBA=45°,∵∠AOD=∠BOC=∠OBA+∠OAB,∴∠AOD=∠BOC=45°,∴∠AOE=∠BOF=45°,∴∠EOF=180°﹣(∠OAB+∠OBA)﹣∠AOE﹣∠BOF=180°﹣45°﹣45°﹣45°=45°,∵AO平分∠BAD,BO=4OD,∴==4,即AB=4AD,∴AE=AB,BE=AB,∵∠EOF=∠BOF=45°,∴OF平分∠BOE,∴===,即EF=BF,∴BF=BE,∴BF=×AB=AB,∵BO平分∠ABC,∴====,故选:B.【点评】此题主要考查全等三角形的判定与性质,角平分线的判定与性质,推理论证过程较难,作出辅助线是解题的关键.二、填空题(18分)11.计算:x2y÷xy2=xy﹣1.【分析】直接利用整式的除法运算法则计算得出答案.【解答】解:x2y÷xy2=xy﹣1.故答案为:xy﹣1.【点评】此题主要考查了整式的除法,正确掌握相关运算法则是解题关键.12.若x2+6x+m是完全平方式,则m=9.【分析】由题意,x2+6x+m是完全平方式,所以,可得x2+6x+m=(x+3)2,展开即可解答.【解答】解:根据题意,x2+6x+m是完全平方式,∴x2+6x+m=(x+3)2,解得,m=9.故答案为9.【点评】本题考查了完全平方公式,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号.13.已知x﹣=3,则x2+=11.【分析】将原式两边平方即可得.【解答】解:∵x﹣=3,∴x2+﹣2=9,∴x2+=11,故答案为:11.【点评】本题主要考查分式的混合运算,解题的关键是掌握完全平方公式和分式的运算法则.14.若某三角形两边长为2,4,第三边上的中线为x,则x的取值范围为1<x<3.【分析】作出图形,延长中线AD到E,使DE=AD,利用“边角边”证明△ACD和△EBD 全等,根据全等三角形对应边相等可得AC=BE,然后根据三角形任意两边之和大于第三边,两边之差小于第三边求出AE的范围,再除以2即可得解.【解答】解:如图,延长中线AD到E,使DE=AD,∵AD是三角形的中线,∴BD=CD,在△ACD和△EBD中,∵,∴△ACD≌△EBD(SAS),∴AC=BE,∵角形两边长为2,4,第三边上的中线为x,∴4﹣2<2x<2+4,即2<2x<6,∴1<x<3.故答案为:1<x<3.【点评】本题考查了三角形的三边关系,全等三角形的判定与性质,根据辅助线的作法,“遇中线加倍延”作出辅助线构造全等三角形是解题的关键.15.若关于x的方程=+1无解,则a的值是2或1.【分析】把方程去分母得到一个整式方程,把方程的增根x=2代入即可求得a的值.【解答】解:x﹣2=0,解得:x=2.方程去分母,得:ax=4+x﹣2,即(a﹣1)x=2当a﹣1≠0时,把x=2代入方程得:2a=4+2﹣2,解得:a=2.当a﹣1=0,即a=1时,原方程无解.故答案是:2或1.【点评】首先根据题意写出a的新方程,然后解出a的值.16.如图,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,D为BC上一动点,EF垂直平分AD分别交AC于E、交AB于F,则BF的最大值为.【分析】要使BF最大,则AF需要最小,而AF=FD,从而通过圆与BC相切来解决问题.【解答】解:∵Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,∴AB=2AC=4,∵EF垂直平分AD,∴AF=DF,若要使BF最大,则AF需要最小,∴以F为圆心,AF为半径的圆与BC相切即可,∴FD⊥BD,∴AB=AF+2AF=4,∴AF=,∴BF的最大值为4﹣=,故答案为:.【点评】本题主要考查了线段垂直平分线的性质、30°角所对直角边是斜边的一半以及圆与直线的位置关系,将BF的最大值转化为AF最小是解决本题的关键,属于压轴题.三、解答题(72分)17.(8分)计算:(1)(2x+y)(2xy);(2)(4x6y﹣6x3)÷2x3.【分析】(1)直接利用单项式乘多项式运算法则计算得出答案;(2)直接利用整式的除法运算法则计算得出答案.【解答】解:(1)原式=(2x•2xy)+(y•2xy)=4x2y+2xy2;(2)原式=(4x6y)÷(2x3)+(﹣6x3)÷(2x3)=2x3y﹣3.【点评】此题主要考查了整式的除法以及单项式乘多项式,正确掌握相关运算法则是解题关键.18.(8分)因式分解:(1)2x2﹣2;(2)x3﹣4x2y+4xy2.【分析】(1)直接提取公因式2,再利用公式法分解因式即可;(2)直接提取公因式x,再利用公式法分解因式即可.【解答】解:(1)原式=2(x2﹣1)=2(x+1)(x﹣1);(2)原式=x(x2﹣4xy+4y2)=x(x﹣2y)2.【点评】此题主要考查了提取公因式法以及公式法分解因式,正确运用乘法公式是解题关键.19.(8分)解方程:﹣1=.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:(x﹣1)2﹣(x2﹣1)=2,整理得:﹣2x+2=2,解得:x=0,检验:x=0时,分母x2﹣1≠0,∴原方程的解为x=0.【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.20.(8分)先化简,再求值:(1﹣)÷,其中a=﹣1.【分析】这是个分式除法与减法混合运算题,运算顺序是先做括号内的减法,此时要注意把各分母先因式分解,确定最简公分母进行通分;做除法时要注意先把除法运算转化为乘法运算,而做乘法运算时要注意先把分子、分母能因式分解的先分解,然后约分.【解答】解:原式=•=,当a=﹣1时,原式==.【点评】考查分式的混合运算需特别注意运算顺序及符号的处理,也需要对通分、分解因式、约分等知识点熟练掌握.21.(8分)如图,是由边长为1的小正方形组成的网格,网格线的交点称为格点,△AOB 的顶点在格点上,以O为原点建立平面直角坐标系.(1)∠OAB=90°;O点关于直线AB的对称点的坐标为(2,2);(2)作A点关于OB的对称点F可按下列操作,要求:仅用无刻度直尺作图(保留作图过程与痕迹);①在网格中取格点C,连接AC,使AC⊥OB,则C的坐标为(0,﹣2);②延长AO使OD=OA,则D的坐标为(﹣1,﹣1);③在网格中取格点E,连接DE,使DE⊥AC,则E的坐标为(2,﹣2),AC与DE的交点F即为A点关于OB的对称点.【分析】(1)利用图象法解决问题即可.(2)根据步骤要求画出图形即可解决问题.【解答】解:(1)观察图象可知∠OAB=90°,O点关于直线AB的对称点的坐标为(2,2),故答案为:90°,(2,2).(2)图形如图所示:①C(0,﹣2);②D(﹣1,﹣1);③E(2,﹣2).故答案为:(0,﹣2),(﹣1,﹣1),(2,﹣2).【点评】本题考查轴对称变换,坐标与图形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.22.(10分)武汉某道路工程项目,若由甲、乙两工程队合作20天可完工;若甲工程队先单独施工40天,再由乙工程队单独施工10天也可完工.(1)求甲、乙两工程队单独完成此项工程各需要多少天?(2)如果甲、乙工程队合作施工时对道路交通有影响,独施工时对交通无影响,且要求整个工期不能超过24天,问如何安排两队施工,对道路交通的影响会最小?【分析】(1)设甲工程队单独完成此项工程需要x天,则甲工程队的工作效率为,乙工程队的工作效率为(﹣),根据“甲工程队先单独施工40天,再由乙工程队单独施工10天也可完工”,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)设甲、乙合作了m天,分剩下的工程由甲工程队单独完成和剩下的工程由乙工程队单独完成两种情况考虑,根据整个工期不能超过24天,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,再结合要求对道路交通的影响最小即可得出结论.【解答】解:(1)设甲工程队单独完成此项工程需要x天,则甲工程队的工作效率为,乙工程队的工作效率为(﹣),依题意得:+10(﹣)=1,解得:x=60,经检验,x=60是原方程的解,且符合题意,∴1÷(﹣)=30.答:甲工程队单独完成此项工程需要60天,乙工程队单独完成此项工程需要30天.(2)设甲、乙合作了m天.①若剩下的工程由甲工程队单独完成还需=(60﹣3m)天,依题意得:m+60﹣3m≤24,解得:m≥18;②若剩下的工程由乙工程队单独完成还需=(30﹣m)天,依题意得:m+30﹣m≤24,解得:m≥12.由①②可知m的最小值为12,∴应安排甲乙合作12天,然后再由乙队单独施工12天,对道路交通影响了会最小.【点评】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.23.(10分)已知△ABC中,∠BAC=60°,以AB和BC为边向外作等边△ABD和等边△BCE.(1)连接AE、CD,如图1,求证:AE=CD;(2)若N为CD中点,连接AN,如图2,求证:CE=2AN;(3)若AB⊥BC,延长AB交DE于M,DB=,如图3,则BM=.(直接写出结果)【分析】(1)先判断出∠DBC=∠ABE,进而判断出△DBC≌△ABE,即可得出结论;(2)先判断出△ADN≌△FCN,得出CF=AD,∠NCF=∠AND,进而判断出∠BAC =∠ACF,即可判断出△ABC≌△CFA,即可得出结论;(3)先判断出△ABC≌△HEB(ASA),得出BH=AC=2,AB=EH,再判断出△ADM≌△HEM(AAS),得出AM=HM,即可得出结论.【解答】(1)∵△ABD和△BCE是等边三角形,∴BD=AB,BC=BE,∠ABD=∠CBE=60°,∴∠ABD+∠ABC=∠CBE+∠ABC,∴∠DBC=∠ABE,∴△ABE≌△DBC(SAS),∴AE=CD;(2)如图2,延长AN使NF=AN,连接FC,∵点N是CD中点,∴DN=CN,∵∠AND=∠FNC,∴△ADN≌△FCN(SAS),∴CF=AD,∠NCF=∠AND,∴∠ACF=∠ACD+∠NCF=∠ACD+∠ADN=60°,∴∠BAC=∠ACF,∵△ABD是等边三角形,∴AB=AD,∴AB=CF,∵AC=CA,∴△ABC≌△CFA(SAS),∴BC=AF,∵△BCE是等边三角形,∴CE=BC=AF=2AN;(3)如图3,∵△ABD是等边三角形,∴AB=AD=DB=,∠BAD=60°,在Rt△ABC中,∠ACB=90°﹣∠BAC=30°,∴AC=2AB=2,过点E作EH∥AD交AM的延长线于H,∴∠H=∠BAD=60°,∵△BCE是等边三角形,∴BC=BE,∠CBE=60°,∵∠ABC=90°,∴∠EBH=90°﹣∠CBE=30°=∠ACB,∴∠BEH=180°﹣∠EBH﹣∠H=90°=∠ABC,∴△ABC≌△HEB(ASA),∴BH=AC=2,AB=EH,∴AD=EH,∵∠AMD=∠HME,∴△ADM≌△HEM(AAS),∴AM=HM,∴BM=AM﹣AB=AH﹣AB=(AB+BH)﹣AB=BH﹣AB=(BH﹣AB)=(2﹣)=,故答案为:.【点评】此题是三角形综合题,主要考查了等边三角形的性质,含30度角的直角三角形的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.24.(12分)已知点A(0,4)、B(﹣4,0)分别为面直角坐标中y、x轴上一点,将线段OA绕O点顺时针旋转至OC,连接AC、BC.(1)如图1,求∠ACB的度数;(2)若∠AOC=60°,∠AOB的平分线OD交BC于D,如图2,求证:OD+BD=CD;(3)若∠AOC=30°,过A作AE⊥AC交BC于E,如图3,求BE的长.【分析】(1)由旋转的性质得出CO=OB=OA,设∠AOC=2α,由等腰三角形的性质得出∠OAC=∠OCA=90°﹣α,可得出答案;(2)在BC上取点H,使∠COH=45°,证明△DOH为等边三角形,由等边三角形的性质得出OD=OH=DH,证明△BOD≌△COH(SAS),由全等三角形的性质得出BD=CH,则可得出结论;(3)过点C作CN⊥AO于点N,过点E作EM⊥AO于点M,连接OE,证明△AEM≌△CAN (AAS),由全等三角形的性质得出AM=CN,由等腰三角形的性质证出∠BOE=∠BEO,则可得出答案.【解答】解:(1)∵A(0,4)、B(﹣4,0),∴OA=OB=4,∵将线段OA绕O点顺时针旋转至OC,∴CO=OB=OA,设∠AOC=2α,∵∠BOC=90°+2α,∴∠OBC=∠OCB=45°﹣α,∵∠AOC=2α,∴∠OAC=∠OCA=90°﹣α,∴∠ACB=∠OCA﹣∠OCB=45°;(2)证明:如图2,在BC上取点H,使∠COH=45°,∵OD平分∠AOB,∠AOB=90°,∴∠BOD=∠AOD=45°,∵∠AOC=60°,∴∠BOC=150°,∵OB=OC,∴∠OBC=∠OCB=15°,∴∠DOH=∠BOC﹣∠BOD﹣∠COH=150°﹣45°﹣45°=60°,∠ODH=∠CBO+∠BOD =15°+45°=60°,∴∠DHO=60°,∴△DOH为等边三角形,∴OD=OH=DH,∴△BOD≌△COH(SAS),∴BD=CH,∴OD+BD=DH+CH=CD;(3)过点C作CN⊥AO于点N,过点E作EM⊥AO于点M,连接OE,由(1)得∠ACB=45°,∵AE⊥AC,∴△AEC为等腰直角三角形,∴AC=AE,∵∠ACN+∠NAC=∠EAM+∠NAC=90°,∴∠ACN=∠EAM,∵∠ANC=∠AME=90°,∴△AEM≌△CAN(AAS),∴AM=CN,∵OB=OA=OC=4,∠AOC=30°,∴CN=CO=2,∴AM=2,∴M为OA的中点,∵EM⊥AO,∴AE=EO,∵∠AOB=90°,∠AOC=30°,∴∠BOC=120°,∴∠CBO=∠OCB=30°,∴∠OAC=∠OCA=75°,∴∠EAO=∠EOA=15°,∴∠BOE=75°,∴∠BEO=180°﹣∠CBO﹣∠BOE=180°﹣30°﹣75°=75°,∴∠BOE=∠BEO,∴BE=BO=4.【点评】本题是几何变换综合题,考查了等边三角形的判定与性质,角平分线的性质,旋转的性质,等腰三角形的判定与性质,等腰直角三角形的性质,坐标与图形的性质,全等三角形的判定与性质,熟练掌握等边三角形的判定与性质及全等三角形的判定与性质是解题的关键.。
八年级第一学期期末考试试卷【含答案】

八年级第一学期期末考试试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪种现象属于光的反射?A. 彩虹B. 镜子中的倒影C. 日食D. 月食2. 在电路中,电阻的单位是?A. 安培B. 伏特C. 欧姆D. 瓦特3. 下列哪个是单质?A. 氧气B. 水C. 二氧化碳D. 盐酸4. 哪个是生物的基本单位?A. 细胞B. 原子C. 分子D. 阳离子5. 地球上最大的生物圈是?A. 海洋生物圈B. 陆地生物圈C. 大气生物圈D. 淡水生物圈二、判断题(每题1分,共5分)1. 地球围绕太阳转是正确的。
()2. 长度单位厘米是国际单位制中的基本单位。
()3. 0℃的水比0℃的冰重。
()4. 人类是由单细胞生物进化而来的。
()5. 光的传播速度在真空中是最慢的。
()三、填空题(每题1分,共5分)1. 地球上最大的生物圈是______。
2. 光的反射定律包括入射角等于______。
3. 电路中,电阻的单位是______。
4. 细胞是生物的______。
5. 地球围绕太阳转是______。
四、简答题(每题2分,共10分)1. 简述光的反射定律。
2. 解释电阻的概念。
3. 什么是单质?4. 生物的基本单位是什么?5. 地球上最大的生物圈是哪个?五、应用题(每题2分,共10分)1. 如果一个物体的质量是5kg,加速度是10m/s²,求物体所受的力。
2. 如果一个电池的电压是9V,电路中的电阻是3Ω,求电路中的电流。
3. 如果一个单质元素的原子量是20,它的分子量是多少?4. 如果一个细胞分裂成两个细胞,每个新细胞的大小是原来细胞的一半,新细胞的数量是多少?5. 如果地球上最大的生物圈是海洋生物圈,那么海洋生物圈中有哪些生物?六、分析题(每题5分,共10分)1. 分析光的反射定律在生活中的应用。
2. 分析电阻在电路中的作用。
七、实践操作题(每题5分,共10分)1. 设计一个实验,验证光的反射定律。
人教版八年级上册数学期末考试试卷含答案

人教版八年级上册数学期末考试试题一、单选题1.下面的图形是轴对称图形的是()A .B .C .D .2.数据0.00000164用科学记数法可表示为()A .51.6410-⨯B .61.6410-⨯C .716.410-⨯D .50.16410-⨯3.下列多项式中,能运用平方差公式分解因式的是()A .22a b +B .22a b-C .22a b -+D .22a b --4.计算:3223x y ⎛⎫-= ⎪⎝⎭()A .632x y-B .63827x y C .53827x y -D .63827x y -5.将分式222x x y+中的x ,y 同时扩大4倍,则分式的值()A .扩大4倍B .扩大2倍C .缩小到原来的一半D .保持不变6.已知2x =是分式方程113k x x x -+=-的解,那么k 的值为()A .0B .1C .2D .47.在ABC 中,AB AC =,AD BC ⊥于点D ,若8AB =,5CD =,则ABC 的周长为()A .13B .18C .21D .268.如图,点E 在AC 上,则A B C D DEB ∠+∠+∠+∠+∠的度数是()A .90°B .180°C .270°D .360°9.如图,两个正方形的边长分别为a 、b ,若7a b +=,3ab =,则阴影部分的面积是()A .40B .492C .20D .2310.如图,已知直角三角形ABC 中,90ACB ∠=︒,60CAB ∠=︒,在直线BC 或AC 上取一点P ,使得ABP △为等腰三角形,则符合条件的点有()A .4个B .5个C .6个D .7个二、填空题11.正五边形的外角和等于_______◦.12.已知221x x -=-,则代数式()52x x +-的值为______.13.已知30x yx -=,则y x=______.14.分式方程:2211x x x+=--的解是___________.15.在ABC 中,AB AC =,AB 的垂直平分线与AC 所在直线相交所得的锐角为42°,则B ∠=______.16.如图,B C ∠=∠,译添加一个条件______使得ABE ACD △△≌.17.如图,5AB AC ==,110BAC ∠=︒,AD 是∠BAC 内的一条射线,且25BAD ∠=︒,P 为AD 上一动点,则PB PC -的最大值是______.18.如图,在平面直角坐标系中,已知()2,0A ,()0,3B ,若在第一象限中找一点C ,使得AOC OAB ≅△△,则C 点的坐标为_______.三、解答题19.计算:()()()323235a a a a a -+-+÷.20.已知23m n=,求224421n mn n m m m ⎛⎫--+÷ ⎪⎝⎭的值.21.在()()223x x a x b -++的运算结果中,2x 的系数为4-,x 的系数为7-,求a ,b 的值并对式子224ax b +进行因式分解.22.如图,AB ,CD 相交于点E 且互相平分,F 是BD 延长线上一点,若2FAC BAC ∠=∠,求证:AC DF AF +=.23.某商场计划在年前用30000元购进一批彩灯,由于货源紧张,厂商提价销售,实际的进货价格比原来提高了20%,结果比原计划少购进100盏彩灯.该商场实际购进彩灯的单价是多少元?24.如图1,射线BD 交△ABC 的外角平分线CE 于点P ,已知∠A=78°,∠BPC=39°,BC=7,AB=4.(1)求证:BD平分∠ABC;(2)如图2,AC的垂直平分线交BD于点Q,交AC于点G,QM⊥BC于点M,求MC的长度.25.如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N.求证:(1)AD=BE;(2)∠BMC=∠ANC;(3)△CMN是等边三角形.26.如图所示,点M是线段AB上一点,ED是过点M的一条直线,连接AE、BD,过点B 作BF//AE交ED于F,且EM=FM.(1)若AE=5,求BF的长;(2)若∠AEC=90°,∠DBF=∠CAE,求证:CD=FE.参考答案1.C 2.B 3.C 4.D 5.A 6.D 7.D 8.B 9.C 10.C 11.36012.413.1314.0x =15.66°或24°16.AB AC =(答案不唯一)【详解】解: B C ∠=∠,,A A ∠=∠添加:,AB AC =∴(),ABE ACD ASA ≌△△故答案为:,AB AC =(答案不唯一)17.5【分析】作点B 关于射线AD 的对称点B ',连接AB '、CB '、B'P .则AB AB '=,PB PB '=,AB C 'V 是等边三角形,在PB C ' 中,PB PC B C -'≤',当P 、B '、C 在同一直线上时,PB PC '-取最大值B C ',即为5.所以PB PC '-的最大值是5.【详解】解:如图,作点B 关于射线AD 的对称点B ',连接AB '、CB ',B'P .则AB AB '=,PB PB '=,25B AD BAD ∠=∠='︒,110252560B AC BAC BAB ∠=∠-∠=︒-︒-︒=''︒.∵5AB AC ==,∴5AB AC '==,∴AB C 'V 是等边三角形,∴5B C '=,在PB C ' 中,PB PC B C -'≤',当P 、B '、C 在同一直线上时,PB PC '-取最大值B C ',即为5.∴PB PC '-的最大值是5.故答案为:5.18.()2,3【详解】根据题意C 点在第一象限内,且AOC OAB ≅△△,如图,又已知OAB 和AOC △有已知公共边AO ,∴(23)C ,.故答案为(2)3,.【点睛】本题考查全等三角形的性质,由已知公共边结合三角形全等的性质找到点C 的位置是解答本题的关键.19.210a --【分析】先利用平方差公式进行整式的乘法运算,同步计算多项式除以单项式,再合并同类项即可.【详解】解:原式222495110a a a =---=--.【点睛】本题考查的是平方差公式的运用,多项式除以单项式,掌握“整式的混合运算”是解本题的关键.20.2【分析】先计算括号内分式的加法,再把除法转化为乘法,约分后可得结果,再把23m n =化为23,n m =再整体代入即可.【详解】解:原式222442n mn m mm n m-+=⋅-()22222n m m n mm n m m--=⋅=-∵23m n=∴23n m =,代入上式,得:原式322m m mm m-===.【点睛】本题考查的是分式的化简求值,掌握“整体代入法求解分式的值”是解本题的关键.21.1a =-,2b =,()()411x x +-【分析】先计算多项式乘以多项式,再结合题意可得64b -=-,327a b -=-,解方程组求解,a b 的值,再利用平方差公式分解因式即可.【详解】解:∵()()223x x a x b -++3223623x bx x bx ax ab =+--++()()323623x b x b a x ab=+-+-++∴64b -=-,327a b -=-解得:1a =-,2b =∴()()222444411ax b x x x +=-+=+-.22.【详解】证明:∵AB ,CD 互相平分∴AE BE =,CE DE =又∵AEC BED ∠=∠∴AEC BED△△≌∴CAE DBE =∠∠,AC BD =∵2FAC BAC ∠=∠∴CAE FAE ∠=∠∴DBE FAE ∠=∠∴AF BF =∵BF BD DF =+∴AC DF AF +=.23.商场实际购进彩灯的单价是60元【分析】设商场原计划购进彩灯的单价为x 元,则商场实际购进彩灯的单价为(120%)x +元,由题意:某商场计划在年前用30000元购进一批彩灯,由于货源紧张,厂商提价销售,实际的进货价格比原来提高了20%,结果比原计划少购进100盏彩灯.列出分式方程,解方程即可.【详解】解:设商场原计划购进彩灯的单价为x 元,则商场实际购进彩灯的单价为(120%)x +元,根据题意得:3000030000100(120%)x x-=+,解得:50x =,经检验,50x =是原分式方程的解,且符合题意,则(120%)60x +=(元),答:商场实际购进彩灯的单价为60元.24.(1)见解析(2)MC=1.5【分析】(1)由∠ACF=∠A+∠ABF ,∠ECF=∠BPC+∠DBF ,得∠ABF=∠ACF-78°,∠DBF=∠ECF-39°,再根据CE 平分∠ACF ,得∠ACF=2∠ECF ,则∠ABF=2∠ECF-78°=2(∠ECF-39°)=2∠DBF ,从而证明结论;(2)连接AQ ,CQ ,过点Q 作BA 的垂线交BA 的延长线于N ,利用HL 证明Rt△QNA≌Rt△QMC,得NA=MC,再证明Rt△QNB≌Rt△QMB(HL),得NB=MB,则BC=BM+MC=BN+MC=AB+AN+MC,从而得出答案.(1)证明:∵∠ACF=∠A+∠ABF,∠ECF=∠BPC+∠DBF,∴∠ABF=∠ACF-78°,∠DBF=∠ECF-39°,∵CE平分∠ACF,∴∠ACF=2∠ECF,∴∠ABF=2∠ECF-78°=2(∠ECF-39°)=2∠DBF,∴BD平分∠ABC;(2)解:连接AQ,CQ,过点Q作BA的垂线交BA的延长线于N,∵QG垂直平分AC,∴AQ=CQ,∵BD平分∠ABC,QM⊥BC,QN⊥BA,∴QM=QN,∴Rt△QNA≌Rt△QMC(HL),∴NA=MC,∵QM=QN,BQ=BQ,∴Rt△QNB≌Rt△QMB(HL),∴NB=MB,∴BC=BM+MC=BN+MC=AB+AN+MC,∴7=4+2MC,∴MC=1.5.25.(1)见解析;(2)见解析;(3)见解析【分析】(1)根据等边三角形的性质和题意,可以得到△ACD ≌△BCE 的条件,从而可以证明结论成立;(2)由△ACD ≌△BCE 得∠CBE=∠CAD ,由△ABC 和△DEC 都是等边三角形得60ACB ECD ∠=∠=︒,由平角定义得60ACN ∠=︒,再由三角形内角和定理可得结论;(3)根据(1)中的结论和等边三角形的判定可以证明△CMN 是等边三角形.【详解】(1)证明:∵△ABC 和△CDE 都是等边三角形,∴BC=AC ,CE=CD ,∠BCA=∠ECD=60°,∴∠BCA+∠ACE=∠ECD+∠ACE ,∠ACE=60°,∴∠BCE=∠ACD ,在△ACD 和△BCE 中AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===,∴△ACD ≌△BCE (SAS );∴AD =BE ;(2)由(1)得△ACD ≌△BCE ∴∠CBE=∠CAD ,∵△ABC 和△DEC 都是等边三角形∴60ACB ECD ∠=∠=︒∴60ACN ∠=︒∵180,180CBM BCM BMC CAN ACN ANC ∠+∠+∠=︒∠+∠+∠=︒∴∠BMC =∠ANC ;(3)由(1)知,△ACD ≌△BCE ,则∠ADC=∠BEC ,即∠CDN=∠CEM ,∵∠ACE=60°,∠ECD=60°,∴∠MCE=∠NCD ,在△MCE 和△NCD 中,MCE NCD MEC NDC CE CD ∠∠⎧⎪∠∠⎨⎪⎩===,∴△MCE≌△NCD(AAS),∴CM=CN,∵∠MCN=60°,∴△MCN是等边三角形.26.(1)BF=5;(2)见解析.【分析】(1)证明△AEM≌△BFM即可;(2)证明△AEC≌△BFD,得到EC=FD,利用等式性质,得到CD=FE.【详解】(1)∵BF//AE,∴∠MFB=∠MEA,∠MBF=∠MAE,∵EM=FM,∴△AEM≌△BFM,∴AE=BF,∵AE=5,∴BF=5;(2)∵BF//AE,∴∠MFB=∠MEA,∵∠AEC=90°,∴∠MFB=90°,∴∠BFD=90°,∴∠BFD=∠AEC,∵∠DBF=∠CAE,AE=BF,∴△AEC≌△BFD,∴EC=FD,∴EF+FC=FC+CD,∴CD=FE.。
人教版八年级上册数学期末考试试卷附答案

人教版八年级上册数学期末考试试题一、单选题1.下列四个图案中,不是轴对称图形的是()A .B .C .D .2.若a+b =6,ab =4,则a 2+4ab+b 2的值为()A .40B .44C .48D .523.分式方程3111x x x =-+-的解是()A .4B .2C .1D .-24.若多项式()()213x x x ax b +-=++,则a ,b 的值分别是()A .2a =,3b =B .2a =-,3b =-C .2a =-,3b =D .2a =,3b =-5.若式子2244x x x -++的值等于0,则x 的值为()A .±2B .-2C .2D .-46.施工队要铺设一段全长2000米的管道,因在中考期间需停工两天,实际每天施工需比原来计划多50米,才能按时完成任务,求原计划每天施工多少米.设原计划每天施工x 米,则根据题意所列方程正确的是()A .20002000250x x -=+B .20002000250x x -=+C .20002000250x x -=-D .20002000250x x -=-7.在4×4的正方形网格中,以格点为顶点的三角形称为格点三角形,在图中画出与△ABC 关于某条直线对称的格点三角形,最多能画()个.A .5B .6C .7D .88.如图是用直尺和圆规作一个角等于已知角的示意图,说明O O ∠'=∠的依据是()A .SASB .SSSC .AASD .ASA9.如图,折叠直角三角形纸片的直角,使点C 落在AB 上的点E 处,已知BC=24,∠B=30°,则DE 的长是()A .12B .10C .8D .610.如图,AE=AF ,AB=AC ,EC 与BF 交于点O ,∠A=60°,∠B=25°,则∠EOB 的度数为()A .60°B .70°C .75°D .85°二、填空题11.269a a -+分解因式得______.12.若正多边形的一个外角是45°,则该正多边形的边数是_________.13.化简1(1)(1)1m m -++的结果是__.14.如图,BD 平分ABC ∠,60ADB ∠=o ,80BDC ∠= ,70C ∠= ,所以ABD ∆是________三角形.15.如图,∠A=30°,∠C'=60°,△ABC 与△A’B'C '关于直线l 对称,则∠B=___________.16.如图,点A 在线段DE 上,AB ⊥AC ,垂足为A ,且AB =AC ,BD ⊥DE ,CE ⊥DE ,垂足分别为D 、E ,若ED =12,BD =8,则CE 长为_____.17.因式分解:22ax ax a -+=_________.18.把一副三角板按如图所示的方式放置,则图中钝角α是______o .三、解答题19.解方程:2133x x x =++.20.如图,每个小正方形的边长均为1,点A 和点B 在小正方形的格点上.(1)在图①中画出ABC ,使ABC 为直角三角形(要求点C 在小正方形的格点上,画一个即可).的面积.(2)求图①中ABC21.某县在“城乡公交一体化改造项目”中,某工程队承接了6千米地下管廊铺设任务,为了赶在年底前完成,实际每天的工作效率比原计划提高20%,结果提前20天完成了任务,问实际每天铺设管廊多少米.22.如图,AB=AC,CD∥AB,点E是AC上一点,且∠ABE=∠CAD,延长BE交AD 于点F.(1)求证:△ABE≌△CAD;(2)如果∠ABC=65°,∠ABE=25°,求∠D的度数.23.已知△ABC是等边三角形,延长BA到点E,延长BC到点D,使得AE=BD,连接CE,DE,求证:CE=DE24.观察下面的因式分解过程:am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(m+n)(a+b)利用这种方法解决下列问题:(1)因式分解:2a+6b﹣3am﹣9bm(2)△ABC三边a,b,c满足a2﹣ac﹣ab+bc=0,判断△ABC的形状.25.如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.求证:AB=AC .26.先阅读下面的内容,再解决问题.例题:若m 2+2mn+2n 2−6n+9=0,求m 和n 的值.解:∵m 2+2mn+2n 2−6n+9=0即:∴m 2+2mn+n 2+n 2−6n+9=0∴22m n n-30++=()()∴即:m+n=0,n-3=0∴m=−3,n=3(1)若2222440x y xy y +-++=,求y x -的值.(2)若三角形三边a ,b ,C 都是正整数,且满足226618|3|0a b a b c +--++-=,判断三角形的形状.27.在△ABC 中,AB=AC ,D 是BC 的中点,以AC 为腰向外作等腰直角△ACE ,∠EAC=90°,连接BE ,交AD 于点F ,交AC 于点G.(1)若∠BAC=40°,求∠AEB 的度数;(2)求证:∠AEB=∠ACF.参考答案1.B【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形进行分析即可.【详解】解:A 、是轴对称图形,不合题意;B 、不是轴对称图形,符合题意;C 、是轴对称图形,不合题意;D 、是轴对称图形,不合题意.故选:B .【点睛】此题主要考查了轴对称图形,正确掌握轴对称图形的性质是解题关键.2.B【分析】将a 2+4ab +b 2化成已知式形式即可解答.【详解】解:a 2+4ab +b 2=(a +b )2+2ab =36+8=44.故选B.【点睛】本题考查完全平方式变式,掌握完全平方式是解题关键.3.B【分析】各项乘以(1)(1)x x +-去分母,然后移项合并,即可求出方程的解.【详解】解:去分母得:22331x x x x -=+-+,移项、合并得:24=x ,解得:2x =,经检验2x =是分式方程的解,故选:B .【点睛】本题考查了解分式方程,解题的关键是掌握解分式方程的方法,注意需要检验.4.B【分析】首先利用多项式乘法将原式展开,进而得出a ,b 的值,即可得出答案.【详解】解:∵(x+1)(x-3)=x 2-2x-3=x 2+ax+b ,故a=-2,b=-3,故选:B .【点睛】本题主要考查了多项式乘法,正确利用多项式乘多项式的法则用将原式展开是解题关键.5.C【详解】2x-=0且x²+4x+4≠0,解得x=2.故选C.6.B【分析】设原计划每天铺设x米,则实际施工时每天铺设(x+50)米,根据:原计划所用时间-实际所用时间=2,列出方程即可.【详解】设原计划每天施工x米,则实际每天施工(x+50)米,根据题意,可列方程:2000200050x x-+=2,故选B.【点睛】本题考查了由实际问题抽象出分式方程,解题的关键是读懂题意,找出合适的等量关系,列出方程.7.C【分析】根据网格结构分别确定出不同的对称轴,然后作出轴对称三角形即可得解.【详解】如图,最多能画出7个格点三角形与△ABC成轴对称.故选:C.【点睛】本题考查了利用轴对称变换作图,熟练掌握网格结构并准确找出对应点的位置是解题的关键,本题的难点在于确定出不同的对称轴.8.B【分析】由作法易得OD=O′D′,OC=O′C′,CD=C′D′,依据SSS 可判定△COD ≌△C'O'D'.【详解】解:由作法易得OD=O′D′,OC=O′C′,CD=C′D′,依据SSS 可判定△COD ≌△C'O'D',故选B .【点睛】本题主要考查了尺规作图—作已知角相等的角,解题的关键在于能够熟练掌握全等三角形的判定条件.9.C【分析】由折叠的性质可知;DC=DE ,∠DEA=∠C=90°,在Rt △BED 中,∠B=30°,故此BD=2ED ,从而得到BC=3BC ,于是可求得DE=8.【详解】解:由折叠的性质可知;DC=DE ,∠DEA=∠C=90°,∵∠BED+∠DEA=180°,∴∠BED=90°.又∵∠B=30°,∴BD=2DE .∴BC=3ED=24.∴DE=8.故答案为8.【点睛】本题考查的是翻折的性质、含30°锐角的直角三角形的性质,根据题意得出BC=3DE 是解题的关键.10.B【详解】,,60.AE AF AB AC A ==∠= .ABF ACE ≌∴25.C B ∴∠=∠= 180602595,AEC ∴∠=--=952570.EOB AEC B ∴∠=∠-∠=-= 故选B .【点睛】本题考查了全等三角形的性质,掌握三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.11.()23a -【分析】利用完全平方公式分解即可.【详解】∵269a a -+=()23a -,故答案为:()23a -.【点睛】本题考查了因式分解,正确理解公式法分解因式是解题的关键.12.8【分析】根据多边形外角和是360度,正多边形的各个内角相等,各个外角也相等,直接用36045︒÷︒可求得边数.【详解】解: 多边形外角和是360度,正多边形的一个外角是45︒,360458∴︒÷︒=即该正多边形的边数是8,故答案为:8.【点睛】本题主要考查了多边形外角和以及多边形的边数,解题的关键是掌握正多边形的各个内角相等,各个外角也相等.13.m【分析】本题需先把(m+1)与括号里的每一项分别进行相乘,再把所得结果相加即可求出答案.【详解】解:(1-11m +)(m+1)=(m+1)-1=m故答案为m14.直角【分析】利用三角形的内角和以及角平分线定理,求出30ABD DBC ∠=∠= ,即可得到∠A ,然后得到结论.【详解】解:∵180180807030DBC BDC C∠=-∠-∠=--=,又∵BD平分ABC∠,∴30ABD DBC∠=∠= ,∵60ADB∠=o,∴180306090A∠=--=,∴ABD∆是直角三角形.故答案为:直角.15.90°【分析】先根据轴对称的性质得出△ABC≌△A′B′C′,由全等三角形的性质可知∠C=∠C′,再由三角形内角和定理可得出∠B的度数.【详解】∵△ABC与△A′B′C′关于直线l对称,∴△ABC≌△A′B′C′,∴∠C=∠C′=60°,∵∠A=30°,∴∠B=180°-∠A-∠C=180°-30°-60°=90°.故答案为90°.16.4【分析】根据已知条件及互余关系可证△ABD≌△CAE,得出BD=AE=8,AD=CE,求出AD=4,即可得出答案.【详解】解:∵BD⊥DE,CE⊥DE,∴∠D=∠E=90°,∠ABD+∠BAD=90°,∵AB⊥AC,∴∠BAD+∠EAC=90°,∴∠ABD=∠EAC,在△ABD和△CAE中,D EAB CA ABD EAC∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABD≌△CAE(ASA),∴BD=AE=8,AD=CE,∴AD=ED﹣AE=12﹣8=4,∴CE =4故答案为:4.【点睛】本题考查了全等三角形的判定与性质、等角的余角相等.找到证明三角形全等的条件,证明三角形全等是解题的关键.17.()21a x -【分析】先提取公因式a ,再利用完全平方公式分解因式.【详解】解:22ax ax a -+=()221a x x -+=()21a x -,故答案为:()21a x -.【点睛】此题考查了因式分解,综合掌握提公因式法及公式法分解因式是解题的关键.18.105【分析】利用三角形内角和定理计算即可.【详解】解:由三角形的内角和定理可知:α=180°-30°-45°=105°,故答案为105.【点睛】本题考查三角形内角和定理,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考基础题.19.23x =【分析】由3x+3=3(x+1),确定最简公分母,解方程即可.【详解】方程两边同时乘以3(1)x +得:32x =,解得:23x =,经检验23x =是分式方程的解.【点睛】本题考查了分式方程的解法,因式分解确定最简公分母是解题的关键.20.(1)见解析(2)6【分析】(1)根据直角三角形的定义画出三角形即可.(答案不唯一)(2)根据三角形面积公式求解即可.(1)解:如图①,△ABC 即为所求.(2)解:图①中,△ABC 的面积为:12AC ⨯BC=12×4×3=6.【点睛】本题考查作图-应用与设计,直角三角形的性质等知识,解题的关键是学会利用数形结合的思想解决问题.21.实际每天铺设管廊60米【分析】设原计划每天铺设管廊x 米,则实际每天铺设管獅(120%)x +米,根据原计划天数-实际天数=20,列方程计算即可.【详解】解:设原计划每天铺设管廊x 米,则实际每天铺设管獅(120%)x +米,根据题意得:6000600020(120%)x x-=+,解得:50x =,经检验,50x =是所列方程的解,且符合题意,∴(120%)60x +=.答:实际每天铺设管廊60米.【点睛】本题考查了分式方程的应用题,正确审题,列出方程是解题的关键.22.(1)见解析;(2)105°【分析】(1)根据ASA 可证明△ABE ≌△CAD ;(2)求出∠BAC =50°,则求出∠BAD =75°,可求出答案.【详解】(1)证明:∵CD ∥AB ,∴∠BAE =∠ACD ,∵∠ABE=∠CAD,AB=AC,∴△ABE≌△CAD(ASA);(2)解:∵AB=AC,∴∠ABC=∠ACB=65°,∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°,又∵∠ABE=∠CAD=25°,∴∠BAD=∠BAC+∠CAD=50°+25°=75°,∵AB∥CD,∴∠D=180°﹣∠BAD=180°﹣75°=105°.【点睛】考核知识点:全等三角形的判定和性质.熟记全等三角形的判定是关键.23.见解析【分析】先过点E作EF//AC,交BD延长线与点F,得出△BEF是等边三角形,进而求出△BCE≌△FDE,从而得出CE=DE.【详解】证明:过点E作EF//AC,交BD延长线与点F∵EF//AC∴∠BAC=∠BEF=60°,∠ACB=∠F=60°∴△BEF是等边三角形∴BE=BF=EF∵△ABC是等边三角形∴AB=BC∴BE-AB=BF-BC即AE=CF∵BD=AE∴BD =CF∴BD -CD =CF -CD即BC =DF在△BCE 和△FDE 中BC DF B F BE EF ⎧⎪∠∠⎨⎪⎩===,∴△BCE ≌△FDE∴CE =DE【点睛】此题主要考查了等边三角形的性质与判定以及全等三角形的判定等知识,解决问题的关键是学会添加常用辅助线,构造全等三角形解决问题.24.(1)(a+3b )(2﹣3m );(2)△ABC 是等腰三角形,见解析【分析】(1)仿照样例,先分组,组内提公因式后组与组之间提取公因式,便可达到分解因式的目的;(2)用样例的方法,把已知等式左边分解因式,再根据几个因式积为0的性质得出一次方程求得a 、b 、c 之间的关系,便可确定△ABC 的形状.【详解】解:(1)2a+6b ﹣3am ﹣9bm=(2a+6b )﹣(3am+9bm )=2(a+3b )﹣3m (a+3b )=(a+3b )(2﹣3m );或2a+6b ﹣3am ﹣9bm=(2a ﹣3am )+(6b ﹣9bm )=a (2﹣3m )+3b (2﹣3m )=(2﹣3m )(a+3b );(2)∵a 2﹣ac ﹣ab+bc =0,∴(a 2﹣ac )﹣(ab ﹣bc )=0,∴a (a ﹣c )﹣b (a ﹣c )=0,∴(a ﹣c )(a ﹣b )=0,∴a ﹣c =0或a ﹣b =0,∴a =c 或a =b ,∴△ABC 是等腰三角形.【点睛】本题考查因式分解的应用,等腰三角形的判定,解题的关键是正确解读样例,根据样例进行因式分解.25.证明见解析.【分析】已知AD 平分∠BAC ,DE ⊥AB 于点E ,DF ⊥AC 于点F ,由角平分线的性质定理可得DE=DF ,再利用HL 证明Rt △BDE ≌Rt △CDF ,即可得∠B=∠C ,由等腰三角形的判定定理即可证得AB=AC.【详解】∵AD 平分∠BAC ,DE ⊥AB 于点E ,DF ⊥AC 于点F ,∴DE=DF ,∵BD=CD ,∴Rt △BDE ≌Rt △CDF ,∴∠B=∠C ,∴AB=AC.【点睛】本题主要考查了角平分线上的点到角两边的距离相等、全等三角形的判定及性质、等腰三角形的判定,比较综合,难度适中.26.(1)4;(2)等边三角形.【分析】(1)把2222440x y xy y +-++=,配方得到22()(2)0x y y -++=,再根据非负数的性质得到x=y=-2,代入即可求得数值;(2)把22661830a b a b c +--++-=,配方得到22(3)(3)30a b c -+-+-=,根据非负数的性质得到a=b=c=3,即可得出三角形的形状.【详解】(1)∵2222440x y xy y +-++=,∴2222440x xy y y y -++++=,∴22()(2)0x y y -++=,即:x-y=0,y=-2,∴x=y=-2,∴y x -=4.(2)∵22661830a b a b c +--++-=,∴22696930a a b b c -++-++-=,∴22(3)(3)30a b c -+-+-=,∴a-3=0,b-3=0,3-c=0,∴a=b=c=3,∴该三角形为等边三角形.27.(1)25°;(2)证明见解析.【分析】(1)已知AB=AC ,△ACE 是等腰直角三角形,可得AB=AE ;再由等腰三角形的性质可得∠ABE=∠AEB ,由已知条件求出∠BAE 的度数,再根据三角形内角和定理即可求出∠AEB 的度数;(2)根据等腰三角形的性质得出∠BAF=∠CAF ,根据SAS 推出△BAF ≌△CAF ,根据全等得出∠ABF=∠ACF ,即可证得结论.【详解】(1)∵AB=AC ,△ACE 是等腰直角三角形,∴AB=AE ,∴∠ABE=∠AEB ,又∵∠BAC=40°,∠EAC=90°,∴∠BAE=40°+90°=130°,∴∠AEB=(180°-130°)÷2=25°.(2)证明:∵AB=AC ,D 是BC 的中点,∴∠BAF=∠CAF .在△BAF 和△CAF 中AF AF BAF CAF AB AC =⎧⎪∠=∠⎨⎪=⎩∴△BAF ≌△CAF (SAS ),∴∠ABF=∠ACF ,∵∠ABE=∠AEB ,∴∠AEB=∠ACF .。
2022-2023人教版八年级数学上册期末统考试题及参考答(WL县统考)

2022-2023人教版八年级数学上册期末统考试题及参考答案(WL 县统考)(满分120分,时间100分钟)第Ⅰ卷(选择题 共36分)一、选择题(本大题共12个小题,每小题3分,满分36分)1.以下冬奥会图标中,是轴对称图形的是( )2.下列运算正确的是( )A.(a+b)2=a 2+b 2B.4a 6b ÷(-2a 2b) =-2a 3C.(−13)−2=−19D.(-3x 3)2=9x 6 3.下列分解因式正确的是( ) A x 2+3x+2=x(x+3)+2 B.4x 2 -9 =(4x+3)(4x -3) C.x 2-5x+6=(x-2)(x-3) D.a 2 -2a+1=(a+1)24.一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是( )A.5B.6C.7D.85.已知a,b,c 是一个三角形的三边长,化简:|a-b-c|+|b-a-c|-|c+b-a|=( )A.a-b+cB.a-b-3cC. 3a+b+cD.a-b-c6.下列分式一定有意义的是( )A. xx 2+1 B. x+2x 2 C. −x x 2−2 D. x 2x+37.若关于x 的分式方程1−mx−1 - 1=21−x 的解为正数,则m 的取值范围是( ) A.m< 4 B.m<4 且m ≠3 C. m> 4 D.m>4 且m ≠58.某工程需要在规定时问内完成,如果甲工程队单独做,恰好如期完成;如果乙工程以单独做,则多用3天,现在甲、乙两队合做2天,剩下的由乙队单独做,恰好如期完成,求规定时间。
如果设规定日期为x 天。
下面所列方程中错误的是( )A. 2x +x x+3=1 B .2x =3x+3 C.(1x +1x+3)×2+x−2x+3=1 D.2x +x−2x+3=19.如图,己知线段AB=40米,MA ⊥AB 于点A ,MA=20米,射线BD ⊥AB 于B ,P 点从B 点向A 运动,每秒走1米,Q 点从B 点向D 运动,每秒走3米,P 、Q 同时从B 出发,则出发x 秒后,在线段MA 上有一点C ,使△CAP 与△PBQ 全等,则x 的值为( )A.10B.20或10C.6D.6或1010.如图,△ABC 中,AD 为中线,AD ⊥BC,∠BAD=30°,AB=3,则AC 长 ( )A.25B.2C.1.8D.1.59题图 10题图 11题图11.如图,锐角∠AOB=x,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=a,∠QNO=β,当MP+PQ+QN最小时,关于a,β,x的数量关系正确的是( )A.a-β=2xB.2β+a=90°+2xC.β+a=90°+xD.β+2a=180°-2x12.已知如图等腰△ABC,AB=AC、∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点0是线段AD上一点,OP =OC,下面的结论:①∠APO+∠DCO=30°②△OPC 是等边三角形③AC=AO+AP ④S△ABC=S四边形AOCP.其中正确的有( )A.①②③B.①②④C.①③④D.①②③④第Ⅱ卷(非选择题共84分)二、填空题(本大题共4个小题,每小题4分,共16分)13.己知a x = 2, a x+y = 12,求a x−y=___________.14.已知a+b=5,ab=3.则ba+ab=___________.15.等愿三角形一腰上的高与另一腰的夹角为50°,则该三角形底角的度数为___________.16.如图,已知:等边△ABC中,D在AC上,E在AB上,且AE=DC,CE,BD 交于点F.过点 E 作EG⊥BD于G,则线段CF,FG和BD的数量关系用等式表示是___________.三、解答题(本大题共6小题,共68分)17.第(1) 题每小题3分,第(2)题4分,第(3)题6分,满分16分.(1)因式分解①a3- 9a ②-3x2 + 18xy-27y2(2)计算 [(x-2y)2+(x-2y)(2y+x)-2x(2x-y)]÷2x(3)先化简再求值.(3a+1-a+1)÷a2−4a2+2a+1,其中a= (2023-π)0-(12)-118.(本题满分9分)如图,平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1.0),B(2,-3),C(4,-2).(1)画出△ABC关于x轴的对称图形△A1B1C1;(2) 画出△A1B1C1向左平移4个单位长度后得到的△A2B2C2;(3) 求出△BA2C2的面积;(4)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标是____________.19.(本题满分9分)文具店王老板用180元购进一批文具,很快售完;王老板又用600元购进第二批文具,所购套数是第一批的3倍,但进价比第一批每套多了2元.(1)第二批文具每套进价多少元?(2)王老板以每本25元的价格销售第二批文具,售出60%后,为了尽快售完,决定打折促销,要使第二批文具的销售总利润不少于60元,剩余的文具每套售价最低打几折?20.(本题满分10分)如图,已知AE⊥AB,AF⊥AC. AE=AB,AF=AC,BF与CE相交于点M.(1)求证:EC=BF(2)求证:EC⊥BF21.(本题满分11分)如图,△ABC 是边长为8cm 的等边三角形,点P 从点A 出发沿AC 边向点C 运动,与此同时点 Q 从点 B 出发以相同的速度沿CB 延长线方向运动,当点P 到达C 点时,P 、Q 停止运动,连接PQ 交AB 于D.(1)设 P 、Q 的运动速度为2cm/s ,求当运动时间为多少时,∠BQD=30°;(2)过P 作PE ⊥AB 于E ,在运动过程中线段ED 的长是否发生变化?如果不变,求出线段ED 的长;如果变化请说明理由.22.(本题满分13分)在平面直角坐标系中,A(-5,0), B (0,5),点C 为x 轴正半轴上一动点,过点A 作AD ⊥BC 交y 轴于点 E.(1)如图1,若C(3,0),求点E 的坐标.(2)如图 2,若点C 在x 轴正半轴上运动,且OC<5,其它条件不变,连接 DO,求证:DO 平分∠ADC.(3) 若点C 在x 轴正半轴上运动,当OC+CD=AD 时,求∠OBC 的度数.参考答案一、选择题CDCCA ABDAD AD二、填空题 13. 1 314. 19315.70°或20°16. BD=2FG+CF三、解答题:17(1)a (a +3)(a −3) ,−3(x −3y )2(2)x-y(3)-418. 如图(3)9.5(4)P 2(m-4,-n ) 19(1)设第二批文具每套进价为x 元, 600x =3×180x−2 x=20,经检验x=20是原方程的解.答:第二批文具每套进价为20元.(2)第二批购进文具的套数为600÷20=30(套)设剩余的文具每套售价打y 折. 25×30×60%+25×y 10×30 ×(1-60%)-600≥60解得 y ≥7 答:剩余的文具每套售价最低打七折.20(1)提示:证ABF ≌△AEC(2)根据(1)提示:△ABF ≌△AEC ∴∠AEC+∠ADE=90°,∠ABF+∠BDM=90°,在△BDM 中,∠BMD=180°-∠ABF-∠BDM=180°-90°=90°∴ EC ⊥BF 21(1) ∵△ABC 是边长为8cm 的等边三角形 ∴ ∠ACB =60°若∠BQD =30°, ∠QPC=90°设运动时间为ts,AP =BQ=2t则 PC =8-2 t,QC = 8+2t在 Rt △QCP 中 ∵ ∠CQP =30°∴CQ==2CP,即8+2t =2(8-2t),t =43s (2)提示:过P 作PF//QC ,证△DBQ ≌△DFP , ED=EF+DF=12AB=4cm22(1)提示:如图∵∠OAE+∠ACD=90°,∠OBC+∠ACD=90° ∴∠OAE=∠OBC∵A(﹣5,0),B(0,5) ∴OA=OB=5 证 △AOE ≌△BOC , E(0,3)(2)如图2过O 作OM ⊥DA 于M,ON ⊥DC 于N由(1)知,△AOE ≌△BOC∴S △AOE =S △BOC∴ 1 2×AE ×OM =12×BC ×ON ∵AE=BC ∴OM=ON ∵OM ⊥AE,ON ⊥BC ∴DO 平分∠ADC(3)如图3,在DA 上截取DP=DC,连接OP∵∠PDO=∠CDO,OD=OD∴△OPD ≌△OCD(SAS)∴OC=OP,∠OPD=∠OCD∵OC+CD=AD∴OC=AD﹣CD∴AD﹣DP=OP 即AP=OP∴∠PAO=∠POA∴∠OPD=∠PAO+∠POA=2∠PAO=∠OCB ∵∠PAO+∠OCD=90°∴3∠PAO=90°∴∠PAO=30°∵∠OAP=∠OBC∴∠OBC=∠PAO=30°。
2021-2022人教版八年级数学上册期末统考试题(WL县统考)

2021-2022人教版八年级数学上册 期末统考试题(WL 县统考)第I 卷(选择题共36分)一、选择题(本大题共12个小题;每小题3分,满分36分) 1.下图为某小区分类垃圾桶上的标识,其图标部分可以看作轴对称图形的有( )A.1个B.2个C.3个D.4个2.下列计算正确的是( )A. A 2·a 3=a 5B. (a 3)2=a 5C.(2ab 2)3=6a 3b6D.3a 2÷4a 2=34a3.芝麻被称为八谷之冠,是世界上最古老的油料作物之一。
它作为食品和药物,得到广泛的使用。
经测算,一粒芝麻的质量约为0.000 002 01 kg ,将100粒芝麻的质量用科学记数法表示约为( )A.20.1X10-3kgB.2.01X10-4kgC.0.201X10-5kgD.2.01x10-6kg 4.若分式x+y xy 中的x 、y 的值都变为原来的3倍,则此分式的值( )A.不变B.是原来的3倍C.是原来的D.是原来的5.已知1a −1b=12,则ab b−a的值是( ) A.12B.−12 C. 2D. -26.一个多边形的内角和等于外角和的两倍,那么这个多边形是( ) A.三边形 B.四边形 C.五边形 D.六边形7.下列因式分解变形正确的是( )A.2a 2-4a=2(a 2-2a)B. a 2-2a+1=(a -1)2C.-a 2+4=(a+2)(a -2)D.a 2-5a -6=(a -2)(a -3)8题图 9题图8.如下图,在 Rt △ABC 中,∠ACB=90°,D 、E 是边AB 上两点,且CE 所在直线垂直平分线段AD ,CD 平分∠BCE ,AC=5cm ,则BD 的长为( ) A.5cm B.6cm C.7cm D.8cm9.如图,已知∠MON=40°,P 为∠MON 内一定点,OM 上有一点A ,ON 上有一点B ,当△PAB 的周长取最小值时,∠APB 的度数是( ) A.40° B.100° C.140° D.50°10.小东一家自驾车去某地旅行,手机导航系统推荐了两条线路,线路一全程75km,线路二全程90km ,汽车在线路二上行驶的平均时速是线路一上车速的1.8倍,线路二的用时预计比线路一用时少半小时,如果设汽车在线路一上行驶的平均速度为xkm/h ,则下面所列方程正确的是( ) A.75x=901.8x+12B.75x=901.8x−12C.751.8x=90x+12D.751.8x=90x−1211.在平面直角坐标系xOy 中,点A 的坐标为(4,-3),且0A=5,在y 轴上确定一点P ,使△AOP 为等腰三角形,则所有正确的点P 的坐标有( ) A.3个 B.4个 C.5个 D.6个12.如图,△ABC 中,∠BAC=60°,∠BAC 的平分线AD 与边BC 的垂直平分线MD 相交于D ,DE ⊥AB 交AB 的延长线于点E ,DF ⊥AC 于点F ,现有下列结论:①DE=DF ②DE+DF=AD ③MD 平分∠EDF ④若AE=3,则AB+AC=6.其中正确的个数为( )A.1个B.2个C.3个D.4个第II 卷(非选择题共84分)二、填空题(本大题共4个小题:每小题4分,共16分) 13.分解因式:m 3-4xy 2=______.14.等腰三角形有一内角的度数为50°,一腰的垂直平分线与另一腰所在直线相交所成的锐角的度数为______. 15.若分式|x|−52x−10的值为0,则x 的值为______.16.如图钢架中,焊上等长的13根钢条来加固钢架,AP 1=P 1P 2=P 2P 3=...=P 13P 14=P 14A,则∠A 的度数是______.三、解答题(本大题共6小题;共68分) 17.(本题满分12分)(1) (−23a 2b)3×(13ab 2)2×34a 3b 2 (2) (a+b)(a -b)+(4ab 3 -8a 2b 2)÷4ab18. (本题满分 12分)(1)解方程12−x=1x−2−6−x3x2−12(2)先化简:(x−1+3−3xx+1)÷x2−xx+1,然后在-1,0,1,2中选取一个合适的数代入求值.19.(本题满分10分)如图,在平面直角坐标系中,△ABC的顶点A,B,C的坐标分别为(2,2),(1,-3),(4,-2),△A'B'C'与△ABC关于y轴对称,点A,B,C的对应点分别为A',B',C'.(1)请在图中作出△A'B'C',并写出点A',B',C'的坐标;(2)若点M(m+2,n-2)是△ABC的边上一点,其关于y轴的对称点为M'(12−n,2m),求m,n的值.(3)请在y轴上找到一点P,使PC-PB的值最大,并在图上标注出来.20.(本题满分10分)为了返校学生的安全,快速筛查体温异常学生,某校在学生返校前购买了一批额温枪发放到班主任及相关人员手中.购买前有A,B两种型号的额温枪可供选择,已知每只A型额温枪比每只B型额温枪贵20元,用5000元购进A型额温枪与用4500元购进B型额温抢的数量相等.(1)每只A型,B型额温枪的价格各是多少元?(2)该校欲购进A,B两种型号的额温枪共30只,购买两种额温枪的总资金不超过5800元.则最多可购进A型号额温枪多少只?21.(本题满分12分)如图,∠BAD=∠CAE=90°,AB=AD,AE=AC, AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE;(2)求∠FAE的度数;(3)求证:CD=2BF+DE.22.(本题满分12分)在平面直角坐标系中,点A的坐标是(0,a),点B 的坐标(b,0) 且a,b 满足a2-12a+36+|a-b|=0.(1)求A,B两点的坐标;(2)如图(1),点C为x轴负半轴一动点,0C<OB,BD⊥AC于D,交y轴于点E.求证:OD 平分∠CDB.(3)如图(2),点F为AB的中点,点G为x正半轴点B右侧的一动点,过点F作FG 的垂线FH,交y轴的负半轴于点H,那么当点G的位置不断变化时,S△AFH-S△FBG 的值是否发生变化?若变化,请说明理由;若不变化,请求出相应结果.参考答案一、选择题BABCC DBABA BC二、填空题13. x(x+2y)(x-2y)14. 40°或10°15. x=—516. ∠A=12° 三、解答题 17(1)−281-a 11b 9(2)a 2-2ab18(1)x =−67 ,经检验:x =−67是分式方程的解.(2)x−2x,因为分式有意义时x≠±1,0.所以当x=2时,原式=x−2x=2−22=019(1)解:如图:∠A′B′C′即为所求;点A′(-2,2),B′(-1,-3),C′(-4,-2)(2)m=12 ,n=3(3)延长CB 交y 轴于点P ,P 为所求.20(1)解:设A 型额温枪的价格是x 元,B 型额温枪的价格是(x ﹣20)元.5000x=4500x−20,x =200,经检验:x =200是原方程的根,x ﹣20=180元.答:A 型额温枪的价格是200元,B 型额温枪的价格是180元.(2)解:设购进A 型号额温枪a 只,200a +180(30﹣a )≤5800,a≤20 答:最多可购进A 型号额温枪20只. 21(1)∠∠BAD=∠CAE=90°∠∠BAC+∠CAD=90°,∠CAD+∠DAE=90° ∠∠BAC=∠DAE 在∠BAC 和∠DAE 中 {AB =AD∠BAC =∠DAE AC =AE∠∠BAC∠∠DAE (SAS )(2)∠∠CAE=90°,AC=AE ∠∠E=45° ∠∠BAC∠∠DAE ∠∠BCA=∠E=45° ∠AF∠BC ∠∠CFA=90° ∠∠CAF=45° ∠∠FAE=∠FAC+∠CAE=45°+90°=135° (3)延长BF 到G ,使得FG=FB ∠AF∠BG ∠∠AFG=∠AFB=90°在∠AFB和∠AFG中{BF=GF ∠AFB=∠AFG AF=AF∠∠AFB∠∠AFG(SAS)∠AB=AG,∠ABF=∠G∠∠BAC∠∠DAE ∠AB=AD,∠CBA=∠EDA,CB=ED ∠AG=AD,∠ABF=∠CDA ∠∠G=∠CDA,在∠CGA和∠CDA中{∠GCA=∠DCA ∠CGA=∠CDA AG=AD∠∠CGA∠∠CDA ∠CG=CD∠CG=CB+BF+FG=CB+2BF=DE+2BF ∠CD=2BF+DE22(1)∠a2-12a+36+|a-b|=0∠(a-6)2+|a-b|=0∠ {a−6=0a−b=0∠a=b=6 ∠A(0,6) ,B(6,0)(2)如图,过点O作OM∠BD于M,ON∠AC于N.根据题意可知∠ACO+∠CAO=90°∠ BD∠AC ∠∠BCD+∠CBE=90° ∠∠CAO=∠CBE∠A(0,6) ,B(6,0) ∠OA=OB=6在∠AOC和∠BOE中{∠CAO=∠EBOOA=OB∠AOC=∠BOE=90°∠∠AOC∠∠BOE ∠OE=OC,AC=BE ,S ∠AOC =S ∠BOE ∠12AC·ON=12BE·OM ∠OM=ON∠点O 一定在∠CDB 的角平分线上 ∠ OD 平分∠CDB (3)解:如图,连接OF∠∠AOB 是等腰直角三角形且点F 为AB 的中点∠OF∠AB ,OF=FB ,OF 平分∠AOB ∠∠OFB=∠OFH+∠HFB=90° ∠FG∠FH ∠∠HFG=∠BFG+∠HFB=90° ∠ ∠OFH=∠BFG ∠ ∠FOB=12∠AOB=45° ∠∠FOH=∠HOB+∠FOB=90°+45°=135°∠∠FBG=180°-∠ABO=180°-45°=135° ∠∠OFH=∠BFG在∠FOH 和∠FBG 中 {∠OFH =∠BFGOF =BF ∠FOH =∠FBG∠∠FOH∠和∠FBG ∠S ∠FOH =S ∠FBG∠S ∠AFH -S ∠FBG =S ∠AFH -S ∠FOH =S ∠FOA =12S ∠AOB =12×12OA·OB=12×6×6=9所以不变,S ∠AFH =S ∠FBG =9。
