工程流体力学答案
工程流体力学课后习题答案

第1章 绪论【1-1】500cm 3的某种液体,在天平上称得其质量为0.453kg ,试求其密度和相对密度。
【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 相对密度330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水,在温度不变的条件下,当压强从98000Pa 增加到4.9×105Pa 时,体积减少1L 。
求水的压缩系数和弹性系数。
【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃,流量为60m 3/h 的水流入加热器,如果水的体积膨胀系数βt =0.00055K -1,问加热到80℃后从加热器中流出时的体积流量变为多少? 【解】根据膨胀系数1t dV V dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。
罐装时液面上压强为98000Pa 。
封闭后由于温度变化升高了20℃,此时汽油的蒸汽压力为17640Pa 。
若汽油的膨胀系数为0.0006K -1,弹性系数为13.72×106Pa ,(1)试计算由于压力温度变化所增加的体积,(2)问灌装时汽油的体积最多不应超过桶体积的百分之多少?【解】(1)由1β=-=P pdV Vdp E可得,由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积,可由1β=tt dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT(2)因为∆∆tp V V ,相比之下可以忽略由压力变化引起的体积改变,则由 200L β+=t V V dT得1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板,其水平运动速度为u =1m/s ,δ=10mm ,油品的粘度μ=0.9807Pa ·s ,求作用在平板单位面积上的阻力。
工程流体力学课后习题答案(第二版)

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
工程流体力学习题及答案

工程流体力学习题及答案(1)1 某种液体的比重为3,试求其比容。
(答:3.3×10-4米3/公斤)2 体积为5.26米3的某种油,质量为4480公斤,试求这种油的比重、密度与重度。
(答:0.85;851公斤/米3;8348牛/米3)3 若煤油的密度为0.8克/厘米3,试求按工程单位计算的煤油的重度、密度与比容。
(答:800公斤力/米3;81.56公斤力·秒2/米4;1.25×10-3米3/公斤力)4 试计算空气在温度t=4℃,绝对压力P=3.4大气压下的重度、密度与比容。
(答:42.4牛/米3;4.33公斤/米3;0.231米3/公斤)5 试计算二氧化碳在温度为t=85℃,绝对压力P=7.1大气压下的重度、密度与比容。
(答:104牛/米3;10.6公斤/米3;0.09厘米3/公斤 )6 空气在蓄热室内于定压下,温度自20℃增高为400℃,问空气的体积增加了多少倍? (答:1.3倍)7 加热炉烟道入口烟气的温度900=t 入℃,烟气经烟道及其中设置的换热器后,至烟道出口温度下降为500=t 出℃,若烟气在0℃时的密度为28.10=ρ公斤/米3,求烟道入口与出口处烟气的密度。
(答:298.0=ρ人公斤/米3;452.0=ρ出公斤/米3) 8 试计算一氧化碳在表压力为0.3大气压、温度为8℃下的重度。
(答:15.49牛/米3)9 已知速度为抛物线分布,如图示 y=0,4,8,12,17厘米处的速度梯度。
又若气体的绝对粘性系数为1013.25-⨯=μ牛·秒/米3,求以上各处气体的摩擦切应力。
9 题图10 夹缝宽度为h ,其中所放的很薄的大平板以定速v 移动。
若板上方流体的粘性系数为μ,下方流体的粘性系数为K μ,问应将大平板放在夹缝中何处,方能使其移动时阻力为最小?(答:h kk kh =++11或)11 如图所示,一正方形b ×b=67×67厘米2、质量为12公斤的平板,在厚3.1=δ毫米的油膜支承下,以匀速v=0.18米/秒沿一斜面滑下,问油的粘性系数是多少?10 题图 11 题图(答:0.728牛·秒/米2)12 如图所示,气缸直径D 1=16厘米,活塞直径D 2=16厘米,质量0.97公斤,若活塞以匀速0.05米/秒在气缺内下降,试求油的粘性系数是多少?12 题图 15 题图(答:0.63牛·秒/米2)13 直径为150毫米的圆柱,固定不动。
工程流体力学经典习题答案

第一章 流体及其主要物理性质1-1.轻柴油在温度15ºC 时相对密度为0.83,求它的密度和重度。
解:4ºC 时所以,33/8134980083.083.0/830100083.083.0mN m kg =⨯===⨯==水水γγρρ1-2.甘油在温度0ºC时密度为1.26g/cm 3,求以国际单位表示的密度和重度。
333/123488.91260/1260/26.1m N g m kg cm g =⨯==⇒==ργρ 1-3.水的体积弹性系数为1.96×109N/m 2,问压强改变多少时,它的体积相对压缩1%?MPa Pa E E VVVV p p6.191096.101.07=⨯==∆=∆=∆β 1-4.容积4m 3的水,温度不变,当压强增加105N/m 2时容积减少1000cm 3,求该水的体积压缩系数βp 和体积弹性系数E 。
解:1956105.2104101000---⨯=⨯--=∆∆-=Pa p V V pβ Pa E p89104105.211⨯=⨯==-β 1-5. 用200L 汽油桶装相对密度为0.70的汽油,罐装时液面上压强为1个大气压,封闭后由于温度变化升高了20ºC ,此时汽油的蒸气压为0.18大气压。
若汽油的膨胀系数为0.0006ºC -1,弹性系数为14000kg/cm 2。
试计算由于压力及温度变化所增减的体积?问灌桶时每桶最多不超过多少公斤为宜?解:E =E ’·g =14000×9.8×104PaΔp =0.18atdp pV dT T V dV ∂∂+∂∂=00V T V T V V T T ββ=∂∂⇒∂∂=00V pVp V V p p ββ-=∂∂⇒∂∂-= 所以,dp V dT V dp pVdT T V dV p T 00ββ-=∂∂+∂∂=从初始状态积分到最终状态得:LL L V p p EV T T V V dpV dT V dV T p pp T TT VV 4.21057.24.2200108.914000108.918.020*******.0)(1)(34400000000≈⨯-=⨯⨯⨯⨯⨯-⨯⨯=---=--=-⎰⎰⎰βββ即()kg V V M 32.13810004.220010007.0=-⨯⨯=∆-=ρ另解:设灌桶时每桶最多不超过V 升,则200=++p t dV dV VV dt V dV t t 2000061.0⨯=⋅⋅=βV dp V dV p p 18.0140001⨯-=⋅⋅-=β(1大气压=1Kg/cm 2)V =197.6升 dV t =2.41升 dV p =2.52×10-3升G =0.1976×700=138Kg =1352.4N 1-6.石油相对密度0.9,粘度28cP ,求运动粘度为多少m 2/s?解:s Pa P s Pa s mPa P cP ⋅=⋅=⋅==--1.0110110132()cSt St s m 3131.0/101.310009.01028253==⨯=⨯⨯==--ρμν1-7.相对密度0.89的石油,温度20ºC 时的运动粘度为40cSt ,求动力粘度为多少?解:89.0==水ρρd ν=40cSt =0.4St =0.4×10-4m 2/sμ=νρ=0.4×10-4×890=3.56×10-2Pa ·s 1-8.图示一平板在油面上作水平运动,已知运动速度u=1m/s ,板与固定边界的距离δ=1,油的动力粘度μ=1.147Pa ·s ,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:233/10147.11011147.1m N dy du ⨯=⨯⨯==-μτ 1-9.如图所示活塞油缸,其直径D =12cm ,活塞直径d =11.96cm ,活塞长度L =14cm ,油的μ=0.65P ,当活塞移动速度为0.5m/s 时,试求拉回活塞所需的力F=?解:A =πdL , μ=0.65P =0.065 Pa ·s , Δu =0.5m/s , Δy=(D-d)/2()N dy du AF 55.821096.11125.010141096.1114.3065.0222=⨯-⨯⨯⨯⨯⨯⨯==---μ第二章 流体静力学2-1. 如图所示的U 形管中装有水银与水,试求:(1)A 、C 两点的绝对压力及表压各为多少? (2)A 、B 两点的高度差为多少?解:① p A 表=γh 水=0.3mH 2O =0.03at =0.3×9800Pa=2940Pa p A 绝=p a + p A 表=(10+0.3)mH 2O =1.03at =10.3×9800Pa=100940Pap C 表=γhg h hg + p A 表=0.1×13.6mH 2O+0.3mH 2O =1.66mH 2O =0.166at= 1.66×9800Pa =16268Pap C 绝=p a + p C 表=(10+1.66)mH 2O =11.66 mH 2O =1.166at =11.66×9800Pa=114268Pa② 30cmH 2O =13.6h cmH 2O ⇒h =30/13.6cm=2.2cm题2-2 题2-32-2.水银压力计装置如图。
工程流体力学课后习题答案

流体及其主要物理性质7 相对密度0.89的石油,温度20ºC 时的运动粘度为40cSt ,求动力粘度为多少?解:89.0==水ρρdν=40cSt =0.4St =0.4×10-4m 2/sμ=νρ=0.4×10-4×890=3.56×10-2Pa ·s8 图示一平板在油面上作水平运动,已知运动速度u=1m/s ,板与固定边界的距离δ=1,油的动力粘度μ=1.147Pa ·s ,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:233/10147.11011147.1m N dy du ⨯=⨯⨯==-μτ9 如图所示活塞油缸,其直径D =12cm ,活塞直径d =11.96cm ,活塞长度L =14cm ,油的μ=0.65P ,当活塞移动速度为0.5m/s 时,试求拉回活塞所需的力F=?解:A =πdL , μ=0.65P =0.065 Pa ·s , Δu =0.5m/s , Δy=(D-d)/2()N dy du AF 55.821096.11125.010141096.1114.3065.0222=⨯-⨯⨯⨯⨯⨯⨯==---μ流体静力学6油罐内装相对密度0.70的汽油,为测定油面高度,利用连通器原理,把U 形管内装上相对密度为1.26的甘油,一端接通油罐顶部空间,一端接压气管。
同时,压气管的另一支引入油罐底以上0.40m 处,压气后,当液面有气逸出时,根据U 形管内油面高差h =0.70m 来推算油罐内的油深H 为多少?解:p -γ甘油Δh =p -γ汽油(H-0.4)H =γ甘油Δh/γ汽油+0.4=1.26×0.7/0.70+0.4=1.66m7为测定油品重度,用如下装置,经过1管或2管输入气体,直至罐内油面出现气泡为止。
用U 形管水银压力计分别量出1管通气时的Δh 1,及2管通气时的Δh 2。
工程流体力学习题及答案

第1章 绪论选择题【1.1】 按连续介质的概念,流体质点是指:(a )流体的分子;(b )流体内的固体颗粒;(c )几何的点;(d )几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
解:流体质点是指体积小到可以看作一个几何点,但它又含有大量的分子,且具有诸如速度、密度及压强等物理量的流体微团。
(d )【1.2】 与牛顿内摩擦定律直接相关的因素是:(a )切应力和压强;(b )切应力和剪切变形速度;(c )切应力和剪切变形;(d )切应力和流速。
解:牛顿内摩擦定律是d d v y τμ=,而且速度梯度d d vy 是流体微团的剪切变形速度d d t γ,故d d t γτμ=。
(b )【1.3】 流体运动黏度υ的国际单位是:(a )m 2/s ;(b )N/m 2;(c )kg/m ;(d )N·s/m 2。
解:流体的运动黏度υ的国际单位是/s m 2。
(a )【1.4】 理想流体的特征是:(a )黏度是常数;(b )不可压缩;(c )无黏性;(d )符合RT p =ρ。
解:不考虑黏性的流体称为理想流体。
(c ) 【1.5】当水的压强增加一个大气压时,水的密度增大约为:(a )1/20 000;(b )1/1 000;(c )1/4 000;(d )1/2 000。
解:当水的压强增加一个大气压时,其密度增大约95d 1d 0.51011020 000k p ρρ-==⨯⨯⨯=。
(a )【1.6】 从力学的角度分析,一般流体和固体的区别在于流体:(a )能承受拉力,平衡时不能承受切应力;(b )不能承受拉力,平衡时能承受切应力;(c )不能承受拉力,平衡时不能承受切应力;(d )能承受拉力,平衡时也能承受切应力。
解:流体的特性是既不能承受拉力,同时具有很大的流动性,即平衡时不能承受切应力。
(c ) 【1.7】下列流体哪个属牛顿流体:(a )汽油;(b )纸浆;(c )血液;(d )沥青。
《工程流体力学》试题及答案

《工程流体力学》试题及答案一、选择题(每题3分,共15分)1. 下列哪个选项不是流体力学的分支?A. 流体静力学B. 流体动力学C. 流体力学实验D. 流体力学数值模拟答案:C2. 下列哪种流体是不可压缩流体?A. 水蒸气B. 液体C. 气体D. 所有流体答案:B3. 下列哪个方程描述了流体运动的基本规律?A. 连续性方程B. 动量方程C. 能量方程D. 上述都是答案:D4. 在伯努利方程中,流速增加时,压力会?A. 增加B. 减少C. 不变D. 无法确定答案:B5. 下列哪个因素对流体流动的影响最小?A. 流体的粘度B. 流体的密度C. 流体的温度D. 流体的流速答案:C二、填空题(每题3分,共15分)1. 流体力学研究的对象是______。
答案:流体2. 流体的连续性方程表达了______与______之间的关系。
答案:流量,流速3. 流体力学中的动量方程是由______和______推导得出的。
答案:牛顿第二定律,动量定理4. 在伯努利方程中,流速与压力之间的关系为:流速越______,压力越______。
答案:大,小5. 流体力学实验中,常用的测量流体流速的仪器是______。
答案:流速仪三、计算题(每题20分,共60分)1. 已知一圆柱形管道,直径为0.2米,管道中水流速度为2米/秒,水的密度为1000千克/立方米,水的粘度为0.001帕·秒。
求管道中的压力分布。
解答:首先,根据连续性方程,计算管道中的流量Q:Q = A v = π (d/2)^2 v = π (0.2/2)^2 2 = 0.0628 m^3/s然后,根据伯努利方程,计算管道中的压力分布:P1 + 1/2 ρ v1^2 + ρ g h1 = P2 + 1/2 ρ v2^2 + ρ g h2由于管道为水平管道,h1 = h2,所以可以简化为:P1 + 1/2 ρ v1^2 = P2 + 1/2 ρ v2^2代入已知数据,得到:P1 + 1/2 1000 2^2 = P2 + 1/2 1000 2^2解得:P1 = P2所以,管道中的压力分布为均匀分布。
(完整版)工程流体力学课后习题答案(第二版)

第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==Θ原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμΘ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=Θ)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yuATmgddsinμθ==001.0145.04.062.22sin8.95sin⨯⨯⨯⨯==δθμuAmgsPa1047.0⋅=μ1-5.已知液体中流速沿y方向分布如图示三种情况,试根据牛顿内摩擦定律yuddμτ=,定性绘出切应力沿y方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
已知导线直径0.9mm,长度20mm,涂料的粘度μ=0.02Pa.s。
《工程流体力学》习题答案

封面作者:Pan Hongliang仅供个人学习第一章流体及其主要物理性质1-1.轻柴油在温度15ºC时相对密度为0.83,求它的密度和重度。
解:4ºC时相对密度:所以,1-2.甘油在温度0ºC时密度为1.26g/cm3,求以国际单位表示的密度和重度。
解:1-3.水的体积弹性系数为1.96×109N/m2,问压强改变多少时,它的体积相对压缩1%?解:1-4.容积4m3的水,温度不变,当压强增加105N/m2时容积减少1000cm3,求该水的体积压缩系数βp和体积弹性系数E。
解:1-5.用200L汽油桶装相对密度为0.70的汽油,罐装时液面上压强为1个大气压,封闭后由于温度变化升高了20ºC,此时汽油的蒸气压为0.18大气压。
若汽油的膨胀系数为0.0006ºC-1,弹性系数为14000kg/cm2。
试计算由于压力及温度变化所增减的体积?问灌桶时每桶最多不超过多少公斤为宜?解:E=E’·g=14000×9.8×104PaΔp=0.18at所以,从初始状态积分到最终状态得:另解:设灌桶时每桶最多不超过V升,则(1大气压=1Kg/cm2)V=197.6升dV t=2.41升dV p=2.52×10-3升G=0.1976×700=138Kg=1352.4N1-6.石油相对密度0.9,粘度28cP,求运动粘度为多少m2/s?解:1-7.相对密度0.89的石油,温度20ºC时的运动粘度为40cSt,求动力粘度为多少?解:ν=40cSt=0.4St=0.4×10-4m2/sμ=νρ=0.4×10-4×890=3.56×10-2 Pa·s1-8.图示一平板在油面上作水平运动,已知运动速度u=1m/s,板与固定边界的距离δ=1,油的动力粘度μ=1.147Pa·s,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:1-9.如图所示活塞油缸,其直径D=12cm,活塞直径d=11.96cm,活塞长度L=14cm,油的μ=0.65P,当活塞移动速度为0.5m/s时,试求拉回活塞所需的力F=?解:A=πdL , μ=0.65P=0.065 Pa·s , Δu=0.5m/s , Δy=(D-d)/2第二章流体静力学2-1. 如图所示的U形管中装有水银与水,试求:(1)A、C两点的绝对压力及表压各为多少?(2)A、B两点的高度差为多少?解:①p A表=γh水=0.3mH2O=0.03at=0.3×9800Pa=2940Pap A绝=p a+ p A表=(10+0.3)mH2O=1.03at=10.3×9800Pa=100940Pap C表=γhg h hg+ p A表=0.1×13.6m H2O+0.3mH2O=1.66mH2O=0.166at=1.66×9800Pa=16268Pap C绝=p a+ p C表=(10+1.66)mH2O=11.66 mH2O=1.166at=11.66×9800Pa=114268Pa② 30c mH2O=13.6h cmH2Oh=30/13.6cm=2.2cm题2-2 题2-32-2.水银压力计装置如图。
(完整版)工程流体力学习题及答案.doc

第 1 章绪论选择题( a )流体的分子; ( b )流体内的固体颗粒; 【1.1 】 按连续介质的概念,流体质点是指:( c )几何的点;( d )几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
解:流体质点是指体积小到可以看作一个几何点,但它又含有大量的分子, 且具有诸如速度、密度及压强等物理量的流体微团。
( d )【1.2 】 与牛顿内摩擦定律直接相关的因素是:( a )切应力和压强; ( b )切应力和剪切变 形速度;( c )切应力和剪切变形; ( )切应力和流速。
ddv dv解:牛顿内摩擦定律是dy,而且速度梯度dy是流体微团的剪切变形速度dddt ,故dt 。
( b )【1.3 】 流体运动黏度 υ 的国际单位是: ( a ) m 2/s ;( ) N/m 2 ;( ) kg/m ;( )N ·s/m 2。
bcd解:流体的运动黏度 υ 的国际单位是 m 2 /s 。
( a )p 【1.4 】 理想流体的特征是:( a)黏度是常数;( b )不可压缩;( c )无黏性;( d )符合RT。
解:不考虑黏性的流体称为理想流体。
( c )【1.5 】当 水的 压 强 增 加一 个 大 气 压 时, 水 的 密 度 增 大约 为 :( a ) 1/20 000 ;( b ) 1/1 000 ;( c ) 1/4 000 ;( d ) 1/2 000 。
解 : 当 水 的 压 强 增 加 一 个 大 气 压 时 , 其 密 度 增 大 约 dkdp0.5 10 9 1 105120 000 。
( a )【1.6 】 从力学的角度分析,一般流体和固体的区别在于流体:( a)能承受拉力,平衡时不能承受切应力; ( )不能承受拉力,平衡时能承受切应力; ( )不能承受拉力,bc平衡时不能承受切应力; (d )能承受拉力,平衡时也能承受切应力。
解:流体的特性是既不能承受拉力, 同时具有很大的流动性, 即平衡时不能承受切应力。
工程流体力学答案..

工程流体力学习题详解第一章 流体的物理性质【1-1】500cm 3的某种液体,在天平上称得其质量为0.453kg ,试求其密度和相对密度。
【解】3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 330.906100.9061.010w ρδρ⨯===⨯【1-2】 体积为5m 3的水,在温度不变的条件下,当压强从98000Pa 增加到4.9×105Pa 时,体积减少1升。
求水的压缩系数和弹性系数。
【解】由压缩系数公式10510.001 5.110 1/Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 9111.9610 Pa 5.1pE β===⨯ 【1-3】温度为20℃,流量为60 m 3/h 的水流入加热器,如果水的体积膨胀系数βt =0.00055K -1,问加热到80℃后从加热器中流出时的体积流量变为多少?【解】根据膨胀系数1t dVV dtβ=则211t Q Q dt Q β=+3600.00055(8020)6061.98 m /h =⨯⨯-+=【1-4】图中表示浮在油面上的平板,其水平运动速度为u =1m/s ,δ=10mm ,油品的粘度μ=0.9807Pa ·s ,求作用在平板单位面积上的阻力。
【解】根据牛顿内摩擦定律=du dy τμ则21=0.980798.07N/m 0.01τ⨯= 【1-5】已知半径为R 圆管中的流速分布为22=(1)r u c R-式中c 为常数。
试求管中的切应力τ与r 的关系。
【解】根据牛顿内摩擦定律=dudy τμ则2222=[(1)]d r r c c dr R Rτμμ-=-第二章 流体静力学【2-1】容器中装有水和空气,求A 、B 、C 和D 各点的表压力?【解】34342223232()()()(2)MA MB MA MC MB MD MC p g h h p p g h h h gh p p gh p p g h h g h h ρρρρρρ=+=-++=-==-=-+=-+【2-2】如图所示的U 形管中装有水银与水,试求:(1)A 、C 两点的绝对压力及表压力各为多少? (2)求A 、B 两点的高度差h ? 【解】(1) ()w 0.3ab A a p p g ρ=+⨯w 0.3MA p g ρ=⨯()w H 0.30.1ab C a p p g g ρρ=+⨯+⨯w H 0.30.1MC p g g ρρ=⨯+⨯(2)选取U 形管中水银的最低液面为等压面,则w H 0.3g gh ρρ⨯= 得 w H0.322 cm h ρρ⨯==【2-3】 在一密闭容器内装有水及油,密度分别为ρw 及ρo ,油层高度为h 1,容器底部装有水银液柱压力计,读数为R ,水银面与液面的高度差为h 2,试导出容器上方空间的压力p 与读数R 的关系式。
(完整版)工程流体力学习题及答案

(完整版)工程流体力学习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第1章 绪论选择题【1.1】 按连续介质的概念,流体质点是指:(a )流体的分子;(b )流体内的固体颗粒;(c )几何的点;(d )几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
解:流体质点是指体积小到可以看作一个几何点,但它又含有大量的分子,且具有诸如速度、密度及压强等物理量的流体微团。
(d )【1.2】 与牛顿内摩擦定律直接相关的因素是:(a )切应力和压强;(b )切应力和剪切变形速度;(c )切应力和剪切变形;(d )切应力和流速。
解:牛顿内摩擦定律是d d v y τμ=,而且速度梯度d d v y 是流体微团的剪切变形速度d d t γ,故d d t γτμ=。
(b )【1.3】流体运动黏度υ的国际单位是:(a )m 2/s ;(b )N/m 2;(c )kg/m ;(d )N·s/m 2。
解:流体的运动黏度υ的国际单位是/s m 2。
(a )【1.4】理想流体的特征是:(a )黏度是常数;(b )不可压缩;(c )无黏性;(d )符合RTp=ρ。
解:不考虑黏性的流体称为理想流体。
(c )【1.5】当水的压强增加一个大气压时,水的密度增大约为:(a )1/20 000;(b )1/1 000;(c )1/4 000;(d )1/2 000。
解:当水的压强增加一个大气压时,其密度增大约95d 1d 0.51011020 000k p ρρ-==⨯⨯⨯=。
(a )【1.6】 从力学的角度分析,一般流体和固体的区别在于流体:(a )能承受拉力,平衡时不能承受切应力;(b )不能承受拉力,平衡时能承受切应力;(c )不能承受拉力,平衡时不能承受切应力;(d )能承受拉力,平衡时也能承受切应力。
解:流体的特性是既不能承受拉力,同时具有很大的流动性,即平衡时不能承受切应力。
工程流体力学课后习题答案

第一章 绪论1-1.20℃的水,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==Θ原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμΘ此时动力粘度μ增加了%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=Θ)(002.0y h g dydu-==∴ρμτ 当h =,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]1-6.为导线表面红绝缘,将导线从充满绝缘涂料的模具中拉过。
已知导线直径,长度20mm ,涂料的粘度μ=.s 。
工程流体力学习题与答案

第1章 绪论选择题【1.1】 按连续介质的概念,流体质点是指:(a )流体的分子;(b )流体内的固体颗粒;(c )几何的点;(d )几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
解:流体质点是指体积小到可以看作一个几何点,但它又含有大量的分子,且具有诸如速度、密度及压强等物理量的流体微团。
(d ) 【1.2】 与牛顿内摩擦定律直接相关的因素是:(a )切应力和压强;(b )切应力和剪切变形速度;(c )切应力和剪切变形;(d )切应力和流速。
解:牛顿内摩擦定律是d d v y τμ=,而且速度梯度d d vy 是流体微团的剪切变形速度d d t γ,故d d t γτμ=。
(b )【1.3】 流体运动黏度υ的国际单位是:(a )m 2/s ;(b )N/m 2;(c )kg/m ;(d )N ·s/m 2。
解:流体的运动黏度υ的国际单位是/s m 2。
(a )【1.4】 理想流体的特征是:(a )黏度是常数;(b )不可压缩;(c )无黏性;(d )符合RTp =ρ。
解:不考虑黏性的流体称为理想流体。
(c )【1.5】当水的压强增加一个大气压时,水的密度增大约为:(a )1/20 000;(b )1/1 000;(c )1/4 000;(d )1/2 000。
解:当水的压强增加一个大气压时,其密度增大约95d 1d 0.51011020 000k p ρρ-==⨯⨯⨯=。
(a )【1.6】 从力学的角度分析,一般流体和固体的区别在于流体:(a )能承受拉力,平衡时不能承受切应力;(b )不能承受拉力,平衡时能承受切应力;(c )不能承受拉力,平衡时不能承受切应力;(d )能承受拉力,平衡时也能承受切应力。
解:流体的特性是既不能承受拉力,同时具有很大的流动性,即平衡时不能承受切应力。
(c )【1.7】下列流体哪个属牛顿流体:(a )汽油;(b )纸浆;(c )血液;(d )沥青。
工程流体力学 课后习题(简精版)答案

第一章 流体及其主要物理性质1-1.轻柴油在温度15ºC 时相对密度为0.83,求它的密度和重度。
解:4ºC 时所以,33/8134980083.083.0/830100083.083.0mN m kg =⨯===⨯==水水γγρρ1-2.甘油在温度0ºC 时密度为1.26g/cm3,求以国际单位表示的密度和重度。
333/123488.91260/1260/26.1m N g m kg cm g =⨯==⇒==ργρ 1-3.水的体积弹性系数为1.96×109N/m 2,问压强改变多少时,它的体积相对压缩1%?MPa Pa E E VVVV p p6.191096.101.07=⨯==∆=∆=∆β 1-4.容积4m 3的水,温度不变,当压强增加105N/m 2时容积减少1000cm 3,求该水的体积压缩系数βp 和体积弹性系数E 。
解:1956105.2104101000---⨯=⨯--=∆∆-=Pa p V V p β Pa E p89104105.211⨯=⨯==-β 1-5石油相对密度0.9,粘度28cP ,求运动粘度为多少m 2/s?()cSt St s m 3131.0/101.310009.01028253==⨯=⨯⨯==--ρμν 1-6 相对密度0.89的石油,温度20ºC 时的运动粘度为40cSt ,求动力粘度为多少? 解:89.0==水ρρd ν=40cSt =0.4St =0.4×10-4m 2/s μ=νρ=0.4×10-4×890=3.56×10-2 Pa ·s1-7 图示一平板在油面上作水平运动,已知运动速度u=1m/s ,板与固定边界的距离δ=1mm ,油的动力粘度μ=1.147Pa ·s ,由平板所带动的油层的运动速度呈直线分布,求作用在平板单位面积上的粘性阻力为多少?解:233/10147.11011147.1m N dy du ⨯=⨯⨯==-μτ 1-8 如图所示活塞油缸,其直径D =12cm ,活塞直径d =11.96cm ,活塞长度L =14cm ,油的μ=0.65P ,当活塞移动速度为0.5m/s 时,试求拉回活塞所需的力F=?解:A =πdL , μ=0.65P =0.065 Pa ·s , Δu =0.5m/s , Δy=(D-d)/2()N dy du AF 55.821096.11125.010141096.1114.3065.0222=⨯-⨯⨯⨯⨯⨯⨯==---μ第二章 流体静力学2-1. 如图所示的U 形管中装有水银与水,试求:(1)A 、C 两点的绝对压力及表压各为多少? (2)A 、B 两点的高度差为多少?解:① p A 表=γh 水=0.3mH 2O =0.03at =0.3×9800Pa =2940Pap A 绝=p a + p A 表=(10+0.3)mH 2O =1.03at =10.3×9800Pa=100940Pap C 表=γhg h hg + p A 表=0.1×13.6m H 2O+0.3mH 2O =1.66mH 2O =0.166at=1.66×9800Pa =16268Pap C 绝=p a + p C 表=(10+1.66)mH 2O =11.66 mH 2O =1.166at =11.66×9800Pa =114268Pa ② 30c mH 2O =13.6h cmH 2O ⇒h =30/13.6cm=2.2cm题2-22-2 今有U 形管,内装水和四氯化碳(CCl 4),如图所示。
工程流体力学答案(整理)
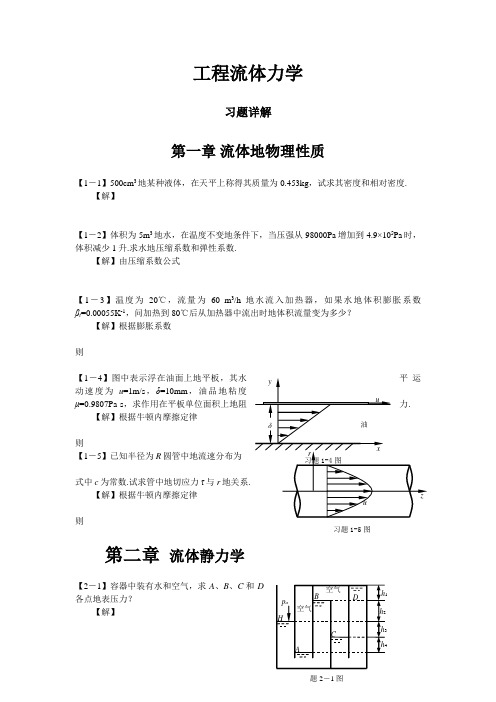
工程流体力学习题详解第一章流体地物理性质【1-1】500cm3地某种液体,在天平上称得其质量为0.453kg,试求其密度和相对密度.【解】【1-2】体积为5m3地水,在温度不变地条件下,当压强从98000Pa增加到4.9×105Pa时,体积减少1升.求水地压缩系数和弹性系数.【解】由压缩系数公式【1-3】温度为20℃,流量为60 m3/h地水流入加热器,如果水地体积膨胀系数βt=0.00055K-1,问加热到80℃后从加热器中流出时地体积流量变为多少?【解】根据膨胀系数则【1-4】图中表示浮在油面上地平板,其水动速度为u=1m/s,δ=10mm,油品地粘度μ=0.9807Pa·s,求作用在平板单位面积上地阻【解】根据牛顿内摩擦定律则【1-5】已知半径为R圆管中地流速分布为式中c为常数.试求管中地切应力τ与r地关系.【解】根据牛顿内摩擦定律则习题1-5图第二章流体静力学【2-1】容器中装有水和空气,求A、B、C和D【解】题2-1图【2-2】如图所示地U 形管中装有水银与水,试求:(1)A 、C 两点地绝对压力及表压力各为多少? (2)求A 、B 两点地高度差h ? 【解】 (1)(2)选取U 形管中水银地最低液面为等压面,则 得 【2-3】在一密闭容器内装有水及油,密度分别为ρw 及ρo ,油层高度为h 1,容器底部装有水银液柱压力计,读数为R ,水银面与液面地高度差为h 2,试导出容器上方空间地压力p 与读数R 地关系式.【解】选取压力计中水银最低液面为等压面,则得 【2-4】油罐内装有相对密度为0.7地汽油,为测定油面高度,利用连通器原理,把U 形管内装上相对密度为 1.26地甘油,一端接通油罐顶部空间,一端接压气管.同时,压力管地另一支引入油罐底以上地0.4m 处,压气后,当液面有气逸出时,根据U 形管内油面高度差△h =0.7m 来计算油罐内地油深H =?【解】选取U 形管中甘油最低液面为等压面,由气体各点压力相等,可知油罐底以上0.4m 处地油压即为压力管中气体压力,则得【2-5】图示两水管以U 形压力计相连,A 、B 两点高差1m ,U 形管内装有水银,若读数△h =0.5m ,求A 、B 两点地压力差为多少?【解】选取U 形管内水银最低液面为等压面,设B 点到水银最高液面地垂直高度为x ,则得【2-6】图示油罐发油装置,将直径为d 地圆管伸进罐内,端部切成45°角,用盖板盖住,盖板可绕管端上面地铰链旋转,借助绳系上来开启.已知油深H =5m ,圆管直径d =600mm ,油品相对密度0.85,不计盖板重力及铰链地摩擦力,求提升此盖板B题2-3图题2-4图所需地力地大小?(提示:盖板为椭圆形,要先算出长轴2b 和短轴2a ,就可算出盖板面积A =πab ).【解】分析如图所示以管端面上地铰链为支点,根据力矩平衡其中可得【2-7】图示一个安全闸门,宽为0.6m ,高为1.0m.距底边0.4m 处装有闸门转轴,使之仅可以绕转轴顺时针方向旋转.不计各处地摩擦力,问门前水深h 为多深时,闸门即可自行打开?水深h 小,即D 点上移.当D 好平衡.即得 【2-8】有一压力贮油箱(见图),其宽度(垂直于纸面方向)b =2m ,箱内油层厚h 1=1.9m ,密度ρ0=800kg/m 3,油层下有积水,厚度h 2=0.4m ,箱底有一U 型水银压差计,所测之值如图所示,试求作用在半径R =1m 地圆柱面AB 上地总压力(大小和方向).【解】分析如图所示,首先需确定自由液面,选取水银压差计最低液面为等压面,则由p B 不为零可知等效自由液面地高度曲面水平受力曲面垂直受力则【2-9】一个直径2m ,长5m 地圆柱体放置在图示地斜坡上.求圆柱体所受地水平力和浮力.【解】分析如图所示,因为斜坡地倾斜角为60°,故/ρo g题2-8题2-9经D 点过圆心地直径与自由液面交于F 点.BC 段和CD 段水平方向地投影面积相同,力方向相反,相互抵消,故 圆柱体所受地水平力圆柱体所受地浮力【2-10】图示一个直径D =2m ,长L =1m 地圆柱体,其左半边为油和水,油和水地深度均为1m.已知油地密度为ρ=800kg/m 3,求圆柱体所受水平力和浮力.【解】因为左半边为不同液体,故分别来分析AB 段和BC 段曲面地受力情况.AB 曲面受力BC 曲面受力则,圆柱体受力(方向向上)【2-11】图示一个直径为 1.2m 地钢球安装在一直径为1m 地阀座上,管内外水面地高度如图所示.试求球体所受到地浮力.【解】分析如图所示,图中实压力体(+)为一圆柱体,其直径为1.0m【2-12】图示一盛水地密闭容器,中间用隔板将其分隔为上下两部分.隔板中有一直径d =25cm 地圆孔,并用一个直径D =50cm 质量M =139kg 地圆球堵塞.设容器顶部压力表读数p M =5000Pa ,求测压管中水面高x 大于若干时,圆球即被总压力向上顶开?【解】分析如图所示,图中虚压力体(-)为一球体和圆柱体体积之和 根据受力分析可知则 ※【2-13】水车长3m ,宽 1.5m ,高1.8m ,盛水深1.2m ,见图2-2.试问为使水不益处,加速度a 地允许值是多少.【解】根据自由夜面(即等压面方程)题2-10图题2-11图图2-13图得第三章 流体运动学【3-1】已知流场地速度分布为 u =x 2y i -3y j +2z 2k(1)属几元流动?(2)求(x , y , z )=(3, 1, 2)点地加速度? 【解】(1)由流场地速度分布可知流动属三元流动. (2)由加速度公式得故过(3, 1, 2)点地加速度其矢量形式为:【3-2】已知流场速度分布为u x =x 2,u y =y 2,u z =z 2,试求(x , y , z )=(2, 4, 8)点地迁移加速度?【解】由流场地迁移加速度得故过(2, 4, 8)点地迁移加速度【3-3】有一段收缩管如图.已知u 1=8m/s ,u 2=2m/s ,l =1.5m.试求2点地迁移加速度.【解】由已知条件可知流场地迁移加速度为其中:则2点地迁移加速度为【3-4】某一平面流动地速度分量为u x =-4y ,u y =4x .求流线方程.【解】由流线微分方程得解得流线方程【3-5】已知平面流动地速度为,式中B 为常数.求流线方程.【解】由已知条件可知平面流动地速度分量题3-3 图代入流线微分方程中,则解得流线方程【3-6】用直径200mm地管输送相对密度为0.7地汽油,使流速不超过1.2m/s,问每秒最多输送多少kg?【解】由流量公式可知则【3-7】截面为300mm×400mm地矩形孔道,风量为2700m3/h,求平均流速.如风道出口处截面收缩为150mm×400mm,求该处断面平均流速.【解】由流量公式可知则如风道出口处截面收缩为150mm×400mm,则【3-8】已知流场地速度分布为u x=y+z,u y=z+x,u z=x+y,判断流场流动是否有旋?【解】由旋转角速度可知故为无旋流动.【3-9】下列流线方程所代表地流场,哪个是有旋运动?(1)2Axy=C(2)Ax+By=C(3)A ln xy2=C【解】由流线方程即为流函数地等值线方程,可得(1)速度分布旋转角速度可知故为无旋流动.(2)速度分布旋转角速度可知故为无旋流动.(3)速度分布旋转角速度可知故为有旋流动.【3-10】已知流场速度分布为u x =-cx ,u y =-cy ,u z =0,c 为常数.求:(1)欧拉加速度a =?;(2)流动是否有旋?(3)是否角变形?(4)求流线方程.【解】(1)由加速度公式得(2)旋转角速度可知故为无旋流动.(3)由角变形速度公式可知为无角变形.(4)将速度分布代入流线微分方程解微分方程,可得流线方程第四章 流体动力学【4-1】直径d =100mm 地虹吸管,位置如附图中所示.求流量和2、3地压力.不计水头损失.【解】选取4点所在断面和1点所在断面列伯努力方程,以过4点地水平线为基准线.得,则选取1、2点所在断面列伯努利方程,以过1点地水平线为基准线(v 2=v 4)得选取1、3点所在断面列伯努利方程,以过1点地水平线为基准线(v 3=v 4)得【4-2】一个倒置地U 形测压管,上部为相对密度0.8地油,用来测定水管中点地速度.若读数△h =200mm ,求管中流速u =?【解】选取如图所示1-1、2-2断面列伯努利方程,以水管轴线为基准线同时,选取U 形测压管中油地最高液面为等压面,则题 4-1图题 4-2图【4-3】图示为一文丘里管和压力计,试推导体积流量和压力计读数之间地关系式.当z 1=z 2时,ρ=1000kg/m 3,ρH =13.6×103kg/m 3,d 1=500mm ,d 2=50mm ,H =0.4m ,流量系数α=0.9时,求Q =?【解】列1-1、2-2所在断面地伯努利方程、以过1-1断面中心点地水平线为基准线.选取压力计中汞地最低液面为等压面,则 又由、,得所以【4-4】管路阀门关闭时,压力表读数为49.8kPa ,阀门打开后,读数降为9.8kPa.设从管路进口至装表处地水头损失为流速水头地2倍,求管路中地平均流速.【解】当管路阀门关闭时,由压力表度数可确定管路轴线到自有液面地高度H当管路打开时,列1-1和2-2断面地伯努利方程,则得【4-5】为了在直径D =160mm 地管线上自动掺入另一种油品,安装了如下装置:自锥管喉道处引出一个小支管通入油池内.若压力表读数为2.3×105Pa ,吼道直径d =40mm ,T 管流量Q =30 l/s ,油品地相对密度为0.9.欲掺入地油品地相对密度为0.8,油池油面距喉道高度H =1.5m ,如果掺入油量约为原输量地10%左右,B 管水头损失设为0.5m ,试确定B 管地管径.【解】列1-1和2-2断面地伯努利方程,则 其中得列3-3和4-4自有液面地伯努利方程,以4-4断面为基准面,则其中、,代入上式,得27mm 【4-6】一变直径地管段AB ,直径d A =0.2m ,d B =0.4m ,高差h =1.0m ,用压力表测得p A =70kPa ,p B =40kPa ,用流量计测得流量Q =0.2m 3/s.试判断水在管段中流动地方向.题 4-4图题 4-5图题 4-3图【解】列A 点和B 点所在断面地伯努利方程则故流动方向为A -B .【4-7】泄水管路如附图所示,已知直径d 1=125mm ,d 2=100mm ,d 3=75mm ,汞比压力计读数h =175mm ,不计阻力,求流量和压力表读数.【解】列1-1、2-2断面地波努利方程又由(即) 可得、、 列压力表所在断面和出口断面地伯努利方程可得【4-8】如图所示,敞开水池中地水沿变截面管路排出地质量流量Q m =14kg/s ,若d 1=100mm ,d 2=75mm ,d 3=50mm ,不计损失,求所需地水头H ,以及第二段管段中央M 点地压力,并绘制测压管水头线.【解】列1-1和3-3断面地伯努利方程,则其中 、 得列M 点所在断面2-2和3-3断面地伯努利方程,则 得【4-9】由断面为0.2m 2和0.1 m 2地两根管子组成地水平输水管系从水箱流入大气中:○1若不计损失,(a )求断面流速v 1及v 2;(b )绘总水头线及测压管水头线;(c )求进口A点地压力.○2计入损失:第一段地水头损失为流速水头地4倍,第二段为3倍,(a )求断面流速v 1及v 2;(b )绘制总水头线及测压管水头线;(c )根据所绘制水头线求各管段中间点地压力.【解】(1)列自有液面和管子出口断面地伯努利方程,则得 又由得列A 点所在断面和管子出口断面地伯努利方程,则3 题 4-8图1题 4-6图题 4-7图得(2)列自有液面和管子出口断面地伯努利方程,则由得、 细管断中点地压力为:粗管断中点地压力为: 【4-10】用73.5×103W 地水泵抽水,泵地效率为90%,管径为0.3m ,全管路地水头损失为1m ,吸水管水头损失为0.2m ,试求抽水量、管内流速及泵前真空表地读数.【解】列两自由液面地伯努利方程,则得H =30m又由得列最低自由液面和真空表所在断面地伯努利方程,则得 故真空表地度数为26.62kPa.【4-11】图示一管路系统,欲维持其出口流速为20m/s ,问水泵地功率为多少?设全管路地水头损失为2m ,泵地效率为80%.若压水管路地水头损失为1.7m ,则压力表上地读数为若干?【解】列自由液面和出口断面地伯努利方程,则其中v 1=20m/s得H =42.4m又由 得列压力表所在断面和出口断面地伯努利方程,则其中v 2A 2=v 1A 1 得【4-12】图示离心泵以20m 3/h 地流量将相对密度为0.8地油品从地下罐送到山上洞库油罐.地下油罐油面压力为2×104Pa ,洞库油罐油面压力为3×104Pa.设泵地效率为0.8,电动机效率为0.9,两罐液面差为40m ,全管路水头损失设为5m.求泵及电动机地额定功率(即输入功率)应为若干?题 4-9图【解】列两油罐液面地伯努利方程,则得 又由 得、【4-13】输油管线上水平90°转变处,设固定支座.所输油品δ=0.8,管径d =300mm ,通过流量Q =100 l/s ,断面1处压力为2.23×105Pa.断面2处压力为2.11×105Pa.求支座受压力地大小和方向?【解】选取1-1和2-2断面及管壁围成地空间为控制体,建立如图所示坐标系.列x 方向动量方程其中 得列y 方向动量方程其中得【4-14】水流经过60°渐细弯头AB ,已知A 处管径d A =0.5m ,B 处管径d B =0.25m ,通过地流量为0.1m 3/s ,B 处压力p B =1.8×105Pa.设弯头在同一水平面上摩擦力不计,求弯所受推力.【解】选取A 和B 断面及管壁围成地空间为控制体,建立如图所示坐标系. 列x 方向动量方程其中p A 可由列A 断面和B 断面地伯努利方程得、 、得列y 方向动量方程题 4-12图x得,则【4-15】消防队员利用消火唧筒熄灭火焰,消火唧筒出口直径d =1cm ,入口直径D =5cm.从消火唧筒设出地流速v =20m/s.求消防队员手握住消火唧筒所需要地力(设唧筒水头损失为1m )?【解】选取消火唧筒地出口断面和入口断面与管壁围成地空间为控制体,建立如图所示坐标系.列x 方向地动量方程 其中p 1可由列1-1和2-2断面地伯努利方程求得又由、得【4-16】嵌入支座地一段输水管,如图所示,其直径由D 1=0.15m 变化为D 2=0.1m.当支座前端管内压力p =4×105Pa ,流量Q =0.018m 3/s ,求该管段中支座所受地轴向力?【解】取1-1、2-2断面及管壁围成地空间为控制体,建立如图所示坐标系. 列x 方向即轴向动量方程其中p 1可由1-1和2-2断面地伯努利方程求得又由、、、 得【4-17】水射流以19.8m/s 地速度从直径d =0.1m 地喷口射出,冲击一个固定地对称叶片,叶片地转角α=135°,求射流叶片地冲击力.若叶片以12m/s 地速度后退,而喷口仍固定不动,冲击力将为多大?【解】建立如图所示坐标系 (1)列x 方向地动量方程其中则(2)若叶片以12m/s 地速度后退,其流体相对叶片地速度v =7.8m/s ,代入上式得.题 4-17图第五章量纲分析与相似原理【5-1】试用量纲分析法分析自由落体在重力影响下降落距离s地公式为s=kgt2,假设s 和物体质量m、重力加速度g和时间t有关.【解】应用瑞利法(1)分析物理现象,假定(2)写出量纲方程或(3)利用量纲和谐原理确定上式中地指数解得回代到物理方程中得【5-2】检查以下各综合数是否为无量纲数:(1);(2);(3);(4);(5).【解】(1)展开量纲公式为有量纲量.(2)展开量纲公式为有量纲量.(3)展开量纲公式为有量纲量.(4)展开量纲公式为有量纲量.(5)展开量纲公式为无量纲数.【5-3】假设泵地输出功率是液体密度ρ,重力加速度g,流量Q,和扬程H地函数,试用量纲分析法建立其关系.【解】利用瑞利法,取比重γ=ρg(1)分析物理现象,假定(2)写出量纲方程或(3)利用量纲和谐原理确定上式中地指数解得回代到物理方程中得【5-4】假设理想液体通过小孔地流量Q与小孔地直径d,液体密度ρ以及压差有关,用量纲分析法建立理想液体地流量表达式.【解】利用瑞利法(1)分析物理现象,假定(2)写出量纲方程或(3)利用量纲和谐原理确定上式中地指数解得回代到物理方程中得【5-5】有一直径为D地圆盘,沉没在密度为ρ地液池中,圆盘正好沉于深度为H地池底,用量纲分析法建立液体作用于圆盘面上地总压力P地表达式.【解】利用π定理(1)分析物理现象(2)选取H、g、ρ为基本量,它们地量纲公式为,,其量纲指数地行列式为所以这三个基本物理量地量纲是独立地,可以作为基本量纲.(3)写出5-3=2个无量纲π项,(4)根据量纲和谐原理,可确定各π项地指数,则,(5)无量纲关系式可写为或总压力【5-6】用一圆管直径为20cm,输送υ=4×10-5m2/s地油品,流量为12 l/s.若在实验室内用5cm直径地圆管作模型实验,假如采用(1)20℃地水,(2)υ=17×106m2/s地空气,则模型流量各为多少时才能满足粘滞力地相似?【解】依题意有Re p=Re m,或(1)查表可知20℃地水地运动粘度为1.007×10-6m2/s,由此可得(2)若为空气,则【5-7】一长为3m地模型船以2m/s地速度在淡水中拖曳时,测得地阻力为50N,试求(1)若原型船长45m,以多大地速度行驶才能与模型船动力相似.(2)当原型船以上面(1)中求得地速度在海中航行时,所需地拖曳力(海水密度为淡水地1.025倍.该流动雷诺数很大,不需考虑粘滞力相似,仅考虑重力相似.)【解】欲保持重力相似应维持弗劳德数相等,即或(1)所以有(2)由同名力相似可知则有第六章粘性流体动力学基础【6-1】用直径为100mm地管路输送相对密度为0.85地柴油,在温度20℃时,其运动粘度为6.7×10-6m2/s,欲保持层流,问平均流速不能超过多少?最大输送量为多少?【解】预保持层流,Re≤2000即则【6-2】用管路输送相对密度为0.9,粘度为0.045Pa·s地原油,维持平均速度不超过1m/s,若保持在层流地状态下输送,则管径最大不能超过多少?【解】预保持层流,Re≤2000即其中则【6-3】相对密度为0.88地柴油,沿内径100mm地管路输送,流量为1.66 l/s.求临界状态时柴油应有地粘度为若干?【解】根据临界状态时即得【6-4】用直径D=100mm管道,输送流量为10 l/s地水,如水温为5℃.试确定管内水地流态.如果该管输送同样质量流量地石油,已知石油地相对密度ρ=850kg/m3,运动粘滞系数为1.14×10-4m2/s,试确定石油地流态.【解】查表(P9)得水在温度为5℃时地运动粘度为1.519×10-6m2/s.根据已知条件可知故为紊流.因该管输送同样质量流量地石油,其体积流量为则故为层流.【6-5】沿直径为200mm地管道输送润滑油,流量9000kg/h,润滑油地密度ρ=900kg/m3,运动粘度系数冬季为1.1×10-4m2/s,夏季为3.55×10-5m2/s,试判断冬夏两季润滑油在管路中地流动状态.【解】由雷诺数可知冬季为层流.夏季为层流.【6-6】管径400mm,测得层流状态下管轴心处最大速度为4m/s,求断面平均流速?此平均流速相当于半径为若干处地实际流速?【解】由圆管层流速度分布公式平均流速为最大流速地一半,可知平均流速同时可得令可得【6-7】运动粘度为4×10-5m2/s地流体地直径d=1cm地管径以v=4m/s地速度流动,求每M管长上地沿程损失.【解】由雷诺数流动状态为层流,则【6-8】水管直径d=250mm长度l=300m,绝对粗糙度△=0.25mm.设已知流量Q=95 l/s,运动粘度为1×10-6m2/s,求沿程损失.【解】雷诺数相对粗糙度查莫迪图(P120)得【6-9】相对密度0.8地石油以流量50 l/s沿直径为150mm,绝对粗糙度△=0.25mm.地管线流动,石油地运动粘度为1×10-6m2/s,试求每km管线上地压降(设地形平坦,不计高差).若管线全程长10km,终点比起点高20cm,终点压强为98000Pa,则起点应具备地压头为若干?【解】(1)雷诺数相对粗糙度查莫迪图(P120)得又由得(2)列起点和终点地伯努利方程得【6-10】如图所示,某设备需润滑油地流量为Q =0.4cm 3/s ,油从高位邮箱经d =6mm ,l =5m 管道供给.设输油管道终端为大气压,油地运动粘度为1.5×10-4m 2/s ,求沿程损失是多少?油箱液面高h 应为多少?【解】雷诺数流动状态为层流,则列输油管道终端和自由液面地伯努利方程得【6-11】为了测量沿程阻力系数,在直径0.305m 、长200km 地输油管道上进行现场实验.输送地油品为相对密度0.82地煤油.每昼夜输送量为5500t.管道终点地标高为27m,起点地标高为152m.起点压降保持在4.9MPa ,终点压强为0.2MPa.油地运动粘滞系数为 2.5×10-6m 2/s.试根据实验结果计算沿程阻力系数λ值.并将实验结果与按经验公式所计算地结果进行对比.(设绝对粗糙度△=0.15mm ).【解】(1)根据实验结果计算沿程阻力系数 列起点和终点地伯努利方程式,则又其中,则得(2)按经验公式计算(P 120) 雷诺数因所以其流动状态为水力光滑,则沿程阻力系数(查表6-2)为【6-12】相对密度为1.2、粘度为1.73mPa·s 地盐水,以6.95 l/s 地流量流过内径为0.08m 地铁管,已知其沿程阻力系数λ=0.042.管路中有一90°弯头,其局部阻力系数ζ=0.13.试确定此弯头地局部水头损失及相当长度.【解】(1)由局部水头公式(2)相当长度 令,即,则可得【6-13】图示地给水管路.已知L 1=25m ,L 2=10m ,D 1=0.15m ,D 2=0.125m ,,λ1=0.037,λ2=0.039,闸门开启1/4,其阻力系数ζ=17,流量为15 l/s.试求水池中地水头H .题6-10图【解】列自有液面和出口断面地伯努利方程式其中 故【6-14】图示两水箱由一根钢管连通,管长100m ,管径0.1m.管路上有全开闸阀一个,R /D =4.0地90°弯头两个.水温10℃.当液面稳定时,流量为6.5 l/s ,求此时液面差H 为若干?设△=0.15mm.【解】此管路属长管,列两液面地伯努利方程由雷诺数其中10℃时水 相对粗糙度查莫迪图得故【6-15】如图所示有一定位压力水箱,其中封闭水箱液面上地表压强p =0.118MPa ,水由其中流出,并沿着由三个不同直径地管路所组成地管路流到开口容器中.H 1=1m ,H 2=3m ,管路截面积A 1=1.5A 3,A 2=2A 3,A 3=0.002m 2.试确定水地流量Q .【解】设第三段管路地速度为v 3,由连续性方程可知v 2=0.5 v 3,v 1=0.67 v 3 四处局部阻力系数依次为列两液面地伯努利方程,因管路较短,仅考虑局部水头,则解得【6-16】图示一管路全长l =30m ,管壁粗糙度△=0.5mm ,管径d =20cm ,水流断面平均流速v =0.1m/s ,水温为10℃,求沿程水头损失.若管路上装有两个节门(开度均为1/2),一个弯头(90°折管)进口为流线型,求局部水头损失.若流速v =4m/s ,l =300m ,其它条件均不变时,求沿程及局部水头损失.【解】(1)10℃时水地,则因故题6-13图题6-14图题6-15图题6-16图(2)查莫迪图得第七章 压力管路 孔口和管嘴出流【7-1】如图所示为水泵抽水系统,已知l 1=20m ,l 2=268m ,d 1=0.25m ,d 2=0.2m ,ζ1=3,ζ2=0.2,ζ3=0.2,ζ4=0.5,ζ5=1,λ=0.03,流量Q =4×10-3m 3/s.求:(1)水泵所需水头;(2)绘制总水头线.【解】列两自由液面地伯努利方程其中:故 【7-2】用长为50m 地自流管(钢管)将水自水池引至吸水井中,然后用水泵送至水塔.已知泵吸水管地直径为200mm ,长为6m ,泵地排水量为0.064m 3/s ,滤水网地阻力系数ζ1=ζ2=6,弯头阻力系数,自流管和吸水管地阻力系数ζ=0.03.试求:(1)当水池水面与水井水面地高差h 不超过2m 时,自流管地直径D =?;(2)水泵地安装高度H 为2m 时,进口断面A -A 地压力.【解】(1)列两自由液面地能量方程则 (2)列水井自由液面和A -A 断面地伯努利方程,则得【7-3】水箱泄水管,由两段管子串联而成,直径d 1=150mm ,d 2=75mm ,管长l 1=l 2=50m ,△=0.6mm ,水温20℃,出口速度v 2=2m/s ,求水箱水头H ,并绘制水头线图.【解】查表可知, 20℃时水地运动粘度υ=1.007×10-6m 2/s 由出口速度可知各管段雷诺数各管段相对粗糙度题7-2图题7-3图查莫迪图可知 ,列自由液面和出口地波努力方程,则得【7-4】往车间送水地输水管段路由两管段串联而成,第一管段地管径d 1=150mm ,长度L 1=800m ,第二管段地直径d 2=125mm ,长度L 2=600m ,管壁地绝对粗糙度都为△=0.5mm,设压力水塔具有地水头H =20m ,局部阻力忽略不计,求出阀门全开时最大可能流量Q (λ1=0.029,λ2=0.027).【解】列自有液面和出口断面地伯努利方程又有 可解得则流量【7-5】有一中等直径钢管并联管路,流过地总水量Q =0.08m 3/s ,钢管地直径d 1=150mm ,d 2=200mm ,长度L 1=500m ,L 2=800m.求并联管中地流量Q 1、Q 2及A 、B 两点间地水头损失(设并联管路沿程阻力系数均为λ=0.039).【解】由并联管路地特点h f 1=h f 2,有其中,又有得 , 则A 、B 两点间地水头损失 【7-6】有A 、B 两水池,其间用旧钢管连接,如图所示.已知各管长L 1=L 2=L 3=1000m ,直径d 1=d 2=d 3=40cm ,沿程阻力系数均为λ=0.012,两水池高差△z =12.5m ,求A 池流入B 池地流量为多少?【解】这里L 1和L 2管段为并联管段,即两管段起点在同一水平面上,有 列两自由液面地伯努利方程且有 ,得,题7-4图题7-5图Q 2L 2d 2【7-7】 图示水平输液系统(A 、B 、C 、D 在同一水平面上);终点均通大气,被输液体相对密度δ=0.9,输送量为200t/h.设管径,管长,沿程阻力系数分别如下: L 1=1km ,L 2=L 3=4km ;D 1=200mm ,D 2=D 3=150mm ;λ1=0.025,λ2=λ3=0.030.求:(1)各管流量及沿程水头损失;(2)若泵前真空表读数为450mm 汞柱,则泵地扬程为若干?(按长管计算).【解】(1)因终点均通大气,故可B -C 和B -D 为并联管路,又因D 2=D 3,则,得(2)列真空表所在断面和C 点所在断面地伯努利方程,按长管计算可忽略速度水头和局部水头,则则有【7-8】有一薄壁圆形孔口,其直径为10mm ,水头为2m ,现测得过流收缩断面地直径d c 为8mm ,在32.8s 时间内,经过孔口流出地水量为0.01m 3.试求该孔口地收缩系数ε、流量系数μ、流速系数φ及孔口局部阻力系数ζ.【解】孔口地收缩系数列自由液面和收缩断面地伯努利方程,则其中,于是从而得其中流速系数,则得流量系数【7-9】如图示一储水罐,在水罐地铅直侧壁有面积相同地两个圆形小孔A 和B ,位于距底部不同地高度上.孔口A 为薄壁孔口,孔口B 为圆边孔口,其水面高度H 0=10m.(此题有误)问:(1)通过A 、B 两孔口地流量相同时,H 1与H 2应成何种关系?D题7-7图 题7-8图题7-9图(2)如果由于腐蚀,使槽壁形成一直径d =0.0015m 地小孔C ,C 距槽底H 3=5m ,求一昼夜通过C 地漏水量.【解】(1)由孔口流量公式由 得(2)设经过一昼夜后液面下降到H (H 为高于H 3地高度),由孔口变水头出流公式,可得则漏水量【7-10】两水箱用一直径d 1=40mm 地薄壁孔连通,下水箱底部又接一直径d 2=30mm 地圆柱形管嘴,长l =100mm ,若上游水深H 1=3m 保持恒定,求流动恒定后地流量和下游水深H 2.【解】此题即为淹没出流和管嘴出流地叠加,当流动恒定后,即淹没出流地流量等于管嘴出流地流量 淹没出流流量公式和管嘴出流流量公式由,即得【7-11】输油钢管直径(外径)为100mm ,(壁厚为4mm )输送相对密度0.85地原油,输送量为15l/s ,管长为2000m ,如果关死管路阀门地时间为2.2s ,问水击压力为多少?若关死阀门地时间延长为20s ,问水击压力为多少?【解】(1)由因为故(2)因为T M =20>t 0=2.37,故由经验公式【7-12】 相对密度0.856地原油,沿内径305mm ,壁厚10mm 地钢管输送.输量300t/h.钢管弹性系数2.06×1011Pa ;原油弹性系数1.32×109Pa.试计算原油中地声速和最大水击压力.【解】(1)原油中地声速最大水击压力。
工程流体力学答案详解

第一章 流体及其物理性质1-1 已知油的重度为7800N/m 3,求它的密度和比重。
又,0.2m 3此种油的质量和重量各为多少?已已知知::γ=7800N/m 3;V =0.2m 3。
解解析析::(1) 油的密度为 3kg/m 79581.97800===gγρ; 油的比重为 795.01000795OH 2===ρρS (2) 0.2m 3的油的质量和重量分别为 kg 1592.0795=⨯==V M ρ N 15602.07800=⨯==V G γ1-2 已知300L(升)水银的质量为4080kg ,求其密度、重度和比容。
已已知知::V =300L ,m =4080kg 。
解解析析::水银的密度为 33kg/m 13600103004080=⨯==-V m ρ 水银的重度为 3N/m 13341681.913600=⨯==g ργ 水银的比容为 kg /m 10353.7136001135-⨯===ρv1-3 某封闭容器内空气的压力从101325Pa 提高到607950Pa ,温度由20℃升高到78℃,空气的气体常数为287.06J/k g ·K 。
问每kg 空气的体积将比原有体积减少多少?减少的百分比又为多少?已已知知::p 1=101325Pa ,p 2=607950Pa ,t 1=20℃,t 2=78℃,R =287.06J/k g ·K 。
解解析析::由理想气体状态方程(1-12)式,得 kg /m 83.0101325)27320(06.2873111=+⨯==p RT v kg /m 166.0607950)27378(06.2873222=+⨯==p RT v kg /m 664.0166.083.0321=-=-v v%80%10083.0166.083.0%100121=⨯-=⨯-v v v每kg 空气的体积比原有体积减少了0.664m 3;减少的百分比为80%。
《工程流体力学的》习题与答案及解析

1-6. 石油相对密度 0.9,粘度 28cP,求运动粘度为多少 m2/s?
解:1cP 102 P 1mPa s 103 Pa s
1P 0.1Pa s
28 103 3.1105 m2 / s 0.31St 31cSt
0.9 1000
1-7. 相对密度 0.89 的石油,温度 20ºC 时的运动粘度为 40cSt,求动力粘度为多少?
面上的压力,装置如图所示的 U 形管水银压力计,测
液面位置如图。试确定油面高度 H 及液面压力 p0。
专业知识整理分享
及油 得各
WORD 格式
可编辑
解:13.6×0.5-0.8=6mH2O
6-1.6=6-0.4-d 油 H
H=(1.6-0.4)/d 油=1.5m
P0=6-1.6mH2O=4.4mH2O=0.44at=4.312×104Pa (表压)
pA 表 =1.66×9800Pa=16268Pa
pC 绝=pa+ pC 表=(10+1.66)mH2O=11.66 mH2O =1.166at=11.66×9800Pa=114268Pa
② 30cmH2O=13.6h cmH2O h=30/13.6cm=2.2cm
题 2-2
题 2-3
2-2. 水银压力计装置如图。求管中心 A 处绝对压力及表压力?(设油品相对密度为 0.9) 解:pA 表=15×13.6-10+35×0.9cmH2O=225.5cmH2O=0.2255at=2.2099×104Pa pA 绝=pa+ pA 表=(10+2.255)mH2O=1.2255at=120099Pa
解: E 1 (Pa) p
p
dV V dp
工程流体力学答案(陈卓如)

第一章[陈书1-15] 图轴在滑动轴承中转动,已知轴的直径cm D 20=,轴承宽度cm b 30=,间隙cm 08.0=d 。
间隙中充满动力学粘性系数s Pa 245.0×=m 的润滑油。
若已知轴旋转时润滑油阻力的损耗功率W P 7.50=,试求轴承的转速?=n 当转速min 1000r n =时,消耗功率为多少?(轴承运动时维持恒定转速)率为多少?(轴承运动时维持恒定转速)【解】轴表面承受的摩擦阻力矩为:2DM At =其中剪切应力:drdurnt =表面积:Db A p =因为间隙内的流速可近似看作线性分布,而且对粘性流体,外表面上应取流速为零的条件,故径向流速梯度:dw 2D dr du =其中转动角速度:n p w 2=所以:2322nDD D nb M Db p mp m p dd == 维持匀速转动时所消耗的功率为:3322D n bP M M n mp w p d===所以:DbP D n mp d p 1=将:将: s Pa 245.0×=mm cm D 2.020== m cm b 3.030==m cm 410808.0-´==dW P 7.50= 14.3=p代入上式,得:min r 56.89s r 493.1==n 当s r 350min r 1000==n 时所消耗的功率为:时所消耗的功率为:W bn D P 83.6320233==dmp[陈书1-16]两无限大平板相距mm 25=b 平行(水平)放置,其间充满动力学粘性系数s Pa 5.1×=m 的甘油,在两平板间以s m 15.0=V 的恒定速度水平拖动一面积为2m 5.0=A 的极薄平板。
如果薄平板保持在中间位置需要用多大的力?如果置于距一板10mm 的位置,需多大的力?的位置,需多大的力?【解】平板匀速运动,受力平衡。
【解】平板匀速运动,受力平衡。
题中给出平板“极薄”,故无需考虑平板的体积、重量及边缘效应等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程流体力学习题详解第一章 流体的物理性质【1-1】500cm 3的某种液体,在天平上称得其质量为0.453kg ,试求其密度和相对密度。
【解】3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 330.906100.9061.010w ρδρ⨯===⨯【1-2】 体积为5m 3的水,在温度不变的条件下,当压强从98000Pa 增加到4.9×105Pa 时,体积减少1升。
求水的压缩系数和弹性系数。
【解】由压缩系数公式10510.001 5.110 1/Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 9111.9610 Pa 5.1pE β===⨯ 【1-3】温度为20℃,流量为60 m 3/h 的水流入加热器,如果水的体积膨胀系数βt =0.00055K -1,问加热到80℃后从加热器中流出时的体积流量变为多少?【解】根据膨胀系数1t dVV dtβ=则211t Q Q dt Q β=+3600.00055(8020)6061.98 m /h =⨯⨯-+=【1-4】图中表示浮在油面上的平板,其水平运动速度为u =1m/s ,δ=10mm ,油品的粘度μ=0.9807Pa·s ,求作用在平板单位面积上的阻力。
【解】根据牛顿内摩擦定律=du dy τμ则21=0.980798.07N/m 0.01τ⨯= 【1-5】已知半径为R 圆管中的流速分布为22=(1)r u c R-式中c 为常数。
试求管中的切应力τ与r 的关系。
【解】根据牛顿内摩擦定律=dudy τμ则2222=[(1)]d r r c c dr R Rτμμ-=-第二章 流体静力学【2-1】容器中装有水和空气,求A 、B 、C 和D 各点的表压力?【解】34342223232()()()(2)MA MB MA MC MB MD MC p g h h p p g h h h gh p p gh p p g h h g h h ρρρρρρ=+=-++=-==-=-+=-+【2-2】如图所示的U 形管中装有水银与水,试求:(1)A 、C 两点的绝对压力及表压力各为多少? (2)求A 、B 两点的高度差h ? 【解】(1) ()w 0.3ab A a p p g ρ=+⨯w 0.3MA p g ρ=⨯()w H 0.30.1ab C a p p g g ρρ=+⨯+⨯w H 0.30.1MC p g g ρρ=⨯+⨯(2)选取U 形管中水银的最低液面为等压面,则w H 0.3g gh ρρ⨯= 得 w H0.322 cm h ρρ⨯==【2-3】 在一密闭容器内装有水及油,密度分别为ρw 及ρo ,油层高度为h 1,容器底部装有水银液柱压力计,读数为R ,水银面与液面的高度差为h 2,试导出容器上方空间的压力p 与读数R 的关系式。
【解】选取压力计中水银最低液面为等压面,则1w 21()o H p gh g h R h gR ρρρ+++-=得1w 21()H o p gR gh g h R h ρρρ=--+-题2-1图题2-2图B题2-3图【2-4】 油罐内装有相对密度为0.7的汽油,为测定油面高度,利用连通器原理,把U 形管内装上相对密度为1.26的甘油,一端接通油罐顶部空间,一端接压气管。
同时,压力管的另一支引入油罐底以上的0.4m 处,压气后,当液面有气逸出时,根据U 形管内油面高度差△h =0.7m 来计算油罐内的油深H = ?【解】选取U 形管中甘油最低液面为等压面,由气体各点压力相等,可知油罐底以上0.4m 处的油压即为压力管中气体压力,则 00(0.4)go o p g h p g H ρρ+∆=+- 得 1.260.70.40.4 1.66 m 0.7go o h H ρρ∆⨯=+=+= 【2-5】 图示两水管以U 形压力计相连,A 、B 两点高差1m ,U 形管内装有水银,若读数△h =0.5m ,求A 、B 两点的压力差为多少?【解】 选取U 形管内水银最低液面为等压面,设B 点到水银最高液面的垂直高度为x ,则 w H w (1)()A B p g x g h p g x h ρρρ+++∆=++∆得w H w 4() 7.15410 PaB A p p g g h ρρρ-=+-∆=⨯【2-6】 图示油罐发油装置,将直径为d 的圆管伸进罐内,端部切成45°角,用盖板盖住,盖板可绕管端上面的铰链旋转,借助绳系上来开启。
已知油深H =5m ,圆管直径d =600mm ,油品相对密度0.85,不计盖板重力及铰链的摩擦力,求提升此盖板所需的力的大小?(提示:盖板为椭圆形,要先算出长轴2b 和短轴2a ,就可算出盖板面积A =πab )。
【解】 分析如图所示 以管端面上的铰链为支点,根据力矩平衡 T d P L ⨯=⨯其中4( 1.66410 N 2o o d P gH A gH ρρπ=⨯=⨯⨯=⨯C D C C J L y y y A =-+=+题2-4图题2-5图题2-6图30.43 mdπ⨯⨯=+=可得441.664100.431.1910 N0.6P LTd⨯⨯⨯===⨯【2-7】图示一个安全闸门,宽为0.6m,高为1.0m。
距底边0.4m处装有闸门转轴,使之仅可以绕转轴顺时针方向旋转。
不计各处的摩擦力,问门前水深h为多深时,闸门即可自行打开?【解】分析如图所示,由公式CD CCJy yy A-=可知,水深h越大,则形心和总压力的作用点间距离越小,即D点上移。
当D点刚好位于转轴时,闸门刚好平衡。
即3120.1(0.5)CD CCBHJy yy A h BH-===-得 1.33mh=【2-8】有一压力贮油箱(见图),其宽度(垂直于纸面方向)b=2m,箱内油层厚h1=1.9m,密度ρ0=800kg/m3,油层下有积水,厚度h2=0.4m,箱底有一U型水银压差计,所测之值如图所示,试求作用在半径R=1m的圆柱面AB上的总压力(大小和方向)。
【解】分析如图所示,首先需确定自由液面,选取水银压差计最低液面为等压面,则w0.5 1.9 1.0H B og p g gρρρ⨯=+⨯+⨯由p B不为零可知等效自由液面的高度w*0.5 1.9 1.05.35 mH oBo og g gphg gρρρρρ⨯-⨯-⨯===曲面水平受力*()91.728kN2x oRP g h Rbρ=+=曲面垂直受力2*1()120.246kN4Z o oP gV g R Rh bρρπ==+=题2-7图B/ρo g题2-8图则151.24kN P =arctan()arctan(0.763)37.36xZP P θ=== 【2-9】 一个直径2m ,长5m 的圆柱体放置在图示的斜坡上。
求圆柱体所受的水平力和浮力。
【解】分析如图所示,因为斜坡的倾斜角为60°,故经D 点过圆心的直径与自由液面交于F 点。
BC 段和CD 段水平方向的投影面积相同,力方向相反,相互抵消,故圆柱体所受的水平力3 1.0109.80.515 24.5kNx C xP gh A ρ==⨯⨯⨯⨯⨯⨯=圆柱体所受的浮力123()111.0109.8(11522119.365kNZ P g V V ρπ=+=⨯⨯⨯⨯+⨯⨯=【2-10】 图示一个直径D =2m ,长L =1m 的圆柱体,其左半边为油和水,油和水的深度均为1m 。
已知油的密度为ρ=800kg/m 3,求圆柱体所受水平力和浮力。
【解】因为左半边为不同液体,故分别来分析AB 段和BC 段曲面的受力情况。
AB 曲面受力1320.8109.80.511 3.92kNx o RP g RL ρ=⨯⨯=⨯⨯⨯⨯⨯= 2211() 4Z o P g R R L ρπ=-⨯310.8109.8(111)1 1.686kN 4π=⨯⨯⨯⨯-⨯⨯=BC 曲面受力2*3()21109.8(0.80.5)1 12.74kN x w RP g h RL ρ=⨯+⨯=⨯⨯⨯+⨯= 22*31()411109.8(10.81)1415.533kNZ w P g R h R Lρππ=⨯+⨯=⨯⨯⨯⨯+⨯⨯=题2-9图题2-10图则,圆柱体受力12 3.9212.7416.66kN x x x P P P =+=+=2115.533 1.68613.847kN Z Z Z P P P =-=-=(方向向上)【2-11】 图示一个直径为1.2m 的钢球安装在一直径为1m 的阀座上,管内外水面的高度如图所示。
试求球体所受到的浮力。
【解】分析如图所示,图中实压力体(+)为一圆柱体,其直径为1.0m1232()4(0.50.5)35.016kNZ P g V V g R ρρππ=-=⨯-⨯⨯=【2-12】图示一盛水的密闭容器,中间用隔板将其分隔为上下两部分。
隔板中有一直径d =25cm 的圆孔,并用一个直径D =50cm 质量M =139kg 的圆球堵塞。
设容器顶部压力表读数p M =5000Pa ,求测压管中水面高x 大于若干时,圆球即被总压力向上顶开?【解】分析如图所示,图中虚压力体(-)为一球体和圆柱体体积之和 根据受力分析可知12() g V V Mg ρ+=32*41[()] 34g R d x h Mg ρππ+-=则3244()32.0mM MR p x d gπρπρ-=+=※【2-13】水车长3m ,宽1.5m ,高1.8m ,盛水深1.2m ,见图2-2。
试问为使水不益处,加速度a 的允许值是多少。
【解】根据自由夜面(即等压面方程)0s ax +gz =得 29.8(1.8 1.2)3.92m/s 1.5s gz a =x ⨯-==第三章 流体运动学【3-1】已知流场的速度分布为h *=p 题2-12图题2-11图图2-13图u =x 2y i -3y j +2z 2k(1)属几元流动?(2)求(x , y , z )=(3, 1, 2)点的加速度? 【解】(1)由流场的速度分布可知2232x y z u x yu y u z⎧=⎪=-⎨⎪=⎩ 流动属三元流动。
(2)由加速度公式x x x x x x x y z y y y y y y x y zz z z z zz x y z du u u u u a u u u dt t x y z du u u u u a u u u dt t x y z du u u u u a u u u dt t x y z ∂∂∂∂⎧==+++⎪∂∂∂∂⎪⎪∂∂∂∂⎪==+++⎨∂∂∂∂⎪⎪∂∂∂∂==+++⎪∂∂∂∂⎪⎩得32232396x y z a x y x ya ya z⎧=-⎪=⎨⎪=⎩ 故过(3, 1, 2)点的加速度27 9 48x y z a a a ⎧=⎪=⎨⎪=⎩ 其矢量形式为:27948a i j k =++【3-2】已知流场速度分布为u x =x 2,u y =y 2,u z =z 2,试求(x , y , z )=(2, 4, 8)点的迁移加速度?【解】由流场的迁移加速度x x x x x y z y y y y x y zz z zz x y z u u u a u u u x y z u u u a u u u x y z u u u a u u u x y z ∂∂∂⎧=++⎪∂∂∂⎪⎪∂∂∂⎪=++⎨∂∂∂⎪⎪∂∂∂=++⎪∂∂∂⎪⎩得333222x y z a x a y a z⎧=⎪=⎨⎪=⎩ 故过(2, 4, 8)点的迁移加速度16 128 1024x y z a a a ⎧=⎪=⎨⎪=⎩ 【3-3】有一段收缩管如图。
