(参考)等截面等跨连续梁在常用荷载作用下的内力系数表
各类梁的弯矩剪力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =m ,每跨各有一集中荷载F =,求中间支座的最大弯矩和剪力。
[解] M B 支=(-××52)+(-××5)=(-)+()=-·mV B 左=(-××5)+(-×)=(-)+(-)=-[例2] 已知三跨等跨梁l =6m ,均布荷载q =m ,求边跨最大跨中弯矩。
[解] M1=××62=·m 。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
3)四跨等跨连续梁内力和挠度系数表2-13注:同三跨等跨连续梁。
4)五跨等跨连续梁内力和挠度系数表2-14注:同三跨等跨连续梁。
连续梁内力系数表等跨计算方法

连续梁内力系数表等跨计算方法标题:连续梁内力系数表等跨计算方法的深入探讨摘要:连续梁是结构工程领域中常见的桥梁形式之一,其设计和分析过程中内力系数表等跨计算方法起着重要的作用。
本文将从深度和广度的角度对内力系数表等跨计算方法进行评估,并介绍其在连续梁设计中的应用。
首页提供一个总结性的概述,然后按照从简到繁、由浅入深的顺序进行讨论,帮助读者更全面、深刻和灵活地理解这一主题。
关键词:连续梁、内力系数表、等跨计算方法、结构工程、设计1. 引言- 简要介绍连续梁及其在桥梁工程中的重要性- 引入内力系数表等跨计算方法的背景和目的2. 内力系数表的概述- 解释内力系数表的含义和作用- 简要介绍不同类型的内力系数表(例如,基于弯矩、剪力等)3. 等跨计算方法的基本原理- 解释等跨计算方法的基本概念- 介绍基于力和位移两种不同方法的计算原理4. 基于力的等跨计算方法- 讨论如何使用力方法计算连续梁的内力系数- 解释基本的力平衡原理和方程- 举例说明力方法的具体应用和计算过程5. 基于位移的等跨计算方法- 介绍位移方法计算内力系数的基本原理- 解释位移平衡原理和方程- 通过示例说明位移方法在连续梁设计中的应用6. 内力系数表等跨计算方法的应用- 详细说明内力系数表在连续梁设计和分析中的具体应用场景 - 比较不同方法的优缺点和适用性- 强调内力系数表等跨计算方法的重要性和价值7. 总结和回顾性的内容- 概括内力系数表等跨计算方法的关键要点- 回顾连续梁设计中的主要问题和挑战- 提供对这些方法的观点和理解- 探讨未来可能的发展方向和研究方向结论:本文深入探讨了内力系数表等跨计算方法在连续梁设计中的应用。
通过从简到繁、由浅入深的方式,读者可以更全面地理解这一主题。
我们总结了内力系数表的基本原理和不同的计算方法,并回顾了其在实际工程中的应用。
我们的文章旨在帮助读者对连续梁设计中的内力系数表等跨计算方法有更深刻的理解,并展示了其对于工程实践的重要性。
等跨连续梁内力系数表

等跨连续梁内力系数表等跨连续梁内力系数表是一种用于计算等跨连续梁内力的工具,它能够帮助工程师在设计等跨连续梁时更加准确地预测梁体的内力。
本文将介绍等跨连续梁内力系数表的基本概念、应用方法以及优缺点。
一、基本概念等跨连续梁内力系数表是一种基于牛顿-拉夫逊法的计算方法,它使用矩形法和梯形法来近似计算等跨连续梁的内力。
计算过程经过多次迭代得到收敛的解,以达到精确计算等跨连续梁内力的目的。
为了使用等跨连续梁内力系数表,需要知道以下参数:1.等跨连续梁的跨度;2.每个跨度的弯矩、剪力、轴力等截面力;3.梁的截面特性(截面形状、面积、惯性矩等)。
二、应用方法使用等跨连续梁内力系数表有以下步骤:1.将每个跨度的弯矩、剪力、轴力等截面力输入到内力系数表中;2.输入梁的截面特性参数;3.计算内力系数表中的系数;4.使用系数和截面特性计算每个跨度的内力。
以下是等跨连续梁内力系数表的一个例子:跨度长度(m)内力系数剪力系数轴力系数3 0.315 0.840 -0.0924 0.403 1.090 -0.0925 0.453 1.270 -0.0926 0.483 1.380 -0.092以第一个跨度为例,假设等跨连续梁跨度长度为3m,该跨度的弯矩为10kN·m,那么根据内力系数表可知,该跨度的内力系数为0.315,截面特性参数也已经给定,因此可以计算出该跨度的弯矩=0.315×10kN·m=3.15kN·m。
三、优缺点等跨连续梁内力系数表具有以下优点:1.计算精准:等跨连续梁内力系数表使用收敛求解方法,能够得出比传统方法精确的结果;2.操作简便:使用等跨连续梁内力系数表只需要输入基本参数和截面特性参数,并按照表格操作,十分简单。
但等跨连续梁内力系数表也有以下缺点:1.只适用于等跨连续梁:内力系数表的名称就表明了它只适用于等跨连续梁的计算,对于其他类型的梁则无法使用;2.不考虑材料非线性:内力系数表仅适用于梁的弹性阶段,无法考虑材料本身的非线性性。
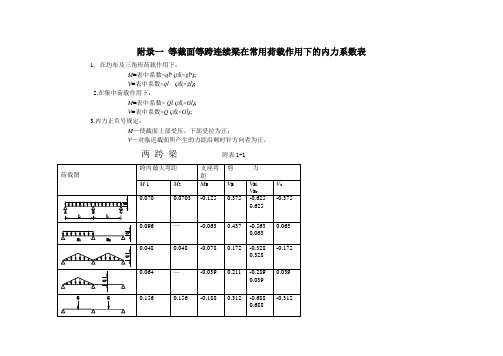
等截面等跨连续梁在常用荷载作用下的内力系数表
-0.060 0.012 0.012
0.178 -0.036 -0.036
荷载图 内力
五跨梁
跨内最大弯距
M1
M2
M3
0.078
0.033
0.046
附表 1-4
MB
-0.105
支座弯距
剪力
MC
-0.079
MD
ME
-0.079 -0.105
VA
0.394
VBl VBr
-0.606 0.526
-0.450 0.050 -0.017 -0.017 -0.188
0
-0.219
0.281
-0.250 0.031 0.051
-0.198 0.021 0.021
0.052 -0.010 -0.010
-0.500 -0.350 0.650
0.213 — 0.162 0.200 0.244 0.289 — 0.229 0.274
— 0.175 0.137 — 0.067 — 0.200 0.170 —
-0.075 -0.075 0.425 -0.575 0
-0.075 -0.075 -0.075 -0.075 0.500
-0.175 -0.050 0.325 -0.675 0.625
-0.100 0.025 -0.267 0.267
-0.550 0 -0.050 0.500 -0.617 0.583 -0.567 0.083 -0.313 0.250
-0.281 0
-0.031 0.250
-0.323 0.302
-0.292 0.052
-0.650 0.500
0 0.550 -0.500 0.050 0.083 -0.017 0.083 -0.017 -0.250 0.313
附录二 等截面附录二等跨连续梁在常用荷载作用下的内力系数表

附录一等截面等跨连续梁在常用荷载作用下的内力系数表 1.在均布及三角形荷载作用下:皿=表中系数 V=表中系数2•在集中荷载作用下: 皿=表中系数 V=表中系数3.内力正负号规定: M —使截面上部受压、下部受拉为正;V —对临近截面所产生的力距沿顺时针方向者为正。
附表1-1 旳12(或旳12);Xql (或XQI (或 XGl ); XQ两跨梁0.203 -0.094 0.406 -0.594 0.0940.0940.222 0.222 -0.333 0.667 -1.333 -0.6671.3330.278 -0.167 0.833 -1.167 0.1670.167a.荷载图三跨梁跨内最大弯距附表1-2M20.080 0.025支座弯距M B M c V A-0.100 -0.100 0.400V BIV Br-0.6000.500剪力V clV er-0.5000.600V D-0.4000.101 -0.050 -0.050 0.450 -0.5500.550-0.4500.075 -0.050 -0.050 0.050 -0.0500.500-0.5000.0500.0500.073 0.054 -0.117 -0.033 0.383 -0.6170.5830.083-0.0170.094-0.017-0.067 0.017 0.433 -0.5670.0830.083-0.017-0.017 A----- A 0.0540.0680.0500.0630.1750.0210.0520.0380.100-0.063 -0.063 0.183 -0.313 -0.250 -0.1880.250 0.313-0.031-0.031-0.073-0.042-0.150-0.031-0.031-0.0210.010-0.1500.2190.0310.1770.2080.350-0.281-0.0310.250-0.3230.302-0.2920.052-0.6500.5000.281-0.2500.051-0.1980.0210.052-0.010-0.5000.650-0.2190.0310.021-0.010-0.350荷载图 0.077 四跨梁 跨内最大弯距 M 2 M 3 M 4 M B 0.036 0.036 0.077 -0.107 附表1-3 支座弯距 剪力 M e M D V A -0.071 -0.107 0.393 0.100 0.081 0.072 0.061 -0.054-0.036 -0.054 0.446 0.098 -0.121 -0.018 -0.058 0.380 V BI V Br -0.607 0.536 Vd V cr -0.464 0.464 V DI V Dr -0.536 0.607 V E -0.393 0.094 Z A0.056 0.056 0.062 0.067 0.049 A 0.071 0.028 -0.036 -0.067 -0.107 -0.036 -0.036 0.018 -0.004 0.433 0.042 0.028 0.055 0.052 0.066 -0.049 -0.054 0.013 -0.049 -0.554 0.018 -0.620 0.603 -0.036 0.429 -0.567 0.085 -0.049 0.496 0.018 0.482 -0.397 -0.040 -0.571 0.571 0.085 -0.022 -0.504 0.067 -0.518 0.054 -0.040 -0.558 -0.429 0.036 0.022 0.004 0.067 0.013 0.054 -0.442 0.036 0.004 -0.013 -0.067-0.045 -0.067 0.183 -0.317 0.272 -0.228 0.228 -0.272 0.317 -0.183 -0.084 -0.075 -0.022 -0.034 0.217 -0.234 0.011 0.011 0.239 -0.261 0.034 0.034 -0.011 -0.036 0.175 -0.325 0.314 -0.186 -0.025 -0.025 0.286 -0.214 0.040 0.040 -0.022-0.067 -0.022 -0.022 -0.022 0.205 -0.295 0.295 -0.205 0.022 0.0224 4u a A s s a 0.274 -0.178 0.048 -0.012 0.822 -1.1780.2260.226-0.060-0.0600.0120.0124 q 川0.198 -0.131 -0.143 0.036 -0.131 -0.1310.988-1.0120.1780.178-0.036-0.036附表1-4荷载图跨内最大弯距支座弯距剪力内力M2 M3 M B M e M D M E V A0.078 0.033 0.046 -0.105 -0.079 -0.079 -0.105 0.394 V BIV Br-0.6060.526V clV cr-0.4740.500V DIV Dr-0.5000.474V EIV Er-0.5260.606V F-0.3940.100 Ml M S M4M S0.085 -0.053 -0.040 -0.040 -0.053 0.447 -0.5530.0130.0130.500-0.500-0.013-0.0130.533-0.4470.079 -0.053 -0.040 -0.040 -0.053 -0.053 -0.0530.513-0.4870.487-0.5130.0530.0530.073(1) 0.0980.094 (2)0.0590.078-0.119 -0.022 -0.044 -0.051 0.3800.0550.0740.064 -0.035-0.067-0.111 -0.020 -0.057 0.0350.018 -0.005 0.001 0.433-0.6200.5980.0350.4240.5670.085-0.402-0.0230.5760.5910.0860.023-0.0230.493-0.409-0.0370.0230.006-0.5070.052-0.0370.5570.006-0.0010.052-0.4430.001-0.049 -0.054 0.014 -0.004 0.019 -0.0490.496-0.5050.0680.068-0.018-0.0180.0040.004。
连续梁按弹性理论五跨梁内力系数及弯矩分配法
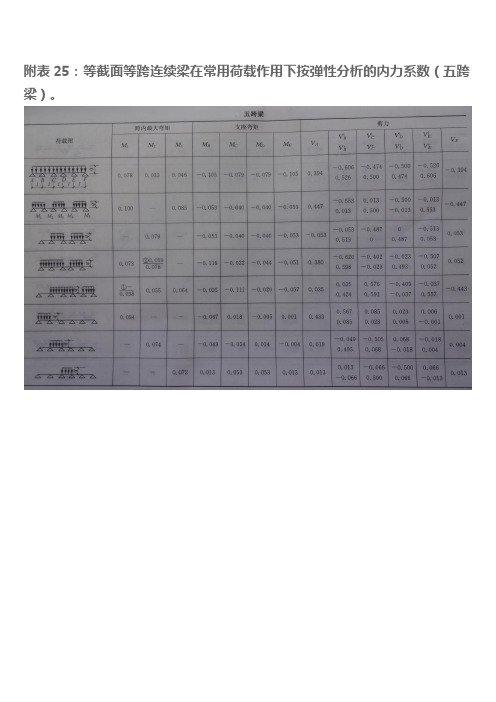
附表25:等截面等跨连续梁在常用荷载作用下按弹性分析的内力系数(五跨梁)。
弯矩分配法(弯矩分配法计算连续梁和刚架及举例)一、名词解释弯矩分配法在数学上属于逐次逼近法,但在力学上属于精确法的范畴,主要适用于连续梁和刚架的计算。
在弯矩分配法中不需要解联立方程,而且是直接得出杆端弯矩。
由于计算简便,弯矩分配法在建筑结构设计计算中应用很广。
(一)线刚度i杆件横截面的抗弯刚度EI 被杆件的长度去除就是杆件的线刚度i :l EI i(a ) 当远端B 为固定支座时,对于A 点处,AB 杆的转动刚度i S AB 4=; (b ) 当远端B 为铰支座时,对于A 点处,AB 杆的转动刚度i S AB 3=; (c ) 当远端B 为滑动支座时,对于A 点处,AB 杆的转动刚度i S AB =; (d ) 当远端B 为自由端时,对于A 点处,AB 杆的转动刚度0=AB S 。
连续梁和刚架的所有中间支座在计算转动刚度时均视为固定支座。
(二)转动刚度S转动刚度表示靠近节点的杆件端部对该节点转动的反抗能力。
杆端的转动刚度以S 表示,等于杆端产生单位转角需要施加的力矩,θ/M S =。
施力端只能发生转角,不能发生线位移。
AB S 中的第一个角标A 是表示A 端,第二个角标B是表示杆的远端是B 端。
AB S 表示AB 杆在A 端的转动刚度。
(三)分配系数μ⎪⎭⎪⎬⎫⋅=⋅=⋅=⋅=⋅=⋅=A AD A AD AD A AC A AC AC A AB A AB AB i S M i S M i S M θθθθθθ34 ⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⋅=⋅=⋅==++=++=++=∑∑∑∑M S S M M S S M M S S M SM S S S M M M M S S S M AD AD AC AC AB AB AD AC AB A AD AC AB A AD A AC A AB θθθθ各杆A 端所承担的弯矩与各杆A 端的转动刚度成正比。
五跨连续梁弯矩系数表静力手册

五跨连续梁弯矩系数表静力手册设置后浇带前后结构的内力系数对比分析为了简化内力系数分析,以等截面等跨连续梁(板)和支座简支均布荷载为例。
不设后浇带前,根据《建筑结构静力计算实用手册》(第二版)可以查到三至五跨等截面连续梁(板)的内力系数。
设置后浇带后,后浇带设置在结构跨1/3处,不考虑后浇带宽度,分析根据结构1/3作为断点,二边分别悬挑1/3和2/3结构跨,根据中国建筑科学研究院编制的多层及高层建筑结构空间有限元分析与设计软件SATWE2010版进行整体计算得到设置后浇带后各跨的内力系数。
1.1三跨等截面连续简支梁(板)内力系数对比分析三跨等截面连续简支梁(板)在AB跨设置后浇带后,荷载图如1.1.2和1.1.4所示,在AB和CD设后浇带后荷载图如1.1.3和1.1.5所示。
从表1中可以看出,当在AB跨设置后浇带后,跨内最大弯矩M2是原来的1.72倍,支座弯矩MC是原来的1.11倍,支座C柱轴力是原来的1.06倍;当在AB和CD跨同时设置后浇带后,跨内最大弯矩M2是原来的2.76倍,支座弯矩MC是原来的0.56倍,支座C柱轴力是原来的0.76倍;其他内力系数不一一比较。
表1三跨等截面连续简支梁(板)设置后浇带前后的内力系数Chat1Theinternalforcecoefficientsofthethree-spancontinuouslybeam(plate)before/aftersettingpost-pouredstrip1.2四跨等截面连续简支梁内力系数对比分析四跨等截面连续简支梁(板)在AB跨设置后浇带后,荷载图如1.2.2和1.2.4所示,在AB和DE设后浇带后荷载图如1.2.3和1.2.5所示。
从表2中可以看出,当在AB跨设置后浇带后,跨内最大弯矩M2是原来的1.56倍,支座弯矩MC是原来的1.08倍,支座C柱轴力是原来的1.09倍;当在AB、和DE跨同时设置后浇带后跨内最大弯矩M2、M3是原来的1.36倍,支座弯矩MC是原来的1.23倍,支座C柱轴力是原来的1.09倍;其他内力系数比原来小不一一比较。
结构力学常用计算公式表
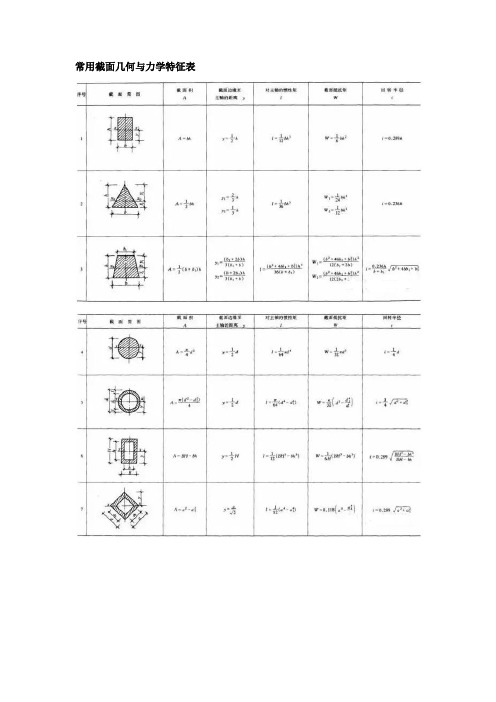
常用截面几何与力学特征表单跨梁的内力及变形表(1)简支梁的反力、剪力、弯矩、挠度(2)悬臂梁的反力、剪力、弯矩和挠度(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度(4)两端固定梁的反力、剪力、弯矩和挠度5)外伸梁的反力、剪力、弯矩和挠度等截面连续梁的内力及变形表二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;w =表中系数×ql4/(100EI)。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;w =表中系数×Fl3/(100EI)。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
=(-0.125×11.76×52)+(-0.188×29.4×5)[解] MB支=(-36.75)+(-27.64)=-64.39kN·mV=(-0.625×11.76×5)+(-0.688×29.4)B左=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
不等跨连续梁的内力系数1)二不等跨梁的内力系数注:1.M=表中系数×ql21;V=表中系数×ql1;2.(Mmax )、(Vmax)表示它为相应跨内的最大内力。
2)三不等跨梁内力系数注:1.M=表中系数×ql21;V=表中系数×ql1;2.(Mmax )、(Vmax)为荷载在最不利布置时的最大内力。
“┌┐”形刚架内力计算表(一)“┌┐”形刚架内力计算表(二)“”形刚架的内力计算表。
等截面等跨连续梁内力系数表

等截面等跨连续梁内力系数表等截面等跨连续梁是一种常见的桥梁结构,它在桥梁工程中广泛应用。
为了确保连续梁的结构安全和有效承载荷载,需要进行内力计算。
而在内力计算过程中,内力系数起着重要的作用。
本文将详细介绍等截面等跨连续梁内力系数表的作用、计算方法及应用。
一、等截面等跨连续梁内力系数表的作用等截面等跨连续梁内力系数表是用来计算连续梁在不同荷载作用下的内力的工具。
通过内力系数表,可以快速、准确地获得连续梁的内力分布,从而判断结构的安全性和合理性。
内力系数表还可以用来指导设计工作和材料选用,以满足设计要求和经济效益。
因此,等截面等跨连续梁内力系数表对于桥梁工程设计和施工具有重要的指导作用。
二、等截面等跨连续梁内力系数的计算方法等截面等跨连续梁内力系数的计算是基于连续梁的结构特点和力学原理的。
一般来说,计算连续梁内力系数需要考虑以下几个关键因素:1. 荷载条件:根据实际使用情况和设计要求,确定连续梁所承受的荷载类型和荷载大小。
常见的荷载类型包括自重、活载、恒载等。
2. 支座条件:根据连续梁的支座形式和约束条件,确定支座在内力计算过程中的影响。
支座条件的确定对于内力计算结果的准确性和结构安全性具有重要意义。
3. 物理参数:包括连续梁的几何参数、材料参数等。
几何参数主要包括跨度、截面形状、弯矩曲率等;材料参数主要包括荷载下的材料强度、刚度等。
基于以上关键因素,可以利用数学公式、力学原理等计算方法,进行连续梁内力系数的计算。
一般来说,连续梁内力系数的计算可以分为初始值的计算和递推计算两个步骤。
初始值的计算是在不考虑变形和位移的情况下进行的,主要通过力学平衡等原理进行计算。
递推计算是通过考虑连续梁的位移和变形等因素,对初始值进行修正和调整,以获得更加准确的内力系数。
三、等截面等跨连续梁内力系数表的应用等截面等跨连续梁内力系数表的应用可以分为两个方面:设计和检验。
在设计方面,内力系数表可以为连续梁的结构设计提供依据。
等跨连续梁内力系数表

等跨连续梁内力系数表1. 引言连续梁是一种常见的结构形式,由多个简支或悬臂梁通过铰链连接而成。
在设计和分析连续梁时,需要考虑各个截面的内力分布情况。
为了简化计算和设计过程,通常使用内力系数表来快速确定各截面的内力。
本文将介绍等跨连续梁内力系数表的编写方法和使用技巧,帮助工程师在设计和分析等跨连续梁时能够更加高效地进行计算。
2. 内力系数的定义在等跨连续梁中,每个截面都受到弯矩和剪力的作用,这些作用可以通过内力系数来表示。
内力系数是一个与连续梁几何形状和受载情况有关的参数,用于计算各截面的弯矩和剪力。
通常情况下,等跨连续梁内力系数表包括以下几个主要参数:•支座处弯矩系数:表示支座处截面的弯矩相对于最大弯矩的比值;•中间处弯矩系数:表示中间截面的弯矩相对于最大弯矩的比值;•支座处剪力系数:表示支座处截面的剪力相对于最大剪力的比值;•中间处剪力系数:表示中间截面的剪力相对于最大剪力的比值。
3. 编写等跨连续梁内力系数表编写等跨连续梁内力系数表需要进行一系列的计算和分析。
下面将介绍编写内力系数表的具体步骤:3.1 确定连续梁几何形状和受载情况首先,需要确定连续梁的几何形状,包括跨度、截面形状和尺寸等参数。
同时,还需要考虑连续梁所受到的荷载情况,包括集中荷载、均布荷载等。
3.2 计算连续梁各截面的弯矩和剪力根据连续梁所受到的荷载情况,可以通过静力学原理计算出各个截面所受到的弯矩和剪力。
这些计算可以使用传统方法或者结构分析软件进行。
3.3 确定最大弯矩和剪力在计算得到各个截面的弯矩和剪力后,需要确定最大的弯矩和剪力值。
这些值将作为基准值,用于计算内力系数。
3.4 计算各截面的内力系数根据已经确定的最大弯矩和剪力,可以计算出各个截面的内力系数。
通常情况下,支座处的内力系数为1,中间处的内力系数小于1。
3.5 编写内力系数表将计算得到的各个截面的内力系数整理成表格形式,编写成等跨连续梁内力系数表。
表格中应包括截面位置、弯矩系数和剪力系数等信息。
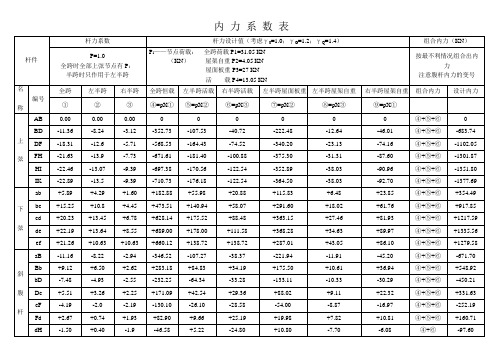
内 力 系 数 表
+51.23
+47.63
-26.10
+98.55
-8.10
+6.68
⑤+⑦+⑧+⑨
+197.81
gK
+2.35
+4.35
-2.6
+72.97
+56.77
-33.93
+117.45
-10.53
+9.52
⑤+⑦+⑧+⑨
+236.67
gI
+0.6
+0.6
0
+18.63
+7.83
0
+16.20
0
+2.43
+10.81
④+⑤+⑥
+160.71
dH
-1.50
+0.40
-1.9
-46.58
+5.22
-24.8008
④+⑥
-97.60
Hg
+0.28
-1.42
+1.70
+8.69
-18.53
+22.19
-38.34
+6.89
+1.13
⑤+⑦+⑧+⑨
-66.87
eg
+1.65
+3.65
全跨荷载p13105knkn屋架自重p2405kn屋面板重p327kn活载p41305kn按最不利情况组合出内力注意腹杆内力的变号名称编号全跨左半跨右半跨全跨恒载左半跨活载右半跨活载左半跨屋面板重左半跨屋架自重右半跨屋架自重组合内力设计内力pxpxpxpxpxpx上弦ab0000000000000000bd113682431235273107534072222481264460168374df1831126571568531644374523402023137416110205fh21631397736716118140100883753031318760130187hi224613079396973817056122543528938039096135180ik22891359397107317618122543645038039270137769下弦ab589429160182885598208811583648238535449bc152510844547351140945807291601802617691785cd20231345678628141755288483631527468193121759de221913648556890017800111583682834638997133556ef2126106310636601213872138722870143058610127958斜腹杆ab111682229434652107273837221941191452067170bb9126502622831884833419175501061369454892bd7484932552322564343328133111033302945021dc55132622517109425429368802911223233163cf4192021913010261028585400887169725219fd267074193829096625191998782108116071dh150040194658522248010807706089760hg0281421708691853221938346891136687eg16536520512347632610985581066819781gk2354352672975677339311745105395223667gi0606018637830162002
