福建省龙岩市2019年质检数学卷及答案
龙岩市2019年高中毕业班教学质量检查数学(理科)参考答案Word版
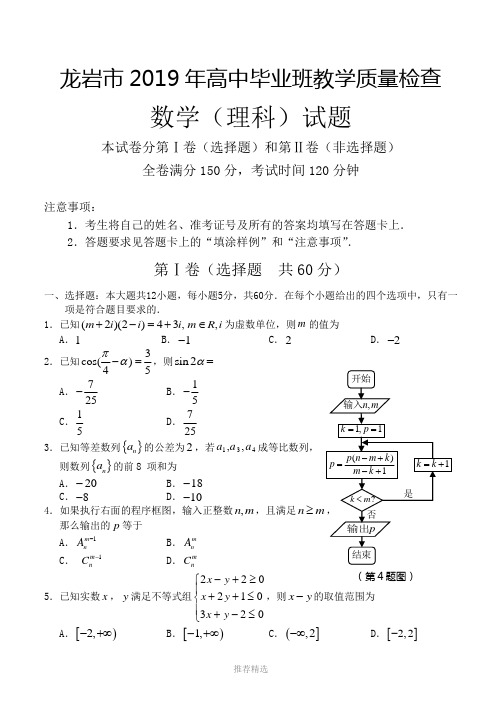
(第4题图) 龙岩市2019年高中毕业班教学质量检查数学(理科)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)全卷满分150分,考试时间120分钟注意事项:1.考生将自己的姓名、准考证号及所有的答案均填写在答题卡上. 2.答题要求见答题卡上的“填涂样例”和“注意事项”.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知(2)(2)43,m i i i +-=+,m R i ∈为虚数单位,则m 的值为 A .1 B .1-C .2D .2-2.已知3cos()45πα-=,则sin 2α= A .725- B .15-C .15D .7253.已知等差数列{}n a 的公差为2,若431,,a a a 成等比数列,则数列{}n a 的前8 项和为A .20-B .18-C .8-D .10- 4.如果执行右面的程序框图,输入正整数,n m ,且满足n ≥那么输出的p 等于 A .1m n A - B .mn AC . 1m n C -D .mnC5.已知实数x ,y 满足不等式组220210320x y x y x y -+≥⎧⎪++≤⎨⎪+-≤⎩,则x y -的取值范围为 A .[)2,-+∞B .[)1,-+∞C .(],2-∞D .[]2,2-2222正视图 侧视图俯视图(第7题图)(第11题图) M P DABC1B 1C 1D 1A (第8题图)AB CDO6.已知双曲线22122:1x y C a b -=()0,0a b >>和双曲线22222:1y x C m n-=()0,0m n >>焦距相等,离心率分别为1e 、2e ,若2212111e e +=,则下列结论正确的是A .1C 和2C 离心率相等B .1C 和2C 渐近线相同 C .1C 和2C 实轴长相等D .1C 和2C 虚轴长相等7.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球表面积为 A 3π B .23π C .43π D .12π 8.如图,AB 和CD 是圆O 两条互相垂直的直径,分别以OA ,OB ,OC ,OD 为直径作四个圆,在圆O 内随机取一点,则此点取自阴影部分的概率是A .21π-B .112π-C .2πD .1π9.已知函数()cos 3f x x ωπ⎛⎫=+ ⎪⎝⎭()0ω>在区间36π5π⎡⎤-⎢⎥⎣⎦,上单调,则ω的取值范围为A .120,15⎛⎤ ⎥⎝⎦B .10,5⎛⎤ ⎥⎝⎦C .112,515⎡⎤⎢⎥⎣⎦D .12,115⎡⎤⎢⎥⎣⎦10.设23451111log log log log s ππππ=+++,||,*T a s a N =-∈,当T 取最小值时a 的值为A .2B .3C .4D .511.如图,已知正方体1111ABCD A B C D -的棱长为4,P 是1AA 的中点,点M 在侧面11AA B B 内,若1D M CP ⊥,则BCM ∆面积的最小值为A .8B .4C .82D 8512.已知数列{}n a 各项均为整数,共有7项,且满足11k k a a +-=,1,2,6k =,其中11a =,7a a =(a 为常数且0a >).若满足上述条件的不同数列个数共有15个,则a 的值为A .1B .3C .5D .7ADBME NFC O(第18题图)第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.已知向量a ,b 的夹角为60°,2a =,37a b -=,则b = . 14.若4(1)()x a x ++的展开式中3x 项的系数为16,则实数a = .15.已知抛物线24y x =的焦点为F ,其准线与x 轴的交点为Q ,过点F 作直线与抛物线交于,A B 两点.若以QF 为直径的圆过点B ,则AF BF -的值为 .16.已知32()||4f x x x =-,若()f x 的图像和y ax =的图像有四个不同的公共点,则实数a 的取值范围是 .三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知2cos 2c B a b =-. (Ⅰ)求角C 的大小;(Ⅱ)设D 为BC 中点,若3AD =,求ABC ∆面积的取值范围.18.(本小题满分12分)如图,已知四边形ABCD 是边长为2的菱形,且060ABC ∠=,BM ABCD ⊥平面,//DN BM ,2BM DN =,点E 是线段MN 上的一点.O 为线段BD 的中点.(Ⅰ)若OF ⊥BE 于F 且1OF =,证明:AF ⊥平面ECB ;(Ⅱ)若4BM =,13NE NM =,求二面角E BC M --的余弦值.19.(本小题满分12分)已知椭圆E 的方程为2221x y a+=,点A 为长轴的右端点.,B C 为椭圆E 上关于原点对称的两点.直线AB 与直线AC 的斜率AB AC k k 和满足:12AB AC k k =-.(Ⅰ)求椭圆E 的标准方程;(Ⅱ)若直线:l y kx t =+与圆2223x y +=相切,且与椭圆E 相交于,M N 两点,求证:以线段MN 为直径的圆恒过原点.20.(本小题满分12分)某医院为筛查某种疾病,需要检验血液是否为阳性,现有n (n N *∈)份血液样本,有以下两种检验方式:(1)逐份检验,则需要检验n 次;(2)混合检验,将其中k (k N *∈且2k ≥)份血液样本分别取样混合在一起检验.若检验结果为阴性,这k 份的血液全为阴性,因而这k 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k 份血液究竟哪几份为阳性,就要对这k 份再逐份检验,此时这k 份血液的检验次数总共为1k +次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为(01)p p <<.(Ⅰ)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过4次检验就能把阳性样本全部检验出来的概率.(Ⅱ)现取其中k (k N *∈且2k ≥)份血液样本,记采用逐份检验方式,样本需要检验的总次数为1ξ,采用混合检验方式,样本需要检验的总次数为2ξ(ⅰ)试运用概率统计的知识,若1E ξ=2E ξ,试求p 关于k 的函数关系式()p f k =;(ⅱ)若1p =,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k 的最大值.参考数据:ln20.6931≈,ln3 1.0986≈,ln4 1.3863≈,ln5 1.6094≈,ln6 1.7918≈21.(本小题满分12分)已知函数1()ln (0)x f x x a R a ax -=+∈≠且,1()(1)()x g x b x xe b R x=---∈ (Ⅰ)讨论函数()f x 的单调性;(Ⅱ)当1=a 时,若关于x 的不等式()()2f x g x +≤-恒成立,求实数b 的取值范围.请考生在22、23两题中任选一题作答. 注意:只能做所选定的题目.如果多做,则按所做第一个题目计分. 作答时,请用2B 铅笔在答题卡上将所选题号后的方框涂黑. 22.(本小题满分10分)选修4-4:坐标系与参数方程已知平面直角坐标系xOy 中,直线l 的参数方程为2cos 1sin x t y t αα=-+⎧⎨=+⎩(t 为参数,02πα≤<),以原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为24cos 2sin 40ρρθρθ---=.(Ⅰ)求直线l 的普通方程、曲线C 的直角坐标方程;(Ⅱ)若直线l 与曲线C 交于A B 、两点,且2AB =.求α的大小.23.(本小题满分10分)选修4-5:不等式选讲已知函数()()f x x m m R =-∈.(Ⅰ)当2m =时,解不等式()1f x x >7--;(Ⅱ)若存在x R ∈,使()1f x x >7+-成立,求m 的取值范围.龙岩市2019年高中毕业班教学质量检查数学(理科)参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有13.1 14.2-或4315. 4 16.(4,0)(0,4)- 三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤. 17.(本小题满分12分) 解:(Ⅰ)由2cos 2c B a b =-,得2sin cos 2sin sin C B A B =- ……………………1分即()2sin cos 2sin sin C B B C B =+-,2sin cos sin B C B ∴=sin 0B >, 1cos 2C ∴=……………………5分0C π<<, 3C π∴=……………………6分(Ⅱ)在ADC ∆中,由余弦定理得:2222cos3ADAC DC AC DC π=+-••……7分即229AC DC AC DC +-•=, 又222AC DC AC DC +≥• 90AC DC ∴≥•>, ……………………9分1sin 23ADCSAC DC π=••0ADC S ∴<≤ …………………10分 2ABC ADC S S = 0ABC S ∴<≤……………………12分18.(本小题满分12分)解:(Ⅰ)四边形ABCD 是边长为2的菱形,且060ABC ∠=∴ AC 与BD 交于点O 且ABC ∆为等边三角形2AC ∴=,BO =又112OF AC ==,AF CF ∴⊥ ………………2分ADBME NxC O (第18题图)yzFBM ABCD ⊥平面,AC BM ∴⊥又AC BD ⊥,∴AC BMND ⊥平面 OF BMND ⊂平面,AC OF ∴⊥在Rt AOF 中,2222AF AO OF =+=在Rt BOF 中,2222FB BO OF =-=∴在ABF ∆中, 24AB =, 224AF FB +=, 222AF FB AB += (4)分AF BE ∴⊥,又,,CF BE CBE CF BE F ⊂=平面,∴AF ECB ⊥平面 ……………………5分 (Ⅱ)在平面BMND 中,过O 作直线l ∥BM , 则l ABCD ⊥面,如图,以l 为z 轴,AC所在直线为x 轴,BD 所在直线为y 轴建立空间直角坐标系, ………………6分()3,0B ∴,()1,0,0C -,()3,4M ,()0,3,2N -13NE NM =,380,33E ⎛⎫∴-⎪⎝⎭, ()1,3,0BC ∴=--,4380,,33BE ⎛⎫=-⎪⎝⎭ 设(),,n x y z =是平面BCE 的法向量,则00n BC n BE ⎧=⎪⎨=⎪⎩,即3043803x y z ⎧--=⎪⎨+=⎪⎩, 取()6,23,3n =-,取BC 中点G ,连结AG ,AG BC ∴⊥,AG BM ⊥, AG BCM ∴⊥面因此,AG 是平面BCM 的法向量,13,,022G ⎛⎫- ⎪⎝⎭,()1,0,0A 3322AG ⎛⎫∴=- ⎪⎝⎭, (10)分设二面角E BC M --的大小为θ,则419cos 19933612944n AG n AGθ===+++ ∴二面角E BC M --419……………………12分19.(本小题满分12分) 解:(Ⅰ)设00(x ,)B y 则00(x ,)C y -- …………………1分由220021x y a +=得,2222000221x a x y a a-=-= …………………2分 由12AB AC k k ⋅=-,即000012y y x a x a -⋅=----得,222002a x y -= …………4分所以22220022a x a x a --=,所以22a = 即椭圆E 的标准方程为:2212x y += …………………5分(Ⅱ)设1122(x ,),(x ,)M y N y由2212x y y kx t ⎧+=⎪⎨⎪=+⎩得: 222(12k )4220x ktx t +++-= 2121222422,1212kt t x x x x k k--+==++ …………………6分 2212121212()()()y y kx t kx t k x x kt x x t =++=+++2222222222(22)42121212k t k t t k t k k k ---=++=+++ 又l 与圆C=22231t k =+ …………………8分 所以2221212222212t t k OM ON x x y y k-+-⋅=+=+ 22222232(1)2(1)2(1)01212t k k k k k-++-+===++ …………………11分 所以,OM ON ⊥,即090MON ∠=所以,以线段MN 为直径的圆经过原点. …………………12分20.(本小题满分12分)解:(Ⅰ) 112223325535C C A A p A ==………………3分 ∴恰好经过4次检验就能把阳性样本全部检验出来的概率为35………………4分(Ⅱ)(ⅰ)由已知得1E k ξ=,2ξ的所有可能取值为1,1k +()()211k P p ξ∴==-, ()()2111kP k p ξ=+=--∴()()21(1)11k k E p k p ξ⎡⎤=-++--⎣⎦=()11kk k p +--……………6分若1E ξ=2E ξ,则1(1)k k k k p =+-- ∴(1)1kk p -=1(1)kp k-= ∴111()k p k -= ∴111()k p k =-∴p 关于k 的函数关系式111()k p k =-(k N *∈且2k ≥) ………………8分(ⅱ)由题意可知21E E ξξ<,得()11,kp k <-31p =-1kk ∴<,1ln 3k k ∴>,设()1ln (0)3f x x x x =->……………10分 ()33xf x x-'=,∴当3x >时,()0f x '<,即()f x 在()3,+∞上单调递减又ln4 1.3863≈,4 1.33333≈,4ln 43∴>,ln5 1.6094≈,5 1.66673≈,5ln53∴< ∴k 的最大值为4. (12)分21.(本小题满分12分) 解:(Ⅰ)11()ln f x x ax a =+- 22111()(0)ax f x x x ax ax -'∴=-=> …………1分 当0a <时,()0f x '∴>,()f x ∴在(0,)+∞单调递增; …………2分当0a >时,由()0f x '>得:1x a >;由()0f x '<得:10x a <<,()f x ∴在1(0,)a单调递减,在1(,)a+∞单调递增 ……………………4分综上:当0a <时,()f x 在(0,)+∞单调递增;当0a >时,()f x 在1(0,)a单调递减,在1(,)a +∞单调递增. ………………5分(Ⅱ)由题意:当0a <时,不等式()()2f x g x +≤-,即11ln 1(1)2x x b x xe x x+-+---≤- 即ln 11xx b e x x -≤--在(0,)+∞恒成立, ……………6分 令ln 1()x x h x e x x =--,则22221ln 1ln ()x xx x e x h x e x x x-+'=-+=, ………7分 令2()ln x u x x e x =+,则21()(2)0xu x x x e x'=++>,()u x ∴在(0,)+∞单调递增又1u(1)e 0,u()ln 2024=>=-<,所以,()u x 有唯一零点0x (0112x <<) 所以,0()0u x =,即0000ln x x x e x =---------(※) ………………9分当0(0,)x x ∈时,()0u x <即h ()0x '<,()h x 单调递减;0(,)x x ∈+∞时,()0u x >即h ()0x '>,()h x 单调递增,所以0()h x 为()h x 在定义域内的最小值. ……10分令1()(1)2xk x xe x =<<则方程(※)等价于()(ln )k x k x =-又易知()k x 单调递增,所以ln x x =-,1xe x=………………11分 所以,()h x 的最小值000000000ln 111()1x x x h x e x x x x x -=--=--= 所以11b -≤,即2b ≤所以实数b 的取值范围是(],2-∞ ………………12分22.(本小题满分10分)选修4-4:坐标系与参数方程解:(Ⅰ)由2cos ,1sin ,x t y t αα+=⎧⎨-=⎩消t 得y 1tan 2x α-=+,直线l 的普通方程为tan 2tan 10x y αα-++=,将222cos ,sin ,x y x y ρθρθρ===+代入24cos 2sin 40ρρθρθ---=得 曲线C 的直角坐标方程为224240x y x y +---= ………………4分 (Ⅱ)曲线C 的方程化为22(2)(1)9x y -+-=,曲线C 是以(2,1)为圆心,3为半径的圆.2AB =,圆心到直线l 的距离d ===又d ==解得tan 1α=±,02πα≤<,∴4πα=……………………10分(注:用21t t -求解一样给分)23.(本小题满分10分)选修4-5:不等式选讲 解:(Ⅰ)由已知21x x -+->7当1x <时,不等式等价于217x x -+->,解得2x <-,∴2x <-; 当12x ≤≤时,217x x -+->,此时不等式无解; 当x >2时,217x x -+->,解得5x >,∴5x >综上:解集为{2x x <-或}5x > ………………………5分 (Ⅱ)∵()()111x m x x m x m ---≤---=-∴11x m x m ---≤-当且仅当()()10x m x --≥且1x m x -≥-时等号成立. 依题意1m ->7,解之得8m >或6m <-,∴m 的取值范围为()(),68,-∞-⋃+∞. ………………………10分(注:可编辑下载,若有不当之处,请指正,谢谢!)。
2019-2020学年福建省龙岩市一级达标校高二下学期期末质检数学试题

福建省龙岩市一级达标校2019-2020学年高二下学期期末质检试题【参考答案】一、单项选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.二、多项选择题:本大题共2小题,每小题5分,共10分,在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,选对但不全的得3分,有选错的得0分. 11.BD 12.BCD三、填空题:本大题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.13.330x y --= 14.28315.21 16.57 9,14四、解答题:本大题共6小题,第17小题10分,其它每小题12分,共70分. 解答应写出文字说明、证明过程或演算步骤. 17. (本题满分10分)解:(1)241mi z i -=+=2-4)(1)(24)(24)(12)(12)1)(1)2mi i m m i m m i i i ---+==--++-((……………………………………………………2分 若z 是纯虚数,则120,120m m -=⎧⎨+≠⎩ 12m ∴=…………………………5分 (2)由(1)得,,)21()21(i m m z +--=im m z )21()21(++-=∴………………6分 2(12)(32)z i m m i+=-++……………………………………………………7分又因为复数2z i +在复平面上对应的点位于第四象限,120,320m m ->⎧∴⎨+<⎩……………………………………………………8分 ∴23m <-. …………………………………………………………10分18. (本题满分12分)解: (1)依题意得,264n =, 6.n ∴=…………………………………………4分(2)6(2x x+展开式的第1r +项为: 616(2)r rr r T C x -+=366262(0,1,2,3,4,5,6)r r rC x r --==……………………7分 则无理项为:995122262192T C x x == …………………………………………8分333322462160T C x x==……………………………………9分3352266212T C xx --== …………………………………………10分∴所有无理项的系数的和为:19216012364++=………………………………12分19. (本题满分12分)解:(1)依题意填写22⨯的列联表如下:…………………………………………2分(备注:有部分对给1分)22100(40202020) 2.78 3.84160406040K ⨯-⨯=≈<⨯⨯⨯,…………………………………4分∴没有95%的把握认为“中学生对这些科学家的了解程度与性别有关”. …………5分(2)抽取的女生人数为40104100⨯=(人),男生人数为60106100⨯=(人).所以X 的可能取值为0,1,2,3,4 …………………………………6分则041322464646444101010183(0),(1),(2),14217C C C C C C P X P X P X C C C =========31446444101041(3),(4)35210C C C P X P X C C ======………………………………9分因此X 的分布列为……………………………………………………10分数学期望为18341()01234 1.61421735210E X =⨯+⨯+⨯+⨯+⨯=.……………12分20.(本题满分12分)(1)证明:2ln 1()x f x x e e '=--在(0,+)∞为减函数, (2)分(备注:利用求导判断减函数也可相应得分)又()0f e '=,(0,)x e ∴∈,()()0f x f e ''>=;(,)x e ∴∈+∞,()()0f x f e ''<=. ()f x ∴在(0,)e 上是增函数,()f x 在(,)e +∞上是减函数,…………………………5分max ()()f x f e ∴=即()()f x f e ≤ ………………………………………………6分(2)解:x 、y 、a 都大于0,由(2)(ln ln )20y a x y x x e ---≤两边同除xa 整理得:2(2)lny ya ex x ≥-…………8分 令(0)y t t x =>,2(2)ln t ta e ∴≥-恒成立,……………………………………………9分 记()(2)ln t g t t e =-,则max2()g t a ≥由(1)知max ()()1g t g e ==, ……………………………………………………11分21a ∴≥,即02a <≤,max 2a = …………………………………………………12分21. (本题满分12分) 解:(1)由题意得1234510121720263,1755x y ++++++++====,51295i i i x y ==∑,52155ii x==∑,则51522152955317ˆ455455i ii ii x y x ybxx ==--⨯⨯===--∑∑,所以ˆˆ17435a y bx =-=-⨯=.…………………………………………3分所以y 关于x 的线性回归方程为ˆ45y x =+令ˆ4550y x =+>解得11.25x >,所以最小的整数为12,2014+12=2026,所以预测该地区新能源汽车的销售量最早在2026年能突破50万量. …………………4分 (2)①由题意知,该地区200名购车车主中,女性车主有200-95-45=60(名),故其中购置新能源汽车的女性车主有60-20=40(名).所以购置新能源汽车的车主中,女性车主所占的比值为408=40+4517,所以该地区购置新能源汽车的车主中女性车主的概率为817,预测该地区2020年新能源汽车的销量为46+5=29⨯(万辆),………………………6分 因此,预测该地区2020年购置新能源汽车的女性车主有82913.617⨯≈(万人) ……………………………………………………8分②由题意知,45,013545p w w =≤≤+则332325()(1)10(12)f p C p p p p p =-=-+34510(2)p p p =-+ ………………………………………9分所以2342'()10(385)10(1)(53)f p p p p p p p =-+=--, 当3(0,)5p ∈时,'()0f p >,函数()f p 单调递增 3(1)5p ∈,时,'()0f p <,函数()f p 单调递减所以当35p =时,()f p 取得最大值3325332216()()()555625f C ==………………10分此时453455w =+,解得30w = ………………………………………………11分所以当30w =时, ()f p 取得最大值216625 …………………………………12分22. (本题满分12分)解:(1)解:2(21)(2)()2(41)px x f x px p x x --'=-++=(0,0)x p >>…………1分当122p <即14p >时,由()0f x '>解得2x >或102x p <<; 当122p =即14p =时,()0f x '≥在(0,)+∞恒成立; 当122p >即104p <<时,由()0f x '>解得12x p >或02x <<…………4分 综上,当14p >时,()f x 的单调递增区间为1(0,)2p ,(2,)+∞; 当14p =时,()f x 的单调递增区间为(0,)+∞;当104p <<时,()f x 的单调递增区间为(0,2),1(,)2p +∞………………5分(2)解:由2()(41)2(1)e xf x px p x q x ≤-+--⋅化简得:ln (1)0x x q x e +-≤在(1,)x ∈+∞时恒成立,…………………………6分 记()ln (1)xg x x q x e =+-,当0q ≥时,()g x 在(1,)x ∈+∞为增函数,(1)0g =,()0g x ∴>,不合题意; ……………………………………………………………7分当0q <时,1()xg x qxe x '=+在(1,)x ∈+∞为减函数,(1)1g qe '=+……………8分 若(1)10g qe '=+≤,即1q e ≤-时,()(1)g x g ''<,()0g x '∴<()g x ∴在(1,)x ∈+∞为减函数,()(1)0g x g ∴<=,1q e ∴≤-合题意. ……9分若(1)10g qe '=+>,即1q e >-时,1()xg x qxe x '=+在(1,)x ∈+∞为减函数,0(1,)x ∴∃∈+∞使得0(1,)x x ∈,()0g x '>, 即()g x 在0(1,)x x ∈为增函数,()(1)0g x g ∴>=与()0g x ∴≤矛盾.1q e∴>-不合题意. …………………………11分综上,1(,q e⎤∈-∞-⎥⎦………………………………………………12分。
福建省龙岩市2019届高三下学期教学质量检查数学理试题(解析版)

龙岩市2019届高三教学质量检查数学(理科)试题2019.2注意事项:1.考生将自己的姓名、准考证号及所有的答案均填写在答题卡上.2.答题要求见答题卡上的“填涂样例”和“注意事项”.第Ⅰ卷(选择题)一、选择题.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知为虚数单位,则的值为()A. B. C. D.【答案】A【解析】【分析】先化简已知的等式,再利用两个复数相等的条件,解方程组求得x的值.【详解】∵∴,∴,即故选:A【点睛】本题考查两个复数的乘法法则的应用,以及两个复数相等的条件,基本知识的考查.2.已知,则()A. B.C. D.【答案】A【解析】,两边平方得:,,即,故选A.3.已知等差数列的公差为,若成等比数列,则数列的前8 项和为()A. -20B. -18C. -8D. -10【答案】C【解析】【分析】运用等比数列中项的性质和等差数列的通项公式,解方程可得首项,再由等差数列求和公式,计算即可得到所求值.【详解】解:等差数列的公差d为2,若,成等比数列,可得a32=,即有(+4)2=(+6),解得=﹣8,则{a n}前8项的和为8×(﹣8)8×7×2=﹣8,故选:C.【点睛】本题考查等差数列的通项公式和求和公式的运用,考查等比数列中项的性质,以及运算能力,属于基础题.4.如果执行下面的程序框图,输入正整数,且满足,那么输出的等于()A. B. C. D.【答案】D【解析】【分析】该程序的作用是利用循环计算并输出变量p的值,模拟程序的运行,用表格对程序运行过程中各变量的值进行分析,不难得到输出结果.【详解】解:第一次循环:k=1,p=1,p=;第二次循环:k=2,p=;第三次循环:k=3,p=…第m次循环:k=m,p=此时结束循环,输出p==故选:D.【点睛】解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.5.已知实数,满足不等式组,则的取值范围为()A. B. C. D.【答案】B【解析】【分析】作出不等式组对应的平面区域,设z=x﹣y,利用目标函数的几何意义,利用数形结合确定z的取值范围.【详解】解:设z=x﹣y,则y=x﹣z,作出不等式对应的平面区域(阴影部分)如图:平移直线y=x﹣z,由图象可知当直线y=x﹣z经过点A(﹣1,0)时,直线y=x﹣z的截距最大,此时z最小,最小值z=﹣1﹣0=﹣1继续向下平移直线y=x﹣z,z值越来越大,∴的取值范围为故选:.【点睛】本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.6.已知双曲线和双曲线焦距相等,离心率分别为、,若,则下列结论正确的是()A. 和离心率相等B. 和渐近线相同C. 和实轴长相等D. 和虚轴长相等【答案】B【解析】【分析】根据可知:,a,从而得到结果.【详解】设两个双曲线的焦距为,∴,又∴,∴∴,即,故又双曲线的渐近线方程为:,双曲线的渐近线方程为:∴和渐近线相同故选:B【点睛】本题考查双曲线的简单几何性质,考查双曲线渐近线方程,考查计算能力,属于基础题.7.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球表面积为()A. B. C. D.【答案】C【解析】【分析】由三视图知几何体是一个侧棱与底面垂直的三棱锥,底面是斜边上的高为的等腰直角三角形,与底面垂直的侧面是个等腰三角形,底边长为,高为,故三棱锥的外接球与以棱长为的正方体的外接球相同,由此可得结论【详解】由三视图知几何体是一个侧棱与底面垂直的三棱锥,底面是斜边上的高为的等腰直角三角形,与底面垂直的侧面是个等腰三角形,底边长为,高为,故三棱锥的外接球与以棱长为的正方体的外接球相同,其直径为,半径为三棱锥的外接球体积为故选【点睛】本题主要考查了三视图,几何体的外接球的体积,考查了空间想象能力,计算能力,属于中档题。
龙岩市2019年高中毕业班教学质量检查数学参考答案
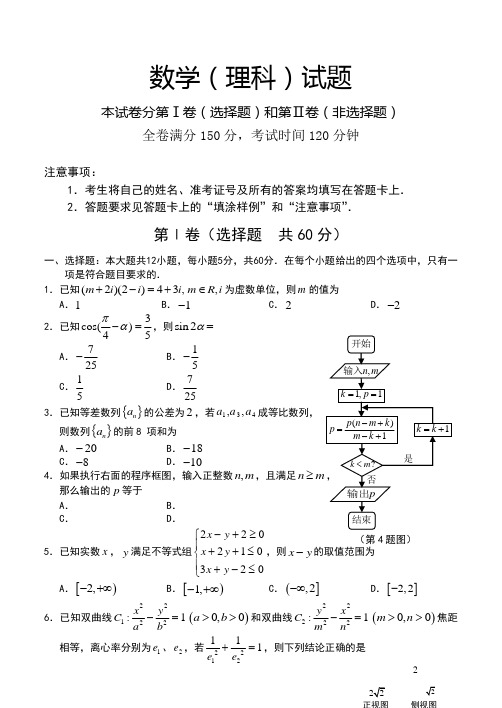
2(第4题图) 数学(理科)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)全卷满分150分,考试时间120分钟注意事项:1.考生将自己的姓名、准考证号及所有的答案均填写在答题卡上. 2.答题要求见答题卡上的“填涂样例”和“注意事项”.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知(2)(2)43,m i i i +-=+,m R i ∈为虚数单位,则m 的值为 A .1 B .1-C .2D .2-2.已知3cos()45πα-=,则sin 2α= A .725- B .15-C .15D .7253.已知等差数列{}n a 的公差为2,若431,,a a a 成等比数列,则数列{}n a 的前8 项和为 A .20- B .18-C .8-D .10-4.如果执行右面的程序框图,输入正整数,n m ,且满足n ≥那么输出的p 等于 A . B .C .D .5.已知实数x ,y 满足不等式组220210320x y x y x y -+≥⎧⎪++≤⎨⎪+-≤⎩,则x y -的取值范围为 A .[)2,-+∞B .[)1,-+∞C .(],2-∞D .[]2,2-6.已知双曲线22122:1x y C a b -=()0,0a b >>和双曲线22222:1y x C m n-=()0,0m n >>焦距相等,离心率分别为1e 、2e ,若2212111e e +=,则下列结论正确的是(第11题图)M P DABC1B 1C 1D 1A (第8题图)ABCD OA .1C 和2C 离心率相等B .1C 和2C 渐近线相同 C .1C 和2C 实轴长相等D .1C 和2C 虚轴长相等7.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球表面积为 AB. C. D .12π 8.如图,AB 和CD 是圆O 两条互相垂直的直径,分别以OA ,OB ,OC ,OD 为直径作四个圆,在圆O 内随机取一点,则此点取自阴影部分的概率是 A . B .C .D . 9.已知函数()cos 3f x x ωπ⎛⎫=+ ⎪⎝⎭()0ω>在区间36π5π⎡⎤-⎢⎥⎣⎦,上单调,则ω的取值范围为 A .120,15⎛⎤ ⎥⎝⎦ B .10,5⎛⎤ ⎥⎝⎦ C .112,515⎡⎤⎢⎥⎣⎦ D .12,115⎡⎤⎢⎥⎣⎦10.设23451111log log log log s ππππ=+++,||,*T a s a N =-∈,当T 取最小值时a 的值为A .2B .3C .4D .511.如图,已知正方体1111ABCD A B C D -的棱长为4,P 是1AA 的中点,点M 在侧面11AA B B 内,若1D M CP ⊥,则BCM ∆面积的最小值为 A .8 B .4C.D.512.已知数列{}n a 各项均为整数,共有7项,且满足11k k a a +-=,1,2,6k =L ,其中11a =,7a a =(a 为常数且0a >).若满足上述条件的不同数列个数共有15个,则a 的值为A .1B .3C .5D .7第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.已知向量a r ,b r的夹角为60°,2a =r,3a b -=r r b =r . 14.若4(1)()x a x ++的展开式中3x 项的系数为16,则实数a = .15.已知抛物线24y x =的焦点为F ,其准线与x 轴的交点为Q ,过点F 作直线与抛物线交于,A B 两点.若以QF 为直径的圆过点B ,则AF BF -的值为 .ADBME NFC O(第18题图)16.已知32()||4f x x x =-,若()f x 的图像和y ax =的图像有四个不同的公共点,则实数a 的取值范围是 .三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知2cos 2c B a b =-. (Ⅰ)求角C 的大小;(Ⅱ)设D 为BC 中点,若3AD =,求ABC ∆面积的取值范围.18.(本小题满分12分)如图,已知四边形ABCD 是边长为2的菱形,且060ABC ∠=,BM ABCD ⊥平面,//DN BM ,2BM DN =,点E 是线段MN 上的一点.O 为线段BD 的中点.(Ⅰ)若OF ⊥BE 于F 且1OF =,证明:AF ⊥平面ECB ;(Ⅱ)若4BM =,13NE NM =u u u r u u u u r,求二面角E BC M --的余弦值.19.(本小题满分12分)已知椭圆E 的方程为2221x y a+=,点A 为长轴的右端点.,B C 为椭圆E 上关于原点对称的两点.直线AB 与直线AC 的斜率AB AC k k 和满足:12AB AC k k =-g .(Ⅰ)求椭圆E 的标准方程;(Ⅱ)若直线:l y kx t =+与圆2223x y +=相切,且与椭圆E 相交于,M N 两点,求证:以线段MN 为直径的圆恒过原点.20.(本小题满分12分)某医院为筛查某种疾病,需要检验血液是否为阳性,现有n (n N *∈)份血液样本,有以下两种检验方式:(1)逐份检验,则需要检验n 次;(2)混合检验,将其中k (k N *∈且2k ≥)份血液样本分别取样混合在一起检验.若检验结果为阴性,这k 份的血液全为阴性,因而这k 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k 份血液究竟哪几份为阳性,就要对这k 份再逐份检验,此时这k 份血液的检验次数总共为1k +次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为(01)p p <<.(Ⅰ)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过4次检验就能把阳性样本全部检验出来的概率.(Ⅱ)现取其中k (k N *∈且2k ≥)份血液样本,记采用逐份检验方式,样本需要检验的总次数为1ξ,采用混合检验方式,样本需要检验的总次数为2ξ(ⅰ)试运用概率统计的知识,若1E ξ=2E ξ,试求p 关于k 的函数关系式()p f k =;(ⅱ)若1p =,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k 的最大值.参考数据:ln20.6931≈,ln3 1.0986≈,ln4 1.3863≈,ln5 1.6094≈,ln6 1.7918≈21.(本小题满分12分)已知函数1()ln (0)x f x x a R a ax -=+∈≠且,1()(1)()x g x b x xe b R x=---∈ (Ⅰ)讨论函数()f x 的单调性;(Ⅱ)当时,若关于x 的不等式()()2f x g x +≤-恒成立,求实数b 的取值范围.请考生在22、23两题中任选一题作答. 注意:只能做所选定的题目.如果多做,则按所做第一个题目计分. 作答时,请用2B 铅笔在答题卡上将所选题号后的方框涂黑. 22.(本小题满分10分)选修4-4:坐标系与参数方程已知平面直角坐标系xOy 中,直线l 的参数方程为2cos 1sin x t y t αα=-+⎧⎨=+⎩(t 为参数,02πα≤<),以原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为24cos 2sin 40ρρθρθ---=.(Ⅰ)求直线l 的普通方程、曲线C 的直角坐标方程;(Ⅱ)若直线l 与曲线C 交于A B 、两点,且2AB =.求α的大小.23.(本小题满分10分)选修4-5:不等式选讲已知函数()()f x x m m R =-∈.(Ⅰ)当2m =时,解不等式()1f x x >7--;(Ⅱ)若存在x R ∈,使()1f x x >7+-成立,求m 的取值范围.龙岩市2019年高中毕业班教学质量检查数学(理科)参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有MEzF13.1 14.2-或4315.4 16.(4,0)(0,4)-U 三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤. 17.(本小题满分12分) 解:(Ⅰ)由2cos 2c B a b =-,得2sin cos 2sin sin C B A B =- ……………………1分即()2sin cos 2sin sin C B B C B =+-,2sin cos sin B C B ∴=sin 0B >Q , 1cos 2C ∴=……………………5分0C π<<Q , 3Cπ∴=……………………6分(Ⅱ)在ADC ∆中,由余弦定理得:2222cos3AD AC DC AC DC π=+-••……7分即229AC DC AC DC +-•=,又222AC DC AC DC +≥•Q 90AC DC ∴≥•>, (9)分1sin 23ADC S AC DC π=••VQ0ADC S ∴<≤V …………………10分2ABCADC S S =V V Q 02ABC S ∴<≤V……………………12分18.(本小题满分12分)解:(Ⅰ)Q 四边形ABCD 是边长为2的菱形,且060ABC ∠=∴ AC 与BD 交于点O 且ABC ∆为等边三角形2AC ∴=,BO =又Q 112OF AC ==,AF CF ∴⊥ ………………2分 Q BM ABCD ⊥平面,AC BM ∴⊥又Q AC BD ⊥,∴AC BMND ⊥平面 OF BMND ⊂Q 平面,AC OF ∴⊥在Rt AOF V 中,2222AF AO OF =+=在Rt BOF V 中,2222FB BO OF =-=∴在ABF ∆中,24AB =, 224AF FB +=, 222AF FB AB+= (4)分AF BE ∴⊥,又Q ,,CF BE CBE CF BE F ⊂=I 平面,∴AF ECB ⊥平面 ……………………5分 (Ⅱ)在平面BMND 中,过O 作直线l ∥BM , 则l ABCD ⊥面,如图,以l 为z 轴,AC所在直线为x 轴,BD 所在直线为y 轴建立空间直角坐标系, ………………6分()B ∴,()1,0,0C -,()M ,()0,N13NE NM =u u u r u u u u r Q,80,33E ⎛⎫∴-⎪⎝⎭,()1,BC ∴=-u u u r,80,,33BE ⎛⎫=- ⎪⎝⎭u u u r 设(),,n x y z =r是平面BCE 的法向量,则 00n BC n BE ⎧=⎪⎨=⎪⎩r u u u r g r u u u r g ,即0803x y z ⎧--=⎪⎨+=⎪⎩,取()n =-r,取BC 中点G ,连结AG ,AG BC ∴⊥,AG BM ⊥, AG BCM ∴⊥面因此,AG uuu r是平面BCM 的法向量,1,,022G ⎛⎫- ⎪⎝⎭Q ,()1,0,0A322AG ⎛⎫∴=- ⎪⎝⎭u u u r , (10)分设二面角E BC M --的大小为θ,则cos 19n AGn AGθ===r u u u r g r u u u r g ∴二面角E BC M --……………………12分19.(本小题满分12分)解:(Ⅰ)设00(x ,)B y 则00(x ,)C y -- …………………1分由220021x y a +=得,2222000221x a x y a a-=-= …………………2分 由12AB AC k k ⋅=-,即000012y y x a x a -⋅=----得,222002a x y -= …………4分所以22220022a x a x a --=,所以22a = 即椭圆E 的标准方程为:2212x y += …………………5分(Ⅱ)设1122(x ,),(x ,)M y N y由2212x y y kx t ⎧+=⎪⎨⎪=+⎩得: 222(12k )4220x ktx t +++-=2121222422,1212kt t x x x x k k--+==++ …………………6分 2212121212()()()y y kx t kx t k x x kt x x t =++=+++2222222222(22)42121212k t k t t k t k k k---=++=+++ 又l 与圆C=22231t k =+ …………………8分 所以2221212222212t t k OM ON x x y y k-+-⋅=+=+u u u u r u u u r 22222232(1)2(1)2(1)01212t k k k k k -++-+===++ …………………11分 所以,OM ON ⊥u u u u r u u u r,即090MON ∠=所以,以线段MN 为直径的圆经过原点. …………………12分20.(本小题满分12分)解:(Ⅰ) 112223325535C C A A p A ==………………3分 ∴恰好经过4次检验就能把阳性样本全部检验出来的概率为35………………4分(Ⅱ)(ⅰ)由已知得1E k ξ=,2ξ的所有可能取值为1,1k +()()211k P p ξ∴==-, ()()2111kP k p ξ=+=--∴()()21(1)11k k E p k p ξ⎡⎤=-++--⎣⎦=()11kk k p +--……………6分若1E ξ=2E ξ,则1(1)k k k k p =+-- ∴(1)1kk p -=1(1)kp k-= ∴111()kp k -= ∴111()k p k =-∴p 关于k 的函数关系式111()k p k =-(k N *∈且2k ≥) ………………8分(ⅱ)由题意可知21E E ξξ<,得()11,kp k <-1p =-Q1kk ∴<,1ln 3k k ∴>,设()1ln (0)3f x x x x =->……………10分 ()33xf x x-'=Q ,∴当3x >时,()0f x '<,即()f x 在()3,+∞上单调递减又ln4 1.3863≈,4 1.33333≈,4ln 43∴>,ln5 1.6094≈,5 1.66673≈,5ln53∴< ∴k 的最大值为4. (12)分21.(本小题满分12分)解:(Ⅰ)11()ln f x x ax a =+-Q 22111()(0)ax f x x x ax ax -'∴=-=> …………1分 当0a <时,()0f x '∴>,()f x ∴在(0,)+∞单调递增; …………2分当0a >时,由()0f x '>得:1x a >;由()0f x '<得:10x a <<,()f x ∴在1(0,)a单调递减,在1(,)a+∞单调递增 ……………………4分综上:当0a <时,()f x 在(0,)+∞单调递增;当0a >时,()f x 在1(0,)a单调递减,在1(,)a+∞单调递增. ………………5分(Ⅱ)由题意:当0a <时,不等式()()2f x g x +≤-,即11ln 1(1)2xx b x xe x x+-+---≤-即ln 11xx b e x x -≤--在(0,)+∞恒成立, ……………6分 令ln 1()x x h x e x x =--,则22221ln 1ln ()x xx x e x h x e x x x-+'=-+=, ………7分 令2()ln xu x x e x =+,则21()(2)0x u x x x e x'=++>,()u x ∴在(0,)+∞单调递增又1u(1)e 0,u()ln 202=>=<,所以,()u x 有唯一零点0x (0112x <<)所以,0()0u x =,即0000ln x x x e x =---------(※) ………………9分 当0(0,)x x ∈时,()0u x <即h ()0x '<,()h x 单调递减;0(,)x x ∈+∞时,()0u x >即h ()0x '>,()h x 单调递增,所以0()h x 为()h x 在定义域内的最小值. ……10分令1()(1)2xk x xe x =<<则方程(※)等价于()(ln )k x k x =-又易知()k x 单调递增,所以ln x x =-,1xe x=………………11分 所以,()h x 的最小值000000000ln 111()1x x x h x e x x x x x -=--=--= 所以11b -≤,即2b ≤所以实数b 的取值范围是(],2-∞ ………………12分22.(本小题满分10分)选修4-4:坐标系与参数方程解:(Ⅰ)由2cos ,1sin ,x t y t αα+=⎧⎨-=⎩消t 得y 1tan 2x α-=+,直线l 的普通方程为tan 2tan 10x y αα-++=,将222cos ,sin ,x y x y ρθρθρ===+代入24cos 2sin 40ρρθρθ---=得 曲线C 的直角坐标方程为224240x y x y +---= ………………4分 (Ⅱ)曲线C 的方程化为22(2)(1)9x y -+-=,曲线C 是以(2,1)为圆心,3为半径的圆.2AB =,圆心到直线l 的距离d ===又d ==解得tan 1α=±,02πα≤<Q ,∴4πα=……………………10分(注:用21t t -求解一样给分)23.(本小题满分10分)选修4-5:不等式选讲 解:(Ⅰ)由已知21x x -+->7当1x <时,不等式等价于217x x -+->,解得2x <-,∴2x <-; 当12x ≤≤时,217x x -+->,此时不等式无解; 当x >2时,217x x -+->,解得5x >,∴5x >综上:解集为{2x x <-或}5x > ………………………5分 (Ⅱ)∵()()111x m x x m x m ---≤---=-∴11x m x m ---≤-当且仅当()()10x m x --≥且1x m x -≥-时等号成立. 依题意1m ->7,解之得8m >或6m <-,∴m 的取值范围为()(),68,-∞-⋃+∞. ………………………10分。
福建省龙岩市2019届高三下学期理数教学质量检测试卷

福建省龙岩市2019届高三下学期理数教学质量检测试卷一、单选题1.已知 (m +2i)(2−i)=4+3i, m ∈R,i 为虚数单位,则 m 的值为( )A .1B .−1C .2D .−22.已知 cos(π4−α)=35,则 sin2α= ( )A .−725B .−15C .15D .7253.已知等差数列 {a n } 的公差为 2 ,若 a 1,a 3,a 4 成等比数列,则数列 {a n } 的前8 项和为( ) A .-20B .-18C .-8D .-104.如果执行下面的程序框图,输入正整数 n,m ,且满足 n ≥m ,那么输出的 p 等于( )A .A n m−1B .A n mC .C n m−1D .C n m5.已知实数 x , y 满足不等式组 {2x −y +2≥0x +2y +1≤03x +y −2≤0 ,则 x −y 的取值范围为( )A .[−2,+∞)B .[−1,+∞)C .(−∞,2]D .[−2,2]6.已知双曲线 C 1:x 2a 2−y 2b2=1 (a >0,b >0) 和双曲线 C 2:y 2m 2−x 2n 2=1 (m >0,n >0) 焦距相等,离心率分别为 e 1 、 e 2 ,若 1e 12+1e22=1 ,则下列结论正确的是( ) A .C 1 和 C 2 离心率相等 B .C 1 和 C 2 渐近线相同 C .C 1 和 C 2 实轴长相等D .C 1 和 C 2 虚轴长相等7.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球表面积为()A.√3πB.2√3πC.4√3πD.12π8.如图,AB和CD是圆O两条互相垂直的直径,分别以OA, OB, OC, OD为直径作四个圆,在圆O内随机取一点,则此点取自阴影部分的概率是()A.1−2πB.12−1πC.2πD.1π9.已知函数f(x)=|cos(ωx+π3)|(ω>0)在区间[−π3,5π6]上单调,则ω的取值范围为()A.(0,1215]B.(0,15]C.[15,1215]D.[1215,1]10.设s=1log2π+1log3π+1log4π+1log5π,T=|a−s|,a∈N∗,当T取最小值时a的值为()A.2B.3C.4D.511.如图,已知正方体ABCD−A1B1C1D1的棱长为4,P是AA1的中点,点M在侧面AA1B1B内,若D1M⊥CP,则ΔBCM面积的最小值为()A.8B.4C.8√2D.8√5512.已知数列{a n}各项均为整数,共有7项,且满足|a k+1−a k|=1, k=1,2,⋯6,其中a1=1 , a 7=a ( a 为常数且 a >0 ).若满足上述条件的不同数列个数共有15个,则 a 的值为( ) A .1B .3C .5D .7二、填空题13.已知向量 a ⇀ , b ⇀ 的夹角为 60° , |a ⇀|=2 , |a ⇀−3b⇀|=√7 ,则 |b ⇀|= . 14.若 (1+x)(a +x)4 的展开式中 x 3 项的系数为16,则实数 a = . 15.已知抛物线 y 2=4x 的焦点为 F ,其准线与 x 轴的交点为 Q ,过点 F 作直线与抛物线交于 A,B 两点.若以 QF 为直径的圆过点 B ,则 |AF|−|BF| 的值为 .16.已知 f(x)=|x|3−4x 2 ,若 f(x) 的图像和 y =ax 的图像有四个不同的公共点,则实数 a的取值范围是 .三、解答题17.在 ΔABC 中,内角 A , B , C 所对的边分别为 a , b , c ,已知 2ccosB =2a −b .(Ⅰ)求角 C 的大小;(Ⅱ)设 D 为 BC 中点,若 AD =3 ,求 ΔABC 面积的取值范围.18.如图,已知四边形 ABCD 是边长为2的菱形,且 ∠ABC =600 , BM ⊥平面ABCD ,DN//BM , BM =2DN ,点 E 是线段 MN 上的一点. O 为线段 BD 的中点.(Ⅰ)若 OF ⊥ BE 于 F 且 OF =1 ,证明: AF ⊥ 平面 ECB ;(Ⅱ)若 BM =4 , NE⇀=13NM ⇀ ,求二面角 E −BC −M 的余弦值. 19.已知椭圆 E 的方程为 x 2a2+y 2=1 ,点 A 为长轴的右端点. B,C 为椭圆 E 上关于原点对称的两点.直线 AB 与直线 AC 的斜率 k AB 和k AC 满足: k AB ·k AC =−12 .(Ⅰ)求椭圆 E 的标准方程;(Ⅱ)若直线 l:y =kx +t 与圆 x 2+y 2=23相切,且与椭圆 E 相交于 M,N 两点,求证:以线段 MN 为直径的圆恒过原点.20.某医院为筛查某种疾病,需要检验血液是否为阳性,现有 n ( n ∈N ∗ )份血液样本,有以下两种检验方式:(1)逐份检验,则需要检验 n 次;(2)混合检验,将其中 k ( k ∈N ∗ 且 k ≥2 )份血液样本分别取样混合在一起检验.若检验结果为阴性,这 k 份的血液全为阴性,因而这 k 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这 k 份血液究竟哪几份为阳性,就要对这 k 份再逐份检验,此时这 k 份血液的检验次数总共为 k +1 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为 p(0<p <1) .(Ⅰ)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过4次检验就能把阳性样本全部检验出来的概率.(Ⅱ)现取其中 k ( k ∈N ∗ 且 k ≥2 )份血液样本,记采用逐份检验方式,样本需要检验的总次数为 ξ1 ,采用混合检验方式,样本需要检验的总次数为 ξ2(ⅰ)试运用概率统计的知识,若 Eξ1= Eξ2 ,试求 p 关于 k 的函数关系式 p =f(k) ;(ⅱ)若 p =1−1√e3 ,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求 k 的最大值.参考数据: ln2≈0.6931 , ln3≈1.0986 , ln4≈1.3863 , ln5≈1.6094 , ln6≈1.791821.已知函数 f(x)=lnx +1−xax (a ∈R 且a ≠0) , g(x)=(b −1)x −xe x −1x(b ∈R) (Ⅰ)讨论函数 f(x) 的单调性;(Ⅱ)当a=1时,若关于 x 的不等式 f(x)+g(x)≤−2 恒成立,求实数 b 的取值范围.22.选修4-4:坐标系与参数方程已知平面直角坐标系 xOy 中,直线 l 的参数方程为 {x =−2+tcosαy =1+tsinα ( t 为参数, 0≤α<π2 ),以原点 O 为极点, x 轴正半轴为极轴建立极坐标系,曲线 C 的极坐标方程为 ρ2−4ρcosθ−2ρsinθ−4=0 .(Ⅰ)求直线 l 的普通方程、曲线 C 的直角坐标方程;(Ⅱ)若直线 l 与曲线 C 交于 A 、B 两点,且 |AB|=2 .求 α 的大小.23.选修4-5:不等式选讲已知函数 f(x)=|x −m|(m ∈R) .(Ⅰ)当 m =2 时,解不等式 f(x)>7−|x −1| ;(Ⅱ)若存在 x ∈R ,使 f(x)>7+|x −1| 成立,求 m 的取值范围.答案解析部分1.【答案】A【解析】【解答】∵(m +2i)(2−i)=4+3i,∴2m +2+(4−m)i =4+3i , ∴{2m +2=44−m =3 ,即 m =1故答案为:A【分析】由复数运算及 复数相等的充要条件即可求出 m 的值 .2.【答案】A【解析】【解答】 cos(π4−α)=√22cosα+√22sinα=35,√22cosα+√22sinα=35两边平方得: 12+cosαsinα=925 , 2cosαsinα=1825−1=−725 , 即 sin2α=−725, 故答案为:A.【分析】 由两角差的余弦函数整理已知等式,两边平方后可得结果.3.【答案】C【解析】【解答】解:等差数列 {a n } 的公差d 为2,若 a 1 , a 3,a 4 成等比数列,可得a 32= a 1a 4 ,即有( a 1 +4)2= a 1 ( a 1 +6), 解得 a 1 =﹣8,则{a n }前8项的和为8×(﹣8) +12× 8×7×2=﹣8,故答案为:C .【分析】利用等比数列的性质可得等差数列 {a n } 的首项,即可得到{a n }前8项的和.4.【答案】D【解析】【解答】解:第一次循环:k =1,p =1,p = 1×(n−m+1)m;第二次循环:k =2,p = (n−m+1)m ×n−m+2m−1 ;第三次循环:k =3,p = (n−m+1)m ×n−m+2m−1×n−m+3m−2 …第m 次循环:k =m ,p = (n−m+1)m ×n−m+2m−1×n−m+3m−2×⋯×n ﹣12×n 1此时结束循环,输出p = (n−m+1)m ×n−m+2m−1×n−m+3m−2×⋯×n ﹣12×n 1 = C n m故答案为:D .【分析】运行程序,当结束循环时,即可得到输出p 的值.5.【答案】B【解析】【解答】解:设z =x ﹣y ,则y =x ﹣z ,作出不等式对应的平面区域(阴影部分)如图:平移直线y =x ﹣z ,由图象可知当直线y =x ﹣z 经过点A (﹣1,0)时,直线y =x ﹣z 的截距最大, 此时z 最小,最小值z =﹣1﹣0=﹣1 继续向下平移直线y =x ﹣z ,z 值越来越大, ∴x −y 的取值范围为 [−1,+∞) 故答案为: B .【分析】作出不等式对应的平面区域,平移直线y =x ﹣z ,由图象可得 x −y 的取值范围.6.【答案】B【解析】【解答】设两个双曲线的焦距为 2c , ∴e 1=c a , e 2=cm又 1e12+1e 22=1 ∴a 2c 2+m 2c2=1 ,∴a 2+m 2=c 2 ∴m 2=c 2−a 2=b 2 ,即 m =b ,故 n =a又双曲线 C 1:x 2a 2−y 2b2=1 的渐近线方程为: y =±ba x ,双曲线 C 2:y 2m 2−x 2n2=1 的渐近线方程为: y =±mn x∴C 1 和 C 2 渐近线相同 故答案为:B【分析】由双曲线方程分别求出他们的离心率 e 1 、 e 2 ,由 1e 12+1e 22=1可计算出 C 1 和 C 2渐近线相同 .7.【答案】C【解析】【解答】由三视图知几何体是一个侧棱与底面垂直的三棱锥,底面是斜边上的高为 √2 的等腰直角三角形,与底面垂直的侧面是个等腰三角形,底边长为 2 ,高为 2 ,故三棱锥的外接球与以棱长为 2 的正方体的外接球相同,其直径为 2√3 ,半径为 √3∴ 三棱锥的外接球体积为 43π×(√3)3=4√3π故答案为: C【分析】由三视图知几何体是一个侧棱与底面垂直的三棱锥,计算可得 该三棱锥的外接球表面积 .8.【答案】A【解析】【解答】解:根据圆的对称性只需看四分之一即可,设扇形的半径为r ,则扇形OBC 的面积为 14πr 2 ,连接BC ,把下面的阴影部分平均分成了2部分,然后利用位移割补的方法,分别平移到图中划线部分,则阴影部分的面积为: 14πr 2−12r 2 ,∴此点取自阴影部分的概率是 14πr 2−12r 214πr2=1−2π .故答案为:A .【分析】分别计算扇形OBC 的面积与阴影部分的面积,利用 几何概型概率计算公式可得结果.9.【答案】B【解析】【解答】令 u =ωx +π3 ,则 y =|cosu| ,其中 u =ωx +π3 在区间 [−π3,5π6] 上单调递增,且 u ∈[−π3ω+π3,5π6ω+π3]y =|cosu| 在 [0,π2] 上单调递减, ∴{ −π3ω+π3≥05π6ω+π3≤π2ω>0,∴0<ω≤15 ,故答案为:B【分析】由余弦函数的图象可得,当函数在区间 [−π3,5π6] 上单调时 ω 的取值范围.10.【答案】C【解析】【解答】 s =1log 2π+1log 3π+1log 4π+1log 5π=ln2lnπ+ln3lnπ+ln4lnπ+ln5lnπ=ln120lnπ=log π120∈(4,5) ,此时 (5−log π120)−(log π120−4)=9−2log π120=log ππ91202>0 ∴T 取最小值时 a 的值为4 故答案为:C【分析】利用对数的运算性质可得 T 取最小值时 a 的值.11.【答案】D【解析】【解答】解:以AB ,AD ,AA 1为坐标轴建立空间坐标系如图所示:则P (0,0,2),C (4,4,0),D 1(0,4,4),设M (a ,0,b ),则 D 1M ⃗⃗⃗⃗⃗⃗⃗⃗⃗ = (a ,﹣4,b ﹣4), CP ⃗⃗⃗⃗⃗ = (﹣4,﹣4,2), ∵D 1M ⊥CP ,∴D 1M ⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅CP⃗⃗⃗⃗⃗ =− 4a+16+2b ﹣8=0,即b =2a ﹣4. 取AB 的中点N ,连结B 1N ,则M 点轨迹为线段B 1N ,过B作BQ⊥B1N,则BQ =4×225=4√55.又BC⊥平面ABB1A1,BC⊥BQ,∴S△PBC的最小值为S△QBC=12×4×4√55=8√55.故答案为:D.【分析】以AB,AD,AA1为坐标轴建立空间坐标系,利用空间向量计算可得S△PBC的最小值. 12.【答案】B【解析】【解答】解:∵|a k+1−a k|=1,∴a k+1−a k=1或a k+1−a k=﹣1设有x个1,则有6x个﹣1∴a7﹣a1=(a7﹣a6)+(a6﹣a5)+…+(a2﹣a1)∴a−1=x+(6﹣x)•(﹣1)∴x=a+52∴这样的数列个数有C6x=15,解得x=2或4,∴a=−1(舍)或a=3故答案为:B.【分析】由题意a k+1−a k=1或a k+1−a k=﹣1,由满足上述条件的不同数列个数共有15个可得a的值 .13.【答案】1【解析】【解答】解:a⃗⋅b⃗=| a⃗|| b⃗|cos60°=| b⃗|,∵|a⇀−3b⇀|=√7,∴|a |2﹣6| b⃗|+9| b⃗|2=7,即9| b⃗|2﹣6| b⃗| −3=0,解得| b⃗|=1或−13(舍去).故答案为:1.【分析】由平面向量数量积的运算即可求得向量b⇀的模.14.【答案】−2或43【解析】【解答】(a+x)4的通项公式为T r+1=C4r a4−r x r,∴(a+x)4展开式的含x3,x2项的系数分别是C43a,C42a2,∴(1+x)(a+x)4的展开式中x3项的系数为C43a+C42a2=16∴3a2+2a−8=0∴a= −2或43故答案为:−2或43【分析】由二项式展开式的通项公式可得展开式中x3项的系数为C43a+C42a2=16,即可解出实数a的值.15.【答案】4【解析】【解答】解:假设k存在,设AB方程为:y=k(x﹣1),与抛物线y2=4x联立得k2(x2﹣2x+1)=4x,即k2x2﹣(2k2+4)x+k2=0设两交点为A(x2,y2),B(x1,y1),∵以QF为直径的圆过点B,∴∠QBA=90°,∴(x1﹣2)(x1+2)+y12=0,∴x12+y12=4,∴x12+4x1﹣1=0(x1>0),∴x1=√5−2,∵x1x2=1,∴x2=√5+2,∴|AF|﹣|BF|=(x2+1)﹣(x1+1)=4,故答案为:4【分析】设AB方程为:y=k(x﹣1),与抛物线y2=4x联立设两交点为A(x2,y2),B(x1,y1),由题意及韦达定理计算可得所求.16.【答案】(−4,0)∪(0,4)【解析】【解答】f(x)的图像和y=ax的图像有四个不同的公共点等价于方程|x|3−4x2=ax 有四个不同的实根,当x=0时,方程显然成立,即x=0为方程的一个实根,问题转化为x≠0时,方程有三个不等的实根,当x>0时,a=x2−4x当x<0时,a=−x2−4x作出图象如图:由图象可得:a∈(−4,0)∪(0,4)故答案为:(−4,0)∪(0,4)【分析】由题意方程|x|3−4x2=ax有四个不同的实根,分离a利用函数图象可得满足题意的实数a的取值范围 .17.【答案】解:(Ⅰ)由2ccosB=2a−b,得2sinCcosB=2sinA−sinB即2sinCcosB=2sin(B+C)−sinB,∴2sinBcosC=sinB∵sinB>0,∴cosC=1 2∵0<C<π,∴C=π3(Ⅱ)在ΔADC中,由余弦定理得:AD2=AC2+DC2−2AC⋅DC⋅cos π3即AC2+DC2−AC•DC=9,又∵AC2+DC2≥2AC•DC∴9≥AC•DC>0,∵S△ADC=12AC•DC•sinπ3∴0<S△ADC≤9√34,∵S△ABC=2S△ADC∴0<S △ABC ≤9√32【解析】【分析】(1)利用三角函数公式计算可得 角 C 的大小 ;(2) 在 ΔADC 中,由余弦定理得 AC 2+DC 2−AC •DC =9 ,则 9≥AC •DC >0,利用三角形面积可得 ΔABC 面积的取值范围.18.【答案】解:(Ⅰ) ∵ 四边形 ABCD 是边长为2的菱形,且 ∠ABC =600∴ AC 与 BD 交于点 O 且 ΔABC 为等边三角形∴AC =2 , BO =√3 又 ∵ OF =1=12AC , ∴AF ⊥CF∵ BM ⊥平面ABCD , ∴AC ⊥BM 又 ∵ AC ⊥BD , ∴ AC ⊥平面BMND ∵OF ⊂平面BMND , ∴AC ⊥OF在 Rt △AOF 中, AF 2=AO 2+OF 2=2 在 Rt △BOF 中, FB 2=BO 2−OF 2=2∴ 在 ΔABF 中, AB 2=4 , AF 2+FB 2=4 , AF 2+FB 2=AB 2 ∴AF ⊥BE ,又 ∵ CF,BE ⊂平面CBE,CF ∩BE =F ,∴ AF ⊥平面ECB(Ⅱ)在平面 BMND 中,过 O 作直线 l ∥ BM , 则 l ⊥面ABCD ,如图,以 l 为 z 轴, AC 所在直线为 x 轴, BD 所在直线为 y 轴建立空间直角坐标系,∴B(0,√3,0) , C(−1,0,0) , M(0,√3,4) , N(0,−√3,2) ∵NE ⇀=13NM ⇀ , ∴E(0,−√33,83) , ∴BC⇀=(−1,−√3,0) , BE ⇀=(0,−4√33,83) 设 n ⇀=(x,y,z) 是平面 BCE 的法向量,则{n ⇀·BC ⇀=0n ⇀·BE⇀=0 ,即 {−x −√3y =0−4√33y +83z =0 , 取 n ⇀=(−6,2√3,3) ,取 BC 中点 G ,连结 AG , ∴AG ⊥BC , AG ⊥BM , ∴AG ⊥面BCM因此, AG⇀ 是平面 BCM 的法向量, ∵G(−12,√32,0) , A(1,0,0) ∴AG ⇀=(−32,√32,0) , 设二面角 E −BC −M 的大小为 θ ,则cosθ=|n ⇀·AG ⇀|n ⇀|·|AG ⇀||=9+3√36+12+9·√94+34=4√1919 , ∴ 二面角 E −BC −M 的余弦值为 4√1919【解析】【分析】(1)由题意 AF ⊥CF , AF ⊥BE ,即可证明 AF ⊥ 平面 ECB ;(2) 以 l 为 z 轴, AC 所在直线为 x 轴, BD 所在直线为 y 轴建立空间直角坐标系, 根据空间向量计算可得 二面角 E −BC −M 的余弦值 .19.【答案】解:(Ⅰ)设 B(x 0,y 0) 则 C(−x 0,−y 0) 由 x 02a2+y 02=1 得, y 02=1−x 02a 2=a 2−x 02a 2由 k AB ⋅k AC =−12 ,即 y 0x 0−a ⋅−y 0−x 0−a =−12 得, y 02=a 2−x 022所以a 2−x 02a2=a 2−x 022 ,所以 a 2=2 即椭圆 E 的标准方程为: x 22+y2=1(Ⅱ)设 M(x 1,y 1),N(x 2,y 2)由 {x 22+y 2=1y =kx +t得: (1+2k 2)x 2+4ktx +2t 2−2=0x 1+x 2=−4kt 1+2k 2,x 1x 2=2t 2−21+2k2y 1y 2=(kx 1+t)(kx 2+t)=k 2x 1x 2+kt(x 1+x 2)+t 2=k 2(2t 2−2)1+2k2+−4k 2t 21+2k 2+t 2=t 2−2k 21+2k2又 l 与圆C 相切,所以 √63=|t|√1+k 即 23=t 21+k2 所以 OM ⇀⋅ON ⇀=x 1x 2+y 1y 2=2t 2−2+t 2−2k 21+2k 2=3t 2−2(1+k 2)1+2k 2=2(1+k 2)−2(1+k 2)1+2k2=0所以, OM⇀⊥ON ⇀ ,即 ∠MON =900 所以,以线段 MN 为直径的圆经过原点.【解析】【分析】(1)由题意可求得, a 2=2,可得椭圆 E 的标准方程;(2) 直线 l:y =kx +t 与圆 x 2+y 2=23联立,由 OM ⇀⋅ON ⇀=0可得以线段 MN 为直径的圆恒过原点.20.【答案】解:(Ⅰ) p =C 21C 31A 32A 22A 55=35∴ 恰好经过4次检验就能把阳性样本全部检验出来的概率为 35(Ⅱ)(ⅰ)由已知得 Eξ1=k , ξ2 的所有可能取值为 1,k +1 ∴P(ξ2=1)=(1−p)k , P(ξ2=k +1)=1−(1−p)k ∴ Eξ2=(1−p)k +(k +1)[1−(1−p)k ] = k +1−k(1−p)k 若 Eξ1= Eξ2 ,则 k =k +1−k(1−p)k ∴k(1−p)k =1(1−p)k =1k ∴1−p =(1k )1k ∴p =1−(1k)1k∴p 关于 k 的函数关系式 p =1−(1k)1k ( k ∈N ∗ 且 k ≥2 )(ⅱ)由题意可知 Eξ2<Eξ1 ,得 1k <(1−p)k , ∵p =1−1√e3∴1k <(1√e3)k , ∴lnk >13k ,设 f(x)=lnx −13x(x >0)∵f ′(x)=3−x3x, ∴ 当 x >3 时, f ′(x)<0 ,即 f(x) 在 (3,+∞) 上单调递减 又 ln4≈1.3863 , 43≈1.3333 , ∴ln4>43 , ln5≈1.6094 , 53≈1.6667 , ∴ln5<53∴ k 的最大值为4.【解析】【分析】(1)由古典概型的计算公式可得结果;(2) 由已知得 Eξ1=k , ξ2 的所有可能取值为 1,k +1 ,由期望运算可得 p 关于 k 的函数关系式 ; 由题意可知 Eξ2<Eξ1 ,得 1k <(1−p)k , 利用单调性可得 k 的最大值.21.【答案】解:(Ⅰ) ∵f(x)=lnx +1ax −1a ∴f ′(x)=1x −1ax 2=ax−1ax 2(x >0) 当 a <0 时, ∴f ′(x)>0 , ∴f(x) 在 (0,+∞) 单调递增;当 a >0 时,由 f ′(x)>0 得: x >1a ;由 f ′(x)<0 得: 0<x <1a,∴f(x) 在 (0,1a ) 单调递减,在 (1a,+∞) 单调递增综上:当 a <0 时, f(x) 在 (0,+∞) 单调递增;当 a >0 时, f(x) 在 (0,1a ) 单调递减,在 (1a,+∞) 单调递增.(Ⅱ)由题意:当 a =1 时,不等式 f(x)+g(x)≤−2 ,即 lnx +1x −1+(b −1)x −xe x −1x≤−2即 b −1≤e x −lnx x−1x 在(0,+∞) 恒成立, 令 ℎ(x)=e x −lnx x −1x ,则 ℎ′(x)=e x −1−lnx x 2+1x 2=x 2e x +lnx x 2, 令 u(x)=x 2e x +lnx ,则 u ′(x)=(x 2+2x)e x +1x >0,∴u(x) 在 (0,+∞) 单调递增又 u(1)=e >0,u(12)=√e4−ln2<0 ,所以, u(x) 有唯一零点 x 0 ( 12<x 0<1 )所以, u(x 0)=0 ,即 x 0e x 0=−lnx0x 0--------(※)当 x ∈(0,x 0) 时, u(x)<0 即 ℎ′(x)<0 , ℎ(x) 单调递减; x ∈(x 0,+∞) 时, u(x)>0 即 ℎ′(x)>0 , ℎ(x) 单调递增,所以 ℎ(x 0) 为 ℎ(x) 在定义域内的最小值.令 k(x)=xe x (12<x <1) 则方程(※)等价于 k(x)=k(−lnx)又易知 k(x) 单调递增,所以 x =−lnx , e x =1x所以, ℎ(x) 的最小值 ℎ(x 0)=e x 0−lnx 0x 0−1x 0=1x 0−−x 0x 0−1x 0=1所以 b −1≤1 ,即 b ≤2 所以实数 b 的取值范围是 (−∞,2]【解析】【分析】(1) 利用导数的符号可得函数的单调性;(2) 当 a =1 时, 分离常数b, 利用导数求函数 ℎ(x)=e x −lnx x −1x 的最值 ,即可得到实数b 的取值范围.22.【答案】解:(Ⅰ)由 {x +2=tcosα, y −1=tsinα, 消 t 得y−1x+2=tanα , 直线 l 的普通方程为 xtanα−y +2tanα+1=0 ,将 ρcosθ=x,ρsinθ=y,ρ2=x 2+y 2 代入 ρ2−4ρcosθ−2ρsinθ−4=0 得 曲线 C 的直角坐标方程为 x 2+y 2−4x −2y −4=0(Ⅱ)曲线 C 的方程化为 (x −2)2+(y −1)2=9 ,曲线 C 是以 (2,1) 为圆心, 3 为半径的圆.|AB|=2,圆心到直线l的距离d=√r2−(AB2)2=√9−1=2√2,又d=|4tanα|√tanα+1,∴|4tanα|√tanα+1=2√2,解得tanα=±1,∵0≤α<π2,∴α=π4【解析】【分析】(1)消参可得直线l的普通方程,利用极坐标与直角坐标互化可得曲线C的直角坐标方程;(2)由直线与圆的位置关系可得α的大小.23.【答案】解:(Ⅰ)由已知|x−2|+|x−1|>7当x<1时,不等式等价于2−x+1−x>7,解得x<−2,∴x<−2;当1≤x≤2时,2−x+x−1>7,此时不等式无解;当x>2时,x−2+x−1>7,解得x>5,∴x>5综上:解集为{x|x<−2或x>5}(Ⅱ)∵||x−m|−|x−1||≤|(x−m)−(x−1)|=|m−1|∴|x−m|−|x−1|≤|m−1|当且仅当(x−m)(x−1)≥0且|x−m|≥|x−1|时等号成立.依题意|m−1|>7,解之得m>8或m<−6,∴m的取值范围为(−∞,−6)∪(8,+∞).【解析】【分析】(1)解绝对值不等式可得其解集;(2)由绝对值三角不等式可将原不等式转化为关于m的不等式,可得m的取值范围.。
福建省龙岩市2019年质检数学卷及答案

2019年龙岩市九年级学业年龙岩市九年级学业((升学升学))质量检查数学试题(满分满分:150:150分考试时间分考试时间:120:120分钟分钟) )一、选择题:本大题共10小题,每小题4分,共40分1.1.如图,数轴上的单位长度为如图,数轴上的单位长度为1,若实数a ,b 所表示的数恰好在整数点上,则a+b = A. 0 B.-1 C. 1 D. 52.2.下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是3.3.下列调查中,适合采用全面调查下列调查中,适合采用全面调查下列调查中,适合采用全面调查((普查普查))方式的是 A.对汀江流域水质情况的调查对汀江流域水质情况的调查B.对端午节期间市场上粽子质量情况的调查对端午节期间市场上粽子质量情况的调查C.对某班对某班40名同学身高情况调查D.对某类烟花爆竹燃放安全情况的调查对某类烟花爆竹燃放安全情况的调查 4.4.是是îíì==b y a x 方程组îíì=-=+72332y x y x 的解,则5a -b 的值是 A. 10 B. -10 C. 14 D.215.5.下列图形中,∠下列图形中,∠下列图形中,∠11一定大于∠一定大于∠22的是ba22221111OC .A .B .D .C .A .B .z yx(第7题)6.6.若关于若关于x 的一元一次不等式组îíì<->-m x x x )2(312的解是x <5<5,则,则m 的取值范围是A.m ≥5 B.m >5 C. m ≤5 D.m <5 7.7.如图,如图,x 、y 、z 分别表示以直角三角形三边为边长的正方形面积,则下列结论正确的是、A. x 2=y 2+z 2 B. x <y +z y+z C.x -y > z D. D. x =y+z 8.8.三个等边三角形的摆放位置如图,若∠三个等边三角形的摆放位置如图,若∠三个等边三角形的摆放位置如图,若∠3=603=603=60°,则∠°,则∠°,则∠1+1+1+∠∠2 的度数是 A.9 0° B. 120° C.270° D. 360°9.9.如图,抛物线如图,抛物线y=ax 2+bx+c 与x 轴交于点A (-1,0)0),顶点,顶点坐标是坐标是(1(1(1,,n ),与y 轴的交点在轴的交点在(0(0(0,,3)3)和和(0(0,,6)6)之间之间之间((包含端 点),则下列结论错误的是A.3a +b a+b <0B. -2≤a ≤-≤-lC.l C. abc >0D.9>0 D.9a +3b +2c >0 10.10.某些整数的所有正约数之和可以按如下方法求得,如某些整数的所有正约数之和可以按如下方法求得,如某些整数的所有正约数之和可以按如下方法求得,如: :6=2×3,则6的所有正约数之和为的所有正约数之和为(1+3)+(2+6)=(1+2)(1+3)+(2+6)=(1+2)(1+3)+(2+6)=(1+2)××(1+3)=12(1+3)=12;;12=22×3,则12的所有正约数之和为的所有正约数之和为(1+3)+(2+6)+(4+12)=(1+2+2(1+3)+(2+6)+(4+12)=(1+2+22)×(1+3)=2836=2×3232,则,则36的所有正约数之和为的所有正约数之和为(1+3+9)+(2+6+18)+(4+12+36)= (1+2+2(1+3+9)+(2+6+18)+(4+12+36)= (1+2+22)×(1+3+32)=91 参照上述方法,那么144的所有正约数之和为yxx =1O A (第9题)321(第8题)A.424B.421C.420D.403 二、填空题:本大题共6小题,每小题4分,共24分11.(11.(--2)--11=_______.12.12.一个不透明的袋子中装有一个不透明的袋子中装有4个黑球,个黑球,22个自球,每个球除颜色个自球,每个球除颜色 外其他都相同,从中任意摸出1个球是白球的概率是个球是白球的概率是_______. _______. 13.13.已知∠已知∠A 是锐角,且sin ∠A =31,则cos ∠A =_______.14.14.当当x=a 与x =b (a ≠b )时,代数式x 2-2x +3的值相等,则x=a+b 时,代数式x 22-2x +3的值为的值为_______. _______.15.15.如图,如图,AB 是⊙O 的直径,点E 是BF 的中点,过点E 的切线分别交AF 、AB 的延长线于点D 、C ,若∠C =30=30°,⊙°,⊙O 的半径是的半径是2,则图形中阴影部分的面积是,则图形中阴影部分的面积是_______. _______.16.16.如图,△如图,△ABC 中,∠ABC =30=30°,°,AB =4=4,,BC =5=5,,P 是△ABC 内部的任意一点,连接PA ,PB ,PC ,则PA+PB+PC 的最 小值为小值为_______. _______. 三、解答题:本大题共9小题,共86分.17. (8分)解方程:1-x x -x2=118.(8分)先化简,再求值:2212xx x ++-÷(x -13+x x ),其中x =31ABCP(第16题)(第15题)19.(8分)在四边形ABCD 中,AB ∥CD . (1)(1)如图如图1,已知∠A =∠B ,求证:AD=BC ;(2)(2)如图如图2,已知∠A =60=60°,∠°,∠B =45=45°,°,AD =2=2,求,求BC 的长的长. .20.(8分)证明:三角形的中位线平行于三角形的第三边,并且等于第三边的一半证明:三角形的中位线平行于三角形的第三边,并且等于第三边的一半. .(要求:在给出的△ABC 中用尺规作出AB 、AC 边的中点M 、N ,保留作图痕迹,不要求写作法,并根据图形写出已知、求证和证明根据图形写出已知、求证和证明) )BDCACDA BABC21.(8分) (1)(1)计算计算计算: :211´+321´+431´+541´+651´(2)(2)求证求证求证: : 31<311´+421´+531´+641´<5422.(10分)小宝大学毕业后回家乡透行园艺创业,第一期培植盆景与花卉各50盆,售后进行统计得知:盆景的平均每盆利润是160元,花卉的平均每盆利润是20元. 调研发现:①盆景每增加1盆,盆景的平均好盆利润减少2元:每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均际盆利润始终不变,小宝计划第二期培植盆景与花齐共100盆,设培植的盆景比第一期增加x 盆,第二期盆景与花卉售完后的利润分别为W 1、W 2(单位:元单位:元) )(1)(1)用含用含x 的代数式分别表示W 1、W 2;(2)(2)当当x 取何们叫时,第二期培植的盆景与花卉作售完行获得的总利润最大?最大总利润是多少?23. (10分)随着互联网、移动终端的迅速发展,数字化阅读越来越普及随着互联网、移动终端的迅速发展,数字化阅读越来越普及. . 公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查((问卷训查表如下图所示如下图所示)),并将调查结果绘制成图①和图②所示的统计图,并将调查结果绘制成图①和图②所示的统计图((均不完整均不完整). ).“您如何看待教化阅读”问卷调查表您好!这是一份关于“您如何看待数字化间读问调查表,请在表格中选择一项您最认 观点,在其后空格内打“√”,非常感谢您的合作观点,在其后空格内打“√”,非常感谢您的合作. . 代码 观点A 获取信息方便获取信息方便,,可以随时随地观看B 价格便宜易得C使得人们成为“低头族”使得人们成为“低头族”,,不利于 人际交往E D 15%C 30%B A 46%人数/人A B C D E 观点2007502502300O5001000150020002500D 内容丰富内容丰富,,比低纸质书涉猎更广 E其他请根据统计图中提供的信息,解答下列问题请根据统计图中提供的信息,解答下列问题: :(1)(1)本次接受词查的总人数是本次接受词查的总人数是本次接受词查的总人数是__________________人,并将条形统计图补充完整;、人,并将条形统计图补充完整;、(2)(2)在扇形统计图中,观点在扇形统计图中,观点E 的百分比是的百分比是_______,_______,_______,表示观点表示观点B 的扇形的圆心角度数为的扇形的圆心角度数为__________________度度. (3)(3)某市共有某市共有300万人,请根据以上调查结果估算该市持A 、B 、D 观点赞成数字化阅读的人数共有多少万人多少万人. .24. (12分)如图,点P 是⊙O 直径AB 上的一点,过P 作直线CD ⊥AB ,分别交⊙O 于C 、D 两点,连接AC ,并将线段AC 绕点A 进时针旋转9090°得到°得到AE ,连接ED ,分别交⊙O 和AB 于F 、G ,连接FC .(1)(1)求证求证求证::∠ACF =∠AED ;(2)(2)若点若点P 在直径AB 上运动上运动((不与点A 、B 重合重合)),其它条件不变,请问AP EG是否为定值是否为定值??若是,请求出其值; 若不是,请说明理由若不是,请说明理由. .PG FO ABEDC25.(14分)已知直线y=x+t 与双曲线y =xk(k >0)>0)交于交于C 、D 两点,过C 作CA ⊥x 轴于点A ,过 D 作DB ⊥y 轴于点B ,连接AB .(1)(1)求求C 、D 两点的坐标两点的坐标; ;(2)(2)试探究直线试探究直线AB 与CD 的位置关系并说明理由的位置关系并说明理由; ;(3)(3)已加点已加点D (3,2)(3,2),且,且C 、D 在抛物线y=ax 2+bx +5(a ≠0) 上,若当m ≤x ≤n(n(其中其中mn <0)<0)时,函数时,函数 y=ax 2+bx +5的最 小值为2m ,最大值为2n ,求m+n 的值,yx–4–3–2–11234–4–3–2–11234ODC参考答案一、一、BACAC ADBCD BACAC ADBCD二、二、111111..12-12.131313..322 14.3 15.32233p - 16.41 三、1717.(本小题满分.(本小题满分8分)解:方程两边同乘以(1)x x -得22(1)(1)x x x x --=-…………………………………………44分整理得:2x -=-,解得2x =………………………………………… 6 6分 检验:当2x =时,(1)20x x -=¹…………………………………………77分 所以2x =是原方程的解……………………是原方程的解……………………88分 1818.(本小题满分.(本小题满分8分)解:原式2223()(1)11x x x x x x x -+=¸-+++…………………………………………33分 =()()21122-+×+-x x x x x …………………………………………55分=()11+x x …………………………………………66分当13x =时,原式1914433==´…………………………………………88分1919.(本小题满分.(本小题满分8分)解:(Ⅰ)证明:如图,过点C 作//CE AD 交AB 于点E …………………………………………11分DNMABC//CE AD ,1A \Ð=Ð,\CE BC = (2)2分 //AB CD ,//CE AD ,∴四边形AECD 为平行四边形……………………为平行四边形……………………33分\AD CE =, AD BC \=…………………………………………44分(Ⅱ)分别过点,D C 作,DE AB CF AB ^^,垂足为,E F ,………………,……………… 5 5分 //DE CF \,//AB CD ,\四边形DEFC 为矩形,∴DE CF =...........................6分 在Rt DAE D 中,60,2A AD Ð=°=,sin 60DEAD\°=,即322DE =,3DE \=………………77分 在Rt CBF D 中,45,3B CF DE Ð=°==,∴26BC CF ==………………88分20. (本小题满分8分)解:如图,点,M N 即为所求作的点………………即为所求作的点………………22分(一个点1分,未标字母不给分)已知:如图,ABC D 中,点,M N 分别是,AB AC 的中点,连接MN . 求证:1//,2MN BC MN BC =.……………….………………44分 证明:延长MN 至点D ,使得MN ND =,连接CD在AMN D 和CDN D 中,AN CDANM DNC MN ND =ìïÐ=Ðíï=î,AMN \D ≌()CDN SAS D (5)5分 AMN D \Ð=Ð,//AM CD \,即//BM CDAM BM CD ==,\四边形BMDC 为平行四边形………………为平行四边形………………66分//MN BC \,MD BC = (7)7分12MN MD =,12MN BC \=………………………………88分2121.(本小题满分.(本小题满分8分)解:(Ⅰ)解:原式11111111511223455666=-+-+-+-=-=………………………………44分(Ⅱ)证明: 解法一:111111111111111+++(1)()()()1324354623224235246=-+-+-+-´´´´ .............6分 1111111117(1)2324354630=-+-+-+-=.....................................7分 110424,330530==,1101724433030305\=<<=,即原式得证,即原式得证 (8).............8分 解法二:111111111111+++++++++233445561324354612233445<<´´´´´´´´´´´´…………………………………………………………………………66分1111111111111111111123344556132435462233445\-+-+-+-<+++<-+-+-+-´´´´………………………………………………………………………77分1111143132435465\<+++<´´´´,即原式得证……………………………………,即原式得证……………………………………88分 2222.(本小题满分.(本小题满分10分)解:(Ⅰ)解:21(1602)(50)2608000W x x x x =-+=-++ ………………………………22分220(50)201000W x x =-=-+………………………………44分(Ⅱ)依题意得:2122409000W W W x x =+=-++………………………………66分22(10)9200x =--+ (8)8分 因为x 为正整数,所以当10x =时,总利润W 最大,最大值为9200………………1010分MNA BCDEFG O P(答:略)2323.(本小题满分.(本小题满分10分)解:(Ⅰ)解:(Ⅰ)500050005000;图略;(Ⅱ);图略;(Ⅱ);图略;(Ⅱ)4%4%4%;;1818°;(每个空格°;(每个空格2分,共8分)(Ⅲ)解:观点B 占的百分比146%30%15%4%5%=----=………………99分300(46%5%15%)30066%198´++=´=万.(答:略(答:略..)………………)………………1010分 2424.(本小题满分.(本小题满分12分)解:(Ⅰ)连接AD ………………………………11分则由同弧所对的圆周角相等可知ACF ADF Ð=Ð………………………………22分又AE 是由线段AC 绕点A 逆时针旋转9090°得到,°得到,AC AE \=,..................,..................33分 AED ADF \Ð=Ð....................................44分 ACF AED \Ð=Ð (5)5分 (Ⅱ)是定值2,理由如下:………………,理由如下:………………66分如图,过点E 作//EN CD ,过点D 作DN CD ^,且EN 与直线AB 交于点M ,与直线DN 交于点N ………………………………77分90EAC CPA Ð=Ð=°,90EAM CAB CAB ACP \Ð+Ð=Ð+Ð=°EAM ACP \Ð=Ð,同理MEA CAB Ð=Ð又AC AE =, EAM ACP \D D ≌....................................88分 ,EM AP AM CP \== (9)9分 DN CD ^,CD AB ^, //DN AB \,又//EN CD ,\四边形MNDP 是矩形, ,MN PD MP ND \==AB 是直径,CD AB ^,所以MN PD CP AM ===,又,EM AP =EM MN AP AM \+=+,即EN MP ND ==,END \D 是等腰直角三角形, =45EDN \а (11)11分 //DN AB , =45EGM EDN \Ð=а,1==2sin EG EG APEMEGM\=Ð (12)12分2525.(本小题满分.(本小题满分.(本小题满分141414分)分) 解:(Ⅰ)直线y x t =+与双曲线kyx =相交,由kx t x =+得20x tx k +-=,所以242t b k x -±+=………………………………22分 设(,)C C C x y ,(,)D D D x y若C D x x <,则2244(,)22t b k t b k C --+-+,2244(,)22t b k t b k D -++++ 若C D x x >,则2244(,)22t b k t b k D --+-+,2244(,)22t b k t b k C -++++ ……………………………………………………………… 4 4分 (注:只写其中一种不扣分)(Ⅱ)//AB CD ,理由如下:………………,理由如下:………………55分不妨设C D x x <,由(Ⅰ)知2244(,)22t b k t b k C --+-+,2244(,)22t b k t b k D -++++ 所以24(,0)2t b k A --+,24(0,)2t b k B ++.................... (66)分设直线AB 的解析式为y px q =+, 则将,A B 两点坐标代入有:2402t b kp q --+×+=,242t b kq ++=,所以1p =,所以直线AB 的解析式为242t b ky x ++=+………………………………77分所以直线AB 与CD 的位置关系是//AB CD .……………….………………88分(Ⅲ)将()32D ,代入双曲线(0)k y k x=>得6k =,将(3,2)D 代入直线y x t =+,得1t =-.\双曲线:by x=,直线1y x =-. 由61x x=-得123,2x x ==-,所以(2,3)C --................................ (9)9分 因为(2,3)C --,()32D ,在抛物线25(0)y ax bx a =++¹上,所以有42539352a b a b -+=-ìí++=î解得12a b =-ìí=î,即2225(1)6y x x x =-++=--+.………………………….………………………… 10 10分 由0mn <,可知0m <,0n >.①当01n <£时,由函数的最小值为2m ,最大值为2n 可知22252252n n nm m m ì-++=ïí-++=ïî,所以,m n 即为一元二次方程2252x x x -++=的两解5x =±, 又m n <,所以5m =-,5n =.又因为01n <£,所以5m =-,5n =不合题意.……………………不合题意.……………………111111分分 ②当1()12m n +£,即2m n £-时,由函数的最小值为2m ,最大值为2n 可知226252n m m m =ìí-++=î所以35n m =ìïí=-ïî,此时51232m n =-£-=-=-满足题意.所以53m n +=-+.………………………….…………………………121212分分③当1()12m n +>,即2m n >-时,由函数的最小值为2m ,最大值为2n 可知226252n n n m =ìí-++=î所以31n m =ìí=î,又因为0m <.1m \=,3n =不合题意...............................不合题意. (13)1313分分 综上所述,满足题意的m n +的值为53-+.…………………….……………………141414分分7、我们各种习气中再没有一种象克服骄傲那麽难的了。
2019学年福建省龙岩市八年级上第二次质检数学试卷【含答案及解析】

2019学年福建省龙岩市八年级上第二次质检数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 下面有4个汽车标志图案,其中是轴对称图形的有()A.1个 B.2个 C.3个 D.4个2. 下列计算正确的是()A.a•a2=a2 B.(a2)2=a4 C.a2•a3=a6 D.(a2b)3=a2•a33. 下列各式从左到右的变形是因式分解的是()A.x2+2x+3=(x+1)2+2B.(x+y)(x-y)=x2-y2C.x2-xy+y2=(x-y)2D.2x-2y=2(x-y)4. 一个三角形的两边的长分别为3和8,第三边的长为奇数,则第三边的长为()A.5或7 B.7 C.9 D.7或95. 如图,∠B=∠D=90°,CB=CD,∠1=30°,则∠2=()A.30° B.40° C.50° D.60°6. 等腰三角形的一个角是80°,则它的底角是()A.50° B.80° C.50°或80° D.20°或80°7. 点(-2,4)关于x轴对称的点的坐标是()A.(-2,-4) B.(-2,4) C.(2,-4) D.(2,4)8. 如图,△A BC中,AB=AC,D为BC的中点,以下结论:(1)△ABD≌△ACD;(2)AD⊥BC;(3)∠B=∠C;(4)AD是△ABC的角平分线.其中正确的有()A.1个 B.2个 C.3个 D.4个9. 若(x+4)(x-3)=x2+mx-n,则()A.m=-1,n=12 B.m=-1,n=-12C.m=1,n=-12 D.m=1,n=1210. 若4x2-mxy+9y2是一个完全平方式,则m的值为()A.6 B.±6 C.12 D.±12二、填空题11. 分解因式:2x2-8= .12. 当x 时,(x-4)0等于1.13. 计算:2xy2•(-3xy)2= .14. 若ax=3,则(a2)x= .15. 若(x+y)2=49,xy=12,则x2+y2= .16. 若(x+m)与(x+3)的乘积中不含x的一次项,则m= .17. 若a-b=1,则代数式a2-b2-2b的值为.18. 探究:观察下列各式,,,…请你根据以上式子的规律填写: = .三、解答题19. 计算(1)(3a-2b)(3a+2b)(2)(x-2y)2(3)(-8m4n+12m3n2-4m2n3)÷(-4m2n)20. 因式分解(1)3x-3x3(2)2a3b-12a2b+18ab(3)x2+2x-3.21. 先化简,再求值:(a+b)(a-b)+(4ab3-8a2b2)÷4ab,其中a=2,b=1.22. 如图,已知△ABC各顶点的坐标分别为A(-3,2),请你画出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1的各顶点坐标.23. 阅读材料:若m2-2mn+2n2-8n+16=0,求m、n的值.【解析】∵m2-2mn+2n2-8n+16=0,∴(m2-2mn+n2)+(n2-8n+16)=0∴(m-n)2+(n-4)2=0,∴(m-n)2=0,(n-4)2=0,∴n=4,m=4.根据你的观察,探究下面的问题:(1)已知x2-2xy+2y2+6y+9=0,求xy的值;(2)已知△ABC的三边长a、b、c都是正整数,且满足a2+b2-10a-12b+61=0,求△ABC的最大边c的值.24. 如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.(1)求证:△COD是等边三角形;(2)当α=150°时,试判断△AOD的形状,并说明理由;(3)探究:当α为多少度时,△AOD是等腰三角形.参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】第24题【答案】。
龙岩市2019高中毕业班教学质量检查文科数学及答案

11 分
所以,当 x 3 1时, g(x)max g( 3 1) 2 e1 3
所以 a 2 e1 3 .即 a 的取值范围为 2 e1 3 , .
…………… …………………
12 分
22.(本小题满分 10 分)选修 4 4:坐标系与参数方程
x 2 t cos,
……………3
分
从而 a 3,b 3 . 22
4分
(Ⅱ)方法一:令 g(x) ae x(x 1) x 2 4x ,
问题转化为 g(x) 0 在 x 0, 上恒成立,
……………
即 g(x)min 0 ,x 0,
5分
g(x) x 2ae x 2 , x 0
抛物线 C 方程 x2 4y 得为 y x2 所以 y x
4
2
切线 l1,l2 的斜率分别为
x1 2
, x2 2
.
………………………9
分
10 分
当 l1
l2 时,
x1 2
x2 2
1 ,即 x1x2
4
………………………
又
x1x2
8k
, 8k
4
解得
k
1 2
合题意,
所以存在直线 l 的方程是 y 1 (x 2) ,即 x 2 y 2 0 . ……………12 2
分
21.(本小题满分 12 分)
数学(文科)答案 第 7页(共 10页)
解:(Ⅰ) f (x) a(x 2) e x
……………1
分 由已知得 f (0) 2a 3 , f (0) b ,
…………… ……………
2019-2019学年福建省龙岩市八年级第二学期期中质量检查数学试卷(含答案)-6页word资料

福建省龙岩市2019-2019学年第二学期期中质量检查八年级数学试卷(满分100分, 考试时间100分钟)一、选择题(每题3分,共30分)1.在式子π xy 2,2334a b c ,x+ 65,y 10 中,分式的个数是( ) A.4 B .3 C .2 D .12. 反比例函数)0(≠=k xk y 的图象经过点(2-,3),则它还经过点( ) A. (1-,6-) B. (6,1-) C. (3,2) D.(2-,-3)3. 下列各式计算正确的是( )A .236x x x = B.0=++y x y x C .b a a b b a =•3234 D .2231634y y =⎪⎪⎭⎫ ⎝⎛. 4. 在反比例函数xk y 3-=图像的每一支曲线上,y 都随x 的增大而减小, 则k 的取值范围是( ) A .3>k B .0>k C .3<kD .0<k 5. 在三边分别为下列长度的三角形中,哪个不是..直角三角形( ). A . 6,8,10a b c === B . 7,24,25a b c ===C . 1.5,2,3a b c === D. 3,4,5a b c ===6、如果方程333-=-x m x x 有增根,那么m 的值为( ) A.0 B.-1 C.3 D.1 7..如果2a=,则b a +的值为 ( ) 折叠,若点D 恰好落在BC 边上点F处,且△ABF 的面积是6平方厘米,则DE 的长为( )A .2cmB .3cmC .2.5cmD .35cm 第8题9.函数m x y +=与xm y =)0(≠m 在同一坐标系内的图像可以是( ) 10、在直线l 上依次摆放着七个正方形(如图所示)。
已知斜放置的三个正方形的面积分别是1、2、3S 1、S 2、S 3、S 4,则S 1+S 2+S 3+S 4的值为( )A .6B .5C .4D .3二、填空题(每题2分,共18分)11. 分式392+-x x 的值为0,则x 的值是 ; 12.科学家发现一种病毒的直径为0.000043米,用科学记数法表示为_________________米.13.计算:ab b b a a -+-= . 14.命题“两直线平行,同位角相等”的逆命题是 。
2019年福建龙岩新罗区小学毕业班数学学业质量检测试卷(word精华版带答案)

2019年福建龙岩新罗区小学毕业班数学学业质量检测试卷时间:90分钟满分:100分一、认真审题,准确选择。
(每小题2分,共24分)1.当a表示所有的自然数0,1,2,3,…时,2a表示()。
A.奇数B.偶数C.质数D.合数2.能与3∶8组成比例的是()。
A.8∶3B.16∶18C.0.2∶0.6D.15∶403.钟面上,时针经过1小时旋转了()度。
A.30B.60C.180D.3604.用6个同样大小的正方体拼成一个立体图形,从上面、正面和左面看到的形状完全一样,这个立体图形是()。
5.下面四句话中,错误的一句是()。
A.0既不是正数也不是负数B.国际儿童节和教师节都在小月C.假分数的倒数不一定是真分数D.在生活中,知道了物体的方向,就能确定物体的位置6.在一个有48名学生的班级里选举班长,选举投票结果如下表。
下面图()表示了这一结果。
7.下面的问题,还需要确定一个信息才能解决,是()。
某花店新进了玫瑰、百合、菊花三种花,已知玫瑰有200朵,是三种花中数量最多的。
这个花店一共新进了多少朵花?A.玫瑰比菊花多20朵B.三种花的总数是百合的6倍C.玫瑰的数量占三种花总数的1 2D.玫瑰、百合的数量比是5∶38.下图中,可以表示35÷4计算过程的是()。
9.一根绳子剪成两段,第一段长37米,第二段占全长的37,两段相比,()。
A.第一段长B.第二段长C.一样长D.无法确定10.等腰三角形两条邻边分别长3厘米、6厘米,这个等腰三角形的周长是()。
A.9厘米B.12厘米C.15厘米D.12厘米或15厘米11.一个底面积是20cm2的圆柱,斜着截去了一段后,剩下的图形如下图。
截后剩下的图形的体积是()cm3。
A.140B.180C.220D.36012.某市规定每户每月用水量不超过6吨时,每吨价格为2.5元;当用水量超过6吨时,超过的部分每吨价格为3元。
下图中能正确表示每月水费与用水量关系的是()。
2019-2020学年第一学期龙岩市质检九年级数学试题及答案

2019-2020学年第一学期期末龙岩市五县(市、区)质量抽测九 年 级 数 学 试 卷(考试时间:120分钟 满分:150分)注意:请把所有答案书写到答题卡上!在本试题上答题无效。
一、选择题(共10小题,每小题4分,共40分) 1.方程x (x ﹣5)=0的根是A .5B .﹣5,5C .0,﹣5D .0,5 2.二次函数y =2(x ﹣3)2﹣6的顶点是 A .(﹣3,6)B .(﹣3,﹣6)C .(3,﹣6)D .(3,6)3.下列交通标志中,是中心对称图形的是A.B.C.D.4.抛掷一枚质地均匀的硬币,正面朝上的概率为0.5,下列说法正确的是A .大量反复抛掷每100次出现正面朝上50次B .连续抛掷10次不可能都正面朝上C .抛掷硬币确定谁先发球的规则是公平的D .连续抛掷2次必有1次正面朝上 5.一元二次方程x 2+2x +m =0有两个不相等的实数根,则 A .m <3B .m >3C .m >-3D .m <-36.圆的直径是8cm ,若圆心与直线的距离是4cm ,则该直线和圆的位置关系是A .相离B .相切C .相交D .相交或相切7.若弦AB ,CD 是⊙O 的两条平行弦,⊙O 的半径为13,AB =10,CD =24,则AB ,CD 之间的距离为A .7B.17C.5或12D.7或178.如图,圆锥的底面半径r 为6cm ,高h 为8cm ,则圆锥的侧面积为 A .30πcm 2 B .48πcm 2 C .60πcm 2 D .80πcm 2 9.如图,⊙O 是△ABC 的内切圆,切点分别相为点D 、E 、F ,设△ABC 的面积、周长分别为S 、l ,⊙O 的半径为r ,则下列等式: ①∠AED +∠BFE +∠CDF =180°;②S =21l r ;③2∠EDF =∠A +∠C ;④2(AD +CF +BE )=l ,其中成立的是A .①②③④B .②③④C .①③④D .①②③O第8题图第9题图10.如图,抛物线的对称轴是直线x =1,与x 轴有两个交点,与y 轴交点的坐标为(0,3),把它向下平移2个单位后,得到新的抛物线的解析式是y =ax 2+bx +c ,以下四个结论:①b 2-4ac <0;②abc <0;③4a +2b +c =1;④a -b +c >10,其中正确的是A .①②③B .②③④C .①③④D .①②③④二、填空题(本大题共6个小题,每小题4分,共24分) 11.一元二次方程x 2﹣x +a =0的一个根是2,则a 的值是 .12.把抛物线y =-2x 2先向上平移1个单位,再向右平移2个单位,所得到的抛物线的解析式是 .13.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是 . 14.已知正六边形ABCDEF 的外接圆半径为2cm ,则正六边形的边心距是_______cm .15.如图是二次函数y =ax 2﹣bx +c 的图象,由图象可知,不等式ax 2﹣bx +c <0的解集是 . 16.“若抛物线y =ax 2+bx +c 与x 轴有两个交点,则一元二次方程ax 2+bx +c =0有两个不等实根。
2019年五月质检理科数学-答案

龙岩市2019年高中毕业班教学质量检查数学(理科)参考答案及评分细则评分说明:1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则。
2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分。
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数。
4.只给整数分数。
选择题和填空题不给中间分。
一、选择题:本大题考查基础知识和基本运算.每小题5分,满分60分.二、填空题:本大题考查基础知识和基本运算.每小题5分,共20分。
13.114.101516.3三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)解:(1)因为方程2230x x+-=的两根为3-和1,且数列{}n a为递增数列,所以243,1a a=-=. ························································································· 1分设数列{}n a的公差为d,则0d>,所以42242a ad-==-,所以()2227na a n d n=+-=-. ···································································· 3分当1n=时,由1121S b+=,解得113b=;····················································· 4分当2n≥时,因为21n nS b+=,所以1121n nS b--+=,以上两式相减得130n nb b--=,······································································ 5分所以113nnbb-=,所以{}n b是首项为13,公比为13的等比数列,所以1111333n n n b -=⨯=. ··················································································· 6分 (2)由(1)得,()()11273nnn c n ⎛⎫=--+- ⎪⎝⎭, ··················································· 7分设数列()(){}127nn --的前2n 项和为2n M ,数列13n⎧⎫⎪⎪⎛⎫-⎨⎬ ⎪⎝⎭⎪⎪⎩⎭的前2n 项和为2n K , 所以()()()()()25314947n M n n =--+---+⋅⋅⋅--+-2n =, ················ 9分所以222111333nn K ⎛⎫⎛⎫⎛⎫=-+-+⋅⋅⋅+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭211133113n +⎛⎫--- ⎪⎝⎭=⎛⎫-- ⎪⎝⎭211434n =-⨯, ······························································································ 11分 所以2222112434n n n nT M K n =+=+-⨯. ······················································ 12分 18.(本小题满分12分)解:(1)证明:因为,AC AB DAC DAB =∠=∠,所以ACD ABD ∆∆≌,所以DC DB =. ····························································································· 1分 取BC 中点O ,连结AO DO ,,所以BC DO ⊥,BC AO ⊥, ··················· 3分 因为AO DO O =I ,所以⊥BC 平面AOD ,所以AD BC ⊥,·················· 4分 又因为AD BM ⊥,BC BM B =I ,所以⊥AD 平面BCM ,所以平面⊥ACD 平面BCM . ······································································· 5分 (2)由(1)知,DOA ∠是二面角A BC D --的平面角,所以2π3DOA ∠=,……6分 过D 作DG AO ⊥交AO 延长线于G ,因为⊥BC 平面AOD ,DG ⊂平面AOD , 所以BC DG ⊥,因为AO BC O =I ,所以DG ⊥平面ABC .如图,以O 为原点,以OA uu r ,OB uu u r ,GD uuu r的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系, ································································································ 7分 设2AB a =()0a >,则AO =,又因为2BCD ABC S S =△△D D ,所以2DO OA ==, 在Rt DGO △中,π3DOG ∠=, 所以3DG a =,OG =,所以(,0,3),(0,,0),(0,,0),,0,0)D a C a B a A -, ···························· 8分所以,0,3)DA a =-uu u r,,,3)DC a a =--u u u r, 设(,,)x y z =n 是平面DCA 的法向量,则0,0,DA DC ⎧⋅=⎪⎨⋅=⎪⎩uu u r uuu r n n即30,30,z y z ⎧-=⎪--=取(3,=-n , ·················································································· 9分 因为点M 是线段AD 的中点 ,所以3(0,0,)2aM , 所以3(0,,)2BM a a =-uuu r , ············································································ 10分设直线BM 与平面DCA 所成角的大小为θ,则sin cos ,||||BM BM BM θ⋅=<>===⋅uuu ruuu r uuu r n n n , 所以直线BM 与平面DCA所成角的正弦值为13································· 12分19.(本小题满分12分)解法一:(1)因为一篇学位论文初评被认定为“存在问题学位论文”的概率为()2233331C p p C p -+,············································································· 2分 一篇学位论文复评被认定为“存在问题学位论文”的概率为()()2213111C p p p ⎡⎤---⎣⎦,······································································ 4分所以一篇学位论文被认定为“存在问题学位论文”的概率为()()()()22223313331111f p C p p C p C p p p ⎡⎤=-++---⎣⎦()()()2223313111p p p p p p ⎡⎤=-++---⎣⎦5432312179p p p p =-+-+. ······················································· 5分(2)设每篇学位论文的评审费为X 元,则X 的可能取值为900,1500. ········ 6分()()21315001P X C p p ==-, ······························································· 7分 ()()21390011P X C p p ==--, ···························································· 8分 所以()()()2211339001115001E X C p p C p p ⎡⎤=⨯--+⨯-⎣⎦()290018001p p =+-. ························································· 9分 令()()()21,0,1g p p p p =-∈,()()()()()2121311g p p p p p p '=---=--.··································· 10分当10,3p ⎛⎫∈ ⎪⎝⎭时,()0g p '>,()g p 在10,3⎛⎫⎪⎝⎭单调递增,当1,13p ⎛⎫∈ ⎪⎝⎭时,()0g p '<,()g p 在1,13⎛⎫⎪⎝⎭单调递减,所以()g p 的最大值为14327g ⎛⎫= ⎪⎝⎭. ······················································· 11分所以实施此方案,最高费用为44100600090018001080027-⎛⎫+⨯+⨯⨯= ⎪⎝⎭(万元). 综上,若以此方案实施,不会超过预算. ················································· 12分解法二:(1)因为一篇学位论文初评时被认定为不是“存在问题学位论文”的概率为()3331C p -,················································································································ 2分 一篇学位论文复评时被认定为不是“存在问题学位论文”的概率为()()221311C p p p --, ············································································ 4分所以一篇学位论文被认定为“存在问题学位论文”的概率为()()()343133111f p C p C p p =----()()341131p p p =----5432312179p p p p =-+-+. ······················································· 5分 (2)同解法一.解法三:(1)因为一篇学位论文初评被认定为“存在问题学位论文”的概率为()2233331C p p C p -+,············································································· 2分 一篇学位论文复评被认定为“存在问题学位论文”的概率为()()2112232211C p p C p p C p ⎡⎤--+⎣⎦, ························································· 4分 所以一篇学位论文被认定为“存在问题学位论文”的概率为()()()()22233112233322111f p C p p C p C p p C p p C p ⎡⎤=-++--+⎣⎦ ()()()223231312p p p p p p p =-++--5432312179p p p p =-+-+. ······················································· 5分(2)同解法一.注明:在(1)问中只要能正确列出表达式,没有化简不扣分. 20.(本小题满分12分)解:(1)因为12(2,0),(2,0)A A -, ················································································ 1分设(,),P x y 00(,),M x y 则00(,),N x y -且2200143x y -=①, 因为动直线l 交双曲线于不同的两点,M N ,所以02x ≠±且2x ≠±,因为直线2A M 的方程为00(2)2y y x x =--②, 直线1A N 的方程为00(2)2y y x x -=++③, ······················································ 2分 ②⨯③得222020(4)4y y x x -=--, 把①代入上式得223(4)4y x =--,化简得22143x y +=, ·························· 4分 所以点P 的轨迹C 的方程为()221243x y x +=≠±. ········································· 5分 (2)依题意得直线DE 与直线FG 斜率均存在且不为0,设直线DE 的方程为()10x my m =+≠,则直线FG 的方程为11x y m=-+, ···························· 6分联立221,3412x my x y =+⎧⎨+=⎩得()2234690m y my ++-=, ··································· 7分 则()()22236363414410m m m ∆=++=+>,设1122(),,,()x y D x y E ,122634m y y m -+=+,()121228234x +x m y +y m =+=+, ··························· 8分 所以DE 的中点2243()34,34mR m m -++,同理FG 的中点22243()433,4m mS m m ++, ························································· 9分 所以直线RS 的斜率为()222222337344344413443RS m mm m m k m m m m --++==--++, 所以直线RS 的方程为()222374343441m m y x m m m ⎛⎫+=- ⎪++-⎝⎭, ··············· 10分 整理得()274741m y x m ⎛⎫=- ⎪-⎝⎭, ··································································· 11分所以直线RS 恒过定点4,07⎛⎫ ⎪⎝⎭,即过两弦,DE FG 中点的直线恒过定点4,07⎛⎫ ⎪⎝⎭.···············································································································12分21.(本小题满分12分)解:(1)因为()f x 的定义域为()0,+∞,又()()()()1+1x x a a f x x a x x++'=++=, ·················································· 1分 所以当0a ≥时,()0f x '>,()f x 在()0,+∞单调递增. ···························· 3分当0a <时,若0x a -<<时,()0f x '<,()f x 在()0,a -单调递减; 若x a ->时,()0f x '>,()f x 在(),a -+∞单调递增. 综上,当0a ≥时,()f x 在()0,+∞单调递增;当0a <时,()f x 在()0,a - 上单调递减,在(),a -+∞单调递增. ············ 5分 (2)当0a <时,由(1)知,()()()2min 1ln 2f x f a a a a a -=--+-=, ···················································· 6分令()()21ln 2g x x x x x =--+-,0x <,则()()ln g x x x '=-+-,令()()ln h x x x =-+-,0x <,则()1110xh x x x-'=-+=<,所以()h x 在(),0-∞单调递减, ····································································· 7分又102h ⎛=- ⎝>,1110e e h ⎛⎫-=- ⎪⎝⎭<,所以存在01e x ⎛⎫∈- ⎪⎝⎭,使得()00h x =,且()00ln 0x x -+-=, ······················································ 8分所以当()0,x x ∈-∞时,()0g x '>,()g x 单调递增; 当()0,0x x ∈时,()0g x '<,()g x 单调递减;所以当0x x =时,()g x 取得最大值, ····························································· 9分因为()()22220000000000111ln 222g x x x x x x x x x x =--+-=--+=- ()2011122x =--, ························································································ 10分 令()211()122k x x =--,1e x ⎛⎫∈- ⎪⎝⎭,则()k x 在1e ⎛⎫- ⎪⎝⎭单调递减, ································································ 11分所以()211121322e 5315k x ⎛⎛⨯-=+= ⎝⎝<<,所以()01315g x <, 因此当0a <时,()min 1315f x <,即1315M <. ············································ 12分22.(本小题满分10分)解:(1)利用1cos sin 22=+ϕϕ消去参数ϕ,得1C 的普通方程为222)(a y a x =+-(0)x a ≤≤. ·········································· 3分由θρ22sin 314+=得4sin 3222=+θρρ,将θρρsin ,222=+=y y x 代入上式并整理得2C 的直角坐标方程为1422=+y x . ····································· 5分 (2)根据对称性知,A 和B 关于x 轴对称,不妨设00(,)A x y ,00x a ≤≤,00y >,因为324||=AB,所以01||23y AB ==, ················································ 7分 代入2C 的直角坐标方程得023x =, ································································ 8分又2(,33A 在1C 上,所以2298)32(a a =+-, ·········································· 9分 解得1=a . ······································································································ 10分注明:在(1)问中没写“0x a ≤≤”扣1分. 23. (本小题满分10分)解法一:(1)当2=a 时,不等式2)(>x f ,即2|2||1|>--+x x ,……………………1分当1x -≤时,原不等式可化为221>-+--x x ,即23>-,此时原不等式无解; ····························································································································· 2分 当12x -<≤时,原不等式可化为221>-++x x ,解得23>x ,所以322x <≤; ·················································································································· 3分 当2>x 时,原不等式可化为221>+-+x x ,即23>,此时原不等式恒成立, 所以2>x ; ····························································································· 4分 综上,原不等式的解集为32x x ⎧⎫>⎨⎬⎩⎭. ······················································· 5分 (2)由()2f x a ≥的解集为空集得|1|||2x x a a +--≥的解集为空集,所以a a x x 2|||1|<--+恒成立. ··························································· 6分 因为0a >,所以()|1||||(1)()|1f x x x a x x a a =+--+--=+≤,……7分 所以当且仅当(1)()0,|1|||,x x a x x a +-⎧⎨+-⎩≥≥即x a ≥时,max [()]1f x a =+, ········· 8分所以a a 21<+, ······················································································ 9分 解得1>a ,即a 的取值范围为(1,)+∞. ·················································· 10分。
福建省龙岩市一级达标校2019-2020学年高二下学期期末质检数学试题含答案

题目要求的.
1. C42 C43 ( )
A. C53
B. A52
C. C54
D. A53
2. 若复数 z 2 2i ,则 z ( )
A. 3 2
B. 3
C. 2 2
D. 2
3. 根据中央对“精准扶贫”的要求,某市决定从 3 名男性党员、2 名女性党员中选派 2 名去甲村调研,则
既有男性又有女性的不同选法共有( )
同,则事件 A 发生的概率为 2 . 3
12. 若函数 f x 1 x3 x2 2 在区间 a 1, a 4 上存在最小值,则整数 a 可以取( )
3
3
A. -3
B. -2
C. -1
D. 0
第Ⅱ卷(非选择题 共 90 分)
三、填空题:本大题共 4 小题,每小题 5 分,共 20 分,其中第 16 题第一空 2 分,第二空 3 分.
13. 曲线 f x x4 ln x 1在点 P 1, 0 处的切线方程是______.
14. 函数 f x 1 x3 4x 4 的极大值为______.
3
2
15.
设
x
2
2 6 x
a0 xm0
a1xm1
a2 xm2
a6 xm6
,则 m0
m1 m2
m6
______.
B. 若四条线段的长度分别是 1,3,5,7,从中任取 3 条,则这 3 条线段能够成三角形的概率为 1 ; 4
C. 线性相关系数 r 越大,两个变量的线性相关性越强;反之,线性相关性越弱;
D. 设两个独立事件 A 和 B 都不发生的概率为 1 , A 发生且 B 不发生的概率与 B 发生且 A 不发生的概率相 9
2019年龙岩市九年级学业(升学)质量检查数学-答案-排(5.10改)

1E ABDC2019年龙岩市九年级学业(升学)质量检查数学试题参考答案11.12-12.1313.322 14.315.32233π- 16.41三、解答题(本大题共9题,共86分)解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分8分)解:方程两边同乘以(1)x x -得22(1)(1)x x x x --=-……………………4分整理得:2x -=-,解得2x =…………………… 6分 检验:当2x =时,(1)20x x -=≠……………………7分 所以2x =是原方程的解……………………8分 18.(本小题满分8分)解:原式2223()(1)11x x x xx x x -+=÷-+++……………………3分 =()()21122-+⋅+-x x x x x ……………………5分 =()11+x x ……………………6分 当13x =时,原式1914433==⨯……………………8分19.(本小题满分8分)解:(Ⅰ)证明:如图,过点C 作//CE AD 交AB 于点E ……………………1分//CE AD ,1A ∴∠=∠, ∴CE BC =……………………2分 //AB CD ,//CE AD ,∴四边形AECD 为平行四边形……………………3分 ∴AD CE =, AD BC ∴=……………………4分DNMABC(Ⅱ)分别过点,D C 作,DE AB CF AB ⊥⊥,垂足为,E F ,……………… 5分//DE CF ∴,//AB CD ,∴四边形DEFC 为矩形, ∴DE CF =...........................6分在Rt DAE ∆中,60,2A AD ∠=︒=, sin 60DEAD∴︒=2DE =,DE ∴=………7分 在Rt CBF ∆中,45,B CF DE ∠=︒==BC ==………8分20. (本小题满分8分)解:如图,点,M N 即为所求作的点………………2分(一个点1分,未标字母不给分)已知:如图,ABC ∆中,点,M N 分别是,AB AC 的中点,连接MN .求证:1//,2MN BC MN BC =.………………4分 证明:延长MN 至点D ,使得MN ND =,连接CD在AMN ∆和CDN ∆中,AN CD ANM DNC MN ND =⎧⎪∠=∠⎨⎪=⎩,AMN ∴∆≌()CDN SAS ∆………………5分AMN D ∴∠=∠,//AM CD ∴,即//BM CDAM BM CD ==,∴四边形BMDC 为平行四边形………………6分 //MN BC ∴,MD BC =………………7分12MN MD =,12MN BC ∴=………………8分21.(本小题满分8分) 解:(Ⅰ)解:原式11111111511223455666=-+-+-+-=-=………………4分 (Ⅱ)证明: 解法一:111111*********+++(1)()()()1324354623224235246=-+-+-+-⨯⨯⨯⨯ .............6分 1111111117(1)2324354630=-+-+-+-= .....................................7分110424,330530==,1101724433030305∴=<<=,即原式得证.............8分 解法二:111111111111+++++++++233445561324354612233445<<⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯……………………………………6分1111111111111111111123344556132435462233445∴-+-+-+-<+++<-+-+-+-⨯⨯⨯⨯……………………………………7分1111143132435465∴<+++<⨯⨯⨯⨯,即原式得证……………………………………8分 22.(本小题满分10分)解:(Ⅰ)解:21(1602)(50)2608000W x x x x =-+=-++ ………………2分220(50)201000W x x =-=-+………………4分(Ⅱ)依题意得:2122409000W W W x x =+=-++………………6分22(10)9200x =--+………………8分因为x 为正整数,所以当10x =时,总利润W 最大,最大值为9200………10分(答:略)23.(本小题满分10分)解:(Ⅰ)5000;图略;(Ⅱ)4%;18°;(每个空格2分,共8分)(Ⅲ)解:观点B 占的百分比146%30%15%4%5%=----=………9分300(46%5%15%)30066%198⨯++=⨯=万.(答:略.)………………10分24.(本小题满分12分) 解:(Ⅰ)连接AD ………………1分则由同弧所对的圆周角相等可知ACF ADF ∠=∠………………2分又AE 是由线段AC 绕点A 逆时针旋转90°得到,AC AE ∴=,………………3分AED ADF ∴∠=∠………………4分 ACF AED∴∠=∠………………5分,理由如下:………………6分如图,过点E 作//EN CD ,过点D 作DN CD ⊥,且EN 与直线AB 交于点M , 与直线DN 交于点N ………………7分90EAC CPA ∠=∠=︒,90EAM CAB CAB ACP ∴∠+∠=∠+∠=︒ EAM ACP ∴∠=∠,同理MEA CAB ∠=∠又AC AE =, EAM ACP ∴∆∆≌………………8分 ,EM AP AM CP ∴==………………9分DN CD ⊥,CD AB ⊥, //DN AB ∴,又//EN CD , ∴四边形MNDP 是矩形, ,MN PD MP ND ∴==AB 是直径,CD AB ⊥,所以MN PD CP AM ===,又,EM AP =EM MN AP AM ∴+=+,即EN MP ND ==,END ∴∆是等腰直角三角形, =45EDN ∴∠︒………………11分 //DN AB , =45EGM EDN ∴∠=∠︒, 1==sin EG EG AP EM EGM∴=∠12分25.(本小题满分14分)解:(Ⅰ)直线y x t =+与双曲线ky x=相交,由k x t x=+得20x tx k +-=,所以x =………………2分设(,)C C C x y ,(,)D D D x y若C D x x <,则(22t t C -,(,22t t D -++若C D x x >,则D ,C ……………………………… 4分(注:只写其中一种不扣分)(Ⅱ)//AB CD ,理由如下:………………5分不妨设C D x x <,由(Ⅰ)知(22t t C -,(,22t t D -++所以A ,B .………………6分 设直线AB 的解析式为y px q =+,则将,A B 两点坐标代入有:0p q +=,q =,所以1p =,所以直线AB的解析式为2t y x +=+………………7分所以直线AB 与CD 的位置关系是//AB CD .………………8分(Ⅲ)将()32D ,代入双曲线(0)ky k x=>得6k =,将(3,2)D 代入直线y x t =+,得1t =-.∴双曲线:by x=,直线1y x =-.由61x x=-得123,2x x ==-,所以(2,3)C --.…………………………9分 因为(2,3)C --,()32D ,在抛物线25(0)y ax bx a =++≠上,所以有42539352a b a b -+=-⎧⎨++=⎩ 解得12a b =-⎧⎨=⎩,即2225(1)6y x x x =-++=--+.………………………… 10分由0mn <,可知0m <,0n >.①当01n <≤时,由函数的最小值为2m ,最大值为2n 可知22252252n n nm m m⎧-++=⎪⎨-++=⎪⎩, 所以,m n 即为一元二次方程2252x x x -++=的两解x =又m n <,所以m =n =又因为01n <≤,所以m =n =11分②当1()12m n +≤,即2m n ≤-时, 由函数的最小值为2m ,最大值为2n 可知226252n m m m=⎧⎨-++=⎩所以3n m =⎧⎪⎨=⎪⎩1232m n =≤-=-=-满足题意.所以3m n +=.…………………………12分③当1()12m n +>,即2m n >-时,由函数的最小值为2m ,最大值为2n 可知226252n n n m=⎧⎨-++=⎩所以31nm=⎧⎨=⎩,又因为0m<. 1m∴=,3n=不合题意.…………………………13分综上所述,满足题意的m n+的值为3.……………………14分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年龙岩市九年级学业(升学)质量检查数学试题(满分:150分考试时间:120分钟)一、选择题:本大题共10小题,每小题4分,共40分1.如图,数轴上的单位长度为1,若实数a ,b 所表示的数恰好在整数点上,则a+b = A. 0 B.-1 C. 1 D. 52.下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是3.下列调查中,适合采用全面调查(普查)方式的是 A.对汀江流域水质情况的调查B.对端午节期间市场上粽子质量情况的调查C.对某班40名同学身高情况调查D.对某类烟花爆竹燃放安全情况的调查 4.是⎩⎨⎧==by ax 方程组⎩⎨⎧=-=+72332y x y x 的解,则5a -b 的值是A. 10B. -10C. 14 5.下列图形中,∠1一定大于∠2的是6.若关于x 的一元一次不等式组⎩⎨⎧<->-mx x x )2(312的解是x <5,则m 的取值范围是A. m ≥5 >5 C. m ≤5 <57.如图,x 、y 、z 分别表示以直角三角形三边为边长的正方形面 积,则下列结论正确的是、A. x 2=y 2+z 2B. x <y+zC. x -y > zD. x =y+z8.三个等边三角形的摆放位置如图,若∠3=60°,则∠1+∠2 的度数是ba22221111OD .C .A .B . D .C . A . B . 321(第8题)z yx(第7题)0° B. 120° ° D. 360°9.如图,抛物线y=ax 2+bx+c 与x 轴交于点A (-1,0),顶点 坐标是(1,n ),与y 轴的交点在(0,3)和(0,6)之间(包含端 点),则下列结论错误的是+b <0 B. -2≤a ≤-l C. abc >0 +3b +2c >0 10.某些整数的所有正约数之和可以按如下方法求得,如: 6=2×3,则6的所有正约数之和为(1+3)+(2+6)=(1+2)×(1+3)=12; 12=22×3,则12的所有正约数之和为(1+3)+(2+6)+(4+12)=(1+2+22)×(1+3)=2836=22×32,则36的所有正约数之和为(1+3+9)+(2+6+18)+(4+12+36)= (1+2+22)×(1+3+32)=91 参照上述方法,那么144的所有正约数之和为二、填空题:本大题共6小题,每小题4分,共24分 11.(-2)-1=_______.12.一个不透明的袋子中装有4个黑球,2个自球,每个球除颜色 外其他都相同,从中任意摸出1个球是白球的概率是_______. 13.已知∠A 是锐角,且sin ∠A =31,则cos ∠A =_______. 14.当x=a 与x =b (a ≠b )时,代数式x 2-2x +3的值相等,则x=a+b 时, 代数式x 2-2x +3的值为_______.15.如图,AB 是⊙O 的直径,点E 是BF 的中点,过点E 的切 线分别交AF 、AB 的延长线于点D 、C ,若∠C =30°,⊙O 的半径是2,则图形中阴影部分的面积是_______.16.如图,△ABC 中,∠ABC =30°,AB =4,BC =5,P 是△ABC 内部的任意一点,连接PA ,PB ,PC ,则PA+PB+PC 的最 小值为_______.三、解答题:本大题共9小题,共86分. 17. (8分)解方程:1-x x -x2=118.(8分)先化简,再求值:2212xx x ++-÷(x -13+x x ),其中x =31ABCP(第16题)(第15题)yxx =1O A(第9题)19.(8分)在四边形ABCD 中,AB ∥CD .(1)如图1,已知∠A =∠B ,求证:AD=BC ;(2)如图2,已知∠A =60°,∠B =45°,AD =2,求BC 的长.20.(8分)证明:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.(要求:在给出的△ABC 中用尺规作出AB 、AC 边的中点M 、N ,保留作图痕迹,不要求写作法,并根据图形写出已知、求证和证明)21.(8分)(1)计算: 211⨯+321⨯+431⨯+541⨯+651⨯ (2)求证: 31<311⨯+421⨯+531⨯+641⨯<5422.(10分)小宝大学毕业后回家乡透行园艺创业,第一期培植盆景与花卉各50盆,售后进行统计得知:盆景的平均每盆利润是160元,花卉的平均每盆利润是20元. 调研发现:①盆景每增加1盆,盆景的平均好盆利润减少2元:每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均际盆利润始终不变,小宝计划第二期培植盆景与花齐共100盆,设培植的盆景比第一期增加x 盆,第二期盆景与花卉售完后的利润分别为W 1、W 2(单位:元) (1)用含x 的代数式分别表示W 1、W 2;(2)当x 取何们叫时,第二期培植的盆景与花卉作售完行获得的总利润最大最大总利润是多少23. (10分)随着互联网、移动终端的迅速发展,数字化阅读越来越普及. 公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷训查表如下图所示),并将调查结果绘制成图①和图②所示的统计图(均不完整).“您如何看待教化阅读”问卷调查表您好!这是一份关于“您如何看待数字化间读问调查表,请在表格中选择一项您最认. (1)本次接受词查的总人数是______人,并将条形统计图补充完整;、(2)在扇形统计图中,观点E 的百分比是_______,表示观点B 的扇形的圆心角度数为______度. (3)某市共有300万人,请根据以上调查结果估算该市持A 、B 、D 观点赞成数字化阅读的人数共有多少万人.24. (12分)如图,点P 是⊙O 直径AB 上的一点,过P 作直线CD ⊥AB ,分别交⊙O 于C 、D 两点,连接AC ,并将线段AC 绕点A 进时针旋转90°得到AE ,连接ED ,分别交⊙O 和AB 于F 、G ,连接FC .(1)求证:∠ACF =∠AED ; (2)若点P 在直径AB 上运动(不与点A 、B 重合),其它 条件不变,请问APEG是否为定值若是,请求出其值; 若不是,请说明理由.25.(14分)已知直线y=x+t 与双曲线y =xk(k >0)交于C 、D 两点,过C 作CA ⊥x 轴于点A ,过 D 作DB ⊥y 轴于点B ,连接AB . (1)求C 、D 两点的坐标;(2)试探究直线AB 与CD 的位置关系并说明理由; (3)已加点D (3,2),且C 、D 在抛物线y=ax 2+bx +5 (a ≠0) 上,若当m ≤x ≤n(其中mn <0)时,函数 y=ax 2+bx +5的最 小值为2m ,最大值为2n , 求m+n 的值,1E A BD CDNMABC参考答案一、BACAC ADBCD二、11.12-12.1313.322 14.3 15.32233π-16.41三、17.(本小题满分8分)解:方程两边同乘以(1)x x -得22(1)(1)x x x x --=-……………………4分整理得:2x -=-,解得2x =…………………… 6分检验:当2x =时,(1)20x x -=≠……………………7分 所以2x =是原方程的解……………………8分 18.(本小题满分8分)解:原式2223()(1)11x x x xx x x -+=÷-+++……………………3分 =()()21122-+⋅+-x x x x x ……………………5分 =()11+x x ……………………6分 当13x =时,原式1914433==⨯……………………8分19.(本小题满分8分)解:(Ⅰ)证明:如图,过点C 作//CE AD 交AB 于点E ……………………1分Q //CE AD ,1A ∴∠=∠, ∴CE BC =……………………2分 Q //AB CD ,//CE AD ,∴四边形AECD 为平行四边形……………………3分 ∴AD CE =, AD BC ∴=……………………4分(Ⅱ)分别过点,D C 作,DE AB CF AB ⊥⊥,垂足为,E F ,……………… 5分//DE CF ∴,//AB CD Q ,∴四边形DEFC 为矩形, ∴DE CF =...........................6分在Rt DAE ∆中,60,2A AD ∠=︒=, sin 60DEAD∴︒=,即322DE =,3DE ∴=………7分 在Rt CBF ∆中,45,3B CF DE ∠=︒==∴26BC CF ==分20. (本小题满分8分)解:如图,点,M N 即为所求作的点………………2分(一个点1分,未标字母不给分)已知:如图,ABC ∆中,点,M N 分别是,AB AC 的中点,连接MN .求证:1//,2MN BC MN BC =.………………4分 证明:延长MN 至点D ,使得MN ND =,连接CD在AMN ∆和CDN ∆中,AN CD ANM DNC MN ND =⎧⎪∠=∠⎨⎪=⎩,AMN ∴∆≌()CDN SAS ∆………………5分AMN D ∴∠=∠,//AM CD ∴,即//BM CDAM BM CD ==Q ,∴四边形BMDC 为平行四边形………………6分 //MN BC ∴,MD BC =………………7分12MN MD =Q ,12MN BC ∴=………………8分21.(本小题满分8分) 解:(Ⅰ)解:原式11111111511223455666=-+-+-+-=-=………………4分 (Ⅱ)证明:解法一:111111*********+++(1)()()()1324354623224235246=-+-+-+-⨯⨯⨯⨯ .............6分 1111111117(1)2324354630=-+-+-+-= .....................................7分110424,330530==Q ,1101724433030305∴=<<=,即原式得证.............8分 解法二:111111111111+++++++++233445561324354612233445<<⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯Q……………………………………6分1111111111111111111123344556132435462233445∴-+-+-+-<+++<-+-+-+-⨯⨯⨯⨯……………………………………7分1111143132435465∴<+++<⨯⨯⨯⨯,即原式得证……………………………………8分 22.(本小题满分10分)解:(Ⅰ)解:21(1602)(50)2608000W x x x x =-+=-++ ………………2分220(50)201000W x x =-=-+………………4分(Ⅱ)依题意得:2122409000W W W x x =+=-++………………6分22(10)9200x =--+………………8分因为x 为正整数,所以当10x =时,总利润W 最大,最大值为9200………10分(答:略)23.(本小题满分10分)解:(Ⅰ)5000;图略;(Ⅱ)4%;18°;(每个空格2分,共8分)(Ⅲ)解:观点B 占的百分比146%30%15%4%5%=----=………9分300(46%5%15%)30066%198⨯++=⨯=万.(答:略.)………………10分24.(本小题满分12分)解:(Ⅰ)连接AD ………………1分则由同弧所对的圆周角相等可知ACF ADF ∠=∠………………2分又AE 是由线段AC 绕点A 逆时针旋转90°得到,AC AE ∴=,………………3分 AED ADF ∴∠=∠………………4分M N A BCDE F G O PACF AED ∴∠=∠………………5分(Ⅱ)是定值2,理由如下:………………6分如图,过点作//EN CD ,过点D 作DN CD ⊥,且EN 与直线AB 交于点M ,与直线DN 交于点N ………………7分90EAC CPA ∠=∠=︒Q ,90EAM CAB CAB ACP ∴∠+∠=∠+∠=︒ EAM ACP ∴∠=∠,同理MEA CAB ∠=∠ 又AC AE =, EAM ACP ∴∆∆≌………………8分 ,EM AP AM CP ∴==………………9分DN CD ⊥Q ,CD AB ⊥, //DN AB ∴,又//EN CD ,∴四边形MNDP 是矩形, ,MN PD MP ND ∴==AB Q 是直径,CD AB ⊥,所以MN PD CP AM ===,又,EM AP =Q EM MN AP AM ∴+=+,即EN MP ND ==, END ∴∆是等腰直角三角形, =45EDN ∴∠︒………………11分 //DN AB Q , =45EGM EDN ∴∠=∠︒, 1==2sin EG EG AP EM EGM∴=∠………………12分25.(本小题满分14分)解:(Ⅰ)直线y x t =+与双曲线ky x=相交, 由k x t x=+得20x tx k +-=,所以24t b k x -±+=………………2分设(,)C C C x y ,(,)D D D x y若C D x x <,则2244(,)22t b k t b k C --+-+,2244(,)22t b k t b kD -++++ 若C D x x >,则2244(,)t b k t b k D --+-+,2244(,)t b k t b kC -++++ ……………………………… 4分(注:只写其中一种不扣分)(Ⅱ)//AB CD ,理由如下:………………5分不妨设C D x x <,由(Ⅰ)知2244(,)22t b k t b k C --+-+,2244(,)22t b k t b kD -++++ 所以24(,0)t b k A --+,24(0,)t b k B ++.………………6分 设直线AB 的解析式为y px q =+,则将,A B 两点坐标代入有:2402t b kp q --+⋅+=,q =,所以1p =,所以直线AB的解析式为2t y x =+………………7分所以直线AB 与CD 的位置关系是//AB CD .………………8分(Ⅲ)将()32D ,代入双曲线(0)ky k x=>得6k =,将(3,2)D 代入直线y x t =+,得1t =-.∴双曲线:by x=,直线1y x =-.由61x x=-得123,2x x ==-,所以(2,3)C --.…………………………9分 因为(2,3)C --,()32D ,在抛物线25(0)y ax bx a =++≠上,所以有42539352a b a b -+=-⎧⎨++=⎩解得12a b =-⎧⎨=⎩,即2225(1)6y x x x =-++=--+.………………………… 10分由0mn <,可知0m <,0n >.①当01n <≤时,由函数的最小值为2m ,最大值为2n 可知22252252n n n m m m⎧-++=⎪⎨-++=⎪⎩,所以,m n 即为一元二次方程2252x x x -++=的两解x =,又m n <,所以m =n =又因为01n <≤,所以m =n =……………………11分 ②当1()12m n +≤,即2m n ≤-时, 由函数的最小值为2m , 最大值为2n 可知226252n m m m=⎧⎨-++=⎩所以3n m =⎧⎪⎨=⎪⎩1232m n =≤-=-=-满足题意.所以3m n +=.…………………………12分③当1()12m n +>,即2m n >-时,由函数的最小值为2m ,最大值为2n 可知226252n n n m=⎧⎨-++=⎩所以31n m =⎧⎨=⎩,又因为0m <.1m ∴=,3n =不合题意.…………………………13分综上所述,满足题意的m n +的值为3.……………………14分。
