完整word版,八年级数学复习计划
(完整word版)北京初二数学知识点与常见题型总结,推荐文档

知识点复习与基本题型总结1.平行四边形的定义两组对边分别平行的四边形叫做平行四边形这个定义包含两层意义:①四边形;②两组对边分别平行2.对角线的定义平行四边形不相邻的两个顶点连成的线段叫做它的对角线3.平行四边形的性质①从边看:平行四边形的对边平行且相等②从角看:平行四边形的对角相等,邻角互补③从对角线看:平行四边形的对角线互相平分,互相平分是指两条线段有公共的中点4.平行四边形的面积平行四边形的面积等于它的底和这个底上的高的积.5.平行四边形的判别方法①两组对边分别平行的四边形是平行四边形②一组对边平行且相等的四边形是平行四边形③两组对边分别相等的四边形是平行四边形④对角线互相平分的四边形是平行四边形⑤两组对角分别相等的四边形是平行四边形6.平行四边形的性质与判定的区别平行四边形的性质是指平行四边形的边,角,对角线等所具有的大小或位置之间的关系,而平行四边形的判定是指四边形具有什么条件就是平行四边形7.矩形的定义有一个角是直角的平行四边形是矩形8.矩形的性质①具有平行四边形的一切性质②矩形的四个角都是直角③矩形的对角线相等④矩形是轴对称图形,它有两条对称轴9.矩形的判定①有一个内角是直角的平行四边形是矩形②对角线相等的平行四边形是矩形③有三个角是直角的四边形是矩形另外还有对角线相等且互相平分的四边形是矩形10.直角三角形的性质直角三角形斜边上的中线等于斜边的一半11.矩形对角线产生的三角形的特点矩形的一条对角线把矩形分成两个全等的直角三角形,两条对角线把矩形分成四个小的全等的等腰三角形12.有关矩形面积的计算①面积公式:矩形面积=长⨯宽②如图.矩形ABCD的两条对角线相交于O,则14 ABO BCO CDO ADOS S S S S∆∆∆∆====矩形ABCDOAB CD13.菱形的定义一组邻边相等的平行四边形叫做菱形14.菱形的性质①具有平行四边形的一切性质②菱形的四条边都相等③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角④菱形是轴对称图形,每条对角线所在的直线都是它的对称轴15.菱形的判定方法①有一组邻边相等的平行四边形是菱形②对角线互相垂直的平行四边形是菱形③四条边都相等四边形是菱形16.有关菱形的面积计算由于菱形的对角线互相垂直平分,11()22ABD CBDS S S BD OA OC BD AC ∆=+=+=⋅ABC DO也可以用平行四边形的面积计算公式=底⨯高17.正方形的定义一组邻边相等的矩形叫做正方形正方形不仅是特殊的平行四边形,而且是特殊的矩形,又是特殊的菱形18.正方形的性质正方形具有平行四边形,矩形,菱形的一切性质①边:四边相等,对边平行②角:四个角都是直角③对角线:互相平分;相等;且垂直;每一条对角线平分一组对角,即正方形的对角线与边的夹角为45︒④正方形是轴对称图形,有四条对称轴19.正方形的判定①菱形+矩形的一条特征②菱形+矩形的一条特征③平行四边形+一个直角+一组邻边相等说明一个四边形是正方形的一般思路是:先判断它是矩形,在判断这个矩形也是菱形;或先判断它是菱形,再判断这个菱形也是矩形20.正方形对角线产生的三角形特点正方形的一条对角线把正方形分成两个全等的等腰直角三角形,两条对角线把正方形分成四个小的全等的等腰直角三角形21.正方形常用的辅助线添加方法①正方形中常连对角线,把四边形的问题转化为三角形的问题②有垂直时做垂线构造正方形③有正方形一边中点时常取另一边中点构造图形来应用④利用旋转法将与正方形有关的题目的分散元素集中起来,从而为解决问题创造条件22.平行四边形,菱形,矩形,和正方形四者之间的关系对角线垂直对角线相等一个内角为直角一组邻边相等正方形菱形平行四边形矩形23.梯形定义:一组对边平行而另一组对边不平行的四边形叫做梯形梯形的底:梯形中平行的两边叫做梯形的底,通常把较短的底叫做上底,较长的底叫做下底梯形的腰:梯形中不平行的两边叫做梯形的腰梯形的高:梯形两底之间的距离叫做梯形的高等腰梯形:两腰相等的梯形直角梯形:一腰垂直于底的梯形24.梯形的判定①判定四边形一组对边平行,另一组对边不平行②一组对边平行但不相等的四边形是梯形25.等腰梯形的性质①两底平行,两腰相等②等腰梯形在同一底上的两个角相等③等腰梯形的两条对角线相等④等腰梯形是轴对称图形,只有一条对称轴,一底的垂直平分线是它的对称轴26.等腰梯形的判定①两腰相等的梯形是等腰梯形②在同一底上的两个角相等的梯形是等腰梯形(以前出现,但是在新课标中没有出现的判定方法:对角线相等的梯形是等腰梯形)27.梯形的面积面积=(上底+下底)×高÷228.三角形中位线:连接三角形两边中点的线段,叫做三角形的中位线,三角形的中位线平行于第三边,并且等于第三边的一半梯形中位线:连接梯形两腰中点的线段,叫做梯形的中位线.梯形中位线平行于两底,并且等于两底和的一半梯形辅助线的添法(图一) (图二) (图三)(图四) (图五) (图六)(图七) (图八)基础题型1.如图在平行四边形ABCD 中,:5:3A B ∠∠=,求这个平行四边形各内角的度数ABCD解:Q 四边形ABCD 是平行四边形∴AD BC ∥,180A B ∠+∠=︒ 由于:5:3A B ∠∠=故设5A x ∠=,则3B x ∠=中点中点即53180x x +=︒解得22.5x =︒ 因此522.5112.5A ∠=⨯︒=︒,322.567.5B ∠=⨯︒=︒ ∴平行四边形各内角度数分别是112.5︒,67.5︒,112.5︒,67.5︒ 2.已知平行四边形ABCD 的周长为38cm ,AC ,BD 相交于O ,且AOB ∆的周长比BOC ∆的周长小于3cm ,如图,求平行四边形ABCD 各边的长 解:Q 四边形ABCD 为平行四边形∴OA OC =,AB CD =,BC AD =Q AOB ∆的周长=OA OB AB ++ BOC ∆的周长=OC OB BC ++且AOB ∆的周长比BOC ∆的周长小于3cm ∴()()3OC OB BC OA OB BC ++-++= 3BC AB ∴-=又Q 平行四边形ABCD 的周长为38cm ∴19BC AB +=∴8AB =cm ,11BC =cm ∴8CD =cm ,11AD =cm3.如图,已知:在平行四边形ABCD 中,BD 是对角线,AE BD ⊥于E ,CF BD ⊥于F 求证:AE CF =DCBAEF证明:方法一:Q 四边形ABCD 是平行四边形 ∴AB CD ∥,AB CD = ∴ABE CDF ∠=∠ Q AE BD ⊥,CF BD ⊥ ∴AEB CFD ∠=∠∴()ABE CDF AAS ∆≅∆ ∴AE CF =O DCBAEF方法二:连接AC ,交BD 于O Q 四边形ABCD 是平行四边形∴OA OC =,又AE BD ⊥,CF BD ⊥ ∴AEO CFO ∠=∠,而AOE COF ∠=∠ ∴AEO CFO ∆≅∆(AAS )∴AE CF = 4.如图所示,在平行四边形ABCD 中,E ,F 分别是AC ,CA 延长线上的点,且CE AF =,则BF 与DE 具有怎么样的位置关系?试说明理由EF ABCD解:BF DE ∥证明:方法一:在平行四边形ABCD 中,AB CD ∥,AB CD =, ∴BAC DCA ∠=∠Q 180BAC BAF ∠+∠=︒,180ACD DCE ∠+∠=︒ ∴BAF DCE ∠=∠又Q AF CE = ∴AFB CED ∆≅∆()SAS方法二.连接BD ,交AC 于O在平行四边形ABCD 中,AO CO =,BO DO = Q AF CE = ∴OF OE =Q FOB EOD ∠=∠ ∴BOF DOE ∆≅∆(SAS ) ∴F E ∠=∠ ∴BF DE ∥OEF ABC DOEF ABCD方法三.连接BD ,交AC 于O ,连接DF ,BE 由方法二知.OF OE =,OB OD = ∴四边形BEDF 为平行四边形 ∴BF DE ∥5.如图,已知O 是平行四边形ABCD 对角线的交点,38AC =cm ,24BD =cm ,14AD =cm ,那么OBC ∆的周长为_____ODCBA解:根据平行四边形对角线互相平分以及对边相等的性质可知14BC AD ==cm ,11241222OB BD ==⨯=cm ,11381922OC AC ==⨯=cm∴OBC ∆的周长为14121945BC OB OC ++=++=cm6.如图平行四边形ABCD 中,EF AB ∥,GH AD ∥,EF 与GH 交于O ,则该图形中的平行四边形的个数共有( )A.7 B.8 C.9 D. 10FED CB AGHO由题意可知图中的平行四边形分别是:DEOH ,EAGO ,HOFC ,OGBF ,DAGH ,HGBC ,DEFC ,EABC ,DABC 所以共有9个7.如图,平行四边形ABCD 中,AF 平分DAB ∠交CD 于N ,交BC 的延长线于F ,DE AF ⊥,交AB 于M ,交CB 延长线于E ,垂足为O ,试证明:BE CF =ON MF EABCD证明:Q 四边形ABCD 为平行四边形 ∴AD BC ∥,AB CD ∥,AB CD =∴DAF F ∠=∠,ADE E ∠=∠,EDC AMD ∠=∠ Q DE AF ⊥,∴90AOM AOD ∠=∠=︒ Q AF 平分DAB ∠,∴DAF BAF ∠=∠ Q OA OA = ∴AOM AOD ∆≅∆(ASA )∴ADM AMD ∠=∠,BAF F ∠=∠,EDC E ∠=∠ ∴AB BF =,CD CE =BF CE ∴=∴BE CF =8.如图,已知:D ,E ,F 分别在ABC 的各边上,DE AF ∥,DE AF =,延长FD 到G ,使2FG FD =.求证:AG 与DE 互相平分.ABCDEFGABC D EF G证明:连接AD ,EGQ DE AF ∥,DE AF =∴四边形AEDF 是平行四边形 ∴DF AE =,DF AE ∥又Q 2FG FD =∴12DG DF FG ==∴DG AE =,而DF AE ∥ ∴四边形AEGD 为平行四边形 ∴AG 与DE 互相平分9.如图,已知D 是ABC ∆的边AB 的中点,E 是AC 上的一点DF BE ∥,EF AB ∥试说明:AE 与DF 互相平分ABCDEFABCDE F证明:连接AF ,DE Q DF BE ∥,EF AB ∥∴四边形BDFE 为平行四边形,∴EF BD = Q D 是AB 中点 ∴BD AD =∴AD EF =,AD EF ∥ ∴四边形ADEF 为平行四边形 ∴AE 与DF 互相平分10.如图,点M ,N 分别在平行四边形ABCD 的边BC ,AD 上,且BM DN =,ME BD ⊥,NF BD ⊥,垂足分别为E ,F ,求证:MN 与EF 互相平分MNABCDEF MNABCDE F证明:连接EN ,MFQ 四边形ABCD 是平行四边形 ∴BC AD ∥,∴CBD ADB ∠=∠Q 90MEF NFE ∠=∠=︒,90MEB NFD ∠=∠=︒ ∴ME NF ∥Q BM DN = ∴BME DNF ∆≅∆()AAS∴ME NF =∴四边形EMFN 是平行四边形(一组对边平行且相等的四边形是平行四边形) ∴MN 与EF 互相平分11.如图,AF 与BE 互相平分,交点为M ,EC 与DF 互相平分,交点为N ,那么,四边形ABCD 是平行四边形么?你是怎么判定的?NM EFABCDNM EFABCD解:四边形ABCD 是平行四边形证明:连接AE ,BF ,EF ,DE ,CF Q AF 与BE 互相平分∴四边形ABFE 是平行四边形 ∴EF AD ∥,EF AD = Q EC 与DF 互相平分∴四边形BCEF 是平行四边形 ∴EF BC ∥,EF BC = ∴AD BC =,AD BC ∥∴四边形ABCD 是平行四边形12.如图,已知BE ,CF 是ABC ∆的高,D 是BC 的中点.求证:DE DF =ABCDEF证明:Q BE ,CF 是ABC ∆的高,∴BFC ∆,BEC ∆均为直角三角形 Q D 是BC 的中点∴DF 是Rt BFC ∆斜边上的中线,DE 是Rt BEC ∆斜边上的中线∴12DF BC =,12DE BC =∴DE DF =13.如图,先将矩形纸片ABCD 对折一次折痕为EF ,展开后又将纸片折叠使点A 落在EF 上,此时折痕为BM ,求NBC ∠度数的大小MNABCDEF GFEDCBAN M提示:根据题意得111222AE BE DF FC CD AB BN ======过点N 作NG BC ⊥,垂足为G则12NG BN =,∴30NBC ∠=︒(直角三角形中30︒角所对的直角边等于斜边的一半,反过来也成立)14.过矩形ABCD 对角线AC 的中点O 作EF AC ⊥分别交AB ,DC 于E ,F ,点G 为AE 的中点,若30AOG ∠=︒,求证:13OG DC =GFEAB CDOODCBAEFG证明:连接CEQ 四边形ABCD 是矩形 ∴OA OC = Q EF AC ⊥∴EF 是线段AC 的垂直平分线 ∴EA EC =Q 30AOG ∠=︒ ∴60ACB ∠=︒,30OCE ∠=︒∴30BCE ∠=︒ ∴12BE EC =Q G 是AE 中点∴1122OG AG GE AE CE ==== ∴OG AG GE EB ===∴13OG DC =15.在矩形ABCD ,6AB =,8BC =,将矩形折叠,使点C 与点A 重合,折痕为EF ,在展开,求折痕EF 的长FEDCBAO解:Q 6AB =,8BC = ∴由勾股定理可得10AC =根据题意有AF CF =,设AF CF x ==,8BF x =-由勾股定理222AB BF AF +=,即2226(8)x x +-= 解得254x = ∴254FC =Q 2575642AFCE S CF AB =⨯=⨯=Y ,12AFCE S AC EF =⨯Y ∴152EF =(提示:对角线互相垂直的四边形面积等于对角线乘积的一半) 16.已知:如图,O 是矩形ABCD 对角线的交点,AE 平分BAD ∠,120AOD ∠=︒,求AEO ∠的度数EODC BA答案:提示ABE ∆为等腰直角三角形,OAB ∆为等边三角形,OBE ∆为等腰三角形 30OBE ∠=︒,75OEB ∠=︒,754530OEA ∠=︒-︒=︒17.如图,MN 为过Rt ABC ∆的直角顶点A 的直线,且BD MN ⊥于D ,CE MN ⊥于点E ,AB AC =,F 为BC 的中点,求证:DF EF =ABCDEFNMABCDEFNM证明:连接AFQ ABC ∆为直角三角形,F 为斜边BC 的中点 ∴BF AF CF ==Q 90BAC ∠=︒ ∴90BAM NAC ∠+∠=︒ Q BD MN ⊥,CE MN ⊥∴90BAM DBA ∠+∠=︒,90BDA AEC ∠=∠=︒∴DBA EAC ∠=∠,又Q AB AC = ∴DBA EAC ∆≅∆(AAS )∴DB AE =Q AB AC =,90BAC ∠=︒,F 为BC 的中点 ∴45ABC FAC ∠=∠=︒∴DBA ABC CAF CAN ∠+∠+∠+∠,即DBF FAE ∠=∠又Q DB AE =,AF BF = ∴DBF EAF ∆≅∆(SAS )∴DF EF =总结:在直角三角形中,出现中点时,常见的辅助线是斜边上的中线以及中位线18.如图E 是菱形ABCD 边AD 的中点,EF AC ⊥于H ,交CB 的延长线于F ,交AB 于G ,求证:AB 与EF 互相平分GHA BC DEFFEDCBAHG证明:Q 四边形ABCD 是菱形∴BAC DAC ∠=∠ Q AC EG ⊥,AH AH = ∴AHE AHG ∆≅∆(ASA )∴AE AG = Q 12AE AD =∴12AG AB = Q AD BC ∥ ∴F AEG ∠=∠Q BGF AGE ∠=∠ ∴AGE BGF ∆≅∆(AAS ) ∴EG FG =,AG GB = 即AB 与EF 互相平分方法二:连接AF ,BE由12AE AD =,12AG AB =得AGE AEG BGF BFG ∠=∠=∠=∠,则AE AG BG BF === ∴AE BF ∥且AE BF =∴四边形AFBE 为平行四边形 ∴AB 与EF 互相平分19.如图,在ABC ∆中,90ACB ∠=︒,AD 是A ∠的平分线,交BC 于点D ,CH 是AB 边上的高,交AD 于F ,DE AB ⊥于E .求证:四边形CDEF 是菱形 ABCDEFH证明:Q AD 是A ∠的平分线 ∴CAD EAD ∠=∠ Q 90ACB ∠=︒,CH AB ⊥∴90CAD CDA ∠+∠=︒,90FAH AFH ∠+∠=︒ ∴CDA AFH ∠=∠ Q AFH CFD ∠=∠∴CFD CDF ∠=∠ ∴CF CD =Q AD 是A ∠的平分线,CD AC ⊥,DE AB ⊥ ∴CD DE = ∴CF DE = Q CH AB ⊥,DE AB ⊥∴CH DE ∥∴四边形CFED 是平行四边形Q CD CF = ∴平行四边形CFED 是菱形20.菱形ABCD 中,120DAB ∠=︒,如果它的一条对角线长为12cm ,求菱形ABCD 的边长 解:AB CDODCBA若对角线12AC =cm ,如图Q 四边形ABCD 为菱形,且120DAB ∠=︒∴60DAC BAC ∠=∠=︒则ADC ∆为等边三角形 ∴菱形ABCD 的边长为12cm 若对角线12BD =cm ,如图Q 四边形ABCD 为菱形,且120DAB ∠=︒∴60DAC BAC ∠=∠=︒则ADC ∆为等边三角形 又Q OD OB =∴6OD OB ==cm 设OA x =,2AD x =, 由勾股定理可得222(2)6x x =+,解得23x =,∴43AD =cm 综上所述:菱形ABCD 的边长为12cm 或43cm22.如图,四边形ABCD 是正方形,E 是CD 的中点,F 是BC 上的一点,且3BF FC = 求证:AE EF ⊥ABCDEFABCDEF证明:连接AF ,设FC k =,则4BC k =Q 四边形ABCD 是正方形 ∴90B C D ∠=∠=∠=︒,4AB BC CD AD k ==== Q E 为CD 中点 ∴2DE EC k ==在Rt ABF ∆中,222225AF AB BF k =+= 在Rt ECF ∆中,22225EF EC FC k =+= 在Rt ADE ∆中,222220AE AD DE k =+= 则222AE EF AF +=,∴AEF ∆是直角三角形∴90AEF ∠=︒ ∴AE EF ⊥(到初三的时候此题还有额外的证明方法)23.如图,过正方形ABCD 对角线BD 上一点P ,作PE BC ⊥于E ,作PF CD ⊥于F ,连接AP ,EF .求证:AP EF =,AP EF ⊥FEPABCDH DCBAPEF证明:连接PC ,延长AP 交EF 于点HQ 四边形ABCD 是正方形∴45ABP CBP ∠=∠=︒,AB BC =Q BP BP = ∴ABP CBP ∆≅∆(SAS ) ∴AP CP =,BAP BCP ∠=∠Q PE BC ⊥,PF CD ⊥,BC CD ⊥∴四边形PECF 为矩形(有三个角为直角的四边形为矩形) ∴PC EF = ∴PA EF =Q PF EC =,90EPF PEC ∠=∠=︒ ∴PEF EPC ∆≅∆(HL )∴PFE PCE ∠=∠ ∴PFE BAP ∠=∠Q AB BC ⊥,PE BC ⊥ ∴AB PE ∥ ∴BAP EPH ∠=∠Q 90PFE PEH ∠+∠=︒ ∴90EPH PEH ∠+∠=︒ ∴AP EH ⊥24.如图正方形ABCD 中,M 是AB 的中点,MN DM ⊥,BN 平分CBE ∠,交MN 于N 求证:DM MN =NABCDEMFM EDCBAN证明:取线段AD 的中点F ,连接FM Q 四边形ABCD 为正方形∴AB AD =,90A ABC ∠=∠=︒ Q F 为AD 中点,M 为AB 中点 ∴DF AF AM MB ===∴45AFM AMF ∠=∠=︒ ∴135DFM ∠=︒ Q BN 平分CBE ∠ ∴45CBN EBN ∠=∠=︒ ∴135MBN ∠=︒ ∴DFM MBN ∠=∠ Q DM MN ⊥ ∴90DMA NMB ∠+∠=︒Q 90DMB ADM ∠+∠=︒ ∴ADM MBN ∠=∠在DMF ∆与MNB ∆中MDF NMB DF MB DFM MBN ∠=∠⎧⎪=⎨⎪∠=∠⎩∴DMF MNB ∆≅∆()ASA ∴DM MN =思考:若点M 是线段AB 上一个动点,其他条件不变,则上面的结论还成立么?M EDCB ANFM EDCBAN请参考上面的解题思路,本题还有额外的证明方法,但是需要初三学习的知识,现在就不列举了25.如图,在梯形ABCD 中,AD BC ∥,AD BC <,E ,F 分别是AD ,BC 的中点,且EF BC ⊥,求证:梯形ABCD 为等腰梯形AB CDEF M NAB CDEF证明:过E 分别作AB ,DC 的平行线交BC 于M ,N ,易知四边形ABME 和四边形DCNE都是平行四边形∴AE BM =,DE NC =,AB EM =,DC EN =Q E ,F 分别是AD ,BC 的中点 ∴AE DE =,BF CF =∴BM CN = ∴BF BM CF NC -=- ∴MF NF ⊥Q EF BC ⊥ ∴EM EN = ∴EF 是线段MN 的垂直平分线 ∴ME NE = ∴AB CD = 故梯形ABCD 是等腰梯形26.已知等腰梯形ABCD 中,AB CD =,60B ∠=︒,15AD =cm ,49BC =cm ,求它的腰长DC B AEAB CD解:方法一:过点A 作AE DC ∥,交BC 于点E Q AD BC ∥ ∴四边形AECD 为平行四边形∴AD EC =,DC AE =Q AB DC = ∴AE AB = Q 60B ∠=︒ ∴四边形ABCD 为等边三角形∴BE AB = Q 15AD =,49BC = ∴491534BE BC CE BC AD =-=-=-= ∴34AB CD ==cm方法二MNABCD过点A 作AM BC ⊥,垂足为M ,过点D 作DN BC ⊥,垂足为N Q 四边形ABCD 为等腰梯形 ∴AB CD =,B C ∠=∠ Q 90AMB DNC ∠=∠=︒ ∴ABM DCN ∆≅∆(AAS ) ∴BM CN =Q 90AMN MND ADN ∠=∠=∠=︒∴四边形AMND 为矩形 ∴AD MN = 49BC =Q ,15AD =∴11()(4915)1722BM CN BC AD ==-=-=Q 60B ∠=︒ ∴30BAM ∠=︒ ∴234AB BM ==cm27.如图,在ABC ∆中,AB AC >,AD 平分BAC ∠,CD AD ⊥,点E 是BC 的中点求证:①DE AB ∥ ②1()2DE AB AC =-ABCD EFE DCBA证明:①延长CD 交AB 于点FQ AD CD ⊥,∴90ADC ADF ∠=∠=︒ Q AD 平分BAC ∠ ∴DAC DAF ∠=∠ Q AD AD =∴ADC ADF ∆≅∆(ASA )(AD 又是高,又是角平分线,很容易联想到“三线合一”) ∴AC AF =,FD DC = Q 点E 是BC 的中点∴DE 是三角形CBF ∆的中位线∴DE BF ∥,12DE BF =②Q AB AF BF -=∴BF AB AC =-∴1()2DE AB AC =-28.如图,在梯形ABCD 中,DC AB ∥,BC DC AB =+,E 是AD 中点 求证:90CEB ∠=︒ABCDEABCDEF证明:取BC 中点F ,连接EF 由梯形中位线性质可知EF DC AB ∥∥且1()2EF DC AB =+Q BC DC AB =+ ∴2EF BC = ∴EF CF FB == ∴90CEB ∠=︒ 基础知识达标一、精心选一选(每小题3分,共30分)1、在□ABCD 中,∠A :∠B :∠C :∠D 的值可以是( )A .1:2:3:4B .1:2:2:1C .2:2:1:1D .2:1:2:1 2、菱形和矩形一定都具有的性质是( )A .对角线相等B .对角线互相垂直C .对角线互相平分D .对角线互相平分且相等 3、下列命题中的假命题是( )A .等腰梯形在同一底边上的两个底角相等B .对角线相等的四边形是等腰梯形C .等腰梯形是轴对称图形D .等腰梯形的对角线相等 4、四边形ABCD 的对角线AC 、BD 交于点O ,能判定它是正方形的是( )A .AO =OC ,OB =OD B .AO =BO =CO =DO ,AC ⊥BD C .AO =OC ,OB =OD ,AC ⊥BD D .AO =OC =OB =OD 5、给出下列四个命题⑴一组对边平行的四边形是平行四边形 ⑵一条对角线平分一个内角的平行四边形是菱形中 点中 点中 点⑶两条对角线互相垂直的矩形是正方形⑷顺次连接等腰梯形四边中点所得四边形是等腰梯形。
初二数学复习计划5篇(实用)

初二数学复习计划5篇(实用)怎样制定详细的复习计划,学生对复习要有起码的安排和目标的制定,对自己的学情进行分析,找到自己的长处和缺陷部分,然后据此进行有目的的复习。
那么你有了解过复习计划吗?这里给大家分享一些关于初二数学复习计划,方便大家学习。
初二数学复习计划1初二阶段是一个分化阶段,为了使初二的数学考试取得理想的成绩,做好期末的复习工作,我们备课组以课标为大纲,以考试规律为指导,现制定教学计划如下:一、复习原则1、基础性原则钻研课标,掌握课标要求,低起点复习。
回归课本,立足基础知识的掌握,基本技能的形成,基本数学思想方法的渗透。
面向所有学生,让所有人都有所收获和提高。
2.框架性原则让学生以树状图形式或表格形式梳理知识,扫除盲点,帮助学生形成知识网络,使学生对所学知识有一个整体认识和提升。
3.规范性原则强调例题的示范作用,通过例题引导学生规范地进行思考和规范地进行书写。
要让学生对几何证明由“有感觉”过度到“有把握”,解题由“会做”到“做对”。
二、复习模式:1、知识点整理,注重基础知识考查。
复习中以印试卷形式为主,按照知识点——例题——跟踪训练——方法总结为主线展开复习。
试卷以填空选择及简单的解答题为主,注重题目多样化,注重层次性,分层训练,让不同的人得到不同的数学教育。
2、加强集体研讨。
通过研讨,进一步总结考试重点和难点,提高团队合作意识。
3、狠抓及格率,提升优秀率。
我所教的七班,八班中八班两极分化现象严重,学困生较多,为此,在复习中我将会更多的关注他们,让他们树立信心,课堂上多提问,多鼓励;作业设计最基础的内容,只有打好基础,才能活用知识。
4、坚持每日小考反馈。
我将会在教学中通过课堂检测来对学生所学知识进行排查,尽可能让百分之八十的同学通过。
5、制定有效的教学策略。
高效课堂是我们的目标,课堂45分钟是关键,复习中我将充分利用4+1教学,提高学生的合作意识,竞争意识,并结合评价表及时表扬和鼓励。
(完整word版)华师大版八年级数学上册知识点总结.doc

八年级数学上册复习提纲第11 章数的开方§11.1 平方根与立方根一、平方根1、平方根的定义:如果一个数的平方等于a,那么这个数叫做a的平方根。
(也叫做二次方根)即:若 x2=a,则 x 叫做 a 的平方根。
2、平方根的性质:(1)一个正数有两个平方根。
它们互为相反数;(2)零的平方根是零;(3)负数没有平方根。
二、算术平方根1、算术平方根的定义:正数 a 的正的平方根,叫做 a 的算术平方根。
2、算术平方根的性质:(1)一个正数的算术平方根只有一个且为正;(2)零的算术平方根是零;(3)负数没有算术平方根;(4)算术平方根的非负性: a ≥0。
三、平方根和算术平方根是记号:平方根± a (读作:正负根号a);算术平方根 a (读作根号a)即:“± a ”表示a的平方根,或者表示求a的平方根;“ a ”表示a的算术平方根,或者表示求 a 的算术平方根。
其中 a 叫做被开方数。
∵负数没有平方根,∴被开方数 a 必须为非负数,即:a≥0。
四、开平方:求一个非负数的平方根的运算,叫做开平方。
其实质就是:已知指数和二次幂求底数的运算。
五、立方根1、立方根的定义:如果一个数的立方等于a,那么这个数叫做a的立方根。
(也叫做三次方根)即:若 x3=a,则 x 叫做 a 的立方根。
2、立方根的性质:(1)一个正数的立方根为正;(2)一个负数的立方根为负;(3)零的立方根是零。
3、立方根的记号:3a(读作:三次根号a),a称为被开方数,“3”称为根指数。
3a 中的被开方数a的取值范围是:a为全体实数。
六、开立方:求一个数的立方根的运算,叫做开立方。
其实质就是:已知指数和三次幂求底数的运算。
七、注意事项:1、“±a ”、“ a ”、“3 a ”的实质意义:“±a ”→问:哪个数的平方是a;“ a ”→问:哪个非负数的平方是a;“3 a ”→问:哪个数的立方是a。
2、注意 a 和3 a 中的a的取值范围的应用。
(完整word版)人教版八年级下册数学教学计划

八年级数学下册教学计划一、指导思想在教学中努力推进九年义务教育,落实新课改,体现新理念,培养创新精神。
通过数学课的教学,使学生切实学好从事现代化建设和进一步学习现代化科学技术所必需的数学基本知识和基本技能;努力培养学生的运算能力、逻辑思维能力,以及分析问题和解决问题的能力。
二、学情分析本班学生数学成绩两极分化比较严重,不少同学基础很差,问题较严重。
在上学期的期末统考中,本班数学只是位列中上游,要在本期获得理想成绩,师生需加倍努力,补缺补差,注重方法,夯实基础。
三、教材分析本学期教学内容共计五章,知识的前后联系,教材的教学目标,重、难点分析如下:第十六章二次根式本章是在数的开方的基础上展开的,是算术平方根概念的抽象与扩展。
本章的重点是二次根式的化简和运算,难点是正确理解二次根式的性质和运算法则的合理性。
第十七章勾股定理直角三角形是一种特殊的三角形,它有许多重要的性质,如两个锐角互余, 30度角所对的直角边等于斜边的一半,本章所研究的勾股定理,也是直角三角形的性质,而且是一条非常重要的性质,本章分为两节,第一节介绍勾股定理及其应用,第二节介绍勾股定理的逆定理。
第十八章平行四边形本章的主要内容是认识平行四边形及几种特殊的四边形,通过对图形的操作或度量,让学生直观认识图形的性质,通过逆命题的猜想、操作验证和逻辑推理的证明等过程,让学生理解并掌握几种图形的判定方法,提高数学思维能力。
第十九章一次函数本章的主要内容是函数的基本知识,以及一次函数的图象、性质和简单应用。
函数是数学中重要的基本概念之一,它揭示了现实世界中数量相互依存和变化的实质,是刻画和研究现实世界变化规律的重要模型。
本章是学习函数的入门,也是进一步学习函数的基础。
第二十章数据的分析本章主要研究平均数、中位数、众数以及极差、方差等统计量的统计意义,学习如何利用这些统计量分析数据的集中趋势和离散情况,并通过研究如何用样本的平均数和方差估计总体的平均数和方差,进一步体会用样本估计总体的思想。
八年级数学期末复习计划(通用6篇)

八年级数学期末复习计划八年级数学期末复习计划(通用6篇)如何进行有效的复习,大家都有写过复习计划吧,对自己的学情进行分析,找到自己的长处和缺陷部分,然后据此进行有目的的复习。
那么大家知道复习计划是怎么写的吗?下面是小编为大家整理的八年级数学期末复习计划(通用6篇),欢迎大家分享。
八年级数学期末复习计划1(一)思想方面的补差。
做好学生的思想工作,经常和学生谈心,关心他们,关爱他们,让学生觉得老师是重视他们的,激发他们学习的积极性。
了解学生们的学习态度、学习习惯、学习方法等。
从而根据学生的思想心态进行相应的辅导。
(二)有效补差措施。
利用课余时间和晚拖班及放学后,对各种情况的同学进行辅导、提高,“因材施教、对症下药”,根据学生的素质采取相应的方法辅导。
具体方法如下:1.课上差生板演,中等生订正,优等生解决难题。
2.安排座位时坚持“好差同桌”结为学习对子。
即“兵教兵”。
3.课堂练习分成三个层次:第一层“必做题”—基础题让差生做,第二层:“选做题”—中等题,满足不同层次学生的需要。
4.培优补差过程必须优化备课,功在课前,效在课上,成果巩固在课后培优。
培优补差尽可能“耗费最少的必要时间和必要精力”。
备好学生、备好教材、备好练习,才能上好课,才能保证补差的效果。
要精编习题、习题教学要有四度。
习题设计(或选编习题)要有梯度,紧扣重点、难点、疑点和热点,面向大多数学生,符合学生的认知规律,有利于巩固“双基”,有利于启发学生思维;习题讲评要增加信息程度,围绕重点,增加强度,引到学生高度注意,有利于学生学会解答;解答习题要有多角度,一题多解,一题多变,多题一解,扩展思路,培养学生思维的灵活性,培养学生思维的广阔性和变通性;解题训练要讲精度,精选构思巧妙,新颖灵活的典型题,有代表性和针对性的题,练不在数量而在质量,训练要有多样化。
(三)在补差中注意几点:1、不歧视学习有困难的学生,不纵容优秀的学生,一视同仁。
2、根据差生的实际情况制定学习方案,学困生则根据他们的程度给与相应的题目进行练习和讲解,已达到循序渐进的目的。
初中八年级复习计划

初中八年级复习计划
一、语文科目
1. 背诵语文课本及语文书在各单元的重要知识点。
如名言警句,典故引文等。
2. 复习材料结构。
如记叙文、议论文、说明文等各种文章类型的结构要点。
3. 学习组织语言。
如并列连词,表递进意思的单词等。
4. 练习阅读理解和写作能力。
选择一个主题,阅读相关资料,归纳论点,写一篇短文。
二、数学科目
1. 方程。
复习一元一次方程和二元一次方程的知识点。
2. 几何图形。
复习点、线、面、角的概念和属性。
复习三角函数定理。
3. 数据处理。
统计问题,概率问题。
4. 练手能力。
每天做十个练习题,掌握基本公式和算法。
三、英语科目
1. 词汇。
背诵单词及其解释,促进语感。
2. 语法。
复习时态、助动词、参词短语等语法知识。
3. 阅读。
阅读短文,理解细节和关键信息。
4. 听力。
每天练习英语广播练习听力能力。
5. 口语。
与家人交流,运用英语表达自己。
6. 写作。
根据给的提示写一篇短文。
以上就是初中八年级复习计划的一个建议模板,望能为同学们提供一个参考。
八年级上册数学复习计划(通用6篇)

八年级上册数学复习计划(通用6篇)八年级上册数学复习计划篇1一、复习内容:第一章:勾股定理第二章:实数第三章:位置与坐标第四章:一次函数第五章:二元一次方程组第六章:数据的分析第七章:平行线的证明二、复习目标:八年级数学本学期知识点多,复习时间又比较短,只有三周的时间。
根据实际情况,应该完成如下目标:(一)、整理本学期学过的知识与方法: 1.第一、七章是几何部分。
这三章的重点是勾股定理的应用以及平行线的性质与判别还有三角形内角和定理及其应用。
所以记住性质是关键,学会判定是重点,灵活应用是目的。
要学会判定方法的选择,不同图形之间的区别和联系要非常熟悉,形成一个有机整体。
对常见的证明题要多练多总结。
2.第四五六章主要是概念的教学,对这几章的考试题型学生可能都不熟悉,所以要以与课本同步的训练题型为主,要列表或作图的,让学生积极动手操作,并得出结论,课堂上教师讲评,尽量是精讲多练,该动手的要多动手,尽可能的让学生自己总结出论证几何问题的常用分析方法。
3.第二章主要是计算,教师提前先把概念、性质、方法综合复习,加入适当的练习,在练习计算。
课堂上逐一对易错题的讲解,多强调解题方法的针对性。
最后针对平时练习中存在的问题,查漏补缺。
(二)、在自己经历过的解决问题活动中,选择一个有挑战问题性的问题,写下解决它的过程:包括遇到的困难、克服困难的方法与过程及所获得的体会,并选择这个问题的原因。
(三)、通过本学期的数学学习,让同学们总结自己有哪些收获;有哪些需要改进的地方。
三、复习方法:1、强化训练,这个学期计算类和证明类的题目较多,在复习中要加强这方面的训练。
特别是一次函数,在复习过程中要分类型练习,重点是解题方法的正确选择同时使学生养成检查计算结果的习惯。
还有几何证明题,要通过针对性练习力争达到少失分,达到证明简练又严谨的效果。
2、加强管理严格要求,根据每个学生自身情况、学习水平严格要求,对应知应会的内容要反复讲解、练习,必须做到学一点会一点,对接受能力差的学生课后要加强辅导,及时纠正出现的错误,平时多小测多检查。
初二期中考试数学复习计划(3篇)

初二期中考试数学复习计划第一部分:知识梳理(500字)1. 复习已学知识点:回顾上学期学习的数学知识点,包括整数、小数、分数、百分数、代数式等。
通过复习,巩固基本概念和运算方法。
2. 查漏补缺:分析自己在上学期学习中容易掌握和容易混淆的知识点,通过查阅教材和参考书的相关内容,进行有针对性的复习。
3. 拓宽知识面:扩展数学知识,了解一些初中数学未教授的高中数学知识和应用领域,提前做好准备。
第二部分:理论性知识强化(____字)1. 题型分类:将已学知识点根据题型进行分类,例如选择题、填空题、解答题等。
对每种题型的解题方法进行总结,明确解题思路和步骤。
2. 练习题量的控制:根据各个题型的难易程度制定合理的练习量。
对于熟练掌握的知识点,适量练习巩固;对于掌握不牢固的知识点,增加相应的练习量。
3. 错题集整理:做题过程中及时记录做错的题目,并将其整理成错题集。
对错题进行分类,分析错误原因,总结解题方法和技巧,并进行针对性的复习和训练。
第三部分:应用性问题解决(____字)1. 实际问题应用:找一些与数学相关的实际问题进行解答。
例如:买卖问题、几何问题等。
通过解答实际问题,巩固数学知识,并将数学知识与实际生活相结合,加深理解。
2. 综合题训练:选取一些综合性较强的题目进行训练,要求综合运用数学知识进行解决。
通过解决综合性题目,能够提高解决问题的能力和思维能力,为应对考试做好准备。
3. 拓展应用领域:尝试解决一些复杂的实际问题,如工程问题、实验问题等,通过解决实际问题,丰富数学应用的领域。
第四部分:模拟考试(500字)1. 模拟试卷:找一些已经出过的模拟试卷进行模拟考试,模拟考试时要求严格按照考试时间和考试规则进行答题,模拟考试环境要尽量接近真实考试环境。
2. 错误分析:模拟考试结束后,认真检查试卷,分析错误原因,并总结出现错误的共性和原因。
并针对性地对有问题的知识点进行复习和强化训练。
3. 时间控制:模拟考试时要重点关注答题时间的控制,熟悉考试时的时间分配,以及有效利用考试时间。
(完整word版)华东师大版八年级数学上册全册教案

第十一章数的开方11。
1平方根与立方根(1)【教学目标】:以实际问题的需要出发,引出平方根的概念,理解平方根的意义,会求某些数的平方根。
【教学重、难点】:重点:了解平方根的概念,求某些非负数的平方根。
难点:平方根的意义【教具应用】:老师:三角板、小黑板学生:【教学过程】:一、提出问题,创设情境.问题1、要剪出一块面积为25cm²的正方形纸片,纸片的边长应是多少?问题2、已知圆的面积是16πcm²,求圆的半径长。
要想解决这些问题,就来学习本节内容二、自学提纲:1、你能解决上面两个问题吗?这两个问题的实质是什么?2、看第2页,知道什么是一个数的平方根吗?3、25的平方根只有5吗?为什么?4、会求110的平方根吗?试一试5、-4有平方根吗?为什么?6、想一想,你是用什么运算来检验或寻找一个数的平方根?7、根据平方根的定义你能指出正数、0、负数的平方根的特征吗?8、什么叫开平方?三、能力、知识、提高同学们展示自学结果,老师点拔①情境中的两个问题的实质是已知某数的平方,要求这个数。
②概括:如果一个数的平方等于a,那么这个数叫做a的平方根。
如5²=25,(-5)²=25 ∴25的平方根有两个:5和-5③ 根据平方根的意义,可以利用平方来检验或寻找一个数的平方根. ④ 任何数的平方都不等于-4,所以-4没有平方根。
⑤ 0的平方等于0。
所以0只有一个平方根为0。
⑥ 概括:一个正数有两个平方根,它们互为相反数;0有一个平方根,它是0本身;负数没有平方根。
⑦ 求一个数a (a ≥0)的平方根的运算,叫做开平方。
四、 知识应用1、 求下列各数的平方根① 49 ②1.69 ③8116④(-0.2)² 2、 将下列各数开平方①1 ②0.09 ③(-53)² 五、 测评1、 说出下列各数的平方根①81 ②0.25 ③1254 2、 求未知数x 的值①(3x )²=16 ②(2x -1)²=9六、 小结:1、 什么叫做平方根?2、 一个正数的平方根有几个?零的平根有几个?负数的平方根呢?3、 平方和开平方运算有什么区别和联系?区别:①平方运算中,已知的是底数和指数,求的是幂。
(完整word版)北师大版八年级数学知识点整理(分单元精校版)(良心出品必属精品)

北师大版八年级全册数学定理知识点汇总八年级上册第一章勾股定理1.勾股定理直角三角形两直角边a, b的平方和等于斜边c的平方, 即2.勾股定理的逆定理如果三角形的三边长a, b, c有关系, 那么这个三角形是直角三角形。
3.勾股数:满足的三个正整数, 称为勾股数。
第二章实数1) 1.实数的概念及分类2)实数的分类正有理数有理数零有限小数和无限循环小数实数负有理数正无理数无理数无限不循环小数负无理数无理数:无限不循环小数叫做无理数。
➢在理解无理数时, 要抓住“无限不循环”这一时之, 归纳起来有四类:➢开方开不尽的数, 如等;➢有特定意义的数, 如圆周率π, 或化简后含有π的数, 如+8等;➢有特定结构的数, 如0。
1010010001…等;某些三角函数值, 如sin60o等1) 2.实数的倒数、相反数和绝对值相反数:实数与它的相反数时一对数(只有符号不同的两个数叫做互为相反数, 零的相反数是零), 从数轴上看, 互为相反数的两个数所对应的点关于原点对称, 如果a与b互为相反数, 则有a+b=0, a=—b,反之亦成立。
绝对值:在数轴上, 一个数所对应的点与原点的距离, 叫做该数的绝对值。
(|a|≥0)。
零的绝对值是它本身, 也可看成它的相反数, 若|a|=a, 则a ≥0;若|a|=-a, 则a ≤0。
倒数:如果a 与b 互为倒数, 则有ab=1, 反之亦成立。
倒数等于本身的数是1和-1。
零没有倒数。
数轴:2) 规定了原点、正方向和单位长度的直线叫做数轴(画数轴时, 要注意上述规定的三要素缺一不可)。
解题时要真正掌握数形结合的思想, 理解实数与数轴的点是一一对应的, 并能灵活运用。
估算:1) 3.平方根、算数平方根和立方根算术平方根:➢ 一般地, 如果一个正数x 的平方等于a, 即x2=a, 那么这个正数x 就叫做a 的算术平方根。
特别地, 0的算术平方根是0。
2) 表示方法:记作“ ”, 读作根号a 。
八年级期末复习计划 (2)

八年级期末复习计划
八年级期末复习计划如下:
1. 制定复习计划:确定每天复习的科目和时间,制定每周的复习目标。
2. 复习时间安排:每天安排固定的复习时间,保证每个科目都有足够的时间进行复习。
3. 整理笔记:回顾每个科目的笔记,整理重点知识点,并做好分类归纳。
4. 逐个科目进行复习:按照复习计划的安排,逐个科目进行复习。
可以从容易的科目
开始,逐渐转向难度较大的科目。
5. 解答题型梳理:针对各个科目的题型进行梳理,解答难题和巩固基础知识。
6. 做模拟试卷:找一些历年的期末试卷进行模拟练习,提前熟悉考试形式和要求。
7. 真题演练:将平时做的错题和漏题进行复习,查缺补漏。
8. 提问答疑:遇到不懂的问题及时向老师或同学请教,通过提问和答疑来弥补自己的
知识漏洞。
9. 复习计划的调整:根据实际情况和复习进展不断调整复习计划,确保每个科目都得
到充分的复习。
10. 注意休息:合理安排休息时间,保证身心健康,提高复习效果。
以上是一个八年级期末复习计划的建议,根据自己的实际情况和需要进行相应的调整。
祝你复习顺利,取得好成绩!。
八年级数学培优资料word版

B AC D EF 第01讲 全等三角形的性质与判定考点·方法·破译1.能够完全重合的两个三角形叫全等三角形.全等三角形的形状和大小完全相同; 2.全等三角形性质:①全等三角形对应边相等,对应角相等;②全等三角形对应高、角平分线、中线相等;③全等三角形对应周长相等,面积相等;3.全等三角形判定方法有:SAS ,ASA ,AAS ,SSS ,对于两个直角三角形全等的判定方法,除上述方法外,还有HL 法;4.证明两个三角形全等的关键,就是证明两个三角形满足判定方法中的三个条件,具体分析步骤是先找出两个三角形中相等的边或角,再根据选定的判定方法,确定还需要证明哪些相等的边或角,再设法对它们进行证明;5..证明两个三角形全等,根据条件,有时能直接进行证明,有时要证的两个三角形并不全等,这时需要添加辅助线构造全等三角形,构造全等三角形常用的方法有:平移、翻折、旋转、等倍延长线中线、截取等等.经典·考题·赏析【例1】如图,AB ∥EF ∥DC ,∠ABC =90°,AB =CD ,那么图中有全等三角形( ) A .5对 B .4对 C .3对 D .2对【解法指导】从题设题设条件出发,首先找到比较明显的一对全等三角形,并由此推出结论作为下面有用的条件,从而推出第二对,第三对全等三角形.这种逐步推进的方法常用到.解:⑴∵AB ∥EF ∥DC ,∠ABC =90. ∴∠DCB =90. 在△ABC 和△DCB 中AB DC ABC DCB BC CB =⎧⎪=⎨⎪=⎩∠∠ ∴△ABC ≌∴△DCB (SAS ) ∴∠A =∠D ⑵在△ABE 和△DCE 中A DAED DEC AB DC =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△ABE ≌∴△DCE ∴BE =CE ⑶在Rt △EFB 和Rt △EFC 中BE CEEF EF=⎧⎨=⎩ ∴Rt △EFB ≌Rt △EFC (HL )故选C . 【变式题组】 01.(天津)下列判断中错误的是( )A .有两角和一边对应相等的两个三角形全等B .有两边和一角对应相等的两个三角形全等C .有两边和其中一边上的中线对应相等的两个三角形全等D .有一边对应相等的两个等边三角形全等A F C E DB 02.(丽水)已知命题:如图,点A 、D 、B 、E 在同一条直线上,且AD =BE ,∠A =∠FDE ,则△ABC ≌△DEF .判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.03.(上海)已知线段AC 与BD 相交于点O , 连接AB 、DC ,E 为OB 的中点,F 为OC 的中点,连接EF (如图所示).⑴添加条件∠A =∠D ,∠OEF =∠OFE ,求证:AB =DC ; ⑵分别将“∠A =∠D ”记为①,“∠OEF =∠OFE ”记为②,“AB =DC ”记为③,添加①、③,以②为结论构成命题1;添加条件②、③,以①为结论构成命题2.命题1是______命题,命题2是_______命题(选择“真”或“假”填入空格).【例2】已知AB =DC ,AE =DF ,CF =FB . 求证:AF =DE .【解法指导】想证AF =DE ,首先要找出AF 和DE 所在的三角形.AF 在△AFB 和△AEF 中,而DE 在△CDE 和△DEF 中,因而只需证明△ABF ≌△DCE 或△AEF ≌△DFE 即可.然后再根据已知条件找出证明它们全等的条件.证明:∵FB =CE ∴FB +EF =CE +EF ,即BE =CF 在△ABE 和△DCF 中, AB DCAE DF BE CF =⎧⎪=⎨⎪=⎩∴△ABE ≌△DCF (SSS ) ∴∠B =∠C在△ABF 和△DCE 中, AB DC B C BF CE =⎧⎪=⎨⎪=⎩∠∠ ∴△ABF ≌△DCE ∴AF =DE【变式题组】01.如图,AD 、BE 是锐角△ABC 的高,相交于点O ,若BO =AC ,BC =7,CD =2,则AO 的长为( ) A .2 B .3 C .4 D .5A B C D O FE A CEFBD02.如图,在△ABC 中,AB =AC ,∠BAC =90°,AE 是过A 点的一条直线,AE ⊥CE 于E ,BD⊥AE 于D ,DE =4cm ,CE =2cm ,则BD =__________. \ 03.(北京)已知:如图,在△ABC 中,∠ ACB =90°,CD ⊥AB 于点D ,点E 在AC 上,CE =BC ,过点E 作AC 的垂线,交CD 的延长线于点F . 求证:AB =FC .【例3】如图①,△ABC ≌△DEF ,将△ABC 和△DEF 的顶点B 和顶点E 重合,把△DEF 绕点B 顺时针方向旋转,这时AC 与DF 相交于点O .⑴当△DEF 旋转至如图②位置,点B (E )、C 、D 在同一直线上时,∠AFD 与∠DCA 的数量关系是________________;⑵当△DEF 继续旋转至如图③位置时,⑴中的结论成立吗?请说明理由_____________.【解法指导】⑴∠AFD =∠DCA⑵∠AFD =∠DCA 理由如下:由△ABC ≌△DEF ,∴AB =DE ,BC =EF , ∠ABC =∠DEF , ∠BAC =∠EDF ∴∠ABC -∠FBC =∠DEF -∠CBF , ∴∠ABF =∠DEC在△ABF 和△DEC 中, AB DE ABF DEC BF EC =⎧⎪=⎨⎪=⎩∠∠∴△ABF ≌△DEC ∠BAF =∠DEC ∴∠BAC -∠BAF =∠EDF -∠EDC , ∴∠FAC =∠CDF∵∠AOD =∠FAC +∠AFD =∠CDF +∠DCA∴∠AFD =∠DCAB (E )OC F 图③DAAE第1题图A BCDEBCDO第2题图AFECB D【变式题组】 01.(绍兴)如图,D 、E 分别为△ABC 的AC 、BC 边的中点,将此三角形沿DE 折叠,使点C落在AB 边上的点P 处.若∠CDE =48°,则∠APD 等于( ) A .42° B .48° C .52° D .58° 02.如图,Rt △ABC 沿直角边BC 所在的直线向右平移得到△DEF ,下列结论中错误的是( )A .△ABC ≌△DEFB .∠DEF =90°C . AC =DFD .EC =CF03.一张长方形纸片沿对角线剪开,得到两种三角形纸片,再将这两张三角形纸片摆成如下图形式,使点B 、F 、C 、D 在同一条直线上. ⑴求证:AB ⊥ED ;⑵若PB =BC ,找出图中与此条件有关的一对全等三角形,并证明.【例4】(第21届江苏竞赛试题)已知,如图,BD 、CE 分别是△ABC 的边A C 和AB 边上的高,点P 在BD 的延长线,BP =AC ,点Q 在CE 上,CQ =AB. 求证:⑴ AP =AQ ;⑵AP ⊥AQ【解法指导】证明线段或角相等,也就是证线段或角所在的两三角形全等.经观察,证AP =AQ ,也就是证△APD 和△AQE ,或△APB 和△QAC 全等,由已知条件BP =AC ,CQ =AB ,应该证△APB ≌△QAC ,已具备两组边对应相等,于是再证夹角∠1=∠2即可. 证AP ⊥AQ ,即证∠PAQ =90°,∠PAD +∠QAC =90°就可以.证明:⑴∵BD 、CE 分别是△ABC 的两边上的高,∴∠BDA =∠CEA =90°, ∴∠1+∠BAD =90°,∠2+∠BAD =90°,∴∠1=∠2. 在△APB 和△QAC 中, 2AB QC BP CA =⎧⎪=⎨⎪=⎩∠1∠ ∴△APB ≌△QAC ,∴AP =AQEFB ACDG第2题图21ABCPQE F D⑵∵△APB ≌△QAC ,∴∠P =∠CAQ , ∴∠P +∠PAD =90° ∵∠CAQ +∠PAD =90°,∴AP ⊥AQ 【变式题组】01.如图,已知AB =AE ,∠B =∠E ,BA =ED ,点F 是CD 的中点,求证:02.直距离MA 为am ,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子顶端距地面的垂直距离NB 为bm ,梯子倾斜角为45°,这间房子的宽度是( )A .2a bm + B .2a bm - C .bm D .am03.如图,已知五边形ABCDE 中,∠ ABC =∠AED =90°,AB =CD =AE =BC +DE =2,则五边形ABCDE 的面积为__________演练巩固·反馈提高01.(海南)已知图中的两个三角形全等,则∠α度数是( )A .72°B .60°C .58°D .50°02.如图,△ACB ≌△A /C /B /,∠ BCB /=30°,则∠ACA /的度数是( )A .20°B .30°C .35°D .40° 03.(牡丹江)尺规作图作∠AOB 的平分线方法如下:以O 为圆心,任意长为半径画弧交OA 、OB 于C 、D ,再分别以点C 、D 为圆心,以大于12CD 长为半径画弧,两弧交于点P ,作射线OP ,由作法得△OCP ≌△ODP 的根据是( )第1题图a αcca50° b72° 58°AECBA 75° C45° BNM第2题图第3题图DA .SASB .ASAC .AASD .SSS 04.(江西)如图,已知AB =AD ,那么添加下列一个条件后,仍无法判定△ABC ≌△ADC 的是( )A . CB =CD B .∠BAC =∠DAC C . ∠BCA =∠DCAD .∠B =∠D =90°05.有两块不同大小的等腰直角三角板△ABC 和△BDE ,将它们的一个锐角顶点放在一起,将它们的一个锐角顶点放在一起,如图,当A 、B 、D 不在一条直线上时,下面的结论不正确的是( )A . △ABE ≌△CBDB . ∠ABE =∠CBDC . ∠ABC =∠EBD =45° D . AC ∥BE06.如图,△ABC 和共顶点A ,AB=AE ,∠1=∠2,∠B =∠E . BC 交AD 于M ,DE 交AC 于N ,小华说:“一定有△ABC ≌△AED .”小明说:“△ABM ≌△AEN .”那么( ) A . 小华、小明都对 B . 小华、小明都不对 C . 小华对、小明不对 D .小华不对、小明对07.如图,已知AC =EC , BC =CD , AB =ED ,如果∠BCA =119°,∠ACD =98°,那么∠ECA 的度数是___________.08.如图,△ABC ≌△ADE ,BC 延长线交DE 于F ,∠B =25°,∠ACB =105°,∠DAC =10°,则∠DFB 的度数为_______.09.如图,在Rt △ABC 中,∠C =90°, DE ⊥AB 于D , BC =BD . AC =3,那么AE +DE =______10.如图,BA ⊥AC , CD ∥AB . BC =DE ,且BC ⊥DE ,若AB =2, CD =6,则AE =_____. 11.如图, AB =CD , AB ∥CD . BC =12cm ,同时有P 、Q 两只蚂蚁从点C 出发,沿CB 方向爬行,P 的速度是0.1cm /s , Q 的速度是0.2cm /s . 求爬行时间t 为多少时,△APB ≌△QDC .DA C .Q P.BA E FB DC 12.如图, △ABC 中,∠BCA =90°,AC =BC ,AE 是BC 边上的中线,过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于D . ⑴求证:AE =CD ;⑵若AC =12cm , 求BD 的长.13.(吉林)如图,AB =AC ,AD ⊥BC 于点D ,AD 等于AE ,AB 平分∠DAE 交DE 于点F , 请你写出图中三对全等三角形,并选取其中一对加以证明.14.如图,将等腰直角三角板ABC的直角顶点C 放在直线l 上,从另两个顶点A 、B 分别作l 的垂线,垂足分别为D 、E .⑴找出图中的全等三角形,并加以证明; ⑵若DE =a ,求梯形DABE 的面积.(温馨提示:补形法)15.如图,AC ⊥BC , AD ⊥BD , AD =BC ,CE ⊥AB ,DF ⊥AB ,垂足分别是E 、F .求证:CE =DF .16.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,那么在什么情况下,它们会全等? ⑴阅读与证明:对于这两个三角形均为直角三角形,显然它们全等;对于这两个三角形均为钝角三角形,可证明它们全等(证明略); 对于这两个三角形均为锐角三角形,它们也全等,可证明如下;已知△ABC 、△A 1B 1C 1均为锐角三角形,AB =A 1B 1,BC =B 1C 1,∠C =∠C 1.求证:△ABC ≌△A 1B 1C 1.(请你将下列证明过程补充完整)⑵归纳与叙述:由⑴可得一个正确结论,请你写出这个结论.ABCDA 1B 1C 1D 1D B A C EF A E B F D CAEF C DB 培优升级·奥赛检测01.如图,在△ABC 中,AB =AC ,E 、F 分别是AB 、AC 上的点,且AE =AF ,BF 、CE 相交于点O ,连接AO 并延长交BC 于点D ,则图中全等三角形有( ) A .4对 B .5对 C .6对 D .7对02.如图,在△ABC 中,AB =AC ,OC =OD ,下列结论中:①∠A =∠B ②DE =CE ,③连接DE , 则OE 平分∠AOB ,正确的是( ) A .①② B .②③ C .①③ D .①②③03.如图,A 在DE 上,F 在AB 上,且AC =CE , ∠1=∠2=∠3, 则DE 的长等于()A .DCB . BC C . ABD .AE +AC04.下面有四个命题,其中真命题是( )A .两个三角形有两边及一角对应相等,这两个三角形全等B .两边和第三边上的高对应相等的两个三角形全等C . 有一角和一边对应相等的两个直角三角形全等D . 两边和第三边上的中线对应相等的两个三角形全等05.在△ABC 中,高AD 和BE 所在直线相交于H 点,且BH =AC ,则∠ABC =_______.06.如图,EB 交AC 于点M , 交FC 于点D , AB 交FC 于点N ,∠E =∠F =90°,∠B =∠C , AE=AF . 给出下列结论:①∠1=∠2;②BE =CF ; ③△ACN ≌△ABM ; ④CD =DB ,其中正确的结论有___________.(填序号)07.如图,AD 为在△ABC 的高,E 为AC 上一点,BE 交AD 于点F ,且有BF =AC ,FD =CD .⑴求证:BE ⊥AC ;⑵若把条件“BF =AC ”和结论“BE ⊥AC ”互换,这个命题成立吗?证明你的判定.08.如图,D 为在△ABC 的边BC 上一点,且CD =AB ,∠BDA =∠BAD ,AE 是△ABD 的中线.求证:AC =2AE .09.如图,在凸四边形ABCD 中,E 为△ACD 内一点,满足AC =AD ,AB =AE , ∠BAE +∠BCEF第6题图2 1AB CE N M3 21ADEBC FADECOA E O BFCD 第1题图B第2题图第3题图ABE D CAB C DEAEBDC=90°, ∠BAC =∠EAD .求证:∠CED =90°.10.(沈阳)将两个全等的直角三角形ABC 和DBE 按图①方式摆放,其中∠ACB =∠DEB =90°,∠A =∠D =30°,点E 落在AB 上,DE 所在直线交AC 所在直线于点F .⑴求证:AF +EF =DE ;⑵若将图①中△DBE 绕点B 顺时针方向旋转角α,且0°<α<60°,其他条件不变,请在图②中画出变换后的图形,并直接写出(1)中结论是否仍然成立;⑶若将图①中△DBE 绕点B 按顺时针方向旋转角β,且60°<β<180°,其他条件不变,如图③你认为(1)中结论还成立吗?若成立,写出证明过程;若不成立,请写出此时AF 、EF 与DE 之间的关系,并说明理由。
(完整word版)初中数学知识点全总结(完美打印版),推荐文档
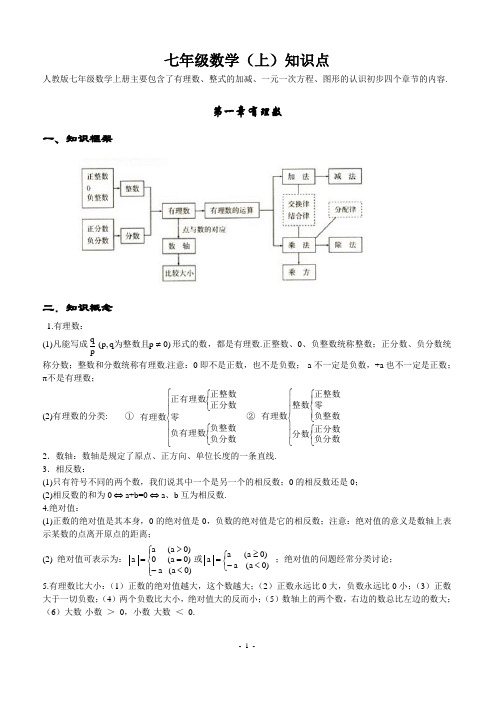
七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一、知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定. 11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a .13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
人教版八年级上册期末数学备考---几何综合 Word版

人教版八年级上册期末数学备考----几何综合(Word版)1.如图,在△ABC 中,AB=AC,∠BAC=90°,点D 是边BC 上的动点,连接AD,点C 关于直线AD 的对称点为点E,射线BE 与射线AD 交于点F.(1)在图中,依题意补全图形;(2)记∠DAC=α(α<45°),求∠ABF的大小;(用含α的式子表示)(3)若△ACE 是等边三角形,猜想EF 和BC 的数量关系,并证明.2.如图,CN 是等边△ABC 的外角∠ACM 内部的一条射线,点A 关于CN 的对称点为D,连接AD,BD,CD,其中AD,BD 分别交射线CN 于点E,P.(1)依题意补全图形;(2)若∠ACN=α,求∠BDC的大小(用含α的式子表示);(3)用等式表示线段PB,PC 与PE 之间的数量关系,并证明.3.数学老师布置了这样一道作业题:在△ABC 中,AB=AC≠BC,点D 和点A 在直线BC 的同侧,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB 的度数.小聪提供了研究这个问题的过程和思路:先从特殊问题开始研究,当α=90°,β=30° 时(如图1),利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形的相关知识便可解决这个问题.(1)请结合小聪研究问题的过程和思路,求出这种特殊情况下∠ADB 的度数;(2)结合小聪研究特殊问题的启发,请解决数学老师布置的这道作业题;(3)解决完老师布置的这道作业题后,小聪进一步思考,当点D 和点A 在直线BC 的异侧时,且∠ADB的度数与(1)中相同,则α,β满足的条件为(直接写出结果).4.如图1,在△ABC 中,∠ACB=2∠B,∠BAC 的平分线AO 交BC 于点D,点H 为AO上一动点,过点H 作直线l⊥AO 于H,分别交直线AB、AC、BC 于点N、E、M.( 1 )当直线l 经过点 C 时(如图 2 ),证明:BN =CD ;(2)当M 是BC 中点时,写出CE 和CD 之间的等量关系,并加以证明;(3)请直接写出BN、CE、CD 之间的等量关系.5.如图1,在等腰直角三角形ABC 中,AB=AC,∠BAC=90°,点D 在BC 边上,连接AD,AE⊥AD,AE=AD,连接CE,DE.(1)求证:∠B=∠ACE;(2)点A 关于直线CE 的对称点为M,连接CM,EM.①补全图形并证明∠EMC=∠BAD;②利用备用图进行画图、试验、探究,找出当D,E,M 三点恰好共线时点D 的位置.请直接写出此时∠BAD 的度数,并画出相应的图形.6.在△ABC 中,AB=AC,在△ABC 的外部作等边三角形△ACD,E 为AC 的中点,连接DE 并延长交BC 于点F,连接BD.(1)如图1,若∠BAC=100°,求∠BDF 的度数;(2)如图2,∠ACB 的平分线交AB 于点M,交EF 于点N,连接BN.①补全图2;②若BN=DN,求证:MB=MN.7.在△ABC 中,∠A=60°,BD,CE 是△ABC 的两条角平分线,且BD,CE 交于点F.(1)如图1,用等式表示BE,BC,CD 这三条线段之间的数量关系,并证明你的结论;小东通过观察、实验,提出猜想:BE+CD=BC.他发现先在BC 上截取BM,使BM=BE,连接FM,再利用三角形全等的判定和性质证明CM=CD 即可.①下面是小东证明该猜想的部分思路,请补充完整:ⅰ)在BC 上截取BM,使BM=BE,连接FM,则可以证明△BEF 与全等,判定它们全等的依据是;ⅱ)由∠A=60°,BD,CE 是△ABC 的两条角平分线,可以得出∠EFB=°;…②请直接利用ⅰ),ⅱ)已得到的结论,完成证明猜想BE+CD=BC的过程.(2)如图2,若∠ABC=40°,求证:BF=CA.8.在等边△ABC 中,点D 在BC 边上,点E 在AC 的延长线上,DE=DA(如图1)(1)求证:∠BAD=∠EDC;(2)点E 关于直线BC 的对称点为M,连接DM,AM.①依题意将图2 补全;②小姚通过观察,实验提出猜想:在点D 运动的过程中,始终有DA=AM,小姚把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:想法1:要证明DA=AM,只需证△ADM 是等边三角形;想法2:连接CM,只需证明△ABD≌△ACM 即可.请你参考上面的想法,帮助小姚证明DA=AM(一种方法即可)9.已知:△ABC 是等边三角形.(1)如图1,点D 在AB 边上,点E 在AC 边上,BD=CE,BE 与CD 交于点F.试判断BF 与CF 的数量关系,并加以证明;(2)点D 是AB 边上的一个动点,点E 是AC 边上的一个动点,且BD=CE,BE 与CD 交于点F.若△BFD 是等腰三角形,求∠FBD 的度数.10.已知:在△ABC 中,∠ABC<60°,CD 平分∠ACB 交AB 于点D,点E 在线段CD 上(点E不与点C、D重合),且∠EAC=2∠EBC.(1)如图1,若∠EBC=27°,且EB=EC,则∠DEB=°,∠AEC=°.(2)如图2,①求证:AE+AC=BC;②若∠ECB=30°,且AC=BE,求∠EBC 的度数.11.在△ABC 中,AD 是△ABC 的角平分线.(1)如图1,过C 作CE∥AD 交BA 延长线于点E,若F 为CE 的中点,连接AF,求证:AF⊥AD;(2)如图2,M 为BC 的中点,过M 作MN∥AD 交AC 于点N,若AB=4,AC=7,求NC 的长.12.如图,在△ABC 中,AC=BC,∠ACB=90°,D 为△ABC 内一点,∠BAD=15°,AD =AC,CE⊥AD 于E,且CE=5.(1)求BC 的长;(2)求证:BD=CD.13.在Rt△ABC 中,∠ACB=90°,∠A=30°,BD 是△ABC 的角平分线,DE⊥AB 于点E.(1)如图1,连接EC,求证:△EBC 是等边三角形;(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG 交DE 延长线于点G.请你在图2 中画出完整图形,并直接写出MD,DG 与AD 之间的数量关系;(3)如图3,点N 是线段AD 上的一点,以BN 为一边,在BN 的下方作∠BNG=60°,NG 交DE 延长线于点G.试探究ND,DG 与AD 数量之间的关系,并说明理由.14.已知:如图,在△ABC 中,如果∠A 是锐角,点D,E 分别在AB,AC 上,且∠DCB=求证:BD=CE.15.在△ABC 中,AB>BC,直线l 垂直平分AC.(1)如图1,作∠ABC 的平分线交直线l 于点D,连接AD,CD.①补全图形;②判断∠BAD 和∠BCD 的数量关系,并证明.(2)如图2,直线l 与△ABC 的外角∠ABE 的平分线交于点D,连接AD,CD.求证:∠BAD=∠BCD.16.在平面直角坐标系xOy 中,△ABO 为等边三角形,O 为坐标原点,点A 关于y 轴的对称点为D,连接AD,BD,OD,其中AD,BD 分别交y 轴于点E,P.(1)如图1,若点B 在x 轴的负半轴上时,直接写出∠BDO 的度数;(2)如图2,将△ABO 绕点O 旋转,且点A 始终在第二象限,此时AO 与y 轴正半轴夹角为α,60°<α<90°,依题意补全图形,并求出∠BDO的度数;(用含α的式子表示)(3)在第(2)问的条件下,用等式表示线段BP,PE,PO之间的数量关系.(直接写出结果17.(1)老师在课上给出了这样一道题目:如图1,等边△ABC边长为2,过AB边上一点P 作PE⊥AC 于E,Q 为BC 延长线上一点,且AP=CQ,连接PQ 交AC 于D,求DE 的长.小明同学经过认真思考后认为,可以通过过点P 作平行线构造等边三角形的方法来解决这个问题.请根据小明同学的思路直接写出DE 的长.(2)【类比探究】老师引导同学继续研究:1.等边△ABC 边长为2,当P 为BA 的延长线上一点时,作PE⊥CA 的延长线于点E,Q 为边BC 上一点,且AP=CQ,连接PQ 交AC 于D.请你在图2 中补全图形并求DE 的长.2.已知等边△ABC,当P 为AB 的延长线上一点时,作PE⊥射线AC 于点E,Q 为(①BC 边上;②BC 的延长线上;③CB 的延长线上)一点,且AP=CQ,连接PQ 交直线AC于点D,能使得DE的长度保持不变.(将答案的编号填在横线上)18.如图,在等边三角形ABC 的外侧作直线AP,点C 关于直线AP 的对称点为点D,连接AD,BD,其中BD 交直线AP 于点E.(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB 的度数;(3)连结CE,写出AE,BE,CE 之间的数量关系,并证明你的结论.19.如图1,在△ABC 中,∠A 的外角平分线交BC 的延长线于点D.(1)线段BC 的垂直平分线交DA 的延长线于点P,连接PB,PC.①利用尺规作图补全图形1,不写作法,保留痕迹;②求证:∠BPC=∠BAC;(2)如图2,若Q 是线段AD 上异于A,D 的任意一点,判断QB+QC 与AB+AC 的大小,并予以证明.第10页(共17页)20.如图,在△ABC 中,BA=BC,点D 为△ABC 外一点,连接DA,∠DAC 恰好为25°,线段AD 沿直线AC 翻折得到线段AD′,过点C 作AD 的平行线交AD′于点E,连接BE.(1)求证:AE=CE;(2)求∠AEB 的度数.21.如图①,在△ABC 中,D、E 分别是AB、AC 上的点,AB=AC,AD=AE,然后将△ADE 绕点A 顺时针旋转一定角度,连接BD,CE,得到图②,将BD、CE 分别延长至M、N,使BD,EN=CE,得到图③,请解答下列问题:(1)在图②中,BD 与CE 的数量关系是;(2)在图③中,猜想AM 与AN 的数量关系,∠MAN 与∠BAC 的数量关系,并证明你的猜想.22.在等边△ABC 中,点E 在AB 上,点D 在CB 的延长线上,且ED=EC.(1)若点E 是AB 的中点,如图1,求证:AE=DB.(2)若点E 不是AB 的中点时,如图2,试确定线段AE 与DB 的大小关系,并写出证明过程.23.在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路,如:在图1 中,若C 是∠MON 的平分线OP 上一点,点A 在OM 上,此时,在ON上截取OB=OA,连接BC,根据三角形全等判定(SAS),容易构造出全等三角形△OBC 和△OAC,参考上面的方法,解答下列问题:如图2,在非等边△ABC 中,∠B=60°,AD,CE 分别是∠BAC,∠BCA 的平分线,且AD,CE 交于点F,求证:AC=AE+CD.24.如图:在Rt△ABC 中,AB=AC,∠BAC=90°,O 为BC 的中点.(1)写出点O 到△ABC 的三个顶点A、B、C 距离之间的关系;(2)如果点M、N 分别在线段AB、AC 上移动,移动中保持AN=BM,请判断△OMN 的形状,并证明你的结论.25.如图,△ABC 是等边三角形,△ADC 与△ABC 关于直线AC 对称,AE 与CD 垂直交BC 的延长线于点E,∠EAF=45°,且AF 与AB 在AE 的两侧,EF⊥AF.(1)依题意补全图形.(2)①在AE 上找一点P,使点P 到点B,点C 的距离和最短;②求证:点D 到AF,EF 的距离相等.26.如图,△ABC 中,AB=AC,AD⊥BC 于点D,延长AB 至点E,使∠AEC=∠DAB.判断CE 与AD 的数量关系,并证明你的结论.27.已知C 是线段AB 垂直平分线m 上一动点,连接AC,以AC 为边作等边三角形ACD,点D 在直线AB 的上方,连接DB 与直线m 交于点E,连接BC,AE.(1)如图1,点C 在线段AB 上.①根据题意补全图1②求证:∠EAC=∠EDC;(2)如图2,点C 在直线AB 的上方,0°<∠CAB<30°,用等式表示线段BE,CE,DE 之间的数量关系,并证明.28.在等边△ABC 外作射线AD,使得AD 和AC 在直线AB 的两侧,∠BAD=α(0°<α<180°),点B关于直线AD的对称点为P,连接PB,PC.(1)依题意补全图1;(2)在图1 中,求∠BPC 的度数;(3)直接写出使得△PBC 是等腰三角形的α的值.29.在△DEF 中,DE=DF,点B 在EF 边上,且∠EBD=60°,C 是射线BD 上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.(1)当点C 在线段BD 上时,①若点C 与点D 重合,请根据题意补全图1,并直接写出线段AE 与BF 的数量关系为;②如图2,若点C 不与点D 重合,请证明AE=BF+CD;(2)当点C 在线段BD 的延长线上时,用等式表示线段AE,BF,CD 之间的数量关系(直接写出结果,不需要证明).30.解决下面问题:如图,在△ABC 中,∠A 是锐角,点D,E 分别在AB,AC 上,且∠A,BE 与CD 相交于点O,探究BD 与CE 之间的数量关系,并证明你的结论.小新同学是这样思考的:在平时的学习中,有这样的经验:假如△ABC 是等腰三角形,那么在给定一组对应条件,如图a,BE,CD 分别是两底角的平分线(或者如图b,BE,CD 分别是两条腰的高线,或者如图c,BE,CD 分别是两条腰的中线)时,依据图形的轴对称性,利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决.请参考小新同学的思路,解决上面这个问题.31.如图,在△ABC 中,AB=AC,P 为△ABC 内一点,且∠BAP=70°,∠ABP=40°,(1)求证:△ABP 是等腰三角形;(2)连接PC,当∠PCB=30°时,求∠PBC 的度数.32.如图,在等边三角形ABC右侧作射线CP,∠ACP=α(0<α<60°),点A关于射线CP 的对称点为点D,BD 交CP 于点E,连接AD,AE.(1)求∠DBC的大小(用含α的代数式表示);(2)在α(0°<α≤60°)的变化过程中,∠AEB 的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB 的大小;(3)用等式表示线段AE,BD,CE 之间的数量关系,并证明.33.如图,在等边△ABC 中,点D 是线段BC 上一点作射线AD,点B 关于射线AD 的对称点为E,连接EC 并延长,交射线AD 于点F.(1)补全图形;(2)求∠AFE 的度数;(3)用等式表示线段AF、CF、EF 之间的数量关系,并证明.34.△ABC 是等边三角形,AC=2,点C 关于AB 对称的点为C',点P 是直线C'B 上的一个动点,连接AP,作∠APD=60°交射线BC 于点D.(1)若点P在线段C'B上(不与点C',点B重合).①如图1,若点P 是线段C'B 的中点,则AP 的长为;②如图2,点P 是线段C'B 上任意一点,求证:PD=PA;(2)若点P 在线段C'B 的延长线上.①依题意补全图3;②直接写出线段BD,AB,BP 之间的数量关系为:.35.等边△ABC 的边长为4,D 是射线BC 上任一点,线段AD 绕点D 顺时针旋转60°得到线段DE,连接CE.(1)当点D 是BC 的中点时,如图1,判断线段BD 与CE 的数量关系,请直接写出结论:(不必证明);(2)当点D 是BC 边上任一点时,如图2,请用等式表示线段AB,CE,CD 之间的数量关系,并证明;(3)当点D 是BC 延长线上一点且CD=1 时,如图3,求线段CE 的长.。
(完整版)湘教版八年级数学上册复习提纲(可编辑修改word版)

⎪那么这个非负数x 就叫做a 的算术平方根,记为 a , a a a a a 2 3-a ⎩ ⎩ ⎩ ⎪ ⎪ ⎪第一章 实数八年级数学上册复习提纲1。
平方根和算术平方根的概念及其性质:(1)概念:如果 x 2 = a ,那么 x 是 a 的平方根,记作: ± ;其中 叫做 a 的算术平方根。
(2)性质:①当 a ≥0 时, ≥0;当 a <0时, 无意义;② ( a )2 = a ;③ = a 。
2。
立方根的概念及其性质:(1)概念:若 x 3 = a ,那么 x 是 a 的立方根,记作: 3 a ;(2)性质:① 3 a 3 = a ;② ( 3 a )3 = a ;③ = - 3 a3。
实数的概念及其分类:(1) 概念:实数是有理数和无理数的统称;(2) 分类:按定义分为有理数可分为整数的分数;按性质分为正数、负数和零。
无理数就是无限不循环小数;小数可分为有限小数、无限循环小数和无限不循环小数;其中有限小数和无限循环小数称为分数。
(书上有图)4、无理数:无限不循环小数 ⎧算术平方根定义如果一个非负数x 的平方等于a ,即x 2 = a ⎪ ⎪ ⎪算术平方根为非负数 ≥ 0 ⎪ ⎧正数的平方根有 2 个,它们互为相反数 ⎪ 平方根⎨0的平方根是 0 ⎪ ⎪ ⎪负数没有平方根 ⎪2. 无理数的表示⎨定义:如果一个数的平方等于a ,即x 2 = a ,那么这个数就 ⎪ ⎪ ⎪ ⎧正数的立方根是正数 ⎪ ⎪ ⎪立方根⎨负数的立方根是负数 ⎪ ⎪0的立方根是 0 ⎪ ⎪定义:如果一个数x 的立方等于a ,即x 3 = a ,那么这个数x ⎪ ⎪⎩5。
与实数有关的概念:在实数范围内,相反数,倒数,绝对值的意义与有理数范围内的意义完全一致;在实数范围内, 有理数的运算法则和运算律同样成立。
每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数,即实数和数轴上的点是一一对应的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级上册数学期末复习计划本学期新课结束,将进入复习阶段。
为了迎接期末检测,实现预定的教学目标,以取得较好的成绩,结合所教学班级学生的情况,对期末复习作以下安排:一、复习内容:第十一章:三角形第十二章:全等三角形第十三章:轴对称第十四章:整式的乘法与因式分解第十五章:分式二、复习目标:八年级数学本学期知识点多,复习时间比较长,有二周的时间。
根据实际情况,应该完成如下复习目标:(一)、全册教学目标:数与代数:了解整数指数幂的意义和基本性质;会用科学记数法表示数(包括在计算器上表示)。
理解整式的概念,掌握合并同类项和去括号的法则,能进行简单的整式加法和减法运算;能进行简单的整式乘法运算(其中多项式相乘仅指一次式之间以及一次式与二次式相乘)。
能推导乘法公式:(a+b)(a-b)=a2- b2;(a±b)2= a2±2ab+b2,了解公式的几何背景,并能利用公式进行简单计算。
能用提公因式法、公式法(直接利用公式不超过二次)进行因式分解(指数是正整数)。
了解分式和最简分式的概念,能利用分式的基本性质进行约分和通分;能进行简单的分式加、减、乘、除运算。
空间与图形:理解三角形及其内角、外角、中线、高线、角平分线等概念,了解三角形的稳定性。
探索并证明三角形的内角和定理。
掌握它的推论:三角形的外角等于与它不相邻的两个内角的和。
证明三角形的任意两边之和大于第三边。
理解全等三角形的概念,能识别全等三角形中的对应边、对应角。
掌握基本事实:两边及其夹角分别相等的两个三角形全等。
掌握基本事实:两角及其夹边分别相等的两个三角形全等。
掌握基本事实:三边分别相等的两个三角形全等。
证明定理:两角及其中一组等角的对边分别相等的两个三角形全等。
探索并证明角平分线的性质定理:角平分线上的点到角两边的距离相等;反之,角的内部到角两边距离相等的点在角的平分线上。
理解线段垂直平分线的概念,探索并证明线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等;反之,到线段两端距离相等的点在线段的垂直平分线上。
了解等腰三角形的概念,探索并证明等腰三角形的性质定理:等腰三角形的两底角相等;底边上的高线、中线及顶角平分线重合。
探索并掌握等腰三角形的判定定理:有两个角相等的三角形是等腰三角形。
探索等边三角形的性质定理:等边三角形的各角都等于60°,及等边三角形的判定定理:三个角都相等的三角形(或有一个角是60°的等腰三角形)是等边三角形。
了解三角形重心的概念。
图形的变化:通过具体实例了解轴对称的概念,探索它的基本性质:成轴对称的两个图形中,对应点的连线被对称轴垂直平分。
能画出简单平面图形(点,线段,直线,三角形等)关于给定对称轴的对称图形。
了解轴对称图形的概念;探索等腰三角形、矩形、菱形、正多边形、圆的轴对称性质。
认识并欣赏自然界和现实生活中的轴对称图形。
(二)、整理本学期学过的知识与方法;就各个单元复习目标重难点具体分述如下:第十一章三角形知识与技能目标1、理解三角形及有关概念,会画任意三角形的高、中线、角平分线;2、了解三角形的稳定性,理解三角形两边的和大于第三边,会根据三条线段的长度判断它们能否构成三角形;3、会证明三角形内角和等于180°,了解三角形外角的性质。
4、了解多边形的有关概念,会运用多边形的内角和与外角和公式解决问题。
过程与方法目标1、在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,逐步养成数学推理的习惯;2、在灵活运用知识解决有关问题的过程中,体验并掌握探索、归纳图形性质的推理方法,提高说理和进行简单推理的能力。
情感、态度与价值观目标1、体会数学与现实生活的联系,增强克服困难的勇气和信心;2、会应用数学知识解决一些简单的实际问题,增强应用意识;3、使学生进一步形成数学来源于实践,反过来又服务于实践的辩证唯物主义思想观念。
单元教学重点、难点1.重点:三角形三边关系、内角和,多边形的外角和与内角和公式是重点;三角形内角和等于1800的证明,2.难点:根据三条线段的长度判断它们能否构成三角形是难点。
第十二章全等三角形单元复习目标:知识与技能目标(1)理解全等三角形的概念,能识别全等三角形中的对应边、对应角,掌握并能运用全等三角形的性质。
(2)经历探索三角形全等条件的过程,掌握判定三角形全等的基本事实(“边边边”“边角边”和“角边角”)和定理(“角角边”),能判定两个三角形全等。
经历探索直角三角形全等的判定定理,并能运用.(3)能利用三角形全等证明一些结论。
(4)探索并证明角平分线的性质定理,能运用角的平分线的性质。
过程与方法目标经历探索三角形全等的判定的过程,发展空间观念和有条理的表达能力,掌握两个三角形全等的判定并应用于实际之中。
情感、态度与价值观目标培养良好的观察、操作、想象、推理能力,感悟几何学的内涵.在探索全等三角形的性质与判定中,提高认知水平,积累数学活动经验。
单元复习重点难点:1.本章复习重点:三角形全等的判定方法。
引导学生分析条件与结论的关系,书写严谨的证明格式。
2.本章复习的难点探索并证明角平分线的性质定理。
第十三章轴对称本单元复习目标:1.通过具体实例认识轴对称、轴对称图形,探索轴对称的基本性质,理解对应点连线被对称轴垂直平分的性质.2.探索简单图形之间的轴对称关系,能够按照要求作出简单图形经过一次或两次轴对称后的图形;认识和欣赏轴对称在现实生活中的应用,能判定一个图形是否为轴对称图形.3.理解线段垂直平分线的概念,探索并掌握其性质;了解等腰三角形、等边三角的有关概念,探索并掌握它们的性质以及判定方法.4.能初步应用本章所学的知识解释生活中的轴对称现象及解决简单的实际问题,在观察、操作、想象、论证、交流的过程中,发展空间观念,提高思维能力。
单元复习重点和难点:1.本章重点:线段的垂直平分线,等腰三角形的性质与判定的应用.2.本章的难点三线合一的理解和应用等腰三角形、等边三角形、垂直平分线的综合解题.第十四章整式的乘法与因式分解本单元复习目标:1. 掌握正整数幂的乘、除运算性质,能用代数式和文字语言正确地表述这些性质,并能运用它们熟练地进行运算。
掌握单项式乘(或除以)单项式、多项式乘(或除以)单项式以及多项式乘多项式的法则,并运用它们进行运算。
2.会推导乘法公式(平方差公式和完全平方公式),了解公式的几何意义,能利用公式进行乘法运算。
3.掌握整式的加、减、乘、除、乘方的较简单的混合运算,并能灵活地运用运算律与乘法公式简化运算。
4.理解因式分解的意义,并感受分解因式与整式乘法是相反方向的运算,掌握提公因式法和公式法(直接运用公式不超过两次)这两种分解因式的基本方法,了解因式分解的一般步骤;能够熟练地运用这些方法进行多项式的因式分解。
本单元复习重点和难点:1.本章重点:整式的乘除运算与因式分解的两种方法.2.本章的难点乘法公式的灵活运用,熟练掌握因式分解的两种方法和变形技巧第十五章分式本单元复习目标:1以描述实际问题中的数量关系为背景抽象出分式的概念体会分式是刻画现实世界中数量关系的一类代数式。
2类比分数的基本性质了解分式的基本性质掌握分式的约分和通分法则。
3类比分数的四则运算法则探究分式的四则运算掌握这些法则。
4结合分式的运算将指数的讨论范围从正整数扩大到全体整数构建和发展相互联系的知识体系。
5结合分析和解决实际问题讨论可以化为一元一次方程的分式方程掌握这种方程的解法体会解方程中的化归思想。
本单元复习重点难点:本章的主要内容包括分式的概念分式的基本性质分式的约分与通分分式的加、减、乘、除运算整数指数幂的概念及运算性质分式方程的概念及可化为一元一次方程的分式方程的解法。
共有三节:11.1分式,11.2分式的运算,11.3 分式方程11.1 节有3个知识点①分式的概念②分式的基本性质③约分、通分。
这是全章的理论基础部分。
11.2节有5个知识点①分式的乘除运算②分式的乘方③分式的加减法运算④分式的四则混合运算⑤零指数和负指数。
分式的四则运算、零指数和负指数是本章的一个重点也是本章学习中的一个难点。
克服这一难点的关键是通过必要的练习掌握分式的各种运算法则及运算顺序。
在这一节中对指数概念的限制从正整数扩大到全体整数这给运算带来便利。
11.3节有4个知识点①分式方程概念②分式方程的解法③分式方程的增根与检验④分式方程的应用。
解分式方程先是应用分式的基本性质通过去分母把解分式方程转化为解整式方程学生的易错点是去分母时找错公分母和漏乘及不检验。
检验、验根是解分式方程时必不可少的最重要的一步,不同于解整式方程。
根据实际问题列出分式方程,是本章教学中的另一个难点,克服它的关键是提高分析问题中数量关系的能力。
1.本章重点:(1)①分式的概念②分式的基本性质③约分、通分。
这是全章的理论基础部分。
(2)①分式的乘除运算②分式的乘方③分式的加减法运算④分式的四则混合运算⑤零指数和负指数。
分式的四则运算、零指数和负指数是本章的一个重点(3)①分式方程概念②分式方程的解法③分式方程的增根与检验④分式方程的应用。
2.本章的难点(1)分式的概念;(2)分式的基本性质;(3)分式的约分、通分。
掌握分式的各种运算法则及运算顺序。
(4)根据实际问题列出分式方程是本章教学中的另一个难点第十一至十三章是几何部分。
这三章的重点是全等三角形和轴对称的性质及其判定定理。
所以记住性质是关键,学会判定是重点,灵活应用是目的。
要学会判定方法的选择,不同图形之间的区别和联系要非常熟悉,形成一个有机整体。
对常见的证明题要多练多总结。
第十四、十五章主要是计算,教师提前先把概念、性质、方法综合复习,加入适当的练习,在练习计算。
课堂上逐一对易错题的讲解,多强调解题方法的针对性。
最后针对平时练习中存在的问题,查漏补缺。
(一)、学生在自己经历过的解决问题活动中,选择一个最具有挑战问题性的问题,写下解决它的过程:包括遇到的困难、克服困难的方法与过程及所获得的体会,并选择这个问题的原因。
(二)、通过本学期的数学学习,让同学们总结自己有哪些收获;有哪些需要改进的地方。
三、复习方法:1、强化训练,这个学期计算类和证明类的题目较多,在复习中要加强这方面的训练。
特别是计算,在复习过程中要分类型练习,重点是解题方法的正确选择同时使学生养成检查计算结果的习惯。
还有几何证明题,要通过针对性练习力争达到少失分,达到证明简练又严谨的效果。
2、加强管理严格要求,根据每个学生自身情况、学习水平严格要求,对应知应会的内容要反复讲解、练习,必须做到学一点会一点,对接受能力差的学生课后要加强辅导,及时纠正出现的错误,平时多小测多检查。
对能力较强的学生要引导他们多做课外习题,适当提高做题难度。
3、加强证明题的训练,通过近阶段的学习,我发现学生对证明题掌握不牢,不会找合适的分析方法,部分学生看不懂题意,没有思路。
