初二常见的几何题
初中数学经典几何题及答案解析

4e d c 经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.FPDE CBAAPCBACBPDEDCA A CBPD经典难题(一)1.如下图做GH⊥AB,连接EO。
初二上册几何专项训练

初二上册几何专项训练题目一:已知在三角形ABC 中,AB = AC,∠A = 40°,求∠B 的度数。
解析:因为AB = AC,所以三角形ABC 是等腰三角形。
根据等腰三角形两底角相等的性质,∠B = ∠C。
又因为三角形内角和为180°,所以∠B = (180° - ∠A)÷2 = (180° - 40°)÷2 = 70°。
题目二:在平行四边形ABCD 中,∠A = 60°,求∠C 的度数。
解析:平行四边形的对角相等,所以∠A = ∠C。
已知∠A = 60°,则∠C = 60°。
题目三:矩形ABCD 的对角线AC、BD 相交于点O,若AB = 3,BC = 4,求AC 的长。
解析:在矩形ABCD 中,∠ABC = 90°。
根据勾股定理,AC² = AB² + BC²。
已知AB = 3,BC = 4,则AC = √(3² + 4²)=5。
题目四:菱形ABCD 的边长为5,一条对角线长为6,求另一条对角线的长。
解析:菱形的对角线互相垂直且平分。
设另一条对角线长为x。
根据菱形的性质和勾股定理可得,(6÷2)² + (x÷2)² = 5²,9 + (x²÷4) = 25,x²÷4 = 16,x² = 64,解得x = 8。
题目五:等腰梯形ABCD 中,AD∠BC,AB = CD,∠B = 60°,AD = 3,BC = 7,求梯形的周长。
解析:过点A 作AE∠DC,因为AD∠BC,所以四边形AECD 是平行四边形,所以AE = CD = AB,EC = AD = 3。
又因为∠B = 60°,所以三角形ABE 是等边三角形,AB = BE = BC - EC = 7 - 3 = 4。
初二几何练习题及答案

初二几何练习题及答案一、选择题1. 下列图形中,边数最多的是:A. 正方形B. 三角形C. 圆形D. 长方形答案:B. 三角形2. 以下哪个选项是一个多边形?A. 圆形B. 长方形C. 椭圆形D. 正方形答案:B. 长方形3. 以下哪个几何图形是三角形的一种?A. 圆B. 梯形C. 正方形D. 椭圆答案:B. 梯形4. 对于一个正方形,边长为a,则它的周长是:A. 2aB. 4aC. a²D. a³答案:B. 4a5. 对于一个圆形,半径为r,则它的周长是:A. 2rB. 4rC. πr²D. 2πr答案:D. 2πr二、填空题1. 一个正方形的边长为5cm,则它的面积是__________。
答案:25cm²2. 一个长方形的长为8cm,宽为4cm,则它的周长是__________。
答案:24cm3. 一个三角形的底边长为7cm,高为4cm,则它的面积是__________。
答案:14cm²4. 一个正方形的周长为12cm,则它的边长是__________。
答案:3cm5. 一个圆形的直径为10cm,则它的半径是__________。
答案:5cm三、解答题1. 如图所示,画出一个正方形,边长为6cm。
(略)2. 如图所示,已知直角三角形的一条直角边长为5cm,斜边长为10cm,求另一条直角边的长度。
解:根据勾股定理,直角三角形的两个直角边的平方和等于斜边的平方。
假设另一条直角边长为a,则有:5² + a² = 10²化简得:25 + a² = 100移项得:a² = 100 - 25计算得:a² = 75开方得:a ≈ 8.66cm答案:约为8.66cm3. 如图所示,计算一个边长为10cm的正方形的面积和周长。
解:面积 = 边长² = 10² = 100cm²周长 = 4 ×边长 = 4 × 10 = 40cm答案:面积为100cm²,周长为40cm4. 如图所示,求一个高为8cm,底边长为6cm的三角形的面积。
初二数学几何题50道,要带答案带过程

初二数学几何题50道,要带答案带过程选择题:1. 若两角互为补角,则它们的差是()。
A.0°B.45°C.60°D.90°2. 在图中,如点S、T分别在边AB的延长线上,且∠ASP=60°,∠BAT=20°,则∠AST为()。
A.40°B.50°C.80°D.110°3. 已知正方形ABCD的边长为5cm,点E、F分别在边AD、AB上,且AE=BF,则三角形CEF的面积为()。
A.(5/8) cm²B.(9/8) cm²C.(13/8) cm²D.(15/8) cm²4. 如果一个圆心角的度数为30°,则它所对的弧度数是()。
A.π/6B.π/3C.π/4D.π/2填空题:1.如图,已知BC平分∠ABD,设∠BAC=a°,∠BCA=b°,则∠CBD=\_\_\_\_°。
2.如图,点A、B、C在同一条直线上,则对于ΔABC来说,以下说法正确的是:①AB=AC;②\angleBAC是钝角;③\angleABC+\angleACB =180^\circ,所以\angleABC=\_\_\_\_°,\angleACB=\_\_\_\_°。
3. 已知直角三角形ABC,其中\angleC=90°,BC=3,AC=4,则AB=\_\_\_\_。
4.如图,长方形ABCD中,点E、F分别为BC、CD上的点,若∠BAE=∠EFD,AB=10cm,则DF=\_\_\_\_cm。
解答题:1.如图,在\triangleABC中,垂足分别为D、E、F。
若AC=6,BD=8,DE=5,EF=9,则BC=()。
2.如图,已知\angleBAC=60°,AD平分\angleBAC,且BD=AD,点E为AD的延长线上的点,且\angleBEC=140°,则\angleACD=\_\_\_\_\_\_°。
几何初二试题及答案

几何初二试题及答案一、选择题1. 已知一个三角形的两边长分别为3和4,第三边的长x满足的不等式是:A. 1 < x < 7B. 4 < x < 7C. 1 < x < 4D. 3 < x < 7答案:D2. 一个圆的半径为5cm,那么这个圆的周长是多少?A. 10π cmB. 15π cmC. 20π cmD. 25π cm答案:D3. 已知一个矩形的长为6cm,宽为4cm,那么这个矩形的面积是多少?A. 20cm²B. 24cm²C. 18cm²D. 16cm²答案:B二、填空题1. 平行四边形的对角线互相______。
答案:平分2. 如果一个角的度数是30°,那么它的余角是______。
答案:60°3. 一个直角三角形的两条直角边分别为3和4,那么它的斜边长是______。
答案:5三、简答题1. 描述如何使用勾股定理来计算直角三角形的斜边长。
答案:首先确定直角三角形的两条直角边的长度,设为a和b。
根据勾股定理,斜边c的长度可以通过公式c = √(a² + b²) 来计算。
2. 解释什么是相似三角形,并给出一个例子。
答案:相似三角形是指两个三角形的对应角相等,对应边的比例相等的三角形。
例如,如果三角形ABC与三角形DEF的角A等于角D,角B等于角E,角C等于角F,并且边AB与边DE、边BC与边EF、边AC与边DF的长度比例相等,那么这两个三角形就是相似的。
四、解答题1. 已知一个等腰三角形的底边长为10cm,两腰的长度为13cm,求这个三角形的面积。
答案:首先,我们可以将等腰三角形分成两个直角三角形,通过底边的中点。
这样,每个直角三角形的底边长度为5cm,斜边为13cm。
根据勾股定理,我们可以计算出高h:h = √(13² - 5²) = √(169 - 25) = √144 = 12cm。
初二数学几何题型练习题

初二数学几何题型练习题在初二数学学习中,几何是一个重点和难点。
为了帮助同学们更好地掌握几何题型,提高解题能力,下面将给出一些初二数学几何题型的练习题。
【题型一:图形的性质】1. 如图所示,矩形ABCD中,AB = 4cm,BC = 3cm。
求AC的长度。
```A _________ B| || |D+-------+C```2. 如图所示,正方形ABCD的边长为x cm,若AB = CD + x cm,则求正方形的边长.```B______C| || |A______D```3. 三角形ABC中,AB = AC = 8cm,BC = 6cm。
求角ABC的度数。
【题型二:圆的性质】1. 如图所示,AB是圆O的直径,C、D分别是圆上的两点,则△ACD是什么类型的三角形?```O/ \A B/ \C-------D```2. 在△ABC中,AB = AC。
角A的角度为x°,角B的角度为y°。
求角C的角度。
3. 如图所示,两条直径AC、BD相交于E,若∠AEB = 30°,求∠AOD的角度。
```A _______ B/ \/ \C /______E_______\ D```【题型三:相似三角形】1. 如图所示,∆ABC和∆AED相似,已知AB = 6cm,BC = 8cm,DE = 12cm,求AC的长度。
```A _______ D\ |\ |\ |\ |\ |\ |\ |\|B```2. 在△ABC和△XYZ中,∠B = ∠Y,∠C = ∠X,已知AB = 5cm,BC = 7cm,XY = 12cm,求AC的长度。
3. 如图所示,∆ABC和∆ADE相似,已知BC = 10cm,AC = 12cm,DE = 15cm,求AD的长度。
```A/ \/ \B-----C| || |D-----E```【题型四:三角形内角和】1. 如图所示,已知△ABC,∠A = 40°,∠B = 60°,用尺子量得BC = 8cm,请问∠C的度数是多少?```B/ \/ \/ \/_______\A C```2. 已知△DEF,∠D = 80°,∠E = 60°,用尺子量得ED = 10cm,请问∠F的度数是多少?3. 如图所示,在△XYZ中,∠X = ∠Y,∠Z = 70°,求∠X和∠Y 的度数。
初二几何试题及答案

初二几何试题及答案1. 已知三角形ABC中,AB=AC,D是BC边上的中点。
求证:AD垂直于BC。
答案:因为AB=AC,所以三角形ABC是等腰三角形。
根据等腰三角形的性质,底边的中线、高线和角平分线重合。
因此,AD既是BC边上的中线,也是高线,所以AD垂直于BC。
2. 一个矩形的长是宽的两倍,且对角线长为10cm。
求矩形的长和宽。
答案:设矩形的宽为x cm,则长为2x cm。
根据勾股定理,对角线的长度满足方程x^2 + (2x)^2 = 10^2。
解得x^2 + 4x^2 = 100,即5x^2 = 100,所以x^2 = 20,x = √20。
因此,矩形的宽为√20 cm,长为2√20 cm。
3. 一个圆的直径是10cm,求这个圆的面积。
答案:圆的面积公式为A = πr^2,其中r是圆的半径。
因为直径是10cm,所以半径r = 10/2 = 5cm。
代入公式得A = π * 5^2 = 25π cm^2。
4. 一个梯形的上底是8cm,下底是12cm,高是5cm。
求梯形的面积。
答案:梯形的面积公式为A = (a + b) * h / 2,其中a和b分别是上底和下底的长度,h是高。
代入数据得A = (8 + 12) * 5 / 2 = 20 * 5 / 2 = 50 cm^2。
5. 已知一个直角三角形的两条直角边分别是6cm和8cm,求斜边的长度。
答案:根据勾股定理,斜边的长度c满足方程c^2 = a^2 + b^2,其中a和b分别是两条直角边的长度。
代入数据得c^2 = 6^2 + 8^2 = 36+ 64 = 100,所以c = √100 = 10cm。
6. 一个正六边形的边长是4cm,求它的面积。
答案:正六边形可以被分成6个等边三角形,每个等边三角形的边长都是4cm。
等边三角形的面积公式为A = (√3 / 4) * a^2,其中a是边长。
因此,正六边形的面积为6 * (√3 / 4) * 4^2 = 6 * √3 * 4 = 24√3 cm^2。
八年级经典几何题

八年级经典几何题一、三角形全等类。
题1:如图,在△ABC中,AB = AC,AD是BC边上的中线,求证:△ABD≌△ACD。
解析:1. 在△ABD和△ACD中:- 已知AB = AC(题目所给条件)。
- 因为AD是BC边上的中线,所以BD = CD(中线的定义)。
- AD = AD(公共边)。
2. 根据SSS(边 - 边 - 边)全等判定定理,可得△ABD≌△ACD。
题2:已知:如图,点B、E、C、F在同一直线上,AB = DE,AC = DF,BE = CF。
求证:∠A = ∠D。
解析:1. 因为BE = CF,所以BE+EC = CF + EC,即BC = EF。
2. 在△ABC和△DEF中:- AB = DE(已知)。
- AC = DF(已知)。
- BC = EF(已证)。
3. 根据SSS全等判定定理,△ABC≌△DEF。
4. 所以∠A = ∠D(全等三角形的对应角相等)。
二、等腰三角形性质类。
题3:等腰三角形的一个角是70°,求它的另外两个角的度数。
解析:1. 当70°角为顶角时:- 因为等腰三角形两底角相等,设底角为x。
- 根据三角形内角和为180°,则2x+70° = 180°。
- 2x = 180° - 70° = 110°,解得x = 55°。
- 所以另外两个角都是55°。
2. 当70°角为底角时:- 则另一个底角也是70°,顶角为180°-70°×2 = 180° - 140° = 40°。
- 所以另外两个角是70°和40°。
题4:已知等腰三角形ABC中,AB = AC,AD⊥BC于D,若∠BAD = 30°,求∠C的度数。
解析:1. 因为AB = AC,AD⊥BC,根据等腰三角形三线合一的性质,AD是∠BAC的平分线。
初二平面几何考试题及答案

初二平面几何考试题及答案一、选择题(每题2分,共20分)1. 下列哪个图形是轴对称图形?A. 正方形B. 圆C. 长方形D. 等边三角形答案:B2. 一个圆的半径为5cm,那么它的周长是多少?A. 10π cmB. 15π cmC. 20π cmD. 25π cm答案:C3. 一个三角形的内角和是多少度?A. 90°B. 180°C. 360°D. 540°答案:B4. 一个平行四边形的对角线互相平分,那么这个平行四边形是:A. 矩形B. 菱形C. 梯形D. 不规则四边形答案:A5. 如果一个角是直角的补角,那么这个角的度数是多少?A. 45°B. 90°C. 135°D. 180°答案:A6. 一个正六边形的内角是多少度?A. 60°B. 90°C. 120°D. 180°答案:C7. 一个圆的面积公式是:A. πr²B. πdC. π(r+d)²D. πr²/48. 一个三角形的外角等于与它相邻的内角的:A. 补角B. 余角C. 相等D. 两倍答案:A9. 一个矩形的对角线相等,那么这个矩形是:A. 正方形B. 长方形C. 梯形D. 不规则四边形答案:A10. 一个圆的内接四边形的对角线互相垂直,那么这个四边形是:A. 矩形B. 菱形C. 梯形D. 平行四边形答案:B二、填空题(每题2分,共20分)11. 一个直角三角形的两条直角边分别为3cm和4cm,那么它的斜边长是________cm。
答案:512. 一个正五边形的每个内角是________度。
答案:10813. 如果一个三角形的三边长分别为a, b, c,且满足a² + b² = c²,那么这个三角形是________三角形。
答案:直角14. 一个圆的半径增加1cm,那么它的面积增加了________πcm²。
初二数学几何试题及答案

初二数学几何试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项不是三角形的内角和?A. 180°B. 360°C. 540°D. 720°2. 如果一个三角形的两条边长分别为3和4,第三边的长度可能为:A. 1B. 5C. 7D. 93. 一个圆的半径为5厘米,那么它的周长是:A. 10π cmB. 20π cmC. 30π cmD. 40π cm4. 一个正方形的对角线长度为10厘米,那么它的边长是:A. 5 cmB. 7.07 cmC. 10 cmD. 14.14 cm5. 一个长方形的长和宽分别是8厘米和6厘米,那么它的面积是:A. 48 cm²B. 36 cm²C. 24 cm²D. 12 cm²二、填空题(每题2分,共10分)6. 一个等腰三角形的底角是45°,那么它的顶角是________度。
7. 如果一个正多边形的每个内角都是120°,那么它是________边形。
8. 一个圆的直径是14厘米,那么它的半径是________厘米。
9. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的斜边长是________厘米。
10. 如果一个平行四边形的对角线互相平分,那么它是一个________。
三、计算题(每题10分,共20分)11. 一个正六边形的边长为2厘米,求它的周长和面积。
12. 已知一个圆的半径为7厘米,求它的面积和周长。
四、解答题(每题15分,共30分)13. 在一个等边三角形ABC中,点D是边AB上的一点,且AD=2,BD=1。
求∠ADC的度数。
14. 一个圆的半径为10厘米,圆心到一个点P的距离为8厘米,求点P到圆上任意一点的距离的最大值和最小值。
答案:一、选择题1. B2. B3. B4. B5. A二、填空题6. 907. 68. 79. 510. 矩形三、计算题11. 周长:2×6=12厘米;面积:(3√3)×2²=12√3平方厘米。
初二几何试题及答案

初二几何试题及答案一、选择题(每题2分,共10分)1. 在直角三角形中,如果一个锐角为30°,那么另一个锐角的度数是多少?A. 30°B. 45°C. 60°D. 90°答案:C2. 一个矩形的长是10厘米,宽是5厘米,那么它的周长是多少厘米?A. 20厘米B. 25厘米C. 30厘米D. 50厘米答案:B3. 一个圆的半径是3厘米,那么它的直径是多少厘米?A. 6厘米B. 9厘米C. 12厘米D. 15厘米答案:A4. 在一个平行四边形中,如果对角线互相平分,那么这个平行四边形是:A. 正方形B. 长方形C. 菱形D. 梯形答案:B5. 如果一个三角形的三边长分别为3厘米、4厘米、5厘米,那么这个三角形是:A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形答案:C二、填空题(每题2分,共10分)6. 一个三角形的内角和等于________度。
答案:1807. 如果一个圆的周长是12.56厘米,那么它的半径是________厘米。
答案:28. 在一个直角三角形中,斜边的长度是两直角边长度的________。
答案:平方和的平方根9. 一个矩形的对角线相等,那么这个矩形是________。
答案:正方形10. 一个平行四边形的对角线互相平分,那么这个平行四边形是________。
答案:矩形三、解答题(每题5分,共10分)11. 已知一个直角三角形的两条直角边分别为6厘米和8厘米,求斜边的长度。
答案:根据勾股定理,斜边长度为√(6² + 8²) = √(36 + 64) = √100 = 10厘米。
12. 一个圆的半径是4厘米,求其面积。
答案:圆的面积公式为A = πr²,所以面积为A = π × 4² = 16π ≈ 50.27平方厘米。
结束语:本试题涵盖了初二几何课程的基础知识和一些基本公式的应用,希望同学们通过练习能够加深对几何概念的理解和运用能力。
几何题目初二数学3篇

几何题目初二数学题目1:求扇形的面积扇形是一个常见的几何图形,它由一个圆心和两条半径组成,圆心角的度数决定了扇形的大小。
我们可以通过以下公式来求解一个扇形的面积:S = (θ / 360) × πr^2其中,θ代表圆心角的度数,r代表扇形的半径,π是一个常数,约等于3.14。
举个例子,如果一个扇形的半径为5cm,圆心角的度数为60°,那么它的面积应该为:S = (60 / 360) × 3.14 × 5^2 ≈ 13.09(cm^2)注意:在使用这个公式时,需要将度数换算成弧度,即用角度×π/180来计算角度的弧度值。
例如60°的弧度值应该是60×π/180=π/3。
题目2:求直角三角形的斜边长度直角三角形是一个有一条直角边的三角形,我们可以利用勾股定理来求解它的斜边长度。
勾股定理指出:在一个直角三角形中,直角边的两个平方和等于斜边的平方,即a^2+b^2=c^2。
(其中a和b分别为直角边,c为斜边)例如,如果一个直角三角形的直角边长度分别为3cm和4cm,那么它的斜边长度应该为:c = √(3^2 + 4^2) ≈ 5(cm)注意:在使用勾股定理时,必须要保证直角边的长度已知,且只能求解斜边长度,不能求解其他两个角或两个边的长度。
题目3:求圆柱的表面积和体积圆柱是一个由一个圆形底面和一个长方形侧面组成的几何体,我们可以通过以下公式来求解一个圆柱的表面积和体积:表面积S = 2πr^2 + 2πrh体积V = πr^2h其中,r代表圆柱的半径,h代表圆柱的高,π是一个常数,约等于3.14。
举个例子,如果一个圆柱的半径为3cm,高为5cm,那么它的表面积应该为:S = 2π×3^2 + 2π×3×5 ≈ 113.1(cm^2)它的体积应该为:V = π×3^2×5 ≈ 141.3(cm^3)注意:在使用这些公式时,需要将所有的长度单位统一转换成同一单位,例如上述例子中,半径和高都是用厘米表示,因此得到的表面积和体积单位也是厘米的平方和立方。
初二上数学几何题10题

初二上数学几何题10题
以下是10道适合初二学生练习的几何题目:
已知等腰三角形的两边长分别为5和2,求该三角形的周长。
在平行四边形ABCD中,若∠A = 60°,AB = 5cm,BC = 8cm,求平行四边形ABCD的面积。
在△ABC中,若∠A = ∠B = ∠C,则△ABC是什么三角形?请说明理由。
在△ABC中,若∠A = 30°,∠B = 60°,AB = 4cm,求BC的长。
在矩形ABCD中,若AB = 6cm,BC = 8cm,E是AD的中点,求CE的长。
在菱形ABCD中,若∠A = 60°,AB = 4cm,求菱形ABCD的面积。
在△ABC中,若∠A = 90°,AB = AC,D为BC的中点,E、F分别为AB、AC上的点,且DE⊥DF,求∠EDF的度数。
已知圆O的半径为5cm,A、B是圆O上的两点,且∠AOB = 60°,求弦AB的长。
在梯形ABCD中,AD∥BC,AB = CD,若∠B = 60°,AD = 2cm,BC = 6cm,求梯形ABCD的面积。
已知一个直角三角形的两条直角边分别为3cm和4cm,求该直角三角形的外接圆的半径。
这些题目涵盖了初二数学几何的多个方面,包括等腰三角形、平行四边形、菱形、矩形、圆等基本图形的性质和计算。
通过练习这些题目,学生可以加深对几何知识的理解和应用,提高解题能力。
希望这些题目对初二学生的数学学习有所帮助!。
(完整版)八年级数学几何经典题【含答案】
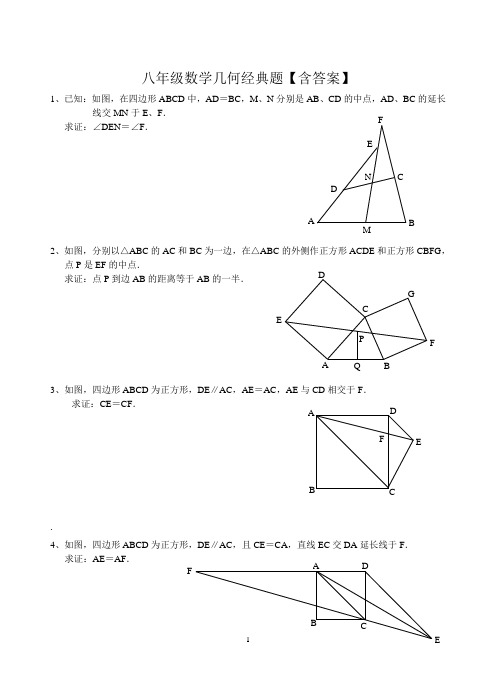
F八年级数学几何经典题【含答案】1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.3、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF ..4、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .B5、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .6、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .7如图,△ABC 中,∠C 为直角,∠A=30°,分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ,DE 与AB 交于F 。
求证:EF=FD 。
8如图,正方形ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD 。
9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA,九年级数学【答案】1.如下图连接AC 并取其中点Q ,连接QN 和QM ,所以可得∠QMF=∠F ,∠QNM=∠DEN 和∠QMN=∠QNM ,从而得出∠DEN =∠F 。
2.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI 。
初二数学几何试题及答案

初二数学几何试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是直角三角形的判定条件?A. 两角之和为90°B. 两边之和大于第三边C. 斜边的平方等于两直角边的平方和D. 任意两边之和大于第三边2. 一个圆的半径是5厘米,那么它的直径是:A. 10厘米B. 15厘米C. 20厘米D. 25厘米3. 如果一个三角形的三个内角分别为40°、60°和80°,那么这个三角形是:A. 直角三角形B. 钝角三角形C. 锐角三角形D. 不能确定4. 一个矩形的长是10厘米,宽是6厘米,那么它的面积是:A. 60平方厘米B. 100平方厘米C. 120平方厘米D. 150平方厘米5. 一个等腰三角形的底边长为8厘米,腰长为5厘米,那么它的高是:A. 3厘米B. 4厘米C. 6厘米D. 8厘米6. 一个正方形的对角线长度为10厘米,那么它的边长是:A. 5厘米B. 7.07厘米C. 8厘米D. 10厘米7. 一个梯形的上底是4厘米,下底是8厘米,高是6厘米,那么它的面积是:A. 12平方厘米B. 24平方厘米C. 30平方厘米D. 40平方厘米8. 一个平行四边形的对角线互相垂直,那么这个平行四边形是:A. 矩形B. 菱形C. 正方形D. 梯形9. 一个正五边形的内角和是:A. 540°B. 720°C. 900°D. 1080°10. 一个圆的周长是62.8厘米,那么它的半径是:A. 10厘米B. 11厘米C. 12厘米D. 13厘米二、填空题(每题4分,共20分)1. 如果一个三角形的两个内角分别为30°和60°,那么第三个内角是______°。
2. 一个圆的周长是31.4厘米,那么它的直径是______厘米。
3. 一个直角三角形的两条直角边长分别为3厘米和4厘米,那么它的斜边长是______厘米。
八年级数学几何题目

八年级数学几何题目一、三角形相关(1 - 10题)题1:在△ABC中,∠A = 50°,∠B = 60°,求∠C的度数。
解析:根据三角形内角和为180°,所以∠C=180° - ∠A - ∠B = 180°- 50° - 60° = 70°。
题2:已知等腰三角形的一个底角为40°,求这个等腰三角形的顶角的度数。
解析:等腰三角形两底角相等,所以另一个底角也是40°。
根据三角形内角和为180°,顶角的度数为180° - 40°×2 = 180° - 80° = 100°。
题3:三角形三边分别为3,4,x。
若该三角形是直角三角形,求x的值。
解析:当x为斜边时,根据勾股定理x=√(3^2)+ 4^{2}=√(9 + 16)=√(25) = 5;当4为斜边时,x=√(4^2)-3^{2}=√(16 - 9)=√(7)。
所以x的值为5或√(7)。
题4:在△ABC中,AB = AC,AD是BC边上的中线,若AB = 10,BC = 12,求AD的长。
因为AB = AC,AD是中线,所以AD⊥BC,BD = BC÷2 = 12÷2 = 6。
在直角三角形ABD中,根据勾股定理AD=√(A B^2)-BD^{2}=√(10^2)-6^{2}=√(100 - 36)=√(64) = 8。
题5:一个三角形的三条高的交点恰是三角形的一个顶点,则这个三角形是()A. 锐角三角形。
B. 直角三角形。
C. 钝角三角形。
D. 以上都有可能。
解析:直角三角形的三条高的交点是直角顶点,锐角三角形三条高的交点在三角形内部,钝角三角形三条高所在直线的交点在三角形外部。
所以答案是B。
题6:如图,在△ABC中,∠ACB = 90°,CD是高,∠A = 30°,AB = 4,求BD的长。
初二几何练习题与答案

初二几何练习题与答案几何学是数学中的一个重要分支,它研究的是形状、大小、相对位置以及其他属性。
对于初二学生来说,几何学的学习尤为关键,因为它是后续高阶数学知识的基础。
为了帮助同学们更好地掌握几何学知识,本文将提供一些初二几何练习题及其答案。
练习题一:平行线与角的关系1. 若两条平行线被一条截线切割,形成的相邻角互补,那么这两条平行线之间的夹角是多少度?答案:180度。
练习题二:三角形内角和定理2. 已知三角形ABC的一个内角为70度,另外两个内角分别为x度和y度。
求x+y的值。
答案:x+y = 180度 - 70度 = 110度。
练习题三:正方形的性质3. 若ABCD是一个正方形,且边长为5cm,求对角线AC的长度。
答案:正方形的对角线长度等于边长的平方根的两倍,即AC = 5√2 cm。
练习题四:平行四边形的性质4. 若ABCD是一个平行四边形,且AB = 6cm,BC = 8cm,求对角线AC的长度。
答案:平行四边形的对角线相等,即AC = BD。
根据勾股定理可得AC的长度为√(AB^2 + BC^2) = √(6^2 + 8^2) = 10cm。
练习题五:圆的周长与面积5. 已知一个圆的半径为3cm,求其周长和面积。
答案:圆的周长等于2πr,其中r为半径。
所以,该圆的周长为2π×3 = 6π cm。
圆的面积等于πr^2,所以该圆的面积为π×3^2 = 9πcm^2。
练习题六:直角三角形的勾股定理6. 在直角三角形ABC中,已知AB = 5cm,BC = 12cm,求AC的长度。
答案:根据勾股定理可得AC的长度为√(AB^2 + BC^2) = √(5^2 +12^2) = 13cm。
练习题七:相似三角形7. 已知三角形ABC与三角形EDF相似,且AB = 6cm,BC = 8cm,DE = 9cm。
求EF的长度。
答案:由相似三角形的性质可知,相似三角形的对应边长度之比相等。
初二几何测试题及答案大全

初二几何测试题及答案大全一、选择题(每题2分,共10分)1. 下列哪个选项表示的是线段?A. 直线的一部分B. 射线的一部分C. 线段的一部分D. 曲线的一部分答案:A2. 一个角的度数是30°,这个角是:A. 锐角B. 直角C. 钝角D. 平角答案:A3. 一个三角形的两边长分别是3厘米和4厘米,第三边的长度可能为:A. 1厘米B. 5厘米C. 7厘米D. 9厘米答案:B4. 一个圆的半径是5厘米,那么这个圆的直径是:A. 10厘米B. 15厘米C. 20厘米D. 25厘米答案:A5. 下列哪个选项是平行四边形的性质?A. 对边相等B. 对角相等C. 对边平行D. 所有选项都是答案:D二、填空题(每题1分,共10分)6. 平行四边形的对角线______。
答案:互相平分7. 如果一个三角形的三边长分别为a、b、c,那么这个三角形的周长是______。
答案:a+b+c8. 一个圆的周长公式是______。
答案:2πr9. 直角三角形的两条直角边的平方和等于______。
答案:斜边的平方10. 如果一个角是直角的一半,那么这个角是______。
答案:45°三、计算题(每题5分,共15分)11. 已知一个三角形的两边长分别为6厘米和8厘米,如果这个三角形是直角三角形,求第三边的长度。
答案:根据勾股定理,第三边的长度为√(8² - 6²) = √(64 - 36) = √28 ≈ 5.29厘米。
12. 已知一个圆的直径为10厘米,求这个圆的面积。
答案:圆的面积公式为πr²,其中r为半径,即直径的一半,所以面积为π×(10/2)² = 25π ≈ 78.54平方厘米。
13. 已知一个平行四边形的对边分别为5厘米和7厘米,求这个平行四边形的面积,如果高为4厘米。
答案:平行四边形的面积公式为底×高,所以面积为5×4 = 20平方厘米。
初中几何常考题目

初中几何常考题目一、在直角三角形ABC中,∠C为直角,若AC=3,BC=4,则AB的长度为:A. 5B. 6C. 7D. 8(答案:A,根据勾股定理,直角三角形的斜边平方等于两直角边的平方和)二、一个圆的半径增加100%,则其面积增加:A. 100%B. 200%C. 300%D. 400%(答案:C,圆的面积与半径的平方成正比,半径增加一倍,面积增加三倍,即增加了200%的原有面积,总共为300%)三、平行四边形ABCD中,若AB=5,BC=8,且∠B=60°,则平行四边形ABCD的面积为:A. 20B. 40C. 60D. 80(答案:B,平行四边形的面积等于任意一边与其对应高之积,高可通过邻边与夹角计算得出)四、等腰三角形的一个底角为40°,则顶角为:A. 40°B. 50°C. 100°D. 140°(答案:C,等腰三角形的两个底角相等,顶角加两个底角等于180°)五、正方形的对角线长与边长的比例是:A. 1:1B. 1:√2C. √2:1D. 2:1(答案:C,正方形的对角线长等于边长乘以√2)六、一个梯形的上底为3cm,下底为7cm,高为4cm,则其面积为:A. 10cm²B. 15cm²C. 20cm²D. 25cm²(答案:C,梯形的面积等于上底加下底之和的一半乘以高)七、若一个三角形的两边长分别为5和8,第三边长为整数,则第三边的可能长度有:A. 2种B. 3种C. 4种D. 5种(答案:C,根据三角形两边之和大于第三边,两边之差小于第三边的原则,第三边长度在3到13之间,且为整数,但考虑到实际情况,应去掉等于两边之差和之和的情况,故为4到12之间的整数,共4种)八、一个圆的周长是20π cm,则圆的半径为:A. 5 cmB. 10 cmC. 15 cmD. 20 cm(答案:B,圆的周长等于2π乘以半径)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如图:在△ABC中,∠ACB=90∘,AC=BC,∠PCQ=45∘,把∠PCQ绕点C旋转,在整个旋转过程中,过点A作AD⊥CP,垂足为D,直线AD交CQ于E.
(1)如图①,当∠PCQ在∠ACB内部时,求证:AD+BE=DE;
(2)如图②,当CQ在∠ACB外部时,则线段AD、BE与DE的关系为___;
(3)在(1)的条件下,若CD=6,S△BCE=2S△ACD,求AE的长。
2.如图,已知B(−1,0),C(1,0),A为y轴正半轴上一点,点D为第二象限一动点,E在BD 的延长线上,CD交AB于F,且∠BDC=∠BAC.
(1)求证:∠ABD=∠ACD;
(2)求证:AD平分∠CDE;
(3)若在D点运动的过程中,始终有DC=DA+DB,在此过程中,
∠BAC的度数是否变化?如果变化,请说明理由;如果不变,
请求出∠BAC的度数?
3.如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60∘,点E在△ABC 外,∠BCE=150∘,∠ABE=60∘.
(1)求∠ADB的度数;
(2)判断△ABE的形状并加以证明;
(3)连接DE,若DE⊥BD,DE=8,求AD的长。
4.在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1)
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②小姚通过观察,实验提出猜想:在点D运动的过程中,始终有DA=AM,小姚把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明DA=AM,只需证△ADM是等边三
角形;
想法2:连接CM,只需证明△ABD≌△ACM即可。
请你参考上面的想法,帮助小姚证明DA=AM(一
种方法即可)
5.如图,已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动).
(1)如图1,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必证明或说明理由;
(2)如图2,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图3中画出相应的图形,并判断(1)的结论中EN与MF 的数量关系是否仍然成立?若成立,请直接写出结论,不必证明或说明理由。
6.如图,已知Rt△ABC,∠ACB=90∘,AD平分∠BAC与BC交于D点,M、N分别在线段AD、AC上的动点,连接MN、MC,当MN+MC最小时,
画出M、N的位置。
已知△ABC的面积为12cm2,AB=6cm,
求MN+MC的最小值。
7.如图1,点A在x轴上,点D在y轴上,以OA、AD为边分别作等边△OAC和等边△ADE,若D(0,4),A(2,0).
(1)若∠DAC=10∘,求CE的长和∠AEC的度数。
(2)如图2,若点P为x轴正半轴上一动点,点P在点A的右边,连PC,以PC为边在第一象限作等边△PCM,延长MA交y轴于N,当点P运动时,
①∠ANO的值是否发生变化?若不变,求其值,若变化,请说明理由。
②AM−AP的值是否发生变化?若不变,求其值,若变化,请说明理由。
8.在等腰直角三角形ABC中,∠BAC=90∘,AB=AC,直线MN过点A且MN∥BC,过点B为一锐角顶点作Rt△BDE,∠BDE=90∘,且点D在直线MN上(不与点A重合),如图1,DE与AC 交于点P,易证:BD=DP.(无需写证明过程)
(1)在图2中,DE与CA延长线交于点P,BD=DP是否成立?如果成立,请给予证明;如果不成立,请说明理由;
(2)在图3中,DE与AC延长线交于点P,BD与DP是否相等?请直接写出你的结论,无需证明。
