上海历年中考数学压轴题复习(试题附答案)
初中数学中考压轴题及答案详解(上海篇)

专题训练125.如图9,在Rt△ABC中,∠ACB=90°.半径为1的圆A与边AB相交于点D,与边AC相交于点E,连结DE并延长,与线段BC的延长线交于点P.(1)当∠B=30°时,连结AP,若△AEP与△BDP相似,求CE的长;(2)若CE=2,BD=BC,求∠BPD的正切值;(3)若1tan3BPD∠=,设CE=x,△ABC的周长为y,求y关于x的函数关系式.图9 图10(备用)参考答案:(1)解:∵∠B=30°∠ACB=90°∴∠BAC=60°∵AD=AE ∴∠AED=60°=∠CEP ∴∠EPC=30°∴三角形BDP为等腰三角形∵△AEP与△BDP相似∴∠EAP=∠EPA=∠DBP=∠DPB=30°∴AE=EP=1∴在RT△ECP中,EC=12EP=12(2)过点D作DQ⊥AC于点Q,且设AQ=a,BD=x ∵AE=1,EC=2∴QC=3-a∵∠ACB=90°∴△ADQ与△ABC相似∴AD AQ AB AC=即113ax=+,∴31 ax=+∵在RT△ADQ中2222328111x x DQ AD AQx x+-⎛⎫=-=-=⎪++⎝⎭∵DQ AD BC AB=∴228111x x x x x +-+=+ 解之得x=4,即BC=4 过点C 作CF//DP∴△ADE 与△AFC 相似,∴AE ADAC AF=,即AF=AC ,即DF=EC=2, ∴BF=DF=2∵△BFC 与△BDP 相似 ∴2142BF BC BD BP ===,即:BC=CP=4 ∴tan ∠BPD=2142EC CP ==(3)过D 点作DQ ⊥AC 于点Q ,则△DQE 与△PCE 相似,设AQ=a ,则QE=1-a ∴QE DQEC CP =且1tan 3BPD ∠= ∴()31DQ a =-∵在Rt △ADQ 中,据勾股定理得:222AD AQ DQ =+ 即:()222131a a =+-⎡⎤⎣⎦,解之得41()5a a ==舍去 ∵△ADQ 与△ABC 相似∴445155AD DQ AQ AB BC AC x x====++ ∴5533,44x xAB BC ++==∴三角形ABC 的周长553313344x xy AB BC AC x x ++=++=+++=+ 即:33y x =+,其中x>0专题训练21.如图,在平面直角坐标系中,二次函数26y ax x c =++的图像经过点()4,0A 、()1,0B -,与y 轴交于点C ,点D 在线段OC 上,=OD t ,点E 在第二象限,∠=90ADE ,1=2tan DAE ∠,EF OD ⊥,垂足为F .(1)求这个二次函数的解析式;(2)求线段EF 、OF 的长(用含t 的代数式表示); (3)当∠ECA =∠OAC 时,求t 的值.参考答案:解:(1)二次函数y=ax 2+6x+c 的图象经过点A (4,0)、B (﹣1,0),∴,解得。
上海市中考数学压轴题总复习(附答案解析)

2021年上海市中考数学压轴题总复习
中考数学压轴题是想获得高分甚至满分必须攻破的考题,得分率低,需要引起重视。
从近10年中考压轴题分析可得中考压轴题主要考查知识点为二次函数,圆,多边形,相似,锐角三角形等。
预计2021年中考数学压轴题依然主要考查这些知识点。
1.如图1,在平而直角坐标系中,直线/:y =勃+m与x轴、y轴分别交于点.4和点
(2)点。
在抛物线上,且点。
的横坐标为f(0Vf<4). 轴交直线/于点£点产在直线/上,且四边形。
FEG为矩形(如图2).若矩形。
尸EG的周长为p,求°与,的函数关系式以及R的最大值:
(3)M是平面内一点,将A4O8绕点M沿逆时针方向旋转90°后,得到△川。
山1,点
A.。
、B的对应点分别是点由、。
1、51.若入41。
1历的两个顶点恰好落在抛物线上,请直
接写出点出的横坐标.
2.已知,抛物线y=aF+Gr+6 (。
#0)与直线y=2rb〃有一个公共点Af (1, 0),且a〈b.
(1)求6与。
的关系式和抛物线的顶点。
坐标(用。
的代数式表示):
(2)直线与抛物线的另外一个交点记为N,求AOMV的面积与。
的关系式:
(3)々=-1时,直线y=-2x与抛物线在第二象限交于点G,点G、H关于原点对称,
现将线段GH沿y轴向上平移,个单位(r>0),若线段GH与抛物线有两个不同的公共点,试求,的取值范围.。
上海历年中考数学压轴题复习(试题附答案)

上海历年中考数学压轴题复习2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC ②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程).27.(1)①证明:∵ ∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴ ∠ABP =∠DPC .∵ 在梯形ABCD 中,AD ∥BC ,AB =CD ,∴ ∠A =∠D .∴ △ABP ∽△DPC .②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252xx -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴ DQ AP PD AB =.即yxx +=-252,得225212-+-=x x y ,1<x <4.②AP=2或AP=3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.图5图6图7 探究:设A、P两点间的距离为x.(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的定义域;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.(图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用)五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分)27.图1 图2 图3(1)解:PQ =PB ……………………(1分) 证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分) ∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB . (2)解法一由(1)△QNP ≌△PMB .得NQ =MP . ∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2. 得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2(1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1. 即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分)解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形.∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN .S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN …(2分)=CN 2=(1-x 22)2=21x 2-x 2+1 ∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形, 此时x =0 ……………………(1分) ②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3) ……………………(1分) 解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴ CQ =QN -CN =x 22-(1-x 22)=x 2-1. 当2-x =x 2-1时,得x =1. ……………………(1分) 解法二 此时∠CPQ =21∠PCN =22.5°,∠APB =90°-22.5°=67.5°, ∠ABP =180°-(45°+67.5°)=67.5°,得∠APB =∠ABP ,∴ AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD中,AB=1,弧AC是点B为圆心,AB长为半径的圆的一段弧。
上海中考数学压轴题专题复习——一元二次方程组的综合

上海中考数学压轴题专题复习——一元二次方程组的综合一、一元二次方程1.使得函数值为零的自变量的值称为函数的零点.例如,对于函数1y x =-,令y=0,可得x=1,我们就说1是函数1y x =-的零点. 己知函数222(3)y x mx m =--+(m m 为常数).(1)当m =0时,求该函数的零点;(2)证明:无论m 取何值,该函数总有两个零点; (3)设函数的两个零点分别为1x 和2x ,且121114x x +=-,此时函数图象与x 轴的交点分 别为A 、B(点A 在点B 左侧),点M 在直线10y x =-上,当MA+MB 最小时,求直线AM 的函数解析式.【答案】(1)当m =0和 (2)见解析,(3)AM 的解析式为112y x =--. 【解析】 【分析】(1)根据题中给出的函数的零点的定义,将m=0代入y=x 2-2mx-2(m+3),然后令y=0即可解得函数的零点;(2)令y=0,函数变为一元二次方程,要想证明方程有两个解,只需证明△>0即可; (3)根据题中条件求出函数解析式进而求得A 、B 两点坐标,个、作点B 关于直线y=x-10的对称点B′,连接AB′,求出点B′的坐标即可求得当MA+MB 最小时,直线AM 的函数解析式 【详解】(1)当m =0和(2)令y=0,得△=∴无论m 取何值,方程总有两个不相等的实数根.即无论m 取何值,该函数总有两个零点. (3)依题意有,由解得.∴函数的解析式为.令y=0,解得∴A(),B(4,0)作点B 关于直线10y x =-的对称点B’,连结AB’, 则AB’与直线10y x =-的交点就是满足条件的M 点.易求得直线10y x =-与x 轴、y 轴的交点分别为C (10,0),D (0,10). 连结CB’,则∠BCD=45° ∴BC=CB’=6,∠B’CD=∠BCD=45° ∴∠BCB’=90° 即B’(106-,)设直线AB’的解析式为y kx b =+,则20{106k b k b -+=+=-,解得112k b =-=-, ∴直线AB’的解析式为112y x =--, 即AM 的解析式为112y x =--.2.已知关于x 的方程24832x nx n --=和()223220x n x n -+-+=,是否存在这样的n 值,使第一个方程的两个实数根的差的平方等于第二个方程的一整数根?若存在,请求出这样的n 值;若不存在,请说明理由?【答案】存在,n=0. 【解析】 【分析】在方程①中,由一元二次方程的根与系数的关系,用含n 的式子表示出两个实数根的差的平方,把方程②分解因式,建立方程求n ,要注意n 的值要使方程②的根是整数. 【详解】 若存在n 满足题意.设x1,x2是方程①的两个根,则x 1+x 2=2n ,x 1x 2=324n +-,所以(x 1-x 2)2=4n 2+3n+2, 由方程②得,(x+n-1)[x-2(n+1)]=0,①若4n 2+3n+2=-n+1,解得n=-12,但1-n=32不是整数,舍.②若4n 2+3n+2=2(n+2),解得n=0或n=-14(舍),综上所述,n=0.3.已知关于x 的一元二次方程()222130x k x k --+-=有两个实数根.()1求k 的取值范围;()2设方程两实数根分别为1x ,2x ,且满足221223x x +=,求k 的值.【答案】(1)134k ≤;(2)2k =-. 【解析】 【分析】()1根据方程有实数根得出()()22[2k 1]41k 38k 50=---⨯⨯-=-+≥,解之可得.()2利用根与系数的关系可用k 表示出12x x +和12x x 的值,根据条件可得到关于k 的方程,可求得k 的值,注意利用根的判别式进行取舍. 【详解】 解:()1关于x 的一元二次方程()222130x k x k --+-=有两个实数根,0∴≥,即()()22[21]4134130k k k ---⨯⨯-=-+≥,解得134k ≤. ()2由根与系数的关系可得1221x x k +=-,2123x x k =-,()222222121212()2(21)23247x x x x x x k k k k ∴+=+-=---=-+, 221223x x +=,224723k k ∴-+=,解得4k =,或2k =-,134k ≤, 4k ∴=舍去, 2k ∴=-. 【点睛】本题考查了一元二次方程2ax bx c 0(a 0,++=≠a ,b ,c 为常数)根的判别式.当0>,方程有两个不相等的实数根;当0=,方程有两个相等的实数根;当0<,方程没有实数根.以及根与系数的关系.4.计算题(1)先化简,再求值:21x x -÷(1+211x -),其中x=2017.(2)已知方程x 2﹣2x+m ﹣3=0有两个相等的实数根,求m 的值.【答案】(1)2018;(2)m=4 【解析】分析:(1)根据分式的运算法则和运算顺序,先算括号里面的,再算除法,注意因式分解的作用;(2)根据一元二次方程的根的判别式求解即可.详解:(1)21xx-÷(1+211x-)=22211 11 x xx x-+÷--=()() 2211 1x xxx x+-⋅-=x+1,当x=2017时,原式=2017+1=2018(2)解:∵方程x2﹣2x+m﹣3=0有两个相等的实数根,∴△=(﹣2)2﹣4×1×(m﹣3)=0,解得,m=4点睛:此题主要考查了分式的混合运算和一元二次方程的根的判别式,关键是熟记分式方程的运算顺序和法则,注意通分约分的作用.5.解方程:(3x+1)2=9x+3.【答案】x1=﹣13,x2=23.【解析】试题分析:利用因式分解法解一元二次方程即可.试题解析:方程整理得:(3x+1)2﹣3(3x+1)=0,分解因式得:(3x+1)(3x+1﹣3)=0,可得3x+1=0或3x﹣2=0,解得:x1=﹣13,x2=23.点睛:此题主要考查了一元二次方程的解法,解题关键是认真观察一元二次方程的特点,然后再从一元二次方程的解法:直接开平方法、配方法、公式法、因式分解法中合理选择即可.6.关于x的方程(k-1)x2+2kx+2=0(1)求证:无论k为何值,方程总有实数根.(2)设x1,x2是方程(k-1)x2+2kx+2=0的两个根,记S=++ x1+x2,S的值能为2吗?若能,求出此时k的值.若不能,请说明理由.【答案】(1)详见解析;(2)S的值能为2,此时k的值为2.【解析】试题分析:(1)本题二次项系数为(k-1),可能为0,可能不为0,故要分情况讨论;要保证一元二次方程总有实数根,就必须使△>0恒成立;(2)欲求k的值,先把此代数式变形为两根之积或两根之和的形式,代入数值计算即可.试题解析:(1)①当k-1=0即k=1时,方程为一元一次方程2x=1, x=有一个解;②当k-1≠0即k≠1时,方程为一元二次方程,△=(2k)²-4×2(k-1)=4k²-8k+8="4(k-1)" ²+4>0方程有两不等根综合①②得不论k为何值,方程总有实根(2)∵x ₁+x ₂=,x ₁ x ₂=∴S=++ x1+x2=====2k-2=2,解得k=2,∴当k=2时,S的值为2∴S的值能为2,此时k的值为2.考点:一元二次方程根的判别式;根与系数的关系.7.已知关于x的一元二次方程x2+(2m+3)x+m2=0有两根α,β.(1)求m的取值范围;(2)若111αβ+=-,则m的值为多少?【答案】(1)14m≥;(2)m的值为3.【解析】【分析】(1)根据△≥0即可求解,(2)化简11αβ+,利用韦达定理求出α+β,αβ,代入解方程即可.【详解】解:(1)由题意知,(2m+3)2﹣4×1×m 2≥0,解得:m≥-34; (2)由根与系数的关系得:α+β=﹣(2m+3),αβ=m 2,∵111αβ+=-,即αβαβ+=-1, ∴2m 3m2+﹣()=-1,整理得m 2﹣2m ﹣3=0解得:m 1=﹣1,m 1=3, 由(1)知m≥-34, ∴m 1=﹣1应舍去, ∴m 的值为3. 【点睛】本题考查了一元二次方程根的判别式以及韦达定理,对根进行判断是正确解题的关键.8.已知x=﹣1是关于x 的方程x 2+2ax+a 2=0的一个根,求a 的值. 【答案】1【解析】试题分析:根据一元二次方程解的定义,把x=﹣1代入x 2+2ax+a 2=0得到关于a 的一元二次方程1﹣2a+a 2=0,然后解此一元二次方程即可. 试题解析:把x=﹣1代入x 2+2ax+a 2=0得1﹣2a+a 2=0, 解得a 1=a 2=1, 所以a 的值为1.9.已知1x 、2x 是关于x 的方程222(1)50x m x m -+++=的两个不相等的实数根. (1)求实数m 的取值范围;(2)已知等腰ABC ∆的一边长为7,若1x 、2x 恰好是ABC ∆另外两边长,求这个三角形的周长.【答案】(1)m>2; (2)17 【解析】试题分析:(1)由根的判别式即可得;(2)由题意得出方程的另一根为7,将x =7代入求出x 的值,再根据三角形三边之间的关系判断即可得.试题解析:解:(1)由题意得△=4(m +1)2﹣4(m 2+5)=8m -16>0,解得:m >2;(2)由题意,∵x 1≠x 2时,∴只能取x 1=7或x 2=7,即7是方程的一个根,将x =7代入得:49﹣14(m +1)+m 2+5=0,解得:m =4或m =10.当m =4时,方程的另一个根为3,此时三角形三边分别为7、7、3,周长为17; 当m =10时,方程的另一个根为15,此时不能构成三角形;故三角形的周长为17.点睛:本题主要考查判别式、三角形三边之间的关系,熟练掌握韦达定理是解题的关键.10.已知关于x的一元二次方程x2﹣mx﹣2=0…①(1)若x=﹣1是方程①的一个根,求m的值和方程①的另一根;(2)对于任意实数m,判断方程①的根的情况,并说明理由.【答案】(1)方程的另一根为x=2;(2)方程总有两个不等的实数根,理由见解析.【解析】试题分析:(1)直接把x=-1代入方程即可求得m的值,然后解方程即可求得方程的另一个根;(2)利用一元二次方程根的情况可以转化为判别式△与0的关系进行判断.(1)把x=-1代入得1+m-2=0,解得m=1∴2--2=0.∴∴另一根是2;(2)∵,∴方程①有两个不相等的实数根.考点:本题考查的是根的判别式,一元二次方程的解的定义,解一元二次方程点评:解答本题的关键是熟练掌握一元二次方程根的情况与判别式△的关系:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根11.已知关于x的方程x2-(m+2)x+(2m-1)=0。
上海历年中考数学压轴题复习

上海历年中考数学压轴题复习2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2.(1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程).27.(1)①证明:∵ ∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴ ∠ABP =∠DPC .∵ 在梯形ABCD 中,AD ∥BC ,AB =CD ,∴ ∠A =∠D .∴ △ABP ∽△DPC . ②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252x x -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴ DQ AP PD AB =.即y x x +=-252,得225212-+-=x x y ,1<x <4. ②AP =2或AP =3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.图5图6图7探究:设A、P两点间的距离为x.(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系试证明你观察得到结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的定义域;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.(图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用)五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分)27.图1 图2 图3(1)解:PQ =PB ……………………(1分) 证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分) ∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB .(2)解法一由(1)△QNP ≌△PMB .得NQ =MP .∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2. 得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2 (1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1. 即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分) 解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形.∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN .S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN…(2分)=CN 2=(1-x 22)2=21x 2-x 2+1∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形,此时x =0 ……………………(1分) ②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3)……………………(1分) 解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴ CQ =QN -CN =x 22-(1-x 22)=x 2-1. 当2-x =x 2-1时,得x =1. ……………………(1分) 解法二 此时∠CPQ =21∠PCN =°,∠APB =90°-°=°, ∠ABP =180°-(45°+°)=°,得∠APB =∠ABP ,∴ AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD 中,AB =1,弧AC 是点B 为圆心,AB 长为半径的圆的一段弧。
上海中考数学压轴题

中考数学试卷一、单项选择题(共12分)1.如图,以A、B、C为顶点的三角形与以D、E、F为顶点的三角形相似,则这两个三角形的相似比为()A.2:1B.3:1C.4:3D.3:22.已知m3=n4,那么下列式子中一定成立的是()A.4m=3n B.3m=4n C.m=4n D.mn=123.在正方形网格中,△ABC的位置如图所示,则tanB的值为()A.1B.√22C.√3D.√334.如图,一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了()A.4圈B.3圈C.5圈D.3.5圈二、填空题(共24分)5.如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B、F的坐标分别为(-4,4)、(2,1)则位似中心的坐标为()。
(x<0)图象上的点,过点6.如图,在平面直角坐标系中,点A是函数y=kxA作y轴的垂线交y轴于点B,点C在x轴上,若△ABC的面积为1,则k的值为()。
三、解答题7.如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(﹣1,﹣1)。
(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;(2)把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C,画出△A2B2C 的图形并写出点B2的坐标;(3)把△ABC以点A为位似中心放大,使放大前后对应边长的比为1:2,画出△AB3C3的图形。
8.如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E。
(1)求证:△ADE∽△MAB;(2)求DE的长。
9.如图,把正方形ABCD绕点A,按顺时针方向旋转得到正方形AEFG,边FG 与BC交于点H.求证:HG=HB.10.已知△ABC和△DEF中,有ABDE =BCEF=CAFD=23,且△DEF和△ABC的周长之差为15厘米,求△ABC和△DEF的周长。
上海历年中考数学压轴题复习试题附答案

上海历年中考数学压轴题复习试题附答案The document was prepared on January 2, 2021上海历年中考数学压轴题复习2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC ②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程). 27.(1)①证明:∵ ∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴ ∠ABP =∠DPC .∵ 在梯形ABCD 中,AD ∥BC ,AB =CD ,∴ ∠A =∠D .∴ △ABP ∽△DPC .②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252xx -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴DQ AP PD AB =.即yxx +=-252,得225212-+-=x x y ,1<x <4.②AP =2或AP =3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD 上,并使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B ,另一边与射线DC 相交于点Q .图5图6图7探究:设A 、P 两点间的距离为x .(1)当点Q 在边CD 上时,线段PQ 与线段PB 之间有怎样的大小关系试证明你观察得到结论;(2)当点Q 在边CD 上时,设四边形PBCQ 的面积为y ,求y 与x 之间的函数解析式,并写出函数的定义域;(3)当点P 在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形如果可能,指出所有能使△PCQ 成为等腰三角形的点Q 的位置,并求出相应的x 的值;如果不可能,试说明理由.(图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用) 五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分) 27.图1 图2 图3(1)解:PQ =PB ……………………(1分) 证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分)∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB . (2)解法一由(1)△QNP ≌△PMB .得NQ =MP . ∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2.得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2(1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1. 即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分) 解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形. ∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN . S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN …(2分)=CN 2=(1-x 22)2=21x 2-x 2+1 ∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形, 此时x =0 ……………………(1分)②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3) ……………………(1分)解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴ CQ =QN -CN =x 22-(1-x 22)=x 2-1.当2-x =x 2-1时,得x =1. ……………………(1分)解法二 此时∠CPQ =21∠PCN =°,∠APB =90°-°=°, ∠ABP =180°-(45°+°)=°,得∠APB =∠ABP ,∴ AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD 中,AB =1,弧AC 是点B 为圆心,AB 长为半径的圆的一段弧。
上海名师马学斌中考数学压轴题

上海名师马学斌中考数学压轴题数学是中学生中考的一门重要科目,也是让很多学生头疼的科目之一。
为了帮助学生更好地备考数学,上海名师马学斌特别准备了一道中考数学压轴题。
本文将为大家详细解析这道题目,并提供解题思路和方法。
题目:已知函数f(x) = 2x^2 - 3x + 1,g(x) = x + 2,h(x) = f(g(x)),求h(3)的值。
解析:首先,我们需要明确题目中给出的函数f(x)、g(x)和h(x)的定义。
函数f(x) = 2x^2 - 3x + 1是一个二次函数,g(x) = x + 2是一个一次函数。
而h(x) = f(g(x))表示将g(x)的结果代入f(x)中,即先计算g(x),再将结果代入f(x)中进行计算。
接下来,我们需要求解h(3)的值。
根据h(x)的定义,我们可以得到h(x) = f(g(x)) = f(x + 2)。
将x + 2代入f(x)中,得到h(x) = 2(x + 2)^2 -3(x + 2) + 1。
将x = 3代入h(x)的表达式中,即可求得h(3)的值。
计算过程如下:h(3) = 2(3 + 2)^2 - 3(3 + 2) + 1= 2(5)^2 - 3(5) + 1= 2(25) - 15 + 1= 50 - 15 + 1= 36因此,h(3)的值为36。
解题思路:解决这道题目的关键在于理解函数的定义和运算规则。
首先,我们要明确每个函数的定义,并根据定义进行计算。
其次,我们要注意函数的运算顺序,先计算g(x),再将结果代入f(x)中进行计算。
最后,根据题目要求,将特定的值代入h(x)的表达式中,求得最终的结果。
解题方法:解决这道题目可以采用代入法和运算法两种方法。
代入法是将给定的值代入函数的表达式中进行计算,而运算法是根据函数的定义和运算规则进行逐步计算。
在本题中,我们采用了运算法的方法。
首先,我们根据h(x)的定义,将g(x)的表达式代入f(x)中,得到h(x) = f(g(x)) = f(x + 2)。
上海中考数学经典必做压轴题及答案
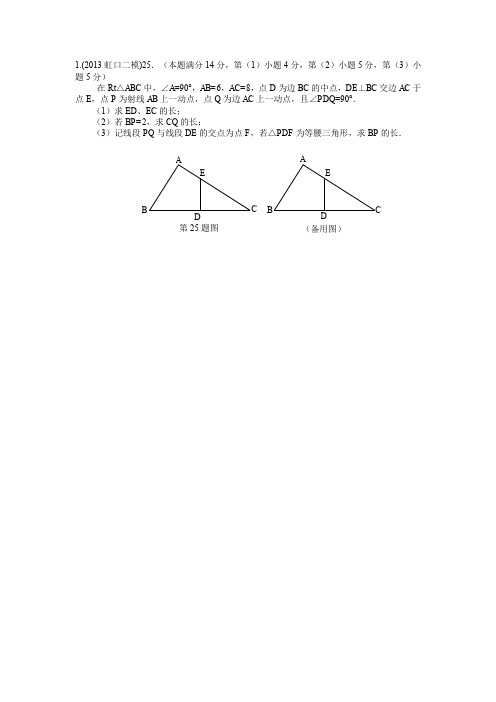
1.(2013虹口二模)25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上一动点,点Q为边AC上一动点,且∠PDQ=90°.(1)求ED、EC的长;(2)若BP=2,求CQ的长;(3)记线段PQ与线段DE的交点为点F,若△PDF为等腰三角形,求BP的长.ABECDAB CED第25题图(备用图)25.解:(1)在Rt△ABC中,∠A=90°,AB=6,AC=8 ∴BC=10……………………(1分)点D为BC的中点∴CD=5可证△ABC∽△DEC∴DE EC CDAB BC AC==,即56108DE EC==………………………………(1分)∴154DE=,254CE=……………………………………………………(2分)(2)①当点P在AB边上时,在Rt△ABC中,∠B+∠C=90°,在Rt△EDC中,∠DEC+∠C=90°,∴∠DEC=∠B∵DE⊥BC,∠PDQ=90°∴∠PDQ=∠BDE=90°∴∠BDP=∠EDQ∴△BPD∽△EQD ……………………………………………………………(1分)∴EQ DEBP BD=,即15425EQ=,∴32EQ=………………………………………………………………………(2分)∴CQ=EC-EQ194 =……………………………………………………………(1分)②当点P在AB的延长线上时,同理可得:32 EQ=,∴CQ=EC+EQ314 =…………………………………………………………(1分)(3)∵线段PQ与线段DE的交点为点F,∴点P在边AB上∵△BPD∽△EQD ∴43 BP BD PD EQ ED QD===若设BP=x ,则34E Q x=,25344CQ x=-…………………………………(1分)可得4cot cot3QPD C∠==∴∠QPD=∠C又可证∠PDE=∠CDQ ∴△PDF∽△CDQ∵△PDF为等腰三角形∴△CDQ为等腰三角形………………………(1分)①当CQ=CD时,可得:253544x-=解得:53x=………………………(1分)②当QC=QD时,过点Q作QM⊥CB于M,∴1522CM CD==,5525248CQ=⨯=∴25325448x-=,解得256x=……………………………………………(1分)③当DC=DQ时,过点D作DN⊥CQ于N,∴4545CN=⨯=,28CQ CN==∴253844x-=,解得73x=-(不合题意,舍去)…………………………(1分)∴综上所述,53BP=或256.2.已知:在梯形ABCD中,AD平行于BC,AB=DC=5,AD=3.5,sinB=4/5,点E是AB边上一点,BE=3,点P是BC边上的一动点,联结EP,作∠EPF,使得∠EPF=∠B,射线PF与AD边交于点F,与CD的延长线交于点G,设BP=x,DF=y(1)求BC的长(2)试求y关于x的函数解析式,并写出定义域(3)联结EF,如果△PEF是等腰三角形,试求BP的长解析(1)BC=9.5 (2)y=9.5-x-x152<x<7.5 (3)分三种情况:①如果PE=PF ,如图,过F 作DC 平行线交底边于H ,则∠FHP=∠C=∠B . ∵在△PEB 与△FPH 中,∠B =∠FHP∠BEP =∠HPF PE =FP∴△PEB ≌△FPH (AAS ),∴EB=PH=3,BP=FH=DC=5;②如果PE=EF ,如图,过F 作DC 平行线交底边于H ,则∠FHP=∠C=∠B .∵在△PEB 与△FPH 中,∠B =∠FHP∠BEP =∠HPF∴△PEB ∽△FPH ,∴PE :PF=PB :FH ,又∵PE=EF ,过E 点做△EFP 的高ET ,则FP :PE=2PT :PE=2cos ∠EPF=2cos ∠B=6/5∵FH=DC=5, ∴5/6=x/5,解得x=25/6③如果PF=EF ,同理可得△PEB ∽△FPH ,∴PE :PF=PB :FH ,∵PE=EF ,过F 点做△EFP 的高FT ,则PE :PF=2PT :PF=2cos ∠EPF=2cos ∠B=6/5,∵FH=DC=5,∴5/6=5/x,解得x=6 ∴综上所述,线x=25/6或x=6。
2021-2019年上海各区中考数学一模压轴题图形的翻折分类汇编答案解析版

2021-2019年上海各区中考数学一模压轴题图形的翻折分类汇编答案解析版【历年真题】1.(2021秋•长宁区期末)如图,在△ABC中,∠C=90°,AC=BC=3,点D、E分别在AC边和AB边上,沿着直线DE翻折△ADE,点A落在BC边上,记为点F,如果CF=1,则BE=4.【考点】翻折变换(折叠问题);等腰直角三角形.【专题】平移、旋转与对称;几何直观.【分析】过F作FG⊥AB于点G.先求出AB=32,BF=3﹣1=2.则FG=GB=BF=2,所以AG=AB﹣BG=32﹣2=22,设AE=x,则EF =x,EG=22﹣x,在Rt△EGF中,EG2+FG2=EF2,利用勾股定理解列出(22﹣x)2+(2)2=x2,解得x=524,即求出BE.【解答】解:过F作FG⊥AB于点G.∵∠C=90°,AC=BC=3,CF=1,∴AB=32,BF=3﹣1=2.∴FG=GB=BF=2,∴AG=AB﹣BG=3,设AE=x,则EF=x,EG=﹣x,在Rt△EGF中,EG2+FG2=EF2,即(﹣x)2+)2=x2,解得x,∴BE=AB﹣AE=.故答案为:4.【点评】本题考查翻折变换,等腰直角三角形的性质等知识,解题的关键是熟练运用勾股定理,属于中考常考题型.2.(2021秋•虹口区期末)如图,在△ABC中,AB=AC=15,sin∠A=45.点D、E分别在AB和AC边上,AD=2DB,把△ADE沿着直线DE翻折得△DEF,如果射线EF⊥BC,那么AE=10.【考点】翻折变换(折叠问题);解直角三角形;等腰三角形的性质.【专题】推理填空题;等腰三角形与直角三角形;平移、旋转与对称;运算能力;推理能力.【分析】先根据折叠得到DE平分∠AEF,根据角平分线过D作∠AEF两边垂线即可.【解答】过D 作DM ⊥AC 于M ,过B 作BH ⊥AC 于H∵AB =AC =15,4sin 5A ∠=,AD =2DB ∴AD =10,DM =8,AM=6,BH=12,AH=9, ∴CH =AC -CH=6∴tan 2,BH C BC CH∠====过D 作DG ⊥EF 交EF 于N ,交AC 于G∵把△ADE 沿着直线DE 翻折得△DEF ∴DE 平分∠AEF ,∴DM =DN =8,EM =EN ,∵EF ⊥BC 于点G ,∴DH ∥BC ,∴23DG AD BC AB ==,∠C =∠NHE ,∴23DG BC ==∴8NG DG DN =-= ∵tan tan 2ENC NGE NG ∠=∠==∴216EM EN NG ===-∴10AE AM EM =+=故答案为:10【点评】本题难度比较大,综合考查折叠的性质、三角函数、相似三角形的性质与判定,解题的关键是由折叠得到角平分线再根据角平分线作垂线.3.(2021秋•金山区期末)在△ABC中,AB=AC=10,sinB=45,E是BC上一点,把△ABE沿直线AE翻折后,点B落在点P处,如果PE∥AC,那么BE= 2 .【考点】翻折变换(折叠问题);解直角三角形;平行线的性质;等腰三角形的判定与性质.【专题】等腰三角形与直角三角形;平移、旋转与对称;解直角三角形及其应用;几何直观;应用意识.【分析】过A作AD⊥BC于D,设AP交BC于F,根据AB=AC=10,sin B=45,AD⊥BC,可得AD=8,BD=CD=6,BC=12,由△ABE沿直线AE翻折后,点B落在点P处,即得∠P=∠B=∠C,∠BAE=∠P AE,而PE∥AC,有∠P=∠F AC,可证得∠AEC=∠EAC,CE=AC=10,即得BE=BC﹣CE=2.【解答】解:过A作AD⊥BC于D,设AP交BC于F,如图:∵AB=AC=10,sin B=45,AD⊥BC,∴4105AD ADAB==,∴AD=8,∴BD=CD=6,∴BC=12,∵△ABE沿直线AE翻折后,点B落在点P处,∴∠P=∠B=∠C,∠BAE=∠P AE,∵PE∥AC,∴∠P=∠F AC,∴∠B=∠F AC,∴∠B+∠BAE=∠F AC+∠P AE,即∠AEC=∠EAC,∴CE=AC=10,∴BE=BC﹣CE=2,故答案为:2.【点评】本题考查等腰三角形中的折叠问题,解题的关键是掌握折叠的性质,能熟练运用锐角三角函数解直角三角形.4.(2021秋•闵行区期末)如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P是AC边上一点,将△ACB沿着过点P的一条直线翻折,使得点A落在边AB上的点Q 处,联结PQ,如果∠CQB=APQ,那么AQ的长为395.【考点】相似三角形的判定与性质;解直角三角形;勾股定理;翻折变换(折叠问题).【专题】几何综合题;压轴题;推理填空题;运算能力;推理能力.【分析】利用三角形内角和180°,以及平角180度,推导出PQ平分∠AQC,设CP=x,则AP=PQ=8﹣x,利用三角形等面积法和相似三角形性质求出AQ 的长,再利用相似三角形的性质构建方程即可解决问题.【解答】解:根据题意如图所示:在Rt△ABC中,∠C=90°,∵AC=8,BC=6,∴AB=10,根据折叠的性质可知∠A=∠PQA,∵∠AQP+∠A+∠APQ=180°,∠AQP+∠PQC+∠CQB=180°,∵∠CQB=∠APQ,∴∠A=∠AQP=∠PQC,∴PQ平分∠AQC,设CP=x,则AP=PQ=8﹣x,如图,过点C作CD⊥AB于点D,PE⊥AB于点E,∴S△ABC =12⨯AC•BC=12⨯AB•CD,∴10CD=6×8,∴CD=245,∵CD⊥AB,PE⊥AB,∴PE∥CD,∴△APE∽△ACD,∴AP PE AC CD=,∴82485x PE-=,∴PE=35(8﹣x),∴AE==45(8﹣x),∴AQ=2AE=85(8﹣x),∵∠PCQ=∠QCA,∠PQC=∠A∴△PCQ∽△QCA,∴CQ CP PQAC CQ AQ==,∴CQ88(8)5xx-=-,∴258x=,∴AQ=85(8﹣x)=395.故答案为:395.【点评】本题属于几何综合题,是中考填空题的压轴题,主要考查了翻折的性质、解直角三角形、相似三角形的判定和性质、勾股定理,三角形等面积法,综合性较强,熟练解直角三角形中线段问题是解题的捷径.5.(2021秋•徐汇区期末)如图,在Rt △ABC 中,∠CAB =90°,AB =AC ,点D 为斜边BC 上一点,且BD =3CD ,将△ABD 沿直线AD 翻折,点B 的对应点为B ′,则sin ∠CB ′D = 10.【考点】翻折变换(折叠问题);平行线分线段成比例;解直角三角形;等腰直角三角形.【专题】平移、旋转与对称;解直角三角形及其应用;运算能力;推理能力.【分析】过点D 作DE ⊥AB 于点E ,由折叠的性质得出AB =AB ',∠BAD =∠B 'AD ,证出∠CB 'D =∠CAD ,由平行线的性质得出∠CAD =∠ADE =∠CB 'D ,13CD AE BD BE ==,设AE =a ,则DE =3a ,求出AD ,由锐角三角函数的定义可得出答案.【解答】解:过点D 作DE ⊥AB 于点E ,∵将△ABD 沿直线AD 翻折,∴AB =AB ',∠BAD =∠B 'AD ,∵AB =AC ,∴AC =AB ',∴∠AB 'C =∠ACB ',设∠B 'AC =x ,∠CB 'D =α,∠CAD =β,∵AB =AC ,∠CAB =90°,∴∠B =∠ACB =∠AB 'D =45°,∴2(α+45°)+x =180°,∴2α=90°﹣x ,又∵∠B 'AD +∠BAD =∠B 'AC +∠CAB ,∴2(x +β)=90°+x ,∴2β=90°﹣x ,∴α=β,∴∠CB 'D =∠CAD ,∵CD ⊥AB ,DE ⊥AB ,∴CA ∥DE ,∴∠CAD =∠ADE =∠CB 'D ,13CD AE BD BE ==, ∵BE =DE ,∴13AE BE =, 设AE =a ,则DE =3a ,∴AD =,∴sin ∠CB ′D =sin ∠ADE =AE DE ==10.【点评】本题考查了折叠的性质,等腰直角三角形的性质,平分线分线段成比例定理,锐角三角函数的定义,熟练掌握折叠的性质是解题的关键.6.(2021秋•崇明区期末)如图所示,在三角形纸片ABC 中,AB =9,BC =6,∠ACB =2∠A ,如果将△ABC 沿过顶点C 的直线折叠,使点B 落在边AC 上的点D 处,折痕为CM ,那么cos ∠DMA = 3132.【考点】翻折变换(折叠问题);解直角三角形.【专题】等腰三角形与直角三角形;平移、旋转与对称;运算能力;推理能力.【分析】由折叠的性质可知,CB =CD =6,∠BCM =∠ACM ,证明△BCM ∽△BAC ,由相似三角形的性质得出CD BM CM AB BC AC==,求出BM 和AC 的长,过点D作DN ⊥AM 于点N ,设MN =x ,则AN =5﹣x ,由勾股定理求出x ,根据锐角三角函数的定义可得出答案.【解答】解:由折叠的性质可知,CB =CD =6,∠BCM =∠ACM ,∵∠ACB =2∠A ,∴∠BCM =∠A ,∵∠B =∠B ,∴△BCM ∽△BAC , ∴CD BM CM AB BC AC ==,∴696BM =, ∴BM =4,∴AM =CM =5,∴659AC=, ∴AC =152,∴AD =AC ﹣CD =152﹣6=32, 过点D 作DN ⊥AM 于点N ,设MN =x ,则AN =5﹣x , ∴22223()(5)42x x +-=-,解得318x =, ∴cos ∠DMA =31318432MN DM ==. 故答案为:3132. 【点评】本题考查了折叠的性质,相似三角形的判定与性质,勾股定理,解直角三角形,证明△BCM ∽△BAC 是解题的关键.7.(2021秋•奉贤区期末)如图,在Rt △ABC 中,∠C =90°,sin B =35.D 是边BC 的中点,点E 在边AB 上,将△BDE 沿直线DE 翻折,使得点B落在同一平面内的点F处.如果线段FD交边AB于点G,当FD⊥AB时,AE:BE的值为 4 .【考点】平行线分线段成比例;解直角三角形;翻折变换(折叠问题).【专题】解直角三角形及其应用;推理能力.【分析】如图,过B点作BH∥DE交GD的延长线于H,如图,利用正弦的定义得到sin B=35DGBD=,则设DG=3x,BD=5x,所以BG=4x,再根据折叠的性质和平行线的性质得到∠H=∠DBH,所以DH=DB=5x,接着根据平行线分线段成比例定理得到35GE DGBE DH==,则BE=52x,然后证明△BDG∽△BAC,利用相似比得到BA=252x,最后计算AE:BE的值.【解答】解:如图,过B点作BH∥DE交GD的延长线于H,如图,∵FD⊥AB,∴∠DGB=90°,∵sin B=35DGBD=,∴设DG=3x,BD=5x,∴BG=4x,∵△BDE沿直线DE翻折得到△FDE,∴∠BDE=∠FDE,∵DE∥BH,∴∠FDE=∠H,∠BDE=∠DBH,∴∠H=∠DBH,∴DH=DB=5x,∵DE∥BH,∴35 GE DGBE DH==,∴BE=58×4x=52x,∵∠BGD=∠C=90°,∠DBG=∠ABD,∴△BDG∽△BAC,∴BD BGBA BC=,即5410x xBA x=,∴BA=252x,∴AE=AB﹣BE=252x﹣52x=10x,∴AE :BE =10x :52x =4. 故答案为:4.【点评】本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.也考查了折叠的性质和解直角三角形.8.(2020秋•崇明区期末)在△ABC 中,AB =,∠B =45°,∠C =60°.点D 为线段AB 的中点,点E 在边AC 上,连接DE ,沿直线DE 将△ADE 折叠得到△A ′DE .连接AA ′,当A ′E ⊥AC 时,则线段AA ′的长为 2【考点】翻折变换(折叠问题).【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;解直角三角形及其应用;运算能力;推理能力.【分析】画出相应的图形,结合图形通过作高构造直角三角形,求出AM =BM =4,进而求出AC ,再利用相似三角形的性质和判定求出AE ,根据对称在Rt △AEF 中求出AF 即可.【解答】解:如图,过点A 作AM ⊥BC ,垂足为M ,在Rt △ABM 中,∠B =45°,AB =,∴AM =BM =AB •sin ∠B =4,在Rt △ACM 中,AM =4,∠C =60°,∴AC =AM 4=sin C sin 60∠=, 又∵A ′E ⊥AC ,∴∠A ′EC =90°,由折叠得∠AED=∠A′ED=12(180°﹣90°)=45°,AA′⊥DE,∵∠AED=45°=∠B,∠DAE=∠CAB,∴△DAE∽△CAB,∴AE AD=AB DC,∵点D为线段AB的中点,∴AD=BD=12AB=AE=在Rt△AEF中,AF=EF=AE•sin∠AED=2,∴AA′=2AF=,故答案为:.【点评】本题考查轴对称的性质,相似三角形的判定和性质,解直角三角形,掌握轴对称、相似三角形的性质以及解直角三角形是解决问题的关键.9.(2020秋•长宁区期末17)如图,矩形ABCD沿对角线BD翻折后,点C落在点E处.联结CE交边AD于点F.如果DF=1,BC=4,那么AE【考点】翻折变换(折叠问题);矩形的性质.【专题】矩形菱形正方形;推理能力.【分析】首先根据题意得到EG=CG,CE⊥BD,证明△CDF∽△BCD和△CDG ∽△BDC,可计算CD和CG的长,再证明△EFD∽△AED,可得AE的长.【解答】解:由折叠得:CE⊥BD,CG=EG,∴∠DGF=90°,∴∠DFG+∠FDG=90°,∵四边形ABCD是矩形,∴∠ADC=∠BCD=90°,∴∠ADG+∠CDG=90°,∴∠CDG=∠DFG,∵∠CDF=∠BCD=90°,∴△CDF∽△BCD,∴CD DF=BC CD,∵AB=4,DF=1,∴CD1=4CD,∴CD=2,由勾股定理得:CFBD,同理得:△CDG∽△BDC,∴CD CG=BD BCCG4,∴CG,∴CE=2CG=5,∴EF=CE﹣CF,∵DF1=ED2,ED21==AD42,且∠EDF=∠AED,∴△EFD∽△AED,∴EF DF=AE DE,即15=AE2,∴AE=【点评】本题主要考查了几何变换中的翻折变换、相似三角形的性质和判定、矩形的性质、勾股定理;熟练掌握翻折变换和矩形的性质,利用相似三角形列比例式是本题的关键.10.(2020秋•虹口区期末)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.D 是BC的中点,点E在边AB上,将△BDE沿直线DE翻折,使得点B落在同一平面内的点B'处,线段B'D交边AB于点F,联结AB'.当△AB'F是直角三角形时,BE的长为2或4017.【考点】翻折变换(折叠问题);相似三角形的判定与性质;勾股定理.【专题】等腰三角形与直角三角形;平移、旋转与对称;运算能力;推理能力.【分析】分两种情况画出图形,①方法一:如图1,当∠AFB′=90°时,由相似三角形的性质及直角三角形的性质可求出答案;方法二:过点E作EH⊥BC 于点H,设EH=3a,BE=5a,则BH=4a,由BF的长列出方程,解方程求出a 即可;②方法一如图2,当∠AB′F=90°时,由相似三角形的性质及直角三角形的性质可求出答案.方法二:过点E作EG⊥BD于点G,设EG=3a,BG=4a,BE=5a,得出9442a a+=,求出a的值则可得出答案.【解答】解:①方法一:如图1,当∠AFB′=90°时.在Rt △ABC 中,∵AC =6,BC =8,∴AB=10==,∵D 是BC 的中点,∴BD =CD =12BC =4, ∵∠AFB '=∠BFD =90°,∠ACB =90°,∴∠DFB =∠ACB , 又∵∠DBF =∠ABC ,∴△BDF ∽△BAC ,∴BF BD BC AB =,即4810BF =, 解得:BF =165, 设BE =B 'E =x ,则EF =165﹣x , ∵∠B =∠FB 'E ,∴sin ∠B =sin ∠FB 'E ,∴'AC EF AB B E =, ∴166510x x-=,解得x =2.∴BE =2. 方法二:过点E 作EH ⊥BC 于点H ,设EH =3a ,BE =5a ,则BH =4a ,∵将△BDE 沿直线DE 翻折,∴EF =3a ,∴BF =8a =BD •cos ∠B =4×45,∴a =25, ∴BE =5a =2;②如图2中,当∠AB ′F =90°时,连接AD ,作EH ⊥AB ′交AB ′的延长线于H .∵AD =AD ,CD =DB ′,∴Rt △ADC ≌Rt △ADB ′(HL ),∴AC =AB ′=6,∵将△BDE 沿直线DE 翻折,∴∠B =∠DB 'E ,∵AB '⊥DB ',EH ⊥AH ,∴DB '∥EH ,∴∠DB 'E =∠B 'EH ,∴∠B =∠B 'EH ,∴sin ∠B =sin ∠B 'EH ,设BE =x ,则B 'H =35x ,EH =45x , 在Rt △AEH 中,AH 2+EH 2=AE 2, ∴22234(6)()(10)55x x x ++=-,解得x =4017,∴BE =4017. 则BE 的长为2或4017. 方法二:过点E 作EG ⊥BD 于点G ,设EG =3a ,BG =4a ,BE =5a ,∴DG =EG ×32=92a , ∵DG +GB =DB ,∴9442a a +=,∴a =817, ∴BE =4017. 故答案为:2或4017. 【点评】本题考查了翻折变换、勾股定理、解直角三角形、相似三角形的判定与性质、全等三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想解决问题.11.(2020秋•松江区期末)如图,已知矩形纸片ABCD ,点E 在边AB 上,且BE =1,将△CBE 沿直线CE 翻折,使点B 落在对角线AC 上的点F 处,联结DF ,如果点D 、F 、E 在同一直线上,则线段AE 的长为 .【考点】翻折变换(折叠问题);矩形的性质.【专题】矩形 菱形 正方形;平移、旋转与对称;运算能力;推理能力.【分析】根据矩形的性质得到AD =BC ,∠ADC =∠B =∠DAE =90°,根据折叠的性质得到CF =BC ,∠CFE =∠B =90°,EF =BE =1,DC =DE ,证明△AEF ∽△DEA ,根据相似三角形的性质即可得到结论.【解答】解:∵四边形ABCD 是矩形,∴AD =BC ,AB =CD ,∠ADC =∠B =∠DAE =90°,∵把△BCE 沿直线CE 对折,使点B 落在对角线AC 上的点F 处,∴CF =BC ,∠CFE =∠B =90°,EF =BE =1,∠CEB =∠CEF ,∵矩形ABCD 中,DC ∥AB ,∴∠DCE =∠CEB ,∴∠CEF =∠DCE , ∴DC =DE ,设AE =x ,则AB =CD =DE =x +1,∵∠AFE =∠CFD =90°,∴∠AFE =∠DAE =90°,∵∠AEF =∠DEA ,∴△AEF ∽△DEA , ∴AF DE EF AE =,∴11x x x+=,解得x 或x ,∴AE =.故答案为:12. 【点评】本题考查了翻折变换(折叠问题),平行线的性质,相似三角形的判定和性质,矩形的性质,正确的识别图形是解题的关键.12.(2020秋•普陀区期末)如图,在▱ABCD 中,点E 在边BC 上,将△ABE 沿着直线AE翻折得到△AFE,点B的对应点F恰好落在线段DE上,线段AF的延长线交边CD于点G,如果BE:EC=3:2,那么AF:FG的值等于214.【考点】相似三角形的判定与性质;平行四边形的性质;翻折变换(折叠问题).【专题】多边形与平行四边形;平移、旋转与对称;图形的相似;推理能力.【分析】延长BC,AG交于点H,设BE=3x,EC=2x,由平行四边形的性质可得AD=BC=5x,AD∥BC,由折叠的性质可得∠AEB=∠AEF,BE=EF=3x,通过证明△ADF∽△HEF,△ADG∽△HCG,可求AF=425y,FG=AG﹣AF=85y,即可求解.【解答】解:如图,延长BC,AG交于点H,∵BE:EC=3:2,∴设BE=3x,EC=2x,∵四边形ABCD是平行四边形,∴AD=BC=5x,AD∥BC,∴∠DAE=∠AEB,∵将△ABE沿着直线AE翻折得到△AFE,∴∠AEB=∠AEF,BE=EF=3x,∴∠DAE=∠AED,∴AD=DE=5x,∴DF=2x,∵AD∥BC,∴△ADF∽△HEF,∴AD DF AFEH EF FH==,∴523x AFEH FH==,∴EH=152x,AF=23FH,∴CH=EH﹣EC=x,∵AD∥BC,∴△ADG∽△HCG,∴AD AGCH GH=,∴51011112x AGGHx==,∴设AG=10y,GH=11y,∴AH=21y,∴AF=215y×2=425y,∴FG=AG﹣AF=85y,∴AF:FG=21:4=214,故答案为214.【点评】本题考查了相似三角形的判定和性质,折叠的性质,平行四边形的性质,灵活运用这些性质进行推理是解题的关键.13.(2019秋•虹口区期末)如图,在等腰梯形ABCD中,AD∥BC,sin C=45,AB=9,AD=6,点E、F分别在边AB、BC上,联结EF,将△BEF沿着EF所在直线翻折,使BF的对应线段B′F经过顶点A,B′F交对角线BD于点P,当B′F⊥AB时,AP的长为247.【考点】相似三角形的判定与性质;解直角三角形;等腰梯形的性质;翻折变换(折叠问题).【专题】图形的相似;解直角三角形及其应用;应用意识.【分析】解直角三角形求出BF,AF,再利用相似三角形的性质求解即可.【解答】解:如图,∵FB′⊥AB,∴∠BAF=90°,∵四边形ABCD是等腰梯形,∴∠ABC=∠C,∴sin∠ABC=sin∠C=AFBF=45,设AF=4k,BF=5k,则AB=9=3k,∴k=3,∴AF=12,BF=15,∵AD∥BF,∴△APD∽△FPB,∴PA AD62===PF BF155,∴P A=27AF=247,故答案为247.【点评】本题考查相似三角形的判定和性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题.14.(2019秋•青浦区期末)已知,在矩形纸片ABCD中,AB=5cm,点E、F分别是边AB、CD的中点,折叠矩形纸片ABCD,折痕BM交AD边于点M,在折叠的过程中,如果点A恰好落在线段EF上,那么边AD.【考点】翻折变换(折叠问题).【专题】平移、旋转与对称;推理能力.【分析】根据已知条件得到AE=DF=BE=CF,求得四边形AEFD是矩形,得到EF=AD,∠AEN=∠BEN=90°,根据折叠的性质得到BN=AB,根据直角三角形的性质得到∠BNE=30°,于是得到EN=2BN即可得到结论.【解答】解:如图,∵在矩形纸片ABCD中,点E、F分别是边AB、CD的中点,∴AE=DF=BE=CF,∴四边形AEFD是矩形,∴EF=AD,∠AEN=∠BEN=90°,∵折叠矩形纸片ABCD,折痕BM交AD边于点M,∴BN=AB,∵BE=12AB,∴BE=12BN,∴∠BNE=30°,∵AB=5cm,∴EN=2BN∴EF≥EN时,点A恰好落在线段EF上,即AD∴边AD【点评】本题考查了翻折变换(折叠问题),矩形的性质,直角三角形的性质,正确的识别图形是解题的关键.15.(2019秋•闵行区期末)如图,在等腰△ABC中,AB=AC=4,BC=6,点D 在底边BC上,且∠DAC=∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E 处,联结BE,那么BE的长为1.【考点】翻折变换(折叠问题);等腰三角形的性质;勾股定理.【专题】平移、旋转与对称;推理能力.【分析】只要证明△ABD∽△MBE,得AB BDBM BE=,只要求出BM、BD即可解决问题.【解答】解:∵AB=AC,∴∠ABC=∠C,∵∠DAC=∠ACD,∴∠DAC=∠ABC,∵∠C=∠C,∴△CAD∽△CBA,∴CA CDCB AC=,∴464CD=,∴CD=83,BD=BC﹣CD=103,∵∠DAM=∠DAC=∠DBA,∠ADM=∠ADB,∴△ADM∽△BDA,∴AD DMBD DA=,即8310833DM=,∴DM=3215,MB=BD﹣DM=65,∵∠ABM=∠C=∠MED,∴A、B、E、D四点共圆,∴∠ADB=∠BEM,∠EBM=∠EAD=∠ABD,∴△ABD∽△MBE,(不用四点共圆,可以先证明△BMA∽△EMD,推出△BME∽AMD,推出∠ADB=∠BEM也可以!)∴AB BD BM BE=,∴BE=BD BMAB=1.故答案为:1.【点评】本题考查翻折变换、等腰三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是充分利用相似三角形的性质解决问题,本题需要三次相似解决问题,题目比较难.16.(2019秋•杨浦区期末)在Rt△ABC中,∠A=90°,AC=4,AB=a,将△ABC沿着斜边BC翻折,点A落在点A1处,点D、E分别为边AC、BC的中点,联结DE并延长交A1B所在直线于点F,联结A1E,如果△A1EF为直角三角形时,那么a=4或【考点】翻折变换(折叠问题);勾股定理;三角形中位线定理.【专题】平移、旋转与对称;推理能力.【分析】当△A1EF为直角三角形时,存在两种情况:①当∠A1EF=90°时,如图1,根据对称的性质和平行线可得:A1C=A1E=4,根据直角三角形斜边中线的性质得:BC=2A1B=8,最后利用勾股定理可得AB 的长;②当∠A1FE=90°时,如图2,证明△ABC是等腰直角三角形,可得AB=AC=4.【解答】解:当△A1EF为直角三角形时,存在两种情况:①当∠A1EF=90°时,如图1,∵△A1BC与△ABC关于BC所在直线对称,∴A1C=AC=4,∠ACB=∠A1CB,∵点D,E分别为AC,BC的中点,∴D、E是△ABC的中位线,∴DE∥AB,∴∠CDE=∠MAN=90°,∴∠CDE =∠A1EF,∴AC∥A1E,∴∠ACB=∠A1EC,∴∠A1CB=∠A1EC,∴A1C=A1E=4,Rt△A1CB中,∵E是斜边BC的中点,∴BC=2A1E=8,由勾股定理得:AB2=BC2﹣AC2,∴AB==②当∠A1FE=90°时,如图2,∵∠ADF=∠A=∠DFB=90°,∴∠ABF=90°,∵△A1BC与△ABC关于BC所在直线对称,∴∠ABC=∠CBA1=45°,∴△ABC 是等腰直角三角形,∴AB =AC =4;综上所述,AB 的长为4;故答案为:4;【点评】本题考查了翻折变换(折叠问题),三角形的中位线定理、勾股定理、轴对称的性质、等腰直角三角形的判定、直角三角形斜边中线的性质,并利用分类讨论的思想解决问题.17.(2019秋•崇明区期末)如图,在Rt △ABC 中,∠C =90°,AB =10,AC =8,D 是AC的中点,点E 在边AB 上,将△ADE 沿DE 翻折,使得点A 落在点A ′处,当A ′E ⊥AB 时,则A ′A = 5或5.【考点】翻折变换(折叠问题).【专题】平移、旋转与对称;解直角三角形及其应用.【分析】分两种情形分别求解,作DF ⊥AB 于F ,连接AA ′.想办法求出AE ,利用等腰直角三角形的性质求出AA ′即可.【解答】解:如图,作DF ⊥AB 于F ,连接AA ′.在Rt △ACB 中,BC 6,∵∠DAF =∠BAC ,∠AFD =∠C =90°,∴△AFD ∽△ACB , ∴DF AD AF BC AB AC ==,∴46108DF AF ==, ∴DF =125,AF =165, ∵A ′E ⊥AB ,∴∠AEA ′=90°,由翻折不变性可知:∠AED =45°,∴EF =DF =125,∴AE =A ′E =125+165=285,∴AA ′=5, 如图,作DF ⊥AB 于F ,当 EA ′⊥AB 时,同法可得AE =165﹣125=45,AA ′AE =5.故答案为5或5. 【点评】本题考查翻折变换,相似三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考填空题中的压轴题.18.(2019秋•静安区期末)如图,有一菱形纸片ABCD ,∠A =60°,将该菱形纸片折叠,使点A 恰好与CD 的中点E 重合,折痕为FG ,点F 、G 分别在边AB 、AD 上,联结EF ,那么cos ∠EFB 的值为 17.【考点】翻折变换(折叠问题);解直角三角形;等边三角形的判定与性质;菱形的性质.【专题】矩形 菱形 正方形;解直角三角形及其应用.【分析】如图,连接BD .设BC =2a .在Rt △BEF 中,求出EF ,BF 即可解决问题.【解答】解:如图,连接BD .设BC =2a .∵四边形ABC都是菱形,∴AB=BC=CD=AD=2a,∠A=∠C=60°,∴△BDC是等边三角形,∵DE=EC=a,∴BE⊥CD,∴BE==,∵AB∥CD,BE⊥CD,∴BE⊥AB,∴∠EBF=90°,设AF=EF=x,在Rt△EFB中,则有x2=(2a﹣x)2+a)2,∴x=74a,∴AF=EF=74a,BF=AB﹣AF=4a,∴cos∠EFB=14774aBFaEF==,故答案为17.【点评】本题考查菱形的性质,解翻折变换,直角三角形等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.。
中考数学压轴题20题(含答案_)

中考数学压轴题复习20题1.在平面直角坐标系xO y 中,抛物线y =-41 m x2+45mx +m2-3m +2与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上.(1)求点B 的坐标;(2)点P 在线段OA 上,从O 点出发向A 点运动,过P 点作x 轴的垂线,与直线OB 交于点E ,延长PE 到点D ,使得ED =PE ,以PD 为斜边,在PD 右侧作等腰直角三角形PCD (当P 点运动时,C 点、D 点也随之运动).①当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求OP 的长;②若P 点从O 点出发向A 点作匀速运动,速度为每秒1个单位,同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动,速度为每秒2个单位(当Q 点到达O 点时停止运动,P 点也同时停止运动).过Q 点作x 轴的垂线,与直线AB 交于点F ,延长QF 到点M ,使得FM =QF ,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当Q 点运动时,M 点、N 点也随之运动).若P 点运动到t 秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,求此刻t 的值.2.在平面直角坐标系中,矩形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,OA =3,OB =4,D 为边OB 的中点.(Ⅰ)若E 为边OA 上的一个动点,当△CDE 的周长最小时,求点E 的坐标;(Ⅱ)若E 、F 为边OA 上的两个动点,且EF =2,当四边形CDEF 的周长最小时,求点E 、F 的坐标.3.在平面直角坐标系中,已知抛物线y =-x2+bx +c 与x 轴交于点A 、B (点A 在点B 的左侧),与y 轴的正半轴交于点C ,顶点为E .(Ⅰ)若b =2,c =3,求此时抛物线顶点E 的坐标;(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC 中满足S △BCE=S △ABC,求此时直线BC的解析式;(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC 中满足S △BCE=2S △AOC,且顶点E 恰好落在直线y =-4x +3上,求此时抛物线的解析式.4.如图1,在Rt △ABC 中,∠ACB =90°,半径为1的圆A 与边AB 相交于点D ,与边AC 相交于点E ,连结DE 并延长,与线段BC 的延长线交于点P . (1)当∠B =30°时,连结AP ,若△AEP 与△BDP 相似,求CE 的长; (2)若CE =2,BD =BC ,求∠BPD 的正切值;(3)若tan ∠BPD =31,设CE =x ,△ABC 的周长为y ,求y 关于x 的函数关系式.5.已知:如图①,在平面直角坐标系xO y 中,边长为2的等边△OAB 的顶点B 在第一象限,顶点A 在x 轴的正半轴上.另一等腰△OCA 的顶点C 在第四象限,OC =AC ,∠C =120°.现有两动点P ,Q 分别从A ,O 两点同时出发,点Q 以每秒1个单位的速度沿OC 向点C 运动,点P 以每秒3个单位的速度沿A →O →B 运动,当其中一个点到达终点时,另一个点也随即停止. (1)求在运动过程中形成的△OPQ 的面积S 与运动的时间t 之间的函数关系,并写出自变量t 的取值范围; (2)在等边△OAB 的边上(点A 除外)存在点D ,使得△OCD 为等腰三角形,请直接写出所有符合条件的点D 的坐标;(3)如图②,现有∠MCN =60°,其两边分别与OB ,AB 交于点M ,N ,连接MN .将∠MCN 绕着C 点旋转(0°<旋转角<60°),使得M ,N 始终在边OB 和边AB 上.试判断在这一过程中,△BMN 的周长是否发生变化?若没变化,请求出其周长;若发生变化,请说明理由.6.已知抛物线y =ax2+bx +c (a >0)的图象经过点B (12,0)和C (0,-6),对称轴为x =2. (1)求该抛物线的解析式:(2)点D 在线段AB 上且AD =AC ,若动点P 从A 出发沿线段AB 以每秒1个单位长度的速度匀速运动,同时另一动点Q 以某一速度从C 出发沿线段CB 匀速运动,问是否存在某一时刻,使线段PQ 被直线CD 垂直平分?若存在,请求出此时的时间t (秒)和点Q 的运动速度;若不存在,请说明理由;AE C B P D 图2(备用) B PE C D A 图3(备用) A B C P E D 图1图②图①(3)在(2)的结论下,直线x =1上是否存在点M ,使△MPQ 为等腰三角形?若存在,请求出所有点M 的坐标;若不存在,请说明理由.7.如图,抛物线y =ax2+bx +1与x 轴交于两点A (-1,0),B (1,0),与y 轴交于点C . (1)求抛物线的解析式;(2)过点B 作BD ∥CA 与抛物线交于点D ,求四边形ACBD 的面积;(3)在x 轴下方的抛物线上是否存在点M ,过M 作MN ⊥x 轴于点N ,使以A 、M 、N 为顶点的三角形与△BCD 相似?若存在,则求出点M 的坐标;若不存在,请说明理由.8.如图,已知抛物线y =21x2+bx +c 与y 轴相交于C ,与x 轴相交于A 、B ,点A 的坐标为(2,0),点C 的坐标为(0,-1).(1)求抛物线的解析式;(2)点E 是线段AC 上一动点,过点E 作DE ⊥x 轴于点D ,连结DC ,当△DCE 的面积最大时,求点D 的坐标;(3)在直线BC 上是否存在一点P ,使△ACP 为等腰三角形,若存在,求点P 的坐标,若不存在,说明理由.9.如图,已知△ABC ∽△A 1B 1C 1,相似比为k (k >1),且△ABC 的三边长分别为a 、b 、c (a >b >c ),△A 1B 1C 1的三边长分别为a 1、b 1、c 1. (1)若c =a 1,求证:a =kc ;(2)若c =a 1,试给出符合条件的一对△ABC 和△A 1B 1C 1,使得a 、b 、c 和a 1、b 1、c 1都是正整数,并加以说明;(3)若b =a 1,c =b 1,是否存在△ABC 和△A 1B 1C 1,使得k =2?请说明理由.10.如图,Rt △ABC 内接于⊙O ,AC =BC ,∠BAC 的平分线AD 与⊙O 交于点D ,与BC 交于点E ,延长BD ,与AC 的延长线交于点F ,连结CD ,G 是CD 的中点,连结OG . (1)判断OG 与CD 的位置关系,写出你的结论并证明; (2)求证:AE =BF ; (3)若OG ·DE =3(2-2),求⊙O 的面积.11.已知:抛物线y =ax2+bx +c (a ≠0)的对称轴为x =-1,与x 轴交于A 、B 两点,与y 轴交于点C ,其中A (-3,0)、C (0,-2). (1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得△PBC 的周长最小.请求出点P 的坐标.(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE ∥PC 交x 轴于点E ,连接PD 、PE .设CD 的长为m ,△PDE 的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.12.(本小题满分12分)如图,BD 是⊙O 的直径,OA ⊥OB ,M 是劣弧上一点,过M 点作⊙O 的切线MP 交OA 的延长线于P 点,MD 与OA 交于N 点. (1)求证:PM =PN ; (2)若BD =4,P A =23AO ,过B 点作BC ∥MP 交⊙O 于C 点,求BC 的长. B C AA 1 a b cB 1C 1 a 1b 1c 1 A C B F D EO G13.如图,在平面直角坐标系中放置一矩形ABCO ,其顶点为A (0,1)、B (-33,1)、C (-33,0)、O (0,0).将此矩形沿着过E (-3,1)、F (-334,0)的直线EF 向右下方翻折,B 、C 的对应点分别为B ′、C ′.(1)求折痕所在直线EF 的解析式;(2)一抛物线经过B 、E 、B ′三点,求此二次函数解析式;(3)能否在直线EF 上求一点P ,使得△PBC 周长最小?如能,求出点P 的坐标;若不能,说明理由.14.已知:甲、乙两车分别从相距300(km )的M 、N回,图1、图2分别是它们离各自出发地的距离y (km )与行驶时间x (h )之间的函数图象. (1)试求线段AB所对应的函数关系式,并写出自变量的取值范围;(2)当它们行驶到与各自出发地的距离相等时,用了29h ,求乙车的速度; (3)在(2)的条件下,求它们在行驶的过程中相遇的时间.y h图1y h图215.如图1,在△ABC 中,AB =BC ,且BC ≠AC ,在△ABC 上画一条直线,若这条直线..既平分△ABC 的面积,又平分△ABC 的周长,我们称这条线为△ABC 的“等分积周线”. (1)请你在图1中用尺规作图作出一条△ABC 的“等分积周线”;(2)在图1中过点C 能否画出一条“等分积周线”?若能,说出确定的方法;若不能,请说明理由; (3)如图2,若AB =BC =5cm ,AC =6cm ,请你找出△ABC 的所有“等分积周线”,并简要说明确定的方法.16.如图,在Rt △ABC 中,∠C =90°,AC =3cm ,BC =4cm ,点P 以一定的速度沿AC 边由A 向C 运动,点Q 以1cm/s 的速度沿CB 边由C 向B 运动,设P 、Q 同时运动,且当一点运动到终点时,另一点也随之停止运动,设运动时间为t (s ). (1)若点P 以43cm/s 的速度运动 ①当PQ ∥AB 时,求t 的值;②在①的条件下,试判断以PQ 为直径的圆与直线AB 的位置关系,并说明理由.(2)若点P 以1cm/s 的速度运动,在整个运动过程中,以PQ 为直径的圆能否与直线AB 相切?若能,请求出运动时间t ;若不能,请说明理由.17.青海玉树发生7.1级强震后,为使人民的生命财产损失降到最低,部队官兵发扬了连续作战的作风。
上海中考数学压轴题专题复习——二次函数的综合

一、二次函数 真题与模拟题分类汇编(难题易错题)1.如图,已知抛物线2(0)y ax bx c a =++≠的对称轴为直线1x =-,且抛物线与x 轴交于A 、B 两点,与y 轴交于C 点,其中(1,0)A ,(0,3)C .(1)若直线y mx n =+经过B 、C 两点,求直线BC 和抛物线的解析式;(2)在抛物线的对称轴1x =-上找一点M ,使点M 到点A 的距离与到点C 的距离之和最小,求出点M 的坐标;(3)设点P 为抛物线的对称轴1x =-上的一个动点,求使BPC ∆为直角三角形的点P 的坐标.【答案】(1)抛物线的解析式为223y x x =--+,直线的解析式为3y x .(2)(1,2)M -;(3)P 的坐标为(1,2)--或(1,4)-或317(+-或317()--. 【解析】分析:(1)先把点A ,C 的坐标分别代入抛物线解析式得到a 和b ,c 的关系式,再根据抛物线的对称轴方程可得a 和b 的关系,再联立得到方程组,解方程组,求出a ,b ,c 的值即可得到抛物线解析式;把B 、C 两点的坐标代入直线y=mx+n ,解方程组求出m 和n 的值即可得到直线解析式;(2)设直线BC 与对称轴x=-1的交点为M ,此时MA+MC 的值最小.把x=-1代入直线y=x+3得y 的值,即可求出点M 坐标;(3)设P (-1,t ),又因为B (-3,0),C (0,3),所以可得BC 2=18,PB 2=(-1+3)2+t 2=4+t 2,PC 2=(-1)2+(t-3)2=t 2-6t+10,再分三种情况分别讨论求出符合题意t 值即可求出点P 的坐标.详解:(1)依题意得:1203b a a b c c ⎧-=-⎪⎪++=⎨⎪=⎪⎩,解得:123a b c =-⎧⎪=-⎨⎪=⎩,∴抛物线的解析式为223y x x =--+.∵对称轴为1x =-,且抛物线经过()1,0A ,∴把()3,0B -、()0,3C 分别代入直线y mx n =+,得303m n n -+=⎧⎨=⎩,解之得:13m n =⎧⎨=⎩, ∴直线y mx n =+的解析式为3y x =+.(2)直线BC 与对称轴1x =-的交点为M ,则此时MA MC +的值最小,把1x =-代入直线3y x =+得2y =,∴()1,2M -.即当点M 到点A 的距离与到点C 的距离之和最小时M 的坐标为()1,2-. (注:本题只求M 坐标没说要求证明为何此时MA MC +的值最小,所以答案未证明MA MC +的值最小的原因).(3)设()1,P t -,又()3,0B -,()0,3C ,∴218BC =,()2222134PB t t =-++=+,()()222213610PC t t t =-+-=-+, ①若点B 为直角顶点,则222BC PB PC +=,即:22184610t t t ++=-+解得:2t =-,②若点C 为直角顶点,则222BC PC PB +=,即:22186104t t t +-+=+解得:4t =,③若点P 为直角顶点,则222PB PC BC +=,即:22461018t t t ++-+=解得: 1317t +=2317t -=. 综上所述P 的坐标为()1,2--或()1,4-或3171,2⎛+- ⎝⎭或3171,2⎛- ⎝⎭. 点睛:本题综合考查了二次函数的图象与性质、待定系数法求函数(二次函数和一次函数)的解析式、利用轴对称性质确定线段的最小长度、难度不是很大,是一道不错的中考压轴题.2.在平面直角坐标系中,我们定义直线y=ax-a 为抛物线y=ax 2+bx+c (a 、b 、c 为常数,a≠0)的“衍生直线”;有一个顶点在抛物线上,另有一个顶点在y 轴上的三角形为其“衍生三角形”.已知抛物线233333y x x =--+“衍生直线”交于A 、B 两点(点A 在点B 的左侧),与x 轴负半轴交于点C .(1)填空:该抛物线的“衍生直线”的解析式为 ,点A 的坐标为 ,点B 的坐标为 ;(2)如图,点M 为线段CB 上一动点,将△ACM 以AM 所在直线为对称轴翻折,点C 的对称点为N ,若△AMN 为该抛物线的“衍生三角形”,求点N 的坐标;(3)当点E 在抛物线的对称轴上运动时,在该抛物线的“衍生直线”上,是否存在点F ,使得以点A 、C 、E 、F 为顶点的四边形为平行四边形?若存在,请直接写出点E 、F 的坐标;若不存在,请说明理由.【答案】(1)2323y=;(-2,231,0); (2)N 点的坐标为(0,3-3),(0,23+3);(3)E (-1,43F (023)或E (-1,43),F (-4103) 【解析】【分析】(1)由抛物线的“衍生直线”知道二次函数解析式的a 即可;(2)过A 作AD ⊥y 轴于点D ,则可知AN=AC ,结合A 点坐标,则可求出ON 的长,可求出N 点的坐标;(3)分别讨论当AC 为平行四边形的边时,当AC 为平行四边形的对角线时,求出满足条件的E 、F 坐标即可【详解】(1)∵2234323y x x =-+a=233-,则抛物线的“衍生直线”的解析式为2323y=; 联立两解析式求交点2234323332323y=y x x ⎧=--+⎪⎪⎨⎪⎪⎩,解得x=-2y=23⎧⎪⎨⎪⎩x=1y=0⎧⎨⎩, ∴A (-2,3B (1,0);(2)如图1,过A 作AD ⊥y 轴于点D ,在223432333y x x =--+中,令y=0可求得x= -3或x=1, ∴C (-3,0),且A (-2,23),∴AC=22-++2133=(23)()由翻折的性质可知AN=AC=13,∵△AMN 为该抛物线的“衍生三角形”,∴N 在y 轴上,且AD=2,在Rt △AND 中,由勾股定理可得DN=22AN -AD =13-4=3,∵OD=23,∴ON=23-3或ON=23+3,∴N 点的坐标为(0,23-3),(0,23+3);(3)①当AC 为平行四边形的边时,如图2 ,过F 作对称轴的垂线FH ,过A 作AK ⊥x 轴于点K ,则有AC ∥EF 且AC=EF ,∴∠ ACK=∠ EFH ,在△ ACK 和△ EFH 中ACK=EFH AKC=EHF AC=EF ∠∠⎧⎪∠∠⎨⎪⎩∴△ ACK ≌△ EFH ,∴FH=CK=1,HE=AK=23∵抛物线的对称轴为x=-1,∴ F 点的横坐标为0或-2,∵点F 在直线AB 上,∴当F 点的横坐标为0时,则F (0,233),此时点E 在直线AB 下方, ∴E 到y 轴的距离为EH-OF=32343,即E 的纵坐标为43∴ E(-1,-433);当F点的横坐标为-2时,则F与A重合,不合题意,舍去;②当AC为平行四边形的对角线时,∵ C(-3,0),且A(-2,23),∴线段AC的中点坐标为(-2.5,3),设E(-1,t),F(x,y),则x-1=2×(-2.5),y+t=23,∴x= -4,y=23-t,23-t=-233×(-4)+233,解得t=43-3,∴E(-1,43-3),F(-4,1033);综上可知存在满足条件的点F,此时E(-1,-433)、(0,233)或E(-1,43 -3),F(-4,1033)【点睛】本题是对二次函数的综合知识考查,熟练掌握二次函数,几何图形及辅助线方法是解决本题的关键,属于压轴题3.已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5)(1)求该函数的关系式;(2)求该函数图象与坐标轴的交点坐标;(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.【答案】(1)y=﹣x2﹣2x+3;(2)抛物线与x轴的交点为:(﹣3,0),(1,0)(3)15.【解析】【分析】(1)已知了抛物线的顶点坐标,可用顶点式设该二次函数的解析式,然后将B 点坐标代入,即可求出二次函数的解析式;(2)根据函数解析式,令x=0,可求得抛物线与y轴的交点坐标;令y=0,可求得抛物线与x轴交点坐标;(3)由(2)可知:抛物线与x轴的交点分别在原点两侧,由此可求出当抛物线与x轴负半轴的交点平移到原点时,抛物线平移的单位,由此可求出A′、B′的坐标.由于△OA′B′不规则,可用面积割补法求出△OA′B′的面积.【详解】(1)设抛物线顶点式y=a(x+1)2+4,将B(2,﹣5)代入得:a=﹣1,∴该函数的解析式为:y=﹣(x+1)2+4=﹣x2﹣2x+3;(2)令x=0,得y=3,因此抛物线与y轴的交点为:(0,3),令y=0,﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,即抛物线与x轴的交点为:(﹣3,0),(1,0);(3)设抛物线与x轴的交点为M、N(M在N的左侧),由(2)知:M(﹣3,0),N(1,0),当函数图象向右平移经过原点时,M与O重合,因此抛物线向右平移了3个单位,故A'(2,4),B'(5,﹣5),∴S△OA′B′=12×(2+5)×9﹣12×2×4﹣12×5×5=15.【点睛】本题考查了用待定系数法求抛物线解析式、函数图象与坐标轴交点、图形面积的求法等知识.熟练掌握待定系数法、函数图象与坐标轴的交点的求解方法、不规则图形的面积的求解方法等是解题的关键.4.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.(1)求抛物线的解析式和直线AC的解析式;(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.【答案】(1)抛物线解析式为y=﹣x2+2x+3;直线AC的解析式为y=3x+3;(2)点M的坐标为(0,3);(3)符合条件的点P的坐标为(73,209)或(103,﹣139),【解析】分析:(1)设交点式y=a(x+1)(x-3),展开得到-2a=2,然后求出a即可得到抛物线解析式;再确定C(0,3),然后利用待定系数法求直线AC的解析式;(2)利用二次函数的性质确定D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(-3,0),利用两点之间线段最短可判断此时MB+MD的值最小,则此时△BDM的周长最小,然后求出直线DB′的解析式即可得到点M的坐标;(3)过点C作AC的垂线交抛物线于另一点P,如图2,利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b,把C点坐标代入求出b得到直线PC的解析式为y=-13x+3,再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩==得此时P点坐标;当过点A作AC的垂线交抛物线于另一点P时,利用同样的方法可求出此时P点坐标.详解:(1)设抛物线解析式为y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,∴﹣2a=2,解得a=﹣1,∴抛物线解析式为y=﹣x2+2x+3;当x=0时,y=﹣x2+2x+3=3,则C(0,3),设直线AC的解析式为y=px+q,把A(﹣1,0),C(0,3)代入得3p qq-+=⎧⎨=⎩,解得33pq=⎧⎨=⎩,∴直线AC的解析式为y=3x+3;(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(﹣3,0),∵MB=MB′,∴MB+MD=MB′+MD=DB′,此时MB+MD的值最小,而BD的值不变,∴此时△BDM的周长最小,易得直线DB′的解析式为y=x+3,当x=0时,y=x+3=3,∴点M的坐标为(0,3);(3)存在.过点C作AC的垂线交抛物线于另一点P,如图2,∵直线AC的解析式为y=3x+3,∴直线PC的解析式可设为y=﹣13x+b,把C(0,3)代入得b=3,∴直线PC的解析式为y=﹣13x+3,解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩==,解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩,则此时P点坐标为(73,209);过点A作AC的垂线交抛物线于另一点P,直线PC的解析式可设为y=﹣x+b,把A(﹣1,0)代入得13+b=0,解得b=﹣13,∴直线PC的解析式为y=﹣13x﹣13,解方程组2231133y x x y x ⎧-++⎪⎨--⎪⎩==,解得10x y =-⎧⎨=⎩或103139x y ⎧=⎪⎪⎨⎪=-⎪⎩,则此时P 点坐标为(103,﹣139). 综上所述,符合条件的点P 的坐标为(73,209)或(103,﹣139). 点睛:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式,理解两直线垂直时一次项系数的关系,通过解方程组求把两函数的交点坐标;理解坐标与图形性质,会运用两点之间线段最短解决最短路径问题;会运用分类讨论的思想解决数学问题.5.如图1,在平面直角坐标系中,直线AB :y =kx +b (k <0,b >0),与x 轴交于点A 、与y 轴交于点B ,直线CD 与x 轴交于点C 、与y 轴交于点D .若直线CD 的解析式为y =﹣1k(x +b ),则称直线CD 为直线AB 的”姊线”,经过点A 、B 、C 的抛物线称为直线AB 的“母线”.(1)若直线AB 的解析式为:y =﹣3x +6,求AB 的”姊线”CD 的解析式为: (直接填空);(2)若直线AB 的”母线”解析式为:2142y x x =-+,求AB 的”姊线”CD 的解析式; (3)如图2,在(2)的条件下,点P 为第二象限”母线”上的动点,连接OP ,交”姊线”CD 于点Q ,设点P 的横坐标为m ,PQ 与OQ 的比值为y ,求y 与m 的函数关系式,并求y 的最大值;(4)如图3,若AB 的解析式为:y =mx +3(m <0),AB 的“姊线”为CD ,点G 为AB 的中点,点H 为CD 的中点,连接OH ,若GH =5,请直接写出AB 的”母线”的函数解析式.【答案】(1)1(6)3y x =+;(2)(2,0)、(0,4)、(﹣4,0);(3)当m =﹣32,y 最大值为338;(4)y =x 2﹣2x ﹣3.【解析】【分析】(1)由k ,b 的值以及”姊线”的定义即可求解;(2)令x =0,得y 值,令y =0,得x 值,即可求得点A 、B 、C 的坐标,从而求得直线CD 的表达式;(3)设点P 的横坐标为m ,则点P (m ,n ),n =﹣12m 2﹣m+4, 从而求得直线OP 的表达式,将直线OP 和CD 表达式联立并解得点Q 坐标, 由此求得P Q y y ,从而求得y =﹣12m 2﹣32m+3,故当m =﹣32,y 最大值为338; (4)由直线AB 的解析式可得AB 的“姊线”CD 的表达式y =﹣1m(x+3),令x =0,得 y 值,令y =0,得x 值,可得点C 、D 的坐标,由此可得点H 坐标,同理可得点G 坐标, 由勾股定理得:m 值,即可求得点A 、B 、C 的坐标,从而得到 “母线”函数的表达式.【详解】(1)由题意得:k =﹣3,b =6, 则答案为:y =13(x+6); (2)令x =0,则y =4,令y =0,则x =2或﹣4,点A 、B 、C 的坐标分别为(2,0)、(0,4)、(﹣4,0),则直线CD 的表达式为:y =12(x+4)=12x+2; (3)设点P 的横坐标为m ,则点P (m ,n ),n =﹣12m 2﹣m+4, 则直线OP 的表达式为:y =n mx , 将直线OP 和CD 表达式联立得122n y x m y x ⎧=⎪⎪⎨⎪=+⎪⎩, 解得:点Q (2438m m m --+,222838m m m m +-+-) 则P Q y y =﹣12m 2﹣32m+4, y =1P Q P Q Q y y y PQ OQ y y -==-=﹣12m 2﹣32m+3, 当m =﹣32,y 最大值为338;(4)直线CD的表达式为:y=﹣1m(x+3),令x=0,则y=﹣3m,令y=0,则x=﹣3,故点C、D的坐标为(﹣3,0)、(0,﹣3m),则点H(﹣32,﹣32m),同理可得:点G(﹣32m,32),则GH2=(32+32m)2+(32﹣32m)2=(5)2,解得:m=﹣3(正值已舍去),则点A、B、C的坐标分别为(1,0)、(0,3)、(﹣3,0),则“母线”函数的表达式为:y=a(x﹣1)(x+3)=a(x2﹣2x﹣3),即:﹣3a=﹣3,解得:a=1,故:“母线”函数的表达式为:y=x2﹣2x﹣3.【点睛】此题是二次函数综合题目,考查了“姊线”的定义,待定系数法求二次函数解析式,二次函数的最值问题,掌握二次函数的有关性质是解答此题的关键.6.如图,抛物线y=ax2+bx过点B(1,﹣3),对称轴是直线x=2,且抛物线与x轴的正半轴交于点A.(1)求抛物线的解析式,并根据图象直接写出当y≤0时,自变量x的取值范围;(2)在第二象限内的抛物线上有一点P,当PA⊥BA时,求△PAB的面积.【答案】(1)抛物线的解析式为y=x2﹣4x,自变量x的取值范图是0≤x≤4;(2)△PAB的面积=15.【解析】【分析】(1)将函数图象经过的点B坐标代入的函数的解析式中,再和对称轴方程联立求出待定系数a和b;(2)如图,过点B作BE⊥x轴,垂足为点E,过点P作PE⊥x轴,垂足为F,设P(x,x2-4x),证明△PFA∽△AEB,求出点P的坐标,将△PAB的面积构造成长方形去掉三个三角形的面积.【详解】(1)由题意得,322a b b a+-⎧⎪⎨-⎪⎩==,解得14a b -⎧⎨⎩==,∴抛物线的解析式为y=x 2-4x , 令y=0,得x 2-2x=0,解得x=0或4, 结合图象知,A 的坐标为(4,0),根据图象开口向上,则y≤0时,自变量x 的取值范围是0≤x≤4;(2)如图,过点B 作BE ⊥x 轴,垂足为点E ,过点P 作PE ⊥x 轴,垂足为F ,设P (x ,x 2-4x ), ∵PA ⊥BA ∴∠PAF+∠BAE=90°, ∵∠PAF+∠FPA=90°, ∴∠FPA=∠BAE 又∠PFA=∠AEB=90° ∴△PFA ∽△AEB,∴PF AF AE BE =,即244213x x x--=-, 解得,x= −1,x=4(舍去) ∴x 2-4x=-5∴点P 的坐标为(-1,-5),又∵B 点坐标为(1,-3),易得到BP 直线为y=-4x+1 所以BP 与x 轴交点为(14,0) ∴S △PAB=115531524⨯⨯+= 【点睛】本题是二次函数综合题,求出函数解析式是解题的关键,特别是利用待定系数法将两条直线表达式解出,利用点的坐标求三角形的面积是关键.7.如图,直线y=﹣x+分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+经过A,B两点.(1)求A、B两点的坐标;(2)求抛物线的解析式;(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC 于点D,求△DMH周长的最大值.【答案】(1)(﹣1,0)(2)y=﹣x2+x+(3)【解析】试题分析:(1)由直线解析式可求得B、C坐标,在Rt△BOC中由三角函数定义可求得∠OCB=60°,则在Rt△AOC中可得∠ACO=30°,利用三角函数的定义可求得OA,则可求得A点坐标;(2)由A、B两点坐标,利用待定系数法可求得抛物线解析式;(3)由平行线的性质可知∠MDH=∠BCO=60°,在Rt△DMH中利用三角函数的定义可得到DH、MH与DM的关系,可设出M点的坐标,则可表示出DM的长,从而可表示出△DMH 的周长,利用二次函数的性质可求得其最大值.试题解析:(1)∵直线y=﹣x+分别与x轴、y轴交于B、C两点,∴B(3,0),C(0,),∴OB=3,OC=,∴tan∠BCO==,∴∠BCO=60°,∵∠ACB=90°,∴∠ACO=30°,∴=tan30°=,即=,解得AO=1,∴A(﹣1,0);(2)∵抛物线y=ax2+bx+经过A,B两点,∴,解得,∴抛物线解析式为y=﹣x2+x+;(3)∵MD∥y轴,MH⊥BC,∴∠MDH=∠BCO=60°,则∠DMH=30°,∴DH=DM,MH=DM,∴△DMH的周长=DM+DH+MH=DM+DM+DM=DM,∴当DM有最大值时,其周长有最大值,∵点M是直线BC上方抛物线上的一点,∴可设M(t,﹣t2+t+),则D(t,﹣t+),∴DM=﹣t2+t+),则D(t,﹣t+),∴DM=﹣t2+t+﹣(﹣t+)=﹣t2+t=﹣(t﹣)2+,∴当t=时,DM有最大值,最大值为,此时DM=×=,即△DMH周长的最大值为.考点:1、二次函数的综合应用,2、待定系数法,3、三角函数的定义,4方程思想8.(本小题满分12分)如图,在平面直角坐标系xOy中,抛物线()与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为,求a的值;(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.【答案】(1)A(-1,0),;(2);(3)P的坐标为(1,)或(1,-4).【解析】试题分析:(1)在中,令y=0,得到,,得到A(-1,0),B(3,0),由直线l经过点A,得到,故,令,即,由于CD=4AC,故点D的横坐标为4,即有,得到,从而得出直线l的函数表达式;(2)过点E作EF∥y轴,交直线l于点F,设E(,),则F(,),EF==,S△ACE=S△AFE-S△CFE==,故△ACE的面积的最大值为,而△ACE的面积的最大值为,所以,解得;(3)令,即,解得,,得到D (4,5a),因为抛物线的对称轴为,设P(1,m),然后分两种情况讨论:①若AD是矩形的一条边,②若AD是矩形的一条对角线.试题解析:(1)∵=,令y=0,得到,,∴A(-1,0),B(3,0),∵直线l经过点A,∴,,∴,令,即,∵CD=4AC,∴点D的横坐标为4,∴,∴,∴直线l的函数表达式为;(2)过点E作EF∥y轴,交直线l于点F,设E(,),则F(,),EF==,S△ACE=S△AFE-S△CFE===,∴△ACE的面积的最大值为,∵△ACE的面积的最大值为,∴,解得;(3)令,即,解得,,∴D(4,5a),∵,∴抛物线的对称轴为,设P(1,m),①若AD是矩形的一条边,则Q(-4,21a),m=21a+5a=26a,则P(1,26a),∵四边形ADPQ为矩形,∴∠ADP=90°,∴,∴,即,∵,∴,∴P1(1,);②若AD是矩形的一条对角线,则线段AD的中点坐标为(,),Q(2,),m =,则P(1,8a),∵四边形APDQ为矩形,∴∠APD=90°,∴,∴,即,∵,∴,∴P2(1,-4).综上所述,以点A、D、P、Q为顶点的四边形能成为矩形,点P的坐标为(1,)或(1,-4).考点:二次函数综合题.9.如图,直线y=﹣3x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c与直线y=c 分别交y轴的正半轴于点C和第一象限的点P,连接PB,得△PCB≌△BOA(O为坐标原点).若抛物线与x轴正半轴交点为点F,设M是点C,F间抛物线上的一点(包括端点),其横坐标为m.(1)直接写出点P的坐标和抛物线的解析式;(2)当m 为何值时,△MAB 面积S 取得最小值和最大值?请说明理由; (3)求满足∠MPO=∠POA 的点M 的坐标.【答案】(1)点P 的坐标为(3,4),抛物线的解析式为y=﹣x 2+3x+4;(2)当m=0时,S 取最小值,最小值为12;当m=3时,S 取最大值,最大值为5.(3)满足∠MPO=∠POA 的点M 的坐标为(0,4)或(247,12449).【解析】【分析】(1)代入y=c 可求出点C 、P 的坐标,利用一次函数图象上点的坐标特征可求出点A 、B 的坐标,再由△PCB ≌△BOA 即可得出b 、c 的值,进而可得出点P 的坐标及抛物线的解析式;(2)利用二次函数图象上点的坐标特征求出点F 的坐标,过点M 作ME ∥y 轴,交直线AB 于点E ,由点M 的横坐标可得出点M 、E 的坐标,进而可得出ME 的长度,再利用三角形的面积公式可找出S=﹣12(m ﹣3)2+5,由m 的取值范围结合二次函数的性质即可求出S 的最大值及最小值;(3)分两种情况考虑:①当点M 在线段OP 上方时,由CP ∥x 轴利用平行线的性质可得出:当点C 、M 重合时,∠MPO=∠POA ,由此可找出点M 的坐标;②当点M 在线段OP 下方时,在x 正半轴取点D ,连接DP ,使得DO=DP ,此时∠DPO=∠POA ,设点D 的坐标为(n ,0),则DO=n ,()()22304n -+-DO=DP 可求出n 的值,进而可得出点D 的坐标,由点P 、D 的坐标利用待定系数法即可求出直线PD 的解析式,再联立直线PD 及抛物线的解析式成方程组,通过解方程组求出点M 的坐标.综上此题得解. 【详解】(1)当y=c 时,有c=﹣x 2+bx+c , 解得:x 1=0,x 2=b ,∴点C 的坐标为(0,c ),点P 的坐标为(b ,c ), ∵直线y=﹣3x+3与x 轴、y 轴分别交于A 、B 两点, ∴点A 的坐标为(1,0),点B 的坐标为(0,3), ∴OB=3,OA=1,BC=c ﹣3,CP=b , ∵△PCB ≌△BOA ,∴BC=OA ,CP=OB , ∴b=3,c=4,∴点P 的坐标为(3,4),抛物线的解析式为y=﹣x 2+3x+4; (2)当y=0时,有﹣x 2+3x+4=0, 解得:x 1=﹣1,x 2=4, ∴点F 的坐标为(4,0),过点M 作ME ∥y 轴,交直线AB 于点E ,如图1所示, ∵点M 的横坐标为m (0≤m≤4),∴点M 的坐标为(m ,﹣m 2+3m+4),点E 的坐标为(m ,﹣3m+3), ∴ME=﹣m 2+3m+4﹣(﹣3m+3)=﹣m 2+6m+1, ∴S=12OA•ME=﹣12m 2+3m+12=﹣12(m ﹣3)2+5, ∵﹣12<0,0≤m≤4, ∴当m=0时,S 取最小值,最小值为12;当m=3时,S 取最大值,最大值为5; (3)①当点M 在线段OP 上方时,∵CP ∥x 轴, ∴当点C 、M 重合时,∠MPO=∠POA , ∴点M 的坐标为(0,4);②当点M 在线段OP 下方时,在x 正半轴取点D ,连接DP ,使得DO=DP ,此时∠DPO=∠POA ,设点D 的坐标为(n ,0),则DO=n ,∴n 2=(n ﹣3)2+16, 解得:n=256, ∴点D 的坐标为(256,0), 设直线PD 的解析式为y=kx+a (k≠0), 将P (3,4)、D (256,0)代入y=kx+a , 342506k a k a +=⎧⎪⎨+=⎪⎩,解得:2471007k a ⎧=-⎪⎪⎨⎪=⎪⎩, ∴直线PD 的解析式为y=﹣247x+1007, 联立直线PD 及抛物线的解析式成方程组,得:2241007734y x y x x ⎧=+⎪⎨⎪=-++⎩﹣,解得:1134x y =⎧⎨=⎩,2224712449x y ⎧=⎪⎪⎨⎪=⎪⎩.∴点M 的坐标为(247,12449). 综上所述:满足∠MPO=∠POA 的点M 的坐标为(0,4)或(247,12449).【点睛】本题考查了待定系数法求一次函数解析式、一次(二次)函数图象上点的坐标特征、全等三角形的性质、二次函数的性质、三角形的面积以及等腰三角形的性质,解题的关键是:(1)利用全等三角形的性质求出b 、c 的值;(2)利用三角形的面积公式找出S=﹣(m ﹣3)2+5;(3)分点M 在线段OP 上方和点M 在线段OP 下方两种情况求出点M 的坐标.10.如图,已知抛物线2y ax bx c =++(a≠0)经过A (﹣1,0)、B (3,0)、C (0,﹣3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P 是直线l 上的一个动点,当点P 到点A 、点B 的距离之和最短时,求点P 的坐标;(3)点M 也是直线l 上的动点,且△MAC 为等腰三角形,请直接写出所有符合条件的点M 的坐标.【答案】(1)223y x x =--;(2)P (1,0);(3).【解析】试题分析:(1)直接将A 、B 、C 三点坐标代入抛物线的解析式中求出待定系数即可; (2)由图知:A .B 点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知,直线l 与x 轴的交点,即为符合条件的P 点;(3)由于△MAC 的腰和底没有明确,因此要分三种情况来讨论:①MA=AC 、②MA=MC 、③AC=MC ;可先设出M 点的坐标,然后用M 点纵坐标表示△MAC 的三边长,再按上面的三种情况列式求解.试题解析:(1)将A (﹣1,0)、B (3,0)、C (0,﹣3)代入抛物线2y ax bx c=++中,得:0{9303a b c a b c c -+=++==-,解得:1{23a b c ==-=-,故抛物线的解析式:223y x x =--.(2)当P 点在x 轴上,P ,A ,B 三点在一条直线上时,点P 到点A 、点B 的距离之和最短,此时x=2b a -=1,故P (1,0); (3)如图所示:抛物线的对称轴为:x=2b a -=1,设M (1,m ),已知A (﹣1,0)、C (0,﹣3),则:2MA =24m +,2MC =2(3)1m ++=2610m m ++,2AC =10;①若MA=MC ,则22MA MC =,得:24m +=2610m m ++,解得:m=﹣1; ②若MA=AC ,则22MA AC =,得:24m +=10,得:m=6±;③若MC=AC ,则22MC AC =,得:2610m m ++=10,得:10m =,26m =-; 当m=﹣6时,M 、A 、C 三点共线,构不成三角形,不合题意,故舍去;综上可知,符合条件的M 点,且坐标为 M (1,6)(1,6-)(1,﹣1)(1,0).考点:二次函数综合题;分类讨论;综合题;动点型.。
上海市中考数学压轴题专项训练(含答案)

上海市20XX 年中考数学压轴题专项训练1.(本题满分12分,第(1)小题满分3分,第(2)小题满分4分,第(3)小题满分5分)如图,已知抛物线2y x bx c =++经过()01A -,、()43B -,两点. (1)求抛物线的解析式; (2 求tan ABO ∠的值;(3)过点B 作BC ⊥x 轴,垂足为点C ,点M 是抛物线上一点,直线MN 平行于y 轴交直线AB 于点N ,如果M 、N 、B 、C 为顶点的四边形是平行四边形,求点N 的坐标.1.解:(1)将A (0,-1)、B (4,-3)分别代入2y x bx c =++得1,1643c b c =-⎧⎨++=-⎩, ………………………………………………………………(1分)解,得9,12b c =-=-…………………………………………………………………(1分) 所以抛物线的解析式为2912y x x =--……………………………………………(1分)(2)过点B 作BC ⊥x 轴,垂足为C ,过点A 作AH ⊥OB ,垂足为点H ………(1分)在Rt AOH ∆中,OA =1,4sin sin ,5AOH OBC ∠=∠=……………………………(1分) ∴4sin 5AH OA AOH =∠=,∴322,55OH BH OB OH ==-=, ………………(1分)在Rt ABH ∆中,4222tan 5511AH ABO BH ∠==÷=………………………………(1分) (3)直线AB 的解析式为112y x =--, ……………………………………………(1分)设点M 的坐标为29(,1)2m m m --,点N 坐标为1(,1)2m m --那么MN =2291(1)(1)422m m m m m -----=-; …………………………(1分)∵M 、N 、B 、C 为顶点的四边形是平行四边形,∴MN =BC =3解方程24m m -=3得2m = ……………………………………………(1分) 解方程243m m -+=得1m =或3m =; ………………………………………(1分)所以符合题意的点N 有4个35(22),(22),(1,),(3,)22---- ……………………………………………………………………………………(1分)2.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)在Rt △ABC 中,∠ACB = 90°,经过点B 的直线l (l 不与直线AB 重合)与直线BC 的夹角等于∠ABC ,分别过点C 、点A 作直线l 的垂线,垂足分别为点D 、点E .(1)如图1,当点E 与点B 重合时,若AE =4,判断以C 点为圆心CD 长为半径的圆C 与直线AB 的位置关系并说明理由;(2)如图2,当点E 在DB 延长线上时,求证:AE =2CD ;(3)记直线CE 与直线AB 相交于点F ,若56CF EF =,CD = 4,求BD 的长.2.解:(1)过点C 作CF ⊥AB ,垂足为点F. ……………………………………………(1分) ∵∠AED =90°,∠ABC =∠CBD ,∴∠ABC =∠CBD =45°,∵∠ACB =90°,∠ABC =45°,AE =4,∴CF =2,BC =1分) 又∵∠CBD =∠ABC =45°,CD ⊥l ,∴CD =2, …………………………………………(1分) ∴CD =CF =2,∴圆C 与直线AB 相切.……………………………………………………(1分) (2)证明:延长AC 交直线l 于点G . ………………………………………………(1分) ∵∠ACB = 90°,∠ABC =∠GBC ,∴∠BAC =∠BGC .∴AB = GB .…………………………………………………………………………………(1分) ∴AC = GC .…………………………………………………………………………………(1分) ∵AE ⊥l ,CD ⊥l ,∴AE ∥CD .A CDB (E )l(第25题图1)(第25题图2)ACD ElB∴12CD GC AE GA ==. …………………………………………………………………………(1分) ∴AE = 2CD . ………………………………………………………………………………(1分) (3)(I )如图1,当点E 在DB 延长线上时:过点C 作CG ∥l 交AB 于点H ,交AE 于点G ,则∠CBD =∠HCB . ∵∠ABC =∠CBD ,∴∠ABC =∠HCB .∴CH = BH .………(1分) ∵∠ACB = 90°,∴∠ABC +∠BAC =∠HCB +∠HCA = 90°. ∴∠BAC =∠HCA .∴CH = AH = BH .∵CG ∥l ,∴56CH CF BE EF ==. 设CH = 5x ,则BE = 6x ,AB = 10x .在Rt △ABE 中,8AE x ==.由(2)知AE = 2CD = 8,∴88x =,得1x =. ∴CH = 5,BE = 6,AB = 10.∵CG ∥l ,∴12HG AH BE AB ==,∴HG =3.……………………(1分) ∴CG = CH + HG = 8.易证四边形CDEG 是矩形,∴DE = CG = 8.∴2BD DE BE =-=.…………………………………………(1分) (II )如图2,当点E 在DB 上时:同理可得CH = 5,BE = 6,HG = 3.…………………………(1分) ∴2DE CG CH HG ==-=.∴BD =DE + BE = 8.…………………………………………………………………………(1分) 综上所述,BD 的长为2或8.3.已知点A (2,﹣2)和点B (﹣4,n )在抛物线y=ax 2(a ≠0)上. (1)求a 的值及点B 的坐标;(2)点P 在y 轴上,且△ABP 是以AB 为直角边的三角形,求点P 的坐标;(3)将抛物线y=ax 2(a ≠0)向右并向下平移,记平移后点A 的对应点为A ′,点B 的对应点为B ′,若四边形ABB ′A ′为正方形,求此时抛物线的表达式.(第25题图1)A CD ElGBHF B(第25题图2)A CD lGE HF【考点】二次函数图象上点的坐标特征;坐标与图形变化-平移.【分析】(1)把点A(2,﹣2)代入y=ax2,得到a,再把点B代入抛物线解析式即可解决问题.(2)求出直线AB解析式,再分别求出过点A垂直于AB的直线的解析式,过点B垂直于直线AB的解析式即可解决问题.(3)先求出点A′坐标,确定是如何平移的,再确定抛物线顶点的坐标即可解决问题.【解答】解:(1)把点A(2,﹣2)代入y=ax2,得到a=﹣,∴抛物线为y=﹣x2,∴x=﹣4时,y=﹣8,∴点B坐标(﹣4,﹣8),∴a=﹣,点B坐标(﹣4,﹣8).(2)设直线AB为y=kx+b,则有,解得,∴直线AB为y=x﹣4,∴过点B垂直AB的直线为y=﹣x﹣12,与y轴交于点P(0,﹣12),过点A垂直AB的直线为y=﹣x,与y轴交于点P′(0,0),∴点P在y轴上,且△ABP是以AB为直角边的三角形时.点P坐标为(0,0),或(0,﹣12).(3)如图四边形ABB′A′是正方形,过点A作y轴的垂线,过点B、点A′作x轴的垂线得到点E、F.∵直线AB解析式为y=﹣x﹣12,∴△ABF,△AA′E都是等腰直角三角形,∵AB=AA′==6,∴AE=A′E=6,∴点A′坐标为(8,﹣8),∴点A到点A′是向右平移6个单位,向下平移6个单位得到,∴抛物线y=﹣x2的顶点(0,0),向右平移6个单位,向下平移6个单位得到(6,﹣6),∴此时抛物线为y=﹣(x﹣6)2﹣6.4.已知,AB=5,tan∠ABM=,点C、D、E为动点,其中点C、D在射线BM上(点C在点D的左侧),点E和点D分别在射线BA的两侧,且AC=AD,AB=AE,∠CAD=∠BAE.(1)当点C与点B重合时(如图1),联结ED,求ED的长;(2)当EA∥BM时(如图2),求四边形AEBD的面积;(3)联结CE,当△ACE是等腰三角形时,求点B、C间的距离.【考点】三角形综合题.【分析】(1)如图1中,延长BA交DE于F,作AH⊥BD于H,先证明BF⊥DE,EF=DF,再利用△ABH∽△DBF,得=,求出DF即可解决问题.=BD•AH,计算即可.(2)先证明四边形ADBE是平行四边形,根据S平行四边形ADBE(3)由题意AC≠AE,EC≠AC,只有EA=EC,利用四点共圆先证明四边形ADBE是平行四边形,求出DH、CH即可解决问题.【解答】解:(1)如图1中,延长BA交DE于F,作AH⊥BD于H.在RT△ABH中,∵∠AHB=90°,∴sin∠ABH==,∴AH=3,BH==4,∵AB=AD,AH⊥BD,∴BH=DH=4,在△ABE 和△ABD中,,∴△ABD≌△ABE,∴BE=BD,∠ABE=∠ABD,∴BF⊥DE,EF=DF,∵∠ABH=∠DBF,∠AHB=∠BFD,∴△ABH∽△DBF,∴=,∴DF=,∴DE=2DF=.(2)如图2中,作AH⊥BD于H.∵AC=AD,AB=AE,∠CAD=∠BAE,∴∠AEB=∠ABE=∠ACD=∠ADC,∵AE∥BD,∴∠AEB+∠EBD=180°,∴∠EBD+∠ADC=180°,∴EB∥AD,∵AE∥BD,∴四边形ADBE是平行四边形,∴BD=AE=AB=5,AH=3,=BD•AH=15.∴S平行四边形ADBE(3)由题意AC≠AE,EC≠AC,只有EA=EC.如图3中,∵∠ACD=∠AEB(已证),∴A、C、B、E四点共圆,∵AE=EC=AB,∴=,∴=,∴∠AEC=∠ABC,∴AE∥BD,由(2)可知四边形ADBE是平行四边形,∴AE=BD=AB=5,∵AH=3,BH=4,∴DH=BD﹣BH=1,∵AC=AD,AH⊥CD,∴CH=HD=1,∴BC=BD﹣CD=3.5.如图,已知二次函数y=x2+bx+c图象顶点为C,与直线y=x+m图象交于AB两点,其中A点的坐标为(3,4),B点在y轴上.(1)求这个二次函数的解析式;(2)联结AC,求∠BAC的正切值;(3)点P为直线AB上一点,若△ACP为直角三角形,求点P的坐标.【分析】(1)先把A点坐标代入y=x+m求出m得到直线AB的解析式为y=x+1,这可求出直线与y轴的交点B的坐标,然后把A点和B点坐标代入y=x2+bx+c中得到关于b、c的方程组,再解方程组求出b、c即可得到抛物线解析式;(2)如图,先抛物线解析式配成顶点式得到C(1,0),再利用两点间的距离公式计算出BC2=2,AB2=18,AC2=20,然后利用勾股定理的逆定理可证明△ABC为直角三角形,∠ACB=90°,于是利用正切的定义计算tan∠BAC的值;(3)分类讨论:当∠APC=90°时,有(2)得点P在B点处,此时P点坐标为(0,1);当∠ACP=90°时,利用(2)中结论得tan∠PAC==,则PC=AC,设P(t,t+1),然后利用两点间的距离公式得到方程t2+(t+1﹣1)2=20,再解方程求出t即可得到时P点坐标.【解答】解:(1)把A(3,4)代入y=x+m得3+m=4,解得m=1∴直线AB的解析式为y=x+1,∵当x=0时,y=x+1=1,∴B(0,1),把B(0,1),A(3,4)代入y=x2+bx+c得,解得,∴抛物线解析式为y=x2﹣2x+1;(2)如图,∵y=x2﹣2x+1=(x﹣1)2,∴C(1,0),∴BC2=12+12=2,AB2=32+(4﹣1)2=18,AC2=(3﹣1)2+42=20,而2+18=20,∴BC2+AB2=AC2,∴△ABC为直角三角形,∠ACB=90°,∴tan∠BAC===;(3)当∠APC=90°时,点P在B点处,此时P点坐标为(0,1);当∠ACP=90°时,∵tan∠PAC==,∴PC=AC,设P(t,t+1),∴t2+(t+1﹣1)2=20,解得t1=﹣,t2=(舍去),此时P点坐标为(﹣,﹣ +1),综上所述,满足条件的P点坐标为(0,1)或(﹣,﹣ +1).【点评】本题考查了二次函数的综合题:熟练掌握二次函数的性质和一次函数图象上点的坐标特征;能运用待定系数法求二次函数解析式;理解坐标与图形性质,记住两点间的距离公式;能利用勾股定理的逆定理证明直角三角形.6.如图,▱ABCD中,AB=8,AD=10,sinA=,E、F分别是边AB、BC上动点(点E不与A、B重合),且∠EDF=∠DAB,DF延长线交射线AB于G.(1)若DE⊥AB时,求DE的长度;(2)设AE=x,BG=y,求y关于x的函数解析式,并写出函数的定义域;(3)当△BGF为等腰三角形时,求AE的长度.【分析】(1)DE⊥AB时,根据sinA=即可解决问题.(2)如图2中,作DM⊥AB于M,根据DG2=DM2+MG2=AGEG,列出等式即可解决问题.(3)分三种情形①BF=BG,②FB=FG,③GB=GF,根据BF∥AD,得出比例式,列方程即可解决.【解答】解:(1)如图1中,∵DE⊥AB,∴sinA==,∵AD=10,∴DE=8.(2)如图2中,作DM⊥AB于M,由(1)可知DM=8,AM=6,MG=AB﹣AM=8﹣6=2,∴DG2=DM2+MG2,∵∠DGE=∠DGA,∠GDE=∠A,∴△DGE∽△AGD,∴=,∴DG2=AGEG,∴DM2+MG2=AGEG,∴82+(2+y)2=(8+y)(8+y﹣x),∴y=(0<x<8)(3)①当BF=FG时,∵BF∥AD,∴=,∴AD=AG=10,∴y=2,即=2,解得x=2,∴AE=2.②当FB=FG时,∵BF∥AD,∴=,∴AD=DG=10,∵DM⊥AG,∴AM=MB=6,∴AG=12,∴y=4,即=4,解得x=.③当GB=GF时,∵BF∥AD,∠GBF=∠BFG,∴∠A=∠GBF,∠ADG=∠BFG,∴∠A=∠ADG,∵∠A=∠EDG,∴∠EDG=∠ADG,∴此时点E与点A重合,不合题意.综上所述AE=2或时,△BFG是等腰三角形.【点评】本题考查四边形综合题、锐角三角函数、相似三角形的判定和性质、平行线分线段成比例定理、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,学会用方程的思想解决问题,属于中考常考题型.。
上海市中考数学压轴题

题目一:某班级有40名学生,其中男生占总人数的3/8。
在这40名学生中,有20人喜欢足球,15人喜欢篮球,10人既喜欢足球又喜欢篮球。
请回答以下问题:1. 该班级男生人数有多少人?2. 喜欢足球但不喜欢篮球的学生有多少人?3. 喜欢篮球的女生有多少人?解答:1. 该班级男生人数= 总人数×男生占比= 40 ×(3/8) = 15人。
2. 喜欢足球但不喜欢篮球的学生= 喜欢足球的学生- 既喜欢足球又喜欢篮球的学生= 20 - 10 = 10人。
3. 喜欢篮球的女生= 喜欢篮球的学生- 既喜欢足球又喜欢篮球的学生= 15 - 10 = 5人。
题目二:在某次数学考试中,小明得到了80分,这个分数在班级中排名第10。
班级共有50名学生参加考试。
请回答以下问题:1. 班级中有多少名学生得到了小明相同的分数?2. 小明超过了班级中多少名学生?解答:1. 班级中得到了小明相同分数的学生人数= 排名-1 = 10 - 1 = 9人。
2. 小明超过了班级中的学生数量= 总人数- 排名+ 1 = 50 - 10 + 1 = 41人。
题目三:在某次数学考试中,小明得到了80分,这个分数在班级中排名第10。
班级共有50名学生参加考试。
请回答以下问题:1. 班级中有多少名学生得到了小明相同的分数?2. 小明超过了班级中多少百分比的学生?解答:1. 班级中得到了小明相同分数的学生人数= 排名-1 = 10 - 1 = 9人。
2. 小明超过了班级中的学生百分比= (总人数- 排名+ 1) / 总人数×100% = (50 - 10 + 1) / 50 ×100% ≈82%。
因此,小明超过了班级中约82%的学生。
上海市2008年—2014年中考数学压轴题图文解析

满分解答
(1)如图 2,过点 A 作 AH⊥BC,垂足为 H.
4 ,所以 BH=4,AH=3. 5 又已知 BC=8,由于 BH=4,所以点 A 在 BC 的垂直平分线上. 所以 CA=BA=5 . 如图 3,当圆 C 经过点 A 时,CP=CA =5.
在 Rt△ABH 中,AB=5 ,cosB=
图2 图3 (2)如图 4,当 AP//CG 时,由于 AE//BC,CP=CE ,所以四边形 AECP 是菱形,边长 为圆的半径 r. 过点 C 作 CQ⊥AD,垂足为 Q. 在 Rt△CEQ 中, CQ=3 ,CE= r, EQ=4-r,由勾股定理,
1 1 8 4 S△BDP= BP DE (t 3) (t 3) , 2 2 3 3
如图 6,过点 D 作 x 轴的平行线交 y 轴于 M,过点 P 作 y 轴的平行线,设两条直线交于 点 N.
8 1 4 由于 S 矩形 OMNP= t ,S△OCP=t,S△OCP= ,S△PND= (t 1) , 3 3 3 8 1 4 4 所以 S△CDP= t t (t 1) t 1 . 3 3 3 3 4 1 解方程 (t 3) t 1 ,得 t=5. 3 3
华东师大出版社荣誉出品 《挑战中考数学压轴题》系列产品·2
上海市 2008 年—2014 年中考数学压轴题图文解析
例1 例2 例3 例4 例5 例6 例7 例8 例9 例 10 例 11 例 12 例 12 2014 年上海市中考第 24 题 / 2 2014 年上海市中考第 25 题 / 4 2013 年上海市中考第 24 题 / 6 2013 年上海市中考第 25 题 / 8 2012 年上海市中考第 24 题 / 10 2012 年上海市中考第 25 题 / 12 2011 年上海市中考第 24 题 / 14 2011 年上海市中考第 25 题 / 16 2010 年上海市中考第 24 题 / 18 2010 年上海市中考第 25 题 / 19 2009 年上海市中考第 24 题 / 21 2009 年上海市中考第 25 题 / 23 2008 年上海市中考第 25 题 / 25
2020-2021上海中考数学压轴题专题复习——相似的综合

2020-2021上海中考数学压轴题专题复习——相似的综合一、相似1.已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.(1)若∠AOB=60°,AB∥x轴,AB=2,求a的值;(2)若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;(3)延长AD、BO相交于点E,求证:DE=CO.【答案】(1)解:如图1,∵抛物线y=ax2的对称轴是y轴,且AB∥x轴,∴A与B是对称点,O是抛物线的顶点,∴OA=OB,∵∠AOB=60°,∴△AOB是等边三角形,∵AB=2,AB⊥OC,∴AC=BC=1,∠BOC=30°,∴OC= ,∴A(-1,),把A(-1,)代入抛物线y=ax2(a>0)中得:a= ;(2)解:如图2,过B作BE⊥x轴于E,过A作AG⊥BE,交BE延长线于点G,交y轴于F,∵CF∥BG,∴,∵AC=4BC,∴ =4,∴AF=4FG,∵A的横坐标为-4,∴B的横坐标为1,∴A(-4,16a),B(1,a),∵∠AOB=90°,∴∠AOD+∠BOE=90°,∵∠AOD+∠DAO=90°,∴∠BOE=∠DAO,∵∠ADO=∠OEB=90°,∴△ADO∽△OEB,∴,∴,∴16a2=4,a=± ,∵a>0,∴a= ;∴B(1,);(3)解:如图3,设AC=nBC,由(2)同理可知:A的横坐标是B的横坐标的n倍,则设B(m,am2),则A(-mn,am2n2),∴AD=am2n2,过B作BF⊥x轴于F,∴DE∥BF,∴△BOF∽△EOD,∴,∴,∴,DE=am2n,∴,∵OC∥AE,∴△BCO∽△BAE,∴,∴,∴CO= =am2n,∴DE=CO.【解析】【分析】(1)抛物线y=ax2关于y轴对称,根据AB∥x轴,得出A与B是对称点,可知AC=BC=1,由∠AOB=60°,可证得△AOB是等边三角形,利用解直角三角形求出OC的长,就可得出点A的坐标,利用待定系数法就可求出a的值。
沪科版九年级数学中考复习:一次函数的综合应用压轴题(含答案)

沪科版九年级数学中考复习:一次函数的综合应用压轴题(含答案)1.甲、乙两家商场平时以同样价格出售相同的商品.新冠疫情期间,为了减少库存,甲、乙两家商场打折促销.甲商场所有商品按9折出售,乙商场对一次购物中超过100元后的价格部分打8折.(1) 以x(元)表示商品原价,y(元)表示实际购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;(2) 新冠疫情期间如何选择这两家商场去购物更省钱?2.某水果市场销售一种香蕉.甲店的香蕉价格为4元/千克;乙店的香蕉价格为5元/千克,若一次购买6千克以上,超过6千克部分的价格打7折.(1) 设购买香蕉x千克,付款金额为y元,分别就两店的付款金额写出y关于x的函数解析式.(2) 到哪家店购买香蕉更省钱?请说明理由.3. 某校举办“创建全国文明城市”知识竞赛,计划购买甲、乙两种奖品共30件.其中甲种奖品每件30元,乙种奖品每件20元.(1) 如果购买甲、乙两种奖品共花费800元,那么这两种奖品分别购买了多少件?(2) 若购买乙种奖品的件数不超过甲种奖品件数的3倍,如何购买甲、乙两种奖品,使得总花费最少?4. 随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,则今年的销售总额将比去年减少10%.(1) 求A型自行车去年每辆售价多少元.(2) 该车行今年计划新进一批A型自行车和新款B型自行车共60辆,且B 型自行车的进货数量不超过A型自行车数量的两倍.已知A型自行车和B型自行车的进货价格分别为1 500元和1 800元,计划B型自行车的销售价格为2 400元,应如何组织进货才能使这批自行车销售获利最多?5. 有一块矩形地块ABCD,AB=20米,BC=30米.为美观,拟种植不同的花卉,如图所示,将矩形ABCD分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形AEHD和BCGF中种植甲种花卉;在等腰梯形ABFE 和CDHG中种植乙种花卉;在矩形EFGH中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米2、60元/米2、40元/米2,设三种花卉的种植总成本为y元.(1) 当x=5时,求种植总成本y;(2) 求种植总成本y与x的函数解析式,并写出自变量x的取值范围;(3) 若甲、乙两种花卉的种植面积之差不超过120平方米,求三种花卉的最低种植总成本.6. 众志成城抗疫情,全国人民在行动.某公司决定安排大、小货车共20辆,运送260吨物资到A地和B地,支援当地抗击疫情.每辆大货车装15吨物资,每辆小货车装10吨物资,这20辆货车恰好装完这批物资.已知这两种货车的运费如下表:现安排上述装好物资的20辆货车(每辆大货车装15吨物资,每辆小货车装10吨物资)中的10辆前往A地,其余前往B地,设前往A地的大货车有x辆,这20辆货车的总运费为y元.(1) 这20辆货车中,大货车、小货车各有多少辆?(2) 求y与x的函数解析式,并直接写出x的取值范围.(3) 若运往A地的物资不少于140吨,求总运费y的最小值7. 为了抗击新冠疫情,某市甲、乙两厂积极生产了某种防疫物资共500吨,乙厂的生产量比甲厂的2倍少100吨.这批防疫物资将运往A地240吨,B地260吨,运费如下表(单位:元/吨).(1) 求甲、乙两厂各生产了这批防疫物资多少吨.(2) 设这批物资从乙厂运往A地x吨,全部运往A,B两地的总运费为y元.求y与x之间的函数解析式,并设计使总运费最少的调运方案.(3) 当每吨运费均降低m元(0<m≤15且m为整数)时,按(2)中设计的调运方案运输,总运费不超过5 200元.求m的最小值.8. 推进农村土地集约式管理,提高土地的使用效率是新农村建设的一项重要举措.某村在小城镇建设中集约了2 400亩土地,计划对其进行平整.经投标,由甲、乙两个工程队来完成平整任务.甲工程队每天可平整土地45亩,乙工程队每天可平整土地30亩.已知乙工程队每天的工程费比甲工程队少500元,当甲工程队所需工程费为12 000元,乙工程队所需工程费为9 000元时,两工程队工作天数刚好相同.(1) 甲、乙两个工程队每天各需工程费多少元?(2) 现由甲、乙两个工程队共同参与土地平整,已知两个工程队工作天数均为正整数,且所有土地刚好平整完,总费用不超过110 000元.①甲、乙两工程队分别工作的天数共有多少种可能?②写出其中费用最少的一种方案,并求出最少费用.9. 天水市某商店准备购进A,B两种商品,A种商品每件的进价比B种商品每件的进价贵20元,用2 000元购进A种商品和用1 200元购进B种商品的数量相同.商店将A种商品每件的售价定为80元,B种商品每件的售价定为45元.(1) A种商品每件的进价和B种商品每件的进价各是多少元?(2) 商店计划用不超过1 560元的资金购进A,B两种商品共40件,其中A 种商品的数量不低于B种商品数量的一半,该商店有几种进货方案?(3) “五一”期间,商店开展优惠促销活动,决定对每件A种商品售价优惠m(10<m<20)元,B种商品售价不变,在(2)的条件下,请设计出m的不同取值范围内,销售这40件商品获得总利润最大的进货方案.10. 倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出A型和B型两款垃圾分拣机器人,已知2台A型机器人和5台B 型机器人同时工作2 h共分拣垃圾3.6吨,3台A型机器人和2台B型机器人同时工作5 h共分拣垃圾8吨.(1) 1台A型机器人和1台B型机器人每小时各分拣垃圾多少吨?(2) 某垃圾处理厂计划向机器人公司购进一批A型和B型垃圾分拣机器人,这批机器人每小时一共能分拣垃圾20吨.设购买A型机器人a台(10≤a≤45),B 型机器人b台,请用含a的代数式表示b.(3) 机器人公司的报价如下表:在(2)的条件下,设购买总费用为w万元,问如何购买使得总费用w最少?请说明理由.11. 甲、乙两地的路程为290 km,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后,按原速继续前进,当离甲地路程为240 km时接到通知,要求中午12:00准时到达乙地.设汽车出发x h后离甲地的路程为y km,如图,折线OCDE表示接到通知前y与x之间的函数关系.(1) 根据图象可知,休息前汽车行驶的速度为______km/h.(2) 求线段DE所表示的y与x之间的函数解析式.(3) 接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.12. “低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地匀速步行前往乙地,同时,小明从乙地沿同一路线匀速步行前往甲地,两人之间的距离y(m)与步行时间x(min)之间的函数关系如图中折线段AB-BC-CD所示.(1) 小丽与小明出发________min相遇.(2) 在步行过程中,若小明先到达甲地.①求小丽和小明步行的速度;②计算出点C的坐标,并解释点C的实际意义.13. 某商店代理销售一种水果,六月份的销售利润y(元)与销售量x(千克)之间函数关系的图象如图中折线所示.请你根据图象及这种水果的相关销售记录提供的信息,解答下面的问题:(1) 截止到6月9日,该商店销售这种水果一共获利多少元?(2) 求图象中线段BC所在直线对应的函数解析式.14. 受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援”,某水果经销商主动从该种植专业户购进甲、乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元/千克的价格出售.设经销商购进甲种水果x千克,付款y元,y与x之间的函数关系如图所示.(1) 直接写出当0≤x≤50和x>50时,y与x之间的函数解析式.(2) 若经销商计划一次性购进甲、乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲、乙两种水果的购进量,才能使经销商付款总金额w(元)最少?(3) 若甲、乙两种水果的销售价格分别为40元/千克和36元/千克.经销商按(2)中甲、乙两种水果购进量的分配比例购进两种水果共a千克,且销售完a 千克水果获得的利润不少于1 650元,求a的最小值.答案1.甲、乙两家商场平时以同样价格出售相同的商品.新冠疫情期间,为了减少库存,甲、乙两家商场打折促销.甲商场所有商品按9折出售,乙商场对一次购物中超过100元后的价格部分打8折.(1) 以x(元)表示商品原价,y(元)表示实际购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;(2) 新冠疫情期间如何选择这两家商场去购物更省钱?解:(1) 由题意,得y甲=0.9x;当0<x≤100时,y乙=x,当x>100时,y乙=100+(x-100)×0.8=0.8x+20,∴y乙={x(0<x≤100),0.8x+20(x>100)(2) 当0<x≤100时,0.9x<x,即y甲<y乙,此时选择甲商场购物更省钱;当x>100时:若0.9x<0.8x+20,即100<x<200时,y甲<y乙,此时选择甲商场购物更省钱;若0.9x=0.8x+20,即x=200时,y甲=y乙,此时在两家商场购物花费一样;若0.9x>0.8x+200,即x>200时,y甲>y乙,此时选择乙商场购物更省钱.综上所述,当0<x<200时,选择甲商场购物更省钱;当x=200时,在两家商场购物花费一样;当x>200时,选择乙商场购物更省钱2.某水果市场销售一种香蕉.甲店的香蕉价格为4元/千克;乙店的香蕉价格为5元/千克,若一次购买6千克以上,超过6千克部分的价格打7折.(1) 设购买香蕉x千克,付款金额为y元,分别就两店的付款金额写出y关于x的函数解析式.(2) 到哪家店购买香蕉更省钱?请说明理由.解:(1) y甲=4x;当0<x≤6时,y乙=5x,当x>6时,y乙=5×6+5×70%(x-6)=3.5x+9,∴y乙={5x(0<x≤6),3.5x+9(x>6)(2) 当0<x≤6时,4x<5x,即y甲<y乙,此时到甲店购买香蕉更省钱;当x>6时:①若4x<3.5x+9,即6<x<18时,y甲<y乙,此时到甲店购买香蕉更省钱;②若4x=3.5x+9,即x=18时,y甲=y乙,此时到甲店、乙店购买香蕉的费用相同;③若4x>3.5x+9,即x>18时,y甲>y乙,此时到乙店购买香蕉更省钱.综上所述,当0<x<18时,到乙店购买香蕉更省钱;当x=18时,到甲店、乙店购买香蕉的费用相同;当x>18时,到乙店购买香蕉更省钱3. 某校举办“创建全国文明城市”知识竞赛,计划购买甲、乙两种奖品共30件.其中甲种奖品每件30元,乙种奖品每件20元.(1) 如果购买甲、乙两种奖品共花费800元,那么这两种奖品分别购买了多少件?(2) 若购买乙种奖品的件数不超过甲种奖品件数的3倍,如何购买甲、乙两种奖品,使得总花费最少?解:(1) 设甲种奖品购买了x件,则乙种奖品购买了(30-x)件.根据题意,得30x +20(30-x)=800,解得x=20,此时30-x=10.答:甲种奖品购买了20件,乙种奖品购买了10件(2) 设甲种奖品购买了y件,乙种奖品购买了(30-y)件.设购买两种奖品的总费用为w 元,则w =30y +20(30-y)=10y +600.根据题意,得 30-y ≤3y ,解得y ≥7.5.在w =10y +600中,∵ 10>0,∴ w 随y 的增大而增大.∴ y =8时,w 有最小值,此时30-y =22,w 最小=10×8+600=680.答:当购买甲种奖品8件、乙种奖品22件时,总花费最少,最少费用为680元4. 随着人们“节能环保,绿色出行”意识的增强,越来越 多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A 型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,则今年的销售总额将比去年减少10%.(1) 求A 型自行车去年每辆售价多少元.(2) 该车行今年计划新进一批A 型自行车和新款B 型自行车共60辆,且B 型自行车的进货数量不超过A 型自行车数量的两倍.已知A 型自行车和B 型自行车的进货价格分别为1 500元和1 800元,计划B 型自行车的销售价格为2 400元,应如何组织进货才能使这批自行车销售获利最多?解:(1) 设去年A 型自行车每辆售价x 元,则今年售价每辆为(x -200)元.由题意,得80 000x =80 000(1−10%)x−200,解得x =2 000.经检验,x =2 000是原方程的根,且符合题意.答:去年A 型自行车每辆售价为2 000元(2) 设今年新进A 型自行车a 辆,则新进B 型自行车(60-a)辆,获利y 元.由题意,得y =(2 000-200-1 500)a +(2 400-1 800)(60-a)=-300a +36 000.∵ B 型自行车的进货数量不超过A 型自行车数量的两倍,∴ 60-a ≤2a ,解得a ≥20.在y =-300a +36 000中,∵ k =-300<0,∴ y 随a 的增大而减小.∴ 当a =20时,y 有最大值,此时60-a =40.答:当新进A 型自行车20辆,B 型自行车40辆时,这批自行车销售获利最多5. 有一块矩形地块ABCD ,AB =20米,BC =30米.为美观,拟种植不同的花卉,如图所示,将矩形ABCD 分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x 米.现决定在等腰梯形AEHD 和BCGF 中种植甲种花卉;在等腰梯形ABFE 和CDHG 中种植乙种花卉;在矩形EFGH 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米2、60元/米2、40元/米2,设三种花卉的种植总成本为y 元.(1) 当x =5时,求种植总成本y ;(2) 求种植总成本y 与x 的函数解析式,并写出自变量x 的取值范围;(3) 若甲、乙两种花卉的种植面积之差不超过120平方米,求三种花卉的最低种植总成本.解:(1) 当x =5时,EF =20-2x =10米,EH =30-2x =20米,∴ y =2×12(EH +AD)x ×20+2×12(GH +CD)x ×60+EF ·EH ×40=(20+30)×5×20+(10+20)×5×60+20×10×40=22 000(元)(2) ∵ EF =(20-2x)米,EH =(30-2x)米,∴ y =2×12(30+30-2x)x ×20+2×12(20+20-2x)x ×60+(30-2x)(20-2x)×40=-400x +24 000(0<x <10)(3) S 甲=2×12(EH +AD)×x =(30-2x +30)x =-2x 2+60x ,同理S 乙=-2x 2+40x.∵ 甲、乙两种花卉的种植面积之差不超过120平方米,∴ -2x 2+60x -(-2x 2+40x)≤120,解得x ≤6.∴ 0<x ≤6.在y =-400x +24 000中,∵ -400<0,∴ y 随x 的增大而减小.∴ 当x =6时,y 的最小值为21 600.答:三种花卉的最低种植总成本为21 600元6. 众志成城抗疫情,全国人民在行动.某公司决定安排大、小货车共20辆,运送260吨物资到A 地和B 地,支援当地抗击疫情.每辆大货车装15吨物资,每辆小货车装10吨物资,这20辆货车恰好装完这批物资.已知这两种货车的运费如下表:现安排上述装好物资的20辆货车(每辆大货车装15吨物资,每辆小货车装10吨物资)中的10辆前往A 地,其余前往B 地,设前往A 地的大货车有x 辆,这20辆货车的总运费为y 元.(1) 这20辆货车中,大货车、小货车各有多少辆?(2) 求y 与x 的函数解析式,并直接写出x 的取值范围.(3) 若运往A 地的物资不少于140吨,求总运费y 的最小值解:(1) 设大货车有m 辆,则小货车有(20-m)辆.根据题意,得15m +10(20-m)=260,解得m =12,此时20-m =8.答:大货车、小货车分别有12辆、8辆(2) ∵ 到A 地的大货车有x 辆,∴ 到A 地的小货车有(10-x)辆,到B 地的大货车有(12-x)辆,到B 地的小货车有(x -2)辆.∴ y =900x +500(10-x)+1 000(12-x)+700(x -2)=100x +15 600,其中2≤x ≤10(3) 根据题意,得运往A 地的物资共有[15x +10(10-x)]吨,∴ 15x +10(10-x)≥140,解得x ≥8.∴ 8≤x ≤10.在y =100x +15 600中,∵ 100>0,∴ y 随x 的增大而增大.∴ 当x =8时,y 有最小值,此时y 最小=100×8+15 600=16 400.答:总运费y 的最小值为16 400元7. 为了抗击新冠疫情,某市甲、乙两厂积极生产了某种防疫物资共500吨,乙厂的生产量比甲厂的2倍少100吨.这批防疫物资将运往A 地240吨,B 地260吨,运费如下表(单位:元/吨).(1) 求甲、乙两厂各生产了这批防疫物资多少吨.(2) 设这批物资从乙厂运往A 地x 吨,全部运往A ,B 两地的总运费为 y 元.求y 与x 之间的函数解析式,并设计使总运费最少的调运方案.(3) 当每吨运费均降低m 元(0<m ≤15且m 为整数)时,按(2)中设计的调运方案运输,总运费不超过5 200元.求m 的最小值.解:(1) 设这批防疫物资甲厂生产了a 吨,乙厂生产了b 吨.根据题意,得{a +b =500,2a −b =100,解得{a =200,b =300.答:这批防疫物资甲厂生产了200吨,乙厂生产了300吨(2) 根据题意,得y =20(240-x)+25[260-(300-x)]+15x +24(300-x)=-4x +11 000.∵ { x ≥0,240−x ≥0,300−x ≥0,x −40≥0,解得40≤x ≤240.在 y =-4x +11 000中,∵ -4<0,∴ y 随x 的增大而减小.∴ 当x =240时,可以使总运费最少,此时调运方案为甲厂的200吨物资全部运往B 地,乙厂运往A 地240吨,运往B 地60吨(3) 根据题意和(2)的解答,得y =-4x +11 000-500m.当x =240时,y 最小=-4×240+11 000-500m =10 040-500m ,∴ 10 040-500m ≤5 200,解得m ≥9.68.∵ 0<m ≤15且m 为整数,∴ m 的最小值为108. 推进农村土地集约式管理,提高土地的使用效率是新农村建设的一项重要举措.某村在小城镇建设中集约了2 400亩土地,计划对其进行平整.经投标,由甲、乙两个工程队来完成平整任务.甲工程队每天可平整土地45亩,乙工程队每天可平整土地30亩.已知乙工程队每天的工程费比甲工程队少500元,当甲工程队所需工程费为12 000元,乙工程队所需工程费为9 000元时,两工程队工作天数刚好相同.(1) 甲、乙两个工程队每天各需工程费多少元?(2) 现由甲、乙两个工程队共同参与土地平整,已知两个工程队工作天数均为正整数,且所有土地刚好平整完,总费用不超过110 000元.① 甲、乙两工程队分别工作的天数共有多少种可能?② 写出其中费用最少的一种方案,并求出最少费用.解:(1) 设甲工程队每天需工程费x 元,则乙工程队每天需工程费(x -500)元.由题意,得12 000x =9 000x−500,解得x =2 000. 经检验,x = 2 000是原方程的解,且符合题意,则x -500=1 500.答:甲工程队每天需工程费2 000元,乙工程队每天需工程费1 500元(2) ① 设甲工程队平整m 天,乙工程队平整n 天.由题意,得45m +30n =2 400①,且2 000m +1 500n ≤110 000②.由①,得n =80-1.5m ③,把③代入②,得2 000m +1 500(80-1.5m)≤110 000,解得m ≥40.∵ n >0,∴ 80-1.5m >0,解得m <5313.∴ 40≤m <5313. ∵ m ,n 是正整数,∴ m =40,n =20或m =42,n =17或m =44,n =14或m =46,n =11或m =48,n =8或m =50,n =5或m =52,n =2.∴ 甲、乙两工程队分别工作的天数共有7种可能② 总费用w =2 000m +1 500(80-1.5m)=-250m +120 000.∵-250<0,∴ w 随m 的增大而减小.∴ 当m =52时,w 有最小值,此时n =2,w 最小=-250×52+120 000=107 000.答:费用最少的方案为甲工程队平整52天,乙工程队平整2天,最少费用为107 000元9. 天水市某商店准备购进A ,B 两种商品,A 种商品每件的进价比B 种商品每件的进价贵20元,用2 000元购进A 种商品和用1 200元购进B 种商品的数量相同.商店将A 种商品每件的售价定为80元,B 种商品每件的售价定为45元.(1) A 种商品每件的进价和B 种商品每件的进价各是多少元?(2) 商店计划用不超过1 560元的资金购进A ,B 两种商品共40件,其中A 种商品的数量不低于B 种商品数量的一半,该商店有几种进货方案?(3) “五一”期间,商店开展优惠促销活动,决定对每件A 种商品售价优惠m(10<m <20)元,B 种商品售价不变,在(2)的条件下,请设计出m 的不同取值范围内,销售这40件商品获得总利润最大的进货方案.解:(1) 设A 种商品每件的进价是x 元,则B 种商品每件的进价是(x -20)元.由题意,得2 000x =1 200x−20,解得x =50. 经检验,x =50是原方程的解,且符合题意,此时x -20=30.答:A 种商品每件的进价是50元,B 种商品每件的进价是30元(2) 设购进A 种商品a 件,则购进B 种商品(40-a)件.由题意,得{50a +30(40−a )≤1 560,a ≥12(40−a ),解得403≤a ≤18.∵ a 为正整数,∴ a =14,15,16,17,18.∴ 该商店共有5种进货方案(3) 设销售A ,B 两种商品共获利y 元.由题意,得y =(80-50-m)a +(45-30)(40-a)=(15-m)a +600.① 当10<m <15时,15-m >0,y 随a 的增大而增大,∴ 当a =18时,获利最大,即方案为购进18件A 种商品,22件B 种商品;② 当m =15时,15-m =0, y 与a 的值无关,即第(2)问中所有进货方案获利相同;③ 当15<m <20时,15-m <0,y 随a 的增大而减小,∴ 当a =14时,获利最大,即方案为购进14件A 种商品,26件B 种商品10. 倡导垃圾分类,共享绿色生活.为了对回收的垃圾进行更精准的分类,某机器人公司研发出A 型和B 型两款垃圾分拣机器人,已知2台A 型机器人和5台B 型机器人同时工作2 h 共分拣垃圾3.6吨,3台A 型机器人和2台B 型机器人同时工作5 h 共分拣垃圾8吨.(1) 1台A型机器人和1台B型机器人每小时各分拣垃圾多少吨?(2) 某垃圾处理厂计划向机器人公司购进一批A型和B型垃圾分拣机器人,这批机器人每小时一共能分拣垃圾20吨.设购买A型机器人a台(10≤a≤45),B 型机器人b台,请用含a的代数式表示b.(3) 机器人公司的报价如下表:在(2)的条件下,设购买总费用为w万元,问如何购买使得总费用w最少?请说明理由.解:(1) 设1台A型机器人和1台B型机器人每小时各分拣垃圾x吨和y吨.由题意,得{(2x+5y)×2=3.6,(3x+2y)×5=8,解得{x=0.4,y=0.2.答:1台A型机器人和1台B型机器人每小时各分拣垃圾0.4吨和0.2吨(2) 由题意,得0.4a+0.2b=20,∴b=100-2a(10≤a≤45)(3) 选购A型机器人35台,B型机器人30台时,总费用w最少理由:①当10≤a<30时,40<b≤80,∴w=20×a+0.8×12(100-2a)=0.8a +960.∵0.8>0,∴当a=10时,w有最小值,w最小=968;②当30≤a≤35时,30≤b≤40,∴w=0.9×20a+0.8×12(100-2a)=-1.2a+960.∵-1.2<0,∴当a=35时,w有最小值,w最小=918;③当35<a≤45时,10≤b<30,∴w=0.9×20a+12(100-2a)=-6a+1 200.∵-6<0,∴当a=45时,w有最小值,w最小=930.∵918<930<968,∴选购A型机器人35台,B型机器人30台时,总费用w最少,此时需要918万元.11. 甲、乙两地的路程为290 km,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后,按原速继续前进,当离甲地路程为240 km时接到通知,要求中午12:00准时到达乙地.设汽车出发x h后离甲地的路程为y km,如图,折线OCDE表示接到通知前y与x之间的函数关系.(1) 根据图象可知,休息前汽车行驶的速度为______km/h.(2) 求线段DE所表示的y与x之间的函数解析式.(3) 接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.解:(1)80(2) 休息后按原速继续前进行驶的时间为(240-80)÷80=2(h),∴点E的坐标为(3.5,240).设线段DE所表示的y与x之间的函数解析式为y=kx+b(1.5≤x≤3.5),则{1.5k+b=80,3.5k+b=240,解得{k=80,b=−40,∴线段DE所表示的y与x之间的函数解析式为y=80x-40(1.5≤x≤3.5) (3) 不能理由:接到通知后,汽车仍按原速行驶,则全程所需时间为290÷80+0.5=4.125(h).∵12:00-8:00=4(h),4<4.125,∴接到通知后,汽车仍按原速行驶不能准时到达.12. )“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地匀速步行前往乙地,同时,小明从乙地沿同一路线匀速步行前往甲地,两人之间的距离y(m)与步行时间x(min)之间的函数关系如图中折线段AB-BC-CD所示.(1) 小丽与小明出发________min相遇.(2) 在步行过程中,若小明先到达甲地.①求小丽和小明步行的速度;②计算出点C的坐标,并解释点C的实际意义.解:(1)30(2) ①设小丽步行的速度为V1 m/min,小明步行的速度为V2 m/min,且V2>V1,则{30V1+30V2=5400,(67.5−30)V1=30V2,解得{V1=80,V2=100.答:小丽步行的速度为80 m/min,小明步行的速度为100 m/min②解法一:设点C的坐标为(x,y),则(100+80)(x-30)+80(67.5-x)=5 400,解得x=54,y=(100+80)×(54-30)=4 320. ∴点C的坐标为(54,4 320).解法二:5 400÷100=54(min),54×80=4 320(m),∴点C的坐标为(54,4 320).点C的实际意义:两人出发54 min时,小明到达甲地,此时两人相距4 320 m13. 某商店代理销售一种水果,六月份的销售利润y(元)与销售量x(千克)之间函数关系的图象如图中折线所示.请你根据图象及这种水果的相关销售记录提供的信息,解答下面的问题:(1) 截止到6月9日,该商店销售这种水果一共获利多少元?(2) 求图象中线段BC 所在直线对应的函数解析式.解:(1) 200×(10-8)=400(元).答:截止到6月9日,该商店销售这种水果一共获利400元(2) 设点B 的坐标为(a ,400).根据题意,得(10-8)×(600-a)+(10-8.5)×200=1 200-400,解得a =350,∴ 点B 的坐标为(350,400).设线段BC 所在直线对应的函数解析式为y =kx +b ,则{350k +b =400,800k +b =1 200,解得{k =169,b =−2 0009,∴ 线段BC 所在直线对应的函数解析式为y =169x -2 000914. 受新冠肺炎疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援”,某水果经销商主动从该种植专业户购进甲、乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按 25元/千克的价格出售.设经销商购进甲种水果x 千克,付款y 元,y 与x 之间的函数关系 如图所示.(1) 直接写出当0≤x ≤50和x >50时,y 与x 之间的函数解析式.(2) 若经销商计划一次性购进甲、乙两种水果共 100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲、乙两种水果的购进量,才能使经销商付款总金额w(元)最少?(3) 若甲、乙两种水果的销售价格分别为40元/千克和36元/千克.经销商按(2)中甲、乙两种水果购进量的分配比例购进两种水果共a 千克,且销售完a 千克水果获得的利润不 少于1 650元,求a 的最小值.解:(1) 当0≤x ≤50时,设y =tx ,根据题意,得50t =1 500,解得t =30,∴ y =30x ;当x >50时,设y =kx +b ,根据题意,得{50k +b =1 500,70k +b =1 980,解得{k =24,b =300,∴ y =24x +300.∴ y ={30x (0≤x ≤50),24x +300(x >50)(2) 设购进甲种水果a 千克,则购进乙种水果(100-a)千克,且40≤a ≤60.① 当40≤a ≤50时,w =30a +25(100-a)=5a +2 500.∵ 5>0,∴ w 随a 的增大而增大.∴ 当a =40 时,w 最小=2 700. ② 当50<a ≤60时,w =24a +300+25(100-a)=-a +2 800.∵ -1<0,∴ w 随a 的增大而减小.∴ 当a =60时,w 最小=2 740.∵ 2 740>2 700,∴ 当a =40时,付款总金额最少,最少付款总金额为2 700元.此时购进乙种水果100-40=60(千克).答:购进甲种水果40千克,购进乙种水果60千克,才能使经销商付款总金额w(元)最少(3) 由(2)可设购进甲种水果为25a 千克,购进乙种水果为35a 千克.当0≤25a ≤50,即0≤a ≤125时,由题意,得25a ×(40-30)+35a ×(36-25)≥1 650,解得a ≥8 25053.∵ 8 25053>125,与0≤a ≤125矛盾,舍去.当25a >50,即a >125时,由题意,得25a ×40-(24×25a +300)+35a ×(36-25)≥1 650,解得a ≥150.∵ 150>125,∴ 这种情况符合题意.∴ a 的最小值为150。
上海初三数学压轴题总结含答案

24.已知抛物线24y ax ax c =-+与y 轴交于点()0,3A ,点B 是抛物线上的点,且满足AB ∥x 轴,点C 是抛物线的顶点.(1)求抛物线的对称轴及B 点坐标;(2)若抛物线经过点()2,0-,求抛物线的表达式; (3)对(2)中的抛物线,点D 在线段AB 上,若以点A 、C 、D 为顶点的三角形与AOC ∆相似,试求点D 的坐标.五、(本题满分14分)25.如图,已知ABC ∆与BDE ∆都是等边三角形,点D 在边AC 上(不与A 、C 重合),DE 与AB 相交于点F .(1)求证:BCD ∆∽DAF ∆; (2)若1BC =,设CD x =,AF y =; ①求y 关于x 的函数解析式及定义域; ②当x 为何值时,79BEF BCD S S ∆∆=?(第24题图)A BCDE F(第25题图)24、(本题满分12分)如图,在平面直角坐标系中,直线AB:44y xa=+(a≠0)分别交x轴、y轴于B、A两点,直线AE分别交x轴、y轴于E、A两点,D是x轴上的一点,OA=OD,过点D作CD⊥x轴,交AE于C,连接BC,当动点B在线段OD上运动(不与点O点D重合)且AB⊥BC时(1)求证:△ABO∽△BCD;(2)求线段CD的长(用a的代数式表示);(3)若直线AE的方程是1316y x b=-+,求tan∠BAC的值.25、(本题满分14分)已知边长为4的正方形ABCD截去一个角后变为五边形ABCFE(如图),其中EF=cot∠DEF=12,(1)求线段DE、DF的长;(2)若P是线段EF上的一个动点,过P做PG⊥AB,PH⊥BC,设PG=x,四边形BHPG的面积为y,求y和x的函数关系式(写出定义域),并画出函数大致图像;2012年上海宝山区一模考试题25.(本题共3小题,4分+5分+3分,满分12分)我们知道,互相垂直且有公共原点的两条数轴构成平面直角坐标系.如果坐标系中两条坐标轴不垂直,那么这样的坐标系称为“斜坐标系”.如图9,P是斜坐标系xOy中的任意一点,与直角坐标系相类似,过点P分别作两坐标轴的平行线,与x轴、y轴交于点M、N,若M、N在x轴、y轴上分别对应实数a、b,则有序数对(a,b)叫做点P在斜坐标系xOy中的坐标.(1)如图10,已知斜坐标系xOy中,∠xOy=60°,试在该坐标系中作出点A(-2,2),并求点O、A之间的距离;(2)如图11,在斜坐标系xOy中,已知点B(4,0)、点C(0,3),P(x,y)是线段BC上的任意一点,试求x、y之间一定满足的一个等量关系式;(3)若问题(2)中的点P在线段BC的延长线上,其它条件都不变,试判断上述x、y之间的等量关系是否仍然成立,并说明理由.(图11)26.(本题共3小题,3分+6分+5分,满分14分)如图12,已知线段AB ,P 是线段AB 上任意一点(不与点A 、B 重合),分别以AP 、BP 为边,在AB 的同侧作等边△APD 和△BPC ,联结BD 与PC 交于点E ,联结CD . (1) 当BC ⊥CD 时,试求∠DBC 的正切值;(2) 若线段CD 是线段DE 和DB 的比例中项,试求这时PBAP 的值;(3) 记四边形ABCD 的面积为S ,当P 在线段AB 上运动时,S 与BD 2是否成正比例, 若成正比例,试求出比例系数;若不成正比例,试说明理由.2011学年第一学期期末考试九年级数学试卷(共4页,第4页)ABP(图12)ABP(备用图)2010奉贤区初三一模考试题24.(本题满分12分,第(1)小题6分,第(2)小题6分)如图,已知抛物线与x 轴交于点(20)A -,,(40)B ,(1)求抛物线的解析式及其顶点D 的坐标;(2)设直线CD 交x 轴于点E .在线段OB 存在点P ,使得点P 到直线CD 的距离等于点P 如果存在,求出点P25.(本题满分14分,第(1)小题3分,第(2)小题4分,第(3)小题7分)如图,直角梯形ABCD 中,AB ∥DC ,∠DAB =90°,AD =2DC =4,AB =6.动点M 以每秒1个单位长的速度,从点A 沿线段AB 向点B 运动;同时点P 以相同的速度,从点C 沿折线C -D -A 向点A 运动.当点M 到达点B 时,两点同时停止运动.过点M 作直线l ∥AD ,与折线A -C -B 的交点为Q .点M 运动的时间为t (秒).(1)当0.5t =时,求线段QM 的长;(2)点M 在线段AB 上运动时,是否可以使得以C 、P 、Q 为顶点的三角形为直角三角形,若可以,请直接写出t 的值(不需解题步骤);若不可以,请说明理由. (3)若△PCQ 的面积为y ,请求y 关于出t 的函数关系式及自变量的取值范围;Q A B CDlMP 第25题图AB CD(备用图1)ABCD(备用图2)2012卢湾区初三一模考试题答案24. 解(1)由题意得,42ax a-=-,∴对称轴为直线2x =;…………………(2分) ∵点()0,3A ,点B 是抛物线上的点,AB ∥x 轴,∴AB 被直线2x =垂直平分,∴()4,3B .………………………………………(1分)(2)∵抛物线经过点()0,3,()2,0-,所以有3,4830c a a =⎧⎨++=⎩,……………(2分)解得1,43.a c ⎧=-⎪⎨⎪=⎩,∴抛物线的表达式为2134y x x =-++.………………………(1分)(3)∵抛物线的对称轴为直线2x =,∴()2,4C ,…………………………(1分) 过点C 作CE y ⊥轴,垂足为点E ,设对称轴与AB 交于点F .……………(1分) ∵AB ∥x 轴,∴90CFA ∠=︒,∴CEO CFA ∠=∠,又∵2142CE OE ==,12CF AF =,∴CE CFOE AF=,∴EOC ∆∽FAC ∆,…………(1分) ∴AOC CAF ∠=∠,………………………………………………………………(1分)当AOC ∆∽DAC ∆时,有AO COAD AC=,∵3,AO CO AC ===,∴32AD =,∴3,32D ⎛⎫⎪⎝⎭;…………………(1分) 当AOC ∆∽CAD ∆时,有AO CO AC AD=, ∴103AD =,∴10,33D ⎛⎫⎪⎝⎭,………………………………………………………(1分) 综上所述满足条件的点D 的坐标为3,32⎛⎫ ⎪⎝⎭或10,33⎛⎫⎪⎝⎭.五、(本题满分14分) 25.(1)证明:∵ABC ∆与BDE ∆都是等边三角形,∴60A C BDE ∠=∠=∠=︒,……………………………………………………(1分) ∵ADF BDE C DBC ∠+∠=∠+∠,∴ADF DBC ∠=∠,……………………(2分) ∴BCD ∆∽DAF ∆.………………………………………………………………(1分) (2)∵BCD ∆∽DAF ∆,∴BC CDAD AF=,………………………………………(1分) ∵1BC =,设CD x =,AF y =,∴11xx y=-,………………………………(1分)∴()201y x x x =-<<.……………………………………………………………(2分) (3)解法一:∵ABC ∆与BDE ∆都是等边三角形,∴60E C ∠=∠=︒,60EBD CBA ∠=∠=︒,∴EBF CBD ∠=∠,…………(1分)∴EBF ∆∽CBD ∆,∴BE BFBC BD=,……………………………………………(1分) ∵BE BD =,1BC =,∴2BE BF =,……………………………………………(1分)∵EBF ∆∽CBD ∆,79BEF BCD S S ∆∆=,∴2279BEF BCD S BE S BC ∆∆==, ……………………(1分) ∴279BE BF ==,∴29AF =,…………………………………………………(1分) ∴229x x -=,解得1221,33x x ==,∴当13x =或23时,79BEF BCD S S ∆∆=.…………(1分)解法二:∵△ABC 与BDE ∆都是等边三角形,∴60E C ∠=∠=︒,60EBD CBA ∠=∠=︒,∴EBF CBD ∠=∠,…………(1分)∴EBF ∆∽CBD ∆,∵79BEF BCD S S ∆∆=,∴2279BEF BCD S BE S BC ∆∆==,……………………(1分) ∵1BC =,BE BD =,∴279BD =. ……………………………………………(1分) 过点B 作BH AC ⊥于点H ,……………………………………………………(1分)∵60C ∠=︒,∴BH =,∴16DH =,12CH =, 当点D 在线段CH 上时,111263CD CH DH =-=-=;………………………(1分)当点D 在线段CH 的延长线上时,112263CD CH DH =+=+=,……………(1分)综上所述,当13x =或23时,79BEF BCD S S ∆∆=2011金山区初三一模24、(1)∵CD ⊥BE ∴∠CDO =∠AOD =90°……………………………………(1分) ∴∠ABO +∠BAO =90°∵CB ⊥AB ∴∠ABO +∠CBD =90° ∴∠BAO=∠CBD …………………………………………………………………………(1分) ∴△ABO∽△BCD …………………………………………………………………………(1分) (2)∵A (0,4) B (﹣a ,0)(a <0) ∴AO=4BO=﹣a ……………………………………………………………………(2分) ∵△ABO ∽△BCD ∴CD BDOB AO=∵OD =AO =4, ∴BD =4+a …………………………………………………………(1分) ∴(4)4a a CD -+=(﹣4<a <0) ………………………………………………………(2分)(3)∵C (4,(4)4a a -+),b =4 ∴(4)1344416a a -+=-⨯+即:21243013a a a a ++==-=- ………………………………………………(2分)∵△ABO ∽△BCD ∴BC BDAB AO=在Rt △ABC 中,∠ABC =90° tan ∠BAC =44BC BD aAB AO +==当11a =-时,tan ∠BAC =34……………………………………………………………(1分) 当23a =-时,tan ∠BAC =14………………………………………………………(1分) 25、(1)∵四边形ABCD 是正方形,∴∠D =90° ∵cot ∠DEF =12DE DF =设DE =m ,则DF =2m ……………………………………………………………(1分) ∴222DE DF EF += ……………………………………………………………………(1分) 即255m = m = 1 ∴DE = 1 DF =2 ……………………………………………(2分) (2)延长GP 交DC 于M ∵PG ⊥AB ,PH ⊥BC∴GP ∥DA ∥BC ∴PH ∥BG ∴PM FMDE FD=……………………………………………………………………………(1分)∵PG =x ,GM =BC =4 PM =4-x FM =2(4-x ) ……………………………(1分) ∴PH=MC=CF+FM=10-2x ………………………………………………………(1分) ∴2(102)210y x x x x=-=-+(3≤x ≤4) ……………………………………………(2分) 画图正确 ……………………………………………………………………………(2分) (3)当23PG PH =时,即21023x x =- ∴207x =(不合题意舍去)…………………(1分) 当23PH PG =时,即10223x x -= ∴154x =…………………………………………(1分) 758y = …………………………………………………………………………………(1分)2012年上海宝山区一模考试题25. (1) 图(略) ----------------(1分)作AM ∥y 轴,AM 与x 轴交于点M ,AN ∥x 轴,AN 与y 轴交于点N ,则四边形AMON 为平行四边形,且OM=ON ,-----(1分)∴ AMON 是菱形,OM=AM ∴OA 平分∠MON ,又∠xOy =60°,∴ ∠MOA =60°,---------------(1分) ∴△MOA 是等边三角形, ∴ OA=OM =2 ----------------(1分) (2) 过点P 分别作两坐标轴的平行线,与x 轴、y 轴交于点M 、N ,----------------(1分) 则 PN=x ,PM=y ,----------------(1分) 由PN ∥OB ,得CBCP OB PN =,即CB CPx =4.--------------(1分) 由PM ∥OC ,得BCBP OC PM =,即BC BPy =3.------------(1分) ∴ 134=+=+BCBP CB CP y x .----------------(1分) 即1243=+y x .(3)当点P 在线段BC 的延长线上时,上述结论仍然成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海历年中考数学压轴题复习2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC ②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程).27.(1)①证明:∵ ∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴ ∠ABP =∠DPC .∵ 在梯形ABCD 中,AD ∥BC ,AB =CD ,∴ ∠A =∠D .∴ △ABP ∽△DPC .②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252xx -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴ DQ AP PD AB =.即yxx +=-252,得225212-+-=x x y ,1<x <4.②AP=2或AP=3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.图5图6图7 探究:设A、P两点间的距离为x.(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的定义域;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.(图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用)五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分)27.图1 图2 图3(1)解:PQ =PB ……………………(1分) 证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分) ∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB . (2)解法一由(1)△QNP ≌△PMB .得NQ =MP . ∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2. 得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2(1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1. 即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分)解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形.∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN .S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN …(2分)=CN 2=(1-x 22)2=21x 2-x 2+1 ∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形, 此时x =0 ……………………(1分) ②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3) ……………………(1分) 解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴ CQ =QN -CN =x 22-(1-x 22)=x 2-1. 当2-x =x 2-1时,得x =1. ……………………(1分) 解法二 此时∠CPQ =21∠PCN =22.5°,∠APB =90°-22.5°=67.5°, ∠ABP =180°-(45°+67.5°)=67.5°,得∠APB =∠ABP ,∴ AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD中,AB=1,弧AC是点B为圆心,AB长为半径的圆的一段弧。
点E是边AD上的任意一点(点E与点A、D不重合),过E作弧AC所在圆的切线,交边DC 于点F,G为切点:(1)当∠DEF=45º时,求证:点G为线段EF的中点;(2)设AE=x,FC=y,求y关于x的函数解析式,并写出函数的定义域;(3)将△DEF沿直线EF翻折后得△D1EF,如图,当EF=65时,讨论△AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由。
2004年上海市中考数学试卷27、(2004•上海)数学课上,老师提出:如图,在平面直角坐标系中,O为坐标原点,A点的坐标为(1,0),点B在x轴上,且在点A的右侧,AB=OA,过点A和B作x轴的垂线,分别交二次函数y=x2的图象于点C和D,直线OC交BD于点M,直线CD交y轴于点H,记点C、D的的横坐标分别为x C、x D,点H 的纵坐标为y H.同学发现两个结论:①S△CMD:S梯形ABMC=2:3 ②数值相等关系:x C•x D=﹣y H(1)请你验证结论①和结论②成立;(2)请你研究:如果上述框中的条件“A的坐标(1,0)”改为“A的坐标(t,0)(t>0)”,其他条件不变,结论①是否仍成立(请说明理由);(3)进一步研究:如果上述框中的条件“A的坐标(1,0)”改为“A的坐标(t,0)(t>0)”,又将条件“y=x2”改为“y=ax2(a>0)”,其他条件不变,那么x C、x D与y H有怎样的数值关系?(写出结果并说明理由)考点:二次函数综合题。
专题:压轴题。
分析:(1)可先根据AB=OA得出B点的坐标,然后根据抛物线的解析式和A,B的坐标得出C,D两点的坐标,再依据C点的坐标求出直线OC的解析式.进而可求出M点的坐标,然后根据C、D两点的坐标求出直线CD的解析式进而求出D点的坐标,然后可根据这些点的坐标进行求解即可;(2)(3)的解法同(1)完全一样.解答:解:(1)由已知可得点B的坐标为(2,0),点C坐标为(1,1),点D的坐标为(2,4),由点C坐标为(1,1)易得直线OC的函数解析式为y=x,故点M的坐标为(2,2),所以S △CMD =1,S 梯形ABMC =32所以S △CMD :S 梯形ABMC =2:3, 即结论①成立.设直线CD 的函数解析式为y=kx+b , 则{k +b =12k +b =4,解得{k =3b =﹣2所以直线CD 的函数解析式为y=3x ﹣2.由上述可得,点H 的坐标为(0,﹣2),y H =﹣2 因为x C •x D =2, 所以x C •x D =﹣y H , 即结论②成立; (2)(1)的结论仍然成立. 理由:当A 的坐标(t ,0)(t >0)时,点B 的坐标为(2t ,0),点C 坐标为(t ,t2),点D 的坐标为(2t ,4t2),由点C 坐标为(t ,t2)易得直线OC 的函数解析式为y=tx , 故点M 的坐标为(2t ,2t2), 所以S △CMD =t3,S 梯形ABMC =32t3. 所以S △CMD :S 梯形ABMC =2:3, 即结论①成立.设直线CD 的函数解析式为y=kx+b ,则{tk +b =t 22tk +b =4t 2,解得{k =3t b =﹣2t 2所以直线CD 的函数解析式为y=3tx ﹣2t 2; 由上述可得,点H 的坐标为(0,﹣2t2),y H =﹣2t 2 因为x C •x D =2t 2, 所以x C •x D =﹣y H , 即结论②成立;(3)由题意,当二次函数的解析式为y=ax 2(a >0),且点A 坐标为(t ,0)(t >0)时,点C 坐标为(t ,at 2),点D 坐标为(2t ,4at 2), 设直线CD 的解析式为y=kx+b ,则:{tk +b =at 22tk +b =4at 2,解得{k =3at b =﹣2at2所以直线CD 的函数解析式为y=3atx ﹣2at 2,则点H 的坐标为(0,﹣2at 2),y H =﹣2at 2. 因为x C •x D =2t 2, 所以x C •x D =﹣1a y H .点评:本题主要考查了二次函数的应用、一次函数解析式的确定、图形面积的求法、函数图象的交点等知识点.2005年上海市初中毕业生统一学业考试数学试卷1、 (本题满分12分,每小题满分各为4分)在△ABC 中,∠ABC =90°,AB =4,BC =3,O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D ,交线段OC 于点E ,作EP ⊥ED ,交射线AB 于点P ,交射线CB 于点F 。
(1) 如图8,求证:△ADE ∽△AEP ;(2) 设OA =x ,AP =y ,求y 关于x 的函数解析式,并写出它的定义域; (3) 当BF =1时,求线段AP 的长.25.1909090AP D ODA PED OD OE ODE OEDODE OED EDA PEA A A ADE AEP∴∠=∠=︒=∴∠=∠∴︒+∠=︒+∠∴∠=∠∠=∠∴∆∆()证明:连结OD切半圆于,又,,又22334,555846416584525555(0)OD CB OA AC OD OD x OE AD x x ADE AEP xAP AE y xy x y xAE AD x x x ==⇒===∆∆∴=⇒=⇒=⇒=>()同理可得:(3)5(46,90512661255E C x AP AB DO BE H DHE DJEHD x PBE PDH PFB PHD PB PB AP x x >>∆≅∆∴=∠=∠=︒∴∆∆∴=⇒=⇒=由题意可知存在三种情况但当在点左侧时BF显然大于4所以不合舍去当时如图)延长,交于易证J54,1261255422x P B DO PE H DHE EJD PBF PDHBP BP x x AP <∆≅∆∆∆∴=⇒=∴=-=当时点在点的右侧延长交于点同理可得2006 年上海市初中毕业生统一学业考试数学试卷25(本题满分14分,第(1)小题满分4分,第(2)小题满分7分,第(3)小题满分3分)已知点P 在线段AB 上,点O 在线段AB 的延长线上。
