2019-2020学年天津市第一中学高二上学期期中考试数学试题 (含答案)

合集下载

天津市第一中学2024-2025学年高二上学期期中质量调查数学试题

天津市第一中学2024-2025学年高二上学期期中质量调查数学试题一、单选题1．直线3260x y -+=在x 轴上的截距为（）A ．2B ．2-C ．3-D ．32．已知直线1l :70x my ++=和2l :()2320m x y m -++=互相平行,则A ．3m =-B ．1m =-C ．1m =或3m =D ．1m =-或3m =3．“4k >”是“方程22(2)50x y kx k y +++-+=表示圆的方程”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．若圆224x y +=与圆222210x y mx m +-+-=相外切，则实数m =（）A ．3-B ．3C ．3±D ．15．双曲线()22210y x b b-=>的渐近线方程是：y =±，则双曲线的焦距为（）A ．3B ．6C ．D 6．曲线221259x y +=与曲线221925x y k k+=--（9k <且0k ≠）的（）A ．长轴长相等B ．短轴长相等C ．焦距相等D ．离心率相等7．已知椭圆22221(0)x y a b a b+=>>与圆222x y c +=在第二象限的交点是P 点，()1,0F c -是椭圆的左焦点，O 为坐标原点，O 到直线1PF 的距离是2c ，则椭圆的离心率是（）A1B 1C D 8．已知12,F F 分别为椭圆22:19x E y +=的左、右焦点，P 是椭圆E 上一动点，G 点是三角形12PF F 的重心，则点G 的轨迹方程为（）A ．2291x y +=B ．2291(0)x y y +=≠C ．221819x y +=D ．221(0)819x y y +=≠9．已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ，圆M 的方程为222(5)2x y b -+=.若直线l 与圆M 切于点()4,1P ，与双曲线C 交于A ，B 两点，点P 恰好为AB 的中点，则双曲线C 的方程为（）A ．2214y x -=B ．2214x y -=C ．2212y x -=D ．2212x y -=10．若曲线2y x =+与曲线22:144x y C λ+=恰有两个不同的交点，则实数λ的取值范围是（）A ．(],1-∞-B ．[)1,+∞C ．(](),11,-∞-+∞ D ．()[),11,∞∞--⋃+二、填空题11．已知直线l 的一个方向向量的坐标是(-，则直线l 的倾斜角为．12．P 、Q 是椭圆C ：22143x y +=的动点，则PQ 的最大值为.13．如图，正方形内的图形来自中国古代的太极图.勤劳而充满智慧的我国古代劳动人民曾用太极图解释宇宙现象.太极图由正方形的内切圆(简称大圆)和两个互相外切且半径相等的圆(简称小圆)的半圆弧组成，两个小圆与大圆均内切.若正方形的边长为8，则以两个小圆的圆心(图中两个黑白点视为小圆的圆心)为焦点，正方形对角线所在直线为渐近线的双曲线实轴长是.14．若1F ，2F 是椭圆C ：22194x y +=的两个焦点，点P ，Q 为椭圆C 上关于坐标原点对称的两点，且12PQ F F =，则四边形12PFQF 的面积为．15．在平面直角坐标系中，()0,1A ，()0,2B ，若动点C 在直线y x =上，圆M 过A 、B 、C 三点，则圆M 的面积最小值为.16．已知双曲线2222:1(0,0)x y C a b a b-=>>的左焦点为F ，过点F 的直线与双曲线C 的左、右支分别交于点A 、B ，若OA ⊥AB ，4AB AF =，则该双曲线的离心率为.三、解答题17．在平面直角坐标系中，三个点(0,0),(2,0),(0,6)O A B -到直线l 的距离均为d ，且1d <．(1)求直线l 的方程；(2)若圆C 过点(1,0)，且圆心在x 轴的正半轴上，直线l 被该圆所截得的弦长为5，求圆C 的标准方程．18．已知椭圆C ：22221x y a b +=()0a b >>过点2322⎫⎪⎪⎝⎭，且离心率e =．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）设C 的左、右焦点分别为1F ，2F ，过点2F 作直线l 与椭圆C 交于A ，B 两点，1112AF BF ⋅= ，求1ABF 的面积．19．如图，在三棱锥111ABC A B C -中，1CC ⊥平面ABC ，12,90CC AC BC ACB ===∠=︒，D 是1CC 的中点.(1)求证：AC BD ⊥；(2)求平面1A BD 与平面ABC 所成锐二面角的余弦值；(3)在线段CD 上是否存在一点P ，使得BP 与平面1A BD 出CP 的长；若不存在，请说明理由20．已知椭圆2222:1(0)x y C a b a b +=>>的左、右焦点分别为1212,,2F F F F =，点M ⎭在椭圆C 上.(1)求椭圆C 的标准方程；(2)过点M 的直线l 与椭圆C 交于点A ，与y 轴交于点B .若AB BM =，求直线l 的斜率；(3)P 为椭圆C 上一点，射线12,PF PF 分别交椭圆C 于点,D E ，试问1212PF PF DF EF +是否为定值?若是，求出该定值；若不是，请说明理由.。

天津市第一中学2024-2025学年高一上学期数学学科期中质量调查试卷

天津市第一中学2024-2025学年高一上学期数学学科期中质量调查试卷一、单选题1．已知全集Z U =，集合{}Z 33A x x x =∈≤->或，()0,3B =，则()U A B ⋂=ð（）A ．()1,2B ．{}1,2,3C ．{}0,1,3D ．{}1,22．已知命题20001:,04∃∈-+≤p x x x R ，则命题p 的否定为（）A ．20001,04∃∈-+>x x x R B ．20001,04∃∈-+<x x x R C ．21,04∀∈-+≤x x x R D ．21,04x x x ∀∈-+>R 3．下列说法正确的是（）.A ．若a b >，则22a b >B ．若0a b >>，0c d <<，则a b d c>C ．若a b >，c d <，则a c b d +>+D ．若0a b >>，0c <，则b c ba c a->-4．不等式11ax x b +>+的解集为{1x x <-或}4x >，则01x abx +≥-的解集为（）A ．164x x ⎧⎫-≤<-⎨⎬⎩⎭B ．{}11x x -≤<C ．164x x ⎧⎫-≤≤-⎨⎬⎩⎭D ．114x x ⎧⎫-≤≤⎨⎬⎩⎭5．函数22()1xf x x =+的图象大致是（）A ．B ．C ．D ．6．命题“213R,022x x x a ∃∈+-<”为真命题的一个必要不充分条件是（）A ．0a ≥B ．1a ≥C ．2a >-D ．3a ≥-7．下列函数中，值域是()0,∞+的是（）A．y =B ．()2,0,1x y x x ∞+=∈++C ．21,21=∈++y x x x ND ．11y x =-8．已知函数()222,02,0x x x f x x x x ⎧+≥=⎨-<⎩，若()22()f m f m ->，则实数m 的取值范围是（）A ．(2,1)-B ．(,1)(2,)-∞-⋃+∞C ．(,2)(1,)-∞-+∞ D ．(1,2)-9．已知函数()2216,2,21x ax x f x a x x ⎧++≤⎪=⎨->⎪-⎩在定义域上单调递减，则实数a 的取值范围是（）A ．[]4,2--B ．(],2-∞-C ．(),0-∞D ．(]4,2--10．若(){}2max 23,32g x x x =--，(){}2max 23,32h x x x =+-，()()(){}min ,f x g x h x =，其中{}max ,,x y z 表示x ，y ，z 中的最大者，{}min ,,x y z 表示x ，y ，z 中的最小者，下列说法不正确的是（）A ．函数()f x 为偶函数B ．当[]1,3x ∈时，有()f x x≤ C ．不等式()1f f x ⎡⎤≤⎣⎦的解集为1,22⎡⎤--⋃⎢⎥⎣⎦⎣⎦D ．当[][]3,22,3x ∈--⋃时，有()()f f x f x ⎡⎤≤⎣⎦二、填空题11．函数()f x =315x +-的定义域为12．设函数()24,24,2x x f x x x ⎧+≤=⎨>⎩，则()1f f -=⎡⎤⎣⎦.13．已知集合{}25A x x =-≤≤，{}121B x m x m =+≤≤-，若B A ⊆，则实数m 的取值范围为.14．已知实数1x >，则函数221y x x =+-的最小值为.15．偶函数()f x 的定义域为R ，且对于任意1x ，(]()212,0x x x ∈-∞≠，均有()()1212f x f x x x -<-成立，若()()121f a f a -<-，则实数a 的取值范围为．16．已知不等式230mx nx -+>的解集为{|1x x <或3}x >，若0,0,3a b ma nb >>+=，并且2112k k a b+≥-恒成立，则实数k 的取值范围是．三、解答题17．已知集合432A xx ⎧⎫=<-⎨⎬-⎩⎭，()(){}170B x x m x m =---->．(1)若0m =，求集合A B ；(2)若A B =∅ ，求实数m 的取值范围．18．已知关于x 的不等式()2320R ax x a ++>∈，(1)若2320ax x ++>的解集为{}|1x b x <<，求实数a ，b 的值；(2)求关于x 的不等式2321ax x ax -+>-的解集．19．已知函数22()4ax bx c f x x ++=+是定义在[2,2]-上的奇函数，且1(1)5f =.(1)求函数()f x 的解析式：(2)判断并用定义法证明()f x 在[]22-,上的单调性：(3)解关于x 的不等式(1)(21)0f x f x -++<20．已知函数()22f x x mx n =++的图象过点(0,1)-，且满足(1)(2)f f -=．(1)求函数()f x 的解析式；(2)设函数()f x 在[],2a a +上的最小值为()h a ，求()h a 的值域；(3)若0x 满足()00f x x =，则称0x 为函数()y f x =的不动点．函数()()g x f x tx t =-+有两个不相等的不动点12,x x ，且120,0x x >>，求1221x x x x +的最小值．。

2022-2023学年天津市第一中学高一上学期期中数学试题(解析版)

2022-2023学年天津市第一中学高一上学期期中数学试题一、单选题1．已知集合{}0,1,2,A B x y⎧===⎨⎩∣，则A B ⋃=（）A ．{}0,1,2B ．{}1,2C ．()0,∞+D ．[)0,∞+【答案】D【分析】先解出集合B ，再求A B ⋃.【详解】{}0B x y xx⎧===>⎨⎩∣∣. 因为{}0,1,2A =，所以A B ⋃=[)0,+∞. 故选：D2．命题“()10,,10x x∞∃∈++<”的否定为（）A ．()10,,10x x∞∃∈++>B ．()10,,10x x ∞∃∈++≥C ．()10,,10x x ∞∀∈++>D ．()10,,10x x∞∀∈++≥【答案】D【分析】特称命题的否定：将存在改任意并否定原结论，即可得答案.【详解】由特称命题的否定为全称命题，则原命题的否定为()10,,10x x ∞∀∈++≥.故选：D3．设x R ∈，则“250x x -<”是“|1|1x -<”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件D ．既不充分也不必要条件【答案】B【解析】分别求出两不等式的解集，根据两解集的包含关系确定. 【详解】化简不等式，可知 05x <<推不出11x -<；由11x -<能推出05x <<，故“250x x -<”是“|1|1x -<”的必要不充分条件，故选B ．【点睛】本题考查充分必要条件，解题关键是化简不等式，由集合的关系来判断条件．4．函数234x x y x --+=的定义域为（）A ．[4,1]-B ．[4,0)-C ．(0,1]D ．[4,0)(0,1]-⋃【答案】D【分析】根据被开方数是非负数，以及分母不为零，列出不等式求得结果即可. 【详解】由2340x x --+≥可得{|41}x x -≤≤，又因为分母0x ≠，所以原函数的定义域为[4,0)(0,1]-⋃．故选：D .【点睛】本题考查具体函数定义域的求解，涉及一元二次不等式的求解，属综合基础题. 5．函数241xy x =+的图象大致为（） A ． B ．C ．D ．【答案】A【分析】由题意首先确定函数的奇偶性，然后考查函数在特殊点的函数值排除错误选项即可确定函数的图象.【详解】由函数的解析式可得：()()241xf x f x x --==-+，则函数()f x 为奇函数，其图象关于坐标原点对称，选项CD 错误；当1x =时，42011y ==>+，选项B 错误. 故选：A.【点睛】函数图象的识辨可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象．利用上述方法排除、筛选选项． 6．已知a ，b 为非零实数，且a ＞b ，则下列不等式成立的是（） A ．a c b c ->- B ．22ac bc > C ．22a b >D ．11a b<【答案】A【分析】利用不等式的性质可判断A ；取特殊值0c 可判断B ；取特殊值1,2a b ==-可判断C ，D 【详解】选项A ，若a ＞b ，利用不等式的性质可得a c b c ->-，正确；选项B ，当0c 时，22ac bc =，不正确；选项C ，当1,2a b ==-时，a ＞b ，但22a b <，不正确; 选项D ，当1,2a b ==-时，a ＞b ，但11a b>，不正确; 故选：A7．若函数,1()27,1x x f x x x x -≤-⎧⎪=⎨+->-⎪⎩，则()2f f -=⎡⎤⎣⎦（） A ．-2 B ．2C ．-4D ．4【答案】C【分析】由()()222f -=--=，得到()()22f f f -=⎡⎤⎣⎦，由此求出()2f f -⎡⎤⎣⎦即可. 【详解】∵函数,1()27,1x x f x x x x -≤-⎧⎪=⎨+->-⎪⎩，∴()()222f -=--=， ()2(2)27422f f f ==+--⎤⎣⎦=-⎡. 故选：C .8．若函数y=f （x)是奇函数，且函数F(x)=af(x)+bx+2在（0，+∞，)上有最大值8，则函数y=F(x)在(－∞，，0)上有 A ．最小值－8 B ．最大值－8 C ．最小值－6 D ．最小值－4【答案】D【分析】利用函数的奇偶性与单调性即可得到结果. 【详解】∵y ＝f （x ）和y ＝x 都是奇函数， ∴af （x ）+bx 也为奇函数，又∵F （x ）＝af （x ）+bx +2在（0，+∞）上有最大值8， ∴af （x ）+bx 在（0，+∞）上有最大值6，∴af （x ）+bx 在（﹣∞，0）上有最小值﹣6，∴F （x ）＝af （x ）+bx +2在（﹣∞，0）上有最小值﹣4，故选D ．【点睛】本题考查的知识点是函数奇偶性与单调性，函数的最值及其几何意义，其中根据函数奇偶性的性质，构造出F （x ）﹣2＝af （x ）+bx 也为奇函数，是解答本题的关键．9．已知函数()f x 的定义域为R ，()2f x +是偶函数，()42f =，()f x 在(),2-∞上单调递增，则不等式()412f x ->的解集为（） A ．15,44⎛⎫ ⎪⎝⎭B ．15,,44⎛⎫⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎭⎝⎭C ．()(),117,-∞-⋃+∞D ．()1,17-【答案】A【分析】由题意判断出函数()f x 关于2x =对称，结合函数的对称性与单调性求解不等式. 【详解】∵()2f x +是偶函数，∴函数()f x 关于2x =对称，∴()()042f f ==，又∵()f x 在(),2-∞上单调递增，∴()f x 在()2,+∞单调递减，∴()412f x ->可化为0414x <-<，解得1544x <<，∴不等式()412f x ->解集为15,44⎛⎫⎪⎝⎭.故选：A10．已知定义在R 上的奇函数()y f x =，当0x ≥时，()||(0)f x x a a a =-->若对于任意的实数x 有(2)()f x f x -≤成立，则正数a 的取值范围是（）A ．[)1+∞，B ．1,2⎡⎫+∞⎪⎢⎣⎭C ．(]01，D ．10,2⎛⎤⎥⎝⎦【答案】D【分析】当0x ≥时，函数()f x 的解析式中含有绝对值，去绝对值化为分段函数，再利用函数在R 上是奇函数，可画出函数()f x 的图像，把函数()f x 向右平移两个单位为(2)f x -，在采用数形结合可知，要想(2)()f x f x -≤恒成立，即(2)f x -的图象始终在()f x 下方，即可得出2(2)2a a --≤，即可得到答案.【详解】0a >，当0x ≥时，2,()=,0x a x af x x a a x x a -≥⎧=--⎨-<<⎩，()f x 为奇函数，即可得到如下图像：对于任意的实数x 有(2)()f x f x -≤成立，采用数形结合把函数()f x 的图象向右平移两个单位得到(2)f x -并使(2)f x -的图象始终在()f x 的图象的下方，即2(2)2a a --≤，即12a ≤，0a >，102∴<≤a . 故选：D.二、填空题11．已知幂函数()()233af x a a x =--在()0,∞+为增函数，则实数a 的值为___________.【答案】4【分析】根据幂函数的定义和单调性，即可求解.【详解】解：()f x 为递增的幂函数，所以23310a a a ⎧--=⎨>⎩，即()()1400a a a ⎧+-=⎨>⎩，解得：4a =，故答案为：412．若命题“x ∃∈R 使()2110x a x +-+<”是假命题，则实数a 的取值范围为_____，【答案】[]1,3-【分析】原命题等价于命题“2R,(1)10x x a x ∀∈+-+≥，”是真命题【详解】由题意得若命题“2R,(1)10x x a x ∃∈+-+<”是假命题，则命题“2R,(1)10x x a x ∀∈+-+≥，”是真命题，则需()2014013a a ∆≤⇒--≤⇒-≤≤,故本题正确答案为[]1,3-．【点睛】本题主要考查全称量词与存在量词以及二次函数恒成立的问题．属于基础题． 13．已知函数221x xy x x -=-+的，则其值域为_____________.【答案】1,13⎡⎫-⎪⎢⎣⎭【分析】首先利用换元，将函数转化为111t y t t-==-，34t ≥，利用函数的单调性，即可求解.【详解】设221331244t x x x ⎛⎫=-+=-+≥ ⎪⎝⎭，即111t y t t -==-，函数在区间34⎡⎫+∞⎪⎢⎣⎭，单调递增，所以113y -≤<.故答案为：113⎡⎫-⎪⎢⎣⎭，14．函数1y =_____．【答案】[3,6]【解析】首先求出函数的定义域，再利用复合函数的单调性即可求解. 【详解】226060x x x x -+≥⇒-≤，解得06x ≤≤，令()()22639x x x x μ=-+=--+，对称轴为3x =，所以函数()x μ在(),3-∞为单调递增；在[)3,+∞上单调递减.所以函数1y =[3,6]. 故答案为：[3,6]15．已知0,0a b >>，且1ab =，则11822a b a b+++的最小值为_________．【答案】4【分析】根据已知条件，将所求的式子化为82a b a b +++，利用基本不等式即可求解. 【详解】0,0,0a b a b >>∴+>，1ab =,11882222ab ab a b a b a b a b∴++=++++842a b a b +=+≥=+，当且仅当a b +=4时取等号，结合1ab =,解得22a b =-=+22a b ==. 故答案为：4【点睛】本题考查应用基本不等式求最值，“1”的合理变换是解题的关键，属于基础题.三、双空题16．已知函数2,0()2,0ax x x f x x x ⎧-≥=⎨-<⎩，①若对任意12,x x R ∈，且12x x ≠都有2121()()0f x f x x x -<-，则实数a 的取值范围为___________；②若()f x 在[1,)t -上的值域为[0,4]，则实数t 的取值范围为___________. 【答案】 0a ≤ 24t <≤【分析】由已知可得()f x 在(),-∞+∞单调递减，利用二次函数的对称轴的位置可得a 的取值范围；分0a >、 0a ≤利用()f x 单调性可得实数t 的取值范围. 【详解】若对任意12,x x R ∈，且12x x ≠都有2121()()0f x f x x x -<-，则()f x 在(),-∞+∞单调递减，则02≤a，即0a ≤，所以实数a 的取值范围(],0-∞；当0a >时，若()f x 在[1,)t -上的值域为[0,4]，224224⎛⎫=-= ⎪⎝⎭a aa f ，解得4a =或4a =-（舍去），又()()()12,040-===f f f ，所以24t <≤；当0a ≤时，因为()f x 在[1,)t -单调递减，则()f x 在[1,)t -上的最大值为()12f -=，不合题意，所以实数t 的取值范围为(]2,4. 故答案为：①(],0-∞；②(]2,4.四、解答题17．已知集合{|25}A x x =-≤≤，集合{|121}B x a x a =+≤≤+， (1)若2a =，求A B ⋃和R A C B ⋂； (2)若A B A ⋃=，求实数a 的取值范围.【答案】(1){|25}A B x x ⋃=-≤≤，(){|23}R A C B x x =-≤< (2)2a ≤【分析】（1）由2a =，得到{|25}A x x =-≤≤，{|35}B x x =≤≤，再利用补集、并集和交集运算求解；（2）由A B A ⋃=，得到B A ⊆，分B =∅， B ≠∅求解. 【详解】（1）解：2a =时，{|25}A x x =-≤≤，{|35}B x x =≤≤ 所以{|35}R C B x x x =<>或，所以{|25}A B x x ⋃=-≤≤ (){|23}R A C B x x =-≤<；（2）∵A B A ⋃=，B A ∴⊆，①若B =∅时，121a a +>+，解得a<0，符合题意；②若B ≠∅时，12121512a a a a +≤+⎧⎪+≤⎨⎪+≥-⎩，解得02a ≤≤.综上可得2a ≤.18．函数()f x 是定义在实数集R 上的奇函数，当0x ≥时，()1f x xx -=+. (1)判断函数()f x 在[0,)+∞的单调性，并给出证明； (2)求函数()f x 的解析式；(3)若对任意的[1,1]t ∈-，不等式22()(223)0f k t f t t -+-->恒成立，求实数k 的取值范围. 【答案】(1)函数()f x 在[)0,∞+上单调递减，证明见解析 (2)(),01,01xx x f x x x x -⎧≥⎪⎪+=⎨⎪<⎪-⎩(3)8,3k k k R ⎧⎫<∈⎨⎬⎩⎭【分析】（1）()f x 在[)0,∞+上单调递减，由定义法证明即可；（2）由奇函数的定义求解即可；（3）由函数的奇偶性与单调性结合二次函数的性质求解即可；【详解】（1）当0x ≥时，()1111x f x x x -==-+++，∴函数()f x 在[)0,∞+上单调递减. 证明如下：任取12,[0,)x x ∈+∞且12x x <， 2112121211()()(1)(1)11(1)(1)x x f x f x x x x x --=-+--+=++++， ∵12,[0,)x x ∈+∞，∴1210,10x x +>+>，又12x x <，∴210x x ->∵()()()()12120,f x f x f x f x ->>， ∴函数()f x 在[)0,∞+上单调递减（2）因为当0x ≥时，()1f x xx -=+，所以，当0x <时，0x ->，又因为()f x 是定义在实数集R 上的奇函数，所以，()()()11x xf x f x x x --=--=-=-+-，即当0x <时，()1x f x x =-. 所以，函数()f x 的解析式为(),01,01xx x f x x x x -⎧≥⎪⎪+=⎨⎪<⎪-⎩；（3）∵函数()f x 在[)0,∞+上单调递减，且()()00f x f ≤=，又因为()f x 是定义在实数集R 上的奇函数，所以，函数()f x 在(),0∞-上单调递减，且0x <时，()()00f x f >=，所以，函数()f x 在实数集R 上单调递减；那么不等式()()222230f k t f t t -+-->，即：()()()222223223f k t f t t f t t ->---=-++，则有22223k t t t -<-++，即2218323333k t t t ⎛⎫<-+=-+ ⎪⎝⎭（[1,1]t ∈-）恒成立，所以，2min 1883333k t ⎡⎤⎛⎫<-+=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦，所以，实数k 的取值范围是8,3k k k R ⎧⎫<∈⎨⎬⎩⎭.19．设函数2()(2)3f x ax b x =+-+（1）若(1)3f =，且0,0a b >>，求14a b+的最小值；（2）若(1)2f =，且()2f x >在(1,1)-上恒成立，求实数a 的取值范围. 【答案】（1）92；（2）[1,1]-.【分析】（1）由()13f =可得2a b +=，再利用基本不等式中乘“1”法的应用计算可得；（2）依题意可得1a b +=，即2(1)10ax a x -++>在(1,1)-上恒成立，等价于(1,1)-是不等式()(1)(1)0g x ax x =-->解集的子集，再对参数a 分类讨论，分别计算可得；【详解】解：（1）函数2()(2)3f x ax b x =+-+，由(1)233f a b =+-+=，可得2a b +=，所以141141419()552222b a a b a b a b a b ⎛⎫⎛⎫⎛⎫+=++=++≥= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，当4b aa b =时等号成立，因为2a b +=，0a >，0b >，解得23a =，43b =时等号成立，此时14a b +的最小值是92.（2）由(1)232f a b =+-+=，即1a b +=，又由2(2)32ax b x +-+>在(1,1)-上恒成立，即2(1)10ax a x -++>在(1,1)-上恒成立，等价于(1,1)-是不等式()(1)(1)0g x ax x =-->解集的子集， ①当0a =时，不等式的解集为(,1)-∞，满足题意；②当a<0时，不等式的解集为1,1a ⎛⎫⎪⎝⎭，则11a ≤-，解得1a ≥-，故有10a -≤<；③当01a <≤时，即11a ≥时，不等式的解集为1(,1),a ⎛⎫-∞⋃+∞ ⎪⎝⎭，满足题意；④当1a >时，即11a <时，不等式的解集为1,(1,)a ⎛⎫-∞+∞ ⎪⎝⎭，不满足题意，（舍去），综上所述，实数a 的取值范围是[1,1]-.【点睛】本题考查基本不等式的应用，以及不等式恒成立问题，考查分类讨论思想，属于中档题. 20．已知函数()21x f x ax b+=+是定义域上的奇函数，且()12f -=-．（1）求函数()f x 的解析式，判断函数()f x 在0,上的单调性并证明；（2）令()()g x f x m =-，若函数()g x 在0,上有两个零点，求实数m 的取值范围；（3）令()()()22120h x x tf x t x =+-<，若对1x ∀，21,22x ⎡⎤∈⎢⎥⎣⎦都有()()12154h x h x -≤，求实数t 的取值范围．【答案】（1）()1f x x x =+；函数()f x 在0,1上单调递减，在1,上单调递增，证明见解析；（2）m>2；（3）302t -≤< 【解析】（1）由()f x 是奇函数，可知()12f -=-，()12f =，进而列出关系式，求出,a b ，即可得到函数()f x 的解析式，然后利用定义法，可判断并证明函数()f x 在0,上的单调性；（2）由函数()g x 在0,上有两个零点，整理得方程210x mx -+=在0,上有两个不相等的实数根，进而可得到24002m m ⎧∆=->⎪⎨>⎪⎩，求解即可；（3）由对任意的1x ∀，21,22x ⎡⎤∈⎢⎥⎣⎦都有()()12154h x h x -≤恒成立，可得()()max min 154h x h x -≤，求出()()max min ,h x h x ，进而可求出t 的取值范围.【详解】（1）()12f -=-，且()f x 是奇函数，()12f ∴=，2222a b a b ⎧=-⎪⎪-+∴⎨⎪=⎪+⎩，解得10a b =⎧⎨=⎩， ()1xf x x ∴=+．函数()f x 在0,1上单调递减，在1,上单调递增，证明如下：任取1x ，()20,1x ∈，且12x x <，则()()()121212*********x x f x f x x x x x x x x x ⎛⎫⎛⎫⎛⎫--=+-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ()12,0,1x x ∈，且12x x <，120x x ∴-<，1201x x <<，∴1210x x -<，()()120f x f x ∴->，即()()12f x f x >，∴函数()f x 在0,1上单调递减.同理可证明函数()f x 在1,上单调递增．（2）函数()g x 在0,上有两个零点，即方程10x m x+-=在0,上有两个不相等的实数根，所以210x mx -+=在0,上有两个不相等的实数根，则24002m m ⎧∆=->⎪⎨>⎪⎩，解得m>2．（3）由题意知()22112h x x t x x x ⎛⎫ ⎪⎝=+-⎭+，令1z x x=+，222y z tz =--，由（1）可知函数1z x x =+在1,12⎡⎤⎢⎥⎣⎦上单调递减，在[]1,2上单调递增， 52,2z ⎡⎤∴∈⎢⎥⎣⎦，函数222y z tz =--的对称轴方程为0z t =<，∴函数222y z tz =--在52,2⎡⎤⎢⎥⎣⎦上单调递增，当2z =时，222y z tz =--取得最小值，min 42y t =-+；当52z =时，222y z tz =--取得最大值，max 1754y t =-+. 所以()min 42h x t =-+，()max 1754h x t =-+，又对任意的1x ∀，21,22x ⎡⎤∈⎢⎥⎣⎦都有()()12154h x h x -≤恒成立， ()()max min 154h x h x ∴-≤，即()171554244t t -+--+≤，解得32t ≥-，又0t <， t ∴的取值范围是302t -≤<．【点睛】方法点睛：已知函数有零点(方程有根)求参数值(取值范围)常用的方法：（1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决；（3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解.。

2022-2023学年天津市滨海新区塘沽第一中学高二上学期期中数学试题(解析版)

2022-2023学年天津市滨海新区塘沽第一中学高二上学期期中数学试题一、单选题1．过()1,2M -、()2,3N -两点的直线的倾斜角为（） A ．π4B ．π3C ．34π D ．2π3【答案】C【分析】求出直线MN 的斜率，结合倾斜角的取值范围可求得结果. 【详解】设直线MN 的倾斜角为α，则0πα≤<，所以，23tan 112α-==--+，3π4α∴=. 故选：C.2．已知向量(1,2,3),(1,2,)a b x =-=-，若a b ，则x 等于（） A ．6- B ． 3- C ．3 D ．6【答案】B【分析】由a b ，列方程求解即可.【详解】因为向量(1,2,3),(1,2,)a b x =-=-，且a b ，所以12123x -==-，得3x =-，故选：B.3．“m>2”是“方程22121x y m m -=--表示双曲线”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A【分析】方程22121x y m m -=--表示双曲线等价于()()210m m --<，求解判断即可【详解】方程22121x y m m -=--表示双曲线等价于()()210m m --<，即1m <或m>2，故“m>2”是“方程22121x y m m -=--表示双曲线”的充分不必要条件. 故选：A4．平行六面体（底面是平行四边形的棱柱）1111ABCD A B C D -中，1160A AB A AD BAD ∠=∠=∠=︒，11AB AD AA ===，则1AC =（）A ．6B ．6C ．3D ．322【答案】A【分析】利用空间向量运算法则得到11AC AB AD AA =++，再利用数量积公式进行运算得到()22116AC AB AD AA =++=，从而求出116AC AC ==.【详解】由空间向量可得：11AC AB AD AA =++，()2222211111222AC AB AD AA AB AD AA AB AD AD AA AA AB =++=+++⋅+⋅+⋅11111112cos 2cos 2cos AB AD AD AA BAD A AD AA A B B A A ∠∠=+++⋅+∠⋅+⋅32cos602cos602cos606=+︒+︒+︒=，所以116AC AC ==故选：A5．已知抛物线C ：()220y px p =>上一点()3M m ，到其焦点F 的距离等于4，则p 的值为（）A ．12B ．1C ．2D ．3【答案】C【分析】利用抛物线上的点到焦点的距离等于到准线距离，列方程求出p 的值. 【详解】依题意可知342pMF =+=，2p ∴=，故选：C6．若点P 是双曲线22:1412x y C -=上一点，1F ，2F 分别为C 的左、右焦点，19PF =，则2PF =（）．A ．5B ．13C ．5或13D ．1或5【答案】C【分析】根据双曲线的定义可得选项.【详解】由题意可知，2a =，4124c =+=，12PF c a ≥-=，若19PF =，则294PF -=，25PF =或13．故选：C.7．已知点()()2,0,0,2A B ，点C 在圆2220x y x ++=上，则△ABC 的面积的最小值为（） A ．32+ B ．3C ．2D ．32-【答案】D【分析】首先求出直线AB 的方程和线段AB 的长度，利用圆心到直线的距离再减去圆的半径得出△ABC 的高的最小值，即可求解.【详解】圆2220x y x ++=的圆心()1,0M -，半径为1 ∵()()2,0,0,2A B ，则22AB =，直线:20AB x y +-= 圆心()1,0M -到直线:20AB x y +-=的距离2210232211d -+-==+ ∵△ABC 的面积最小时，点C 到直线AB 的距离最短，该最短距离即圆心到直线AB 的距离减去圆的半径∴ABC 边AB 上高的最小值为3212-，则ABC 的最小值为1321223222⎛⎫⨯-⨯=- ⎪ ⎪⎝⎭故选：D.8．如图，111A B C ABC -是直三棱柱，90BCA ∠=，点1D ，1F 分别是11A B ，11A C 的中点，若1BC CA CC ==，则1BD 与1AF 所成角的余弦值是（）A ．3010B ．12C ．3015D ．1510【答案】A【分析】以C 为原点，建立空间直角坐标系，然后坐标运算即可. 【详解】以C 为原点，建立如图所示空间直角坐标系，设12BC CA CC ===，则()2,0,0A ，()0,2,0B ，()11,1,2D ，()11,0,2F ，可得()11,1,2BD =-，()11,0,2AF =-， 11111130cos ,65BD AF BD AF BD AF ⋅=〉〈==⋅ 此时，1BD 与1AF 30故选：A9．如果椭圆221369x y +=的弦被点(4,2)平分，则这条弦所在的直线方程是（）A ．20x y -=B ．280x y +-=C ．23140x y +-=D ．2100x y +-=【答案】B【分析】判断点(4,2)在椭圆内，再借助“点差法”求出这条弦所在直线的斜率即可计算作答. 【详解】依题意，点(4,2)在椭圆221369x y +=内，设这条弦的两个端点1122(,),(,)A x y B x y ，由22112222436436x y x y ⎧+=⎨+=⎩得：12121212()()4()()0x x x x y y y y +-++-=，又121284x x y y +=⎧⎨+=⎩，于是得弦AB 所在直线斜率1212121214()2y y x x k x x y y -+==-=--+，方程为：1242()y x -=--，即280x y +-=，所以这条弦所在的直线方程是280x y +-=. 故选：B10．若双曲线2222:1(0,0)y x C a b a b-=>>的一条渐近线被圆()2224x y +-=所截得的弦长为则C的离心率为（）A ．2BCD ．4【答案】B【分析】取渐近线方程为0ax by -=，根据圆心到直线距离公式结合勾股定理计算得到答案. 【详解】不妨取渐近线为ay x b=，即0ax by -=，圆心到渐近线的距离为1d ，得到2c b =，故3a b ，故离心率为c e a ==. 故选：B11．以下四个命题表述正确的个数（）①圆222x y +=上有且仅有3个点到直线:10l x y -+= ②曲线22120C :x y x ++=与曲线222480C :x y x y m +--+=，恰有四条公切线，则实数m 的取值范围为4m >；③已知圆22:2C x y +=，P 为直线0x y ++上一动点，过点P 向圆C 引一条切线PA ，其中A 为切点，则||PA 的最小值为2；④已知圆22:4C x y +=，点P 为直线:280l x y +-=上一动点，过点P 向圆C 引两条切线PA ，PB ，A ，B 为切点，则直线AB 经过点1(1,)2.A ．1个B ．2个C ．3个D ．4个【答案】C【分析】①根据圆心到直线的距离与半径的关系来确定所求点的个数；②根据两曲线有四条公切线，确定曲线类型为圆，再由两圆外离列不等式求解；③利用圆心与切点的连线垂直切线列等式，转化为求圆心到直线上的点的距离的最小值问题；④利用切线的性质得切点弦方程，再根据切点弦方程求定点.【详解】①：圆222x y +=的圆心为()0,0O ，半径r =.圆心()0,0O 到直线:10l x y -+=的距离12O d r ==，所以圆222x y +=上有且仅有3个点到直线:10l x y -+=故①正确；②：方程22+20x y x +=可化为()2211x y ++= ，故曲线1C 表示圆心为()11,0C -，半径11r =的圆.方程22480x y x y m +--+=可化为()()222420x y m -+-=- 因为圆1C 与曲线2C 有四条公切线，所以曲线2C 也为圆，且圆心为()22,4C，半径2r ()20m <，同时两圆的位置关系为外离，有1212C C r r >+，即51>420m <<，故②错误；③：圆22:2C x y +=的圆心()0,0C，半径r = 圆心()0,0C到直线0x y ++=的距离C d r =>，所以直线与圆相离.由切线的性质知，PAC △为直角三角形，2PA ，当且仅当PC与直线0x y ++=垂直时等号成立，所以PA 的最小值为2，故③正确；④：设点()00,P x y ，因为点()00,P x y 在直线280x y +-=上，所以00280x y +-=，0082y x =- ，由圆的切线性质知，直线AB 的方程为 004xx yy +=，即()00824xx y x +-=，整理得()02840x y x y -+-=，要求直线AB 过定点，则应满足20840x y y -=⎧⎨-=⎩，解得112x y =⎧⎪⎨=⎪⎩.所以直线AB 过定点11,2⎛⎫⎪⎝⎭，故④正确.故选：C.12．如图为陕西博物馆收藏的国宝——唐金筐宝钿团花纹金杯，杯身曲线内收，玲珑娇美，巧夺天工，是唐代金银细作的典范之作．该杯的主体部分可以近似看作是双曲线()2222:10,0x y C a b a b-=>>的右支与直线0x =，4y =，=2y -围成的曲边四边形ABMN 绕y 轴旋转一周得到的几何体．若该金杯主体部分的上口外直径为1033，下底外直径为2393，则下列曲线中与双曲线C 有共同渐近线的是（）A ．22193y x -=B ．22193x y -=C ．22163y x -=D ．22136x y -=【答案】A【分析】根据给定条件求出双曲线C 的渐近线方程，再逐一分析各个选项判断作答.【详解】依题意，双曲线C ：22221(0,0)x y a b a b -=>>过点5339(4),(2)M N -，则有222225163113431a b a b ⎧⎪-=⎪⎪⎨⎪⎪-=⎪⎩，解得3,3a b ==，因此，双曲线C 的渐近线方程为3y x =，对于A ，双曲线22193y x -=的渐近线方程为3y x =，A 正确；对于B ，双曲线22193x y -=的渐近线方程为3y x =，B 不正确；对于C ，双曲线22163y x -=的渐近线方程为2y x =±，C 不正确；对于D ，双曲线22136x y -=的渐近线方程为2y x =，D 不正确. 故选：A二、填空题13．圆224x y +=与圆22x +44120y x y -+-=的公共弦所在直线的方程为_______.【答案】x y 20-+=【分析】将圆的方程作差即可求得公共弦方程.【详解】将所给的两圆的方程作差可得圆224x y +=与圆2244120x y x y +-+-=的公共弦所在直线的方程为：4480x y -+=，即20x y -+=.【点睛】本题主要考查圆与圆的位置关系，公共弦方程的求解等知识，意在考查学生的转化能力和计算求解能力.14．过点(的直线l 与圆224x y +=相切，则直线l 在y 轴上的截距为__________．【答案】4【分析】根据题意，分析可得点(在圆224x y +=上，根据垂直关系求出切线的斜率，由点斜式求出切线方程，根据截距的定义可得结果.【详解】因为22(14+=，所以点(在圆224x y +=上，∴切线l的斜率110k =-=- 则切线l的方程为1y x -=，变形可得4y =+，所以直线l 在y 轴上的截距为4；故答案为：4.【点睛】本题考查了点与圆的位置关系，考查了求圆的切线方程，考查了直线的截距，属于基础题. 15．直线y x b =+与曲线1x =有且只有一个公共点，则b 的取值范围是_____. 【答案】[){}2,021--【解析】根据图形表示当直线与半圆有一个交点时，求b的取值范围. 【详解】曲线1x =()2211x y -+= ()1x ≤，所以曲线表示如图的半圆，直线y x b =+表示斜率为1的平行线，当直线与半圆只有一个公共点时，直线与半圆相切时，有一个交点，此时1d==，解得：1b =，或1b =（舍）当直线过点,O A 时，有两个交点，此时0b =，当直线过点B 时，有一个交点，此时112b b -=+⇒=-，根据图象可知，当直线有一个交点时，b 的取值范围是[){}2,021--.故答案为：[){}2,021--【点睛】本题考查直线与圆相交问题，重点考查数形结合分析问题，属于基础题型，本题的关键是正确画出对应的图形.16．已知()1,0,0A ，()0,1,0B ，()0,0,1C ，若点(),1,1P x 在平面ABC 内，则x =______. 【答案】1-【分析】求出平面的法向量，由法向量求参数值．【详解】设平面ABC 的一个法向量是(,,)n x y z =，又(1,1,0),(1,0,1)AB AC =-=-，所以00n AB x y n AC x z ⎧⋅=-+=⎨⋅=-+=⎩，取1x =得(1,1,1)n =，(,1,1)P x 在平面ABC 上，则1110n AP x ⋅=-++=，=1x -．故答案为：1-．17．设1F 、2F 分别为椭圆22221(0)x y a b a b +=>>与双曲线22221(0,0)x y m n m n-=>>的公共焦点，P 为它们的一个公共点，且1260F PF ∠=︒，则当这两条曲线的离心率之积最小时，双曲线的渐近线的方程是 ________．【答案】2y = 【分析】设12(,0),(,0)F c F c -，在12F PF △中，由余弦定理可得22243c a m =+，再利用椭圆和双曲线的几何性质列方程求解即可.【详解】设12(,0),(,0)F c F c -，不妨设120PF PF ->，由椭圆和双曲线的性质可得121222PF PF aPF PF m +=⎧⎨-=⎩，解得12PF a m PF a m =+⎧⎨=-⎩，又椭圆的离心率1c e a =，双曲线的离心率2c e m =，212c e e am=，在12F PF △中，由余弦定理得222121212122cos F F PF PF PF PF F PF =+-⨯⨯⨯∠，解得22243c a m =+，即243c a mam m a=+，根据均值不等式可得243c a m am m a =+≥当且仅当3a m m a =，即a =时，等号成立，即当两条曲线的离心率之积212c e e am=最小时，a =，所以由双曲线性质22222243c a m c m n a ⎧=+⎪=+⎨⎪=⎩解得n m =即双曲线的渐近线方程为y =，根据椭圆和双曲线的对称新，当120PF PF -≤仍成立，故答案为：2y x =.三、双空题18．已知抛物线y ＝ax 2过点（4，2），则a ＝_____，准线方程为_____ 【答案】18=2y - 【分析】先由抛物线所过点的坐标，得到a ，进而可得出准线方程. 【详解】依题意，得：162a =，解得：18a =，抛物线方程为：218y x =，即28x y =，所以，准线方程为：2y =-．故答案为(1).18(2). 2y =- 【点睛】本题主要考查抛物线的准线方程，熟记抛物线的性质即可，属于常考题型.四、解答题19．已知点(2,0)P ，圆C 的圆心在直线50x y --=上且与y 轴切于点(0,2)M -， (1)求圆C 的方程；(2)若直线l 过点P 且被圆C 截得的弦长为l 的方程；(3)设点Q 在圆C 上运动，求线段PQ 的中点N 的轨迹方程．【答案】(1)22(3)(2)9x y -++=(2)3460x y +-=或2x = (3)2259()(1)24x y -++=．【分析】(1)先设出圆心，再根据圆C 的圆心在直线50x y --=上且与y 轴切于点(0,2)M -建立方程即可求解.(2)先讨论斜率存在，设出直线方程，根据弦长公式建立方程，求出斜率k ;再讨论斜率不存在时，求出直线方程，验证是否存在即可.(3)先设点N 的坐标为(,)x y ，根据相关点法即可求出N 的轨迹方程.【详解】（1）圆C 的圆心在直线50x y --=上且与y 轴切于点(0,2)M -， ∴设圆心坐标为(,)C a b ，则502a b b --=⎧⎨=-⎩，解得3a =，2b =-，∴圆心(3,2)C -，半径||3r MC =，故圆的方程为22(3)(2)9x y -++=.（2）点(2,0)P ，直线l 过点P ，∴设直线l 的斜率为(k k 存在）则方程为0(2)y k x -=-，又圆C 的圆心为(3,2)-，半径3r =，弦长为故弦心距1d ==，故1d ==，解得34k =-，所以直线方程为3(2)4y x =--，即3460x y +-=，当l 的斜率不存在时，l 的方程为2x =，经验证2x =也满足条件，故l 的方程为3460x y +-=或2x =.（3）设点N 的坐标为(,)x y ，Q 点的坐标为0(x ，0)y ．由于(2,0)P ，且N 为PQ 的中点，∴002,22x y x y +==，于是有00222x x y y=-⎧⎨=⎩①， Q 在圆C 上运动，∴2200(3)(2)9x y -++=，将①代入上式得22(25)(22)9x y -++=，即点N 的轨迹方程为2259()(1)24x y -++=．20．如图，已知梯形ABCD 中，//AD BC ，90DAB ∠=︒，22AB BC AD ===，四边形EDCF 为矩形，2DE =，平面EDCF ⊥平面ABCD ．(1)求证：//DF 平面ABE ；(2)求平面ABE 与平面BEF 的夹角的余弦值；(3)若点P 在线段EF 上，且直线AP 与平面BEF 14，求线段AP 的长．【答案】(1)证明见解析25 214【分析】（1）使用空间向量证明：只需证明DF 与平面ABE 的法向量垂直即可；（2）分别求出两个平面的法向量，使用空间向量求两面夹角的余弦值；（3）设EP EF λ=，根据直线AP 与平面BEF 所成角的正弦值使用空间向量求出λ值.【详解】（1）证明：四边形EDCF 为矩形，DE CD ∴⊥，又平面EDCF ⊥平面ABCD ，平面EDCF ⋂平面ABCD CD =，DE ⊂面EDCFED ∴⊥平面ABCD ．取D 为原点，DA 所在直线为x 轴，DE 所在直线为z 轴建立空间直角坐标系，如图，则(1A ，0，0)，(1B ，2，0)，(1C -，2，0)，(0E ，0，2)，(1F -，2，2)，设平面ABE 的法向量(,,)m x y z =，(1,2,2)BE =--，(0,2,0)AB =，由22020m BE x y z m AB y ⎧⋅=--+=⎪⎨⋅==⎪⎩，取1z =，得(2,0,1)m =，又(1,2,2)DF =-，∴2020DF m =-++=，则DF m ⊥，又DF ⊄平面ABE ，//DF ∴平面ABE ；（2）设平面BEF 的法向量111(,,)n x y z =，(1,2,2)BE =--，(1,2,0)EF =-，由1111122020n BE x y z n EF x y ⎧⋅=--+=⎪⎨⋅=-+=⎪⎩，取11y =，可得(2,1,2)n =， 4225cos ,||||35m n m n m n +∴<>===，即平面ABE 与平面BEF 25；（3）点P 在线段EF 上，设EP EF λ=，[0λ∈，1]，∴(1AP AE EF λ=+=-，0，2)(1λ+-，2，0)(1λ=--，2λ，2)，又平面BEF 的法向量(2,1,2)n =，设直线AP 与平面BEF 所成角为θ， ∴22|||2(114sin |cos ,|||||3(1)44AP n AP n AP n θλλ-=<>==--++， 24518110λλ∴+-=，即(31)(1511)0λλ-+=，[0λ∈，1]，∴13λ=． ∴4(3AP =-，23，2)，则2242214||()()433AP =-++AP ∴的长为2143． 21．如图，椭圆2222:1(0)x y E a b a b +=>>经过点(0,1)A -，且离心率为22. (I )求椭圆E 的方程；(II )经过点(1,1)，且斜率为k 的直线与椭圆E 交于不同两点,P Q （均异于点A ），问：直线AP 与AQ 的斜率之和是否为定值？若是，求出此定值；若否，说明理由．【答案】(1) 2212x y += (2)2 【详解】（Ⅰ）由题意知21c b a ==，综合222a b c =+，解得2a =所以，椭圆的方程为2212x y +=. （Ⅱ）由题设知，直线PQ 的方程为(1)1(2)y k x k =-+≠，代入2212x y +=，得 22(12)4(1)2(2)0+--+-=k x k k x k k ，由已知0∆>，设()()1122,P x y Q x y ，120x x ≠则1212224(1)2(2),1212k k k k x x x x k k --+==++，从而直线AP 与AQ 的斜率之和121212111122AP AQ y y kx k kx k k k x x x x +++-+-+=+=+ 121212112(2)2(2)x x k k k k x x x x ⎛⎫+=+-+=+- ⎪⎝⎭()4(1)222(21)22(2)k k k k k k k k -=+-=--=-. 【解析】1.椭圆的标准方程；2.圆锥曲线的定值问题.22．设椭圆2222:1(0)x y C a b a b+=>>的右顶点为A ，离心率为12，且以坐标原点为圆心，椭圆C 的短半轴长为半径的圆与直线60x y +=相切．(1)求椭圆C 的方程；(2)设直线2x =-上两点M ，N 关于x 轴对称，直线AM 与椭圆C 相交于点(B B 异于点)A ，直线BN与x 轴相交于点D ，若AMD，求直线AM 的方程； (3)P 是y 轴正半轴上的一点，过椭圆C 的右焦点F 和点P 的直线l 与椭圆C 交于G ，H 两点，求||||||PG PH PF +的取值范围．【答案】(1)22143x y +=；(2)20x y -=或20x y -=或20x y +-=或20x -=； (3)8[,4)5．【分析】（1）根据已知得到关于,,a b c 的方程组，解方程组即得解；（2）设直线AM 方程为2x my =+，0m ≠，求出直线BN方程，再解方程AMD S 即得解；（3）设直线l 的方程为(1)y k x =-，其中0k <，1(G x ，1)y ，2(H x ，2)y ，联立直线和椭圆方程得到韦达定理，求出12||||||||||PG PH x x PF +=+，再就点P 的位置分两种情况讨论得解. 【详解】（1）由题意可得12c e a ==，且点()0,0到直线0x y +=b = 又2222134a abc =+=+，解得2a =，所以椭圆C 的方程为22143x y +=. （2）设直线AM 方程为2x my =+，0m ≠，与直线l 的方程2x =-联立可得点4(2,)M m --，4(2,)N m-，联立直线AM 方程和椭圆方程2234122x y x my ⎧+=⎨=+⎩消去x ，整理得22(34)120m y my ++=，解得10y =，221234m y m =-+，可得22486(3m B m +-，21234m m -+)，由4(2,)N m -，22221243234648223BN m m m m k m m m --++==--++，则直线BN 方程2432(2)2m y x m m +-=-+，令0y =，解得224326m x m =+-，即2246(,0)32m D m +-，所以有22146483223||32AMD m S m m ⎛⎫-=-= ⎪⎝⎭+，整理得29||0m -+，解得m =或m = 所以直线AM的方程为20x y -=或20x y -=或20x -=或20x y -=. （3）设直线l 的方程为(1)y k x =-，其中0k <，1(G x ，1)y ，2(H x ，2)y ，联立22(1)143y k x x y =-⎧⎪⎨+=⎪⎩，得2222(43)84120k x k x k +-+-=， 2122843k x x k ∴+=+，212241243k x x k -=+，∆4222644(43)(412)144(1)k k k k =-+-=+， ∴1212||||||||||||||||||||||11x x PG PH PG PH x x PF PF PF +=+=+=+，当点P 在椭圆及外部，即3k -时，10x ，20x >， ∴2121222||||888||||[,2)3||4354PG PH k x x x x PF k k+=+=+==∈++；当点P在椭圆内部，即0k <<时，10x <，20x >，∴1212||||||||||PG PH x x x x PF +=+=-+，m =，则12m <<，21221212128(,4)14(1)34154m m x x m m m m∴-===∈-+--，综上所述，||||||PG PH PF +的取值范围为8[,4)5．【点睛】关键点睛：解答本题的关键有两点，关键一，是就点P 的位置分两种情况讨论；关键二是灵活运用方法求函数的取值范围.。

天津市第一中学2022-2023学年高三上学期第三次月考数学试题(解析版)

天津一中2022-2023-1高三年级第三次月考数学试卷（答案）本试卷总分150分，考试用时120分钟。

考生务必将答案涂写在答题卡上，答在试卷上的无效。

一、选择题：本题共9小题，每小题5分，共45分．在每小题给出的四个选项中，只有一项是符合题目要求的．1、已知集合3{Z |Z}1A x x=∈∈-，2{Z |60}B x x x =∈--≤，则A B ⋃=（） A ．{2} B ．}{2,0,2- C ．{}2,1,0,1,2,3,4-- D ．}{3,2,0,2,4--【详解】{A x =∈2Z |x x --{2,1,0,1,2,3,4--．，b ，c 为非零实数，则“A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【分析】根据不等式的基本性质可判定“a ＞b ＞c ”能推出“a +b ＞2c ”，然后利用列举法判定“a +b ＞2c ”不能推出“a ＞b ＞c ”，从而可得结论．【解答】解：∵a ＞b ＞c ，∴a ＞c ，b ＞c ，则a +b ＞2c ，即“a ＞b ＞c ”能推出“a +b ＞2c ”，但满足a +b ＞2c ，取a ＝4，b ＝﹣1，c ＝1，不满足a ＞b ＞c ，即“a +b ＞2c ”不能推出“a ＞b ＞c ”，所以“a ＞b ＞c ”是“a +b ＞2c ”的充分不必要条件，故选：A ．3、已知2log 0.8a =，0.12b =，sin 2.1c =，则（）A ．a b c <<B ．a c b <<C ．c a b <<D ．b<c<a 【答案】B【详解】因为22log 0.8log 10<=，0.10122>=，0sin 2.11<<，所以a c b <<，故选：B 4、函数2sin ()1x xf x x -=+的图象大致为（）A ．B ．C ．D ．【答案】A 【解析】【分析】根据函数的定义域、奇偶性以及2f π⎛⎫⎪⎝⎭的值来确定正确选项. 【详解】由题意，函数2sin ()1x xf x x -=+的定义域为R ，且22sin()sin ()()()11x x x xf x f x x x -----===--++，所以函数()f x 奇函数，其图象关于原点对称，所以排除C 、D 项，2120212f πππ-⎛⎫=> ⎪⎝⎭⎛⎫+ ⎪⎝⎭，所以排除B 项．故选：A5、已知1F 、2F 分别为双曲线2222:1x y E a b-=的左、右焦点，点M 在E 上，1221::2:3:4F F F M F M =，则双曲线E 的渐近线方程为（） A ．2y x =± B ．12y x =±C．y = D．y =【答案】C【解析】由题意，1F 、2F 分别为双曲线2222:1x y E a b-=的左、右焦点，点M 在E 上，且满足1221:||:2:3:4F F F M F M =，可得122F F c =，23F M c =，14F M c =，由双曲线的定义可知21243a F M F M c c c =-=-=，即2c a =，又由b ==，所以双曲线的渐近线方程为y =．故选：C ．6、设n S 是等比数列{}n a 的前n 项和，若34S =，4566a a a ++=，则96S S = （）A ．32B ．1910 C ．53D ．196【答案】B【解析】设等比数列{}n a 的公比为q ，若1q =，则456133a a a a S ++==，矛盾．所以，1q ≠，故()()33341345631111a q a q q a a a q S qq--++===--，则332q=，所以，()()()63113631151112a q a q S q S qq--==+⋅=--， ()()()9311369311191114a q a q S q q S qq--==++=--，因此，9363192194510S S S S =⋅=．故选：B ． 7、直线1y kx =-被椭圆22:15x C y +=截得最长的弦为（） A ．3 B ．52C ．2D【答案】B【解析】联立直线1y kx =-和椭圆2215xy +=，可得22(15)100k x kx +-=，解得0x =或21015kx k =+，则弦长21015kl k =+，令215(1)k t t +=≥，则10l === 当83t =，即k =，l 取得最大值55242⨯=，故选：B8、设函数()sin()(0)4f x x πωω=->，若12()()2f x f x -=时，12x x -的最小值为3π，则（）A ．函数()f x 的周期为3πB ．将函数()f x 的图像向左平移4π个单位，得到的函数为奇函数 C ．当(,)63x ππ∈，()f x的值域为D ．函数()f x 在区间[,]-ππ上的零点个数共有6个【答案】D【解析】由题意，得23T π=，所以23T π=，则23T πω==，所以()sin(3)4f x x π=-选项A 不正确；对于选项B ：将函数()f x 的图像向左平移4π个单位，得到的函数是 ()sin[3()]cos344f x x x ππ=+-=为偶函数，所以选项B 错误；对于选项C ：当时(,)63x ππ∈，则33444x πππ<-<，所以()f x的值域为，选项C 不正确；对于选项D ：令()0,Z 123k f x x k ππ=⇒=+∈，所以当3,2,1,0,1,2k =---时，[,]x ππ∈-，所以函数()f x 在区间[,]-ππ上的零点个数共有6个，D 正确，故选：D ．9、设函数()(),01,,10,1xx mf x x x m x ⎧≤<⎪⎪=⎨-⎪-<<+⎪⎩，()()41g x f x x =--.若函数()g x 在区间()1,1-上有且仅有一个零点，则实数m 的取值范围是（）A ．(]11,1,4⎡⎫--⋃+∞⎪⎢⎣⎭B ．(]1,1,4⎡⎫-∞-+∞⎪⎢⎣⎭C ．{}11,5⎡⎫-⋃+∞⎪⎢⎣⎭D ．{}11,15⎛⎫-⋃ ⎪⎝⎭【答案】C 【详解】令()()410g x f x x =--=，则()41f x x =+，当01x ≤<时，41xx m=+，即4x mx m =+，即函数1y x =与24y mx m =+的交点问题，其中24y mx m =+恒过A 1,04⎛⎫- ⎪⎝⎭.当10x -<<时，()411x x m x -=++，即1114mx m x -+=++，即函数3111x y =-++与24y mx m =+的交点问题分别画出函数1y ，2y ，3y 在各自区间上的图象：当2y 与3y 相切时，有且仅有一个零点，此时()411xx m x -=++，化简得：()24510mx m x m +++=，由()2251160m m ∆=+-=得：11m =-，219m =-（舍去）当直线2y 的斜率，大于等于直线1y 的斜率时，有且仅有一个零点，把()1,1B 代入24y mx m =+中，解得：15m =，则15m ³综上，m 的取值范围是{}11,5⎡⎫-⋃+∞⎪⎢⎣⎭故选：C二、填空题：本大题共6小题，每小题5分，共30分．试题中包含两个空的，答对1个的给3分，全部答对的给5分．10、已知复数z 满足()2i i z -=，则5i z -=___________．【答案】3【解析】因为圆22:20(0)C x ax y a -+=>的标准方程为：()222x a y a -+=，所以圆必坐标为(,0)a ，半径为a ，由题意得：32a a += 解得：3a = ，故答案为：3.12、已知3π3sin 85α⎛⎫-= ⎪⎝⎭，则πcos 24α⎛⎫+= ⎪⎝⎭________．【答案】725-【解析】2πcos 2cos 22cos 1488ππααα⎡⎤⎛⎫⎛⎫⎛⎫+=+=+- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦232cos 182ππα⎡⎤⎛⎫=-+- ⎪⎢⎥⎝⎭⎣⎦223372sin 1218525πα⎛⎫⎛⎫=--=⨯-=- ⎪ ⎪⎝⎭⎝⎭，故答案为：725- 13、直线l 与双曲线2222:1(0,0)x y E a b a b -=>>的一条渐近线平行，l 过抛物线2:4C y x =的焦点，交C 于A ，B 两点，若||5AB =，则E 的离心率为_______．【详解】依题意，点F 的坐标为(1,0)，设直线l 的方程为1x my =+，联立方程组214x my y x=+⎧⎨=⎩，消去x 并整理得：2440y my --=，设1(A x ，1)y ，2(B x ，2)y ，则124y y m +=，124y y =-，则2212||()4(1)5AB y y m ++=，解得：12m =±，∴直线l 的方程为220x y +-=或220x y --=；直线的斜率为：2±．直线l 与双曲线2222:1(0,0)x y E a b a b -=>>的一条渐近线平行，可得2b a =，所以22224b a c a ==-，1e >，解得e =故14、已知1a >，1b >，且lg 12lg a b =-，则log 2log 4a b +的最小值为_______．【答案】9lg2【解析】由已知，令lg 2log 2lg a m a ==，lg 4log 4lg b n b==，所以lg 2lg a m =，lg 42lg 2lg b n n ==，代入lg 12lg a b =-得：lg 24lg 21m n+=，因为1a >，1b >，所以lg 24lg 24log 2log 4()1()()5lg 2(lg 2lg 2)a b m nm n m n m n n m+=+⨯=++=++ 2lg 25lg 25lg 24lg 29lg 2n m≥+=+=．当且仅当4lg 2lg 2m n n m=时，即1310a b ==时等号成立． log 2log 4a b +的最小值为9lg2．故答案为：9lg2．15、在Rt ABC 中，90C ∠=，若ABC 所在平面内的一点P 满足0PA PB PC λ++=，当1λ=时，222PA PB PC+的值为；当222PA PB PC+取得最小值时，λ的值为．【答案】5；-1【解析】（1）如图5-26，以C 为坐标原点建立直角坐标系，因为0PA PB PC λ++=，所以点P 为ABC 的重心，设BC a =，AC b =，所以(),0A b ，()0,B a ，易得,33a b P ⎛⎫⎪⎝⎭，所以222222222411499991199a b a b PA PBPC b a ++++=+5=．（2）设(,)P x y ,则(,),(,),(,)PA b x y PB x a y PC x y =--=--=--, 所以2,2,b x x a y y λλ-=⎧⎨-=⎩可得(2),(2),b x a y λλ=+⎧⎨=+⎩于是222222222||||()()||PA PB x b y x y a x y PC +-+++-=+()222222222x y bx ay a b x y +--++=+ 22222222(2)(2)2(2)2(2)2x y x y x y λλλλ+++-+-+=++()()222222222x y x y λλλλ+++=++ 2222(1)11λλλ=++=++…当1λ=-时取等号,所以222||||||PA PB PC +的最小值为1．故答案为：5；-1．三、解答题：本大题共5小题，共75分．解答应写出文字说明，证明过程或演算步骤．16、如图，在平面四边形ABCD 中，对角线AC 平分BAD ∠，ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，cos cos cos 0B a C c A ++=．（1）求B ；（2）若2AB CD ==，ABC 的面积为2，求AD ．【答案】（1）34B π=；（2）4=AD ．【分析】（1）利用正弦定理将边化角，再根据两角和的正弦公式及诱导公式即可得到cos B=出B；（2）由三角形面积公式求出a，再利用余弦定理求出AC，即可求出cos CAB∠，依题意cos cosCAB CAD∠=∠，最后利用余弦定理得到方程，解得即可；【详解】（1）cos cos cos0B aC c A++=，cos sin cos cos sin0B B AC A C++=，()cos sin0B B A C++=，cos sin0B B B+=，因为0Bπ<<，所以sin0B>，所以cos B=34Bπ=．（2）因为ABC的面积2S=，所以1sin22==ABCS ac B，2=，所以a=由余弦定理得AC==所以222cos2AB AC BCCABAB AC+-∠==⋅因为AC平分BAD∠，所以cos cosCAB CAD∠=∠，所以2222cosCD AC AD AC AD CAD=+-⋅⋅∠，所以24202AD AD=+-⨯28160AD AD-+=，所以4=AD．17、如图，在五面体ABCDEF中，四边形ABEF为正方形，DF⊥平面ABEF，//CD EF，2DF=，22EF CD==，2EN NC=，2BM MA=．（1）求证：//MN平面ACF；（2）求直线AD与平面BCE所成角的正弦值；（3）求平面ACF与平面BCE夹角的正弦值．【答案】（1）见解析；（2；（3）45【详解】（1）证明：在EF上取点P，使2EP PF=，因为2EN NC=，所以//NP FC，于是//NP平面ACF，因为2BM MA=，四边形ABEF为正方形，所以//MP AF，所以//MP平面ACF，因为MP PN P =，所以平面//MNP 平面ACF ，因为MN ⊂平面MNP ，所以//MN 平面ACF ；（2）解：因为DF ⊥平面ABEF ，所以DF FA ⊥，DF EF ⊥，又因为四边形ABEF 为正方形，所以AF EF ⊥，所以FA 、FE 、FD 两两垂直，建立如图所示的空间直角坐标系， (2AD =-，0，2)，(2EB =，0，0)，(0EC =，1-，2)，设平面BCE 的法向量为(m x =，y ，)x ， 2020EB m x EC m y z ⎧⋅==⎪⎨⋅=-+=⎪⎩，令1z =，(0m =，2，1)，所以直线AD 与平面BCE所成角的正弦值为||2||||22AD m AD m ⋅=⋅⋅ （3）解：(2FA =，0，0)，(0FC =，1，2)，设平面ACF 的法向量为(n u =，v ，)w ，2020FA n u FC n v w ⎧⋅==⎪⎨⋅=+=⎪⎩，令1w =-，(0n =，2，1)-，由（1）知平面BCE 的法向量为(0m =，2，1)，设平面ACF 与平面BCE 所成二面角的大小为θ，||33cos ||||55m n m n θ⋅===⋅⋅，4sin 5θ==．所以平面ACF 与平面BCE 所成二面角的正弦值为45． 18、已知椭圆2222:1(0)x y C a b a b +=>>的左、右焦点为12,F F ，P 为椭圆上一点，且212PF F F ⊥，12tan PF F ∠=．（1）求椭圆C 的离心率；（2）已知直线l 交椭圆C 于,A B 两点，且线段AB 的中点为11,2Q ⎛⎫- ⎪⎝⎭，若椭圆C 上存在点M ，满足234OA OB OM +=，试求椭圆C 的方程．【答案】（1）e =（2）22551164x y +=．【分析】（1）由212tan 2b a PF F c ∠==222a c b -=，建立关于e 的方程，即可得到结果；（2）设()()()112200,,,,,A x y B x yM x y ，由（1）可知224a b =，可设椭圆方程为22244x y b +=，根据234OA OB OM +=，可得120120234234x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩，设1:(1)2AB y k x =--将其与椭圆方程联立，由韦达定理和点M 满足椭圆方程，可求出2b ，进而求出结果.【详解】（1）解：因为2212tan 22b b a PF F c ac ∠==26b =，即()226a c -=，则()261e -=，解得e =（2）设()()()112200,,,,,A x y B x y M x y ，由22234c e a ==，得2243a c =，所以222221134b a c c a =-==，所以224a b =设2222:14x y C b b+=，即22244x y b +=由于,A B 在椭圆上，则2221144x y b +=，2222244x y b +=，①由234OA OB OM +=，得120120234234x x x y y y +=⎧⎨+=⎩，即120120234234x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩ 由M 在椭圆上，则2220044x y b +=,即212222144232344x x y y b ⎛⎫+= ⎪++⎛⎫ ⎪⎝⎝⎭⎭，即()()()222211121222441249464x y x x y y x y b +++++=，②将①代入②得：212124x x y y b +=，③线段AB 的中点为11,2Q ⎛⎫- ⎪⎝⎭，设1:(1)2AB y k x =--可知()22211244y k x x y b⎧=--⎪⎨⎪+=⎩ ()()22222148444410k x kk x k k b +-+++-+=212284121142k k x x k k ++==⨯⇒=+，所以222220x x b -+-=，其中0∆>，解得212b >，所以21222x x b ⋅=-，AB 方程为112y x =-又()2121212121111111122422b y y x x x x x x -⎛⎫⎛⎫=--=-++= ⎪⎪⎝⎭⎝⎭，④ 将④代入③得：22221422425b b b b --+⋅=⇒=，经检验满足212b >，所以椭圆C 的方程为22551164x y +=. 19、已知等差数列}{n a 的前n 项和为n S ，且455=S 455=S ，40342=+a a .数列}{n b 的前n 项和为n T ，满足n n b T 413=+)(*N n ∈.（1）求数列}{n a 、}{n b 的通项公式；（2）若1)23(+⋅-=n n n n n a a a b c ，求数列}{n c 的前n 项和n R ；（3）设n n n b S d =，求证：11248-=+-<∑n n k k n d . 【答案】（1）32+=n a n ，14-=n n b ；（2）51524-+=n R n n ；（2）证明见详解．【详解】（2）；（3）124n n n n n b c b b ++=， 112(3)44n n n n n n b n n c b b +-++∴==，则12124)2(444--+=++<n n n n n n c ，122-+<n n ．设1122n n k k k S '-=+=∑， 11123422122nn k n k k n S '--=++∴==++⋯+∑ 213422222n n n S +'∴=++⋯+ 12111(1)121112422334122222221()2n n n n n n n n n S ---+++'∴=-+++⋯+=-+=--，1482n n n S -+'∴=- 综上，11248-=+-<∑n n k k n c ． 20、已知函数()e cos x f x x =，()cos (0)g x a x x a =+<，曲线()y g x =在π6x =处的切线的斜率为32．（1）求实数a 的值；（2）对任意的π,02x ⎡⎤∈-⎢⎥⎣⎦，()'()0f x g x -≥恒成立，求实数t 的取值范围；（3）设方程()'()f x g x =在区间()ππ2π,2π32n n n +⎛⎫++∈ ⎪⎝⎭N 内的根从小到大依次为1x 、2x 、…、n x 、…，求证：12n n x x +->π．【答案】（1）1a =-；（2）1t ≥；（2）证明见详解．【分析】（1）由'π362g ⎛⎫= ⎪⎝⎭来求得a 的值. （2）由()'()0f x g x -≥，对x 进行分类讨论，分离常数t 以及构造函数法，结合导数求得t 的取值范围.（3）由()'()f x g x =构造函数()e cos sin 1x x x x ϕ=--，利用导数以及零点存在性定理，结合函数的单调性证得12n n x x +->π.【详解】（1）因为()cos (0)g x a x x a =+<，则()'1sin g x a x =-，由已知可得'π131622g a ⎛⎫=-= ⎪⎝⎭，解得1a =-．（2）由（1）可知()'1sin g x x =+，对任意的π,02x ⎡⎤∈-⎢⎥⎣⎦，()'()0tf x g x -≥恒成立，即e cos 1sin x t x x ≥+对任意的π,02x ⎡⎤∈-⎢⎥⎣⎦恒成立，当2x π=-时，则有00≥对任意的R t ∈恒成立；当π02x -<≤时，cos 0x >，则1sin e cos x x t x+≥，令1sin ()e cos x x h x x +=，其中π02x -<≤， ()()2'2e cos e (cos sin )(1sin )e cos x x x x x x x h x x --+=2(1cos )(1sin )0e cos x x x x-+=≥且()'h x 不恒为零，故函数()h x 在π,02⎛⎤- ⎥⎝⎦上单调递增，则max ()(0)1h x h ==，故1t ≥．综上所述，1t ≥．（3）由()'()f x g x =可得e cos 1sin x x x =+，e cos 1sin 0x x x --=，令()e cos sin 1x x x x ϕ=--，则()'e (cos sin )cos x x x x x ϕ=--，因为()ππ2π,2π32x n n n +⎛⎫∈++∈ ⎪⎝⎭N ，则sin cos 0x x >>，所以，()'0x ϕ<，所以，函数()ϕx 在()ππ2π,2π32n n n +⎛⎫++∈ ⎪⎝⎭N 上单调递减，因为π2π3ππ2πe cos 2π33n n n ϕ+⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭πsin 2π13n ⎛⎫-+- ⎪⎝⎭π2π31e 12n +=π2π3e 102+≥>，π2π202n ϕ⎛⎫+=-< ⎪⎝⎭，所以，存在唯一的()ππ2π,2π32n x n n n +⎛⎫∈++∈ ⎪⎝⎭N ，使得()0n x ϕ=，又1ππ2(1)π,2(1)π32n x n n +⎛⎫∈++++ ⎪⎝⎭()n +∈N ，则()1ππ2π2π,2π32n x n n n ++⎛⎫-∈++∈ ⎪⎝⎭N 且()10n x ϕ+=，所以，()()12π112πe cos 2πn x n n x x ϕ+-++-=-()1sin 2π1n x +---12π11e cos sin 1n x n n x x +-++=--112π11e cos e cos n n x x n n x x ++-++=-()112π1e e cos 0n n x x n x ++-+=-<()n x ϕ=，因为函数()ϕx 在()ππ2π,2π32n n n +⎛⎫++∈ ⎪⎝⎭N 上单调递减，故12n n x x +-π>，即12n n x x +->π．。

天津市第一中学高一上学期期中考试数学试题含答案

天津一中2019－2020－1高一年级数学学科期中质量调查试卷本试卷分为第I 卷（选择题）、第II 卷（非选择题）两部分，共100分，考试用时120分钟。

第Ⅰ卷为第1页，第Ⅱ卷为第2至3页。

考生务必将答案涂写规定的位置上，答在试卷上的无效。

祝各位考生考试顺利!第Ⅰ卷一．选择题：（每小题3分，共30分）在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集为R ，集合{}1,0,1,2,3A =-，201x B xx ⎧⎫-=≥⎨⎬+⎩⎭，则A B 中元素的个数为()A ．1B ．2C ．3D ．42．命题“012,2≥+-∈∀x x R x ”的否定是（）A.∃012,2≤+-∈x x R x B.012,2≥+-∈∃x x R x C.D.012,2<+-∈∀x x R x 3.下列关系中正确的是（）A.221333111252⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭B.122333111225⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C.212333111522⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D.221333111522⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭4．函数2()21,f x ax x =+-在[1,2]上是増函数，则a 的取值范围是()A ．1[,0]2-B ．1[,)2-∞C ．1[,0)(0,)2-+∞ D ．(0,)+∞012,2<+-∈∃x x R x5.若不等式02>++c bx ax 的解集为},21|{<<-x x 那么不等式ax c x b x a 2)1()1(2>+-++的解集为（）A.}12|{<<-x xB.{2|-<x x 或1>x }C.}30|{<<x x D.0|{<x x 或}3>x 6.使不等式0)1|)(|1(>-+x x 成立的充分不必要条件是（）A.),1(+∞∈x B.),2(+∞∈x C.),1()1,(+∞--∞∈ x D.)1,(--∞∈x 7．已知函数()9411y x x x =-+>-+，当x a =时，y 取得最小值b ，则a b +等于（）A.3-B ．2C ．3D ．88.若定义运算=Θb a ,,b a ba ab ≥⎧⎨<⎩，则函数)2()(x x x f -Θ=的值域为（）A.(0,1]B ．(,1]-∞C ．(0,1)D ．[1,)+∞9．若函数)(x f y =是奇函数，且函数2)()(++=bx x af x F 在（0，+∞，)上有最大值8，则函数)(x F y =在(－∞，，0)上有()A.最小值－8B.最大值－8C.最小值－6D.最小值－410.高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设x ∈R ，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，例如：[3.5]4-=-，[2.1]2=，已知函数1()12x xe f x e =-+，则函数()()y f x f x =+-⎡⎤⎡⎤⎣⎦⎣⎦的值域是（）A.{0,1}B.{1}C.{1,0,1}- D.{1,0}-第Ⅱ卷二．填空题：（本大题共6小题，每小题4分，共24分）11．计算=+⎪⎭⎫ ⎝⎛+331125833416___．12.已知函数，，则的值为.________13.若()f x 为奇函数，且在(,0)-∞上是减函数，又(2)0f -=，则()0x f x ⋅<的解集为________。

2022-2023学年天津市实验中学滨海学校高二年级上册学期期中质量调查数学试题解析版

2022-2023年度第一学期高二年级期中质量调查（数学）试卷满分： 150分时长：100分钟第I 卷（选择题）一、单选题（本大题共12小题，共60.0分。

在每小题列出的选项中，选出符合题目的一项）1.直线的倾斜角为( )50x +-=A. B. 30︒-60︒C. D. 120︒150︒2.圆的圆心到直线( )22(1)1x y ++=y =A. 0B. 1C.3.已知抛物线上一点到其焦点的距离为，则实数的值y 2=2px(p >0)M(1,m)(m >0)5m 是( )A. B. C. D. ‒42484.已知是椭圆的两个焦点，过的直线l 交椭圆于两点，若12(1,0),(1,0)F F -1F ,M N 的周长为8，则椭圆方程为( )∆MF 2N A. B. C. D. 22143x y +=22143y x +=2211615x y +=2211615y x +=5.已知双曲线上有一点M 到右焦点的距离为18，则点M 到左焦点的22=1259x y -1F 2F 距离是( )A. 8B. 28C. 12D. 8或286.若点在圆的内部，则a 的取值范围是( )(2,1)a a +22+(1)=5x y -A. B. C. D. (1,1)-(0,1)1(1,)5-1(,1)5-7.是方程表示双曲线的( )9k >22+=194x y k k --A. 充要条件 B. 充分不必要条件C. 必要不充分条件D. 既不充分又不必要条件8.P 是椭圆上一点，，分别是椭圆的左、右焦点，若221169x y +=1F 2F ，则的大小为 ( )12||||12PF PF ⋅=12F PF ∠A. B. C. D. 60︒30︒120︒150︒9.若点，，直线l 过点且与线段AB 相交，则l 的斜率k 的(2,3)A --(3,2)B --(1,1)P 取值范围是( )A. B.k ≤34或k ≥43k ≤‒43或k ≥‒34C. D. 34≤k ≤43‒43≤k ≤‒3410.已知圆截直线所得线段的长度是M 与22:20(0)M x y ay a +-=>0x y +=圆的位置关系是( )22:(1)(1)1N x y -+-=A. 内切 B. 相离 C. 外切 D. 相交11.以下四个命题表述错误的的是( )A. 圆上有且仅有3个点到直线222x y +=:10l x y -+=B. 曲线与曲线，恰有四条公切线，221:20C x y x ++=222:480C x y x y m +--+=则实数m 的取值范围为4m >C. 已知圆，P 为直线上一动点，过点P 向圆C 引一22:2C x y +=0x y ++=条切线PA ，其中A 为切点，则的最小值为2||PA D. 已知圆，点P 为直线上一动点，过点P 向圆C 引22:4C x y +=:280l x y +-=两条切线PA ，PB ，A ，B 为切点，则直线AB 经过点1(1,212.已知椭圆C ：的左焦点为F ，点A 是椭圆C 的上顶点，直线22221(0)x y a b a b+=>>l ：与椭圆C 相交于M ，N两点．若点A 到直线l 的距离是1，且2y x =，则椭圆C 的离心率的取值范围是( )|MF |+|NF |≤6A. B. C. D.第II 卷（非选择题）二、填空题（本大题共8小题，共40.0分）13.以点为圆心，并且与y 轴相切的圆的方程是__________.(2,3)P -14.设m 是常数，若点是双曲线的一个焦点，则__________.(0,5)F 2219y x m -=m =15.已知直线过点，它在x 轴上的截距是在y 轴上的截距的2倍，则此直线的方程为(2,3)__________.16.在平面直角坐标系Oxy 中，若双曲线经过点，则该双曲线的2221(0)y x b b-=>(3,4)渐近线方程是__________.17.直线l 过点且与圆相切，那么直线l 的方程为(4,0)-22(1)(2)9x y ++-=__________.18.设圆的圆心为A ，点P 在圆上，则PA 的中点M 的轨迹方2242110x y x y +-+-=程是__________.19.已知F 为双曲线-的右焦点，A 为C 的右顶点，B 为C 上:C 22x a 22y b1(0,0)a b =>>的点且BF 垂直于x 轴.若AB 的斜率为3，则C 的离心率为__________.20.在平面直角坐标系xOy 中，已知双曲线C ：的左、右焦点分别为，2228x y -=1F ，过点作一直线与双曲线C 的右支交于P ，Q 两点，使得，则2F 2F 190F PQ ︒∠=的内切圆的半径为__________.1F PQ 三、解答题（本大题共4小题，共50.分。

天津市第一中学2020-2021学年高二上学期期中数学试题

天津市第一中学2020-2021学年高二上学期期中数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．直线l 1：ax +2y +6=0与直线l 2：x +(a -1)y +a 2-1=0平行，则a 等于（） A ．-1 B ．-1或2 C ．2 D ．12．过点P (1，2)引直线使两点A (2，3)､B (4，-5)到它的距离相等，则直线方程是（） A ．4x +y -6=0B ．x +4y -6=0C ．2x +3y -7=0或x +4y -6=0D ．4x +y -6=0或3x +2y -7=03．过点P(1，4)且在x 轴，y 轴上的截距的绝对值相等的直线共有 ( )A ．1条B ．2条C ．3条D ．4条4．圆x 2+y 2-4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是（） A ．36 B ．18 C ． D ．5．若圆x 2+y 2+ax -by =0的圆心在第二象限，则直线x +ay -b =0一定不经过（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 6．已知圆C ：x 2+y 2-8x +15=0，若直线y =kx -2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的最大值是（）A ．32B ．43C ．53D ．54 7．过椭圆9x 2+25y 2=225的右焦点且倾斜角为45°的弦长AB 的长为（） A ．5 B ．6 C ．9017 D ．78．已知椭圆x 2+4y 2=12的左、右焦点分别为F 1､F 2，点P 在椭圆上，线段PF 1的中点在y 轴上，则∣PF 1∣是∣PF 2∣的（）A ．3倍B ．4倍C ．5倍D ．7倍 9．若椭圆2a 2x 2-ay 2=2的一个焦点是(-2，0)，则a =（）A B C D 10．已知A ､B 为椭圆的左、右顶点，F 为左焦点，点P 为椭圆上一点，且PF ⊥x 轴，过点A 的直线与线段PF 交于M 点，与y 轴交于E 点，若直线BM 经过OE 中点，则椭圆的离心率为（）A ．12 B C ．13 D二、填空题11．已知点(1,2),(3,1)A B ，则线段AB 的垂直平分线的方程是________________ 12．如果x 2+y 2-2x +y +k =0是圆的方程，则实数k 的取值范围是_____.13．已知圆C 过点（1,0），且圆心在x 轴的正半轴上，直线l ：1y x =-被该圆所截得的弦长为C 的标准方程为 .14．过直线:0l x y +-=上一点P 作圆：221x y +=的两条切线的夹角为60°，则点P 的坐标为__________．15．椭圆的两焦点为F 1(－4,0)，F 2(4,0)，点P 在椭圆上，若△PF 1F 2的面积最大为12，则椭圆方程为________.16．椭圆2212516x y +=的左、右焦点为F 1､F 2，点P 在椭圆上，若Rt F 1PF 2，则点P 到x 轴的距离为_____.三、解答题17．在三棱锥P -ABC 中，∠APB =90°，∠P AB =60°，AB =BC =CA ，平面P AB ⊥平面ABC . （1）求直线PC 与平面ABC 所成角的正弦值；（2）求二面角B -AP -C 的余弦值.18．已知直线x +y -1=0与椭圆C ：b 2x 2+a 2y 2=a 2b 2(a >b >0)相交于A ，B 两点，且线段AB 的中点在直线l ：x -2y =0上.（1）求此椭圆C 的离心率；（2）若椭圆C 的右焦点关于直线l 的对称点在圆x 2+y 2=4上，求此椭圆C 的方程. 19．已知(0,3)A ，直线:24=-l y x ，设圆C 的半径为1，圆心在l 上.（1）若圆心C 也在直线1y x =-上，过A 作圆C 的切线，求切线方程；（2）若圆C 上存在点M ，使||2||MA MO =，求圆心C 的横坐标a 取值范围. 20．已知直线l ：x =my +1过椭圆C ：b 2x 2+a 2y 2=a 2b 2(a >b >0)的右焦点F ，且交椭圆C 于A ､B 两点，点A ､B 在直线G ：x =a 2上的射影依次为点D ､E .（1）若22113||e OF OA FA +=，其中O 为原点，A 2为右顶点，e 为离心率，求椭圆C 的方程；（2）连接AF ，BD ，试探索当m 变化时，直线AE ，BD 是否相交于一定点N ？若交于定点N ，请求出N 点的坐标，并给予证明；否则说明理由.参考答案1．A【分析】根据直线平行关系可得方程组，解方程组求得结果.【详解】由1l 与2l 平行得：()()()21202161a a a a ⎧--=⎪⎨-≠-⎪⎩，解得：1a =- 故选：A .【点睛】本题考查两直线1111:+0l A x B y C +=与2222:+0l A x B y C +=平行时有12212112=A B A B B C B C ⎧⎨≠⎩，易错点是忽略直线不能重合，造成增根.2．D【分析】当直线l 的斜率不存在时，直线l 的方程为x =1，不成立；当直线l 的斜率存在时，设直线l 的方程为20kx y k --+=，由此利用点到直线的距离公式能求出直线方程.【详解】当直线l 的斜率不存在时，直线l 的方程为x =1，不成立；当直线l 的斜率存在时，设直线l 的方程为2(1)y k x -=-，即20kx y k --+=，∵直线l 与两点A (2，3)， B (4，-5）的距离相等，=解得4k =-或32k =- .:.直线l 的方程为4420x y --++=或332022x y --++= 整理，得：460x y +-=或3270x y +-=故选：D【点睛】解决本题要注意设直线方程时，分直线的斜率存在、不存在两种情况讨论，然后根据点到直线的距离相等即可求解.3．C【详解】当直线经过原点时，横、纵截距都为0，符合题意，当直线不经过原点时，设直线方程为1x y a b+=. 由题意得141,,a b a b ⎧+=⎪⎨⎪=⎩解得33a b =-⎧⎨=⎩或55a b =⎧⎨=⎩综上，符合题意的直线共有3条.故选：C ．【点睛】首先明白直线的截距的概念，就是直线和坐标轴的交点的坐标，可正，可负，可0，截距不是距离．截距绝对值相等，截距互为相反数，横截距是纵截距的两倍，都要考虑过原点的情况．4．C【分析】先看直线与圆的位置关系，如果相切或相离最大距离与最小距离的差是直径；相交时，圆心到直线的距离加上半径为所求．【详解】圆x 2+y 2-4x-4y-10=0的圆心为（2，2），半径为r =，圆心到到直线x+y-14=0=，所以圆上的点到直线的距离的最大值为d r +=d r -= 因此最大距离与最小距离的差是，故选C ．5．C【分析】由圆心位置确定a ，b 的正负，再结合一次函数图像即可判断出结果.【详解】因为圆22+0x y ax by +-=的圆心坐标为,22a b ⎛⎫-⎪⎝⎭，由圆心在第二象限可得0,0a b >>，所以直线0x ay b +-=的斜率10a -<，y 轴上的截距为0b a>，所以直线不过第三象限.故选：C6．B【分析】圆C 化成标准方程，得圆心为C （4，0）且半径r =1，根据题意可得C 到直线y =kx ﹣2的距离小于或等于2，利用点到直线的距离公式建立关于k 的不等式，即可得到k 的最大值．【详解】∵圆C 的方程为x 2+y 2﹣8x +15=0，∴整理得：（x ﹣4）2+y 2=1，可得圆心为C （4，0），半径r=1．又∵直线y =kx ﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点， ∴点C 到直线y =kx ﹣2的距离小于或等于22≤，化简得：3k 2﹣4k ≤0，解之得0≤k ≤43，可得k 的最大值是43．故选：B7．C【分析】求出焦点坐标和直线方程，与椭圆方程联立，利用韦达定理和弦长公式可得答案.【详解】由9x 2+25y 2=225得，221259x y +=，2225,9a b ==，所以216c =，右焦点坐标为(4,0)，直线AB 的方程为4y x =-，所以2241259y x x y =-⎧⎪⎨+=⎪⎩得2342001750x x -+=，设1122(,),(,)A x y B x y ，所以1212100175,1734x x x x +==，||AB ==9017==. 故选：C.【点睛】本题主要考查直线与椭圆的弦长公式||AB =应用.8．D【分析】由已知得到焦点坐标，设(,)P x y ，根据中点坐标公式得到横坐标等于零得到P 点坐标，再利用两点间的距离公式可得答案.【详解】由椭圆x 2+4y 2=12得，221123x y += ，2222212,3,9a b c a b ===-=，所以1(3,0)F F （-3,0),，设(,)P x y ，则线段1PF 的中点坐标为3,22x y -⎛⎫ ⎪⎝⎭，因为线段PF 1的中点在y 轴上，所以302x -=，所以3x =，所以2231123y +=，解得y =P ⎛ ⎝⎭，1||PF ==2||2PF ==，所以12||7||PF PF =，当3,2P ⎛- ⎝⎭，1||2PF ==，2||2PF ==，所以12||7||PF PF =，故选：D.9．C【分析】方程化为椭圆的标准方程，根据焦点求解即可.【详解】由原方程可得222y 112x a a-=，因为椭圆焦点是(-2，0)，所以2124a a ⎛⎫--= ⎪⎝⎭，解得14a =±，因为20a->，即0a <，所以14a =，故选：C10．C【分析】根据已知条件求出,,B H M 三点坐标，再由三点共线可得斜率相等，从而得出3a c =可得答案.【详解】由题意可设(,0),(,0),(,0)F c A a B a --，设直线AE 的方程（由题知斜率存在）为()y k x a =+，令x c =-，可得(),()M c k a c --，令0x =，可得(0,)E ka ，设OE 的中点为H ，可得0,2ka H ⎛⎫ ⎪⎝⎭，由,,B H M 三点共线，可得BH BM k k =，即()2ka k a c a c a-=---，即为3a c =，可得13c e a ==，故选：C.【点睛】本题考查求椭圆的离心率，解题关键是根据三点共线找到关于,a c 的等量关系.11．4250x y --=【解析】试题分析：先求出中点的坐标，再求出垂直平分线的斜率，点斜式写出线段AB 的垂直平分线的方程，再化为一般式解：线段AB 的中点为(2，32)，垂直平分线的斜率 k=1AB k -=2，∴线段AB 的垂直平分线的方程是 y-32=2（x-2），4x-2y-5=0，故答案为4250x y --=．考点：直线方程点评：本题考查两直线垂直的性质，线段的中点坐标公式，以及用直线方程的点斜式求直线方程的求法．12．5-4∞⎛⎫ ⎪⎝⎭，【分析】根据2240D E F +->即可求解.【详解】由2240D E F +->即(-2)2+12-4k >0，解得k <54. 所以实数k 的取值范围是5-4∞⎛⎫ ⎪⎝⎭，.故答案为：5-4∞⎛⎫ ⎪⎝⎭，. 【点睛】本题考查了圆的一般方程，考查了基本运算求解能力，属于基础题. 13．22(3)4x y -+= 【详解】设圆心为(,0)a ，则圆心到直线10x y --=的距离为d =因为圆截直线所得的弦长根据半弦、半径、弦心距之间的关系有222(1)a +=-，即2(1)4a -=，所以3a =或1a =-（舍去），半径r=3-1=2所以圆C 的标准方程为22(3)4x y -+=14．【详解】设切断为E 、F60EPF ∠=由切线的性质可知30OPF ∠=，因为,OE PE ⊥所以设，由故点P 的坐标为()2,2.【考点定位】此题考查了直线与圆的位置关系，直角三角形的性质，以及切线的性质．已知切线往往连接圆心与切点，借助图形构造直角三角形解决问题，培养了学生数形结合的思想，分析问题，解决问题的能力15．221259x y +=【解析】当点P 为椭圆的短轴顶点时，△PF 1F 2的面积最大，此时△PF 1F 2的面积为S ＝12×8×b ＝12，解得b ＝3.又a 2＝b 2＋c 2＝25，所以椭圆方程为22259x y ＋＝1.16．165或163【分析】设点P (x ,y )，表示出点P 到x 轴的距离为||y ，由哪一个角是直角来分类讨论，在第一类中直接令x =士3得结果，在第二类中要列出方程组，再用等面积法求y. 【详解】设点(,)P x y ，则到x 轴的距离为||y 由于5a =，4b =，3c ∴=，（1）若1290PF F ∠=︒或2190PF F ∠=︒，令3x =±得29y =291616(1)2525-=，16||5y ∴=，即P 到x 轴的距离为165．（2）若1290F PF ∠=︒，则122221210||6PF PF PF PF ⎧+=⎪⎨+=⎪⎩， 22121||||(106)322PF PF ∴=-=，121211||||||||22PF PF F F y =， 6|1|3y ∴=，由（1）（2）知：P 到x 轴的距离为165或163，故答案为：165或163．【点睛】解决本题的关键是要注意分类讨论的思想，题目中的直角三角形，要分清楚那个角是直角，是解决问题的先决条件. 17．（12【分析】(1)设AB 中点为D ，AD 中点为O ，连接,,OC OP CD ，可以证出∠OCP 为直线PC 与平面ABC 所成的角.不妨设P A =2,则OD = 1 , OP AB =4，在Rt △OCP 中求解；（2）过D 作DE AP ⊥于E ，连接CE ，可证明CED ∠就是二面角B -AP -C 的平面角，解三角求解即可. 【详解】（1）设AB 中点为D ，取AD 中点为O ，连接OC ，连接PD 、CD . 如图，因为∠APB =90°，∠P AB =60°，1,2AP AB AD PD AD ===, 所以PAD 为等边三角形，所以PO AB ⊥，因为平面P AB ⊥平面ABC ，AB 为交线，所以PO ⊥平面ABC所以OCP ∠为直线PC 与平面ABC 所成的角因为AB =BC =CA ，所以CD ⊥AB . 因为∠APB =90°，∠P AB =60°，不妨设P A =2，则OD =1，OP AB =4.所以，OC ==在Rt OCP 中，13tan OP O C C O P ===∠，所以sin 4OCP ∠=故直线PC 与平面ABC （2）过D 作DE AP ⊥于E ，连接CE . 如图，由已知可得，CD ⊥平面P AB. 根据三垂线定理可知，CE ⊥P A ，所以，CED ∠就是二面角B -AP -C 的平面角.由（1）知，DE 在Rt △CDE 中， tan 2CED CDDE==∠，所以cos CED ∠=故二面角B AP C --. 【点睛】求立体几何中空间的角，利用传统做法把握好两方面即可：一是要找到或作出所求角，并要适当证明，二是要把角放在合适的三角形中求解.18．（1）2（2）22184x y +=【分析】（1）联立直线方程与椭圆方程，利用韦达定理以及中点坐标公式解得线段AB 中点M 坐标，代入直线l 的方程，解得离心率；（2）利用方程组解得右焦点关于直线l 的对称点坐标，代入圆方程，结合（1）解得a ，b ,即可求出椭圆标准方程. 【详解】椭圆C ：b 2x 2+a 2y 2=a 2b 2(a >b >0)，即22221x y a b+=，（1）设A ，B 两点的坐标分别为（x 1，y 1），（x 2，y 2），由2222101x y x y a b +-=⎧⎪⎨+=⎪⎩得：()222222220a b x a x a a b +-+-=． ()()()222222220aab a a b ∆=--+->，即221a b +>．x 1+ x 2=2222a a b+， y 1+ y 2＝-( x 1+ x 2)+2=2222b a b +，∴点M 的坐标为（222a a b +，222b a b +）．又点M 在直线l 上，∴2222222a b a b a b -++=0， ∴()222222a b a c ==-，∴222a c =，∴c e a ==．（2）由（1）知b c =，设椭圆的右焦点F （b ，0）关于直线l ： 12y x =的对称点为（x 0，y 0），由000001121222y x b y x b -⎧⋅=-⎪-⎪⎨+⎪=⋅⎪⎩，解得003545x b y b ⎧=⎪⎪⎨⎪=⎪⎩ ∵22004x y +=，∴2234455b b ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭， ∴24b =，222822b a c =∴==，显然有221a b +>．∴所求的椭圆的方程为22184x y +=．【点睛】解决此题的关键在于求出A ，B 两点的中点坐标，利用中点坐标在直线l ：x -2y =0上，建立关于,a b 的方程，结合222a b c =+，转化为关于,a c 的方程，求出椭圆的离心率e . 19．（1）3y =或34120x y +-=；（2）1205a . 【分析】（1）根据圆心在直线:24=-l y x 上也在直线1y x =-上，求得圆心坐标，可得过A 的圆C 的切线方程.（2）设圆C 的方程为22()(24)1x a y a -+-+=，再设(,)M x y ，根据2MA MO =，求得圆22:(1)4D x y ++=，根据题意，圆C 和圆D 有交点，可得2112CD -+，即221(241)3a a +-+，由此求得a 的范围.【详解】解：（1）根据圆心在直线:24=-l y x 上，若圆心C 也在直线1y x =-上，则由241y x y x =-⎧⎨=-⎩，求得32x y =⎧⎨=⎩，可得圆心坐标为(3,2).设过(0,3)A 的圆C 的切线方程为3(0)y k x -=-，即30kx y -+=，根据圆心到直线30kx y -+=的距离等于半径11=，求得0k =，或34k =-，故切线方程为3y =，或34120x y +-=.（2）根据圆心在直线:24=-l y x 上，可设圆的方程为22()(24)1x a y a -+-+=.若圆C 上存在点M ，使||2||MA MO =，设(,)M x y ，2MA MO =，∴=化简可得22(1)4x y ++=，故点M 在以(0,1)D -为圆心、半径等于2的圆上.根据题意，点M 也在圆C 上，故圆C 和圆D 有交点，2112CD ∴-+，即221(241)3a a +-+，求得251280a a -+，且25120a a -，解得1205a . 【点睛】本题主要考查直线和圆的位置关系的应用，点到直线的距离公式，圆的标准方程，考查学生的数学抽象能力与计算能力，属于中档题.20．（1）22143x y +=（2）相较于定点5(2N ，0)，证明见解析.【分析】（1）设椭圆的半焦距为c ，由题意可得1c =，由已知等式可得e ，进而得到a ，b ，即可得到椭圆方程；（2）当0m =时，求得AE ，BD 的交点，猜想定点5(2N ，0)．当0m ≠时，分别设A ，B 的坐标为1(x ，1)y ，2(x ，2)y ，由题意可得1(4,)D y ，2(4,)E y ，联立直线l 的方程和椭圆方程，运用韦达定理，结合三点共线的性质，计算直线BN ，DN 的斜率，可判断B ，N ，D 共线，同理可判断A ，E ，N 共线，即可得到定点N ．【详解】（1）椭圆的方程为22221(0)x y a b a b+=>>，设椭圆的半焦距为c ，由题意可得1c =，由22113||||||e OF OA FA +=，可得113ec a a c+=-，即有113a ce c a -+-=，即14e e =，解得12e =，则2a =，b ==所以椭圆的方程为22143x y +=；（2）当0m =时，直线AB 垂直于x 轴，可得四边形ABED 为矩形，直线AE ，BD 相交于点5(2，0)，猜想定点5(2N ，0)；当0m ≠时，分别设A ，B 的坐标为1(x ，1)y ，2(x ，2)y ，由题意可得1(4,)D y ，2(4,)E y ，由2213412x my x y =+⎧⎨+=⎩可得22(43)690m y my ++-=， 122643m y y m+=-+，122943y y m =-+，由2252BN y k x =-，1542DN y k =-，由212235()2235()22BN DNy y x k k x ---=-，又212121222353369(1)()()()022224343m y y my y y my y m m m -+-=+-=---=++，则0BN DN k k -=，即BN DN k k =，所以B ，D ，N 三点共线；同理可得A ，E ，N 三点共线．则直线AE ，BD 相交于一定点5(2N ，0)．【点睛】本题考查椭圆的方程和性质，以及直线和椭圆的位置关系，注意联立直线方程和椭圆方程，运用韦达定理和直线的斜率公式，考查方程思想和运算能力，属于中档题．。

天津经济技术开发区第一中学2024-2025学年高二上学期11月期中考试数学试题

天津经济技术开发区第一中学2024-2025学年高二上学期11月期中考试数学试题一、单选题1．已知向量()()1,,1,1,1,1a m b =-=-，若()a b b +⊥ ，则m =（）A ．4B ．3C ．2D ．12．正方体1111ABCD A B C D -中，E 为AB 中点，则直线1A E ，1C D 所成角的正弦值为（）A B ．12C D ．15153．在棱长为6的正四面体ABCD 中，点P 与Q 满足23AP AB =uu u r uu u r ，且2CD CQ =，则PQ 的值为（）AB C D 4．过抛物线22y x =的焦点，且与直线230x y -+=垂直的直线方程为（）A ．210x y +-=B ．4210x y +-=C ．8410x y +-=D ．16810x y +-=5．直线:1l y =+与圆22:1O x y +=相交于A ，B 两点，则OAB ∆的面积为A ．14B C ．12D 6．已知线段AB 的端点B 的坐标()4,3，端点A 在圆224x y +=上运动，求线段AB 的中点M 的轨迹所围成图形的面积（）A ．4πB ．2πC ．πD ．9π47．“12m <<”是“方程22113x y m m+=--表示的曲线是焦点在y 轴上的椭圆”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件8．已知O 为坐标原点,抛物线y 2=2x 与过焦点的直线交于A ,B 两点,则OA OB ⋅的值是A ．34B ．34-C ．3D ．-39．在数列{}n a 中，12a =，且11,N 1n na n a *+=∈-，则2020a =（）A ．2B ．1-C ．12D ．110．已知双曲线221(0)x y m n m n-=>>和椭圆22154x y +=有相同的焦点，则41m n +的最小值为（）A ．2B ．4C ．6D ．911．双曲线()2222:10,0x y C a b a b-=>>的左右焦点分别为1F ，2F ，过1F 的直线与双曲线C 的左右两支分布交于两点M ，N ，若1114F M F N =，2F M MN =，则双曲线的离心率为（）A ．2BC ．3D 12．已知点A 是抛物线x 2=4y 的对称轴与准线的交点，点B 为抛物线的焦点，点P 在抛物线上且满足|PA |=m |PB |，当m 取最大值时，点P 恰好在以A ，B 为焦点的双曲线上，则双曲线的离心率为（）AB +1CD -1二、多选题13．在空间直角坐标系O xyz -中，已知点()()()2,0,0,1,1,2,2,3,1A B C -，则（）A ．AC =B ．异面直线OB 与AC 所成角的余弦值为30C ．5AB BC ⋅=-D ．OB 在BC 上的投影向量的模为1114．已知a ∈R ，直线1l ：0x ay a +-=，直线2l ：()2320ax a y a --+-=，则（）A ．若12//l l ，则1a =或3-B ．若12//l l ，则1l 与2lC ．若12l l ⊥，则0a =或2D ．若2l 在x 轴和y 轴上的截距相等，则1a =15．已知椭圆E ：()222210x y a b a b+=>>的离心率为23，长轴长为6，F ，F '分别是椭圆的左、右焦点，()1,1A 是一个定点，P 是椭圆E 上的动点，则下列说法正确的是（）A ．6PF PF +'=B ．椭圆E 的标准方程为22195x y +=C ．AF '=D ．PA PF +的最大值为616．已知抛物线28y x =的焦点为F ，过原点O 的动直线l 交抛物线于另一点P ，交抛物线的准线于点Q ，下列说法正确的是（）A ．若4PF =，则O 为线段PQ 中点B ．若OP =||6PF =C ．存在直线l ，使得PF QF⊥D ．PFQ △面积的最小值为8三、填空题17．已知(),,2u a b a b =+-r是直线l 的一个方向向量，()2,3,1n = 是平面α的一个法向量，若l ⊥α，则a ，b 的值分别为.18．已知圆()22:44C x y +-=，直线()():31140l m x m y ++--=，直线被圆所截的最短弦长为19．抛物线24y x =上的点到直线40x y -+=的最小距离为．20．数列{}n a 的前n 项和记为n S ，若231n S n n =-+，则n a =.21．已知抛物线2:2(0)C y px p =>的焦点为F ，其准线与x 轴交点为K ，2FK =，直线l 过点K ，且与抛物线C 交于A ，B 两点，若BF =，则AF BF +=22．若椭圆C ：()222210+=>>x y a b a b 的离心率是2，一个顶点是(0,1)B ，且P ，Q 是椭圆C 上异于点B 的任意两点，BP BQ ⊥，则直线PQ 过定点．四、解答题23．已知圆C 的圆心在直线30x y -=上，且经过点(1,3),(1,5)A B -．(1)求圆C 的标准方程；(2)过点(2,1)P的直线l 与圆C 相交于,M N 两点，且||MN =l 的方程．24．如图所示，在直三棱柱111ABC A B C -中，侧面11AAC C 为长方形，11AA =，2AB BC ==，120ABC ∠= ，AM CM =.(1)求证：平面11AA C C ⊥平面1C MB ；(2)求直线1A B 和平面1C MB 所成角的正弦值；(3)在线段1A B 上是否存在一点T ，使得点T 到直线1MC 的距离是3，若存在求1AT 的长，不存在说明理由.25．已知椭圆2222:1(0)x y C a b a b +=>>的离心率为3，左、右焦点分别为1F 、2F ，过右焦点2F 的直线与椭圆交于P 、Q 两点，且1PQF △的周长为(1)求椭圆C 的方程；(2)过点1F 的直线与椭圆C 相交于,A B 两点．且AB =2AF B 的面积．26．已知椭圆2222:1(0)x y E a b a b +=>>的离心率为3，A 、C 分别是E 的上、下顶点，B ，D分别是E 的左、右顶点，||4AC =．(1)求E 的方程；(2)设P 为第一象限内E 上的动点，直线PD 与直线BC 交于点M ，直线PA 与直线2y =-交于点N ．求证：//MN CD ．。

天津市第一中学2023-2024学年高一上学期11月期中数学试题

所以 (ðU P) È Q = {4} È{2, 4} = {2, 4} .
故选：B 2．B 【分析】根据已知条件，分别检验充分性与必要性即可.
【详解】
a
=
b
<
0
时，
a
+ 2
b
=
ab
不成立，“
a
=
b
”不是“
a
+ 2
b
=
ab ”的充分条件；
( ) a
+b 2
=
ab 时，有 a ³ 0 且 b ³ 0 ， a + b - 2 ab = 0 ，即
答案第51 页，共22 页
【详解】解 2 + x - x2 < 0 ，即 x2 - x - 2 > 0 可得， x < -1或 x > 2 .
（）
A．{0, 2,3, 4} C．{2,3, 4}
B．{2, 4} D．{1, 2, 4}
2．“
a
=
b
”是“
a
+ 2
b
=
ab ”的（
）
A．充分不必要条件 C．充要条件
B．必要不充分条件 D．既不充分也不必要条件
3．存在量词命题 p： $x Î[-1,1] , x2 -1 £ 0 的否定是（）
A． "x Î[-1,1] , x2 -1 > 0
f
(a)
=
.
15．已知函数
f
(
x)
=
ìïx2 - (a + 4) x íïî(2a - 3) x，x
+ ³
5，x 2
<
2

2023-2024学年天津市耀华中学高二上学期期中数学试卷+答案解析(附后)

2023-2024学年天津市耀华中学高二上学期期中数学试卷一、单选题：本题共10小题，每小题4分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知空间四边形ABCD 的每条边和对角线的长都等于a ，点E ，F 分别是BC ，AD 的中点，则的值为( )A. B.C.D.2.若直线与圆有公共点，则( )A. B.C.D.3.圆和圆的公切线的条数为( )A. 1B. 2C. 3D. 44.已知直线过点，且被圆截得的弦长是8，则该直线的方程为( )A. B.或C.D.或5.若两条直线与互相垂直，则a 的值等于( )A. 3B. 3或5C. 3或或2D.6.作直线l 与圆相切且在两轴上的截距相等，这样的直线l 有( )A. 4条B. 3条C. 2条D. 1条7.已知椭圆以及椭圆内一点，则以P 为中点的弦所在直线的斜率为( )A. B. C. 2D.8.过椭圆的一个焦点F 作弦AB ，若，，则的数值为( )A. B.C. D. 与弦AB 斜率有关9.椭圆的两焦点为，，以为边作正三角形，若椭圆恰好平分正三角形的另两条边，则椭圆的离心率为( )A.B.C.D.10.设椭圆的方程为，斜率为k的直线不经过原点O，且与椭圆相交于A，B两点，M为线段AB 的中点.下列说法正确的个数( )①直线AB与OM垂直②若点M的坐标为，则直线方程为③若直线方程为，则点M的坐标为④若直线方程为，则A. 4B. 3C. 2D. 1二、填空题：本题共5小题，每小题4分，共20分。

11.直线与曲线有两个公共点，则b的取值范围是__________.12.若圆上恰有相异两点到直线的距离等于1，则r的取值范围是__________13.已知P是直线上的动点，PA，PB是圆的切线，A，B为切点，C为圆心，那么四边形PACB面积的最小值是__________14.已知椭圆的离心率为，短轴长为2，点P为椭圆上任意一点，则的最小值是__________.15.已知椭圆C：的左焦点为F，经过原点的直线与C交于A，B两点，总有，则椭圆C离心率的取值范围为__________.三、解答题：本题共3小题，共40分。

天津第一中学高二下学期期中考试数学试题Word版含答案

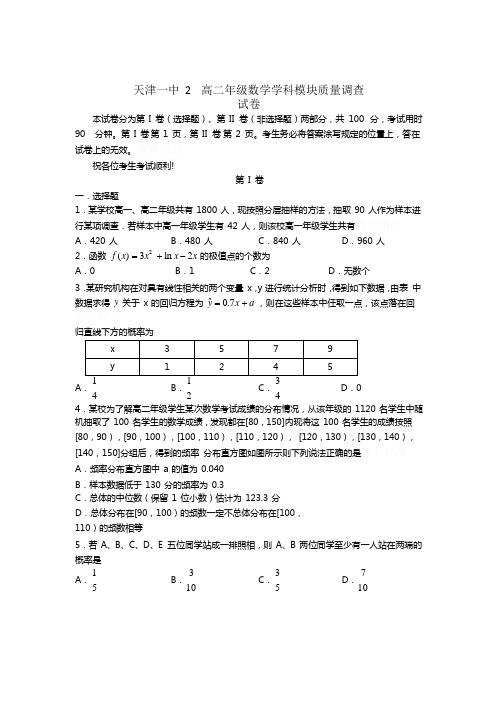
天津一中2 高二年级数学学科模块质量调查试卷本试卷分为第 I 卷（选择题）、第 II 卷（非选择题）两部分，共100 分，考试用时90 分钟。

第 I 卷第 1 页，第 II 卷第 2 页。

考生务必将答案涂写规定的位置上，答在试卷上的无效。

祝各位考生考试顺利!一．选择题第 I 卷1．某学校高一、高二年级共有 1800 人，现按照分层抽样的方法，抽取 90 人作为样本进行某项调查．若样本中高一年级学生有 42 人，则该校高一年级学生共有A．420 人B．480 人C．840 人D．960 人2．函数f (x) = 3x2 + ln x - 2x 的极值点的个数为A．0 B．1 C．2 D．无数个3．某研究机构在对具有线性相关的两个变量x，y 进行统计分析时，得到如下数据，由表中数据求得y 关于x 的回归方程为yˆ= 0.7x +a ，则在这些样本中任取一点，该点落在回x3579y12451 1 A．B．4 23C．D．0 44．某校为了解高二年级学生某次数学考试成绩的分布情况，从该年级的 1120 名学生中随机抽取了 100 名学生的数学成绩，发现都在[80，150]内现将这 100 名学生的成绩按照[80，90），[90，100），[100，110），[110，120），[120，130），[130，140），[140，150]分组后，得到的频率分布直方图如图所示则下列说法正确的是A．频率分布直方图中a 的值为 0.040B．样本数据低于 130 分的频率为 0.3C．总体的中位数（保留 1 位小数）估计为 123.3 分D．总体分布在[90，100）的频数一定不总体分布在[100，110）的频数相等5．若A、B、C、D、E 五位同学站成一排照相，则A、B 两位同学至少有一人站在两端的概率是1 3 3 7 A．B．C．D．5 10 5 106．函数 f ( x) = sin xln( x+ 2)的图象可能是A. B.C. D.7．某校为了增强学生的记忆力和辨识力，组织了一场类似《最强大脑》的PK 赛，A，B 两队各由 4 名选手组成，每局两队各派一名选手PK，比赛四局．除第三局胜者得 2 分外，其余各局胜者均得 1 分，每局的负者得 0 分．假设每局比赛A 队选手获胜的概率均为2，且各局比赛结果相互独立，比赛结束时A 队的得分高于B 队的得分的概率为316 52 A．B．27 81⎧20 7C．D．27 9 0 , 0 <x ≤18．函数f ( x) = | l n x |, g (x) =| x2 4 | 2,x，若关于x 的方程f (x) +m =g(x) 恰有1⎨- - >三个丌相等的实数解，则m 的取值范围是A．[0,ln 2] B．(-2 -ln 2,0]C．(-2 -ln 2,0)D．[0, 2 + ln 2)二．填空题第 II 卷9．从区间（﹣2，3）内任选一个数m，则方程mx2+y2＝1 表示的是双曲线的概率为．10．一批排球中正品有m 个，次品有n 个，m+n＝10（m≥n），从这批排球中每次随机取一个，有放回地抽取 10 次，X 表示抽到的次品个数若DX＝2.1，从这批排球中随机一次取两个，则至少有一个次品的概率p＝11．已知直线y = 2x -1不曲线y = ln(x +a)相切，则a 的值为12．某公司 16 个销售店某月销售产品数量（单位：台）的茎叶图如图，已知数据落在[18，22]中的频率为 0.25，则这组数据的中位数为．13．函数f（x）＝e x﹣3x+2 的单调增区间为．14．已知函数f（x）＝ax+lnx，若f（x）≤1 在区间（0，+∞）内恒成立，实数a 的取值范围为．。

天津市天津中学2023-2024学年高二上学期第一次月考数学试题

为
．
11．不论 m 为何实数，直线 l：(m 1)x (2m 3) y m 0 恒过定点
.
12．已知直线 l1 ： ax y 3 0 与 l2 ： 2x a 1 y a 1 0 平行，则 a
.
13．点 P 1, 2 到直线 3x 4y 6 0 的距离为
．
14．点 0, 1 到直线 y k x 1 距离的最大值为
值为
．
25．数学家华罗庚说：“数缺形时少直观，形少数时难入微”，事实上，很多代数问题可
以转化为几何问题加以解决．例如：与 x a2 y b2 相关的代数问题，可以转化
为点 A x, y 与点 B a,b 之间的距离的几何问题．结合上述观点：对于函数
f x x2 2x 2 x2 2x 2 ， f x 的最小值为
．
二、证明题 26．在三棱台 ABC - A1B1C1 中，若 A1A 平面 ABC, AB AC, AB AC AA1 2, A1C 1 1, M ， N 分别为 BC, AB 中点．
(1)求证： A1N // 平面 C1MA ； (2)求平面 C1MA 与平面 ABB1A1 所成角的余弦值； (3)求点 B1 到平面 C1MA 的距离； (4)求点 B1 到直线 C1M 的距离． 27．直三棱柱 ABC - A1B1C1 中，AA1 AB AC 2, AA1 AB, AC AB, D 为 A1B1 中点，E
．
3．已知直线 l 斜率的取值范围是 3,1 ，则 l 的倾斜角的取值范围是
．
4．两直线 3x＋y－3＝0 和 6x＋my－1＝0 平行，则它们之间的距离为
.
5．已知直线 l1 : (a 1)x 2 y 1 0与直线 l2 : x ay 3 0 垂直，则 a 等于

2023-2024学年天津市第一中学高二上学期期中数学试卷+答案解析(附后)

2023-2024学年天津市第一中学高二上学期期中数学试卷一、单选题：本题共10小题，每小题3分，共30分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.设直线l的斜率为k，且，则直线l的倾斜角的取值范围为( )A. B.C. D.2.设点，，直线l过点且与线段AB相交，则l的斜率k的取值范围是( )A.或 B. 或 C. D.3.“”是“直线和直线互相垂直”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件4.已知圆，若直线与圆C相交于A，B两点，则的最小值为( )A. B. C. 3 D.5.某广场的一个椭球水景雕塑如图所示，其横截面为圆，过横截面圆心的纵截面为椭圆，，分别为该椭圆的两个焦点，PQ为该椭圆过点的一条弦，且的周长为若该椭球横截面的最大直径为2米，则该椭球的高为( )A. 米B. 米C. 米D. 米6.已知双曲线C的焦点与椭圆E：的上、下顶点相同，且经过E的焦点，则C的方程为( )A. B. C. D.7.圆关于直线对称，则的最小值是.( )A. B. C. 4 D.8.双曲线C：的左、右焦点分别为，，过的直线与双曲线C的右支在第一象限的交点为A，与y轴的交点为B，且B为的中点，若的周长为6a，则双曲线C的渐近线方程为( )A. B. C. D.9.已知椭圆与双曲线有相同的焦点、，椭圆的离心率为，双曲线的离心率为，点P为椭圆与双曲线的交点，且，则的值为( )A. B. C. D. 410.椭圆的左、右焦点分别是、，斜率为1的直线l过左焦点且交C于A，B两点，且的内切圆的面积是，若椭圆C离心率的取值范围为，则线段AB的长度的取值范围是( )A. B. C. D.二、填空题：本题共6小题，每小题4分，共24分。

11.若椭圆的焦点在y轴上，则实数k的取值范围是__________.12.若圆与双曲线的渐近线相切，则双曲线的离心率为__________.13.直线l过点，且在两坐标轴上截距相等，则直线l的方程为__________14.若直线与曲线有两个交点，则实数k的取值范围是__________.15.已知O为坐标原点，设，分别是双曲线的左、右焦点，P为双曲线左支上任意一点，过点作的平分线的垂线，垂足为H，则__________.16.已知点是函数的图象上的动点，则的最小值为__________.三、解答题：本题共4小题，共46分。

2019-2020学年天津市第一中学高二上学期期中考试数学试题 (含答案)

天津市第一中学2024-2025学年高二上学期期中质量调查数学试题

天津市第一中学2024-2025学年高一上学期数学学科期中质量调查试卷

2022-2023学年天津市第一中学高一上学期期中数学试题(解析版)

2022-2023学年天津市滨海新区塘沽第一中学高二上学期期中数学试题(解析版)

天津市第一中学2022-2023学年高三上学期第三次月考数学试题(解析版)

天津市第一中学高一上学期期中考试数学试题含答案

2022-2023学年天津市实验中学滨海学校高二年级上册学期期中质量调查数学试题 解析版

天津市第一中学2020-2021学年高二上学期期中数学试题

天津经济技术开发区第一中学2024-2025学年高二上学期11月期中考试数学试题

天津市第一中学2023-2024学年高一上学期11月期中数学试题

2023-2024学年天津市耀华中学高二上学期期中数学试卷+答案解析(附后)

天津第一中学高二下学期期中考试数学试题Word版含答案

天津市天津中学2023-2024学年高二上学期第一次月考数学试题

2023-2024学年天津市第一中学高二上学期期中数学试卷+答案解析(附后)

2022-2023学年天津市实验中学滨海学校高二年级上册学期期中质量调查数学试题解析版