2019遂宁中考真题
中考真题生物试题分项汇编05生物体的结构层次(解析版)

母题05 生物体的结构层次【母题来源一】2019年四川省遂宁市中考生物【母题原题】2015年12月10日瑞典国王为诺贝尔奖得主屠呦呦颁奖,以表彰她从野生植物黄花蒿中提取青蒿素治疗由疟原虫引起的疟疾,挽救了数百万人的生命。
下列有关黄花蒿的说法错误的是A.黄花蒿的细胞有细胞壁,而疟原虫的细胞没有细胞壁B.黄花蒿的结构层次是:细胞→器官→组织→植物体C.黄花蒿细胞内指导青蒿素形成的控制中心是细胞核D.黄花蒿植株生长离不开细胞的分裂、生长和分化【答案】B【解析】黄花篙属于植物,疟原虫属于动物,黄花蒿的细胞有细胞壁,而疟原虫的细胞没有细胞壁,A 正确;黄花蒿的结构层次是:细胞→组织→器官→植物体,B错误;细胞核是遗传物质的控制中心,黄花蒿细胞内指导青蒿素形成的控制中心是细胞核,C正确;黄花蒿植株生长离不开细胞的分裂、生长和分化,D正确。
【母题来源二】2019年海南省中考生物【母题原题】关于如图的描述错误的是A.甲中的细胞壁和液泡是植物细胞具有而动物细胞没有的结构B.乙所示的胃的结构层次是器官C.丙中叶片的上、下表皮分布有保护组织D.丁和丙的生物体结构层次是相同的【答案】D【解析】植物细胞与动物细胞的不同点:植物细胞具有细胞壁、叶绿体和液泡,动物细胞不具有细胞壁、液泡、叶绿体。
植物体的结构层次由小到大依次是细胞→组织→器官→植物体.人体的结构层次由小到大依次是细胞→组织→器官→系统→人体。
图中甲是细胞,B是胃(器官),丙是植物体,丁是动物体(人体)。
植物细胞具有细胞壁、叶绿体和液泡,动物细胞不具有细胞壁、液泡、叶绿体。
所以甲图中的细胞壁和液泡是植物细胞具有而动物细胞没有的结构,故A正确;乙图中的胃是由不同的组织构成的,属于器官,故B正确;丙图中的植物体,在其叶片的上、下表层分布的表皮细胞具有保护叶片内部的功能,属于保护组织,故C正确;丁图表示人体,在结构层次上动物体具有系统,植物体没有,所以丙图和丁图代表的生物体的结构层次是不相同的,故D错误。
四川省各市2019年中考语文卷【古诗文默写与鉴赏类题】及答案解析汇集

四川省各市2019年中考语文卷【古诗文默写及鉴赏类题】汇集2019年乐山市中考题名篇名句默写(8分)13.根据提示,补写出下列句子中的空缺部分。
(1)大漠孤烟直,______________________________(2)落红不是无情物,o (3),却话巴山夜雨时。
(4),心忧炭贱愿天寒。
(5)长风破浪会有时,_________________________(6)马作的卢飞快,o (7)欧阳修《醉翁亭记》中“,。
(王维《使至塞上》)(龚自珍《己亥杂诗》(李商隐《夜雨寄北》(白居易《卖炭翁》)(李白《行路难》)(辛弃疾《破阵子•为陈同甫赋壮词以寄之》)"两句描绘了色彩鲜明的春夏之景。
答案13.(1)长河落日圆(2)化作春泥更护花(3)何当共剪西窗烛(4)可怜身上衣正单(5)直挂云帆济沧海(6)弓如霹雳弦惊(7)野芳发而幽香,佳木秀而繁阴(-)古代诗歌阅读(本题共2小题,7分)阅读下面这首唐诗,完成11〜12题。
归雁①(其一)唐•杜甫万里衡阳雁,今年又北归。
双双瞻②客上,一一背人飞。
云里相呼疾,沙边自宿稀。
系书元浪语③,愁寂故山④薇。
【注】①杜甫晚年漂泊于湖北、湖南一带时,写下此诗。
②瞻:往前看。
③浪语:妄说。
④故山:喻家乡。
11.下列对诗句的理解恰当的一项是(3分)A.首联开篇点题,如今大雁又要从衡阳飞回万里之外的北方了,与范仲淹“衡阳雁去”四字意思相同。
B.颔联和颈联描写归雁一双双,一只只往北飞去,很少栖息,表现出大雁北归途中急切的心情。
C.尾联说大雁传书原来是一句空话,惶急的大雁不能代我问问家乡薇草采了没有,表现了诗人对家乡农事的关心。
D.诗人采用比兴的手法,由雁及人,伤感自己年迈力衰,无法像归雁一样自由翱翔,施展抱负。
12.从内容上看,《归雁》属于什么类型的诗歌?这首诗抒发了诗人怎样的情感?(4分)答案:(二)古代诗歌阅读(本题共2小题,7分)11.B12.羁旅怀乡诗(咏物诗);苦于漂泊羁旅的孤独凄凉之情和对家乡亲人无限思念的愁绪。
2019年中考物理真题集锦——专题三:力学作图(含答案)
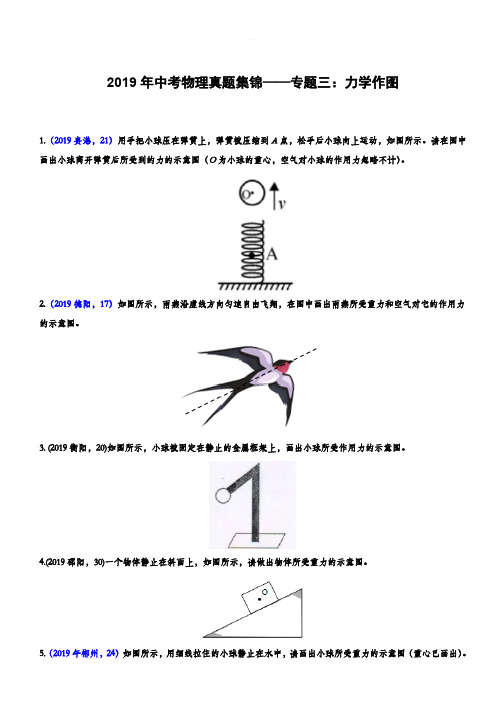
2019年中考物理真题集锦——专题三:力学作图1.(2019贵港,21)用手把小球压在弹簧上,弹簧被压缩到A点,松手后小球向上运动,如图所示。
请在图中画出小球离开弹簧后所受到的力的示意图(O为小球的重心,空气对小球的作用力忽略不计)。
2.(2019德阳,17)如图所示,雨燕沿虚线方向匀速自由飞翔,在图中画出雨燕所受重力和空气对它的作用力的示意图。
3. (2019衡阳,20)如图所示,小球被固定在静止的金属框架上,画出小球所受作用力的示意图。
4.(2019邵阳,30)一个物体静止在斜面上,如图所示,请做出物体所受重力的示意图。
5.(2019年郴州,24)如图所示,用细线拉住的小球静止在水中,请画出小球所受重力的示意图(重心已画出)。
6.(2019临沂,28)如图所示,一瓶饮料静置在停止运转的传送带上。
请在图中画出饮料瓶受重力的示意图。
(图中的A点为饮料瓶的重心)7.(2019常德,24)画出下图中小球所受重力的示意图。
8.(2019怀化,29)如图所示,小球悬挂在天花板上静止不动,请画出小球所受重力的示意图;9.(2019上海,16)重为10牛的物体静止在水平地面上,用力的图示法在图4中画出它所受的重力G。
10.(2019徐州,34)如图乙所示,一个实心球静止在水平地面上,请画出它所受重力G的示意图.11.(2019襄阳,19)请画出正方体木块所受的重力的示意图12.(2019新疆,18)请在图中画出足球所受重力的示意图。
13.(2019淮安,20)画出图中靜止在斜面上的茶杯所受重力的示意图.14. (2019扬州,23)如图,是一块质量分布均匀的半圆形量角器,将其用细线悬挂在天花板上。
请你用作图的方法找出重心O 点的位置。
15.(2019攀枝花,24)小球在竖直平面内摆动,请画出小球摆动到A时所受重力的示意图。
16.(2019海南,18)在图中画出茶壶受重力的示意图。
17.(2019重庆B卷,14)在图中画出静止在水平面上的木块所受重力的示意图;18.(2019聊城,)用一根细线的一端系一个小钢球就做成了一个摆。
2019中考真题——特殊的平行四边形

2019中考真题——特殊的平行四边形一、选择题1.(安顺)如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于CD的长为半径作弧,两弧相交于M、N两点;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE.则下列说法错误的是()A.∠ABC=60°B.S△ABE=2S△ADEC.若AB=4,则BE=4D.sin∠CBE=2.(毕节)如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为()A.B.3C.D.53.(毕节)平行四边形ABCD中,AC、BD是两条对角线,现从以下四个关系①AB=BC;②AC=BD;③AC⊥BD;④AB⊥BC中随机取出一个作为条件,即可推出平行四边形ABCD是菱形的概率为()A.B.C.D.14.(贵阳)如图,菱形ABCD的周长是4cm,∠ABC=60°,那么这个菱形的对角线AC的长是()A.1cm B.2 cm C.3cm D.4cm5.(黔东南)平行四边形ABCD 中,AC 、BD 是两条对角线,现从以下四个关系①BC AB =、②B D AC = ③BD AC ⊥、④BC AB ⊥中随机取出一个作为条件,即可推出平行四边形ABCD 是菱形的概率为( ) A.41 B.21 C.43 D.1 6. (铜仁)如图为矩形ABCD ,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a 和b ,则a +b 不可能是( )A .360°B .540°C .630°D .720°7. (铜仁)如图,四边形ABCD 为菱形,AB =2,∠DAB =60°,点E 、F 分别在边DC 、BC 上,且CE =CD ,CF =CB ,则S △CEF =( )A .B .C .D .8. (铜仁)如图,正方形ABCD 中,AB =6,E 为AB 的中点,将△ADE 沿DE 翻折得到△FDE ,延长EF 交BC 于G ,FH ⊥BC ,垂足为H ,连接BF 、DG .以下结论:①BF ∥ED ;②△DFG ≌△DCG ;③△FHB ∽△EAD ;④tan ∠GEB =;⑤S △BFG =2.6;其中正确的个数是( )A .2B .3C .4D .59.(广元)如图,点P 是菱形ABCD 边上的动点,它从点A 出发沿A →B →C →D 路径匀速运动到点D ,设△P AD 的面积为y ,P 点的运动时间为x ,则y 关于x 的函数图象大致为( )A .B .C .D .10. (广元)如图,在正方形ABCD 的对角线AC 上取一点E .使得∠CDE =15°,连接BE 并延长BE 到F ,使CF =CB ,BF 与CD 相交于点H ,若AB =1,有下列结论:①BE =DE ;②CE +DE =EF ;③S △DEC =﹣;④=2﹣1.则其中正确的结论有( )A .①②③B .①②③④C .①②④D .①③④11.(乐山) 把边长分别为1和2的两个正方形按图3的方式放置.则图中阴影部分的面积为 ()A 61 ()B 31 ()C 51 ()D 4112. (乐山)如图4,在边长为3的菱形ABCD 中,︒=∠30B ,过点A 作BC AE ⊥于点E ,现将△ABE 沿直线AE 翻折至△AFE 的位置,AF 与CD 交于点G .则CG 等于 ()A 13- ()B 1 ()C 21 ()D 2313. (四川泸州)一个菱形的边长为6,面积为28,则该菱形的两条对角线的长度之和为( )A .8B .12C .16D .322图3图414.(四川眉山)如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是()A.1B.C.2D.15.(四川眉山)如图,在菱形ABCD中,已知AB=4,∠ABC=60°,∠EAF=60°,点E在CB的延长线上,点F在DC的延长线上,有下列结论:①BE=CF;②∠EAB=∠CEF;③△ABE∽△EFC;④若∠BAE=15°,则点F到BC的距离为2﹣2.则其中正确结论的个数是()A.1个B.2个C.3个D.4个16.(四川绵阳)如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点E的坐标为()A. B. C. D.17.(四川遂宁)如图,四边形ABCD是边长为1的正方形,△BPC是等边三角形,连接DP并延长交CB的延长线于点H,连接BD交PC于点Q,下列结论:①∠BPD=135°;②△BDP∽△HDB;③DQ:BQ=1:2;④S△BDP=.其中正确的有()A .①②③B .②③④C .①③④D .①②④18. (四川雅安)如图,在四边形ABCD 中,AB=CD ,AC 、BD 是对角线 ,E 、F 、G 、H 分别是AD 、BD 、BC 、AC 的中点,连接EF 、FG 、GH 、HE ,则四边形EFGH 的形状是( )A .平行四边形B .矩形C .菱形D .正方形19. (四川达州)矩形OABC在平面直角坐标系中的位置如图所示,已知2)B ,点A 在x 轴上,点C 在y 轴上,P 是对角线OB 上一动点(不与原点重合),连接PC ,过点P 作PD PC ⊥,交x 轴于点D.下列结论:①OA BC ==D 运动到OA 的中点处时,227PC PD +=;③在运动过程中,CDP ∠是一个定值;④当△ODP 为等腰三角形时,点D的坐标为⎫⎪⎪⎝⎭.其中正确结论的个数是( )A. 1个B. 2个C. 3个D. 4个 20. (四川攀枝花)下列说法错误的是( )A. 平行四边形的对边相等B. 对角线相等的四边形是矩形C. 对角线互相垂直的平行四边形是菱形D. 正方形既是轴对称图形、又是中心对称图形 21. (四川攀枝花)如图,在正方形ABCD 中,E 是BC 边上的一点,4BE =,8CE =,将正方形边AB 沿AE 折叠到AF ,延长EF 交DC 于G 。
2019年中考物理真题集锦——专题一:声现象(含答案)

2019年中考物理真题集锦——专题一:声现象一、选择题1.(2019湘潭,17)图展示了我国古代劳动人民的智慧成果,对其中涉及的物理知识,说法错误的是()A.孔明灯在上升过程中,只受浮力B.紫砂壶属于连通器C.司南能够指南北是利用了磁体受地磁场的作用D.正在发声的编钟在振动2.(2019徐州,1)机械手表放在耳朵附近,听到表针走动的声音较小;把一个气球放在手表与耳朵之间相互贴紧,听到表针走动的声音较大.这两种情况声音的主要差别是A.音调B.响度C.音色D.频率3.(2019天水,1)下列有关声现象的实验中,能用来探究决定音调高低因素的是()A.手指蘸水摩擦杯口发声,同时增加杯中的水量B.响铃时,不断抽出瓶内的空气C.室内收音机播音时,导致喇叭前方的烛焰摇晃D.敲鼓时,用大小不同的力4.(2019孝感,1)如图,是四个与声现象相关的图形,下列说法正确的是()A.图甲可以说明真空能够传声B.图乙可以探究音色与频率的关系C.图丙可以探究响度与振幅的关系D.图丁的倒车雷达可以说明声能够传递能量5.(2019益阳,2) 有关声音的知识,下列说法正确的是( )A.演奏古筝时按压不同的弦是为了改变其响度B.用大小不同的力击打鼓面是为了改变其音调C.摩托车安装消音器是为了在传播过程中减弱噪声D.能分辨出《二泉映月》是用二胡演奏的,是因为不同乐器发声时音色不同6.(2019咸宁,14)远古时代,鼓被赋予神秘色彩。
如图是湖北崇阳出土的商代铜鼓史。
关于鼓声,下列说法正确的是()A.鼓声能在真空中传播B.鼓面振动的幅度越大,响度越大C.鼓声的音色与鼓的材料、结构无关D.区分鼓声和其他乐器声是根据音调不同7.(2019绵阳,2)如图所示,将一把钢尺紧按在桌面边缘,一端伸出桌边。
先用较小的力拨动钢尺,听它振动发出的声音;保持钢尺位置不动,再用较大的力拨动钢尺,听到的声音A.响度变大B. 响度变小C. 音调变高D. 音调变低8.(2019赤峰,5)关于图中的声现象,下列分析正确的是()A.甲中敲打鼓面,附近的烛焰跳动,说明声音可以传递信息B.乙中车间工人佩戴耳罩,是在声源处减弱噪声C.丙中弹吉它时,增大拨动弦的力度可以增大声音的响度D.丁中抽出罩内空气,听到钟声音变小,说明发声体振动减弱9.(2019东营,7)如图所示,我国自主研发的彩虹﹣4无人机正在进行航空物探试验飞行,下列说法正确的是()A.无人机在空中飞行时,始终受到平衡力的作用B.无人机匀速下降时,重力势能转化为动能C.地面操作人员通过超声波向无人机传递信息D.试验飞行中的无人机相对于地面是运动的10.(2019东营,2)如图所示,目前声纹锁在门禁系统得到很好的应用,实现了传说中“芝麻开门”的神话。
数与式的计算100题(真题专练)备战2023年中考数学考点微专题

考向1.9 数与式的计算100题(真题专练)1.(2019·四川遂宁·中考真题)计算:201920(1)(2)(3.14)4cos30|212|π-︒-+-+--+- 2.(2019·四川乐山·中考真题)如图,点A 、B 在数轴上,它们对应的数分别为2-,1xx +,且点A 、B 到原点的距离相等.求x 的值.3.(2021·湖南张家界·中考真题)计算:2021(1)222cos608-+-︒4.(2021·广东深圳·中考真题)先化简再求值:2169123x x x x ++⎛⎫+÷ ⎪++⎝⎭,其中1x =-. 5.(2021·湖南湘潭·中考真题)计算:011|2|(2)()4tan 453π----+-︒6.(2021·内蒙古呼伦贝尔·中考真题)计算:2122sin 60133---︒+7.(2021·广西柳州·中考真题)计算:391-8.(2021·黑龙江大庆·()2222sin 451+︒-- 9.(2021·上海·中考真题)计算: 1129|1228-+- 10.(2021·青海西宁·中考真题)计算: 121(2)|3|2-⎛⎫-+-- ⎪⎝⎭.11.(2020·新疆·中考真题)计算:()()2012π34-++-12.(2020·青海·中考真题)计算:10311345( 3.14)273π-⎛⎫+︒+- ⎪⎝⎭13.(2020·甘肃天水·中考真题)(1)计算:114sin 6032|2020124-︒⎛⎫-+ ⎪⎝⎭.(2)先化简,再求值:21111211a a a a a a ---÷-+++,其中3a = 14.(2020·北京·中考真题)计算:11()18|2|6sin 453---︒15.(2020·山东菏泽·中考真题)计算:20201202012|63|2345(2)2-⎛⎫++︒--⋅ ⎪⎝⎭.16.(2020·四川乐山·中考真题)计算:022cos60(2020)π--︒+-.17.(2020·浙江·﹣1|.18.(2020·浙江嘉兴·中考真题)(1)计算:(2020)0﹣3|; (2)化简:(a +2)(a ﹣2)﹣a (a +1).19.(2020·浙江台州·中考真题)计算:3-20.(2019·山东东营·中考真题)(1)计算:()101 3.142019π-⎛⎫+- ⎪⎝⎭2sin 4512+-;(2)化简求值:22222a b a ab b a b a ab a ⎛⎫++-÷⎪--⎝⎭,当1a =-时,请你选择一个适当的数作为b 的值,代入求值.21.(2021·甘肃兰州·中考真题)先化简,再求值:22611931m m m m m --÷--+-,其中4m =.22.(2021·河南·中考真题)(1)计算:013(3--; (2)化简:21221x x x -⎫⎛-÷⎪⎝⎭. 23.(2021·湖北鄂州·中考真题)先化简,再求值:2293411x x x x x x -+÷+--,其中2x =.24.(2021·广西玉林·()()01416sin30π--+--°.25.(2021·广西玉林·中考真题)先化简再求值:()2112a a a a -⎛⎫-+÷ ⎪⎝⎭,其中a 使反比例函数ay x=的图象分别位于第二、四象限. 26.(2021·北京·中考真题)已知22210a b +-=,求代数式()()22-++a b b a b 的值.27.(2021·北京·中考真题)计算:02sin60(5π--.28.(2021·江苏宿迁·中考真题)计算:()0π1-4sin45°29.(2021·湖北荆州·中考真题)先化简,再求值:2221211a a a a a ++⎛⎫÷+ ⎪--⎝⎭,其中a =30.(2021·浙江衢州·中考真题)先化简,再求值:2933x x x +--,其中1x =.31.(2021·浙江衢州·01()|3|2cos602--+︒.32.(2021·湖北随州·中考真题)先化简,再求值:2141122x x x -⎛⎫+÷⎪++⎝⎭,其中1x =. 33.(2021·山东菏泽·中考真题)先化简,再求值:22221244m n n m m n m mn n--+÷--+,其中m ,n满足32m n =-. 34.(2021·湖北十堰·中考真题)化简:22214244a a a a a a a a +--⎛⎫-÷⎪--+⎝⎭.35.(2021·湖北十堰·1133-⎛⎫︒+-- ⎪⎝⎭.36.(2021·湖南常德·中考真题)化简:2593111aa a a a a ++⎛⎫+÷⎪---⎝⎭37.(2021·湖南常德·中考真题)计算:012021345-+︒.38.(2021·湖南郴州·中考真题)先化简,再求值:2213111a a a a a a --⎛⎫-÷⎪+--⎝⎭,其中a =39.(2021·湖南郴州·中考真题)计算:11(2021)|2tan 602π-⎛⎫--+⋅︒ ⎪⎝⎭.40.(2021·湖南怀化·中考真题)计算:021(3)()4sin 60(1)3π--+︒--41.(2021·湖北黄冈·中考真题)计算:0|12sin 60(1)π-︒+-.42.(2021·新疆·中考真题)先化简,再求值:22414421x x x x x x ⎛⎫-+⋅⎪+++-⎝⎭,其中3x =.43.(2021·湖南长沙·中考真题)计算:(02sin 451-+°44.(2021·四川广安·中考真题)先化简:2221211a a a a a a -+⎛⎫÷- ⎪-+⎝⎭,再从-1,0,1,2中选择一个适合的数代入求值.45.(2021·四川广安·中考真题)计算:()03.1414sin 60π-︒.46.(2021·湖南邵阳·中考真题)先化简,再从1-,0,1,21中选择一个合适的x 的值代入求值.2211121x x x x x -⎛⎫-÷ ⎪+++⎝⎭.47.(2021·四川眉山·中考真题)计算:(1143tan 602-⎛⎫-︒-- ⎪⎝⎭48.(2021·江苏苏州·中考真题)先化简再求值:21111x x x-⎛⎫+⋅⎪-⎝⎭,其中1x =.49.(2021·江苏苏州·223--.50.(2021·江苏扬州·中考真题)计算或化简:(1)013|tan603⎛⎫-++︒ ⎪⎝⎭; (2)()11a b a b ⎛⎫+÷+ ⎪⎝⎭.51.(2021·湖南邵阳·中考真题)计算:()020212tan 60π--︒.52.(2021·甘肃武威·中考真题)先化简,再求值:2224(2)244x x x x x --÷--+,其中4x =. 53.(2021·甘肃武威·中考真题)计算:011(2021)()2cos 452π--+-︒.54.(2021·云南·中考真题)计算:201tan 452(3)1)2(6)23-︒-++-+⨯-. 55.(2021·浙江金华·中考真题)已知16x =,求()()()2311313x x x -++-的值.56.(2021·浙江金华·中考真题)计算:()202114sin 45+2-︒-.57.(2021·浙江温州·中考真题)(1)计算:()0438⨯-+-.(2)化简:()()215282a a a -++.58.(2021·四川南充·中考真题)先化简,再求值:2(21)(21)(23)x x x +---,其中1x =-. 59.(2021·四川凉山·中考真题)已知112,1x y x y-=-=,求22x y xy -的值.60.(2021·四川泸州·中考真题)计算:120211423cos304.61.(2021·重庆·中考真题)计算:(1)2(23)()a a b a b ++-;(2)22293211x x x x x x ⎛⎫--÷+ ⎪+++⎝⎭.62.(2021·四川自贡·0|7|(2-+.63.(2021·浙江丽水·中考真题)计算:0|2021|(3)-+-64.(2020·广西贺州·中考真题)计算:()24π345+-︒--+︒.65.(2020·福建·中考真题)先化简,再求值:211(1)22x x x --÷++,其中1x =.66.(2020·四川广安·中考真题)计算:202011(1)12cos 45()2--+-.67.(2020·四川广安·中考真题)先化简,再求值:221(1)11x x x -÷+-,其中x=2020.68.(2020·广西柳州·中考真题)计算:11682⨯-+.69.(2020·广西·中考真题)计算:(0+(﹣2)2+|﹣12|﹣sin30°.70.(2020·贵州黔南·中考真题)(1)计算()1013tan602cos6020202-⎛⎫--︒+-︒- ⎪⎝⎭;(2)解不等式组:312324xx -⎧⎪⎨⎪+⎩.71.(2020·辽宁鞍山·中考真题)先化简,再求值:2344111x x x x x ++⎛⎫--÷⎪++⎝⎭,其中2x =. 72.(2020·内蒙古呼伦贝尔·中考真题)计算:1012cos60-(-1)2π-⎛⎫- ⎪⎝⎭.73.(2020·内蒙古呼伦贝尔·中考真题)先化简,再求值:222442342x x x x x x -+-÷+-+,其中4x =-. 74.(2020·江苏宿迁·中考真题)先化简,再求值:2x x -÷(x ﹣4x),其中x﹣2. 75.(2020·四川眉山·中考真题)先化简,再求值:229222a a a -⎛⎫-÷⎪--⎝⎭,其中3=a . 76.(2020·四川眉山·中考真题)计算:(2122sin 452-⎛⎫+-+︒ ⎪⎝⎭77.(2020·云南昆明·中考真题)计算:12021(π﹣3.14)0﹣(﹣15)-1.78.(2020·江苏南通·中考真题)计算: (1)(2m +3n )2﹣(2m +n )(2m ﹣n );(2)22⎛⎫--÷+ ⎪⎝⎭x y y xy x x x 79.(2021·福建·1133-⎛⎫- ⎪⎝⎭.80.(2021·四川达州·中考真题)计算:()02120212sin 601π-+-+︒-.81.(2020·江苏徐州·中考真题)计算:(1)120201(1)2|2-⎛⎫-+- ⎪⎝⎭;(2)2121122a a a a -+⎛⎫-÷⎪-⎝⎭82.(2020·湖南邵阳·中考真题)已知:|1|0m -=, (1)求m ,n 的值;(2)先化简,再求值:22(3)(2)4m m n m n n -++-.83.(2020·湖南怀化·222cos 45|2-︒-+ 84.(2020·湖南张家界·中考真题)阅读下面的材料:对于实数,a b ,我们定义符号min{,}a b 的意义为:当a b <时,min{,}a b a =;当a b 时,min{,}a b b =,如:min{4,2}2,min{5,5}5-=-=.根据上面的材料回答下列问题: (1)min{1,3}-=______;(2)当2322min ,233x x x -++⎧⎫=⎨⎬⎩⎭时,求x 的取值范围. 85.(2020·四川自贡·中考真题)我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”;数形结合是解决数学问题的重要思想方法.例如,代数式2x -的几何意义是数轴上x 所对应的点与2所对应的点之间的距离;因为()+=--x 1x 1,所以1x +的几何意义就是数轴上x 所对应的点与1-所对应的点之间的距离. ⑴. 发现问题:代数式12x x ++-的最小值是多少?⑵. 探究问题:如图,点,,A B P 分别表示的是-1,2,x ,3AB =.∵12x x ++-的几何意义是线段PA 与PB 的长度之和∴当点P 在线段AB 上时,+=PA PB 3;当点点P 在点A 的左侧或点B 的右侧时 +>PA PB 3 ∴12x x ++-的最小值是3. ⑶.解决问题:①.-++x 4x 2的最小值是 ;②.利用上述思想方法解不等式:314x x ++->③.当a 为何值时,代数式++-x a x 3的最小值是2.86.(2021·四川内江·中考真题)计算:0216sin 45|128(2021)()2π-︒----. 87.(2021·青海西宁·中考真题)计算:2(53)(53)(31)-.88.(2021·辽宁盘锦·中考真题)先化简,再求值:2233816164x x xx x x x --÷--+--,其中24x =89.(2021·青海·中考真题)先化简,再求值:2121a a a a a -+⎛⎫-÷ ⎪⎝⎭,其中21a =.90.(2021·江苏南京·中考真题)计算222ab a b b ab a b a ab ab-⎛⎫-+÷⎪+++⎝⎭. 91.(2021·四川成都·中考真题)先化简,再求值:2269111a a a a ++⎛⎫+÷⎪++⎝⎭,其中33=a .92.(2021·四川资阳·中考真题)先化简,再求值:222211111x x x x x x ⎛⎫++-÷ ⎪---⎝⎭,其中30x -=. 93.(2021·重庆·中考真题)计算(1)()()22x y x x y -++; (2)2241244a a a a a -⎛⎫-÷ ⎪+++⎝⎭. 94.(2021·浙江嘉兴·中考真题)(1)计算:12sin 30-︒; (2)化简并求值:11a a -+,其中12a =-. 95.(2021·四川遂宁·中考真题)先化简,再求值:322293443m m m m m m -⎛⎫÷++ ⎪-+-⎝⎭,其中m 是已知两边分别为2和3的三角形的第三边长,且m 是整数. 96.(2021·四川泸州·中考真题)化简:141()22a a a a a --+÷++.97.(2021·山东枣庄·中考真题)先化简,再求值:21(1)11x x x ÷+--,其中1x =.98.(2020·广西贵港·中考真题)(1()0236cos30π+-︒; (2)先化简再求值:221239m m m ÷--,其中5m =-.99.(2020·内蒙古赤峰·中考真题)先化简,再求值:221121m m m m m m ---÷++,其中m 满足:210m m --=.100.(2021·重庆·中考真题)如果一个自然数M 的个位数字不为0,且能分解成A B ⨯,其中A 与B 都是两位数,A 与B 的十位数字相同,个位数字之和为10,则称数M 为“合和数”,并把数M 分解成M A B =⨯的过程,称为“合分解”.例如6092129=⨯,21和29的十位数字相同,个位数字之和为10, 609∴是“合和数”.又如2341813=⨯,18和13的十位数相同,但个位数字之和不等于10, 234∴不是“合和数”.(1)判断168,621是否是“合和数”?并说明理由;(2)把一个四位“合和数”M 进行“合分解”,即M A B =⨯.A 的各个数位数字之和与B 的各个数位数字之和的和记为()P M ;A 的各个数位数字之和与B 的各个数位数字之和的差的绝对值记为()Q M .令()()()P M G M Q M =,当()G M 能被4整除时,求出所有满足条件的M .1.74-【分析】先根据整数指数幂、负指数幂、零指数幂、三角函数和绝对值进行化简,再进行加减运算.解:原式131142324=-++-+ 111232324=-++- 74=-.【点拨】本题考查指数幂、三角函数和绝对值,解题的关键是掌握指数幂、三角函数和绝对值.2.2x =-【分析】根据点A 、B 到原点的距离相等可知点A 、B 表示的数值互为相反数,即21xx =+,解分式方程即可.解:∵点A 、B 到原点的距离相等 ∴A 、B 表示的数值互为相反数 即21xx =+,去分母,得2(1)x x =+, 去括号,得22x x =+, 解得2x =-经检验,2x =-是原方程的解.【点拨】本题考查了相反数,绝对值的定义,解分式方程,解本题的关键是读懂题意,根据题中点A 、B 到原点的距离相等可知点A 、B 表示的数值互为相反数3【分析】先运用乘方、绝对值、特殊角的三角函数值以及平方根的性质化简,然后计算即可.解:2021(1)22cos60-+︒+11222=-+⨯+=【点拨】本题主要考查了乘方、绝对值、特殊角的三角函数值、平方根的性质等知识点,灵活运用相关知识成为解答本题的关键.4.12x +;1 【分析】先把分式化简后,再把x 的值代入求出分式的值即可. 解:原式212331122(3)232x x x x x x x x x +++⎛⎫=+⋅=⋅= ⎪++++++⎝⎭ 当1x =-时,原式1112==-+. 【点拨】本题考查了分式的化简求值,熟练分解因式是解题的关键. 5.0【分析】根据绝对值的性质、零指数幂、负整指数幂的性质及45°角的正切值计算解题即可.解:011|2|(2)()4tan 453π----+-︒21341=-+-⨯0=.【点拨】本题考查实数的混合运算,涉及绝对值、零指数幂、负整指数幂、正切等知识,是基础考点,难度较易,掌握相关知识是解题关键.6. 【分析】分别进行负整数指数幂运算、特殊角的三角函数值运算、绝对值运算、二次根式运算即可解答解:222sin 601---︒+=1214--=54-=. 【点拨】本题考查负整数指数幂、特殊角的三角函数值、绝对值、二次根式,熟记特殊角的三角函数值,掌握运算法则是解答的关键.7.1【分析】根据绝对值的定义及算术平方根的定义即可解决. 解:原式331=-+1=【点拨】本题考查了绝对值的定义、算术平方根的定义及实数的运算,关键是掌握绝对值和算术平方根的定义.8.1【分析】直接利用去绝对值符号、特殊角度的三角函数值、负整数的平方运算计算出结果即可.()222sin 451+︒--221= 1=故答案是:1.【点拨】本题考查了去绝对值符号、特殊角度的三角函数值、负整数的平方运算法则,解题的关键是:掌握相关的运算法则.9.2【分析】根据分指数运算法则,绝对值化简,负整指数运算法则,化最简二次根式,合并同类二次根式以及同类项即可.解:1129|12-+-,(112-⨯=31 =2.【点拨】本题考查实数混合运算,分指数运算法则,绝对值符号化简,负整指数运算法则,化最简二次根式,合并同类二次根式与同类项,掌握实数混合运算法则与运算顺序,分指数运算法则,绝对值符号化简,负整指数运算法则,化最简二次根式,合并同类二次根式与同类项是解题关键.10.3【分析】由乘方、负整数指数幂、绝对值的意义进行化简,即可得到答案.解:原式423=+-3=.【点拨】本题考查了乘方、负整数指数幂、绝对值的意义,解题的关键是掌握运算法则,正确的进行化简.11【分析】按照绝对值的性质、乘方、零指数幂、二次根式的运算法则计算.解:原式112=-=【点拨】本题考查绝对值的性质、乘方、零指数幂、二次根式的运算法则,比较基础.12【分析】根据负整数指数幂,绝对值的性质,零指数幂,立方根,特殊角的三角函数值进行计算即可解:101145( 3.14)3π-⎛⎫+︒+- ⎪⎝⎭3|11|13=++-3113=+-=【点拨】本题考查了负整数指数幂,绝对值的性质,零指数幂,立方根,特殊角的三角函数值,熟知以上计算是解题的关键.13.(13;(2)221a -,1. 【分析】(1)先代入三角函数值、去绝对值符号、计算零指数幂、化简二次根式、计算负整数指数幂,再计算乘法、去括号,最后计算加减可得;(2)先根据分式的混合运算顺序和运算法则化简原式,再将a 的值代入计算可得.解:(1)原式4(214=-+-,214=-,3;(2)原式21111(1)1a a a a a -+=-⨯-+-, 1111a a =--+, 11(1)(1)a a a a +-+=-+, 221a =-,当a ==()222213121===--. 【点拨】本题主要考查实数的混合运算与分式的化简求值,解题的关键是熟练掌握分式的混合运算顺序和运算法则.14.5【分析】分别计算负整数指数幂,算术平方根,绝对值,锐角三角函数,再合并即可得到答案.解:原式=3262+-⨯32=+-5.= 【点拨】本题考查的是负整数指数幂,算术平方根,绝对值,锐角三角函数,以及合并同类二次根式,掌握以上的知识是解题的关键.15.52【分析】根据负整数指数幂,绝对值,特殊角的三角函数值,积的乘方公式的逆向应用进行计算即可.解:202012020123|45(2)2-⎛⎫++︒--⋅ ⎪⎝⎭202011(3(2)22=++-⨯ 1312=+ 52=. 【点拨】本题考查了负整数指数幂,绝对值,特殊角的三角函数值,积的乘方公式的逆向应用,熟知以上运算是解题的关键.16.2【分析】根据绝对值,特殊三角函数值,零指数幂对原式进行化简计算即可.解:原式=12212-⨯+ =2.【点拨】本题考查了绝对值,特殊三角函数值,零指数幂,掌握运算法则是解题关键.17. 1【分析】根据算术平方根定义和绝对值的性质计算,再合并同类二次根式即可.解:原式1.【点拨】本题考查了算术平方根和绝对值以及同类二次根式的合并,解题的关键是正确理解定义.18.(1)2;(2)﹣4﹣a【分析】(1)直接利用零指数幂的性质和二次根式的性质、绝对值的性质分别化简得出答案;(2)直接利用平方差公式以及单项式乘以多项式计算得出答案.解:(1)(2020)0﹣3|=1﹣2+3=2;(2)(a +2)(a ﹣2)﹣a (a +1)=a 2﹣4﹣a 2﹣a=﹣4﹣a .【点拨】本题主要考查了实数的运算,准确运用零指数幂、二次根式的性质和绝对值的性质是解题的关键.19.3【分析】按照绝对值的概念、平方根的概念逐个求解,然后再用二次根式加减运算即可.解:原式=3=故答案为:3.【点拨】本题考查了绝对值的概念、平方根的概念、二次根式的加减运算等,熟练掌握运算公式及法则是解决此类题的关键.20.(1)2020;(2)1【分析】(1)根据负指数幂、零指数幂、绝对值和三角函数、二次根式,即可得到答案;(2)根据分式的性质进行化简,再代入1a =-,即可得到答案.解:1()原式201912++=2020+=2020=;2()原式()()222a b a a a b a b -=-+ ()()()()2a b a b aa ab a b -+=-+ 1a b =+, 当1a =-时,取2b =,原式1112==-+. 【点拨】本题负指数幂、零指数幂、绝对值、三角函数、二次根式和分式的化简,解题的关键是掌握负指数幂、零指数幂、绝对值、三角函数、二次根式和分式的化简.21.11m -,13【分析】先将除法转化为乘法,因式分解,约分,分式的减法运算,再将字母的值代入求解即可. 解:22611931m m m m m --÷--+- 2(3)31(3)(3)11m m m m m m -+=⋅-+--- 2111m m =--- 11m =-. 当4m =时, 原式11413==-. 【点拨】本题考查了分式的化简求值,掌握因式分解是解题的关键.22.(1)1;(2)2x . 【分析】(1)实数的计算,根据实数的运算法则求解即可;(2)分式的化简,根据分式的运算法则计算求解.解:(1)013(3-- 11133=-+ 1=.(2)21221x x x -⎫⎛-÷ ⎪⎝⎭212(1)x x x x -=⨯- 2x =. 【点拨】本题考查了实数的混合运算,负指数幂,二次根式的化简,零次幂的计算,分式的化简等知识,牢记公式与定义,熟练分解因式是解题的关键.23.1x x +,32【分析】先通过约分、通分进行化简,再把给定的值代入计算即可.解:原式()()()313341x x x x x x x -=⨯++--+ 1x x+=, 当2x =时,原式32=. 【点拨】本题主要考查分式的化简求值,解题的关键是熟练掌握因式分解,正确进行约分、通分.24.1【分析】先算算术平方根,零指数幂,负整数指数幂以及特殊角三角函数值,再算加减法,即可求解.解:原式=141162+--⨯ =1【点拨】本题主要考查实数的混合运算,掌握算术平方根,零指数幂,负整数指数幂以及特殊角三角函数值,是解题的关键.25.1-【分析】由题意易得0a <,然后对分式进化简,然后再求解即可.解:∵a 使反比例函数a y x=的图象分别位于第二、四象限, ∴0a <, ∴()2112a a a a -⎛⎫-+÷ ⎪⎝⎭ =()22211a a a a a -+-⨯- =1-.【点拨】本题主要考查反比例函数的图象与性质及分式的化简求值,熟练掌握反比例函数的图象与性质及分式的运算是解题的关键.26.1【分析】先对代数式进行化简,然后再利用整体思想进行求解即可.解:()()22-++a b b a b=22222a ab b ab b -+++=222a b +,∵22210a b +-=,∴2221a b +=,代入原式得:原式=1.【点拨】本题主要考查整式的乘法运算及完全平方公式,熟练掌握利用整体思想进行整式的化简求值是解题的关键.27.4【分析】根据特殊三角函数值、零次幂及二次根式的运算可直接进行求解.解:原式=2514-=. 【点拨】本题主要考查特殊三角函数值、零次幂及二次根式的运算,熟练掌握特殊三角函数值、零次幂及二次根式的运算是解题的关键.28.1【分析】结合实数的运算法则即可求解.解:原式=1411+=+. 【点拨】本题考察非0底数的0次幂等于1、二次根式的化简、特殊三角函数值等知识点,属于基础题型,难度不大.解题的关键是掌握实数的运算法则.29.1a a +【分析】先计算括号内的加法,然后化除法为乘法进行化简,继而把a =即可.解:原式=()()21111a a a a a ++⎛⎫÷ ⎪--⎝⎭()()211=1+1a a a a a +-⎛⎫ ⎪-⎝⎭1=a a +当a =【点拨】本题主要考查分式的化简求值,解题的关键是掌握分式混合运算顺序和运算法则.30.3x +;4【分析】先将这两个分式转化为同分母的分式,再将分母不变,分子相加减,最后化简即可. 解:原式29(3)(3)333x x x x x x +-=-=--- 3x =+当1x =时,原式4=.【点拨】本题考查了分式的化简求值问题,涉及到了分式的通分和约分,解决本题的关键是牢记相关概念与法则,并灵活运用,最后的结果记得化简即可.31.2.【分析】由特殊的三角函数值得到1cos602︒=,由零指数幂公式算出01()=12,,最后算出结果即可. 解:原式13+1322 2=【点拨】本题考查了实数的混合运算,关键注意零指数幂的运算和特殊的三角函数值.32.22x -,-2 【分析】(1)先把括号里通分合并,括号外的式子进行因式分解,再约分,将x=1代入计算即可.解:原式()()()21221222x x x x x x ++=⋅=++-- 当1x =时,原式2212==-- 【点拨】本题考查了分式的化简求值,用到的知识是约分、分式的加减,熟练掌握法则是解题的关键.33.3n m n+;-6. 【分析】先变除法为乘法,后因式分解,化简计算,后变形32n m =-代入求值即可 解:∵22221244m n n m m n m mn n --+÷--+=2(2)12()()m n m n m n n m n m --+⨯--+ =21m n n m --+ =3n m n+, ∵32m n =-, ∴32n m =-, ∴原式=332nn n -+= -6. 【点拨】本题考查了分式的化简求值,熟练掌握分式混合运算的基本顺序,基本计算方法是解题的关键.34.21(2)a - 【分析】先算分式的减法,再把除法化为乘法运算,进行约分,即可求解.解:原式=221(2)(2)4a a a a a a a ⎛⎫+--⋅ ⎪---⎝⎭=()()()22221(2)(2)4a a a a a a a a a a +--⎛⎫-⋅ ⎪---⎝⎭=2224(2)4a a a a a a a --+⋅-- =24(2)4a a a a a -⋅-- =21(2)a - 【点拨】本题主要考查分式的化简,掌握分式的通分和约分,是解题的关键. 35.1【分析】利用特殊角的三角函数值、负整数指数幂、绝对值的性质逐项计算,即可求解.解:原式33=- 1=.【点拨】本题考查实数的运算,掌握特殊角的三角函数值、负整数指数幂、绝对值的性质是解题的关键.36.31a a ++【分析】直接将括号里面的分式,通分运算进而结合分式的混合运算法则,计算得出答案. 解:2593111a a a a a a ++⎛⎫+÷ ⎪---⎝⎭ 222591=113a a a a a a a ++-⨯--+(+) 2691=(1)(1)3a a a a a a ++-⨯+-+ 2(3)1=(1)(1)3a a a a a +-⨯+-+ 31a a +=+ 故答案为:31a a ++. 【点拨】本题考查了分式的化简,分式的通分,因式分解,平方差公式,完全平方公式,分式的混合运算,熟练运用公式和分式的计算法则是解题关键.37.1.【分析】直接利用零次幂的运算法则,负次幂的运算法则、二次根式及特殊角的三角函数值进行计算即可.解:012021345-+︒3132=+ 111=+-1=故答案是:1.【点拨】本题考查了零次幂的运算法则,负次幂的运算法则、二次根式及特殊角的三角函数值,解题的关键是:熟练掌握相关运算法则.38 【分析】先算分式的减法运算,再把除法化为乘法,进行约分化简,最后代入求值,即可.解:原式=2213111a a a a a a --⎛⎫-÷ ⎪+--⎝⎭=131(1)(1)(1)1a a a a a a a ⎛⎫----⋅ ⎪++-⎝⎭=()()2131(1)(1)(1)(1)1a a a aa a a a a a⎛⎫----⋅⎪⎪+-+-⎝⎭=()()2131(1)(1)1a a a aa a a----⋅+-=222131(1)(1)1a a a a aa a a-+-+-⋅+-=11(1)(1)1a aa a a+-⋅+-=1a,原式.【点拨】本题主要考查分式的化简求值,熟练掌握分式的通分和约分,是解题的关键.39.3【分析】先算零指数幂,绝对值,负整数指数幂以及锐角三角函数,再算加减法,即可求解.解:原式=12+-=3.【点拨】本题主要考查实数的混合运算,熟练掌握零指数幂,绝对值,负整数指数幂以及锐角三角函数,是解题的关键.40.11【分析】根据非零实数0二次根式、负整数次幂、特殊角三角函数值根据实数加减混合运算法则计算即可.解:原式=191=11-+.【点拨】本题主要考查非零实数0次幂、二次根式、负整数次幂、特殊角三角函数值根据实数加减混合运算法则,正确掌握每个知识点是解决本题的关键.41.0.【分析】先化简绝对值、计算特殊角的正弦值、零指数幂,再计算实数的混合运算即可得.解:原式121-=,==.【点拨】本题考查了化简绝对值、特殊角的正弦值、零指数幂等知识点,熟练掌握各运算法则是解题关键.42.22x ;25【分析】根据分式混合运算的法则进行化简计算,然后代入条件求值即可.解:原式()()()2221212x x x x x x ⎡⎤+-=+⎢⎥+-+⎢⎥⎣⎦ 21221x x x x x -⎛⎫=+ ⎪++-⎝⎭ 22121x x x -=+- ()21121x x x -=+- 22x =+ 将3x =代入得:原式22325==+. 【点拨】本题考查分式的化简求值问题,掌握分式混合运算法则是解题关键. 43.5.【分析】先化简绝对值、特殊角的正弦值、零指数幂、二次根式的乘法,再计算实数的混合运算即可得.解:原式21=++14=+, 5=. 【点拨】本题考查了化简绝对值、特殊角的正弦值、零指数幂、二次根式的乘法等知识点,熟练掌握各运算法则是解题关键.44.1a ,12【分析】先根据分式的混合运算法则化简,再取使得分式有意义的a 的值代入计算即可.解:2221211a a a a a a -+⎛⎫÷- ⎪-+⎝⎭ =()()()()21112111a a a a a a a a -+⎡⎤÷-+-⎢+⎣+⎥⎦ =()()()()211111a a a a a a +-+⨯-- =1a由原式可知,a 不能取1,0,-1,∴a =2时,原式=12.【点拨】此题考查了分式的化简求值,解题的关键是记住分式的混合运算,先乘方,再乘除,然后加减,有括号的先算括号里面的.45.0【分析】分别化简各数,再作加减法.解:()03.1414sin 60π-+︒=114-+=11-+=0【点拨】本题考查了实数的混合运算,特殊角的三角函数值,解题的关键是掌握运算法则.46.1;11x --(答案不唯一) 【分析】小括号先通分合并,再将除法变乘法并因式分解即可约分化简,再结合分式有意义的条件和除数不为0,即可代值计算. 解:原式()()()()()()2211111=1111111x x x x x x x x x x x +++-⨯=⨯=++-++-- 代数式有意义,分母和除数不为0∴()()110x x +-≠即1x ≠±∴当0x =时,原式=111101x ==---(答案不唯一). 【点拨】本题考察分式的化简求值、分式有意义的条件、因式分解和分母有理化,属于基础题,难度不大.解题的关键是掌握分式的运算法则和分式有意义的条件.47.3【分析】依次计算“0次方”、tan 60︒等,再进行合并同类项即可.解:原式=()132123--+=-+=【点拨】本题综合考查了非零数的零次幂、特殊角的三角函数、负整数指数幂以及二次根式的化简等内容,解决本题的关键是牢记相关计算公式等,本题易错点为对112-⎛⎫-- ⎪⎝⎭的化简,该项出现的“ -”较多,因此符号易出错,因此要注意.48.1x +【分析】先算分式的加法,再算乘法运算,最后代入求值,即可求解. 解:原式()()111111x x x x x x+--+=⋅=+-.当1x =时,原式【点拨】本题主要考查分式的化简求值,熟练掌握分式的通分和约分,是解题的关键.49.-5【分析】分别化简算术平方根、绝对值和有理数的乘方,然后再进行加减运算即可得到答案.223--229=+-5=-.【点拨】此题主要考查了实数的混合运算,熟练掌握运算法则是解答此题的关键. 50.(1)4;(2)ab【分析】(1)分别化简各数,再作加减法;(2)先通分,计算加法,再将除法转化为乘法,最后约分计算.解:(1)013|tan603⎛⎫-++︒ ⎪⎝⎭=13+=4;(2)()11a b a b ⎛⎫+÷+ ⎪⎝⎭ =()a b a b ab ++÷=()ab a b a b+⨯+ =ab 【点拨】本题考查了实数的混合运算,特殊角的三角函数值,零指数幂,分式的混合运算,解题的关键是熟练掌握运算法则.51.﹣1.【分析】根据零指数幂运算法则、绝对值符号化简、特殊角的三角函数值代入计算,然后根据同类二次根式合并求解即可.解:()020212tan 60π--︒=(12-=12-+=﹣1.【点拨】本题主要考查了实数的综合运算能力,是中考题中常见的计算题型.熟练掌握零指数幂、特殊角的三角函数值、绝对值化简方法,同类二次根式是解题关键.52.42,23x --+ 【分析】小括号内先通分计算,将除法变成乘法并因式分解,根据乘法法则即可化简,再代值计算即可. 解:原式2242(2)()22(2)(2)x x x x x x x --=-⨯--+- 4222x x x --=⨯-+ 42x =-+ 当4x =时,原式42423=-=-+. 【点拨】本题考察分式的化简求值,难度不大,属于基础题型.解题的关键在于熟悉运算法则和因式分解.53.3【分析】先进行零指数幂和负整数指数幂,余弦函数值计算,再计算二次根式的乘法,合并同类项即可. 解:011(2021)()2cos 452π--+-︒,122=+-3=【点拨】本题主要考查零指数幂和负整数指数幂,特殊角三角函数值,掌握零指数幂和负整数指数幂的运算法则,特殊角锐角三角函数值是解题的关键.54.6【分析】原式分别利用乘方,特殊角的三角函数值,零指数幂,负整数指数幂,乘法法则分别计算,再作加减法.解:201tan 452(3)1)2(6)23-︒-++-+⨯- =1191422++-- =6【点拨】此题考查了实数的混合运算,熟练掌握运算法则是解本题的关键.55.1【分析】直接利用完全平方差公式展开及平方差公式展开后,合并同类项化简,再将16x =代入进去计算. 解:原式229611962x x x x =-++-=-+ 当16x =时,原式16216=-⨯+=. 故答案是:1.【点拨】本题考查了代数式的化简求值,解题的关键是:先利用完全平方差公式,平方差公式,合并同类项运算法则化简,然后代值计算.56.1【分析】利用乘方的意义,二次根式的化简,特殊角的函数值,绝对值的化简,化简后合并计算即可解:原式142=-+12=-+ 1=.【点拨】本题考查了二次根式的化简,特殊角的三角函数值,绝对值的化简等知识,熟练运用各自的运算法则化简是解题的关键.57.(1)-6;(2)22625a a -+.【分析】(1)直接利用有理数乘法法则以及绝对值的性质、二次根式的性质、零指数幂的性质分别化简得出答案;(2解:(1)()0438⨯-+- 12831=-+-+6=-;(2)()()215282a a a -++ 2210254a a a a =-+++22625a a =-+.【点拨】此题主要考查了实数运算、整式的混合运算,正确掌握相关运算法则是解题关键.58.1210x -,-22【分析】利用平方差公式和完全平方公式,进行化简,再代入求值,即可求解. 解:原式=2241(4129)x x x ---+=22414129x x x --+-=1210x -,当x =-1时,原式=()12110⨯--=-22.【点拨】本题主要考查整式的化简求值,熟练掌握完全平方公式和平方差公式,是解题的关键.59.-4【分析】根据已知求出xy =-2,再将所求式子变形为()xy x y -,代入计算即可. 解:∵2x y -=, ∴1121y x x y xy xy---===, ∴2xy =-,∴()()22224xy x x y xy y ==---⨯=-.【点拨】本题考查了代数式求值,解题的关键是掌握分式的运算法则和因式分解的应用.60.12.【分析】根据零指数幂,负整指数幂,去括号法则,特殊角的三角函数值化简,然后再计算即可.解:0120211423cos3043144232144312=.【点拨】本题考查了零指数幂,负整指数幂,去括号法则,特殊角的三角函数值等知识点,熟悉相关知识点是解题的关键61.(1)223++a ab b ;(2)-31x x + 【分析】(1)根据单项式乘以多项式以及完全平方公式计算即可;(2)利用分式的混合运算法则进行计算即可.解:(1)2(23)()a a b a b ++-2222+3+2+=a ab a ab b -22=3++a ab b(2)22293211x x x x x x ⎛⎫--÷+ ⎪+++⎝⎭()()()222+3-3+3=11+x x x x x x x ⎛⎫-÷ ⎪++⎝⎭()()()2+3-31=31x x x x x +++ -3=1x x + 【点拨】本题考查了整式的混合运算和分式的混合运算,熟练掌握运算法则是解题的关键.62.1-【分析】利用算术平方根、绝对值的性质、零指数幂分别计算各项即可求解. 解:原式5711=-+=-.【点拨】本题考查实数的混合运算,掌握算术平方根、绝对值的性质、零指数幂是解题的关键.63.2020【分析】先计算绝对值、零指数幂和算术平方根,最后计算加减即可;解:0|2021|(3)-+-202112=+-,2020=.【点拨】本题主要考查实数的混合运算,解题的关键是掌握实数的混合运算顺序及相关运算法则.64.2.【分析】直接利用零指幂的性质、绝对值的性质、特殊角的三角函数值分别化简得出答案.解:()24π345+-︒--︒313=+-+ 3131=+-+2=.【点拨】此题主要考查了实数运算,正确化简各数是解题关键.65.11x - 【分析】先将括号内的项进行通分化简,再分式的除法法则,结合平方差公式因式分解,化简,最后代入数值解题即可.解:原式=2122(1)(1)x x x x x +-+⋅++- 1(1)(1)x x x +=+-。
2020年中考数学复习:数与式、化简求值问题 专项练习题(含答案解析)

2020年中考数学复习:数与式、化简求值问题 专项练习题1. (2019遂宁第18题)先化简,再求值:÷﹣,其中a ,b 满足(a ﹣2)2+=02.(2019·本溪)先化简,再求值:a a a a a a 2221444222-÷⎪⎪⎭⎫ ⎝⎛--+--. 其中a 满足 a 2+3a -2=0.3.观察下列等式:第1个等式:a 1=11+2=2-1, 第2个等式:a 2=12+3=3-2, 第3个等式:a 3=13+2=2-3, 第4个等式:a 4=12+5=5-2, 按上述规律,回答以下问题:(1)请写出第n 个等式:a n = ;(2)a 1+a 2+a 3+…+a n = .4.(2019·凉山)先化简,再求值:(a +3)2-(a +1)(a -1)-2(2a +4),其中a =-12.53+22,我们可以如下做:∵3+22=2+1+22=(2)2+2×2×1+12=(2+1)2, ∴3+22=(2+1)2=2+1. 仿照上例化简下列各式: (1)4+23= ;(2)13-242= ;(3)14+65-14-65= .6.阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+22=(1+2)2.善于思考的小明进行了以下探索:设a +b 2=(m +n 2)2(其中a 、b 、m 、n 均为整数),则有a +b 2=m 2+2n 2+2mn 2. ∴a =m 2+2n 2,b =2mn .这样小明就找到了一种把类似a +b2的式子化为平方式的方法. 请你仿照小明的方法探索并解决下列问题:(1)当a ,b ,m ,n 均为正整数时,若a +b 3=(m +n 3)2,用含m ,n 的式子分别表示a ,b 得:a = ,b = ; (2)利用所探索的结论,找一组正整数a ,b ,m ,n 填空: +( +2;(3)若a +43=(m +n 3)2,且a ,m ,n 均为正整数,求a 的值.7.化简:x -3x -2÷(x +2-5x -2).8.先化简,再求值:(a +b )2+b (a -b )-4ab ,其中a =2,b =-12.。
2019年全国中考化学真题分类 考点34 物质的共存、鉴别、鉴定、转化(简单转化)

15.(2019·衡阳)下列鉴别物质所用的方法或试剂中,错误的是()A.水和白醋﹣观察颜色 B.氯化钾和氯化铵﹣氢氧化钠C.合成纤维和羊毛纤维﹣点燃闻气味 D.一氧化碳和二氧化碳﹣灼热的氧化铜【答案】A【解析】水和白醋均为无色液体,用观察颜色的方法不能鉴别,A错误;氯化铵能与氢氧化钠混合研磨产生有刺激性气味的气体,氯化钾不能,可以鉴别,B正确;点燃闻气味,产生特殊气味的是合成纤维,产生烧焦羽毛气味的是羊毛纤维,可以鉴别,C正确;一氧化碳能与灼热的氧化铜反应生成铜和二氧化碳,二氧化碳不能,可以鉴别,D正确。
14.(2019·湘西)下列鉴别或区分物质的方法不正确...的是()A.用肥皂水鉴别硬水和软水B.用灼烧法区分羊毛和合成纤维C.用食酷鉴别纯碱和食盐D.通过观察颜色区分黄铜和黄金【答案】D【解析】A.加入肥皂水,泡沫多的是软水,泡沫少的是硬水,方法正确;B.灼烧时有烧焦羽毛的味道的是羊毛,刺激性气味的是合成纤维,方法正确;C.加入食醋,有气泡冒出的是碳酸钠(纯碱),无现象的是氯化钠,方法正确; D. 黄铜和黄金都是黄色的,观察颜色无法鉴别,方法错误。
【答案】C【解析】氮气和二氧化碳都不能支持燃烧,燃着的木条插入都会熄灭,A错误;氯化铵、硝酸铵都是铵态氮肥,加熟石灰研磨都放出氨气,故无法鉴别,B错误;稀盐酸pH<7,碳酸钠溶液pH>7,氯化钠溶液pH=7,可以鉴别,C正确; Fe2(SO4)3溶液溶液为黄色,可以直接鉴别,再将其加入其余溶液,生成红褐色沉淀为氢氧化钠,但是硝酸钠、氯化钾溶液就无法鉴别了,D错误.14.(2019·泰州)下列有关物质的检验、鉴别以及分离、提纯的做法,正确的是()A.检验食品中是否含有淀粉:用碘化钾溶液B.鉴别K2SO4和(NH4)2SO4两种固体:加熟石灰研磨C.除去CaCO3固体中的少量Na2CO3:加入足量稀盐酸充分反应后过滤D.分离Fe和CuSO4固体混合物:加人足量的水溶解,过滤【答案】B【解析】碘遇淀粉变成蓝色,而不是碘化钾,故不能用碘化钾淀粉溶液检验食品中是否含有淀粉,故A错误;鉴别K2SO4和(NH4)2SO4两种固体,加熟石灰研磨,能产生刺激性气味气体的为硫酸铵,B正确;除去CaCO3固体中的少量Na2CO3,加人足量稀盐酸充分反应后过滤,会把碳酸钠和碳酸钙都反应掉了,C错误;分离Fe和CuSO4固体混合物,加人足量的水溶解,过滤,得到铁粉和硫酸铜的溶液,故溶解、过滤、洗涤、蒸发,D错误。
中考物理真题选及答案:照相机

中考物理真题选及答案:照相机1.(2019南充,11)小明在探究“凸透镜成像规律”的实验中,他把蜡烛放在距透镜30cm 时,在光屏上形成清晰缩小的像,此时的成像特点可应用于___________(填“照相机”、“投影仪”或“放大镜”)。
现将蜡烛向透镜方向移动10cm,要使光屏上再次形成清晰倒立的像,应将光屏___________透镜(填“远离”或“靠近”)。
2.( 2019深圳,2)下列与照相机成像原理相同的设备是()A. 放大镜B. 近视眼镜C. 监控摄像头D. 投影仪3.(2019北部湾,8)为加强校园安全管理,在校内安装监控摄像机。
来自物体的光经过摄像机的镜头后形成()A.倒立、缩小的实像 B.正立、放大的实像C.倒立、放大的虚像 D.正立、缩小的虚像4.(2019潍坊,8)小明通过透镜观察“美丽潍坊”四个字,看到的情形如图所示,下列说法正确的是()A.该透镜只能成放大的像B.该透镜可以用作近视眼镜C.该透镜可以用作照相机镜头D.字到透镜的距离小于此透镜的焦距5.(2019咸宁,23)用如图所示装置探究凸透镜成像规律,调整物距u,测量对应的像距v,部分数据如下表所示。
根据表中数据可知该凸透镜的焦距是 cm;如果u=27cm,移动光屏可得到倒立、 (选填“放大”或“缩小”)的实像, (选填“幻灯机”或“照相机”)应用了这一原理。
6.(2019株洲,14)为使倒车更安全,车辆通常会配置倒车可视和倒车雷达。
倒车时,可视系统自动接通车尾摄像头,将车后状况显示在液晶屏上(图甲):保险杠上的超声波探头(图乙)探测到障碍物进入危险距离时,蜂鸣器就开始鸣叫,提醒司机及时停车。
关于摄像头和探头的作用,下列说法正确的是()A.摄像头相当于凸透镜B.摄像头相当于凹透镜C.探头相当于声呐D.探头相当于喇叭7.(2019北海,8)为加强校园安全管理,在校内安装监控摄像机,来自物体的光经过摄像机的镜头后形成()A.倒立、缩小的实像B.正立、放大的实像C.倒立、放大的虚像D.正立、缩小的虚像8. (2019衡阳,5)当汽车经过十字路口时,监控摄像头就会拍下照片,摄像头相当于一个透镜,影像传感器相当于光屏,下列说法正确的是A. 监控摄像头和近视眼镜的镜片都对光有会聚作用B. 拍照时,汽车位于摄像头二倍焦距以外C. 当汽车远离摄像头时,影像传感器上的像变大D. 影像传感器上成的是正立的虚像9.(2019株洲)图为某同学游酒埠江时拍下的一张照片。
2019年中考物理真题集锦——专题二:光学作图(word版含答案)
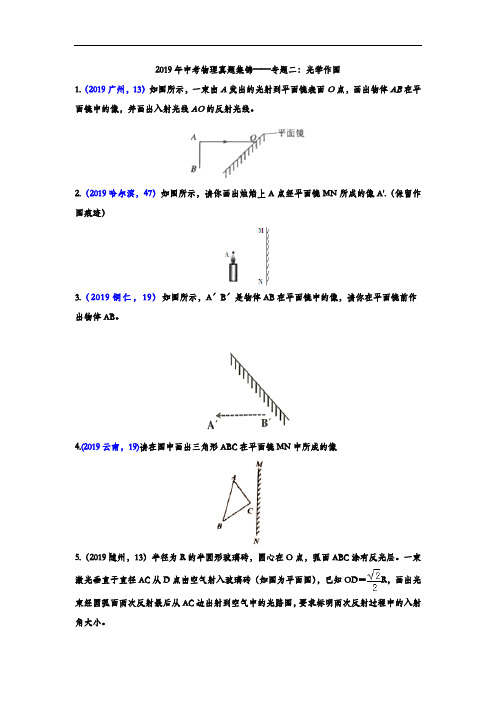
2019年中考物理真题集锦——专题二:光学作图1.(2019广州,13)如图所示,一束由A发出的光射到平面镜表面O点,画出物体AB在平面镜中的像,并画出入射光线AO的反射光线。
2.(2019哈尔滨,47)如图所示,请你画出烛焰上A点经平面镜MN所成的像A'.(保留作图痕迹)3.(2019铜仁,19)如图所示,A'B'是物体AB在平面镜中的像,请你在平面镜前作出物体AB。
4.(2019云南,19)请在图中画出三角形ABC在平面镜MN中所成的像5.(2019随州,13)半径为R的半圆形玻璃砖,圆心在O点,弧面ABC涂有反光层。
一束激光垂直于直径AC从D点由空气射入玻璃砖(如图为平面图),已知OD=R,画出光束经圆弧面两次反射最后从AC边出射到空气中的光路图,要求标明两次反射过程中的入射角大小。
6.(2019娄底,19)如图所示,S'为发光点S在平面镜MN中所成的像,请在图中画出发光点S 的位置,并画出一条由S点发出,经平面镜反射后通过P点的光线。
7.(2019聊城,)如图所示,画出物体AB在平面镜中的像A′B′。
8.(.2019烟台,21)汉代的《淮南万毕术》中记载:“取大镜高悬,置水盆于下,则见四邻矣。
”(如图)。
请在答题卡指定位置,通过作图确定“大镜”的位置。
9.(2019山西,22)如图甲所示,家用小轿车的前挡风玻璃都是斜的,这样可以保证夜间行车时,车内景物通过挡风玻璃所成的像,成在司机前面斜上方避免干扰司机视线,保证驾驶安全。
请你在图乙中画出司机眼睛(B点)通过挡风玻璃MN看到车内装饰物(A点)的像的光路图。
10.(2019泰安,21)如图所示,从点光源S发出的一条光线射向平面镜,经平面镜反射后射向墙壁上的O点处。
请作出这条入射光线并完成光路图。
11.(2019济宁,)如图10所示,一束光水平射入潜望镜镜口后,通过潜望镜进入小明的眼睛。
请画出光的传播路径12.(2019沈阳,2)舞蹈教室内有一面非常大的平面镜,一位同学先后站在镜前甲、乙、丙、丁的四个位置,如图所示。
2019年中考物理真题集锦——专题三十六:简单机械实验(含答案)

2019年中考物理真题集锦——专题三十六:简单机械实验1.(2019攀枝花,30)某同学在河边玩耍时捡到一块石头,估测石头质量大约800g。
回家后,他用弹簧测力计、玻璃杯、细绳和足量的水等器材测量石头的密度。
观察弹簧测力计量程后,发现该测力计不能直接测得石头的质量。
通过思考,该同学利用一根质量分布均匀的细木杆和上述实验器材设计如图所示实验:(1)将木杆的中点O悬挂于线的下端,使杆在水平位置平衡,这样做的好处是可以消除对杆平衡的影响;(2)将左端A与弹簧测力计相连,用细线把石头挂于OA的中点C,弹簧测力计竖直向上提起A端,使杆保持水平,测力计示数如图所示,则拉力大小为N;将石头浸没于装有水的玻璃杯中且不与杯子接触,保持杆水平,记下弹簧测力计此时示数为2.7N;(3)通过计算,浸没后石头受到的浮力大小为N,石头的密度为kg/m3(已知ρ水=1.0×103kg/m3);(4)若上述(2)步骤中,只是杆未保持水平,则测量结果(填“偏大”、“偏小”或“不变”)。
2.(2019齐齐哈尔,19)小红和小君探究“杠杆的平衡条件”时,使用的每个钩码质量均为50g,杠杆上相邻刻度线间的距离相等。
如图甲所示,为使杠杆在水平位置平衡,应将杠杆两端的平衡螺母向端调节(选填“A”或“B“)。
如图乙所示,杠杆水平平衡后,在杠杆的C点挂4个钩码,在D点用弹簧测力计竖直向上拉杠杆,使杠杆仍保持水平平衡,则弹簧测力计的示数为N。
3.(2019包头,10)下图是“利用杠杆测量石块密度”的实验。
(ρ水=1.0×103kg/m3)(1) 在实验前,杠杆静止在图甲所示的位置,此时杠杆处于(选填“平衡”或“不平衡”)状态;要使杠杆在水平位置平衡,应将平衡螺母向调节,这样做的目的是,并消除杠杆自重对实验的影响。
(2) 在溢水杯中装满水,如图乙所示,将石块缓慢浸没在水中,让溢出的水流入小桶A中,此时小桶A中水的体积石块的体积。
【中考真题】四川省遂宁市2019年中考生物试卷(含答案)

2019年四川省遂宁市中考生物试卷一、选择题(本大题共10小题,共20.0分)1.下列所描述的生命现象与其实例不相符合的是()A. 生物的生命活动需要营养--螳螂捕蝉,黄雀在后B. 生物能对外界刺激作出反应--朵朵葵花向太阳C. 生物需要排出体内的代谢废物--蜻蜓点水D. 生物能生长和繁殖--离离原上草,一岁一枯荣2.下列有关实验或探究活动的叙述,错误的是()A. 使用显微镜时,选用10倍目镜和40倍物镜,所观察的物像放大了400倍B. 利用澄清石灰水可以验证植物呼吸作用是否产生二氧化碳C. 用显微镜观察小鱼尾鳍内血液的流动时,红细胞单行通过的血管是毛细血管D. “绿叶在光下合成淀粉实验”中,直接加热酒精对叶片进行脱色处理3.2015年12月10日瑞典国王为诺贝尔奖得主屠呦呦颁奖,以表彰她从野生植物黄花蒿中提取青蒿素治疗由疟原虫引起的疟疾,挽救了数百万人的生命。
下列有关黄花蒿的说法错误的是()A. 黄花蒿的细胞有细胞壁,而疟原虫的细胞没有细胞壁B. 黄花蒿的结构层次是:细胞→器官→组织→植物体C. 黄花蒿细胞内指导青蒿素形成的控制中心是细胞核D. 黄花蒿植株生长离不开细胞的分裂、生长和分化4.大棚种植的西瓜喜获丰收,合成西瓜中甜味物质的原料是()A. 二氧化碳和水B. 二氧化碳和氧气C. 水和有机物D. 氧气和无机盐5.如图表示农作物种植密度与光合作用和呼吸作用强度的关系,下列分析错误的是()A. A点时,光合作用和呼吸作用强度相等B. 种植密度越大,光合作用强度越大C. 种植密度为m3时,对农作物增产最有利D. 种植密度在m4之后,农作物将会减产6.如图是哺乳动物心脏内部结构及与其相连的血管示意图。
有关分析正确的是()A. ③是右心室,其肌肉壁最发达B. ④收缩时部分血液可流到⑤中C. 图中①是将血液运往全身去的血管D. ②是肺静脉,流动脉血7.下列有关人体生命活动调节的描述中,不正确的是()A. 醉酒人的动作不协调,主要原因是酒精麻痹了此人的小脑B. 幼年生长激素分泌不足会患呆小症C. 成年人能有意识地排尿,该反射的神经中枢在大脑皮层D. “谈虎色变”“谈梅止渴”是人特有的复杂反射8.在人体的呼吸系统中,下列表述不正确的是()A. 人体呼吸时,呼出的气体全部是二氧化碳B. 吸气时,膈肌收缩,膈顶部下降,气体进入肺C. 肺是呼吸系统的主要器官,是完成气体交换的重要场所D. 北欧人的鼻子明显比生活在赤道附近的人大,这有利于预热冬天寒冷的空气9.下列关于染色体,DNA和基因的描述中,正确的是()A. 正常人体的所有细胞中染色体都是成对存在的B. 染色体是由DNA和基因组成的C. 每个DNA分子上只含有1个基因D. 男性含Y染色体的精子只传给儿子,不传给女儿10.如图表示生态系统中几种生物的关系图,下列有关说法不正确的是()A. 能量沿食物链单向流动,逐级递减B. ②与③之间是捕食关系C. ①②③④共同构成了生态系统D. 该生态系统只有一条食物链二、实验题(本大题共1小题,共5.0分)11.果蝇是遗传学的重要实验材料,请据图分析回答:(1)图一为雌果蝇的体细胞染色体示意图。
遂宁市船山区中考语文真题试卷

遂宁市船山区中考语文真题试卷姓名:________ 班级:________ 成绩:________一、积累(14分) (共3题;共14分)1. (4.0分) (2019八上·义乌月考) 阅读下面这段文字,完成后面的题目。
学习《人民解放军百万大军横渡长江》,让我们领略了战士们冲破敌人重重阻遏,歼灭和击溃一切顽抗敌人的气势,那气势只能用“锐不可dāng”来形容;学习《首届诺贝尔奖bān发》,让我们了解那些像诺贝尔一样为人类做出伟大贡献的人;朗读《“飞天”凌空》,让我们仿佛又听到了观众那震耳欲聋的掌声和欢呼声;朗读《一着惊海天》,让我们心潮澎湃,豪情万丈,信念与梦想,在同一时刻汇聚:我们的祖国真正强大起来了!(1)根据拼音写出相应的汉字。
dāng bān锐不可________________发(2)选择划线字的正确读音。
①“飞天”凌空________(A.líng B.léng)②澎湃________(A.bài B.pài)2. (8分) (2018九上·桐乡期中) 古诗文名句积累。
(1)露从今夜白,________。
(2) ________,雪拥蓝关马不前。
(3)李白在《行路难》中“闲来垂钓碧溪上,________”典故表达自己希望能够得到重用的愿望;刘禹锡在《酬乐天初逢席上见赠》中借“________,到乡翻似烂柯人。
”的典故来感叹人事变迁之快。
(4)作家梁衡称张岱的《湖心亭看雪》用42个字创造了一幅淡雅、高洁的画轴,是我国古典文学宝库中的精品。
请在下面的方框内默写描写雪景的42个字,书写要工整、美观。
3. (2分)我国历史上著名故事《完璧归赵》的主人公是()A . 诸葛亮B . 蔺相如C . 曹操D . 越王勾践二、阅读(48分) (共6题;共48分)4. (4分)阅读名著片段,回答下列问题。
鲁提辖假意道:“你这厮诈死,酒家再打!”只见面皮渐渐的变了。
01鱼我所欲也中考语文复习“决胜古诗文”专题讲义(学生版)

【原文呈现】鱼我所欲也鱼,我所欲也;熊掌,亦我所欲也。
二者不可得兼,舍鱼而取熊掌者也。
生,亦我所欲也;义,亦我所欲也。
二者不可得兼,舍生而取义者也。
生亦我所欲,所欲有甚于生者,故不为苟得也;死亦我所恶(w ù),所恶有甚于死者,故患有所不辟(bì)也。
如使人之所欲莫甚于生,则凡可以得生者何不用也?使人之所恶莫甚于死者,则凡可以辟患者何不为也?由是则生而有不用也,由是则可以辟患而有不为也。
是故所欲有甚于生者,所恶有甚于死者。
非独贤者有是心也,人皆有之,贤者能勿丧耳。
一箪食,一豆羹,得之则生,弗得则死。
呼尔而与之,行道之人弗受;蹴(cù)尔而与之,乞人不屑也。
万钟则不辩礼义而受之,万钟于我何加焉!为宫室之美、妻妾之奉、所识穷乏者得我与?乡(xiàng)为身死而不受,今为宫室之美为之;乡为身死而不受,今为妻妾之奉为之;乡为身死而不受,今为所识穷乏者得我而为之:是亦不可以已乎?此之谓失其本心。
【诵读点拨】鱼我所欲也鱼,我/所欲/也;熊掌,亦/我/所欲/也。
二者/不可/得兼,舍/鱼/而取/熊掌/者也。
生,亦/我/所欲/也;义,亦/我/所欲/也。
二者/不可/得兼,舍生/而/取义/者也。
生/亦/我/所欲,所欲/有甚于/生者,故/不为/苟得/也;死/亦/我/所恶,所恶/有甚于死/者,故/患/有所/不辟也。
如使/人之所欲/莫甚于/生,则/凡可以/得生者/何不用也?使/人之所恶/莫甚于/死者,则/凡可以/辟患者/何不为/也?由是则/生/而有不用/也,由是则/可以辟患/而有/不为也。
是故/所欲/有甚于/生/者,所恶/有甚于/死/者。
非/独贤者/有/是心/也,人/皆有之,贤者/能/勿丧/耳。
一箪食,一豆羹,得之/则/生,弗得/则/死。
呼/尔/而与之,行道/之人/弗受;蹴/尔/而与之,乞人/不屑/也。
万钟/则/不辩/礼义/而/受之,万钟/于/我/何加焉!为/宫室/之美、妻妾/之奉、所识/穷乏者/得/我与?乡/为/身死/而/不受,今/为/宫室/之美/为之;乡/为/身死/而/不受,今/为/妻妾/之奉/为之;乡/为/身死/而/不受,今/为/所识/穷乏者/得我/而/为之:是/亦不可以/已乎?此之谓/失其本心。
2019年中考物理真题集锦——专题五十五:浮力(含答案)

2019年中考物理真题集锦——专题五十五:浮力1.(2019泸州,11)三个相同的轻质弹簧,一端固定在容器底部,另一端分别与甲、乙、丙三个体积相同的实心球相连。
向容器内倒入水,待水和球都稳定后,观察到如图所示的情况,此时乙球下方弹簧长度等于原长。
下列判断正确的是()A. 乙球的重力与它受到的浮力相等B. 甲球的重力大于它受到的浮力C. 甲、乙、丙三个球的密度大小关系为ρ甲<ρ乙<ρ丙D. 甲、乙、丙三个球受到的浮力大小关系为F甲<F乙<F丙【答案】AC2.(2019枣庄,8)在木棒的一端缠绕一些细铜丝制成简易的液体密度计,将其分别放入盛有甲乙两种液体的烧杯中处于静止状态,如图所示,若密度计在甲乙液体中受到的浮力分别是F甲、F乙,甲乙两种液体的密度分别为ρ甲、ρ乙.则()A.F甲<F乙B.F甲>F乙C.ρ甲>ρ乙D.ρ甲<ρ乙【答案】C3.(2019湘潭,17)图展示了我国古代劳动人民的智慧成果,对其中涉及的物理知识,说法错误的是()A.孔明灯在上升过程中,只受浮力B.紫砂壶属于连通器C.司南能够指南北是利用了磁体受地磁场的作用D.正在发声的编钟在振动【答案】A4.(2019达州,4)下列关于力的说法中正确的是()A.两个物体不接触就一定不产生力B.摩擦力的方向一定与物体的运动方向相反C.浸没在水中向上运动的物体浮力可能小于重力D.随着生产力的提高人类将会制造出既省力又省距离的机械【答案】C。
5.(2019达州,6)如图所示,甲、乙两个底面积不同的圆柱形容器中分别盛有两种不同的液体A、B,液体对两个容器底的压强相等。
现将两个质量相等的物体分别放入两个容器中,静止时个漂浮、一个悬浮(液体均无溢出,则液体密度ρA、ρB和液体对容器底部的压强p甲、p乙的大小关系正确的是()A.ρA<ρB p甲<p乙B.ρA>ρB p甲>p乙C.ρA>ρB p甲<p乙D.ρA<ρB p甲>p乙【答案】C。
2019年四川省遂宁中考数学试卷(附答案与解析)

数学试卷 第1页(共20页) 数学试卷 第2页(共20页)绝密★启用前四川省遂宁市2019年初中毕业会考、高级中等学校招生考试数 学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,总分150分,考试时间120分钟.第Ⅰ卷(选择题,满分40分)一、选择题(本大题共10个小题,每小题4分,共40分,在每个小题给出的四个选项中,只有一个符合题目要求.) 1.-的值为( ) AB. C. D .2 2.下列等式成立的是( )A.2=B .()22346a ba b =C .()222a a a a +÷=D .22523x y x y -=3.如图为正方体的一种平面展开图,各面都标有数字,则数字为2-的面与其对面上的数字之积是( )A .12-B .0C .8-D .10-4.某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本是( )A .100B .被抽取的100名学生家长C .被抽取的100名学生家长的意见D .全校学生家长的意见5.已知关于x 的一元二次方程2212)10(a x x a --+-=有一个根为0x =,则a 的值为( )A .0B .1±C .1D .1- 6.如图,ABC △内接于O ⊙,若45A ∠=︒,O ⊙的半径4r =,则阴影部分的面积为( )A .48π-B .2πC .4πD .88π- 7.如图,ABCD 中,对角线AC 、BD 相交于点O ,OE BD ⊥交AD 于点E ,连接BE ,若ABCD 的周长为28,则ABE △的周长为( )A .28B .24C .21D .14 8.关于x 的方程1242k xx x -=--的解为正数,则k 的取值范围是( )A .4k >-B .4k <C .4k >-且4k ≠D .4k <且4k ≠- 9.二次函数2 y x ax b =-+的图象如图所示,对称轴为直线2x =,下列结论不正确的是( )A .4?a =B .当4?b =-时,顶点的坐标为(2,)8-C .当1x =-时,5b >-D .当3x >时,y 随x 的增大而增大10.如图,四边形ABCD 是边长为1的正方形,BPC △是等边三角形,连接DP 并延长交CB 的延长线于点H ,连接BD 交PC 于点Q ,下列结论:①135BPD ∠=︒;②BDP HDB △∽△;③:1:2DQ BQ =;④BDP S =△ 其中正确的有( )毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共20页) 数学试卷 第4页(共20页)A .①②③B .②③④C .①③④D .①②④第Ⅱ卷(非选择题,满分110分)二、填空题(本大题共5个小题,每小题4分,共20分)11.2018年10月24日,我国又一项世界级工程——港珠澳大桥正式建成通车,它全长55000米,用科学记数法表示为 米.12.若关于x 的方程220x x k -+=有两个不相等的实数根,则k 的取值范围为 . 13.某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为92分、85分、90分,综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为 分.14.阅读材料:定义:如果一个数的平方等于1-,记为21i =-,这个数i 叫做虚数单位,把形如a bi +(a ,b 为实数)的数叫做复数,其中a 叫这个复数的实部,b 叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似. 例如计算:462461()()()()210i i i i ++-++--==;2()()2363261(7)i i i i i i i -+-+-----===; 2441616117()()()i i i +----===; 22(24444134)i i i i i ++++-+===根据以上信息,完成下面计算:2()(22(2)1)i i i +-+-= .15.如图,在平面直角坐标系中,矩形OABC 的顶点O 落在坐标原点,点A 、点C 分别位于x 轴,y 轴的正半轴,G 为线段OA 上一点,将OCG △沿CG 翻折,O 点恰好落在对角线AC 上的点P 处,反比例函数12y x=经过点B 二次函数2()0y ax bx c a =++≠的图象经过()0,3C 、G 、A 三点,则该二次函数的解析式为 .(填一般式)三、计算或解答题(本大题共10小题,满分90分) 16.(本小题满分7分)计算:20192012 3.144()()cos3()|02π---++--︒+17.(本小题满分7分)解不等式组:3561162x x x x <+⎧⎪+-⎨≥⎪⎩,把它的解集在数轴上表示出来,并写出其整数解.18.(本小题满分7分)先化简,再求值:2222222a ab b a ab a b a a b-+-÷--+,其中a ,b满足2(2)0a -.19.(本小题满分9分)如图,在四边形ABCD 中,AD BC ∥,延长BC 到E ,使=CE BC ,连接AE 交CD 于点F ,点F 是CD 的中点.求证: (1)ADF ECF △≌△.(2)四边形ABCD 是平行四边形.数学试卷 第5页(共20页) 数学试卷 第6页(共20页)20.(本小题满分9分)汛期即将来临,为保证市民的生命和财产安全,市政府决定对一段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡坡面从A 至A 共有30级阶梯,平均每级阶梯高30cm ,斜坡AB 的坡度1:1i =;加固后,坝顶宽度增加2米,斜坡EF的坡度i =,问工程完工后,共需土石多少立方米?(计算土石方时忽略阶梯,结果保留根号)21.(本小题9分)仙桃是遂宁市某地的特色时令水果.仙桃一上市,水果店的老板用2 400元购进一批仙桃,很快售完;老板又用3 700元购进第二批仙桃,所购件数是第一批的32倍,但进价比第一批每件多了5元. (1)第一批仙桃每件进价是多少元?(2)老板以每件225元的价格销售第二批仙桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批仙桃的销售利润不少于440元,剩余的仙桃每件售价至少打几折?(利润=售价-进价)22.(本小题满分10分)我市某校为了让学生的课余生活丰富多彩,开展了以下课外活动:代号 活动类型 A 经典诵读与写作 B 数学兴趣与培优 C 英语阅读与写作 D 艺体类 E其他为了解学生的选择情况,现从该校随机抽取了部分学生进行问卷调查(参与问卷调查的每名学生只能选择其中一项),并根据调查得到的数据绘制了如图所示的两幅不完整的统计图.请根据统计图提供的信息回答下列问题(要求写出简要的解答过程).(1)此次共调查了 名学生. (2)将条形统计图补充完整.(3)“数学兴趣与培优”所在扇形的圆心角的度数为 .(4)若该校共有2 000名学生,请估计该校喜欢A 、B 、C 三类活动的学生共有多少人?(5)学校将从喜欢“A ”类活动的学生中选取4位同学(其中女生2名,男生2名)参加校园“金话筒”朗诵初赛,并最终确定两名同学参加决赛,请用列表或画树状图的方法,求出刚好一男一女参加决赛的概率.23.(本小题满分10分)如图,一次函数3y x =-的图象与反比例函数(0)ky k x=≠的图象交于点A 与点(),4B a -. (1)求反比例函数的表达式; (2)若动点P 是第一象限内双曲线上的点(不与点A 重合),连接OP ,且过点P 作y 轴的平行线交直线AB 于点C ,连接OC ,若POC △的面积为3,求出点P 的坐标.毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第7页(共20页) 数学试卷 第8页(共20页)24.(本小题满分10分)如图,ABC △内接于O ⊙,直径AD 交BC 于点E ,延长AD 至点F ,使2DF OD =,连接FC 并延长交过点A 的切线于点G ,且满足AG BC ∥,连接OC ,若1cos 3BAC ∠=,6BC =.(1)求证:COD BAC ∠=∠;(2)求O ⊙的半径OC ; (3)求证:CF 是O ⊙的切线.25.(本小题满分12分)如图,顶点为()3,3P 的二次函数图象与x 轴交于点()6,0A ,点B 在该图象上,OB 交其对称轴l 于点M ,点M 、N 关于点P 对称,连接BN 、ON . (1)求该二次函数的关系式.(2)若点B 在对称轴l 右侧的二次函数图象上运动,请解答下列问题: ①连接OP ,当12OP MN =时,请判断NOB △的形状,并求出此时点B 的坐标. ②求证:BNM ONM ∠=∠.数学试卷 第9页(共20页) 数学试卷 第10页(共20页)四川省遂宁市2019年初中毕业会考、高级中等学校招生考试数学答案解析第Ⅰ卷一、选择题 1.【答案】B【解析】-=B 2.【答案】B【解析】A、2,无法计算,故此选项错误;B 、()22346a b a b =,正确;C 、()2221aa a a +÷=+,故此选项错误;D 、故222523x y x y x y -=,此选项错误。
四川省遂宁市2019-2020学年中考中招适应性测试卷地理试题(1)含解析

四川省遂宁市2019-2020学年中考中招适应性测试卷地理试题(1)一、选择题(本题包括25个小题,每小题2分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的。
)1.西藏打造世界级精品旅游地的主要限制性因素是①气候高寒缺氧②旅游资源的游览价值低③交通不便④旅游环境的承载量小A.①②B.③④C.①③D.②④【答案】C【解析】【分析】【详解】西藏位于青藏高原上,独特的高原环境,旅游资源丰富价值高,但是由于海拔高,气温低,空气稀薄,高寒缺氧,再加上,地形崎岖,交通不便,成为限制该地区的旅游业发展的主要因素。
故选C。
【点睛】该题考查西藏地区旅游业发展的条件,分析解答即可。
2.下列建筑能体现北京城市政治职能的是A.B.C.D.【答案】B【解析】【分析】【详解】北京是我国的首都,是我国的政治中心和文化中心,以上四幅图片中,只有B图表示的人民大会堂能够体现北京是我国的政治中心,其他三个是北京历史上留下的文化遗产,不能体现北京政治中心的职能,故选B。
3.“一江春水向东流”“滚滚长江东逝水”这些话反映的我国的地势特征与下图中哪一图示相符()A.B.C.D.【答案】B【解析】【分析】【详解】由题目可知,“一江春水向东流”“滚滚长江东逝水”反映我国大部分河流自西向东注入海洋,这是由于我国西高东低的地势造成的,除此之外,我国地势呈三级阶梯状分布,与图中B表示的地势图相符,故选B。
4.日月星辰东升西落现象形成的原因是()A.日月星辰都绕着地球转B.地球绕太阳自西向东公转C.地球自西向东自转D.地球公转时,地轴是倾斜的【答案】C【解析】【分析】【详解】地球绕地轴不停转动,叫地球自转.地球自转的方向是自西向东,自转的周期是一天.地球自转产生的现象是昼夜交替和时间差异.日月星辰每天绕着地球东升西落属于昼夜交替现象,其原因是地球自西向东不停自转造成.故选项C符合题意.故选:C.【点睛】本题考查的是地球自转产生的地理现象。
吴小军《月亮村的月亮》中考现代文阅读练习及答案(2019年四川省遂宁市中考题)

13.阅读《月亮村的月亮》,完成下列各题,月亮村的月亮吴小军①月亮三年没回他那粤北深山里的家了,他已经在邻近深圳的一个小县城安了家,实现了进城的梦想。
前几天突然接到村民小组长从家乡的县城打来的电话,说他爸有些不得劲了。
月亮决定,趁着中秋请假回一趟,把母亲去世后一直不肯离开村子的老父亲接过去住。
要不,还真拿不准啥时才回家。
②一跨上山坳,他就真切地想起了老人讲的月亮村的名是怎么来的了。
真是好大个月亮!就这样银光光、亮爽爽、突兀兀地从两座大山坳处撞入他的眼帘,撞入他的心房。
③“我回来了!”坐了几个钟头的火车,坐了一个多钟头的汽车,坐了近一个钟头的小四轮,又走了一个钟头的山路的月亮,忘了所有的疲惫,心里豁然亮堂了起来。
④转过这个坳,是一起做泥水工的广财的家,墙头有的塌了,瓦破了,屋顶上露着的椽子黑了。
房门上还挂着几片纸,残的,月光虽然很亮,却看不出红白了。
广财的孩子在城里上民办学校,前些年他爸也没了,他可能有四五年没回村了。
⑤月亮沿着那条走了三十多年,眼下却觉有些陌生的小路下坳。
陌生?是呀,怎么就陌生了呢?是三年没走了?哦,是杂草太盛了,反射着月光,银灿灿的一片,草间这条由乱石铺成的小路,显得瘦了。
⑥下了坳,有一片稍缓的坡地,错落着几座屋子,分别是广发、兴利、黑牛、中坤等人的家,除了兴利是木工,其他几个原先也和月亮一起做泥水工、杂工,后来各自分开,也不知散落到哪处去了。
一路上,经过了秋英、亚菊的家,屋子的窗都黑着,想是也没人在屋。
这些年,村里的人像蒲公英的种子一样,陆陆续续飘进城里去了,有大城市,也有县城,最差的也到镇上去了。
去了,也慢慢扎下了脚跟。
大家都不愿意回来。
⑦又转过一个山包,是一大片连着的庄稼地,现在全荒了。
转过得水家,月亮看见祠堂了。
守祠堂的孤老头七叔公会点香火。
都是岁月,都是故事。
前些年,祠堂香火很盛,除了年节、醮会,村里红事、白事都在那里上香鸣炮,禀告先人。
祠堂,是一个村的中枢,是圣地哩。
2019年中考试题汇编一元二次方程填空题(解析版)

2019年中考试题汇编一元二次方程填空题1.(2019年湖北省荆门市)已知x1,x2是关于x的方程x2+(3k+1)x+2k2+1=0的两个不相等实数根,且满足(x1﹣1)(x2﹣1)=8k2,则k的值为1.【分析】根据根与系数的关系结合(x1﹣1)(x2﹣1)=8k2,可得出关于k的一元二次方程,解之即可得出k的值,根据方程的系数结合根的判别式△>0,可得出关于k的一元二次不等式,解之即可得出k的取值范围,进而即可确定k值,此题得解.【解答】解:∵x1,x2是关于x的方程x2+(3k+1)x+2k2+1=0的两个实数根,∴x1+x2=﹣(3k+1),x1x2=2k2+1.∵(x1﹣1)(x2﹣1)=8k2,即x1x2﹣(x1+x2)+1=8k2,∴2k2+1+3k+1+1=8k2,整理,得:2k2﹣k﹣1=0,解得:k1=﹣,k2=1.∵关于x的方程x2+(3k+1)x+2k2+1=0的两个不相等实数根,∴△=(3k+1)2﹣4×1×(2k2+1)>0,解得:k<﹣3﹣2或k>﹣3+2,∴k=1.故答案为:1.【点评】本题考查了根与系数的关系以及根的判别式,利用根与系数的关系结合(x1﹣1)(x2﹣1)=8k2,求出k值是解题的关键.2.(2019年四川省遂宁市)若关于x的方程x2﹣2x+k=0有两个不相等的实数根,则k的取值范围为k<1.【分析】利用根的判别式进行计算,令△>0即可得到关于k的不等式,解答即可.【解答】解:∵关于x的方程x2﹣2x+k=0有两个不相等的实数根,∴△>0,即4﹣4k>0,k<1.故答案为:k<1.【点评】本题考查了根的判别式,要知道一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.3.(2019年江西省)设x1,x2是一元二次方程x2﹣x﹣1=0的两根,则x1+x2+x1x2=0.【分析】直接根据根与系数的关系求解.【解答】解:∵x1、x2是方程x2﹣x﹣1=0的两根,∴x1+x2=1,x1×x2=﹣1,∴x1+x2+x1x2=1﹣1=0.故答案为:0.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=﹣,x1•x2=.4.(2019年山东省威海市)一元二次方程3x2=4﹣2x的解是x1=,x2=.【分析】直接利用公式法解方程得出答案.【解答】解:3x2=4﹣2x3x2+2x﹣4=0,则b2﹣4ac=4﹣4×3×(﹣4)=52>0,故x=,解得:x1=,x2=.故答案为:x1=,x2=.【点评】此题主要考查了公式法解方程,正确掌握公式法是解题关键.5.(2019年四川省攀枝花市)已知x1,x2是方程x2﹣2x﹣1=0的两根,则x12+x22=6.【分析】根据根与系数的关系变形后求解.【解答】解:∵x1、x2是方程x2﹣2x﹣1=0的两根,∴x1+x2=2,x1×x2=﹣1,∴x12+x22=(x1+x2)2﹣2x1x2=22﹣2×(﹣1)=6.故答案为:6.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=﹣,x1•x2=.6.(2019年四川省成都市)已知x1,x2是关于x的一元二次方程x2+2x+k﹣1=0的两个实数根,且x12+x22﹣x1x2=13,则k的值为﹣2.【分析】根据“x1,x2是关于x的一元二次方程x2+2x+k﹣1=0的两个实数根,且x12+x22﹣x1x2=13”,结合根与系数的关系,列出关于k的一元一次方程,解之即可.【解答】解:根据题意得:x1+x2=﹣2,x1x2=k﹣1,+﹣x1x2=﹣3x1x2=4﹣3(k﹣1)=13,k=﹣2,故答案为:﹣2.【点评】本题考查了根与系数的关系,正确掌握一元二次方程根与系数的关系是解题的关键.7.(2019年江苏省扬州市)一元二次方程x(x﹣2)=x﹣2的根是1或2.【分析】移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.【解答】解:x(x﹣2)=x﹣2,x(x﹣2)﹣(x﹣2)=0,(x﹣2)(x﹣1)=0,x﹣2=0,x﹣1=0,x1=2,x2=1,故答案为:1或2.【点评】本题考查了解一元二次方程的应用,能把一元二次方程转化成一元一次方程是解此题的关键.8.(2019年四川省资阳市)a是方程2x2=x+4的一个根,则代数式4a2﹣2a的值是8.【分析】直接把a的值代入得出2a2﹣a=4,进而将原式变形得出答案.【解答】解:∵a是方程2x2=x+4的一个根,∴2a2﹣a=4,∴4a2﹣2a=2(2a2﹣a)=2×4=8.故答案为:8.【点评】此题主要考查了一元二次方程的解,正确将原式变形是解题关键.9.(2019年甘肃省天水市)中国“一带一路”给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年人均年收入20000元,到2018年人均年收入达到39200元.则该地区居民年人均收入平均增长率为40%.(用百分数表示)【分析】根据题意可以列出相应的方程,从而可以求得该地区居民年人均收入平均增长率,本题得以解决.【解答】解:设该地区居民年人均收入平均增长率为x,20000(1+x)2=39200,解得,x1=0.4,x2=﹣2.4(舍去),∴该地区居民年人均收入平均增长率为40%,故答案为:40%.【点评】本题考查一元二次方程的应用,解答本题的关键是明确题意,列出相应的方程,求出相应的增长率.10.(2019年四川省宜宾市)某产品每件的生产成本为50元,原定销售价65元,经市场预测,从现在开始的第一季度销售价格将下降10%,第二季度又将回升5%.若要使半年以后的销售利润不变,设每个季度平均降低成本的百分率为x,根据题意可列方程是65×(1﹣10%)×(1+5%)﹣50(1﹣x)2=65﹣50.【分析】设每个季度平均降低成本的百分率为x,根据利润=售价﹣成本价结合半年以后的销售利润为(65﹣50)元,即可得出关于x的一元二次方程,此题得解.【解答】解:设每个季度平均降低成本的百分率为x,依题意,得:65×(1﹣10%)×(1+5%)﹣50(1﹣x)2=65﹣50.故答案为:65×(1﹣10%)×(1+5%)﹣50(1﹣x)2=65﹣50.【点评】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.11.(2019年江苏省盐城市)设x1、x2是方程x2﹣3x+2=0的两个根,则x1+x2﹣x1•x2=1.【分析】由韦达定理可知x1+x2=3,x1•x2=2,代入计算即可;【解答】解:x1、x2是方程x2﹣3x+2=0的两个根,∴x1+x2=3,x1•x2=2,∴x1+x2﹣x1•x2=3﹣2=1;故答案为1;【点评】本题考查一元二次方程根与系数的关系;牢记韦达定理是解题的关键.12.(2019年江苏省连云港市)已知关于x的一元二次方程ax2+2x+2﹣c=0有两个相等的实数根,则+c的值等于2.【分析】根据“关于x的一元二次方程ax2+2x+2﹣c=0有两个相等的实数根”,结合根的判别式公式,得到关于a和c的等式,整理后即可得到的答案.【解答】解:根据题意得:△=4﹣4a(2﹣c)=0,整理得:4ac﹣8a=﹣4,4a(c﹣2)=﹣4,∵方程ax2+2x+2﹣c=0是一元二次方程,∴a≠0,等式两边同时除以4a得:c﹣2=﹣,则+c=2,故答案为:2.【点评】本题考查了根的判别式,正确掌握根的判别式公式是解题的关键.13.(2019年浙江省绍兴市)x为何值时,两个代数式x2+1,4x+1的值相等?【分析】利用题意得到x2+1=4x+1,利用因式分解法解方程即可.解:x2+1=4x+1,x2﹣4x=0,x(x﹣4)=0,x1=0,x2=4.【点评】考查了实数的运算,因式分解法解一元二次方程.因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).14.(2019年浙江省嘉兴市)在x2+±4x+4=0的括号中添加一个关于x的一次项,使方程有两个相等的实数根.【分析】要使方程有两个相等的实数根,即△=0,则利用根的判别式即可求得一次项的系数即可.【解答】解:要使方程有两个相等的实数根,则△=b2﹣4ac=b2﹣16=0得b=±4故一次项为±4x故答案为±4x【点评】此题主要考查一元二次方程的根的判别式,利用一元二次方程根的判别式(△=b2﹣4ac)可以判断方程的根的情况:一元二次方程的根与根的判别式有如下关系:①当△>0时,方程有两个不相等的实数根;②当△=0 时,方程有两个相等的实数根;③当△<0 时,方程无实数根,但有2个共轭复根.上述结论反过来也成立.15.(2019年江苏省南京市)已知2+是关于x的方程x2﹣4x+m=0的一个根,则m=1.【分析】把x=2+代入方程得到关于m的方程,然后解关于m的方程即可.【解答】解:把x=2+代入方程得(2+)2﹣4(2+)+m=0,解得m=1.故答案为1.【点评】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.16.(2019年山东省泰安市)已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+3=0有两个不相等的实数根,则实数k的取值范围是k.【分析】根据方程有两个不相等的实数根可得△=(2k﹣1)2﹣4(k2+3)>0,求出k 的取值范围;【解答】解:∵原方程有两个不相等的实数根,∴△=(2k﹣1)2﹣4(k2+3)=﹣4k+1﹣12>0,解得k;故答案为:k.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.17.(2019年甘肃省武威市、陇南市)关于x的一元二次方程x2+x+1=0有两个相等的实数根,则m的取值为4.【分析】要使方程有两个相等的实数根,即△=b2﹣4ac=0,则利用根的判别式即可求得一次项的系数.【解答】解:由题意,△=b2﹣4ac=()2﹣4=0得m=4故答案为4【点评】此题主要考查一元二次方程的根的判别式,利用一元二次方程根的判别式(△=b2﹣4ac)可以判断方程的根的情况:一元二次方程的根与根的判别式有如下关系:①当△>0时,方程有两个不相等的实数根;②当△=0 时,方程有两个相等的实数根;③当△<0 时,方程无实数根,但有2个共轭复根.上述结论反过来也成立.18.(2019年山东省青岛市)若关于x的一元二次方程2x2﹣x+m=0有两个相等的实数根,则m的值为.【分析】根据“关于x的一元二次方程2x2﹣x+m=0有两个相等的实数根”,结合根的判别式公式,得到关于m的一元一次方程,解之即可.【解答】解:根据题意得:△=1﹣4×2m=0,整理得:1﹣8m=0,解得:m=,故答案为:.【点评】本题考查了根的判别式,正确掌握根的判别式公式是解题的关键.19.(2019年山东省枣庄市)已知关于x的方程ax2+2x﹣3=0有两个不相等的实数根,则a的取值范围是a>且a≠0.【分析】由方程有两个不相等的实数根,则运用一元二次方程ax2+bx+c=0(a≠0)的根的判别式是b2﹣4ac>0即可进行解答【解答】解:由关于x的方程ax2+2x﹣3=0有两个不相等的实数根得△=b2﹣4ac=4+4×3a>0,解得a>则a>且a≠0故答案为a>且a≠0【点评】本题重点考查了一元二次方程根的判别式,在一元二次方程ax2+bx+c=0(a≠0)中,(1)当△>0时,方程有两个不相等的实数根;(2)当△=0时,方程有两个相等的实数根;(3)当△<0时,方程没有实数根.20.(2019年山东省济宁市)已知x=1是方程x2+bx﹣2=0的一个根,则方程的另一个根是﹣2.【分析】根据根与系数的关系得出x1x2==﹣2,即可得出另一根的值.【解答】解:∵x=1是方程x2+bx﹣2=0的一个根,∴x1x2==﹣2,∴1×x2=﹣2,则方程的另一个根是:﹣2,故答案为﹣2.【点评】此题主要考查了一元二次方程根与系数的关系,得出两根之积求出另一根是解决问题的关键.。
古蜀栈道—阅读答案(2019四川遂宁中考试题)

古蜀栈道—阅读答案(2019四川遂宁中考试题)古蜀栈道刘小方①打开古旧地图,我们就会发觉,关中通往汉中的陈仓道、褒斜道、傥骆道、子午道以及由汉中通往四川的金牛道、米仓道和荔枝道,犹如一张精致斜织在秦岭山脉和大巴山脉中的大网,连接着八百里秦川与四川盆地这两个古代的天府之国。
②秦中自古帝王之都。
长期作为国家政治经济文化中心的关中地区,面临着人口剧增与生产生活资料短缺的冲突,而四川盆地物产丰富,两地的沟通势在必定。
〔《史记货殖列传》记载:"〔秦〕昭治咸阳,因以汉都,长安诸陵,四方辐凑并至而会,地小人众,故其民益玩巧而事末也。
南则巴蜀。
巴蜀亦沃野,地饶卮、姜、丹沙、石、铜、铁、竹、木之器。
然四塞。
'〕对于古蜀先民而言,闭塞成为其进展的最大障碍,关中地区是经济文化最发达的地区,来自北边的吸引力巨大。
而北面呈东西向的米仓山和大巴山脉成为南北相通的第一道自然屏障,汉中以北的秦岭成为第二道屏障。
因此,需要穿越米仓山、大巴山,再穿越秦岭,巴蜀先民才有可能与关中地区沟通联系。
所以,打通北边的交通线是蜀道的关键。
③战国时,秦国为打通陕西到四川的道路,于公元前267年开始修筑褒斜栈道。
这条起自秦岭北麓眉县西南15千米的斜水谷,到达秦岭南麓褒城县北5千米的褒水河谷,全长大约200千米的栈道,是在峭崖陡壁上开山破石,钻孔架木并在其上铺板而成。
当时火药还没有发现,在上为绝壁、下为激流的自然条件下,先民们先是采纳"火焚水激'的方法开山破石,然后再岩壁上凿成30厘米见方、50厘米深的孔洞,分上、中、下三排,均插上木桩,接着在上排木桩上搭遮雨棚,中排木桩上铺板成路,下排木桩上支木为架,最究竟公元前259年完成,历时八年之久。
修筑者因地制宜,制造了标准式、石积式、千梁无柱式、依坡搭架式、凹槽式和多层立柱平梁式等多种栈道形制。
这些都反映了古人在修建古蜀栈道过程中付出的聪慧和汗水。
〔好语文网搜集〕④蜀道的通行,使得大批钱粮赋税源源不断由四川运往长安,使先后在长安建都的周秦汉唐获得殷实富足的统治管理基础。
