四则混合运算及运算定律资料讲解学习
小学数学四年级四则混合运算及运算法则知识点整理附练习题

小学数学四年级四则混合运算及运算法则知识点整理附练习题文章目录四则运算(一)加法运算定律:1、两个加数交换位置,和不变,这叫做加法交换律。
字母公式:a+b=b+a2、先把前两个数相加,或者先把后两个数相加,和不变,这叫做加法结合律。
字母公式:(a+b) +c=a+(b+c)(二)乘法运算定律:1、交换两个因数的位置,积不变,这叫做乘法交换律。
字母公式:a×b=b×a2、先乘前两个数,或者先乘后两个数,积不变,这叫做乘法结合律。
字母公式:(a×b)×c=a×(b×c)3、两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律。
用字母公式:(a+b)×c=a×c+b×c或a×(b+c) =a×b+a×c拓展:(a-b)×c=a×c-b×c或a×(b-c) =a×b-a×c(三)减法简便运算:1、一个数连续减去两个数,可以用这个数减去这两个数的和。
用字母表示:a-b-c=a-(b+c)2、一个数连续减去两个数,可以用这个数先减去后一个数再减去前一个数。
用字母表示:a-b-c=a—c-b(四)除法简便运算:1、一个数连续除以两个数,可以用这个数除以这两个数的积。
用字母表示:a÷b÷c=a÷(b×c)2、一个数连续除以两个数,可以用这个数先除以后一个数再除以前一个数。
用字母表示:a÷b÷c=a÷c÷b小学四年级数学“四则运算”知识点详解知识点一:四则运算的概念和运算顺序1、加法、减法、乘法和除法统称四则运算。
2、在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要从左往右按顺序计算。
3、在没有括号的算式里,既有乘、除法又有加、减法的,要先算乘除法,再算加减法。
四则混合运算的运算法则和运算顺序

四则混合运算的运算法则和运算顺序1.运算法则:在进行四则混合运算时,需要遵循以下几个基本的运算法则:1.1加法法则:两个数相加,结果等于这两个数的和。
例如:2+3=51.2减法法则:两个数相减,结果等于第一个数减去第二个数。
例如:5-3=21.3乘法法则:两个数相乘,结果等于这两个数的乘积。
例如:2×3=61.4除法法则:两个数相除,结果等于第一个数除以第二个数。
例如:6÷3=21.5括号法则:在括号中的运算先于其他运算进行。
例如:(2+3)×4=20。
2.运算顺序:在进行四则混合运算时,需要按照一定的运算顺序来进行。
具体的运算顺序如下:2.1先进行括号内的运算:括号内的运算优先级最高,要先计算括号内的运算。
例如:(2+3)×4,先计算括号内的2+3,得到5,再将5与4相乘,最终结果为20。
2.2其次进行乘法和除法运算:乘法和除法运算的优先级高于加法和减法运算。
例如:5×3+2÷4,先计算5×3得到15,再计算2÷4得到0.5,最后将15加上0.5,得到15.52.3最后进行加法和减法运算:加法和减法运算的优先级较低,要在前面的运算完成后进行。
例如:15+5-3,先计算15+5得到20,再将20减去3,最终结果为17需要注意的是,当存在同一优先级的运算时,按照从左到右的顺序进行计算。
例如:6÷3×2,先计算6÷3得到2,再将2与2相乘,最终结果为4综上所述,四则混合运算的运算法则包括加法、减法、乘法和除法法则,运算顺序为先进行括号内的运算,然后进行乘法和除法运算,最后进行加法和减法运算。
遵循这些法则和顺序,能够正确地进行四则混合运算,得出正确的结果。
四则混合运算和运算律的知识点归纳

混合运算 必背概念:1.整数、小数、分数的四则混合运算的运算顺序是相同的。
3. 计算简算注意点:①审清题目要求:计算下面各题 如果是这种要求,一般按顺序计算。
用简便方法计算 如果是这种要求,说明都要用简便方法计算。
计算下面各题,能简算的要用简算 如果是这种要求,说明题目会有两种,可以简算的题目,也有不可以简算的题目。
做的时候,先学会观察分析,进行分辨,能简算的一定要简算,不简算的话即使算对也算错。
怎样算简便就怎样算 如果是这种要求,说明不管怎样算,只要算对就行。
②先观察,再计算。
(有些题是可以简算的,简算会使题目变得简单而且准确率高)③有依据,才能简算。
(有总结过的运算律或性质进行一一比对,找到依据才能进行简算)④没依据,按规定的运算顺序算。
简算例子:例子1: 28.9+52+2.1+513 例子2: 311-3.76+310-1.24 =(28.9+2.1)+(52+513) =(311+310)-(3.76+1.24) =31+3 =7-5=34(同时运用加法交换律和结合律) =2(同时运用加法交换律和结合律、减法的性质)例子3: 12.5×4.8 12.5×4.8 12.5×4.8+1.2×12.5=12.5×8×0.6 =12.5×(4+0.8) =12.5×(4.8+1.2)=100×0.6 =12.5×4+12.5×0.8 =12.5×6=60 =50+10 =75=60(把4.8拆成8×0.6运用乘 (把4.8拆成4+0.8运用乘 (找到公因数12.5,运用乘法分配律 法结合律简算) 法分配律简算) 进行简算) 例子4: 49×2423 (52+34-61)÷901 =(48+1)×2423 =(52+34-61)×90 =48×2423+1×2423 =52×90+34×90-61×90 =46+2423 =36+120-15 =462423 =141 (把49拆成48+1运用乘法分配律简算) (把除法转化成乘法,运用乘法分配律简算)例子5: 31.2÷1.25÷8 28.7÷1.4=31.2÷(1.25×8) =(28.7÷7)÷(1.4÷7)=31.2÷10 =4.1÷0.2=3.12 =20.5(运用除法的性质进行简算) (运用商不变性质进行简算)一些特殊的简算172×4+174×32 12.4×2.7-1.24×7 39.4-1.9×3.1-3.11 =174×2+174×32 =12.4×2.7-12.4×0.7 = 39.4- 5.89 -3.11 =174×(2+32) =12.4×(2.7-0.7) = 39.4-(5.89 +3.11) =174×34 =12.4×2 = 39.4 - 9=8 =24.8 = 30.4(创造公因数,运用乘法分配律进行简算) 有些简算并不在第一步,在做题的过程中要学会观察。
小升初 数学 暑假课14讲 第1讲 四则运算及运算定律 讲义
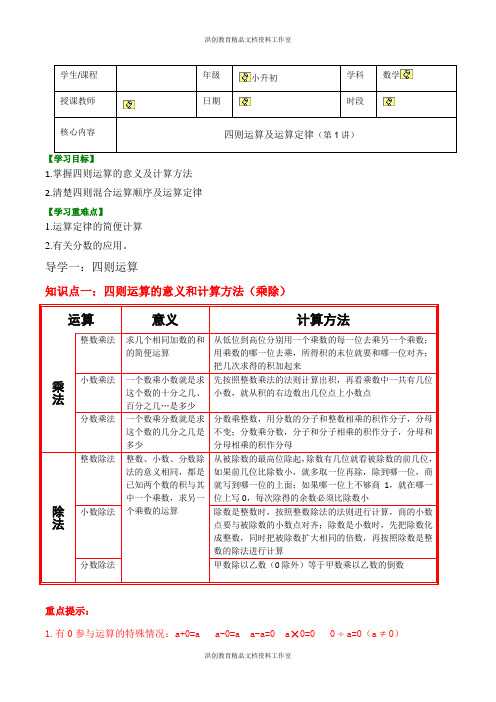
1.掌握四则运算的意义及计算方法2.清楚四则混合运算顺序及运算定律【学习重难点】1.运算定律的简便计算2.有关分数的应用。
导学一:四则运算知识点一:四则运算的意义和计算方法(乘除)运算 意义 计算方法乘法 整数乘法 求几个相同加数的和的简便运算 从低位到高位分别用一个乘数的每一位去乘另一个乘数;用乘数的哪一位去乘,所得积的末位就要和哪一位对齐;把几次求得的积加起来小数乘法 一个数乘小数就是求这个数的十分之几、百分之几…是多少 先按照整数乘法的法则计算出积,再看乘数中一共有几位小数,就从积的右边数出几位点上小数点分数乘法 一个数乘分数就是求这个数的几分之几是多少 分数乘整数,用分数的分子和整数相乘的积作分子,分母不变;分数乘分数,分子和分子相乘的积作分子,分母和分母相乘的积作分母除法整数除法 整数、小数、分数除法的意义相同,都是已知两个数的积与其中一个乘数,求另一个乘数的运算从被除数的最高位除起,除数有几位就看被除数的前几位,如果前几位比除数小,就多取一位再除,除到哪一位,商就写到哪一位的上面;如果哪一位上不够商1,就在哪一位上写0,每次除得的余数必须比除数小小数除法 除数是整数时,按照整数除法的法则进行计算,商的小数点要与被除数的小数点对齐;除数是小数时,先把除数化成整数,同时把被除数扩大相同的倍数,再按照除数是整数的除法进行计算分数除法甲数除以乙数(0除外)等于甲数乘以乙数的倒数重点提示:1.有0参与运算的特殊情况:a+0=a a-0=a a-a=0 a ×0=0 0a=0(a 0)学生/课程 年级 小升初 学科 数学授课教师日期时段核心内容 四则运算及运算定律(第1讲)2.有1参与运算的特殊情况:a×1=a a 1=a a a=1(a0)知识点二:四则运算中各部分间的关系运算各部分间的关系加法加数十加数=和一个加数=和一另一个加数减法被减数一减数=差减数=被减数一差被减数=减数+差乘法乘数×乘数=积一个乘数=积另一个乘数除法没有余数的除法商=被除数除数除数=被除数商被除数=除数×商有余数的除法被除数÷除数=商……余数被除数=商×除数+余数商=(被除数-余数)除数除数=(被除数-余数)商余数=被除数-商×除数1.小数乘法转化为整数乘法,除数为小数的除法转化为除数为整数的除法,分数除法转化为分数乘法,都体现了转化的数学思想。
完整版)四则运算和运算定律知识点

完整版)四则运算和运算定律知识点四则运算和运算定律是数学中的基础知识点。
首先,四则运算包括加法、减法、乘法和除法,没有括号的算式中,单独的加减法或乘除法按顺序从左往右计算,有混合运算的先算乘除法再算加减法。
如果有括号,要先算括号里面的,再算括号外面的,括号的计算顺序为小→中→大,括号里面的运算遵循以上的计算顺序。
其次,运算定律包括加法交换律、加法结合律、乘法交换律、乘法结合律和乘法分配律。
这些定律可以简化计算,例如交换加数位置不影响和的大小,三个数相加可以先把前两个数相加或后两个数相加,积的顺序也可以交换,两个数的和与一个数相乘可以先分别相乘再相加,两个数的差与一个数相乘可以先分别相乘再相减。
此外,还有连减定律和连除定律,也可以简化计算。
最后,我们可以通过简便计算来练四则运算和运算定律的应用,例如常见乘法计算、加法交换律、加法结合律和乘法交换律的简算例题。
掌握好这些知识点,可以帮助我们更快更准确地进行数学计算。
五、乘法结合律的应用:99×125×8可以改写为99×(125×8),再进行简算得到.六、加法交换律和结合律的应用:65+286+35+714可以改写为(65+35)+(286+714),再进行简算得到1100.七、乘法交换律和结合律的应用:25×0.125×4×8可以改写为(25×4)×(0.125×8),再进行简算得到100.八、乘法分配律的应用:1.分解式25×(40+4)可以拆分为25×40+25×4,再进行简算得到1100.2.合并式135×12.3—135×2.3可以拆分为135×(12.3—2.3),再进行简算得到1350.3.特殊例题1:99×25.6+25.6可以拆分为99×25.6+25.6×1,再进行简算得到2560.4.特殊例题2:45×102可以拆分为45×(100+2),再进行简算得到4590.5.特殊例题3:99×26可以拆分为(100—1)×26,再进行简算得到2574.6.特殊例题4:35.3×8+35.3×6—4×35.3可以拆分为35.3×(8+6—4),再进行简算得到353.九、连减的简便运算例子:1.528—6.5—3.5可以拆分为528—(6.5+3.5),再进行简算得到518.2.528—89—128可以拆分为528—128—89,再进行简算得到311.3.52.8—(40+12.8)可以拆分为52.8—12.8—40,再进行简算得到0.十、连除的简便运算例子:3200÷25÷4可以拆分为3200÷(25×4),再进行简算得到32.十一、其他简便运算例子:1.256—58+44可以拆分为256+44—58,再进行简算得到242.2.250÷8×4可以拆分为250×4÷8,再进行简算得到125.。
四则混合运算知识总结

四则混合运算知识总结.DOC1、加法、减法、乘法和除法统称四则运算。
2、在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要从左往右按顺序计算。
3、在没有括号的算式里,既有乘、除法又有加、减法的,要先算乘除法,再算加减法。
4、算式有括号,要先算括号里面的,再算括号外面的;大、中、小括号的计算顺序为小→中→大。
括号里面的计算顺序遵循以上1、2、3条的计算顺序。
知识点二:0的运算1、0不能做除数;字母表示:无,a÷0是错误的表达2、一个数加上0还得原数;字母表示:a+0 = a3、一个数减去0还得原数;字母表示:a-0 = a4、一个数减去它本身,差是0;字母表示:a-a =05、一个数和0相乘,仍得0;字母表示:a×0 =06、0除以任何非0的数,还得0;字母表示:0÷a =0(a≠0)知识点三:运算定律1、加法交换律:在两个数的加法运算中,交换两个加数的位置,和不变。
字母表示:a+b=b+a2、加法结合律:三个数相加,先把前两个数相加,再加另一个加数;或者先把后两个数相加,再加另一个加数,和不变。
字母表示:(a+b)+c=a+(b+c)3、乘法交换律:两个数相乘的乘法运算中,交换两个乘数的位置,积不变。
字母表示:a×b=b×a4、乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
字母表示:(a×b)×c=a×(b×c)5、乘法分配律:两个数相加(或相减)再乘另一个数,等于把这个数分别同两个加数(减数)相乘,再把两个积相加(相减),得数不变。
字母表示:①(a+b)×c=a×c+b×c;a×c+b×c=(a+b)×c;②a×(b—c)=a×b—a×c;a×b—a×c=a×(b—c)6、连减定律:①一个数连续减两个数, 等于这个数减后两个数的和,得数不变;字母表示:a—b—c=a—(b+c);a—(b+c)=a—b—c;②在三个数的加减法运算中,交换后两个数的位置,得数不变。
四则混合运算知识点讲解学习

四则混合运算知识点讲解学习
1.运算顺序:按照运算顺序进行四则混合运算是解决问题的基本原则。
运算顺序是指先乘除后加减,如果有多个乘法或除法运算,按照从左到右
的顺序进行。
括号里的运算按照特定的顺序进行。
例如,表达式2+3×4
的运算顺序是先进行乘法3×4得到12,再加2得到14
2.加法和减法:加法是将两个数或多个数相加,减法是将一个数减去
另一个数。
在进行加法和减法时,只需要按照运算顺序进行即可。
例如,20+15-8的运算顺序是先进行加法20+15得到35,再进行减法35-8得到
27
3.乘法:乘法是将两个数相乘得到积。
在进行乘法运算时,只需要将
两个数相乘即可。
例如,5×6的结果是30。
4.除法:除法是将一个数除以另一个数得到商。
在进行除法运算时,
需要注意除数不能为0。
除数为0会导致无法得到有效的结果。
例如,
10÷2的结果是5
5.括号运算:在四则混合运算中,括号运算是最先进行的运算。
在有
括号的表达式中,先计算括号内的表达式再进行其他运算。
例如,表达式
2×(3+4)的括号运算先计算括号内的3+4得到7,再进行乘法2×7得到
14
通过对四则混合运算的学习,我们能够在面对复杂的数学问题时能够
清晰地进行思考解决。
若要在四则混合运算中迅速准确地得出结果,需要
灵活运用运算顺序和基本运算法则,注意数学中的特殊情况,如除数不能
为0等。
此外,还需要多做练习,通过不断实践提高运算的速度和准确性。
小学数学六年级第6讲 四则混合运算的运算顺序和运算律(学生版)

第6讲四则混合运算的运算顺序和运算律知识点一:四则混合运算的运算顺序1.分级的标准四则混合运算分为两级,加法和减法叫作第一级运算;乘法和除法叫作第二级运算。
2.四则混合运算的运算顺序(1)在没有括号的算式里,如果只含有同一级运算,要从左往右依次计算;如果含有两级运算,要先算第二级运算,再算第一级运算(也就是先算乘除法,再算加减法)。
(2)算式里有括号的,要先算小括号里面的,再算中括号里面的,最后算括号外面的知识点二:四则混合运算定律知识点三:运算性质1.减法的性质:a-b-c=a-(b+c) a-b+c=a-(b-c)2.除法的性质(除数不等于0): a÷(b×c)=a÷b÷c a÷b÷c=a÷c÷b3.商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商不变。
a÷b=(a×m)÷(b×m)(m≠0,b≠0) a÷b=(a÷m)÷(b÷m)(m≠0,b≠0)重点提示:在利用减法和除法的运算性质进行简便计算时,等式的两边可以颠倒过来,要根据算式的特点灵活地进行去括号或添括号。
知识点四:四则混合运算中的速算技巧:1.加减法中的速算与巧算(1)分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减去,或先减去那些与被减数有相同尾数的减数.(“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”)(2)加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.(3)数值原理法:先把加在一起为整十、整百、整千…的数相加,再与其它的数相加.(4)“基准数”法,基准当几个数比较接近于某一整数的数相加时,选这个整数为“基准数”(要注意把多加的数减去,把少加的数加上)2.乘法凑整技巧:先把能凑成整十、整百、整千的几个乘数结合在一起,最后再与前面的数相乘,使得运算简便。
四则运算及运算律详解

(1)运算公式:加数+加数=和和-一个加数=另一个加数(2)加法交换律:两个数相加,交换加数的位置,它们的和不变。
a +b =b +a(3)加法结合律:三个数相加,先把前两个数相加,再同第三个数相加;或者先把后两个数相加,再同第一个数相加,和不变。
a +b +c =a +(b +c)=(a +b )+c(1)运算公式:被减数-减数=差被减数-差=减数 减数+差=被减数(2)减法的运算性质:一个数连续减去几个数,可以从这个数里减去这几个数的和,差不变。
a -b -c =a -(b +c)a -(b -c )=a -b +c(1)运算公式:因数(被乘数)×因数(乘数)=积积÷一个因素=另一个因素(2)乘法交换律:两个数相乘,因数交换位置,积不变。
a ×b =b ×a(3)乘法结合律:三个数相乘,先乘前两个数,再同第三个数相乘;或者先把后两个数相乘,再同第一个数相乘,积不变。
a ×b ×c =a ×(b ×c) (4)乘法分配律:两个数与一个数相乘,可以先把它们与这个数分别相乘,再相加。
(a +b)×c =a×c +b ×c(1)运算公式:①没有余数的除法:被除数÷除数=商被除数÷商=除数商×除数=被除数②有余数的除法:被除数÷除数=商……余数除数=(被除数-余数)÷商商=(被除数-余数)÷除数余数=被除数-除数×商(2)0不能作除数,0除以任何不是0的数都得0。
(3)除法的验算(没有余数):计算法则:(1)用除法验算,即交换除法和商的位置(2)用乘法验算(逆运算)(4)除法的性质(没有余数):一个数连续除以几个数,可以除以后几个数的积,也可以先除以第二个数,再除以第一个数。
a÷b÷c=a÷(b×c)(b,c ≠0)(a+b)÷c=a÷c+b÷c (b,c ≠0)(a-b)÷c=a÷c-b÷c (b,c ≠0)(5)商不变性质:①没有余数的除法:被除数和除数都乘(或除以)一个非0的数,商不变。
四则混合运算定律

四则混合运算定律同级运算时,从左到右依次计算;两级运算时,先算乘除,后算加减。
有括号时,先算括号里面的,再算括号外面的;有多层括号时,先算小括号里的,再算中括号里面的,再算大括号里面的,最后算括号外面的。
要是有乘方,最先算乘方。
在混合运算中,先算括号内的数,括号从小到大,如有乘方先算乘方,然后从高级到低级。
运算定律1、加法交换律:在两个数的加法运算中,交换两个加数的位置,和不变。
字母表示:a+b=b+a2、加法结合律:三个数相加,先把前两个数相加,再加另一个加数;或者先把后两个数相加,再加另一个加数,和不变。
字母表示:(a +b)+c=a+(b+c)3、乘法交换律:两个数相乘的乘法运算中,交换两个乘数的位置,积不变。
字母表示:a×b=b×a4、乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
字母表示:(a×b)×c=a×(b×c)5、乘法分配律:两个数相加(或相减)再乘另一个数,等于把这个数分别同两个加数(减数)相乘,再把两个积相加(相减),得数不变。
字母表示:①(a+b)×c=a×c+b×c;a×c+b×c=(a+b)×c;②a×(b—c)=a×b—a×c;a×b—a×c=a×(b—c)6、连减定律:①一个数连续减两个数,等于这个数减后两个数的和,得数不变;字母表示:a—b—c=a—(b+c);a—(b+c)=a—b—c;②在三个数的加减法运算中,交换后两个数的位置,得数不变。
字母表示:a—b—c=a—c—b;a—b+c=a+c—b7、连除定律:①一个数连续除以两个数,等于这个数除以后两个数的积,得数不变。
字母表示:a÷b÷c=a÷(b×c);a÷(b×c)=a÷b÷c;②在三个数的乘除法运算中,交换后两个数的位置,得数不变。
第一讲:整数四则混合运算及简便运算

一、整数四则运算定律(1) 加法交换律:a b b a +=+(2) 加法结合律:()()a b c a b c ++=++ (3) 乘法交换律:a b b a ⨯=⨯(4) 乘法结合律:()()a b c a b c ⨯⨯=⨯⨯(5) 乘法分配律:()a b c a b a c ⨯+=⨯+⨯;()b c a b a c a +⨯=⨯+⨯ (6) 减法的性质:()a b c a b c --=-+ (7) 除法的性质:()a b c a b c ÷⨯=÷÷;(8) 除法的“左”分配律:()a b c a c b c +÷=÷+÷;()a b c a c b c -÷=÷-÷,这里尤其要注意,除法是没有“右”分配律的,即()c a b c a c b ÷+=÷+÷是不成立的! 备注:上面的这些运算律,既可以从左到右顺着用,又可以从右到左逆着用.二、 加减法中的速算与巧算速算巧算的核心思想和本质:凑整。
常用的思想方法总结如下:(1) 分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减去,或先减去那些与被减数有相同尾数的减数.“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”.(2) 加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.三、乘法凑整思想核心:先把能凑成整十、整百、整千的几个乘数结合在一起,最后再与前面的数相乘,使得运算简便。
例如:425100⨯=,81251000⨯=,520100⨯=理论依据:乘法交换律:a ×b=b ×a 乘法结合律:(a ×b) ×c=a ×(b ×c) 乘法分配律:(a+b) ×c=a ×c+b ×c知识点拨第一讲 整数四则混合运算的简便运算积不变规律:a ×b=(a ×c) ×(b ÷c)=(a ÷c) ×(b ×c)四、乘、除法混合运算的性质⑴商不变性质:被除数和除数乘(或除)以同一个非零数,其商不变.即: ()()()()0a b a n b n a m b m m ÷=⨯÷⨯=÷÷÷≠ ,0n ≠⑵在连除时,可以交换除数的位置,商不变.即:a b c a c b ÷÷=÷÷⑶在乘、除混合运算中,被乘数、乘数或除数可以连同运算符号一起交换位置(即带着符号搬家).例如:a b c a c b b c a ⨯÷=÷⨯=÷⨯⑷在乘、除混合运算中,去掉或添加括号的规则去括号情形:①括号前是“×”时,去括号后,括号内的乘、除符号不变.即()()a b c a b c a b c a b c ⨯⨯=⨯⨯⨯÷=⨯÷ ②括号前是“÷”时,去括号后,括号内的“×”变为“÷”,“÷”变为“×”.即()()a b c a b c a b c a b c ÷⨯=÷÷÷÷=÷⨯ 添加括号情形:加括号时,括号前是“×”时,原符号不变;括号前是“÷”时,原符号“×”变为“÷”,“÷”变为“×”.即()()()()a b c a b c a b c a b c a b c a b c a b c a b c ⨯⨯=⨯⨯⨯÷=⨯÷÷÷=÷⨯÷⨯=÷÷ ⑸两个数之积除以两个数之积,可以分别相除后再相乘.即 ()()()()()()a b c d a c b d a d b c ⨯÷⨯=÷⨯÷=÷⨯÷ 上面的三个性质都可以推广到多个数的情形.一、加法【例1】:278+463+22+37举一反三:732+580+268二、减法【例2】:2871-299例题精讲举一反三:(1)157-99 (2)363-199 (3)968-599三、连减(5种)【例3】:528-53-47举一反三:(1)489-134-76 (2)470-254-46 (3)545-167-133【例4】:496-(296+144)举一反三:(1)675-(175+89)(2)466-(66+125)(3)354-(154+77)【例5】:496-(144+296)举一反三:(1)675-(89+175)(2)466-(125+66)(3)354-(77+154)【例6】:528-72-28举一反三:(1)489-77-389 (2)465-267-65 (3)545-167-145【例7】:824-224-176-124举一反三:(1)643-164-133-243 (2)487-187-139-61 (3)545-167-145四、乘法分配律(8种)【例8】:计算:125×(80+32)(24+40)×25举一反三:(1)125×(64+80)(2)(80+32)×125 (3)(16+32)×25【例9】:(1)125×(100-8)(2)(125-40)×8举一反三:(1)125×(100-48)(2)(100-16)×25【例10】:(1)117×56+117×44举一反三:(1)269×26+74×269 (2)521×65+35×521 (3)126×72+126×12+126×16【例11】:125×69-125×61举一反三:(1)25×127-25×119 (2)365×251-365×151(3)156×59-156×27-156×22 (4)137×97-44×137-137×43【例12】:45×102举一反三:(1)25×44 (2)125×168 (3)125×18【例13】:36×99举一反三:(1)45×98 (2)125×92 (3)35×99【例14】:(1)81+9×391 (2)9+9×999 (3)99+9×99【例15】:(1)9×107-63 (2)6×108-48 (3)134×101-134五、连除(2种)【例16】:1250÷25÷5举一反三:(1)2000÷125÷8 (2)1280÷16÷8 (3)1300÷5÷20(4)840÷5÷8 (5)1700÷25÷4 (6)4800÷50÷2【例17】:630÷(63×5)举一反三:(1)780÷(78×2)(2)1250÷(125×5)(3)6300÷(63×5)六、四则混合运算(1)(24+24)÷24×24 (2)24+24÷24×24 (3)16+4-16+4 (4)(16+4)-(16+4)(5)25×6÷25×6 (6)120-(72+48)÷24(7)45+55÷5-20 (8)12×(280-80÷4)(9)218+324÷18×5(10)(488+32×5)÷12 (11)4500÷(170-60×2)(12)(28+41)÷(92÷4)(13)80+320÷4-30 (14)18×(420-320÷20)(15)48-2×8÷8×2 (16)480÷(144-960÷8)(17)120+480÷(43-28)(18)(273+562)÷5-96 (19)4500÷(150-40×3)(20)812÷(532-36×14)(21)(12+12)÷12×12(22)625÷(54-522÷18)(23)17+13-17+13 (24)60-15×7÷15×7 (25)12×(289-84÷4)(26)218+702÷18×5 (27)45000÷(150-40×3)(28)(77+38)÷(92÷4)(29)58-28×2+40 (30)56×4-175÷5(31)(73-59)×(6+13)(32)(85-40)÷(15÷3)(33)71-17×7÷17×7课堂检测:(1)43×202 (2) 59×299 (3) 134×51-51×34 (4) 7200÷36 (5)68×32—784÷56 (6)3000÷125÷8 (7)98×35 (8) 960×46÷48 (9)480×46÷48 (10)302×99+302 (11)756+483-556(12)230×54+540×77 (13)887×25-87×25 (14)(825+25×8)×4(15)325-225÷5+145 (16)35×102 (17)498+(201-154)(18)125×89×8 (19)428×78+572×78 (20)8800÷(25×88)(21)3600÷50÷2(22)25×(20+4)容易出错类型(共五种类型)600-60÷15 20×4÷20×4736-35×20 25×4÷25×498-18×5+25 56×8÷56×8280-80÷ 4 12×6÷12×6175-75÷25 25×8÷25×880-20×2+60 36×9÷36×936-36÷6-6 25×8÷(25×8)。
(完整版)混合运算和运算定律

混合运算和运算定律甘肃甘南合作市藏族小学徐忠一、四则运算四则运算:四则是指加法、减法、乘法、除法的计算法则,四则运算就是指加、减、乘、除运算。
1.整数加减:数位对齐相加减,从最低位算起。
2.整数乘法:数位对齐从个位乘起,错位相加。
3.整数除法:被除数大于除数,看除数位数,从高位除起,试商定商;被除数小于除数,整数部分补0占位,点上小数点再除。
4.分数加减:分数单位相同,分母不变,分子相加减;分数单位不同,通分后再加减。
5.分数乘法:分子乘分子,分母乘分母。
6.分数除法:被除数乘以除数的倒数。
二、混合运算四则混合运算:在一个算式中,含有加、减、乘、除四种运算中的两种或两种以上的运算,便称四则混合运算。
四则混合运算的顺序1.四则运算分为两级:加法和减法叫做第一级运算;乘法和除法叫做第二级运算。
2.(1)在没有括号的算式里,如果只含有同一级运算,要从左往右依次计算;如果含有两级运算,要先做第二级运算,在做第一级运算。
(2)在有括号的算式里,要先算小括号里面的,后算中括号里面的,再算大括号里面的,最后算括号外面的。
(3)如果有乘方开方,要先算乘方开方,乘方开方是三级运算。
三、运算定律1.加法的运算定律(1)加法交换律:两个数相加,交换加数的位置,它们的和不变,用字母表示:a+b=b+a。
(2)加法结合律:三个数相加,先把前两个数相加,再加上第三个数,或者先把后两个数相加,再和第一个数相加,它们的和不变,用字母表示是:(a+b)+c=a+(b+c)。
2.乘法的运算定律(1)乘法交换律:两个数相乘,交换因数的位置,它们的积不变。
用字母表示是:a×b=b×a。
(2)乘法结合律:三个数相乘,先把前两个数相乘,再与第三个数相乘,或者先把后两个数相乘,再与第一个数相乘,它们的积不变。
用字母表示是:(a×b)×c=a×(b×c)。
(3)乘法分配律:两个数的和与一个数相乘,可以把两个加数分别与这个数相乘,再把所得的积相加。
第一讲:整数四则混合运算 及简便运算

第一讲 整数四则混合运算的简便运算知识点拨1、整数四则运算定律(1) 加法交换律:(2) 加法结合律:(3) 乘法交换律:(4) 乘法结合律:(5) 乘法分配律:;(6) 减法的性质:(7) 除法的性质:;(8) 除法的“左”分配律:;,这里尤其要注意,除法是没有“右”分配律的,即是不成立的!备注:上面的这些运算律,既可以从左到右顺着用,又可以从右到左逆着用.2、加减法中的速算与巧算速算巧算的核心思想和本质:凑整。
常用的思想方法总结如下:(1) 分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减去,或先减去那些与被减数有相同尾数的减数.“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”.(2) 加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.三、乘法凑整思想核心:先把能凑成整十、整百、整千的几个乘数结合在一起,最后再与前面的数相乘,使得运算简便。
例如:,,理论依据:乘法交换律:a×b=b×a乘法结合律:(a×b) ×c=a×(b×c)乘法分配律:(a+b) ×c=a×c+b×c积不变规律:a×b=(a×c) ×(b÷c)=(a÷c) ×(b×c)四、乘、除法混合运算的性质⑴商不变性质:被除数和除数乘(或除)以同一个非零数,其商不变.即:,⑵在连除时,可以交换除数的位置,商不变.即:⑶在乘、除混合运算中,被乘数、乘数或除数可以连同运算符号一起交换位置(即带着符号搬家).例如:⑷在乘、除混合运算中,去掉或添加括号的规则去括号情形:①括号前是“×”时,去括号后,括号内的乘、除符号不变.即 ②括号前是“÷”时,去括号后,括号内的“×”变为“÷”,“÷”变为“×”.即添加括号情形:加括号时,括号前是“×”时,原符号不变;括号前是“÷”时,原符号“×”变为“÷”,“÷”变为“×”.即⑸两个数之积除以两个数之积,可以分别相除后再相乘.即上面的三个性质都可以推广到多个数的情形.例题精讲一、加法【例1】:278+463+22+37举一反三:732+580+268二、减法【例2】:2871-299举一反三:(1)157-99 (2)363-199 (3)968-599三、连减(5种)【例3】:528-53-47举一反三:(1)489-134-76 (2)470-254-46 (3)545-167-133 【例4】:496-(296+144)举一反三:(1)675-(175+89)(2)466-(66+125)(3)354-(154+77)【例5】:496-(144+296)举一反三:(1)675-(89+175)(2)466-(125+66)(3)354-(77+154)【例6】:528-72-28举一反三:(1)489-77-389 (2)465-267-65 (3)545-167-145【例7】:824-224-176-124举一反三:(1)643-164-133-243 (2)487-187-139-61 (3)545-167-145四、乘法分配律(8种)【例8】:计算:125×(80+32)(24+40)×25举一反三:(1)125×(64+80)(2)(80+32)×125 (3)(16+32)×25【例9】:(1)125×(100-8)(2)(125-40)×8举一反三:(1)125×(100-48)(2)(100-16)×25【例10】:(1)117×56+117×44举一反三:(1)269×26+74×269 (2)521×65+35×521 (3)126×72+126×12+126×16【例11】:125×69-125×61举一反三:(1)25×127-25×119 (2)365×251-365×151(3)156×59-156×27-156×22 (4)137×97-44×137-137×43【例12】:45×102举一反三:(1)25×44 (2)125×168 (3)125×18【例13】:36×99举一反三:(1)45×98 (2)125×92 (3)35×99【例14】:(1)81+9×391 (2)9+9×999 (3)99+9×99【例15】:(1)9×107-63 (2)6×108-48 (3)134×101-134五、连除(2种)【例16】:1250÷25÷5举一反三:(1)2000÷125÷8 (2)1280÷16÷8 (3)1300÷5÷20(4)840÷5÷8 (5)1700÷25÷4 (6)4800÷50÷2【例17】:630÷(63×5)举一反三:(1)780÷(78×2)(2)1250÷(125×5)(3)6300÷(63×5)六、四则混合运算(1)(24+24)÷24×24 (2)24+24÷24×24 (3)16+4-16+4(4)(16+4)-(16+4)(5)25×6÷25×6 (6)120-(72+48)÷24(7)45+55÷5-20 (8)12×(280-80÷4)(9)218+324÷18×5(10)(488+32×5)÷12 (11)4500÷(170-60×2)(12)(28+41)÷(92÷4)(13)80+320÷4-30 (14)18×(420-320÷20)(15)48-2×8÷8×2(16)480÷(144-960÷8)(17)120+480÷(43-28)(18)(273+562)÷5-96 (19)4500÷(150-40×3)(20)812÷(532-36×14)(21)(12+12)÷12×12(22)625÷(54-522÷18)(23)17+13-17+13 (24)60-15×7÷15×7(25)12×(289-84÷4)(26)218+702÷18×5 (27)45000÷(150-40×3)(28)(77+38)÷(92÷4)(29)58-28×2+40 (30)56×4-175÷5(31)(73-59)×(6+13)(32)(85-40)÷(15÷3)(33)71-17×7÷17×7课堂检测:(1)43×202 (2)59×299 (3) 134×51-51×34 (4)7200÷36(5)68×32—784÷56 (6)3000÷125÷8 (7)98×35 (8) 960×46÷48(9)480×46÷48 (10)302×99+302 (11)756+483-556(12)230×54+540×77 (13)887×25-87×25 (14)(825+25×8)×4(15)325-225÷5+145 (16)35×102 (17)498+(201-154)(18)125×89×8(19)428×78+572×78 (20)8800÷(25×88)(21)3600÷50÷2(22)25×(20+4)容易出错类型(共五种类型)600-60÷15 20×4÷20×4736-35×20 25×4÷25×498-18×5+25 56×8÷56×8280-80÷ 4 12×6÷12×6175-75÷25 25×8÷25×880-20×2+60 36×9÷36×936-36÷6-6 25×8÷(25×8)。
初中数学《整数四则混合运算综合》讲义及练习

本讲主要是通过一些速算技巧,培养学生的数感,并通过一些大数运算转化为简单运算,让学生感受学习的成就感,进而激发学生的学习兴趣一、运算定律 ⑴加法交换律:a b b a +=+的等比数列求和⑵加法结合律:()()a b c a b c ++=++⑶乘法交换律:a b b a ⨯=⨯⑷乘法结合律:()()a b c a b c ⨯⨯=⨯⨯⑸乘法分配律:()a b c a b a c ⨯+=⨯+⨯(反过来就是提取公因数)⑹减法的性质:()a b c a b c --=-+⑺除法的性质:()a b c a b c ÷⨯=÷÷()a b c a c b c +÷=÷+÷()a b c a c b c -÷=÷-÷上面的这些运算律,既可以从左到右顺着用,又可以从右到左逆着用.二、要注意添括号或者去括号对运算符号的影响⑴在“+”号后面添括号或者去括号,括号内的“+”、“-”号都不变;⑵在“-”号后面添括号或者去括号,括号内的“+”、“-”号都改变,其中“+”号变成“-”号,“-”号变成“+”号;⑶在“⨯”号后面添括号或者去括号,括号内的“⨯”、“÷”号都不变,但此时括号内不能有加减运算,只能有乘除运算;⑷在“÷”号后面添括号或者去括号,括号内的“⨯”、“÷”号都改变,其中“⨯”号变成“÷”号,“÷”号变成“⨯”号,但此时括号内不能有加减运算,只能有乘除运算.【例 1】 计算:315325335345÷+÷+÷+÷.【考点】四则混合运算之提取公因数 【难度】1星 【题型】计算【关键词】第二届,希望杯,四年级,第二试【解析】 原式313233345=+++÷() 130526=÷= 【答案】26【巩固】 计算:⑴ 36196419⨯+⨯⑵ 361964144⨯+⨯【考点】四则混合运算之提取公因数 【难度】2星 【题型】计算【解析】 ⑴原式3664191900=+⨯=() 例题精讲 知识点拨教学目标整数四则混合运算⑵原式36196419125=⨯+⨯+()36641964125190088125190080009900=+⨯+⨯=+⨯⨯=+=()【答案】⑴1900 ⑵9900【例 2】 计算: 。
四则混合运算知识点讲解学习

48 ÷
12
=
4
4 x 12 = 48 (积)÷(一个因数) =(另一个因数)
(因数) x(因数) =(积) 48 ÷
4
=
12
(积)÷(一个因数) =(另一个因数)
已知两个因数的积和其中一个因数,用除法计算;一个因数 =积÷另一个因数
2、被除数÷除数 =商 (求两个数的商用除法)
48 ÷ 12 = 4
65+28.6+35+71.4
25× 0.125 × 4× 8
= (65+35)+(28.6+71.4)
= (25 ×4) ×(0.125 ×8)
= 100+100
=100×1
ห้องสมุดไป่ตู้
= 200
=100
四、特殊例题
99× 25.6+25.6
45× 102
99× 26
5.3 × 8+35.3 —×46× 35.3
知识点二: 0 的运算
1、一个数加上 0 还得原数;字母表示: a+0 = a
2、一个数减去 0 还得原数;字母表示: a-0 = a
3、一个数减去它本身,差是 0;字母表示: a-a =0
4、一个数和 0 相乘,仍得 0;字母表示: a× 0 =0
5、0 除以任何非 0 的数,还得 0;字母表示: 0÷ a =0(a ≠ 0)
a—b—c=a—(b+c);a—(b+ c)=a—b—c;
② 在三个数的加减法运算中,交换后两个数的位置,得数不变。字母表示:
a—b—c=a—c—b;a—b+c=a+c—b
7、连除定律:
① 一个数连续除以两个数 , 等于这个数除以后两个数的积, 得数不变。字母表示:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、四则运算性质
1、加法运算性质
(1)一个数加上几个数的和,可以用这个数加和里的第一个加数,再加第二,三,…个加数。
用字母表示是:a+(b+c+d)=a+b+c+d
(2)几个数的和加上一个数,可以把这个加数加到和里的任意一个加数上去,再加和里的其他加数。
用字母来表示:(a+b+c)+d=(a+d)+b+c=a+(b+d)+c=a+b+(c+d)
(3)几个数的和加上几个数的和,可以把两个和里的所有数依次相加。
用字母表示是:
2、加减混合运算性质
“加减混合运算性质”也可称为“和与差的性质”。
这些性质有以下几条:
⑴第一个数加上(或减去)第二个数,再减去第三个数,可以把第一个数先减去第三个数,再加上(或减去)第二个数。
这就是说,在加减混合运算中,改变运算的顺序,得数不变。
这常被称之为加减混合运算的“交换性质”。
用字母表示:a+b-c=a-c+b或a-b-c=a-c-b
(2)一个数加上两个数的差,等于这个数加上差里的被减数,再减去差里的减数。
这可以称之为加减混合运算的“结合性质”。
用字母表示:a+(b-c)=a+b-c
(3)一个数减去几个数的和,等于这个数依次减去和里的每一个加数。
这也可称之为“结合性质”。
用字母表示:a—(b+c+d+e)=a-b-c-d-e
(4)一个数减去两个数的差,等于这个数先加上差里的减数,再减去差里的被减数。
这也是加减混合运算的“结合性质”。
用字母表示:a-(b-c)=a+c-b
(5)几个数的和减去一个数,可以用和里的等于或大于这个数的一个加数,先减去这个数,然后再加和里的其他加数。
这也是“结合性质”。
用字母表示:(a+b+c+d)-e=(a-e)+b+c+d(a、b、c、d≥e)
=a+(b-e)+c+d=a+b+(c-e)+d=a+b+c+(d-e)
(6)几个数的和减去几个数的和,可以用第一个和里的各个加数,分别减去第二个和里不比它大的各个加数,然和相加。
这也可称为“结合性质”。
用字母表示是:(a+b+c+d)-(e+f+g+h)=(a-e)+(b-f)+(c-g)+(d-h)(a≥e,b≥f,c≥g,d≥h) 3、乘除混合运算性质
“乘除混合运算性质”也可称之为“积与商的性质”。
它们的性质可分为三大类:
(1)交换性质:在乘除混合运算或连除的算式中,变更它们的运算顺序,得数的大小不变。
用字母表示是: ab÷c+=a÷cb(c≠0)
a÷bc=ac÷b(b≠0)
a÷b÷c=a÷c÷b( b≠0, c≠0)
(2)“结合性质”。
结合性质有以下几条:
①一个数乘以两个数的商,等于这个数先乘以商里的被除数,再用积除以商里的除数。
用字母表示是:a(b÷c)=ab÷c(c≠0)
②一个数除以两个数(或若干个)因数的积,等于这个数除以积里的一个因数,再依次除以其他的因数。
用字母表示是:a÷(bc)=a÷b÷c(b、c≠0)
a÷(bcm)=a÷b÷c÷…÷m(b,c,…,m≠0)
③一个数除以两个数的商,等于这个数除以商里的被除数,再乘以商里的除数。
用字母表示是:a÷(b÷c)=a÷b×c(b≠0,c≠0)
(3)“分配性质”。
分配性质有以下几条:
①两个数的差与一个数相乘,可以用被减数与减数分别与这个数相乘,然后再相减。
用字母表示是:(a-b)c=ac-bc或a(b-c)=ab-ac
②几个数的和除以一个数,可以用和里的每个加数分别除以这个数,再把所得的商相加。
用字母表示是:(a+b+c)÷d=a÷d+b÷d+c÷d(d≠0)
注意:此性质不适用于“一个数除以几个数的和”,即a÷(b+c+d)≠a÷b+a÷c+a÷d。
③两个数的差除以一个数,可以把被减数和减数分别除以这个数,再把所得的商相减。
用字母表示是:(a-b)÷m=a÷m-b÷m(m≠0)
注意:此性质也不适用于“一个数除两个数的差”,即m÷(a-b)≠m÷a-m÷b。
④几个数的积除以一个数,可以把积里的任何一个因数除以这个数,然后再与其他的因数相乘。
用字母表示是:(abc)÷m=(a÷m)bc=a(b÷m)c=ab(c÷m)(m≠0)
⑤几个数的积除以几个数的积,可以把第一个积里的各个因数,分别除以第二个积里的各个因数,然后把所得的商相乘。
用字母表示是:(abcd)÷(efg)=(a÷e)(b÷f)(c÷g)d (e、f、g≠0)。
