种常用逻辑门的实用知识逻辑表达式逻辑符真值表逻辑运算规则
数字逻辑电路基础知识整理

数字逻辑电路基础知识整理数字逻辑电路是电子数字系统中的基础组成部分,用于处理和操作数字信号。
它由基本的逻辑门和各种组合和顺序逻辑电路组成,可以实现各种功能,例如加法、减法、乘法、除法、逻辑运算等。
下面是数字逻辑电路的一些基础知识整理:1. 逻辑门:逻辑门是数字逻辑电路的基本组成单元,它根据输入信号的逻辑值进行逻辑运算,并生成输出信号。
常见的逻辑门包括与门、或门、非门、异或门等。
2. 真值表:真值表是描述逻辑门输出信号与输入信号之间关系的表格,它列出了逻辑门的所有输入和输出可能的组合,以及对应的逻辑值。
3. 逻辑函数:逻辑函数是描述逻辑门输入和输出信号之间关系的数学表达式,可以用来表示逻辑门的操作规则。
常见的逻辑函数有与函数、或函数、非函数、异或函数等。
4. 组合逻辑电路:组合逻辑电路由多个逻辑门组合而成,其输出信号仅取决于当前的输入信号。
通过适当的连接和布线,可以实现各种逻辑操作,如加法器、多路选择器、比较器等。
5. 顺序逻辑电路:顺序逻辑电路由组合逻辑电路和触发器组成,其输出信号不仅取决于当前的输入信号,还取决于之前的输入信号和系统状态。
顺序逻辑电路可用于存储和处理信息,并实现更复杂的功能,如计数器、移位寄存器、有限状态机等。
6. 编码器和解码器:编码器将多个输入信号转换成对应的二进制编码输出信号,解码器则将二进制编码输入信号转换成对应的输出信号。
编码器和解码器可用于信号编码和解码,数据传输和控制等应用。
7. 数字信号表示:数字信号可以用二进制表示,其中0和1分别表示低电平和高电平。
数字信号可以是一个比特(bit),表示一个二进制位;也可以是一个字(word),表示多个二进制位。
8. 布尔代数:布尔代数是逻辑电路设计的数学基础,它通过符号和运算规则描述了逻辑门的操作。
布尔代数包括与、或、非、异或等基本运算,以及与运算律、或运算律、分配律等运算规则。
总的来说,数字逻辑电路是由逻辑门和各种组合和顺序逻辑电路组成的,它可以实现各种基本逻辑运算和数字信号处理。
八种逻辑门电路真值表

以下是八种逻辑门电路的真值表:1. 与门(AND):所有输入为高时,才会有输出高。
真值表如下:* 输入A
* 输入B
* 输出Y
* 0
* 0
* 0
* 0
* 1
* 0
* 0
* 1
* 1
* 1
2. 或门(OR):所有输入为低时,才会有输出低。
真值表如下:
* 输入A
* 输入B
* 输出Y
* 0
* 0
* 0
* 0
* 1
* 1
* 1
* 0
3. 非门(NOT):逆转输入的高低状态。
真值表如下:
* 输入A
* 输出Y
* 0
* 1
4. 与非门(NAND):所有输入为高时,才会有输出低。
真值表如下:
* 输入A
* 输入B
* 输出Y
* 0
* 0
* 1
* 0
* 1
* 1
5. 或非门(NOR):所有输入为低时,才会有输出高。
真值表如下:
* 输入A
* 输入B
* 输出Y
* 0
* 0
* 0
6. 异或门(XOR):输入相同时输出为低,否则为高。
真值表如下:
* 输入A
* 输入B
* 输出Y
* 0
* 0
7. 同或门(XNOR):与异或门相反。
输入相同时输出为高,否则为低。
真值表如下:
8. 与门的逻辑符号为AND,或门的逻辑符号为OR,非门的逻辑符号为NOT,与非门的逻辑符号为NAND,或非门的逻辑符号为NOR,异或门的逻辑符号为XOR,同或门的逻辑符号为XNOR。
八种常用逻辑门的实用知识逻辑表达式逻辑符真值表逻辑运算规则

全1得0
B
F
1 1 1 0
或 非 门
A
0 0 1 1
0 1 0 1
有1得0
全0得1
B
F
1 0 0 0
与 或 非 门
A
0 0…1
0 0…1
0 0…1
0 1…1
AB或CD有一组或两组全是1结果得0
其余输出全得1
B
C
D
F
1 1 0
异 或 门
A
0 0 1 1
0 1 0 1
不同得1
相同得0
B
F
0 1 1 0
八种常用逻辑门的实用知识逻辑表达式逻辑符真值表逻辑运算规则
名称
逻辑表达式
逻辑符号
真值表
逻辑运算规则
与门
A
0 0 1 1
0 1 0 1
有0得0
全1得1
B
F
0 0 0 1
或门
A
0 0 1 1
0 1 0 1
有1得1
全0得0
B
F
0 1 1 1
非门
A
0 1
有0得1
有1得0
F
1 0
与 非 门
A
0 0 1 1
0 1 0 1
同 或 门
⊙
A
0 0 1 1
0 1 0 1
不同得0
相同得1
B
F
1 0 01
色 环 电 阻 的 表 示
颜色
黑
棕
红
橙
黄
绿蓝紫ຫໍສະໝຸດ 灰白金银
无
有效数字
0
1
2
3
4
5
6
基本逻辑运算及集成逻辑门多图.

将0, 1值代入多变量的异或式中可得出如下结论。 (1) 奇数个“1”相异或结果为1; 偶数个1相异或结果为0。 (2) 偶数个变量的“同或”,等于这偶数个变量的
“异或”之非。如:
B
NP
A
C
NP
B C
1
+VCC ( +5V) Rb1
3
T1
1. 电路基本结构
Rb1 4kΩ
Rc 2 1.6kΩ
Vc 2
1
+VCC( +5V) Rc4 130Ω
3
T2 4
1
3 31
D
A
B
T1
C
2T2
Vo
Ve 2
1
3
2T 3
Re2
1kΩ
输入级
中间级
输出级
2.功能分析
(1)输入全为高电平3.6V时。
T2、T3饱和导通,
由图2 - 11(b)得:F1 A B F2 C D
F F1 F2 (A B) (C D) ABCD
Y1 A B 由图2 - 12(a)得:Y Y1 ⊙ C ( A ⊙ B) ⊙ C A ⊙ B ⊙ C
Y1 A ⊙ B Y2 C ⊙ D
A⊙B=
________
A B
_____________________
A⊙B⊙C⊙D= A B C D
奇数个变量的“同或”, 等于这奇数个变量的 “异或”。如:
A⊙B⊙C= A B C
2.2.5逻辑运算的优先级别
逻辑运算的优先级别决定了逻辑运算的先后顺序。 在 求解逻辑函数时, 应首先进行级别高的逻辑运算。 各种逻 辑运算的优先级别, 由高到低的排序如下:
基本逻辑门电路符号和口诀

无论多么复杂的单片机电路,都是由若干基本电路单元组成的。
2.2.1 常用的逻辑门电路最基本的门电路是与、或、非门,把它们适当连接可以实现任意复杂的逻辑功能。
用小规模集成电路构成复杂逻辑电路时,最常用的门电路是与(AND)、或(OR)、非(INV BUFF)、恒等(BUFF)、与非(NAND)、或非(NOR)、异或(XOR)。
主要是因为这7种电路既可以完成基本逻辑功能,又具有较强的负载驱动能力,便于完成复杂而又实用的逻辑电路设计。
1.与门与门是一个能够实现逻辑乘运算的、多端输入、单端输出的逻辑电路,逻辑函数式:F = A·B其记忆口诀为:有0出0,全1才1。
2.或门或门是一个能够实现逻辑加运算的多端输入、单端输出的逻辑电路,逻辑函数式:F = A+B其记忆口诀为:有1出1,全0才0。
3.非门实现非逻辑功能的电路称为非门,有时又叫反相缓冲器。
非门只有一个输入端和一个输出端,逻辑函数式是:F =A非非门逻辑符号4.恒等门实现恒等逻辑功能的电路称为恒等门,又叫同相缓冲器。
恒等门只有一个输入端和一个输出端,逻辑函数式是:F = A同相缓冲器和反相缓冲器在数字系统中用于增强信号的驱动能力。
5.与非门与和非的复合运算称为与非运算,逻辑函数式是:F = A.B非其记忆口诀为:有0出1,全1才0。
6.或非门或与非的复合运算称为或非运算,逻辑函数式是:F = A+B非其记忆口诀为:有1出0,全0才1。
7.异或门异或逻辑也是一种广泛应用的复合逻辑,其记忆口诀为:相同出0,不同出1。
逻辑门电路是单片机外围电路运算、控制功能所必需的电路。
在单片机系统中我们经常使用集成逻辑电路(常称为集成电路)。
一片集成逻辑门电路中通常含有若干个逻辑门电路,如7400为4重二输入与非门,即7400内部有4个二输入的与非门。
高速CMOS74HC逻辑系列集成电路具有低功耗、宽工作电压、强抗干扰的特性,是单片机外围通用集成电路的首选系列。
高二通用技术---逻辑门

00
1
01 4
6
14
11
10
9
(2) 四个相邻最小项合并可以消去两个因子
CD AB 00 01 11 10
00 0
32
01 4
11 12
10 8
11 10
CD AB 00 01 11 10
00 0
2
01
57
11
13 15
10 8
10
(3) 八个相邻最小项合并可以消去三个因子
CD AB 00 01 11 10
[例] 证明: 德 摩根定理
A+A=A
A B AB
A B A B 00 0 1 01 0 1 10 0 1 11 1 0
AB
A B
11 1 0 1 1
10 1 1 0 0
01 1 1 0 0
00 0 1 0 0
相等
相等
五、关于等式的三个规则
1. 代入规则: 等式中某一变量都代之以一个逻 辑函数,则等式仍然成立。
A BC ( A B) ( A C)
[例 ] 证明公式 [解] 方法一:公式法
右式 ( A B)( A C) A A A C A B B C A AC AB BC A(1 C B) BC A BC 左式
证明公式 方法二:真值表法(将变量的各种取值代入等式
(2) 或非逻辑
(NOR)
A ≥1
B
Y2 A B
(3) 与或非逻辑
A
(AND – OR – INVERT) B
Y3 AB CD
C D
Y1、Y2 的真值表
Y1
A B Y1 Y2
00 11
01 10
Y2 1 0 1 0 11 00
3种基本逻辑门的符号和逻辑关系

在写这篇文章之前,我想先向大家简单介绍一下逻辑门。
逻辑门是数字电路中常用的基本元件,它们用于执行布尔逻辑运算,可以实现数字信号的处理和控制。
逻辑门有很多种类,但在这篇文章中,我将主要讨论三种基本逻辑门:与门、或门和非门,它们分别代表了与、或、非三种基本的逻辑运算。
让我们来看一下与门。
与门是最基本的逻辑门之一,它有两个输入端和一个输出端。
当且仅当所有输入端为高电平时,输出端才为高电平。
与门的符号通常用“∧”表示,逻辑关系可以用真值表来表示。
与门的逻辑关系其实就是“与”的逻辑关系,即如果A和B都为真,输出才为真。
接下来,让我们看一下或门。
或门也是一种基本的逻辑门,它同样有两个输入端和一个输出端。
当任意一个输入端为高电平时,输出端就为高电平。
或门的符号通常用“∨”表示,逻辑关系同样可以用真值表来表示。
或门的逻辑关系就是“或”的逻辑关系,即如果A和B中有一个为真,输出就为真。
让我们了解一下非门。
非门只有一个输入端和一个输出端,它的作用是对输入信号取反。
如果输入端为高电平,输出端就为低电平;反之,如果输入端为低电平,输出端就为高电平。
非门的符号通常用“¬”表示,逻辑关系同样可以用真值表来表示。
非门的逻辑关系就是“非”的逻辑关系,即输入的反向。
以上就是对三种基本逻辑门的符号和逻辑关系的简单介绍。
通过真值表和逻辑关系的分析,我们可以更深入地理解这些逻辑门的工作原理。
在实际应用中,我们可以通过组合这些逻辑门来实现更加复杂的逻辑功能,从而构建出各种数字电路和系统。
总结回顾:在这篇文章中,我们深入探讨了三种基本逻辑门:与门、或门和非门,以及它们的符号和逻辑关系。
透过逻辑门的工作原理的理解,我们可以更好地应用它们,构建出各种数字电路和系统。
在实际应用中,逻辑门的灵活运用可以带来更多的创新和发展。
个人观点和理解:逻辑门作为数字电路中的基本元件,扮演着至关重要的角色。
通过对逻辑门的深入理解,我们可以更好地应用它们,实现各种复杂的逻辑功能。
逻辑表达式是逻辑函数常用的表示方法

逻辑表达式是逻辑函数常用的表示方法一、什么是逻辑表达式逻辑表达式是一种表示逻辑函数的方式,用来描述逻辑关系和条件。
它由变量、运算符和常数构成,表示了变量之间的逻辑关系和条件约束。
二、逻辑运算符逻辑运算符是用于组合逻辑表达式的基本元素,包括逻辑与(AND)、逻辑或(OR)和逻辑非(NOT)。
2.1 逻辑与(AND)逻辑与操作符表示逻辑关系的交集,只有所有操作数都为真,结果才为真。
用符号“∧”表示,例如:A∧B。
2.2 逻辑或(OR)逻辑或操作符表示逻辑关系的并集,只要至少有一个操作数为真,结果就为真。
用符号“∨”表示,例如:A∨B。
2.3 逻辑非(NOT)逻辑非操作符表示逻辑关系的否定,对操作数的结果取反。
用符号“¬”表示,例如:¬A。
三、逻辑表达式的表示方法逻辑表达式可以使用多种方式表示,下面介绍常见的几种方法。
3.1 布尔代数布尔代数是逻辑表达式的一种常见表示方法,它使用变量和逻辑运算符来进行逻辑推理和计算。
通过布尔代数的运算法则,可以将复杂的逻辑关系简化为简单的逻辑表达式。
3.2 真值表真值表是逻辑表达式的另一种常见表示方法,它列出了逻辑表达式的所有可能取值情况,并指示了每种情况下逻辑表达式的结果。
通过真值表可以分析逻辑表达式的真值情况,从而得出逻辑关系。
3.3 逻辑电路图逻辑电路图是逻辑表达式的图形化表示方法,它使用逻辑门和连线表示逻辑关系和条件。
逻辑门表示逻辑运算符,连线表示变量和运算符之间的逻辑关系。
通过逻辑电路图可以直观地理解逻辑表达式的计算过程。
四、逻辑表达式的应用领域逻辑表达式在计算机科学、电子电路设计和人工智能等领域有着广泛的应用。
4.1 计算机科学在计算机科学中,逻辑表达式被用于逻辑编程、条件判断和逻辑运算等方面。
例如,在编程语言中可以使用逻辑运算符进行条件判断,根据逻辑表达式的结果执行相应的代码。
4.2 电子电路设计逻辑表达式在电子电路设计中起着重要的作用,可以用来描述逻辑门的功能和布尔代数的运算法则。
7种逻辑门电路的逻辑符号和逻辑表达式

序在现代电子学和计算机科学中,逻辑门电路是至关重要的基础组成部分。
而逻辑门电路最基本的形式就是7种逻辑门,它们分别是与门、或门、非门、异或门、与非门、或非门以及同或门。
每种逻辑门都有其独特的逻辑符号和逻辑表达式,它们在数字电子电路中扮演着不可或缺的角色。
接下来,我们将深入探讨这7种逻辑门电路的逻辑符号和逻辑表达式,并从浅到深逐步分析它们的原理和应用。
一、与门与门是最简单的逻辑门之一,它的逻辑符号是一个“Λ”形状,而其逻辑表达式可以用“Y=A·B”来表示。
在与门电路中,只有当输入的布尔值均为1时,输出才会为1;否则输出为0。
这个逻辑表达式实际上就表明了与门的原理,即只有当所有输入为真时,输出才为真。
二、或门或门的逻辑符号是一个“V”形状,而其逻辑表达式可以用“Y=A+B”来表示。
与与门相反,或门只要有一个输入为1,输出就为1;只有当所有输入为0时,输出才为0。
可以看出,或门的逻辑表达式和与门的逻辑表达式是相对应的。
三、非门非门的逻辑符号是一个“¬”形状,而其逻辑表达式可以用“Y=¬A”来表示。
非门的原理是将输入的布尔值取反,即如果输入为1,则输出为0;如果输入为0,则输出为1。
四、异或门异或门的逻辑符号是一个带有一个加号的“⊕”形状,而其逻辑表达式可以用“Y=A⊕B”来表示。
异或门的原理是只有当输入不同时为1时,输出为1;否则输出为0。
异或门也常被用于比较两个输入是否相等的情况。
五、与非门与非门实际上是与门和非门的组合,其逻辑符号是一个与门后加上一个小圆点的符号,而其逻辑表达式可以用“Y=¬(A·B)”表示。
与非门的原理是先进行与运算,再对结果取反。
六、或非门或非门实际上是或门和非门的组合,其逻辑符号是一个或门后加上一个小圆点的符号,而其逻辑表达式可以用“Y=¬(A+B)”表示。
或非门的原理是先进行或运算,再对结果取反。
七、同或门同或门的逻辑符号是一个带有一个加号和一个横线的“⊙”形状,而其逻辑表达式可以用“Y=¬(A⊕B)”表示。
八种常用逻辑门的实用知识(逻辑表达式逻辑符号真值表逻辑运算规则)

百度文库- 让每个人平等地提升自我1名称逻辑表达式逻辑符号真值表逻辑运算规则与门ABF=A 0 0 1 10 1 0 1有0得0全1得1BF 0 0 0 1或门BAF+=A 0 0 1 10 1 0 1有1得1全0得0BF 0 1 1 1非门AF=A 0 1 有0得1有1得0F 1 0与非门ABF=A 0 0 1 10 1 0 1有0得1全1得0BF 1 1 1 0或非门BAF+=A 0 0 1 10 1 0 1有1得0全0得1BF 1 0 0 0与或非门CDABF+=A 0 0 (1)0 0 (1)0 0 (1)0 1 (1)AB或CD有一组或两组全是1结果得0其余输出全得1BCDF 1 1 0异或门BAF⊕=BABA+=A 0 0 1 10 1 0 1不同得1相同得0BF 0 1 1 0同或门AF=⊙BABBA+=A 0 0 1 10 1 0 1不同得0相同得1BF 1 0 0 1色环电阻的表示颜色黑棕红橙黄绿蓝紫灰白金银无有效数字0 1 2 3 4 5 6 7 8 9 -1 -2 -3 乘数10010110210310410510610710810910-110-2精确度±1﹪±2﹪±﹪±﹪±﹪±5﹪±10﹪±20﹪注:四色环电阻:1、2环表示是有效数照写,3环表示是乘数(就是要乘与这个乘数),4环表示是精确度。
五色环电阻:1、2、3环表示是有效数照写,4环表示是乘数(就是要乘与这个乘数),5环表示是精确度。
例:四色环电阻五色环电阻1 2 103±10﹪ 2 0 3 101±5﹪式子:12x103=12x1000=12000Ω=12KΩ±10﹪式子:203X101=203X10=2030Ω=Ω±5﹪。
基本逻辑门电路符号和口诀【最新资料】

无论多么复杂的单片机电路,都是由若干基本电路单元组成的。
2.2.1 常用的逻辑门电路最基本的门电路是与、或、非门,把它们适当连接可以实现任意复杂的逻辑功能。
用小规模集成电路构成复杂逻辑电路时,最常用的门电路是与(AND)、或(OR)、非(INV BUFF)、恒等(BUFF)、与非(NAND)、或非(NOR)、异或(XOR)。
主要是因为这7种电路既可以完成基本逻辑功能,又具有较强的负载驱动能力,便于完成复杂而又实用的逻辑电路设计。
1.与门与门是一个能够实现逻辑乘运算的、多端输入、单端输出的逻辑电路,逻辑函数式:F = A·B其记忆口诀为:有0出0,全1才1。
2.或门或门是一个能够实现逻辑加运算的多端输入、单端输出的逻辑电路,逻辑函数式:F = A+B其记忆口诀为:有1出1,全0才0。
3.非门实现非逻辑功能的电路称为非门,有时又叫反相缓冲器。
非门只有一个输入端和一个输出端,逻辑函数式是:F =A非非门逻辑符号4.恒等门实现恒等逻辑功能的电路称为恒等门,又叫同相缓冲器。
恒等门只有一个输入端和一个输出端,逻辑函数式是:F = A同相缓冲器和反相缓冲器在数字系统中用于增强信号的驱动能力。
5.与非门与和非的复合运算称为与非运算,逻辑函数式是:F = A.B非其记忆口诀为:有0出1,全1才0。
6.或非门或与非的复合运算称为或非运算,逻辑函数式是:F = A+B非其记忆口诀为:有1出0,全0才1。
7.异或门异或逻辑也是一种广泛应用的复合逻辑,其记忆口诀为:相同出0,不同出1。
逻辑门电路是单片机外围电路运算、控制功能所必需的电路。
在单片机系统中我们经常使用集成逻辑电路(常称为集成电路)。
一片集成逻辑门电路中通常含有若干个逻辑门电路,如7400为4重二输入与非门,即7400内部有4个二输入的与非门。
高速CMOS74HC逻辑系列集成电路具有低功耗、宽工作电压、强抗干扰的特性,是单片机外围通用集成电路的首选系列。
基本逻辑门电路符号和口诀word精品

无论多么复杂的单片机电路,都是由若干基本电路单元组成的。
2.2.1常用的逻辑门电路最基本的门电路是与、或、非门,把它们适当连接可以实现任意复杂的逻辑功能。
用小规模集成电路构成复杂逻辑电路时,最常用的门电路是与(AND )、或(OR)、非(INV BUFF)、恒等(BUFF )、与非(NAND )、或非(NOR)、异或(XOR )。
主要是因为这7种电路既可以完成基本逻辑功能,又具有较强的负载驱动能力,便于完成复杂而又实用的逻辑电路设计。
1•与门与门是一个能够实现逻辑乘运算的、多端输入、单端输出的逻辑电路,逻辑函数式:F二A •其记忆口诀为:有0出0,全1才1。
2•或门或门是一个能够实现逻辑加运算的多端输入、单端输出的逻辑电路,逻辑函数式:F二A+B其记忆口诀为:有1出1,全0才0。
3•非门实现非逻辑功能的电路称为非门,有时又叫反相缓冲器。
非门只有一个输入端和一个输出端,逻辑函数式是:F二A非非门逻辑符号4•恒等门实现恒等逻辑功能的电路称为恒等门,又叫同相缓冲器。
恒等门只有一个输入端和一个输出端,逻辑函数式是:F二A同相缓冲器和反相缓冲器在数字系统中用于增强信号的驱动能力。
5•与非门与和非的复合运算称为与非运算,逻辑函数式是:F二A.B非其记忆口诀为:有0出1,全1才0。
6•或非门或与非的复合运算称为或非运算,逻辑函数式是:F二A+B非其记忆口诀为:有1出0,全0才1。
7•异或门异或逻辑也是一种广泛应用的复合逻辑,其记忆口诀为:相同出0,不同出1。
逻辑门电路是单片机外围电路运算、控制功能所必需的电路。
在单片机系统中我们经常使用集成逻辑电路(常称为集成电路)。
一片集成逻辑门电路中通常含有若干个逻辑门电路,如7400为4重二输入与非门,即7400内部有4个二输入的与非门。
高速CMOS74HC逻辑系列集成电路具有低功耗、宽工作电压、强抗干扰的特性,是单片机外围通用集成电路的首选系列。
随着单片机内部功能的不断增强和硬件软件化,外部所用的逻辑门电路将越来越少。
基本逻辑门电路符号和口诀

无论多么复杂的单片机电路,都是由若干基本电路单元组成的。
2.2.1 常用的逻辑门电路最基本的门电路是与、或、非门,把它们适当连接可以实现任意复杂的逻辑功能。
用小规模集成电路构成复杂逻辑电路时,最常用的门电路是与(AND)、或(OR)、非(INV BUFF)、恒等(BUFF)、与非(NAND)、或非(NOR)、异或(XOR)。
主要是因为这7种电路既可以完成基本逻辑功能,又具有较强的负载驱动能力,便于完成复杂而又实用的逻辑电路设计。
1.与门与门是一个能够实现逻辑乘运算的、多端输入、单端输出的逻辑电路,逻辑函数式:F = A·B 其记忆口诀为:有0出0,全1才1。
2.或门或门是一个能够实现逻辑加运算的多端输入、单端输出的逻辑电路,逻辑函数式:F = A+B其记忆口诀为:有1出1,全0才0。
3.xx实现非逻辑功能的电路称为xx,有时又叫反相缓冲器。
xx 只有一个输入端和一个输出端,逻辑函数式是:F =A非xx逻辑符号4.恒等门实现恒等逻辑功能的电路称为恒等门,又叫同相缓冲器。
恒等门只有一个输入端和一个输出端,逻辑函数式是:F = A同相缓冲器和反相缓冲器在数字系统中用于增强信号的驱动能力。
5.与xx与和非的复合运算称为与非运算,逻辑函数式是:F = A.B 非其记忆口诀为:有0出1,全1才0。
6.或xx或与非的复合运算称为或非运算,逻辑函数式是:F = A+B非其记忆口诀为:有1出0,全0才1。
7.异或门异或逻辑也是一种广泛应用的复合逻辑,其记忆口诀为:相同出0,不同出1。
逻辑门电路是单片机外围电路运算、控制功能所必需的电路。
在单片机系统中我们经常使用集成逻辑电路(常称为集成电路)。
一片集成逻辑门电路中通常含有若干个逻辑门电路,如7400为4重二输入与xx,即7400内部有4个二输入的与xx。
高速CMOS74HC逻辑系列集成电路具有低功耗、宽工作电压、强抗干扰的特性,是单片机外围通用集成电路的首选系列。
【卓顶精品】最新基本逻辑门电路符号和口诀.doc

无论多么复杂的单片机电路,都是由若干基本电路单元组成的。
2.2.1 常用的逻辑门电路最基本的门电路是与、或、非门,把它们适当连接可以实现任意复杂的逻辑功能。
用小规模集成电路构成复杂逻辑电路时,最常用的门电路是与(AND)、或(OR)、非(INV BUFF)、恒等(BUFF)、与非(NAND)、或非(NOR)、异或(POR)。
主要是因为这7种电路既可以完成基本逻辑功能,又具有较强的负载驱动能力,便于完成复杂而又实用的逻辑电路设计。
1.与门与门是一个能够实现逻辑乘运算的、多端输入、单端输出的逻辑电路,逻辑函数式:F = A·B其记忆口诀为:有0出0,全1才1。
2.或门或门是一个能够实现逻辑加运算的多端输入、单端输出的逻辑电路,逻辑函数式:F = A+B其记忆口诀为:有1出1,全0才0。
3.非门实现非逻辑功能的电路称为非门,有时又叫反相缓冲器。
非门只有一个输入端和一个输出端,逻辑函数式是:F =A非非门逻辑符号4.恒等门实现恒等逻辑功能的电路称为恒等门,又叫同相缓冲器。
恒等门只有一个输入端和一个输出端,逻辑函数式是:F = A同相缓冲器和反相缓冲器在数字系统中用于增强信号的驱动能力。
5.与非门与和非的复合运算称为与非运算,逻辑函数式是:F = A.B非其记忆口诀为:有0出1,全1才0。
6.或非门或与非的复合运算称为或非运算,逻辑函数式是:F = A+B非其记忆口诀为:有1出0,全0才1。
7.异或门异或逻辑也是一种广泛应用的复合逻辑,其记忆口诀为:相同出0,不同出1。
逻辑门电路是单片机外围电路运算、控制功能所必需的电路。
在单片机系统中我们经常使用集成逻辑电路(常称为集成电路)。
一片集成逻辑门电路中通常含有若干个逻辑门电路,如7400为4重二输入与非门,即7400内部有4个二输入的与非门。
高速CMOS74HC逻辑系列集成电路具有低功耗、宽工作电压、强抗干扰的特性,是单片机外围通用集成电路的首选系列。
八种常用逻辑门的实用知识逻辑表达式逻辑符真值表逻辑运算规则.docx
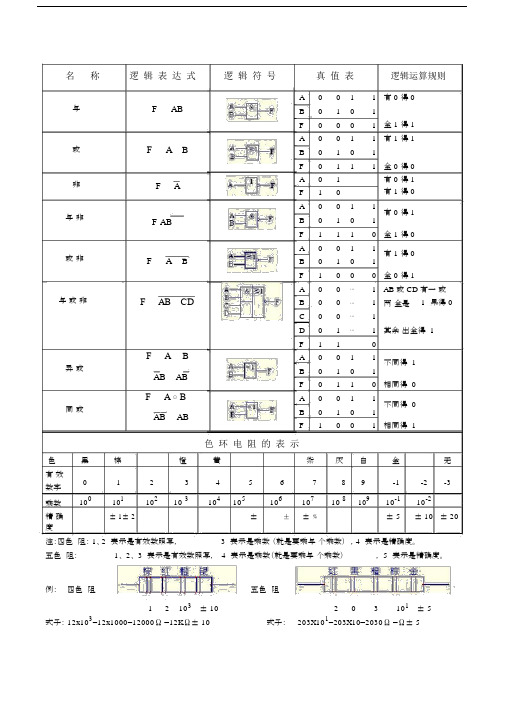
名称逻辑表达式逻辑符号真值表逻辑运算规则与或非与非或非与或非异或同或F ABF A BF AF ABF A BF AB CDF A BAB ABF A ⊙ BAB ABA0011有 0 得 0B0101F0001全 1 得 1A0011有 1 得 1B0101F0111全 0 得 0A01有 0 得 1F10有 1 得 0A0011有 0 得 1B0101F1110全 1 得 0A0011有 1 得 0B0101F1000全 0 得 1A00⋯1AB 或 CD 有一或B00⋯1两全是 1 果得 0C00⋯1D01⋯1其余出全得 1F110A0011不同得 1B0101F0110相同得 0A0011不同得 0B0101F1001相同得 1色环电阻的表示色黑棕橙黄紫灰白金无有效0123456789-1-2-3数字乘数10010110210 310410********* 810910-110-2精确± 1± 2± ±± ﹪± 5± 10 ± 20度注:四色阻: 1、2 表示是有效数照写, 3 表示是乘数(就是要乘与个乘数),4 表示是精确度。
五色阻:1、 2、 3 表示是有效数照写, 4 表示是乘数(就是要乘与个乘数), 5 表示是精确度。
例:四色阻五色阻1 2 103± 10203101± 5式子: 12x103=12x1000=12000Ω =12KΩ± 10式子:203X101=203X10=2030Ω =Ω± 5。
各种逻辑门的符号及表达式

各种逻辑门的符号及表达式逻辑门是计算机系统中的重要组成部分。
它们是用来处理和处理数字信号的数字电子设备,可以实现基本的逻辑函数操作。
本文将介绍各种逻辑门的符号及表达式,以帮助读者更好地理解它们是如何工作的。
第一步,介绍逻辑门的符号。
逻辑门通常由一个矩形表示,有输入和输出。
输入通常有两个,标记为A和B,而输出标记为Q。
最常见的逻辑门有四种,分别是与门(AND),或门(OR),非门(NOT)和异或门(XOR)。
与门的符号是一个点,或门的符号是一个加号,非门的符号是一个倒置的三角形,异或门的符号是一个带有加号和圆圈的符号。
第二步,介绍逻辑门的表达式。
逻辑门可以用公式表示。
一个与门的表达式是Q = A AND B,这意味着当输入A和B都为1时输出Q才能为1。
一个或门的表达式是Q = A OR B,这意味着当输入A或B任何一个为1时输出Q就为1。
一个非门的表达式是Q = NOT A,这意味着如果输入A为1,则输出Q为0,反之亦然。
一个异或门的表达式是Q = A XOR B,这意味着当输入A和B不同时输出Q才会为1,如果输入A和B相同则输出Q为0。
第三步,介绍逻辑门的组合。
一系列逻辑门可以组合在一起以执行不同的任务。
例如,一个与非门(NAND)是由一个与门和一个非门组合而成的,可以使用公式Q = NOT(A AND B)表示。
一个或非门(NOR)是由一个或门和一个非门组合而成,可以使用公式Q = NOT(A OR B)表示。
其他复杂的逻辑门也可以由几个简单的逻辑门组合而成,以实现更多的电路功能。
综上所述,本文介绍了各种逻辑门的符号及表达式。
通过该文,你应该可以更好地理解逻辑门是如何工作的。
逻辑门是计算机系统中不可或缺的重要组成部分,能够执行一系列逻辑函数操作,以实现各种不同的任务。
逻辑门电路的基本应用—基本逻辑关系

图2.5 由开关组成的非逻辑门电路
表6.2.3 非逻辑的真值表
A
Y
0
1
1
0
Y A B
与逻辑的 逻辑符号如图6.2.2所示。
图2.2
2.或逻辑 当决定某一事件的一个或多个条件满足时,事件便能发生。
图2.3 由开关组成的或逻辑门电路
表2.1 或逻辑的真值表
A
B
Y
0
0
0
1
0
1
0
1
1
1
1
1
或逻辑的关系式为
Y AB
或逻辑的逻辑符号如图6.2.4所示
图2.4
3.非逻辑 条件具备时,事件不能发生;条件不具备时,事件一定发生。
2 基本逻辑关系
2.1 逻辑代数的运算
逻辑运算的基本运算有3种:与、或和非运算。 1.与逻辑 当决定某一事件的所有条件都具备时,事件才能发生。
图2.1 由开关组成的与逻辑门电路
表2.1 与逻辑的真值表
A
B
Y
0
0
0
1
0
00Βιβλιοθήκη 1011
1
在逻辑代数中,用运算符号表示各种逻辑的输出与输 入之间的关系,形成了逻辑函数表达式。与逻辑的关 系式为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
1 0 01
色 环 电 阻 的 表 示
颜色
黑
棕
红
橙
黄
绿
蓝
紫
灰
白
金
银
无
有效数字
0
1
2
3
4
5
6
7
8
9
-1
-2
-3
乘数
100
101
102
103
104
105
106
107
108
109
10-1
10-2
精确度
±1﹪
±2﹪
±﹪
±﹪
±﹪
±5﹪
±10﹪
±20﹪
注:四色环电阻:1、2环表示是有效数照写,3环表示是乘数(就是要乘与这个乘数),4环表示是精确度。五色环电阻:1、2、3环表示是有效数照写,4环表示是乘数(就是要乘与这个乘数),5环表示是精确度。
名称
逻辑表达式
逻辑符号
真值表
逻辑运算规则
与门
A
0 0 1 1
0 1 0 1
有0得0
全1得1
B
F
0 0 0 1Βιβλιοθήκη 或门A0 0 1 1
0 1 0 1
有1得1
全0得0
B
F
0 1 1 1
非门
A
0 1
有0得1
有1得0
F
1 0
与 非 门
A
0 0 1 1
0 1 0 1
有0得1
全1得0
B
F
1 1 10
或 非 门
A
0 0 1 1
例:四色环电阻 五色环电阻
1 2 103±10﹪2 0 3 101±5﹪
式子:12x103=12x1000=12000Ω=12KΩ±10﹪式子: 203X101=203X10=2030Ω=Ω±5﹪
0 1 0 1
有1得0
全0得1
B
F
1 0 0 0
与 或 非 门
A
0 0…1
0 0…1
0 0…1
0 1…1
AB或CD有一组或两组全是1结果得0
其余输出全得1
B
C
D
F
1 1 0
异 或 门
A
0 0 1 1
0 1 0 1
不同得1
相同得0
B
F
0 1 1 0
同 或 门
⊙
A
0 0 1 1
0 1 0 1
不同得0
相同得1
