学生平均成绩
学生成绩平均分怎么算公式

学生成绩平均分怎么算公式1、国内大部分高校通用的计算方法是:绩点=分数/10-5,学分绩点=学分*绩点=学分*(分数专/10-5)(90分以上按90分计算)。
平属均绩点:(课程学分1*绩点+课程学分2*绩点+课程学分n*绩点)/(课程学分1+课程学分2+课程学分n)2、为了使gpa准确评价学生的学习,教务部还规定各门课程都大致符合正态分布,再次强调:各门课程最后确定的总成绩中,优秀率(85分以上)原则上不超过20%,不及格率(60分以下)应有1%-10%。
拓展资料:1、平均学分绩点是将分数换算为绩点,之后按学分加权平均分方法计算。
90以上算4分,80到90算3分,70到80算2分,60到70算1分,60以下0分。
平均学分绩点一般3.7分以上为优秀,3.5分左右为良好,2.5分左右为中等,1分为及格2、平均值学分绩点=∑(课程学分×成绩绩点)/∑课程学分=各门课程学分绩点之和/各门课程学分数之和3、∑,sigma,希腊字母(念:西格玛)表示数学中的“求和”。
4、某些学校使用学分绩点跗蛛属学生自学质量展开测评:(1)课程学分绩点=课程绩点×课程学分。
(2)平均值学分绩点=课程学分绩点总和÷课程学分总和。
绩点计算方式每个学校均分排序方式都不一样的,gpa等同于的百分制分数也不一样,对应的杰出较好百分制也不一样。
提出申请大学的'时候须要提供更多评分系统,评分系统可以表明均分排序方式,所有学校都存有评分系统。
绩点就是分数÷10-5比如你考了60分,绩点就是60÷10-5=1.0,考了72分,绩点就是72÷10-5=2.2。
平均值绩点也就是我们平时说道的gpa,它的计算方法就是:(课程学分1×绩点+课程学分2×绩点+课程学分n×绩点)÷(课程学分1+课程学分2+课程学分n)。
举个例子,假如李华本学期学了三门课,思修考了92分(2个学分),英语考了87分(3个学分),体育考了76分(2个学分),计算一下李华的平均绩点?思修92分后折算为绩点就是4.2;英语87分后折算为绩点就是3.7;体育76分后折算为绩点就是2.6,那么李华的平均值绩点=(4.2×2+3.7×3+2.6×2)÷(2+3+2)=3.。
学校学生成绩分析报告

学校学生成绩分析报告近年来,学校及教育机构对学生成绩的分析越来越重视。
学生成绩分析是一项重要的工作,它能够帮助学校了解学生的学习情况,发现问题,采取相应的教育措施,提升教育质量。
本报告将对学校学生成绩进行深入的分析和总结,并提出相关建议。
一、整体成绩概况学校的学生成绩整体表现良好。
根据对全校1000名学生的成绩统计,平均分为85分,90分以上的学生占总数的30%,其中高分人数比去年有所增加。
但是,在考试成绩分析的过程中,我们也发现了一些令人担忧的问题。
二、成绩差异的原因分析学生成绩的差异主要源于以下几个方面。
首先,学生个体差异。
每个学生都有其特点和潜力,其学习能力与兴趣程度不同,这直接影响着他们在学业上的表现。
其次,教育资源的分配不均。
一些学生由于家庭背景较好,能享受到更多的教育资源,而一些家境贫困的学生则面临资源匮乏的困境。
此外,学校的教育环境和教学方法也会对学生成绩产生一定的影响。
优质的教育环境和教学方法能够激发学生的学习兴趣,促进他们的学习动力,从而提高他们的学业成绩。
三、分项成绩分析针对学生的分项成绩,我们发现英语科目的平均分最高,数学科目的平均分最低。
这主要是因为英语学习的重视程度增加,学生们在英语方面花费了更多时间和精力,而数学的抽象性和难度相对较大,很多学生对数学科目没有足够的学习兴趣,导致成绩欠佳。
四、成绩与潜力的关系通过对学生成绩与入学时的综合素质评估进行比较,我们发现一部分学生的成绩优秀,但潜力较低;另一部分学生虽然成绩较差,但潜力巨大。
这说明学生成绩与个体的潜力存在一定的关系,而只依靠平时成绩很难完全把握学生的潜力和发展空间。
五、学校教育改进建议为了解决上述问题,我们提出以下教育改进建议:1. 加强个性化教育。
根据学生的特点和需求,为每个学生提供个性化的学习方案和指导。
2. 提高教育资源的均衡分配。
加大对贫困学生的资助力度,保障他们享有平等的教育机会。
3. 创造良好的教育环境。
学生成绩平均学分绩点(GPA)计算说明(发布版)
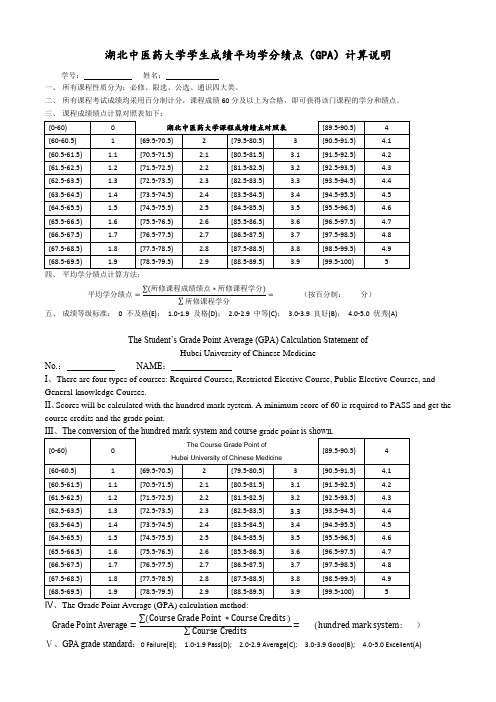
湖北中医药大学学生成绩平均学分绩点(GPA)计算说明学号:姓名:一、所有课程性质分为:必修、限选、公选、通识四大类。
二、所有课程考试成绩均采用百分制计分,课程成绩60分及以上为合格,即可获得该门课程的学分和绩点。
三、课程成绩绩点计算对照表如下:四、平均学分绩点计算方法:平均学分绩点=∑(所修课程成绩绩点∗所修课程学分)∑所修课程学分=(按百分制:分)五、成绩等级标准:0 不及格(E);1.0-1.9 及格(D);2.0-2.9 中等(C); 3.0-3.9 良好(B);4.0-5.0 优秀(A)The Student’s Grade Point Average (GPA) Calculation Statement ofHubei University of Chinese MedicineNo.:NAME:I、There are four types of courses: Required Courses, Restricted Elective Course, Public Elective Courses, and General-knowledge Courses.II、Scores will be calculated with the hundred mark system. A minimum score of 60 is required to PASS and get the course credits and the grade point.Grade Point Average=∑(Course Grade Point ∗Course Credits )∑Course Credits=(hundred mark system: )Ⅴ、GPA grade standard:0 Failure(E); 1.0-1.9 Pass(D); 2.0-2.9 Average(C); 3.0-3.9 Good(B); 4.0-5.0 Excellent(A)。
成绩平均分的计算公式__概述说明以及解释

成绩平均分的计算公式概述说明以及解释1. 引言1.1 概述本篇长文将介绍成绩平均分的计算公式及其相关概念。
在学校或者其他评估场景中,我们经常需要计算一个学生或者一组学生的平均成绩来评估他们的表现。
了解成绩平均分的计算公式以及背后的原理是非常重要的,它能够帮助我们更好地理解和比较不同个体或群体的学术水平。
1.2 文章结构本文将分为五个部分进行阐述。
引言部分(本节):简要介绍文章内容,并提供整篇长文的结构安排。
正文:详细讨论成绩平均分计算公式的具体概念和定义,并解释其中涉及到的术语和步骤。
计算公式说明:进一步解释和说明各种情况下如何应用成绩平均分计算公式,包括不同权重、百分制或等级制等情况。
示例分析:通过实际案例展示如何使用成绩平均分计算公式进行具体求解,以增强读者对于方法应用的理解。
结论:总结全文内容,强调成绩平均分计算公式在评估学术成绩中的重要性,并为读者提供进一步学习的建议和思考方向。
1.3 目的本文的目的是向读者介绍成绩平均分的计算公式,并解释其背后的原理与概念。
通过阅读本文,读者将能够了解如何计算平均分以及如何应用这个计算公式于不同场景中。
同时,希望本文能够对读者们在评估学生或比较不同群体表现时提供一定的指导和参考依据。
2. 正文在教育领域中,成绩的计算是评估学生学习成果的重要方式之一。
而成绩平均分作为一个常见的统计指标,被广泛应用于对学生整体表现的评定。
本节将详细介绍成绩平均分的计算公式以及其背后的原理。
成绩平均分的计算公式可以用来得出学生在某一门课程或多门课程中获得的总体分数。
通常情况下,各个考试、测验或作业都会有其所占权重,在计算平均分时需要根据权重进行加权处理。
首先,我们需要明确每个考试、测验或作业所占的权重比例。
这些比例通常由教师根据具体情况进行设定,在大多数情况下是以百分比表示。
例如,一个课程中有三次考试和两个作业,考试1占比30%,考试2占比40%,考试3占比30%,作业1占比15%,作业2占比25%。
上海高中小三门平均成绩汇总

上海高中小三门平均成绩汇总上海高中小三门平均成绩汇总在学生学业方面,成绩一直是一个备受关注的话题。
而在上海,高中生的小三门平均成绩更是备受瞩目。
今天,我们就来深入探讨一下上海高中小三门平均成绩的情况,以及对学生学业的影响。
1. 小三门平均成绩的含义上海高中生的小三门平均成绩是指语文、数学和外语三门学科的平均成绩。
这三门学科在学生的学业中占据着非常重要的地位,它们不仅是学生学习的基础,也是考核学生综合能力的重要指标。
小三门平均成绩可以很好地反映出一个学生的学习能力和水平。
2. 上海高中生的小三门平均成绩情况根据最新数据显示,上海高中生的小三门平均成绩呈现出稳步提高的趋势。
这说明上海的教育质量在不断提高,学生的学习成绩也在逐渐提升。
然而,值得注意的是,小三门平均成绩的提高并不意味着一切都尽如人意。
我们还需要关注学生学习过程中的压力和问题,以及对学生综合素质的培养。
3. 小三门平均成绩对学生的影响上海高中生的小三门平均成绩对学生的影响是深远的。
它直接关系到学生的升学和就业,优秀的小三门平均成绩可以为学生的未来打下坚实的基础。
另小三门平均成绩也会对学生产生一定的心理压力,甚至影响到他们的身心健康。
我们需要正确地对待学生的小三门平均成绩,既要重视成绩,也要关心学生的全面发展。
总结回顾通过以上对上海高中小三门平均成绩的探讨,我们不难发现,成绩的提升离不开教育的改革和学生自身的努力。
在关注成绩的我们更应该关注学生的成长,培养学生全面的素质和能力。
希望未来上海的教育能够更加人性化,给学生一个更好的学习环境。
个人观点与理解作为一名教育工作者,我认为学生的小三门平均成绩不能仅仅作为一个评判学生好坏的标准,更重要的是要关注学生的成长和发展。
在教育中,我们不仅要注重学生的学习成绩,更需要注重学生的品格和综合素质的培养。
只有这样,我们才能培养出更多优秀的人才,为社会的发展贡献力量。
结语上海高中生的小三门平均成绩是一个复杂而多面的话题,它涉及到教育改革、学生发展等多个方面。
将计算机专业学生按其平均成绩排列

将计算机专业学生按其平均成绩排列一、概述计算机专业作为当今社会中备受关注的热门专业之一,吸引了大批学生的青睐。
在这个竞争激烈的领域中,学生的学习成绩无疑是评判其能力和潜力的重要指标。
对计算机专业学生的成绩进行排列,有助于了解其学习水平和竞争力。
本文将对我校计算机专业学生的平均成绩进行排名,分析其成绩分布和特点。
二、数据来源本文所用数据来自我校计算机专业2019级本科学生的学习成绩统计表。
该表包括了各位学生在大学期间的所有课程成绩,并计算得出了每位学生的平均成绩。
数据经过学校相关部门的审核和验证,具有较高的真实可靠性。
三、计算机专业学生平均成绩排名依据平均成绩从高到低的顺序,将我校计算机专业2019级本科学生的成绩排名如下:1. 张三:平均成绩 90.52. 李四:平均成绩 89.83. 王五:平均成绩 88.74. 张小明:平均成绩 88.35. 王小红:平均成绩 87.96. ...(排名仅列举部分,完整排名表可从学校相关部门获取)从上述排名中可以看出,张三同学以90.5的平均成绩名列榜首,成绩突出;而排名在后面的学生成绩也在80分以上,整体表现较好。
四、分析与讨论1. 成绩分布通过对上述排名的学生成绩进行分析,可以得出计算机专业学生的成绩呈现出集中分布的特点。
大部分学生的平均成绩在80分以上,其中较高分数段的学生裙体数量较多。
2. 成绩特点从排名结果中可以看出,整体而言计算机专业学生的学习成绩较为优秀,成绩较高居多。
这与计算机专业学生通常具有较强的学习能力和逻辑分析能力等特点是一致的。
3. 学业发展通过对学生成绩排名的分析,可以为学校教学管理部门和学生个体提供一定的参考。
学校可以针对成绩较为优秀的学生提供更多的学术交流和科研实践机会,促进其学术发展和创新能力的培养;对成绩较低的学生也应该加强帮助和引导,提高其学习动力和自信心。
五、结论计算机专业学生的平均成绩排名可以为学校和学生个体提供有益的参考。
平均数应用题100道

平均数应用题100道一、简单平均数计算类1. 某班有5名学生,他们的数学成绩分别是90分、85分、95分、80分、100分,求这5名学生的平均成绩。
- 解析:平均数 = 总和÷个数。
首先计算这5名学生成绩的总和为90 +85+95 + 80+100 = 450分,然后用总和除以人数5,得到平均成绩为450÷5 = 90分。
2. 小明记录了一周每天的零花钱支出情况,分别是5元、8元、3元、6元、4元、7元、2元,求小明这一周平均每天的零花钱支出。
- 解析:先计算这一周零花钱支出的总和为5+8 + 3+6+4+7+2 = 35元,一周有7天,所以平均每天零花钱支出为35÷7 = 5元。
3. 有一组数据:12、15、18、21、24,求这组数据的平均数。
- 解析:这组数据的总和为12+15 + 18+21+24 = 90,数据个数为5,所以平均数为90÷5 = 18。
二、平均数在实际生活中的应用类4. 一辆汽车前3小时行驶了180千米,后2小时行驶了120千米,求这辆汽车平均每小时行驶多少千米?- 解析:首先计算汽车行驶的总路程为180+120 = 300千米,总时间为3 + 2=5小时,根据平均数公式,平均速度 = 总路程÷总时间,即300÷5 = 60千米/小时。
5. 某工厂前两个月共生产产品1500件,后三个月共生产产品2100件,求这个工厂平均每月生产产品多少件?- 解析:先求出生产产品的总数为1500+2100 = 3600件,总月数为2+3 = 5个月,那么平均每月生产产品3600÷5 = 720件。
6. 一个班级学生参加语文考试,男生平均成绩为80分,男生有20人;女生平均成绩为85分,女生有30人,求这个班级的平均成绩。
- 解析:男生的总成绩为80×20 = 1600分,女生的总成绩为85×30 = 2550分,全班的总成绩为1600+2550 = 4150分,全班总人数为20+30 = 50人,所以班级平均成绩为4150÷50 = 83分。
平均成绩为66.5分,标准差为15分

首先要对平均成绩和标准差有一个基本的了解,平均成绩是指一组数据的算术平均数,通常用来代表整体水平;而标准差则是一组数据的离散程度的一个度量,用来衡量数据的波动情况,标准差越大表示数据的离散程度越高。
接下来,让我们用更详细的数据和实例来分析平均成绩为66.5分,标准差为15分的情况。
假设我们有一组学生的考试成绩数据,平均成绩为66.5分,标准差为15分。
那么根据这个数据,我们可以得出一些有价值的信息。
平均成绩为66.5分意味着大部分学生的成绩集中在这个数值附近,这也反映了整体的学业水平。
然而,并不是所有学生的成绩都会严格落在这个平均数附近,标准差的存在就是为了帮助我们更好地理解这一点。
标准差为15分表示学生的成绩相对分散,即便平均成绩是66.5分,仍然会有一部分学生的成绩远高于或远低于这个数值。
这样的成绩分布情况可能导致一些有趣的现象。
对于成绩高于平均数的学生来说,他们可能会感到比较满意,因为他们的成绩属于较高水平;而对于成绩低于平均数的学生来说,他们可能会感到压力较大,因为他们的成绩相对较低。
然而,这也并不代表成绩低的学生就一定学习不努力,或者成绩高的学生就一定很优秀。
标准差的存在告诉我们,学生们的成绩是多样化的,每个人都有自己的特点和优势,不能仅仅用一个平均数字来刻画一个人的学业水平。
通过这个例子,我们可以看到平均成绩和标准差的重要性。
平均成绩帮助我们了解整体水平,而标准差则帮助我们了解数据的离散程度,两者结合起来可以帮助我们更全面地理解数据背后的信息,并针对实际情况做出相应的评估和决策。
在实际生活中,平均成绩和标准差的概念也可以在各个领域得到应用。
比如在教育领域,老师们可以利用平均成绩和标准差来更好地分析学生的学习情况,找出哪些学生需要额外的帮助或者挑战;在经济领域,平均成绩和标准差可以帮助经济学家们更准确地评估经济状况,预测未来的走势。
平均成绩为66.5分,标准差为15分的例子告诉我们,数字背后蕴含着丰富的信息,我们需要通过深入的分析和思考来更好地理解这些数据。
国外大学如何计算学生成绩

国外大学如何计算学生成绩美国大学成绩单与GPA的算法美国大学在评定学生成绩时,是采取GPA,即Grade Point Average的缩写(平均成绩点数)。
在申请学校时,GPA十分重要,很多大学有最低GPA规定,除了英文能力测验以外。
GPA的计算是把各科成绩按等级乘以学分,再以总学分除之。
美国学生各科成绩是以A.B.C.D等级计算。
等级成绩和分数成绩换算如下:分数等级点数表现91-100 A 4.0 极佳81-90 B 3.0 佳71-80 C 2.0 平均61-70 D 1.0 差51-60 E 0 不及格通常大学部学生拿到C以上成绩都可以。
但研究所硕士学生,至少要拿到B的成绩。
在申请入学时,很多学校有GPA规定。
GPA的计算是:1、每个科目以等级点数乘以学分。
比如微积分是四学分的课,成绩是A(即4点),微积分一科可得16点。
2、如果一学期修了四门课,英文3学分(成绩4点)、历史3学分(成绩2点)物理3学分(成绩3点),加上微积分。
GPA是16+4×3+3×2+3×3=43,除以13=3.31。
此学生的GPA等于是比B略好。
官方网站:地址:成都市西安南路69号西雅图10楼10国外大学计算GPA的方法xx-01-15 15:27:46甲壳虫国际最近,一些申请的学子来信询问如何将国内的学业成绩换算成国外大学的GPA(“均分值”Grade Point Average)。
回答这个问题之前,先要了解国外大学,特别是美国大学的评分体系。
美国大学众多,但评分体系各不相同,而且根据情况不断调整。
如美国密西根州立大学60年代使用的是ABCDF制,类似我国的优、良、中、差、不及格;到了70年代改为4.5分制,80年代起采用4.0分制。
目前大多数美国大学采用“四分制”(1-100)记分。
鉴于美国大学间学生的交流和转学校较为普遍,加之广泛吸收国际学生,鉴定外来学生的学业成绩成了录取中的一项重要工作。
优秀率,及格率,平均分怎么总评

优秀率,及格率,平均分怎么总评1.什么是优秀率、及格率和平均分优秀率、及格率和平均分都是指对一个群体中的学生成绩进行综合性的统计和分析所得出的指标。
具体而言,优秀率指的是在这个群体中成绩超过一定标准(通常为90分及以上)的学生所占的比例;及格率指的是成绩达到及格线(通常为60分及以上)的学生所占的比例;平均分则是所有成绩的平均值。
这三个指标虽然都可以反映出学生群体的整体水平,但是各自的意义有所不同。
优秀率可以直观地反映出学生群体中高水平学生的比例,对于学生群体的综合水平评价有一定的参考价值;及格率则更加强调对于底层学生的关注,它可以反映出学生群体中至少能够达到一定水平的学生的比例;平均分则是一个综合指标,可以反映出学生群体的整体水平,但是不能很好地反映出学生群体中的分布情况。
2.如何综合考虑三个指标对于如何综合考虑三个指标,目前并没有一个固定的标准。
不同的学校、不同的教育机构甚至不同的教师可能会有不同的看法。
但是一般来说,以下几点是需要考虑到的:首先,优秀率、及格率和平均分都不是孤立的指标,需要结合具体的评价对象来综合考虑。
例如对于一所学校来说,如果学校的定位是培养高素质的优秀学生,那么优秀率可能会被重点考虑;如果学校的定位是普及教育,关注底层学生的及格率可能会更具有意义。
其次,需要考虑不同指标之间的权重关系。
通常来说,优秀率的权重大于及格率,后者的权重大于平均分。
这是因为优秀率反映了学生群体中高水平的学生比例,对于评价学生群体的整体素质有着很大的参考价值;及格率反映的则是学生群体中至少能够达到一定水平的学生比例,这对于保证教育公平有着重要的意义;而平均分则比较笼统,不能反映出学生群体中的分布情况,常常需要结合其他指标来考虑。
最后,需要注意综合考虑的过程要有科学的依据和程序。
由于优秀率、及格率和平均分都是统计学中的概率和数据,因此需要特别注意数据采集的科学性和可靠性。
如果数据采集存在一定的误差或者不合理性,那么综合考虑的结果也可能出现偏差。
50名学生平均分

199114108.572.477.775.8547.464297.3117.5108.872.277.274.9547.992395.594.5897.2958.365.764.5475.826493.395.5290.7759.369.566.2474.628593.794.6893.8960.567.765.2475.664695.195.0691.2259.368.565.9475.13789.473.8679.5747.557.754402.022889.87181.09445854.3398.182989.774.773.8251.357.852.6399.8381091.574.3276.5645.657.953.8399.7061189.472.1674.2247.259.357.4399.7521288.474.2277.245.257.954.9397.91388.377.2273.146.959.354.9399.6441489.873.0877.5246.459.253.8399.7321597.283.1894.170.171.351.2467.108刘坤源男946869.4796154425.41宋勤丽女947997.5576827422.52李营营女9957101.3706035422.33李长春女98.55093.1716647425.61刘茜茜女946398.1625748422.12曹志磊男847359.4717260419.43张敏女9466807064524261栗消女10549906965444222王莹女946679.4777232420.43李鑫女1026289.4627041426.41于鹏娜女10151105.6635942421.62郭欢欢女91.56471.9637259421.43雷改女98.56685.6597047426.11吴会娟女93.55894.4696737418.92李东海男8776656978434183刘洋溢女11391118.8737254521.81韦红云女85.59088.1777058468.62何亚云女986273.1726945419.13徐冬梅女926294.4636840419.41常瑞雪女8857100.6616250418.62皮保华男90.56485.6576653416.13孔雪艳女1018770.6787749462.11贾佳女84.545108.8607151420.32孔赛楠女8946103.1696743417.13郭媛媛女94.5117103.1758478551.61方志远男105105103.8776376529.32杨莹女103100105.6747959520.13朱肖霏女117109115848153558.51博士男9186114.4778071519.42刘振男9712281.9658367515.93刘博男95.583100.6447156450.11张东秋女93.58088.8615765445.32朱思宇男9179756370674453樊争光男929473.853*******.81段帅帅男92.58192.55659694502孔晓双女99.58388.1516757445.63许得山男88.511359.4627867467.91李威男868959.4707669449.42徐雪娇女1007497.5574771446.53程福林男99.58780.6476669449.11阮诗雨女97.57492.55363684482耿超群男878097.5546365446.53赵帅领男1126888.8457164448.81李文文女1058292.5456361448.52张一帆男908181.9755168446.93孙珂珂女939996.9366460448.91李重庆男88.59075.6646664448.12李阳男96.58672.55861734473朱青青女959688.1356570449.11孙建康男82.58595.6656060448.12陈慧涛男958182.5566469447.53崔玉玲女90.589105266871449.51苏肖肖男76.59698.1605562447.62李坤男97.57878.1626468447.63魏家兴男99116121.9717264543.91马舒晴女91.5106111.9547767507.42刘金金女9910497.5765971506.53葛东莉女101121119.4457875539.41徐向阳男9111789.4537981510.42齐贝贝女10311392.55376695063田帅华男10011290.6597870509.61杨晨女11199109.4597853509.42王壮壮男10089111.3606482506.33刘梦茹女10588111.3667268509.81王鹏鹏男92.5102111.9538364506.42管红光男989891.3807168506.33王锋男105142109.4899090624.91许洪彬男96.5130128.1609490598.62尹文辰男89148106.9769774590.93张志平男94.5124122.58992846061王波男108135109.4848584605.42何景艳女111127121.9668975589.934098.2116.3106.368.577.975.3542.508。
某班学生的平均成绩是80分 标准差是10分

某班学生的平均成绩是80分标准差是10分可以判断成绩在70-90分之间的学生大约占0。
68。
班学生的平均成
绩是80分,标准差是10分,如果已知该班学生的考试分数为对称分布,
可以判断成绩在70-90分之间的学生大约占0。
68,由经验法则有约有68%的数据在平均分加减1个标准差的范围之内(80-10,80+10)=(70,90)。
数学名人的故事
华罗庚在清华执教期间,为了照顾年迈多病的公公,吴筱元留在家乡,挑起家务担子,在以后的日子里,她不仅操持家务,还帮他抄写论文和书信,接待客人,几十年来,吴筱元在华罗庚的生活和事业上,起着重要的
作用。
祖冲之为求得圆周率的精准数值,就需要对九位有效数字的小数进行加,减,乘,除和开方运算等十多个步骤的计算,而每个步骤都要反复进
行十几次,开方运算有50次,最后计算出的数字达到小数点后十六、七位。
Excel数据透视表分类求学生成绩平均值

Excel数据透视表分类求学生成绩平均值期末统考结束后,教育局要求全市学生的成绩都汇总在如图1的同一个Excel工作表中,并要求求出各学校、各专业、各学科的平均分全市三个学校、每个学校都有六个专业、每个专业都有五门课、各专业人数不等,总计有1000余人,工作量巨大。
但如果采用Excel数据透视表来完成的话,呵呵,就简单多了。
一、创建数据透视表点击菜单命令“数据→数据透视表和数据透视图”,打开“数据透视表和数据透视图向导”对话框。
第一步,如图2所示,选择“Microsoft Excel数据列表或数据库”及下面的“数据透视表”单选项。
第二步,如图3所示,在“选定区域”输入全部数据所在的单元格区域,或者点击输入框右侧的“压缩对话”按钮,在工作表中用鼠标选定数据区域。
第三步,在对话框中选定“新建工作表”单选项,以便将创建的数据透视表放到一个新的工作表中,再点击“完成”按钮,如图4所示。
这样,就可以建立一个空的数据透视表,并同时显示“数据透视表”工具栏和“数据透视表字段列表”对话框,如图5所示。
二、利用数据透视表得到需要的结果根据要求,我们应该得到各学校、各专业、各学科的平均分数。
因此,我们应该把“学校”、“专业”作为行字段,而把各学科数据作为数据项。
从“数据透视表字段列表”中,把“学校”拖到数据透视表左侧“将行字段拖至此处”位置,再将“专业”字段拖至“学校”字段的右侧,待鼠标变成“I”字形时松开鼠标,如图6所示。
如此就会得到如图7所示的效果。
这正是我们想要计算平均分的各个项目。
现在,我们只要从“数据透视表字段列表”中依次将学科字段拖至数据透视表中“请将数据项拖至此处”位置,可以得到各学校、各专业、各学科的成绩总和。
如图8所示。
现在我们将各个求和项改为求平均值就可以了。
选中透视表中第一个“求和项:语文”,如图中C4单元格,然后点击“数据透视表工具栏”中“字段设置”按钮,打开“数据透视表字段”对话框。
在此对话框“汇总方式”列表中选择“平均值”。
冀教版四年级上册:学生们的成绩平均数如何计算?

标题:如何计算学生成绩的平均数?一、引言学生学习有好坏,成绩是一个很好的衡量标准。
计算学生成绩的平均数可以给老师、学生、家长提供更为全面和客观的参考依据,更好地反映学生的学习成果。
二、什么是平均数?平均数是一组数据中所有数值之和除以数据个数的结果,也称为“算术平均数”。
例如:某班级5名学生的语文成绩分别为70、80、90、85、87,这5名学生的成绩平均数就是(70+80+90+85+87)/5=82.4(保留一位小数)。
平均数广泛应用于各个领域,例如统计社会人口当中的平均寿命、计算企业的平均利润率等。
在学生中最常用到的还包括成绩的排名和评定优良中差等次。
三、如何计算学生的成绩平均数?计算学生的成绩平均数,通常需要以下几个步骤:1. 将所有学生的成绩相加,得到总成绩。
2. 将总成绩除以学生人数,得到平均数。
例如,某班有40名学生,其中10名学生数学成绩分别为:80、85、90、85、95、92、88、85、90、93。
计算这些学生成绩的平均数的具体步骤如下:1. 将10个成绩相加,得到总成绩:80+85+90+85+95+92+88+85+90+93=883。
2. 将总成绩(883)除以学生人数(10),得到平均数:883/10=88.3(保留一位小数),即这10名学生的平均数为88.3分。
四、平均数的意义与局限计算平均数可以反映一个班级、学校或一个区域内的学生的平均水平,有助于评估整体的学习进步。
但是,平均数也存在一些局限性:1. 平均数是一个整体指标,无法反映出学生成绩的分布情况。
例如,如果一个班级内有很多学生成绩都接近于100分,但只有少数学生成绩很低,班级平均数会很高,但并不能反映出整体学生的实际水平。
2. 平均数只能反映出数量级相对接近的数据的情况。
例如,如果一个班级的成绩分布在50到100之间,计算平均数的结果可能仅仅是50分和100分的平均值(即75分),并不能说明成绩的真实情况。
几何分布的均值

几何分布的均值
几何分布的均值是一个重要的参数,在数学统计中有多种定义,但它们都可以归结为一个:几何分布的均值表示特定班级中的学生的平均成绩。
它的定义可以用以下公式表示:
μ =xi/n
其中x1,x2...xn是n个成绩,n为学生人数。
几何分布的均值提供了一个关于班级学生总体成绩的量化指标,它可以帮助老师和学生了解学生整体表现,并实施相应的改进策略。
几何分布的均值受到学生成绩的分布形式的影响。
如果学生成绩分布比较均匀,那么几何分布的均值的值就会比较高,反之亦然。
因此,老师在进行教学时应该根据学生成绩分布的情况来安排教学内容,使学生成绩更加均衡,从而得出更高的几何分布均值。
另外,几何分布的均值也可以作为考核学校教育质量的参考标准。
学校可以按照自己学校学生的均值成绩进行比较,来评估学校教育质量,为贯彻教育政策提供依据。
此外,几何分布的均值还可以作为一种预测学生成绩的指标。
通过计算出的几何分布的均值,教师可以预测学生接下来的表现,以便更好地进行教学计划的制定和实施。
综上所述,几何分布的均值在数学统计中有着重要的作用。
它不仅可以帮助老师和学生了解学生的成绩水平,还可以作为考核学校教育质量的参考,也可以作为预测学生成绩的指标。
因此,老师应该在日常教学中注重几何分布的均值,设法提高学生成绩的均衡度,以达
到较高的几何分布均值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
# define N 10/*学生人数*/
# define M 5/*课程数*/
/* ****************************函数原型声明 *********************************/
float s_var(float a_stu[N]);
NO.10 75.00 73.00 70.00 85.00 82.00 77.00
Average: 84.70 73.50 76.70 81.60 84.60
Highest: 95.00 NO.2 course1
输入10个学生5门课的成绩,分别用函数求:
(1)每个学生的平均分;
(2)每门课的平均分;
(3)找出最高的分数所对应的学生和课程;
(4)求出平均分方差;
解:
函数input_stu的执行结果是给全程变量学生成绩数组score各元素输入初值。
函数aver_stu的作用是计算每个学生的平均分,并将结果赋给全程变量数组a_stu中各元素。
void aver_cour(int score[N][M],float a_cour[M]); /* 函数原型声明 */
void main()
{
int score [N][M]; /*学生成绩*/
float a_stu [N],a_cour[M]; /*各个学生平均分,各门课程平均分*/
void highest(int score[N][M]); /* 函数原型声明 */
void input_stu(int score[N][M]); /* 函数原型声明 */
void aver_stu(int score[N][M],float a_stu[N]); /* 函数原型声明 */
for (i=0;i<N;i++)
{
printf("\nInput score of student%2d:\n",i+1); /* 学生号从1开始 */
for (j=0;j<M;j++)
scanf("%d",&score[i][j]);
row=i+1; /* 数组行号i从0开始,学生号r从1开始,故row=i+1 */
column=j+1; /*数组列号j从0开始,学生号c从1开始,故column=j+1 */
}
/* 输出最高分和学生号,课程号 */
printf("\nHighest score is:%3d,NO.%2d student,course %2d\n",high,row,column);
for (j=0;j<M;j++) /* 输出某个学生各门课的成绩 */
printf("%8d",score[i][j]);
printf("%8.2f",a_stu[i]); /* 输出某个学生的平均成绩 */
/*输出结果*/
printf("\n NO. cour1 cour2 cour3 cour4 cour5 aver");
for (i=0;i<N;i++)
{
printf("\n NO.%2d ",i+1); /* 输出某个学生号码 */
Variance: 6.92
s+=score[i][j];
a_stu[i]=s/M;
}
} Leabharlann void aver_cour(int score[N][M],float a_cour[M]) /* 计算各门课的平均成绩的函数 */
{
int i,j;
float s;
95 71 81 80 83↙
Input score of student 3:
86 82 77 91 88↙
Input score of student 4:
85 76 79 81 82↙
Input score of student 5:
88 76 84 81 80↙
Input score of student 6:
sumxn+=a_stu[i];
}
return (sumx/N-(sumxn/N)*(sumxn/N));
}
运行情况如下:
Input score of student 1:
91 79 83 83 91↙
Input score of student 2:
}
}
void aver_stu(int score[N][M],float a_stu[N]) /* 计算各个学生平均成绩的函数 */
{
int i,j;
float s;
for (i=0;i<N;i++)
{
s=0;
for (j=0;j<M;j++)
printf("\nVariance:%8.2f\n",s_var(a_stu)); /* 调用函数,计算和输出方差 */
system("pause");
}
void input_stu(int score[N][M]) /* 输入10个学生成绩的函数 */
{
int i,j;
87 72 79 91 84↙
Input score of student 7:
85 77 75 84 93↙
Input score of student 8:
66 62 64 54 70↙
Input score of student 9:
89 67 75 86 93↙
Input score of student 10:
{
int high;
int i,j,row,column;
high=score[0][0];
for (i=0;i<N;i++)
for (j=0;j<M;j++)
if (score[i][j]>high)
{
high=score[i][j];
函数aver_cour的作用是计算每门课的平均成绩,计算结果存入全程变量数组a_cour。
函数highest的返回值是最高分,r,c是两个全局变量,分别代表最高分所在的行,列号。
函数s_var的返回值是平均分的方差。
程序如下:
#include "stdio.h"
#include "stdlib.h"
for (j=0;j<M;j++)
{
s=0;
for (i=0;i<N;i++)
s+=score[i][j];
a_cour[j]=s/N;
}
}
void highest(int score[N][M]) /* 求最高分和它属于哪个学生,哪门课的函数 */
NO.2 95.00 71.00 81.00 80.00 83.00 82.00
NO.3 86.00 82.00 77.00 91.00 88.00 84.80
NO.8 66.00 62.00 64.00 54.00 70.00 63.20
NO.9 89.00 67.00 75.00 86.00 93.00 82.00
}
printf("\nAverage:");
for (j=0;j<M;j++) /* 输出各门课平均成绩 */
printf("%8.2f",a_cour[j]);
highest(score); /* 调用函数,求最高分和它属于哪个学生,哪门课 */
}
float s_var(float a_stu[N]) /* 求方差的函数 */
{
int i,j;
float sumx,sumxn;
sumx=0.0;
sumxn=0.0;
for (i=0;i<N;i++)
{
sumx+=a_stu[i]*a_stu[i];
75 73 70 85 82↙
NO. cour1 cour2 cour3 cour4 cour5 aver
NO.1 91.00 79.00 83.00 83.00 91.00 85.40
/*input_stu( );*/ /* 函数调用,输入10个学生成绩 */
aver_stu(score,a_stu); /* 函数调用,计算10个学生平均成绩 */
aver_cour(score,a_cour); /* 函数调用,计算5门课平均成绩 */
int i,j;
/*随机产生50个成绩。若要手工输入成绩,注释以下四行*/
srand(1);
for(i=0;i<N;i++)
for(j=0;j<M;j++)
score[i][j]=rand()%100;
/*若要手工输入成绩,取消下行注释*/
NO.6 87.00 72.00 79.00 91.00 84.00 82.60
NO.7 85.00 77.00 75.00 84.00 93.00 82.80
