材料力学能量法最经典解析课件

合集下载

演示课件材料力学能量法.ppt

.精品课件.
14
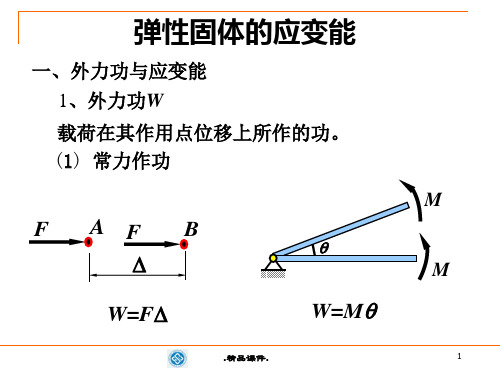
先加F1后加F2 F1
F2
先加F2后加F1 F1
F2
不同加载次序外力功均相同，若按比例同时加载，外力同时达到最终值，即比例加载，外力功不变。
.精品课件.
15
三、克拉贝依隆（Clapeyron)原理线弹性体上，作用有载荷F1,F2 , … Fi, … Fn 与外力方向相应的位移为D1, D2, … Di, … Dn 由线弹性体的叠加原理，各位移是载荷的线性函数
……
Di*= di1F1 * +di2 F2 * + … +diiFi * … +dinFn *= lDi
……
注意：带星号上标的载荷和位移都是中间值，所以是变数，随着l的变化而变化。
.精品课件.
18
Ve
W
n i 1
1 2
Fi Di
线弹性体的外力功或变形能等于每一外力与其对应位移乘积之半的总和。
20
组合变形
M
据Clapeyron原理，
微段dx上
dVe
dW
1 2
FNd (Dl )
1 Mdq
2
1 Tdj
2
FN2dx M 2dx T 2dx
dx
2EA 2EI 2GIP
整个杆件的应变能为
Ve
FN2
(
x
)
dx
l 2EA
M2 (x)
dx l 2EI
T2 (x)
dx l 2GIP
T
FN
.精品课件.
9
已知：EI = 常数，用功能原理
F
计算A点的挠度。
A
B
解：①建立坐标系
wA

材料力学第三章能量法

三、卡氏第二定理（线弹性体）
Di
Vc Fi
在线弹性范围内
余能定理 Vc V
Di
V Fi
卡氏第二定理：线弹性杆件或杆系的应变能对于作用在该杆件或杆系上的某一荷载的变化率，就等于与该荷载相应的位移。
卡氏第二定理适用于一切受力状态下的线弹性体。
卡氏第二定理公式D及i 含义VF：i
若结构的应变能 V 表示为F1、F2 …Fi …的函数，则应变能对任一载荷Fi的偏导数等于Fi作用点沿Fi方向位移。
C
与需求位移相应的虚设外力
F。求偏导后令其为零。
（2）列弯矩方程
M
x
F 2
ql 2
x
qx 2 2
0
x
l 2
M
x
F 2
ql 2
x
qx 2 2
0
x
l 2
（3）求梁的应变能
M 2 l/2
x
1
V 2 0
dx
2EI
EI
l/2
0
F 2
ql 2
x
qx 2 2
2 dx
1 EI 1 EI
V W
一、杆件基本变形的应变能
(一)轴向拉伸(压缩)
1、杆的应变能
轴力沿轴线不变的情况:
dW Fd(Dl) W Dl1 Fd(Dl) 0
线弹性范围内 W 1 FDl
1
2
V
F
W
FN
2
F Dl Dl
FNl EA
应变能
V
FN2l 2EA
F
l
Dl
F
Dl d (Dl)
Dl1
Dl
(一)轴向拉伸(压缩)

008-材料力学_能量法

U i Fi
U i Fi
Fj Fj
M M M2 M M ( dx) dx L EI F L EI F Fi L 2EI i i Fj Fj Fj Fj
dx T T L GI p Fi Fj Fj
8.1 杆件的应变能
二、杆件的应变能 FN dx
dx d
克拉贝隆原理
U
L 2 FN 1 dx FN d L 2 2 EA
克拉贝隆原理
FN 拉压杆的应变能
d
FN dx EA
2 FN l U 2 EA
圆轴扭转的应变能
d
T
T2 1 U dx T d L 2GI L2 p T2l U 2GI p
拉压杆的应变能 F F
U dUV udV
V V
or U dU l
L

l l +Δ l FN dx
dx d
FN ( x) F ( x) N A( x) E EA( x)
1 u 2
2 FN ( x) 1 U udV dA dx dA dx V L A2 L 2 EA2 ( x) A
A F
Ay
2U 2 2 Fl1 ( ) () F E1 A1 2E2 A2
例：图示悬臂梁 AB 的 EI 是常数，在自由端作用一横力 F 和一力偶矩 m ，求梁的应变能。
F m
解：由外力功计算应变能横力的相应位移为自由端的挠度，力偶矩的相应位移为自由端的转角，分别为：
B x l
例：图示悬臂梁 AB 的 EI 是常数，在跨中作用一横力 F ，求 yC 、 θA 。解：F 是与 yC 相应的广义力，与 θA 相应的 F 广义力为作用在自由端的力偶矩，可虚设一个“附加力” m ，最后在位移表达式中令其 m 为零即可。( 附加力法 ) C A B 2 l/2 l M dx 梁的应变能 U 0 2 EI l 由卡氏第二定理

第十章能量法材料力学课件

§10.2 杆件变形能计算
一. 杆件基本变形的变形能 U=W
F
F
线弹性 U W 1F
2
特殊情况
F
F UW1Fl FN2l
2
2EA
Me
Me UW12Me2M Gx2Ilp
Me 广义表达式
Me UW12Me2M E2lI
UW
1F
2
内力2
2刚度
l
注意：当内力或刚度发生变化时要用
积分或分段计算
(内力)2(x)
必须强调 U W 1F 只适用于线弹性结构 2
面积= 1 底高 2
对非线性材料 U=W=曲线下的面积
可利用积分计算
U uW 0d0Fd
未作特殊说明,均假定材料在线弹性范围内
F
F
例10.2 已知d F E G
解
求 fc=? 1 U W 2Ffc
2U
A
2a
F
C
a
B
fc F
UUCBUBA
aM 1 2(x)d x2aM 2 2(x)d x2aM x2(x)d
l M x M x dx tan l xM x dx
tan x c
M c
Mx
C•
x
Mx
l
M
lMxMxdx
tanxM(x)dx
l
tanxc
M
x xc
.c
dx
x
M M ( x) M c xc l
lM xE M Ixdx E M cI
lM xE M Ixdx E M cI
若需要分段,则: i Mci
M(x) ql x qx2(0 x l) 22
A1
。。。

材料力学第十三章能量法

单元体上外力作功： W s e1 d e 0
应变能密度：
ve
e1 s d e
0
边长为dx、dy、dz的单元体： dVe ve d x d y d z
杆： Ve dVe V ve dV
线性弹性体：
ve
s e1
0
de
1 2
s
1e1
1 2
Ee12
1 2E
s
2 1
ve
1 d
0
1 2
1
AF
Fl 2 16 EI
应变能：
Vε
1 2
M AM
(1 2
FDCF
M AF )
1
F 2l3 (
M
2l
MFl 2
)
EI 96 6 16
④ M、F 分别单独作用
F
A
DCF
B
A M AM
B
DCF
Fl 3 48 EI
AM
Ml 3EI
应变能之和： VεF VεM
1 2
FDCF
1 2
M AM
1 EI
VεS
l
s
FS2 (x) d x 2GA
s — 剪切形状因数
S
S
通常，梁的剪切应变能远小于弯曲应变能。
杆件发生组合变形
在线弹性、小变形的条件下，每一基本变形的内力仅在其相应的基本变形上作功，在其他基本变形上不作功。
Vε
l FN2 (x) d x 0 2EA
l T 2 (x) dx
0 2GIp
材料是线弹性的，但变形 D 与力F 不是线性的
几何非线性弹性问题
材料是非线性弹性的
物理非线性弹性问题

材料力学第12章能量方法及应用PPT课件

给一个增量d，外力做元功为
d W F 1 1 d F 2 2 d F n n d
( F 1 1 F 2 2 F n n )d
可得
W(F11F22
Fnn)
1d
0
12F1112F22 12Fnn
根据功能原理，物体的应变能应为
U W 1 2F 1 11 2F 2 2 1 2F n n
例：试求图示悬臂梁的应变能，并利用功能原理求自由
端B的挠度。
A x
解：
M (x)Px
U M 2(x)dx l 2EI
l (Px)2 dx
0 2EI
P 2l3 6EI
W
1 2
P
fB
由UW,得f B
Pl3 3EI
例：试求图示梁的应变能，并利用功能原理求C截面的挠度。
解： U
l
M 2(x)dx 2EI
第十二章能量原理及其应用
§12-1 杆件的应变能
在弹性范围内，弹性体在外力作用下发生变形而在体内积蓄的能量，称为弹性应变能，简称应变能。
物体在外力作用下发生变形，物体的应变能在数值上等于外力在加载过程中在相应位移上所做的功，即
UW (功能原理）
能量法：从功和能的角度出发，分析
杆件的内力、应力和位移。
一、杆件应变能计算
1、轴向拉伸和压缩
UW
1 2
P
l
1 2
P
Pl EA
P2l FN2l 2EA 2EA
FN或A变化时
UV
l
FN2 (x) 2 EA( x)
dx
P
l l
P
2、扭转
m
m
UW 1 m 1mml m2l MTT 2l

材料力学刘鸿文第六版最新课件第十三章能量方法

13-3 应变能的普遍表达式
基础知识
广义
线弹性结构上受一个外力作用，任一点的位移与该力成正比。
线弹性结构上任意一点的广义位移与各广义力成线性齐次关系。
比例加载时，线弹性结构上任一外力作用点沿外力方向的位移与该点的广义力成正比。
F1
1
应变能只取决于受力变形的最终状态，因
此可采用便于计算的方式计算应变能。
P1
P2
1 dV 2 M( x )d
一般情况下：剪力对变形的影响很小，剪切应变能远远小于弯曲应变能。
M 2( x )dx dV 2EI
w = M(x) = dθ EI dx
d M( x) dx
EI
M 2( x )dx
V l 2EI
应变能的特点：
（1）基本变形的应变能通式：
1
V
W
F 2
F2
F3
采用比例加载
2 3
外力
比例
0
位移
比例
F1、F2、F3
1、 2、 3
0
V
W
1 2
F11
1 2
F2 2
1 2
F33
n i1
1 2
Fii
即：线弹性体的变形能等于每一外力与其相应位移乘
积的二分之一的总和。
克拉贝依隆原理
对于组合变形
M (x)
Fs(x)
FN (x)
T (x)
M (x)
FN (x)
Me
⑵ 应变能
V
L
M 2 (x) dx
2EI
L
1 2EI
(M e
Fx)2 dx
M
2 e
L
M e FL2

材料力学第26讲 Chapter3-1第三章能量法(应变能余能)

利用功和能的概念求解可变形固体的位移、变形及内力等的方法，统称为能量方法。
能量方法是用有限元法解固体力学问题的重要基础。
4
能量方法用途很广：
不仅适用于线弹性问题；也可用于非线性弹性问题；曲杆问题；
5
本章要介绍的几种能量方法：
应变能原理－卡氏第一定理余能原理－卡氏第二定理虚位移原理及单位力法
6
§3–2 应变能余能
应变能的计算：
I. 应变能
外力缓慢做功W ，无损失地转化为应变能（不
转化成动能、热能），贮存于弹性体内部。
V W
7
一、线弹性问题
1. 轴向拉压杆件应变能的计算
W 1 Fl
2
l Fl
W F 2l 2EA
F
EA
W＝V 功能原理
V
EAl2
2l
F 2l V 2 EA
5P1P2l3 48EI
23
进一步分析
21
P1
P2
12
l
l
2
2
21P16(E 2l)Il2(3l2l)458P1E l3I
l
l
2
2
12P26(E 2l)Il2(3l2l)4 58 P2 E lI3
P112 P221 ====== 功的互等定理 ======
第一组力在第二组力作用所产生位移上做的功等于第二组力在第一组力作用所产生位移上做的功。
17
4.3 弯曲杆件应变能的计算
V
V vdV
V
1 2
dV
V
1 2E
2dV
l
A21E(M Izy)2dAdl l
A21E(M Iz )2y2dAdl
d l dx M 2 l 2EIz

材料力学之能量法

A
l/2
F C 1
l/2
B
l/2 1 1 Fl 3 W Fδ1 F F 2 2 48 EI C A 2) 力偶由零增至最后值 Me Mel B 截面的转角为 θ 3 EI 1 1 Mel 力偶 Me 所作的功为 W2 M eθ M e 2 2 3 EI
l/2 Me B
由 V =W 得
( FRsin ) 2 πF 2 R3 Rd 2 EI 8EI
Δ BV
πFR 4 EI
3
A
O
例: 简支梁, 两种载荷按同样比例加载, 计算其变形能。梁中点的挠度为梁右端的转角为
Fl 3 M el 2 δ1 48EI 16 EI Fl 2 M el δ2 θ 16 EI 3EI
Fb 2 Fa 2 ( x1 ) ( x2 ) a b l dx1 l dx2 0 0 2 EI 2 EI
2
B
x1 a l C x2
b
F 2b2 a3 F 2a 2 b3 F 2a 2b 2 2 2 2 EIl 3 2 EIl 3 6 EIl
1 W F vC 2
由 V =W 得
(( ))
1
q A
RA
F=qa B
C
x
A x 1/2a
B
C x
x
2a
a
2a
a
(2) 求 C 截面的转角 ( 在 C 处加一单位力偶） 2 qa qx x AB: M ( x) x (0 x 2a) M ( x) 2 2 2a BC: M ( x) qa x (0 x a) M ( x) 1 a 1 2 a qa qx 2 x 5qa3 c [ ( x )( )dx (qax)(1)d x] 0 EI 0 2 2 2a 6 EI （

材料力学课件：12 第十二章能量法(一)

广义位移：线位移，角位移，相对线位移，相对角位移等。
7
第十二章能量法(一）
例：试确定图a均布载荷q 对应的广义位移，图b铰链两侧
横截面相对转角对应的广义力。
q
F
A
B
l
A
B
C
(a)
(b)
l
相应广义位移：面积
MM
对应广义力：一对力偶 M
8
第十二章能量法(一）
➢ 克拉比隆定理：(线弹性体上作用有多个广义力的情况)
引言
弹性体的能量原理
在外载荷作用下，构件发生变形
载荷在相应位移上做功构件因变形储存了能量
F
F
能量守恒
从零开始，缓慢加载
忽略动能与热能的损失
V W
能量原理：是固体力学的重要原理
4
第十二章能量法(一）
§12-1 外力功与应变能的一般表达式
一、计算外力功的基本公式
刚体线性弹簧
W F
V
M2( x )y2
2EI
2 z
dxdydz
1 2
M 2(x ) dx
l EIz
非对称弯曲沿两主轴分解计算应变能
Vε =
M
2 y
(x)dx
l 2EI y
M
2 z
(x)dx
l 2EIz
注：忽略了弯曲剪力的应变能
l
C
z
F y
18
第十二章能量法(一）
利用功能原理计算应变能
•单向拉压
dVε
dW
FN (x)dδ 2
第十二章能量法(一）
求节点A的铅垂位移的两条研究途径
FN1 F sin（拉）, FN2 F tan（压）

材料力学第十二章能量法精品PPT课件

应变能只与外力的最终值有关与加载过程和加载次序无关。
13
注意：
1、注意常力做功与变力做功的区别；
2、多个外力引起的同种变形能不能简单叠加而是要算出合内力后，再用变形能公式计算；如果各外力相互独立，即引起的变形互不相同，此时不同的变形能可以叠加。
3、功能原理只能计算构件只作用一个力，力的作用点沿力作用 F 线方向的位移。
纯弯曲
U M e2l 2EI
T 2(x)
U
dx
l 2GIp (x)
横力弯曲
U Me2(x)dx l 2EI(x)
变形能等于内力的平方乘以构件的长度再除以2倍的刚度，若内力或刚度为变量时，将长度取为微量再积分
5
4、组合变形的变形能
截面上存在几种内力，力独立作用原理成立，各个内力只对其相应的位移做功。
端B的挠度。
F
解：
A
B
M(x) F x
x l
U
M 2(x )
dx
l ( Fx)2 dx
F 2l3
2EI
0 2EI
6EI
1 W 2 F wB
Fl3 由U=W 得： w B 3 E I
7
例12-2、试求图示梁的变形能，并利用功能原理求C截面的挠度。
解：
F
U
M 2(x )
2EI
dx
A
W3
F1δB2
F 1F 2a EA
所以应变能为：
U 1 W W1W2W3 F12aF22(ab)F1F2a 2EA 2Eb C
W1
F
2 1
a
2EA
F2
W2
F22(a b) 2EA
12

材料力学第9章能量法

1 1 1 1 ' Vε 2 F1δ1 F2 δ2 F3 δ3 F4 δ4 F3 δ'3 F4 δ4 2 2 2 2
由于应变能只决定于力和位移的最终值,与加力的次序无关,故 F1 F2
3

' 3
F3
Vε1 Vε 2
Fδ Fδ Fδ Fδ
' 1 1 ' 2 2 ' 3 3 ' 4 4
0 xM ( x )dx 为图M(x)对 y 轴坐标的静矩 M(x) 0 M ( x )dx ωxC l M ( x ) M ( x )dx
A M ( x )dx B x M ( x )dx
0 0 l l
l
ω
l
C
xC
M (x )
（c）弯曲
Vε M 2 ( x )dx M ( x ) M ( x ) δi 2 EI EI Fi dx Fi Fi
（4）平面桁架
n FNj l j FNj Vε δi Fi j 1 EA Fi
（5）组合变形
2 Vε FN ( x )dx T 2 ( x )dx M 2 ( x )dx δi [ ] l 2GI l Fi Fi l 2 EA 2 EI p
n
2
M l 1 Vε W M θ 2 2 EI
M ( x) Vε dx l 2 EI ( x )
2
横力弯曲
4.组合变形的变形能截面上存在几种内力,各个内力及相应的各个位移相互独立,
力独立作用原理成立,各个内力只对其相应的位移做功.
2 FN ( x ) T 2 ( x) M 2 ( x) Vε dx dx dx l 2 EA( x ) l 2GI ( x ) l 2 EI ( x ) p

材料力学第11章能量法讲解

x Me
A
l FAy
B FBy
(1) 应变能计算
梁的约束力
FA

FB

Me l
梁的弯矩方程
代入应变能公式
M (x)

FA x M e

x Me(l
1)
Vε
M 2(x) dx
l 2EI
1 2EI
l 0
M
2 e
(
x l
1)2 dx

M e2l 6EI
15/65
11.1 外力功与应变能【例11-1】解
10/65
11.1 外力功与应变能
11.1.3 克拉贝依隆原理
F1Δ12 F2 Δ21
W

1 2
F1 Δ11

1 2
F2 Δ22

F1 Δ12

上式可推广到有多个广义力共同作用于线性弹性体的情况 Vε W
Vε
W

1 2
Fi Δi
上式称为克拉贝依隆原理。
式中为全部外力（F1，F2，…，Fi，…，Fn）在广义力Fi处
l GI p
M xdq
2
w M EI
12/65
11.1 外力功与应变能
M(x)
T(x) FN(x) FN(x)
11.1.4 杆件的应变能
dq
T(x) M(x)
dj
dx
dx dd
dx
dx
dVε

FN2 (x)dx 2EA

T 2 (x)dx 2GIp

M 2 (x)dx 2EI
则整个圆截面杆的应变能 Vε
FN2 (x) dx l 2EA

材料力学_能量法_课件

拉压杆
E
u
1 0
1 2 d E1 2 2E
2 1
扭转杆
G
u
1
0
1 1 2 d G 1 2 2G
2
例题：水平杆系如图所示，两杆的长度均为 l,横截面面积
为A，弹性模量为E，且均为线弹性。试计算在P1作用下的
应变能。
l
2
2
（3）弯曲梁内的变形能（略去剪力的影响）
1 M l l M ( x )dx U m 0 2 2EI 2EI
（4）组合变形的变形能
N ( x )dx T ( x )dx M ( x )dx U l l l 2 EA 2GI p 2 EI
2 2 2
2
2
2、非线性弹性体，通过比能求应变能
1 1
d
3
1 P1d 1 4
二. 余能 1、非线性弹性材料（拉杆）
P
P1

1
O
P
1

O
ε1
ε
P
P1
dP

P
P1
O
1

Δ1 Δ dP + 0 PdΔ 0
=矩形面积
余功公式
P1 W C 0 Δ dP
P
P1
dP

P
O
1

余能公式
UC W C 0 Δ dP
P1
UC V ucdV
§3.1
概述
可变形固体在受外力作用而变形时，外力和内力均将作功。对于弹性体，外力在相应位移上作的功，在数值上就等于
积蓄在物体内的应变能。
U=W
能量方法：利用功能原理 U = W 来求解可变形固体的位移、变形和内力等的方法。

材料力学第10章能量法

§10.3 互等定理
1.先在1点作用F1
A 1 1 U1 F1 11 F2 22 F1 12 2 2
F1 1
11 12
2.先在2点作用F2
21 22 F2
F2 2
B
1 外力功： F2 22 2
再在1点作用F1
A
F1 1
12 11
22 21
F2 2
V W
弹性范围内应变能可逆
第十章能量法
§10.2 弹性应变能的计算
一、线弹性问题的应变能线弹性体的应变能等于每一外力与其相应位移乘积的二分之一的总和即：
1 3
F1 F2
2
F3
1 1 1 U W F1 1 F2 2 F3 3 2 2 2
变形能是外力或位移的二次函数

例1
求图示简支梁的变形能，并求yC
a A F b C B
解： 1.求支反力 2.列弯矩方程
Fb x1 AC段： M x1 l Fa M x x2 CB段： 2 l
RA = Fb l
x1
x1
l
x2
RB = Fa l
例1
求图示简支梁的变形能，并求fC
a A F b C B
解： 1.求支反力 2.列弯矩方程
3. 梁应变能
Vε W M e d
ε1 0 0
1
应变能密度 vε d 式中， Me为外力偶矩，为弯曲转角，为正应力，为线应变。应变能和应变能密度之间的关系为
Vε vε d x d y d z vε dV
V V
式中，V 为体积。
例题 3-1
Me

材料力学能量法最经典解析课件

演示课件材料力学能量法.ppt

材料力学第三章 能量法

008-材料力学_能量法

第十章 能量法 材料力学课件

材料力学第十三章 能 量 法

材料力学 第12章 能量方法及应用PPT课件

材料力学刘鸿文第六版最新课件第十三章 能量方法

材料力学第26讲 Chapter3-1第三章 能量法(应变能 余能)