参数变量函数
数值函数、参数函数、通用函数

数值函数、参数函数、通用函数数学中的函数是一种特殊的关系,它将一个或多个输入值映射到唯一的输出值。
函数是数学建模和问题求解的基础,在各个领域都有广泛的应用。
本文将介绍数值函数、参数函数和通用函数的概念及其在实际问题中的应用。
一、数值函数数值函数是指将一个或多个实数作为输入,返回一个实数作为输出的函数。
它可以用一个数学式子来表示,也可以用一张表格或图像来表示。
数值函数的定义域是实数集,值域是实数集。
常见的数值函数包括线性函数、二次函数、指数函数、对数函数等。
线性函数是最简单的数值函数之一,其表达式为f(x) = ax + b,其中a和b为常数。
线性函数的图像是一条直线,斜率a决定了直线的倾斜程度,常数b决定了直线与y轴的交点。
二次函数是一种重要的数值函数,其表达式为f(x) = ax^2 + bx + c,其中a、b和c为常数,且a ≠ 0。
二次函数的图像是一个抛物线,开口方向由二次项系数a的正负决定,常数c决定了抛物线与y轴的交点。
指数函数是以指数为变量的函数,其表达式为f(x) = a^x,其中a 为常数。
指数函数的图像是一条逐渐增加或逐渐减小的曲线,常数a决定了曲线的增长速度。
对数函数是指数函数的反函数,其表达式为f(x) = loga(x),其中a 为常数且a > 0,且a ≠ 1。
对数函数的图像是一条逐渐平缓或逐渐陡峭的曲线,常数a决定了曲线的陡峭程度。
数值函数在实际问题中有着广泛的应用。
例如,在经济学中,利润函数、成本函数和供需函数都属于数值函数,用于分析和预测市场行为。
在物理学中,速度函数、加速度函数和力函数都是数值函数,用于描述物体的运动规律。
在生物学中,生长函数和衰减函数也是数值函数,用于研究生物体的生长和衰老过程。
二、参数函数参数函数是指函数中含有一个或多个参数的函数。
参数是函数中可变的量,通过改变参数的值,可以得到不同的函数。
参数函数可以用一个数学式子来表示,也可以用一张表格或图像来表示。
第三讲 参变量函数

u
(nk )
v
(k )
uv
Cnu
k
(nk )
v
(k )
k0
公式(3)称为 莱布尼兹公式
几个初等函数的高阶导数
(1 ) ( a )
x (n)
a
(n)
x
ln
n
n
a
(a 0)
(e )
x
(n)
e
x
( 2 ) (sin kx ) ( 3 ) (cos kx )
(4) ( x )
2
设函数
y f ( x ) 有导数
,
f ( x ),
( 1 ) 若 x 是自变量时
dy f ( x ) dx ;
( 2 ) 若 x 是中间变量时 微函数
, 即另一变量
t 的可
x ( t ), 则 dy f ( x ) ( t ) dt
dy f ( x ) dx .
x e 2 t 3t 1 3 2 y 4t 2t 6
t x 1 t y 1 t 1 t
第四讲 微分
1、定义:
设函数 y
y f
f
x 定义在 x 0 的改变量是 y 与自变数 x 的改变量 x ,有下列关系
f
x 的 n 1 阶微分在 x 的微分,称为函数 f x 在 x 的 n 阶微
分,表为 d n y 或 d n f x
dy f ' x dx
d y d dy
2
f ' x dx ' dx
2
f '' x d x
comsol内置参数变量函数

保留函数的名称可以被用于变量和参数名,反之同样。
描述名称值双精度浮点数、机器精度eps2-52(~2.2204·10-16)虚数单位i,j i,sqrt(-1)无穷大,∞Inf,inf一个大于能被计算机处理的值非数字值NaN,nan未定义或者不能表示出来到值如0/0或者inf/infπpi 3.141592653589793描述名称值重力加速度g_const9.80665[m/s^2]阿伏伽德罗常数N_A_const 6.02214129e23[1/mol]玻耳兹曼常量k_B_const1.3806488e-23[J/K]真空特性阻抗Z0_const376.73031346177066[ohm]电子质量me_const9.10938291e-31[kg]元电荷e_const 1.602176565e-19[C]法拉第常数F_const96485.3365[C/mol]精细结构常数alpha_const7.2973525698e-3万有引力常数G_const 6.67384e-11[m^3/(kg*s^2)]标准状态下想气体体积V_m_const 2.2413968e-2[m^3/mol]中子质量mn_const 1.674927351e-27[kg]真空磁导率mu0_const4*pi*1e-7[H/m]真空介电常数epsilon0_const8.854187817000001e-12[F/m]普朗克常数h_const 6.62606957e-34[J*s]普朗克常数/2πhbar_const 1.05457172533629e-34[J*s]质子质量mp_const 1.672621777e-27[kg]真空中的光速c_const299792458[m/s]斯忒藩—玻耳兹曼常数sigma_const 5.670373e-8[W/(m^2*K^4)]通用气体常数R_const8.3144621[J/(mol*K)]维恩位移定律常数b_const 2.8977721e-3[m*K]参数化几何尺寸参数化网格元素大小参数扫描变量,主要有两种类型变量:内部保留变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
参数变量函数的导数

dy dy dt dy 1 ψ ′( t ) = ⋅ = ⋅ = dx dt dx dt dx ϕ ′( t ) dt
dy dy dt 即 = dx dx dt
x = ϕ( t ) 若函数 二阶可导, y = ψ( t )
d ψ ′( t ) dt d 2 y d dy ) = ( )= ( 2 dx dx dt ϕ′( t ) dx dx
x = ϕ( t ) 在方程 中, y = ψ( t )
设函数 x = ϕ ( t )具有单调连续的反函数 t = ϕ ( x ),
−1
∴ y = ψ [ϕ −1 ( x )]
再设函数 x = ϕ ( t ), y = ψ ( t )都可导, 且ϕ ( t ) ≠ 0,
由复合函数及反函数的求导法则得
ψ ′′( t )ϕ ′( t ) − ψ ′( t )ϕ ′′( t ) 1 = ⋅ 2 ϕ ′ (t ) ϕ ′( t )
d2 y ψ′′(t )ϕ′(t ) −ψ′(t )ϕ′′(t ) . 即 = 2 3 dx ϕ′ (t)
π x = a ( t − sin t ) 例1 求摆线 在t = 处的切线 2 y = a (1 − cos t ) 方程 .
即 y = x + a( 2 − ) 2
π
π
例7 不计空气的阻力, 以初速度 v0 , 发射角 α
发射炮弹 , 其运动方程为 x = v0 t cosα , 1 2 y v t sin α − gt , = 0 2 求 (1)炮弹在时t 0的速度大小 .
v 0 sin α − gt 0 . = v 0 cos α
( 2) 炮弹在 t 0时刻沿 x , y轴方向的分速度为
Comsol内置参数变量函数

C o m s o l内置参数变量
函数
Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】
Comsol 内置表达式:参数、变量、函数
表达式:?
参数
一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
?
变量
个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
?
函数?
一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
注:保留函数的名称可以被用于变量和参数名,反之同样。
内置的物理常数
变量:主要有两种类型变量:内部保留变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
有一组有趣的变量,即空间坐标变量和因变量,这些基于空间维度和所选物理场的变量有默认的名称,comsol会创建一张变量表来表示这些变量。
称。
所以可以生产下列变量:Tx、Ty、Txx、Txy
Tyx、Tyy、Tt、Txt、Tyt、Txxt、Txyt、Tyxt、Tyyt、Ttt、Txtt、Tytt、Txxtt、Txytt、Tyxtt、Tyytt.其中Tx是T对x的导数,Ttt是T 对t的二阶导数,如果空间坐标系有其他的名字,同理置换相应变量。
acosh,acoth,acsch,asech,asinh,atanh,besselj,bessely,besseli,bes selk,
erf,gamma,和psi。
内置操作函数:。
Comsol内置参数变量函数

Comsol 内置表达式:参数、变量、函数
表达式:?
参数
一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
?
变量
个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
?
函数?
一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
注:保留函数的名称可以被用于变量和参数名,反之同样。
内置的数学常数
内置的物理常数
变量:主要有两种类型变量:内部保留变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
有一组有趣的变量,即空间坐标变量和因变量,这些基于空间维度和所选物理场的变量有默认的名称,comsol 会创建一张变量表来表示这些变量。
内置变量
称。
所以可以生产下列变量:Tx、Ty、Txx、Txy
Tyx、Tyy、Tt、Txt、Tyt、Txxt、Txyt、Tyxt、Tyyt、Ttt、Txtt、Tytt、Txxtt、Txytt、Tyxtt、Tyytt.其中Tx是T对x的导数,Ttt是T对t的二阶导数,如果空间坐标系有其他的名字,同理置换相应变量。
内置数字函数
acosh,acoth,acsch,asech,asinh,atanh,besselj,bessely,besseli,bes selk,
erf,gamma,和psi。
内置操作函数:
这些内置的函数不同于内置的数学函数,详细见用户指南。
表示函数的三种方法

表示函数的三种方法函数是数学中的一个重要概念,它描述了一个变量如何依赖于另一个变量。
在数学和计算机科学中,表示函数的方法有很多种,本文将介绍其中的三种方法,显式函数、隐式函数和参数方程。
首先,我们来谈谈显式函数。
显式函数是最为常见的一种表示函数的方法。
当一个函数可以被直接表示为一个变量的函数时,我们称之为显式函数。
比如,y =2x + 3就是一个显式函数的例子,其中y是x的线性函数。
在这种表示方法中,我们可以直接通过函数表达式来计算函数值,非常直观和方便。
其次,我们来看看隐式函数。
与显式函数相对应,隐式函数是一种不能直接表示为一个变量的函数的方法。
在隐式函数中,通常会包含多个变量之间的关系,而这种关系不容易用单一的函数表达式来表示。
比如,x^2 + y^2 = 1就是一个隐式函数的例子,它表示了一个单位圆的方程。
在这种情况下,我们不能直接通过一个函数表达式来表示函数值,需要通过其他方法来求解。
最后,我们来介绍参数方程。
参数方程是一种使用参数来表示函数的方法。
在参数方程中,一个变量的取值由另一个参数决定,而这个参数可以是一个或多个变量。
比如,x = cos(t)、y = sin(t)就是一个参数方程的例子,它表示了一个单位圆的参数方程。
在这种表示方法中,我们通过改变参数t的取值来得到不同的函数值,非常适合描述一些复杂的曲线和图形。
总结一下,表示函数的三种方法分别是显式函数、隐式函数和参数方程。
显式函数是最为直观和常见的一种方法,隐式函数适用于描述多个变量之间的复杂关系,而参数方程则适合描述曲线和图形的特定形式。
不同的表示方法适用于不同的情况,我们可以根据具体的问题来选择合适的方法来表示函数。
希望本文的介绍能够帮助读者更好地理解表示函数的方法。
函数调用中的数据传递方法

函数调用中的数据传递方法在编程中,函数是一种独立的代码块,它封装了特定的功能,可以在程序中被重复调用。
当我们调用函数时,有几种方法可以传递数据给函数。
1.传递参数参数是函数定义中声明的变量,用于接收传递给函数的数据。
参数可以是必选参数、默认参数或可变参数。
-必选参数:在函数定义时,需要明确指定参数的名称和类型,函数调用时必须传递对应数量和类型的参数。
例如:```pythondef add(x, y):return x + yresult = add(2, 5) # 传递两个整数参数```-默认参数:在函数定义时,可以为参数提供默认值。
调用函数时,如果没有传递对应参数,则使用默认值。
例如:```pythondef greet(name, greeting="Hello"):print(greeting + ", " + name)greet("Alice") # 传递一个参数,使用默认的问候语greet("Bob", "Hi") # 传递两个参数,使用自定义的问候语```-可变参数:在函数定义时,可以使用`*`符号指定一个可变长度的参数。
这样的参数可以接收任意数量的传递参数,并将其作为元组处理。
例如:```pythondef average(*numbers):return sum(numbers) / len(numbers)avg = average(1, 2, 3, 4, 5) # 传递任意数量的参数```2.传递关键字参数关键字参数是传递给函数的具有特定名称的参数。
这种方式使用关键字作为参数名,与其对应的值一起传递给函数。
关键字参数可用于任何参数类型(必选、默认、可变)。
```pythondef greet(name, greeting):print(greeting + ", " + name)greet(greeting="Hello", name="Alice") # 通过关键字传递参数```使用关键字参数具有以下好处:-可以跳过默认参数:通过指定参数名,我们可以只传递关心的参数,而跳过其他参数。
参数(parameter)和变量(argument)的区别

参数(parameter)和变量(argument)的区别(Argument is the actual value of this variable that gets passed to function. argument变量是传给⽅法的实际数据,即实参;parameter参数是⼀个⽅法所定义的变量,即形参;变量variable在函数定义中出现的参数可以看做是⼀个占位符,它没有数据,只能等到函数被调⽤时接收传递进来的数据,所以称为形式参数,简称形参。
函数被调⽤时给出的参数包含了实实在在的数据,会被函数内部的代码使⽤,所以称为实际参数,简称实参。
形参和实参的功能是传递数据,发⽣函数调⽤时,实参的值会传递给形参。
形参和实参有以下⼏个特点:形参变量只有在函数被调⽤时才会分配内存,调⽤结束后,⽴刻释放内存,所以形参变量只有在函数内部有效,不能在函数外部使⽤。
实参可以是常量、变量、表达式、函数等,⽆论实参是何种类型的数据,在进⾏函数调⽤时,它们都必须有确定的值,以便把这些值传送给形参,所以应该提前⽤赋值、输⼊等办法使实参获得确定值。
实参和形参在数量上、类型上、顺序上必须严格⼀致,否则会发⽣“类型不匹配”的错误。
当然,如果能够进⾏⾃动类型转换,或者进⾏了强制类型转换,那么实参类型也可以不同于形参类型。
函数调⽤中发⽣的数据传递是单向的,只能把实参的值传递给形参,⽽不能把形参的值反向地传递给实参;换句话说,⼀旦完成数据的传递,实参和形参就再也没有⽠葛了,所以,在函数调⽤过程中,形参的值发⽣改变并不会影响实参。
)形参:proc过程被定义时的参数称为形参,它没有数据只是个占位符。
但它毕竟也是个参数所以它也是个变量,可以在过程内部当成变量使⽤。
实参:当proc过程被调⽤的时候所使⽤的数据称为实参。
当函数被调⽤时,数值的传递是单向的,只能从实参à形参。
函数的初学知识点总结

函数的初学知识点总结1. 函数的定义和调用函数是一段可以反复调用的代码块。
定义一个函数时,需要给函数取一个名字,并且可以传入一些参数。
例如:```pythondef greet(name):print("Hello, " + name)```上面的代码定义了一个名为greet的函数,它接受一个参数name,并打印出"Hello, "加上参数name的值。
要调用这个函数,只需要写出函数的名字并且传入对应的参数:```pythongreet("Alice")```2. 函数的参数函数的参数可以分为两种,一种是必需参数,一种是默认参数。
必需参数是在函数定义时就需要指定的,而默认参数是在函数定义时就有默认值的参数。
例如:```pythondef greet(name, greeting="Hello"):print(greeting + ", " + name)```在这个例子中,name是一个必需参数,而greeting是一个默认参数,它的默认值是"Hello"。
如果调用greet函数时只传入name参数,那么greeting参数就会使用默认值:```pythongreet("Bob")```3. 函数的返回值函数可以返回一个值,这个值可以在函数被调用的地方使用。
使用关键字return来返回一个值。
例如:```pythondef add(a, b):return a + b```在上面的代码中,add函数接受两个参数a和b,然后返回它们的和。
要使用这个返回值,可以在函数被调用的地方将它赋给一个变量:```pythonresult = add(3, 5)print(result) # 输出8```4. 局部变量和全局变量在函数内部定义的变量叫做局部变量,它们只能在函数内部使用。
Comsol-内置参数变量函数
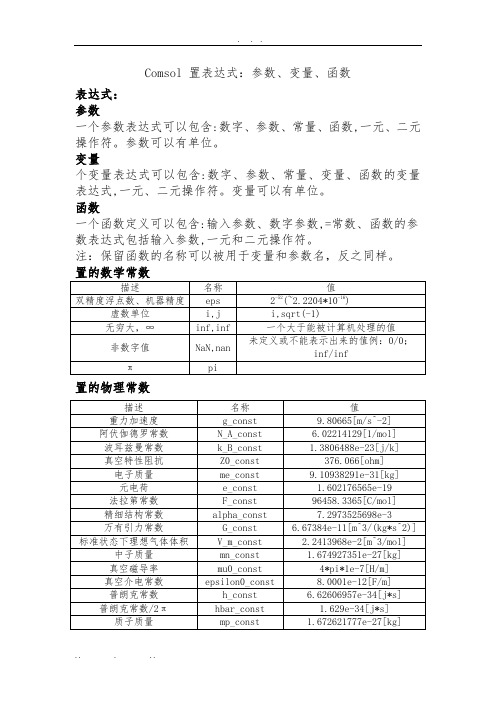
Comsol 置表达式:参数、变量、函数
表达式:
参数
一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
变量
个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
函数
一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
注:保留函数的名称可以被用于变量和参数名,反之同样。
置的物理常数
数扫描。
变量:主要有两种类型变量:部保留变量和用户自定义变量,变量可以是标量也可以是字段,可以有单位。
有一组有趣的变量,即空间坐标变量和因变量,这些基于空间维度和所选物理场的变量有默认的名称,comsol会创建一变量表来表示这些变量。
坐标的名称。
所以可以生产下列变量:Tx、Ty、Txx、Txy Tyx、Tyy、Tt、Txt、Tyt、Txxt、Txyt、Tyxt、Tyyt、Ttt、Txtt、Tytt、Txxtt、Txytt、Tyxtt、Tyytt.其中Tx是T对x的导数,Ttt是T对t的二阶导数,如果空间坐标系有其他的名字,同理置换相应变量。
acosh,acoth,acsch,asech,asinh,atanh,besselj,bessely,bes seli,besselk,
erf,gamma,和psi。
置操作函数:。
Comsol-内置参数变量函数

Comsol-内置参数变量函数Comsol 内置表达式:参数、变量、函数表达式:参数一个参数表达式可以包含:数字、参数、常量、函数,一元、二元操作符。
参数可以有单位。
变量个变量表达式可以包含:数字、参数、常量、变量、函数的变量表达式,一元、二元操作符。
变量可以有单位。
函数一个函数定义可以包含:输入参数、数字参数,=常数、函数的参数表达式包括输入参数,一元和二元操作符。
注:保留函数的名称可以被用于变量和参数名,反之同样。
内置的数学常数描述名称值双精度浮点数、机器精度eps 2-52(~2.2204*10-16)虚数单位i,j i,sqrt(-1)无穷大,∞inf,inf 一个大于能被计算机处理的值非数字值NaN,nan未定义或不能表示出来的值例:0/0;inf/infπpi内置的物理常数描述名称值重力加速度g_const9.80665[m/s^-2]阿伏伽德罗常数N_A_const 6.02214129[1/mol]波耳兹曼常数k_B_const 1.3806488e-23[j/k]真空特性阻抗Z0_const 376.73031346177066[ohm] 电子质量me_const 9.10938291e-31[kg]元电荷e_const 1.602176565e-19 法拉第常数F_const 96458.3365[C/mol]精细结构常数alpha_const 7.2973525698e-3万有引力常数G_const 6.67384e-11[m^3/(kg*s^2)]标准状态下理想气体体积V_m_const 2.2413968e-2[m^3/mol] 中子质量mn_const 1.674927351e-27[kg]真空磁导率mu0_const 4*pi*1e-7[H/m]真空介电常数epsilon0_const 8.854187817000001e-12[F/m]普朗克常数h_const 6.62606957e-34[j*s]普朗克常数/2πhbar_const 1.05457172533629e-34[j*s] 质子质量mp_const 1.672621777e-27[kg] 真空中的光速c_const 299792458[m/s]斯忒潘—波耳兹曼常数sigma_const 5.670373e-8[W/(m^2*k^4)] 通用气体常数R_const 8.3144621[j/(mol*k)] 维恩位移定律常数b_const 2.8977721e-3[m*k]参数有以下用途:参数化几何尺寸、参数化网格元素大小、参数扫描。
matlab 参数变量

matlab 参数变量
MATLAB中的参数变量是指在函数定义中用于接收输入参数值的
变量。
当你定义一个函数时,你可以指定一个或多个参数变量,这
些参数变量用于接收函数调用时传入的实际参数值。
在函数体内部,你可以使用这些参数变量来进行计算、处理数据等操作。
在MATLAB中,定义函数时可以指定输入参数和输出参数。
输入
参数即为参数变量,用于接收函数调用时传入的值。
这些参数变量
可以是任何合法的变量名,通常用来表示函数需要处理的数据或者
进行计算所需的参数。
例如,你可以定义一个计算两个数之和的函数,其参数变量可以是x和y,用来接收两个数值。
在函数定义中,参数变量可以有默认值,也可以指定参数的类型。
默认值可以在定义函数时给参数变量赋值,如果调用函数时没
有传入该参数的值,就会使用默认值。
参数的类型可以指定为特定
的数据类型,这样可以在函数内部对参数进行类型检查或者进行特
定类型的操作。
另外,在MATLAB中,还可以使用可变参数列表来接收不定数量
的参数值。
这可以通过在参数变量前加上三个点(...)来实现,这样
函数就可以接收任意数量的参数值,并将其存储在一个特殊的变量中,你可以在函数内部对这个变量进行处理。
总之,MATLAB中的参数变量是用来接收函数调用时传入的实际参数值的变量,可以通过设置默认值、指定类型或者使用可变参数列表来灵活地处理不同情况下的参数传递。
希望这些信息能够帮助你更好地理解MATLAB中的参数变量。
c++ 参数和函数中变量命名规则

c++ 参数和函数中变量命名规则
在C++中,参数和函数中的变量遵循以下命名规则:
1. 变量名只能由字母、数字和下划线组成。
2. 第一个字符必须是一个字母或下划线。
3. 变量名区分大小写。
4. 变量名不能是C++关键字。
5. 变量名应该能够清楚地表达其含义,以增加代码的可读性。
6. 变量名应遵循驼峰命名规则,即除了第一个单词之外,后续的每个单词的首字母大写。
例如,以下是一些符合C++变量命名规则的示例:
```cpp
int age;
double height;
string firstName;
```
虽然C++对于变量命名没有硬性规定,但是遵循这些规则可以帮助编写更清晰、易读和维护的代码。
变量作为函数参数和返回值的使用示例

变量作为函数参数和返回值的使用示例电脑编程中,变量作为函数参数和返回值是非常常见和重要的概念。
通过合理地使用变量,我们可以实现更高效、灵活和可维护的代码。
本文将通过一些具体的使用示例,探讨变量作为函数参数和返回值的应用。
1. 传递变量作为函数参数在编程中,我们经常需要将某些数据传递给函数进行处理。
这时,我们可以使用变量作为函数的参数,以便将数据传递给函数并在函数内部进行操作。
例如,我们有一个函数`calculate_sum`,用于计算两个数的和。
我们可以将这两个数作为函数的参数传递进去,然后在函数内部进行求和操作,并返回结果。
```pythondef calculate_sum(num1, num2):sum = num1 + num2return sumresult = calculate_sum(5, 3)print(result) # 输出:8```在这个示例中,`num1`和`num2`就是作为函数参数传递的变量。
通过传递变量作为参数,我们可以在函数内部使用这些变量进行相应的计算,并将结果返回。
2. 使用变量作为函数的返回值除了将变量作为函数参数传递外,我们还可以将变量作为函数的返回值。
这样,函数就可以将处理后的结果返回给调用者。
例如,我们有一个函数`calculate_average`,用于计算一组数的平均值。
我们可以在函数内部进行计算,并将结果通过返回值的方式返回给调用者。
```pythondef calculate_average(numbers):total = sum(numbers)average = total / len(numbers)return averagemy_numbers = [1, 2, 3, 4, 5]result = calculate_average(my_numbers)print(result) # 输出:3.0```在这个示例中,`numbers`是作为函数参数传递的变量,而`average`则是作为函数的返回值。
参数函数求导

参数函数求导一、参数函数的概念参数函数是指函数中参数是变量的一种函数形式,即函数不是写成y=f(x),而是写成y=f(x,a)的形式,其中a是函数中的参数。
例如:y=x^a,其中a是参数,x是自变量,y是因变量。
二、参数函数的导数参数函数的导数是指将函数中的参数当作常数来对函数求导。
例如:对于函数y=x^a,y'=a*x^(a-1)。
其中,a是参数,x是自变量,y 是因变量。
当求导时,a被视为常数,x被视为自变量。
三、参数函数的求导方法1. 将参数视为常数,对自变量求导。
2. 将自变量视为常数,对参数进行求导。
3. 将函数中的参数进行化简,再对自变量进行求导。
四、参数函数的例题例1:求参数函数y=x^a在x=2处的导数。
解:y'=a*x^(a-1),将x=2代入得:y'=a*2^(a-1)。
例2:求参数函数y=a*sin(x)关于参数a的导数。
解:y'=sin(x),因为x是自变量,所以a被视为常数。
所以y关于a的导数是sin(x)。
例3:求参数函数y=ax^(b-1)在x=2处的导数。
解:将y=ax^(b-1)化简得:y'=ab*x^(b-2)。
将x=2代入得:y'=ab*2^(b-2)。
五、总结参数函数在函数中的参数是变量的一种函数形式,函数不是写成y=f(x),而是写成y=f(x,a)的形式。
对于参数函数的求导,我们可以将参数视为常数,对自变量求导;也可以将自变量视为常数,对参数进行求导;还可以将函数中的参数进行化简,再对自变量进行求导。
函数参数中有变量TROUGHBARS解决的方法

函数参数中有变量TROUGHBARS解决的方法TROUGHBARS可以理解为一种数学函数,它将输入的参数进行处理,
然后输出一个结果。
参数有四个,第一个参数是4,第二个参数是ZF,第
三个参数是2,第四个参数是K。
TROUGHBARS函数的工作原理可以如下描述:
首先,TROUGHBARS函数根据第一个参数4,从左到右分割第二个参数ZF,得到4个子串。
比如如果ZF是“ABCDEFG”,那么TROUGHBARS这个
函数会分割出“AB”,“CD”,“EF”,“G”四个子串。
然后,TROUGHBARS函数根据第三个参数2,从左到右将每个子串反转,得到4个反转后的子串,比如“ABCDEFG”将会变成“BA”,“DC”,“FE”,“G”四个字符串。
接着,TROUGHBARS函数根据第四个参数K,从右到左合并反转后的子串,得到一个结果字符串。
例如“BA”,“DC”,“FE”,“G”四个子
串反转后,合并后的结果字符串就是“GDCFEBA”。
最终,TROUGHBARS函数会输出这个结果字符串“GDCFEBA”。
这就是TROUGHBARS函数的工作原理。
由此可见,TROUGHBARS函数是一种非常有效的数学函数,它可以通
过处理参数,将输入的字符串变成一个新的字符串,这与普通的字符串变
换函数大不相同。
同时,由于TROUGHBARS函数的参数是可以自定义的,
因此它可以满足不同的应用场景。
例如,在字符串加密时,我们可以使用TROUGHBARS函数来变换明文,将其变成密文。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
验证函数 y arcsin x 满足微分方程 (1 x 2 ) y ( n 2 ) (2 n 1) xy( n 1 ) n 2 y ( n ) 0. ( n3 )
并依此求 y ( n ) ( 0). 解 y 1 1 x2 , 1 x 2 y 1. xy 1 x
(1 x 2 ) y ( n 2 ) (2 n 1) xy( n 1 ) n 2 y ( n ) 0. 可见函数 y arcsin x 满足所指方程. y (n 2 ) n 2 y (n ). 注意到 y (0) 0 和 y (0) 1 , n 2k 时, n 2k 1 时, y (n ) ( 0) 0; y (n ) ( 0) ( 2k 1) 2 ( 2k 3) 2 3 2 12 f ( 0) 就有 在上式中令 x 0, 得递推公式
2 3 C1 C54 5, C 5 C5 10. 5
y (5 ) e x (cos x 5 sin x 10 cos x 10 sin x 5 cos x sin x) 4e x (sin x cos x ).
例3 解
y x 2 sin x, ( x 2 ) 2 x,
求 三.
f (x) .
高阶导数的运算性质: n 阶可导. 则
设函数 u (x) 和 v (x ) 均 1. 2. 3.
ku( x ) ( n)
ku( n ) ( x). u ( n ) ( x ) v ( n ) ( x).
u( x) v( x) ( n )
乘积高阶导数的 Leibniz 公式:
数为 t 1 ( x ),
有 y (t ) 1 ( x ) , 用复合函数求导法, 并注
意利用反函数求导公式. 就有
dy dy dy dt ψ (t) dt . dx dx dt dx (t) dt
例1 解
x a cos t , dy dy dx dt
y (80 ) ( x 2 sin x) (80 ) x 2 sin x 80 2 x( cos x)
( x 2 6320) sin x 160 x cos x. 例4 例5 y f (arctgx), 其中 f (x ) 二阶可导. d2 y 求 . dx 2
d2 y y b sin t. 求 . 2 dx d2y b 2 . 2 3 dx a sin t
解
( 50)
e x 50 e 3 x C 50 e 6 x C 50 e 6
x 3 x 2 2 x 3 x
注意:利用萊布尼兹公式时要注意 u 与 v 的选取次序,否则会使计 算复杂。 例2 解 y e x cos x, C50 C55 1, 求 y (5 ) .
2 即在对数螺线上任意一点的切线 与向径的夹角等于 arctg 2
O
MP
P
x
§ 4 一. 高阶导数的概念 我们知道,加速度 a (t ) lim
高阶导数
v (t ) v(t 0 ) t t 0 t t0
因此加速度函数是速度函数的导数,从而是路程函数的导数的导数,这就 产生了高阶导数的概念。 定义: f ( x 0 ) lim f ( x 0 x) f ( x0 ) . x f ( n ) ( x) f ( n 1) ( x ) .
§3 参数变量函数的导数 平面曲线 C 一般的可表示为参变量方程形式: x ( t ), y ( t ) , t ( , ) 设 t t 0 对应曲线上的 P 点,如果 P 点由切线,那么切线斜率也可由 割线斜率去极限得到
Q P
x
y
割线 PQ 的斜率为
y ( t 0 t ) ( t 0 ) x ( t 0 t ) (t 0 ) 取极限得切线斜率 lim y t 0 (t 0 t ) (t 0 ) ( t 0 ) tg lim x 0 x lim (t 0 t ) ( t 0 ) (t 0 )
(3)
(3) 式表示在曲线 ( ) 上的点 M ( , ) 处切线 MT 与极轴 OX 轴的夹角 的正切,如图所示。 过点 M 的射线 OH 与切线 MT 的交角 的正切是 tan tan( ) tan tan 1 tan tan (4)
求 y (80 ) . ( x 2 ) 2, ( x 2 ) ( x 2 ) ( n ) 0; (sin x) (79 ) cos x, (sin x ) ( 78 ) sin x.
80 79 2( sin x) 2
(sin x) (80 ) sin x,
四.
参数方程所确定函数的高阶导数:
d dy d 2 y dt dx dx dx 2 dt 例6 x a cos t , dy b ctgt. dx a
(t ) (t ) (t ) (t ) (t ) (t ) . (t ) (t) 3
3. ex 4. 5 和 e kx 的高阶导数:
1 的高阶导数: x
2 15
多项式的高阶导数. Q( x ) 3 2 x Q ( 49 ) ( 0.235) .
2x 1 ,
18
求 Q ( 48) ( 0 ) 和
6
1 的高阶导数: ( x a)( x b)
为例,
x 2 , x 0, 7 分段函数在分段点的高阶导数:以函数 f ( x ) 2 x , x 0.
dy ( ( ) sin ) ( ) sin ( ) cos ( ) tan ( ) dx ( ( ) cos ) ( ) cos ( ) sin ( ) ( ) tan
y b sin t.
求
dy . dx
dx (b sin t}) b cot t dt ( aost ) a
若曲线 C 由极坐标 参量方程
( ) 表示,则可转化为一极角 为参数的
x cos ( ) cos y sin ( ) sin
2 (uv) (n) u (n) v (0) C1 u (n 1) v (1) Cn u (n 2) v (2) Ck u (n k) v (k) u (0) v n n
例1
设
y x 3 e x 求 y (50 )
利用萊布尼兹公式 , 取 u e x , v x 3 y
x 0
f ( x ) f ( x) , 注意区分符号 f ( x0 ) 和
f ( x0 ) .
二. 几个特殊函数的高阶导数:
1 2.
求幂函数 y x n 的各阶导数 正弦和余弦函数: 计算
sin x ( n) 、 cos x ( n) 、 sin kx( n) 、 cos kx( n)
2
两端求导
1 x 2 y
0,
即
(1 x 2 ) y xy 0. 对上式两端求 n 阶导数, 利用 Leibniz 公式, 有
2 (1 x 2 ) y ( n 2 ) C1 ( 2 x) y ( n 1) Cn ( n
t 0
于是得到下面结论 dy (t ) 结论:设函数 x (t ), y (t ) 可导且 (t ) 0 ,则 . dx (t ) 证 ( 法一 ) 用定义证明. (法二 ) 由 ( t ) 0, 恒有 ( t ) 0 或 (t ) 0. (t ) 严格单调. (这些事实的证明将在下一章给出.) 因此, (t ) 有反函数, 设反函
T H T
将(3)代入(4)得向径与切线夹角的正切
O
tan
( ) ( )
(5)
例 2 证明:对数螺线 e / 2 上所有点的切线与向径的夹角 为一常 量 证明 由(5),对每一个 都有
( ) e / 2 tan 2 ( ) 1 e / 2
