曲线曲面的插值与拟合方法(2次课
曲线曲面的插值与拟合方法次课共45页文档

11、用道德的示范来造就一个人,显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
45
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪Байду номын сангаас
28、知之者不如好之者,好之者不如乐之者。——孔子
插值拟合的原理和步骤

插值拟合的原理和步骤嘿,朋友们!今天咱来聊聊插值拟合这玩意儿,听起来是不是挺高深莫测的呀?其实啊,没那么玄乎!你就想想看,插值拟合就像是给数据搭积木!咱手里有一堆数据点,就好比是一堆形状各异的积木块。
而插值拟合呢,就是要把这些积木块巧妙地连接起来,组成一个好看又实用的模型。
比如说,咱有一些气温的数据,在不同时间点上的气温不一样。
那怎么才能知道中间那些时间点的气温大概是多少呢?这时候插值拟合就派上用场啦!它就像个神奇的魔法师,能在这些已知的数据点之间“填补”出合理的数值来。
那它具体是怎么做到的呢?这就好比是走钢丝,得小心翼翼地找到那个平衡点。
不同的插值拟合方法就像是不同的走钢丝技巧。
有的方法简单直接,就像大步流星地走过去;有的方法则细致入微,像是一小步一小步稳稳地挪。
咱常见的插值拟合方法有多项式插值啦,样条插值啦等等。
多项式插值呢,就像是用一条弯弯的曲线去尽量贴合那些数据点,让它们乖乖地待在曲线上。
样条插值呢,则更像是把数据点串起来的一条光滑丝带,既好看又实用。
那插值拟合有啥用呢?哎呀,用处可多啦!在科学研究中,它能帮助科学家们更好地理解数据背后的规律。
在工程领域,它能让工程师们更准确地设计出各种东西。
就好比建筑师盖房子,得先把地基打好,插值拟合就是那个帮他们打好地基的工具。
你想想,如果没有插值拟合,很多数据就只是孤立的点,很难看出个所以然来。
但有了它,这些点就像被施了魔法一样,变成了有意义的曲线、模型。
咱平时生活中其实也能看到插值拟合的影子呢!比如说天气预报,那可不是随便猜猜的,背后就有插值拟合的功劳。
它能根据已有的气象数据,推测出未来的天气情况。
这不是很神奇吗?总之呢,插值拟合就像是一把神奇的钥匙,能打开数据背后的神秘大门。
它让那些看似杂乱无章的数据变得有秩序、有意义。
所以啊,朋友们,可别小瞧了它哟!这玩意儿可厉害着呢!。
插值与拟合方法

插值与拟合方法在实际中,常常要处理由实验或测量所得到的一批离散数据.插值与拟合方法就是要通过这些数据去确定某一类已知函数的参数或寻找某个近似函数,使所得到的近似函数与已知数据有较高的拟合精度.插值问题:要求这个近似函数(曲线或曲面)经过所已知的所有数据点.通常插值方法一般用于数据较少的情况.数据拟合:不要求近似函数通过所有数据点,而是要求它能较好地反映数据的整体变化趋势。
共同点:插值与拟合都是根据实际中一组已知数据来构造一个能够反映数据变化规律的近似函数的方法,由于对近似要求的准则不同,因此二者在数学方法上有很大的差异.插值问题的一般提法:已知某函数)(x f y =(未知)的一组观测(或试验)数据),,2,1)(,(n i y x ii⋅⋅⋅=,要寻求一个函数)(x φ,使iiy x =)(φ),,2,1(n i ⋅⋅⋅=,则)()(x f x ≈φ.实际中,常常在不知道函数)(x f y =的具体表达式的情况下,对于i x x =有实验测量值iy y =),,2,1,0(n i ⋅⋅⋅=,寻求另一函数)(x φ使满足:)()(i i i x f y x ==φ),,2,1,0(n i ⋅⋅⋅=称此问题为插值问题,并称函数)(x φ为)(x f 的插值函数,nx x x x ,,,,21⋅⋅⋅称为插值节点,),,2,1,0()(n i y x ii⋅⋅⋅==φ称为插值条件,即)()(iiix f y x ==φ),,2,1,0(n i ⋅⋅⋅=,则)()(x f x ≈φ.(1) 拉格朗日(Lagrange )插值设函数)(x f y =在1+n 个相异点nx x x x ,,,,21⋅⋅⋅上的函数值为ny y y y ,,,,21⋅⋅⋅,要求一个次数不超过n 的代数多项式nnnx a x a x a a x P +⋅⋅⋅+++=221)(使在节点i x 上有),,2,1,0()(n i y x P ii n ⋅⋅⋅==成立,称之为n 次代数插值问题,)(x P n称为插值多项式.可以证明n 次代数插值是唯一的.事实上: 可以得到j n j n i i j in y x x xx x P j i ∑∏==⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛--=≠00)()( 当1=n 时,有二点一次(线性)插值多项式:101001011)(y x x x x y x x x x x P --+--=当n =2时,有三点二次(抛物线)插值多项式:2120210121012002010212))(())(())(())(())(())(()(y x x x x x x x x y x x x x x x x x y x x x x x x x x x P ----+----+----=(2)牛顿(Newton ) 插值牛顿插值的基本思想:由于)(x f y =关于二节点10,x x 的线性插值为)()()()()()()()()(00101000010101x x x x x f x f x p x x x x x f x f x f x p ---+=---+= 假设满足插值条件)2,1,0()()(2===i x p y x f iii的二次插值多项式一般形式为))(()()(1212x x x x c x x c c x p --+-+= 由插值条件可得⎪⎩⎪⎨⎧=--+-+=-+=)())(()()()()(21202202101011000x f x x x x c x x c c x f x x c c x f c 可以解出⎪⎪⎪⎩⎪⎪⎪⎨⎧------=--==020101121220101100)()()()()()(),(x x x x x f x f x x x f x f c x x x f x f c x f c所以))(()())(()()(10211020102x x x x c x p x x x x c x x c c x p --+=--+-+=类似的方法,可以得到三次插值多项式等,按这种思想可以得到一般的牛顿插值公式.函数的差商及其性质对于给定的函数)(x f ,用),,,(10n x x x f ⋅⋅⋅表示关于节点nx x x ,,,1⋅⋅⋅的n 阶差商,则有一阶差商:01011)()(),(x x x f x f x x f --=,121221)()(),(x x x f x f x x f --= 二阶差商:021021210),(),(),,(x x x x f x x f xx x f --=n 阶差商:0110211),,,(),,,(),,,(x x x x x f x x x f x x x f n n n n -⋅⋅⋅-⋅⋅⋅=⋅⋅⋅-差商有下列性质:(1)差商的分加性:∑∏=≠=-=⋅⋅⋅nk nk j j j kk n x xx f xx x f 0)(01)()(),,,(.(2)差商的对称性:在),,,(1nx x x f ⋅⋅⋅中任意调换jix x ,的次序其值不变.牛顿插值公式: 一次插值公式为))(,()()(01001x x x x f x f x p -+=二次插值公式为))()(,,()())()(,,())(,()()(1021011021001002x x x x x x x f x p x x x x x x x f x x x x f x f x p --+=--+-+=于是有一般的牛顿插值公式为)())()(,,,()()())()(,,,())()(,,())(,()()(11010111010102100100----⋅⋅⋅--⋅⋅⋅+=-⋅⋅⋅--⋅⋅⋅+⋅⋅⋅+--+-+=n n n n n n x x x x x x x x x f x p x x x x x x x x x f x x x x x x x f x x x x f x f x p可以证明:其余项为))(())()(,,,,()(11010n n n x x x x x x x x x x x x f x R --⋅⋅⋅--⋅⋅⋅=-实际上,牛顿插值公式是拉格朗日插值公式的一种变形,二者是等价的.另外还有著名的埃尔米特(Hermite )插值等.(3)样条函数插值方法样条,实质上就是由分段多项式光滑连接而成的函数,一般称为多项式样条.由于样条函数的特殊性质,决定了样条函数在实际中有着重要的应用.样条函数的一般概念定义 设给定区间],[b a 的一个分划b x x x a n=<⋅⋅⋅<<=∆1:,如果函数)(x s 满足条件:(1) 在每个子区间),,2,1](,[1n i x x ii ⋅⋅⋅=-上是k 次多项式; (2) )(x s 及直到k -1阶的导数在],[b a 上连续.则称)(x s 是关于分划△的一个k 次多项式样条函数,nx x x ,,,1⋅⋅⋅称为样条节点,121,,,-⋅⋅⋅n x x x 称为内节点,nx x ,0称为边界节点,这类样条函数的全体记作),(k S P∆,称为k 次样条函数空间.若),()(k S x s P∆∈,则)(x s 是关于分划△的k 次多项式样条函数.k 次多项式样条函数的一般形式为∑∑=-=+-+=ki n j k j jii k x x k i x x s 011)(!!)(βα其中),,1,0(k i i=α和)1,,2,1(-=n j jβ均为任意常数,而)1,,2,1(,0,)()(-=⎪⎩⎪⎨⎧<≥-=-+n j x x x x x x x x jj kj kj在实际中最常用的是2=k 和3的情况,即为二次样条函数和三次样条函数. 二次样条函数:对于],[b a 上的分划b x x x a n=<⋅⋅⋅<<=∆1:,则)2,()(!2!2)(11222102∆βαααP n j j jS x x x x x s ∈-+++=∑-=+其中)1,2,1(,0,)()(22-=⎪⎩⎪⎨⎧<≥-=-+n j x x x x x x x x j j j j . 三次样条函数:对于],[b a 上的分划b x x xa n =<⋅⋅⋅<<=∆10:,则)3,()(!3!3!2)(1133322103∆βααααP n j j jS x x x x x x s ∈-++++=∑-=+其中)1,2,1(,0,)()(33-=⎪⎩⎪⎨⎧<≥-=-+n j x x x x x x x x jjj j .1 二次样条函数插值)2,()(2∆∈P S x s 中含有2+n 个待定常数,故应需要2+n 个插值条件,因此,二次样条插值问题可分为两类:问题(1):已知插值节点ix 和相应的函数值),,2,1,0(n i y i⋅⋅⋅=,以及端点0x (或n x )处的导数值0'y (或ny '),求)2,()(2∆∈PS x s 使得⎩⎨⎧'=''='⋅⋅⋅==))(()(),,2,1,0()(20022n n i i y x s y x s n i y x s 或(5.1)问题(2):已知插值节点ix 和相应的导数值),,2,1,0(n i y i⋅⋅⋅=',以及端点0x (或n x )处的函数值0y (或ny ),求)2,()(2∆∈P S x s 使得⎩⎨⎧==⋅⋅⋅='='))(()(),,2,1,0()(20022n n i i y x s y x s n i y x s 或(5.2)事实上,可以证明这两类插值问题都是唯一可解的.对于问题(1),由条件(5.1)⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧'=+='==-+++==++==++=∑-=00210211222102121211112020201002)(,,3,2,)(2121)(21)(21)(y x x s n j y x x x x x s yx x x s y x x x s j j i i j i jj j ααβααααααααα 引入记号T n ),,,,,(11210-=ββααα X 为未知向量,T nn y y y y ),,,,(10'= C 为已知向量, ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---=-0010)(21)(21211)(212110211211021212212222211200x x x x x x x x x x x x x x x n n n n n A 于是,问题转化为求方程组C AX =的解Tn ),,,,,(1121-=ββααα X 的问题,即可得到二次样条函数的)(2x s 的表达式.对于问题(2)的情况类似.2.三次样条函数插值由于)3,()(3∆∈P S x s 中含有3+n 个待定系数,故应需要3+n 个插值条件,因此可将三次样条插值问题分为三类: 问题(1):已知插值节点jx 和相应的函数值),,2,1,0(n j y j⋅⋅⋅=,以及两个端点0x ,n x 处的导数值0'y ,ny ',求)3,()(3∆∈PS x s 使满足条件⎪⎩⎪⎨⎧='='⋅⋅⋅==),0()(),,1,0()(33n j y x s n j y x s j j j j(5.3)问题(2):已知插值节点jx 和相应的函数值),,2,1,0(n j y j⋅⋅⋅=,以及两个端点0x ,nx 处的二阶导数值0y '',n y '',求)3,()(3∆∈PS x s 使满足条件⎪⎩⎪⎨⎧=''=''⋅⋅⋅==),0()(),,1,0()(33n j y x s n j y x s j j j j(5.4)问题(3):类似地,求)3,()(3∆∈PSx s 使满足条件⎪⎩⎪⎨⎧=+=-==)2,1,0)(0()0(),,1,0()(0)(3)(33k x s x s n j y x s k n k j j(5.5)这三类插值问题的条件都是3+n 个,可以证明其解都是唯一的〔8〕.一般的求解方法可以仿照二次样条的情况处理方法,在这里给出一种更简单的方法.仅依问题(1)为例,问题(2)和问题(3)的情况类似处理.由于在)3,()(3∆PS x s ∈区间],[b a 上是一个分段光滑,且具有二阶连续导数的三次多项式,则在子区间],[1+j jx x 上)(3x s ''是线性函数,记),,,1,0)((3n j x s d jj =''=为待定常数.由拉格朗日插值公式可得nj x x h h x x d h x x d x s j j j jj j jj j ,,1,0,,)(1113=-=-+-=''+++显然jjj h d dx s -='''+13)(在],[1+j jx x上为常数.于是在],[1+j j x x 上有31233)(6)(2))(()(j jjj j j j j j x x h d d x x d x x x s y x s --+-+-'+=+(5.6)则当1+=j x x 时,由(5.6)式和问题(1)的条件得121231362)()(+++=-++'+=j j jj j j j j j j y h d d h d h x s y x s故可解得)2(6)(113+++--='j j j jjj j d d h h y y x s(5.7)将(5.7)式代入(5.6)式得)1,,1,0](,[,)(6)(2)()2(6)(1312113-=∈--+-+-⎥⎥⎦⎤⎢⎢⎣⎡+--+=++++n j x x x x x h d d x x d x x d d h h y y y x s j j j jj j j jj j j j j j j j(5.8) 在],[1j j x x-上同样的有),,2,1](,[,)(6)(2)()2(6)(131112111111113n j x x x x x h d d x x d x x d d h h y y y x s j j j j j j j j j j j j j j j j =∈--+-+-⎥⎥⎦⎤⎢⎢⎣⎡+--+=------------(5.9) 根据)(3x s的一阶导数连续性,由(5.9)式得)()2(6)0(311113j j j j j j j j x s d d h h y y x s '=++-=-'---- 结合(5.7)式整理得⎪⎪⎭⎫ ⎝⎛---+=++++--+-+----11111111162j j j j j j j j j j j j j j j j j h y y h y y h h d h h h d d h h h 引入记号⎪⎪⎭⎫ ⎝⎛---+=+=--+--111116,j j j j j j j j j j j j j h y y h y y h h c h h h a ,111--+=-j j j j h h h a .则)1,,2,1(,2)1(11-==++-+-n j c d a d d a j j j j j j(5.10)再由边界条件:nny x s y x s '=''=')(,)(33得⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛--'=+⎪⎪⎭⎫ ⎝⎛'--=+----111100010106262n n n n n n n h y y y h d d y h y y h d d(5.11)联立(5.10),(5.11)式得方程组C D A =⋅(5.12)其中⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---=----2121212112112200n n n n a a a a a aA ,⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=-n n d d d d 110 D ,⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--'⎪⎪⎭⎫ ⎝⎛'--=----111110001066n n n n n n hy y y h c c y h y y h C 由方程组(6.12)可以唯一解出),,1,0(n j d j=,代入(5.8)式就可以得三次样条函数)(3x s 的表达式.B样条函数插值方法磨光函数实际中的许多问题,往往是既要求近似函数(曲线或曲面)有足够的光滑性,又要求与实际函数有相同的凹凸性,一般插值函数和样条函数都不具有这种性质.如果对于一个特殊函数进行磨光处理生成磨光函数(多项式),则用磨光函数构造出样条函数作为插值函数,既有足够的光滑性,而且也具有较好的保凹凸性,因此磨光函数在一维插值(曲线)和二维插值(曲面)问题中有着广泛的应用.由积分理论可知,对于可积函数通过积分会提高函数的光滑度,因此,我们可以利用积分方法对函数进行磨光处理.定义 若)(x f 为可积函数,对于0>h ,则称积分⎰+-=22,1)(1)(hx h x h dt t f h x f为)(x f 的一次磨光函数,h 称为磨光宽度.同样的,可以定义)(x f 的k 次磨光函数为)1()(1)(22,1,>=⎰+--k dt t f h x f hx h x h k h k事实上,磨光函数)(,x f h k 比)(x f 的光滑程度要高,且当磨光宽度h 很小时)(,x f h k 很接近于)(x f .等距B样条函数对于任意的函数)(x f ,定义其步长为1的中心差分算子δ如下:⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=2121)(x f x f x f δ在此取0)(+=x x f ,则002121+++⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=x x x δ是一个单位方波函数(如图5-1),记0)(+=Ωx x δ.并取1=h ,对)(0x Ω进行一次磨光得++++-+++-+++--+-+=-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+==⎰⎰⎰⎰)1(2)1(2121)()(11212100212101x x x dt t dt t dt t t dt t x x xx x x x x x ΩΩ显然)(1x Ω是连续的(如图5-2).)(1x Ωo1-1/2 0 1/2 x -1 0 1 x 图5-1图5-2类似地可得到k 次磨光函数为kk j jk j k j k x k C x ++=+⎪⎭⎫ ⎝⎛-++-=Ω∑21!)1()(11 实际上,可以证明:)(x kΩ是分段k 次多项式,且具有1-k 阶连续导数,其k 阶导数有2+k个间断点,记为)1,,2,1,0(21+⋅⋅⋅=+-=k j k j x j.从而可知)(x kΩ是对应于分划+∞<<⋅⋅⋅<<<-∞∆+110:k x x x 的k 次多项式样条函数,称之为基本样条函数,简称为k 次B样条.由于样条节点为)1,,2,1,0(21+⋅⋅⋅=+-=k j k j xj是等距的,故)(x k Ω又称为k 次等距B样条函数.对于任意函数)(x f 的k 次磨光函数,由归纳法可以得到 [4,8] :⎪⎭⎫⎝⎛+≤≤--Ω=⎰∞+∞--22)()(1)(1,h x t h x dt t f htx h x f k h k 特别地,当1)(=x f 时,有1)(11⎰+∞∞--=-dt htx hk Ω,从而1)(⎰+∞∞-=dx x k Ω,且当k ≥1时有递推关系⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-Ω⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛+Ω⎪⎭⎫ ⎝⎛++=Ω--212121211)(11x x k x k x k x k k k一维等距B样条函数插值等距B样条函数与通常的样条如下的关系: 定理设有区间],[b a 的均匀分划nab h n j jh x x j -=⋅⋅⋅=+=),,,1,0(:0∆,则对任意 k 次样条函数),()(k S x S p k ∆∈都可以表示为B样条函数族1021-=-=⎭⎬⎫⎩⎨⎧⎪⎭⎫⎝⎛+---n j k j k k j h x x Ω的线性组合[14].根据定理 5.1,如果已知曲线上一组点()jjy x ,,其中),,1,0,0(0n j h jh x x j⋅⋅⋅=>+=,则可以构造出一条样条磨光曲线(即为B样条函数族的线性组合)⎪⎭⎫⎝⎛--=∑--=j h x x c x S n kj k j k 01)(Ω 其中)1,,1,(-⋅⋅⋅+--=n k k j c j为待定常数.用它来逼近曲线,既有较好的精度,又有良好的保凸性.实际中,最常用的是3=k 的情况,即一般形式为⎪⎭⎫ ⎝⎛--=∑+-=j h x x c x S n j j 01133)(Ω 其中3+n 个待定系数)1,,0,1(+⋅⋅⋅-=n j c j可以由三类插值条件确定.由插值条件(5.3)得()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧'=-'='==-='=-'='∑∑∑+-=+-=+-=n n j j n i n j j i n j j y j n c h x S ni y j i c x S y j c h x S 113311330113031)(,,1,0,)(1)(ΩΩΩ(5.13)注意到)(3x Ω的局部非零性及其函数值:61)1(,32)0(33=±=ΩΩ,当2≥x 时0)(3=x Ω;且由)21()21()(223--+='x x x ΩΩΩ知,21)1(,0)0(33=±'='ΩΩ,当2≥x 时0)(3='x Ω.则(5.13)中的每一个方程中只有三个非零系数,具体的为⎪⎩⎪⎨⎧'=+-==++'=+-+-+--n n n i i i i y h c c n i y c c c y h c c 2,,1,0,6421111011(5.14)由方程组(5.14)容易求解出)1,,0,1(+⋅⋅⋅-=n j c j,即可得到三次样条函数)(3x S 表达式.类似地,由插值条件(5.4)得待定系数的)1,,0,1(+⋅⋅⋅-=n j c j所满足的方程组为⎪⎩⎪⎨⎧''=+-==++''=+-+-+--nn n n i i i i y h c c c n i y c c c y h c c c 21111021012,,1,0,642(5.15)由插值条件(5.5)得待定系数的)1,,0,1(+⋅⋅⋅-=n j cj所满足的方程组为⎪⎪⎩⎪⎪⎨⎧==++=-+---=-++-=-+-+-+-+--+--+--ni y c c c c c c c c c c c c c c c c c c c i i i i n n n n n n n n ,,1,0,640)()(2)(0)(0)(0)()(4)(1111011111111011(5.16)方程组(5.15),(5.16)也都是容易求解的.注:上述等距B样条插值公式也适用于近似等距的情形,但在端点0x 和n x 处误差可能较大,实际应用时,为了提高在端点0x 和nx 处的精度,可以适当向左右延拓几个节点.二维等距B样条函数插值设有空间曲面),(y x f z =(未知),如果已知二维等距节点()()τj y ih x y x ji++=0,,)0,(>τh 上的值为),,2,1,0;,,2,1,0(m j n i z ij⋅⋅⋅=⋅⋅⋅=,则相应的B样条磨光曲面的一般形式为⎪⎭⎫ ⎝⎛--⎪⎭⎫⎝⎛--=∑∑--=--=j y y i h x x c y x s l m lj k ij n ki τΩΩ0011),( 其中),,2,1,0;,,2,1,0(m j n i c ij⋅⋅⋅=⋅⋅⋅=为待定常数,l k ,可以取不同值,常用的也是2,=l k 和3的情形.这是一种具有良好保凸性的光滑曲面(函数),在工程设计中是常用的,但只能使用于均匀分划或近似均匀分划的情况.(4) 最小二乘拟合方法最小二乘拟合方法的思想:由于一般插值问题并不总是可解的(即当插值条件多于待定系数的个数时,其问题无解),同时,问题的插值条件本身一般是近似的,为此,只要求在节点上近似地满足插值条件,并使它们的整体误差最小,这就是最小二乘拟合法.最小二乘拟合方法可以分为线性最小二乘拟合方法和非线性最小二乘拟合方法.线性最小二乘拟合方法设{}m k kx 0)(=φ是一个线性无关的函数系,则称线性组合∑==mk k k x a x 0)()(φφ为广义多项式.如三角多项式:∑∑==+=mk k mk kkx b kx ax 0sin cos )(φ.设由给定的一组测量数据),(iiy x 和一组正数),,2,1(n i w i⋅⋅⋅=,求一个广义多项式∑==mk k k x a x 0)()(φφ使得目标函数[]21)(∑=-=ni i i i y x w S φ(5.17)达到最小,则称函数)(x φ为数据),,2,1)(,(n i y x ii⋅⋅⋅=关于权系数),,2,1(n i w i⋅⋅⋅=的最小二乘拟合函数,由于)(x φ关于待定系数ia 是线性的,故此问题又称为线性最小二乘问题. 注意:这里{}m k kx 0)(=φ可根据实际来选择,权系数iw 的选取更是灵活多变的,有时可选取1=i w ,或nw i 1=,对于nw i1=,则相应问题称为均方差的极小化问题.最小二乘拟合函数的求解要使最小二乘问题的目标函数(5.17)达到最小,则由多元函数取得极值的必要条件得),,2,1,0(0m k a Sk==∂∂ 即),,2,1,0(0)()(10m k x y x a w i k ni i m k i k k i ⋅⋅⋅⋅==⎥⎦⎤⎢⎣⎡-∑∑==φφ 亦即),,2,1,0()()()(001m k x y w a x x w n i i k i i j mj n i i k i j i ⋅⋅⋅⋅==⎥⎦⎤⎢⎣⎡∑∑∑===φφφ(5.18)是未知量为ma a a a ,,,,21⋅⋅⋅的线性方程组,称(5.18)式为正规方程组.实际中可适当选择函数系{}m k kx 0)(=φ,由正规方程组解出ma a a a ,,,,210⋅⋅⋅,于是可得最小二乘拟合函数∑==mk kk x a x 0)()(φφ.一般线性最小二乘拟合方法将上面一元函数的最小二乘拟合问题推广到多元函数,即为多维线性最小二乘拟合问题.假设已知多元函数),,,(21nx x x f y ⋅⋅⋅=的一组测量数据);,,,(21iniiiy x x x ⋅⋅⋅),,2,1(m i ⋅⋅⋅=和一组线性无关的函数系{}N k nk x x x 021),,,(=⋅⋅⋅φ,求函数∑=⋅⋅⋅=⋅⋅⋅Nk n k k n x x x a x xx 02121),,,(),,,(φφ对于一组正数mw w w ,,,21⋅⋅⋅,使得目标函数[]2121),,,(∑=⋅⋅⋅-=mi ni i i i i x x x y w S φ达到最小.其中待定系数N a a a a,,,,210⋅⋅⋅由正规方程组),,2,1,0(),(),(0N k y a Nj k j k j⋅⋅⋅==∑=φφφ确定,此处ini i i k mi i k ni i i k mi ni i i j i k j y x x x w y x x x x x x w ),,,(),(),,,(),,,(),(21121121⋅⋅⋅=⋅⋅⋅⋅⋅⋅=∑∑==φφφφφφ注:上面的函数φ关于ia 都是线性的,这就是线性最小二乘拟合问题,对于这类问题的正规组总是容易求解的.如果φ关于ia 是非线性的,则相应的问题称为非线性最小二乘拟合问题.非线性最小二乘拟合方法假设已知多元函数),,,(21nx x x f y ⋅⋅⋅=的一组测量数据);,,,(21iniiiy x x x ⋅⋅⋅),,2,1(m i ⋅⋅⋅=,要求一个关于参数),,2,1,0(N j a j⋅⋅⋅=是非线性的函数),,,;,,,(1021Nn a a a x x x ⋅⋅⋅⋅⋅⋅=φφ对一组正数mw w w ,,,21⋅⋅⋅使得目标函数[]21102110),,,;,,,(),,,(∑=⋅⋅⋅⋅⋅⋅-=⋅⋅⋅mi N ni i i i i N a a a x x x y w a a a S φ达到最小,则称之为非线性最小二乘问题.这类问题属于无约束的最优化问题,一般问题的求解是很复杂的,通常情况下,可以采用共轭梯度法、最速下降法、拟牛顿法和变尺度法等方法求解.实例:黄河小浪底调水调沙问题问题的提出2004年6月至7月黄河进行了第三次调水调沙试验,特别是首次由小浪底、三门峡和万家寨三大水库联合调度,采用接力式防洪预泄放水,形成人造洪峰进行调沙试验获得成功.整个试验期为20多天,小浪底从6月19日开始预泄放水,直到7月13日恢复正常供水结束.小浪底水利工程按设计拦沙量为75.5亿立方米,在这之前,小浪底共积泥沙达14.15亿吨.这次调水调试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪,在小浪底形成人造洪峰,冲刷小浪底库区沉积的泥沙.在小浪底水库开闸泄洪以后,从6月27日开始三门峡水库和万家寨水库陆续开闸放水,人造洪峰于29日先后到达小浪底,7月3日达到最大流量2700立方米/每秒,使小浪底水库的排沙量也不断地增加.下面是由小浪底观测站从6月29日到7月10日检测到的试验数据:表5-1: 试验观测数据单位:水流为立方米/每秒,含沙量为公斤/立方米·84··85·注:以上数据主要是根据媒体公开报道的结果整理而成的,不一定与真实数据完全相符.现在,根据试验数据建立数学模型研究下面的问题:(1) 给出估算任意时刻的排沙量及总排沙量的方法;(2) 确定排沙量与水流量的变化关系.模型的建立与求解对于问题(1),根据所给问题的试验数据,要计算任意时刻的排沙量,就要确定出排沙量随时间变化的规律,可以通过插值来实现.考虑到实际中排沙量应该是随时间连续变化的,为了提高精度,我们采用三次B样条函数进行插值.下面构造三次B样条函数)(x S y =.由试验数据,时间是每天的早8点和晚8点,间隔都是12个小时,共24个点)24,,2,1(⋅⋅⋅=i t i.为了计算方便,令)23,,,1,0(122128⋅⋅⋅=+⎥⎦⎤⎢⎣⎡⋅+-=i i t x i i(5.19)则it 对应于)23,,1,0(1⋅⋅⋅=+=i i x i.于是以)23,,1,0(⋅⋅⋅=i x i为插值节点(等距),步长1=h .其相应的排沙量为)23,,1,0(⋅⋅⋅=i y i 对应关系如下表:·86·表5-2: 插值数据对应关系单位:排沙量为公斤函数)(x S y =所满足的条件为 (1)23,,1,0,)(⋅⋅⋅==i y x S ii;(2) 3500)(,56400)(2223222323231212-=--≈'='=--≈'='x x y y x S y x xy yx S y .取)(x S 的三次B样条函数一般形式为∑-=⎪⎭⎫⎝⎛--=24103)(j j j h x x c x S Ω·87·其中)24,,1,0,1(⋅⋅⋅-=j cj为待定常数,1=h .在这里⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<<+-+-≤+-=Ω2,021,342611,3221)(23233x x x x x x x x x且易知⎪⎪⎪⎩⎪⎪⎪⎨⎧≥±===Ω2,01,610,32)(3x x x x和⎪⎪⎩⎪⎪⎨⎧≥±===Ω'2,01,210,0)(3x x x x 根据B样条函数的性质,)(x S ''在[]23,x x 上连续,则有()∑-=--'='='2413)(j jj xx c x S y Ω由插值条件(1),(2)可得到下列方程组()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧'=-'=''=-'='⋅⋅⋅==-=∑∑∑-=-=-=23241323024130241323)()(23,,1,0,)(y j c x S y j c x S i y j i c x S j j j j i j j i ΩΩΩ 即⎪⎩⎪⎨⎧'=+-'=+-⋅⋅⋅==++-+-23242311112223,,1,0,64y c c y c c i y c c c i i i i 将232324112,2y c c y c c '+='-=-代入前24个方程中的第一个和最后一个,便可得到方程组F AC =,其中·88·⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⋅⋅⋅⋅⋅⋅=⨯232102424,421410141014124c c c c C A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡'-'+=3400048000684000458400266626232322100 y y y y y y F显然A 为满秩阵,方程组F AC =一定有解,用消元法求解可得问题的解为56044.39830=c , 4117111.2031=c , 2159510.7882=c , 9189845.6433=c ,1203106.6364=c , 8239727.8115=c ,8249182.1166=c , 1263543.7217=c ,9287842.9988=c , 2302284.2839=c ,4317419.86810=c , 1304836.24311=c ,3307635.15912=c ,6305423.11913=c ,2270672.36214=c ,4240287.43115=c ,0154177.91216=c ,4103000.92017=c ,99818.406218=c , 43725.454719=c ,49279.775020=c ,32155.445221=c , 2098.444222=c ,7450.777923=c ,-450.777924311.2034,2232324011='+=='-=-y c c y c c . 将)24,,1,0,1(⋅⋅⋅-=j c j代入()∑-=--==24131)(j jj x c x S y Ω(5.20)即得排沙量的变化规律.由(5.19)和(5.20)式可得到第i 时间段(12小时为一段)内,任意时刻]12,0[∈t 的排沙量.则总的排沙量为()dt j t c dx x S Y j j⎰∑⎰-=--Ω==284824132411)(经计算可得1110844.1⨯=Y 吨,即从6月29日至7月10日小浪底水库排沙总量大约为1.844亿吨,此与媒体报道的排沙量基本相符.对于问题(2),研究排沙量与水量的关系,从试验数据可以看出,开始排沙量是随着水流量的增加而增长,而后是随着水流量的减少而减少.显然,变化规律并非是线性的关系,为此,我们问题分为两部分,从开始水流量增加到最大值2720立方米/每秒(即增长的过程)为一段,从水流量的最大值到结束为第二段,分别来研究水流量与排沙量的关系.具体数据如表5-3和5-4.表5-3: 第一阶段试验观测数据 单位:水流为立方米/每秒,含沙量为公斤/立方米表5-4: 第二阶段试验观测数据单位:水流为立方米/每秒,含沙量为公斤/立方米对于第一阶段,由表5-3用Matlab作图(如图5-3)可以看出其变化趋势,我们用多项式作最小二乘拟合.·90··91·图5-3设拟合函数为∑==mk kk x a x 1)(φ确定待定常数),,1,0(m k ak=使得211111102])([∑∑∑===⎥⎦⎤⎢⎣⎡-=-=i i i m k k i k i i y x a y x S φ有最小值.于是可以得到正规方程组为m k x y a x mj i k i i j i j k i ,,1,0,0111111 ==⎪⎭⎫⎝⎛∑∑∑===+ 当3=m 时,即取三次多项式拟合,则3,2,1,0,1113111321112111110111==⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛∑∑∑∑∑==+=+=+=k x y a x a x a x a x i k i i i k i i k i i k i i k i求解可得73321108423.1,103172.1,3.1784,-2492.9318--⨯=⨯-===a a a a .于是可得拟合多项式为332213)(x a x a x a a x +++=φ,最小误差为847.72=S ,拟合效果如图所示.·92·图:三次拟合效果,带*号的为拟合曲线.类似地,当4=m 时,即取四次多项式拟合,则正规方程组为4,3,2,1,0111411143111321112111110111==⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛∑∑∑∑∑∑==+=+=+=+=k x y a x a x a x a x a x i ki i i k i i k i i k i i k i i k i求解可得104633210109312.1,1094.1,102626.7,12.0624,-7434.6557---⨯-=⨯=⨯-===a a a a a 于是可得拟合多项式为443322104)(x a x a x a x a a x ++++=φ,最小误差为102.66=S ,拟合效果如图5-5所示.图5-5:四次拟合效果,带*号的为拟合曲线.从上面的三次多项式拟合和四次多项拟合效果来看,差别不大.基本可以看出排沙量与水流量的关系.图5-6:第二段三·93··94· 次多项式拟合效果对于第二阶段,由表5-4可以类似地处理.我们用线性最小二乘法作三次和四多项式拟合.拟合效果如图5-6和5-7所示,最小误差分别为5.459=S 和1.236=S . 从拟合效果来看,显然四次多项式拟合要比三次多项式拟合好的多.图5-7:第二段四次多项式拟合效果。
曲线拟合和插值
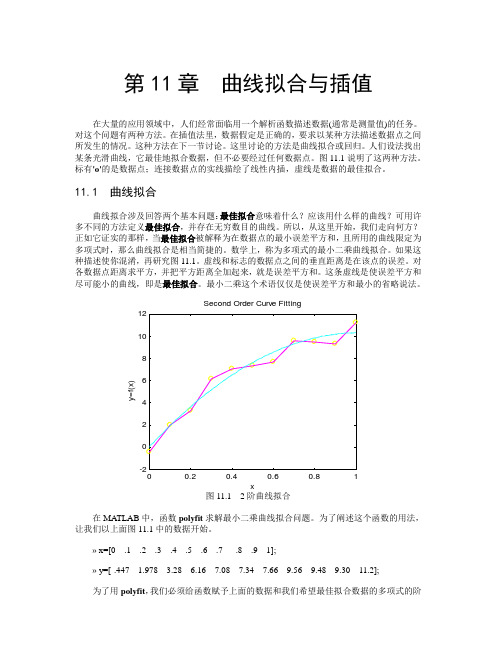
第11章曲线拟合与插值在大量的应用领域中,人们经常面临用一个解析函数描述数据(通常是测量值)的任务。
对这个问题有两种方法。
在插值法里,数据假定是正确的,要求以某种方法描述数据点之间所发生的情况。
这种方法在下一节讨论。
这里讨论的方法是曲线拟合或回归。
人们设法找出某条光滑曲线,它最佳地拟合数据,但不必要经过任何数据点。
图11.1说明了这两种方法。
标有'o'的是数据点;连接数据点的实线描绘了线性内插,虚线是数据的最佳拟合。
11.1 曲线拟合曲线拟合涉及回答两个基本问题:最佳拟合意味着什么?应该用什么样的曲线?可用许多不同的方法定义最佳拟合,并存在无穷数目的曲线。
所以,从这里开始,我们走向何方?正如它证实的那样,当最佳拟合被解释为在数据点的最小误差平方和,且所用的曲线限定为多项式时,那么曲线拟合是相当简捷的。
数学上,称为多项式的最小二乘曲线拟合。
如果这种描述使你混淆,再研究图11.1。
虚线和标志的数据点之间的垂直距离是在该点的误差。
对各数据点距离求平方,并把平方距离全加起来,就是误差平方和。
这条虚线是使误差平方和尽可能小的曲线,即是最佳拟合。
最小二乘这个术语仅仅是使误差平方和最小的省略说法。
图11.1 2阶曲线拟合在MA TLAB中,函数polyfit求解最小二乘曲线拟合问题。
为了阐述这个函数的用法,让我们以上面图11.1中的数据开始。
» x=[0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1];» y=[-.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];为了用polyfit,我们必须给函数赋予上面的数据和我们希望最佳拟合数据的多项式的阶次或度。
如果我们选择n=1作为阶次,得到最简单的线性近似。
通常称为线性回归。
相反,如果我们选择n=2作为阶次,得到一个2阶多项式。
现在,我们选择一个2阶多项式。
第四章插值和曲线拟合

在实际问题和科学实验中所遇到的函数y=f(x),往往
没有解析表达式 , 只能根据试验观察或其它方法提供一
系列点的函数值; 有时尽管可以写出表达式,但是比较
复杂, 直接使用它感到不方便。我们经常需要利用已知
的数据去寻求某个简单的函数φ (x)来逼近f(x),即用φ (x)
作为f(x)的近似表达式。本章的插值法和曲线拟合就是
φ (xi) = yi ,
插值法的几何意义
插值法的几何意义就是通过n+1个点: (xi,yi) (i=0,1,2,…,n) 作一条近似曲线y= φ (x) 代替y=f(x)。如下图所示。 y=f(x) (xn,yn) y= φ (x) y
(x1,y1) (x0,y0) (x2,y2)
(xn-1,yn-1)
三、n次拉格朗日插值
仿照P2 (x)的构造方法,可得出 Pn(x)=L0(x)y0+L1(x)y1+…+Ln(x)yn 其中 L0(x)=[(x-x1)(x-x2)…(x-xn)]/ [(x0-x1)(x0-x2)…(x0-xn)] Lk(x)= [(x-x0)…(x-xk-1)(x-xk+1) …(x-xn)] /[(xk-x0)…(xk-xk-1)(xk-xk+1) …(xk-xn)] ( k = 0, 1, …, n ) 这就是n次拉格朗日插值多项式。 也可写为 n n n x x k P ( x ) L ( x ) y y n i i i x x i 0 i 0 k 0 , k i i 或 k
线性插值举例
例 解 或 已知 1001/2 =10,1211/2 =11 求 1151/2 P1(x) = y0+(y1-y0)/(x1-x0)*(x-x0) P1(115) = 10+(11-10)/(121-100)*(115-100)
数学建模插值法与曲线拟合讲课

插值法的matlab实现—一维插值
命令:interp1(x0,y0,x,’method’) 其中:x0:插值节点;
y0:插值节点处的函数值; x:要计算函数值的点;
method:
l i n e a r :分段线性插值; c u b i c :分段三次埃尔米特插值; s p l i n e :三次样条插值。
z4
8
686
8
8
x 157.5 107.5 77 81 162 162 117.5
y -6.5 -81 3 56.5 -66.5 84 -33.5
z9
9
88
94
9
水深和流速的问题
在水文数据测量中,不同水深的流速是不同的. 水文数据的测量 时天天进行的,为了减少测量的工作,希望得到确定的水深和水 流之间的关系. 为此测量了一系列不同水深和流速值. 下表给出了 对某河流的测量数据,其中水深和流速根据适当的单位进行了规 范化,共10个值.
插值与拟合的不同点
插值: 过节点; ; 拟合: 不过点, 整体近似;
插值法
拉格朗日插值 牛顿插值 三次埃尔米特插值法 分段线性插值 分段三次埃尔米特插值法 三次样条插值
1、 拉格朗日插值公式
(1)定义
对给定的n+1个节点x0 , x1,x2,…,xn及对应的函数值y0 , y1,y2,…,yn, 构造一个n次插值多项式:
f(x)=1/(1+x2) , 但对于3.63≤∣x∣≤1的x,Pn(x)严重发散。 用图形分析问题。
for n=10:2:20
%从10等份到20等份
x0=[-5:10/n:5]; %插值节点
y0=1./(1+x0.^2); %插值节点处的精确函数值
曲线拟合与插值

1、曲线拟合在许多应用领域中,人们经常需要从一系列已知离散点上的数据集[(x1,y1),(x2,y2)],…(x n,y n)]得到一个解析函数y=f (x)。
得到的解析函数f(x)应当在原离散点x i上尽可能接近给定的y i的值,这一过程称为曲线拟合。
最常用的曲线拟合是最小二乘法曲线拟合。
似合结果可使误差的平方和最小,MATLAB提供的函数polyfit,根据给定的自变量数组x和函数数组y,按照拟合的阶数要求自动求解满足最小二乘意义的一阶或高阶解析函数f(x),使用很方便。
为了说明这个问题,我们取以下函数为例:2-y⨯=25.0xx=0:0.1:1;for i=1:length(x);y(i)=0.5-2*x(i)^2;end将y值进行一定的修改,输入如下的程序y=[0.52 0.45 0.4 0.35 0.18 0.02 -0.25 -0.4 -0.81 -1.1 -1.5]m=1;fxy1=polyfit(x,y,m) %获得拟合的多项式系数,存储在fxy1m=2;fxy2=polyfit(x,y,m)y1=poly val(fxy1,x) %多项式求值,x为输入值,y1为作图使用。
此处为了画出拟合之后的曲线,是运用了离散点的形式绘图,也可以直接使用函数形式来画图,与未拟合的离散点对比。
指令为:fun1=poly2sym(fxy1);ezplot(fun1,[x(1),x(2)]);y2=polyval(fxy2,x)plot(x,y,'o',x,y1,'k:',x,y2,'k')2、插值运算与曲线拟合不同,插值运算不是试图找出适合于所有自变量数组x的全局最优拟合函数Y=f(x〕,而是要找到一个解析函数连接自变量相邻的两个点(xi,xi十1),由此还可以找到两点间的数值。
根据自变量的维数不同,插值方法可以分为一维插值y=f(x)和二维插值z=f(x,y)等。
数学实验8-曲线拟合及插值

23
a =1.0e+006 *
-0.00000000000014
0.00000000107892 -0.00000304878595
0.00381927346813
-1.79012132225427
仿真结果表明, 人口增加的模型用多项式拟合能 比较准确地反映人口自然增长的规律,对长期预 测具有指导意义。
8
7 0 2 4 6 8 10 12 14 16 18 20
The length of the label is
L= 26.3809 (m)
% prog45.m This program is to fit the data by polynomial %
format long t=linspace(0,20,21); x=linspace(0,20,100); P=[9.01,8.96,7.96,7.97,8.02,9.05,10.13,11.18,12.26,13.2 8,13.32,12.61,11.29,10.22,9.15,7.90,7.95,8.86,9.81,10.8 0,10.93]; [a,s]=polyfit(t,P,12); yy=polyval(a,x); plot(x,yy,'r*--',t,P,'b+-'); L=0; for i=2:100 L=L+sqrt((x(i)-x(i-1))^2+(yy(i)-yy(i-1))^2); end disp('The length of the label is L=');disp(L);
实验13 人口数量预测模型实验
实验目的
1、学会用MATLAB软件 进行数据拟合 2、掌握在最小二乘意 义下数据拟合的理论和 方法. 3、通过对实际问题的 分析和研究,初步掌 握建立数据拟合数学 模型的方法
数值计算方法 曲线拟合2 - 曲线拟合2

曲 a1=-0.2347;
线
a2=2.9943; d=300;
拟 v=1/Exp[a2]* D0
合 k=-a1
c1=10;
c0=25;
D0=v*c0
p=v*(c0-c1)
T=N[1/k*Log[c0/c1],8]
参考数据
初始剂量:
D0=(mg)
中心室血液容积: V=15.02 (L)
重复注入固定剂量: D=225.3(mg)
大学:
创新的活水
大学:
真理的福地
大学:
文化的酵母
大学:
知识的源泉
大学:
道德的高地
大学:
良心的堡垒
学府:学者的共同体 学术:教师的活动 学业:学生的活动 学人:追求学问的人
雅典神庙门廊石碑上的警世名言:
人对社会的贡献
= k*F(广度、深度、准确度)
古希腊思想家苏格拉底 :我们必须自知”,“我们必须自觉自己的无知”
k2=Plot[y,{x,0,2}]
Show[k1,k2]
程序设计
课后实验课题
已知某模型快速静脉注射下的血药浓度数据 (t=0 注射300mg ) t (h) 0.25 0.5 1 1.5 2 3 4 6 8 g (g/ml) 19.21 18.15 15.36 14.10 12.89 9.32 7.45 5.24 3.01
认识自己, 方能认识人生。
智慧意味着自知无知 !
我平生只知道一件事: 我为什么是那么无知。
感悟:品质建设最重要
1 做什么?
境界 1
境界 2
2 怎样做?
境界 3
境界 4
境界 5
3 怎样做好 ?
4 怎样做精 ?
曲线拟合和插值运算原理和方法

实验10 曲线拟合和插值运算一. 实验目的学会MATLAB 软件中软件拟合与插值运算的方法。
二. 实验内容与要求在生产和科学实验中,自变量x 与因变量y=f(x)的关系式有时不能直接写出表达式,而只能得到函数在若干个点的函数值或导数值。
当要求知道观测点之外的函数值时,需要估计函数值在该点的值。
要根据观测点的值,构造一个比较简单的函数y=t (x),使函数在观测点的值等于已知的数值或导数值,寻找这样的函数t(x),办法是很多的。
根据测量数据的类型有如下两种处理观测数据的方法。
(1) 测量值是准确的,没有误差,一般用插值。
(2) 测量值与真实值有误差,一般用曲线拟合。
MATLAB 中提供了众多的数据处理命令,有插值命令,拟合命令。
1.曲线拟合已知离散点上的数据集[(1x ,1y ),………(n x ,n y )],求得一解析函数y=f (x),使f(x)在原离散点i x 上尽可能接近给定i y 的值,之一过程叫曲线拟合。
最常用的的曲线拟合是最小二乘法曲线拟合,拟合结果可使误差的平方和最小,即使求使21|()|n i ii f x y =-∑ 最小的f(x).格式:p=polyfit(x,Y ,n).说明:求出已知数据x,Y 的n 阶拟合多项式f(x)的系数p ,x 必须是单调的。
[例 1.9]>>x=[0.5,1.0,1.5,2.0,2.5,3.0]; %给出数据点的x 值>>y=[1.75,2.45,3.81,4.80,7.00,8.60]; %给出数据点的y 值>>p=polyfit (x,y,2); %求出二阶拟合多项式f(x)的系数>>x1=0.5:0.05:3.0; %给出x 在0.5~3.0之间的离散值>>y1=polyval(p,1x ); %求出f(x)在1x 的值>>plot(x,y,‟*r ‟, 11,x y ‟-b ‟) %比较拟合曲线效果计算结果为:p=0.5614 0.8287 1.1560即用f(x)=0.56142x +0.8287x+1.1560拟合已知数据,拟合曲线效果如图所示。
拉格朗日插值(线性、二次、n次多项式插值)

1 x0 x V ( x 0 , x 1 , , x n ) 1 x1 x 1 xn x
2 0 2 1
x x x
n 0 n 1
2 n
n n
0 j i n
(x x )
i j
因为x0, x1,…,xn的互不相同,故系数行 列式不等于0,因此方程组有唯一解, 即Pn(x)存在并唯一。
j 0 ji n
x xj xi x j
是n次插值基函数
思考1 设f(x)=x2,求f(x)的次数不超 过1、2、3、…的插值多项式各是什 么?在哪些点处会有误差? 思考2 设f(x)=sinx,求f(x)的次数不超 过1、2、3、…的插值多项式各是什 么?在哪些点处会有误差?
思考 1 答案:当 f(x) 是次数不超过 n 的 多项式时,其 ≥ n 次的插值多项式就 是f(x)本身。此时误差为0!
定义: 设插值基点 x0,x1,…,xn 中最小者为 a 、 最大者为b,当插值点x∈(a, b)时我们 称为内插,否则称为外插
例1 给定数据表
x 2 3 4 5 6 7 f(x) 10 15 18 22 20 16 要用插值方法计算 f(4.8) 的近似值。 问线性插值、二次插值和三次插值应 选哪些基点?
2. 线性插值的几何意义
用通过两点 (x0, y0) 、 (x1, y1) 的直线 y=L1(x) 近似代替曲线 y=f(x) ,如下图 所示。
y y=f(x)
y0 o x0
y=L1(x) y1
x1 x
3. 线性插值公式的推导
根据直线的点斜式,有
y1 y 0 L1 ( x ) y 0 ( x x0 ) x1 x 0
插值和拟合

插值和拟合都是函数逼近或者数值逼近的重要组成部分他们的共同点都是通过已知一些离散点集M上的约束,求取一个定义在连续集合S(M包含于S)的未知连续函数,从而达到获取整体规律的目的,即通过"窥几斑"来达到"知全豹"。
简单的讲,所谓拟合是指已知某函数的若干离散函数值{f1,f2,…,fn},通过调整该函数中若干待定系数f(λ1, λ2,…,λ3), 使得该函数与已知点集的差别(最小二乘意义)最小。
如果待定函数是线性,就叫线性拟合或者线性回归(主要在统计中),否则叫作非线性拟合或者非线性回归。
表达式也可以是分段函数,这种情况下叫作样条拟合。
而插值是指已知某函数的在若干离散点上的函数值或者导数信息,通过求解该函数中待定形式的插值函数以及待定系数,使得该函数在给定离散点上满足约束。
插值函数又叫作基函数,如果该基函数定义在整个定义域上,叫作全域基,否则叫作分域基。
如果约束条件中只有函数值的约束,叫作Lagrange插值,否则叫作Hermite插值。
从几何意义上将,拟合是给定了空间中的一些点,找到一个已知形式未知参数的连续曲面来最大限度地逼近这些点;而插值是找到一个(或几个分片光滑的)连续曲面来穿过这些点。
一、概念的引入1. 插值与拟合在现实生活中的应用l 机械制造:汽车外观设计l 采样数据的重新建构:电脑游戏中场景的显示,地质勘探,医学领域(CT)2.概念的定义l 插值:基于[a,b]区间上的n个互异点,给定函数f(x),寻找某个函数去逼近f(x)。
若要求φ(x)在xi处与f(xi)相等,这类的函数逼近问题称为插值问题,xi即是插值点l 逼近:当取值点过多时,构造通过所有点的难度非常大。
此时选择一个次数较低的函数最佳逼近这些点,一般采用最小二乘法l 光顾:曲线的拐点不能太多,条件:①二阶几何连续②不存在多余拐点③曲率变化较小l 拟合:曲线设计过程中用插值或通过逼近方法是生成的曲线光滑(切变量连续)光顾二、插值理论设函数y=f(x)在区间[a,b]上连续,在[a,b]上有互异点x0,x1,…,xn处取值y 0,y1,…,yn。
插值法与曲线拟合

故用线性插值求得的近似值为
y
(x , y ) 00
y L2x
(x , y ) 11
y f x
(x , y ) 22
0
x0
x1
x
图2-3
11515 100
121 121
11*115 100 121 100
10.714
15
仿上,用抛物插值公式(2.7)所求得的近似值为
例1 已知 100 10, 121 11, 144 12分别用线性插值和抛物插值
求 115 的值。
14
解 因为115在100和121之间,故取节点x0=100,x1=121相应地有
y0=10,y1=11,于是,由线性插值公式(2.5)可得
L1
(x)
10
*
x 121 100 121
11*
x 100 121 100
为插值多项式Pn (x) 的余项。
17
关于误差有如下定理2中的估计式。
定理2 设 f (x) 在区间 a,b
上有直到n+1阶导数,x0, x1,, xn
为区间 a,b 上n+1个互异的节点, Pn (x) 为满足条件:
Pn (xi ) f (xi )(i 0,1,, n)
(2.9)
的n次插值多项式,则对于任何 x a,b ,有
的n次插值多项式(2.2),这样,由(2.2)式可以求出n+1个n次插 插多项式 l0 (x), l1(x),,ln (x) 。容易看出,这组多项式仅与节点的取
法有关,称它们为在n+1个节点上的n次基本插值多项式或n次插值
基函数。
11
2.2 拉格朗日插值多项式
利用插值基函数立即可以写出满足插值条件(1.3)的n次插值
曲线插值算法

曲线插值算法一、概述曲线插值算法是一种数学方法,用于在给定的控制点之间生成平滑的曲线。
该算法可以应用于各种领域,如计算机图形学、CAD和工程设计等。
曲线插值算法通过计算控制点之间的曲线来创建平滑的曲线,并且可以根据需要进行调整。
二、常见的曲线插值算法1. 贝塞尔曲线插值算法贝塞尔曲线插值是一种基于控制点的方法,它通过连接多个控制点来生成平滑的曲线。
该方法使用贝塞尔函数来计算两个相邻控制点之间的曲线。
这种方法通常用于计算机图形学中,用于绘制二维和三维图像。
2. 样条曲线插值算法样条曲线插值是一种基于函数逼近的方法,它通过拟合多项式函数来生成平滑的曲线。
该方法使用分段多项式函数来连接相邻控制点,并且保证函数在连接处连续可导。
这种方法通常用于CAD和工程设计中。
3. B样条曲线插值算法B样条曲线插值是一种基于参数化表示的方法,它通过计算参数化函数来生成平滑的曲线。
该方法使用B样条基函数来计算控制点之间的曲线,并且可以通过调整参数来改变曲线的形状。
这种方法通常用于计算机图形学和CAD中。
三、贝塞尔曲线插值算法详解1. 原理贝塞尔曲线插值是一种基于控制点的方法,它通过连接多个控制点来生成平滑的曲线。
该方法使用贝塞尔函数来计算两个相邻控制点之间的曲线。
贝塞尔函数是一种多项式函数,它可以用于生成平滑的曲线。
2. 计算公式在贝塞尔曲线插值中,每个控制点都有一个权重系数,称为贝塞尔权重。
假设有n个控制点,第i个控制点的坐标为(Pi, Qi),则第i个控制点的贝塞尔权重为Bi(n,t),其中t是一个0到1之间的参数。
当t=0时,Bi(n,t)等于1;当t=1时,Bi(n,t)等于1;当0<t<1时,Bi(n,t)可以通过递归公式计算得出:Bi(n,t)= (1-t)*Bi-1(n-1,t)+t*Bi(n-1,t)对于两个相邻的控制点Pi和Pi+1,它们之间的曲线可以用下面的公式计算得出:P(t)= (1-t)*Pi+t*Pi+1其中,t是一个0到1之间的参数。
第五章插值法与曲线拟合插值法精品PPT课件

f (n1) (x
(n 1)!
)
wn1(x)
,
x (a,b)
n
Ln(x) f (xi)li(x)
i0
其中
li(x ) (( x x i x x 0 0 ))(( x x i x x ii 1 1 ) )( (x x i x x ii 1 1 ) )
(x x n ) ,i
(x i x n )
计算各阶差分可按如下差分表进行.
向前差分表
xi fi fi 2 fi 3 fi
n fi
x0 f0 x1 f1 f0 x2 f2 f1 2 f0 x3 f3 f2 2 f1 3 f0
xn fn fn1 2 fn2 3 fn3
n f0
差分具有如下性质:
.
性质1(差分与函数值的关系) 各阶差分均可表示为函值
(1)
使满足
cn(xx0)(xx1)(xx2) (xxn 1)
N n (x i) f(x i), i 0 ,1 , n
(2)
为了使 N n ( x ) 的形式得到简化,引入如下记号
0(x)1
i(x)(xxi1)i1(x)
(3)
(xx0)(xx1) (xxi1), i1,2, n
定义 由式(3)定义的n+1个多项式 0(x),1(x), ,n(x)
表示f(x)在x0及x1两点的一阶差商. 用记号 f[x0,x1,x2]f[x0,xx10 ] xf2[x1,x2]
表示f(x)在x0,x1,x2三点的二阶差商. 一般地,有了k-1阶差商之后, 可以定义f(x)在x0,x1,..,xk的k阶差商
f[x 0 ,x 1 ,
,x k] f[x 0 ,x 1 ,
2 f (xi ) (f (xi )) ( f (xi h) f (xi )) f (xi h) f (xi ) f (xi 2h) 2 f (xi h) f (xi )
曲线曲面的计算机数学处理

(x2 x0 )(x2 x1)
(x2 x0 )(x2 x1)
f (x0 , x2 ) f (x0 , x1) x2 x1
上式含义为一阶均差的均差,称为函数f(x)的 二阶均差,记为f(x0,x1,x2)
依次类推,可得
p (x) 2
f
(x0 )
f
(x0 , x1)( x x0 )
之,三次样条函数就是全部通过型值点,二阶连续 可导的分段三次多项式函数。
3、三次样条函数插值解
1)利用公式
M M 2
0
0
1
0
(1
)
1
M
0
2M
1
1
M
2
1
(1
)
2
M
1
2M
2
2
M
3
2
M 2M M (1 )
n1
n2
n1
n1
n
n1
M M
(1 )
2
n
n1
n
n
2
1 1
f
(x0 , x1, x2 )( x x0 )( x x2 )
经直接计算可得
y
y
y
f
(x0 ,
x1,
x2)
( x0
0
x1)(x0
x2)
( x1
1
x0)(x1
x2)
( x2
2
x0)(x2
x1)
由上式可以推知,二阶均差也与点的排序无关,也 具有对称性。由此可以归纳出高阶均差的定义:k-1 阶均差的均差称为k阶均差,即
2、插值的基本思路
插值的基本思路是先设法对列表函数f(x)构 造一个简单函数y=p(x)作为近似表达式,然 后再计算p(x)的值来得到f(x)的近似值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比如 在三个点[x0,x1,x2]上lagrange插值函数为 (线性插值是拉格朗日插值最简单的情形)
插第
值四
与讲
拟 合 方 法
曲 线 曲 面
的
2
L 2 ( x )
y k lk ( x )
k0
y 0 l 0 ( x ) y 1l1 ( x ) y 2 l 2 ( x )
L2(x)
(x (x0
x1 )( x x 2 ) x1 )( x 0 x 2 )
y0
(x ( x1
x0 )( x x 0 )( x1
x2 ) x2 )
y1
(x (x2
x0 )( x x0 )( x 2
x1 ) x1 )
y2
分段三次埃尔米特插值条件数 9
插第
值四
与讲
拟 合 方 法
曲 线 曲 面
的
分段三次埃尔米特插值: 线性插值在每一小段上(两点之间),用到2个条件 q(xi)=yi,所以确定了一个线性插值函数;三次埃 尔米特插值在每一小段上,用到4个条件q(xi)=yi, q'(xi)=y'i,所以确定一个3次多项式插值函数。
插第
值四
与讲
拟 合 方 法
曲 线 曲 面
的
(2.34)=0.99036
(2.35)=0.99061
求~
(2.3457)=?
(2.3457) ≈(2.35-2.3457)/(2.35-2.34)* (2.34)+
(2.3457-2.34)/(2.35-2.34)* (2.35)
引例2 地图绘制问题: 假如我们在地图边界获取了一些边界点的坐标, 连接这些边界点形成闭合曲线,可以用来近似表 示真实边界线,如何更准确地逼近真实边界线?
➢了解拉格朗日和分段线性插值的基本思想 ➢了解三次样条插值的提法和思路 ➢掌握插值函数 interp interp1 interp2 griddata ➢掌握水塔用水量的计算(水位-体积-流速-积分)
关于插值与拟合的区别…
2
插第
值四
与讲
拟 合 方 法
曲 线 曲 面
的
面对工程实践和科学计算中的采集得到数据 (xi,yi),我们总是试图去揭示x与y之间的关系,即 用近似的y=f(x)来表示,那么我们通常可以采用两 种方法:插值与拟合
插第
值四
与讲
拟 合 方 法
曲 线 曲 面
的
三次样条(spline法
曲 线 曲 面
的
首先从段数n=2分析:我们知道在每一小段的 三次多项式有4个系数,所以如下图,总共需要有 4*2=8个方程来确定; 由q(xi)=yi可以确定2*2=4个 方程,又由内部节点q1'(xi)= q2'(xi)和q1''(xi)= q2''(xi)可以确定2*(2-1)=2个方程,看来剩下的8(4+2)=2个方程只有靠外部给定(边界条件)了
插值与拟合的区别在于—— 插值试图去通过已知点了解未知
点处的函数值;而拟合则在于在
整体上用某种已知函数去拟合数
据点列所在未知函数的性态。
关键区别在于插值要求必须经过已知点列,拟 合只求尽量靠近不必经过!拟合将在本讲下介绍~
函数查表与地图边界线绘制 3
引例1 函数查表问题: 已知标准正态分布函数表,求表中没有的值
第四讲 插值与拟合之插值(上)1
插第
值四
与讲
拟 合 方 法
曲 线 曲 面
的
内容:插值是离散函数逼近的重要方法,利用它 可通过函数在有限个点处的取值状况,估 算出函数在其他点处的近似值
目的:学习插值的基本思想和方法,掌握Matlab 的一维/二维等距和非等距插值函数
要求:掌握Matlab插值函数,处理插值应用问题
插第 值四 与讲
q(x) xxi xi1 xi
yi1
xxi1 xi xi1
yi
拟 合 方 法
曲 线 曲 面
的
x[xi1,xi],i 0,1,2,...,n
拉格朗日插值: 用n次拉格朗日插值多项式
n
Ln (x)
yklk (x)
k 0
连接数据点列上相邻的n+1个点。Pszjs71
拉格朗日插值基函数的构造 8
x1
q2
x2
q1
x0
一维曲线等距插值函数interp 12
interp's syntax One-dimensional r times longer data interpolation y = interp(y,r)
插第
值四
与讲
拟 合 方 法
曲 线 曲 面
的
题例 在原始数据点中增倍插值
x=0:0.001:1; y=sin(2*pi*30*x)+sin(2*pi*60*x); yi=interp(y,4); subplot(1,2,1); stem(y(1:30)); title('Original Points'); subplot(1,2,2); stem(yi(1:120)); title('Interpolated Points');
分段插值主要是为了避免高次插值可能出现的 大幅度振荡现象,在实际应用中通常采用分段低 次插值来提高近似程度,比如可用分段线性插值 或分段三次埃尔米特插值来逼近已知函数,但它 们的总体光滑性较差,为了克服这一缺点,三次 样条插值成为比较理想的工具。
三次样条(spline)插值的概念 10
样条的概念出自工程设计和机械加工(飞机、船 舶外形曲线设计)中的绘图工具(曲线尺),简单说 就是具有连续二阶导数的三次插值多项式函数。
如何更准确地逼近真实边界线?4
插第
值四
与讲
拟 合 方 法
曲 线 曲 面
的
插值在数码图像放大中的应用 5
引例3 图像插值放大:
数码相机运用插值的方法可以创造出比传感器实 际像素更多的图像,这种处理称为“数码变焦”。
插第
值四
与讲
拟 合 方 法
曲 线 曲 面
的
106*40原始图像:
右边: 双三次插值 放大450%
左边: 最近邻插值 放大450%
插值在图像三维重建中的应用 6
Surface recostruction from scattered points cloud
插第
值四
与讲
拟 合 方 法
曲 线 曲 面
的
分段线性插值和拉格朗日插值 7
分段线性插值:
用直线(线性)连接数据点列上相邻的两点。 比如~在两点[xi-1,xi]上线性插值函数为~
一维曲线等距插值函数interp1 13
interp1's syntax
One-dimensional data interpolation
yi = interp1(x,y,xi,method)
