回归分析例题SPSS求解过程
用SPSS进行曲线回归分析实例

用SPSS进行曲线回归分析实例曲线回归分析在一元回归中,若因变量和自变量相关的趋势不是线性分布,呈现曲线关系。
这种情况可以利用SPSS提供的曲线估计过程(Curve Estimation)方便地进行线性拟合,选出最佳的回归模型来拟合出相应曲线。
下面以一个实例来介绍曲线拟合的基本步骤和使用方法。
例子台湾稻螟蚁螟侵入不同叶龄稻茎后的生存率数据(表4-1)。
拟合出适合的曲线模型,来表达不同叶龄稻茎对台湾稻螟蚁螟侵入的生存关系。
表4-1 台湾稻螟蚁螟侵入不同叶龄稻茎后的生存率数据本例子数据保存在DATA6-3.SAV。
1)准备分析数据在SPSS数据编辑窗口建立变量“生存率”和“叶龄”两个变量,把表6-13中的数据输入到对应的变量中。
或者打开已经存在的数据文件(DATA6-3.SAV)。
2)启动线性回归过程单击SPSS主菜单的“Analyze”下的“Regression”中“Curve Estimation”项,将打开如图4-1所示的线回归对话窗口。
图4-1 线回归对话窗口3) 设置分析变量设置因变量:从左侧的变量列表框中选择一个或多个因变量进入“Dependent(s)”框。
本例子选“生存率”变量为因变量。
设置自变量:选择一个变量为自变量,进入“Independent”框,也可选取“Independent”框中的“Time”项,即以时间为自变量。
本例子选“叶龄”变量为自变量。
选择标签变量: 选择一个变量进入到“Case Labels”框中,该变量为标签变量,可以利用该变量的值在图上查找观测值。
本例子没有标签变量。
4)选择曲线方程模型在“Models”框中选择一个或多个回归方程模型,这11个模型都可化为相应的线性模型。
其中各项的意义分别为:(1) Linear 线性模型(2) Quadratic 二次模型(3) Compound 复合模型(4) Growth 生长模型(5) Logarithmic 对数模型(6) S 形模型(7) Cubic 抛物线模型(8) Exponential 指数的模型(9) Inverse 倒数模型(10) Power 幂函数模型(11) Logistic 逻辑斯蒂模型在各项模型上单击鼠标右键,可以得到模型的方程类型。
SPSS多元线性回归分析实例操作步骤
SPSS 统计分析多元线性回归分析方法操作与分析实验目的:引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量,来研究上海房价的变动因素。
实验变量:以年份、商品房平均售价(元/平方米)、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。
实验方法:多元线性回归分析法软件:spss19.0操作过程:第一步:导入Excel数据文件1.open data document——open data——open;2. Opening excel data source——OK.第二步:1.在最上面菜单里面选中Analyze——Regression——Linear ,Dependent(因变量)选择商品房平均售价,Independents(自变量)选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率;Method 选择Stepwise.进入如下界面:2.点击右侧Statistics,勾选Regression Coefficients(回归系数)选项组中的Estimates;勾选Residuals(残差)选项组中的Durbin-Watson、Casewise diagnostics默认;接着选择Model fit、Collinearity diagnotics;点击Continue.3.点击右侧Plots,选择*ZPRED(标准化预测值)作为纵轴变量,选择DEPENDNT(因变量)作为横轴变量;勾选选项组中的Standardized Residual Plots(标准化残差图)中的Histogram、Normal probability plot;点击Continue.4.点击右侧Save,勾选Predicted Vaniues(预测值)和Residuals(残差)选项组中的Unstandardized;点击Continue.5.点击右侧Options,默认,点击Continue.6.返回主对话框,单击OK.输出结果分析:1.引入/剔除变量表Variables Entered/Removed aModel Variables Entered Variables Removed Method1 城市人口密度(人/平方公里) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).2 城市居民人均可支配收入(元) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).a. Dependent Variable: 商品房平均售价(元/平方米)该表显示模型最先引入变量城市人口密度(人/平方公里),第二个引入模型的是变量城市居民人均可支配收入(元),没有变量被剔除。
SPSS多元线性回归分析报告实例操作步骤

SPSS 统计分析多元线性回归分析方法操作与分析实验目的:引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量,来研究上海房价的变动因素。
实验变量:以年份、商品房平均售价(元/平方米)、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。
实验方法:多元线性回归分析法软件:spss19.0操作过程:第一步:导入Excel数据文件1.open data document——open data——open;2. Opening excel data source——OK.第二步:1.在最上面菜单里面选中Analyze——Regression——Linear ,Dependent(因变量)选择商品房平均售价,Independents(自变量)选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率;Method 选择Stepwise.进入如下界面:2.点击右侧Statistics,勾选Regression Coefficients(回归系数)选项组中的Estimates;勾选Residuals(残差)选项组中的Durbin-Watson、Casewise diagnostics默认;接着选择Model fit、Collinearity diagnotics;点击Continue.3.点击右侧Plots,选择*ZPRED(标准化预测值)作为纵轴变量,选择DEPENDNT(因变量)作为横轴变量;勾选选项组中的Standardized Residual Plots(标准化残差图)中的Histogram、Normal probability plot;点击Continue.4.点击右侧Save,勾选Predicted Vaniues(预测值)和Residuals(残差)选项组中的Unstandardized;点击Continue.5.点击右侧Options,默认,点击Continue.6.返回主对话框,单击OK.输出结果分析:1.引入/剔除变量表Variables Entered/Removed aModel Variables Entered Variables Removed Method1 城市人口密度(人/平方公里) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).2 城市居民人均可支配收入(元) . Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove >=.100).a. Dependent Variable: 商品房平均售价(元/平方米)该表显示模型最先引入变量城市人口密度(人/平方公里),第二个引入模型的是变量城市居民人均可支配收入(元),没有变量被剔除。
SPSS实验6-回归分析

SPSS作业6:回归分析(一)回归分析多元线性回归模型的基本操作:(1)选择菜单Analyze-Regression-Linear;(2)选择被解释变量(能源消费标准煤总量)和解释变量(国内生产总值、工业增加值、建筑业增加值、交通运输邮电业增加值、人均电力消费、能源加工转换效率)到对应框中;(3)在Method框中,选择Enter方法;在Statistics框中,选择Estimates、Model fit、Covariancematrix、Collinearity diagnostics选项;在Plots框中,选择ZRESED到Y框,ZPRED到X框,再选择Histogram和Normal plot;(4)选择菜单Analyze-Non Test-1-Sanple K-S;选择菜单Analyze-Correlate-Brivariate;结果如下:Regression能源消费需求的多元线性回归分析结果(强制进入策略)(一)Model Summary bModel R R Square Adjusted R Square Std. Error of the Estimate1 .990a.980 .973 8480.38783a. Predictors: (Constant), 能源加工转换效率/%, 交通运输邮电业增加值/亿元, 工业增加值/亿元, 人均电力消费/千瓦时, 建筑业增加值/亿元, 国内生产总值/亿元b. Dependent Variable: 能源消费标准煤总量/万吨分析:被解释变量和解释变量的复相关系数为0.990,判定系数为0.980,调整的判定系数为0.973,回归方程的估计标准误差为8480.38783。
该方程有6个解释变量,调整的判定系数为0.973,,接近于1,所以拟合优度较高,被解释变量可以被模型解释的部分较多,未能解释的部分较少。
分析:由上可知,被解释变量的总离差平方和为5.882E10,回归平方和及均方分别为5.766E10和9.611E9,剩余平方和及均方分别为1.151E9和7.192E7,F检验统计量的观测值为133.636,对应的概率p值近似为0。
SPSS实验8-二项Logistic回归分析
SPSS作业8:二项Logistic回归分析为研究和预测某商品消费特点和趋势,收集到以往胡消费数据.数据项包括是否购买,性别,年龄和收入水平。
这里采用Logistic回归的方法,是否购买作为被解释变量(0/1二值变量),其余各变量为解释变量,且其中性别和收入水平为品质变量,年龄为定距变量。
变量选择采用Enter方法,性别以男为参照类,收入以低收入为参照类。
(一)基本操作:(1)选择菜单Analyz e-Regression-Binary Logistic;(2)选择是否购买作为被解释变量到Dependent框中,选其余各变量为解释变量到Covariates框中,采用Enter方法,结果如下:消费的二项Logistic分析结果(一)(强制进入策略)Categorical Variables CodingsFrequency Parameter coding (1) (2)收入低收入132 .000 .000中收入144 1.000 。
000高收入155 。
000 1。
000性别男191 。
000女240 1.000分析:上表显示了对品质变量产生虚拟变量的情况,产生的虚拟变量命名为原变量名(编码)。
可以看到,对收入生成了两个虚拟变量名为Income(1)和Income(2),分别表示是否中收入和是否高收入,两变量均为0时表示低收入;对性别生成了一个虚拟变量名为Gedder(1),表示是否女,取值为0时表示为男。
消费的二项Logistic 分析结果(二)(强制进入策略)Block 0: Beginning BlockClassification Table a,bObserved Predicted是否购买 Percentage Correct不购买购买Step 0是否购买不购买 269 0 100。
购买162。
0 Overall Percentage62。
4a 。
Constant is included in the model 。
SPSS(第7章回归分析)

表7—23 回归模型的一般性统计量表 Model 1 2 R .831a .985b R square .690 .970 Adjusted Square .662 .965 Std.Error of the Estimate 8.671 2.808
a.Predictors(Constant),x4 b.Predictors(Constant),x4,x1 c.Dependent Variable:Y
表中第一列:列出了回归方程模型的编号;第二列表示回归方程的 复相关系数;第三列为回归方程的复相关系数的平方;第四列表示调 整了的复相关系数的平方。第五列为预测值的标准差。 从表中可看出,随着自变量个数的增加,复相关系数及其平方相 应增加,这表明回归效果是越来越好。还可看出,预测值的标准差越 来越来小,这也正表明回归方程越来越符合观测情况。
Total 2670.523 a.Predictors(Constant),x4 b.Predictors(Constant),x4,x1 c.Dependent Variable:Y
表中第一列为回归方程模型的编号;第二列列出了回归的平方和; 第三列为回归的自由度;第四列为均值平方;第五列为F值;第六列为 统计量大于F值的概率。 从表中可看出,当只有变量x4进入回归方程时,自变量与因变量 之间完全无线性关系的概率为0.001 ;当x1也进入方程之后,自变量 与因变量之间完全无线性关系的概率为0.000,这表明拒绝假设;所有 的回归因子的系数为0。
输出相关残差的durbinwatson统计量残差和预测值的统计量输出满足选择条件的观测量诊断表设置奇异值的判断条件输出所有有关测量的残差值选择回归系输出有关回归系数及其相关测量输出回归系数的95的置信区间输出协方差和相关矩图73statistics对话框201566图74plots对话框x轴和y轴中有一个是源变量标准化的预测值标准化的残差删除的残差修正后的预测值
SPSS—回归—多元线性回归结果分析(二)

SPSS—回归—多元线性回归结果分析(二)2011-10-27 14:44,最近一直很忙,公司的潮起潮落,就好比人生的跌岩起伏,眼看着一步步走向衰弱,却无能为力,也许要学习“步步惊心”里面“四阿哥”的座右铭:“行到水穷处”,”坐看云起时“。
接着上一期的“多元线性回归解析”里面的内容,上一次,没有写结果分析,这次补上,结果分析如下所示:结果分析1:由于开始选择的是“逐步”法,逐步法是“向前”和“向后”的结合体,从结果可以看出,最先进入“线性回归模型”的是“price in thousands"建立了模型1,紧随其后的是“Wheelbase"建立了模型2,所以,模型中有此方法有个概率值,当小于等于0.05时,进入“线性回归模型”(最先进入模型的,相关性最强,关系最为密切)当大于等 0.1时,从“线性模型中”剔除结果分析:1:从“模型汇总”中可以看出,有两个模型,(模型1和模型2)从R2 拟合优度来看,模型2的拟合优度明显比模型1要好一些(0.422>0.300)2:从“Anova"表中,可以看出“模型2”中的“回归平方和”为115.311,“残差平方和”为153.072,由于总平方和= 回归平方和+残差平方和,由于残差平方和(即指随即误差,不可解释的误差)由于“回归平方和”跟“残差平方和”几乎接近,所有,此线性回归模型只解释了总平方和的一半,3:根据后面的“F统计量”的概率值为0.00,由于0.00<0.01,随着“自变量”的引入,其显著性概率值均远小于 0.01,所以可以显著地拒绝总体回归系数为0的原假设,通过ANOVA方差分析表可以看出“销售量”与“价格”和“轴距”之间存在着线性关系,至于线性关系的强弱,需要进一步进行分析。
结果分析:1:从“已排除的变量”表中,可以看出:“模型2”中各变量的T检的概率值都大于“0.05”所以,不能够引入“线性回归模型”必须剔除。
SPSS多元线性回归分析报告实例操作步骤
SPSS 统计分析多元线性回归分析方法操作与分析实验目的:引入1998~2008年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量,来研究上海房价的变动因素。
实验变量:以年份、商品房平均售价(元/平方米)、上海市城市人口密度(人/平方公里)、城市居民人均可支配收入(元)、五年以上平均年贷款利率(%)和房屋空置率(%)作为变量。
实验方法:多元线性回归分析法软件:spss19.0操作过程:第一步:导入Excel数据文件1.open data document——open data——open;2. Opening excel data source——OK.第二步:1.在最上面菜单里面选中Analyze——Regression——Linear ,Dependent (因变量)选择商品房平均售价,Independents(自变量)选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率;Method选择Stepwise.进入如下界面:2.点击右侧Statistics,勾选Regression Coefficients(回归系数)选项组中的Estimates;勾选Residuals(残差)选项组中的Durbin-Watson、Casewise diagnostics默认;接着选择Model fit、Collinearity diagnotics;点击Continue.3.点击右侧Plots,选择*ZPRED(标准化预测值)作为纵轴变量,选择DEPENDNT(因变量)作为横轴变量;勾选选项组中的Standardized Residual Plots(标准化残差图)中的Histogram、Normal probability plot;点击Continue.4.点击右侧Save,勾选Predicted Vaniues(预测值)和Residuals(残差)选项组中的Unstandardized;点击Continue.5.点击右侧Options,默认,点击Continue.6.返回主对话框,单击OK.输出结果分析: 1.引入/剔除变量表该表显示模型最先引入变量城市人口密度 (人/平方公里),第二个引入模型的是变量城市居民人均可支配收入(元),没有变量被剔除。
曲线回归估计的spss分析
上机操作8 曲线回归估计的SPSS分析习题:落叶松林单位面积的蓄积量(V)和胸高断面积(D)的测定数据如下表,V(m3) 46 56 67 65 89 86 103 108 121 118D(m2) 4.7 5.4 6.3 7.2 7.8 8.8 9.9 11.7 11.4 11.8(1)定义变量:打开SPSS数据编辑器,点击“变量视图”,在名称列下输入“V”、“D”,改“类型”栏均为“数字”,“小数”栏分别保留0位和1位。
(2)输入数据:在“数据视图”模式下,在各名称列输入相应的数据,如图所示:二、分析过程分析→回归→曲线估计,将“V”添加到“因变量”中,将“D”添加到“变量”中,勾选模型中的“二次模型”、“复合”、“对数”、“立方模型”、“指数”、“幂”、“”、“Logistic”,→确定。
三、输出结果分析曲线拟合MODEL: MOD_1.Dependent variable.. V Method.. LOGARITH(对数曲线模型)Listwise Deletion of Missing DataMultiple R (负相关系数) .97210R Square(决定系数) .94498Adjusted R Square .93811Standard Error 6.59944Analysis of Variance(方差分析):DF(自由度) Sum of Squares Mean Square(均方)Regression(回归) 1 5984.4787 5984.4787Residuals(残差) 8 348.4213 43.5527F = 137.40787 Signif F = .0000 (小于0.05,具有极显著性)-------------------- Variables in the Equation (方程中的变量)--------------------Variable B(系数) SE B Beta T Sig T(T的显著性水平)D 78.152283 6.667083 .972102 11.722 .0000(小于0.05)(Constant) -77.682919 14.110257 -5.505 .0006(小于0.05)分析可知:蓄积量(V)与胸高段面积(D)的相关性为0.97210,它们的F 检验Sig.<0.01,说明蓄积量(V)与胸高段面积(D)达到极显著水平,即蓄积量(V)与胸高段面积(D)的方程具有统计学意义。
用spss软件进行一元线性回归分析

step2:做散点图
给散点图添加趋势线的方法: • 双击输出结果中的散点图 • 在“图表编辑器”的菜单中依次点击“元素”—“总计拟合线”,由此“属性”中加载了 “拟合线” • 拟合方法选择“线性”,置信区间可以选95%个体,应用
step3:线性回归分析
从菜单上依次点选:分析—回归—线性 设置:因变量为“年降水量”,自变量为“纬度” “方法”:选择默认的“进入”,即自变量一次全部进入的方法。 “统计量”:
step4:线性回归结果
【Anova】 (analysisofvariance方差分析) • 此表是所用模型的检验结果,一个标准的方差分析表。 • Sig.(significant )值是回归关系的显著性系数,sig.是F值的实际显著性概率即P值。 当sig. <= 0.05的时候,说明回归关系具有统计学意义。如果sig. > 0.05,说明二者 之间用当前模型进行回归没有统计学意义,应该换一个模型来进行回归。 • 由表可见所用的回归模型F统计量值=226.725 ,P值为0.000,因此我们用的这个回 归模型是有统计学意义的,可以继续看下面系数分别检验的结果。 • 由于这里我们所用的回归模型只有一个自变量,因此模型的检验就等价与系数的检验, 在多元回归中这两者是不同的。
• 勾选“模型拟合度”,在结果中会输出“模型汇总”表 • 勾选“估计”,则会输出“系数”表 “绘制”:在这一项设置中也可以做散点图 “保存”: • 注意:在保存中被选中的项目,都将在数据编辑窗口显示。 • 在本例中我们勾选95%的置信区间单值,未标准化残差 “选项”:只需要在选择方法为逐步回归后,才需要打开
利用spss进行一元线性回归
step1:建立数据文件 打开spss的数据编辑器,编辑变量视图
SPSS实验回归分析
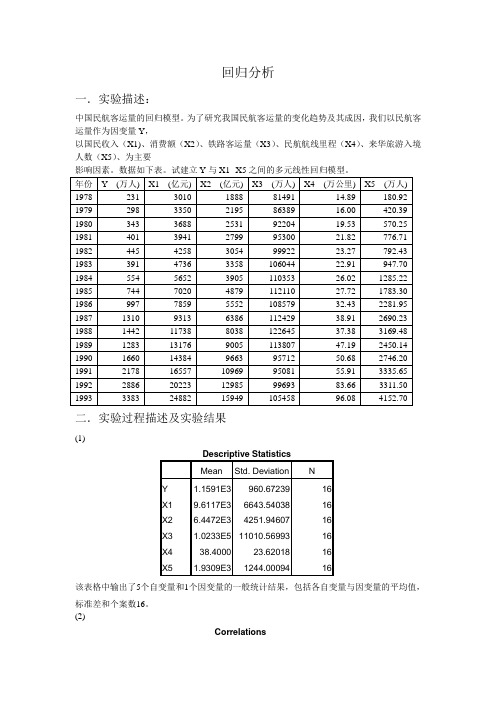
回归分析一.实验描述:中国民航客运量的回归模型。
为了研究我国民航客运量的变化趋势及其成因,我们以民航客运量作为因变量Y,以国民收入(X1)、消费额(X2)、铁路客运量(X3)、民航航线里程(X4)、来华旅游入境人数(X5)、为主要影响因素。
数据如下表。
试建立Y与X1--X5之间的多元线性回归模型。
二.实验过程描述及实验结果(1)该表格中输出了5个自变量和1个因变量的一般统计结果,包括各自变量与因变量的平均值,标准差和个案数16。
该表格中列出了各个变量之间的相关性,从该表格可以看出因变量Y和自变量X1之间的相关系数为0.989,相关性最大,。
因变量Y与自变量X3之间相关系数为0.227,相关性最小。
(3)该表格输出的是被引入或从回归方程中被剔出的各变量。
说明进行线性回归分析时所采用的方法是全部引入法Enter。
因变量为Y。
(4)该表格输出的是常用统计量。
从该表看出相关性系数R为0.999,判定系数R2为0.998,调整的判定系数为0.997,回归估计的标准误差为49.49240。
该表格输出的是方差分析表。
从这部分结果看出:统计量F为1.128E3;相伴概率值小于0.01,拒绝原假设说明多个自变量与因变量Y之间存在线性回归关系。
Sum of Squares一栏中分别代表回归平方和(1.382E7),残差平方和(24494.981)以及总平方和(1.384E7),df为自由度。
判定系数R2=0.99855。
该表格为回归系数分析。
其中Unstandardized Coefficients为非标准化系数,Standardized Coefficients为标准化系数,t为回归系数检验统计量,sig为相伴概率值。
由表知t检验的相伴概率值均小于0.01,拒绝原假设,说明个变量与因变量之间均有显著线性相关关系。
从表格中可以看出该多元线性回归方程为:y=450.909+0.354 X1-0.561 X2-0.007 X3+21.578 X4+0.435 X5该表格为残差统计结果表。
线性回归spss分析

线性回归分析的具体步骤SPSS软件中进行线性回归分析的选择项为Analyze→Regression→Linear。
如图3.9所示。
下面通过例题介绍线性回归分析的操作过程。
图3.9 Regression 分析功能菜单例3. 仍然用例2的数据,考察火柴销售量与各影响因素之间的相关关系,建立火柴销售量对于相关因素煤气户数、卷烟销量、蚊香销量、打火石销量的线性回归模型,通过对模型的分析,找出合适的线性回归方程。
解:建立线性回归模型的具体操作步骤如下:1、打开数据文件SY-9,单击Analyze → Regression → Linear打开Linear 对话框如图3.10所示。
2、从左边框中选择因变量Y进入Dependent 框内,选择一个或多个自变量进入Independent框内。
从Method 框内下拉式菜单中选择回归分析方法,有强行进入法(Enter),消去法(Remove),向前选择法(Forward),向后剔除法(Backward)及逐步回归法(Stepwise)五种。
本例中选择逐步回归法(Stepwise)。
图3.10 Linear Regression对话框3、单击Statistics,打开Linear Regression: Statistics对话框,可以选择输出的统计量如图3.11所示。
●Regression Coefficients栏,回归系数选项栏。
Estimates (系统默认): 输出回归系数的相关统计量:包括回归系数,回归系数标准误、标准化回归系数、回归系数检验统计量(t值)及相应的检验统计量概率的P值(sig)。
本例中只选择此项。
Confidence intervals:输出每一个非标准化回归系数95%的置信区间。
Covariance matrix: 输出协方差矩阵。
●与模型拟合及拟合效果有关的选择项。
Model fit是默认项。
能够输出复相关系数R、R2及R2修正值,估计值的标准误,方差分析表。
SPSS如何进行线性回归分析操作 精品

SPSS如何进行线性回归分析操作本节内容主要介绍如何确定并建立线性回归方程。
包括只有一个自变量的一元线性回归和和含有多个自变量的多元线性回归。
为了确保所建立的回归方程符合线性标准,在进行回归分析之前,我们往往需要对因变量与自变量进行线性检验。
也就是类似于相关分析一章中讲过的借助于散点图对变量间的关系进行粗略的线性检验,这里不再重复。
另外,通过散点图还可以发现数据中的奇异值,对散点图中表示的可能的奇异值需要认真检查这一数据的合理性。
一、一元线性回归分析用SPSS进行回归分析,实例操作如下:1.单击主菜单Analyze / Regression / Linear…,进入设置对话框如图7-9所示。
从左边变量表列中把因变量y选入到因变量(Dependent)框中,把自变量x选入到自变量(Independent)框中。
在方法即Method一项上请注意保持系统默认的选项Enter,选择该项表示要求系统在建立回归方程时把所选中的全部自变量都保留在方程中。
所以该方法可命名为强制进入法(在多元回归分析中再具体介绍这一选项的应用)。
具体如下图所示:2.请单击Statistics…按钮,可以选择需要输出的一些统计量。
如RegressionCoefficients(回归系数)中的Estimates,可以输出回归系数及相关统计量,包括回归系数B、标准误、标准化回归系数BETA、T值及显著性水平等。
Model fit 项可输出相关系数R,测定系数R2,调整系数、估计标准误及方差分析表。
上述两项为默认选项,请注意保持选中。
设置如图7-10所示。
设置完成后点击Continue返回主对话框。
回归方程建立后,除了需要对方程的显著性进行检验外,还需要检验所建立的方程是否违反回归分析的假定,为此需进行多项残差分析。
由于此部分内容较复杂而且理论性较强,所以不在此详细介绍,读者如有兴趣,可参阅有关资料。
3.用户在进行回归分析时,还可以选择是否输出方程常数。
SPSS--回归-多元线性回归模型案例解析

SPSS--回归-多元线性回归模型案例解析多元线性回归,主要是研究⼀个因变量与多个⾃变量之间的相关关系,跟⼀元回归原理差不多,区别在于影响因素(⾃变量)更多些⽽已,例如:⼀元线性回归⽅程为:毫⽆疑问,多元线性回归⽅程应该为:上图中的 x1, x2, xp分别代表“⾃变量”Xp截⽌,代表有P个⾃变量,如果有“N组样本,那么这个多元线性回归,将会组成⼀个矩阵,如下图所⽰:那么,多元线性回归⽅程矩阵形式为:其中:代表随机误差,其中随机误差分为:可解释的误差和不可解释的误差,随机误差必须满⾜以下四个条件,多元线性⽅程才有意义(⼀元线性⽅程也⼀样)1:服成正太分布,即指:随机误差必须是服成正太分别的随机变量。
2:⽆偏性假设,即指:期望值为03:同共⽅差性假设,即指,所有的随机误差变量⽅差都相等4:独⽴性假设,即指:所有的随机误差变量都相互独⽴,可以⽤协⽅差解释。
今天跟⼤家⼀起讨论⼀下,SPSS---多元线性回归的具体操作过程,下⾯以教程教程数据为例,分析汽车特征与汽车销售量之间的关系。
通过分析汽车特征跟汽车销售量的关系,建⽴拟合多元线性回归模型。
数据如下图所⽰:点击“分析”——回归——线性——进⼊如下图所⽰的界⾯:将“销售量”作为“因变量”拖⼊因变量框内,将“车长,车宽,耗油率,车净重等10个⾃变量拖⼊⾃变量框内,如上图所⽰,在“⽅法”旁边,选择“逐步”,当然,你也可以选择其它的⽅式,如果你选择“进⼊”默认的⽅式,在分析结果中,将会得到如下图所⽰的结果:(所有的⾃变量,都会强⾏进⼊)如果你选择“逐步”这个⽅法,将会得到如下图所⽰的结果:(将会根据预先设定的“F统计量的概率值进⾏筛选,最先进⼊回归⽅程的“⾃变量”应该是跟“因变量”关系最为密切,贡献最⼤的,如下图可以看出,车的价格和车轴跟因变量关系最为密切,符合判断条件的概率值必须⼩于0.05,当概率值⼤于等于0.1时将会被剔除)“选择变量(E)" 框内,我并没有输⼊数据,如果你需要对某个“⾃变量”进⾏条件筛选,可以将那个⾃变量,移⼊“选择变量框”内,有⼀个前提就是:该变量从未在另⼀个⽬标列表中出现!,再点击“规则”设定相应的“筛选条件”即可,如下图所⽰:点击“统计量”弹出如下所⽰的框,如下所⽰:在“回归系数”下⾯勾选“估计,在右侧勾选”模型拟合度“ 和”共线性诊断“ 两个选项,再勾选“个案诊断”再点击“离群值”⼀般默认值为“3”,(设定异常值的依据,只有当残差超过3倍标准差的观测才会被当做异常值)点击继续。
用SPSS做回归分析

当自变量和 因变量选好 后,点击 OK 键
结果说明——常用统计量:
P (1 R 2 ) R R N P 1 ( P为 自 变 量 个 数 ,为 样 本 数 N )
2 a 2
1. Model为回归方程模型编号(不同方法对应不同模型) 2. R为回归方程的复相关系数 3. R Square即R2系数,用以判断自变量对因变量的影响有 多大,但这并不意味着越大越好——自变量增多时,R2 系数会增大,但模型的拟合度未必更好 4. Adjusted R Square即修正R2,为了尽可能确切地反映模 型的拟合度,用该参数修正R2系数偏差,它未必随变量 个数的增加而增加 5. Std. Error of the Estimate是估计的标准误差
xi yi
y 106.3094 1.7172ln x
112
首先绘出散点图:
步骤: Graphs →Scatter… →Simple
111
110
109
108
ð ô ¬ ¿ ½ ʺ Á
0 10 20
107 106
à ë ¾ À
根据散点图的形态可以认为变量X与Y之间具 有对数曲线类型的回归方程:
y a b ln x
操作步骤:Analyze→Regression →Curve Estimation… 通过点击右键观看选择适当的 类型:Logarithmic 结果如右:
例. 《概率论与数理统计》P280 例9.3.1
在汽油中加入两种化学添加剂,观察它们对汽车消 耗1公升汽油所行里程的影响,共进行9次试验,得到 里程Y与两种添加剂用量X1、X2之间数据如下: xi1 0 1 0 1 2 0 2 3 1 xi2 0 0 1 1 0 2 2 1 3 yi 15.8 16.0 15.9 16.2 16.5 16.3 16.8 17.4 17.2 试求里程Y关于X1、X2的经验线性回归方程,并求 误差方差σ2的无偏估计值。
SPSS多元线性回归分析实例操作步骤

SPSS多元线性回归分析实例操作步骤在数据分析领域,多元线性回归分析是一种非常实用且强大的工具,它可以帮助我们探究多个自变量与一个因变量之间的线性关系。
下面,我将为您详细介绍使用 SPSS 进行多元线性回归分析的实例操作步骤。
首先,打开 SPSS 软件,我们需要准备好数据。
假设我们有一组关于房屋价格的数据集,其中包含房屋面积、房间数量、地理位置等自变量,以及房屋的销售价格作为因变量。
在 SPSS 中,通过“文件”菜单中的“打开”选项,找到并导入我们的数据文件。
确保数据的格式正确,并且变量的名称和类型都符合我们的预期。
接下来,选择“分析”菜单中的“回归”,然后点击“线性”选项,这就开启了多元线性回归分析的设置窗口。
在“线性回归”窗口中,将我们的因变量(房屋销售价格)放入“因变量”框中,将自变量(房屋面积、房间数量、地理位置等)放入“自变量”框中。
然后,我们可以点击“统计”按钮,在弹出的“线性回归:统计”窗口中,根据我们的需求选择合适的统计量。
通常,我们会勾选“估计”“置信区间”“模型拟合度”等选项,以获取回归系数的估计值、置信区间以及模型的拟合优度等信息。
接着,点击“图”按钮,在“线性回归:图”窗口中,我们可以选择绘制一些有助于分析的图形,比如“标准化残差图”,用于检查残差的正态性;“残差与预测值”图,用于观察残差的分布是否均匀。
再点击“保存”按钮,在这里我们可以选择保存一些额外的变量,比如预测值、残差等,以便后续的进一步分析。
设置完成后,点击“确定”按钮,SPSS 就会开始进行多元线性回归分析,并输出相应的结果。
结果中首先会给出模型的汇总信息,包括 R 方(决定系数)、调整后的 R 方等。
R 方表示模型对因变量的解释程度,越接近 1 说明模型的拟合效果越好。
调整后的 R 方则考虑了自变量的个数,对模型的拟合优度进行了更合理的修正。
接着是方差分析表,用于检验整个回归模型是否显著。
如果 F 值对应的显著性水平小于设定的阈值(通常为 005),则说明回归模型是显著的,即自变量整体上对因变量有显著的影响。
SPSS多元线性回归分析实例操作步骤

SPSS多元线性回归分析实例操作步骤SPSS(Statistical Package for the Social Sciences)是一种统计分析软件,广泛应用于社会科学研究领域。
其中,多元线性回归分析是SPSS中常用的一种统计方法,用于探讨多个自变量与一个因变量之间的关系。
本文将演示SPSS中进行多元线性回归分析的操作步骤,帮助读者了解和掌握该方法。
一、数据准备在进行多元线性回归分析之前,首先需要准备好数据。
数据应包含一个或多个因变量和多个自变量,以及相应的观测值。
这些数据可以通过调查问卷、实验设计、观察等方式获得。
确保数据的准确性和完整性对于获得可靠的分析结果至关重要。
二、打开SPSS软件并导入数据1. 启动SPSS软件,点击菜单栏中的“文件(File)”选项;2. 在下拉菜单中选择“打开(Open)”选项;3. 导航到保存数据的文件位置,并选择要导入的数据文件;4. 确保所选的文件类型与数据文件的格式相匹配,点击“打开”按钮;5. 数据文件将被导入到SPSS软件中,显示在数据编辑器窗口中。
三、创建多元线性回归模型1. 点击菜单栏中的“分析(Analyse)”选项;2. 在下拉菜单中选择“回归(Regression)”选项;3. 在弹出的子菜单中选择“线性(Linear)”选项;4. 在“因变量”框中,选中要作为因变量的变量;5. 在“自变量”框中,选中要作为自变量的变量;6. 点击“添加(Add)”按钮,将自变量添加到回归模型中;7. 可以通过“移除(Remove)”按钮来删除已添加的自变量;8. 点击“确定(OK)”按钮,创建多元线性回归模型。
四、进行多元线性回归分析1. 多元线性回归模型创建完成后,SPSS将自动进行回归分析并生成结果;2. 回归结果将显示在“回归系数”、“模型总结”和“模型拟合优度”等不同的输出表中;3. “回归系数”表显示各个自变量的回归系数、标准误差、显著性水平等信息;4. “模型总结”表提供模型中方程的相关统计信息,包括R方值、F 统计量等;5. “模型拟合优度”表显示模型的拟合优度指标,如调整后R方、残差平方和等;6. 可以通过菜单栏中的“图形(Graphs)”选项,绘制回归模型的拟合曲线图、残差图等。
多元线性回归spss案例

多元线性回归spss案例【篇一:多元线性回归spss案例】多元线性回归,主要是研究一个因变量与多个自变量之间的相关关系,跟一元回归原理差不多,区别在于影响因素(自变量)更多些而已,例如:一元线性回归方程为:毫无疑问,多元线性回归方程应该为:上图中的x1, x2, xp分别代表自变量xp截止,代表有p个自变量,如果有 n组样本,那么这个多元线性回归,将会组成一个矩阵,如下图所示:那么,多元线性回归方程矩阵形式为:其中:代表随机误差,其中随机误差分为:可解释的误差和不可解释的误差,随机误差必须满足以下四个条件,多元线性方程才有意义(一元线性方程也一样)1:服成正太分布,即指:随机误差必须是服成正太分别的随机变量。
2:无偏性假设,即指:期望值为03:同共方差性假设,即指,所有的随机误差变量方差都相等4:独立性假设,即指:所有的随机误差变量都相互独立,可以用协方差解释。
今天跟大家一起讨论一下,spss---多元线性回归的具体操作过程,下面以教程教程数据为例,分析汽车特征与汽车销售量之间的关系。
通过分析汽车特征跟汽车销售量的关系,建立拟合多元线性回归模型。
数据如下图所示:点击分析回归线性进入如下图所示的界面:将销售量作为因变量拖入因变量框内,将车长,车宽,耗油率,车净重等10个自变量拖入自变量框内,如上图所示,在方法旁边,选择逐步,当然,你也可以选择其它的方式,如果你选择进入默认的方式,在分析结果中,将会得到如下图所示的结果:(所有的自变量,都会强行进入)如果你选择逐步这个方法,将会得到如下图所示的结果:(将会根据预先设定的 f统计量的概率值进行筛选,最先进入回归方程的自变量应该是跟因变量关系最为密切,贡献最大的,如下图可以看出,车的价格和车轴跟因变量关系最为密切,符合判断条件的概率值必须小于0.05,当概率值大于等于0.1时将会被剔除)选择变量(e) 框内,我并没有输入数据,如果你需要对某个自变量进行条件筛选,可以将那个自变量,移入选择变量框内,有一个前提就是:该变量从未在另一个目标列表中出现!,再点击规则设定相应的筛选条件即可,如下图所示:点击统计量弹出如下所示的框,如下所示:在回归系数下面勾选估计,在右侧勾选模型拟合度和共线性诊断两个选项,再勾选个案诊断再点击离群值一般默认值为 3 ,(设定异常值的依据,只有当残差超过3倍标准差的观测才会被当做异常值)点击继续。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
回归分析例题SPSS求解过程1、一元线性回归
SPSS求解过程:
判别:x y 202.0173.2ˆˆˆ1
0+=+=ββ,且x 与y 的线性相关系数为R=0.951 ,回归方程的F 检验值为75.559,对应F 值的显著性概率是0.000<0.05,表示线性回归方程具有显著性 ,当对应F 值的显著性概率>0.05,表示回归方程不具有显著性。
每个系数的t 检验值分别是3.017与8.692,对应的检验显著性概率分
别为:0.017(<0.05)和0.000(<0.05),即否定
H,也就是线性假设是显著
的。
二、一元非线性回归
SPSS求解过程:
1、Y与X的二次及三次多项式拟合:
所以,二次式为:2
029.07408.00927.6x x Y -+=
三次式为:320046.01534.07068.1118.4x x x Y +-+=
2、把Y 与X 的关系用双曲线拟合:
作双曲线变换:x
V y U 1,1==
判别:V U 131.0082.0-=,x
V y U 1
,1==
,V 与U 的相关系数为R=0.968,回归方程系数的F 检验值为196.227,对应F 值的显著性概率是0.000(<0.05),表示线性回归方程具有显著性 ,每个系数的t 检验值分别是440514与14.008,对应的检验显著性概率分别为:0.000(<0.05)和0.000(<0.05),即否定0H ,也就是线性假设是显著的。
3、把Y 与X 的关系用倒指数函数拟合: x
b
ae Y =,则x
b a Y 1ln ln +=
令U1=LN (Y ),V1=V=1/x,有 U1=c+b V1.
判别:V
=,x
1-
U的相关系数为R=0.979,.2
U111
.1
458
1=
=,V与1
ln
,
U/1
V
y
回归方程的F检验值为303.190,对应F值的显著性概率是0.000(<0.05),表示线性回归方程具有显著性,每个系数的t检验值分别是195.221与-17.412,对应的检验显著性概率分别为:0.000(<0.05)和0.000(<0.05),即否定
H,
0也就是线性假设是显著的。
三、多元线性回归
判别:
321036.0108.0161.0695.0x x x y +++=,321,,x x x 与y 的复相关系
数为R=0.582,回归方程的F 检验值为7.702,对应F 值的显著性概率是0.000(<0.05),表示线性回归方程具有显著性 ,每个系数的t 检验值分别是0.803、2.663、2.876与3.401,对应的检验显著性概率分别为:0.426(>0.05)、0.011(<0.05)、0.006(<0.05)和0.001(<0.05),即对于3,2,1,0:0==i H i β,否定0H ,也就是Y 关于各自变量的线性假设是显著的,而对于0:00=βH ,接受0H 。
书解特点:
01.0=α,1x 关于y 的线性关系不显著(Sig=0.011>0.01),剔除1x ,结果
是:
由于结果中又出现2x 关于y 的线性关系不显著(Sig=0.278>0.01),剔除2x ,结果是:
显然,
x关于y的线性关系显著(Sig=0.001<0.01)
3。
