一元一次不等式应用题汇总

合集下载

中考复习一元一次(组)不等式应用(四大类型)

中考复习一元一次（组）不等式应用（四大类型）考点1 盈利问题1.（2021春•饶平县校级期末）八年级某班级部分同学去植树，若每人平均植树7棵，还剩9棵，若每人平均植树9棵，则有1位同学植树的棵数不到8棵．若设同学人数为x人，植树的棵数为（7x+9）棵，下列各项能准确的求出同学人数与种植的树木的数量的是（）A．7x+9≤8+9（x﹣1）B．7x+9≥9（x﹣1）C．D．2.（磁县期末）现在有住宿生若干名，分住若干间宿舍，若每间住4人，则还有19人无宿舍住；若每间住6人，则有一间宿舍不空也不满，若设宿舍间数为x，则可以列得不等式组为（）A．B．C．D．3.把一些书分给几名同学，如果每人分3本，那么余6本；如果前面的每名同学分5本，那么最后一人就分不到3本，这些书有______本，共有______人．（）A．27本，7人B．24本，6人C．21本，5人D．18本，4人考点2 行程问题4.（2020春•嘉祥县期末）某人要完成2.1千米的路程，并要在18分钟内到达，已知他每分钟走90米．若跑步每分钟可跑210米，问这人完成这段路程，至少要跑（）A．3分钟B．4分钟C．4.5分钟D．5分钟5.（2020春•濮阳期末）爆破员要爆破一座旧桥，根据爆破情况，安全距离是70米（人员要撤到70米或70米以外），下面是已知的一些数据，人员撤离速度是7米/秒，导火索的燃烧速度是10.3厘米/秒，请问这次爆破的导火索至少多长才能确保安全？（）A．100厘米B．101厘米C．102厘米D．103厘米6.（春•番禺区期末）张翔上午7：30出发，从学校骑自行车去县城，路程全长20km，中途因道路施工步行一段路他步行的平均速度是5km/h．（1）若张翔骑车的平均速度是15km/h，当天上午9：00到达县城，则他骑车与步行各用多少时间？（2）若张翔必须在当天上午9：00之前赶到县城，他的步行平均速度不变，则他骑车的平均速度应在什么范围内？7.（市北区二模）小颖和小华进行百米赛跑，小颖的平均速度是7m/s，小华的平均速度是6m/s，小颖让小华先跑10米．（1）求小颖何时追上小华；（2）求从什么时间开始，小颖到终点的距离不超过16米；（3）求小颖何时和小华相距5米．考点3 经济问题8.（春•金水区校级月考）某商品进价是6000元，标价是9000元，商店要求利润率不低于5%，需按标价打折出售，最低可以打（）A．8折B．7折C．7.5折D．8.5折9.（2021•金水区校级开学）某商品进价是400元，标价是500元，商店要求利润不低于10%，需按标价打折出售，最多可以打（）A．8折B．7折C．7.5折D．8.8折10.（春•荷塘区期末）已知某品牌的饮料有大瓶与小瓶装之分．某超市花了2100元购进一批该品牌的饮料共800瓶，其中，大瓶和小瓶饮料的进价及售价如表所示．大瓶小瓶进价（元/瓶） 3 2售价（元/瓶） 5 3（1）问：该超市购进大瓶和小瓶饮料各多少瓶？（2）当大瓶饮料售出了200瓶，小瓶饮料售出了100瓶后，商家决定将剩下的小瓶饮料的售价降低0.5元销售，并把其中一定数量的小瓶饮料作为赠品，在顾客一次性购买大瓶饮料时，每满2瓶就送1瓶小瓶饮料，送完即止．请问：超市要使这批饮料售完后获得的利润为1075元，那么小瓶饮料作为赠品送出多少瓶？11.（防城港）蔬菜经营户老王，近两天经营的是青菜和西兰花．（1）昨天的青菜和西兰花的进价和售价如表，老王用600元批发青菜和西兰花共200市斤，当天售完后老王一共能赚多少元钱？青菜西兰花进价（元/市斤） 2.8 3.2售价（元/市斤）4 4.5（2）今天因进价不变，老王仍用600元批发青菜和西兰花共200市斤．但在运输中青菜损坏了10%，而西兰花没有损坏仍按昨天的售价销售，要想当天售完后所赚的钱不少于昨天所赚的钱，请你帮老王计算，应怎样给青菜定售价？（精确到0.1元）考点4 方案问题12.（武汉模拟）某自行车专卖店销售A，B两种型号的自行车，其进价与售价如表进价（元/辆）售价（元/辆）自行车A200250自行车B160200（1）一季度，自行车专卖店购进这两种型号的自行车共30辆，用去了5600元，并且全部售完，该自行车专卖店在该买卖中赚了元；（2）为了满足市场需求，二季度自行车专卖店决定用不超过9000元的资金采购A、B 两种型号的自行车共50辆，且自行车A的数量不少于自行车B的数量的，问自行车专卖店有哪几种进货方案？并说明理由；（3）在（2）的条件下，请你通过计算判断，哪种进货方案自行车专卖店赚钱最多？13.（资阳）为了解决农民工子女就近入学问题，我市第一小学计划2012年秋季学期扩大办学规模．学校决定开支八万元全部用于购买课桌凳、办公桌椅和电脑，要求购买的课桌凳与办公桌椅的数量比为20：1，购买电脑的资金不低于16000元，但不超过24000元．已知一套办公桌椅比一套课桌凳贵80元，用2000元恰好可以买到10套课桌凳和4套办公桌椅．（课桌凳和办公桌椅均成套购进）（1）一套课桌凳和一套办公桌椅的价格分别为多少元？（2）求出课桌凳和办公桌椅的购买方案．14．（黔东南州）去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．（1）求饮用水和蔬菜各有多少件？（2）现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来；（3）在（2）的条件下，如果甲种货车每辆需付运费400元，乙种货车每辆需付运费360元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？培优特训专项2.2 一元一次（组）不等式应用（四大类型）考点1 盈利问题1.（2021春•饶平县校级期末）八年级某班级部分同学去植树，若每人平均植树7棵，还剩9棵，若每人平均植树9棵，则有1位同学植树的棵数不到8棵．若设同学人数为x人，植树的棵数为（7x+9）棵，下列各项能准确的求出同学人数与种植的树木的数量的是（）A．7x+9≤8+9（x﹣1）B．7x+9≥9（x﹣1）C．D．【答案】D【解答】解：（x﹣1）位同学植树棵数为9（x﹣1），∵有1位同学植树的棵数不到8棵．植树的总棵数为（7x+9）棵，∴可列不等式组为：．故选：D．2.（磁县期末）现在有住宿生若干名，分住若干间宿舍，若每间住4人，则还有19人无宿舍住；若每间住6人，则有一间宿舍不空也不满，若设宿舍间数为x，则可以列得不等式组为（）A．B．C．D．【答案】D【解答】解：∵若每间住4人，则还有19人无宿舍住，∴学生总人数为（4x+19）人，∵一间宿舍不空也不满，∴学生总人数﹣（x﹣1）间宿舍的人数在1和5之间，∴列的不等式组为：故选：D．3.把一些书分给几名同学，如果每人分3本，那么余6本；如果前面的每名同学分5本，那么最后一人就分不到3本，这些书有______本，共有______人．（）A．27本，7人B．24本，6人C．21本，5人D．18本，4人【答案】C【解答】解：设有x名同学，则就有（3x+6）本书，由题意，得：0≤3x+6﹣5（x﹣1）＜3，解得：4＜x≤5.5，∵x为非负整数，∴x＝5．∴书的数量为：3×5+6＝21．故选：C．考点2 行程问题4.（2020春•嘉祥县期末）某人要完成2.1千米的路程，并要在18分钟内到达，已知他每分钟走90米．若跑步每分钟可跑210米，问这人完成这段路程，至少要跑（）A．3分钟B．4分钟C．4.5分钟D．5分钟【答案】B【解答】解：设这人跑了x分钟，则走了（18﹣x）分钟，根据题意得：210x+90（18﹣x）≥2100，解得：x≥4，答：这人完成这段路程，至少要跑4分钟．故选：B．5.（2020春•濮阳期末）爆破员要爆破一座旧桥，根据爆破情况，安全距离是70米（人员要撤到70米或70米以外），下面是已知的一些数据，人员撤离速度是7米/秒，导火索的燃烧速度是10.3厘米/秒，请问这次爆破的导火索至少多长才能确保安全？（）A．100厘米B．101厘米C．102厘米D．103厘米【答案】D【解答】解：设这次爆破的导火索需要xcm才能确保安全，•7≥70x≥103．这次爆破的导火索至少103cm才能确保安全．故选：D．6.（春•番禺区期末）张翔上午7：30出发，从学校骑自行车去县城，路程全长20km，中途因道路施工步行一段路他步行的平均速度是5km/h．（1）若张翔骑车的平均速度是15km/h，当天上午9：00到达县城，则他骑车与步行各用多少时间？（2）若张翔必须在当天上午9：00之前赶到县城，他的步行平均速度不变，则他骑车的平均速度应在什么范围内？【答案】（1）骑车用了1.25小时，步行用了0.25小时，（2）大于15km/h．【解答】解：（1）设他骑车用了x小时，步行用了y小时，依题意得：，解得，答：他骑车用了1.25小时，步行用了0.25小时，（2）设骑车的平均速度为vkm/h，依题意得：1.25v+5×0.25＞20，解得：v＞15，答：骑车的平均速度大于15km/h．7.（市北区二模）小颖和小华进行百米赛跑，小颖的平均速度是7m/s，小华的平均速度是6m/s，小颖让小华先跑10米．（1）求小颖何时追上小华；（2）求从什么时间开始，小颖到终点的距离不超过16米；（3）求小颖何时和小华相距5米．【答案】（1）10秒（2）12秒开始（3）5秒【解答】解：（1）设经过x秒小颖追上小华，由题意得7x﹣6x＝10解得：x＝10答：经过10秒小颖追上小华．（2）设经过y秒后，小颖到终点的距离不超过16米，由题意得0≤100﹣7y≤16解得：12≤y≤14答：从12秒开始，小颖到终点的距离不超过16米．（3）设小颖追上小华之前，经a秒小颖和小华相距5米，7a﹣6a＝10﹣5解得：a＝5设小颖追上小华之后，经b秒小颖和小华相距5米，7b﹣6b＝10+5解得：b＝15（不合题意，舍去）答：经5秒小颖和小华相距5米．考点3 经济问题8.（春•金水区校级月考）某商品进价是6000元，标价是9000元，商店要求利润率不低于5%，需按标价打折出售，最低可以打（）A．8折B．7折C．7.5折D．8.5折【答案】B【解答】解：设商店可以打x折出售此商品，根据题意可得：，解得：x≥7，故选：B．9.（2021•金水区校级开学）某商品进价是400元，标价是500元，商店要求利润不低于10%，需按标价打折出售，最多可以打（）A．8折B．7折C．7.5折D．8.8折【答案】D【解答】解：设可以打x折，根据题意可得：500×﹣400≥400×10%，解得：x≥8.8，故选：D．10.（春•荷塘区期末）已知某品牌的饮料有大瓶与小瓶装之分．某超市花了2100元购进一批该品牌的饮料共800瓶，其中，大瓶和小瓶饮料的进价及售价如表所示．大瓶小瓶进价（元/瓶） 3 2售价（元/瓶） 5 3（1）问：该超市购进大瓶和小瓶饮料各多少瓶？（2）当大瓶饮料售出了200瓶，小瓶饮料售出了100瓶后，商家决定将剩下的小瓶饮料的售价降低0.5元销售，并把其中一定数量的小瓶饮料作为赠品，在顾客一次性购买大瓶饮料时，每满2瓶就送1瓶小瓶饮料，送完即止．请问：超市要使这批饮料售完后获得的利润为1075元，那么小瓶饮料作为赠品送出多少瓶？【答案】（1）大瓶饮料500瓶，小瓶饮料300瓶（2）50瓶【解答】解：（1）设该超市购进大瓶饮料x瓶，小瓶饮料y瓶，依题意，得：，解得：．答：该超市购进大瓶饮料500瓶，小瓶饮料300瓶．（2）设小瓶饮料作为赠品送出m瓶，依题意，得：（5﹣3）×500+（3﹣2）×100+（3﹣0.5﹣2）×（300﹣100﹣m）﹣2m＝1075，解得：m＝50．答：小瓶饮料作为赠品送出50瓶．11.（防城港）蔬菜经营户老王，近两天经营的是青菜和西兰花．（1）昨天的青菜和西兰花的进价和售价如表，老王用600元批发青菜和西兰花共200市斤，当天售完后老王一共能赚多少元钱？青菜西兰花进价（元/市斤） 2.8 3.2售价（元/市斤）4 4.5（2）今天因进价不变，老王仍用600元批发青菜和西兰花共200市斤．但在运输中青菜损坏了10%，而西兰花没有损坏仍按昨天的售价销售，要想当天售完后所赚的钱不少于昨天所赚的钱，请你帮老王计算，应怎样给青菜定售价？（精确到0.1元）【答案】（1）赚250元钱（2）不低于4.5元/市斤【解答】解：（1）设批发青菜x市斤，西兰花y市斤；根据题意得：，解得：，即批发青菜100市斤，西兰花100市斤，∴100×（4﹣2.8）+100×（4.5﹣3.2）＝120+130＝250（元）；答：当天售完后老王一共能赚250元钱；（2）设给青菜定售价为a元/市斤；根据题意得：100×（1﹣10%）a+100×4.5﹣600≥250，解得：a≥≈4.44；答：给青菜定售价为不低于4.5元/市斤．考点4 方案问题12.（武汉模拟）某自行车专卖店销售A，B两种型号的自行车，其进价与售价如表进价（元/辆）售价（元/辆）自行车A200250自行车B160200（1）一季度，自行车专卖店购进这两种型号的自行车共30辆，用去了5600元，并且全部售完，该自行车专卖店在该买卖中赚了元；（2）为了满足市场需求，二季度自行车专卖店决定用不超过9000元的资金采购A、B 两种型号的自行车共50辆，且自行车A的数量不少于自行车B的数量的，问自行车专卖店有哪几种进货方案？并说明理由；（3）在（2）的条件下，请你通过计算判断，哪种进货方案自行车专卖店赚钱最多？【答案】（1）1400 （2）三种方案（3）当a＝25时，W最大，此时购进自行车A、自行车B各25台．【解答】解：（1）设自行车专卖店购进自行车Ax辆，自行车By辆，依题意得，解得，所以，20×（250﹣200）+10×（200﹣160）＝1400（元）．答：自行车专卖店在该买卖中赚了1400元；（2）设购买自行车Aa台，则购买自行车B（50﹣a）台，依题意得，解得22≤a≤25．又∵a为正整数，∴a可取23，24，25．故有三种方案：①购买自行车A23台，则购买自行车B27台；②购买自行车A24台，则购买自行车B26台；③购买自行车A25台，则购买自行车B25台．（3）设自行车专卖店赚钱数额为W元，当a＝23时，W＝23×（250﹣200）+27×（200﹣160）＝2230；当a＝24时，W＝24×（250﹣200）+26×（200﹣160）＝2240；当a＝25时，W＝25×（250﹣200）+25×（200﹣160）＝2250；综上所述，当a＝25时，W最大，此时购进自行车A、自行车B各25台．故答案为：1400．13.（资阳）为了解决农民工子女就近入学问题，我市第一小学计划2012年秋季学期扩大办学规模．学校决定开支八万元全部用于购买课桌凳、办公桌椅和电脑，要求购买的课桌凳与办公桌椅的数量比为20：1，购买电脑的资金不低于16000元，但不超过24000元．已知一套办公桌椅比一套课桌凳贵80元，用2000元恰好可以买到10套课桌凳和4套办公桌椅．（课桌凳和办公桌椅均成套购进）（1）一套课桌凳和一套办公桌椅的价格分别为多少元？（2）求出课桌凳和办公桌椅的购买方案．【答案】（1）一套课桌凳和一套办公桌椅的价格分别为120元、200元（2）略【解答】解：（1）设一套课桌凳和一套办公桌椅的价格分别为x元、y元，得：，解得∴一套课桌凳和一套办公桌椅的价格分别为120元、200元；（2）设购买办公桌椅m套，则购买课桌凳20m套，由题意得：16000≤80000﹣120×20m﹣200×m≤24000，解得：，∵m为整数，∴m＝22、23、24，有三种购买方案：方案一方案二方案三课桌凳（套）440460480办公桌椅（套）22232414．（黔东南州）去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．（1）求饮用水和蔬菜各有多少件？（2）现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来；（3）在（2）的条件下，如果甲种货车每辆需付运费400元，乙种货车每辆需付运费360元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？【答案】（1）饮用水和蔬菜分别为200件和120件（2）①甲车2辆，乙车6辆；②甲车3辆，乙车5辆；③甲车4辆，乙车4辆；（3）选择甲车2辆，乙车6辆，可使运费最少，最少运费是2960元．【解答】解：（1）设饮用水有x件，则蔬菜有（x﹣80）件．x+（x﹣80）＝320，解这个方程，得x＝200．∴x﹣80＝120．答：饮用水和蔬菜分别为200件和120件；（2）设租用甲种货车m辆，则租用乙种货车（8﹣m）辆．得：，解这个不等式组，得2≤m≤4．∵m为正整数，∴m＝2或3或4，安排甲、乙两种货车时有3种方案．设计方案分别为：①甲车2辆，乙车6辆；②甲车3辆，乙车5辆；③甲车4辆，乙车4辆；（3）3种方案的运费分别为：①2×400+6×360＝2960（元）；②3×400+5×360＝3000（元）；③4×400+4×360＝3040（元）；∴方案①运费最少，最少运费是2960元．答：运输部门应选择甲车2辆，乙车6辆，可使运费最少，最少运费是2960元．。

一元一次不等式15道应用题

一、综合题（共15题；共160分）1.（2015•凉山州）2015年5月6日，凉山州政府在邛海“空列”项目考察座谈会上与多方达成初步合作意向，决定共同出资亿元，建设40千米的邛海空中列车．据测算，将有24千米的“空列”轨道架设在水上，其余架设在陆地上，并且每千米水上建设费用比陆地建设费用多亿元．（1）求每千米“空列”轨道的水上建设费用和陆地建设费用各需多少亿元（2）预计在某段“空列”轨道的建设中，每天至少需要运送沙石1600m3，施工方准备租用大、小两种运输车共10辆，已知每辆大车每天运送沙石200m3，每辆小车每天运送沙石120m3，大、小车每天每辆租车费用分别为1000元、700元，且要求每天租车的总费用不超过9300元，问施工方有几种租车方案哪种租车方案费用最低，最低费用是多少》2.（2015•攀枝花）某超市销售有甲、乙两种商品，甲商品每件进价10元，售价15元；乙商品每件进价30元，售价40元．（1）若该超市一次性购进两种商品共80件，且恰好用去1600元，问购进甲、乙两种商品各多少件!（2）若该超市要使两种商品共80件的购进费用不超过1640元，且总利润（利润=售价﹣进价）不少于600元．请你帮助该超市设计相应的进货方案，并指出使该超市利润最大的方案．3.（2015•钦州）某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球（每个气排球的价格都相同，每个篮球的价格都相同）．经洽谈，购买1个气排球和2个篮球共需210元；购买2个气排球和3个篮球共需340元．|（1）每个气排球和每个篮球的价格各是多少元（2）该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个，总费用不超过3200元，且购买气排球的个数少于30个，应选择哪种购买方案可使总费用最低最低费用是多少元》4.某商店购买60件A商品和30件B商品共用了1080元，购买50件A商品和20件B商品共用了880元．（1）A、B两种商品的单价分别是多少元（2）已知该商店购买B商品的件数比购买A商品的件数的2倍少4件，如果需要购买A、B两种商品的总件数不少于32件，且该商店购买的A、B两种商品的总费用不超过296元，那么该商店有哪几种购买方案&5.在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要万元，购买2台电脑和1台电子白板需要万元．（1）求每台电脑、每台电子白板各多少万元（2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低．/"6.某超市销售甲、乙两种商品，五月份该超市第一次购进甲商品50件，乙商品30件，用去1400元，第二次购进甲商品40件，乙商品40件，用去1600元．（1）求两种商品进价分别是多少元．（2）由于商品受到市民欢迎，六月份决定再购进甲乙两种商品共80件，且进价不变，甲种商品售价15元，乙种商品售价40元，该超市为使甲、乙两种商品共80件的总利润（利润=售价﹣进价）不少于600元，但又不超过610元．请你帮助该超市设计相应的进货方案．^7.师生积极为地震灾区捐款，在得知灾区急需帐篷后，立即到当地的一家帐篷厂采购，该厂生产的帐篷有两种规格：可供3人居住的小帐篷，价格每顶160元；可供10人居住的大帐篷，价格每顶400元。

10道一元一次不等式应用题和答案过程

一元一次不等式解应用题一、某水产品市场管理部门规划建造面积为2400平方米的大棚，大棚内设A种类型和B 种类型的店面共80间，每间A种类型的店面的平均面积为28平方米，月租费为400元，每间B种类型的店面的平均面积为20平方米，，月租费为360元，全部店面的建造面积不低于大棚总面积的85%。

（1）试确定A种类型店面的数量？（2）该大棚管理部门通过了解，A种类型店面的出租率为75%，B种类型店面的出租率为90%，为使店面的月租费最高，应建造A种类型的店面多少间？解：设A种类型店面为a间，B种为80-a间根据题意28a+20（80-a）≥2400×85%28a+1600-20a≥20408a≥440a≥55A型店面至少55间设月租费为y元y=75%a×400+90%（80-a）×360=300a+25920-324a=25920-24a很明显，a≥55，所以当a=55时，可以获得最大月租费为25920-24x55=24600元二、水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖，他了解到情况：1、每亩地水面组建为500元，。

2、每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗；3、每公斤蟹苗的价格为75元，其饲养费用为525元，当年可或1400元收益；4、每公斤虾苗的价格为15元，其饲养费用为85元，当年可获160元收益；问题：1、水产养殖的成本包括水面年租金，苗种费用和饲养费用，求每亩水面虾蟹混合养殖的年利润（利润=收益—成本）；2、李大爷现有资金25000元，他准备再向银行贷款不超过25000元，用于蟹虾混合养殖，已知银行贷款的年利率为10％，试问李大爷应租多少亩水面，并向银行贷款多少元，可使年利润达到36600元？解：1、水面年租金=500元苗种费用=75x4+15x20=300+300=600元饲养费=525x4+85x20=2100+1700=3800元成本=500+600+3800=4900元收益1400x4+160x20=5600+3200=8800元利润（每亩的年利润）=8800-4900=3900元2、设租a亩水面，贷款为4900a-25000元那么收益为8800a成本=4900a≤25000+250004900a≤50000a≤50000/4900≈10.20亩利润=3900a-（4900a-25000）×10%3900a-（4900a-25000）×10%=366003900a-490a+2500=366003410a=34100所以a=10亩贷款（4900x10-25000）=49000-25000=24000元三、某物流公司，要将300吨物资运往某地，现有A、B两种型号的车可供调用，已知A 型车每辆可装20吨，B型车每辆可装15吨，在每辆车不超载的条件下，把300吨物资装运完，问：在已确定调用5辆A型车的前提下至少还需调用B型车多少辆?解：设还需要B型车a辆，由题意得20×5+15a≥30015a≥200a≥40/3解得a≥13又1/3 ．由于a是车的数量，应为正整数，所以x的最小值为14．答：至少需要14台B型车．四、某城市平均每天产生生活垃圾700吨，全部由甲，乙两个垃圾厂处理，已知甲厂每小时处理垃圾55吨，需费用550元；乙厂每小时处理垃圾45吨，需费用495元。

一元一次不等式应用题集锦

（） A.11辆 B.10辆
C.9辆
D.8辆
7、 (2001荆州)在双休日,某公司决定组织48名员工到附近一水上公园坐船游园,公司先派一个人去了解船只的租金情况,这个人看到的租金价格表如下:
船型
每只限载人数 (人)
租金 (元)
大船 5
3
小船 3
2
那么,怎样设计租船方案才能使所付租金最少?(严禁超载)
了节约资金应选择哪种方案？
18、某商店需要购进一批电视机和洗衣机，根据市场调查，决定电视机进货量不少于洗衣机的进货量的一半．电视机与洗衣机的进价和售价如下表：
类别
电视机洗衣机
进价（元/ 台）
1800
1500
售价（元/ 台）
2000
1600
计划购进电视机和洗衣机共100台，商店最多可筹集资金161 800 元．
（1）、求y与x之间的函数关系式，并画出函数的图象。（2）、求弹簧所挂物体的最大质量是多少？
29、某人点燃一根长度为25㎝的蜡烛，已知蜡烛每小时缩短5㎝，设xh后蜡烛剩下的长度为y㎝。（1）、求y与x的函数关系式。（2）、几个小时以后，蜡烛的长度不足10㎝？
30、一艘轮船以20km/h的速度从甲港驶往160km远的乙港，2h后，一艘快艇以40km/h的速度也从甲港驶往乙港。分别列出轮船和快艇行驶的路程y km与时间x h的函数关系式，并在直角坐标系中画出函数的图象，观察图象回答下列问题：（1）何时轮船行驶在快艇的前面？（2）何时快艇行驶在轮船的前面？（3）哪一艘船先驶过60km？哪一艘船先驶过100km？
③每千克蟹苗的价格为75元，其饲养费用为525元，当年可获1 400 元收益；
④每千克虾苗的价格为15元，其饲养费用为85元，当年可获160元收益．

10道一元一次不等式应用题和答案过程

10道一元一次不等式应用题和答案过程1.某水产品市场管理部门计划建造2400平方米的大棚，内设有A种和B种店面各80间。

A种店面的平均面积为28平方米，月租费为400元；B种店面的平均面积为20平方米，月租费为360元。

全部店面的建造面积不低于大棚总面积的85%。

现在要确定A种店面的数量。

解：设A种店面为a间，B种店面为80-a间。

根据题意，28a+20(80-a)≥2400×85%，化简得8a≥440，即a≥55.因此，A种店面至少应有55间。

为使店面的月租费最高，设月租费为y元，根据题意可得y=75%a×400+90%(80-a)×360=300a+-24a=-24a。

因为a≥55，所以当a=55时，y取最大值，即月租费最高为元。

2.水产养殖户XXX计划进行大闸蟹与河虾的混合养殖。

每亩地水面租金为500元，每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗。

每公斤蟹苗的价格为75元，饲养费用为525元，当年可获得1400元收益；每公斤虾苗的价格为15元，饲养费用为85元，当年可获得160元收益。

现在要求出每亩水面虾蟹混合养殖的年利润，并确定XXX应租多少亩水面，向银行贷款多少元，才能使年利润达到元。

解：每亩水面的成本包括水面年租金、苗种费用和饲养费用，即成本=500+75×4+15×20+525×4+85×20=4900元。

每亩水面的收益为1400×4+160×20=8800元。

因此，每亩水面的年利润为8800-4900=3900元。

设租a亩水面，贷款为4900a-元。

根据题意，收益为8800a，成本不超过元，即4900a≤，解得a≤10.2亩。

为使年利润达到元，可列出方程3900a+0.1(4900a-)=，解得a≈13.08亩，即XXX应租13亩水面，向银行贷款约为元。

某手机生产厂家决定对一款原售价为2000元的彩屏手机进行调价，按新单价的八折优惠出售。

一元一次不等式应用题汇总

不等式应用练习题1、某商店第一天以每件10元的价格购进某商品15件,第二天又以12元的价格购进同种商品35件,然后以相同的价格卖出,如果销售这些商品时,至少要获得10%的利润,这种商品每件的售价应不低于多少元？2、一家三口准备参加旅行团外出旅游，甲旅行社告知：“父母买全票，小孩按半价优惠”，乙旅行社告知：“家庭旅游可按团体计价，即每人均按全价的8折收费”，若这两家旅行社每人的原价相同，那么可以算出（）A．甲比乙优惠B．乙比甲优惠C．甲与乙相同D．与原票价有关3、甲乙两家超市以相同的价格出售同样的商品.为吸引顾客各自推出不同的优惠方案.甲超市累计购买商品超出500元之后.超出部分按原价八五折优惠.在乙超市累计购买商品超出300元之后.超出部分按原价九折优惠.（1）是用含x的代数式分别表示,顾客在两家超市购物所付的费用.（2）试比较顾客到哪家超市购物更优惠,并说明你的理由.4、按国家有关规定，个人发表文章、出版图书获得的稿费的纳税计算方法是：(1)稿费不高于4000元的不纳税；国家规定个人发表文章、出版图书所得稿费的纳税计算方法是：（1）稿费不高于800元的不拿税；（2）稿费高于800元而低于4000元的应缴纳超过800元那部分稿费的14％的税；（3）稿费等于或高于4000元的应缴纳全部稿费的11％的税。

王老师获得一笔稿费，并交纳个人所得税不超过420元，问他这笔稿费最多是多少元？5、今秋，某市白玉村水果喜获丰收，果农王灿收获枇杷20吨，桃子12吨．现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售，已知一辆甲种货车可装枇杷4吨和桃子1吨，一辆乙种货车可装枇杷和桃子各2吨．（1）王灿如何安排甲、乙两种货车可一次性地运到销售地？有几种方案？（2）若甲种货车每辆要付运输费300元，乙种货车每辆要付运输费240元，则果农王灿应选择哪种方案，使运输费最少？最少运费是多少？6、某校初三年级春游，现有36座和42座两种客车供选择租用，若只租用36座客车若干辆，则正好坐满；若只租用42座客车，则能少租一辆，且有一辆车没有坐满，但超过30人；已知36座客车每辆租金400元，42座客车每辆租金440元．（1）该校初三年级共有多少人参加春游？（2）请你帮该校设计一种最省钱的租车方案？7、某射击运动员在一次训练中，打靶10次的成绩为89环，已知前6次射击的成绩为50环，则他第七次射击时，击中的环数至少是______环．8、某县出租车计费规则：2公里以内3元,超过两公里部分另按每公里1.2元收费（不足1公里按1公里收费）,李立同学从家出发坐出租车到新华书店购书,下车时付费9元,那么李立家离书店最多有几公里?9、甲从一个鱼摊上买了三条鱼,平均每条a元,又从另一个鱼摊买了两条鱼,平均每条b元,后来他又以每条a+b/2元的价格把鱼全部地卖给了乙,结果发现赔钱,你知道为什么吗?10、为了加强学生的交通安全意识,某中学和交警大队联合举行了“我当一日小交警”活动.星期天选派部分学生到交通路口值勤,协助交通警察维持交通秩序.若每一个路口安排4人,那么剩下78人；若每一个路口安排8人,那么最后一个路口不足8人,但不少于4人,求这个中学共选派值勤学生多少人?共在多少个交通路口安排值勤?11、足球比赛的记分规则为：胜一场得3分，平一场得1分，负一场得0分，一支足球队在某个赛季比赛共需14场，现已比赛8场，输了一场，得17分，请问：（1）前8场比赛中，这支球队共胜了多少场？（2）这支球队打满14场比赛，最高能得多少分？（3）通过对比赛的分析，这支球队打满14场比赛，得分不低于29分，就可达到预期的目的，请你分析一下，在后面的6场比赛中，这支球队至少要胜几场，才能达到预期的目标？12、2012年我市某县筹备20周年县庆，园林部门决定利用现有的3 490盆甲种花卉和2 950盆乙种花卉搭配两种园艺造型共50个摆放在迎宾大道两侧，已知搭配一个种造型需甲种花卉80盆，乙种花卉40盆，搭配一个种造型需甲种花卉50盆，乙种花卉90盆．（1）某校九年级（1）班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来．（2）若搭配一个种造型的成本是800元，搭配一个种造型的成本是960元，试说明（1）中哪种方案成本最低？最低成本是多少元？13、某园林的门票每张10元，一次性使用．考虑到人们的不同需求，也为了吸引更多的游客，该园林除保留原来的售票方法外，还推出了一种“购买个人年票”的售票方法（个人年票从购买日起，可供持票者使用一年）．年票分A、B、C 三类，A类年票每张120元，持票者进人园林时，无需再购买门票；B类年票每张60元，持票者进入该园林时，需再购买门票，每次2元；C类年票每张40元，持票者进入该园林时，需再购买门票，每次3元．（1）如果你只选择一种购买门票的方式，并且你计划在一年中用80元花在该园林的门票上，试通过计算，找出可使进入该园林的次数最多的购票方式；（2）求一年中进入该园林至少超过多少次时，购买A类年票比较合算．14、某种出租车的收费标准是：起步价7元(即行驶距离不超过3千米都需付7元车费),超过3千米,每增加1千米,加收2.4元(不足1千米接1千米计)．某人乘这种出租车从甲地到乙地共支付车费19元,设此人从甲地到乙地经过的路程是x千米,那么x的最大值是？15、某次数学测验中共有16道题目,评分方法：答对一道得6分,答错一道扣3分,不答得0分.某学生有两道题未答那么这个同学至少要答对多少道题,成绩才能在60分以上?16、娃哈哈矿泉水每瓶售价1.2元,现甲、乙两家超市分别给出优惠政策,甲商场全部九折,乙商场20瓶以上的部分8折,若你是消费者,选哪家商场比较合适?.17、某校为了奖励在数学竞赛中获奖的学生，买了若干本课外读物准备送给他们，如果每人送3本，则还余8本；如果前面每人送5本，则最后一人得到的课外读物不足3本，设该校买了m本课外读物，有x名学生获奖，请解答下列问题：（1）用含x的代数式表示m；（2）求出该校的获奖人数及所买课外读物的本数\19、某射击运动员在一次比赛中前8次射击共中72环，如果他要打破89环（10次射击）的记录，第九次射击不能少于多少环？20、学校将若干间宿舍分配给七年级一班女生住宿，已知该班女生人数少于35人。

解一元一次不等式专项练习 (80题,附答案)

解一元一次不等式专项练习（80 题、附答案）（1）3（x+2）﹣8≥1﹣2（x﹣1）；（2）x ﹣≤2﹣．（3）2（x﹣1）+2＜5﹣3（x+1）（4）．（5）﹣＜1；（6）3﹣（3y﹣1）≥（3+y）（7）x ﹣≥﹣1（8）﹣＞﹣1 （9）﹣1≤．（10）﹣3x+2≤8．（11）﹣3x﹣4≥6x+2．（12）﹣8x﹣6≥4（2﹣x）+3．（13）（14）（15）．（16）2（x﹣1）＜﹣3（1﹣x）（17）≤﹣1 （18）10﹣3（x﹣2）≤2（x+1）（19）﹣2≤．（20）﹣3x＞2（21）x ＞﹣x﹣2（22）3（x+1）＜4（x﹣2）﹣3 （23）≤1．（24）≥；（25）﹣＞﹣2．（26）5x﹣4＞3x+2（27）4（2x﹣1）＞3（4x+2）（28）≤（29）﹣2≥．（30）4（x﹣1）+3≥3x；（31）2x﹣3＜；（32）≤1．（33）3[x﹣2（x﹣2）]＞6+3 （34）（35）（36）．（37）3（x+2）﹣8≥1﹣2（x﹣1）；（38）＞；（39）≤；（40）＜．（41）3（2x﹣3）≥2（x﹣4）（42）≥0（43）7（1﹣2x）＞10﹣5（4x﹣3）（44）．（45）﹣＜0；（46）1﹣≤﹣x．（47）5x﹣12≤2（4x﹣3）；（48）≥x﹣2．（49）4x﹣2（3+x）＜0 （50）﹣≥0．（51）3x﹣2＜﹣4（x﹣5）；（52）﹣1＜＜2．（53）；（54）．（55）5x+15＞4x﹣13（56）≤．（57）7（4﹣x）﹣2（4﹣3x）＜4x；（58）10﹣4（x﹣3）≥2（x﹣1）；（59）3[x﹣2（x﹣2）]＞x﹣3（x﹣3）；（60）（2x﹣1）+x﹣1+（1﹣2x）≤0；（61）﹣y ﹣；（62）．（63）x（x+1）＞（x﹣2）2；（64）．（65）3（y﹣3）＜7y﹣4（66）﹣21＜6﹣3x≤9．（67）；（68）；（69）0.5x+3（1﹣0.2x）≥0.4x﹣0.6；（70）x ﹣＜1﹣；（71）2[x﹣（x﹣1）+2]＜1﹣x；（72）．（73）3x﹣7＜5x﹣3；（74）．（75）（76）（77）≤．（78）3x﹣9≤0；（79）2x﹣5＜5x﹣2；（80）2（﹣3+x）＞3（x+2）；参考答案：（1）3（x+2）﹣8≥1﹣2（x﹣1），3x+6﹣8≥1﹣2x+2，3x+2x≥1+2﹣6+8，5x≥5，x≥1；（2）x ﹣≤2﹣，6x﹣3（x﹣1）≤12﹣2（x+2），6x﹣3x+3≤12﹣2x﹣4，3x+2x≤8﹣3，5x≤5，x≤1（3）2（x﹣1）+2＜5﹣3（x+1）2x﹣2+2＜5﹣3x﹣3，2x+3x＜5﹣3+2﹣2，5x＜2，x，（4），3（1+x）≤2（2x﹣1）+6，3+3x≤4x﹣2+6，3x﹣4x≤﹣2+6﹣3，﹣x≤1，x≥﹣1（5）去分母得，2x﹣3（x﹣1）＜6，去括号得，2x﹣3x+3＜6，移项、合并同类项得，﹣x＜3，把x的系数化为1得，x＞﹣3．（6）去分母得，24﹣2（3y﹣1）≥5（3+y），去括号得，24﹣6y+2≥15+5y，移项、合并同类项，﹣11y≥﹣11，把x的系数化为1得，y≤1（7）去分母得，6x﹣2（2x﹣1）≥3（2+x）﹣6去括号得，6x﹣4x+2＞6+3x﹣6，移项得，6x﹣8x﹣3x＞6﹣6﹣2，合并同类项得，﹣5x＞﹣2，把x的系数化为1得，x ＜﹣，（8）去分母得，6（2x﹣1）﹣4（2x+5）＞3（6x﹣1），去括号得，12x﹣6﹣8x﹣20＞18x﹣3，移项得，12x﹣8x﹣18x＞﹣3+6+20，合并同类项得，﹣14x＞23，把x的系数化为1得，x ＜﹣，（9）分子与分母同时乘以10得，﹣1≤，去分母得，2（2x﹣1）﹣6≤3（5x+2），去括号得，4x﹣2﹣6≤15x+6，移项得，4x﹣15x≤6+2+6，合并同类项得，﹣11x≤14，把x的系数化为1得，x ≥﹣（10）移项合并得：﹣3x≤6，解得：x≥﹣2，（11）移项合并得：9x≤﹣6，解得：x ≤﹣，（12）去括号得：﹣8x﹣6≥8﹣4x+3，移项合并得：﹣4x≥17，解得：x ≤﹣（13）去分母得：4x﹣8＞6x+2，移项合并得：﹣2x＞10，解得：x＜﹣5；（14）去分母得：2x﹣4x+1＜3，移项合并得：﹣2x＜2，解得：x＞﹣1；（15）去分母得：12+3x﹣6≥8x+8，移项合并得：5x≥﹣2，解得：x ≤﹣（16）去括号得，2x﹣2≤﹣3+3x，移项得，2x﹣3x≤﹣3+2，合并同类项得，﹣x≤﹣1把x的系数化为1得，x≥1，（17）去分母得，3（2﹣3x）≤2x﹣1﹣6，去括号得，6﹣9x≤3x﹣7，移项得，﹣9x﹣3x≤﹣7﹣6，合并同类项得，﹣12x≤13，x的系数化为1得，x ≥﹣，（18）去括号得，10﹣3x+6≤2x+2，移项得，﹣3x﹣2x≤2﹣10﹣6，合并同类项得，﹣5x≤﹣24把x的系数化为1得，x ≥﹣，（19）去分母得，2（1﹣5x）﹣24≤3（3﹣x）去括号得，2﹣10x﹣24≤9﹣3x，移项得，﹣10x+3x≤9﹣2+24，合并同类项得，﹣7x≤31，x的系数化为1得，x ≥﹣（20）﹣3x＞2，解得：x ＜﹣；（21）去分母得：x＞﹣2x﹣6，解得：x＞﹣2；（22）去括号得：3x+3＜4x﹣8﹣3，解得：x＞14；（23）去分母得：2（2x﹣1）﹣3（5x+1）≤6，去括号得： 4x﹣2﹣15x﹣3≤6，解得： x≥﹣1（24）去分母得，3（x+4）≥﹣2（2x+1），去括号得，3x+12≥﹣4x﹣2，移项、合并同类项得，7x≥﹣14，把x的系数化为1得，x ≥﹣．（25）去分母得，4（x﹣1）﹣3（2x+5）＞﹣24，去括号得，4x﹣4﹣6x﹣15＞﹣24，移项、合并同类项得，﹣2x＞﹣5，把x的系数化为1得，x ＜（26）移项得，5x﹣3x＞2+4，合并同类项得，2x＞6，把x的系数化为1得，x＞3．（27）去括号得，8x﹣4＞12x+6，移项得，8x﹣12x＞6+4，合并同类项得，﹣4x＞10，把x的系数化为1得，x＜﹣．（28）去分母得，3（4x﹣1）≤1﹣5x，去括号得，12x﹣3≤1﹣5x，移项得，12x+5x≤1+3，合并同类项得，17x≤4，把x的系数化为1得，x ≤．（29）去分母得，2（5x+1）﹣24≥3（x﹣5），去括号得，10x+2﹣24≥3x﹣15，移项得，10x﹣3x≥﹣15﹣2+24，合并同类项得，7x≥7，把x的系数化为1得，x≥1（30）去括号得，4x﹣4+3≥3x，移项得，4x﹣3x≤4﹣3，合并同类项得，x≤1，（31）去分母得，3（2x﹣3）＜x+1，去括号得，6x﹣9＜x+1，移项得，6x﹣x＜1+9，合并同类项得，5x＜10，x的系数化为1得，x＜2，（32）去分母得，2（2x﹣1）﹣（9x+2）≤6，去括号得，4x﹣2﹣9x﹣2≤6，移项得，4x﹣9x≤6+2+2，合并同类项得，﹣5x≤10，x的系数化为1得，x≥﹣2（33）3[x﹣2（x﹣2）]＞6+3x解：去小括号，3[x﹣3x+4]＞6+3x合并，3[﹣x+4]＞6+3x去中括号，﹣3x+12＞6+3x移项，合并，﹣6x＞﹣6化系数为1，x＜1．（34）解：去分母，2（2x﹣5）≤3（3x+1）﹣8x去括号，4x﹣10≤9x+3﹣8x移项合并，3x≤13化系数为1，x ≤．（35）解：去分母，3（2﹣x）﹣3（x﹣5）＞2（﹣4x+1）+8 去括号，6﹣9x﹣3x+15＞﹣8x+2+8移项合并，﹣4x＞﹣11化系数为1，x ＜．（36）解：利用分数基本性质化小数分母为整数去括号，4x﹣1﹣10x+7＞2﹣4x移项合并，﹣2x＞﹣4化系数为1，x＜2（37）去括号，得：3x+6﹣8≥1﹣2x+2，移项、合并同类项，得：5x≥5，系数化成1得：x≥1；（38）去分母，得：3（x﹣3）﹣6＞2（x﹣5），去括号，得：3x﹣9﹣6＞2x﹣10，移项、合并同类项得：x＞5；（39）去分母，得：6x﹣3（x﹣1）≤12﹣2（x+2），去括号，得：6x﹣3x+3≤12﹣2x﹣4，移项、合并同类项得：5x≤5系数化成1得：x≤1；（40）去分母，得：6x﹣3x＜6+x+8﹣2（x+1），去括号，得：6x﹣3x＜6+x+8﹣2x﹣2，移项得：6x﹣3x﹣x+2x＜6﹣2+8合并同类项得：4x＜12系数化成1得：x＜3（41）去括号，得6x﹣9≥2x﹣8，移项，得6x﹣2x≥﹣8+9，合并同类项，得4x≥1，两边同除以4，得x ≥，（42）去分母，得4﹣8x≥0，移项得﹣8x≥﹣4，两边同除以﹣8，得x ≤，（43）去括号，得7﹣14x＞10﹣20x+15，移项，得﹣14x+20x＞10+15﹣7，合并同类项得6x＞18，两边同除以6得x＞3，（44）去分母，得2x+6＜﹣6x﹣3（x+10），去括号，得2x+6＜﹣6x﹣3x﹣30，移项，得2x+6x+3x＜﹣30﹣6，合并同类项，得11x＜﹣36，两边同除以11得x ＜﹣（45）去分母得：2（2x+1）﹣（5﹣2x）＜0，去括号得：4x+2﹣5+2x＜0，移项合并得：6x＜3，解得：x ＜，表示在数轴上，如图所示：；（46）去分母得：6﹣2（x﹣1）≤3（2x+3）﹣6x，去括号得：6﹣2x+2≤6x+9﹣6x，移项合并得：﹣2x≤1，解得：x ≥﹣（47）去括号得，5x﹣12≤8x﹣6，移项得，5x﹣8x≤﹣6+12，合并同类项得，﹣3x≤6，x的系数化为1得，x≥﹣2；（48）去分母得，x﹣3≥2（x﹣2），去括号得，x﹣3≥2x﹣4，移项得，x﹣2x≥﹣4+3，合并同类项得，﹣x≥﹣1，x的系数化为1得，x≤1（49）去括号得4x﹣6﹣2x＜0，移项、合并同类项得2x＜6，系数化为1得x＜3；这个不等式的解集在数轴上表示如图1：（50）去分母得3（2x﹣3）﹣4（x﹣2）≥0，去括号得6x﹣9﹣4x+8≥0，移项、合并同类项得2x≥1，系数化为1得x≥0.5（51）3x﹣2＜﹣4（x﹣5）；去括号得3x﹣2＜﹣4x+20，移项得3x+4x＜20+2合并同类项得7x＜22未知项的系数化为1得x ＜，（52）﹣1＜＜2，去分母得﹣3＜2﹣x＜6，移项得﹣3﹣2＜﹣x＜6﹣2，合并同类项得﹣5＜﹣x＜4未知项的系数化为1得﹣4＜x＜5（53）去分母得，2（x﹣1）﹣3（x+4）＞﹣12，去括号得，2x﹣2﹣3x﹣12＞﹣12，移项、合并同类项得﹣x＜2，化系数为1得x＜﹣2．（54）去分母得，（x﹣2）﹣3（x﹣1）＜3，去括号得，x﹣2﹣3x+3＜3，移项、合并同类项得﹣2x＜2，化系数为1得x＞﹣120．解：（55）移项，得：5x﹣4x＞﹣13﹣15，合并同类项，得：x＞﹣28；（56）去分母，得：2（2x﹣1）≤3x﹣4，去括号，得：4x﹣2≤3x﹣4，移项，得：4x﹣3x≤﹣4+2，合并同类项，得：x≤﹣2（57）去括号得，28﹣7x﹣8+6x＜4x，移项得，﹣7x+6x﹣4x＜8﹣28，合并同类项得，﹣5x＜﹣20，系数化为1得，x＞4．（58）去括号得，10﹣4x+12≥2x﹣2，移项得，﹣4x﹣2x≥﹣2﹣10﹣12，合并同类项得，﹣6x≥﹣24，系数化为1得，x≤4．（59）去括号得，3x﹣6x+12＞x﹣3x+9，移项得，x﹣6x﹣x+4x＞9﹣12，合并同类项得，﹣3x＞﹣3，系数化为1得，x＜1．（60）去分母得，（2x﹣1）+3x﹣3+（1﹣2x）≤0，去括号得，2x﹣1+3x﹣3+1﹣2x≤0，移项得，2x+3x﹣2x≤3+1﹣1，合并同类项得，3x≤3，系数化为1得，x＞1．（61）去分母得，﹣10y﹣5（y﹣1）≥20﹣2（y+2），去括号得，﹣10y﹣5y+5≥20﹣2y﹣4，移项得，﹣10y﹣5y+2y≥20﹣4﹣5，合并同类项得，﹣13y≥11，系数化为1得，y ≤﹣．（62）去分母得，2（3x+2）﹣（7x﹣3）＞16，去括号得，6x+4﹣7x+3＞16，移项得，6x﹣7x＞16﹣4﹣3，合并同类项得，﹣x＞9，系数化为1得，x＜﹣9（63）由原不等式，得x2+x＞x2﹣4x+4，移项、合并同类项，得5x＞4，不等式两边同时除以5，得x ＞，即原不等式的解集是x ＞；（64）由原不等式，得﹣17x+1＜12﹣10x，移项、合并同类项，得﹣7x＜11，不等式两边同时除以﹣7（不等号的方向发生改变），得x ＞﹣，即原不等式的解集是x ＞﹣（65）去括号，得：3y﹣9＜7y﹣4，移项，得：3y﹣7y＜9﹣4，即﹣4y＜5，；（66）﹣21＜6﹣3x≤9两边同时减去6再除以﹣3，不等号的方向改变，得：﹣1≤x＜9（67）去分母得，2（1﹣2x）≥4﹣3x，去括号得，2﹣4x≥4﹣3x，移项得，﹣4x+3x≥4﹣2，合并同类项得，﹣x≥2，化系数为1得，x≤﹣2；（68）去分母得，2（x+4）﹣3（3x﹣1）＜6，去括号得，2x+8﹣9x+3＜6，移项得，2x﹣9x＜6﹣8﹣3，合并同类项得，﹣7x＜﹣5，化系数为1得，x ＞；（69）去括号得，0.5x+3﹣0.6x≥0.4x﹣0.6，移项得，0.5x﹣0.6x﹣0.4x≥﹣0.6﹣3，合并同类项得，﹣0.5x≥﹣3.6，化系数为1得，x≤7.2．（70）去分母得，6x﹣3x﹣（x+8）＜6﹣2（x+1），去括号得，6x﹣3x﹣x﹣8＜6﹣2x﹣2，移项得，6x﹣3x﹣x+2x＜6﹣2+8，合并同类项得，4x＜12，化系数为1得，x＜3；（71）去括号得，2x﹣2x+2+4＜1﹣x，移项得，2x﹣2x+x＜1﹣2﹣4，合并同类项得，x＜﹣5；（72）去分母得，2（2x﹣1）﹣3（5x+1）≤6，去括号得，4x﹣2﹣15x﹣3≤6，移项得，4x﹣15x≤6+2+3，合并同类项得，﹣11x≤11，化系数为1得，x≥﹣1（73）移项合并得：﹣2x＜4，解得：x＞﹣2；（74）去分母得：3（x+5）﹣2（2x+3）≥12，去括号得：3x+15﹣4x﹣6≥12，移项合并得：﹣x≥3，解得：x≤﹣3（75）原不等式的两边同时乘以6，得2x+6＞21﹣3x，移项，合并同类项，得5x＞15，不等式的两边同时除以5，得x＞3，∴原不等式的解集是x＞3．（76）原不等式的两边同时乘以6，得8x+2≤14﹣x，移项，合并同类项，得9x≤16，不等式的两边同时除以9，得x≤；所以，原不等式的解集是x≤；（77）原不等式的两边同时乘以6，得8﹣2x≤9，移项，合并同类项，得﹣2x≤1，不等式的两边同时除以﹣2，得x≥﹣，所以，原不等式的解集是x≥﹣（78）移项得，3x≤9，x的系数化为1得，x≤3．（79）移项得，2x﹣5x＜﹣2+5，合并同类项得，﹣3x＜3，把x的系数化为1得，x＞﹣1．。

一元一次不等式应用题专题

一元一次不等式应用题专题(附答案)1、某校王校长暑假将带领该校市级三好学生去北京旅游。

甲旅行社说如果校长买全票一张，则其余学生可享受半价优惠，乙旅行社说包括校长在内全部按全票价的6折优惠（按全票价的60％收费，且全票价为1200元） ①设学生数为x，甲旅行社收费为y甲，乙旅行社收费为y乙，分别计算两家旅行社的收费（写出表达式） ②当学生数是多少时，两家旅行社的收费一样？ ③就学生数x讨论哪家旅行社更优惠。

解：设设学生数为x，甲旅行社收费为y甲，乙旅行社收费为y乙，根据题意，得①y甲=1200+1200×50%×x=1200+600xy乙=(x+1)×1200×60%=720(x+1)=720x+720②当学生数是多少时，两家旅行社的收费一样？当y甲=y乙时，即1200+600x=720x+720120x=480x=4所以，当学生数为4人时，两家旅行社的收费一样！③就学生数x讨论哪家旅行社更优惠。

若y甲＞y乙，即1200+600x＞720x+720120x＜480x＜4，此时乙旅行社便宜。

若y甲＜y乙，即1200+600x＜720x+720解得，x>4,此时甲旅行社便宜。

答：当学生人数少于4人时，乙旅行社更优惠；当学生人数多于4人时，甲旅行社更优惠；当学生人数等于4人时，两个旅行社一样优惠。

2、李明有存款600元，王刚有存款2000元，从本月开始李明每月存款500元，王刚每月存款200元，试问到第几个月，李明的存款能超过王刚的存款。

解：设到第x个月李明的存款超过王刚的存款，根据题意，得600+500x＞2000+200x300x＞1400x＞14/3因为x为整数，所以x=5答：到第5个月李明的存款超过王刚的存款。

3、暑假期间，两名家长计划带领若干名学生去旅游，他们联系了报价为每人500元的两家旅行社，经协商，甲旅行社的优惠条件是：两名家长全额收费，学生都按七折；乙旅行社的优惠条件是：家长，学生都按八折收费。

一元一次不等式组应用题专题

• • • • •
解：依题意，甲店B型产品有（70﹣x）件，乙店A型有（40﹣x）件，B型有（x﹣10）件，则（1）W=200x+170（70﹣x）+160（40﹣x）+150（x﹣10）=20x+16800．解得10≤x≤40．（2分）由
• • • • • • • • • • •
（2）由W=20x+16800≥17560， ∴x≥38 ． ∵ 10≤x≤40 ∴38≤x≤40，x=38，39，40． ∴有三种不同的分配方案． ①x=38时，甲店A型38件，B型32件，乙店A型2件，B型28件； ②x=39时，甲店A型39件，B型31件，乙店A型1件，B型29件； ③x=40时，甲店A型40件，B型30件，乙店A型0件，B型30件．（3）依题意：W=（200﹣a）x+170（70﹣x）+160（40﹣x）+150（x﹣10）=（20﹣a） x+16800． ①当0＜a＜20时，x=40，即甲店A型40件，B型30件，乙店A型0件，B型30件，能使总利润达到最大； ②当a=20时，10≤x≤40，符合题意的各种方案，使总利润都一样； ③当20＜a＜30时，x=10，即甲店A型10件，B型60件，乙店A型30件，B型0件，能使总利润达到最大．（8分）
• 3、（2013•湛江）某工厂现有甲种原料280kg，乙种原料190kg，计划用这两种原料生产A，B 两种产品50件，已知生产一件A产品需甲种原料 7kg、乙种原料3kg，可获利40可获利350 元． • （1）请问工厂有哪几种生产方案？ • （2）选择哪种方案可获利最大，最大利润是多少？
• • • •
解：（1）60﹣x﹣y；（2）由题意，得900x+1200y+1100（60﹣x﹣y）=61000，整理得y=2x﹣50．（3）①由题意，得P=1200x+1600y+1300（60﹣x﹣y） ﹣61000﹣1500， • 整理得P=500x+500． • ②购进C型手机部数为：60﹣x﹣y=110﹣3x．根据题意列不等

一元一次不等式组应用题及答案

一元一次不等式组应用题及答案一元一次不等式应用题一．分配问题：6.一群女生住若干家间宿舍，每间住4人，剩下191.把若干颗花生分给若干只猴子。

如果每只猴子分3人无房住；每间住6人，有一间宿舍住不满。

颗，就剩下8颗；如果每只猴子分5颗，那么最后一(1)如果有x间宿舍，那么可以列出关于x的不等式组：只猴子虽分到了花生，但不足5颗。

问猴子有多少只，花生有多少颗？2.把一些书分给几个学生，如果每人分3本，那么余8本；如果前面的每个学生分5本，那么最后一人就分不到3本。

问这些书有多少本？学生有多少人？3.某中学为八年级寄宿学生安排宿舍，如果每间4人，那么有20人无法安排，如果每间8人，那么有一间不空也不满，求宿舍间数和寄宿学生人数。

4．将不足40只鸡放入若干个笼中，若每个笼里放4只，则有一只鸡无笼可放；若每个笼里放5只，则有一笼无鸡可放，且最后一笼缺乏3只。

问有笼多少个？有鸡多少只？5.用若干辆载重量为8吨的汽车运一批货色，若每辆汽车只装4吨，则剩下20吨货物；若每辆汽车装满8 吨，则最后一辆汽车不满也不空。

请问：有多少辆汽车？(2)可能有多少间宿舍、多少逻辑学生？你得到几个解？它符合题意吗？2、其他问题1.有一个两位数，其十位上的数比个位上的数小2，已知这个两位数大于20且小于40，求这个两位数2.一次知识竞赛共有15道题。

竞赛规则是：答对1题记8分，答错1题扣4分，不答记分。

XXX有2道题没答，飞艇队答了所有的题，两队的成绩都超过了90分，两队分别至少答对了几道题？3.某公司需刻录一批光盘（总数不超过100张），若请专业公司刻录，每张需10元（包括空白光盘费）；若公司自刻，除设备租用费200元以外，每张还需成本5元（空白光盘费）。

问刻录这批光盘，是请专家公司刻录费用省，还是自刻费用省？4.考试共有25道选择题，做对一题得4分，做错一题减2分，不做得分，若XXX想确保考试成绩在60分以上，那么，他至少做对X题，应满足的不等式是什么？5.有红、白颜色的球若干个，已知白球的个数比红球少，但白球的两倍比红球多，若把每个白球都记作数2，每一个红球都记作数3，则总数为60，求白球和红球各几个？三、方案选择与设计1．某厂有甲、乙两种原料配制成某种饮料，已知这两种质料的维生素C含量及购买这两种质料的价格如下表：原料甲种原维生素C及价格料乙种原料维生素C/（单位/千克）原料价格/（元/千克）84现配制这种饮料10千克，要求至少含有4200单位的维生素C，并要求购买甲、乙两种原料的费用不超过72元，（1）设需用x千克甲种原料，写出x应满足的不等式组。

一元一次不等式(销售问题)应用题专题(附答案)

一元一次不等式（销售问题）应用题专题（销售问题）1、商场购进某种商品m件，每件按进价加价30元售出全部商品的65%，然后再降价10%，这样每件仍可获利18元，又售出全部商品的25%。

(1)试求该商品的进价和第一次的售价；(2)为了确保这批商品总的利润率不低于25%，剩余商品的售价应不低于多少元？解：（1）设进价是x元, （一件商品）(1-10%)×(x+30)=x+18x=90第一次的售价x+30=90+30=120该商品的进价和第一次的售价分别是90元和120元（2）设剩余商品售价应不低于y元,(90+30)×m×65%+(90+18)×m×25%+y×m×(1-65%-25%)≥90×(1+25%) ×my≥75剩余商品的售价应不低于75元2.水果店进了某中水果1t，进价是7元/kg。

售价定为10元/kg，销售一半以后，为了尽快售完，准备打折出售。

如果要使总利润不低于2000元，那么余下的水果可以按原定价的几折出售？解：方法一：设按原价的x折出售所以：1000×1/2×10+1000×1/2×10×x/10>=7×1000+20005000+500x>=90005x>=40x>=8所以至多打8折方法二：1.货款：7.00*1000=7000.00元2、已销售产生的利润：（10.00*500）-（7.00*500）=5000.00-3500.00=1500.00元3、剩余商品需要产生的利润：2000-1500.00=500.00元4、产生利润需要的单价：7.00+500/500=8元5、需要在10元基础上打折：8/10=0.8，也就是八折3.“中秋节”期间苹果很热销，一商家进了一批苹果，进价为每千克1.5元，销售中有6%的苹果损耗，商家把售价至少定为每kg多少元，才能避免亏本？解：设这批苹果有 a千克，商家把售价至少定为每千克 x元a（1-6%）×x≥a×1.5解得：x≥1.60(哟等于)2、某电影院暑假向学生优惠开放，每张票2元。

一元一次不等式(组)应用题及练习(含答案)

一元一次不等式组的典型应用题例1.某校初三年级春游，现有36座和42座两种客车供选择租用，若只租用36座客车若干辆，则正好坐满；若只租用42座客车，则能少租一辆，且有一辆车没有坐满，但超过30人；已知36座客车每辆租金400元，42座客车每辆租金440元．(1)该校初三年级共有多少人参加春游?(2)请你帮该校设计一种最省钱的租车方案．【思路点拨】本题的关键语句是：“若只租用42座客车，则能少租一辆，且有一辆车没有坐满，但超过30人”．理解这句话，有两层不等关系．(1)租用36座客车x辆的座位数小于租用42座客车(x-1)辆的座位数．(2)租用36座客车x辆的座位数大于租用42座客车(x-2)辆的座位数+30．【答案与解析】解：(1)设租36座的车x辆．据题意得：3642(1)3642(2)30x xx x<-⎧⎨>-+⎩，解得：79xx>⎧⎨<⎩．由题意x应取8，则春游人数为：36×8＝288(人)．(2)方案①：租36座车8辆的费用：8×400＝3200(元)，方案②：租42座车7辆的费用：7×440＝3080(元)，方案③：因为42×6+36×1＝288，所以租42座车6辆和36座车1辆的总费用：6×440＋1×400＝3040(元) ．所以方案③：租42座车6辆和36座车1辆最省钱．练习一：1.将一筐橘子分给几个儿童，若每人分4个，则剩下9个橘子；若每人分6个，则最后一个孩子分得的橘子将少于3个，则共有_______个儿童，_______个橘子．2. 5.12四川地震后，怀化市立即组织医护工作人员赶赴四川灾区参加伤员抢救工作．拟派30名医护人员，携带20件行李（药品、器械），租用甲、乙两种型号的汽车共8辆，日夜兼程赶赴灾区．经了解，甲种汽车每辆最多能载4人和3件行李，乙种汽车每辆最多能载2人和8件行李．(1) 设租用甲种汽车x辆，请你设计所有可能的租车方案；(2) 若甲、乙汽车的租车费用每辆分别为8000元、6000元，请你选择最省钱的租车方案．类型二例2.某市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐赠一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．（1）求饮用水和蔬菜各有多少件？（2）现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．（3）在（2）的条件下，如果甲种货车每辆需付运费400元，乙种货车每辆需付运费360元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？解：（1）设饮用水有x件，蔬菜有y件，依题意，得320,80, x yx y+=⎧⎨-=⎩解得200,120.xy=⎧⎨=⎩所以饮用水和蔬菜分别为200件和120件．（2）设租用甲种货车m辆，则租用乙种货车(8-m)辆．依题意得4020(8)200,1020(8)120.m mm m+-≥⎧⎨+-≥⎩解得2≤m≤4．又因为m为整数，所以m＝2或3或4．所以安排甲、乙两种货车时有3种方案．设计方案分别为：①2×400+6×360＝2960（元）；②3×400+5×360＝3000（元）；③4×400+4×360＝3040（元）．所以方案①运费最少，最少运费是2960元．练习二：1.户种植的两类蔬菜的种植面积与总收入如下表：种植户种植A类蔬菜面积（单位：亩）种植B类蔬菜面积（单位：亩）总收入（单位：元）甲 3 1 12500乙 2 3 16500说明：不同种植户种植的同类蔬菜每亩平均收入相等．⑴求A、Ｂ两类蔬菜每亩平均收入各是多少元？⑵某种植户准备租20亩地用来种植A、Ｂ两类蔬菜，为了使总收入不低于63000元，且种植Ａ类蔬菜的面积多于种植Ｂ类蔬菜的面积（两类蔬菜的种植面积均为整数），求该种植户所有租地方案.2、某公司为了更好得节约能源，决定购买一批节省能源的10台新机器。

一元一次不等式组应用题汇总

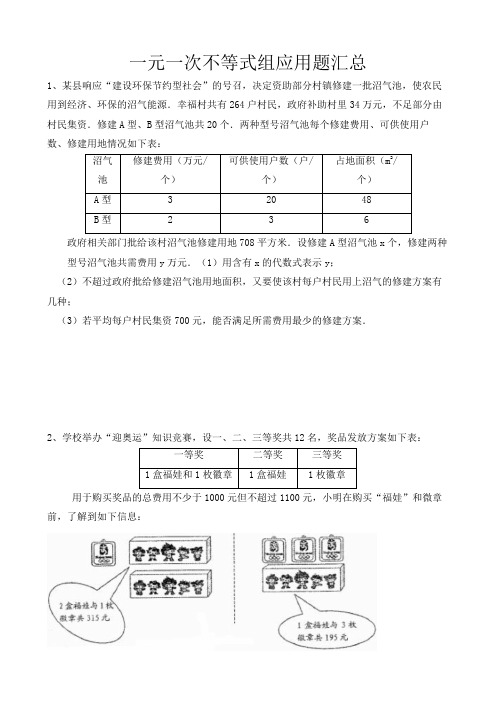
一元一次不等式组应用题汇总1、某县响应“建设环保节约型社会”的号召，决定资助部分村镇修建一批沼气池，使农民用到经济、环保的沼气能源．幸福村共有264户村民，政府补助村里34万元，不足部分由村民集资．修建A型、B型沼气池共20个．两种型号沼气池每个修建费用、可供使用户数、修建用地情况如下表：沼气池修建费用（万元/个）可供使用户数（户/个）占地面积（m2/个）A型 3 20 48B型 2 3 6 政府相关部门批给该村沼气池修建用地708平方米．设修建A型沼气池x个，修建两种型号沼气池共需费用y万元．（1）用含有x的代数式表示y；（2）不超过政府批给修建沼气池用地面积，又要使该村每户村民用上沼气的修建方案有几种；（3）若平均每户村民集资700元，能否满足所需费用最少的修建方案．2、学校举办“迎奥运”知识竞赛，设一、二、三等奖共12名，奖品发放方案如下表：一等奖二等奖三等奖1盒福娃和1枚徽章1盒福娃1枚徽章用于购买奖品的总费用不少于1000元但不超过1100元，小明在购买“福娃”和微章前，了解到如下信息：（1）求一盒“福娃”和一枚徽章各多少元？（2）若本次活动设一等奖2名，则二等奖和三等奖应各设多少名？3.某超市销售有甲、乙两种商品，甲商品每件进价10元，售价15元；乙商品每件进价30元，售价40元。

(1)若该超市同时一次购进甲、两种商品共80件，恰好用去1600元，求能购进甲乙两种商品各多少件？(2)该超市为使甲、乙两种商品共80件的总利润(利润=售价-进价)不少于600元，但又不超过610元，请你帮助该超市设计相应的进货方案。

4.惊闻5月12日四川汶川发生强烈地震后，某地民政局迅速地组织了30吨食物和13吨衣物的救灾物资，准备于当晚用甲、乙两种型号的货车将它们快速地运往灾区.已知甲型货车每辆可装食物5吨和衣物1吨，乙型货车每辆可装食物3吨和衣物2吨，但由于时间仓促，只招募到9名长途驾驶员志愿者.① 3名驾驶员开甲种货车，6名驾驶员开乙种货车，能否将救灾物资一次性地运往灾区？②要使救灾物资一次性地运往灾区，共有哪几种运货方案？5.某地为四川省汶川大地震灾区进行募捐，共收到粮食100吨，副食品54吨. 现计划租用甲、乙两种货车共8辆将这批货物全部运往汶川，已知一辆甲种货车同时可装粮食20吨、副食品6吨，一辆乙种货车同时可装粮食8吨、副食品8吨.(1) 将这些货物一次性运到目的地，有几种租用货车的方案？(2) 若甲种货车每辆付运输费1300元，乙种货车每辆付运输费1000元，要使运输总费用最少，应选择哪种方案？6. 5．12四川地震后，怀化市立即组织医护工作人员赶赴四川灾区参加伤员抢救工作．拟派30名医护人员，携带20件行李（药品、器械），租用甲、乙两种型号的汽车共8辆，日夜兼程赶赴灾区．经了解，甲种汽车每辆最多能载4人和3件行李，乙种汽车每辆最多能载2人和8件行李．（1）设租用甲种汽车x辆，请你设计所有可能的租车方案；（2）如果甲、乙两种汽车的租车费用每辆分别为8000元、6000元，请你选择最省钱的租车方案．7．某超市销售甲、乙两种商品．甲商品每件进价10元，售价15元；乙商品每件进价30元，售价40元．（1）若该超市同时一次购进甲、乙两种商品共80件，恰好用去1600元，求能购进甲、乙两种商品各多少件？（2）该超市为使甲、乙两种商品共80件的总利润（利润=售价-进价）不少于600元，但又不超过610元．请你帮助该超市设计相应的进货方案．8. 某校师生积极为汶川地震灾区捐款，在得知灾区急需帐篷后，立即到当地的一家帐篷厂采购，帐篷有两种规格：可供3人居住的小帐篷，价格每顶160元；可供10人居住的大帐篷，价格每顶400元。

(完整版)一元一次不等式应用题分类专题(10种)

一元一次不等式应用题专题（分配问题）1、一堆玩具分给若干个小朋友，若每人分3件，则剩余4件，若前面每人分4件，则最后一人得到的玩具最多3件，问小朋友的人数至少有多少人？。

2、用若干辆载重量为8吨的汽车运一批货物，若每辆汽车只装4吨，则剩下20吨货物；若每辆汽车装满8吨，则最后一辆汽车不满也不空。

请问：有多少辆汽车？（积分问题）1、一次知识竞赛有15道题。

规则是：对1题记8分，错1题扣4分，不答0分。

神箭队2道题没答，飞艇队全答了，两队的成绩都超过了90分，两队分别至少答对了几道题？2、在比赛中，每名射手打10枪，每命中一次得5分，每脱靶一次扣1分，得到的分数不少于35分的射手为优胜者，要成为优胜者，至少要中靶多少次？（比较问题）1、某校校长暑假将带领该校“三好学生”去三峡旅游，甲旅行社说：如果校长买全票一张，则其余学生可享受半价优惠；乙旅行社说：包括校长在内全部按全票的6折优惠。

已知两家旅行社的全票价都是240元，至少要多少名学生选甲旅行社比较好？2、李明有存款600元，王刚有存款2000元，从本月开始李明每月存款500元，王刚每月存款200元，试问到第几个月，李明的存款能超过王刚的存款。

（行程问题）1、爆破施工时，导火索燃烧的速度是0.8cm/s，人跑开的速度是5m/s，为了使点火的战士在施工时能跑到100m以外的安全地区，导火索至少需要多长？2、王凯家到学校2.1千米，现在需要在18分钟内走完这段路。

已知王凯步行速度为90米/ 分，跑步速度为210米/分，问王凯至少需要跑几分钟？（工程问题）1 .一个工程队规定要在6天内完成300土方的工程，第一天完成了60土方，现在要比原计划至少提前两天完成，则以后平均每天至少要比原计划多完成多少方土？3.某工人计划在15天里加工408个零件，最初三天中每天加工24个，问以后每天至少要加工多少个零件，才能在规定的时间内超额完成任务？（浓度问题）1、在1千克含有40克食盐的海水中，在加入食盐，使他成为浓度不底于20%的食盐水，问：至少加入多少食盐？（增减问题）1、一根长20cm的弹簧，一端固定，另一端挂物体。

一元一次不等式试题（大全5篇）

一元一次不等式试题（大全5篇）第一篇：一元一次不等式试题10.（2012湖北随州4分）若不等式组⎨⎧x-b<0⎩x+a>0的解集为2A.－2，3B.2，－3C.3，－2D.－3，2【答案】A。

【考点】解一元一次不等式组【分析】∵解不等式x－b＜0得：x＜b，解不等式x＋a＞0得：x ＞－a，∴不等式组的解集是：－a＜x＜b，∵不等式组⎨⎧x-b<0 ⎩x+a>0解集为2＜x＜3，∴－a=2，b=3，即a=－2，b=3。

故选A。

11.（2012湖北孝感3分）若关于x的一元一次不等式组⎨范围是【】⎧x-a>0⎩1-2x>x-2无解，则a的取值A．a≥1B．a＞1C．a≤－1D．a＜－1【答案】A。

【考点】解一元一次不等式组。

【分析】解出两个不等式，再根据“大大小小找不到”的原则解答即可：⎧x-a>0①，由①得：x＞a，由②得：x＜1。

⎨1-2x>x-2②⎩∵不等式组无解，∴a≥1。

故选A。

12.（2012湖北襄阳3分）若不等式组⎨⎧1+x>a⎩2x-4≤0有解，则a的取值范围是【】A．a≤3B．a＜3C．a＜2D．a≤2【答案】B。

【考点】解一元一次不等式组。

【分析】先求出不等式的解集，再不等式组有解根据“同大取大，同小取小，大小小大中间找，大大小小解不了（无解）”即可得到关于a的不等式，求出a的取值范围即可：由1+x>a得，x＞a﹣1；由2x-4≤0得，x≤2。

∵此不等式组有解，∴a﹣1＜2，解得a＜3。

故选B。

20.（2012四川凉山4分）设a、b、c表示三种不同物体的质量，用天枰称两次，情况如图所示，则这三种物体的质量从小到大排序正确的是【】A．c<b<aB．b<c<aC．c<a<bD．b<a<c【答案】A。

30.（2012山东淄博4分）若a>b，则下列不等式不一定成立的是【】(A)a+m>b+m(B)a(m2+1)>b(m2+1)(C)-a2<-b2(D)a2>b2x+2⎧4+x>⎪32的解集为x<2，则a的取值范9.（2012湖北鄂州3分）若关于x的不等式组⎪⎨⎪x+a<0⎪⎩2围是▲.12.（2012四川广安3分）不等式2x+9≥13.（2012四川达州3分）若关于x、y的二元一次方程组⎨⎧2x+y=3k-1⎩x+2y=-2的解满足x＋y＞1，则k的取值范围是▲.3（x+2）的正整数解是14.（2012四川绵阳4分）如果关于x的不等式组：⎨⎧3x-a≥0⎩2x-b≤0，的整数解仅有1，2，那么适合这个不等式组的整数a，b组成的有序数对（a，b）共有▲个。

八年级上册数学-一元一次不等式应用题集锦

八年级上册数学-一元一次不等式应用题集锦.1、一元一次不等式应用题集锦1.1、混合糖果问题甲种糖果每千克价格为20元，乙种糖果每千克价格为18元。

现在要将8千克甲种糖果和若干千克乙种糖果混合，使得总价不超过400元，且糖果总量不少于15千克。

问：混合的乙种糖果最多是多少？最少是多少？1.2、安排宿舍问题某中学为八年级寄宿学生安排宿舍。

每间宿舍可以住4人或8人。

如果每间住4人，则会有20人无法安排宿舍；如果每间住8人，则会有一间宿舍不满也不空。

问：这个中学有多少间宿舍？可以安排多少名学生住宿？1.3、水产养殖问题一块水面每亩年租金为500元，每亩水面可以混合投入4千克蟹苗和20千克虾苗。

蟹苗每千克价格为75元，饲养费用为525元，当年可获得1,400元收益；虾苗每千克价格为15元，饲养费用为85元，当年可获得160元收益。

问：1）租用n亩水面的年租金共需多少元？2）每亩水面混合养殖蟹虾的年利润是多少？（利润=收益-成本）3）XXX现有资金25,000元，他准备向银行贷款不超过25,000元，用于蟹虾混合养殖。

已知银行贷款的年利率为8%。

问：XXX应该租多少亩水面，向银行贷款多少元，才能使年利润超过35,000元？1.4、课外读物问题某校为了奖励在数学竞赛中获奖的学生，买了若干本课外读物准备送给他们。

如果每人送3本，则还有8本余下；如果每人送5本，最后一人得到的课外读物不足3本。

设该校买了m本课外读物，有x名学生获奖。

问：1）用含x的代数式表示m；2）该校获奖人数和所买课外读物的本数分别是多少？1.5、蔬菜种植问题有10名菜农，每人可以种3亩甲种蔬菜或2亩乙种蔬菜。

已知甲种蔬菜每亩可收入0.5万元，乙种蔬菜每亩可收入0.8万元。

现在要使总收入不低于15.6万元，应该如何安排人员？1.6、出租车费用问题某出租车起价为10元，行驶路程在5公里以内需付10元车费。

超过5公里后，每增加1公里加价1.2元（不足1公里按1公里计算）。

完整整理一元一次不等式组应用题练习含答案

一元一次不等式组应用题练习A1、我市一山区学校为部分家远的学生安排住宿，将部分教室改造成若干间住房. 如果每间住5人，那么有12人安排不下；如果每间住8人，那么有一间房还余一些床位，问该校可能有几间住房可以安排学生住宿？住宿的学生可能有多少人？解：设住房有x间，住宿的学生有5x＋12人，根据题意：0＜（5x＋12）－8(x－1)＜826＜x 4＜36，x＝5 ∵x为整数，∴克，造一140、一玩具厂生产甲、乙两种玩具，已知造一个甲种玩具需用金属80克，塑料2克，计划用6440若工厂有金属4600克，塑料100克，塑料120克.个乙种玩具需用金属. 件，求甲种玩具件数的取值范围两种材料生产甲、乙两种玩具共50 根据题意得：）件.x件，则甲种玩具为（50－x 解：设甲种玩具为4600?x)100(50?80x???6440)?(50?x?140x120?22x≤解得：20≤ 22个答：甲种玩具不少于20个，不超过、已知这列货车挂在A吨和乙种货物880吨用一列货车运往某地，3、现计划把甲种货物1240型车厢每节B型车厢每节费用为6000元，使用B两种不同规格的货车厢共40节，使用A.元费用为8000节，试定出用车厢节x A型车厢1（）设运送这批货物的总费用为y万元，这列货车挂.的公式表示总费用y数x型车厢最多吨，每节B型车厢最多可装甲种货物35吨和乙种货物152 （）如果每节A两种车厢的节数，那么共B、35吨，装货时按此要求安排A可装甲种货物25吨和乙种货物有哪几种安排车厢的方案？2000x－＝32000（解：1）y节、2615节或2524、B两种车厢的节数分别为节、16节或节、A2 （）共有三种方案， 14节4、为了保护环境，某企业决定购买10台污水处理设备，现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如下表：A型 B型价格（万元／台） 12 10200240处理污水量（吨／月）年消耗费（万元／台） 1 1经预算，该企业购买设备的资金不高于105万元.（1）请你设计该企业有几种购买方案；（2）若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案；（3）在第（2）问的条件下，若每台设备的使用年限为10年，污水厂处理污水费为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？（注：企业处理污水的费用包括购买设备的资金和消耗费）解：（1）共有三种购买方案，A、B两种型号的设备分别为0台、10台或1台、9台或2台、8台.（2）A、B两种型号的设备分别1台、9台；（3）10年节约资金42.8万元5、某厂计划2004年生产一种新产品，下面是2003年底提供的信息，人事部：明年生产工人不多于800人，每人每年可提供2400个工时；市场部：预测明年该产品的销售量是10000～12000件；技术部：该产品平均每件需要120个工时，每件要4个某种主要部件；供应部：2003年低库存某种主要部件6000个.预测明年能采购到这种主要部件60000个.根据上述信息，明年产品至多能生产多少件？解：设明年可生产产品x件，根据题意得：120x?800?2400??10000?x?12000解得： 10000≤x≤12000 ??4x?6000?60000?6、某宾馆底层客房比二楼少5间，某旅行团有48人.若全部住底层，每间4人，房间不够；每间住5人，有房间没有住满5人.若全部安排在二楼，每间住3人，房间不够；每间住4人，有房间没有住满4人.问该宾馆底层有客房多少间？解：设宾馆底层有客房x间，则二楼有客房（x+5）间.根据题意得：4x?48??5x?48?解得：9.6＜x＜11 ?3(x?5)?48??4(x?5)?48?所以： x = 10答：该宾馆底层有客房x间.年眉山市）某县响应“建设环保节约型社会”的号召，决定资助部分村镇修建一7、（200734批沼气池，使农民用到经济、环保的沼气能源．幸福村共有264户村民，政府补助村里个．两种型号沼气池每个修建费型、B型沼气池共20万元，不足部分由村民集资．修建A 用、可供使用户数、修建用地情况如下表：2/个）个）占地面积（m沼气池修建费用（万元/个）可供使用户数（户/48 型A 3 2062B型 3政府相关部门批给该村沼气池修建用地708平方米．设修建A型沼气池x个，修建两种型号沼气池共需费用y万元．（1）用含有x的代数式表示y；（2）不超过政府批给修建沼气池用地面积，又要使该村每户村民用上沼气的修建方案有几种；（3）若平均每户村民集资700元，能否满足所需费用最少的修建方案．y?3x?2(20?x)?x?40）解：（1（2）由题意可得20x?3(20?x)≥264①??②≤708?6(20?x)48x?解①得x≥12解②得x≤14∴不等式的解为12≤x≤14Qx是正整数∴x的取值为12，13，14即有3种修建方案：①A型12个，B型8个；②A型13个，B型7个；③A型14个，B型6个x y的增加而增加，要使费用最少，则x＝40中，12 随x（3）∵y＝＋∴最少费用为y＝x＋40＝52（万元）村民每户集资700元与政府补助共计：700×264＋340000＝524800＞520000∴每户集资700元能满足所需要费用最少的修建方案8、（2007年常州市）学校举办“迎奥运”知识竞赛，设一、二、三等奖共12名，奖品发放方案如下表：一等奖二等奖三等奖1枚徽章1盒福娃 11盒福娃和枚徽章用于购买奖品的总费用不少于1000元但不超过1100元，小明在购买“福娃”和微章前，了解到如下信息：（1）求一盒“福娃”和一枚徽章各多少元？（2）若本次活动设一等奖2名，则二等奖和三等奖应各设多少名？x y元，根据题意得元，一枚徽章1）设一盒“福娃”（解：2x?y?315x?150??解得??x?3y?195y?15??答：一盒“福娃”150元，一枚徽章15元．（2）设二等奖m名，则三等奖（10—m）名，2?165?150m?15(10?m)≥1000??2?165?150m?15(10?m)≤1100?104124≤m≤解得．2727Qm是整数，∴m＝4，∴10－m＝6．答：二等奖4名，三等奖6名．。

10道一元一次不等式应用题和答案过程

一元一次不等式解应用题1.某水产品市场管理部门规划建造面积为2400平方米的大棚.大棚设A 种类型和B种类型的店面共80间.每间A种类型的店面的平均面积为28平方米.月租费为400元.每间B种类型的店面的平均面积为20平方米..月租费为360元.全部店面的建造面积不低于大棚总面积的85%。

(1) 试确定A种类型店面的数量？（2）该大棚管理部门通过了解.A种类型店面的出租率为75%.B种类型店面的出租率为90%.为使店面的月租费最高.应建造A种类型的店面多少间？. . . 资料. .解：设A种类型店面为a间.B种为80-a间根据题意28a+20（80-a）≥2400×85%28a+1600-20a≥20408a≥440a≥55 A型店面至少55间设月租费为y元y=75%a×400+90%（80-a）×360=300a+25920-324a=25920-24a很明显.a≥55.所以当a=55时.可以获得最大月租费为25920-24x55=24600元. . . 资料. .二、水产养殖户大爷准备进行大闸蟹与河虾的混合养殖.他了解到情况：每亩地水面组建为500元;每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗；每公斤蟹苗的价格为75元.其饲养费用为525元.当年可获1400元收益；每公斤虾苗的价格为15元.其饲养费用为85元.当年可获160元收益；问题：1、水产养殖的成本包括水面年租金.苗种费用和饲养费用.求每亩水面虾蟹混合养殖的年利润（利润=收益—成本）；2、大爷现有资金25000元.他准备再向银行贷款不超过25000元.用于蟹虾混合养殖.已知银行贷款的年利率为10％.试问大爷应租多少亩水面.并向银行贷款多少元.可使年利润达到36600元？. . . 资料. .解：1、水面年租金=500元苗种费用=75x4+15x20=300+300=600元饲养费=525x4+85x20=2100+1700=3800元成本=500+600+3800=4900元收益1400x4+160x20=5600+3200=8800元利润（每亩的年利润）=8800-4900=3900元2、设租a亩水面.贷款为4900a-25000元那么收益为8800a成本=4900a≤25000+250004900a≤50000a≤50000/4900≈10.20亩利润=3900a-（4900a-25000）×10%3900a-（4900a-25000）×10%=36600. . . 资料. .3900a-490a+2500=366003410a=34100所以a=10亩贷款（4900x10-25000）=49000-25000=24000元三、某物流公司.要将300吨物资运往某地.现有A、B两种型号的车可供调用.已知A型车每辆可装20吨.B型车每辆可装15吨.在每辆车不超载的条件下.把300吨物资装运完.问：在已确定调用5辆A型车的前提下至少还需调用B型车多少辆?解：设还需要B型车a辆.由题意得20×5+15a≥30015a≥200a≥40/3解得a≥13又1/3 ．. . . 资料. .由于a是车的数量.应为正整数.所以x的最小值为14．答：至少需要14台B型车．四、某城市平均每天产生生活垃圾700吨.全部由甲.乙两个垃圾厂处理.已知甲厂每小时处理垃圾55吨.需费用550元；乙厂每小时处理垃圾45吨.需费用495元。

一元一次不等式应用题汇总

中考复习 一元一次(组)不等式应用(四大类型)

一元一次不等式15道应用题

10道一元一次不等式应用题和答案过程

一元一次不等式应用题集锦

10道一元一次不等式应用题和答案过程

一元一次不等式应用题汇总

解一元一次不等式专项练习 (80题,附答案)

一元一次不等式应用题专题

一元一次不等式组应用题专题

一元一次不等式组应用题及答案

一元一次不等式(销售问题)应用题专题(附答案)

一元一次不等式(组)应用题及练习(含答案)

一元一次不等式组应用题汇总

(完整版)一元一次不等式应用题分类专题(10种)

一元一次不等式试题（大全5篇）

八年级上册数学-一元一次不等式应用题集锦

完整整理一元一次不等式组应用题练习含答案

10道一元一次不等式应用题和答案过程

中考复习一元一次(组)不等式应用(四大类型)