(完整版)信号与系统习题答案.docx

(完整版)信号与系统(吴大正)--完整版答案--纠错修改后版本

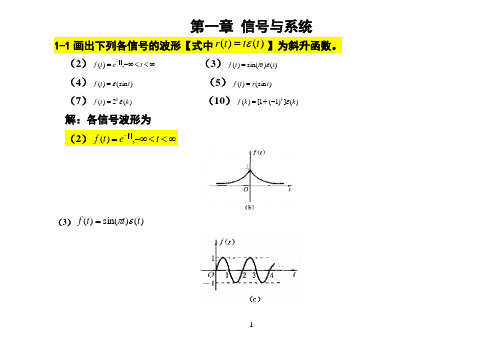
第一章信号与系统1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为（2）∞<<-∞=-t e t f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)(sin )(t r t f =（7）)(2)(k t f k ε=（10）)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε 解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

《信号与系统》课后习题参考答案

《信号与系统》课后习题参考答案第二章连续信号与系统的时域分析2-9、（1）解：∵系统的微分方程为：)(2)(3)(t e t r t r '=+'，∴r(t)的阶数与e(t) 的阶数相等，则h(t)应包含一个)(t δ项。

又∵系统的特征方程为：03=+α，∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程（此时e(t)= )(t δ），得：)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。

∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。

2-11、解：①求)(t r zi ： ∵系统的特征方程为：0)3)(2(652=++=++αααα，∴特征根：21-=α，32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs ：t t e A eA t h 3221)(--+= (t ≥0)，可求得：11=A ，12-=A （求解过程略） ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r ：)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=，21=C 21=C ∴ 011=-C ， ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi ， ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解：（1）依题意，得：)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---，两边求导得：)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ （2）∵系统的起始状态保持不变，∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+，∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证：∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时：u(t-3k)为非零值又∵0≤t ≤3，∴k 取负整数，则：3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(，且311--=e A 。

(完整word版)信号与系统专题练习题及答案

信号与系统专题练习题一、选择题1．设当t 〈3时，x(t)=0，则使)2()1(t x t x -+-=0的t 值为 C 。

A t>-2或t>-1 B t=1和t=2 C t>—1 D t 〉-22．设当t 〈3时，x （t)=0，则使)2()1(t x t x -⋅-=0的t 值为 D 。

A t>2或t 〉-1 B t=1和t=2 C t>—1 D t>—23．设当t<3时，x(t ）=0，则使x （t/3)=0的t 值为 C 。

A t>3 B t=0 C t<9 D t=34．信号)3/4cos(3)(π+=t t x 的周期是 C 。

A π2 B π C 2/π D π/2 5．下列各表达式中正确的是 BA. )()2(t t δδ= B 。

)(21)2(t t δδ= C. )(2)2(t t δδ= D 。

)2(21)(2t t δδ=6. 已知系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B . A 线性时不变系统 B 线性时变系统 C 非线性时不变系统 D 非线性时变系统 7。

已知系统的激励e(t ）与响应r （t)的关系为:)()(2t e t r = 则该系统为 C .A 线性时不变系统B 线性时变系统C 非线性时不变系统D 非线性时变系统8。

⎰∞-=t d ττττδ2sin )( A 。

A 2u （t ） B )(4t δ C 4 D 4u （t) 10. dt t t )2(2cos 33+⋅⎰-δπ等于 B 。

A 0 B —1 C 2 D —211．线性时不变系统输出中的自由响应的形式由 A 决定A 系统函数极点的位置；B 激励信号的形式;C 系统起始状态；D 以上均不对。

12．若系统的起始状态为0，在x （t)的激励下，所得的响应为 D . A 强迫响应;B 稳态响应；C 暂态响应;D 零状态响应。

(完整版)信号与系统练习及答案

信号与系统练习及答案一、单项选择题1．已知信号f (t )的波形如题1图所示，则f （t ）的表达式为（）A ．tu(t)B ．(t-1)u(t-1)C ．tu(t-1)D ．2(t-1)u(t-1)2．积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是（） A ．14 B ．24 C ．26 D ．283．已知f(t)的波形如题3（a ）图所示，则f (5-2t)的波形为（）4．周期矩形脉冲的谱线间隔与（）A ．脉冲幅度有关B ．脉冲宽度有关C ．脉冲周期有关D ．周期和脉冲宽度有关 5．若矩形脉冲信号的宽度加宽，则它的频谱带宽（） A ．不变 B ．变窄 C ．变宽D ．与脉冲宽度无关 6．如果两个信号分别通过系统函数为H （j ω）的系统后，得到相同的响应，那么这两个信号（）A ．一定相同 B ．一定不同 C ．只能为零 D ．可以不同7．f(t)=)(t u e t 的拉氏变换为F （s ）=11-s ，且收敛域为（） A ．Re[s]>0B ．Re[s]<0C ．Re[s]>1D ．Re[s]<1 8．函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F （s ）等于（） A ．1 B ．s 1 C ．e -2s D ．s1e -2s 9．单边拉氏变换F （s ）=22++-s e )s (的原函数f(t)等于（） A ．e -2t u(t-1) B ．e -2(t-1)u(t-1) C ．e -2t u(t-2)D ．e -2(t-2)u(t-2)答案: BCCCBDCDA二．填空题1．如果一线性时不变系统的单位冲激响应为h(t)，则该系统的阶跃响应g(t)为_________。

2．已知x(t)的傅里叶变换为X （j ω），那么x (t-t 0)的傅里叶变换为_________________。

3．如果一线性时不变系统的输入为f(t)，零状态响应为y f (t )=2f (t-t 0)，则该系统的单位冲激响应h(t)为_________________。

信号与系统题库答案(完整版)

1 −2( s +1) 1 −2 s e (2) e s +1 s +1 e2 2cos 2 + s sin 2 − s (3) (4) ie s +1 s2 + 4 1 ⎛ 1 1⎞ ⎛ 1 2⎞ (5) 2 [1 − (1 + s )e − s ]e − s (6) ⎜ 2 + ⎟ e − s − ⎜ 2 + ⎟ e −2 s s s⎠ s⎠ ⎝s ⎝s (1)
[3]解 A 点： FA (ω ) =
1 [G1 (ω + ω0 ) + G1 (ω − ω0 )] 2 j B 点： FB (ω ) = [G1 (ω + ω0 ) − G2 (ω − ω0 )] 2 1 C 点： FC (ω ) = [ FA (ω ) + FB (ω )] ⋅ π [δ (ω + ω0 ) + δ (ω − ω0 )] 2π 1 1 1 j j = [ G1 (ω + 2ω0 ) + G1 (ω ) + G2 (ω + 2ω0 ) − G2 (ω )] 2 2 2 2 2 1 1 1 j j + [ G1 (ω ) + G1 (ω − 2ω0 ) + G2 (ω ) − G2 (ω − 2ω0 )] 2 2 2 2 2
1 1 1 j j = [ G1 (ω + 2ω0 ) + G1 (ω ) + G2 (ω + 2ω0 ) − G2 (ω )] 2 2 2 2 2 1 1 1 j j + [ G1 (ω ) + G1 (ω − 2ω0 ) + G2 (ω ) − G2 (ω − 2ω0 )] 2 2 2 2 2

《信号与系统》(郑君里)课后习题答案

2
(t )
2
非线性：设 r1 ( t ) = e1
( t ) 、 r2 ( t ) = e2 2 ( t ) ，
2 2 2 2
则⎡ ⎣ c1e1 ( t ) + c2 e2 ( t ) ⎤ ⎦ = c1 e1 ( t ) + c2 e2
2
( t ) + 2c1c2e1 ( t ) e2 ( t ) ≠ c1r1 ( t ) + c2 r2 ( t )
5
即输入 x1 ( t ) ， x2 ( t ) 得到的输出分别为 y1 ( t ) ， y2 ( t ) ， T ⎡ ⎣ x1 ( t ) ⎤ ⎦ = y1 ( t ) ，
T⎡ 。 ⎣ x2 ( t ) ⎤ ⎦ = y2 ( t ) ，则 T ⎡ ⎣ c1 x1 ( t ) + c2 x2 ( t ) ⎤ ⎦ = c1 y1 ( t ) + c2 y2 ( t ) （ c1 ， c2 为常数）
解题过程：
(a-1)
(a-2)
(a-3)
4
(a-4)
(b) f ( t ) 为偶函数，故只有偶分量，为其本身
(c-1)
(c-2)
(c-3)
(c-4)
(d-1)
(d-2)
(d-3)
(d-4)
1-20 分析过程：本题为判断系统性质：线性、时不变性、因果性（1）线性（Linearity）：基本含义为叠加性和均匀性
f (t )
1 1
f ( 3t )
→
→
-2
-1
0
1
-2/3
f ( 3t − 2 )
→
1/3
f ( −3t − 2 )

信号与系统复习题含答案完整版

信号与系统复习题含答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】（C ）)(t δ+(-6e -t +8e -2t)u(t) （D ）3)(t δ +(-9e -t +12e -2t)u(t)6、连续周期信号的频谱具有（A ）连续性、周期性（B ）连续性、收敛性（C ）离散性、周期性（D ）离散性、收敛性7、周期序列2)455.1(0+k COS π的周期N 等于(A) 1 （B ）2 （C ）3 （D ） 48、序列和()∑∞-∞=-k k 1δ等于（A ）1 (B) ∞ (C) ()1-k u (D) ()1-k ku9、单边拉普拉斯变换()se s s s F 2212-+=的愿函数等于10、信号()()23-=-t u te t f t的单边拉氏变换()s F 等于二、填空题（共9小题，每空3分，共30分） 1、卷积和[（）k+1u(k+1)]*)1(k -δ=________________________2、单边z 变换F(z)= 12-z z的原序列f(k)=______________________ 3、已知函数f(t)的单边拉普拉斯变换F(s)=1+s s，则函数y(t)=3e -2t·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、单边拉普拉斯变换s s s s s F +++=2213)(的原函数 f(t)=__________________________6、已知某离散系统的差分方程为)1(2)()2()1()(2-+=----kf k f k y k y k y ，则系统的单位序列响应h(k)=_______________________7、已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=2)()(t dxx f t y 的单边拉氏变换Y(s)=______________________________ 8、描述某连续系统方程为该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ，=k t 22三（8分）已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(),dtt df t s =求⎪⎭⎫ ⎝⎛2ωs 的傅里叶逆变换。

信号与系统考试题及答案(共8套)

信号与系统考试题及答案（一）1．系统的激励是)t (e ，响应为)t (r ，若满足dt)t (de )t (r =，则该系统为线性、时不变、因果。

（是否线性、时不变、因果？） 2．求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。

3．当信号是脉冲信号f(t)时，其低频分量主要影响脉冲的顶部，其高频分量主要影响脉冲的跳变沿。

4．若信号f(t)的最高频率是2kHz ，则t)f(2的乃奎斯特抽样频率为 8kHz 。

5．信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为一常数相频特性为_一过原点的直线（群时延）。

6．系统阶跃响应的上升时间和系统的截止频率成反比。

7．若信号的3s F(s)=(s+4)(s+2)，求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。

8．为使LTI 连续系统是稳定的，其系统函数)s (H 的极点必须在S 平面的左半平面。

9．已知信号的频谱函数是））00(()j (F ωωδωωδω--+=，则其时间信号f(t)为01sin()t j ωπ。

10．若信号f(t)的211)s (s )s (F +-=，则其初始值=+)(f 0 1 。

二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。

（每小题2分，共10分）1.单位冲激函数总是满足)()(t t -=δδ （ √ ）2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。

（ × ） 3.非周期信号的脉冲宽度越小，其频带宽度越宽。

（ √ ）4.连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。

（ √ ）5.所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。

（ × ）三、计算分析题（1、3、4、5题每题10分，2题5分， 6题15分，共60分）1.信号)t (u e )t (f t-=21，信号⎩⎨⎧<<=其他，01012t )t (f ，试求)t (f *)t (f 21。

信号与系统课后习题附参考答案

1-1试分别指出以下波形是属于哪种信号？题图1-11-2 试写出题1-1图中信号的函数表达式。

1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示，试作出下列各信号的波形图，并加以标注。

题图1-3t)(2t x )(b 12112t)(1t x )(a 121123122T T2TEt)(t x )(a t)(t x )(b 13124023412t)(t x )(c n)(n x )(d 2213012112344⑴)2(1t x ⑵)1(1t x ⑶)22(1t x ⑷)3(2tx ⑸)22(2t x ⑹)21(2t x ⑺)(1t x )(2t x ⑻)1(1t x )1(2tx ⑼)22(1t x )4(2tx 1-4 已知信号)(1n x 与)(2n x 波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。

题图1-4⑴)12(1n x ⑵)4(1n x ⑶)2(1n x ⑷)2(2n x ⑸)2(2n x ⑹)1()2(22n x n x ⑺)2(1nx )21(2n x ⑻)1(1n x )4(2nx ⑼)1(1nx )3(2nx 1-5 已知信号)25(t x 的波形如题图1-5所示，试作出信号)(t x 的波形图，并加以标注。

题图1-5t)25(t x 110232523n)(2n x )(b 2213121124n)(1n x )(a 22131142134212321231-6 试画出下列信号的波形图：⑴)8sin()sin()(t t t x ⑵)8sin()]sin(211[)(t t t x ⑶)8sin()]sin(1[)(t t t x ⑷)2sin(1)(t tt x 1-7 试画出下列信号的波形图：⑴)(1)(t u e t x t⑵)]2()1([10cos )(t u t u t e t x t⑶)()2()(t u e t x t⑷)()()1(t u et x t ⑸)9()(2tu t x ⑹)4()(2tt x 1-8试求出以下复变函数的模与幅角，并画出模与幅角的波形图。

信号与系统复习题(答案全)

1、若系统的输入f (t ）、输出y （t) 满足()3()4t y t e ft -=，则系统为线性的（线性的、非线性的)、时变的 (时变的、时不变）、稳定的 (稳定的、非稳定的).2、非周期、连续时间信号具有连续、非周期频谱；周期、连续时间信号具有离散、非周期频谱；非周期、离散时间信号具有连续、周期频谱；周期、离散时间信号具有离散、周期频谱。

3、信号f(t)的占有频带为0-10KHz,被均匀采样后,能恢复原信号的最大采样周期为 5×10—5 s 。

4、 )100()(2t Sa t f =是能量信号（功率信号、能量信号、既非功率亦非能量信号）。

5、 ()2cos()f t t =+是功率信号 (功率信号、能量信号、既非功率亦非能量信号)。

6、连续信号f(t ）=sint 的周期T 0= 2π ,若对f （t ）以fs=1Hz 进行取样，所得离散序列f(k)=sin(k ），该离散序列是周期序列？否。

7、周期信号2sin(/2)()j n tn n f t e n ππ+∞=-∞=∑，此信号的周期为 1s 、直流分量为 2/π 、频率为5Hz 的谐波分量的幅值为 2/5 。

8、 f (t) 的周期为0。

1s 、傅立叶级数系数**03355532F F F F F j --=====、其余为0。

试写出此信号的时域表达式f (t ） = 5 + 6 cos （ 60 π t ) - 4 sin （100 π t ) . 9、 f (k ）为周期N=5的实数序列，若其傅立叶级数系数()205=F ()52511,πjeF -+=()54512πjeF -+=、则F 5 （3 )= ()54512πjeF +=- 、F 5 （4 )= ()52511πj eF +=- 、F 5 （5 ）= 2 ；f(k ） =())1.7254cos(62.052)9.3552cos(62.152525140525︒-⨯+︒-⨯+=∑=k k e n F n k jn πππ。

(完整版)信号与系统课后题答案

《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4～2-10,2-12～2-15,2-17～2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。

图(a)：微分方程：11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图（b ）：微分方程：⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程：dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程：⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件，求系统的零输入响应。

信号与系统课后习题参考答案

信号与系统课后习题参考答案精心整理1-试分别指出以下波形是属于哪种信号？题图1-11-2试写出题1-1图中信号的函数表达式。

1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示，试作出下列各信号的波形图，并加以标注。

题图1-3⑴(1x ⑷2x ⑺1x 1-4 题图1-4⑴(1x ⑷2x ⑺1x 1-51-6⑴(t x 2⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t t t x =1-7试画出下列信号的波形图：⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --= ⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角，并画出模与幅角的波形图。

⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X1-9已知信号)]()([sin )(π--=t u t u t t x ，求出下列信号，并画出它们的波形图。

⑴)()()(221t x dtt x d t x +=⑵ττd x t x t ?∞-=)()(21-101-11⑴?∞-⑶?∞-⑸?∞-1-12⑴x 1⑶x 31-13⑴t y =)(⑶)2()(t x t y =⑷)1()1()(t x t x t y ---=⑸?∞-=2)()(t d x t y ττ⑹2()(n x n y =⑺)()(n nx n y =⑻)1()()(-=n x n x n y1-14如题图1-14中已知一线性时不变系统当输入为)(t x 时，响应为)(t y 。

试做出当输入为)(1t x 时，响应)(1t y 的波形图。

(完整版)信号与系统复习试题(含答案)

电气《信号与系统》复习参考练习题一、单项选择题：14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为（） A ．400rad ／s B 。

200 rad ／s C 。

100 rad ／s D 。

50 rad ／sf如下图（a）所示，其反转右移的信号f1(t) 是（ d ）15、已知信号)(tf如下图所示，其表达式是（）16、已知信号)(1tA、ε（t）＋2ε(t－2)－ε(t－3)B、ε(t－1)＋ε(t－2)－2ε(t－3)C、ε(t)＋ε(t－2)－ε(t－3)D、ε(t－1)＋ε(t－2)－ε(t－3)17、如图所示：f（t）为原始信号，f1(t)为变换信号，则f1(t)的表达式是（）A、f(－t+1)B、f(t+1)C、f(－2t+1)D、f(－t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（ c ）19。

信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为（）A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ，则该系统是（）＞－系统的系统函数．已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（）A 、常数B 、实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（）A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( ) A )0(f B )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( )A.)(t δB.)2(t δC. )(t fD.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应 D .全响应与强迫响应之差2A 、1-eB 、3eC 、3-e D 、1 27.信号〔ε(t)－ε(t －2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28．已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为t t Be Ae 2--+，则其2个特征根为( )A 。

电子教案《信号与系统》(第三版)信号系统习题解答.docx

《信号与系统》（第 3 版）习题解析高等教育出版社目录第 1 章习题解析 (2)第 2 章习题解析 (6)第 3 章习题解析 (16)第 4 章习题解析 (23)第 5 章习题解析 (31)第 6 章习题解析 (41)第 7 章习题解析 (49)第 8 章习题解析 (55)第 1 章习题解析1-1题 1-1 图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c)(d)题 1-1图解 (a)、(c)、(d)为连续信号； (b)为离散信号； (d)为周期信号；其余为非周期信号； (a)、(b)、(c)为有始（因果）信号。

1-2 给定题 1-2 图示信号 f( t )，试画出下列信号的波形。

[提示： f( 2t )表示将 f( t )波形压缩，f( t)表示将 f( t )波形展宽。

]2(a) 2 f( t 2 )(b) f( 2t ) (c) f(t)2(d) f( t +1 )题1-2图解以上各函数的波形如图 p1-2 所示。

图 p1-21-3如图1-3图示，R、L、C元件可以看成以电流为输入，电压为响应的简单线性系统S R、S L、 S C，试写出各系统响应电压与激励电流函数关系的表达式。

S RS LS C题 1-3图解各系统响应与输入的关系可分别表示为u R (t)R i R (t )u L (t)di L (t )L1dttu C (t )i C ( )dC1-4如题1-4图示系统由加法器、积分器和放大量为 a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

题 1-4图解系统为反馈联接形式。

设加法器的输出为 x( t )，由于x(t ) f (t) ( a) y(t)且y(t ) x(t)dt ,x(t) y (t)故有y (t) f (t ) ay (t)即y (t ) ay(t ) f (t)1-5已知某系统的输入 f( t )与输出 y( t )的关系为 y( t ) = | f( t )|，试判定该系统是否为线性时不变系统？解设 T 为系统的运算子，则可以表示为y(t) T[ f (t )]f (t)不失一般性，设 f( t ) = f 1( t ) + f 2 ( t )，则T[ f 1 (t)]f 1 (t)y 1 (t )T[ f 2 (t)] f 2 (t )y 2 (t )故有T[ f (t)] f 1 (t )f 2 (t ) y(t)显然f 1 (t ) f 2 (t)f 1 (t ) f 2 (t )即不满足可加性，故为非线性时不变系统。

《信号与系统》习题参考答案

《信号与系统》习题参考答案（1）2—1（1） 01()()()()(1)()ta at x t h t x u t d e d e u t aτττττ∞---∞*=⋅-==-⎰⎰ （2） 00()()(cos sin )()x t h t t d ωτωτδττ∞-∞*=+⋅-⎰0000(cos sin )()cos sin t t t d t t ωωδττωω∞-∞=+⋅-=+⎰（3）当0t <时 ()()0x t h t *=当01t ≤<时 20()()(1)2tt x t h t d t ττ*=+=+⎰当12t ≤<时 13()()(1)2x t h t d ττ*=+=⎰ 当23t ≤<时 12213()()(1)22t x t h t d t t ττ-*=+=-++⎰ 当3t ≥时 ()()0x t h t *= （4）当0t <时 ()()0x t h t *=当0t ≥时 01()()sin 2(1cos 2)2tx t h t d t ττ*==-⎰ （5） 22222(2)2(4)241()()(2)2t t t t t t t x t h t e d e d e ee ττττ-----*=-=-+⎰⎰ （6）()x t at b =+11212()()()()()(2)3363tt x t h t a b d a tb t a t a bττδ-*=+++*--=++⎰2—2（1） [][][][2](2)[2]x n h n nu n n n u n δ*=*-=--（2） 10[][](2)[](21)[]nin i x n h n u n u n +=*==-∑（3）当0n ≥时 1111[][]2()()232i n in i x n h n --=-∞*==∑ 当0n <时 111[][]2()223n i n i n i x n h n --=-∞*==⋅∑ （4）当0n <时 [][]0x n h n *=当0n ≥时 110[][]()[]n n nin ii x n h n u n βααββα++-=-*==-∑（5）当07n ≤≤时 071[][](1)[1(1)]2in i n x n h n -=-*=-=--∑ 当70n -≤≤时 71[][](1)[(1)1]2ni n i x n h n -=-*=-=--∑ 2—3（1） 12()()[(1)(1)][(5)(5)]x t x t u t u t t t δδ*=+--*++- (6)(4)(4)(6)u t u t u t u t =++--+-- （2） 123()()()x t x t x t **{[(6)(4)][(4)(6)]}*[u t u t u t u t =+-++---11()()]22t t δδ++- ( 6.5)( 4.5)( 5.5)( 3.5)( 3.5)( 5.5)u t u t u t u t u t u t =+-+++-++--- ( 4.5)( 6.5)u t u t +---（3） 1311()()[(1)(1)][()()]22x t x t u t u t t t δδ*=+--*++- ( 1.5)(0.5)(0.5)( 1.5)u t u t u t u t =+--++-- 2—4 0(3)331()(3)1t k k t tk k y t eu t k e e e e∞-----=-∞=-∞=-=⋅=-∑∑311A e-=- 2—5（1）当2t ≥时 ()()0x t h t *= 当20t -<<时 11()()2t x t h t d t τ+-*==+⎰当02t <<时 11()()2t x t h t d t τ-*==-⎰（2）当01t <<时 1()()22(1)tx t h t d t τ*==-⎰ 当10t -<<时 01()()22(1)2t tx t h t d d t t t ττ+*=+=-++=+⎰⎰当21t -<<-时 11()()2t x t h t d t τ+-*==+⎰当 1t ≥ 或 2t <-时 ()()0x t h t *=此题也可利用性质，先对()x t 积分，对()h t 微分，'()()()y t x t dt h t =*⎰（3）当0t <时 (1)1()()1t x t h t e dt +∞--*==⎰当0t ≥时 1(1)(1)11()()22t t t t t x t h t e dt e dt e ++∞-----+*=+=-⎰⎰（4）当t π< 或 5t π>时 ()()0x t h t *= 当3t ππ<<时 0()()sin 1cos t x t h t d t πττ-*==+⎰当35t ππ<<时 23()()sin 1cos t x t h t d t ππττ-*==--⎰（5）当01t <<时 2211()()222()22x t h t t t t *=-=--当12t <≤时 2231()()264[2()]22x t h t t t t *=-+-=---()()x t h t *是以2为周期的周期函数 2—7（1） 111[][1]()[]()[1]22nn h n Ah n u n A u n ---=--111()[()()][1]()22nn n A u n n δδ-=+--=12A =（2） 111[][][][1][][]h n h n Ah n h n h n n δ---*-*-=*11[][][1]2h n n n δδ-∴=-- （3） 11[][][]2[[][1]][]nx n h n h n u n u n h n --**=--* 2[]2[[][4]]2[[1][5]]nn x n u n u n u n u n -∴=------2—8（1） 0()3()y t y t =（2） 00()()(2)y t y t y t =-- （3） 0()(1)y t y t =- （4） 0()()y t y t =-（5） 0()()dy t y t dt=（6） 202()()d y t y t dt =2—9 12111[][]()[]()[1]222n n x n h n u n u n -*=-+--1()([][1])[]2nu n u n n δ=---=1221[][][][]([][])*[]y n x n h n h n x n h n h n =**=* []*([][])[][]n n n n n u n u n u n u n δαβαβ=+=+ 2—10（1） 341201[][]((0.5))[3]2(1())[3]2n nn n x n x n u n u n ++=*=+=-+∑ （2） 4123[][][]2(1(0.5))[3]([][1])n x n x n x n u n n n δδ+**=-+*-- 43312(1(0.5))[3]2(1(0.5))[2]()[3]2n n n u n u n u n +++=-+--+=+ （3） 23[][][3]([][1])[3][2][3]x n x n u n n n u n u n n δδδ*=+*--=+-+=+ 2—11（1） 12345[][]([][][])[]h n h n h n h n h n h n =*-*+ （2） 34[][][1]h n h n nu n *=- 234[][][](1)[][1][]h n h n h nn u n n u n u n -*=+--= 12345[][]([][][])[]h n h n h n h n h n h n =*-*+514()([][3])*[][]2nu n u n u n hn =--+ 4[]6[1]7[2][]4[3]5[]6[1]7[2]4[3]n n u n n n n n u n n δδδδδδδ=+-+-++-=+-+---（1）'()()(2)(2)()(2)tt y t e x d x t y t x t τττ---∞=--+-=-+-⎰(2)()(2)t h t eu t --=- （2）当1t ≤时 ()0y t =当14t <≤时 1(2)(1)2()1t t y t e d e ττ+----==-⎰当4t >时 1(2)(4)(1)2()t t t t y t e d e e ττ+-------==-⎰2—13（1）213()()()()(1)[()](1)[()](1)h t h t h t u t t t u t t u t δδδ**=*-*-=-*-=-- 1213()()()()()()(1)h t h t h t h t h t u t u t =+**=--（2）1(10)1(02)()3(23)0t t t y t t t +-<<⎧⎪<<⎪=⎨-<<⎪⎪⎩其余2—14（1）因果、稳定（2）非因果、非稳定（3）非因果、稳定（4）非因果、稳定（5）非因果、稳定（6）因果、稳定（7）因果、非稳定 2—15（1）因果、稳定（2）非因果、稳定（3）非因果、非稳定（4）非因果、稳定（5）因果、非稳定（6）非因果、稳定（7）因果、稳定 2—16（1）对（2）对()h t dt ∞-∞=+∞⎰（3）错例如单位冲激响应(1)t δ-是因果的，但LTI 系统的逆系统(1)t δ+不是因果的。

(完整版)信号与系统练习及答案

信号与系统练习及答案一、单项选择题1．已知信号f (t )的波形如题1图所示，则f （t ）的表达式为（）A ．tu(t)B ．(t-1)u(t-1)C ．tu(t-1)D ．2(t-1)u(t-1)2．积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是（） A ．14 B ．24 C ．26 D ．283．已知f(t)的波形如题3（a ）图所示，则f (5-2t)的波形为（）4．周期矩形脉冲的谱线间隔与（）A ．脉冲幅度有关B ．脉冲宽度有关C ．脉冲周期有关D ．周期和脉冲宽度有关 5．若矩形脉冲信号的宽度加宽，则它的频谱带宽（） A ．不变 B ．变窄 C ．变宽D ．与脉冲宽度无关 6．如果两个信号分别通过系统函数为H （j ω）的系统后，得到相同的响应，那么这两个信号（）A ．一定相同 B ．一定不同 C ．只能为零 D ．可以不同7．f(t)=)(t u e t 的拉氏变换为F （s ）=11-s ，且收敛域为（） A ．Re[s]>0B ．Re[s]<0C ．Re[s]>1D ．Re[s]<1 8．函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F （s ）等于（） A ．1 B ．s 1 C ．e -2s D ．s1e -2s 9．单边拉氏变换F （s ）=22++-s e )s (的原函数f(t)等于（） A ．e -2t u(t-1) B ．e -2(t-1)u(t-1) C ．e -2t u(t-2)D ．e -2(t-2)u(t-2)答案: BCCCBDCDA二．填空题1．如果一线性时不变系统的单位冲激响应为h(t)，则该系统的阶跃响应g(t)为_________。

2．已知x(t)的傅里叶变换为X （j ω），那么x (t-t 0)的傅里叶变换为_________________。

3．如果一线性时不变系统的输入为f(t)，零状态响应为y f (t )=2f (t-t 0)，则该系统的单位冲激响应h(t)为_________________。

(完整)信号与系统西安邮电习题答案

第一次1.1 画出下列各个信号的波形[式中()()r t t t ε=为斜升函数]知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。

解题方法:首先考虑各信号中普通函数的波形特点，再考虑与()t ε或()k ε结合时的变化情况；若()t f 只是普通信号与阶跃信号相乘,则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形；若()t f 是普通函数与阶跃信号组合成的复合信号，则需要考虑普通函数值域及其对应的区间。

（1) ()()()t t t f εsin = 解:正弦信号周期ππωπ2122===T 1-12ππt()f t(2） ()()sin f t t επ= 解：()0 sin 01 sin 0t f t t ππ<⎧=⎨>⎩，正弦信号周期22==ππT(3）()()cosf t r t=解:()0 cost0 cos cos0f tt t <⎧=⎨>⎩，正弦信号周期221Tππ==（4) ()()kkkfε)12(+=-1-212k3135()f k …………(5) ()()()111k f k k ε+⎡⎤=+-⎣⎦-2-412k312()f k …………45-1-31。

2 画出下列各信号的波形[式中()()r t t t ε=为斜升函数］知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。

解题方法：首先考虑各信号中普通函数的波形特点,再考虑与()t ε或()k ε结合时的变化情况；若()t f 只是普通信号与阶跃信号相乘，则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形；若()t f 是普通函数与阶跃信号组合成的复合信号,则需要考虑普通函数值域及其对应的区间。

(完整版)信号与系统习题答案.docx

(完整版)信号与系统(吴大正)--完整版答案--纠错修改后版本

《信号与系统》课后习题参考答案

(完整word版)信号与系统专题练习题及答案

(完整版)信号与系统练习及答案

信号与系统题库答案(完整版)

《信号与系统》(郑君里)课后习题答案

信号与系统复习题含答案完整版

信号与系统考试题及答案(共8套)

信号与系统课后习题附参考答案

信号与系统复习题(答案全)

(完整版)信号与系统课后题答案

信号与系统课后习题参考答案

(完整版)信号与系统复习试题(含答案)

电子教案《信号与系统》(第三版)信号系统习题解答.docx

《信号与系统》习题参考答案

(完整版)信号与系统练习及答案

(完整)信号与系统 西安邮电 习题答案

(完整)信号与系统西安邮电习题答案