习题四参考答案

合集下载

现代工程设计制图习题集(第四版)参考答案

强化了实践应用
第四版习题集更加注重实践应用，增加了大量来自于实际工程案例的题目，帮助学生更好地将理论知识应用于实践中。
提高了题目质量
第四版习题集的题目经过了精心的设计和筛选，质量更高、更具代表性，能够更好地帮助学生掌握工程设计制图的核心技能。
习题集使用方法和建议
系统性使用
建议学生按照章节顺序，系统性地完成习题集中的题目，以全面掌握工程设计制图的知识和技能。
透视图的分类
根据观察者和物体之间的相对位置关系以及投影面的选择不同，透视图可分为一点透视、两点透视和三点透视三种类型。其中，一点透视和两点透视是常用的透视图类型。
06
工程图样的表达方法
视图表达方法
基本视图向视图局部视图斜视图
根据正投影法绘制出物体的六个基本视图，即主视图、俯视图、左视图、右视图、仰视图和后视图。
三视图的投影规律
长对正、高平齐、宽相等。即主视图与俯视图长度相等且对正，主视图与左视图高度相等且平齐，俯视图与左视图宽度相等。
基本几何体的三视图
平面立体的三视图
棱柱、棱锥等平面立体的三视图，要注意各视图的形状和尺寸标注。
回转体的三视图
圆柱、圆锥、圆球等回转体的三视图，要注意各视图的形状、尺寸标注和截交线、相贯线的画法。
AutoCAD软件的操作界面及工具栏介绍
AutoCAD软件的基本操作技巧与快捷键使用
二维图形绘制与编辑命令
尺寸标注、文字标注等
二维图形标注命令
移动、旋转、缩放、镜像等
二维图形编辑命令
直线、圆、圆弧、多边形等
二维图形绘制命令
三维建模与渲染技术
三维建模命令
拉伸、旋转、放样、布尔运算等
三维渲染技术

高教高职版《财务会计习题与全真实训》(第四版)习题部分参考答案

第1章总论一、单选题1、【答案】：C2、【答案】：A3、【答案】：C4、【答案】：D5、【答案】：A6、【答案】：B7、【答案】：B8、【答案】：C9、【答案】：B10、【答案】：B二、多选题1、【答案】：ABCD2、【答案】：ABCD3、【答案】：BCD4、【答案】：BC5、【答案】：ABD6、【答案】：BD7、【答案】：ABCD8、【答案】：ABD9、【答案】：ABC10、【答案】：AC三、判断题1、【答案】√2、【答案】×3、【答案】×4、【答案】×5、【答案】×6、【答案】×7、【答案】×8、【答案】×9、【答案】×10、【答案】√第2章货币资金一、单选题1、【答案】：D2、【答案】：C3、【答案】：B4、【答案】：B5、【答案】：A6、【答案】：A7、【答案】：B8、【答案】：A9、【答案】：B10、【答案】：C11、【答案】：C12、13【答案】：C14【答案】：D二、多选题1【答案】：ABC2【答案】：ABD 3【答案】：BCD 4【答案】：ABC 5【答案】：ABC 6【答案】：ABCD 7【答案】：ABD 8【答案】：CD9【答案】：ABC 10【答案】：ACD 11【答案】：ABCD 12【答案】：AB三、判断题1、【答案】：√【解析】：2、【答案】：×3、【答案】：√4、【答案】：×5、【答案】：×6、【答案】：×7、【答案】：×8.【答案】：√9.【答案】：√10.【答案】：×11.【答案】：×12.【答案】：×四、计算分析题1、【答案】（1）银行存款余额调节表2019年1月31日单位：元（2）如果调节后的银行存款余额仍不相等，则应进一步逐笔核对，发现错账、漏账应立即予以纠正。

（3）该企业可动用的银行存款为264 000元。

计量经济学精要习题参考答案(第四版)

计量经济学（第四版）习题参考答案第一章绪论1.1 一般说来，计量经济分析按照以下步骤进行：（1）陈述理论（或假说）（2）建立计量经济模型（3）收集数据（4）估计参数（5）假设检验（6）预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量，但它（它们）仅是影响因变量的主要因素，还有很多对因变量有影响的因素，它们相对而言不那么重要，因而未被包括在模型中。

为了使模型更现实，我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素，这些因素包括相对而言不重要因而未被引入模型的变量，以及纯粹的随机因素。

1.3时间序列数据是按时间周期（即按固定的时间间隔）收集的数据，如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。

横截面数据是在同一时点收集的不同个体（如个人、公司、国家等）的数据。

如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。

1.4 估计量是指一个公式或方法，它告诉人们怎样用手中样本所提供的信息去估计总体参数。

在一项应用中，依据估计量算出的一个具体的数值，称为估计值。

如Y 就是一个估计量，1nii YY n==∑。

现有一样本，共4个数，100，104，96，130，则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。

第二章计量经济分析的统计学基础2.1 略，参考教材。

2.2 NS S x ==45=1.25 用α=0.05，N-1=15个自由度查表得005.0t =2.947，故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说，根据样本，我们有99%的把握说，北京男高中生的平均身高在170.316至177.684厘米之间。

2.3 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即此样本不是取自一个均值为120元、标准差为10元的正态总体。

计算机网络课后习题参考答案第四章

第四章网络层1.网络层向上提供的服务有哪两种？是比较其优缺点。

网络层向运输层提供“面向连接”虚电路（Virtual Circuit）服务或“无连接”数据报服务前者预约了双方通信所需的一切网络资源。

优点是能提供服务质量的承诺。

即所传送的分组不出错、丢失、重复和失序（不按序列到达终点），也保证分组传送的时限，缺点是路由器复杂，网络成本高；后者无网络资源障碍，尽力而为，优缺点与前者互易2.网络互连有何实际意义？进行网络互连时，有哪些共同的问题需要解决？网络互联可扩大用户共享资源范围和更大的通信区域进行网络互连时，需要解决共同的问题有：不同的寻址方案不同的最大分组长度不同的网络接入机制不同的超时控制不同的差错恢复方法不同的状态报告方法不同的路由选择技术不同的用户接入控制不同的服务（面向连接服务和无连接服务）不同的管理与控制方式3.作为中间设备，转发器、网桥、路由器和网关有何区别？中间设备又称为中间系统或中继(relay)系统。

物理层中继系统：转发器(repeater)。

数据链路层中继系统：网桥或桥接器(bridge)。

网络层中继系统：路由器(router)。

网桥和路由器的混合物：桥路器(brouter)。

网络层以上的中继系统：网关(gateway)。

4.试简单说明下列协议的作用：IP、ARP、RARP和ICMP。

IP协议：实现网络互连。

使参与互连的性能各异的网络从用户看起来好像是一个统一的网络。

网际协议IP是TCP/IP体系中两个最主要的协议之一，与IP协议配套使用的还有四个协议。

ARP协议：是解决同一个局域网上的主机或路由器的IP地址和硬件地址的映射问题。

RARP：是解决同一个局域网上的主机或路由器的硬件地址和IP地址的映射问题。

ICMP：提供差错报告和询问报文，以提高IP数据交付成功的机会因特网组管理协议IGMP：用于探寻、转发本局域网内的组成员关系。

5.IP地址分为几类？各如何表示？IP地址的主要特点是什么？分为ABCDE 5类;每一类地址都由两个固定长度的字段组成，其中一个字段是网络号net-id，它标志主机（或路由器）所连接到的网络，而另一个字段则是主机号host-id，它标志该主机（或路由器）。

化工专业英语练习题参考答案

练习一参考答案1将下列句子或段落翻译成英语1)A process is any operation or series of operations that causes a physical or chemical change in asubstance or a mixture of substances .The material that enters a process is referred to as input or feed the process,and that which leaves is called output or product.2)As a chemical engineer,you might be called on to design individual process units (such as reactors,distillation columns,heat exchangers),supervise the operation of a process,or modify a process design to accommodate a change in the feed or in the desired product characteristics.As a rule,to any of these things you must know the amounts,compositions,and conditions of the materials that enter and leave each process unit,and if you are working with an existing units,you must be able to measure enough of these quantities to verify that the process is doing what it was designed to do.3)Founded in 1839from a small production firm for pharmaceutical products,B.Braun has grown steadilyinto a multinational company dealing with medical products,medical technology,pharmaceutical and biotechnology.2将下列句子或段落翻译成汉语1）包括的一系列操作，如混合、蒸发、过滤，无论产物是什么，这些操作都基本同，从而导致了单元操作的概念。

习题-4-参考答案'

高分子化学与物理习题习题四（共聚合，开环聚合部分）1. 写出两种不同形式的二元聚合微分方程，简述其应用条件。

答：浓度表示的二元共聚微分方程式：])[][]([])[][]([][][1222211121M M r M M M r M M d M d ++= 摩尔分数表示式：222212112121112f r f f f r f f f r F +++= 应用条件：稳态，等活性，分子量大（引发和终止对共聚物的组成影响不大），低转化率（一般小于10%）2. 为什么不研究r 1>1, r 2>1的二元共聚体系？答：根据r 的定义，r>1不利于共聚；r 1>1，r 2>1的体系进行共聚合，一般情况下得到的大多数为两种单体的均聚物的混合物，也可能是含有少量嵌段聚合物（视二者的投料比和均聚合的速度而定）3. 等摩尔M 1, M 2共聚合，若r 1<1, r 2>1，分析聚合后期产物组成情况。

答：r 1<1, r 2>1时，F 1<f 1，单体M 2比单体M 1更易于进入大分子链，M 2消耗很快。

若二者等摩尔混合，聚合前期会形成M 2单体含量多的共聚物，而反应后期M 2已经消耗完，剩余单体M 1发生均聚得到均聚物。

4. 下列单体：St, MMA, V Ac （醋酸乙烯酯）, VCl （氯乙烯），B （丁二烯）间，选出自由基共聚合（二元共聚）好的单体组，简要说明理由。

答：按共轭单体/共轭单体，非共轭单体/非共轭单体配对易于形成共聚合的原则来考虑，下列单体对易于共聚合：St/MMA, St/B, MMA/B, V Ac/VC 。

5. F 1-f 1图是如何做出来的？何谓恒比共聚点，此时共聚合的特点是什么？答：根据二元共聚摩尔微分方程，已知r 1和r 2，将不同的f 1值代入方程则可以得到系列F 1值，画出F 1~ f 1图。

r 1和r 2均小于1时，F 1~ f 1图与对角线有交点，此点为恒比共聚点；此时F 1= f 1计算方法为：()212121r r r f C ---= 在恒比共聚点进行投料聚合，可以得到含量明确的共聚物。

财务管理习题四答案

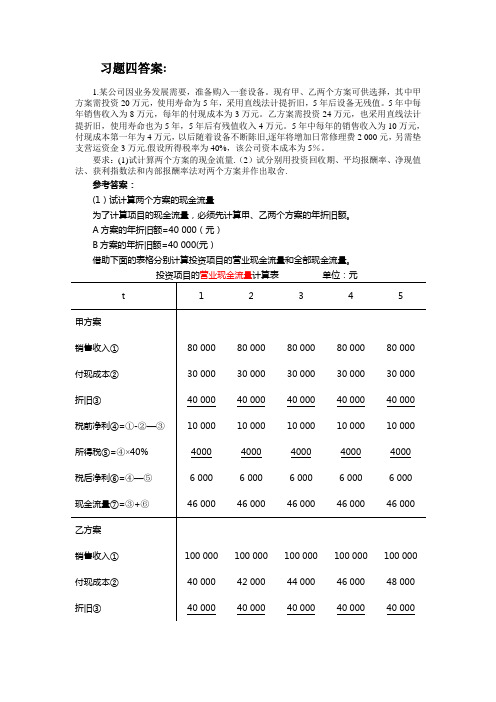
习题四答案:1.某公司因业务发展需要，准备购入一套设备。

现有甲、乙两个方案可供选择，其中甲方案需投资20万元，使用寿命为5年，采用直线法计提折旧，5年后设备无残值。

5年中每年销售收入为8万元，每年的付现成本为3万元。

乙方案需投资24万元，也采用直线法计提折旧，使用寿命也为5年，5年后有残值收入4万元。

5年中每年的销售收入为10万元，付现成本第一年为4万元，以后随着设备不断陈旧,逐年将增加日常修理费2 000元，另需垫支营运资金3万元.假设所得税率为40%，该公司资本成本为5％。

要求：(1)试计算两个方案的现金流量.（2）试分别用投资回收期、平均报酬率、净现值法、获利指数法和内部报酬率法对两个方案并作出取舍.参考答案：(1）试计算两个方案的现金流量为了计算项目的现金流量，必须先计算甲、乙两个方案的年折旧额。

A方案的年折旧额=40 000（元）B方案的年折旧额=40 000(元）借助下面的表格分别计算投资项目的营业现金流量和全部现金流量。

方案作出取舍①投资回收期甲方案每年NCF相等，故：②平均报酬率投资报酬率甲=46000100%23%200000⨯=投资报酬率乙=()520005080049600484001172005100%23.56%270000++++÷⨯=③净现值甲方案的各年NCF 相等，可按年金形式用公式计算：甲方案NPV=未来报酬的总现值–初始投资额=NCF ×（5％，5年）年金现值系数﹣200000 =46 000×(P/A,5％，5) – 2000 00=46 000×4.329﹣200 000=199134—200000=-866（元)未来报酬的总现值 1+2+3+4+5= 270 152减：初始投资 270 000净现值（NPV）152从上面计算中我们可以看出,甲方案的净现值小于零,不可取；乙方案的净现值大于零，可进行投资.④现值指数甲方案的现值指数= （200000-866)/200000= =0。

概率论与数理统计第四章习题参考答案

=
⎡ E⎢
1
⎢⎣ n −1
n i =1
(Xi
−
⎤ X )2 ⎥
⎥⎦
=
1 n −1
⎡ E⎢
⎢⎣
n i =1
X
2 i
−
nX
2⎤ ⎥ ⎥⎦
=
1 n −1
⎡n ⎢ ⎢⎣ i=1
E
(
X
2 i
)
−
nE( X
2⎤ )⎥ ⎥⎦
∑[ ] [ ] =
1 n −1
⎧ ⎨ ⎩
n i =1
D(X i ) + E 2 (X i )
X −µ 3/2
<
⎫ 1.96⎬
=
0.95
⎭
故，正态总体均值 µ 的 95%的置信区间为 (X − 2.94, X + 2.94)
代入样本值得正态总体均值 µ 的 95%的置信区间为（-2.565，3.315）。
（2）当σ 未知时，由 T = X − µ ~ t(n − 1) 即T = X − µ ~ t(3) ，所以
n
−a n
=0 =0
无解。由此不能求得
a,
b
的极大似然估计量。
⎩ ∂b
b−a
解：X
的概率密度为
f
(x)
=
⎪⎧ ⎨b
1 −
a
,
a
≤
x
≤
b
，
⎪⎩ 0, 其它
似然函数为 L(a, b) = 1 , θ1 ≤ xi ≤ θ 2 ,i = 1,2,L, n ， (b − a)n
对于给定的样本值 (x1 , x2 ,L, xn )
−
n
D(

《宏观经济学》课后练习题参考答案4

第四章货币与通货膨胀一、选择题二、名词解释1、M1与M2：都是美联储计算货币存量的指标，M1是指通货加活期存款、旅行支票和其它支票性存款，被称为狭义的货币；M2是指加货币市场基金余额、储蓄存款以及小额定期存款，被称为广义的货币。

M1具有完全的流动性，但没有利息。

M2有利息但不具有完全的流动性。

M1与经济关联性强，而M2与货币政策关联性强。

2、货币需求函数：（1）货币需求函数是为了分析货币需求量的决定因素及其变动规律而建立的一种函数关系。

通常将决定和影响货币需求的各种因素作为自变量，而将货币需求本身作为因变量。

（2）比较典型的货币需求函数有：①传统货币数量论的交易方程式：PV=MY，其中M为货币数量，V为货币流通速度，P为一般物价水平，Y为实际国民收入；②剑桥方程式：M= kPY，其中M为货币数量，k为以货币形式持有的国民收入的比例，P为一般物价水平，Y为实际国民收入；③凯恩斯的货币需求函数：L=L1（Y）+L2（i）。

其中由交易动机和预防动机而产生的货币需求用L1表示，是收入Y的递增函数，即L1=L1（Y）；投机性货币需求L2则与利率有关，是利率的递减函数，即L2=L2（i）；④弗里德曼的货币需求函数：M=f｛P，r b，r c，1/P·dP/dt，w，y，u｝，其中，M表示名义货币量，P表示价格水平，r b表示债券的预期收益率，r c表示股票的预期收益率，1/P·dP/dt表示物价的预期变动率，w表示人力财富与非人力财富的比率，y表示货币收入，u为其他随机因素。

3、数量方程式：数量方程式是用来表示交易量与货币之间的关系的方程。

它有以下表示形式：MV=PT式中，M为流通中的货币数量，V为货币的流通速度，P为一般物价水平，T为社会总交易额。

交易方程式直观地表示了流通中的货币数量与一般物价水平之间的关系。

如果用Y代表实际GDP，P是GDP平减指数，而PY是名义GDP，数量方程式变为MV=PY。

习题四：植物生长、生殖、成熟衰老及逆境生理-参考答案

一、名词解释1、细胞全能性：指植物体的每一个生活细胞携带着一套完整的基因组，并具有发育成完整植株的潜在能力。

2、光周期：自然界一昼夜间的光暗交替，即白天和黑夜的相对长度称为光周期。

3、生长大周期：植物在不同生育时期的生长速率表现出慢-快-慢的变化规律，呈现“S”型的生长曲线，这个过程称为生长大周期。

4、光敏色素：在植物体内存在着一种吸收红光和远红光并且可以相互转化的光受体蛋白，具有红光吸收型（Pr）和远红光吸收型（Pfr）两种形式，其中Pfr 型具有生理活性，参与光形态建成，调节植物生长发育。

5、光形态建成：光控制植物生长、发育和分化的过程。

6、光受体：是指植物体中存在的一些微量元素，能够感受到外界的光信号，并把光信号放大使植物做出相应的反应，从而影响植物的光形态建成。

7、抗逆性：植物对逆境的抵抗和忍耐能力，简称抗性。

抗性是植物对环境的一种适应性反应，是在长期进化过程中形成的。

8、冻害：温度下降到零度以下，植物体内发生冰冻，因而受伤甚至死亡，这种现象称为冻害。

9、临界暗期：昼夜周期中，引起短日植物成花的最短暗期长度或引起长日植物成花的最长暗期长度。

10、后熟：是指成熟种子离开母体后，需要经过一系列的生理生化变化后才能完成生理成熟，而具备发芽的能力。

11、跃变型果实：指在成熟期出现呼吸跃变现象的果实，如：香蕉、苹果等。

12、衰老：是植物生命周期的最后阶段，是成熟的细胞、组织、器官和整个植株自然地终止生命活动的一系列技能衰败过程。

13、自由基：带有未配对电子的离子、原子、分子以及集团的总称。

根际自由基中是否含有氧，可将其分为氧自由基和非氧自由基。

14、交叉抗性：植物经历了某种逆境后，能提高对另一些逆境的抵抗能力，这种对不同逆境间的相互适应作用，称为交叉适应。

15、集体效应：在一定面积内，花粉数量越多，花粉萌发和花粉管的生长越好的现象。

16、程序性细胞死亡：是指胚胎发育、细胞及许多病理过程中，细胞遵循其自身的“程序”，主动结束其生命的生理性希望过程。

《大数据技术原理与操作应用》习题解答(四)

《大数据技术原理与操作应用》习题解答（四）第六章一、单选题1、Hadoop2.0集群服务启动进程中，下列选项不包含的是（）。

A、NameNodeB、JobTrackerC、DataNodeD、ResourceManager参考答案:B2、关于SecondaryNameNode哪项是正确的？A、它是NameNode的热备B、它对内存没有要求C、它的目的是帮助NameNode合并编辑日志，减少NameNode启动时间D、SecondaryNameNode应与NameNode部署到一个节点参考答案:C3、HDFS中的Block默认保存（）份。

A、3份B、2份C、1份D、不确定参考答案:A答案解析:HDFS中的Block默认保存3份。

4、一个gzip文件大小75MB，客户端设置Block大小为64MB，占用Block的个数是（）。

A、1B、2C、3D、4参考答案:B5、下列选项中，Hadoop2.x版本独有的进程是（）。

A、JobTrackerB、TaskTrackerC、NodeManagerD、NameNode参考答案:C6、下列哪项通常是集群的最主要的性能瓶颈？A、CPUB、网络C、磁盘D、内存参考答案:C二、判断题1、NameNode的Web UI端口是50030，它通过jetty启动的Web服务。

对错参考答案:错答案解析:端口号为500702、NodeManager会定时的向ResourceManager汇报所在节点的资源使用情况，并接受处理来自ApplicationMaster的容器启动、停止等各种请求对错参考答案:对3、Hadoop HA是集群中启动两台或两台以上机器充当NameNode，避免一台NameNode节点发生故障导致整个集群不可用的情况。

对错参考答案:对答案解析:Hadoop HA是集群中启动两台或两台以上机器充当NameNode，避免一台NameNode节点发生故障导致整个集群不可用的情况。

现代汉语课后习题参考答案

第四章词汇“词汇”思考和练习一三、用“替代法”证明“驼绒”是两个语素，“骆驼”是一个语素。

“驼绒”中的“驼”跟“绒”都可为已知语素所代替，也可跟已知合，如：（1）驼绒平绒呢绒鸭绒（2）驼绒驼毛驼峰驼铃(1)组说明“驼”被“平、呢、鸭”替换，“绒”可跟上述语素组合，(2)组说明可以被“毛、峰、铃”替换；所以“驼”、“绒”是两个语素。

“驼绒中”的“驼”不能被替换，也就是说“骆”不能跟任何其他语素组合，它不具备语素的资格。

由于语言中同一层次的单位才能组合，语素不能跟非语素组合，所以在这里“驼”也不是语素，“骆驼”只能算一个语素。

四、分别指出下列字中的自由语素、半自由语素、不自由语素单独作语素的字。

柿素眉蜻狗羊鸭习鹃祝闪平虎狼自由语素：狗、羊、学、祝、闪、平、狼半自由语素：绩、柿、素、眉、虎、鸭、习没有不自由语素。

不能单独作语素的字：蜻、鹃五、划分出下文中的词(在词下划一横线，成语不划，不分析)。

如果是合成词就注明它的构成方式。

（略）六、指出下列的双声词、叠韵词、音译词。

仓促灿烂沙发孑孓恍惚婆娑铿锵扑克涤纶秋千踟蹰拮据婀娜腼腆双声词：仓促孑孓恍惚秋千踟蹰拮据叠韵词：灿烂婆娑腼腆音译词：沙发扑克涤纶’七、指出下列复合式合成词的类型。

痛快认真抓紧房间革命飞快解剖石林开关领袖工人碰壁戳穿司令雪崩动静无论烧饼粉饰体验奶牛牛奶功用用功(一)联合型：人民解剖开关领袖美好丝毫伟大动静衣服功用(二)偏正型：痛快飞快石林雪白工人烧饼粉饰(三)补充型：抓紧房间照明戳穿(四)动宾型：认真革命碰壁司令无论用功(五)主谓型：雪崩体验八、试举出yi音的五个同音语素，用每个语素各造三个合成词，同时注明其结构类型(一)一一定(偏正) 一律(偏正) 统一(补充)(二)衣衣服(联合) 大衣(偏正) 衣领(偏正)(三)依依靠(联合) 依赖(联合) 依然(附加)(四)医医院(偏正) 医术(偏正) 医疗(联合)(五)揖揖让(联合) 作揖(动宾) 拜揖(联合)十、下面句子里加着重点的词中间也插进了其他成分，你认为对吗?①为了完成全年计划，昨天厂里又动了一次员。

采购与供应链管理习题库04第四章习题及参考答案

同步测试一、单项选择题1. 供应链的( )体现了战略伙伴关系和企业内外资源的集成与优化利用。

BA. 决策机制B. 合作机制C. 自律机制D. 激励机制2. 供应链合作伙伴关系发展的主要特征就是从以产品/物流为核心转向以( )为技心。

DA.产品/合作B.物流/资金C产品/服务 D.集成/合作3. 基于战略合作伙伴关系的企业集成模式在宏观层面上主要是实现企业之间的（）。

AA.信息共享B.资源配置C同步作业 D.服务协作4. 建立基于信任、合作、开放性交流的供应商长期合作关系，首先( )。

BA.分析市场竞争环境B.建立供应商选择目标C.建立供应商评价标准D.评价供应商5. 1974年，日本本田汽车公司通知一些零部件厂商，未来五年内本田不希望零部件涨价，本田将密切同供应商合作，帮助他们改革和优化零部件设计，而且本田还将新的生产方法技术提供给供应商。

这里供应商与采购商是（）。

CA.买卖关系B.竞争关系C.战略合作伙伴关系D.兼并关系6. 现代采购企业与供应商的关系是（）DA.零和B. 单赢C. 双赢D.共赢7. 供应商是指（）AA.提供产品的组织和个人，他们可以是制造商、批发商、产品的零售商，也可以是服务或信息的提供者B.强调公司之间的过程与关系C.原材料采购到产品分销给顾客的整个过程中对产品和服务的管理。

D.以上都不对8. 以下不属于按照供应商分类模块法，将供应商划分的类型是（）BA.伙伴型B. 合作型C. 优先型D. 重点商业型9. （）是一种互利共赢的关系。

BA.竞争关系模式B.合作伙伴关系C.互利供需关系D.以上都不对10. 供应商伙伴关系的特点不包括（）AA. 供应商数量增多B. 信息和知识共享C. 降低成本D. 准时交货E. 高度信任二、多项选择题1. 基于合作伙伴关系的企业集成模式在宏观上主要是实现企业之间的（）。

ABCDA.信息共享B. 资源配置C. 同步作业D. 服务协作2. 以下属于是横向供应链联盟的是（）。

(第4章进程及进程管理)习题四答案介绍

4-16 图 4-30(a)、4-30(b)分别给出了两个进程流图。试用信号灯的 P、V 操作实现如图中所示进程之间的同步，并写出程序描述。
s p5 P1 s p6
P2
P3
P4
p7
f 图4.22(a)
f 图4.22(b)
答：(a) main() { var s12, s13, s14 : semaphore := 0, 0, 0; cobegin
Email: nancy78733@ 8
《操作系统原理与 Linux 系统实验》课后习题参考答案
沈华
湖北工业大学计算机学院
P1(); P2(); P3(); P4(); coend } P1() { p1 execute; V(s12); V(s13); V(s14); } P2() { P(s12); p2 execute; } P3() { P(s13); p3 execute; } P4() { P(s14); p4 execute; }
Email: nancy78733@
2
《操作系统原理与 Linux 系统实验》课后习题参考答案
沈华
湖北工业大学计算机学院
4-5 如下图所示，设一誊抄程序，将 f 中记录的序列正确誊抄到 g 中，这一程序由 get、copy、put 三个程序段组成，它们分别负责获得记录、复制记录、输出记录。请指出这三个程序段对 f 中的 m 个记录进行处理时各种操作的先后次序，并画出誊抄此记录序列的先后次序图。（假设 f 中有 1,2，…，m 个记录，s，t 为设置在主存中的软件缓冲区，每次只能装一个记录。）
沈华
湖北工业大学计算机学院
P 对公共变量 Q 的访问 V
end coend 信号量 mutex 的取值范围为：mutex.value ∈[1, - (n-1)]。 ①值为 1 时，表示没有进程访问公共变量 Q； ②值为 0 时，表示有一个进程正在访问公共变量 Q； ③值<0 时，表示有一个进程正在访问公共变量 Q，同时又| mutex.value |个进程等待访问公共变量 Q。

C语言程序设计课后习题1-8参考答案

C语言程序设计课后习题1-8参考答案习题1参考答案一、简答题1、冯诺依曼计算机模型有哪几个基本组成部分各部分的主要功能是什么？答：冯诺依曼计算机模型是由运算器、控制器、存储器、输入设备、输出设备五大功能部件组成的。

运算器又称算术逻辑部件，简称ALU，是计算机用来进行数据运算的部件。

数据运算包括算术运算和逻辑运算。

控制器是计算机的指挥系统，计算机就是在控制器的控制下有条不紊地协调工作的。

存储器是计算机中具有记忆能力的部件，用来存放程序和数据。

输入设备是用来输入程序和数据的部件。

输出设备正好与输入设备相反，是用来输出结果的部件。

2、简述计算机的工作原理。

答：计算机的工作原理可简单地概括为：各种各样的信息，通过输入设备，进入计算机的存储器，然后送到运算器，运算完毕把结果送到存储器存储，最后通过输出设备显示出来。

整个过程由控制器进行控制。

3、计算机软件系统分为哪几类答：软件内容丰富，种类繁多，通常根据软件用途将其分为两大类：系统软件和应用软件。

系统软件是指管理、监控、维护计算机正常工作和供用户操作使用计算机的软件。

这类软件一般与具体应用无关，是在系统一级上提供的服务。

系统软件主要包括以下两类：一类是面向计算机本身的软件，如操作系统、诊断程序等。

另一类是面向用户的软件，如各种语言处理程序（像BC、VC等）、实用程序、字处理程序等。

应用程序是指某特定领域中的某种具体应用，供最终用户使用的软件，它必须在操作系统的基础上运行。

4、什么叫软件说明软件与硬件之间的相互关系。

答：软件是指计算机程序及有关程序的技术文档资料。

两者中更为重要的是程序，它是计算机进行数据处理的指令集，也是计算机正常工作最重要的因素。

在不太严格的情况下，认为程序就是软件。

硬件与软件是相互依存的，软件依赖于硬件的物质条件，而硬件则需在软件支配下才能有效地工作。

在现代，软件技术变得越来越重要，有了软件，用户面对的将不再是物理计算机，而是一台抽象的逻辑计算机，人们可以不必了解计算机本身，可以采用更加方便、更加有效地手段使用计算机。

2013春季数学集训四队C教材每周习题(4)参考答案

2013春季数学集训四队C教材每周习题(4)参考答案星期一1、希望小学四(1)班同学进行队列表演，排成一个8行8列的正方形方阵。

如果去掉一行一列，要减少多少人？解：8×2－1＝15(人)或(8－1)×2＋1＝15(人)答：如果去掉一行一列要减少15人。

2、装饰一个形状是正方形的舞台，四周等距离插上彩旗，四个角上都要插，每边插25面。

一共要插多少面？解：(25－1)×4＝96(面)或25×4－4＝96(面)答：一共插了96面。

3、参加小学生运动会团体操表演的运动员组成了一个正方形队列，共排了18行，每行18人。

后因场地原因，把最外一圈的同学去掉了。

去掉了多少人？还剩下多少人？解：去掉的人数：(18－1)×4＝68(人)或18×4－4＝68(人)剩下的人数：18×18－68＝256(人)或(18－2)×(18－2)＝256(人)答：去掉了68人；还剩下256人。

星期二4、棋子被摆成一个实心方阵，最外层有80枚。

这个方阵最外层每边有多少枚棋子？共用了多少枚棋子？解：最外层每边的棋子数：80÷4＋1＝21(枚)或(80－4)÷4＋2＝21(枚)共用棋子数：21×21＝441(枚)答：这个方阵最外层每边有21枚棋子；共用了441枚棋子。

5、为了庆祝国庆节，同学们组成了一个鲜花队方阵。

已知第一横行和第一竖列共有25人，则这个鲜花队方阵共有多少人？解：最外层每边人数：(25＋1)÷2＝13(人)或(25－1)÷2＋1＝13(人)共有人数：13×13＝169(人)答：这个鲜花队方阵共有169人。

6、小丽用棋子摆成一个实心方阵。

后来她又加上11枚棋子，使横竖各增加了一排，成为一个较大的实心方阵。

原来的实心方阵有多少枚棋子？解：原来的实心方阵最外层有棋子：(11－1)÷2＝5(枚)或(11＋1)÷2－1＝5(枚) 原来的实心方阵有棋子：5×5＝25(枚)答：原来的实心方阵有25枚棋子。

高等数学课后习题及参考答案(第四章)

高等数学课后习题及参考答案（第四章）习题4-11. 求下列不定积分:(1)⎰dx x 21;解 C x C x dx x dx x +-=++-==+--⎰⎰112111222.(2)⎰dx x x ; 解 C x x C x dx x dx x x +=++==+⎰⎰212323521231. (3)⎰dx x1;解C x C x dx xdx x+=++-==+--⎰⎰21211112121. (4)⎰dx x x 32; 解 C x x C x dx x dx x x+=++==+⎰⎰3313737321031371. (5)⎰dx xx 21;解C x x C x dx xdx xx +⋅-=++-==+--⎰⎰12312511125252. (6)dx x m n ⎰; 解C x m n m C x mn dx x dx x mn m m nm nmn++=++==++⎰⎰111.(7)⎰dx x 35;解 C x dx x dx x +==⎰⎰4334555.(8)⎰+-dx x x )23(2;解 C x x x dx dx x dx x dx x x ++-=+-=+-⎰⎰⎰⎰2233123)23(2322.(9)⎰ghdh 2(g 是常数);解C ghC h gdh hgghdh +=+⋅==⎰⎰-22212122121. (10)⎰-dx x 2)2(;解 C x x x dx dx x dx x dx x x dx x ++-=+-=+-=-⎰⎰⎰⎰⎰423144)44()2(23222.(11)⎰+dx x 22)1(;解 C x x x dx dx x dx x dx x x dx x +++=++=++=+⎰⎰⎰⎰⎰3524242232512)12()1(.(12)dx x x ⎰-+)1)(1(3;解 ⎰⎰⎰⎰⎰⎰-+-=-+-=-+dx dx x dx x dx x dx x x x dx x x 23212323)1()1)(1(C x x x x +-+-=25233523231.(13)⎰-dx xx 2)1(;解C x x x dx x x xdx xx x dx xx ++-=+-=+-=-⎰⎰⎰-2523212321212252342)2(21)1(. (14)⎰+++dx x x x 1133224; 解C x x dx x x dx x x x ++=++=+++⎰⎰arctan )113(1133322224.(15)⎰+dx x x 221;解⎰⎰⎰+-=+-=+-+=+C x x dx xdx xx dx x x arctan )111(111122222.(16)⎰+dx xe x )32(;解 C x e dx xdx e dx x e x x x ++=+=+⎰⎰⎰||ln 32132)32(.(17)⎰--+dx xx )1213(22;解 ⎰⎰⎰+-=--+=--+C x x dx xdx x dx xx arcsin 2arctan 3112113)1213(2222.(18)dx xe e x x⎰--)1(;解 C x edx xe dx xe e xxx x+-=-=-⎰⎰--21212)()1(.(19)⎰dx e x x 3;解 C e C e e dx e dx e xx x xxx++=+==⎰⎰13ln 3)3ln()3()3(3.(20)⎰⋅-⋅dx xxx 32532; 解 C x C x dx dx x xx xxx+--=+-=-=⋅-⋅⎰⎰)32(3ln 2ln 5232ln )32(52])32(52[32532. (21)⎰-dx x x x )tan (sec sec ;解 ⎰⎰+-=-=-C x x dx x x x dx x x x sec tan )tan sec (sec )tan (sec sec 2.(22)⎰dx x2cos 2;解 C x x dx x dx x dx x ++=+=+=⎰⎰⎰)sin (21)cos 1(212cos 12cos 2.(23)⎰+dx x 2cos 11;解 ⎰⎰+==+C x dx xdx x tan 21cos 212cos 112.(24)⎰-dx xx xsin cos 2cos ;解 ⎰⎰⎰+-=+=--=-C x x dx x x dx xx xx dx x x x cos sin )sin (cos sin cos sin cos sin cos 2cos 22.(25)⎰dx x x x22sin cos 2cos ;解 ⎰⎰⎰+--=-=-=C x x dx xx dx x x x x dx x x x tan cot )cos 1sin 1(sin cos sin cos sin cos 2cos 22222222.(26)⎰-dx x x x)11(2;解 ⎰⎪⎭⎫ ⎝⎛-dx x x x 211⎰++=-=--C x x dx x x 41474543474)(.2. 一曲线通过点(e 2, 3), 且在任一点处的切线的斜率等于该点横坐标的倒数, 求该曲线的方程.解设该曲线的方程为y =f (x ), 则由题意得xx f y 1)(='=',所以 C x dx xy +==⎰||ln 1.又因为曲线通过点(e 2, 3), 所以有=3-2=1 3=f (e 2)=ln|e 2|C =2C ,C =3-2=1. 于是所求曲线的方程为 y =ln|x | 1.3. 一物体由静止开始运动, 经t 秒后的速度是3t 2(m/s ), 问 (1)在3秒后物体离开出发点的距离是多少？ (2)物体走完360m 需要多少时间？解设位移函数为s =s (t ), 则s '=v =3 t 2, C t dt t s +==⎰323. 因为当t =0时, s =0, 所以C =0. 因此位移函数为s =t 3. (1)在3秒后物体离开出发点的距离是s =s (3)=33=27.(2)由t 3=360, 得物体走完360m 所需的时间11.73603≈=t s. 4. 证明函数x e 221, e x sh x 和e x ch x 都是x x e xsh ch -的原函数.证明 x x xx x x x x x e ee e e e e e x x e 222sh ch ==--+=----. 因为x x e e 22)21(=', 所以x e 221是x x e xsh ch -的原函数.因为(e x sh x )'=e x sh x e x ch x =e x (sh x ch x )x xx x x x e e e e e e 2)22(=++-=--, 所以e x sh x 是xx e xsh ch -的原函数.因为(e x ch x )'=e x ch x e x sh x =e x (ch x sh x )x xx x x x e e e e e e 2)22(=-++=--, 所以e xch x 是xx e x sh ch -的原函数.习题4-21. 在下列各式等号右端的空白处填入适当的系数, 使等式成立(例如: )74(41+=x d dx :(1) dx = d (ax );解dx = a 1d (ax ).(2) dx = d (7x -3);解dx = 71d (7x -3).(3) xdx = d (x 2); 解xdx = 21 d (x 2).(4) x d x = d (5x 2);解x d x = 101d (5x 2).(5))1( 2x d xdx -=;解 )1( 212x d xdx --=.(6)x 3dx = d (3x 4-2);解x 3dx = 121d (3x 4-2).(7)e 2x dx = d (e 2x ); 解e 2x dx = 21 d (e 2x ).(8))1( 22x x ed dxe --+=;解 )1( 2 22x xe d dx e --+-=.(9))23(cos 23sin x d xdx =;解 )23(cos 32 23sin x d xdx -=.(10)|)|ln 5( x d xdx=; 解 |)|ln 5( 51x d x dx =. (11)|)|ln 53( x d xdx-=; 解|)|ln 53( 51x d x dx --=. (12))3(arctan 912x d x dx=+; 解 )3(arctan 31912x d x dx =+. (13))arctan 1( 12x d xdx -=-;解)arctan 1( )1( 12x d xdx --=-.(14))1( 122x d x xdx -=-.解)1( )1( 122x d x xdx --=-.2. 求下列不定积分(其中a , b , ω, ϕ均为常数): (1)⎰dt e t 5; 解 C e x d e dt e xx t +==⎰⎰55551551. (2)⎰-dx x 3)23(; 解 C x x d x dx x +--=---=-⎰⎰433)23(81)23()23(21)23(. (3)⎰-dx x 211; 解C x x d x dx x +--=---=-⎰⎰|21|ln 21)21(21121211.(4)⎰-332xdx ;解C x C x x d x xdx+--=+-⋅-=---=-⎰⎰-3232313)32(21)32(2331)32()32(3132. (5)⎰-dx e ax bx)(sin ;解C be ax ab x d e b ax d ax a dx e ax b xb xbx+--=-=-⎰⎰⎰cos 1)()(sin 1)(sin .(6)⎰dt tt sin ;解⎰⎰+-==C t t d t dt tt cos 2sin 2sin .(7)⎰⋅xdx x 210sec tan ;解 ⎰⋅xdx x 210sec tan C x x xd +==⎰1110tan 111tan tan . (8)⎰xx x dxln ln ln ;解C x x d x x d x x x x x dx +===⎰⎰⎰|ln ln |ln ln ln ln ln 1ln ln ln ln 1ln ln ln .(9)⎰+⋅+dx xx x 2211tan ;解 ⎰+⋅+dx x x x 2211tan 2222211cos 1sin 11tan x d x x x d x +++=++=⎰⎰C x x d x ++-=++-=⎰|1cos |ln 1cos 1cos 1222.(10)⎰xx dxcos sin ;解 C x x d xdx x x x x dx +===⎰⎰⎰|tan |ln tan tan 1tan sec cos sin 2. (11)⎰-+dx e e xx 1;解 ⎰-+dx e e xx 1C e de edx e e x x xx x +=+=+=⎰⎰arctan 11122.(12)⎰-dx xe x 2; 解 .21)(212222C e x d e dx xe x x x +-=--=---⎰⎰ (13)⎰⋅dx x x )cos(2;解 C x x d x dx x x +==⋅⎰⎰)sin(21)()cos(21)cos(2222. (14)⎰-dx xx 232;解C x C x x d x dx x x+--=+--=---=-⎰⎰-2212221223231)32(31)32()32(6132.(15)⎰-dx xx 4313; 解⎰⎰+--=---=-C x x d x dx x x |1|ln 43)1(11431344443.(16)⎰++dt t t ))sin((cos 2ϕωϕω; 解 C t t d t dt t t ++-=++-=++⎰⎰)(cos 31)cos()(cos 1)sin()(cos 322ϕωωϕωϕωωϕωϕω. (17)⎰dx x x3cos sin ; 解 C x C x x xd dx xx +=+=-=--⎰⎰2233sec 21cos 21cos cos cos sin . (18)⎰-+dx x x xx 3cos sin cos sin ; 解 )sin cos (cos sin 1cos sin cos sin 33x x d x x dx x x x x +--=-+⎰⎰ C x x x x d x x +-=--=⎰-3231)cos (sin 23)cos (sin )cos (sin .(19)⎰--dx xx 2491;解dx xx dx xdx xx ⎰⎰⎰---=--22249491491)49(49181)32()32(1121222x d x x d x --+-=⎰⎰C x x +-+=2494132arcsin 21.(20)⎰+dx xx 239; 解 C x x x d xx d x x dx x x ++-=+-=+=+⎰⎰⎰)]9ln(9[21)()991(21)(9219222222223. (21)⎰-dx x 1212;解⎰⎰⎰+--=+-=-dx x x dx x x dx x )121121(21)12)(12(11212 ⎰⎰++---=)12(121221)12(121221x d x x d x C x x C x x ++-=++--=|1212|ln 221|12|ln 221|12|ln 221.(22)⎰-+dx x x )2)(1(1;解C x x C x x dx x x dx x x ++-=++--=+--=-+⎰⎰|12|ln 31|1|ln |2|(ln 31)1121(31)2)(1(1.(23)⎰xdx 3cos ;解 C x x x d x x d x xdx +-=-==⎰⎰⎰3223sin 31sin sin )sin 1(sin cos cos .(24)⎰+dt t )(cos 2ϕω; 解 C t t dt t dt t +++=++=+⎰⎰)(2sin 4121)](2cos 1[21)(cos 2ϕωωϕωϕω. (25)⎰xdx x 3cos 2sin ; 解 ⎰xdx x 3cos 2sin C x x dx x x ++-=-=⎰cos 215cos 101)sin 5(sin 21. (26)⎰dx xx 2cos cos ;解 C x x dx x x dx x x ++=+=⎰⎰21sin 23sin 31)21cos 23(cos 212cos cos .(27)⎰xdx x 7sin 5sin ; 解 C x x dx x x xdx x ++-=--=⎰⎰2sin 4112sin 241)2cos 12(cos 217sin 5sin . (28)⎰xdx x sec tan 3;解 x d x xdx x x xdx x sec tan tan sec tan sec tan 223⎰⎰⎰=⋅=C x x x d x +-=-=⎰sec sec 31sec )1(sec 32.(29)⎰-dx xx2arccos 2110;解C x d x d dx xx xxx+-=-=-=-⎰⎰⎰10ln 210)arccos 2(1021arccos 10110arccos 2arccos 2arccos 22arccos 2.(30)⎰+dx x x x )1(arctan ;解C x x d x x d x xdx x x x +==+=+⎰⎰⎰2)(arctan arctan arctan 2)1(arctan 2)1(arctan .(31)⎰-221)(arcsin xx dx;解C xx d x x x dx+-==-⎰⎰arcsin 1arcsin )(arcsin 11)(arcsin 222.(32)⎰+dx x x x 2)ln (ln 1; 解C xx x x d x x dx x x x+-==+⎰⎰ln 1)ln ()ln (1)ln (ln 122. (33)⎰dx xx xsin cos tan ln ;解⎰⎰⎰=⋅=x d x x xdx x x dx x x x tan tan tan ln sec tan tan ln sin cos tan ln 2C x x d x +==⎰2)tan (ln 21tan ln tan ln .(34)⎰-dx x a x 222(a >0);解⎰⎰⎰⎰-===-dt t a dt t a tdt a t a t a t a x dx xa x 22cos 1sin cos cos sin sin 22222222令, C x a xa x a C t a t a +--=+-=222222arcsin 22sin 421. (35)⎰-12x x dx ;解C x C t dt tdt t t t tx x x dx +=+==⋅⋅=-⎰⎰⎰1arccos tan sec tan sec 1sec 12令.或C x x d x dx xx x x dx +=--=-=-⎰⎰⎰1arccos 111111112222.(36)⎰+32)1(x dx ;解C t tdt t d t tx x dx +==+=+⎰⎰⎰sin cos tan )1(tan 1tan )1(3232令C x x ++=12.(37)⎰-dx xx 92; 解⎰⎰⎰=-=-tdt t d tt t x dx x x 222tan 3)sec 3(sec 39sec 9sec 39令 C x x C t t dt t+--=+-=-=⎰3arccos 393tan 3)1cos 1(322.(38)⎰+xdx 21;解C x x C t t dt t tdt t t x xdx ++-=++-=+-=+=+⎰⎰⎰)21ln(2)1ln()111(11221令.(39)⎰-+211x dx ;解⎰⎰⎰⎰-=+-=+=-+dt tdt t tdt t tx x dx)2sec211()cos 111(cos cos 11sin 1122令 C xxx C t t t C t t +-+-=++-=+-=211arcsin cos 1sin 2tan . (40)⎰-+21x x dx .解⎰⎰⎰+-++=⋅+=-+dt tt tt t t tdt t t tx x x dx cos sin sin cos sin cos 21cos cos sin 1sin 12令C t t t t t d t t dt +++=+++=⎰⎰|cos sin |ln 2121)cos (sin cos sin 12121 C x x x ++-+=|1|ln 21arcsin 212.习题4-3求下列不定积分: 1. ⎰xdx x sin ; 解C x x x xdx x x x xd xdx x ++-=+-=-=⎰⎰⎰sin cos cos cos cos sin .2. ⎰xdx ln ;解 C x x x dx x x x xd x x xdx +-=-=-=⎰⎰⎰ln ln ln ln ln . 3. ⎰xdx arcsin ;解 ⎰⎰-=x xd x x xdx arcsin arcsin arcsin ⎰--=dx xx x x 21arcsinC x x x +-+=21arcsin . 4. ⎰-dx xe x ;解 ⎰⎰⎰----+-=-=dx e xe xde dx xe x x x x C x e C e xe x x x ++-=+--=---)1(. 5. ⎰xdx x ln 2; 解 ⎰⎰⎰-==x d x x x xdx xdx x ln 31ln 31ln 31ln 3332 C x x x dx x x x +-=-=⎰332391ln 3131ln 31.6. ⎰-xdx e x cos ; 解因为⎰⎰⎰⎰------+=-==xdx e x e xde x e x d e xdx e x x x x x x sin sin sin sin sin cos ⎰⎰-----+-=-=x x x x x xde x e x e x d e x e cos cos sin cos sin⎰-----=xdx e x e x e x x x cos cos sin ,所以 C x x e C x e x e xdx e x x x x +-=+-=----⎰)cos (sin 21)cos sin (21cos .7. ⎰-dx xe x 2sin 2;解因为⎰⎰⎰-----==x x x x de xx e x d e dx x e 22222cos 22cos 22cos 22sin⎰⎰----+=+=2sin 82cos 22cos 42cos 22222xd e x e dx x e x e x x x x⎰----+=x x x de xx e x e 2222sin 82sin 82cos 2⎰---++=dx xe x e x e x x x 2sin 162sin 82cos 2222,所以 C xx e dx x e x x ++-=--⎰)2sin 42(cos 1722sin 22.8. ⎰dx xx 2cos ;解 C xx x dx x x x x xd dx x x ++=-==⎰⎰⎰2cos 42sin 22sin 22sin 22sin 22cos .9. ⎰xdx x arctan 2; 解 ⎰⎰⎰+⋅-==dx x x x x xdx xdx x 233321131arctan 31arctan 31arctan ⎰⎰+--=+-=2232223)111(61arctan 31161arctan 31dx xx x dx x x x x C x x x x +++-=)1ln(6161arctan 31223.10. ⎰xdx x 2tan解 ⎰⎰⎰⎰⎰+-=-=-=x xd x xdx xdx x dx x x xdx x tan 21sec )1(sec tan 2222C x x x x xdx x x x +++-=-+-=⎰|cos |ln tan 21tan tan 2122.11. ⎰xdx x cos 2;解 ⎰⎰⎰⎰+=⋅-==x xd x x xdx x x x x d x xdx x cos 2sin 2sin sin sin cos 2222C x x x x x xdx x x x x +-+=-+=⎰sin 2cos 2sin cos 2cos 2sin 22. 12. ⎰-dt te t 2;解 ⎰⎰⎰----+-=-=dt e te tde dt te t t tt 2222212121 C t e C e te t t t ++-=+--=---)21(214121222.13. ⎰xdx 2ln ;解 ⎰⎰⎰-=⋅⋅-=xdx x x dx xx x x x xdx ln 2ln 1ln 2ln ln 222C x x x x x dx x x x x x x ++-=⋅+-=⎰2ln 2ln 12ln 2ln 22.14. ⎰xdx x x cos sin ; 解 ⎰⎰⎰⎰+-=-==xdx x x x xd xdx x xdx x x 2cos 412cos 412cos 412sin 21cos sin C x x x ++-=2sin 812cos 41.15. ⎰dx xx 2cos 22; 解 ⎰⎰⎰⎰-+=+=+=xdx x x x x x d x x dx x x dx x x sin sin 2161sin 2161)cos 1(212cos 2323222⎰⎰-++=++=xdx x x x x x x xd x x x cos cos sin 2161cos sin 21612323C x x x x x x +-++=sin cos sin 216123.16. ⎰-dx x x )1ln(; 解 ⎰⎰⎰-⋅--=-=-dx x x x x dx x dx x x 1121)1ln(21)1ln(21)1ln(222 ⎰-⋅++--=dx x x x x )111(21)1ln(212C x x x x x +-----=)1ln(212141)1ln(2122.17. ⎰-xdx x 2sin )1(2;解 ⎰⎰⎰⋅+--=--=-xdx x x x x d x xdx x 22cos 212cos )1(212cos )1(212sin )1(222 ⎰+--=x xd x x 2sin 212cos )1(212⎰-+--=xdx x x x x 2sin 212sin 212cos )1(212C x x x x x +++--=2cos 412sin 212cos )1(212.18. ⎰dx x x 23ln ;解⎰⎰⎰⎰+-=+-=-=xdx xx x x d x x x x xd dx x x22333323ln 13ln 1ln 1ln 11ln ln⎰⎰+--=--=x d xx x x x x xd x x 22323ln 13ln 3ln 11ln 3ln 1⎰⎰---=+--=x xd x x x x dx x x x x x x 1ln 6ln 3ln 1ln 16ln 3ln 123223⎰+---=dx xx x x x x x 22316ln 6ln 3ln 1C x x x x x x x +----=6ln 6ln 3ln 123.19. ⎰dx e x3;解 ⎰⎰⎰==t t xde t dt e t t x dx e223333令⎰⎰-=-=t t t t tde e t dt te e t 636322 ⎰+-=dt e te e t t t t 6632 C e te e t t t t ++-=6632 C x x ex ++-=)22(33323.20. ⎰xdx ln cos ; 解因为⎰⎰⋅⋅+=dx xx x x x xdx 1ln sin ln cos ln cosdx xx x x x x x xdx x x 1ln cos ln sin ln cos ln sin ln cos ⋅⋅-+=+=⎰⎰⎰-+=xdx x x x x ln cos ln sin ln cos , 所以 C x x xxdx ++=⎰)ln sin ln (cos 2ln cos .21. ⎰dx x 2)(arcsin ;解 ⎰⎰-⋅⋅-=dx xx x x x dx x 22211arcsin 2)(arcsin )(arcsin⎰-+=221arcsin 2)(arcsin x xd x x ⎰--+=dx x x x x 2arcsin 12)(arcsin 22 C x x x x x +--+=2arcsin 12)(arcsin 22. 22. ⎰xdx e x 2sin . 解 ⎰⎰⎰-=-=xdx e e dx x e xdx e xx x x 2cos 2121)2cos 1(21sin 2, 而 dx x e x e xde xdx e x x x x ⎰⎰⎰+==2sin 22cos 2cos 2cos⎰⎰-+=+=xdx e x e x e de x x e x x x x x 2cos 42sin 22cos 2sin 22cos ,C x x e xdx e x x ++=⎰)2sin 22(cos 512cos ,所以 C x x e e xdx e x x x ++-=⎰)2sin 22(cos 10121sin 2.习题4-4求下列不定积分:1. dx x x ⎰+33;解 dx x x x x dx x x dx x x ⎰⎰⎰+-+-+=+-+=+327)93)(3(327273233 ⎰⎰+-+-=dx x dx x x 3127)93(2 C x x x x ++-+-=|3|ln 279233123.2. ⎰-++dx x x x 103322;解 C x x x x d x x dx x x x +-+=-+-+=-++⎰⎰|103|ln )103(1031103322222.3. ⎰--+dx xx x x 3458; 解 ⎰⎰⎰--++++=--+dx xx x x dx x x dx x x x x 3223458)1(8 ⎰⎰⎰--+-+++=dx x dx x dx x x x x 13148213123C x x x x x x +--+-+++=|1|ln 3|1|ln 4||ln 8213123.4. ⎰+dx x 133;解 ⎰⎰⎰+-⋅++--⋅-+=+-+-++=+dx x x x x x x dx x x x x dx x )11231122111()1211(132223⎰⎰-+-++-+--+=)21()23()21(123)1(1121|1|ln 2222x d x x x d x x xC x x x x +-++-+=312arctan31|1|ln2. 5. ⎰+++)3)(2)(1(x x x xdx;解dx x x x x x x xdx )331124(21)3)(2)(1(+-+-+=+++⎰⎰C x x x ++-+-+=|)1|ln |3|ln 3|2|(ln 21.6. ⎰-++dx x x x )1()1(122;解 ⎰⎰+--⋅++⋅=-++dx x x x dx x x x ])1(111211121[)1()1(1222 C x x x +++-+-=11|1|ln 21|1|ln 21C x x +++-=11|1|ln 212.7. dx x x )1(12+⎰; 解 C xx dx x x x dx x x ++-=+-=+⎰⎰)1ln(21||ln )11()1(1222.8. ⎰++))(1(22x x x dx;解⎰⎰+⋅-++⋅-=++dx x x x x x x x dx )112111211())(1(222⎰++-+-=dx x x x x 1121|1|ln 21||ln 2⎰⎰+-+-+-=dx x dx x x x x 11211241|1|ln 21||ln 22C x x x x +-+-+-=arctan 21)1ln(41|1|ln 21||ln 2.9. ⎰+++)1)(1(22x x x dx; 解dx x xx x x x x x dx )111()1)(1(2222⎰⎰+-+++=+++)1ln(21112111221222+-++++++=⎰⎰x dx x x x x x ⎰++++-++=dx x x x x x 1121)1ln(21|1|ln 21222C x x x x ++++-++=312arctan 33)1ln(21|1|ln 2122. 10. ⎰+dx x 114;解dx x x x x dx x ⎰⎰+-++=+)12)(12(111224⎰⎰+-+-++++=dx x x x dx x x x 12214212214222⎰⎰+----++++=dx x x x dx x x x 1222)22(21421222)22(214222 )1212(41]12)12(12)12([82222222⎰⎰⎰⎰+-+++++-+--++++=x x dxx x dx x x x x d x x x x d C x x x x x x +-++++-++=)12arctan(42)12arctan(42|1212|ln 8222. 11. ⎰++--dx x x x 222)1(2; 解 ⎰⎰⎰++-++-=++--dx x x dx x x x dx x x x 11)1(1)1(2222222 ⎰⎰⎰++-++-+++=dx x x dx x x dx x x x 11)1(123)1(122122222 ⎰⎰++-++-++⋅-=dx x x dx x x x x 11)1(12311212222, 因为)312arctan(32)312()312(11321122+=+++=++⎰⎰x x d x dx x x , 而⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1由递推公式 ⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx ,得⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1312arctan 323211231)1121()23(212222+⋅++++⋅=++++++=⎰x x x x x x dx x x x , 所以 ⎰++--dx x x x 222)1(2C x x x x x x x ++-+-+++-++⋅-=312arctan 32312arctan 3211221112122C x x x x ++-+++-=312arctan34112.12. ⎰+x dx2sin 3;解⎰⎰⎰+=-=+x d x dx x x dx tan 3tan 41cos 41sin 3222C x x d x +=+=⎰3tan 2arctan321tan )23(tan 14122.13.⎰+dx x cos 31;解 ⎰⎰⎰+=+=+)2sec 1(2cos )2(2cos 121cos 31222x x x d x dx dx x ⎰+=+=C x x x d 22tanarctan 212tan 22tan 2. 或⎰⎰+⋅++=+du u u u xu dx x221212312tancos 31令 C xC u du u +=+=+=⎰22tan arctan212arctan21)2(122. 14.⎰+dx x sin 21;解 ⎰⎰⎰+=+=+)2cot 2(csc 2sin )2(2cos 2sin 22sin 2122x x x x d x x dx dx x⎰⎰+++-=++-=222)23()212(cot )212(cot 12cot 2cot )2(cot x x d x x x dC x ++-=312cot 2arctan 32. 或⎰⎰+⋅++=+du u u u xu dx x221212212tansin 21令 ⎰⎰++=++=du u du u u 222)23()21(111C xC u ++=++=312tan 2arctan 32312arctan 32. 15.⎰++x x dxcos sin 1;解 ⎰⎰⎰+=+=+=++C x x xd x x dx x x dx |2tan |ln 2tan1)2(tan )2tan 1(2cos 21cos sin 12. 或⎰⎰+⋅+-+++=++du u u u u ux u xx dx2222121112112tancos sin 1令C xC u du u ++=++=+=⎰|12tan |ln |1|ln 11. 16.⎰+-5cos sin 2x x dx; 解⎰⎰⎰++=+⋅++--+=+-du u u du u u u u ux u x x dx2231125111412tan5cos sin 222222令C xC u du u ++=++=++=⎰512tan 3arctan 51513arctan 51)35()31(13122. 或⎰⎰+⋅++--+=+-du uu uu u x u x x dx2222125111412tan5cos sin 2令⎰⎰++=++=du u du u u 222)35()31(1312231C xC u ++=++=512tan 3arctan 51513arctan 51. 17.⎰++dx x 3111;解⎰⎰⎰++-=⋅+=+=++du uu du uu ux dx x )111(33111111233令 C x x x C u u u +++++-+=+++-=)11ln(313)1(23|1|ln 332333322.18.⎰++dx x x 11)(3;解C x x x dx x x dx x x ++-=+-=++⎰⎰232233221]1)[(11)(.19.⎰++-+dx x x 1111;解⎰⎰⎰++-=⋅+-=+++-+du u u udu u u u x dx x x )122(221111111令 C u u u +++-=|)1|ln 2221(22C x x x +++++-+=)11ln(414)1(. 20.⎰+4xx dx ;解⎰⎰⋅+=+du uu u u x xx dx 324441令C u u u du uu +++-=++-=⎰|1|ln 442)111(42 C x x x +++-=)1ln(4244.21.⎰+-xdxx x 11;解令u x x=+-11, 则2211u u x +-=, du u u dx 22)1(4+-=,⎰⎰⎰++-=+-⋅-+⋅=+-du uu du u u u u u x dx x x )1111(2)1(41111222222 C u u u +++-=arctan 2|11|ln C xxxx x x ++-+++-+--=11arctan2|1111|ln . 22.⎰-+342)1()1(x x dx .解令u x x =-+311, 则1133-+=u u x , 232)1(6--=u udx , 代入得C x x C u du x x dx +-+-=+-=-=-+⎰⎰334211232323)1()1(.总习题四求下列不定积分(其中a , b 为常数):1. ⎰--x x e e dx;解 C e e de e dx e e e e dxx x xx x xxx ++-=---=-⎰⎰⎰-|11|ln 2111122.2. dx x x ⎰-3)1(; 解C x x dx x dx x dx x x+-⋅+-=----=-⎰⎰⎰2323)1(12111)1(1)1(1)1(. 3. ⎰-dx xa x 662(a >0);解 C ax a x a x d x a dx x a x +-+=-=-⎰⎰||ln 61)()()(1313333332323662.4. ⎰++dx x x xsin cos 1;解 C x x x x d x x dx x x x ++=++=++⎰⎰|sin |ln )sin (sin 1sin cos 1.5. ⎰dx xxln ln ; 解 C x x x dx x x x x x x xd dx x x +-⋅=⋅⋅-⋅==⎰⎰⎰ln ln ln ln 1ln 1ln ln ln ln ln ln ln ln ln .6.⎰+dx x xx 4sin 1cos sin ; 解 C x x d x x d xx dx x x x +=+=+=+⎰⎰⎰222244sin arctan 21)(sin )(sin 1121sin sin 1sin sin 1cos sin . 7. ⎰xdx 4tan ; 解 xxd x x d xx xdx tan sin tan tan cos sin tan 22244⎰⎰⎰==⎰⎰++-=+=x d x x x d x x tan )1tan 11(tan tan 1tan tan 2224c x x x c x x x ++-=++-=tan tan 31tan arctan tan tan 3133.8. ⎰xdx x x 3sin 2sin sin ; 解 ⎰⎰--=xdx x x xdx x x 3sin )cos 3(cos 213sin 2sin sin ⎰⎰+-=xdx x xdx x 3sin cos 213sin 3cos 21 ⎰⎰++=dx x x x xd )2sin 4(sin 41)3(cos 3cos 61 C x x x +--=2cos 814cos 1613cos 1212. 9.⎰+)4(6x x dx;解 C x x dx x x x x x dx++-=+-=+⎰⎰)4ln(241||ln 41)41(41)4(6656.10.)0(>-+⎰a dx xa xa ; 解⎰⎰⎰⎰-+-=-+=-+dx xa xdx x a a du x a x a dx x a x a 2222221C x a a xa +--=22arcsin .11.⎰+)1(x x dx ;解C x x C x x x d x x x dx +++=+++=+=+⎰⎰)1ln(2))(1ln(2)(112)1(22.12. ⎰xdx x 2cos ; 解 ⎰⎰⎰+=+=x xd x dx x x x xdx x 2sin 4141)2cos (21cos 22 C x x x x xdx x x x +++=-+=⎰2cos 812sin 41412sin 412sin 414122.13. ⎰bxdx e ax cos ; 解因为dx bx e a b bx e a bxde a bxdx e ax axax ax ⎰⎰⎰+==sin cos 1cos 1cos dx bx e ab bx e a b bx e a de bx a b bx e a ax ax ax axax ⎰⎰-+=+=cos sin cos 1sin cos 12222,所以 C bx e ab bx e a b a a bxdx e axax ax+++=⎰)sin cos 1(cos 2222C bx b bx a e ba ax +++=)sin cos (122.14.⎰+xedx 1;解⎰⎰⎰⎰+--=-=-=++du u u du u u d u u e edx xx)1111(112)1ln(11122令.c e e c u u x x +++-+=++-=1111ln |11|ln .15.⎰-122x xdx ;解C t tdt tdt t t t tx x x dx+==⋅⋅=-⎰⎰⎰sin cos tan sec tan sec 1sec 1222令C xx +-=12.16.⎰-2/522)(x a dx;解⎰⎰⋅=-tdt a t a ta x x a dx cos )cos (1sin )(52/522令⎰⎰+==t d t adt ta tan )1(tan1cos 112444C t at a++=tan 1tan 31434C xa x ax a x a+-+-⋅=224322341)(31.17.⎰+241xxdx;解tdt t t tx x xdx 2424secsec tan 1tan 1⋅⋅=+⎰⎰令⎰⎰==t d t tdt t tsin sin cos sin cos 4243 C t tt d t t ++-=-=⎰sin 1sin 31sin )sin 1sin 1(324 C xx x x ++++-=233213)1(.18.⎰dx x x sin ;解⎰⎰⎰=⋅=tdt t tdt t t t x dx x x sin 22sin sin 2令⎰⎰⋅+-=-=tdt t t t t d t 2cos 2cos 2cos 222⎰⎰-+-=+-=tdt t t t t t td t t sin 4sin 4cos 2sin 4cos 222 C t t t t t +++-=cos 4sin 4cos 22C x x x x x +++-=cos 4sin 4cos 2. 19. ⎰+dx x )1ln(2;解 ⎰⎰+⋅-+=+dx xx x x x dx x 22212)1ln()1ln(⎰+--+=dx x x x )111(2)1ln(22C x x x x ++-+=arctan 22)1ln(2. 20.⎰dx x x32cos sin ;解 x d x xx x d x x dx x xtan )1tan tan (tan tan cos sin cos sin 2232⎰⎰⎰+-== C x x ++-=)1ln(tan 21tan 2122.21. ⎰dx x arctan ;解 x d xx x x dx x ⎰⎰+⋅-=11arctan arctan x d xx x ⎰+⋅--=)111(arctan C x x x x ++-=arctan arctan C x x x +-+=arctan )1(. 22.dx xx⎰+sin cos 1;解C x x x d x dx x x xdx x x +-===+⎰⎰⎰|2cot 2csc |ln 222csc 22cos2sin 22cos2sin cos 1. 23.⎰+dx x x 283)1(;解 C x x x dx x dx x x +++⋅=+=+⎰⎰]arctan 1[2141)1(141)1(484428283. 提示: 已知递推公式⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx . 24. ⎰++dx x x x 234811; 解 ⎰⎰⎰++=++=++dt t t t t x dx x x x dx x x x 234123412322444884811令 ⎰⎰+++-=+++-=dt t t dt t t t )11241(41)23231(412 C t t t ++++-=|1|ln 41|2|ln 41C x x x ++++=21ln 414444.25.⎰-416x dx;解⎰⎰⎰++-=+-=-dx x x dx x x x dx)4141(81)4)(4(11622224C xx x ++-+=)2arctan 21|22|ln 41(81C x x x ++-+=2arctan 161|22|ln 321. 26.dx x x⎰+sin 1sin ;解 ⎰⎰⎰-=--=+dx xxx dx x x x dx x x 222cos sin sin sin 1)sin 1(sin sin 1sinC x x x dx x x x++-=+-=⎰tan sec )cos 11cos sin (22.27. dx xxx ⎰++cos 1sin ;解⎰⎰⎰⎰+=+=++dx x xdx x x dx x x x dx x x x 2cossin 212cos 212cos 2sin cos 1sin 222 ⎰⎰+=dx xx xd 2tan 2tanC xx dx x dx x x x +=+-=⎰⎰2tan 2tan 2tan 2tan .28. ⎰-dx x x x x e x23sin cos sin cos ;解 ⎰⎰⎰⋅⋅-⋅⋅=-xdx x e xdx e x dx xx x x ex x xsec tan cos cos sin cos sin sin 23sin⎰⎰-=x d e x d xe x x sec sin sin sin ⎰⎰+⋅-=x x x xde e x xde sin sin sin sec sec⎰⎰⋅⋅+⋅--=xdx e x e x dx e xe x x x x cos sec sec sin sin sin sin C e x xe x x +⋅-=sin sin sec .29.⎰+dx x x x x)(33;解dt t t dt t t t t t t x dx x x x x)111(66)()(52362633+-=⋅+=+⎰⎰⎰令C x x C t t ++=++=66)1(ln 1ln6. 30.⎰+2)1(x e dx;解⎰⎰⎰---=-⋅=++dt t t t dt t tt e e dxx x )1111(1111)1(222令 C tt t ++--=1ln )1ln(C ee x xx ++++-=11)1ln(.31. ⎰+-+dx e e e e x x xx 1243;解)()(1111222243x xx x x x xx x x x x e ed e e dx e e e e dx e e e e ------+=+-+=+-+⎰⎰⎰C e e x x +-=-)arctan( C x +=)sh 2arctan(. 32.⎰+dx e xe xx 2)1(;解⎰⎰⎰+-=++=+11)1()1()1(22x x x x xe xd e d e x dx e xe⎰⎰+++-=+++-=x x x x x x de e e e x dx e e x )1(11111⎰+-++-=x xxxde e ee x )111(1 C e e e xx x x ++-++-=)1ln(ln 1C e e xe x x x++-+=)1ln(1.33. ⎰++dx x x )1(ln 22;解 dx x x x x x x dx x x ])1([ln )1(ln )1(ln 222222'++⋅-++=++⎰⎰ ⎰+⋅++-++=dx xx x x x x x 22221)1ln(2)1(ln⎰+++-++=22221)1ln(2)1(ln x d x x x x x⎰'++⋅+++++-++=dx x x x x x x x x x ])1[ln(12)1ln(12)1(ln 222222 ⎰++++-++=dx x x x x x x 2)1ln(12)1(ln 2222 C x x x x x x x +++++-++=2)1ln(12)1(ln 2222.34.⎰+dx x x2/32)1(ln ;解因为⎰⎰⎰++=+==⋅=+C xx C t tdt tdt t t x dx x 2232/321sin cos sec sec 1tan )1(1令,所以⎰⎰⎰⋅+-+=+=+dx x x xx x x x x xd dx x x111ln )1(ln )1(ln 2222/32 C x x x x x +++-+=)1ln(1ln 22.35. ⎰-xdx x arcsin 12;解⎰⎰⎰+=⋅=-dt t t t tdt t t x xdx x )2cos (21cos sin arcsin 122令⎰⎰-+=+=tdt t t t t t t 2sin 412sin 41412sin 414122C t t t t +++=2cos 812sin 41412122241arcsin 121)(arcsin 41C x x x x x +--+=.36.⎰-dx xx x 231arccos ;解⎰⎰⎰--=-⋅=-2222231arccos 1arccos 1arccos x xd x dx x x x x dx x x x⎰'⋅-+--=dx x x x x x x )arccos (1arccos 12222 ⎰-⋅-⋅-+--=dx xx x x x x x x )11arccos 2(1arccos 122222⎰⎰-⋅-+--=dx x xdx x x x x x 2222arccos 12arccos 1⎰-----=32322)1(arccos 3231arccos 1x xd x x x x⎰-------=dx x x x x x x x )1(32arccos )1(3231arccos 1232322。