§7.4刚体定轴转动的动能定理
刚体转动的动能定理

一、力矩的功 1 力矩的定义若作用的质点上的力为F ,则将r ×F 定义为力F 对O 点的力矩,记为M 。
M r F =⨯M 、F 、r 三者的方向构成右手螺旋关系。
M大小:方向:右手法则2 力矩的功设:;转盘上的微小质量元Δm 在力F 作用下以R 为半径绕O 轴转动,在dt 时间内转过角度d ,对应位移d r,路程ds,此时F 所做的元功为则总功为二、转动惯量设初速为零,质量元Δm 的动能为转盘的总动能1 定义:为物体的转动惯量。
意义:由质量和质量对于转轴的分布情况决定。
描述转动的惯性。
o z FtF nF tF ord rd θt t d d d d A F r F s F r θ=⋅==d d A M θ=21d A M θθθ=⎰αrsin t M Fr F rα==d θFtF ord r12ki i iE m v =212k ki i i i i E E m ==∆∑∑v 221()2i i i m r ω=∆∑2i i iI m r =∆∑单位:SI 制 kg m 22 定轴转动物体转动惯量的计算质量不连续分布的质点系:转动惯量定义为各个质点对该定轴的转动惯量之和2i i iI m r =∑质量连续分布的刚体:转动惯量定义为各个质点对该定轴的转动惯量的积分。
2mI r dm =⎰转动惯量的大小不仅取决于物体的质量,还与质量的分布和轴线的位置有关。
例1 求小球m 的转动惯量。
解:m 看作质点 I = m R 2例2 质量为m 的细圆环,求I 。
解:把环分成无限多个质量为dm 的小段,对每个d m 有d J = R 2对整个环有I = R 2d m = mR 2例3质量m ,半径 R 的薄圆盘,求I 。
解:把盘分成无限多个环。
取其中的一个环(半径r ,宽d r ,质量 d m ), 其转动惯量 d I = r 2d m22mdm rdr Rππ=整个盘的转动惯量d rd md SrRd mRRm22322200002122R R R Rm m I dI r dm r rdr r dr mR R R ππ=====⎰⎰⎰⎰例4 长为L 、质量为m 的细长直杆,转轴垂直于细杆且通过杆中心 解:杆长为L,质量为m, 则密度为=m / L 。
刚体绕定轴转动的动能定理

刚体绕定轴转动的动能定理1. 引言刚体是指其内部各点之间的相对位置关系在运动过程中不会发生改变的物体。
刚体绕定轴转动是指刚体在固定轴线上做圆周运动的情况。
动能定理是物理学中的一条重要定理,描述了物体运动过程中动能的变化与外力做功之间的关系。
本文将对刚体绕定轴转动的动能定理进行全面详细、完整且深入的阐述。
2. 刚体绕定轴转动在刚体绕定轴转动的情况下,我们需要考虑刚体的转动惯量和角速度等因素。
转动惯量是描述刚体对转动运动抵抗程度的物理量,通常用符号I表示。
角速度是描述刚体旋转快慢程度的物理量,通常用符号ω表示。
根据牛顿第二定律和角动量守恒定律,我们可以得到刚体绕定轴转动时的基本方程:τ=Iα其中,τ表示作用于刚体上产生转矩(力矩)大小,α表示角加速度。
刚体绕定轴转动的运动规律与作用在刚体上的转矩和转动惯量有关。
3. 动能定理的推导根据刚体绕定轴转动的基本方程,我们可以推导出刚体绕定轴转动的动能定理。
我们来考虑刚体上某一质点的动能T。
由于刚体上各质点都在绕着同一个轴旋转,因此它们具有相同的角速度ω。
设某一质点到轴心的距离为r,则该质点具有的线速度v为v=rω。
该质点的动能T′可以表示为:T′=12mv2=12m(rω)2=12mr2ω2其中,m表示质点的质量。
由于刚体是由众多质点组成的,因此整个刚体的动能T 可以表示为所有质点动能之和:T=∑Tni=1′i其中,n表示刚体上质点的总数。
根据牛顿第二定律和角动量守恒定律,我们知道刚体绕定轴转动时转动惯量I和角加速度α之间存在关系τ=Iα。
将该关系代入动能的表达式中,得到:T=12Iω2其中,ω表示整个刚体的角速度。
刚体绕定轴转动的动能可以表示为12Iω2。
这就是刚体绕定轴转动的动能定理。
4. 动能定理的物理意义刚体绕定轴转动的动能定理描述了刚体在转动过程中动能的变化与外力做功之间的关系。
根据动能定理,我们可以得出以下物理结论:1.外力对刚体做功会改变刚体的动能。
刚体定轴转动的动能定理

3 2
g.
又因棒在竖直位置时的角加速度 0(因此时合力矩为(4)可以由质心运动定理求出棒在竖直位置时,O 轴对棒的 反力 Fx 和 Fy:
Fy
Fx mact 0
Fx O
Fy mg macn
对于刚体,因其内部质点间无相对位移, 任何一对内力作功为零(对刚体的任何运动形式都 是成立的)。
若A外 A内非 0 E Ek EP 常量
则刚体系统的机械能守恒。
直线运动与定轴转动规律对照
质点的直线运动
v dx dt
a dv d2 x dt dt2
P mv F
EK
1 2
mv2
m
dA Fdx Fdt
A
Ek 2
Ek1
1 2
I22
1 2
I12
合外力矩对绕定轴转动的刚体做的功 = 刚体转动动能的增量
—— 刚体绕定轴转动的动能定理
刚体的重力势能:
刚体受保守力作用也有势能概念.
对于一个不太大的质量为 m 的物体,它的重
力势能应是组成刚体的各个质点的重力势能之和。
C • mi
hc
EP 0
h Epi mi ghi i
力的空间累积效应 力的功,动能,动能定理.
力矩的空间累积效应 力矩的功,转动动能,动能定理.
§7.4 定轴转动中的功能关系
F 一、力矩的功:
α
(设力F 在转动平面内)
dr P
d r
Z
rd
x dA F dr F dr sin rF sin d
力矩的元功:dA Ftrd Md
力矩作功:当刚体在外力矩作用下绕定轴转
B、对于定轴转动刚体,所有内力的功总和在任何过程 中均为零。(内力成对,大小相等方向相反,一对内力矩 的的功代数dA和为F零2 ;dr∴ 内相力对矩位的移功为总零和.)为零。另一角度,内力
刚体定轴转动动能定理公式

刚体定轴转动动能定理公式刚体定轴转动动能定理是描述刚体绕某一固定轴转动时动能变化的物理定理。
在物理学中,刚体定轴转动动能定理是非常重要的定理之一,它能够帮助我们更好地理解物体在转动时的能量变化规律。
我们需要了解一下刚体的概念。
刚体是指在运动或者受力作用下不会发生形变的物体,也就是说,在运动或者受力作用下,刚体的形状和大小都不会发生任何改变。
我们可以将刚体分为两种类型,一种是平面刚体,另一种是空间刚体。
平面刚体指的是只有面积,没有厚度的物体,空间刚体指的是有一定大小和形状的物体。
接下来,我们来了解一下刚体定轴转动动能定理。
刚体定轴转动动能定理的表达式是:E = 1/2 * I * ω²,其中E表示刚体定轴转动的动能,I表示刚体对于轴的转动惯量,ω表示刚体绕轴的角速度。
从这个公式中,我们可以看出,刚体定轴转动动能与刚体的转动惯量和角速度的平方成正比。
那么,什么是转动惯量呢?转动惯量是描述物体转动惯性的物理量,它表示物体绕着某一轴旋转时所具有的旋转惯性。
不同形状的刚体,其转动惯量也是不同的。
例如,对于一个质量均匀分布的球体,其转动惯量为2/5 * m * r²,其中m表示球体的质量,r表示球体的半径。
刚体定轴转动动能定理的应用非常广泛。
例如,在机械制造和工程设计中,我们可以通过刚体定轴转动动能定理来计算物体旋转时所需要的能量和功率。
同时,在运动学和动力学研究中,刚体定轴转动动能定理也是非常重要的工具。
刚体定轴转动动能定理是描述刚体绕某一固定轴转动时动能变化的重要定理。
通过刚体定轴转动动能定理,我们可以更好地理解物体在转动时的能量变化规律,这对于物理学的研究和应用都具有非常重要的意义。
刚体的能量定轴转动的动能定理
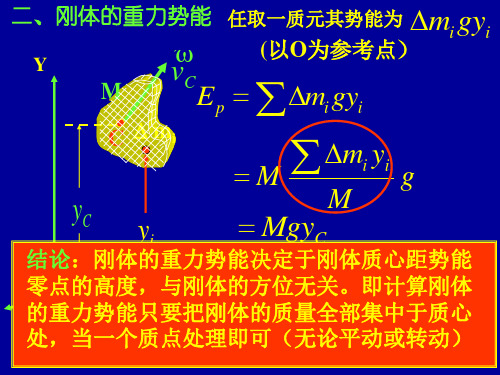
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ,则该质元动能:
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能:
n
Ek Ek
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程,设
在力矩作用下,刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用,力矩越 大,在空间转过的角度越大,作的功就越大。 这种力矩对空间的积累作用的规律是什么呢?
/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL 1 mL2
3g L
3
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例)设一细杆的质量为m,长为L,一端支以
枢轴而能自由旋转,设此杆自水平静止释放。
求: 当杆过铅直位置时的角速度:
N
YZ
XO
r
mg
第7章-刚体力学

d
3g
cos
d
0
0 2l
=
3g sin
l
运用质心运动定理,对质心C:
nˆ F1
F
F2
l
O C
ˆt
mg
x
nˆ : F1 mg sin man ˆt : F2 mg cos mat
F
an
r2
l 2 2
3g sin 2l
l 3g cos
at
r
2
4
F12 F22
arctan F1 F2
(7.5.2)
即刚体相对于质心的轴的转动同样服从定轴转 动定律. 式(7.5.1)和(7.5.2)称刚体平面运动的基本动 力学方程.
§7.5.2 作用于刚体上的力
1.作用于刚体上力的两种效果 ·滑移矢量
(1) 施于刚体的力的特点 施于刚体的某个点的力,决不可以随便移到另一点去.
A
F
作用力通过质心,对质心轴上的 力矩为零,使刚体产生平动.
FT
11 10
mg
比较上面结果,可见提升弧形闸门
所用的拉力较小.
W
图(b)
[例题3]如图表示一种用实验方法测量转动惯量的装置。
待测刚体装在转动架上,线的一端绕在转动架的轮轴上,
线与线轴垂直,轮轴的轴体半径为r,线的另一端通过定
滑轮悬挂质量为m的重物,已知转动架惯量为I0 ,并测得 m自静止开始下落 h 高度的时间为 t ,求待测物体的转动
L
r1
r1
L2
L1
r2
O r2
m2
k
2mr 2
v1 v2 r
2如.转图轴, 为非对称k 轴对O点同样有
刚体定轴转动的动能定理

它的动能为 ΔEki
1 2
Δmi vi2
1 2
Δmi
ri 2 2
整个刚体的动能为全部质元的动能之和,即 Ek
1
2
n i 1
Δmi
ri2
2
1 2
J2
式即为刚体转动动能的表达式。
刚体定轴转动的动能定理
1.3 刚体定轴转动的动能定理
将式的转动定律代入可得 dW Md J d J d d Jd
式中 ds ——位移元 dr 对应的弧长,其与对应角位移 dθ 的关系为 ds rd
刚体定轴转动的动能定理
1.1 力矩的功
于是,式可写为 dW Fτrd Md
当刚体的角位置由1 变为2 时,外力矩所做功为W
2 Md
1
式中,M 若是合外力矩,则 W 就是合外力矩的功。
刚体定轴转动的动能定理 1.2 转动动能
大学物理
刚体定轴转动的动能定理 1.1 力矩的功
如图所示,一个绕固定轴 OO 转动的圆盘状刚体,在圆盘平面上有外力 F 作用于 A 点。外力 F 可分解 为切向分力 Fτ 和法向分力 Fn 。
刚体定轴转动的动能定理 1.1 力矩的功
由于法向分力 Fn 垂直于 A 点的角位移,不做功,因此,外力 F 所做的功等于切向分力 Fτ 所做的功,则 外力 F 所做的元功为 dW F dr Fτds
静止下降 h 距离时物体的速率 v。
【解】 由题意可知,以滑轮、物体和地球组成的系统机械能守恒。
取物体在 h 处时系统的重力势能为零,设物体下降到 h 处时滑轮的角速度为 ω,
则根据机械能守恒定律可得
m2 gh
1 2
J2
1 2
m2v2
根据表可知,滑轮的转动惯量为
论述刚体定轴转动的新转动动能定理

论述刚体定轴转动的新转动动能定理力作功就伴随系统机械能的转化,而目前的物理学只定义了非保守作用力对相对参考系有位移的受力体作的耗散功,却忽视了非保守反作用力对相对参考系没有位移的受力体作的耗散功,从而使经典功能方程对系统损失的机械能的去向不能正确的解释,使理论不能正确反映和指导客观实践,需要加以研究解决。
本文依照“论对系统功能原理的推论”[1]、“作用力作功、反作用力也作功”[2]的规律,推导出了刚体定轴转动的新转动动能定理。
使每一对非保守力对各自受力体同时作耗散功,同时消耗系统的机械能的规律如实体现。
1 刚体的新定轴转动动能定理1.1 刚体定轴转动的运动学描述为了在功能方程中既体现非保守力一般情况下作耗散功、又同时作非耗散功的双重特性,又体现非保守力作耗散功、非保守反作用力也伴随着作等值的耗散功的规律性,将质点的绝对运动、相对运动和牵连运动理念[3]引入转动参考系。
以相对于转轴静止的惯性参考系作为S系;刚体相对于S系绕定轴转动的角位移微元为绝对角位移微元;以定轴转动刚体所受非保守力(力矩)的第j个施力体相对于S系绕定轴转动的角位移微元为牵连角位移微元(j=1,2,…,m),这第j个施力体是绕定轴相对于S系转动的转动参考系Sj′的参照物;定轴转动刚体相对转动参考系Sj′的角位移微元是相对角位移微元,而第j个施力体(转动参考系Sj′)相对定轴转动刚体的相对角位移微元,且=-;=+。
1.2 刚体的新定轴转动动能定理设:在惯性参考系O-XYZ中(S系),质量为m0的刚体对定轴oo’的转动惯量为J,刚体受的非保守外力在其作用点所在转动平面的分量依次为f0j,其反作用力在转动平面的分量依次为f0j(j=1,2,…,m),这些非保守外力作用点在各自的转动平面对圆心的位置矢量依次为rj;刚体受的保守外力在各自作用点所在的转动平面内的分量依次为F0i,这些力对定轴oo’的力矩依次为(i=1,2,…,n)。
则保守外力F0i对定轴oo’的合力矩为:=,这继承了保守力矩功的传统定义。
漆安慎《力学》教案第07章 刚体力学

Δt0 Δt dt
在定轴转动中, 只有两个转向
第七章 刚体力学
P(t+t )
+ P(t)
O
x
逆时针转动时 >0; 顺时针转动时 < 0.
角速度用每分 n 转表示时: 2πn πn rad/s
60 30
类似地可得: 角加速度
lim Δ d
d (t)dt
t
0
(t)dt
0
d (t) dt
t
0
(t)dt
0
匀速转动时 =常量
匀变速转动时 =常量
0 t 0 t
0
t
1 t2
2
2 02 2( 0)
与质点作匀速或匀变速直线运动的公式完全对应!!!
特点
(1) 刚体可以看成由许多质点组成的质点 系,每一个质点叫做刚体的一个质元
(2) 刚体内任意两点间的距离保持不变. 所以将刚体称为“不变质点系”.
研究刚体的基本方法 将刚体看作质点系,并运用已知的质
点系的运动规律去研究.
上页 下页 返回 结束
第七章 刚体力学
§7.1 刚体运动的描述
刚体最基本的运动形式有: ⑴平动;⑵绕固定轴的转动;⑶平面运动
r j
z
r k
其中
x
dx
dt
y
dy
dt
z
dz
dt
当刚体作定轴转动时,可令转轴与 z 轴重合,
则有
x y 0 x y
r
z
r k
刚体力学_功 动能定理
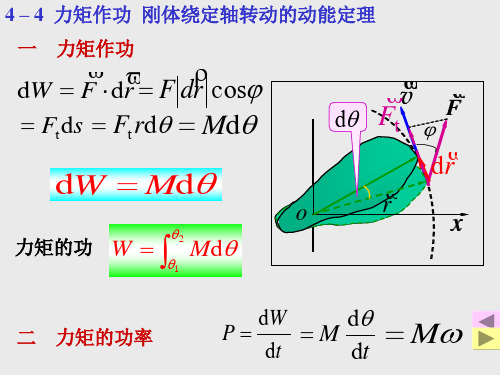
m
.
N
R
m1
m2 解: 把m1、m2和m看作一系统 系统所受 m g 看作一系统,系统所受 看作一系统 1 m2 g 合外力有重力m 、 合外力有重力 1g、m2g,这两个力对轴 这两个力对轴 支撑力N通过转轴 的力矩分别为m 的力矩分别为 1gR、m2gR;支撑力 通过转轴 对轴的力 、 支撑力 通过转轴,对轴的力 矩为零.加上阻力矩 加上阻力矩M 系统所受合外力矩为 顺时针为正) 系统所受合外力矩为(顺时针为正 矩为零 加上阻力矩 f ,系统所受合外力矩为 顺时针为正 M=m2gR-m1gR-Mf 系统的总角动量为(顺时针为正 顺时针为正) 系统的角 m: Jω 系统的总角动量为 顺时针为正 动量包括 m1: Rm1v L=Jω+Rm1v+Rm2v m2: Rm2v
1 1 1 2 2 2 mv 0 = mv + Jω 2 2 2
的圆盘, 例 一质量为 m' 、半径为 R 的圆盘,可绕一垂 圆盘上绕有轻绳, 直通过盘心的无摩擦的水平轴转动 . 圆盘上绕有轻绳, 问物体由静止下落高度 一端挂质量为m 一端挂质量为 的物体 . 问物体由静止下落高度 h 时, 其速度的大小为多少? 其速度的大小为多少 设绳的质量忽略不计 . v 对圆盘做功, 解1 拉力 FT 对圆盘做功,由刚体绕定轴转动的动 v 能定理可得, 能定理可得,拉力 FT 的力矩所作的功为
o
圆 锥 摆
o
v θ T
'
m
v v
v p
o
v v
R
以子弹和杆为系统 守恒; 动量不守恒; 守恒; 角动量 守恒; 机械能 不守恒 .
圆锥摆系统 守恒; 动量不守恒; 对 O'O 轴角动量 守恒; 守恒; 机械能 守恒 .
08 刚体定轴转动的动能定理和转动定律

3-1 刚体定轴转动的动能定理和转动定律
n
定义转动惯量 J miri2 i1
对质量连续分布的刚体,任取质量元dm,其到轴的距离为 r,则转动惯量
J r2dm 单位:kg ·m2(千克·米2)
dm:质量元
dmdl :线密度 dmdS :面密度
dmdV :体密度
3-1 刚体定轴转动的动能定理和转动定律
刚体定轴转动的动能定理
W12M d1 2J2 21 2J12
合外力矩对绕定轴转动的刚体所作的功等于刚体转动动能 的增量.
注意
1. 如果刚体在运动过程中还有势能的变化,可用质点组的功能
原理和机械能转换与守恒定律讨论. 总之,刚体作为特殊的质
点组,它服从质点组的功能转换关系.
2. 刚体的定轴转动的动能应用 Ek
m1(2m2
1 2
m)g
m1
m2
1 2
m
,
FT 2
m2
(2m1
1 2
m)
g
m1
m2
1 2
m
决定刚体转动惯量的因素 ⑴与刚体的密度有关(即与m有关); ⑵与刚体的几何形状有关(即与m的分布有关); ⑶与刚体的转轴位置有关。
3-1 刚体定轴转动的动能定理和转动定律
求质量为m、长为l的均匀细长棒,对通过棒中心和过端点 并与棒垂直的两轴的转动惯量.
O
Or
l 2 O´ dr l 2
O´ dr l
M
1.力矩
动 点平P面刚, 且的体在交绕转点O动z,轴平力旋面F 转内作,,用Or 为在轴刚为与体由上转点
O 到力的作用点 P 的位矢.
O
M zr*
dP
F
F对转轴z的力矩 M Fsrin Fd
05-3刚体绕定轴转动的动能定理

2
物体下滑的速率 是物体在斜面上 位置的函数
2)物体在斜面上能滑多远 ) 物体的速率
R
m
2
2mgx sin θ − kx v= 2 m+ J /R
2
m
θ
x
k
当v= 0 时物体在斜面上停止下滑
2mgx sin θ − kx = 0
2mg sin θ x= k
1 2 2 = (∑ mi ri )ω 2
z
1 2 2 Ek = (∑ mi ri )ω 2 i =1
刚体对定轴 的转动惯量
n
ω
vi
mi
J = ∑ mi ri
i =1
n
2
v o ri
1 2 Ek = Jω 2
对比质点 的动能
——刚体的转动动能 刚体的转动动能
1 2 Ek = mv 2
v dr
v F
当力作用在质点上使它在力的方向发 生位移, 生位移,该力就对质点做功
v v dW = F ⋅ dr
z
刚体绕固定轴转动时, 刚体绕固定轴转动时,外力使刚体上 的质点都作圆周运动, 的质点都作圆周运动,外力也在做功 外力对刚体做功要用力矩和角位移 的乘积形式来表示, 的乘积形式来表示,称为力矩的功
ω
vi
4-4 刚体绕定轴转动的动能定理 -
力矩是改变刚体转动状态的原因
刚体定轴 转动定律
M = Jα
——力矩的瞬时作用效应 力矩的瞬时作用效应 还应该研究力矩的累积效应—— 还应该研究力矩的累积效应 力矩对时间累积效应 刚体的角动量定理 力矩对空间的累积 刚体定轴转动的动能定理 如何表示刚体的转动动能呢? 如何表示刚体的转动动能呢? 高速转动的砂轮具有 转动动能, 转动动能,它能通过 摩擦转化为热能
刚体的能量定轴转动的动能定理

/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL
1 mL2
3g L
3
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ,则该质元动能:
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能:
n
Ek Ek
力 F 作的功:
ds rd
dA F ds F sin rd Md
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程,设
在力矩作用下,刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用,力矩越 大,在空间转过的角度越大,作的功就越大。 这种力矩对空间的积累作用的规律是什么呢?
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例)设一细杆的质量为m,长为L,一端支以
枢轴而能自由旋转,设此杆自水平静止释放。
大物刚体力学-2

13
解法二: 解法二:选取 m、M、k 为系统,由动能定理
∫
v v v v 1 2 1 2 f ⋅ dx + ∫ mg ⋅ dx = mv + I M ω − 0 2 2
绳子的张力为内力。 所以有
1 2 1 2 ∫0 −kxdx + ∫0 mg sin θ dx = 2 mv + 2 I M ω
R
O
M
m
x
m
EP = 0
θ
11
设 m 未释放时为 初态,此时重力 势能为零。当m 下滑 x 后为终态。
R
O
M
m
x
m
EP = 0
θ
初态能量:
Eko + E p 0 = 0 + 0
(滑轮的重力势 能不变)
终态能量:
1 2 1 2 1 2 Ek + Ep = kx − mgx sinθ + mv + IM ω 2 2 2
两边积分得
∫
t2
t1
v v L2 v v v M z dt = ∫ dL = ∆L = I 2ω2 − I1ω1
L1
定轴转动刚体在t1 → t 2时间内所受合外力 矩的冲量矩等于该时间内刚体角动量的增量。
——角动量(动量矩)定理 角动量(动量矩)
单位(SI ):米 ⋅ 牛顿 ⋅ 秒(m ⋅ N ⋅ s )
vc = dω
即:刚体绕某定轴的转动动能等于刚体绕质心以 角速度ω 角速度ω 转动的动能与质心携带总质量 m 以质 心速度
vc 平动动能之和。 平动动能之和。
2
• 力矩的功和功率
(一)力矩的功
力对刚体做的功是各个力对 各相应质元做功的总和。 各相应质元做功的总和。 内力、垂直转动平台的力均不做功。 内力、垂直转动平台的力均不做功。
刚体定轴转动的动能定理

dm 积分遍及刚体体积V,
分几种情况:
dV , ( x, y, z )
1、刚体具有对称中心,对称中心就是质心;
2、若刚体无对称中心,但可以划分为几部分,而每一部 分都有对称中心,各部分的中心就是各部分的质心,这些质心 形成为分立的质点组,则刚体的质心就归结为这一质点组的质 心; 3、前二个条件都不具备,这时就必须求积分,计算刚体 的质心。
dri j r j ri rij (为什么?) dt dt r r ij j 2 2 d r j d ri i 2 2 即 v j v i , a j ai O ri dt dt
dr j
由于 i ,j 是任意两个质元,所以刚体上所有质元均有相同的速 度和加速度,各质元的运动轨迹的形状也相同。这里很自然想 到一个代表性的质元——质心。
二、刚体的转动
如果刚体上各质元都绕同一直线作圆周运动就称为刚体转 动,这条直线称为转轴,转轴固定于参考系的情况称为定轴转 动。例如机器上齿轮的运动,门窗等都是定轴转动。若转轴上 有一点静止于参考系,而转轴的方向在变动,这种转动称为定 点转动。例如玩具陀螺的转动就属于定点转动。
分析表明:刚体的任何复杂运动总可以分解为平动和转动(定 轴转动或定点转动)的叠加,例如车轮的滚动、螺帽的运动。 研究刚体绕定轴转动时,通常取任一垂直于定轴的平面作 为转动平面,如图所示,通过分析,转动平面内各个质点的运 动情况搞清楚了,整个刚体的运动情况就知道了。取任一质点 P,P在这一转动平面内绕O点作圆周运动,用矢径 r 与Ox 轴间
唯一确定。总之,为描述平面运动,必须给出
rB rB (t ) xB (t )i yB (t ) j, 或 xB xB (t ), yB yB (t )
力矩的功 刚体绕定轴转动的动能定理

mg
df πR2 drdl
此力对点o的力矩为
rdf
mg
πR2 rdrdl
df
dl dr
or
R
4-4 力矩的功 刚体绕定轴转动的动能定理
于是,在宽为dr的
圆环上,唱片所受的摩
擦力矩为
mg
o
dM πR2 rdr(2πr)
R
2mg
R2
r 2dr
M
2mg
R2
R r 2dr 2 Rmg
v g(2 3)(ml 2ma)(ml2 3ma2 ) 6 ma
4-4 力矩的功 刚体绕定轴转动的动能定理
作 业第144页 4 - 30 4 - 31 4 - 36
第四章
刚体的转动
2019/7/14
14
一、刚体定轴转动的运动学
z
角坐标 (t) 角位移 (t t) (t)
质量为m的细棒可绕其
一端自由转动,开始
时棒处于水平位置,
mg
求棒转到与水平线成
角度 时的角速 度、角加速度.
第四章 刚体的转动
33
物理学
第五版
第四章补充例题
解 应用转动定律
L
M J 求β
M L mg cos
2
mg
J 1 mL2 3
3g cos
2L
第四章 刚体的转动
34
物理学
ox
dx x
第四章 刚体的转动
25
物理学
第五版
第四章补充例题
解 dm m dx l
dM x(dmg)
M
xdmg
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5mg 解得: N N n 2
小 结 刚体定轴转动
M I
质点直线运动
F ma
0
Mdt I I
功
Fdt mv mv
0
1 转动动能 Ek I 2 2 A Md 1 1 2 2 Md I I 0 2 2 重力势能 E p mghc
例2
解法二:刚体定轴转动的机械能守恒定律
[分析:以杆和地球为一系统,只有 mg 作功, 机械能守恒.] 选择水平位置为杆的势能零点,开始时 E0 0 1 2 l 至杆与水平线夹角为 时 E I mg sin 2 2 1 l 2 N I mg sin 0 2 2 O mg 3g sin 解得: l 1 mg vc 3 gl sin 2
mghc
决定于刚体重心距势能零点的高度。
五、刚体的机械能
1 2 E Ek E p I z mghc 2
刚体的机械能守恒定律:
若只有重力做功,则刚体机械能保持不变。
例1
已知:滑轮为匀质圆柱,质量为m1,半径为R质量 为m2的重物由静止下落h,求重物下落h后的速度。 解1:质点和刚体定轴转动的动能定理
外 k
k0
由于刚体内力作功的代数和为零
1 1 2 2 A外 2 I z 2 I z 0
内容: 刚体绕定轴转动时,转动动能的增量 等于刚体所受外力矩做功的代数和。
四、刚体的重力势能
E pi mi ghi mi gyi E p mi gyi
my mg m
i i i
m 2 gh v 2 m1 2m 2
例1
解2:质点系动能定理:
质点系:滑轮、重物
在下落过程中只有重力做功, 由质点系动能定理:
2 2 1 m2 gh 1 m v I 2 2 2 2 2 2 1 1 1 m v ( m R )( v / R ) 2 1 2 2 2
m 2 gh v 2 m1 2m 2
§7.4刚体定轴转动的动能定理
一、刚体定轴转动的动能
所有质元作圆周运动的动能之和
1 Ek mi vi2 i 2
vi ri
1 Ek ( mi ri2 ) 2 2 i
1 I z 2 2
二、力矩的功
F Fn Ft dA F dr Ft ds Ft rd
l 2 2
1 4 Ic 4(12 ml 2 m l4 ) 3 ml 2
2
2
o
Ep= 0 B A
A B
Io 7 3 ml 2 2 2 l 1 1 7 1、据机械能守恒定律:4mg 2 2 Io 2 ( 3 ml )
2
12 g 7l
N 分析:以杆为研究对象,它受到 重力 mg 和转轴的作用力 N 。N O 不作功,只有 mg 作功。 1 2 mg I l sin 2 2 mg 1 2 3g I ml 代入,得 sin 3 l l 1 3 gl sin 质心的速度为 vc 2 2 mg
例1
解3:隔离滑轮和重物,受力、运动情况如图,
2 m R ) 据转动定理: TR I ( 1 1 2
R T
T
据牛顿第二定律: m2 g T m2a 联系方程:
a
m2g
=a/R.
设重物落下h后的速度为v:
m2 gh v2 m1 2m2
v 2 2ah
例2
已知: m, l , 求: (1) vC (1)解法一:刚体定轴转动的动能定理
R T
T
a m2g
据质点动能定理:
m2 gh Th m2v
1 2
2
例1
据质点动能定理:
2 m2 gh Th 1 m v 2 2
R T
T a m2g
据刚体定轴转动的动能定理:
2 TR 1 I 2
2 Th 1 m v 1 4
因悬线不可伸长: R h; v R
A Ft rd M z d
0 0
z
Ft
O
F
r
s
P
Fn
力矩的功:当刚体定轴转动时,力所做的功等于
该力对转轴的力矩对角坐标的积分。
特例: 恒力矩的功 A M z
本质?
三、刚体定轴转动的动能定理
质点系动能定理:
A A内 E E
3
en
mg
mg
例2
l l 3 g cos 3 g cos aCt 2 2 2l 4 2 v 3 g sin 1 C vc 3 gl sin aCn l 2 2 2
3 g sin N n mg sin m 2
3 g cos mg cos N t m 4 mg cos 5mg sin Nt 解得: N n 4 2
例2
(2)求:杆在下摆到 位置时,杆对支点的作用力 N .
解:据质心运动定理,得
en et
O
Nn mg sin maCn
N
mg cos N t maCt 2 vC l aCn l ;aCt et 2 2 l 据转动定理,得 mg cos I 2 1 2 I ml 代入,得 3g cos 2l
1 平动动能 Ek mv 2 2 功 A F ds 1 1 2 2 F ds mv mv 0 2 2 重力势能 E p mgh
7.5.2 求:当AB边达到水平时,框架质心的线速度vc及 框架作用于支点的压力N.
解:正方形框架对转轴的转动惯量:
Io Ic 4m( ) Ic ml
N
2 Nn N t2 ; tan N n N t
例2
特殊:杆摆到竖直位置时,杆对支点的作用力
N
3 g sin N n mg sin m 2
3 g cos mg cos N t m 4
N
900
3g N n mg m 2
Nt 0
mg
