自发对称性破缺
标准模型 U(1)规范对称自发破缺机制

标准模型 U(1)规范对称自发破缺机制标准模型 U(1) 规范对称自发破缺机制标准模型是粒子物理学中描述基本粒子及其相互作用的理论框架,而 U(1) 规范对称自发破缺机制则是标准模型中的重要概念之一。
本文将重点探讨 U(1) 规范对称自发破缺机制的原理和影响。
一、U(1) 规范对称性U(1) 是表示一个单位长度的圆周的数学结构,而在粒子物理学中,U(1) 规范对称性表示物理理论在 U(1) 变换下不变。
具体来说,它要求物理系统的拉格朗日量在 U(1) 变换下具有不变性。
二、规范场和轴子U(1) 规范对称性导致存在一个相应的规范场,该规范场传播着一种被称为轴子(axion)的粒子。
轴子是一种中性粒子,不带电荷,但会参与强相互作用。
它的存在对物理现象具有重要影响。
三、规范对称自发破缺在自发对称破缺机制中,物理系统在低温下的真空态会选择一个不再具有 U(1) 对称性的状态,这导致了规范对称自发破缺。
具体来说,当轴子的势能曲线形状呈现双井势时,真空态会从对称的零场态转变为一个能量较低的非零场态。
四、轴子的重要性轴子在理论和实验中都具有重要的作用。
首先,在量子色动力学中,由于有轴子的存在,QCD 的拓扑缺陷能够得到解释。
其次,轴子在宇宙学中也扮演着关键角色,可以解释暗物质、强子谱问题等。
此外,轴子还可以通过实验证据进行探测,例如通过引力波的观测等手段。
五、实验探测轴子的探测是当今粒子物理学的热点研究之一。
科学家们使用了多种方法来寻找轴子。
例如,实验室中可以通过高强度的磁场和激光场等手段来产生和探测轴子。
此外,一些天文观测设备,如望远镜和引力波探测器等,也可以用于轴子的间接探测。
六、未来展望随着技术的不断发展和实验手段的改进,对于 U(1) 规范对称自发破缺机制和轴子的研究将进一步深入。
科学家们将不断探索轴子的性质和行为,并希望最终验证轴子的存在,以进一步完善理论框架。
总结:U(1) 规范对称自发破缺机制是标准模型的重要概念之一,涉及到轴子的产生和相应的物理现象。
标准模型U(1)规范自发对称破缺

标准模型U(1)规范自发对称破缺标准模型U(1)规范自发对称破缺标准模型是描述了基本粒子和相互作用的物理理论,其中U(1)规范对称是标准模型的一部分。
本文将探讨U(1)规范自发对称破缺的概念以及其在物理学中的应用。
1. U(1)规范对称简介U(1)规范对称是指标准模型中的一种对称性,它描述了基本粒子之间的相互作用。
在U(1)规范对称下,拉格朗日量是不变的,即它在规范变换下保持不变。
2. 自发对称破缺自发对称破缺是指系统在哈密顿量的基态中具有一种对称性,但在物理过程中该对称性被破坏。
在标准模型中,U(1)规范对称是通过希格斯机制实现的,即通过希格斯场的真空期望值的产生。
3. 希格斯机制与自发对称破缺希格斯机制是标准模型中实现U(1)规范自发对称破缺的机制。
希格斯场是一个复标量场,通过希格斯势的形式确定了希格斯场在真空中的期望值。
希格斯场的真空期望值的非零值导致了U(1)规范对称的破缺,同时赋予了电子、夸克等基本粒子质量。
4. U(1)规范自发对称破缺的实验观测U(1)规范自发对称破缺的实验证据来自于希格斯粒子的发现。
2012年,CERN的ATLAS和CMS实验室通过对大型强子对撞机产生的高能粒子进行观测,成功发现了希格斯粒子。
这一发现证实了标准模型中U(1)规范对称的自发破缺,进一步巩固了标准模型的有效性。
5. 应用和意义U(1)规范自发对称破缺是理解基本粒子质量来源的重要机制。
通过希格斯场的真空期望值,能够给基本粒子赋予质量,进而解释了它们在物理过程中的相互作用。
这一机制的理解对于现代粒子物理学的发展至关重要。
6. 总结U(1)规范自发对称破缺是标准模型中描述基本粒子相互作用的重要部分。
通过希格斯机制,U(1)规范对称被破坏,希格斯场的真空期望值赋予了基本粒子质量。
实验证据和应用表明,U(1)规范自发对称破缺的理解对于解释基本粒子之间的相互作用至关重要,对于推动粒子物理学的发展具有重要意义。
本文简要介绍了标准模型U(1)规范自发对称破缺的概念,并阐述了希格斯机制在其中的作用。
量子力学中的対称性破缺

量子力学中的対称性破缺量子力学中的对称性破缺量子力学作为现代物理学的重要分支,研究微观粒子的行为规律和性质,是理解自然界的基础。
在量子力学中,对称性破缺是一个关键的概念,它揭示了微观世界中的一些非常奇特的现象和规律。
本文将介绍量子力学中的对称性破缺现象,并探讨其在物理学研究中的重要意义。
1. 对称性与物理定律对称性是自然界中普遍存在的一种特性,它指的是在某种变换下,物理系统保持不变。
例如,空间平移对称性表明物体在空间位置的变化下具有不变性;时间平移对称性表明物体在时间的演化过程中具有不变性。
在经典物理学中,对称性常常与守恒定律相联系,如能量守恒、动量守恒和角动量守恒等。
2. 连续对称性与自发对称性破缺在量子力学中,对称性的破缺可以分为连续对称性和自发对称性破缺两种情况。
连续对称性是指系统在某种变换下具有对称性,但这种对称性在某个特定的条件下被破坏。
例如,考虑一个具有旋转对称性的系统,当外界施加一个不同于系统自身对称轴的力时,系统的旋转对称性即被破坏。
自发对称性破缺是指系统的基态并不具有与系统哈密顿量对称的性质。
一个典型的例子是铁磁体的顺磁-铁磁相变。
在高温下,铁磁体的自旋是呈无序排列的,系统的基态具有旋转对称性;而在低温下,铁磁体的自旋呈有序排列,系统的基态不再具有旋转对称性。
3. 对称性破缺与粒子质量对称性破缺与粒子质量之间存在着密切的关系。
根据标准模型理论,粒子的质量是通过与希格斯场的耦合来实现的。
希格斯场的自发对称性破缺导致了粒子质量的存在,并解释了为什么不同粒子具有不同的质量。
这一发现被认为是物理学史上的一次重大突破,为解释微观世界的质量问题提供了重要线索。
4. 对称性破缺在粒子物理学中的应用对称性破缺不仅在理论物理学中具有重要意义,也在实验物理学中得到了广泛应用。
其中一个典型的例子是超导现象的解释。
超导材料在低温下表现出电阻为零的特性,这种现象是由于超导材料的自发对称性破缺造成的。
此外,对称性破缺还在凝聚态物理学、粒子物理学和宇宙学等领域有着广泛的应用。
对称性破缺

对称性破缺对称性破缺是一个跨物理学、生物学、社会学与系统论等学科的概念,狭义简单理解为对称元素的丧失;也可理解为原来具有较高对称性的系统,出现不对称因素,其对称程度自发降低的现象。
对称破缺是事物差异性的方式,任何的对称都一定存在对称破缺。
对称性是普遍存在于各个尺度下的系统中,有对称性的存在,就必然存在对称性的破缺。
对称性破缺也是量子场论的重要概念,指理论的对称性为真空所破坏,对探索宇宙的本原有重要意义。
它包含“自发对称性破缺”和“动力学对称性破缺”两种情形。
中文名对称性破缺外文名Symmetry Breaking目录1. 1简介2. 2系统3. 3物理4. ▪超对称5. ▪弱作用规范6. ▪ 11维空间1. 4生物2. ▪手性破缺3. ▪ Salam 假说4. ▪局限性5. 5耗散分岔6. 6反馈机制1. 7举例2. ▪宇称不守恒3. ▪贝纳德对流4. ▪意大利怪钟5. ▪重子与反重子6. ▪生物界应用1. ▪真空不空2. ▪对称性破缺也叫CP破缺3. 8社会简介李政道认为对称性原理均根植于“不可观测量”的理论假设上;不可观测就意味着对称性,任何不对称性的发现必定意味着存在某种可观测量。
李政道说:“这些‘不可观测量’中,有一些只是由于我们目前测量能力的限制。
当我们的实验技术得到改进时,我们的观测范围自然要扩大。
因而,完全有可能到某种时候,我们能够探测到某个假设的‘不可观测量’,而这正是对称破坏的根源。
这和“对称性破缺则是由‘宏观’走向‘微观’而展现事物差异性的方式”哲学观点是一致的。
假如没有对称性破缺,这个世界将会失去活力,也将是单调、黯淡的,也不会有生物。
自然界同样也存在着诸多对性破缺的例子。
比如:弱作用力下的宇称不守恒、粒子与反粒子的不对称、手性分子的对称性破缺等等。
系统耗散理论在解释生命分子手性起源中取得了较大成功,这也是本书所拥护的观点;近些年也得到更多的实验支持。
普利高津(Prigogine)认为,在远离平衡的条件下,一个开放的物理化学体系可以通过分支现象,从原先空间均匀的各向同性状态发展到集中都是稳定的但时空特性可能不同的有序状态,即由无序中产生有序。
强子物理中的对称性破缺机制

强子物理中的对称性破缺机制在物理学的研究中,对称性一直是一种非常重要的概念。
对称性意味着系统在某种变换下保持不变,而对称性破缺则是指系统在某些条件下不再具有对称性。
而在强子物理中,对称性破缺机制是解释强子之间相互作用的重要理论。
强子物理研究的对象是由夸克组成的粒子,其中最为著名的是质子和中子。
而这些夸克粒子之间的相互作用是由强相互作用力驱动的。
根据强相互作用力的理论,即量子色动力学(QCD),夸克之间的相互作用是由一种被称为胶子的粒子传递的。
而在量子色动力学中,存在着一种被称为色荷的量子数来描述夸克和胶子之间的相互作用。
在强相互作用力的理论中,存在着一个重要的对称性,即SU(3)对称性。
这个对称性是指夸克和胶子的相互作用法则在变换下保持不变。
在理论中,SU(3)对称性是通过引入八个生成元来描述的,分别对应于八种不同的胶子。
这些生成元的线性组合可以构成SU(3)群,而夸克和胶子的相互作用可以由这个群对称性的变换规则来描述。
然而,现实中我们并不能观察到强子之间完全对称的状态。
实验观测表明,强子之间存在着一种称为手征对称性的破缺。
手性是夸克自旋与运动方向之间的关系,手征对称性破缺意味着系统在不同的方向上具有不同的性质。
这种对称性破缺是如何发生的呢?对称性破缺的机制可以通过引入一种叫做“自发对称性破缺”的机制来解释。
这个机制认为,在系统的基态中,系统的真实状态并不是具有完全对称的状态,而是具有一种破缺了对称性的状态。
这种破缺可以通过引入一种叫做“规范场”的粒子来实现。
规范场是描述系统中对称性变换的场,它的存在使得系统的基态具有了对称性的破缺。
在强子物理中,胶子场就是典型的规范场。
胶子场的存在导致了强子之间的对称性破缺。
具体来说,胶子场在系统的基态中形成了一种被称为色荷凝聚态的状态。
色荷凝聚态是指胶子场在夸克之间形成了一种非零的期望值,使得系统的基态具有了对称性的破缺。
对称性破缺的机制不仅可以解释强子物理中的现象,还可以应用于其他物理学领域。
对称性破缺

对称性破缺是一个跨物理学、生物学、社会学与系统论等学科的概念,狭义简单理解为对称元素的丧失;也可理解为原来具有较高对称性的系统,出现不对称因素,其对称程度自发降低的现象。
对称破缺是事物差异性的方式,任何的对称都一定存在对称破缺。
对称性是普遍存在于各个尺度下的系统中,有对称性的存在,就必然存在对称性的破缺。
对称性破缺也是量子场论的重要概念,指理论的对称性为真空所破坏,对探索宇宙的本原有重要意义。
它包含“自发对称性破缺”和“动力学对称性破缺”两种情形。
简介李政道认为对称性原理均根植于“不可观测量”的理论假设上;不可观测就意味着对称性,任何不对称性的发现必定意味着存在某种可观测量。
李政道说:“这些‘不可观测量’中,有一些只是由于我们目前测量能力的限制。
当我们的实验技术得到改进时,我们的观测范围自然要扩大。
因而,完全有可能到某种时候,我们能够探测到某个假设的‘不可观测量’,而这正是对称破坏的根源。
这和“对称性破缺则是由‘宏观’走向‘微观’而展现事物差异性的方式”哲学观点是一致的。
假如没有对称性破缺,这个世界将会失去活力,也将是单调、黯淡的,也不会有生物。
自然界同样也存在着诸多对性破缺的例子。
比如:弱作用力下的宇称不守恒、粒子与反粒子的不对称、手性分子的对称性破缺等等。
物理学中几何对称与抽象对称对称性破缺可以理解为原来具有较高对称性的系统,出现不对称因素,其对称程度自发降低的现象。
或者用物理语言叙述为:控制参量λ跨越某临界值时,系统原有对称性较高的状态失稳,新出现若干个等价的、对称性较低的稳定状态,系统将向其中之一过渡。
和前面群论提到几何对称操作中旋转、反映、反演相似,在物理学中则是电荷对称、时间反演、空间反映,的对称操作就是C、T、P。
CTP也存在对称与破缺。
按照诺特定理,守恒量意味着对称性;在物理学上不仅仅有几何的对称还有抽象的对称。
比如:电荷守恒定律涉及抽象的性质而非动力学的性质,它对应着抽象的对称性;还有保守力在保守场中的做功,这些就是规范对称。
论自发对称破缺

论自发对称破缺在物理学中,自发对称破缺是一种非常重要的现象。
它描述了一种物质系统从一个对称状态发生变化,变成另一个非对称状态的过程。
这种现象首先在基本粒子物理学中被描述出来,然后又被广泛应用于凝聚态物理学、化学、生物学等领域。
本文将对自发对称破缺现象进行探讨和分析。
一、自发对称破缺的基本原理自发对称破缺是指在一个系统中出现了由于局域过程引起的全局非对称性,而这个非对称性并没有在系统的宏观物理规律中体现出来。
例如,一个完全对称的圆形塑料薄膜,在贴附在一个光滑表面上后弯曲成一个圆锥形,这时圆锥的轴线就代表了一个显著的方向,这个方向是原本对称的圆形塑料薄膜所不具备的。
同样的,破坏水平对称的平衡位置,一个弹簧会有向下的趋势。
从整个系统的角度来看,弹簧有向下方向的倾向,这个方向就是系统的非对称性。
但是,在弹簧弹性势能和外加力之间的平衡关系中,并没有出现这个非对称性。
二、自发对称破缺现象的应用自发对称破缺现象的应用非常广泛,尤其是在凝聚态物理学方面。
磁性、超导、自旋玻璃转变等现象都是由于自发对称破缺造成的。
例如,C60分子在低温下可以表现出超导的性能,这个超导现象就是由于自发对称破缺造成的。
同样的,在铁磁性材料中,铁磁自旋规整的极化方向也是由于自发对称破缺的结果。
生物学研究中自然界的一些对称破缺现象,如对称的草丛中,有些面向更多阳光的方向,这也和自发对称破缺原理有关。
三、自发对称破缺的意义自发对称破缺的意义在于它提供了很多重要的物理学解释。
例如,在超导这个领域,我们只需要关心电路中电流的宏观运动规律,而不必考虑每一个电子的细节。
同样的,对于一个磁体,我们只需关注宏观磁场的产生规律,并且不必对每一个电子的磁性定向进行复杂的计算。
这种宏观物理学模型建立的前提就是对称性的破缺。
当对称性被破坏时,我们就能更快、更有效地预测出现的现象。
四、自发对称破缺和普适性自发对称破缺现象具有普适性,它是不依赖于物质的种类的。
有些物理现象只在某些物质体系中出现,而自发对称破缺并不在乎物质的种类。
探寻自然界的对称性与对称破缺机制(精品)

探寻自然界的对称性与对称破缺机制日常生活中处处可见对称和对称破缺的例子。
自然界本身就充满了各种对称性,如许多动物的左右对称性、太阳的转动对称性、海星的五重对称性和雪花的六重对称性等。
然而,不同种类的粒子、不同种类的相互作用,乃至人类生存的时空和物质世界以及整个复杂纷纭的自然界(包括人类自身),却都是对称性破缺的产物,如生命起源过程中DNA的左右镜像对称破缺等。
杨振宁曾以“20世纪物理学的主旋律:量子化、对称性和相因子”为题做专题报告。
李政道也曾多次强调指出:“21世纪物理学的挑战是:夸克禁闭,对称和对称破缺。
”周光召也曾多次谈到:“对称性和对称破缺是世界统一性和多样性的根源。
”事实上.对称性和对称破缺在自然科学研究中起着非常重要的作用,对称性破缺已成为具有普适性的重大科学问题。
对称性、守恒律和对称破缺物理学中的对称性是指一个系统的一组不变性。
数学上利用群论来研究对称性。
自然界的许多对称性本身就是物理的,如分子的转动与反射、晶格的平移等。
对称性可以是分离的(即具有有限的数目,如八面体分子的转动),也可以是连续的(即具有无限的数目,如原子或核子的转动),还可以是更一般的和抽象的,如CPT不变性(即粒子一反粒子变换、左右镜像变换和时间反演对称性),以及与规范理论相关的对称性。
对空间性质进行变换所对应的对称性称为空间对称性.对时间性质进行变换所对应的对称性称为时间对称性。
与时间和空间相独立的变换所体现的对称性称为内部对称性。
内部对称性又分为整体对称性和局域对称性。
揭示宇宙世界所具有的各种类型的对称性是物吴岳良:研究员,副所长,中国科学院理论物理研究所,北京100080。
WuYueliang:Professor,ViceDirector,Institute0f.11leoreticalPhys—ics,CAS,Beqing100080.◆吴岳良理学的重要任务之一。
在粒子物理学中,对称性决定了相互作用。
爱因斯坦的狭义相对论就是由庞加莱(P0incar6)群结构所决定的描述时间与空间对称性的理论。
对称破缺和相变的关系
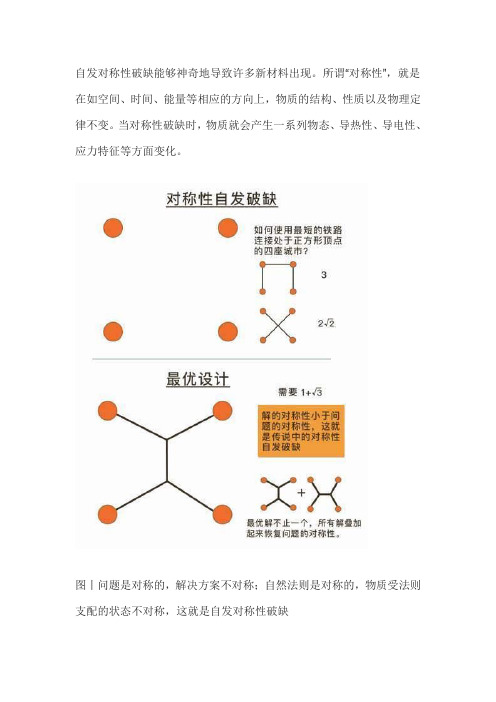
自发对称性破缺能够神奇地导致许多新材料出现。
所谓“对称性”,就是在如空间、时间、能量等相应的方向上,物质的结构、性质以及物理定律不变。
当对称性破缺时,物质就会产生一系列物态、导热性、导电性、应力特征等方面变化。
图丨问题是对称的,解决方案不对称;自然法则是对称的,物质受法则支配的状态不对称,这就是自发对称性破缺如果把这个话题应用在我们在日常生活中,其最直接的表现就是物态变化。
如冰晶体中的水分子从左到右、从上到下的排列呈现一个高度有序的状态,也就是在空间上具有平移对称性。
举例而言,冰融化成水的过程实为一个平移对称性破缺的过程,破缺后的液态水高度无序,并达成了所谓的相变。
毫无疑问,在数学上,高度有序的晶体浅显易懂的——它们在标准大气压下有着确定的熔点和沸点,且物理学家早已提出了一系列理论以概括其物理性质。
但对于包括玻璃、冷冻食物、塑料等非晶体的相变过程,目前还没有得出普遍接受的理论。
不得不承认,在长达30 年的时间里,物理学家们一直对于非晶体是否有相变过程的问题争论不休,该相变过程仅存在于理论模型中,还无法在现实非晶体物质中得到验证。
然而,在粒子物理学的帮助下,杜克大学研究员Sho Yaida 不久前终于通过几十页的长篇手算解决了这个持续了30 年的争论。
对此,Sho Yaida 的导师、杜克大学化学系教授Patrick Charbonneau 表示,他们找到了这种相变存在的线索,但换做以前没人敢这么说,因为学术界认为这种相变是不可能存在的。
无论如何,他们的研究结果已经证明了,这种相变完全有可能存在。
对于这位化学系教授而言,这项研究最奇异的地方在于:把玻璃和其他无序系统的数学模型放在假想的高维宇宙中其实更容易解。
在维度无限的情况下,他们的性质能被展开得更加简单易懂,就像我们在三维图像上解决晶体的相位问题一样。
然而,这一相变也在三维中存在吗?在上世纪八十年代就有一个研究团队通过数学计算否定了这一可能。
所以,在过去三十年中,学界的普遍观点仍然是,存在于高维的计算结果在三维世界中无效。
物理中的对称性破缺现象

物理中的对称性破缺现象引言对称性在自然界中起着举足轻重的作用,无论是宏观世界中的几何和时间对称性,还是微观世界中的基本粒子对称性,都对物理现象的产生和演化起到重要的决定性作用。
然而,物理学界发现了一种被称为对称性破缺的现象,从而揭示了自然界中隐藏的规律。
对称性破缺的概念对称性破缺是指系统的基本方程或基本规则在某种条件下失去对称性的现象。
物理学家通过研究对称性破缺现象,成功解释了许多重要的物理现象,拓展了物理学的边界。
自发对称性破缺最常见的对称性破缺现象是自发对称性破缺。
自发对称性破缺是指系统的基本方程或基本规则具有某种对称性,但所观察到的现象却没有这种对称性,即在宏观层面上表现为对称性破缺。
一个著名的例子是自旋系统的顺磁性与反磁性转变。
在高温下,磁体的微观自旋方向是无规则的,整个磁体表现出无磁性;但在低温下,磁体的自旋方向趋向于一致,整个磁体表现出有磁性。
这是自发对称性破缺的典型例子。
Higgs机制Higgs机制是对称性破缺的重要机制之一。
在标准模型中,物质粒子的质量是由Higgs场通过与粒子相互作用产生的,而Higgs场自身的存在和性质又与自发对称性破缺有关。
Higgs机制的提出成功解决了电弱相互作用的问题,并预言了存在一种被称为Higgs玻色子的新粒子。
2012年,Higgs玻色子在CERN的大型强子对撞机实验中被发现,验证了Higgs机制的存在。
强相互作用的对称性破缺除了电弱相互作用外,强相互作用也涉及到对称性破缺。
量子色动力学(QCD)是描述强相互作用的理论,其中的夸克和胶子之间通过交换胶子相互作用。
然而,在低能量下,QCD表现出自发对称性破缺,即夸克和胶子不再以自由态存在,而是在胶子构成的束缚态中。
这种对称性破缺导致了夸克的局域束缚和色荷禁闭效应。
这一现象对于我们理解夸克胶子等离子体和强子的行为非常重要。
拓展和应用对称性破缺的研究不仅仅局限于理论物理领域,还涉及到许多其他领域。
例如,在凝聚态物理中,对称性破缺被广泛应用于描述相变和物质性质的变化。
对称性自发破缺

对称性自发破缺物理体系从高温到低温的过程中,或者从高能级到基态的过程中,从一个对称的体系变得不对称的过程,称为对称性自发破缺最简单的对称性自发破缺将一根火柴棍直立在桌上,这时火柴棍与重力,桌面构成的体系具有以火柴棍为轴的旋转对称性。
火柴棍如果圆头朝下,那肯定是立不稳的,总会倒下,指向某个特定的方向,破坏先前的旋转对称性。
这一过程中,对称性从有到无,自发地消失,因此叫做对称性自发破缺。
顺磁铁磁相变中的对称性自发破缺大家常见的永磁铁通常都是铁磁体。
铁磁体随着温度的升高,磁性会逐渐下降。
直到超过某个特定的温度后,磁性会完全消失。
在这个温度以上,只要没有外界磁场,磁体不能自己产生磁场,这时铁磁体已经变成顺磁体。
这个转变温度称为居里温度。
将居里温度以上的材料逐渐降温,材料会由不能自己保留磁场的顺磁体变回能够自己产生磁场的铁磁体。
只要温度降得足够缓慢,恢复后的铁磁体往往会带有磁场。
考虑材料在居里温度以上到居里温度下这个转变。
在居里温度以上,磁体是往往是各向同性的(某些特殊材料除外)。
物理体系具有很大的对称性。
从宏观上看,这时材料没有磁性,因此也不存在特定的方向。
当温度降低时,磁体恢复磁性。
如果没有外界磁场诱导,恢复的磁场方向将是随机的,这跟之前处在一个没有特殊方向的状态相关。
材料恢复磁场,说明它内部选择了某一个特定的方向作为体系的特定方向。
对称性不再保持。
这一相变,由具有对称性的状态,自动变到了不具有对称性的状态,就是对称性自发破缺粒子物理中的对称性自发破缺我们所处的世界粒子物理学家认为,我们所处的世界相对于理论物理中的某些能标,是一个能量很低的状态。
因此,只要构成我们世界的基本规律允许,我们完全有可能处在一个对称性自发破缺了的世界。
理论物理学家用对称性自发破缺解释弱相互作用和电磁相互作用的分离,其中最重要的机制是希格斯机制。
涉及到的一系列理论被称为粒子物理的标准模型。
在该理论下,电磁相互作用和弱相互作用原本是同一个相互作用,称为电弱相互作用。
标准模型U(1) 规范自发对称破缺机制

标准模型U(1) 规范自发对称破缺机制在理论物理学中,标准模型是描述基本粒子和它们之间相互作用的理论框架。
标准模型的一个关键特征是U(1)规范对称破缺机制,它解释了为什么某些基本粒子具有质量,而其他粒子则没有。
本文将介绍U(1)规范自发对称破缺机制的基本原理和应用。
一、U(1)规范对称破缺机制的基本原理在标准模型中,电磁相互作用是由U(1)规范对称性描述的。
U(1)表示一个无穷小的变换矩阵,它描述了电磁相互作用下的粒子状态的变化规律。
然而,根据电磁相互作用的观测结果,我们知道电子具有质量,但光子却是无质量的。
这表明U(1)规范对称性在自然界中自发破缺。
U(1)规范自发对称破缺机制的基本思想是通过引入一个带电标量场,也称为Higgs场,来实现对称性破缺。
Higgs场与电磁场和W、Z玻色子相互作用,使得光子和W、Z玻色子获得质量。
在对称破缺之前,Higgs场和电磁场是通过U(1)规范对称性联系在一起的,而在对称破缺之后,Higgs场获得了真空期望值,导致U(1)规范对称性破缺。
二、U(1)规范对称破缺机制的应用U(1)规范自发对称破缺机制在标准模型中的应用非常广泛。
它解释了为什么光子是无质量的,而W、Z玻色子却具有质量。
这一机制还预言了一个新的粒子,即Higgs玻色子,在2012年Large HadronCollider的实验证实。
Higgs玻色子的发现进一步验证了U(1)规范自发对称破缺机制的有效性,并为标准模型的完善提供了重要线索。
除了在标准模型中的应用,U(1)规范对称破缺机制还在其他物理理论中发挥重要作用。
例如,在超对称理论中,U(1)规范自发对称破缺机制被用来解释超对称粒子的质量来源。
这些超对称粒子被认为是标准模型粒子的超对称伴侣,其存在能够解释一些现有问题,并为物理学的进一步发展提供了新的方向。
三、总结标准模型U(1)规范自发对称破缺机制是理论物理学中重要的概念之一,它解释了为什么某些基本粒子具有质量,而其他粒子则没有。
弦理论T对称性自发破缺

弦理论T对称性自发破缺弦理论是现代超弦理论的一个组成部分,它被广泛认为是统一所有基本粒子和相互作用的理论。
在弦理论中,T对称性是一个重要的性质,它指的是理论在时间反演下保持不变。
然而,研究表明,在某些情况下,弦理论的T对称性会自发地破缺,这给我们对宇宙的理解带来了新的挑战。
首先,让我们来了解一下T对称性的概念。
T对称性是指物理系统在时间反演下具有不变性,即如果我们将时间反过来,物理系统的行为保持不变。
这意味着物理过程在正向和反向的时间流动下是等价的。
在弦理论中,T对称性是非常重要的,因为它是保证弦理论的相容性和一致性的基本原则之一。
然而,根据最新研究成果,我们发现在某些情况下,弦理论中的T对称性会自发地破缺。
这意味着在特定的条件下,弦理论中的物理过程在时间反演下并不保持不变。
这种自发破缺可能与我们观察到的自然界现象有关,例如宇宙的起源和演化。
弦理论中T对称性自发破缺的一个重要机制是通过弦的背景场实现的。
背景场指的是弦理论中描述时空背景的一组场。
当这些背景场的取值满足特定条件时,T对称性会自发地破缺。
这种自发破缺可能会导致我们观察到的宇宙中一些重要的性质,例如时间箭头的存在和宇宙的不对称性。
在研究弦理论中的T对称性自发破缺时,我们还需要考虑到量子效应的影响。
量子效应是指在微观尺度下粒子的行为受到量子力学规律的影响。
在弦理论中,量子效应可能会导致T对称性自发破缺的出现。
因此,我们需要将量子力学和弦理论相结合,来进一步研究T对称性自发破缺的机制和性质。
弦理论T对称性自发破缺的研究还有很多待解决的问题。
例如,我们需要确定T对称性自发破缺的条件以及如何在实验中进行验证。
同时,我们还需要进一步研究T对称性自发破缺对宇宙演化的影响,以及它与其他基本力和粒子的关系。
这些问题的研究将有助于我们更深入地理解弦理论和宇宙的基本性质。
总之,弦理论是一种具有T对称性的理论,但在特定条件下,它的T对称性会自发地破缺。
这对于我们理解宇宙的起源、演化和基本粒子的行为具有重要的意义。
对称破缺 序参量 -回复

对称破缺序参量-回复什么是对称破缺?对称破缺(spontaneous symmetry breaking)是物理学中的一个重要概念,涉及到基本粒子的自发对称性破缺以及相对应的序参量。
在许多自然现象中,这种对称破缺可以解释为一种原因,例如超导体中的超导相变或者新兴材料中的自旋流体阶段。
在接下来的文章中,我将对对称破缺和序参量进行更详细的阐述,并探讨它们在物理学中的应用。
首先,让我们来了解什么是对称破缺。
在自然界中,许多系统表现出某种对称性,例如空间对称性、时间对称性等。
然而,在一些情况下,这种对称性并不完全成立,系统可能会选择某个特定的状态破坏对称性。
这种自发的破坏被称为对称破缺。
对称破缺的概念最早由物理学家费曼(Richard Feynman)在20世纪60年代提出,并得到了后来的实验证实。
接下来,我们来了解一下什么是序参量。
序参量是对称破缺的一个量化表征,用于描述系统在对称破缺后所选择的状态。
在对称破缺之前,系统具有高度对称性,而在对称破缺之后,系统会选择一个特定的状态作为系统的基态。
这个特定的状态或者说序参量将成为描述系统的重要参数,它具有一定的关联性,并可以用来解释一些宏观现象。
举个例子来说明对称破缺和序参量的概念。
假设有一个铁磁体,它在高温下具有旋转对称性,也就是说,磁场可以沿任意方向取向。
然而,在低温下,这个对称性会被打破,系统会选择一个特定的磁化方向,例如指向上方。
这个选择的方向就是序参量,它是描述系统状态的重要参数。
对称破缺和序参量在物理学中具有广泛的应用。
例如,在粒子物理学中,序参量被用来解释了为什么基本粒子会具有质量。
在标准模型中,通过固定希格斯场的期望值为非零值,电弱对称性自发破缺,从而使得光子和弱质子获得了质量。
这个期望值即是序参量,它对应着自发对称性破缺后的基态。
此外,对称破缺和序参量还有很多其他的应用。
在凝聚态物理学中,许多现象可以通过对称破缺和序参量来解释,例如超导、铁磁性、铁电性等。
从量子场论角度研究自发对称性破缺现象

从量子场论角度研究自发对称性破缺现象自发对称性破缺是物理学中一个重要的现象,它涉及到了量子场论的基本原理和自然界的基本规律。
在量子场论中,对称性是一个核心概念,它描述了系统在各种变换下的不变性。
然而,自然界中存在着许多自发对称性破缺的现象,这些现象揭示了我们对自然界的认识还有很多不完善之处。
首先,让我们来了解一下量子场论的基本原理。
量子场论是描述自然界微观粒子行为的理论,它将粒子看作是场的激发态。
在量子场论中,对称性是一个非常重要的概念。
对称性可以分为连续对称性和离散对称性两种。
连续对称性是指系统在无穷小变换下的不变性,而离散对称性则是指系统在有限变换下的不变性。
自发对称性破缺是指系统在整体对称性的情况下,出现了局部对称性破缺的现象。
简单来说,就是系统在整体对称性下的基态并不是完全对称的。
这一现象最早由安德森在1958年提出,他通过研究超导现象发现了自发对称性破缺的存在。
自发对称性破缺不仅在超导领域有重要应用,还广泛存在于其他物理系统中,如相变、强子物理等。
量子场论提供了一种理论框架来研究自发对称性破缺现象。
在量子场论中,自发对称性破缺可以通过引入一个称为“场的真空期望值”的概念来描述。
在整体对称性下,场的真空期望值为零,即系统处于对称的基态。
而在自发对称性破缺的情况下,场的真空期望值不再为零,系统处于非对称的基态。
自发对称性破缺的机制可以通过量子场论中的相互作用项来解释。
相互作用项可以看作是描述场与场之间相互作用的项,它会引起场的真空期望值的变化。
当相互作用项满足一定条件时,场的真空期望值会发生非零的变化,从而导致自发对称性破缺的现象出现。
自发对称性破缺的一个重要例子是电弱对称性破缺。
在标准模型中,电弱对称性是描述电磁力和弱力统一的理论。
然而,实验观测到的粒子质量并不完全符合电弱对称性的预言,这就需要引入自发对称性破缺来解释。
通过引入希格斯场并研究其真空期望值的变化,可以解释电弱对称性破缺的现象。
对称破缺

对称破缺的系统学诠释武杰、李润珍引言19世纪的最后一天,欧洲著名的科学家欢聚一堂,会上德高望重的开尔文勋爵致新年贺辞。
他在回顾物理学的发展时说:“物理大厦已经落成,所剩只是一些修饰工作。
”而在展望20世纪物理学前景时,他若有所思地讲道:“动力理论肯定了热和光是运动的两种方式,现在它的美丽而晴朗的天空却被两朵乌云笼罩了,第一朵乌云出现在光的波动理论上,第二朵乌云出现在关于能量均分的麦克斯韦-玻尔兹曼理论上。
”[1]出乎意料的是,这两朵乌云不久就酿成了两场风暴,掀起了20世纪物理学上的两次革命。
同样,在20世纪和21世纪之交,李政道教授在《展望21世纪科学发展前景》时也提出了两个疑问:“第一,目前我们的物理理论都是对称的,而实验表明有些对称性在弱作用过程中被破坏了;另外一个疑问是一半的基本粒子是永远独立不出来的。
”[2]他还认为,20世纪的文明是微观的,21世纪微观和宏观应该结合成一体。
这也就是说,20世纪自然科学的迅猛发展,一方面使对称性思想愈发彰显自身的光彩和魅力,由此展现了理论创新的威力,解释了原子构造、分子构造、核能、激光、半导体、超导体、X光、超级计算机等等;另一方面,大量的经验事实和理论探索一再展示对称破缺的重大意义。
事实上,每一次对称破缺都有新质的突现,都在创造一个更加丰富多彩的现象世界。
因此,我们将它概括为自然界演化发展的一条基本原理。
[3]在这样的背景下,我们应该从系统科学的视角出发,立足于关系,就有可能看到整体中的区分,以达到对现存事物的理解、说明和解释。
当代著名物理学家盖尔曼也曾指出:“今天……我们必须对整个系统进行研究,即使这种研究很粗糙也是必要的,因为对复杂的非线性系统的各个部分不作紧密联系的研究,我们对整体行为就不会有正确的思想。
”[4]有鉴于此,我们试图对对称破缺这一自然界演化发展的基本原理进行一次系统学的解读。
一非线性是对称破缺的动力源泉20世纪40年代以来,科学上的转向是难以与文化和社会变迁截然分开的,它一再向人们表明这样一个事实:每一种重要科学分支的前缘正在大大地扩展着。
物理学中的序参量

物理学中的序参量序参量是物理学中的一个重要概念,它在许多领域都有着广泛的应用,涉及到超导、磁性、液晶、量子霍尔效应等许多现象。
具体来说,序参量是指描述系统自发对称性破缺的物理量,例如磁化强度、相角、自旋等。
它不仅在物理学中起着重要的作用,也在材料科学、纳米科技等领域中有非常广泛的应用。
序参量的概念最初是由著名物理学家里奥·兰道提出的。
他指出,距离绝对零度,物质的基态是具有最高对称性的状态。
如果温度升高,原子或分子的运动就会造成对称性的破缺,形成一些新的有序结构,这些结构被称为序。
此时,系统可以用序参量来描述自身的对称性破缺情况。
在物理学中,序参量通常是一个复数,它表示量子态的复杂相互作用,也可以用来描述关联态之间的转化。
例如,在超导领域中,序参量可以用来描述超导态的形成,这是一种完全由电子间相互作用导致的现象。
在这种状态下,电子组成了一种特殊的集体行为,它们的运动可以被看做是一种相干的整体运动,而序参量则描述了这种相干运动的特征。
类似地,在磁性、液晶等领域中,序参量也可以用来描述物质中自旋或分子的有序排列。
序参量的研究对于物理学和材料科学的发展具有极其重要的意义。
它不仅可以帮助我们深入理解许多自旋相互作用、电子动力学、磁性、液晶等现象的本质,还有助于我们设计新的材料和开发新的技术。
例如,通过控制序参量的变化,我们可以制备出一些具有特殊电子性质的材料,从而产生一些新的物理现象。
同时,序参量的研究也有助于我们在纳米尺度上控制物质的自组装过程,从而为纳米科技的发展带来新的机遇。
总之,序参量是物理学中一个非常重要且广泛应用的概念。
它可以用来描述自身对称性的破缺,探究量子态的复杂相互作用和关联态之间的转化。
序参量的研究有助于我们深入理解许多重要的物理现象,促进材料科学和纳米科技等领域的发展。
未来,序参量的研究将会有更加广泛的应用,并将继续推动我们对自然界的认识和探索。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自发对称性破缺[编辑]维基百科,自由的百科全书跳转至:导航、搜索墨西哥帽势能函数的电脑绘图,对于绕着帽子中心轴的旋转,帽顶具有旋转对称性,帽子谷底的任意位置不具有旋转对称性,在帽子谷底的任意位置会出现对称性破缺。
自发对称性破缺(spontaneous symmetry breaking)是某些物理系统实现对称性破缺的模式。
当物理系统所遵守的自然定律具有某种对称性,而物理系统本身并不具有这种对称性,则称此现象为自发对称性破缺。
[1]:141[2]:125这是一种自发性过程(spontaneous process),由于这过程,本来具有这种对称性的物理系统,最终变得不再具有这种对称性,或不再表现出这种对称性,因此这种对称性被隐藏。
因为自发对称性破缺,有些物理系统的运动方程或拉格朗日量遵守这种对称性,但是最低能量解答不具有这种对称性。
从描述物理现象的拉格朗日量或运动方程,可以对于这现象做分析研究。
对称性破缺主要分为自发对称性破缺与明显对称性破缺两种。
假若在物理系统的拉格朗日量里存在着一个或多个违反某种对称性的项目,因此导致系统的物理行为不具备这种对称性,则称此为明显对称性破缺。
如右图所示,假设在墨西哥帽(sombrero)的帽顶有一个圆球。
这个圆球是处于旋转对称性状态,对于绕着帽子中心轴的旋转,圆球的位置不变。
这圆球也处于局部最大引力势的状态,极不稳定,稍加微扰,就可以促使圆球滚落至帽子谷底的任意位置,因此降低至最小引力势位置,使得旋转对称性被打破。
尽管这圆球在帽子谷底的所有可能位置因旋转对称性而相互关联,圆球实际实现的帽子谷底位置不具有旋转对称性──对于绕着帽子中心轴的旋转,圆球的位置会改变。
[3]:203大多数物质的简单相态或相变,例如晶体、磁铁、一般超导体等等,可以从自发对称性破缺的观点来了解。
像分数量子霍尔效应(fractional quantum Hall effect)一类的拓扑相(topological phase)物质是值得注意的例外。
目录[隐藏]∙ 1 概述∙ 2 凝聚态物理学∙ 3 粒子物理学o 3.1 手征对称性破缺o 3.2 希格斯机制▪ 3.2.1 外显的对称性案例▪ 3.2.2 自发对称性破缺案例∙ 4 实例∙ 5 诺贝尔奖∙ 6 数学范例:墨西哥帽势能∙7 参见∙8 注释∙9 参考文献∙10 外部链接概述[编辑]量子力学的真空与一般认知的真空不同。
在量子力学里,真空并不是全无一物的空间,虚粒子会持续地随机生成或湮灭于空间的任意位置,这会造成奥妙的量子效应。
将这些量子效应纳入考量之后,空间的最低能量态,是在所有能量态之中,能量最低的能量态,不具有额外能量来制造粒子,又称为基态或“真空态”。
最低能量态的空间才是量子力学的真空。
[4]设想某种对称群变换,只能将最低能量态变换为自己,则称最低能量态对于这种变换具有“不变性”,即最低能量态具有这种对称性。
尽管一个物理系统的拉格朗日量对于某种对称群变换具有不变性,并不意味着它的最低能量态对于这种对称群变换也具有不变性。
假若拉格朗日量与最低能量态都具有同样的不变性,则称这物理系统对于这种变换具有“外显的对称性”;假若只有拉格朗日量具有不变性,而最低能量态不具有不变性,则称这物理系统的对称性被自发打破,或者称这物理系统的对称性被隐藏,这现象称为“自发对称性破缺”。
[5]:116-117回想先前提到的墨西哥帽问题,在帽子谷底有无穷多个不同、简并的最低能量态,都具有同样的最低能量。
对于绕着帽子中心轴的旋转,会将圆球所处的最低能量态变换至另一个不同的最低能量态,除非旋转角度为360°的整数倍数,所以,圆球的最低能量态对于旋转变换不具有不变性,即不具有旋转对称性。
总结,这物理系统的拉格朗日量具有旋转对称性,但最低能量态不具有旋转对称性,因此出现自发对称性破缺现象。
[3]:203凝聚态物理学[编辑]大多数物质的相态可以通过自发对称性破缺的透镜来理解。
例如,晶体是由原子以周期性矩阵排列形成,这排列并不是对于所有平移变换都具有不变性,而只是对于一些以晶格矢量为间隔的平移变换具有不变性。
磁铁的磁北极与磁南极会指向某特定方向,打破旋转对称性。
除了这两个常见例子以外,还有很多种对称性破缺的物质相态,包括液晶的向列相(nematic phase)、超流体等等。
类似的希格斯机制应用于凝聚态物质会造成金属的超导体效应。
在金属里,电子库柏对的凝聚态自发打破了电磁相互作用的U(1)规范对称性,造成了超导体效应。
更详尽细节,请参阅条目BCS理论。
有些物质的相态不能够用自发对称性破缺来解释。
例如,分数量子霍尔液体(fractional quantum Hall liquid)、旋液体(spin liquid)这一类物质的托普有序相态。
这些相态不会打破任何对称性,是不同种类的相态,没有比较通用的理论论述来描述这些相态。
粒子物理学[编辑]在粒子物理学里,描述基本粒子的方程可能遵守某种对称性,可是方程的解并不能满足这对称性,例如,假设某种场方程可以用来估算两种夸克A、B的质量,并且对于这两种夸克具有对称性,解析这场方程或许给出了两个解,在第一个解里,夸克A比夸克B沉重,而在第二个解里,以同样的重量差,夸克B比夸克A 沉重。
对于这案例,场方程的对称性并没有被场方程的每一个单独解反映出来,而是被所有解共同一起反应出来。
由于每一次做实际测量只能得到其中一个解,这表征了所倚赖理论的对称性被打破。
对于这案例,使用术语“隐藏”可能会比术语“打破”更为恰当,因为对称性已永远嵌入在场方程里。
由于物理学者并未找到任何外在因素涉及到场方程的对称性破缺,这现象称为“自发”对称性破缺。
[6]:194-195手征对称性破缺[编辑]主条目:手征对称性破缺在粒子物理学里,手征对称性破缺指的是强相互作用的手征对称性被自发打破,是一种自发对称性破缺。
假若夸克的质量为零(这是手征性(chirality)极限),则手征对称性成立。
但是,夸克的实际质量不为零,尽管如此,跟强子的质量相比较,上夸克与下夸克的质量很小,因此可以视手征对称性为一种“近似对称性”。
在量子色动力学的真空里,夸克与反夸克彼此会强烈吸引对方,并且它们的质量很微小,生成夸克-反夸克对不需要用到很多能量,因此,会出现夸克-反夸克对的夸克-反夸克凝聚态,就如同在金属超导体里电子库柏对的凝聚态一般。
夸克-反夸克对的总动量与总角动量都等于零,总手征荷不等于零,所以,夸克-反夸克凝聚的真空期望值(vacuum expectation value)不等于零,促使物理系统原本具有的手征对称性被自发打破,这也意味着量子色动力学的真空会将夸克的两个手征态混合,促使夸克在真空里获得有效质量。
[7]:669-672根据戈德斯通定理,当连续对称性被自发打破后必会生成一种零质量玻色子,称为戈德斯通玻色子。
手征对称性也具有连续性,它的戈德斯通玻色子是π介子。
假若手征对称性是完全对称性,则π介子的质量为零;但由于手征对称性为近似对称性,π介子具有很小的质量,比一般强子的质量小一个数量级。
这理论成为后来电弱对称性破缺的希格斯机制的初型与要素。
[7]:669-672根据宇宙学论述,在大爆炸发生10-6秒之后,开始强子时期,由于宇宙的持续冷却,当温度下降到低于临界温度KT≈173MeV之时,会发生手征性相变(chiralcphase transition),原本具有的手征对称性的物理系统不再具有这性质,手征对称性被自发性打破,这时刻是手征对称性的分水岭,在这时刻之前,夸克无法形成强子束缚态,物理系统的有序参数反夸克-夸克凝聚的真空期望值等于零,物理系统遵守手征对称性;在这时刻之后,夸克能够形成强子束缚态,反夸克-夸克凝聚的真空期望值不等于零,手征对称性被自发性打破。
[8][9]希格斯机制[编辑]设定直角坐标系的x-坐标与y-坐标分别为复值希格斯场的实部与虚部,z-坐标为希格斯势,则参数为希格斯场的希格斯势,其猜想形状好似一顶墨西哥帽。
主条目:希格斯机制在标准模型里,希格斯机制是一种生成质量的机制,能够使基础粒子获得质量。
为什么费米子、W玻色子、Z玻色子具有质量,而光子、胶子的质量为零?[10]:361-368希格斯机制可以解释这问题。
希格斯机制应用自发对称性破缺来赋予粒子质量。
在所有可以赋予规范玻色子质量,而同时又遵守规范理论的可能机制中,这是最简单的机制。
[10]:378-381根据希格斯机制,希格斯场遍布于宇宙,有些基础粒子因为与希格斯场之间相互作用而获得质量。
更仔细地解释,在规范场论里,为了满足局域规范不变性,必须设定规范玻色子的质量为零。
由于希格斯场的真空期望值不等于零,[注 1]造成自发对称性破缺,因此规范玻色子会获得质量,同时生成一种零质量玻色子,称为戈德斯通玻色子,而希格斯玻色子则是伴随着希格斯场的粒子,是希格斯场的振动。
通过选择适当的规范,戈德斯通玻色子会被抵销,只存留带质量希格斯玻色子与带质量规范矢量场。
[注 2][10]:378-381费米子也是因为与希格斯场相互作用而获得质量,但它们获得质量的方式不同于W玻色子、Z玻色子的方式。
在规范场论里,为了满足局域规范不变性,必须设定费米子的质量为零。
通过汤川耦合,费米子也可以因为自发对称性破缺而获得质量。
[7]:689ff外显的对称性案例[编辑]假定遍布于宇宙的希格斯场是由两个实函数、组成的复值标量场:;其中,是四维坐标。
假定希格斯势的形式为;其中,、都是正值常数。
则这物理系统只有一个最低能量态,其希格斯场为零()对于这自旋为零、质量为零、势能为的标量场,克莱因-戈尔登拉格朗日量为[7]:16-17。
注意到这拉格朗日量的第一个项目是动能项目。
由于拉格朗日量对于全域相位变换具有不变性,而最低能量态对于全域相位变换也具有不变性:,所以,这物理系统对于全域相位变换具有外显的对称性。
自发对称性破缺案例[编辑]假定遍布于宇宙的希格斯场是由两个实函数、组成的复值标量场:;其中,是四维坐标。
假定希格斯势的形式为;其中,、都是正值常数。
对于这自旋为零、质量为零、势能为的标量场,克莱因-戈尔登拉格朗日量为[7]:16-17。
如墨西哥帽绘图所示,这势能的猜想形状好似一顶墨西哥帽。
希格斯势与拉格朗日量在、空间具有旋转对称性。
位于z-坐标轴的帽顶为希格斯势的局域最大值,其复值希格斯场为零(),但这不是最低能量态;在帽子的谷底有无穷多个简并的最低能量态。
从无穷多个简并的最低能量态中,物理系统只能实现出一个最低能量态,标记这最低能量态为。
这物理系统的拉格朗日量对于全域相位变换具有不变性,即在、空间具有旋转对称性,而最低能量态对于全域相位变换不具有不变性:,通常,不等于,除非角弧是的整数倍数。
