环球城市数学竞赛试题2002环球城市数学竞赛秋季赛高中组初级卷
2001_2002年国内外数学竞赛题选解二

(1 ,3 ,4) , (2 ,3 ,4) , (1 ,2 ,3 ,4) . 如果能讲语言 1 , 2 , 3 的会议代表少于60 %, 用 xij …表示会讲语言 i , j , …的会议代表的数目 ,则有
2. 设 A 是集合{ 1 ,2 ,3 , …,16} 的一个 k 元子集 , 且 A 的任意两个子集的元素之和互不相等. 而对于 集合{ 1 ,2 ,3 , …,16} 的包含集合 A 的任意 k + 1 元子 集 B ,则存在 B 的两个子集 ,它们的元素之和相等.
(1) 证明 : k ≤5 ; (2) 求集合 A 的元素之和的最大值和最小值. (2002 ,保加利亚冬季数学竞赛) 证明 : (1) 因为 A 有 2 k 个子集 (包括空集) , 且任 意两个子集的元素之和互不相等 , 所以 A 的元素之 和至少有 2 k - 1 个. 若 k ≥7 ,则 2 k - 1 > 16 k ,不可能. 若 k = 6 , 考虑 A 的一 、二 、三 、四元子集 , 共有 C16 + C26 + C36 + C46 = 56 个不同的和 ,且最小的和是 1 , 最大的和是 16 + 15 + 14 + 12 = 57 (其中 16 + 13 = 15 + 14 ,故这 4 个数不能同在 A 中) . 若 1 ∈A ,则最大的和是 16 + 14 + 12 + 9 = 51 (其 中 16 = 15 + 1 ,故这 3 个数不能同在 A 中 ; 14 = 13 + 1 ,故这 3 个数不能同在 A 中 ; 12 = 11 + 1 , 故这 3 个 数不能同在 A 中 ;16 + 10 = 14 + 12 , 故这 4 个数不能 同在 A 中) ,最多有 51 个不同的和 ,矛盾. 若 2 ∈A ,则最大的和是 16 + 15 + 12 + 9 = 52 , 最 多有 51 个不同的和 ,矛盾. 若 1 ¢A ,2 ¢A ,则在[3 ,57 ]中至多有 55 个和 , 矛盾. 故 k ≤5. 解 : (2) 若 A = { a1 , a2 , …, ak} 元素的和小于 16 , 则集合 { a1 , a2 , …, ak , 16} 中无元素的和相等的子
数学书籍

shkwen上传的数学电子书,坛友们若有兴趣,可以到中报论坛去看看,他的这个帖子《数学书吧》现在置顶,容易找。
大家若不愿多走一步,我可以厚着脸皮传输一下。
001——《从单位圆谈起》华罗庚002——丘成桐中学数学奖推荐参考书(英文版的都没有传,以下同)由高等教育出版社出版,目前已出版了5本:1.《莫斯科智力游戏359 道数学趣味题》(俄)Б. А. 柯尔捷姆斯基著2.《趣味密码术与密写术》M·加德纳著3.《著名几何问题及其解法尺规作图的历史》B. 波尔德(Benjamin Bold)著4.《第一届丘成桐中学数学奖获奖论文集(英文版)》5.《恒隆数学奖获奖论文集(英文版)》003——好玩的数学,目前已经出了13种:1.《不可思议的e》2.《幻方及其他》第二版3.《乐在其中的数学》4.《七巧板、九连环和华容道》5.《趣味随机问题》6.《数学聊斋》7.《数学美拾趣》8.《数学演义》9.《说不尽的π》10.《中国古算解趣》11.《数学志异》12.《进位制与数学**》13.《古算诗题探源》14.《幻方与素数》第三版注:前10本xuguoyun 于“数学丛书”帖上传;《幻方及其他》第二版已经改成《幻方与素数》第三版004——科普作家别莱利曼,三类一、中国青年出版社最近出版的1.《趣味代数学第4版》(俄)别莱利曼著丁寿田朱美琨译2.《趣味几何学第3版》(俄)别莱利曼著符其珣译(将2个压缩文件放在一起解压!)3.《趣味物理学第5版》(俄)别莱利曼著符其珣译4.《趣味物理学:续编第3版》(俄)别莱利曼著滕砥平译二、中国青年出版社5、60年代出版的(有的是繁体字)5.《趣味代数学》(俄)别莱利曼著丁寿田朱美琨译(无)6.《趣味几何学(上册)》(俄)别莱利曼著符其珣译(无)7.《趣味几何学(下册)》(俄)别莱利曼著符其珣译(无)8.《趣味力学》(苏)别莱利曼著;符其珣译9.《趣味天文学》(苏)别列利曼撰;滕砥平,唐克译10.《趣味物理学》(苏)别莱利曼撰;符其珣译(无)11.《趣味物理学续编》(苏)别莱利曼撰;腾砥平译(无)12.《行星际的旅行》(苏)别莱利曼著;符其珣译三、其他出版社出版的13.《物理万花筒》(苏)别莱利曼著;王昌茂译14.《趣味思考题》(苏)别莱利曼著;符其珣译15.《有趣的游戏》(苏)别莱利曼原著;王昌茂翻译005——《数学试卷分析方法》华东师范大学出版社,许世红,胡中锋编著006——《七彩数学》专辑,科学出版社第一批1.《数学走进化学与生物》姜伯驹钱敏平龚光鲁著2.《数论与密码》冯克勤著3.《迭代浑沌分形》李忠著4.《数学的力量——漫话数学的价值》李文林任辛喜著5.《古希腊名题与现代数学》张贤科著第二批6.《离散几何欣赏》宗传明著7.《通信纠错中的数学》冯克勤著8.《趣话概率》安鸿志著9.《画图的数学》齐东旭著10.《整数分解》颜松远著007——《中学数学教学参考书》,1956年新知识出版社编辑出版,初中部分一、算术:1.《整数》2.《分数》3.《小数与百分数》4.《比例》二、代数5.《有理数》6.《有理整式的恒等变换》7.《分式与比例》8.《一元一次方程》9.《一次方程组及开平方》三、几何10.《体面线点》11.《全等三角形》12.《基本轨迹与作图》13.《平行四边形》14.《圆》(缺)008——《中学数学教学参考书》,1956年新知识出版社编辑出版,高中部分一、代数:1.《无理数与无理式》2.《一元二次方程》3.《函数图象及二元二次联立方程》4.《数列与极限》(缺)5.《指数与对数》6.《联合二项式定理及复数》7.《不等式》8.《高次方程》二、几何9.《相似形》10.《勾股定理》11.《多边形面积》12.《正多边形与圆》13.《直线与平面》14.《多面体》(缺)15.《回转体》(缺)三、三角16.《三角函数》17.《加法定理》18.《解三角形》19.《三角方程》(缺)注:部分书籍以内容完全相同的上教版代替009——《中学数学教学参考丛书》,上海教育出版社1.《多项式的乘法和因式分解》茅成栋编2.《一元二次方程》赵宪初编3.《绝对值》陈汝作编(缺,这里该书的封面用附件传上)4.《代数方程组》李大元武成章等编5.《指数函数和对数函数》徐美琴许三保编6.《三角函数》姚晶编7.《幂的运算和幂函数》顾鸿达朱成杰王致平编8.《解不等式》张福生赵国礼编9.《实数》张镜清霍纪良编10.《直线形》陶成铨编11.《圆与正多边形》黄承宏编12.《相似形和比例线段》杨荣祥黄荣基编13.《轨迹》毛鸿翔左铨如编14.《解三角形》黄汉禹编15.《直线与平面》夏明德编16.《排列和组合》翟宗荫编17.《高次方程》李传芳陈汝作陈永明编18.《复数》顾忠德管锡培编19.《数列与极限》刘文编20.《直线和圆》陈森林揭方琢编21.《二次曲线》张泽湘编22.《参数方程和极坐标方程》刘世伟编23.《概率初步》上海师范大学数学系应用数学组编24.《矩阵初步》张弛编25.《集合论初步》沈石山俞鑫泰编010——教学工具书1.《代数学辞典问题解法上》笹部贞市郎编蒋声等译2.《代数学辞典问题解法下》笹部贞市郎编张明梁等译3.《三角学辞典问题解法》笹部贞市郎编肖乐编译4.《几何学辞典问题解法》笹部贞市郎编高清仁等译5.《解析几何辞典问题解法》笹部贞市郎编关桐书等译6.《微积分辞典问题解法》笹部贞市郎编蒋声等译011——《中学生数学课外读物》,上海教育出版社1.《速算与验算》姚人杰著2.《数学归纳法》华罗庚著3.《不等式》张驰著4.《谈谈怎样学好数学》苏步青著5.《π和е》夏道行著6.《复数的应用》莫由著7.《怎样用复数解题》程其坚著8.《圆和二次方程》马明著9.《怎样列方程解应用题》赵宪初著10.《怎样应用数学归纳法》洪波著11.《最大值和最小值》谷超豪著12.《图上作业法》管梅谷著13.《谈谈怎样编数学墙报》华东师范大学第一附属中学数学教研组编012——上海教育出版社1978年12月到2002年5月出版一套初等数学小丛书,一共29本,如下:1.《抽屉原则及其他》常庚哲2.《谈谈怎样学好数学》苏步青3.《函数方程》田增伦4.《几何不等式》单壿5.《一百个数学问题》[波兰]史坦因豪斯6.《又一百个数学问题》[波兰]史坦因豪斯7.《从单位根谈起》蒋声8.《从正五边形谈起》严镇军9.《集合论与连续统假设浅说》张锦文10.《矩阵对策初步》张盛开11.《趣味的图论问题》单壿12.《母函数》史济怀13.《代数方程与置换群》李世雄14.《中学生数学分析》[苏]庞特里亚金15.《覆盖》单壿16.《计数》黄国勋李炯生17.《对称和群》朱水林18.《平方和》冯克勤19.《不定方程》单壿余红兵20.《凸函数与琴生不等式》黄宣国21.《有趣的差分方程》李克大李尹裕22.《柯西不等式与排序不等式》南山23.《组合几何》单壿24.《奇数、偶数、完全平方数》南秀全余石25.《棋盘上的组合数学》冯跃峰26.《十个有趣的数学问题》单壿27.《染色:从**到数学》柳柏濂28.《集合及其子集》单壿29.《平面几何中的小花》单壿013——《中学生文库》数学部分:1.《怎样列方程解应用题》赵宪初2.《面积关系帮你解题》张景中3.《怎样用配方法解题》奚定华4.《根与系数的关系及其应用》毛鸿翔5.《怎样添辅助线》余振棠谢传芳6.《圆和二次方程》马明7.《几何作图不能问题》邱贤忠沈宗华8.《从勾股定理谈起》盛立人严镇军9.《从√2谈起》张景中10.《不等式》张弛11.《不等式的证明》吴承鄫李绍宗12.《奇数和偶数》常庚哲苏淳13.《射影几何趣谈》冯克勤14.《数学万花镜》[波]史坦因豪斯著裘光明译15.《递归数列》陈家声徐惠芳16.《从平面到空间》蒋声17.《平面向量和空间向量》吕学礼18.《几何变换》蒋声19.《一些不像“几何”的几何学》沈信耀20.《复合推理与真值表》戴月仙21.《数学归纳法》华罗庚22.《凸图形》吴立生庄亚栋23.《三角恒等式及应用》张运筹24.《三角不等式及应用》张运筹25.《抽屉原则及其他》常庚哲26.《初等极值问题》程龙27.《图论中的几个极值问题》管梅谷28.《趣味的图论问题》单墫29.《矩阵对策初步》张盛开30.《从单位根谈起》蒋声31.《形形色色的曲线》蒋声32.《反射和反演》严镇军33.《极坐标与三角函数》陈福泰34.《反证法》孙玉清35.《棋盘上的数学》单墫程龙36.《谈谈数学中的无限》谷超豪37.《模糊数学》刘应明任平38.《人造卫星轨道的分析和计算》俞文陈守吉39.《谈谈怎样学好数学》苏步青40.《世界数学名题选》陆乃超袁小明41.《生物数学趣谈》李金平苏淳42.《漫话电子计算机》张根法43.《运动场上的数学》黄国勋李炯生44.《SOS编码纵横谈》谈祥柏45.《数学探奇》(西班牙)米盖尔.德.古斯曼著周克希译46.《三角形趣谈》杨世明47.《思维的技巧》吴宣文48.《魔方》朱兆毅沈庆海著在/thread-23988-1-10.html/thread-29576-7-1.html这两个帖子中传有部分书籍014——《初中学生课外阅读系列》,上海教育出版社1.《漫游勾股世界》吴深德2.《绝对值》陈汝作3.《多项式的乘法和因式分解》刘渝瑛4.《怎样列方程解应用题》赵宪初5.《怎样解不等式》张福生赵国礼6.《怎样用配方法解题》奚定华7.《面积关系帮你解题》张景中8.《怎样添辅助线》余振棠射传芳9.《根与系数的关系及其应用》毛鸿翔10.《反证法》孙玉清015——《高中学生课外阅读系列》,上海教育出版社1.《从平面到空间》蒋声2.《三角恒等式及其应用》张运筹3.《直线和平面》夏明德4.《不等式的证明》吴承鄫李绍宗5.《参数方程和极坐标方程》刘世伟6.《从单位根谈起》蒋声7.《二次曲线》张泽湘8.《排列与组合》翟宗荫9.《数列与极限》刘文10.《集合和映射》康士凯张海森(缺)11.《随机世界探秘概率统计初步》茆诗松魏振军016——《自然科学小丛书》,北京出版社出版1.《轨迹》赵慈庚编著2.《三角形内角和等于180°吗?》梅向明著3.《谈勾股定理》严以诚孟广烈编著4.《有趣的偶然世界》张文忠著5.《中学数学中的对称》张文忠著017——《北京市中学生数学竞赛辅导报告汇集》,北京出版社1.《谈谈与蜂房结构有关的数学问题》华罗庚著2.《无限的数学》秦元勋著3.《谈谈解答数学问题》赵慈庚著018——数学中译本,科学普及出版社1.《高次方程解法》程乃栋编译2.《力学在数学上的一些应用》高天青编译3.《怎样作图象》刘远图编译4.《逐次逼近法》赵根榕编译5.《最简单的极值问题》潘德松编译019——趣味数学书籍,上海教育出版社1.《趣味算术》蒋声陈瑞琛编2.《趣味代数》蒋声陈瑞琛编3.《趣味几何》蒋声陈瑞琛编4.《趣味代数(续)》蒋声陈瑞琛编5.《趣味立体几何》蒋声陈瑞琛编6.《趣味解析几何》蒋声陈瑞琛编020——《数学精品库》,民主与建设出版社1.《决策致胜思维训练》郑应文著2.《难题精解思维训练》王志雄汪启泰余文竑詹方玮著3.《平面几何思维训练》余文竑詹方玮著4.《数学宫趣游》王志雄著5.《数学竞赛题的背景》王志雄汪启泰著6.《组合几何思维训练》林常著7.《诺贝尔奖中的数学方法》高鸿桢等著(缺)021——由一些数学专家写的小册子,上海教育出版社1.《初等数论100例》柯召孙琦编著2.《复数计算与几何证题》常庚哲编著3.《运动群》张远达编著022——《数学奥林匹克命题人讲座》,上海科技教育出版社1.《解析几何》陆洪文著(缺)2.《代数函数与多项式》施咸亮著(缺)3.《函数迭代与函数方程》王伟叶熊斌著(缺)4.《代数不等式》陈计季潮丞著(缺)5.《重心坐标与平面几何》曹纲叶中豪著(缺)6.《初等数论》冯志刚著7.《集合与对应》单壿著8.《数列与数学归纳法》单壿著9.《组合问题》刘培杰,张永芹著著(缺)10.《图论·组合几何》任韩田廷彦著(缺)11.《向量与立体几何》唐立华著(缺)12.《复数·三角函数》邵嘉林著(缺)023——反例相关书籍1.《初中数学中的反例》朱锡华编2.《高中数学中的反例》马克杰编3.《从反面考虑问题反例·反证·反推及其他》严镇军陈吉范编4.《代数中的反例》胡崇慧编5.《高等代数的265个反例》李玉文编著6.《高等数学中的反例》朱勇编7.《数学分析中的问题和反例》汪林编8.《数学分析中的反例》王俊青编著9.《分析中的反例》(美)盖尔鲍姆(美)奥姆斯特德著高枚译10.《实分析中的反例》汪林编11.《实变函数论中的反例》程庆汪远征编著12.《泛函分析中的反例》汪林编13.《概率统计中的反例》张文忠但冰如编14.《概率论与数理统计中的反例》陈俊雅王秀花编著15.《概率统计中的反例》张尚志刘锦萼编著16.《概率论中的反例》张朝金编17.《图论的例和反例》(美)卡波边柯(美)莫鲁卓著聂祖安译18.《拓扑空间中的反例》汪林杨富春编著19.《点集拓扑学题解与反例》陈肇姜编著024——精品书系第一批,哈尔滨工业大学出版社1.《最新世界各国数学奥林匹克中的平面几何试题》刘培杰主编2.《走向国际数学奥林匹克的平面几何试题诠释:历届全国高中数学联赛平面几何试题一题多解上》沈文选主编杨清桃步凡昊凡副主编3.《走向国际数学奥林匹克的平面几何试题诠释:历届全国高中数学联赛平面几何试题一题多解下》沈文选主编杨清桃步凡昊凡副主编4.《世界著名平面几何经典著作钩沉几何作图专题卷上》刘培杰主编5.《世界著名平面几何经典著作钩沉几何作图专题卷下》刘培杰主编(缺)6.《历届CMO中国数学奥林匹克试题集1986-2009》刘培杰主编7.《历届IMO试题集》刘培杰主编8.《全国大学生数学夏令营数学竞赛试题及解答》许以超陆柱家编著9.《历届PTN美国大学生数学竞赛试题集1938-2007》冯贝叶许康侯晋川等编译10.《历届俄罗斯大学生数学竞赛试题及解答》(即将出版)11.《数学奥林匹克与数学文化第1辑》刘培杰主编12.《数学奥林匹克与数学文化第2辑文化卷》刘培杰主编13.《数学奥林匹克与数学文化第2辑竞赛卷》刘培杰主编14.《数学奥林匹克与数学文化第3辑竞赛卷》刘培杰主编(即将出版)15.《500个最新世界著名数学智力趣题》刘培杰马国选主编16.《400个最新世界著名数学最值问题》刘培杰主编17.《500个世界著名数学征解问题》冯贝叶编译18.《400个中国最佳初等数学征解老问题》刘培杰主编(缺)19.《500个世界著名几何名题及1000个著名几何定理》(即将出版)20.《从毕达哥拉斯到怀尔斯》刘培杰主编21.《从迪利克雷到维斯卡尔迪》刘培杰主编22.《从哥德巴赫到陈景润中国解析数论群英谱》刘培杰主编23.《从庞加莱到佩雷尔曼》刘培杰主编(即将出版)24.《精神的圣徒别样的人生:60位中国数学家成长的历程》刘培杰主编25.《数学我爱你大数学家的故事》(美)吕塔·赖默尔维尔贝特·赖默尔著26.《俄罗斯平面几何问题集原书第6版》波拉索洛夫编著025——精品书系第二批,哈尔滨工业大学出版社1.《初等数学研究Ⅰ》甘志国著—数学·统计学系列2.《初等数学研究Ⅱ上》甘志国著—数学·统计学系列3.《初等数学研究Ⅱ下》甘志国著—数学·统计学系列4.《数学眼光透视》沈文选杨清桃编著—中学数学拓展丛书5.《数学思想领悟》沈文选杨清桃编著—中学数学拓展丛书6.《数学应用展观》沈文选杨清桃编著—中学数学拓展丛书7.《数学建模导引》沈文选杨清桃编著—中学数学拓展丛书8.《数学方法溯源》沈文选杨清桃编著—中学数学拓展丛书9.《数学史话览胜》沈文选杨清桃编著—中学数学拓展丛书10.《博弈论精粹》刘培杰执行主编11.《初等数论难题集第1卷》刘培杰主编12.《多项式和无理数》冯贝叶著—数学·统计学系列13.《数学奥林匹克不等式研究》杨学枝著—数学·统计学系列14.《解析不等式新论》张小明,褚玉明著—数学·统计学系列15.《模糊数据统计学》王忠玉吴柏林著—数学·统计学系列16.《三角形的五心》贺功保叶美雄编著17.《中国初等数学研究2009卷第1辑》杨学枝主编18.《高等数学试题精选与答题技巧》杨克劭主编19.《运筹学试题精选与答题技巧》徐永仁主编20.《空间解析几何及其应用》徐阳,杨兴云编著026——精品书系第三批,哈尔滨工业大学出版社1.《中考数学专题总复习》陈晓莉主编2.《中考几何综合拔高题解法精粹》李双臻李春艳编著3.《数学奥林匹克超级题库初中卷上》刘培杰数学工作室编著(缺)4.《新编中学数学解题方法全书初中版上》刘培杰主编5.《新编中学数学解题方法全书高中版上》刘培杰主编6.《新编中学数学解题方法全书高中版中》刘培杰主编7.《新编中学数学解题方法全书高中版下1》刘培杰主编8.《新编中学数学解题方法全书高中版下2》刘培杰主编9.《新编中学数学解题方法全书高考真题卷》张广民王世堑主编(缺)10.《新编中学数学解题方法全书高考复习卷》张永辉主编(缺)11.《最新全国及各省市高考数学试卷解法研究及点拨评析》邵德彪主编12.《高考数学真题分类解读第1册》刘松丽张坯东杨婷婷等本册主编13.《高考数学真题分类解读第2册》高考真题研究组编14.《高考数学真题分类解读第3册》阎丽红孙宏宇牟晓永等本册主编15.《高考数学真题分类解读第4册》王小波董亮本册主编16.《高考数学真题分类解读第5册》高考真题研究组编17.《向量法巧解数学高考题》赵南平编著18.《高考数学的理论与实践》高慧明著19.《中学数学解题方法》吕凤祥主编20.《中学数学方法论》鲍曼主编027——《当代数学园地》,科学出版社出版1.《Kac-Moody代数导引》万哲先著2.《哈密顿系统的指标理论及其应用》龙以明著3.《分形-美的科学复动力系统图形化》(德)派特根(德)P.H.里希特著井竹君章祥荪译4.《哈密顿系统与时滞微分方程的周期解》刘正荣李继彬著5.《群类论》郭文彬著6.《代数几何码》冯贵良吴新文著7.《正规形理论及其应用》李伟固著8.《测度值分枝过程引论》赵学雷著9.《完备李代数》孟道骥朱林生姜翠波著028——《通俗数学名著译丛》,上海教育出版社出版1.《数学:新的黄金时代》2.《数论妙趣:数学女王的盛情款待》3.《数学娱乐问题》4.《数学趣闻集锦》上、下册5.《数学与联想》6.《计算出人意料:从开普勒到托姆的时间图景》7.《当代数学为了人类心智的荣耀》8.《近代欧氏几何学》9.《站在巨人的肩膀上》10.《无穷之旅:关于无穷大的文化史》11.《数:科学的语言》12.《20世纪数学的五大指导理论》13.《数学**与欣赏》14.《数学旅行家:漫游数王国》15.《蚁迹寻踪及其他数学探索》16.《圆锥曲线的几何性质》17.《拓扑实验》18.《数学*国界:国际数学联盟的历史》19.《意料之外的绞刑和其他数学娱乐》20.《稳操胜券》上、下册21.《现代世界中的数学》22.《**:自然规律支配偶然性》23.《解决问题的策略》24.《东西数学物语》25.《黎曼博士的零点》26.《奇妙而有趣的几何》27.《虚数的故事》28.《悭悭宇宙:自然界里的形态和造型》029——《走进教育数学丛书》,科学出版社1.《数学的神韵》李尚志著(缺)2.《数学不了情》谈祥柏著(缺)3.《微积分快餐》林群著4.《走进教育数学》沈文选著5.《数学解题策略》朱华伟钱展望著(缺)6.《绕来绕去的向量法》(缺)7.《直来直去的微积分》张景中著(缺)8.《一线串通的初等数学》张景中著9.《几何新方法和新体系》张景中著10.《从数学竞赛到竞赛数学》朱华伟编030——关于匈牙利奥林匹克数学竞赛的几本书,后两本是台湾出的繁体字书:1.《匈牙利奥林匹克数学竞赛题解》(匈)库尔沙克(Й.Кюршак)等编胡湘陵译2.《匈牙利数学问题详解第1册》王昌锐译(将2个压缩文件放在一起解压!)3.《匈牙利数学问题详解第2册》王昌锐译(将2个压缩文件放在一起解压!)031——原新知识出版社出版的一些老书,书目如下:1.《平面几何作图题解法中的讨论》金品编著2.《上海市1956-57年中学生数学竞赛习题汇编》中国数学会上海分会中学数学研究委员会编3.《什么是非欧几何》吴宗初著4.《数学试题汇集·附解法》(苏)沙赫诺(Шахно.К.У.)编著赵越李伯尘译5.《同解方程》程志国编6.《统计平均数》邹依仁编著7.《因式分解及其应用》郁李编8.《有趣的算术题》(苏)巴梁克(Г.Б.Поляк)编盛帆译9.《整式与分式》郁李编10.《整数四则和分数四则》刘永政著11.《正定理和逆定理》(苏)格拉施坦(И.С.Градштейн)著许梅译12.《中学课程中的无理方程》(苏)吉布什(И.А.Гибш)著管承仲译13.《中学数学课外活动》张运钧编著032——《中学数学奥林匹克丛书》,北京师范学院出版社1.《立体几何向量及其变换》何裕新孙维刚著2.《平面几何及变换》梅向明主编唐大昌等编写3.《代数恒等变形》梅向明主编4.《初等数论初中册》梅向明主编5.《北京市中学生数学竞赛试题解析》梅向明主编6.《数学奥林匹克解题研究初中册》梅向明主编7.《数学奥林匹克解题研究高中册》周春荔等编8.《组合基础》周沛耕张宁生著9.《初等数论高中册》米道生吴建平编写033——《数理化竞赛丛书》数学部分,科学普及出版社1.《北京市中学数学竞赛题解1956-1964》北京市数学会编2.《全国中学数学竞赛题解1978》全国数学竞赛委员会编3.《美国及国际数学竞赛题解1976-1978》(美)格雷特编中国科学院应用数学研究推广办公室译4.《匈牙利奥林匹克数学竞赛题解》(匈)库尔沙克(Й.Кюршак)等编胡湘陵译5.《北京市中学数学竞赛题解1956-1979》北京市数学会6.《全国中学数学竞赛题解1979》科学普及出版社编034——《数学奥林匹克题库》,新蕾出版社1.《美国中学生数学竞赛题解1》(缺)2.《美国中学生数学竞赛题解2》3.《国际中学生数学竞赛题解》4.《中国中学生数学竞赛题解1》(缺)5.《中国中学生数学竞赛题解2》(缺)6.《加拿大中学生数学竞赛题解》7.《苏联中学生数学竞赛题解》035——《中学数学》丛书,湖北省暨武汉市数学会组织编写、湖北人民出版社1.《代数解题引导》杨挥陈传理编2.《初等几何解题引导》江志著3.《三角解题引导》车新发编4.《解析几何解题引导》刘佛清张硕才编5.《国际数学竞赛试题讲解Ⅰ》江仁俊编6.《国际数学竞赛试题讲解Ⅱ》江仁俊等编036——《数学圈丛书》,湖南科技出版社1.《数学圈》1 【美】H.W.伊佛斯2.《数学圈》2 【美】H.W.伊佛斯3.《数学圈》3 【美】H.W.伊佛斯4.《数学爵士乐》【美】爱德华.伯格、迈克尔.斯塔伯德5.《素数的音乐》【英】马科斯.杜.索托伊6.《无法解出的方程》【美】马里奥.利维奥7.《数学家读报》【美】约翰·艾伦·保罗斯037——一套数学竞赛书籍,上海科学技术出版社1.《初中数学竞赛妙题巧解》常庚哲编2.《初中数学竞赛辅导讲座》严镇军等编3.《高中数学竞赛辅导讲座》常庚哲等编4.《中、美历届数学竞赛试题精解》刘鸿坤等编038——国外数学奥林匹克俱乐部丛书,湖北教育出版社1.《美国数学邀请赛试题解答与评注》朱华伟编译2.《俄国青少年数学俱乐部》苏淳朱华伟译039——《国内外数学竞赛题解》,陕西师范大学图书馆编辑组编写《国内外数学竞赛题解》上、中、下三册040——开明出版社出版由中国数学奥林匹克委员会编译的两本书,书目如下:1.《环球城市数学竞赛问题与解答第1册》2.《环球城市数学竞赛问题与解答第2册》041——数学奥林匹克试题集锦,华东师范大学出版社,IMO中国国家集训队教练组编写1.《走向IMO 数学奥林匹克试题集锦2003》2003年IMO中国国家集训队教练组编2.《走向IMO 数学奥林匹克试题集锦2004》2004年IMO中国国家集训队教练组,选拔考试命题组编3.《走向IMO 数学奥林匹克试题集锦2005》2005中国国家集训队教练组、选拔考试命题组编4.《走向IMO 数学奥林匹克试题集锦2006》2006年IMO中国国家集训队教练组编5.《走向IMO 数学奥林匹克试题集锦2007》2007年IMO中国国家集训队教练组编6.《走向IMO 数学奥林匹克试题集锦2008》2008年IMO中国国家集训队教练组编(缺)7.《走向IMO 数学奥林匹克试题集锦2009》2009年IMO中国国家集训队教练组编(缺)042——国外、国际数学竞赛试题方面的书籍1.《奥林匹克数学竞赛题集》(苏)罗什柯夫等编著张兴烈刘承明译2.《波兰数学竞赛题解1-27届》(波)耶·勃罗夫金(波)斯·斯特拉谢维奇著朱尧辰译3.《初中中外数学竞赛集锦》刘鸿坤编著4.《第26届国际数学奥林匹克》中国数学会普及工作委员会编5.《第一届至第二十二届国际中学生数学竞赛题解1959-1981》杨森茂陈圣德编译6.《国际奥林匹克数学竞赛题及解答1978-1986》中国科协青少年工作部中国数学会编译7.《国际数学奥林匹克1-20届》江苏师范学院数学系编译8.《国际数学竞赛题解》(德)H.D.霍恩舒赫编潘振亚等译9.《国际数学竞赛选载》江西省中小学教材编写组编10.《国内外高中数学竞赛汇编》杭州市第一中学高中数学教研组编11.《基辅数学奥林匹克试题集》(苏)维申斯基等编著刘鸿坤等译12.《加拿大美国历届中学生数学竞赛题解》福建师范大学数学系资料室编译13.《历届奥林匹克数学竞赛试题分析》闫建平编14.《美国历届数学竞赛题解1950-1972》梁伟强编15.《美国中学数学竞赛试题及题解》朱鉴清编译16.《普特南数学竞赛1938-1980》刘裔宏译17.《苏联中学数学竞赛题汇编》(苏)别尔尼克编仁毅志译18.《1981年国内外数学竞赛题解选集》顾可敬编19.《通用数学竞赛100题附:第27届国际数学奥林匹克试题》张运筹刘一宏左宗琰编译20.《最新国外数学竞赛分类题解》王连笑编著21.《国际数学奥林匹克30年为迎接1990年第31届IMO在我国举办》梅向明主编22.《国外高中数学竞赛真题库》《数学竞赛之窗》编辑部主编23.《全苏数学奥林匹克试题》(苏)Н.Б.瓦西里耶夫(苏)А.А.叶戈罗夫著李墨卿等译24.《数学奥林匹克1987-1988 高中版》单墫胡大同25.《数学奥林匹克1989 第30届国际数学竞赛预选题》单墫等编26.《数学奥林匹克1990 第31届国家集训队资料》单墫葛军编27.《北美数学竞赛100题》(加)威廉(加)哈迪著侯晋川张秀玲译28.《第1-50届莫斯科数学奥林匹克》(苏)Г.А.嘎尔别林(苏)А.К.托尔贝戈编苏淳等译29.《国际数学奥林匹克三十年1959-1988试题集解》胡炳生等编著30.《第一届数学奥林匹克国家集训队资料选编1986》胡大同严镇军编31.《国际中学生数学竞赛试题集粹初中版中英文对照》戴筱逄主编乌实译043——国内数学竞赛试题及方法等方面的书籍部分书目如下:1.《1978年全国部分省市中学数学竞赛试题解答汇集》福建教育学院数学组编2.《1978年全国部分省市中学数学竞赛题解汇集》山西省数学学会编3.《1979年数学竞赛试题解答》襄樊市教育局教研室编4.《奥林匹克数学教程》刘凯年编著5.《奥林匹克数学竞赛解谜初中部分》康纪权主编6.《奥林匹克数学竞赛解谜高中部分》康纪权编著。
2年全国高中数学联赛试题及解答

2000年全国高中数学联合竞赛试卷(10月15日上午8:00?9:40)一、选择题(本题满分36分,每小题6分)1.设全集是实数,若A={x|≤0},B={x|10=10x},则A∩?R B是()(A){2}(B){?1}(C){x|x≤2}(D)?2.设sin?>0,cos?<0,且sin>cos,则的取值范围是()(A)(2k?+,2k?+),k?Z(B)(+,+),k?Z(C)(2k?+,2k?+?),k?Z(D)(2k?+,2k?+)∪(2k?+,2k?+?),k?Z3.已知点A为双曲线x2?y2=1的左顶点,点B和点C在双曲线的右分支上,△ABC 是等边三角形,则△ABC的面积是()(A)(B)(C)3(D)64.给定正数p,q,a,b,c,其中p?q,若p,a,q是等比数列,p,b,c,q 是等差数列,则一元二次方程bx2?2ax+c=0()(A)无实根(B)有两个相等实根(C)有两个同号相异实根(D)有两个异号实根5.平面上整点(纵、横坐标都是整数的点)到直线y=x+的距离中的最小值是()(A)(B)(C)(D)6.设ω=cos+i sin,则以?,?3,?7,?9为根的方程是()(A)x4+x3+x2+x+1=0(B)x4?x3+x2?x+1=0(C)x4?x3?x2+x+1=0(D)x4+x3+x2?x?1=0二.填空题(本题满分54分,每小题9分)1.arcsin(sin2000?)=__________.2.设a n是(3?)n的展开式中x项的系数(n=2,3,4,…),则(++…+))=________.3.等比数列a+log23,a+log43,a+log83的公比是____________.4.在椭圆+=1(a>b>0)中,记左焦点为F,右顶点为A,短轴上方的端点为B.若该椭圆的离心率是,则∠ABF=_________.5.一个球与正四面体的六条棱都相切,若正四面体的棱长为a,则这个球的体积是________.6.如果:(1)a,b,c,d都属于{1,2,3,4};(2)a?b,b?c,c?d,d?a;(3)a是a,b,c,d中的最小值,那么,可以组成的不同的四位数的个数是_________三、解答题(本题满分60分,每小题20分)1.设S n=1+2+3+…+n,n?N*,求f(n)=的最大值.2.若函数f(x)=-x2+在区间[a,b]上的最小值为2a,最大值为2b,求[a,b].3.已知C0:x2+y2=1和C1:+=1(a>b>0).试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为顶点,与C0外切,与C1内接的平行四边形?并证明你的结论.2000年全国高中数学联赛二试题 (10月15日上午10∶00-12∶00)一.(本题满分50分)如图,在锐角三角形ABC 的BC 边上有两点E 、F ,满足∠BAE=∠CAF ,作FM ⊥AB ,FN ⊥AC (M 、N 是垂足),延长AE 交三角形ABC 的外接圆于D .证明:四边形AMDN 与三角形ABC 的面积相等.二.(本题满分50分)设数列{a n }和{b n }满足a 0=1,a 1=4,a 2=49,且n=0,1,2,……证明a n (n=0,1,2,…)是完全平方数. 三.(本题满分50分) 有n 个人,已知他们中的任意两人至多通电话一次,他们中的任意n -2个人之间通电话的次数相等,都是3k次,其中k 是自然数,求n 的所有可能值.2000年全国高中数学联合竞赛试题解答第一试 一.选择题(本题满分36分,每小题6分)1.设全集是实数,若A={x |≤0},B={x |10=10x },则A ∩?R B 是() (A ){2}(B ){?1}(C ){x |x ≤2}(D )? 解:A={2},B={2,-1},故选D .2.设sin ?>0,cos ?<0,且sin >cos ,则的取值范围是() (A )(2k ?+,2k ?+),k ?Z (B )(+,+),k ?Z(C )(2k ?+,2k ?+?),k ?Z (D )(2k ?+,2k ?+)∪(2k ?+,2k ?+?),k ?Z解:满足sin ?>0,cos ?<0的α的范围是(2k ?+,2k ?+π),于是的取值范围是(+,+),满足sin >cos 的的取值范围为(2k ?+,2k ?+).故所求范围是(2k ?+,2k ?+)∪(2k ?+,2k ?+?),k ?Z .选D .3.已知点A 为双曲线x 2?y 2=1的左顶点,点B 和点C 在双曲线的右分支上,△ABC 是等边三角形,则△ABC 的面积是()(A )(B )(C )3(D )6 解:A (-1,0),AB 方程:y=(x +1),代入双曲线方程,解得B (2,),∴S=3.选C .4.给定正数p ,q ,a ,b ,c ,其中p ?q ,若p ,a ,q 是等比数列,p ,b ,c ,q 是等差数列,则一元二次方程bx 2?2ax +c=0()(A )无实根(B )有两个相等实根(C )有两个同号相异实根(D )有两个异号实根 解:a 2=pq ,b +c=p +q .b=,c=;△=a 2-bc=pq -(2p +q )(p +2q )=-(p -q )2<0.选A .5.平面上整点(纵、横坐标都是整数的点)到直线y=x +的距离中的最小值是() (A )(B )(C )(D )A CBy x OA B C DE FM N解:直线即25x -15y +12=0.平面上点(x ,y )到直线的距离==.∵5x -3y +2为整数,故|5(5x -3y +2)+2|≥2.且当x=y=-1时即可取到2.选B . 6.设ω=cos+i sin ,则以?,?3,?7,?9为根的方程是() (A )x 4+x 3+x 2+x +1=0(B )x 4?x 3+x 2?x +1=0 (C )x 4?x 3?x 2+x +1=0(D )x 4+x 3+x 2?x ?1=0 解:ω5+1=0,故?,?3,?7,?9都是方程x 5+1=0的根.x 5+1=(x +1)(x 4-x 3+x 2-x +1)=0.选B . 二.填空题(本题满分54分,每小题9分)1.arcsin(sin2000?)=__________.解:2000°=180°×12-160°.故填-20°或-. 2.设a n 是(3?)n 的展开式中x 项的系数(n=2,3,4,…),则(++…+))=________. 解:a n =3n -2C .∴==,故填18.3.等比数列a +log 23,a +log 43,a +log 83的公比是____________. 解:q=====.填.4.在椭圆+=1(a >b >0)中,记左焦点为F ,右顶点为A ,短轴上方的端点为B .若该椭圆的离心率是,则∠ABF=_________.解:c=a ,∴|AF |=a .|BF |=a ,|AB |2=|AO |2+|OB |2=a 2.故有|AF |2=|AB |2+|BF |2.即∠ABF=90°.填90°. 或由b 2=a 2-c 2=a 2=ac ,得解.5.一个球与正四面体的六条棱都相切,若正四面体的棱长为a ,则这个球的体积是________.解:取球心O 与任一棱的距离即为所求.如图,AE=BE=a ,AG=a ,AO=a ,BG=a ,AB ∶AO=BG ∶OH . OH==a .V=πr 3=πa 3.填πa 3..6.如果:(1)a ,b ,c ,d 都属于{1,2,3,4}; (2)a ?b ,b ?c ,c ?d ,d ?a ;(3)a 是a ,b ,c ,d 中的最小值,那么,可以组成的不同的四位数的个数是_________解:a 、c 可以相等,b 、d 也可以相等.⑴当a 、c 相等,b 、d 也相等时,有C=6种; ⑵当a 、c 相等,b 、d 不相等时,有A +A=8种; ⑶当a 、c 不相等,b 、d 相等时,有CC +C=8种;⑷当a 、c 不相等,b 、d 也不相等时,有A=6种;共28种.填28. 三、解答题(本题满分60分,每小题20分)1.设S n =1+2+3+…+n ,n ?N *,求f (n )=的最大值. 解:S n =n (n +1),f (n )==+34)≤错误!未指定书签。
历年全国高中数学竞赛试卷及答案(77套)

9.若 是双曲线 上的点,则 的最小值是_________.
10. 如图,设正方体 的棱长为1,α为过直线 的平面,则α截该正方体的截面面积的取值范围是_________.
11.已知实数 满足: 的最大值是____.
12.设集合 则集合A中元素的个数是___________
二.填空题(本大题共4小题,每小题10分):
1.设x≠y,且两数列x,a1,a2,a3,y和b1,x,b2,b3,y,b4均为等差数列,那么 =.
解:a2-a1= (y-x),b4-b3= (y-x), = .
2.( +2)2n+1的展开式中,x的整数次幂的各项系数之和为.
解:( +2)2n+1-( -2)2n+1=2(C 2xn22n+1).
1.设x≠y,且两数列x,a1,a2,a3,y和b1,x,b2,b3,y,b4均为等差数列,那么 =.
2.( +2)2n+1的展开式中,x的整数次幂的各项系数之和为.
3.在△ABC中,已知∠A=α,CD、BE分别是AB、AC上的高,则 =.
4.甲乙两队各出7名队员,按事先排好顺序出场参加围棋擂台赛,双方先由1号队员比赛,负者被淘汰,胜者再与负方2号队员比赛,……直至一方队员全部淘汰为止,另一方获得胜利,形成一种比赛过程.那么所有可能出现的比赛过程的种数为.
⑴ 点(1,1)∈ln,(n=1,2,3,……);
⑵kn+1=an-bn,其中kn+1是ln+1的斜率,an和bn分别是ln在x轴和y轴上的截距,(n=1,2,3,……);
⑶knkn+1≥0,(n=1,2,3,……).
2023年青少年数学国际城市邀请赛个人赛试题

BIMC 2023Bulgaria International Mathematics Competition 2023(Virtual)Bulgaria , 1st to 7th July 20232023年青少年数学国际城市邀请赛个人赛试题1. 已知x 是实数,且知y=43+x +x 34−,请问y 2的最小可能值是什么?[新加坡供题]2.一个半径为1 cm 的圆与一个等边三角形的三边都相切。
从这个圆开始,然后绘制三个无限小圆序列,每个角一个,使得每个圆都与序列中的前一个圆以及三角形的两条边相切,如图所示。
请问所有圆的周长之和为多少cm? (取π=3.14)[尼泊尔供题]3.若ABCDEF 与AGHIJK 为不重迭的两个正六边形,如图所示。
假设∠FAK = 90°并且.满足面积关系: 3×[AGHIJK]=4×[ABCDEF]。
请问[ABG]:[AGHIJK]为何? (注: [P]表示多边形P 的面积) [墨西哥供题]4.以下的53位数37,984,318,966,591,152,105,649,545,470,741,788,308,402,068,827,142,719可以写成n 21的形式,其中n 是正整数。
请问n 之值为何? [ 泰国供题]5. 考虑方程10y2-9x222=y4,其中x、y为整数。
假设m是x+y的最大可能值,n是解(x,y)的数量,请问m+n之值为何? [ 印度尼西亚供题]6.已知非零实数a、b、c满足a+b+c=0。
请问之值为何?[越南供题]7.如果一个数可以写成2a+2b,其中a、b为不同的非负整数,那么称这个数为「幸运数」。
将所有幸运数以递增方式列出,请问第64个幸运数是什么? [中国供题]8.己知等边三角形ABC的面积为36 cm2,且知等腰三角形EFD中,EF=FD,点F是三角形ABC 的中心,并且点B与点C分别位于EF与FD的中点,如图所示。
2019年第41届环球城市高中数学竞赛秋季赛

第41届环球城市数学竞赛秋季赛 O 级别海亮高级中学 龙崎钢 译比赛时间: 2019年秋高级组1. (3分)魔术师表演如下魔术: 他在桌上将52张扑克牌摆成一排.在每一步中, 一位观众被邀请上台,说出一个整数, 随后魔术师从牌堆一侧开始数, 数到这个整数时, 将其所对应位置那张牌丢掉. 当然, 从左侧还是右侧开始数由魔术师决定. 在魔术开始之前, 魔术师宣布, 经过若干步操作之后, 桌上只会留下一张牌, 就是草花三. 那么, 魔术师在魔术开始时, 应该把草花三放在什么位置, 才能确保魔术一定成功?2. (4分)凸五边形ABCDE 中, AE ∥CD, AB =BC. ∠A 和∠C 的平分线交于点K. 求证: BK ∥AE.3. (4分)黑板上写有一个整数. 智多星对这个数字进行若干次操作, 每次他可以将原数字x 替换为3x +1或者2x ⎡⎤⎢⎥⎣⎦,即不大于2x 的最大整数. 证明: 若一开始的数字为1, 那么智多星可以进行有限步操作之后, 将其变为任意一个数字.4. (5分)在一个多边形中, 任意两个相邻的边都互相垂直. 如果有两个点所对应的角平分线互相垂直, 就称这两个点为”不统一的”. 证明: 对多边形的任意一个顶点, 跟它成”不统一的”点的个数为偶数.5. (5分)一行100个单元格里各有一枚互不相同的筹码. 向荷官付1元可以交换两个相邻的筹码的位置. 同时, 如果两个筹码之间有4个筹码, 那么你可以免费交换它们的位置. 智多星想要通过若干次交换,使得这些筹码的顺序正好与初始的顺序相反, 那么他至少需要付给荷官多少元?初级组1. (4分,与高级组第一题相同)魔术师表演如下魔术: 他在桌上将52张扑克牌摆成一排.在每一步中, 一位观众被邀请上台,说出一个整数, 随后魔术师从牌堆一侧开始数, 数到这个整数时, 将其所对应位置那张牌丢掉. 当然, 从左侧还是右侧开始数由魔术师决定. 在魔术开始之前, 魔术师宣布, 经过若干步操作之后, 桌上只会留下一张牌, 就是草花三. 那么, 魔术师在魔术开始时, 应该把草花三放在什么位置, 才能确保魔术一定成功?2. (4分)圆ω的圆心为O, 圆上有两个不重合的点A和C. 对圆上任意一点P, 设X和Y分别为AP和CP的中点, H 为△OXY的垂心. 证明: H的位置与P点无关.3. (4分,高级组第五题削弱版)一行100个单元格里各有一枚互不相同的筹码. 向荷官付1元可以交换两个相邻的筹码的位置. 同时, 如果两个筹码之间有3个筹码, 那么你可以免费交换它们的位置. 智多星想要通过若干次交换,使得这些筹码的顺序正好与初始的顺序相反, 那么他至少需要付给荷官多少元?4. (5分)已知有1000个数字121000,,...a a a . 智多星将它们的平方2211000,...a a 写在一个圆周上, 使得圆周上任意连续41个数的和正好是241的倍数. 那么, 是否121000,,...a a a 都一定是41的倍数?5. (5分)智多星有两种砖头, 一种是1×1×3型的, 另一种是Γ型的,由3块1×1×1的立方体组成, 如下图所示. 已知智多星用这两种砖头填满了一个m ×n ×k 的盒子, 其中m,n,k 都是大于1的整数. 证明: 智多星可以只用Γ型砖头填满这个盒子.第41届环球城市数学竞赛秋季赛 A 级别海亮高级中学 龙崎钢 译比赛时间: 2019年秋初级组1. (4分)对大于1的正整数n, 设n 的素因数分解中因子的个数为n 的复杂度. 例如, 数字4和6的复杂度都是2.(1) (2分)若所有位于n 和2n 之间的整数, 其复杂度不大于n 的复杂度, 求n 所有的可能的值.(2) (2分)求所有位于n 和2n 之间的整数, 其复杂度小于n 的复杂度, 求n 所有的可能的值.2. (7分)在锐角三角形ABC 边BC 上取两个点11,B C , 再在△ABC 内部取一个点1A , 使得111A B C 也为锐角三角形.证明: 1111111A B C ABC S S AB AC A B AC >++. 3. (7分,与高级组第三题相同)有100枚外观完全相同的硬币, 分为金银铜三种, 每种至少有一枚. 每个金币重3克, 每个银币重2克, 每个铜币重1克. 现有一个无砝码的天平, 允许称重不超过101次, 如何分辨出每一枚硬币的材质?4. (7分)已知O 为△ABC 的外心, 过O 作∠B 的内角平分线和外角平分线的垂线, 垂足分别为P , Q. 连接CB 中点M 和AB 的中点N, 证明线段MN 被直线PQ 等分.5. (8分)若两个不同的正整数m,n满足mn和(m+1)(n+1)都是完全平方数, 就称(m,n)是一对好对子.证明: 对任意正整数m, 至少存在一个正整数n大于m, 使得(m,n)是一对好对子.6. (8分)智多星有若干张百元大钞, 且没有其他现金. 他用这些钱去书店买书, 每本书的价格都是正整数, 且他获得的找零都是1元硬币. 当智多星购买价格为100元或以上的书籍时, 他只用百元大钞付款. 当他购买价格不超过100元的书籍时, 他尽可能地使用零钱付款. 当智多星所有百元大钞都被用掉时, 他所剩的现金为之前的一半. 那么, 智多星是否可能花费了超过5000元?7. (10分)智多星有一枚方格子印章, 他将其中102个格子涂上了黑色墨水. 之后呢, 他用这枚印章在一张白纸上盖了100次章, 每次盖章时, 都只有这102个黑格子在纸上留下了黑色印记. 那么, 是否可能在智多星盖了100次章之后, 纸上的一个101×101的方格中, 除了一个角落之外,其他所有的格子都是黑色的?高级组1. (5分)多项式P(x,y)满足: 对任意非负整数n, 多项式P(n,y)和P(x,n)要么为次数不超过n 的多项式, 要么为常数0. 那么, 多项式P(x,x)的次数是否可能为奇数?2. (5分)锐角△ABC 内部有一点P . 直线AP , BP , CP 分别和BC, AC, AB 边交于点A ’, B ’, C ’. 以AA ’, BB ’, CC ’为直径作圆, 再在每个圆内, 过P 点作垂直于直径的弦.若所有的弦长相等, 求证: P 为△ABC 垂心.3. (6分) 有100枚外观完全相同的硬币, 分为金银铜三种, 每种至少有一枚. 每个金币重3克, 每个银币重2克, 每个铜币重1克. 现有一个无砝码的天平, 允许称重不超过101次, 如何分辨出每一枚银币的材质?4. (10分)递增数列21012......a a a a a --<<<<<在两个方向都有无穷项. 对常数k, 设k b 表示这个数列中, 任意k 项的和除以其中最大的一项的比值的上界. 证明: 数列123,,...b b b 要么与1,2,3…一致, 要么在某一项之后为常数.5. (12分)凸四边形ABCD 内的一点M 到直线AB 和CD 的距离相等, 到直线BC 和AD 的距离也相等. 已知ABCD 的面积等于MA ∙MC +MB ∙MD. 求证:(1) (6分)四边形ABCD 存在内切圆.(2) (6分)四边形ABCD 存在外接圆.6. (12分)一个由3N个单位立方体组成的大立方体被若(2)干平行于它的边的针穿过, 每根针恰好穿过2N个单位立方体, 且每个单位立方体都至少被一根针穿过. 对这些针所组成的集合的某个子集, 如果其中任意两根针都没有穿过相同的单位立方体, 就称这个子集是”常规”的.(1) (6分)证明: 存在一个由22N根针组成的”常规”的子集, 其中所有的针的方向至多只有2个.(2) (6分)对不同的刺穿方法, ”常规”的子集的元素个数的最大值至少是多少?7. (12分)将整数1,2,3…n中的一部分染成红色, 使得其中任意三个红色数a,b,c(不一定互不相同)满足()-是n的倍a b cϕ.数的必要条件是b=c. 证明: 红色数的个数不超过()n ϕ表示1,2,…n中与n互素的正整数的个数.注: ()n。
2020年环球城市春季赛 O级别奥林匹克竞赛数学试题
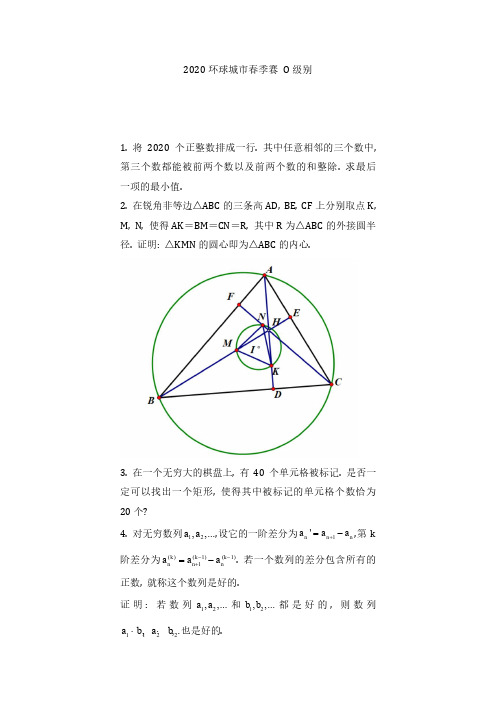
2020环球城市春季赛 O 级别1. 将2020个正整数排成一行. 其中任意相邻的三个数中, 第三个数都能被前两个数以及前两个数的和整除. 求最后一项的最小值.2. 在锐角非等边△ABC 的三条高AD, BE, CF 上分别取点K, M, N, 使得AK =BM =CN =R, 其中R 为△ABC 的外接圆半径. 证明: △KMN 的圆心即为△ABC 的内心.3. 在一个无穷大的棋盘上, 有40个单元格被标记. 是否一定可以找出一个矩形, 使得其中被标记的单元格个数恰为20个?4. 对无穷数列12,,...a a ,设它的一阶差分为1'n n n a a a +=-,第k阶差分为()(1)(1)1k k k n n na a a --+=-. 若一个数列的差分包含所有的正数, 就称这个数列是好的.证明: 若数列12,,...a a 和12,,...b b 都是好的, 则数列1122,,...a b a b⋅⋅也是好的.5. 在半径为1的球的球面上取一个球面三角形, 它的三条边均为球面上半径为1,长度不超过π的弧,(即这段弧所在的平面过球心), 其面积正好是球面积的14. 证明: 将这个球面三角形复制4份,可以覆盖整个球面.6. 将N个红色, 白色或蓝色的立方体放在圆圈上. 机器人从圆圈上的某个位置出发, 顺时针移动并执行如下操作, 直到只剩一个立方体为止: 机器人摧毁自己前方最靠近自己的两个立方体, 并将一个立方体放置在自己身后,该立方体的颜色由被摧毁的两个立方体决定: 若这两个立方体颜色相同, 则被放置的立方体颜色与他们也相同. 若这两个立方体颜色不同, 则被放置的立方体颜色与他们均不同.若放置好立方体后, 无论机器人从哪个位置出发, 最终所得的立方体颜色都不变, 就称这个放置法是好的. 若对整数N, 所有的放置法都是好的, 就称N是成功的.求所有成功的N.。
2019第41届环球城市数学竞赛秋季赛 O级别 高级组(无答案)

2019第41届环球城市数学竞赛秋季O 级别高级组
1.魔术师表演如下魔术:他在桌上将52张扑克牌摆成一排,在每一步中,一位观众被邀请上台,说出一个整数,随后魔术师从牌堆一侧开始数,数到这个整数时,将其所对应位置那张牌丢掉。
当然,从左侧还是右侧开始数由魔术师决定。
在魔术开始之前,魔术师宣布,经过若干步操作之后,桌上只会留下一张牌,就是草花三。
那么,魔术师在魔术开始时,应该把草花三放在什么位置,才能确保魔术一定成功。
2.凸五边形 ABCDE 中,AE ∥CD,AB=BC 。
∠A 和∠C 的平分线交于点K 。
求证:BK ∥AE 。
3. 黑板上写有一个整数.玛丽对这个数字进行若干次操作,每次他可以
将原数字x 替换为3x+1或者⎥⎦⎤⎢⎣⎡2x ,即不大于2x 的最大整数。
证明:若一开始的数字为1,玛丽可以进行有限步操作之后,将其变为任意一个数字。
4.在一个多边形中,任意两个相邻的边都互相垂直。
如果有两个点所对应的角平分线互相垂直,就称这两个点为“不团结的”。
证明:对多边形的任意一个顶点,跟它成“不团结的”点的个数为偶数。
5.一行100个单元格里各有一枚互不相同的筹码。
向荷官付1元可以交换两个相邻的筹码的位置。
同时,如果两个筹码之间有4个筹码,那么你可以免费交换它们的位置.威廉想要通过若干次交换,使得这些筹码的顺序正好与初始的顺序相反,那么他至少需要付给荷官多少元?。
青少年数学国际城市邀请赛试题解答

目 录张景中谈奥数前言第1章 第一届青少年数学国际城市邀请赛1……………………………………………………………………………………………1畅1 个人竞赛试题11畅2 个人竞赛试题解答4………………………………………………………………………………………………………………1畅3 队际竞赛试题8…………………………………………………1畅4 队际竞赛试题解答10第2章 第二届青少年数学国际城市邀请赛13…………………………………………………………………………………………2畅1 个人竞赛试题13…………………………………………………2畅2 个人竞赛试题解答142畅3 队际竞赛试题19…………………………………………………………………………………………………………2畅4 队际竞赛试题解答20…………………………………第3章 第三届青少年数学国际城市邀请赛26………………………………………………………3畅1 个人竞赛试题26…………………………………………………3畅2 个人竞赛试题解答27………………………………………………………3畅3 队际竞赛试题323畅4 队际竞赛试题解答34……………………………………………………………………………………第4章 第四届青少年数学国际城市邀请赛42………………………………………………………4畅1 个人竞赛试题42…………………………………………………4畅2 个人竞赛试题解答44………………………………………………………4畅3 队际竞赛试题51…………………………………………………4畅4 队际竞赛试题解答53…………………………………第5章 第五届青少年数学国际城市邀请赛59………………………………………………………5畅1 个人竞赛试题59…………………………………………………5畅2 个人竞赛试题解答61青少年数学国际城市邀请赛试题解答………………………………………………………5畅3 队际竞赛试题69…………………………………………………5畅4 队际竞赛试题解答71…………………………………第6章 第六届青少年数学国际城市邀请赛796畅1 个人竞赛试题79…………………………………………………………………………………………………………6畅2 个人竞赛试题解答81………………………………………………………6畅3 队际竞赛试题85…………………………………………………6畅4 队际竞赛试题解答86…………………………………第7章 第七届青少年数学国际城市邀请赛91………………………………………………………7畅1 个人竞赛试题917畅2 个人竞赛试题解答93…………………………………………………………………………………………………………7畅3 队际竞赛试题97…………………………………………………7畅4 队际竞赛试题解答99………………………………第8章 第八届青少年数学国际城市邀请赛105………………………………………………………8畅1 个人竞赛试题105…………………………………………………8畅2 个人竞赛试题解答1088畅3 队际竞赛试题113…………………………………………………………………………………………………………8畅4 队际竞赛试题解答116………………………………第9章 第九届青少年数学国际城市邀请赛122………………………………………………………9畅1 个人竞赛试题122…………………………………………………9畅2 个人竞赛试题解答124………………………………………………………9畅3 队际竞赛试题1309畅4 队际竞赛试题解答133…………………………………………………………………………………第10章 第十届青少年数学国际城市邀请赛141……………………………………………………10畅1 个人竞赛试题141………………………………………………10畅2 个人竞赛试题解答143……………………………………………………10畅3 队际竞赛试题147………………………………………………10畅4 队际竞赛试题解答149第11章 第十一届青少年数学国际城市邀请赛154…………………………………………………………………………………11畅1 个人竞赛试题154………………………………………………11畅2 个人竞赛试题解答156目 录……………………………………………………11畅3 队际竞赛试题162………………………………………………11畅4 队际竞赛试题解答164第12章 第十二届青少年数学国际城市邀请赛170…………………………………………………………………………………12畅1 个人竞赛试题17012畅2 个人竞赛试题解答172……………………………………………………………………………………………………12畅3 队际竞赛试题177………………………………………………12畅4 队际竞赛试题解答179第1章 第一届青少年数学国际城市邀请赛1畅1 个人竞赛试题第一部分填空题,共12题,每题5分畅1畅设数a=122333444455555666666777777788888888999999999,那么a除以9的余数为畅2畅图1-1中角a、b、c、d的度数之和为畅图1-13畅在12,22,…,19992中,十位上的数字为奇数的数共有个畅4畅有一幢建筑物高60m,在白天某时刻的影子长40m,这个建筑物的顶楼插着一根旗杆,长2m,在这个时刻,旗杆的影子长m畅5畅计算19992-19982+19972-19962+…+32-22+12=畅6畅如果一个4位数中正好有两位上的数字相同,称为“好数”,例如:3445、3231是好数,但3443、3233不是好数,那么所有的四位数中千位是3的好数有个畅7畅如图1-2所示,已知等边三角形的边长为1,若在三角形内有3个大小相等的圆彼此相切且与三角形的边相切,那么圆的半径为畅青少年数学国际城市邀请赛试题解答图1-2 8畅设A、B、C为3个正整数,A的平方加160等于B的平方加5,且A的平方加320等于C的平方加5,那么A=畅9畅设x为一个两位数,f(x)为x加上其数字和再减去其数字积,例如:x=32,那么f(x)=32+3+2-6=31,当x为时,f(x)有最大值畅10畅如图1-3所示,在直角△ABC中,AB长为15,AC长为8,点E、G在AC上,点D、F在AB上,若CD、DE、EF、FG将△ABC分成5个面积相等的部分,且CD、DE、EF、FG中只有一条线段的长度为整数,这个整数等于畅11畅如图1-4所示,图中不包含阴影部分的正方形共有个畅图1-4 第1章 第一届青少年数学国际城市邀请赛12畅设有A、B两个委员会,其中A委员会有13名委员,B委员会有6名委员畅在本年度召开的会议期间,若每位委员出席会议的天数在30天以内(含30天),那么每天可以支领6000元车马费,若会议超过30天,超出的天数每天支领9000元车马费,已知B委员会开会的天数是A委员会开会的天数的2倍,在本年度会议两个委员会所支出的车马费都相同,且这两个委员会车马费的总开支超过3000000元,那么这两个委员会实际支领的车马费总共元畅第二部分解答题,共3题,每题20分畅1畅如图1-5所示,用铁丝围成棱长为1的正方体,有一只蚂蚁从点A出发,沿着这个正方体的棱(铁丝)爬行但不能走重复的路线,如果它要回到原来的A点,请问这只蚂蚁所经过的路径最长为多少?(说明理由)图1-52畅如图1-6所示,已知AC=8CE、BC=4BD畅若AD=164、BE=52,试求AB的长畅图1-63畅将一个6位数分别乘以2、3、4、5、6后得到的数还是由原来的6位数的数字组成,只是改变了原来数字排列的位置,试求原来的数是多少?青少年数学国际城市邀请赛试题解答1畅2 个人竞赛试题解答第一部分1畅答案:6畅解 直接运算,余数为6畅评注 被除数比较大,直接运算较复杂,考虑到除数为9,利用同余,计算数a的数字和除以9的余数畅数a的数字和为1+2×2+3×3+…+9×9=1+22+32+…+92=1+4+9+…+81=285畅数字和为285,285除以9的余数为6,即数a除以9的余数为6畅2畅答案:540°畅解 如图1-7所示,角c等于∠1+∠2,角a等于∠3+∠4,因此a+b+c+d=∠3+∠4+b+∠1+∠2+d畅又因为∠3+∠1=180°、b+∠2=180°、∠4+d=180°,因此a+b+c+d=540°畅图1-73畅答案:400畅解 一个正整数的平方的十位上的数字为奇数,当且仅当这个正整数的个位为4或6,因此满足条件的数共有400个畅4畅答案:43m畅解 设旗杆的影子长xm,6040=2x,第1章 第一届青少年数学国际城市邀请赛解得x=43畅5畅答案:1999000畅解 由平方差公式:19992-19982+19972-19962+…+32-22+12=(19992-19982)+(19972-19962)+…+(32-22)+12=1999+1998+1997+1996+…+3+2+1=(1999+1)19992=1999000畅6畅答案:432个畅解 有两种情况:第一,相同的数字为3:共有C31×C91×C81=216种;第二,相同的数字不为3:共有C32×C91×C81=216种;满足条件的好数共有432个畅7畅答案:3-14畅解 如图1-8所示添加辅助线,设圆的半径为x,∠ABC=30°,那么AC=3x、BC=2x,因为三角形边长为1,即2x+23x=1,解得x=3-14畅图1-88畅答案:13畅解 由题意得A2+160=B2+5、A2+320=C2+5,即青少年数学国际城市邀请赛试题解答B2-A2=(B+A)(B-A)=155、C2-A2=315畅因为155=31×5,因此B+A=31、B-A=5,即B=18、A=13、C=22畅9畅答案:90畅解 设x=ab=10a+b,那么f(x)=10a+b+a+b-ab=11a+2b-ab=(a-2)(11-b)+22畅要使f(x)有最大值,那么a-2、11-b都要有最大值,即a=9、b=0,f(x)最大值为99畅因此x为90畅10畅答案:10畅解 AGGE=△GFA△EFG=11、AECE=△ADE△EDC=31,所以EC=2、AE=6、AG=GE=3畅同理,AFFD=△AEF△FED=21、ADDB=△ACD△DCB=41,所以BD=3、AD=12、AF=8、FD=4畅由勾股定理:GF=AF2+AG2=82+32=73,FE=AF2+AE2=82+62=100=10,DE=AD2+AE2=122+62=180,DC=AD2+AC2=122+82=208畅长度为整数的线段为FE,FE=10畅11畅答案:150畅解 不包含阴影部分的正方形有大小不同的几种类型:面积为1的正方形:9×9-3×3=81-9=72;面积为4的正方形:8×8-4×4=64-16=48;面积为9的正方形:7×7-5×5=49-25=24;面积为16的正方形:6;共有:72+48+24+6=150个畅12畅答案:14040000畅解 设A委员会开会的天数为x天:(1)假设x≤15:13×6000x≤1170000,由条件知A委员会至少支出车马费1500000,矛盾;(2)假设15<x≤30:第1章 第一届青少年数学国际城市邀请赛A委员会支出:13×6000x,B委员会支出:6[6000×30+9000(2x-30)]畅由题意:13×6000x=6[6000×30+9000(2x-30)],x=18,总车马费为2808000元,小于3000000元,不合题意;(3)假设x>30:A委员会支出:13[6000×30+9000(x-30)]=117000x-1170000,B委员会支出:6[6000×30+9000(2x-30)]=108000x-54000,由题意:117000x-1170000=108000x-54000,解得x=70,总支出为(117000×70-1170000)×2=14040000畅第二部分1畅答案:8cm畅解 因为要求最长的路径,则蚂蚁经过的顶点最多为8个点(图1-9),即路径小于或等于8cm,如A→B→F→G→C→D→H→E→A畅图1-92畅答案:16109畅解 设CE=x、BD=y,则AC=8x、BC=4y、CD=3y畅在直角△ACD中,AD2=AC2+CD2,即(3y)2+(8x)2=1642,在直角△BCE中,BE2=BC2+CE2,即(4y)2+x2=522,解得x=20、y=12,即AC=160、BC=48,在直角△ACB中,AB=BC2+AC2=16109畅3畅答案:142857畅解 设这个6位数为abcdef,由题意,6个数字互不相同,且都不为0;因为这个数乘以5、6后还是6位数,因此a=1畅因为abcdef×5个位不为0,那么f为奇数,且不为5畅青少年数学国际城市邀请赛试题解答8 当f=3时,分别乘以1、2、3、4、5、6,末位分别为3、6、9、2、5、8,即出现7个不同数字,不合题意;当f=7时,分别乘以1、2、3、4、5、6,末位分别为7、4、1、8、5、2,恰出现6个不同数字,且包含1;当f=9时,分别乘以1、2、3、4、5、6,末位分别为9、8、7、6、5、4,出现7个不同数字,不合题意;因此f=7畅所以这6个不同数字分别为1、4、8、5、2、7,而17=0畅142857,恰好相同,且以7为分母的真分数均为循环小数,且循环节的数字相同,即这个六位数为142857畅1畅3 队际竞赛试题1畅(1)试将98+76+54+32+1分解成质因子的乘积畅(2)试找出230+330任意两个不同的质因子畅2畅请在所附的空白卡片上分别写上整数1、3、5、…、59,每张卡片上只写一个数畅(1)试问编号为1、3、5、7、9、11、13、15、17、19的10张卡片如何排列,使得这些卡片满足下列条件:如果从这叠卡片最上面取出第一张放到最下面,第二张卡片出现1,则将这张卡片取出放在旁边,然后在剩下的卡片中最上面取出3张依次放到最下面,接着最上面的卡片为3,把这张卡片取出放在旁边,依此方式重复上面的步骤,从最上面取出2k+1张卡片,其中2≤k≤8,并依次放到最下面,则最上面的卡片上出现2k+1,再把2k+1这张卡片取出放在旁边,最后一张是19畅请写出原来数字卡片的排列顺序畅(2)试仿照题(1)的做法,若这叠卡片编号为1、3、5、…、59,请问怎么排列这叠卡片,使得这叠卡片满足下列条件:如果从这叠卡片最上面取出第一张卡片放到最下面,第二张卡片出现1,则将这张卡片取出放在旁边,然后在剩下的卡片中最上面取出3张依次放到最下面,接着最上面的卡片为3,把这张卡片取出放在旁边,依此方式重复上面的步骤,从最上面取出2k+1张卡片,其中2≤k≤28,并依次放到最下面,则最上面的卡片上出现2k-1,再把2k+1这张卡片取出放在旁边,最后一张是59畅第1章 第一届青少年数学国际城市邀请赛9 请写出原来数字卡片的排列顺序畅3畅(1)试找出一组相异的正整数,包含5,使得它们的倒数之和是1畅(2)试找出一组相异的正整数,包含1999,使得它们的倒数之和是1畅4畅(1)试将一个正方形刚好分割成1999个内部没有重叠部分的小正方形,这些正方形的大小可以不相等,须写出解题过程畅(2)试将图1-10中的阴影部分剪开,用最少的片数填满图1-11(中间有2×2的洞),写出切开的片数,粘贴时允许部分图片翻转,须说明理由畅图1-10图1-115畅如图1-12所示,一个边长为5的正方形分割成25个小正方形,使每一行每一列都有5个单位长的正方形,把数字1,2,3,4,5填入这些小正方形中,使得1,2,3,4,5在每一行、每一列和每一条对角在线的5个小正方形中恰好出现一次,从左上到右下的对角线正下方的4个小正方形上的数字之和称为这个正方形的分数畅试问这个正方形的最高分数是多少?说明理由,并构造出这样的正方形填数畅青少年数学国际城市邀请赛试题解答10 图1-121畅4 队际竞赛试题解答1畅答案:(1)43165005=3×5×13×41×5399;(2)13和61畅解 (1)98+76+54+32+1=43165005,43165005=3×5×13×41×5399畅(2)由于x5+y5=(x+y)(x4-x3y+x2y2-xy3+y4),故对任意正整数x、y,x+y整除x5+y5,特别地,26+36整除230+330畅因为26+36=13×61,因此所求的两个质因子为13和61畅2畅答案:(1)11、1、5、7、17、3、13、15、9、19;(2)13、1、47、33、25、3、57、45、49、55、43、5、19、39、11、17、21、51、29、7、41、15、31、23、27、59、35、53、37、9畅解 (1)我们先把10张卡片排列好,按照操作一次一次拿出,再将需要拿出的卡片填上它应有的数字畅例如第一次操作将第一张卡片移到最下面,原来的第二张卡片将被拿出,在它上面填上1,接着将原来的第三、第四、第五张卡片移到最下面,原来第六张卡片将被拿出,在它上面写上3,以此类推,最终10张卡片上的数依次为11、1、5、7、17、3、13、15、9、19畅(2)仿照题(1)的做法,得到最终的排列为13、1、47、33、25、3、57、45、49、55、43、5、19、39、11、17、21、51、29、7、41、15、31、23、27、59、35、53、37、9畅3畅答案:(1)2、5、8、12、20、24;(2)1×2、2×3、3×4、4×5、…、1998×1999、1999畅解 (1)因为1=12+14+18+18,其中14=15+120,18=112+124,即符合题意的一组正整数为2、5、8、12、20、24畅(2)因为1=11×2+12×3+13×4+…+1n-1n+1n,当n=1999时,这组的正整数分别是1×2、2×3、3×4、4×5、…、1998×1999、1999,共1999个数畅第1章 第一届青少年数学国际城市邀请赛11 4畅解 (1)因为一个正方形可被分割成4个正方形,只要将其中一个正方形再分割成4个正方形,就可得到7个正方形;重复将其中一个正方形分割成4个正方形,就可得到10个正方形;……畅重复这些动作,每次都会增加3个正方形,即一个正方形被分割成不规定大小的正方形的个数是N=4,7,10,13,…,即3的倍数加1的正整数,1999正好是3的倍数加1,就可以按照这个方法分割畅(2)将图1-10剪成9小片,如图1-13所示畅图1-13拼入图1-11中,如图1-14所示畅图1-145畅答案:17畅解 首先我们证明阴影部分不能有3个或者4个5畅显然,若是有4个5,则左上-右下对角在线不会有5;若是有3个5,则分情况讨论易知剩下两个5无法满足两条对角在线各有一个5(由对称性,只需讨论两种情况)畅假设阴影部分是两个5和两个4,由对称性讨论3种情况:(1)由左上到右下依次为5、5、4、4;(2)由左上到右下依次为5、4、5、4;(3)由左上到右下依次为5、4、4、5畅青少年数学国际城市邀请赛试题解答12 对于(1)和(2),原大正方形的左下-右上对角在线,左下方的4个格子都不能是4或5,因此右上角的格子必须既是4又是5,矛盾;对于(3),大正方形左上-右下的对角在线中间的3个格子已经不能是4,故不妨设左上角的格子为4,而剩下两个4的位置要使各行各列都恰有一个4,则只能在第二行第四列及右下角各放一个4,这样左上-右下对角在线有两个4,矛盾畅综上,阴影部分最多有两个5,也不能是两个5和两个4,因此正方形的分数最高为5+5+4+3=17畅图1-15是取到17的一个例子畅图1-15第2章 第二届青少年数学国际城市邀请赛2畅1 个人竞赛试题第一部分填空题,共12题,每题5分畅1畅172000个位上的数字是畅2畅从13、16、19、112、115、118中去掉两项,使得余下各项的和等于23,那么去掉的那两项乘积等于畅3畅设A为小于1000大于100的奇数,若A的百位数字大于它的个位数字,且A是11的倍数,那么满足这些条件所有可能的值中最小值为畅4畅将150至650之间除以10余4的整数全部相加,总和为畅5畅设N=111…1222…2,其中有2000个1,2000个2;则N被666…62000除时,商为畅6畅著名的哥德巴赫(Goldbach)猜想是:对于任意一个大于7的偶数一定可以表示为两个不同的质数之和,例如10=3+7,我们希望找到两个不同的质数p,q使得p+q=192,且使2p-q越大越好,那么数对(p,q)=畅7畅在△ABC中,点D为BC上一点,若AC=CD,且∠CAB=∠ABC+45°,则∠BAD的度数为畅8畅已知:100000035811ab12=1000000cde2247482444265735361,其中a、b、c、d、e均为小于10的非负整数,那么a+b+c-d-e的值为畅9畅在长方形ABCD中,P为此长方形内部的一点畅若PA=4、PB=6、PD=9,则PC的长度为畅10畅某种新的温度计在水结冰时显示的度数为20℃,煮沸时为160℃,摄氏温度计显示冰点为0℃,沸点为100℃,那么在215℃时,新温度计显示℃畅13青少年数学国际城市邀请赛试题解答14 11畅已知正方形ABCD内接于圆O,将这个圆对折成半圆,作这个半圆的内接正方形EFGH,那么正方形EFGH的面积与正方形ABCD的面积之比是畅12畅有一叠纸牌共10张,每张纸牌上都印有一个正整数,已知任意连续的3张纸牌上的正整数之和都是20,且第一张纸牌上的数字为2,第九张纸牌上的数为8,则第五张纸牌上的数为畅第二部分计算证明题,共3题,每题20分畅1畅如图2-1所示,将一张正方形纸片ABCD折叠,使得A点落在BC边上A′图2-1点处,D点落在D′点处,折线为EF,其中点E在AB边上,点F在CD边上,折叠后,A′D′与CD交于点G畅试证:A′E+FG=A′G畅2畅有10张卡片,每张卡片的正反两面都各写了一个正整数,这20个正整数互不相同,每张卡片正反面的数字和都相等,且这10张卡片正面的数字总和等于这10张卡片反面的数字总和,其中9张卡片上正面的数字分别为2、5、17、21、24、31、35、36、42,请问第10张卡片正面的数为多少?3畅从100到999的每一个正整数均称为3位数,从1000到9999的每个正整数均称为4位数,组成任一个正整数的各位数字相加之和称为这个正整数的数字和,例如312的数字和为6畅假设a、b、c均为正整数,其中a、b为3位数、c为4位数,若a+b、b+c、c+a的数字和都等于3,请问a+b+c的最大值为多少?2畅2 个人竞赛试题解答第一部分1畅答案:1畅解 考虑7的幂:71=7、72=49、73=343、74=2401、75=16807、…,发现规律,7的幂个位数以4为周期,即2000÷4=500,余数为0,即172000个位上的数字为1畅2畅答案:1180畅解 这6个数之和为4960,要去掉2项,余下4项和为23,即4060,即去掉的2项第2章 第二届青少年数学国际城市邀请赛15 之和为960,即112、115,这2项的乘积为1180畅3畅答案:231畅解 因为A是11的倍数,设A=11x,要使A为小于1000大于100的奇数且A的百位数字大于它的个位数字,那么x为奇数,且x>20,当x=21,A=231畅4畅答案:19950畅解 150至650之间除以10余4的整数为个位数字为4的数,即154、164、174、…、644,共50个数,这些数的和为(154+644)×502=19950畅5畅答案:166…67198畅解 观察n=12=3×4,n=1122=33×34,n=111222=333×334,⁝因此N=111…1222…2=333…3×33…34,其中333…3有2000个3,33…34有1999个3,1个4畅因此N被666…62000除的商为166…619987畅6畅答案:(181,11)畅解 使2p-q越大,那么p要越大,q要越小畅相加为192的两个质数,符合题意的p=181、q=11畅即(p,q)=(181,11)畅7畅答案:22畅5°畅解 设∠ABC=x、∠BAD=y、∠CAD=∠CDA=z(图2-2),图2-2由题意得x+y=z,青少年数学国际城市邀请赛试题解答16 x+45°-y=z,解得y=22畅5°畅8畅答案5畅解 100000035811ab12=(1014+35811ab1)2=1028+2×1014×35811ab1+35811ab12畅因为35811ab12是15位数,而c、d、e是原数中第22、23、24位数,由2×1014×35811ab1决定,因此cde=2×358=716;35811ab12=(35811×103+ab1)2=35811×106+2×35811×103×ab1+ab12;那么得数的后五位只与2×35811×103×ab1和ab12有关,后两位只与ab12有关,那么2b=6,b=3;百位的3为2a+b2的个位数,即a=2,因此a+b+c-d-e=2+3+7-1-6=5畅9畅答案:101畅解 过P点作两条互相垂直的线段,且分别与AD、AB平行,交长方形的四边分别为E、F、G、H,如图2-3所示畅图2-3设PE=a、PF=b、PG=c、PH=d,由题意得a2+d2=42,a2+b2=92,d2+c2=62,第2章 第二届青少年数学国际城市邀请赛17 PC=b2+c2=92+62-42=101畅10畅答案:321℃畅解 设215℃时该新温度计为x℃,100140=215x,解得x=301畅因此新温度计上显示的度数为301+20=321℃畅11畅答案:2∶5畅解 如图2-4所示,设圆O的半径为r,OG=x、HG=2x,由勾股定理:x2+(2x)2=r2,x2=r25畅正方形EFGH的面积为4r25,正方形ABCD的面积为2r2,那么两个面积之比为2∶5畅图2-412畅答案:10畅解 设前3张纸牌上的数为2、a、b,第四张纸牌为x,由题意:2+a+b=a+b+x,即x=2,那么这列数为2、a、b、2、a、b、2、a、b、2,因为第九张纸牌上的数为8,即b=8,第五张纸牌上的数为a=20-2-8=10畅第二部分1畅解 如图2-5所示,连接AA′,显然AA′⊥EF,因此AE-DF=BA′(做E或F到对边CD或AB的垂足即可以看出来)畅因此BE+DF+BA′=AB-AE+(DF+BA′)=AB畅青少年数学国际城市邀请赛试题解答18 两边同时减去BA′得BE+DF=A′C畅显然DF=D′F,故BE+D′F=A′C畅注意到3个△EBA′、△A′CG和△D′FG彼此相似,且BE、D′F、A′C为它们对应的一条直角边,EA′、A′G、FG为它们的斜边,因此有BEEA′=A′CA′G=D′FFG,故A′E+FG=A′G畅图2-52畅答案:37畅解 设第十张卡片正面的数为x,每张卡片正反面的数之和为y:10张卡片正面的数总和为2+5+17+21+24+31+35+36+42+x;10张卡片反面的数总和为10y-(2+5+17+21+24+31+35+36+42)-x;即x+213=10y-x-213,化简得5y=x+213,因为y-x≥0,即x+2135-x≥0,x≤5314畅因此,x所有可能的取值为7、12、22、27、32、37、47、52,但这20个数互不相同畅经检验,x=37符合题意畅即第十张卡片正面的数为37畅3畅答案:10800畅解 由于a、b为3位数,故200≤a+b≤1998,结合a+b的数码和为3知a+b的最大可能值为1200畅由于a为3位数、c为4位数,故1100≤a+c≤10998,结合a+c的数码和为3知a+c的最大可能值为10200畅同理b+c的最大可能值也为10200畅故a+b+c=12[(a+b)+(a+c)+(b+c)]第2章 第二届青少年数学国际城市邀请赛19 ≤12(1200+10200+10200)=10800畅其中,等号当且仅当a=b=600、c=9600时取到畅评注 若要求a、b不等,则a+c与b+c中有一个最多为10200,另一个最多为10110,故a+b+c的最大值为10755,此值为当a=555、b=645、c=9555时取到畅2畅3 队际竞赛试题1畅已知正方形ABCD,点E为BC边上的中点,H为AE上一点,使得BE=EH,X为AB上一点使得AH=AX,试证:AB·BX=AX2畅2畅在下面5×5的表格中(表2-1),已经填入了4个非负整数,请在余下21个空格中填入正整数使得每行每列之和相等畅表2-1 827910303畅对于任意n≥1,定义an=1000+n2,若dn为an和an+1的最大公约数,n=1、2、…,试求dn的最大值畅4畅某校初一有A、B、C、D、E5个班级,5个班级的导师分别为a(A班),b(B班),c(C班),d(D班),e(E班),考试后,5名导师预测5个班级的排名情况见表2-2畅表2-2 项目第一名第二名第三名第四名第五名导师aABCDE导师bEDABC导师cEBCDA。
第41届环球城市数学竞赛秋季赛O水平

41st INTERNATIONAL MATHEMATICAL TOURNAMENT OF TOWNS Junior O-Level Paper,Fall2019Grades8–9(ages13-15)(The result is computed from the three problems with the highest scores.) points problems41.An illusionist performs the following trick:he lays a full deck of52cards in a row.On each step a spectator selects some integer number, and the card lying on the place with this number in the row is thrown away.However,each time after the number is selected the illusionist chooses from which side of the row it is counted.The illusionist announced beforehand that in the end only a definite card,namely the Three of Clubs,should remain.For which initial positions of the Three of Clubs the illusionist can guarantee the success of the trick?Alexey Voropaev42.Letωbe a circle with the center O and A and C be two differentpoints onω.For any third point P of the circle let X and Y be the midpoints of the segments AP and CP.Finally,let H be the orthocenter(the point of intersection of the altitudes)of the triangle OXY.Prove that the position of the point H does not depend on the choice of P.Artemiy Sokolov43.There is a row of100cells each containing a token.For1dollar itis allowed to interchange two neighbouring tokens.Also it is allowed to interchange with no charge any two tokens such that there are exactly3tokens between them.What is the minimum price for arranging all the tokens in the reverse order?Egor Bakaev54.There are given1000integers a1,...,a1000.Their squaresa21,...,a21000are written in a circle.It so happened that the sum of any41consecutive numbers on this circle is a multiple of412.Is it necessarily true that every integer a1,...,a1000is a multiple of41?Boris Frenkin55.Basil has an unrestricted supply of straight bricks1×1×3andΓ-shape bricks made of three cubes1×1×1.Basil filled a whole box m×n×k with these bricks,where m,n and k are integers greater than1.Prove that it was sufficient to use onlyΓ-shape bricks.Mikhail Evdokimov。
02奥赛及解答

2002年中国数学奥林匹克试题及解答(考试时间:2002年1月27号、28号)试题:一、△ABC 的三边长分别为a ,b ,c ,b<c ,AD 是角A 的内角平分线,点D 在边BC 上。
(1)求在线段AB ,AC 内分别存在点EF (不是顶点)满足BE=CF 和∠BDE=∠CDF 的充分必要条件(用角A 、B 、C 表示);(2)在点E 和F 存在的情况下,用a ,b ,c 表示BE 的长。
二、设多项式序列)}x (P {n 满足:)1x (x 2)x (P 1x )x (P 2221-=-=,,且222n 1n 1n )1x())x (P ()x (P )x (P --=-+,n=2,3,…。
设n S 为)x (P n 各项系数的绝对值之和,对于任意正整数n ,求非负整数n k 使得n knS 2-为奇数。
三、18支足球队进行单循环赛,即每轮将18支球队分成9组,每组的两队赛一场,下一轮重新分组进行比赛,共赛17轮,使得每队都与另外17支球队各赛一场,按任意可行的程序比赛了n 轮之后,总存在4支球队,它们之间总共只赛了1场,求n 的最大可能值。
四、对平面上任意四个不同点4321P P P P ,,,,求ji j i j i j i P P P P 4141min≤≤≤≤≤≤∑的最小值。
五、平面上横纵坐标都为有理数的点称为有理点,证明平面上的全体有理点可分为三个两两不相交的集合,满足条件:(1)在以每个有理点为圆心的任一圆内一定包含这三个集合中每个集合的点; (2)在任意一条直线上不可能有三个点分别属于这三个集合。
六、给定)1 21(c ,∈,求最小常数M ,使得对任意整数n ≥2及实数n 21a a a 0≤⋯≤≤<,只要满足∑∑===n1k kn1k kackan1,总有∑∑==⋅≤n1k m1k k k a M a ,其中m 是不超过cn 的最大整数。
解答:一、(1)由条件BE=CF ,∠BDE=∠CDF …①,得CDF BDE S S ∆∆=,∴BD ·DE=CD ·DF …②, C D Fc o s DF CD 2DFCDCFBEBDE cos DE BD 2DEBD 222222∠⋅-+===∠⋅-+…③由①、②、③,得2222DFCDDEBD+=+…④由②、④得BD+DE=CD+DF …⑤以及22)DF CD ()DE BD (-=-…⑥由⑥知,BD-DE=CD-DF …⑦,或BD-DE=DF-CD …⑧ 若⑦成立,则由⑤,BD=CD 这与条件b<c 矛盾。
数学竞赛题-世界各国最新平几竞赛题

数学竞赛题(第一章 有关直线的试题)1.设ABC ∆的三边长分别为,,.,,AB c BC a CA b a b c ===互不相等,,,AD BE CF 分别为ABC ∆的三条内角平分线,且DE DF =,证明:⑴a b c b c c a a b=++++; ⑵90BAC ∠>︒. (2003年中国女子数学奥林匹克)2.证明:若凸四边形ABCD 内任意一点P 到边AB ,BC ,CD ,DA 的距离之和为定值,则ABCD 是平行四边形. (2003年中国西部数学奥林匹克)3.已知ABC ∆的外接圆半径为R ,若c o s c o sc o s s i n s i n s i n 9a b c a b c a b c R αβγβγα⋅+⋅+⋅++=⋅+⋅+⋅,其中,,,a b c为ABC ∆的三边长,,,αβγ分别为,,A B C ∠∠∠的角度数,求,,αβγ的值.(2002—2003年匈牙利数学奥林匹克)4.由小三角形12,,,n H H H 拼成三角形H ,它们的内切圆半径分别为12,,,n r r r 和r ,证明:r ≤12.n r r r +++ (2002—2003年匈牙利数学奥林匹克)5.已知ABC ∆,由顶点A 分别向B ∠和C ∠的平分线引垂线,垂足分别为1A 和2A ,同理,定义12,B B 和12,.C C 证明:1212122().A A B B C C AB BC CA ++=++(2002—2003年匈牙利数学奥林匹克)6.平面上的点集H 称为是好的,如果H 中任意3个点都存在一条对称轴,使得这3个点关于这条对称轴对称,证明:⑴一个好的集合不一定是轴对称的;⑵如果一个好的集合中恰有2003个点,则这2003个点在一条直线上7.设H 是锐角△ABC 的高线CP 上的任一点,直线AH ,BH 分别交BC ,AC 于点M ,N .⑴证明:∠NPC=∠MPC ;⑵设O 是MN 与CP 的交点,一条通过O 的任意的直线交四边形CNHM 的边于D ,E 两点,证明:∠EPC=∠DPC8.P 是△ABC 内的一点,直线AC ,BP 相交于Q ,直线AB ,CP 相交于R ,已知AR=RB=CP ,CQ=PQ ,求∠BRC9.在锐角△ABC 中,点A ,B 到对边垂线的垂足分别为,.,a b H H A B ∠∠的平分线分别交对边点,a b W W ,证明:ABC ∆的内心I 在线段a b H H 上当且仅当外心O 在a b W W 上10.在ABCD 中,,M N 分别在AB ,BC 上,且,M N 不与端点重合,AM=NC ,设AN 与CM 交于点Q ,证明:DQ 平分∠ADC11.对于任意三角形都有两条边的边长之差不超过这个三角形周长的六分之一,请判断此命题是否成立12.已知△ABC ,且边AC ,BC 中点的连线为,,c l A B ∠∠的平分线分别交直线c l 于M ,N ,同理,在直线b l 上定义K ,L ;在直线a l 上定义P ,Q ,证明:2(MN+KL+PQ)=AB+BC+CA13.如图,已知锐角△ABC 的三边BC ,CA ,AB 的中点分别为A 1,B 1,C 1,分别由A 1,B 1,C 1向△ABC 的的另外两条边作垂线,相应的交点分别为A 2,B 2,C 2,证明:六边形A 1C 2B 1A 2C 1B 2的面积等于△ABC 面积的一半14.在一条直线上按A ,B ,C 的次序排列着三个点,且AB=8,AC=18,D 为直线外一点,且DA ⊥AB ,求AD 等于多少时,∠BDC 有最大值?15.已知梯形ABCD ,AB ∥CD ,若高为2,AB=2,CD=4,且AB 的中点为M ,当边CD 上的点N 移动时,求△ANB 和△DMC 公共部分的面积的最大值16.已知一个角的一条边上有1001个不同的点A 0,A 1,…,A 1000,另一条边上也有1001个不同的点B 0,B 1,…,B 1000,且满足A 0A 1=A 1A 2=…=A 999A 1000,B 0B 1=B 1B 2=…=B 999B 1000,若四边形A 0A 1B 1B 0和四边形A 1A 2B 2B 1的面积分别为5和7,求四边形A 999A 1000B 1000B 999的面积17.已知圆内接四边形ABCD 满足AB=BC=AD+CD ,∠BAD=a ,AC=d ,求△ABC 的面积18.若三角形和矩形有相等的周长和面积,则称它们是“孪生的”,证明:对于给定的三角形,存在“孪生的”矩形,该矩形不是正方形,且较长的边与较短的边之比至少为1λ-+λ= 19.已知凸五边形ABCDE 满足AB=BC ,CD=DE ,∠ABC=150°,∠CDE=30°,BD=2,求五边形ABCDE 的面积20.锐角△ABC 中,H 是垂心,O 是外心,I 是内心,已知∠C >∠B >∠A ,求证:I 在 △BOH 内部21.设D 为锐角△ABC 内部一点,且满足条件:DA ·DB ·AB+DB ·DC ·BC+DC ·DA ·CA=AB ·BC ·CA ,试确定点D 的几何位置,并证明你的结论22.如图,在四边形ABCD 中,对角线AC 平分∠BAD ,在CD上取一点E ,BE 与AC 相交于F ,延长DF 交BC 于G ,求证明:∠GAC=∠EAC23.平面上给定凸四边形ABCD 及其内点E 和F ,适合AE=BE ,CE=DE ,∠AEB=∠CED ,AF=DF ,BF=CF ,∠AFD=∠BFC ,求证:∠AFD+∠AEB=π24.给定正△ABC ,D 是BC 边上任意一点,△ABD 的外心、内心分别为O 1,I 1,△ADC 的外心、内心分别为O 2,I 2,直线O 1I 1与O 2I 2相交于P ,试求:当点D 在BC 边上运动时,点P 的轨迹25.设锐角△ABC 的外心为O ,从A 作BC 的高,垂足为P ,且∠BCA ≥∠ABC+30°,证明:∠CAB+∠COP <90°26.设点I ,H 分别为锐角△ABC 的内心垂心,点B 1,C 1分别为AC ,AB 的中点,已知射线B 1I 交边AB 于点B 2(B 2≠B),射线C 1I 交AC 的延长线于点C 2,B 2C 2与BC 相交于K ,A 1为△BHC 的外心,试证:A ,I ,A 1三点共线的充分必要条件是△BKB 2和△CKC 2的面积相等27.锐角△ABC 有三条高分别为AD ,BE ,CF ,求证:△DEF 的周长不超过△ABC 周长的一半28.凸四边形ABCD 的对角线交于点M ,点P ,Q 分别是△AMD 和△CMB 的重心,R ,S 分别是△DMC 和△MAB 的垂心,求证:PQ ⊥RS29.设D ,E ,F 分别为△ABC 的边BC ,CA ,AB 上的点,,,,αβγδ分别是△AEF ,△BFD ,△CDE 和△DEF 的面积,求证:111αββγγα++≥23δ30.在给定梯形ABCD 中,AD ∥BC ,E 是AB 边上的动点,O 1,O 2分别是△AED 和△BEC 的外心,求证:O 1O 2的长为一定值31.设一个凸n 边形没有两条边互相平行,求证:过其内部一点O 平分该n 边形的面积的直线至多n 条32.△ABC 中,AC >AB ,P 为BC 的垂直平分线和∠A 的内角平分线的交点,作PX ⊥AB ,交AB 的延长线于点X ,PY ⊥AC ,交AC 于点Y ,Z 为XY 和BC 的交点,求BZ ZC的值 33.设D 为△ABC 的边AC 上一点,E 和F 分别为线段BD 和BC 上的点,满足∠BAE=∠CAF ,再设P ,Q 为线段BC 和BD 上的点,使得EP ∥QF ∥DC ,求证:∠BAP=∠QAC34.已知△ABC 的三个顶点A ,B ,C 分别在锐角△A 1B 1C 1的边B 1C 1,C 1A 1,A 1B 1上,使得∠ABC=∠A 1B 1C 1,∠BCA=∠B 1C 1A 1,∠CAB=∠C 1A 1B 1,求证:△ABC 和△A 1B 1C 1的垂心到△ABC 的外心距离相等35.设△ABC 的三边,,a b c 上对应的中线为,,a b c m m m ,内角平分线为,,a b c w w w ,且,,a b b c c a w m P w m Q w m R ===,记△PQR 的面积为δ,△ABC 的面积为F ,求使不等式F δλ<成立的最小正常数λ36.⑴设D 为△ABC 内任一点,求证:2sin ,902,90min{,,}A A BC A AD BD CD ∠<︒⎧≥⎨∠≥︒⎩ ⑵设E 为凸四边形ABCD 内任一点,A ,B ,C ,D ,E 五点中任意两点间的最大距离与最小距离之比记为k ,求证:k ≥2sin70︒,并说明等号能否成立37.在锐角△ABC 中,AD 是∠A 的内角平分线,点D 在边BC 上,过点D 分别作DE ⊥AC ,DF ⊥AB ,垂足分别为E ,F ,联结BE ,CF ,它们相交于点H ,△AFH 的外接圆交BE 于点G ,求证:线段BG ,GF 和BF 组成的三角形是直角三角形38.以△ABC 的三边向形外分别作正方形ABHI ,BCDE 和CAFG ,设XYZ 是线段EF ,DI和GH 围出的三角形,求证:(4XYZ ABC S S ∆∆≤-39.锐角△ABC 中,AB ≠AC ,H ,G 分别为该三角形的垂心和重心,已知11HAB HAC S S ∆∆+2HBC S ∆=,求证:90AGH ∠=︒40.在△ABC 中是否存在一点P ,使得过点P 的任意直线都将△ABC 分成面积相等的两部分?为什么?41.AD ,BE ,CF 是△ABC 的高,K ,M ,N 分别为△AEF ,△BFD ,△CDE 的垂心,求证:△DEF 和△KMN 是全等三角形42.已知过锐角△ABC 顶点A ,B ,C 的高线分别交对边于D ,E ,F ,AB >AC ,直线EF 交BC 延长线于P ,过点D 且平行EF 的直线分别交AC 延长线和AB 于Q ,R ,N 是BC 上的一点,且∠NQP+∠NRP <180°,求证:BN >CN43.点A 在∠KMN 内,点B 在KM 上,点C 在MN 上,如果∠CBM=∠ABK ,∠BCM= ∠CAN ,求证:△BCM 的外心在AM 上44.如图,△AEF 是矩形ABCD 的内接直角三角形,E ,F 分别在边BC ,CD 上,且∠AEF= 90°,AE= 4,EF=3,求矩形ABCD 面积的最小值45.已知I 为△ABC 的内心,联结AI ,BI ,CI ,若△BIC ,△CIA ,△AIB 中有一个三角形与△ABC 相似,求△ABC 各角的大小46.设P 为锐△ABC 内一点,P 到三条边BC ,CA ,AB 的垂足分别为D ,E ,F ,求出(并加以证明)使PD 2+PE 2+PF 2达到最小值的点P47.已知△ABC 是边长为1的正三角形,D 是边BC 上一点且BD= p ,r 1,r 2分别是△ABD 和△ADC 的内切圆的半径,请用p 表示r 1r 2,并求r 1r 2的最大值48.已知D 是△ABC 的边AB 上的任意一点,E 是边AC 上的任意一点,联结DE ,F 是线段DE 上的任意一点,设,,AD AE DF x y z AB AC DE===,证明: ⑴(1),(1)(1)BDF ABC CEF ABC S x yzS S x y z S ∆∆∆∆=-=--49.在锐角△ABC 中,点A ,B ,C 在边BC ,CA ,AB 上的投影分别为D ,E ,F ,点A ,B ,C 在边EF ,FD ,DE 上的投影分别为P ,Q ,R ,记△ABC ,△PQR ,△DEF 的周长分别为p 1,p 2,p 3,证明:p 1p 2≥p 2350.P 是凸四边形ABCD 所在平面上一点,∠APB ,∠BPC ,∠CPD ,∠DPA 的平分线分别交AB ,BC ,CD ,DA 于点K ,L ,M ,N⑴寻找一点P ,使KLMN 是平行四边形;⑵求所有这样点P 的轨迹51.设D是△ABC的边BC上的一点,点P在线段AD上,过点D作一直线分别与线段AB,PB交于点M,E,与线段AC,PC的延长线交于点F,N,已知DE=DF,求证:DM=DN 52.在凸四边形ABCD中,AB=a,BC=b,CD=c,DA=d,AC=e,BD=f,且max{a,b,c,d,e,f}=1,求abcd的最大值53.点D,E,F分别在锐角△ABC的边BC,CA,AB上(均不是端点),满足EF∥BC,D1是边BC上一点(不同于B,D,C),过D1作D1E1∥DE,D1F1∥DF,分别交AC,AB 两边于点E1,F1,联结E1F1,再在BC上方(与A同侧)作△PBC,使得△PBC∽△DEF,联结PD1,求证:EF,E1F1,PD1三线共点54.设a,b,c是周长不超过2π的三角形的三条边长,证明:长为sina,sinb,sinc的三条线段可构成三角形55.已知等腰△ABC的边长BC= a,AB=AC =b,M,N分别是边AC和AB上的动点,满足a2·AM·AN= b2·BN·CM,直线BM和CN相交于点P,求动点P的轨迹56.△ABC在平面π上,周长为3+π上与△ABC全等的三角形内部或边界上至少有一个整点,证明:△ABC是等边三角形57.设E为凸四边形ABCD的对角线的交点,F1,F2,F3分别为△ABE,△CDE,四边形ABCD58.已知一个凸多边形x的边长和对角线均为有理数,凸多边形x被它的所有对角线分成一些小凸多边形,证明这些小凸多边形的边长都是有理数59.在△ABC中,∠A=90°,AC>AB,我们在边AC上取点E,在边BC上取点D,使得AB=AE=BD,求证:∠ADE=90°的充分必要条件是AB∶AC∶BC=3∶4∶560.△ABC的边BC和边AC分别取定长a和b,而边AB的长度可变动,以边AB作正方形的一边向三角形外作正方形,设O是所作正方形的中心,并设BC和AC的中点分别为M 和N,试求OM+ON的最大值61.给定凸四边形ABCD,若在四边形ABCD内有点M,使得△AMB和△CMD为等腰三角形(即AM=MB,CM=MD),且∠AMB=∠CMD=120°,试证存在一点N,使得△BNC 和△DNA都是正三角形62.设CM和BN为△ABC的中线,在边AB及AC上可分别取点P及Q,使得∠ACB的角平分线也是∠MCP的角平分线,且∠ABC的角平分线也是∠NBQ的角平分线,试问AP=AQ 是否蕴含△ABC为等腰三角形?63.设△ABC为锐角三角形,它的外心为O,将△AOC的外心记为T,将边AC的中点记为M,在边AB和BC上分别取点D和E,使得∠BDM=∠BEM=∠ABC,证明BT⊥DE 64.已知正△ABC内一点D,满足∠ADC=150°,证明:由线段AD,BD,CD为边构成的三角形是直角三角形65.△ABC的外心为O,三条高线AH,BK,CL的垂足分别为H,K,L,A0,B0,C0分别是AH,BK,CL的中点,以I为圆心的内切圆分别切△ABC的三边BC,CA,AB于点D,E,F,证明:A0D,B0E,C0F,OI四线共点(当O,I重合时,直线OI视作任一条过点O 的直线)66.M,N,P分别是△ABC的三边BC,CA,AB的中点,M1,N1,P1在△ABC的边上,且满足MM1,NN1,PP1分别平分△ABC的周长,证明:⑴MM 1,NN 1,PP 1交于同一点K ; ⑵,,KA KB KCBC CA AB 67.证明:一个三角形可以被分割成三个多边形(包括三角形),其中之一为钝角三角形,且能重新拼为一个矩形(多边形允许被翻转)68.已知△ABC 中,∠C 为直角,D 为边AC 上一点,K 为边BD 上一点,且∠ABC=∠KAD=∠AKD ,证明:BK=2DC69.将平面过点O 的n (n >2)条直线作上标记,对于任意如上过点O 的两条直线,总存在一条作过标记的直线平分这两条直线所成的角,证明:这n 条直线满足相邻直线的夹角相等70.已知凸四边形ABCD 的对角线AC 上一点K ,满足KD=DC ,∠BAC=12∠KDC ,∠DAC= 12∠KBC ,证明:∠KDA=∠BCA 或∠KDA=∠KB ′A 71.在R △ABC ,∠A=90°,∠A 的平分线交边BC 于点D ,点D 在边AB ,AC 上的投影分别为P ,Q ,若BQ 交DP 于点M ,CP 交DQ 于点N ,BQ 交CP 于点H ,证明:⑴PM=DN ;⑵MN ∥BC ;⑶AH ⊥BC72.一个凸多边形P 被它所有的对角线分成一些小凸多边形,且P 满足:它的所有的边和对角线的长度都为有理数,证明:所有小凸多边形的边长都是有理数73.在锐角△ABC 中,|BC|<|AC|<|AB|,点D ,E 分别在边AB ,AC 上,且满足|BD|=|BC|=|CE|,证明:△ADE 的外接圆半径等于△ABC 的内心到外心的距离74.设四边形ABCD 是矩形,E ,F 分别是边BC ,CD 上的点,且满足△AEF 是正三角形,证明:ECF ABE AFD S S S ∆∆∆=+75.对于由平面上任意5个点构成的集合S ,满足S 中的任意三点不共线,设M (S )和m (S )分别为由S 中的3个点构成的三角形的面积的最大值和最小值,求()()M S m S 的最小值 76.设ABCDEF 是凸六边形,360B D F ∠+∠+∠=︒,且1AB CD EF BC DE FA⋅⋅=,证明:1BC AE FD CA EF DB⋅⋅= 77.设M ,N 分别是△ABC 的边AC ,BC 上的点,且∠ACB=90°,设AN 与BM 交于点L ,证明:△AML ,△BNL 的垂心与点C 三点共线78.设E ,F 是ABCD 的边AD ,CD 上的点,∠AEB=∠AFB=90°,EG ∥AB ,且EG 与BF 交于点G ,若AF 交BE 于点H ,DH 交BC 于点I ,证明:FI ⊥GH79.如图,已知△ABC 的∠ACB ,∠BAC ,∠ABC 的外角平分线分别为A 1C ,B 1A ,C 1B ,点A ,B ,C 在A 1C ,B 1A ,C 1B 上的投影分别为A 1,B 1,C 1,若d 是△A 1B 1C 1外接圆的直径,r 和p 分别为△ABC 的内切圆半径和半周长,证明:r 2+p 2=d 280.求最小的数k ,使得a b t t k a b+<+,其中,a b 是三角形的两条边长,,a b t t 分别是与这两条边相对应的角平分线长81.已知△KLM ,A 在LK 的延长线上,试构造矩形ABCD ,使得B ,C ,D 分别在边KM ,LM ,KL 所在的直线上82.已知CH 是Rt △ABC 的高(∠C=90°),且与角平分线AM ,BN 分别交于P ,Q 两点,证明:通过QN ,PM 中点的直线平行于斜边AB83.假设ABCD 是边长为a 的正方形纸板,平面上有两条距离为a 的平行线1l 和2l ,将正方形ABCD 放在这个平面上,使得边AB ,AD 与1l 的交点分别为E ,F ,边CB ,CD 与2l 的交点分别为G ,H ,设△AEF ,△CGH 的周长分别为1m ,2m ,证明:无论怎样放置正方形纸板ABCD ,12m m +是定值84.假设平面上的n 个点中任意三点不共线,且满足下列性质:无论怎样将这n 个点分别记为A 1,A 2,…,A n ,折线A 1A 2…A n 自身不相交,求n 的最大值85.△ABC 中,O 为外心,三条高AD ,BE ,CF 交于点H ,直线ED 和AB 交于点M ,FD 和AC 交于点N ,求证:⑴OB ⊥DF ,OC ⊥DE ;⑵OH ⊥MN86.已知△ABC 的三边长分别为,,a b c ,点P 在△ABC 的内部,P 到三条边的距离分别为,,p q r ,证明:R 222R 为△ABC 的外接圆半径,并确定等号成立的条件 87.已知△ABC 覆盖凸多边形M ,证明:存在一个与△ABC 全等的三角形,能够覆盖M ,并且它的一条边所在的直线与M 的一条边所在的直线平行或者重合88.设P 是一个凸多边形,证明:在P 内存在一个凸六边形,其面积至少是P 的面积的3489.设K ,M 是△ABC 的边AB 上的两点,L ,N 是边AC 上的两点,K 在M ,B 之间,L 在N ,C 之间,且BK CL KM LN=,求证:△ABC ,△AKL ,△AMN 的垂心在一条直线上 90.设点O 是锐角△ABC 的外心,B C ∠<∠,直线AO 交边BC 于点D ,△ABD ,△ACD 的外心分别为点E ,F ,延长BA 和CA ,在延长线上分别取点G ,H ,使得AG=AC ,AH=AB ,证明:四边形EFGH 是矩形的充分必要条件是60ACB ABC ∠-∠=︒91.如图所示,在△ABC 中,90,,ABC D G ∠=︒是边CA 上的两点,联结BD ,BG ,过点A ,G 分别作BD 的垂线,垂足分别为E ,F ,联结CF ,已知BE=EF ,求证:ABG DFC ∠=∠92.在△ABC 中,P ,Q 分别是边AB ,AC 上的点,且使得45APC AQB ∠=∠=︒,过点P 作边AB 的垂线与BQ 交于点S ,过点Q 作边AC 的垂线与CP 交于点R ,设D 是BC 上的点,且使得AD ⊥BC ,证明:PS ,AD ,QR 三线共点,且SR ∥BC93.在等腰直角△ABC 中,CA=CB=1,点P 是△ABC 边界上任意一点,求PA ·PB ·PC 的最大值94.已知正n 边形12n A A A ,定义点121,,,n B B B -如下:⑴如果1i =或1i n =-,则i B 是边1i i A A +的中点;⑵如果1,1,i i i n S ≠≠-是11i A A +和n i A A 的交点,则i B 是1i i i A S A +∠的角平分线与1i i A A +的交点;证明:111211180n n n n A B A A B A A B A -∠+∠++∠=︒95.给定实数,,0a b a b >>,将长为a 宽为b 的矩形放入一个正方形内(包含边界),问正方形的边至少为多长?96.证明:三角形的三条中线的和大于其三边之和的34倍 97.已知△ABC 的三边BC ,CA ,AB 上各有一点D ,E ,F ,且满足AD ,BE ,CF 交于一点G ,若△AGE ,△CGD ,△BGF 的面积相等,证明:G 是△ABC 的重心98.如图,四边形ABCD 中,点P 满足12,,,PAB CAD PCB ACD O O ∠=∠∠=∠分别是 △ABC ,△ADC 的外心,求证:△PO 1B ∽△PO 2D99.已知X 是△ABC 的边AB 上的一点,P 为△ACX 的内心,Q 是△BCX 的内心,M 是线段PQ 的中点,证明:MC >MX100.设I 为△ABC 的内心,P 是△ABC 内部的一点,满足∠PBA+∠PCA=∠PBC+∠PCB ,证明:AP ≥AI ,并说明等号成立的充分必要条件是P=I101.已知△ABC 满足,B C A ∠>∠∠的平分线和过顶点A 的高线,中线与边BC 分别交于点L ,H ,D ,证明:HAL DAL ∠=∠的充分必要条件是90BAC ∠=︒102.已知△ABC ,△PAB 和△QAC 为△ABC 外面的两个三角形,满足AP=AB ,AQ=AC 以及∠BAP=∠CAQ ,线段BG 与CP 相交于点R ,设O 是△BCD 的外接圆圆心,证明:AO ⊥PQ103.已知非等边△ABC ,,,A B C ∠∠∠的平分线分别交对边于点'''',,,A B C AA 的中垂线与BC 交于点''',A BB 的中垂线与AC 交于点''',B CC 的中垂线与AB 交于点''C ,证明:'''''',,A B C 三点共线104.已知P 是△ABC 内一点,过P 作BC ,CA ,AB 的垂线,其垂足分别为D ,E ,F ,又Q 是△ABC 内的一点,且使得∠ACP=∠BCQ ,∠BAQ=∠CAP ,证明:∠DEF=90°的充分必要条件是Q 为△BDF 的垂心105.已知斜边为AC 的Rt △ABC ,B 在AC 上的投影为H ,若AB ,BC ,BH 可以构成一个直角三角形,求AH HC的所有可能的值 106.在方格纸上画有一个矩形,它的边与方格线交成45°的角,它的顶点都不在方格线上,试问:矩形的各余边能否都刚好穿过奇数条方格线?107.一个三角形的三个内角的余弦分别等于另一个三角形的三个内角的正弦,试求这六个内角的最大值108.将梯形的各个顶点均作关于不包含该顶点的对角线的对称点,证明:如果所得到的四个像点也形成四边形,则必为一个梯形109.设凸四边形的面积为S ,对它的每个顶点,都作其关于不经过它的对角线的对称点,将所得到的四个像点组成的四边形的面积记作S ‘,证明:'3S S < 110.已知梯形ABCD 满足AB ∥CD ,E 为边AB 上一点,且满足EC ∥AD ,直线AC ,BD ,DE 交出的三角形的面积记为t ,梯形ABCD 的面积记为T ,当t T 取最大值时,求AB CD 的值 111.已知锐角△ABC ,求△ABC 内的点M 的轨迹,使得MF AG MG BF AB FG CM⋅+⋅-=,其中F ,G 分别是点M 在边BC ,AC 上的投影 112.以点C 为旋转中心,将ABC ∆旋转为'''A B C ∆,设线段'',,BA AC B C 的中点分别为M ,E ,F ,若AC ≠BC ,且EM=FM ,求∠EMF 的度数113.设△ABC 的边AB 的中点为N ,A B ∠>∠,D 是射线AC 上一点,满足CD=BC ,P 是射线DN 上一点,且与点A 在边BC 的同侧,满足,PBC A PC ∠=∠与AB 交于点E ,BC 与DP 交于点T ,求表达式BC EA TC EB-的值 114.已知凸四边形ABCD ,AD ∩BC={E},AC ∩BD={I},证明:当且仅当AB ∥CD ,且IC 2=IA ·AC 时,△EDC 重心与△IAB 的重心重合115.设△ABC 为非直角三角形,其垂心为H ,M 1,M 2,M 3分别为边BC ,CA ,AB 的中点,令A 1,B 1,C 1分别为H 关于M 1,M 2,M 3的对称点,A 2,B 2,C 2分别为△BA 1C ,△CB 1A ,△AC 1B 的垂心,求证:⑴△ABC 与△A 2B 2C 2的重心重合;⑵由△AA 1A 2,△BB 1B 2,△CC 1C 2的重心所构成的三角形与△ABC 相似116.已知锐角△ABC ,对其内部或边界的任意点T 而言,,,a b c T T T 是由点T 分到边BC ,CA ,AB 所作垂线的垂足,若()c a b a b cAT BT CT f T TT TT TT ++=++,证明:当且仅当△ABC 为等边三角形时,()f T 不依赖于点T 的选择117.设S 为锐角△ABC 的边AB 上的点,P ,Q 分别为△ASC 和△BSC 的外接圆的圆心,问:点S 在边AB 上的什么位置时,使得△PQS 的面积最小?118.已知△ABC 的内切圆的半径为r ,圆心为O ,过点O 的直线分别交边BC ,CA 于点D ,E ,记△CDE 的面积为S ,求证:S ≥22r ,并指出等号成立的条件119.已知E ,F 分别是平行四边形ABCD 的边AB ,AD 上的点,且满足EF ∥BD ,证明:△BCE 和△CDF 的面积相等120.求满足下列条件的最小实数t :存在两个边长都是整数的三角形,这两个三角形不全等,而且这两个三角形的面积都是t121.在凸四边形ABCD 中,∠ADC=∠BCD >90°,BE 平行于AD 交AC 延长线于点E ,AF 平行于BC 交BD 延长线于点F ,联结E ,F ,证明:EF ∥CD122.已知凸四边形ABCD ,P ,Q 分别为边BC ,CD 上的点,且使得∠BAP=∠DAO ,求证:当且仅当过△ABP 与△ADQ 垂心的直线垂直于AC 时,△ABP 与△ADQ 的面积相等 123.已知U 为△ABC 的内切圆的圆心,O 1,O 2,O 3分别为△BCU ,△CAU ,△ABU 的外接圆的圆心,求证:△ABC 的外接圆圆心与△O 1O 2O 3的外接圆圆心重合124.联结三角形内切圆的圆心和它的顶点的直线将原三角形分为三个三角形,若它们之中的一个三角形与原三角形相似,求三角形三个角的度数125.给定一个凸四边形ABCD ,P 为其内一点,求满足条件PAB PCD PBC PDA S S S S ∆∆∆∆⋅=⋅的点P 的轨迹126.已知在一条直线上依次排列着A ,B ,C 三个点,','A B 是在直线AB 同侧的两个点,且满足'AA ∥'BB ,点',',A B C 不在一条直线上,设'AA C ∆和'BB C ∆的外心分别为O 1,O 2,若12''A CB O CO S S ∆∆=,求'CAA ∠的度数127.设D ,E ,F 分别是△ABC 边BC ,CA ,AB 上的内点,并且△AEF ,△BFD 与△CDE 的内切圆半径都等于△ABC 内切圆半径的一半,证明:D ,E ,F 恰好是△ABC 各边的中点数学竞赛题(第二章 有关圆的试题)1.设ABCD 是面积为2的长方形,P 为边CD 上的一点,Q 为△PAB 的内切圆与边AB 的切点,PA ·PB 的值随着长方形ABCD 及点P 的变化而变化,当PA ·PB 取最小值时,⑴证明:AB ≥2BC ;⑵求AQ ·BQ 的值2.已知等腰△ABC (AB=BC )中,平行于BC 的中位线交△ABC 的内切圆于点F ,其中F 不在底边AC 上,证明:过F 的切线与∠C 的平分线的交点在边AB 上3.已知△ABC 为锐角三角形,AB ≠AC ,以BC 为直径的圆分别交边AB ,AC 于点M ,N ,记BC 的中点为O ,∠BAC 的平分线和∠MON 的平分线相交于点R ,求证:△BMR 的外接圆和△CNR 的外接圆有一个交点在边BC 上4.在凸四边形ABCD 中,对角线BD 既不是∠ABC 的平分线,也不是∠CDA 的平分线,点P 在四边形ABCD 内部,满足∠PBC=∠DBA 和∠PDC=∠BDA ,证明:ABCD 为圆内接四边形的充分必要条件是AP=CP5.设P 为△ABC 内一点,A 1,B 1和C 1分别是PA 和BC ,PB 和CA ,PC 和AB 的交点,A 2,B 2和C 2分别是B 1C 1和BC ,C 1A 1和CA ,A 1B 1和AB 的交点,W 1,W 2和W 3分别是以A 1A 2,B 1B 2和C 1C 2为直径的圆,求证:W 1,W 2和W 3有一个公共点的充要条件是W 1和W 2有公共点6.点O 为一个单位圆的圆,A 1A 2…A 2n 为该单位圆的内接凸2n 边形, 求证:123421221212sin2n n n i ii AOA A OA A OA A A --=∠+∠++∠≤∑7.给定2a a <<,内接于单位圆Γ的凸四边形ABCD 适合以下条件:⑴圆心在这凸四边形内部;⑵最大边长是a A ,B ,C ,D 依次作圆Γ的4条切线,∠A ,∠B ,∠C ,∠D ,已知∠A 与∠B ,∠B 与∠C ,∠C 与∠D ,∠D 与∠A 分别交于',',','A B C D ,求面积之比''''A B C D ABCDS S 四边形四边形的最大值与最小值 8.已知凸四边形ABCD 的对角线AC 和BD 互相垂直,且交于点O ,设△AOB ,△BOC ,△COD ,△DOA 的内切圆的圆心分别为O 1,O2,O 3,O 4,证明:⑴圆O 1,圆O 2,圆O 3,圆O 4的直径之和不超过(2)AC BD -+;⑵O 1O 2+O 2O 3+O 3O 4+O 4O 1<1)()AC BD +9.设I 是△ABC 的∠BAC 平分线上的一点,M ,N 分别是边AB ,AC 上的点,且使得∠ABI=∠NIC ,∠ACI=∠MIB ,证明:当且仅当点M ,N ,I 共线时,I 是△ABC 的内切圆圆心10.凸四边形ABCD 有内切圆,该内切圆切边AB ,BC ,CD ,DA 的切点分别为A 1,B 1,C 1,D 1,联结A 1B 1,B 1C 1,C 1D 1,D 1A 1,点E ,F ,G ,H 分别为A 1B 1,B 1C 1,C 1D 1,D 1A 1的中点,证明:四边形EFGH 为矩形的充分必要条件是A ,B ,C ,D 四点共圆11.已知△ABC 的外接圆为圆S ,且满足AB <AC ,过点A 的高线交圆S 于点P ,X 为线段AC 上的点,且BX 交圆S 于Q ,证明:BX=CX 的充分必要条件是PQ 为圆S 的直径12.设I 为△ABC 的内心,射线AI ,BI ,CI 与△ABC 的外接圆分别交于点D ,E ,F ,证明:AD ⊥EF13.已知D 为△ABC 的边AB 上一点,使得4AD=AB ,过D 的射线l 满足与DA 的夹角ACB θ=∠,且射线l 与点C 在直线AB 的同侧,若l 与△ABC 的外接圆交于点P ,证明:PB=2PD14.锐角△ABC 的外接圆的圆心为O ,M ,N 为直线AC 上的两点,且满足MN=AC ,设点D 是点M 在直线BC 上的射影,点E 是点N 在直线AB 上的射影,证明:⑴△ABC 的垂心位于以'O 为圆心的△BED 的外接圆上;⑵线段AN 的中点与点B 关于线段'OO 的中点对称15.两圆圆O 1,圆O 2相切于点M ,圆O 2的半径大于圆O 1的半径,点A 是圆O 2上的一点,且满足O 1和O 2和A 三点不共线,AB ,AC 是点A 到圆O 1的切线,切点分别为B ,C ,直线MB ,MC 与圆O 2的另一个交点分别为E ,F ,点D 是线段EF 和圆O 2的以A 为切点的切线的交点,证明:当点A 在圆O 2上移动且保持O 1,O 2和A 三点不共线时,点D 沿一条固定的直线移动16.如图,3个圆有公共弦AB ,任一条过点A 的直线l 与3个圆的交点依次为X ,Y ,Z ,其中X ≠B ,证明:XY YZ为定值 17.已知五边形ABCDE 的内切圆与边AE 切于点P ,且∠B=∠C=∠D=∠E ,证明:AD ,PC ,EB 三线交于一点18.已知△ABC 的∠C 内的旁切圆与边AB 切于点'C ,设Z 为由点C 引出的△ABC 的高的中点,证明:△ABC 的内心在直线'C Z 上19.如图,在△ABC 的内部有四个半径相等的圆K 1,圆K 2,圆K 3,圆K 4,其中圆K 1,圆K 2,圆K 3均与△ABC 的两条边相切,且与圆K 4外切,证明:△ABC 的内心,外心和K 4在一条直线上20.已知圆内接正△ABC ,在劣弧BC 上有一点P ,若AP 与BC 交于点D ,且PB=21,PC=28,求PD21.已知凸六边形的对角线1425,A A A A 和36A A 交于一点K ,且2123243,A A A A A K A A == 45465616,A A A K A A A A A K ====,证明:该六边形为圆内接六边形22.已知AB 是O 的弦,M 是弧AB 的中点,C 是O 外任一点,过点C 作O 的切线CS ,CT ,联结MS ,MT 分别交AB 于点E ,F ,过点E ,F 作AB 的垂线,分别交OS ,OT于点X ,Y ,再过点C 任作O 的割线,交O 于点P ,Q ,联结MP交AB 于点R ,设Z 是△PQR 的外心,求证:X ,Y ,Z 三点共线23.在锐角△ABC ,C B ∠>∠,点D 是边BC 上一点,使得ADB ∠是钝角,H 是△ABD 的垂心,点F 在△ABC 内部且在△ABD 的外接圆圆周上,如图所示,求证:点F 是△ABC 的垂心的充要条件是HD ∥CF且H 在△ABC 的外接圆圆周上24.某圆分别与凸四边形ABCD 的AB ,BC 两边相切于G ,H 两点,与对角线AC 相交于E ,F 两点,问ABCD 应满足怎样的充要条件,使得存在另一圆过E ,F 两点,且分别与DA ,DC 的延长线相切?证明你的结论25.如图,在锐角△ABC 的BC 边上有两点E ,F ,满足BAE CAF ∠=∠,作,FM AB FN AC ⊥⊥(M ,N 是垂足),延长AE 交△ABC 的外接圆于点D ,证明:四边形AMDN 与△ABC 的面积相等26.设,,a b c 为△ABC 的三条边,a b c ≤≤,R 和r 分别为△ABC 的外接圆半径和内切圆半径,令22f a b R r =+--,试用C ∠的大小来判定f 的符号27.如图,在△ABC 的中,AB=AC ,线段AB 上有一点D ,线段AC的延长线上有一点E ,使得DE=AC ;线段DE 与△ABC 外接圆交于点T ,P 是线段AT 的延长线上的一点,证明:点P 满足PD+PE=A T 的充分必要条件是点P 在△ADE 的外接圆上28.设A ,B ,C ,D 是圆周上依顺时针方向排布的四点,满足AB <AD ,BC >CD ,∠BAD 的平分线交圆周于点X ,∠BCD 的平分线交圆周于点Y ,考虑圆周上这六点组成的六边形,如果六边形六条边中的四条长度相等,证明BD 是圆的直径29.圆1Γ和圆2Γ相交于点M 和N ,设l 是圆1Γ和圆2Γ的两条公切线中距离M 较近的那条公切线,l 与圆1Γ相交于点A ,与圆2Γ相切于点B ,设经过点M 且与l 平行的直线与圆1Γ还相交于点C ,与圆2Γ还相交于点D ,直线CA 和DB 相交于点E ,直线AN 和CD 相交于点P ,直线BN 和CD 相交于点Q ,证明:EP=EQ30.设AH 1,BH 2,CH 3是锐角△ABC 的三条高线,△ABC 的内切圆与边BC ,CA ,AB 分别相结切于点T 1,T 2,T 3,设直线123,,l l l 分别是直线H 2H 3,H 3H 1,H 1H 2关于直线T 2T 3,T 3T 1,T 1T 2的对称直线,证明:123,,l l l 所确定的三角形,其顶点都在△ABC 的内切圆上31.设锐角△ABC 的的外心为O ,从A 作BC 的高,垂足为P ,且30BCA ABC ∠≥∠+︒,证明:∠CAB+∠COP <90°32.圆O 1和圆O 2相交于B ,C 两点,且BC 是圆O 1的直径,过点C 作圆O 1的切线,交圆O 2于另一点A ,联结AB ,交圆O 1于另一点E ,联结CE 并延长,交圆O 2于点F ,设点H 为线段AF 上的任意一点,联结HE 并延长,交圆O 1于点G ,联结BG 并延长,与AC 的延长线交于点D ,求证:AH AC HF CD= 33.设O 为锐角△ABC 的外心,P 为△AOB 内部一点,P 为△ABC 的三边BC ,CA ,AB。
2002年全国高中数学联赛试题+解析(含加试题)

二○○二年全国高中数学联合竞赛试题参考答案及评分标准说明:1. 评阅试卷时,请依据本评分标准,选择题只设6分的0分两档,填空题只设9分和0分两档,其它各题的评阅,请严格按照本评分标准规定的评分档次给分,不要再啬其他中间档次。
2. 如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准适当档次评分,可以5分为一个档次,不要再增加其它中间档次。
一、 选择题(本题满分36分,每小题6分) 1、 函数f(x)=)32(log 221--x x 的单调递增区间是(A) (-∞,-1) (B) (-∞,1) (C) (1,+∞) (D) (3,+∞) 解:由x 2-2x -3>0⇒x<-1或x>3,令f(x)=u 21log , u= x 2-2x -3,故选A2、 若实数x, y 满足(x+5)2+(y -12)2=142,则x 2+y 2的最小值为 (A) 2 (B) 1 (C) 3 (D) 2解:B 3、 函数f(x)=221xx x -- (A) 是偶函数但不是奇函数 (B) 是奇函数但不是偶函数 (C) 既是奇函数又是偶函数 (D) 既不是奇函数又不是偶函数 解:A4、 直线134=+yx 椭圆191622=+y x 相交于A ,B 两点,该圆上点P ,使得⊿PAB 面积等于3,这样的点P 共有(A) 1个 (B) 2个 (C) 3个 (D) 4个 解:设P 1(4cos α,3sin α) (0<α<2π),即点P 1在第一象限的椭圆上,如图,考虑四边形P 1AOB 的面积S 。
S=11OBP OAP S S ∆∆+=ααcos 4321sin 3421⨯⨯+⨯⨯=6(sin α+cos α)=)4sin(26πα+ ∴S max =62 ∵S ⊿OAB =6∴626)(max 1-=∆AB P S ∵626-<3∴点P 不可能在直线AB 的上方,显然在直线AB 的下方有两个点P ,故选B5、 已知两个实数集合A={a 1, a 2, … , a 100}与B={b 1, b 2, … , b 50},若从A 到B 的映射f 使xy OA B P 1得B 中的每一个元素都有原象,且f(a 1)≤f(a 2)≤…≤f(a 100),则这样的映射共有(A) 50100C (B) 5090C (C) 49100C (D) 4999C解:不妨设b 1<b 2<…<b 50,将A 中元素a 1, a 2, … , a 100按顺序分为非空的50组,定义映射f :A →B ,使得第i 组的元素在f 之下的象都是b i (i=1,2,…,50),易知这样的f 满足题设要求,每个这样的分组都一一对应满足条件的映射,于是满足题设要求的映射f 的个数与A 按足码顺序分为50组的分法数相等,而A 的分法数为4999C ,则这样的映射共有4999C ,故选D 。
青少年数学国际城市邀请赛试题与答案

1. 34+ 44+54+…..+2004=╴201762╴╴╴╴╴╴解:可以看作30+40+50+…+2000+4×198=10×(()12002002+÷-1-2)+792=200970+792=2017622. 將分数313化为小数后,则小数点后第2004位数字为何?9╴解:將3除以13可知其小数以230769为一循环,所以將2004÷6=334…..0所以可知小数点后第2004位数字为93. 在一条道路上,测得A, B, C, D四个城市之间的某些距離资料,列表如下:请问城市A和城市B之间的距離为╴╴22╴╴╴╴╴解:因为上述资料可知程式顺序为ADBC,所以可知道AB=AD+BD=14+8=224. 设X为一实数,定义﹝X﹞表示不大于X的最大整数,例如:﹝3.5﹞=3,﹝4﹞=4 ,則+〔++ …. +=╴╴561╴╴╴╴.解:可將上式改为1×(4-1)+2×(9-4)+3×(16-9)+….+8×(81-64)+9×13=3+2×5+3×7+4×9+5×11+6×13+7×15+8×17+9×13=5615. 右图中,已知BDEF 为一菱形,且AB=10,BC=15则DE=╴╴╴6╴╴╴╴.解:因为AFE 和ABC 相似且BDEF 为一菱形所以另DE=BF=x ,101015x x -=,所以DE=6 6. 一长方形的长与宽各增加20%,则其面积增加的百分率为╴44%. 解:120%×120%=144%7. 平面上两个全等的正三角形,若其中一个三角形的顶点恰好落在另一个三角形的重心,则兩个三角形重疊部分的可能最大面积与可能最小面积之比值为╴2╴解:由于顶点是在正三角形的重心上所以重疊的部分最小为一个高为原來1/3的正三角形而最大会如右图,出現兩个正三角形所以最大会是最小的兩倍8. 已知一正方形与一正三角形的周长相等,且该正三角形则该正方形面积为╴9/4╴╴╴╴╴.解:正三角形面积为2,所以可以知道其边长为2,周长为6,所以正方形边长为3/2所以正方形面积为9/49. 设q p ,为实数,若方程式02=+-q px x 有正整数解b a ,,那么a b p q b a q p +++之值为╴╴20╴╴╴╴.解:因为方程式02=+-q px x 有正整数解a,b ,所以由根于系数关系知ab=q 且a+b=p (其中a,b 为正整数,p,q 为实数)所以a=1或b=1。
创界学校国高中数学联赛试题及解析2

智才艺州攀枝花市创界学校二零零二年全国高中数学联赛试卷一试题(2021年10月13日上午8:00—9:40)一.选择题(本小题总分值是36分,每一小题6分):1.函数f (x )=log(x 2-2x -3)的单调递增区间是A .(-∞,-1)B .(-∞,1)C .(1,+∞)D .(3,+∞)2.假设实数x ,y 满足(x +5)2+(y -12)2=142,那么x 2+y 2的最小值为A .2B .1C .D .3.函数f (x )=-A .是偶函数但不是奇函数B .是奇函数但不是偶函数C .既是奇函数也是偶函数D .既不是奇函数也不是偶函数4.直线+=1与椭圆+=1相交于A 、B 两点,该椭圆上点P ,使得ΔPAB 面积等于3.这样的点P 一共有A .1个B .2个C .3个D .4个5.两个实数集合A={a 1,a 2,a 3,…,a 100},与B={b 1,b 2,…,b 50},假设从A 到B 的映射f 使得B 中每个元素都有原象,且f (a 1)≤f (a 2)≤…≤f (a 100),那么这样的映射一共有A .CB .CC .CD .C6.由曲线x 2=4y ,x 2=-4y ,x=4,x=-4围成的图形绕y 轴旋转一周所得的旋转体的体积为V 1;满足x 2+y 2≤16,x 2+(y -2)2≥4,x 2+(y +2)2≥4的点绕y 轴旋转一周所得的旋转体的体积为V 2,那么A .V 1=V 2B .V 1=V 2C .V 1=V 2D .V 1=2V 2二.填空题(此题总分值是54分,每一小题9分)7.复数Z 1、Z 2满足|Z 1|=2,|Z 2|=3,假设它们所对应的向量的夹角为60,那么=;8.将二项式的展开式按x 的降幂排列,假设前三项的系数成等差数列,那么该展开式中x 的幂指数是整数的项一共有个;9.如图,点P 1、P 2、…,P 10分别是四面体顶点或者棱的中点,那么在同一平面上的四点组(P 1,P i ,P j ,P k )(1<i <j <k ≤10)有个;10.f (x )是定义在R 上的函数,f (1)=1且对任意x R 都有f (x +5)≤f (x )+5,f (x +1)≥f (x )+1,.假设g (x )=f (x )+1-x ,那么g (2021)=;11.假设log 4(x +2y )+log 4(x -2y )=1,那么|x |-|y |的最小值是;12.使不等式sin 2x +a cos x +a 2≥1+cos x 对于一切x R 恒成立的负数a 的取值范围是;三.解答题(此题总分值是60分,每一小题20分):13.点A (0,2)和抛物线y 2=x +4上两点B ,C ,使得AB ⊥BC ,求点C的纵坐标的取值范围.14.如图,有一列曲线P 0,P 1,P 2,…,P 0是面积为1的等边三角形,P k +1是对P k 进展如下操作得到的:将P k 的每条边三等分,以每边中间局部的线段为边向形外作等边三角形,再将中间局部的线段去掉(k=0,1,2,…).记S n 为曲线Pn 所围成图形的面积.⑴求数列{S n }的通项公式; ⑵求S n .15.设二次函数f (x )=ax 2+bx +c (a ,b ,c R ,a ≠0)满足条件:⑴当x R 时,f (x -4)=f (2-x ),且f (x )≥x ;⑵当x(0,2)时,f (x )≤;P P P P P P P P P 12345678109(0,2)(-4,0)ABCyO x⑶f(x)在R上的最小值为0.求最大的m(m>1),使得存在t R,只要x[1,m],就有f(x+t)≤x.二试题(本卷一共三个大题,一共150分,每一小题50分)一.在ΔABC 中,∠BAC=60,AB >AC ,点O 为ΔABC 的外心,两条高BE 、CF 的交于点H ,点M 、N 分别在线段BH 与HF 上,且满足BM=CN .求的值.二.实数a ,b ,c 和正数λ使得f (x )=x 3+ax 2+bx +c 有三个实根x 1,x 2,x 3,且满足⑴x 2-x 1=λ; ⑵x 3>(x 1+x 2). 求的最大值.三.在世界杯足球赛前,F 国的教练员为了考察A 1、A 2、A 3、A 4、A 5、A 6、A 7这七名队员,准备让他们在三场训练比赛(每场比赛90分钟)中都上场,假设在比赛的任何时刻,这些队员都有且只有一人在场上,并且A 1、A 2、A 3、A 4每人上场的总时间是(以分钟为单位)均被7整除,A 5、A 6、A 7每人上场的总时间是(以分钟为单位)均被13整除.假设每场换人的次数不限,那么,按每名队员上场的总时间是计,一共有多少种不同的情况?AH EF MN O2021年全国高中数学联赛解答一试题(2021年10月13日上午8:00—9:40)一.选择题(本小题总分值是36分,每一小题6分):1.函数f(x)=log(x2-2x-3)的单调递增区间是A.(-∞,-1)B.(-∞,1)C.(1,+∞)D.(3,+∞)解:由x2-2x-3>0,得x<-1或者x>3.在x∈(-∞,-1)时,u=x2-2x-3单调减,f(x)单调增;在x∈(3,+∞)时,u=x2-2x-3单调增,f(x)单调减.应选A2.假设实数x,y满足(x+5)2+(y-12)2=142,那么x2+y2的最小值为A.2B.1C.D.解:令x+5=14cosθ,y-12=14sinθ,那么x2+y2=196+28(5cosθ-12sinθ)+169=365+364sin(θ+φ)≥1.选B.(亦可用几何意义解:圆上点到原点间隔平方的最小值)3.函数f(x)=-A.是偶函数但不是奇函数B.是奇函数但不是偶函数C.既是奇函数也是偶函数D.既不是奇函数也不是偶函数解:f(x)定义域为(-∞,0)∪(0,+∞);f(x)-f(-x)=--+=-x=0.即f(x)是偶函数.选A.4.直线+=1与椭圆+=1相交于A、B两点,该椭圆上点P,使得ΔPAB面积等于3.这样A.1个B.2个C.3个D.4个解:直线与椭圆的交线长=5.直线方程3x+4y-12=0.设点P(4cosθ,3sinθ).点P与直线的间隔d=,当0≤θ≤时,d ≤(-1),S ABC ≤6(-1)<3.即此时没有三角形面积=3; 当<θ<2π时,d ≤(+1),S ABC ≤6(+1).即此时有2个三角形面积=3.选B .5.两个实数集合A={a 1,a 2,a 3,…,a 100},与B={b 1,b 2,…,b 50},假设从A 到B 的映射f 使得B 中每个元素都有原象,且f (a 1)≤f (a 2)≤…≤f (a 100),那么这样的映射一共有A .CB .CC .CD .C解:不妨设b 1≤b 2≤…≤b 50,在a 1,a 2,…,a 100的每两个数间有1个空档,一共99个空档,其中任选49个空档插入1条竖杠,把a 1,a 2,…,a 100分成50段,从前向后的第i 段中的数映射到b i ,即满足要求.一共有C 种插法,选D .6.由曲线x 2=4y ,x 2=-4y ,x=4,x=-4围成的图形绕y 轴旋转一周所得的旋转体的体积为V 1;满足x 2+y 2≤16,x 2+(y -2)2≥4,x 2+(y +2)2≥4的点绕y 轴旋转一周所得的旋转体的体积为V 2,那么A .V 1=V 2B .V 1=V 2C .V 1=V 2D .V 1=2V 2解:作平面y=h (0≤h ≤4).与图形⑴交于一个圆环,圆环面积=π(42-x 2)=π(16-4h );与图⑵交得一个圆环,面积=π(16-h 2)-π(4-(h -2)2)=π(16-h 2-(-h 2+4h ))=π(16-4h ).说明该平面与两个旋转体截得的面积相等.由祖暅原理知,V 1=V 2,选C . 二.填空题(此题总分值是54分,每一小题9分)7.复数Z 1、Z 2满足|Z 1|=2,|Z 2|=3,假设它们所对应的向量的夹角为60,那么=;解:由余弦定理知|Z 1+Z 2|==;|Z 1-Z 2|==, ∴==.8.将二项式的展开式按x 的降幂排列,假设前三项的系数成等差数列,那么该展开式中x 的幂指数是整数的项一共有个;解:前三项系数为1,n ,n (n -1),于是得n=1+n (n -1),解得,n=8,和n=1(舍去).y x O yxO当n=8时,T r +1=C ()rx=C ()rx ,当r=0,4,8时x 的指数为整数,∴一共有3个.9.如图,点P 1,P 2,…,P 10分别是四面体顶点或者棱的中点,那么在同一平面上的四点组(P 1,P i ,P j ,P k )(1<i <j <k ≤10)有个;解:同在某一侧面上:除P 1外另外5点中任取3点与P 1一共4点组成一个四点组,有3C=30组,每条侧棱上三点与对棱中点:3组.∴一共有33组.10.f (x )是定义在R 上的函数,f (1)=1且对任意x R 都有f (x +5)≤f (x )+5,f (x +1)≥f (x )+1,.假设g (x )=f (x )+1-x ,那么g (2021)=;解:由后式,f (x +5)≥f (x +4)+1≥f (x +3)+2≥f (x +2)+3≥f (x +1)+4≥f (x )+5.比较前式得f (x +1)=f (x )+1.∴f (x )=x 对一切x ∈N *成立,∴对于x ∈N *,g (x )=f (x )+1-x=x +1-x=1 ∴g (2021)=1.11.假设log 4(x +2y )+log 4(x -2y )=1,那么|x |-|y |的最小值是; 解:x >-2y ,x >2y ,x 2-4y 2=4.由对称性,只考虑x >0,y >0的情况.令x=2sec θ,y=tan θ,(0<θ<),u=x -y=表示点(0,2)与点(-cos θ,sin θ)连线的斜率,当直线与单位圆相切时,u 最小为.即所求最小值为.(或者用判别式法解)12.使不等式sin 2x +a cos x +a 2≥1+cos x 对于一切xR 恒成立的负数a 的取值范围是;解:即(cos x -)2≤a 2+()2,假设(1-)2≤a 2+()2,那么a 2+a -2≥0. ∴a ≤-2或者a ≥1,但a <0,故a ≤-2. 三.解答题(此题总分值是60分,每一小题20分):13.点A (0,2)和抛物线y 2=x +4上两点B ,C ,使得AB ⊥BC ,求点C 的纵坐标的取值范围.解:设B (y 02-4,y 0),C (y 12-4,y 1).那么P P P P P P P P P 12345678109k AB ==.k BC ==.由k AB ·k BC =-1,得(y 1+y 0)(y 0+2)=-1.∴y 02+(y 1+2)y 0+(2y 1+1)=0.∴△=(y 1+2)2-4(2y 1+1)=y 12-4y 1≥0,∴y 1≤0,y 1≥4.当y 1=0时,得B (-3,-1),当y 1=4时,得B (5,-3)均满足要求,故点C 的纵坐标的取值范围是(-∞,0]∪[4,+∞).14.如图,有一列曲线P 0,P 1,P 2,…,P 0是面积为1的等边三角形,P k +1是对P k 进展如下操作得到的:将P k 的每条边三等分,以每边中间局部的线段为边向形外作等边三角形,再将中间局部的线段去掉(k=0,1,2,…).记S n 为曲线P n 所围成图形的面积.⑴求数列{S n }的通项公式; ⑵求S n .解:⑴对P 0操作后,每条边变为4条边,一共有4×3条边;对P 1操作,也是每条边变为4条边,故P 2一共有42×3条边,即P k 有3×4k条边.S 0=1,S 1=S 0+3×=1+,S 2=S 1+4×3×=1++;S 3=1+++;依此类推,得S k =1+++…+=1+·=1+[1-()k]=-()k.用数学归纳法易证上式正确. ⑵S n =.15.设二次函数f (x )=ax 2+bx +c (a ,b ,c R ,a ≠0)满足条件:⑴当x R 时,f (x -4)=f (2-x ),且f (x )≥x ;⑵当x(0,2)时,f (x )≤;⑶f (x )在R 上的最小值为0.求最大的m (m >1),使得存在t R ,只要x[1,m ],就有f (x +t )≤x .(0,2)(-4,0)ABCyO x解:由f (x -4)=f (2-x ),知f (x )关于x=-1对称.于是-=-1.b=2a .此时,f (x )有最小值0,∴a -b +c=0.c=a .f (x )=ax 2+2ax +a .由⑴f (1)=4a ≥1.由⑵4a ≤1.∴a=c=,b=.f (x )=(x +1)2. 假设对于x ∈[1,m ],f (x +t )-x ≤0,f (1+t )-1=(t +2)2-1≤0,得-4≤t ≤0.f (m +t )-m ≤0,m 2+2(t -1)m +(t +1)2≤0.解得-(t -1)-2≤m ≤-(t -1)+2.∴m ≤1-t +2≤9.而当t=-4时,f (x -4)-x=(x 2-10x +9)=(x -1)(x -9)在x ∈[1,9]时,恒有f (x -4)-x ≤0成立.∴m 的最大值为9.二试题(本卷一共三个大题,一共150分,每一小题50分)一.在ΔABC 中,∠BAC=60,AB >AC ,点O 为ΔABC 的外心,两条高BE 、CF 的交于点H ,点M 、N 分别在线段BH 与HF 上,且满足BM=CN .求的值.解:记∠ACB=α,连OB 、OC ,那么∠BOC=∠BHC=120,∴B 、O 、H 、C 四点一共圆.设此圆的半径为R ', 那么2R '===2R .HM +NH=(BH -BM )+(CN -CH )=BH -CH .在ΔBCH 中,∠CBH=90-α.∠HCB=90-(120-α)=α-30,∴HM +NH=BH -CH=2R (sin(α-30)-sin(90-α))=2R (sin αcos30-cos αsin30-cos α)=2R sin(α-60).在ΔOCH 中,OH=2R sin ∠HCO=2R sin(α-30-30)=2R sin(α-60).∴=.二.实数a ,b ,c 和正数λ使得f (x )=x 3+ax 2+bx +c 有三个实根x 1,x 2,x 3,且满足AH EF MN O⑴x2-x1=λ;⑵x3>(x1+x2).求的最大值.解:设x1=m-λ,x2=m+λ,x3=m+k(k>λ).a=-(x1+x2+x3)=-(3m+k);b=x1x2+x1x3+x2x3=3m2+2mk-λ2;c=-x1x2x3=-m3-m2k+λ2m+λ2k.那么2a3+27c-9ab=-3(m+k)3+27(-m3-m2k+λ2m+λ2k)+9(3m+k)(3m2+2mk-λ2)=-2k3+λ2k.令=t,那么(2a3+27c-9ab)=-2t3+t.取g(t)=-2t3+t.那么g'(t)=-6t2+,g"(t)=-12t.令g'(t)=0,得t=±,而当t=时g"(t)<0.∴当t=时,g(t)获得最大值g()=-2()3+()=.假设取λ=1,此时得,k=.令a=0,得m=-,代入b、c的表达式得b=-,c=此时得f(x)=x3-x+满足题意.三.在世界杯足球赛前,F国的教练员为了考察A1、A2、A3、A4、A5、A6、A7这七名队员,准备让他们在三场训练比赛(每场比赛90分钟)中都上场,假设在比赛的任何时刻,这些队员都有且只有一人在场上,并且A1、A2、A3、A4每人上场的总时间是(以分钟为单位)均被7整除,A5、A6、A7每人上场的总时间是(以分钟为单位)均被13整除.假设每场换人的次数不限,那么,按每名队员上场的总时间是计,一共有多少种不同的情况?解:设各人上场时间是分别为7t1,7t2,7t3,7t4,13t5,13t6,13t7,(t i为正整数).得方程7(t1+t2+t3+t4)+13(t5+t6+t7)=90×3.令t1+t2+t3+t4=x,t5+t6+t7=y,得方程7x+13y=270.即求此方程满足4≤x≤38,3≤y≤20的整数解.即6y≡4(mod7),3y≡2(mod7),y≡3(mod7)∴y=3,10,17,相应的x=33,20,7.t5+t6+t7=3的解只有1种,t5+t6+t7=10的解有C种,t5+t6+t7=17的解有C种;t1+t2+t3+t4=33的解有C种,t1+t2+t3+t4=20的解有C种,t1+t2+t3+t4=7的解有C种.∴一共有1·C+C·C+C·C=42244种.。
