基于离散单元法球形颗粒碰撞破碎行为的数值模拟_黄令军
工程流体力学中的悬浮颗粒物运动模拟研究

工程流体力学中的悬浮颗粒物运动模拟研究悬浮颗粒物在工程流体中的运动模拟研究是工程流体力学领域的重要课题之一。
随着计算机技术的发展和数值模拟方法的成熟,研究人员可以通过数值模拟来了解悬浮颗粒物在工程流体力学中的行为,从而为实际工程应用提供理论依据和技术支持。
悬浮颗粒物的运动模拟可以通过流体力学和颗粒力学相结合的方法来实现。
这种方法通常称为欧拉-拉格朗日法,即将流体作为连续介质来描述,并用Navier-Stokes方程组来模拟流体流动;同时,将颗粒物作为离散物体,并通过牛顿第二定律来描述其受力和运动。
通过求解Navier-Stokes方程组和颗粒物运动方程,可以计算出悬浮颗粒物在工程流体中的运动轨迹、速度、压力等参数。
在进行悬浮颗粒物运动模拟研究时,需要考虑一系列因素,如颗粒物的物理性质、流体的流动性质、颗粒物之间的相互作用等。
首先,颗粒物的物理性质包括颗粒粒径、密度、形状等,这些参数对颗粒物运动的速度和轨迹都有重要影响;其次,流体的流动性质包括流速、粘性、密度等,这些参数决定了颗粒物在流体中的受力情况;最后,颗粒物之间的相互作用则影响颗粒物的聚集和分散行为,直接影响到颗粒物的整体运动。
悬浮颗粒物运动模拟研究在多个工程领域具有广泛应用。
在环境工程领域,可以通过模拟颗粒物在气流中的运动来研究大气扩散和颗粒物污染物的输送;在石油工程领域,可以模拟颗粒物在油井中的运动来研究油气产能和油井堵塞等问题;在化工工程领域,可以模拟颗粒物在流体中的运动来研究颗粒物的分离和混合等过程。
当前,研究人员在悬浮颗粒物运动模拟方面面临一些挑战和难题。
首先,悬浮颗粒物的运动是一个多尺度和多物理过程耦合的问题,需要建立合适的数值模型和求解方法;其次,悬浮颗粒物的运动受到流动的影响,需要考虑颗粒物与流体之间的相互作用;最后,大规模悬浮颗粒物运动模拟需要高性能计算资源的支持,需要开发高效的并行计算算法。
为了解决这些问题,研究人员采用了各种方法和技术。
基于有限元法催化剂颗粒撞击壁面的数值模拟

从而为企业 带来更 多的利益 。为 了使碰撞造成 的催 化剂 颗 粒 和构 件 损耗 更 小 , 国内外 的学者 进行 了相关 方面的研究 , 中, .r n 其 DGi 等 利用有限元法模拟了 i f 多颗颗粒撞击对壁面造成的磨损 ; . ukr 模拟 M Jna等
节 点发生 的最 大位移 如 图 8 所示 。
参考文 献 ( frne) Reeecs :
[ ] 杨 勇刚 , 勇. 1 罗 催化剂磨 损和再生器催化 剂跑损 的控制 [] 炼油设 计 ,0 13 ( )1ቤተ መጻሕፍቲ ባይዱ— 8 J. 2 0 ,19 :5 1. [ ] 刘仁桓 , 2 魏耀东 , 催化裂化装置跑损催化剂 的颗粒粒度分 析[] 石油化工设备 ,0 6 3 ( )9 1 . J. 20 ,5 2 :- 1
p r ce a a t r r p i z d n o d r t e u e c t y t p r ce e o mai n a d e o i e o h u f c t e t c n c a u e a il s p r me e s we e o t t mie .I r e o r d c aa s a t ls d fr t n r sv ft e s r e,h e h ia me s r s l i o a l
[ ] 陈学 东 , 3 王
冰, 关卫和 , 我国石化企业在用压力容器 等.
与管道使用现状和缺 陷状况分 析及失效预防对策 [] 压 J.
力容 器 ,0 1 1( )4 — 3 20 ,8 5 :3 5 . [ ] 万古军 , 4 魏耀东 , 时铭显. 化裂化再生器 树枝状 主风分 催
布管磨损 的气相流场分 析[ ]炼油技 术与工程 ,0 6 3 J. 2 0 ,6
PFC课件(经典)

所以颗粒流程序只存在颗粒-颗粒接触模型和颗粒-墙接触模型。
4、颗粒流方法的特点
PFC可以直接模拟圆形/球形颗粒的运动和相互作用问题。颗料可以 代表材料中的个别颗粒,例如砂粒,也可以代表粘结在一起的固体材料, 例如混凝土或岩石。当粘结以渐进的方式破坏时,它能够破裂。粘结在 一起的集合体可以是各向同性,也可以被分成一些离散的区域或块体。 这类物理系统可以用处理角状块体的离散单元程序UDEC和3DEC来模拟。
举例
①允许粒子发生有限位移和转动,粒子间可以完全脱离 ②在计算过程中能够自动辩识新的接触
PFC 优点:
1、它有潜在的高效率。因为圆形物体间的接触探测比角状物体间的更简单。 2、对可以模拟的位移大小实质上没有限制。
3、由于它们是由粘结的粒子组成,采用其模拟时块体单元可以破裂,而UDEC和 3DEC模拟的块体不能破裂。
最关键的优势
• 平衡方程 • 变形协调方程 • 本构方程
变形协调方程保证介质的变形连续性(材料在变形过程中应 当是连续的,而不能出现撕裂或重叠的现象),本构方程即 物理方程(应力分量与应变分量之间关系),它表征介质应 力和应变的物理关系。
对于颗粒流而言,由于介质一开始就假定为离散颗粒体的
集合,故颗粒之间没有变形协调的约束,但必须满足平衡 方程。
PFC (Particle Follow Code) 是通过离散单元方法来模拟 圆形颗粒介质的运动及其相互作用。最初,这种方法是研究 颗粒介质特性的一种工具,它采用数值方法将物体分为有代 表性的数百个颗粒单元,期望利用这种局部的模拟结果来研 究边值间题连续计算的本构模型。
以下两种因素促使PFC方法产生变革与发展: (1)通过现场实验来得到颗粒介质本构模型相当困难; (2)随着微机功能的逐步增强,用颗粒模型模拟整个问题成为
弹体贯穿钢筋混凝土数值模拟

第23卷 第6期爆炸与冲击Vol.23,No.6 2003年11月EXPLOSION AND SHOCK WAV ES Nov., 2003 文章编号:100121455(2003)0620545206弹体贯穿钢筋混凝土数值模拟Ξ武海军1,黄风雷1,金乾坤2,张庆明1(1.北京理工大学爆炸与安全科学国家重点实验室,北京 100081;2.北京理工大学软件技术开发有限公司,北京 100081) 摘要:详细描述了依据损伤原理建立的连续损伤模型,并对该模型进行了改进。
在L S2D YNA程序用户自定义材料模型中加入改进的连续损伤模型,并对弹体侵彻钢筋混凝土的穿孔过程进行了数值模拟,其结果与实验结果相吻合,模型可以用于钢筋混凝土的动态破坏预报。
关键词:固体力学;贯穿;连续损伤模型;钢筋混凝土;数值模拟 中图分类号:O346.5 国标学科代码:130・1540 文献标志码:A1 引 言 钢筋混凝土作为一种重要的建筑和防护材料,被广泛地应用于军事与民用领域。
当弹丸穿透钢筋混凝土靶后,靶板破坏严重,在靶的背面形成比正面大的弹坑,此时钢筋混凝土靶的断裂破坏有两种形式:靶表面部分由于稀疏波引起的层裂和中间部分由于剪切和挤压引起的断裂破碎。
侵彻过程及弹坑形状与靶厚度、弹丸头部几何形状和撞击速度有关。
对于很厚的靶板,穿深过程起主导作用,关于这点, V.K.Luk等[1~2]作出了满意的解答。
从S.J.Hanchak等[3]的钢筋混凝土侵彻实验中可以清楚地观察到上述的破坏形式。
因此要得到钢筋混凝土穿孔的理想结果,必须考虑混凝土的拉伸破坏。
近年来,人们对混凝土本构关系进行了大量研究。
由于Johnson2Cook模型能够较好地描述混凝土的断裂破坏,目前国内多采用此模型[4]。
T.J.Holmquist等[5]利用Ottosen模型,并考虑了应变率的影响,研究了混凝土的动态冲击过程。
E.P.Chen[6]将连续损伤模型引入混凝土材料的动态响应,也较好地描述了混凝土的动态冲击特性。
爆炸驱动球形破片飞散的数值模拟

第4期邓吉平.等爆炸驱动球形破片飞散的数值模拟97钢球,在对称面上施加了相应的约束.采用Ira—grange算法,计算中单元类型均选用8节点实体单元solidl64.有限元模型如图1所示.图1弹体有限元模型1.2材料模型及参数该弹丸在数值模拟时涉及的材料包括:炸药、钢和硬铝合金.对于炸药材料‘43采用高能炸药材料模型和JwI.状态方程描述.内衬和端盖选用钢材料[5]。
采用Johnson—Cook模型;状态方程为Gruneisen状态方程.蒙皮采用硬铝合金LY-12cz[6],用塑性随动模型MAT—PLASTIC-KINEMATIC进行模拟.钢球破片采用刚性材料模型MAT—RIGID,钢球破片的密度为7.85g/cma,弹性模量为210GPa,泊松比为0.3.炸药和铝合金材料参数及状态方程参数如表1、表2所示.表中,|0为密度;D为爆速;P。
I为爆轰压力;A,B,R。
,R!,叫为材料参数;E0为单位体积初始内能;砜为初始相对体积;E为弹性模量;肚为泊松比弧为屈服极限;E:为切线模量;h为硬化参数.£f为失效应变.表1TNT炸药的爆炸性能及状态方程参数1.3计算结果分析图2为弹丸在炸药中心起爆后钢球破片的飞散过程.结合文献[7,8]分析,上述弹丸破片的飞散情况良好,在中心起爆的情况下,破片沿径向均匀飞散.弹丸破片的飞散速度直接决定了破片的杀伤动能.图3为破片的速度历程曲线.图中,节点A~E分别取自弹丸不同位置的破片.(c)t=24.987p.s图2破片驱动过程图3破片速度历程曲线将上面计算所得的破片初速与文献[-3-1的实验结果进行对比,如表3所示,妒为实验中各靶到弹丸中心连线与弹轴形成的夹角.表3钢球破片的初速分布序号由图3可知,其破片初速大致分布在l330~1670m/s之间,只相差8%左右。
从而说明本文建立的有限元计算模型是合理的.在弹丸设计中,破片飞散角也是极为重要的,它直接关系到破片飞散密度的大小,以及对于打击目标是否有足够的杀伤概率.图4为计算所得的静态98弹道学报第20卷飞散角a,图上节点取自不同位置破片.图4轴向不同位置破片的飞散角由图4可以看出,沿轴向不同位置破片的飞散角有所不同。
基于CFD-DEM耦合的径向移动床反应器数值模拟

10.3969/j.i s s n.1008-5548.2013.03.003基于C FD-D EM耦合的径向移动床反应器数值模拟吴臻刘雪东黄令军常州大学机械工程学院,江苏常州213016摘要:针对径向移动床反应器内颗粒及流体分布不均的问题,采用计算流体力学(CFD)-离散单元法(D E M)耦合的方法,对6种不同开口面积和分布形式的中心管的移动床反应器内的颗粒与流体的运动行为进行数值模拟,分析反应器内部气体流场特性及颗粒运动特性的变化。
结果表明,开孔面积与进口面积的适宜比例为0.8~1.12,最优比为0.96;改变中心管两端开孔的分布能使流场均布,避免端效应的产生。
计算流体力学-离散单元法耦合;移动床反应器;数值模拟TQ132A1008-5548(2013)03-0009-05N um e r i ca l Si m ul at i on of Radi a l Fl owM ovi ng-be d Re a c t or U s i ng CFD-D EMC oupl i ng A ppr oac hW U Zh e n L I U X uedong H U A N G Li ngj unS c hool of M e c ha ni ca l Engi ne er i ng,C hangzhou U ni ver si t y,C hangzhou213016,Chi naA bs t r act:The fl ow behavi or of par t i cl es and f l ui d i n radi al f l owm ovi ng-bed r eact or w i t h6cent er pi pes of di ff erent open ar ea anddi s t r i but i on f or m s w er e s i m ul a t e d usi ng C FD-D E M coupl i ng m e t hod duet o t h ei r uneve n di st r i but i on.T he chang i ng char act er i st i s of gas f l ow f i el dand par t i cl e m ovem ent w er e anal yzed.The r es ul t s s how t hat t heapp r o pr i at e r a t i o o f o pen i ng h ol e ar e a and i m por t ar e a i s bet ween0.8and1.12,an d t he op t i m al r at i o i s0.96.Changi ng t he di st r i but i on of t he o penhol es on c ent er pi pe e nds c a n uni f or m t he f l ow f i e l d and a voi d t heocc ur r enc e of e nd ef f e ct.K ey w or ds:C FD-DEM coupl i ng;m ovi ng-bed r eact or;num er i cals i m ul at i on2012-11-052012-11-18第一作者简介:吴臻(1988-),男,硕士研究生,研究方向为化工过程机械、粉体工程技术及应用。
韧性金属圆球壳的动态膨胀和碎裂过程的数值模拟
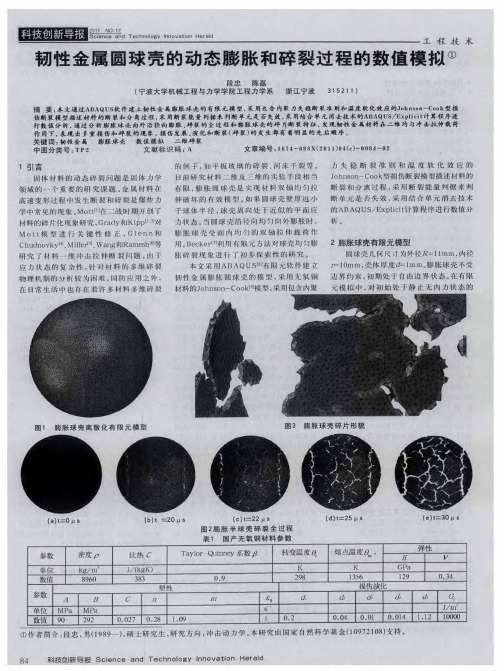
以通过 将球壳体 刨分平均 的两个半 球壳 ,
推 得 另 一 个 半 球 壳 的 膨 胀 碎 裂 规 律 。 球 半
观 察 一 个 半 球 壳 的 膨 胀 碎 裂 过 程 , 应 地 材 料 由 于 塑 性 变 形 产 生 的 局 部 升 温 。 以 对 可
发 现 单 个 碎 片 的 断 口不 均 匀 , 现 非 连 续 呈
坏 。 过 分 析 半 球 壳 膨 胀 碎 裂 过 程 图2, 通 在
图2 b中观 察 到 了材 料 损 伤 区域 的 形 成 , 然
后 演 化 为 图2 c中 的 微 裂 纹 成 形 , 图 2 到 d中 多 微 裂 纹 的 产 生 , 每 个 裂 纹 产 生 的 时 间 但
5 结 论
1 通 过 分 析 半 球 壳 膨 胀 碎 裂 的分 幅 图 )
碎 片 分 布 表 现 出 随 机 性 , 口不 光 滑 。 断 整个过 程可分为 : 启动 , 匀 弹 性 变 形 , 均 均 伤 区 域 并 没 有 演 化 成 为 断 口 。 球 壳 内部 圆
匀 塑 性 膨 胀 , 均 匀 塑性 膨 胀 , 裂 起 始 , 非 断
完 全 碎 裂 , 由 飞行 等 各个 阶 段 。 过 改 变 自 通
2 1 N0 01 1 2
工 程 技 术
球 壳 沿 径 向 施 加 均 匀 初 始 速 度 , 其 自 由 使
S in e a d Te h oo y In v c e c n c n lg n o a
丽
— ,8 3 u一 t ∞
中 某 个 区 域 首 先 产 生 了 微 裂 纹 , 外 载 荷 在 的破坏; 一部分实验出现的现象是 , 另 材料
的 温 升 由 塑 性 变 形 功 转 换 而 来 , 映 了各 反
基于响应曲面法与离散元法的破碎过程能耗仿真分析

基于响应曲面法与离散元法的破碎过程能耗仿真分析黄鹏鹏;李成;胡明亮【摘要】以降低破碎机的破碎能耗为目标,建立以PE250*400颚式破碎机为原型的的几何模型及颗粒物料模型,以梯形齿上底边长、动颚板与定颚板的啮角、动颚板的水平行程和动颚板的运动速度等4个因素作为优化变量,根据响应曲面法(RSM)设计原理对其进行分组试验,结合EDEM软件对物料破碎过程中能量的消耗以及断裂键数进行数值模拟.研究结果表明:破碎机破碎过程中单位能耗的破碎效果受梯形齿上底边长、啮角、动颚板的水平行程影响显著,而运动速度则次之,影响程度从大到小排列为动颚板的水平行程、上底边长、啮角、运动速度.另外,破碎过程中最优参数为梯形齿上底边长5mm、动颚板与定颚板的啮角17°、动颚板的水平行程40mm和动颚板的运动速度1m/s.【期刊名称】《机械设计与制造》【年(卷),期】2016(000)010【总页数】5页(P78-82)【关键词】响应曲面法;EDEM;破碎能耗;仿真【作者】黄鹏鹏;李成;胡明亮【作者单位】江西理工大学机电工程学院,江西赣州341000;江西理工大学机电工程学院,江西赣州341000;江西理工大学机电工程学院,江西赣州341000【正文语种】中文【中图分类】TH16随着经济的快速发展,物料的需求越来越大,破碎机的应用也越来越广泛,全国每年都需要破磨大量的矿石和岩石,消耗大量的电能。
以矿山生产为例,破碎作为选矿的第一道工序,其耗电量就占到了选矿厂总耗电量的50%以上[1],并且大量的电能由于破碎过程中的摩擦等转化为热能被耗散。
因此,为了提高能量利用率以降低能耗,对破碎过程中的能耗进行研究具有必要性。
为了最大程度地提高破碎机的能量利用率,文献[2]运用离散元法研究了能量的消耗与转速、行程的影响关系,研究表明随着转速的降低和行程的增加,消耗的能量呈先增后减的趋势;文献[3]运用离散元法模拟立方体物料与球体物料在两颚板之间的挤压破碎过程,研究模拟的应变能与由Bong破碎系数估计的应变能之间的关系,并进一步研究证实了大量的球形岩石情形下,颚板吸收的能量与颗粒特定的粉碎能量相近,但是颚板吸收的能量与立方岩的断裂能量之间呈现着多样性的特点[4];文献[5]运用离散元法模拟了不同粒径颗粒在颚式破碎机中的破碎过程,并得出了颗粒能量吸收与碰撞频率的关系曲线,指出当每秒碰撞800次时,在能量为1mJ的能量级水平上将出现一个大致的正态分布;某大学的母福生运用EDEM对单颗粒物料单向压缩下的能耗进行了研究,得到了压板的冲击速度、齿板厚度以及两齿间水平距离对能耗及破碎概率的影响次序[6];破碎过程中衬板直接挤压物料,其齿形对破碎效果及破碎过程中能量消耗起着非常重要的作用,目前大多数研究者主要研究了齿形对破碎效果以及破碎力的影响,如文献[7]运用有限元软件分析齿板的受力情况,得出齿顶距越小,物料越容易破碎,但会减弱破碎齿的强度;文献[8]基于离散元法和正交试验设计进行数值仿真,获得齿形参数多因素对破碎力的综合影响规律,获得最优齿形参数组合。
离散元数值模型对颗粒颗粒摩擦力仿真

离散元数值模型对颗粒颗粒摩擦力仿真摘要:离散元数值模型(DEM)是一种用于模拟颗粒颗粒间相互作用的数值模型。
在DEM模型中,粒子被视为离散的实体,通过考虑颗粒颗粒之间的力学相互作用来模拟实际颗粒体系的动力学行为。
本文讨论了DEM模型在颗粒颗粒摩擦力仿真中的应用,并介绍了一些常用的方法和技术。
1. 引言离散元数值模型是一种基于颗粒间力学相互作用的数值模拟方法。
它广泛应用于颗粒流动、颗粒堆积、颗粒颗粒碰撞等领域。
颗粒颗粒摩擦力是DEM模型中的一个重要参数,它对颗粒系统的力学行为具有重要影响。
2. DEM模型简介DEM模型将颗粒视为离散的实体,通过求解颗粒间的力学相互作用来模拟实际颗粒体系的运动。
在DEM模型中,每个颗粒被建模为具有质量、形状和位置的刚体。
力学相互作用包括弹性力、摩擦力、粘聚力等。
3. 颗粒颗粒摩擦力模型颗粒颗粒之间的摩擦力是DEM模型中的一个重要参数。
颗粒颗粒间的摩擦力可以通过多种方式建模,常见的方法包括:- 接触力模型:常用的接触力模型包括线性弹簧-阻尼模型、Mohr-Coulomb模型等。
这些模型通过使用弹簧和阻尼元件来模拟颗粒颗粒之间的摩擦力。
- 离散元模型:离散元模型通过将颗粒视为离散的刚体,使用力学相互作用来模拟颗粒颗粒之间的碰撞和摩擦。
- 其他模型:还有一些其他的方法可以用于建模颗粒颗粒之间的摩擦力,例如基于颗粒形状的模型、基于接触表面特征的模型等。
4. DEM模型在颗粒颗粒摩擦力仿真中的应用DEM模型在颗粒颗粒摩擦力仿真中有广泛的应用。
它可以用于研究颗粒颗粒之间的摩擦力对颗粒流动、颗粒堆积等行为的影响。
DEM模型可以提供关于颗粒流动性质、颗粒堆积形态等方面的定量信息。
5. DEM模型中摩擦力参数的确定在使用DEM模型进行颗粒颗粒摩擦力仿真时,摩擦力参数的确定是一个重要的问题。
常见的方法包括实验测定、摩擦力系数调整等。
实验测定方法可以通过直接测量颗粒颗粒之间的摩擦力来获得参数值。
软式空中加油系统鞭甩现象多体动力学分析

软式空中加油系统鞭甩现象多体动力学分析作者:赵振军谭兴宇史晓军张昌荣郭鹏来源:《振动工程学报》2024年第04期摘要软管‑锥套式空中加油系统的柔性结构经常发生不同程度的软管鞭甩现象,极大影响空中加油任务的安全性。
基于柔性多体动力学,建立了空中加油系统动力学模型,其中,利用基于任意拉格朗日‑欧拉描述方式和绝对结点坐标法的索/梁模型描述管线的大变形、大范围运动以及软管收放,并对空中加油系统受到的气动力进行建模,建立的模型能够反映加油机和受油机运动、软管和锥套的变形与气动力的耦合影响。
基于建立的空中加油系统动力学模型,复现飞行状态下的软管鞭甩现象,获得了鞭甩现象的形成机理。
研究表明,对接冲击下,软管平衡状态改变所形成的剪切波向后传播与反射是鞭甩现象产生的主要原因。
通过多工况计算结果,分析了软管刚度、对接速度、Ma数各因素对鞭甩现象引起的软管剪切力、纵波与剪切波传播速度的影响规律,并分别分析了软管收放控制和加缓冲的受油插头两种措施对鞭甩现象振动抑制的有效性。
关键词多体动力学; 空中加油; 鞭甩现象; 软管‑锥套组合体引言空中加油是飞行器在不着陆情况下,实现燃油快速补给、提升战机滞空时间、及时投入战场作战的主要技术手段。
根据加油管路方案的不同,空中加油可以分为软管式加油和硬管式加油两种方式[1],中国主要采用软管式加油方式。
软管是一根长达数十米的柔性体,在对接过程中受到多种内外部干扰因素影响,比如加油对接操纵方式、软管柔性材料、飞行Ma数、加油机尾流、姿态变化、受油机头波等[2]。
软管鞭甩现象是造成空中加油失败的主要原因之一[3],在空中加油的对接和输油阶段,受油机高速对接引起软管松弛,有可能发生软管鞭甩现象,轻则导致加油行动失败,重则使受油机受损、危及飞行安全。
因此,深刻揭示软管鞭甩现象的内在机理,提出有效的抑制/解决措施,对于提高空中加油的安全性、可靠性具有十分重要的意义。
对空中加油管线系统动力学建模方法主要有两种:多刚体动力学链式模型、有限元梁/索模型。
基于有限元法催化剂颗粒撞击壁面的数值模拟

基于有限元法催化剂颗粒撞击壁面的数值模拟
袁健;沈文君
【期刊名称】《机电工程》
【年(卷),期】2012(029)010
【摘要】为解决催化裂化装置中的许多构件因为催化剂颗粒长期不断冲击而导致失效等的问题,将有限元法应用到其模拟仿真中,分析了单颗催化剂颗粒参数(角度、速度、材料)对不同壁面材料的撞击而造成壁面磨损的影响,建立了催化剂颗粒撞击壁面的数值分析模型,研究了催化剂颗粒以不同的速度、撞击角度,以及不同的催化剂颗粒的材料撞击不同材料的壁面对壁面造成的影响,并分析了催化剂颗粒变形对壁面磨损的影响,根据计算的结果,对催化剂颗粒参数进行了优化控制,提出了减少催化剂颗粒变形和构件磨损的技术措施.研究结果表明,该方法能够使催化裂化装置长期安全稳定地运行.
【总页数】4页(P1179-1182)
【作者】袁健;沈文君
【作者单位】浙江工业大学特种装备制造与先进加工技术教育部重点实验室,浙江杭州310032;浙江工业大学特种装备制造与先进加工技术教育部重点实验室,浙江杭州310032
【正文语种】中文
【中图分类】TE963;TH117
【相关文献】
1.大水滴撞击壁面的动态特性数值模拟 [J], 郭宇翔;刘荫泽;董威;雷桂林;朱剑鋆
2.催化剂颗粒撞击壁面的有限元分析 [J], 刘冬玉;周迪峰
3.稠密颗粒射流撞击壁面颗粒膜表面波纹特征∗ [J], 钱文伟;李伟锋;施浙杭;刘海峰;王辅臣
4.剪切变稀液滴撞击不同浸润性壁面的数值模拟研究 [J], 沈学峰; 曹宇; 王军锋; 刘海龙
5.基于计算流体力学-离散单元法耦合的粗糙壁面颗粒趋壁沉积过程的数值模拟 [J], 刘岩;秦攀;洪文鹏
因版权原因,仅展示原文概要,查看原文内容请购买。
大颗粒与壁面碰撞的离散单元法模拟与分析

大颗粒与壁面碰撞的离散单元法模拟与分析张鹤;李天津;刘马林;黄志勇;薄涵亮【摘要】颗粒与壁面碰撞普遍存在于散体物料输送过程,研究颗粒与壁面碰撞有助于优化输送系统、减小物料磨损或提高输送经济性.本文基于离散单元法(DEM),采用Hertz-Mindlin无滑移接触模型,对单个6 mm直径大颗粒与壁面碰撞进行了数值模拟和分析,研究了碰撞速度、碰撞角度和剪切模量对碰撞过程和法向最大接触力的影响.研究结果表明,Hertz-Mindlin无滑移接触理论描述的法向接触过程具有自相似特性,法向卸载时长与法向加载时长比值为定值.模拟的接触时长与Thornton等的关系式预测值相符.碰撞速度和碰撞角度对碰撞过程中的法向最大接触力均有明显影响,法向最大接触力随法向碰撞速度的增加近似线性增加;碰撞速度不变时,法向最大接触力随碰撞角度的增大而减小.剪切模量对法向接触力具有重要影响,在考虑颗粒磨损和破碎的DEM模拟时,不宜采用降低剪切模量加快计算速度.本研究对颗粒磨损和破碎研究以及高温气冷堆吸收球气力输送过程优化均具有重要意义.%Particle-wall collisions widely exist in bulk solidstransportation .Investiga-tions on particle-wall collisions are helpful to optimize transporting system ,decrease product attrition or improve transportation economy .Collisions between a single coarse particle (6 mm in diameter) and a wall were investigated by Hertz-Mindlin no-slip con-tact model based on discrete element method (DEM ) .Effects of impact velocity ,impact angle and shear modulus on contact processes and maximum normal contact forces were studied .Results show that the normal contact process described by Hertz-Mindlin no-slip contact model shows self-similarity feature ,and the ratio of unloading to loadingduration in normal direction keeps as a certain value .The numerical contact durations agree well with the predictions by the correlation of Thornton et al .The impact velocity and impact angle show obvious effects on maximum contact forces .The normal maxi-mum contact force increases almost linearly with normal impact velocity .For the certain impact velocity of 2 m/s ,the normal maximum contact force decreases with the increase of impact angle .The shear modulus is a key factor to normal contact force ,which sug-gests that speeding up DEM simulation by decreasing shear modulus should be avoided when particle attrition and/or breakage are in consideration .The results in the present study are important for investigation of particle attrition and/or breakage ,as well as optimization of absorber sphere pneumatic conveying process in high temperature gas-cooled reactor .【期刊名称】《原子能科学技术》【年(卷),期】2017(051)012【总页数】6页(P2212-2217)【关键词】颗粒碰撞;颗粒磨损;颗粒破碎;离散单元法;气力输送【作者】张鹤;李天津;刘马林;黄志勇;薄涵亮【作者单位】清华大学核能与新能源技术研究院 ,先进核能技术协同创新中心 ,先进反应堆工程与安全教育部重点实验室,北京 100084;清华大学核能与新能源技术研究院 ,先进核能技术协同创新中心 ,先进反应堆工程与安全教育部重点实验室,北京 100084;清华大学核能与新能源技术研究院 ,先进核能技术协同创新中心 ,先进反应堆工程与安全教育部重点实验室,北京 100084;清华大学核能与新能源技术研究院 ,先进核能技术协同创新中心 ,先进反应堆工程与安全教育部重点实验室,北京100084;清华大学核能与新能源技术研究院 ,先进核能技术协同创新中心 ,先进反应堆工程与安全教育部重点实验室,北京 100084【正文语种】中文【中图分类】TL33吸收球停堆系统是高温气冷堆的第二停堆系统[1]。
可破碎颗粒体在动力载荷下的耗能特性

可破碎颗粒体在动力载荷下的耗能特性祁原;黄俊杰;陈明祥【摘要】采用离散元的数值方法,通过连接键将若干小颗粒绑定为一个具有不规则外形的大颗粒体,设置不同连接键强度模拟了颗粒体在外加动力载荷下破碎过程,并探讨其中系统能量耗散特性.计算结果表明,颗粒体的破碎程度决定了系统能量耗散率,即内部耗能占外界输入能量的比例.破碎率越高,颗粒间相互摩擦和碰撞越剧烈,系统能量耗散率越高.同时,在循环载荷下系统内颗粒体破碎绝大部分发生在加载初期,随着颗粒体的分解破碎速率逐渐减小,系统耗能能力也随之降低.【期刊名称】《力学学报》【年(卷),期】2015(047)002【总页数】8页(P252-259)【关键词】离散元;颗粒破碎;破碎率;能量耗散【作者】祁原;黄俊杰;陈明祥【作者单位】武汉大学工程力学系,武汉430072;武汉大学工程力学系,武汉430072;武汉大学工程力学系,武汉430072【正文语种】中文【中图分类】TU43颗粒材料作为典型的离散介质广泛地存在于实际的工程中,如土石坝堆料[1]、路基填料[2]、颗粒阻尼器[3].它在静力加载下的应力应变关系[4-5]、组构张量的演化[6-7]、循环加载[8-9]下的力学特性等数值和模型试验已经存在很多相关的研究,而对于颗粒材料的动力学特性[10-11],尤其是系统内部能量的关系却很少涉及.近年来,堆石坝由于其取料方便、施工简单、抗震性能强等特性,在我国的经济建设中尤其是地震较为频繁的地区得到越来越多的应用,因此对于离散介质的动力学响应以及其耗能机制的研究有着极其重要的意义.传统的有限元方法在讨论岩土材料的动力学特性时,一般采用设置阻尼系数来研究结构内部的能量耗散.这种方法虽然简便,然而对其物理机制的描述却很模糊.事实上,离散介质内部能量耗散的形式主要体现在颗粒表面相互滚动和滑动导致的摩擦耗能,以及颗粒间非弹性碰撞引起的阻尼耗能.文献[12]以二维圆形颗粒为模型研究了无黏性土在动力载荷下系统能量的耗散,指出在各种外界激励下摩擦耗能占据内部能耗的绝大部分;文献[3]通过研究两种阻尼器模型,从数值模拟的角度研究阻尼和摩擦耗能的关系,然而其模型的基本单元局限在等直径圆形颗粒;文献[13]通过研究非阻碍性颗粒阻尼(non-obstructive particle damping)时发现颗粒摩擦耗能与碰撞阻尼耗能处于同一等级,并且随着颗粒半径的减小摩擦耗能在系统能耗中增加,但是在讨论颗粒粒径的对于耗能的影响时,所研究的颗粒的数目并不是固定的;黄俊宇等[14]通过改变外界加载应变率的变化讨论了脆性颗粒材料的应变率效应,却没有明确指出阻尼和摩擦的影响.事实上,在实际的工程中颗粒材料往往不是规则的圆形,并且在外界激励下尤其是粗粒料往往会发生破碎,引起系统内颗粒级配的改变,从而显著的影响结构强度、内部结构等特性[15-19],这些变化对系统能量的吸收和耗散的影响是一个值得关心的课题.本文采用离散元的方法,通过设置连接键将若干基本颗粒绑定为一个具有不规则外形的整体,以此为模型模拟了二维颗粒体随外界循环动力载荷的破碎过程,并从微观的角度探讨颗粒体破碎对于系统耗能的影响.具体的,第1节对颗粒体连接键的设置、破碎率的定义以及能量的组成部分作简要介绍;第2节给出数值试验的模型和参数,以及外加动力载荷的模式;第3节在给定的细观参数以及加载方式下进行一系列数值试验,并对结果加以解释;第4节总结本文得出的结论.离散元方法(discreteelementmethod)首先由文献[20]提出,假设最基本单元是一个个能够产生局部变形的刚性小球,通过局部接触模型和牛顿第二定律来研究物体的运动和变形.与传统的有限元相比,它更贴近实际物理模型并且能从微观的角度提供更多的信息来解释宏观的力学行为.关于颗粒流离散元的基本原理在文献[21-22]中已经做出了详细的介绍,不再赘述.这里给出的基本概念包括:颗粒体连接键、能量以及破碎率.1.1 颗粒体连接键传统的离散元方法对颗粒做出了刚性假设,允许颗粒间接触发生重叠但颗粒本身无法变形以及破碎.为了实现颗粒的破碎过程,一般设置具有一定强度的连接键将若干基本颗粒绑定为一个整体.本文的重点在于描述颗粒破碎对于能量耗散的影响,简单起见,采用与文献[15,23-24]类似的方法,粗略地将样本中原始粒径超过细沙范围的颗粒等质量地替换为7个颗粒绑定的颗粒体,如图1所示.颗粒间连接键设置有两种,接触键和平行键[22].其中接触键不允许绑定的颗粒间发生滚动,其接触集中在一个点,如果超过接触力临界值接触键断裂,但是这种接触模型无法记录接触键的弹性变形以及能量的变化;平行键相当于颗粒间的黏结物质(比如混凝土中粗骨料间的水泥砂浆),允许其在一定界限内发生弹性变形并储存弹性能,超出强度极限即发生脆断,连接键失效,但是这种连接键允许颗粒间接触“脱落”,并且颗粒间可以发生相对滑动.本文采用两种键混合的形式来实现颗粒破碎前颗粒体内部不发生相对滑动,同时记录断裂前能量的变化和颗粒破碎消耗的能量.这种混合键的形式在很多研究中均得到了采用,但是,大多的数值模拟关于两种键参数的设定并不严谨:其中一个键的失效并不能同时保证另外一个键的失效.事实上,在颗粒破碎后,脱离原集合体的颗粒变为“自由颗粒”,从而不再与“本体”有键的连接.为了保证使数值模拟的过程更加贴近实际情况,本文中涉及的计算均设定当接触键失效的同时设定平行键强度参数为零,即平行键失效.1.2 破碎率破碎率是衡量颗粒破碎程度的重要指标,刘汉龙等[19]总结了多种根据粒径级配曲线变化的定义,指出这类方法只能反映某个粒径下颗粒数目的变化,不能从整体上反映系统颗粒破碎的情况.在实际的数值模拟中,颗粒体是由事先定义好的小粒径颗粒连接组成,所以初始设定组成等效颗粒体中小颗粒的直径对于破碎后的颗粒粒径的分布有很大的影响,从而影响到破碎程度判断.本文采用刘君等[15]的定义,即通过断裂的连接键与初始设定的总连接键的比值来定义破碎率其中,N br,N ini分别是断裂的连接键数目和初始连接键的数目.1.3 能量本文涉及的能量组成部分[12,25]包括:重力做功E b其中,Np,mp,g,d u p分别为颗粒数,颗粒的质量,重力加速度和颗粒质心的位移增量. 边界施加的外力功Ew其中,Nw是边界的数目,f w和t w分别为外力和外力矩,d u w,dθw为相应的位移增量和角度增量.颗粒平移和旋转的动能Ek其中,Ip和ωp分别为转动惯量和相应的角速度.数值模拟中颗粒假设为不可变形的刚体,其等效应力通常由颗粒表面各接触点的接触力获得[4-6],颗粒的应变也集中在接触点并由接触弹簧的变形来体现.于是,颗粒接触应变能E s等效为接触部分的法向与切向弹簧变形能之和,其表达式为其中,N c为接触数,f n和f t分别为接触力的法向和切向分量,k n和k t为相应的接触刚度.颗粒摩擦耗能E f是指由于颗粒间的相互滚动和滑动使得接触表面产生摩擦力而耗散的能量,其表达式为其中d u slip是扣除弹性变形后的位移增量.颗粒碰撞阻尼耗能E d是指颗粒间的非弹性碰撞耗散的能量,其表达式为其中,c n和c t分别为法向和切向的阻尼系数.连接键弹性能E pb其中,N pb表示连接键数目,f pbn,f pbt和t pb分别表示连接键所受法向力、切向力以及扭矩,k pbn和k pbt分别为连接键法向刚度和切向刚度,A pb和I pb分别表示连接键的横截面积以及转动惯量.连接键失效瞬间,记录该时刻E pb作为外界激励使该连接键失效所需要的能量,于是颗粒体破碎所消耗的能量E br可以表示为其中,c br为失效的连接键的数量.上述能量分量中,施加在边界墙上的载荷为外界激励,重力势能、颗粒动能、摩擦耗能、阻尼耗能、颗粒间以及连接键间的应变能为内部的能量.由能量守恒,可得本文研究的对象为粒径在2.0~15.0mm范围的二维无黏性颗粒.样本生成的过程是:首先将底部和左右两侧的边界固定,接着在较大区域内均匀生成上述粒径范围内的颗粒,并且将粒径大于6mm的颗粒用同等质量的颗粒体代替,如下图2所示,其中绿色颗粒表示的为小于6mm的颗粒,蓝色表示的为等效的颗粒体.颗粒体中颗粒间连接键用球心间红色连线表示,若连接键失效红线也随之消除.接着施加重力使颗粒沉降同时检测底部边界受力,当其受力稳定后即认为系统平衡,删除高出范围的颗粒,使样本的尺寸为360mm×360mm;继续循环直至底部边界受力再次稳定,样本生成完毕.由1.1节的假设可知在设置颗粒体破碎准则时,只用定义接触键的极限值.接触键的强度是影响颗粒体破碎的重要参数,其值的大小直接影响到颗粒体破碎的程度.黄俊宇等[26]在研究颗粒体时设定平行键强度法向强度为30MPa,对应于本文不同粒径的颗粒体连接键极限值范围约为485~3000 N.本文的研究重点在于颗粒体破碎对于系统耗能的影响,故不区分接触键拉伸破坏或剪切破坏.考虑到连接键极限值过低,系统在加载至初始固结应力下会过早的发生颗粒体破碎,故设置5组不同强度的接触键其值分别为1 kN,1.5 kN,2.0 kN, 3.0 kN,5.0 kN以模拟在相同加载条件下系统颗粒体不同程度的破碎.其余微观参数参照文献 [12,25]对石英沙土的取值,即颗粒间法向和切向刚度均取10MN/m,颗粒间摩擦系数为0.5,法向阻尼系数比例为0.1,颗粒密度取2650 kg/m3.为了模拟样本在循环动力载荷下的运动过程,采用土工试验中动三轴双向激振的方法.在初始应力为σx=70 kPa,σy=100 kPa的状态下,固定底部边界和左边边界,同时对顶部边界和右边边界分别施加速度激励,速度激励形式为其中,αp=2πf,f为加载频率取4Hz.vp为速度激励幅值取0.674m/s,这样样本在竖直方向达到最大压缩时,其工程应变正好为15%.本节主要对颗粒体在外加动力载荷下的破碎过程进行数值模拟,同时探讨该过程中系统微观结构的变化以及能量耗散的机理.3.1 颗粒体破碎及系统耗能在外界激励下,颗粒不断与周围颗粒或者边界碰撞,通过相互间的摩擦和挤压,颗粒体中连接键受力达到极限值时失效,颗粒体逐渐破碎并分解为粒径较小的颗粒,如图3所示.图4(a)显示的是颗粒体破碎率随时间的变化,可以看出加载阶段在A点0.035 s前破碎率增加较慢,随后颗粒体加速破碎,B点0.125 s即1/2周期开始卸载,破碎率增加减缓,到C点约0.22 s颗粒体破碎率不再增加,D点0.25 s完成一个加载循环后外界停止速度激励.在这个过程中,系统内应力的竖向方向分量随时间的变化如图4(b)所示.虽然在加载初期已有少部分连接键失效,但是颗粒体其他连接键的约束以及颗粒表面摩擦阻力使得颗粒之间没有较大的相对运动,系统内部结构没有较大的变化,整体表现为弹性变形,于是应力稳定变化.E点0.043 s后破碎率继续增加,颗粒的内部连接减弱,颗粒之间的相互运动使原有的结构发生变化,使得系统的承载力有所下降,应力出现跌落.随后系统又形成新的构型,系统接触数目增加,颗粒排列更加紧密使应力回升,如此反复使得应力在加载阶段出现较大波动.B点后底部边界向下运动,卸载过程中颗粒几乎不再破碎,系统内部结构相对稳定,于是应力曲线变化较为光滑.同时,由于内部颗粒的排列发生变化,经过一个周期的运动回到初始状态时,系统内平均应力竖直方向分量由初始100 kPa减小到约30 kPa.在能量方面,图5(a)表明外部输入的能量与内部吸收耗散的能量大致相等,保证整个计算过程能量守恒.图5(b)显示了各能量组成部分随时间变化的过程,其中颗粒间摩擦耗能在加载阶段约为卸载阶段的2倍,阻尼耗能只是在加载阶段增加随后保持不变,应变能由于初始应力场在加载前不为零,在经历一段与应力同样的波动达到峰值随后减小.由前面的讨论可知,加载阶段颗粒体发生破碎,颗粒间的相对运动加剧,并且颗粒接触表面积增加,促进了系统内摩擦和阻尼耗能;0.125 s系统达到最大形变后卸载,与加载阶段相比,系统内力降低,颗粒几乎不再发生破碎,系统内部结构稳定减少了颗粒间的相对运动,整体表现为弹性变形,摩擦和阻尼耗能增量也随之降低.同时可以发现,经过一个循环的加载,由于系统内部颗粒体的破碎使得颗粒间的排列更加紧凑,相同宏观应变的情况下系统内部的应力减小,系统的应变能相对于加载之前有所降低.3.2 破碎对系统耗能的影响为进一步探讨颗粒体的破碎程度对系统耗能的影响,在保证其他参数相同的情况下将连接键强度分别设置为1.5 kN,2.0 kN,3.0 kN,5.0 kN.图6表明不同连接键强度下,系统能量各分量随时间变化的情况大致相同.随着连接键强度的增加,边界输入的能量和应变能也随之增加,并且应变能在加载阶段逐渐变得光滑.这是由于,连接键强度越高,颗粒体越难以破碎,系统内部结构越稳定,内部扰动引起的卸载现象就越难以发生,宏观上应变能波动就越小.同时,由于破碎率的降低,颗粒间的相对运动受到限制,颗粒间的阻尼耗能逐渐减少,应变能峰值也随着连接键强度的增加而逐渐超过摩擦耗能.这说明颗粒破碎率的变化改变了系统储能以及耗能的比例.为了量化这一现象,引入能量耗散率的概念,即系统耗散的能量与外界输入能量的比值.图7显示的是外界累计输入能量达到最大值时能量耗散率随连接键强度的变化情况,可以看出,连接键强度为5.0 kN时,系统内部颗粒没有发生破碎,外界输入的能量只有大约26%被颗粒间相互摩擦消耗,其余约74%的能量储存为应变能;连接键强度减小至1.0 kN时破碎率提高到32%时,摩擦和阻尼消耗的能量占据外部输入能量的比值提高至62%.也就是说,颗粒体破碎程度越严重系统消耗的能量的越多,储存为系统的应变能就相对减少.而对于具体的结构来说,系统储存的应变能越高其稳定性越低.颗粒体破碎提高了系统的能量耗散能力,进而提高了其稳定性,使得结构更加安全.3.3 循环载荷下破碎率和系统耗能的变化为讨论循环加载对于破碎率的变化及其对系统能耗的影响,在相同的条件下将载荷激励时间延长至8 s.图8显示的是连接键强度为1.0 kN时颗粒体破碎率随时间变化的过程,可以看出,破碎率是随时间单调增加的,并且在加载初期不规则的颗粒外形使得应力集中现象较为严重,颗粒体破碎速率较快;随后由于大的颗粒体逐渐分解为小的颗粒,系统颗粒级配分布更加合理,接触点的应力集中现象得到了缓解,颗粒间接触力分布更加均匀,使得连接键足以抵抗外界的激励,破碎率逐渐减缓.该结果与文献[27]在动力三轴试验仪下观察的颗粒在循环加载初期阶段发生大多数破碎的现象相吻合.图9显示的是在各加载周期外界输入能量最大时,系统能量耗散率的变化.如图可知,能量耗散率在第1个周期达到约62%,随后下降,到第7个周期后停留在33%左右.不难看出,系统能量耗散率的变化与颗粒体破碎情况相同步.第1个加载循环中,颗粒体破碎较为剧烈,颗粒间的内部连接变弱,结构的变形主要由系统内颗粒间的相互运动、空隙填塞主导,这个阶段颗粒间的摩擦和阻尼耗能相对较多;颗粒体破碎减缓后,由颗粒破碎导致系统内部结构扰动作用减小,结构的变形形式转换为整体颗粒的弹性变形,外界输入的能量主要储存为内部应变能,于是能量耗散率也随之降低.本文采用离散元的方法,模拟出颗粒体在外界动力激励下的破碎过程,并以此探讨颗粒体破碎对于系统能量耗散的影响.结果表明,在动力载荷下外部输入的能量主要转化为应变能以及被颗粒间的摩擦和碰撞阻尼所消耗,并且在相同载荷条件下系统内颗粒破碎率越高,能量耗散率越高;在循环载荷下,颗粒在加载初期破碎较为剧烈,系统能量耗散率较高,随后颗粒破碎速率降低,能量耗散率也随之降低,进一步说明了颗粒破碎程度与系统耗能能力成正相关关系.本文仅对一组微观参数和加载模式下进行数值分析,而颗粒材料的微观参数(如刚度、阻尼系数、密度、摩擦系数),以及加载模式(加载周期、频率、振幅等)对于颗粒材料耗能特性的影响将会在接下来的研究中做进一步探讨.1)Thisprojectwassupported by TheHubeiProvincialKey Laboratory of Safety for Structuraland GeotechnicalEngineering(HBKLCIV201207),the Young Faculty ResearchGrantatWuhan University(2042014KF0007),and TheNationalKey Basic Research DevelopmentProgram(973Program) sub-project(2014CB046902).2)Chen M ingxiang,professor,research interests:solidmechanics.E-mail:**************.cn【相关文献】1 Deluzarche R,Cambou B.Discrete numericalmodelling of rockfil dams.International Journalfor Numericaland AnalyticalMethods in Geomechanics,2006,30(11):1075-10962石云,郑月秀.大粒径填石路堤碾压试验研究.公路交通技术, 2011,6:13-15(Shi Yun,Zheng Yuexiu.Experimental research on rolling compaction of large particle size rock fillin roadbed.Technology ofHighway and Transport,2011,6:13-15(in Chinese))3 Bai XM,Keer L,Wang QJ,et al.Investigation of particle dampingmechanism viaparticledynam icssimulations.GranularMatter, 2009,11(6):417-4294 BagiK.Stressand strain in granular assemblies.Mechanics ofMaterials,1996,22(3):165-1775 Li X,Yu HS,Li XS.Macro–micro relations in granularmechanics.International Journal of Solids and Structures,2009,46(25–26):4331-43416 Li X,Li XS.M icro-macro quantificatio of the internal structure of granularmaterials.Journal of Engineering Mechanics,2009, 135(7):641-6567 M illet O,Gu S,Kondo D.A 4th order fabric tensor approach applied to puters and Geotechnics,2009,36(5): 736-7428 Sitharam TG.Discrete elementmodelling of cyclic behaviour of granularmaterials.Geotechnical&Geological Engineering,2003, 21(4):297-3299 Ng T,Dobry R.Numerical simulations of monotonic and cyclic loading of granular soil.Journal of Geotechnical Engineering, 1994,120(2):388-40310孔宪京,刘君,韩国城.面板堆石坝模型动力破坏试验与数值仿真分析.岩土工程学报,2003,25(1):26-30(Kong Xianjing,Liu Jun,Han Guocheng.Dynam ic failure testand numericalsimulation ofmodel concrete-faced rockfil dam.Chinese J.Geot.Eng.,2003,25(1):26-30(in Chinese))11杨庆华,姚令侃,杨明.地震作用下松散堆积体崩塌的颗粒流数值模拟.西南交通大学学报,2009,44(4):580-584(Yang Qinghua, Yao Lingkan,Yang M ing.Particle fl w numerical simulation of landslip of loose slope under seism ic loading.JournalofSouthwest Jiaotong University,2009,44(4):580-584(in Chinese))12 Huang JJ,Qi Y,Chen MX,M icromechanical response of granular geomaterialssubjected to earthquake groundmotions.In:Proc.of International Conference on Science and Technology of HeterogeneousMaterialsand Structures,Wuhan.2013.13 Chen T,Mao K,Huang X,etal.,Dissipationmechanismsofnonobstructive particle damping using discrete elementmethod.Smart Structuresand Materials:DampingandIsolation,2001.4331:294-301.14黄俊宇,徐松林,胡时胜.脆性颗粒材料的应变率效应机理研究.固体力学学报,2013,34(3):247-250(Huang Junyu,Xu Songlin, Hu Shisheng.Inverstifation on the intrinsic mechanisms of strain rate e f ects of brittle granularmaterials.Chinese Journal of SolidMechanics,2013,34(3):247-250(in Chinese))15刘君,刘福海,孔宪京.考虑破碎的堆石料颗粒流数值模拟.岩土力学,2008,29(增1):107-112(Liu Jun,Liu Fuhai,Kong Xianjing.Particle fl w code numerical simulation of particle breakage of rockfill Rock and SoilMechanics,2008,29(sup.1):107-112(in Chinese))16马刚,周伟,常晓林,等.考虑颗粒破碎的堆石体三维随机多面体细观数值模拟.岩石力学与工程学报,2011,30(8):1671-1682 (Ma Gang,Zhou Wei,Chang Xiaolin,et al.Mesoscopic numeiacal simulation of rockfil considering particle breakage by using three-dimensional stochaticpolyhedrons.Chinese Journal ofRock Mechancsand Engineering,2011,30(8):1671-1682(in Chinese))17 Huang J,Xu S,Hu S.E f ectsof grain size and gradation on the dynam ic responses of quartz sands.International Journal of Impact Engineering,2013,59:1-1018 Huang JY,Xu SL,Hu SS.Influenc of particle breakage on the dynam ic compression responsesofbrittlegranularmaterials.MechanicsofMaterials,2014,68:15-2819刘汉龙,孙逸飞,杨贵,等.粗粒料颗粒破碎特性研究述评.河海大学学报(自然科学版),2012,40(4):361-369(Liu Hanlong, Sun Yifei,Yang Gui,etal.A review of particle breakage characteristicsof coarseaggregates.JournalofHohaiUniversity(NaturalSciences),2012,40(4):361-369(in Chinese))20 Cundall PA,Strack ODL,A discrete numericalmodel for granular assemblies.G Technique,1979,29:47-65.21 Cho N,Martin CD,Sego DC.A clumped particlemodel for rock.International JournalofRock Mechanicsand Mining Sciences,2007, 44(7):997-101022 Potyondy DO,Cundall PA.A bonded-particlemodel for rock.International JournalofRock Mechanicsand Mining Sciences,2004, 41(8):1329-136423 Jensen R,Edil T,Bosscher P,et al.E f ect of particle shape on interface behavior of DEM—simulated granularmaterials.International JournalofGeomechanics,2001,1(1):1-1924 Jensen R,PleshaM,Edil T,etal.DEM simulation of particle damage in granularmedia—structure interfaces.International Journal ofGeomechanics,2001,1(1):21-3925 ElShamy U,Denissen C.M icroscale characterization ofenergy dissipation mechanisms in liquefiabl granular puters and Geotechnics,2010,37(7–8):846-85726黄俊宇,徐松林,王道荣,等.脆性颗粒材料的动态多尺度模型研究.岩土力学,2013,34(4):922-932(Huang Junyu,Xu Songlin, Wang Daorong,etal.Investigation of dynamicmultiscalemodel for brittle granularmaterials.Rock and Soil Mechanics,2013,34(4): 922-932(in Chinese))27 Lackenby J,Indraratna B,M cDowell G,etal.E f ect of confinin pressure on ballast degradation and deformation under cyclic triaxial loading.G Technique,2007,57:527-536。
基于EDEM的物料破碎效果仿真分析_黄鹏鹏

破 ・ 磨
Fig. 1
图 1 大颗粒被小颗粒团替换示意 Sketch of replacing one big grain with small grains
1.2 破碎机几何模型及破碎参数设定
以 PE400×600 型颚式破碎机结构尺寸为参考, 在不影响仿真的前提下,对颚式破碎机做相应简化, 运用 SolidWorks 三维绘图软件建立颚式破碎机的几何 模型,如图 2 所示。在 EDEM 界面中仿真需对颗粒 和几何体材料的物理参数进行设置 (如表 1 所列),再 对接触模型、颗粒工厂、颗粒体力插件和时间步长等 进行定义后,进行模拟仿真。
料的缓冲作用,噪声较小;另外,轮锤式破碎机安装 前需要现场加装破碎机固定支架,必要时要对输送机 出料端进行现场改造。但总体上看,破碎机改进后明 显利大于弊,具有较大的应用价值。
参 考 文 献
[1] 中国煤炭工业协会.MT/ T 493—2002 顺槽用破碎机 [S].北 京:中国煤炭工业出版社,2002. [2] 哈尔滨工业大学理论力学教研室.理论力学 (Ⅱ) [M].7 版. 北京:高等教育出版社,2009:40-55. [3] 杨丙乾,任小中.锤式破碎机的打击平衡计算 [J].矿山机 械,2006,34(1):61-62. [4] 李正峰.锤式破碎机锤头销孔碰撞反力的定量计算 [J].煤矿 机械,2006,27(2):185-186. □ (收稿日期:2014-06-06) (修订日期:2014-07-09)
因素
Fig. 3
所用的颗粒模型为软球模型edem界面中建立半径为90mm的颗粒破碎南大学的李云龙等人对高压状态下矿物颗粒破碎的模型运用api插件将若干个小颗粒黏结成大的颗粒基本规律进行了研究得出粉碎过程可以划分为预每个大颗粒球团由70个半径为18mm损碎裂压实3个阶段以及若干种矿物的挤压的小颗粒通过附有正应力及切应力的黏结键黏结而阻力大小顺序
液滴碰撞Janus颗粒球表面的行为特征

液滴碰撞Janus颗粒球表面的行为特征*彭家略 郭浩 尤天涯 纪献兵† 徐进良(华北电力大学低品位能源多相流与传热北京市重点实验室, 北京 102206)(2020 年8 月18日收到; 2020 年9 月10日收到修改稿)为研究液滴碰撞Janus颗粒(双亲性)球表面的独特行为特征, 以粒径为5.0 mm铜球为材料制备了Janus 颗粒, 用直径为2.0 mm的液滴, 在韦伯数(We)为2.7, 10, 20, 30的测试情况下对Janus颗粒球表面进行了碰撞实验. 结果表明: 液滴碰撞Janus颗粒球表面后的运动可分为铺展、回缩、振荡和回弹4个过程. 在不同We下, 液滴碰撞Janus颗粒后的运动状态主要与表面润湿性相关, 在Janus颗粒亲水侧表现为铺展特性且铺展系数g随着时间t的增大而逐渐增大并趋于稳定; 但在疏水侧, 表现为回弹现象, 铺展系数g会出现类似“抛物线”形状; 当液滴碰撞Janus颗粒球表面亲-疏水分界线时, 液滴铺展和回弹同时发生. 基于能量平衡和受力分析发现, 液滴动能和表面能的互相转化是液滴铺展的关键, 液滴会在重力、惯性力、表面张力、黏性力、接触力等力的综合作用下展现其独特的行为特征并最终达到平衡状态.关键词:润湿性, 液滴, 碰撞, Janus颗粒PACS:47.55.Ca, 47.55.nd, 47.55.df DOI: 10.7498/aps.70.202013581 引 言液滴碰撞壁面现象广泛存在于大自然中, 与MEMS、喷涂、农药喷洒和喷雾冷却等[1−5]农业、工业过程息息相关, 因此液滴碰撞壁面的行为特征引起了研究者的极大关注. 液滴碰撞后的行为受液体性质、表面几何形状、表面润湿性、液滴碰撞速度[6−10]等多种因素的综合影响, 会发生铺展、回缩、液滴分离、飞溅等行为. 目前, 液滴碰撞壁面的研究主要集中在平滑的刚性表面上[11−13], 并取得很好的成果, 但由于液滴碰撞球表面的复杂性, 液滴碰撞球壁面的研究并没有取得较为系统的总结.因此通过实验、模拟和理论分析等方法对液滴碰撞球壁面行为进行研究也成为当下的热点. 郑志伟等[14]采用CLSVOF (couple level-set and volume of fluid)方法建立了液滴冲击球形凹曲面的数值计算模型, 发现其先后呈现出铺展、收缩、振动及回弹等状态, 同碰撞平面过程基本一致; 并在不同雷诺数下对平面与凹曲面的液滴最大铺展系数进行了系统研究. Khurana等[15]利用实验和理论相结合的方法对亲水性和疏水性球表面进行了液滴碰撞行为研究, 并提出了一种基于能量平衡原理的数学模型预测了球形物体的最大铺展角, 其理论值与实验结果吻合较为良好. Amirfazli和Banitabaci[16]研究了液滴碰撞速度对于液滴动力学的影响, 并对较大参数范围 (0.1 < We < 1146)内的碰撞问题进行了研究, 且首次对球直径小于液滴直径的情况进行了实验研究, 当球与液滴直径大小比值不同时, 液滴碰撞后运动状态也会随之发生变化, 甚至出现液滴穿透球的现象. Bakshi等[17]首次对液滴撞击球形目标进行了实验和理论研究, 通过球形表面的液膜变化将液滴碰撞过程划分为: 初始液滴变形、惯性控制和黏性主导3个阶段, 建立了球面液膜的流动模型, 理论分析得出球面薄膜厚度的演化方程, 并且理论预测与实验结果具有良好的一致性.* 国家自然科学基金(批准号: 51676071)和国家重点研发计划(批准号: 2017YFB0601801)资助的课题.† 通信作者. E-mail: jxb@© 2021 中国物理学会 Chinese Physical Society 虽然液滴碰撞球表面已取得一些研究成果, 但其大多数集中在单一润湿性表面, 对液滴碰撞两种润湿性表面集于1个的球面的研究较少. 近年来,由于人们对亲疏水性的认知应用的扩展, 人们对具有两种不同性质的同一粒子 (Janus颗粒)产生了浓厚的兴趣并逐渐应用于实际. “Janus”(古罗马神话中的双面神)一词, 首次在1991年, 由Gennes[18]在诺贝尔颁奖大会上提出并使用. 后来Janus粒子被定义成表面具有不同化学性质或物理性质的不对称粒子. 本文的Janus颗粒是指颗粒具有一半亲水, 一半疏水特性. 目前国内外对液滴碰撞Janus 颗粒的研究较少, 正确的认知液滴碰撞Janus颗粒球表面的行为特征对深化Janus颗粒的应用具有重要的价值. 因此本文制备了Janus颗粒并搭建了液滴碰撞Janus颗粒球面的实验装置, 测试了液滴在不同韦伯数下分别碰撞Janus颗粒球表面亲水侧、疏水侧和Janus亲疏水分界线的行为特征, 详细分析了液滴碰撞的行为动态变化过程, 并对液滴在运动过程中的受力进行分析.2 实验材料与方法2.1 表面制备及表征制备Janus颗粒所使用的材料粒径为5.0 mm 的紫铜球, 将紫铜球先后经过去离子水、丙酮、乙醇、稀盐酸和去离子水超声波清洗过程, 得到表面干净的紫铜球颗粒; 然后将其均匀放置在丝网上,对裸露在上方的半球喷涂超疏水喷雾剂 (美国超技术公司生产), 下半球不做处理, 再将其置于通风口处1.5 h后则得到Janus颗粒. 为了进一步确定液滴在Janus颗粒球面上的润湿性, 对液滴在球表面上的静态接触角进行了多次测量, 发现液滴在亲水侧的静态接触角为66°, 在疏水侧的静态接触角为150°.本实验环境温度为25 ℃, 所使用的液滴为去离子水, 液滴体积为4.0 µL, 等效直径约为2.0 mm,其密度r为998.2 kg/m3, 黏度µ为1.005 × 103 pa·s,表面张力s为72.75 × 10–3 N/m.2.2 实验系统与方法实验装置如图1所示, 主要由玻璃注射器、高速摄影仪、微流量液滴控制器、挡风玻璃、LED背光灯和实验样品组成. 其中玻璃注射器(带有不锈钢的疏水针头)容量为5.0 ml, 针头外径为0.2 mm.微流量液滴控制器可通过调整升降台使液滴获取不同的滴落高度, 从而赋予液滴不同的碰撞速度0.3, 0.6, 0.8, 1.1 m/s, 所对应的韦伯数分别为2.7, 10, 20, 30, 对应的雷诺数分别为621.8, 1191.9, 1589.2, 2185.1.12453图 1 液滴碰撞球面实验装置系统 1. 计算机; 2. 高速摄影仪; 3. 微流量液滴控制器; 4. Janus球; 5. 可调节底柱Fig. 1. Experimental set up of the droplet collision on spherical surface. 1. Computer; 2. high speed camera; 3. di-gitized microliter droplet dispenser; 4. Janus sphere; 5. ad-justable bottom column.实验时, 首先利用计算机精确设定液滴直径大小及玻璃注射器的推进速度, 达到预定体积后液滴会从针头处脱落, 以自由落体状态碰撞颗粒球表面, 碰撞的整个过程由高速摄影仪进行记录, 拍摄帧率为4000 Hz、像素为1016 × 1016. 实验中可以通过调整升降台使液滴获得不同的滴落高度. 为获得液滴碰撞球表面的瞬时速度u, 利用Photoshop 的图像处理功能, 选取液滴碰撞壁面前D t, 2D t, 3D t, 4D t时间间隔的4张图片, 测量液滴距壁面碰撞点的距离h, 再通过时间t和距离h, 则可得出液滴碰撞表面的瞬时速度u. 此外液滴在下降过程中由于空气阻力的影响会使液滴表面形态发生一些变化, 为了确保实验结果的精确性, 整个实验过程都将在封闭环境中进行.在液滴碰撞颗粒球表面过程中, 液滴碰撞行为特征会受到工质物性、液滴直径大小等许多因素影响, 因此为了简化分析, 采用韦伯数和雷诺数对液滴碰撞壁面过程进行无量纲分析. 其中韦伯数表示惯性力和表面张力的比值, 当We > 1时, 表示在碰撞过程中液滴的动能占据主导地位.其中, r f为液滴密度, u为液滴碰撞速度, s为液滴的表面张力系数.雷诺数表示惯性力和黏性力的比值, 当Re > 1时表示碰撞过程中惯性力起主导作用.其中, µ为液滴的黏性系数.同时为了更加形象地描绘出液滴碰撞壁面后的铺展特性, 提出了液滴碰撞壁面的无量纲铺展因子g :其中, a 为液滴在球面的铺展半径, d 为液滴直径.3 实验结果与讨论3.1 液滴碰撞Janus 颗粒疏水侧的行为特征如图2所示为液滴碰撞Janus 颗粒疏水侧时的具体运动状态, 可发现在韦伯数介于2.7至30下液滴的运动过程几乎一致, 先在表面铺展然后迅速回弹, 直至液滴脱离颗粒球表面. 因此可将液滴在疏水侧的运动大致划分为: 液滴铺展初期(I)、缓慢铺展 (II)、回弹 (III)及完全脱离 (IV)4个过程.过程I (0—0.75 ms)中, 由于液滴从一定高度滴落, 因此液滴碰撞Janus 颗粒球表面时, 会以碰撞点为中心迅速向四周铺展, 在此过程中液滴的动能逐渐向表面能和黏性扩散能[19]转化. 在We =20, t = 0.75 ms 时 (如图2所示)液滴出现分层现象, 形成“球冠状”, 造成这种现象的主要原因是:在碰撞过程中, 由于液滴本身具有的冲击动能和颗粒表面的亲疏水特性造成了液滴在表面的快速铺展; 但液滴在铺展过程中会产生毛细波[20], 毛细波向液滴的传播则阻碍了上部液滴的惯性铺展过程.过程II (0.75—3 ms)中, 从图2可发现液滴在表面张力和黏性力的共同作用下, 铺展变慢, 意味着速度的减小. 那么这种现象的原因究竟是表面张力主导还是黏性力主导呢?为了探究这个问题,Clanet 等[21]提出了可以区分表面张力主导和黏性主导两种流动机制的参数P :得出了在P < 0.3时表面张力主导; 相反则是黏性力主导. 经过计算临界速度为v r = 3.667 m/s, 而本实验中液滴的速度分别为v = 0.313, 0.6, 0.85,1.05 m/s, 显然均小于临界速度, 则过程II 中主要由于表面张力的作用使液滴扩散速度减小. 当液滴在t = 3 ms 时, 液滴达到最大铺展长度, 此时液滴的动能为零, 表面能最大.但过程III (3—8 ms) 中, 不论We 大小液滴都会沿球壁面方向运动 (如图2蓝色箭头所示),在表面张力的作用下液滴发生回弹现象. 过程IV (t > 8 ms)中液滴完全脱离颗粒表面.为了更全面分析We 对铺展因子g 的影响, 图3给出了液滴在4种韦伯数下撞击球颗粒的情况, 曲线大致呈现出“抛物线”形状, 我们的结果与Khoj-asteh 等[22]文献中的具有相同性, 在液滴碰撞超疏水球面时, 不同韦伯数下铺展因子g 随时间的变化趋势几乎相同. 可看出在过程I 中液滴铺展因子g 基本相同, 表明在液滴铺展初期We 变化对铺展因子g 影响较小, 几乎可以忽略. 过程II 中不同We 下达到最大铺展长度所需要的时间基本相同, 说明We 变化对液滴铺展速率影响较小. 针对这种现5.00 ms 3.00 ms 2.25 ms 1.50 ms 0.75 ms 0 ms6.50 ms8.00 ms=0=0=0=0IIIIII图 2 不同We 下液滴碰撞疏水侧球面行为的动态过程Fig. 2. Dynamic behavior of droplet collision on the hydrophobic spherical surface under different We .W =4πr 3sub (1−cos ϕ)µϕuδ象Mitra 等[19]和Khurana 等[15]计算出液滴碰撞球壁面的黏性扩散能 , 可知虽然液滴碰撞壁面动能越大, 但铺展过程中黏性扩散能也增大, 故在不同We 下液滴达到最大铺展因子时所需时间较为接近. 过程III 中铺展因子g 随时间增加呈指数下降. 直到过程IV 时, 液滴完全脱离颗粒球表面, g = 0.3.2 液滴碰撞Janus 颗粒亲水侧的行为特征与液滴碰撞Janus 颗粒疏水侧的表现有所不同, 液滴碰撞Janus 颗粒亲水侧后, 液滴的行为特性在0 < t < 3 ms 内, 表现为铺展特性; 但在t > 3 ms 中, 与碰撞疏水侧呈现出截然不同的现象, 液滴在达到最大铺展长度后只有小幅度的波动, 并不会呈现回弹现象, 如图4所示.为了更加清晰表达液滴撞击亲水侧的铺展因化, 图5给出了液滴在4种韦伯数下撞击球颗粒表面的情况: 在0—3 ms 内, 液滴以; 在3—12 ms 与液滴碰撞疏水侧的行为明显不同的是液滴在, 并没有呈现出指数下降的趋而是发生振荡现象. 且最大铺展因子g值不同,时, g = 0.91; We= 30时, g = 1.77. 发We 的最大铺展因子差值不同(H 1 > H 2 >H 3), 汪焰恩等[23]对液滴正向撞击亲水球面的过程进行了数值模拟, 可发现在不同We 下达到最大铺展系数时所需时间较为接近, 且最大铺展因子g 值不同. 即最大铺展因子随着We 的增大, 差值H 会逐渐减小, 表明g 的变化程度主要受惯性影响.3.3 液滴碰撞Janus 颗粒亲疏水分界线的行为特征图6展示了液滴碰撞Janus 颗粒亲疏水分界线的动态特性, 在0—3 ms, 液滴在亲水侧和疏水侧都表现为铺展特性, 达到最大铺展长度时所需时间相同; 在3—8 ms, 分界线两侧开始呈现出截然不同的现象, 分界线左侧液滴依然铺展在球颗粒表面, 而右侧液滴开始收缩团聚成椭圆形液滴 (We =30, t = 5 ms); 随着时间增大, 可发现右侧液滴脱离球表面, 在t = 6.5 ms (如图6所示) 蓝色箭头所示, 处于腾空状态, 铺展和回弹现象同时发生.造成这种现象的原因为左右两侧的亲疏水差异, 使两侧液滴受力不同./ms图 3 不同We 下的动态铺展因子变化(疏水侧)Fig. 3. Dynamic spreading factor of droplet collision under different We (hydrophobic side).5.00 ms3.00 ms 2.25 ms 1.50 ms 0.75 ms 0 ms 6.50 ms 8.00 ms=0 =0=0图 4 不同We 下液滴碰撞亲水侧球面行为的动态过程Fig. 4. Dynamic behavior of droplet collision on the hydrophilic spherical surface under different We..而图7更加充分的展示了液滴碰撞Janus颗粒亲疏水分界线的具体情况, 在Janus颗粒亲水侧g随时间逐渐增大然后有小幅度的波动现象, 表明液滴亲水侧表面过程后期会发生小幅度的波动(回弹-铺展-回弹过程); 而在Janus颗粒疏水侧g随时间逐渐增大, 达到最大铺展长度时呈指数减小, 表明液滴在疏水侧表面快速铺展后会发生回弹现象. 随着We的增大, 在液滴铺展初期Janus颗粒亲水侧和疏水侧的g值基本一致, 但随着时间的增加二者之间的差值也逐渐增大, 此外两侧重合时间也随We增大而增大: We = 2.7时, 重合时间为0.75 ms; We = 10时, 重合时间为1 ms; We = 20时, 重合时间为1.5 ms; We = 30时, 重合时间为1.75 ms.造成上述现象的主要原因为g的变化趋势是由Janus颗粒表面润湿性决定的, 而最大扩展因子g值的大小主要受液滴碰撞速度影响. We越大,液滴撞击Janus颗粒球表面的惯性动能越大, 即液滴在球面铺展的动能越大, 液滴在球面的最大铺展长度越大.3.4 液滴在Janus颗粒不同表面的受力为了更好探究造成液滴具有不同行为特征的原因, 对液滴进行受力分析, 如图8所示.(F g)(F t)(F contact)图8(a)为液滴刚接触颗粒球表面, 此时液滴只受重力、惯性力[24] 和接触力[25],它们的表达式为:r subδηni其中, 为颗粒半径, 为液膜厚度, 为球颗粒表面的碰撞系数,ϕ可以发现液滴在初期铺展过程图8(a)和图8(b)中, 不管是碰撞Janus颗粒亲水侧、疏水侧还是亲疏水分界线, 其在整个碰撞的过程所受的重力、惯性力和接触力基本一致, 且角几乎为零即表面张力可忽略不计, 从而使液滴在铺展过程初期g值几乎一致.液滴在持续铺展图8(b)和图8(c)过程中, 液滴会在表面张力和黏性力的作用下铺展速度逐渐放缓, 但在疏水侧、亲水侧和亲疏水分界线3种情况下液滴达到最大铺展长度时所需时间相等, 表明在此过程中表面润湿性对液滴铺展速率影响较小./ms图 5 不同We下的动态铺展因子变化(亲水侧) Fig. 5. Dynamic spreading factor of droplet collision under different We (hydrophilic side).5.00 ms2.25 ms1.50 ms0.75 ms0 ms 6.50 ms8.00 ms=0图 6 不同We下液滴碰撞亲疏水分界线行为的动态过程Fig. 6. Dynamic behavior of droplet collision on the hydrophilic-hydrophobic boundary under different We..图8(c)—图8(e)为液滴的回缩过程表面张力为驱动力, 惯性力和黏性力为阻力, 作用在液滴接触线处受到的黏性阻力可以用Gennes[26]的润滑理论近似得出, 我们这里只考虑沿球面切线方向上的流体剪切运动, 因此黏性力为ξ其中为液滴在球颗粒表面的滑移长度.此过程液滴在亲水侧、疏水侧和亲疏水分界线时的行为特性开始出现差别, 可发现亲水侧铺展长度随着时间的增加并没有大幅度的增加或下降趋势, 而是呈现出小幅度的上下波动现象; 而疏水侧液滴克服自身重力的影响形成“椭圆形”离开疏水表面; 液滴碰撞亲疏水分界线时, 分界线两侧的液滴呈现出截然不同的运动特性, 疏水侧的液滴受到亲水侧的牵引力跃向亲水侧. 因此液滴离开疏水侧表面的主要原因是表面张力不同, 如图9所示.而线张力是研究液滴润湿行为的关键参数, 液滴三相接触线上的能量组成仅采用两相表面自由能无法解释清楚, 线张力的概念最早可以追溯到1878年, Gibbs[27]研究发现, 液滴三相接触线上的能量组成仅采用两相表面自由能无法解释清楚, 为解决这一难题, 定义了一种类似于表面张力、在三相接触线上具有线性能量密度的作用力, 即线张力./ms/ms图 7 不同We下的动态铺展因子变化 (亲疏水分界线) (a) 液滴在Janus亲水侧的变化; (b) 液滴在Janus疏水侧的变化Fig. 7. Dynamic spreading factor of droplet collision under different We (the hydrophilic-hydrophobic boundary): (a) Dynamic spreading factor of droplet on the hydrophilic side; (b) dynamic spreading factor of droplet on the hydrophobic side.疏水侧亲水侧contacta,0疏水侧亲水侧a,0(a)(b)(c)(d)(e)疏水侧亲水侧图 8 液滴在疏水侧、亲水侧和亲疏水分界线的受力Fig. 8. Force analysis of the droplet on the hydrophobic side, hydrophilic side and hydrophilic-hydrophobic boundary.1977年, Pethica [28]定义了理想固体表面上液滴的线张力, 通过恒定体积下的能量最小化分析推导出修正Young 方程:σsl σsg σlg 其中, q 为Young 接触角, 、 和 分别为固液表面张力、固气表面张力和气液表面张力.στ且Guzzardi 和Rosso [29]推导出张力分量 :根据(9)式和(10)式可推导出理想固体球表面上液滴的线张力, 亲水侧三相接触点沿固液界面切线方向受力平衡为θ1ϕ1στσsl 其中, 为Young 接触角, 为线张力所对应的张力分量 和固液表面张力 的夹角.疏水侧三相接触点沿固液界面切线方向受力平衡为θ2ϕ2στσsl 其中, 为Young 接触角, 为线张力所对应的张力分量 和固液表面张力 的夹角.根据(11)式和(12)式可得:ϕ1≈ϕ2θ1<π/2<θ2στ1<στ2液滴碰撞亲疏水分界线 (如图7所示), 在达到最大铺展因子前在两侧的铺展长度基本相等, 即, 且因为 , 代入(12)式和(13)式可得 , 故液滴由于牵引力的作用从疏水侧弹跳到亲水侧, 进而导致随着时间的增大两侧之间的铺展因子g 差值也逐渐增大, 直到疏水侧液滴完全跳跃到亲水侧.4 结 论在不同We 下, 探究了液滴碰撞Janus 颗粒疏水侧、亲水侧和亲疏水分界线时的行为特征, 并进行了机理分析, 具体结果如下:1) 液滴碰撞Janus 颗粒疏水侧时, 铺展系数g 随时间增大会出呈现类似“抛物线”形状, 且不同We 下达到最大铺展因子所需要的时间较为接近.2) 而当液滴碰撞Janus 颗粒亲水侧时, 铺展系数g 随着时间的增大而逐渐增大并趋于稳定, 且最大铺展因子随着We 的增大也增大.στ1<στ23) 但当液滴碰撞Janus 颗粒亲疏水分界线时,分界线两侧呈现出截然不同的运动特性, 液滴铺展和回弹会同时发生, 且疏水侧液滴会弹跳到亲水侧. 而铺展系数g 的变化趋势由表面润湿性决定,大小则主要受液滴惯性影响. 且对两侧液滴受力分析发现亲水侧线张力小于疏水侧, 即 , 进而导致了疏水侧液滴弹跳到亲水侧.4) 液滴动能和表面能的互相转化是液滴铺展和回弹的关键, 液滴在碰撞Janus 球表面时, 会在重力、惯性力、表面张力、黏性力和接触力等力的综合作用下展示出其独特的行为特征.参考文献K im S Y, Choi B G, Baek W K, Park S H, Park S W, Shin JW 2019 Smart Mater. Struct. 28 035025[1]D erby B 2010 Annu. Rev. Mater. Sci. 40 395[2]Z hou Z F, Chen B, Wang R, Wang G X 2017 Exp. Therm.Fluid Sci. 82 189[3]G yeongrak C, Jong L, Ju C, Young J K, Yeon S C, Mark SChang M, Kwon L, Sung K, Inpil K 2016 Sensors. 16 1171[4]A guilar G, Vu H, Nelson J S 2004 Phys. Med. Biol. 49 147[5]D ai C, Ji X B, Zhou D D, Wang Y, Xu J L 2018 Journal ofZhejiang Univ. (Engineering Science). 1 36 (in Chinese) [代超, 纪献兵, 周冬冬, 王野, 徐进良 2018 浙江大学学报(工学版)1 36][6]K awahara N, Kintaka K, Tomita E 2017 Spie. 10328 1032817[7]R ioboo R, Voue M, Vaillant A, Coninck D J 2008 Langmuir.24 14074[8]B iance A L, Clanet C, Quéré D 2004 Phys. Rev. E. 69 016301[9]J osserand C, Thoroddsen S T 2016 Annu. Rev. Fluid Mech.48 365[10]H amlett C A E, Atherton S, Shirtcliffe N J, Mchale G, AhnS, Doerr S H 2013 Eur. J. Soil. Sci. 64 324[11]K ang B S, Lee D H 2000 Exp. Fluids. 29 380[12]B i F F, Guo Y L, Shen S Q, Chen J X, Li Y Q 2012 Acta.Phys. Sin. 61 293 (in Chinese) [毕菲菲, 郭亚丽, 沈胜强, 陈觉先, 李熠桥 2012 物理学报 61 293][13]Z heng Z W, Li D S, Qiu X Q, Zhu X L, Cui Y J 2015 J.[14] 1 2 2 1 12 sg1gsgslsllg 亲水侧疏水侧图 9 球面的线张力效应Fig. 9. Line tension effect of sphere.Chem. Ind. Eng. 5 48 (in Chinese) [郑志伟, 李大树, 仇性启,朱晓丽, 崔运静 2015 化工学报 5 48]K hurana G, Sahoo N, Dhar P 2019 Phys. Fluids. 31 072003[15]A mirfazli A, Banitabaei S A 2017 Phys. Fluids. 29 419[16]B akshi S, Roisman I V, Tropea C 2007 Phys. Fluids. 19032102[17]G ennes D P G 1992 Rev. Mod. Phys. 64 645[18]M itra S, Nguyen T B, Doroodchi E, Pareek V, Joshi J B,Evans G M 2016 Chem. Eng. Sci. 149 181[19]Y ang W L 2017 Ph. D. Dissertation (Beijing: North China Electric Power University) (in Chinese) [杨卧龙 2017 博士学位论文 (北京: 华北电力大学)][20]C lanet C, BéGUIN, CéDRIC, Richard D, QUéRéD 2004 J.Fluid Mech. 517 199[21]K hojasteh D, Bordbar A, Kamali R, Marengo M 2017 Int. J.Comput. Fluid D. 31 310[22]W ang Y E, Zhou J H, Qing Y L, Li P L, Yang M M, Han Q,Wang Y B, Wei S M 2012 J. Vib. Shock. 31 51 (in Chinese)[汪焰恩, 周金华, 秦琰磊, 李鹏林, 杨明明, 韩琴, 王月波, 魏生民 2012 振动与冲击 31 51][23]W ang H R 2013 M. S. Thesis (Dalian: Dalian University ofTechnology) (in Chinese) [王辉 2013硕士学位论文 (大连: 大连理工大学)][24]Y asmin D, Mitra S, Evans G M 2019 Miner. Eng. 131 111[25]G ennes P G D 1985 Rev. Mod. Phys. 57 827[26]G ibbs J W 1948 Nature. 124 119[27]P ethica B A 1977 J. Colloid Interf. Sci. 62 567[28]G uzzardi L, Rosso R 2007 J. Food Compos. Anal. 40 19[29]Behavioral characteristics of droplet collisionon Janus particle spheres*Peng Jia -Lue Guo Hao You Tian -Ya Ji Xian -Bing † Xu Jin -Liang(Beijing Key Laboratory of Multiphase Flow and Heat Transfer for Low Grade Energy,North China Electric Power University, Beijing 102206, China)( Received 18 August 2020; revised manuscript received 10 September 2020 )AbstractTo acquire the unique behavioral characteristics that droplets impact the Janus particle (amphiphilicity) sphere surface, a series of collision experiments is conducted by using Janus particles with a diameter of 5.0 mm. These Janus particles are prepared by chemical treatment of the copper particles. Water droplets with a diameter of 2.0 mm are used to impact hydrophbilic surface, hydrophobic surface and hydropholic-hydropholic boundary of Janus particle, under four Weber numbers which are 2.7, 10, 20 and 30, the corresponing Reynold numbers are 621.8, 1191.9, 1589.2 and 2185.1. The results show that the collision process can be divided into four stages: spread, retraction, oscillation and rebound. Under different Weber numbers, the behavioral characteristics of droplets are mainly affected by the surface wettability. On the hydrophbilic surface, the droplets exhibit the spreading characteristics, with increasing time the spreading coefficient gradually increases and finally tends to be stable. As Weber number increases, the difference in spreading coefficient for droplet under adjacent Weber number gradually decreases, indicating that droplets spreading is mainly affected by inertia. On the hydrophobic surface, the spreading coefficient on the figure presents a "parabola" shape. Droplets spreading takes the same time to reach the maximum spreading coefficient under different Weber numbers. However, when droplets impact the hydropholic-hydropholic boundary, droplets show spreading and rebound behavioral characteristics simultaneously. At the beginning of droplets spreading, the spreading coefficient has almost the same value on both sides of the hydropholic-hydropholic boundary. With the increase of time, part of droplets on the hydrophobic are attracted by the hydrophbilic side surface and go into hydrophbilic side zone. In order to explain this phenomenon, the concept of line tension is introduced and the line tension on the hydrophilic side is found to be less than that on the hydrophobic side by analyzing the forces on both sides of the droplets. Based on energy balance and force analysis, it is found that the mutual conversion of droplet kinetic energy and surface energy are the key factor to make droplets spread. The droplets possess the unique behavioral characteristics and reach an equilibrium state under the combined influence of gravity, inertial force, surface tension, viscous force, and contact force.Keywords: wettability, droplet, collision, Janus particlePACS: 47.55.Ca, 47.55.nd, 47.55.df DOI: 10.7498/aps.70.20201358* Project supported by the National Natural Science Foundation of China (Grant No. 51676071) and the National Key R&D Program of China (Grant No. 2017YFB0601801).† Corresponding author. E-mail: jxb@。
声场中PM2.5颗粒碰撞运动模型

2840 垂直方向上颗粒的运动方程为:
Abstract A model that describes the collision of PM2. 5 driven by level sound wave in gravitational field was sugand gested. The angle θ of speed of particle and horizontal is one of important factors that affect the movement of PM2. 5 , its change will determine whether the collision will happen, the position of collision and how the particles will move after collision. The speed of particles before collision will determine whether particles will move along the direction of sound waves, against direction of the sound waves or will vibrate in their original position. The different frequency of sound field and, it also will change the swing. The change will change the tendency of movement of particles when collision happens, of intensity of sound field influences the swing of PM2. 5 and the movement tendency of particles after collision. Key words energy and power engineering; PM2. 5 ; twoparticle system; model 近年来, 火电厂燃煤锅炉基本都安装了除尘效 率达 99% 以上的静电除尘器, 但这些除尘器对可吸 入颗粒物 PM2. 5 的捕获率很低。 而这些颗粒易于富 集有毒金属、 酸性氧化物、 有机污染物、 细菌和病毒, 对环境和人体健康危害严重。 正由于此, 近年来国 内外学者针对 PM2. 5 的理化特性及控制方法, 开展了 [16 ] 。 许多的研究 利用声场来使 PM2. 5 颗粒产生团聚从而进行处 理是目前非常引人关注的一项技术 。国内外对于声 场中颗粒系碰撞研究多是讨论的颗粒的碰撞 [710 ] , 率 讨论的是一定声强和一定频率声场对颗粒 但颗粒间的碰撞过程讨论 间相互碰撞的影响情况, 的较少。本研究以双颗粒体系为例, 以数值模拟的 方法讨论了颗粒间的碰撞情况, 为声波法脱除 PM2. 5 提供进一步理论依据。 提供了彼此接近的机会, 这是发生凝聚现象的必要 条件。除了布朗运动和流体宏观动力作用外, 本模 Born 斥力和 型中考虑的作用力还括: 扩散双电层、 。 : 范德华力 颗粒间的引力势能为 d1 d2 A U ss = - ( 1) 12 Z0 d1 + d2 式中: 负号代表引力势能; d1 和 d2 分别是 2 颗粒的 - 10 m; A 粒径; Z0 是颗粒间的距离, 通常取用 4 ˑ 10 是 Hamaker 常数。 1. 2 2 颗粒碰撞前的运动 在我们前面所建立的单颗粒模型中, 给出了单颗 [ 11 ] 粒的运动方程 。但当 2 个颗粒接近时, 由于颗粒 , 2 间作用力的影响 个颗粒的速度和位移都将发生改 这些改变在单颗粒模型的基础上可结合上述几种 变, 力得出。下面以颗粒 1 为例给出颗粒运动方程。
球形颗粒系统的连续介质力学模型及数值模拟

本文采用Porous Elasticitynl和Drucker—Prager-Cap模型表征颗粒介质的力学本构关系,使 用ABAOUS进行数值模拟,得到的实验结果与数值模拟结果见图2。
图1实验结果与数值结果对比图
三、结论
考虑颗粒介质在加载和卸载过程中所表现出的弹塑性及非线性弹性特征,本文基于连续介质理 论,构建了球形颗粒介质的力学模型。通过辅助力学实验来确定模型中的待定参数,对球形颗粒介 质在机械载荷作用下的非线性力学特性进行了研究,最后本文将采用ABAOUS对含球形颗粒介质的实 际工程结构进行数值模拟,为该类T程结构的设计和可靠性分析提供理论依据.
beds in fusion blankets[J].Fusion Eng.Des.2007;82(2):189-206 3 D.Hofer.1I.Kamlah.Drucker-Prager-Cap creep modell ing of pebble beds in fusion blankets[J].Fusion
参考文献
l ABAOOS。Analysis User’s ganual,Volume III:Materials。2009;Version 6.9 2 YIXIANG ran.MARC Kamlah.1dentification of material parameters of a thermomeehanical model for pebble
戈键词颗粒介质:连续舟质^学岩t山学订m元:q啦忡
、前言
相对J。考虑单一颗粒与苴周囝颗粒问相百作用的离敞兀方法而言,采用将颗粒介质整体连续化 的理论研究其宏观力学特性更具有I:程意义。本文将颗粒介质作为均匀连续体进行考虑,采用岩上
混凝土细观刚体弹簧元法在劈裂试验中的应用

混凝土细观刚体弹簧元法在劈裂试验中的应用邢立坤;王立成;侯宇星【摘要】Authors systematically summarized the theoretical frame of the mesoscopic rigid-body-spring method, which included the generation process of random aggregates, the meshing technique of elements, the construction of the mesoscopic rigid-body-spring model and the development of constitutive law of the springs.In addition, the latest research advances and results on the application of mesoscopic rigid-body-spring method at home and abroad were reviewed.At the end, regarding of the loading characteristics of splitting test, the adjustment of meshing method of element was adopted for the sample in order to represent the test condition.The results indicate that the mesoscopic rigid-body-spring method can be applied to the numerical simulation process of splitting test of concrete.%系统总结了细观刚体弹簧元法的理论框架,即随机骨料的生成过程、细观刚体单元的划分原理、刚体弹簧元模型的确定方法、本构关系的建立过程等,并评述了各国细观刚体弹簧元法的最新研究进展及成果;在模拟混凝土劈裂试验时,考虑劈裂试验的加载特点,对劈裂试件刚体单元的划分方法进行了局部调整.结果表明:细观刚体弹簧元法能够应用于混凝土劈裂试验的数值模拟.【期刊名称】《建筑科学与工程学报》【年(卷),期】2011(028)001【总页数】8页(P83-90)【关键词】细观层次;刚体弹簧元模型;本构关系;劈裂试验;数值模拟【作者】邢立坤;王立成;侯宇星【作者单位】大连理工大学海岸和近海工程国家重点实验室,辽宁大连116024;大连理工大学海岸和近海工程国家重点实验室,辽宁大连116024;大连理工大学海岸和近海工程国家重点实验室,辽宁大连116024【正文语种】中文【中图分类】TU5280 引言混凝土根据其内部结构组成和分析的需要,可分为宏观、细观和微观3个不同层次。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
;< 为粘结半径 !7 &
收稿日期 $*)0&*Q&)* ! 修回日期 $*)0&))&)+ & 第一作者简介 黄令军 *)Q+% ,#! 男 ! 硕士研究生 ! 研究方向为化工过程 机械 ' 粉体工程及技术应用 & =RI:<6S4B:;>T6UQ*V)$1&35I & 通信作者简介 刘雪东 *)Q1, ,#! 男 ! 教授 ! 研究方向为化工过程机械及 粉体工程技术 & =RI:<6S6WHQQV)$1&35I &
!"#$%&'() *&+")(,&-. -. /%$(0&.1 /$2(3&-% -4 562$%-&7() 8(%,&')$9 :+6(', /(9$7 -. ;&9'%$,$ <)=+=., >=,2-?
"#$%& '()*+,)! -./ 0,123)*! 4/ 45(6()*
"234556'57'8934:;<3:6'=;><;99?<;> ! @4:;>A45B'C;<D9?E<FG !
,
对象颗粒模型建立及相关参数设置
以花岗岩材料为例 ! 采用 ?@?' ,.A 软件构建对
象颗粒 ! 利用 B;; 程序编写颗粒体力 C=D 插件 & 颗粒
第期
黄令军 等 基于离散单元法球形颗粒碰撞破碎行为的数值模拟
-(
体力的作用是在用户给定的某一时间 + 时将所有的 大颗粒移除 同时根据对象颗粒的每个小颗粒的坐标 位置数据文件生成小颗粒 并替换原来的大颗粒 利 用 23456789:;<9: 粘结接触模型 把替换后的小颗粒 球团在某一时间 ,,=( 时按照一定的 粘结键 粘结 起来 得到对象颗粒 对象颗粒构建过程及对象颗粒 粘结键如图 ( 所示 对象颗粒为粒径为 ' ## 的球体 该颗粒由 ')> 个粒径为 >&' ## 的 小 颗 粒 粘 结 而 成 对象颗粒内部小颗粒之间的粘结键总个数为 * (,*
小颗粒之间的粘结参数
>)-% !
替换时间 ( "@
<+,6#,$ 4)/)8'*'/ )8+,$ 58)(( 4)/*#1('5
粘结时间 , "@ 法向刚度系数 : " B #7( 切向刚度系数 5 ? B #7(
>&>>(
最大法向应力
>&>>,
)(>
/
*(>/
粘接半径 ! ?#
&7) ; ,8$ : ! < 789 $ 9 &7$ ; ,8) ; ! < 789 $ 9
式中 $ 789'
789
*- # *, #
分别为最大法向 ' 切向应力 !=8 % 7)'7$
分别为法向 ' 切向粘结力 !> % 8)'8$ 分别为法向 ' 切向 力矩 !>+ 7 % $ 为 接 触 区 域 面 积 !7,% 9 为 惯 性 矩 !7/%
A 小颗粒群代替大颗粒
于 (,> #?@ 时 对象颗粒撞击时产生的冲击力使粘结 的小颗粒的粘结键部分发生断裂 小颗粒没有从对象 颗粒脱落下来 颗粒破碎率为 > 表明颗粒碰撞接触以 后 颗粒虽然未发生破碎 但是颗粒内部粘结 键 部 分 发生断裂 宏观表现为颗粒表面出现裂纹 相 对 速 度 大于 (,> #"@ 时 碰撞产生的冲击力使所有粘结小颗 粒的粘结键断裂 , 个颗粒碰撞接触面开始有小颗粒 脱落 随着相对速度的增大 越来越多的单个 小 颗 粒
表; 对象颗粒与小颗粒的相关参数
粉 体 加 工 与 p;'('0),* 4)/)8'*'/ +3 +-='1*'6 4)/*#1('5 ),6 58)(( 4)/*#1('5
小颗粒 粒径 "## 粒径比 小颗粒 总个数 粘结键 总个数
对象颗粒 粒径 "##
(&% +&, +&* +&-
) 0& *
中 国 粉 体 技 术
D-A E
GCHI 年 J 月 H5<)*&)0%0$XU&<EE;&#**+&,,-+&Y*#-&*0&*#-
F".A GCHI
基于离散单元法球形颗粒碰撞破碎行为的数值模拟
黄令军 刘雪东 苏世卿
* 常州大学 机械工程学院 ! 江苏 常州
,-A:-0 #
摘要 采用离散单元法 基于 !"#$%&'()*+() 粘结接触模型 对 , 个球形 颗粒在水平方向上的对心碰撞破碎过程进行数值模拟研究 分析相对 速度及粒径比 ! 为 -., -./ -.0 对颗粒破碎行为的影响 结果表明 撞 击速度较小时 颗粒碰撞后未破碎 但 是 内 部 出 现 局 部 粘 结 键 的 断 裂 宏观表现为裂纹 随着撞击速度的增大 颗 粒 出 现 破 裂 或 完 全 破 碎 不 同粒径比的 , 个颗粒碰撞时 小 颗 粒 比 大 颗 粒 破 碎 严 重 粒 径 比 为 -.0 时 粒 径 较 小 的 颗 粒 碰 撞 后 获 得 的 动 量 最 大 粒 径 比 为 -./ 时 次 之 粒 径比为 -., 时最小 关键词 颗粒碰撞 破碎 离散单元法 数值模拟 中图分类号 !"#$%&$' ' ' 文献标志码 ( 文章编号 )**+&,,-+.$*)-/*0&**1*&*-
网络出版时间:2014-06-24 10:21 网络出版地址:/kcms/doi/10.13732/j.issn.1008-5548.2014.03.014.html
第 GC 卷
第E期
KL:DM 8NOPQR STUQDTQ MDP VQTWDXYXZ[
@-)A BC
颗粒物料冲击破碎一直是 粉 体 工 程 技 术 领 域 所 关注的课题 & 破碎过程的随机性 ' 多样性和复杂性使 理论分析十分困难 & 研究者通过实验或数值模拟对此 类问题进行了探索 ! 这些研究主要集中在颗粒物料冲 击靶板的破碎 1-&/2或颗粒物料挤压破碎 13&02& 牟赛杰等 142 研究了颗粒物料相互冲击破碎的情况 ! 认为尺寸不同 的 , 个颗粒撞击时小颗粒比大颗粒破碎严重 & 离散单 元法及计算机技术的进步使颗粒破碎行 为 的 数 值 模 拟得以实现 ! 但是目前有关利用离散单元法模拟颗粒 物料之间破碎行为的研究报道很少 & 本文中利用离散 单元法对 , 个球形颗粒在水平方向上的 对 心 碰 撞 破 碎行为进行模拟 ! 为研究在冲击载荷作用下颗粒物料 之间的破碎过程和机理提供参考 &
#AC ?DA '(>-
最大切向应力 #AC ?DA
,&'(>-
'(>7*
.
结果与讨论
图: 颗粒相对速度与破碎率的关系
在小颗粒本身性质及小颗粒之间粘 结 参 数 相 同
"#$% : &'()*#+, -'*.'', /'()*#0' 0'(+1#*2 +3 4)/*#1('5 ),6 $/#,6#,$ /)*#+
的情况下 根据建立的对象颗粒模型及相关参数的设 定 对不同粒径比 的 , 个对象颗粒在水平方向上以 相同速度对心碰撞进行数值模拟 对模拟结果进行分 析与讨论
.&(
相同粒径的颗粒碰撞 对粒径为 ' ## 的 , 个颗粒进行碰撞模拟 , 个
对象颗粒在水平方向上以相同速度对碰 得到颗粒相 对速度 4 与破损粘结键数 及颗粒相对速度 4 与破 碎率 的关系如图 , . 所示 破碎率为从对象颗粒脱 落的单个小颗粒的个数与构成对象 颗 粒 的 小 颗 粒 总 数之比 对象颗粒中小颗粒的位置是不规则排列的 因此对象颗粒两半球的小颗粒分布不均 使 , 个对象 颗粒对碰后的破损粘结键数和破碎率有略微偏差 但 是呈现一致的变化趋势 由图 , . 可知 相对速度小
! 对象颗粒内部粘结键 图; 对象颗粒构建过程及对象颗粒粘结键
"#$% ;
<7#(6#,$ 4/+1'55 ),6 -+,6#,$ +3 +-='1*'6 4)/*#1('5
通过相同的方法得到对象颗粒与小 颗 粒 的 相 关 参数如表 ( 所示 粒径比 是不同粒径的对象颗粒与 粒径为 ' ## 的对象颗粒的粒径之比 离散单元法模 拟中花岗岩材料小颗粒之间的粘结参数如表 , 所示
球形颗粒组成 ! 这是颗粒离散单元法的一个很大的局 限性 ! 因此颗粒单元无法直接破碎152& 假设球形颗粒是 由无数个更小的球形颗粒组成! 离散单元法中的
!"#$%&'()*+() 粘结接触模型 162 通过 一 定 尺 寸 的 ( 粘 结
