基础巩固练13
适用于新高考新教材备战2025届高考数学一轮总复习课时规范练13指数与对数运算新人教A版

课时规范练13 指数与对数运算基础巩固练1.(2024·浙江温州模拟)下列算式计算正确的是()A.(=1B.42×4-2=0C.log2=1D.lg 3·lg 5=lg 152.(2024·福建福州联考)已知2a=5,则lg 20=()A. B.C. D.3.(2024·安徽临泉模拟)已知4·3m=3·2n=1,则()A.m>n>-1B.n>m>-1C.m<n<-1D.n<m<-14.(2024·江苏徐州模拟)要测定古物的年头,可以用放射性碳法:在动植物的体内都含有微量的放射性14C.动植物死亡后,停止了新陈代谢,14C不再产生,且原来的14C会按确定的比率衰减(称为衰减率).大约经过5730年(14C的半衰期),它的残余量只有原始量的一半.现用放射性碳法测得某古物中14C含量为原来的,推算该古物约是m年前的遗物(参考数据:(lg 2)-1≈3.321 9),则m的值约为(结果保留整数)()A.12 302B.13 304C.23 004D.24 0345.已知3x=5,log3=y,则x+2y=()A.3B.4C.5D.66.(2024·山西大同模拟)(0.064+[(-2)3-16-0.75= .7.(2024·北京顺义模拟)计算log315-log35-+ln = .8.(2024·四川眉山模拟)18世纪数学家欧拉探讨调和级数得到了以下的结果:当n很大时,1++…+=ln n+γ(常数γ=0.557…).利用以上公式,可以估计+…+的值为.综合提升练9.(多选题)(2024·河南豫南名校检测)设a=log0.20.3,b=log0.30.4,则下列结论中正确的是()A.2a<1+abB.2a>1+abC.a>bD.b>a10.(2024·重庆巴蜀中学模拟)随着新一代人工智能技术的快速发展和突破,以深度学习计算模式为主的AI算力需求呈指数级增长.现有一台计算机每秒能进行×1015次运算,用它处理一段自然语言的翻译,须要进行2128次运算,那么处理这段自然语言的翻译所需时间约为(参考数据:lg2≈0.301,100.431≈2.698)()A.2.698×1022秒B.2.698×1023秒C.2.698×1024秒D.2.698×1025秒11.(2024·山东济南模拟)为落实党的二十大提出的“加快建设农业强国,扎实推动乡村振兴”的目标,银行拟在乡村开展小额贷款业务.依据调查的数据,建立了实际还款比例P关于还款人的年收入x(单位:万元)的Logistic模型:P(x)=.已知当贷款人的年收入为9万元时,其实际还款比例为50%.若银行希望实际还款比例为40%,则贷款人的年收入约为()(参考数据:ln3≈1.1,ln 2≈0.7)A.4万元B.5万元C.6万元D.8万元12.(2024·重庆一中检测)设p>0,q>0,满意log2p=log4q=log8(2p+q),则= .创新应用练13.(2024·湖北恩施联考)数学家纳皮尔独创了对数,对数的思想方法是把乘方和乘法运算分别转化为乘法和加法运算.已知lg 2≈0.301 0,lg 3≈0.477 1,设N=810×95,则N所在的区间为() A.(1011,1012) B.(1012,1013)C.(1013,1014)D.(1014,1015)14.(多选题)已知正数x,y,z满意3x=4y=12z,则()A. B.6z<3x<4yC.xy<4z2D.x+y>4z课时规范练13指数与对数运算1.C解析因为()0=1,所以(1,故A错误;42×4-2=42-2=40=1,故B错误;log2=log22=1,故C正确;因为lg3+lg5=lg15,所以lg3·lg5≠lg15,故D错误,故选C.2.C解析由2a=5,得a=log25,故lg20=lg=2-lg5=2-=2-=2-,故选C.3.D解析由已知得m=-log34<-1,n=-log23<-1,∵32>23,∴3>,log23>∵34>43,∴4<,log34<,∴log23>log34,-log23<-log34,∴n<m<-1,故选D.4.B解析设该古物中14C原始量为x,每年衰减率为a,∴xa5730=x,∴a=(,∴a m=(,=lo=log25=(lg10-lg2)=-1≈2.3219,∴m≈5730×2.3219≈13304,故选B.5.B解析∵3x=5⇔x=log35,y=log3,∴x+2y=log35+2log3=log3(5)=log381=4.6解析原式=(0.43-1+(-2)-4-(24)-0.75=0.4-1-1+7.-解析 log315-log35-+ln=log33-3+ln=1-3+=-8.ln 3解析由题意,可得+…+=(1++…+)-(1++…+)=ln30000+γ-(ln10000+γ)=ln30000-ln10000=ln=ln3.9.AD解析+b=log0.30.2+log0.30.4=log0.30.08>log0.30.09=2,因为a=log0.20.3>log0.21=0,所以2a<1+ab,故A正确,B错误;4a=log0.20.0081<log0.20.008=3,4b=log0.30.0256>log0.30.027=3,所以b>a,故C错误,D正确,故选AD.10.B解析设所需时间为t秒,则t1015=2128,lg t+lg5-2lg2+15=128lg2,∴lg t=131lg2-16,∴lg t≈131×0.301-16=23.431,∴t≈1023.431=100.431×1023≈2.698×1023秒,故选B.11.B解析由题意得当x=9时,P=50%,则=50%,得e-0.9+9k=1,所以9k-0.9=0,得k=0.1,因此P(x)=当P=40%时,由=40%,得3e-0.9+0.1x=2,所以e-0.9+0.1x=,所以-0.9+0.1x=ln=ln2-ln3≈0.7-1.1=-0.4,解得x=5,所以当银行希望实际还款比例为40%时,贷款人的年收入约为5万元,故选B.12解析由log2p=log4q,可知log2p=log2q=log2,即p=,由log2p=log8(2p+q),可知log2p==log2,即p=,消去q得p2-p-2=0,解得p=2或p=-1(舍去),当p=2时,q=4,所以13.C解析∵N=810×95,∴lg N=lg810+lg95=lg230+lg310=30lg2+10lg3≈9.030+4.771=13.801,∴N=1013.801∈(1013,1014),故选C.14.ABD解析设3x=4y=12z=t,t>1,则x=log3t,y=log4t,z=log12t,所以=log t3+log t4=log t12=,A正确;因为=log129<1,则6z<3x,因为=log8164<1,则3x<4y,所以6z<3x<4y,B正确;因为x+y-4z=log3t+log4t-4log12t=>0,则x+y>4z,D正确;因为,则=x+y>4z,所以xy>4z2,C错误.故选ABD.。
部编版2021-2022学年六年级下册语文基础知识巩固练习

部编版2021-2022学年六年级下册语文基础知识巩固练习一、字音、字形过关(共7题;共18.8分)1.(2分)给加点字选择正确的读音。
勉强.(qiáng qiǎng ) 强.烈(qiáng qiǎng ) 烧掉.(diào dào ) 哀悼.(diào dào ) 哽咽.(yān yè) 咽.喉(yān yè) 强劲.(jìn jìng ) 暂.时(zhàn zàn ) 2.(3分)给下列加点字注音。
栀.子花( ) 稚.嫩( ) 沮丧.( ) 模.仿( ) 呐.喊( ) 白皙.( ) 懵.懂( ) 教诲.( ) 猝.死( ) 歧.途( ) 憧.憬( ) 告诫.( ) 3.(4.5分)看拼音写词语míng mèibō nòng cǎo cóng huà bào niàn daotíng dùnhuàng dòng dān gē chén yù màn chángxiū zhǐshí guāng jīng huáng qīn wěn yī wēiwǎn huíhuāng liáng fān xiāng dǎo guì4.(2.3分)看拼音,写字词。
(1)(0.3分)zhuān()缝里的小草随着wēi fēng()轻轻huàng dòng (),仿佛在向路过的mǎ yǐ()打招呼。
(2)(0.3分)妹妹笑着把珍cáng()的zhēng()糕递给妈妈,那笑容míng mèi()动人。
妈妈亲wěn()了一下妹妹的额头,轻轻róu rou()她的头发,也跟着笑了。
串、并联电路的电流规律-巩固练习(基础)

【巩固练习】一、选择:1。
有关电路中的电流正确的说法是()A.电流从正极流出时最大,回到负极时最小B.用电器工作时会消耗电流,从而使电流减小C.在并联电路中,干路上的电流比任一支路上的电流都大D.在串联电路中,流过用电器的电流比流过导线的电流大2。
有L1和L2两只灯泡串联在电路中,闭合开关后发现L1很亮,L2很暗,那么()A。
L1中电流较大 B。
L2中电流较大C。
L1和L2中的电流一样大 D.由于灯的亮度不同故无法比较电流的大小3.(多选)小明用电流表测量串联电路的电流时,闭合开关后发现两灯泡时亮时暗,电流表指针来回摆动,则发生故障的原因可能是()A。
导线断开 B。
开关接触不良 C。
灯泡与灯座接触不良 D。
电流表损坏4。
在“探究串联电路中的电流”实验中,某同学用电流表分别测出图中a、b、c三处的电流大小,并初步得到它们之间关系的结论。
为了进一步探究它们之间的关系,下一步他的操作是( )A.将电源两极对调,再次测量a、b、c三处的电流B.改变开关S的位置,再次测量a、b、c三处的电流C.将图中两只灯泡位置对调,再次测量a、b、c三处的电流D.换用不同规格的灯泡,再次测量a、b、c三处的电流5. 如图甲所示,L1和L2是两只完全相同的灯泡,闭合开关S后,电流表的示数如图乙所示,则通过L1的电流为()A。
0.5 A B.0.25 A C.2.5 A D.1。
25 A6。
(2015•陕西中考)如图所示电路,闭合开关S1、S2,下列对电路的分析正确的是()A.L1与L2串联B.电流表A1测L1的电流C.当开关S2断开时,通过L1的电流变小D.当开关S2断开时,电流表A2的示数变小二、填空7.(2015•邵阳中考)学了串、并联电路后,小红用“顺口溜”对电路的特点进行了总结。
如:“电流走向多条路,各自为政不相顾,支路要由干路管,就像排长管班长"。
这里描述的是(选填“串联”或“并联”)电路的特点。
8. 节日用小彩灯由28个小灯泡串联而成,接入电路,现测得第1只小灯泡的电流为0。
度执业药师考前基础巩固练习题

度执业药师考前基础巩固练习题2017年度执业药师考前基础巩固练习题知识不常常巩固是很容易就忘记了,现在店铺分享2017年度执业药师考前基础巩固练习题给大家,希望对您有帮助!1.下列最容易水解的是(B)A.2-氨基糖苷B.2-去氧糖苷C.2-羟基糖苷D.6-去氧糖苷2.提取原生苷类成分,为抑制酶常用方法之一是加入适量(C)A.H2SO4B.NaOHC.CaCO3D.Na2CO33.下列化合物属于碳苷的是(B)A.芦丁B.芦荟苷C.芥子苷D.天麻苷4.研究苷中糖的种类宜采用哪种水解方法(A)A.强烈酸水解B.Smith降解法C.乙酸解D.全甲基化甲醇解5.不同苷原子的苷水解速度由快到慢顺序是(C)A.S-苷>N-苷>C-苷>O-苷B.C-苷>S-苷>O-苷>N-苷C.N-苷>O-苷>S-苷>C-苷D.O-苷>N-苷>C-苷>S-苷6.下列物质中水解产生糖与非糖两部分的是(B)A.二萜B.黄酮苷C.双糖D.二蒽酮7.根据苷原子分类,属于C-苷的是( D )A.山慈菇苷AB.黑芥子苷C.巴豆苷D.芦荟苷E.毛茛苷8.根据苷原子分类,属于醇-苷的是( E )A.山慈菇苷AB.黑芥子苷C.巴豆苷D.芦荟苷E.毛茛苷9.根据苷原子分类,属于N-苷的是(A )A.巴豆苷B.黑芥子苷C. 山慈菇苷AD.芦荟苷E.毛茛苷10.根据苷原子分类,属于S-苷的是(B )A.山慈菇苷AB.黑芥子苷C.巴豆苷D.芦荟苷E.毛茛苷11.根据苷原子分类,属于酯苷的是(A )A.山慈菇苷AB.黑芥子苷C.巴豆苷D.芦荟苷E.毛茛苷12.提取原生苷时,首先要设法破坏或抑制酶的`活性,为保持原生苷的完整性,常用的提取溶剂是(A)A 乙醇B 酸性乙醇C 水D酸水E碱水13.与Molisch反应呈阴的化合物为(C)A氮苷B硫苷C碳苷D氰苷E酚苷14. Molisch反应的阳性特征是( C )A上层显红色,下层有绿色荧光B上层绿色荧光,下层显红色C 两液层交界面呈紫色环D 有红色沉淀产生15.有关苷类性质叙述错误的是( C )A 有一定亲水性B 多呈左旋光性C 多具还原性D 可被酶酸水解E 除酯苷、酚苷外,一般苷键对碱液是稳定的。
2022年人教版初中数学9年级上册正多边形和圆—巩固练习(基础)及答案

2022年人教版初中数学9年级上册正多边形和圆—巩固练习(基础)【巩固练习】一、选择题1.一个正多边形的一个内角为120°,则这个正多边形的边数为()A.9B.8C.7D.62.如图所示,正六边形螺帽的边长是2cm,这个扳手的开口a 的值应是()A.23cmB.3cmC.233cm D.1cm第2题图第5题图3.(2020•广州)已知圆的半径是2,则该圆的内接正六边形的面积是()A.3B.9C.18D.364.正三角形、正方形、圆三者的周长都等于l ,它们的面积分别为S 1,S 2、S 3,则().A.S 1=S 2=S 3B.S 3<S 1<S 2C.S 1<S 2<S 3D.S 2<S 1<S 35.中华人民共和国国旗上的五角星的画法通常是先把圆五等分,然后连接五个等分点而得到的(如图所示).五角星的每一个角的度数是().A.30°B.35°C.36°D.37°第6题图第7题图第9题图6.如图所示,是由5把相同的折扇组成的“蝶恋花”(如图①)和梅花图案(如图②)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为()A.36°B.42°C.45°D.48°二、填空题7.如图所示,平面上两个正方形与正五边形都有一条公共边,则∠ 等于________.8.要用圆形铁片裁出边长为4的正方形铁片,则选用的圆形铁片的直径最小是________.9.如图所示,等边△ABC 内接于⊙O,AB=10cm,则⊙O 的半径是________.10.(2020•铁岭)如图,点O 是正五边形ABCDE 的中心,则∠BAO 的度数为.11.正六边形的半径是5cm,则边长6a =________,周长6P =________,边心距6r =________,面积6S =________.12.正六边形的外接圆的半径与内切圆的半径之比为.三、解答题13.如图所示,正△ABC 的外接圆的圆心为O,半径为2,求△ABC 的边长a,周长P,边心距r,面积S.14.如图所示,半径为R 的圆绕周长为10πR 的正六边形外边作无滑动滚转,绕完正六边形后,圆一共转了多少圈?一位同学的解答过程:圆的周长为2πR,所以它绕完正六边形后一共转了102RRππ圈,结果一共转了5圈.你认为这位同学的解答有无错误?如有错误,请更正.15.(2020秋•吴江市校级期中)如图,已知等边△ABC 内接于⊙O,BD 为内接正十二边形的一边,CD=5cm,求⊙O 的半径R.【答案与解析】一、选择题1.【答案】D;【解析】可求每个外角为60°,∴360÷60=6或(2)180120n n-⨯=°°∴n=6.2.【答案】A;【解析】较长对角线与较短对角线及一边长构成一直角三角形,用勾股定理求解.3.【答案】C;【解析】连接正六边形的中心与各个顶点,得到六个等边三角形,等边三角形的边长是2,高为3,因而等边三角形的面积是3,∴正六边形的面积=18,故选C.4.【答案】C;【解析】当周长一定时,边数越多的正多边形其面积越大,当它成为圆时面积最大.5.【答案】C;【解析】五角星的每一个角所对的弧为圆的15,∴弧的度数为72°,因而每个角的度数为36°,故选C.6.【答案】D.【解析】如图③所示,正五边形ABCDE 的中心角为72°,各内角为108°,故五角星五个锐角均为48°.二、填空题7.【答案】72°;【解析】α=360°-90°-90°-108°=72°.8.【答案】42;【解析】如图所示,△ABC 为等腰Rt△,242AC AB ==.9.【答案】1033cm;【解析】过O 作OD⊥BC 于D,连接OB,在Rt△BOD 中,BD=12BC=1102⨯=5(cm).∠BOD=180603=°°,∴32BD OB =.∴BO=5103332=(cm).10.【答案】54°;【解析】连接OB,则OB=OA,∴∠BAO=∠ABO,∵点O 是正五边形ABCDE 的中心,∴∠AOB==72°,∴∠BAO=(180°﹣72°)=54°;故答案为:54°.11.【答案】6a =5cm,666P a ==30cm,6532r =cm,26753cm 2s =;12.【答案】2:.【解析】设正六边形的半径是r,则外接圆的半径r,内切圆的半径是正六边形的边心距,因而是,因而正六边形的外接圆的半径与内切圆的半径之比为2:.三、解答题13.【答案与解析】作AD⊥BC 于D.∵△ABC 是正三角形,∴点O 在AD 上,a=BC=2CD,∠OCD=30°,在Rt△COD 中,112r OD OC ===,2222213CD OC OD =-=-=,∴223a BC CD ===,363P a ==.又∵AD=OA+OD=2+1=3,∴112333322S BC AD ==⨯⨯= ,∴23a =,63P =,1r =,33S =.14.【答案与解析】有错误,由正六边形的每个顶点外圆要转60°角,应转了10162RRππ+=(圈).15.【答案与解析】解:连接OB,OC,OD,∵等边△ABC 内接于⊙O,BD 为内接正十二边形的一边,∴∠BOC=×360°=120°,∠BOD=×360°=30°,∴∠COD=∠BOC﹣∠BOD=90°,∵OC=OD,∴∠OCD=45°,∴OC=5×=5(cm).即⊙O 的半径R=5cm.正多边形和圆—知识讲解(基础)【学习目标】1.了解正多边形和圆的有关概念及对称性;2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会应用正多边形和圆的有关知识画正多边形;3.会进行正多边形的有关计算.【要点梳理】知识点一、正多边形的概念各边相等,各角也相等的多边形是正多边形.要点诠释:判断一个多边形是否是正多边形,必须满足两个条件:(1)各边相等;(2)各角相等;缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).知识点二、正多边形的重要元素1.正多边形的外接圆和圆的内接正多边形正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.2.正多边形的有关概念(1)一个正多边形的外接圆的圆心叫做这个正多边形的中心.(2)正多边形外接圆的半径叫做正多边形的半径.(3)正多边形每一边所对的圆心角叫做正多边形的中心角.(4)正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.3.正多边形的有关计算(1)正n边形每一个内角的度数是;(2)正n边形每个中心角的度数是;(3)正n边形每个外角的度数是.要点诠释:要熟悉正多边形的基本概念和基本图形,将待解决的问题转化为直角三角形.知识点三、正多边形的性质1.正多边形都只有一个外接圆,圆有无数个内接正多边形.2.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形.3.正多边形都是轴对称图形,对称轴的条数与它的边数相同,每条对称轴都通过正n边形的中心;当边数是偶数时,它也是中心对称图形,它的中心就是对称中心.4.边数相同的正多边形相似。
专题13初高中衔接阅读理解(练习)-2023年初高中衔接英语精品课件专项训练(新高一适用)

专题13 初高中衔接阅读理解一.基础巩固练1. “I think we can make a difference,”says Sparks, who points out that his love of comics inspired him.〖明句式〗“I think we can make a difference,”为says宾语,who引导的定语从句修饰主语Sparks.〖句子翻译〗____________________________________________________________________________2. It’s a symbol of honor, particularly because the lawn on the top deck of the ship has special challenges with growth at sea, including “burns” from the salt water, which must be washed off immediately and clearance checks before the ship can pull in to the shore.〖明句式〗It’s a symbol of honor是主句,because 引导原因状语,which引导定语从句修饰“burns” from the salt water。
〖句子翻译〗________________________________________________________________________________________________________________________________________________________3.Though the option of walking barefoot through a grassy field on a moving cruise ship seems terrific , there are many other ships that are trying to outdo one another with even more surprising guest options. 〖扫清词汇〗 barefoot adv. 赤着脚地 ; outdo one another 超过对方;option n.选择 ;terrific adj.极好的,极其的〖明句式〗Though 引导让步状语从句,there be...为主句〖句子翻译〗________________________________________________________________________________________________________________________________________________________4. Once identified , lands with minimal or no earthworm damage should be protected.〖明句式〗Once identified为状语从句中的省略,充当条件状语。
角的平分线的性质(基础)巩固练习【名校学案word打印版+详细解答】
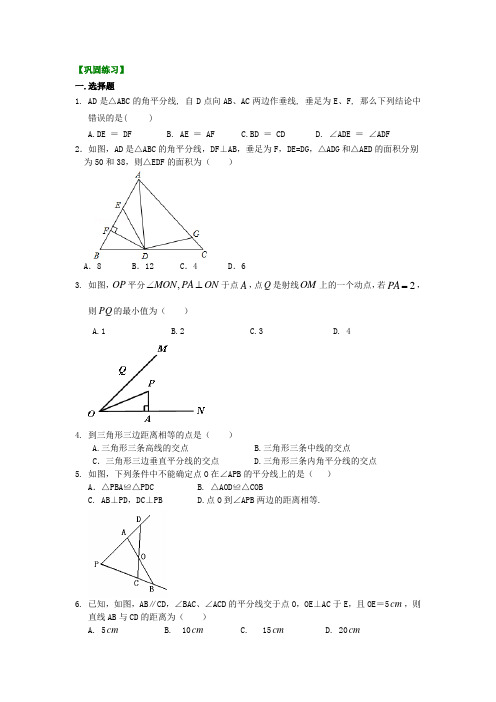
【巩固练习】一.选择题1. AD 是△ABC 的角平分线, 自D 点向AB 、AC 两边作垂线, 垂足为E 、F, 那么下列结论中错误的是( )A.DE = DFB. AE = AFC.BD = CDD. ∠ADE = ∠ADF2.如图,AD 是△ABC 的角平分线,DF⊥AB,垂足为F ,DE=DG ,△ADG 和△AED 的面积分别为50和38,则△EDF 的面积为( )A .8B .12C .4D .63. 如图,OP 平分,MON PA ON ∠⊥于点A ,点Q 是射线OM 上的一个动点,若2PA =,则PQ 的最小值为( ) A.1 B.2 C.3 D. 44. 到三角形三边距离相等的点是( )A.三角形三条高线的交点B.三角形三条中线的交点C .三角形三边垂直平分线的交点 D.三角形三条内角平分线的交点5. 如图,下列条件中不能确定点O 在∠APB 的平分线上的是( )A .△PBA ≌△PDC B. △AOD ≌△COBC. AB ⊥PD ,DC ⊥PBD.点O 到∠APB 两边的距离相等.6. 已知,如图,AB ∥CD ,∠BAC 、∠ACD 的平分线交于点O ,OE ⊥AC 于E ,且OE =5cm ,则直线AB 与CD 的距离为( )A. 5cmB. 10cmC. 15cmD. 20cm二.填空题7.如图,已知∠C =90°,AD 平分∠BAC ,BD =2CD ,若点D 到AB 的距离等于5cm ,则BC 的长为_____cm .8. 如图,在△ABC 中,∠C =90°,DE ⊥AB ,∠1=∠2,且AC =6cm ,那么线段BE 是△ABC 的 ,AE +DE = 。
9. 已知:如图,在ΔABC 中,BD 、CE 分别平分∠ABC 、∠ACB ,且BD 、CE 交于点O ,过O 作OP ⊥BC 于P ,OM ⊥AB 于M ,ON ⊥AC 于N ,则OP 、OM 、ON 的大小关系为_____.10.如图,直线1l 、2l 、3l 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,可供选择的地址有 处.11.如图,DE⊥AB 于点E ,DF⊥BC 于点F ,且DE=DF ,若∠DBC=50°,则∠ABC= (度).12.已知如图点D 是△ABC 的两外角平分线的交点,下列说法(1)AD =CD (2)D 到AB 、BC 的距离相等(3)D到△ABC的三边的距离相等(4)点D在∠B的平分线上其中正确的说法的序号是_____________________.三.解答题13.已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)求证:AM平分∠BAD;(2)试说明线段DM与AM有怎样的位置关系?(3)线段CD、AB、AD间有怎样的关系?直接写出结果.14.如图,在ΔABC中,∠C=90°,BD平分∠ABC,DE⊥AB于E,若△BCD与△BCA的面积比为3∶8,求△ADE与△BCA的面积之比.15. 已知:如图,ΔABC的外角∠CBD和∠BCE的平分线BF、CF交于点F.求证:一点F必在∠DAE的平分线上.【答案与解析】一.选择题1.【答案】C;2.【答案】D;【解析】解:如图,过点D作DH⊥AC于H,∵AD是△ABC的角平分线,DF⊥AB,∴DF=DH,在Rt△DEF和Rt△DGH中,,∴Rt△DEF≌Rt△DGH(HL),∴S△EDF=S△GDH,设面积为S,同理Rt△ADF≌Rt△ADH,∴S△ADF=S△ADH,即38+S=50﹣S,解得S=6.故选D.3.【答案】B;【解析】PQ的最小值就是过P点作PQ⊥OM,此时PQ=PA=2.4.【答案】D;【解析】三角形角平分线的交点到三边的距离相等.5.【答案】C ;【解析】C项中,仅表示了到两边的距离,没说明相等.6.【答案】B;【解析】由题意知点O到AC、AB、CD的距离相等,都等于5cm,所以两平行线间的距离为5+5=10cm.二.填空题7. 【答案】15;【解析】点D到AB的距离等于CD,BC=3CD=15.8. 【答案】角平分线,6cm;【解析】AE+DE=AE+EC=AC=6cm.9. 【答案】OP=OM=ON【解析】三角形角平分线的交点到三边的距离相等.10.【答案】4;【解析】内角平分线交点一个,外角平分线交点三个.11.【答案】100;【解析】解:∵DE⊥AB于点E,DF⊥BC于点F,且DE=DF,∴BD平分∠ABC,∴∠ABC=2∠DBC,∵∠DBC=50°,∴∠ABC=100°,故答案为:100.12.【答案】(2)(3)(4).三.解答题13.【解析】(1)证明:作ME⊥AD于E,∵MC⊥DC,ME⊥DA,MD平分∠ADC,∴ME=MC,∵M为BC中点,∴MB=MC,又∵ME=MC,∴ME=MB,又∵ME⊥AD,MB⊥AB,∴AM平分∠DAB.(2)解:DM⊥AM,理由是:∵DM平分∠CDA,AM平分∠DAB,∴∠1=∠2,∠3=∠4,∵DC∥AB,∴∠CDA+∠BAD=180°,∴∠1+∠3=90°,∴∠DMA=180°﹣(∠1+∠3)=90°,即DM⊥AM.(3)解:CD+AB=AD,理由是:∵ME⊥AD,MC⊥CD,∴∠C=∠DEM=90°,在Rt△DCM和Rt△DEM中∴Rt△DCM≌Rt△DEM(HL),∴CD=DE,同理AE=AB,∵AE+DE=AD,∴CD+AB=AD.14.【解析】解:∵∠C=90°,BD平分∠ABC,DE⊥AB于E∴DE=CD可证Rt△BCD≌Rt△BED(HL)设△BCD的面积=△BED的面积=3x,△BCA的面积为8x,△ADE的面积为8x-6x=2x,∴△ADE与△BCA的面积之比为2x:8x=1:4.15.【解析】证明:过F点作FM⊥AD,FN⊥AE,FP⊥BC∵ΔABC的外角∠CBD和∠BCE的平分线BF、CF交于点F.∴FM =FP, FN=FP(角平分线上的点到角两边的距离相等)∴FM = FN∴点F必在∠DAE的平分线上.(到角两边的距离相等的点在角的平分线上)。
用尺规作三角形及三角形全等应用(基础)巩固练习

【巩固练习】一.选择题1.尺规作图是指( )A.用量角器和刻度尺作图 B.用圆规和有刻度的直尺作图C.用圆规和无刻度的直尺作图 D.用量角器和无刻度的直尺作图2.如图,两钢条中点连在一起做成一个测量工件,AB的长等于内槽宽A'B',那么判定△OAB≌△OA'B'的理由是( )A.SSS B.SAS C.ASA D.AAS3.(2015•邵阳一模)如图,点C落在∠AOB边上,用尺规作CN∥OA,其中弧FG的( )A. 圆心是C,半径是OD B.圆心是C,半径是DMC.圆心是E,半径是OD D.圆心是E,半径是DM4.如图,∠1=∠2,∠3=∠4,下面结论中错误的是()A.△ADC≌△BCD B.△ABD≌△BACC.△ABO≌△CDO D.△AOD≌△BOC5.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )A.SSS B.SAS C.ASA D.AAS6.角平分线的性质:角平分线上的点到这个角的两边距离相等,其理论依据是全等三角形判定定理( )A.SAS B.HL C.AAS D.ASA二.填空题7.如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=_________.8.小明做了一个如图所示的风筝,其中∠EDH=∠FDH,ED=FD=a,EH=b,则四边形风筝的周长是 .9.用尺规作一个直角三角形,使其两直角边分别等于已知线段,则作图的依据是.10.如图所示,已知线段a,用尺规作出△ABC,使AB=a,BC=AC=2a.作法:(1)作一条线段AB= ;(2)分别以 、 为圆心,以 为半径画弧,两弧交于C点;(3)连接 、 ,则△ABC就是所求作的三角形.11.作图题的书写步骤是、、,而且要画出和结论,保留.12.(2015•淮安)将一副三角尺按如图所示的方式放置,使含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,则∠1的度数是 .三.解答题:13.(2015•陕西模拟)如图,已知△ABC,用尺规作出△ABC的角平分线BD.(保留作图的痕迹,不写作法)14.如图所示,要测量河两岸相对的两点A,B的距离,因无法直接量出A,B两点的距离,请你设计一种方案,求出A,B的距离,并说明理由.15.如图,已知AB=DC,AC=DB,BE=CE求证:AE=DE.【答案与解析】一.选择题1.【答案】C;【解析】尺规作图所用的作图工具是指不带刻度的直尺和圆规.故选:C.2.【答案】B;【解析】∵两钢条中点连在一起做成一个测量工件,∴OA′=OB,OB′=OA,∵∠AOB=A′OB′,∴△AOB≌△A′OB′.所以AB的长等于内槽宽A'B',用的是SAS的判定定理.3.【答案】D;【解析】图中要作CN∥OA,就是作∠NCB=∠AOD,根据作一个角等于已知角的方法可得弧FG是以圆心是E,半径是DM所画的弧.4.【答案】C;【解析】根据已知所给条件,结合图形中隐含的公共边条件,可以得到A、B、D中的三角形是可以全等,唯有C答案中的两个三角形不能全等,所以答案为C.5.【答案】D;【解析】根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角角边”定理作出完全一样的三角形.故选D.6.【答案】C ;【解析】作出图形,利用“角角边”证明全等三角形的判定即可.二.填空题7.【答案】66°;【解析】可由SSS 证明△ABC≌△DCB,∠OBC=∠OCB=, 所以∠DCB=82412︒=︒∠ABC=25°+41°=66°.8.【答案】2a+2b ;【解析】△DEH 和△DFH 中ED=FD ,∠EDH=∠FDH,DH=DH∴△DEH≌△DFH∴EH=FH=b又∵ED=FD=a,EH=b∴该风筝的周长=2a+2b.9.【答案】SAS ;【解析】 用尺规做直角三角形,已知两直角边.可以先画出两条已知线段和确定一个直角,作图的依据为SAS .10.【答案】a ;A ;B ;2a ;AC ,BC ;【解析】作法:(1)作一条线段AB=a ;(2)分别以A 、B 为圆心,以 2a 为半径画弧,两弧交于C 点;(3)连接AC 、BC ,则△ABC 就是所求作的三角形.11.【答案】已知、求作、作法,图形,作图痕迹;【解析】作图题的书写步骤是 已知、求作、作法,而且要画出 图形和 结论,保留 作图痕迹.12. 【答案】75°.【解析】如图,∵含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,∴AB ∥CD ,∴∠3=∠4=45°,∴∠2=∠3=45°,∵∠B=30°,∴∠1=∠2+∠B=30°+45°=75°.三.解答题13. 【解析】解:如图:14.【解析】解:在AB 的垂线BF 上取两点C ,D ,使CD=BC ,再作出BF 的垂线DE ,使A ,C ,E 在一条直线上,这时测得的DE 的长就是AB的长.15. 【解析】证明:在△ABC 和△DCB 中AB DC AC DBBC =CB ⎧⎪⎨⎪⎩== ∴△ABC≌△DCB(SSS )∴∠ABC=∠DCB,在△ABE 和△DCE 中ABC DCBAB DC BE CE =∠=∠=⎧⎪⎨⎪⎩∴△ABE≌△DCE(SAS )∴AE=DE.。
初中物理--电流的测量(基础)巩固练习【名校学案word版+详细解答】
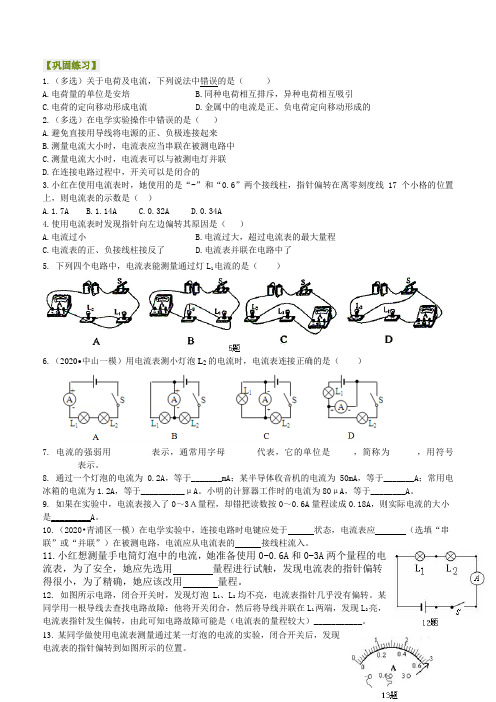
【巩固练习】1.(多选)关于电荷及电流,下列说法中错误的是()A.电荷量的单位是安培B.同种电荷相互排斥,异种电荷相互吸引C.电荷的定向移动形成电流D.金属中的电流是正、负电荷定向移动形成的2.(多选)在电学实验操作中错误的是()A.避免直接用导线将电源的正、负极连接起来B.测量电流大小时,电流表应当串联在被测电路中C.测量电流大小时,电流表可以与被测电灯并联D.在连接电路过程中,开关可以是闭合的3.小红在使用电流表时,她使用的是“-”和“0.6”两个接线柱,指针偏转在离零刻度线17个小格的位置上,则电流表的示数是()A.1.7AB.1.14AC.0.32AD.0.34A4.使用电流表时发现指针向左边偏转其原因是()A.电流过小B.电流过大,超过电流表的最大量程C.电流表的正、负接线柱接反了D.电流表并联在电路中了5.下列四个电路中,电流表能测量通过灯L1电流的是()6.(2020•中山一模)用电流表测小灯泡L2的电流时,电流表连接正确的是()7. 电流的强弱用_________表示,通常用字母_______代表,它的单位是_____,简称为______,用符号________表示。
8. 通过一个灯泡的电流为0.2A,等于_______mA;某半导体收音机的电流为50mA,等于_______A;常用电冰箱的电流为1.2A,等于__________μA。
小明的计算器工作时的电流为80μA,等于________A。
9. 如果在实验中,电流表接入了0~3A量程,却错把读数按0~0.6A量程读成0.18A,则实际电流的大小是_________A。
10.(2020•青浦区一模)在电学实验中,连接电路时电键应处于状态,电流表应(选填“串联”或“并联”)在被测电路,电流应从电流表的接线柱流入。
11.小红想测量手电筒灯泡中的电流,她准备使用0-0.6A和0-3A两个量程的电流表,为了安全,她应先选用量程进行试触,发现电流表的指针偏转得很小,为了精确,她应该改用量程。
《二次函数》全章复习与巩固—巩固练习(基础)

《二次函数》全章复习与巩固—巩固练习(基础)【巩固练习】 一、选择题1.将二次函数2y x =的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( ).A .2(1)2y x =-+ B .2(1)2y x =++ C .2(1)2y x =-- D .2(1)2y x =+- 2.二次函数y=ax 2与一次函数y=ax+a 在同一坐标系中的大致图象为( )3.(2016•永州)抛物线y=x 2+2x +m ﹣1与x 轴有两个不同的交点,则m 的取值范围是( ) A .m <2 B .m >2 C .0<m ≤2 D .m <﹣24. 抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )A .22y x x =-- B .211122y x x =-++ C .211122y x x =--+ D .22y x x =-++5.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,有下列结论:①240b ac ->;②abc>0;③8a+c >0;④9a+3b+c <0.其中,正确结论的个数是( ). A .1 B .2 C .3 D .4第4题 第5题6.已知点(1x ,1y ),(2x ,2y )(两点不重合)均在抛物线21y x =-上,则下列说法正确的是( ). A .若12y y =,则12x x = B .若12x x =-,则12y y =- C .若120x x <<,则12y y > D .若120x x <<,则12y y >7.二次函数y=ax 2+bx+c 与一次函数y=ax+c ,它们在同一直角坐标系中的图象大致是( )8.(2015•黔东南州)如图,已知二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c >0,③a >b ,④4ac ﹣b 2<0;其中正确的结论有( )A .1个B . 2个C . 3个D .4个二、填空题9.已知抛物线2(0)y ax bx c a =++>的对称轴为直线1x =,且经过点1(1,)y -,2(2,)y ,试比较1y 和2y 的大小:1y ________2y (填“>”,“<”或“=”).10.如图,已知抛物线y=﹣x 2+bx+c 的对称轴为直线x=1,且与x 轴的一个交点为(3,0),那么它对应的函数解析式是 .11.抛物线22(2)6y x =--的顶点为C ,已知y =-kx+3的图象经过点C ,则这个一次函数图象与两坐标轴所围成的三角形面积为________.12.已知二次函数22y x x m =-++的部分图象如图所示,则关于x 的一元二次方程220x x m -++=的解为___ _____.13.如图所示的抛物线是二次函数2231y ax x a =-+-的图象,那么a 的值是________.14.烟花厂为扬州“4·18”烟花三月经贸旅游节特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是252012h t t =-++,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为________.15.已知抛物线2y ax bx c =++经过点A(-1,4),B(5,4),C(3,-6),则该抛物线上纵坐标为-6的另一个点的坐标是________.16.若二次函数26y x x c =-+的图象过A(-1,y 1)、B(2,y 2)、C(32+,y 3)三点,则y 1、y 2、y 3大小关系是 .三、解答题17.(2016•河南)某班“数学兴趣小组”对函数y=x 2﹣2|x |的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x 的取值范围是全体实数,x 与y 的几组对应值列表如下: x … ﹣3 ﹣ ﹣2 ﹣1 0 1 2 3 … y…3m﹣1﹣13…其中,m= .(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.(3)观察函数图象,写出两条函数的性质. (4)进一步探究函数图象发现:①函数图象与x 轴有 个交点,所以对应的方程x 2﹣2|x |=0有 个实数根;②方程x 2﹣2|x |=2有 个实数根;③关于x 的方程x 2﹣2|x |=a 有4个实数根时,a 的取值范围是 .18. 如图所示,要设计一个等腰梯形的花坛,花坛上底长120米,下底长180米,上、下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上、下底之间有两条纵向甬道,各甬道的宽度相等,设甬道的宽为x 米.(1)用含x 的式子表示横向甬道的面积;(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?19.为迎接第四届世界太阳城大会,德州市把主要路段路灯更换为太阳能路灯.已知太阳能路灯售价为5000元/个,目前两个商家有此产品.甲商家用如下方法促销:若购买路灯不超过100个,按原价付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但太阳能路灯的售价不得低于3500元/个.乙店一律按原价的80%销售.现购买太阳能路灯x 个,如果全部在甲商家购买,则所需金额为y 1元;如果全部在乙商家购买,则所需金额为y 2元. (1)分别求出y 1、y 2与x 之间的函数关系式;(2)若市政府投资140万元,最多能购买多少个太阳能路灯?20.(2015•温州模拟)已知:如图,抛物线y=﹣x 2+bx+c 与x 轴交于点A (﹣1,0),B (3,0),与y 轴交于点C .过点C 作CD ∥x 轴,交抛物线的对称轴于点D . (1)求该抛物线的解析式;(2)若将该抛物线向下平移m 个单位,使其顶点落在D 点,求m 的值.【答案与解析】 一、选择题 1.【答案】A ;【解析】2y x =向右平移1个单位后,顶点为(1,0),再向上平移2个单位后,顶点为(1,2),开口方向及大小不变,所以1a =,即2(1)2y x =-=.2.【答案】C ;【解析】①当a >0时,二次函数y=ax 2的开口向上,一次函数y=ax+a 的图象经过第一、二、三象限,排除A 、B ;②当a <0时,二次函数y=ax 2的开口向下,一次函数y=ax+a 的图象经过第二、三、四象限,排除D . 故选C .3.【答案】A.【解析】∵抛物线y=x 2+2x +m ﹣1与x 轴有两个交点,∴△=b 2﹣4ac >0, 即4﹣4m +4>0, 解得m <2, 故选A .4.【答案】D ;【解析】由图象知,抛物线与x 轴两交点是(-1,0),(2,0),又开口方向向下,所以0a <,抛物线与y 轴交点纵坐标大于1.显然A 、B 、C 不合题意,故选D . 5.【答案】D ;【解析】抛物线与x 轴交于两点,则0b <. 由图象可知a >0,c <0, 则b <0,故abc >0.当x =-2时,y =4a-2b+c >0. ∵ 12bx a=-=,∴ b =-2a , ∴ 4a-(-2a)×2+c >0,即8a+c >0.当x =3时,y =9a+3b+c <0,故4个结论都正确. 6.【答案】D ;【解析】画出21y x =-的图象,对称轴为0x =,若12y y =,则12x x =-;若12x x =-,则12y y =;若120x x <<,则21y y >;若120x x <<,则12y y >.7.【答案】A ; 8.【答案】C ;【解析】∵二次函数y=ax 2+bx+c 图象经过原点,∴c=0,∴abc=0 ,∴①正确;∵x=1时,y <0,∴a+b+c<0,∴②不正确; ∵抛物线开口向下,∴a<0,∵抛物线的对称轴是x=﹣,∴﹣,b <0,∴b=3a,又∵a<0,b <0,∴a>b ,∴③正确;∵二次函数y=ax 2+bx+c 图象与x 轴有两个交点,∴△>0,∴b 2﹣4ac >0,4ac ﹣b 2<0,∴④正确; 综上,可得正确结论有3个:①③④.故选:C .二、填空题 9.【答案】>;【解析】根据题意画出抛物线大致图象,找出x =-1,x =2时的函数值,比较其大小,易如12y y >. 10.【答案】y=﹣x 2+2x+3;【解析】∵抛物线y=﹣x 2+bx+c 的对称轴为直线x=1,∴=1,解得b=2,∵与x 轴的一个交点为(3,0), ∴0=﹣9+6+c , 解得c=3,故函数解析式为y=﹣x 2+2x+3.11.【答案】1; 【解析】92k =,932y x =-+,与坐标轴交点为(0,3),2,03⎛⎫⎪⎝⎭. 12.【答案】 x 1=3或x 2=-1 ;【解析】由二次函数22y x x m =-++部分图象知,与x 轴的一个交点为(3,0).代入方程得m =3,解方程得x 1=3或x 2=-1.13.【答案】-1;【解析】因为抛物线过原点,所以210a -=,即1a =±,又抛物线开口向下,所以a =-1. 14.【答案】4s ; 【解析】204(s)522t =-=⎛⎫⨯- ⎪⎝⎭.15.【答案】(1,-6);【解析】常规解法是先求出关系式,然后再求点的坐标,但此方法繁琐耗时易出错,仔细分析就会注意到:A 、B 两点纵坐标相同,它们关于抛物线对称轴对称,由A(-1,4),B(5,4)得,对称轴1522x -+==,而抛物线上纵坐标为-6的一点是(3,-6),所以它关于x =2的对称点是(1,-6).故抛物线上纵坐标为-6的另一点的坐标是(1,-6).16.【答案】y 1>y 3>y 2. 【解析】因为抛物线的对称轴为6323x -==⨯.而A 、B 在对称轴左侧,且y 随x 的增大而减小,∵ -1<2,∴ y 1>y 2,又C 在对称轴右侧,且A 、B 、C 三点到对称轴的距离分别 为2,1,2,由对称性可知:y 1>y 3>y 2.三、解答题17.【答案与解析】解:(1)把x=﹣2代入y=x 2﹣2|x |得y=0, 即m=0,故答案为:0; (2)如图所示;(3)由函数图象知:①函数y=x 2﹣2|x |的图象关于y 轴对称;②当x >1时,y 随x 的增大而增大;(4)①由函数图象知:函数图象与x 轴有3个交点,所以对应的方程x 2﹣2|x |=0有3个实数根;②如图,∵y=x 2﹣2|x |的图象与直线y=2有两个交点,∴x 2﹣2|x |=2有2个实数根;③由函数图象知:∵关于x 的方程x 2﹣2|x |=a 有4个实数根, ∴a 的取值范围是﹣1<a <0, 故答案为:3,3,2,﹣1<a <0.18.【答案与解析】 (1)横向甬道的面积为1201801502x +=(m 2). (2)依题意:2112018028015028082x x x +⨯+-=⨯⨯,整理得21557500x x -+=,解得x 1=5,x 2=150(不合题意,舍去).∴ 甬道的宽为5米.(3)设建花坛的总费用为y 万元,则21201800.0280(1601502) 5.72y x x x x +⎡⎤=⨯⨯-+-+⎢⎥⎣⎦. ∴ y =0.04x 2-0.5x+240. 当0.56.25220.04b x a =-==⨯时,y 的值最小. ∵ 根据设计的要求,甬道的宽不能超过6 m .∴ 当x =6m 时,总费用最少,为0.04×62-0.5×6+240=238.44(万元).19.【答案与解析】(1)由题意可知,当x ≥100时,因为购买个数每增加一个,其价格减少10元,但售价不得低于3500元/个,所以5000350010025010x -≤+=,即100≤x ≤250时,购买一个需5000-10(x-100)元.故y 1=6000x-10x 2;当x >250时,购买一个需3500元. 故y 1=3500x .所以215000(0100),600010(100250),3500(250),x x y x xx x x ≤≤⎧⎪=-<≤⎨⎪>⎩y 2=5000×80%x =4000x .(2)当0<x ≤100时,y 1=5000x ≤500000<1400000;当100<x ≤250时,y 1=6000x-10x 2=-10(x-300)2+900000<1400000; 所以,由3500x =1400000,得x =400. 由4000x =1400000,得x =350.故选择甲商家,最多能购买400个路灯.20.【答案与解析】(1)设y =kx ,把(2,4)代入,得k =2,所以y =2x ,自变量x 的取值范围是:0≤x ≤30.(2)当0≤x <5时,设y =a(x-5)2+25, 把(0,0)代入,得25a+25=0,a =-1, 所以22(5)2510y x x x =--+=-+. 当5≤x ≤15时,y =25.即210(05),25(515).x x x y x ⎧-+≤<=⎨≤≤⎩(3)设王亮用于回顾反思的时间为x(0≤x <5)分钟,学习收益总量为Z ,则他用于解题的时间为(30-x)分钟.当0≤x <5时,222102(30)860(4)76Z x x x x x x =-++-=-++=--+. 所以当x =4时,76Z =最大.当5≤x ≤15时,Z =25+2(30-x)=-2x+85. 因为Z 随x 的增大而减小, 所以当x =5时,75Z =最大.综合所述,当x =4时,76Z =最大,此时30-x =26.即王亮用于解题的时间为26分钟,用于回顾反思的时间为4分钟时.学习收益总量最大.。
2020版高中物理高一必修1教案及练习归纳整理13巩固练习相遇和追及问题(基础)

【巩固练习及参考答案与试题解析】一选择题:1、(2015 山西忻州一中期末考)a、b、c三个物体在同一条直线上运动,三个物体的位移-时间图象如右图所示,图象c是一条抛物线,坐标原点是抛物线的顶点,下列说法中正确的是A.a、b两物体都做匀速直线运动,两个物体的速度相同B.a、b两物体都做匀速直线运动,两个物体的速度大小相同方向相反C.在0~5 s的时间内,t=5 s时,a、b两个物体相距最远D.物体c做匀加速运动,加速度为0.2 m/s22、(2015 沈阳市期末考)甲、乙两物体同时从同一位置出发沿同一直线运动,它们的v﹣t 图象如图所示,则下列判断正确的是()A.甲做匀速直线运,乙做匀变速直线运动B.两物体两次相遇的时刻分别是1S末和4S末C.乙在前2s内做匀加速直线运动,2S后做匀减速直线运动D.第2s末乙物体的运动方向改变二解答题:0.5m s的加速度从停车线启动做匀加速运动,恰好有一辆自行车以1、在十字路口,汽车以25m s的速度匀速驶过停车线与汽车同方向行驶,求:(1)什么时候它们相距最远?最远距离是多少?(2)在什么地方汽车追上自行车?追到时汽车的速度是多大?2、甲、乙两个同学在直跑道上练习4 100m接力,他们在奔跑时有相同的最大速度。
乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀变速运动。
现甲持棒以最大速度向乙奔来,乙在接力区伺机全力奔出。
若要求乙接棒时奔跑达到最大速度的80%,则: (1)乙在接力区须奔出多大距离?(2)乙应在距离甲多远时起跑?3、(2015 湖北孝感高级中学期末考)甲、乙两辆汽车沿平直公路同向匀速行驶,甲车在乙车前面,它们之间相距x0=40m,速度均为v0=10m/s。
某时刻,甲车刹车作匀减速直线运动,加速度大小为5m/s2。
从此时刻起,求:(1)甲车经过多长时间停止运动;(2)当甲车静止时,甲、乙两辆汽车之间的距离为多大;(3)经多长时间两车相遇?4、在水平直轨道上有两列火车A和B相距s。
人教版七年级数学下册三元一次方程组(基础) 巩固练习及答案.doc

【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】【巩固练习】 一、选择题1. (2015春•沙坪坝区期末)下列四组数值中,为方程组的解是( )A .B .C .D .2.已知方程组329a b b c a c +=⎧⎪+=-⎨⎪+=⎩,则a+b+c 的值为( ).A .6B .-6C .5D .-5 3.已知532y x y z xab c ++-与254x ya b c -是同类项,则x-y+z 的值为 ( ) .A .1B .2C .3D .44.若x+2y+3z =10,4x+3y+2z =15,则x+y+z 的值为 ( ) .A .2B .3C .4D .55.已知甲、乙、丙三个人各有一些钱,其中甲的钱是乙的2倍,乙比丙多1元,丙比甲少11元,则三人共有( ).A .30元B .33元C .36元D .39元 6.(2016春•南京校级期末)关于x ,y 的方程组的解是方程3x+2y=10的解,那么a 的值为( )A .﹣2B .2C .﹣1D .1 二、填空题7. 解三元一次方程组的基本思路是 .8. (2015春•高新区期末)方程组的解为 .9. (2016春•吴江区期末)已知,则= .10. 若方程-3x-my+4z=6是三元一次方程,则m的取值范围是 .11. 如果方程组864x yy zz x+=⎧⎪+=⎨⎪+=⎩的解满足方程kx+2y-z=10,则k=________.12.已知方程组2334823x y zx y zx y z-+=⎧⎪+-=⎨⎪+-=-⎩,若消去z,得到二元一次方程组________;若消去y,得到二元一次方程组________,若消去x,得到二元一次方程组________.三、解答题13.解方程组:(1)2321122x y zx yx y z-=⎧⎪⎪+=⎨⎪⎪-=+⎩(2)32522642730x y zx y zx y z++=⎧⎪--=⎨⎪+-=⎩14. (2015春•镇江校级期末)已知y=ax2+bx+c,当x=1时,y=3;当x=﹣1时,y=1;当x=0时,y=1.求a,b,c的值.15. 2003年全国足球甲A联赛的前12轮(场)比赛后,前三名比赛成绩如下表.胜(场)平(场)负(场)积分大连实德队8 2 2 26上海申花队 6 5 1 23北京现代队 5 7 0 22【答案与解析】一、选择题1. 【答案】D.【解析】,①+②得:3x+y=1④,①+③得:4x+y=2⑤,⑤﹣④得:x=1,将x=1代入④得:y=﹣2,将x=1,y=﹣2代入①得:z=3,则方程组的解为.2. 【答案】C;【解析】将方程组中的三个方程左右分别相加,得2()10a b c ++=,两边同除以2便得答案.3. 【答案】D ;【解析】由同类项的定义得:5235y x x y z x y +=⎧⎪+=⎨⎪-=⎩,解得:211x y z =⎧⎪=-⎨⎪=⎩,所以4x y z -+=.4. 【答案】D ;【解析】将三个等式左右分别相加,可得5()25x y z ++=,进而得 5x y z ++= . 5. 【答案】D ;【解析】解:设甲乙丙分别有,,x y z 元元元,则有:2111x y y z x z =⎧⎪-=⎨⎪-=⎩,解得:20109x y z =⎧⎪=⎨⎪=⎩,所以三人共有:39x y z ++=(元). 6. 【答案】B ;【解析】解:本题的实质是解三元一次方程组,用加减法或代入法来解答.(1)﹣(2)得:6y=﹣3a ,∴y=﹣,代入(1)得:x=2a ,把y=﹣,x=2a 代入方程3x+2y=10, 得:6a ﹣a=10, 即a=2. 故选B .二、填空题7. 【答案】消元;8.【答案】.9. 【答案】;【解析】解:,①×7﹣②×6得:2x ﹣3y=0, 解得:x=y ,①×2+②×3得:11x ﹣33z=0 解得:x=3z , ∵x=y ,x=3z , ∴y=2z , ∴===.故答案为:.10.【答案】0m ≠;【解析】三元一次方程的定义. 11.【答案】13; 【解析】解原方程组得:351x y z =⎧⎪=⎨⎪=⎩,代入kx+2y-z =10得,13k =.12. 【答案】531153x y x y +=⎧⎨-=⎩3011320x z x z -=⎧⎨+=⎩ 539517z y y z -=⎧⎨+=⎩;【解析】加减或代入消元.三、解答题 13.【解析】解:(1) 2321122x y z x y x y z ⎧⎪-=⎪+=⎨⎪⎪-=+⎩①②③由①得:2x y z=+④,将④代入②③,整理得:831132y z y z +=⎧⎪⎨+=⎪⎩,解得:121y z ⎧=⎪⎨⎪=-⎩, 代入④得:0x =,所以,原方程组的解是0,1,21.x y z =⎧⎪⎪=⎨⎪=-⎪⎩(2)32522642730x y z x y z x y z ++=⎧⎪--=⎨⎪+-=⎩①②③ 由①+②得:448x z +=,即2x z +=④,由②+③得:5836x z -=⑤, 由④×5-⑤,整理得:2z =-, 将2z =-代入④,解得:4x =, 将4x =,2z =-代入①,解得0y =,所以,原方程组的解是4,0,2.x y z =⎧⎪=⎨⎪=-⎩14.【解析】解:∵y=ax 2+bx+c ,当x=1时,y=3;当x=﹣1时,y=1;当x=0时,y=1,∴代入得:把③代入①和②得:,解得:a=1,b=1, 即a=1,b=1,c=1. 15.【解析】解:设每队胜一场、平—场、负—场分别得x 分,y 分,z 分根据题意,得8222665235722x y z x y z x y ++=⎧⎪++=⎨⎪+=⎩①②③由①得4x+y+z =13 ④②一④,得x+2y =5 ⑤ ⑤×5-③,得y =1.把y =1代入⑤,得x =5-2×1=3,即x =3.把x =3,y =1代入④,得z =0.∴310x y z =⎧⎪=⎨⎪=⎩答:每队胜一场得3分,平一场得1分,负一场得0分.初中奥数题试题一一、选择题(每题1分,共10分)1.如果a,b都代表有理数,并且a+b=0,那么 ( )A.a,b都是0 B.a,b之一是0C.a,b互为相反数 D.a,b互为倒数2.下面的说法中正确的是 ( )A.单项式与单项式的和是单项式B.单项式与单项式的和是多项式C.多项式与多项式的和是多项式D.整式与整式的和是整式3.下面说法中不正确的是 ( )A. 有最小的自然数 B.没有最小的正有理数C.没有最大的负整数 D.没有最大的非负数4.如果a,b代表有理数,并且a+b的值大于a-b的值,那么 ( )A.a,b同号 B.a,b异号 C.a>0 D.b>05.大于-π并且不是自然数的整数有 ( )A.2个 B.3个 C.4个 D.无数个6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身。
中考总复习:圆的有关概念、性质与圆有关的位置关系--巩固练习(基础)

中考总复习:圆的有关概念、性质与圆有关的位置关系—巩固练习(基础)【巩固练习】一、选择题1. 已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ,若12O O =7 cm ,则⊙1O 与⊙2O 的位置关系是( )A .相交B .相离C .内切D .外切2.如图,AB 是⊙O 的直径,点C 、D 在⊙O 上 ,∠BOD=110°,AC∥OD,则∠AOC 的度数 ( )A. 70°B. 60°C. 50°D. 40°3.如图所示,AB 是⊙O 的直径,CD 为弦,CD ⊥AB 于点E ,则下列结论中不成立的是( )A .∠COE =∠DOEB .CE =DEC .OE =BED .»»BDBC第2题 第3题 第5题 第6题4.(2015•黑龙江)如图,⊙O 的半径是2,AB 是⊙O 的弦,点P 是弦AB 上的动点,且1≤OP≤2,则弦AB 所对的圆周角的度数是( )A .60°B .120°C .60°或120°D .30°或150°5.如图所示,△ABC 内接于圆O ,∠A =50°;∠ABC =60°,BD 是圆O 的直径,BD 交AC 于点E ,连接DC ,则∠AEB 等于( )A .70°B .110°C .90°D .120°6.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配成与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )A .第①块B .第②块C .第③块D .第④块二、填空题7.(2015•雁江区模拟)如图,MN 是半径为2的⊙O 的直径,点A 在⊙O 上,∠AMN=30°,B 为弧AN 的中点,P 是直径MN 上一动点,则PA+PB 的最小值为 .8.如图所示,⊙O的直径AC=8 cm,C为⊙O上一点,∠BAC=30°,则BC=________cm.第8题第9题9.两圆有多种位置关系,图中(如图所示)不存在的位置关系是__________.10.如图所示,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=36°,则∠C=______.11.如图,直线PA过半圆的圆心O,交半圆于A,B两点,PC切半圆与点C,已知PC=3,PB=1,则该半圆的半径为 .第10题第11题第12题12.如图所示.B是线段AC上的一点,且AB:AC=2:5.分别以AB、AC为直径画圆,则小圆的面积与大圆的面积之比为________.三、解答题13.已知AB与⊙O相切于点C,OA=OB.OA、OB与⊙O分别交于点D、E.(1) 如图①,若⊙O的直径为8,AB=10,求OA的长(结果保留根号);(2)如图②,连接CD、CE,若四边形ODCE为菱形.求ODOA的值.14. 如图所示,在Rt△ABC中,∠C=90°,O为直角边BC上一点,以O为圆心、OC为半径的圆恰好与斜边AB相切于点D,与BC交于另一点E.(1)求证:△AOC≌△AOD;(2)若BE=1,BD=3,求⊙O的半径及图中阴影部分的面积S.15.(2015•上城区二模)如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.(1)若∠DFC=40°,求∠CBF的度数;(2)求证:CD⊥DF.l16. 如图,已知∠ABC=90°,AB=BC.直线与以BC为直径的圆O相切于点C.点F是圆O上异于B、Cl的动点,直线BF与相交于点E,过点F作AF的垂线交直线BC与点D.(1)如果BE=15,CE=9,求EF的长;(2)证明:①△CDF∽△BAF;②CD=CE;(3)探求动点F在什么位置时,相应的点D位于线段BC的延长线上,且使CD,请说明你的理由.【答案与解析】一、选择题1.【答案】D;O O=7,根据圆与圆位置关系的判定可知两圆外切.【解析】两圆半径之和3+4=7,等于两圆圆心距122.【答案】D;【解析】由AB是⊙O的直径,点C、D在⊙O上,知OA=OC,根据等腰三角形等边对等角的性质和三角形内角和定理,得∠AOC=180°-2∠OAC.由AC∥OD,根据两直线平行,内错角相等的性质,得∠OAC=∠AOD.由AB是⊙O的直径,∠BOD=110°,根据平角的定义,得∠AOD=180°-∠BOD=70°.∴∠AOC=180°-2×70°=40°.故选D.3.【答案】C;【解析】由垂径定理知A、B、D都正确.4.【答案】C;【解析】作OD⊥AB,如图,∵点P是弦AB上的动点,且1≤OP≤2,∴OD=1,∴∠OAB=30°,∴∠AOB=120°,∴∠AEB=∠AOB=60°,∵∠E+∠F=180°,∴∠F=120°,即弦AB所对的圆周角的度数为60°或120°.故选C.5.【答案】B;【解析】∵∠A=50°,∴∠D=50°,又∵BD是直径,∴∠BCD=90°,∴∠DBC=90°-50°=40°,∠ABD=60°-40°=20°,∴∠BEC=50°+20°=70°,∴∠AEB=180°-70°=110°.6.【答案】B;【解析】因为第②块含有圆周的一部分,可以找到圆心,量出半径.其他块都不行.二、填空题7.【答案】2;【解析】如图,作点B关于MN的对称点B′,连接OA、OB′、AB′,由轴对称确定最短路线问题可知,AB′与M的交点即为所求的使PA+PB的值最小的点,∵∠AMN=30°,∴∠AON=2∠AMN=2×30°=60°,∵B为弧AN的中点,∴∠NOB′=×60°=30°,∴∠AOB′=90°,∴△AOB′是等腰直角三角形,∵⊙O的半径为2,∴AB′=2,即PA+PB的最小值为为2.8.【答案】4;【解析】因为AC为直径,根据直径所对的圆周角为直角,得∠ABC=90°,则BC=AC·sin∠BAC=4(am).9.【答案】相交;【解析】认真观察、判断可发现每两圆间不存在的位置关系是:相交.10.【答案】27°;【解析】如图,连结OB,由AB与⊙O相切于点B,得∠ABO=90°,因为∠A=36°,所以∠AOB=54°,所以∠C=27°.11.【答案】4;【解析】连接OC,则由直线PC是圆的切线,得OC⊥PC.设圆的半径为x,则在Rt△OPC中,PC=3,OC= x,OP=1+x,根据地勾股定理,得OP2=OC2+PC2,即(1+x)2= x2+32,解得x=4.即该半圆的半径为4.12.【答案】4:25;三、解答题13.【答案与解析】(1) 如图①,连接OC ,则OC=4.∵AB 与⊙O 相切于点C ,∴OC⊥AB. ∴在△OAB 中,由OA=OB ,AB=10得1AC AB 52==.∴ 在△RtOAB 中,OA ===.(2)如图②,连接OC ,则OC=OD.∵四边形ODCE 为菱形,∴OD=DC.∴△ODC 为等边三角形.∴∠AOC=60°.∴∠A=30°.∴1OC 1OD 1OC OA 2OA 2OA 2===,,即.14.【答案与解析】解:(1)∵ AB 切⊙O 于D ,∴OD ⊥AB .在Rt △AOC 和Rt △AOD 中,,.OC OD AO AO =⎧⎨=⎩ ∴Rt △AOC ≌Rt △AOD(HL).(2)设半径为r ,在Rt △ODB 中,,解得r =4.2223(1)r r +=+ 由(1)有AC =AD ,∴,2229(3)AC AC +=+ 解得AC =12,∴.22111112945482222S AC BC r πππ=-=⨯⨯-⨯=-g 15.【答案与解析】解:(1)∵∠ADB=∠ACB ,∠BAD=∠BFC ,∴∠ABD=∠FBC ,又∵AB=AD ,∴∠ABD=∠ADB ,∴∠CBF=∠BCF ,∵∠BFC=2∠DFC=80°,∴∠CBF==50°;(2)令∠CFD=α,则∠BAD=∠BFC=2α,∵四边形ABCD 是圆的内接四边形,∴∠BAD+∠BCD=180°,即∠BCD=180°﹣2α,又∵AB=AD ,∴∠ACD=∠ACB ,∴∠ACD=∠ACB=90°﹣α,∴∠CFD+∠FCD=α+(90°﹣α)=90°,∴∠CDF=90°,即CD ⊥DF .16.【答案与解析】解:(1)∵直线与以BC 为直径的圆O 相切于点C ,l ∴∠BCE=90°,又∵BC 为直径,∴∠BFC=∠CFE=90°.∴∠CFE=∠BCE.∵∠FEC=∠CEB,∴△CEF∽△BEC.∴CE EF BE EC =.∵BE=15,CE=9,即:9EF 159=,解得:EF=275.(2)证明:①∵∠FCD+∠FBC=90°,∠ABF+∠FBC=90°,∴∠ABF=∠FCD.同理:∠AFB=∠CFD.∴△CDF∽△BAF.②∵△CDF∽△BAF,∴CF CD BF BA =.又∵△CEF∽△BCF,∴CF CE BF BC =.∴CD CE BA BC=.又∵AB=BC,∴CE=CD.(3)当F 在⊙O 的下半圆上,且»»2BF BC 3=时,相应的点D 位于线段BC 的延长线上,且使CD.理由如下:CE.在Rt△BCE 中,tan∠CBE=CEBC =,∴∠CBE=30°,∴»CF所对圆心角为60°.∴F 在⊙O 的下半圆上,且»»2BF BC 3=.。
2022年中考物理专项《声现象》基础巩固练习(附答案)

专题01 声现象〔解析版〕2021年中考物理回归课本根底稳固练习一、知识导图二、易混易错判断1.课堂上能听到老师讲课声,是由于空气能够传声。
( √)2.用大小不同的力先后敲击同一音叉,音叉发生的音调会不同。
( ×)3.“闻其声而知其人〞主要是根据音色来判断的。
( √)4.根据音色可以区分不同乐器发出的声音。
( √)5.物体只要振动就能听见声音。
( ×)6.按动笛子不同的孔,声音的音调会变化。
( √)7.超声波、超声波的传播不需要介质。
( ×)8.窃窃私语不是噪声。
( ×)9.公路旁安装隔音墙是为了在传播途径上减弱噪声。
( √)三、稳固练习1.关于声音的产生和传播的说法正确的选项是〔〕。
A.声音的传播不需要介质;B.只要物体振动,我们就能听见声音;C.物体的振动一旦停止,发声也随之停止;D.声音在空气中传播最快【答案】C。
【解析】A、声音传播需要介质,真空不能传声,故A错误;B、声音是由物体振动产生的,但振动的频率范围如果不在人耳的听觉范围之内,人也听不到声音。
故B错误。
C、声音是由物体振动产生的,振动停止,发声也随之停止,故C正确;D、声音传播需要介质,真空不能传声,故D错误。
应选:C。
2.我国的宇航员费俊龙和聂海盛已乘坐着宇宙飞船“神舟6号〞邀游太空。
宇航员在太空舱中可以直接对话,但在飞船外作业时,他们之间不能直接对话,必须借助电子通信设备进行交流,其原因是〔〕。
A.用通信设备对话是为了方便;B.声音的传播需要介质;C.太空中噪声太大;D.声音只能在地面上传播【答案】B。
【解析】声音的传播需要介质,真空不能传播声音。
飞船内有空气,可以直接对话,但在飞船外是真空,所以工作时,必须借助电子通讯设备才能进行对话。
应选:B。
3.在门窗关闭的空教室里说话,会感到声音比在门窗翻开放有桌椅的教室里声音响亮,原因是〔〕。
A.声音的响度大些B.声音的音调高些C.声音与回声分开了D.声音与回声混在一起了【答案】D。
2020_2021学年八年级物理上学期寒假作业巩固练13长度和时间的测量含解析沪科版

巩固练13长度和时间的测量一、单选题(共5小题)1.在进行长度测量时,下列操作正确的是()A.读数时视线应与刻度尺面平行B.刻度尺的零刻度线如果磨损,仍可以继续使用C.测量长度时,只需要读到刻度尺的分度值D.测量长度时,必须从刻度尺的零刻度线起,否则测量就是错误的【解答】解:A、读取刻度尺数值时,视线与刻度尺相垂直,故A错误;BD、如果0刻度线磨损,测量的始端可以与其它整格刻线对齐,测量结果要减去前面的数值,故B正确,D错误;C、记录长度测量结果时,应估读到分度值的下一位,故C错误。
故选:B。
【知识点】刻度尺的使用2.估测在实际生活中的应用十分广泛,下列所估测的数据中最接近实际的是()A.一张试卷厚度大约1mmB.课桌的高度大约是0.75cmC.人体感觉舒适的环境温度约为37℃D.1min内人的脉搏跳动的次数约是70次【解答】解:A、人的头发的直径在75μm左右,试卷的厚度与此差不多,在75μm=0.075mm左右。
故A 不符合实际;B、中学生的身高在160cm左右,课桌的高度大约是中学生身高的一半,在80cm左右。
故B不符合实际;C、人体正常体温在37℃左右,感觉舒适的温度在23℃左右。
故C不符合实际;D、正常情况下,人的脉搏跳动一次的时间接近1s,1min跳动的次数在70次左右。
故D符合实际。
故选:D。
【知识点】长度的估测、温度、时间的估测3.小明同学用同一把刻度尺对同物体的长度进行了4次测量,结果如下7.34cm、7.36cm、7.37cm、7.85cm,则该物体的长度应记为()A.7.34cm B.7.35cm C.7.36cm D.7.48cm【解答】解:从题干中提供数据可知,7.75cm与其它数据相差较大,准确值与其他数据不同,所以7.85cm是错误的,应该去掉;为减小长度测量的误差,通常采用的方法是取多次测量的平均值;故物体的长度最终应记录为:L=≈7.36cm。
故选:C。
【知识点】长度的测量4.如图所示是四种用厚刻度尺测量长方体长度的方法,其中正确的是()A.B.C.D.【解答】解:A、图中刻度尺的零刻度线未与被测物体的边缘对齐,故A错误;B、图中刻度尺有刻度线的一侧紧贴被测物体,而且放正,零刻度线与被测物体的边缘对齐,视线与刻度尺垂直,故B正确。
初级审计师-《审计相关基础知识》(初级)巩固练习(2021年12月)

初级审计师《审计相关基础知识》(初级)巩固练习(2021年12月1日-2021年12月31日)正确答案:B答案解析期末所有者权益=年初所有者权益+本年净利润=6000+800=6800万元。
以资本公积转增资本不影响所有者权益。
资本公积转增资本的分录为:借:资本公积贷:实收资本企业提取盈余公积不影响所有者权益,会计分录为:借:利润分配——提取法定盈余公积贷:盈余公积——法定盈余公积考察知识点资本公积核算概述正确答案:A答案解析对于确实无法支付的应付账款,直接转入营业外收入,借记“应付账款”科目,贷记“营业外收入”科目。
营业外收入不影响营业利润。
考察知识点应付账款正确答案:D答案解析短期薪酬具体包括:职工工资、奖金、津贴和补贴,职工福利费,医疗保险费、工伤保险费和生育保险费等社会保险费,住房公积金,工会经费和职工教育经费,短期带薪缺勤,短期利润分享计划,非货币性福利以及其他短期薪酬。
选项D,属于离职后福利。
考察知识点短期薪酬4、对有限责任公司而言,如有新投资者加入,新加入的投资者缴纳的出资额大正确答案:C答案解析新加入的投资者缴纳的出资额大于其在注册资本中所占份额的部分应作为资本溢价,记入“资本公积——资本溢价”科目。
考察知识点资本溢价(或股本溢价)5、权益法核算时,被投资单位其他综合收益增加,企业按持股比例计算应享有正确答案:D答案解析权益法下,如果被投资方的其他综合收益增加,投资方应做分录:借:长期股权投资——其他综合收益贷:其他综合收益考察知识点其他综合收益6、某股份有限公司2017年度实现净利润400万元,法定盈余公积的提取率为1正确答案:A答案解析本题考核“盈余公积”知识点。
计提盈余公积时的基数为当期实现的净利润。
应计提法定盈余公积金额=400×10%=40(万元)。
借:利润分配——提取法定盈余公积 400 000贷:盈余公积 400 000考察知识点盈余公积正确答案:D答案解析发放股票股利,按实际发放的股票股利金额借记“利润分配”,按股票票面金额,贷记“股本”,如有差额,贷记“资本公积---股本溢价”。
有理数的加减法(基础)巩固练习

【巩固练习】一、选择题1.某市一天的最高气温为2℃,最低气温为﹣8℃,那么这天的最高气温比最低气温高()A.﹣10℃ B.﹣6℃ C.10℃D.6℃2.(2015•吉林)若等式0□1=﹣1成立,则□内的运算符号为()A. + B.﹣C.×D.÷3.两个有理数相加,和小于其中一个加数而大于另一个加数,需满足()A.两个数都是正数 B.两个数都是负数C.一个是正数,另一个是负数 D.至少有一个数是零4.下列说法中正确的是A.正数加负数,和为0B.两个正数相加和为正;两个负数相加和为负C.两个有理数相加,等于它们的绝对值相加D.两个数的和为负数,则这两个数一定是负数5.下列说法正确的是( )A.零减去一个数,仍得这个数B.负数减去负数,结果是负数C.正数减去负数,结果是正数D.被减数一定大于差6.某粮店出售的三种品牌的面粉袋上,分别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差( )A.0.8kg B.0.6kg C.0.5kg D.0.4kg7. -3+5的相反数是( ).A.2 B.-2 C.-8 D.8二、填空题8.有理数,,a b c c在数轴上对应点位置如图所示,用“>”或“<”(1)|a|______|b|;(2)a+b+c______0:(3)a-b+c______0;(4)a+c______b;(5)c-b______a.9.(2015•上海)计算:|﹣2|+2=________.10.某月股票M开盘价20元,上午10点跌1.6元,下午收盘时又涨了0.4元,则股票这天的收盘价是_______.11.列出一个满足下列条件的算式:(1)所有的加数都是负数,和为-5,________;(2)一个加数是0,和是-5________;(3)至少有一个加数是正整数,和是-5,________.12. 数学活动课上,王老师给同学们出了一道题:规定一种新运算“☆”对于任意两个有理数a和b,有a☆b=a-b+1,请你根据新运算,计算(2☆3)☆2的值是 .13.计算(﹣3)+(﹣9)的结果为.三、解答题14.计算题(1)232(1)(1)( 1.75)343-----+-(2)132.1253(5)(3.2)58-+---+(3)21772953323+--- (4)231321234243--++-+ (5)2312()()3255---+--+- (6)123456782001200220032004-+-+-+-+--+-+15. 已知:|a|=2,|b|=3,求a+b 的值.16.某人用400元购买了8套儿童服装,准备以一定价格出售,如果以每套儿童服装55元的价格为标准,超出的记作正数,不足的记作负数,记录如下:+2,﹣3,+2,+1,﹣2,﹣1,0,﹣2.(单位:元)(1)当他卖完这八套儿童服装后是盈利还是亏损?(2)盈利(或亏损)了多少钱?【答案与解析】一、选择题1. 【答案】C【解析】解:2﹣(﹣8)=2+8=10℃.故选C .2.【答案】B3. 【答案】C【解析】举例验证.4.【答案】B【解析】举反例:如5+(-2)=+3≠0,故A 错;如:(-2)+(-3)≠|-2|+|-3|,故C 错;如(+2)+(-8)=-6,故D 错误.5.【答案】C【解析】举反例逐一排除.6.【答案】B【解析】因为最低重量为24.7kg ,最大重量为25.3kg ,故质量最多相差25.3-24.7=0.6kg .7.【答案】B二、填空题8. 【答案】<,<,>,>,> 【解析】由图可知:b a c >>,且0,0b a c <<>,再根据有理数的加法法则可得答案.9.【答案】4.10.【答案】18.8元【解析】跌 1.6元记为-1.6元,涨0.4元记为+0.4元,故有收盘价为20+(-1.6)+0.4-18.8.11.【答案】(1)(-2)+(-3)=-5 (2)(-5)+0=-5 (3)2+(-7)=-5【解析】答案不唯一.12. 【答案】-1【解析】(2☆3)☆2=(2☆3)-2+1=2-3+1-2+1=-113. 【答案】-12.【解析】同号两数相加的法则是取相同的符号,并把绝对值相加. 原式=﹣(3+9)=﹣12.三、解答题14. 【解析】(1)原式22(1)( 1.75 1.75)133=-++-+=;(2)原式131 [3( 3.2)][(5) 2.125]3 584 =+-++---=(3)原式21729771 9)533326 =+---=-(4)原式223311 ()()12334422 =-++-++-=-(5)原式23122312231283[()][()]32553255325530 =------=--------=----=-(6)原式=12342001200220032004-+-++-+-+(12)(34)(20032004)110021002=-++-+++-+=⨯=15. 【解析】由题意知:a=±2, b=±3,所以要分四种情况代入求值.∵|a|=2, ∴ a=±2, ∵|b|=3, ∴b=±3.当a=+2, b=+3时, a+b=(+2)+(+3)=+5;当a=+2, b=-3时, a+b=(+2)+(-3)=-1;当a=-2,b=+3时, a+b=(-2)+(+3)=+1;当a=-2, b=-3时, a+b=(-2)+(-3)=-5.16. 【解析】解:根据题意得(1)2﹣3+2+1﹣2﹣1+0﹣2=﹣3,55×8+(﹣3)=437元,∵437>400,∴卖完后是盈利;(2)437﹣400=37元,故盈利37元.。
(基础)坐标系知识 巩固练习全部整理 含参考

平面直角坐标系(基础)一、选择题1.为确定一个平面上点的位置,可用的数据个数为().A.1个B.2个C.3个D.4个2.下列说法正确的是().A.(2,3)和(3,2)表示的位置相同B.(2,3)和(3,2)是表示不同位置的两个有序数对C.(2,2)和(2,2)表示两个不同的位置D.(m,n)和(n,m)表示的位置不同3.(2016•大连)在平面直角坐标系中,点M(1,5)所在的象限是().A.第一象限B.第二象限C.第三象限D.第四象限4.若点P(m,n)在第三象限,则点Q(-m,-n)在().A.第一象限B.第二象限C.第三象限D.第四象限5.知点P(m+3,2m+4)在y轴上,那么点P的坐标是().A.(-2,0)B.(0,-2)C.(1,0)D.(0,1)二、填空题7.已知有序数对(2x-1,5-3y)表示出的点为(5,2),则x=________,y=________.8.某宾馆一大楼客房是按一定规律编号的,例如房间403号是指该大楼中第4层第3个房间,则房间815号是指第________层第________个房间;第6层第1个房间编号为________.9.点P(-3,4)到x轴的距离是________,到y轴的距离是________.10.指出下列各点所在象限或坐标轴:点A(5,-3)在_______,点B(-2,-1)在_______,点C(0,-3)在_______,点D(4,0)在_______,点E(0,0)在_______.11.(2016•黔南州)在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:①△(a,b)=(﹣a,b);②○(a,b)=(﹣a,﹣b);③Ω(a,b)=(a,﹣b),按照以上变换例如:△(○(1,2))=(1,﹣2),则○(Ω(3,4))等于.12.(2015•安溪县模拟)若点(3﹣x,x﹣1)在第二象限,则x的取值范围是.三、解答题13.在图中建立适当的平面直角坐标系,使A、B两点的坐标分别为(-4,1)和(-1,4),写出点C、D的坐标,并指出它们所在的象限.14.(2014春•夏津县校级期中)根据要求解答下列问题:设M(a,b)为平面直角坐标系中的点.(1)当a>0,b<0时,点M位于第几象限?(2)当ab>0时,点M位于第几象限?(3)当a为任意实数,且b<0时,点M位于何处?15.已知A,B,C,D的坐标依次为(4,0),(0,3),(-4,0),(0,-3),在平面直角坐标系中描出各点,并求四边形ABCD的面积.答案、分析一、选择题1.答案B.2.答案B.3.答案B;析:四个象限的点的坐标符号分别是(+,+),(-,+),(-,-),(+,-).4.答案A;析:因为点P(m,n)在第三象限,所以m,n均为负,则它们的相反数均为正.5.答案B;析:m+3=0,∴m=-3,将其代入得:2m+4=-2,∴P(0,-2).二、填空题7.答案3,1;析:由2x-1=5,得x=3;由5-3y=2,得y=1.8.答案8,15,601;9.答案4,3;析:到x轴的距离为:│4│=4,到y轴的距离为:│-3│=3.10.答案第四象限,第三象限,y轴的负半轴上,x轴的正半轴上,坐标原点.11.答案(﹣3,4)析:解:○(Ω(3,4))=○(3,﹣4)=(﹣3,4).12.答案x>3;析:解:∵点(3﹣x,x﹣1)在第二象限,∴,解不等式①得,x>3,解不等式②得,x>1,所以不等式组的解集是x>3.故答案为:x>3.三、解答题13.解:建立平面直角坐标系如图:得C(-1,-2)、D(2,1).由图可知,点C在第三象限,点D在第一象限.14.解:∵M(a,b)为平面直角坐标系中的点.(1)当a>0,b<0时,点M位于第四象限;(2)当ab>0时,即a,b同号,故点M位于第一、三象限;(3)当a为任意实数,且b<0时,点M位于第三、四象限和纵轴的负半轴.15.解:描点如下:14443242ABCD AOBS S==⨯⨯⨯=四边形三角形坐标平面内图形的轴对称和平移(基础)一、选择题1.如图,在平面直角坐标系xOy 中,点P(-3,5)关于y 轴的对称点的坐标为()A.(-3,-5)B.(3,5)C.(3.-5)D.(5,-3)2.平面直角坐标系中,点P 的坐标为(-5,3),则点P 关于x 轴的对称点的坐标是()A.(5,3)B.(-5,-3)C.(3,-5)D.(-3,5)3.如图,△COB 是由△AOB 经过某种变换后得到的图形,请同学们观察A 与C 两点的坐标之间的关系,若△AOB 内任意一点P 的坐标是(a,b),则它的对应点Q 的坐标是().A.(a,b)B.(-a,b)C.(-a,-b)D.(a,-b)4.(2016•贵港)在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是()A.(-1,1)B.(-1,-2)C.(-1,2)D.(1,2)5.在平面直角坐标系中,将某个图象上各点的横坐标都加上3,得到一个新图形,那么新图形与原图形相比().A.向右平移3个单位B.向左平移3个单位C.向上平移3个单位D.向下平移3个单位6.(2015春•赵县期末)线段CD 是由线段AB 平移得到的.点A(﹣1,4)的对应点为C(4,7),则点B(﹣4,﹣1)的对应点D 的坐标为()A.(2,9)B.(5,3)C.(1,2)D.(﹣9,﹣4)二、填空题7.点A(-3,0)关于y 轴的对称点的坐标是______.8.点P(2,-1)关于x 轴对称的点P′的坐标是______.9.在平面直角坐标系中,点A(1,2)关于y 轴对称的点为B(a,2),则a=_____.10.通过平移把点A(1,-3)移到点A 1(3,0),按同样的平移方式把点P(2,3)移到点P 1,则点P 1的坐标是__________.11.(2016•广安)将点A (1,﹣3)沿x 轴向左平移3个单位长度,再沿y 轴向上平移5个单位长度后得到的点A′的坐标为.12.(2014秋•嘉鱼县校级月考)点P(1,2)关于直线y=1对称的点的坐标是;关于直线x=1对称的坐标是.三、解答题13.已知点P(a+1,2a-1)关于x 轴的对称点在第一象限,求a 的取值范围.14.如图,正方形ABCD 关于x 轴、y 轴均成轴对称,若这个正方形的面积为100,请分别写出点A、B、C、D 的坐标.15.(2014春•环翠区校级期末)如图,回答下列问题:(1)将△ABC 沿x 轴向左移一个单位长度,向上移2个单位长度,则A 1的坐标为,B 1的坐标为,C 1的坐标为.(2)若△ABC 与△A 2B 2C 2关于x 轴对称,则A 2的坐标为,B 2的坐标为,C 2的坐标为.答案、分析一、选择题1.答案B;2.答案B;3.答案D;析:观察图形可得,△COB 与△AOB 关于x 轴对称,则P (a,b)关于x 轴对称点坐标为(a,-b).4.答案A;析:将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,即坐标变为(1-2,-2+3),即点A′的坐标为(-1,1).故选A.5.答案A .6.答案C;析:解:平移中,对应点的对应坐标的差相等,设D 的坐标为(x,y);根据题意:有4﹣(﹣1)=x﹣(﹣4);7﹣4=y﹣(﹣1),解可得:x=1,y=2;故D 的坐标为(1,2).故选:C.二、填空题7.答案(3,0);8.答案(2,1);9.答案-1;析:∵点A(1,2)关于y 轴对称的点为B (a,2),∴a=-1.10.答案(4,6);析:从点A 到A 1点的横坐标从1到3,说明是向右移动了3-1=2,纵坐标从-3到0,说明是向上移动了0-(-3)=3,那点P 的横坐标加2,纵坐标加3即可得到点P 1.则点P 1的坐标是(4,6).11.答案(﹣2,2).12.答案(1,0),(1,2);析:解:如图所示:点P(1,2)关于直线y=1对称的点的坐标是(1,0);关于直线x=1对称的坐标是:(1,2).故答案为:(1,0),(1,2).三、解答题13.解:依题意得p 点在第四象限,∴10210a a +>⎧⎨-<⎩,解得:-1<a<12,即a 的取值范围是-1<a<12.14.解:设正方形的边长为a.则2a =100∴a=10∴A(5,5),B(-5,5),C(-5,-5),D(5,-5).15.解:(1)A(3,0),B(﹣2,4),C(0,﹣1),将△ABC 沿x 轴向左移一个单位长度,向上移2个单位长度,则A 1的坐标为(3﹣1,0+2),B 1的坐标为(﹣2﹣1,4+2),C 1的坐标为(0﹣1,﹣1+2),即:A 1的坐标为(2,2),B 1的坐标为(﹣3,6),C 1的坐标为(﹣1,1),故答案为:(2,2),(﹣3,6),(﹣1,1);(2)若△ABC 与△A 2B 2C 2关于x 轴对称,则A 2的坐标为(3,0),B 2的坐标为(﹣2,﹣4),C 2的坐标为(0,1),故答案为:(3,0),(﹣2,﹣4),(0,1).《平面直角坐标系》全章复习与巩固(基础)巩固练习一、选择题1.点P(0,3)在().A.x轴的正半轴上B.x的负半轴上C.y轴的正半轴上D.y轴的负半轴上2.(2016•雅安)已知△ABC顶点坐标分别是A(0,6),B(﹣3,﹣3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为()A.(7,1)B.B(1,7)C.(1,1)D.(2,1)3.将某图形的横坐标减去2,纵坐标保持不变,可将图形().A.横向向右平移2个单位B.横向向左平移2个单位C.纵向向右平移2个单位D.纵向向左平移2个单位4.(2015•威海)若点A(a+1,b﹣2)在第二象限,则点B(﹣a,b+1)在()A.第一象限B.第二象限 C.第三象限 D.第四象限5.点P的坐标为(3a-2,8-2a),若点P到两坐标轴的距离相等,则a的值是().A.23或4B.-2或6C.23 或-4D.2或-66.如图是被墨迹污染的旅游区各景点地图,隐约可见,第一景点的坐标为(0,3),第二景点的坐标为(5,3),景区车站坐标为(0,0),则车站大约在().A.点A B.点B C.点C D.点D7.若点A(m,n)在第二象限,则点B(|m|,-n)在().A.第一象限B.第二象限C.第三象限D.第四象限8.点P(m+3,m+1)在直角坐标系的x轴上,则P点的坐标为().A.(0,-2)B.(2,0)C.(4,0)D.(0,-4)二、填空题9.如图,若点E坐标为(-2,1),点F坐标为(1,-1),则点G的坐标为.GEF10.点P(-5,4)到x轴的距离是,到y轴的距离是.11.若点M在第二象限,到x轴的距离是2,到y轴的距离是3,则M的坐标是.12.若点(a,b)在第二象限,则点(b,a)在第象限.13.将点P(-1,-2)向下平移2个单位,再向右平移3个单位,得到P1,则点P1的坐标是.14.点B与点C的横坐标相同,纵坐标不同,则直线BC与x轴的关系为.15.(2015春•道县校级期中)在平面直角坐标系中,坐标轴上到点A(3,4)的距离等于5的点有个.三、解答题17.(2016春•潮南区月考)已知三角形ABC的两个顶点坐标为A(﹣4,0),B(2,0),如图,且过这两个点的边上的高为4,第三个顶点的横坐标为﹣1,求顶点C的坐标及三角形的面积.18.(2015春•和县期末)如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(﹣1,﹣2),解答以下问题:(1)在图中试找出坐标系的原点,并建立直角坐标系;(2)若体育馆位置坐标为C(1,﹣3),请在坐标系中标出体育馆的位置;(3)顺次连接学校、图书馆、体育馆,得到三角形ABC,求三角形ABC的面积.19.已知A(0,0),B(9,O),C(7,5),D(2,7),求四边形ABCD的面积.答案、分析一.选择题1.答案C;析:横坐标为0,说明点在y 轴上,又纵坐标大于0,说明点在y 轴的正半轴上.2.答案C;析:∵点A (0,6)平移后的对应点A 1为(4,10),4﹣0=4,10﹣6=4,∴△ABC 向右平移了4个单位长度,向上平移了4个单位长度,∴点B 的对应点B 1的坐标为(﹣3+4,﹣3+4),即(1,1).3.答案B.4.答案A;析:解:由A (a+1,b ﹣2)在第二象限,得a+1<0,b ﹣2>0.解得a <﹣1,b >2.由不等式的性质,得﹣a >1,b+1>3,点B (﹣a ,b+1)在第一象限,故选:A .5.答案D ;析:由题意得:3282a a -=-,解得:2a =或6-.6.答案B;析:根据已知的坐标,可建立平面直角坐标系,如图,由此可得答案.7.答案D;析:第二象限的点横坐标为负,纵坐标为正,所以m<0且n>0,所以|m|>0,-n<0,点B(|m|,-n)在第四象限,故选D.8.答案B;析:在x 轴上点的纵坐标为0,所以m+1=0,可得m=-1,m+3=2,所以P 点的坐标为(2,0),故选B.二.填空题9.答案(1,2);析:由图可知,点G 的横坐标与点F 的横坐标相同,均为1,而纵坐标比点E 的纵坐标大1,所以点点G 的坐标为(1,2).10.答案4,5.11.答案(-3,2).12.答案四;析:由点(a,b)在第二象限,可得a<0,b>0,即得点(b,a)的横坐标大于0,而纵坐标小于0,所以点(b,a)在第四象限.13.答案(2,-4);析:-1+3=2,-2-2=-4.14.答案垂直.15.答案3;析:解:点A 的坐标是(3,4),因而OA=5,坐标轴上到点A (3,4)的距离等于5的点就是以点A 为圆心,以5为半径的圆与坐标轴的交点,圆与坐标轴的交点是原点,另外与两正半轴有两个交点,共有3的点.所以坐标轴上到点A (3,4)的距离等于5的点有3个.故答案填:3.16.答案1.析:∵点A(1-2k,k-2)在第三象限,∴1-2k<0,k-2<0,解得:0.5<k<2,又∵k 为整数,∴k=1.三.解答题17.解:(1)∵AB 边上的高为4,∴点C 的纵坐标为4或﹣4,∵第三个顶点C 的横坐标为﹣1,∴点C 的坐标为(﹣1,4)或(﹣1,﹣4);(2)∵A (﹣4,0),B (2,0),∴AB=2﹣(﹣4)=2+4=6,∴△ABC 的面积=×6×4=12.18.解:(1)如下图;(2)如下图;(3)S △ABC =3×4﹣×2×1﹣×1×4﹣×3×3=4.5.19.解:过点C 作CF⊥x 轴于点F,过D 作DE⊥x 轴于点E 则AE=2,DE=7,BF=2,CF=5,EF=5∴ADE BCFABCD DEFC S S S S ∆∆=++四边形梯形11127(75)52542222=⨯⨯+⨯+⨯+⨯=.。
专题13一次函数及其应用(基础巩固练习)练习版

2021年中考数学专题13 一次函数及其应用(基础巩固练习,共46个小题)一、选择题(共20小题):1.(2020秋•章丘区期末)下列关系式中,一次函数是()−1 B.y=x2+3A.y=2xC.y=k+b(k、b是常数)D.y=3x2.(2019•梧州)下列函数中,正比例函数是()C.y=8x2D.y=8x﹣4 A.y=﹣8x B.y=8x3.(2020•广安)一次函数y=﹣x﹣7的图象不经过的象限是()A.第一象限B.第二象限C.第三象限D.第四象限4.(2020•桂林)直线y=kx+2过点(﹣1,4),则k的值是()A.﹣2 B.﹣1 C.1 D.25.(2020•泰州)点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b+1的值等于()A.5 B.3 C.﹣3 D.﹣16.(2018•辽阳)如图,直线y=ax+b(a≠0)过点A(0,4),B(﹣3,0),则方程ax+b=0的解是()A.x=﹣3B.x=4C.x=−43D.x=−347.(2020•济宁)数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是()A.x=20B.x=5C.x=25D.x=158.(2020•广州)一次函数y=﹣3x+1的图象过点(x1,y1),(x1+1,y2),(x1+2,y3),则()A.y1<y2<y3B.y3<y2<y1C.y2<y1<y3D.y3<y1<y29.(2020•济南)若m<﹣2,则一次函数y=(m+1)x+1﹣m的图象可能是()10.(2020•沈阳)一次函数y=kx+b(k≠0)的图象经过点A(﹣3,0),点B(0,2),那么该图象不经过的象限是()A.第一象限B.第二象限C.第三象限D.第四象限11.(2020•凉山州)若一次函数y=(2m+1)x+m﹣3的图象不经过第二象限,则m的取值范围是()A.m>−12B.m<3 C.−12<m<3 D.−12<m≤312.(2020•陕西)在平面直角坐标系中,将直线y=kx﹣6沿x轴向左平移3个单位后恰好经过原点,则k的值为()A.﹣2 B.2 C.﹣3 D.313.(2020•内江)将直线y=﹣2x﹣1向上平移两个单位,平移后的直线所对应的函数关系式为()A.y=﹣2x﹣5 B.y=﹣2x﹣3 C.y=﹣2x+1 D.y=﹣2x+314.(2020•湖州)已知在平面直角坐标系xOy中,直线y=2x+2和直线y=2x+2分别交3 x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是()x+2 A.y=x+2 B.y=√2x+2 C.y=4x+2 D.y=2√3315.(2020•西宁)全民健身的今天,散步是大众喜欢的运动.甲、乙两人在绿道上同时从同一起点以各自的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行.甲乙两人之间的距离s(米)与他们出发后的时间t(分)的函数关系如图所示,已知甲步行速度比乙快.由图象可知,甲、乙的速度分别是()A.60米/分,40米/分B.80米/分,60米/分C.80米/分,40米/分D.120米/分,80米/分16.(2020•西藏)如图,一个弹簧不挂重物时长6cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所挂物体质量x (单位:kg)的函数图象如图所示,则图中a的值是()A.3 B.4 C.5 D.617.(2020•鄂尔多斯)鄂尔多斯动物园内的一段线路如图1所示,动物园内有免费的班车,从入口处出发,沿该线路开往大象馆,途中停靠花鸟馆(上下车时间忽略不计),第一班车上午9:20发车,以后每隔10分钟有一班车从入口处发车,且每一班车速度均相同.小聪周末到动物园游玩,上午9点到达入口处,因还没到班车发车时间,于是从入口处出发,沿该线路步行25分钟后到达花鸟馆.离入口处的路程y(米)与时间x(分)的函数关系如图2所示,下列结论错误的是()A.第一班车离入口处的路程y(米)与时间x(分)的解析式为y=200x﹣4000(20≤x≤38)B.第一班车从入口处到达花鸟馆所需的时间为10分钟C.小聪在花鸟馆游玩40分钟后,想坐班车到大象馆,则小聪最早能够坐上第四班车D.小聪在花鸟馆游玩40分钟后,如果坐第五班车到大象馆,那么比他在花鸟馆游玩结束后立即步行到大象馆提前了7分钟(假设小聪步行速度不变)18.(2020•恩施)甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是()A.甲车的平均速度为60km/hB.乙车的平均速度为100km/hC.乙车比甲车先到B城D.乙车比甲车先出发1h19.(2020•武汉)一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始4min内只进水不出水,从第4min到第24min内既进水又出水,从第24min 开始只出水不进水,容器内水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则图中a的值是()A.32 B.34 C.36 D.3820.(2020•连云港)快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程y(km)与它们的行驶时间x(h)之间的函数关系.小欣同学结合图象得出如下结论:①快车途中停留了0.5h;②快车速度比慢车速度多20km/h;③图中a=340;④快车先到达目的地.其中正确的是()A.①③B.②③C.②④D.①④二、填空题(共15小题):21.(2020秋•浦东新区期末)如果函数y=(m−√2)x m2−1是正比例函数,那么m=.时,y=﹣1,则y关于22.(2020秋•九龙县期末)已知y与x﹣1成正比例,且当x=12x的函数解析式为.23.(2020秋•会宁县期末)当k=时,函数y=(k+3)x k2−8−5是关于x的一次函数.24.(2020秋•雁塔区校级月考)若y=(m﹣2)x m2−3+5是一次函数函数,则其解析式为.25.(2020秋•金东区期中)已知一次函数y=2x+b图象与正比例函数y=kx图象交于点(2,3)(k,b是常数),则关于x的方程2x=kx﹣b的解是.26.(2020•宿迁)已知一次函数y=2x﹣1的图象经过A(x1,1),B(x2,3)两点,则x 1x2(填“>”“<”或“=”).27.(2020秋•潮阳区期末)如图所示,在平面直角坐标系中,A(4,0),B(0,2),AC由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是.28.(2018•邵阳)如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是.29.(2020•广安)一次函数y=2x+b的图象过点(0,2),将函数y=2x+b的图象向上平移5个单位长度,所得函数的解析式为.30.(2020•黔东南州)把直线y=2x﹣1向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的解析式为.31.(2020•南京)将一次函数y=﹣2x+4的图象绕原点O逆时针旋转90°,所得到的图象对应的函数表达式是.32.(2020•宁夏)如图,直线y=52x+4与x轴、y轴分别交于A、B两点,把△AOB绕点B逆时针旋转90°后得到△A1O1B,则点A1的坐标是.33.(2020•重庆)周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的85继续骑行,经过一段时间,甲先到达B地,乙一直保持原速前往B地.在此过程中,甲、乙两人相距的路程y(单位:米)与乙骑行的时间x (单位:分钟)之间的关系如图所示,则乙比甲晚分钟到达B地.34.(2019•济南)某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中l1、l2分别表示去年、今年水费y(元)与用水量x(m3)之间的关系.小雨家去年用水量为150m3,若今年用水量与去年相同,水费将比去年多元.35.(2019•重庆)一天,小明从家出发匀速步行去学校上学.几分钟后,在家休假的爸爸发现小明忘带数学书,于是爸爸立即匀速跑步去追小明,爸爸追上小明后以原速原路跑回家.小明拿到书后以原速的54快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小明家到学校的路程为米.三、解答题(共11小题):36.(2020•南通)如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.(1)求直线l2的解析式;(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.37.(2020•北京)在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=x的图象平移得到,且经过点(1,2).(1)求这个一次函数的解析式;(2)当x>1时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b 的值,直接写出m的取值范围.38.(2020•陕西)小蕾家与外婆家相距270km,她假期去看望外婆,返回时,恰好有一辆顺路车可以带小蕾到A服务区,于是,小蕾与爸爸约定,她先搭乘顺路车到A服务区,爸爸驾车到A服务区接小蕾回家.两人在A服务区见面后,休息了一会儿,然后小蕾乘坐爸爸的车以60km/h的速度返回家中.返回途中,小蕾与自己家的距离y(km)和时间x(h)之间的关系大致如图所示.(1)求小蕾从外婆家到A服务区的过程中,y与x之间的函数关系式;(2)小蕾从外婆家回到自己家共用了多长时间?39.(2020•大连)甲、乙两个探测气球分别从海拔5m和15m处同时出发,匀速上升60min.如图是甲、乙两个探测气球所在位置的海拔y(单位:m)与气球上升时间x (单位:min)的函数图象.(1)求这两个气球在上升过程中y关于x的函数解析式;(2)当这两个气球的海拔高度相差15m时,求上升的时间.40.(2020•长春)已知A、B两地之间有一条长240千米的公路.甲车从A地出发匀速开往B地,甲车出发两小时后,乙车从B地出发匀速开往A地,两车同时到达各自的目的地.两车行驶的路程之和y(千米)与甲车行驶的时间x(时)之间的函数关系如图所示.(1)甲车的速度为千米/时,a的值为.(2)求乙车出发后,y与x之间的函数关系式.(3)当甲、乙两车相距100千米时,求甲车行驶的时间.41.(2020•鸡西)A,B两城市之间有一条公路相连,公路中途穿过C市,甲车从A市到B市,乙车从C市到A市,甲车的速度比乙车的速度慢20千米/时,两车距离C市的路程y(单位:千米)与行驶的时间t(单位:小时)的函数图象如图所示,结合图象信息,解答下列问题:(1)甲车的速度是千米/时,在图中括号内填入正确的数;(2)求图象中线段MN所在直线的函数解析式,不需要写出自变量的取值范围;(3)直接写出甲车出发后几小时,两车距C市的路程之和是460千米.42.(2020•福建)某公司经营甲、乙两种特产,其中甲特产每吨成本价为10万元,销售价为10.5万元;乙特产每吨成本价为1万元,销售价为1.2万元.由于受有关条件限制,该公司每月这两种特产的销售量之和都是100吨,且甲特产的销售量都不超过20吨.(1)若该公司某月销售甲、乙两种特产的总成本为235万元,问这个月该公司分别销售甲、乙两种特产各多少吨?(2)求该公司一个月销售这两种特产所能获得的最大总利润.43.(2020•乐山)某汽车运输公司为了满足市场需要,推出商务车和轿车对外租赁业务.下面是乐山到成都两种车型的限载人数和单程租赁价格表:车型每车限载人数(人)租金(元/辆)商务车 6 300轿车 4(1)如果单程租赁2辆商务车和3辆轿车共需付租金1320元,求一辆轿车的单程租金为多少元?(2)某公司准备组织34名职工从乐山赴成都参加业务培训,拟单程租用商务车或轿车前往.在不超载的情况下,怎样设计租车方案才能使所付租金最少?44.(2020•广安)某小区为了绿化环境,计划分两次购进A,B两种树苗,第一次购进A种树苗30棵,B种树苗15棵,共花费1350元;第二次购进A种树苗24棵,B种树苗10棵,共花费1060元.(两次购进的A,B两种树苗各自的单价均不变)(1)A,B两种树苗每棵的价格分别是多少元?(2)若购买A,B两种树苗共42棵,总费用为W元,购买A种树苗t棵,B种树苗的数量不超过A种树苗数量的2倍.求W与t的函数关系式.请设计出最省钱的购买方案,并求出此方案的总费用.45.(2020•宜昌)已知函数y1=x+2m﹣1,y2=(2m+1)x+1均为一次函数,m为常数.(1)如图1,将直线AO绕点A(﹣1,0)逆时针旋转45°得到直线l,直线l交y轴于点B.若直线l恰好是y1=x+2m﹣1,y2=(2m+1)x+1中某个函数的图象,请直接写出点B坐标以及m可能的值;(2)若存在实数b,使得|m|﹣(b﹣1)√1−b=0成立,求函数y1=x+2m﹣1,y2=(2m+1)x+1图象间的距离;(3)当m>1时,函数y1=x+2m﹣1图象分别交x轴,y轴于C,E两点,y2=(2m+1)x+1图象交x轴于D点,将函数y=y1•y2的图象最低点F向上平移562m+1个单位后刚好落在一次函数y1=x+2m﹣1图象上.设y=y1•y2的图象,线段OD,线段OE围成的图形面积为S,试利用初中知识,探究S的一个近似取值范围.(要求:说出一种得到S的更精确的近似值的探究办法,写出探究过程,得出探究结果,结果的取值范围两端的数值差不超过0.01.)46.(2020•广西)如图1,在平面直角坐标系中,直线l1:y=x+1与直线l2:x=﹣2相交于点D,点A是直线l2上的动点,过点A作AB⊥l1于点B,点C的坐标为(0,3),连接AC,BC.设点A的纵坐标为t,△ABC的面积为s.(1)当t=2时,请直接写出点B的坐标;(2)s关于t的函数解析式为s={14t2+bt−54,t<−1或t>5a(t+1)(t−5),−1<t<5,其图象如图2所示,结合图1、2的信息,求出a与b的值;(3)在l2上是否存在点A,使得△ABC是直角三角形?若存在,请求出此时点A的坐标和△ABC的面积;若不存在,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基础巩固练(十三)
阅读下面的文字,完成1~3题。
随着暗物质粒子探测卫星“悟空”号成功飞天,推开了一扇寻找暗物质幽灵的新窗口,确保在距离地面大约500千米的太阳同步轨道上分辨出高能电子和测量它们的能量来源奠定坚实的基础。
人们赋予它这个诗意的别称“悟空”,()。
中科院院士吴岳良说,根据最新天文观测结果,宇宙是由27%的暗物质、68%的暗能量和5%的普通物质组成的。
暗物质不发光,不发出电磁波,从来没有被直接“看”到过。
对于神秘的暗物质,科学家迫切想知道它到底是什么,对它们的研究很可能会引发科学上的革命。
与暗物质________的,不只有光,还有普通物质,他们靠分子和原子之间的电磁力组装在一起。
也正是通过这样的电磁作用,我们才能够触摸到这个大千世界。
而暗物质,对这样的电磁作用,根本就________。
在运行的头530天里,“悟空”号果然________,一共记录到28亿个高能粒子,从中分辨出150万个高能电子,测量了它们的能量和来源方位。
以高置信度观测到了能谱在TeV 处的拐折行为,从________的乱象中抓住了一条关键线索,或许能够帮助我们认清这个幽灵的真面目。
中科院院长白春礼认为,“悟空”成果的取得,表明中国科学家已经从自然科学前沿理论的学习者、继承者、围观者,逐渐走到了舞台中央。
1.文中画横线的句子有语病,下列修改最恰当的一项是()
A.暗物质粒子探测卫星“悟空”成功飞天,推开了一扇寻找暗物质幽灵的新窗口,确保在距离地面大约500千米的太阳同步轨道上分辨出高能电子和测量它们的能量来源奠定坚实的基础。
B.随着暗物质粒子探测卫星“悟空”成功飞天,推开了一扇寻找暗物质幽灵的新窗口,为在距离地面大约500千米的太阳同步轨道上分辨出高能电子和测量它们的能量来源奠定坚实的基础。
C.随着暗物质粒子探测卫星“悟空”成功飞天,推开了一扇寻找暗物质幽灵的新窗口,确保在距离地面大约500千米的太阳同步轨道上分辨出高能电子和测量它们的能量来源。
D.暗物质粒子探测卫星“悟空”成功飞天,推开了一扇寻找暗物质幽灵的新窗口,为在距离地面大约500千米的太阳同步轨道上分辨出高能电子和测量它们的能量来源奠定坚
实的基础。
D[A项,“确保”和“奠定坚实的基础”杂糅;B、C项,“随着”淹没主语。
]
2.下列在文中括号内补写的语句,最恰当的一项是()
A.科学家内心惊叹于它的火眼金睛,似乎隐隐看到了这个暗物质幽灵留下的半个身影。
B.它的出现,让科学家似乎隐隐看到了这个物质幽灵留下的半个身影,内心激动不已。
C.科学家似乎隐隐看到了这个暗物质幽灵留下的半个身影,内心惊叹于它的火眼金睛。
D.它的出现,让科学家内心激动不已,似乎隐隐看到了这个暗物质幽灵留下的半个身影。
B[“悟空”号卫星是语段的叙述对象,据此可排除A、C两项。
按照认知事物的逻辑顺序,科学家应该先看到,然后才激动,据此可排除D项。
]
3.依次填入文中横线上的成语,全都恰当的一项是()
A.素昧平生不屑一顾不孚众望浩如烟海
B.形同陌路不屑一顾不负众望纷繁复杂
C.素昧平生不足挂齿不负众望浩如烟海
D.形同陌路不足挂齿不孚众望纷繁复杂
B[素昧平生:彼此一向不了解,指与某人从来不认识,指过去没见过面的人。
形同陌路:指以前曾经熟悉的人因为一些事情而不再交往,把一切都当没发生过以后各自走各自的人生路。
第一处,强调暗物质与光、普通物质相处在一起但各自走各自的路,应选用“形同陌路”。
不屑一顾:认为不值得一看,形容极端轻视。
不足挂齿:不值得一提。
谦虚的用词。
比喻自己做的事不够重大。
第二处没有谦虚的意思,应选用“不屑一顾”。
不负众望:为人所信服,很争气,不负大家的期望。
不孚众望:意思是不能使大家信服,未符合大家的期望。
第三处强调“悟空”号果然不负大家的期望,应选用“不负众望”。
浩如烟海:形容文献资料、书籍等多得无法计算,只用于形容书籍、文献多等。
纷繁复杂:复杂事物的种类、头绪等多而杂。
第四处强调乱象多而杂,应选用“纷繁复杂”。
]
4.下列对古代文化常识的解说,不正确的一项是()
A.礼部,我国古代的官署名,主要掌管典礼事务与学校教育、科举考试以及文职官员的考察、选拔、嘉奖等事务。
B.薨,古代称诸侯或有爵位的大官死去,也可称皇帝的高等级妃嫔和所生育的皇子公主以及封王贵族的死亡。
C.士大夫,旧时指官吏或较有声望、地位的知识分子,如《师说》“士大夫之族,曰
师曰弟子云者,则群聚而笑之”。
D.日昃,古人根据太阳的影子来确定时间,如太阳正中叫做日中,而太阳偏西,下午两点左右时,就叫做日昃。
A[文职官员的考察、选拔、嘉奖等事务不属于礼部职权范围。
]
5.下面是某毕业学生在教师节前夕给老师发来的短信,其中有四处不得体,请找出并加以修改。
恩师无恙,毕业之后,学生垂念师恩。
曾经我是您的高足,现在学生也没让恩师失望!值此教师节到来之际:谨祝恩师节日快乐,万事如意!以后还请恩师继续斧正我的不足,如有事需要学生效劳,我当鼎力相助!
答案(1)“垂念”改为“常念”“思念”(2)“高足”改为“学生”(3)“斧正”改为“指出”(4)“鼎力”改为“全力”或“大力”
6.清代画家郑板桥在描述自己的画竹经验时曾说过:“江馆清秋,晨起看竹,烟光、日影、露气,皆浮动于疏枝密叶之间。
胸中勃勃遂有画意。
其实胸中之竹,并不是眼中之竹也。
”下面是郑板桥竹画创作过程的简图,请用简洁的文字表述这一创作过程,要求内容完整,表述准确,语言连贯,不超过90个字。
审美选择改造加工形诸画卷
现实之竹→眼中之竹→胸中之竹→画中之竹
答案竹画创作的过程是这样的:现实生活中的竹子,经过画家的审美选择,成为画家眼中的竹子,再经过改造加工,成为画家胸中的竹子,最后经画家之手便成为画卷中的竹子。
7.补写出下列句子中的空缺部分。
(1)诸葛亮在《出师表》中力荐向宠,认为军中之事,都应与他商议,这样“________________,________________”。
(2)郦道元《三峡》中“________________,________________”两句描写了春冬之时三峡的美丽的景象。
(3)《赤壁赋》中,苏轼企望同神仙一起自由飞行,情愿长伴明月的诗句是“________________,________________”。
答案(1)必能使行阵和睦优劣得所(2)素湍绿潭回清倒影(3)挟飞仙以遨游抱明月而长终。
